4. fejezet - A csúszómód szabályozás
- 4.1. Rövid történeti áttekintés
- 4.2. Bevezető példa
- 4.3. Jobboldalán nem folytonos differenciál egyenletek megoldása
- 4.4. Relés szabályozók
- 4.5. A bevezető példa differenciálegyenletének megoldása
- 4.6. Több bemenetű rendszerek csúszómódban
- 4.7. A csúszómód szabályozók tervezési lépései
- 4.8. A csúszómód szabályozók tervezési lépéseinek kísérleti alkalmazása
- 4.9. Kéttömeg rendszer közvetlen elcsavarodás szabályozása csúszómódban
-
- 4.9.1. A nem modellezett dinamika hatása a csúszómódra
- 4.9.2. Kéttömeg rendszer egyenletei
- 4.9.3. Állapottér egyenletek
- 4.9.4. A csúszófelület tervezése
- 4.9.5. Megfigyelőre alapozott csattogásmentes szabályozási törvény
- 4.9.6. A kéttömeg rendszer csúszómód alapú közvetlen elcsavarodás szabályozásának kísérleti alkalmazása
- 4.10. Következtetés
4.1. Rövid történeti áttekintés
A csúszómód szabályozás sajátos helyet foglal el szabályozáselméletben. Egyrészről az egzakt matematikai kezelése számos érdekes kihívást jelentett és mind a mai napig jelent a matematikusok számára. Másrészről e komoly matematikai háttér mélyebb ismerete nélkül is sok esetben viszonylag könnyen alkalmazható, ezért széles körben alkalmazzák is a mérnöki gyakorlatban. Jelen fejezet célja, hogy hidat képezzen az egzakt matematikai leírásmód és a mérnöki alkalmazások között, ahol első helyen a teljesítményelektronikát és az ehhez sok szálon szorosan kapcsolódó mechatronikát kell említenünk.
Napjainkban a legtöbb szabályozott rendszert villamos energiával táplálunk, mert a villamos energia az egyik legtisztább és a legkönnyebben (legkisebb időállandóval) változtatható (szabályozható) energiaforrás. A villamos energia átalakítására a teljesítményelektronika szolgál. A teljesítményelektronikai berendezések egyik legjellemzőbb közös tulajdonsága a kapcsoló üzemmód, vagyis a teljesítményelektronikai berendezésekben található félvezető elemeket ki- vagy bekapcsolhatjuk a veszteségek csökkentése érdekében, hiszen ha a kapcsolóelemnek vagy a feszültsége vagy az árama közel nulla, akkor a vesztesége is közel nulla. Így a teljesítményelektronikai berendezések tipikusan a változó struktúrájú rendszerek (variable structure system: VSS) csoportjába tartoznak. A változó struktúrájú rendszerek rendelkeznek néhány érdekes szabályozástechnikai tulajdonsággal. Egy VSS akkor is lehet aszimptotikusan stabilis, ha a VSS–t alkotó valamennyi struktúra önmagában labilis. Egy további fontos tulajdonság, hogy egy VSS – megfelelő szabályozással ellátva – egy olyan állapotba kerülhet, amikor a rendszer dinamikája az eredetihez képest csökkentett szabadságfokú differenciálegyenlettel írható le. Ebben az állapotban a rendszer elméletileg teljesen független bizonyos típusú paraméterek változásától és bizonyos típusú külső zavarok (pl. nemlineáris terhelés) hatásától. Ezt az állapotot csúszómódnak (sliding mode) és az erre alapozott szabályozást csúszómód szabályozásnak nevezik, amely kiemelten fontos szerepet játszik a teljesítményelektronikai eszközök szabályozása területén.
A változó struktúrájú rendszerek - és ehhez kapcsolódva a csúszómód szabályozás- elméletét először a Szovjetunióban, évtizedekkel ezelőtt dolgozták ki. Az elmélet kidolgozása elsősorban Vadim I. Utkin [1] és David K. Young [2] nevéhez fűződik. Első alkalmazási területe a repülés és a rakétatechnika volt, majd egyre szélesebb körben terjedt a robotirányítás [3], [4] és a szervohajtások [5], [6] területén. A csúszómód a ’70-es évek végén jelent meg a robotok és manipulátorok vezérléseinek tervezésénél [2]. Célja ezeknél az alkalmazásoknál az volt, hogy a robot nemlineáris dinamikáját kézben tarthassuk, és a robot pályakövetési pontosságát érzéketlenné tegyük paraméterváltozások és külső terhelésekkel szemben. A 80-as évek elején a csúszómód megjelent az indukciós motoros hajtások szabályozásában [4], [5] is. Előnye ebben az összetettebb alkalmazásban, hogy közvetlen beavatkozást tesz lehetővé a teljesítményelektronikai eszközökben az indukciós motor nemlineáris és csatolt jellemzőinek ellenére, mert a szabályozó megtervezése szétcsatolható egy nemlineáris és egy alacsonyabb rendű lineáris szabályozó tervezési problémájára. A csúszómód szabályozás két korai alkalmazása rámutatott néhány nagyon előnyös tulajdonságára. E kezdeti munkákat számos tudományos kutatás és gyakorlati alkalmazás követte a robotok vezérlésének és a motoros hajtások szabályozásának területén [3], [4]. A nyolcvanas évektől kezdődően a csúszómód szabályozás a teljesítményelektronikai és mozgásszabályozási alkalmazások egyik kedvelt eszközévé vált és mind a mai napig gyakran alkalmazzák ezen a területen [7], [8], [9]. A ötvenes–hatvanas években Rácz István professzor a Park vektor bevezetésével a teljesítményelektronikába egy máig ható iskolát teremtett. E magyar iskola egy újabb eredményének tekinthető a Park vektoros szemlélet bevezetés a csúszófelületek tervezésének területére [10], [11], és e módszert alkalmazva a szünetmentes áramforrások aszimmetrikus terhelés okozta problémái is kezelhetővé váltak [10], [11].
Az elmélet alapján arra lehetett következtetni, hogy a csúszómód szabályozás nagyszerű és robosztus viselkedést mutat, azonban a kísérletek azt igazolták, hogy ennek komoly korlátjai vannak. A csúszómód alkalmazásának a legnagyobb problémája a csúszófelület körüli nagy frekvenciás oszcilláció, az ún. csattogást (chattering), amely a szabályozás teljesítőképességét erősen csökkenti. Keveseknek sikerült a gyakorlatban is megvalósítani az elmélet által jósolt robusztus viselkedést. Sokan arra a következtetésre jutottak, hogy a csattogás jelenléte miatt a csúszómód szabályozás egy jó elméleti játék, amely a gyakorlatban nem alkalmazható. A következő időszakban a kutatók legnagyobb energiáját a csattogásmentes alkalmazások kötötték le. Erre számos megoldás született.
Tüneti kezelést adhat, ha a kapcsolófelületek éles határvonalát egy folytonos (boundary-layer) átmenettel helyettesítjük [12], vagy a beavatkozó jel nagyfrekvenciás összetevőit egy alul-áteresztő szűrővel szűrjük [13]. Ezek a megoldások értelemszerűen csökkentik a csúszómód robosztusságát. Léteznek olyan módszerek, amelyek a csattogás okait keresik meg, és azt próbálják orvosolni, így elméletileg nem adják fel a rendszer robosztusságát. A csattogás egyik oka, hogy a nagy frekvenciával kapcsolgatott beavatkozó jel gerjesztheti a szabályozott szakasznak a szokásos tervezések során elhanyagolt nagyfrekvenciás tartományba eső sajátfrekvenciáit. Ennek kiküszöbölésére szolgál az ún. megfigyelő alapú csúszómód, melynek lényege, hogy csúszómód szabályozóba egy általunk alkotott megfigyelő állapotváltozóit csatoljuk vissza, és így a csúszómód szabályozó–megfigyelő hurokban egy ideális csúszómód alakulhat ki. Ezt a módszert kísérletileg is sikerült alkalmazni egy olyan - nevezetesen két-tömeg - rendszerre, amely különösen hajlamos a rezgésekre [14]. A megfigyelő nem csak eszköz lehet, hanem cél is. A csúszómód szabályozás elméletére alapozva robosztus és nemlineáris megfigyelő is tervezhető [15], [16]. Egy ugyancsak elméletileg robosztus és gyakorlatban is megvalósított módszer az ún. szektoros csúszómód [17], [18], [19]. A közelmúltban a nemlineáris rendszerek egy új reprezentációja jelent meg, amely a tenzor szorzat modell transzformáción alapszik. A tenzor szorzat modell transzformáció bevezetése a csúszómód szabályozók területére a szektoros csúszómód egy új szemléletű tervezéséhez vezetett [20]. Az analóg csúszómód szabályozók csattogás elkerüléséről egy összefoglaló található a [21] -ben. A csattogás egy másik előidézője lehet a beavatkozó jel korlátozott kapcsolási frekvenciája. A folytonos idejű csúszómód szabályozás robosztusságát nagy frekvenciájú kapcsolgatással megvalósított nagy körerősítéssel érjük el. Ahhoz, hogy ezt a filozófiát a digitális szabályozók világában is alkalmazhassuk, a mintavételezési frekvenciát növelni kell más szabályozásokéhoz képest. Ennek a problémának megoldására a [22] irodalomban a csúszófelület aszimptotikus elérését ajánlják a kommutáció elkerülésére. Egy alternatív megoldást követ [23], ahol a mintavételezett állapotváltozók véges mintavételezési szám után elérik a csúszófelületet. A kilencvenes években az egyszerű pólusáthelyezéstől a különböző optimális szabályozó tervezési módszerekig szinte minden állapot visszacsatolásos algoritmust adaptáltak csúszófelület tervezésére. Ezek közül kiemelhetjük a frekvenciaformálást [24] és a H∞ normára alapozott optimális tervezést [25]. Az előbbi egy frekvenciafüggő súlyozással bünteti az állapotváltozók időfüggvényében megjelenő nagyfrekvenciás összetevőket, az utóbbi a H∞ norma segítségével közvetlen korlátot ad meg a nagyfrekvenciás összetevőkre. Az optimális csúszófelület tervezésére egy összefoglaló található [26] -ben. A közelmúltban az ún. „back stepping” módszert [27] és a legkülönbözőbb lágyszámítási módszereket alkalmazták a csúszófelület tervezésére [28], [29].
4.2. Bevezető példa
Először egy olyan példát mutatunk be, amelyhez hasonlóval többször találkozhatunk a mérnöki gyakorlatban. Tegyük fel, hogy van egy ideális elemekből álló soros L-C körünk, amelyet vagy rövidre zárhatunk, vagy rákapcsolhatjuk egy akkumulátor feszültségét egy tranzisztor kapcsoló segítségével (ld. 41. ábra, ahol a tranzisztoros kapcsoló részletei nincsenek feltüntetve).
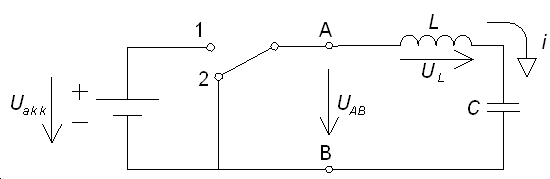
Tegyük fel, hogy energiamentes állapotból indulunk és az a célunk, hogy a tranzisztor kapcsolgatásával a kondenzátort az akkumulátor feszültségének felére töltsük fel. A két áramköri elemre felírható differenciálegyenlet:
|
és |
(4.1) |
A soros kapcsolás miatt , így a rendszert leíró differenciálegyenlet:
|
|
(4.2) |
Vezessünk be relatív egységeket oly módon, hogy és legyen. Vezessük be az feszültség hibajelet, ahol a kondenzátor referencia feszültsége. Így a hibajelre vonatkozó differenciálegyenlet a következő alakú:
|
, ahol |
(4.3) |
Könnyen belátható, hogy a (4.3) egyenlet megoldásához tartozó állapot az fázissíkon mindig egy kör mentén haladhat az óramutatóval megegyező irányban (ld 4-2. ábra)
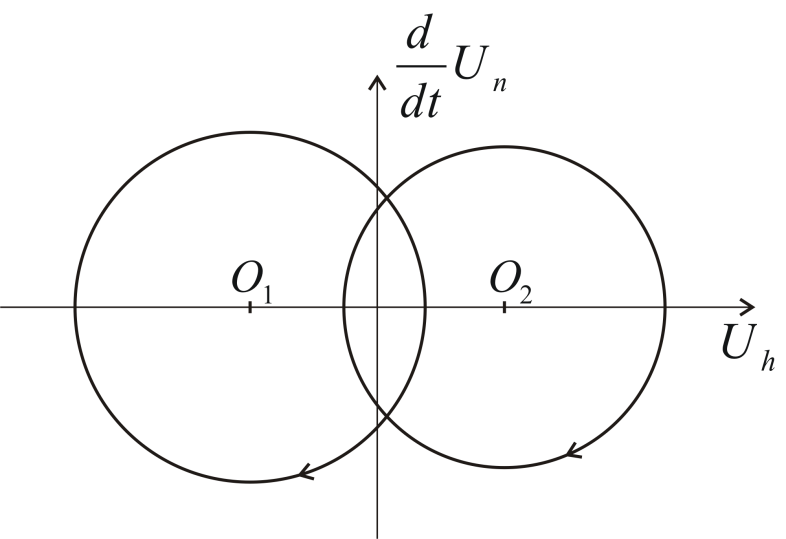
A kör középpontja a tranzisztorkapcsoló állapotától függ. Az állapottrajektória folytonos, így a kör sugarát az határozza meg, hogy az utolsó kapcsolás pillanatában a rendszer éppen milyen állapotban volt. Tegyük fel, hogy az állapotból indulunk és megfelelő kapcsolgatással az állapotba kívánunk eljutni. Vezessük be a következő kapcsolási stratégiát:
|
ahol |
(4.4) |
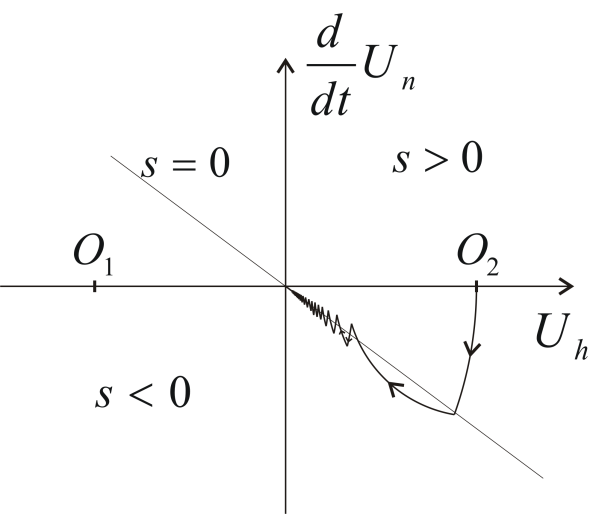
Ez azt jelenti, hogy ha az állapottrajektória az egyenes felett tartózkodik, akkor O1 középpontú kört, ha az egyenes alatt van, akkor O2 középpontú kört kell kapcsolnunk. Vizsgáljuk meg, hogy miként szüntethetjük meg a hibát. Tekintsük a 4-3. ábrat, a (4.4) értelmében először az egyenes felett O1 középpontú kör mentén indulunk el. Az egyenest elérve átkapcsolunk egy O2 középpontú körre úgy, hogy közben a trajektória folytonos marad. A második kapcsolás után egy érdekes jelenséget tapasztalunk. Az állapottrajektória amint elindul az O1 középpontú kör mentén, azonnal visszatér arra a térrészre, ahol O2 középpontú kört kell kapcsolni, de e körön sem maradhat tovább az állapottrajektória, újabb kapcsolás következik. Az ábrázolhatóság kedvéért a 4-3. ábran az állapottrajektória az egyenes mindkét oldalán jelentősen belenyúlik az egyenes feletti és alatti tartományba. Ideális esetben az állapottrajektória az egyenest végtelenül nagy frekvenciával kapcsolgatott és végtelenül rövid szakaszokból álló, minden pontjában megtört görbe mentén követi, más szavakkal a hibajel trajektóriája az egyenes mentén csúszik és ezért nevezik csúszómódnak.
A mérnöki, illetve geometriai szemlélet alapján érezzük, hogy a második kapcsolás után a hibajel viselkedését a másodrendű (4.3) helyett a következő elsőrendű differenciálegyenlet írja le:
|
|
(4.5) |
Ez azért különösen érdekes, mert (4.5)-ben nem szerepel az eredeti rendszer egyetlen paramétere sem, csak az általunk megadott , így egy olyan robosztus szabályozáshoz jutottunk, amely bizonyos feltételek mellett érzéketlen bizonyos zavarások és paraméterek változására. A teljesség igénye nélkül vizsgáljuk meg, hogy a rendszer néhány tulajdonságának, illetve paraméterének megváltozása milyen hatással lehet. Ha az ideális veszteségmentes elemeket valóságos veszteséges elemekkel helyettesítjük, akkor az állapottrajektória kör helyett csökkenő sugarú spirál mentén halad, ha pedig az akkumulátor feszültség ingadozik, akkor a kör középpontja vándorol. Mindkét változás hatással van a csúszómódot megelőző szakaszra és módosítja a csúszómód fennmaradásának feltételét, de mindkét esetben a csúszómód fennmaradhat (az állapottrajektória nem tudja elhagyni a kapcsolóegyenest), és ha fennmarad, akkor a fent említett változások nem befolyásolják a rendszer csúszómódbeli viselkedését.
4.3. Jobboldalán nem folytonos differenciál egyenletek megoldása
Tekintsük a következő autonóm differenciálegyenlet-rendszert:
|
és |
(4.6) |
ahol és . Ha folytonos, akkor (4.6) helyett a következő integrál egyenletet írhatjuk:
|
|
(4.7) |
A (4.6) differenciálegyenlet (4.7) alakú megoldását Carathéodory megoldásnak szokás nevezni, amely bizonyos feltételek mellett akkor is létezhet, ha nem folytonos [30]. A közelmúltban több cikk és Ph.D. dolgozat foglalkozott azzal, hogy miként lehet enyhíteni az -re vonatkozó és a (4.7) létezését garantáló előfeltételezéseket, de a bemutatott példára egyik eset sem alkalmazható, teljesen más jellegű megoldással kell próbálkozni.
Filippov egy olyan megoldást javasolt, amely talán közelebb áll az előző pontban bemutatott mérnöki szemlélethez [31], [32]. Filippov a (4.6) megoldását egy adott pontban annak alapján kereste, hogy miként viselkedik a derivált az adott pont környezetében, megengedve még azt is, hogy egy nulla mértékű halmazon a derivált viselkedése teljesen eltérjen a környezetétől, és a megoldás szempontjából figyelmen kívül hagyja a deriváltat ez utóbbi halmazon. Filippov eredeti definíciója nem-autonóm differenciálegyenletekre vonatkozott, de e fejezetben csak autonóm differenciálegyenletekkel foglalkozunk.
Tekintsük a (4.6) differenciálegyenlet-rendszert és tegyük fel, hogy az tér egy nyitott tartományán majdnem mindenütt értelmezett, mérhető és helyileg korlátos vektorfüggvény, amelyik x-ben nem folytonos. Az vektor értékkészletéből adott x mellett definiáljunk egy halmazt:
|
|
(4.8) |
ahol az x pont δsugarú környezetét, μa Lebesgue értelemben vett mértéket, N a Lebesgue értelemben vett nulla mértékű halmazt és a „konv” szócska az adott halmaz konvex lezárását jelöli.
Filippov a nem folytonos differenciálegyenlet-rendszerek megoldására a következő definíciót vezette be:
Definíció
Egy abszolút folytonos vektorfüggvény akkor megoldása a (4.6) differenciálegyenlet- rendszernek, ha tartományon majdnem minden t-re felírható
|
|
(4.9) |
Megjegyezzük, ha folytonos, akkor halmaznak minden x-re csak egyetlen eleme van, mégpedig , így Filippov definíciója összhangban van a szokásos (jobb oldalán folytonos) differenciálegyenletek megoldásával. Ugyanakkor, ha nem folytonos, akkor ez a definíció megengedi, hogy (4.6) megoldását olyan tartományban keressük, ahol nincs értelmezve.
4.4. Relés szabályozók
Alkalmazzuk Filippov definícióját a bevezető példa általánosításaként olyan állapot visszacsatolásos szabályozókörre, amelynek a visszacsatoló ágában egyetlen relé található (ld. 4-4. ábra). Tegyük fel, a rendszer állapotát (4.6) alakú differenciálegyenlet írja le, olyan módon, hogy a jobb oldalon álló vektorfüggvény a relé állapotától függően ugrásszerűen változik. A szabályozási (kapcsolási) stratégia legyen a következő. A visszacsatolt állapotváltozók által kifeszített tér tartományában definiáljunk egy n-1 dimenziós sima reguláris S hiperfelületet (amelyet kapcsoló felületnek is nevezhetünk) egy folytonos skalár-vektor függvény segítségével a következő módon:
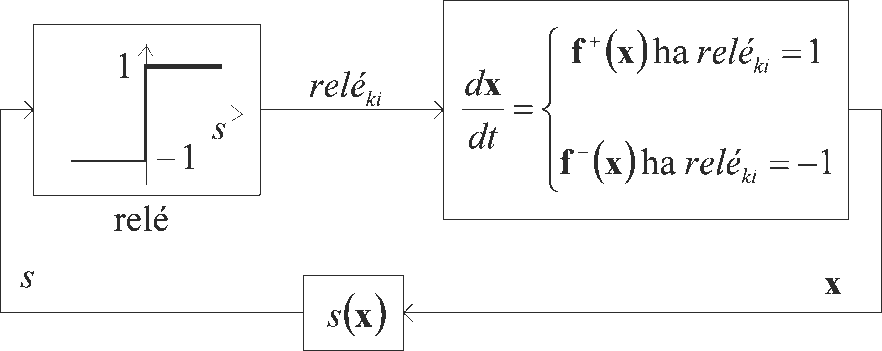
|
|
(4.10) |
A szabályozás célja, hogy az állapottrajektóriát erre a felületre kényszerítsük. Az ezzel kapcsolatos feltételeket a 2.3.1 fejezet tárgyalja. Az S felület pontjait jelöljük xs-sel. E felület segítségével osszuk két részre a G tartományt:
|
|
(4.11) |
A G tartományon legyen az x-re vonatkozó differenciálegyenlet a következő alakú:
|
|
(4.12) |
ahol mind , mind egy egyenletesen folytonos vektor-vektor függvény. Vegyük észre, hogy az S felületen nincs értelmezve, és nem tettünk olyan kikötést, hogy és az S felület két oldalán egyezzen meg.
Az S felületen kívül egy közönséges differenciálegyenlettel van dolgunk. A (2.12) megoldása az S felület xs(t) pontjaiban okozhat gondot. A (4.9) definíció szerint K az a legkisebb zárt konvex halmaz, melyet úgy kapunk, hogy az S felület xs(t) pontjaiban vesszük xs egy tetszőleges környezetét, ebből kizárjuk -t, vagyis egy olyan nullamértékű N tartományt, ahol nincs értelmezve, s az így kapott tartományhoz tartozó vektorok halmazát zárt konvex halmazzá egészítjük ki. Nyilvánvaló, hogy értéke minél kisebb, annál kisebb lesz az így kapott zárt konvex halmaz. Végül vennünk kell a zárt konvex halmazok közös részét az összes és N mellett. Mivel f(x) abszolút folytonos, ezért az S felület bármely pontján léteznek a következő határértékek:
|
|
(4.13) |
Ebből az következik, hogy az S felület bármely xs(t) pontjához tartozó halmaznak csak két eleme van, és . E két vektornak kell venni a konvex lezárását, amelyik az összes értékhez tartozó legkisebb részhalmaz lesz. Összefoglalva, a (4.6) differenciálegyenlet a (4.12) alakú nem-folytonossággal az S felület xs(t) pontjaiban a (4.9) definíció értelmében a következő alakban írható le:
|
|
(4.14) |
A (4.14) szemléltetéséhez tekintsük a 4-5. ábrat, ahol az S felület P pontjához tartozó és vektort rajzoltuk fel. Az pontban az állapottrajektória változását az ekvivalens vektor adja meg, amely az és vektorok konvex összege.
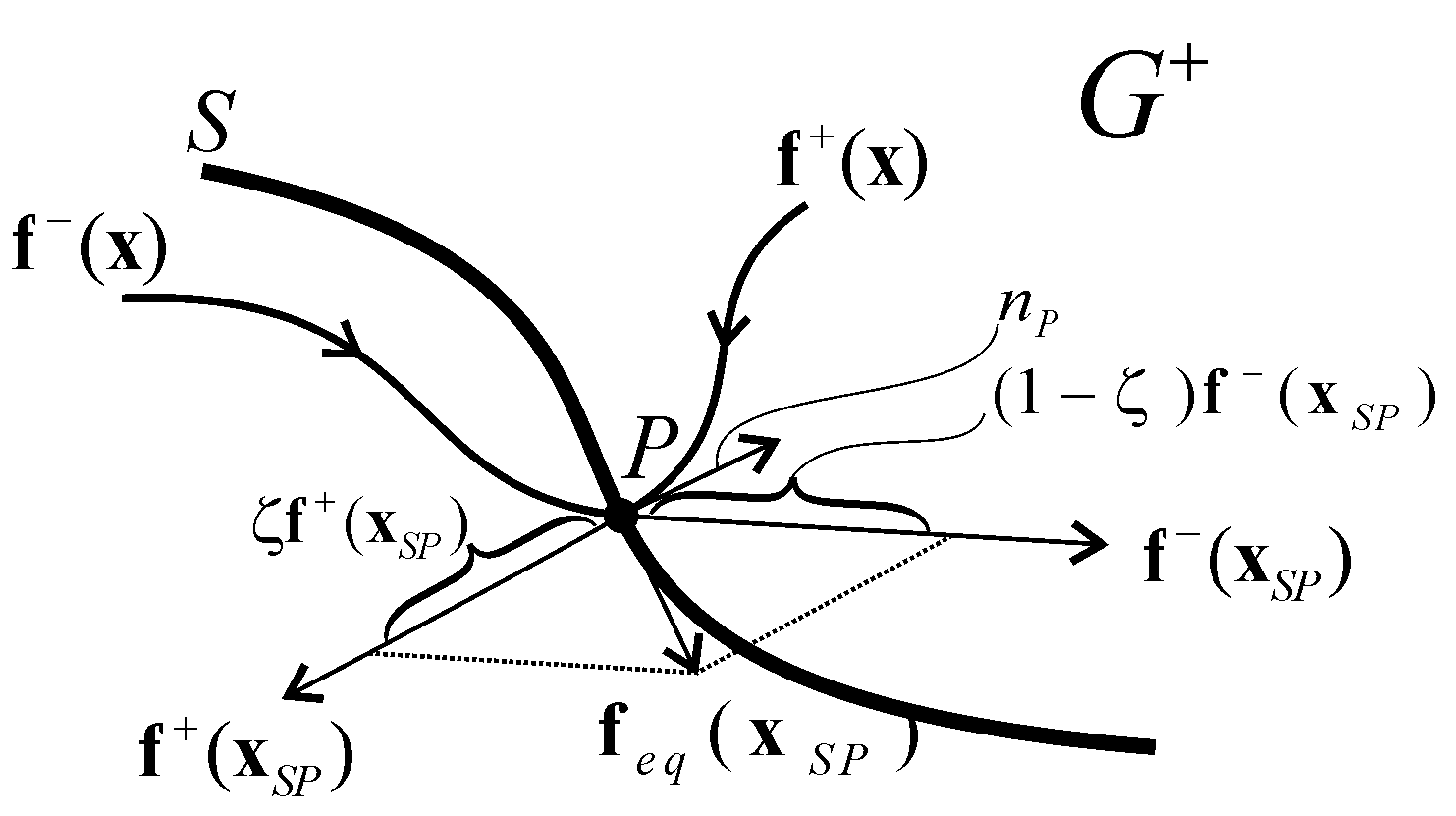
Jelöljük Lfs(x)-szel az s(x) skalár függvénynek az vektortérre vonatkozó irány menti deriváltját.
|
|
(4.15) |
ahol (a●b) az a és b vektorok skalárszorzatát jelöli. Mivel s(x) egyenletesen folytonos, ezért az S felület bármely pontján léteznek a következő határértékek:
|
|
(4.16) |
értékét úgy kell meghatározni, hogy , illetve merőleges legyen az S felület normálisára (ld. Filippov 3. Lemma [32]).
|
|
(4.17) |
(4.17) úgy értelmezhető, hogy a csúszómódban a csúszófelület pontjaiban az állapottrajektória változását egy olyan ekvivalens vektor függvénnyel írhatjuk le, amely kielégíti a (4.17) feltételt. A (4.14) és (4.17) alapján:
|
|
(4.18) |
A (4.18)-ből kifejezhető
|
|
(4.19) |
4.4.1. A csúszómód fennmaradásának feltétele
Ha és , akkor az S felület mindkét oldalán az f(x) vektortér az S felület felé mutat (ld. 4-6. ábra). Ezért, ha az állapottrajektória egyszer elérte az S felületet, akkor nem tudja elhagyni azt. Az állapottrajektória a felület mentén csúszik, és ezért nevezik ezt az állapotot csúszómódnak.
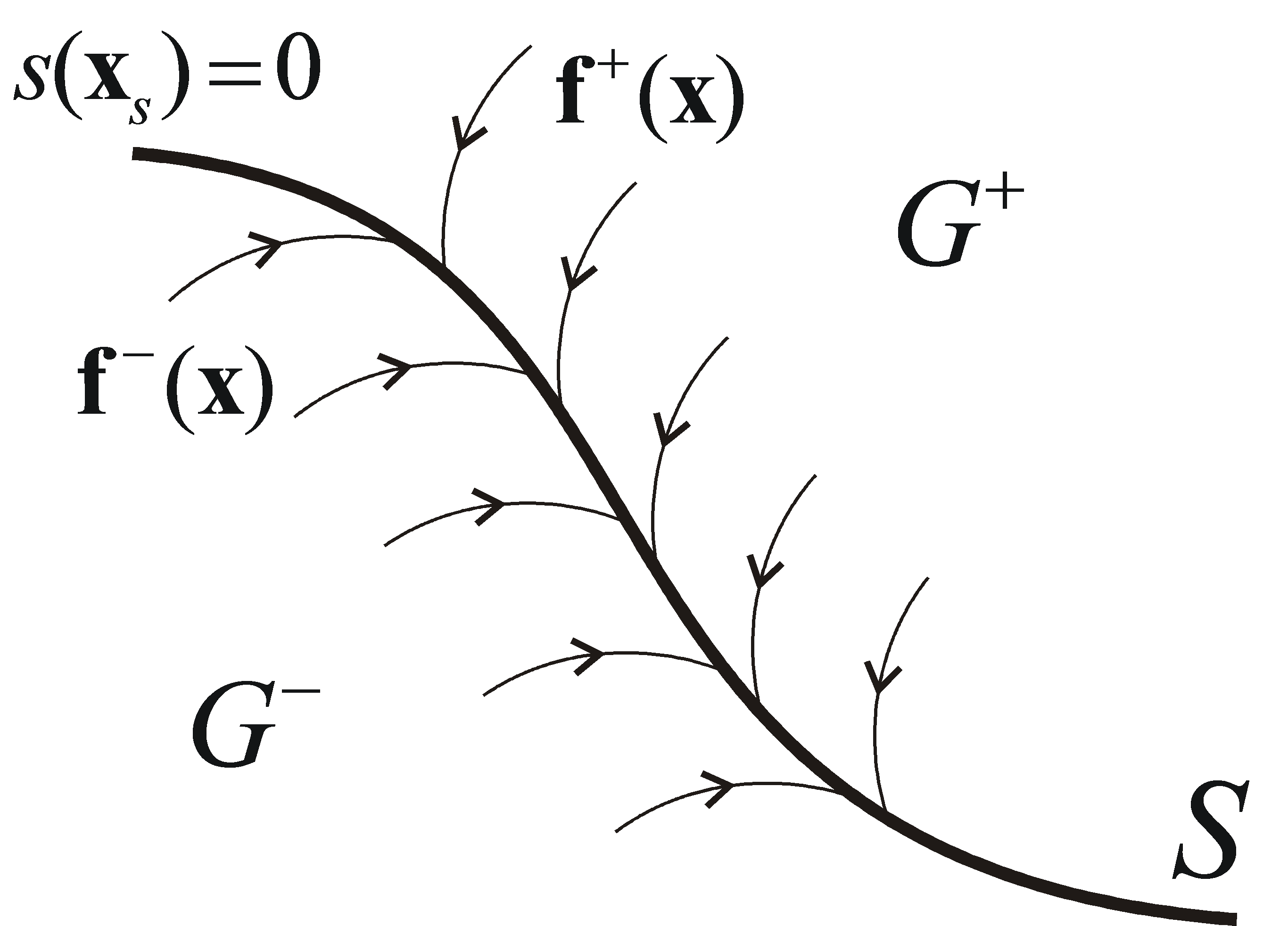
Megjegyezzük, hogy az S felület két oldalán külön-külön felírt két feltétel:
|
|
(4.20) |
egyetlen egyenlőtlenséggel is helyettesíthető:
|
|
(4.21) |
amely értelmezhető úgy is, mint a rendszernek az S felületen maradására vonatkozó Lyapunov-féle stabilitás kritérium.
4.5. A bevezető példa differenciálegyenletének megoldása
A bevezető példa áramkörében két energiatároló elem van (L és C), ezért az áramkör viselkedését két állapotváltozó segítségével írhatjuk le. A szabályozás célja az, hogy a hibajelet megszüntessük, ezért célszerű a hibajelet és annak időszerinti első deriváltját választani állapotváltozónak.
|
|
(4.22) |
A hibajelre vonatkozó állapotegyenlet konstans alapjel mellett a szokásos mátrixos alakban a következő:
|
, |
(4.23) |
ahol , ha ideális L-C elemeket feltételezve a veszteségeket elhanyagoljuk, és ha egy soros ellenállással modellezzük az áramkör veszteségeit. A (4.4) alapján, legyen a csúszófelületet definiáló skalár függvény
|
|
(4.24) |
A (4.23) mátrixegyenletet átírva (4.12) alakúra:
|
|
(4.25) |
Ahol
|
, |
(4.26) |
Az s(x) skalár függvénynek az vektortérre vonatkozó irány menti deriváltja az S felület két oldalán:
|
|
(4.27) |
Megjegyezzük, hogy esetünkben mind , mind értelmezhető magán az S felületen is, ezért nincs szükség a (4.16)-ban leírt határérték számításra, az S felülethez tartozó pontok közvetlenül behelyettesíthetők. Ugyanakkor a (2.21) feltétel csak a következő tartományban teljesül.
|
|
(4.28) |
Ebből az következik, hogy az adott relés szabályozó mellett az S felületnek csak egy korlátozott részén alakulhat ki a csúszómód. A relés szabályozási törvény további tagokkal kiegészítve a teljes S felületére kiterjeszthető a csúszómód kialakulásának feltétele [3]. Maradva a relés szabályozónál, a (4.19) és (4.27) alapján:
|
|
(4.29) |
A (4.13), (2.51), (2.53), valamint (2.56) alapján a csúszómódban a rendszert leíró differenciálegyenlet a következő alakú lesz:
|
|
(4.30) |
A (4.30) differenciálegyenlet lényegében megegyezik a csúszóegyenes egyenletével.
|
|
(4.31) |
Ezzel beláttuk, hogy a sima reguláris S csúszóegyenes előállítható végtelenül nagy frekvenciával kapcsolgatott és végtelenül rövid szakaszokból álló, minden pontjában megtört görbe segítségével. A (4.30) megoldása:
|
|
(4.32) |
ahol az hibajel kezdeti értéke abban a pillanatban, amikor az állapottrajektória eléri az S felületet. A (4.32)-ből az is látható, hogy a csúszóegyenesre jellemző időállandó. Vegyük észre, hogy a (4.32) egyenletben nem szerepel az eredeti áramkör egyetlen paramétere sem. Ez azt jelenti, hogy a fent vázolt ideális csúszómódban a relés szabályozási törvény a rendszer bizonyos paramétereire és bizonyos jellegű zavarójelekre érzéketlen robosztus szabályozóhoz vezet. A fenti levezetés csak azzal foglalkozik, hogy a rendszer miként viselkedik magán a csúszófelületen, de nem foglalkoztunk azzal a gyakorlatban nagyon fontos kérdéssel, hogy miként lehet gondoskodni arról, hogy az állapottrajektória mindig elérje a csúszófelületet, és a csúszófelületen maradjon.
Természetesen a valóságban egy ilyen ideális csúszómód nem alakulhat ki. Mérnöki szempontból ennek egy közelítő és azon belül is az ún. csattogásmentes megvalósítása jelenti a kihívást.
4.6. Több bemenetű rendszerek csúszómódban
Az előző pontban azt feltételeztük, hogy a rendszernek egyetlen bemenete van, ezért a tartományt egyetlen hiperfelülettel két részre osztottuk és a rendszert relés jelleggel e felület mentén kapcsolgattuk. Tegyük fel, hogy a rendszernek m bemenete van és minden bemenetet relés jelleggel kapcsolgatunk. Ennek megfelelően atartományban definiálunk m db n-1 dimenziós sima reguláris Si hiperfelületet m db folytonos skalár-vektor függvény segítségével a következő módon:
|
|
(4.33) |
Minden egyes felület segítségével más-más módon oszthatjuk ketté a G tartományt:
|
|
(4.34) |
Általános esetben a G tartományt 2m részre osztjuk és a (4.12) kiterjesztéseként minden tartományban más-más alakot vehet fel.
|
|
(4.35) |
A csúszómód kialakulhat részlegesen minden Si felületen a többi felülettől függetlenül. Globális csúszómódról akkor beszélünk, ha minden felületen kialakult a csúszómód, vagyis a globális csúszómód a hiperfelületek közös S metszésvonalán alakulhat ki.
|
, |
(4.36) |
ahol az egyes skalár-vektor függvények oszlopvektora:
|
, |
(4.37) |
Csúszómódban az állapottrajektória az S metén halad. Az S felület 2m résztartománnyal határos és a (4.9) definíciónak megfelelően az S felület bármely xs(t) pontjához tartozó halmaznak 2m eleme van, . E vektoroknak kell venni a konvex lezárását, amelyik az összes értékhez tartozó legkisebb részhalmaz lesz. A (4.35) differenciálegyenlet az S felület xs(t) pontjaiban a következő alakú:
|
ahol , |
(4.38) |
Csúszómódban a értékeinek meghatározásához a (4.19)-et kell általánosítanunk.
|
|
(4.39) |
A fenti definíció az jelenti, hogy az állapottrajektória az S felület mentén, az S felület normálisára merőleges irányban halad. A 4-7. ábra a részleges és globális csúszómódot szemlélteti m=2 esetre. A P1 és P2 pontban részleges, valamint P3 pontban globális csúszómód alakulhat ki. A csúszómód kialakulásának feltételét kétféle megközelítésben írhatjuk elő. Az első megközelítésben a részleges csúszómódot lokálisan az egyes Si felületek mentén külön-külön írhatjuk elő.
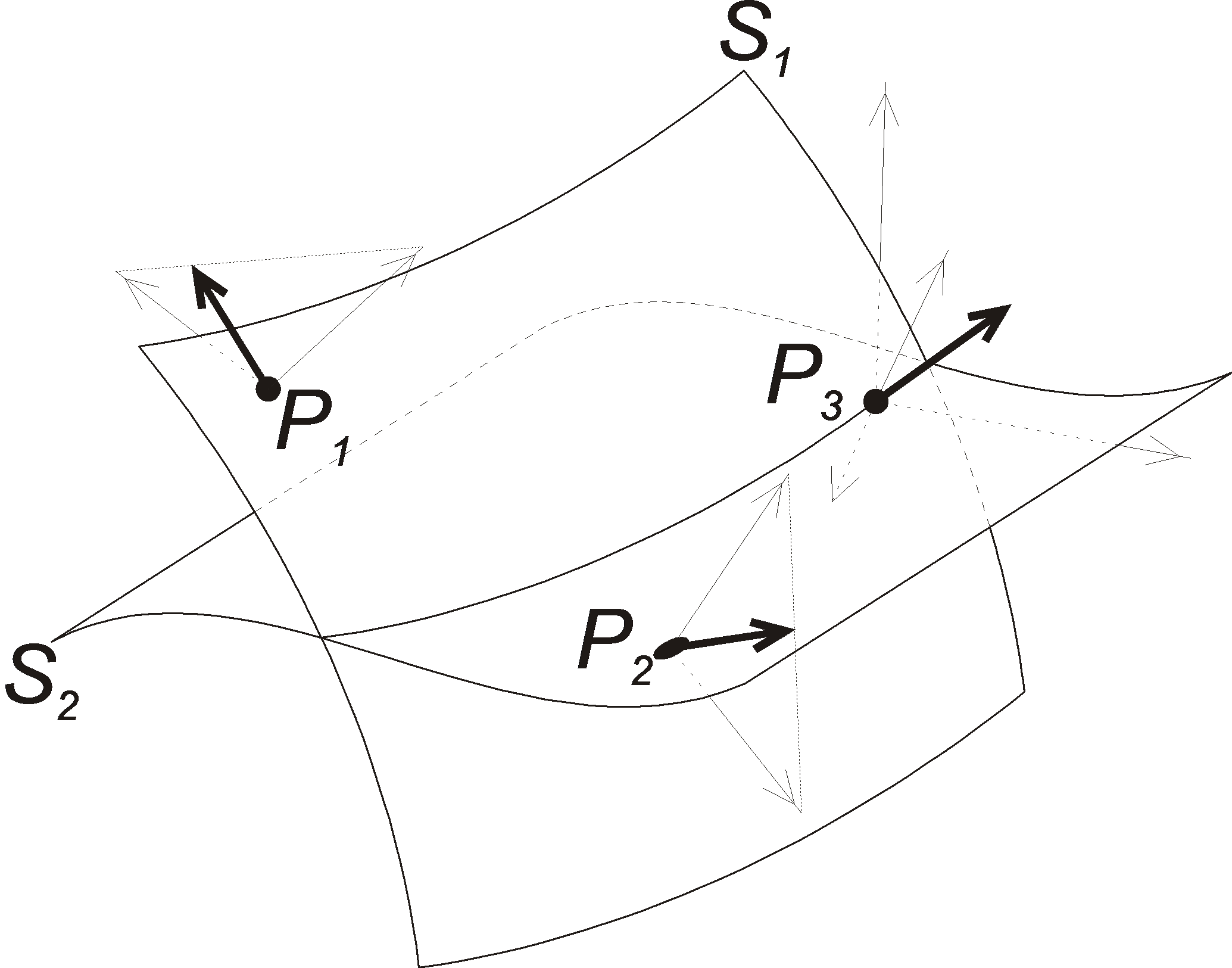
|
|
(4.40) |
Meg kell jegyezni, hogy a rendszeregyenlet belső struktúrájától függően az egyes bemenetek nem minden esetben függetleníthetőek egymástól. A másik és általánosabban alkalmazható megközelítésben a csúszómód kialakulását globálisan, az Si hiperfelületek közös metszéspontjában írjuk elő.
|
|
(4.41) |
Ennek megfelelően a szabályozási törvényt is kétféle megközelítésben kereshetjük. Az egyik megközelítésben minden bemenetnél a többi bemenettől függetlenül a (4.40) kielégítése a cél. A másik megközelítésben az összes bemenetet együttesen úgy változtatjuk, hogy a (4.41) teljesüljön. A teljesítményelektronika területén tipikusan a háromfázisú rendszerek említhetők meg, mint a több bemenetű-több kimenetű rendszerek. A [10], [11] -ban mind a (4.40), mind (4.41) megközelítésre találunk példát.
4.7. A csúszómód szabályozók tervezési lépései
A csúszómód szabályozó megtervezése három fő lépésből áll: első lépés a csúszófelület megtervezése, a második lépés egy olyan szabályozási törvény kiválasztása, amely az állapotváltozók trajektóriáját a csúszófelületre kényszeríti, majd azon tartja, végül a harmadik - a legfontosabb - lépés, a csattogás (lengés) mentesen történő megvalósítás.
Tekintsük a következő lineáris időinvariáns rendszert:
|
, |
(4.42) |
ahol ,és . Célunk a rendszert egy adott kezdeti állapotból eljuttassuk egy előírt egyensúlyi állapotba, és ehhez feltételezzük, hogy szabályozható párt alkot. Ha az állapotváltozókat szétválasztjuk, a (4.42) rendszer átírható az alábbi,
|
|
(4.43) |
reguláris alakra, ahol az beavatkozó jel közvetlenül csak az állapotváltozókra tud hatni, -re csak közvetetten, -n keresztül.
4.7.1. A csúszófelület tervezése
Csúszómód szabályozásnál általában a rendszer állapotváltozóinak számával megegyező dimenziójú fázistérben kijelölünk egy S csúszófelületet (kapcsolófelületet), amelyre rá akarjuk kényszeríteni a rendszerünket. A csúszófelülettel egyben megválasztjuk a visszacsatolt rendszer dinamikus tulajdonságait is. Természetesen ennek vannak elvi, és egy valós rendszernél egyéb fizikai korlátai is. A csúszófelületet klasszikusan az állapotváltozók lineáris kombinációjaként írjuk fel:
|
|
(4.44) |
ahol és . Ha a rendszer csúszómódban van, akkor s = 0, vagyis . A csúszófelület megtervezése gyakorlatilag mátrix megválasztását jelenti, tehát a tervezési probléma leegyszerűsíthető egy kisebb dimenziójú altér
|
|
(4.45) |
állapot visszacsatolásának a megtervezésére. Ebben az altérben x1 az állapotváltozó és x2 a bemenőjel, amelyet alakú állapot visszacsatolással határozhatunk meg. Csúszómódban a rendszer viselkedését a
|
|
(4.46) |
differenciálegyenlet írja le. Az eredeti szabályozási célunkat csak akkor érhetjük el, ha (4.46) stabilis. Így minden olyan állapot visszacsatoláson alapuló lineáris szabályozó tervezési algoritmus alkalmazható a kapcsolófelület megtervezésére, amely a (4.45)-öt stabilizálja (4.46) formában. Erre vonatkozóan a bevezető fejezet számos referenciát tartalmaz. Ez a tervezési módszer lineáris rendszerekre, illetve nemlineáris rendszerek linearizált modelljére alkalmazható.
4.7.2. A szabályozási törvény megválasztása
Ha a csúszófelületünk már megvan, akkor u értékét kell helyesen megválasztani. A visszacsatolt rendszer Ljapunov értelemben vett aszimptotikus stabilitásának, illetve annak a feltétele, hogy az adott rendszer mindig a csúszómód (s = 0 állapot) felé tartson és onnan ne térjen ki, a (4.40), illetve (4.41) feltételnek kell teljesüljön. Az egyszerűség kedvéért alkalmazzuk az első feltételt. A legegyszerűbb szabályozó elem, amely gondoskodhat a (4.41) teljesüléséről és a csúszómód kialakulásához vezethet, a relé (ld. 48. ábra):
|
|
(4.47) |
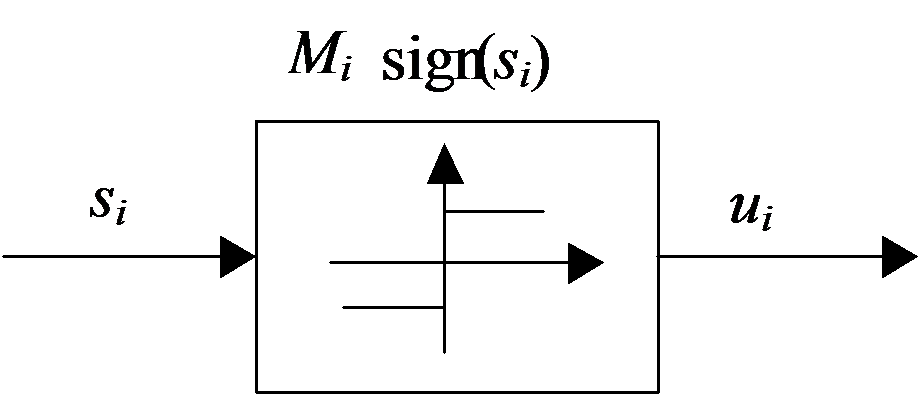
Megjegyezzük, hogy a csúszómód szabályozó a robusztusságát a nagy (ideális esetben végtelenül nagy) körerősítésének köszönheti. Erről a visszacsatoló ágban lévő relé gondoskodik, amelynek erősítését a ki- és bemenőjelének hányadosával definiálhatjuk:
|
|
(4.48) |
Csúszómódban si = 0, tehát a relé bemenetére 0 nagyságú jel érkezik, míg a kimenetén egy 0-tól különböző jel távozik, ezért ezt értelmezhetjük úgy, hogy a relé csúszómódban végtelenül nagy körerősítést kölcsönöz a szabályozási körnek.
|
|
(4.49) |
A (4.47) nem tud gondoskodni a csúszómód kialakulásáról a teljes állapottérben. (4.47) szabályozási törvényt megfelelő tagokkal kiegészítve elérhető, hogy a csúszómód kialakulásának és fennmaradásának feltétele az egész állapottérben teljesüljön. Az esetben a következő szokásos szabályozási törvény gondoskodik a csúszómód fenntartásáról, megfelelő megválasztásával [26]:
|
|
(4.50) |
Amennyiben a csúszómód bekövetkezett, akkor létezik egy olyan folytonos, úgynevezett ekvivalens beavatkozó jel, , amely a csúszófelületen képes tartani a rendszert. A (4.42) rendszeregyenletbe helyettesítve -t, kapjuk az ekvivalens vektort, amely az állapotváltozók mozgását írja le a csúszófelület mentén. Ennek megfelelően is (4.17)-ből számítható ki. A (4.43) és (4.44) egyenletekből meghatározható értéke:
|
|
(4.51) |
Ennek alapján felírható az beavatkozó jel:
|
|
(4.52) |
A gyakorlatban azonban ez nem használható, ugyanis a rendszer paramétereinek, illetve A és B rendszermátrixok pontos ismeretét feltételezi, ezért helyett annak csak becsült értékét tudjuk kiszámítani. Mivel sem , sem még önmagában nem biztosítja a csúszómód kialakulását (a zavarok távol tarthatják a rendszert csúszófelülettől), így egy olyan relés jellegű nem folytonos beavatkozó jelet adunk a becsült ekvivalens beavatkozó jelhez, amely képes kompenzálni a zavarok hatását.
|
|
(4.53) |
Ebben az esetben a relének csak becslési hibáját kell kompenzálni, ezért minél pontosabban becsüljük értékét, annál kisebbre választhatjuk az M értékét és ezzel együtt annál kisebb csattogásra számíthatunk.
A gyakorlati alkalmazás szempontjából a (4.47) relés szabályozási törvénynek az a legnagyobb előnye, hogy könnyen megvalósítható akár egyszerű analóg műveleti erősítővel is, ezért relatívan nagy kapcsolási frekvencia érhető el, s ennek köszönhetően (4.47) közvetlenül vezérelheti a teljesítményelektronikai félvezető kapcsoló elemeket. Ezért ott is alkalmazható, ahol a szabályozott szakasz legnagyobb időállandója viszonylag kicsi (ms alatt van), s ahol gyors beavatkozásra van szükség, így jelenleg még a digitális szabályozók nem alkalmazhatók, illetve alkalmazásuk esetén sincs idő bonyolult számításra két mintavételezés között. Ezzel szemben a hátránya az, hogy a (4.47) nem tud gondoskodni a csúszómód kialakulásáról a teljes állapottérben. értékére vonatkozóan két egymásnak ellentmondó elvárás van. Minél nagyobb értéke, az állapottérnek annál nagyobb tartományában gondoskodhat a csúszómód kialakulásáról, de ezzel együtt annál nagyobb csattogást eredményezhet a csúszófelület körül. A (4.52) és (4.53) által leírt szabályozási törvények közvetlenül nem vezérlik a félvezető kapcsoló elemeket, egy ISZM (Impulzus Szélesség Moduláció) is szükséges az elméletileg folytonosan változó , illetve előállításához. Ez általában mechanikai rendszerek szabályozásakor nem probléma, mert a szabályozott mechanikai rendszerek (robotok, manipulátorok) mozgásának meghatározó frekvenciája 100 Hz-nél kisebb. A digitális szabályozók napjainkban elérhető mintavételezési (vagyis (4.52) és (4.53) szabályozási törvényben a relé kapcsolási) frekvenciája legalább egy nagyságrenddel nagyobb és 1kHz körül van. A félvezető elemek kapcsolási frekvenciáját az akusztikus zaj csökkentése érdekében 20 kHz-nél nagyobbra szokás beállítani és ez ismét legalább egy nagyságrendi különbséget jelent a modulált , illetve és a moduláló jel frekvenciája között.
4.7.3. A csattogás elkerülése
A gyakorlati alkalmazhatóság szempontjából ez a fejezet meghatározó fontosságú.
4.7.3.1. A szakadásos jel folytonossá tétele
Több csattogás elkerülési módszer arra irányul, hogy az szakadását a kapcsoló felület környékén egy folytonos átmenettel helyettesítse. A legegyszerűbb és talán ezért a leggyakoribban alkalmazott módszer, amikor a relét egy telítődéssel helyettesítjük (ld. 4-9. ábra).
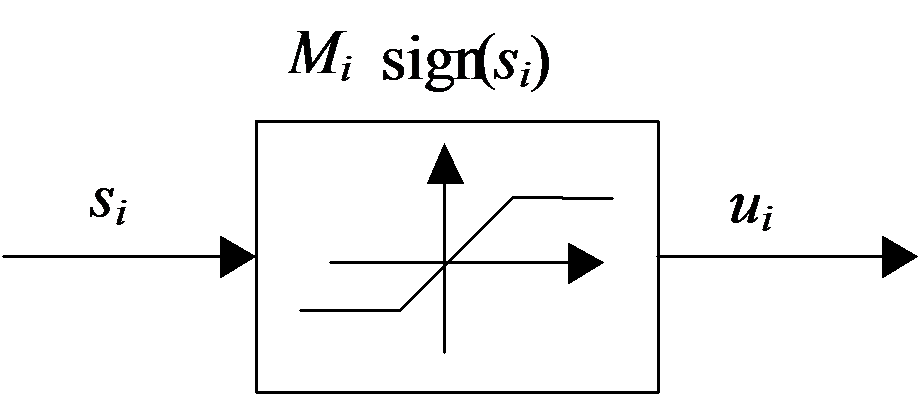
Egy másik fontos megközelítés az ún. szektoros csúszómód. Ennek is több változata létezik. Furuta [20,21] abból indul ki, hogy a csúszófelület közelében bizonyos esetekben található egy olyan szektor, ahol már nulla beavatkozó jel mellett is a rendszer a felület felé tart. Ő ezt PR szektornak nevezte el, mert a szektort a P norma csökkenése alapján jelöli ki. Kiderült, hogy vannak esetek, amikor annak ellenére, hogy a P norma csökken, az állapottrajektória kiléphet a PR szektorból, ezért további módosításokat javasolt [33].
A szektoros csúszómódnak egy teljesen más megközelítése található [17], [34] -ben. A csúszó szektort két felület határolja. A felületeket úgy választjuk ki, hogy a szektor Ljapunov értelemben stabilis legyen. A szektoron kívül a szokásos módon egy olyan csúszófelületre próbáljuk az állapottrajektóriát kényszeríteni, amelyik a szektort határoló két felület középértéke. Ez gondoskodik arról az állapottrajektória belépjen a szektorba, és ha egyszer belépett oda, akkor ott is maradjon. A szektoron belül a feltételül szabott stabilitásnak megfelelően az állapottrajektória automatikusan konvergál az origóhoz, ezért egy olyan folytonos beavatkozó jelet adunk ki, amely az aktuális állapotnak a szektort határoló két felülettől mért távolságának középértékével arányos, így az origóhoz közeledve automatikusan egyre kisebb lesz a beavatkozó jel. Az 5. fejezet részletesen foglalkozik ezzel.
4.7.3.2. Állapot-megfigyelő alapú csúszómód szabályozás
A csúszómód szabályozás legnagyobb problémája, hogy minden mérnöki modell a valósághoz képest elhanyagolásokon alapul. Bizonyos elhanyagolások egy folytonos beavatkozás esetén is okozhatnak gondot, például nem várt lengéseket, de ezeknek sokkal nagyobb a veszélye a csúszómód szabályozás esetén, ahol a nem folytonos beavatkozó jel nagyfrekvenciás összetevője rezonanciába kerülhet a valós rendszernek a tervezés során elhanyagolt kis időállandójú dinamikai tulajdonságával. A csattogásnak ez lehet az egyik oka. Más jellegű probléma, hogy a csúszómód szabályozás teljes állapot visszacsatoláson alapul és legtöbbször nem mérhető az összes állapotváltozó. Az utóbbi probléma megoldása az állapot-megfigyelő, abban az esetben, ha rendszerünk megfigyelhető. Bizonyos esetekben állapot-megfigyelő megoldást jelenthet a csattogási problémákra [1] is. Ilyenkor az állapot-megfigyelő egyfajta szűrő szerepét látja el, a kapcsolási felületet és a beavatkozó jelet az állapotváltozók megfigyelt (becsült) értékéből számítjuk, még akkor is, ha a tényleges állapotváltozók mérhetőek. A szabályozó vázlata a 4-10. ábran látható. Miután a megfigyelő struktúrája és paraméterei ismertek, a megfigyelő – VSS szabályozó hurokban ideális csúszómód jöhet létre (VSS=Variable Structure Systems).
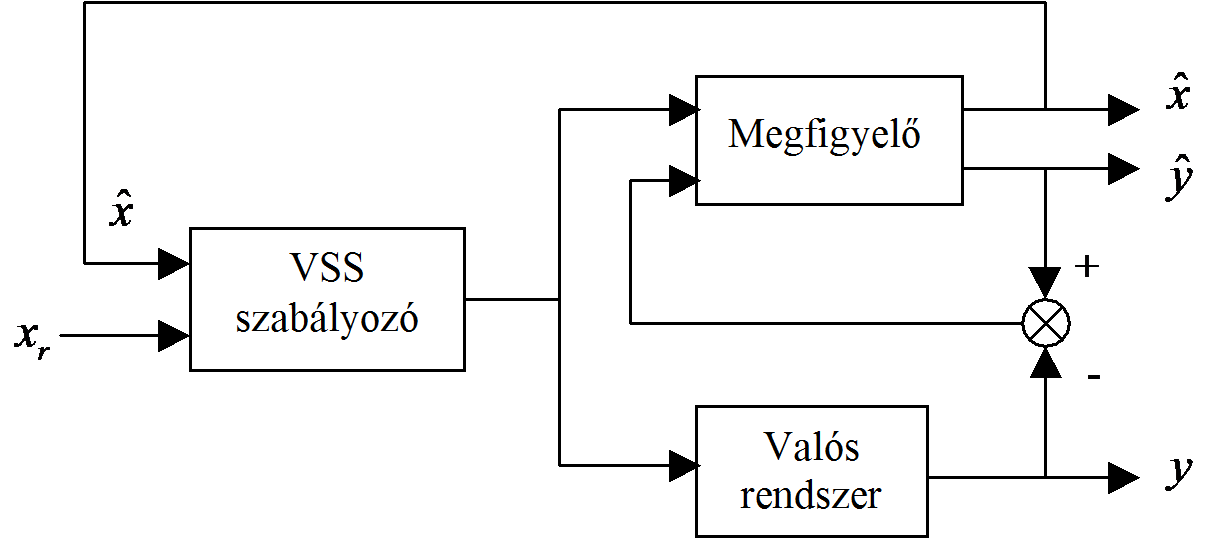
A szinguláris perturbáció elvének megfelelően [35] a valós rendszer gyors időállandói elhagyhatók a megfigyelő modelljéből. Ily módon a megfigyelt állapotváltozók száma jelentősen lecsökkenthető. A megfigyelőt leíró egyenletek:
|
|
(4.54) |
Az n index a névleges értékeket jelöli. A dinamika elhanyagolt gyors összetevőinek tranziens hatása miatt a valós rendszer és a megfigyelő kimenetei között lesz egy aszimptotikusan megszűnő eltérés, de a mozgásban a nem modellezett dinamika nem okoz oszcillációt.
4.7.4. Diszkrét idejű csúszómód szabályozás
A csattogás egy másik előidézője lehet a beavatkozó jel korlátozott kapcsolási frekvenciája. A folytonos idejű csúszómód szabályozás robosztusságát nagy frekvenciájú kapcsolgatással megvalósított nagy körerősítéssel érjük el. Ahhoz, hogy ezt a filozófiát a digitális szabályozók világában is alkalmazhassuk, a mintavételezési frekvenciát növelni kell más szabályozásokéhoz képest. Ennek a problémának megoldására a [22] irodalomban a csúszófelület aszimptotikus elérését ajánlják a kommutáció elkerülésére. Egy alternatív megoldást követ [23], ahol a mintavételezett állapotváltozók véges mintavételezési szám után elérik a csúszófelületet.
Definíció: Az
|
|
(4.55) |
diszkrét idejű dinamikai rendszerben az felület részhalmazára akkor állhat elő diszkrét idejű csúszómód, ha létezik -nek olyan U nyílt környezete, amelyre -ból következik, hogy .
A fenti definíciónak megfelelően a (4.43) állapotegyenlet diszkretizálható minden mintavételezési pillanatban.
|
, |
(4.56) |
ahol a k index a k-adik mintavételezési időt jelöli, azaz ( a mintavételezési időállandó) és
|
, |
(4.57) |
A csúszófelület az mintavételezési pontban:
|
|
(4.58) |
A definícióból következik, hogy
|
|
(4.59) |
minden -ra. A diszkrét idejű csúszómód megvalósul, ha a mátrix invertálható, és az beavatkozó jelet úgy kell megválasztani, hogy kielégítse a (4.59)-at.
|
|
(4.60) |
A folytonos idejű esethez hasonlóan a (4.60)-ből számított megoldást ekvivalens beavatkozó jelnek nevezzük:
|
|
(4.61) |
A szabályozási törvényt a következőképpen lehet definiálni:
|
|
(4.62) |
ahol az beavatkozó jel fizikai korlátja.
4.8. A csúszómód szabályozók tervezési lépéseinek kísérleti alkalmazása
Egy olyan alkalmazást kerestünk, amelynek a matematikai leírása hasonló a 4.2 példa leírásához, és amelyhez megvoltak a kísérleti eszközök. Célunk az, hogy egy permanens mágneses szervomotor forgórészét csúszómódban eljuttassuk az egyik pozícióból egy másikba [26] alapján. Elhanyagolva a motor armatúra induktivitását (más megközelítésben a villamos időállandót), a rendszer két állapotváltozóval írható le. A motor aktuális pozícióját tekintsük zéró értéknek, és legyen a referencia jel egy konstans nullától különböző pozícióérték r. Válasszuk állapotváltozónak a motor szögelfordulásának és szögsebességének hibajelét.
|
|
(4.63) |
A motor hibajelére vonatkozó differenciálegyenlet konstans pozíció alapjel mellett:
|
, |
(4.64) |
ahol és Fv a szervorendszer másodrendű nyomatéka, illetve viszkózus súrlódást figyelembe vevő paramétere. A a motor fluxusa, k a motor felépítésére jellemző konstans, R az armatúrakör ellenállása és Uk a motor kapocsfeszültsége. Legyen a csúszófelületet definiáló skalár függvény:
|
, |
(4.65) |
Ez a állapotsíkon egy egyenest határoz meg (ld. 4-11. ábra).
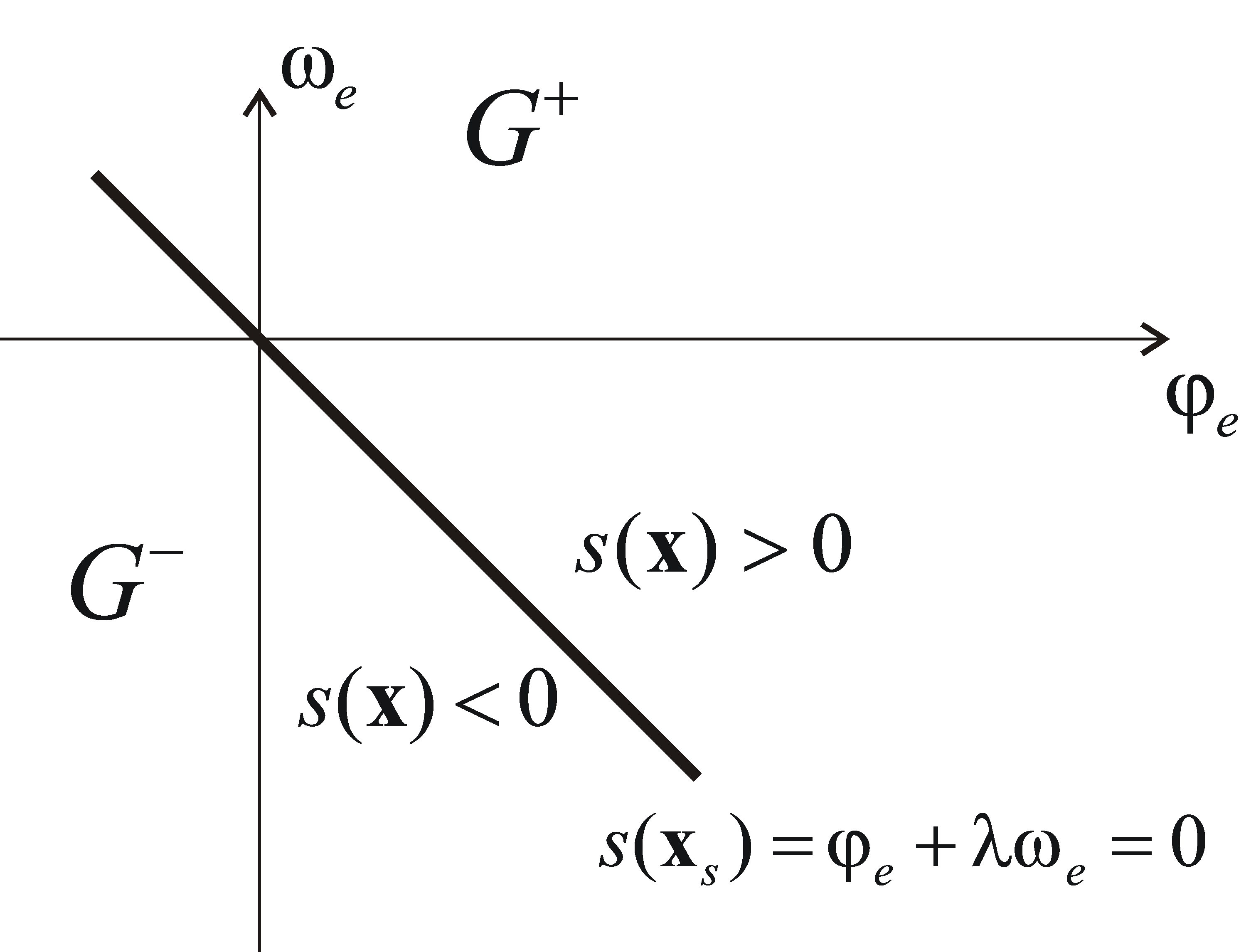
A legegyszerűbb relés szabályozót feltételezve:
|
|
(4.66) |
A (4.12), (4.62) és (4.64) alapján
|
, |
(4.67) |
ahol
|
és . |
(4.68) |
Ez jellegében megegyezik a (4.25) egyenlettel, ezért (4.64) megoldása:
|
|
(4.69) |
ahol a szögelfordulás hibájának az értéke abban a pillanatban, amikor az állapottrajektória eléri az S felületet. A bevezető példához hasonlóan itt is egy robosztus szabályozáshoz jutottunk. Vizsgáljuk meg a csúszómód kialakulásának feltételét (4.21) alapján. Ehhez szükségünk van az S idő szerinti első deriváltjára, a (4.64) és (4.65) alapján:
|
|
(4.70) |
Az értékét a (4.46) relé segítségével határozzuk meg. A (2.21) a következő feltételek mellett teljesül:
|
|
(4.71) |
4.8.1. Mérési eredmények
A kísérleti eszköz egy DSP-vel vezérelt egy-szabadságfokú szervorendszer (ld. ???
4-12. ábra). A fényképpel ellentétben ezeknél a méréseknél a zavarójelet megvalósító rúdra szerelt tömeget is felszereltük. A motorhoz egy merev tengelyen keresztül kapcsoljuk a terhelést.
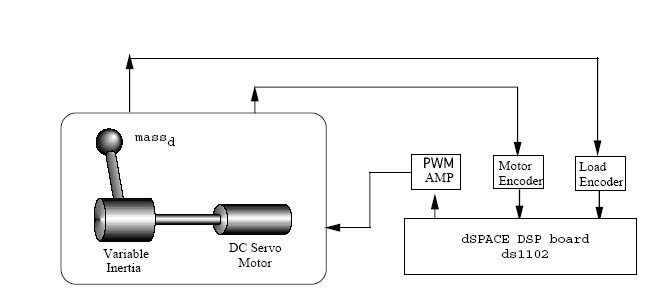

A névleges értékekből számított egyszerűsített rendszer egyenlet az előző pontban bevezetett jelölésekkel
|
|
(4.72) |
A csúszófelületre jellemző időállandó:
|
|
(4.73) |
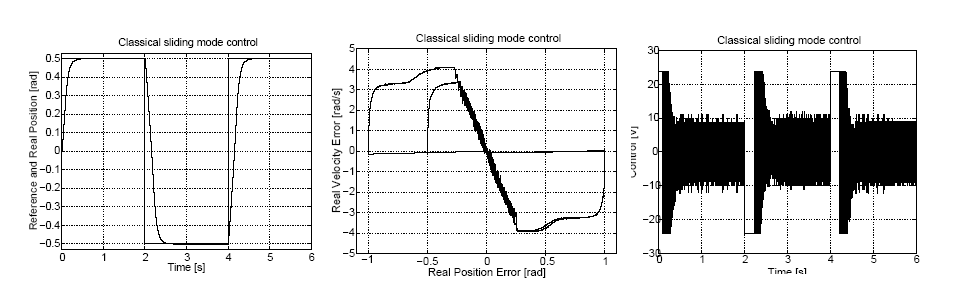
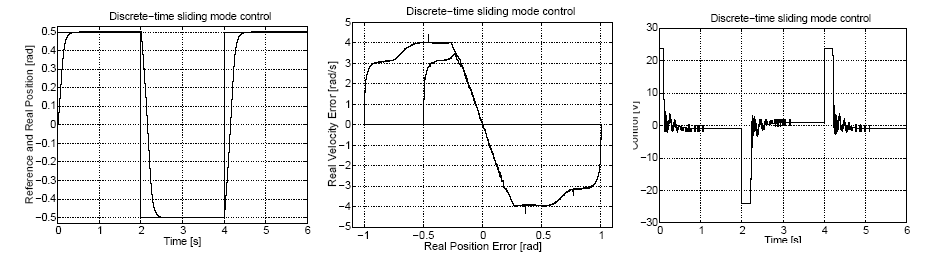
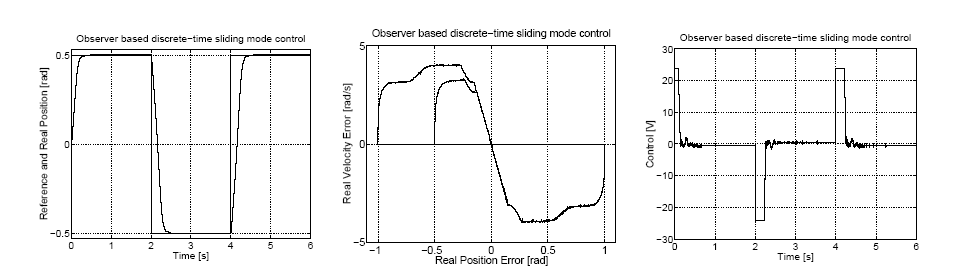
Három különböző mérési sorozatot végeztünk el az első esetben (klasszikus csúszómód) a (4.50), a második (diszkrét idejű csúszómód) és a harmadik (megfigyelőre alapozott diszkrét idejű csúszómód) esetben a (4.62) szabályozási törvényt alkalmaztuk. A második és a harmadik eset között az a különbség, hogy a harmadik esetben a 4-10. ábra alapján a (4.54) megfigyelőből kapott állapotváltozó értékeket helyettesítettük a (4.62) képletbe a mért értékek helyett. Mindhárom esetben a szabályozási törvényben megtalálható folytonosan változó összetevőjét Impulzus Szélesség Moduláció segítségével állítottuk elő. A mintavételezési frekvencia 1 Hz és a felvezetők kapcsolási frekvenciája 20 kHz volt. Mindhárom esetben a szögelfordulás időfüggvényét, az állapottrajektóriát és a beavatkozó jel (amely esetünkben a motorra kapcsolt feszültség, amely egy 24 V maximális értékű modulált jel) időfüggvényét ábrázoltuk (ld. 4-13. ábra, 4-14. ábra és 4-15. ábra). Megfigyelhető, hogy a szögelfordulás időfüggvényében nincs jelentős eltérés a három esetben, és ez összhangban van azzal, hogy elméletileg a három eset azonos eredményt ad. Ezzel szemben a beavatkozó jel aktivitása sokkal nagyobb a klasszikus csúszómódban ennek elméletileg is így kell lennie – ez a (4.50) szabályozási törvény sajátossága – és ami a mérés során hallható, a mintavétellel megegyező frekvenciájú zajt eredményezett. Megjegyezzük, hogy a 20 kHz-es moduláló jel természetesen nem volt hallható. Elméletileg a diszkrét idejű csúszómódban – a modulációtól eltekintve – egy folytonos, sima beavatkozó jelet kellett volna kapnunk, de a valóságban (ld. 4-14. ábra) határozottan észlelhetők a beavatkozó jel gyors előjelváltásai, bár ez füllel már alig érzékelhető zajt eredményezett. A beavatkozó jel aktivitása a megfigyelő alkalmazásával tovább csökkenthető, ennek a hallható zajra már nem volt észlelhető hatása.
4.9. Kéttömeg rendszer közvetlen elcsavarodás szabályozása csúszómódban
A fejezet egy rugalmas tengellyel összekötött ún. kéttömeg rendszer csúszómód szabályozásával foglalkozik. A kihívást az jelenti, hogy a kéttömeg rendszer önmagában lengésre hajlamos, és a csúszómód szabályozás legnagyobb problémája, hogy lengéseket gerjeszt. Ezért mérnöki szempontból nem a csúszómód szabályozás a legalkalmasabb e szabályozási feladatra, de pont ezért fontos annak bizonyítása, hogy egy ilyen lengésre hajlamos rendszert is lehet csattogás mentesen szabályozni csúszómódban. A következőkben megvizsgáljuk, hogy miként befolyásolja az előző fejezet végén tárgyalt kísérleti berendezés működését, ha a mozgatott tömeget egy rugalmas tengely segítségével kapcsoljuk a motorhoz, majd javaslatot teszünk a tengely elcsavarodásának közvetlen csúszómód szabályozására, és bemutatjuk a lengések elkerülésének módját.
4.9.1. A nem modellezett dinamika hatása a csúszómódra
Tegyük fel, hogy a 411. ábran a motort és a terhelést egy rugalmas tengely köti össze a 416. ábran látható módon, ahol az egyik tömeg az egyenáramú motor, a másik tömeg a terhelés. Az őket összekötő rugalmas tengelyt egy rugóval modellezzük.
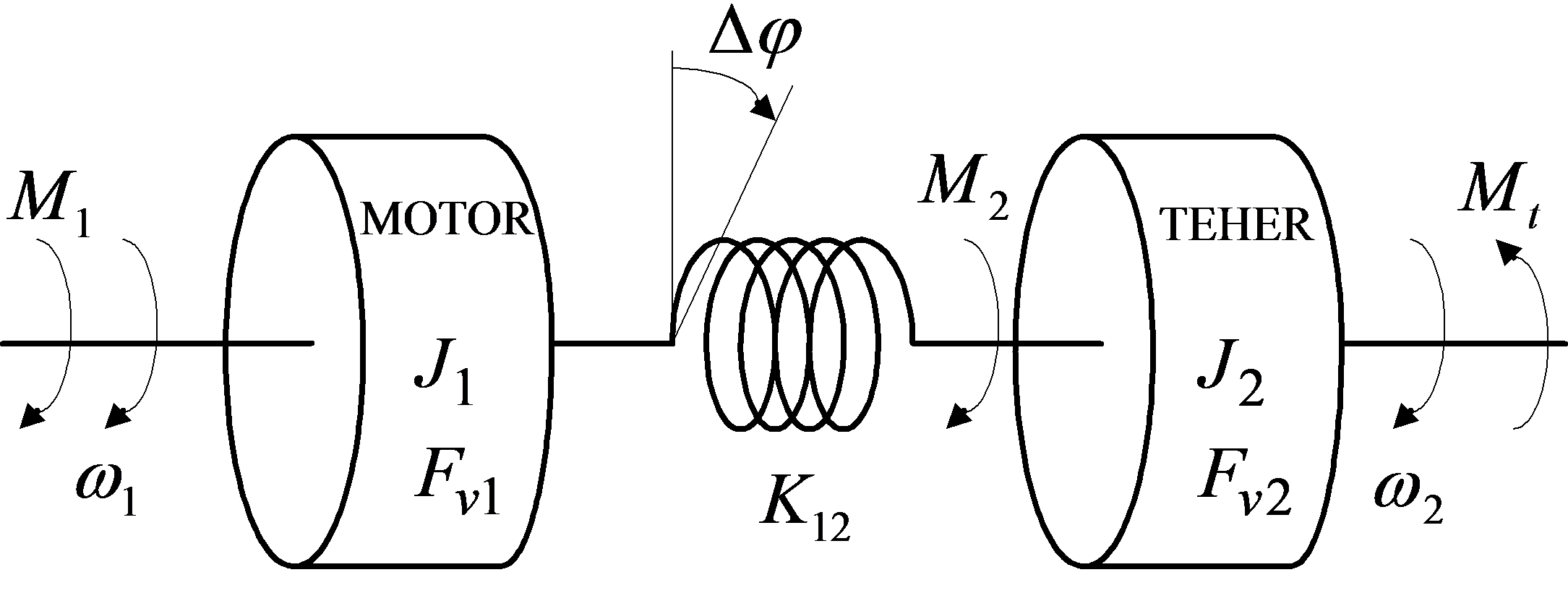
A jelölések: a motor nyomatéka, a fordulatszáma és az elfordulása, a rugóról a teherre ható nyomaték, és a teher fordulatszáma és elfordulása, pedig a terhelő nyomaték (zavarásként fogjuk fel). a rugóállandó, a rugó elcsavarodása (), , , és pedig értelemszerűen a motor illetve a teher másodrendű nyomatéka, illetve viszkózus súrlódást figyelembe vevő paraméter. a korábban alkalmazott eredő J-t két részre osztjuk
|
|
(4.74) |
A (4.64) rendszeregyenletet kell módosítanunk. Tegyük fel, hogy a motorra és a terhelésre az ún. illesztési feltételnek megfelelően írjuk elő a referencia jelet, és legyen az állapotváltozók vektora:
|
|
(4.75) |
A módosított állapotegyenlet:
|
|
(4.76) |
Az előző példához hasonlóan itt is a motor pozíció és fordulatszámjeléből számítjuk a csúszófelületet:
|
|
(4.77) |
Vizsgáljuk meg a csúszómód kialakulásának feltételét a (4.21) alapján. Ehhez szükségünk van az s idő szerinti első deriváltjára, a (4.76) és (4.77) alapján:
|
|
(4.78) |
Az értékét a (4.46) relé segítségével határozzuk meg. A (4.21) a következő feltételek mellett teljesül:
|
|
(4.79) |
Látható, hogy a paraméterek megválaszthatók úgy, hogy az origó környékén ne alakulhasson ki stabilis csúszómód. Az előző példában szereplő J tehetetlenségi nyomatékot 2:3 arányban osztjuk meg a motor és a terhelés között, a rugalmassági tényező értékét 800Nm/rad-nak választjuk. A csúszómód korábbi három vizsgált megvalósítása között már lényeges különbség tapasztalható. Ilyen méréseket nem állt módunkban elvégezni, így csak szimulációra hagyatkozhatunk. A szimulációs eredmények a 4-17. ábran láthatók. Mind a klasszikus, mind a diszkrét idejű csúszómódban jól láthatóak a lengések. Ez a (4.79) alapján nem meglepő. Az igazán fontos üzenetet a 4-17. ábra/c. ábrája hordozza. Esetünkben a motornak mind a pozíciója, mind a szögsebessége mérhető és ezeket csatoltuk vissza az első két szabályozásnál, ha ezeket a jeleket egy olyan megfigyelő jelével helyettesítjük, amelyik merev tengelyt feltételez a motor és a terhelés között, akkor ezek a lengések eltűnnek.
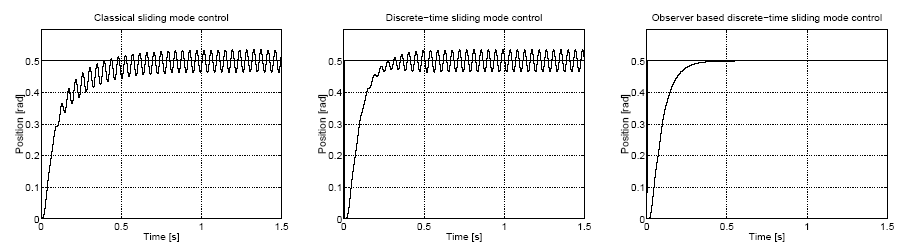
A lengések az első két esetben is kiküszöbölhetőek lennének, ha a (4.64) helyett a (4.76) rendszeregyenletből kiindulva a csúszófelületet kiegészítenénk egy, a rugalmas tengelyre vonatkozó állapotváltozóval és azt a négy állapotváltozó négy dimenziós fázisterében terveznénk meg. Ekkor viszont problémát jelentene a három állapotváltozó mérése. Ha nem tudjuk mérni a három állapotváltozót, akkor egy megfigyelőt kell terveznünk a nem mérhető állapotváltozóhoz, tehát mindenképp szükségünk van egy megfigyelőre. A szinguláris perturbáció elvének megfelelően elegendő lehet, ha a megfigyelőt pusztán az eredeti merev tengellyel rendelkező rendszerhez tervezzük, így a megfigyelőre alapozott diszkrét idejű csúszómód szabályozó egyaránt jól működik merev, illetve rugalmas tengellyel összekötött terhelés esetén (ld. 4-14. ábra és 4-17. ábra. c.). Ha a tengely rugalmasságát tovább növeljük, akkor az elhanyagolt villamos időállandó okozhat problémát.
4.9.2. Kéttömeg rendszer egyenletei
Célunk a teher fordulatszámának szabályozása a motor nyomatékán keresztül. Technológiai okok miatt csak a motor fordulatszáma mérhető, továbbá a tengely elcsavarodása egy bizonyos értéket nem haladhat meg.
|
|
(4.80) |
4.9.3. Állapottér egyenletek
Legyen az állapotváltozók vektora:
|
, |
(4.81) |
A rendszer hibajelére vonatkozó állapottér egyenletei:
|
, |
(4.82) |
ahol a motor fluxusa, R az armatúraellenállás és L az armatúrainduktivitás.
A mérhető állapotváltozó a motor fordulatszáma, , így
|
, . |
(4.83) |
4.9.4. A csúszófelület tervezése
Klasszikusan a csúszófelületet, amely mentén a beavatkozó jelnek szakadása van, az állapotváltozók lineáris kombinációjával definiálják, esetünkben:
|
|
(4.84) |
ahol az állandósult állapotot, illetve a tranziens viselkedést határozza meg. A és paramétereket úgy kell megválasztani, hogy ha a rendszer trajektóriája a csúszófelület mentén mozog, akkor a rendszer a kívánt módon (dinamikával) viselkedjen. A (4.84) alakú csúszófelület megtervezésekor a következő problémákkal állunk szemben:
Nehéz a (4.84) megszorítást a szabályozó tervezésekor számításba venni.
Az ún. illesztési feltételeknek megfelelően, az áram és a nyomaték állandósult állapotbeli pontos értékeinek ismeretére van szükségünk értékének megfelelő megválasztásához.
Nem mérhető az összes állapotváltozó.
Az első két probléma megoldására a tengelyelcsavarodás közvetlen szabályozását vezettük be [35]. A 3. problémára a 4.9.5 pontban térünk vissza. A szabályozási körben két hurok található, egy belső szabályozó hurok ügyel a tengely elcsavarodására. Mivel a belső hurok önmagában még nem vezeti a rendszert az állandósult állapotba, ezért van szükségünk a külső hurokra. A szabályozókör egyszerűsített felépítése a 4-18. ábran látható.A belső hurok szabályozása valósul meg csúszómódban, míg a külsőnél egy PI szabályozót alkalmaztunk. A külső fordulatszámszabályozó hurok szolgáltatja az alapjelet a belső hurok számára, és egyben impliciten értékére vonatkozó információt is tartalmaz.
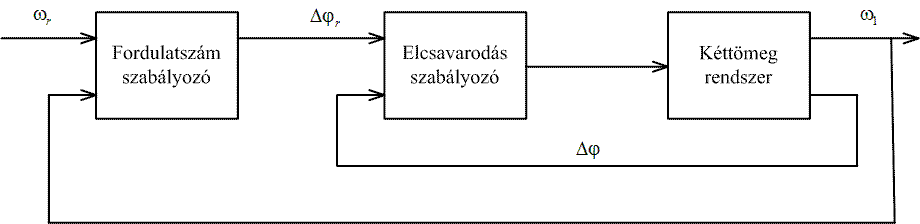
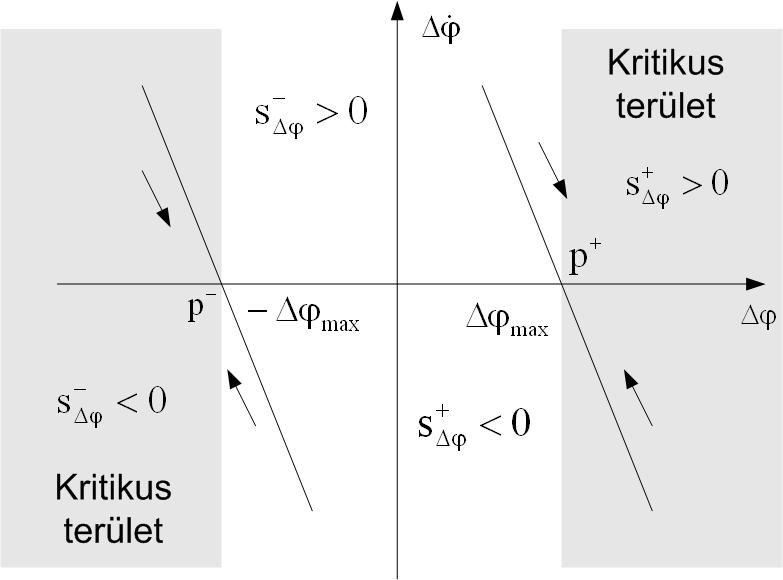
A belső hurok fázisterének dimenziója, ahol a csúszófelületet kell megtervezni 5-ről 2-re csökken. E csökkentett dimenziójú fázisteret a 419. ábraán látjuk. A működés szempontjából nem megengedhető területet szürkén jelöltük.
A legrövidebb felgyorsulási időt úgy tudjuk elérni, ha a gyorsítási szakaszban a tengely elcsavarodása a maximális értéket veszi fel, (negatív alapjel esetén ), tehát az állapottarjektóriának a (vagy ) ponton kell ekkor tartózkodnia. Az állapottarjektóriát vastag egyenesek (nevezhetjük csúszóegyeneseknek) mentén lehet a (vagy ) pontba juttatni. A csúszóegyenesek egyenletét a következőképpen írhatjuk fel:
|
, |
(4.85) |
|
, |
(4.86) |
ahol a csúszómód időállandóját jelenti. Könnyen belátható, hogy ha (ahol i=+,-), akkor az adott kapcsoló egyenes alatt tartózkodik a trajektória, ha , akkor felette.
4.9.5. Megfigyelőre alapozott csattogásmentes szabályozási törvény
A szinguláris perturbáció elvét alkalmazva a szabályozó tervezésénél a szervomotor villamos időállandóját elhanyagoljuk. (A konkrét esetben ez egy ismert paraméter és számításba is tudnánk venni, de az a célunk, hogy elhanyagolások és a nem modellezett dinamika hatását bemutassuk).
A megfigyelő csökkentett számú állapotváltozói és állapotegyenletének mátrixai:
|
, |
(4.91) |
A megfigyelő diszkretizált egyenlete:
|
, |
(4.92) |
ahol és (4.88) és (4.89)-ból (4.57) alapján értelemszerűen következnek. A csúszófelület a következőképpen diszkretizálható:
|
, |
(4.93) |
ahol a külső hurok által számított alapjel. A csúszófelület együtthatóit pedig egy sorvektorral leírhatjuk:
|
. |
(4.94) |
Esetünkben (4.84) a következőképp módosul
|
, |
(4.95) |
amelyből kiszámítható az ekvivalens beavatkozó jel:
|
|
(4.96) |
A szabályozási törvény (4.62) alakú.
A teljes szabályozó felépítése a 420. ábran tekinthető meg.
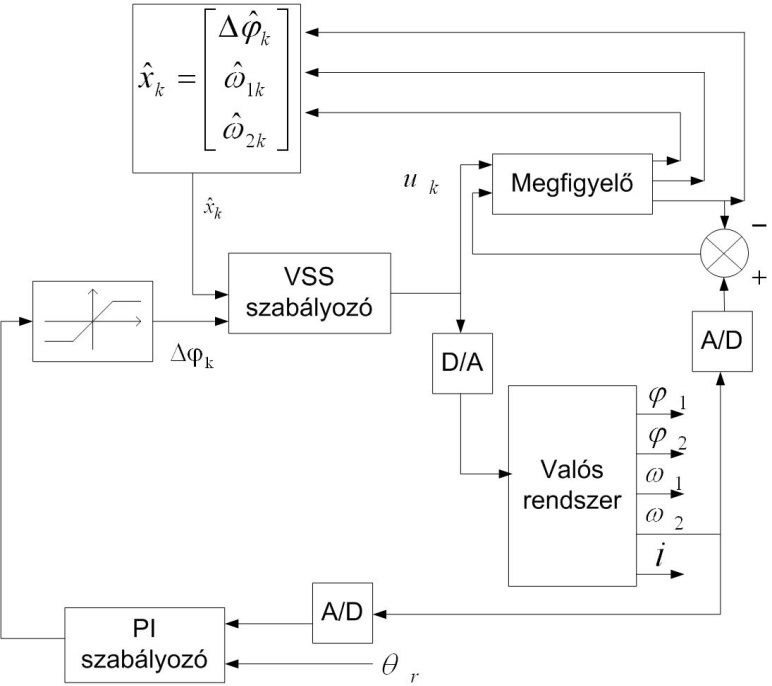
4.9.6. A kéttömeg rendszer csúszómód alapú közvetlen elcsavarodás szabályozásának kísérleti alkalmazása
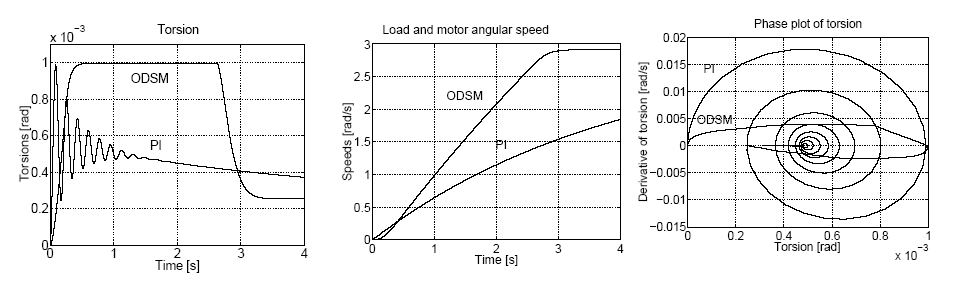
Először az általunk javasolt megfigyelőre alapozott diszkrét idejű csúszómód szabályozót (továbbiakban ODSM) egy PI szabályozóval szimuláció útján hasonlítottuk össze (ld. 421. ábra). A 421. ábran megfigyelhető, hogy a PI szabályozó is behangolható úgy, hogy a gyorsítási szakaszban a tengely elcsavarodása nem haladja meg a megengedett maximális értéket, de ekkor a beállási idő többszöröse az ODSM szabályozó beállási idejének ld. 421. ábra/b. A 421. ábra/c-n jól megfigyelhető, hogy a PI szabályozó esetén a tengelyelcsavarodás lengése, míg az ODSM szabályozó esetén a tarjektória először a csúszóegyenes felé tart, majd a csúszóegyenes mentén eléri a maximálisan megengedhető tengelyelcsavarodást, végül a tengelyelcsavarodás referencia jele az állandósult értékre csökken, amit a trajektória is követ.
Korábban kihangsúlyoztuk, hogy a csattogás egyik legfontosabb forrása a nem modellezett nagy sajátfrekvenciájú dinamika. A 4-22. ábra ezt a hatást demonstrálja. Ahogy említettük a szimulációnkban a valóságos és a megfigyelő modellje abban különbözik egymástól, hogy az elsőben számításba vettük a motor villamos időállandóját, a másodikban viszont elhanyagoltuk azt. Elvégeztünk egy olyan szimulációt, amely pusztán abban különbözik 421. ábra ODSM szimulációjától, hogy a szabályozóba a motor fordulatszámát nem a megfigyelőtől, hanem a tényleges modelltől csatoltuk vissza. A motor villamos időállandójának elhanyagolása a csúszómód szabályozó teljes csődjéhez vezet. A 4-22. ábran r a referenciaszögsebesség, m motor szögsebessége és l a terhelés szögsebessége. A 4-22. ábra arra is magyarázatot ad, hogy sok kutatónak miért nem sikerült a klasszikus csúszómódszabályozót a gyakorlatban alkalmazni.
|
a. Tengelyelcsavarodásb. Szögsebességc. Állapottrajektória |
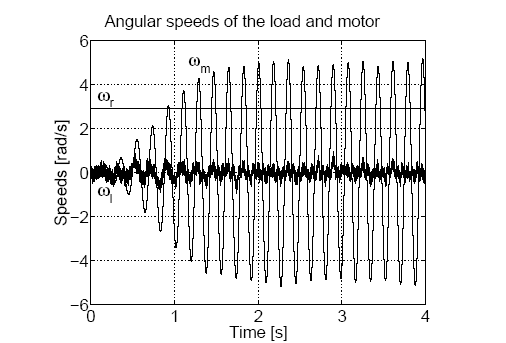
A szimulációs eredmények után bemutatunk néhány mérési eredményt is. A kísérleti eszközt a 423. ábra mutatja.
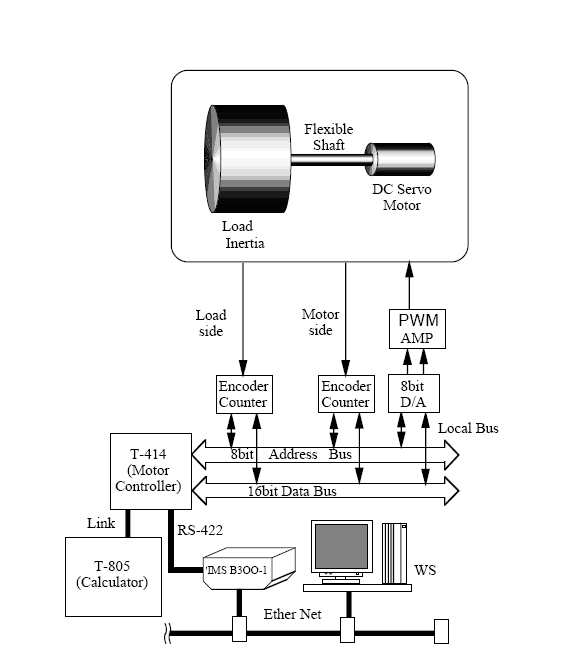
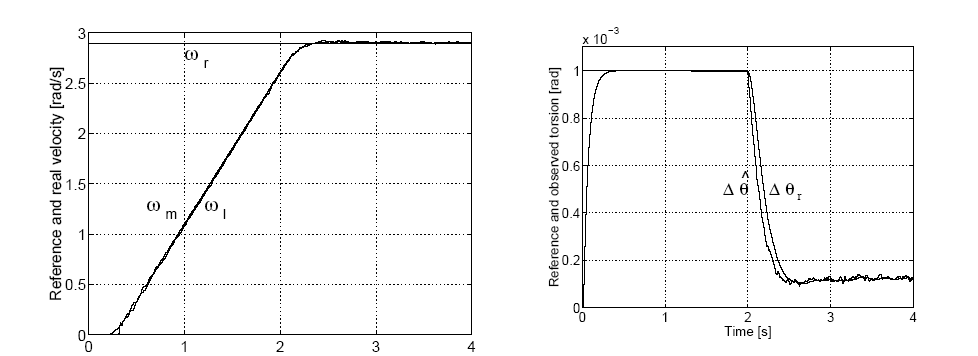
A szabályozáshoz szükséges számításokat egy transputeres rendszeren végeztük el. A fordulatszám érzékeléséhez a motor oldalon egy nagy felbontású inkrementális enkódert alkalmaztunk (fordulatonként 36 000 impulzus). A terhelés oldali érzékelőnek a felbontása 3000 impulzus/fordulat volt. Az egyenáramú szaggató kapcsolási frekvenciája 20 kHz, a mintavételezési frekvencia 1.5 kHz volt. A 4-24. ábra/a-n az r a referenciaszögsebességet, m motor szögsebességét és l a terhelés szögsebességét, a 4-24. ábra/b-n a tengelyelcsavarodás referencia és becsült értékét láthatjuk.
|
a. Szögsebesség |
b. Tengelyelcsavarodás |
4.10. Következtetés
A csúszómód szabályozással kapcsolatos biztató elméleti eredmények után a gyakorlati próbálkozások jelentős része kudarcot vallott, ennek okát jól példázza a 4-22. ábra. Sok kutató ezért arra a következtetésre jutott, hogy a csúszómód egy érdekes elméleti eszköz, de gyakorlati jelentősége nincs, a leírt példában ennek ellenkezőjét bizonyítottuk. Természetesen a valóságban ideális csúszómód nem alakulhat ki. Mérnöki szempontból ennek egy közelítő és azon belül is az ún. csattogás mentes megvalósítása jelenti a kihívást. Példánkban sikerült egy gyakorlatban is működő csúszómódszabályozót megvalósítani egy lengésekre hajlamos, rugalmas tengellyel összekötött ún. kéttömeg rendszer szabályozására.