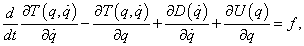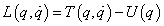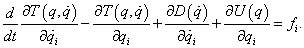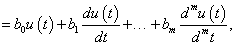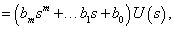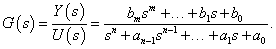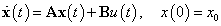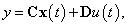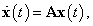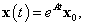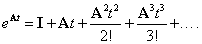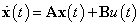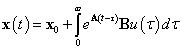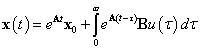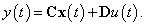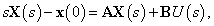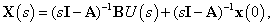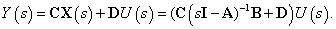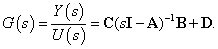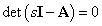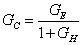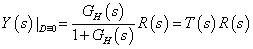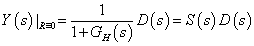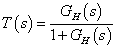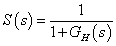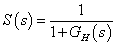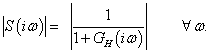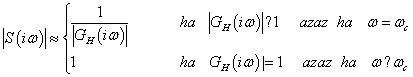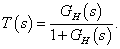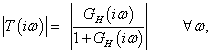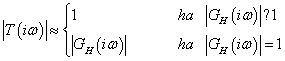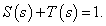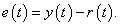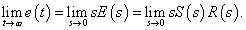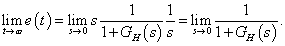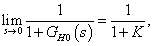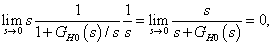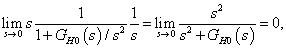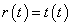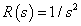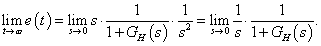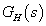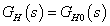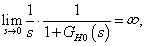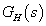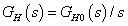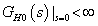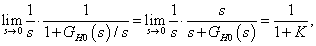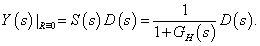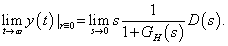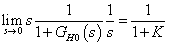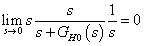1. fejezet - Bevezetés
1.1. A rendszer modellezés általános elvei
A modell jellege a modellezésnél használt módszerek és eszközök függvénye. Ezzel összefüggésben a modellezés kiindulási pontjai szerint a valós fizikai rendszerről szerzett információk forrásai lehetnek elméleti ismeretek illetve gyakorlati ismeretek és feltevések. Az elméleti ismeretek sorába tartoznak az egyes jelenségekről alkotott fizikai elméletek által szolgáltatott leírások, amelyek általában (közönséges/parciális) differenciálegyenletek formájában öltenek testet. A gyakorlati ismeretek a rendszerről megfigyelések és mérések által gyűjtött adatok összességét, az elméleti modellekben szereplő egyes paraméterek mért értékeinek ismeretét jelentik. A feltevések sorába tartozik az alkalmazott modell megbízhatóságáról, érvényességi tartományáról alkotott vélemény.
Szimulációs cél esetén a modellezés célja rendszer viselkedésének minél pontosabb reprodukálása, amikor is a bonyolultságnak csak a futtatási idővel szemben támasztott követelmények szabnak határt. Irányítási cél esetén azonban csak azok a rendszertulajdonságok érdekesek, amik az irányítási célt befolyásolják, és a bonyolultságnak az elérhető irányítástervezési eljárások lehetőségei szabnak gátat.
A lehetséges modellosztályokat tekintve megkülönböztethetünk statikus és dinamikus modelleket: statikus modell időben nem változó állapotot ír le: a rendszer állapotát algebrai egyenletekkel, vagy idő szerinti deriváltakat nem tartalmazó (parciális) differenciál-egyenletekkel írható le. Elterjedt még a stacionárius, állandósult, illetve egyensúlyi modell kifejezés is. A dinamikus modell a vizsgált rendszer, folyamat jellemzőinek időbeni változását írja le, ami legtöbbször egy közönséges vagy parciális differenciálegyenlet, vagy egyenletrendszer. Lehetséges, hogy a tárgyalás nem az időtartományában, hanem valamely célszerűen megválasztott transzformált tartományában (frekvencia tartomány) valósul meg.
Az egyik legfontosabb osztályozó elv a lineáris illetve nemlineáris viselkedés megkülönböztetése: lineáris modell esetén a folyamatot leíró egyenletrendszer kielégíti a szuperpozíció elvét. A szuperpozíció elvéből következik, hogy lineáris matematikai modellek alakja csak homogén, lineáris egyenlet, illetve egyenletrendszer lehet. Egy nemlineáris modell használatakor a rendszerben lejátszódó folyamatot leíró egyenletek legalább egyike nemlineáris függvényt is tartalmaz. A nemlineáris modellek az egyszerűbb vizsgálat és tervezés érdekében valamilyen linearizálási eljárással lineáris modellekké alakíthatók át.
A modellben szereplő jelek természete szerint modellezhetünk folytonos illetve diszkrét időben: folytonos idejű modell esetén a modellezett rendszert vagy folyamatot leíró jellemzők, független és függő változók a vizsgált idő alatt bármelyik pillanatban vehetnek fel valamilyen értéket: a bemeneti és kimeneti jelei egyaránt folytonos idejű jelek. A folytonos paraméterű/folytonos állapotterű modellekben a változók egy adott tartományon, értékhatáron belül bármilyen értéket felvehetnek. A diszkrét idejű modellben a jellemzők csak adott, konkrét időpillanatokban vehetnek fel értékeket. Diszkrét paraméterű/diszkrét állapotterű modellek esetén a változók csak meghatározott diszkrét értékeket vehetnek fel.
1.2. Newton-Lagrange modellezés
A Lagrange módszer a rendszer modelljét általánosított elmozdulás és sebesség komponensekkel fogalmazza meg:
|
|
(1) |
ahol 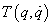 a kinetikai (mozgási) energia,
a kinetikai (mozgási) energia, 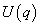 a potenciális (helyzeti) energia,
a potenciális (helyzeti) energia, 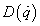 a disszipációs (csillapítás által elnyelt) energia és
a disszipációs (csillapítás által elnyelt) energia és 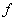 egy külső erő. A kinetikus energia a sebességvektoron kívül a helyzetvektortól is függhet, míg a potenciális energia egyedül a helyzetvektortól függ. A kinetikus energia és a potenciális energia különbsége az úgynevezett Lagrange állapotfüggvényt adja meg:
egy külső erő. A kinetikus energia a sebességvektoron kívül a helyzetvektortól is függhet, míg a potenciális energia egyedül a helyzetvektortól függ. A kinetikus energia és a potenciális energia különbsége az úgynevezett Lagrange állapotfüggvényt adja meg:
|
|
(2) |
A Lagrange egyenlet felírható az egyes komponensekre bontott alakban is, azaz 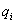 komponensre felírva:
komponensre felírva:
|
|
(3) |
Megjegyezzük, hogy a Newtoni mechanikában a rendszer modelljét erő és nyomaték egyensúlyi egyenletekkel fogalmazzuk Newton törvényeinek felhasználásával.
1.3. Átviteli függvény
Egy lineáris időinvariáns rendszer modelljének leírása lineáris, állandó együtthatós közönséges differenciál egyenlettel történik:
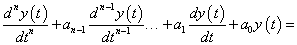
|
|
(4) |
ahol 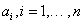 és
és 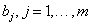 együtthatók konstansok, nem függnek az időtől. Tekintsük a differenciálegyenlet Laplace transzformáltját (
együtthatók konstansok, nem függnek az időtől. Tekintsük a differenciálegyenlet Laplace transzformáltját (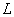 - transzformált) zérus kezdeti feltételekkel. Ekkor a következő egyenlethez jutunk:
- transzformált) zérus kezdeti feltételekkel. Ekkor a következő egyenlethez jutunk:
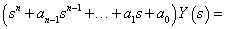
|
|
(5) |
ahol 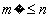 .
.
A 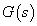 racionális törtfüggvényt a rendszer átviteli függvényének nevezzük. Az átviteli függvény tehát a kimenőjel és a bemenőjel zérus kezdeti feltételekkel vett
racionális törtfüggvényt a rendszer átviteli függvényének nevezzük. Az átviteli függvény tehát a kimenőjel és a bemenőjel zérus kezdeti feltételekkel vett 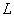 - transzformáltjainak hányadosa.
- transzformáltjainak hányadosa.
|
|
(6) |
1.4. Az állapottér elmélet alapjai
A rendszer állapota egy 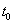 időpontbeli információ (olyan jelek ismerete), amelyből az
időpontbeli információ (olyan jelek ismerete), amelyből az  ,
, 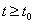 bemenőjel ismeretében a rendszer válasza minden
bemenőjel ismeretében a rendszer válasza minden 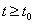 időpontra meghatározható. A rendszer válasza a jövőbeli,
időpontra meghatározható. A rendszer válasza a jövőbeli, 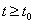 időpontra vonatkozó állapotokat és a kimenőjeleket jelenti. A rendszer állapotait leíró jeleket, illetve ezek függvényeit, a rendszer állapotváltozóinak nevezzük.
időpontra vonatkozó állapotokat és a kimenőjeleket jelenti. A rendszer állapotait leíró jeleket, illetve ezek függvényeit, a rendszer állapotváltozóinak nevezzük.
Általánosan egy lineáris dinamikus rendszer állapottér reprezentációját a következő alakban írhatjuk:
|
|
(7) |
|
|
(8) |
ahol 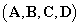 a rendszermátrixok,
a rendszermátrixok, 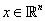 az állapotvektor,
az állapotvektor, 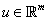 az irányító bemenetek vektora és
az irányító bemenetek vektora és  a mért kimenetek vektora. A mátrixok méretei a jelek méreteihez illeszkednek.
a mért kimenetek vektora. A mátrixok méretei a jelek méreteihez illeszkednek.
Az állapotegyenlet, mint egy elsőrendű differenciálegyenlet megoldása két lépésben történik. Előbb megoldjuk a homogén egyenletet, majd megkeressük az inhomogén egyenlet egy partikuláris megoldását. A homogén egyenlet alakja:
|
|
(9) |
az 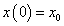 kezdeti feltétellel és megoldása:
kezdeti feltétellel és megoldása:
|
|
(10) |
ahol az 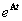 mátrix-exponenciális függvényt a következőképpen értelmezzük:
mátrix-exponenciális függvényt a következőképpen értelmezzük:
|
|
(11) |
Például diagonál reprezentációk esetén, azaz 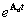 (
(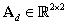 ) választással ennek alakja:
) választással ennek alakja:
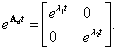
Az inhomogén egyenlet alakja:
|
|
(12) |
ahol 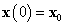 egyenlet megoldása a következő:
egyenlet megoldása a következő:
|
|
(13) |
A fentiek alapján az elsőrendű differenciálegyenlettel leírt állapotegyenlet megoldása:
|
|
(14) |
|
|
(15) |
Az állapottér reprezentáció alapján a rendszer átviteli függvényét a Laplace transzformáció alkalmazásával kapjuk meg:
|
|
(16) |
ebből az állapot Laplace transzformáltja:
|
|
(17) |
ahol 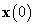 a kezdő állapot a
a kezdő állapot a 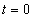 időpontban. Az
időpontban. Az 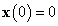 feltétel mellett
feltétel mellett
|
|
(18) |
A 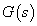 átviteli függvény:
átviteli függvény:
|
|
(19) |
Az átviteli függvény pólusai tehát az
|
|
(20) |
egyenlet gyökei.
1.5. Minőségi tulajdonságok elemzése
A minőségi kritériumok vizsgálata mindig a szabályozott rendszer (zárt kör) vizsgálatával történik: A zárt rendszer átviteli függvénye:
|
|
(21) |
ahol 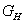 a hurokátviteli függvény és
a hurokátviteli függvény és 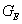 az előrevezető ág eredő átviteli függvénye. Az alábbiakban az időtartományi és frekvencia tartományi jellemzőket soroljuk fel.
az előrevezető ág eredő átviteli függvénye. Az alábbiakban az időtartományi és frekvencia tartományi jellemzőket soroljuk fel.
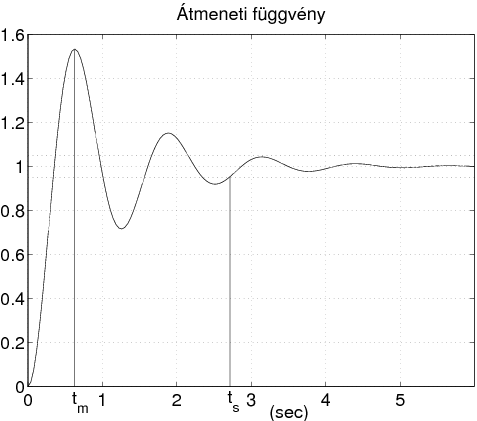
1.5.1. Időtartományi jellemzők
-
A rendszer állandósult állapotban felvett értékét beállási értéknek nevezzük, amit
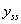 -sel jelölünk.
-sel jelölünk. -
A szabályozási idő (
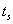 ) annak időtartama, amely eltelte után a rendszer kimenete a beállási értéktől
) annak időtartama, amely eltelte után a rendszer kimenete a beállási értéktől 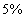 -nál nagyobb mértékben nem tér el.
-nál nagyobb mértékben nem tér el. -
A szabályozási eltérés a megkívánt érték és az állandósult állapotbeli érték különbsége:
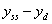 .
. -
Túllendülési idő (
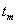 ): a kimeneti jel maximális értékének időpontja.
): a kimeneti jel maximális értékének időpontja. -
A túllendülés mértéke (
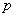 ): százalékban kifejezett viszonyszám, ami a maximális és beállási érték közötti különbség beállási értékhez való viszonyát fejezi ki:
): százalékban kifejezett viszonyszám, ami a maximális és beállási érték közötti különbség beállási értékhez való viszonyát fejezi ki: 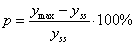 .
.
1.5.1.1. Frekvencia tartományi jellemzők
-
rezonancia csúcs
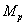 : az amplitúdó görbe maximális értéke;
: az amplitúdó görbe maximális értéke; -
rezonancia frekvencia
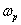 : a rezonancia csúcshoz tartozó frekvencia érték;
: a rezonancia csúcshoz tartozó frekvencia érték;
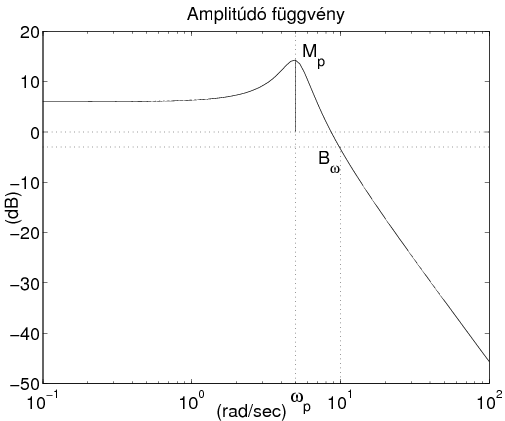
-
A sávszélesség fogalmát a kiegészítő érzékenységi függvény segítségével a következőképp adhatjuk meg. A rendszer sávszélessége az a
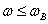 frekvencia tartomány, amelyben a
frekvencia tartomány, amelyben a 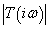 kiegészítő érzékenységi függvény Bode diagramja
kiegészítő érzékenységi függvény Bode diagramja 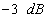 -re csökken.
-re csökken.
1.6. Érzékenységfüggvény
Vizsgáljuk a zárt rendszer kimenetét különböző bemenetek esetén:
|
|
(22) |
|
|
(23) |
ahol  .
.
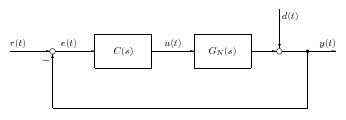
Bevezetjük a szabályozási körben értelmezett 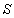 érzékenységi függvényt és a
érzékenységi függvényt és a 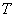 kiegészítő érzékenységi függvényt:
kiegészítő érzékenységi függvényt:
|
|
(24) |
|
|
(25) |
Az érzékenységi függvény azt mutatja meg, hogy a zavaró jellemző hogyan befolyásolja a zárt rendszer kimenetét.
|
|
(26) |
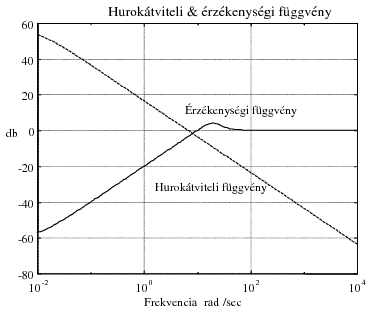
Az 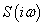 érzékenységi függvény közelítő ábrázolását Bode-diagramon a felnyitott hurok
érzékenységi függvény közelítő ábrázolását Bode-diagramon a felnyitott hurok 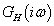 frekvenciafüggvénye alapján a következőképp végezhetjük el.
frekvenciafüggvénye alapján a következőképp végezhetjük el.
Az érzékenységi függvény definíció szerint:
|
|
(27) |
Kis és nagy körfrekvenciákra a következő közelítést használhatjuk:
|
|
(28) |
A kiegészítő érzékenységi függvény a referencia jel és a kimenő jel közötti átviteli függvény.
|
|
(29) |
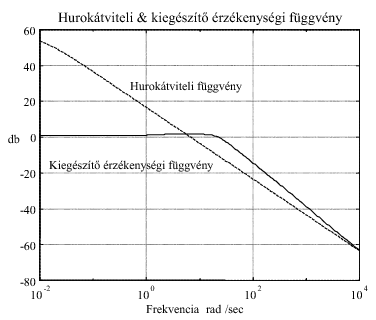
A 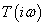 kiegészítő érzékenységi függvény közelítő ábrázolását Bode-diagramon a felnyitott hurok
kiegészítő érzékenységi függvény közelítő ábrázolását Bode-diagramon a felnyitott hurok 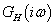 frekvenciafüggvénye alapján a következőképp végezhetjük el. A kiegészítő érzékenység függvény definíció szerint:
frekvenciafüggvénye alapján a következőképp végezhetjük el. A kiegészítő érzékenység függvény definíció szerint:
|
|
(30) |
Kis és nagy körfrekvenciákra a következő közelítést használhatjuk:
|
|
(31) |
Az érzékenységi és kiegészítő érzékenységi függvények közötti összefüggés az alábbi:
|
|
(32) |
1.7. Aszimptotikus jelkövetés
Követő szabályozásoknál a kimenőjelnek a referencia jeltől való eltérését követési hibának nevezzük:
|
|
(33) |
Vizsgáljuk meg, hogy adott 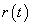 referencia jelre aszimptotikusan mekkora lesz az eltérés, azaz a követési hiba. A követési hiba jel és a referencia jel Laplace-transzformáltjai közötti kapcsolatot az
referencia jelre aszimptotikusan mekkora lesz az eltérés, azaz a követési hiba. A követési hiba jel és a referencia jel Laplace-transzformáltjai közötti kapcsolatot az 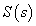 érzékenységi függvény írja le. Alkalmazva a határérték tételeket:
érzékenységi függvény írja le. Alkalmazva a határérték tételeket:
|
|
(34) |
Vizsgálhatjuk a tipikus referencia jelek, mint egységugrás vagy egység sebesség ugrás jelek aszimptikus követését.
1.7.1. Egységugrás bemenetre adott válaszfüggvény
Vizsgáljuk meg a válaszfüggvényt 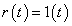 ,
, 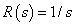 bemenetre. Ekkor
bemenetre. Ekkor
|
|
(35) |
Ha 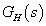 arányos jellegű, azaz ha
arányos jellegű, azaz ha 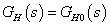 , akkor
, akkor
|
|
(36) |
ahol 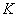 a hurokerősítési tényező. A követési hiba értéke függ a hurokerősítési tényező értékétől.
a hurokerősítési tényező. A követési hiba értéke függ a hurokerősítési tényező értékétől.
Ha 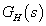 integráló jellegű, azaz ha
integráló jellegű, azaz ha 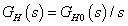 ,
, 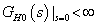 alakú, akkor
alakú, akkor
|
|
(37) |
tehát a követési hiba aszimptotikusan zérus.
Ha 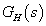 2 típusú (kétszeres integrátort tartalmaz), azaz ha
2 típusú (kétszeres integrátort tartalmaz), azaz ha 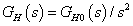 ,
, 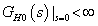 alakú, akkor
alakú, akkor
|
|
(38) |
tehát a követési hiba aszimptotikusan zérus.
1.8. Zavarkompenzálás
Az aszimptotikus zavarkompenzálást az aszimptotikus alap- vagy referencia jelkövetéshez hasonlóan vizsgálhatjuk. Tipikus zavaró jelek, mint egységugrás, egység sebességugrás jelek, a zavaró jel hatását a kimenő jelben zérus referencia jel feltételezése mellett vizsgáljuk. Ehhez felírjuk a kimenő jel és a zavaró jel Laplace - transzformáltjai közötti összefüggéseket és alkalmazzuk a határérték tételeket.
A kimenő és a zavaró jel közötti átviteli függvény az 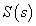 érzkenységi függvény. Ennek alapján a kimenőjel Laplace – transzformáltja
érzkenységi függvény. Ennek alapján a kimenőjel Laplace – transzformáltja
|
|
(42) |
Alkalmazva a határérték tételt:
|
|
(43) |
Legyen például 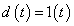 ,
, 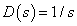 .
.
Arányos rendszer vizsgálata: vizsgáljuk meg az arányos rendszer viselkedését. A hurokátviteli függvény alakja 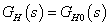 . Ekkor
. Ekkor
|
|
(44) |
ahol 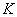 a hurokerősítés tényező. Tehát a zavaró jel hatása megjelenik a kimeneten.
a hurokerősítés tényező. Tehát a zavaró jel hatása megjelenik a kimeneten.
Integráló rendszer vizsgálata: legyen például 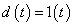 ,
, 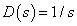 és tegyük fel, hogy a hurokátviteli függvény integráló alakú, azaz
és tegyük fel, hogy a hurokátviteli függvény integráló alakú, azaz 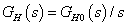 . Ekkor
. Ekkor
|
|
(45) |
tehát a zavaró jel hatását a rendszer aszimptotikusan teljesen elnyomja, kompenzálja. Megjegyezzük, hogy a 2-típusú integráló tulajdonságú rendszer is kompenzálja a hibajelet.