2. fejezet - Modellezés mért jelek alapján

Példa 3.1 Írjuk fel az alábbi negyedjármű modellt a nemlinearitások figyelembe vételével.

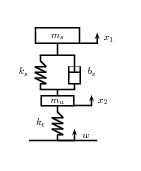
Erők, egyensúlyi egyenletek, nemlinearitások

$F_{m_s}=F_{k_s}+F_{b_s},$

$F_{m_u}=-F_{k_s}-F_{b_s}-F_{k_t}.$

ahol az egyes komponensek alakja:

$F_{m_s}=m_s{\ddot{x}}_1;$

$F_{m_u}=m_u{\ddot{x}}_2;$

$F_{b_s}=b_s^l\left({\dot{x}}_2-{\dot{x}}_1\right)-b_s^{sym}\left|{\dot{x}}_2-{\dot{x}}_1\right|+b_s^{nl}\sqrt{\left|{\dot{x}}_2-{\dot{x}}_1\right|}sgn\left({\dot{x}}_2-{\dot{x}}_1\right);$

$F_{k_s}=k_s^l\left(x_2-x_1\right)+k_s^{nl}{(x_2-x_1)}^3;$

$F_{k_t}=k_t\left(x_2-w\right).$

Az állapottér reprezentáció

$\dot{x}=f\left(x\right)+gu+hw$

Ha az állapotvektor elemeit az alábbi formában vesszük fel:

$x={\left[\begin{array}{llll}{x}_1\hfill & x_2\hfill & {\dot{x}}_1\hfill & {\dot{x}}_2\hfill \end{array}\right]}^T$

akkor a komponensek:

$f\left(x\right)=\left[\begin{array}{l}{\dot{x}}_1\hfill \\ {\dot{x}}_2\hfill \\ \frac{1}{m_s}\left(F_{k_s}+F_{b_s}\right)\hfill \\ \frac{1}{m_u}\left(-F_{k_s}-F_{k_t}-F_{b_s}\right)\hfill \end{array}\right]$

$g=\left[\begin{array}{l}0\hfill \\ 0\hfill \\ \frac{1}{m_s}\hfill \\ -\frac{1}{m_u}\hfill \end{array}\right],h=\left[\begin{array}{l}0\hfill \\ 0\hfill \\ 0\hfill \\ \frac{k_t}{m_u}\hfill \end{array}\right]$

A qLPV állapottér modell

ahol ${\dot{x}}_1=x_3$ és ${\dot{x}}_2=x_4.$

Nemlinearitások virtuális linearizálása:

$F_{b_s}\left({\rho }_b\right)=b_s^l\left(x_4-x_3\right)-b_s^{sym}\left|{\rho }_b\right|+b_s^{nl}\sqrt{\left|{\rho }_b\right|}sgn\left({\rho }_b\right)$

$F_{k_s}\left({\rho }_k\right)=k_s^l\left(x_2-x_1\right)+k_s^{nl}{\rho }_k^3$

Mért ütemezési változók:

${\rho }_b=x_4-x_3$

${\rho }_k=x_2-x_1$

Fiktív input:

$\varphi \left({\rho }_k,{\rho }_b\right)={\left[\begin{array}{lll}{\rho }_k^3\hfill & \left|{\rho }_b\right|\hfill & \sqrt{\left|{\rho }_b\right|}sgn\left({\rho }_b\right)\hfill \end{array}\right]}^T.$

Grey-box qLPV modell:

$\dot{x}=\left[\begin{array}{llll}0\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill \\ -p_{11}\hfill & p_{11}\hfill & -p_{12}\hfill & p_{12}\hfill \\ p_{21}\hfill & -p_{21}-p_t\hfill & p_{22}\hfill & -p_{22}\hfill \end{array}\right]x$

$+\left[\begin{array}{lll}0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ p_{13}\hfill & -p_{14}\hfill & p_{15}\hfill \\ -p_{23}\hfill & p_{24}\hfill & -p_{25}\hfill \end{array}\right]\varphi \left({\rho }_k,{\rho }_b\right)+\left[\begin{array}{l}0\hfill \\ 0\hfill \\ 0\hfill \\ p_t\hfill \end{array}\right]w$

ahol

$p_t=\frac{k_t}{m_u}$

Legyen $y={\text{Φ}}_{x_0}\left(u,p\right)$ az $x\left(0\right)=x_0$ kezdeti értékű és

$\dot{x}=f\left(x,p\right)+g\left(x,p\right)u$

$y=h\left(u,x,p\right)$

rendszer input/output leképezése ( $p$ vektor paraméter).

A $p=p^{\text{*}}$ paraméter globálisan identifikálható az input/output adatokból, ha létezik legalább egy $u$ bemenő jel, hogy ${\text{Φ}}_{x_0}\left(u,p\right)={\text{Φ}}_{x_0}\left(u,p^{\text{*}}\right)$ egyértelműen megoldható legyen minden $x_0$ kezdeti értékre.

A lineáris rendszer:

$\dot{x}=A\left(t\right)x+B\left(t\right)u$

$y=C\left(t\right)x,$

A ${\text{Φ}}_{x_0}\left(u,p\right)$ input/output leképezés (alapmátrix) ismerete nem szükséges az identifikálhatóság eldöntéséhez. Helyette egy implicit $\text{Ψ}\left(y,u,p\right)=0$ identifikálhatósági kifejezést használhatunk.

$\text{Ω}$ kiszámítása: legyen $U\left(t\right)=B\left(t\right)u$ és

$\tilde{U}:=\left[U\cdots U^{\left(n-1\right)}{]}^T,\tilde{y}:=\right[y\cdots y^{\left(n-1\right)}{]}^T$

Ekkor

$\tilde{y}=\text{Ω}\left(t\right)x+\text{Γ}\left(t\right)\tilde{U}.$

ahol ${\text{Ω}}^T\left(t\right)=\left[C_0^T\left(t\right)\cdots C_{n-1}^T\left(t\right)\right]$ és

$C_0\left(t\right):=C\left(t\right),$

$C_{i+1}\left(t\right):=C_i\left(t\right)A\left(t\right)+\frac{d}{dt}{C}_i\left(t\right).$

$\text{Γ}$ kiszámítása: legyen ${\gamma }^k$ vektor sorai:

${\gamma }_0^{k+1}={\gamma }_0^k+C_k,$

${\gamma }_j^{k+1}={\gamma }_j^k+{\dot{\gamma }}_{j-1}^k,j=k,\cdots ,1$

${\gamma }_j^k=0,j\ge k.$

Ekkor $\text{Γ}\left(t\right)$ sorai a ${\gamma }_k,k=0,\cdots n-1$ vektorok.

Identifikálhatósági feltétel: egy analitikus dinamikus rendszer megfigyelhető az $I$ intervallum minden nemtriviális részintervallumán akkor és csak akkor, ha $rank\text{ Ω}\left(t\right)=n$.

$y^{\left(n\right)}-C_n\left(p\right){\text{Ω}}^{\#}\left(p\right)\tilde{y}=\left({\gamma }^n\left(p\right)-C_n\left(p\right){\text{Ω}}^{\#}\left(p\right)\text{Γ}\left(p\right)\right)\tilde{U}\left(p\right),$

ahol ${\text{Ω}}^{\#}\left(p\right)$ az $\text{Ω}\left(p\right)$ egy általánosított inverze.

Ez az egyenlet egy implicit leképezés $\text{Ψ}\left(y,u,p\right)=0,$ ahol a kezdeti érték

$\tilde{y}\left(0\right)=\text{Ω}\left(0\right)x\left(0\right)+\text{Γ}\left(0\right)\tilde{U}\left(0\right).$

Átparaméterezés: az egyenleteket átparaméterezve ($\text{Π}:=\left[{\pi }_l\left(p,x_0\right)\right]$):

${\text{Ψ}}_1\left(u,y\right)+\text{Π}\left(p,x_0\right){\text{Ψ}}_2\left(u,y\right)=0.$

Példa 3.2 Vizsgáljuk meg a rugózott tömeg identifikálhatóságát. Átparaméterezett modell: legyen $\gamma :=\frac{m_u}{m_s}$.

$\dot{x}=\left[\begin{array}{llll}0\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill \\ -\mu {\pi }_1\hfill & \mu {\pi }_1\hfill & -\mu {\pi }_2\hfill & \mu {\pi }_2\hfill \\ {\pi }_1\hfill & -{\pi }_1-{\pi }_t\hfill & {\pi }_2\hfill & -{\pi }_2\hfill \end{array}\right]x+$

ahol $\pi :=\left[{\pi }_1{\pi }_2{\pi }_3{\pi }_4{\pi }_5]=[\frac{k_s^l}{m_u}\frac{b_s^l}{m_u}\frac{k_s^{nl}}{m_u}\frac{b_s^{sym}}{m_u}\frac{b_s^{nl}}{m_u}\right]$ és ${\pi }_t=\frac{k_t}{m_u}$ ismert paraméterek. Mivel $m_s$ változhat, $\gamma$ ismeretlen. $\text{Λ}\left(y\right):={\pi }_1{y}_1+{\pi }_2{y}_2+\left[{\pi }_3-{\pi }_4{\pi }_5\right]\varphi \left(y\right)$ jelöléssel a dinamikai egyenlet

Ekkor

és

Ha $\text{Λ}\left(y\right)$ nem azonosan zéró és a bemenetek perszisztensek akkor a $\gamma$ paraméter, legalább is elméletben, identifikálható.

A modell ellenőrzése a mért eredményekkel való összevetést modell validációnak nevezzük. A vizsgált rendszer viselkedésének leírására felállított matematikai modell jósága igazolásának legegyszerűbb módja az, hogy az eredeti rendszerben méréseket végzünk, és azok eredményeit összevetjük a modell által szolgáltatott eredményekkel. A modellalkotás során a modell és a mérések által szolgáltatott eredmények eltéréseit kell minimalizálni (identifikáció): a feladat megoldására leggyakrabban az legkisebb négyzetek módszerét alkalmazzuk.

Iteratív séma: ha az ellenőrzés során kiderül, hogy a feltételezett modell nem teljesíti a megkövetelt pontossági előírásokat, akkor egy iterációs feladatot kell megoldanunk: vissza kell térnünk a modellalkotási algoritmus elejére, és esetleg újabb paraméterek bevonásával, figyelembevételével egy újabb, javított felépítéssel kell elvégezni a modell azonosítását majd végre kell hajtanunk a modell validálásához leírt feladatokat.

Szimuláció során a matematikai modellel a rendszer kimenő változóit a bemenetek különböző értékéi függvényében határozzuk meg. Fontos, hogy gondot fordítsunk azon paraméterek azonosítására, amelyek a rendszer viselkedését döntően befolyásolják, amelyekre a rendszer a legérzékenyebben reagál. Paraméter-érzékenységi vizsgálat alkalmával a kapott eredményekből vonhatunk le következtetéseket a rendszer viselkedésére.