4. fejezet - Hosszirányú modellezés és irányítás
Vissza		Előre

4. fejezet - Hosszirányú modellezés és irányítás

Tartalom

A hosszirányú járműdinamikai modellezés két fő témaköre a következő: egyrészt a menetellenállások, mint például a gördülési ellenállás, kanyarellenállás, légellenállás, emelkedési ellenállás, gyorsítási ellenállás, vizsgálata. Másrészt, mivel a gumiabroncsnak kitüntetett szerepe van a hajtóerők és fékerők átvitele szempontjából, a modellezés célja a gumiabroncs és a talaj közötti erőátvitel leírása.

A dinamikai hatások jó része a jármű és környezet kölcsönhatásaként jön létre, például súrlódás, légellenállás, út és kerék kontaktus. Szimulációk során cél ezeknek a hatásoknak minél élethűbb modellezése és reprodukálása. A járműirányítás tervezése során azonban a cél ezeknek a hatásoknak minél egyszerűbb, de a tervezési célok tekintetében releváns modellezése.

Amíg az útmodellek célja az útgerjesztés leírása, addig a kerékmodellek az út-kerék kölcsönhatás leírását adják meg. A vízszintes úton gördülő járműkerékre ható erők lehetnek egyrészt aktív erők, másrészt passzív erők.

Az aktív erők közül a kerék középpontján halad keresztül a függőleges terhelőerő, ami a kerék együttes tömegéből és a gépjármű tömegének a kerékre eső részéből tevődik össze. Aktív erő a vízszintes vonóerő, amivel a gépjármű tengelye tolja vagy húzza a kereket (valójában a kerék és az út érintkezési pontján ébred). A kereket a középpontja körül igyekszik elforgatni a forgató/fékező-nyomaték

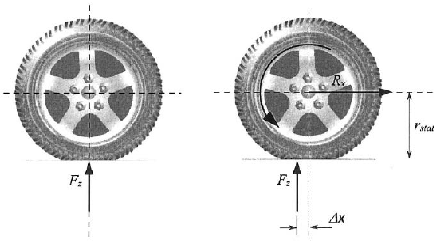
Vízszintes úton gördülő járműkerékre ható passzív erők csak akkor ébrednek, ha valamilyen aktív erő hat. Így például a reakcióerő, a kerék és a talaj felfekvési felületén ébred: mivel a kerék nem pontban, hanem felületen érintkezik a talajjal, a reakcióerő egy elosztott erőként jelentkezik, amelyet azonban a számításokban egy koncentrált erővel helyettesítenek. A reakcióerő támadáspontja a függőleges szimmetriatengelyhez viszonyítva a haladás irányában eltolódik.

Passzív erőként jelentkezik a légellenállás: a levegő ellenállást fejt ki a kerék haladásával szemben, valamint a vonóerő reakcióereje, azaz a tapadási erő.

Egyenletes sebességet feltételezve a kerék szempontjából az alábbi tipikus eseteket különböztethetjük meg:

Forgatott (hajtott) vontató kerék, emelkedőn felfele: ilyenkor a motornak nyomatékot kell kifejtenie a kerékre, hogy a jármű meg ne álljon. A hajtott kerék toló/vonóerőt fejt ki a tengelyen keresztül a járműre.A reakcióerő eredője a kerék talppontjától a menetirányban eltolva hat, s függőleges komponense a súlyerővel tart egyensúlyt. A reakcióerő vízszintes komponense előre mutat és a vonóerővel tart egyensúlyt.
Csak forgatott (hajtott) kerék, vízszintes úton: ekkor a motornak nyomatékot kell kifejtenie a kerékre az egyenletes haladás érdekében. Ebben az esetben nincs vonóerő, s a reakcióerő eredője a függőleges terhelőerővel tart egyensúlyt, nyomatéka pedig a forgatónyomatékkal.
Forgatott (hajtott) és vontatott kerék enyhe lejtőn: ebben az esetben a jármű súlyából adódik egy haladás irányú vonóerő, de ez még nem akkora, hogy a motornak ne kelljen nyomatékot kifejtenie a kerékre. A reakcióerő függőleges komponense a terhelőerővel tart egyensúlyt a vízszintes komponense a haladással ellentétes irányba mutat és a vonóerővel tart egyensúlyt.
Csak vontatott kerék, lejtőn: ilyenkor a jármű súlyából adódó vonóerő éppen legyőzi a gördülési ellenállást, azaz ekkor nincs forgatónyomaték.
Fékezett és vontatott kerék meredek lejtőn: ebben az esetben a jármű motornyomaték kifejtése nélkül is gyorsulna. Az egyenletes sebesség biztosításához tehát a járművet fékezni kell. Ez eredményezi a keréken a fékező nyomatékot. Ekkor ugyan van forgatónyomaték, de most a kerék forgásirányával ellentétes irányban hat.

Mint azt már láttuk, a gumiabroncs biztosítja az erőátvitelt a jármű és az út között. A jármű súlya képviseli a függőleges irányú (útra merőleges) erőket, a gyorsulás/lassulás a hosszirányúakat, a kanyarodáskor pedig oldalirányú erők hatnak. Ezeket az erőket az abroncs egy igen kis helyen adja út illetve veszi fel, ezért a gumiabroncsnak olyannak kell lennie, hogy mindezeket az intenzív erőhatásokat elviselje.

4.1. Tapadás és csúszás modellezése

A kerék és útfelület kölcsönhatását tekintve általában az jellemző, hogy csak a gumiabroncs nyomódik be, az útfelület nem deformálódik. A kerék és a pálya érintkezése nem egy pont, hanem ellipszis és a nyomás egy ellipszoid mentén oszlik el. Ha a kerék áll és a függőleges terhelőerőn kívül más aktív erő nem hat, a reakcióerő a kerék talppontjánál szimmetrikusan hat, eredője függőleges és átmegy a kerék középpontján.

A függőleges terhelés következtében a gumiabroncs deformálódik: egy adott része hol összenyomódik, hogy megnyúlik és a talajon egy felfekvő felületet alkot. Ha a kerék gördül, akkor a gördülés alatt a nyomás eloszlása a felfekvő felületen nem egyenletes. Így a fellépő erő már nem szimmetrikus a függőleges terhelőerőhöz képest, az eredő vertikális erő nem a kerék talppontjában, a felület középpontjánál, hanem attól a haladás irányában eltolva, előtte hat. Ez lesz a gördülési ellenállás karja. Ennek az eltolódásnak a következtében a reakcióerő nyomatékot fejt ki a kerékre, ezért kell egy aktív forgatónyomaték a kerék forgásban tartásához: ez nem más, mint a gördülési ellenállás.

A deformáció során a befektetett mechanikai energia egy része elnyelődik, azaz hővé alakul. Ennyivel több energiát kell befektetni a gumiabroncs mozgásban tartásához, gördüléséhez. Ezért ha nem fektetnünk be folyamatosan energiát, akkor a gördülési ellenállástól egy idő után megállna a gördülő kerék, ugyanúgy, mint a súrlódástól. A gördülő ellenállás általában sokkal kisebb, mint a száraz csúszó súrlódás. A gumiabroncs deformációja miatt a befektetett energia nem nyerhető vissza teljesen, egy része elvész. A gumiabroncs deformációja a normál kerékterhelés aszimmetrikus eloszlását is eredményezi.

4.1. ábra - Gördülési ellenállás

A mechanikából ismeretes a tiszta csúszósúrlódás valamint a tiszta nyugvósúrlódás. Mindkettőt azzal a fajlagos erővel jellemezhetjük, amely szükséges a csúszás fenntartásához, illetve megindításához. A kerék gördülésekor fellépő tapadás nem egyszerűen a nyugvósúrlódáson alapszik. Vannak gumiabroncsszemcsék, amelyek pillanatnyilag mozdulatlanok, de vannak olyan szemcsék is az abroncs és az út érintkezési felületén, amelyek csúsznak. A talaj és a gumiabroncs között fellép egy vákuumos szívóhatás is, ami az abroncsfelület elválását nehezíti meg. Így a gördülő kerék tapadását nem jellemzi egyértelműen sem a csúszó-, sem a nyugvósúrlódási tényező. Erre a célra külön tényező, tapadási tényező bevezetése szükséges, mely alatt azt a maximális vonóerőt értjük, amelynél a gördülés éppen tiszta csúszásba megy át.

Az így bevezetett tapadási tényező értéke több elemtől függ: például az út minőségétől és állapotától, a gumiabroncs minőségétől és állapotától, bizonyos mértékig függ a jármű sebességétől valamint kisebb mértékben függ a gumiabroncs légnyomásától. Ugyancsak kismértékben függ a függőleges terhelőerőtől.

Csúszó súrlódásról akkor beszélünk, ha a kerekek nem gördülnek, hanem csúsznak a felületen. A csúszó súrlódási tényező értéke mindig kisebb, mint a tapadási tényezőé. A két érték közötti átmenet folytonos, amit az úgynevezett szlippel lehet kifejezni.

4.2. ábra - Erőhatások

A tapadási és súrlódási tényezők a hosszirányú és oldalirányú komponensek vektoriális eredőjeként foghatók fel, amelyek segítségével a hosszirányú gyorsulások (gyorsítás, fékezés) és az oldalirányú mozgások leírhatók.

Ennek megfelelően a jármű mozgásához szükséges hajtóerő összességében az alábbi ellenállás komponenseket győzi le:

$F_{A} = R_{x f} + R_{x r} + F_{a e r o} + F_{s l o p e} + F_{c o r n} + F_{a c c}$

(144)

ahol

$R_{x f}, R_{x r}$ : gördülési ellenállások az első és hátsó kerekeken,
$F_{a e r o}$ : a légellenállás,
$F_{s l o p e}$ : az emelkedési ellenállás,
$F_{c o r n}$ : a kanyarellenállás,
$F_{a c c}$ : pedig a gyorsítási ellenállás.

A gördülés során a terhelés eloszlása nem egyenletes, az $F_{z}$ eredő vertikális erő a felület középpontja előtt $Δ x$ távolságban hat.

$R_{x f} + R_{x r} = f (F_{z f} + F_{z r}),$

(145)

ahol $f$ a gördülés ellenállási tényező.

A gyorsulás nélkül gördülő keréken a nyomatékok egyensúlya alapján: $R_{x} r_{s t a t} = F_{z} Δ x$ , ahol $r_{s t a t}$ a statikailag terhelt kerék sugara. Ebből a gördülési ellenállás: $R_{x} = Δ x / r_{s t a t} F_{z} = f F_{z}$ , ahol $f = Δ x / r_{s t a t}$ . Mivel $Δ x$ változó nem mért, ezért $R_{x}$ ellenállást az $F_{z}$ normálerővel arányosan modellezzük.

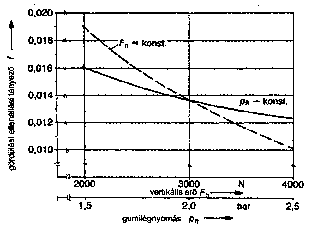
4.3. ábra - Gördülési ellenállási tényező

A gördülési ellenállás tényezője a gumi légnyomásától, a gumiabroncs típusától (összetételétől) és a kerékterhelésétől függ. Ezeken a gumi összetétele van rá hatással. Terepen a talaj minősége játszik fontos szerepet. A gördülési ellenállási tényező egy a sebességtől független állandóból és a sebességtől függő tagokból tevődik össze:

$f = f_{0} + f_{1} (v) + f_{n} v^{n}$

(146)

Normális (150 $k m / h$ ) sebességig az összefüggés lineáris ( $f_{n} \approx 0)$ . Nagy sebességnél a tapasztalati összefüggés:

$f = f_{0} + f_{1} v + f_{4} v^{4} .$

(147)

4.4. ábra - Kerékösszetartás

Nedves talajon, bizonyos vízrétegvastagság felett a gördülési ellenállást növeli a lökéshullámból adódó ellenállás, amely a talaj és a gumiabroncs közé ékszerűen benyomuló víz kiszorítása miatt lép fel. A lökéshullám ellenállása a sebességtől, az abroncs szélességétől és a vízréteg vastagságától függ. magasabb vízréteg és nagyobb sebesség esetén a kerék felúszhat és vízen csúszás keletkezhet.

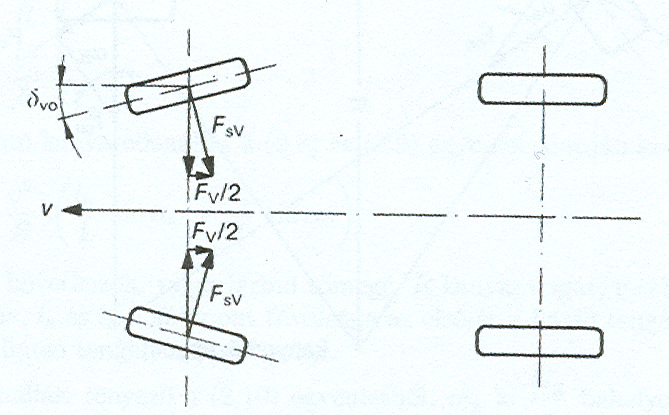
A gördülési ellenállást növeli a kerékösszetartásból eredő ellenállás is. A kerékösszetartási ellenállás ( $F_{v}$ ) a gumi felfekvő felületének oldalirányú deformációja miatt keletkezik.

4.5. ábra - Kanyarellenállás

A kerékösszetartási szögből ( $δ_{v 0}$ ) eredő oldalerő ( $F_{s v}$ ) hosszirányú komponense a menetiránnyal ellentétesen hat, ezért növeli a kerékellenállást:

$F_{v} = 2 F_{s v} sin δ_{v 0} .$

(148)

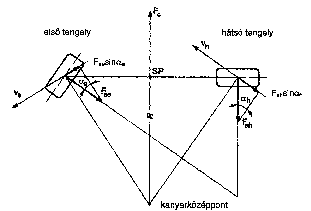
A kanyarellenállás ívmenetben a gumiabroncs oldalirányú deformációja következtében keletkezik. A kanyarellenállás a kerekeken ívmenetben fellépő oldalerők ( $F_{s i}$ ) mozgással ellentétes irányban ható komponenseiből számítható.

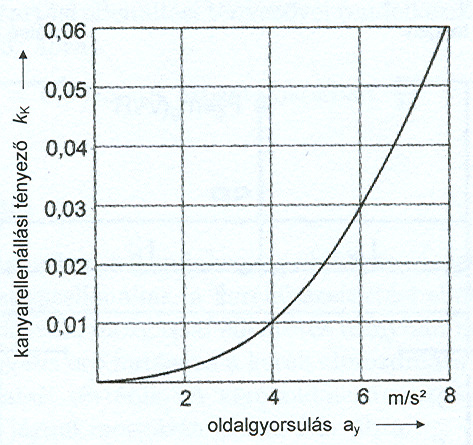
A kerékoldalerő mozgással ellentétes irányú komponense $F_{s i} sin α_{i}$ a jármű mozgását fékezi. A kanyarellenállás ekkor

$F_{c o r n} = F_{s e} sin α_{e} + F_{s h} sin α_{h},$

(149)

ahol $α_{e}, α_{h}$ az első és hátsó tengely kúszási szöge.

A kanyarmenetben fellépő centrifugális erő ( $F_{c}$ ) által generált nyomaték egyensúlyban van a tengely oldalerők ( $F_{s i}$ ) által generált nyomatékkal.

$F_{s e} l = F_{c} l_{h}, F_{s h} l = F_{c} l_{e}$

(150)

ahol a centrifugális erő közelítése: $F_{c} = m_{g} v^{2} / R$ , ahol $m_{g}$ a jármű tömege, $R$ a kanyarsugár, $v$ sebesség, $l$ tengelytáv, $l_{e}, l_{h}$ a súlypont távolsága az első és hátsó tengelytől.

A járműre ható kanyarellenállás:

$F_{c o r n} = F_{s e} sin α_{e} + F_{s h} sin α_{h} = m_{g} \frac{v^{2}}{R} (\frac{ℓ_{h}}{l} sin α_{e} + \frac{ℓ_{e}}{l} sin α_{h})$

(151)

azaz

$F_{c o r n} = k_{K} m_{g} g$

(152)

ahol $k_{K}$ kanyarellenállási tényező:

$k_{K} = \frac{v^{2}}{g R} (\frac{ℓ_{h}}{l} sin α_{e} + \frac{ℓ_{e}}{l} sin α_{h}) .$

(153)

A 31. ábra a kanyarellenállási tényező változását mutatja az oldalgyorsulás függvényében.

A mozgásban lévő járművön a menetszél következtében a mozgás irányával ellentétesen ható erő, $F_{a e r o}$ légellenállás keletkezik. A légellenállás nagysága a jármű alakján kívül elsősorban az áramlási sebességtől függ. Az eredő áramlási sebesség a menetszélből ( $v$ ) és a természetes szélből ( $w$ ) tevődik össze: $v_{r e s} = v \pm w$ .

Ha a természetes szél iránya nem egyezik meg a menetszél irányával, az eredő erő háromszögeléssel számolható:

$v_{r e s} = \sqrt{v^{2} + w^{2} + 2 v w cos τ}$

(154)

ahol $τ$ a természetes szélsebesség iránya és a jármű hossztengelye közötti szög.

Oldalszél esetén az eredő áramlási sebesség és az áramlási szög:

$v_{r e s} = \sqrt{v^{2} + w^{2}} .$

(155)

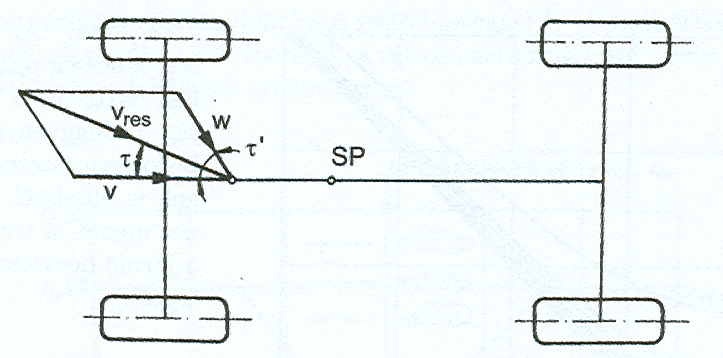
4.6. ábra - Áramlási sebesség

A természetben az áramlási szög állandóan változik, mert a szélsebesség és az útirány is változik. Az áramlási veszteségek az áramlási sebesség négyzetével nőnek. A légellenállás a következő összefüggésből számítható:

$F_{a e r o} = \frac{ρ}{2} C_{d} A_{f} v_{r e s}^{2}$

(156)

ahol $ρ$ a levegő sűrűsége, $C_{d}$ a légellenállási tényező, $A_{f}$ a jármű homlokfelülete, $v_{r e s}$ az áramlási szélsebesség. Megjegyzés: $C_{d}$ értéke a jármű hosszirányába ható szélsebességgel egy szélcsatornában határozható meg.

Az emelkedési ellenállás a jármű tömegéből és a lejtő szögéből számítható.

$F_{s l o p e} = m_{g} g sin α_{s}$

(157)

Gyorsításkor a jármű transzlációs és rotációs mozgást végző tömegeinek tehetetlenségi ellenállását kell leküzdeni. Ezek alapján a gyorsítási ellenállás két részből tevődik össze:

(158)

ahol $m_{g}$ a jármű tömege, $a_{x}$ a gyorsulás, a forgó tömegeknek a kerékre redukált tehetetlenségi nyomatéka, ${\dot{ω}}_{R}$ a kerék szöggyorsulása és $r_{d y n}$ a dinamikus keréksugár. A kerék szöggyorsulását átszámíthatjuk transzlációs gyorsulássá: ${\dot{ω}}_{R} = a_{x} / r_{d y n}$ . A gyorsítási ellenállás:

(159)

ahol $k_{m}$ forgási tömegtényező a rotációs és transzlációs tömegek viszonyát fejezi ki.

$J_{i}$ meghatározásához a forgó tömegek tehetetlenségi nyomatékát az $ω_{R}$ szögsebességgel forgó kerékre kell redukálni.

A hajtótengely $ω_{T}$ és a motor $ω_{M}$ szögsebességét a differenciálmű áttételével ( $i_{D}$ ) és a hajtóműáttétellel ( $i_{G}$ ) kell a kerékre átszámítani: $ω_{T} = i_{D} ω_{R},$ $ω_{M} = i_{D} i_{G} ω_{R}$

A kerékre redukálandó tehetetlenségi nyomatékok összege ennek megfelelően

(160)

ahol $J_{T, r e d} = i_{D}^{2} J_{T}$ a hajtótengely kerékre redukált tehetetlenségi nyomatéka és $J_{M, r e d} = i_{D}^{2} i_{G}^{2} J_{M}$ a motor forgó részeinek kerékre redukált tehetetlenségi nyomatéka.

4.2. Kerék és út

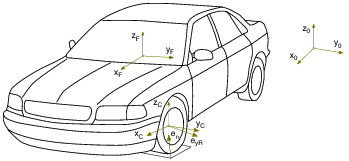
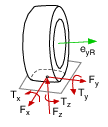
4.7. ábra - Koordináta rendszerek és kerék erők

A kerék erők leírása során több koordináta rendszert használhatunk. Ezek lehetnek például földhöz rögzített $(x_{0}, y_{0}, z_{0})$ , a járműhöz rögzített $(x_{F}, y_{F}, z_{F})$ , kerék hordozóhoz rögzített $(x_{c}, y_{c}, z_{c})$ , kerék forgéstengelyhez rögzített $(e_{y R})$ , valamint a lokális útfelület dőléséhez rögzített $(e_{n})$ koordináta rendszerek.

Minden ponton, ahol a gumiabroncs érintkezik az út felületével merőleges (normális) erők és súrlódási erők ébrednek. Az abroncs profiljának kialakítása miatt azonban a felfekvő felület nem feltétlenül alkot összefüggő területet. A kontakterők hatása leírható egyetlen eredő erővel ami az érintkezési felület egy rögzített pontján hat és egy nyomaték vektorral. Mivel egyenetlen úton a $P$ kontakt pont meghatározása nem egyszerű, ezért a kontakt pont geometriáját úgy kaphatjuk meg, hogy egy becsült $P_{*}$ pontot a tényleges útra vetítve kapunk egy $P_{0}$ közelítést a kontakt pontra, ahol a kerékre ható erőket tételezzük.

4.2.1. Kerékre ható erők és nyomatékok

A vektorok komponenseit egy, a pályához rögzített, koordináta rendszerben fejezhetjük ki, ahol a $z$ tengely merőleges a pályára, az $x$ tengely merőleges a $z$ tengelyre és a kerekek $e_{y R}$ forgási tengelyére. Az $y$ tengely irányát a jobbkezes rendszer szerint rögzítjük.

Ebben a koordináta rendszerben a kerék erő és nyomaték komponensei a következőek:

$F_{x}$ hosszirányú, síkbeli longitudinális (fék, hajtás) erő,
$F_{y}$ oldalirányú, síkbeli laterális (kanyarodás) erő
$F_{z}$ függőleges (kerék-terhelés) erő,
$M_{x}$ dőlési/billenő, (kerék dőlését létrehozó) nyomaték,
$M_{y}$ gördülő nyomaték
$M_{z}$ nyomaték, ami a síkbeli erőkből jön létre azáltal, hogy azok támadáspontja nem közvetlenül a kerék középpontja alatt van.

A függőleges (kerék-terhelés) erőnek van egy statikus és egy dinamikus komponense:

$F_{z} = F_{z, s t a t} + F_{z, d y n},$

(161)

ahol a statikus komponens a kerék elhajlás (tire deflection, $Δ z$ ) és a kerék elhajlás változási sebességének ( $Δ \dot{z}$ ) nemlineáris függvénye, míg a dinamikus komponens kifejezése $F_{z, d y n} = d_{R} Δ \dot{z}$ .

A kerék síkja általában nem merőleges az útra. A kerékdőlési szög ( $γ$ ) a kerék síkjának oldalirányú kitérését méri. Ez főleg motorkerékároknál jelentős, de bizonyos felfüggesztési megoldások hatására is jelentkezhet, amikor a tengelyterhelés változik. A rugalmas kapcsolatok eredményeképp kanyarodáskor is jelentkezik oldalirányú kitérés.

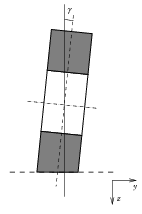
4.8. ábra - Kerékdőlési szög

$M_{x}$ dőlési/billenő, (kerék dőlését létrehozó) nyomaték kifejezése

$M_{x} = y F_{z} .$

(162)

A dőlés hatására akkor is lesznek oldalirányú erők, ha nincs csúszás. Kis dőlési szögekre ennek közelítése

$M_{x} \approx s_{T} γ,$

(163)

ahol $s_{T}$ dőlési együttható (tipping stiffness).

Az $M_{y}$ gördülő nyomatékot általában lineáris tagként modellezzük:

$M_{y} = q_{0} R | F_{z} | .$

(164)

Pontosabb modelleknél a kerékspecifikus $q_{0}$ faktor a jármű sebességétől is függ. Egy további veszteségforrás lehet a hosszirányú erő nyomatéka:

$M_{y, a d d} = (R_{e} - R) F_{x},$

(165)

ahol $R_{e}$ az effektív gördülési sugár.

4.2.2. A kerék kinematikája

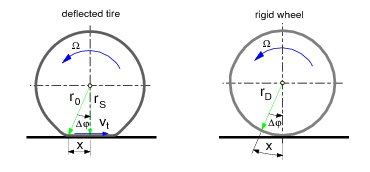
4.9. ábra - Kontakt pont sebessége

A gumiabroncs kerületén ébredő hosszirányú erők a következő tényezőktől függnek: hosszirányú szlip, a függőleges kerékterhelés és a tapadási tényező. Hajtónyomaték vagy fékező nyomaték hatása alatt a gumiabroncs felfekvő felületén lévő gumirészecskék parciális csúszása miatt sebességkülönbség keletkezik a jármű sebessége és a kerék gördülési sebessége között. Emiatt kerék által megtett távolság nem egyezik meg a kerék forgási szögéből számítható távolsággal, úgynevezett hosszirányú szlip keletkezik.

A hosszirányú szlip ( $λ_{x}$ ) a $v_{x}$ menetsebesség és a kerék/talaj közötti $r_{d y n} ω$ relatív sebesség különbségéből határozható meg. A dinamikus keréksugár $r_{d y n}$ a gumiabroncs legördülési kerületéből adódik. A legördülési kerület egyenlő a szabadon gördülő kerék által egy fordulat alatt megtett úttal. Így a kerék dinamikus gördülési sugarát a következő definíció alapján határozhatjuk meg:

$v_{x} = r_{d y n} ω,$

(166)

ahol $ω$ a kerék fordulatszáma. Tehát a dinamikus keréksugár az az effektív $r_{d y n}$ keréksugár, amivel az $ω$ fordulatszámmal a kerék által elért sebesség adódna.

A dinamikus keréksugár összefüggése alapján:

$r_{d y n} = r_{w} \frac{sin ϕ}{ϕ} = r_{w} \frac{sin {{cos}^{- 1} (r_{s t a t} / r_{w})}}{{cos}^{- 1} (r_{s t a t} / r_{w})}$

(167)

ahol $r_{w}$ a terheletlen kerék sugara és $r_{s t a t}$ a terhelt kerék sugara. Ennek egy közelítő értékét az alábbiak szerint kaphatjuk meg:

$r_{d y n} \approx \frac{2}{3} r_{0} + \frac{1}{3} r_{S} (F_{z}) .$

(168)

Látható, hogy

$r_{s t a t} < r_{d y n} < r_{w} .$

(169)

Egy meghajtó kerék esetén (elsőkerék hajtású jármű első kereke) a forgásból számított sebesség nagyobb a jármű sebességénél, azaz $r_{d y n} ω_{R} > v_{x}$ . Egy meghajtott kerék esetén a jármű sebessége nagyobb a kerék forgásából számított sebességénél, tehát $v_{x} > r_{d y n} ω_{R}$ . Hajtás esetén a következő sebességkülönbség adódik: $r_{d y n} ω_{R} - v_{x}$ .

A dinamikai jármű modellekben szereplő egyik legfontosabb paraméter a $λ$ longitudinális csúszási együttható (szlip), ahol:

$λ = \frac{v_{x} - R_{e} ω}{v_{x}} = \frac{ω_{0} - ω}{ω_{0}} .$

(170)

A hosszirányú szlip hajtás és fékezés esetén a következőképpen definiálható: a fékezési szlip

$λ_{x b} = \frac{v_{x} - r_{d y n} ω_{R}}{v_{x}},$

(171)

míg a hajtási szlip

$λ_{x a} = \frac{r_{d y n} ω_{R} - v_{x}}{r_{d y n} ω_{R}} .$

(172)

Az álló járművön kipörgő kerék, illetve a fékezéskor blokkoló kerék egyaránt $1$ szlipet jelent.

Összefoglalva, a kerék kinematikáját meghatározó legfontosabb tényezők az alábbiak: a jármű $v = (v_{x}, v_{y})$ sebessége, a $v_{c} = ω R_{e}$ kerék kerületi sebessége valamint a $v_{s} = (v_{x} - v_{c}, v_{y})$ csúszási sebesség. Az $R_{e} = \frac{v_{x}}{ω_{0}}$ effektív gördülési sugár értékét a szabadon futó (fék/hajtás= $0$ ) kerék $ω_{0}$ szögsebessége határozza meg. Bevezetjük még az $α = arctan \frac{v_{y}}{v_{x}}$ a csúszási szöget valamint a csúszási sebesség $β = arctan \frac{v_{s y}}{v_{s x}}$ irányát.

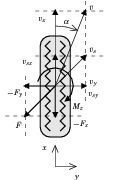
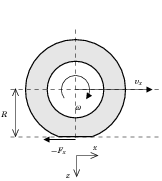
4.10. ábra - Kerék kinematikája

A kerékerők a tapadási és csúszási együtthatók függvényei. A különböző együtthatók definíciói és a köztük levő kapcsolatok az alábbiak:

$σ = (σ_{x}, σ_{y}) = (\frac{v_{x}}{v_{c}} - 1, \frac{v_{y}}{v_{c}}),$

(173)

$κ = (κ_{x}, κ_{y}) = (1 - \frac{v_{c}}{v_{x}}, \frac{v_{y}}{v_{x}}),$

(174)

$s = (s_{x}, s_{y}) = (\frac{v_{x} - v_{c}}{| v |}, \frac{v_{y}}{| v |}), | v | = \sqrt{v_{x}^{2} + v_{y}^{2}} .$

(175)

Mivel $λ = κ_{x}$ a csúszási együttható (slip ratio):

$σ = (\frac{λ}{1 - λ}, tan (α)),$

(176)

$κ = (λ, tan (α)),$

(177)

$s = (λ cos (α), sin (α))) .$

(178)

Az ISO és SAE szabványok szerint a hosszirányú csúszás kifejezése $- 100 κ_{x}$ [%] míg az oldalirányú csúszás $α$ [deg].

A gyakorlatban használt irányítási célú járműmodellek linearizált erőkkel és nyomatékokkal számolnak:

$F_{x} = C_{x} s_{x}, C_{x} = \frac{d F_{x}}{d s_{x}} |_{s_{x} = 0, s_{y} = 0},$

(179)

$F_{y} = C_{y} s_{y}, C_{y} = \frac{d F_{y}}{d s_{y}} |_{s_{x} = 0, s_{y} = 0},$

(180)

azaz

$F_{x} = C_{F_{x}} λ,$

(181)

$F_{y} = C_{F_{α}} α + C_{F_{γ}} γ,$

(182)

$M_{Z} = C_{M_{α}} α + C_{M_{γ}} γ,$

(183)

ahol például $C_{F_{x}}$ longitudinális merevség (szlip) és $C_{F_{α}}$ pedig a kanyarodási (cornering) merevség.

4.3. Erőátvitel modellezés

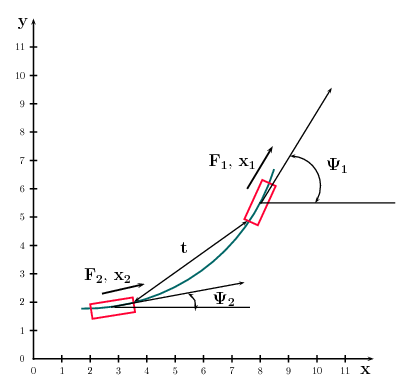
A kerékre ható, úttartást és menetstabilitást befolyásoló tényezők a csúszási szög az oldalerő és az általa generált nyomaték. Amennyiben a jármű a tapadási viszonyokhoz képest nagy sebességgel halad az ívben, a tapadás jelentős részét felemészti az íven tartás biztosítása: a tapadási tényező oldalirányú komponense megközelíti az útpálya és gumiabroncs közötti tapadási tényező értékét. Ha a két komponenst összegezzük, előfordulhat, hogy nincs akkora tapadás, mint amekkorára az adott manővernél szükség lenne: a jármű kicsúszik a kanyarban.

A horizontális síkban maximálisan átvihető erőt az abroncs és a talaj érintkezési síkjában ható súrlódási viszonyok határozzák meg. A jármű hosszirányú mozgásához szükséges erők:

$m \ddot{x} = F_{x f} + F_{x r} - F_{A}$

(184)

ahol $F_{A}$ a leküzdendő menetellenállások összege, $F_{x f}$ és $F_{x r}$ a hosszirányú erő az első és hátsó kerekeken.

Mint azt már láttuk, a maximális hosszirányú erő ( $F_{x}$ ) arányos a függőleges erővel ( $F_{n}$ ):

$F_{x} = μ_{H} F_{n}$

(185)

ahol $μ_{H}$ arányossági tényező a gumiabroncs és az út közötti tapadási tényező. Ha a keréken ennél nagyobb hajtó vagy fékerő lép fel, akkor a gumiabroncs nem tud a talajon tapadni és kipörög vagy blokkol. Ebben az állapotban átvihető erő a $μ_{G}$ csúszási tényező nagyságától függ:

$F_{x G} = μ_{G} F_{n} .$

(186)

Egy tipikus $μ$ szlip görbe maximuma a $μ_{H}$ tapadási tényező, ami a maximális erőkapcsolat kihasználást jelenti. Fékezéskor a tapadási tényező növekvő kerékcsúszás esetén intenzíven, kezdetben lineárisan majd kevésbé növekedve éri el maximális értékét. Ezt stabil tartománynak tekintjük.

Ha a szlip görbe maximumán túl növekszik, akkor a súrlódási tényező leesik a $μ_{G}$ csúszási tényező értékére. A görbének ez a szakasza az instabil tartomány, ami azt jelenti, hogy a szlip a görbe maximumának átlépésekor növekszik és a kerék a csúszás állapotába megy. Ez egy önmagát gerjesztő folyamat, melynél ha nem csökkentik a fékező nyomást, a kerék hamarosan blokkolni fog.

A jármű iránytartása szempontjából a gumiabroncs oldalvezetési tulajdonságai jelentősek. A kormány működtetésével a kerék elfordul eredeti síkjától. Ekkor a gumiabroncs felfekvő felületében a talajon tapadó gumirészecskék rugalmas deformációja lép fel.

A kerék emiatt nem a középsíkja irányában, hanem az úgynevezett $α$ kúszási szög alatt gördül le. A kerék sebességvektora a kerék középsík tengelyével $α$ szöget zár be. A felfekvő felületen fellépő $v sin α$ oldalcsúszási sebesség oldalirányú szlipet okoz.

$λ_{y} = \frac{v sin α}{v} .$

(187)

A kúszási szög az első és hátsó kerekeken a következő:

$α_{f} = δ - θ_{v f}$

(188)

$α_{r} = - θ_{v r}$

(189)

ahol $δ$ a kormányszög. Kis szögek esetén a kúszási szögek a következő módon közelíthetők:

$θ_{v f} = \frac{v_{y} + l_{f} \dot{ψ}}{v_{x}}$

(190)

$θ_{v r} = \frac{v_{y} - l_{r} \dot{ψ}}{v_{x}}$

(191)

ahol $v_{x}, v_{y}$ a hosszirányú és oldalirányú sebességek, $\dot{ψ}$ a perdülés szöge.

Az oldalirányú erő a függőleges normál erőtől függ:

$F_{l a t} = μ_{s} F_{n}$

(192)

ahol $μ_{s}$ az arányossági oldalsúrlódási tényező. Az oldalerő kis szögek esetén arányos a kúszási szöggel

$F_{l a t} = C_{R} α .$

(193)

Az oldalvezető erő nem a gumiabroncs talajérintkezési felületének közepén hat, hanem $n_{R}$ távolságban mögötte. Emiatt egy visszatérítő kúszási nyomaték keletkezik, ami a kúszási szöget csökkenteni akarja:

$M_{s R} = n_{R} F_{l a t} .$

(194)

A $γ$ kerékdőlés is oldalerőt generál, amely irányától függően kanyarban növeli vagy csökkenti a centrifugális erőből adódó oldalerőt. Kis dőlésszögek esetén jó közelítéssel

$F_{l a t} = sin γ F_{n} .$

(195)

4.4. Kerékmodellek

Szimulációs célból a keréknek különböző bonyolultságú modelljeit használhatjuk. Vannak strukturális, komplex kerék modellek, mint például a végeselem modellek, ahol a kerék kis elemekre van bontva, az egyes elemekre és kölcsönhatásaira felírt (parciális) differenciálegyenletekkel. Ezeknek a modelleknek azonban igen nagy a számítási igényük.

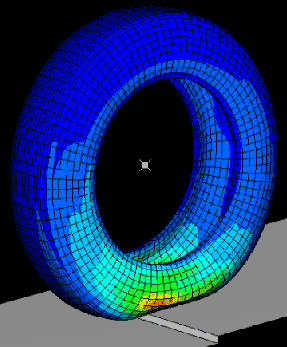
4.11. ábra - Komplex kerék modell

Az ennél valamivel egyszerűbb dinamikus kerék modellek közül megemlíthetők a kefe modellek, ahol a gumiabroncs szeletekre van bontva, és ezeknek a szeleteknek a mozgása, mintha egy kefe sörtéi lennének, van modellezve. Ebben a modellben az egyes cellákra vonatkoztatott erők és a szlip alakja:

$F_{x i} = k δ_{i}, k = c_{p} d x_{c}, F_{x i, m a x} = μ F_{z i}$

(196)

$F_{z i} = q (x_{c}) d x_{c}, q (x) = \frac{3 F_{z}}{4 a} (1 - \frac{x^{2}}{a^{2}})$

(197)

$μ q (x_{s}) = c_{p} σ_{x} (a - x_{s})$

(198)

(199)

$σ_{x} = \frac{λ}{1 + λ} .$

(200)

A dinamikus szemi-empirikus modellek figyelembe veszik, hogy a manőverezés során a kerékerők kialakulásához idő kell, azaz

$\frac{σ_{x}}{v_{x}} \frac{d λ}{d t} = λ - \bar{λ},$

(201)

ahol $λ$ a kerékerőket meghatórozó slip, $\bar{λ}$ a tényleges (mért) slip, míg $\frac{σ_{x}}{v_{x}}$ az úgynevezett relaxációs hossz. Az $r_{y}$ oldalirányú relaxációs hossz az $F_{z}$ kerékerő és az oldalirányú szlip függvénye.

Egy egyszerüsített kefe modell a LuGre modell, ahol

$F_{x} (v_{x} + {\dot{x}}_{e}) \approx {\bar{F}}_{x} (v_{x}) + \frac{\partial F_{x}}{\partial v_{x}} {\dot{x}}_{e}$

(202)

$F_{y} (v_{y} + {\dot{y}}_{e}) \approx {\bar{F}}_{y} (v_{y}) + \frac{\partial F_{y}}{\partial v_{y}} {\dot{y}}_{e}$

(203)

A dinamikus kerék modellek általában túl bonyolultak ahhoz, hogy irányítási célú modellekben használjuk őket. Ilyen célokra megfelelőbbek a stacionárius kerék modellek, ahol a szlip egy stacionárius nemlineáris kifejezésként van modellezve. Ilyen például a Pacejka féle "mágikus" formula:

$y (x) = D sin [C arctan [(1 - E) x + (\frac{E}{B}) arctan (B x)]]$

(204)

ahol $(x, y)$ a $(λ, F_{x})$ , $(α, F_{y})$ , $(α, M_{z})$ párok valamelyike és

$B = \frac{(a_{3} F_{z}^{2} + a_{4} F_{z})}{(C D e^{a_{5} F_{z}})}$ merevségi faktor;
$C = a_{0}$ alak faktor;
$D = a_{1} F_{z}^{2} + a_{2} F_{z}$ csúcs faktor;
$E = a_{6} F_{z}^{2} + a_{7} F_{Z} + a_{8}$ görbületi faktor.

A teljes szimulációs célú modell jóval több (kb. $85$ ) paramétert tartalmaz amit mért adatokkal való összevetéssel kalibráltak be. Tervezés során természetesen a paraméterek számának csökkentése a kívánatos.

4.5. Egyszerű hosszirányú jármű modell

Egy egészen egyszerű longitudinális jármű modell egyenletei

$m \dot{v} = F_{x},$

(205)

$Θ \dot{ω} = T - r F_{x},$

(206)

ahol $m$ a jármű tömege, $v$ a jármű sebessége, $Θ$ az inercia együttható és $r$ a kerék sugara. Ebben az egyszerű modellben a kerék felfüggesztését és a gumiabroncs összenyomódási mértékét nem vesszük figyelembe. $T$ a hajtási vagy fékezési nyomaték.

Az állandósult állapotban a keletkezett kerék erők és nyomatékok a hosszirányú és oldalirányú csúszás függvényei. Ennek megfelelően az $F_{x}$ hosszirányú erő a hosszirányú $s_{x}$ csúszási együttható függvénye, ahol

$s_{x} = \frac{v - r ω}{r | ω |},$

(207)

és ahol $r$ szolgál, ebben ez az egyszerű megközelítésben, dinamikus gördülési sugárként is.

Normál vezetési körülmények között $s_{x}$ igen kicsi, és a kerék közel áll a

$Ω \approx \frac{v}{r}$

(208)

szabadon gördülési feltételhez. Ekkor a $v = v_{0}$ és $ω = \frac{v_{0}}{r}$ állapottól való eltérés

$v = v_{0} + Δ v$

(209)

és

$ω = \frac{v_{0}}{r} + Δ ω .$

(210)

Kis eltérések esetén a hosszirányú csúszási együttható alakja

$s_{x} = \frac{v_{0} + Δ v - v_{0} - r Δ ω}{| v_{0} + r Δ ω |} \approx \frac{Δ v - r Δ ω}{| v_{0} |} .$

(211)

A már látott módon a linearizált longitudinális erő $F_{x} = C_{x} s_{x}$ így a kapott longitudinális modell

(212)

4.5.1. Példa: vasúti kerék szimulált fékezése

Ennek az egyszerű longitudinális modellnek az alkalmazására álljon itt a vasúti kerék csúszásának vizsgálata fékezéskor. Láttuk, hogy a $ν = \frac{R ω - v}{v}$ szlip értékei $0$ (szabadon futó kerék) és $1$ (blokkolt kerék) között lehetnek. A valós és a modellezett $μ (ν)$ adhéziós görbát, ahol a tribológiai környezet a $ν_{0}, μ_{0}, ν_{e}, μ_{\infty}$ paraméterekkel van modellezve, a 38. ábra szemlélteti.

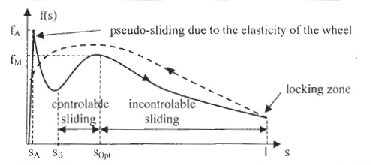
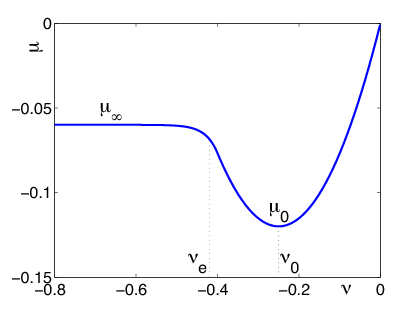
4.12. ábra - Valós és modellezett adhéziós görbe

A szimulációhoz használt modell alakja

$μ = {\begin{array}{l} s i g n (ν) (4 μ_{0} \frac{| ν |}{2 ν_{0}} (1 - \frac{| ν |}{2 ν_{0}})) & h a | ν | < ν_{e} \\ s i g n (ν) (η e^{- χ (| ν | - ν_{e})} + μ_{\infty}) & h a | ν | \geq ν_{e} \end{array}$

(213)

ahol

$η = 4 μ_{0} \frac{ν_{e}}{2 ν_{0}} (1 - \frac{ν_{e}}{2 ν_{0}}) - μ_{\infty},$

(214)

$χ = - \frac{2 μ_{0}}{ν_{0} η} (1 - \frac{ν_{e}}{ν_{0}}) .$

(215)

A modell alapján egy blokkolásgátló fékezés lett tervezve. Ennek a fékezésnek a működését szemlélteik az 40 és 41 ábrák. A szimuláció során beállított tribológiai paraméterek értékei az alábbiak voltak:

$ν_{0} = 0.25, ν_{e} = 0.4, μ_{0} = 0.12, μ_{\infty} = 0.06;$
$ν_{0} = 0.1, ν_{e} = 0.18, μ_{0} = 0.08, μ_{\infty} = 0.012;$
$ν_{0} = 0.2, ν_{e} = 0.35, μ_{0} = 0.04, μ_{\infty} = 0.01.$

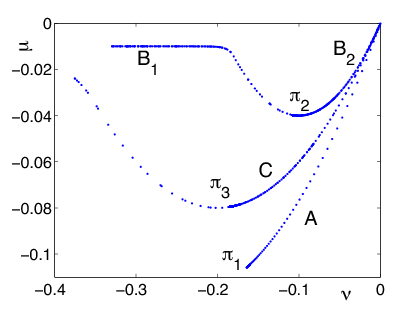
4.13. ábra - Szimuláció:

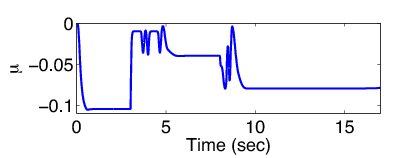
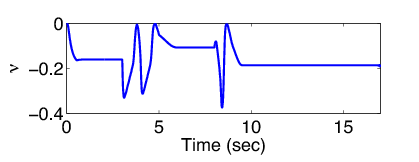
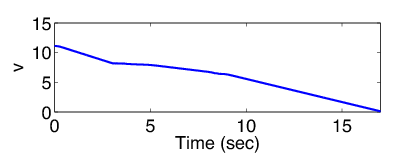
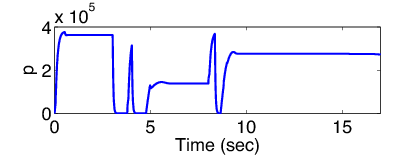
4.14. ábra - Szimuláció: jelek

4.6. Sebesség és távolságtartó irányítások

Egy hagyományos sebességtartó irányítás a vezető által megadott sebességérték tartására képes. Az adaptív sebességszabályozás feladata a hagyományos menetsebesség szabályozáson nyugszik, ami tartja a megadott sebességet. A szabályozás képes váltakozó forgalmi körülményekhez automatikusan igazodni: gyorsítani, gázadást csökkenteni, fékezni. Ezáltal képes egy előtte haladó jármű sebességéhez is igazodni egy hosszirányú követési távolság figyelembe vételével.

A szabályozási feladat az igényelt sebesség ( $v_{r e f}$ ) és az aktuális sebesség ( $v_{x}$ ) közötti különbség csökkentéséhez kiszámítja a szükséges gyorsulás (lassulás) értékét és azt realizálja:

$v_{x} - v_{r e f} \to m i n .$

(216)

A jármű mozgásához szükséges hajtóerő komponensei:

$F = F_{a c c} + F_{d i s t}$

(217)

ahol $F_{a c c}$ a gyorsítási ellenállás és $F_{d i s t}$ a zavaró tényezők eredője (gördülési ellenállás, légellenállás, kanyarellenállás, emelkedési ellenállás). Az $F$ hosszirányú erő egyszerűsített összefüggése:

$F_{=} m \ddot{x}$

(218)

ahol $m$ a jármű tömege, $\ddot{x}$ pedig a jármű gyorsulása.

Az irányítási feladatot például egy PI típusú szabályozóval oldhatjuk meg. A szabályozó struktúrája ekkor

$C = k_{p} + \frac{k_{i}}{s} .$

(219)

A szabályozó bemenete a megkívánt sebesség ( ${\dot{x}}_{d e s} = v_{r e f}$ ) és az elért sebesség ( $\dot{x} = v_{x}$ ) közötti különbség: A szabályozó komponenseinek hatása a sebességekre:

(220)

Definiáljuk a referencia pozíciót: (folyt.)

ahol $x_{d e s} (t)$ az igényelt referencia sebességhez tartozó pozíció. Az $x$ aktuális pozíció hasonlóan felírható.

Az igényelt gyorsulás és a szabályozó komponenseinek hatása:

${\ddot{x}}_{d e s} (t) = - k_{p} (\dot{x} - {\dot{x}}_{d e s}) - k_{I} (x - x_{d e s}) .$

(221)

A felsőszintű szabályozás tervezése rutinfeladat. Ha az irányítójel nagyságát meg akarjuk szorítani, akkor az elérendő minőségi tulajdonságokat bővítjük:

megfelelő referenciajel-követést kell biztosítania;

$v_{x} - v_{r e f} \to m i n$

azaz az előírt sebesség és a tényleges sebesség közötti különbség legyen minimális,

minél kisebb hosszirányú erőt használjon a rendszer.

$| F_{l} | \to m i n$

A szabályozótervezés kritériuma a következőképpen fogalmazható meg:

(222)

ahol $q$ és $r$ a skalár tervezési súlyok.

A hosszirányú erőt a hajtási vagy a fékezési rendszerekkel kell létrehozni. Hajtáskor a motor fojtószelep beállításával állítjuk elő a hajtáshoz szükséges nyomatékot (táblázat). A sebességváltásról a fordulatszám és az optimális fogyasztás alapján döntünk. Fékezéskor a féknyomásokat állítjuk be ( például táblázat alapján).

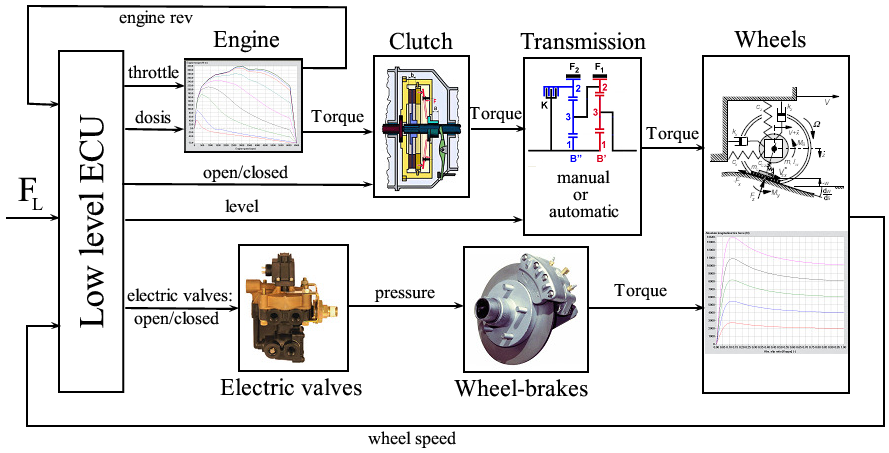
4.15. ábra - Összetett szabályozási séma

Ha a jármű előtt nem halad másik jármű, akkor standard sebességtartó irányítási feladatot kell megoldani. Ha a jármű előtt egy másik jármű jelenik meg, akkor döntési feladatot kell először megoldani. Ha az előttünk lévő jármű távolsága és sebessége alapján nincs szükség a sebesség változtatására, akkor továbbra is sebességtartó irányítást kell megoldani. Ha az aktuális sebesség nem tartható, akkor a továbbiakban egy távolságtartó irányítási feladatot kell megoldani.

Az irányítási feladatban közúti járműhöz tervezünk szabályozót, amely képes a járművet egy előző járműtől előre megadott távolságban vezetni. Az irányítástervezés feladata a szükséges hosszirányú erő (hajtáslánc és fékrendszer) meghatározása. A szabályozási feladat a két jármű közötti relatív távolság minimalizálása:

$x_{1} - x_{2} \to m i n$

(223)

ahol $x_{1}$ és $x_{2}$ az egyes járművek elmozdulásai.

A járművek $F_{i}$ hosszirányú erőinek összefüggése:

$F_{1} = m_{1} {\ddot{x}}_{1}$

(224)

$F_{2} = m_{2} {\ddot{x}}_{2}$

(225)

ahol $m_{i}$ a jármű tömege, $x_{i}$ a járművek elmozdulása. Az egyenleteket a következő alakban célszerű megfogalmazni:

$\dot{d} = {\dot{x}}_{1} - {\dot{x}}_{2}$

(226)

$\ddot{d} = {\ddot{x}}_{1} - {\ddot{x}}_{2} = \frac{1}{m_{1}} F_{1} - \frac{1}{m_{2}} F_{2}$

(227)

ahol $d = x_{1} - x_{2}$ relatív távolság.

4.16. ábra - Követési feladat

A szabályozott rendszernek a következő minőségi tulajdonságokat kell kielégítenie:

megfelelő referenciajel-követést kell biztosítania

$| d_{r e f} - d | \to m i n$

(228)

azaz az előírt relatív távolság és a tényleges közötti különbség legyen minimális

minél kisebb hosszirányú erőt használjon a rendszer

$| F_{l} | \to m i n$

(229)

A szabályozótervezés kritériuma a következőképpen fogalmazható meg:

(230)

ahol $q$ és $r$ a skalár tervezési súlyok.

Az adaptív távolságtartó irányítási feladatban a járműnek egy előre megadott követési távolságot kell tartania.

4.17. ábra - Oszlopban haladó járművek

Az oszlopban haladó járművek irányítása azt a jellegzetes forgalmi szituációt kísérli meg automatizálás által biztonságosabbá és költséghatékonyabbá tenni, amikor több jármű, hosszú távon, azonos útszakaszon halad. Emellett a környező járművek aktuális pozíciójának pontos ismerete segítheti a ráfutásos balesetek kiküszöbölését is. Az oszlopban haladó járművek esetén a cél a minél kisebb követési távolság megvalósítása. Az oszlopban haladó járművek közötti kommunikáció kihasználásával a követési távolságot a normál követési távolságnál lényegesen kisebbre választjuk.

Normál működési körülmények esetén a követőjárművek irányítása szétcsatolható egy sebességszabályozási feladatra (hosszirányú irányítás) és a sávon belüli pozícionálásra (oldalirányú irányítás). A sebességszabályozó kimenete a féknyomás vagy a pillangószelep-állás, amelyek a jármű gyorsulásának beállítására szolgálnak. A szabályozó bemenetei az alkalmazott irányítási módszertől függően változhatnak, de a vezető vagy közvetlenül a vizsgált jármű előtt haladó jármű gyorsulás, sebesség és pozíció (távolság) adatai rendszerint szükségesek.

Ebben a feladatban alapvető szerepet játszanak a szenzorfúziós eljárások és a járművek közötti kommunikációs módszerek. A szokásos pozíciómeghatározási módszereket (GPS) a járművön megtalálható egyéb érzékelők (sebesség, oldalgyorsulás, radar) adataival kiegészítve kezeljük. Az oszlopban haladó járművek közötti kommunikáció kihasználásával a követési távolságot a normál követési távolságnál lényegesen kisebbre csökkentjük.

Kétféle stabilizálási feladatot kell megoldani: az egyedi járműveknek meg kell oldaniuk, hogy az őt megelőző járműtől való távolság minél kisebb (illetve az előírt értékű) legyen. Meg kell oldani a teljes járműoszlop stabilitását, az úgynevezett string stabilitási feladatot. A string stabilitás biztosítja, hogy az egyes járművek elérjék a számukra előírt pozíciót a járműoszlopon belül, továbbá garantálja, hogy a konvoj elején - például a vezető jármű hirtelen fékezése miatt - keletkező követési hiba folyamatosan csökkenő hibát okozzon a járműoszlop mentén. Ezzel elkerülhető, hogy egy hirtelen fékezés ráfutásos ütközést váltson ki a konvoj végén.

Az egyedi járműveknek meg kell oldaniuk, hogy az őt megelőző járműtől való távolság minél kisebb (illetve az előírt értékű) legyen. Legyen $x_{i}$ az $i$ -edik jármű aktuális pozíciója. A járművek között $L_{d e s}$ távolságot akarunk tartani, melynek meghatározása során figyelembe vettük a járművek hosszát is. A követő járművek közötti távolság hibája

$δ_{i} = x_{i} - x_{i - 1} + L_{d e s} .$

(231)

Az egyedi irányítás biztosítja a stabilitást, ha a következő követelmény teljesül:

${\ddot{x}}_{i - 1} \to 0 \Rightarrow δ_{i} \to 0.$

(232)

Az irányítási feladat a megadott távolság tartása az előző jármű mozgását figyelembe véve.

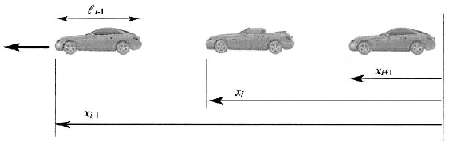
4.18. ábra - Adaptív string

Meg kell oldani a teljes járműoszlop stabilitását, az úgynevezett string stabilitási feladatot. A string stabilitási feladat azt jelenti hogy a konvoj elején keletkező követési hiba ne növekedjen a járműoszlop mentén a később érkező járművek irányában. A string stabilitásra többféle megoldás létezik: állandó távolság tartása vagy állandó időköz tartása, amikor a távolság nem állandó, hanem a sebességgel arányosan változik.

A szabályozó bemenetei az alkalmazott irányítási módszertől függően változhatnak, de a vezető vagy közvetlenül a vizsgált jármű előtt haladó jármű gyorsulás, sebesség és pozíció (távolság) adatai rendszerint szükségesek. Ha az irányítási stratégia a vezető jármű alapján (1. módszer) történik, akkor

(233)

ahol $x_{l}$ a vezető jármű pozíciója. Ekkor a követési hiba dinamikája: ${\ddot{ε}}_{i} = {\ddot{x}}_{i} - {\ddot{x}}_{i - 1} = u_{i} - u_{i - 1}$ azaz ${\ddot{ε}}_{i} + k_{v} {\dot{ε}}_{i} + k_{p} ε_{i} = 0$ . String stabilitás szempontjából ez biztosítja a leghatékonyabb megoldást, hiszen hibamentes megoldást ad. A stratégia nem biztonságos, mivel nem veszi figyelembe a vizsgált jármű előtt haladó jármű adatait.

Ha az irányítási stratégia csak a vizsgált jármű előtt haladó jármű adatai alapján (2. módszer) történik, akkor a módszer a vizsgált jármű előtt haladó jármű pozíció és sebesség adatai alapján dolgozik:

$u = - k_{v} {\dot{e}}_{i} - k_{p} e_{i} .$

(234)

Ekkor a követési hiba dinamikája ${\ddot{ε}}_{i} = u_{i} - u_{i - 1}$ alapján

${\ddot{ε}}_{i} + k_{v} {\dot{ε}}_{i} + k_{p} ε_{i} = k_{v} {\dot{ε}}_{i - 1} + k_{p} ε_{i - 1}, \forall i � 2.$

(235)

Az első járműre

${\ddot{ε}}_{i} + k_{v} {\dot{ε}}_{i} + k_{p} ε_{i} = - {\ddot{x}}_{l},$

(236)

ahol ${\ddot{x}}_{l}$ az első jármű gyorsulása. Az átviteli és a frekvencia függvény:

$H (s) = \frac{k_{v} s + k_{p}}{s^{2} + k_{v} s + k_{p}} \to H (i ω) = \frac{k_{v}^{2} ω^{2} + k_{p}^{2}}{{(k_{p} - ω^{2})}^{2} + k_{v}^{2} ω^{2}} .$

(237)

Azokon a frekvenciákon, ahol $H (i ω) � 1$ a hiba erősítve terjed tovább a járművek mentén. Ilyenkor a string stabilitás nem teljesül.

Ha az irányítási stratégia csak a vizsgált jármű előtt haladó jármű adatai alapján (3. módszer) történik, és a módszer a vizsgált jármű előtt haladó jármű pozíció és sebesség adatain kívül a vizsgált jármű előtt haladó jármű gyorsulás adatát is figyelembe veszi, akkor:

$u = k_{a} {\ddot{x}}_{i - 1} - k_{v} {\dot{e}}_{i} - k_{p} e_{i} .$

(238)

A követési hiba dinamikája ekkor ${\ddot{ε}}_{i} = u_{i} - u_{i - 1}$ alapján

${\ddot{ε}}_{i} + k_{v} {\dot{ε}}_{i} + k_{p} ε_{i} = k_{a} {\ddot{ε}}_{i - 1} + k_{v} {\dot{ε}}_{i - 1} + k_{p} ε_{i - 1}, \forall i � 2.$

(239)

Az első járműre ${\ddot{ε}}_{i} + k_{v} {\dot{ε}}_{i} + k_{p} ε_{i} = (k_{a} - 1) {\ddot{x}}_{l}$ , i=1, ahol ${\ddot{x}}_{l}$ az első jármű gyorsulása. Az átviteli függvény:

$H (s) = \frac{k_{a} s^{2} + k_{v} s + k_{p}}{s^{2} + k_{v} s + k_{p}} .$

(240)

Ha $H (i ω) � 1$ , akkor lehetnek frekvenciák, amelyeknél a hiba erősítve terjed tovább a járművek mentén. Ezért $k_{a} = 1$ ( $H (i ω) = 1$ ) választás célszerű a string stabilitáshoz.

Ha az irányítási stratégia a vezető jármű és a közvetlenül a vizsgált jármű előtt haladó jármű adatait egyaránt felhasználja. (4. módszer), akkor

(241)

A módszer nagyszámú információt használ, azonban ebben az esetben a string stabilitás garantálható.

A változó távolságot biztosító irányítási stratégiában minden jármű a közvetlenül előtte haladó jármű pozíció, sebesség és gyorsulás adatából dolgozik (5. módszer).

Ekkor

$u = k_{a} {\ddot{x}}_{i - 1} - k_{i} {\dot{x}}_{i} - k_{v} {\dot{e}}_{i} - k_{p} e_{i} .$

(242)

Ez a módszer is nagyszámú információt használ, azonban ebben az esetben is a string stabilitás garantálható.

A továbbiakban az ezekben a feladatokban felmerülő jelkövető irányítástervezésre adunk néhány módszer.

4.6.1. Állapot szeparálás módszere

Induljunk ki az alábbi integráló tulajdonságú rendszerből, melynek állapottér reprezentációja a következő:

$\dot{x} = A x + b u$

(243)

$y = c x$

(244)

Integráló tulajdonságú rendszerhez jelkövetést biztosító szabályozó struktúra egy output visszacsatolt soros kompenzátort kombinál az állapot-visszacsatolással.

Ha a rendszer maga integráló tulajdonságú, és a rendszer kimenetét is visszacsatoljuk, akkor ez a struktúra automatikusan biztosítja a referencia jelkövetést és az állapot-visszacsatolás a pólusok megfelelő elhelyezését.

Válasszuk meg az állapotvektort úgy, hogy az első komponense éppen a rendszer kimenete legyen. Ebben a rendszerben az $x_{1}$ állapotjelet nem csatoljuk vissza, helyette a rendszer kimenőjelét csatoljuk vissza negatívan és az így képzett különbséget erősítjük a $k_{n - 1}$ értékkel.

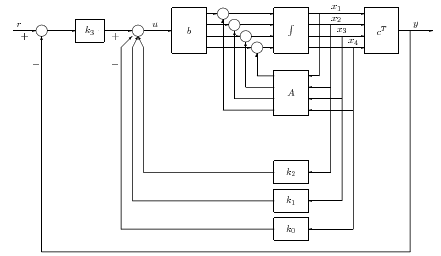
Ekkor a bemenőjel és a kimenőjel az állapotvektor elemeivel a következőképpen írható fel:

$u = - k_{n - 1} (y - r) - k_{n - 2} x_{2} - \dots - k_{1} x_{n - 1} - k_{0} x_{n}$

$= - k_{n - 1} x_{1} - k_{n - 2} x_{2} - \dots - k_{1} x_{n - 1} - k_{0} x_{n} + k_{n - 1} r$

$= - k^{T} x + k_{n - 1} r$

(245)

$y = x_{1}$

(246)

ahol

$k^{T} = [\begin{array}{l} k_{n - 1} & ... & k_{1} & k_{0} \end{array}]$

(247)

az állapotvisszacsatolás komponensei.

Az input jelet az állapotegyenletbe helyettesítve a következő egyenletet kapjuk:

$\dot{x} = A x + b (- k^{T} x + k_{n - 1} r)$

$= (A - b k^{T}) x + b k_{n - 1} r .$

(248)

A követési hiba:

$e = r - y = r - x_{1} .$

A szabályozott rendszer pólusai az $A - b k^{T}$ mátrix sajátértékei, ami azt jelenti, hogy a fenti struktúra alkalmazásával a pólus allokációs technika gyakorlatilag változtatás nélkül használható.
A szabályozott rendszer állapotmátrixa: $A_{c} = A - b k^{T}$ és input vektora: $b_{c} = b k_{n - 1}$ .

Példa 5.1: Tekintsük példaként a következő integráló tulajdonságú rendszert:

$\dot{x} = [\begin{array}{l} 0 & - 2 & - 3 \\ 0 & 1 & 2 \\ 0 & 2 & 0 \end{array}] x + [\begin{array}{l} 1 \\ 2 \\ - 1 \end{array}] u$

(249)

$y = [\begin{array}{l} 1 & 0 & 0 \end{array}] x$

(250)

Az első állapot azonos a rendszer kimenetével. Tervezzünk jelkövető szabályozást LQ módszerrel. Az LQ tervezés súlyozó tényezői:

$Q = [\begin{array}{l} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}] R = 1$

(251)

Az LQ tervezés eredménye:

$k^{T} = [\begin{array}{l} - 1 & 8 & 7 \end{array}] .$

(252)

A zárt rendszer állapottér reprezentációja:

$\dot{x} = [\begin{array}{l} 1 & - 10 & - 10 \\ 2 & - 15 & - 12 \\ - 1 & 10 & 7 \end{array}] x + [\begin{array}{l} - 1 \\ - 2 \\ 1 \end{array}] r$

(253)

$y = [\begin{array}{l} 1 & 0 & 0 \end{array}] x$

(254)

A megoldás szimulációját az alábbi ábrasor illusztrálja:

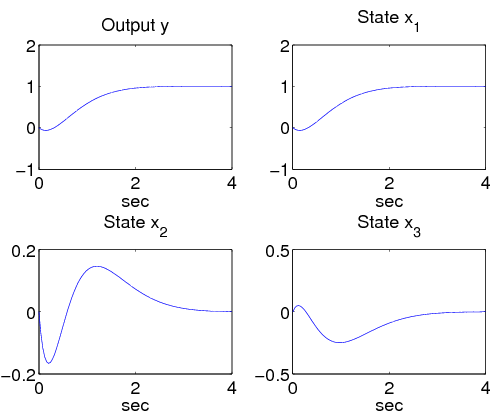
4.19. ábra - A megoldás szimulációja

Megjegyzés: állapottér átalakítása

A megoldásban feltételeztük, hogy az állapotváltozókat sikerült úgy összeállítani, hogy a rendszer kimenete azonos az első állapotváltozóval.

Ha ez nincs így, akkor egy transzformációt kell végrehajtani.

Tegyük fel, hogy a rendszer átviteli függvénye a következő:

$Y (s) = \frac{b_{1} s^{n - 1} + ... + b_{n - 1} s + b_{n}}{s^{n} + a_{1} s^{n - 1} + ... + a_{n - 1} s + a_{n}} U (s)$

(255)

Az első állapotváltozót úgy választjuk meg, hogy az azonos legyen a rendszer kimenetével: $x_{1} = y$ . A többi állapotváltozó megválasztása a következőképpen történik:

$x_{2} = {\dot{x}}_{1} - β_{1} u$

$x_{3} = {\dot{x}}_{2} - β_{2} u$

$...$

$x_{n} = {\dot{x}}_{n - 1} - β_{n - 1} u$

(256)

ahol $β_{1} = b_{1}$ , $β_{2} = b_{2} - a_{1} β_{1}$ , $β_{3} = b_{3} - a_{1} β_{2} - a_{2} β_{1}$ , ..., $β_{n - 1} = b_{n - 1} - a_{1} β_{n - 2} - ... - a_{n - 2} β_{1}$ .

Végül az $x_{n}$ elsőrendű deriváltjára a következő alakot kapjuk:

${\dot{x}}_{n} = - a_{n} x_{1} - a_{n - 1} x_{2} - ... - a_{1} x_{n} + β_{n} u .$

(257)

ahol $β_{n} = b_{n} - a_{1} β_{n - 1} - ... - a_{n - 1} β_{1}$ .

A fentiek alapján az állapottér reprezentáció a következő alakot kapjuk:

(258)

$y = [\begin{array}{l} 1 & 0 & 0 & ... & 0 \end{array}] x$

(259)

A hasonlósági transzformációval kapott állapottérben az első állapotváltozó a kimenőjellel azonos.

4.6.1.1. Struktúra módosítás

Egy integrátort nem tartalmazó rendszer esetén a jelkövetést úgy kell megoldani, hogy integráló típusú soros kompenzátort alkalmazunk a visszacsatolásban.

Ez állapot-visszacsatolást tartalmazó rendszerben azt jelenti, hogy az állapot-visszacsatolt struktúrát egy olyan output visszacsatolással kombináljuk, amely integráló tulajdonságú. Ebben a struktúrában valamennyi állapot vektort visszacsatoljuk a rendszer bemenetére. Ezen túlmenően egy integráló elemet építünk a rendszer előrevető ágába és ezt $k_{i}$ -vel erősítjük. Fentiek miatt ebben a struktúrában $n + 1$ számú erősítést alkalmazunk.

Egy új állapotváltozót definiálunk:

(260)

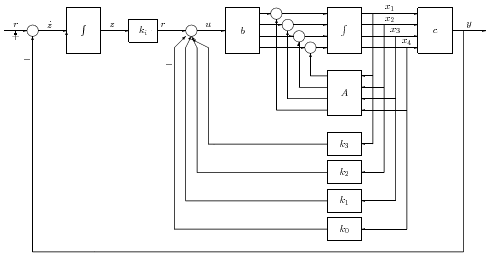
4.20. ábra - Struktúra modosítása

Az állapot-visszacsatolt struktúrával a rendszer állapottér reprezentációja a következő:

$\dot{x} (t) = A x (t) + b u (t)$

(261)

$y (t) = c^{T} x (t)$

(262)

$u (t) = - k^{T} x (t) + k_{i} z (t)$

(263)

$\dot{z} (t) = r (t) - y (t)$

(264)

Az állapot-visszacsatolt struktúrában a bemenőjelet az $x_{1}$ , $x_{2}$ , $x_{n}$ komponenseken kívül az $r - y$ hibajel figyelembe vételével állítjuk elő. A rendszer állapottér struktúráját a $z$ komponenssel bővítjük és ebben a bővített rendszerben végezzük el a tervezést.

Az állapotegyenletek a következők:

$\dot{x} (t) = A x (t) + b u (t)$

(265)

$\dot{z} (t) = - c x (t) + r (t)$

(266)

A kimeneti egyenlet:

$y = c x (t)$

(267)

A bővített rendszer állapottér reprezentációja:

$[\begin{array}{l} \dot{x} (t) \\ \dot{z} (t) \end{array}] = [\begin{array}{l} A & 0 \\ - c^{T} & 0 \end{array}] [\begin{array}{l} x (t) \\ z (t) \end{array}] + [\begin{array}{l} b \\ 0 \end{array}] u (t) + [\begin{array}{l} 0 \\ 1 \end{array}] r (t)$

(268)

$y (t) = [\begin{array}{l} c^{T} & 0 \end{array}] [\begin{array}{l} x (t) \\ z (t) \end{array}]$

(269)

Az irányítójel összefüggése:

$u = - k^{T} x (t) + k_{i} z (t)$

(270)

Az állapottér reprezentáció:

$= [\begin{array}{l} A - b k^{T} & b k_{i} \\ - c^{T} & 0 \end{array}] [\begin{array}{l} x (t) \\ z (t) \end{array}] + [\begin{array}{l} 0 \\ 1 \end{array}] r (t),$

(271)

$y (t) = [\begin{array}{l} c^{T} & 0 \end{array}] [\begin{array}{l} x (t) \\ z (t) \end{array}] .$

(272)

A követési hiba:

$e = r - y = r - c x_{1} .$

Ezzel a struktúrával automatikusan elérjük, hogy a szabályozott rendszer jelkövetést biztosítson. A pólus allokációt a bővített rendszerben végezzük el. A továbbiakban a hagyományos pólus allokációs technika használható.

Az állapotvisszacsatoilt erősítés $n + 1$ komponensű:

$k_{a}^{T} = [\begin{array}{l} k_{n - 1} & ... & k_{1} & k_{0} & k_{i} . \end{array}]$

(273)

Az állapotvisszacsatolás tervezésének feltétele, hogy az irányíthatósági mátrix teljes rangú legyen:

$r a n g ([\begin{array}{l} A - b k^{T} & b k_{i} \\ - c^{T} & 0 \end{array}]) = n + 1$ .

Példa 5.2:

Tekintsük példaként a rendszert:

$\dot{x} = [\begin{array}{l} - 3 & - 2 & - 1 \\ 2 & - 1 & 0 \\ - 1 & 1 & 2 \end{array}] x + [\begin{array}{l} 1 \\ 0.5 \\ 2 \end{array}] u$

(274)

$y = [\begin{array}{l} 1 & 0 & 0 \end{array}] x$

(275)

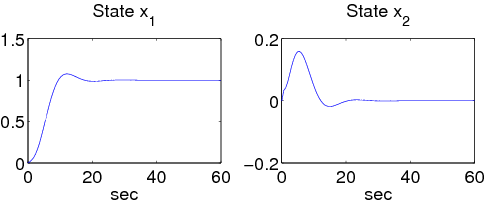
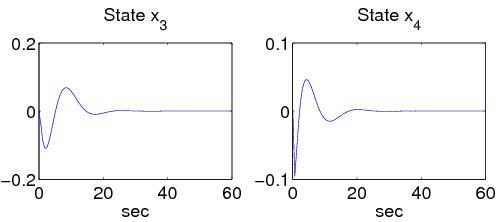
4.21. ábra - Az 5.2 példa megoldása

A bővített rendszer állapottér reprezentációja:

$\dot{x} = [\begin{array}{l} - 3 & - 2 & - 1 & 0 \\ 2 & - 1 & 0 & 0 \\ - 1 & 1 & 2 & 0 \\ - 1 & 0 & 0 & 0 \end{array}] x + [\begin{array}{l} 1 \\ 0.5 \\ 2 \\ 0 \end{array}] u$

(276)

$y = [\begin{array}{l} 1 & 0 & 0 & 0 \end{array}] x$

(277)

Az LQ tervezés súlyozó tényezői:

$Q = [\begin{array}{l} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}] R = 1$

(278)

Az LQ tervezés eredménye:

$k^{T} = [\begin{array}{l} - 0.4535 & 1.1147 & 2.7423 & 1 \end{array}] .$

(279)

A zárt rendszer állapottér reprezentációja:

$\dot{x} = [\begin{array}{l} - 2.5465 & - 3.1147 & - 3.7423 & - 1.0000 \\ 2.2267 & - 1.5573 & - 1.3712 & - 0.5000 \\ - 0.0931 & - 1.2294 & - 3.4846 & - 2.0000 \\ - 1.0000 & 0 & 0 & 0 \end{array}] x + [\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \end{array}] u$

(280)

$y = [\begin{array}{l} 1 & 0 & 0 & 0 \end{array}] x$

(281)

A megoldás szimulációját az 5.2 ábrasor illusztrálja.

Vissza		Előre
3. fejezet - Bizonytalanságok modellezése	Főoldal	5. fejezet - Keresztirányú modellezés és irányítás