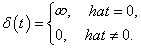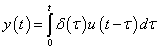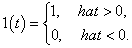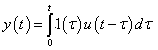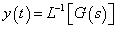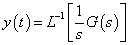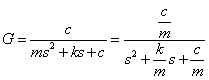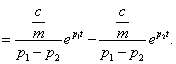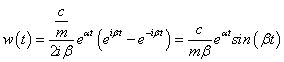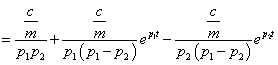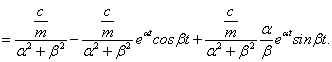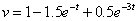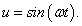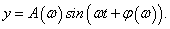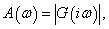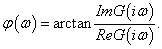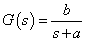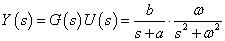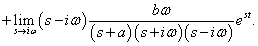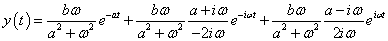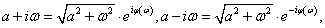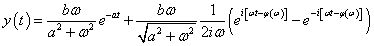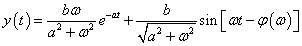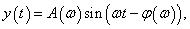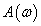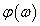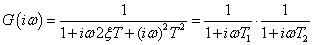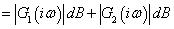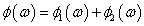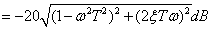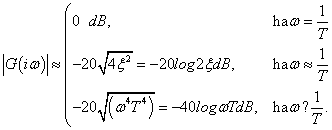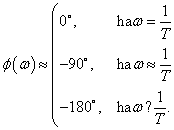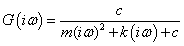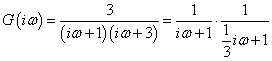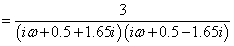4. fejezet - Rendszerek elemzése idő és frekvencia tartományban
4.1. Időtartományi elemzés
Definíció 3.1 (Súlyfüggvény)
A bemenőjel -- kimenőjel kapcsolatot leírhatjuk az ún. Dirac-delta függvényre adott válaszfüggvény segítségével is.
A Dirac-delta függvényt a következőképp definiáljuk:
|
|
(196) |
A Dirac-delta bemenőjelre adott válaszfüggvény a rendszer súlyfüggvényének nevezzük.
A súlyfüggvény segítségével egy tetszőleges bemenőjelre adott válaszfüggvény:
|
|
(197) |
Definíció 3.2
A bemenőjel - kimenőjel kapcsolatot leírhatjuk az egységugrás függvényre adott válaszfüggvény segítségével is.
Az egységugrás függvényt a következőképp definiáljuk:
|
|
(198) |
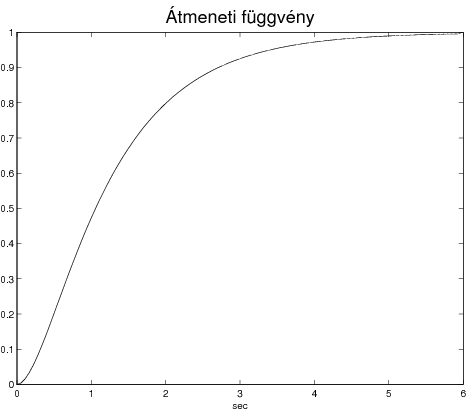
Az egységugrás bemenőjelre adott válaszfüggvény a rendszer átmeneti függvényének nevezzük.
Az átmeneti függvény segítségével egy tetszőleges bemenőjelre adott válaszfüggvény:
|
|
(199) |
A Dirac-delta bemenőjelre adott válaszfüggvény a rendszer súlyfüggvényének nevezzük. A Dirac-delta függvény (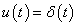 ) Laplace transzformáltja:
) Laplace transzformáltja: 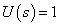 . Emiatt
. Emiatt 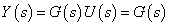 .
.
|
|
(200) |
Az egységugrás bemenőjelre adott válaszfüggvény a rendszer átmeneti függvényének nevezzük. A egységugrás függvény (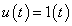 ) Laplace transzformáltja:
) Laplace transzformáltja: 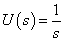 .Emiatt
.Emiatt 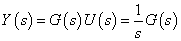 .
.
|
|
(201) |
Példa 3.1
Írjuk fel a 3.1 ábrán látható tömegből, rugóból és csillapítóból álló mechanikai rendszer átviteli függvényét.
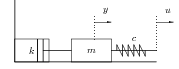
Az átviteli függvény Laplace transzformációval:
|
|
(202) |
Két pólusa van, amelyek a fizikai paraméterektől függően valósak, vagy komplexek lehetnek: 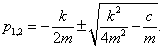 Súlyfüggvény számítása
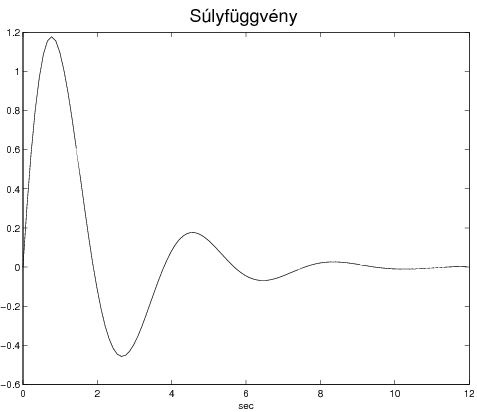
Súlyfüggvény számítása
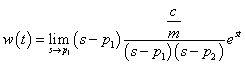
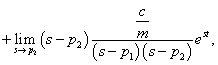
|
|
(203) |
Komplex pólusok esetén (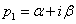 és
és 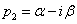 ) további számítások szükségesek:
) további számítások szükségesek:
|
|
(204) |
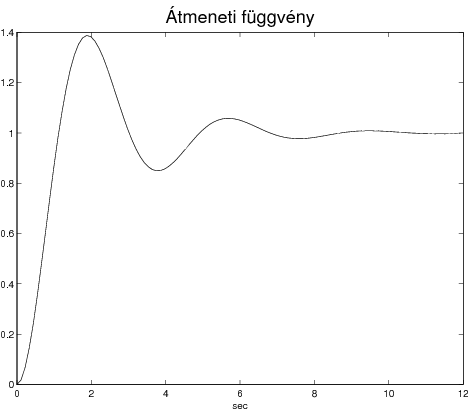
Kihasználtuk a szögfüggvényekre vonatkozó 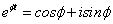 Euler összefüggést. Átmeneti függvény számítása:
Euler összefüggést. Átmeneti függvény számítása:
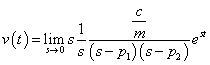
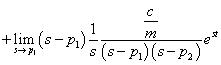
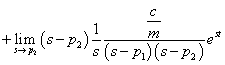
|
|
(205) |
Komplex pólusok esetén (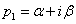 és
és 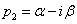 ) további számítások szükségesek:
) további számítások szükségesek:
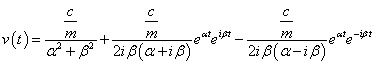
|
|
(206) |
Komplex pólusok esete: az adatok: 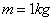 ,
, 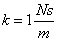 ,
, 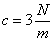 .
.
Két komplex konjugált pólus van: a 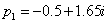 és
és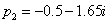 . A súlyfüggvény és az átviteli függvény a reziduum tétel alkalmazásával számítható:
. A súlyfüggvény és az átviteli függvény a reziduum tétel alkalmazásával számítható:
|
|
(207) |
|
|
(208) |
Valós pólusok esetén az adatok: 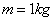 ,
, 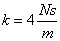 ,
, 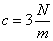 .
.
Valós pólusai vannak: 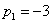 és
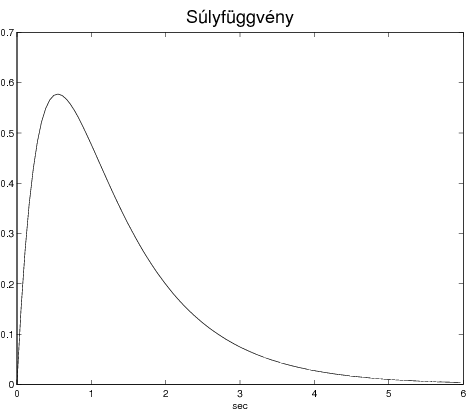
és 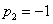 . A súlyfüggvény és átviteli függvény a reziduum tétel alkalmazásával számítható:
. A súlyfüggvény és átviteli függvény a reziduum tétel alkalmazásával számítható:
|
|
(209) |
|
|
(210) |
4.2. Frekvencia tartományi elemzés
Egy rendszer frekvencia függvényének a rendszernek szinuszos bemenőjelre, állandósult állapotban adott válaszfüggvényét nevezzük.
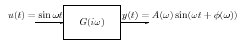
Itt a bemenőjel egy egységnyi amplitúdójú szinusz lefutású jel, amelynek körfrekvenciája 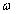 .
.
|
|
(211) |
A kimenőjel:
|
|
(212) |
Az 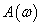 függvényt amplitudó függvénynek, a bemenőjel és a kimenőjel közötti fáziseltolást jelentő
függvényt amplitudó függvénynek, a bemenőjel és a kimenőjel közötti fáziseltolást jelentő 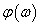 függvényt pedig fázisfüggvénynek nevezzük, mindkettő a bemenőjel
függvényt pedig fázisfüggvénynek nevezzük, mindkettő a bemenőjel 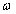 körfrekvenciájától függ.
körfrekvenciájától függ.
Az amplitudó függvény a 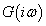 függvény abszolút értékeként kapható:
függvény abszolút értékeként kapható:
|
|
(213) |
a fázisfüggvény pedig 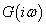 fázisfüggvényeként:
fázisfüggvényeként:
|
|
(214) |
Legyen egy rendszer átviteli függvénye:
|
|
(215) |
A rendszer bemenete egy egységnyi amplitúdójú szinusz lefutású jel 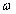 körfrekvenciával:
körfrekvenciával: 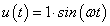 .
.
A 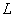 -transzformáció alkalmazásával vizsgáljuk meg a rendszer kimenőjelét.
-transzformáció alkalmazásával vizsgáljuk meg a rendszer kimenőjelét.
|
|
(216) |
Időtartományba transzformálva:
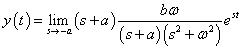
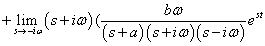
|
|
(217) |
Elvégezve a megfelelő határértékképzéseket:
|
|
(218) |
Megjegyzés 3.1
Egy
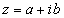 komplex szám exponenciális alakja
komplex szám exponenciális alakja
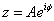 ahol
ahol
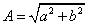 és
és
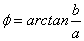 .
.
Alkalmazva az összefüggést:
|
|
(219) |
ahol 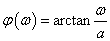 .
.
|
|
(220) |
majd felhasználva az Euler-összefüggést (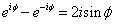 ):
):
a kimenőjelre a következő adódik:
|
|
(221) |
A kimenőjel első tagja a tranziens időtartamában exponenciálisan nullához tart. Az állandósult állapotot a második tag határozza meg.
Az állandósult állapotra azt kapjuk, hogy
|
|
(222) |
ahol 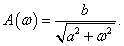 Állandósult állapotban tehát a rendszer egy adott körfrekvenciájú szinuszos lefolyású bemenőjelre egy szinuszos lefolyású kimenőjellel válaszol, amelynek amplitúdóját az
Állandósult állapotban tehát a rendszer egy adott körfrekvenciájú szinuszos lefolyású bemenőjelre egy szinuszos lefolyású kimenőjellel válaszol, amelynek amplitúdóját az 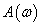 függvény, a bemenőjel és a kimenőjel közötti fáziseltolást pedig a
függvény, a bemenőjel és a kimenőjel közötti fáziseltolást pedig a 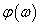 függvény méri.
függvény méri.
Definíció 3.3
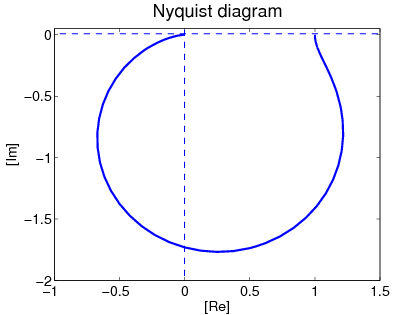
Nyquist diagram A frekvencia függvény ábrázolásának egyik módja az, amikor az amplitudó függvényt mint vektort egy polár koordináta rendszerben ábrázoljuk a hozzátartozó
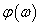 függvény segítségével, ahol az
függvény segítségével, ahol az
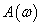 hosszúságú vektornak a pozitív valós tengellyel bezárt szöge épp a
hosszúságú vektornak a pozitív valós tengellyel bezárt szöge épp a
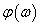 szög. A frekvencia függvénynek ezt az ábrázolásmódját Nyquist -- diagramnak nevezzük.
szög. A frekvencia függvénynek ezt az ábrázolásmódját Nyquist -- diagramnak nevezzük.
Definíció 3.4
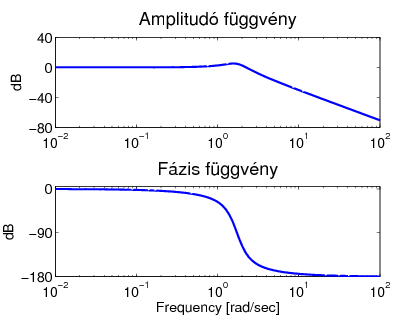
Bode diagram A frekvencia függvények egy másik ábrázolásmódja az, amikor az
|
|
(223) |
amplitúdó függvényt a 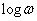 függvényében ábrázoljuk, decibelben. Ennek alapján a függőleges tengelyen
függvényében ábrázoljuk, decibelben. Ennek alapján a függőleges tengelyen 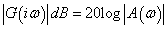 szerepel. Ebben az esetben a
szerepel. Ebben az esetben a
|
|
(224) |
fázisfüggvényt külön diagramban, a 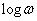 függvényében ábrázoljuk. Ezt az ábrázolást a rendszer Bode -- diagramjának nevezzük.
függvényében ábrázoljuk. Ezt az ábrázolást a rendszer Bode -- diagramjának nevezzük.
Példa 3.2
A kéttárolós arányos tag (2TP) Nyquist diagramját a két különböző időállandójú egytárolós tag Nyquist diagramjának összeszorzásával kapjuk. (Az eredő vektor abszolút értéke a két vektor abszolút értékeinek szorzata, fázisszöge a két vektor fázisszögének összege.)
|
|
(225) |
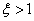
eset (valós pólusok):
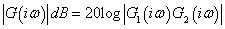
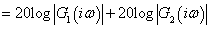
|
|
(226) |
|
|
(227) |
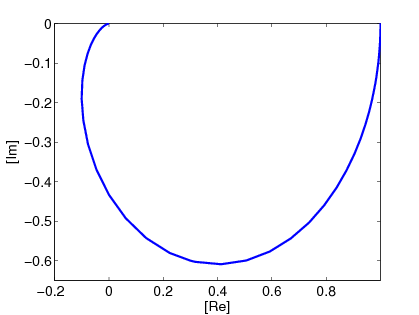
A frekvenciafüggvény két egytárolós tag frekvencia függvényének szorzataként írható fel. Mivel logaritmikus síkon a szorzásnak összeadás felel meg, a két egytárolós tag Bode diagramját összegezve kapjuk az eredő Bode diagramot.
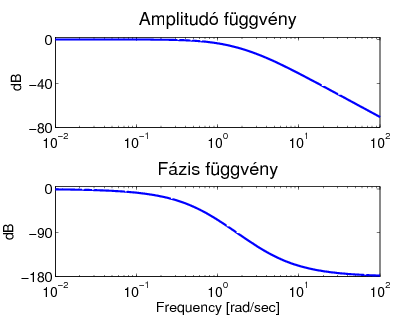
Komplex pólusok esete: 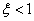 eset (komplex pólusok):
eset (komplex pólusok):
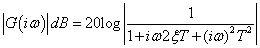
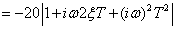
|
|
(228) |
Vizsgáljuk meg a jelleggörbe menetét:
|
|
(229) |
Ha 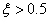 a pontos görbe a közelítő egyenesek alatt fut, ha
a pontos görbe a közelítő egyenesek alatt fut, ha 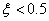 a pontos görbe az egyenesek fölött halad, míg
a pontos görbe az egyenesek fölött halad, míg 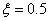 esetén a pontos és a közelítő érték
esetén a pontos és a közelítő érték 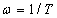 -nél megegyezik.
-nél megegyezik.
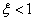
eset (komplex pólusok): A fázis görbe alakja ugyancsak a 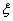 -től függ:
-től függ:
|
|
(230) |
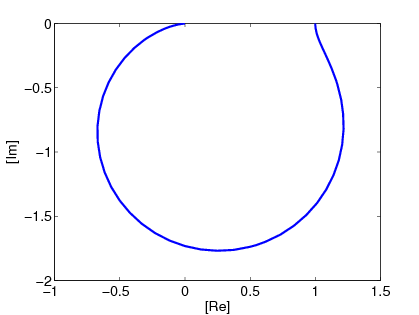
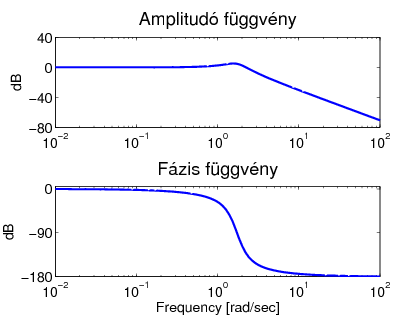
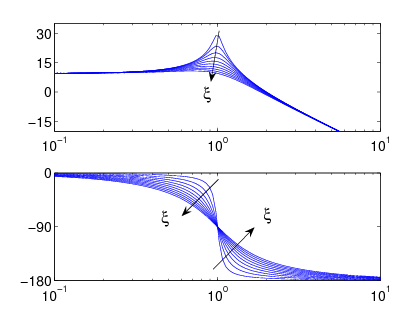
A 3.2 ábra  változó különböző értékeinek hatását illusztrálja az amplitúdó és fázisgörbe függvényekben.
változó különböző értékeinek hatását illusztrálja az amplitúdó és fázisgörbe függvényekben.
Példa 3.3
Tömeg, rugó és csillapító Írjuk fel a tömegből, rugóból és csillapítóból álló mechanikai rendszer frekvencia függvényét. A frekvencia függvény:
|
|
(231) |
Két pólusa van, amelyek a fizikai paraméterektől függően valósak, vagy komplexek lehetnek: 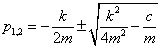 . Frekvencia diagramok valós pólusok esetén: Adatok:
. Frekvencia diagramok valós pólusok esetén: Adatok: 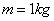 ,
, 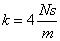 ,
, 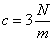 .
.
|
|
(232) |
Valós pólusai vannak: 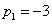 és
és 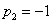 . Időállandók:
. Időállandók: 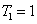 és
és 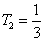 .
.
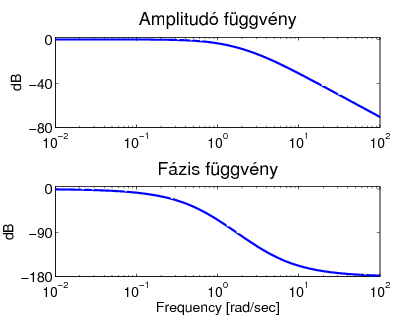
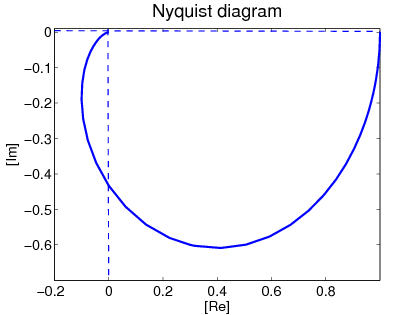
Frekvencia diagramok komplex pólusok esetén: A numerikus adatok: 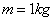 ,
, 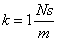 ,
, 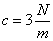 .
.
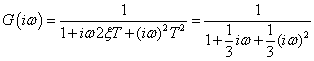
|
|
(233) |
Két komplex konjugált pólus van: 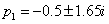 . Az időállandó és a csillapítási együttható:
. Az időállandó és a csillapítási együttható: 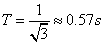 és
és 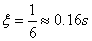 .
.