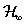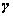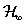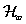15. fejezet - Nemlineáris irányítások
Vissza		Előre

15. fejezet - Nemlineáris irányítások

Tartalom

Az irányításelmélet kezdeti korszakában a nemlineáris irányításelmélet legtöbb fogalma, mint a stabilitást, optimalitást és bizonytalanságot leíró fogalmak inkább leíró jellegűek voltak mint konstruktívak, azaz arra használták őket, hogy leírják a rendszer tulajdonságai ahelyett, hogy alkalmasak legyenek egy rendszer tervezésére, amely rendelkezik ezekkel a tulajdonságokkal. Később ezek a leíró fogalmak néhány módósítással alkalmasak lettek eléggé általános nemlineáris tervezési feladatok kezelésére is. A hangsúly ezen fogalmak és a visszacsatolás kapcsolatának explicit megfogására került, így például a Lyapunov technikát a kontroll Lyapunov függvényekre alapozott módszerek helyettesítik. Másik példa a rendszer visszacsatolással való passzívvá tétele vagy a disszipativitásra alapozott eljárások, mint a lineáris robusztus technikák nemlineáris kiterjesztései. A továbbiakban ezeknek a fogalmaknak és eljárásoknak a rövid bemutatására kerül sor.

15.1. Stabilitás

Definíció 14.1

Egy folytonos $α : [0, a) \to [0, \infty)$ függvény $K$ osztálybeli, ha szigorúan növekvő és $α (0) = 0$ . Ha $a = \infty$ és $l i m_{t \to \infty} α (t) = \infty$ , akkor a függvény $K_{\infty}$ osztálybeli.

Egy folytonos $β : [0, a) \times [0, \infty) \to [0, \infty)$ függvény $K ℒ$ osztálybeli, ha minden rögzített $s$ -re a $β (\cdot, s)$ függvény eleme $K$ -nak és minden rögzített $r$ esetén a $β (r, \cdot)$ függvény csökkenő és ${lim}_{s \to \infty} β (r, s) = 0$ .

Tekintsük a következő nemlineáris rendszert:

$\dot{x} = f (x)$

(781)

ahol $x \in ℝ^{n}, f (0) = 0$ és $f$ lokálisan Lipschitzes. A rendszer $x = 0$ egyensúlyi helyének (asszimptotikus) stabilitása az ismert Lyapunov kritériummal jellemezhető:

Tétel 14.1 (Lyapunov) Legyen $V : B_{d} \to ℝ$ egy folytonosan differenciálható függvény úgy, hogy valamely $K$ osztálybeli $[0, d)$ -n értelmezett $\underline{α}, \bar{α}$ függvényekkel

$\underline{α} (| | x | |) \leq V (x) \leq \bar{α} (| | x | |) .$

$\partial_{x} V (x) f (x) \leq 0$

minden $| | x | | < d$ esetén, akkor az $x = 0$ egyensúlyi hely stabilis.

Ha valamely $K$ -beli $[0, d)$ -n értelmezett $α$ függvényre

$\partial_{x} V (x) f (x) \leq - α (| | x | |)$

mindenl $| | x | | < d$ esetén, akkor az $x = 0$ egyensúlyi hely lokálisan asszimptotikusan stabilis (LAS).

Ha $d = \infty$ és $\underline{α}, \bar{α} K_{\infty}$ -beli függvények, akkor az $x = 0$ egyensúlyi hely globálisan asszimptotikusan stabilis (GAS).

$\underline{α} (s) = a s^{2}, α (s) = b s^{2}, a, b > 0,$

akkor az $x = 0$ egyensúlyi hely lokálisan exponenciálisan stabilis (LES).

Külső zavarással gerjesztett rendszerekre a stabilitás lokális fogalmát a sokkal hasznosabb bemenetről--állapotra (input-to-state) stabilitás váltja fel.

Tekintsük a

$\dot{x} = f (x, u)$

(782)

nemlineáris rendszert, ahol $x \in ℝ^{n}, u \in ℝ^{m}, f (0, 0) = 0$ és $f$ lokálisan Lipschitzes az $ℝ^{n} \times ℝ^{m}$ halmazon.

Definíció 14.2

A (782) rendszer bemenetről--állapotra (input-to-state) stabilis ha létezik egy $K ℒ$ osztálybeli $β$ függvény és egy $K$ osztálybeli $γ$ függvény (erősítés) úgy, hogy minden lokálisan korlátos $u$ bemenet és minden $x (0) = x_{0}$ kezdeti érték esetén az $x (t)$ válaszfüggvény kielégíti az

$| | x (t) | | \leq β (| | x_{0} | |, t) + γ (| | u | |_{\infty})$

egyenlőtlenséget minden $t \geq 0$ esetén.

Tétel 14.2 (ISS--Lyapunov) Egy folytonosan differenciálható $V : ℝ^{n} \to ℝ$ függvényt ISS--Lyapunov függvénynek nevezünk, ha léteznek $K_{\infty}$ osztálybeli $\underline{α}, \bar{α}, α$ függvények és egy $K$ osztálybeli $σ$ függvény úgy, hogy:

$\underline{α} (| | x | |) \leq V (x) \leq \bar{α} (| | x | |),$

minden $x \in ℝ^{n}$ esetén és

$\partial_{x} V (x) f (x) \leq - α (| | x | |) + σ (| | u | |)$

(783)

minden $x \in ℝ^{n}$ és $u \in ℝ^{m}$ esetén.

Az (782) rendszer akkor és csak akkor bemenetről--állapotra stabilis ha létezik hozzá ISS--Lyapunov függvény.

A nemlineáris esetben alkalmazott leggyakoribb módszer a kontrol Lyapunov függvényre alapozott eljárás, ami analóg a homogén rendszerekre alkalmazott Lyapunov eljárással.

Definíció 14.3

Legyen egy

$\dot{x} = f (x) + g (x) u$

input affin nemlineáris rendszer, ahol $f (0) = 0$ valamint $f$ és $g$ sima függvények. Feltesszük, hogy a szabályozó jelek $ℝ^{m}$ egy $U$ részhalmazából valók. Egy $V : ℝ^{n} \to ℝ^{+}$ pozitív definit függvényt, amelyre minden $c > 0$ -ra a ${x | V (x) \leq c}$ halmaz kompakt kontrol Lyapunov függvénynek nevezünk, ha

$inf_{u \in U} {\partial_{x} V (x) (f (x) + g (x) u)} < 0.$

$V$ rendelkezik a kis erősítési tulajdonsággal, ha minden $ε > 0$ esetén létezik $δ > 0$ úgy, hogy $x \neq 0$ kielégíti $| | x | | < δ$ egyenlőtlenséget akkor létezik $u \in U$ úgy, hogy $| | u | | < ε$ amire $\partial_{x} V (x) (f (x) + g (x) u) < 0$ .

A sima stabilizáló visszacsatolás léte feltételezi egy kontrol Lyapunov függvény meglétét és fordítva, elég általános $U$ halmazokra ha létezik $V$ az adott tulajdonságokkal, akkor van $u = k (x)$ , a rendszert globálisan stabilizáló sima visszacsatolás.

Ezek a fogalmak általánosíthatók zavarással terhelt

$\dot{x} = f (x, d) + g (x, d) u$

rendszerek esetére is. A $d$ zavarások egy kompakt $D$ halmazbeli értékeket felvevő mérhető függvények. Feltételezzük, hogy $f (0, d) = 0$ minden $d \in D$ esetén.

Definíció 14.4

$V : ℝ^{n} \to ℝ^{+}$ kontrol Lyapunov függvény egyenletes, ha

$inf_{u \in U} {\partial_{x} V (x) (f (x, d) + g (x, d) u)} < 0$

minden $x \neq 0$ és $d \in D$ esetén.

$V$ rendelkezik az egyenletes kis erősítési tulajdonsággal, ha minden $ε > 0$ -ra van $δ > 0$ úgy, hogy ha $x \neq 0$ -ra $| | x | | < δ$ , akkor létezik $u \in U$ amire $| | u | | < ε$ úgy, hogy $\partial_{x} V (x) (f (x, d) + g (x, d) u) < 0$ minden $d \in D$ esetén.

15.2. Disszipatív rendszerek

Tekintsünk egy

$\dot{x} = f (x, u)$

(784)

$y = h (x, u) .$

nemlineáris rendszert.

Egy, az ISS tulajdonsághoz nagyon hasonló fogalmat kaphatunk, ha annak definíciójában az (783) egyenletben a $K$ osztalybeli $σ$ függvény helyett egy tetszőleges $q (u, y)$ függvényt veszünk, amelyre $q (0, 0) = 0$ . Ezt a függvényt disszipativitási függvénynek nevezzük.

Definíció 14.5

A(784)rendszer disszipatív a $q (u, y)$ disszipativitási függvényre nézve ha van egy folytonosan differenciálható $V (x)$ függvány, amelyre

$\underline{α} (| | x | |) \leq V (x) \leq \bar{α} (| | x | |)$

min $x \in ℝ^{n}$ esetén, ahol $\underline{α}$ és $\bar{α} K_{\infty}$ -beli függvények úgy, hogy

$\partial_{x} V f (x, u) \leq q (u, y)$

(785)

minden $x \in ℝ^{n}, u \in ℝ^{m}$ és $y = h (x, u)$ esetén.

A rendszer szigorúan disszipatív, ha valamely $K_{\infty}$ -beli $α$ függvénnyel

$\partial_{x} V f (x, u) \leq - α (| | x | |) + q (u, y) .$

(786)

$V (x)$ -t tároló függvénynek nevezzük, az (784) és (785),(786) egyenlőtlenségeket pedig disszipativitási egyenlőtlenségeknek.

A disszipációs egyenlőtlenség még a

$V (x (T)) - \int_{0}^{T} q (u, y) d t \leq V (x (0)), T \geq 0,$

formába is írható.

Bevezethető még a rendelkezésre álló energia függvény mint

$V_{a v} (x_{0}) = sup_{T \geq 0, u \in U} {- \int_{0}^{T} q (u, y) d t}$

és a szükséges energi függvény, mint

$V_{r q} (x_{0}) = sup_{T \geq 0, u \in U} {- \int_{T}^{0} q (u, y) d t},$

ahol $x (0) = x_{0}$ .

A rendszer akkor és csak akkor disszipatív, ha ezek a függvények valós véges értékű függvények. Ekkor $V_{a v}$ a legkisebb és $V_{r q}$ a legnagyobb lehetséges $V$ tároló függvény, azaz minden $V$ előáll ezek konvex kombinációjaként: $V = α V_{a v} + (1 - α) V_{r q}, 0 \leq α \leq 1$ .

A disszipatív rendszerek nem tudnak több energiát leadni mint a betáplált energia.

Általában kvadratikus

$q (u, y) = [\begin{array}{l} u^{T} & y^{T} \end{array}] [\begin{array}{l} R & S^{T} \\ S & Q \end{array}] [\begin{array}{l} u \\ y \end{array}]$

(787)

disszipativitási függvényeket használunk, ahol $R$ és $Q$ szimmetrikus mátrixok.

Tétel 14.3 A

$\dot{x} = f (x) + g (x) u$

$y = h (x) + k (x) u$

nemlineáris rendszer akkor és csak akkor disszipatív a (787) disszipativitási függvényre nézve, ha

- az alábbi

$W (x) = R + k^{T} (x) S + S^{T} k (x) + k^{T} (x) Q k (x)$

mátrix mindeb $x \in ℝ^{n}$ -re pozitív szemidefinit,

- létezik egy folytonosan differenciálható pozitív szemidefinit $V (x)$ függvény, amelyre minden $x \in ℝ^{n}$ esetén az

$U (x) = {u \in ℝ^{m} | W (x) u = \frac{1}{2} {(\partial_{x} V g (x) - 2 h^{T} (x) (Q k (x) + S))}^{T}}$

halmaz nem üres, és minden $u \in U (x)$ -ra

$\partial_{x} V f (x) - h^{T} (x) Q h (x) + u^{T} W (x) u \leq 0.$

15.3. Passzív rendszerek

Definíció 14.6

Tekintsünk egy $q (u, y)$ disszipativitási függvényt, melyre $q (u, 0) = 0$ minden $u$ -ra és $q (0, y) = 0$ minden $y$ -ra.

A (784) rendszer, ahol $m = p$ passzív a $q (u, y)$ disszipativitási függvényre nézve, ha létezik egy $V$ tároló függvény amelyre

$V (x (t_{f})) - V (x (t_{0})) \leq \int_{t_{0}}^{t_{f}} q (u, y) d t$

(788)

minden $t_{0} < t_{f}$ , $x$ és $u$ esetén.

Általában $q (u, y) = y^{T} u$ választással élünk.

Pozitív definit tároló függvénnyel rendelkező passzív rendszerek asszimptotikusan stabilisak.

Tétel 14.4 (Kalman--Yakubovich--Popov) Egy passzív (784) rendszer esetén:

$L_{f (x, 0)} V \leq 0$

$L_{\partial_{u} f} V = \partial_{u} q + \partial_{y} q \partial_{u} h .$

Ezek a feltételek egy

$\dot{x} = f (x) + g (x) u$

$y = h (x) + k (x) u$

input affin rendszer esetén a

$L_{f} V \leq 0, L_{g} V = h (x) + 2 k (x) u = y + k (x) u$

formába írhatók.

A (784) nemlineáris rendszer passzívá tehető, ha létezik egy $u = γ (x, v)$ visszacsatolás, amire a zárt kör passzív.

15.4. Nemlineáris $ℋ_{\infty}$ szabályozás

A nemlineáris $ℋ_{\infty}$ szabályozás a már ismert $ℋ_{\infty}$ elmélet egy nemlineáris kiterjesztése.A tervezés célja, hogy egy olyan nelineáris szabályozót kapjunk, melyre a zárt kör stabilis és az $ℒ_{2}$ erősítése a legkisebb.

15.4.1. $γ$ -disszipativitás

Definíció 14.7

Egy rendszer $ℒ_{2}$ erősítése véges ( $γ$ --disszipatív) ha valamely $γ$ -ra disszipatív a

$q (u, y) = γ^{2} | | u | |^{2} - | | y | |^{2}$

(789)

disszipativitási függvényre nézve.

Ha a rendszer zérus-állapot detektálható és az $ℒ_{2}$ erősítése véges, akkor globálisan asszimptotikusan stabilis.

Definíció 14.8

Egy rendszer zérus-állapot detektálható ha minden $x_{0}$ esetén a $\dot{x} = f (x, 0, x (0) = x_{0}$ egyenlet $x^{0}$ megoldása minden $t \geq 0$ esetén létezik és $h (x^{0}, 0) = 0$ fennállása $t \geq 0$ -ön implikálja, hogy $l i m_{t \to \infty} x^{0} (t) = 0$ .

Ebben a speciális esetben a 14.3 Tétel az alábbi formára egyszerűsödik:

Lemma 14.1 (Bounded Real Lemma) A

$\dot{x} = f (x) + g (x) u$

$y = h (x) + k (x) u$

rendszer akkor és csak akkor $γ$ --disszipatív, ha

- a

$W (x) = γ^{2} I - k^{T} (x) k (x)$

(790)

mátrix minden $x \in ℝ^{n}$ -re pozitív definit és

- létezik egy folytonosan differenciálható pozitív szemidefinit $V (x)$ függvény, hogy minden $x \in ℝ^{n}$ -re fennáll az alábbi Hamilton-Jacobi egyenlőtlenség

$\partial_{x} V f (x) + h^{T} (x) h (x) +$

$+ (\frac{1}{2} \partial_{x} V g (x) + h^{T} (x) k (x)) W {(x)}^{- 1} {(\frac{1}{2} \partial_{x} V g (x) + h^{T} (x) k (x))}^{T} \leq 0.$

(791)

15.4.2. Nemlineáris $ℋ_{\infty}$ feladat

Tekintsük az alábbi input affin alakban adott

$\dot{x} = f (x) + g_{1} (x) w + g_{2} (x) u, x (0) = x_{0},$

(792)

$z = h_{1} (x) + k_{12} (x) u,$

$y = h_{2} (x) + k_{21} (x) w,$

nemlineáris rendszert, ahol az egyes függvények legalább kétszer folytonosan differenciálhatók és az egyensúlyi pontban $f (0) = 0$ , $h_{1} (0) = 0$ és $h_{2} (0) = 0$ . Feltesszük továbbá, hogy

$e_{1} (x) : = k_{12} {(x)}^{T} k_{12} (x) > 0, e_{2} (x) : = k_{21} (x) k_{21} {(x)}^{T} > 0,$

vagyis a feladat reguláris.

A $K$ szabályozó alakja

$\dot{ξ} = a (ξ) + b (ξ) y, ξ (0) = 0,$

(793)

$u = c (ξ) .$

Ez a szabályozó megoldása a disszipatív irányítási feladatnak, ha a zárt kör $γ$ -disszipatív. Ha a rendszer lineáris, ez épp azt jelenti, hogy a zárt kör $ℋ_{\infty}$ normája kisebb mint $γ$ . Ha a rendszer zérus-állapot detektálható akkor a $γ$ -disszipatívitás garantálja a rendszer globális asszimptotikus stabilitását is.

15.4.2.1. Állapotvisszacsatolásos $ℋ_{\infty}$ feladat

Tekintsük az alábbi egyszerüsített rendszert:

$\dot{x} = A (x) + B_{1} (x) w + B_{2} (x) u, x (0) = x_{0},$

(794)

$z = C_{1} (x) + D_{11} (x) w + D_{12} (x) u,$

$y = x,$

ahol feltesszük, hogy $r a n k [\begin{array}{l} B_{2} (x) \\ D_{12} (x) \end{array}] = m$ és $D_{11}^{T} (x) D_{11} (x) < I$ minden $x$ -re.

Az $u = F (x) x$ állapotvisszacsatolás alkalmazásával kapjuk, hogy

$[\begin{array}{l} A_{c l} (x) & B_{c l} (x) \\ C_{c l} (x) & D_{c l} (x) \end{array}] = [\begin{array}{l} A_{1} (x) & B_{1} (x) \\ C_{1} (x) & D_{11} (x) \end{array}] + [\begin{array}{l} B_{2} (x) \\ D_{12} (x) \end{array}] F (x) [\begin{array}{l} I & 0 \end{array}] .$

Ekkor a $γ$ --disszipativitási feltételből (Baounded Real Lemma) a zárt körre

$[\begin{array}{l} \partial_{x} V (x) A_{c l} (x) & \partial_{x} V (x) B_{c l} (x) & C_{c l}^{T} (x) \\ B_{c l}^{T} (x) \partial_{x} V {(x)}^{T} & - γ I & D_{c l}^{T} (x) \\ C_{c l} (x) & D_{c l} (x) & - γ I \end{array}] \leq 0$

(795)

feltétel adódik, ami általában nemlineáris a $\partial_{x} V (x)$ és $F (x)$ ismeretlenekben.

Az $A (x) = a (x) x, C_{1} (x) = c_{1} (x) x$ stb. és a $\partial_{x} V (x) = 2 x^{T} P (x)$ ahol $P (x) > 0$ feltételezéssel élve, valamint az $X (x) = P^{- 1} (x)$ transzformáció alkalmazásával kapjuk, hogy:

$[\begin{array}{l} X (x) a_{c l}^{T} (x) + a_{c l} (x) X (x) & B_{c l} (x) & c_{c l}^{T} (x) X (x) \\ B_{c l}^{T} (x) & - γ I & D_{c l}^{T} (x) \\ X (x) c_{c l} (x) & D_{c l} (x) & - γ I \end{array}] \leq 0$

(796)

ami már lineáris az $X (x) = P^{- 1} (x)$ és $Z (x) = X (x) F (x)$ ismeretlenekben. Ebből az egyenletből kapható a következő konvex feltétel:

${\tilde{B}}_{⊥}^{T} (x) [\begin{array}{l} X (x) a^{T} (x) + a (x) X (x) & B_{1} (x) & X (x) c_{1}^{T} (x) \\ B_{1}^{T} (x) & - γ I & D_{11}^{T} (x) \\ c_{1} (x) X (x) & D_{11} (x) & - γ I \end{array}] {\tilde{B}}_{⊥} (x) \leq 0,$

(797)

ahol ${\tilde{B}}^{T} (x) = [\begin{array}{l} B_{2}^{T} (x) & 0 & D_{12}^{T} (x) \end{array}]$ a $γ^{2} I - D_{11}^{T} D_{11} > 0$ feltétellel.

15.4.2.2. Kimenet visszacsatolásos $ℋ_{\infty}$ feladat

Ha az állapotvisszacsatolás helyett adott méréseket felhasználó szabályozót akarunk használni, tekintsük a következő rendszert

$\dot{x} = a (x) x + b_{1} (x) w + b_{2} (x) u, x (0) = x_{0},$

(798)

$z = c_{1} (x) x + d_{11} (x) w + d_{12} (x) u,$

$y = c_{2} (x) x + d_{21} (x) w + d_{22} (x) u,$

ahol feltesszük, hogy $r a n k [\begin{array}{l} B_{2} (x) \\ D_{12} (x) \end{array}] = m$ , valamint $r a n k [\begin{array}{l} C_{1} (x) & D_{21} (x) \end{array}] = p$ és $D_{11}^{T} (x) D_{11} (x) < I$ minden $x$ esetén.

Erre az esetre a dinamikus visszacsatolás létezési feltételei a következők:

${\tilde{B}}_{⊥}^{T} (x) [\begin{array}{l} X (x) A^{T} (x) + A (x) X (x) & B_{1} (x) & X (x) C_{1}^{T} (x) \\ B_{1}^{T} (x) & - γ I & D_{11}^{T} (x) \\ C_{1} (x) X (x) & D_{11} (x) & - γ I \end{array}] {\tilde{B}}_{⊥} (x) \leq 0,$

(799)

${\tilde{C}}_{⊥}^{T} (x) [\begin{array}{l} A^{T} (x) Y (x) + Y (x) A (x) & Y (x) B_{1} (x) & C_{1}^{T} (x) \\ B_{1}^{T} (x) Y (x) & - γ I & D_{11}^{T} (x) \\ C_{1} (x) & D_{11} (x) & - γ I \end{array}] {\tilde{C}}_{⊥} (x) \leq 0,$

(800)

és

$[\begin{array}{l} X (x) & 0 \\ 0 & Y (x) \end{array}] \geq 0,$

ahol $\tilde{B} (x) = [\begin{array}{l} B_{2}^{T} (x) & 0 & D_{12}^{T} (x) \end{array}]$ és $\tilde{C} (x) = [\begin{array}{l} B_{2}^{T} (x) & 0 & D_{12}^{T} (x) \end{array}]$ .

15.5. Nemlineáris megfigyelők

15.5.1. Állapotfüggetlen Lyapunov függvények (SIELF)

Ha adott a

$\dot{x} = f (x), y = h (x)$

(801)

rendszer, arra a kérdésre keressük a választ, hogy milyen feltételekkel létezik egy

$\hat{x} = F (\hat{x}, y)$

megfigyelő úgy, hogy legyen hozzá olyan $V$ Lyapunov függvény, ami csak az $e = \hat{x} - x$ becslési hibától függ, azaz

$\partial_{e} V (F (x + e, h (x)) - f (x)) < 0$

minden $x$ és $e \neq 0$ esetén.

Tegyük fel, hogy

$F (x + e, y) = f (x + e) + k (x + e, y) (h (x + e) - y) .$

Tétel 14.5 Ha $V$ egy SIELF Lyapunov függvény, akkor

${h (x + e) = y, e \neq 0} \Rightarrow \partial_{e} V (f (x + e) - f (x)) < 0$

minden $x$ -re.

Ha a $V$ függvény $C^{2}$ -beli, akkor $\partial_{e^{2}}^{2} V (0)$ nemnegatív és

$\partial_{x} h (x) = 0 \Rightarrow e^{T} \partial_{e^{2}}^{2} V (0) \partial_{x} f (x) e \leq 0$

minden $x$ -re.

Definíció 14.9

Egy radiálisan nemkorlátos $V$ függvény egy megfigyelési Lyapunov függvény (OLF) ha

${h (x + e) = y, e \neq 0} \Rightarrow \partial_{e} V (f (x + e) - f (x)) < 0$

minden $x$ -re.

Tétel 14.6 Ha a mérési egyenlet lineáris és $V = \frac{1}{2} e^{T} P e$ valamint

${C^{T} e = 0, e \neq 0} \Rightarrow e^{T} V \partial_{x} f e < 0$

minden $x$ -re akkor $V$ egy kvadratikus SIELF $ℝ^{n}$ minden kompakt $E$ részhalmazán, és létezik $F$ melyre

$\partial_{e} V (F (x + e, h (x)) - f (x)) < 0$

minden $x$ -re és $e \neq 0, e \in E$ esetén.

Tétel 14.7 Ha a mérési egyenlet lineáris és létezik egy pozitív definit $P$ mátrix, egy $D (y)$ vektor és pozitív $σ (y), ρ (y)$ függvények úgy, hogy

$C^{T} P^{- 1} D \neq 0, | D^{T} \partial_{x} f (x) | \leq σ$

és

$C^{T} e = 0 \Rightarrow e^{T} V \partial_{x} f e 〈 - ρ | | e | |^{2}$

minden $x$ -re akkor $V = \frac{1}{2} e^{T} P e$ egy SIELF.

Megjegyzés 14.1 Tekintsük példaként a

${\dot{x}}_{1} = x_{2}$

${\dot{x}}_{2} = x_{2}^{2}$

(802)

$y = x_{1}$

rendszert.

Ekkor a

$x_{1} = z_{1}, x_{2} = z_{2} e^{y}$

transzformációval kapjuk, hogy

${\dot{z}}_{1} = z_{2} e^{y} = z_{2} e^{z_{1}}$

${\dot{z}}_{2} = 0$

(803)

$y = z_{1} .$

A (803) rendszerhez tartozik kvadratikus SIELF, például

$k (y) = [\begin{array}{l} - e^{y} \\ - e^{y} \end{array}], V (e) = e^{T} e .$

Azonban az eredeti rendszerhez nincs ilyen Lyapunov függvény.

15.5.2. Passzivitásos technika

Tekintsük a

$\dot{x} = f (x, d) + g (x, d) u$

(804)

$y = h (x, d)$

(805)

dinamikus rendszert, ahol $d$ egy időben változó külső bemenet.

Definíció 14.10

A (804) rendszer egyenletesen $C^{1}$ passzív a $A, d$ párra nézve, ha létezik egy $V$ tároló függvény és $K_{\infty}$ -beli $α_{1}, α_{2}$ függvények valamint egy $α_{3}$ folytonos pozitív definit függvény amelyre:

$α_{1} (| | x | |_{A}) \leq V (x) \leq α_{2} (| | x | |_{A})$

$L_{f} V (x, d) \leq - α_{3} (| | x | |_{A})$

$L_{f} V (x, d) = h {(x, d)}^{T}$

minden $x$ és $d$ esetén.

Az állapottér egy adott $x = (x_{1}, x_{2})$ particionálására és ha $A = {x | x_{1} = 0}$ a rendszer parciálisan egyenletesen $C^{1}$ passzív (PSUP) az $(x_{2}, d)$ párra nézve és $| | x | |_{A} = | | x_{2} | |$ választással.

Ha a

$\dot{x} = f (x, u)$

(806)

$y = h (x, u)$

rendszerhez létezik állapotmegfigyelő, annak alakját vehetjük a

$\dot{\hat{x}} = f (\hat{x}, u) + l (\hat{x}, u, δ_{y}) k (u, y, δ_{y}) δ_{y}$

(807)

formában, ahol $δ_{y} : = h (\hat{x}, u) - y$ és $k$ nemszinguláris. Ekkor a kapcsolódó hiba dinamika alakja

$\dot{x} = f (x, u)$

(808)

$\dot{e} = Δ_{f} (e, x, u) + l (e + x, u, Δ_{h} (e, x, u)) v$

(809)

$y_{o} = Δ_{h} (e, x, u)$

(810)

ahol $e = \hat{x} - h, Δ_{f} (e, x, u) = f (\hat{x}, u) - f (x, u)$ és $Δ_{h} (e, x, u) = h (\hat{x}, u) - h (x, u)$ valamint $v = - k (u, y, y_{o}) y_{o}$ .

A (807) rendszer egy passzivitásos megfigyelője (PSO) a rendszernek, ha a hiba dinamika PSUP a $(e, u)$ párra nézve $\bar{v}$ -ről $y_{o}$ -ra a

$v = - k (u, y, y_{o}) y_{o} + \bar{v}$

visszacsatolással.

A továbbiakban tegyük fel, hogy $x = (x_{1}, x_{2})$ és $y = x_{2}$ valamint létezik $V (x, e_{1})$ tárolófüggvény, $L_{1}$ és invertálható $L_{2}$ mátrixok úgy, hogy

$ψ_{1} (| | e_{1} | |) \leq V (x, e_{1}) \leq ψ_{2} (| | e_{1} | |)$

$\partial_{x} V f (x, u) + \partial_{e_{1}} V (Δ_{f_{1}} (e_{1}, 0, x_{1}, x_{2}, u) - L_{1} L_{2}^{- 1}) Δ_{f_{2}} (e_{1}, 0, x_{1}, x_{2}, u)) \leq ψ_{3} (| | e_{1} | |)$

minen $x, e_{1}$ és $u$ esetén, ahol $ψ_{1}, ψ_{2}$ függvények $K_{\infty}$ -beliek és $ψ_{3}$ egy folytonos pozitív függvény.

Tegyük fel továbbá, hogy $ϕ_{1}$ és $ϕ_{2}$ nemnegatív függvényekkel

$| | \partial_{e_{1}} V ({\tilde{Δ}}_{f_{1}} (e, x, u) - L_{1} L_{2}^{- 1} {\tilde{Δ}}_{f_{2}} (e, x, u)) + {\tilde{Δ}}_{f_{2}}^{T} (e_{1} + L_{1} L_{2}^{- 1} e_{2}, e_{2}, x, u) L_{2}^{- T} | | \leq$

$\leq ϕ_{1} (u, x_{2}, e_{2}) | | e_{2} | |^{2} + ϕ_{2} (u, x_{2}, e_{2}) \sqrt{ψ_{3} (| | e_{1} | |)} | | e_{2} | |,$

minden $x, e$ és $u$ esetén, ahol

${\tilde{Δ}}_{f_{i}} (e, x, u) =$

$= \int_{0}^{1} (\partial_{β_{1}} f_{i} (β_{1}, β_{2}, u) L_{1} L_{2}^{- 1} + \partial_{β_{2}} f_{i} (β_{1}, β_{2}, u)) |_{β_{1} = θ L_{1} L_{2}^{- 1} e_{e} + e_{1} + x_{1}, β_{2} = θ e_{2} + e_{1}} d θ .$

Tétel 14.8 A fenti feltevések mellet a PSO rendszer a

$k (u, y, y_{o}) = ε + ϕ_{1} (u, y, y_{o}) + ϕ_{2}^{2} (u, y, y_{o})$

mellet minden $y > 0$ -ra egy PSUP hibadinamikával rendelkezik a $(e, u)$ párra nézve és a $v = - k (u, y, y_{o}) y_{o} + \bar{v}$ visszacsatolással.

A tétel második feltétele helyettesíthető az alábbival:

$| \partial_{e_{1}} V (Δ_{f_{1}} (L_{1} L_{2}^{- 1} e_{2}, e_{2}, e_{1} + x_{1}, x_{2}, u) - L_{1} L_{2}^{- 1} Δ_{f_{2}} (L_{1} L_{2}^{- 1} e_{2}, e_{2}, e_{1} + x_{1}, x_{2}, u)) +$

$+ e_{2}^{T} L_{2}^{- 1} Δ_{f_{2}} (e_{1} + L_{1} L_{2}^{- 1} e_{2}, e_{2}, x, u) | \leq$

$\leq ϕ_{1} (u, x_{2}, e_{2}) | | e_{2} | |^{2} + ϕ_{2} (u, x_{2}, e_{2}) \sqrt{ψ_{3} (| | e_{1} | |)} | | e_{2} | | .$

15.5.3. Lipschitz nemlineáris rendszerek

Tekintsük az alábbi Lipschitz nemlineáris rendszert:

$\dot{x} = A x + B u + Φ (x, u)$

$y = C x,$

ahol

$| | Φ (x_{1}, u) - Φ (x_{2}, u) | | \leq c | | x_{1} - x_{2} | |, | | Φ (x, u) | | \leq c | | x | |$

minden $x, x_{1}, x_{2}$ és $u$ esetén.

Tekintsük egy

$\dot{\hat{x}} = A \hat{x} + B u + Φ (\hat{x}, u) + L (y - C \hat{x}),$

megfigyelőt, amelyhez a

$\dot{e} = (A - L C) e + Φ (\hat{x}, u) - Φ (x, u) .$

(811)

hibaegyenletek tartoznak. Tegyük fel, hogy a (811) megfigyelőhöz tartozik egy kvadratikus $V (e) = e^{T} Q e$ SIELF. Mivel

$2 e^{T} Q (Φ (\hat{x}, u) - Φ (x, u)) \leq 2 | | Q e | | | | Φ (\hat{x}, u) - Φ (x, u) | | \leq$

$\leq 2 c | | Q e | | | | e | | \leq γ_{1} | | P e | |^{2} + γ_{2} | | e | |^{2},$

(812)

ahol $γ_{1}, γ_{2}$ alkalmas pozitív állandók úgy, hogy $γ_{1} γ_{2} = c^{2}$ , következik, hogy

$\dot{V} (e) = e^{T} (Q A_{o} + A_{o}^{T} Q) e + 2 e^{T} Q (Φ (\hat{x}, u) - Φ (x, u)) \leq$

$\leq e^{T} (Q A_{o} + A_{o}^{T} Q + γ_{1} Q Q + γ_{2} I) e \leq 0$

(813)

ahol $A_{0} = A - L C$ , azaz

$Q (A - L C) + {(A - L C)}^{T} Q + γ_{1} Q Q + γ_{2} I \leq 0.$

(814)

$L = L_{1} + \frac{γ}{2} Q C^{T}$

(815)

választással kapjuk, hogy

$Q (A - L_{1} C) + {(A - L_{1} C)}^{T} Q + Q (γ_{1} I - γ C^{T} C) Q + γ_{2} I \leq 0.$

(816)

$R : = γ_{1} I - γ C^{T} C \geq 0,$

(817)

akkor (816) az alábbi formában írható:

$[\begin{array}{l} Q (A - L_{1} C) + {(A - L_{1} C)}^{T} Q + γ_{2} I & Q R^{\frac{1}{2}} \\ R^{\frac{1}{2}} Q & - I \end{array}] \leq 0.$

(818)

Vissza		Előre
14. fejezet - Rekonfiguráló és hibatűrő irányítások tervezése	Főoldal	16. fejezet - Mintavételezett rendszerek irányítása

15. fejezet - Nemlineáris irányítások

15.1. Stabilitás

15.2. Disszipatív rendszerek

15.3. Passzív rendszerek

15.4. Nemlineáris ℋ ∞ szabályozás

15.4.1. γ -disszipativitás

15.4.2. Nemlineáris ℋ ∞ feladat

15.4.2.1. Állapotvisszacsatolásos ℋ ∞ feladat

15.4.2.2. Kimenet visszacsatolásos ℋ ∞ feladat

15.5. Nemlineáris megfigyelők

15.5.1. Állapotfüggetlen Lyapunov függvények (SIELF)

15.5.2. Passzivitásos technika

15.5.3. Lipschitz nemlineáris rendszerek

15.4. Nemlineáris $ℋ_{\infty}$ szabályozás

15.4.1. $γ$ -disszipativitás

15.4.2. Nemlineáris $ℋ_{\infty}$ feladat

15.4.2.1. Állapotvisszacsatolásos $ℋ_{\infty}$ feladat

15.4.2.2. Kimenet visszacsatolásos $ℋ_{\infty}$ feladat