6. fejezet - Szórás analízis (ANOVA analízis)

Ha Q1, Q2, …, Qk független, rendre f1, f2, …, fk szabadsági fokú χ2 eloszlású valószínűségi változó, akkor a

Q = Q1 + Q2 + … + Qk

összeg ugyancsak χ2 eloszlású változó f1 + f2 +, …, + fk szabadsági fokkal (paraméterrel).

Bontsuk fel „f” darab független, χ2 eloszlású valószínűségi változó Q négyzetösszegét „k” számú kifejezés összegére:

Q = Q1 + Q2 + Q3 + … Qi + … + Qk

Ekkor annak a szükséges és elegendő feltétele, hogy a Qi-k függetlenek és mind χ2 eloszlásúak legyenek, rendre fi paraméterrel az, hogy fennálljon:

n = f1 + f2 + f3 + … fi + … + fk

A parametrikus modell a következő:

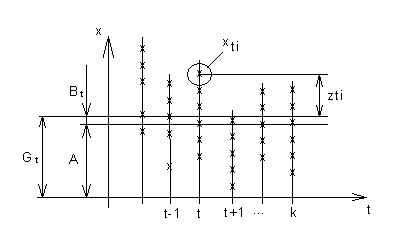
xti = A + Bt + zti

aholxtia megfigyelt értékek

t = 1…ka faktor szintek sorszáma

i = 1…ntaz egyes megfigyelések sorszáma

Aa teljes sokaság várható értéke

és

$$A=\frac{1}{N}{\displaystyle \sum _{t=1}^k}{\displaystyle \sum _{i=1}^{{{}_n}_t}{x}_{{}_{ti}}}$$

továbbá N az összes megfigyelés száma:

$$N={\displaystyle \sum _{t=1}^k{n}_{{}_t}}$$

Btaz egyes csoportok várható értékének eltérése a teljes átlagtól

Gt = A + Bta csoportátlag várható értéke

$${{\displaystyle z}}_{ti}={{\displaystyle x}}_{ti}-{{\displaystyle \overline{x}}}_{ti}$$

ztiaz egyes adatok eltérése a csoportátlagtól:

A zti reziduál (vagy reziduális eltérés) az adatok véletlen hibáját testesíti meg.

Mindezt a 6.1. ábra szemlélteti:

Egyszeres osztályozásnál az adatokat a XL.táblázat szerint szokás megadni.

XL. táblázat

Adatok elrendezése egyszeres osztályozáshoz

Feltételezések:

$${\displaystyle \sum _{t=1}^k{n}_t{B}_t}=0$$

$$A=\frac{1}{N}{\displaystyle \sum _{t=1}^k{n}_t{s}_t}$$

Részletezve az összefüggéseket, a csoport átlagok:

$${{\displaystyle B}}_t={{\displaystyle \overline{x}}}_{t•}=\frac{1}{n_t}{\displaystyle \sum _{i=1}^{n_t}{x}_{ti}}$$

A csoportokon belüli átlagok:

$${{\displaystyle \overline{x}}}_{t•}=A+B_t+{\overline{z}}_{t•}$$

A reziduál átlaga:

$${{\displaystyle \overline{z}}}_{t•}=\frac{1}{n_t}{\displaystyle \sum _{i=1}^{n_t}{z}_{ti}}$$

A reziduál M várható értéke:

$$M({{\displaystyle \overline{z}}}_{t•})=0$$

Ezekkel a jelölésekkel

$$A={\overline{x}}_{••}=\frac{1}{N_t}{\displaystyle \sum _{t=1}^k{n}_t}\overline{x_{t•}}$$

$${\overline{z}}_{••}={\displaystyle \sum _{i=1}^{n_t}}{\displaystyle \sum _{t=1}^k}\overline{z_{ti}}$$

Nullhipotézis: B1 = B2 = … Bt = 0

Ellenhipotézis:Bt ≠ 0

Az előzőek szerint:

Az egyes adatok eltérése a teljes átlagtól:

$$x_{ti}-{\overline{x}}_{••}$$

A csoportátlagok eltérése a teljes átlagtól:

$$x_{t•}-{\overline{x}}_{••}$$

Az egyes adatok eltérése a csoport átlagtól:

$$x_{ti}-{\overline{x}}_{t•}$$

Ezekre pedig fenn áll az alábbi összefüggés:

$$x_{ti}-{\overline{x}}_{••}=({\overline{x}}_{t•}-{\overline{x}}_{••})+({\overline{x}}_{ti}-{\overline{x}}_{t•})$$

Ahol

$${\overline{x}}_{••}=A+{\overline{z}}_{••}$$

Ezekből képezzük a eltérés négyzetösszegeket:

A teljes eltérés-négyzetösszeg:

$$Q={\displaystyle \sum _{t=1}^k}{\displaystyle \sum _{i=1}^{n_t}(x_{ti}}-{\overline{x}}_{••}{)}^2$$

A csoportok közötti eltérés-négyzetösszeg:

$$Q_1={\displaystyle \sum _{t=1}^k{n}_t(\overline{x_{t•}}}-{\overline{x}}_{••}{)}^2$$

A csoportokon belüli (maradék vagy reziduális) eltérés-négyzetösszeg:

$$Q_e={\displaystyle \sum _{t=1}^k}{\displaystyle \sum _{i=1}^{n_t}({\overline{x}}_{ti}}-x_{t•}{)}^2$$

És ezekre fenn áll az alábbi összefüggés:

Q = Q1 + Qe

Most meghatározzuk, hogy a minket érdeklő jel (a csoport-hatás, azaz az oszlopok közötti eltérés) szignifikánsan kiemelkedik-e a zajból (azaz a csoportokon belüli ingadozásból). Ehhez a szórásokat F-próbával fogjuk összehasonlítani.

A szórást az eltérés négyzetösszegből képezhetjük: az eltérés négyzetösszeget osztani kell a szabadságfokok számával.

A csoportok közötti eltérés négyzet összeg szabadságfoka k-1, mert k csoport van, és a csoport átlagok képzéséhez 1 szabadságfokot felhasználtunk.

A csoporton belüli négyzetösszegek szabadságfoka N-k, mert az összes N adatból k csoport átlagot képeztünk, tehát k szabadságfokot használtunk fel.

A totál négyzetösszeg szabadságfoka N-1, mert N adatból képeztük és az N adat átlagához 1 szabadság fokot használtunk fel.

A számítás áttekintéséhez az adatokat ANOVA táblában szokták összefoglalni.

Az ANOVA (Analysis of Variances) tábla segít eldönteni, hogy valamely hatás befolyásolja-e a kísérleti eredményt, vagy sem. Az összes mérési adatot a vizsgált hatás különböző szintjei szerint csoportosítjuk, és ha ezek között a csoportok között szignifikáns eltérés van, azt csak a vizsgált hatás okozhatja. A mérési adatoknak egy-egy csoporton belüli ingadozását viszont csakis a véletlen hiba okozhatja. Meg kell határozni, hogy a jel nagyobb-e a zajnál, azaz a csoport-hatás nagyobb-e a véletlen hibánál. Vagyis az a kérdés, hogy a csoportok közötti ingadozás (a csoport-átlagok szórása) szignifikánsan nagyobb-e a csoporton belüli adatok ingadozásánál (a csoportokon belüli szórások átlagánál). Ezt a kérdést egy F-próbával dönthetjük el.

Az egyszeres osztályozás ANOVA táblája a XLI. táblázatban látható.

XLI. táblázat

Az egyszeres osztályozás ANOVA táblája

Az Fszám értéket összehasonlítjuk az F-táblázatban található Fkrit értékkel, és ha Fszám> Fkrit, akkor a csoporthatás szignifikáns, ellenkező esetben nem.

A műszaki gyakorlatban 95% szignifikancia szinten (p=0,05) szokás a próbát elvégezni.

A kétszeres osztályozás két hatás együttes vizsgálatát teszi lehetővé. (Az együttes vizsgálatot jelzi a „keresztosztályozás” kifejezés.) Eljárhatnánk úgy is, hogy két független egyszeres osztályozást végzünk, azaz először az egyik hatás szignifikanciáját vizsgáljuk meg, azután a másikét. Ekkor azonban egyszerre csak az egyik hatás szórását vennénk figyelembe, és így nagyobbnak tűnne a véletlen hiba, mint valójában, mert a másik hatás okozta szórást is bele számolnánk.

Kétszeres osztályozásnál lehetőség van a kereszt-hatás vizsgálatára is, amennyiben a cellákon belül több adat – minimum két adat – van.

Kétszeres keresztosztályozásnál az adatokat a XLII. táblázat szerint szokás elrendezni.

XLII. táblázat

Kétszeres keresztosztályozás adatainak elrendezése

Az elrendezésnek megfelelően az egyik hatást sor-hatásnak (Row), a másikat oszlop-hatásnak (Column) nevezik. A sorok és oszlopok keresztezésénél vannak a cellák. A cellákban lévő adatok azonos sorok azonos oszlopa szerint végzett ismételt mérési adatok, tehát ingadozásukat (szórásukat) csak a véletlen okozhatja. Ezért a cellák szórásának átlaga a véletlen hatást tartalmazza.

A kétszeres kereszt osztályozás parametrikus modellje az alábbi:

xtij = A + Rt + Ci + (RC)ti + ztij

t=1…rta sorok száma

i=1…craz oszlopok száma

j=1…nn a cellák száma

A cellák átlaga:

$${\overline{x}}_{ti}=A+R_t+C_i+{(RC)}_{ti}+\overline{z_{ti}}$$

A sorok átlaga:

$${\overline{x}}_{t••}=A+R_t+\overline{z_{t••}}$$

Az oszlopok átlaga:

$${\overline{x}}_{•i•}=A+C_i+\overline{z_{•i•}}$$

A sorok közötti eltérés négyzetösszeg (sor-hatás):

$$Q_r=nc{\displaystyle \sum _{t=1}^r({\overline{x}}_{t••}}-{\overline{x}}_{•••}{)}^2$$

Az oszlopok közötti eltérés négyzetösszeg (oszlop-hatás):

$$Q_c=nr{\displaystyle \sum _{i=1}^c({\overline{x}}_{•i•}}-{\overline{x}}_{•••}{)}^2$$

A cellák közötti eltérés négyzetösszeg (kereszt-hatás vagy kölcsön-hatás):

$$Q_{rc}=n{\displaystyle \sum _{t=1}^r}{{\displaystyle \sum _{i=1}^c\left[\overline{x_{ti•}}-\overline{x_{•••}}\right]}}^2$$

A cellán belüli („maradék” vagy „reziduális”) négyzetösszeg:

$$Q_e={\displaystyle \sum _{t=1}^r{\displaystyle \sum _{i=1}^c{\displaystyle \sum _{j=1}^n(x_{tij}}}}-\overline{x_{ti•}}{)}^2$$

A teljes eltérés négyzetösszeg:

$$Q={\displaystyle \sum _{t=1}^r}{\displaystyle \sum _{i=1}^c{\displaystyle \sum _{j=1}^n}(x_{tij}}-\overline{x_{ti•}}{)}^2$$

A teljes eltérés négyzetösszegre pedig fennáll, hogy:

Q = Qr + Qc + Qrc + Qe

A véletlen (másképpen „maradék”, „reziduális”) eltérés négyzetösszegének meghatározásához elegendő a másik négy eltérés négyzetösszeget kiszámolni, mert ezekből a reziduál meghatározható:

Qe = Q – Qr – Qc - Qrc

A fenti kifejezésekkel a kétszeres keresztosztályozás ANOVA táblája a XLIII. táblázatban látható.

XLIII. táblázat

A kétszeres keresztosztályozás ANOVA táblája

Az eltérés négyzetösszegek összege megegyezik a Teljes eltérés-négyzetösszeggel, és a szabadságfokok összege megegyezik a Teljes szabadságfok-számmal.

Minden egyes hatás szignifikanciáját külön F-próbával kell ellenőrizni, mindig a reziduális eltérés négyzetösszeghez képest.

Célszerű először megvizsgálni, hogy van-e kereszthatás. Ha nincs, a kereszthatást (a cellák közötti eltérés-négyzetösszeget) hozzá adjuk a véletlen hatáshoz (a cellákon belüli eltérés négyzetösszeghez), és most már csak a sor- és oszlop-hatást vizsgáljuk a véletlenhez képest.