6. fejezet - Szenzorok és aktuátorok dinamikai modelljei és tervezésük
Vissza		Előre

6. fejezet - Szenzorok és aktuátorok dinamikai modelljei és tervezésük

Tartalom

A szenzorokat és az aktuátorokat nem véletlenül szokás együtt tárgyalni. Ennek sok egyéb mellett, két oka van. Az egyik az, hogy néhány un. aktív szenzor inverz üzemmódban aktuátorként viselkedik. Erről a témáról egy áttekintést láthatunk a fejezet első ábráján. A másik az, hogy a két csoport a mechatronika „klasszikus” definícióját gyakran önmagában is megjeleníteni képes. Az aktuátorok és a szenzorok képezik a „határfelületet” a gépészet és az elektrotechnika/elektronika között, hiszen a szenzor feladata a mérendő fizikai (mechanikai) mennyiségekből villamos úton mérhető mennyiséget létrehozni, míg az aktuátor villamos bemenő jel (teljesítmény) segítségével hatni képes a mechanikai rendszerben zajló folyamatokra. Ezek a rendszer építőelemek tehát a legtöbb esetben elektromechanikus rendszerek, és ráadásul az intelligens szenzorok és aktuátorok esetében az elektronika is integrálva van hozzájuk (Embedded Systems: beágyazott rendszerek). A teljesség kedvéért azonban tudni kell, hogy nem minden szenzor és aktuátor feltétlenül elektromechanikus rendszer. Vannak különleges eszközök, amelyek egymagukban szenzorok és aktuátorok. Sok esetben ez nem valamiféle bonyolult rendszer, hanem egyszerűen egy speciális anyag. Példaként megemlítjük, hogy vannak olyan speciális anyagok, amelyek alakjukat a folyadékban található alkohol egy bizonyos küszöbértékének meghaladása után ugrásszerűen változtatják, térfogatuk megnő. Segítségükkel például elzáró, vagy adagoló szelepeket építenek. Más jellegű példa, és lomha viselkedése miatt korlátozottan alkalmazható, de egy időben például számos publikáció látott napvilágot az SMA (alakemlékező fémötvözet) mechatronikában való alkalmazhatóságáról. Ezek az anyagok hőmérsékletváltozás hatására nagymértékben és ugrásszerűen változtatják alakjukat. Ezeket az anyagokat a különleges szenzorok és aktuátorok csoportban tárgyalja a szakirodalom.

Még a mérés-és műszertechnikában járatos szakemberek számára is gyakran nehézséget okoz a mérőátalakító és a szenzor fogalmának megkülönböztetése. A kérdés tisztázása különösen akkor lett aktuális, amikor a mechatronika eszköztárának fejlődésével, elsősorban konferencia szekciók elnevezésében kialakult és megerősödött a „szenzortechnika” területe. A mechatronikai mérnök a rendszerek szintézise során túlnyomó részben kész termékeket, valójában mérőátalakítókat használ, amelyek „lelke”, legfontosabb alkotórésze a „szenzor” (érzékelő). Miben áll tehát a különbség? Van-e minden esetben különbség a két fogalom között? Ezt kíséreljük meg néhány sorban tisztázni.

A gépészeti méréstechnikában és a mechatronikában a szenzor feladata az alakváltozásnak, az elmozdulásnak, a fényintenzitás változásnak, a mágneses tér és a mágneses jellemzők változásának, anyagjellemzők változásának stb. átalakítása olyan fizikai mennyiséggé, amelyet villamos úton mérni lehet. A villamos átalakítás nem kizárólagos, hiszen napjainkra jellemző a fény, mint információhordozó erőteljes elterjedése, és vannak mérőrendszerek, amelyek levegőnyomással működnek. Vannak aktív szenzorok, amelyek működésükhöz nem igényelnek segédenergiát (ez a kisebbség) és igen sokféle passzív, tehát segédenergiával működő szenzort ismerünk. A szenzorok tárháza a technika fejlődésével folyamatosan bővül.

Egy adott szenzor típust sokféle mérőátalakítóba lehet beépíteni, ettől a szenzor még eredeti funkciója alapján nem válik többféle fizikai mennyiség mérésére közvetlenül alkalmassá. A szenzorok többsége ugyanis csak közvetett mérést tesz lehetővé. A közvetett mérést a nemzetközi méréstechnikai irodalomban is ismert „mérőlánc” testesíti meg. Igen gyakran fizikai mennyiségek közötti átalakítások sora szükséges ahhoz, hogy a mérőlánc végén a bemenő mennyiséggel szoros kapcsolatot mutató villamos jelhez jussunk.

Példaképpen emeljünk ki egy passzív szenzort a sorból, ez a nyúlásmérő bélyeg. Napjainkban kétféle változata létezik, fémréteg és félvezető. Mit „mér” tulajdonképpen a nyúlásmérő bélyeg? Nevében is mutatja, hogy alakváltozást, nyúlást és zsugorodást! Minden olyan fizikai mennyiség mérésére alkalmas tehát, amelyek egy megfelelően méretezett gépészeti elemen reprodukálható módon, és a tervezett mérési tartományban alakváltozást képesek létrehozni. Ezért nyúlásmérő bélyeg, mint szenzor található – többek között – a következő mérőátalakítókban: elmozdulás érzékelő, erőérzékelő, gyorsulásérzékelő, nyomásérzékelő, nyomatékmérő, hogy a mechatronikában legismertebbeket említsük.

Ugyanakkor tudni kell, hogy a fent felsorolt fizikai mennyiségek többsége egy megfelelően kialakított mechanikai elem segítségével elmozdulássá is alakíthatóak, így mindegyikük mérhető induktív elmozdulás szenzorok felhasználásával is.

A példából világosan látszik, hogy a szenzor és a mérőátalakító nem azonos műszaki fogalmak, tehát a szenzor a mérőátalakító „szíve”. Ezért helytelen pl. erőmérő szenzorról beszélni, hiszen az erő többféle szenzorral, pl. elmozdulás, alakváltozás, optikai stb. szenzorokkal egyaránt mérhető. Az ugyanakkor lehetséges, hogy a különféle szenzorokkal megvalósított mérőeszközök működési frekvenciatartománya, és mérési tartománya erősen különböző. Néhány jellegzetes, és a mechatronikában fontos fizikai mennyiség érzékelésére alkalmas szenzor összefoglalása látható az alábbi táblázatban. A mátrixban látható jelek magyarázata alul található.

6.1. táblázat - A gépészetre jellemző mennyiségek és a mérésükre alkalmas szenzorok

A helyszűke miatt nem lehet feltüntetni azt, hogy melyik szenzor, milyen „köztes elem” segítségével teszi lehetővé az átalakítást, a tisztelt olvasóra bízzuk, hogy felismeri-e, hogy adott esetben alakváltozást, elmozdulást, fényintenzitás, esetleg anyagjellemző változást alakít át a szenzor villamos úton mérhető mennyiséggé.

6.1. Piezoelektromos gyorsulásérzékelő. Fordító váltó a gyakorlatban.

A piezoelektromos átalakítók fordító váltó jellegű energia átalakítók . A fordító váltó két eltérő típusú fizikai rendszer eltérő típusú változói között teremt kapcsolatot (ld.: 2. fejezet).

A piezoelektromos effektus energia átalakítók formájában előkelő helyet foglal el a mechatronikai rendszerek szintézise, tervezése folyamatában. A piezoelektromos átalakító tökéletesen megvalósítja az energia átalakítás mindkét irányát, hiszen mechanikai bemenetre villamos kimenettel, illetve villamos bemenetre mechanikai kimenettel válaszol. Az első irány általában a szenzorokra jellemző, míg a második az aktuátorokra. Ezek megvalósítási formái igen változatosak.

Piezoelektromos szenzor olyan aktív, tehát működéséhez segédenergiát nem igénylő eszköz, amely alakváltozást alakít át villamos töltéskülönbséggé. Alkalmas tehát minden olyan fizikai, mechatronikai mennyiség mérésére, amely reprodukálható alakváltozást idéz elő a piezoelektromos átalakítón. Ilyenek például az erő, a nyomás, és a gyorsulás. Fontos tudni, hogy ez az eszköz statikus mérésekre napjainkig még nem alkalmas, mert az alakváltozás (kristály deformáció) hatására létrejövő töltések idővel elszivárognak, részben a kerámián, részben pedig a töltéserősítőn keresztül. Megfelelő tokozásban közvetlenül lehet vele erőt mérni, és ha szeizmikus tömeget helyeznek rá, majd házba foglalják, akkor a ház gyorsulása detektálhatóvá válik. Ez a régóta ismert piezoelektromos gyorsulásérzékelő elve. A szeizmikus tömeg f_a(t)=ma gyorsulással arányos tömegerőt hoz létre, amely erő a kerámiát deformáló rugóerővel f_pie(t)=kΔx tart egyensúlyt. A Δx elmozdulás különbség a ház és a szeizmikus tömeg közötti relatív elmozdulás, vagyis alakváltozás. Amint a modell bemutatásánál látni fogjuk, az alakváltozáshoz szükséges erőt a gyorsulás, mint bemenet hozza létre. A hatására kialakuló piezo-feszültség, a kimenő mennyisé. Ezt a gyorsulásérzékelőt a későbbiekben részletesen elemezzük. A piezokerámia, mechanikai szilárdsága miatt, nélkülözhetetlen az extrém nagy nyomások mérése során, pl. belsőégésű motorok hengereiben. Az átalakító anyaga régebben a természetes kristályok (kvarc, turmalin, Rochell só) köréből került ki, napjainkban azonban az báriumtitanát, ólomtitanát és ólomcirkonát kerámiákat a nagyobb érzékenységük miatt alkalmazzák. Ezeket porkohászati úton állítják elő, majd megfelelő elektromos térerő segítségével állítják be a piezoelektromos dipólusokat a kívánt irányba. A piezokerámia „n_F” átalakítási tényezőjét négy paraméter alkotja. Az indexben lévő „F” a fordító váltó jellegű tulajdonságra utal.

$n_{F} = \frac{ε_{0} ε_{r} A}{K_{P} \cdot l} = e_{p} \frac{A}{l}$

Az összefüggésben „K_p[C/N], vagy [m/V]” a piezoelektromos együttható, „l” a kerámia vastagsága, „A” a felülete, ε_r a kerámia relatív permittivitása. Néhány irodalomban a piezoelektromos anyagra jellemző tényezőket „e_p” együtthatóként foglalják össze. A fordító váltó itt látható képletét a későbbiekben a fizikai egyenletekből fogjuk levezetni. Az energia átalakítás iránya megfordítható. Ezt a második jelenséget aknázzák ki, ha a piezokerámia segítségével aktuátorokat akarnak létrehozni. Ezek közül a legismertebb a piezomotor, amely kereskedelemben kapható eszköz, lineáris és forgó mozgások létrehozására a nanométeres tartománytól a néhány mikrométeresig. Mobiltelefonjainkban, elektroakusztikai átalakítóként, a rezgő piezo tárcsa hangszóró szerepét játssza el, azzal együtt, hogy frekvencia átvitele korlátozott, de a beszédhang átvitelére alkalmas. Az autóipar ma már elképzelhetetlen villamosan vezérelt piezoelektromos adagoló nélkül (mechanikai alakváltozás).

Nem szabad ugyanakkor arról sem elfeledkezni, hogy a kerámia felületein egy fémréteg segítségével gyűjtik össze a keletkezett töltéseket, és ehhez csatlakozik a villamos vezeték is. A kerámia, mint villamosan szigetelő anyag a fémrétegek között egy C_p kapacitású piezo-kondenzátort képez, ezt a modellezésnél figyelembe kell venni. Később látni fogjuk az egyenletekből, hogy ennek a kapacitásnak a növelése mechanikai oldalon a rendszer rugómerevségének növekedését eredményezi, hiszen fordító váltóról van szó, és ebben az esetben a „két oldal” energiatárolói típus szerint ellentétükre „váltanak” át.

Foglaljuk össze egyenletek formájában a piezoelektromos energia átalakítót.

Az energia átalakításra jellemző fizikai összefüggések a szakirodalomban megtalálhatóak, itt csak egyet említünk, pl. A. Lenk: Elektromechanische Systeme Bd. 2. [6.1.]:

$\begin{array}{l} P = K_{p} σ + ε_{0} (ε_{r} - 1) E_{d} \\ \frac{Δ l}{l} = \frac{1}{E} σ + K_{p} E_{d} \end{array}$

A két egyenletben az alábbi jelöléseket alkalmaztuk:

	P[C/m²]	elektromos polarizáció
	K_p[C/N], [m/V]	piezoelektromos együtth. (kvarc: 2.3·10^-12 C/N; báriumtitanát: 2.5·10^-12 C/N)
	σ[N/m²]	mechanikai feszültség
	ε₀[C/Vm]	vákuum dielektromos állandója
	ε_r	relatív dielektromos együttható
	E_d[V/m]	dielektromos térerő
	E[N/m²]	Young-modulus

A második egyenlet dimenzió nélküli, ezért van szükség az „K_p” piezoelektromos együttható kétféle dimenziójára, és az ezek közötti azonosság bemutatására.

Ha az átalakító két egyenletét úgy vizsgáljuk, hogy keressük a mechanikai és a villamos oldalak közötti összefüggéseket, akkor a két egyenlet egyszerűbb alakba írható:

$\begin{array}{l} P = K_{p} σ \\ \frac{Δ l}{l} = K_{p} E_{d} \end{array}$

Tehát a kerámia (piezoelektromos anyag, legtöbbször kerámia) kontaktust adó fémréteg fegyverzetein létrejövő „P” töltéspolarizáció a piezoelektromos együtthatóval és a kerámián létrehozott „σ” mechanikai feszültséggel függ össze. A kerámia mechanikai alakváltozása viszont a piezoelektromos együttható révén az elektromos térerővel függ össze.

Adott minden az átalakító szokásos módon, átmenő és keresztváltozókkal való leírásához. A keresett alakhoz átalakítások és helyettesítések révén jutunk el.

A polarizáció adott „A” felületen megjelenő „Q” töltéskülönbséget jelent. Ha a töltésre fejezzük ki az első egyenletet, és figyelembe vesszük, hogy a töltés a fémfelületek miatti un. piezo-kondenzátor fegyverzetein jelenik meg, úgy ezek között „u_p” villamos feszültség alakul ki:

$\begin{array}{l} Q = C_{p} \cdot u_{p} = K_{p} \cdot A \cdot \frac{F}{A} \\ u_{p} = \frac{K_{p}}{C_{p}} \cdot F = \frac{K_{p} \cdot l}{ε_{0} \cdot ε_{r} \cdot A} \cdot F = \frac{1}{n_{F}} \cdot F \end{array}$

Az átalakító első egyenlete mutatja, hogy rendszer típus váltás mellett változó típus váltás is történt.

Az átalakító második egyenletében az alakváltozást „Δx” fogja jelölni, a kerámia nyugalmi hossza pedig marad „l”. Átrendezés után az alábbi forma jön létre:

$Δ x = K_{p} \cdot l \cdot E_{d}$

Az elektromos erőtér hatására létrejövő eltolási áramsűrűség „J_d”.

Definíció szerint: $J_{d} = ε_{0} \cdot ε_{r} \frac{\partial E_{d}}{\partial t}$ , továbbá az áramsűrűség és az áram kapcsolata $J_{d} = \frac{d I}{d A}$ .

Ha a második átalakító egyenletét idő szerint deriváljuk, akkor az alakváltozási sebesség és az eltolási áramsűrűség közötti kapcsolatot kapjuk:

$Δ v = K_{p} \cdot l \cdot \frac{1}{ε_{0} \cdot ε_{r}} J_{d}$

Figyelembe véve az áram és az áramsűrűség közötti kapcsolatot, amely lényegében a kerámia felületével függ össze, végül a következő alakhoz jutunk:

$Δ v = \frac{K_{p} \cdot l}{ε_{0} \cdot ε_{r} \cdot A} \cdot I = \frac{1}{n_{F}} \cdot I$

Immár az átalakító második egyenlete is azokat a jellegzetességeket mutatja, mint az első.

Írjuk fel végezetül a két átalakító egyenletet olyan formában, hogy szokás szerint az egyik oldalon a mechanikai, a másikon pedig a villamos változók szerepeljenek:

$\begin{array}{l} u_{p} = \frac{1}{n_{F}} \cdot f \\ i = n_{F} \cdot v \end{array}$

Az átalakító egyenleteiben a változókat kisbetűvel jelöltük, utalva arra, hogy ezek időbeli változók. Látható, hogy két eltérő típusú fizikai rendszert úgy köt össze a piezoelektromos átalakító, hogy az összekapcsolt változók ellentétes típusúak.

Az energia átalakító átalakítási tényezője:

$n_{F} = \frac{ε_{0} \cdot ε_{r} \cdot A}{K_{p} \cdot l}$

Megjegyezzük, hogy a különféle szakirodalmak a fordító váltó átalakítási tényezőjét másként is definiálhatják. Előfordul, hogy a fent látható összefüggés reciprok értéke az átalakítási tényező. A lényegen ez nem változtat.

Rendkívül fontos meggyőződnünk arról, hogy az eddig felírt egyenletek dimenziójukat tekintve helyesek-e? A „K_p” piezoelektromos együtthatónak két dimenzióját is láttuk: C/N és m/V.

Elsőként ellenőrizzük ezek azonosságát:

$\frac{C}{N} = \frac{A s}{k g \frac{m}{s^{2}}} = \frac{\frac{W}{V} s}{k g \frac{m}{s^{2}}} = \frac{\frac{k g m^{2}}{s^{3} V} s}{k g \frac{m}{s^{2}}} = \frac{m}{V}$

Majd megvizsgáljuk a fordító váltó átalakítási tényezőjének dimenzió helyességét:

$\begin{array}{l} \frac{1}{n_{F}} [] = \frac{K_{p} \cdot l}{A \cdot ε} [] = \frac{1}{n_{F}} [\frac{\frac{C}{N} \cdot m}{m^{2} \frac{A s}{V m}}] = \frac{1}{n_{F}} [\frac{C \cdot V}{N \cdot A s}] = \frac{1}{n_{F}} [\frac{V}{N}] \\ u_{p} [V] = \frac{1}{n_{F}} [\frac{V}{N}] \cdot f [N] \\ n_{F} [] = n_{F} [\frac{N}{V}] = n_{F} [\frac{k g \frac{m}{s^{2}}}{V}] = n_{F} [\frac{k g \cdot m}{V s^{2}}] \\ i [A] = n_{F} [\frac{k g \cdot m}{V s^{2}}] \cdot v [\frac{m}{s}] = i [\frac{W}{V}] = i [A] \end{array}$

Mindkét esetben helyes eredményeket kaptunk, az átalakítási tényezővel egymásba átszámíthatjuk az eltérő típusú rendszerekhez tartozó impedanciákat.

A dinamikai tulajdonságok tervezésének bemutatására nézzük először a piezoelektromos gyorsulásérzékelő szerkezeti vázlatát és az abból megszerkeszthető gráfját. A műszerházban látható szeizmikus tömeget vagy csavarkötéssel, vagy nagy merevségű rugóval szorítják a piezokerámiához. Csavarkötés esetén, a kerámia közepén furat található. A szerkezeti vázlaton látszik, hogy 3 független keresztváltozó definiálható, egy a referencia, egy a műszerház sebessége, ami a referenciához viszonyítva a bemenő mennyiség integráltja (gyorsulást mérünk), és a szeizmikus tömeg referenciához viszonyított sebessége.

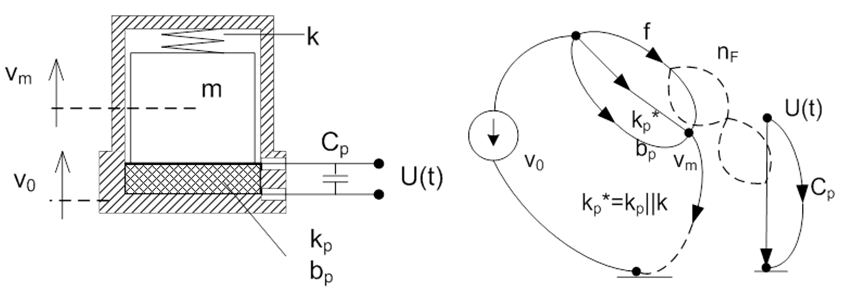
6.1. ábra - Piezoelektromos szeizmikus gyorsulásérzékelő modellje és gráfja

A fordító váltót a ház és a tömeg sebessége közé kell kötni, hiszen a gyorsító erő (F_a=m·a) hozza létre a kerámia deformációját a tömeg és a műszerház fala között, és ezzel az „u_p” kimeneti feszültséget. Ez a feladat annak illusztrálására is jó, hogy nem szabad mechanikusan szerkeszteni a gráfokat. Jelen esetben a fordító váltó bal oldalán a gráf éle nincs a referenciához kötve.

A rendszer annyira egyszerű, hogy a megoldáshoz kínálkozik az impedancia módszer. Az eredeti bemenet keresztváltozóból származtatott mennyiség (gyorsulás), a kimenet pedig az átalakító egyenletével adódik a ház és a szeizmikus tömeg közötti alakváltozási sebesség (kerámia alakváltozása) felhasználásával. A jobb oldalon egyetlen villamos elem, a kerámia villamos kapacitása szerepel. Éppen ezért célszerűen ezt a kapacitást számoljuk át egyenértékű mechanikai elemmé. Az átszámítás módját az energia átalakítók általános tárgyalásánál már megmutattuk. Az impedanciák közötti átszámítás érdekében osztjuk egymással az átalakító két egyenletét:

$\begin{array}{l} U_{p} (s) = \frac{1}{n_{F}} F (s) \\ I (s) = n_{F} \cdot V (s) \\ Z_{v i l l} = \frac{1}{n_{F}^{2}} \cdot Y_{m e c h} (s) = \frac{1}{n_{F}^{2}} \cdot \frac{1}{Z_{m e c h}} \end{array}$

Ezek szerint olyan energia tárolókat kell összeválogatnunk, amelyek esetében az „s” operátor egyszerűsítése révén eltűnik a paraméterek közötti átszámítás képletéből. A kondenzátor villamos impedanciája 1/sC, ehhez csak olyan mechanikai admittancia párosítható, amelynek a nevezőjében van az operátor:

$\frac{1}{s C_{p}} = \frac{1}{n_{F}^{2}} \cdot \frac{k_{c}}{s}$

Ezek szerint a piezo-kondenzátornak, a mechanikai oldalon, egy rugómerevség felel meg.

$k_{c} = \frac{n_{F}^{2}}{C_{p}}$

Az energia tárolók ellentétes típusra való „fordulását” tetézi az, hogy a dualógia (duálisan analóg) szabályai miatt a két oldalon szereplő impedancia kapcsolások is ellenpárjukra váltanak. Sorosból párhuzamos és fordítva lesz az ellenkező oldalon. Ennek következtében a kapacitásból számított rugómerevség a mechanikai rugómerevségekkel párhuzamosan kapcsolva, azok eredő értékét növeli:

$k_{e} = k_{p} + k + k_{C}$

Ezek után már felrajzolható a legegyszerűbb impedancia hálózat, és felírható a keresztváltozó osztó, mint implicit átviteli függvény.

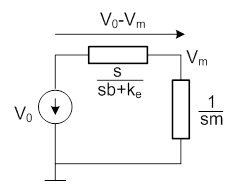
6.2. ábra - Az átviteli függvényhez „vezető” legegyszerűbb kapcsolás

$\begin{array}{l} G (s) = \frac{V_{0} (s) - V_{m} (s)}{V_{0} (s)} = \frac{\frac{s}{s b + k_{e}}}{\frac{s}{s b + k_{e}} + \frac{1}{s m}} = \frac{s^{2} m}{s^{2} m + s b + k_{e}} = \frac{s^{2} \frac{m}{k_{e}}}{s^{2} \frac{m}{k_{e}} + s \frac{b}{k_{e}} + 1} \\ G (s) = \frac{(V_{0} (s) - V_{m} (s))}{\frac{1}{s} a (s)} = \frac{s V_{k i}}{a (s)} = \frac{s^{2} \frac{m}{k_{e}}}{s^{2} \frac{m}{k_{e}} + s \frac{b}{k_{e}} + 1} \\ G (s) = \frac{V_{k i}}{a (s)} = \frac{s \frac{m}{k_{e}}}{s^{2} \frac{m}{k_{e}} + s \frac{b}{k_{e}} + 1} \end{array}$

A „V_ki(s) alakváltozási sebesség az átalakító egyik egyenlete segítségével villamos mennyiséggé számítható át, és ez az eltolási áram „I”.

$I (s) = n_{F} \cdot V (s)$

Tudjuk, hogy az áram a töltés idő szerinti deriváltja, valamint azt, hogy a töltések révén a „C_p” piezo-kapacitás fegyverzetein létrejövő feszültségkülönbség „U_p”, éppen a keresett villamos kimenet:

$\begin{array}{l} \begin{matrix} \frac{d Q}{d t} = i & \to & s Q (s) = I (s) \end{matrix} \\ U_{p} (s) = \frac{1}{C_{p}} Q (s) = \frac{1}{s C_{p}} I (s) = \frac{n_{F}}{s C_{p}} V (s) \\ V_{k i} (s) = \frac{s C_{p}}{n_{F}} U_{p} (s) \end{array}$

Behelyettesítve a kapott átviteli függvénybe:

$\frac{U_{p} (s) \frac{s C_{p}}{n_{F}}}{a (s)} = \frac{s \frac{m}{k_{e}}}{s^{2} \frac{m}{k_{e}} + s \frac{b}{k_{e}} + 1}$ ,

És végül, a valójában keresett átviteli függvényt kapjuk, gyorsulás bemenetre és villamos feszültség kimenetre:

$G (s) = \frac{U_{p} (s)}{a (s)} = \frac{n_{F}}{C_{p}} \frac{m}{k_{e}} \cdot \frac{1}{s^{2} \frac{m}{k_{e}} + s \frac{b}{k_{e}} + 1}$

A modell helyességét legegyszerűbben dimenzió analízissel ellenőrizhetjük. Az első dimenzió egyenlet az átviteli függvény bal, a második a jobb oldalának dimenzióját mutatja:

$\begin{array}{l} \frac{V s^{2}}{m} = \frac{\frac{m^{2} k g}{s^{3} A} \cdot s^{2}}{m} = \frac{k g m}{A s} \\ \frac{\frac{k g \cdot m}{V s^{2}} \cdot k g}{\frac{A^{2} s^{4}}{k g m^{2}} \cdot \frac{k g \cdot m}{s^{2}} \cdot \frac{1}{m}} = \frac{\frac{k g^{2} m}{s^{2}} \cdot \frac{1}{V}}{\frac{A^{2} s^{2}}{m^{2}}} = \frac{\frac{k g^{2} m}{s^{2}} \cdot \frac{s^{3} A}{m^{2} k g}}{\frac{A^{2} s^{2}}{m^{2}}} = \frac{k g m}{A s} \end{array}$

Dinamikai szempontból a piezoelektromos gyorsulásérzékelő másodrendű rendszer, un. PT2-tag. A méréstechnikában szokásos a Bode-diagramot normált formában megadni, így látjuk ezt az adatlapokon is. Ez azt jelenti, hogy a frekvencia-függő átviteli tényezőt |G(ω)| egy igen alacsony frekvencián mért átviteli tényezőre |G(ω=ω_ref)| vonatkoztatják, és így egyrészt dimenzió nélküli lesz a Bode-diagram függőleges tengelye, másrészt a görbe a zérus dB szinten indul. Mindaddig, amíg a görbe ±0.1 dB értékkel nem tér el a vízszintestől – ez mintegy ±1% hibát jelent, - az eszköz átvitelének arányos szakaszán „vagyunk”, és a mérés az adott frekvenciatartományban lehetséges. Azt a frekvenciát, ahol az eltérés meghaladja a ±0.1 dB értéket, a mérési tartomány felső határfrekvenciájának nevezzük. A bevezetőben már jeleztük, hogy ez a felső határfrekvencia magas lehet, esetenként, akár f_f=50 kHz (vagy ω_f=50·2π r/s), ugyanakkor hátrányos, hogy alacsony frekvenciás gyorsulások mérésére az eszköz nem alkalmas a töltések elszivárgása miatt. Használatba vétel előtt meg kell győződni a gyorsulásérzékelő és a hozzá kapcsolt töltéserősítő működési frekvenciatartományáról.

6.3. ábra - Brüel&Kjaer gyártmányú piezoelektromos gyorsulásérzékelő adatlapja

A modellezést három fontos aktuátorral folytatjuk. Tekintettel arra, hogy az előzőekben bemutatott piezoelektromos szenzor fordító váltót tartalmazott, didaktikai okok miatt az aktuátorok közül is azt vesszük elsőként, amelyik fordító váltóval épül fel.

6.2. Pneumatikus és hidraulikus munkahenger. Fordító váltók a gyakorlatban

A pneumatikus és hidraulikus átalakítók fordító váltó jellegű energia átalakítók. A fordító váltó két eltérő típusú fizikai rendszer eltérő típusú változói között teremt kapcsolatot (ld.: 2. fejezet).

A mechatronika egyik legfontosabb építőeleme a munkahenger. A hidraulikus munkahengereket kifejezetten erő, energia átvitelére tervezik, és működtetésük folyadék térfogatárammal, míg a pneumatikus munkahengerek működtetése a sűrített levegő nyomásával történik. A két aktuátor forrása tehát eltérő típusú. A pneumatikus munkahengerek (lineáris és rotációs) ugyancsak képesek az elektromechanikus rendszerekre jellemzőtől nagyobb erők kifejtésére, de túlnyomórészt csak „digitális” üzemmódban alkalmazzák őket, a lökethossz tetszőleges pozíciójában megállítani csak igen körülményes szabályozó rendszer segítségével lehet. Ilyen a szervopneumatikus pozicionáló, amelynek egy megvalósítási formáját a 18. fejezet fejezetben találjuk.

6.2.1. Hidraulikus munkahenger modellje

A működési vázlaton látható, hogy legegyszerűbb lineáris forma egy hengerből és a dugattyúhoz csatlakozó rúdból áll. A beömlő csonk áramlási ellenállása nem játszik szerepet, mert átmenő változó forrásból térfogatáram van rákényszerítve. A henger belsejének folyadék kapacitása zérus, mert a közeg összenyomhatatlan, a fluid oldalon energiatárolás nincs.

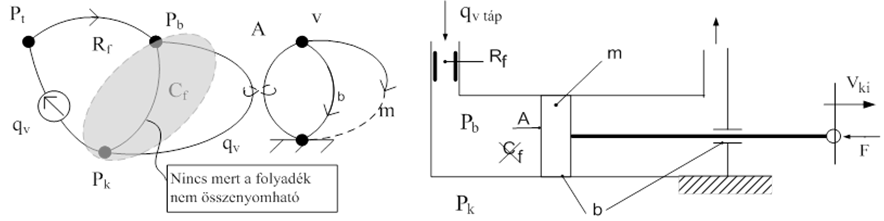
6.4. ábra - Hidraulikus munkahenger modellje és gráfja

A gráf egyszerűsíthető, a „q_v” bemenőjel teljes egészében megjelenik a fordító váltó bal oldalán. A váltó 2 egyenlete közül az, amelyik a térfogatáram és a dugattyú sebesség között írja le a kapcsolatot, megadja a mechanikai oldal sebesség forrását. Ilyen módon a mechanikai oldal elemei sem játszanak szerepet, hiszen a referenciától eltérő csomópont keresztváltozójának értékét előírjuk.

A munkahenger, mint fordító váltó egyenleteinek felírása nem igényel hosszadalmas levezetéseket, hiszen a változók közötti kapcsolat közismert. Annyi kiegészítés szükséges, hogy az erő és a nyomás közötti összefüggés tartalmaz egy negatív előjelet. Ez a csomóponti egyenletek felírása során nélkülözhetetlen, és egyben utal arra, hogy az erővektor és az „A” felület normálisa ellentétes irányúak.

$\begin{array}{l} f (t) = - A \cdot [p_{b} (t) - p_{k} (t)] \\ v (t) = \frac{1}{A} \cdot q_{V} (t) \end{array}$

A hidraulikus munkahenger dugattyújának sebességét és elmozdulását az alábbi összefüggés írja le:

$\begin{array}{l} v (t) = \frac{1}{A} \cdot q_{V} \\ x (t) = \frac{1}{A} \int_{0}^{T_{\max}} q_{V} d t \end{array}$

Amint a következő ábrán is látjuk, a hidraulikus munkahenger integráló típusú tag, amennyiben a dugattyú elmozdulását választjuk kimeneti változónak, és a bemeneti mennyiség a munkahengerre kapcsolt állandó térfogatáram, egységugrás-függvény formájában.

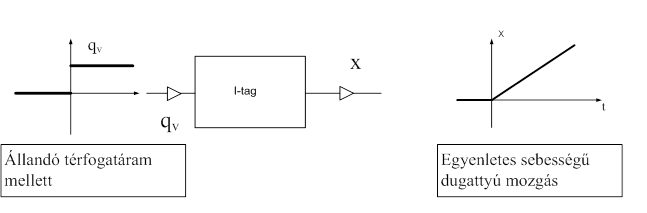
6.5. ábra - Hidraulikus munkahenger átmeneti függvénye

6.2.2. Pneumatikus munkahenger modelljei (átviteli függvény és ÁTM)

Lényegesen bonyolultabb a helyzet, ha a pneumatikus munkahenger modelljét akarjuk meghatározni. A rendszer fluid oldalán megmarad a belépő csonk (szűkület) által előidézett áramlási ellenállás, és megmarad a henger üregének energiatároló képessége is. A forrás, mint már jeleztük, nyomás, tehát keresztváltozó.

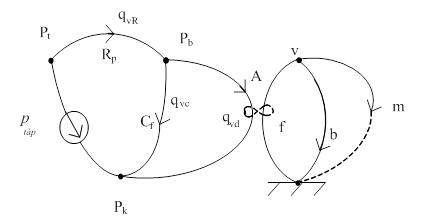
6.6. ábra - Pneumatikus munkahenger gráfja

Mechanikai oldalon a tömeg és a dugattyú tömítései által létrehozott, nem kis értékű csillapítás az identifikálható két elem. A két energiatároló, a fliud kapacitás és a tömeg típusra azonosak lennének, de a két rendszerrész közötti fordító váltó miatt másodrendű lesz a rendszer.

Elsőként impedancia módszerrel vezetjük le a rendszer átviteli függvényét, mert az átszámítás tanulságos. A keresett kimenet a dugattyú sebessége, illetve elmozdulása, tehát célszerű a pneumatikus rendszerrész elemeit és forrását átszámítani a mechanikai oldalra. Annál is inkább, mert ez az átszámítás jól mutatja a dualóg rendszerek esetében adódó feladatokat. A végső, legegyszerűbb alak egy keresztváltozó osztó lesz. A végső hálózat terhelő impedanciája a mechanikai rendszerrészben látható két párhuzamos impedancia eredője.

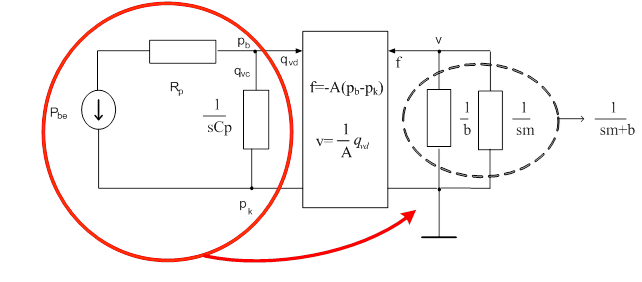
6.7. ábra - Pneumatikus munkahenger impedancia hálózata

Az egyszerű keresztváltozó osztó kapcsolást mutatja a következő ábra. Az aktív rész „Z_b” belső impedanciáját és az új „V₀”keresztváltozó forrást a következő lépésekben fogjuk meghatározni.

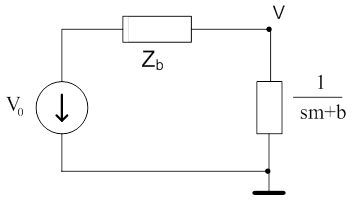
6.8. ábra - Az átviteli függvényt adó legegyszerűbb kapcsolás általános impedanciákkal

Az átviteli függvény formájában megadott modell az alábbi lesz:

$G (s) = \frac{V (s)}{V_{0} (s)} = \frac{\frac{1}{s m + b}}{Z_{b} + \frac{1}{s m + b}}$

A pneumatikus impedanciák átszámításához a már ismert módon kell a fordító váltó egyenleteit felhasználni. Az átalakító egyenleteit Laplace transzformált alakban írjuk fel:

$\begin{array}{l} F (s) = - A \cdot [p_{b} (s) - p_{k} (s)] \\ v (s) = \frac{1}{A} \cdot q_{V} (s) \end{array}$

A külső nyomást a vizsgálat idejére állandónak, sőt referenciának tekintjük. Mindkét oldalon elvégezzük az osztást, amelynek eredményeként a mechanikai oldalon admittanciát, a pneumatikuson impedanciát kapunk:

$\frac{F (s)}{V (s)} = Y_{m e c h} (s) = A^{2} \cdot \frac{p (s)}{q_{V} (s)} = A^{2} \cdot Z_{p n e u} (s)$

Feladatunk megtalálni azokat az elemeket, amelyek esetében az átszámítás során egyszerűsíthető az operátor.

$Y_{m e c h} (s) = s m = A^{2} \cdot Z_{p n e u} = A^{2} \cdot s L_{p n e u}$

Első próbálkozásunk eredménytelen, mert a pneumatikus rendszerekben nincsen „induktív” jellegű energiatároló. Ugyan a vizsgált pneumatikus rendszerben nem is találunk ilyen tárolót, de a teljesség kedvéért lefolytattuk a próbát. A másik mechanikai energiatárolóval már más a helyzet:

$Y_{m e c h} (s) = \frac{k}{s} = A^{2} \cdot Z_{p n e u} = A^{2} \cdot {\frac{1}{s C}}_{p n e u}$

A pneumatikus rendszerrészben van kapacitív tároló, és látjuk, hogy ennek a mechanikai oldalon rugómerevség felel meg. Ezt a műszaki érzékünk alapján eddig is tudtuk, hiszen a pneumatikus kapacitás a légrugó szemléletes példája.

Az új mechanikai keresztváltozó forrás az átalakító egyenletéből adódik. Az átszámításnál, akárcsak az impedanciák esetében, nem vesszük figyelembe az előjelet.

$F_{P} (s) = A \cdot (p_{t á p} - p_{k}) = A \cdot p_{b e}$

Átszámítjuk tehát a pneumatikus kapacitást és az ellenállást, valamint azt is figyelembe kell vennünk, hogy a pneumatikus oldal kapcsolása is ellentétesre fordul a másik oldalon.

	$k_{C} = \frac{A^{2}}{C_{p n e u}}$
	$b_{R p} = A^{2} \cdot R_{p n e u}$

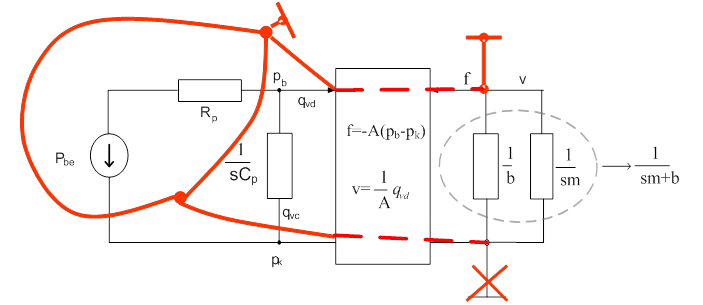
6.9. ábra - A legegyszerűbb kapcsoláshoz vezető út részletezése

A dualóg (duálisan analóg) kapcsolás megszerkesztését segíti a fenti ábra. A pneumatikus oldalon kijelölünk a hurok helyére egy (ellentétes) csomópontot, és az új referencia is megjelenik csomópontként, ami az eredeti kapcsoláson kívüli teret helyettesíti. Az új csomópontokat úgy kötjük össze, hogy közben „átvágjuk” az eredeti kapcsolás impedanciáit, és az energiatárolók esetében ellentéteset teszünk a helyére. A disszipatív elem (ellenállás) jellegre nem változik. A fordító váltó szerepe megszűnik, az ábrán látható piros vonalat továbbhúztuk a mechanikai oldal felé. A mechanikai oldalon a rajztechnikai okok miatt felülre rajzoltuk át a referenciát.

A következő ábra az egyenértékű mechanikai rendszer impedancia hálózatát mutatja. Bejelöltük az aktív és passzív rész

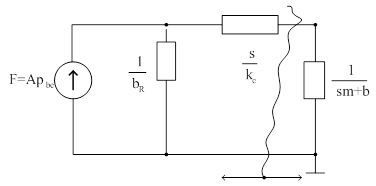
6.10. ábra - Balra az aktív, jobbra a passzív rész

Az aktív rész „Z_b” belső impedanciáját a szétválasztás után szabaddá váló kapcsok felől az aktív rendszerrész felé „benézve” határozzuk meg:

$Z_{b} = \frac{s}{k_{C}} + \frac{1}{b_{R}} = \frac{s b_{R} + k_{C}}{k_{C} \cdot b_{R}}$

Az aktív rész egyenértékű keresztváltozó forrásának kiszámítása a következő feladat. Ebben az esetben a terheletlen aktív rész maximális keresztváltozó értéke az üresjárat, és ezért az s/k_C impedancia nem játszik szerepet. Az erőforrás Thevenin ekvivalense az Ohm törvény révén számítható:

$V_{0} (s) = F \cdot \frac{1}{b_{R}} = A \cdot p_{b e} \cdot \frac{1}{b_{R}}$

Minden együtt áll a legegyszerűbb kapcsolás megrajzolásához, és az átviteli függvény (keresztváltozó osztó) felírásához:

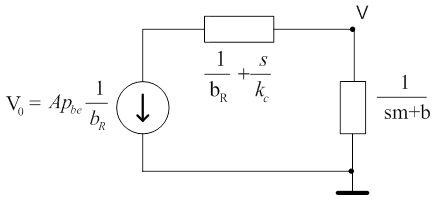
6.11. ábra - A keresztváltozó osztó konkrét impedanciákkal

$G (s) = \frac{V (s)}{p_{b e} (s)} = \frac{A}{b_{R}} \cdot \frac{\frac{1}{s m + b}}{\frac{s b_{R} + k_{C}}{b_{R} k_{C}} + \frac{1}{s m + b}} = \frac{A k_{C}}{s^{2} m b_{R} + s (m k_{C} + b_{R} b) + k_{C} (b + b_{R})}$

Az átviteli függvény szabályozástechnikai alakja, amely nevezőjében az operátortól független tag egyre van normálva, segíti a dimenzió ellenőrzést is.

	$G (s) = \frac{V (s)}{p_{b e} (s)} = \frac{A}{(b + b_{R})} \frac{1}{s^{2} \frac{m b_{R}}{k_{C} (b + b_{R})} + s \frac{m k_{C} + b_{R} b}{k_{C} (b + b_{R})} + 1}$
	$G (s) = \frac{V (s)}{p_{b e} (s)} \approx \frac{A}{(b + b_{R})} \frac{1}{s^{2} T_{p n e u} T_{m e c h} + s (T_{p n e u} + T_{m e c h}) + 1}$

A pneumatikus munkahenger túlcsillapított másodrendű tag. Az átviteli függvény karakterisztikus polinomjából a túlcsillapítás miatt két valós gyök származik, és ebből következően két időállandó. Az időállandók elkülöníthetőek: T_pneu= b_R/k_C és T_mech≈m/b. A mechanikai időállandó esetében jó közelítés jelölés azért indokolt, mert b»b_R. Olyan rendszerben, ahol van visszahatás is, pl. két RC elemből álló, soros villamos rendszer esetében, az elsőfokú operátor együtthatója két időállandót és egy vegyes tagot is tartalmaz. Ebben az esetben viszont a dugattyúsúrlódást modellező „b” csillapítási tényező értéke meghatározó, vegyes tag elhanyagolható. A következő ábra az átmeneti függvényt (dugattyú sebesség) és annak integráltját (elmozdulás) mutatja, kissé torzított formában, mert a tranziens szakasz fel van nagyítva.

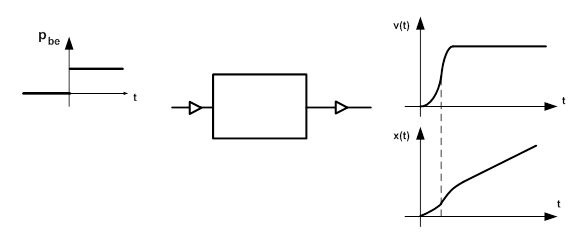
6.12. ábra - Pneumatikus munkahenger átmeneti függvénye

A lappangási idő oka kettős: A kamra belső nyomása az R_pC_p=b_R/k_C pneumatikus időállandó miatt fokozatosan alakul ki, és, ha az „A” felületre ható erő eléri azt a szintet, amely mellett a tömítés miatti súrlódási erőt képes legyőzni, megindul a dugattyú. E folyamatok miatt a pneumatikus munkahenger nem alkalmazható precíziós pozicionálásra. Ilyen jellegű feladatot a bevezetőben említett szervopneumatikus szabályozással, a dugattyú mindkét oldalán létrehozott, és szabályozott nyomásértékekkel lehet megvalósítani, ld.: 18. fejezet. Költségessége miatt az iparban eddig nem tudott átütő módon elterjedni.

6.3. Egyenáramú szervomotor és tachogenerátor modelljei. Váltók a gyakorlatban

A DC motor és a tachogenerátor az elektrodinamikus váltók csoportjába tartozik. A váltó olyan energia átalakító, amely két eltérő típusú fizikai rendszer azonos típusú változói között teremt kapcsolatot. (ld.: 2. fejezet).

Az elektrodinamikus átalakító (forgó és egyenes vonalú) működésének fizikai háttere a Lorentz erő és a mozgási indukció. E két törvény adja az adott konstrukció átalakítási tényezőjét, amelyet „n_v” jelöléssel látunk el, az indexben utalva a váltó jellegre. A dinamikai modellezés eszköztárával foglalkozó fejezetben ismertettük az energia átalakítók három változatát.

Az elektrodinamikus váltó egyenleteinek meghatározásához először is vissza kell nyúlnunk a Lorentz erőhöz. A magyarázó szövegben megjelennek vektorok (dF, B, v, ds) és skalármennyiségek (i, q), ahogy ezt a törvény eredeti formájában bemutatjuk. Ismert, hogy a „B” mágneses indukciójú térben „v” sebességgel mozgó „q” elemi töltésre (definíciószerűen ez pozitív) dF részerő hat. Ha a töltés nem szabad térben, hanem vezetőben mozog, akkor áramról beszélünk. Ezért az előbbi mondat kiegészíthető azzal, hogy az „i” árammal átjárt vezető „ds” darabjára dF erő hat a „B” indukciójú mágneses térben.

$d \vec{F} = q (\vec{v} \times \vec{B}) + i (d \vec{s} \times \vec{B})$

A mechatronikában szokásos rendszerek esetében a tekercs, mint fő alkotórész egyértelműsíti, hogy az erőegyenlet második része az, amelyre jelen esetben építünk. Az összefüggés igen gyakran hibásan szerepel katalógusokban, mert az áramot vektorként tüntetik fel, holott nem az áram, hanem az áramsűrűség a vektormennyiség. Helyesebb a képletből kiindulni a magyarázatban. Ott ugyanis a „ds” vezetődarab a gépész számára egyértelműen vektort jelent, amelynek irányát a töltések mozgásának irányával lehet összefüggésbe hozni. Ismét óvatosnak kell lenni, mert a definíció pozitív „q⁺” töltésekről és nem a negatívakról „q-” szól. A keletkező erő irányának meghatározásánál ezért pozitív töltések mozgási irányának ismeretében a „jobbsodrású”, a negatív töltések esetében pedig a „balsodrású” vektorszámítást használjuk. A kezünk hüvelyk, mutató, és középső ujját egymásra merőlegesen „rendezzük”. Pozitív töltések esetében a jobb kéz hüvelykujja a töltések mozgásának iránya, a mutatóujj a mágneses indukció iránya, és a középső ujj a vektor-szorzás eredményeként megjelenő erő iránya. Történelmileg, és megállapodás szerint az elektromos áramlás iránya a pozitív töltéshordozók (valóságos vagy elképzelt) áramlásának irányával egyezik meg. Az áram irányának ilyen, hagyományos értelmezése a legtöbb vezetőben (pl. fémekben) ellentmond a valóságnak, mivel azokban a negatív töltéshordozók (elektronok) áramlanak. Gyakorlati okok miatt, e tény ellenére, áramirányon ma is a hagyományosan definiált áramirányt értjük. A szakirodalom beszél „műszaki” áram irányról is, ez az elektronok mozgása a negatív pólus felől a pozitív pólus irányába.

Ez az irány-probléma a keletkező erő irányának egyértelmű meghatározása miatt lényeges.

Az összefüggés alapján, a „ds” vezetődarabokból álló tekercsrész eredő, vagy „aktív” hosszára összegzés segítségével kapjuk a teljes „F” erőt. Mi is lesz a tekercs „aktív” része, az átalakításban résztvevő összes vezetőhossz? Az egyenlet választ ad erre a kérdésre is, mert abban a „ds” és a „B” mennyiségek vektorszorzata szerepel. Az erő létrehozásában tehát csak azok a „ds” vezetődarabok vesznek részt, amelyek metszik a „B” indukcióvonalakat. A szorzás vektoriális, tehát az erővonalak által bezárt szög szinusza határozza meg a szorzat nagyságát, amely így 90º esetében maximális.

Az összefüggés skalár és egyszerűbb alakban tehát így írható fel:

$F = (l_{a k t} B) \cdot i$

A csomóponti szabályok miatt ezt az egyenletet „ellátjuk” egy negatív előjellel. Ugyanakkor azt is tudjuk, hogy az „i” elektronáramot tekintve ez a negatív előjel a „valóságot” is tükrözi.

A zárójeles kifejezés a váltó egyik egyenlete:

$F = - n_{v} \cdot i$

A fejezet elején már említettük, hogy az áram hatására megmozduló vezetőben, a mágneses tér jelenlétében feszültség indukálódik. Az adott szerkezet felépítéstől függően a tekercs mozgása lehet forgó és lehet egyenes vonalú.

Az átalakító másik egyenlete a mozgási indukción alapul:

$u_{i n d} = \int_{s_{1}}^{s_{2}} \vec{E} \cdot d \vec{s} = \int_{s_{1}}^{s_{2}} (\vec{v} \times \vec{B}) \cdot d \vec{s}$

Tudjuk, hogy az elektromos és a mágneses terek egymással összefüggenek. Ha a „ds” vektor ismét az áram által átjárt vezetődarab, akkor a fenti összefüggést a következőképpen magyarázhatjuk. A „ds” vezetődarabban, azzal egy irányban „E” villamos erőtér jön létre, ha a vezetődarab „v” sebességgel mozogva metszi a „B” indukcióvonalakat. Definícióból tudjuk, hogy az „E” erőtér a pozitív villamos töltésekre hat. Ebből következően tudjuk, hogy a teljes, a mágneses erőteret merőlegesen metsző, tehát aktív vezetőhosszban az integrál alapján létrejövő u_ind indukált feszültség mely irányban mozgatja az elektronokat, és milyen lesz a teljes vezetőn fellépő polaritás.

Írjuk ezt az összefüggést is egyszerűbb alakba:

$u_{i n d} = (l_{a k t} B) \cdot v$

Fentebb láttuk, hogy a zárójeles kifejezés az átalakítási tényező:

$u_{i n d} = n_{v} \cdot v$

Az elektrodinamikus átalakító két egyenlete a szokásos formában felírva mutatja, hogy a két irány között számértékét tekintve ugyanaz a tényező szerepel, és azonosak a dimenziók is, az eltérés csupán látszólagos. Ezt az impedancia módszer alkalmazásánál és a dimenzió ellenőrzésnél kell tudni. A „r” (radián) dimenzió nélküli mennyiség.

$\begin{matrix} M_{v} = - n_{v} \cdot i & \to n_{v} [\frac{N m}{A} = \frac{\frac{k g m}{s^{2}} \cdot m}{A} = \frac{k g m^{2}}{s^{2} A}] \\ Ω = \frac{1}{n_{v}} \cdot u & \to n_{v} [\frac{V s}{r} = \frac{\frac{k g m^{2}}{s^{3} A} \cdot s}{r} = \frac{k g m^{2}}{s^{2} A}] \end{matrix}$

Az átszámítás során, az átalakítási tényező négyzetének esetében, a gyorsabb ellenőrzés érdekében, a következő dimenzióval célszerű számolni:

$n_{v}^{2} [\frac{N m \cdot V s}{A \cdot r}]$

A következő alfejezetekben példákat mutatunk be elektrodinamikus váltót tartalmazó rendszerekre

Az alcímben szereplő aktuátor és szenzor mellett a mechatronikában, és általában a műszaki életben sok ilyen típusú váltót tartalmazó eszközzel találkozunk. Ilyen az elektrodinamikus hangszóró, a dinamikus mikrofon, az elektrodinamikus rázóasztal, a merülő tekercses lineáris motor.

6.3.1. A DC motor (aktuátor)

A mechatronikában jelenleg talán leggyakrabban alkalmazott aktuátor és szenzor a DC motor, és „inverze” a tachogenerátor. A működésük fizikai elvei szétválaszthatatlanok, de méretre és műszaki paramétereiket tekintve természetesen jelentősen eltérnek egymástól. Alapvetően mindkét esetben elektrodinamikus energia átalakítóról van szó, ami annyit jelent, hogy működésükhöz kettő plusz egy dolog szükséges: Az első kettő a mágneses tér (állandó, vagy változó) és villamos vezetőből megfelelően kiképzett tekercs. A tekercsben megjelenő áram és a mágneses tér kölcsönhatására a tekercsre erő hat, és létrejön a mechanikai mozgás, amelynek fizikai alapja a Lorentz erő. Ugyanakkor abban a pillanatban, amikor az áram hatására „megmozdul” a tekercs, hat az elektrodinamika másik törvénye, és a mozgási indukció miatt, a tekercs két végpontja között megjelenik az indukált feszültség. Gépész alapokon álló szakember nem felejtheti el, hogy szabályos mozgások csak vezetékkel biztosíthatók. Ez a „plusz” feltétel. Motor és tachogenerátor esetében csapágyazás, lineáris, merülő tekercses motor esetében pedig többnyire rugalmas egyenes vezeték.

A motor esetében a „kivehető” mechanikai teljesítmény érdekében nagyobb áramokra tervezik a tekercseket és a keféket, míg a tachogenerátor esetében az eszköz „jelet” és nem teljesítményt szolgáltat. Méretezése is ennek megfelelően történik.

Meg kell jegyezni, hogy ez a „kettősség” az elektronikusan kommutált DC motorokra nem áll fenn. Az elektronikusan kommutált DC motorok felépítésben is eltérnek, mert ezeknél a forgórész állandó mágnes, tehetetlenségi nyomatéka ennek megfelelően nagyobb, és az állórész tekercseit szekvenciálisan gerjesztve hozzák létre a forgó mágneses teret, mozgásba hozva a forgórészt.

A klasszikus DC motor állórésze állandó mágnesből és lágyvasból álló mágneses kör, amelynek a légrésében forog a tekercs, a forgórész. A tekercselés lehet serleg alakú, és lehet lapos kivitelű. Az állandó forgásirány biztosítása un. kommutátor és érintkező kefék segítségével történik. A kefék anyaga kopásálló ezüst ötvözet, nagyobb gépeknél grafit. A kereskedelemben kapható kisebb, a mechatronikában alkalmazott kefés DC motorok esetében leggyakrabban 3, 5, vagy 7 tekercs bekezdés található a forgórészen. A több bekezdéssel a motor villamos forgatónyomatékának egyenletesebbé tétele érhető el. A valóságban ezek a motorok „lüktetve” járnak, a Lorentz erő által létrejövő nyomaték kisebb-nagyobb mértékben ingadozik a forgórész körülfordulása során. A modellezés során, ennek ellenére a szögelfordulás függvényében állandónak tekintjük a villamos eredetű forgatónyomatékot. A motorra jellemző váltó állandót gépállandónak, vagy nyomatékállandónak nevezik. Definíciója szerint, és skalár alakban:

$K_{M} = c \cdot Φ = \frac{z \cdot p}{a} \cdot Φ$

ahol „Φ” a légrés fluxus, „c” a motor műszaki jellemzőit foglalja magába: „z” a forgórész kerületén lévő vezetők száma, „p” az állórész mágnese pólusainak száma (2p a pólus-pároknak felel meg) és „a” a párhuzamos ankerág-párok száma (hullámtekercselésnél a=1, huroktekercselésnél a˃1).

Tehát a DC motor, mint elektrodinamikus váltó esetében, a váltó állandója n_v=K_M. Ezzel az alábbi összefüggéseket kapjuk:

$\begin{array}{l} M_{v} = - K_{M} \cdot i \\ Ω = \frac{1}{K_{M}} \cdot u \end{array}$

A motor általános felépítését az alábbi ábra mutatja. A képen látható tekercselés speciális, ennél a serleges kialakításnál a Faulhaber licenc alapján készült. Tulajdonképpen önhordó kompozitról van szó, amelyben a mátrix műgyanta, a villamos vezető pedig a szálmerevítés. A tekercselés menetei a merevség növelése érdekében szimmetrikusan keresztezik egymást, a menet a motor hossztengelyéhez viszonyítva szöget zár be. Az emiatt keletkező axiális erőkomponensek párban kiegyenlítik egymást.

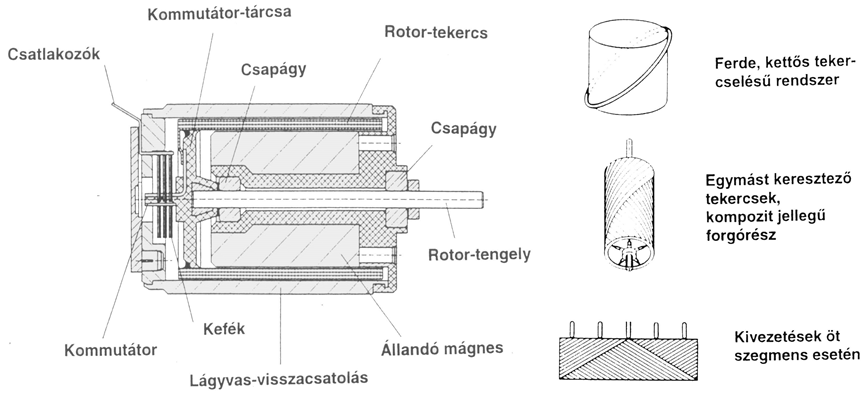
6.13. ábra - DC mikromotor metszete és a forgórész tekercselése (Faulhaber)

A szerkezeti vázlat alapján megszerkeszthető a motor gráfja. A villamos rész két elemet tartalmaz, a tekercs ellenállását és a nyugalmi induktivitását. Ez utóbbi azt a fizikai jelenséget modellezi, amely szerint a mágneses térhez képest nyugalomban lévő tekercsben villamos feszültség indukálódik, amely a tekercsben fellépő áram időbeli változásával függ össze. Induláskor, ha a motor bemenetére u_be(t) villamos feszültséget, „kapocsfeszültséget” kapcsolunk, a forgórész (armatúra) tekercsében exponenciálisan felfutó áram maximális értékű lesz, majd a mozgási indukció révén indukálódó feszültség miatt ez az áram korlátozódik a fordulatszám növekedésével, hiszen a kapocsfeszültség és az indukált feszültség egymás ellen hatnak.

A váltó mechanikai oldalán két passzív elem van, a tekercs tehetetlenségi nyomatéka és a csapágysúrlódást modellező csillapítási tényező. A gráfban a mechanikai oldalon egy átmenő változó forrás képében megjelenítettük az időben változó terhelő nyomatékot. Ha ezt a gráf élet elhagyjuk, a motor üresjárati modelljét kapjuk. Az összetett mechatronikai rendszerekben ezt a terhelő nyomatékot jelképező gráf élet például a valós hajtómű eredő torziós rugalmassága váltja fel, és utána következik a hajtómű többi eleme.

A következő ábra egy kisebb teljesítményű, a mechatronikában, főként a robottechnikában alkalmazott motortípus nyomaték-fordulatszám jelleggörbéjét mutatja.

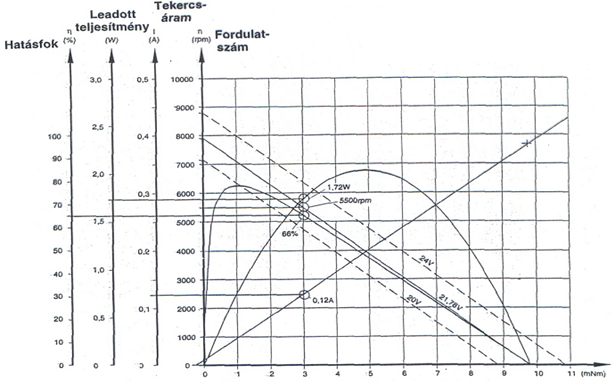
6.14. ábra - Egy DC mikromotor jelleggörbéi (Faulhaber)

A teljesség kedvéért, és a módszerek összehasonlítása érdekében mindhárom módszert bemutatjuk a matematikai modellek felírásához, és bemutatjuk modellek közötti átszámítási lehetőségeket is:

Hurok/csomóponti módszer→Mátrix-egyenlet→Átviteli függvény →Differenciálegyenlet→Állapottér modell
Hurok/csomóponti módszer→Állapottér modell→Átviteli mátrix→Átviteli függvény
Impedancia módszer→ Átviteli függvény→(Differenciálegyenlet)

6.3.1.1. Hurok és csomóponti módszer

A DC motor példája és gráfja egy lényeges, gyakorlati modellezési szabály bemutatását teszi lehetővé. Ismeretes, hogy egy gráf esetében a változók meghatározására csomóponti, vagy hurok egyenleteket írunk fel. Az egyenlet típusok nem keverhetőek. Az összes keresztváltozó a csomóponti, míg valamennyi átmenő változó a hurok egyenletek alkalmazásával írható fel.

Olyan gráfok esetében azonban, amelyekben energia átalakító található, ez a megkötés felesleges, és csak a különböző rendszerrészekre korlátozódik. Miután a rendszerrészeket egy konstans köti össze, lehetséges minden részben más-más módszert alkalmazni.

A DC motor esetében a villamos részre célszerű hurok egyenletet felírni, míg a mechanikai oldalra csomópontit. A villamos „i” hurokváltozót egy konstans, a „K_M” köti a mechanikai oldal csomóponti egyenleteibe. A két egyenlet alatt megjelenítettük a váltó egyenleteit is, hiszen ezek nélkül az egyenletek nem köthetők egymáshoz.

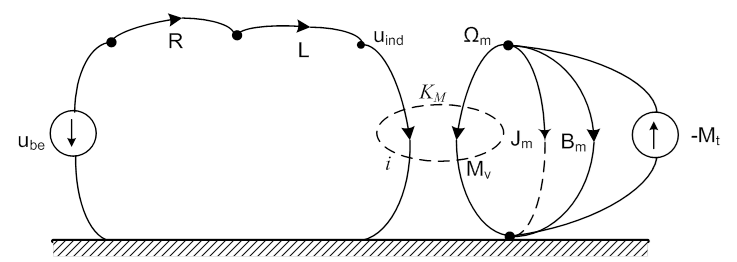
6.15. ábra - DC szervomotor gráfja

Az „i” hurokváltozó célszerűen kijelölt iránya meghatározza a keresztváltozó különbségek előjelét, ami egyezik, pozitív, ami nem, negatív. Az „Ω” csomóponti változóra felírt egyenleteknél legyen pozitív a kifelé mutató élek, és negatív a befelé mutató élek előjele. A szimulált terhelő nyomatékot a gráfban átmenő változó forrásként modellezzük, mert nincsen más szimbólum, de a negatív előjel utal arra, hogy nem gerjesztésről, hanem forgatónyomaték „kivételről” van szó.

$\begin{array}{l} - u_{b e} + u_{R} + u_{L} + u_{i n d} = 0 \\ M_{V} + M_{B} + M_{J} - (- M_{t}) = 0 \\ M_{V} = - K_{M} i \\ u_{i n d} = K_{M} Ω \end{array}$

Behelyettesítve a fizikai és a váltó egyenleteket, az alábbi differenciálegyenlet rendszert kapjuk:

$\begin{array}{l} i R + L \frac{d i}{d t} + K_{M} Ω = u_{b e} \\ - K_{M} i + B Ω + J \frac{d Ω}{d t} = (- M_{t}) \end{array}$

Ezt az alakot minden hasonló esetben „forrás-értékű” alaknak tekinthetjük, és megtaláljuk több szakirodalomban, például a B. C. Kuo Önműködő szabályozott rendszerek című munkájában [6.2.] is. Megjegyezzük azt is, hogy hálózati módszerrel kevesebb munkával tudtuk ezt a differenciálegyenlet rendszert felírni, mint az energia módszerrel, lásd: 1. fejezet. Forrás-forma, mert ezen a ponton elválhatnak ugyanis a további utak:

Ha állapottér modellt kell felírnunk, akkor ezt a legcélszerűbb ebből a formából kiindulva megtenni.
Ha átviteli függvény, és/vagy differenciálegyenlet keresett, akkor Laplace transzformálás után algebrai egyenletrendszert hozunk létre, majd a további lépések a mátrix-vektor műveletek alkalmazásával lehetségesek.

Elsőként legyen keresett az átviteli függvény, és a vele kapcsolatos differenciálegyenlet, ezért Laplace-transzformáljuk a két differenciálegyenletet. A nagybetűk a változók Laplace transzformáltját jelentik:

$\begin{array}{l} R I + s L I + K_{M} Ω = U_{b e} \\ - K_{M} I + B Ω + s J Ω = (- M_{t}) \end{array}$

Mátrixos alakba írjuk az egyenletrendszert:

$[\begin{matrix} R + s L & K_{M} \\ - K_{M} & B + s J \end{matrix}] \cdot [\begin{matrix} I \\ Ω \end{matrix}] = [\begin{matrix} U_{b e} \\ - M_{t} \end{matrix}]$

Bizonyos szabályosságok azonnal felismerhetők. A hurokegyenletből származó sorvektor impedanciákat és az átalakító konstansát, a csomóponti egyenletből származó sorvektor admittanciákat és az átalakító konstansát tartalmazza. A főátló elemei pozitívak.

Tovább lépve el kell dönteni, hogy mindkét változót keressük, vagy csak az egyiket. Ha mindkettőt, akkor a mátrixot invertálni kell:

$[\begin{matrix} I \\ Ω \end{matrix}] = {\underline{\underline{M}}}^{- 1} [\begin{matrix} U_{b e} \\ - M_{t} \end{matrix}] = \frac{a d j \underline{\underline{M}}}{\det \underline{\underline{M}}} [\begin{matrix} U_{b e} \\ - M_{t} \end{matrix}]$

Az invertáláshoz kijelölt műveleteket ebben a feladatban nem végezzük el, először a motor jellegzetes kimenőjelére, a szögsebességre írjuk fel a modelleket. Ha csak egy változó keresett, akkor célszerű a Cramer szabályt alkalmazni:

$Ω = \frac{| \begin{matrix} R + s L & U_{b e} \\ - K_{M} & - M_{t} \end{matrix} |}{\det \underline{\underline{M}}} = \frac{K_{M} U_{b e} - (R + s L) M_{t}}{(R + s L) (B + s J) + K_{M}^{2}}$

Elvégezzük a műveleteket, és az operátor csökkenő hatványai szerint rendezzük a nevezőt:

$Ω = \frac{K_{M} U_{b e} - (R + s L) M_{t}}{s^{2} L J + s (R J + L B) + R B + K_{M}^{2}}$

Az operátortól független taggal beosztva két átviteli függvényre és a hozzájuk kapcsolódó bemenőjelekre választjuk szét a kapott alakot:

$Ω = \frac{\frac{K_{M}}{R B + K_{M}^{2}}}{s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1} U_{b e} - \frac{\frac{s L + R}{R B + K_{M}^{2}}}{s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1} M_{t}$

Felismerhető a szuperpozíció szabálya, amelyet az impedancia módszer esetében kell, majd alkalmazunk, több forrás előfordulása esetén. A szuperpozíció felhasználása természetesen csak lineáris rendszerek esetében jöhet szóba.

A két átviteli függvény a két forrás felől nézve külön-külön adja meg a kimenőjel egy-egy részét:

$Ω = {Ω_{U} |}_{M_{t} = 0} - {Ω_{M}_{t} |}_{U = 0} = G_{U} U_{b e} - G_{M} M_{t}$

Mindkét átviteli függvény karakterisztikus polinomja azonos, hiszen egyazon rendszer viselkedését írják le. A rendszer másodrendű, hiszen két energia tárolója van, „L” és „J”. Szép példája ez a mechatronikai részrendszerek energia átalakítón keresztül megvalósuló egymásra hatásának, hiszen egymás mellett szerepelnek az eltérő típusú rendszerekhez tartozó paraméterek.

Az átviteli függvényekből a differenciálegyenlet inverz Laplace transzformáció segítségével előállítható. Nézzük a „G_U” átviteli függvényt:

$G_{U} (s) = \frac{Ω}{U_{b e}} (s) = \frac{\frac{K_{M}}{R B + K_{M}^{2}}}{s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1} = \frac{b_{0}}{a_{2} s^{2} + a_{1} s + a_{0}}$

Az átviteli függvényben az általános paraméteres jelölést alkalmaztuk, mert az operátor négyzetes tagja melletti „a₂” paraméterben összefoglalt összefüggés nem azonos az időállandó négyzetével. Itt ugyanis megjelennek a disszipatív paraméterek. Az „átszorzás” eredményeként először a differenciálegyenlet operátor térbeli formáját kapjuk, majd inverz Laplace transzformálás után a keresett időtartománybeli modellt.

$\begin{array}{l} a_{2} s^{2} Ω (s) + a_{1} s Ω (s) + a_{0} Ω (s) = b_{0} U_{b e} (s) \\ a_{2} \ddot{Ω} (t) + a_{1} \dot{Ω} (t) + a_{0} Ω (t) = b_{0} u_{b e} (t) \end{array}$

Az állapottér modell ebből a másodrendű differenciálegyenletből is előállítható, visszavezetéssel. A kapott modellt az állapotirányításban „normál” alaknak is nevezik. A német szakirodalomban a „normál alak” megjelölést azért alkalmazzák, mert a stabilitás tervezése, a gyökök elhelyezkedésének megadása révén, e forma alkalmazásával egyszerű. Megjegyezzük, hogy magasabb rendszámú differenciálegyenletek esetében ez a módszer szükségképpen olyan állapottér modellhez is vezethet, amelyben az állapotjelzők egyike-másika mögött nincs valós, mérhető fizikai jellemző. Jelen esetben, a visszavezetés módszerével, a szögsebesség és a szöggyorsulás lesz a két állapotjelző. Ha gyakorlatban nem is minden esetben, de ez a két fizikai mennyiség legalább elvben mérhető.

	$\begin{array}{l} Ω = x_{1} \\ \dot{Ω} = {\dot{x}}_{1} = x_{2} \end{array}$
	$\begin{array}{l} {\dot{x}}_{1} = x_{2} \\ {\dot{x}}_{2} = - \frac{a_{0}}{a_{2}} x_{1} - \frac{a_{1}}{a_{2}} x_{2} + \frac{b_{0}}{a_{2}} u_{b e} \end{array}$

Az állapottér modellre a későbbiekben még visszatérünk.

A mechatronikában, különösképpen a robottechnikában alkalmazott kisméretű DC motorok „L” nyugalmi induktivitása igen csekély, és a jó csapágyazásnak, valamint a kis kefesúrlódásnak köszönhetően szintén kicsi a „B” csillapítási tényező értéke is. Ezért találjuk meg a gyártók katalógusaiban az un. elektromechanikus időállandót az adatok között, és azt az ajánlást is, hogy a motort elsőrendű rendszerként célszerű modellezni.

A motor un. üresjárati átviteli függvénye, ha „L” és „B” paraméterektől eltekintünk:

$G (s) = \frac{Ω}{U_{b e}} (s) = \frac{\frac{1}{K_{M}}}{s \frac{R J}{K_{M}^{2}} + 1} = \frac{A}{s T_{e l m e c h} + 1}$

A szabályozástechnikában gyakran a fenti átviteli függvénnyel közelítik a DC motor dinamikai viselkedését. Ha a motorhoz „ideális” hajtómű is csatlakozik, akkor az átviteli függvény alakja nem változik, csak az időállandó. Annak ellenére, hogy a nagyobb tehetetlenségi nyomaték hatásaként elvárható lenne az időállandó csekély növekedése, a hajtómű súrlódásai miatt az időállandó a gyakorlatban kisebb lesz, a motor-hajtómű egység „kifutási görbéje” megrövidül. Erről részletes magyarázat található az 1. fejezet fejezetben, és a jelenségről könnyű kifutási mérésekkel meggyőződni.

6.3.1.2. DC motor állapottér modellje

Ahogy a hurok-és csomóponti egyenletek felírásánál jeleztük, ott található az a „stratégiai” pont, ahol a célnak megfelelő utak szétválnak. Láttuk, hogy az egyenletek Laplace transzformálása révén algebrai egyenletrendszert kapunk, és a keresett változó(k) meghatározása mátrix-vektor műveletekkel történik.

Ha a másik utat kell járnunk, mert a cél az állapottér modell felírása valós, mérhető fizikai változók formájában megjelenő állapotjelzőkkel, akkor a hurok és csomóponti egyenletekben kell definiálni az állapotjelzőket:

$\begin{array}{l} i R + L \frac{d i}{d t} + K_{M} Ω = u_{b e} \\ - K_{M} i + B Ω + J \frac{d Ω}{d t} = (- M_{t}) \end{array}$

Az induktivitás, mint energiatároló állapota az átmenő változó segítségével (i) írható le. A tehetetlenségi nyomaték állapotjelzője a keresztváltozó (Ω) lesz. A bemeneti vektor két függvényt tartalmaz.

$\begin{array}{l} {\underline{x}}^{T} = [\begin{matrix} i & Ω \end{matrix}] \\ {\underline{u}}^{T} = [\begin{matrix} u_{b e} & - M_{t} \end{matrix}] \end{array}$

Az állapottér modell (ÁTM) főegyenlete a fentiekkel így írható fel:

$\begin{array}{l} \frac{d i}{d t} = - \frac{R}{L} i + \frac{K_{M}}{L} Ω - \frac{1}{L} u_{b e} \\ \frac{d Ω}{d t} = \frac{K_{M}}{J} i + \frac{B}{J} Ω - \frac{1}{J} M_{t} \end{array}$

A főegyenletet mátrixos alakban is felírhatjuk, mert a paraméterek állandók és az egyenletrendszer lineáris:

$\underline{\dot{x}} = [\begin{matrix} - \frac{R}{L} & - \frac{K_{M}}{L} \\ \frac{K_{M}}{J} & - \frac{B}{J} \end{matrix}] \cdot \underline{x} + [\begin{matrix} \frac{1}{L} & 0 \\ 0 & \frac{1}{J} \end{matrix}] \cdot \underline{u}$

Az „A” rendszermátrix és „B” bemeneti mátrix vizsgálata révén azonnal eldönthetjük, hogy helyesen írtuk-e fel a modellt? A rendszermátrix négyzetes (nxn, ahol n a rendszám), a főátlójának elemei negatívak, ez a stabilitás egyik előfeltétele. Az egyes tagok dimenzió analízise is helyes eredményt ad, érdemes tehát továbblépni.

Ha a kimenetek között kíváncsiak vagyunk a motor tengelyének szögelfordulására is, akkor bővíteni kell a rendszermátrixot. Ez több mechanikai rendszert, vagy rendszerrészt tartalmazó feladatban problémaként merülhet fel. A lineáris és rotációs mechanikai rendszerekben van ugyanis egy természetes „származtatási” rend. A keresztváltozóból integrálással és deriválással további változók állíthatók elő. Ilyen más rendszerben nincs, csak a villamos rendszerben az áram és a töltés kapcsolata. Kezdeti feltételek nélkül tekintsük át a kapcsolatokat:

$\begin{array}{l} v = \frac{d}{d t} x = \int a \cdot d t \\ a = \dot{v} = \ddot{x} \\ Ω = \frac{d}{d t} ϕ = \int ε \cdot d t \\ ε = \dot{Ω} = \ddot{ϕ} \end{array}$

Az így bevezetett új „φ” állapotjelző nem valós állapotjelző, mert a rendszerben nincsen olyan energia átalakító, amelynek leírásához szükség lenne rá, ugyanakkor előfeltétele az újabb kimenet felírásának. A módosított ÁTM harmadrendű rendszert „sugall”, de ez csak a fentiekben leírtak miatt van így, a rendszám marad 2, csak az állapotjelzők száma nőtt 3-ra.

$\underline{\dot{x}} = [\begin{matrix} \frac{d i}{d t} \\ \frac{d Ω}{d t} \\ \frac{d ϕ}{d t} \end{matrix}] = [\begin{matrix} - \frac{R}{L} & - \frac{K_{M}}{L} & 0 \\ \frac{K_{M}}{J} & - \frac{B}{J} & 0 \\ 0 & 1 & 0 \end{matrix}] \cdot \underline{x} + [\begin{matrix} \frac{1}{L} & 0 \\ 0 & \frac{1}{J} \\ 0 & 0 \end{matrix}] \cdot \underline{u}$

Az állapottér modell nagy előnye, hogy a főegyenlet megoldása után minden releváns változó kifejezhető az állapotjelzők lineáris kombinációjával. A kimeneti változók csoportja az alábbi lehetséges, lényeges változókat tartalmazhatja:

${\underline{y}}^{T} = [\begin{matrix} i & Ω & u_{R} & u_{L} & u_{i n d} & M_{B} & M_{J} & ε & π \end{matrix}]$

Az állapotjelzők természetszerűen elsők a sorban. Ügyelni kell arra, hogy az u_L és az M_J kimenetek esetében deriválás nem lehet a formulában, tehát ezeket a kimeneteket a hurok és a csomóponti egyenletek újbóli felhasználásával lehet csak megadni.

$\begin{array}{l} y_{1} = i \\ y_{2} = Ω \\ y_{3} = R \cdot i \\ y_{4} = L \frac{d i}{d t} = - R \cdot i - K_{M} Ω + u_{b e} \\ y_{5} = K_{M} Ω \\ y_{6} = B \cdot Ω \\ y_{7} = K_{M} \cdot i - B Ω - M_{t} \\ y_{8} = \frac{d Ω}{d t} = \frac{M_{J}}{J} = \frac{K_{M}}{J} i - \frac{B}{J} Ω - \frac{1}{J} M_{t} \\ y_{9} = J \cdot Ω \end{array}$

A kimeneti, vagy segédegyenlet is felírható mátrixos alakban, ahol a „C” a kimeneti és „D” a segédmátrix.

$\underline{y} = [\begin{matrix} 1 & 0 \\ 0 & 1 \\ R & 0 \\ - R & - K_{M} \\ 0 & K_{M} \\ 0 & B \\ K_{M} & - B \\ \frac{K_{M}}{J} & - \frac{B}{J} \\ 0 & J \end{matrix}] \cdot \underline{x} + [\begin{matrix} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 1 \\ 0 & \frac{1}{J} \\ 0 & 0 \end{matrix}] \cdot \underline{u}$

6.3.1.3. Műveletek a DC motor állapottér modelljével

Ennek az aktuátornak a modellje alkalmas arra, hogy olyan műveleteket mutassunk berajta, amelyek a rendszerek dinamikai viselkedésének vizsgálatához szükségesek.

Az átviteli mátrix W(s) meghatározása

Ha valamennyi bemenet és valamennyi kimenet között keressük az átvitelt, akkor az állapotegyenletek segítségével felírható az átviteli mátrix. Ebben az esetben operátor tartományban kell dolgoznunk, és nem vesszük figyelembe a kezdeti értékeket, mert általános, frekvencia-függő kapcsolatot keresünk.

A főegyenlet Laplace transzformálása után elhagyjuk a kezdeti feltéteket, és az állapotvektort behelyettesítjük a kimeneti egyenletbe. Az egységmátrixot $\underline{\underline{E}}$ -vel jelöljük:

$\begin{array}{l} s \underline{X} (s) - \underline{x} (0) = \underline{\underline{A}} \underline{X} + \underline{\underline{B}} \underline{u} \\ s \underline{X} - \underline{\underline{A}} \underline{X} = \underline{x} (0) + \underline{\underline{B}} \underline{u} \\ [s \underline{\underline{E}} - \underline{\underline{A}}] \underline{X} = \underline{x} (0) + \underline{\underline{B}} \underline{u} \\ \underline{x} (0) = 0 \\ \underline{X} (s) = {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} \underline{\underline{B}} \underline{u} = \underline{\underline{Φ}} \underline{\underline{B}} \underline{u} \end{array}$

A DC motor esetében nem jelent gondot a 2x2-es mátrix determinánsának felírása.

$\begin{array}{l} {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} = \frac{a d j [s \underline{\underline{E}} - \underline{\underline{A}}]}{\det [s \underline{\underline{E}} - \underline{\underline{A}}]} \\ \det [s \underline{\underline{E}} - \underline{\underline{A}}] = (s + \frac{R}{L}) (s + \frac{B}{J}) - (- \frac{K_{M}^{2}}{L J}) \end{array}$

Nagyobb rendszám esetén, egy n·n méretű mátrix invertálásánál ügyelni kell az aldeterminánsok célszerű megválasztására.

Adott tehát az alábbi egyenlet:

$\underline{X} (s) = {[s E - \underline{\underline{A}}]}^{- 1} \underline{\underline{B}} \underline{u}$

Következő lépésben az „X” állapotvektort behelyettesítjük a kimeneti egyenletbe, csoportosítjuk a műveleteket és előállítjuk a „ $\underline{\underline{W}} (s)$ ” átviteli mátrixot:

$\begin{array}{l} \underline{Y} (s) = \underline{\underline{C}} {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} \underline{\underline{B}} \underline{U} + \underline{\underline{D}} \underline{U} = [\underline{\underline{C}} {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} \underline{\underline{B}} + \underline{\underline{D}}] \underline{U} \\ \underline{Y} (s) = \underline{\underline{W}} \cdot \underline{U} \\ \underline{\underline{W}} (s) = \underline{\underline{C}} \cdot \underline{\underline{Φ}} (s) \cdot \underline{\underline{B}} + \underline{\underline{D}} \end{array}$

ahol $\underline{\underline{Φ}} (s) = {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1}$ , a rezolvens mátrix Lapace transzformáltja.

Az állapotváltozók időfüggésének meghatározása Laplace transzformációval

A főegyenlet Laplace transzformálásával a következő alakhoz jutunk:

$\begin{array}{l} s \underline{X} (s) - \underline{x} (0^{-}) = \underline{\underline{A}} \underline{X} + \underline{\underline{B}} \underline{u} \\ s \underline{X} - \underline{\underline{A}} \underline{X} = \underline{x} (0^{-}) + \underline{\underline{B}} \underline{u} \\ [s \underline{\underline{E}} - \underline{\underline{A}}] \underline{X} = \underline{x} (0^{-}) + \underline{\underline{B}} \underline{u} \\ \underline{X} (s) = {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} \underline{x} (0^{-}) + {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} \underline{\underline{B}} \underline{u} \end{array}$

Az utolsó sorban látható egyenlet első tagja a homogén, míg a második a partikuláris megoldás Laplace transzformáltja. Az időtartománybeli műveletekkel való összehasonlítás érdekében most csak a homogén megoldást vizsgáljuk.

Észre kell venni azt is, hogy a Laplace transzformációs szabályok a deriválás esetében a 0^- kezdeti értéket tartalmazzák. Ezen a helyen ismételten utalunk Fodor György munkájára, amely különbséget tesz a kiindulási x(0-) és a kezdeti x(0+) értékek között [3.1.]. Ez abban az esetben nem jelent gondot, ha a rendszer állapotjelzőinek „bekapcsolást” megelőző értékei azonosak a „bekapcsolás” utánival, tehát

$\underline{x} (0^{-}) = \underline{x} (0^{+})$ .

Az állapotjelzők időbeli lefutásának inverz Laplace transzformációval történő meghatározásához az x(0-) értékekre van szükség. Fodor György megfogalmazása szerint a Laplace transzformáció a kezdeti érték kiszámítását „automatikusan” elvégzi helyettünk.

Abban az esetben, ha a változók nem „kanonikus” változók (állapotjelzők), és valamilyen okból szükség van a jobboldali kezdeti értékekre, az x_i(0⁺) értékek az operátor térben a Laplace transzformáció kezdeti érték tétele segítségével határozhatók meg. A témáról bővebben Korondi Péter Rendszertechnika [2.4.] című elektronikus jegyzetében, és Fodor György fentebb említett könyvében olvashatunk.

A mátrix inverzió első lépésében képezzük a zárójelben található kifejezés eredményét:

$s [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] - [\begin{matrix} - \frac{R}{L} & - \frac{K_{M}}{L} \\ \frac{K_{M}}{J} & - \frac{B}{J} \end{matrix}] = [\begin{matrix} s + \frac{R}{L} & \frac{K_{M}}{L} \\ - \frac{K_{M}}{J} & s + \frac{B}{J} \end{matrix}]$

Kiszámítjuk az adjungáltat, majd a determinánst. Az adjungált számítása általános esetben két lépésben történik. Először meghatározzuk minden mátrix elem aldeterminánsát, majd sor-oszlop cserét hajtunk végre. Az aldetermináns képzésnél ügyelni kell az elemek indexeitől függő előjelekre. 2x2-es mátrix esetében egyszerűen lehet eljárni, de végighaladunk a lépéseken:

Aldeterminánsok:

$[\begin{matrix} s + \frac{B}{J} & - (- \frac{K_{M}}{J}) \\ - \frac{K_{M}}{L} & s + \frac{R}{L} \end{matrix}]$

Majd a sor-oszlop cserét követően:

$a d j [s \underline{\underline{E}} - \underline{\underline{A}}] = [\begin{matrix} s + \frac{B}{J} & - \frac{K_{M}}{L} \\ \frac{K_{M}}{J} & s + \frac{R}{L} \end{matrix}]$

A következő lépésben meghatározzuk a determinánst:

	$\det [s \underline{\underline{E}} - \underline{\underline{A}}] = \det [\begin{matrix} s + \frac{R}{L} & \frac{K_{M}}{L} \\ - \frac{K_{M}}{J} & s + \frac{B}{J} \end{matrix}] = (s + \frac{R}{L}) (s + \frac{B}{J}) - (- \frac{K_{M}^{2}}{L J})$
	$\det [s \underline{\underline{E}} - \underline{\underline{A}}] = s^{2} + s (\frac{R}{L} + \frac{B}{J}) + \frac{R}{L} \frac{B}{J} + \frac{K_{M}^{2}}{L J}$

Ha a szokásos módon átalakítjuk az összefüggést, akkor összehasonlíthatjuk a karakterisztikus polinomot azzal az alakkal, amelyet a hurok-és csomóponti módszerrel kaptunk:

$\det [s \underline{\underline{E}} - \underline{\underline{A}}] = \frac{s^{2} L J + s (R J + L B) + R B + K_{M}^{2}}{L J} = \frac{(R B + K_{M}^{2})}{L J} (s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1)$

Az invertált mátrix az alábbi formát veszi fel:

${[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} = \frac{\frac{L J}{R B + K_{M}^{2}} [\begin{matrix} s + \frac{B}{J} & - \frac{K_{M}}{L} \\ \frac{K_{M}}{J} & s + \frac{R}{L} \end{matrix}]}{(s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1)}$

Az inverz mátrixot felhasználva érdemes ellenőrzésképpen az Ω(s)/U_be(s) átviteli függvényt kiszámítani, mert így lehetőség nyílik az összehasonlításra. Ezt az átviteli függvényt korábban a hurok-és csomóponti egyenletekből írtuk fel.

Tehát korábbról, az átviteli mátrixról tudjuk, hogy

$\underline{Y} (s) = [\underline{\underline{C}} {[s E - \underline{\underline{A}}]}^{- 1} \underline{\underline{B}} + \underline{\underline{D}}] \underline{U}$ ,

és ebből a mátrix-vektor egyenletből az U_bebemenetet és az Ω kimenetet választjuk ki. Ennek megfelelően a kimeneti mátrix második sorára és a bemeneti mátrix első oszlopára lesz csak szükség a számításokhoz. A segédmátrixra nem lesz szükség.

	$Y_{2} (s) = Ω (s) = [[\begin{matrix} 0 & 1 \end{matrix}] {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} [\begin{matrix} \frac{1}{L} \\ 0 \end{matrix}]] U_{b e} (s)$
	$Ω (s) = [\begin{matrix} 0 & 1 \end{matrix}] \frac{\frac{L J}{R B + K_{M}^{2}} [\begin{matrix} s + \frac{B}{J} & - \frac{K_{M}}{L} \\ \frac{K_{M}}{J} & s + \frac{R}{L} \end{matrix}]}{(s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1)} [\begin{matrix} \frac{1}{L} \\ 0 \end{matrix}] U_{b e} (s)$

A vektor-mátrix-vektor szorzás eredménye két szorzat tagként (K_M/J és 1/L) jelenik meg az alábbi függvény számlálójában, a tört többi része skalár volt:

$Ω (s) = \frac{\frac{L J}{R B + K_{M}^{2}} \cdot \frac{K_{M}}{J} \cdot \frac{1}{L}}{(s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1)} U_{b e} (s)$

Ha a megszokott formában írjuk fel az átviteli függvényt, akkor meggyőződhetünk, hogy az eredmény megegyezik a hurok-és csomóponti egyenletekből kapottal.

$G (s) = \frac{Ω (s)}{U_{b e} (s)} = \frac{K_{M}}{R B + K_{M}^{2}} \cdot \frac{1}{(s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1)}$

Dimenzióellenőrzés:

$\begin{array}{l} \frac{Ω}{U_{b e}} [\frac{1}{V s} = \frac{A s^{3}}{m^{2} k g \cdot s} = \frac{A s^{2}}{k g m^{2}}] \\ \frac{K_{M}}{R B + K_{M}^{2}} [\frac{A}{N m} = \frac{A s^{2}}{k g m^{2}}] \end{array}$

A sikeres ellenőrzés után az eredeti kérdés még nyitott, nevezetesen, hogy miként kapjuk meg a keresett állapotjelzők időfüggvényét az inverz mátrix felhasználásával. Amint fentebb láttuk, a homogén megoldás az operátor térben a következő:

$\underline{X} (s) = {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} \underline{x} (0^{-})$

Az előzőekben már írtunk arról, hogy állapotjelzők időbeli alakjának kiszámításában, Laplace inverz transzformáció alkalmazása esetén, a legnagyobb könnyebbséget az jelenti, hogy nincsen szükség a kezdeti értékek meghatározására, elegendő a kiindulási értékek ismerete. Kanonikus változók esetén – ezeket a jegyzetünk keresztváltozónak, vagy átmenő változónak nevezi, másként ezek a „természetes” állapotjelzők, a kiindulási érték és a kezdeti érték meg kell, hogy egyezzen, mert semmilyen energiatárolót nem lehet zérus idő alatt feltölteni, állapotát megváltoztatni, olvashatjuk Fodor György: Lineáris rendszerek analízise című munkájában [3.1.]. Ezt az alábbi módon lehet kifejezni:

$\underline{x} (t = 0^{-}) = \underline{x} (t = 0^{+})$

Kérdés, mi történik valós technikai rendszerekben akkor, ha van kiindulási érték x(0-), de ezen felül t=0 időpillanatban impulzus-szerű gerjesztés éri?

Idézzük Fodor Györgyöt az energiatárolók impulzus gerjesztéssel történő feltöltésével kapcsolatban. „Ha impulzust kívánunk vizsgáló gerjesztésként alkalmazni, akkor célszerű valamilyen előírással szabványosítani. Normalizáljuk impulzusunkat úgy, hogy egységnyi intenzitású legyen, és egyetlen jellemzője a $τ$ hosszúsága, hiszen amplitúdója $x_{0} = 1 / τ$ . …Célszerű az impulzushosszat is „szabványosítani”, mégpedig minél kisebbnek választani, mert ekkor az impulzus-válasz egyre kisebb „t” értékektől kezdve tekinthető függetlennek a gerjesztő impulzus hosszától. …Mit értsünk a formális alakban megadható – de matematikailag közvetlenül nem értelmezhető - $δ (t)$ Dirac-impulzuson? …Határesetben egy végtelenül rövid és végtelenül nagy amplitúdójú, egységnyi erősségű impulzust kapunk. Ez azonban nem függvény, és semmilyen fizikai mennyiség nem változhat ilyen törvényszerűség szerint. … A Dirac-impulzus tehát csak rövid jelölése annak a $δ (t, τ)$ egységnyi erősítésű impulzusnak, amelynek $τ$ hosszúsága igen kicsi, mégpedig jóval kisebb a rendszer legkisebb időállandójánál is. …Fizikai szempontból a Dirac-impulzus semmivel sem absztraktabb a véges hosszúságú impulzusnál, vagy az egységugrásnál, hiszen a valóságban ilyen lefutású jelek sem hozhatók pontosan létre. A közelítést akkor alkalmazhatjuk, ha az állandó érték eléréséhez szükséges idő jóval kisebb a rendszer legkisebb időállandójánál.”

Eddig az idézet szöveg, amely többször is hangsúlyozza, hogy a valóságos energiatárolók feltöltését csak akkor lehet Dirac-impulzussal modellezni, ha a rendszer legkisebb időállandója lényegesen kisebb, mint a „feltöltéshez” alkalmazott impulzus időtartama. Ezért alkalmazzák például a modálanalízis méréstechnikájában (pl. rudak, lemezek sajátfrekvenciáinak felderítése céljából) az „impulzus-kalapácsot”, amellyel a Dirac-impulzust lehet a gyakorlatban közelíteni.

Ugyanakkor kétségtelen tény, hogy elméletben a Dirac-impulzus segítségével lehet a gerjesztés nélküli rendszerek súlyfüggvényét, modern szóhasználattal impulzus-válaszát meghatározni. Ez a függvény igen fontos rendszerjellemző függvény.

Behelyettesítve az ellenőrzött inverz mátrixot, az alábbi Laplace transzformált függvényeket kapjuk. A nagy méret miatt ismét alkalmazzuk az átviteli függvények esetében szokásos „a_i” jelöléseket, de ezúttal a későbbi gyöktényezős alak előállítása miatt másként rendezzük:

$\underline{X} (s) = [\begin{matrix} I (s) \\ Ω (s) \end{matrix}] = \frac{\frac{L J}{R B + K_{M}^{2}} [\begin{matrix} s + \frac{B}{J} & - \frac{K_{M}}{L} \\ \frac{K_{M}}{J} & s + \frac{R}{L} \end{matrix}]}{(s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1)} [\begin{matrix} i (0^{-}) \\ Ω (0^{-}) \end{matrix}] = \frac{[\begin{matrix} s + \frac{B}{J} & - \frac{K_{M}}{L} \\ \frac{K_{M}}{J} & s + \frac{R}{L} \end{matrix}]}{s^{2} + s \frac{a_{1}}{a_{2}} + \frac{a_{0}}{a_{2}}} [\begin{matrix} i (0^{-}) \\ Ω (0^{-}) \end{matrix}]$

Az armatúra áram operátor térbeli alakja a fenti összefüggésből számítható ki. Az inverz transzformáció eredménye mindkét esetben a konkrét számértékektől függ, ettől függően, vagy exponenciálisan lecsengő lengéssel, vagy aperiodikus lefolyással kell számolni.

Az időfüggvények természetesen paraméteres formában is megadhatóak. Feltételezzük, hogy a két gyök konjugált komplex, tehát a DC motor másodrendű, és alulcsillapított, ha kis mértékben is. Az állapotvizsgálat üresjáratban történik, és csak az impulzusválaszt, más néven homogén megoldást adjuk meg, a Cannon: Dynamics of Physical Systems [2.2.] című, alapvető szakirodalom alapján.

Tehát legyenek a pólusok lengő esetre: s₁=σ_a+jω_a és s₂=σ_a-jω_a.

Paraméteres alakban ez a következőket jelenti:

$s_{1,2} = - \frac{R J + L B}{2 L J} \pm \sqrt{{(\frac{R J + L B}{2 L J})}^{2} - \frac{R B + K_{M}^{2}}{L J}} = - \frac{R J + L B}{2 L J} \pm \sqrt{\frac{{(R J + L B)}^{2} - 4 L J (R B + K_{M}^{2})}{{(2 L J)}^{2}}}$

Ha tehát lengő, alulcsillapított esetet feltételezünk, akkor teljesülnie kell az alábbi feltételnek:

$4 L J (R B + K_{M}^{2}) 〉 {(R J + L B)}^{2}$

Ezekkel a csillapított rendszer rezonancia körfrekvenciáját a következő formulával határozhatjuk meg:

$ω_{a} = \sqrt{\frac{4 L J (R B + K_{M}^{2}) - {(R J + L B)}^{2}}{{(2 L J)}^{2}}}$

Az időfüggvények meghatározásához fontos még az alábbi két összefüggés:

$\begin{matrix} ϕ_{m e c h} = t g \frac{ω_{a}}{| σ_{m e c h} - σ_{a} |} & ϕ_{v i l l} = t g \frac{ω_{a}}{| σ_{v i l l} - σ_{a} |} \end{matrix}$

A fenti irodalomban található Laplace transzformációs táblázat szerint az alábbi időfüggvények tartoznak az operátor térbeli alakhoz, ahol σ_mech=1/T_mech és σ_vill=1/T_vill.

Az állapotjelzők általános megoldására a Φ(s) mátrix alkalmazásával az alábbi Laplace transzformált kifejezéseket kapjuk:

	$I (s) = \frac{(s + \frac{B}{J})}{s^{2} + s \frac{a_{1}}{a_{2}} + \frac{a_{0}}{a_{2}}} \cdot i (0^{-}) - \frac{K_{M}}{L} \frac{1}{s^{2} + s \frac{a_{1}}{a_{2}} + \frac{a_{0}}{a_{2}}} \cdot Ω (0^{-})$
	$I (s) = \frac{s + σ_{m e c h}}{(s - s_{1}) (s - s_{2})} i (0^{-}) - \frac{K_{M}}{L} \cdot \frac{1}{(s - s_{1}) (s - s_{2})} Ω (0^{-})$
	$I (s) = L^{- 1} {\frac{s + σ_{m e c h}}{(s - s_{1}) (s - s_{2})}} i (0^{-}) - \frac{K_{M}}{L} \cdot L^{- 1} {\frac{1}{(s - s_{1}) (s - s_{2})}} Ω (0^{-})$

Paraméteres formában visszatranszformálás után az alábbi általános alakot kapjuk:

$i (t) = i (0^{-}) \frac{\sqrt{{(σ_{m e c h} - σ_{a})}^{2} + ω_{a}^{2}}}{ω_{a}} \cdot e^{- σ_{a} t} \sin (ω_{a} t + ϕ_{m e c h}) - Ω (0^{-}) \frac{K_{M}}{L} \frac{1}{ω_{a}} e^{- σ_{a} t} \sin ω_{a} t$

Kérdés, hogy mihez kezdünk műszaki értelemben ezzel a függvénnyel?

Például választ kapunk arra a kérdésre, hogy ha az i(0^-) és Ω(0^-) kiindulási értékek t=0+ időpillanatban, tehát az időtengely jobboldalán megszűnnek, a magára hagyott rendszer árama milyen módon fog az idő függésében változni.

Elméletben ezt homogén megoldásnak nevezzük.

Kérdés még, hogy a függvény második tagja valóban „A” (Amper) dimenziójú?

$\frac{\frac{1}{s} \cdot \frac{k g m}{s^{2}} m \frac{1}{A}}{\frac{m^{2} k g}{s^{2} A^{2}}} = \frac{A}{s}$

Figyelembe véve az inverz Laplace transzformált együtthatóját, amelynek dimenziója „s”, (ω_a[1/s]) megnyugodhatunk, a függvény második része is „A (Amper)” dimenziójú.

Jól látható, hogy az kiindulási értékekről „elengedett” elektromechanikus rendszer áram függvényében a mechanikai rendszerelemek is „éreztetik” a hatásukat: Jelen van σ_mech=1/T_mech formában a mechanikai időállandó, és az ω_a rezonancia frekvencia

$ω_{a} = \sqrt{\frac{4 L J (R B + K_{M}^{2}) - {(R J + L B)}^{2}}{{(2 L J)}^{2}}}$

ugyancsak elektromechanikus, vegyes kifejezés alakjában. A rezonancia körfrekvencia értéke csillapítatlan esetre könnyen ellenőrizhető, ha a két disszipatív elemet (R, B) zérusnak választjuk:

$ω_{a} = \sqrt{\frac{K_{M}^{2}}{L J}} = \sqrt{\frac{1}{L C_{J}}}$

Az összefüggésben C_J=J/K_M², azaz a tehetetlenségi nyomatékkal egyenértékű villamos kapacitás. A képlet ismert a szakirodalomból, esetünkben nevezzük „elektromechanikus” Thomson képletnek.

Az előzőekhez hasonlóan járunk el a másik állapotjelző esetében is. Az Ω(s) Laplace transzformáltja ugyancsak a Φ(s) alapmátrix segítségével határozható meg:

$\begin{array}{l} Ω (s) = \frac{\frac{K_{M}}{J}}{s^{2} + s \frac{a_{1}}{a_{2}} + \frac{a_{0}}{a_{2}}} \cdot i (0^{-}) + \frac{s + \frac{R}{L}}{s^{2} + s \frac{a_{1}}{a_{2}} + \frac{a_{0}}{a_{2}}} \cdot Ω (0^{-}) \\ Ω (s) = \frac{K_{M}}{J} \frac{1}{(s - s_{1}) (s - s_{2})} i (0^{-}) + \frac{s + σ_{v i l l}}{(s - s_{1}) (s - s_{2})} Ω (0^{-}) \end{array}$

Visszatranszformálással kapjuk a keresett időfüggvényt:

$Ω (s) = \frac{K_{M}}{J} L^{- 1} {\frac{1}{(s - s_{1}) (s - s_{2})}} i (0^{-}) + L^{- 1} {\frac{s + σ_{v i l l}}{(s - s_{1}) (s - s_{2})}} Ω (0^{-})$

$Ω (t) = i (0^{-}) \frac{K_{M}}{J} \frac{1}{ω_{a}} e^{- σ_{a} t} \sin ω_{a} t + Ω (0^{-}) \frac{\sqrt{{(σ_{v i l l} - σ_{a})}^{2} + ω_{a}^{2}}}{ω_{a}} \cdot e^{- σ_{a} t} \sin (ω_{a} t + ϕ_{v i l l})$

A kapott időfüggvényben az áram esetéhez hasonlóan az tükröződik, hogy milyen lesz a forgórész szögsebességének időfüggvénye, ha az állapotjelzők kiindulási értékekeit t(0⁺) időpillanatban megszüntetjük.

6.3.1.4. Impedancia módszer

Az alábbi ábrán látható a DC motor impedancia hálózata.

6.16. ábra - A DC szervomotor impedancia hálózata

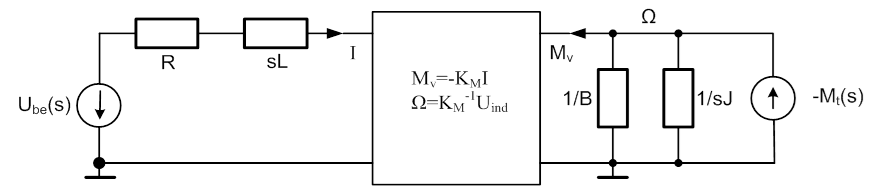
A hurok és csomóponti módszernél bemutatottakhoz hasonlóan, most is a motor normál üzemi jellemzőjére vagyunk kíváncsiak, azaz az Ω(s) szögsebességre. Két forrás van a rendszerben, ezért az impedancia módszer alkalmazása során a szuperpozíció szabályára támaszkodunk. Ennek szellemében, külön-külön vizsgáljuk a keresett változót, először az U_be(s) kapocsfeszültséget, majd az –M_t(s) terhelő nyomatékot választjuk bemenetnek, és a hatásokat összegezzük. Két átviteli függvényt kell tehát felírnunk. Az éppen aktuális bemenet a másik forrást nem forrásként, hanem annak belső ellenállásaként érzékeli. Ezt a megfelelő ábrákon jeleztük is, a nyomaték helyén szakadással, a kapocsfeszültség helyén rövidzárral.

Az első átviteli függvény legyen Ω_u(s)/U_be(s)=G_u(s). Az indexek arra utalnak, hogy ebben az esetben nem a teljes keresett kimenetre kapunk összefüggést, hanem csupán az egyik bemenet felől nézve. Úgy kell tekinteni, hogy a másik forrás értéke jelenleg zérus.

A kapcsolást a keresett átviteli függvénynek alárendelve vontuk össze, alakítottuk át. Ennek lépéseit a modellezéssel részletesen foglalkozó fejezetben már bemutattuk. A mechanikai oldal párhuzamos impedanciáit eredőben vontuk össze. Ezen az eredőn jelenik meg a keresett változó, ezért célszerű az aktív részhez tartozó villamos oldalt a forrással együtt a mechanikai részre redukálni. Ha ez megtörtént, akkor a kapcsolás igen egyszerű lesz, mert egy keresztváltozó osztót képez.

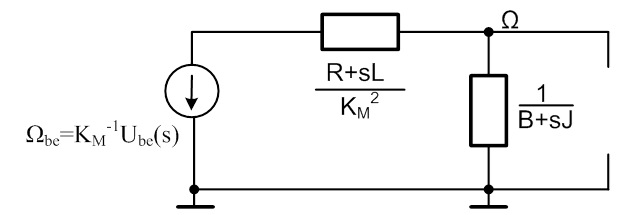
6.17. ábra - A keresett Ω kimenet és az Ube forrás közötti kapcsolatot leíró hálózat

A két soros villamos impedancia eredőjét a mechanikai oldalra redukáljuk, és ehhez a váltó egyenleteit használjuk fel:

$\begin{array}{l} \frac{Ω}{M {}_{v}} = \frac{\frac{1}{K_{M}} u_{i n d}}{(-) K_{M} I} \\ Z_{m e c h} = \frac{1}{K_{M}^{2}} Z_{v i l l} \end{array}$

A keresztváltozó osztó a mechanikai impedanciák eredőjének meghatározása után már felírható:

$\begin{array}{l} \frac{Ω_{u}}{Ω_{b e}} (s) = \frac{\frac{1}{B + s J}}{\frac{R + s L}{K_{M}^{2}} + \frac{1}{B + s J}} = \frac{K_{M}^{2}}{(R + s L) (B + s J) + K_{M}^{2}} \\ G_{u} (s) = \frac{Ω_{u}}{U_{b e}} (s) = \frac{K_{M}}{(R + s L) (B + s J) + K_{M}^{2}} = \frac{K_{M}}{s^{2} L J + s (R J + L B) + R B + K_{M}^{2}} \end{array}$

Ellenőrizhető, hogy a kapott eredmény egyezik azzal az alakkal, amit a hurok és csomóponti módszer segítségével vezettünk le.

A következő lépésben a terhelő nyomaték „felől” vizsgáljuk a rendszert, miközben kiiktatjuk a kapocsfeszültséget és azt rövidzárral helyettesítjük, hiszen az ideális keresztváltozó forrás belső ellenállása zérus. Az így kialakuló kapcsolás még egyszerűbb, mint az előző, hiszen a terhelő és a belső impedancia párhuzamosan vannak kapcsolva, az átviteli függvény egyszerűen az eredő impedancia lesz.

$G_{M} (s) = \frac{Ω_{M}}{- M_{t}} (s) = \frac{1}{B + s J + \frac{K_{M}^{2}}{R + s L}} = \frac{R + s L}{(R + s L) (B + s J) + K_{M}^{2}}$

A két átviteli függvény felhasználásával felírható a végeredmény operátor tartományban:

$Ω (s) = \frac{K_{M}}{(R + s L) (B + s J) + K_{M}^{2}} U_{b e} - \frac{R + s L}{(R + s L) (B + s J) + K_{M}^{2}} M_{t}$

Az átviteli függvények esetében szokásos alakra hozva:

$Ω (s) = \frac{\frac{K_{M}}{R B + K_{M}^{2}}}{s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1} U_{b e} (s) - \frac{\frac{s L + R}{R B + K_{M}^{2}}}{s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1} M_{t} (s)$

Didaktikai szempontból célszerű az állapottér modellel kapott eredményt összevetni az impedancia módszerrel kiszámítottal. Mindkét bemenet szerepel az állapottér modellben is, de csak az Ω állapotjelző a „közös” kimenet a két eljárásban.

Válasszuk ezúttal a fenti függvényből a második tagot összeghasonlításul, hiszen az U_be(s) bemenet felől már felírtuk korábban az állapottér segítségével az átviteli függvényt, és összehasonlítottuk a hurok és csomóponti módszerrel kapott eredménnyel.

Az összehasonlítás érdekében vissza kell térnünk az állapottér modellből felhasználni kívánt egyenletekre. Ezekből az átviteli mátrixra van szükségünk, mert ez adja meg a minden bemenet és kimenet közötti kapcsolatot:

	$\underline{Y} (s) = [\underline{\underline{C}} {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} \underline{\underline{B}} + \underline{\underline{D}}] \underline{U}$
	$Ω (s) = [\begin{matrix} 0 & 1 \end{matrix}] {[s \underline{\underline{E}} - \underline{\underline{A}}]}^{- 1} [\begin{matrix} \frac{1}{L} & 0 \\ 0 & \frac{1}{J} \end{matrix}] [\begin{matrix} U_{b e} (s) \\ - M_{t} (s) \end{matrix}]$

Behelyettesítjük az alapmátrixot, majd elvégezzük a kijelölt mátrix-vektor műveleteket:

	$Ω (s) = [\begin{matrix} 0 & 1 \end{matrix}] \frac{\frac{L J}{R B + K_{M}^{2}} [\begin{matrix} s + \frac{B}{J} & - \frac{K_{M}}{L} \\ \frac{K_{M}}{J} & s + \frac{R}{L} \end{matrix}]}{s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1} [\begin{matrix} \frac{1}{L} & 0 \\ 0 & \frac{1}{J} \end{matrix}] [\begin{matrix} U_{b e} (s) \\ - M_{t} (s) \end{matrix}]$
	$\begin{array}{l} Ω (s) = \frac{\frac{L J}{R B + K_{M}^{2}} [\begin{matrix} \frac{K_{M}}{J} & s + \frac{R}{L} \end{matrix}]}{s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1} [\begin{matrix} \frac{1}{L} & 0 \\ 0 & \frac{1}{J} \end{matrix}] [\begin{matrix} U_{b e} (s) \\ - M_{t} (s) \end{matrix}] \\ Ω (s) = \frac{\frac{L J}{R B + K_{M}^{2}} (s + \frac{R}{L}) \cdot \frac{1}{J}}{s^{2} \frac{L J}{R B + K_{M}^{2}} + s \frac{R J + L B}{R B + K_{M}^{2}} + 1} (- M_{t} (s)) \end{array}$

Az állapottér modellből kapott átviteli függvényt úgy rendeztük, hogy a karakterisztikus polinom alakja megegyezzen azzal, amit az inverz Laplace transzformálásnál alkalmaztunk. Ehhez a számlálót és a nevezőt beszorozzuk az operátor négyzete mellett szereplő együttható reciprokával.

	$\frac{Ω (s)}{- M_{t} (s)} = \frac{(s + \frac{R}{L}) \cdot \frac{1}{J}}{s^{2} + s \frac{R J + L B}{L J} + \frac{R B + K_{M}^{2}}{L J}}$
	$\frac{Ω (s)}{M_{t} (s)} = - \frac{1}{J} \frac{(s + σ_{v i l l})}{s^{2} + s \frac{R J + L B}{L J} + \frac{R B + K_{M}^{2}}{L J}} = - \frac{1}{J} \frac{(s + σ_{v i l l})}{(s - s_{1}) (s - s_{2})}$

A kapott eredmény meggyőző, mert látható, hogy mind az impedancia, mind pedig az állapottér módszerrel kapott eredmény megegyezik egymással. A visszatranszformálástól eltekintünk, annak eredményét láttuk az állapottér modellnél.

Összefoglalva elmondhatjuk, hogy a DC motor modelljén, mint demonstrációs példán bemutattunk két hálózati módszert az egyenletek gyors és hatékony felírásához, majd bemutattuk az átszámítás lehetőségeit, és összehasonlítottuk a kapott eredményeket is. Ezek az alábbiak voltak:

Hurok/csomóponti módszer→Mátrix-egyenlet→Átviteli függvény →Differenciálegyenlet→Állapottér modell
Hurok/csomóponti módszer→Állapottér modell→Átviteli mátrix→Átviteli függvény
Impedancia módszer→ Átviteli függvény→(Differenciálegyenlet)

Ezeken túlmenően megmutattuk az állapotjelzők időbeli alakjának meghatározását a Laplace transzformáció segítségével. Az időtartománybeli megoldástól (Taylor sorfejtés) a modellezésben bemutatott nehézségek miatt „eltekintettünk”.

6.3.2. Tachogenerátor (szenzor)

Az „inverz” DC motor, a tachogenerátor (tacho: görög szó, sebesség) szögsebesség (fordulatszám) mérésére szolgáló aktív szenzor, működéséhez nem szükséges segédenergia, és a bemenő forgó mechanikai keresztváltozót közvetlenül villamos keresztváltozóvá alakítja, tehát váltóról van szó. Ebben az esetben a szenzor és a jelátalakító azonos fogalmat takarnak. Ha azonban a tachogenerátort egyenes vonalú mozgást végző tömeg sebességének mérésére alkalmaznak, pl. terelőgörgőkön átvezetett vonóelem segítségével, akkor a szenzor ugyan tachogenerátor, de a transzlációs sebességmérő rendszer már jelátalakító.

Az „inverz” jelzővel természetesen csupán az energia átalakító jelleget akartuk hangsúlyozni. Bár szerkezeti felépítésében megegyezik a DC motorral, lényeges különbségek is vannak. A forgórész tekercsein a motorhoz képest lényegesen kisebb áram folyik, itt nincs szó teljesítményről, csupán „jel” generálás a feladat. Ebből következik, hogy méretei, főként a vezető keresztmetszete kisebb.

Dinamikai szempontból ez az eszköz arányos tag, és ez igen nagy előny a szabályozástechnikában. A DC motor gráfjának segítségével azonnal érthető lesz ez a megállapítás. Szögsebesség bemenőjel mérése esetében a mechanikai oldalon előírt a forrás, és ennek értéke van „rákényszerítve” a két párhuzamos elemre. Így ezekre nem kell, és nem is lehet egyenletet felírni. A villamos oldalon az induktivitás a tachogenerátor esetében sokkal kisebb, mint a motornál, így ezt már végképp nem szükséges a modellbe bevonni.

A tachogenerátor a kefés egyenirányítás miatt pulzáló fél-szinusz hullámokat szolgáltat. A jel frekvenciája és amplitúdója a fordulatszámtól függ. A tachogenerátor jelét aktív, vagy passzív villamos kapcsolással szokták „simítani”. A legegyszerűbb egy megfelelően méretezett, ellenállásból és kondenzátorból álló aluáteresztő szűrő.

6.4. Merülő tekercses lineáris motor konstrukciója. Váltó a gyakorlatban.

A lineáris motorok között speciális helyet foglal el. Mielőtt megvizsgáljuk a lineáris motorok egy kiválasztott típusát, érdemes röviden áttekinteni a motoroknak (aktuátoroknak) e családját is.

Lényegében három típust lehet megkülönböztetni:

Elektrodinamikus (merülőtekercses)
Szinkron
Aszinkron

Az első típust kis teljesítményigény, rövid lökethossz és általánosságban kisméretű szerkezetek esetében alkalmazzák. A CD és DVD fejeken kívül lényegében ilyen szerkezet található a hangszórókban és az elektrodinamikus mikrofonokban is.

A szinkron és aszinkron lineáris motorokat a szerszámgépiparban és az elektronikai gyártóberendezésekben alkalmazzák. Kis méretekben ezekkel nem lehet találkozni.

Érdemes áttekinteni előnyeiket és hátrányaikat is, hiszen joggal merül fel a kérdés, miért kell forgó motorokat, hajtóműveket és mozgásátalakítókat tartalmazó, bonyolult rendszereket építeni pozicionálási célra, ha egyszer az egyenes vonalú direkt hajtás rendelkezésre áll?

6.2. táblázat - Lineáris motorok jellemző tulajdonságai

Előnyök	Hátrányok
Nagy gyorsítási képesség (10 g-ig)	Rossz hatásfok, a veszteségi teljesítmény miatt jelentős hőforrás a rendszerben
Nagy pozicionálási pontosság (szabályozással 0.1-1 μm)	Erőt módosító áttétre nincs lehetőség, mindent a motor határoz meg
Típustól függően légcsapágyazás és mágneses lebegtetés lehetséges	Bizonyos típusoknál az erős mágneses tér miatt jelentős a szánra és a vezetékre ható erő
Igény szerinti mozgatási hossz	Pozícióban tartáshoz energia szükséges
Nagy előtoló erő (20 kN-ig)	Aszinkron változatnál pozícióban tartásnál nagy hőterhelés
Nincs mozgásátalakító	Terheléstől függő dinamika
Nagy mozgatási sebesség (100 m/s –ig)	Ferromágneses anyagok megmunkálásánál gond van a forgáccsal

Egy jelentős gyártó által készített összehasonlító táblázaton láthatjuk a további szempontokat, amelyek mérlegelésével érthetővé válik az, hogy miért nem vált egyeduralkodóvá a piacon a lineáris motorok családja.

6.3. táblázat - Jellegzetes mechatronikai hajtások összehasonlítása

Hajtás jellemzői	Fogazott szíj	Golyósorsó	Lineáris motor
Mozgatási hossz	10 m-ig	2 m-ig	10 m-ig
Mozgatás sebessége	5…10 m/s	3…5 m/s	…100 m/s
Gyorsítás	100 m/s²	50 m/s²	100 m/s²
Pozicionálás	10 μm	2 μm	1 μm
Merevség	közepes	nagy	nagy
Ár	alacsony	magas	magas-nagyon magas

A fejezetben példaként, a merülő tekercses lineáris motort fogjuk elemezni.

A CD és DVD eszközök optikai rendszerének fókuszáló lencséjét merülő tekercses lineáris motor mozgatja. Az eszköz jellegzetesen mechatronikai, sőt optomechatronikai, különlegessége a méreteiben és a megkívánt pozicionálási pontosságban van. Ezen túlmenően olyan példája az elektromechanikus váltónak, amelynél jól tanulmányozható, hogy melyek egy eltérő típusú rendszert összekapcsoló átalakító szerves részét képező passzív elemek. Azok az elemek, amelyek nélkül a rendszer működésképtelenné válna. A villamos elemek megléte magától értetődő, hiszen tekercs és mágneses mező nélkül nincs átalakító. Azonban a mechanikai oldal sem érdektelen. A tekercs és az optika a foglalattal együtt természetesen a tömeg, de a kettős célú rugalmas konstrukció nélkül nincsen sem pozíciótartás, sem egyenes vezetés. Ha ugyanis ezt a rugós vezetéket elhagynánk, a tekercs árama által létrehozott erő vagy kilökné, vagy ütközésig behúzná a foglalatot. A mikrométer törtrészére is lehetséges pozíciót a rugófeszítés által keletkező ellenerő biztosítja, hiszen a foglalat azt a pillanatnyi pozíciót veszi fel, amelynél az adott áram által létrehozott Lorentz erővel (elektromágneses erő) a rugóerő egyensúlyt tart. A finommechanikában jól ismert, hogy a felületi érdesség és egyéb technológiai korlátok miatt a mikrométer tartományban, de főként az alatt, kizárólag deformációs elven működő vezetékeket lehet alkalmazni, csúszó és gördülő vezetékek ilyen célra nem használhatók. Legalábbis a tudomány és technika jelen állása szerint.

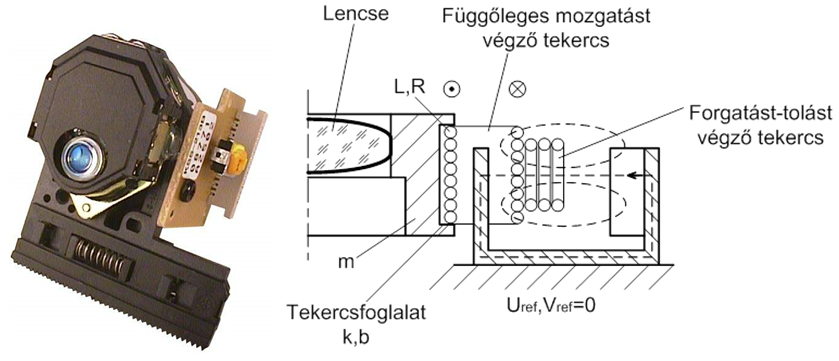
6.18. ábra - CD fej képe és szerkezeti modellje

A fenti fotón egy híradástechnikai CD fej látható összeszerelt állapotban, jobboldalon pedig a modellezést lehetővé tevő szerkezeti vázlat félnézet-félmetszet szerű rajz (magyarázó ábra, nem egzakt műszaki rajz) formájában azzal, hogy rugalmas vezeték éppen nem látható, mert az a rajz síkjára merőleges. Egyszerűbb CD és DVD szerkezetekben négy db kör keresztmetszetű, rugóbronzból készült huzaldarab képezi a vezetéket, amelyeknek egyik vége a kerethez, a másik pedig a foglalathoz van rögzítve. Igényesebb kialakításokban speciálisan kiképzett csuklópontokkal rendelkező, kettős műanyag vezeték (négycsuklós mechanizmus) található.

A következő képen egy ilyen komplex kialakítású, rugalmas egyenes vezeték felülnézeti fotóját látjuk. A bemutatott vezeték valójában négycsuklós mechanizmus, a négy csapágyazás helyén rugalmas csuklókkal – ezért ezt a szerkezetet is rugalmas vezeték egy speciális formájának tekintjük. A vezeték monolitikus (egy darabból készült) és lényegében két párhuzamos, merev műanyag lemezből áll, a rugalmas csapágyazásokat az anyag elvékonyításával, és speciális, hornyos kialakításával hozták létre. Ez a vezeték nem csak függőleges mozgást, hanem bizonyos mértékű oldalirányú elmozdulást és szögben történő elfordítást is lehetővé tesz. A kép baloldalán a rugós vezeték befogása, míg a jobboldalon a lencsefoglalat egy kicsiny része látszik. A kör alakú jelölés „1”-es számmal jelzi azokat a csuklópontokat, amelyek a lencsefoglalat oldalirányú pozicionálását és szögben való elfordítását biztosítják. A méhsejt formával kijelölt, és „2”-es számmal jelzett csuklók a párhuzamos rugós vezeték függőleges mozgását teszik lehetővé.

A rugalmas vezetéken kívül jól kivehetőek további szerkezeti elemek is, így például a szimmetrikusan elhelyezett, két lineáris motor „fő” tekercsei, amelyek a lencse függőleges pozicionálását teszik lehetővé. A nagy tekercsek közepén a mágneskör „vas” része látható, az „U”-alak egyik szára, felülről. A permanens mágnes az U-forma belső oldalára van ragasztva, ez a fotón már nem látszik, de a fenti szerkezeti ábrán bemutattuk. A nagy tekercsek külső oldalán két-két további, kisebb tekercset is találunk, ezekkel a lencsefoglalat oldalirányú elmozdítását és szögben való elfordítását lehet biztosítani.

(„1” elfordulás, „2” függőleges mozgás)

6.19. ábra - A CD fejben található rugalmas vezeték elemei

A rugalmas kettős vezeték működésének jobb érthetősége miatt a két következő kép a rugós vezeték két szélső pozícióját mutatják be. A baloldali képen az alsó ütközési helyzet látható, és figyelmes szemlélő nem csak az egyik lemezt, hanem a kép alján a párhuzamos, második lemez csuklópontjait is fel tudja ismerni. A jobboldali képen a vezeték felső ütközési pozíciója van bemutatva.

6.20. ábra - A rugalmas vezeték főmozgásának két szélső pozíciója

A működési vázlat alapján megszerkesztett gráf erősen emlékeztet a DC motor gráfjára. A villamos oldal azonos, ott a tekercs ellenállása és a nyugalmi induktivitása alkotják a hurok passzív elemeit, a mechanikai oldalon egyenes vonalú mozgást végző elemeket láthatunk. A rugalmas vezeték „k” rugómerevsége, és a deformációból eredő belső súrlódási veszteséget modellező „b” csillapítási tényezője (veszteséges rugó, Kelvin modell) valamint az eredő tömeg található. A mechanikai oldalon forrás nincsen.

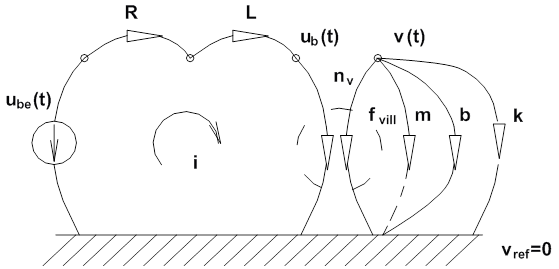
6.21. ábra - A CD fej gráfja

Keresett a hagyományos szabályozókör megtervezéséhez szükséges X(s)/U_be(s)=G(s) átviteli függvény. Ilyen esetben legcélszerűbb, ha impedancia módszert alkalmazunk. A következő ábrákon először az impedancia hálózat, majd a kimeneti változónak alárendelt összevonások eredményeként kapott kapcsolás látható. Mechanikai keresztváltozó keresett, ezért a villamos oldal impedanciáit átszámítjuk mechanikai egyenértékű impedanciákká, és felrajzoljuk a keresztváltozó osztót. A feladatot ennél egyszerűbb kapcsolással nem lehet megoldani.

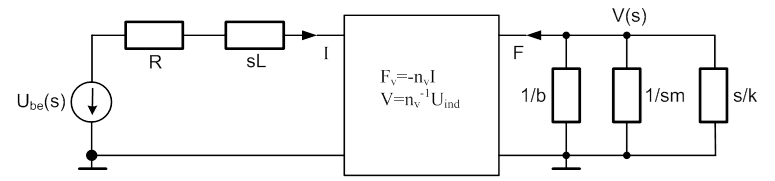
6.22. ábra - A CD fej impedancia hálózata

A korábbi példáknál bemutatott módon összevonjuk a villamos oldal impedanciáit, majd a mechanikaim oldalra számítjuk át az eredőt, hiszen mechanikai változó a keresett.

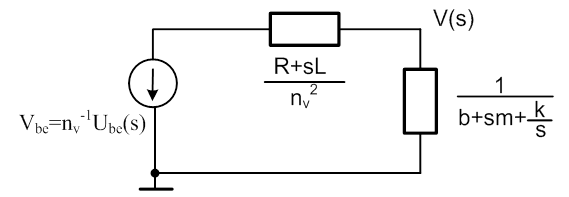
6.23. ábra - Egyszerűsített kapcsolás az átviteli függvény felírásához

Az egyszerűsített kapcsolás alapján, feszültségosztó formájában felírjuk az átviteli függvényt:

$\frac{V (s)}{V_{b e} (s)} = \frac{V (s)}{\frac{1}{n_{v}} U_{b e} (s)} = \frac{\frac{s}{s^{2} m + s b + k}}{\frac{R + s L}{n_{v}^{2}} + \frac{s}{s^{2} m + s b + k}}$

A kijelölt műveletek elvégzése a következő feladat:

$G (s) = \frac{V (s)}{U_{b e} (s)} = \frac{1}{n_{v}} \cdot \frac{n_{v}^{2} \cdot s}{\frac{R + s L}{n_{v}^{2}} + \frac{s}{s^{2} m + s b + k}} = \frac{s \cdot n_{v}}{s^{3} \frac{L}{R} \frac{m}{k} + s^{2} (\frac{m}{k} + \frac{L}{R} \frac{b}{k} + \frac{n_{v}^{2}}{R k}) + s (\frac{L}{R} + \frac{b}{k}) + 1}$

Végül a szakasz átviteli függvénye már nem tartalmaz deriváló jelleget, tekintettel arra, hogy az optikai foglalatnak nem a sebessége, hanem a pozíciója a szabályozott jel. A sebességre felírt átviteli függvényt tehát be kell szorozzuk 1/s kifejezéssel:

$G (s) = \frac{X (s)}{U_{b e} (s)} = \frac{n_{v}}{s^{3} \frac{L}{R} \frac{m}{k} + s^{2} (\frac{m}{k} + \frac{L}{R} \frac{b}{k}) + s (\frac{L}{R} + \frac{b}{k} + \frac{n_{v}^{2}}{R k}) + 1}$

Az átviteli függvényben szándékosan elkülönítettük a mechanikai és a villamos időállandókat, valamint a mechanikai rész csillapítatlan rezonancia frekvenciájával összefüggő tagot:

$ω_{0} = α = \sqrt{\frac{k}{m}}$

Az operátor első hatványához tartozó együttható harmadik tagja jellegzetesen mechatronikai, hiszen ez egy vegyes időállandó. A redukció alapján a n_v²/k=L_k kifejezés nem más, mint a mechanikai rugómerevséggel egyenértékű induktivitás. Így valójában egy L_k/R elektromechanikus időállandóval van dolgunk.

Az általunk eddig megvizsgált híradástechnikai CD fejek mindegyikének mechanikai rezonancia frekvenciája a 17 Hz<ω₀ <30 Hz tartományban volt található. A szabályozókör tervezése szempontjából ezt a szakaszt mindenképpen másodrendűnek célszerű tekinteni, hiszen az L/R időállandó elhanyagolhatóan kicsi a mechanikai rész időállandójához viszonyítva. A szakasz dinamikai szimulációját bemutatjuk a 15. fejezet elején. Szimulációval és méréssel győződtünk meg arról, hogy a szabályozás szempontjából „éppen” a motor induktivitása lesz elhanyagolható. Érdekességként említjük, hogy van olyan munka, amelyben a szerző nem vesz tudomást a domináns jellegű mechanikai építőelemekről, munkájában olyan villamos kapcsolás látható, amelyen a lineáris motorból kizárólag a tekercs induktivitása van feltüntetve. Éppen az az elem, amely a dinamikus viselkedésben nem játszik szerepet: Claus Biaesch-Wiebke CD-Player und R-DAT-Recorder [6.3.]. Ilyen alapról indulva természetesen nem lehet megfelelő szabályozókört méretezni. Az idézett munka célja nem is ez volt, hanem a CD-DVD fejek felépítésének és működésének bemutatása, bár a teljeséghez mechatronikai szemlélet esetében az elektrodinamikus váltó, és a mechanikai építőelemek is hozzátartoznak.

Szakirodalom

[6.1.] Lenk, A.. Elektromechanische Systeme Bd. 2. Verlag Technik. Berlin . 1975.

[6.2.] Kuo, B. C.. Önműködő szabályozott rendszerek. Műszaki Könyvkiadó. Budapest . 1979.

[6.3.] Biaesch-Wiebke, Claus. CD-Player und R-DAT-Recorder. Vogel Verlag. Würzburg . 1988.

Vissza		Előre
5. fejezet - Az állapotegyenlet megoldása idő és operátor tartományban	Főoldal	7. fejezet - Hajtómű dinamikai modelljei, a mechanikai időállandó kérdése