16. fejezet - Golyósorsós pozícionáló szabályozásának tervezése és szimulációja
Vissza		Előre

16. fejezet - Golyósorsós pozícionáló szabályozásának tervezése és szimulációja

Tartalom

A 9. fejezet fejezetben szereplő golyósorsós mozgásátalakító matematikai modell struktúrájának előállítására mutatunk egyet a lehetséges módszerek közül.

A matematikai modell (átviteli függvény) paraméterezéséhez katalógusból válogatott adatokat használunk.

A matematikai modellel adott rendszer dinamikai (idő- és frekvenciatartománybeli) vizsgálata után szabályozót tervezünk, az ilyen jellegű valóságos rendszerekkel szemben támasztott irányítási célok figyelembe vételével. Elsődleges elvárás természetesen a stabilitás, mégpedig aperiodikus viselkedéssel, túllendülések nélküli, gyors és pontos (hibamentes) alapjel követéssel.

16.1. Matematikai modell előállítása

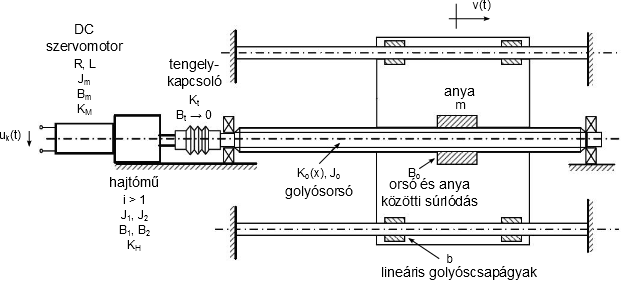
16.1. ábra - A rendszer felépítése a figyelembe vett fizikai jellemzőkkel

A vázlat nem géprajzi, hanem a működést szemlélteti. Ugyanakkor érdekes konstrukciós probléma a vezetékek rögzítése a keretben, és a tengely csapágyazása. Erről a 11. fejezet fejezet elején találunk rövid ismertetést. A rendszer működését ábrázoló „műszaki vázlat” alapján elkészíthetjük a struktúragráfot.

16.2. ábra - A rendszer vázlata alapján készített struktúragráf

Az ábrán (és a további modellekben) szereplő fizikai mennyiségek:

	u [V]	feszültség
	R [Ω]	ellenállás
	L [H=Vs/A]	induktivitás
	n_v1=K_M [Nm/A=Vs/rad]	az elektrodinamikai energiaátalakító (váltó) ún. motorállandója
	Ω [rad/s]	szögsebesség
	J [kg m²]	tehetetlenség
	B [Ns/rad]	transzlációs mechanikai rendszerben értelmezett csillapítási tényező
	K [Nm/rad]	torziós rugómerevség
	n_t = i	a hajtómű mint energiaátalakító (transzformátor) állandója
	n_v2=h/2π [m/rad]	a forgó és haladó mozgás közötti energiaátalakító (váltó) állandója
	m [kg]	tömeg
	b [Ns/m]	transzlációs mechanikai rendszerben értelmezett csillapítási tényező

Ugyan már a vázlatban is alkalmaztunk elhanyagolásokat (például a tengelykapcsolóban fellépő veszteséget elhanyagoljuk, B_t → 0), de modellünk még mindig igen összetett. Az energiatárolók száma: egy villamos (L), összevonással két torziós rugalmas (K), négy torziós tehetetlenség (J), valamint egy transzlációs mechanikai (m). Összesen nyolc energiatárolót számolhatunk össze, sőt ha külön részmodellként kezeljük a rugalmasságokat, még magasabb rendű rendszermodellt kapunk. Eddigi – legalább részrendszerenként értelmezhető – domináns póluspárokra vonatkozó ismereteinket és tapasztalatainkat megerősítik a konkrét katalógusadatok (fizikai mennyiségek) helyettesítésével számított matematikai modellek.

Az összevonható mennyiségek és az egyes részegységek sajátságai figyelembe vételével egyszerűsíthetjük a gráfot és két részrendszerre bonthatjuk.

Az alábbi konstrukciós adottságokból indulunk ki:

a DC motor induktivitása mint energiatároló a rendszerben lévő többi tárolóhoz képest gyors dinamikájú (nagyságrendekkel kisebb időállandójú), ezért elhanyagoljuk.
a hajtómű K_Hrugómerevsége nagy, ezért Ω_més Ω₁ szögsebességek azonosak. A motor mechanikai paraméterei közül a B_mcsapágycsillapítást és a J_m tehetetlenséget a hajtómű hasonló, de nagyobb értékű paramétereivel összevonva vesszük figyelembe (B₁, B₂ csillapítások és J₁, J₂ tehetetlenségek). Az egyszerűbb jelölés miatt a továbbiakban J_e és B_e paraméterekkel számolunk, de tudjuk, hogy:

$\begin{array}{l} J_{e} = J_{m} + J_{1} + \frac{1}{i^{2}} J_{2} \\ B_{e} = B_{m} + B_{1} + \frac{1}{i^{2}} B_{2} \end{array}$

A hajtómű módosítása legyen olyan nagy értékű, hogy az Ω₂ kimenő szögsebesség értékét a terhelés ingadozása nem befolyásolja. A hajtómű kimenetét ezért az Ω₂ jelű generátorként vesszük figyelembe, mint a második részrendszer gerjesztését. A motor-hajtómű egység lehetséges modell-formáiról szól a 8. fejezet fejezet. A példában a 8.1.1. szakasz fejezetben bemutatott változatot alkalmazzuk, a tulajdonságok részletes leírását ott találjuk meg.
A golyósorsó és mechanikai környezete összes rugómerevségét egyetlen eredővel, K_o-val vesszük figyelembe. A részletes modellezés a 11. fejezet fejezetben látható. Az itt bemutatott példa a 11.2. szakasz fejezetben van részletesebben leírva, az „Elsőrendű motor és hajtómű egységgel” bekezdésben.

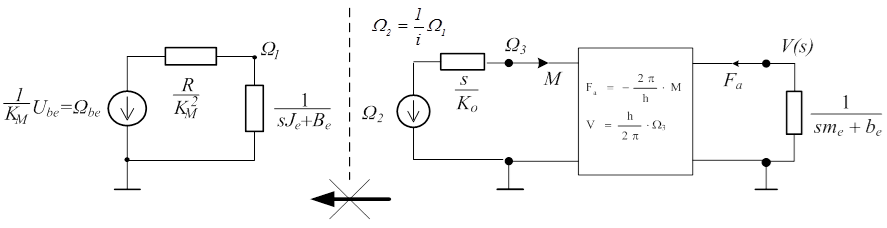
16.3. ábra - A két alrendszer egyszerűsített impedancia modellje

A fenti ábrán a bal oldali részrendszer a motort és a hajtómű hajtott oldalát tartalmazza, a második részrendszer tartalmazza a hajtott részrendszert.

A két részrendszer matematikai modelljét célszerű az átviteli függvényt eredményező hálózati (más néven impedancia) módszerrel, esetleg csomóponti vagy hurokmódszerrel előállítani, hiszen a sorba kapcsolt részrendszerek eredő átviteli függvénye az összetevők átviteli függvényének szorzata.

Az átviteli függvényes felírás miatt az időfüggvényként adott jeleket Laplace-operátoros tartományba transzformáljuk. Ha a csomóponti módszert (vagy a hurokmódszert) választjuk, szintén transzformálnunk kell a jeleket, sőt a modell jellegétől függően integráljukat és deriváltjukat. (A második részrendszer modelljét csomóponti módszerrel állítjuk elő.)

16.1.1. A hajtó részrendszer modellje

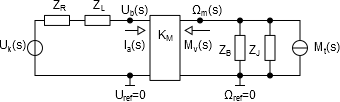
16.4. ábra - A hajtó alrendszer elhanyagolás nélküli impedanciahálózat modellje

Az impedancia a keresztváltozó és az átmenő változó hányadosaként írható fel Laplace-operátoros tartományban.

a villamos rendszer általános impedanciája így $Z_{v i l l a m o s} = \frac{U (s)}{I (s)}$
a rotációs mechanikai általános impedanciája így $Z_{r o t á c i ó s} = \frac{Ω (s)}{M (s)}$

Az egyes impedanciák:

a villamos oldalon
- a disszipatív elem impedanciája $Z_{R} = R$
- az induktív energiatárolót elhanyagoljuk, (impedanciája egyébként $Z_{L} = s \cdot L$ )
a mechanikai oldalon
- a disszipatív elem impedanciája $Z_{B} = \frac{1}{B_{e}}$
- az energiatároló impedanciája $Z_{J} = \frac{1}{s \cdot J_{e}}$
- a párhuzamosan kapcsolt elemek eredő impedanciája: $Z_{M} = \frac{1}{\frac{1}{Z_{B}} + \frac{1}{Z_{J}}} = \frac{Z_{B} \cdot Z_{J}}{Z_{B} + Z_{J}} = \frac{\frac{1}{B_{e}} \cdot \frac{1}{s \cdot J_{e}}}{\frac{1}{B_{e}} + \frac{1}{s \cdot J_{e}}} = \frac{1}{B_{e} + s \cdot J_{e}}$

A rendszerben forrásként jelenik meg a villamos motorra kapcsolt U_k feszültség. A visszahatásból származó M_t terhelő nyomatékot elhanyagoljuk.

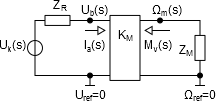
16.5. ábra - A hajtó alrendszer elhanyagolás és összevonás utáni impedanciahálózat modellje

Az elektrodinamikai energiaátalakító (váltó) egyenletei

	$Ω_{m} (s) = \frac{1}{K_{M}} \cdot U_{b} (s)$	(16.1)
	$M_{v} (s) = - K_{M} \cdot I_{a} (s)$	(16.2)

ahol M [Nm] a forgatónyomaték, I [A] a villamos áram, Ω [rad/s] a szögsebesség, U [V] a feszültség és K_M [Nm/A=Vs/rad] az energiaátalakító állandója.

A váltó egyenleteivel felírhatjuk a villamos résznek megfeleltethető mechanikai impedanciát

$Z_{m R} = \frac{Ω_{m} (s)}{M_{v} (s)} = \frac{\frac{U_{b} (s)}{K_{M}}}{- K_{M} \cdot I_{a} (s)} = (-) \frac{1}{K_{M}^{2}} \cdot \frac{U_{b} (s)}{I_{a} (s)} = (-) \frac{R}{K_{M}^{2}}$

(16.3)

Mivel a forgatónyomaték felel meg a villamos áramnak, a feszültségforrást szögsebesség forrással helyettesíthetjük. Így az egyszerűsített modellt villamos feszültségosztó analógiájaként szögsebesség osztóként (keresztváltozó osztóként) modellezhetjük.

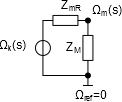
16.6. ábra - A hajtó alrendszer egyszerűsített és mechanikai szögsebesség osztóként előállított impedancia hálózat modellje

A szögsebesség-osztó egyenlete és egyben a hajtó részrendszer átviteli függvénye

$\frac{Ω_{m} (s)}{Ω_{k} (s)} = \frac{Z_{M}}{Z_{M} + Z_{m R}} = \frac{\frac{1}{B_{e} + s \cdot J_{e}}}{\frac{1}{B_{e} + s \cdot J_{e}} + \frac{R}{K_{M}^{2}}}$

(16.4)

Egyszerűsítve

$G_{1} (s) = \frac{\frac{1}{B_{e} + s \cdot J_{e}}}{\frac{1}{B_{e} + s \cdot J_{e}} + \frac{R}{K_{M}^{2}}} = \frac{\frac{1}{B_{e} + s \cdot J_{e}}}{\frac{K_{M}^{2} + R \cdot (B_{e} + s \cdot J_{e})}{K_{M}^{2} \cdot (B_{e} + s \cdot J_{e})}} = \frac{K_{M}^{2}}{(K_{M}^{2} + R \cdot B_{e}) + s \cdot R \cdot J_{e}}$

(16.5)

Időállandós alakra átírva (és a szögsebességgel helyettesített feszültséget visszaírva) látszik a modell jellege (elsőrendű, azaz P-T1)

$G_{1} (s) = \frac{Ω_{m} (s)}{U_{k} (s)} = \frac{\frac{K_{M}^{2}}{K_{M}^{2} + R \cdot B_{e}}}{\frac{R \cdot J_{e}}{K_{M}^{2} + R \cdot B_{e}} \cdot s + 1} = \frac{A}{T \cdot s + 1}$

(16.6)

16.1.2. A hajtott részrendszer modellje

Oktatási célból a hajtott rendszer átviteli függvényét időtartományból kiindulva, csomóponti egyenletek felhasználásával határozzuk meg. Ezt azért tesszük, mert a 11. fejezet fejezetben, ahol a golyósorsós szakasz tervezését és méretezését találjuk, az átviteli függvényt impedancia módszerrel határoztuk meg. A két módszer lépései és munkaigénye így összehasonlíthatóvá válnak.

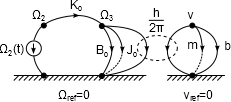
16.7. ábra - A hajtott alrendszer struktúragráf modellje

A stuktúragráf alapján a csomóponti egyenletek:

	$- M_{K o} (t) + M_{B o} (t) + M_{J o} (t) + M (t) = 0$	(16.7)
	$- f (t) + f_{m} (t) + f_{b} (t) = 0$	(16.8)

Az egyes passzív elemekre vonatkozó összefüggések idő- és Laplace-operátoros tartományban (a deriválásnál zérus kezdeti értéket feltételezve):

a rotációs mechanikai rendszerben (figyelembe véve, hogy $Ω_{r e f} = 0$ )
- az egyik energiatároló (torziós rugó) egyenlete:
  
  $M_{K o} (t) = K_{o} \cdot \int Ω_{23} (t) d t = K_{o} \cdot \int (Ω_{2} (t) - Ω_{3} (t)) d t$
  
  $M_{K o} (s) = \frac{K_{o}}{s} \cdot (Ω_{2} (s) - Ω_{3} (s))$
- a másik energiatároló egyenlete:
  
  $M_{J o} (t) = J_{o} \cdot \frac{d Ω_{3 R} (t)}{d t} = J_{o} \cdot \frac{d (Ω_{3} (t) - Ω_{r e f})}{d t} = J_{o} \cdot \frac{d Ω_{3} (t)}{d t}$
  
  $M_{J o} (s) = s \cdot J_{o} \cdot Ω_{3} (s)$
- a passzív elem egyenlete:
  
  $M_{B o} (t) = B_{o} \cdot Ω_{3 R} (t) = B_{o} \cdot (Ω_{3} (t) - Ω_{r e f}) = B_{o} \cdot Ω_{3} (t)$
  
  $M_{B o} (s) = B_{o} \cdot Ω_{3} (s)$
a transzlációs mechanikai rendszerben (figyelembe véve, hogy $v_{r e f} = 0$ )
- az energiatároló (tömeg) egyenlete:
  
  $f_{m} (t) = m \cdot \frac{d v_{1 R} (t)}{d t} = m \cdot \frac{d (v (t) - v_{r e f})}{d t} = m \cdot \frac{d v (t)}{d t}$
  
  $F_{m} (s) = s \cdot m \cdot V (s)$
- a passzív elem egyenlete:
  
  $f_{b} (t) = b \cdot v_{1 R} (t) = b \cdot (v (t) - v_{r e f}) = b \cdot v (t)$
  
  $F_{b} (s) = b \cdot V (s)$

A csomóponti egyenletekbe helyettesítjük a Laplace-operátoros tartománybeli összefüggéseket:

	$- \frac{K_{o}}{s} \cdot (Ω_{2} (s) - Ω_{3} (s)) + B_{o} \cdot Ω_{3} (s) + s \cdot J_{o} \cdot Ω_{3} (s) + M (s) = 0$	(16.9)
	$- F (s) + s \cdot m \cdot V (s) + b \cdot V (s) = 0$	(16.10)

Átrendezve

	$(\frac{K_{o}}{s} + B_{o} + s \cdot J_{o}) \cdot Ω_{3} (s) + M (s) = \frac{K_{o}}{s} \cdot Ω_{2} (s)$	(16.11)
	$(s \cdot m + b) \cdot V (s) = F (s)$	(16.12)

Az rotációs-transzlációs mechanikai energiaátalakító (transzformátor) egyenletei

	$Ω_{3} (s) = \frac{2 π}{h} \cdot V (s)$	(16.13)
	$M (s) = - \frac{h}{2 π} \cdot F (s)$	(16.14)

Behelyettesítve a váltóegyenleteket

	$(\frac{K_{o}}{s} + B_{o} + s \cdot J_{o}) \cdot \frac{2 π}{h} \cdot V (s) + M (s) = \frac{K_{o}}{s} \cdot Ω_{2} (s)$	(16.15)
	$(s \cdot m + b) \cdot V (s) = \frac{2 π}{h} \cdot M (s)$	(16.16)

Mindkét egyenletből kifejezve az M forgatónyomatékot az átviteli függvény meghatározására alkalmas egyenletet kapunk (egyik változó kimenő jel, azaz a v sebesség V(s) Laplace-transzformáltja, a másik a bemenő jel, az Ω₂(s) szögsebesség).

$M (s) = \frac{K_{o}}{s} \cdot Ω_{2} (s) - (\frac{K_{o}}{s} + B_{o} + s \cdot J_{o}) \cdot \frac{2 π}{h} \cdot V (s) = \frac{h}{2 π} (s \cdot m + b) \cdot V (s)$

(16.17)

A változókat csoportosítva és együtthatóikat s-hatványai szerint rendezve

$\frac{K_{o}}{s} \cdot Ω_{2} (s) = (\frac{2 π}{h} \cdot \frac{K_{o}}{s} + (\frac{h}{2 π} \cdot b + \frac{2 π}{h} \cdot B_{o}) + (\frac{h}{2 π} \cdot m + \frac{2 π}{h} \cdot J_{o}) \cdot s) \cdot V (s)$

(16.18)

Az egyenlet mindkét oldalát s-sel szorozva

$K_{o} \cdot Ω_{2} (s) = (\frac{2 π}{h} \cdot K_{o} + (\frac{h}{2 π} \cdot b + \frac{2 π}{h} \cdot B_{o}) \cdot s + (\frac{h}{2 π} \cdot m + \frac{2 π}{h} \cdot J_{o}) \cdot s^{2}) \cdot V (s)$

(16.19)

A hajtott részrendszer átviteli függvénye

$G_{2} (s) = \frac{V (s)}{Ω_{2} (s)} = \frac{K_{o}}{\frac{2 π}{h} \cdot K_{o} + (\frac{h}{2 π} \cdot b + \frac{2 π}{h} \cdot B_{o}) \cdot s + (\frac{h}{2 π} \cdot m + \frac{2 π}{h} \cdot J_{o}) \cdot s^{2}}$

(16.20)

Átrendezve

$G_{2} (s) = \frac{K_{o}}{\frac{2 π}{h} \cdot K_{o} \cdot (1 + \frac{h}{2 π \cdot K_{o}} \cdot (\frac{h}{2 π} \cdot b + \frac{2 π}{h} \cdot B_{o}) \cdot s + \frac{h}{2 π \cdot K_{o}} \cdot (\frac{h}{2 π} \cdot m + \frac{2 π}{h} \cdot J_{o}) \cdot s^{2})}$

$G_{2} (s) = \frac{\frac{h}{2 π}}{1 + (\frac{b}{K_{o} \cdot {(\frac{2 π}{h})}^{2}} + \frac{B_{o}}{K_{o}}) \cdot s + (\frac{m}{K_{o} \cdot {(\frac{2 π}{h})}^{2}} + \frac{J_{o}}{K_{o}}) \cdot s^{2}}$

Időállandós alakra átírva látszik a modell jellege (másodrendű, azaz P-T2)

$G_{2} (s) = \frac{V (s)}{Ω_{2} (s)} = \frac{\frac{h}{2 π}}{1 + \frac{b + B_{o} \cdot {(\frac{2 π}{h})}^{2}}{K_{o} \cdot {(\frac{2 π}{h})}^{2}} \cdot s + \frac{m + J_{o} \cdot {(\frac{2 π}{h})}^{2}}{K_{o} \cdot {(\frac{2 π}{h})}^{2}} \cdot s^{2}} = \frac{A}{1 + 2 \cdot ξ \cdot T \cdot s + T^{2} \cdot s^{2}}$

(16.21)

16.1.3. A hajtómű modellje

A hajtómű egyszerűsített modellje az i áttételnek megfelelő arányos (P) taggal állítható elő, a hajtó részrendszer Ω_m szögsebességét és hajtott rendszer Ω₂ szögsebességét felhasználva az átviteli függvény felírásához.

$G_{i} (s) = \frac{Ω_{2} (s)}{Ω_{m} (s)} = \frac{1}{i} = A$

(16.22)

16.1.4. A teljes szakasz modellje

A kapott három átviteli függvény (G₁ hajtó részrendszer, G_i hajtómű és G₂ hajtott részrendszer) soros eredőjeként (szorzataként) állítható elő a bemenő U_k feszültség és a mozgatott rendszer v sebessége közötti kapcsolat.

$\frac{V (s)}{U_{k} (s)} = G_{1} (s) \cdot G_{i} (s) \cdot G_{2} (s) = \frac{Ω_{m} (s)}{U_{k} (s)} \cdot \frac{Ω_{2} (s)}{Ω_{m} (s)} \cdot \frac{V (s)}{Ω_{2} (s)}$

(16.23)

Mivel számunkra nem a sebesség, hanem az elmozdulás lényeges, az x elmozdulás és v sebesség közötti összefüggést is figyelembe kell vennünk (a sebesség az elmozdulás idő szerinti deriváltja).

$V (s) = s \cdot X (s)$

(16.24)

Ezzel a x elmozdulás és az U_k feszültség között felírható átviteli függvény

$G_{s} (s) = \frac{X (s)}{U_{k} (s)} = \frac{V (s)}{U_{k} (s)} \cdot \frac{1}{s} = G_{1} (s) \cdot G_{i} (s) \cdot G_{2} (s) \cdot \frac{1}{s}$

(16.25)

Behelyettesítve

$G_{s} (s) = \frac{X (s)}{U_{k} (s)} = \frac{\frac{K_{M}^{2}}{K_{M}^{2} + R \cdot B_{m}}}{\frac{R \cdot J_{m}}{K_{M}^{2} + R \cdot B_{m}} \cdot s + 1} \cdot \frac{1}{i} \cdot \frac{\frac{h}{2 π}}{1 + \frac{b + B_{o} \cdot {(\frac{2 π}{h})}^{2}}{K_{o} \cdot {(\frac{2 π}{h})}^{2}} \cdot s + \frac{m + J_{o} \cdot {(\frac{2 π}{h})}^{2}}{K_{o} \cdot {(\frac{2 π}{h})}^{2}} \cdot s^{2}} \cdot \frac{1}{s}$

(16.26)

A rendszer harmadrendű integráló (I-T3) típusú

$G_{s} (s) = \frac{A_{1}}{T_{1} \cdot s + 1} \cdot A_{i} \cdot \frac{A_{2}}{1 + 2 \cdot ξ \cdot T_{2} \cdot s + T_{2}^{2} \cdot s^{2}} \cdot \frac{1}{s}$

(16.27)

16.2. Szimulációs modell

A matematikai modell előállításához és a szabályozó tervezéséhez konkrét komponensek kiválasztása és a szükséges paraméterek behelyettesítése után kapott átviteli függvényt használunk.

16.1. táblázat - Az átviteli függvény számításához használt értékek

Elektromechanikus energiaátalakító (váltó) állandója	K_M = 0,022 Nm/A
Hajtómű áttétele	i = 134
Motor ellenállása	R = 2,05 Ω
A motor és hajtómű tehetetlenségi nyomatéka	J_e = 13*10^-7 kg/m²
A motor és hajtómű csillapítási tényezője	B_e = 5*10^-5 Ns/rad
A golyósorsó menetemelkedése	h = 0,002 m
A mozgatandó tömeg	m = 1,35 kg
Az anya és orsó közötti csillapítási tényező	b = 2*10^-4 Ns/m
Az orsóra számított eredő torziós rugómerevség	K_o = 2,107 Nm/rad
Az orsó csillapítási tényezője	B_o = 3,5*10^-3 Ns/rad
Az orsó tehetetlenségi nyomatéka	J_o = 1,2*10^-6 kg/m²

A GNU GPL licenc által szabályozott hozzáférésű Maxima (http://maxima.sourceforge.net/) számítógépes algebra rendszerrel számoljuk a katalógusadatok alapján az átviteli függvény együtthatóit. A Maxima rendszer hivatalos dokumentációja [16.4.] mellett az interneten igen sok oktatóanyag és mintapélda található. A COMA (COntrol engineering with MAxima) szabályozástechnikai számításokat megkönnyítő kiegészítő [16.5.] angol és német leírása mellett mintapéldákat is letölthetünk.

Az átviteli függvény együtthatóinak meghatározása wxMaxima programmal:

A National Instruments cég LabVIEW (Laboratory Virtual Instrumentation Engineering Workbench) szoftvercsomagja (http://www.ni.com/labview/) 2009-es verziójában, a Control Design and Simulation Module (http://www.ni.com/labview/cd-sim/) elemkészletével készült az átviteli függvény szimbolikus leképezése. A LabVIEW és a kiegészítő használatában a [16.1.], [16.2.], [16.3.] hivatalos források mellett szintén találhatunk interneten hozzáférhető segédanyagokat és mintapéldákat.

Az áttekinthetőség érdekében a G₁(s), G_i(s) átviteli függvények soros eredőjéhez szükséges számláló és nevező együttható képletek külön szerepelnek a hajtott részrendszer G₂(s) átviteli függvény előállításához szükséges összefüggésektől.

A két – szimbolikus átviteli függvényével adott – sorba kapcsolt rendszer eredőjét előállító programrészletet könnyen elkészíthetjük a Control Design & Simulation/Control Design/Model Interconnection/CD Series.vi használatával.

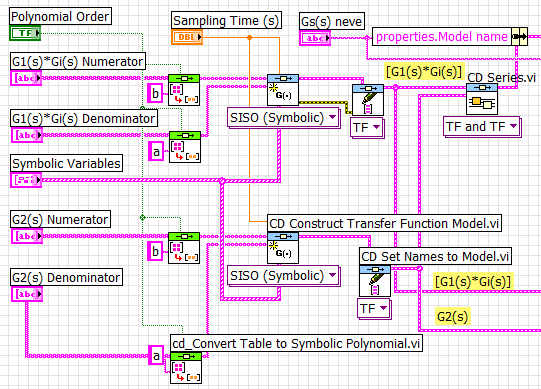
Az átviteli függvény előállítása a hajtó rendszer+hajtómű G1(s)*Gi(s) és a hajtott rendszer G2(s) szimbolikusan adott átviteli függvényének soros eredőjeként

16.8. ábra - Az átviteli függvény előállítása a hajtó rendszer+hajtómű G1(s)*Gi(s) és a hajtott rendszer G2(s) szimbolikusan adott átviteli függvényének soros eredőjeként

A sebesség-elmozdulás átalakításhoz szükséges integrálást 1/s átviteli függvényével, az előzőleg kapott átviteli függvénnyel szintén sorba kapcsolva vesszük figyelembe. A későbbiekben erre „szakasz integrálással” néven hivatkozunk.

Valamennyi szimuláció SI mértékegységekkel történt. A soron következő, „.vi” fájlokkal megjelenített diagramokon az alábbi SI prefixum jelöléseket látjuk:

u: mikro; n: nano; m: mili

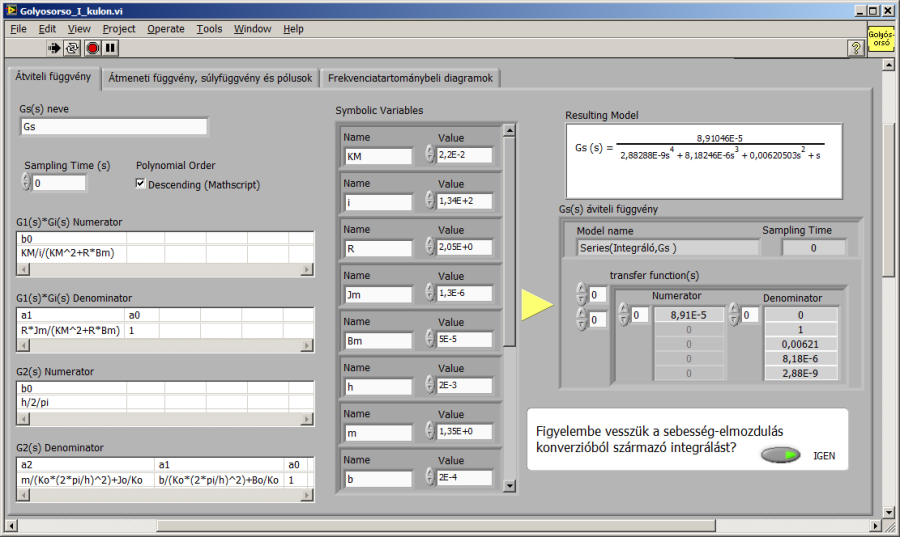
Az átviteli függvény szimbolikus megadása a sebesség-elmozdulás átalakításhoz szükséges integrátorral („szakasz integrálással” átviteli függvény számítása)

16.9. ábra - Az átviteli függvény szimbolikus megadása a sebesség-elmozdulás átalakításhoz szükséges integrátorral („szakasz integrálással” átviteli függvény számítása)

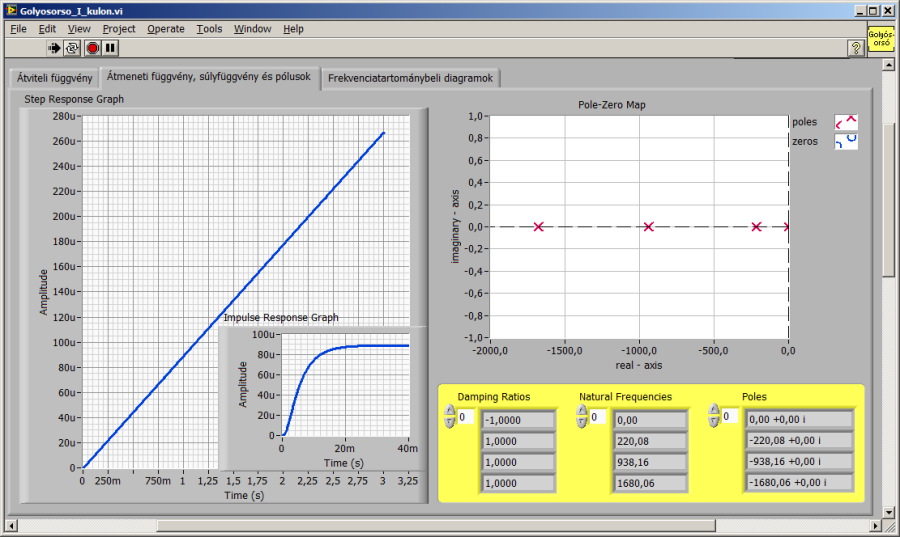
A „szakasz integrálással” átmeneti- és súlyfüggvénye és a zérus-pólus térkép a pólusok paramétereivel (csillapítási tényezők, sajátfrekvenciák és komplex számsíkbeli koordináták)

16.10. ábra - A „szakasz integrálással” átmeneti- és súlyfüggvénye és a zérus-pólus térkép a pólusok paramétereivel (csillapítási tényezők, sajátfrekvenciák és komplex számsíkbeli koordináták)

A későbbiek szempontjából fontos megjegyeznünk, hogy az integrátor nélküli szakaszban nincs konjugált komplex gyökpár, azaz a szakasz nem lengő jellegű.

A következő ábrán a „szakasz integrálással” frekvenciatartománybeli leképezései szerepelnek.

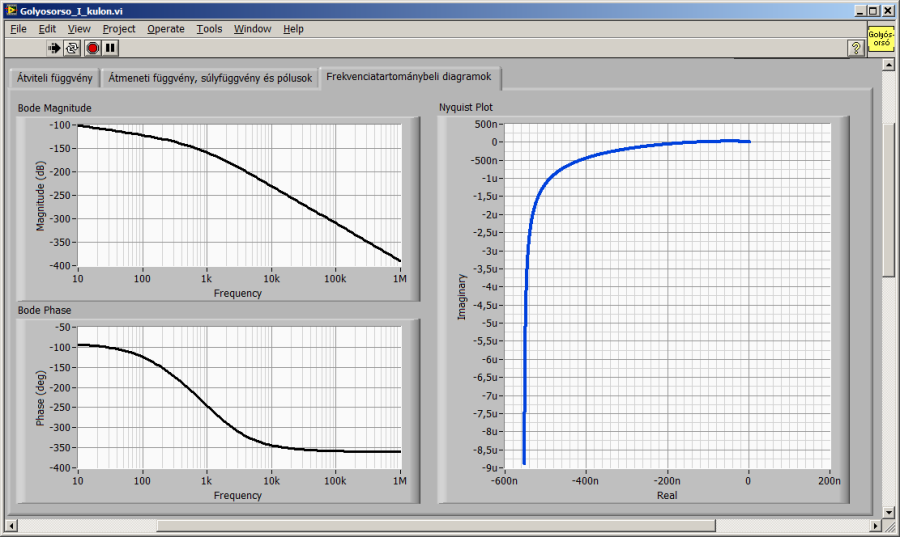
16.11. ábra - A „szakasz integrálással” Bode-diagrampárja és Nyquist-diagramja

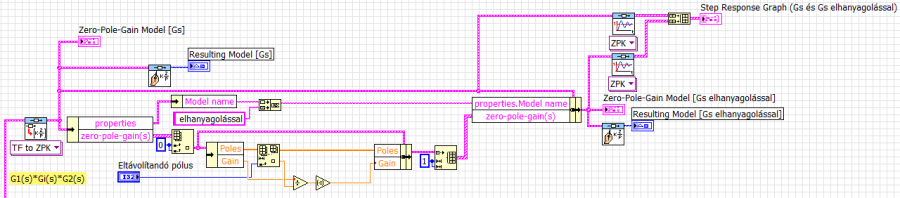
A szakasz dinamikai tulajdonságainak szemléletes ábrázolása miatt érdemes az integrálás nélkül is ábrázolni a jellegzetes idő- és frekvenciatartománybeli diagramokat. A sebesség-elmozdulás konverzió miatt szükséges integrálást a programunk előlapján lévő kapcsolóval vehetjük figyelembe. A megoldás az alábbi programrészleten látható, az előlapi logikai (Boolean adattípusú) kapcsoló neve „Integráló tag?”, az elágazás (Case struktúra) igaz (True) lapján a konstansként összeállított integráló tag és a G₁(s)·G_i(2) G₂(s) integráló nélküli szakasz soros eredője. A hamis (False) lapon az integráló hatást nem vesszük figyelembe, a G₁(s)·G_i(2) G₂(s) átviteli függvényt vezetjük tovább.

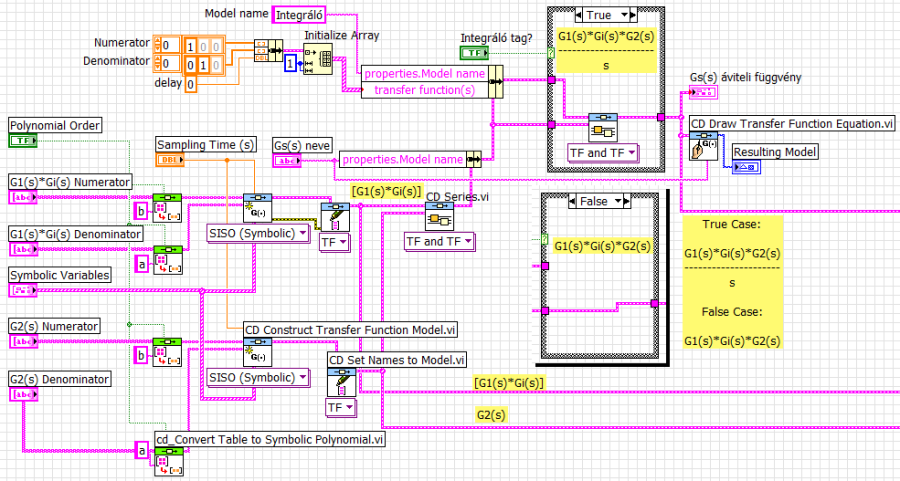
16.12. ábra - Az integrálás figyelembe vétele a szakasz átviteli függvényében az előlapi („”Integráló tag?) gomb logikai értéke alapján

Az alábbi ábrákon az integráló hatás nélküli átviteli függvény és az idő- és frekvenciatartománybeli leképezései szerepelnek.

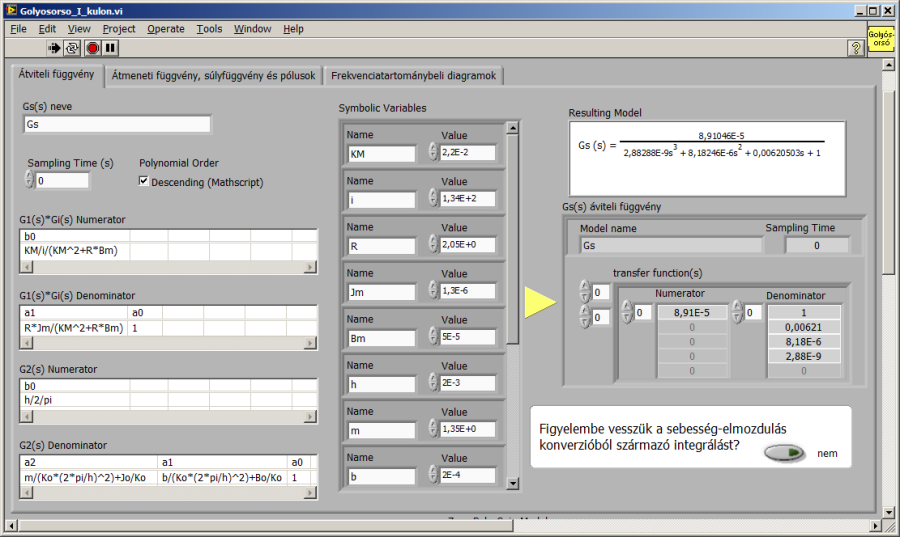
16.13. ábra - A szakasz (integrálás nélküli) átviteli függvény adatai

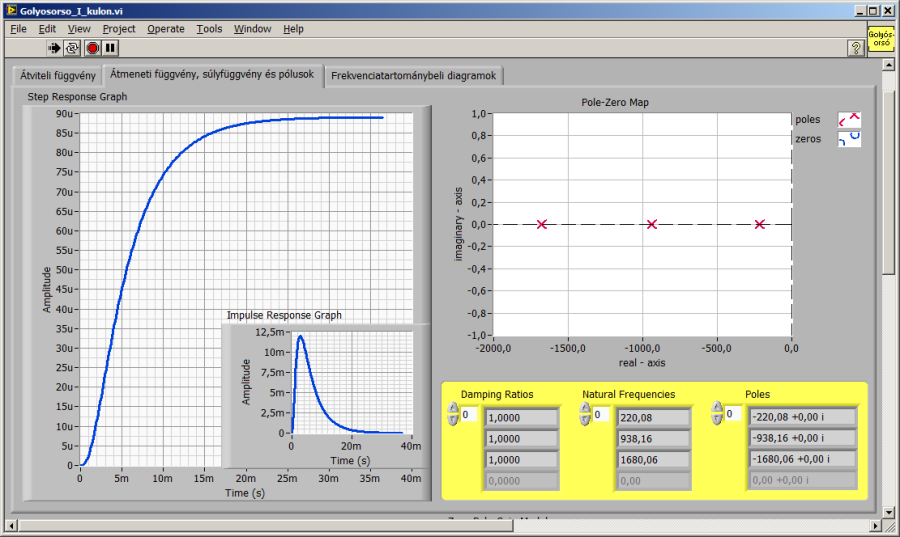
16.14. ábra - A szakasz (integrálás nélküli) jellegzetes időfüggvényei és pólusai

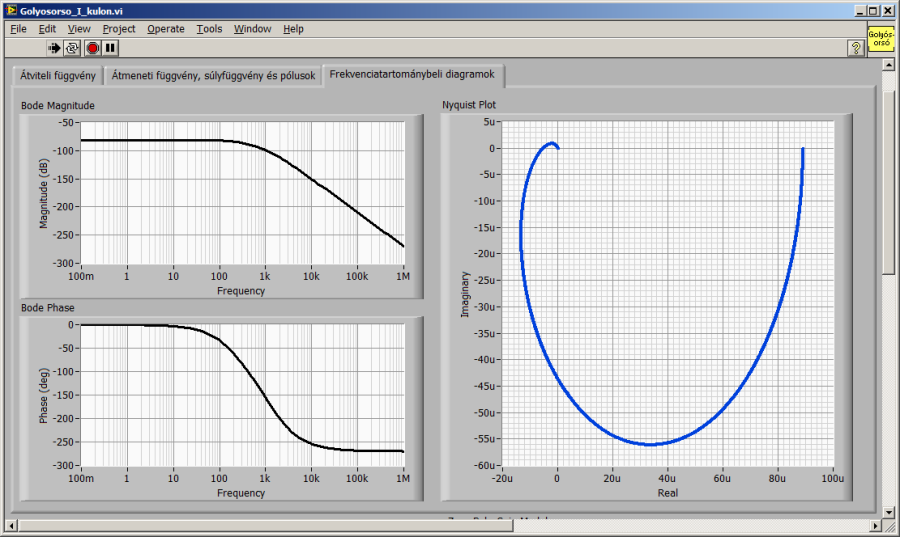
16.15. ábra - A szakasz (integrálás nélküli) frekvenciatartománybeli leképezései

16.3. A modell egyszerűsítése a számított eredmények alapján

A szabályozó tervezéshez vizsgáljuk meg a szakasz hajtó részrendszerének egyetlen, valamint a hajtott részrendszer két pólusát (és a belőlük számítható időállandókat). Az átviteli függvényből (TF, Transfer Function) a zérus-pólus-erősítés (ZPK, Zero-Pole-Gain) matematikai modellt a Control Design & Simulation/Control Design/Model Conversion/CD Convert to Zero-Pole-Gain model.vi használatával kapjuk. A három időállandót egyszerűen számíthatjuk a pólusokból.

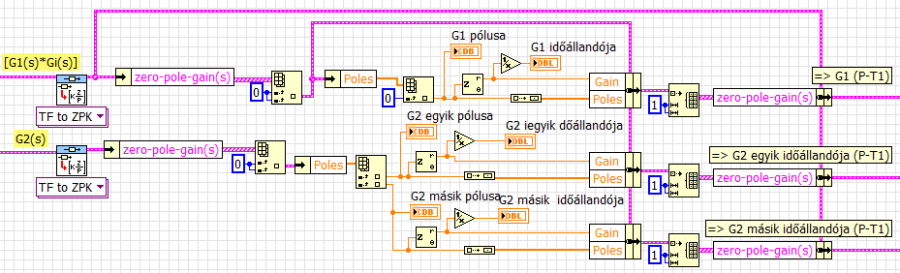
G1 egyetlen és G2 két valós pólusának (és ebből az időállandó) számítása, majd a pólusoknak megfelelő időállandójú egységnyi erősítésű egytárolós arányos tagok előállítása ZPK modellként

16.16. ábra - G1 egyetlen és G2 két valós pólusának (és ebből az időállandó) számítása, majd a pólusoknak megfelelő időállandójú egységnyi erősítésű egytárolós arányos tagok előállítása ZPK modellként

A pólusokból számított időállandóakkal megrajzolhatjuk a három, egységnyi erősítésűnek választott elsőrendű rendszer alább látható átmeneti függvényét.

16.2. táblázat - Az integráló hatás nélküli szakasz átviteli függvény pólusai és a megfelelő időállandók

	pólusa	időállandója
G1	-220,075 +0 i	4,544E-3
G2 egyik	-1680,06 +0 i	5,952E-4
G2 másik	-938,163 +0 i	1,066E-3

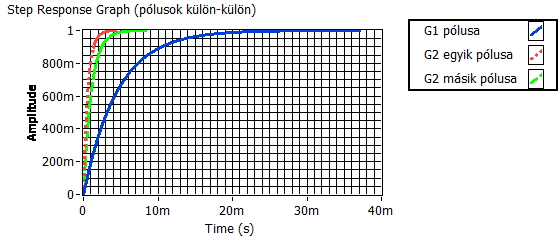
A harmadrendű szakasz három jellemző időállandójának megfelelő, egységnyi erősítésűnek választott elsőrendű rendszer átmeneti függvénye

16.17. ábra - A harmadrendű szakasz három jellemző időállandójának megfelelő, egységnyi erősítésűnek választott elsőrendű rendszer átmeneti függvénye

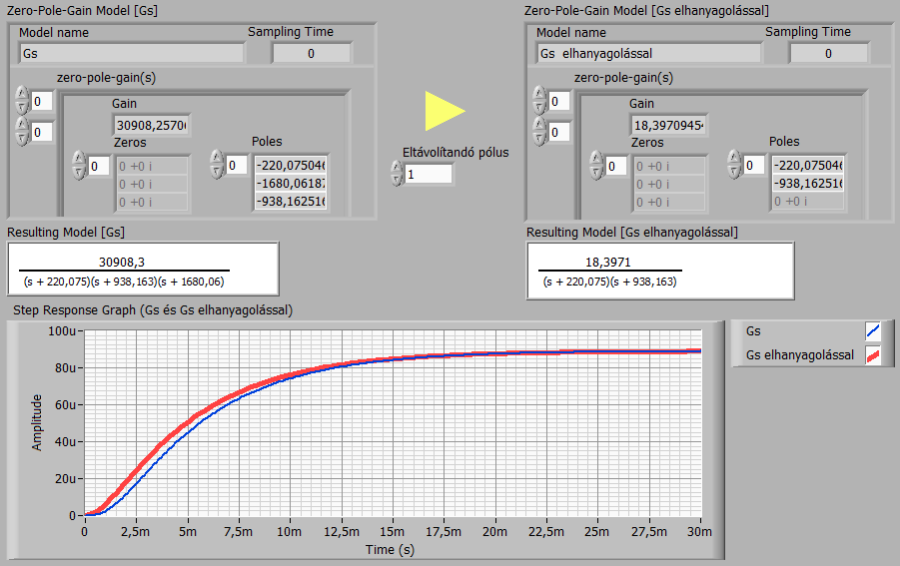
A szabályozótervezéshez figyelembe vehető elhanyagolást az átmeneti függvények ábrázolása alapján is indokolhatjuk. Az alábbiakban a két „lassú” pólusú másodrendű rendszert hasonlítjuk össze a háromtárolós modellel és feltüntetjük a szabályozásba nem bevont „gyors” pólus dinamikáját, szintén átmeneti függvényen.

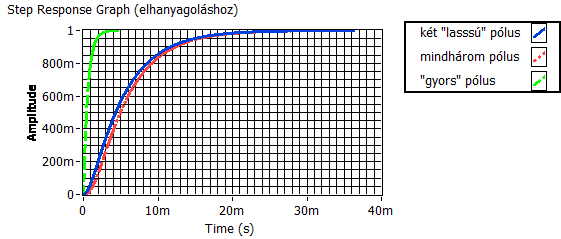
16.18. ábra - A harmadrendű szakasz, a másodrendű közelítés és az elhagyott elsőrendű rész átmeneti függvénye

Az elhanyagoláshoz szükséges számításokat a wxMaxima munkafüzetben is elvégezzük és ebben ábrázoljuk az eredeti és az elhanyagolás utáni rendszer átmeneti függvényének különbségét.

A harmadrendű szakasz egyszerűsítése másodrendűvé és az elhanyagolás létjogosultsága wxMaxima programmal:

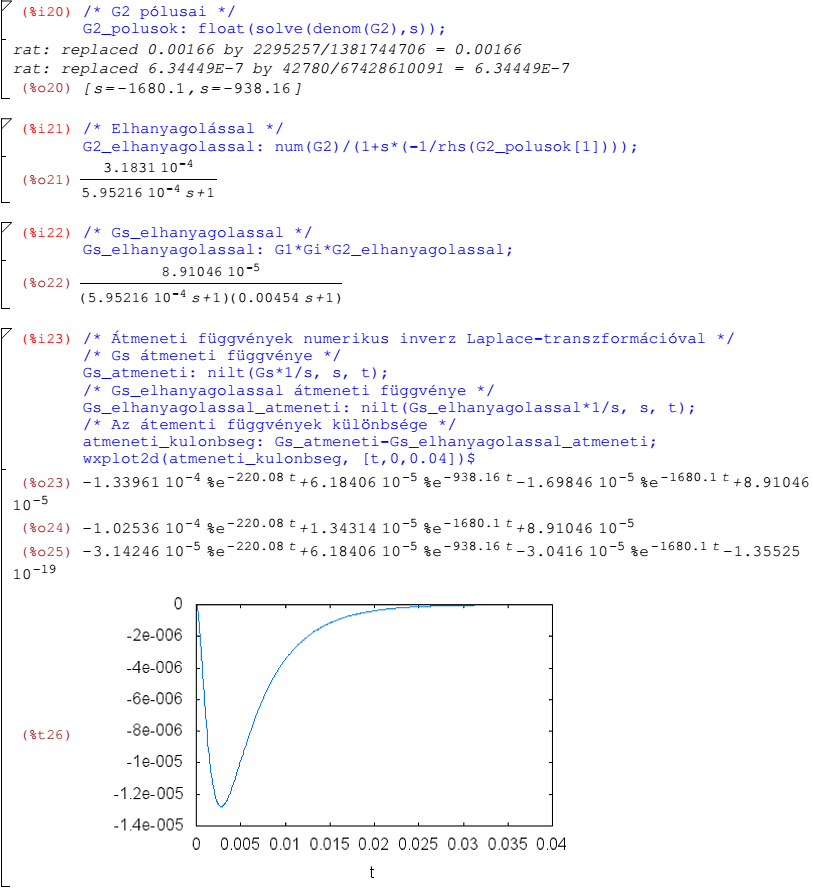
Az elhanyagolás indoklását alátámaszthatjuk a három elsőrendű rendszer Bode-diagramjával is. Az alábbi diagramokon látszik, hogy a két „lassú” pólus („G1 pólusa” és „G2 egyik pólusa”) között nincs jelentős eltérés (az időállandók viszonya durván 4,3). A „gyors” pólusnak („G2 másik pólusa”) megfelelő töréspont viszont hozzávetőleg egy dekáddal jobbra esik az előzőektől.

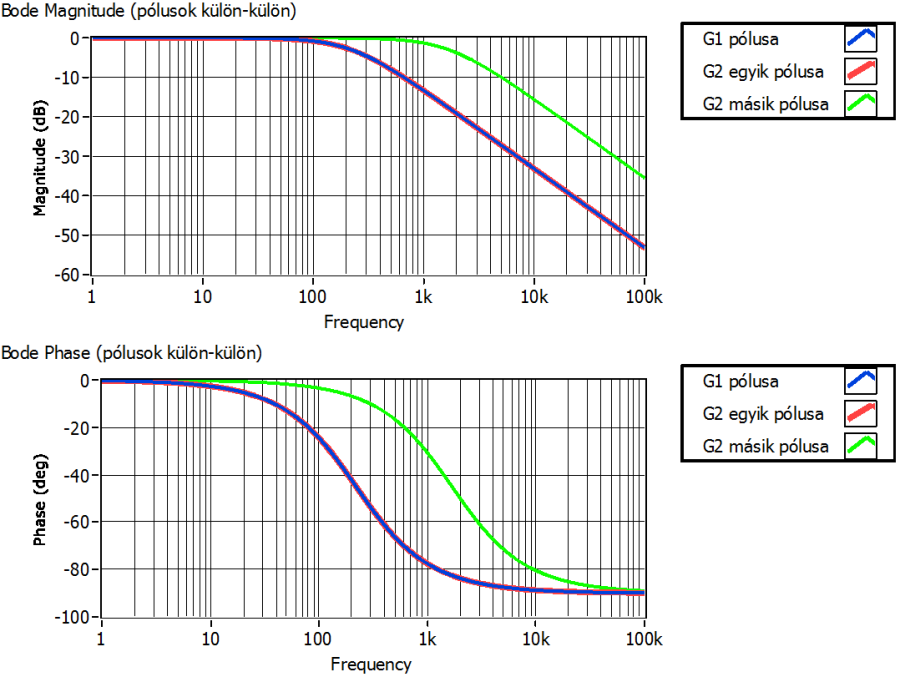
16.19. ábra - A harmadrendű szakasz időállandóinak megfelelő három elsőrendű tag Bode-diagramja

E megfontolás alapján a szakaszt a G₁(s) hajtó rész, a G_i(s) hajtómű és a G₂(s) hajtott rész domináns időállandót tartalmazó elsőrendűvé? (csak a gyors pólust hagytuk el, tehát másodrendű lett a szakasz) egyszerűsített modelljével közelítjük.

16.20. ábra - A „gyors” pólus elhanyagolását megvalósító LabVIEW programrészlet

16.21. ábra - A „gyors” pólus elhanyagolása és a kapott átmeneti függvény a kiindulási harmadrendűhöz hasonlítva

16.4. Szabályozás tervezése

Először szabályozó nélkül (tulajdonképpen egységnyi átviteli tényezőjű P-szabályozóval), a szabályozási kör visszacsatoló ágában szintén egységnyi átviteli tulajdonságot feltételezve vizsgáljuk az egyszerűsített másodrendű rendszert.

A visszacsatoló ágban lévő egységnyi átvitel megfelelően közelíti az egyébként szabályozási körökben használatos érzékelő és jelátalakító dinamikai tulajdonságait.

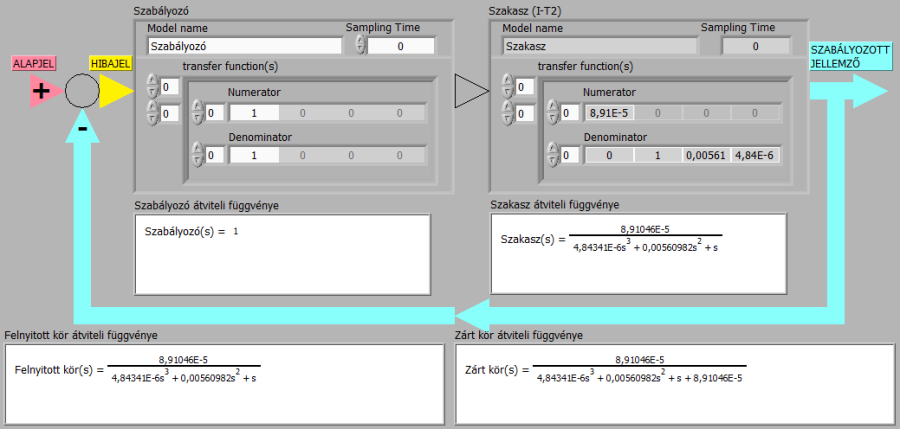
16.22. ábra - A másodrendű szakasz és egységnyi erősítésű arányos szabályozó: átviteli függvények

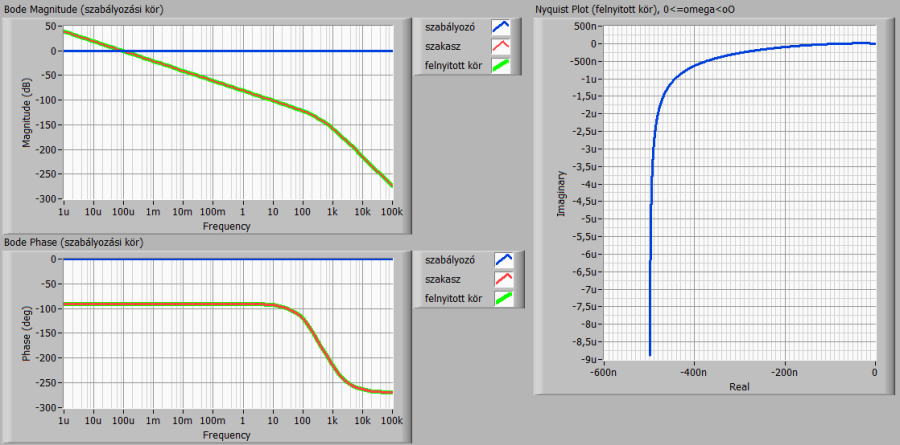
A másodrendű szakasz és egységnyi erősítésű arányos szabályozó: frekvenciatartománybeli diagramok (szakasz, szabályozó és felnyitott kör Bode-diagram, felnyitott kör Nyquist-diagram)

16.23. ábra - A másodrendű szakasz és egységnyi erősítésű arányos szabályozó: frekvenciatartománybeli diagramok (szakasz, szabályozó és felnyitott kör Bode-diagram, felnyitott kör Nyquist-diagram)

A szabályozás minőségét a tartalékok (fázis- és erősítési tartalék), a zárt kör átmeneti függvénye, valamint a szakasz és a zárt pólusaival értékelhetjük.

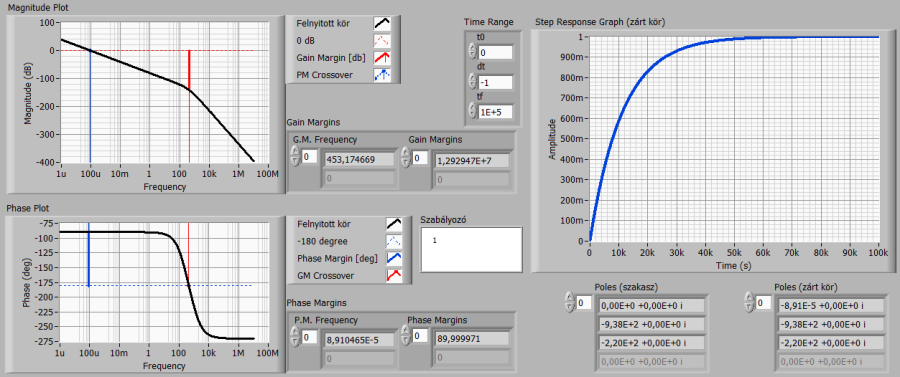
A másodrendű szakasz és egységnyi erősítésű arányos szabályozó: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

16.24. ábra - A másodrendű szakasz és egységnyi erősítésű arányos szabályozó: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

A kapott eredményekből – főleg a zárt kör átmeneti függvényéből – látszik, hogy az egységnyi erősítésű P-szabályozóval

ugyan a kívánt aperiodikus beállást érjük el,
nincs maradó követési hiba a szakasz melletti (a sebesség-elmozdulás konverzió miatt szükséges) integrálás miatt, azonban
a szabályozás rendkívül lassú!

Az arányos szabályozó erősítését növelve a vágási körfrekvencia jobbra tolódik, a zárt kör gyorsul. 100-szoros erősítésű arányos szabályozót választva az eredmény az alábbi ábrán látható.

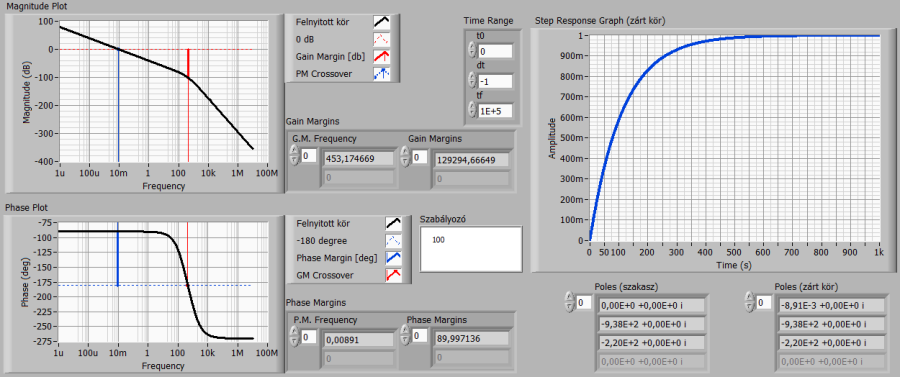
A másodrendű szakasz és százszoros erősítésű arányos szabályozó: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

16.25. ábra - A másodrendű szakasz és százszoros erősítésű arányos szabályozó: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

Az elméleti – pontosabban szimulációs – vizsgálódást folytatva, az arányos szabályozó erősítését 10000-re választva tovább gyorsíthatjuk a rendszert. Az alábbi ábrán látható, hogy a szakasz másodrendű részének dinamikáját még mindig nem tudtuk eléggé megközelíteni.

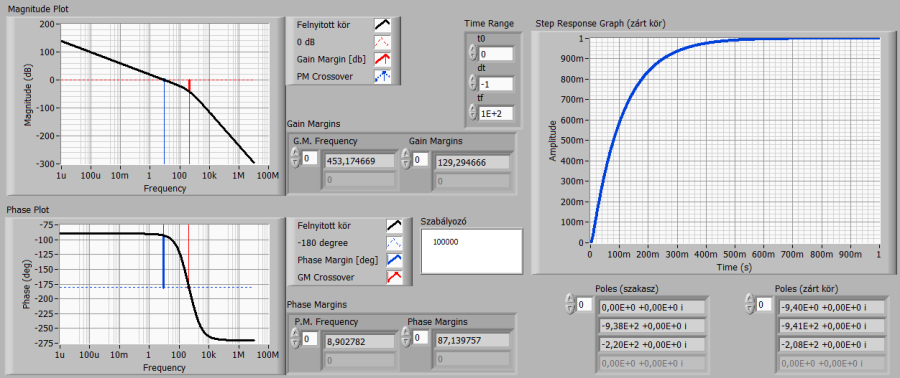
A másodrendű szakasz és tízezerszeres erősítésű arányos szabályozó: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

16.26. ábra - A másodrendű szakasz és tízezerszeres erősítésű arányos szabályozó: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

Próbálkozzunk az erősítés további növelésével! AZ előző érték 20-szorosát, vagyis 2000000-szoros erősítést választva még mindig nem értük el a szakasz gyorsaságát, viszont a rendszerünk lengő beállást mutat. Az erősítés további növelése fokozza a lengési hajlamot. A golyósorsós pozícionáló esetében lengéseket semmiképpen nem engedhetünk meg, így a legegyszerűbb arányos szabályozónál összetettebb struktúrára lesz szükségünk.

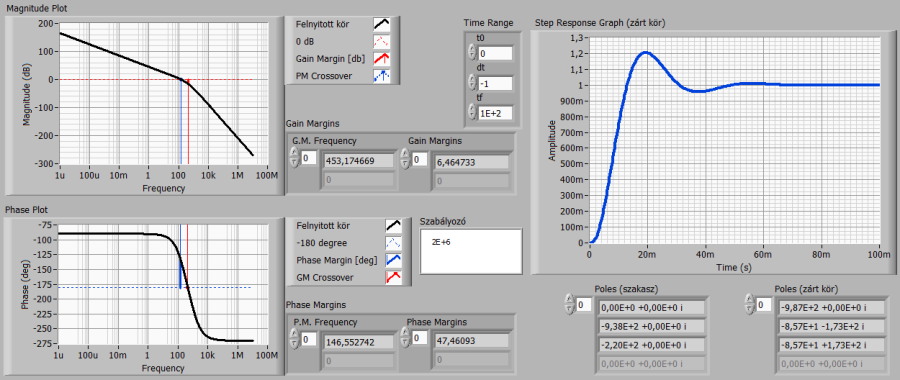
A másodrendű szakasz és kétmilliószoros erősítésű arányos szabályozó: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

16.27. ábra - A másodrendű szakasz és kétmilliószoros erősítésű arányos szabályozó: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

Válasszunk PD-jellegű töréspontáthelyező algoritmust (azaz párhuzamosan kapcsolt arányos és megvalósítható differenciáló tulajdonságú tagból álló szabályozót)!

$G_{c} (s) = A_{c} \cdot \frac{1 + T_{A} \cdot s}{1 + T_{B} \cdot s}$

(16.28)

A szabályozó (1+T_As) gyöktényezőjével „semlegesítjük” a szakasz kisebb törésponti körfrekvenciájú (vagyis nagyobb időállandójú) elsőrendű komponensét. A T_B időállandó reciprokának megfelelő töréspontot és az A_c erősítést úgy választjuk meg, hogy a zárt kör továbbra is aperiodikusan követi az egységugrás alapjelet és gyorsasága legyen összemérhető a szakasz integrálás nélküli, másodrendűként közelített részével.

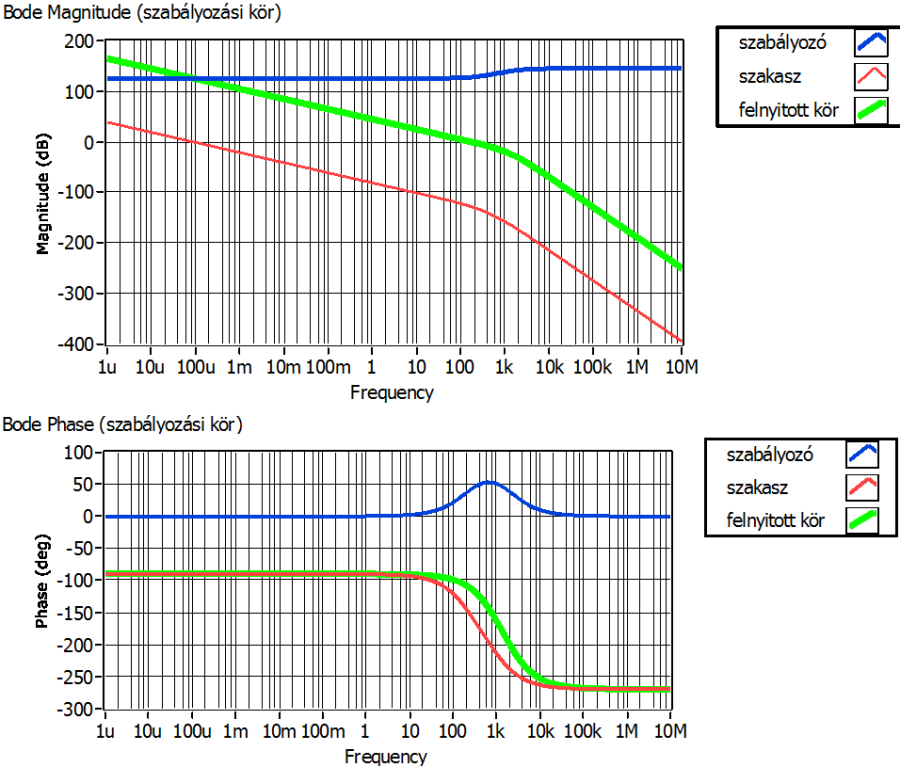
A másodrendű szakasz PD-jellegű töréspontáthelyezővel (Ac=2*106 és TB=0,0005): szakasz, szabályozó és felnyitott kör Bode-diagram

16.28. ábra - A másodrendű szakasz PD-jellegű töréspontáthelyezővel (Ac=2*10⁶ és TB=0,0005): szakasz, szabályozó és felnyitott kör Bode-diagram

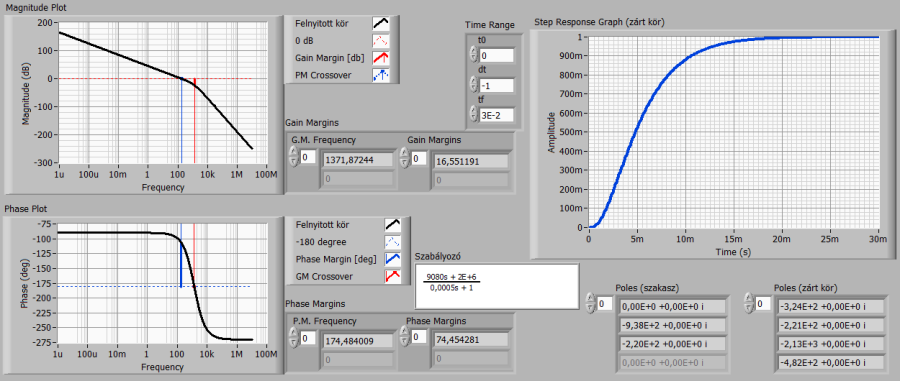
A másodrendű szakasz PD-jellegű töréspontáthelyezővel (Ac=2*106 és TB=0,0005): tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

16.29. ábra - A másodrendű szakasz PD-jellegű töréspontáthelyezővel (Ac=2*10⁶ és TB=0,0005): tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

A PD-jellegű töréspontáthelyező további hangolásával (erősítés növelése, töréspont további jobbra mozgatása) elérhetjük a szabályozó lehetőségeinek határát. Ekkor célszerű olyan PID-jellegű struktúrát választani, amiben nincs soros integráló hatás, hiszen az a szakaszban már van. Így a szakasz másodrendűen közelített részében lévő pólusok áthelyezését biztosító szabályozó struktúrát választunk.

A választott PID-jellegű struktúra a kettős töréspontáthelyező algoritmus. A szakasz két töréspontját (pólusát) a szabályozó két (a T_A és T_C időállandónak megfelelő) zérusa kompenzálja, az előírt dinamikai tulajdonságokat biztosító felnyitott szabályozási körbeli gyököket pedig a szabályozó (T_B és T_D időállandónak megfelelő) zérusai adják. Az A_C erősítési tényezővel biztosíthatjuk, hogy a vágási körfrekvencia az előírt stabilitási és gyorsasági feltételeket biztosítsa. A szakaszban lévő integráló tulajdonság miatt az ugrásszerű alapjelet a szabályozás mindenképpen hiba nélkül követi.

$G_{c} (s) = A_{c} \cdot \frac{1 + T_{A} \cdot s}{1 + T_{B} \cdot s} \cdot \frac{1 + T_{C} \cdot s}{1 + T_{D} \cdot s}$

(16.29)

A szakasz (egyszerűsített) átviteli függvény két elsőrendű és egy integráló tag soros eredőjeként felírva

$G_{s} (s) = \frac{A_{s}}{(1 + T_{1} \cdot s) \cdot (1 + T_{2} \cdot s)} \cdot \frac{1}{s}$

(16.30)

A felnyitott kör átviteli függvénye a szabályozó G_c(s) és a szakasz G_s(s) átviteli függvényének soros eredője (szorzata)

$G_{0} (s) = G_{c} (s) \cdot G_{s} (s) = (A_{c} \cdot \frac{1 + T_{A} \cdot s}{1 + T_{B} \cdot s} \cdot \frac{1 + T_{C} \cdot s}{1 + T_{D} \cdot s}) \cdot (\frac{A_{s}}{(1 + T_{1} \cdot s) \cdot (1 + T_{2} \cdot s)} \cdot \frac{1}{s})$

(16.31)

Először vizsgáljuk meg a szakasz T₁ és T₂ időállandójának megfelelő pólust közömbösítő, nem megvalósítható szabályozó átviteli függvényt.

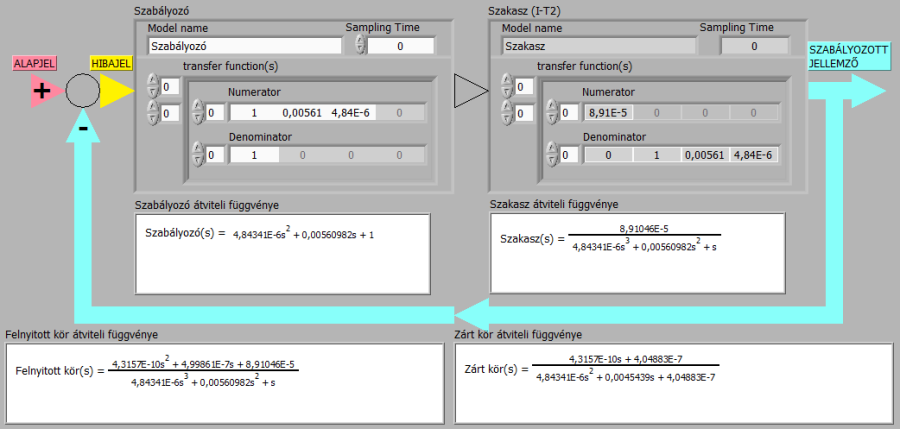
16.30. ábra - A szakasz nullától különböző pólusait kompenzáló másodrendű zérus polinommal adott szabályozó: átviteli függvények

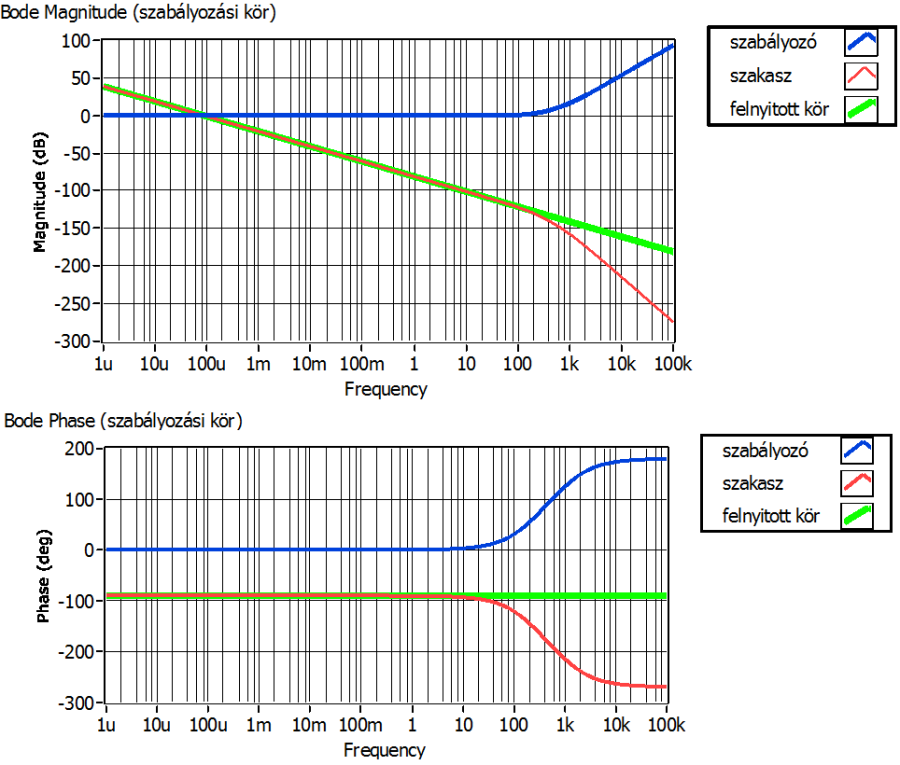
A másodrendű szakasz és a szakasz pólusait kompenzáló másodrendű zérus polinommal adott szabályozó: szakasz, szabályozó és felnyitott kör Bode-diagram

16.31. ábra - A másodrendű szakasz és a szakasz pólusait kompenzáló másodrendű zérus polinommal adott szabályozó: szakasz, szabályozó és felnyitott kör Bode-diagram

Ezzel a – hangsúlyozottan nem megvalósítható – szabályozóval a felnyitott kör integráló, a zárt kör egytárolós arányos jellegű. A zárt kör előírt dinamikáját biztosító – a vágási körfrekvencia reciprokaként értelmezhető – zárt kör időállandót a szabályozó megfelelő értékű erősítésével lehetne beállítani.

A szabályozó megvalósíthatóságához elengedhetetlen, hogy átviteli függvényében a számláló polinom fokszáma ne legyen alacsonyabb a nevező polinom fokszámánál. Ha az előző ábrákon látható módon a szabályozó zérusaival semlegesítjük a szakasz nullától különböző pólusait, a szabályozó pólusaival definiálhatjuk a felnyitott kör és természetesen ezen keresztül a kör zárt pólusait.

A szakasz integráló jellegét figyelembe véve úgy kell a pólusokat áthelyeznünk, hogy az előírt gyorsaságot biztosító vágási körfrekvenciától elegendően messze jobbra essenek a felnyitott kör töréspontjai a Bode-diagramon.

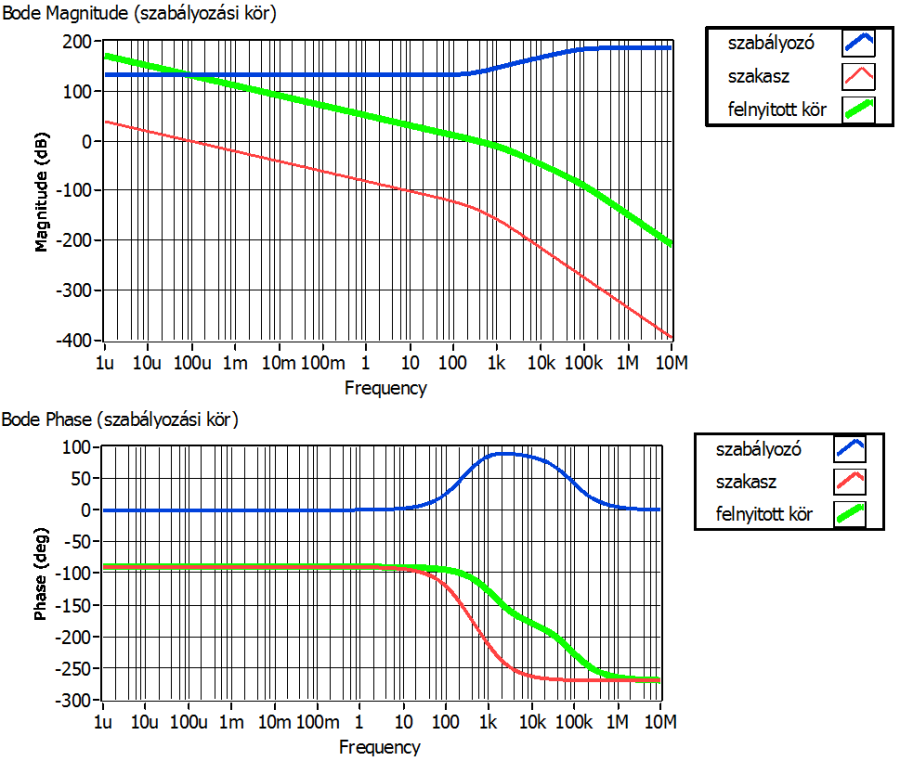
16.32. ábra - A másodrendű szakasz kettős töréspontáthelyezővel: szakasz, szabályozó és felnyitott kör Bode-diagram

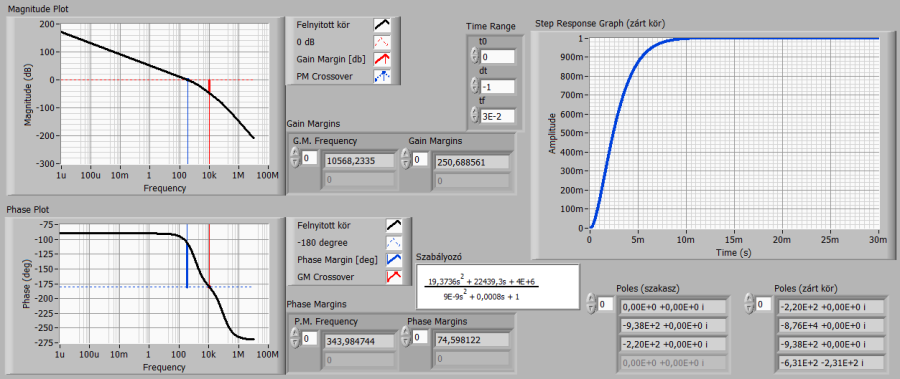
A másodrendű szakasz kettős töréspontáthelyezővel: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

16.33. ábra - A másodrendű szakasz kettős töréspontáthelyezővel: tartalékok ábrázolása a felnyitott kör Bode-diagramján, a zárt kör átmeneti függvénye, valamint a szakasz és a zárt kör pólusai

A szabályozó paramétereit folyamatosan változtatva és futtatva a szimulációs programot tovább tudjuk alakítani a zárt kör válaszát, hogy a célul kitűzött zárt rendszer dinamikai sajátságokat elérhessük.

Szakirodalom

[16.1.] LabVIEW 2009 Help http://www.ni.com/pdf/manuals/371361f.zip.

[16.2.] LabVIEW Control Design User Manual, June 2009 http://www.ni.com/pdf/manuals/371057g.pdf.

[16.3.] LabVIEW 2009 Control Design and Simulation Module Help http://www.ni.com/pdf/manuals/371894d.zip.

[16.4.] Maxima, a Computer Algebra System: Documentation http://maxima.sourceforge.net/documentation.html.

[16.5.] Haager, Wilhelm. COMA, Control Engineering with Maxima és Regelungstechnik mit Maxima http://www.austromath.at/daten/maxima/zusatz/Control_Engineering_with_Maxima.pdf.

Vissza		Előre
15. fejezet - CD-fej fókusztávolság szabályozásának tervezése és szimulációja	Főoldal	17. fejezet - Vonóelemes pozícionáló szabályozásának tervezése és szimulációja