19. fejezet - Módszeres tervezés a mechatronikában
Vissza		Előre

19. fejezet - Módszeres tervezés a mechatronikában

Tartalom

19.1. A rendszertervezés természete és metodológiája

19.1.1. A rendszertervezés fogalma és típusai

A rendszertechnika fogalmait használva egy rendszert és környezetét a 19.1. ábra alapján szoktuk modellezni, ahol a rendszert annak struktúrájával, állapotával és paramétereivel, azaz állapotterével és paraméterterével írjuk le, amely környezetéhez a bemenetekkel és kimenetek-kel, valamint a környezet-rendszer és rendszer-környezet zavarokkal kapcsolódik. Itt a bemeneteket és kimeneteket a rendszer oldaláról akaratlagos, azaz tudatos és eltervezett rendszer- elemekként kezeljük, míg a zavarok többnyire véletlenszerű, a rendszert és/vagy a környezetet nem tervezetten befolyásoló események. Ez a megközelítés természetesen érvényes valamely eszközre vagy berendezésre – nevezzük ezeket egyszerű rendszereknek –, de összetett, több berendezés csatolásával kialakított technológiai hálózatokra is, melyeket nagyrendszereknek fogunk nevezni. Másképpen egyetlen, adott feladatot – műveletet – végrehajtó berendezésre használjuk a műveleti egység elnevezést is.

Ha most azt nézzük, hogy az ilyen rendszerekkel kapcsolatos mérnöki feladatokat általánosságban hogyan lehet csoportosítani, akkor (Bemenet-Rendszer-Kimenet) rendezett hármasból kiindulva a következő három csoportot tudjuk megkülönböztetni.

Rendszerelemzés, melyben adottak a Rendszer és a Bemenet, és meghatározandó a bemenethez tartozó Kimenet. Ez lényegében egy meglévő rendszerrel kapcsolatos kísérletezést jelent a rendszer tulajdonságainak vizsgálatára a stimuláló jel-rendszerreakció párok elemzé-sével.
Rendszerirányítás, melyben adottak a Rendszer és a Kimenet, és meghatározandó az a Bemenet, amely a megszabott kimenetet generálja. Ez lényegében egy meglévő rendszerrel kapcsolatosan annak vizsgálatát jelenti, hogy milyen módon tudjuk a rendszert stimulálni annak kedvező, vagy akár optimális válaszára.
Rendszertervezés, melyben adottak a Bemenet és a Kimenet, és meghatározandó az a Rendszer, amely adott bemenetből a megszabott kimenetet produkálja – lehetőleg a legkedvezőbb módon. Ez tehát egy adott feladat megvalósítására képes rendszer elképzelését és konstrukcióját jelenti.

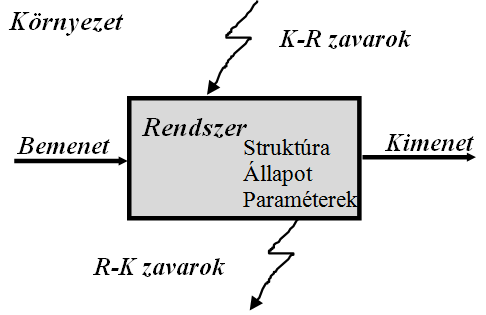
19.1. ábra - Rendszer és környezete

A három feladatcsoport közül kettőben – a rendszerelemzésben- és irányításban – egy-egy meglévő rendszerrel van dolgunk és ezek erősen összefüggő feladatokat jelentenek: az adott rendszert kell kiismerni, tulajdonságait és reakcióit meghatározni, kiválasztani-meghatározni azokat a bemenő jeleket, amelyek a rendszerről a legtöbb információt szolgáltatják vagy a rendszert jól meghatározott, kedvező, esetleg optimális működésre késztetik. A harmadikban, azaz a rendszertervezés során magát a rendszert – akármit is jelent ez adott esetben, mivel ez lehet egy eszköz, berendezés, sőt egy teljes technológiai hálózat – kell létrehozni, mégpedig egy jól meghatározott cél és működés érdekében. Ez tehát jól illusztrálja, hogy a rendszer-tervezés, illetve általában a tervezés lényegében a mérnöki munka talán legösszetettebb alapfeladata: a gyakorlatban még nem létező dolgok elképzelése, részleteinek kidolgozása és – ami ezzel nagyon is összefügg – megvalósítása.

Definíció. A tervezés a célok és lehetőségek közötti keresési folyamat valamely a) funkcioná-lis, b) teljesítmény, és c) esztétikai jellegű követelmények teljesítésére.

Egy adott cél elérését általában különböző szerkezetű, változatú, minőségű és teljesítményű, és nem utolsósorban különböző értékű rendszerekkel lehet megvalósítani. A tény-legesen megvalósítandó változat kiválasztása és részletezése során tehát akkor járunk el megfelelő gondossággal, ha a tervezés folyamatában az összes lehetséges változatot számba vesszük és megvizsgáljuk, és azok összehasonlításával, megfelelő mérlegeléssel választjuk ki a célnak legjobban megfelelő variánst.

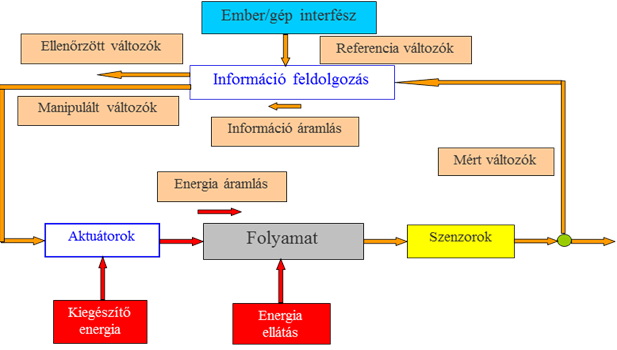
A mechatronikai rendszerek struktúrájának és folyamatainak a (19.2. ábra) ábrán bemutatott vázlatos képe jól mutatja a tervezési tevékenység sokrétűségét. A (19.2. ábra) ábrán a folyamat a rendszer által végzett tevékenységet jelenti, amit különböző jellegű és kivitelű aktuátorokkal lehet megvalósítani, aminek a célzatos megvalósítását különböző jellegű és kivitelű szenzorokkal lehet érzékelni, nem beszélve a megfelelő működést biztosító információfeldolgozás és –kezelés változatairól.

19.2. ábra - Egy mechatronikai rendszer nagyvonalú struktúrája

Az összes megoldás tehát általában nagyszámú lehetőséget jelent, melyet azonban sokrétű – alapjában véve objektv – korlátozásokkal gyorsan lehet szűkíteni a lehetséges megoldások, amjd a plauzibilis megoldások tartományára, ahogy ezt a 19.3. ábra szemlélteti. Ez az ábra a krolátozások bizonyos mértékű hierarchiáját is megadja, mivel pl. a fizikai törvények és a hatósági előírások – különösen a technológiai nagyrendszerek esetében – nagyjából azonos szinten kezelendők.

A nagyszámú lehetőség és korlátozás miatt a tervezés folyamata a legtöbb esetben lénye-gében egy iterációs eljárás, ahogy azt a 19.4. ábra mutatja. Itt a feladat megfogalmazásától a vég-leges megoldás kidolgozásáig vezető direkt utat különböző próbálkozások, javítások és visszalépések tarkítják és szakítják meg. A 19.4. ábra egyes pontjainak részletese.

A tervezési feladat precíz megfogalmazása: ez természetesen különböző részletességű lehet az eszközök, berendezések vagy technológiai hálózatok esetén. Itt természetesen a szükséges precizitásra kell gondolni, mivel elégséges megfogalmazást csak a legegyszerűbb esetekben lehet elérni. Ennek a következménye az iterációs eljárás alkalmazásának a szükségessége.

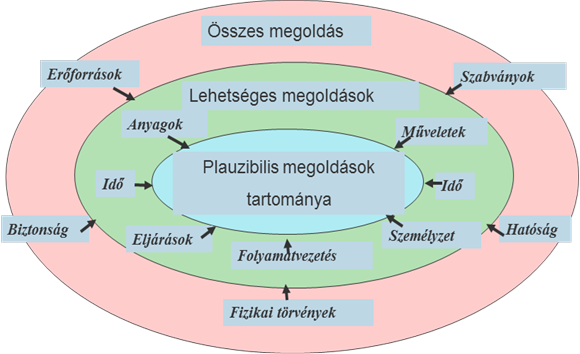19.3. ábra - A tervezési variánsok halmazának szűkítése a korlátozások alkalmazásával

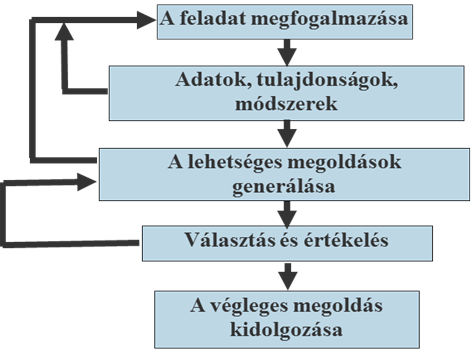19.4. ábra - A tervezési probléma iterációs megoldása
Adatok, tulajdonságok, módszerek összegyűjtése: ez a lépés többnyire nagyon széles információhalmazban történő kutatást jelenti az alapkönyvektől egészen az internetig. Jellegzetessége, hogy ennek az információhalmaznak a tervező nem ismeri a terjedelmét és határait, mivel minden egyes mozzanat bővítheti a felhasználható ismereteket.
A lehetséges megoldások generálása: ez lényegében a szintézis-lépés, melyben fontos szerepet játszanak a mérnöki tapasztalat, egyes részletek számításait irányító algoritmusok, vagy akár szakértői rendszerek alkalmazása is. A rendszer komplexitásától függően a lehetséges megoldások száma rendkívül nagy is lehet: minél nagyobb, annál szélesebb változathalmazból kereshetjük ki a kedvező, esetleg optimális megoldást, de ez annál összetettebb értékelési és választási feladatot jelent.
Választás és értékelés: ez lényegében a szintetizált változatok analízisének a lépése, amelynek során figyelembe vesszük a különböző jellegű korlátozásokat, elemezzük a rendszer egyes tulajdonságaira és viselkedésére vonatkozó becsléseket és számításokat. Modell-alapú tervezés esetén szimulációs vizsgálatokkal a részleteket is elemezni tudjuk. Ez a lépés a lehetséges megoldásokból a kedvező, vagy adott feltételek esetén a legjobb megoldást eredményezi
A végleges megoldás kidolgozása: a 3. lépésben kiválasztott – a legjobb megoldásnak tekintett – rendszer-változat részletezése az adott diszciplinának megfelelő sajátos követelmények figyelembevételével.

19.1.2. A tervezés szerkezete és fázisai

Egy tervezési feladat szerkezetét a (19.7. ábra) ábrán bemutatott kérdés-csoporttal, illetve az azokra elvárt válaszokkal tudjuk felvázolni. Az első kérdés nyilván a Miért, hiszen itt ember alkotta, mesterséges, tehát megfelelő célból készülő, nem pedig önmagukban való rendszerekről van szó.

A Mit kérdésre adandó válasz lényegében azt a tevékenységet vagy dolgot specifikálja, melyet a tervezendő rendszernek el kell látnia vagy produkálnia – gyártania – kell. Ez a rendszer (19.1. ábra) ábrán bemutatott kimenetét, azaz a rendszer célját, feladatát specifikálja, és így a következő logikus kérdés: Miből kell, vagy lehetséges a kimenetet alkotó entitást a rendszernek megvalósítania? Ez tehát a bemenet specifikációját jelenti. Természetesen a kimenet meghatározása minden esetben egyértelmű, a bemenet már nem feltétlenül az, mivel itt már alternatív lehetőségek is felmerülhetnek. Ez tehát annyi rendszer-változatot jelenthet, ahány kimenet-bemenet párt találunk, azaz elkezdődhet a lehetőségek számának növekedése.

19.5. ábra - A tervezési feladat szerkezete

A következő kérdésre adandó válasz általában már jóval összetettebb, mivel ez jelenti a rendszer-változatok generálását, azaz a szintézist, melynek fázisai nagyrendszer esetén a 19.6. ábrán látható koncepcionális és előzetes tervezési lépések, míg egyszerű eszköz vagy berendezés esetén a specifikációs fázisból és a koncepcionális és előzetes tervezési lépésekből áll. Ezek részletezése a (19.6. ábra) ábrán kerül bemutatásra.

A tényleges tervezés lényegében a Mivel kérdés megválaszolását jelenti, melynek során az előzetes tervezésben kialakított tulajdonságú és viselkedésű modell-elemeknek fizikai rendszerelemekkel történő behelyettesítése történik, kiválasztva és részletezve azokat a fizikai elemeket, amelyek a lehető legjobban megfelelnek a tervezés korábbi fázisaiban meghatározott tulajdonságú modell-elemeknek. Ebben a részben a (19.6. ábra és 19.7. ábra) ábrákon a Részletes tervezés és fejlesztés cím alatt felsorolt fő szempontokat vesszük figyelembe a fizikai elemek kiválasz-tásával, vagy egyes fizikai elemek aktuális fizikai tervezésével.

Végezetül az utolsó kérdésként megfogalmazott Mennyiért megválaszolása azonban igazából nem lehet utolsó kérdés, mivel ezt a kérdést a tervezési folyamat bármelyik fázisában újra és újra fel kell tenni.

19.6. ábra - A tervezési fázisai nagyrendszer, vagy technológiai hálózat esetén

Ennek a kérdésnek a megválaszolása természetesen mindig viszonylagos, ugyanis itt igazából nem az abszolút érték az érdekes, hanem az, hogy adott esetben költségeket tekintve megéri-e? Ennek a kérdésnek a megválaszolása a tervezés során attól is függ, hogy mennyiben állnak rendelkezésre az egyes eszközök, vagy akár teljes technológiák költségeire vonatkozó, hosszabb időszakra feldolgozott statisztikai adatok. A végső megtervezett változatra természetesen az aktuális árak alapján lehet választ adni, ami nem már nem igényel becslést.

Jegyezzük meg, hogy az egyszerű rendszerek és nagyrendszerek tervezési eljárásai között az a jelentős különbség, hogy míg a technológiai hálózatok lényegében egyedi darabok, addig az egyes eszközök és berendezések jelentős része, mint termék, sokszorosításra kerül, így a prototípus megalkotása és a tervezés eredményének ez által történő ellenőrzése egyszerűbb és biztosabb megoldást jelent. Természetesen a nagyrendszerek tervezését is lehet bizonyos mértékig fizikai modelleken, azaz kismintákon keresztül ellenőrizni, de az első megvalósított változat tapasztalatai is sok információt adnak az esetleges későbbi változatok tervezéséhez.

19.1.3. A tervezés modellje

A rendszertervezés, vagy akár általánosabban is fogalmazhatunk a tervezés lényege a problémamegoldás. Ennek alapján a tervezés következő típusait tudjuk megkülönböztetni:

19.7. ábra - A tervezés fázisai egyszerű rendszer, mint gyártandó termék esetén

Rutinszerű tervezés, amelyben a tervezendő rendszer komponensei adottak és az ismert komponensekből – az adott célnak és korlátozásoknak megfelelő – rendszer létrehozására szolgáló eljárás is adott.
Innovatív tervezés, amelyben a tervezendő rendszer komponensei adottak, de nem ismert olyan eljárás, amellyel a komponensekből – az adott célnak és korlátozásoknak megfelelő – rendszert létre lehet hozni.
Kreatív tervezés, melynek során sem a tervezendő rendszer komponensei, sem a komponensekből – az adott célnak és korlátozásoknak megfelelő – rendszer létrehozására szolgáló eljárás sem ismeretes.

Természetesen az említett tervezési típusoktól is függ, hogy a tervezés során milyen stratégiát célszerű követni:
Ez lehet cél-vezérelt vagy top-down stratégia, melynek lényege a következő sorrend: a (globális) feladat megfogalmazása, a feladat felbontása részfeladatokra, ameddig csak lehet az aktuális ismeretek alapján, majd a tartomány-specifikus adatok felhasználásával keressük a részfeladatok megoldásait. Ezt a stratégiát elsősorban a rutinszerű tervezésben lehet alkalmazni.
Ez lehet adat-vezérelt vagy bottom-up stratégia, melynek lényege: először az elérhető, tartomány-specifikus adatok összegyűjtése, minden adat alapos vizsgálata és az ezekből történő következtetések végig vitele mindaddig, amíg meg nem találjuk a megoldást. Ezt a stratégiát elsősorban innovatív és kreatív tervezés esetén tudjuk alkalmazni.

Általánosságban azt mondhatjuk, hogy a tervezési folyamatok többnyire a két stratégia kombinációjaként alakulnak ki, mivel a top-down stratégiát tisztán csak rutinszerű tervezésben lehet alkalmazni, míg a bottom-up stratégia önmagában csak algoritmikus tervezés esetén alkalmazható, azaz amikor a tartomány-specifikus adatok ismeretéből kiindulva a teljes további tervezés algoritmusok alkalmazásával megy végbe.

Az eddigiekből (is) jól látható, hogy egy tervezési feladat megvalósítása – különösen a nagyrendszerek esetében – meglehetősen összetett probléma, ezért több absztrakciós szinten célszerű, sőt szükséges megvalósítani. Ezeket az absztrakciós szinteket és kölcsönhatásaikat a 19.8. ábra mutatja be, míg a módszer alapelveit a következő módon foglaljuk össze.

19.8. ábra - A többszintű tervezés szerkezete

A rendszer terve több absztrakciós szinten kerül kifejtésre.
A tervezés során a magasabb absztrakciós szintektől az alacsonyabb szintek felé haladunk egy hierarchikus tervezési folyamattal.
A hierarchikus tervezési folyamatban a tervezési specifikációk fokozatos finomítása – bővítése – megy végbe.
A tervezési specifikációk fokozatos finomítása során a korlátozásoknak az alsóbb szintek-re való transzformációja biztosítja a szintek közötti konzisztenciát.

Ez két tényezőből áll:
- Valamely szint korlátozásainak az alsóbb szintre való közvetítése.
- Az alsóbb szint részletesebb specifikációi által indukált új korlátozások kielégítése.
A finomítási lépések végrehajtása a dekompozíció és koordináció elve alapján történik.
Minden absztrakciós szint terv-implementációjának a kidolgozásában a szintézis-analízis-értékelés lépéssorból álló transzformációs tervezési metodika kerül alkalmazásra.
Minden absztrakciós szint terv-implementációja a következő szint implementációjának a specifikációjaként szolgál, egyúttal meghatározva a szintek közötti hatásköri relációkat is.

Az egyes szintek gazdasági potenciálja:

$E P_{i} = {\begin{cases} Bevétel - költségek, ha i = 0 \\ {EP}_{i - 1} - i -edik szint költségei, ha i > 0 \end{cases}$

ahol i – az i-edik szintet jelenti

19.2. Modell-bázisú rendszertervezés

19.2.1. Rendszertervezési módszerek

A tervezést két nagy módszerbeli csoportba sorolhatjuk:

Konvencionális tervezés, melynek lépései a következők.

1. lépés.	A tervezendő rendszer struktúrájának és méreteinek specifikációja a tervező aktuális ismeretei – tudásbázisa – alapján.
2. lépés.	A specifikált rendszer számításokkal történő értékelése.
3. lépés.	A változók és paraméterek számított értékei a megengedett értékhatárokon belül vannak?
4. lépés.	Nem. A tervezendő rendszer méreteinek, esetleg struktúrájának módosítása a tervező aktuális ismeretei – tudásbázisa – alapján. Ugrás a 2. lépésre.
5. lépés.	Igen. A tervezés befejeződött. Stop.

Modell-bázisú tervezés, melynek lépései a következők.

1. lépés.	A tervezendő rendszer matematikai modelljének – struktúrájának és viselkedésének, továbbá korlátozásainak a – specifikációja a tervező aktuális ismeretei – tudásbázisa – alapján.
2. lépés.	A specifikált rendszer struktúrájának és méreteinek meghatározása számítógépi modell-kísérletekkel, szimulációval.
3. lépés.	Elfogadhatók az eredmények?
4. lépés.	Nem. A matematikai modell és/vagy a korlátozások módosítása a tervező aktuális ismeretei – tudásbázisa - alapján. Ugrás a 2.lépésre.
5. lépés.	Igen. A tervezés befejeződött. Stop.

Összehasonlítva a két algoritmust mind a kettő az un. trial and error eljáráson alapul, ami a (19.4. ábra) ábrán bemutatott iteratív megoldást jelzi. Ugyanakkor a két módszer alapvetően különbözik egymástól, mivel a konvencionális módszer rögtön a fizikai rendszerre kérdez rá, azaz a fizikai rendszerelemekkel kezdi a tervezést és a későbbiekben – a rész-számítások alapján – szükség esetén ezeket cseréli ki a célnak megfelelően.

A modell-alapú tervezést alapjában véve a tervezendő rendszer egy alkalmas modelljével kezdjük, melynek rendszer-elemei, a csatolásukkal megadott struktúrája és paraméterei megfelelnek a koncepcióban kialakított nagyvonalú tervnek. Ennek a modellnek természetesen tartalmaznia kell a rendszer tulajdonságait és viselkedését visszatükröző szükséges információkat, és a szimulációs vizsgálatok részeredményeit értékelve kell azt módosítani. E módosítást először a paraméterek változtatásával, esetleg a rendszerelemek cseréjével, de szükség

esetén a rendszer elképzelt struktúrájának a változtatásával visszük végbe. Jegyezzük meg, hogy a legnagyobb változásokat a rendszerek struktúrájának módosításával lehet elérni.

A modell-alapú tervezésben a matematikai modelleket, mint a korszerű tervezés alapeszközeit használjuk, így ennek a tervezési módszernek a lényege a modellekkel való manipulációs eljárás. A modell-egyenletek megoldása természetesen megfelelő algoritmusok alkalmazásával történik, azonban az egyes lépések közötti döntések gyakran a mérnöki tapasztalat, bizonyos heurisztikák alapján megy végbe. Itt heurisztikának szigorúan nem igazolt, vagy nem igazolható, tapasztalati tényeken, megfigyeléseken alapuló szabályokat értünk. Ezzel mindjárt meg is jegyezhetjük, hogy a

konvencionális tervezési módszer nagy részben mérnöki heurisztikák alkalmazására épül, de azért természetesen sok számítással, azaz algoritmussal kevert metódus, míg a
modell-alapú tervezés lényegileg használja az algoritmusokat, de azért nem nélkülözheti a mérnöki heurisztikákat. Jelenleg elsősorban az optimális rendszerek tervezésében találkozunk tisztán algoritmusokat használó módszerekkel, amikor is adat-vezérelt módon meghatározzuk a szükséges kiindulási adatokat, valamint az egyenlőségi és egyenlőtlenségi korlátozásokat, és ezzel a többnyire nemlineáris programozást, vagy esetleg vegyes egészértékű nemlineáris programozást alkalmazó optimalizáló módszerre bízzuk a számítások lebonyolítását. Itt az egészértékű, azaz diszkrét programozás a tervezendő rendszer strukturálisan különböző változatainak a generálásához szükséges. Jegyezzük azonban meg, hogy a mérnöki intuíció általában ezekben az esetekben is szükséges, mivel az optimum erősen függ a korlátozó fel-tételektől, és így a modell-bázisú algoritmus 4. lépésében a nem-kielégítő eredmények megfelelő modell és/vagy korlátozó feltételek módosítását igénylik, amit igazából csak a tervező mérnök tud végigvinni.

A rutinszerű tervezés nagymértékben algoritmizálható, míg az innovatív és kreatív tervezési eljárásokban gyakran játszik szerepet a mérnöki heurisztika. A tervezés (19.4. ábra) ábrán bemutatott folyamatában a lehetséges megoldások előállításáig, amely többnyire nagy mennyiségű információ előállítását jelenti, a heurisztikus metodika dominál, míg a további fázisokat már gyakran algoritmikusan is meg lehet oldani.

Figyelembe véve, hogy a felvázolt tervezési algoritmusok lényegében azonos logikán alapulnak, azt mondhatjuk, hogy a tervezés fejlődése elsősorban a felhasználható eszközök és információbázisok fejlődését jelenti. A tervezés kialakítandó modelljének részletes sémát kell tartalmaznia arról, hogy a jól leírt végállapotot hogyan kell elérnie az adott adatbázis keretében. Ehhez a tervező rendszernek következtetéseket kell levonnia a tervezés tárgyának

korlátozó feltételeiből,
oksági viszonyairól, és a
tervezési stratégiákról.

Ehhez az előzőekben vázolt modell-bázisú tervezés mindegyik lépését algoritmizálni szükséges az absztrakciós szinteknek a (19.8. ábra) ábrán bemutatott csatolásával együtt. A fejlesztés tehát ebben az irányban folyik.

19.2.2. A modell-bázisú tervezés formális meghatározása

19.2.2.1. Egyszerű rendszerek tervezése

Egy rendszer modell-bázisú tervezéséhez, ahogy ez a (19.1. ábra) ábrán bemutatott séma és a tervezési feladat értelmezése alapján látható, a rendszer belső világát és a környezettel való kapcsolatait részletesen leíró modell szükséges. Erre a célra a rendszertechnikából ismeretes és ott részletesen vizsgált állapottér modelleket tudjuk felhasználni, amelyek általános alakja a következő egyenletekből áll.

Az állapot-átmeneti, vagy belső egyenlet-rendszer

$\frac{d x}{d t} = f (x, u, p)$

(19.1)

egy közönséges differenciálegyenlet-rendszer az $x (t = 0) = x_{0}$ kezdeti feltételekkel. Itt az $x = (x_{1}, x_{2} ... x_{N})$ az N-dimenziós rendszer állapota, az $f = (f_{1}, f_{2} ... f_{N})$ nemlineáris függvények a rendszer struktúráját leíró állapot-átmeneti függvényrendszert alkotják, az $u = (u_{1}, u_{2} ... u_{M})$ a bemeneti változók vektora és $p = (p_{1}, p_{2} ... p_{P})$ a paraméterek vektora.

A rendszer kimeneteit meghatározó algebrai egyenletek az

$y = g (x, u, p)$

(19.2)

formában adottak, ahol $y = (y_{1}, y_{2} ... y_{L})$ a kimeneti változók vektora és a $g = (g_{1}, g_{2} ... g_{L})$ a kimenet struktúráját meghatározó függvényrendszer.

A korlátozó egyenlőtlenségi relációk:

$s (x, u, p) - v \leq 0$

(19.3)

ahol az $s = (s_{1}, s_{2} ... s_{K})$ a korlátozó függvények vektora és $v = (v_{1}, v_{2} ... v_{K})$ a korlátozások értékeit meghatározó vektor.

Az (19.1)-(19.3) dinamikus rendszerben az

f leírja a rendszer struktúráját és viselkedését, a
p leírja az f struktúrájú és viselkedésű rendszer megvalósulási változatait, míg az
(s,v) páros meghatározza a rendszer állapotváltozóinak, bemeneti változóinak és paramétereinek a korlátait. A (19.2) kimeneti egyenleteken keresztül természetesen a kimeneti változókra is megadhatjuk azok korlátozásait.

A p paraméterek egy részét az anyagi – konstitutív – mennyiségek alkotják, ezt az a vektorral jelöljük és a rendszerelemek tulajdonságait jellemzik, míg a másik része a rendszerelemek kapcsolatait határozza meg, azaz a rendszer struktúráját jellemzik. Ezeket a tervezés során a d vektorral jelöljük így a paraméterek vektorát a

$p = (a, d)$

(19.4)

A rendszerek tervezését elsősorban az állandósult állapotokra, azaz tulajdonképpen a rend-szerek üzemelési állapotaira tervezzük, ami azt jelenti, hogy a tervezési összefüggéseket az s indexszel jelölt állandósult – stacionárius – változókra érvényes

	$f (x_{s}, u_{s}, p) = 0$	(19.5)
	$y_{s} = g (x_{s}, u_{s}, p)$	(19.6)
	$s (x_{s}, u_{s}, p) - v \leq 0$	(19.7)

algebrai egyenletek és korlátozások jelentik.

A modell-bázisú tervezés egyik fontos fogalma a modell szabadsági foka, amit a következő módon határozunk meg.

Legyen az (19.5)-(19.7) összefüggésekben az összes változó, azaz $x_{s}, u_{s}, y_{s} és p$ száma N_v=N+ M+L+P, és legyen a változók közötti független és ellentmondásmentes (19.5)-(19.6) egyenletek száma N_r=N+L. Akkor a rendszer szabadsági fokát az N_sz=N_v-N_r=M+P különbség adja meg, amely a tervezés során megválasztható változók maximális számát jelenti. Ha most N_d-vel jelöljük a rendszer tervezéséhez felhasznált változók számát, akkor érvényes az $N_{d} \leq N_{s z}$ feltétel.

Ha N_d=0, akkor az (19.5)-(19.6) egyenletrendszer megoldása egyértelmű és nincs valódi tervezési probléma.
Ha N_d<0, akkor a probléma túldefiniált, azaz csak triviális megoldás létezhet, és a modellünk hibás, azaz ellentmondásos.
Ha N_d>0, akkor rendszer tervezője N_d változó értékét választhatja meg a tervezés szempontjainak megfelelően.

Jegyezzük meg, hogy a tervezési változók közül az $u_{s}$ bemeneti változókat sok esetben már a részletes tervezési fázis előtt, a Miből kérdésre adandó válasz esetén rögzítjük, ezért ekkor gyakorlatilag csak a paraméterekkel gazdálkodhatunk. Valójában ez jelenti a rendszer tényleges tervezését, mivel a rögzített kimenethez a bemenet megválasztása többnyire erősen determinált, amit szükség esetén az iterációs lépésekben tudunk módosítani.

Definíció. Az ( 19.5 )-( 19.7 ) dinamikus rendszer tervezése során a feladat a rendszer struktúráját meghatározó f , és mellette a kimenetet generáló g függvények, valamint a p paraméterek meg-határozása megadott y _s és u _s kimeneti és bemeneti változók és a korlátozások ( s , v ) ismeretében.

Ennek a folyamatnak a lépései a következők.

Megadjuk a rendszer belső modelljét és a korlátozó feltételeket

	$f (x_{s}, u_{s}, p) = 0$	(19.8)
	$s (x_{s}, u_{s}, p) - v \leq 0$	(19.9)

és rögzítjük a bemeneti változók és a paraméterek kezdeti értékeit.

Megoldjuk a (19.8) egyenletrendszert az x_s állapotra:

$x_{s} = ϕ (u_{s}, p)$

(19.10)

A kapott x_s állapotot behelyettesítjük a kimeneti egyenletbe

$y_{s} = g (ϕ (u_{s}, p), u_{s}, p)$

(19.11)

és a korlátozó feltételekbe

$s (ϕ (u_{s}, p), u_{s}, p) - v \leq 0$

(19.12)

Teljesülnek-e a korlátozó feltételek?

Nem. Módosítjuk a paraméterek és/vagy a bemeneti változók értékeit és ugrás a 2^o lépésre.

Igen: Ugrás az 5^o lépésre.
Kedvezőek az állapot és kimeneti értékek?

Nem. Módosítjuk a paraméterek és/vagy a bemeneti változók értékeit és ugrás a 2^o lépésre.

Igen. Ugrás az 6^o lépésre.
Az eredmények adminisztrálása. Stop.

Ezt az eljárást nemlineáris rendszerekre mutattuk be, de természetesen a lineáris dinamikus rendszerekre is közvetlenül értelmezhető, mivel (19.1)-(19.3), illetve (19.8)-(19.11) összefüggéseknek a rendszertechnikából jól ismertek a lineáris megfelelői.

19.2.2.2. Összetett rendszerek

Az egyszerű rendszerek tervezési kérdéseit tárgyaló előző szakaszban nem határoztuk meg a

változók és egyenletek számát, ami azt mutatja, hogy az egyszerű rendszer fogalom modell-szinten nem attól függ, hogy hány változó van a modellben. Ezt a problémát röviden már értelmeztük a 19.1. ábrakapcsán, ahol az egyszerű rendszer fogalmat egy műveleti egységgel társítottuk, míg a műveleti egységek technológiai sorba szervezett csoportját neveztük összetett rendszernek. Modell-szinten egy rendszert akkor nevezünk összetettnek, ha az megfelelően csatolt kompakt alrendszerekből épül fel, vagy – ha most az (19.1)-(19.3) összefüggésekből indulunk ki – abban kompakt, hálózatba csatolt alrendszereket tudunk elkülöníteni. Ezeket az alrendszereket feleltetjük meg a műveleti egységeknek, míg maga az összetett rendszer a teljes technológiai hálózatnak felel meg.

Egy összetett rendszer, a továbbiakban egyszerűen hálózat, struktúráját a (19.9. ábra) ábrán bemutatott (U,S) szerkezeti gráffal tudjuk megadni. Itt az U=(u₁,u₂,u₃,u₄,u₅) szögpontok a műveleti egységek halmazát, míg az S=(s₁,s₂,s₃,s₄,s₅,s₆,s₇,s₈,s₉,s₁₀,s₁₁) irányított élek a műveleti egységek közötti kapcsolatokat reprezentálják. A szögpontok önmagukban (19.8)-(19.11) típusú dinamikus rendszereket reprezentálnak, melyek a bemenet-kimenet párokkal kapcsolódnak egymáshoz. Ezek a kapcsolatok többnyire teljesítmény-kapukon keresztül jönnek létre, amikor is a teljesítmény-konjugált változók közül az irányított élek a megfelelő áramokat jelölik. Azonban ezek az élek lehetnek információ-áramok is információ-kapukon keresztül.

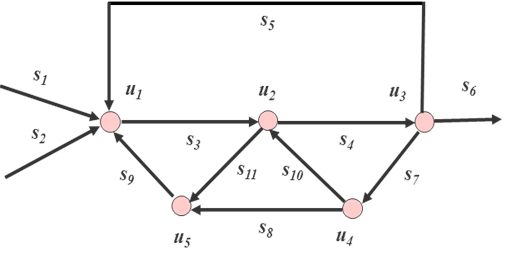
19.9. ábra - Egy technológiai hálózat szerkezeti gráfja

A technológiai hálózatok struktúrájának (19.9. ábra) ábrán látható geometriai képe nagyon szemléletes és a koncepció kialakításánál jól használható, de a számításokban többnyire az algebrai reprezentációkat használjuk. Ezek közül – a 19.9. ábra szerkezeti gráfjára vonatkozóan – az A illeszkedési mátrix az

$\begin{array}{l} \begin{matrix} u_{1} \\ u_{2} \\ u_{3} \\ u_{4} \\ u_{5} \end{matrix} [\begin{matrix} + 1 & + 1 & - 1 & 0 & + 1 & 0 & 0 & 0 & + 1 & 0 \\ 0 & 0 & + 1 & - 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & + 1 & - 1 & - 1 & - 1 & 0 & 0 & + 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & + 1 & - 1 & 0 & - 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & + 1 & - 1 & 0 \end{matrix} \begin{matrix} 0 \\ 0 \\ - 1 \\ 0 \\ + 1 \end{matrix}] \\ \begin{matrix} s_{1} & s_{2} & s_{3} & s_{4} & s_{5} & s_{6} & s_{7} & s_{8} & s_{9} & s_{10} \begin{matrix} s_{11} \end{matrix} \end{matrix} \end{array}$

(19.13)

alakú, amelyben az egyes irányított éleknek a szögpontokra való illeszkedéseit jelöljük úgy, hogy a kimenet kapcsolatot -1-gyel, míg a bemenet kapcsolatot +1-gyel jelöljük.

A másik jellegzetes algebrai leírást a N szomszédossági mátrix jelenti, melyet a következő mátrix ad meg

$\begin{array}{l} \begin{matrix} u_{1} \\ u_{2} \\ u_{3} \\ u_{4} \\ u_{5} \end{matrix} [\begin{matrix} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \end{matrix}] \\ \begin{matrix} u_{1} & u_{2} & u_{3} & u_{4} & u_{5} \end{matrix} \end{array}$

(19.14)

ahol a szomszédosságot azzal jelöljük, hogy valamely szögpontból vezet-e közvetlen él valamelyik másik, azaz ebben az értelmezésben a szomszédos szögpontba. Jegyezzük meg, hogy itt a szomszédosság nem szimmetrikus reláció.

Végül vegyük a C körmátrixot, amely az irányított élek által alkotott irányított köröket, azaz hurkokat jelöli meg az alábbi módon

$\begin{array}{l} \begin{matrix} C_{1} \\ C_{2} \\ C_{3} \\ C_{4} \end{matrix} [\begin{matrix} 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \end{matrix}] \\ \begin{matrix} s_{1} & s_{2} & s_{3} & s_{4} & s_{5} & s_{6} & s_{7} & s_{8} & s_{9} & s_{10} & s_{11} \end{matrix} \end{array}$

(19.15)

Vegyük észre, hogy a rendszerben megjelenő szomszédosságokat és hurkokat már az illeszkedési mátrixból elő tudjuk állítani, ezért elemzés esetén elégséges az illeszkedési mátrix megadása. Azonban mind a szomszédossági mátrixot, mind a körmátrixot hasznosan lehet felhasználni a számítások szervezése során, ezért célszerű azokat is explicite megadni.

Az összetett rendszer teljes leírásához természetesen szükség van a szögpontok által reprezentált alrendszerek modelljeinek a megadására, ami az

	$f^{i} (x_{s}^{i}, u_{s}^{i}, p^{i}) = 0, i = 1,2... N_{u}$	(19.16)
	$y_{s}^{i} = g^{i} (x_{s}^{i}, u_{s}^{i}, p^{i}), i = 1,2... N_{u}$	(19.17)
	$s^{i} (x_{s}^{i}, u_{s}^{i}, p^{i}) - v^{i} \leq 0, i = 1,2... N_{u}$	(19.18)

függvény kapcsolatok specifikációját jelenti. Itt N_u az alrendszerek – szögpontok – száma.

A (19.16)-(19.17) egyenleteket természetesen kiegészítik a struktúrát meghatározó kapcsolati egyenletek

$K \cdot (\begin{matrix} y_{s} \\ u_{s} \end{matrix}) = 0$

(19.19)

ahol K a kapcsolati mátrix, amely lényegében a bővített A illeszkedési mátrix transzponáltja-ként határozható meg, $y_{s} = {(y_{s}^{1}, y_{s}^{2},... y_{s}^{L})}^{T}$ és $u_{s} = {(u_{s}^{1}, u_{s}^{2},... u_{s}^{M})}^{T}$ pedig az összes kimenet és bemenet vektorai. A bővítés tehát azt jelenti, hogy az illeszkedést az összes bemeneti és kimeneti változóra ki kell jelölni, figyelembe véve magának a rendszernek a bemeneteit és kimeneteit is.

Most a rendszer szabadsági fokát az

$N_{s z} = \sum_{i = 1}^{N_{u}} N_{s z}^{i} - \sum_{k = 1}^{N_{K}} N_{s z}^{k}$

(19.20)

képlettel számoljuk, ahol $N_{s z}^{i}$ az i-edik alrendszer szabadsági foka, $N_{s z}^{k}$ a csatolt bemenetek és kimenetek szabadsági fokai, mivel azokat a hálózat struktúráját megadó NK kapcsolati egyenlettel már lekötöttük.

Az összetett rendszerek szerkezeti gráfjában az élek irányítása egyúttal megadja az alrend-szerek közötti számítási sorrendet is, mivel a (19.16)-(19.17) egyenletek azt mutatják, hogy valamely alrendszer – a számítások tárgyalásában ezeket számítási moduloknak nevezzük – bemeneteinek ismerete lehetővé teszi a kimenetek számítását. Azonban, mivel ezek össze vannak kötve a kapcsolásban következő modul(ok) bemeneteivel, így most már azok is számíthatók. Ezt figyelembe véve az összetett rendszerek számítását struktúrájuktól függően a következő módon végezhetjük.

Ha a rendszerben nincs hurok, azaz mindegyik számítási modul elérhető szekvenciálisan a korábbi modulokból, akkor azt a moduláris vagy egyszerű szekvenciális módszerrel, azaz direkt módon számolhatjuk. Erre mutat példát a 19.10. ábra, ahol csak azt kell megkeresni, hogy a rendszer melyik bemenetével vagy bemeneteivel kell, illetve lehet a számításokat elkezdeni. Ezt a számítási sorrend meghatározásának nevezzük.

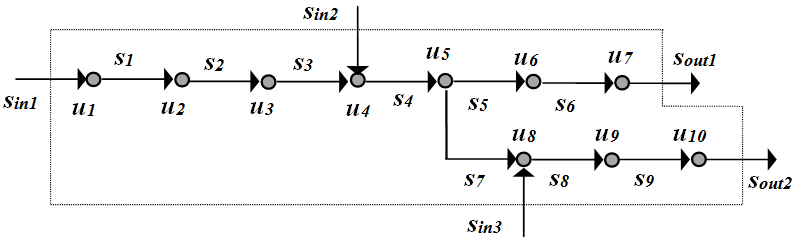
19.10. ábra - Az összetett rendszerek egyszerű szekvenciális számításához

A (19.11. ábra) ábrán bemutatott rendszer már csak un. iterációs-szekvenciális számítással érté-kelhető, mivel két kör vagy hurok is található a rendszerben. Ezért, pl. a számítás már az u₁-nél megakad, mivel annak számításához szükséges lenne az s₁₀ bemenet ismeretére, de ezt csak az s₃, majd – visszafelé – az s₂, s₁ és az s₁₀ismeretében tudjuk meghatározni, ami zárja a kört: az s₁₀-et akkor tudjuk kiszámítani, ha ismerjuk az s₁₀-et!

Ezt az ellentmondást a hurok felvágásával és iterációval tudjuk feloldani, ami a 19.11. ábra alapján a következőket jelenti: megbecsülve s₁₀” értékét végig tudjuk számolni a hurkot, ami megadja az s₁₀’ értékét.

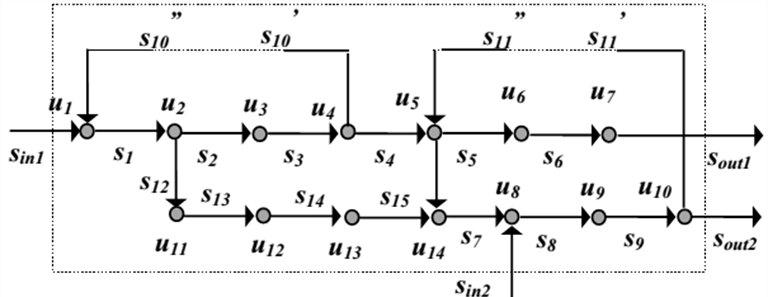
19.11. ábra - A hálózatok iterációs szekvenciális számításához

Az $| s_{10} " - s_{10}' |$ különbség alapján újabb becslést adva az s₁₀” értékére ismételten számolhatunk, és megfelelő iterációs stratégiát választva a cél az $| s_{10} " - s_{10}' | < ε$ feltétel elérése, ahol az ε elégségesen kis pozitív szám. Hasonló módon tudjuk feloldani az esetleges további köröket vagy hurkokat.

A (19.11. ábra) ábrán látható rendszer rendelkezik egy fontos tulajdonsággal: a két kör egymástól független, azaz az első kör számításába nem kell a második kör iterálását bevonni, miközben

második kör az elsőt követően szekvenciálisan számolható. Ezt úgy nevezzük, hogy a hálózat két partícióra bontható, melynek lényege, hogy a partíciók önállóan, megfelelő szekvenciákban számíthatók

Nem rendelkezik ezzel a hasznos tulajdonsággal a (19.12. ábra) ábrán látható hálózat, ahol a két kör az u₃ szögponton keresztül kapcsolódik. Ezek a körök csak egyidejű felvágással számíthatók, ami általában több iterációs változót és bonyolultabb számításokat jelent.

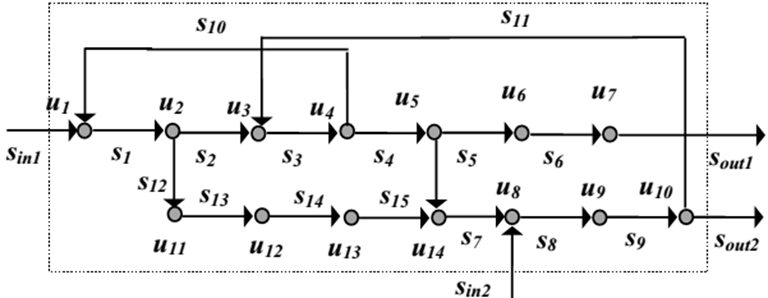
19.12. ábra - A hálózatok iterációs szekvenciális számításához

A (19.11. ábra és 19.12. ábra) ábrák hálózatai között azonban van még egy jelentős különbség: a 19.11. ábra esetén nem egyidejűleg, de mindkét hurkot fel kell vágni, míg a 19.12. ábra hálózatában elég az s₃ él felvágását elvégezni, mivel ezzel egyidejűleg mind a két hurkot felvágjuk.

Definíció. Független körök. Egy technológiai hálózatban egy kör független a többitől, ha legalább egy olyan éle van, amelyik a többi kör egyikének sem éle.

Definíció. Minimális felvágás. Egy hálózatban legfeljebb annyi élt kell felvágni, amennyi a független körök száma. A felvágások száma csökkenthető a független körök közös éleinek kiválasztásával.

Összefoglalva, a hálózatok moduláris számításának lépései:

1. lépés.	Körkeresés a hálózat részletes átvizsgálásával. Ha nincs kör, akkor ugrás a 4. lépésre, ha van, akkor ugrás a 2. lépésre.
2. lépés.	Hálózat-particionálás.
3. lépés.	Minimális felvágás meghatározása.
4. lépés.	Számítási sorrend meghatározása.
5. lépés.	Számítások.

19.2.3. Tervezési példa 1: Meghajtás tervezése egyenáramú motorral

A rendszertechnikai szempontból villamos teljesítmény → mechanikai teljesítmény transz-formációt végző, azaz zsirátor jellegű egyenáramú motorok a mechatronikai rendszerek, elsősorban az aktuátorok alapvető elemeit alkotják. Az egyenáramú (DC) motorok lényegé-ben két villamos alrendszerből és egy mechanikai alrendszerből állnak, ahogy ezt a 19.13. ábra szemlélteti. Jellemzőik:

Jól szabályozható sebesség.
Jó forgásirány reverzibilitás.
Gyors válasz (nagy forgató nyomaték/rotor-inercia arány).
Dinamikus fékezés vagy regeneratív fékezési lehetőség a gyors megállás biztosí-tására.

19.2.3.1. A koncepció

A mechatronikában természetesen nem az egyenáramú motorok tervezésével foglalkozunk, hanem a rendszer céljának a megfelelő karakterisztikájú motorok kiválasztása, a rendszerbe történő beépítésük, valamint a motorok irányításának a tervezése a feladat.

Az egyenáramú motorok szelekciója során a következő lépések szerint haladhatunk:

Mi a cél: pontos helyzet-beállítás vagy megadott forgási sebesség?
A cél elérésének módja: vezérléssel vagy szabályozással?
A feladat: egyenletes forgási sebesség?
Mekkora legyen a maximális sebesség?
A feladat: diszkrét vagy folytonos helyzet-beállítás?
Ha nem kell állandó működés, akkor milyen ciklusidővel kell a motornak működnie?
Mekkora a tervezett terhelés tehetetlensége?
Mekkora teljesítmény szükséges?
Mekkora forgatónyomaték szülkséges?
Szükséges-e a forgási irány változtatása?
Kell a hajtáshoz mechanikai transzformáció? (Transzmisszió, áttétel, hajtómű)
Van méret vagy súlykorlát?
Milyen legyen a motor karakterisztikája?
A terhelés és a motor karakterisztikája ismeretében hogyan alakul a munkapont?
Megfelelő a motor indulása és gyorsulása?

Az első tizenhárom pont tehát a rendelkezésre álló motorok szelekciójára vonatkozik, amit többnyire un. ököl-szabályok, azaz mérnöki heurisztikák alkalmazásával hajtunk végre. Ez azonban meghatározza a kiválasztott motor vagy motorok karakterisztikáit és a további mo-dell-számításokhoz szükséges paramétereit is.

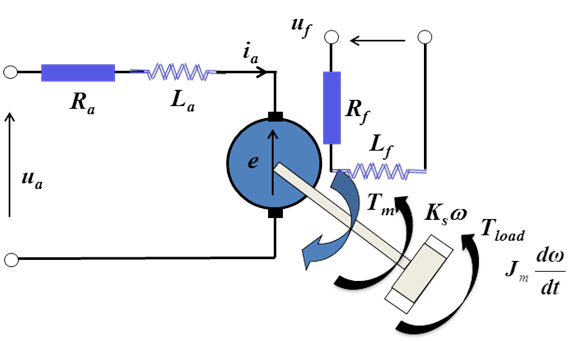
19.13. ábra - Egy egyenáramú motor strukturális vázlata

A választáshoz felhasznált alapvető karakterisztikák a forgatónyomaték-szögsebesség valamint az armatúra áramerősség-forgatónyomaték állandósult állapotbeli függvények. Ezek gyakran lineáris összefüggések, azaz az egyenáramú motorok lineáris rendszerekként kezelhetők, ami jelentősen megkönnyíti a tervezést.

Az egyenáramú motorok karakterisztikákat meghatározó strukturális változatai.

Az állórész állandó mágnes:

Nincs az állórészben hő-disszipáció, könnyű és kisebb a többi motornál, egyszerű kapcsolással változtatható a forgásirány, kitűnően lehet alkalmazni a számítógépes szabályozásban a lineáris karakterisztikák következtében (19.14. ábra)
Külső gerjesztésű motor:

Az armatúrát és állórészt egymástól független feszültségforrásból tápláljuk, a gerjesztő áram erőssége nem függ a terheléstől, karakterisztikái hasonlóak – lineárisak – az állandó mágnes-állórészű motor karakterisztikáihoz (19.14. ábra)

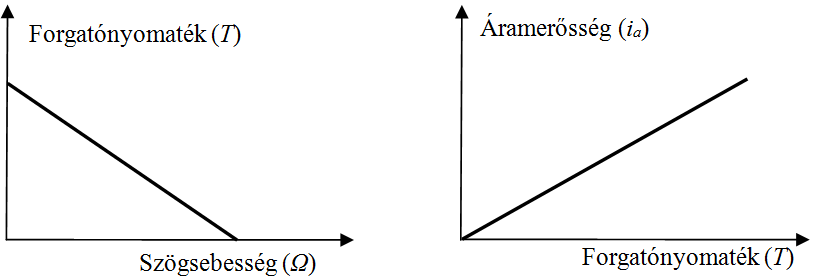19.14. ábra - Az állandó mágneses és külső gerjesztésű DC motorok lineáris karakterisztikái
Párhuzamos (mellékáramkörű) gerjesztésű:

Az áramterhelés az armatúra- és állórész-áram összege, a forgási sebesség széles terhelés-tartományban állandó, az indító forgatónyomaték a munkapontnak kb. 1.5-szerese, az indító forgatónyomaték a legkisebb az egyes változatok közül, ezért az indítást változtatható ellenállással lehet megfelelően szabályozni.
Soros (főáramkörű) gerjesztésű:

Nagy az indító forgatónyomatéka, a forgási sebesség erősen változik a terhelés függvényében, kis terhelés esetén nagy forgási sebességet érhet el. Sebesség-elfutás veszélye áll fenn (a hiperbolikus karakterisztika miatt).
Vegyes gerjesztésű (a soros és párhuzamos kapcsolás kombinációja):

Az indító forgatónyomaték valamivel kisebb a hasonló méretű soros motoroknál, a forgási sebessége korlátos, rosszabb a sebesség-szabályozhatósága a párhuzamos motorokénál.

19.2.3.2. Motor-szelekció és az indítás tervezése

Feladat: viszonylag könnyen szabályozható, állandó fordulatszámot biztosító egyenáramú motor modell-alapú tervezése, Ehhez a gép matematikai modelljének kidolgozását és elemzését kell elvégezni az eszköz tulajdonságainak és működésének vizsgálata céljából.

Az előzőekben megadott rövid jellemzések alapján egy megfelelő paraméterekkel rendelkező mellékáramkörű egyenáramú motort célszerű választani, amelynek kapcsolási vázlatát a 19.15. ábra szemlélteti. A kedvező teljesítmény elérése érdekében a motort úgy célszerű megválasztani, hogy a terhelés tehetetlensége legyen hasonló a motor saját tehetetlenségéhez. Ha a motor és a terhelés között reduktort tervezünk, akkor az a terhelés J_l tehetetlenségét a motorra a J_l/N² értékkel közvetíti, ahol az N az áttételt jelöli. Ha ezt a motor J_m saját tehetetlenségével egyenlőnek választjuk, akkor a maximális gyorsulást érhetünk el, azonban a forgatónyomaték értéke minimális lesz. Egy jó kompromisszumot jelent a

$2.5 J_{m} \leq J_{l} / N^{2} \leq 5 J_{m}$

(19.21)

ökölszabály szerinti választás.

A kedvező üzemelés érdekében természetesen elégséges forgatónyomatékot szükséges biztosítani a terhelés által keltett súrlódás legyőzésére és valamely távolság – a motor tengelyére vonatkoztatott a_m=Na_l szöggyorsulás – gyors elérését jelentő gyorsulás biztosítására. Itt a

19.15. ábra - A mellékáramkörű egyenáramú motor kapcsolási vázlata

$a_{l} = d Ω_{l} / d l$ a terhelés elvárt szöggyorsulását jelöli. A motor forgatónyomatékát a

$T_{m} = N [T_{s} + a_{l} (J_{l} + N^{2} J_{m})]$

(19.22)

képlettel számolhatjuk (T_s a súrlódás legyőzéséhez szükséges forgatónyomaték), és az így kapott értéket általában 50 százalékkal célszerű megnövelni.

A kedvező forgatónyomaték-érték mellett a terhelés megfelelő forgási sebességének eléréséhez teljesítményt is biztosítani szükséges. Ennek becsléséhez általában elhanyagolható értékkel járul hozzá a súrlódási komponens és lényegében a terhelés megfelelő gyorsításához szükséges

$P = T_{m} Ω = \frac{4 J s^{2}}{τ^{3}}$

(19.23)

teljesítményt kell figyelembe venni, ahol J a teljes mozgatott tehetetlen nyomatékot, míg az s a τ idő alatt elérendő elmozdulást jelöli. A (19.23) képlet azt mutatja, hogy a J tehetetlen nyomaték mozgatásának fele időre való felgyorsításra nyolcszoros teljesítmény szükséges.

A (19.15. ábra) ábrán bemutatott kapcsolási vázlat alapján a mellékáramkörű motor dinamikus modelljét az alábbi elsőrendű differenciálegyenlet-rendszer alkotja:

	$L_{a} \frac{d i_{a}}{d t} + R_{a} i_{a} + K_{e} Ω = u_{i n}, e = K_{e} Ω$	(19.24)
	$L_{f} \frac{d i_{f}}{d t} + R_{f} i_{f} = u_{i n}$	(19.25)
	$(J_{a} + J_{l}) \frac{d ω}{d t} + T_{s} + T_{l} = K_{m} i_{a}, T = K_{m} i_{a}$	(19.26)

ahol $i = i_{a} + i_{f}$ , $K_{e} = K_{m} = K$ a motor villamos és mechanikai együtthatói (gépállandó), és

	J _a	– a forgórész tehetetlen nyomatéka
	J _l	– a terhelés tehetetlen nyomatéka
	T _s	– súrlódási forgató nyomaték
	T _l	– a terhelés által generált súrlódási forgató nyomaték.

A villamos kapun keresztül bevitt teljesítmény $P = u_{i n} i = u_{i n} (i_{a} + i_{f})$ , és itt feltételeztük, hogy az armatúra áramkörben $R_{v} = 0$ .

Állandósult állapotban

$R_{a} i_{a} + K ω = u_{i n}$

(19.27)

ahonnan

$T = \frac{K}{R_{a}} u_{i n} - \frac{K^{2}}{R_{a}} ω$

azaz az indító forgatónyomaték és a motor maximális szögsebessége

$T_{i n} = \frac{K}{R_{a}} u_{i n}$ $Ω_{\max} = \frac{1}{K} u_{i n}$ .

Ezért a forgatónyomaték-szögsebesség karakterisztika a

$T = T_{i n} (1 - \frac{Ω}{Ω_{\max}})$

(19.28)

formát ölti, míg az áramerősség-szögsebesség karakterisztika az

$Ω = \frac{u_{i n} - R_{a} i_{a}}{K}$

(19.29)

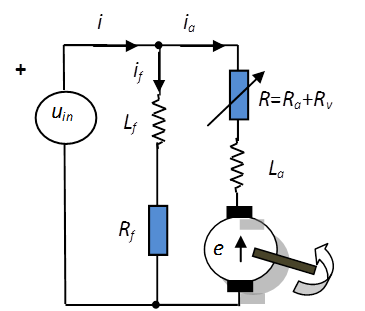
alakú, amely a szögsebességnek u_in tápfeszültséggel és R_a ellenállással való szabályozhatóságát mutatja. Természetesen itt nem az armatúra R_a adott ellenállásának a változtatására kell gondolni, hanem – ahogy ezt a 19.15. ábra szemlélteti – az armatúra áramkörbe beépített R_v pót-ellenállás értékének megfelelő modulálására.

A motor által leadott teljesítmény a

$P (Ω) = T Ω = Ω T_{i n} (1 - \frac{Ω}{Ω_{\max}})$

(19.30)

képlettel fejezhető ki, és így a leadott teljesítmény maximumát az

$Ω_{o p t} = \frac{Ω_{\max}}{2}$

szögsebességnél éri.

A (19.29) képletből jól látható, hogy – mivel az R_a ellenállás kicsi – az indító armatúra-áramerősség meglehetősen nagy, és ha (19.16. ábra) ábrán jelölt szögsebesség-áramerősség munkapontot szeretnénk elérni, akkor ez túlságosan nagy kezdeti és hosszantartó áramfelvétellel, ráadásul lassan lenne lehetséges. Felhasználva azonban, hogy egy egyenáramú motort rövid ideig túl lehet terhelni a nominális áramerősség felett akár 2.5-szeres erősségű árammal is, megfelelően megtervezett R_v változtatható ellenállás-sorral fel tudjuk gyorsítani az indítási folyamat a 19.16. ábra által bemutatott módon a szögsebesség-áramerősség karakterisztikának az

$Ω = \frac{u_{i n} - (R_{a} + R_{v, k}) i_{a}}{K}, k = 1,2,3...$

(19.31)

összefüggés szerinti modulálásával.

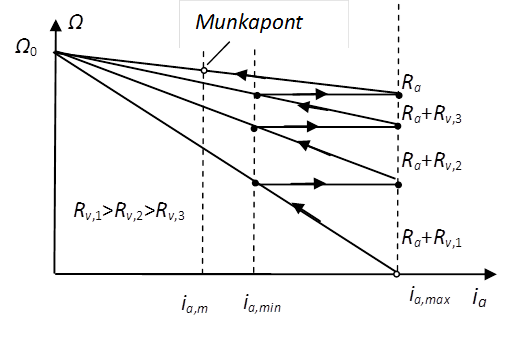
19.16. ábra - A mellékáramkörű egyenáramú motorok indítása változtatható ellenállás-sorral

Itt az i_a,min áramerősség-értéket elérve egy kapcsoló segítségével az $R_{v, k} \to R_{v, k + 1}$ kapcsolásokat kell megvalósítani, ami az egyes karakterisztikák közötti ugrásszerű átmeneteket jelenti. A 19.16. ábra jól mutatja azt is, hogyan lehet a motor paramétereinek felhasználásával, valamint az i_a,min és i_a,max áramerősségek rögzítésével meghatározni a kapcsolások számát és az ellenállás-sor értékeit.

Jegyezzük még meg, hogy a mellékáramkörű egyenáramú motor fékezése is történhet ezen ellenállások felhasználásával az armatúra áramkör ellenkapcsolásával, vagy rövidre zárásával.

19.2.4. Tervezési példa 2: Lineáris elektromechanikai erőgép

Egy másik egyszerű, de nemlineáris rendszerként modellezett mechatronikai eszköz tervezését mutatjuk be, illusztrálva ezzel az általánosan megfogalmazott lépéseket és felhasználva az elektromechanikai Lagrange-egyenleteket.

Feladat: táv-irányítható, megfelelően nagy erősűrűséget biztosító erőgép modell-alapú tervezése, amely lineáris – transzlációs – mozgással alkalmas emelésre és kapcsolásra. Ehhez a gép matematikai modelljének kidolgozását és elemzését kell elvégezni az eszköz tulajdonságainak és működésének vizsgálata céljából.

19.2.4.1. A koncepció

A 19.17. ábra mutatja be az elektromechanikai eszköz koncepciójának vázlatos rajzát, amely egy rögzített vasmag-állórészből, a középső részen egy bronz betéttel, valamint egy mozgatható – mobil – vasmagból áll. Az állórész középső részén található N menetszámú tekercsen átfolyó i erősségű elektromos áram hatására a mobil vasmag kétirányú függőleges mozgást végezhet megfelelő mechanikai erőhatást kifejtve.

Induljunk ki abból a feltételezésből, hogy a vasmag mágneses permeabilitása nagyságrendekkel nagyobb a levegőrés mágneses permeabilitásánál, amely egyenlőnek vehető a bronzbetét permeabilitásával. Ugyanakkor tételezzük fel, hogy a – főleg a könyökökben fellépő – szórt mágneses fluxus mértéke elhanyagolható.

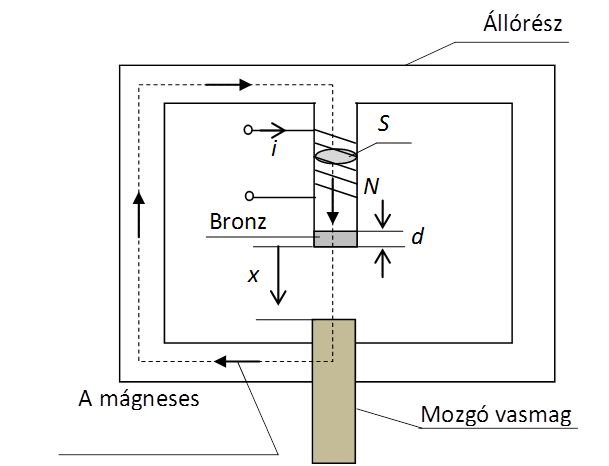
19.17. ábra - A lineáris elektromechanikai erőgép vázlatos képe

Az ok-okozati kapcsolatokat elemezve: ha a tekercsen elektromos áramot bocsátunk át, akkor az a vasmagok – levegőrés - bronzbetét mágneses körben megfelelő mágneses fluxust generál, és ez a mobil vasmagra történő erőhatással annak elmozdulását hozza létre. A mobil vas-mag transzlációs mozgása a mágneses térre történő indukciós visszahatást eredményezi, és ez adott feltételek esetén a két hatás egyensúlyához, azaz a mobil vasmag valamely helyzetben történő rögzülését jelentheti.

A modell kidolgozása során természetesen feltételezzük, hogy adottak a szükséges konstitutív mennyiségek, ami egyúttal azt is megmutatja, hogy a tervezendő rendszer előzetes vizsgálatát jelentő szimulációs vizsgálatokhoz milyen adatok szükségesek.

19.2.4.2. A mágneses tér leírása

A levegőrésben és bronzbetétben kialakuló mágneses mező térerősség-vektorát az Ampére- törvényből kapjuk meg

$\oint_{C} H \cdot d l = \int_{S} J \cdot d S$

(19.32)

ahol a C a fluxus zárt középvonalát és az S felületet a 19.13. ábra értelmezi. Az ábra alapján figyelembe véve a geometriai viszonyokat a (19.32) egyenlet az egyszerű

$H_{l} x + H_{b} d = - N \dot{q} = - N i$

(19.33)

formában írható. Mivel a levegőrés és a bronzbetét mágneses térerősségét azonosnak tételeztük fel, ezért a mágneses indukció vektorát a

$B = μ_{0} H_{l} e_{x} = μ_{0} H_{b} e_{x}$

(19.34)

kifejezéssel adhatjuk meg, és ezt a (19.33) egyenletbe behelyettesítve a

$B = - \frac{μ_{0} N \dot{q}}{d + x} e_{x}$

(19.35)

kifejezést kapjuk, ahonnan a keletkezett fluxust a

$Φ = \int_{S} B \cdot d S = \int_{S} - \frac{μ_{0} N \dot{q}}{d + x} e_{x} \cdot d S = - \frac{μ_{0} N A i}{d + x}$

(19.36)

integrállal kapjuk meg. Itt az A a légrés és a bronzbetét, tehát a mágneses erővonalakra merő-leges felület területét jelenti. Így a kapcsolt fluxust a

$ψ (i, x) = - N Φ = \frac{μ_{0} N^{2} A i}{d + x}$

(19.37)

lineáris összefüggés adja meg.

A ψ fluxus változása az i áramerősség és a légrés x magassága, mint paraméter függvényében.

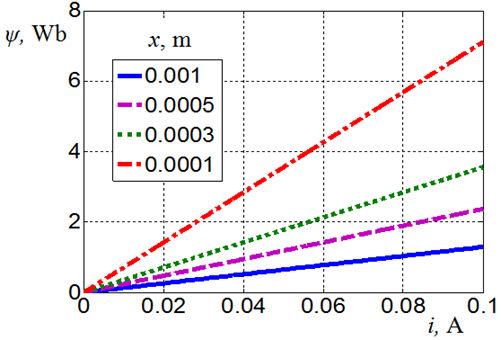
19.18. ábra - A légrés fluxusának változása az áramerősség és légrés magassága függvényében

Az N-elemű tekercs kapcsolt fluxusának ismeretében a (19.17. ábra) ábrán bemutatott mágneses rendszert helyettesítő sémáját a (19.19. ábra) ábrán mutatjuk be.

A (19.37) fluxus-kifejezésből a mágneses koenergiát a

$W_{m}^{c} (i, x) = \int_{0}^{i} ψ (i', x) d i' = \int_{0}^{i} \frac{μ_{0} N^{2} A i'}{d + x} d i'$

(19.38)

integrállal kapjuk meg, ami a

$W_{m}^{c} (i, x) = \frac{μ_{0} N^{2} A i^{2}}{2 (d + x)}$

(19.39)

eredményt szolgáltatja.

A mágneses tér energiáját a (19.26) kifejezés inverzével számolhatjuk, amely az áramerősségre az

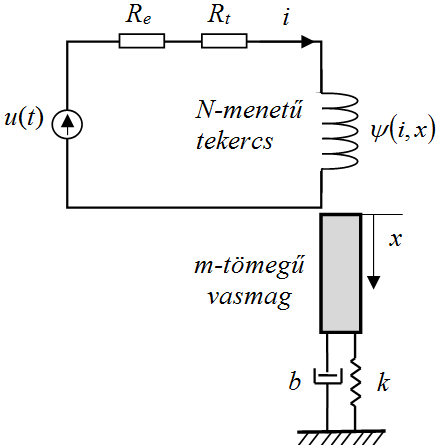
19.19. ábra - A 19.17. ábra mágneses rendszerének helyettesítő sémája

$i (ψ, x) = \frac{(d + x) ψ}{μ_{0} N^{2} A}$

(19.40)

összefüggést adja, és ennek alapján a

$W_{m} (ψ, x) = \int_{0}^{ψ} \frac{(d + x) ψ'}{μ_{0} N^{2} A} d ψ'$

(19.41)

integrállal az eredmény a

$W_{m} (ψ, x) = \frac{(d + x) ψ^{2}}{2 μ_{0} N^{2} A}$

(19.42)

alakú.

Ha a $\dot{q} = i$ töltésáramot behelyettesítjük a mágneses koenergia-állapotfüggvénybe azt kapjuk, hogy a koenergia és energia értékei egyenlők, azaz

$W_{m}^{c} = W_{m}$

(19.43)

ami a (19.37) lineáris kapcsolat következménye. Könnyen belátható, hogy a mágneses energia és koenergia összegére az elvárható

$W_{m}^{c} + W_{m} = ψ \dot{q}$

(19.44)

kifejezést kapjuk.

19.2.4.3. Matematikai modell: Mérlegegyenletek

Az erőmérlegeket az elektromechanikai Lagrange-egyenletekből határozzuk meg, melynek tagjai az alábbi kifejezésekkel adhatók meg.

A vizsgált rendszerben – a 19.19. ábra alapján – két általánosított koordinátát tudunk kijelölni: az egyik a mechanikai alrendszer x változója, míg a villamos alrendszer általánosított koordinátáját az i áramerősség, vagy a $\dot{q} = i$ töltésáram adja meg.

Ezekkel a koordinátákkal a teljes elektromechanikai kinetikus energia a

$T_{e m} (\dot{x}, x, \dot{q}) = \frac{1}{2} m {\dot{x}}^{2} + \frac{μ_{0} N^{2} A {\dot{q}}^{2}}{2 (d + x)}$

(19.45)

alakú, míg a teljes elektromechanikai potenciális energiát a

$V_{e m} (x, q) = \frac{{(x - b)}^{2}}{2 K}$

(19.46)

függvény adja meg, mivel a rendszer villamos energiája zérus értékű, ui. nincs benne kapacitív energiatároló. Így tehát a Lagrange-függvény az

$L_{e m} (\dot{x}, x, \dot{q}) = \frac{1}{2} m {\dot{x}}^{2} + \frac{μ_{0} N^{2} A {\dot{q}}^{2}}{2 (d + x)} - \frac{{(x - b)}^{2}}{2 K}$

(19.47)

formájú, a rendszer Rayleigh-féle disszipációs függvényét az

$R_{e m} (\dot{x}, \dot{q}) = \frac{1}{2} D {\dot{x}}^{2} + \frac{1}{2} (R_{e} + R_{t}) {\dot{q}}^{2}$

(19.48)

forma, míg a külső elektromechanikai erőket együttesen az

$F_{e m} (t) = m g + u (t)$

(19.49)

kifejezés adja meg.

Mindezen függvényeket felhasználva a mechanikai Lagrange-egyenletet a

$\frac{d}{d t} \frac{\partial L_{e m} (\dot{x}, x, \dot{q})}{\partial \dot{x}} - \frac{\partial L_{e m} (\dot{x}, x, \dot{q})}{\partial x} + \frac{\partial R_{e m} (\dot{x}, \dot{q})}{\partial \dot{x}} = F_{e m} (t)$

(19.50)

míg a villamos Lagrange-egyenletet a

$\frac{d}{d t} \frac{\partial L_{e m} (\dot{x}, x, \dot{q})}{\partial \dot{q}} - \frac{\partial L_{e m} (\dot{x}, x, \dot{q})}{\partial q} + \frac{\partial R_{e m} (\dot{x}, \dot{q})}{\partial \dot{q}} = F_{e m} (t)$

(19.51)

formában kapjuk meg.

Nem részletezve a matematikai levezetéseket az (19.50)-(19.51) egyenletekből a mechanikai erő-mérleget az

$m \frac{d^{2} x}{d t^{2}} + D \frac{d x}{d t} + \frac{x - b}{K} + \frac{a i^{2}}{{(d + x)}^{2}} = m g$

(19.52)

míg a villamos töltés-mérleget a

$\frac{2 a}{d + x} \frac{d^{2} q}{d t^{2}} + (R_{e} + R_{t}) \frac{d q}{d t} - \frac{2 a \dot{q}}{{(d + x)}^{2}} \frac{d x}{d t} = u$

(19.53)

nemlineáris negyedrendű differenciálegyenlet-rendszer formájában kapjuk meg.

Írjuk fel a (19.53) egyenletet az áramerősség felhasználásával

$\frac{2 a}{d + x} \frac{d i}{d t} + (R_{e} + R_{t}) i - \frac{2 a i}{{(d + x)}^{2}} \frac{d x}{d t} = u$

(19.54)

így a (19.52) és (19.54) egyenletekből álló harmadrendű differenciálegyenlet-rendszert kapjuk.

A rendszer mechanikai és elektromos erőmérlegeit tartalmazó modelljét tehát az (19.52) és (19.54) közönséges differenciálegyenletekből álló egyenletrendszer adja meg, melynek megoldását az

$x (t = 0) = x_{0}, \dot{x} (t = 0) = {\dot{x}}_{0}, i (t = 0) = i_{0}$

(19.55)

kezdeti feltételekkel kell meghatározni.

19.2.4.4. A rendszer analízise

A rendszer állandósult állapotait az

	$\frac{x_{s} - b}{K} + \frac{a i_{s}^{2}}{{(d + x_{s})}^{2}} = m g$	(19.56)
	$(R_{e} + R_{t}) i_{s} = u_{s}$	(19.57)

algebrai egyenletrendszerből tudjuk meghatározni, amiből az

$u_{s}^{2} = {(R_{e} + R_{t})}^{2} \frac{{(d + x_{s})}^{2}}{a} [m g - \frac{x_{s} - b}{K}]$

(19.58)

nemlineáris algebrai egyenlethez jutunk.

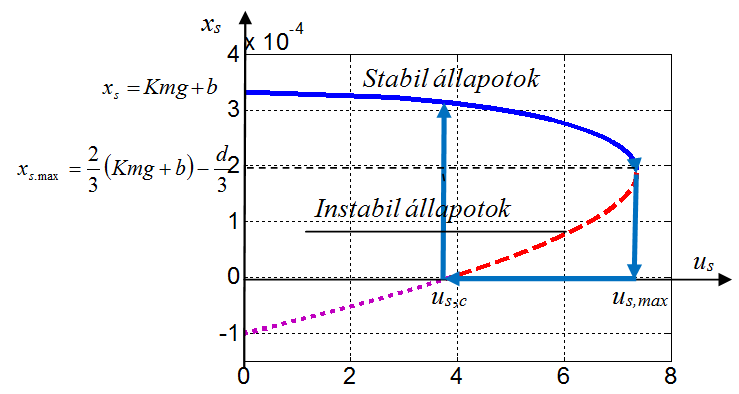
Az (19.58) egyenlet alapján ábrázolva az x_s változót az u_s függvényében a rendszer karakterisztikáját állítjuk elő, amely a (19.20. ábra) ábrán látható. Ezt a karakterisztikát a K=1.28e-5 m/N, D=0.004 N s/m, a=μ₀N²A/2, μ₀=4πe-7 H/m, R_e=120 Ω, m=5.00e-4 kg, N=1200, R_t=520 Ω, b=3.33e-4 m, g=9.81 m/s², u=24 V értékekkel számoltuk.

A (19.20. ábra) ábrán látható karakterisztika meglehetősen komplex, melyen három jól elkülöníthető szakaszt figyelhetünk meg. Az u_s=0 értéknél i_s nyilván zérus, így a légrés a maximális x_s=Kmg+b értéket veszi fel a két mechanikai erő, azaz a rugóerő és a gravitációs erő egyen-súlyánál. Ha bekapcsoljuk a feszültségforrást, a feszültség fokozatos növelésével csökken a légrés egészen az x_s,max=2(Kmg+b)/3-d/3 értékig, amikor is a feszültség akármilyen kismértékű további növelése a légrés ugrásszerűen zérusra-váltását idézi elő. A mágneses erő hirtelen teljesen legyőzi a mechanikus erők ellenállását és a mobil vasmagot az állórészhez rántja. Ha ezt követően elkezdjük csökkenteni a feszültséget, akkor a mobil vasmag mozdulatlan marad egészen az $u_{s, c} = (R_{e} + R_{t}) d \sqrt{K m g + b / K a}$ értékig, ahol helyzete ismét ugrásszerűen megváltozik és az u_s_,c feszültségértéknek megfelelő légrés-helyzetbe ugrik, azaz a karakterisztika felső szakaszára ugrik vissza. A jelenség magyarázata – ahogy ezt a 19.16. ábra mutatja –, hogy az (u_s_,c,u_s_,max) feszültség intervallumon a szaggatott vonallal jelölt karakterisztika szakasz végig instabil állapotokból áll. Tovább csökkentve a feszültséget az u_s<u_s_,c értékekre a légrés a negatív értéktartományba kerülne át – (19.20. ábra) ábrán ezt a tiltott szakaszt a pontozott görbe jelöli –, ami nyilván lehetetlen. Tehát a u_s_,c feszültségértéknél a mágneses erő elengedi a mobil vasmagot és a megfelelő stabil állapotba ugrik át.

Mindezt igazolhatjuk a (19.52)-(19.54) nemlineáris rendszer állapotainak stabilitás vizsgálatával, amit az (x_s,i_s) állandósult állapot körül linearizálással és a Routz-Hurwith kritérium alkalmazásával érhetünk el.

A linearizálást a nemlineáris tagok Taylor-sorba fejtésével és csak a lineáris tagok meg-tartásával érjük el. Bevezetve az $i = i_{s} + Δ i$ és $x = x_{s} + Δ x$ jelöléseket, a lineáris modellt

	$m \frac{d^{2} Δ x}{d t^{2}} + D \frac{d Δ x}{d t} + \frac{Δ x}{K} - \frac{2 a i_{s}^{2}}{{(d + x_{s})}^{3}} Δ x + \frac{2 a i_{s}}{{(d + x_{s})}^{2}} Δ i = 0$	(19.59)
	$\frac{2 a}{d + x_{s}} \frac{d Δ i}{d t} + (R_{e} + R_{t}) Δ i - \frac{2 a i_{s}}{{(d + x_{s})}^{2}} \frac{d Δ x}{d t} = Δ u$	(19.60)

19.20. ábra - A rendszer feszültség-légrés karakterisztikája

egyenletek alkotják, ahonnan a rendszer Jacobi-mátrixa a

$J = [\begin{matrix} 0 & 1 & 0 \\ \frac{2 a i_{s}^{2}}{m {(d + x_{s})}^{3}} - \frac{1}{K m} & - \frac{D}{m} & \frac{2 a i_{s}}{m {(d + x_{s})}^{2}} \\ 0 & \frac{i_{s}}{(d + x_{s})} & - \frac{(d + x_{s}) (R_{e} + R_{t})}{2 a} \end{matrix}]$

(19.61)

formájú.

Az állandósul állapotokra vonatkozó (19.56)-(19.57) egyenletekből a 19.20. ábra karakterisztikájának felső szakaszához tartozik az x_s=2.6089e-4 és i_s=8.5697e-4 állapot, melyet a (19.61) Jacobi-mátrixba behelyettesítve λ₁=-4.0151+j 1.2488e4, λ₂=-4.0151-j 1.2488e4 és λ₃=-1.6205e1 három sajátértéket kapjuk, ami az állapot stabilitását igazolja.

Hasonlóan kapjuk az x_s=9.4354e-5 és i_s=9.9565e-3 állapotra, amely a 19.20. ábra karakterisztikájának középső, szaggatottan ábrázolt szakaszához tartozik, és ezt behelyettesítve a Jacobi-mátrixba az eredményt a λ₁=1.2747e1, λ₂=-1.4741e1+j 1.2488e4 és λ₃=-1.4741e1-j 1.2488e4 sajátértékek szolgáltatják. Tehát az első valós sajátérték pozitív, így ez az állapot instabilis.

Végezetül nézzük az x_s=0 tengelyen fekvő karakterisztika szegmenshez tartozó x_s=0 és i_s=3.6617e-5 állapot esetében a három sajátértéket. Ezek a λ₁=-3.9926+j 1.2488e4, λ₂=-3.9926 –j 1.2488e4 és λ₃=-4.5021 értékek, azaz ismét stabilis állapotot kaptunk.

Ezek az eredmények azt illusztrálják, hogy a vizsgált rendszerben egy állapot-hiszterézis fordul elő, ahol két stabil állandósult állapot-szakasz között egy instabil állapot-szakasz található, aminek az eredménye, hogy különböző kezdeti feltételekből indítva az eszköz az alsó, légrés nélküli állapotba, vagy a felső, határozott méretű légrés helyzetbe, vagy munkaállapotba kerülhet.

Szakirodalom

[19.1.] Alciatore, D.G. és Histand, M.B.. Introduction to Mechatronics and Measurement Systems. McGraw-Hill. Boston . 2003.

[19.2.] Bishop, R.H.. The Mechatronics Handbook. CRC Press. Boca Raton, Washington, D.C . 2002.

[19.3.] Blanchard, B.S és Fabrycky, W.J.. Systems Engineering and Analysis. Prentice Hall. Upper Saddle River. New Jersey . 1998..

[19.4.] Borutzky, W.. Bond graph modelling and simulation of multidisciplinary systems – An intro-duction. Simulation Modelling Practice and Theory. 17 (2009) 3–21..

[19.5.] Bronstejn, I.N, Szemengyajev, K.A., Musiol, G., és Mühlig, H.. Matematikai kézikönyv. TypoTEX Kiadó. Budapest . 2000.

[19.6.] Cellier, F.E.. Continuous System Modeling. Springer-Verlag. New York . 1991.

[19.7.] Chhabra, R. és Emami, M.R.. Holistic system modeling in mechatronics. Mechatronics. Vol.21. pp.166–175.. 2011.

[19.8.] Damić., V. és Montgomery, J.. Mechatronics by Bond Graphs. An Object-Oriented Approach to Modelling and Simulation. Springer-Verlag. Berlin . 2003.

[19.9.] de Silva, C,W. és Behbahani S.. A design paradigm for mechatronic systems http://dx.doi.org/10.1016/j.mechatronics.2012.08.004. Mechatronics. 2012.

[19.10.] Gershenfield, N.. The Nature of Mathematical Modeling. Cambridge University Press. Cambridge, UK . 1999.

[19.11.] Isermann, R.. Mechatronic systems—Innovative products with embedded control. Control Engineering Practice. Vol.16. pp.14–29.. 2008.

[19.12.] Meisel, J.. Principles of Electromechanical Energy Conversion. McGraw Hill. New York . 1966.

[19.13.] Onwulobu, G.C.. Mechatronics. Principles and Applications. Elsevier Butterworth-Heine-mann. Amstredam . 2005.

[19.14.] Rzevski, G.. On conceptual design of intelligent mechatronic systems. Mechatronics. Vol.13. pp.1029–1044.. 2003.

[19.15.] Simonyi, K.. Elméleti villamosságtan. Tankönyvkiadó. Budapest . 1967.

[19.16.] Simonyi, K.. Villamosságtan. Akadémiai Kiadó. Budapest . 1973.

[19.17.] Stiffler, A.K.. Design with Microprocessors for mechanical Engineers. McGraw-Hill. New York . 1992.

[19.18.] Wang, Y., Ying, Y., Xie, C., Zhang, X., és Jiang, W.. A proposed approach to mechatronics design education: Integrating design methodology, simulation with projects http://dx.doi.org/10.1016/j.mechatronics.2012.10.002. Mechatronics (2012).

Vissza		Előre
18. fejezet - Szervopneumatikus pozícionáló szabályozásának tervezése és szimulációja	Főoldal	FÜGGELÉK