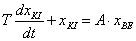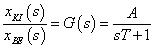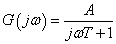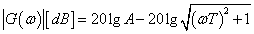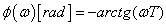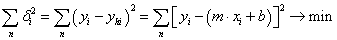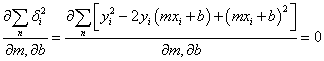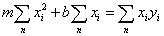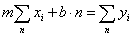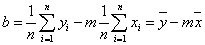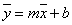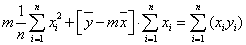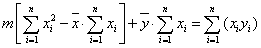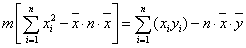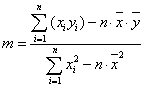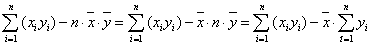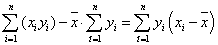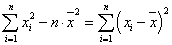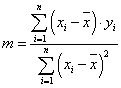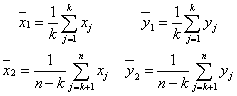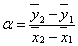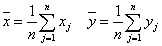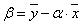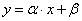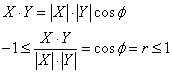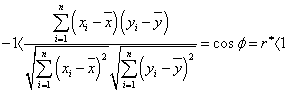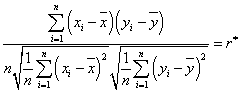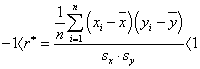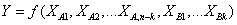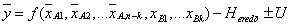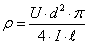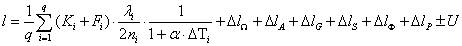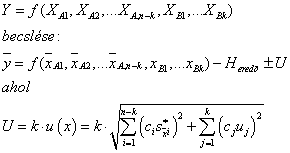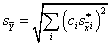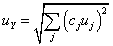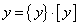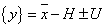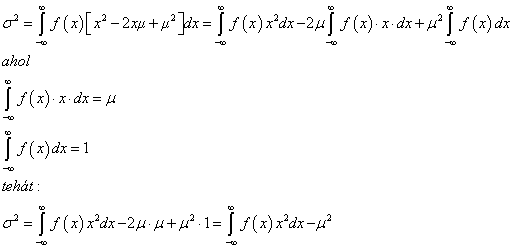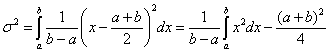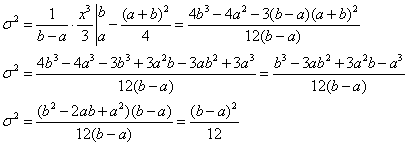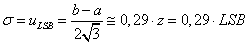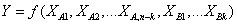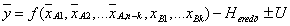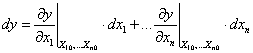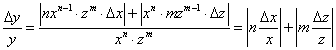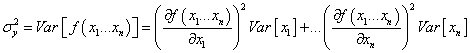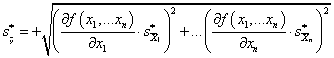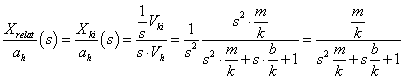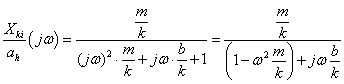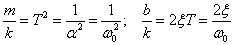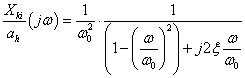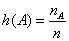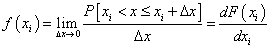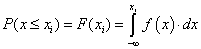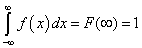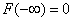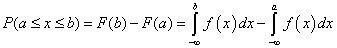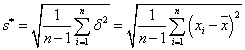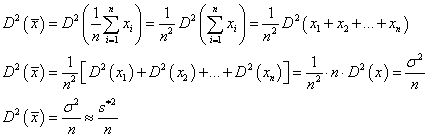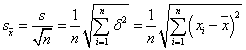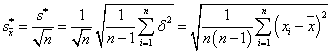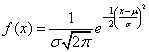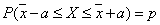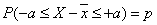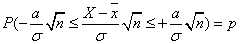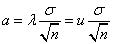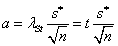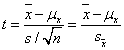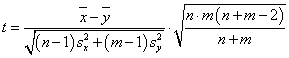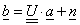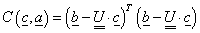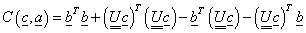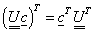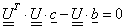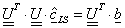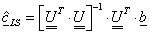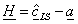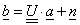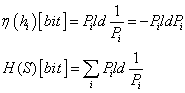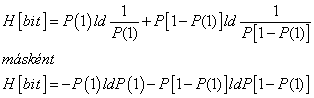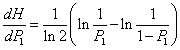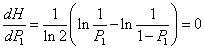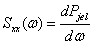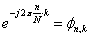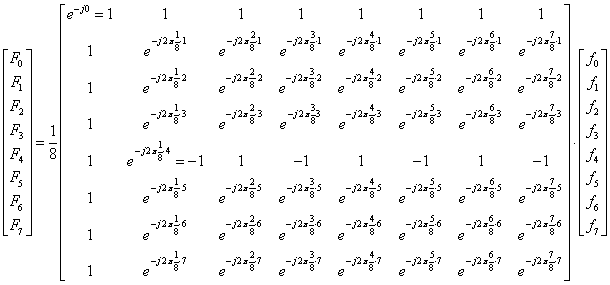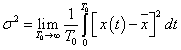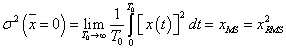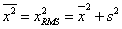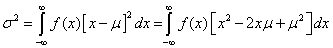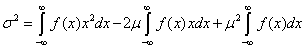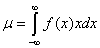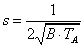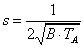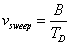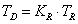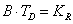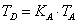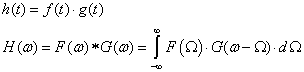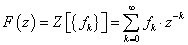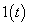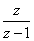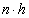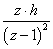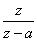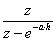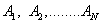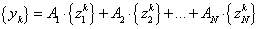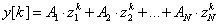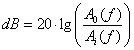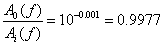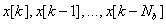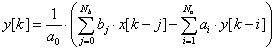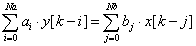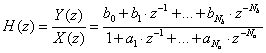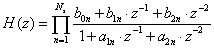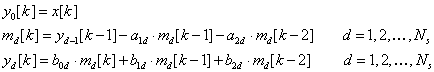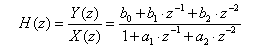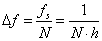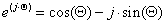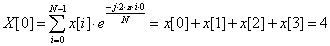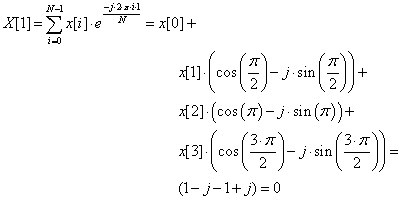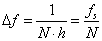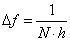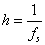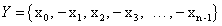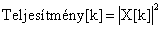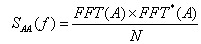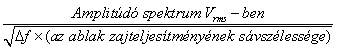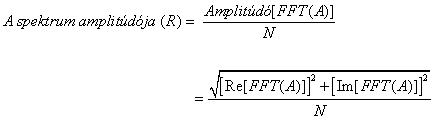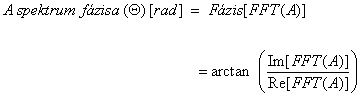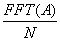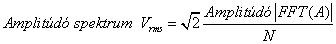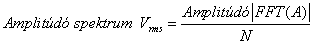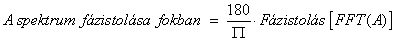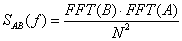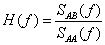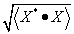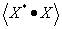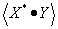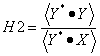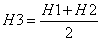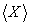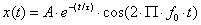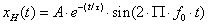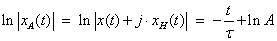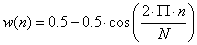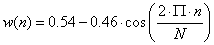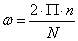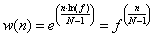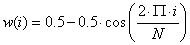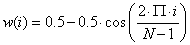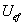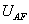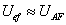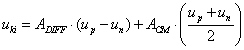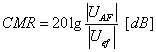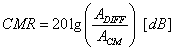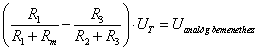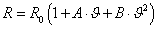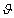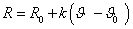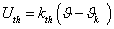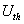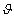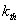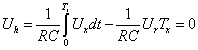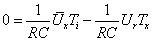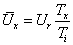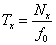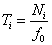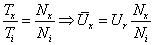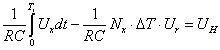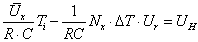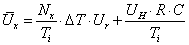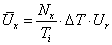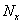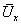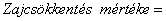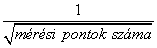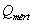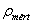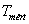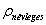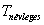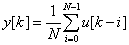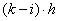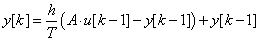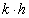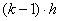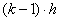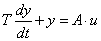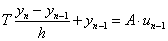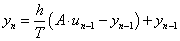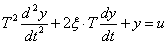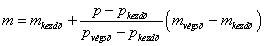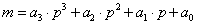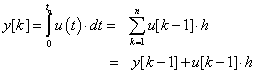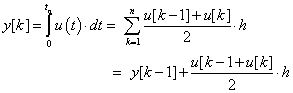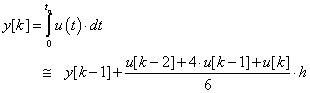Méréselmélet
Szerzői jog © 2014 Dr. Huba Antal, Dr. Lipovszki György

A tananyag a TÁMOP-4.1.2.A/1-11/1-2011-0042 azonosító számú „ Mechatronikai mérnök MSc tananyagfejlesztés ” projekt keretében készült. A tananyagfejlesztés az Európai Unió támogatásával és az Európai Szociális Alap társfinanszírozásával valósult meg.

Dr. Huba Antal (1-7. fejezetek) c. egyetemi tanár, BME-MOGI
Dr. Lipovszki György (8-16. fejezetek) egyetemi docens, BME-MOGI
Kézirat lezárva: 2014 február
Lektorálta: Dr. Pataki Péter
További közreműködők: Dr. Vass József, Dr. Samu Krisztián, Dr. Antal Ákos
A kiadásért felel a(z): BME MOGI
Felelős szerkesztő: BME MOGI
2014
- 1. Méréselmélet és méréstechnika
- 2. Mérés-és műszertechnika
- 3. Mérési hibák
- 4. Mérés és valószínűség számítás
- 4.1. Mérési adat, mint valószínűségi változó
- 4.2. Relatív gyakoriság és a valószínűség
- 4.3. Eloszlásfüggvény, sűrűségfüggvény
- 4.4. Egydimenziós eloszlások elméleti és empirikus paraméterei
- 4.5. Normál eloszlás, vagy Student eloszlás
- 4.6. Az eredményképlet konfidencia intervallumának meghatározása
- 4.7. Statisztikai próbákról röviden
- Irodalmak
- 5. Mérés és modellezés
- 6. Mérőjelek idő és frekvencia tartományban
- 7. Spektrum analízis a méréstechnikában
- 8. Bevezetés a digitális jelfeldolgozásba és analízisbe
- 9. Jelgenerálás
- 10. Digitális szűrés
- 10.1. Bevezetés a digitális szűrés gyakorlati alkalmazásába
- 10.2. A Z transzformáció
- 10.3. Egyszerű digitális szűrők
- 10.4. Egy ideális szűrő jellemzői
- 10.5. Valóságos (nem ideális) szűrők
- 10.6. Mintavételi idő
- 10.7. Véges impulzus válasz (FIR) szűrők
- 10.7.1. Leágaztatások (Taps)
- 10.7.2. Véges impulzus válasz szűrők (FIR szűrők) tervezése
- 10.7.3. Véges impulzus válasz szűrők (FIR szűrők) tervezése ablakozással
- 10.7.4. Optimális FIR szűrők tervezése a Parks-McClellan algoritmussal
- 10.7.5. Egyenletes hullámosságú FIR szűrők tervezése Parks-McClellan algoritmus alkalmazásával
- 10.7.6. Keskeny sávú FIR szűrők tervezése
- 10.7.7. Széles sávú FIR szűrők tervezése
- 10.8. Végtelen impulzus válasz (IIR) szűrők
- 10.8.1. Az IIR szűrés kaszkádképlete
- 10.8.2. Másodfokú szűrés
- 10.8.3. Negyedfokú szűrés
- 10.8.4. IIR szűrő konstrukciók
- 10.8.5. Csúcshiba minimalizálása
- 10.8.6. Butterworth-szűrők
- 10.8.7. Csebisev-szűrők
- 10.8.8. Csebisev II - szűrők
- 10.8.9. Elliptikus szűrők
- 10.8.10. Bessel-szűrők
- 10.8.11. IIR szűrők tervezése
- 10.8.12. IIR szűrők jellemzői
- 10.8.13. Átmeneti függvény
- 10.9. A FIR és az IIR szűrők összehasonlítása
- 10.10. Nemlineáris szűrők
- 10.11. Digitális szűrő típus kiválasztása
- Irodalom
- 11. Diszkrét frekvencia analízis
- 11.1. A frekvencia és az időtartomány közötti különbségek
- 11.2. Fourier transzformáció, mint a DFT alapja
- 11.3. (Időben) Diszkrét Fourier transzformáció (DFT)
- 11.4. Frekvencia lépés a DFT minták között
- 11.5. Gyors Fourier transzformáció alapjai (FFT= Fast Fourier Transformation)
- 11.6. A frekvencia információ megjelenítése a Fourier transzformáció után
- 11.7. Kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció
- 11.8. Teljesítmény Spektrum SAA(f)
- 11.9. A spektrumokkal végzett számítások
- 11.10. Amplitúdó és fázis spektrumok kiszámítása
- 11.11. Frekvencia válasz függvény
- 11.12. Kereszt teljesítmény spektrum SAB(f) (Cross Power Spectrum)
- 11.13. Frekvencia válasz és hálózat analízis
- 11.14. Ablakozási technika
- 11.15. Átlagolás a mérési eredmények ábrázolásához
- 11.16. Visszhang észlelése
- Irodalom
- 12. Simító ablakok
- 13. Számítógépes mérésadatgyűjtés és beavatkozás
- 14. Analóg bemenetek
- 14.1. A jelforrások típusai
- 14.2. Jelvevő áramkörök
- 14.3. Az illesztés legfontosabb szabályai
- 14.4. Zavarjelek
- 14.4.1. A csatolások típusai
- 14.4.2. A zavarjelek kiküszöbölésének általános módszerei
- 14.4.3. A zavarjelek típusai, időbeni változásuk alapján
- 14.4.4. A zavarjelek típusai áramkörökben való megjelenési formájuk szerint
- 14.4.5. A zavarjelek típusai keletkezési ok szerint és a zajcsökkentés módszerei
- 14.4.5.1. Csatlakozási potenciál
- 14.4.5.2. Termikus potenciál (termoelem)
- 14.4.5.3. Átmeneti ellenállás, átvezetés
- 14.4.5.4. Elektromágneses (induktív) zavarjel
- 14.4.5.5. Elektrosztatikus (kapacitív) zavarjel
- 14.4.5.6. Villamos áramkörök be és kikapcsolásakor keletkező zavarjel
- 14.4.5.7. Kábelhajlításból származó zavarjel
- 14.4.5.8. Rádiófrekvenciás zavarjel
- 14.4.5.9. Tápforrásból származó zavarjel
- 14.5. Földelések
- 14.6. A nemkívánatos föld áramkörök kiküszöbölésének módjai
- 14.7. Analóg bemenetek elemei
- 14.8. Analóg jel kondicionálása
- 14.9. Small Computer Extended Interface (SCXI)
- 14.10. Analóg méréspont váltók (multiplexerek)
- 14.11. Mintavevő tartó és erősítő
- 14.12. Analóg digitális (A/D) átalakítók
- 14.13. Mérés-adatgyűjtés általános áttekintése
- 14.13.1. Mérés-adatgyűjtő rendszerek komponensei
- 14.13.2. Analóg bemenet
- 14.13.3. Egy kimenetű jelek (Single-Ended Inputs)
- 14.13.4. Különbségi bemenetek (Differential Inputs)
- 14.13.5. Felbontás (Resolution)
- 14.13.6. Mérési határok (Range)
- 14.13.7. Erősítés (Gain)
- 14.13.8. Mintavételezés sebessége (Sampling Rate)
- 14.13.9. Átlagolás (Averaging)
- 14.13.10. Analóg bemenet eljárása a számítógépben
- 14.13.11. Analóg bemenet csatorna mintavételezés
- 14.13.12. Hullámforma bemenet (Waveform Input)
- 14.13.13. Analóg input hullámforma adatgyűjtő
- 14.14. Az analóg bemeneti perifériák perifériavezérlő egysége
- 14.15. Folytonos idejű mérésadatgyűjtés
- Irodalmak
- 15. Analóg kimenetek
- 16. A mérésadatgyűjtő számítógép algoritmusai
- Tárgymutató
- 1.1. A mérés szerepe a modern gépészetben
- 2.1. Az etalonok hierarchiája
- 2.2. Példák a nyomás etalonok megvalósítására
- 2.3. Dinamikus kalibrálás idő tartományban (elsőrendű rendszer)
- 2.4. Dinamikus kalibrálás eredményének ábrázolása frekvencia tartományban (Elsőrendű rendszer)
- 2.5. Regressziós egyenes és a kalibrációs pontok
- 2.6. A Wald-módszer grafikus szemléltetése
- 3.1. A mérési hibák rendszerező áttekintése
- 3.2. A legfontosabb mérési módszerek áttekintése
- 3.3. Az amplitúdó kvantálásból eredő f(x) egyenletes sűrűségfüggvény
- 3.4. A kvantálásból származó hiba
- 3.5. Egyenletes eloszlás függvényei
- 3.6. A mérőlánc felépítése és szerepe
- 3.7. Induktív gyorsulásérzékelő felépítése (Hottinger és Baldwin)
- 3.8. Részletek a H&B B12 gyorsulásérzékelő adatlapjából
- 3.9. A dinamikus hiba szemléltetése
- 3.10. Másodrendű rendszer átmeneti függvénye (step response)
- 3.11. A gyorsulásérzékelő működési modellje és impedancia hálózata
- 3.12. Méréstechnikában fontos dB értékek és az ábrázolás előnyei
- 3.13. Amplitúdó kvantált jel
- 3.14. Időben mintavételezett analóg jel
- 3.15. Mintavételezett és amplitúdó kvantált analóg jel
- 3.16. A négyszög impulzus és spektruma
- 3.17. A Dirac impulzus spektrumának közelítése
- 3.18. Anti-aliasing szűrés ábrázolása
- 3.19. Az ωm mintavételi körfrekvenciával mintavételezett és anti-aliasing szűrőn átengedett impulzus sorozat spektruma
- 3.20. Impulzus sorozat túl alacsony körfrekvenciával mintavételezett „összecsúszott” spektruma
- 3.21. A mintavételezés szemléltetése a legmagasabb harmonikus összetevőn
- 4.1. A relatív gyakoriság és a valószínűség kapcsolata
- 4.2. Hisztogram, relatív gyakoriság, valószínűség eloszlás és valószínűség sűrűség-függvény
- 4.3. Jellegzetes konfidencia szintekhez tartozó faktorok
- 4.4. A konfidencia intervallum szemléltetése
- 4.5. A normál és a standard normál eloszlás. Felül a sűrűségfüggvény, alul az eloszlásfüggvény látható
- 4.6. Hipotézis és ellenhipotézis egy feltételezett eloszláson
- 5.1. A mérési tevékenység modellezése folyamatként
- 5.2. A mérés folyamat-modelljének részletezése
- 5.3. A mérés valószínűségelméleti modellje
- 5.4. A H=ĉ – a becslési hiba szemléltetése
- 5.5. Az abszolút és a négyzetes hiba költségfüggvényei
- 5.6. A becslési hiba számításának szemléltetése
- 5.7. Hatás, amelyet az f(a) sűrűségfüggvény varianciájának növelése okoz
- 5.8. A legkisebb négyzetes hibájú becslő tömbvázlata
- 5.9. Információelméleti (hírközlési) modell értelmezése a mérésre
- 5.10. A mérőlánc általános struktúrája
- 5.11. Gyorsulásérzékelő jelátalakító induktív elmozdulás érzékelővel (szenzorral)
- 5.12. A mérés információelméleti modellje
- 5.13. A bináris hírforrás entrópiája a valószínűség függvényében
- 5.14. Sűrűségfüggvények digitális mérőműszerrel történő mérésnél
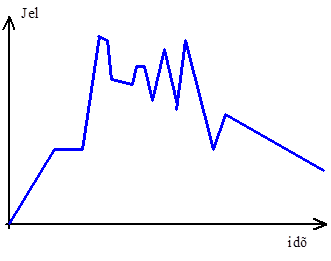
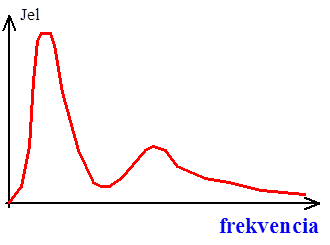
- 6.1. Harmonikus jel idő és frekvencia tartományban
- 6.2. Egy tetszőleges, periodikus jel spektrum formái
- 6.3. A jelek felosztása
- 6.4. A Fourier analízis összefoglaló bemutatása
- 6.5. A Heaviside függvény felbontása
- 6.6. A Heaviside-függvény komplex spektruma
- 6.7. A mintavételezés folyamatának matematikai modellje
- 6.8. Mintavételező áramkör elvi képe
- 6.9. Mintavételezést követő „értéktartás” nulladrendű tartótaggal
- 6.10. Sztochasztikus jel
- 6.11. Normál jelszint-eloszlású sztochasztikus jel
- 6.12. Az auto-korrelátor elvi vázlata
- 6.13. A komplex vektor (fazor) ábrázolása, a szokásoshoz képest 90 fokkal pozitív irányba elforgatva
- 6.14. Egy általános, „ϕ” fázistolású cos függvény időbeli alakja és komplex formája
- 6.15. Determinált jelek Fourier összetevői
- 6.16. Általános, folytonos periodikus jel diszkrét komplex spektruma
- 6.17. Analóg és mintavételezett jelek idő és frekvencia tartományban
- 6.18. Tetszőleges válaszjel felbontása
- 6.19. A Fourier és a Hilbert transzformáció képi ábrázolása
- 6.20. A komplex spektrum fázisforgatása Hilbert transzformációval
- 6.21. Az F1 komplex együttható részvektorainak forgása
- 7.1. Szűrt jel amplitúdó és teljesítmény spektruma
- 7.2. Szűrő (analizátor) tömbvázlata
- 7.3. Lineáris és log lépték, konstans és konstans relatív sávszélesség
- 7.4. Ideális és valós szűrő átviteli karakterisztikája
- 7.5. Szűrő alaktényezőjének meghatározása
- 7.6. Szűrő oktáv szelektivitása
- 7.7. Tercszűrő tranziens viselkedése
- 7.8. Léptető szűrős analizátor tömbvázlata
- 7.9. 10 db szomszédos tercszűrő által „lefedett” dekád
- 7.10. Terc-analizátorral felvett spektrum szintírón regisztrált képe
- 7.11. Hangolható szűrős analizátor tömbvázlata
- 7.12. Keskenysávú analízis eredménye
- 7.13. Real-time analizátor tömbvázlata
- 7.14. B&K 3347 típusú tercsávos real-time analizátor monitorja
- 7.15. Az idő-kompressziós analízis eredménye
- 7.16. Az átlagolási idő és az empirikus szórás kapcsolata
- 7.17. A jelminta és az átlagolási idő kapcsolata
- 7.18. Átlagolási idő és a spektrum felbontása közötti összefüggés
- 7.19. Sávonkénti átlagolási idő kvázi-folytonos analízis esetében
- 7.20. Gauss-időablak „simító” hatása a jelmintaperiodikus visszajátszása során
- 7.21. Időfüggvények szorzása – spektrumok konvoluciója
- 7.22. Négyszög és Gauss ablak hatása a spektrumra
- 7.23. Jellegzetes időablakok és frekvenciamenetük
- 7.24. Tranziens analízis döntési folyamatábrája
- 7.25. Tranziens analízis gyakorlati kivitelezésének lehetőségei
- 7.26. Tranziens jel visszajátszási idejének hatása a spektrumra
- 7.27. Kitartott „Á” hang spektruma és cepstruma
- 7.28. A komplex cepstrum alkalmazása visszhang eltávolítására
- 8.1. A nyers mérési adatok
- 8.2. A feldolgozott (szűrt) mérési adatok
- 8.3. DSP alkalmazások
- 8.4. Analóg jel és annak mintavételezett értékei ( h = a mintavételezések között eltelt idő az időtengelyen )
- 8.5. Alul-mintavételezés okozta látszólagos frekvencia jelensége
- 8.6. Aktuális jel frekvencia komponensei
- 8.7. A jel frekvenciakomponensei és a látszólagos frekvenciák
- 8.8. A különböző mintavételi frekvenciák hatása
- 8.9. Ideális és megvalósítható anti-aliasing szűrő
- 9.1. Egyszerű vizsgáló jelek
- 9.2. További gyakran használt vizsgáló jelek
- 9.3. Többfrekvenciás jel a szomszédos frekvenciák közötti fázis különbség változtatásával
- 9.4. Többfrekvenciás jel véletlenszerű fáziseltolássala szomszédos frekvenciák között
- 9.5. Homogén fehér zaj
- 9.6. Gauss-eloszlású fehér zaj
- 9.7. Véletlenszerű periodikus zaj és átlagolt fehér zaj spektrális ábrázolása
- 10.1. Analóg jelek mintavételezése és a mintavétel értéke
- 10.2. Analóg jelek mintavételezése és a mintavétel értéke
- 10.3. Diszkrét jel érték eltolása az időtengelyen negatív irányban
- 10.4. Diszkrét jel érték eltolása az időtengelyen pozitív irányban
- 10.5. A különböző típusú szűrő karakterisztikák
- 10.6. Ideális szűrők frekvencia válaszai
- 10.7. Átviteli sáv és vágási sáv
- 10.8. Nem ideális szűrők
- 10.9. FIR szűrő amplitúdó és fázis függvénye összehasonlítva a normalizált frekvenciával
- 10.10. Leágaztatás
- 10.11. Egyenletes hullámosságú sáváteresztő FIR szűrő frekvenciafüggvénye
- 10.12. Egy egyenletes hullámosságú sáváteresztő FIR szűrő amplitúdó és fázisfüggvénye
- 10.13. Hamming-ablakkal ablakozott jel
- 10.14. Keskeny sávú FIR szűrő frekvenciaválaszának becslése
- 10.15. Szűk sávú sáváteresztő FIR szűrő, 0-tól a Nyquist frekvenciáig tartó, becsült frekvenciagörbéje
- 10.16. Keskeny sávú sáváteresztő FIR szűrő becsült frekvenciamenetének részlete
- 10.17. Szélessávú aluláteresztő szűrő frekvenciaválasza 0-tól a Nyquist frekvenciáig
- 10.18. Kaszkád szűrés sorba kapcsolt fokozatai
- 10.19. Aluláteresztő Butterworth-szűrő amplitúdó-frekvencia függvénye
- 10.20. Aluláteresztő Csebisev-szűrő amplitúdó-frekvencia függvénye
- 10.21. Aluláteresztő Csebisev II -szűrő amplitúdó-frekvencia függvényét
- 10.22. Aluláteresztő Elliptikus-szűrő amplitúdó-frekvencia függvénye
- 10.23. Egy aluláteresztő Bessel-szűrő amplitúdó-frekvencia függvénye
- 10.24. Aluláteresztő Bessel-szűrő fázis-frekvencia függvénye
- 10.25. IIR szűrő frekvenciaválasza
- 10.26. Egy sáváteresztő elliptikus IIR szűrő amplitúdó és fázis függvénye
- 10.27. Átmeneti (tranziens) válaszfüggvény és egy IIR szűrő állandósult állapota
- 10.28. A Medián szűrő alkalmazása, hogy meghatározzuk az impulzus információit
- 10.29. Zajos impulzus és Medián szűrővel szűrt impulzus
- 10.30. A megfelelő szűrő kiválasztásának folyamatábrája
- 11.1. Három frekvencia komponens összeadásával kialakult jel
- 11.2. A VI diagram panelje, amely meghatározza a Parseval tételt
- 11.3. A Parseval VI eredményei
- 11.4. A Diszkrét Fourier Transzformáció
- 11.5. A DFT példa időtartománybeli jelsorozata
- 11.6. A jel páros és páratlan szimmetriája
- 11.7. X komplex kimeneti sorozat N=8 esetén
- 11.8. X[p] komplex kimeneti sorozat N=7 esetén
- 11.9. Számítási időtartam arány a DFT és FFT algoritmus között N=128-nál
- 11.10. Számítási időtartam arány a DFT és FFT algoritmus között N=512-nél
- 11.11. Nulla értékekkel történő feltöltés
- 11.12. Moduláció komplex exponenciális jel segítségével
- 11.13. Pontos adatokkal ellátott frekvencia transzformáció
- 11.14. A frekvencia transzformáció eredményeinek megjelenítése
- 11.15. A jelgenerátor felépítése
- 11.16. A Nyquist Shift VI blokk diagrammja
- 11.17. Időtartománybeli jelsorozat előállítása, 0(nulla) frekvencia középpontú spektrum
- 11.18. Az időtartománybeli bemenő adatok és a 0(nulla) frekvencia középpontú amplitúdó spektrum
- 11.19. A jel kétoldalas teljesítmény spektruma
- 11.20. Egyoldalas teljesítmény spektrum
- 11.21. Kétcsatornás frekvencia analízis
- 11.22. A hálózat mérés felépítése
- 11.23. Egy jel kétoldalas vonalas teljesítmény spektruma
- 11.24. Egy zajos szinuszos jel egyoldalas folytonos teljesítmény spektruma
- 11.25. Visszhang jel
- 11.26. Az xA(t) jel nagyságának logaritmikus léptékű ábrázolása
- 11.27. A visszhang detektálásának blokk diagramja
- 12.1. Mintavételi periódusból alkotott periodikus hullámforma
- 12.2. Szinusz hullám és Fourier transzformáltja
- 12.3. Spektrális ábra, amikor a mintavétel nem egész számú periódusból történt
- 12.4. A spektrum szóródás elfedi a közeli frekvencia komponenseket
- 12.5. Az ablakozott spektrum frekvencia karakterisztikája
- 12.6. Hanning-ablakkal ablakozott jel
- 12.7. Egy 1 Vrms-os 256 Hz-es jel teljesítmény-spektrumaállandó, Hanning és ”Flat top” ablakokkal
- 12.8. Egy 1 Vrms-os 256.5 Hz-es jel teljesítmény-spektruma állandó, Hanning és ”Flat top” ablakokkal
- 12.9. Két szinusz jel összegeként kapott jel spektrumának mérése
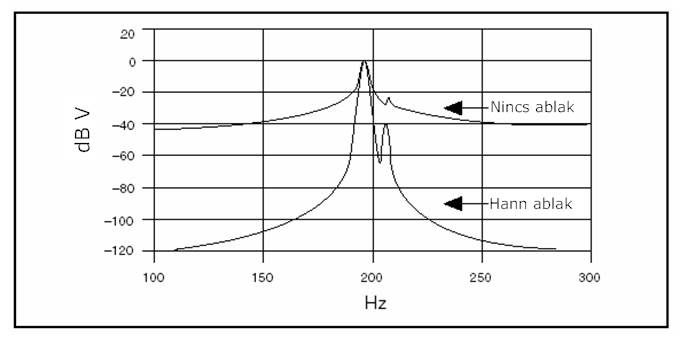
- 12.10. Két szinusz jel összegének ablakozott és ablakozás nélküli spektruma
- 12.11. Simító ablak frekvencia válasza
- 12.12. Négyszögletes ablak
- 12.13. Hanning ablak
- 12.14. Hamming ablak
- 12.15. Kaiser-Bessel ablak
- 12.16. Háromszög ablak
- 12.17. Flat Top ablak
- 12.18. Exponenciális ablak
- 12.19. Hanning ablak 8 mintavételi ponttal
- 12.20. Szinusz hullám 8 mintavételi ponttal
- 13.1. A számítógépes irányítás blokkdiagramja
- 13.2. Az irányítási feladatra alkalmazott jelátalakítási és transzformációs egységek és eljárások
- 13.3. A digitális jel szabályozástechnikai alkalmazása
- 13.4. Digitális TTL logikai szint értékek
- 13.5. Digitális kimenet/bemenet TTL logikai szint értékek
- 13.6. Relés digitális bemenet
- 13.7. Digitális bemenet fotodióda segítségével
- 13.8. Digitális bementi pozicionáló eszköz
- 13.9. Digitális CMOS bemenet kapcsolása
- 13.10. MOS tranzisztor felépítése
- 13.11. Digitális kimenet TTL logikai szint értékek
- 13.12. Digitális kimenet három logikai szint értékkel
- 13.13. Relés digitális kimenet
- 13.14. Digitális félvezetős kimenet
- 13.15. Optikai vezérlésű CMOS kapcsolók
- 13.16. Solid State relé
- 13.17. Digitális bemenetek (összefoglalás)
- 13.18. Digitális kimenetek (összefoglalás)
- 13.19. Távvezeték elosztott paraméterű modelljének helyettesítő kapcsolása
- 13.20. Hálózat rövidzárási és üresjárási impedanciájának mérése
- 13.21. Az analóg egyenfeszültségű jel szabályozástechnikai alkalmazása
- 13.22. Az analóg időfüggvény szabályozástechnikai alkalmazása
- 13.23. Az analóg időfüggvény mintavételezése
- 13.24. Az analóg frekvenciafüggvény szabályozástechnikai alkalmazása
- 14.1. Analóg bemenet(ek) blokk diagramja
- 14.2. Analóg jel mintavételezései között elvégzett feladatok
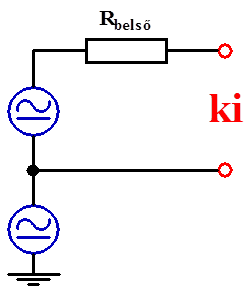
- 14.3. Aszimmetrikus földelt jelforrás
- 14.4. Aszimmetrikus földfüggetlen jelforrás
- 14.5. Aszimmetrikus földelt eltolt nullszintű jelforrás
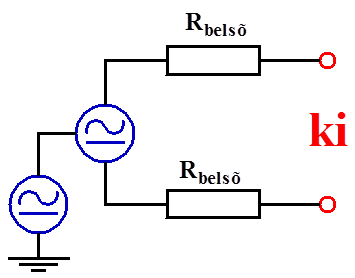
- 14.6. Szimmetrikus földelt jelforrás
- 14.7. Szimmetrikus földfüggetlen jelforrás
- 14.8. Szimmetrikus földelt eltolt nullszintű jelforrás
- 14.9. Az ideális műveleti erősítő
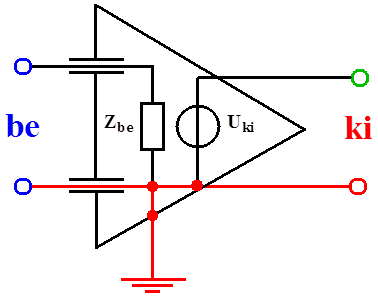
- 14.10. Aszimmetrikus földelt jelvevő áramkör
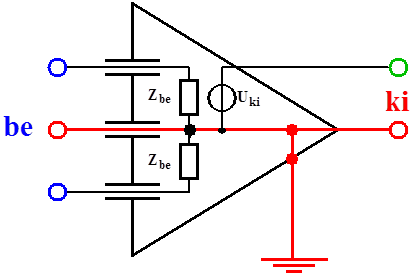
- 14.11. Szimmetrikus földelt jelvevő áramkör
- 14.12. Aszimmetrikus földfüggetlen jelvevő áramkör
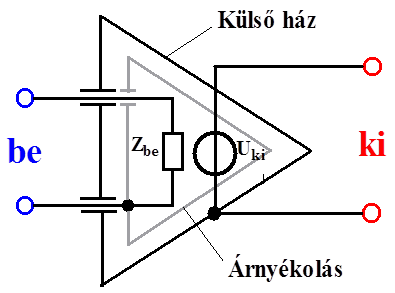
- 14.13. Szimmetrikus földfüggetlen védőárnyékolt jelvevő áramkör
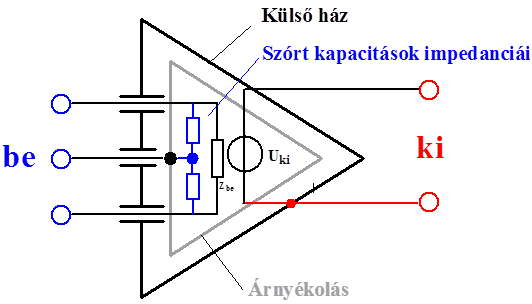
- 14.14. Aszimmetrikus földfüggetlen védőárnyékolt jelvevő áramkör
- 14.15. Aszimmetrikus földfüggetlen jelforrás és aszimmetrikus földelt jelvevő bemenet összekapcsolása
- 14.16. Aszimmetrikus földfüggetlen jelforrás és szimmetrikus földelt jelvevő bemenet összekapcsolása
- 14.17. Szimmetrikus földfüggetlen jelforrás és szimmetrikus földelt jelvevő bemenet összekapcsolása
- 14.18. Aszimmetrikus földelt jelforrás és aszimmetrikus földfüggetlen árnyékolt jelvevő bemenet összekapcsolása
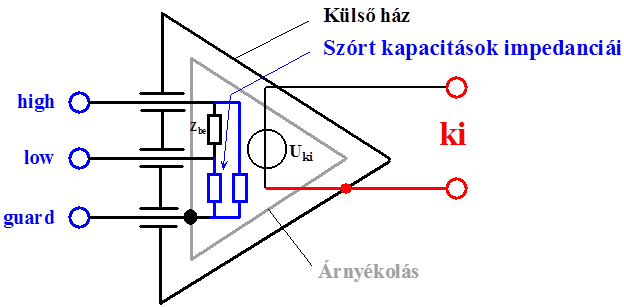
- 14.19. Aszimmetrikus földelt jelforrás és szimmetrikus földfüggetlen védőárnyékolt jelvevő bemenet összekapcsolása
- 14.20. Aszimmetrikus földelt jelforrás és szimmetrikus földfüggetlen védőárnyékolt jelvevő bemenet összekapcsolása
- 14.21. Analóg jelforrás és jelvevő összekapcsolásának összefoglalása
- 14.22. A zavarjel hatásvázlata
- 14.23. Ellenfázisú zavarjel blokkvázlata
- 14.24. Azonos fázisú zavarjel blokkvázlata
- 14.25. Két ponton földelt áramkör blokkvázlata
- 14.26. Kapcsolás az azonos fázisú zavarjel elnyomás meghatározásához
- 14.27. Helyettesítő kapcsolás az azonos fázisú zavarjel elnyomás meghatározásához
- 14.28. Szimmetrikus kapcsolás az azonos fázisú zavarjel elnyomás növelésére
- 14.29. Védőárnyékolás alkalmazása
- 14.30. Elektromágneses zavarjel keletkezése
- 14.31. A vezetékek megcsavarásakor kialakuló elektromágneses jelek
- 14.32. R_C áramkör be és kikapcsolásakor keletkező tranziens jelek
- 14.33. R_L áramkör be és kikapcsolásakor keletkező tranziens jelek
- 14.34. Sugaras (egy pontban történő) földelési rendszer
- 14.35. Repülő kondenzátoros galvanikus leválasztás
- 14.36. Transzformátoros galvanikus leválasztás
- 14.37. Fotodiódás galvanikus leválasztás
- 14.38. Galvanikus leválasztás feszültség frekvencia átalakítással
- 14.39. Analóg bemenet(ek) blokk diagramja
- 14.40. Analóg bemenet elemeinek blokkdiagramja
- 14.41. Analóg bemeneti érzékelő: bolométer
- 14.42. Analóg bemeneti érzékelő: ellenállás mérés Wheathstone híddal
- 14.43. Pitot csöves érzékelő
- 14.44. Mérőperemes érzékelő
- 14.45. Rosemount mérőperemes érzékelő (Típus: 1595P)
- 14.46. Analóg bemeneti szivattyú: köböző mennyiségmérő
- 14.47. Analóg mennyiségmérő szivattyú: köböző mennyiségmérő
- 14.48. Analóg mennyiségmérő szivattyú: köböző mennyiségmérő nyomatéki viszonyai mérés alatt
- 14.49. Analóg bemeneti érzékelő: ellenállás-hőmérő karakterisztikája (a másodfokú tag elhanyagolásával)
- 14.50. Analóg bemeneti érzékelő: félvezetős ellenállás-hőmérő karakterisztikája
- 14.51. Analóg bemeneti érzékelő: hőelem blokkdiagramja
- 14.52. Analóg bemenet elemeinek blokkdiagramja
- 14.53. Analóg bemeneti jel szűrés: passzív szűrő
- 14.54. Analóg bemeneti jel szűrése: időzítéses integrálással
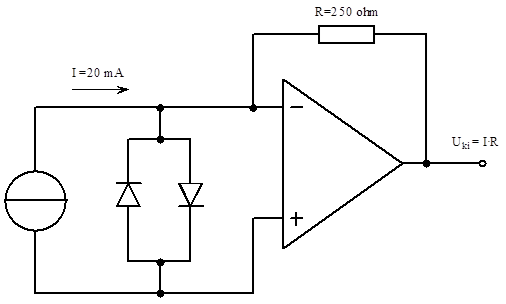
- 14.55. Analóg bemeneti jel átalakítás: áram – feszültség átalakító
- 14.56. Analóg bemeneti jel átalakítás: áram – feszültség átalakító
- 14.57. Analóg bemeneti jel átalakítás: feszültség osztó
- 14.58. Analóg bemeneti jel szűrése: egyszerű RC (passzív) szűrő
- 14.59. Analóg bemeneti jel szűrés: egyszerű RC (passzív) szűrő Bode amplitúdó diagramja
- 14.60. Analóg bemeneti jel átalakítás: változtatható feszültség osztó
- 14.61. Analóg bemeneti jel átalakítás: feszültség osztó és szűrő kapcsolás
- 14.62. Analóg bemeneti jel szűrés: kettős RC (passzív) szűrő
- 14.63. Analóg bemeneti jel szűrése: kettős RC (passzív) szűrő Bode (amplitúdó) diagramja
- 14.64. Analóg bemeneti jel szűrésének megvalósítása
- 14.65. Analóg bemenet elemeinek blokkdiagramja
- 14.66. Analóg multiplexer blokkdiagramja
- 14.67. Reed relé szerkezeti felépítése
- 14.68. Analóg multiplexer blokkok összekapcsolása
- 14.69. Félvezetős méréspont váltó
- 14.70. élvezetős méréspont váltó (földfüggő)
- 14.71. Analóg bemenet elemeinek blokkdiagramja
- 14.72. Mintavevő és tartó áramkör
- 14.73. Analóg bemenet elemeinek blokkdiagramja
- 14.74. Analóg digitális átalakítók: digitális-analóg visszacsatolásos
- 14.75. Digitális-analóg visszacsatolásos átalakító idődiagramja
- 14.76. Analóg digitális átalakítók: fokozatos közelítésű átalakító
- 14.77. Fokozatos közelítésű átalakító működési ábrája
- 14.78. Analóg digitális átalakítók: több komparátoros
- 14.79. Analóg digitális átalakítók: kettős meredekségű (integráló)
- 14.80. Kettős meredekségű (integráló) átalakító idő diagramja
- 14.81. Feszültség frekvencia átalakító működési ábrája
- 14.82. Analóg digitális átalakítók: feszültség frekvencia átalakító
- 14.83. Földelt bemenet
- 14.84. Földeletlen különbségi (differenciális) bemenet
- 14.85. Digitális felbontás
- 14.86. A jel erősítése
- 14.87. Helyes (fent) és helytelen (lent) mintavételezési frekvencia választása
- 14.88. Analóg bemenet ikonja
- 14.89. Analóg bemenet megadott mintavételi darabszám esetén
- 14.90. Analóg bemenet(ek) blokk diagramja
- 14.91. Analóg bemenet elemeinek blokkdiagramja
- 14.92. Kettős pufferelésű bemenet, sorrendi adat átvitellel
- 14.93. Kettős pufferelésű bemenet felülírása mielőtt kimásoltuk volna a tartalmát
- 14.94. Kettős pufferelésű bemenet egy adat felülírással
- 15.1. Analóg kimenet blokkdiagramja
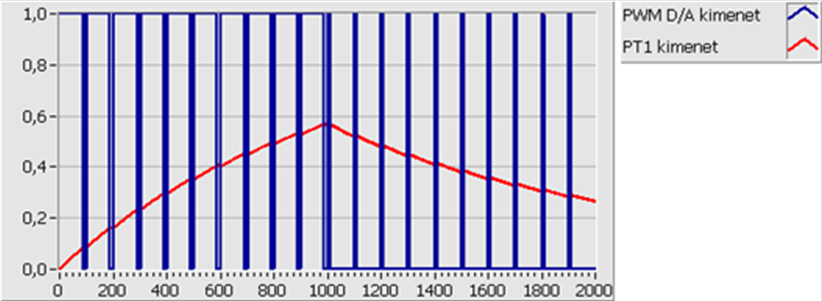
- 15.2. Digitális analóg átalakítók: Pulzus szélesség moduláció
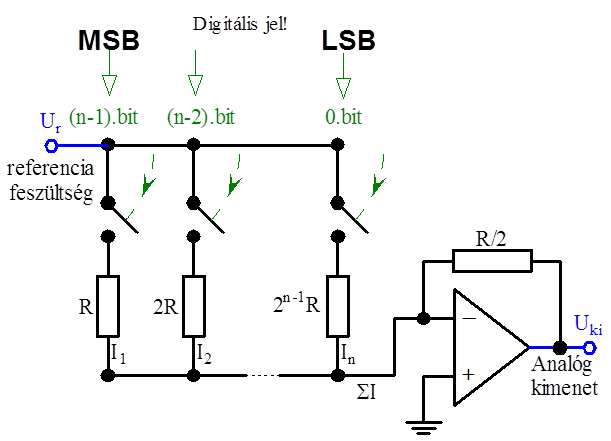
- 15.3. Digitális analóg átalakítók: 2^i ellenállás osztó segítségével
- 15.4. Digitális analóg átalakítók: R-2R ellenállás osztó segítségével
- 15.5. Analóg kimenet ikonja
- 15.6. Analóg kimenet létrehozása vektor típusú adatból
- 16.1. Analóg mintavételezés
- 16.2. A szinuszos jel mintavételezése
- 2.1. Az SI alapmennyiségek és alapegységek
- 2.2. Az SI alapmennyiségek definíciói
- 2.3. Származtatott mennyiségek és egységek.
- 8.1. Referencia érték és kiszámíthatók a decibel értékek
- 8.2. Decibelek , teljesítmény és feszültség arányok viszonya
- 9.1. Gyakran előforduló mérések és jelek
- 10.1. Jelek Z transzformációja
- 10.2. Ideális és valóságos szűrők jellemzői
- 11.1. X[p] értékei N = 8 esetén
- 11.2. X[p] értékei N = 7 esetén
- 12.1. A simító ablakok jellemzői
- 12.2. Jelek és javasolt ablakok
- 12.3. Simító ablakok korrekciós tényezői és a legrosszabb esetben fellépő amplitúdó hibák
- 13.1. Logikai (digitális) jelek
- 13.2. Analóg jelek
- 13.3. Időzítés mérése
- 14.1. Árnyékolások zajcsökkentő hatása
- 14.2. Analóg bemeneti csatorna eljárás paraméterei
- 14.3. Analóg hullámforma bemeneti csatorna eljárás paraméterei
- 15.1. Analóg kimeneti csatorna frissítés eljárás paraméterei
- 15.2. Analóg kimeneti hullámforma létrehozása eljárás paraméterei
- 16.1. Átszámítás fizikai értékekre
1. fejezet - Méréselmélet és méréstechnika
Miért éppen ilyen a fejezetcímben szereplő sorrend? A jegyzet tanulmányozása során mindenki számára világossá kell válnia, hogy alapos elméleti megfontolások nélkül igényes mérést nem lehet végezni. A mérési folyamat (ennek modelljét látni fogjuk egy későbbi fejezetben) minden egyes fázisa, tehát a modellalkotás , a mérési eljárás kiválasztása , a mérés kivitelezése és a kiértékelés feltételezi azokat az elméleti ismereteket, amelyeket a méréstudomány napjainkig felhalmozott. Ebbe a hatalmas, és más területekkel szorosan összefüggő ismeretanyagba szeretnénk e jegyzet keretei között betekintést nyújtani. A jegyzet tartalmi felépítésnél figyelembe vettük a mechatronikai mérnöki és gépészmérnöki BSc képzések számára összeállított Méréstechnika című [1.1.] elektronikus jegyzet anyagát, amely ugyancsak TÁMOP támogatással jött létre. A jelen jegyzet 2., 3., és 4. fejezetében azokat az ismereteket, amelyek a mérési tevékenység szempontjából alapvető jelentőségűek, röviden átismételtük, és kiegészítettük az MSc követelményeinek megfelelő ismeretanyagokkal.
1.1. Mit és miért mérünk?
Bernard Orth [1.2.] azt írja, hogy „A mérés, történetét és metodikáját tekintve a tudomány egyik alappillére. Egzakt mérések nélkül a gyakorlati tudományok, különösképpen a természettudományok, elképzelhetetlenek. A mérések elősegítik új tudományos elméletek kifejlődését, és a meglévők finomítását. Mérések segítenek az empirikus összefüggések felismerésében, és lehetővé teszik különböző elméletek valósággal történő összevetését.”
Nincs mérnöki területeken olyan tudományos igényű munka, diplomaterv, PhD dolgozat, vagy tudományos cikk, amelyben ne találkoznánk az elmélet és a gyakorlat összehasonlításával. A gyakorlati eredmények dokumentálása és az elméletek alátámasztása mérésekkel történik.
Mindennapjaink is elképzelhetetlenek a mérések nélkül, bár gyakran ez nem is tudatosodik. A konyhai tevékenységektől az egészségügyi szolgáltatásokon át a gépjárművek sebességméréséig életünk szinte minden percében jelen van valamilyen formában a mérés.
Ugyanakkor nem szabad azt gondolnunk, hogy a természet a mi saját fáradozásaink igénybevétele nélkül „tálcán kínálja” az ismereteket. Mielőtt egy ismeretlen, vagy többé-kevésbé ismert mennyiség mérésének nekilátunk, jó előre tisztázni, hogy az adott jellemző egyáltalán mérhető-e, és milyen hibák fogják befolyásolni a mérést? A méréselmélet többek között erre a két alapvető kérdésre próbál választ adni.
Méréselmélet alatt napjainkban a különböző tudományterületeken, szakterületeken létrejött olyan tudományos ismeretek összességét lehet érteni, amelyek lényegében a mérési problémák megoldásához szükséges eszköztárat képezik.
Minden szakterület a saját fejlődésével szoros kapcsolatban és azzal kölcsönhatásban, kialakította a saját mérési technikáját és a hozzá tartozó elméleti hátteret. Amíg a mérési módszerek tekintetében a diverzifikáció, a szakra jellemző specializáció a jellemző, addig megfigyelhető, hogy a méréselméleti háttér egyre több területen közeledik egymáshoz. A közeledés a modellezés területén mutatható ki leginkább, és ez a modellezés végső soron a jel-és rendszerelmélethez kötődik. A mérési eljárások általános megfogalmazásához szükséges matematikai apparátust tágabban a jel-és rendszerelmélet, valamint társtudományai (pl. becslés- és információelmélet) szolgáltatják. Jegyzetünkben a „méréselmélet” fogalom alatt, a fentiekre való hivatkozással, és a fenti meghatározás által biztosított szabadsággal élve, a gépészet és a mechatronika szempontjából fontos ismeretanyag kerül előtérbe. Ez nyilvánvalóan más témákat érint, mint egy olyan méréselméleti munka, amely a villamosmérnök, építőmérnök, vagy akár közgazdász képzés számára készült.
El kell fogadni továbbá, hogy a műszertechnika és a méréstechnika a fejlődése során produkálhat meglepő súlyponteltolódásokat, de akár új tudományos irányok is megjelenhetnek.
1.2. Mérés a gépészetben és a mechatronikában
Az előzőek szerint a szerzők tehát feltételezik, hogy e jegyzet olvasója BSc tanulmányai során már megismerte és használta a Méréstechnika című elektronikus jegyzetet [1.1.] . Az alapvető ismereteket ennek ellenére szükségesnek látjuk összefoglalni, mert az alapképzésben tanult ismeretekre szeretnénk alapozni. Az említett munka négy nagy ismeretkört tartalmaz. Az elsőben a metrológiai alapismeretekről van szó, és a valószínűség számítás segítségével a mérési eredmény megadásának szabályairól. A második témakör az időben változó mennyiségek, a harmadik a geometriai mennyiségek mérése. A negyedik csoport a mérésügyi szabályozásokat és a minőségbiztosítás alapismereteit mutatja be.
A gépész és a mechatronikai mérnök jellemzően az alábbi területeken fejt ki mérési tevékenységeket:
Mérőeszköz kalibrálás, hitelesítés
Műszaki ismeretszerzés (ez a legszélesebb terület)
Minőség-ellenőrzés - minőségbiztosítás
Folyamatirányítás
Automatizálás
A mérőeszközökkel kapcsolatos tevékenységek az első helyen szerepelnek, hiszen eszközök nélkül lehetetlen egy mérés kivitelezése. Látnunk kell ugyanakkor, hogy a felsorolásban másodikként szereplő „műszaki ismeretszerzés” kiemelt jelentőséggel bír. Ez a legalapvetőbb mérési-mérnöki tevékenység, mert számtalan és igen eltérő jellegű a mérési feladat a tervezés, az anyagtudomány, a gyártás, a gépészeti folyamatok, energetika, stb. területén.
A teljesség igénye nélkül , néhány kiválasztott gépészeti és mechatronikai területen, példákkal illusztráljuk azt, hogy az időben változó mennyiségek mérésének igénye miként vezet ezeken a szakterületeken a bevezetőben említett jel-és rendszertechnikai matematikai apparátus szükségszerű alkalmazásához.
A modern gépiparban a gyártóeszközök - gyártóberendezések elképzelhetetlenek valamilyen szintű automatizáltság és robotika nélkül. Az önműködő, és várhatóan egyre bonyolultabb adaptív rendszerek szerves része a méréstechnika. Mind a klasszikus gépészeti berendezések, mind pedig a mechatronikai rendszerek lényege és középpontja az összetett mechanikai, elektromechanikai, stb. dinamikus rendszer (szabályozott rendszerekben a „szabályozott szakasz”).
A dinamikus rendszerekkel kapcsolatban két féle megközelítést látunk az (1.1. ábra - A mérés szerepe a modern gépészetben) ábrán.
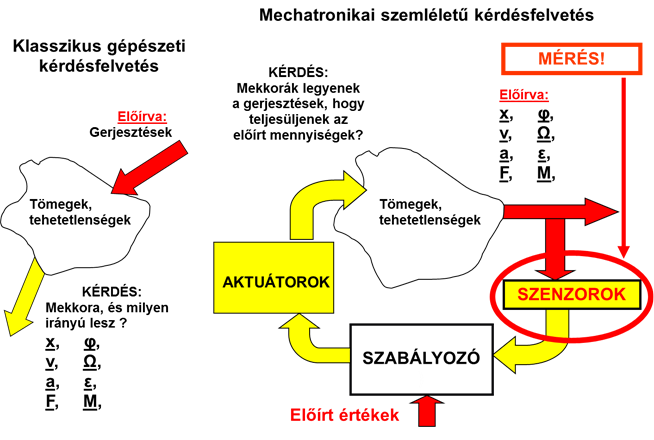
A hagyományos gépészeti kérdésfelvetés, a klasszikus műszaki mechanikai megfogalmazásban baloldalon látható. Ebben a megközelítésben azokat a válaszokat keressük, amelyeket valamilyen, a rendszert, berendezést érő külső-belső gerjesztés hatására kapunk. A „kimeneti” mennyiségek ellenőrző mérése itt is elengedhetetlen. Ezzel szemben a jobboldali ábrarészen látható mechatronikai rendszer esetében a kérdésfelvetés és a válasz sorrendje pont fordított. A gépészeti, mechatronikai rendszer válaszai, kimenetei vannak előírva, és arra keressük a megoldást, hogy a középpontban álló összetett rendszert hogyan lehet az előírt válaszokra „rákényszeríteni”. Ennek előfeltétele a szabályozás, amelyhez viszont alapkövetelmény a szabályozott jellemzők időben folytonos mérése, visszacsatolás, vagy visszacsatolások formájában. A modern, mesterséges intelligenciával ellátott gépészeti berendezések ezért nem nélkülözhetik a méréstechnikát.
A gyártástechnológia, gyártásautomatizálás területén napjainkban az egyik legalapvetőbb mechatronikai rendszer a szabályozott pozícionáló. Ez szerves része minden NC és CNC gépnek, mérőgépnek és hasonló berendezésnek. Ezek a pozicionálók lehetnek egyszerű, kaszkád szabályozó rendszerek. Napjaink korszerű szabályozástechnikájára és mechatronikájára az un. állapotszabályozás jellemző. Annyi közös mindkét változatban, hogy az állapot-visszacsatolások (többnyire) ugyancsak méréssel történnek. A „többnyire” kifejezés azért szerepel, mert pozíció mérések alapján, elvileg, számítással is meghatározható például a mozgó gépszerkezet sebessége. Elvileg, mert ez a módszer hibákkal jár, és korlátozza két tetszőlegesen beállított pozíció közötti távolság beállíthatóságát. A pozíciószabályozásban a szabályozott szakasz többnyire elektromechanikus, hiszen az általában egyenáramú szervomotort, hajtóművet, tengelykapcsolót és egy golyósorsós mozgás-átalakítót foglal magába, de alkalmaznak lineáris motorral történő mozgatást is. A szabályozott kimenőjel (előírt kimenet, lásd: 1.1. ábra - A mérés szerepe a modern gépészetben) a pozicionáló (asztal) elmozdulása. A mozgatás egyszerű, nyílt láncú vezérléssel is megoldható valamilyen szintű pontossággal, de ebben az esetben nem lenne visszajelzés a mozgatott eszköz valóságos helyzetéről. Szabályozás segítségével javítható a dinamika és csökkenthető a maradó hiba . A szabályozás visszacsatolása, nevezetesen a visszacsatoló tag szolgáltatja a helyzettel kapcsolatos információt. Ha a hivatalos nevén alapjelként előírt érték, és az asztal megmért, aktuális pozíciója nem egyeznek, akkor a szabályozó tag a különbségi jel feldolgozása után „parancsot” küld a szervomotornak a különbség megszüntetésére, és ez természetesen a különbség előjelét figyelembe véve, a megfelelő irányban fog bekövetkezni.
Tehát mérés és mérőrendszer nélkül egy ilyen szabályozókör nem elképzelhető.A gyártástudományban az NC és CNC berendezéseket az ipari robotok „kategóriájába” sorolják, nem alaptalanul. A szerelő és hegesztő robotok, a gyártócellák egy része ugyancsak szabályozott mozgású mechanikai egységekből épül fel. Vannak természetesen vezérelt berendezések is ezek között, de ezek manipulációs pontossága korlátozott.
A szabályozás, és a vele járó mérés már rég megjelent a gépszerkezetek területén is. Kétségtelen, hogy a klasszikus gépészet régi törekvése a sok gondot okozó súrlódások leküzdése, csökkentése. A csapágyak mágneses tehermentesítése régről ismert módszer, de a komolyabb igényeket kielégíteni képes mágneses csapágyazás csak szabályozás segítségével valósítható meg. Az elektromágneses tér segítségével aktívan csapágyazott forgó tengely tulajdonképpen elektromágnesek vaskörének záró elemét képezi. Az elektromágnesektől való távolságot induktív, vagy más típusú útadóval mérik, és amennyiben az előírt távolság valamilyen irányban megváltozik, az ellen-oldali elektromágnes - a mágneses gerjesztés növelése révén – visszahúzza a tengelyt a helyes pozícióba. A tengely helyzetét nem csupán radiális, hanem axiális irányban is szabályozzák, ez utóbbi szabályozókörének visszacsatoló ágában egy váll két oldalán elhelyezkedő útadók mérőjelei szolgáltatják a helyzet-információt, és ugyancsak elektromágnesek biztosítják a szükséges erőket. A tengely, forgás közben „lebeg” az aktív mágneses mezőben.
A gépészetben a mérés természetesen nem csupán szabályozókörökben jelenik meg, hanem a minőség-ellenőrzés számtalan formájában, például geometriai mennyiségek mérése során. Kihagyhatatlan a felsorolásból az áramlásmérés, a nyomásmérés, a hőmérsékletmérés, vagy éppen a zaj-és rezgésmérés . A műszaki mechanikában sokszor gondot jelent a rezgő felületek „letapogatása” (szkennelése) úgy, hogy a mérendő rendszert a mérőberendezés, vagy a jelátalakító ne befolyásolja. Ez kisméretű tárgyak esetében különösen fontos, de nem mellékes a mérési pontok száma sem, ha az érzékelőt minden mérési ponton külön kell rögzíteni. A mért adatok feldolgozása (spektrum analízis, stb.) hagyományos mérőeszközökkel gyakran igen nehézkes, sőt extrém kis méretek esetén gyakran egyáltalán nem megoldható feladat. A lézer-optika ma már megoldást nyújt ezekre a problémákra is, még ha nem is olcsón. A lézer Doppler-effektus fizikai elvén alapuló rezgéssebesség-mérő érintésmentes (terhelésmentes), kiváló felbontású és hatalmas mérési tartományú mérést tesz lehetővé. Példaként egy katalógusban olvashatjuk [1.3.] , hogy a rezgés amplitúdója, azaz elmozdulás (relatív is) mérése 2·10-12 m – 10 m tartományban, míg a rezgéssebesség mérése 50 nm/s – 30 m/s tartományban lehetséges. A megfigyelt jelek frekvencia analízise természetesen lehetséges a mérőrendszerrel.
Irodalmak
[1.1.] Méréstechnika. TÁMOP-4.1.2-08/A/KMR-0029 Elektronikus jegyzet. 2013.
[1.2.] Einführung in die Theorie des Messens.
[1.3.] Polytec Waldbronn, Laser Doppler Vibrometer Termékismertető . 2008.
2. fejezet - Mérés-és műszertechnika
2.1. SI rendszer
A CIPM (Nemzetközi Méteregyezmény) tagországaiban törvénnyel szabályozott módon kötelező az SI (Système International d’Unités) alapegységek és alap mértékegységek használata. Az egyezményt 1971-ben a General Conference on Weight and Measures (Általános Súly-és Mértékügyi Értekezlet) kötötték. Meghatározott feltételek mellett más, törvényes egységek és mértékegységek is alkalmazhatóak, tekintettel a kereskedelemre, és egyéb, fontos területekre. Magyarországon - a korábbi évek rendeleti szabályozása helyett - 1991-ben lépett hatályba a Mérésügyi Törvény (1991. évi XLV. törv.)
2.2. SI alapmennyiségek és származtatott mennyiségek.
Minden méréstechnikával és méréselmélettel foglalkozó szakembernek tisztában kell lennie a törvényes egységekkel és mértékegységekkel, és igen hasznos egy áttekintés a származtatott mennyiségekről is. Ezért a következőkben bemutatjuk ezeket, valamint közöljük az alapegységek jelenleg érvényes definícióit is, rövidített formában.
|
Alapmennyiség |
Jelölés |
Alapegység |
|---|---|---|
|
Hosszúság |
l |
méter (m) |
|
Tömeg |
m |
kilogramm (kg) |
|
Idő |
t |
másodperc (s) |
|
Áram |
I |
amper (A) |
|
Termodinamikai hőmérséklet |
T |
kelvin (K) |
|
Anyagmennyiség |
n |
mol (mol) |
|
Fényerősség |
IV |
kandela (cd) |
|
1 m |
A fény által vákuumban 1/299 792 458 s idő alatt megtett út. |
|
1 kg |
1889 óta Sèvres-ben őrzött platinum-iridium henger, mint a kilogramm nemzetközi ősetalonja, (az egyetlen prototípus alapú alapetalon!) |
|
1 s |
Az alapállapotú cézium-133 atom két hiperfinom energiaszintje közötti átmenetnek megfelelő sugárzás 9 192 631 770 periódusának időtartama. |
|
1 A |
1 A konstans áram folyik két párhuzamos, végtelen hosszú, egymástól 1 m távolságban lévő, elhanyagolható keresztmetszetű vezetőben, ha közöttük vákuumban, méterenként 2x10-7 N erő mérhető. |
|
1 K |
A víz hármaspontja termodinamikai hőmérsékletének 1/273.16-szorosa. |
|
1 mol |
Egy rendszer anyagának azon mennyisége, amely ugyanannyi elemi egységet tartalmaz, ahány atom van a 12-es tömegszámú szén 0,012 kg-jában. |
|
1 cd |
Olyan fényforrás fényerőssége adott irányban, amely 540×1012 Hz frekvenciájú monokromatikus sugárzást bocsát ki, és sugárerőssége ebben az irányban 1/683 W/steradian. |
|
Származtatott mennyiség |
Elnevezés |
Jel |
Más SI egységgel kifejezve |
SI alap-egységgel kifejezve |
|---|---|---|---|---|
|
Síkszög |
radian (a) |
rad |
- |
m·m-1 = 1 (b) |
|
Térszög |
steradian (a) |
sr (c) |
- |
m2·m-2 = 1 (b) |
|
Frekvencia |
hertz |
Hz |
- |
s-1 |
|
Erő |
newton |
N |
- |
m·kg·s-2 |
|
Nyomás, Mechanikai feszültség |
pascal |
Pa |
N/m2 |
m-1·kg·s-2 |
|
Energia, Munka, Hőmennyiség |
joule |
J |
N·m |
m2·kg·s-2 |
|
Teljesítmény, Sugárteljesítmény |
watt |
W |
J/s |
m2·kg·s-3 |
|
Elektromos töltés |
coulomb |
C |
- |
s·A |
|
Elektromos feszültség |
volt |
V |
W/A |
m2·kg·s-3·A-1 |
|
Kapacitás |
farad |
F |
C/V |
m-2·kg-1·s4·A2 |
|
Elektromos ellenállás |
ohm |
V/A |
m2·kg·s-3·A-2 | |
|
Elektromos vezetőképesség |
siemens |
S |
A/V |
m-2·kg-1·s3·A2 |
|
Mágneses fluxus |
weber |
Wb |
V·s |
m2·kg·s-2·A-1 |
|
Mágneses fluxussűrűség |
tesla |
T |
Wb/m2 |
kg·s-2·A-1 |
|
Induktivitás |
henry |
H |
Wb/A |
m2·kg·s-2·A-2 |
|
Celsius hőmérséklet |
degree Celsius (e) |
°C |
- |
K |
|
Fényáram |
lumen |
lm |
cd·sr (c) |
m2·m-2·cd = cd |
|
Megvilágítás |
lux |
lx |
lm/m2 |
m2·m-4·cd = m-2·cd |
|
Aktivitás (Nukleáris) |
becquerel |
Bq |
- |
s-1 |
|
Elnyelt sugárdózis |
gray |
Gy |
J/kg |
m2·s-2 |
|
Ekvivalens sugárdózis(d) Dózisegyenérték |
sievert |
Sv |
J/kg |
m2·s-2 |
Magyarázat a származtatott mennyiségek táblázatában alkalmazott jelölésekhez:
(a)A radián és a steradián két jellemző kifejezés arra az esetre, amikor eltérő természetű származtatott mennyiségeknek azonos a dimenziója, pontosabban nincs dimenziója. Egy radián az a szög, amely alatt a sugárral megegyező nagyságú ívhossz a középpontból látszik. Másképp a radián a sugárnyi hosszúságú ívhosszhoz tartozó középponti szög 57.2958°. Egy szteradián az a középponti szög, amely a gömbsugár négyzetével egyenlő területű gömbfelületrészhez tartozik.
(b) A gyakorlatban a „rad” és „sr” mértékegységek használatosak, annak ellenére, hogy a definícióból mindkét esetben "1" adódna.
(c) A fotometriában a mértékegység neve steradian, jele „sr”.
(d) Más mennyiségek „sieverts”-ben kifejezve: személyi dózis, effektív dózis, irányított ekvivalens dózis
(e) A Celsius hőmérséklet egysége a Celsius fok, jele °C. A Celsius hőmérséklet „t” numerikus értéke Celsius fokban kifejezve: t/°C = T/K - 273.15. Megjegyzés: Az összefüggésben 273,15 K a víz olvadási hőmérséklete, ami nem azonos a víz-hármaspont 273,16 K hőmérsékletével. Az egyszázados eltérés oka, hogy a zárt víz-hármaspontban a három halmazállapot együtt van jelen, szemben a nyílt edényben olvadó jég két halmazállapotával.
2.3. Metrológiai definíciók
A metrológia legfontosabb meghatározásait a NAT (Nemzeti Akkreditáló Testület) NAR-EA-4/02. jelű anyaga [2.1.] alapján, az alábbiakban gyűjtöttük össze:
Alapmennyiség
Megállapodásszerűen, egy adott rendszerben egymástól függetlennek tekintett mennyiségek
Származtatott mennyiség
Alapmennyiségek függvényeként definiált mennyiségek
Mértékegység
Ugyanolyan fajtájú, más mennyiség nagyságának kifejezésére definiált konkrét mennyiség
Egységrendszer
Az alap és származtatott egységek összessége
Koherens egység
Alapegységek hatványainak szorzataként kifejezhető egység, az arányossági tényező: 1 (egy)
Inkoherens egység
Mint előbb, de az arányossági tényező nem 1 (egy)
Etalon
Mérték, mérőeszköz, anyagminta, vagy mérőrendszer, amelynek az a rendeltetése, hogy egy mennyiség egységét, illetve egy, vagy több ismert értékét definiálja, megvalósítsa, fenntartsa, vagy reprodukálja és referenciaként szolgáljon.
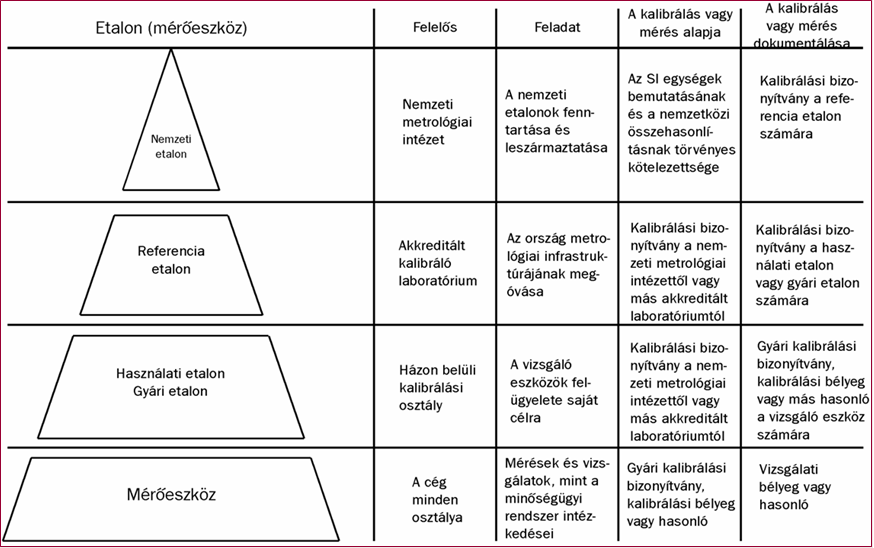 2.1. ábra - Az etalonok hierarchiája
2.1. ábra - Az etalonok hierarchiája
Visszavezethetőség
Egy mérés eredményének, vagy etalon értéknek az a tulajdonsága, hogy ismert bizonytalanságú összehasonlítások láncolatán keresztül kapcsolódik megadott referenciákhoz, általános nemzeti (ld. ehhez a magyarázatot a (2.5. szakasz - Statikus és dinamikus kalibrálás) fejezetben), vagy nemzetközi etalonhoz. A visszavezetési láncban a kevésbé pontos etalonok felől haladunk a pontosabbak felé.
Leszármaztathatóság
A visszavezetéssel ellentétes műveletsor.
Etalonok csoportosítása
Jogi státuszuk szerint:
Nemzetközi etalon
Megállapodás alapján elfogadott etalon
Nemzeti etalon
Adott országban választott viszonyítási alap
Referencia etalon
Adott szervezet legpontosabb etalonja
Használati etalon
Mérőeszközök ellenőrzésére rendszeresen használt etalon
Metrológiai státuszuk szerint:
Elsődleges etalon
Nem lehet más etalonból leszármaztatni
Másodlagos etalon
Leszármaztatott etalon
Jellegük szerint:
Egyedi etalon
Etalon műszer, mérték, anyagminta
Etalon csoport
Pl.: Súlysorozat, mérőhasáb készlet
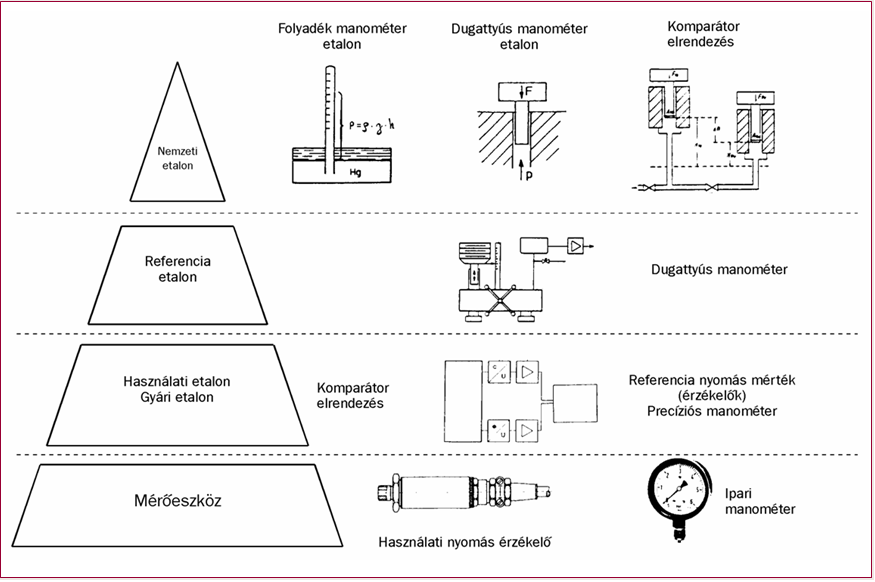 2.2. ábra - Példák a nyomás etalonok megvalósítására
2.2. ábra - Példák a nyomás etalonok megvalósítására
Illeszkedés
Összefügg a műszertechnikai alapfogalmak között szereplő reprodukálhatósággal és ismételhetőséggel (ld.: ott). Az illeszkedés azt jelenti, hogy különböző helyen és időben végzett mérések eredményei egymással összevethetőek.
Joghatással járó mérések
Az ilyen típusú méréseket csak hitelesített mérőeszközökkel lehet elvégezni. Ebbe a körbe a következő tevékenységek tartoznak:
Jogi érdekeket érintő mérések
Minőség tanúsítást célzó mérések
Hatósági bizonyítás céljából végzett mérések
Ellenszolgáltatás mértékének megállapítása (kereskedelmi mérések)
Életvédelem, egészségügy, környezet-és vagyonvédelem területén végzett mérések
Hitelesítés
Közigazgatási eljárás. Annak elbírálása, hogy a mérőeszköz megfelel-e a vele szemben támasztott mérésügyi előírásoknak.
Kalibrálás
Metrológiai tevékenység. Azon műveletek összessége, amelyekkel meghatáro-zott feltételek mellett megállapítható az összefüggés egy mérőeszköz, vagy egy mérőrendszer értékmutatása, illetve egy mértéknek vagy anyagmintának tulajdonított érték és a mérendő mennyiség etalonnal reprodukált megfelelő értéke között.
Valódi érték
Egy adott konkrét mennyiség definíciójának megfelelő érték, amelyet csak „tökéletes” méréssel lehetne meghatározni.
Sajnos, kevés ilyen érték jeleníthető meg. Példaként a Nemzetközi Kilogramm Prototípusát, a víz hármaspontjának hőmérsékletét (273,16 K), a fény vákuumbeli sebességét (299 792 458 m/s), vagy a háromszög szögeinek összegét lehetne felhozni.
Helyes érték
Valamely konkrét mennyiségnek tulajdonított, gyakran megegyezés alapján elfogadott olyan érték, amely az adott célnak megfelelő bizonytalanságú. Egy referencia etalon által megvalósított mennyiségnek tulajdonított érték az adott helyen a mennyiség konvencionális helyes értékének tekinthető.
Abszolút hiba
Elméletileg ez a mért és a valódi érték közötti különbség. A gyakorlatban a valódi érték helyére a helyes érték kerül.
Relatív hiba
Elméletben az abszolút hiba osztva a valódi értékkel. Miután azonban az utóbbit nem ismerjük, helyére osztóként a helyes érték kerül.
Redukált hiba
Az abszolút hiba osztva a terjedelemmel, azaz a legnagyobb és legkisebb mért érték közötti különbséggel.
2.4. Fontosabb műszertechnikai alapfogalmak
A mérési adatok kiértékelését természetesen megelőzi az adatok felvétele és rendszerezése. Ehhez mérőeszközök, műszerek, mérőberendezések szükségesek, így a mérés- és a műszertechnika elválaszthatatlanok. Mindenekelőtt tehát tisztázni kell néhány igen fontos műszertechnikai fogalmat.
Osztálypontosság
Más néven „Pontossági osztály”, a mérőeszköz hibájának, pontosságának egyik elterjedt megadási módja (ld.: 3. fejezet - Mérési hibák fejezet, Mérési hibák). Meghatározása szerint az abszolút hiba osztva a mérőeszköz maximális értékmutatásával (végkitérésének értékével), százalékban kifejezve.
Mérési tartomány
A mérendő mennyiség azon halmaza, amelyre a mérőműszer hibája a megadott határok között marad.
Felbontás
A kijelzőn biztonságosan megjeleníthető értékek közül a legkisebb. A felbontás mindig nagyobb tartományt kell, hogy jelentsen, mint a feloldás, jellemzően a felbontás a feloldás 3-5-szöröse. Ha ez nem teljesül, akkor a kijelzett legkisebb érték „eltűnik” a feloldásból származó bizonytalanságban.
Feloldás, érzékenységi küszöb
A bemenet lassú és egyenletes változtatása mellett az a legnagyobb tartomány, amelyben nem tapasztalható értékelhető műszerválasz (kimenet). A nullpont környezetében ezt a jellemzőt érzékenységi küszöb kifejezéssel jelöljük. A feloldás a teljes mérési tartományban változó lehet, de mindig a legnagyobb értéket kell a felbontás meghatározásához figyelembe venni.
Műszerállandó
Az a tényező, amellyel a műszeren kijelzett értéket szoroznunk kell, hogy a mérendő fizikai mennyiséget megkapjuk.
Érzékenység
A műszer kimenőjele és bemenőjele változásának hányadosa.
Érzéketlenségi sáv
Az a maximális tartomány, amelyben a bemenőjel mindkét irányú változása nem hoz létre kimenőjelet a műszeren.
Ismétlőképesség
Azonos mérési eljárással (fizikai elv és módszer), azonos mérőeszközökkel, azonos körülmények között, ugyanazon mérőszemély(ek) által elvégzett két mérés közötti eltérés nagysága. Iparvállalatoknál ez a jellemző igen kiemelkedő fontosságú lehet, bizonyos méréseket csak olyan személyre bíznak, akinél az ismétlőképesség egy megadott határon belül marad.
Reprodukálhatóság
Azonos mérési eljárással (fizikai elv és módszer), eltérő mérőeszközökkel és eltérő körülmények mellett, más mérőszemély által elvégzett mérés és az eredeti mérés közötti különbség.
Stabilitás
A mérőműszer azon tulajdonsága, amely hosszabb időre alkalmassá teszi az eszközt a metrológiai jellemzőinek megőrzésére.
Drift
A mérőműszer metrológiai jellemzőinek lassú időbeli változása. Oka lehet termikus, mechanikai, stb. hatás.
Pontosság
A méréstechnikában ritkábban használt jellemző. Lényegében azt fejezi ki, hogy a mérőeszköz milyen eltéréssel képes a mérendő mennyiség valós értékét megjeleníteni.
Átviteli függvény
Dinamikus rendszerek, így műszerek és mérőrendszerek modellezésére alkalmas matematikai összefüggés. Definíciója szerint harmonikus kimenő és bemenő jelek Laplace transzformáltjainak hányadosa. Csak lineáris és állandó együtthatójú rendszerek viselkedésének leírására alkalmas, ennek ellenére széleskörűen alkalmazzák a mérés- és irányítástechnikában. Minden technikai jel harmonikus összetevőkre bontható, ez a téma a frekvencia analízissel foglalkozó, (6. fejezet - Mérőjelek idő és frekvencia tartományban) fejezetben van kibontva. Az átviteli függvény a rendszer differenciálegyenletével és állapottér modelljével „rokon”, mert előbbiből Laplace transzformálással, a másodikból pedig mátrix műveletekkel származtatható. A Laplace operátort helyettesítve annak jelentésével, azaz az „s=jω” kifejezéssel, kapjuk a rendszer körfrekvenciától függő, un. átviteli tulajdonságait leíró „frekvencia átviteli függvényt”. Ezt a méréstechnikában Bode-diagramon szokás ábrázolni, amelynek két része van: Az egyik a bemenő és kimenő jel amplitúdó arányát mutatja decibelben (dB), a másik a két jel közötti fáziskülönbséget. Ha a bemenő és kimenő jelek fizikai dimenziói nem azonosak, akkor egy célszerűen választott alacsony körfrekvencián számított (mért) átviteli értékhez „normálják” (viszonyítják) a különféle körfrekvenciákon meghatározott értékeket, így „dimenziótlanítva” az arányt.
Átviteli tényező
Az átviteli függvény abszolút értéke (harmonikus kimenőjel és bemenőjel amplitúdóinak aránya) valamely körfrekvencián.
Időállandó
Adott műszer egyik fontos dinamikai jellemzője. Első és másodrendű (vagy ilyen rendszámú átviteli tagokra bontható) műszer (mérőrendszer) esetében van szerepe. Elsőrendű rendszer esetében a kimenőjel időbeli lefutásáról és a reciprok értéke az arányos amplitúdó átvitel frekvenciatartományáról ad információt. Időtartományban az ugrásszerű bemenő mennyiségre adott műszer válasz csak késleltetve jelenik meg. Egy elsőrendű műszer (egyetlen) energiatárolójának feltöltődése miatt, a kijelzett érték az időállandóval egyező időpillanatban az állandósult műszerválasz értékének csupán 63,2%-a lesz. Ezért ajánlatos a műszert az időállandó (3-5)-szörösének eltelte után leolvasni. A másodrendű műszer két (független) energiatárolót tartalmaz. Alulcsillapított másodrendű rendszer esetében az időállandó reciprok értéke a csillapítatlan rezonancia frekvencia négyzetgyöke. Túlcsillapított másodrendű rendszer két soros elsőrendű átviteli tag eredőjével írható le, ennek folytán két időállandó jelenik meg. A kritikus csillapítás esetén az időállandók azonosak.
Letörési körfrekvencia
Elsőrendű műszer időállandójának reciprok értéke. Az amplitúdó átvitel ezen a körfrekvencián méréstechnikai szempontból már elfogadhatatlan, mert a kimenőjel amplitúdója csupán közel 70%-a a bemenőjel amplitúdójának.
Felső határ(kör)frekvencia
A méréstechnikában szokásos 1%-os amplitúdó átviteli hiba a felső határ(kör)frekvenciánál jelenik meg, és ez a körfrekvencia lényegesen alacsonyabb érték, a letörési körfrekvenciának ≈0.14-szerese.
Csillapítási fok
Másodrendű rendszer dinamikai tulajdonságaira jellemző szám, amelytől lengő (rezgő) rendszer esetén, rezonancia frekvencián az amplitúdó nagyítás függ.
Rezonancia körfrekvencia (csillapított rendszeré)
Az a körfrekvencia, amelynél másodrendű rendszer esetében maximális az amplitúdó nagyítás. Kisebb érték, mint a csillapítatlan másodrendű rendszer rezonancia körfrekvenciája, amely az időállandó reciprok értéke (ld.: Időállandó).
Beállási idő
Első és másodrendű műszerek (rendszerek) esetében azon időtartam, amely addig telik el, amíg az ugrásszerű bemenőjelre adott válaszfüggvény az állandósult állapotbeli értékhez viszonyított ±5%-os sávban vesz fel értékeket, és ezt a sávot a kimenőjel már nem hagyja el.
Fázistolás
A harmonikus kimenőjel fázisából kivonva a harmonikus bemenőjel fázisa.
2.5. Statikus és dinamikus kalibrálás
A méréstechnikában alapszabály, hogy „ne higgyünk vakon” a mérőberendezések által kijelzett értékekben. A kalibrálás metrológiai definíciója a 2.3. szakasz - Metrológiai definíciók fejezetben található meg. A témához szorosan kötődik két másik fogalom is, a leszármaztathatóság és a visszavezethetőség.
Tekintettel arra, hogy kalibrálást szinte minden méréstechnikához kapcsolódó munkahelyen végeznek, ez az egyik legáltalánosabb és legfontosabb metrológiai feladat, hiszen a konkrét mérési feladat végrehajtása előtt kalibrálnunk kell, ha
ismeretlen mérőeszközt veszünk használatba,
elkallódtak a műszer(ek) adatlapjai,
régebben volt használatban egy alkalmazni kívánt műszer,
saját tervezésű mérőeszközt készítettünk, vagy
megterveztünk és összeállítottunk egy mérőláncot.
A fenti néhány kiragadott példa csak szemléltetésül szolgál, ennél sokkal szélesebb ez a terület. Ha a munkaeszköz jellegű mérőműszert kalibrálunk, akkor a használati etalonokkal kell ezeket összehasonlítani, mert a visszavezetési láncban a kevésbé pontos etalonok felől haladunk a pontosabbak felé. A visszavezethetőség metrológiai szabálya általánosságban megköveteli, hogy használati mérőeszközünk ismert bizonytalanságú összehasonlítások láncolatán keresztül kapcsolódjon a nemzeti etalonhoz.
A referencia etalonokat rendszerint az adott ország nemzeti metrológiai laboratóriumában (NMI) kalibráltatják a nemzeti etalonok segítségével. Ezeknek a nemzeti etalonoknak és az adott NMI által kiadott kalibrálási bizonyítványoknak kölcsönös elismerése kötelező, ha az adott ország aláírója az 1998-as CIPM-MRA–nak, vagyis a CIPM Kölcsönös Elismerési Megállapodásának.
A használati etalon ellenőrzése olyan referencia etalon (műszer) segítségével történjen, amelyet a legjobbnak tekintünk az adott mérőlaborban. A használati etalonok referencia etalonnal való összevetésének időtervét az adott szervezet (üzem) metrológiai szabályzata írja elő. Ha nem vagyunk meggyőződve a referencia etalon megbízhatóságáról, akkor helyi, vagy országos mérésügyi szervezethez célszerű fordulni.
Kétféle kalibrálás történhet, statikus és dinamikus, azonban a dinamikus esetében is első lépcső a statikus kalibrálás. A statikus kalibrálás célja főként a műszer karakterisztikájának ellenőrzése, de fontos más metrológia jellemzők vizsgálata is. Ennek során célszerűen választott lépcsőzéssel a vizsgált műszer teljes mérési tartományában összehasonlítjuk a kijelzett értéket a referenciaként használt etalon értékmutatásával. A leolvasás csak a műszer állandósult állapotában történhet. Annak eldöntése, hogy a kalibrálási lépcsők mekkorák legyenek, vagy műszerkönyvek, előírások segítenek eligazodni, vagy a tapasztalatunkra kell hagyatkozni. Fontos a feloldást (érzékenységi küszöböt) több tartományban ellenőrizve meggyőződni arról, hogy a felbontás (legkisebb kijelzett érték) megfelelő-e? A (2.4. szakasz - Fontosabb műszertechnikai alapfogalmak) fejezetben felsorolt műszerjellemzők közül szükség szerint kell továbbiakat kiválasztani.
A dinamikus kalibrálás különösen fontos, ha időben változó mennyiségek mérésére szolgál a vizsgált műszer, vagy mérőrendszer. A dinamikus kalibrálás célja annak eldöntése, hogy a mérőeszköz rendszáma, időállandói, beállási ideje, frekvencia menete, alsó és felső határfrekvenciája, rezonancia frekvenciája, stb. valóban egyeznek-e a feltételezett értékekkel, illetve ezek egyeznek-e az adatlapon megadott értékekkel?
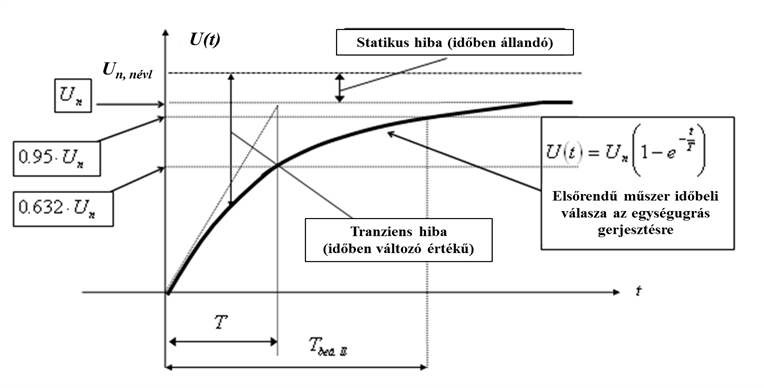
Ismeretes, hogy az elsőrendű rendszer (műszer) egy energiatárolót tartalmaz. Tudjuk, hogy a rendszámot az adott rendszer független energiatárolóinak száma határozza meg.
Az elsőrendű rendszer dinamikus viselkedését leíró differenciálegyenlet általános alakjában megjelenik két olyan fontos műszertechnikai jellemző, amelyek metrológiai szempontból is fontosak, ez a „T” időállandó és az „A” érzékenység (erősítés). A műszer időtartománybeli matematikai modellje az alábbi:
|
|
(2.1) |
A (2.3. ábra - Dinamikus kalibrálás idő tartományban (elsőrendű rendszer)) ábrán az x KI kimenőjelet U(t) villamos feszültségként értelmeztük.
A differenciálegyenlet Laplace transzformálása és megfelelő átrendezése után kapjuk az átviteli függvényt. Az átviteli függvényben s=jω helyettesítéssel kapjuk azt a körfrekvenciától függő formát, amely segítségével a Bode diagram megszerkeszthető:
|
|
(2.2) | |
|
|
(2.3) | |
|
|
(2.4) | |
|
|
(2.5) |
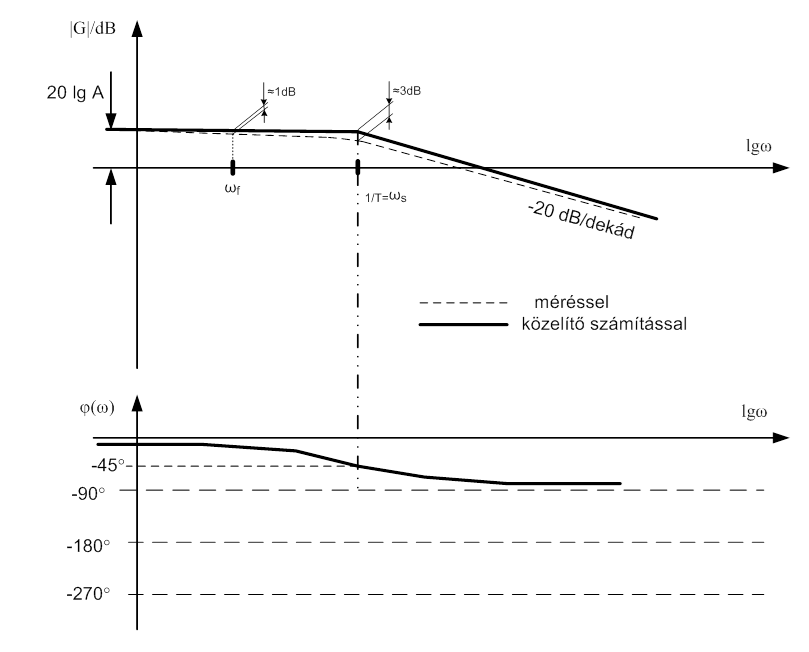
A (2.4. szakasz - Fontosabb műszertechnikai alapfogalmak) fejezetben ismertetett műszertechnikai metrológiai jellemzők felismerhetőek a két ábrán.
2.6. Regresszió
A regresszió alkalmazásával az ismert etalon értékek és a vizsgált műszer által jelzett értékek közötti kapcsolatot szándékozunk kimutatni. A legismertebb forma a lineáris regresszió, amelynek esetében az etalon értékek és a vizsgált műszer által mutatott értékek között lineáris kapcsolatot feltételezünk. A kapcsolatot egy egyenes egyenletének formájában adjuk meg, és ehhez szükség van a regressziós egyenes „m” meredekségére és a „b” nullpont-hibára.
Két változatot kell megkülönböztetnünk. Az egyik esetben az etalon bizonytalansága kisebb, mint a vizsgált műszeré. Az etalon beállított „xi” értékei jelentik a független változót, megadható az ehhez az értékhez tartozó „δi” hiba és alkalmazható a legkisebb négyzetek módszere. A másik esetben – és ez gyakran előfordul a gépészeti méréstechnikában – az etalon és a vizsgált műszer bizonytalansága összemérhető, hasonló. Ilyenkor nem lehet a legkisebb négyzetek módszerét alkalmazni, helyette a „Wald-módszer” nyújt lehetőséget a regressziós egyenes két paraméterének meghatározására. (Wald Ábrahám a XX. sz. elején a kolozsvári Ferenc József Tudományegyetem matematika tanára volt.)
Amennyiben tehát az etalon kisebb bizonytalanságú, pontosabb, mint a vizsgált műszer, a két paraméter meghatározására alkalmazható a Gauss által javasolt „legkisebb négyzetek módszere”. Ilyen típusú kalibrálási feladat például egy olyan finomtapintó ellenőrzése, amelyik 1 μm felbontással rendelkezik, és etalonként mérőhasáb készletet alkalmazunk.
A (2.5. ábra - Regressziós egyenes és a kalibrációs pontok) ábrán látható egy lineáris regresszió, ahol xBE=x és xKI=y:
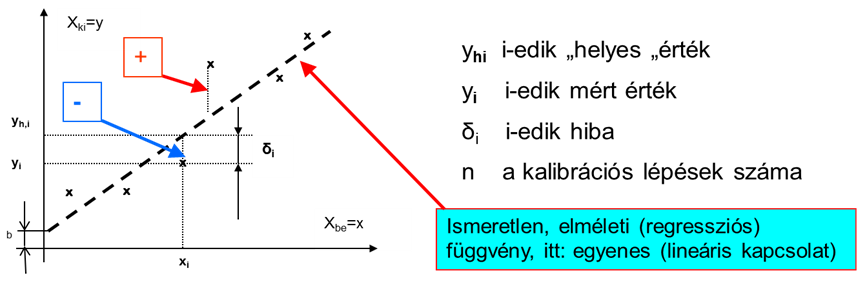
Az ábrán látható eltérések négyzetösszegének minimumát keressük. A pontpárok ismeretében a regressziós egyenes „m” meredekségét és a „b” nullpont-hibát szélsőérték-kereséssel határozhatjuk meg.
|
|
(2.6) |
Az összefüggést „m” és „b” szerint külön-külön parciálisan deriváljuk, és egyenlővé tesszük zérussal.
|
|
(2.7) |
Olyan egyenletrendszert kapunk, amelyik kétszer „n” db egyenletből áll:
|
|
(2.8) | |
|
|
(2.9) |
A második „csoportból”, azaz egyenletrendszerből „b” azonnal kifejezhető, és meghatározásához már csak az átlagokat kell kiszámítani:
|
|
(2.10) | |
|
|
(2.11) |
A továbbiakban „m” meghatározása a feladat. Az első egyenletrendszerbe behelyettesítjük a „b”-re kapott eredményt:
|
|
(2.12) | |
|
|
(2.13) | |
|
|
(2.14) |
Végül a fenti egyenletből „m”-re rendezve kapjuk az első eredményt, ami ebben a formájában algoritmizálásra egyelőre nem alkalmas.
|
|
(2.15) |
A számláló azonban tovább alakítható:
|
|
(2.16) |
Végül olyan alakhoz jutunk, amely már algoritmizálásra is alkalmas.
|
|
(2.17) |
A nevezőt is át kell formálni. A következő egyenlet már több lépés eredményét mutatja. Ha az egyenlet jobb oldalán elvégezzük a kijelölt műveletet, akkor belátható, hogy az összefüggés helyes.
|
|
(2.18) |
Így mind a számlálóban, mind a nevezőben olyan formákhoz jutottunk, amelyek áttekinthető és jól alkalmazható számítási módot kínálnak a regressziós egyenes meredekségének meghatározására:
|
|
(2.19) |
Az előzőekben bemutatott számítási módszer csak akkor alkalmazható, ha az etalon bizonytalansága kisebb, mint a vizsgált eszközé.
A Wald-módszer viszont segít abban az esetben, ha mind az etalonként alkalmazott eszközt, mind pedig a vizsgált műszert normális eloszlású, véletlen hiba terheli.
Az eljárás lépései a következőek:
Az értékpárokat nagyság szerint sorba rendezzük. Lehetőleg a mérési tartomány két végének környezetében végezzünk méréseket. A halmazt két részre osztjuk, és mindkét részhalmaz súlypontját képezzük.
A két súlypontot (S1, S2) összekötve a regressziós egyenes meredekségét kapjuk.
A teljes halmaz „S” súlypontjának kiszámítása után a 2. pontban meghatározott meredekséggel húzunk egyenest az „S” súlyponton keresztül.
A különbségtétel kedvéért a meredekséget „α” és a nullpont-hibát „β” szimbólummal jelöljük.
A két részhalmaz súlypontjának meghatározása a következők szerint történik:
|
|
(2.20) |
Az átlagok segítségével már kijelölhető a meredekség:
|
|
(2.21) |
Végül meg kell határoznunk a nullpont-hibát, az egyenes és a függőleges tengely metszéspontját. Most valamennyi értékpár felhasználásával kiszámítjuk a teljes ponthalmaz súlypontját, és az így kapott átlagértékkel a keresett metszéspontot:
|
|
(2.22) | |
|
|
(2.23) |
A Wald-módszerrel meghatározott regressziós egyenes egyenletének paramétereivel kapjuk a végeredményt:
|
|
(2.24) |
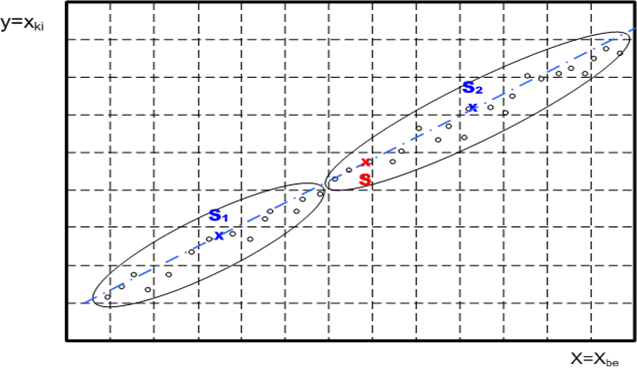
A regresszió analízis természetesen a fentiekben bemutatottaknál lényegesen szélesebb körű. Ebben a fejezetben csak a méréstechnikában legfontosabb ismeretekre szorítkoztunk.
2.7. Korreláció
Az ipari gyakorlatban sokszor elengedhetetlenül fontos a mérési adatok közötti lineáris kapcsolat objektív kimutatása, a matematika eszköztárának igénybevételével. Gyakori feladat annak eldöntése, hogy két, különböző mérési sorozatból származó mintasokaság, azaz adathalmaz között van-e lineáris összefüggés? A függőség mértékének meghatározása a korrelációszámítással történik.
Ilyen gyakorlati feladat lehet a gépészetben például annak eldöntése, hogy egy tengely vállbeszúrásának megadott erőhatással történő körkörös zömítése (görgőzés) és a görgőzés eredményeként létrejövő alakváltozás között van-e összefüggés? Összefügg-e továbbá a görgőzés (zömítés) mélysége a tengely szilárdságának növekedésével?
A módszer alapja a vektorszámítás. Két vektor között egy pozitív, vagy negatív előjelű szorzó, azaz konstans, akkor teremt kapcsolatot, ha a vektorok között bezárt szög 0°, vagy 180°. Ha két vektor egymáshoz képest 90°-ot zár be, akkor nincsen közöttük egy konstanssal kifejezhető lineáris kapcsolat.
A vektorokra érvényes szabály kiterjeszthető a mérési adatok halmazára is, ha a mért értékek és a várható érték közötti különbségeket egy n-dimenziós vektor elemeinek tekintjük.
A vektor-térben ugyanis egyszerűbb a korreláció (kapcsolat) értelmezése.
Ha ugyanis a két vektor egymással φ szöget zár be, akkor a szög értékével kifejezhető minden lényeges összefüggés:
φ=90º, akkor nincs a ponthalmazok között lineáris függés
φ=0º, akkor van lineáris összefüggés, a két n-dimenziós vektor között konstans szorzóval kifejezhető a kapcsolat: y=ax
φ=180º, akkor a két n-dimenziós vektor között negatív konstans szorzóval kifejezhető lineáris kapcsolat van: y= - ax, a két vektor ellentétesen korrelált
φ≈0º, ill. φ≈180º akkor lehet lineáris a kapcsolat, de van egy korrekciós tag is, amelyet „e” szimbólummal jelölünk: y= ax + e, ahol |e|→0
A korrelációs tényező számításhoz szükséges összefüggéshez a következő megfontolások alapján jutunk.
A két vektor közötti hajlásszög cosinus-a -1 és +1 között mozoghat, ezt nevezzük „r” korrelációs tényezőnek (faktornak).
|
|
(2.25) |
Behelyettesítve az előző képletbe a kijelölt matematikai műveleteknek megfelelő alakokat, és figyelembe véve azt, hogy a gyakorlatban a mért adatok felhasználásával nem a korrelációs tényezőt, hanem a tapasztalati korrelációs tényezőt tudjuk csak meghatározni, a következő formát kapjuk:
|
|
(2.26) |
Látható, hogy az egyenlőtlenségből eltűnt az egyenlőség jel, hiszen az elméleti értéket empirikus adatokból nem lehet meghatározni. További átformálások „kínálják” magukat, amelyek révén a számításhoz lényegesen egyszerűbb alakhoz jutunk:
|
|
(2.27) |
A tapasztalati korrelációs tényező kiszámítására alkalmas célszerű alakban a két mérési adathalmaz abszolút hibái mellett a tapasztalati szórások szerepelnek. Ez előnyös, mert ezekre az adatokra, paraméterekre a statisztikai feldolgozás során más célból is szükség van.
|
|
(2.28) |
Végül fontos megjegyezni, hogy a műszaki gyakorlatban csak akkor feltételezzük a lineáris kapcsolatot, ha az empirikus korrelációs tényező értéke 0,7 felett van, de sok esetben már csak a 0,8 feletti értékek elfogadhatóak. A statisztikai szakirodalomban megtalálható „Pearson-táblázatok” a konfidenciaszint és a minta elemszámának függvényében adják meg azt a tapasztalati korrelációs tényezőt, amely mellett a kapcsolat hipotézise elfogadható. E táblázatok azonban nem a műszaki területek sajátosságait veszik alapul, és ezért a gépészetben ajánlatos a fent jelzett szigorúbb vizsgálat.
2.8. Mérés egyenlete, közvetlen és közvetett mérés
Mielőtt az eredmény szokásos alakjait tárgyalnánk – erre a következő, (2.9. szakasz - Az eredmény szokásos alakja) fejezetben kerül sor - emlékeztetnünk kell arra, hogy a mérési eredményt nem mindig egyetlen ismeretlen mennyiség mérésével kapjuk. A mérési feladatok tekintélyes része olyan, hogy az eredmény többféle mennyiség méréséből származó adat felhasználásával határozható meg. Ezt a szakirodalom közvetett mérésnek nevezi.
Az eredményt egyenlet formájában megadott matematikai modell reprezentálja. Az eredmény általános egyenletében a nagybetűk a valódi értékeket reprezentálják. Az „A” indexű tagok a mérendő bemenő mennyiségeket, míg a „B” indexűek a különböző tényezőket jelentik.
|
|
(2.29) |
Méréseink eredményeként ezt az elméleti „Y” kimenetet becsüljük az „y” átlagértékével:
|
|
(2.30) |
Egy ilyen matematikai modellnek lehet ismert fizikai törvényszerűség az alapja, de ezek mellett, számos esetben, tapasztalati úton nyert összefüggések is megjelenhetnek, mint eredményképlet. Fizikai törvényen alapszik például egy kör keresztmetszetű villamos vezető fajlagos ellenállásának meghatározása:
|
|
(2.31) |
Az ismert képletben négyféle mennyiség mérése szükséges az eredmény meghatározásához. Ha az „ℓ” hosszúságú, „d” átmérőjű vezető két vége közötti villamos feszültség „U” és ennek hatására „I” áram folyik a vezetőben, akkor a fajlagos ellenállás „ρ” meghatározható. Az eredmény egyenletben nem szerepeltettük a korrekciókat (rendszeres hibák) és az eredő mérési bizonytalanságot. Ezekkel külön alfejezetben foglalkozunk.
Egy mérőhasáb hosszának meghatározása a mérőhasábok kalibrálása során interferométerben, optikai úton történik. Az eredmény megadásához alkalmazott eredményegyenletben, a fizikai törvényszerűségeken (pl.: hő okozta alakváltozás hatása) kívül egyéb empirikus ismereteket is felhasználnak:
|
|
(2.32) |
Az eredményképletben a jelölések az alábbiak:
|
l: |
a hasáb hossza 20 °C hőmérsékletre vonatkoztatva | |
|
q: |
a végzett mérések száma | |
|
λ i: |
az egyes mérésekhez használt fény névleges hullámhossza | |
|
n i: |
a levegő egyes mérésekhez kiszámolt törésmutatójának az értéke | |
|
K i: |
a hasáb hosszon a fény fél hullámhossz számának egészrésze | |
|
F i: |
a hasáb hosszon a fény fél hullámhossz számának törtrésze | |
|
α: |
a hasáb lineáris hőtágulási együtthatója | |
|
ΔT i: |
a hasáb hőmérsékletének 20 °C – tól való eltérése az egyes mérések alkalmával |
A fizikai törvényszerűségeken alapuló összefüggés tartalmaz ezeken felül hétféle Δℓ k tapasztalati korrekciót (ezek ismert, rendszeres hibák), továbbá megjelenik az „U” kiterjesztett mérési bizonytalanság is.
Közvetett mérés esetében tehát ismernünk kell az eredmény egyenletét (matematikai modellt), azaz a matematikai függvényt az eredmény kiszámítására. A szakirodalom helyenként „modellfüggvénynek ” nevezi az eredmény egyenletét, egyébként nagyon helyesen, hiszen a mérés valójában modellalkotási folyamat , ahogy azt a (3. fejezet - Mérési hibák) fejezetben bemutatjuk.
2.9. Az eredmény szokásos alakja
A mérendő mennyiségek a mérés tárgyát képező tényleges mennyiségek, általában az egyetlen Y mérendő vagy kimenő mennyiség több (i=1,2,…n) Xi bemeneti mennyiség függvénye az Y=f(X1, X2, … Xn) összefüggésnek megfelelően.
A soron következő összefüggések a NAT (Nemzeti Akkreditációs Testület) hivatalos kiadványában megtalálhatóak [2.1.] .
A mérési eljárást és a kiértékelési módszert az „f” modell-függvény képviseli. Az esetek többségében ez egy analitikus kifejezés, de lehet ilyen összefüggések csoportja is, amely a rendszeres hatásokra alkalmazott korrekciós tagokat és korrekciós tényezőket tartalmaz, és ezért olyan összetettebb kapcsolatra vezet, amely egyértelműen nem írható le egyetlen függvénnyel. Lehet továbbá, hogy kísérleti úton vagy csak számítási algoritmusként van meghatározva, vagy „f” lehet mindezek kombinációja is.
A mérendő mennyiség egy becslése az y-nal jelölt kimeneti becslés, amit a modellfüggvényből kapunk, ha az Xi bemeneti mennyiséget az xi bemeneti becsléssel helyettesítjük:
|
|
(2.33) |
A becslésre felírt összefüggésben kétféle bemeneti mennyiséget látunk. Az egyik típus a bemeneti mennyiségek a modell szempontjából fontos összes hatásnak megfelelően korrigált legjobb becslései, ezeknél „A” betűvel való jelölés látható az indexekben. A másik típus azon korrekciók csoportja, amelyeket önálló bemenő mennyiségként veszünk figyelembe, itt „B” betűt látunk az indexekben.
Tehát értékük és bizonytalanságuk meghatározásának módjától függően az Xi bemeneti mennyiségek két csoportra oszthatók:
Azokra a mennyiségekre, amelyek értékét és a hozzájuk tartotó bizonytalanságot közvetlenül az adott mérésből határozták meg. Ezek az értékek származhatnak például egyetlen leolvasásból, ismételt leolvasásokból vagy tapasztalaton alapuló döntésekből. Tartalmazhatják az eszközök leolvasási korrekcióit, a befolyásoló mennyiségek miatti korrekciókat, amilyen például a környezeti hőmérséklet, légnyomás, nedvességtartalom.
Azokra a mennyiségekre, amelyek becslései és a hozzájuk tartozó bizonytalanságok az adott mérés esetén külső forrásból származnak. Ilyen mennyiségek a kalibrált etalonok vagy a tanúsított anyagminták értékei, vagy a kézikönyvekből származó adatok.
Az előírások a bizonytalanságokat annak megfelelően, hogy a modellfüggvényben szereplő egyes mennyiségek melyik csoporthoz tartoznak, „A” és „B” típusba sorolják.
Ha alaposan megvizsgáljuk az „Y” kimeneti mennyiség becslésére felírt fenti összefüggést, akkor látható, hogy a mérési eredményben szereplő „mérőszám” alapvetően három tagból tevődik össze, amelyek a következőek:
Helyes érték, azaz a valódi érték legjobb becslése a modellfüggvény szerint kiszámított átlaggal (egy bemeneti mennyiség esetében egyszerűen a mért adatok átlagával)
Korrekciók, azaz a rendszeres hibák előjeles eredője, jele H
A két fenti érték az eredményben különbség formájában jelenik meg. Elkülönítésük csak akkor lehetséges, ha ismerjük az átlagot, vagy a korrekciók eredőjét.
(Kiterjesztett) bizonytalanság, azaz a konfidencia szinthez tartozó faktorral és a tapasztalati szórással számított konfidencia intervallum, jele U.
Szembetűnő, hogy a mérőszám 2/3 részben hibákkal kapcsolatos adatokat tartalmaz.
Ez is alátámasztja azt, amit a hibákkal kapcsolatos fejezetben jeleztünk, miszerint jogosan merül fel az igény a mérési hibák okozóinak megismerésére, és a véletlen hibák minél határozottabb visszaszorítására.
A korrekciókról fentebb már írtunk, az „U” kiterjesztett mérési bizonytalanság értelmezése az European Cooperation for Accreditation of Laboratories” útmutatója (Mérésügyi Közlemények XXXIX./3. 1998.) [2.2.] alapján történik.
Ha ismert az eredmény egyenlete (modell-függvény), tehát közvetett mérésről van szó, és adott az eredmény egyenlete, akkor az „u” eredő bizonytalanság meghatározásánál – a bemeneti mennyiségek mért adatainak becslése (átlagok: xAi) és korrigált tapasztalati szórásaik mellett - meg kell határozni az un. ci súlyfaktorokat is. A súlyfaktorok az eredmény egyenlet (modell-függvény) bemeneti mennyiségek szerinti parciális deriválásával állíthatók elő, ezt a közvetett mérés modellfüggvénye kapcsán már láttuk. Az így kapott (eredő) bizonytalanság „A” típusú.
Az eredmény egyenletben lehetnek olyan bemeneti mennyiségek is (xBj), amelyeknek a bizonytalansága a „B” típusba sorolható. Ezekre a bemenő mennyiségekre is meg kell állapítani súlyfaktorokat, ezeknél cj jelölést alkalmaztunk. Előfordulhatnak olyan további bizonytalanságok is, amelyek a bemenő mennyiségek mellett származhatnak a mérési eljárásból (fizikai elv és módszer), továbbá a mérés kivitelezéséből is. (Pl.: az ismétlőképesség bizonytalansága).
A gyakorlatban alkalmazott méréstechnikai előírásokban „k” faktor értéke 95%-os valószínűségi szint mellett ≈2, ha labormérésekről és ipari mérésekről van szó, és a mintasokaság eloszlását Gauss-eloszlásnak feltételezzük. Megjegyezzük azonban, hogy a faktor értéke – 120 mérési adat esetében - Student-eloszlást feltételezve, 95%-os valószínűségi szinten 1.98, normál eloszlás esetében pedig - a mérések számától függetlenül - 1,96 lenne. Látható, hogy kerekítéssel ezek az értékek is kellően reprezentálva vannak az előírásokban található k=2 esetén.
2.9.1. A mérés „A” típusú (eredő) bizonytalanságának megadása
A variancia, és az abból számított szórás elméleti érték, az eloszlást jellemző un. funkcionál. A variancia a véges számú mérések alapján a gyakorlatban nem meghatározható, ehhez ugyanis az eloszlás sűrűségfüggvényének pontos ismerete szükséges. Helyette a tapasztalati szórást, esetleg a korrigált tapasztalati szórást, és az átlag szórását tudjuk a mérési adatokból meghatározni.
A méréstechnikai szakirodalomban látható képletek és kifejezések gyakran nem tesznek különbséget sem a fogalmak jelölésénél, sem azok megnevezésénél. Ezért készítettünk a (2.3. szakasz - Metrológiai definíciók) és (2.4. szakasz - Fontosabb műszertechnikai alapfogalmak) fejezetben egy metrológiai-műszertechnikai fogalmi összefoglalót. A legfontosabb valószínűség számítási összefüggések pedig a (3. fejezet - Mérési hibák) fejezetben találhatók.
Ennek ellenére ezen a helyen is fontosnak tartjuk az első előfordulásuk, felhasználásuk alkalmával rögzíteni a következő fontos fogalmakat:
Elméleti középérték, várható érték: Jelölése: μ, vagy ξ.
Átlag: A minta középértéke. Empirikus, tapasztalati átlag. A várható érték, azaz elméleti középérték, vagy első centrális momentum legjobb becslése. Az empirikus eloszlás elhelyezkedését mutatja. Jelölése: x, vagy y felülvonás.
Szórás: Elméleti érték, a második momentum, más néven a variancia pozitív négyzetgyöke. Jelölése: σ. A variancia a szóródás (koncentráció) mértékszáma.
Tapasztalati szórás: A szórás torzított becslése, kiszámítása az átlagtól való eltérések négyzetösszegéből történik úgy, hogy azt „n”-nel osztjuk, majd a kapott értékből négyzetgyököt vonunk. Jelölése: s
Korrigált tapasztalati szórás: Az előzőhöz hasonló módon számítjuk, de az osztás „n-1”-gyel történik, mert az átlag felhasználása miatt csökken a szabadságfok. Jelölése: s*
Látható, hogy helyes, ha az elméleti jellemzőket (funkcionálok) görög betűvel, és az empirikus úton kapottakat latin betűkkel jelöljük, így az elnevezések és a számítási módok nem keverednek.
Az „A” típusú bizonytalanság ismert modellfüggvényt felhasználva, egymástól független bemenő mennyiségek esetében, amelyek valószínűségi változók, a következő képlettel határozható meg:
|
|
(2.34) |
Látható, hogy a képletben következetesen az átlagok korrigált tapasztalati szórásával, mint az elméleti szórás torzítatlan becslésével számoltunk. Az összefüggés hátterében az eredő variancia számításának módja áll.
2.9.2. A mérés „B” típusú bizonytalanságának megadása
A „B” típusú bizonytalanságok megadása már nehezebb, és mérési munkában való komolyabb jártasságot, műszerismeretet, stb. feltételez. Ebben a formában ugyanis lehetőség van minden olyan tényező figyelembe vételére, amely az adott ismereti szinten számba vehető. Elsődlegesen az eredmény egyenletben (modell-függvény) szereplő olyan bemeneti mennyiségek bizonytalanságát kell megbecsülni, amelyek esetében nem meghatározható a tapasztalati szórás. Ezeken felül figyelembe lehet venni további bizonytalanságokat is.
Az „uj” bizonytalanságokat a következő módon lehet becsülni:
A korábbi mérések adataiból,
Az anyagok és eszközök tulajdonságainak ismeretéből, az ezekre vonatkozó tapasztalatokból,
A kalibrálási és egyéb bizonyítványokban megadott adatokból,
A kézikönyv/műszerkönyv adatokhoz tartozó bizonytalanságokból,
A mérés körülményeiből,
A mérést végző személy ismétlőképessége alapján, stb.
A „B” típusú bizonytalanságok eredője, ha ezek a bizonytalanságok egymástól független véletlen mennyiségek, a következő módon számítható:
|
|
(2.35) |
A szakirodalomban a jelölésre szándékos az „u” betű alkalmazása, hiszen itt bizonytalanságról (uncertainty) van szó.
Irodalmak
[2.1.] A mérési bizonytalanság meghatározása kalibrálásnál. Nemzeti Akkreditáló Testület, NAR-EA-4/02. sz. kiadvány . 2003.
[2.2.] Mérésügyi Közlemények XXXIX/3. Nemzeti Akkreditáló Testület. 1998.
3. fejezet - Mérési hibák
Közismert a méréstechnikával foglalkozók számára a szabály, hogy a mérési munka csak akkor befejezett, ha a hibaszámítást is elvégeztük. Ha tehát egy „eredmény” közlésében nem szerepel „±” előjellel egy bizonytalanságot megjelenítő tag, akkor az adott mérés „finoman szólva” nem lehetett igényesen megtervezett munka.
Az eredményben alapvetően két hiba típusnak kell tükröződnie. Az egyik a rendszeres hibák eredője, amit korrekcióként ismert előjellel és nagysággal veszünk figyelembe, és éppen ezért az eredményben az átlaggal összevonva szerepel, hacsak valamilyen okból nem tüntetik különállóan fel. A másik hibatípus a véletlen hibák eredője, ami közvetlenül nem észlelhető, mert a mérési bizonytalanságba van „beágyazva”, sok összetevőjű, és a bizonytalanság meghatározásában már a megbízhatósági szintet is figyelembe vesszük.
3.1. A mérési hibák az eredményben, a hibák rendszerezése
A mérési eredmény a mérőszám és a mértékegység szorzata, de maga a mérőszám három tagból áll:
|
|
(3.1) | |
|
|
(3.2) |
A második egyenletben szereplő 3 tag jelentése az alábbi:
„Helyes érték”, azaz a valódi érték legjobb becslése az átlaggal
„H” a korrekció, azaz a rendszeres hibák előjeles eredője
Kiterjesztett bizonytalanság, azaz a megadott konfidencia szinthez tartozó faktorral, a tapasztalati szórások eredőjével és az egyéb mérési bizonytalanságok figyelembe vételével számított konfidencia intervallum. A bizonytalanság un. „A” és „B” típusú megadásáról később még lesz szó.
Szembetűnő, hogy a mérőszám 2/3 részben hibákkal kapcsolatos adatokat tartalmaz. Ezek után jogosan merül fel az a kérdés, hogy mik a mérési hibák okozói, és főként az, miként lehet a véletlen hibákat minél jobban visszaszorítani, és ezzel a bizonytalanságot csökkenteni?
A jelen fejezet a hibák rendszerezésével, ismertetésével foglalkozik, hiszen visszaszorításuk, esetleges megszűntetésük, vagy csökkentésük attól függ, mennyire vagyunk tisztában eredetükkel. Erről a témáról részletesen a Halász G. - Huba A.: Műszaki mérések című jegyzetben [3.1.] olvashatunk.
A mérési hibákat három szempont alapján lehet vizsgálni, és csoportosítani:
eredetük,
jellegük, és
formájuk szerint.
A három csoport nem egymást kizáró, hanem egymást szinergikusan értelmező megközelítést jelent. Példaként tekintsük egy digitális műszer kijelzési bizonytalanságát, ami a legkisebb megjeleníthető (LSB=Least Significant Bit) érték 29 %-a (lásd 3.9 képlet). Véletlen jellegű hibákat a szakirodalom gyakran „bizonytalanság” kifejezéssel is illet. Ez a hiba eredete szerint a mérés kivitelezéséből adódik (digitális kijelzővel ellátott mérőeszköz miatt jelentkezik), jellegét tekintve véletlen, és forma szerint abszolút hiba.
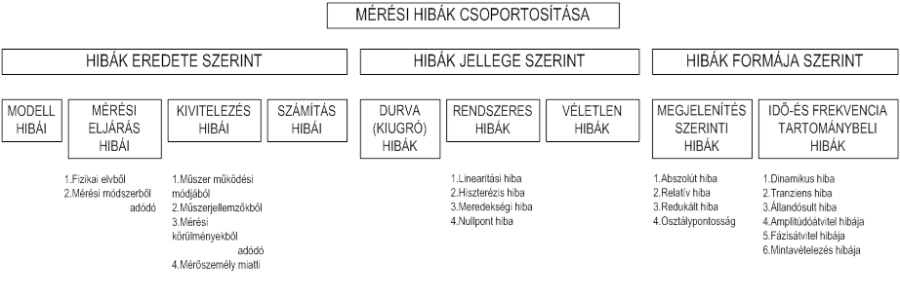
Látjuk az ábrán, hogy eredetük szerint a hibákat négy csoportba lehet sorolni. Ezek ismerete döntő jelentőségű a mérési munka minőségére vonatkozóan. Adott esetben ugyanis minden más, a mérési adatokkal való statisztikai „bűvészkedés” sem képes már közömbösíteni a mérési munka elején, a tervezés során elkövetett hibákat.
3.2. A mérési hibák eredete
A modell általánosságban a mérés „modellfüggvényét” jelenti, azt a matematikai összefüggést (ld.: Mérés egyenlete), amelynek alapján az eredményt a bemenő mennyiségek és az állandók segítségével ki lehet számítani.
A mérési eljárás definíciója szakirodalmanként változhat, de abban teljes az egyetértés, hogy az eljárás a mérési tevékenység „műszaki dokumentációja”. Ebben rögzítik a modellre alapozva a mérés fizikai elvét, és a mérési módszert. Néha a módszerek közé sorolják a közvetett és közvetlen mérést is, de az azért felesleges, mert az eredmény egyenlet (modellfüggvény) már önmagában jelzi, hogy melyik formáról van szó. A mérési módszerek száma nagy, a gépészetben és a mechatronikában minimum 6 módszer ismerete elengedhetetlenül fontos. Ezek a következő ábrán vannak röviden összefoglalva.

A mérés kivitelezése igen tekintélyes hibák forrása lehet. Ebbe a csoportba egyrészt a műszer, mérőrendszer működési módja, tehát a gépészetben konkrétan az, hogy a mérés során az mérőeszköz a vizsgált objektummal kontaktusba kerül-e, befolyásolja-e valamilyen módon annak energia állapotát? Köznapi megfogalmazással érintéses, vagy érintésmentes a mérőeszköz működési módja.
Ebben a csoportban a hibák további forrásait a műszerjellemzők, a mérés körülményei (nyomás, páratartalom, rezgések, stb.) és a mérést végző személyek körében kell keresnünk.
A kiértékelés, a számítások során is követhetünk el hibákat, ezek mértéke igen változó lehet. Kezdve a legdurvább „elszámolások” eseteitől, a becslési hibákig. Ez utóbbira jó példa lehet a konfidencia intervallum téves megadása. Normál eloszlást feltételezünk olyan esetben, amikor sem a mérési adatok értékei, sem a mérések száma ezt nem támasztják alá, és ennek következtében kisebb faktor alkalmazásával határozzuk meg a bizonytalansági tartományt.
3.3. A mérési hibák vizsgálata jellegük szerint
3.3.1. Rendszeres hibák
A rendszeres hibák a mérési eljárás (fizikai elv és mérési módszer) és a mérés kivitelezésének (mérőeszközök és mérési körülmények) elvi hibái, amelyek az eredményt torzítják. Ennek a torzításnak a mértéke és előjele megfelelő elméleti felkészültséggel és megfelelő mérőeszközök alkalmazásával megállapítható. Az eredményben a rendszeres hibák eredője korrekcióként jelenik meg, az eredő nagysága és előjele ismert .
A rendszeres hibák megjelenhetnek mind az időben állandó, mind pedig az időben változó mennyiségek mérése során.
A rendszeres hibák közül négyet érdemes kiemelni.
A linearitási hiba kompenzálása a modern számítástechnikai eszközök birtokában már nem jelent műszaki problémát. Ez a torzítás egy adott mérési tartomány bármely pontjában állandó, de a mérési tartományonként eltérő is lehet. Nem definiálható műszerállandó, ha a műszer jelleggörbéje négyzetes, exponenciális stb. függvénykapcsolatot mutat.
A nullpont hiba az un. regressziós egyenes és a függőleges tengely metszéspontja. Ezt a torzítást a regressziós egyenes paramétereinek meghatározásakor részben már megismertük, de természetesen felléphet nemlineáris karakterisztikájú műszer esetében is.
Hiszterézis hiba elsősorban mechanikus, vagy elektromechanikus mérőeszközöknél jelentkezik. Lényegében a fel-és leterhelés, azaz kitérítés és visszatérítés között kijelzett értékek közötti különbség formájában mutatkozik. A két karakterisztika nem esik egybe, sőt gyakran előfordul, hogy a kiinduló pont sem. A maradó eltérést a súrlódás okozza, és ezért ajánlott például tapintós mechanikus mérőeszközökkel történő mérés esetén, a mérendő felületet következetesen egy irányból megközelíteni (pl. felülről, a tapintó felemelésével).
A meredekségi hiba elektronikus és elektromechanikus műszerek esetében leginkább hőmérsékleti drift hatására jelentkezik. Ennek oka az elektronikus egységek jellemzőinek – így például az erősítésnek, hő okozta megváltozása. A műszer karakterisztikájának meredeksége változik meg. Kis mérési tartományban kisebb, a végkitérés tartományában maximális mértékű az erősítés megváltozásából eredő hiba
A fentieken kívül más rendszeres hibák is torzíthatják az eredményt, ezek részletes tárgyalása a műszertechnika témakörébe tartozik.
3.3.2. Véletlen hibákból adódó bizonytalanságok
A véletlen hibák hatása többségében a mérés bizonytalanságában, „beágyazottan” jelenik meg. A beágyazottság azt jelenti, hogy ezeket a hibákat nem „direkt” formában láthatjuk, hanem az „U” szimbólummal jelzett, un. kiterjesztett mérési bizonytalanság foglalja őket magába. A kiterjesztés az eredő mérési bizonytalanságok meghatározott faktorral való súlyozását jelenti. Ez a faktor a megbízhatósági szinttől és az eloszlás típusától függően a minta elemszámától is függhet. A kérdéssel a 4. fejezet - Mérés és valószínűség számítás fejezetben részletesebben foglalkozunk.
A véletlen hiba oka vagy ismeretlen, vagy a hibaokozók felderítése a mérés egészét tekintve aránytalanul nagy munkával és anyagi befektetéssel járna, ezért ésszerűtlen lenne keresésük. E hibatípus pontos értéke és előjele nem ismert, csak az alsó és felső korlátja valószínűsíthető.
Az eredmény bizonytalanságai azt tükrözik, hogy a mérendő mennyiségre vonatkozó ismereteink hiányosak. A „teljes” ismerethez „végtelen” mennyiségű információra lenne szükség. Nézzük ezek után egy-egy jellemző példán, hogy melyek azok a legfontosabb tényezők, amelyek a bemeneti mennyiségek véletlenszerű ingadozásait, bizonytalanságait okozzák:
A mérendő mennyiség hiányos meghatározása. (Nincs definiálva, hogy egy alkatrész átmérőjét mely keresztmetszetben kell mérni.)
A mérés nem tökéletes megvalósítása. (Hibás lehet a modellfüggvény, a mérési eljárás, a mérés kivitelezése és az alkalmazott számítási módszerek.)
A nem reprezentatív mintavétel. (Egy gyártóberendezés beállítási pontosságát kívánjuk ellenőrizni adott időpontban, de az ellenőrzésbe bevont munkadarabok gyártási ideje ismeretlen, vagy bizonytalan.)
A környezeti feltételek hatásának nem tökéletes ismerete. (Nincs adat a hőmérsékletről, páratartalomról, stb.)
A mérést végző személy hibájából adódó eltérések. (Annyira fontos tényező, hogy nagyobb üzemekben meghatározzák, kik azok a személyek, akik a minőségellenőrzésben egymást váltva végezhetik a méréseket. Ld.: Ismétlőképesség)
A műszer véges felbontása, küszöbérzékenysége. (A műszer nem alkalmas a felbontása alatti eltéréseket kimutatni.)
Az etalonok és anyagminták pontatlan értékei.
Az állandók és az algoritmusban alkalmazott faktorok pontatlansága
A mérési eljárásban alkalmazott közelítések. (Kúposság mérése mérőhasábokkal és görgőkkel. A módszer általában két keresztmetszet magasságában vett átmérőkkel számítja ki a kúpszöget, egyéb adatok híján nincs pontos információ a munkadarab valódi alakjáról, hiszen az alkatrész alkotói nem feltétlenül egyenesek.)
A mérés ismétlőképességéből adódó eltérések. (Az ismétlőképesség nem csupán a mérést végző személytől függ, ld.: 2. fejezet - Mérés-és műszertechnika fejezet.)
A fentiek mellett nem szabad elfeledkeznünk a korszerű méréstechnika digitális kijelző eszközeinek kijelzési bizonytalanságáról sem. A közvetlen A/D konverziós (átalakítási) eljárás kvantálást, azaz értékekhez rendelést jelent mind az amplitúdókra, mind pedig az időre nézve. Az időbeli kvantálást nevezzük mintavételezésnek. A kvantálás miatt a jelszinteket egy adott tartományban azonos értékűnek vesszük, ebből következik, hogy egy kvantum teljes tartományában a sűrűségfüggvény egyenletes. Ezt mutatjuk be a következő ábrán.
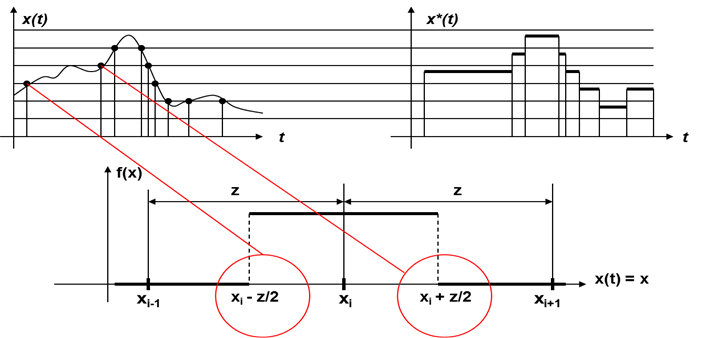
A digitális kijelzésű műszerek esetében az abszolút hiba egy „kvantumon” belül változó, és maximális értéke a kvantum fele. Ezt látjuk a következő ábrán.
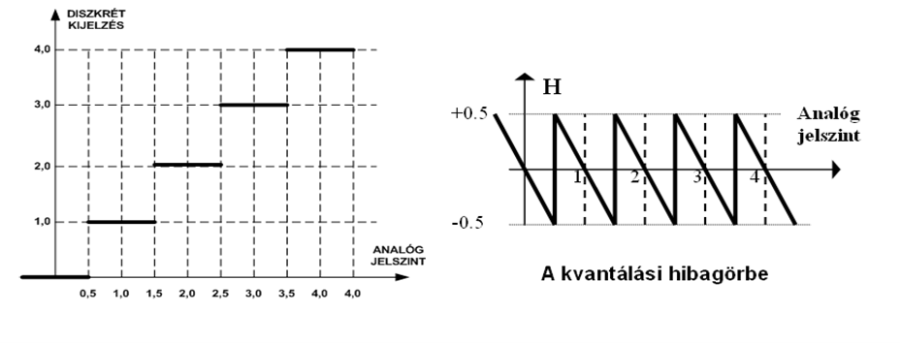
Ez a maximum azonban nyilvánvalóan „pesszimista” becslés, hiszen a mért értékek és a kijelzett értékek között nem mindig ez az eltérés adódik. Kérdés, hogy digitális műszereknél milyen bizonytalansággal jellemezhetjük a kijelzést? A megoldást az egyenletes eloszlás sűrűségfüggvényének segítségével keressük meg.
A következő ábrán az egyenletes eloszlás függvényeit látjuk folytonos változó esetére. Az ábra a levezetés megértését igyekszik segíteni.
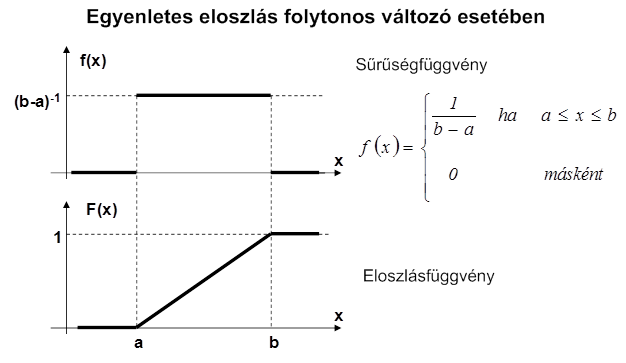
A várható érték kiszámítása az első lépés:
|
|
(3.3) | |
|
|
(3.4) |
Ezt követően a varianciát (szórásnégyzet) határozzuk meg úgy, hogy felhasználjuk az alábbi azonosságot is. Ez a szórás lesz a digitális kijelzés bizonytalansága, a legkisebb digitre (LSB:Least Significant Bit) vonatkoztatva:
|
|
(3.5) |
Az összefüggés jobb oldalán kijelölt matematikai műveleteket kibontva igazoljuk, hogy az azonosság fennáll:
|
|
(3.6) |
Felhasználva az azonosságot, a könnyebben integrálható kifejezésbe behelyettesítjük a várható értéket:
|
|
(3.7) |
Az integrálás elvégzése után úgy alakítjuk át a kapott kifejezést, hogy az egyszerűsítés lehetővé válhasson:
|
|
(3.8) |
A digitális kijelzés bizonytalansága tehát a legkisebb digitre vonatkoztatva:
|
|
(3.9) |
A kijelzés bizonytalanságaként tehát nem a legkedvezőtlenebb esetet, azaz 0,5·LSB értéket kell alkalmaznunk, hanem ennél jóval kisebbet.
3.3.3. Közvetett mérés rendszeres hibája, rendszeres hiba terjedése
Láttuk a (2.8. szakasz - Mérés egyenlete, közvetlen és közvetett mérés) fejezetben, hogy a mérés egyenletének segítségével adjuk meg a bemenő mennyiségek ismeretében a keresett kimenő mennyiséget.
|
|
(3.10) |
A becslésben megjelenik a korrekció, azaz a rendszeres hibák eredője, valamint a kiterjesztett mérési bizonytalanság is:
|
|
(3.11) |
Kérdés, hogy több bemenő mennyiség esetében miként lehet az eredő rendszeres hibát meghatározni. Ezt a hibát a szakirodalom hibaterjedésnek nevezi.
A feladatunk megkeresni „y0” azon „dy0” változását, amely azért lép fel, mert „xi0” helyett „xi” volt a mérésünk eredménye. Az ilyen típusú feladatok megoldására szolgál a Taylor sor, amely fontos szerepet játszik, ha egy függvényt hatványsorral kell közelítenünk.
A méréstechnikában és a fizikai kísérletek kiértékelésénél Taylor-sorfejtést akkor alkalmaznak, ha egy mérendő mennyiség valamilyen hatás miatti megváltozása nagyságrendekkel kisebb, mint maga a mérendő mennyiség. A hangsúly a kis mértéken van, ezért elegendőek a vizsgálathoz a Taylor sor első tagjai. A hatványsor magasabb fokú tagjai ugyanis a kis változás miatt már nem befolyásolják az eredményt.
Az eredmény egyenletének (modellfüggvénynek) parciális deriválása révén lehet megállapítani az egyes változókhoz (bemeneti mennyiségekhez) tartozó súlyfaktorokat.
|
|
(3.12) |
Az eredmény (matematikai) egyenletének „xi” változó szerinti parciális deriváltjába behelyettesítve az adott változó legvalószínűbb értékének becslésére használt átlagértéket, kapjuk az un. súlyfaktort (ci), ami az adott változó hatásának mértékét jelzi, mind a rendszeres , mind pedig a véletlen hiba terjedésének , valamint az eredő (tapasztalati) szórásnak meghatározásában.
A rendszeres hibák terjedését a szakirodalom két alap képletforma segítségével magyarázza. Az egyiket az összeg/különbség jellegű, míg a másikat szorzás/osztás/hatványozás alakú modellfüggvényre írják fel.
Nézzük elsőként azt a modellfüggvényt, amelyben az „y” kimenet az „x” és „z” bemenő mennyiség összege vagy különbsége. Az eredő maximális abszolút hiba a fentebb ismertetett parciális deriválással határozható meg:
|
|
(3.13) |
A legtöbb méréstechnikai szakirodalom összeg-képlet esetére az eredő abszolút, más néven eredő maximális hiba számítását alkalmazza (például a német szakirodalomban ennek neve: Größtfehler). Ez a lehetséges legnagyobb hiba, vagyis a legkedvezőtlenebb eset.
Előfordul azonban, hogy nem az abszolút értéket, hanem a tagokat a deriválásból adódó előjellel használják a hiba meghatározására. Ez különbség esetén természetesen optimistább becslést ad. Szélsőséges esetben - különbség-jellegű modellfüggvény mellett – a hibák kompenzálhatják egymást.
Az előírásokon (szabványokon), esetleg a mérést végző, képzett személyen múlik, hogy adott esetben melyik formát alkalmazza. Egyéb előírás hiányában ajánlott az eredő abszolút hiba kiszámítása a fent látható képlettel.
Szorzat és hatványfüggvény formájú eredmény egyenlet esetében az alábbi általános formából indulunk ki, ahol „x” és „z” megint csak a bemenő mennyiségek:
|
|
(3.14) |
ahol „n” és „m” pozitív, vagy negatív előjelű, egynél kisebb, vagy nagyobb valós szám lehet.
Parciális deriválás révén jutunk az eredő abszolút hibához, ami a legkedvezőtlenebb eset:
|
|
(3.15) |
Mérlegelés tárgya, hogy az előjelek figyelembevétele milyen torzítást okoz, és megengedhető-e? Ha a deriválásból származó előjeleket is figyelembe vesszük, akkor a hibát csökkentheti az osztóként megjelenő bemenő mennyiség:
|
|
(3.16) |
Nézzük ezt egy egyszerű példán:
|
|
(3.17) |
Csupán a teljesség kedvéért említjük meg, hogy számos szakirodalomban találkozhatunk a hibaterjedés kapcsán az eredő relatív hibákkal is. Összeg esetében két bemenő mennyiséggel (x,z) az alább látható formát kapjuk. Felhívjuk a figyelmet az összefüggésben rejlő veszélyre. Ha ugyanis a két bemenő mennyiség értéke közel esik egymáshoz, netán azonosak, akkor különbség esetén a nevező nullává is válhat. Ezért ezzel a formával óvatosan kell bánni.
|
|
(3.18) |
Szorzat és hatvány modellfüggvényeknél az abszolút relatív hiba megadását ajánlja a szakirodalom, mert a deriválásból adódó előjelek indokolatlanul csökkenthetik az eredő hiba nagyságát.
|
|
(3.19) |
Az eredő relatív hiba, amely hibaterjedéssel, tehát több bemenő mennyiséget tartalmazó modellfüggvényre adódik, általában a legkedvezőtlenebb eset.
3.3.4. Közvetett mérés bizonytalansága, véletlen hiba terjedése
Láttuk, hogy valamennyi részeredményt a rendszeres hibák mellett véletlen hibák is terhelnek. A rendszeres hibákat a korrekcióban vesszük figyelembe, a véletlen hibákat az empirikus szórásukkal jellemezhetjük.
A leghelyesebb, ha újra a modellfüggvényt vesszük alapul, és az „U” kiterjesztett bizonytalanságban az eredő tapasztalati (korrigált) szórást vesszük figyelembe. A hibaterjedésnél azt vizsgáljuk, hogy az eredmény kismértékű változásához a részadatok milyen mértékben járulnak hozzá.
Ismeretes a valószínűség számításból, hogy ha az x1, x2, …xi,…xn valószínűségi változók egymástól függetlenek, akkor az alábbi képlettel határozható meg az eredő variancia:
|
|
(3.20) |
Az eredő variancia tehát független változók esetében a súlyozott varianciák összege.
Mivel x1, x2, … xn valószínűségi változók, a képletben szereplő y=f(x1, x2, … xn) modellfüggvény (eredményegyenlet) természetesen maga is valószínűségi változó lesz.
A közvetett mérés várható értékét a részeredmények átlagaival becsüljük. Ezért nyilvánvaló, hogy a hibaterjedés eredő szórásának becslésére használt számítási képletben, az egyes összetevőkben, az átlagok korrigált tapasztalati szórását használtuk fel.
Tehát a közvetett mérés eredő (korrigált) tapasztalati szórása jellemzi majd az átlagos érték ingadozását.
|
|
(3.21) |
Az eredő korrigált tapasztalati szórás meghatározásában is láthatók a „súlyfaktorok” (ci), amelyeket az eredményfüggvény Taylor sorának elsőrendű tagjaiból nyertünk, parciális deriválás révén.
3.4. A mérési hibák formai megjelenése
A hibák csoportosításánál látott harmadik megközelítés a hibák formájára, megadási módjára vonatkozott. Ebben az aspektusban két alcsoportot lehet megkülönböztetni: Az egyik alcsoport a hiba megadási módját jelenti, és ide tartoznak olyan fogalmak, mint az
abszolút hiba,
relatív hiba,
redukált hiba, és
osztálypontosság.
Ezek magyarázatát korábbi fejezetekben, a metrológiai és a műszertechnikai fogalmak között már megadtuk, és néhányat közülük az eddigiek során már rendszeresen alkalmaztunk is. További taglalásuk tehát nem indokolt. A hangsúlyt az időben változó mennyiségek méréstechnikájára helyezzük.
3.4.1. Időben változó mennyiségek mérésének jellegzetes hibái
Az időben változó mennyiségek mérése a gépészetben rendkívüli fontosságú, és ezért a másik alcsoporttal, az időbeli és frekvencia tartománybeli hibákkal a következőkben részletesebben foglalkozunk. A méréstechnika egyik jellegzetes ellentmondása talán éppen ezen a területen jelentkezik a legszembetűnőbben. Nevezetesen az, hogy már a mérés megtervezésekor „à priori” (előzetes) ismeretekkel kell rendelkeznünk nem csak a mérendő jelek nagyságát, hanem azok spektrumát illetően is. Magyarul: Ismernem kell a megismerni kívánt mennyiség bizonyos jellemzőit. A jelekkel és a jelanalízissel külön fejezetekben foglalkozunk.
A jelek spektrumának és az adott mérőrendszer dinamikai tulajdonságainak figyelmen kívül hagyása súlyos mérési hibákhoz vezethet, mind analóg, mind pedig a mintavételezett jelek esetében. Sajnos, gyakran találkozhatunk a mérőrendszer, mérőlánc, vagy egy-egy mérőműszer frekvenciafüggő átvitelének figyelmen kívül hagyásából származó hamis eredményekkel.
Az időben változó gépészeti mennyiségek mérésének bemutatására a nemzetközi gyakorlatban is előszeretettel alkalmazott megközelítés a „mérőlánc”. A jellegzetes villamos mérésektől ez a struktúra alapvetően különbözik, hiszen ennek igen fontos részét képezi a bemenő (mérendő) mennyiségek villamos jellé történő átalakítása. Ezt a műveletet a szakirodalom sokféle módon nevezi, de alapvetően „jelátalakítás” ami itt végbemegy. A következő ábra a mérőlánc tagjait és ezek legfontosabb feladatait mutatja be.
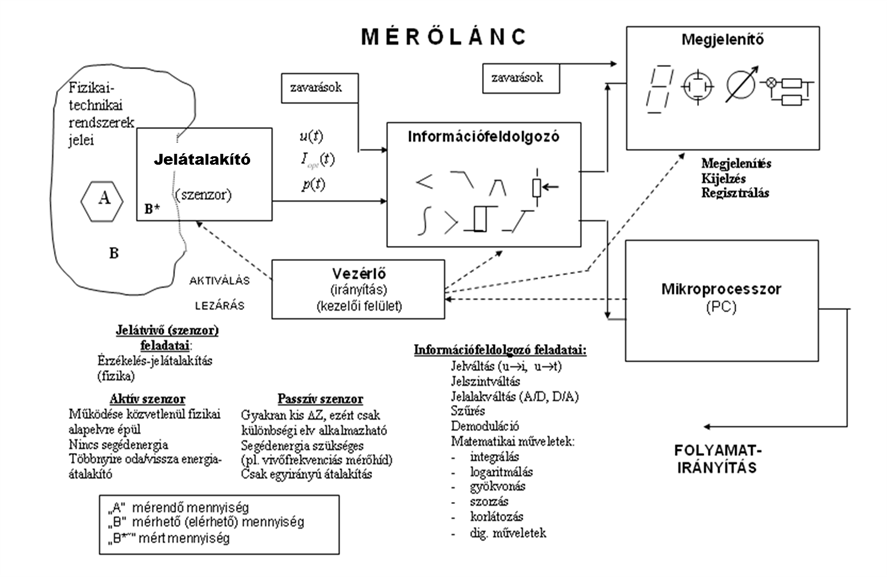
A hibaanalízis szempontjából fontos, hogy a mérőlánc és a mérendő fizikai mennyiségek, jelek közötti kapcsolatot dinamikai szempontok figyelembe vételével megvilágítsuk.
Tehát, nagyvonalakban össze kell gyűjtenünk előzetesen minden lehetséges és fontos ismeretet arról a mennyiségről, amit meg akarunk „ismerni”. Az ok a dinamikában, rendszertechnikában és rezgéstanban járatos gépészek, mechatronikusok számára világos. A jelátalakítók (jeltovábbítók) többségében vegyes, mechanikai-villamos rendszerelemek találhatóak, és ezek között is meghatározó jelentőségűek az energiatárolók . A példákat igen hosszan lehetne sorolni, legyen elegendő ezen a helyen csak a különféle gyorsulásérzékelőkre (induktív, nyúlásmérő bélyeges, piezoelektromos, vagy a MEMS-technikában /Micro Electro Mechanics/ a kapacitív) utalni, amelyekben valamilyen formában szeizmikus tömeg csillapított rugalmassággal van felfüggesztve, és így mindegyik azonnal másodrendű lengő rendszert képez. A következő ábra egy induktív útadós szenzorral ellátott szeizmikus gyorsulásérzékelő kitöréses metszetét mutatja.
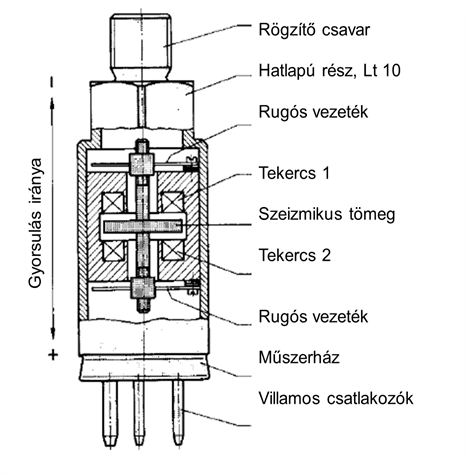
A jelátalakító (jeltovábbító) és annak induktív útadó szenzorja nagyszerű példa annak illusztrálására, hogy a mérőlánc tagjai bizony tartalmazhatnak energiatárolókat, amelyek az eszköz dinamikus tulajdonságait – értsd alatta: jelátvitelét – alapvetően meghatározzák. A műszertechnikában szokás arányos, egytárolós és kéttárolós tagokról beszélni. Nem, mintha kettőnél több független energiatároló nem lehetne egy rendszerben. Helyesebb is lenne egytárolós helyett páratlan és kéttárolós helyett páros jellegről beszélni, mert ezek kombinációjával a gyakorlatban előforduló – magasabb rendszámú - műszertechnikai átviteli tagok „összerakhatóak”.
Ezt olvashatjuk le a következő ábrán látható diagramról, amelyet, egy valós eszköz műszerkönyvéből vettünk.
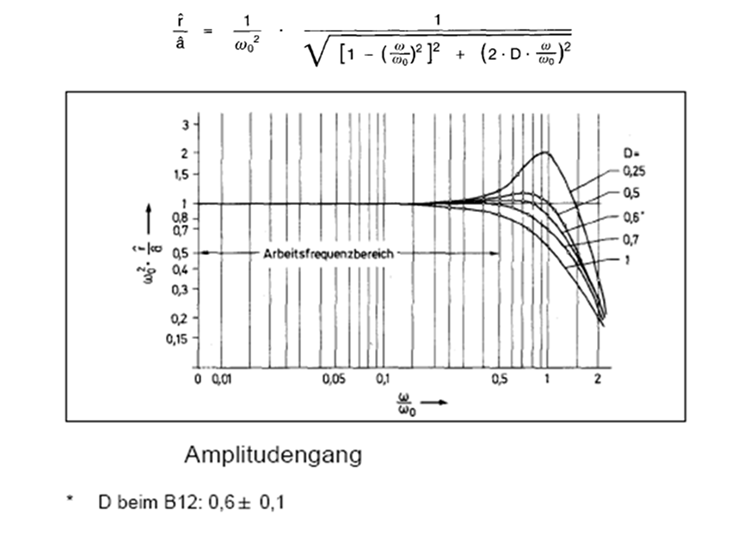
A fenti ábrán a H&B B12 gyorsulásérzékelő „amplitúdó menete”, és felül az átviteli függvény abszolút értékének kiszámításához szükséges összefüggés látható. A diagram se nem un. Bode-diagram, se nem normalizált frekvenciamenet, ahogy a műszaki mechanika ismeri, hanem egy vegyes kép, de jól szemlélteti a dinamikai problémát. A jelátalakító másodrendű, mert rugalmas vezetéken felfüggesztett, szeizmikus tömeget tartalmaz. A csillapítást igen körülményes módon 0.6 értékre állítják be. Ez a másodrendű rendszer alul-áteresztő szűrőként működik, azaz 0.6-es csillapítási fok esetén 0≤f≤0.5frez frekvencia sávban arányos működésű, tehát mérésre alkalmas. Ebben a frekvencia tartományban minden harmonikus jelet - ezek a mérendő gyorsulás jel Fourier összetevői - a műszerkönyvben megadott arányossági tényezővel súlyozva alakít át elmozdulássá. Ugyanakkor f>0.5frez frekvenciákon egy szűk tartományt, a rezonancia sávot kivéve, csökken az arányossági tényező, frekvencia dekádonként (frekvencia megtízszereződése) 40 dB-lel, ami jelszintben 0.01-es szorzót jelent.
Mindez jól leolvasható a diagramról, és tájékoztatja a felhasználót a dinamikai szempontból fontos alkalmazhatósági feltételekről.
Összefoglalva tehát az energiatároló elemek (tömeg, rugómerevség, induktivitás, kapacitás, stb.) hatása idő tartományban dinamikai hibák , a frekvencia tartományban pedig az amplitúdó átvitel és fázis átvitel hibáknak forrása lehet.
3.4.2. Dinamikus hiba
Már a dinamikus kalibrálással foglalkozó fejezetben is találkozhattunk a problémával. A lényeg tehát az, hogy a műszerek, mérőrendszerek a bennük lévő energiatárolók miatt csak időben késleltetve, esetleg amplitúdóban nagyobb eltéréssel képesek követni a mérendő bemenő jelet. A dinamikus hiba a következő ábrán látható módon, amplitúdóját tekintve időbeli késésként, vagy adott időpillanatban amplitúdó hibaként jelentkezik.

A dinamikus hiba különösen nagy problémákat okozhat másod, vagy annál magasabb rendű rendszerek esetében. A műszer, vagy mérőrendszer csillapítási fokától függően hosszabb-rövidebb ideig tartó lengésekre kell számítani, esetenként tekintélyes túllendüléssel. A kalibrálással foglalkozó fejezetben már leírtuk, hogy a leolvasás csak az állandósult állapotban lehetséges. Egy jellegzetes finommechanikai méretekkel rendelkező másodrendű műszer ugrásfüggvény bemenetre (ez is látható az oszcilloszkóp kép alsó részén) adott válaszát (un.: step response) látjuk a következő ábrán. A kép baloldalán a pozitív, a jobboldalán a negatív irányú kitérítés dinamikája figyelhető meg.
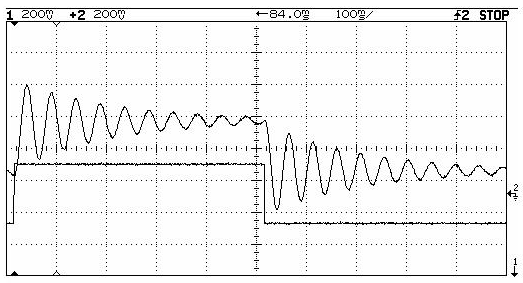
3.4.3. Mérőlánc frekvenciafüggő átviteléből adódó hibák
Az „Időben változó mennyiségek mérésének jellegzetes hibái” című fejezet bevezetőjében már jeleztük, hogy a mérendő mennyiség várható nagysága (amplitúdója) mellett ismerni kell a mérendő mennyiség (jel) időbeli alakját, és ebből következően a frekvencia spektrumát, hogy a mérőlánc minden tagjának frekvencia-átvitelét ehhez a spektrumhoz illeszthessük, hiszen a mérőlánc dinamikai tulajdonságainak figyelmen kívül hagyása a létező legdurvább hibákat eredményezheti.
A problémát frekvencia tartományban jól szemlélteti a (3.8. ábra - Részletek a H&B B12 gyorsulásérzékelő adatlapjából) ábrán látható diagram, amelyet, egy valós eszköz műszerkönyvéből vettünk.
A 3.7. ábra - Induktív gyorsulásérzékelő felépítése (Hottinger és Baldwin) felső részén látható frekvencia átviteli függvény (r/a, azaz a ház és a tömeg közötti relatív elmozdulás amplitúdója osztva a bemenő gyorsulás amplitúdójával) levezetése igen egyszerű, ha feltételezzük, hogy a rugós vezeték rugómerevsége (k) és a csillapítási tényező (b) lineáris és idő-invariáns rendszerelemek. Ebben az esetben a műszerház és a szeizmikus tömeg közötti relatív elmozdulás, valamint a bemenő gyorsulás közötti összefüggést, e két mennyiséggel matematikai kapcsolatban álló sebességek alkalmazásával, és impedancia módszerrel írhatjuk fel. Az általános impedancia a keresztváltozó (mechanikában sebesség) és az átmenő változó (mechanikában erő) Laplace transzformáltjának hányadosa.
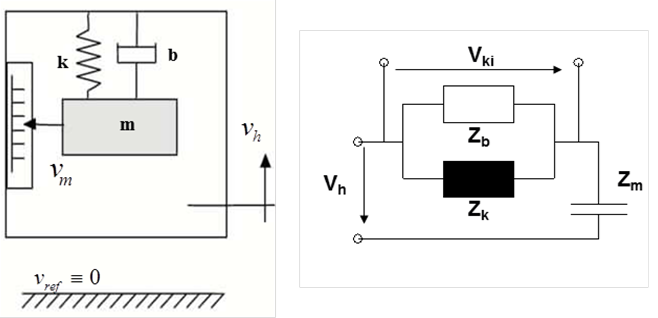
A fenti ábra jobb oldalán látható impedancia kapcsolásban meghatározzuk a kimenő sebességhez tartozó impedanciák párhuzamos eredőjét és a keresztváltozó-osztó szabályt alkalmazva azonnal az implicit átviteli függvényt kapjuk:
|
|
(3.22) |
A sebességek helyére a Laplace transzformáció szabályit figyelembe véve (integrálás, deriválás) az elmozdulás és a gyorsulás helyettesíthető:
|
|
(3.23) |
Ha az átviteli függvényben a Laplace operátor helyére annak „jelentését” írjuk s=jω, akkor nyilvánvalóvá válik számunkra az átvitel körfrekvenciától való függése:
|
|
(3.24) |
Bevezetve a mechanikában, műszertechnikában szokásos jelöléseket azzal, hogy a nemzetközi szakirodalom a csillapítatlan rezonancia körfrekvenciát hol „α”, hol „ω0” szimbólummal jelöli,
|
|
(3.25) |
majd az átviteli függvény abszolút értékét képezve a műszer adatlapon szereplő összefüggéshez jutunk:
|
|
(3.26) | |
|
|
(3.27) |
Az átviteli függvény abszolút értéke „normálás”, azaz „dimenziótlanítás” után alkalmas a Bode diagram megrajzolására, hiszen a bemenő és kimenő jelek fizikai dimenziója nem azonos. A normálásra azért van szükség, mert az átviteli függvény dimenziója, a dB nem fizikai mennyiségekből adódik.
A méréstechnikában a normálás úgy történik, hogy az átviteli függvény adott körfrekvencián vett értékét osztják egy célszerűen igen alacsony körfrekvencián vett átvitel értékével, esetünkben:
|
|
(3.28) |
Erre az arányra már képezhető a „lg” és az eredmény megadható dB-ben.
A „frekvencia-átviteli” tulajdonságok Bode diagramon történő ábrázolása elterjedt és jellemző a mérés-és szabályozástechnikai gyakorlatban. Alkalmazása több előnnyel jár. Mindkét tengely „komprimált”, azaz széles frekvencia tartományban, és nagy amplitúdó arány átfogással jeleníthetőek meg az átviteli tagok frekvencia-függő tulajdonságai. Ezen túlmenően igen szemléletes, mert „első ránézésre” megállapítható, hogy az átviteli tag egy adott körfrekvencián milyen mértékben változtatja meg a harmonikus jel (összetevő) amplitúdóját. A körfrekvencia tengely log léptéke körfrekvencia-dekádonként azonos távolságot jelent, és így nem gond számos dekád, tehát nagy frekvencia tartomány ábrázolása. Zérus körfrekvencia természetesen nem jeleníthető meg, csak valamely tetszőleges, nagyon alacsony körfrekvencia érték. A fázis-átvitelt külön diagramon ábrázolják, de a frekvencia tengely léptéke megegyezik az amplitúdó átvitelével.
A kalibrációs Bode diagramot a legtöbb dinamikus műszer esetében közlik a gyártók, de ha mégsem, akkor az arányos átviteli tartományt mindenképpen megadják.
A kimenő és bemenő harmonikus jelek amplitúdó arányának logaritmusa 20-szal szorozva adja azt a dimenzió nélküli mértékegységet, amit a mérés- és híradástechnikában decibel-nek (dB) nevezünk. A „bel” (rövidítése: B) egységet a Bell Telephone Laboratory mérnökei alkalmazták először, a szabványos telefonkábel 1 mérföld (1,6 km) hosszú darabja okozta hangerősség-csökkenés mértékének meghatározásához. Eredetileg „transmission unit” vagy TU (átviteli egység) volt az egység neve, majd az 1920-as évek közepén nevezték el a labor alapítójáról (A. G. Bell). A „bel”, mint egység, túl nagy a műszaki alkalmazásra, ezért használjuk a tizedét.
A dB mértékegységet alkalmazzák az akusztikában, az optikában is, de vigyázat, az akusztikai dB számítása egészen más alapon történik, csak a logaritmus számítás bennük a közös, nem átviteli függvényről van szó! Az akusztikai dB-t hangnyomásszint és hangteljesítményszint megadására alkalmazzák. A tört számlálójában az aktuális érték (hangnyomás, teljesítmény), míg a nevezőben egy vonatkoztatási érték szerepel!
Kétféle dB használatos a műszertechnikában, az egyik az jelszint-decibel, a másik a teljesítmény-decibel. Ez utóbbi esetében a tízes alapú logaritmus előtt azonban nem 20-as, hanem 10-es a szorzó áll. A jelek frekvencia analízise kapcsán a teljesítményre még visszatérünk. Egyébként ez az eredeti formája is a dB definíciónak, mert a kimenő és bemenő teljesítmény közötti viszony meghatározására hozták létre. Teljesítmény viszonyok esetében a szorzó tehát 10, míg a teljesítményben négyzetesen szereplő - többnyire keresztváltozó - amplitúdók arányát behelyettesítve (pl.: P=U2 / R) a szorzat a log előtt 2·10 lesz.
Érdemes néhány fontos dB értéken és a mögöttük lévő amplitúdó arányon, és ezek diagramon való megjelenésén elgondolkodni, mert a méréstechnikában a használatuk mindennapos, és ezért ezeket összefoglalva bemutatjuk.
A méréstechnikában gyakran alkalmazott 1%-os hibakorlát (amplitúdó) dB-ben kifejezett értékét is megtaláljuk a táblázatban, célszerűen kerekítve 0.1 dB-t szokás megadni.
|
Amplitúdó arány |
dB |
Amplitúdó arány |
dB |
|---|---|---|---|
|
1000 |
60 |
10-3 |
-60 |
|
100 |
40 |
10-2 |
-40 |
|
10 |
20 |
10-1 |
-20 |
|
3,3 |
10 |
0,33 |
-10 |
|
2 |
6 |
0,5 |
-6 |
|
1,4 |
3 |
0,7(=1/1,4) |
-3 |
|
1 |
0 | ||
|
1.01 |
0.09 |
0.99 |
-0.09 |
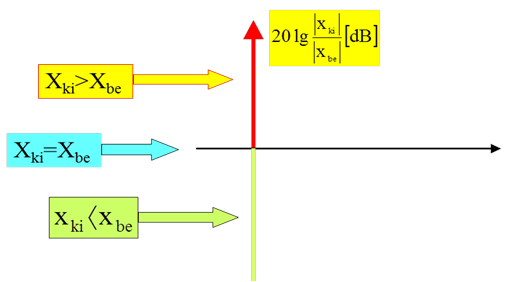
A gyorsulásérzékelő esetében a Bode diagram függőleges tengelyén ábrázolt átviteli tényező értékek normálás nélkül az alábbi összefüggéssel számíthatók ki:
|
|
(3.29) |
Az amplitúdó átvitel hibája tehát jól leolvasható a Bode diagramról, és tájékoztatja a felhasználót a dinamikai szempontból fontos alkalmazhatósági feltételekről.
3.4.4. Mintavételezési hiba
A digitális kijelzésből származó bizonytalansággal egy korábbi fejezetben már foglalkoztunk, és láttuk, hogy ez a legkisebb kijelzett érték mintegy 30 %-a. Hiba azonban nem csak az amplitúdó léptékezés (kvantálás) során keletkezik, hanem az időben történő kvantálás, más elterjedt kifejezéssel „mintavételezés” miatt is. Ebben a fejezetben röviden arra világítunk rá, hogy adott, időben változó jel spektrumának ismeretében milyen szabályt kell figyelembe venni a jel mintavételezése során a hiba elfogadható szinten tartása érdekében.
Az első ábrán egy analóg jel amplitúdó kvantálását látjuk.
A kvantálási szabály a következő:
|
|
(3.30) |
Ahol „N” az analóg jelhez rendelt diszkrét szintet, „A” pedig az analóg jel pillanatnyi értékét jelenti az adott tartományban.
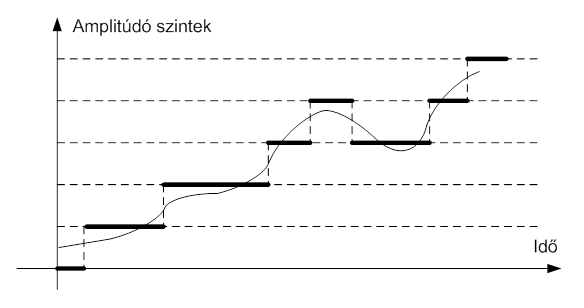
A fenti ábrán az eredeti analóg jelet vékony folytonos vonallal, az amplitúdó kvantáltat pedig vastagabb vonallal jelöltük. Az amplitúdó kvantálás szemmel láthatóan önmagában eléggé torzítja a jelet. A torzítás a kvantálási szinttől függ, ez a szakirodalom által emlegetett „LSB”, azaz legkisebb kijelezhető bit.
Az A/D konverzió (analóg-digitális átalakítás) sokféle módon történhet, ezek alapvetően közvetett, vagy közvetlen csoportba sorolhatók. A közvetett A/D átalakítás során az időalapra, mint köztes mennyiségre vezetik vissza az átalakítást, ilyen volt a régebben alkalmazott fűrészfog-generátoros, napjainkban pedig a dual-slope (kettős integrálás) konverzió. A közvetlen átalakítók, amint az elnevezés is mutatja, időalap igénybevétele nélkül végzik az átalakítást. Ilyen a szimultán A/D konverter és a szukcesszív approximációs átalakító. Különböznek az A/D átalakítók abban is, hogy a jel pillanatnyi értékét, vagy a jel egy meghatározott idő alatti integrálásának eredményét méri. Pillanatnyi értéket mér a szimultán és a szukcesszív approximációval dolgozó átalakító, és a régi fűrészfog-generátoros rendszer is. A szukcesszív approximációs átalakítónál szükség van a pillanatnyi jel értékének tárolására is, mert a közelítés és a kódolás több lépcsőben történik. A dual-slope átalakító viszont nem pillanatnyi értéket mér, hanem adott időállandóval és meghatározott ideig integrálja a bemenő jelet.
Az A/D átalakítás, és az ezt követő kódolás mindenképpen időt vesz igénybe. A vizsgálandó jel átalakítását ezért nem folyamatosan, hanem „idő-kvantumokban” végzik el. Az időbeli kvantálás a mintavételezés. Az előző ábrán már látott analóg jel (vékony vonal) egy lehetséges Tm idővel történő mintavételezését mutatja az alábbi ábra:
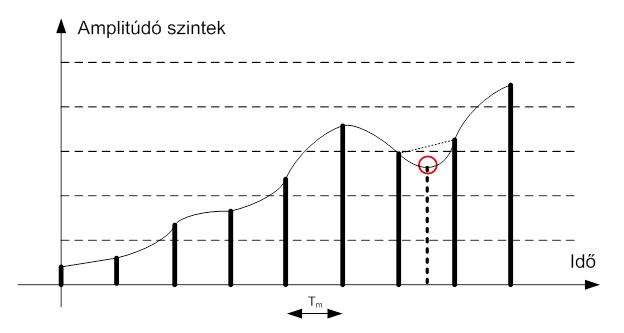
A fenti ábrán érzékeltetni akartuk, hogy a mintavételi idő nagy ahhoz, hogy a jelben meglévő, pirossal körülrajzolt információ elvesszen. A mintavételi értékek csúcsait képzeletben összekötve láthatjuk, hogy az eredeti jelhez képest itt komoly eltérés lenne.
A helyzet tovább romolhat, ha a kétféle kvantálást együttesen alkalmazzák, márpedig ez a helyzet minden A/D átalakító esetében! A gyakorlatban tehát mintavételezett és amplitúdó kvantált jelekből származó információt jelenítenek meg a digitális kijelzésű eszközök. A következő ábrán az eddigiekben alkalmazott analóg jelen mutatjuk be a kettős torzító hatást:
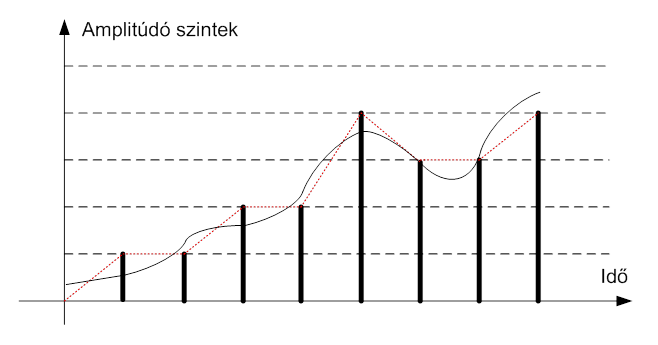
Ha szemléltetési célból most is összekötjük a mintavételezés csúcsait, amint ez az ábrán piros szaggatott vonallal megtörtént, akkor az eredeti analóg jelhez képest jól kivehető a különbség.
Mindenképpen kell tehát hibával számolnunk, a kérdés az, hogy miként lehet a mintavételezéssel járó hibát minimalizálni?
Első látásra világos, hogy a jel változásának követése csak megfelelően kis mintavételi időkkel valósítható meg. Shannon volt az, aki a mintavételezés róla elnevezett szabályát kidolgozta. Abból kell kiindulnunk, hogy minden jel harmonikus összetevőkre bontható.
Minél meredekebb a jel változása, annál több és nagyobb frekvenciájú harmonikus összetevőből épül fel a jel. Jó példája ennek a Dirac-impulzus, illetve ennek közelítése valós impulzusokkal.
A jelek Fourier analízisével a 6. fejezet - Mérőjelek idő és frekvencia tartományban fejezet részletesen foglalkozik, de a dinamikus okokra visszavezethető hibák nem tárgyalhatóak bizonyos ismeretek ismétlő áttekintése nélkül. A Fourier analízissel a BSc tanulmányok során feltehetően már mindenki találkozott, ezen a helyen csupán a hibák vizsgálatához nélkülözhetetlen ismeretekre szorítkozunk.
Az időben kétoldalasan határolt jelek spektruma folytonos, így az elméleti és a valós impulzus spektruma is. Az impulzusspektrumának abszolút értéke eredetileg |sinx/x| függvény jellegű, amelynek zérus helyei egy [-Timp/2;+Timp/2 ] időtartamú és „A” magasságú négyszög impulzus esetében ωn=n2π/Timp körfrekvenciáknál vannak. Ebből adódóan, ha minden határon túl csökkentjük a négyszög impulzus időtartamát, akkor az első zérushely a végtelen körfrekvencia irányába tolódik el, és a spektrum egyenletesen „kisimul” és az összetevők értéke is zérushoz tart.
Ezt a jelenséget érdemes nyomon követni a négyszög impulzus Fourier transzformálásának bemutatásával.
A négyszög impulzus függvény és spektruma az alábbi ábrán látható:
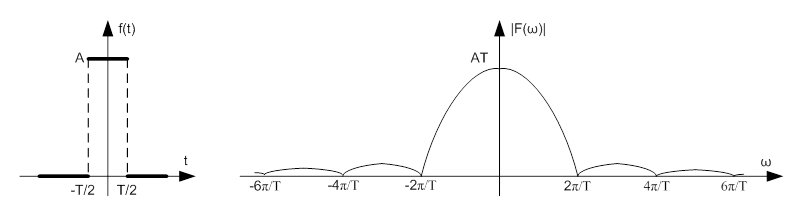
Az ábra baloldalán látható időfüggvényt Fourier transzformáljuk:
|
|
(3.31) |
Célszerű átformálással kapjuk a fent leírt eredményt:
|
|
(3.32) |
A függvény értéke a ω=0+ helyen, valamint zérus helyei csak a L’Hospital szabállyal határozhatók meg:
|
|
(3.33) |
A spektrum legfontosabb értékeit az alábbi táblázatban foglaltuk össze:
|
ω |
0 |
n·2π/T |
|
|F(ω)| |
AT |
0 |
Gondolati kísérletként az impulzus ”T” idejét csökkentve látjuk, hogy az első zérus hely egyre távolabb kerül az origótól, miközben a függvény értéke ω=0 helyen folyamatosan csökken. Végül - legalábbis elméletben - eljutunk az ideális Dirac impulzushoz, amelynek, mint ismeretes, az időtartama zérus, és a spektruma folytonos, a frekvencia tengellyel párhuzamos egyenes.
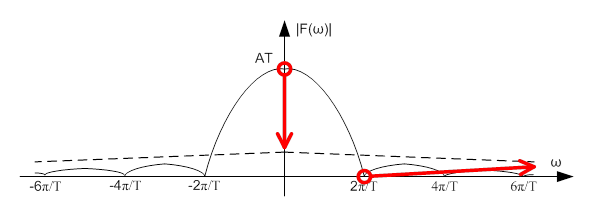
Fontos tudni, hogy amíg egyetlen négyszög impulzus spektruma |sinx/x| jellegű addig az impulzus sorozat spektruma periodikus. A mintavételezett analóg jel a mintavételi időpillanatokban vett nagyságú impulzusok sorozata.
A jegyzet terjedelme nem teszi lehetővé, hogy bemutassuk az impulzus sorozat spektrum ának kiszámítását a Fourier transzformáció segítségével, de az érdeklődők a Fodor Gy.: Jelek és rendszerek című munkában [3.2.] részletes bemutatót találhatnak.
A későbbiek megértéséhez azt viszont tudni kell, hogy az impulzus sorozat spektrumának periódusa a körfrekvencia tengely mentén éppen ωm, azaz a periódus éppen a mintavétel körfrekvenciája lesz.
Nincs olyan műszer, mérőrendszer, amely egy impulzus, vagy egy impulzus sorozat hibátlan leírásához szükséges valamennyi, elméletben végtelen számú harmonikus összetevőt képes lenne átvinni. Nincs is gyakorlati szempontból jelentősége egy bizonyos felső határ(kör)frekvencia feletti összetevők átvitelének, mert azok a visszaállítható jel alakját érdemben már nem befolyásolják. Az elterjedt gyakorlat az, hogy az első zérus hely környékén adják meg azt a felső határ(kör)frekvenciát, amelynél az impulzus spektrumát levágják. Ezt a körfrekvenciát a következőkben „Ω”-val jelöljük. A frekvencia-korlátozást angol kifejezéssel „anti-aliasing” szűrésnek nevezik. A következő ábrán egyetlen impulzus spektrumának anti-aliasing szűrését szemléltetjük.
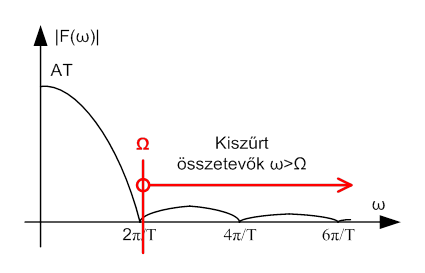
Említettük, hogy az impulzus sorozat spektruma a mintavétel körfrekvenciájával periodikus. Az anti-aliasing szűrésen átesett impulzusokból álló sorozat spektrumát látjuk a következő ábrán:
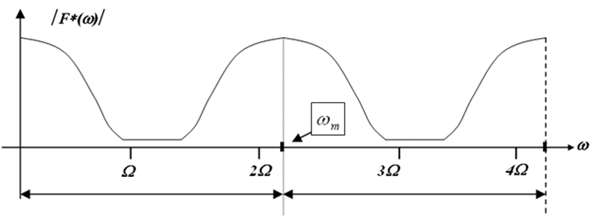
A fenti ábrán látjuk, hogy az impulzus-sorozat periodikus spektrumában, szűrés után, a 0≤ω≤Ω körfrekvencia tartományban a legfontosabb harmonikus összetevők maradtak. A görbe alakja hasonlít az egyetlen impulzus spektrumára jellemző sinx/x jellegű függvényből az első zérus helyig terjedő részhez. Az impulzus-spektrumból tehát már hiányzik az a tartomány, amelyet az anti-aliasing szűrővel vágási, vagy sávkorlátozó körfrekvencia felett kiszűrtünk.
Ha tehát nem egyetlen impulzus, hanem impulzus sorozat spektrumát vizsgáljuk, ez a sávkorlátozott spektrumkép jól láthatóan ismétlődik. Az impulzus sorozat spektruma szabályosan periodikus, a periódus körfrekvenciája éppen ωm .
Az ábrán úgy viszonylik egymáshoz mintavételi ωm körfrekvencia és Ω vágási körfrekvencia (antialiasing szűrő), hogy minimális mértékben, de teljesül a Shannon-szabály, mert a mintavétel körfrekvenciája nagyobb, mint a vágási körfrekvencia kétszerese.
A Shannon szabály tehát a következő módon adható meg:
|
|
(3.34) |
A mintavétel (kör) frekvenciája legyen a mintavételezett jelben megtalálható legmagasabb (kör)frekvenciájú harmonikus összetevő kétszeresénél nagyobb. Másként fogalmazva a mintavételi idő legyen kisebb, mint a jelben található legmagasabb (kör)frekvenciájú összetevő periódusidejének fele.
A következő ábrán látható, hogy mi történik a Shannon-szabály figyelmen kívül hagyása esetén? Ha tehát ωm körfrekvencia kisebb, mint az Ω vágási körfrekvencia kétszerese, akkor a spektrum „összecsúszik”. Az így torzult spektrumot úgy kell elképzelni, mintha a görbék felső szakaszai felett haladnánk végig. Az összecsúszott eredő spektrumot piros vonallal jelöltük. Ha a mintavételi frekvencia még a vágási körfrekvenciánál is kisebb, akkor a spektrum közelíthet egy egyeneshez.
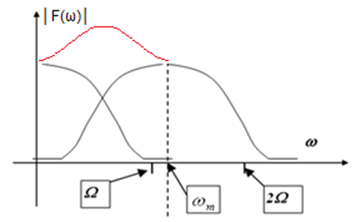
A Shannon szabály gyakorlati alkalmazásához nyújt segítséget a következő ábrán látható összeállítás. Tévedés lenne azt gondolni, hogy a mintavételezésből adódó hiba már azzal megszűntethető, ha a mintavételezési frekvencia nagyobb, mint a még átvinni (mérni) kívánt legmagasabb harmonikus összetevő kétszerese. Mekkora legyen a gyakorlatban elégséges körfrekvencia?
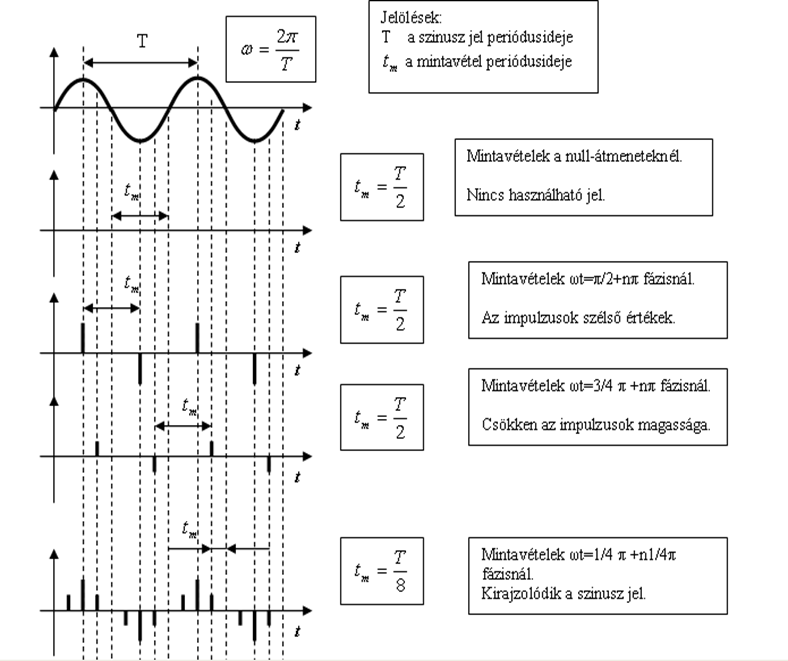
A fenti ábra-soron első helyen azt az esetet látjuk, amikor a Shannon szabály nem teljesül, mert a mintavételi idő éppen a fele a legnagyobb frekvenciájú harmonikus periódusidejének. Előállhat olyan eset, hogy a mintavételezés éppen a null-átmeneteknél következik be, és ezért erről az összetevőről semmilyen információnk nem lesz. Ezért helytelen az a megfogalmazás, amelyet bizonyos internetes oldalakon is olvashatunk, miszerint a mintavételezés frekvenciája „legalább” kétszerese legyen a jelben megtalálható legnagyobb, még releváns összetevő frekvenciájának. A „legalább” kifejezésbe az „=2” is beleértendő, és ezért ez a megfogalmazás nem helyes.
Némiképp javul a helyzet, ha a mintavétel a null-átmenetekhez képest fázisban eltolt, ugyanakkor nagy képzelőerő kell a szinuszos jel rekonstrukciójához periódusonként kettő mintából. Ha a mintavétel frekvenciája már nyolcszorosa a legmagasabb frekvenciájú összetevőnek, akkor a harmonikus jel tűrhetően kirajzolódik. Gyakorlati szempontból tehát arra kell törekedni, hogy a mintavételi (kör)frekvencia legalább tízszerese legyen a legmagasabb (kör)frekvenciájú harmonikus összetevő (kör)frekvenciájának:
|
|
(3.35) |
A mintavételezés gyakorlati kivitelezésére a (8.3. szakasz - Alul-mintavételezés (Aliasing)) és (8.4. szakasz - A mintavételi frekvencia növelése az alul-mintavételezéselkerüléséhez) fejezetben visszatérünk.
Irodalmak
[3.1.] Műszaki mérések. Műegyetemi kiadó. 2008.
[3.2.] Jelek és rendszerek. Műegyetemi kiadó. 2006.
4. fejezet - Mérés és valószínűség számítás
- 4.1. Mérési adat, mint valószínűségi változó
- 4.2. Relatív gyakoriság és a valószínűség
- 4.3. Eloszlásfüggvény, sűrűségfüggvény
- 4.4. Egydimenziós eloszlások elméleti és empirikus paraméterei
- 4.5. Normál eloszlás, vagy Student eloszlás
- 4.6. Az eredményképlet konfidencia intervallumának meghatározása
- 4.7. Statisztikai próbákról röviden
- Irodalmak
A Méréstechnika című jegyzetben közölt [1.1.] olyan fontosabb valószínűség számítási ismereteket, amelyek e jegyzet megértése szempontjából nélkülözhetetlennek tartunk, ebben a fejezetben tömören összefoglaljuk. A valószínűségszámítási vonatkozásokra az eredmény alakjának ismertetésénél már utaltunk.
4.1. Mérési adat, mint valószínűségi változó
A véletlen változókat – ilyenek a mért értékek is – okok rendszere hozza létre, illetve befolyásolja. Ez az „okság törvénye”. Ha valamennyi okot, körülményt és hatótényezőt módunkban állna figyelembe venni, akkor a mérés eredményében e befolyásoló tényezők hatását korrekció formájában meg lehetne adni. Ez azonban tapasztalataink szerint lehetetlen, ezért csak az ismert hatásokat vesszük figyelembe a korrekcióban. Az előre nem ismert, véletlen hatások következményeit mérési bizonytalanságok formájában foglaljuk össze.
A mérés modellezésében beszélnek ú.n. kauzuális és sztochasztikus szkémáról. A méréselméletben a kauzalitás azt jelenti, hogy amennyiben a meghatározott feltételek összessége fennáll, akkor az esemény biztosan bekövetkezik. Ebbe a kategóriába sorolhatók a fizikai törvények által leírt jelenségek, hiszen például, ha ismerjük egy test tömegét és gyorsulását, akkor az erő statisztikai módszerekkel kiszámított bizonytalansággal mérési adatokból meghatározható. A sztochasztikus jelenségek egzakt leírása nehezebb, mert az ismereteink hiányosak. Ennek műszaki-tudományos, vagy gazdaságossági okai lehetnek. Jól példázza ezt a szkémát a rezgő gépi berendezések által kibocsátott zaj spektruma és hangnyomásszintje. Ismert a fizikai kapcsolat, de az azt leíró modellek csak közelítő jellegűek.
A mérési adatot véletlen elemi eseményként kell felfogni. A gépészetben vannak időben állandó mérési adatok, ilyenek például az alkatrészek hosszméretei, és vannak időben folytonosan változó adatok, ezek közé tartozik az előbbiekben említett rezgés amplitúdó, vagy a géprezgések által keletkező hangnyomásszint ingadozása. Valószínűség számítási szempontból mindkét típust folytonos változónak kell tekinteni, mert adott határok között elvben végtelen sok érték előfordulhat.
Ha az azonos mérési adatok, vagy egy osztály elemeinek abszolút gyakoriságát az összes mérési adatra vonatkoztatjuk, akkor kapjuk a relatív gyakoriságot.
4.2. Relatív gyakoriság és a valószínűség
A mért értékeket – kerekítés után - szokás úgy osztályokba (részintervallumokba) sorolni, hogy a legnagyobb és legkisebb mért érték közötti tartományt - ezt nevezzük terjedelemnek – felosztjuk intervallumokra. Ezek az intervallumok lehetnek azonos szélességűek, ez a méréstechnikában a gyakorlat, de lehetnek különbözőek is. Célszerűen az intervallum-határok középértékével jellemezzük az adott osztályt.
Csoportosított, osztályba sorolt adatok esetén a számításokat leegyszerűsíti, ha a részintervallumok egyforma Δx szélességűek, amint arról G.A. Korn és T.M. Korn a Matematikai kézikönyv műszakiaknak című munkájukban írnak [4.1.] .
A statisztikai jellemzők (korrigált tapasztalati szórás, átlag) értéke csupán a méréstechnikában szokásos hibahatáron belül különbözik, ha osztályba sorolással kapott, vagy az egyedi mérési adatokkal számítjuk ki ezeket.
A relatív gyakoriság alatt az adott osztályban való előfordulás összes mérési adathoz való viszonyítását értjük. A relatív gyakoriság definíciója:
|
|
(4.1) |
ahol n a mintanagyság, nA pedig az „A” esemény előfordulásának száma.
A hasonlóság miatt nagyon fontos kihangsúlyozni ezen a helyen, hogy a valószínűségre Laplace által adott értelmezést (t.i.: A kedvező események száma osztva az összes lehetséges esemény számával) a modern matematika másként fogalmazza meg. A matematika a valószínűséget nem a bekövetkezés relatív gyakoriságának segítségével értelmezi, hanem definiáló axiómákkal .
A matematikában a valószínűség fogalma ugyanis nem azonos a szó köznapi jelentésével! Ugyanakkor ezek az axiómák a relatív gyakorisággal kapcsolatban vannak, annak lényeges tulajdonságait absztraháljuk segítségükkel. A valószínűség és a relatív gyakoriság közötti kapcsolat az, hogy ha egy kísérletet egymástól függetlenül végtelen sokszor megismételnénk , akkor a bekövetkezés relatív gyakorisága minden eseményre a megfelelő valószínűséghez tartana. Ezt mutatja be a 4.1. ábra - A relatív gyakoriság és a valószínűség kapcsolata.
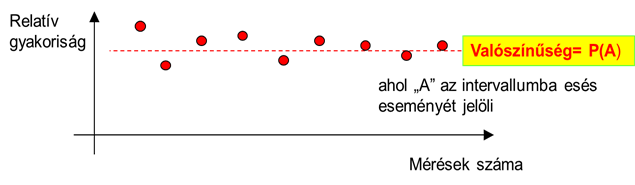
Fontos ugyanakkor hangsúlyozni, hogy a fent ábrázolt összefüggés nem azt jelenti, hogy a relatív gyakoriság limese (analízisbeli határértéke) a valószínűség lenne. E jelenség mögött egy másfajta konvergencia húzódik meg, amelyet sztochasztikus limesnek neveznek.
Az ábrán látható, hogy a relatív gyakoriság maga is valószínűségi változó , és a mérések számának növelésével, ideális esetben, csillapodik a relatív gyakoriság ingadozása. Az ábrán a valószínűséget az angol „probability” kifejezés miatt jelöltük a valószínűség számításban szokásos „P” betűvel.
Kolmogorov munkásságára alapozva a valószínűséget halmazelméleti alapon közelítik meg. Eszerint a P(A) valószínűségek az eseménytér halmazain adott halmazfüggvénynek, a valószínűségfüggvénynek értékei. Ez a függvény valószínűség eloszlást definiál az eseménytérben. A „T” halmaz a méréselméletben egy adott kísérlethez tartozó eseménytér , más kifejezéssel valószínűségi alaphalmaz . A „T” eseménytérben értelmezett, mérhető „x” függvényt valószínűségi változónak nevezzük. A valószínűségi változó értékkészletének részhalmazain ennek révén létesített valószínűség eloszlást az „x” valószínűségi változó eloszlásának nevezzük.
A méréstechnikában az „x” változó minden mintavételi értékét egy elemi eseményt definiáló mérési eredménynek feleltethetjük meg. Az adott kísérlethez tartozó valószínűségeket a valószínűségi változó egyértelműen meghatározza.
A témával mélyebben foglalkozni kívánók számára a Prékopa A.: Valószínűségelmélet című munkáját is [4.2.] ajánljuk.
4.3. Eloszlásfüggvény, sűrűségfüggvény
A relatív gyakoriság hisztogramon ábrázolható. A vízszintes tengelyen állandó, vagy változó Δx osztályszélesség, a függőlegesen a relatív gyakoriság jelenik meg. A hisztogramon látható négyszögek (oszlopok) területe a relatív gyakoriságnak felel meg:
|
|
(4.2) |
Az összefüggésben megjelenő f(x) függvény a sűrűségfüggvény . Definíciószerűen az f(x) sűrűség függvényt az F(x) eloszlásfüggvényből származtatják. Legyen „x” folytonos valószínűségi változó eloszlásfüggvénye F(x), és ha ez a függvény deriválható, akkor a sűrűségfüggvény:
|
|
(4.3) |
minden xi értékre.
Az „x” változó [-∞, xi] tartományban való előfordulásának valószínűsége az alábbi összefüggéssel számítható:
|
|
(4.4) |
A P(x≤xi) valószínűség tehát a valószínűségsűrűség-függvény értéke xi helyen.
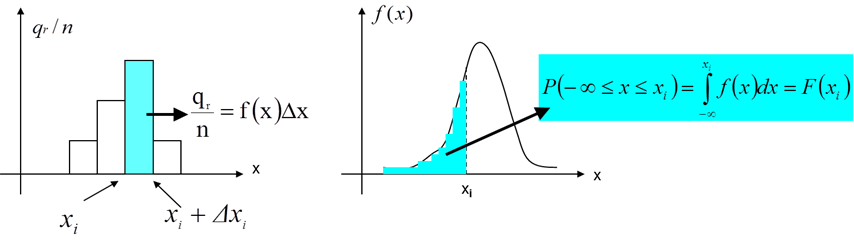
Belátható, hogy a valószínűségi változó a [-∞,+∞] tartományban bizonyosan megtalálható, és az alábbi összefüggés rendkívüli fontossággal bír a számítások során:
|
|
(4.5) |
Továbbá a fentiek alapján:
|
|
(4.6) |
A fenti valószínűségszámítási definíciók méréstechnikai alkalmazása során fontos, hogy tisztán lássuk az integrálási határokat. A méréstechnikában általában az a kérdés, hogy egy olyan adott tartományban keressük egy változó előfordulásának valószínűségét, amely tartomány alsó határa nem „-∞”. Ezért, ha azt vizsgáljuk, hogy egy változó (mérési adat) mekkora valószínűséggel fordul elő az [a, b] tartományban, akkor az alábbi összefüggést kell valamilyen formában alkalmaznunk:
|
|
(4.7) |
4.4. Egydimenziós eloszlások elméleti és empirikus paraméterei
Ha tehát az előbbiek szerint az „x” egydimenziós, folytonos valószínűségi változó, amint az a mérési adatok esetében is jellemző, akkor a változó f(x) sűrűségfüggvényének elméleti, várható értékét az alábbi képlettel lehet meghatározni:
|
|
(4.8) |
Jelölésként a szakirodalomban mind az „E”, mind pedig az „M” betű előfordul. Az utóbbi arra utal, hogy a várható érték más néven az első centrális momentum. Ugyancsak előfordul a „ξ” szimbólum mellett a „μ” jelölés is.
Ugyanezen változó varianciáját (szórásnégyzetét) pedig a következő összefüggéssel definiálják:
|
|
(4.9) |
Fontos tudni, hogy „E{x}” és „D2{x}” nem függvényei „x”-nek, hanem ezek olyan paraméterek, amelyek az „x” valószínűségi változó eloszlásának két fontos tulajdonságát jelenítik meg. A matematika nyelvén kifejezve ezek un. funkcionálok . A változó eloszlásának elhelyezkedésére az „x” tengely mentén az E{x}, és az „x” változó szóródásának mértékére a D2{x} ad jellemzést. Az egydimenziós eloszlásoknak további tulajdonságainak leírására szolgálnak még más paraméterek is, úgymint a „ kvantilisek ”, amelyek egyik formája a „medián”, vagy a „ferdeség” és a „lapultság” mérőszámai. Különböző szakterületeken (biológia, szociológia, statisztika, stb.) e további paraméterek segítségével a vizsgált jelenségek nélkülözhetetlen jellemzését biztosítják.
A méréstechnikában az empirikus (tapasztalati úton) szerzett adatok feldolgozása során nem a fenti elméleti paraméterekkel, hanem empirikus paraméterekkel dolgozunk, amelyeket más összefüggésekkel nyerhetünk. Előfordul természetesen, hogy korábbi tapasztalatok alapján ismert a valószínűségi változó f(x) sűrűségfüggvénye, vagy egy gyártási folyamatban, a műszaki rajzon rögzített (előírt) egy várható érték. Ez utóbbi esetben például az lehet a kérdés, hogy a munkadarab vizsgált mérete a gyártmányok ellenőrző mérése során milyen empirikus átlagértéket mutat, és ez milyen mértékben tér el az előírt értéktől.
Az átlag az empirikus eloszlást jellemző paraméter:
|
|
(4.10) |
Az átlag meghatározása után már sor kerülhet a tapasztalati (empirikus) szórás, vagy a korrigált tapasztalati szórás kiszámítására is. Ezek ugyancsak paraméterek:
Tapasztalati szórás:
|
|
(4.11) |
A képletben „δ” az abszolút hibát jelöli. Az összefüggés alkalmazása kellő óvatosságot igényel. Az átlagértékhez viszonyítva kis eltérések és nagyszámú mérési adat esetében mutat elfogadható egyezést a tapasztalati szórás és a korrigált tapasztalati szórás értéke. Nincs tehát általánosan érvényes szabály, de megjegyezzük, hogy statisztikai szempontból a „nagyszámú” adat 100-nál többet jelent.
A mindennapos mérési gyakorlatban használatos paraméter a korrigált tapasztalati szórás :
|
|
(4.12) |
A „szabadságfok” n-1, hiszen az átlag számításához már felhasználtunk „n” mérési adatot, és a fenti képletben szerepel az „n” adatból kiszámított átlag maga is.
Bizonyos feltételek teljesülése mellett használatos a méréstechnikában az átlag szórása is. Ha több, legalább 3 mérési sorozatot végeztünk el, és a sorozatok hossza egyenként legalább 10, továbbá az egyes sorozatok szórása kellő mértékben megegyező, akkor lehetséges a teljes minta szóródásának jellemzésére az átlag szórását is megadni. A mérési sorozatokból ugyanis külön-külön meghatározható egy-egy „xi” átlagérték. Ezek az átlagok maguk is valószínűségi változók, de nyilvánvalóan kisebb mértékben szóródnak, mint az egyes adatok.
Az átlag diszperziójának meghatározását a következő levezetésben láthatjuk, ha a leírt feltételek teljesülnek:
|
|
(4.13) |
A (minimálisan) három átlagértékből meghatározható az átlagok átlaga és az átlag szórása is. Az átlag szórása kisebb bizonytalanságot eredményez, mint a teljes minta szórása.
Az átlag szórásának becslése tehát a tapasztalati szórással és a korrigált tapasztalati szórással történhet, ha a megfelelő feltételek teljesülése adott:
|
|
(4.14) | |
|
|
(4.15) |
4.5. Normál eloszlás, vagy Student eloszlás
A normál eloszlás sűrűségfüggvényében két paraméter (funkcionál) látható, μ „várható érték” és σ „szórás”. Ezek becslésére szolgál az átlag és a tapasztalati szórás.
Mindenekelőtt fel kell tenni a kérdést, hogy a mérési eredményeinkből számított átlagérték és a tapasztalati szórás mennyire adnak megbízható információt a valóságról?
|
|
(4.16) |
Láttuk, hogy mérési sorozatok esetében az átlagok átlagával becsüljük a várható értéket.
A szórást általában sajnos nem ismerjük, helyette a korrigált tapasztalati szórást alkalmazzuk az eredményben , a kiterjesztett bizonytalanság meghatározásához. Az eredmény szokásos alakjaival a (2.9. szakasz - Az eredmény szokásos alakja) fejezetben találkozhattunk. Az eredményben két fajta bizonytalanság becsléssel dolgozhatunk (A és B típus), az eredmény forma egységesítését nemzetközi szabványok írják elő.
Az eredményben látható a kiterjesztett bizonytalanság faktora, amelyet az ipari méréstechnikai előírások 95 %-os konfidencia (megbízhatósági) szintre általában k=2 értékben határoznak meg. Joggal felmerül a kérdés, miért éppen ez az előírásokban javasolt érték?
A statisztikai táblázatokból látszik, hogy n=30 darabos minta esetében, Student-eloszlást feltételezve, a bizonytalansági intervallum meghatározásához szükséges faktor 95 %-os konfidencia szinten jó közelítéssel 2. A normál eloszlás faktora nem függ a minta számától, és ismeretes, hogy 95,45 % esetén értéke éppen 2. Az összehasonlíthatóság érdekében, a következő ábrán látható a két eloszlás típushoz 95 %-os konfidencia szinten tartozó faktorok értéke. Az is látható egyúttal, hogy Student eloszlás esetében nem várható a bizonytalansági tartomány jelentősebb csökkenése, ha a minta nagyságát 30-ról 100-ra növeljük, és közben megtartjuk a 95 %-os konfidencia szintet.
Az elvégzendő munka mennyisége nincs arányban a remélhető „hozammal”.
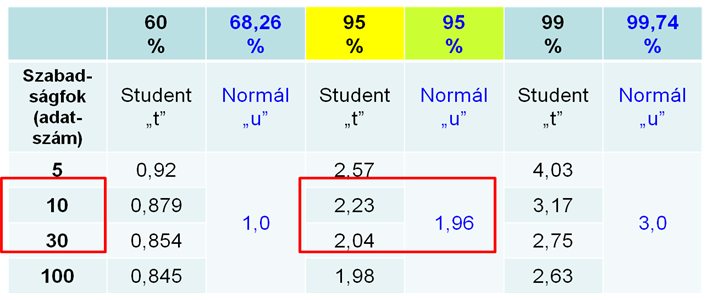
Látva a faktorok a (4.3. ábra - Jellegzetes konfidencia szintekhez tartozó faktorok) ábrán kiragadva bemutatott értékeinek feltűnő különbözőségét, joggal merül fel a kérdés: Milyen esetben feltételezhető normál és mikor Student eloszlás? Lehet a mintából következtetni az eloszlás típusára és paramétereire?
A gépészeti méréstechnikában alapvetően két eloszlás típussal találkozunk, a normál eloszlással és a Student eloszlással . Tapasztalható ugyanakkor, hogy a mérésekkel foglalkozó szabványok, előírások gyakran indoklás nélkül feltételezik a normál eloszlást a mintákra. Ez a feltételezés a központi határeloszlás tételen alapszik. A központi határeloszlás tétel azt mutatja meg, hogy nagyszámú, független valószínűségi változó összegének eloszlása közelítően normális eloszlást követ, ha ezen összeg minden egyes tagja külön-külön elhanyagolhatóan kicsiny az összeghez képest.
A tételre tipikus alkalmazási példaként ugyanis a véletlen mérési hibákat szokták felhozni. A mérési eredményre elméletben „végtelenül” sok, egymástól független zavaró, véletlenszerű tényező gyakorol hatást. Ezen összetett hatások eredményeként alakul ki a véletlen mérési hiba, és a gyakorlat azt igazolja, hogy az esetek túlnyomó többségénél a véletlen hibák normális eloszlást követnek.
Ha azonban a véletlen hatások nem összegződnek, hanem például szorzódnak, akkor már csak az adott mennyiség logaritmusa lesz megközelítően normális eloszlású.
Az eloszlás típusának ellenőrzésére statisztikai próbák léteznek, ezzel a témakörrel ebben a fejezetben később röviden foglalkozunk.
A gépészeti méréstechnikai gyakorlatban sokszor előfordul, hogy a rendelkezésre álló, viszonylag kisszámú adat miatt, tudományos módszerrel nem igazolható megnyugtatóan a normál eloszlás hipotézise. A Gauss-féle normál eloszlás mellett ezért kell ismerni a „t”, vagy Student eloszlás tulajdonságait is. A véletlen „x” változóra Gauss-féle eloszlást feltételezve, W. S. Gosset 1908-ban publikálta az un. „t” paraméter sűrűség és eloszlás függvényét. A „Student” elnevezés onnan ered, hogy Gosset ezen a szerzői néven jelentette meg munkáit. A „t”-eloszlás összefügg a standardizált normál eloszlással, ott, az „u” veszi át a „t” paraméter szerepét.
Ugyanakkor a gyakorlat számára érdemes tudni, hogy un. nagy elemszámok esetén, pl. 100 felett, már jogos lehet a normál eloszlás feltételezése, ha egymástól független tényezők befolyásolják a mérési hibát, és ennek alapja a központi határeloszlás tétel. Nincs éles határvonal az elemszám tekintetében, de ha – és a gépészetben ez a gyakoribb eset – nem áll rendelkezésre „nagyszámú” minta, azaz a mérési adatok száma jóval 50, pontosabban 30 alatt van, akkor járunk el helyesen, ha Student eloszlást feltételezünk. Így ugyanolyan konfidencia szint mellett nagyobb lesz a bizonytalansági tartomány, de kisebb a tévedés kockázata.
4.6. Az eredményképlet konfidencia intervallumának meghatározása
Empirikus (gyakorlati) mérési adataink alapján a várható értéket nem tudjuk meghatározni, hiszen láttuk, hogy ehhez ismerni kellene az f(x) sűrűség függvényt, és „végtelen” számú mérést kellene végrehajtani. Ezért természetesen felmerül a kérdés, hogy ebben az esetben miként lehet az átlag és a várható érték közötti eltérést megbecsülni? A várható értéket „X”-szel jelöljük. A becslés „bizonytalansági tartománya” lesz adott valószínűségi szinten a konfidencia intervallum, amint a (4.4. ábra - A konfidencia intervallum szemléltetése) ábrán látható. Sőt, tovább is lépünk. Az átlag ebben az esetben az átlagok átlaga lesz, azaz a számegyesen látható x1, x2, és x3 értékek egy-egy részhalmaz átlagai. Láttuk ugyanis a (4.4. szakasz - Egydimenziós eloszlások elméleti és empirikus paraméterei) fejezetben, hogy a várható érték legjobb becslését az átlagok átlaga adja, és az átlag szórása kisebb, mint egy részhalmaz adatainak szórása. A konfidencia intervallum szemléltető ábrája Halász G. előadási anyagának alapján készült.
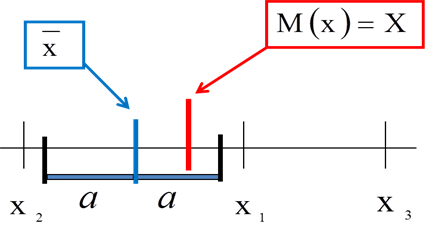
A konfidencia intervallum, akár csak az átlagérték, véletlen helyzetű, ezért csak azt tudjuk megadni, hogy „X” az adott tartományon belül mekkora valószínűséggel helyezkedik el. Az átlag körül rajzolható egy „a” sugarú intervallum, amely adott „p” valószínűséggel tartalmazza majd a várható értéket.
|
|
(4.17) |
Méréstechnikai feladtatok kiértékelése során gyakran másként fogalmazzuk meg a feladatot, de a lényeg nem változik. Meg kell keresnünk egy adott konfidencia szinthez tartozó „a” értéket.
A megoldáshoz első lépésben kissé átrendezzük az összefüggést:
|
|
(4.18) |
A továbbiakhoz szükséges két esetet megkülönböztetni:
Ismert a minta σ szórása (korábbi mérések, stb. alapján)
A szórás ismeretlen, a minta alapján kell becsülnünk: s*
Ha ismert a minta szórása, akkor a fenti összefüggésben osztunk a korábbiakban már megismert átlag szórásával (ld.: 4.4. szakasz - Egydimenziós eloszlások elméleti és empirikus paraméterei fejezet):
|
|
(4.19) |
A következő lépésben olyan jelöléseket vezetünk be, amelyeket a későbbiekben még alkalmazni fogunk. A szakirodalomban kétféle jelöléssel találkozhatunk, „λ” helyett gyakran „u” szerepel, ha az eloszlás normális.
|
|
(4.20) |
Megfordítható az egyenlőtlenségben középen álló összefüggés számlálója
|
|
(4.21) |
mert a kifejezésből adódó érték egyik esetben az alsó, a másikban a felső határhoz esik közelebb. A táblázatokban ugyanakkor az eltérés (hiba) szabályos alakja szerepel, ez pedig a második változat.
Ha feltételezhető, hogy az „x” változó normál eloszlású, akkor a fentiekkel juthatunk el az un. standardizált normál eloszláshoz, amely egyparaméteres, a paraméter u, vagy λ. Többféle változatban és jelöléssel látható ez a szakirodalomban, és a szórás lehet az átlag szórása is:
|
|
(4.22) |
A következő ábrán a normál eloszlás sűrűségfüggvénye és az eloszlásfüggvénye van ábrázolva úgy, hogy a standardizált normál eloszlás paraméter értékeit piros színnel jelöltük.

Ha a szórás ismeretlen, és a minta alapján a korrigált tapasztalati szórással (s*) becsüljük a szórás elméleti értékét, akkor η-ról sem állíthatjuk, hogy normál eloszlású, ezért η* jelölést kap. Ezzel az egyenlőtlenségben látható kifejezés az alábbi alakú lesz:
|
|
(4.23) |
A (3. fejezet - Mérési hibák) fejezetben, a hibák bemutatásánál már említettük, hogy W. S. Gosset igazolta, hogy η * (más jelölése „t” ) eloszlása kis mintaszámok esetében jelentősen eltér a normálistól. A λ st vagy t faktor függ a szignifikancia szinttől és a mérések számától. A szabadsági fok „DF” eggyel kevesebb, mint a minta elemszáma. A különbség jelentős, mert a normál eloszlás esetében a faktor független az elemszámtól.
Összefoglalva a konfidencia intervallum „a” sugarának meghatározását a két esetre az alábbiakat állapítjuk meg:
Ha a szórás ismert, és normál eloszlást feltételezhetünk, akkor a konfidencia intervallum sugara csak a konfidencia szinttől függ. Adott „p” valószínűséghez megkeressük F(u) értékét (más jelöléssel Φ(λ)), és ezzel „a” értéke kiszámítható:
|
|
(4.24) |
Ha a kisszámú adat áll rendelkezésre, és szórás ismeretlen, becslésére a s* korrigált tapasztalati szórást alkalmazzuk, akkor adott „p” valószínűség és a szabadságfok (DF) ismeretében (DF=n-1) kiválasztjuk λSt, vagy „t” értékét, és az alábbi összefüggéssel számolunk:
|
|
(4.25) |
A „λ”faktor két tényezőtől való függését szokás a következőképpen jelölni: λ(p, n-1).
4.7. Statisztikai próbákról röviden
A következőkben G. A. Korn és T. M. Korn: Matematikai kézikönyv műszakiaknak c. [4.1.] munkájára támaszkodva összefoglaljuk azokat a próbákkal kapcsolatos legfontosabb ismereteket, amelyek a méréselmélet és méréstechnika szempontjából fontosnak tartunk.
Gyakori feladat a méréstechnikában annak eldöntése, hogy a mért adatok eloszlásával kapcsolatban egy „nullhipotézis” (kiinduló feltételezés) „kiállja-e” a próbát.
Paraméteres próba:
Ismert az eloszlás, csak az eloszlásra jellemző paramétereket kell ellenőrizni. A próba elutasítja a hipotézist, ha a minta egy előre kijelölt kis valószínűségű tartományba esik.
Nemparaméteres próba:
Az elméleti eloszlásfüggvény paraméterekkel nem kifejezhető tulajdonságaira irányul, ilyen pl.: két eloszlás azonossága, két valószínűségi változó függetlensége. Különösen előnyös a méréstechnikai gyakorlatban, mert nem követeli meg a minta sűrűségfüggvénye alakjának ismeretét.
A próba egy „ null-hipotézis ” (jele: H 0 ) felállításával indul.
A hipotézis vizsgálat során lényegében arról van szó, hogy az adott minta (mérési adatsor: X1, X2,…Xn) alapján elfogadjuk, vagy elvetjük-e a „H 0 ” feltételezést , hipotézist . Ezt nevezi a szakirodalom statisztikai próbának.
A feltételezés, idegen szóval hipotézis (jelölése „H”) lehet egyszerű és összetett. Az „egyszerű” hipotézis a vizsgált eloszlás paramétereinek μ, σ, … stb. egy-egy meghatározott értékét μ=μ0, σ=σ0, stb., azaz a paramétertér egy pontját jelöli ki. Az összetett hipotézis a μ, σ, … stb. pontok egy halmazát, illetve tartományát jelöli ki a paramétertérben.
Fejezetünkben a legegyszerűbb forma, az egyszerű hipotézis vizsgálatával foglalkozunk.
A hipotézist empirikus (kísérleti úton nyert) adatok alapján ellenőrizzük. A statisztika tudományterülete definiált egy S c kritikus tartományt, amely a statisztikai próbához tartozó azon pontok halmaza, amelyek esetében a H hipotézist elutasítjuk, ha bebizonyosodik mintáról, hogy elemei az S c –hez tartoznak. Más mintapontok esetén a hipotézist elfogadjuk.
Megjegyzés: Az elfogadás, illetve elutasítás még elvileg végtelen elemszámú minta esetén sem jelenti azt, hogy a H hipotézis teljesülése logikailag bizonyítást nyert, illetve, hogy a H nem teljesülése bizonyított.
A hipotézissel kapcsolatban következő ábrán látható esetek lehetségesek (Az ábra G. A. Korn és T. M. Korn: Matematikai kézikönyv műszakiaknak c. könyvéből származik):
H igaz, és a próba elfogadja. Ennek valószínűsége „1-α”
H hamis, és a próba elutasítja. Ennek valószínűsége „1-β”
H igaz, de a próba elutasítja (elsőfajú hiba). Ennek valószínűségét „α” jelöli.
H hamis, de a próba elfogadja (másodfajú hiba). Ennek valószínűségét „β” jelöli.
A 4.6. ábra - Hipotézis és ellenhipotézis egy feltételezett eloszláson egy feltételezett eloszlás esetére a fenti eseteket szemlélteti.
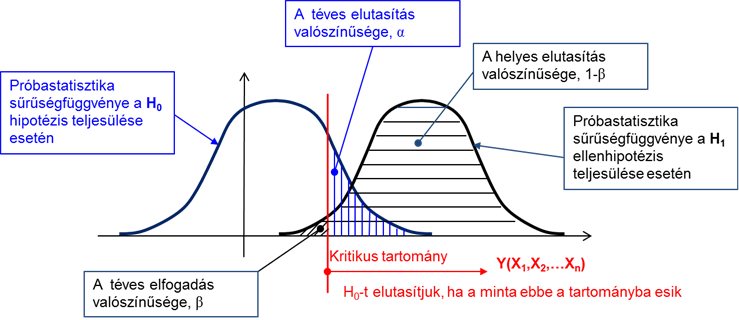
Az ábrán H0 jelöli az un. null hipotézist (kiindulási feltételezés) míg H1 az alternatív, vagy ellenhipotézist. Ugyancsak jól látható, hogy a sűrűségfüggvények alatt jól elkülöníthető módon, α, β görög betűkkel és ezek komplementerjeivel (1-α, 1-β) területeket jelöltünk meg. Ezek a területek a fejezet elején megismert definíció szerint valószínűséget jelentenek. Az α és β szimbólumokkal jelzett valószínűségek mutatják meg a hipotézisvizsgálat során, hogy mennyire jelentős, idegen kifejezéssel szignifikáns a feltételezés és a mérési adatokból nyert „valóság” közötti eltérés?
A méréstechnikában és a műszaki életben sokszor előfordul, hogy az elméleti sokaságnak paraméterekkel kifejezett tulajdonságait kell hipotézisként vizsgálni. Ilyen paraméterek lehetnek például a várható érték és a szórás, μ=μ0, σ=σ0, …stb., miközben a minta tulajdonságait empirikus adatok felhasználásával, az μ=y1(X1, X2, … Xn), σ=y2(X1, X2, … Xn) becslések írják le.
A paraméterek esetében, amint az előzőekben már láttuk, az indexben szereplő „0” jelöli a hipotetikus értéket, az index nélküli paraméter pedig a mintából nyert adatokat.
A H0 ≡ [μ=μ0, σ=σ0, …] egyszerű hipotézist adott „α” szignifikancia szinten elutasítjuk (tehát az eltérés szignifikáns), ha y értéke kívül van egy [yP1, yP2,] elfogadási intervallumon, amelyre
|
P[y P1 ≤ y ≤ y P2 ,] = P 2 – P 1 = 1-α |
(4.26) |
Az így definiált próbákat szignifikancia vizsgálatnak nevezik a statisztikában.
Illusztrálás céljából bemutatunk néhány jellegzetes, a méréstechnikában gyakran előforduló statisztikai próbát:
F-próba (paraméteres próba)
A próba alkalmazásával eldönthető, hogy két normális eloszlású statisztikai sokaság szórása azonos-e, vagy nem?
χ 2 -próba (paraméteres próba)
A méréstechnikában lényegében alább felsorolt vizsgálatokra alkalmazzák:
Normalitás (illeszkedés vizsgálat, azaz a várt értékek összehasonlítása a megfigyelt adatokkal)
Függetlenség (Két adatsor független-e egymástól?)
Homogenitás (Az alapsokaságból két eltérő időben vett minta között van-e kapcsolat?) Ilyen vizsgálatra például akkor lehet szükség, ha egy gyártóberendezés esetében a beállításokból, vagy a szerszámkopásokból eredő hibák után kell nyomozni.
Egymintás t-próba (paraméteres próba)
Különösen fontos a szerepe a minőség-ellenőrzés területén. Segítségével eldönthető, hogy egy mintasokaságból számított átlag szignifikánsan különbözik-e egy adott értéktől (Pl. a műszaki dokumentációban megadott mérettől)?
Legyen vizsgálat tárgya, hogy egy „n” elemszámú minta esetében teljesül-e a H0 hipotézis, miszerint az adatokból számított átlag megegyezik az előírt értékkel, vagy az eltérés szignifikáns (lényeges)? A t-eloszlás szabadságfoka ebben az esetben f=n-1. A tp érték előírt szignifikancia szinten táblázatból vehető, míg a μx az előírt érték.
|
|
(4.27) |
Ha |t| ≥ tp , akkor a H0 hipotézist el kell vetni Ha |t| < tp akkorH0 hipotézist megtartjuk.
Kétmintás t-próba (paraméteres próba)
Kalibrálás során előfordulhat a kérdés, hogy két külön mintában egy-egy változó átlagai szignifikánsan különböznek-e egymástól? (Pl.: Ugyanazt a mintát két különböző műszerrel mérték.)
Vizsgáljuk meg azt a H0 hipotézist, miszerint az „n” és az „m” elemszámú minták átlagértékei adott konfidencia szinten lényegesen (szignifikánsan) nem különböznek egymástól. A szabadságfok ebben a kétmintás próbában f=n+m-2, és táblázatból keressük meg az előírt konfidencia szinthez és az f szabadságfokhoz tartozó tp értéket.
|
|
(4.28) |
Ha a számítás alapján |t| ≥ tp akkor a H0 hipotézist elvetjük. Ha |t| < tp akkor a H0 hipotézist megtartjuk.
Egymintás u-próba (paraméteres próba)
Az átlag és a várható érték közötti különbség a mintavétel hibája miatt van, vagy szignifikáns az eltérés? A „σ” ismert, pl. korábbi mérésekből. Hasonlít a t-próbára.
Jelentőség ugyancsak a minőségellenőrzésben van, ebben az esetben a várható érték alatt a műszaki dokumentációban megadott értékeket kell érteni.
Példaképpen első lépésben felállítjuk a H0 nullhipotézist: Szignifikáns-e az átlag és az előírt érték közötti eltérés? Legyen „σ” a minta (itt sorozat) ismert szórása, és μx az ismert (itt: előírt) várható érték, esetünkben a műszaki rajzon szereplő hosszméret, az átlagértéket pedig a kész darabokon végzett mérésekkel, az „n” elemszámú minta alapján határoztuk meg.
Behelyettesítve az u-próba összefüggésébe, amely tulajdonképpen ismert a konfidencia intervallum számításából
|
|
(4.29) |
és megvizsgáljuk, hogy a kapott érték hogyan viszonyul az alábbi táblázatban szereplő feltételekhez?
Ha a kiszámított értékre teljesül valamelyik ellenhipotézis, akkor az ellenhipotézis elfogadásával elvetjük nullhipotézist, a téves elutasítást valószínűsítő „α” szinten. A szignifikancia szinteket a táblázat első oszlopában tüntettünk fel.
|
Szignifikancia szint |
Baloldali ellenhipotézis |
Kétoldali ellenhipotézis |
Jobboldali ellenhipotézis |
|---|---|---|---|
|
0.05 |
u < -uα = -1,64 |
u < - uα/2 = -1,96 vagy 1,96 = uα/2 < u |
1,64 = uα < u |
|
0.01 |
u < - uα = -2,32 |
u < - uα/2 = -2,57 vagy 2,57 = uα/2 < u |
2,32 = uα < u |
|
0.005 |
u < - uα = -2,57 |
u < - uα/2 = -2,81 vagy 2,81 = uα/2 < u |
2,57 = uα < u |
Ha a számítással kapott „u” értékre nem teljesül valamelyik H1 ellenhipotézis, akkor szakszerű kifejezéssel élve „meggyőző ellenhipotézis H1 hiányában” megtartjuk H 0 -t.
Irodalmak
[4.1.] Matematikai kézikönyv műszakiaknak. Műszaki Könyvkiadó. 1975.
[4.2.] Valószínűségelmélet műszaki alkalmazásokkal. Műszaki Könyvkiadó. 1974.
5. fejezet - Mérés és modellezés
5.1. A modellezés szerepe a metrológiában
A mérés, legyen szó bármilyen fizikai, kémiai, időben állandó, vagy változó mennyiségekről, a legáltalánosabban megismerési folyamatként fogható fel. Ebben a folyamatban a modellalkotás döntő jelentőséggel bír a tevékenységünk minősége szempontjából.
A modern rendszerszemlélet kialakulásával összefüggésben, az 1960-as évektől kezdődően, alig találunk olyan mértékadó méréselméleti, vagy rendszertechnikai és irányításelméleti szakirodalmat, amelyben a megismerési tevékenység középpontjában ne a modellalkotás állana. A tudománytörténet Galileo Galileit tartja a modellezés atyjának, mivel pl. a szabadesést lejtőn való mozgatással modellezve mutatott utat a tudományos megismerés alapvető módszeréhez, a modellezéshez és az absztrakcióhoz. A mérés és modellezés elválaszthatatlanságának a Schnell László által szerkesztett Jelek és rendszerek méréstechnikája című, alapvető fontosságú magyar nyelvű, összefoglaló méréselméleti és méréstechnikai munkában két fejezetet szenteltek a szerzők [5.1.] .
A modellezés fontosságát jelzi, hogy a metrológiában (méréstudomány) már magának a mérésnek is legalább négy modellje ismert és használatos, amelyekkel magát a mérési tevékenységet kísérlik meg leírni.
Ez a négy modell a következő:
Hagyományos, un. „szabványos” modell
Folyamat modell
Valószínűségelméleti modell
Információelméleti modell
A négy modellt kifejezetten méréselméleti megközelítésként ismertetjük. Ezek az elméletek szolgálnak műszerek és mérőrendszerek tervezésének alapjául. A négy modell taglalása különböző terjedelmű , mert a valószínűségelméleti modell önmagában többféle változatot is magába foglal, aszerint, hogy milyen előzetes ismeretekkel rendelkezünk a mérendő mennyiségekről, vagy a mérőrendszer átviteli tulajdonságairól.
Mind a négy modell más-más aspektusból világítja meg a mérési tevékenység komplexitását. Egyik modell sem kizárólagos, mindegyik ismerete elengedhetetlen feltétele a mérési tevékenység helyes megtervezésének, akár tudományos kutatásról, akár ipari ellenőrzésről van szó.
A „mi megközelítésünk” – tekintettel arra, hogy a szerzők mérnökök, valamint mérnökhallgatók számára készült a jegyzet, természetesen alapvetően mérnöki. A mérnökök vagy kutató tevékenységet végeznek, vagy az ipari termelésben vesznek részt, termékeket és gyártórendszereket terveznek, és a termelést irányítják. A mérés négy modellje közül az egyik az un. „folyamat modell”, amely a legszemléletesebben mutatja be azt, hogy a mérési tevékenység tudományos síkon a bennünket körülvevő „világ megismerésének” eszköze, ipari szinten pedig a minőségbiztosítás elengedhetetlen eszköze. Az (5.1. ábra - A mérési tevékenység modellezése folyamatként) ábrán látjuk a mérés folyamat modelljét, de „rejtetten” megjelenik az ábrán a hagyományos, szabványos meghatározás is, amely szerint a mérés tervszerű, összehangolt tevékenységek sorozata, amely arra irányul, hogy ismeretlen mennyiséget ismert etalonokkal hasonlítsunk össze.
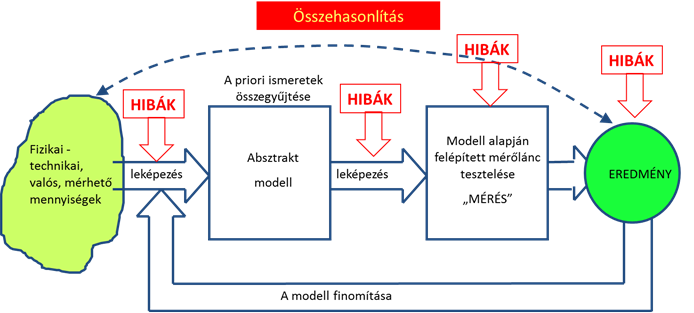
A gépészmérnöki szemléletet és megközelítést egyrészt a folyamat modell, másrészt az információelméleti modell tükrözi legjobban, míg a villamosmérnöki és informatikai szakmában a valószínűségelméleti modellt tekintik a legjobb általános leírásnak.
Az (5.1. ábra - A mérési tevékenység modellezése folyamatként) ábrán a mérendő mennyiségek halmazát és az eredményt eltérő színnel és formával jelöltük. Ezzel kívánjuk kifejezésre juttatni, hogy a fizikai technikai valóság teljes körű megismerése legfeljebb elméletben lehetséges, hiszen a jellemzőkre és a mérési tevékenységre ható, és azokat befolyásoló tényezők száma végtelenül nagy, erről a 4. fejezet - Mérés és valószínűség számítás fejezetben már volt szó. Valamennyi befolyásoló tényező gyakorlati megismerésére nincsenek eszközeink, de nem is lenne gazdaságilag indokolható minden hatótényező figyelembe vétele. Ezért minden eredmény leegyszerűsített, és valamilyen „pontossági szintű” – helyesebben hibákkal terhelt - modellje a valóságnak.
Érdemes kiemelni azt is, hogy az ábrán a hibák eredete is nyomon követhető. A hibákat a metrológia ugyanis háromféle szempont szerint csoportosítja: Eredetük, jellegük és megjelenési formájuk szerint. Az (5.1. ábra - A mérési tevékenység modellezése folyamatként) ábrán a hibák eredete is jól látható, a modellalkotástól a mérés kivitelezéséig és ellenőrzéséig. Eredetük szerint a hibák természetesen már a folyamat első fázisában, a modellalkotás során megjelennek és továbbiak lépnek be a mérési eljárás megválasztásából (ide tartozik a mérés fizikai elve és a mérési módszer), a mérés kivitelezéséből (eszközök jellemzői, mérési körülmények, stb.), végül a számításokból, az eredmény közléséből adódóan. A szakirodalom szerint a mérés „autonóm” (önálló) szakasza a modell alapján felépített mérőlánc tesztelése. Sajnálatos módon, a méréstechnikát sokan úgy képzelik el, hogy a méréstechnika egyszerűen csak erre az autonóm szakaszra korlátozódik, holott az a modellalkotástól és a kiértékeléstől elválaszthatatlan.
5.2. Modellalkotás
A bennünket körülvevő világ mérnöki szempontból megismerni kívánt töredék részét, a jelenségek közötti kapcsolatokat modellek segítségével kíséreljük meg leírni. A modellek nagyvonalakban három kategóriába sorolhatók: fizikai, esetleg kémiai modellek, funkcionális modellek és matematikai (absztrakt) modellek. A műszaki életben manapság használatos modellezési alapokat 1975-ben megjelent művükben Mesarovic és Takahara [5.2.] fektették le.
A fizikai modellek általános alkalmazása főként régebbi időkben volt elterjedt, ugyanakkor még ma is nélkülözhetetlenek az áramlástechnikai vizsgálatok esetében a kicsinyített, hasonlóság alapján megalkotott modellek. Ugyanakkor összetett mechanikai lengő rendszerek dinamikai vizsgálatának céljából már csak elvétve találkozhatunk analóg villamos áramkörökkel (analóg számítógéppel), hiszen a szilárdsági és dinamikai analízis területén szinte egyeduralkodóvá vált a végeselem módszer.
A funkcionális modellek mind a mai napig általánosan elterjedtek a mechanikában, valamint a mérés-és szabályozástechnikában. Ebben az esetben a vizsgálat alá vett rendszert felépítő elemeket idealizált szerepük alapján jelenítjük meg. Minden, alapozó mérnöki ismeretekkel rendelkező szakember tudja, hogy egy rugalmas szerkezeti elem sokféleképpen írható le, de a „legidealizáltabb” változat az, ha helyette egy rugót jelenítünk meg. Azonban sem a fémek, sem a műanyagok viselkedésének pontosabb leírása nem lehetséges egy ilyen módon. Fémek esetében minimálisan egy rugó és egy csillapítás párhuzamos kapcsolásával, de relaxációt és kúszást mutató, nemlineáris tulajdonságú elasztomerek esetében – bizonyos követelmények mellett - még ez a forma sem lenne elegendő.
A matematikai modellek absztrakciós lépések eredményeként jönnek létre. Ezeknek napjainkban kiemelt szerepük van, ami a számítástechnika fejlettségének köszönhető. A vizsgált rendszerekben a mérhető és nem mérhető mennyiségeket változók formájában jelenítjük meg, a rendszerre jellemző műszaki tulajdonságokat paraméterek (ezek állandóak és változóak lehetnek) formájában írjuk le. Tudjuk alapozó ismereteink alapján, hogy időben változó mennyiségek villamos jellé történő átalakítása és mérése nélkül bármely mechatronikai rendszer elképzelhetetlen, ezért a méréstechnika kiemelt fontosságú.
A mechatronikai rendszerek megtervezéséhez elengedhetetlen a négy matematikai modell-típus ismerete.
Ezek
a differenciálegyenlet (idő tartomány)
az átviteli függvény (operátor, vagy frekvencia tartomány)
az állapottér modell (idő és operátor tartomány) és
a logikai függvények.
5.3. A modellezés korlátai
A modell soha nem képes a valóságot teljes komplexitásában leírni. Mindig annak egy részét, vagy bizonyos aspektusait ragadjuk ki, esetenként leegyszerűsítjük a valóságot. A jelenségről alkotott fizikai elképzeléseink korlátozottak, sok a bizonytalansági forrás. A modell mindig célorientált. Bonyolultságát a megoldandó feladat jellege, a műszaki feltételek, az ésszerűség és gyakran az anyagi lehetőségek korlátozhatják. A mérnöki gyakorlatban a modellek a kutatást, a tervezést és az elemzést segítik, és ide sorolhatók a mérésekhez alkalmazott modellek is.
A modellezés során gyakran körül kell határolni a valós rendszernek azt a részét, amellyel az adott feladat megoldása érdekében foglalkoznunk kell. Ez a rész általában un. „zárt rendszert” képez, és ez a modellezési problémáink első forrása. A valóságban a műszaki rendszerek nem zártak , a környezettel és más rendszerekkel kölcsönhatásban állnak. Ezeket a hatásokat bizonyos mértékben természetesen figyelembe lehet, és kell is venni, de a teljesség igénye nélkül.
A méréstechnikában egy modell megalkotásához a vizsgálat kezdetén rendelkezésre álló ismeretek összességét „à priori” ismereteknek nevezik. A francia kifejezések a mérésügyben a XVIII. század végétől kezdődően igen elterjedtek, ennek kultúrtörténeti okait röviden a „Méréstechnika” c. TÁMOP által megjelentetett elektronikus jegyzetben érintettük [1.1.] . A modellezési és mérési munka végeztével ismereteink jelentősen bővülnek, és ezek következtében immár „à posteriori” információkkal is rendelkezünk. Az à priori ismeretek meghatározóak a modell minősége szempontjából, mert meghatározzák a modell típusát, bonyolultságát, a megkívánt pontosságot, és a költségeket, és ezek következtében magát a mérési eljárást és a mérés kivitelezését. A korábban ismertetett modellformákra közösen vonatkozik, hogy szükséges egy struktúra és szükségesek hozzá paraméterek. E tekintetben mindegy ugyanis, hogy fizikai, funkcionális, vagy matematikai modellről van szó
A legnagyobb probléma az, hogy az à priori ismeretek nem elegendőek a struktúra kiválasztására. Ebben még igen nagy a szerepe a mérnöki tapasztalatnak, a próbáknak és az un. mérnöki intuíciónak. A paraméterek becslésére és identifikációjára már objektívnek tekinthető módszerek állnak rendelkezésre.
A döntően, vagy kizárólagosan à priori ismeretekre támaszkodó modellalkotást „deduktív” szemléletnek, míg az à posteriori ismeretekkel, tehát kísérleti, mérési adatokkal operáló megközelítést „induktív” módszernek nevezik. Normál mérnöki gyakorlatban elvétve alkalmazzák kizárólagosan csak az egyik változatot.
5.4. A mérés hagyományos modellje és értelmezése
Az 5.1. szakasz - A modellezés szerepe a metrológiában fejezetben már röviden ismertettük a hagyományos megfogalmazást, amely szerint a mérés tervszerű, összehangolt tevékenységek sorozata, amely arra irányul, hogy ismeretlen mennyiséget ismert etalon mennyiségekkel hasonlítsunk össze. A mérés ezért fizikai vagy kémiai mennyiségek nagyságának jellemzése, a választott mértékegységben kifejezett számértékével. A mérési eredmény egy szám és egy mértékegység szorzata, amely az egységet és az egységhez való viszonyt fejezi ki. A mérési tevékenység csak akkor tekinthető befejezettnek, ha elvégeztük a kiértékelést és a hibaszámítást is.
5.5. A mérés folyamat modellje
A mérés második, un. „folyamat modellje” a deduktív és az induktív személet váltakozva történő alkalmazásán alapul. Ezt igen jól szemlélteti a korábban bemutatott 5.1. ábra - A mérési tevékenység modellezése folyamatként és az ebben az alfejezetben látható 5.1. ábra - A mérési tevékenység modellezése folyamatként.
Mind az 5.1. ábra - A mérési tevékenység modellezése folyamatként, mind pedig az (5.2. ábra - A mérés folyamat-modelljének részletezése) ábrán felismerhető, hogy a modellalkotás iterációs folyamat. A kitűzött célnak meghatározott bizonytalanság mellett eleget tenni képes modell, vagy eredmény csak több, pontosítást eredményező lépésben jöhet létre. Látható, hogy amennyiben a modell még nem a megkívánt bizonytalansági határokon belül „dolgozik”, akkor kiértékelést követően, három helyen lehet beavatkozni. A legegyszerűbb esetben „belép” az első visszacsatolás, növelni kell a mérések számát. Ha ez nem bizonyul elegendőnek, akkor hozzá kell nyúlni a mérési eljáráshoz (módszer és kivitelezés), és ha ez sem éri el a kellő hatást, akkor bizony az „à priori” modellel van baj.
Felül kell vizsgálni a modell specifikálásánál tett hipotéziseket, strukturális, vagy a paramétereket érintő módosításokat kell végrehajtani.
A mérnökhallgató évközi feladatainak megoldása során, de legkésőbb a szakdolgozat, vagy a diplomaterv elkészítésénél szembesül a folyamat modell lépéseivel. A gépészetben és a mechatronikában a műszaki munkák elsöprő többségénél ugyanis mérésekkel kell igazolni a téma kapcsán megalkotott elméleti modellek helyességét.
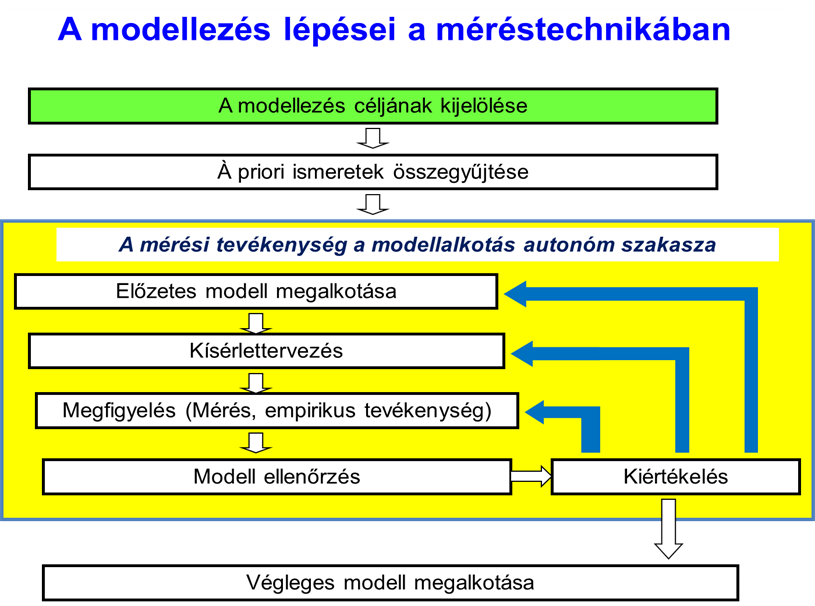
5.6. A valószínűségelméleti modell és sajátosságai a gépészetben
Az [5.1.] jelű, már korábban említett szakirodalmi munka arra törekszik, hogy jel- és rendszerelméleti alapon általános meghatározásokat adjon a modern méréstechnikában előforduló legtöbb feladatra. Már az első fejezetben megállapítja, hogy a mérés hagyományos értelmezése, „modellje”, miszerint a mérési eredmény egy szám és egy mértékegység szorzata, továbbá a mérési hiba az eredmény tényleges és ideális értéke közötti különbség, a napjainkban felmerülő mérési problémák jó részére nem alkalmazható. Példaként egy, a digitális rendszerek méréstechnikájában szokásos feladatot hoz fel, amikor egy digitális vezérlő belső állapotának felmérését kell elvégezni. Ebben a feladatban – és főként a villamosmérnöki gyakorlatban – nem egy mennyiség nagyságát kell megmérni, az eredmény nem is szám, és a mértékegység sem megszokott formájú.
Jegyzetünkben kísérletet teszünk arra, hogy a fent említett szakirodalomban ismertetett jel-és rendszerelméleti megközelítést kiterjesszük a gépészeti mérések világára is.
Az idézett szakirodalomi munka alapján a mérési folyamat a jel-és rendszerelméleti értelmezés szerint nem más, mint a leképezést megvalósító rendszer, azaz a mérőeszköz. A mérendő objektum a modellezés tárgya, a modell leírását az objektum bemenő és kimenő (információhordozó) jelei teszik lehetővé. A mérőeszköz feladata az információhordozó jelek begyűjtése és feldolgozása. A jelek feldolgozása egy műveletlánc, és az idézett munka a továbbiakban ezt tekinti mérési eljárásnak . A mérendő objektum jelei, mielőtt eljutnának a mérőeszköz bemenetére, különböző eredetű torzító hatásoknak, zavarásoknak vannak kitéve, olvashatjuk a munkában. Ennek a jelenségnek a matematikai leírására vezették be a jelátviteli csatorna fogalmát. Ezek szerint a jelátviteli csatorna kimenetén jelenik meg a mérőeszköz bemenetére kerülő „megfigyelt” jel. A mérőeszköz kölcsönhatásba kerül a mérendő objektummal, energia és információ átadás formájában. A mérőeszköz begyűjti a jeleket, és feldolgozza az ezek által hordozott információt. A jelfeldolgozás műveletlánc, amely a jeleket a mérés célkitűzésének megfelelő alakra hozza. Ez a jelfeldolgozás tehát az idézett munka szerint a mérési eljárás, amely műszaki teljességében egy mérőrendszerben mutatkozik meg, mert ebbe a fogalomba már a jellemzők informatikai feldolgozása is beleértendő.
Ebből a leírásból, megközelítésből kitűnik, hogy a mérőeszköz alatt villamos mennyiségeket (feszültség, áram, frekvencia, stb.) mérő műszert értenek.
Ezzel szemben a gépészeti mennyiségek mérésénél többnyire egy átalakítási láncolat segítségével jut el az információt hordozó villamos jel a jelfeldolgozó villamos egység, vagy villamos mérőrendszer bemenetére.
A valószínűségelméleti modellt a gépészet és a mechatronika esetében például úgy értelmezhetjük, hogy a jelátviteli csatorna reprezentálja azt az átalakítási láncolatot, amely a jellegzetes gépészeti mennyiségekből (elmozdulás, sebesség, gyorsulás, erő, szögelfordulás, szögsebesség, fordulatszám, szöggyorsulás, forgatónyomaték, nyomás, térfogatáram, hőmérséklet, stb.) mérhető villamos mennyiségeket állít elő. Ebben az esetben teljesen nyilvánvaló a valószínűségelméleti modellben szereplő torzítások és zavarások szükségszerű megjelenése, és hatásaikkal bizony komolyan kell számolnunk.
Elfogadva és alkalmazva az idézett jel-és rendszerelméleti, azaz valószínűségelméleti modellt a következő megállapításokat tehetjük a gépészet és a mechatronika területén jellemző mérési feladatokkal kapcsolatban.
Az a mérendő jellemző (paraméter) és az azt jelképező szimbólum – azaz c eredmény - között leképezésekkel teremtünk kapcsolatot. A mérés valószínűségelméleti modellje két fontos leképezést tartalmaz. A paraméter térben találhatóak a mérendő mennyiségek, a megfigyelési tér a paraméterek zajjal (torzítással) terhelt leképezésével jön létre, és itt találhatók a b megfigyelések. Ennek az első leképezésnek a tulajdonságait a jelkibocsátó rendszer és a megfigyelések közötti jelátviteli csatorna jellemzői határozzák meg, ennek elnevezése a csatorna karakterisztika .
A mérési eljárások a mérendő objektumon végzett b megfigyelések feldolgozásával állítják elő a mérési eredményt, c =f( b ) összefüggés szerint. Ha a mérés eredménye folytonos, tehát egy adott tartományban tetszőleges értéket vehet fel, akkor az eljárás tervezésében a becsléselmélet apparátusa alkalmazható. Ha megszámlálható (diszkrét) eredmény lehetséges, akkor a döntéselmélet módszereit kell alkalmazni. E jegyzetben a gépészetre jellemző folytonos jellemzők és az ezekhez rendelt folytonos eredmények kapcsolatára szorítkozunk.
Tehát a jelfeldolgozó egység (mérőműszer, mérőrendszer) bemenetére kerülő jelek feldolgozása révén jutunk az eredményhez. A jelfeldolgozás kifejezés igen sokféle műveletet takar, a matematikai műveletektől kezdve az erősítésen, az A/D átalakításon át a különféle szűrési feladatokig. A szűrést külön azért érdemes kihangsúlyozni, mert éppen a jel-és rendszerelméleti aspektusra alapozták a szűrők elméleti tervezését, gondolunk itt a Wiener és a Kálmán szűrőre.
A jelfeldolgozáshoz tartozik ebben a modellben a gépészeti mérések eredményeinek valószínűség számítási módszerekkel történő meghatározása. Mindez tehát a második leképezés során történik, és ennek révén jutunk a becslési térben az eredményhez. A becslő, vagy becslési eljárás olyan fizikai rendszert (műszert, mérőrendszert) modellez, amelynek bemenetén a megfigyelés, kimenetén az eredmény található.
Az (5.3. ábra - A mérés valószínűségelméleti modellje) ábrán az a , b , és c vektorok eltérő színűek és helyzetűek, szimbolizálva a zajok és torzítások, valamint a leképezések hatásait.
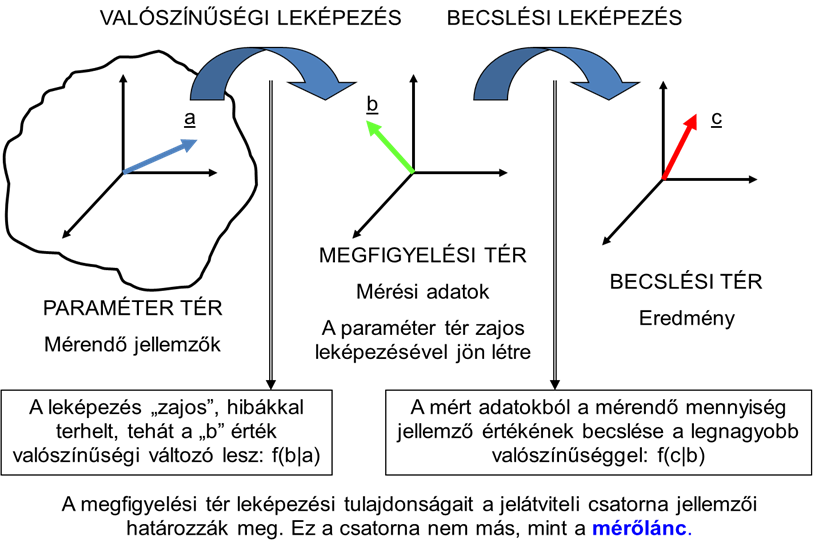
Feltételezzük, hogy a mérendő mennyiség véletlen változó, amelynek eloszlását az f( a ) függvény írja le. Értelmezésünk szerint, a gépészeti méréstechnikában legyen az első leképezés az a láncolat, amelynek révén tetszőleges fizikai mennyiségekből villamos jellemzőket hozunk létre. Ennek a láncolatnak az információ átviteli „képességét” nevezhetjük csatornakarakterisztikának . Az átvitel minőségét az f( b | a ) a feltételes sűrűség függvény írja le. A feltételes valószínűség megmutatja, hogy egy adott a paraméterhez milyen sűrűség függvénnyel rendelhető hozzá a b megfigyelt paraméter. A mérés elvégzése után természetesen már bővebb ismereteink vannak, így egy újabb feltételes valószínűséggel, amelyet f( a | b ) jelöl, már azt is le tudjuk írni a matematika nyelvén, hogy egy megfigyelt b paraméterhez a mérendő a paraméter milyen eloszlása van hozzárendelve. A valószínűség számítás nyelvén ez „à posteriori” (utólagos) ismeret, ami megfelel a valóságnak.
5.6.1. Becslési módszerek
A következőkben három olyan információelméleti módszert mutatunk be, amelyek az eredmény matematikai eszközökkel történő becslését teszik lehetővé – a becslési térben.
A becslési módszereket úgy állítjuk sorrendbe, hogy az első helyen a legtöbb „à priori” ismeretet igénylő módszer álljon, és ez után csökkenő előzetes ismeret szerint a Maximum Likelihood (ML), majd végül a „Legkisebb négyzetes hiba” (LMS) következzen.
5.6.2. Bayes-féle becslési módszer
A legtöbb előzetes ismeret a Bayes-féle becslési eljáráshoz szükséges. Ebben az esetben ismerni kell
a mérendő jellemző ( a paraméter) f( a ) sűrűségfüggvényét (eloszlását)
a mérendő jellemző és a megfigyelések közötti f( b | a ) feltételes valószínűség sűrűségfüggvényt
és a K( c , a ) költségfüggvényt.
A Bayes becsléshez szükséges, hogy a mérendő jellemző f( a ) eloszlásfüggvényének és a csatornakarakterisztikának ismeretében meghatározhassuk az à posteriori (utólagos) feltételes sűrűségfüggvényt. Ezen utólagos ismeret, azaz az f( a | b ) feltételes sűrűségfüggvény, rögzített (ismert) b megfigyelt érték mellett adja az a paraméter statisztikai leírását.
Az f( a | b ) feltételes valószínűség (utólagos tapasztalaton alapuló) a valószínűség számítás szabályainak alkalmazásával és a Bayes-becsléssel előre megadható, ha ismert a mérendő mennyiség sűrűségfüggvénye f(a) és a mérőrendszer csatornakarakterisztikája.
|
|
(5.1) |
Becslésnek a paraméter megfigyelése utáni legvalószínűbb ĉ értéket tekintjük. A becslésnek mindig lesz „H” hibája
|
H=ĉ – a |
(5.2) |
Tekintettel arra, hogy ez a hiba maga is változó, függ a „ c ” és „ a ” értékeitől, bevezetik az átlagos hiba fogalmát, és ez „R” jelölést kap.
A Bayes becslés – „költségfüggvények” alkalmazásával, amelyeket K( c , a ) jelöléssel látunk a következő képletben - az „ a ” paraméter olyan „ ĉ = c B ” becsült értékét keresi, amely az „R” hibát minimalizálja.
A költségfüggvény K( c , a ) fogalom itt tehát hibakritériumot, optimum kritériumot takar. A becslés átlagos hibája a költségfüggvénnyel (optimum kritérium) súlyozott à posteriori (utólagos) feltételes sűrűségfüggvénnyel a következő módon adható meg. Az átlagos hiba minimumát kell tehát keresni:
|
|
(5.3) |
Az ilyen módon kiszámítható R B minimális átlagos hibát Bayes-hibának nevezik. A becslési hiba látható a következő ábrán:
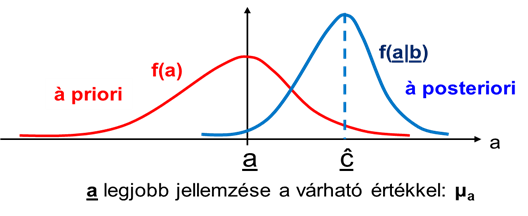
A „költségfüggvény” hatása két példán jól szemléltethető. Ha az abszolút hibát tartjuk fontosnak a becslési hiba csökkentésére, akkor abszolút érték költségfüggvényt alkalmazunk. Ha a nagyobb eltéréseket határozottabban kívánjuk súlyozni, akkor pedig a négyzetes hibafüggvényt célszerű használni.
Ezeket látjuk a következő ábrán.
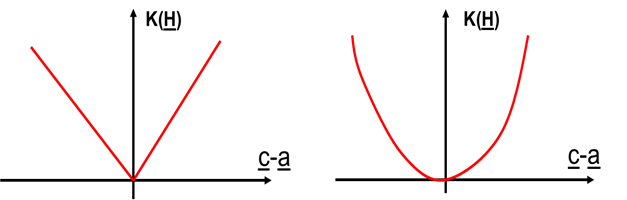
Az „à posteriori” (utólagos) feltételes sűrűségfüggvény négyzetes költségfüggvénnyel történő súlyozását és a minimális hibát mutatja az alábbi ábra.
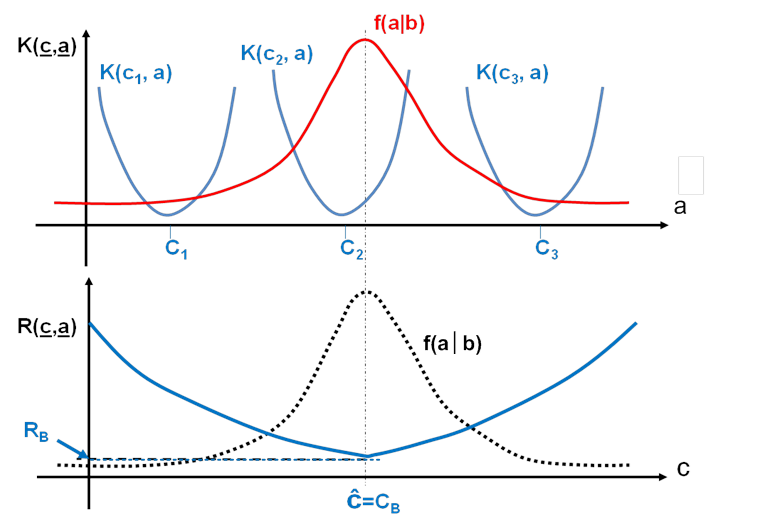
5.6.3. Maximum Likelihood becslés (ML)
Előfordulhat a sokféle mérési feladat során, hogy nincs előzetes ismeretünk a mérendő paraméter f( a ) sűrűségfüggvényéről, és csak az f( b | a ) feltételes sűrűségfüggvény, a megfigyelés, azaz a csatornakarakterisztika adott. Ilyen esetben a Bayes becslő nem alkalmazható. Helyette a szakirodalom a Maximum Likelihood (ML) becslőt javasolja.
Az ML becslés előállításához definiálni kell az un. „likelihood” függvényt f ML ( b | c ), amelynek c szerinti maximum helyéhez tartozik az optimális becslés:
|
|
(5.4) |
A Maximum Likelihood becslésnél tehát nem ismerjük az f( a ) sűrűségfüggvényt. Ezt a műszaki tényállást a matematika nyelvén úgy közelítik, hogy az f( a ) sűrűségfüggvény varianciáját egyre nagyobbá teszik, határátmenetben végtelen varianciát feltételeznek. Ennek következménye az (5.7. ábra - Hatás, amelyet az f(a) sűrűségfüggvény varianciájának növelése okoz) ábrán látható, azaz az f( a ) függvény egyre jobban „szétterül”. Ezért az f( a ) sűrűségfüggvénynek nincs hatása az à priori sűrűségfüggvényre, és a ML becslés majdan a f ML ( b | c ) függvény maximumához tartozó érték lesz.
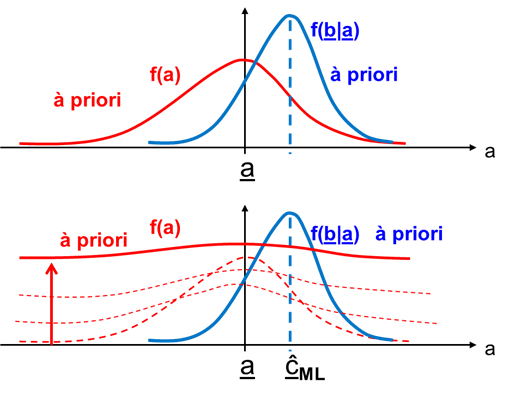
Ehhez a megállapításhoz azonban még szükség van néhány lépésre. A Maximum Likelihood becslő a maximum à posteriori (utólagos) sűrűségfüggvényből vezethető le, felhasználva az ismert csatornakarakterisztikát. Felhasználva a Bayes becslőnél látott összefüggést, az alábbiakat írhatjuk fel:
|
|
(5.5) |
A továbbiak megértéséhez fontos, hogy az f( a | b ) à posteriori sűrűségfüggvényben a konstans „ a ” helyére „ c ” változó kerül, hiszen ennek a függvényében kell megkeresni a maximumhelyet. Tekintettel a változó cserére, és arra, hogy a minden határon túl megnövelt varianciájú f( a ) sűrűségfüggvény konstans lesz, f( c ) ugyancsak konstans. Ugyanakkor tudjuk, hogy f( b ) nem függ c -től, ezért az „à posteriori” sűrűségfüggvény maximum helye megegyezik a ML függvény szélső értékével, amint azt a fejezet elején láttuk.
|
|
(5.6) |
Összefoglalva megállapítható, hogy mivel nem ismerjük a mérendő paraméter eloszlását, csak a megfigyelésekre lehet a becslésnél támaszkodni. A Maximum Likelihood becslésnek azt az a = ĉ ML paraméter értéket vesszük, amely mellett a kapott f( b | a = c ) megfigyelés a legvalószínűbb, ezt szemlélteti az 5.7. ábra - Hatás, amelyet az f(a) sűrűségfüggvény varianciájának növelése okoz, ahol látható, hogy a f( b | a ) „à priori” sűrűségfüggvény maximuma az a paraméter ĉ ML értékénél van.
5.6.4. Legkisebb négyzetes hibájú becslés (LMS)
Láttuk, hogy a Bayes becslésnél a paraméter sűrűségfüggvényére és a megfigyelések (csatornakarakterisztika) sűrűségfüggvényére volt szükség, míg a ML becslésnél már csak az utóbbi áll rendelkezésre.
Ha semmilyen „à priori” ismerettel nem rendelkezünk, akkor a becslés alapja kizárólag a feltételezett modell és maga a mérendő rendszer lehet, és nyilvánvalóan az e kettő közötti eltérést kell minimalizálni.
A legkisebb négyzetes hibájú becslés (LMS) négyzetes hibakritériuma mellett sok műszaki tapasztalat szól, hiszen könnyen kezelhető, fizikailag jól megjeleníthető, és a becslő viszonylag könnyen megvalósítható.
A becslési feladat lényege tehát az, hogy a mérendő rendszer a paraméterének olyan ĉ becslését keressük, amely mellett a mérendő rendszerről nyert b megfigyelés és a modell y kimenőjelének négyzetes eltéréseként meghatározott C( a , c ) hiba minimális lesz. Tekintettel arra, hogy a paraméter, a megfigyelések, az eredmények vektor formában vannak felírva, ezt a meghatározást a következő egyenlettel lehet leírni:
|
|
(5.7) |
A C( a , c ) hibafüggvény minimumához tartozó c érték, azaz a legkisebb négyzetes hibájú becslés szélsőérték meghatározással állapítható meg:
|
|
(5.8) |
A becslési hibára vonatkozó összefüggés megjeleníthető tömbvázlat segítségével is, ezt mutatja következő ábra.
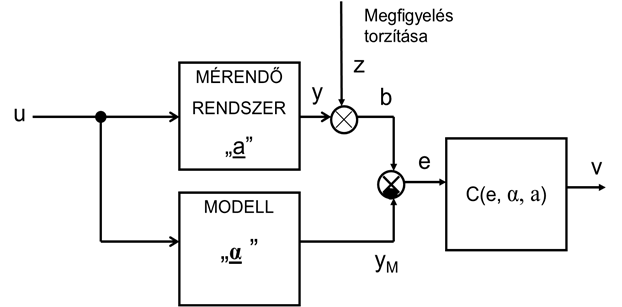
A legkisebb négyzetes hibájú becslő megvalósítására célszerű lineáris modellel való közelítést alkalmazni akkor is, ha a modell nemlineáris. Ha feltételezzük, hogy az a mérendő paraméter és a b megfigyelés közötti kapcsolat lineáris, és létezik az n torzítás, vagy zaj, akkor felírható a következő összefüggés:
|
|
(5.9) |
Az optimumkereséshez szükséges a hibafüggvény létrehozása:
|
|
(5.10) |
Az összefüggés tovább formálható:
|
|
(5.11) |
Az egyenlet c szerinti deriválásával nyerhetjük a legkisebb négyzetes hibájú becslést. Elvégezve a deriválást és figyelembe véve a számítási szabályokat, felírható, hogy
|
|
(5.12) |
és ezzel a következő feltételt kapjuk:
|
|
(5.13) |
Átrendezés után
|
|
(5.14) |
Amennyiben az U mátrix nem szinguláris, akkor az inverzió elvégezhető, és megkapjuk az a paraméter LS becslését:
|
|
(5.15) |
Ezzel az eredménnyel kiszámítható a becslés hibája is:
|
|
(5.16) |
Tekintettel arra, hogy
|
|
(5.17) |
volt, behelyettesítéssel felírhatjuk a becslés hibáját is:
|
|
(5.18) |
Jól látható, hogy a becslési hiba nem függ a paraméter eloszlásfüggvényétől, hiszen ez amúgy is ismeretlen, viszont megjelenik benne a megfigyelés és a mérendő mennyiség lineáris kapcsolatának leírása és a zavarás hatása.
5.7. A mérés információelméleti modellje
5.7.1. A hírközlés modellje és a mérőlánc
Azon kivételektől eltekintve, ahol a mérendő mennyiség és a kijelzett villamos mennyiség között fizikai törvény formájában direkt kapcsolat létezik, általánosságban elmondható, hogy a mérendő mennyiség és a mérőeszközökre eljutó jelek között hosszabb-rövidebb átviteli láncra van szükség. Fontos kihangsúlyozni, hogy ez esetben nem villamos jelvezetékre, hanem köztes fizikai mennyiségekre gondolunk. A kijelzett érték igen sokféle zavarás torzító hatását foglalja magába. A mérés információelméleti modellje ezeket a hatásokat szemlélteti.
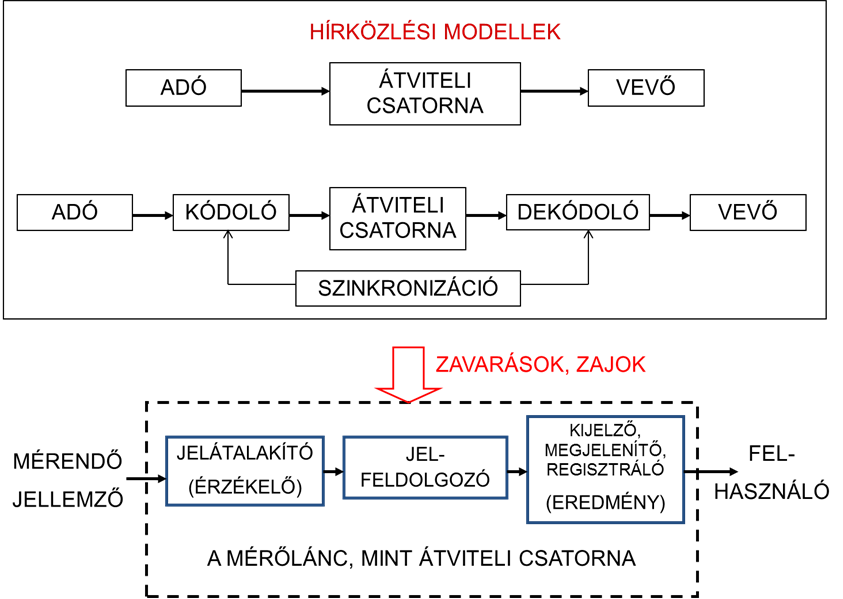
Az információelméleti modell központi része a jelátviteli csatorna, amelyet mérési feladat esetében a mérőlánc valósít meg. A mérőlánc a valóságban természetesen lényegesen több tagot tartalmazhat, esetenként átviteli tagok soros, párhuzamos és visszacsatolt formájában. A mérőlánc ebben a modellben magába foglalja a valószínűségelméleti modellben megismert mérőrendszert is, tehát az adatfeldolgozó egységet is. Az közismert, hogy a kijelzett (megjelenített) eredmény napjainkban döntően villamos jellegű mennyiség. A mérendő jellemző villamos jellé történő átalakítása már a jelfeldolgozó egység előtt megtörténik. A jelfeldolgozás alatt analóg, vagy diszkrét jelekkel való műveleteket kell érteni, amelyeket áramkörökkel, vagy számítástechnikai eszközökkel (pl. PC, adatfeldolgozó kártyák, mikrokontroller) végeznek el, de napjainkban a kijelzés és megjelenítés is gyakran már PC monitoron történik. A legfontosabb műveletek az erősítés, demoduláció, A/D és D/A átalakítás, szűrés, összegzés, integrálás, logaritmus műveletek, stb.
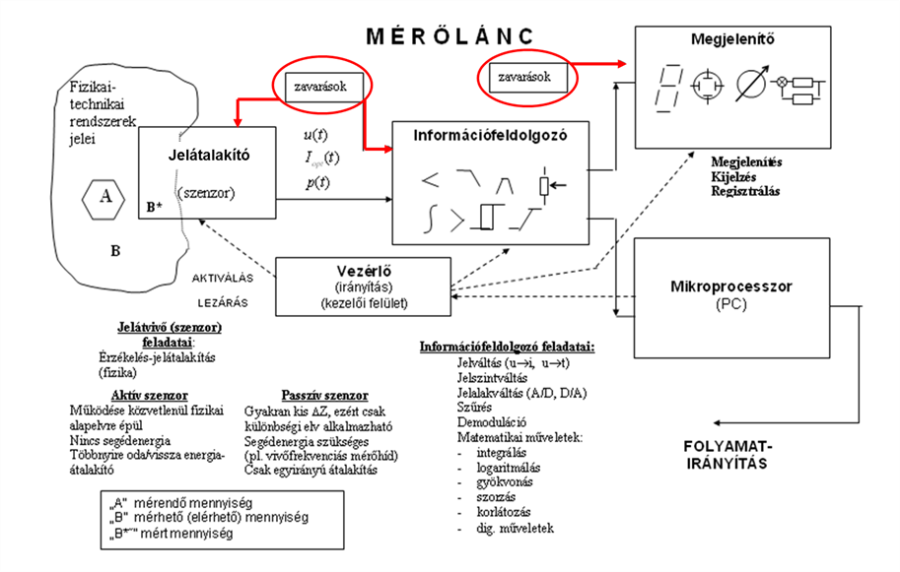
A jelátalakító a mérőlánc első tagja. Megnevezésére használatos még a jelátalakító, mérő-átalakító kifejezés is. Többnyire komplex egység, amely a mérendő fizikai mennyiséget olyan reprodukálhatóan detektálható változássá formálja, amely egy alkalmasan választott szenzor segítségével villamos (esetleg optikai, pneumatikus, stb.) jellé alakítható át.
A jelátalakító lehet persze egyben szenzor is, főként aktív (segédenergia nélkül működő) eszközök esetében, mint például a tachogenerátor esetében láthatjuk. Ez az eszköz a mozgási indukción alapulva közvetlenül, köztes mennyiségek beiktatása nélkül lehetővé teszi a fordulatszám (szögsebesség) mérését.
Igen csekély kivételtől eltekintve azonban az érzékelő (szenzor) a jelátalakítónak „csupán” egy részét képezi, és amint az előbbiekből látható, többféle mennyiség mérésére ugyanazon szenzor típus alkalmas lehet. Általában elmondható, hogy egy gépészeti mennyiség passzív szenzorokkal akkor alakítható át villamos jellé, ha olyan mérőelemet tudunk tervezni, létrehozni, amely reprodukálhatóan és kellő felbontással elmozdulássá, alakváltozássá, vagy anyagjellemző (pl. permeabilitás, optikai törésmutató, stb.) változássá képes átalakítani az eredeti mérendő mennyiséget.
Az aktív és passzív fogalmakat különböző módon lehet értelmezni . Lehet a műszer szempontjából, és lehet önmagában, a szenzor működési módja szerint vizsgálni és besorolni az eszközöket. Az [5.1.] jelű irodalomban, annak 7.1.1 fejezetében, ezt a két fogalmat a mérőeszköz „szempontjából” vizsgálják. Ezért passzív érzékelést úgy értelmezik, hogy egy fizikai rendszer energiát ad le a mérőeszköz felé. Ebben az esetben a műszer valóban passzívan viselkedik, mert kívülről „kap” energiát. Aktív az érzékelés ebben az értelmezésben akkor, ha az érzékelő működtetéséhez a mérőeszköznek energiát kell szolgáltatnia, majd információt hordozó energiát „kap vissza”, tehát az energiafolyam kétirányú.
Mi ebben a jegyzetben nem a fentiek szerint, hanem a működési módjuk szempontjából vizsgáljuk a szenzorokat . Ilyen megközelítésben teszünk különbséget „aktív” és a „passzív” érzékelők között. Működési módja szerint az aktív szenzor nem igényel segédenergiát, és a jelátalakítás többnyire fizikai törvényszerűségen alapul, amint azt a piezoelektromos, vagy elektrodinamikus eszközöknél látjuk. A passzív szenzorok ezzel ellentétben csak segédenergiával működtethetők, és gyakori a moduláció valamilyen formájának alkalmazása is. Passzív szenzorok jellegzetes példái az impedancia változáson alapuló eszközök, ilyenek az induktív, kapacitív, rezisztív elemeket tartalmazó átalakítók, mint pl. az induktív elmozdulás érzékelő, vagy a nyúlásmérő bélyeg.
A gépészeti és mechatronikai mérési feladatokra jellemző, hogy a mérendő jellemző gyakran több közvetítő mennyiségen, elérhető mennyiségen keresztül hoz létre villamosan mérhető mennyiséget, és ilyen módon villamos kimenő jelet. Ezt szemlélteti a gyorsulásérzékelés egy lehetséges formáján a következő ábra. A gyorsulást, mint mérendő jellemzőt lehet ugyanis elmozdulás, (ld.: következő ábra), vagy alakváltozás (aktív piezoelektromos szenzor, vagy passzív nyúlásmérő bélyeges szenzor), mint elérhető mennyiségek révén mérhető mennyiséggé alakítani.
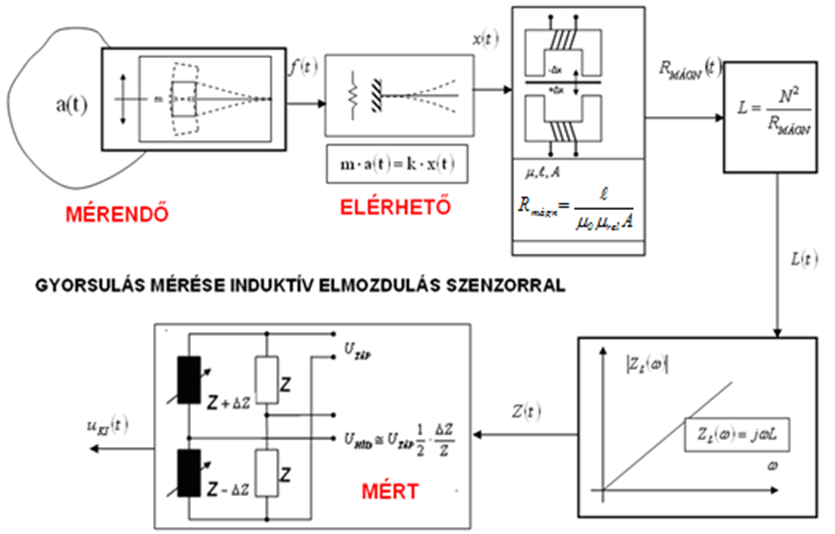
Az (5.11. ábra - Gyorsulásérzékelő jelátalakító induktív elmozdulás érzékelővel (szenzorral)) ábrán bemutatott példa szemlélteti azt, hogy mérőlánc első tagja már önmagában is milyen bonyolult felépítésű lehet, és azt, hogy a többszörös átalakítás mindegyike természetesen növeli a zavarások, torzítások fellépésének eshetőségét. Az ábrán Utáp híd-tápfeszültség ω körfrekvenciájú harmonikus jel.
A bemutatott mérőlánc-részlet például önmagában már két, különböző mérési módszert is tartalmaz. Óvatosaknak kell lennünk tehát a „besorolásokkal”, mert eszközeink gyakran bonyolult felépítésűek! Meg kell jegyezni természetesen még azt is, hogy az ábrán látható Wheatstone-híd fehér színnel jelzett két impedanciája már a mérőlánc második tagjához, a vivőfrekvenciás mérőerősítőhöz tartozik, és ez a mérőerősítő szolgáltatja a híd tápfeszültségét is (UTÁP).
Mivel jelenleg nem ismeretes olyan fizikai kapcsolat, amely révén a gyorsulás közvetlenül villamos jellé átalakítható lenne, szükség van köztes mennyiségekre. A példában a szeizmikus tömegre ható gyorsító erővel tart egyensúlyt a tömeg rugalmas vezetékében ébredő rugóerő. Ez a formáció a klasszikus méréstechnika szerint „kitérítéses módszer” alapján mér. Ugyanakkor a további átalakítások végén, az előidézett impedancia változást „ különbségi módszerrel” mérjük. A műszerház és a tömeg közötti relatív elmozdulás a mérendő gyorsulással arányos. Végül a relatív távolság változását induktív elmozdulás szenzorral érzékelik, és tekintettel az így létrehozott impedancia változás rendkívül kis mértékére, az impedancia változás különbségi módszeren alapuló Wheatstone-híd szolgál.
A legdurvább, a mérési eredményt súlyos mértékben befolyásoló zavarok a híd tápfeszültségének és a vivőfrekvencia ingadozásából származhatnak, hiszen ezek a mennyiségek az eredmény részét képezik. Ha a rugalmas vezeték konstrukciója megfelelő, akkor ebből a részből jelentős zavarás nem várható, de mechanikai szempontból nagyon lényeges a jelátalakító és a csatlakozó kábel rögzítésére vonatkozó gyártói előírások betartása. Elektromágneses hatások, és földelési problémák további zavaró veszélyforrás lehetnek.
Az információelméleti modell természetesen nem csupán arra szorítkozik, hogy a mérőláncot a jelátviteli csatornának megfeleltesse, hanem elméleti megfontolásokat is tartalmaz.
Érdekesség, hogy az információelméleti modell nélkül nem lehetne például némely speciális eloszlásfüggvény esetében kiszámítani a második centrális momentumot, mert improprius integrált kapunk.
A továbbiak részletezéséhez lássuk még egyszer az információelméleti modell „méréstechnikai értelmezését”.
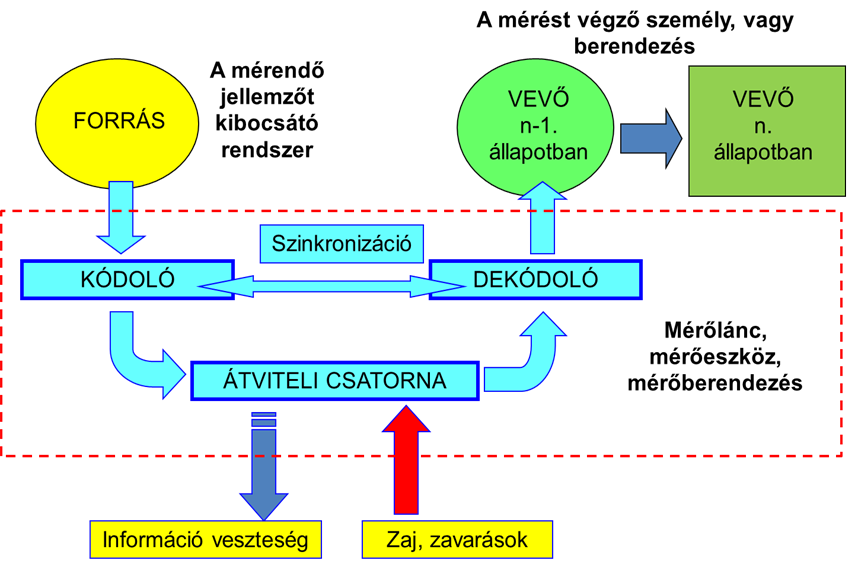
Shannon klasszikus információ átviteli modelljének „lefordítását” látjuk a fenti ábrán. Shannon szerint az információ átvitel nem öncélú, hanem a vevő (fogadó, felhasználó) oldalán a meglévő bizonytalanság, azaz információ hiány csökkentésére irányul.
5.7.2. A műszaki információ mérése
Tekintettel arra, hogy a mérést információelméleti szempontból úgy kell értelmezni, mint olyan tevékenységet, amely a mérés előtt meglévő ismerethiány (bizonytalanság) megszüntetésére irányul, természetes, hogy nézetünk szerint a műszaki információ fogalmába beletartozik a mérés útján szerzett információ is .
Ez a szemlélet a mérési tevékenység céljával tökéletes összhangban van, hiszen a mérés a hiányzó ismereteink pótlását szolgálja. Ezért nem kell meglepődni, ha a későbbiekben a méréssel szerezhető információmennyiséget a hírközlésben szokásos módon „entrópiának” nevezzük.
Az információ műszaki értelemben – látjuk a következőkben – pontosan ezt jelenti: Információ entrópia = a bizonytalanság (ismerethiány) megszűntetésének mértéke.
Méréstechnikus szemével nézve a forrás tehát a mérendő fizikai-technikai mennyiséget kibocsátó rendszer (gépi berendezés, stb.), a vevő a mérést végző személy, vagy az irányítástechnikában maga a szabályozott rendszer, pontosabban a különbségképző tag, hiszen a visszacsatolás minden szabályozott mechatronikai rendszerben mérés.
Az átviteli csatorna maga a mérőlánc, amelybe a kódoló és dekódoló is beletartozik. Ha jól meggondoljuk, nincs ebben semmi erőltetettség, hiszen például a vivőfrekvenciás mérőerősítők a legszembetűnőbben szemléltetik még a kódolás/dekódolás és ezek szinkronjának szükségességét is. A vivőfrekvenciáról csak jól szinkronozott (fázisban lévő) generátorjel segítségével lehet a hasznos, és információt hordozó moduláló jelet dekódolással leválasztani.
Az is természetes, hogy a „vevő” állapota (ismerethalmaza) a mérés eredményének függvényében megváltozik. (Másként minek fektetnénk pénzt és munkát a mérésbe, információszerzésbe?)
Mielőtt a mérés entrópiájára rátérnénk, szükséges néhány ismeret rövid összefoglalása, hiszen ahhoz, hogy a méréssel szerezhető információmennyiség „mérhető” legyen, meg kell ismernünk az információ alapegységét és mértékegységét is.
A modern információelmélet kialakulását a valószínűség számítás fejlődése alapozta meg. A valószínűség matematikai megfogalmazása régóta foglalkoztatta a gondolkodókat. Úgy tudjuk, hogy a valószínűség első tudományos igényű tárgyalása Pascal levelében olvasható, amelyet 1654. júl. 29-én Fermat-hoz írt. Bernoulli is foglalkozott a témával, és a következő megközelítést adta: „A valószínűség olyan bizonyossági fok, amely úgy viszonyul a teljes bizonyossághoz, mint rész az egészhez.” Laplace-tól származik az a formula, amelyre napjainkban is hivatkoznak: A valószínűség a „kedvező” események osztva az „összes lehetséges” eseménnyel, amennyiben minden esemény azonos valószínűséggel következhet be. Láttuk ugyanakkor a 4. fejezet - Mérés és valószínűség számítás fejezetben, hogy a modern valószínűségszámítás már axiómák segítségével definiál. Többek mellett Gauss, Poisson, Markov, Kotelnyikov, Hincsin, Feinstein és Fano is foglalkozott a legfontosabb véletlen folyamatok és valószínűségi eloszlások kutatásával.
Kolmogorovtól származik az a közismert egyenlőtlenség, amely az események bekövetkezésének valószínűségét a biztos (P=1) és a lehetetlen (P=0) események közé helyezte, és ezzel „számszerű” megfogalmazást tett lehetővé. Ez a gondolat „ihlette” a hírtartalom, vagy információmennyiség fogalmának megalkotóit. Már csupán olyan matematikai összefüggést kellett találni, amely jól visszatükrözi azt a felfogást, hogy a biztos eseményt sugárzó „hírforrás” (előre ismert hírtartalommal, információval) entrópiája (hírtartalma) zérus legyen, viszont, ha a hírforrás teljes bizonytalanságban hagy, azaz bármilyen hírt azonos valószínűséggel kibocsáthat, akkor az entrópiája maximális legyen. A matematikai összefüggést először Hartley javasolta 1928-ban, majd Shannon fejlesztette tovább.
H. Nyquist (1920) és R. Hartley (1928), a Bell Labs munkatársai publikáltak elsőként olyan elméleteket, amelyek később az információ „méréséhez” vezettek.
A Hartley iránti tisztelet miatt a tízes alapú logaritmus segítségével kiszámított információt „hartley (h)”-ben mérik. A „bit”-be való átszámítás a logaritmus alapok közötti áttérés segítségével lehetséges, 1 h ≈ 3,32 bit.
Az információ mérésére szolgáló mennyiség és mértékegysége nem köthető abszolút természeti állandóhoz , hanem logikai úton lett meghatározva. A Hartley, majd Shannon által javasolt „információ entrópia” (mint mennyiség) és a Tukey-féle „bit” , mint mértékegység első sorban arra való, hogy általuk a műszaki rendszerek , átviteli csatornák, tárolók, stb. műszaki kapacitásának egymás közötti objektív összehasonlítása lehetővé váljon. Az entrópia elnevezés azért került az információelmélet szótárába, mert a számításának Hartley és Shannon által javasolt módja erősen emlékeztet a termodinamikai entrópia meghatározásának módjára.
Gépészek és mechatronikusok számára ismeretes, hogy a termodinamikai entrópia gondolata R. Clausiustól származik (1822-1888), aki ezzel jellemezte a termodinamikában az anyagi rendszerek molekuláris rendezetlenségét, illetve a termodinamikai állapot valószínűségének a mértékét. Ebből következtetni lehet a maguktól végbemenő folyamatok irányára: Mindennapos tapasztalat, hogy a természetben az „egyre valószínűbb” állapotok következnek be. Például annak az állapotnak a valószínűsége, amelynél egy zárt teret úgy töltenek ki gázmolekulák, hogy azok kizárólag a tér egy meghatározott részében helyezkednek el, kisebb, mint annak a valószínűsége, hogy a molekulák a rendelkezésre álló teret egyenletesen kitöltik. Így tehát, ha P1 és P2 azokat a valószínűségeket jelzik, amelyekkel adott termodinamikus rendszer különböző állapotban való tartózkodását lehet leírni, akkor a képlet az entrópia megváltozását tükrözi („k” a Boltzmann-állandó) valamilyen folyamat során.
|
|
(5.19) |
Ilyen meggondolásból a termodinamikai entrópia a „rendezetlenség” mértéke, amely annál nagyobb, minél nagyobb az adott állapot valószínűsége.
A fentiekkel analóg módon hír (vagy hírforrás) entrópiája , azaz információmennyisége annál nagyobb, minél nagyobb a bizonytalanság, amelyet a hír közlése révén el tudunk oszlatni. Másként fogalmazva, annak a hírnek nagyobb az entrópiája, amelynek a bekövetkezési valószínűsége kisebb. Az információ tartalom mérésére szolgáló mennyiség definíciója megszületését tehát a termodinamikai rendezetlenség és az információelméleti bizonytalanság közötti hasonlóság ihlette.
Shannon, 1948-ban közölt munkájában, csak a műszaki értelemben vett információk (elsősorban digitális villamos jelek által hordozott hírtartalom) mérésére – összehasonlítás céljából - dolgozott ki módszert.
Az információmennyiségre alkalmazott „entrópia” elnevezés tehát logikai és formai okokra vezethető vissza. Az információelmélet és a valószínűségszámítás szorosan összefüggnek. A biztos esemény (itt: hír) a fogadó/vevő számára nem rendelkezik információ tartalommal (csak műszaki értelemben!), míg a lehetetlen esemény információ tartalma végtelen nagy lenne. Ezt a matematika nyelvén a valószínűség reciprokával lehetne a legjobban kifejezni.
Ugyanakkor azonban gond, hogy a biztos esemény információ tartalma ez esetben nem zérus, hanem egy lenne. Ezért a hír bekövetkezésének valószínűségét nem csak reciprokként, hanem a reciprok logaritmusaként vesszük.
Az „S” (source) hírforrás „P” valószínűséggel kibocsátott, egyetlen „h” hírének információ tartalma, más elnevezéssel hírértéke, vagy entrópiája az alábbi formula segítségével állapítható meg:
|
|
(5.20) |
Így azután az elméleti megfontolást a képlet már jobban tükrözi, és a termodinamikai entrópia képletével való formai hasonlóság szembetűnő.
Az információ alapmennyisége az „információ entrópia” (ez nem SI alapmennyiség) és alapegysége a „bit” .
Egy „S” hírforrás egyetlen „hi” hírének, valamint a hírforrás teljes jelkészletének entrópiáját a következőképpen lehet meghatározni:
|
|
(5.21) |
(ahol ld = log2 : logarithmus dualis (latin), a kettes alapú logaritmus)
Érdekesség, hogy az információ napjainkban játszott óriási szerepe ellenére, sokáig nem szerepelt az információ entrópia az SI egységek között. Ennek oka feltehetően az, hogy az információ jelenleg használt mértékegységének (bit) átszámítása anyag és/vagy energia ekvivalensbe, a kapott érték rendkívül kicsiny volta miatt, egyelőre még nehezen interpretálható. A „bit” ma már SI származtatott egység és jelenlegi energia ekvivalense 9,569940(16) × 10−24 J/K. (A Boltzmann állandó értéke 2006-ban kB = 1,380 6504(24)·10−23 J/K volt.)
Az információ mértékegységének megértéséhez és az előzőekben ismertetett összefüggések gyakorlati illusztrálásának céljából mutatunk be egy fontos számítást, mert ugyan a napi gyakorlatban ismételten használjuk információelméleti mértékegységet a „ bit ”-et, de nem biztos, hogy minden esetben világos az, hogy ez a mértékegység valójában mit takar?
Legyen egy hírforrás bináris, azaz csak két féle információt képes kibocsátani, ezek legyenek a 0, vagy 1 szintek. Ebből következően, ha rögzítjük az egyik szint valószínűségét, akkor a másik szint kiadódik: P(1)=1-P(0) és fordítva. A két jel információtartalma láthatóan nem független egymástól. Az alábbi táblázat első sorában az „1” szint valószínűségét adtuk meg 9 értékkel P(1). A második sorban ennek a jelnek az információtartalmát, míg a harmadikban a „0” jel információtartalmát tüntettük fel. Jól látszik, hogy csak a két jel valószínűsége komplementer, de az információtartalmuk már nem .
A bináris hírforrás átlagos információtartalma az előző képlet szerint összegként adódik:
|
|
(5.22) |
Megjegyezzük, hogy a táblázatban az előjelek és a log–ld átszámítás tekintetében figyelembe vettük a log azonosságokból adódó lehetőségeket.
|
P(1) |
0,00 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,4 |
0,5 |
|
H(1)= -[P(1) ld P(1)] |
0,00 |
0,22 |
0,33 |
0,41 |
0,46 |
0,5 |
0,52 |
0,53 |
0,5 |
|
P[1-P(1) ]=P(0) |
1,00 |
0,95 |
0,9 |
0,85 |
0,8 |
0,75 |
0,7 |
0,6 |
0,5 |
|
H(0)= -[1-P(1)]ld [1- P(1)] |
0,00 |
0,07 |
0,14 |
0,2 |
0,26 |
0,31 |
0,36 |
0,44 |
0,5 |
|
H [bit]=H(1)+H(0) |
0,00 |
0,29 |
0,47 |
0,61 |
0,72 |
0,81 |
0,88 |
0,97 |
1 |
Jól látható a táblázatból, hogy ha valamelyik esemény (0 és 1) bekövetkezésének valószínűsége előre tudottan nagyobb, mint 50 %, azaz P>0.5, akkor csökken a bizonytalanság a várható eseménnyel kapcsolatban, így csökken a hír entrópiája is. Így tehát ha P(1)=0.2, akkor P(0)=0.8, azaz 80%-ban előre bizonyosak vagyunk, hogy a „0” lesz a kimenet (esemény). Ezért az erről „szóló hír” entrópiája csupán 0.72 bit. A forrás információtartalma akkor lesz maximális, ha semmilyen előzetes ismeretünk nincsen arról, hogy melyik jelszint előfordulása valószínűbb. Ugyanakkor a táblázat első oszlopában látszik, hogy amennyiben az 1 jel egyáltalán nem fordulhat elő, azaz P(1)=0, akkor a 0 jel valószínűsége 100 %-os, azaz P(0)=1. A hírtartalom mindkét jelre vonatkozóan nulla – amit az eddigi fejtegetések alapján már sejtettünk is.
Maximális lesz a hír entrópiája, azaz 1 bit, ha mindkét esemény bekövetkezési valószínűsége azonos.
Az értéktáblázat alapján készített diagram látható a következő ábrán.
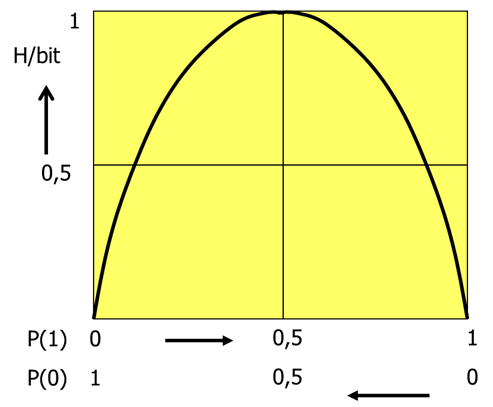
A maximális hír entrópia természetesen nem csak értéktáblázattal mutatható ki. A függvényvizsgálat szabályi szerint kereshetjük az átlagos hírtartalom szélsőértékét, és első lépésben a differenciálási szabályok miatt áttérünk természetes logaritmusra:
|
|
(5.23) |
Az utolsó sor egyszerűbben is írható:
|
|
(5.24) |
A függvénynek szélső értéke van, ha
|
|
(5.25) |
Ez csak akkor lehetséges, ha a zárójelben lévő kifejezés lesz zérus, így felírható, hogy
|
|
(5.26) |
Befejezésként ellenőrizzük, hogy maximum, vagy minimum helyről van szó? A második derivált P1=0.5 értékre negatív lesz, tehát maximumot találtunk.
|
|
(5.27) |
Nagyon fontos az is, hogy a hír és az információ fogalmai ne keveredjenek! A „hír” kifejezés hétköznapi használata miatt gyakran téves képzetek keletkezhetnek.
Műszaki értelemben a hír megléte még nem feltétlenül jelenti azt, hogy annak van információtartalma is. (Némi szarkazmussal, persze ez a megállapítás tágabb értelemben is igaz lehet.)
Először tehát néhány fontos információelméleti fogalom rövidített, tömör leírása következik:
A jel időben és/vagy térben lezajló fizikai, vagy kémiai folyamat, információhordozó.
A műszaki „hír” időben és/vagy térben korlátozott jel.
A hírkészlet az összes lehetséges hír.
Az információ a bizonytalanság mértéke, amelyet a hír megszűntet.
5.7.3. Entrópia a méréstechnikában
A mérés és a mérési hiba entrópiájának objektív meghatározása lehetővé teszi, hogy a mérési tevékenység minősítésével kapcsolatban megalapozott elméleti megállapításokat tehessünk. Ezek alapja a mérés információelméleti modellje.
Méréssel csökkentjük az adott méréstechnikai probléma információelméleti entrópiáját (Az „ismeretlen” felderítésével csökken a bizonytalanság.)
Ha a mérési adatokról, amelyek valószínűségi változók, van előzetes ismeret, akkor viszont a „forrás” entrópiája csökken, és ezáltal a méréssel szerezhető információ entrópiája is csökken.
A hiba információelméleti entrópiája tovább csökkentheti a méréssel megszerezhető entrópiát.
A mérés kivitelezésére nézve fontos útmutatás, hogy az entrópia bármilyen csökkenése azt jelenti , hogy az elvégzett méréssel az adott mérési feladatról (mérendő mennyiségről) az optimálisnál kevesebb információt tudunk majd csak megszerezni.
A méréssel szerezhető információmennyiség meghatározásához támaszkodnunk kell a mérés valószínűségelméleti modelljénél megismert à posteriori ismeretek matematikai megfogalmazására, amit az f(a|b) feltételes sűrűségfüggvény ír le. Ennek a sűrűségfüggvénynek a felhasználásával meghatározható a valószínűség, és az előzőekben bemutatott összefüggésekkel az entrópia is. Az à posteriori sűrűségfüggvény segítségével tulajdonképpen a mérési hiba írható le, hiszen egy adott, megfigyelt (megismert) „b” értékhez rendeli hozzá a mérendő „a” jellemző sűrűségfüggvényét.
A mérendő jellemzőt ebben a modellben a méréstechnikában szokásos módon „a” helyett „x” és a megfigyelt mennyiséget „b” helyett xm” betűvel jelöljük. A mérési hiba entrópiáját jelöljük H(x|xm) és a mérendő jellemző sűrűségfüggvényével kiszámítható à priori (előzetes) ismerethiányunk entrópiáját H(x) függvénnyel.
A mérés eredményeként megkapható „Q” információmennyiség számítása ezekkel:
|
|
(5.28) |
A mérés információtartalmának számítását egy egyszerű példán lehet illusztrálni. Legyen a csupán egy digitális kijelzésű mérőműszerről szó, amelynek bizonytalansága a teljes mérési tartomány bármely részén egyformán 2Δ (±Δ). A mérés előtt a mérendő mennyiségről csak annyi információval rendelkezünk, hogy az [x1; x2] tartományba esik.
Az entrópiák számításához szükséges sűrűségfüggvények ezek alapján megadhatók, ezt mutatja a következő ábra.
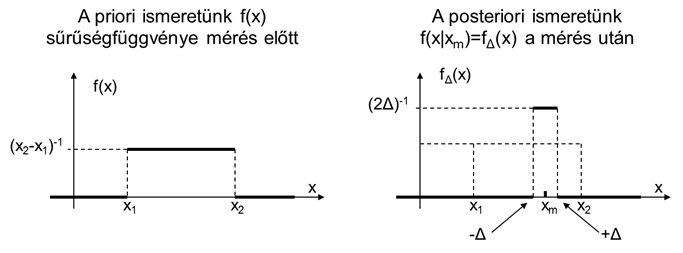
Az ábrák alapján a sűrűségfüggvények megadhatók, hiszen egyenletes eloszlásról van szó:
|
|
(5.29) |
Az entrópiák kiszámításához a valószínűségekre van szükség. Ismeretes a valószínűségszámításból, hogy:
|
|
(5.30) |
Ezzel meghatározható a mérés előtti bizonytalanság entrópiája H(x) (az ismerethiány) entrópiája:
|
|
(5.31) | |
|
|
(5.32) |
Továbbá a hiba entrópiája H(x|xm):
|
|
(5.33) |
Ezekkel azután a méréssel szerezhető információmennyiség (entrópia) a következő lesz:
|
|
(5.34) |
Ha az így meghatározott entrópiát konkrét mérőműszer esetére alkalmazzuk, akkor a legegyszerűbb egy digitális kijelzésű finomtapintóra gondolni.
Legyen az egyszerű számítás miatt a műszer mérési (kijelzési) tartománya ±64 μm, a kijelzés bizonytalansága pedig ±1 μm. Ezekkel az értékekkel a méréssel szerzett információ mennyisége 6 bit:
|
|
(5.35) |
Már az információelméleti modell bevezető soraiban jeleztük, hogy az ilyen jellegű mérési eredmény interpretálása önmagában nem egyszerű. A modell nyújtotta lehetőség inkább abban rejlik, hogy mérőeszközöket és mérőrendszereket egymás között a matematika eszköztárával objektíven össze tudjunk hasonlítani. Akkor ugyanis, ha olyan mérőműszert választunk, amelynek mérési tartománya változatlan mérési bizonytalansággal már 200 mm lesz, ami egyébként az előzőhöz képest egy elég magas ár-kategóriájú mérőműszert jelent, a fenti információnyereség már 16,7 bit lesz.
Irodalmak
[5.1.] Jelek és rendszerek méréstechnikája. Műszaki Könyvkiadó. 1985.
[5.2.] General Systems Theory. Matematical Foundation . Academic Press. New York . 1975.
6. fejezet - Mérőjelek idő és frekvencia tartományban
A jeleket azért kell idő és frekvencia tartományban ábrázolni és értelmezni, mert mindkét tartománybeli kép más-más információt közöl. Ha a mérési hibákat formájuk szerint vizsgáljuk (Ld.: Hibák rendszerezését a 3. fejezet - Mérési hibák fejezetben: Eredet- jelleg – forma), akkor a mérőlánc tagjait és magát a teljes mérőláncot minősíthetjük átviteli tulajdonságaik alapján is, nevezetesen aszerint, hogy idő tartományban és frekvencia tartományban milyen hibákkal képesek „átvinni” a jeleket.
A legfontosabb jeltípus a harmonikus , azaz „tisztán” szinuszos jel, mert ez minden jeltípus „építőköve”. A harmonikus jel, idő tartományban, három információ segítségével tetszőleges időpillanatban rekonstruálható: Ismerni kell az „A” amplitúdót, az „ω0” körfrekvenciát és a „φ(t=0)” értéket. E háromból kettő különösen fontos szerepet játszik: az amplitúdó és a körfrekvencia. A frekvencia tartományban ugyanezt a harmonikus jelet úgy ábrázoljuk, hogy az amplitúdó (további formák: amplitúdó négyzet, komplex amplitúdó sűrűség, teljesítmény sűrűség) a körfrekvencia függvénye. Az amplitúdó és a fázis körfrekvenciától való függését nevezik spektrumnak . Ezt a kapcsolatot mutatja a következő ábra. A jobboldalon a harmonikus jel „A” nagyságú amplitúdója ω0 körfrekvenciánál egy spektrális „vonal”.
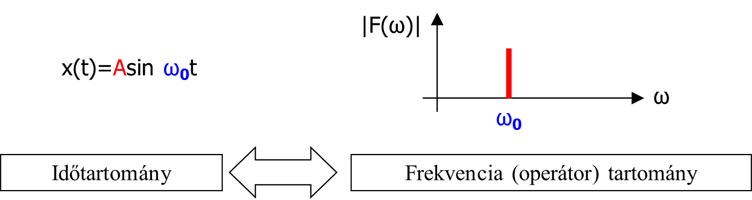
A spektrumot a Fourier transzformáció segítségével lehet meghatározni, ha a Dirichlet feltétel teljesül. A problémára a 6.1.2. szakasz - Nem periodikus (tranziens) jelek fejezetben, a „Heaviside” függvény kapcsán visszatérünk.
A Fourier sor és a Fourier transzformáció közötti kapcsolat
|
|
(6.1) | |
|
|
(6.2) |
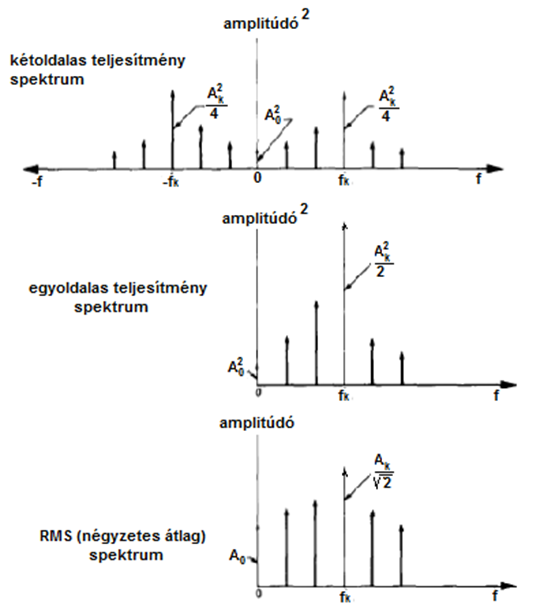
Az ábra részletes magyarázatával a 6.3. szakasz - A Fourier sor komplex alakja fejezetben szolgálunk, ezen a helyen csak a spektrum képének és formáinak érzékeltetése a cél.
Idő tartományban a lappangási idő, felfutási idő, beállási idő, időállandó, dinamikus hiba, tranziens hiba és az állandósult hiba jellemzik a műszerek, mérőláncok jelátviteli tulajdonságait. Frekvencia tartományban a jel spektrumának (vagy a spektrum legfontosabb összetevőinek) lehetőség szerint hibátlan átvitelét kell biztosítani a mérőeszközeinkkel.
Az időben változó mennyiségek mérése tehát azért igényes feladat, mert a mérendő mennyiség nagyságának előzetes (à priori) ismeretén kívül ismerni kell a mérendő mennyiség időbeli lefolyását is - legalább hozzávetőleges formában - hogy olyan mérőláncot tudjunk összeállítani, amely az adott jel rekonstruálásához elengedhetetlenül fontos harmonikus összetevők amplitúdóit minimális hibával képes átvinni.
6.1. Jelek és felosztásuk
A jel időben (esetenként térben) változó fizikai, kémiai, biokémiai folyamat. A jel hordozza a hírt, amely időben (és térben) korlátozott jel. A híradástechnikában a hír által „átvitt” információ mennyisége alatt a korábban meglévő ismerethiány (bizonytalanság) nagyságát értik, amelyet a hír megszüntetett.
A jelek idő és frekvencia tartományban történő elemzése előtt elengedhetetlen a jelek rendszerező bemutatása, annál is inkább, mert más fejezetben már jeleztük, hogy minden jeltípus alapvető építőköve a harmonikus jel, amelyet a következő táblázatban pirossal emeltünk ki.
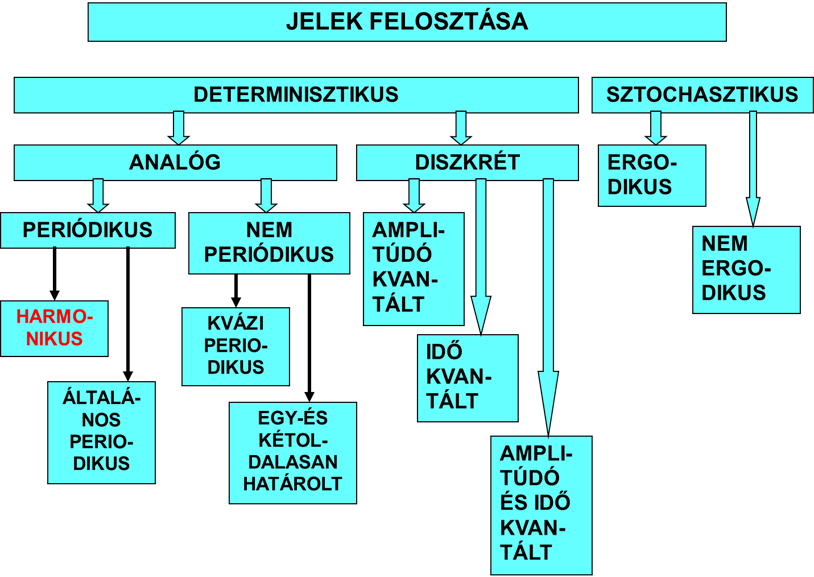
A következőkben tömören összefoglaljuk a táblázatban látható fogalmak leírását, felülről lefelé haladó sorrendben.
Ha a determinisztikus jel pillanatnyi értéke t0 időpillanatban ismert, akkor értéke t0+Δt időpillanatban matematikai összefüggés segítségével meghatározható. A sztochasztikus jelek pillanatnyi értéke előre nem határozható meg, mert amplitúdója, frekvenciája és fázisa véletlen változó. Nagy szerepe van e jeltípusnak a gépészetben, a rezgés és akusztikai mérések esetében. Ezeket a véletlenszerű jeleket stacionárius sztochasztikus jeleknek tekintjük, és méréük során megfelelő „ablakozással” mintákat „vágunk” ki belőlük. Stacionárius sztochasztikus a jel, ha a sokaság szerinti momentumai idő-invariánsak (ti.: átlag és szórás a mérés pontossági előírásainak szempontjából lényeges mértékben nem ingadozik). Ergodikus a stacionárius sztochasztikus jel, ha időtartománybeli momentumai egyenlőek a sokaságszerinti momentumaikkal. Az ergodikus sztochasztikus jel jövőbeli alakjára a „múltbeli” jelek csak a jelenbeli állapoton keresztül gyakorolhatnak hatást. Az ergodikus sztochasztikus jelet ezért egyetlen, megfelelően választott időhosszúságú minta értékelésével lehet analizálni. A nem ergodikus, de stacionárius sztochasztikus jelet tetszőleges időpontokban vett „n” db pillanatnyi érték alapján lehet megismerni.
Az analóg jelre jellemző, hogy két szélsőérték – pl. ±15 V – között minden lehetséges jelszint előfordulhat. A diszkrét jelek csak meghatározott szinten és/vagy meghatározott időpillanatban vehetnek fel értékeket. A szint szerinti beosztást amplitúdó kvantálásnak, az idő szerinti beosztást idő kvantálásnak, gyakrabban mintavételezésnek nevezik. A periodikus jel pillanatnyi értéke meghatározott idő (periódusidő) eltelte után újra megjelenik. A harmonikus jel minden jeltípus építőköve, ezért van a táblázatban piros színnel jelölve. Az általános periodikus jel lehet bármilyen bonyolult időbeli lefutású, de olyan szabályosságot mutat, hogy esetében a periódusidő értelmezhető. Egyszerűbb esetben ilyen például egy fűrészfog, vagy egy folytonos négyszögjel. A kétoldalasan határolt jelekhez sorolhatjuk a változatos lefutású, impulzus formájú jeleket, így ide tartozik a fontos tesztfüggvény, a Dirac impulzus (régebbi nevén: egység lökés jel) is. Az egyoldalasan határolt jelek közül legfontosabb az egységugrás jel, amellyel a műszereket, rendszereket gerjesztve, kimenetükön az átmeneti függvényt kapjuk válaszként.
A bonyolultabb jelek többsége előállítható a fenti csoportosításban szereplő jeltípusok kombinációjaként.
A jelek frekvencia tartománybeli alakjának meghatározására alkalmazzuk a Fourier analízist. Ez a matematikai fogalmat a Fourier sorfejtésre és a Fourier transzformációra egyaránt alkalmazzák, sőt a mérnöki gyakorlatban a frekvencia analizátorokkal végzett műveleteket is ide sorolják.
A Fourier sor és a Fourier transzformáció áttekintő bemutatása megkönnyíti az a táblázat, amit összefoglalásként a következőkben bemutatunk.
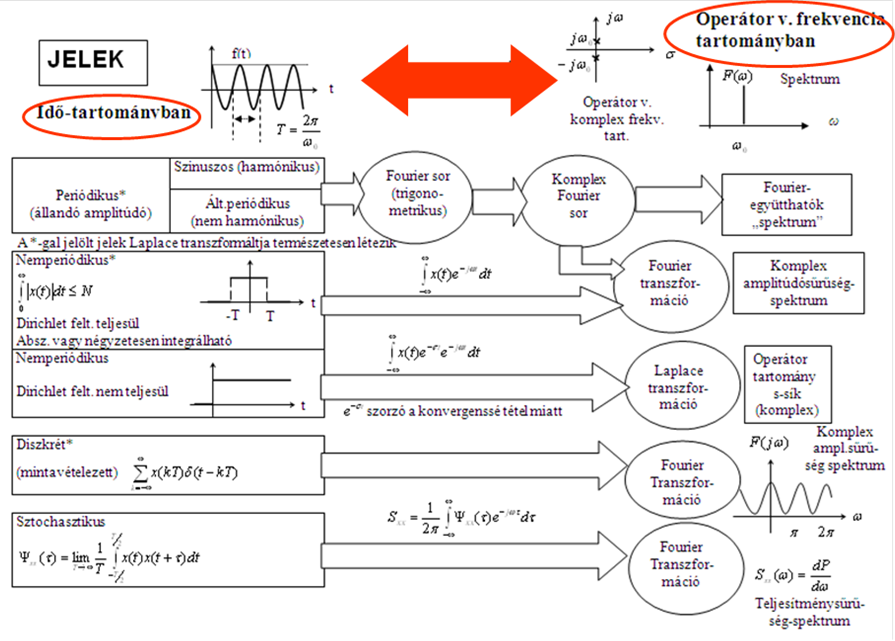
A táblázatban legalul látható „sztochasztikus” jel alatt ergodikus sztochatikus jelet kell érteni, és nyilakkal jelöltük, hogy az egyes jeltípusokból milyen matematikai eljárással lehet az adott jeltípus spektrumát meghatározni. Különleges helyet foglalnak el azok a függvények, amelyek esetében nem teljesül a Dirichlet feltétel. Egy példát látunk erre a típusra, a „Heaviside” függvényt, régebbi nevén egységugrás függvényt. Az integrálási határok, vagy egyéb okok miatt nem integrálható függvények Fourier transzformálása nem közönséges feladat. A szakirodalomban, így például R. Unbehauen Systemanalyse 1. [6.1.] című művében több ilyen típusú függvény transzformálását mutatja be.
6.1.1. Periodikus jelek
A folytonos és kvázi folytonos periodikus jelek Fourier sorba fejthetők trigonometrikus és komplex formában, így tehát meghatározhatók a Fourier-együtthatók . Ha ezeket a Fourier együtthatókat grafikusan ábrázoljuk, a spektrum ot kapjuk. A Fourier sor spektruma valós együtthatókat tartalmaz. A függőleges tengely az együttható nagyságának, a vízszintes tengely a kiszámított körfrekvencia (frekvencia) értékének ábrázolását teszi lehetővé, így egy frekvencia-amplitúdó összefüggés szemléltetésére nyílik mód. Egy diszkrét (kör)frekvenciához húzott függőleges vonal magassága az amplitúdó. Ha viszont a teljesítmény spektrumot számítottunk ki, vagy erre van szükség, akkor a függőleges tengelyt természetesen a teljesítményre kell léptékezni.
A nehézkes és hosszadalmas sorfejtés helyett, ezek a jelek Fourier transzformálhatók is, ebben az esetben eredményül a komplex amplitúdó sűrűség spektrumot kapjuk, itt már, amint a neve is mutatja, komplex lesz a spektrum.
Hasznos gyakorlati tudnivaló, hogy a frekvencia analízis műszaki eszközei (real-time analizátor, FFT analizátor) által megjelenített, mért spektrumok ettől az elméleti függvényábrázolástól eltérnek. A grafikus kép vagy különböző magasságú keskeny oszlopokat mutat, vagy olyan függvényt, amely egy, vagy több, „sátorra” emlékeztető fel-és lefutású, és kiemelkedő csúcsokban végződő formával bír. Ez utóbbi forma folytonos függvény, és alakja műszaki okra vezethető vissza. Technikailag nem lehetséges olyan sávszűrők létrehozása, amelyek szelektivitása egy adott sáv mindkét oldalán „végtelen” meredekséget lehetővé tenne, ezért a szomszédos frekvencia sávokhoz tartozó összetevők – ha elnyomva is – de megjelennek a vizsgált sávban is. Ezért nem keskeny vonal, hanem csúcsban végződő, „sátorszerű” egy spektrális összetevő képi megjelenítése. Az analóg szűrés gyakorlati ismereteivel és a szűrő karakterisztikákkal foglalkozik a 7. fejezet - Spektrum analízis a méréstechnikában fejezet.
6.1.2. Nem periodikus (tranziens) jelek
A nem periodikus jelek közül azok, amelyek kétoldalasan határoltak , és teljesítik a Dirichlet-féle feltételt, Fourier transzformálhatóak. Ilyen jelek a méréstechnikai gyakorlatban a négyszög vagy egyéb formájú impulzusok, és az impulzus-szerűen korlátozott periodikus jelek. A négyszög impulzus Fourier transzformáltjának kiszámítását a 3.4.4. szakasz - Mintavételezési hiba fejezetben láthattuk. A jellegzetes impulzus-szerű jelek időbeli és frekvencia tartománybeli alakjának összehasonlító bemutatása a 6.2. szakasz - A Fourier sortól a Fourier és a Laplace transzformációig fejezetben látható.
Méréstechnikában fontos szerepük miatt kiemelten kell foglalkozni az egyoldalasan határolt jelek közül azokkal, amelyeken nem lehet integrál-transzformációt (Fourier transzformáció) végrehajtani, amelyek nem abszolút, vagy négyzetesen integrálhatóak (Dirichlet-feltétel). Ilyen például az egység ugrás függvény. Újabban magyar szakkönyvekben is a „Heaviside” függvény elnevezést alkalmazzák erre a speciális, és a mérés-és híradástechnikában nagy szerepet játszó függvényre, amellyel egy bekapcsolása matematikailag szimulálható.
A függvény Fourier transzformáltja annak ellenére létezik, hogy a szabályok szerint nem lehetne alkalmazni a függvény transzformációt. Sokféle módon tárgyalja a megoldást a szakirodalom, de abban megegyeznek, hogy az eredeti időfüggvényt két részre bontják, egy időben konstans ½ értékű függvényre, és egy szignum függvényre, amelynek szintje ±½.
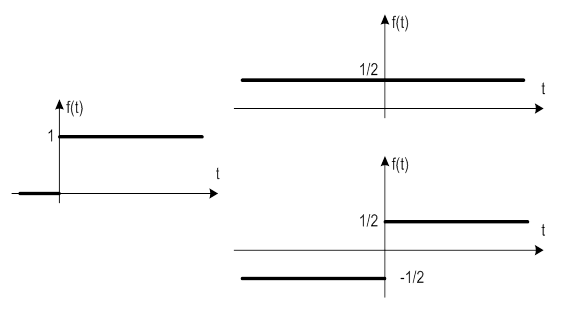
A Fourier transzformáció szabályai szerint az egységnyi, időben konstans jel transzformáltja egy 2π nagyságú impulzus az ω=0 helyen. Ha ez a jel csak ½ értékű, akkor a linearitási szabály miatt a transzformáltja π·δ(ω) lesz, továbbá a két időbeli függvényt külön-külön lehet transzformálni.
A szignum függvény sem integrálható, csak improprius integrálként. Többek mellett R. Unbehauen a Systemtechnik 1. című munkájában [6.1.] foglalkozik a „Heaviside” függvény Fourier transzformálásával, és a jel két részre bontása után a szignum függvény transzformálását a következők szerint mutatja:
|
|
(6.3) |
F(ω=0)=0. Ha ω nem zérus, akkor a fenti integrál a következő eredményt adja:
|
|
(6.4) |
A második tag határértéke disztribúciós elmélet szerint zérus, így a szignum függvény Fourier transzformáltja az alábbi lesz:
|
|
(6.5) |
A két részre bontott Heaviside függvény Fourier transzformáltja, figyelembe véve az ½-es szorzókat, végül a következő alakú lesz:
|
|
(6.6) |
A spektrum imaginárius része ω=0 helyen eltűnik, és itt a reális rész „π” nagyságú Dirac impulzus lesz. Ez természetes, hiszen ismert, hogy az f(t)=1 konstans időfüggvény Fourier transzformáltja ω=0 helyen „2π” nagyságú Dirac impulzusként van definiálva.
A spektrum imaginárius része ugyanakkor folytonos, tehát az 1/x-jellegű függvény alatti terület „ki van töltve” harmonikus összetevőkkel.
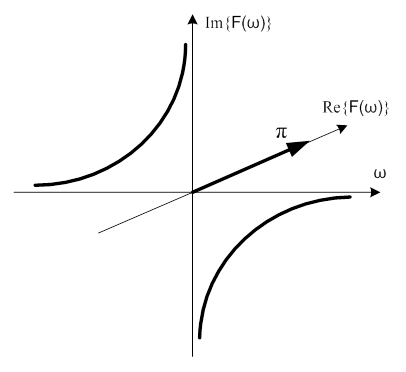
Ha Heaviside függvényt megszorozzuk egy e-σt konvergens függvénnyel, akkor megváltozik a transzformáció „törzsfüggvénye”, és a Fourier transzformáció e-jωt törzsfüggvényéből e-σt·e-jωt=e-st törzsfüggvény lesz, ami viszont már egy másik, nevezetesen a Laplace transzformáció törzsfüggvénye, és ahol s=σ±jω.
A Laplace transzformáció eredményeként azonban nem a spektrum valamilyen formáját, hanem a jel operátor (s) tartománybeli alakját kapjuk. Erről részletesen írunk a 6.2. szakasz - A Fourier sortól a Fourier és a Laplace transzformációig fejezetben.
6.1.3. Diszkrét jelek
Az időben diszkrét (mintavételezett) jel , vagy más néven impulzus sorozat Fourier transzformálható, és eredményül a komplex amplitúdó sűrűség spektrumot kapjuk. A mintavételezett jel amplitúdósűrűség-spektruma a mintavételezés frekvenciájával periodikus. A hibákkal foglalkozó 3. fejezet - Mérési hibák fejezetben részletesen elemeztük a mintavételezésből származó hibákat. Itt csak emlékeztetnénk arra, hogy ha a mintavételezés frekvenciája kisebb, vagy egyenlő, mint az eredeti, nem mintavételezett jelben még éppen megtalálható legnagyobb harmonikus összetevő frekvenciájának kétszerese, akkor ez a periodikus amplitúdó sűrűség spektrum eltorzul, az átvitt jel nagy hibával lesz terhelt. A Shannon által adott mintavételezési szabály kimondja, hogy a mintavételezés frekvenciája legyen nagyobb, mint a jelben megtalálható, maximális frekvenciájú összetevő frekvenciájának kétszerese. Ez az elmélet, a méréstechnikai gyakorlatban ajánlatos a tízszeres szorzó alkalmazása .
A mintavételezés folyamatának elméleti hátterét foglalja össze a következő három ábra.
Először azt látjuk, hogy az „x(t)” (szakaszosan) folytonos analóg jel időbeli „kvantálása”, azaz mintavételezése eredményeként „nT” időpillanatokban megjelenik egy-egy Dirac impulzus, amelynek magassága a mintavételezett jel aktuális értéke nT időpillanatban.
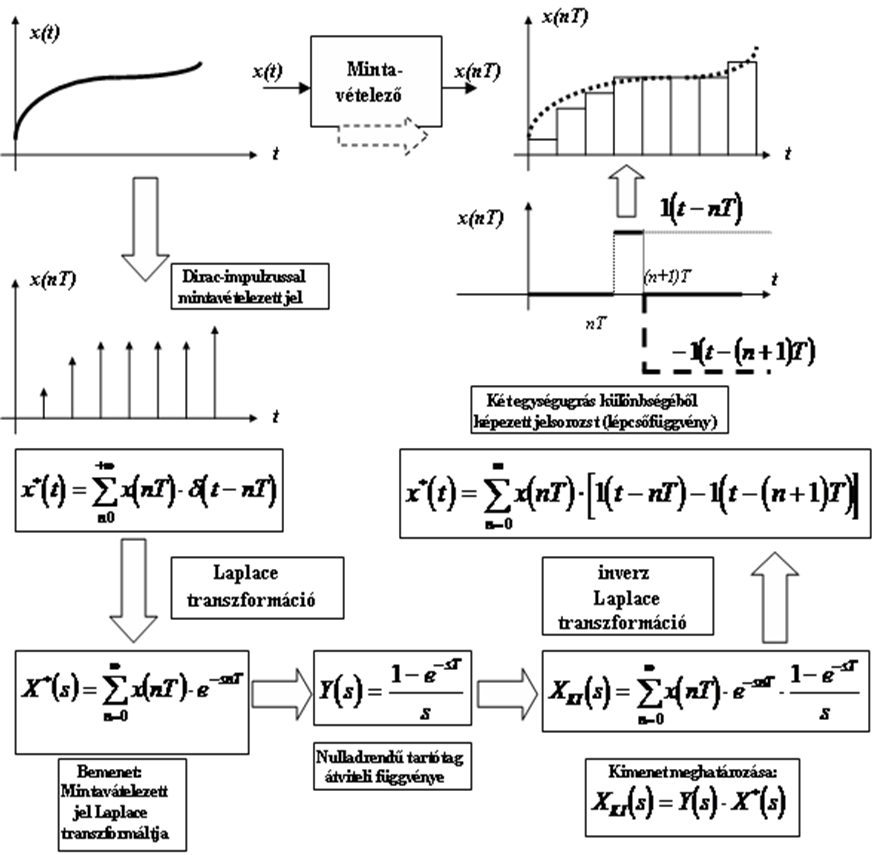
A műveletet elektronikus áramkörrel valósítják meg, ennek elvi képét látjuk a (6.8. ábra - Mintavételező áramkör elvi képe) ábrán. A mintavételezett jelet, a diagram függőleges tengelyén látható módon megkülönböztetjük az eredeti analóg jeltől: x*(t)=x(nT). Az impulzus sorozat spektruma lényegesen különbözik az eredeti analóg jel spektrumától. Amíg annak vonalas, diszkrét spektruma van, addig az impulzus sorozaté folytonos és periodikus. Ezt már bemutattuk a 3. fejezet - Mérési hibák fejezetben, a mintavételezés hibáival kapcsolatos részben.
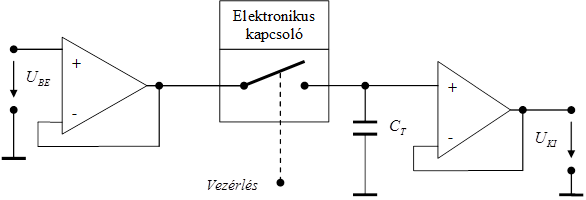
Az impulzus sorozat csak akkor helyettesítheti az eredeti függvényt, ha a mintavétel kellően sűrű, és az egyes Dirac impulzusok közötti „tér” ki van töltve. ezért az impulzus sorozatot egy speciális átviteli egységen kell átengedni, hogy annak kimenetén az eredeti analóg jel legjobb közelítését kaphassuk. Ebben a fejezetben később lesz szó a Laplace transzformáció műszaki alkalmazásairól. Egy ilyen ragyogó alkalmazási példa azon átviteli egység megtervezése, amely a Dirac impulzus aktuális értékét előírt ideig „tartani” képes. Tudott a Laplace transzformáció szabályai alapján, hogy a bemeneti jel Laplace transzformáltjának és az átviteli tag (egység) átviteli függvényének szorzata a kimeneti jel Laplace transzformáltját adja. Tudjuk, hogy a kimenő jel ideálisan egy függőleges téglalap, amelynek magassága a mintavételezett jel, szélessége pedig a minta tartásának ideje. Ez a függvény idő tartományban két Heaviside (egységugrás) függvénnyel valósítható meg. Az egyik egy normál egységugrás, amely nT időpillanatba van eltolva, a másik egy olyan egységugrás, amelyik (n+1)T időpillanatig eltolt, de éppen negatív előjelű. A két függvény összege éppen kiadja a keresett szélességű impulzust, ha összegüket megszorozzuk a mintavételezett jel aktuális értékével. Ez az időfüggvény az ábrán, jobb oldalon látható:
|
|
(6.7) |
A megfelelő átviteli tag átviteli függvényének szintéziséhez (meghatározásához) szükség van ennek a kimeneti függvénynek a Laplace transzformáltjára. Ismeretes az is a speciális jelekkel foglalkozó disztribúciós elméletből, hogy az egységugrás (Heaviside) függvény a Dirac impulzus integrálásával jön létre. A Dirac impulzus Laplace transzformáltja közismerten „1”, ezt külön nem érzékeljük a kifejezésben, de a kimenő jelben lennie kell integrálásnak is. A következő Laplace transzformált függvényben felismerjük a bemenő jel nT időpillanatban vett értékét „x(nT)”, azt, hogy integráljuk a Dirac impulzust, és azt, hogy az integrálás útján kapott két egységugrás jelet két különálló, párhuzamos „úton” kell átvezetnünk, mielőtt előjelhelyes összegzésük megtörténik. Tehát az egyik ágon nT, a másik ágon ellentétes előjellel és (n+1)T idővel eltolva kell átereszteni, majd összegezni:
|
|
(6.8) |
A kimenő jel Laplace transzformáltjában szerencsésen elkülöníthető egymástól a keresett átviteli tag átviteli függvénye és a bemenő jel Laplace transzformáltja, ami az ábrán, baloldalon legalul is látható. A bemenő jel Laplace transzformáltja könnyen meghatározható az impulzus sorozatból:
|
|
(6.9) |
Ebből következik, hogy a keresett átviteli függvény, amely integrál és két „úton” vezeti át a jelet, csak az alábbi lehet:
|
|
(6.10) |
Az átviteli függvény alapján szintetizálható a keresett átviteli egység, amelyet a szakirodalom „nulladrendű tartótagként” ismer. Nulladrendű, mert a tartás alatt nem változik a jel szintje. Létezik elsőrendű tartótag is, ez további integráló elemet is tartalmaz, a tartási idő alatt a minta értékét integrálja, és így közelíti az analóg jelet.
A nulladrendű tartótag tömbvázlatos kapcsolása a következő ábrán látható.
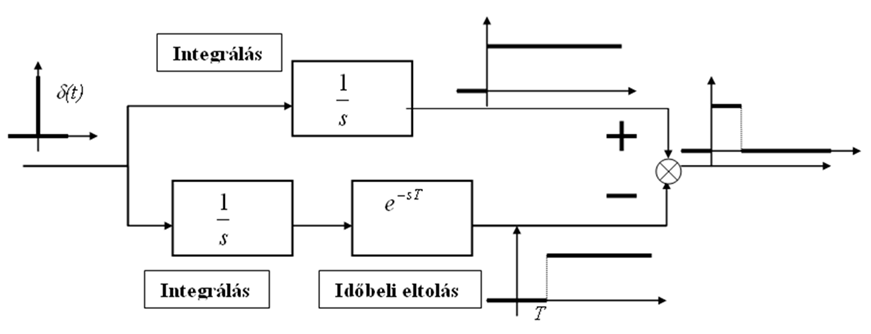
6.1.4. Folytonos sztochasztikus jelek
A sztochasztikus jelek – minthogy ezekre éppen az jellemző, hogy semmilyen részletükben nem periodikusak – közvetlenül nem Fourier transzformálhatóak. Erre a jeltípusra az jellemző, hogy amplitúdója, frekvenciája (frekvencia összetevői és ezek fázisa) véletlenszerűen változik. Éppen ezért ez a jeltípus csak statisztikai jellemzőivel, írható le. Ilyenek lehetnek a jelszintek statisztikai eloszlásának típusa, továbbá a „kvantilisek”, mint pl. a tapasztalati szórás és az átlag. A mérendő mennyiség valószínűség számítási aspektusból ebben az esetben folytonos változó, a valószínűséggel kapcsolatos legfontosabb tudnivalókat a 4. fejezet - Mérés és valószínűség számítás fejezetben foglaltuk össze. Ha az ezen a helyen a leírtakkal kapcsolatban kérdések merülnek fel, célszerű az említett fejezetben a kérdéses fogalmat megkeresni.
A téma tömör leírását többek között Fodor Gy. Lineáris rendszerek analízise című könyvében [6.2.] találhatjuk meg.
Egy sztochasztikus jelszint megjelenésének valószínűsége az f(x) valószínűségsűrűség-függvénnyel írható le. Ez azt mutatja meg, hogy egy „x” jelszint mekkora valószínűséggel fordul elő az „xi” és az „xi +Δx” tartományban:
A P(x) valószínűséget, az f(x) sűrűségfüggvényt és az F(x) eloszlásfüggvényt a szokásos módon kell értelmezni:
|
|
(6.11) |
Az elektronika eszközeivel, a komparálás révén, könnyen mérhető, hogy egy adott jel mikor halad meg egy bizonyos jelszintet, pontosabban azt, hogy a jel mennyi ideig „tartózkodik” egy megadott értéksávban.
Éppen ezért a fenti egyenlet ergodikus folyamatoknál átalakítható idő alapra:
|
|
(6.12) |
Az ábrán az „x” jelszint ingadozását a lineáris átlagra vonatkoztatva vizsgáljuk. A sűrűségfüggvény azt mutatja, hogy a jel átlagértékéhez képest milyen a (jelszintek) amplitúdók eloszlása.
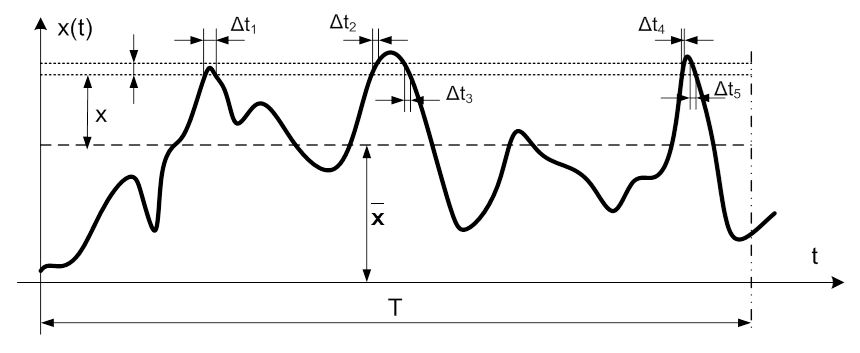
Ezzel a műszaki mérések szempontjából igazán lényeges ergodikus sztochasztikus jel sűrűségfüggvénye is megadható:
|
|
(6.13) |
A sztochasztikus jelek sűrűségfüggvénye elvben sokféle lehet, a gyakorlati tapasztalatok mégis azt mutatják, hogy a Gauss-féle normál eloszlás modellezi ezt a jeltípust a legjobban.
A normál eloszlás tehát arra vonatkozik, hogy a jel átlagértékéhez viszonyított aktuális amplitúdók (jelszintek) mennyi időt „tartózkodnak” egy adott Δx szintsávban, a teljes „T” vizsgálati időre vonatkoztatva. A következő ábrán az előző ábrán látható sztochasztikus jelet használtuk fel, és belerajzoltuk a valószínűség sűrűség függvényét és a hozzá tartozó tengelyeket.
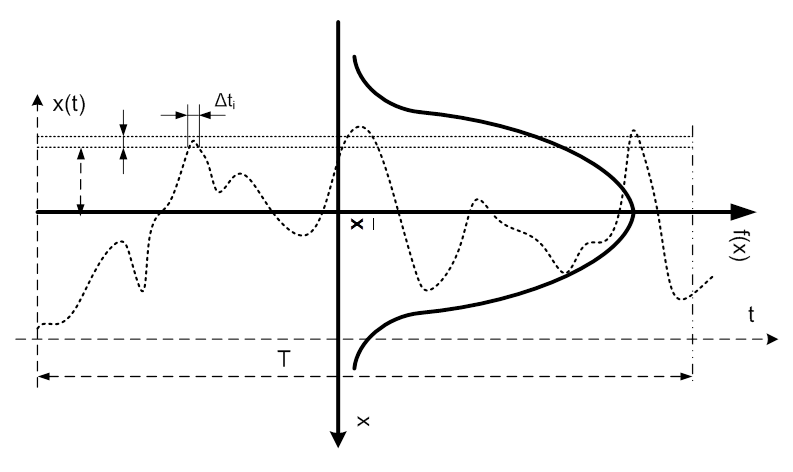
A sztochasztikus jel spektruma folytonos, és, ha kellő mértékben „lapos”, akkor keskenysávú szűréssel jól analizálható. Ez a méréstechnikai oldal. Elméletben a sztochasztikus jel spektruma Fourier transzformációval közvetlenül nem határozható meg, csak két lépésben.
Közvetett lépésként létre kell hozni az autókorrelációs függvényüket .
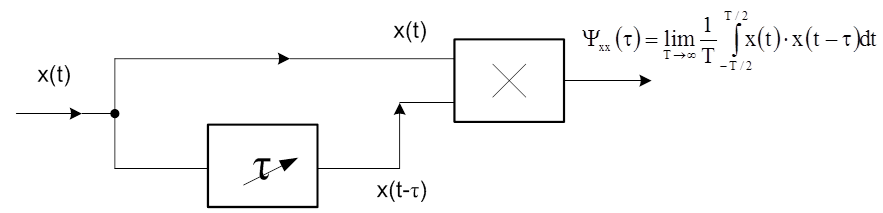
A Ψxx(τ) autókorrelációs függvény ideális sztochasztikus jel esetében kizárólag τ=0 időbeli eltolás esetében ad nullától eltérő eredményt. Ez tulajdonképpen azt jelenti, hogy a jel négyzetét képezzük, tehát eljutottunk a jel teljesítményhez .
A sztochasztikus jel autókorrelációs függvénye ideálisan impulzus formájú, tehát csak akkor kapunk eredményt, ha a jelet eltolás nélkül önmagával szorozzuk. Ez az impulzus alakú autokorrelációs függvény ψxx(ω) azután természetesen már Fourier transzformálható, és eredményül a teljesítménysűrűség-spektrumot Sxx(ω) kapjuk.
|
|
(6.14) |
Az eljárás a szakirodalomban Wiener-Hincsin tételként ismeretes, és segítségével az érzékeltethető, hogy a jel teljesítménye miként oszlik meg adott sávszélességre vonatkoztatva:
|
|
(6.15) |
6.2. A Fourier sortól a Fourier és a Laplace transzformációig
A Fourier és a Laplace transzformációk a függvény transzformációk csoportjába tartoznak, közöttük szoros a kapcsolat. A Laplace transzformáció a Fourier transzformáció ismeretében már megérthető.
A kulcs tehát a Fourier transzformációban rejlik, ennek elfogadásához egy gépész, vagy egy mechatronikus esetében, meglátásunk szerint, a Fourier sorból célszerű kiindulunk. Annál is inkább, mert tudománytörténeti tény, hogy a tudósok mechanikai rezgéstani és hőtani problémák megoldására kerestek megoldásokat, és ez vezetett a Fourier-féle leíráshoz.
A matematikatörténettel foglalkozó irodalomban előkelő helyet foglal el a Fourier-sorok elméletének kialakulása. Az elmélet létrejöttében két fizikai probléma játszott főszerepet: a rezgő húr problémája, és a hővezetés egyenlete.
Három vezető matematikus, d'Alembert, Bernoulli és Euler között az 1700-as évek végén vita folyt egy mechanikai probléma, a két végpontjában rögzített, kifeszített rugalmas húr rezgésének matematikai leírásáról. Meg is született a probléma egy mai szemmel nézve is korrekt megoldása, de ez nem vált széles körben elfogadottá. Nem törődve a kor kételyeivel Joseph Fourier francia matematikus az 1800-as évek elején igen sikeresen alkalmazta a három matematikus által kidolgozott, illetve vitatott eljárást a hő terjedésének matematikai leírására.
Egy 1822-ben megjelent művében Fourier azt elemezte, hogy a környezetétől elszigetelt rúd belsejében zajló hőmérséklet-változást hogyan írhatjuk le. A felvetés szerint a hő csak a rúdban áramlik; a rúd és a környezete között nem.
A matematikusok, beleértve korunk matematikusait is, rengeteg átgondolnivalót kaptak a Fourier-analízissel kapcsolatban. Akadnak még mindig nyitott kérdések, elméleti problémák. Ugyanakkor különösképpen a mérés-és híradástechnika számára a gyakorlati alkalmazásokban jól felhasználható módszerek, technikák jöttek létre.
A Fourier-sorokkal kapcsolatban már a kezdet kezdetén is számos kérdés vetődött fel, s ezek alapvetően megszabták az elméleti kutatások irányát. Dirichlet 1829-ben bebizonyította, hogy szakaszonként monoton függvények trigonometrikus Fourier-sora előállítja a függvényt. Ezzel igazolást nyert, hogy egy fontos függvényosztály elemei rekonstruálhatók Fourier-együtthatóikból, ha a végtelen sor összegét a szokásos módon, vagyis a részletösszegek sorozatának határértékeként határozzuk meg.
A trigonometrikus Fourier-együtthatók kiszámítását az a felismerés tette lehetővé, hogy a trigonometrikus rendszer bármely két különböző tagjának szorzatintegrálja nulla. Ha két függvény szorzatának integrálját a két függvény skaláris szorzatának tekintjük, akkor az imént említett tulajdonság azt jelenti, hogy ezek a függvények páronként merőlegesek (ortogonálisak) egymásra, ortogonális rendszert alkotnak. A függvény Fourier-sora pedig felfogható egy így létrejött végtelen dimenziós koordináta-rendszerben való megjelenítésnek. Ezen szemléletből kiindulva kezdték el vizsgálni a skaláris szorzattal ellátott vektortereket, és ezek fontos osztályát David Hilbert német matematikusról „Hilbert tereknek” nevezték el.
Hilbert a trigonometrikus rendszer szerinti Fourier-szintézis problémáival összefüggésben további elméleti kérdéseket vetett fel, többek között a Fourier-sor konvergenciájával kapcsolatosakat is.
Ahogy már említettük, a Fourier analízis a méréstechnikában alapvető fontosságú, mert a megfelelő átviteli tulajdonságokkal rendelkező technikai mérőláncot a vizsgált jel spektrumához kell illeszteni. Kérdés mi az elméleti háttere a jelek harmonikus összetevői, amplitúdó, vagy teljesítmény spektruma meghatározásának?
Az f(t) periodikus, állandó amplitúdójú jel harmonikus összetevőkre bontható, azaz elméletileg végtelen számú, különböző amplitúdójú és frekvenciájú szinusz és koszinusz jelek összegeként írható fel.
|
|
(6.16) |
Az Ak és Bk együtthatókat a következő módon határozzuk meg:
|
|
(6.17) |
Az Ak és Bk együtthatók meghatározása igen hosszadalmas, még akkor is, ha egy adott feladatban, a gyakorlatban nincsen szükség minden (végtelen számú) együtthatóra, csak bizonyos számú összetevő kiszámítására. Ezen kívül bonyodalmat jelenthet a trigonometrikus függvények és az adott f(x) jel szorzatának integrálása is.
Ez a probléma küszöbölhető ki azzal, hogy a trigonometrikus függvények helyett komplex exponenciális függvényeket alkalmazunk. Így csak egyetlen, C k együttható marad, ami azonban komplex, tehát most már nem a spektrum együtthatóiról, hanem komplex amplitúdó spektrumról beszélünk. A trigonometrikus függvények helyére az Euler-formula segítségével komplex exponenciális függvények írhatók.
A fentiek miatt a mérés-és híradástechnikában a Fourier analízis nem trigonometrikus függvényekkel, hanem forgó vektorok – „fazorok” segítségével történik. Ezért az első mozzanat, hogy bemutatjuk a kétdimenziós komplex vektort a komplex síkon, és ennek kapcsolódását a trigonometrikus alakokhoz.
|
|
(6.18) | |
|
|
(6.19) |
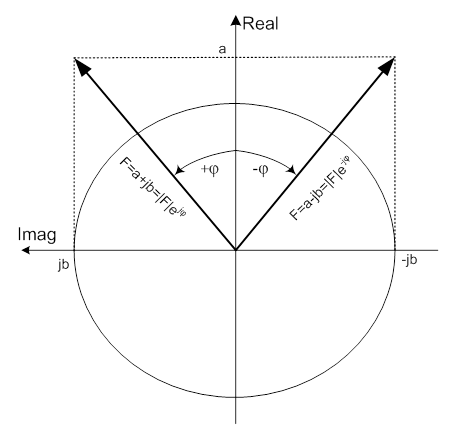
|
|
(6.20) |
Az Euler formulák szemléltetése céljából egy általános „cos” időfüggvényt ábrázoltunk két formában a következő ábrán:
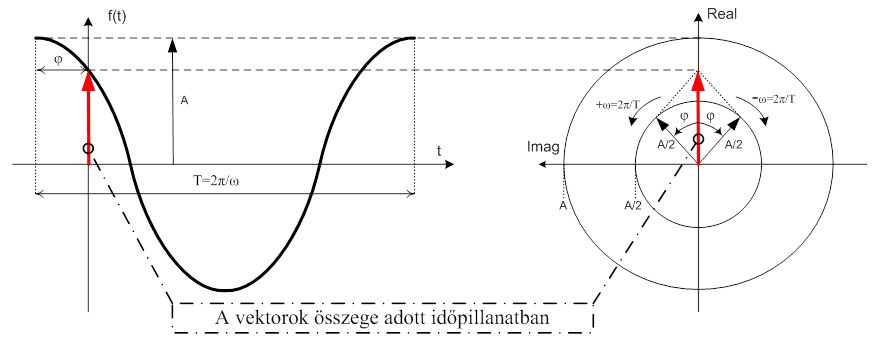
A fenti ábrán egy általános cos függvény időbeli és komplex alakját látjuk. A jel „A” amplitúdójú és „φ” fázistolású. Az ábrán a függvény t=0 időpillanatbeli értékéhez tartozó vektor piros színnel van jelölve. A jel Euler formula szerinti átírása az alábbi módon történt:
|
|
(66.21) |
Behelyettesítve az exponenciális alakot a trigonometrikus formába a Fourier sor komplex alakjához jutunk:
|
|
(6.22) |
A két exponenciális függvény összevonása, és az átrendezés után kétféle komplex együtthatót kapunk, ezek Ak és Bk:
|
|
(6.23) |
A cél az, hogy ezt a summát egy kompaktabb, és egyszerűbben számítható alakra hozzuk. Ehhez azonban egy megállapodás is szükséges:
Amint igaz az, hogy -(-1)=1, ugyanúgy legyen –k=k’, azaz –k’=k, ahol k’=-1,-2,-3,…
E megállapodás a Fourier együtthatók előjeleire nézve következményekkel jár:
|
|
(6.24) | |
|
(páros függvény) | ||
|
|
(6.25) | |
|
(páratlan függvény) |
|
Behelyettesítve, és az A 0 együtthatót is befoglalva, továbbá felhasználva, hogy –k=k’, két lépésben olyan alakhoz jutunk, amely lehetővé teszi az összevonást:
|
|
(6.26) | |
|
|
(6.27) |
Most már lehetséges egyszerűbb formában is felírni a komplex Fourier sort:
|
|
(6.28) |
Megjelenik viszont ezzel egy időben egy műszaki szemszögből bizarrnak tűnő jelenség is, ez a negatív körfrekvencia . Ilyen frekvenciák a valóságban természetesen nem léteznek, de bevezetésükért cserében, a kétféle, és elméletben végtelen sok együttható helyett, csupán egyféle, a Ck (persze ugyancsak végtelen sok) kiszámítására van szükség.
Mihez kezdünk azonban a negatív körfrekvenciákkal? Ezek bizonyos, numerikus úton meghatározott komplex amplitúdó spektrumok esetében úgy jelennek meg grafikus formában, hogy a zérus körfrekvenciára szimmetrikusan, kétoldalasan láthatók az együtthatók a körfrekvencia tengely mentén. Ilyen esetben nincs más teendő, mint bal oldali összetevőket a jobb oldali, pozitív körfrekvenciákhoz tartozó együtthatókhoz hozzáadni, és készen van a „műszakilag értelmezhető” spektrum.
A Ck komplex együtthatók kiszámításához ugyancsak felhasználjuk az Euler-formulákat.
|
|
(6.29) | |
|
|
(6.30) | |
|
|
(6.31) | |
|
|
(6.32) |
A C k komplex mennyiségek tehát a komplex Fourier sor együtthatóinak felelnek meg.
A periodikus jelek spektruma a k=1,2,3,… egész értékek miatt un. „vonalas” spektrum, más néven diszkrét spektrum.
Egy ilyen, képzeletbeli periodikus jel vonalas komplex spektrumát mutatja a 6.16. ábra - Általános, folytonos periodikus jel diszkrét komplex spektruma ábra, három dimenzióban, érdemes a szemléletesség kedvéért „hátrább lapozni”. Adott körfrekvencián megjelenő komplex együttható valós és képzetes részre bontható. A legtöbb spektrum ábrázolás azonban nem 3D-s, hanem az együttható abszolút értékét mutatják a megfelelő körfrekvenciáknál: |F(ω)|.
A Fourier sor komplex alakjára és az ennek felírásához szükséges C k komplex együtthatókra különleges jelentőségük miatt a 6.3. szakasz - A Fourier sor komplex alakja fejezetben még visszatérünk. Ha ugyanis a C k együtthatók komplexek, akkor vektorként is felfoghatók, amint azt a (6.16. ábra - Általános, folytonos periodikus jel diszkrét komplex spektruma) ábrán láthatjuk.
A Fourier transzformációhoz vezető úton azonban itt még nem állhatunk meg. Eddig ugyanis csak periodikus, vagy szakaszosan periodikus jelek sorát tudtuk meghatározni. A technikai jelek világában azonban nem csak összetett periodikus, hanem egy-és kétoldalasan határolt jelek is előfordulnak. Olyan nem periodikus jeleknek (függvények), amelyek teljesítik a Dirichlet-feltételt, tehát abszolút, vagy négyzetesen integrálhatóak nem a Fourier együtthatóit, hanem a Fourier transzformáltját határozzuk meg.
C k felhasználásával – és az amplitúdó sűrűség spektrum c(ω) bevezetésével - jön létre a Fourier transzformáció.
Bevezetjük elsőször is a diszkrét körfrekvenciákon megjelenő együtthatók helyett az amplitúdó sűrűség fogalmát. Ez alatt a Δω sávszélességre eső Ck együtthatókat kell érteni:
|
mert |
(6.33) |
Ha most Δωk helyére behelyettesítjük a 2π/T összefüggést, akkor a T→∞kiterjesztés révén, az impulzus-szerű, időben határolt, nem periodikus függvények is bevonhatók a vizsgálatba azzal, hogy ezek a függvényeket T→∞ időtartamban „legalább egyszer periodikusnak” tekintjük. Ck helyére a kiszámításához korábban meghatározott összefüggést helyettesítjük be.
|
|
(6.34) |
A „T” periódusidő tehát eltűnik az összefüggésből, és átrendezés után kapjuk a komplex amplitúdó sűrűség spektrumot, aminek jelölése F(ω).
|
|
(6.35) |
A Fourier transzformáció tehát minden olyan függvényre alkalmazható, amelyekre teljesül a Dirichlet feltétel, azaz általános periodikus és időben kétoldalasan határolt jelekre is.
A fejezet (6.5. ábra - A Heaviside függvény felbontása) ábráján látható Heaviside-függvény, és a hozzá hasonló, önmagában nem integrálható függvények Fourier transzformálása komoly apparátust igénylő matematikai feladat. A szakirodalomban található Fourier transzformációs táblázatok a gyakorlatban sokszor előforduló, továbbá jó néhány „kritikus” függvény transzformáltját tartalmazzák.
Már csupán az utolsó lépés hiányzik ahhoz, hogy a Laplace transzformációhoz eljussunk. A (6.4. ábra - A Fourier analízis összefoglaló bemutatása) ábrán látható táblázatos összefoglalásban az egységugrás, azaz Heaviside függvényt beszoroztuk egy olyan exponenciális függvénnyel, amely a kritikus egyoldalasan határolt, és nem integrálható függvényt konvergenssé teszi. Ez a függvény e-σt lesz, ahol |σ| egy zérustól eltérő, bármilyen kis szám.
|
|
(6.36) |
A fenti összefüggésben „s” a Laplace-operátor . Az f(t) időfüggvényt a transzformáció segítségével az operátor tartományba képezzük le, és az F(s) racionális törtfüggvényt kapjuk eredményül. A mérnöki gyakorlatban a Laplace transzformáció nélkülözhetetlen szerepet játszik a lineáris, állandó együtthatós differenciálegyenletek megoldása során, valamint a mérés-és műszertechnikában az átviteli függvények meghatározásában, az amplitúdó és fázismenet kiszámításában. Erre látunk fontos gyakorlati példát egy másodrendű műszer dinamikai vizsgálatánál, a 3.4.3. szakasz - Mérőlánc frekvenciafüggő átviteléből adódó hibák fejezetben.
Befejezésül egy összefoglaló táblázatban mutatjuk be a legfontosabb jeltípusok Fourier együtthatóinak, illetve Fourier transzformáltjainak jellemző képeit. Az időben folytonos jelek spektruma vonalas (diszkrét), az időben kétoldalasan határolt jeleké pedig folytonos.

A táblázat csak a jelek felosztása során megjelenő, determinált jeltípusokat mutatja. A szakirodalomban közölt táblázatokban megtaláljuk valamennyi fontos időfüggvény Fourier transzformált alakjait.
6.3. A Fourier sor komplex alakja
Levezettük a Fourier sor trigonometrikus alakjából, hogy az Euler formula segítségével a Fourier sor komplex alakja tömörebben felírható:
|
|
(6.37) | |
|
|
(6.38) |
A levezetésben a jelölések logikája világos: A trigonometrikus alak Ak és Bk együtthatóiból a komplex alakban Ck lesz.
A továbbiakban az egyszerűség kedvéért, és a (6.16. ábra - Általános, folytonos periodikus jel diszkrét komplex spektruma) ábrán látható jelöléssel összhangban az időbeli jelet f(t)-vel és ennek Fourier transzformáltját F(ω)-val jelöljük. Ennek szellemében a komplex Fourier együtthatókat az alábbi általános jelölésekkel kapjuk:
|
|
(6.39) |
ahol a (6.16. ábra - Általános, folytonos periodikus jel diszkrét komplex spektruma) ábrán ωk=kω1, azaz az alap harmonikus k-szorosa.
A Méréstechnika című [1.1.] elektronikus jegyzetben egy páratlan periodikus függvény Fourier sorfejtésének példáján megmutattuk, miként tűnnek el bizonyos összetevők együtthatói az integrálás eredményeként a sorból.
Ezt a jelenséget a komplex együtthatók és a komplex síkban forgó vektorok segítségével általános formában is le lehet írni.
Láttuk korábban, hogy az általános periodikus időfüggvény egy tetszőleges harmonikus (k-adik) összetevője két ellentétese forgó vektor összegeként, az alábbi formában írható fel:
|
|
(6.40) |
Ha az f(t) függvény tartalmaz egy olyan komponenst, mint a fenti egyenlet, akkor a komplex Fourier együttható kiszámításánál az alábbiakat tapasztalhatjuk:
|
|
(6.41) |
Látjuk, hogy az adott integrálási határok miatt az első tag megmarad, mert a két komplex exponenciális függvény kompenzálja egymást, míg a második tag, tekintettel arra, hogy az
e-jkωt szorzó koszinusz és szinusz függvényekre bontható, tehát
|
|
(6.42) |
a teljes periódusra vett integráljuk zérust fog eredményezni, bármilyen függvény is álljon szorzandóként előttük. Ezért tehát az alábbi eredmény kapjuk:
|
|
(6.43) |
Az Fk(ω) együttható értéke tehát az integrálás elvégzése után egy „kimerevített” (nem forgó) Ak/2 nagyságú, φk fázishelyzetű komplex vektor.
Az is látható a részletesen bemutatott integrálásból, hogy eltűnnek azok az együtthatók is, amelyek nem egész számú többszörösei az alap harmonikusnak, hiszen ezekben az esetekben az első tagban sem kompenzálják egymást a komplex exponenciális függvények.
A komplex Fourier sor tehát valóban az alábbi általános alakban írható fel:
|
|
(6.44) |
A komplex együtthatók képe a (6.16. ábra - Általános, folytonos periodikus jel diszkrét komplex spektruma) ábrán látható, és korábban már jeleztük, hogy a probléma részletes bemutatására sor fog kerülni.
A komplex együtthatók meghatározásából két fontos következtetést kell levonni.
Az egyiket már említettük, nevezetesen azt, hogy a sorozatban csak az alap harmonikus egész számú többszörösei jelennek meg.
A másik az, hogy a valós fizikai jelek komplex együtthatókkal történő leírása esetében minden pozitív körfrekvenciájú együttható kell rendelkezzen egy negatív körfrekvenciájú párral is, hiszen azt láttuk a (6.13. ábra - A komplex vektor (fazor) ábrázolása, a szokásoshoz képest 90 fokkal pozitív irányba elforgatva) ábrán, hogy az „A” amplitúdójú jel két A/2 amplitúdójú vektoriális összetevőre volt bontható.
Az általános periodikus jel (6.16. ábra - Általános, folytonos periodikus jel diszkrét komplex spektruma) ábrán látható spektrumán igyekeztünk érzékeltetni azt is, hogy a pozitív körfrekvenciákhoz tartozó komplex együtthatók konjugált komplexei a negatív körfrekvenciákhoz tartozó együtthatóknak. Másként a két együttható összege nem adhatna ki reális eredményt, de így a konjugált komplex imaginárius részek kompenzálják egymást. A két reális együttható nagysága külön-külön Ak/2, tehát összegük kiadja a k-adik harmonikus Ak amplitúdóját.
Ennek viszont nagyon fontos általános következménye van, amit az alábbiak szerint lehet megfogalmazni:
|
|
(6.45) |
ahol F* az F konjugált komplexe.
Ezt az összefüggést a Hilbert transzformáció ismertetése során is fel fogjuk használni.
A gyakorlatban két féle spektrális ábrázolás létezik. Az egyiken csak a pozitív körfrekvenciákhoz tartozó Ak együtthatókat látjuk, míg a másikon zérus körfrekvenciára szimmetrikusan, a pozitív és negatív körfrekvenciákhoz tartozó Ak/2 együtthatókat. Ezt láttuk a 6.15. ábra - Determinált jelek Fourier összetevői ábra összefoglaló táblázatában, a négyszögrezgés spektrumán.
A komplex Fourier együtthatók, illetve a Fourier transzformált szemléltetésére iktattuk be a már többszörösen is hivatkozott, következő, azaz 6.16. ábra - Általános, folytonos periodikus jel diszkrét komplex spektruma ábrát.
(Néhány igen szemléletes ábra ötletét átrajzolva és némileg módosítva, a Brüel & Kjaer műszergyártó cég 1977-ben megjelent kézikönyvéből vettünk át [6.3.] . A hasznos kézikönyv a frekvencia analizátor műszerek felhasználói számára készült.)
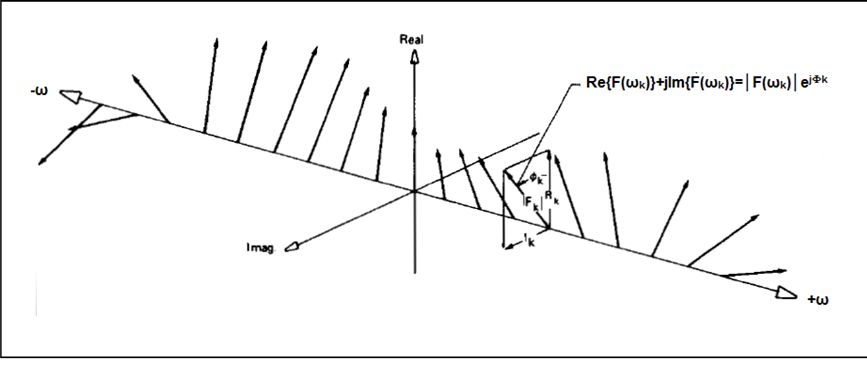
A méréstechnikai szakirodalomban nagyon ritka a spektrum komplex megjelenítése. Helyette vagy a spektrum abszolút értékét, vagy a jel teljesítmény spektrumát ábrázolják.
A következő, összefoglaló ábrán négy olyan időfüggvény látható, amelyek vagy Fourier sorba fejthetők, vagy van Fourier transzformáltjuk, amelyeket az időfüggvények alatt találunk.
Az első páros egy időben diszkrét analóg (időben kétoldalasan határolt) jel képe, és Fourier transzformáltja, amely folytonos spektrumot eredményez. Fourier sorfejtés itt nem lehetséges.
A második páros egy időben periodikus analóg jel és annak diszkrét spektruma, amelyik Fourier transzformációval határozható meg, de amelynek Fourier együtthatói is kiszámíthatók.
A harmadik páros egy időben diszkrét (kétoldalasan határolt) jel mintavételezése (impulzus sorozat) és annak folytonos, periodikus spektruma, amelyet Fourier transzformációval lehet meghatározni.
A negyedik páros egy periodikus mintavételezett jel és annak diszkrét periodikus spektruma, amely diszkrét Fourier transzformációval (lásd 6.5. szakasz - Diszkrét Fourier transzformáció (DFT) fejezetet) lett meghatározva.
A mérnöki gondolkodáshoz közel áll a képekben való összefüggés-keresés, ezért úgy gondoljuk, a megértésben sokat segíthet az ábra vizsgálata.
Láttuk, hogy az analóg jelek csoportjában, az időben kétoldalasan határolt jelek spektruma folytonos, míg időben folytonos, periodikus, stacionárius jelek spektruma diszkrét lesz.
A mintavételezett jelek esetében azt látjuk, hogy az időben korlátozott impulzus sorozat hagyományos módon meghatározott Fourier spektruma folytonos és a mintavétel körfrekvenciájával (ωm) periodikus.
A negyedik ábrán a mintavételezett jelet nem hagyományos Fourier transzformációnak vetettük alá, hanem a diszkrét Fourier transzformációt végeztük el.
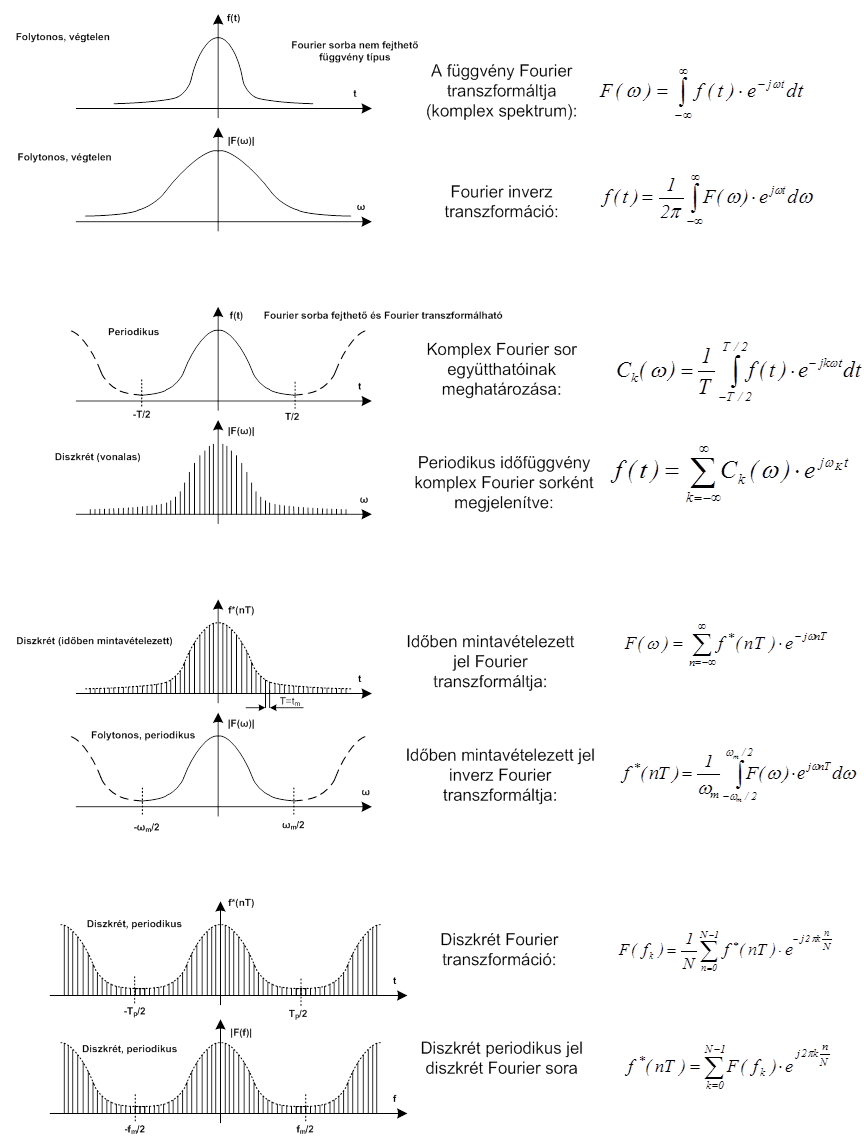
Az ábrán bemutatott jelek időtartománybeli alakja szándékosan „rokon” egymással, légyeges pontokon mégis különbözőek.
6.4. A Hilbert transzformáció
A Hilbert transzformáció az egyoldalas Fourier transzformáció valós és képzetes részei közötti kapcsolatot reprezentálja. A kapcsolat a soron következő lépések bemutatásával nyilvánvalóvá válik.
A gyakorlatban előforduló válaszjelek un. „okozati” jelek függvényértéke negatív időtartományban zérus:
|
|
(6.46) |
Erre a jeltípusra jellemző példa egy technikai (elsőrendű) rendszer impulzus válasza, hiszen a kimeneten csak akkor jelenhet meg válasz, ha a bemenetre került t=0 időpillanatban a gerjesztés.
Az általános válaszjelet, vagyis „okozati” jelet fel lehet írni úgy is, mint egy páros a**(t) és egy páratlan a*(t) függvény összegét. A két részre való bontást természetesen úgy értjük, hogy a pozitív időkhöz tartozó részek megegyeznek. A páros és páratlan részre való bontás a szignum függvény alkalmazásával is kifejezhető:
|
|
(6.47) |
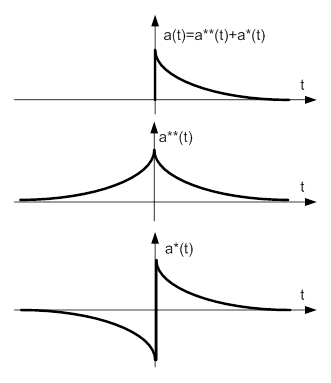
Ahhoz, hogy ezeket a páros és páratlan időfüggvényeket a Fourier transzformáció valós és képzetes részeivel kapcsolatba lehessen hozni, szükséges a Fourier transzformáció összefüggéseit felidézni:
|
|
(6.48) |
Látható, hogy a transzformáció törzsfüggvényében az „előre”- és „vissza”transzformálás közötti különbség az e-függvény kitevőjének előjelében jelentkezik. Ez a különbség eltűnik, ha az idő, mint független változó előjele ellentétesre változik. Így az f(t) függvény „előre” transzformálásánál megjelenő törzsfüggvény megegyezik az f(-t) függvény visszatranszformálásának törzsfüggvényével, ha az integrál kifejezés előtti 1/2π konstanstól eltekintünk.
|
|
(6.49) |
A fentiek alapján általánosságban felírható az alábbi gondolatsor:
|
|
(6.50) |
Végezzük el a Fourier transzformációt az a(t) függvényre:
|
|
(6.51) | |
|
|
(6.52) |
Fontos az információelméleti átalakítások, szűrők tervezése, stb. szempontjából, hogy a spektrum reális és imaginárius része között kapcsolat van, tehát ezek nem függetlenek egymástól.
E kapcsolat matematikai kifejezése tulajdonképpen a Hilbert transzformáció , mint a függvény transzformáció egyik speciális formája.
Láttuk a fejezet bevezetőjében, hogy
|
|
(6.53) |
Behelyettesítve a fenti összefüggést a spektrum reális részére felírt egyenletbe látjuk, hogy a spektrum imaginárius része konvolucióval felírható a spektrum reális részeként:
|
|
(6.54) |
A konvolució mindkét tagja Fourier transzformációból áll. Az első tagja tulajdonképpen a „j” komplex egységvektorral megszorzott imaginárius spektrum-rész, amint ez a néhány sorral feljebb bemutatott egyenletből látható. A második tag a szignum függvény Fourier-transzformáltja. Ezt a transzformáltat a Heaviside függvény kapcsán már tárgyaltuk. Ezeket az összefüggéseket behelyettesítve, a spektrum reális és imaginárius része közötti kapcsolatra az alábbi egyenletet kapjuk:
|
|
(6.55) |
Tekintettel arra, hogy a konvoluciós integrál elé „kihozhatók” a konstansok, esetünkben a „j”, végül az alábbi összefüggést kapjuk. Az egyenletben felhasználtuk az ω=2πf összefüggést is, mert a szakirodalom nem a körfrekvencia, hanem a frekvencia használatát preferálja a Hilbert transzfor-máció esetében:
|
|
(6.56) |
A Hilbert transzformáció általános formája frekvencia tartományban a következő:
|
|
(6.57) |
A Hilbert transzformáció a Fourier transzformációval ellentétben nem változtatja meg a független változót, az eredmény ugyanabban a tartományban marad. A transzformáció létezik természetesen az idő tartományban is, amint azt később látni fogjuk.
Azért a frekvencia tartománybeli összefüggést írtuk fel először, mert a Hilbert transzformáció lényege könnyebben megérthető a frekvencia tartományban, mint az idő tartományban. Ez a transzformáció ugyanis nem változtatja meg F(f), illetve F(ω) amplitúdóit, hanem csupán a fázisukat tolja el.
A Fourier transzformáció pozitív (kör)frekvenciákon vett értékeit „–j”-vel szorozzuk (ez a fázis „-π/2” nagyságú módosítását jelenti), míg a negatív (kör)frekvenciákhoz tartozó Fourier transzformált értékeket „j”-vel szorozva „+π/2” fázismódosítást kapunk.
Lényegét tekintve a Hilbert transzformáció „kicseréli” F(ω) reális és a valós részeit, miközben ezek előjelét is megváltoztatja:
|
|
(6.58) |
Említettük korábban, hogy a Hilbert transzformáció idő tartományban is elvégezhető:
|
|
(6.59) |
A következő két ábrán a transzformáció folyamatát világítjuk meg.
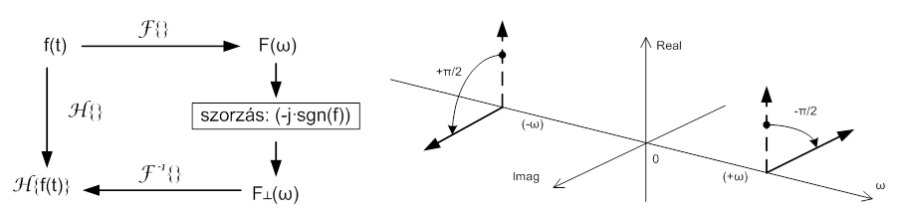
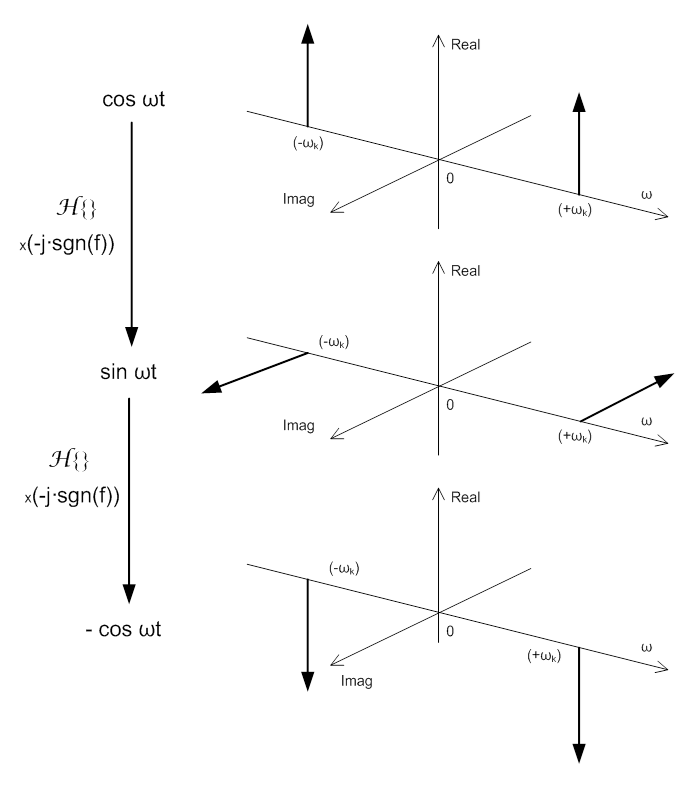
6.5. Diszkrét Fourier transzformáció (DFT)
A modern méréstechnikában kiemelt szerepe van a számítástechnikának, és így nem meglepő, hogy a jól algoritmizálható matematikai műveletek viszonylag hamar megjelentek programok formájában.
Az előző fejezetekben elmondottakra alapozva bemutatjuk, hogy milyen összefüggések érvényesek, ha mind a mintavételezett jel, mind pedig a spektruma diszkrét. Ez az eset a (6.17. ábra - Analóg és mintavételezett jelek idő és frekvencia tartományban) ábrán látható változatok közül az alsó, sorrendben a negyedik.
A jel tehát periodikus, a digitális technikában, ebben az esetben frekvencia helyett szekvenciát, sorrendet emlegetnek, és impliciten periodikus a spektrum is.
A Fourier sor képe a 6.3. szakasz - A Fourier sor komplex alakja fejezetben látható komplex alakhoz hasonló, de természetesen itt nem a folytonos időfüggvény, hanem annak „n” időpillanatban történő mintavételezéséből származó impulzus-sorozat szerepel. A transzformáció törzsfüggvényében az „ωt” folytonos fázis helyett k·n/N diszkrét fázisértékek szerepelnek. Az összefüggésben „N” azt jelzi, hogy a komplex egységvektor egy körülfordulása (2π) hány részre van felosztva. A gyakorlatban ez azt jelenti, hogy a periodikus jel egy periodusából „N” mintát veszünk, egyenletes mintavételezéssel. Az összefüggésben „k” a diszkrét körfrekvenciákra utal, míg „f(n)” az n-edik időpillanathoz tartozó minta értéke.
A diszkrét Fourier transzformáció képlete:
|
|
(6.60) |
Az inverz diszkrét Fourier transzformáció képlete segítségével természetesen az időfüggvény n-edik időpillanatban vett értékét kapjuk:
|
|
(6.61) |
Az integrálok helyére szummák kerültek, innen már csak egy lépés a számítás algoritmizálása a digitális számítógépes feldolgozáshoz. Ahhoz, hogy az N darab mintából N frekvencia komponenst kapjunk (vagy fordítva), N2 komplex szorzásra van szükség. Maga a számítási eljárás a „Gyors Fourier Transzformáció”, „Fast Fourier Transformation – FFT”, néven ismert, amely elvégzéséhez N·log2N komplex szorzási művelet szükséges.
Bár az FFT bemutatására a 11. fejezet - Diszkrét frekvencia analízis fejezetben kerül sor, a jelekkel való műveletek teljessége érdekében, a bemutatásból nem hiányozhat a DFT sem.
A diszkrét Fourier transzformáció fentebb látható képlete felírható mátrix-vektor egyenlet formájában is, hiszen szorzásokról és összeadásokról van szó:
|
|
(6.62) |
Nézzük egy áttekinthető méretű mátrix esetén, mit is jelent ez a formula. Legyen N=8.
A négyzetes „A” mátrix minden eleme egy egységvektort jelent, különböző szöghelyzetekben:
|
|
(6.63) |
Minden mátrix sor k=0…7 (kör)frekvenciát tartalmaz, míg az oszlopok n=0…7 időpillanatnak felelnek meg. Ha k=0 és n=0, akkor a szög zérus, és ez a mátrixban +1 értékű elemet eredményez.
Mivel a mátrix első sora a k=0 körfrekvenciához van rendelve, azt mondhatjuk, hogy az így kiadódó F0 az fn időpillanatokban mintavételezett jel szintjei összegének 1/8 része, hiszen N=8.
A második mátrix sor a k=1 miatt a legalacsonyabb frekvenciájú összetevőt adja. Az „előre” transzformálásnál az exponenciális függvény kitevőjének negatív előjele az óramutató járásával megegyező vektor forgásirányt jelöl.
|
|
(6.64) |
Példaként nézzük egy ábrán az F1 komplex együtthatót kiadó vektorok forgását, ha az fn mintavételi értékek állandók:
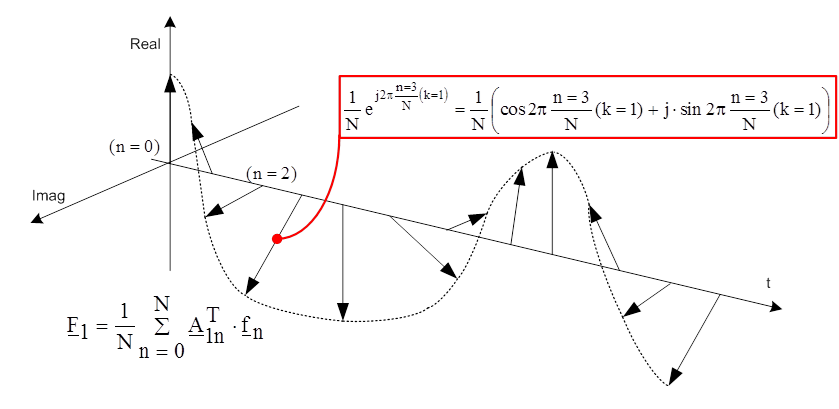
A mintavételezett jelek spektrumának periodicitása világossá válik, ha a mátrix-vektor egyenletet nézzük. A mátrix első sora az fm mintavételi frekvenciát jól reprezentálja, hiszen a vektor egy teljes körülfordulása tartozik egy időbeli mintához, majd következik a 2fm mintavételi frekvencia, és így tovább. Mivel a forgó vektorok diszkrét időpillanatokhoz tartoznak, a köztes információk „elvesznek”, így azt sem lehet tudni, hogy egy adott szöghelyzet eléréséig a vektor hányszor forgott körbe. Ezt a problémát a 3.4.4. szakasz - Mintavételezési hiba fejezetben taglalt, Shannon-féle mintavételezési szabállyal lehet kiküszöbölni.
A fent bemutatott mátrix-vektor egyenlet képezi az FFT (Gyors Fourier Transzformáció) alapját azzal, hogy a korszerű rendszerekben N=1024, vagy ennél nagyobb érték. Az algoritmus igen bonyolult, az első fázisban az „A” mátrixot szorzatokra bontják, ami a mátrix műveleteket leegyszerűsíti.
A 11.5. szakasz - Gyors Fourier transzformáció alapjai (FFT= Fast Fourier Transformation) fejezetben az itt leírt algoritmusok gyakorlati alkalmazását találhatja meg.
Irodalmak
[6.1.] Systemanalyse 1.. Oldenburg Verlag. 2002.
[6.2.] Lineáris rendszerek analízise. Műszaki Könyvkiadó. 1967.
[6.3.] Application of B&K Equipment to Frequency Analysis. Brüel & Kjaer. 1977.
7. fejezet - Spektrum analízis a méréstechnikában
7.1. Analóg frekvenciaanalízis
Ebben a fejezetben az ábra és képanyagok tekintetében a Brüel és Kjaer műszergyártó cég által forgalmazott analizátorokat és tartozékaikat felhasználó műszaki szakemberek részére készült kézikönyvre támaszkodtunk: R. B. Randall: Application of B&K Equipment to Frequency Analysis, 1977. [6.3.] . (A „B & K” cég napjainkban már mintegy 70 éves múltra tekinthet vissza, és vezető a hang-és rezgésmérés mérőeszközeinek gyártásában. Korszerű gyártmányai mellett, a felhasználókat tudományos igényességgel elkészített segédletekkel is támogatja.)
Villamos jelek frekvencia spektrumának meghatározása „klasszikus” analóg formában úgy történik, hogy az analizálni kívánt jelet különböző középfrekvenciájú analóg szűrőkön, vagy egyetlen, de középfrekvenciáját adott (vizsgált) frekvencia tartományban folyamatosan változtatni képes szűrőn bocsátják át, miközben mérik a jel teljesítményét (amplitúdóját).
Egy rögzített középfrekvenciájú szűrő válasza a bemenő jelre a bemenő jel és a szűrő (mint átviteli tag) súlyfüggvényének konvoluciója, amint az a rendszertechnikából ismert. Ennek az időtartománybeli folyamatnak, a Laplace transzformációs szabályok szerint, az operátor térben két komplex függvény szorzata felel meg, nevezetesen a bemenőjel Laplace transzformáltjának és a szűrő-súlyfüggvény Laplace transzformáltjának szorzata. A „frekvencia térben” ezért úgy tekinthetjük, hogy a szűrőn átengedett jel amplitúdó spektruma két individuális jel amplitúdó spektrumának szorzata. Amennyiben a bemenő jel és a szűrő teljesítmény spektruma adott, akkor a kimenő jel a két teljesítmény spektrum szorzata lesz, amint a következő ábrán szemléltetjük.
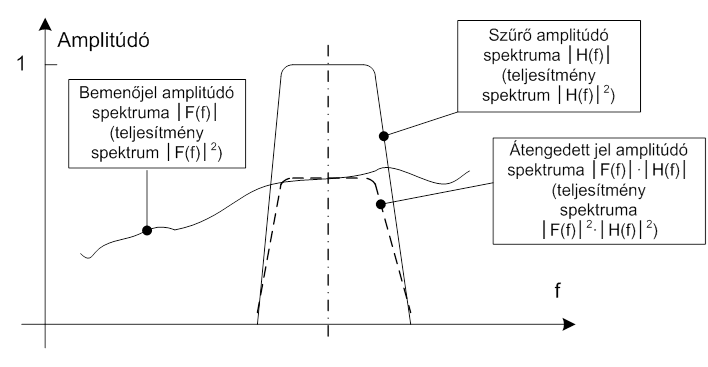
Ugyanakkor a bemenő jel összetevőinek fázisát is befolyásolja a szűrő, ennek azonban nincsen hatása a jel teljesítményére, és a méréstechnikában a fázishelyzetet - kivételektől eltekintve - a nem is szokás ábrázolni.
7.1.1. Analóg szűrők jellemzői
A 7.2. ábra - Szűrő (analizátor) tömbvázlata ábra egy egyszerű analóg szűrő tömbvázlatát mutatja.

A vizsgált jel teljes spektrumát csak úgy kaphatjuk meg, ha a szűrő középfrekvenciát léptetjük, esetleg célszerűen választott sebességgel „csúsztatjuk” a kérdéses frekvencia tartományban. A léptetés, illetve csúsztatás sebességét a tömbvázlatban látható átviteli tagok jelet késleltető tulajdonságai határozzák meg. Éppen ezért az analizálás helyessége érdekében részletesen meg kell vizsgálnunk az átviteli tagok dinamikai tulajdonságait, mert ezek hatása döntő az eredményre.
7.1.1.1. Szűrők és szűrő átviteli karakterisztikák
Alapvetően meg kell különböztetni konstans abszolút sávszélességű és konstans relatív (százalékos) sávszélességű szűrőket. A konstans relatív sávszélességet mindig a hangolható középfrekvencia bizonyos meghatározott százalékában kapjuk. A (7.2. ábra - Szűrő (analizátor) tömbvázlata) ábrán, összehasonlítás céljából, a kétféle sávszélességet lineáris és logaritmikus frekvencia tengely mentén ábrázoltuk, mert így világítható meg legjobban a két szűrő típus, és az ábrázolás közötti különbség. Az esetlegesen zavaró arányeltolódások logaritmikus lépték és konstans relatív sávszélesség alkalmazása esetében szűnnek meg. A logaritmikus lépték egyben az ábrázolható frekvencia tartomány nagyságát is megnöveli.
A konstans sávszélesség nagyjából egységes felbontást biztosít a lineáris frekvencia skálán, ami akkor előnyös, ha a harmonikus komponensek egyforma felbontását és elkülöníthetőségét kell biztosítani. Megjegyezzük, hogy a régi analóg regisztrálók és megjelenítők sajátosságai miatt, lineáris skála esetében, a lineáris frekvencia skála erősen korlátozta a vizsgált frekvenciatartomány nagyságát. A korszerű, digitális adatrögzítés ezt a problémát kiküszöbölte, mert a tárolt adatokból a tetszőlegesen választott frekvencia tartomány kiemelhető. Ha viszont a spektrumot ki kell nyomtatnunk, akkor a probléma természetesen továbbra is fennáll, és ilyen esetben lineárisan legfeljebb két-három frekvencia dekádot szoktak megjeleníteni.
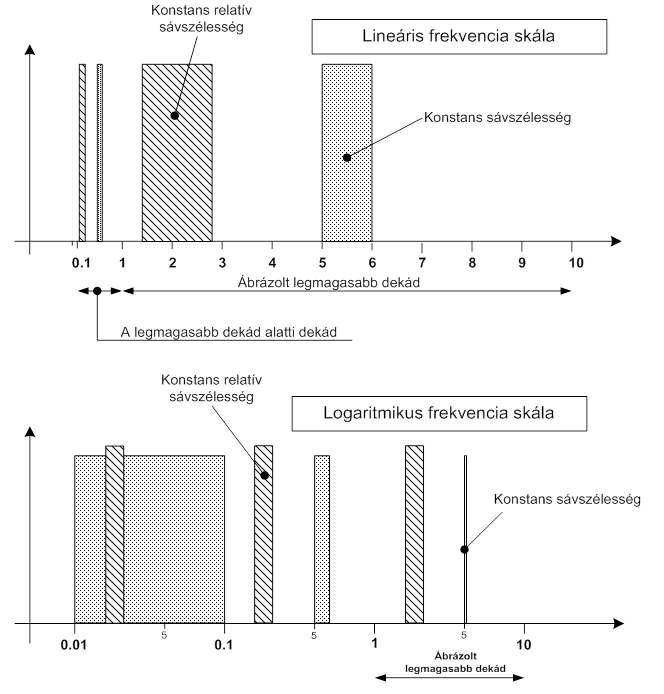
A konstans relatív sávszélesség egyenletes felbontást eredményez a logaritmikus frekvencia skálán, és ezért a nyomtatott protokollok esetében (pl. műszer kalibrálás) egy nagyobb frekvencia tartomány megjelenítése sem okoz gondot. A konstans relatív sávszélesség másik előnye az, hogy a jósági tényezővel (Q) közvetlen kapcsolatban áll. A Q faktor a rezonancia csúcsok nagyságát (magasságát) jellemzi. Ezért olyan spektrumok elemzése során, amelyeknél várhatóan számos rezonancia csúcs fog megjelenni, és ezek kiértékelése fontos a feladat szempontjából, célszerű konstans relatív sávszélességű analízist végezni. Természetesen olyan sávszélességgel kell analizálni, amely kisebb, mint a legkeskenyebb rezonancia csúcs szélessége.
Más okok is a logaritmikus frekvencia skála alkalmazása mellett szólnak:
Bizonyos összefüggések jobban érzékeltethetők log-log léptékű skálán, ilyen például a vizsgált átviteli tag (műszer, mérőlánc) integráló jellege, amely ilyen léptékezés mellett egy -20 dB/dekád meredekségű egyenest eredményez.
Több soros tag eredő frekvencia átvitele egyszerűen meghatározható.
Megkülönböztetett figyelmet érdemel a konstans relatív sávszélességű szűrők két csoportja, mert ezeket az akusztika és a rezgésvizsgálat területén rendszeresen alkalmazzák, ezek az oktáv- és tercszűrők. Az oktávszűrő esetében a szűrő áteresztő sávjának felső határfrekvenciája kétszerese az alsó határfrekvenciának, ami relatív sávszélességként 70.7 %-ot eredményez. Ez az alábbiak szerint adódik:
|
|
(7.1) |
A sávközép frekvencia a felső és alsó határfrekvencia mértani közepe:
|
|
(7.2) |
Az abszolút sávszélesség megegyezik az alsó határfrekvenciával:
|
|
(7.3) |
A relatív sávszélesség a fentiek felhasználásával:
|
|
(7.4) |
A sávközép frekvenciákat nemzetközi szabványokban rögzítették, valamint azt, hogy a referencia középfrekvencia 1000 Hz legyen.
Látható, hogy ilyen módon három frekvencia dekáddal és ezeken belül 10 oktáv sávval az akusztikában fontos frekvenciasáv lefedhető (itt: 22.5 Hz – 22.5 kHz). Az 1000 Hz-es referenciát viszonyításul véve 22.5 Hz a legalacsonyabb alsó határfrekvencia, és ennek a legalsó oktávsávnak 31.5 Hz a középfrekvenciája. A legfelső (legmagasabb) oktávsáv felső határfrekvenciája 22.5 kHz és 16 kHz a középfrekvenciája.
A szűrés finomítható a terc sávok létrehozásával, amelynek során minden oktávsávban három aláosztott, un. terc sávot képeznek, az alábbi formula szerint:
|
|
(7.5) |
A tercsávok középfrekvenciáját az oktávokhoz hasonlóan ugyancsak a geometriai középérték segítségével határozzuk meg.
|
|
(7.6) |
A (7.9. ábra - 10 db szomszédos tercszűrő által „lefedett” dekád) ábrán látható módon, egy frekvencia dekádban 10 terc sáv kap helyet, mert:
|
|
(7.7) |
A relatív sávszélesség pedig a következők szerint állapítható meg:
|
|
(7.8) |
7.1.1.2. Szűrő karakterisztikák a gyakorlatban
A gyakorlatban megépíthető szűrők karakterisztikái sajnos eltérnek az ideálistól.
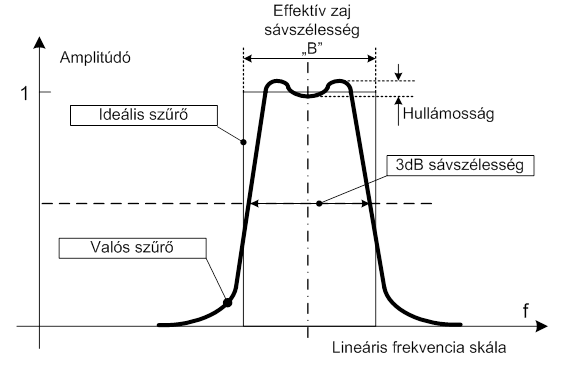
Ha az áteresztő sávban látható „hullámosságot” elfogadható határok között lehet tartani, akkor a gyakorlati szűrő a szelektivitásával és a sávszélességével jellemezhető.
Bevezetőben meg kell említeni a szűrők Beff „effektív zaj sávszélességét” is. Az effektív zaj sávszélességet úgy számítják ki, hogy a valós szűrő karakterisztikája és a frekvencia tengely által bezárt terület értékét (a karakterisztika integrálja a frekvencia szerint) osztják a referencia szinttel. Az effektív zaj sávszélesség másként fogalmazva az a frekvenciasáv, amely egy olyan ideális szűrőhöz tartozik, amely az ideális fehér zajból ugyanakkora teljesítményt enged át, mint az azonos referencia szinttel rendelkező valós szűrő. Ennek a jellemzőnek fontos szerepe van a véges idejű jelminták analízise során. A véges „T” idejű jelmintához (valós méréstechnikai helyzet) tartozó effektív zaj sávszélesség az alábbi szerint állapítható meg:
|
|
(7.9) |
Egy másik sávszélességet is szokás a szűrőkkel kapcsolatban emlegetni, ez pedig a 3 dB sávszélesség. Ez a sávszélesség ahhoz a teljesítmény szinthez tartozik, amely 3 dB értékkel van a szűrő átengedő sávjának csúcsértéke alatt. Tekintettel arra, hogy ennek értéke igen közel van az effektív zaj sávszélességhez, és könnyebben mérhető is, a gyakorlatban előszeretettel alkalmazzák ezt az értéket a szűrő jellemzőjeként. Csak igen gyenge szelektivitással rendelkező szűrők esetében van a két érték között szignifikáns eltérés.
A sávszélesség arról ad információt, hogy a szűrő mennyire képes szeparálni az egyes frekvencia komponenseket, megközelítőleg azonos szinten.
A szelektivitás azt írja le, hogy a szűrő mennyire képes szeparálni a komponenseket eltérő szinteken. A szelektivitást az „alaktényezővel” szokás jellemezni. Rendeljük egyszerűség kedvéért a szűrő átengedési sávjának maximumához a 0 dB értéket (1:1 átvitel). Az alaktényezőt általában, mint a szűrő -60 dB átviteli szintjéhez tartozó sávszélességének és a 3 dB sávszélességének arányát szokták definiálni. Ha a szűrő dinamikája kisebb, mint 60 dB (1000-szeres szorzó), akkor az alaktényező meghatározásához a -40 dB szinthez tartozó sávot alkalmazzák.
|
|
(7.10) |
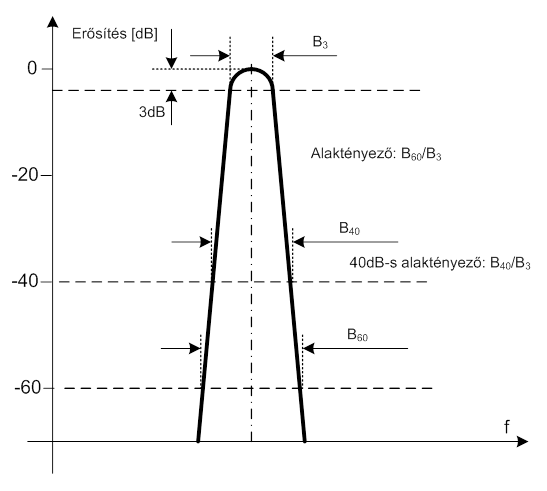
Az alaktényezőt általában a lineáris frekvencia tengelyre szimmetrikus és állandó sávszélességű szűrők jellemzésére használják, de más alkalmazás is ismert.
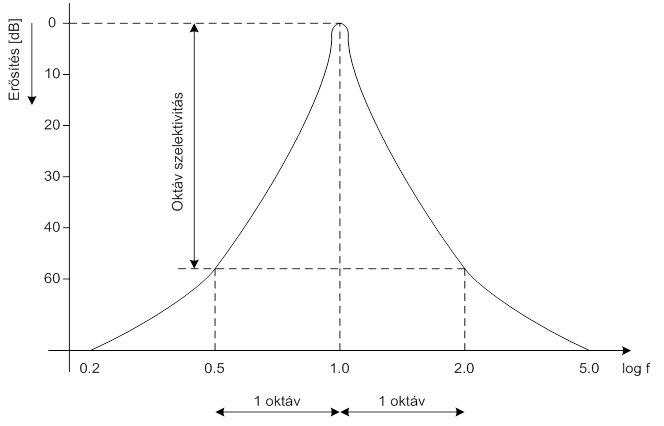
A konstans relatív sávszélességű szűrők jellemzésére, amelyek karakterisztikája a logaritmikus frekvencia tengelyre nézve szimmetrikus, az oktáv, vagy terc szelektivitás fogalmakat alkalmazzák. Ez a szűrő csillapítását adja meg a sávközép frekvenciához viszonyítva egy oktávnyira, vagy egy tercnyire.
7.1.1.3. A szűrő válaszideje
Ha a jel „hirtelen” kerül a szűrő bemenetére, az energiatárolók miatt, nyilvánvalóan idő szükséges ahhoz, hogy a kimeneten a válasz megjelenjen. Legyen a jel harmonikus, és frekvenciája a szűrő átengedési sávján belüli. Ebben az esetben a harmonikus jel amplitúdóját a szűrő 1:1 arányban átengedi, de a kimeneten a jel állandósult értéke csak T=1/B idő eltelte után jelenik meg, ahol „B” a szűrő sávszélessége.
A szűrő „TR válaszideje” mellett, szokás még a szűrő „felfutási idejéről” és „beállási idejéről” is beszélni, de ez utóbbinak csak akkor van jelentősége, ha a szűrő válaszában van egy jelentősebb lappangási idő is. A felfutási idő természetesen rövidebb, mint a válaszidő.
Általánosságban:
|
|
(7.11) |
Ezt az összefüggést a konstans sávszélességű szűrők esetében alkalmazzák.
A konstans relatív sávszélességű szűrők esetében kissé módosul ez a formula:
|
|
(7.12) |
ahol
|
b |
relatív sávszélesség | |
|
n R |
az „f” frekvencia TR válaszidőben történő előfordulása |
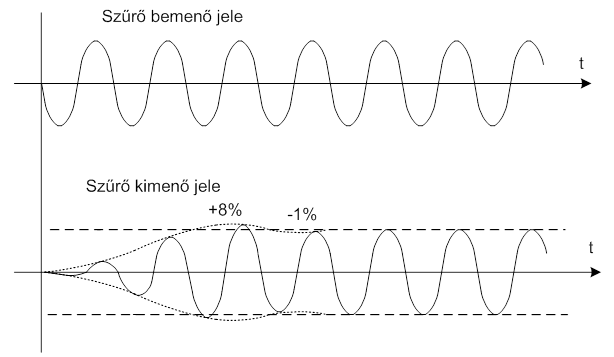
Ez azt jelenti, hogy b=1% esetén nR~100 lesz. Ezek a megfogalmazások más módon írják le azt a szabályt, hogy „B” sávszélességgel történő analízishez minimálisan 1/B idő szükségeltetik.
A 7.7. ábra - Tercszűrő tranziens viselkedése ábra egy tercszűrő időbeli válaszát mutatja „hirtelen” ráadott harmonikus jel esetében. Mivel a relatív sávszélesség 23.1% azt gondolnánk, hogy 4.3 periódus után állandósul a szűrő kimenete. Ugyanakkor az ábrán az látszik, hogy a kellő pontossághoz 5-6 periódus szükséges. A két, becsléshez alkalmazott összefüggést valójában extrém esetre írtuk fel, arra, hogy a szűrő bemenetére „hirtelen” kerül a harmonikus gerjesztés. Ha olyan analóg szűrőt alkalmaznak, amelynél az analízis „csúsztatással” történik, tehát a szűrő átviteli sávját meghatározott sebességgel mozgatják a frekvencia tengely „mentén”, a gerjesztés nem ugrásszerű. Ezzel együtt, becslés céljára, még „sweep”-elés (csúsztatás) esetén is ezeket a formulákat szokás alkalmazni.
7.1.1.4. Analóg detektorok és rekorderek
Az analóg szűrési technika „hőskorában” természetesen szükség volt olyan analóg áramkörökre is, amelyek az analizált jelekkel a szükséges és meghatározott matematikai műveleteket el tudták végezni. Ezeknek az analóg detektoroknak a mai digitális technikák birtokában megszűnt a jelentősége, de a teljesség kedvéért tömören ismertetjük ezeket is.
A híradástechnikában a zajokat a hasznos jelre szuperponálódó, olyan véletlen feszültség, vagy áram „jelekként” interpretálják, amelynek lineáris átlagértéke zérus.
A zaj teljesítményének mérőszáma tehát a négyzetes átlag lesz, ami tulajdonképpen a zaj varianciája, hiszen a zaj-jel csak AC komponenseket tartalmaz. Az átlagolás „kellően” hosszú idő alatt történik, erre utal a T0 bevezetése. Minél hosszabb ugyanis az átlagolási idő, annál kevésbé függ a kapott érték a T0 időtartamtól. Határértékként így valóban a varianciát kapjuk:
|
|
(7.13) |
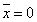 feltételezéssel:
feltételezéssel:
|
|
(7.14) |
ahol
|
x MS |
négyzetes átlag (Mean Square) | |
|
x RMS |
négyzetes átlag gyöke (Root Mean Square), más néven effektív érték |
A fentieket általánosítva az alábbiakat mondhatjuk:
|
Össz-jelteljesítmény=DC teljesítmény+AC teljesítmény |
(7.15) |
Tekintettel arra, hogy a jell (feszültség, vagy áram) négyzete a teljesítménnyel arányos, másként is fogalmazhatunk:
|
Négyzetes átlag=Átlag négyzete+ Variancia |
(7.16) |
Ha tehát általánosságban 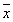 az x(t) időben változó jel átlaga, „σ” a jel szórása, és „s” a jel tapasztalati szórása, akkor a négyzetes átlag a valós, a gyakorlatban mérhető (empirikus) jelek esetében az alábbi képlet szerint számítható:
az x(t) időben változó jel átlaga, „σ” a jel szórása, és „s” a jel tapasztalati szórása, akkor a négyzetes átlag a valós, a gyakorlatban mérhető (empirikus) jelek esetében az alábbi képlet szerint számítható:
|
|
(7.17) |
A fentiek alapján, a mérnöki gyakorlatban az xRMS2 négyzetes átlagot a standard eltérésnek is tekintik, ha a jel lineáris átlaga zérus. A műszerek bementén ezért gyakran látható az alábbi megjelölés: „AC” (vagy „AC only”) és „DC”, ami azt jelenti, hogy a jel egyen-összetevője nélkül, vagy azzal együtt történik a mérés.
A valószínűségszámításból ismert összefüggéssel is igazolható a fenti összefüggés.
Legyen f(x) az „x” valószínűségi változó sűrűségfüggvénye. A variancia számítása a következő módon történik:
|
|
(7.18) |
Felbontva a zárójelet három tagot kapunk:
|
|
(7.19) |
Ismeretes, hogy:
|
|
(7.20) |
Behelyettesítve látjuk, hogy a variancia számításának kifejezése igen leegyszerűsödik:
|
|
(7.21) |
Az összefüggés a sűrűségfüggvénytől függetlenül érvényes, és esetünkben célszerű a funkcionálok helyett az empirikus mérési adatokból számolható átlagértékkel és a tapasztalati szórással dolgozni. Ennek figyelembevételével a fenti összefüggés átalakul:
|
|
(7.22) |
Átrendezve igazolva látjuk azt az összefüggést, amelyet a jel DC és AC összetevőire bontva bemutattunk:
|
|
(7.23) |
A szűrő kimenetén tehát megjelenik egy időben változó AC jel. Egyrészt ahhoz, hogy a jel teljesítmény spektrumának komponenseit megkapjuk, a kimenő jel négyzetére van szükség. Másrészt az időben ingadozó amplitúdójú és változó előjelű jel statisztikai mérőszáma a négyzetes középérték. Vigyázat! Változó előjelű harmonikus jel lineáris átlaga ugyanis zérus is lehet, ha a jel szimmetrikus az idő tengelyre!
Diszkrét értékek esetében a négyzetes átlag gyökét az alábbi módon számoljuk:
|
|
(7.24) |
Az időben változó jel folytonos változó, ezért a négyzetes átlag gyökét integrálással határozzuk meg. Ha az átlagolás időtartama T1≤t≤T2, akkor az összefüggés az alábbi lesz:
|
|
(7.25) |
Említettük, hogy a harmonikus jel lineáris átlaga zérus, ezért a villamosságtanban a váltakozó áram és feszültség esetében a négyzetes átlag gyökét alkalmazzák, és hasonlóképpen van ez az információhordozó jel esetében is.
Tanulságos egy U0 amplitúdójú harmonikus jel esetében bemutatni a négyzetes átlag gyökének számítását:
|
|
(7.26) | |
|
|
(7.27) | |
|
|
(7.28) |
Tekintettel arra, hogy a négyzetes átlagot definíciója szerint a periódusidőre, és annak egész számú többszörösére számítjuk, a zárójeles kifejezés második tagja kiesik.
|
|
(7.29) |
A négyzetes jel előállítása analóg áramkörök alkalmazásával történhet úgy, hogy a jel pillanatnyi értékét négyzetre emeljük, így megkapjuk a pillanatnyi teljesítményt, és egy meghatározott idejű átlagolással ennek integrálját képezzük (MS: mean square). Minél hosszabb az átlagolási idő, annál kisebb a kapott értékek ingadozása, de persze, hosszú az analízishez szükséges időtartam.
Ha a bemenő jel dimenziójának megfelelően szeretnénk a spektrális tartalmat megjelentetni, tehát az amplitúdó spektrumra van szükség, akkor az előzőekben képzett négyzetes átlagból gyököt kell vonni, így kapjuk az RMS: Root Mean Square értéket.
Gyakran szükség van a kimenet-bemenet arány logaritmikus megjelenítésére is, méghozzá dB értékben. Ilyenkor logaritmikus áramkörök alkalmazására van szükség.
Az analóg technikában a jel négyzetes átlagának gyökét többféle módon képezik:
Analóg szorzó áramkör alkalmazásával a jelet önmagával megszorozzák, majd egy kapacitás segítségével megtörténik az átlagolás. A négyzetgyökvonást a visszacsatolásba iktatott négyzetre emelő szorzóáramkörrel valósítják meg. Egy precíziós egyenirányító áramkörrel először képezik a jel abszolút értékét, majd az így kapott jel egy logaritmikus erősítő bemenetére kerül. Az erősítő kimenő jelét megkétszerezik, és ezt követően egy exponenciális átviteli jellegű műveleti erősítő bemenetére kapcsolják. Az átlagolás és négyzetgyökvonás az előbbiekhez hasonló módon történik.
FET tranzisztor segítségével közvetlenül megtörténik a bemenőjel négyzetre emelése, ezt követi az átlagolás és a gyökvonás.
Termo-csatolásos módszerrel úgy, hogy a bemenő jelet, vele arányos árammá konvertálva egy parányi fűtőszálat melegítenek. A fűtőszál hőmérséklete a váltakozó jel négyzetével arányos. A fűtőszál hőmérséklet változását termisztor, termoelem, vagy egy kettős tranzisztoros kapcsolás figyeli.
Az analóg feldolgozó áramkörök (detektorok) kimenő jelét régebben
kijelzőre
megjelenítőre, vagy/és
regisztrálóra
kapcsolták. Az analóg, vagy digitális kijelző tette lehetővé az analizátorok beállítását, a mért értékek real-time megfigyelését. A megjelenítésben a mai napig is használatos oszcilloszkópok játszották a fő szerepet, míg a regisztrálók családja volt hivatott a szűrés eredményét papír alapú regisztrátumon megörökíteni. A regisztrálók a korabeli műszertechnika és finommechanika csúcstechnikáját képviselték, mert előírt pontossággal és igen nagy frekvencia tartományban képesek voltak a jelszintek rögzítésére. Az igényes regisztrálók mindegyike szabályozókörre épült. A bemenetükre kerülő jel a szabályozókör alapjeleként funkcionált, és a papíron mozgó írótoll (vagy fehér viasszal bevont felületű színes papíron csúszó karcoló tű) pozíciója volt tekinthető a szabályozott jelnek. Az írótoll pozícióját mérték, és szabályozási eltérés esetén a kívánt helyzetbe mozgatták. Magasabb frekvenciák mérése esetében (akusztika, rezgések) a karcoló tűt rugalmas vezetékkel csapágyazták. A rekordereket minden esetben egyfajta aluláteresztő szűrőként kellett kezelni.
A regisztrátum (papír) mozgatásáról külön, precíziós elektromechanikus szerkezet gondoskodott, hiszen a papír mozgása az idő tengelyt, vagy spektrumok esetében a frekvencia tengelyt jelenítette meg. Az akusztikában ezen felül lehetséges volt polár-koordinátás szintrögzítésre is, mert a hangszórók és mikrofonok iránykarakterisztikáját csak így lehetett megjeleníteni. Ebben az esetben a kör alakú papír síkban történő forgatásával a szöghelyzetnek megfelelően lehetett a mért értéket rögzíteni. Az analóg szűrők (analizátorok) használata során külön kellett ügyelni a regisztrálás (írás) sebességére is, figyelembe véve a rekorder adta lehetőségeket. Nagyobb írássebesség magasabb vágási frekvenciát eredményezett, de ez szükségképpen rövidítette az átlagolási időt. A kisebb átlagolási idők kismértékű, míg a nagyobb átlagolási idők jelentősebb jelszint ingadozást eredményeztek.
7.1.2. Analóg analizátor (szűrő) típusok
Az analóg technikában az alábbi analizátor típusok voltak jellemzőek:
Diszkrét (léptető szűrős) analizátorok
Csúsztatott szűrős analizátorok
Párhuzamos (real-time) analizátorok
Idő-kompressziós analizátorok (real-time).
Az idő-kompressziós analizátorok tulajdonképpen már átvezetnek a digitális technikába, de a működésük alapját még az analóg heterodin analizátor adja.
A négy analizátor típus felépítését tömören összefoglaljuk.
Az első két típus esetében feltételeznünk kell, hogy az analizálandó jel stacionárius , mert az analízist a sávokban nem egyszerre, hanem időben eltolva végezzük.
7.1.2.1. Diszkrét (léptető szűrős) analizátorok
A 7.8. ábra - Léptető szűrős analizátor tömbvázlata ábra a rögzített középfrekvenciájú sávszűrőkkel felépített analizátor tömbvázlatát mutatja. A jel ebben az analizátorban a kondicionálás (erősítő fokozat) után közvetlenül egy sorozat párhuzamosan kapcsolt sávszűrőre kerül, amelyek együttesen lefedik az analízis szempontjából érdekes frekvencia tartományt, ld.: 7.8. ábra - Léptető szűrős analizátor tömbvázlata
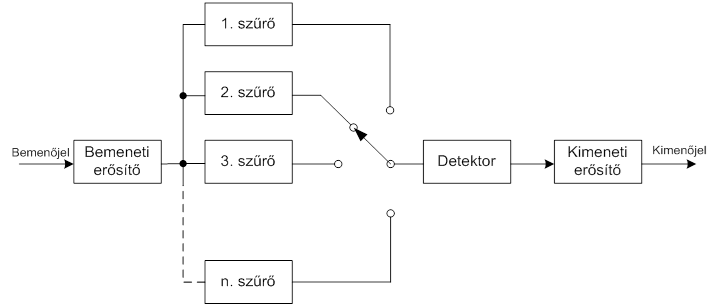
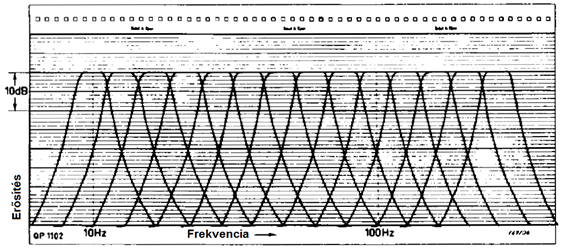
A detektort szekvenciálisan kapcsolják a sávszűrőhöz, amely sorban egymás után méri a sávszűrők kimenetén megjelenő jelet. Az egyes sávokban való tartózkodás idejét az analizálandó jel becsült spektruma alapján kellett beállítani, hasonlóképpen tekintettel kellett lenni a detektorok „feléledési” idejére is. A sávszűrők kimenetének léptetését szinkronizálták az analizátorhoz kapcsolt rekorderrel, pontosabban annak papírsebességével, és az írás sebességével.
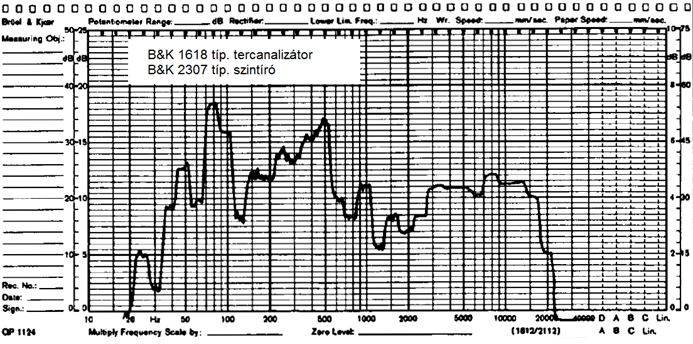
A 7.10. ábra - Terc-analizátorral felvett spektrum szintírón regisztrált képe ábra egy léptető szűrős analizátorral felvett terc spektrumot mutat. Ilyen felépítésű analizátorokat kizárólag oktáv és terc sávos szűrésre alkalmaztak, mert a keskeny sávú analízis, a nagyszámú szűrő alkalmazása miatt, az analizátor előállítási költségeit aránytalanul megnövelte volna.
7.1.2.2. Hangolható, „csúsztatott” szűrős analizátorok
A keskenysávú analízis céljaira sokkal jobban megfelel a hangolható középfrekvenciájú szűrő, amelynek tömbvázlatát a (7.11. ábra - Hangolható szűrős analizátor tömbvázlata) ábrán láthatjuk. A szűrőt igény szerint be lehet állítani mind konstans sávszélességre, mind pedig konstans relatív sávszélességre.

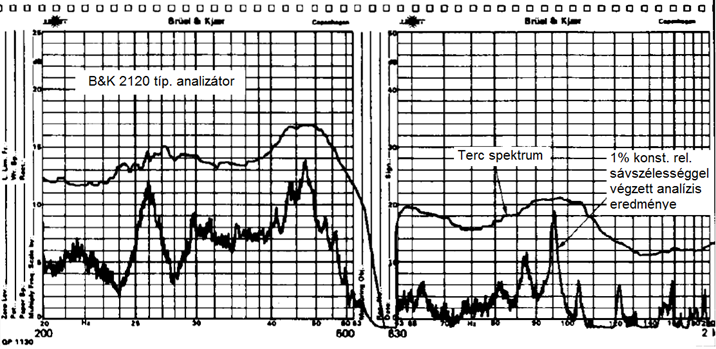
A 7.12. ábra - Keskenysávú analízis eredménye ábra ugyannak a jelnek a spektrumát mutatja, amelyet a 7.12. ábra - Keskenysávú analízis eredménye ábrán láthatunk tercsávos analízis után, annyi módosítással, hogy csak a 200…2 kHz tartományt mutatjuk be. Sajnos a regisztráló papír más célra készült, de így is látható, hogy 600 Hz után 630 Hz sávközép frekvenciával folytatódik. A regisztrátum felső görbéje a konstans sávszélességű tercsávos, míg az alsó az 1%-os relatív sávszélességgel végzett analízis eredményét mutatja. Látjuk, hogy a hangolható (csúszatott) szűrős analízis eredményeként folytonos spektrumot kapunk, persze tudnunk kell, hogy a görbe minden egyes pontja az adott szűrő sávszélességben megjelenő spektrum integrálját adja.
7.1.2.3. Real-time párhuzamos analizátorok
Ez az analizátor típus lehetővé teszi, hogy a vizsgált jelről folyamatosan, és egyszerre kapjunk spektrumképet. Lényegesen gyorsabb a vizsgálat, és természetesen jobban igazodik a jel gyors változásaihoz. Az analizátor tömbvázlatát a 7.13. ábra - Real-time analizátor tömbvázlata ábra mutatja.
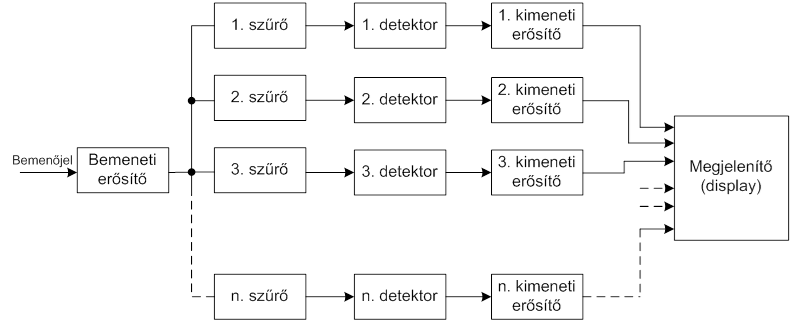
A tömbvázlatnak megfelelő módon épültek fel az első tercsávos real-time analizátorok. Tekintettel a jel spektrumának gyors időbeli változására, a megjelenítésre olyan monitorokat építettek, amelyek a spektrumot világító oszlopok formájában mutatták (a megjelenített kép a hisztogramokra emlékeztetett).
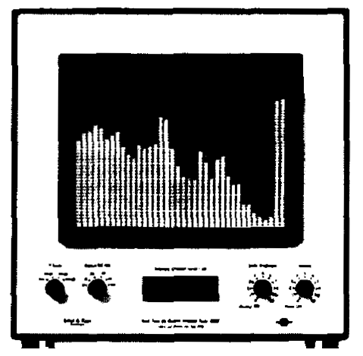
Az analóg real-time analizátorokat a digitális szűrési technika „legyőzte” ugyan, de elszórtan még lehet ilyen eszközökkel munkahelyeken találkozni. A korszerű digitális analizátorok által a számítógép monitorára adott eredmény nagyjából ma is ugyanolyan, mint az egykori analóg berendezések esetében volt.
7.1.2.4. Idő-kompressziós, real-time analizátorok
A tercsávos real-time analizátorok a megvalósíthatóság szempontjából még éppen a technikai ésszerűség határán helyezkednek el. A frekvencia sávot tovább csökkentve, keskenysávú analizátort párhuzamos szűrőkkel és detektorokkal építeni egyszerűen nem lenne gazdaságos, a készülék a magas ár miatt nem lett volna piacképes. A keskenysávú real-time analízist más módon kellett megoldani, így születtek az első idő-kompressziós analizátorok, amelyek működésének alapját a következőkben röviden ismertetjük.
A rendszer működésének alapja az, hogy a vizsgálandó jelet rögzítik (régen FM magnetofonokkal, manapság természetesen korszerű jelrögzítőkkel, illetve számítógépben), majd a felvett jelet ismert sebességre felgyorsítva analizálják a folyamatot, tercsávos párhuzamos analizátorokkal. A real-time analízis ugyanis megköveteli a párhuzamos működést.
A szűrönkénti, egyenként történő analízishez szükséges időt (szűrő „feléledési” ideje) már bemutattuk korábban. Determinisztikus jel esetében a szűréshez szükséges idő a szűrő TR válaszidejével megegyező, ezt láttuk a 7.1.1.3. szakasz - A szűrő válaszideje fejezetben:
|
|
(7.30) |
Ugyanakkor sztochasztikus jeleknél , keskenysávú analízis esetében, a szűréshez szükséges időt tekintve a szűrő válaszidejét a szűrőben való tartózkodás TD ideje váltja fel. Ennek következtében már nem a válaszidő, hanem a TA átlagolási idő határozza meg a szűréshez szükséges időt. Az átlagolási idő és a szűrő sávszélessége befolyásolják az analízissel kapott eredmény bizonytalanságát (pontosságát), amit az „s” empirikus szórás jellemez. Az RMS detektorral végzett keskenysávú analízis esetében, az analizált jel empirikus szórását, a sávszélességből és az átlagolási időből az alábbi összefüggés révén kapjuk:
|
|
(7.31) |
ahol
|
B |
sávszélesség | |
|
T A |
átlagolási idő |
A sztochasztikus jelek esetében általában normál amplitúdó eloszlást feltételezhetünk . Az analízis eredménye a helyes értéket annál jobban megközelíti, minél nagyobb az átlagolási idő. Végső soron ez az egyetlen paraméter, amellyel az empirikus szórást befolyásolni lehet. A sávszélességhez ugyanis nem lehet „hozzányúlni”, mert adott esetben ez az analizátor fix jellemzője, amely vagy terc/oktáv, vagy keskenysáv.
Az empirikus szórás értékét mutatja a BTA szorzat függvényében, az alábbi táblázat:
|
BT A |
10 |
20 |
30 |
40 |
50 |
80 |
100 |
|
s [dB] |
1.5 |
1.0 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
Azért, hogy mind a determinisztikus, mind pedig a sztochasztikus jelekre egyaránt alkalmazható feltételt találjunk, az előzőekben ismertetett szabályt némiképpen módisítani kell. Az átlagolás két feltételét összefoglaljuk a szűrőben való TD tartózkodási idő segítségével. A tapasztalati összefüggés a következő:
|
|
(7.32) |
ahol
|
B |
a szűrő sávszélessége | |
|
T D |
a szűréshez szükséges idő (tartózkodási idő) | |
|
K |
tapasztalati állandó |
Az idő-kompressziót az analóg analizátorokban egy igen szellemes és egyszerű úton valósítják meg.
Tekintettel arra, hogy a TD idő és a „B” sávszélesség szorzata állandó, a sávszélesség virtuális csökkentésének (tehát a keskeny sáv irányába történő elmozdulásnak) egyik lehetséges módja az, ha a TD időt M-szeresére megnöveljük. Ennek olyan hatása van, mintha a sávszélességet M-ed részére csökkentettük volna. Ezt úgy érik el, hogy a vizsgálandó jelet tárolják, majd M-szeresére felgyorsítva kapcsolják az analizátor bemenetére. Ilyen módszerrel lehetségessé vált a jelek keskenysávú real-time analízise. Napjaink digitális technikája esetében ez nem jelent problémát, az analóg technikában a jelrögzítés mérőmagnetofonok segítségével történt, és a szalag sebességét gyorsították fel a visszajátszás során.
Gyakran okoz gondot a csatornánkénti TD tartózkodási idő szükséges (előírt) hossza is, mert az analízis összes ideje tetemesé válhat. Az idő-kompressziós módszerrel a csatornánkénti TD időt is lehet csökkenteni, mégpedig úgy, hogy virtuálisan megnöveljük a „B” sávszélességet. Ezt a felbontás lerontása nélkül kell biztosítani azáltal, hogy a jelet adott sebességgel (valós időben) rögzítik, majd azt az analízis céljára „M”-szer gyorsabban visszajátsszák.
A 7.15. ábra - Az idő-kompressziós analízis eredménye ábra mutatja, hogy ebben az esetben minden frekvenciát meg kell szorozni M-mel, és emiatt a felbontás ugyanolyan lesz, mintha a szűrő sávszélessége M-szer nagyobb lenne. Ennek eredményeként viszont a TD időt osztani lehet M-mel, ami virtuálisan annak felel meg, mintha az analízist M-szer gyorsabban végeztük volna. Ez volt végső soron az idő-kompresszió célja.
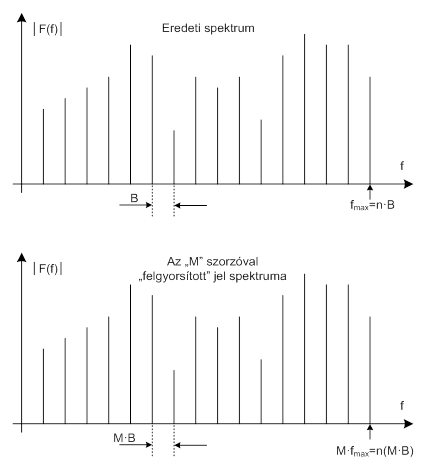
A nehézkes jelrögzítést napjainkban kiváltotta a digitalizálás, és a rendelkezésre álló tekintélyes memóriakapacitás. A módszert „kvázi” real-time analízisnek nevezték, mert a jel egy részét „ki kellett vágni” a jelfolyamból. A mai, korszerű digitális technikában a mintavétel és a feldolgozás megfelelő ütemezésével a real-time üzemmód valósággá válhatott.
7.1.3. Stacionárius jelek analízise a gyakorlatban
A következőkben röviden összefoglaljuk a determinisztikus és sztochasztikus stacionárius jelek analóg analízisével kapcsolatos gyakorlati tudnivalókat.
7.1.3.1. Diszkrét (léptetős) szűrős analízis
Az analízis sávszélességét a szűrő sávszélessége határozza meg, ami terc és oktáv lehet. Már jeleztük korábban, hogy a keskenysávú szűrés ebben a verzióban műszakilag nem megoldható. Az analízis során – a rekordereket is figyelembe véve - jellemzően az alábbi paramétereket lehetett beállítani:
Átlagolási idő
DC vagy AC jelrögzítés
és régebbi, írószerkezetekhez kapcsolt analizátorok esetében ezeken felül:
Rekorder írási sebessége
Papírsebesség
Példaként megjegyezzük, hogy 100 mm szélességű („függőleges tengely”) regisztráló papír esetében egy tercsáv 5 mm szélességűnek adódott a vízszintes tengely mentén.
Átlagolási idő megválasztása
Determinisztikus jelek esetében fő követelmény, hogy a szűrő okozta hullámosság elfogadható mértékű legyen. Ha egy adott sávban egyetlen harmonikus komponens fordul elő, akkor a hullámosság kisebb lesz, mint 0.25 dB, ha
|
|
(7.33) |
ahol „f” a harmonikus jel frekvenciája. Rendes körülmények között sok harmonikus komponens fordul elő egy tercsávon belül. Ilyen esetben „f” az a minimális frekvencia különbség, amely két komponens között előre becsülhető.
Magasabb frekvenciákon, ahol már igen sok komponens jelenik meg egy tercsávon belül, célszerűbb a sztochasztikus jelek esetében szokásos átlagolási idővel kalkulálni.
Sztochasztikus jelek esetében a jel amplitúdójának „s” empirikus szórása, tehát a megkívánt (előírt) bizonytalanság ismeretében meg lehet megbecsülni az átlagolási időt, az összefüggést az idő-kompressziós analízisnél már láttuk:
|
|
(7.34) |
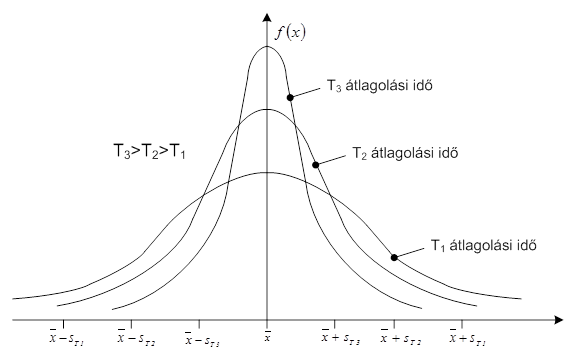
Tájékozódás céljából, táblázatosan összefoglaltuk az empirikus szórás értékeit decibelben, az átlagolási idő függvényében, adott terc sávközép frekvenciákon:
|
Terc sávközép frekvencia [Hz] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
TA [s] |
2 |
6.3 |
20 |
63 |
200 |
630 |
2k |
6.3k |
20k |
|
0.1 |
1.2 |
0.7 |
0.4 |
0.2 | |||||
|
0.3 |
1.2 |
0.7 |
0.4 |
0.2 | |||||
|
1 |
1.2 |
0.7 |
0.4 |
0.2 | |||||
|
3 |
1.2 |
0.7 |
0.4 |
0.2 | |||||
|
10 |
1.2 |
0.7 |
0.4 |
0.2 | |||||
|
30 |
1.2 |
0.7 |
0.4 |
0.2 | |||||
|
100 |
0.7 |
0.4 |
0.2 | ||||||
|
300 |
0.4 |
0.2 | |||||||
Oktávsávok esetében a sávszélesség háromszor nagyobb, ezért a fenti táblázatban látható átlagolási időket értelem szerűen harmadolni kell.
A jelminta hosszának megválasztása
Ha a sztochasztikus jelből rögzített hosszúságú (analóg, vagy digitális) mintát készítettünk, akkor a minta idejénél (Trec) mindenképpen legyen nagyobb az átlagolási idő (TA). Az integrálás effektív (Teff) idejére, a jelminta hosszúsága és az átlagolási idő által gyakorolt hatást mutatja a következő ábra. Látható, hogy exponenciális (analóg RC) jellegű, más néven felejtő átlagolás esetén, ha a jelminta hossza és az átlagolási idő megegyeznek, akkor az effektív integrálási idő ezen idők 76%-ára csökken. A szakirodalomban találunk leírást arra vonatkozóan, hogy semmilyen további javulás nem várható statisztikai funkcionálok (jellemzők) esetében, ha az átlagolási időt az RC jellegnél, a jelminta kétszeresénél nagyobbra választják. Lineáris átlagolásnál az átlagolási idő és a jelminta hossza célszerűen legyen azonos.
A jelrögzítésre, ha csak lehetséges, a DC üzemmód volt ajánlott, mert az átlagolási időt erre specifikálták és az analízis gyorsabb volt ebben az üzemmódban. A DC üzemmód egyik feltétele ugyanakkor a detektor és erősítő 50 dB-nél nagyobb dinamikája volt.
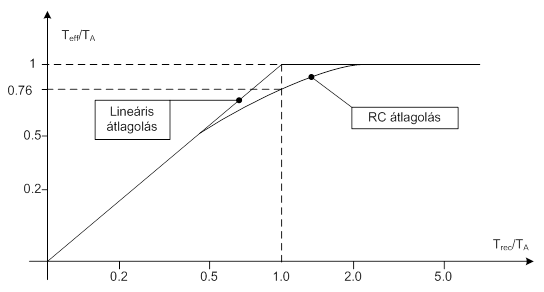
7.1.3.2. Hangolható szűrős (csúsztatott) analizátorok alkalmazása a gyakorlatban
Ennek az analizátor típusnak alkalmazásakor igen sok szempontra kellett figyelemmel lenni. Ezek a következők:
Konstans abszolút sávszélességű, vagy konstans relatív sávszélességű szűrőt alkalmazunk
Lineáris, vagy logaritmikus a frekvencia skála
Aktuális sávszélesség Hz-ben, vagy százalékban
Átlagolási idő
Sávban tartózkodás ideje (ez határozza meg a csúsztatás - sweep - idejét)
Régebbi időkben ezeken felül
Rekorder írási sebessége
Papírsebesség
Az első öt feltételt részletesebben is megvizsgáljuk, az írássebességgel és papírsebességgel nem foglalkozunk, ezek jórészt aktualitásukat vesztették.
Konstans sávszélességet akkor alkalmaznak, ha a frekvencia skála lineáris, ha a várható frekvencia spektrumra harmonikus, vagy más determinisztikus összetevők jellemzőek, és, ha más, konstans sávszélességű analízis eredményével kell a kapott értékeket összehasonlítani.
Konstans relatív sávszélességet akkor kell alkalmazni, ha a frekvencia lépték logaritmikus, ha a jel stacionárius sztochasztikus jellegű, és domináns rezonancia frekvenciák is előfordulnak. Például akkor, ha akusztikai, vagy rezgésmérésről van szó, és akkor, ha más, tercsávos analízissel kapott eredménnyel kell az analízis eredményét összehasonlítani.
Lineáris frekvencia skála alkalmazása akkor célszerű, ha a spektrumban egymáshoz kapcsolódó harmonikus összetevők várhatóak, esetleg egymáshoz képest azonos frekvencia-távolságban, mint például az oldalsávok. Alkalmazható akkor is, ha a frekvencia tartomány korlátozott, és, ha más, hasonló módon kapott eredményekkel való összevetés szükséges.
Logaritmikus frekvencia skála ajánlott, ha konstans relatív sávszélességű szűrőket alkalmazunk az analizátorban, ha a frekvencia tartomány nagy, ha kisebb frekvenciaingadozásokat is meg kell jeleníteni, vagy, ha olyan átviteli tulajdonságokat kell kimutatni, amelyek például 10, vagy 20 dB/dekád meredekség formájában jelentkeznek.
Sávszélesség tekintetében is vannak kötöttségek. Determinisztikus jelek esetében kívánatos, hogy az egymáshoz közeli frekvencia komponenseket minél jobban el lehessen különíteni. Ennek feltétele, hogy az alkalmazott sávszélesség a minimális sávfelbontás 1/3 része legyen.
Sztochasztikus jelek esetében a megkívánt relatív sávszélesség legyen kisebb, mint a becsült spektrum legkeskenyebb csúcsához tartozó frekvencia sáv. A legtöbb esetben ez csak léptető szűrős analizátorral érhető el, mert az 1%-os relatív konstans sávszélesség a legkisebb, amely a kereskedelmi analizátorok esetében adott. Determinisztikus és sztochasztikus jelek szuperpozíciója esetében a sávszélességet a determinisztikus jelhez célszerű igazítani.
Átlagolási idő tekintetében a korábbiakban leírtak a mértékadók.
Sávban tartózkodás ideje (T D ) egy egyszerű összefüggésből számítható ki:
|
|
(7.35) |
ahol
|
v sweep |
a csúsztatás sebessége | |
|
B |
sávszélesség | |
|
T D |
sávban tartózkodás ideje |
A T D időt több tényező befolyásolja. Ezek a szűrő válaszideje (feléledési ideje), az átlagolási idő és régebbi rendszereknél a rekorder papírsebessége.
Ha a T D idő megegyezik a szűrő feléledési idejével, akkor az egész szűréssel kapott spektrum a frekvencia tengely mentén azonos mértékben jobbra lesz eltolódva. Ez a gyakorlatban nem elfogadható. A sáveltolódással kapcsolatos általános összefüggés az alábbi:
|
|
(7.36) |
Ha KR=4, akkor például a sáveltolódás 1/4 lesz, ami rögzített szűrők esetében, az átlagos frekvencia hiba tekintetében még egy elfogadható kompromisszum is lehet. A KR érték megválasztásánál tudni kell, hogy a sáveltolódás „B” sávszélesség esetében a B/KR aránnyal adható meg.
|
|
(7.37) |
Az átlagolási idő is befolyásolja a szűrőben való tartózkodás idejét. A következő táblázat bemutatja több jellemző, közöttük a sáveltolódás lehetséges mértékét a KA tényező függvényében.
|
|
(7.38) |
A KA tényező nagyságát a detektor karakterisztikájának maximális változása határozza meg, ennek értéke jellemzően 8.7 dB/TA. Az átlagolási idő szokott jelölése és TA.
A következő táblázat a KA tényező kiválasztásában ad támpontokat.
|
KA |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
Szűrő alaktényezője |
15 |
8 |
5.6 |
4.5 |
3.8 |
|
Csúcsdetektálási hiba [dB] |
1.2 |
0.5 |
0.4 |
0.2 |
0.15 |
|
Csúcseltolódás [×B] |
0.3 |
0.2 |
0.13 |
0.1 |
0.1 |
|
Minimumok hibája [dB] |
3 |
1 |
0.5 |
0.25 |
0.2 |
|
Minimumok eltolása [×B] |
0.5 |
0.25 |
0.17 |
0.13 |
0.1 |
7.1.3.3. Idő-kompressziós real-time analízis a gyakorlatban
A real-time analízis révén keletkező spektrummal kapcsolatban fontos korlátozásokat kell figyelembe venni:
Az eredeti időbeli jelből kivett minta időtartama (hossza) korlátozza a felső határfrekvenciát.
A jelminta időtartama véges, ez alapvetően négyszög időablakot jelent, és vonalas (diszkrét) spektrumot eredményez.
Ezeken felül, régebben, a jelminta hosszát az adott memória nagysága korlátozta.
Az idő-kompressziós analizátor műveleti idejének meghatározása a következő tényezők figyelembe vételét teszi még szükségessé:
Sávszélesség
Négyszög súlyozó függvénnyel végzett analízis esetében az analizáló sávszélesség megegyezik a spektrum felbontásával, amelynek értéke „β”. Már jeleztük, hogy a spektrum vonalas lesz, a vonalak közötti távolság (frekvencia sáv) pedig egyszerűen úgy adódik, hogy a kiválasztott frekvencia tartományt osztjuk a vonalak számával. A digitális korszakban a „β” értéket a jelminta idejének hossza dönti el, hiszen a jelminta idejének reciproka a sávszélesség:
|
|
(7.39) |
Megjegyezzük, hogy Hanning-súlyozó függvény alkalmazása esetében 1.5·β zaj sávszélességet kell alkalmazni.
Átlagolási idő
Az átlagolás 1/β időintervallumokban történik, amint az alábbi ábrán látható.
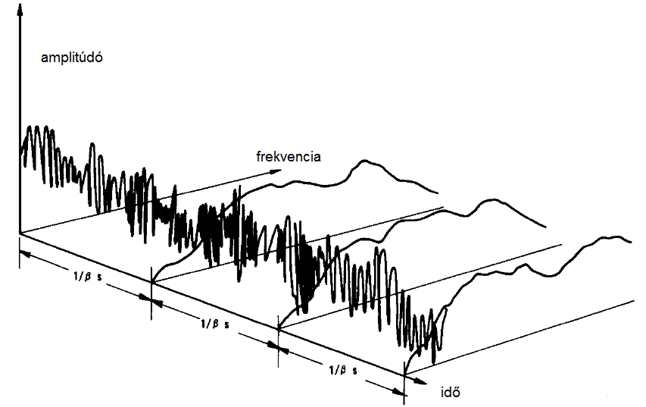
Minden különálló spektrum a tárolt (tárolható) jelminta átlagából keletkezik. Ezért úgy tekinthető, hogy a spektrumok teljessége a teljes analízis idejének átlagából származik. Az átlagolást minden különálló spektrumban lineáris súlyozással is el lehet végezni, de ez azt jelenti idő tartományban, hogy a jelről „pillanatfelvételt” készítünk, ezt analizáljuk, és figyelmen kívül hagyjuk a jel időbeli folytonosságát.
A folytonos analízist ezért úgy programozzák, hogy a szomszédos idősávok bizonyos hányadát figyelembe veszik. A módszert a korszerű digitális szűrés esetében is alkalmazzák, megfelelő rekurzív algoritmussal.
A szomszédos idősávok súlyozása analóg technikában a következő algoritmus szerint történik:
Az új spektrum 10 %-át hozzáadják az addig meghatározott spektrum 90%-ához, és így egy hhoz hasonló kép áll elő, mint amit analóg RC szűrővel történő átlagolásnál kaphatunk. A súlytényezők csökkenése ugyan nem exponenciális, de megközelíti azt.
|
|
(7.40) |
ahol „S” a teljes spektrum és „Sn” az új sáv átlaga.
A jobb érthetőség kedvéért az algoritmust a következő ábrán rajzos formában is bemutatjuk:
Az „effektív” átlagolási idő tehát a már figyelembe vett és az új sáv arányának függvénye. Részletes levezetés nélkül jelezzük, hogy a 0.9 – 0.1 arány a mintavételi idő 10-szereződését, és az effektív átlagolási idő 20-szorozódását jelenti. Ha az arányokat 0.99 – 0.01 értékre módosítják, akkor az előbbi mintavételi idők további látszólagos 10-szereződése lesz ennek eredménye.
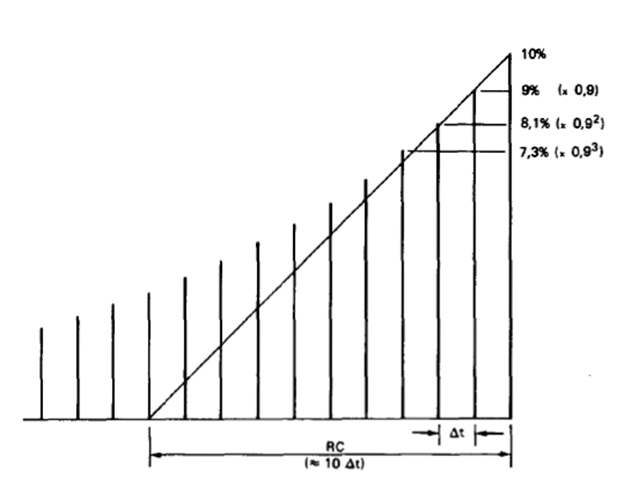
7.1.3.4. Folytonos, nem stacionárius jelek analízise a gyakorlatban
Az idő-ablakot a nem stacionárius folytonos jelek mentén mozgatva, meg lehet határozni az ablakozott rész frekvencia spektrumát. Az eredmény megjelenítése 3D-ben célszerű, mert így egyrészt a frekvenciától való függés (spektrum), másrészt a spektrum-kép időbeli változása is megjeleníthető.
A nem stacionárius időbeli jelek analízise esetében az időbeli ablakozásnak nagy szerepe van. Ha az időablak négyszög formájú, akkor a két végén „hirtelen” változás történik. (Elméletben végtelen meredekséggel, a gyakorlatban persze bizonyos átmenettel.) A szakadás megszüntethető, és lényegesen jobb eredmény kapható, ha az ablak „lágyabb” átmenetű, például Gauss-függvény alakú.
A gyakorlatban használatos ablakok a jelminta más-más részét hangsúlyozzák ki, de mindegyik ablak jobb, mint a négyszög ablak. A nem stacionárius folytonos jelből vett mintát akkor lehet a legkönnyebben analizálni, ha a minta a teljes jelhez képest rövid, mert így hasonló a helyzet, mintha stacionárius jelet vizsgálnánk.
Az ilyen típusú jelek analízise során az alábbi tényezőket kell figyelni:
Az időablak típusát
Az időablak hosszát
Az inkrementális lépések megválasztását
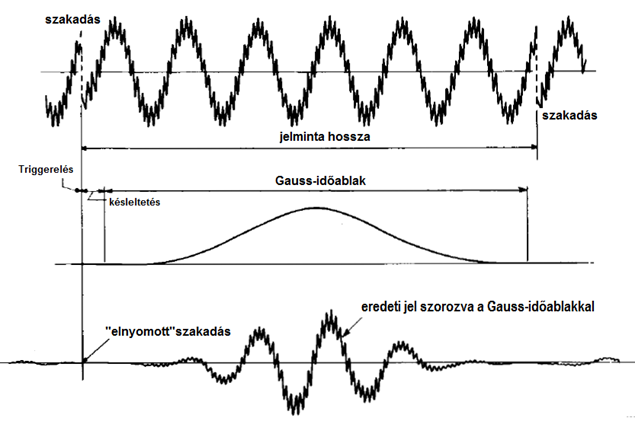
Az időablakozás és a hozzá kapcsolódó spektrum nem érthető a Fourier transzformáció néhány fontos összefüggésének felelevenítése nélkül.
A legfontosabb az ablakozás szempontjából a konvoluciós tétel, amelynek révén a konvolúciós integrál szorzattá transzformálható . A tételt a leggyakrabban a Laplace operátor térben alkalmazzuk, amikor a bemenőjel Laplace transzformáltját az átviteli függvénnyel megszorozva a kimenőjel Laplace transzformáltját állítjuk elő. Időtartományban ennek a műveletnek a konvoluciós integrál felel meg. A konvolució jelölése a két függvény között egy csillaggal történik.
|
|
(7.41) |
A konvolució azonban nem csak a Laplace transzformációhoz kapcsolódik.
A Fourier transzformáció is tartalmaz ennek megfelelő szabályokat. A legfontosabbak ezek közül a témához kapcsolódóan az alábbiak:
|
|
(7.42) |
A kimenőjel spektrumát tehát egyszerűen úgy állíthatjuk elő, hogy a bemenőjel spektrumát a frekvencia átviteli függvénnyel megszorozzuk. A folyamatot egyetlen kiragadott részlet segítségével könnyen elképzelhetjük, ha kiválasztunk egy összetevőt a bemenőjel spektrumából ωi körfrekvenciánál, és ezt a frekvencia átviteli függvény ωi körfrekvenciához tartozó értékével megszorozzuk. Az időtartományban az integrálszámítás lényegesen bonyolultabb.
A megszokott formájú konvolucióban a g(t) függvény az átviteli tag súlyfüggvénye, tehát maga is időfüggvény. A konvoluciót tehát időtartományban végezzük.
Ha egy lépéssel továbbmegyünk, és a konvoluciót a frekvenciatartományra is kiterjesztjük a Fourier transzformációs szabályoknak megfelelően, akkor az időablakozás frekvenciatérbeli hatása érthetővé válik.
A konvolucióban felcseréljük az idő és a frekvencia tartományt, azaz a változókat, és így az alábbi összefüggéseket kapjuk:
|
|
(7.43) |
Tekintettel arra, hogy F(jω) és G(jω) komplex függvények, a szorzatuk is komplex szorzat, ami azt jelenti, hogy szorozzuk az amplitúdókat, és összegezzük a fázisszögeket. Az integrálás ebben az esetben vektor-összegzést jelent.
Ha tehát egy f(t) folytonos időbeli jelből ki akarunk „vágni” egy meghatározott hosszúságú mintát, akkor egy g(t) négyszög időablakkal kell az f(t) függvényt megszorozni. A két időtartománybeli jel szorzata a frekvenciatartományban a megfelelő jelek spektrumainak konvolucióját eredményezi.
A folyamat képi megjelenítése a (7.21. ábra - Időfüggvények szorzása – spektrumok konvoluciója) ábrán követhető nyomon. Felülről sorrendben az első két függvény egy-egy koszinusz, illetve szinusz függvény, mellettük jobbra a komplex Fourier transzformáltjuk, amelyek Dirac-impulzusok +ωi és -ωi körfrekvenciáknál. Láttuk, hogy 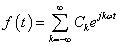 , tehát
a komplex Fourier transzformált valós része koszinusz, képzetes része pedig szinusz függvény,
ha figyelembe vesszük az Euler-összefüggést. Ez tükröződik vissza a spektrumokon is. A harmadik függvény egy négyszög időablak (T időtartamú impulzus), amellyel a folytonos harmonikus függvényekből egy-egy mintát szeretnénk „kimetszeni”. Az impulzus spektruma a jobboldalon látható, és csak valós résszel rendelkezik. A koszinusz jellel való szorzás (ablakozás) eredménye a spektrumban az, hogy az impulzus spektruma a koszinusz függvény -ωi és +ωi körfrekvenciáinál jelenik meg, és csak valós része van. Jól látszik, hogy az ablakozott koszinusz jel lineáris átlaga nem zérus (a pozitív és negatív hullám-felek eredője nem zérus), ezért jelenik meg a spektrumban zérus körfrekvenciánál is összetevő.
, tehát
a komplex Fourier transzformált valós része koszinusz, képzetes része pedig szinusz függvény,
ha figyelembe vesszük az Euler-összefüggést. Ez tükröződik vissza a spektrumokon is. A harmadik függvény egy négyszög időablak (T időtartamú impulzus), amellyel a folytonos harmonikus függvényekből egy-egy mintát szeretnénk „kimetszeni”. Az impulzus spektruma a jobboldalon látható, és csak valós résszel rendelkezik. A koszinusz jellel való szorzás (ablakozás) eredménye a spektrumban az, hogy az impulzus spektruma a koszinusz függvény -ωi és +ωi körfrekvenciáinál jelenik meg, és csak valós része van. Jól látszik, hogy az ablakozott koszinusz jel lineáris átlaga nem zérus (a pozitív és negatív hullám-felek eredője nem zérus), ezért jelenik meg a spektrumban zérus körfrekvenciánál is összetevő.
A szinusz függvény ablakozása imaginárius spektrumot eredményez, ugyancsak a függvény -ωi és +ωi körfrekvenciáin, és ismét az impulzus spektruma jelenik meg. A spektrumnak nincs összetevője a zérus körfrekvencián, mert az ablakozott szinusz jel lineáris átlaga zérus.
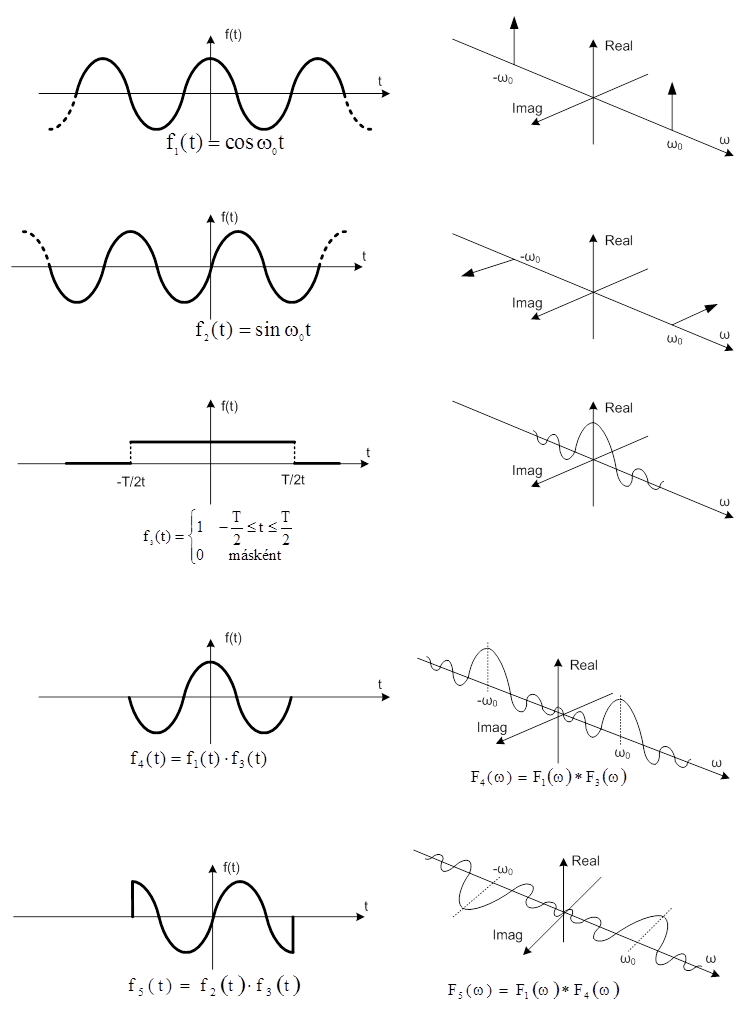
A konvolucióval létrejött spektrum megjelenítése lényegesen egyszerűbb, ha a teljesítmény spektrum közlése a feladat, mert ebben az esetben a 3D-s kép helyett csak a valós koordinátarendszerben kell ábrázolni az eredményt.
A következő ábrán ugyancsak harmonikus jelen történő „ablakozást” látunk két időablak esetében, és jobboldalon a teljesítmény spektrum látható. A folytonos, periodikus harmonikus függvény Fourier transzformáltja (komplex spektruma) ±f0 frekvenciáknál egy-egy Dirac-impulzus. A nem periodikus négyszög-impulzus és a Gauss-függvény spektruma folytonos, és a függőleges tengelyre szimmetrikus. A frekvenciatérbeli konvolució eredményeként az ablakok spektruma a harmonikus jel ±f0 frekvenciáin jelenik meg. Látható, hogy a négyszögjel két végén végbemenő hirtelen változás (végtelen meredekség) igen széles sávú spektrumot eredményez. Az eredeti harmonikus jel frekvenciáján van ugyan egy jól elkülöníthető csúcs, de az oldalsávok teljesítménye nem elhanyagolható. A Gauss-függvénnyel történő ablakozás a harmonikus jelből fokozatosan növekvő amplitúdójú részletet „vág ki”, a hirtelen ugrás megszűnik, és a spektrum ennek következtében „szűkebb” lesz. A teljesítmény spektrumban a megjelenő Gauss-spektrum csúcsaihoz tartozó ±f0 frekvenciák felelnek meg az eredeti folytonos jel frekvenciáinak. Az oldalsávok persze itt sem elhanyagolható mértékűek, ennek nagysága a Gauss-függvény alakjától, pontosabban annak szórásától függ.
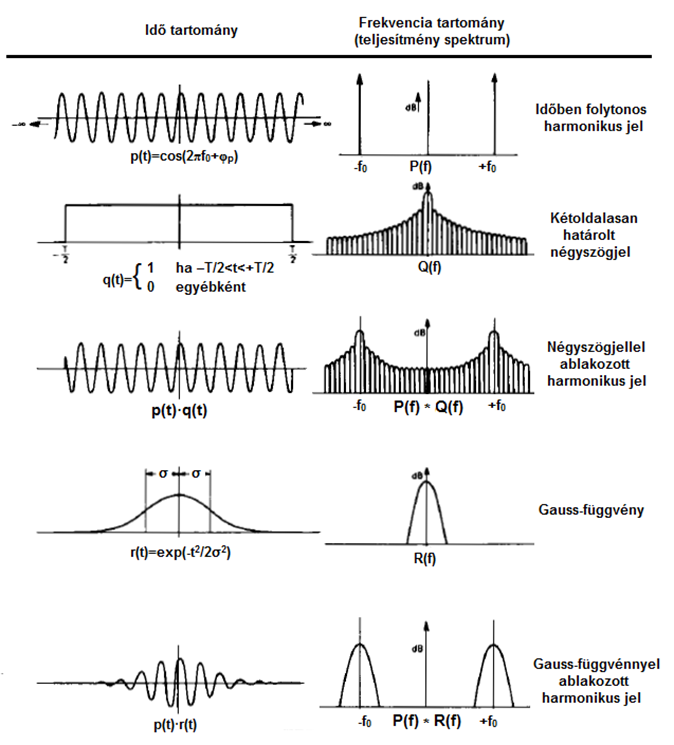
Az időablak típusának megválasztása
Az analóg szűrési gyakorlatban az alábbi időablakokat szokás alkalmazni:
Négyszög ablak T időtartammal
Hanning (cos2) ablak
Hamming ablak (Hanning ablak egy kismértékű emeléssel)
Gauss ablak
Táblázatban foglaltuk össze a fenti időablakokhoz tartozó szűrési tulajdonságokat:
|
Típus |
3dB sávszélesség β=1/T |
Zaj sávszélesség B eff |
Legmagasabb oldalsáv [dB] |
Oldalsávok csúcsainak meredeksége |
|---|---|---|---|---|
|
Négyszög |
0.9 β |
1.0 β |
-13 |
-20 dB/dekád |
|
Hanning |
1.4 β |
1.5 β |
-32 |
-60 dB/dekád |
|
Hamming |
1.3 β |
1.4 β |
-42 |
-20 dB/dekád |
|
Gauss |
1.8 β |
1.9 β |
nincs |
nincs |
A különböző típusú és „T” időtartamú időablakok frekvencia menetét hasonlítjuk össze a következő ábrán:
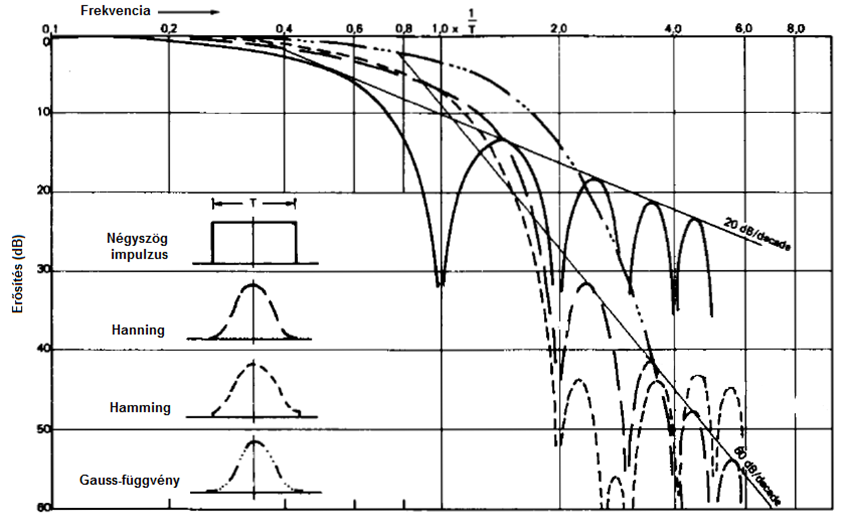
Az időablak hosszának megválasztása
Természetes, hogy az ablak hossza az analizálni kívánt nem stacionárius, folytonos jel hosszától függ, gondoljunk példaképpen a beszédben kiejtett hangzókra, amelyek időtartama átlagban 40 ms körüli. A rövid minta következménye természetesen nagy sávszélesség lesz a frekvenciatartományban, gondoljunk az impulzus spektrumára. A különböző ablak típusok Teff effektív hossza (összehasonlítás céljából) az effektív, vagy zaj sávszélességgel határozható meg, ha a jelminta véletlenszerű, és nagyjából stacionárius:
|
|
(7.44) |
A Teff érték tulajdonképpen a TA helyettesítésére szolgál abban a korábban már megismert összefüggésben, amely az átlagolási idő és a hiba várható eloszlása közötti kapcsolatot adja meg.
|
|
(7.45) |
Láttuk, hogy minél hosszabb az átlagolási idő, annál kisebb a hiba, az eredmény bizonytalansága, empirikus szórása.
Konstans relatív sávszélességű analízis esetében előfordulhat, hogy a kapott eredményt nem a szűrő sávszélessége, hanem az időablak alakja határozza meg.
Az inkrementális lépések megválasztása
Láttuk, hogy Teff dönti el az inkrementális lépések szélességét. Ugyanakkor, ha a fenti elméleti képlet szerint állapítjuk meg a frekvencia inkrementumot, akkor a gyakorlatban hibát követhetünk el.
A lépések sávszélességét célszerű keskenyebbre választani, például a következő minta szerint:
Egy Hanning ablak effektív sávszélessége 1.5β, a képlet alapján számítható Teff=0.67T. Az inkrementális lépések számításához 0.5T értéket célszerű választani.
7.1.4. Tranziens jelek analízise
A gyakorlatban sokféle módszer ismert, és gondot jelent, hogy ezek nem adnak azonos értékű eredményt. Ezért az alkalmazott módszer kiválasztásához több szempontot kell figyelembe venni. A helyes módszer kiválasztásához az alábbi két ábra szolgálhat segítségül:
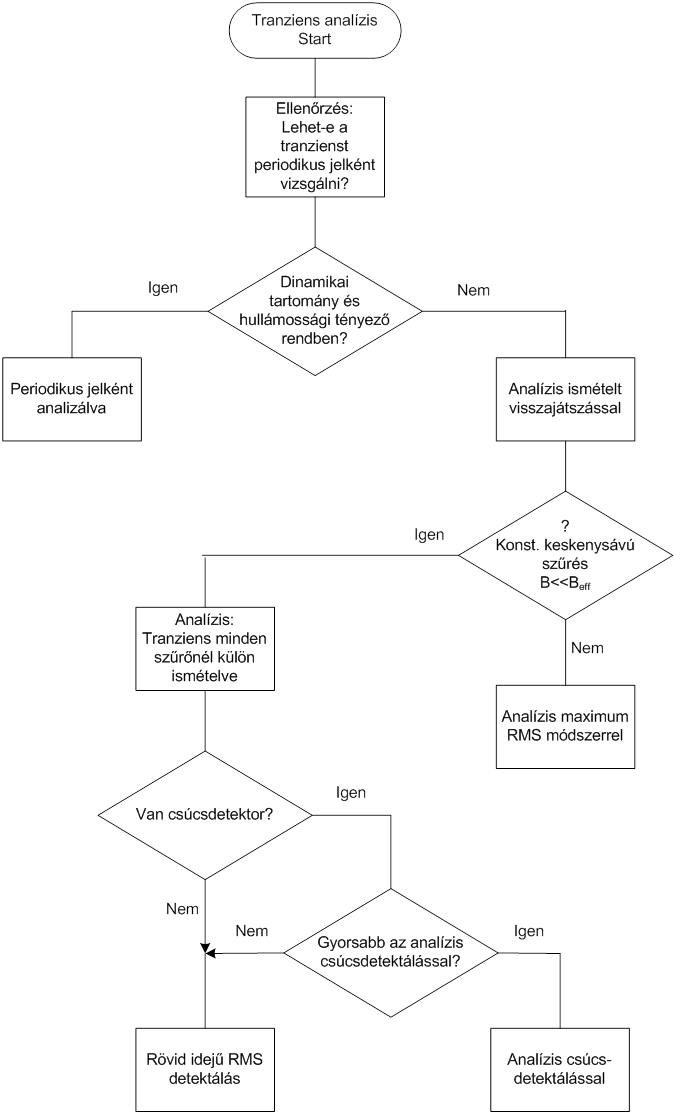
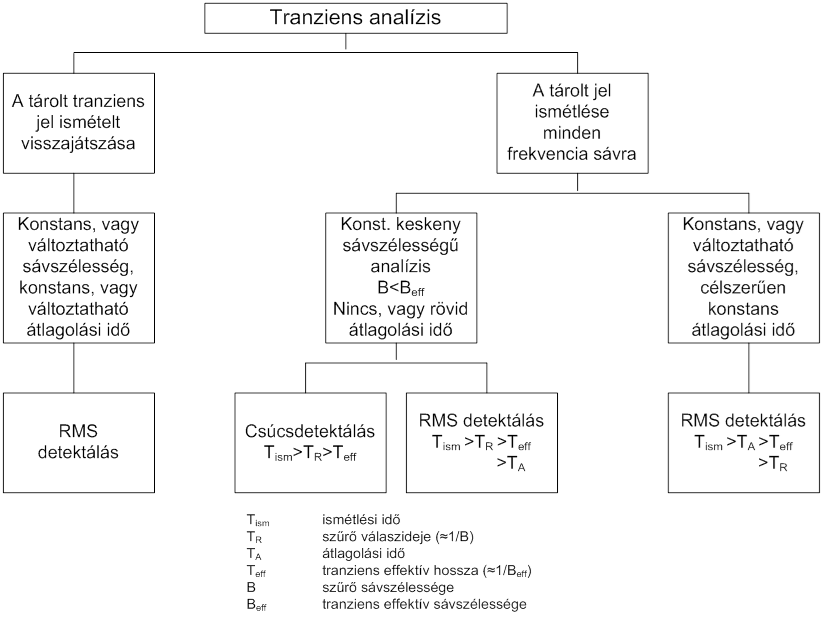
Analízis periodikus jelként
Ebben az esetben a tárolt tranziens jelet „Tism” ismétlési idővel periodikusan visszajátsszák, ügyelve arra, hogy a Tism hosszabb legyen, mint maga a tranziens jel. Ezt láthatjuk a (7.24. ábra - Tranziens analízis döntési folyamatábrája) ábrán. Ilyen módon a tranzienst mesterségesen periodikussá alakítják, és az így kapott vonalas spektrum alakja könnyen rokonítható az eredeti tranziens jel folytonos spektrumával. A detektorokkal RMS átlagolást kell végezni, TA átlagolási idővel, amely nagyobb, mint az ismétlés ideje, mert így csillapíthatók az ingadozások.
A periodikus jelként történő analízis módszerének előnyei:
Hasonló analizálási technikák alkalmazhatóak, mint a folytonos jelek esetében.
A kapott eredményt a sávszélesség kevéssé befolyásolja, mind konstans sávszélesség, mind pedig konstans relatív sávszélesség alkalmazható.
Feltéve, hogy az átlagolási idő elegendően nagy (ismétlés idejének figyelembe vételével), az átlagolási idő növelése már nem befolyásolja az eredményt.
A spektrum inkább folytonosnak látszik, mert a csúcsok közel esnek egymáshoz.
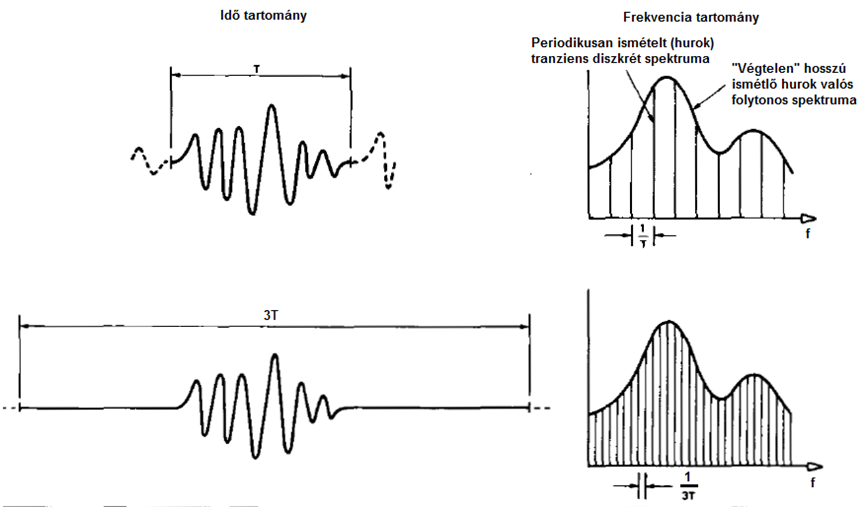
Az analizátor sávszélességével kapcsolatban fontos követelmény viszont, hogy az legyen nagyobb, mint az analízissel kapott vonalas spektrum vonaltávolsága:
|
|
(7.46) |
A spektrumvonalak távolságát viszont az ismétlési idő határozza meg.
Az átlagolási idő T A legyen lényegesen nagyobb, mint az ismétlési idő, a hullámosság csökkentése érdekében. Az elméletben alátámasztható gyakorlati érték az alábbi:
|
|
(7.47) |
Általában 3-nál nagyobb értékkel szokás indulni, és a kapott eredmény szemrevételezése után növelik a szorzót.
A szűrési, vagy TD tartózkodási időt hasonló módon kell megállapítani a sweep-eléshez, amint a stacionárius jelek esetében láttuk.
Tranziens analízis állandó keskeny sávszélességgel
Ezt a módszert akkor szükséges választani, ha az ismétlési időt nem lehet a szükséges mértékben lerövidíteni. Ebben az esetben a tranziens jelet minden egyes szűrő beállítás mellett ismételni kell, megvárva a szűrő válaszát. A szűrő válaszideje jellemzően hosszabb, mint a tranziens jel hosszának ötszöröse, mint ahogy a méréstechnikában is szokásos a leolvasási időt az időállandó ötszörösének venni. Frekvencia térben kifejezve a feltételt a következőképpen lehet megfogalmazni:
|
|
(7.48) |
Teff ebben az esetben a tranziens effektív időtartama, amely nem azonos az ismétlési idővel. A módszer lassú és körülményes, de a kapott spektrum pontos. A spektrumvonalak csúcsain át húzott burkológörbe a tulajdonképpeni jelspektrum.
Ha a szűrési, vagy TD tartózkodási idő nem kisebb, mint az ismétlési idő, akkor a spektrumvonalak távolsága éppen a szűrő sávszélességének felel meg:
|
|
(7.49) |
Tranziens analízis állandó változó sávszélességgel
A keskenysávú analízist a rendelkezésre álló szűrő sávszélessége és a jelminta effektív időbeli hosszának reciprokja közötti arány korlátozza. Szükség esetén az analízist el lehet végezni konstans relatív sávszélességű szűréssel is, például tercsáv-analizátorral.
Az átlagolási időnek a jelmintánál alapvetően hosszabbnak kell lennie, így természetesen az analízishez szükséges idő is hosszabb, mint a keskenysávú módszernél.
Az átlagolási idő meghatározásához az alábbi formula áll rendelkezésre:
|
|
(7.50) |
ahol Teff a jelminta (impulzus) hossza.
Az ismétlési idő és az átlagolási idő közötti kapcsolat pedig az alábbi:
|
|
(7.51) |
A szűrési idő TD (szűrőben töltött idő) rögzített középfrekvenciájú tercszűrők esetében legyen legalább akkora, mint az ismétlési idő.
7.1.5. Cepstrum analízis
B. P. Bogert, M. J. R. Healy, J. W. Tukey „The Quefrency Analysis of Time Series for Echoes: Cepstrum, Pseudo-Autocovariance, Cross-ceprstrum and Saphe Cracking” című, a Proceedings of the Symposium on Time Series Analysis kiadványban megjelent (M. Rosenblatt, Ed. Wiley, New York, 1963 [7.1.] cikke 1963-ban mutatta be azt a módszert, amelynek segítségével a földrengések igen összetett rezgésképéből szét lehetett „választani” az epicentrumban (forrás) kipattant lökéshullámokat, a földkéreg, mint bonyolult átviteli tulajdonságokkal rendelkező passzív rendszer válaszát (kvázi „súlyfüggvényét”), és az echókat (visszahatásokat, „visszhangokat”). Rendszertechnikai kifejezésekkel fogalmazva: el kellett különíteni a földkéreg impulzus-válaszától a forrás által kibocsátott rezgésjeleket.
Bogert újítása azért nagyon fontos újdonság és nélkülözhetetlen gyakorlati módszer a jelanalízisben, mert J. Trampe Broch „On the Applicability and Limitations of the Cross-Corelation and the Cross-Spectral Density Techniques” című, a B&K Technical Review No 4. 1970 [7.2.] megjelent publikációjában, a későbbiekben megmutatta, hogy a hagyományos módszerrel, nevezetesen az autokorrelációs függvény segítségével felderített csúcsok, amelyek például a visszhanggal kapcsolatba hozhatók lennének, sajnálatos módon erősen függenek a frekvencia spektrum alakjától. Ráadásul a földkéregben való terjedés különféle szűrő hatásoknak is ki van téve. A teljesítmény spektrum logaritmusának felhasználásával is történtek próbálkozások, de ezek az eredmények is hasonlóan érzékenyek a szűrésre. Csak a cepstrum képes olyan késleltetett csúcsokat is kimutatni, amire az auto-és keresztkorreláció már nem volt alkalmas.
A gépészeti méréstechnika szempontjából természetesen nem a cepstrum analízis eredeti célja fontos, hanem az, hogy a Bogert-féle publikációt követően szédítő sebességgel kezdték a módszert alkalmazni különböző tudományterületeken, ahol hasonló dekonvoluciós problémákkal küzdöttek. A szeizmikus vizsgálatok után, másodikként, a beszédanalízis területén alkalmazták, mert a cepstrum alkalmas a hangképző szervek frekvencia átviteli tulajdonságainak, és önmagában a „tiszta” hang frekvenciaspektrumának szétválasztására. A hangképző szervek esetleges deformitásai, betegségei ennek segítségével beazonosíthatóvá váltak.
A gépészeti méréstechnika szempontjából természetesen nem ez a két alkalmazás, hanem az alábbi műszaki lehetőségek játszanak szerepet:
géprezgések periodikus összetevőinek detektálása és azonosítása,
turbinalapátok hibái,
csapágyak hibái,
a megfelelő felharmonikusak és oldalsávok elkülönítésének segítségével.
Bogert és társai a bevezetőben említett publikációjukban az általuk javasolt cepstrum analízis eljárás fogalmaira és egységeire olyan elnevezéseket találtak ki, amelyek az eredeti frekvencia analízisből származtak, de néhány betű felcserélésével teljesen új szavak születtek az új fogalmak megjelölésére. Mindeközben persze, a megjelölések hangalakja a felhasználóban a hagyományos frekvencia analízissel való rokonság érzetét kelti, nem alaptalanul.
Nézzünk ezek közül néhányat, angol nyelven, mert így érzékelhető a betűk cseréje. A quefrencia dimenziója idő, ez a soron következő definícióból is nyilvánvaló lesz.
|
Frekvencia analízis |
Cepstrum analízis |
|---|---|
|
frequency [Hz] |
quefrency [s] |
|
spectrum |
cepstrum |
|
filtering |
liftering |
|
harmonic |
rahmonic |
|
phase |
saphe |
A cepstrum analízist több szakirodalom joggal nevezi dekonvoluciónak . Az elnevezés jogos, és igen szemléletesen tükrözi a cepstrum analízis lényegét. Az idő tartományban mért „válaszjelek”, amelyet a földrengéseket észlelő szeizmológiai állomások regisztrálnak, valójában konvoluciós integrálok „eredményei”. Ugyanis, a rendszertechnikában megszokott módon, időtartományban az „y(t)” kimenőjel (válaszjel) az alábbi módon adható meg az átviteli tag „g(t)” impulzus válaszának (súlyfüggvény) és az „u(t)” gerjesztő jelnek ismeretében:
|
|
(7.52) |
A gépészeti méréstechnikai alkalmazásokban legyen az u(t) függvény egy gép (géprendszer) belső zaja, vagy rezgésforrásának jele, g(t) pedig az impulzusválasz, amely a gép belsejétől a mérési pontig terjedő összetett, és nehezen modellezhető rendszert jellemzi.
A méréssel detektálható y(t) válaszjelből idő tartományban nem lehet az eredeti két összetevőt szétválasztani, de amint olvashattuk, az autokorrelációs spektrum sem volt erre alkalmas.
Bogert és társai a konvoluciós integrál frekvencia tartománybeli megfelelőjéből indultak ki, és arra alapozva, hogy a szorzatból logaritmusképzéssel összeg állítható elő, megalkották a cepstrum fogalmát. A cepstrum lényegében az átviteli függvény és a gerjesztés spektrumának logaritmikus összege. Ezt mutatjuk be a következőkben.
A konvolució megfelelője frekvencia tartományban a frekvencia függvények szorzata. Az egyenlet logaritmusát képezve, az egyenlet összeggé alakul.
|
|
(7.53) |
A két összetevő a linearitási törvény alapján külön-külön Fourier transzformálható, így áll elő a cepstrum, amely a két kérdéses időfüggvényből származó spektrum összege:
|
|
(7.54) |
Az egyenlet lényegében a „dekonvolució”, azaz az időfüggvényekhez rendelt spektrumok szétválasztásának folyamatát mutatja.
Napjainkban a cepstrum két formája ismeretes és alkalmazott, ezek a
teljesítmény cepstrum és a
komplex cepstrum.
Ez utóbbi elnevezésben ugyan benne foglaltatik a komplex jelző, de a cepstrum valójában nem komplex, csak reális része van, erről a későbbiekben még lesz szó.
A következő ábra baloldalán a kitartott emberi „Á” hangméréssel felvett spektrumát (válasz spektruma), jobboldalán pedig a cepstrumát mutatja. A spektrumból az eredeti hang frekvenciája nem szűrhető ki, mert a hang több felharmonikussal együtt jelenik meg. A hangképző szervek frekvencia átviteléről egyszerűen pedig nincsen információ.
A jobboldali cepstrumban viszont a hangképző szervek frekvencia átvitele és az eredeti „Á” hang már jól elkülönítetten jelenik meg. Az átviteli tagra (láncra) jellemző quefrenciák általában alacsonyabb értéknél jelennek meg (kisebb a spektrum fluktuációja), így könnyen felismerhetőek, erre jó példa az alábbi ábra jobboldala.
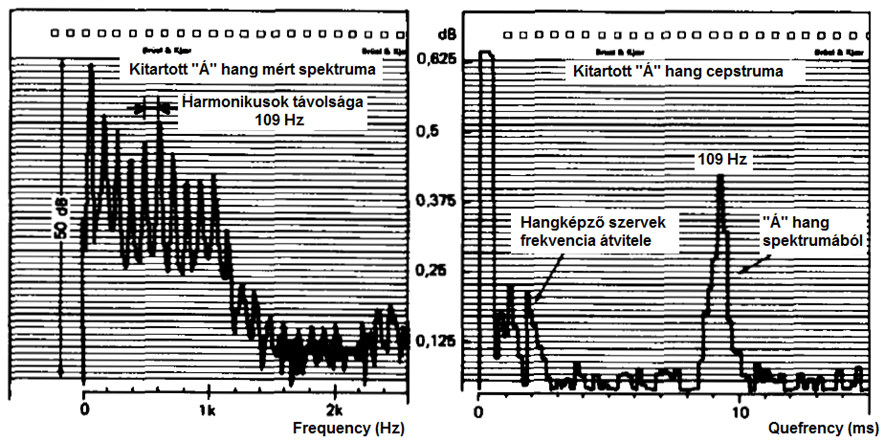
Teljesítmény cepstrum
Matematikailag és történelmileg ez az első forma, hiszen az idézett munkában a cepstrum mint „A teljesítmény spektrum logaritmusának teljesítmény spektruma” van definiálva.
A „miért” kérdésre azonnal érthető a válasz: A bevezetőben ismertetett összefüggések általános formában mutatták be a cepstrum analízis lényegét. Tudomásul kell azonban vennünk, hogy az analizálandó jelek túlnyomó része sztochasztikus jellegű. Az ilyen jeltípusok frekvencia analízise „egyszerű” Fourier transzformációval nem lehetséges, csak az autokorreláció révén.
Nézzük az egyes lépéseket sorjában:
Az időbeli jel Fourier transzformáltja a szokott módon képezhető:
|
|
(7.55) |
A jel teljesítmény spektruma:
|
|
(7.56) |
Végezetül a cepstrum:
|
|
(7.57) |
Fontos egy másik megközelítésben, a quefrency dimenziója miatt, hogy az „R xx (τ)” autokorrelációs függvény és a teljesítmény spektrum között az alábbi összefüggés áll fenn (Wiener-Hincsin tétel):
|
|
(7.58) |
Az autokorrelációs függvény stacionárius és ergodikus folyamat esetében az időközépérték segítségével meghatározható. Meg kell jegyezni, hogy nem stacionárius jelek esetében az autokorrelációs függvény nem csak „τ” eltolási időnek, hanem a „t 0 ” kiindulási időpontnak függvénye is.
|
|
(7.59) |
Ezért az eltolási idő „τ” nem csupán az autokorrelációra, hanem a cepstrumra is jellemző.
A quefrency dimenziója tehát idő .
Nem is lehet más, hiszen a módszer a konvoluciós integrál eredményeként kapott válaszfüggvény dekonvolucióját jelenti. A konvoluciós integrálban ugyanis az átviteli tag súlyfüggvényét ugyancsak folytonosan „τ” idővel toljuk el a bemenő függvényhez képest, és „τ” szerint integrálunk.
A cepstrum megítélésénél fontos, hogy magas quefrency értékek a spektrum gyors fluktuációját jelentik, míg kis quefrency értékek éppen az ellenkezőjét, lassú változásokat mutatnak a jel spektrumában.
Hátra van még a cepstrum mértékegységének kérdése. Tekintettel arra, hogy spektrumot leginkább logaritmikus léptékben adjuk meg, és a mértékegység „dB”, a cepstrum mértékegysége „(dB)2 ” lesz. (Eredetileg a cepstrum megalkotói a teljesítmény második Fourier transzformáltjára „amplitúdó spektrum” elnevezést használtak, amelynek dimenziója viszont „dB” lenne. A második transzformáció a későbbi szerzőknél vagy előre, vagy vissza Fourier transzformáció, ahol csak a léptékek különböznek.)
Komplex cepstrum
Ezt a cepstrum formát A. V. Oppenheim, R. W. Schafer, és T.G. Stockham írták le publikációjukban, amely a „Nonlinear Filtering of Multiplied and Convolved Signals IEEE Trans. Audio & Electroacoustics, Vol. AU-16. No 3, Sept. 1968 [7.3.] jelent meg.
A nevétől eltérően ez egy valós értékű függvény, az elnevezésnek az oka abban áll, hogy a komplex cepstrumot a komplex spektrumból eredeztetik. A legfontosabb tulajdonsága az, hogy a fázis információ nem „vész el”. Ennek következtében a szűrési műveletek után az eredeti jel teljes egészében visszaállítható. Lényegében alkalmas lineáris szűrési technikák alkalmazásával a konvolucióval és szorzással képezett jelek eredeti összetevőinek szétbontására.
A szerzők a komplex cepstrumot a következőképpen definiálták:
„Az időbeli jel komplex spektruma komplex logaritmusának inverz Fourier transzformáltja”.
A szöveg az alábbi műveletekkel írható le:
|
|
(7.60) |
A szerzők a teljesítmény cepstrumtól való eltérés hangsúlyozására a komplex cepstrumot K x (τ) formában jelölték.
Ismeretes, hogy a komplex spektrum F x (f) a következő alakban írható fel:
|
|
(7.61) |
A transzformált F x (f) a Fourier transzformáció eredményeként jött létre:
|
|
(7.62) |
A komplex exponenciális függvény a valós és képzetes részre való bontás helyett amplitúdót és fázist ad meg. Ha az F x (f) transzformált természetes logaritmusát képezzük a komplex cepstrum eredeti definíciója szerint, akkor az amplitúdó és fázis információ szétválnak:
|
|
(7.63) |
A komplex spektrum a definíciója szerint tehát:
|
|
(7.64) |
A komplex spektrum A(f) és e jΦ(f) szorzat alakjából tehát e komplex cepstrum esetében is összeg lesz a logaritmus révén.
Valós f x (t) függvény komplex spektruma páros konjugált lesz. Így A(f) és lnA(f) páros is páros lesz, Φ(f) pedig páratlan. Ezért a komplex L(f) függvény konjugált páros, amelynek inverz Fourier transzformáltja valós időfüggvény lesz.
A komplex cepstrum révén lehetővé válik az, hogy a mérhető válaszjel komplex cepstrumából kivonva az átviteli függvény komplex cepstrumát megkapjuk a forrás eredeti jelének komplex cepstrumát, amelyből azután a jel időbeli alakja visszaállítható. Az átviteli függvény komplex cepstruma jellemzően alacsony quefrency értékeken jelentkezik, így könnyű az azonosítás és az eltávolítás.
A következő példán jól követhető a visszhang megszűntetése.
A következő ábra legfelül látható, 1. képén három, periodikusan lecsengő szinuszos jel látható, egymástól τ 0 időbeli távolságra. Az első eredeti jelnek tehát két, csökkenő amplitúdójú visszhangja van. Ez az additív jellegű periodicitás megjelenik a logaritmikus amplitúdó spektrumon (2. kép) és fázismeneten (3. kép) is. Ez a két kép tehát már nem a megszokott spektrum, hanem azok logaritmusa. Az amplitúdó spektrumban látható kiemelés a harmonikus jel frekvenciája, a folytonos, sinx/x jellegű spektrum összetevő pedig az időbeli jel impulzus formája miatt jelenik meg.
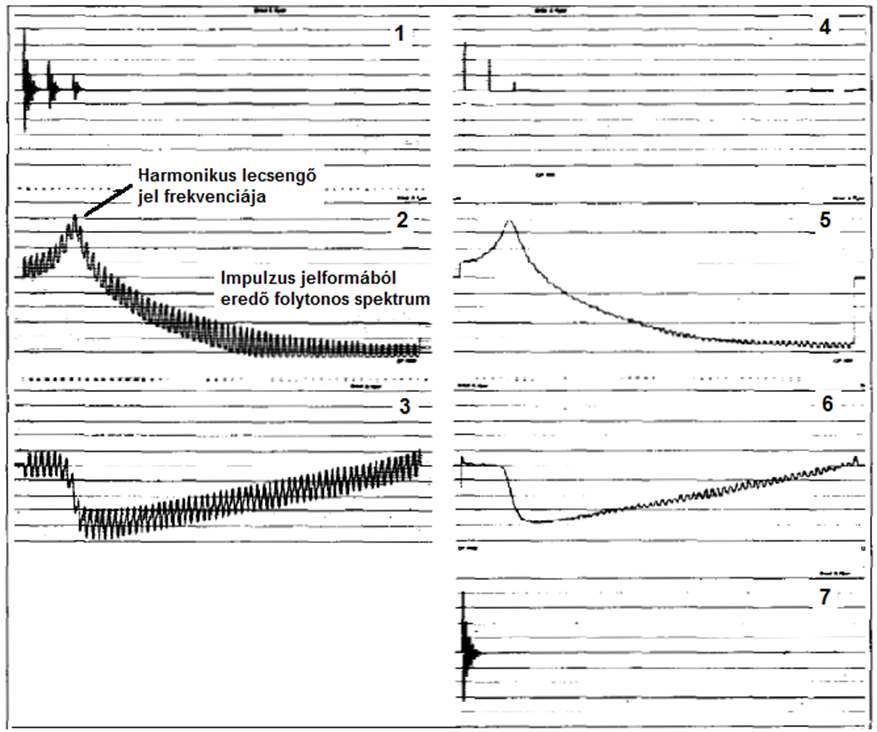
Az inverz Fourier transzformálás után, tehát a komplex cepstrumban , az ismétlődést olyan formában látjuk viszont a 4. képen, hogy a harmonikus jelhez tartozó Dirac-impulzusok τ 0 távolságra helyezkednek el. Eltávolítva a két visszhangot jelentő impulzust (második és harmadik), a „kijavított” komplex cepstrumot visszatranszformálják logaritmikus spektrummá (5. és 6. kép), majd egy inverz logaritmusképzést követően sor kerül a második inverz Fourier transzformálásra is. A folyamat végén, a 7. képen látható az eredeti, visszhangmentes jel időbeli alakja.
Irodalmak
[7.1.] The Quefrency Analysis of Time Series for Echoes: Cepstrum, Pseudo-Autocovariance, Cross-ceprstrum and Saphe Cracking. Proceedings of the Symposium on Time Series Analysis . Wiley. 1963.
[7.2.] On the Applicability and Limitations of the Cross-Corelation and the Cross-Spectral Density Techniques. B&K Technical Review No 4.. 1970.
[7.3.] Nonlinear Filtering of Multiplied and Convolved Signals . IEEE Trans. Audio & Electroacoustics. Sept. 1968.
8. fejezet - Bevezetés a digitális jelfeldolgozásba és analízisbe
A digitális jelek (digitalizált analóg jelek) napjainkban minden műszaki területen megtalálhatók a világban. A telefontársaságok digitális jeleket alkalmaznak, hogy az emberi hangot feldolgozzák, rádió, televízió, Hi-Fi hangrendszerek mind fokozatosan állnak át a digitális működésre, mert így kedvezőbb a hangvisszaadás és a zajcsökkentés valamint a jelfeldolgozás is rugalmasabb. Az adatok a műholdakról a földi vevőállomásokra szintén digitális formában jutnak el. A NASA a távoli bolygók, a világűr képeit gyakran digitálisan dolgozza fel, hogy eltávolítsa róluk a zajt, és kiemelje a lényeges információkat. Népességi adatok, népszámlálás eredményei, az értéktőzsde árfolyamok mind-mind digitális formában érhetőek el. Mivel a digitális jelfeldolgozásnak számos előnye van, az analóg jeleket is átalakítjuk digitális formába, hogy a számítógéppel feldolgozhatóak legyenek. Ez a fejezet alapvető ismereteket ad a digitális jelfeldolgozás alapjainak megértéséhez.
8.1. Az adatelemzés jelentősége
A részletes elemzést végző könyvtáraknak az a feladatuk, hogy bejuttassák a berendezésekbe a nyers mérési adatokat. A nyers mérési adatok amint azt a 8.1. ábra - A nyers mérési adatok ábra mutatja, nem mindig csak a közvetlen az információt hordozzák. Gyakran át kell alakítanunk a jelet, el kell távolítanunk belőle a zavarjeleket, ki kell javítanunk a hibás részeket, kompenzálnunk kell a káros környezeti hatásokat, mint például a hőmérséklet és a páratartalom változásának következményeit.
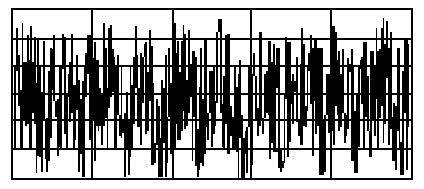
A digitális jel feldolgozásával és analízisével tudjuk „kibányászni” a felhasználható információt a zavarjellel terhelt mért jelből, és megjeleníthetjük egy olyan függvényként, amely jobban érthető, mint a nyers bejövő adatok (8.1. ábra - A nyers mérési adatok).
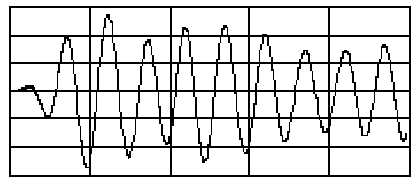
A LabVIEW blokkdiagramos programozási stílusa és a jel feldolgozásának helyes (pontos) beállítása , valamint a VI-s (Virtual Instrument) mérés lényegesen leegyszerűsítik a jeleket elemző alkalmazásokat.
A mai korszerű intelligens rendszereknél — úgy is mondhatjuk, mechatronikai rendszereknél — rendkívüli jelentősége van a mérésnek. Mérés nélkül nincs szabályozás, szabályozás nélkül pedig nincs intelligens rendszer. A legszemléletesebben ezt úgy lehet megérteni, ha megnézzük a különbséget a klasszikus gépészeti szemlélet és a korszerű mechatronikai szemléletmód között.
8.2. Vizsgáló jelek
Egy jel frekvencia összetételének meghatározásához először digitalizálni kell a folytonos jelet. Ahhoz hogy alkalmazhassuk a digitális jelfeldolgozás módszereit, digitális formába kell (át)konvertálnunk az analóg jelet. A gyakorlatban ezt az átalakítást egy analóg-digitál (A/D) átalakítóval valósítják meg.
Tekintsünk egy analóg jelet x(t), amelyből minden h másodpercben veszünk mintát. A h időintervallum a mintavételi intervallum vagy mintavételi periódus . Ennek reciproka 1/h a mintavételi frekvencia . Mértékegysége: minta/másodperc. Az x(t) minden egyes függvényértéke diszkrét érték a t=0,h, 2h, 3h -nál és így tovább, ezek az egyes minták. Így x(0), x(h), x(2h), … az összes minta. Az x(t) jelet a mintavételezés után a mintavételi értékekből álló halmaz írja le:
|
{ x(0), x(h), x(2.h), x(3.h), …, x(k.h), …} |
(8.1) |
A 8.4. ábra - Analóg jel és annak mintavételezett értékei ( h = a mintavételezések között eltelt idő az időtengelyen ) egy analóg jelet és a hozzá tartozó megfelelő mintavételi értékeket mutatja.
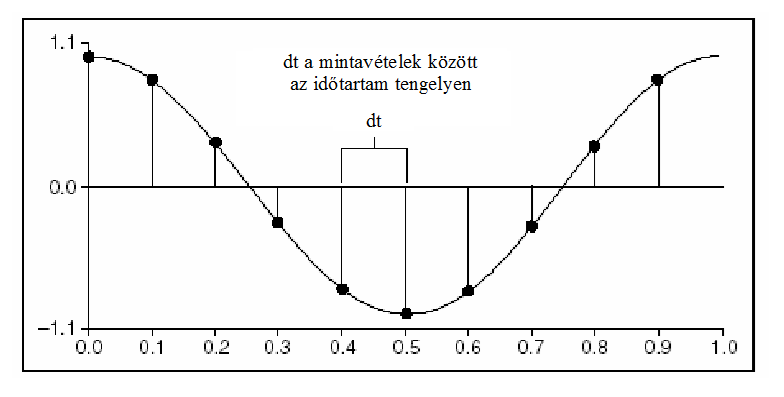
A következő kifejezés leírja az egyes mintavételi értékeket:
|
x[k] = x( k.h ) , ahol k = 0, 1, 2, … |
(8.2) |
Ha az x(t) jelből N darab értéket veszünk, akkor x(t) előállítható a következő jelsorozatból:
|
X = { x[0], x[1], x[2], x[3], …., x[N–1] }. |
(8.3) |
A fenti sorozat x(t) digitális leképezése, vagyis x(t) mintavételezett alakja. Az X = { x[k] } sorozat k egész értékei szerint van sorszámozva, és nem tartalmaz információt a mintavételezés gyakoriságáról. Tehát a mintáknak csak az értékét ismerjük, és nem tudjuk, hogy milyen frekvenciával történt a mintavételezés. Egy (digitális) számítógépes analóg bemenet egyik legfontosabb jellemzője hogy a mintavevő berendezés mekkora frekvenciával vesz mintát a bejövő jelből. Alacsony frekvenciájú mintavételezés alul mintavételezett jelet eredményezhet!
8.3. Alul-mintavételezés (Aliasing)
Ha a jel alul-mintavételezett, akkor minimális információt tartalmaz az analóg jelről. Az alul-mintavételezés eredményeként úgy tűnik, mintha egy megtévesztő kisebb frekvenciájú jel is megjelenne a mintavételezett jelben. A 8.5. ábra - Alul-mintavételezés okozta látszólagos frekvencia jelensége egy megfelelő módon mintavételezett és egy alul-mintavételezett jelet mutat be.
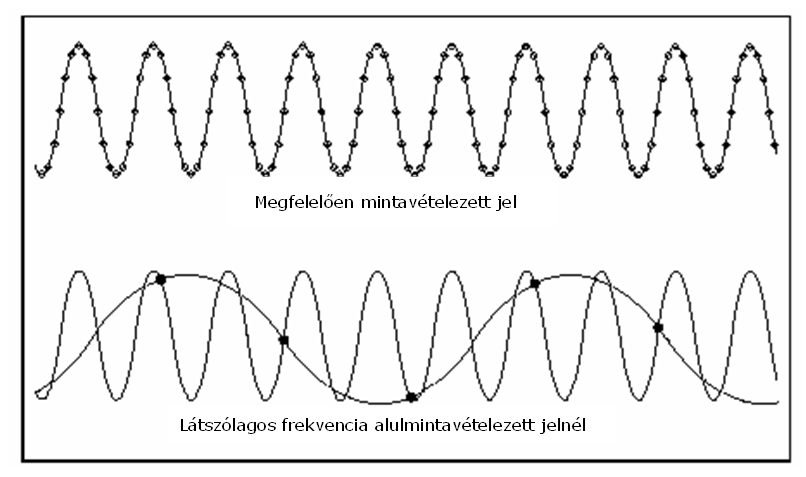
A (8.5. ábra - Alul-mintavételezés okozta látszólagos frekvencia jelensége) ábrán az alul-mintavételezett jelnél úgy tűnik mintha volna egy alacsonyabb frekvenciájú komponense is, ahol az eredeti tíz periódusból csak kettő látszik. Ha megnöveljük a mintavételi frekvenciát, ezzel megnöveljük a mintavételi pontok számát is az adott időtartam alatt. A nagyobb mintavételezési frekvencia az eredeti analóg jel egy jobb, több információt tartalmazó (átalakítása) megjelenítése, a kisebb frekvenciájú mintavételezéshez képest. Meg lehet adni egy olyan mintavételi frekvenciát, amellyel a mintavételezett jelben lévő maximális frekvenciát is mindig pontosan elő tudjuk állítani alul-mintavételezés (aliasing) nélkül, ez az úgynevezett Nyquist frekvencia .
A Nyquist frekvencia megegyezik az alkalmazott mintavételi frekvencia felével, amelyet a következő képlettel írhatunk le:
|
|
(8.4) |
ahol
|
f N |
a Nyquist frekvencia, | |
|
f S |
a mintavételi frekvencia (sampling frequency). |
Az olyan jelek, amelyeknek bizonyos frekvencia komponensei a Nyquist frekvencia felett vannak, vonalasnak, szaggatottnak látszanak a tényleges és a Nyquist frekvencia között. A Nyquist frekvencia feletti komponensek az alatt látszanak a vonalas jelben. Például egy frekvencia komponens f N <f 0 <f S , f S- f 0 frekvenciaként jelentkezik.
A (8.6. ábra - Aktuális jel frekvencia komponensei) és (8.7. ábra - A jel frekvenciakomponensei és a látszólagos frekvenciák) ábra illusztrálja az alul-mintavételezés jelenségét.
A 8.7. ábra - A jel frekvenciakomponensei és a látszólagos frekvenciák a bejövő jel frekvencia komponenseit mutatja, és a mintavételi frekvenciát, amely 100 Hz.
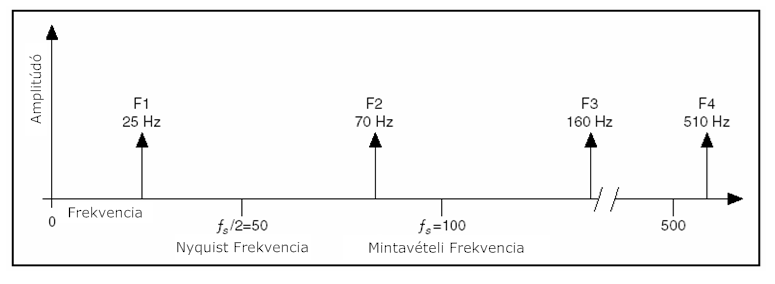
A 8.6. ábra - Aktuális jel frekvencia komponensei a bejövő jel látszólagos és a tényleges frekvencia komponenseit mutatja.
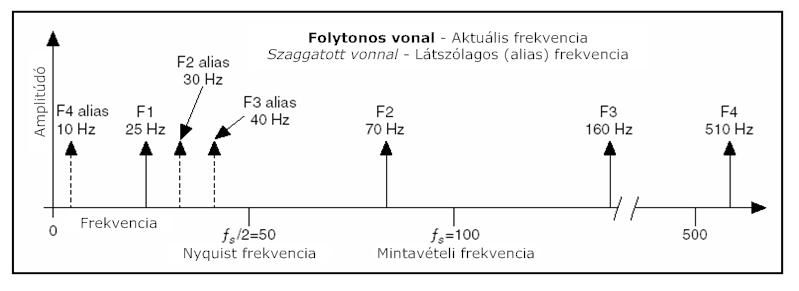
A 8.6. ábra - Aktuális jel frekvencia komponensei szerint f S /2=50Hz alatti komponensek helyesen vannak mintavételezve, például F1 jó helyen van. A Nyquist frekvencia feletti frekvenciájú komponensek viszont máshol látszódnak . Például az F2, F3 és F4 frekvencia komponensek 30 Hz-en, 40 Hz-en és 10 Hz-en látszanak külön-külön.
A látszólagos frekvencia értéke egyenlő a mintavételi frekvencia legközelebbi egészszámú többszöröse és a bejövő frekvencia különbségének abszolút értékével.
|
|
(8.5) |
ahol
|
AF |
a látszólagos frekvencia, (Alias Frequency) | |
|
CIMSF |
a mintavételi frekvencia legközelebbi egészszámú többszöröse, (Closest Integer Multiple of the Sampling Frequency) | |
|
IF |
a bejövő frekvencia (Input Frequency) |
Például meghatározhatjuk a látszólagos frekvenciákat F2, F3 és F4-ből a következő képletek szerint:
|
|
(8.6) |
8.4. A mintavételi frekvencia növelése az alul-mintavételezéselkerüléséhez
A Shannon-féle mintavételi elv szerint (lásd 3.4.4. szakasz - Mintavételezési hiba fejezetben) a mintavételi frekvenciának a minta-vételezett jel maximális frekvencia komponens legalább a duplájának kell lennie, hogy elkerüljük a látszólagos frekvencia jelenségét. A 8.8. ábra - A különböző mintavételi frekvenciák hatása különböző mintavételi frekvenciák hatását mutatja be.
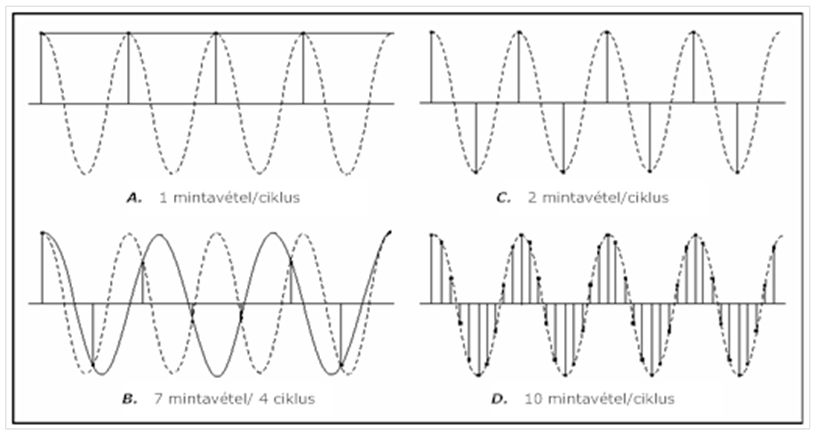
A 8.8. ábra - A különböző mintavételi frekvenciák hatása szerinti A esetben az f S mintavételi frekvencia egyenlő a mintavételezett szinusz hullám f frekvenciájával. f S mértékegysége minta/másodperc. f mértékegysége periódus/másodperc. Tehát A esetben 1 mintavételi érték 1 periódusnak felel meg. A leképezett hullámforma az eredeti jel látszólagos frekvenciáját mutatja be, amely egy egyenfeszültség (minden mintavételezésnél állandó értékű jel).
A 8.8. ábra - A különböző mintavételi frekvenciák hatása szerinti B esetben f S =7/4f, azaz 7 minta esik 4 periódusra. A B esetben tehát a mintavételi gyakoriság növelésére emelkedik a hullám frekvencia. Azonban a látszólagos frekvencia kisebb mint az eredeti jel frekvenciája , 4 helyett csak 3 periódus jelenik meg.
A 8.8. ábra - A különböző mintavételi frekvenciák hatása szerinti C esetben a mintavételi gyakoriság f S =2f-re való növelésére a digitalizált hullámformát helyes frekvenciával kapjuk. A periódusok száma az eredeti jellel azonos. A C esetben az előállított hullámforma pontosabb leképezése az eredeti szinusz hullámnak, mint A vagy B esetben. Ha a mintavételi gyakoriságot kellő mértékben f fölé növeljük, például f S =10f-re, azaz 10 minta/periódusra, akkor megfelelően és precízen mintavételeztük a jelet.
A 8.8. ábra - A különböző mintavételi frekvenciák hatása szerinti D esetben a mintavételi frekvencia tízszerese az eredeti jel frekvenciájának, amelynek eredménye látható az ábrán.
8.5. Szűrő az alul mintavételezés elkerüléséhez
A digitális átalakításnál a 0 és a Nyquist frekvencia közötti tartományban nem tudjuk megkülönböztetni a látszólagos frekvenciát a valóditól. Ha a mintavételi frekvencia éppen duplája a Nyquist frekvenciának, az elszórt jelekből eredő zavarjelek - például a villamos vezetékekből vagy a rádióadókból érkező jelek - tartalmazhatnak magasabb frekvenciájú komponenseket, mint a Nyquist frekvencia. Az elszórt jel Nyquist frekvencia feletti komponensei a vizsgáló jel által megkívánt frekvencia tartományába eshetnek és látszólagosan hibás eredményt hozhatnak létre. Ezért el kell tüntetnünk az analóg jelből a látszólagos frekvenciákat, mielőtt a jel A/D átalakítását elvégezzük.
Használjunk anti-aliasing analóg alul áteresztő szűrőt az A/D átalakítás előtt, hogy eltüntessük a Nyquist frekvenciánál magasabb látszólagos frekvenciákat. Egy alul áteresztő szűrő az alacsony frekvenciákat átengedi, de elnyomja a magas frekvenciákat. A Nyquist frekvenciánál magasabb frekvenciák gyengítésével az anti-aliasing alul áteresztő szűrő megelőzi a látszólagos komponensek mintavételezését. Az ilyen szűrő egy teljes frekvenciasávot le fog vágni, megfelelő nagyfrekvencia levágást az átmeneti sávban egy gyors lefutás biztosít . Mivel az anti-aliasing szűrőt az analóg jelhez alkalmazzuk mielőtt átalakítottuk volna digitális jellé, ezért ez a szűrő egy analóg szűrő.
8.8. ábra - A különböző mintavételi frekvenciák hatása egy ideális és egy megvalósítható anti-aliasing szűrőt mutat be. A következő információk az ábrára vonatkoznak:
f 1 a legnagyobb bejövő frekvencia.
f 1 -nél kisebb frekvenciák, amelyeket át akarunk engedni.
f 1 -nél nagyobb frekvenciák, amelyeket nem akarunk átengedni.
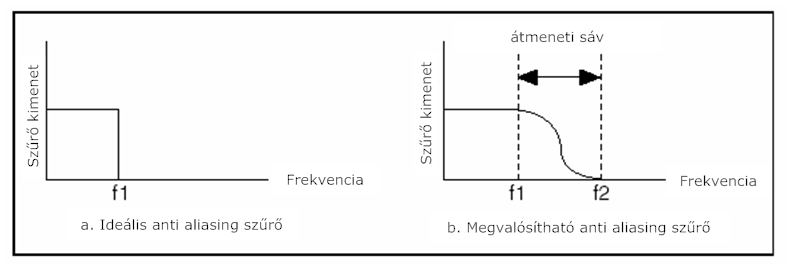
Egy ideális alul áteresztő szűrő, ahogy az a (8.9. ábra - Ideális és megvalósítható anti-aliasing szűrő) ábrán látható, átengedi az összes alkalmazni kívánt bejövő frekvenciát, és levágja az összes nem kívánt komponenst. Az ideális alul áteresztő szűrő azonban fizikailag megvalósíthatatlan.
A (8.9. ábra - Ideális és megvalósítható anti-aliasing szűrő) b ábra a megfelelő anti-aliasing szűrő viselkedését szemlélteti. Egy valós alul áteresztő szűrő minden f<f 1 frekvenciát átenged, és minden f>f 2 frekvenciát levág. Az f 1 és f 2 közötti tartomány az átmeneti sáv, ahol a bemenő frekvenciák fokozatos elnyomása történik. Habár mi csak f<f 1 frekvenciájú jeleket akarjuk átereszteni, az átmeneti sávban lévő jelek előidézhetnek látszólagos frekvenciákat. Ezért a gyakorlatban több mint kétszeres mintavételező frekvenciát alkalmazunk, képlettel: f S >2f 1 .
8.6. Áttérés logaritmikus mértékegységekre
Néhány berendezésen ki lehet íratni az amplitúdót lineáris és decibel(dB ) skálán egyaránt. A lineáris skála az amplitúdót tényleges értékét írja ki. A decibel skála egy arány kifejezése. A decibel skála egy transzformáció lineáris léptékről logaritmikus léptékre (lásd 3.4.3. szakasz - Mérőlánc frekvenciafüggő átviteléből adódó hibák fejezetet).
A következő egyenlőségek definiálják a decibel értékét. Az 8.7 egyenlet teljesítmény arányban írja le a deciBell (dB P ) meghatározását.
|
|
(8.7) |
ahol
|
P ki |
a mért (kimeneti) teljesítmény, | |
|
P be |
a bemeneti teljesítmény |
Az 8.8 egyenlet pedig amplitúdók arányaként írja le a deciBell (dB A ) értékét.
|
|
(8.8) |
ahol
|
A ki |
a mért (kimeneti) amplitúdó, | |
|
A be |
a bemeneti amplitúdó |
A 8.7 és 8.8 egyenletek igényelnek egy referencia értéket, hogy kifejezhessük a teljesítmény és az amplitúdó arányát decibel-ben. A vonatkoztatási érték adja a 0 (nulla) decibeles szintet. Különféle egyezmények léteznek a referencia érték megállapítására.
A következő megállapodásokkal meghatározható a referencia érték, és kiszámíthatók a decibel értékek.
|
Mértékegység |
Magyarázat |
|---|---|
|
dBVrms |
A referencia 1 Volt-RMS a négyzeten (1 |
|
dBV |
A referencia 1 Volt-RMS ampitudóra |
|
dBm |
A referencia 1 mW rádió frekvenciákra és 50 Ohm-os kimenetre, ahol 0 dB -> 0.22 Vrms, |
|
dBm |
a referencia 1 mW audió frekvenciákra és 600 Ohm-os kimenetre, ahol 0 dB -> 0.78 Vrms |
Amikor a teljesítményt és amplitúdót úgy alkalmazzuk, mint ugyanaz a jel amplitúdó négyzete, akkor a decibel arány pontosan ugyanaz az érték. Ha a decibel arányt 2-vel megszorozzuk, ugyanazt érjük el, mintha az eredeti jelet négyzetre emeltük volna. Éppen ezért alkalmazhatjuk ugyanazt a decibel értéket és műszer beosztást, akár amplitúdó akár teljesítmény spektrumot mérünk.
8.7. Eredmény kijelzése decibel léptékben
Amplitúdó vagy teljesítmény spektrumot általában decibel skálán ábrázolnak. Decibel skálán ábrázolva e spektrumokat, áttekinthetővé válnak széles dinamikus értéktartományok, és apró jel összetevők jelenlétét is lehet látni a nagyok között. Például tegyük fel, hogy olyan jelet akarunk ábrázolni, amely amplitúdója 0.1 V és 100 V közötti értéket vehet fel, egy 10 cm magas kijelzős készüléken. Ha lineáris léptéket használunk, abban az esetben a berendezés teljes kijelző magasságát kitölti a 100 V, a kijelzőn 1 cm távolság 10 V-os amplitúdónak felel meg. Ha a műszerállandó 10 V/cm, akkor a 0.1 V amplitúdójú jel csak 0.1 mm nagyságú. Mivel a 0.1 mm távolság nehezen látható a képernyőn, ezért ember ezt a komponenst nem fogja észre venni.
A logaritmikus decibel lépték használata lehetővé teszi, hogy a 0.1 V amplitúdójú elemet is láthatóvá tegyük.
|
dB |
Teljesítmény arány |
Amplitudó arány |
|---|---|---|
|
+40 |
10 000 |
100 |
|
+20 |
100 |
10 |
|
+6 |
4 |
2 |
|
+3 |
2 |
1.4 |
|
0 |
1 |
1 |
|
–3 |
1/2 |
1/1.4 |
|
–6 |
1/4 |
1/2 |
|
–20 |
1/100 |
1/10 |
|
–40 |
1/10 000 |
1/100 |
A 8.2. táblázat - Decibelek , teljesítmény és feszültség arányok viszonya táblázat bemutatja, hogyan lehet az amplitúdók széles tartományát összehúzni egy kisebb értékkészletbe a logaritmikus decibel léptékkel.
Irodalom
[8.1.] LabVIEW Control Design User Manual. 2009.
9. fejezet - Jelgenerálás
A tesztelő- vagy mérő-rendszerek nagyon fontos eleme a jelgenerátor .
A következő feladatok mintapéldák a jelgenerátorok alkalmazására:
Jelek szimulálása akkor fontos egy folyamat tesztelése céljából, amikor valós jelek nem állnak rendelkezésre, amikor nem áll rendelkezésünkre mérés-adatgyűjtő berendezés, hogy valós jeleket megmérjük vagy egyáltalán nincsenek valós jelek.
Jelek generálása digitális analóg (D/A) átalakítóval történik.
Ez a fejezet a jelgenerálás alapjait mutatja be.
9.1. Egyszerű vizsgáló jelek
Az egyszerű vizsgáló jelek a következők:
szinusz hullám,
négyszögjel,
háromszögjel,
fűrészjel,
zavarjelek néhány típusa,
több szinusz hullámból álló jeleket.
A hangerősítő rendszerek tesztelésre általánosan használt jel a szinusz hullám. Az egyszerű szinusz hullámot gyakran használják a rendszerből származó harmonikus torzítás meghatározására is. Több szinusz hullámból álló jelet széles körben alkalmaznak az intermodulációs torzítás mérésére, vagy frekvencia válasz meghatározására.
A 9.1. táblázat - Gyakran előforduló mérések és jelek táblázat néhány gyakran előforduló mérésnél használt jelet sorol fel.
|
Mérés |
Az alkalmazott bemeneti jel |
|---|---|
|
Szinusz hullám | |
|
Multitone (két szinusz hullám) | |
|
Multitone (több szinusz hullám, impulzus, frekvencia-változtatással), szélessávú zaj | |
|
Intermoduláció |
Sinc |
|
Egységugrás | |
|
Négyszög jel |
Ezen jelformák számos vizsgálat alapjául szolgálnak egy rendszer egyedi gerjesztésre adott válaszának mérésekor. A (9.1. ábra - Egyszerű vizsgáló jelek) és (9.1. ábra - Egyszerű vizsgáló jelek) ábrán látható vizsgáló jelek megtalálhatók a jelgenerátorokban.
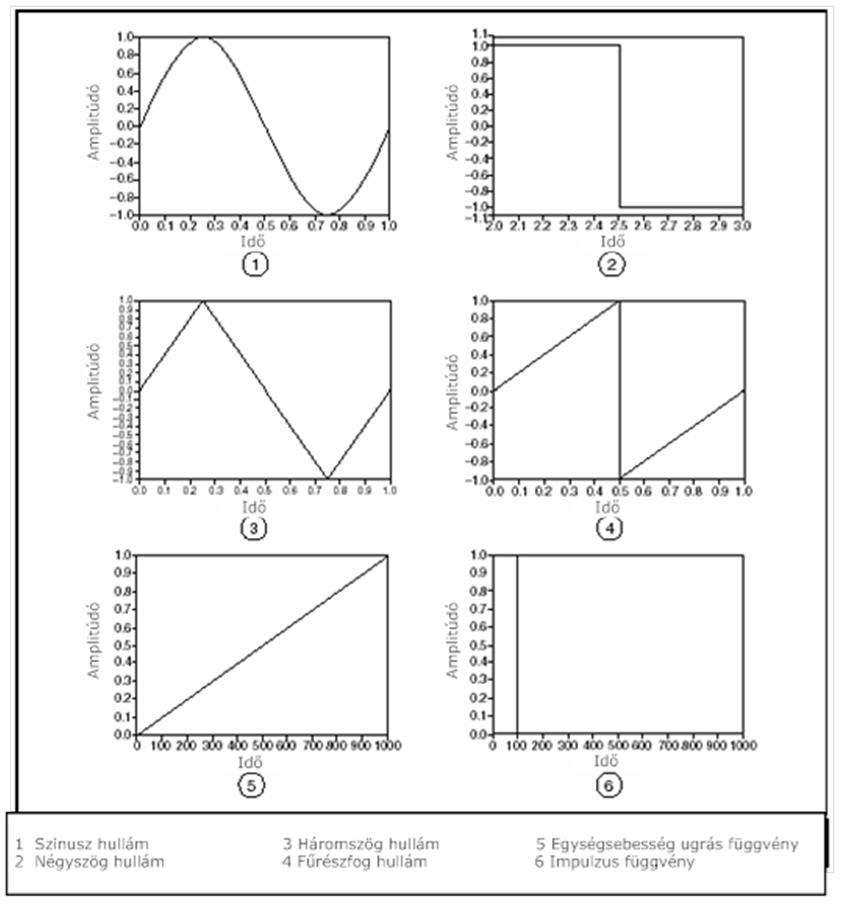
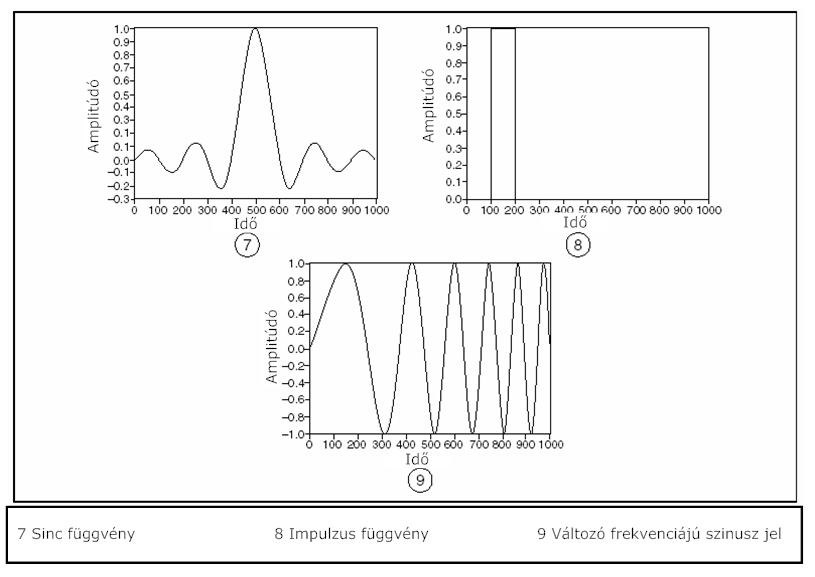
A legfontosabb, hogy az egyszerű vizsgáló jeleket frekvencia összetevőik alapján megismerjük.
A szokásos vizsgáló jelek frekvencia összetevőinek jellemzői:
A négyszög hullámok az alapfrekvencia páratlan rendszámú felharmonikusainak szuperpozíciójából keletkezik.
A háromszög és fűrész jeleknek olyan felharmonikus komponensei vannak, melyek az alapfrekvencia többszörösei.
Egy impulzus jel tartalmazza az összes frekvenciát, amelyeket egy adott mintavételi számmal és gyakorisággal reprezentálni lehet.
A változó frekvenciájú szinusz jelnél egy szinusz görbe jelenik meg egy indítási frekvenciától a megállási frekvenciáig, ily módon állít elő energiát egy adott frekvencia tartományban. A frekvencia végigsöprés jelalakjának diszkrét frekvenciái függnek a mintavételi gyakoriságtól, az indítási és megállási frekvenciáktól valamint a mintavételek számától.
9.2. Frekvencia átvitel mérése
Ahhoz, hogy egy frekvenciafüggvény mérést jól végezhessünk el, a mérési frekvenciatartománynak jelentős gerjesztő energiával kell rendelkeznie. Két alapvető jel használatos frekvenciafüggvény mérésekre, a változó frekvenciájú jel, valamint egy széles sávú zavarjel , az úgynevezett fehér zaj . Ebben a fejezetben az Egyszerűvizsgáló jelekről szóló rész ad bővebb információt a frekvencia végigsöpréses jelről. A Zavarjel generálás-ról szóló részben találhatók információk a fehér zajról.
Legjobb, ha nem használunk ablakokat (lásd 7.1.3.4. szakasz - Folytonos, nem stacionárius jelek analízise a gyakorlatban fejezetben) a frekvencia átviteli jelek vizsgálatakor. Amennyiben generálunk egy változó frekvenciájú gerjesztő jelet ugyanazzal a gyakorisággal, ahogyan kapjuk a választ, akkor hozzá tudjuk illeszteni az adatgyűjtés keret méretét a frekvencia végigsöpréses hosszához. Általában az ablak nélküli elemzés a legjobb választás szélessávú jelforrásokhoz. Mivel némelyik gerjesztő jel nem folytonos az időjel rögzítésen keresztül, ablak használatával eltompulhatnának a fontos tranziens függvényrészek.
9.3. Többtónusú jelgenerálás
A szinusz hullámon kívül az egyszerű vizsgáló jeleket a spektrális összetételükön túl nem lehet teljesen szabályozni. Például a négyszögjel harmonikus komponensei a frekvenciában, a fázisban és amplitúdóban viszonylag rögzítettek. Azonban létre tudunk hozni többtónusú jeleket külön-külön egyedi frekvencia komponensekkel adott amplitúdóval és fázistolással.
Egy többfrekvenciás jel különféle szinusz hullámok vagy hangfrekvenciás jelek összegzéséből állítható elő, egyenként egy határozott amplitúdóval, fázistolással és frekvenciával. Egy többfrekvenciás jel tipikusan úgy jön létre, hogy az önálló frekvenciájú komponensek meghatározott amplitúdóval szerepelnek a jelben. Ha a bejövő többfrekvenciás jel FFT-jét (Fast Fourier Transformation) meghatározzuk, a frekvencia komponensek mindegyike pontosan beleesik egy egyedi frekvencia sávba, amely nem ad módot színkép szóródására, vagy veszteség megjelenésére. A többfrekvenciájú jelekkel szokták meghatározni egy berendezés frekvencia átviteli-függvényét, és a megfelelő frekvenciák kiválasztásával, szintén mérni lehet olyan mennyiséget, mint az intermodulációs torzítás.
9.3.1. Csúcstényező
A jelet alkotó komponensek egymáshoz viszonyított fázisai határozzák meg az adott amplitúdójú többfrekvenciás jel csúcstényezőjét. A csúcsfaktort a jel RMS értékének ( Root Mean Square = négyzetes középérték ) és maximális kitérésének arányaként definiálják.
Például egy szinusz hullám csúcstényezője 1.414 : 1
Egy nagy csúcstényezőjű többfrekvenciás jel ugyanakkora maximális amplitúdó mellett, kevesebb energiát tartalmaz mint egy kisebb csúcstényezőjű jel.
Más szóval a nagyobb csúcstényező azt jelenti, hogy egy adott szinusz komponens amplitúdója kisebb, mint egy kisebb csúcstényezőjű ugyanolyan szinusz frekvencia egy többfrekvenciás jelben. Egyedi szinusz frekvenciák esetében egy magasabb csúcstényező alacsonyabb jel-zaj viszonyt eredményez. Ezért a fázisok megfelelő kiválasztása kritikus pont, amikor egy használható többfrekvenciás jelet akarunk létrehozni.
Hogy elkerüljük a csúcslevágást, a többtónusú jel legnagyobb értéke nem lépheti túl a jelgeneráló készülék maximális lehetőségét, tehát a jel legnagyobb amplitúdójára vonatkozó határértéket. Létrehozhatunk egy adott amplitúdójú többtónusú jelet az alkotó szinusz tónusok fázisviszonyai és amplitúdói különböző kombinációjának változtatásával. Egy jel generálásához megfelelő közelítésnek úgy kell megválasztani az amplitúdókat és a fázisokat, hogy a csúcstényező minél kisebb legyen.
9.3.2. Fázis jel generálás
A következő leírás szerint szokás a többfrekvenciás jelek frekvenciáinak fázisait előállítani:
A szomszédos frekvenciák közötti fáziskülönbséget 0-tól 360 fokig lineárisan változtatva, a frekvenciák közötti fázisok véletlenszerű változtatásával.
A szomszédos frekvenciák közötti fáziskülönbséget 0-tól 360 fokig lineárisan változtatva elő lehet állítani nagyon alacsony csúcsfaktorú többfrekvenciás jeleket.
Azonban a kapott többfrekvenciás jel a következő nem kívánt jellemzőkkel rendelkezik:
A többfrekvenciás jel fázistorzításra nagyon érzékeny.
Ha a jelgenerálás folyamán a készülékben vagy a vezetékekben nemlineáris fázistorzítás jön létre, akkor a csúcsfaktor jelentősen megváltozhat.
A többfrekvenciás jelnél jelentkezhetnek időtartománybeli ismétlődő jellegzetességek, melyeket a (9.3. ábra - Többfrekvenciás jel a szomszédos frekvenciák közötti fázis különbség változtatásával) ábrán követhetünk nyomon.
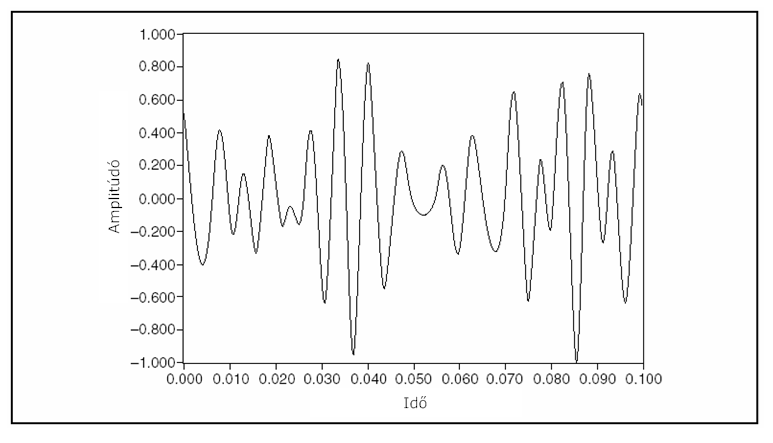
A 9.3. ábra - Többfrekvenciás jel a szomszédos frekvenciák közötti fázis különbség változtatásával ábra szerinti jel egy olyan frekvencia végigsöpréses jelre hasonlít, amelynek a frekvenciája csökkenni látszik balról jobbra. A látszólagos balról jobbra mutató frekvenciacsökkenés jellemző azokra a többfrekvenciás jelekre, amelyeket a szomszédos frekvenciák fáziskülönbségének lineáris változtatásával hoznak létre. Gyakran kívánatosabb egy olyan jelet használni, ami sokkal zajosabb mint a (9.3. ábra - Többfrekvenciás jel a szomszédos frekvenciák közötti fázis különbség változtatásával) ábrán lévő.
Véletlenszerűen változtatva a fázisokat, olyan többfrekvenciás jelet kapunk, amelynek amplitúdói majdnem Gauss eloszlást követnek, ahogy a frekvenciák száma növekszik. A 9.4. ábra - Többfrekvenciás jel véletlenszerű fáziseltolássala szomszédos frekvenciák között a frekvencia fázisok véletlenszerű változtatásával létrehozott jelet szemlélteti.
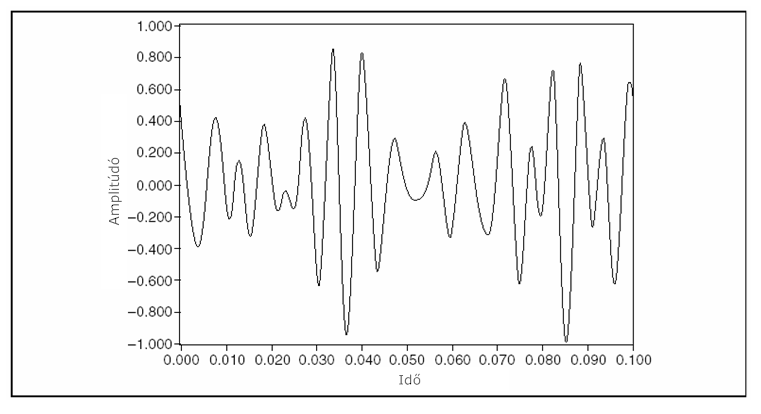
Azon túl, hogy a (9.4. ábra - Többfrekvenciás jel véletlenszerű fáziseltolássala szomszédos frekvenciák között) ábrán látható jel sokkal zajosabb, kevésbé érzékeny a fázistorzításra.
A 9.4. ábra - Többfrekvenciás jel véletlenszerű fáziseltolássala szomszédos frekvenciák között ábra szerinti fázis viszonyú többfrekvenciás jelek általában egy 10 és 11 dB közötti csúcsfaktort érnek el. (Vagyis a csúcsérték az effektív érték három, négyszerese.)
9.3.3. Változó frekvenciájú szinusz jel, illetve többfrekvenciás jel
Ahhoz hogy egy rendszert jellemezhessünk, általában meg kell mérni a rendszer jelátviteli tényezőjét több különböző frekvencián. Ebben segítenek a következőkben felsorolt eljárások.
A változó frekvenciájú szinusz függvény simán és folytonosan változtatja a szinusz hullám frekvenciáját egy megadott frekvencia tartományban.
A léptető szinusz függvény egy állandó frekvenciájú szinusz jelet szolgáltat addig, amíg egy bizonyos gerjesztés tart, aztán növeli a frekvenciát egy diszkrét értékkel. A folyamat addig tart, amíg az összes érdekelt frekvencián végig nem halad.
A többfrekvenciás hullám olyan jelet szolgáltat, amely egyedi szinusz hullámú komponensekből áll.
A többfrekvenciás jeleknek van egy jelentős előnyük a végigsöprő szinusz és a léptető szinusz jelekkel szemben. Egy adott frekvencia tartományra vonatkozóan, a többfrekvenciás megközelítés sokkal gyorsabb lehet, mint az annak megfelelő végigsöprő szinusz mérés, amely főleg a kimenetek véges beállási idejének következménye (lásd 7. fejezet - Spektrum analízis a méréstechnikában fejezet sávszélesség és analízis idő kapcsolatáról szóló meggondolásait).
Minden szinusz jelnél a léptető szinusz mérésekor várakozni kell a rendszer beállási idejének leteltéig, mielőtt elkezdhetjük a mérést.
Egy végigsöprő szinusz mérés kimeneti beállási ideje még bonyolultabb lehet. Ha a rendszernek vannak kis frekvenciájú pólusai és/vagy zérusai illetve Q-rezonanciái, a rendszer ilyenkor egy viszonylag hosszabb beállási időt vesz igénybe. Egy többfrekvenciás jelnél viszont csak egyszer kell megvárni a beállási időt. A többfrekvenciás jel legkisebb frekvenciájának egy periódusa rendszerint elegendő a beállási idő szempontjából. A többfrekvenciás jelre kapott válasz feldolgozása már nagyon gyors lehet. Használhatunk egy egyszerű gyors Fourier transzformációt számos frekvencia pont, amplitúdó és fázis egyidejű mérésére.
A változó frekvenciájú szinusz közelítés bizonyos helyzetekben alkalmasabb, mint a többfrekvenciás közelítés. Az egyenként megmért frekvenciák a többfrekvenciás jelben érzékenyebbek a zajra, mivel az egyes frekvenciák energiaszintje alacsonyabb, mint egy egyedülálló frekvenciájú jelnek. Például tekintsünk egy 10V-os maximális amplitúdójú önálló szinusz jelet, amelynek 100 Hz a frekvenciája. Egy többfrekvenciás jel 10 frekvenciát tartalmaz, (köztük a 100 Hz-est is), legnagyobb amplitúdója szintén csak 10V lehet. Ezért a 100 Hz-es frekvencia-komponensnek amplitúdója kisebb lesz mint 10V. A 100 Hz-es frekvenciájú összetevő alacsonyabb amplitúdója abból az eljárásból következik, hogy az összes szinusz jel összegződik. Feltéve, hogy a zaj azonos szintű, a 100 Hz-es komponens jel-zaj viszonya (SNR = Signal Noise Rate) kedvezőbb a végigsöprő szinusz közelítés esetén. A többfrekvenciás közelítésben az egyes jelek amplitúdóinak és fázisainak beállításával mérsékelhetjük a redukált jel-zaj viszonyt úgy, hogy ahol szükséges nagyobb energiát használunk, a kevésbé kritikus frekvenciáknál pedig kisebbet.
Amikor egy rendszer többfrekvenciás gerjesztésre adott válaszát vizsgáljuk, az FFT közben elhasznált energia a zajnak, vagy a vizsgálat alatt álló berendezés indukált torzításának tulajdonítható.
Az FFT frekvenciafelbontása a mérési idő miatt korlátozott. Ha meg akarjuk mérni a rendszerünket 1.000 kHz-en és 1.001 kHz-en, a legjobb a közelítést két független szinusz jel alkalmazásával kapunk. Két önálló szinusz jel alkalmazásával el tudjuk végezni a mérést néhány ezredmásodperc alatt, míg ugyanez a többfrekvenciás mérés legalább 1 másodpercig tart.
Némely alkalmazásnál, mint például egy kristály rezonancia frekvenciájának meghatározásánál, kombinálni kell egy durvább többfrekvenciás mérést egy szűk tartományú finomabb méréssel.
9.4. Zavarjel generálás
Zavar jeleket alkalmazhatunk a frekvencia függvény mérésének elvégzéséhez, vagy bizonyos folyamatok szimulálására.
A zajok néhány típusa gyakran használt, amelyek a következők:
homogén fehér zaj,
Gauss-eloszlású zaj,
véletlenszerű periódikus zaj.
A fehér szó a zaj elnevezésében a jellemző frekvencia tartományára utal. Az ideális fehér zaj teljesítménye egyenletes az adott sávszélességben, és egyenletes teljesítmény eloszlást eredményez a megfigyelt frekvencia tartományban. Ilyenformán pl. a 100 Hz-től 110 Hz-ig terjedő frekvenciatartomány teljesítménye egyenlő az 1000 Hz és 1010 Hz közötti intervallum teljesítményével. Gyakorlati mérésekben az egyenletes teljesítmény eloszlás megvalósításához végtelen számú mintavételre volna szükség. Tehát amikor fehér zajjal végzünk méréseket, a teljesítmény spektrum rendszerint átlagolt, minél több átlagértékkel számolunk, annál egyenletesebb teljesítmény spektrumot kapunk.
A homogén és a Gauss elnevezések a valószínűségi sűrűség függvényre ( PDF = Probability Density Function ) utalnak, ami a zaj időtartománybeli mintái amplitúdójának függvénye. A homogén fehér zajhoz tartozó valószínűségi sűrűség függvény a megadott maximális és minimális szinteken belül homogén. Más szóval bizonyos határok között valószínűleg minden amplitúdó értéke egyenlő. Az elektronikus elemekben létrejött termikus zaj eloszlásban hasonlít a homogén fehér zajhoz.
A 9.4. ábra - Többfrekvenciás jel véletlenszerű fáziseltolássala szomszédos frekvenciák között ábra a homogén fehér zaj mintáinak eloszlását mutatja.
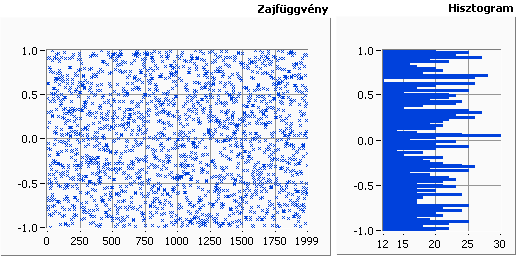
A Gauss-eloszlású zajra vonatkozó valószínűségi sűrűség függvény Gauss-féle függvény (haranggörbe).
Ha a homogén fehér zajt bevezetjük egy lineáris rendszerbe, a kimeneten Gauss-eloszlású zajt kapunk eredményül. A 9.6. ábra - Gauss-eloszlású fehér zaj ábra a Gauss zaj mintáinak eloszlását mutatja.
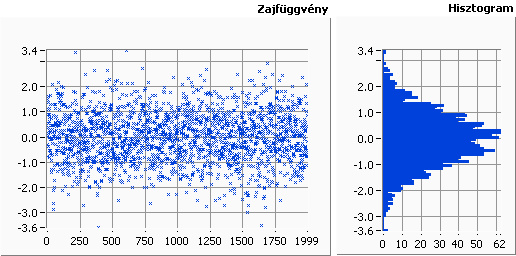
A véletlenszerű periodikus zaj (PRN = Periodic Random Noise) szinuszos jelek összegződése azonos amplitúdókkal, de véletlenszerű fázissal. A véletlenszerű periodikus zaj tartalmazza az összes olyan frekvenciájú szinusz hullámot, amelyeket egész számú periódusokon ábrázolni lehet a szükséges számú mintával. Mivel a véletlenszerű periodikus zaj csak egész periódusú szinusz hullámot tartalmaz, nincs szükségünk véletlenszerű periodikus zaj ablakra, mielőtt elvégezzük a spektrum analízisét. A véletlenszerű periodikus zaj ön-ablakozó ,ezért nincs benne színkép-szóródás.
A véletlenszerű periodikus zajnak nincs minden frekvencián azonos energiája, mint a fehér zajnak, hanem csak diszkrét frekvenciákon, amelyek az alapfrekvencia harmonikus összetevőinek felelnek meg. Az alapfrekvencia egyenlő a mintavételi frekvenciának és a minták számának hányadosával. A zajszint azonban minden egyes diszkrét frekvencián azonos nagyságú.
A véletlenszerű periodikus zajt alkalmazhatjuk egy lineáris rendszer frekvencia függvényének meghatározására egyszeri adatsorral, ahelyett hogy néhány mérés után a frekvenciafüggvényeket átlagolnánk, ahogy azt tennünk kell nem periodikus véletlenszerű források esetében. A 9.6. ábra - Gauss-eloszlású fehér zaj ábra a véletlenszerű periodikus zaj spektrumát és a fehér zaj átlagolt színképét mutatja.
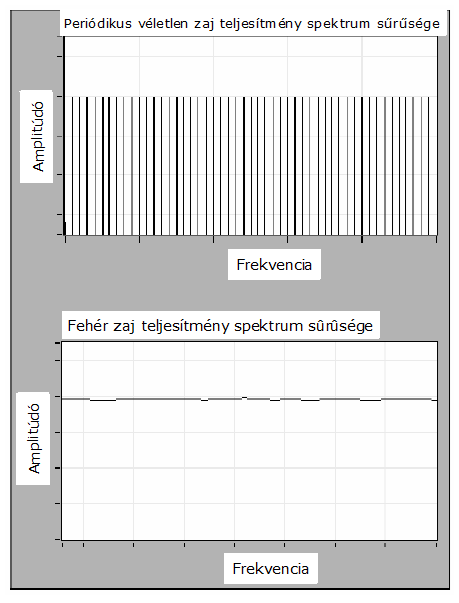
9.5. Normalizált frekvencia
Az analóg rendszerekben egy jel analóg frekvenciáját Hertzben (Hz) mérik vagy periódus/másodperc-ben. A digitális rendszerekben azonban gyakran egy digitális frekvenciát használnak, amely az analóg frekvencia és a mintavételező frekvencia arányát jelenti, ahogy azt a következő egyenlet bemutatja:
|
|
(9.1) |
periódus/minták száma. Néhány jelgeneráló VI használ egy f frekvencia bemenetet, amelyen periódus/minta mértékegységben kéri a normalizált frekvencia értékét.
A normalizált frekvencia értékkészlete 0.0-tól 1.0-ig tart, amely megfelel a 0-tól f s mintavételező frekvenciáig terjedő valós tartománynak. A normalizált frekvencia burkolja az 1-et, ezért az 1.1-nek a normalizált frekvenciája 0.1. Például ha egy jelet az f s /2 Nyquist frekvenciával mintavételezünk, ez periódusonként szimpla mintavételezést eredményez, azaz 1 minta/periódust. Ez a mintavételi gyakoriság megegyezik a 1 periódus/minta normalizált frekvenciával.
A normalizált frekvencia reciproka 1/f értéke megadja, hogy a jel egy periódusában hányszor mintavételeztük, amely a periódusonkénti minták száma.
Amikor olyan VI-t használunk amelyen van normalizált frekvencia bemenet, át kell váltani a frekvencia mértékegységét normalizált periódus/minta egységre. Ilyen normalizált mértékegységeket kell használnunk a következő jel generáló VI alkalmazásokban:
Szinusz hullám
Négyszög hullám
Fűrészfog hullám
Háromszög hullám
Tetszőleges hullám
Változó frekvenciájú szinusz jel
Ha a periódusok frekvencia mértékegységét használjuk, mindig át kell alakítani a periódusokat a periódusok per mintavételekre, amelyet úgy határozunk meg, hogy a periódusok számát elosztjuk a létrehozott minták számával.
Például 2 periódus frekvenciája osztva 50 mintával, eredmény normalizált frekvenciában f=1/25 periódus/minta. Ez azt jelenti, hogy a szinusz hullám egy periódusában f reciproka, azaz 25 mintát veszünk.
Ha azonban Hertz-et kell használnunk frekvencia mértékegységként. Ha át akarjuk alakítani a Hertz-et periódus/minta egységre, osszuk el a Hz-ben mért értéket a mintavételi gyakorisággal (minta/másodperc), ahogy azt a következő képlet mutatja:
|
|
(9.2) |
Például ha 60 Hz-et elosztunk a mintavételi frekvenciával 1000 Hz-el, a normalizált frekvencia f=0.06 periódus/minta lesz az eredmény. Tehát ez majdnem 17 vagy 1/0.06 , a szinusz hullám az egy periódusra eső minták száma.
A jelgeneráló programok sok általános jelet előállítanak, amelyekre a hálózatok elemzésénél és a szimulációnál van szükség. Használhatja a jelgeneráló alkalmazásokat, és előállíthat analóg gerjesztő jeleket.
Irodalom
[9.1.] LabVIEW Control Design User Manual. 2009.
10. fejezet - Digitális szűrés
- 10.1. Bevezetés a digitális szűrés gyakorlati alkalmazásába
- 10.2. A Z transzformáció
- 10.3. Egyszerű digitális szűrők
- 10.4. Egy ideális szűrő jellemzői
- 10.5. Valóságos (nem ideális) szűrők
- 10.6. Mintavételi idő
- 10.7. Véges impulzus válasz (FIR) szűrők
- 10.7.1. Leágaztatások (Taps)
- 10.7.2. Véges impulzus válasz szűrők (FIR szűrők) tervezése
- 10.7.3. Véges impulzus válasz szűrők (FIR szűrők) tervezése ablakozással
- 10.7.4. Optimális FIR szűrők tervezése a Parks-McClellan algoritmussal
- 10.7.5. Egyenletes hullámosságú FIR szűrők tervezése Parks-McClellan algoritmus alkalmazásával
- 10.7.6. Keskeny sávú FIR szűrők tervezése
- 10.7.7. Széles sávú FIR szűrők tervezése
- 10.8. Végtelen impulzus válasz (IIR) szűrők
- 10.8.1. Az IIR szűrés kaszkádképlete
- 10.8.2. Másodfokú szűrés
- 10.8.3. Negyedfokú szűrés
- 10.8.4. IIR szűrő konstrukciók
- 10.8.5. Csúcshiba minimalizálása
- 10.8.6. Butterworth-szűrők
- 10.8.7. Csebisev-szűrők
- 10.8.8. Csebisev II - szűrők
- 10.8.9. Elliptikus szűrők
- 10.8.10. Bessel-szűrők
- 10.8.11. IIR szűrők tervezése
- 10.8.12. IIR szűrők jellemzői
- 10.8.13. Átmeneti függvény
- 10.9. A FIR és az IIR szűrők összehasonlítása
- 10.10. Nemlineáris szűrők
- 10.11. Digitális szűrő típus kiválasztása
- Irodalom
Ez a fejezet bemutatja a digitális jelek szűrését, összehasonlítja a digitális és analóg szűrőket, bemutatja a véges impulzus válasz (FIR = Finite Impulse Response) és a végtelen impulzus válasz (IIR = Infinite Impulse Response) szűrőket, valamint bemutatja, hogyan kell kiválasztani a megfelelő digitális szűrőt egy adott feladathoz.
10.1. Bevezetés a digitális szűrés gyakorlati alkalmazásába
A szűrési eljárás megváltoztatja a jelet alkotó frekvencia komponensek amplitúdóit. Például a mély hangszín szabályzó a sztereo rendszereken megváltoztatja a jel alacsony frekvenciáinak amplitúdóját, a magas hangszín szabályzó pedig a magas frekvenciás komponensek amplitúdóit alakítja át. A mély és magas szabályzók beállításával kiszűrhetjük vagy kiemelhetjük a különböző frekvenciájú hang jeleket. Két általános szűrő alkalmazás csökkenti a zajt és csonkítja a sávszélességet. A csonkítás egy aluláteresztő szűrőt tartalmaz, és csökkenti a mintavétel frekvenciáját.
A szűrési folyamat lehetővé teszi, hogy a jel számunkra lényeges részeit kiválasszuk a nyers (zajos) jelből. Egy klasszikus lineáris szűrő a frekvencia tartományban kiemeli a lényeges részeket az eredeti jelből.
A digitális szűrés előnyei az analóg szűréssel szemben :
Egy analóg szűrő bemenetén analóg jel x(t) jut be és kimenetén szintén analóg jel y(t) jelenik meg. Az x(t) is és y(t) is a t folytonos (idő)változó függvényei, és végtelen sok értéket felvehetnek. Analóg szűrők tervezéséhez komoly matematikai ismeretek szükségesek, és ismerni kell a szűrők rendszerekben kifejtett hatásának bonyolult folyamatát is.
A modern mintavételező és digitális jelfeldolgozó eszközök térhódítása miatt az analóg szűrőket (majdnem mindenütt) helyettesíthetjük digitális szűrőkkel. Olyan alkalmazásokban, amelyek megkövetelik a szűrők programozhatóságát, mint például az hangtechnikában, a híradástechnikában, a geofizikában valamint számos egyéb területen.
A digitális szűrők a következő előnyökkel rendelkeznek az analóg szűrőkkel szemben:
nagyobb pontosság érhető el velük, mint R-L-C áramkörökkel,
olyan szűrők is megvalósíthatók, amelyeknek nem létezik valós, R-L-C elemekből készíthető megfelelőjük,
A digitális szűrők paraméterei programozhatók, így könnyen változtathatók és az eredmény gyorsan tesztelhető.
A digitális szűrők egyszerű számtani műveletekkel dolgoznak, amelyek az összeadás, kivonás, szorzás, osztás.
A digitális szűrők működését nem befolyásolja a hőmérséklet és a páratartalom változása, illetve nem tartalmaznak különleges pontosságot igénylő alkatrészeket.
A digitális szűrőknek különlegesen jó a teljesítmény/költség aránya.
A digitális szűrők tulajdonságai nem függnek a gyártási verzióktól és tulajdonságaik nem "öregszenek".
Készíthetők ún. adaptív, vagyis a feladathoz automatikusan alkalmazkodó szűrők is.
10.2. A Z transzformáció
A Z-transzformáció a Laplace-transzformáció diszkrét idejű megfelelője. Általánosabb a 6.5. szakasz - Diszkrét Fourier transzformáció (DFT) fejezetben tárgyalt diszkrét Fourier-transzformációnál (DFT), mert kevésbbé szigorúak a konvergencia feltételek.
Általánosan egy {f k } diszkrét számsorozat Z transzformáltja definíció szerint:
|
|
(10.1) |
ahol:
|
|
(10.2) |
|
t k =k.h |
az k.-ik mintavételezési időpont | |
|
h |
a mintavételezési időtartam | |
|
k |
pozitív egész szám |
Itt is belépő függvény van, amely ugyanolyan szerepű, mint a Laplace transzformációnál volt.
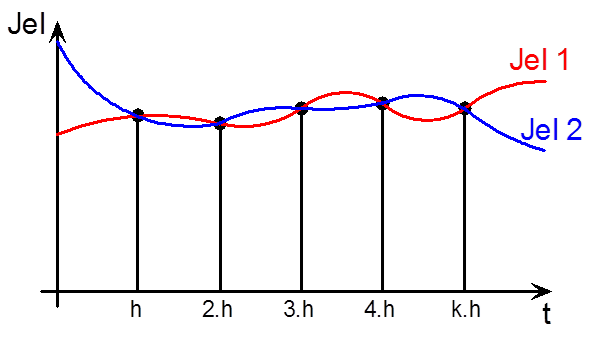
A Z transzformációval meghatározott értékek csak a mintavételi időpontokban adnak információt , hogy két mintavétel között mi történik, arra nem.
A jelek Z transzformációjának összefüggései alapján meghatározható függvények táblázatba foglalhatók:
|
f(t) |
f(n.h) |
F(z) |
|---|---|---|
|
|
1 |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A Z transzformált értékek mindegyike egy 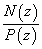 alakú polinom.
alakú polinom.
Ezek csak a legfontosabb transzformációs összefüggések, további kiszámított Z transzformációs összefüggések mintavételes szabályozási kézikönyvekben találhatók.
Mintapélda:
Egységugrás-függvény Z transzformáltja:
|
|
(10.3) |
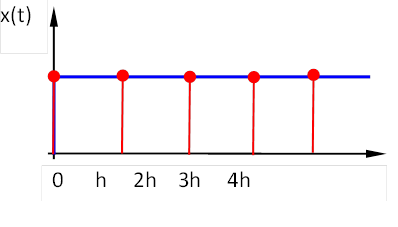
|
|
(10.4) |
Magyarázat:
A mértani sor összege:
|
|
(10.5) |
amelybe behelyettesítve az a
1
= 1 és 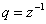 (q = quotient = kvóciens) értékeket,
(q = quotient = kvóciens) értékeket, 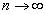 esetén kapjuk a
esetén kapjuk a 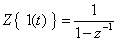 összeget:
összeget:
|
|
(10.6) |
10.2.1. A Z transzformáció legfontosabb tulajdonságai
Linearitás:
|
|
(10.7) |
A Laplace transzformáció és a Z transzformáció kapcsolata:
|
|
(10.8) |
Eltolási tételek:
Eltolás az időtengelyen negatív irányban
|
|
(10.9) |
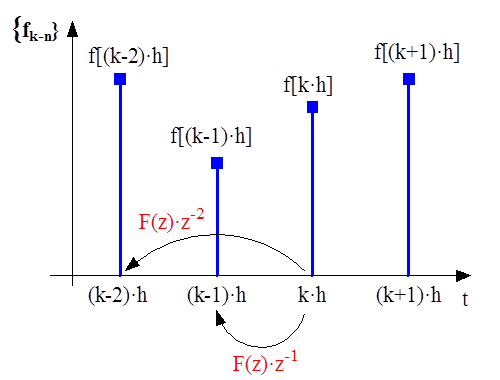
Eltolás az időtengelyen pozitív irányban
|
|
(10.10) |
Például n=2 esetén
|
|
(10.11) |
ahol
|
f 0 |
a függvény értéke t=0.h időpontban | |
|
f 1 |
a függvény értéke t=1.h időpontban |
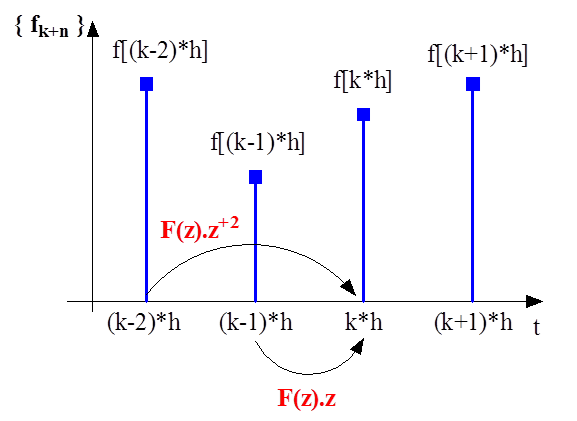
Végérték tételek:
|
|
(10.12) | |
|
| ||
|
|
(10.13) | |
|
|
az 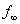 ilyen módon történő meghatározása akkor igaz, ha az
ilyen módon történő meghatározása akkor igaz, ha az 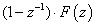 -nek nem helyezkedik el egyetlen pólusa sem az egység sugarú körön, illetve azon kívül.
-nek nem helyezkedik el egyetlen pólusa sem az egység sugarú körön, illetve azon kívül.
A megoldás módszere hasonló a Laplace transzformációnál megismert módszerhez. A bemenő jelet és az átvitelt leíró függvényt transzformáljuk (Z transzformáció), majd az eredményt visszatranszformáljuk.
10.2.2. Az inverz Z transzformációs módszerek
10.2.2.1. Táblázatból való visszakereséssel
Ilyenkor a 10.1. táblázat - Jelek Z transzformációja táblázat F(z) oszlopát alkalmazzuk bementként és az f(t) időfüggvényt határozzuk meg a táblázatból.
10.2.2.2. Résztörtekre bontással
A számítások eredményeként általában a kimenő jel z transzformáltját határozzuk meg, amely az Y(z). Ezt bonthatjuk fel a nevező (Y(z)) gyökei szerint felírt résztörtekre.
|
|
(10.14) |
alakra hozzuk, ahol
|
|
a nevező egyszeres gyökei, | |
|
|
állandók. |
A meghatározott 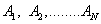 együtthatók segítségével a megoldás idő tartományban
együtthatók segítségével a megoldás idő tartományban
|
|
(10.15) | |
|
|
(10.16) |
alakú lesz.
Egy tag rekurzív formulává történő visszaalakításánál az 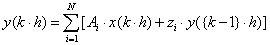 alakú kifejezésben az A
i
és z
i
értékek a meghatározó paraméterek. N az elemek száma.
alakú kifejezésben az A
i
és z
i
értékek a meghatározó paraméterek. N az elemek száma.
A résztörtekre bontás a nevező többszörös gyökei esetén is alkalmazható, ilyenkor a reziduum tétel segítségével határozzuk meg a függvényt.
10.2.2.3. Sorba fejtéssel
Az Y(z) függvényt, amely általában egy számláló (NUM(z)) és egy nevező (DEN(z)) polinomok hányadosaként jelenik meg, z-1 hatványsorba fejtjük.
|
|
(10.17) |
A z-1 hatványsor együtthatói a diszkrét számsorozat mintavételi időpontokban felvett értékeit fogják megadni. Ha Y(z) racionális törtfüggvény, a sorfejtést a számláló nevezővel való osztásával végezhetjük.
10.2.2.4. Diszkrét konvolúcióval
A diszkrét konvolúciós összeget ugyanúgy alkalmazhatjuk az inverz Z transzformáció meghatározásához a mintavételes rendszereknél, mint a koncolúciós integrált az inverz Laplace transzformációnál a folytonos rendszereknél.
Az inverz Z transzformációhoz alkalmazzuk az Y(z) függvényt, amelyet bontsuk fel két Z transzformált függvény szorzatára, (amelyek egyszerűbbek Y(z)-nél).
|
|
(10.18) |
Így Y(z) kifejezhető, mint a szorzatban szereplő Y 1 (z) és Y 2 (z) függvények z-1 hatványaival felírt komponenseinek sorozatával.
|
|
(10.19) |
A két függvény sorozat összeszorzásával a következő függvényt kapjuk:
|
|
(10.20) |
Az y[k] általánosan leírható függvénye időtartományban:
|
|
(10.21) |
ami nem más mint y 1 [k] és y 2 [k] diszkrét konvolúció függvénye.
Ezt az inverz Z transzformációs eljárást akkor érdemes alkalmazni, ha az y 1 [k] és y 2 [k] már eleve idősorozatként áll rendelkezésünkre.
A diszkrét konvolúciót általánosan a következő összefüggéssel határozhatjuk meg:
|
|
(10.22) |
A * a konvolúciós szorzat, amelynek definícióját a 10.21 képlettel adtuk meg.
10.3. Egyszerű digitális szűrők
A digitális szűrők következő alaptípusait különböztetjük meg:
Véges impulzus válasz szűrő ( FIR = Finite Impulse Response ), más néven mozgó átlag szűrő ( MA = Moving Average )
Végtelen impulzus válasz szűrő ( IIR = Infinite Impulse Response ), más néven autoregressziós mozgó-átlag szűrő ( ARMA = Autoregressive Moving-Average )
Nemlineáris szűrő
A szűrők csoportosítása általában az impulzus bemeneti jelre adott válaszuk alapján történik.
10.3.1. Impulzusválasz
Az impulzus egy rövid idő alatt 0-tól a maximum értékig felfutó, majd szintén nagyon gyorsan a 0 értékre visszatérő jel. A 10.17. egyenlet matematikai alakban írja le az impulzust.
|
|
(10.23) |
Egy szűrő impulzus válasza a szűrő egy impulzusra adott válasza, és alakja függ a szűrő működési paramétereitől illetve a szűrő típusától. A 10.5. ábra - A különböző típusú szűrő karakterisztikák ábra a különböző típusú szűrőket mutatja be.
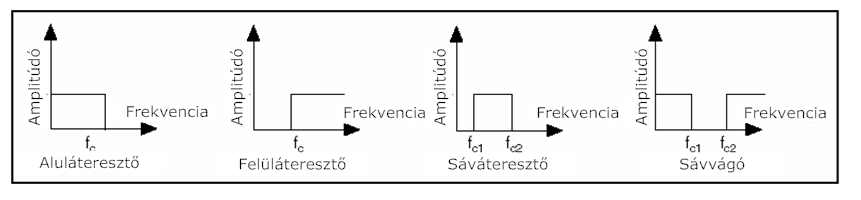
Az impulzus válasz Fourier transzformáltja a szűrő frekvencia válasza.
A szűrő frekvencia válasza információt ad a szűrő frekvencia áteresztő képességéről a különböző frekvenciákon. Más szóval egy szűrő frekvenciaválasza megmutatja a szűrő erősítését különböző frekvenciákon. Egy ideális szűrő erősítése az átviteli sávban 1, a csillapítási sávban pedig 0. Egy ideális szűrő az átviteli sávban lévő összes frekvenciát változatlanul átengedi a kimenetre, illetve a csillapítási sáv frekvenciáit nem engedi a kimenetre.
10.3.2. Szűrők osztályozása impulzusválaszuk alapján
A szűrő impulzusválasza eldönti, hogy egy adott szűrő véges impulzus válaszú szűrő (FIR) vagy végtelen impulzus válaszú szűrő (IIR).
A véges impulzus válasz szűrő (FIR) kimeneti jele csak a jelenlegi és az előző bemeneti értékektől függ.
A végtelen impulzus válasz szűrő (IIR) kimeneti jele függ a jelenlegi és az ezt megelőző bemeneti értékektől, valamint a megelőző kimeneti értékektől is.
Egy pénztárgép példájával jól lehet szemléltetni a véges impulzus válasz szűrők (FIR) és a végtelen impulzus válasz szűrők (IIR) működése közötti különbséget.
A példában a következő feltételek adottak:
|
x[k] |
az aktuális árucikk ára, amelyet éppen beütöttünk a gépbe | |
|
x[k–1] |
eggyel korábban beütött árucikk ára | |
|
1 ≤ k ≤ N | ||
|
N |
az összes beütött árucikk darabszáma |
A következő szabály leírja a pénztárgép működését:
A pénztárgép összeadja minden egyes (eddig) eladott árucikk árát, meghatározva ezzel az úgynevezett futó összeget y[k]-t.
A következő 10.18 egyenlet megadja az y[k]–t a k-dik árucikkig.
|
|
(10.24) |
Tehát N árucikk összege az y[N] lesz.
y[k] egyenlő 1-től a k-adik árucikkig az árak összegével. y[k-1] egyenlő (k-1)-ig bezáróan az árak összegével. Tehát a 10.24 egyenlet felírható a következő alakban is.
|
|
(10.25) |
Az összeghez hozzáadva 27.0% adót és leírva újra a 10.24 és 10.25 egyenletet, a következőket kapjuk.
|
|
(10.26) | |
|
|
(10.27) |
A 10.26 és 10.27 egyenletek azonos módon írják le a pénztárgép működését. Azonban a 10.26 egyenlet csak a bementet alkalmazza a működési leírásához, míg a 10.27 egyenlet a bemeneteket és kimeneteket egyaránt alkalmazza a folyamat jellemzéséhez.
A 10.26 egyenlet egy nem rekurzív , vagy FIR műveletet mutat be.
A 10.27 egyenlet egy rekurzív vagy IIR műveletet mutat be.
Azok az egyenletek, amelyek leírják a szűrő működését és olyan alakúak (felépítésűek), mint a 10.24, 10.25, 10.26 és 10.27 egyenletek, differencia-egyenletek .
A szűrők közül a véges impulzus válasz szűrőket (FIR) a legegyszerűbb tervezni. Ha egy egyszerű impulzus jelenik meg a véges impulzus válasz szűrő bemenetén, és az összes későbbi bemenő érték nulla, akkor a véges impulzus válasz szűrő kimenete véges idő múlva szintén nulla értékű lesz. Azt az időtartamot, amely alatt a szűrő kimenete beáll a nulla értékre, a szűrő együtthatóinak darabszáma határozza meg.
További információkat a véges impulzus válasz szűrőkről ezen fejezet FIR szűrők című részéből ismerhetünk meg.
Mivel a végtelen impulzus válasz szűrők (IIR) a jelenlegi és a korábbi bemeneti- valamint a korábbi kimeneti értékek alapján működnek, az ilyen szűrő impulzusválasza sohasem éri el a nulla értéket ezért, ezek végtelen válaszfüggvények. Ezzel az IIR szűrők című fejezet rész foglalkozik bővebben.
10.3.3. Szűrő együtthatók
A 10.24 egyenlet minden egyes tagjának 1.27 volt a szorzótényezője. A 10.25 egyenletben y[k–1] tagnak 1.0, az x[k] tagnak pedig 1.27 az szorzótényezője. Ezek a szorzótényezők a szűrő együtthatói . A végtelen impulzus válasz (IIR) szűrőre vonatkozó bemeneti szorzó tényezői az előreható együtthatók a kimeneti szorzóegyütthatók pedig a visszaható együtthatók .
10.4. Egy ideális szűrő jellemzői
Az ideális szűrőt nem lehet megvalósítani!
Az ideális szűrők lehetővé teszik egy megadott frekvenciasáv teljes (veszteségmentes) áteresztését, míg a nem kívánt frekvenciatartomány jeleit teljes egészében (maximálisan) elnyomják. Következő csoportosításban aszerint osztályozzuk a szűrőket, hogy egy frekvenciatartomány jeleit átengedik vagy elnyomják.
Aluláteresztő szűrők: átengedik az alacsony, és levágják a magas frekvenciájú jeleket
Felüláteresztő szűrők: átengedik a magas, és levágják az alacsony frekvenciájú jeleket
Sáváteresztő szűrők : egy bizonyos frekvenciatartomány jeleit átengedik
Sávvágó szűrők: egy bizonyos frekvencia tartomány jeleit nem engedik át
A 10.6. ábra - Ideális szűrők frekvencia válaszai ábra az egyes szűrő típusok frekvencia válaszait mutatja be. (fc = fcut)
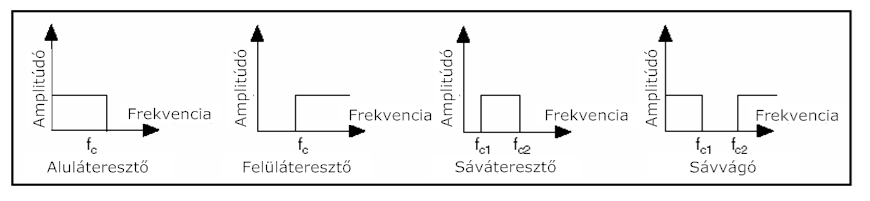
A (10.6. ábra - Ideális szűrők frekvencia válaszai) ábrán bemutatott szűrők a következő módon viselkednek:
Az aluláteresztő szűrő f c alatt minden frekvenciát átenged.
A felüláteresztő szűrő f c felett minden frekvenciát átenged.
A sáváteresztő szűrő f c1 és f c2 között minden frekvenciát átenged.
A sávvágó szűrő f c1 és f c2 között minden frekvenciát csillapít (levág).
Az f c , f c1 , és f c2 frekvencia pontok kijelölik a különféle szűrők határfrekvenciáit.
A szűrők tervezésénél ezeket a határfrekvenciákat kell megadnunk bemeneti adatként.
A szűrő átviteli sávja az a frekvenciatartomány, amelyet a szűrő átenged. Az ideális szűrő erősítése az átviteli sávban 1 (amely megfelel 0 dB erősítésnek), így a jel amplitúdója sem nem növekszik sem nem csökken.
A szűrő vágási sávja az a frekvenciatartomány, amelyet a szűrő teljes egészében levág. A (10.7. ábra - Átviteli sáv és vágási sáv) ábra az átviteli (PB = PassBand) és vágási sávot (SB = StopBand) mutatja az egyes szűrő típusokra.
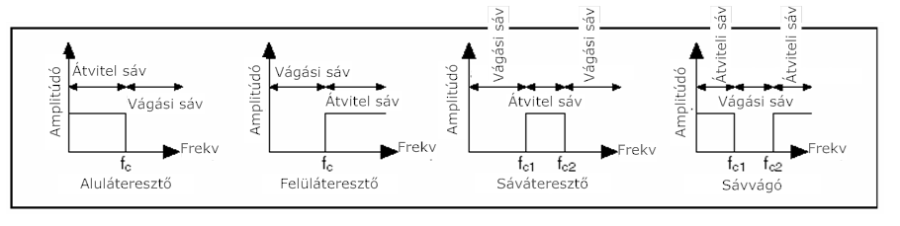
A (10.7. ábra - Átviteli sáv és vágási sáv) ábrán látható szűrők átviteli és vágási sávjait a következőképpen jellemezhetjük:
Az alul- és a felül-áteresztő szűrőknek egy átviteli és egy vágási sávjuk van.
A sáváteresztő szűrőnek egy átviteli és két vágási sávja van.
A sávvágó szűrőnek két átviteli és egy vágási sávja van.
10.5. Valóságos (nem ideális) szűrők
Ideális esetben egy szűrőnek egységnyi (0 dB) az erősítése az átviteli sávban, és nulla ( dB) az erősítése a vágási sávban. A valóságos szűrők nem tudják teljesíteni egy ideális szűrővel szemben támasztott követelményeket. A gyakorlatban mindig van egy véges
átmeneti sáv
az átviteli és vágási sáv között. Az átmeneti sávban a szűrő erősítése fokozatosan változik egytől (0 dB) nulláig
dB) az erősítése a vágási sávban. A valóságos szűrők nem tudják teljesíteni egy ideális szűrővel szemben támasztott követelményeket. A gyakorlatban mindig van egy véges
átmeneti sáv
az átviteli és vágási sáv között. Az átmeneti sávban a szűrő erősítése fokozatosan változik egytől (0 dB) nulláig 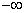 dB) átviteli sávtól a vágási sávig.
dB) átviteli sávtól a vágási sávig.
10.5.1. Átmeneti sáv
A 10.8. ábra - Nem ideális szűrők ábra bemutatja az átviteli, a vágási és az átmeneti sávokat a valós szűrő típusokra.
A (10.8. ábra - Nem ideális szűrők) ábrán az x-tengelyen ábrázoljuk a frekvenciát, y-tengelyen pedig a jel amplitúdó átvitelének arányát deciBel-ben (dB). Az átviteli sáv tartományában a szűrő erősítése 0 dB-től -3 dB-ig változik.
10.5.2. Átviteli sáv ingadozása és vágási sáv csillapítása (ripple)
Sok alkalmazásban megengedhetjük, hogy az átviteli sáv erősítése kis mértékben eltérjen az egységnyi (1) értéktől. Ez az eltérés az átviteli sáv ingadozása , vagyis a különbség a valóságos és az ideális egységnyi erősítés között. A gyakorlatban nem valósítható meg, hogy a vágási sáv csillapítása végtelen legyen, ezért meg kell állapítani egy megfelelő nagyságú értéket. Az átviteli sáv ingadozását, és a határfrekvencia csillapítását megadhatjuk dB egységben. 10.28 egyenlet szerint.
|
|
(10.28) |
Ahol lg a 10-es alapú logaritmust jelenti, 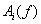 egy f részfrekvencia amplitúdója szűrés előtt, és
egy f részfrekvencia amplitúdója szűrés előtt, és 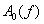 egy f részfrekvencia amplitúdója szűrés után.
egy f részfrekvencia amplitúdója szűrés után.
Ha ismerjük az átviteli sáv hullámosságát, vagy a vágási sáv csillapítását, akkor a 10.28 egyenlettel meghatározhatjuk a bemenő és kimenő amplitúdók arányát. Az amplitúdók aránya megmutatja, hogy az átviteli vagy vágási sáv milyen mértékben térnek el az ideálistól.
Például amikor az átviteli sáv ingadozása 0.02 dB, a 10.29 egyenletből a következő összefüggés írható fel.
|
|
(10.29) | |
|
|
(10.30) |
A 10.29 és 10.30 egyenletek megmutatják, hogy a bemenő és kimenő amplitúdók arányának mekkora az eltérése az egytől, amely az átviteli sáv ideális esetben. A gyakorlatban, szűrő tervezésekor megpróbálják megközelíteni a megkívánt ideális intenzitásfüggvényt, bizonyos megszorításokkal korlátozva.
A 10.2. táblázat - Ideális és valóságos szűrők jellemzői táblázat összehasonlítja a valós és az ideális szűrők jellemzőit.
|
Jellemző |
Ideális szűrő |
Valós szűrő |
|---|---|---|
|
Átviteli sáv |
Lapos és állandó |
Hullámos lehet |
|
Csillapítási sáv |
Lapos és állandó |
Hullámos lehet |
|
Átmeneti sáv |
Nincs |
Van(nak) átmeneti sáv(ok) |
A valós szűrők tervezésekor kompromisszumra törekszünk, hogy a kívánt szűrő jellemzőt kiemeljük a kevésbé kívánt jellemzők rovására. Választásunkat két dolog befolyásolja, azaz hogy véges impulzus válasz szűrőről (FIR) vagy végtelen impulzus válasz szűrőről (IIR) van-e szó, illetve, hogy milyen a szűrőalgoritmus felépítése.
10.6. Mintavételi idő
A szűrő sikeres működéshez fontos a megfelelően megválasztott mintavételi idő. A vizsgált jel maximális frekvencia összetevője általában meghatározza a szükséges mintavételi frekvenciát.
Rendszerint a vizsgált jel Fourier transzformáltja legnagyobb frekvenciájú összetevőjének 10-szeresét (általában) már elegendő mintavételi frekvenciának választani!
Ha a határfrekvencia túl közel van a Nyquist frekvenciához, növelni kell a mintavételi frekvenciát. Ha a határfrekvencia túl közel van az egyenfeszültséghez (0 Hertz), akkor csökkenteni kell a mintavételi frekvenciát.
Általában csak akkor változtassunk a mintavételi frekvencián, ha ütközési problémák fordulnak elő.
10.7. Véges impulzus válasz (FIR) szűrők
Véges impulzus válasz szűrők ( FIR szűrők ) olyan digitális szűrők, amelyeknek időben véges hosszúságú impulzusválaszuk van. A véges impulzus válasz szűrők működésükkor csak az aktuális és az előző bemeneti értéket veszik figyelembe a szűrő algoritmusában. Az ilyen típusú szűrőket a legegyszerűbb megtervezni. A véges impulzus válasz szűrők más néven is ismertek, mint nem visszatérő (nem rekurzív), konvolúciós , vagy mozgó átlag (MA) szűrők .
A véges impulzus válasz szűrők a szűrő-együtthatók konvolúcióját végzik a bemenő értékek egy sorozatán, és létrehozzák a kimeneti értékek (azonosan sorszámozott) sorozatát. A 10.25. egyenlet egy véges impulzus válasz szűrő véges konvolúcióját adja meg.
|
|
(10.31) |
ahol
|
x[k-i] |
a szűrő bemenő jelének értéke az [k-i]-ik időpillanatban, | |
|
y[k] |
a szűrt kimenő jel értéke az [k]-ik időpillanatban, | |
|
b i |
a szűrő (FIR szűrő) i-ik együtthatója | |
|
N b |
a szűrő együtthatóinak száma (fokszáma). |
A véges impulzus válasz szűrők (FIR szűrők) a következő tulajdonságokkal rendelkeznek:
A FIR szűrők lineáris fázismenetet valósítanak meg, mert a szűrő együtthatói szimmetrikusak.
A FIR szűrők mindig stabil működésűek.
A FIR szűrők a jelek szűrését a konvolúció alkalmazásával teszik lehetővé. Ezért általában a kimenő sorozat mindig tartalmaz késleltetést , amelyet a következő egyenletben láthatunk
A kimenő jel késleltetése mintavételi lépésben =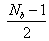 .
.
A 10.9. ábra - FIR szűrő amplitúdó és fázis függvénye összehasonlítva a normalizált frekvenciával ábra bemutatja egy FIR szűrő tipikus amplitúdó- és fázisfüggvényét, összehasonlítva a normalizált frekvenciával.
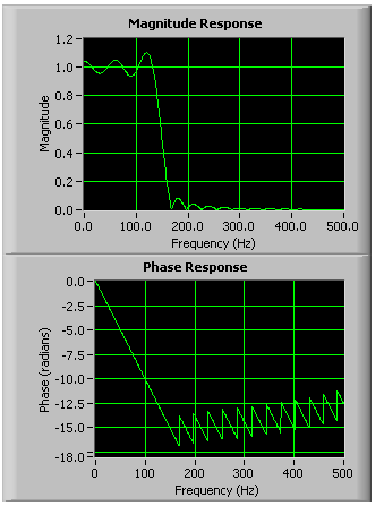
A (10.9. ábra - FIR szűrő amplitúdó és fázis függvénye összehasonlítva a normalizált frekvenciával) ábrán, a fázis-függvényben lévő szakadások akkor keletkeznek, amikor az abszolút értéket használjuk az amplitúdó függvény meghatározásához. A fázis jelleggörbe szakadásai PI (π = 3.14) egész számú többszöröseinél vannak, bár a fázisfüggvény teljesen lineáris.
10.7.1. Leágaztatások (Taps)
A leágaztatás kifejezés gyakran feltűnik a véges impulzus válasz szűrők (FIR szűrők) leírásaiban. A 10.10. ábra - Leágaztatás ábra illusztrálja a leágaztatás műveletét.
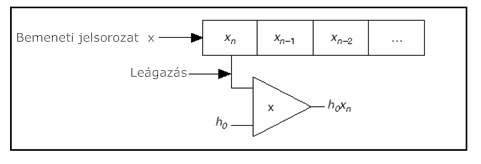
A 10.10. ábra - Leágaztatás ábra bemutatja a bemenő mintákat
|
{
|
(10.32) |
tartalmazó Nb-elemű shift regisztert.
A leágaztatás kifejezés a shift regiszter leágaztatásának működéséből ered.
A taps kifejezés általában a FIR szűrő együtthatóinak számára utal.
10.7.2. Véges impulzus válasz szűrők (FIR szűrők) tervezése
Egy diszkrét rendszer előírt frekvenciafüggvényét (legjobban) közelítve tervezünk véges impulzus válasz szűrőket (FIR). A legtöbb általános tervezési módszer jól közelíti a kívánt amplitúdó függvényt, emellett, hogy egy jó lineáris fázis menetet biztosít.
A lineáris fázis menet azt jelenti, hogy a jel terjedési késleltetése azonos minden frekvencián a rendszerben.
A 10.11. ábra - Egyenletes hullámosságú sáváteresztő FIR szűrő frekvenciafüggvénye ábra egy VI blokkdiagramot mutat be, amely egy egyenletes hullámosságú sáváteresztő véges impulzus válasz szűrő (FIR szűrő) frekvenciafüggvényét adja meg.
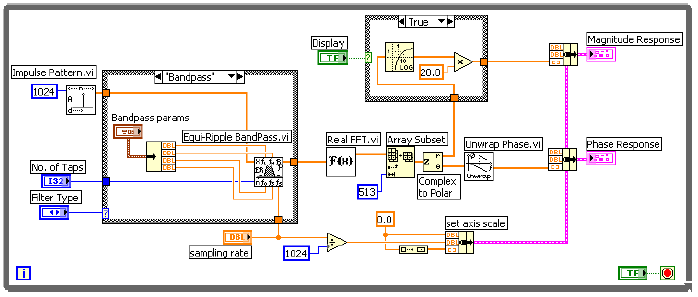
A (10.11. ábra - Egyenletes hullámosságú sáváteresztő FIR szűrő frekvenciafüggvénye) ábrán látható VI a következő lépéseket hajtja végre, amikor kiszámítja a szűrő frekvenciafüggvényét:
Egy impulzus jellel gerjesztjük a szűrőt.
A case-struktúra (case = eset) meghatározza a szűrő típusát, hogy az alul- vagy felül-áteresztő, sávvágó vagy sáváteresztő. A case-struktúrából kijövő jel a szűrő impulzusválasza.
A case-struktúrából kijövő impulzusválaszon a FFT.VI diszkrét Fourier-transzformációt végez, és meghatározza a szűrő frekvenciafüggvényét úgy, hogy az impulzusválasz és a frekvenciafüggvény alkotják a Fourier-transzformáltat, h(t) az impulzusválasz. H(w) a frekvenciafüggvény.
Az FFT.VI által kibocsátott adatokat redukálja a Array Subset függvénnyel. A valódi FFT eredményeinek fele ismétlődik, ezért a VI – nek elegendő az FFT.VI által kibocsátott adatok felét feldolgoznia.
A Complex to Polar függvénnyel előállítja az FFT.VI-ből kapott adatok amplitúdó és fázis függvényét. Az FFT.VI komplex kimenetének amplitúdó/fázis alakját egyszerűbb értelmezni, mint az FFT Descartes koordinátájú komponenseit.
A fázis értékeket átalakítja fokokra.
Az amplitúdó értékeket átalakítja deciBel-ekké (dB).
A 10.12. ábra - Egy egyenletes hullámosságú sáváteresztő FIR szűrő amplitúdó és fázisfüggvénye ábra a VI által, a 10.11. ábra - Egyenletes hullámosságú sáváteresztő FIR szűrő frekvenciafüggvénye ábra szerint megvalósított szűrő amplitúdó-és fázisfüggvénye.
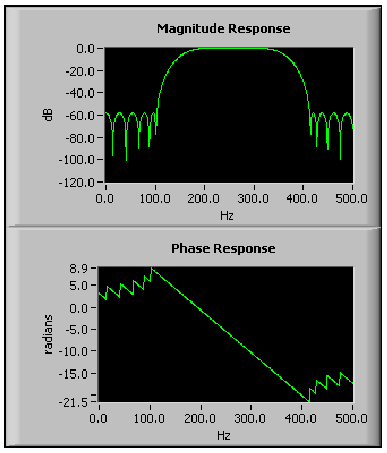
A (10.12. ábra - Egy egyenletes hullámosságú sáváteresztő FIR szűrő amplitúdó és fázisfüggvénye) ábrán, amikor az abszolút értéket alkalmazunk, hogy kiszámítsuk az amplitúdó függvényt, szakadások keletkeznek, ezek okoznak a fázisgörbén is szakadásokat. A fázisgörbe azonban egy lineáris függvény, mivel a rendszerben minden frekvenciának azonos a terjedési késleltetése.
Mivel a véges impulzus válasz szűrők (FIR szűrők) intenzitásgörbéje hullámos, a FIR szűrők tervezésekor a következő feladatokat kell megoldani:
Szűrő tervezése az ideálishoz lehető legközelebb eső amplitúdó függvénnyel;
Szűrő tervezése , amely a hullámosságot előírt módon osztja el;
Például egy aluláteresztő szűrő rendelkezik egy ideális amplitúdó függvény alakkal. Egy valóságos alkalmazás megengedhet egy kis hullámosságot az átviteli sávban, és egy kicsivel többet a vágási sávban. A szűrő konstrukció algoritmusának egyensúlyban kell tartania a viszonylagos hullámosságot és az éles átmeneti sávot.
A leggyakrabban alkalmazott módszerek a véges impulzus válasz szűrők (FIR szűrők) tervezéséhez az ablakozás és a Parks-McClellan algoritmus , amely úgy is ismert, mint a Remez-csere módszer .
10.7.3. Véges impulzus válasz szűrők (FIR szűrők) tervezése ablakozással
A témakör elméletét a 7.1.3.4. szakasz - Folytonos, nem stacionárius jelek analízise a gyakorlatban fejezetben már tárgyaltuk, most a gyakorlati alkalmazást tekintjük át.
A legegyszerűbb módszer véges impulzus válasz szűrők (FIR szűrők) tervezésére az ablakozás, mert a megvalósítása kényelmes és egyszerű. A FIR szűrők ablakozással való tervezése az amplitúdó függvény inverz FFT-ját adja és egy simító ablakot alkalmaz.
A simító ablak egy idő dimenziójú ablak.
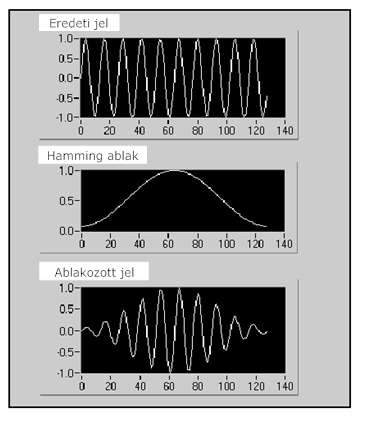
Egy FIR szűrő ablakozással történő tervezéséhez a következő lépéseket kell elvégezni:
Meg kell határozni egy ideális frekvenciafüggvényt;
Meg kell határozni az ideális frekvenciafüggvény impulzusválaszát;
Az impulzusválaszt le kell rövidíteni, hogy véges számú együtthatóból álljon;
Szimmetrikus simító ablakot kell alkalmazni.
Az ideális impulzusválasz megcsonkítása a Gibbs-jelenségben nyilvánul meg. A Gibbs-jelenség a határfrekvenciák közelében lengő viselkedésként jelenik meg a FIR szűrő frekvenciafüggvényében. Ezt a jelenséget tudjuk gyengíteni olyan módon, hogy simító ablakot használunk, így ”kisimítjuk” az ideális impulzusválasz frekvencia vágását. A FIR együtthatókat csökkentve a végeken, csökkenthetjük a frekvenciafüggvény oldalsó hurkainak magasságát. Azonban ha csökken a hurkok magassága, akkor kiszélesedik a főhurok, és a határfrekvenciáknál szélesebb lesz az átmeneti sáv.
Egy simító ablak kiválasztásához kompromisszum szükséges a határfrekvenciák közelében lévő oldalhurkok magassága, és az átmeneti sáv szélessége között. Csökkentve az oldalhurkok magasságát, növekszik az átmeneti sáv szélessége. Csökkentve az átmeneti sáv szélességét, növekszik az oldalhurkok magassága a határfrekvenciák közelében.
Az ablakozásos FIR szűrő tervezésnek a következő hátrányai vannak:
Nincs figyelemmel a következőkre
Az ablakozás egyenlőtlen fodrozódás eloszlást okoz.
Az ablakozás szélesebb átviteli sávot eredményez, mint más tervezési módszerek.
Nehézségek jelentkeznek a paraméterek pontos meghatározásban
Az ablakozás nehezíti a határfrekvencia meghatározását, amely egy megadott csillapítással rendelkezik.
A szűrő tervezőjének meg kell határoznia:
az ideális vágási frekvenciát.
a mintavételi frekvenciát.
a leágazások számát.
az alkalmazott ablak típusát.
A FIR szűrők ablakozással való tervezése nem igényel bonyolult számítási műveleteket. Ezért az ablakozás a leggyorsabb módszer FIR szűrők tervezésénél. Viszont az ablakozás nem a legjobb technika FIR szűrők tervezéséhez.
10.7.4. Optimális FIR szűrők tervezése a Parks-McClellan algoritmussal
A Parks-McClellan algoritmus, vagy a Remez-csere módszer, egy hiba kritériumon alapuló iteráló módszert alkalmaz a FIR szűrő együtthatóinak meghatározására. A Parks-McClellan algoritmust a legkedvezőbb lineáris fázismenetű FIR szűrő együtthatóinak tervezésére alkalmazhatjuk. A Parks-McClellan algoritmussal tervezett szűrők optimálisak lesznek, mert a szűrő aktuális amplitúdó függvénye és a szűrő ideális amplitúdó függvénye között minimálisra csökkennek a hibák.
Az optimális FIR szűrők lecsökkentik az ellentétes hatásokat a határfrekvenciáknál. Az optimális FIR szűrők tervezése nagyobb ellenőrzési lehetőséget kínál közelítési hibák felett, különböző frekvencia sávokban, mint egyéb más FIR szűrő tervező technikák, mint például az ablakozás, amely nem nyújt ellenőrzési lehetőséget a különböző frekvencia sávokban a közelítési hibákra.
Optimális FIR szűrőket a Parks-McClellan algoritmussal tervezhetünk, amelyeknek a következő a jellemzői vannak:
Az amplitúdó függvény súlyozott hullámossága egyenletesen oszlik el az átviteli és a vágási sávokban.
Éles átmeneti sávja van.
Ha a FIR szűrőket a Parks-McClellan algoritmussal tervezzük, egy optimális amplitúdó függvényt kapunk. A tervezés folyamata bonyolultabb és számításigényesebb, mint az ablakozásnál.
10.7.5. Egyenletes hullámosságú FIR szűrők tervezése Parks-McClellan algoritmus alkalmazásával
A Parks-McClellan algoritmust használhatjuk egyenletes hullámosságú FIR szűrők tervezésére. Az egyenletes hullámosságú konstrukció egyenlően osztja el az átviteli és a vágási sáv ingadozását, és lineáris fázismenetű szűrőket hoz létre.
Ahhoz, hogy egy egyenletes hullámosságú szűrőt tervezzünk, meg kell határozni a következő jellemzőket:
Határfrekvencia
Leágazások száma
Szűrő típusa, azaz aluláteresztő, felüláteresztő, sáváteresztő, vagy sávvágó
Átmeneti frekvencia
Vágási frekvencia
Az egyenletes hullámosságú szűrők határfrekvenciája megszabja az átviteli sáv, vagy a vágási sáv élét, vagy mindkettőt. Az egyenletes hullámosságú szűrők vágási és átviteli sávjának ingadozása okozza a következő impulzusválaszokat:
Átviteli sáv - az intenzitásfüggvény nagyobb vagy egyenlő, mint 1
Vágási sáv - az intenzitásfüggvény kisebb vagy egyenlő, mint a vágási sáv csillapítása
Például ha veszünk egy aluláteresztő szűrőt, az átviteli sáv határfrekvenciája a legnagyobb frekvencia, amelyre az átviteli sáv feltételei teljesülnek. Hasonlóképpen a vágási sáv határfrekvenciája a legalacsonyabb frekvencia, amelyre a vágási sáv feltételei teljesülnek
10.7.6. Keskeny sávú FIR szűrők tervezése
A különlegesen szűk sávszélességű FIR szűrők hagyományos módszerekkel történő tervezése nagy elemszámú szűrőt eredményezne. A nagy elemszámú FIR szűrők hosszú tervezési és kivitelezési időt igényelnek, valamint számítási pontatlanságra hajlamosak. Néhány esetben a hagyományos tervezési módszerek, mint a Parks-McClellan algoritmus, sem tudnak elfogadható szűk sávú FIR szűrőt meghatározni.
Az interpolációs véges impulzus válasz (IFIR) típusú szűrőtervezési módszer egy hatékony algoritmust ajánl a keskeny sávú FIR szűrők tervezésére. Az IFIR módszert alkalmazva olyan keskeny sávú szűrőket lehet tervezni, amelyek kevesebb együtthatót, és számítást igényelnek, mint ha a Parks-McClellan algoritmust közvetlenül végrehajtva tervezünk szűrőt. A „FIR keskeny sáv együtthatók.VI” (FIR Narrowband Coefficients.VI) az IFIR módszert alkalmazza a keskeny sávú FIR szűrő együtthatók meghatározására.
A következő paramétereket kell megadnunk, amikor keskeny sávú szűrőt tervezünk:
Szűrő típus: aluláteresztő, felüláteresztő, sáváteresztő, sávvágó
Átviteli sáv ingadozás egy lineáris skálán
Mintavételi frekvencia
Átviteli sáv frekvencia, ami a sáváteresztő és sávvágó szűrők átviteli sávjára vonatkozik
Vágási sáv frekvencia, ami a sáváteresztő és sávvágó szűrők vágási sávjára vonatkozik
Sáváteresztő és sávvágó szűrők középfrekvenciája
Vágási sáv csillapítása dB-ben
A 10.14. ábra - Keskeny sávú FIR szűrő frekvenciaválaszának becslése ábra annak a VI–nek a blokkdiagramját mutatja, amely egy keskeny sávú sáváteresztő FIR szűrő frekvenciafüggvényének becslését állítja elő, az impulzusválaszt frekvenciatartományba transzformálva.
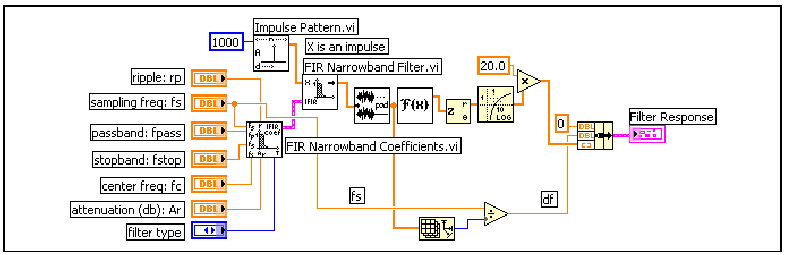
A 10.15. ábra - Szűk sávú sáváteresztő FIR szűrő, 0-tól a Nyquist frekvenciáig tartó, becsült frekvenciagörbéje ábra bemutatja azt a válaszfüggvényt 0-tól a Nyquist frekvenciáig, ami a (10.14. ábra - Keskeny sávú FIR szűrő frekvenciaválaszának becslése) ábrán lévő VI impulzusgerjesztésre adott eredménye .
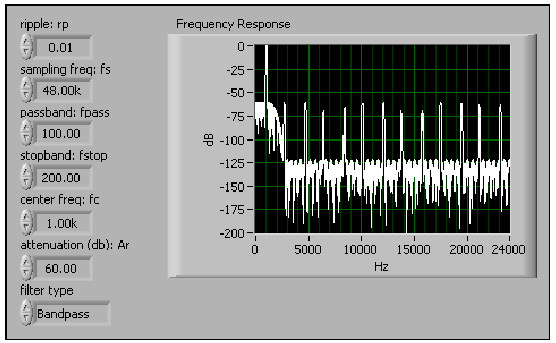
A (10.15. ábra - Szűk sávú sáváteresztő FIR szűrő, 0-tól a Nyquist frekvenciáig tartó, becsült frekvenciagörbéje) ábrán a főpanel szabályzóival beállított szűrő válaszfüggvénye az 1 kHz középvonalú keskeny átviteli sáv.
A 10.16. ábra - Keskeny sávú sáváteresztő FIR szűrő becsült frekvenciamenetének részlete ábra a szűrő válaszfüggvényének részletét mutatja.
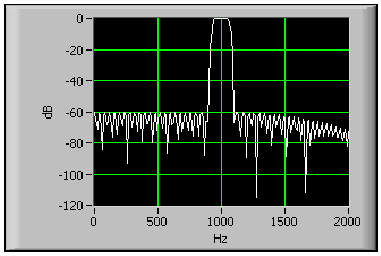
A (10.16. ábra - Keskeny sávú sáváteresztő FIR szűrő becsült frekvenciamenetének részlete) ábrán a keskeny átviteli sáv pontosan 1 kHz-re központosítva és a jel csillapítása 60 dB-lel az átviteli sáv alatt van.
10.7.7. Széles sávú FIR szűrők tervezése
Az IFIR technikát alkalmazhatjuk a széles sávú alul-, és felüláteresztő FIR szűrő tervezéséhez is. Egy széles sávú aluláteresztő FIR szűrőnek egy határfrekvenciája van, közel a Nyquist frekvenciához. A szélessávú felüláteresztő FIR szűrőnek egy 0-hoz közeli határfrekvenciája van. Használhatjuk szélessávú alul, -és felüláteresztő FIR szűrők tervezésére a FIR keskeny sávú együtthatók VI–t. A 10.16. ábra - Keskeny sávú sáváteresztő FIR szűrő becsült frekvenciamenetének részlete ábra bemutatja azt a frekvenciafüggvényt, amelyet a (10.14. ábra - Keskeny sávú FIR szűrő frekvenciaválaszának becslése) ábrán látható VI hoz létre, amikor arra használjuk, hogy egy szélessávú aluláteresztő FIR szűrő frekvenciafüggvényét meghatározzuk.
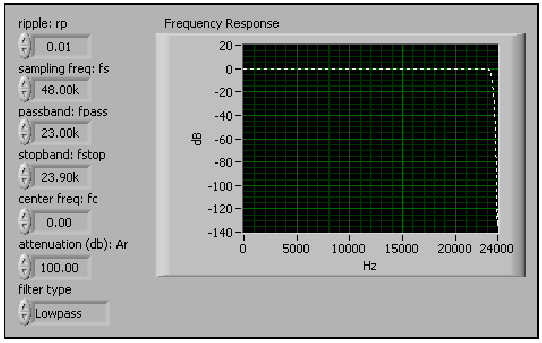
A (10.17. ábra - Szélessávú aluláteresztő szűrő frekvenciaválasza 0-tól a Nyquist frekvenciáig) ábrán lévő főpanel szabályzói beállítanak egy szűk sávszélességet a 23.9 kHz-es vágási sáv és a 24 kHz-es Nyquist frekvencia között. Azonban a frekvenciafüggvény 0-tól 23.9 kHz-ig fut, amely miatt a szűrő szélessávúvá válik.
10.8. Végtelen impulzus válasz (IIR) szűrők
A végtelen impulzus válasz szűrők (IIR = Infinite Impulse Response), más néven rekurzív vagy autoregresszív mozgó átlag (ARMA) szűrők az aktuális és a korábbi bementi értékek, valamint a korábbi kimeneti értékek szerint működnek.
Egy IIR szűrő impulzusválasza alatt értjük az általános IIR szűrőnek egy olyan impulzusra adott válaszfüggvényét, amelyet a 10.27. egyenlet definiál. Elméletileg egy IIR szűrő impulzusválasz függvénye soha nem éri el a nulla értéket, ez tehát egy végtelen válaszfüggvény. A következő általános differencia-egyenlet az IIR szűrő működését írja le:
|
|
(10.33) |
ahol
|
b j |
az előreható szűrőegyütthatók halmaza, | |
|
N b |
az előreható szűrőegyütthatók száma, | |
|
a i |
a visszafelé ható szűrőegyütthatók halmaza, | |
|
N a |
pedig a visszaható szűrőegyütthatók száma. |
Ezt impulzusátviteli függvény formában felírva:
|
|
(10.34) |
ahol
|
| ||
|
|
állandó együtthatók, | |
|
N b, Na |
pedig pozitív egészek |
Ha a nevezőkkel elvégezzük a beszorzásokat, akkor
|
|
(10.35) |
Behelyettesítve az
|
|
(10.36) | |
|
|
(10.37) |
a következő összefüggést kapjuk:
|
|
(10.38) | |
|
|
(10.39) |
Az eltolási tételt és az inverz Z transzformációt alkalmazva a kifejezés a következő alakú lesz:
|
|
(10.40) |
A kifejezést összegzési alakban felírva a következő kifejezést kapjuk:
|
|
(10.41) |
Az egyenletben szereplő 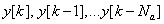 a (szabályozó) kimeneti számsorozatának,
a (szabályozó) kimeneti számsorozatának, 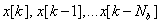 , pedig a bemeneti számsorozat pillanatnyi és megelőző értékei.
, pedig a bemeneti számsorozat pillanatnyi és megelőző értékei.
Ha kifejezzük a kimeneti számsorozat aktuális értékét, akkor ehhez az alábbi rekurzív összefüggést kapjuk:
|
|
(10.42) |
Ha tehát H(z) racionális törtfüggvény, akkor H(z)-nek megfelelő számítási egyenlet lineáris differenciaegyenlet.
A z-1 hatványaival felírt racionális törtfüggvény alakban megadott H(z) átviteli függvény realizálhatóságának feltétele: a0<>0.
A mintavételes rendszereknél
nem szükséges
az Nb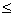 Na feltétel a megvalósításhoz z-1 hatványaival felírt racionális törtfüggvény alakban megadott H(z) esetén.
Na feltétel a megvalósításhoz z-1 hatványaival felírt racionális törtfüggvény alakban megadott H(z) esetén.
A 10.33. egyenlet egy olyan szűrőt ír le, amelynek elméletileg végtelen hosszúságú az impulzusválasza és értéke nem egyenlők nullával. Azonban a gyakorlati szűrési feladatokban egy stabil IIR szűrő impulzusválasza véges számú mintavétel után gyakorlatilag közel 0 szintre csökken.
A legtöbb IIR szűrő konstrukcióban és az összes LabVIEW IIR szűrőnél az a 0 együtthatójuk egyenlő 1-el . Az aktuális k indexű kimenő mintaérték, a előreható együtthatókkal megszorzott aktuális bemenetek és korábbi bemeneti értékeket, valamint a kimeneti együtthatókkal megszorzott korábbi kimeneti értékek összegeként adódik, ahogy azt a 10.43. egyenlet is mutatja.
|
|
(10.43) |
ahol
|
x[k] |
az aktuális bemeneti érték, | |
|
y[k] |
az aktuális kimeneti érték, | |
|
x[k-j] |
a korábbi bemeneti értékek, | |
|
y[k-i] |
a korábbi kimeneti értékek. |
Az IIR szűrőknek ingadozásaik lehetnek az átviteli sávban, a vágási sávban, vagy mindkettőben.
Az IIR szűrőknek nemlineáris fázisfüggvénye van.
10.8.1. Az IIR szűrés kaszkádképlete
A 10.44. egyenlet egy IIR szűrő közvetlen formájú impulzus-átviteli függvénye (a0=1 esetén).
|
|
(10.44) |
A 10.44. egyenletnél a 10.33. differencia-egyenlet alakjából nyert formájú szűrőt nevezzük közvetlen alakú IIR szűrőnek .
Egy közvetlen alakú szűrő érzékeny az együtthatók számából és a számítási pontosság határaiból adódó hibákra. Egy eredetileg stabil konstrukciójú szűrő is instabillá válhat, ha megnöveljük az együtthatók számát. Ahogy a szűrő fokszáma növekszik, a szűrő egyre instabilabbá válik.
Csökkenthetjük egy szűrő hibákra való érzékenységét, ha felírjuk a 10.44. egyenletet, mint a Z transzformált tényezők szorzatát. Így alacsonyabb fokú részekre osztjuk fel a közvetlen alakú átviteli függvényt.
A 10.44. egyenlet tényezőkre bontásával, a szűrő impulzus-átviteli függvénye átalakul másodfokú impulzus-átviteli függvények szorzatává, ahogy a 10.45. egyenletben láthatjuk.
|
|
(10.45) |
ahol Ns a másodfokú részfüggvény sorszáma, 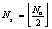 a legnagyobb egész szám
a legnagyobb egész szám 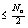 , és
, és 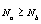 .
.
A 10.39. egyenlet szerint definiált szűrő felépítését úgy ábrázolhatjuk, mint egy olyan szűrőt, amely másodfokú szűrők sorba kapcsolásából áll. A 10.18. ábra - Kaszkád szűrés sorba kapcsolt fokozatai ábra a kaszkádszűrést mutatja be.
Az egyes önálló szűrő tagokból a 10.18. ábra - Kaszkád szűrés sorba kapcsolt fokozatai ábra alapján felépíthetjük a végtelen impulzusválasz (IIR) közvetlen alakú szűrő struktúrát.
A végtelen impulzusválasz (IIR) közvetlen alakú szűrő struktúrát úgy kell kialakítani, hogy a szűrőben szereplő egyes tagok a következő feltételek szerint működjenek:
A végtelen impulzusválasz (IIR) közvetlen alakú szűrő felépítése minimális számú matematikai műveletet igényel,
Minimális számú késleltető elemre, és belső szűrő állapotra van szüksége.
Minden egyes k-adik tagnak van egy bemenete, egy kimenete, és két előző belső állapota amelyek:
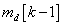 és
és 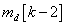 .
.
Ha n a minták száma a bementő sorozatban, akkor a szűrés a következő egyenletek szerint zajlik:
|
|
(10.46) |
Minden egyes mintára ahol k= 0, 1, 2, … , n–1 .
az egyenletek a következő függvényből erednek:
|
|
(10.47) |
egy új bevezetett változóval M(z)-vel kifejezzük Y(z)-t:
|
|
(10.48) |
amely időtartományban
|
|
(10.49) |
ahol
|
|
(10.50) | |
|
|
(10.51) | |
|
|
(10.52) |
ami időtartományban
|
|
(10.53) |
10.8.2. Másodfokú szűrés
Alul-, és felüláteresztő szűrők helyett, amelyeknek egy határfrekvenciájuk van, tervezhetünk közvetlenül másodfokú szűrő fokozatokat. Az így kapható alul-, és felül áteresztő végtelen impulzusválasz ( IIR ) szűrők sorba kapcsolt másodfokú szűrőkből épülnek fel.
Minden másodfokú szűrő fokozat a következő jellemzőkkel rendelkezik:
d = 1,2, …,Ns, ahol k a másodfokú szűrő fokozat sorszáma,
Ns a fokozatok száma = (Na+1)/2.
Minden másodfokú szűrő fokozatnak két visszaható együtthatója van, (a1d, a2d).
Az összes visszaható együtthatók száma =2·Ns
Minden másodfokú szűrő fokozatnak három előreható együtthatója van, (b0d, b1d, b2d).
Az összes előreható együtthatók száma =3·Ns.
A jelfeldolgozó VI – okban, amelyek előre-, és visszaható együttható paraméterekkel működnek, vektorok tartalmazzák minden egyes másodfokú szűrő fokozat együtthatóit. Például egy IIR szűrőnél, amelynek két szűrő fokozata van, összesen 4 visszaható és 6 előreható együtthatót szükséges megadni, ahogy az alábbi egyenletek is mutatják.
|
Visszaható együtthatók száma = 2·Ns =4 | ||
|
Visszaható együtthatók: {a11, a12, a21, a22 } | ||
|
Előreható együtthatók száma = 3·Ns =6 | ||
|
Előreható együtthatók: {b01, b11, b21, b02, b12, b22 } |
10.8.3. Negyedfokú szűrés
A sáváteresztő és sávvágó szűrőknek , amelyeknek két határfrekvenciájuk van, a negyedfokú szűrő konstrukció jobb hatásfokú, mint a másodfokú szűrő fokozatok. A végtelen impulzusválasz ( IIR ) sávvágó, sáváteresztő szűrők a negyedfokú szűrők összekapcsolásával készíthetők, amelyek negyedfokú tagok sorba kapcsolásával jönnek létre.
Minden negyedfokú szűrő tag a következő jellemzőkkel rendelkezik:
d = 1,2, …,Ns, ahol d a negyedfokú szűrő fokozat sorszáma,
Ns a fokozatok száma = (Na+1)/4.
Minden negyedfokú szűrő fokozatnak négy visszaható együtthatója van, (a1d, a2d, a3d, a4d).
Az összes visszaható együtthatók száma =4·Ns
Minden negyedfokú szűrő fokozatnak öt előreható együtthatója van, (b0d, b1d, b2d , b3d, b4d).
Az összes előreható együtthatók száma =5·Ns.
A sorba kapcsolt fokozatokat összeépítjük egy negyedfokú szűrő struktúrába, olyan módon, ahogyan azt a másodfokú szűrésnél is tettük.
A következő egyenletek mutatják be, hogyan működik a szűrés negyedfokú tagok esetén.
|
|
(10.54) |
ahol
|
d = 1,2, …,Ns. |
az egyenletek a következő függvényből erednek:
|
|
(10.55) |
egy új bevezetett változóval M(z)-vel kifejezzük Y(z)-t:
|
|
(10.56) |
amely időtartományban
|
|
(10.57) |
ahol
|
|
(10.58) | |
|
|
(10.59) | |
|
|
(10.60) |
ami időtartományban
|
|
(10.61) |
10.8.4. IIR szűrő konstrukciók
A digitális végtelen impulzus válasz (IIR) szűrő típusok a klasszikus analóg szűrő típusok digitális megfelelői, amelyek a következők:
Butterworth-szűrők
Csebisev-szűrők
Csebisev II-szűrők, Inverz Csebisev vagy II-es típusú Csebisev szűrőként is ismert
Elliptikus-szűrők, más néven Cauer-szűrők
Bessel-szűrők
Az IIR szűrő típusok abban különböznek egymástól, hogy az átviteli sáv és a vágási sáv között milyen éles az átmenet illetve hogy milyen tulajdonságuk van-az átviteli és a vágási sávban.
10.8.5. Csúcshiba minimalizálása
A Csebisev , a Csebisev II , és Elliptikus szűrők minimalizálják a csúcshibát úgy, hogy közben az előírt hibát biztosítják a frekvencia válasz függvényben.
A csúcshiba alatt az ideális és aktuális szűrő frekvenciafüggvénye közötti különbségének abszolút érték maximumát értjük. A szűrő frekvencia függvényében megengedett hullámosság mértéke dB-ben kifejezve, meghatározza a tűréshatáron belüli hibát. Típustól függően a szűrő minimálisra csökkenti a csúcshibát az átviteli, a vágási sávban, vagy mindkettőben.
10.8.6. Butterworth-szűrők
A Butterworth-szűrők a következő jellemzőkkel rendelkeznek:
Csillapított amplitúdó függvény minden frekvencián
Az amplitúdó függvény monoton csökkenő egy adott határfrekvenciától
Maximális laposság, az átviteli sávban a válaszfüggvény egységnyi értékű, a vágási sávban pedig nulla.
Fél-teljesítmény frekvencia vagy 3 dB-s csökkenési frekvencia összefüggés-ben van a vágási frekvenciával.
A Butterworth-szűrők előnyei, a simaságuk és monoton csökkenő frekvencia függvényük. A 10.19. ábra - Aluláteresztő Butterworth-szűrő amplitúdó-frekvencia függvénye ábra egy aluláteresztő Butterworth-szűrő amplitúdó-frekvencia függvényét mutatja be.
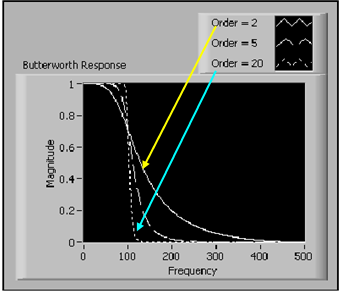
Ahogy a (10.19. ábra - Aluláteresztő Butterworth-szűrő amplitúdó-frekvencia függvénye) ábrán látható, mi határozzuk meg a Butterworth-szűrő vágási frekvenciáját, a LabVIEW beállítja az átmenet meredekségét annak arányában, hogy hányad fokú a szűrő. A magasabb fokú Butterworth-szűrő görbéje megközelíti az ideális aluláteresztő szűrő függvényét.
A Butterworth-szűrők nem mindig nyújtanak jó közelítést az ideális szűrő válaszfüggvényhez képest, mert lassú a lecsengésük az átviteli és vágási sáv között.
10.8.7. Csebisev-szűrők
A Csebisev szűrőknek a következő jellemzőik vannak:
Minimális csúcshiba az átviteli sávban
Egyenletes ingadozású amplitúdó függvény az átviteli sávban
Monoton csökkenő amplitúdó függvény a vágási sávban
Élesebb frekvencia levágású, mint a Butterworth-szűrők
A Butterworth-szűrőhöz hasonlítva egy Csebisev-szűrő élesebb frekvencia levágás valósít meg az átviteli és vágási sáv között, alacsonyabb fokú szűrővel. A Csebisev-szűrő éles átmenete kisebb abszolút hibát, gyorsabb végrehajtást eredményez, mint egy Butterworth-szűrőé. A (10.20. ábra - Aluláteresztő Csebisev-szűrő amplitúdó-frekvencia függvénye) ábra egy aluláteresztő Csebisev-szűrő amplitúdó-frekvencia függvényét mutatja.
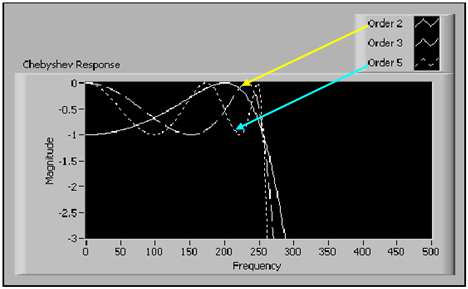
A (10.20. ábra - Aluláteresztő Csebisev-szűrő amplitúdó-frekvencia függvénye) ábrán az átviteli sávban a tűréshatár bekorlátozza az ingadozó görbét. az éles frekvencia levágás a vágási sávban jelentkezik.
10.8.8. Csebisev II - szűrők
A Csebisev II szűrőknek a következő jellemzői vannak:
Minimális csúcshiba a vágási sávban
Egyenletes ingadozású amplitúdó függvény a vágási sávban
Monoton csökkenő amplitúdó függvény az átviteli sávban
Élesebb frekvencia levágású, mint a Butterworth-szűrők
A Csebisev II - szűrők hasonlítanak a Csebisev-szűrőkre. A következőkben viszont eltérnek a Csebisev-szűrőktől : - A Csebisev II - szűrők az átviteli sáv helyett a vágási sávban csökkentik a csúcshibát.
A Csebisev-II szűrőknek egyenletes ingadozású amplitúdó függvénye van az átviteli sáv helyett a vágási sávban.
A Csebisev-II szűrőknek monoton csökkenő amplitúdó függvénye van az átviteli sávban a vágási sáv helyett.
A 10.20. ábra - Aluláteresztő Csebisev-szűrő amplitúdó-frekvencia függvénye ábra egy aluláteresztő Csebisev II – szűrő amplitúdó-frekvencia függvényét mutatja be.
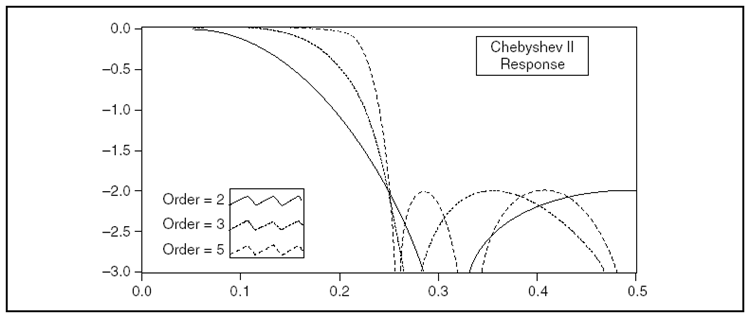
A (10.21. ábra - Aluláteresztő Csebisev II -szűrő amplitúdó-frekvencia függvényét) ábrán látható módon a hiba tűréshatára bekorlátozza az ingadozó görbét a vágási sávban. Szintén a vágási sávban látszik a sima, monoton lecsengés.
A Csebisev II –szűrőknek ugyanazok az előnyeik a Butterworth-szűrőkkel szemben, mint a Csebisev-szűrőknek, azaz élesebb átmenetük van egy alacsonyabb fokú szűrővel, kisebb abszolút hiba, gyorsabb működés mellett.
10.8.9. Elliptikus szűrők
Az elliptikus szűrők jellemzői:
Minimális csúcshiba a vágási és átviteli sávban
Egyenletes ingadozású amplitúdó függvény a vágási és átviteli sávban
Összehasonlítva a Butterworth vagy Csebisev-szűrőkkel, az Elliptikus szűrők adják a legélesebb átmenetet az átviteli és vágási sáv között, amely megmagyarázza, hogy miért annyira elterjedtek.
A 10.22. ábra - Aluláteresztő Elliptikus-szűrő amplitúdó-frekvencia függvénye ábra egy aluláteresztő Elliptikus szűrő amplitúdó-frekvencia függvényét mutatja.
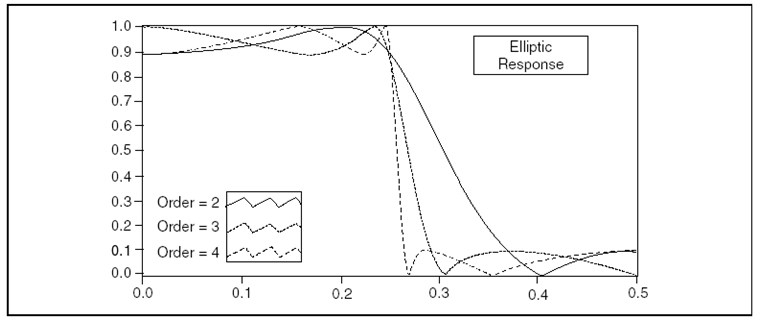
A (10.22. ábra - Aluláteresztő Elliptikus-szűrő amplitúdó-frekvencia függvénye) ábrán az azonos maximális elfogadható hiba (csúcshiba) bekorlátozza a hullámosságot a átviteli és a vágási sávban egyaránt. Még az alacsony fokú Elliptikus szűrőknek is meredek átmeneti élük van.
10.8.10. Bessel-szűrők
A Bessel-szűrők a következő tulajdonságokkal rendelkeznek:
Maximálisan lapos amplitúdó- és fázisfüggvény
Közel lineáris fázisfüggvény az átviteli sávban
A Bessel-szűrőket arra használhatjuk, hogy az összes IIR szűrőre jellemző nemlineáris fázistorzítást lecsökkentsük a segítségével. A nagy rendszámú IIR szűrőknek határozott, meredek lefutású nemlineáris fázistorzításuk van, különösen a szűrők átmeneti tartományában. Előállíthatjuk a lineáris fázisfüggvényt FIR szűrőkkel is.
A 10.23. ábra - Egy aluláteresztő Bessel-szűrő amplitúdó-frekvencia függvénye ábra egy aluláteresztő Bessel-szűrő amplitúdó-, és fázisfüggvényét ábrázolja.
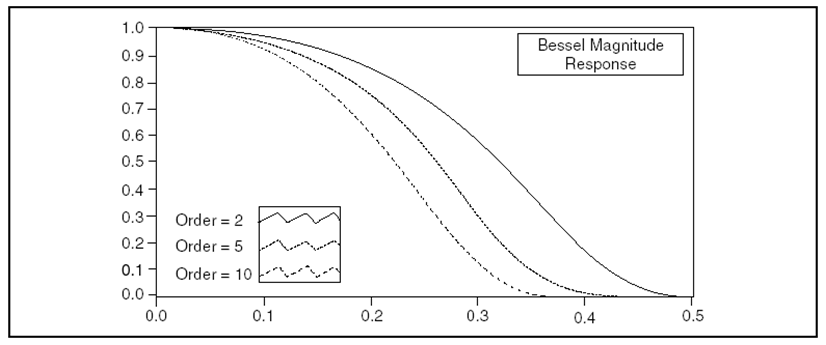
A (10.23. ábra - Egy aluláteresztő Bessel-szűrő amplitúdó-frekvencia függvénye) ábrán látható, hogy az amplitúdó görbe sima és monoton csökkenő minden frekvencián.
A 10.24. ábra - Aluláteresztő Bessel-szűrő fázis-frekvencia függvénye ábra egy aluláteresztő Bessel-szűrő fázis-frekvencia függvényét mutatja.
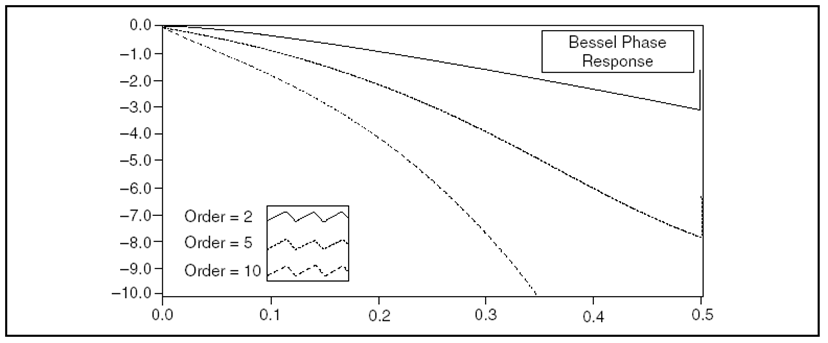
A 10.24. ábra - Aluláteresztő Bessel-szűrő fázis-frekvencia függvénye ábra közel lineáris fázismenetet mutat az átviteli sávban. A fázisfüggvény monoton csökkenő minden frekvencián.
A Butterworth-szűrőkhöz hasonlóan a Bessel-szűrőknél is magas fokszámú szűrőre van szükség, hogy lecsökkentsük a csúcshibát, amely korlátozott használatot tesz lehetővé.
10.8.11. IIR szűrők tervezése
Amikor egy feladatra kiválasztunk egy IIR szűrőt , ismernünk kell a szűrő válaszfüggvényét. A 10.25. ábra - IIR szűrő frekvenciaválasza ábra egy olyan VI blokkdiagramja, amely egy IIR szűrő impulzusra adott válaszfüggvényét határozza meg.
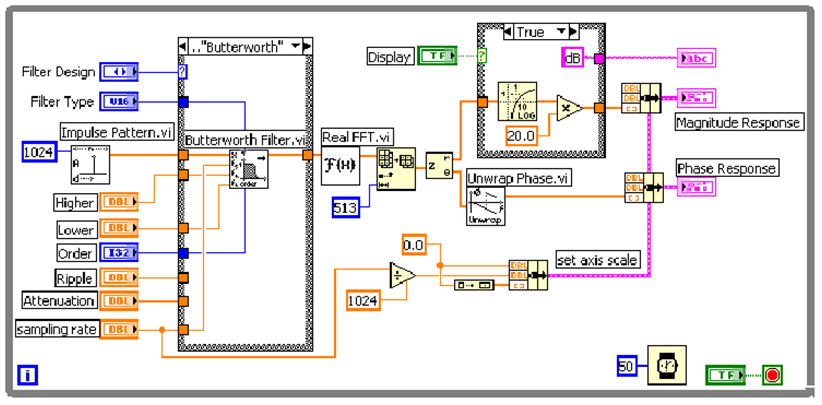
Azonos matematikai elméleteket alkalmaznak az IIR és FIR szűrők tervezésére, a (10.25. ábra - IIR szűrő frekvenciaválasza) ábrán látható VI blokkdiagram, amely egy IIR szűrő frekvenciaválaszát határozza meg, és a (10.11. ábra - Egyenletes hullámosságú sáváteresztő FIR szűrő frekvenciafüggvénye) ábrán látható VI blokkdiagram, amely egy FIR szűrő frekvenciaválaszát adja, közös tervező elemekből épülnek fel. A legfőbb különbség a két VI között az, hogy a 10.25. ábra - IIR szűrő frekvenciaválasza ábra bal oldalán lévő case struktúrában van, amelyik az IIR szűrő konstrukcióját is megadja a szűrő típusa mellett. A 10.25. ábra - IIR szűrő frekvenciaválasza ábra szerinti VI kiszámítja az IIR szűrő frekvenciaválaszát, közben ugyanazokat a lépéseket végzi el, amelyeket a FIR szűrők tervezése című fejezetben már bemutattunk.
A 10.26. ábra - Egy sáváteresztő elliptikus IIR szűrő amplitúdó és fázis függvénye ábra egy sáváteresztő elliptikus IIR szűrő amplitúdó- és fázisfüggvényét mutatja be.
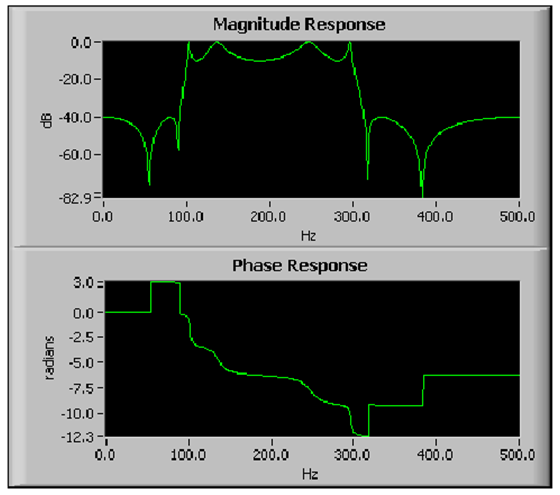
A (10.26. ábra - Egy sáváteresztő elliptikus IIR szűrő amplitúdó és fázis függvénye) ábrán látható fázis információ nyilvánvalóan nemlineáris. Amikor eldöntjük, hogy IIR vagy FIR szűrőt alkalmazunk az adatok feldolgozásához, jussanak eszünkbe a nemlineáris fázis információt nyújtó IIR szűrők. Bővebb információval szolgálhat az IIR és FIR közötti választásról ezen fejezet FIR és IIR szűrők összehasonlítása című és a Digitális szűrő típus kiválasztása című részei.
10.8.12. IIR szűrők jellemzői
Az IIR szűrők a következő tulajdonságokkal rendelkeznek:
Az IIR szűrő VI–k az első hívás alkalmával a 10.26. egyenlet szerint a negatív előjelű indexekkel jelölt értékeket nulla értéknek veszik.
Az átmeneti-függvény válasz vagy késleltetés, arányosan a szűrő fokszámával, és lezajlik mielőtt a szűrő eléri az állandósult állapotát. Bővebb információt erről a témáról ezen fejezet „ Átmeneti függvény ” című része ad.
A szűrt jelsorozat elemeinek száma megegyezik a bemenő sorozat elemeinek számával.
A szűrő megtartja a belső állapot értékeit, amikor a szűrési művelet befejeződik.
10.8.13. Átmeneti függvény
Az átmeneti válasz (függvény) azért jelenik meg, mert a szűrő kezdeti állapota nulla, vagy értékek vannak a negatív előjelű indexeknél. Az átmeneti válasz függvény késleltetése függ a szűrő típusától.
Az átmeneti válasz (függvény) késleltetése alul- és felüláteresztő szűrőnél egyenlő a szűrő rendszámával (mintavételi időlépésekben).
|
Késleltetés alul,felül áteresztő szűrő = a szűrő_rendszáma |
(10.62) |
Az átmeneti válasz (függvény) késleltetése sáváteresztő és sávvágó szűrőnél egyenlő a szűrő rendszámának kétszeresével (mintavételi időlépésekben).
|
Késleltetés sáváteresztő sávvágó szűrő = 2·a_szűrő_rendszáma |
(10.63) |
Eltüntethetjük az átmeneti választ (függvényt) egy IIR szűrő VI sorozatos meghívásával, ha engedélyezzük az állapot memóriát.
Hogy a folyamatos szűrés számára engedélyezzük az állapot memóriát, az IIR szűrő VI init/cont bementére kapcsoljunk egy IGAZ (TRUE) értéket.
A 10.27. ábra - Átmeneti (tranziens) válaszfüggvény és egy IIR szűrő állandósult állapota ábra bemutat egy átmeneti választ (függvényt) és az IIR szűrő állandósult állapotát.
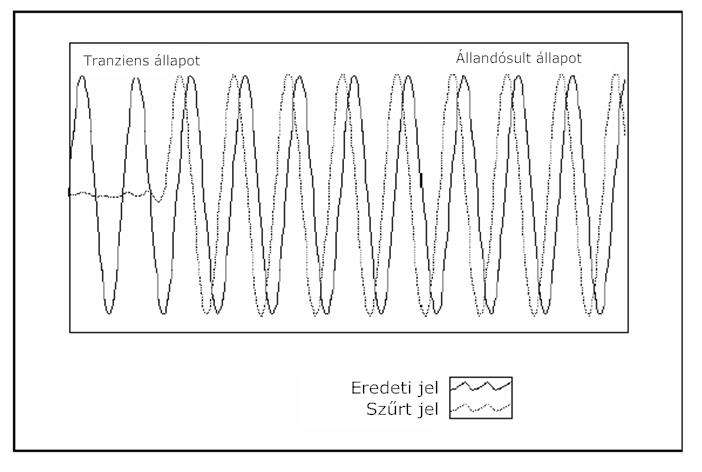
10.9. A FIR és az IIR szűrők összehasonlítása
Mivel a digitális szűrők tervezésekor kompromisszumokat kell kötnünk, hogy egy számunkra fontos szűrő jellemzőt kiemeljünk a kevésbe fontos jellemzők közül, a FIR és IIR szűrők összehasonlítása segítséget nyújthat egy adott feladat megoldásához szükséges szűrő kiválasztásában.
Az IIR szűrők ugyanolyan mértékű csillapításra képesek, mint a FIR szűrők, de sokkal kevesebb együttható alkalmazásával. Ebből kifolyólag az IIR szűrők sokkal gyorsabban működnek, és hatásosabb szűrő eljárást valósítanak meg, mint egy FIR szűrő.
Lineáris fázisfüggvényhez alkalmazzunk FIR szűrőt. Az IIR szűrők nemlineáris fázisfüggvényt hoznak létre. Lineáris fázisfüggvényt igénylő feladatokhoz tehát FIR szűrőt használjunk!.
A fázis információt nem igénylő feladatokhoz használjunk IIR szűrőt.
Bővebb információval szolgál erről a témáról ezen fejezet Digitális szűrő típus kiválasztása című része.
10.10. Nemlineáris szűrők
A simító ablakok, az IIR szűrők és a FIR szűrők lineárisak, mert eleget tesznek a szuperpozíció és az arányosság elvének, ahogy a 10.64. egyenlet leírja.
|
L {a·x(t) + b·y(t)} = a·L {x(t)} + b·L {y(t)} |
(10.64) |
ahol a és b állandók , x(t) és y(t) villamos jelek (időfüggvények) , L{} egy lineáris szűrő művelet, a bemenetek és kimenetek közötti összefüggés műveleteken keresztül valósul meg, ahogy azt a 10.31. és 10.43. egyenlet leírja.
Egy nemlineáris szűrő nem tesz eleget a 10.64. egyenletnek. Ezen kívül nem határozhatjuk meg a nemlineáris szűrő kimenő jeleit konvolúciós művelet segítségével, mert az együtthatók egy összeállítása és a szűrő impulzusválasza között nincs (nem állapítható meg) egyértelmű kapcsolat. A nemlineáris szűrők sajátos szűrőkarakterisztikával rendelkeznek, amelyeken nagyon bonyolult a lineáris számolási eljárások alkalmazása.
A medián szűrő egy olyan nemlineáris szűrő, amely egyesíti magában az aluláteresztő szűrő és egy magas frekvenciájú szűrő jellemzőit. Az aluláteresztő tulajdonságok lehetővé teszik a nagy frekvenciás zaj ”eltűntetését”. A nagyfrekvenciás tulajdonságok lehetővé teszik, hogy a medián szűrő megtartsa az éleket és megkímélje azok információtartalmát.
Példa:
Zajos impulzus szűrése Medián szűrővel
Az “Impulzus paraméter.VI” (Pulse Parameters.VI) elemezi egy impulzus diagram bemenő sorozatát, és előállítja azokat az impulzus paramétereket, amelyek legjobban leírják ezt az impulzust. Miután a VI elvégzi a jelalak elemzését, azért hogy meghatározza az időtengelyt és a bemenő sorozat csúcsát, további információ nélkül a jel és a zaj megkülönböztetése nehézkessé válik. Ezért az impulzus paraméterek pontos meghatározásához a bemenő jelsorozat zajrésze maximális amplitúdójának kisebbnek vagy egyenlőnek kell lennie az impulzus átlagos amplitúdójának 50%-ánál. Számos gyakorlati alkalmazásnál nehéz elérni az 50%-os jel/zaj viszonyt. A szükséges jel/zaj viszony teljesítéséhez még el kell végezni egy sor számítási műveletet, hogy kiemeljük az impulzus lényeges információit.
Ha az impulzus olyan zajjal rendelkezik, amelynek átlagos amplitúdó maximuma meghaladja az impulzus átlagos amplitúdójának 50%-át, akkor aluláteresztő szűrőt használhatunk a nem kívánatos zaj eltávolításra. Azonban a szűrő időben eltolja (késlelteti) a jelet, és eltompítja az impulzus éleit, mivel ”levágja” az átmeneti élek magas frekvenciájú információt. A Medián szűrő hatásosabban tudja az impulzust szűrni, mint egy aluláteresztő szűrő, mert megóvja az élek információtartalmát, miközben eltünteti a magas frekvenciájú zajt.
A 10.28. ábra - A Medián szűrő alkalmazása, hogy meghatározzuk az impulzus információit ábra egy VI blokk diagramját mutatja, amely létrehoz, és analizál egy zajos impulzust.
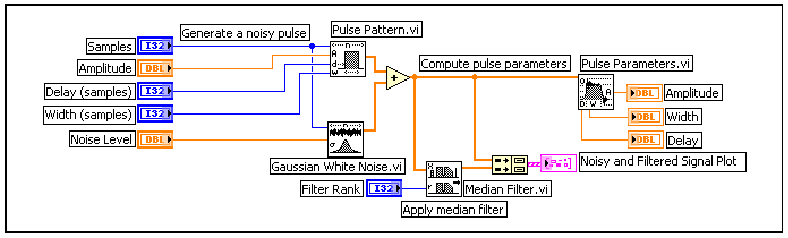
A (10.28. ábra - A Medián szűrő alkalmazása, hogy meghatározzuk az impulzus információit) ábrán látható VI létrehoz egy zajos impulzust, amelyben az átlagos zaj csúcs amplitúdó az impulzus amplitúdó 100%-ánál nagyobb. A (10.28. ábra - A Medián szűrő alkalmazása, hogy meghatározzuk az impulzus információit) ábrán lévő VI által generált jel a következő ideális impulzus értékekkel rendelkezik:
5.0 V –os amplitúdó
64 mintavételnyi késleltetés
32 mintavételnyi szélesség
A 10.29. ábra - Zajos impulzus és Medián szűrővel szűrt impulzus ábra bemutatja a zajos impulzust, a szűrt impulzust, és a (10.28. ábra - A Medián szűrő alkalmazása, hogy meghatározzuk az impulzus információit) ábrán lévő VI-ből visszatérő becsült impulzus paramétereket.
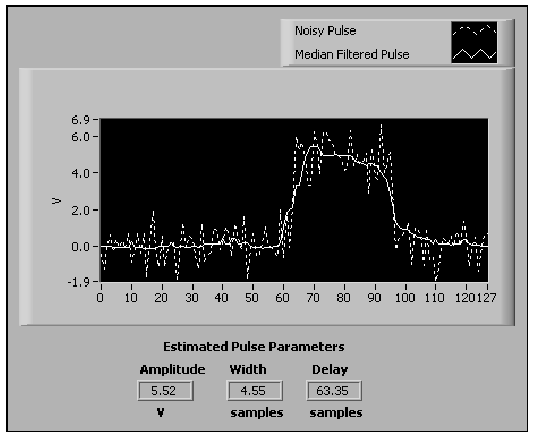
A (10.29. ábra - Zajos impulzus és Medián szűrővel szűrt impulzus) ábrán a Medián szűrővel létrehozott impulzus jelet kísérhetjük figyelemmel, úgy hogy a zaj eltorzítja az impulzust.
Az elemzés szabályos elvégzéséhez a Medián szűrő.VI–al eltávolíthatjuk a magas frekvenciájú zajt. Az 50%-os jel/zaj viszony eléréséhez, az „Impulzus paraméter VI”-t alkalmazzuk.
10.11. Digitális szűrő típus kiválasztása
Egy konkrét feladathoz legalkalmasabb szűrő kiválasztásához a következő kérdésekre kell választ adni:
A szűrés eredménye lineáris fázisfüggvényt igényel?
Az elemzés elviseli az amplitúdó függvény ingadozásait?
Szűk frekvencia átviteli sávra van szükség?
Egy gyakorlati feladatban alkalmazhatjuk a 10.30. ábra - A megfelelő szűrő kiválasztásának folyamatábrája ábrát segítségként, a megfelelő szűrő típus kiválasztásához.
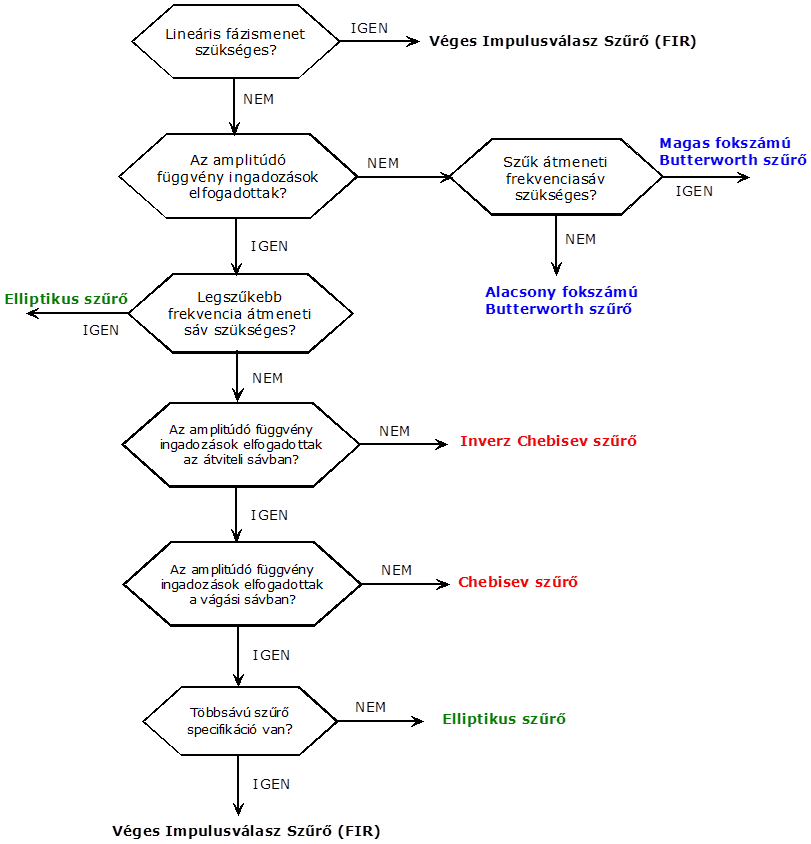
A 10.30. ábra - A megfelelő szűrő kiválasztásának folyamatábrája ábra egy kiválasztási módszert mutat be az adott feladathoz legjobban megfelelő szűrő kiválasztására. Általában több szűrő típust is ki kell kipróbálni, hogy közülük megtaláljuk a legalkalmasabbat.
Irodalom
[10.1.] LabVIEW Control Design User Manual. 2009.
11. fejezet - Diszkrét frekvencia analízis
- 11.1. A frekvencia és az időtartomány közötti különbségek
- 11.2. Fourier transzformáció, mint a DFT alapja
- 11.3. (Időben) Diszkrét Fourier transzformáció (DFT)
- 11.4. Frekvencia lépés a DFT minták között
- 11.5. Gyors Fourier transzformáció alapjai (FFT= Fast Fourier Transformation)
- 11.6. A frekvencia információ megjelenítése a Fourier transzformáció után
- 11.7. Kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció
- 11.8. Teljesítmény Spektrum SAA(f)
- 11.9. A spektrumokkal végzett számítások
- 11.10. Amplitúdó és fázis spektrumok kiszámítása
- 11.11. Frekvencia válasz függvény
- 11.12. Kereszt teljesítmény spektrum SAB(f) (Cross Power Spectrum)
- 11.13. Frekvencia válasz és hálózat analízis
- 11.14. Ablakozási technika
- 11.15. Átlagolás a mérési eredmények ábrázolásához
- 11.16. Visszhang észlelése
- Irodalom
Ez a fejezet tárgyalja a diszkrét Fourier transzformáció (DFT = Discrete Fourier Transformation) alapjait, a gyors Fourier transzformációt (FFT = Fast Fourier Transform), az alapvető jelanalízis számításokat, a teljesítmény spektrumon végrehajtott számításokat, és azt hogy hogyan kell alkalmazni az FFT-alapú függvényeket hálózatok mérésére. Használjuk az NI = National Instruments Példakeresőt, hogy megtaláljuk azokat a mintapéldákat, amelyek alkalmazzák a digitális jelfeldolgozó VI-ket és a mérés analízis VI-ket, FFT és frekvenciaanalízis elvégzéséhez.
11.1. A frekvencia és az időtartomány közötti különbségek
Az időtartománybeli ábrázolás a mintavételi időpontokban megadja a jel amplitúdóját, amelyet mintavételeztünk. Bár sok esetben inkább a jel frekvencia tartalmát kell ismernünk, mint az egyedi minták amplitúdóit.
A Fourier-tétel kimondja , hogy bármely időtartománybeli hullámalakot le lehet írni sinus és cosinus függvények súlyozott összegeként. Ugyanazt a hullámalakot megjeleníthetjük frekvencia tartományban is, mint az egyes frekvencia összetevők amplitúdóját és fázisát.
Előállíthatunk bármely hullámalakot szinusz hullámok összegeként, ahol az egyes szinuszos tagok önálló amplitúdó és fázis értékkel rendelkeznek. A 11.1. ábra - Három frekvencia komponens összeadásával kialakult jel ábra bemutatja az eredeti hullámalakot, és az összetevő tag frekvenciákat. Az alapfrekvencia 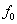 -lal van jelölve, a második felharmonikus 2·
-lal van jelölve, a második felharmonikus 2·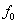 frekvenciájú, a harmadik felharmonikus pedig 3·
frekvenciájú, a harmadik felharmonikus pedig 3·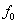 frekvenciájú.
frekvenciájú.
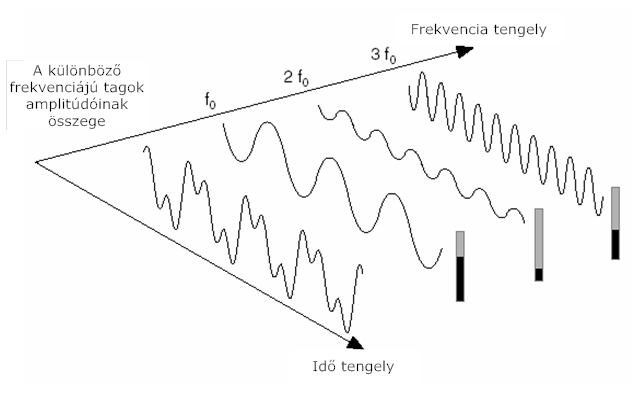
A frekvencia tartományban meghatározhatók azok a szinusz komponens függvények, amelyek létrehozznak egy komplex időtartománybeli hullámalakot.
A 11.1. ábra - Három frekvencia komponens összeadásával kialakult jel ábra egy olyan hullámalakot mutat be, amely az időtartományban úgy bontható fel komponensekre, mint a frekvencia tartományban különböző szinuszos komponensekre. Minden frekvencia komponens amplitúdója megegyezik az ehhez a frekvencia komponenshez tartozó időtartománybeli hullámalak amplitúdójával. A jel megjelenítése egyéni frekvencia komponensek segítségével a frekvencia tartománybeli megjelenítés . A frekvencia tartománybeli megjelenítés általában számos lényeges információt ad meg a jelről és arról a rendszerről, amellyel létrehoztuk.
A jelátalakítóból (analóg/digitális átalakítóból) érkező minták időtartományban írják le a jelet. Néhány analízis adat, mint például a harmonikus torzítás értékét nehéz pontosan meghatározni az időtartománybeli hullámalak tanulmányozásával. Amikor ugyanazt a jelet egy FFT analizátor (Dinamikus Jel analizátorként is ismert) műszer segítségével megjelenítjük frekvencia tartományban, könnyen megállapíthatjuk a harmonikus frekvenciákat és az amplitúdókat.
A Parseval tétel
A Parseval-tétel kimondja, hogy az időtartományban meghatározott (kiszámított) összes energiának meg kell egyeznie a frekvenciatartományban kiszámított összes energiával. Ez az energia-megmaradás tétele . A 11.1 egyenlet a Parseval tétel folytonos alakja. A 11.2 egyenlet pedig a Parseval tétel időben diszkrét alakja.
|
|
(11.1) | |
|
|
(11.2) |
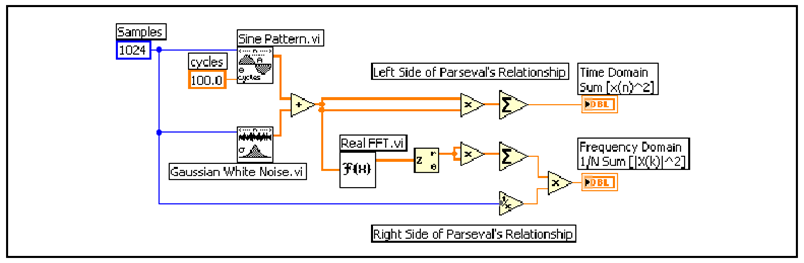
A (11.2. ábra - A VI diagram panelje, amely meghatározza a Parseval tételt) ábrán látható VI Diagram panel egy valós bemeneti jelsorozaton végzett műveleteket mutat be. A blokkdiagram felső része az időtartománybeli jel energiáját határozza meg a 11.1 egyenlet bal oldalát alkalmazva. A blokk diagram alsó része átkonvertálja az időtartománybeli jelet frekvencia tartományba és meghatározza a frekvenciatartománybeli jel energiáját a 11.1 egyenlet jobb oldalát alkalmazva.
A 11.3. ábra - A Parseval VI eredményei ábra a (11.2. ábra - A VI diagram panelje, amely meghatározza a Parseval tételt) ábrán bemutatott VI számított eredményeit mutatja be.
A 11.3. ábra - A Parseval VI eredményei ábra bemutatja, hogy az összes számított energia az időtartományban megegyezik a frekvencia tartományban meghatározott értékkel.
11.2. Fourier transzformáció, mint a DFT alapja
A 6.2. szakasz - A Fourier sortól a Fourier és a Laplace transzformációig fejezetben részletesen bemutattuk a Fourier transzformáció kialakulásának történetét és kapcsolatát a Fourier sorral. Jelen fejezetben felhasználva ezeket ez elméleti ismereteket, a mintavételes jelek Fourier transzformációját mutatjuk be.
A Fourier transzformáció egy olyan eljárás, amellyel a jel tulajdonságait és azok kapcsolatait vizsgálhatunk meg frekvencia tartományban. A Fourier transzformáció leggyakoribb alkalmazása a lineáris idő-invariáns rendszerek vizsgálata valamint a spektrum analízis.
A következő egyenlet a kétoldalas Fourier transzformációt definiálja:
|
|
(11.3) |
A következő egyenlet a kétoldalas inverz Fourier transzformációt adja meg:
|
|
(11.4) |
A kétoldalas Fourier transzformáció azt jelenti, hogy a Fourier transzformáció és az Inverz Fourier transzformáció figyelembe veszi az összes negatív és pozitív frekvenciájú és időpontú jelet a transzformációnál. Az egyoldalas transzformáció azt jelenti, hogy a transzformáció matematikai leírása csak a jel pozitív frekvenciáit és időtartománybeli történéseit veszi figyelembe.
A Fourier transzformáció pár tartalmazza a jel reprezentációját mind idő mind pedig frekvencia tartományban. A következő összefüggés általánosan mutatja be a Fourier transzformáció párt.
|
|
(11.5) |
11.3. (Időben) Diszkrét Fourier transzformáció (DFT)
Az algoritmust, amelyet arra használunk, hogy időtartománybeli mintavételezett jel értékeket frekvencia tartományba transzformáljunk (időben) Diszkrét Fourier transzformációnak (DFT) nevezzük (lásd 6.5. szakasz - Diszkrét Fourier transzformáció (DFT) fejezet). A DFT kapcsolatot állít fel az időtartománybeli jel mintavételezett értékei (minta-értékek) és frekvencia tartománybeli reprezentációjuk között. A DFT-t széles körben alkalmazzák a spektrum analízisben, az alkalmazott mechanikában, hang-elemzéseknél, képfeldolgozásoknál, numerikus analízisnél, műszer és telekommunikációs feladatoknál.
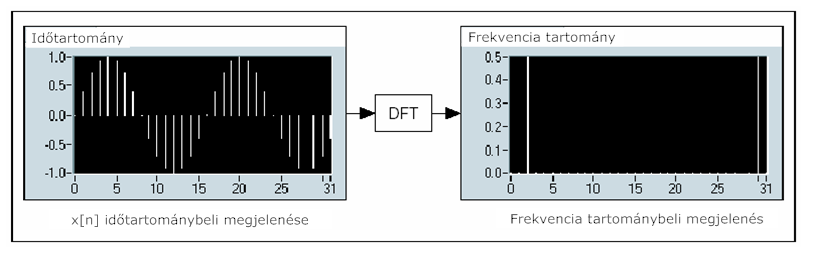
Tételezzük fel, hogy rendelkezésünkre áll egy N mintából álló adatcsomag egy mérésadatgyűjtő berendezésből. Ha alkalmazzuk a diszkrét Fourier transzformációt (DFT) erre az időtartománybeli N mintára , az eredmény szintén N értéket fog tartalmazni és a jel frekvencia tartománybeli tulajdonságait jeleníti meg.
11.3.1. Kapcsolat az N mintát tartalmazó időtartománybeli és frekvenciatartománybeli jel értékek között
Ha a jelből egy megadott mintavételi frekvenciával veszünk mintákat, a 11.6 egyenlet megadja az egyes minták közötti időtartamot, vagy más néven mintavételi időt .
|
|
(11.6) |
ahol
|
h |
a mintavételi időtartam, | |
|
f s |
pedig a mintavételi frekvencia (minta/másodperc). |
A mintavételi időből lehet meghatározni azt a legkisebb frekvenciát, amelyet a rendszer még meg tud vizsgálni a DFT illetve a hozzá kapcsolódó eljárások segítségével.
A 11.7 egyenlet definiálja a diszkrét Fourier transzformációt . A függvény eredményei az X[k] értékek, amelyek a frekvencia tartományban adják meg a mintavételezett jel Fourier transzformált értékét.
|
|
(11.7) |
ahol
|
x[i] |
értékek a mintavételezett jel időtartománybeli értékei | |
|
N |
a minta értékeinek száma. |
Hasonlóan a h időlépéshez, amely az időtartományban adja meg az x mintái közötti időtartamot az X frekvenciatartománybeli megjelenítésében is van egy frekvencia lépés vagy frekvencia felbontás, amely a 11.8 egyenlet ad meg.
|
|
(11.8) |
ahol
|
Δf |
a frekvencia felbontás, | |
|
f S |
a mintavételi frekvencia, | |
|
N |
a minták száma, | |
|
h |
a mintavételi idő, | |
|
N.h |
pedig a teljes vizsgálati időtartam. |
A frekvencia felbontás növeléséhez, azaz Δf csökkentéséhez, növelni kell a minták számát (N) mialatt a mintavételi frekvenciát (f S ) állandó értéken tartjuk, vagy csökkenteni kell a mintavételi frekvenciát mialatt az N értékét tartjuk állandó értéken. Mindkét megközelítés az N·h vizsgálati időtartam megnövelését jelenti.
11.3.2. Mintapélda a Diszkrét Fourier Transzformáció (DFT) meghatározására
Ez a fejezet egy mintapéldát mutat be, amely alkalmazza a 11.3 diszkrét jelekre érvényes alakját, a 11.7 egyenletet azért, hogy meghatározzuk egy egységugrás jel diszkrét Fourier transzformált értékét. A példában a következő feltételezéseket alkalmazzuk:
X[0] a jel átlagértéke vagy 0(nulla) frekvenciájú komponense.
A 0(nulla) frekvenciájú komponensnek állandó +1 V amplitúdója van.
4 mintavételi értékünk van.
Minden minta értéke +1 V nagyságú, ahogy azt a 11.5. ábra - A DFT példa időtartománybeli jelsorozata ábra mutatja.
Az eredményként kapott idősort a következő egyenlet adja meg:
|
x[0] = x[1] = x[2] = x[3]= 1 |
(11.9) |
/Mivel ez az idősor véges, ezért a konvergencia feltétel automatikusan teljesül. Ilyen értelemben beszélhetünk itt az egységugrás Fourier transzformáltjáról. Általános értelemben a folyamatosan mintavételezett egységugrásnak csak Z transzformáltja létezik. (lásd 11.1. táblázat - X[p] értékei N = 8 esetén táblázatot)/
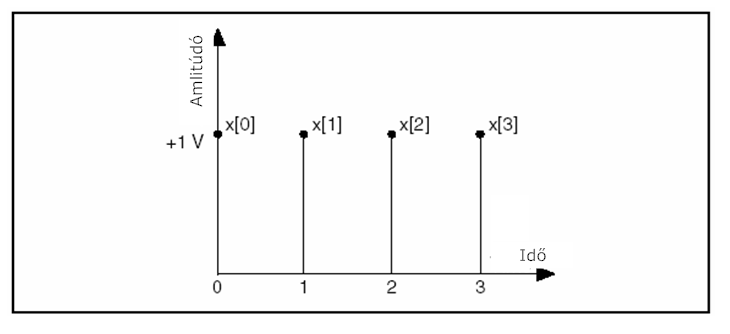
A DFT alkalmazza az Euler összefüggést, amelyet a következő egyenlet ad meg:
|
|
(11.10) |
Ha a 11.3 egyenletet alkalmazzuk, hogy meghatározzuk a DFT sorozatot a (11.5. ábra - A DFT példa időtartománybeli jelsorozata) ábrán bemutatott jelsorozathoz és alkalmazzuk az Euler összefüggést, a következő egyenleteket kapjuk:
|
|
(11.11) | |
|
|
(11.12) | |
|
|
|
(11.13) |
|
|
|
(11.14) |
ahol
|
X[0] |
a 0 frekvenciájú komponens amplitúdója, | |
|
N |
a minták száma. |
Így a 0 frekvenciájú komponenst kivéve minden további érték 0 (nulla) értékű a DFT sorozatban, ahogy azt feltételeztük. Az X[0] értéke a DFT elvégzése után meghatározóan függ N értékétől. Mivel a példánkban N=4 volt, így X[0]=4. Ha N=10 lett volna a transzformáció után X[0]=10 lett volna.
Ez a függőségi viszony X[0] és N között megjelenik az összes további frekvencia komponensnél is. Ezért a DFT után kapott kimeneti értékeket rendszerint elosztjuk N-el, hogy a frekvencia komponensek korrekt amplitúdóit kapjuk meg.
11.3.3. Amplitúdó és fázis információ
A bemeneti időtartománybeli jel N minta értéke N értéket fog meghatározni a Diszkrét Fourier transzformáció segítségével. A 11.3 egyenlet bemutatja, hogy a bemeneti jel x[i] lehet valós vagy komplex érték , az X[k] azonban mindig komplex érték , bár az imaginárius rész lehet nulla értékű is. Más megfogalmazásban minden frekvencia komponensnek van amplitúdója és fázistolása.
Leggyakrabban az amplitúdó spektrumot szoktuk megjeleníteni egy diagramban, amely nem más, mint X[k] valós és képzetes rész négyzetének összegéből vont négyzetgyök (a komplex szám abszolút értéke).
A fázistolás az időrekordok kezdetére vonatkozik vagy egy egyciklusú cosinus hullám kezdetére, amely az időrekordok kezdeténél indul el. Egycsatornás fázistolás mérések csak akkor stabilak, ha bemeneti jel triggerelt jelérték. Kétcsatornás fázis mérésnél meghatározható a fáziseltérés a csatornák jelei között, így ha a csatornákat egyszerre mintavételezzük triggerelés rendszerint nem szükséges.
A fázistolás a képzetes és a valós rész hányadosának arcus tangense, rendszerint π és -π értékek közötti számérték radiánban, vagy 180° és –180° közötti érték fokban.
A valós jel (x[i] valós) Diszkrét Fourier transzformáltja a következő szimmetrikus tulajdonságokkal rendelkezik:
|
|
(11.15) | |
|
|
(11.16) |
Az amplitudó X[k] páros szimmetriájú , míg a fázis(X[k]) páratlan szimmetriával rendelkezik. A páros szimmetriájú jel szimmetrikus az y tengelyre, míg a páratlan szimmetriájú jel az origóra szimmetrikus.
A 11.6. ábra - A jel páros és páratlan szimmetriája ábra a páros és páratlan szimmetriát mutatja be.
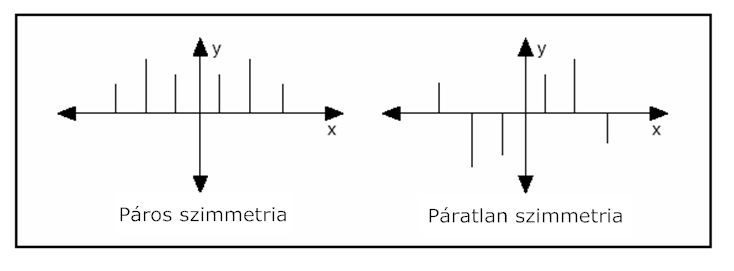
A szimmetria miatt a Diszkrét Fourier Transzformáció N értéke az információt duplikáltan tartalmazza. Emiatt a DFT értékeinek csak a felét kell kiszámítani, mivel a másik fél értékeinek meghatározásánál felhasználhatjuk a már kiszámított értékeket.
Ha a bemeneti jel ( x[i] ) komplex érték és a DFT aszimmetrikussá válik, ekkor az előbb javasolt számítási eljárás nem alkalmazható.
11.4. Frekvencia lépés a DFT minták között
Ha a mintavételi időintervallum h másodperc és az első mintaadat (k=0) a 0-dik másodpercbeli mérési adat és a (k>0) akkor a k-dik mintavételi adat a k.h másodpercnél mért jel értéke. Hasonlóan, ha a frekvencia felbontás Δf, akkor a DFT k-dik eleme a k×Δf Hz frekvenciájú komponens lesz. Ez a megállapítás a frekvencia komponensek első felére érvényes, a komponensek másik felében a negatív frekvencia komponensek találhatók.
Meg lehet adni egy olyan mintavételi frekvenciát, amellyel a mintavételezett jelben lévő maximális frekvenciát is mindig pontosan elő tudjuk állítani alul-mintavételezés (aliasing) nélkül, ez az úgynevezett Nyquist frekvencia .
A Nyquist frekvencia megegyezik az alkalmazott mintavételi frekvencia felével , amelyet a következő képlettel írhatunk le:
|
|
(11.17) |
ahol 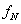 a Nyquist frekvencia,
a Nyquist frekvencia, 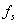 a mintavételi frekvencia (sampling frequency) (sample/secundum = minta /másodperc).
a mintavételi frekvencia (sampling frequency) (sample/secundum = minta /másodperc).
Attól függően, hogy az N értéke páros vagy páratlan különböző a DFT k-dik komponense. Például, ha N=8 és p adja meg a Nyquist frekvencia indexét, p = N/2 = 4.
A 11.1. táblázat - X[p] értékei N = 8 esetén táblázat mutatja be a Δf lépéssel a komplex X sorozatot.
|
X[p] |
Δf |
|
X[0] |
0 frekvencia |
|
X[1] |
Δf |
|
X[2] |
2×Δf |
|
X[3] |
3×Δf |
|
X[4] |
4×Δf (Nyquist frekvencia) |
|
X[5] |
-3×Δf |
|
X[6] |
-2×Δf |
|
X[7] |
-Δf |
A negatív értékek a második oszlopban a Nyquist frekvencia felett negatív frekvenciákat jelentenek, ezek azok az elemek, amelyeknek az indexe nagyobb mint p.
Ha N=8, X[1]-nek és X[7]-nek ugyanaz az amplitúdója; X[2]-nek és X[6]-nak ugyancsak azonos az amplitúdója; X[3]-nak és X[5]-nek hasonlóan azonos az amplitúdója. A különbség csupán az, hogy X[1], X[2] és X[3] pozitív frekvenciákhoz tartozik, míg az X[5], X[6] és X[7] negatív frekvenciákhoz. X[4] értéke a Nyquist frekvenciánál mérhető.
A 11.7. ábra - X komplex kimeneti sorozat N=8 esetén ábra a X komplex kimeneti sorozatot mutatja N=8 esetén.
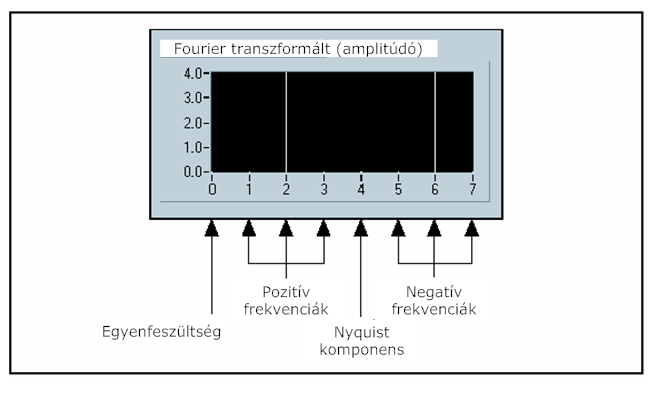
Ez egy reprezentáció, ahol láthatók a kétoldalas transzformáció pozitív és negatív frekvenciái.
Amikor N páratlan, akkor nincs komponens a Nyquist frekvenciánál. A 11.2. táblázat - X[p] értékei N = 7 esetén táblázat bemutatja az X[p] értékeket Δf lépéssel, amikor N=7 és p = (N-1)/2 (7-1)/2= 3.
|
X[p] |
Δf |
|
X[0] |
0 frekvencia (állandó jel érték, egyenfeszültség) |
|
X[1] |
Δf |
|
X[2] |
2×Δf |
|
X[3] |
3×Δf |
|
X[4] |
-3×Δf |
|
X[5] |
-2×Δf |
|
X[6] |
-Δf |
Ez egy reprezentáció, ahol láthatók a kétoldalas transzformáció pozitív és negatív frekvenciái.
Ha N=7, X[1]-nek és X[6]-nek ugyanaz az amplitúdója; X[2]-nek és X[5]-nak ugyancsak azonos az amplitúdója; X[3]-nek és X[4]-nek hasonlóan azonos az amplitúdója. A különbség csupán az, hogy X[1], X[2] és X[3] pozitív frekvenciákhoz tartozik, míg az X[4], X[5] és X[6] negatív frekvenciákhoz. Mivel N értéke páratlan nincs komponens a Nyquist frekvenciánál .
A 11.8. ábra - X[p] komplex kimeneti sorozat N=7 esetén ábra a X komplex kimeneti sorozatot mutatja N=7 esetén.
![X[p] komplex kimeneti sorozat N=7 esetén](images/image_XI_8.png)
Ez egy reprezentáció, ahol láthatók a kétoldalas transzformáció pozitív és negatív frekvenciái.
11.5. Gyors Fourier transzformáció alapjai (FFT= Fast Fourier Transformation)
A Diszkrét Fourier transzformáció közvetlen megvalósításánál N minta esetén közelítőleg N 2 komplex műveletet kell elvégeznünk, amely nagyon időigényes számítási művelet.
A Gyors Fourier transzformáció (FFT) egy olyan (gyors) algoritmus, amellyel kiszámíthatjuk a DFT-at. A következő egyenlet adja meg a DFT transzformációs képleltét:
|
|
(11.18) |
ahol
|
x[i] |
értékek a mintavételezett jel időtartománybeli értékei | |
|
N |
a minta értékeinek száma. |
A következő mérések magukba foglalják az FFT alapú jelanalízis alapfüggvényeit:
FFT
Teljesítmény spektrum
Kereszt teljesítmény spektrum
Ezek az alapfüggvények felhasználhatók, hogy segítségükkel létrehozzunk további mérési függvényeket, mint például a frekvencia válaszfüggvényt vagy az impulzus választ illetve a koherencia függvényt valamint az amplitúdó illetve a fázis spektrumot .
Az FFT és a teljesítmény spektrum nagyon hasznos az állandósult és a tranziens jelek frekvencia tartalmának mérésénél. Az FFT egy átlagos frekvencia tartalmat ad meg a teljes mérési tartományban. Ezért az FFT-t akkor célszerű alkalmazni, ha a jel állandósult állapotban van vagy abban az esetben, ha egy átlagos energiatartalomra van szükség mindegyik frekvenciánál.
Egy FFT megegyezik egy olyan párhuzamosan kapcsolt szűrő csoporttal, amelynek a sávszélessége Δf középpontú és minden frekvencia komponense 0 (nulla) frekvenciától növekszik 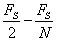 lépésközzel. Ezért a frekvencia komponenseket frekvencia tárolóknak vagy FFT tárolóknak nevezzük.
lépésközzel. Ezért a frekvencia komponenseket frekvencia tárolóknak vagy FFT tárolóknak nevezzük.
A Teljesítmény spektrum alfejezet még ebben a fejezetben további információkat közöl a teljesítmény spektrumról.
11.5.1. A frekvencia komponensek kiszámítása
Minden frekvencia komponens egy időtartománybeli jel amplitúdó értékének és egy exponenciális alakban felírt komplex számnak a szorzata, ahogy azt a következő egyenlet megadja:
|
|
(11.19) |
ahol
|
k=0, 1, 2,....., N-1 |
A 0 (k=nulla) frekvenciájú komponens az 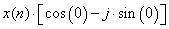 értékek sorozata különböző n értékeknél.
értékek sorozata különböző n értékeknél.
Az első (k=1) frekvencia komponens az 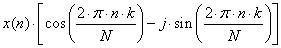 értékek sorozata különböző n értékeknél. Mivel ilyenkor k=1 a
értékek sorozata különböző n értékeknél. Mivel ilyenkor k=1 a  függvény egy egyszeres frekvenciájú cosinus jelet, míg a
függvény egy egyszeres frekvenciájú cosinus jelet, míg a 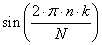 függvény egy egyszeres frekvenciájú sinus jelet fog eredményezni.
függvény egy egyszeres frekvenciájú sinus jelet fog eredményezni.
Általánosan, a k-ik tároló az x(n) jelek szorzata k ciklusú cosinus függvényekkel, amelyekből az X(k) valós részét, míg a sinus jelek segítségével az X(k) képzetes részét állítjuk elő.
Az FFT alkalmazása frekvencia analízisre további két fontos összefüggéssel rendelkezik .
Az első összefüggés megadja a legmagasabb analizálható frekvencia és a mintavételezési frekvencia közötti kapcsolatot.
|
|
(11.20) |
ahol 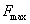 a legmagasabb frekvencia, amely még analizálható,
a legmagasabb frekvencia, amely még analizálható, 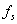 a mintavételezési frekvencia. Az
Ablakozás
alfejezet ebben a fejezetben további adatokat ad meg
a mintavételezési frekvencia. Az
Ablakozás
alfejezet ebben a fejezetben további adatokat ad meg 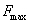 -ról.
-ról.
A második összefüggés kapcsolatot ad meg a frekvencia felbontás és a teljes mintavételezési idő között, amely kapcsolatban áll a mintavételezési frekvenciával és az FFT blokk méretével a következő egyenlet szerint:
|
|
(11.21) |
ahol 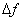 a frekvencia felbontás, h (az időtartománybeli) két minta közötti mintavételi idő,
a frekvencia felbontás, h (az időtartománybeli) két minta közötti mintavételi idő, 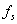 a mintavételezési frekvencia és végül N az FFT blokk mérete vagyis a minták száma.
a mintavételezési frekvencia és végül N az FFT blokk mérete vagyis a minták száma.
11.5.2. Gyors FFT transzformáció számítási időszükséglete
Amikor a bemeneti jelsorozat mérete kettő egész hatványa N=2
m
, aDFT számításai elvégezgetők olyan módon, hogy közelítően csak 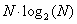 műveletet végezzünk el, amely az DFT kiszámításának leggyorsabb módja.
műveletet végezzünk el, amely az DFT kiszámításának leggyorsabb módja.
A DSP (Digital Signal Processing ) irodalom utal olyan algoritmusokra, amelyek gyorsabbak, mint a gyors FFT számítás. Általánosan a bemeneti jelsorozat mérete, amelyet alkalmaznak mindenütt kettő egész kitevős hatványai, például az 512, a 1024 vagy a 2048 értékek.
A következő ábrákon (11.9. ábra - Számítási időtartam arány a DFT és FFT algoritmus között N=128-nál és 11.10. ábra - Számítási időtartam arány a DFT és FFT algoritmus között N=512-nél) a DFT konvencionális kiszámítási módjának és a kettő egész hatványa esetén alkalmazható FFT számítás időszükségleteit láthatjuk ugyanolyan méretű mintákon.
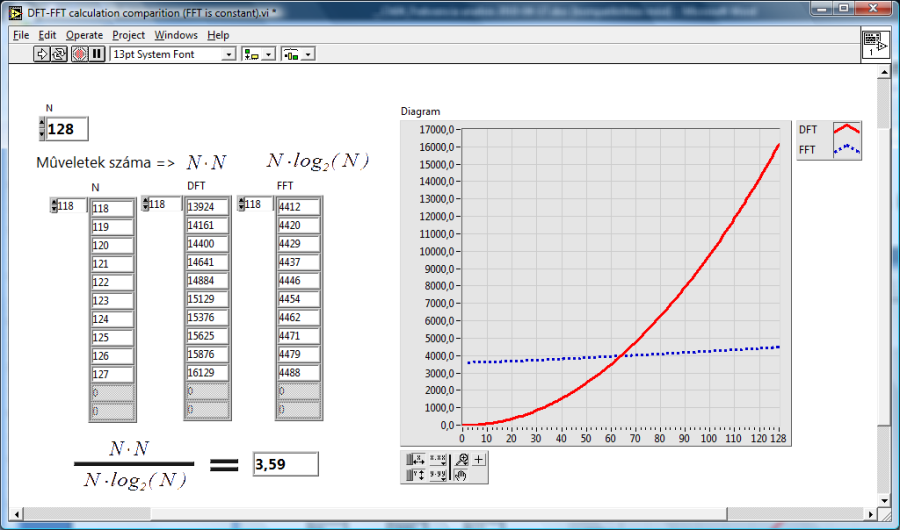
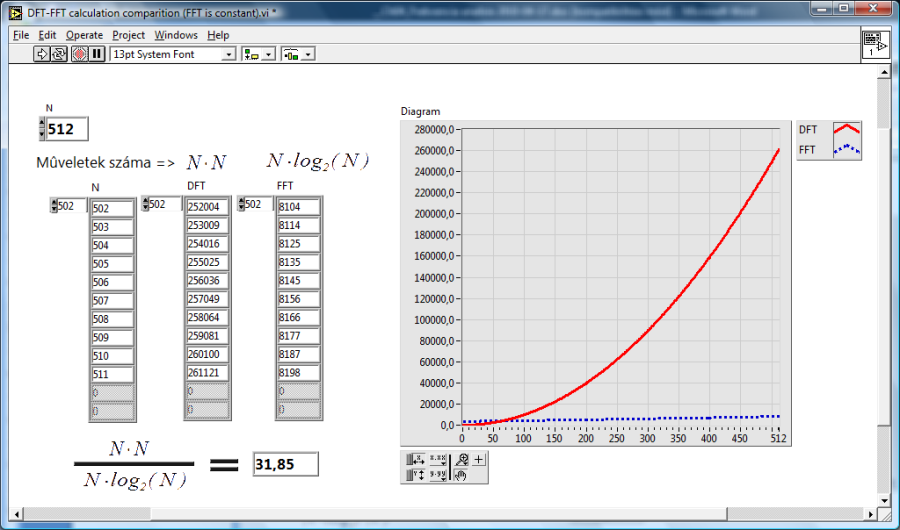
Amikor a bemeneti jelsorozat mérete nem kettő egész kitevős hatványa, de felbontható mint kis prímszámok egész kitevős hatványai, akkor alkalmazhatunk egy olyan speciális algoritmust (Cooley-Tukey algorithm), amely ilyen esetben is a lehető leggyorsabban kiszámítja a bemeneti jelsorozat DFT értékét.
Például a 11.22 egyenlet egy bemeneti jelsorozatot ad meg, amelynek mérete N felbontható kis prímszámok szorzatára.
|
|
(11.22) |
ahol
|
m, j, k = 0,1,2,3,... |
Arra a bemeneti (mért) jelsorozatra, amelyet a 11.22 egyenlettel adtunk meg, az FFT alapú .VI a DFT számításokat közelítőleg olyan sebességgel végzi el, mintha a jelsorozat mérete kettő egész kitevős hatványa volna.
A gyakran használt bementi jelsorozat méretek, amelyek (könnyen) felbonthatók kis prímszámok szorzatára a következők: 480, 640, 1000 és 2000.
11.5.3. Nulla értékekkel történő feltöltés (Zero Padding)
A nulla értékkel történő feltöltés technikáját akkor alkalmazunk, amikor a bemeneti sorozat méretét szeretnénk kettő egész számú hatványának megfelelő méretűvé tenni. A megoldásnál nulla jel értékeket adunk hozzá a bemeneti jelsorozat végéhez, így a teljes jelsorozat hosszúságát kettő következő egész számú kitevőjének megfelelő hosszúságúra növeljük. Például, ha van 10 mintánk a vizsgált jelből 6 nulla értéket hozzáadva a sorozat végéhez 16 minta hosszúságú sorozatot kapjunk, amely 2 negyedik hatványa. A 11.11. ábra - Nulla értékekkel történő feltöltés ábra bemutatja a 10 mintából álló sorozat kiegészítését 16 minta hosszúságú sorozattá.
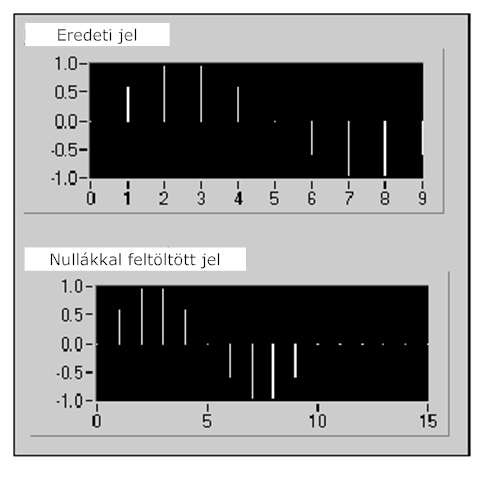
Az időtartománybeli jelsorozat végéhez hozzáadott nulla értékek nem befolyásolják a frekvencia felbontást. A frekvencia felbontás növelésének módja, hogy az időtartománybeli jelnél megnöveljük a mérés időtartamát és így hosszabb mérési rekordokkal dolgozzunk.
A mért értékek számának kettő hatványának megfelelő értékére történő növelése rövidebb számítási időt jelent az FFT számításánál. A nullákkal történő kiegészítés egy interpolációs FFT meghatározását teszi lehetővé, amely nagyobb képernyő felbontást eredményez.
11.5.4. Az FFT VI
A több adattípus fogadására alkalmas FFT VI meghatározza a jel gyors Fourier transzformáltjának(FFT) két típusát, amelyek a következők:
valós FFT (Real FFT) és a
komplex FFT (Complex FFT).
A két típusú FFT között az a különbség, hogy a valós FFT (Real FFT) a valós értékű jel Fourier transzformáltját határozza meg, míg a komplex FFT (Complex FFT) a komplex jel FFT értékét számítja ki.
Az eredmény mind a valós, mind a komplex FFT számítás esetében komplex érték.
A mért jelek legnagyobb része valós értékű jel. Ezért ezekhez a valós FFT számítást kell alkalmazni. Ha a komplex bemeneti jel képzetes részét nullává tesszük, akkor a komplex FFT-t is alkalmazhatjuk a valós FFT számításához. A következőkben egy példát mutatunk be, amelynél alkalmazzuk a komplex FFT-t és a bemeneti jel tartalmaz valós és képzetes részű komponenst. Ilyen jelek gyakran fordulnak elő a telekommunikációban, amikor a bemeneti jelet egy komplex exponenciális értékkel moduláljuk. A modulációs eljárás egy komplex jelet eredményez, amelyet a (11.12. ábra - Moduláció komplex exponenciális jel segítségével) ábrán láthatunk.
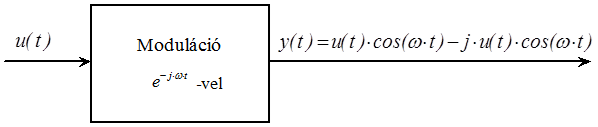
11.6. A frekvencia információ megjelenítése a Fourier transzformáció után
A Fourier transzformáció diszkrét implementációja, a digitális jel Fourier együtthatóinak (vagy harmonikusainak) térképe. Sajnálatos, de sem idő- sem pedig frekvenciainformáció nincs közvetlen kapcsolatban a FFT-vel.
Ezért a mintavételi időt, a h-t a felhasználónak kell megadnia.
Mivel egy bemeneti jel vektorának értékei a jel változását adják meg, azonos mintavételi időlépéssel meghatározható a jellel kapcsolatos frekvencia (sáv) Hertz-ben. A 11.23 egyenlet megadja a frekvencia felbontás Δf értékét a h-hoz viszonyítva.
|
|
(11.23) |
A 11.13. ábra - Pontos adatokkal ellátott frekvencia transzformáció ábra egy blokk diagramot mutat be, amely pontosan adja meg a frekvencia információt és Δf-et egy megadott mintavételi idő ( 1.000 E-3 ) esetén.
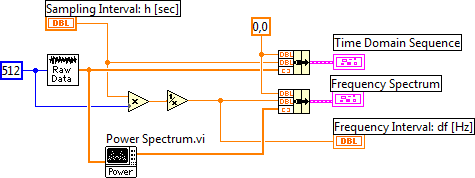
A 11.14. ábra - A frekvencia transzformáció eredményeinek megjelenítése ábra mutatja Δf függvényében azt a képernyőt, amely a (11.13. ábra - Pontos adatokkal ellátott frekvencia transzformáció) ábrán bemutatott VI eredményeként jelenik meg.
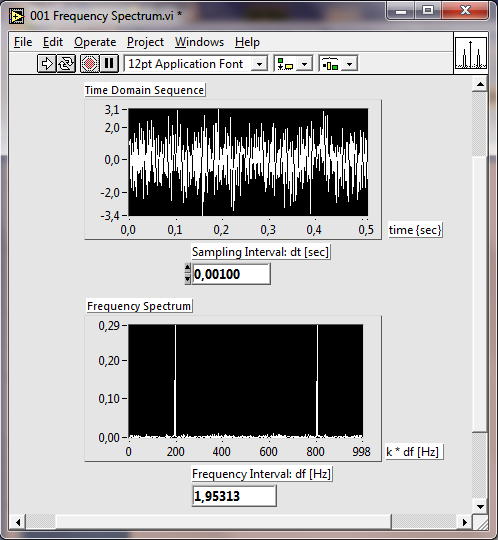
Fontos még az is, hogy milyen bementi adat alapján jött létre a 11.14. ábra - A frekvencia transzformáció eredményeinek megjelenítése ábra ezt a következő ábrán láthatjuk.
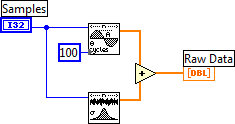
Az ábra egy olyan szinuszos jelet kibocsájtó jelgenerátort mutat be, amely a ”Samples” változóban megadott darabszámú (512) mintát tartalmaz, és amely 100 darab teljes szinuszos ciklust tartalmaz. A második generátor egy Gauss eloszlású zajgenerátor (0 várható értékkel és szigma=1 szórással), amely hasonlóan 512 mintát hoz létre. A két jel összege, amelyet a zajos jelként adunk ki a kimeneten.
Két további általános lehetőség a frekvencia információ megjelenítéséhez a 0 frekvenciás komponens megjelenítése a kétoldalas spektrum közepén.
A továbbiakban a Kétoldalas 0 frekvencia középpontú FFT transzformáció című részben információkat közlünk a 0 frekvenciás komponens megjelenítéséről. A Teljesítmény spektrum fejezetben pedig az egyoldalas spektrum megjelenítésről közlünk adatokat.
11.7. Kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció
A kétoldalas 0 frekvencia középpontú FFT egy olyan eljárást biztosít, amellyel mind a pozitív, mind pedig a negatív frekvenciák megjeleníthetők. A legtöbb transzformációs kézikönyv úgy tárgyalja a Fourier transzformációt és annak tulajdonságait, hogy bemutatja a kétoldalas Fourier transzformáció párokat. Alkalmazhatjuk a Fourier transzformáció frekvencia eltolás (shiftelés) tulajdonságát, hogy meghatározzuk a 0 frekvencia középpontú értékeket. Egy kétoldalas 0 frekvencia középpontú FFT 0 frekvenciás komponense az adatokat tároló puffer közepén helyezkedik el (a puffer maximális indexének felénél).
11.7.1. A kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció matematikai leírása
Ha 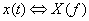 egy Fourier transzformációs páros, akkor legyen
egy Fourier transzformációs páros, akkor legyen
|
|
(11.24) |
ahol 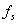 az időfüggvény diszkrét reprezentációjának mintavételi frekvenciája.
az időfüggvény diszkrét reprezentációjának mintavételi frekvenciája.
Határozzuk meg a 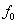 -t mint indexet a megfelelő Nyquist komponenshez
-t mint indexet a megfelelő Nyquist komponenshez 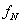 -hez, ahogy azt következő egyenlet mutatja
-hez, ahogy azt következő egyenlet mutatja
|
|
(11.25) |
Az 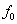 egy beállított index a megfelelő
egy beállított index a megfelelő 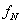 -hez, hogy azt eredményezze, hogy a 0(nulla) frekvenciás komponens a Nyquist komponens helyén jelenjen meg, vagyis egy frekvencia eltolást valósít meg
-hez, hogy azt eredményezze, hogy a 0(nulla) frekvenciás komponens a Nyquist komponens helyén jelenjen meg, vagyis egy frekvencia eltolást valósít meg 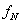 értékkel.
értékkel.
Ha az 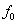 egy beállított index
egy beállított index 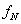 -hez képest, a diszkrét Fourier transzformáció párosban a következő kapcsolatot valósítja meg.
-hez képest, a diszkrét Fourier transzformáció párosban a következő kapcsolatot valósítja meg.
|
|
(11.26) |
ahol i az elemek száma a diszkrét szekvenciában (sorrendben);  az időtartománybeli jelsorozat;
az időtartománybeli jelsorozat;  pedig
pedig  reprezentációja frekvencia tartományban.
reprezentációja frekvencia tartományban.
Ha az exponenciális kifejezést kifejtett alakban írjuk fel, a következő összefüggést kapjuk:
|
|
(11.27) |
A 11.26 egyenlet egy +1 és –1 függvény értékű alternáló sorozat. A 11.26 egyenlet azt mutatja, hogy az eredeti időtartománybeli jelsorozat páratlan elemeit negáljuk és végrehajtunk egy FFT-t az új sorozaton, amelynek 0(nulla) frekvenciás komponense a jelsorozat közepén jelenik meg.
Ezért az eredeti bemeneti jelsorozat, amely a következő:
|
|
(11.28) |
után létrehozott Y jelsorozat
|
|
(11.29) |
létrehoz egy 0(nulla) frekvencia középpontú spektrumot.
11.7.2. A kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció létrehozása
Egy jelet úgy is modulálhatunk a Nyquist frekvenciával, hogy ehhez nem használunk fel semmilyen külső puffert. A 11.16. ábra - A Nyquist Shift VI blokk diagrammja ábra egy olyan blokk diagramot mutat, amely a 11.26 kifejezéssel bemutatott jelsorozatot hozza létre.
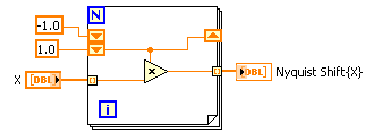
A (11.16. ábra - A Nyquist Shift VI blokk diagrammja) ábrán a For Loop a bementi szekvencia minden elemét alternálva megszorozza +1.0-el illetve –1.0-el. A műveletet a bemeneti vektor minden elemére elvégzi.
A 11.17. ábra - Időtartománybeli jelsorozat előállítása, 0(nulla) frekvencia középpontú spektrum ábra egy VI blokk diagramját mutatja be, amely létrehozza az időtartománybeli jelsorozatot és felhasználja a Nyquist Shift VI és a Power Spectrum VI-okat, hogy létrehozza a 0(nulla) frekvencia középpontú spektrumot.
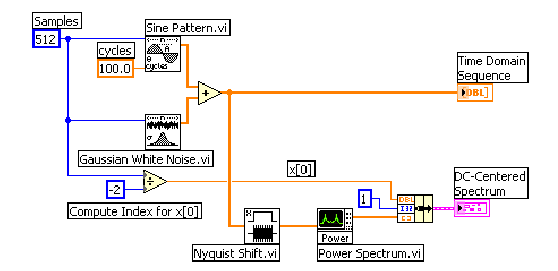
A (11.17. ábra - Időtartománybeli jelsorozat előállítása, 0(nulla) frekvencia középpontú spektrum) ábrán Nyquist Shift VI előkészíti az időtartománybeli jelsorozatot, úgy hogy –1.0-el megszoroz minden további elemet a jelsorozatban. A Power Spectrum VI transzformálja az adatokat frekvencia tartományba.
Ahhoz, hogy a frekvencia tengelyt valós frekvencia értékekkel mutathassa a képernyő meg kell adni az  értékét, amely az x tengely kezdőfrekvenciájának értéke. A 0(nulla) frekvencia középpontú spektrum számára a következő egyenlet határozza meg
értékét, amely az x tengely kezdőfrekvenciájának értéke. A 0(nulla) frekvencia középpontú spektrum számára a következő egyenlet határozza meg  értékét.
értékét.
|
|
(11.30) |
A 11.18. ábra - Az időtartománybeli bemenő adatok és a 0(nulla) frekvencia középpontú amplitúdó spektrum ábra mutatja az időtartománybeli jelsorozatot és a 0(nulla) frekvencia középpontú spektrumot, amely a (11.18. ábra - Az időtartománybeli bemenő adatok és a 0(nulla) frekvencia középpontú amplitúdó spektrum) ábrán bemutatott műveletek végrehajtása után megjelenik a kijelzőkön.
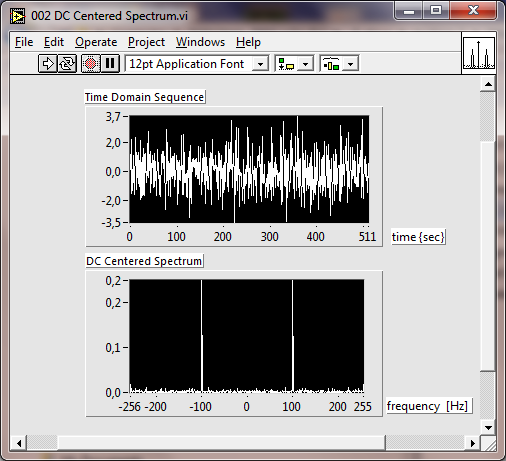
A 0(nulla) frekvencia középpontú frekvenciaspektrum megjelenítésénél, amelyet a 11.18. ábra - Az időtartománybeli bemenő adatok és a 0(nulla) frekvencia középpontú amplitúdó spektrum ábra mutat be a 0(nulla) frekvenciájú komponens, az f=0 a képernyő közepénél jelenik meg.
Létrehozhatunk 0(nulla) frekvencia középpontú frekvenciaspektrumot páros adatmennyiséggel rendelkező bemeneti jelsorozatból ha a páratlan indexű adatokat negáljuk (szorozzuk –1-el).
Nem hozhatunk létre 0(nulla) frekvencia középpontú frekvenciaspektrumot, ha a bemeneti adatok száma páratlan (a páratlan indexű adatokat negálásával), mivel ilyenkor a Nyquist frekvencia két frekvencia tartománybeli FFT érték közé esik. Ilyen esetben rotálnunk kell az FFT tömböt egy olyan index eltolás értékkel, amelyet a következő összefüggés ad meg:
|
|
(11.31) |
A 0(nulla) frekvencia középpontú frekvenciaspektrum megjelenítésénél, páratlan bementi adatszám esetén a következő kifejezés adja meg 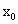 értékét:
értékét:
|
|
(11.32) |
11.8. Teljesítmény Spektrum SAA(f)
Ahogyan azt az Amplitúdó és fázis információ fejezetben leírtuk a DFT vagy FFT transzformáció után a valós bemeneti jelből komplex transzformált értéket hozunk létre, amelynek van valós és képzetes része.
A teljesítmény meghatározható az egyes frekvencia komponensekben, amelyet a DFT vagy az FFT reprezentál, ha négyzetre emeljük a frekvencia komponens amplitúdó értékét. Ezek alapján a k. frekvencia komponens teljesítménye – a DFT vagy FFT k. elemével – a következő egyenlettel írható le:
|
|
(11.33) |
ahol 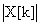 a frekvencia komponens amplitúdója.
a frekvencia komponens amplitúdója.
A 11.3.3. szakasz - Amplitúdó és fázis információ fejezetben megadtuk, hogy hogyan kell meghatározni egy frekvencia komponens amplitúdójának értékét.
A teljesítmény spektrum egy olyan vektort ad eredményül, amely tartalmazza, az időtartománybeli bementi jel kétoldalas teljesítmény spektrumát a frekvencia tartományban.
A 11.34 egyenlettel meghatározható a kétoldalas teljesítmény spektrum az FFT-ből:
|
|
(11.34) |
ahol FFT*(A) az FFT(A) komplex konjugált értéke.
(Az FFT(A) komplex konjugált értéke az FFT(A) imaginárius részének negálásával és a reális rész megtartásával kapott komplex érték.)
Az elemek értéke a teljesítmény spektrum vektorban minden frekvencia komponensnél arányos az időtartománybeli jel egyes komponenseinek amplitúdó négyzetével.
Mivel egy valós jel DFT vagy az FFT transzformáltja szimmetrikus érték, a teljesítmény a pozitív a 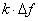 frekvenciáknál, és ugyanaz a teljesítmény van a megfelelő negatív frekvenciáknál
frekvenciáknál, és ugyanaz a teljesítmény van a megfelelő negatív frekvenciáknál 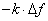 -nél is, a 0(nulla) frekvenciás és a Nyquist komponenst kizárva.
-nél is, a 0(nulla) frekvenciás és a Nyquist komponenst kizárva.
A kétoldalas teljesítmény spektrum ábrája a negatív és pozitív frekvencia komponenseket mutatja, amelyek magasságát a következő összefüggés adja meg:
|
|
(11.35) |
ahol A
k
a szinuszos komponens amplitúdója (csúcsértéke) a k. frekvencia komponensnél. A 0(nulla) komponensnek olyan magassága van, mint az 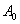 értékének az időjelben.
értékének az időjelben.
A 11.19. ábra - A jel kétoldalas teljesítmény spektruma ábra azt a teljesítmény spektrumot mutatja, amelynek az időtartománybeli függvénye 3 Veff szinuszos jelet tartalmaz 128 Hz-nél, 3 Veff szinuszos jelet tartalmaz 256 Hz-nél és egy 2 V-os jelet tartalmaz 0(nulla) Hz-nél. A 3 Veff szinuszos jel megfelel egy 4,2426V amplitúdójú szinuszos jelnek (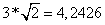 ).
).
A teljesítmény spektrumot a 11.34 egyenlettel leírt alap FFT függvény segítségével határoztuk meg.
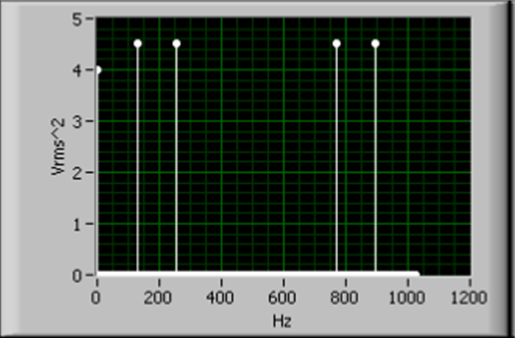
11.8.1. Kétoldalas teljesítmény spektrum konvertálása egyoldalas teljesítmény spektrummá
A legtöbb frekvencia analízist végző berendezés csak a frekvencia spektrum pozitív részét jeleníti megmert a negatív frekvenciákra vonatkozó információ redundáns, mivel a valóságos jelek szimmetrikusak a 0(nulla) frekvenciájú jel körül.
Az analízis függvény kétoldalas eredményei magukba foglalják a pozitív fél spektrumot, amelyet a negatív fél spektrum követ, ahogy azt a 11.19. ábra - A jel kétoldalas teljesítmény spektruma ábra mutatja.
|
|
(11.36) |
ahol 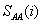 a kétoldalas teljesítmény spektrum,
a kétoldalas teljesítmény spektrum, 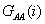 az egyoldalas teljesítmény spektrum, és Na kétoldalas teljesítmény spektrum hosszúsága. Emlékeztetőül a kétoldalas teljesítmény spektrum
az egyoldalas teljesítmény spektrum, és Na kétoldalas teljesítmény spektrum hosszúsága. Emlékeztetőül a kétoldalas teljesítmény spektrum 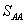 „eldobott értékei” az N/2-től (N-1) indexekkel jelölt elemekben találhatók.
„eldobott értékei” az N/2-től (N-1) indexekkel jelölt elemekben találhatók.
A nem 0(nulla) frekvenciás értékek az egyoldalas teljesítmény spektrumban az egyes súly értékek a következő összefüggéssel adhatók meg:
|
|
(11.37) |
a 11.37 kifejezés a következő összefüggéssel egyezik meg:
|
|
(11.38) |
ahol 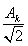 a k. frekvenciájú szinuszos
komponens négyzetes középértékének
(rootmean square = rms) amplitúdója.
a k. frekvenciájú szinuszos
komponens négyzetes középértékének
(rootmean square = rms) amplitúdója.
A teljesítmény spektrum dimenziója rendszerint a négyzetes középérték négyzetének mennyiségi dimenziója, ahol a mennyiség az időtartománybeli jel dimenziója.
Például egy [V] (Volt) dimenziójú jelalak egyoldalas teljesítmény spektruma a négyzetes középérték (rms) négyzete 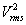 .
.
A 11.20. ábra - Egyoldalas teljesítmény spektrum ábra annak a jelnek az egy egyoldalas spektrumát mutatja, amelynek kétoldalas spektruma a 11.19. ábra - A jel kétoldalas teljesítmény spektruma ábrán látható.
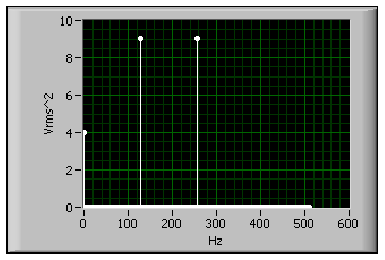
A (11.20. ábra - Egyoldalas teljesítmény spektrum) ábrán a nem nulla frekvenciájú komponensek nagysága kétszerese a (11.19. ábra - A jel kétoldalas teljesítmény spektruma) ábrán látható nem nulla frekvenciájú komponenseknek. Ugyancsak látható, hogy a (11.20. ábra - Egyoldalas teljesítmény spektrum) ábrán látható spektrum csak a (11.19. ábra - A jel kétoldalas teljesítmény spektruma) ábrán látható spektrum frekvenciájának feléig tart.
11.8.2. A fázismenet információ elvesztése
Mivel a teljesítményt rendszerint a DFT vagy FFT amplitúdóinak négyzetre emelésével kapjuk, a teljesítmény spektrum rendszerint valós érték. A valós érték (mivel nincs imaginárius és valós értéke külön-külön) nem tartalmaz fázis információt. Ha mégis szükség van a fázis információra, akkor azokat a DFT vagy FFT eljárásokat kell alkalmaznunk, amelyek komplex kimentet adnak.
A teljesítményspektrum információ szabadon felhasználható azokban az alkalmazásokban, amelyekben a fázisinformáció nem játszik szerepet, ilyen például a harmonikus teljesítmény egy jelben. Ha szinuszos jelet adunk egy nemlineáris rendszer bemenő jeleként, meghatározhatjuk az egyes felharmonikus frekvencia komponensek teljesítményét a rendszer kimenetén.
11.9. A spektrumokkal végzett számítások
Ha rendelkezünk az amplitúdó vagy a teljesítmény spektrummal , a bemeneti jel számos hasznos tulajdonságát határozhatjuk meg, mint például a teljesítményt és a frekvenciát , zaj szintet vagy a teljesítmény spektrális sűrűségét.
11.9.1. A teljesítmény és a frekvencia közelítése
Ha egy frekvencia komponens két frekvencia vonal között helyezkedik el, akkor ez a frekvencia komponens úgy jelenik meg. hogy energiája megoszlik a két szomszédos frekvencia komponens energiájának arányosan csökkentett értékével. Az aktuális csúcs a két frekvencia vonal között helyezkedik el.
Az aktuális frekvenciát nagyobb felbontással közelíthetjük a diszkrét frekvencia komponensek segítségével, mint az a 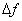 frekvencia, amely az FFT eljáráshoz tartozik, ha végrehajtjuk a frekvencia egy súlyozott átlaggal való számítását egy meghatározott csúcsérték környezetében a teljesítmény spektrumban, ahogy azt a következő függvény mutatja:
frekvencia, amely az FFT eljáráshoz tartozik, ha végrehajtjuk a frekvencia egy súlyozott átlaggal való számítását egy meghatározott csúcsérték környezetében a teljesítmény spektrumban, ahogy azt a következő függvény mutatja:
|
|
(11.39) |
ahol j a látszólagos frekvencia csúcs vektor indexe, amelyre kíváncsiak vagyunk.
A j±3 elfogadható, mivel egy olyan frekvencia kiterjedést reprezentál, amely szélesebb mint a simító ablak legszélesebb sávja a 12.3. táblázat - Simító ablakok korrekciós tényezői és a legrosszabb esetben fellépő amplitúdó hibák táblázatban, a Simító ablakok korrekciós tényezői és a legrosszabb esetben fellépő amplitúdó hibák az 12. fejezet - Simító ablakok fejezetben.
A diszkrét csúcs frekvencia komponensek összegzésével közelíthető a teljesítmény az elemek között a csúcsérték közelében. Más szavakkal, kiszámíthatunk egy területet a csúcsérték alatt. A következő összefüggést felhasználhatjuk, hogy a segítségével közelítsük a diszkrét csúcs frekvencia komponensek teljesítményét.
|
|
(11.40) |
A 11.40 egyenlet csak akkor érvényes, ha a spektrum diszkrét frekvenciájú komponenseket tartalmaz!
Az összefüggés nem érvényes folytonos frekvencia spektrumra!
Ha két vagy több frekvencia csúcs van egymáshoz képest azonosan a hat vonalban, akkor ezek jelentős hatással vannak arra, hogy a teljesítmény és a meredekség az aktuális frekvencián megnövekedjen.
Csökkenthető ez a hatás, ha csökkentjük a frekvenciavonalak számát a 11.40 egyenletben.
Ha a teljesítményt akarjuk meghatározni egy adott frekvencia tartományban, összegezzünk minden tagot a frekvencia tartományban és osszuk el a csillapító ablak zajteljesítményének sávszélességével. A továbbiakban az 12. fejezet - Simító ablakok fejezetben (Simító ablakok) kapunk részletesebb tájékoztatást a simító ablak zajteljesítményének sávszélességéről.
11.9.2. A zajszint és a teljesítmény spektrum sűrűségének meghatározása
A mérés zajszintje szoros kapcsolatban van a mérés sávszélességével. Amikor egy teljesítmény spektrum alap zajszintjét vizsgáljuk akkor minden keskenysávú zajszintet meg kell vizsgálnunk az összes FFT sávban. Ezért egy adott spektrum zajszintje függ a spektrumhoz tartozó 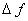 értéktől, amelyet a mintavételi idő és a mérésben szereplő mintavételi pontok száma határoz meg. Más szavakkal a zajszint minden frekvencia vonalnál egyenlő azzal a zajszinttel, amelyet úgy kaphatunk meg, hogy egy
értéktől, amelyet a mintavételi idő és a mérésben szereplő mintavételi pontok száma határoz meg. Más szavakkal a zajszint minden frekvencia vonalnál egyenlő azzal a zajszinttel, amelyet úgy kaphatunk meg, hogy egy 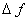 Hz-es szűrőt alkalmazunk az adott frekvencia-vonal körül. Ezért, ha egy meghatározott mintavételi idő mellett megduplázzuk a mintavételi adatok számát, csökkenthetjük a zaj teljesítményt 3 dB-el, amely az egyes frekvencia sávokban megjelenik. Elméletileg a diszkrét frekvencia komponenseknek zérus sávszélessége van ezért nem skálázhatók a pontok számával vagy a FFT frekvencia tartományával.
Hz-es szűrőt alkalmazunk az adott frekvencia-vonal körül. Ezért, ha egy meghatározott mintavételi idő mellett megduplázzuk a mintavételi adatok számát, csökkenthetjük a zaj teljesítményt 3 dB-el, amely az egyes frekvencia sávokban megjelenik. Elméletileg a diszkrét frekvencia komponenseknek zérus sávszélessége van ezért nem skálázhatók a pontok számával vagy a FFT frekvencia tartományával.
Ahhoz, hogy kiszámolhassuk a jel / zaj viszonyt (SNR = Signal to Noise Ratio) hasonlítsuk össze a vizsgált frekvenciákhoz tartozó teljesítmény csúcsértékeket a szélessávú zaj szintjével. A szélessávú zajszint számítása az összes teljesítmény spektrum sávban történő összegzéssel történik, kivéve a csúcsokat és a 0(nulla) frekvenciájú komponenst, majd osztjuk az összeget az ablak ekvivalens zaj szélességével.
Mivel a zajszint skálázása 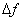 -el, a zaj spektrumának mérése pedig normalizált formában jelenik meg, ezért a
teljesítmény vagy amplitúdó spektrum sűrűségnek
nevezzük.
-el, a zaj spektrumának mérése pedig normalizált formában jelenik meg, ezért a
teljesítmény vagy amplitúdó spektrum sűrűségnek
nevezzük.
A teljesítmény vagy amplitúdó spektrum sűrűség normalizálja a teljesítmény vagy amplitúdó spektrumot egy olyan spektrumhoz, amelyet egy 1 Hz szélességű négyszög típusú (ideális) szűrő mér, amely egy megállapodás a zajszint mérésekre. A szint minden frekvencia vonalnál megegyezik azzal a szinttel, amelyet úgy kapnánk, ha egy 1 Hz-es szűrőt alkalmaznánk az adott frekvencia vonal körül.
A következő összefüggés a teljesítmény spektrum sűrűséget adja meg:
|
Teljesítmény spektrum sűrűség=
|
(11.41) |
A következő összefüggés az amplitúdó spektrum sűrűséget adja meg:
|
Amplitúdó spektrum sűrűség=
|
(11.42) |
A spektrális sűrűség formátum alkalmazható véletlen-értékű vagy zajos jelekre egyaránt.
A spektrális sűrűség formátum nem alkalmazható diszkrét frekvencia komponensekre, mivel a diszkrét frekvencia komponenseknek elvileg 0(nulla) sávszélessége van.
11.10. Amplitúdó és fázis spektrumok kiszámítása
A teljesítmény spektrum a teljesítményt úgy mutatja, mint az amplitúdó négyzetes átlag értékét minden frekvencia vonalon, de nem tartalmaz fázis információt. Mivel a teljesítmény spektrum elveszíti a fázis információt, az FFT-t (Fast Fourier Transformation) kell alkalmazni, hogy megnézhessük a jel frekvencia és a fázis információját.
Az a fázis információ, amelyet az FFT biztosít egy relatív fázis információ az időtartománybeli jel kezdetéhez viszonyítva. Ezért ugyanettől a ponttól kell indítani mindent a jelnél, hogy helyes fázismenet értéket kapjunk. Egy szinusz hullám 90 fokos fázistolást mutat a szinuszos hullámú frekvencián. Egy cosinus hullám 0 fokos fázistolást mutat. Az analízis feladatok elsődleges feladata rendszerint meghatározni a relatív fázistolást a komponensek között vagy a fázis eltérést két jel között, amelyeket azonos időpontban mérünk. Két jel közötti fázis eltérést meghatározhatunk valamelyik magas szintű FFT alkalmazásával. Tekintse át a Frekvencia válasz és hálózat analízis fejezetet ebben a könyvben, hogy további információkat kapjon a magas szintű FFT alkalmazásáról.
Az FFT kétoldalas spektrumot hoz létre komplex formátumban valós és képzetes résszel. A kétoldalas spektrum konvertálható polár formátumba, hogy meghatározhassuk a jel amplitúdó és a fázis értékét. A polár formátum frekvencia tengelye megegyezik a kétoldalas spektrum frekvencia tengelyével. Az FFT amplitúdója arányos az időtartománybeli jel pontjainak számával. (Lásd 11.14 képlethez fűzött magyarázatot!) Alkalmazzuk a következő egyenleteket, hogy meghatározzuk az amplitúdó és a fázis értékeket adott frekvencián az FFT elvégzése után.
|
|
(11.43) | |
|
|
(11.44) |
ahol az arctangens függvény –PI és +PI közötti fázis értékkel tér vissza egy 2·PI radián szélességű értékhatárban.
A következő összefüggés megadja a derékszögű koordinátákból polár koordinátába történő átszámítás függvényét.
|
|
(11.45) |
A derékszögű koordinátákból polár koordinátába történő átszámításhoz alkalmazzuk a 11.43 és 11.44 egyenleteket.
A kétoldalas amplitúdó spektrum az amplitúdó (csúcsérték) felét mutatja a pozitív és negatív frekvenciáknál. Ahhoz, hogy átkonvertáljuk az egyoldalas alakot – kivéve a 0(nulla) frekvenciájú komponenst – kettővel(2-vel) szorzunk és töröljük a vektor második felét. Az egyoldalas amplitúdó spektrum egysége azon amplitúdó érték, amely megadja minden szinuszos amplitúdó komponens csúcsértékét, felhasználva ehhez az időfüggvény értékeit.
Hogy megkapjuk az egyoldalas fázis spektrumot töröljük a kimeneti vektor második felét.
11.10.1. Az amplitúdó meghatározása Vrms-ben valamint a fázis meghatározása fokban
Hogy megnézhessük az amplitúdó spektrumot Vrms-ben (négyzetes középérték [
rms
=
r
oot
m
ean
s
quare]) osszuk el a nem egyenfeszültség komponenseket négyzetgyök 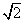 -vel, majd konvertáljuk a spektrumot egy egy-oldalas formulába. Mivel a nem egyenfeszültségű komponenseket megszoroztuk kettővel, amikor a kétoldalas spektrumot átkonvertáltuk egyoldalas spektrummá, az rms (rms = root mean square => négyzetes középérték) amplitúdó spektrumot közvetlenül meghatározhatjuk a kétoldalas amplitúdó spektrumból úgy, hogy megszorozzuk a nem egyenfeszültségű komponenseket négyzetgyök 2-vel (
-vel, majd konvertáljuk a spektrumot egy egy-oldalas formulába. Mivel a nem egyenfeszültségű komponenseket megszoroztuk kettővel, amikor a kétoldalas spektrumot átkonvertáltuk egyoldalas spektrummá, az rms (rms = root mean square => négyzetes középérték) amplitúdó spektrumot közvetlenül meghatározhatjuk a kétoldalas amplitúdó spektrumból úgy, hogy megszorozzuk a nem egyenfeszültségű komponenseket négyzetgyök 2-vel (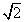 -vel) és töröljük a vektor második felét. A következő egyenlet bemutatja az alapvető számításokat a kétoldalas FFT-ből egyoldalas amplitúdó spektrumba.
-vel) és töröljük a vektor második felét. A következő egyenlet bemutatja az alapvető számításokat a kétoldalas FFT-ből egyoldalas amplitúdó spektrumba.
|
|
(11.46) |
|
i =1 ..((N/2)-1) -nél |
|
|
(11.47) |
|
i =0-nál (egyenfeszültségnél) |
ahol
i a frekvencia sor száma; vagy vektor index az A mintavételes jel FFT-jában
A számértékek a Vrms-ben megadják az effektív (rms) feszültség értékért az időfüggvény minden szinuszos komponenséhez.
Az amplitúdó spektrum nagyon hasonlít a teljesítmény spektrumhoz. Az egyoldalas teljesítmény spektrumot kiszámíthatjuk, ha négyzetre emeljük az egyoldalas rms amplitúdó spektrum minden egyes elemét. Következésképpen meghatározhatjuk az amplitúdó spektrumot, ha négyzetgyököt vonunk a teljesítmény spektrum minden egyes eleméből. A teljesítmény spektrum számításáról további részleteket ezen fejezet „Teljesítmény spektrum” alfejezetében talál.
Alkalmazzuk a következő egyenletet, hogy meghatározzuk a spektrum fázistolását szög dimenzióban:
|
|
(11.48) |
11.11. Frekvencia válasz függvény
Amikor két darab, egy időben mintavételezett csatornát elemzünk, rendszerint jobban szeretnénk ismerni a különbségeket a két csatorna között, mint az egyes csatornák tulajdonságait.
Egy tipikus két csatornás analizátor berendezésben, amilyen a (11.21. ábra - Kétcsatornás frekvencia analízis) ábrán látható, meghatározható a nem-állandósult spektrum, amelyet ablak függvény alkalmazásával számítunk, valamint a két csatorna külön-külön számított FFT függvénye. Az átlagolt FFT spektrum , az auto-teljesítmény (auto-power) spektrum valamint a kereszt-teljesítmény (cross-power) spektrum számított értékek, amelyek segítségével a frekvencia válasz függvény közelítése történik. A koherencia függvényt szintén alkalmazhatjuk, hogy ellenőrizzük segítségével a frekvencia válasz függvény érvényességét.
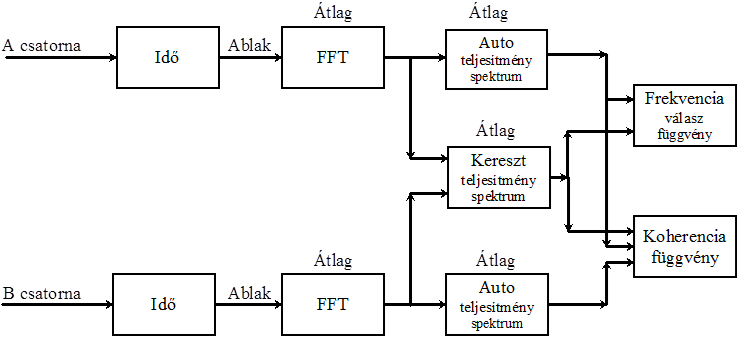
Egy rendszer
frekvencia válasz függvényét
adott frekvencián a függvény amplitúdójának nagyságával 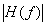 és fázis-szögével
és fázis-szögével 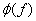 írhatjuk le.
írhatjuk le.
A rendszer erősítése a kimeneti jel amplitúdó értéke osztva a bemeneti jel amplitúdó értékével minden frekvencián. A rendszer fázistolása a kimeneti jel és a bemeneti jel fázistolásainak különbsége minden frekvencián.
11.12. Kereszt teljesítmény spektrum SAB(f) (Cross Power Spectrum)
A kereszt teljesítmény spektrumot { SAB(f) } nem alkalmazzuk közvetlenül a mérésekhez, de nagyon hasznos építőelem más mérési típusokhoz.
Alkalmazzuk a következő egyenletet, hogy meghatározzuk a kétoldalas kereszt teljesítmény spektrumot két időfüggvényhez A-hoz és B-hez.
|
|
(11.49) |
A kereszt teljesítmény spektrum egy kétoldalas komplex formula, amelynek van valós és képzetes része. Ahhoz, hogy a kereszt teljesítmény spektrum erősítés és fázistolás információit áttranszformáljuk Descartes koordináta rendszerbe (x,y koordinátákba), alkalmazzuk a polárból derékszögű koordinátákba átalakító szubrutint, amelynek algoritmusát a 11.43 és a 11.44 függvények mutattak be.
Ahhoz, hogy a teljesítmény spektrumot a kétoldalas komplex formátumból átalakítsuk egyoldalas formátumra alkalmazzuk azokat az eljárásokat és függvényeket, amelyeket a „Kétoldalas teljesítmény spektrum átalakítása egy oldalas spektrumba” alfejezet mutat be ebben a fejezetben.
Az egyoldalas kereszt teljesítmény spektrum létrehoz még négyzetes középérték (rms = root mean square) amplitúdókat valamint fázis differenciákat a két jel A és B között. Az egyoldalas kereszt teljesítmény spektrum egysége megegyezik a négyzetes középérték (rms) négyzetével, amely a 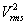 .
.
A teljesítmény spektrum megegyezik a kereszt teljesítmény spektrummal, amikor a két jel A és B ugyanaz a jel. Ezért a teljesítmény spektrumra rendszerint úgy hivatkoznak, mint az auto teljesítmény spektrumra vagy auto spektrumra .
11.13. Frekvencia válasz és hálózat analízis
A következő függvényeket alkalmazhatjuk, hogy meghatározzuk egy adott hálózat frekvencia átviteli tulajdonságait:
Frekvencia válasz függvény
Impulzus válasz függvény
Koherencia függvény
11.13.1. Frekvencia válasz függvény H(f)
A 11.22. ábra - A hálózat mérés felépítése ábra bemutatja egy hálózat frekvencia válasz függvényének mérési metódusát:

A (11.22. ábra - A hálózat mérés felépítése) ábrán egy gerjesztő függvényt alkalmazunk a vizsgált hálózathoz és mérjük a gerjesztést valamint a válasz jelet. A mért gerjesztő jelből és a válasz jelből kiszámítható a frekvencia válasz függvény. A frekvencia válasz függvény egy adott frekvencián megadja a hálózat erősítését és fázistolását.
A 11.50 egyenletet alkalmazzuk a frekvencia válaszfüggvény meghatározásához.
|
|
(11.50) |
ahol H(f) a frekvencia válasz függvény. Az A jel a gerjesztés, B jel pedig a válasz jel, SAB(f) az A és B jel kereszt teljesítmény spektruma, SAA(f) az A jel teljesítmény spektruma.
A frekvencia válasz függvény egy kétoldalas komplex alak, amelynek van valós és képzetes része. Ahhoz, hogy konvertáljuk a frekvencia válasz függvényt erősítéssé és fázistolássá, alkalmazzuk a derékszögű- polár konverziós függvényt a 11.44 egyenlet alapján.
Ahhoz átkonvertáljuk az adatokat egyoldalas formára a válaszfüggvény vektorának második felét el kell hagynunk.
Ha a mérési adatok frekvencia válaszfüggvényeinek átlagértékét szeretnénk meghatározni, a következő lépéseket javasoljuk:
Számítsuk ki az S AB (f) függvény átlagát a következő módon: összegezzük a komplex adatokat és osszuk a mérések számával.
Számítsuk ki az S AA (f) függvény átlagát úgy, hogy összegezzük a komplex adatokat és osszuk a mérések számával.
Határozzuk meg az S AB (f), S AA (f) függvények átlagai segítségével a H(f) frekvencia válasz függvény átlagát az 11.50 egyenlet szerint.
11.13.2. Impulzus válasz függvény FFT1( H(f) )
A hálózat impulzus válasz függvénye a hálózat frekvencia válasz függvényének időtartománybeli reprezentációja.
A hálózat impulzus válasz függvénye egy olyan idő alapú kimeneti jel, amelyet akkor kapunk, ha a hálózatot egy impulzussal gerjesztjük a t=0 időpillanatban.
A hálózat impulzus válaszfüggvényének meghatározásához inverz Fourier transzformálnunk kell a kétoldalas komplex frekvencia válasz függvényt a 11.50 egyenlet alapján.
Az impulzus válaszfüggvény átlagának meghatározásához inverz Fourier transzformálnunk kell a frekvencia válasz függvény átlagát.
11.13.3. Koherencia függvény K(f)
A koherencia függvény arról ad információt, hogy milyen a frekvencia válasz függvény mérésének minősége, valamint, hogy a válasz energiája milyen korrelációban (kapcsolatban) van a gerjesztés energiájával. Ha további jel jelenik meg a válaszban, amely lehet akár egy különlegesen nagy amplitúdójú zaj jel vagy egyéb más jel, akkor a hálózat válaszának mérése nagyon rossz minőségű lesz.
A koherencia függvényt arra használhatjuk, hogy azonosítsuk a különböző zajokat valamint a többi jelforrást, amely hozzájárul a válasz jelhez.
A koherencia függvény a 11.51 egyenlet szerint határozzuk meg:
|
|
(11.51) |
ahol
|
S AB (f) |
a kereszt teljesítmény spektrum, | |
|
S AA (f) |
az A jel teljesítmény spektruma, | |
|
S BB (f) |
a B jel teljesítmény spektruma. |
A 11.51 egyenlet egy nulla (0.0) és egy (1.0) közötti értékkel rendelkező koherencia tényezőt is meghatároz a jel frekvenciájának függvényében. A koherencia tényező akkor egy (1.0), ha frekvencia vonal azt mutatja, hogy a válasz energiájának 100%-a megegyezik a gerjesztő jel energiájával és nem lép fel semmiféle zavaró hatás az adott frekvencián.
A koherencia függvény pontos meghatározásához a gerjesztő jelet és az erre adott válasz jelet kettő vagy ennél több esetben célszerű megmérni. Ha csak egy mérés történik, a koherencia függvény minden frekvenciához egységnyi értéket rendel hozzá.
11.14. Ablakozási technika
A gyakorlati alkalmazásokban a vizsgált jel mintavételi értékeiből véges számú értéket tudunk megmérni. Az FFT feltételezi, hogy ez az időfüggvény rekord (felvétel) ismétlődik. Ha a mérési adatok száma egy meghatározott érték az időadatok rekordjában, az ismétlődésnél egy csillapítási hatás lép fel az időtartománybeli jelsorozat határainál.
A gyakorlati alkalmazásokban általában rendelkezünk a mérési adatok ciklusszámának értékével (hozzárendelt értékkel). Ebben az esetben a ciklusok egy nem hozzárendelt értéke, az eredmény rekordok ismétlődésekor egy folytonossági hiányt mutat a mérési adatok határainál. (lásd 12.1. ábra - Mintavételi periódusból alkotott periodikus hullámforma ábrát) Ezek a mesterséges folytonossági hiányok eredetileg nem voltak jelen a mért jelben és ezért egy „energia maszatolást” vagy „energia átszivárgást” jelentenek az aktuális frekvenciából más frekvenciákba.
Ez a jelenség a spektrális energia átszivárgás . Az átszivárgás mennyisége függ a folytonossági hiány amplitúdójának nagyságától, nagyobb amplitúdó nagyobb mennyiségű energia szivárgást eredményez.
Egy periodikus típusú jel időfüggvényének rekordja szinuszos komponensekből áll, ami azt jelenti, hogy rendelkezik egy meghatározott ciklussal az időfüggvény rekordjában. Így egy tökéletesen periodikus jel olyan spektrummal rendelkezik, amely az energiát meghatározott frekvenciájú komponensekben tartalmazza. (11.23. ábra - Egy jel kétoldalas vonalas teljesítmény spektruma)
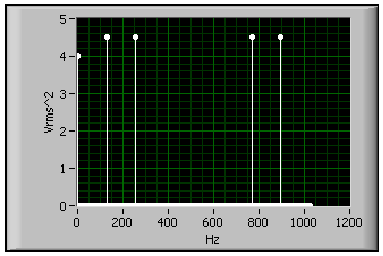
Egy olyan jelnek, amely nem periodikus időfüggvénnyel rendelkezik az energiája eloszlik a különböző frekvenciájú komponensek között. Az FFT spektrum azt az állapotot modellezi, mintha az időfüggvény örökké saját magát ismételné. Ez azt jelenti, hogy az analizált rekordok egy-egy periódus hosszúságú, végtelenül ismétlődő periodikus jel.
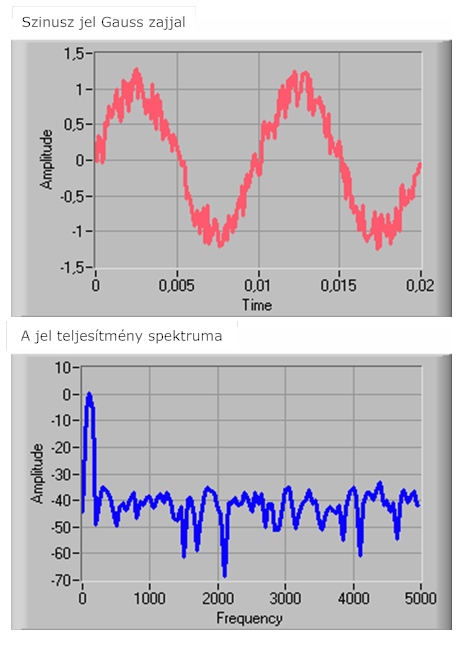
Mivel az energia átszivárgás nagysága a folytonossági hiány amplitúdójával arányos a jel határainál, ablakozási technikát alkalmazhatunk , hogy csökkentsük a folytonossági hiányt és ezzel együtt csökkentsük a spektrális energia (át)szivárgást. Az ablakozás az időtartománybeli jelet egy másik időtartománybeli jellel szorozza meg, amelyet ablaknak nevezünk, melynek amplitúdója folyamatosan csökken és csillapított módon viszi (le) 0 értékűre a vizsgált jel éleit. Az eredmény egy olyan ablakozott jel, amelynél nagyon csekély vagy egyáltalán nincs folytonossági hiány a rekordok között, és ezért nagyon kicsiny a spektrális energia (át)szivárgása. Az ablakozás megvalósításához számos ablak típus közül választhatunk. Az ablak kiválasztása függ az alkalmazás jellegétől és valamilyen elsődleges információt arról a jelről, amelyet analizálunk.
A 12. fejezet - Simító ablakok fejezetben további információkat talál az ablakozásról.
11.15. Átlagolás a mérési eredmények ábrázolásához
A mérési eredmények egymást követő folyamatos átlagolása rendszerint javítja a mérési eredmények pontosságát.
Az átlagolást a mérési eredményeken vagy egy egyéni spektrumon hajtjuk végre, de sohasem egy, hanem több idő rekordon. Választhatunk a következő általános átlagolási módok közül:
Négyzetes (effektív) átlagolás (RMS Average= Root Mean Square Average)
Vektoros átlagolás
Csúcsérték megtartása
11.15.1. Négyzetes (effektív) átlagolás (RMS Averaging)
A négyzetes átlagolás csökkenti a jel ingadozást, de nem csökkenti a zaj alapszintjét. A zaj alapszintje nem csökken, mert a négyzetes átlagolás, átlagolja a jel energiáját vagy a teljesítményét. Az átlagolás eredményeként egy csatornás mérésnél a fázistolás nulla(0) értékű. A négyzetes átlagolás két csatornás mérésnél megőrzi a fontos fázistolási információt.
A négyzetes (effektív) átlagolás metódus szerint történő átlagolásnál a következő egyenleteket alkalmazzuk:
|
FFT spektrum |
|
|
Teljesítmény spektrum |
|
|
Kereszt teljesítmény spektrum |
|
|
Frekvencia válaszfüggvény |
|
ahol
|
X |
az x gerjesztés komplex Fourier transzformáltja | |
|
X* |
az X komplex konjugáltja | |
|
Y |
az y válasz komplex Fourier transzformáltja | |
|
Y* |
az Y komplex konjugáltja | |
|
|
az X átlaga; a valós és a képzetes rész átlag képzése külön-külön történik |
11.15.2. Vektoros átlagolás
A vektoros átlagolás megszünteti a zajt az egyidejű jelekben. A vektoros átlagolás a komplex mennyiségeket direkt módon átlagolja. A valós rész és a képzetes rész átlagolása külön-külön történik. A valós rész és a képzetes rész külön-külön történő átlagolása csökkenti a zaj alapszintet véletlen jeleknél, mivel a véletlen jelek nem fázis koherensek (összefüggők) az egyik idő rekordból a következőbe történő átlépéskor. Ha a valós és képzetes részt külön-külön átlagoljuk, csökkentjük a zaj értékét, de szükségünk van egy indító (trigger) jelre.
|
FFT spektrum |
|
|
Teljesítmény spektrum |
|
|
Kereszt teljesítmény spektrum |
|
|
Frekvencia válaszfüggvény |
|
ahol
|
X |
az x gerjesztés komplex Fourier transzformáltja | |
|
X* |
az X komplex konjugáltja | |
|
Y |
az y válasz komplex Fourier transzformáltja | |
|
Y* |
az Y komplex konjugáltja | |
|
|
az X átlaga; a valós és a képzetes rész átlag képzése külön-külön történik |
11.15.3. A csúcsérték megtartása
A csúcsérték megtartása (rögzítése) az átlagolt értékek csúcsértékével tér vissza. A csúcsérték megtartott átlagolása minden frekvencián (frekvenciavonalon) külön-külön történik, a csúcsérték szintjét megtartja az egyik FFT értékből (rekordból) a következőbe történő átlépéskor.
|
FFT spektrum |
|
|
Teljesítmény spektrum |
|
ahol
|
X |
az x gerjesztés komplex Fourier transzformáltja | |
|
X* |
az X komplex konjugáltja |
11.15.4. Súlyozás
Amikor egy négyzetes vagy vektoros átlagolást hajtunk végre minden új spektrális rekordot súlyozunk vagy lineáris vagy exponenciális súlyozással.
A lineáris súlyozás az N darab spektrális rekordot azonos súlyozással látja el. Amikor a megadott számú átlagolás befejeződik, az algoritmus megállítja az átlagolást és megjeleníti az átlagolt eredményt
Az exponenciális súlyozás jobban kiemel egy új spektrális adatot, mint a korábbit és ezeket egy folytonos eljárással minden lépésben újra számolja.
Az exponenciáis súlyozással történő (új) érték meghatározásához a következő formulát alkalmazzuk:
|
|
(11.52) |
ahol
|
X[k] |
a k. rekordból származó bemeneti adat | |
|
Y[k] |
az átlagolási eljárás eredménye X[1]-től X[k]-ig, |
ahol
|
N = k-val |
lineáris súlyozás esetén; | |
|
N = konstans |
exponenciális súlyozás esetén | |
|
( N = 1 ha k = 1 ). |
11.16. Visszhang észlelése
A visszhang észleléséhez általában modulált rendszerek analíziséhez általánosan használt Hilbert transzformációt alkalmazzuk. (lásd 6.4. szakasz - A Hilbert transzformáció fejezetet)
A 7.1.5. szakasz - Cepstrum analízis fejezetben pedig látható, hogy a cepstrum analízis milyen módon alkalmazható a visszhang megszüntetésére.
A 11.53 egyenlet az időtartománybeli jelet írja le. Míg a 11.54 egyenlet az időtartománybeli jel Hilbert transzformáltját adja meg.
|
|
(11.53) | |
|
|
(11.54) |
ahol
|
A |
az amplitúdó | |
|
|
a természetes rezonancia frekvencia | |
|
|
az idő-csillapítási konstans |
A 11.55 egyenlet az analizált jel 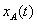 amplitúdójának természetes alapú logaritmusát adja meg.
amplitúdójának természetes alapú logaritmusát adja meg.
|
|
(11.55) |
A 11.55 egyenlet eredménye egy egyenes egyenlete, amelynek 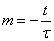 a meredeksége.
a meredeksége.
Ezért eltávolítható a rendszer idő-konstansa 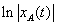 ábrázolásakor.
ábrázolásakor.
A 11.25. ábra - Visszhang jel ábra egy időtartománybeli jelet mutat, amely tartalmaz visszhang jelet.
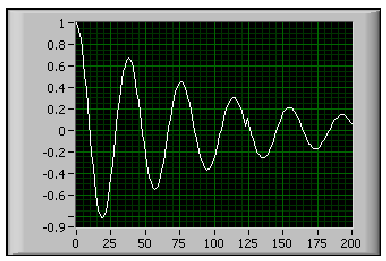
A következő feltételek akadályozzák a visszhang jel felfedezését a (11.25. ábra - Visszhang jel) ábrán:
Az időkésés a forrás és a visszhang jel között nagyon kis érték és relatív érték a rendszer idő-késleltetési konstans értékéhez képest.
A visszhang amplitúdója kis értékű a forrás amplitúdójához képest.
A visszhang jelet láthatóvá tehetjük, ha az 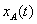 nagyságát logaritmus léptékben ábrázoljuk, mint az a (11.26. ábra - Az xA(t) jel nagyságának logaritmikus léptékű ábrázolása) ábrán látható.
nagyságát logaritmus léptékben ábrázoljuk, mint az a (11.26. ábra - Az xA(t) jel nagyságának logaritmikus léptékű ábrázolása) ábrán látható.
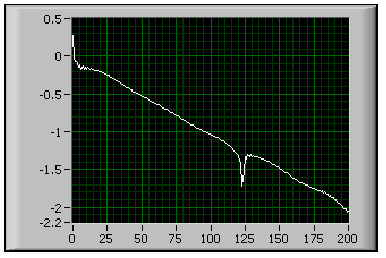
A (11.26. ábra - Az xA(t) jel nagyságának logaritmikus léptékű ábrázolása) ábrán a folytonossági hiány világosan látható és kijelöli a visszhang késleltetésének helyét.
A 11.27. ábra - A visszhang detektálásának blokk diagramja ábra bemutatja egy olyan VI blokk diagramját, amely létrehozta a 11.25. ábra - Visszhang jel és 11.26. ábra - Az xA(t) jel nagyságának logaritmikus léptékű ábrázolása ábrákat.
A 11.27. ábra - A visszhang detektálásának blokk diagramja ábra a következő lépéseket tartalmazza a visszhang detektálásához:
Meghatározza a bemeneti jel Gyors Hilbert Transzformáltját, amely az 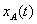 jelet adja eredményül.
jelet adja eredményül.
Meghatározza az 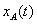 jel amplitúdóját 1D derékszögű-Polár VI segítségével.
jel amplitúdóját 1D derékszögű-Polár VI segítségével.
Kiszámítja az 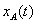 jel természetes alapú logaritmusát, hogy megállapíthassuk a visszhang létezését.
jel természetes alapú logaritmusát, hogy megállapíthassuk a visszhang létezését.
Irodalom
[11.1.] LabVIEW Control Design User Manual. 2009.
12. fejezet - Simító ablakok
Ez a fejezet bemutatja a spektrális szóródás jelenségét, hogy hogyan kell simító ablakokat használni a spektrális szóródás csökkentésére, a simító ablakok típusait, illetve, hogy hogyan kell a megfelelő típusú simító ablakot kiválasztani, a spektrális analízishez, a szűrő együtthatók tervezéséhez.
Bemutatja a simító ablakok skálázásának fontosságát. (lásd 7.1.3.4. szakasz - Folytonos, nem stacionárius jelek analízise a gyakorlatban fejezetet)
Ablakozási vizsgálatokat a következő esetekben alkalmazhatunk:
A megfigyelés időtartamának meghatározása.
A spektrális lebegés csökkentése.
Egy kis amplitúdójú jel elválasztása egy nagy amplitúdójú jeltől, melyek frekvenciái nagyon közel vannak egymáshoz.
FIR szűrő együtthatók tervezése.
A Windows VI-k egyszerű eljárást biztosítanak a mintavételezett jel spektrális karakterisztikájának javítására.
12.1. Spektrális szóródás
A Shannon mintavételezési tétel értelmében, egy időben folytonos jel teljes mértékben rekonstruálható diszkrét, egyenlő időközű mintákból, ha a mintavételezett jel legmagasabb frekvenciájú összetevője kisebb, mint a mintavételi frekvencia fele. A mintavételi frekvencia felét Nyquist frekvenciának nevezzük. A Shannon tétel áthidalja a szakadékot az időben folytonos és a digitális jelek között. A Shannon tétellel kapcsolatos további információk az 8. fejezet - Bevezetés a digitális jelfeldolgozásba és analízisbe fejezetben találhatók.
Gyakorlatilag az időjelet digitalizáló alkalmazások véges számú adatból álló jelsorozatot eredményeznek még akkor is, ha betartjuk a Shannon tételt és gondosan megválasztjuk a mintavételezés körülményeit. Még akkor is, ha az adatok megfelelnek a Nyquist kritériumnak, a véges számú minta energia szóródást okozhat, amit spektrális szóródásnak nevezünk. Emiatt, még megfelelő mintavételezési technikával is előfordulhat, hogy a mérés nem eredményez egy skálázott, egyoldalas spektrumot a spektrum szóródás miatt. Spektrum szóródásnál úgy tűnik, mintha egy adott frekvencia energiája szétszóródna az összes többi frekvencián. A spektrum szóródás az FFT és a DFT algoritmus egyik feltételének az eredménye, annak, hogy az időtartománybeli jelsorozat mindig pontosan ismétlődik (a rekordok többszöri ismétlése miatt). Így a jelek egy időtartománybeli jelsorozatban periodikusan ismétlődnek olyan intervallummal, amely megegyezik az jelsorozat (rekordok) hosszával. Amikor FFT-t vagy DFT-t használunk a jel frekvencia összetevőinek meghatározásához, a transzformáció azt feltételezi, hogy a véges adathalmaz egy periodikus jel egyetlen periódusa. Ezért a jelsorozat végessége (meg)csonkított hullámformát eredményez az eredeti folytonos időfüggvénytől eltérő spektrális karakterisztikával és a végesség éles átmeneti változásokat hozhat létre a mért adatokban. Ezek az éles átmenetek által okozott szakadásokat a 12.1. ábra - Mintavételi periódusból alkotott periodikus hullámforma ábra mutatja be.
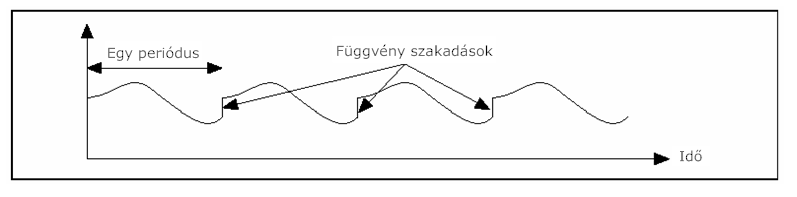
A (12.1. ábra - Mintavételi periódusból alkotott periodikus hullámforma) ábrán látható szakadások (folytonossági hiány) a spektrális információk szóródását eredményezik. A spektrális szóródás egy diszkrét idő spektrumot hoz létre, ami az eredeti folytonos idő spektrum „elkenődött” változataként jelenik meg.
12.1.1. Egész számú periódus mintavétele
A spektrális szóródás csak akkor jön létre, ha az adathalmaz (rekord) nem egész számú periódust tartalmaz. A 12.2. ábra - Szinusz hullám és Fourier transzformáltja ábra egy egész periódusból álló szinusz hullám mintát és Fourier transzformáltját mutatja.
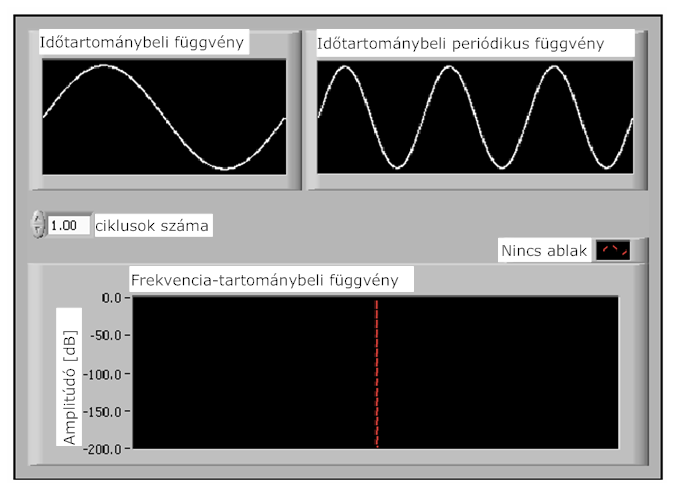
A 12.2. ábra - Szinusz hullám és Fourier transzformáltja ábra 1. diagramja a minta időtartománybeli hullámalakját mutatja. A 2. diagramon az 1. diagram szinusz hullámjának periodikusan ismétlődő időfüggvénye látható. A 2. diagramban a hullám periodikusan ismétlődik, ezáltal teljesíti a Fourier transzformáció periodicitásra vonatkozó feltételét. A 3. diagram a jel frekvencia-tartománybeli ábrázolása látható.
Mivel a 2. diagramban a jel periodikus és nincs benne szakadás, a spektruma a 3. diagramban egyetlen vonalként jelenik meg, ami a szinusz hullám frekvenciáját mutatja. A 2. diagram hullámalakjában nincs szakadás, mivel az adatok egész számú periódusból származtak, - esetünkben egyből.
Kizárólag az alábbi eljárások biztosítják, hogy mindig egész számú periódusokat nyerjünk:
A mintavételezésnek szinkronban kell lenni a mért jellel. Így szándékosan egész számú periódus kapható.
A tranziens jelek mérésénél a rögzítés idejének teljesen illeszkedni kell a jelhez.
12.1.2. Nem egész számú periódus mintavételezése
Általában a mérni kívánt ismeretlen jel időben állandó jel. Egy időben állandó jel létezik a mintavétel előtt, alatt és után is. Ebben az esetben nem lehet biztosítani, hogy mintavételezéskor egész számú periódust kapjunk. Ha a minta nem egész számú periódust tartalmaz, spektrum szóródás jön létre, mivel a jel nem egészszámú periódusának frekvencia komponense nem egyezik meg pontosan a spektrum egyetlen frekvenciájával sem. A spektrum szóródás eltorzítja a mérést oly módon, mintha egy adott frekvenciakomponens energiája szétterjedne a szomszédos frekvencia vonalakon vagy sávokon, ami egy “szétkenődött” spektrumot eredményez. Simító ablakok használatával minimalizálni lehet a nem egész számú perióduson végrehajtott FFT miatt kialakuló hatásokat.
A jel periodicitására vonatkozó feltétel miatt mesterséges szakadások jelennek meg az egymást követő periódusok között, amikor a mintavétel nem egész számú periódusból történik. Ezek a szakadások nagyon magas frekvenciájú komponensekként jelennek meg a jel spektrumában. Ezek olyan frekvenciák, amelyeket az eredeti jel nem tartalmaz. A szakadások frekvenciája sokkal nagyobb lehet, mint a Nyquist frekvencia, ezért látszólagos frekvenciaként valahol 0 és fs/2 között jelenik meg. E miatt lép fel a spektrum szóródás. A DFT-vel vagy FFT-vel kapott spektrum ezért „elkenődött” lesz, nem az eredeti jel valódi spektruma.
A 12.3. ábra - Spektrális ábra, amikor a mintavétel nem egész számú periódusból történt ábrán egy szinusz hullám, melynek nem egész számú periódusából történt a mintavétel, valamint a szinusz hullám Fourier transzformáltja látható.
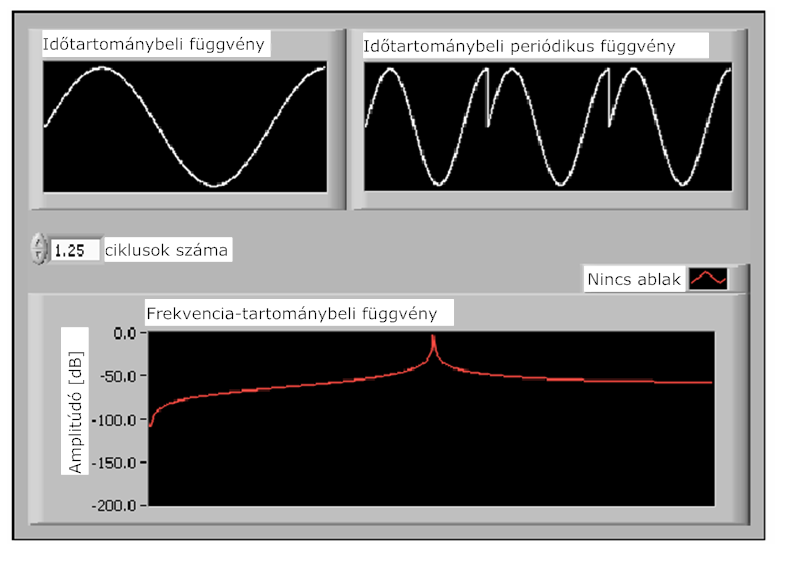
A (12.3. ábra - Spektrális ábra, amikor a mintavétel nem egész számú periódusból történt) ábrán az 1. diagram a szinusz hullám 1,25 periódusát tartalmazza. A 2. diagramban a jel periodikusan ismétlődik, a Fourier transzformáció periodicitási feltétele miatt. A 3. diagram mutatja a jel spektrális ábráját. Az energia szétterjed vagy ”szétkenődik” egy széles frekvencia tartományban. Az energia „kiszivárog” az egyetlen frekvencia komponensből és szétterül a többi frekvencián és ezáltal spektrum szóródást okoz.
A spektrum szóródás azért jött létre, mert a bemenő jel rögzítési időtartama véges. A spektrum szóródás legyőzéséhez végtelen mérési időtartamot kellene vennünk –∞-től +∞-ig. Végtelen jelsorozattal az FFT egyetlen vonalat eredményezne, a megfelelő frekvencián. Azonban a gyakorlatban végtelen idejű mérés nem valósítható meg. A véges jelsorozat korlátainak legyőzésére ablakozást használunk a spektrum szóródás csökkentésére.
Ezen kívül a spektrum szóródás amplitúdó pontossági hibát is okozva elfedheti a szomszédos frekvencia csúcsokat. A (12.4. ábra - A spektrum szóródás elfedi a közeli frekvencia komponenseket) ábrán a spektrum két közeli frekvencia komponense látható simító ablak használata nélkül és Hanning ablak alkalmazásával.
A (12.4. ábra - A spektrum szóródás elfedi a közeli frekvencia komponenseket) ábrán a második csúcs sokkal jobban kiemelkedik az ablakozott jelnél, mint amikor nem használunk simító ablakot.
12.2. Ablakozott jelek
A mintavételezett jel spektrális karakterisztikájának javítására általában simító ablakot használunk. Amikor Fourier vagy spektrális analízist hajtunk végre véges hosszúságú (időtartománybeli) adatokon, simító ablakok használatával minimalizálni lehet a csonka hullámforma szakadásait, és ezáltal csökkenteni lehet a spektrum szóródást.
A spektrum szóródás mértéke a szakadás amplitúdójától függ. Ha a szakadás nagyobb lesz, a spektrum szóródás nő, és fordítva. A simító ablak csökkenti a szakadás amplitúdóját minden periódus határán és úgy viselkedik, mint egy előre meghatározott alul-áteresztő szűrő.
Egy jel ablakozásának művelete a véges hosszúságú jelsorozat megszorzását jelenti egy véges hosszúságú simító ablakkal, melynek amplitúdója egyenletesen és fokozatosan nullához tart a széleknél. A simító ablak hossza vagy időintervalluma a minták számával van megadva. Az időtartománybeli szorzás egyenértékű frekvencia tartománybeli konvolúcióval . Emiatt az ablakozott jel spektruma az eredeti jel és a simító ablak spektrumának konvoluciójából adódik. Az ablakozás megváltoztatja a jel alakját az időtartományban, valamint hatással van a spektrumra, amit látunk.
A 12.5. ábra - Az ablakozott spektrum frekvencia karakterisztikája ábra az jel eredeti és egy simítóablak spektrumának konvolúcióját mutatja.
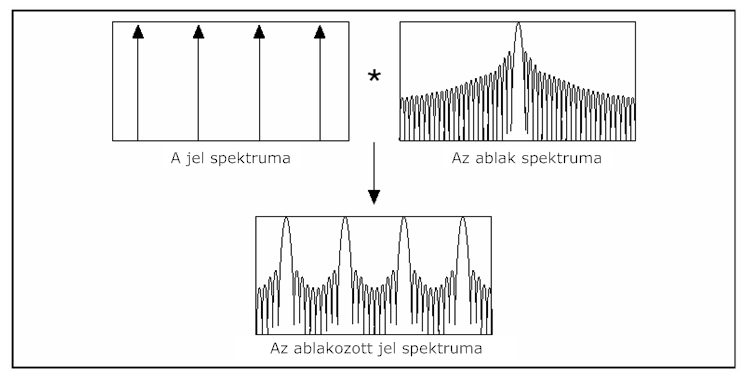
Az ablakozás-hatás akkor is fellép, ha nem alkalmazunk simító ablakot. Egy bemenő jel véges jelsorozatának mérése a jel egy állandó ablakkal való megszorzását jelenti az időtartományban. Az állandó ablak alakja négyszögletes és a magassága állandó. A bemenő jel állandó ablakkal való megszorzása az időtartományban megfelel a jel és az állandó ablak spektrumának konvolúciójával a frekvencia tartományban, amelynek sinc függvény karakterisztikája van.
A 12.6. ábra - Hanning-ablakkal ablakozott jel ábra egy Hanning ablak alkalmazásának hatását mutatja egy időfüggvényen
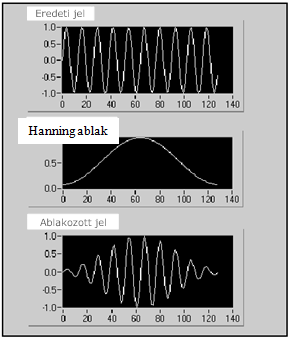
A (12.6. ábra - Hanning-ablakkal ablakozott jel) ábrán az ablakozott jel időfüggvénye fokozatosan nullára csökken a végein, mivel a Hanning-ablak minimalizálja a szakadásokat a hullámforma átmeneti végeinél. Simítóablak alkalmazása időtartománybeli adatoknál a frekvenciatartományba való transzformálás előtt minimalizálja a spektrum szóródást.
A 12.7. ábra - Egy 1 Vrms-os 256 Hz-es jel teljesítmény-spektrumaállandó, Hanning és ”Flat top” ablakokkal ábra az alábbi simítóablakok hatásait mutatja:
Ablak nélkül (négyszög ablak)
Hanning ablakkal
„Flat top” ablakkal (Lásd később a 12.3.8. szakasz - “Flat Top” ablak fejezetben)
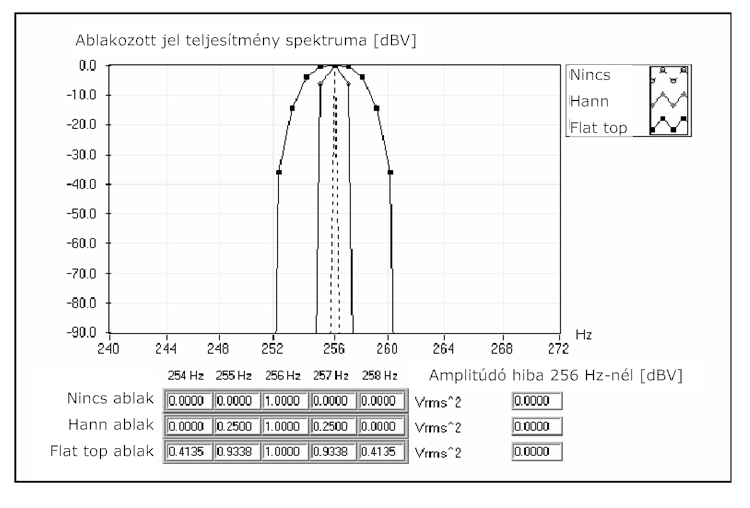
A (12.7. ábra - Egy 1 Vrms-os 256 Hz-es jel teljesítmény-spektrumaállandó, Hanning és ”Flat top” ablakokkal) ábrán látható jel adathalmaza egészszámú (256) periódust tartalmaz egy 1024 pontból álló jelsorozatban. Ha az eredeti jel frekvencia összetevő pontosan illenek egy frekvenciavonalra, - ez az az eset, mikor az adathalmaz egészszámú periódust tartalmaz - akkor csak a spektrum fő-szárnya látható.
A simító ablaknak van egy fő-szárnya a vizsgált frekvencia körül. A fő-szárny az ablakok egy frekvenciatartománybeli karakterisztikája. Az állandó ablaknak van a legkeskenyebb fő-szárnya. A Hanning és a „flat top” ablakok némileg szélesebbek. A „flat top” ablaknak van a legszélesebb fő-szárnya az állandó és a Hanning ablakhoz képest. Egészszámú periódus esetén az összes simító ablak ugyanazt a csúcs amplitúdó értéket adja és kitűnő amplitúdó pontosságot biztosít. Az oldal-szárnyak nem jelennek meg, mivel a simítóablak spektruma eléri a nullát Δf intervallumokban a fő-szárny mindkét oldalán.
A 12.7. ábra - Egy 1 Vrms-os 256 Hz-es jel teljesítmény-spektrumaállandó, Hanning és ”Flat top” ablakokkal ábra a 254 Hz és 258 Hz közötti értékeket is mutatja mindegyik simítóablaknál. Az amplitúdó hiba 254 Hz-en mindhárom simítóablak esetén 0 dB. A diagram a spektrum értékeket mutatja 240 és 272 Hz között. Az aktuális értékek mindhárom simító ablakra nézve 254-258 Hz között a diagram alatt láthatók. Δf egyenlő 1Hz.
Ha a jelsorozat nem egész számú periódust tartalmaz , a simítóablak folyamatos spektruma eltolódik a fő-szárny közepétől Δf frekvencia osztással, ami megegyezik frekvencia összetevő és az FFT frekvencia vonal közötti különbséggel. Ez az eltolódás eredményezi az oldal-szárnyakat, amelyek megjelennek a spektrumban. Továbbá amplitúdó hiba lép fel a frekvencia csúcsnál, mivel a fő-szárnya mintavétele kívül esik a középponttól és „elkenődik” a spektrumban. A 12.8. ábra - Egy 1 Vrms-os 256.5 Hz-es jel teljesítmény-spektruma állandó, Hanning és ”Flat top” ablakokkal ábra a spektrális szóródás hatását mutatja meg egy olyan jelnél, mely jelsorozata 256,5 periódust tartalmaz.
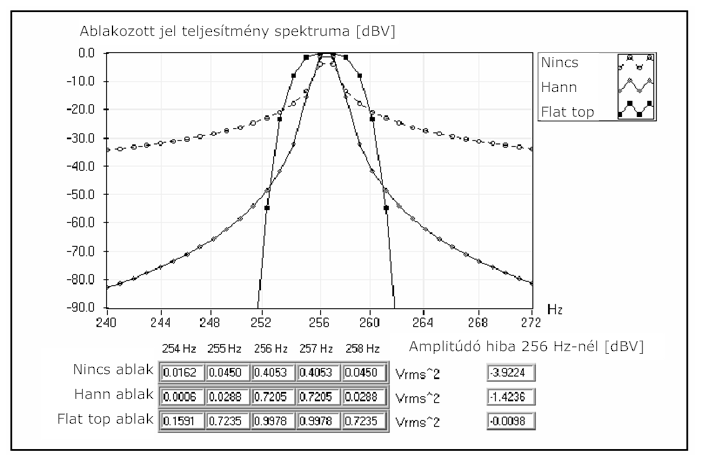
A (12.8. ábra - Egy 1 Vrms-os 256.5 Hz-es jel teljesítmény-spektruma állandó, Hanning és ”Flat top” ablakokkal) ábrán nem egész számú periódusoknál a Hanning és a „flat top” ablak sokkal kisebb spektrumszivárgást mutat, mint az állandó ablak. Ezen kívül az amplitúdó hiba is kisebb a Hanning és a „flat top” ablakok esetén. A „flat top” ablak nagyon jó amplitúdó pontosságot mutat, de szélesebb és magasabb oldal lebenyei vannak, mint a Hanning ablaknak.
A (12.9. ábra - Két szinusz jel összegeként kapott jel spektrumának mérése) ábra egy VI blokkdiagramját mutatja, ami két szinusz jel összegeként kapott jel ablakozott és ablakozás nélküli spektrumát méri.
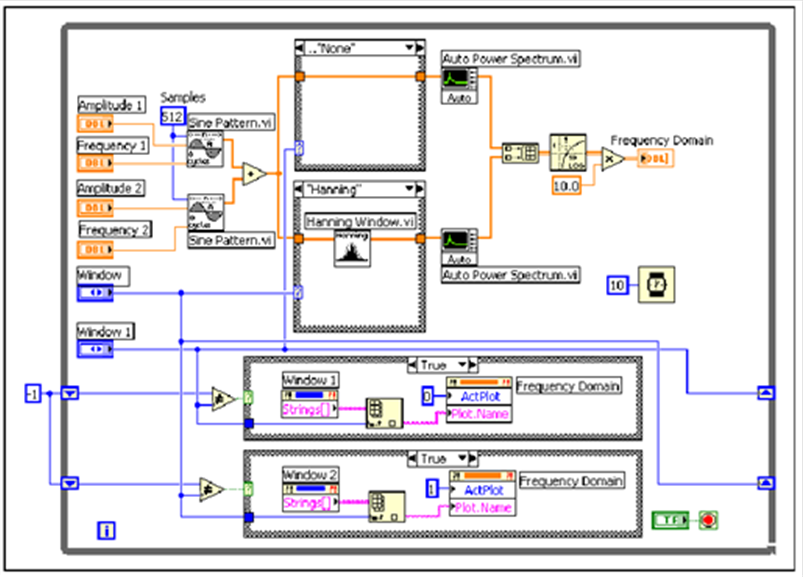
A 12.10. ábra - Két szinusz jel összegének ablakozott és ablakozás nélküli spektruma ábra a két szinusz jel amplitúdóját és frekvenciáját valamint a mérések eredményeit mutatja. A frekvenciák kijelzése a periódusok dimenzióval történik.
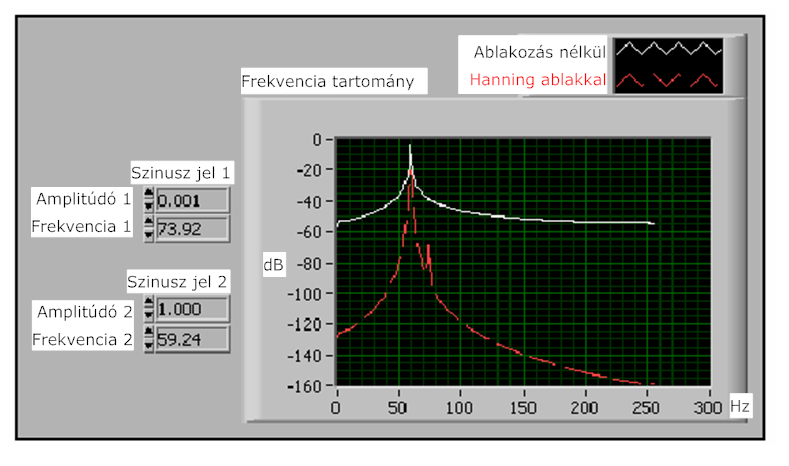
A (12.10. ábra - Két szinusz jel összegének ablakozott és ablakozás nélküli spektruma) ábrán az ablakozás nélküli spektrum 20 dB-nél nagyobb spektrális szóródást mutat a kisebb szinusz jel frekvenciájánál. Lehet ennél kifinomultabb technikát is alkalmazni az eredeti időfüggvény frekvencia tartománybeli leírásához. Azonban a legtöbb esetben elegendő simító ablak alkalmazása a frekvenciafüggvény jobb ábrázolásához.
12.3. A különböző simító ablakok tulajdonságai
A simító ablak kiválasztásának egyszerűsítése érdekében szükség van a különböző frekvencia karakterisztikák definiálására, hogy a simító ablakokat egymással össze lehessen hasonlítani. Egy simító ablak aktuális ábrája azt mutatja, hogy a simítóablak frekvencia karakterisztikája egy folyamatos spektrum egy fő és számos oldal szárnnyal. A 12.11. ábra - Simító ablak frekvencia válasza ábra egy tipikus simító ablak spektrumot mutat.
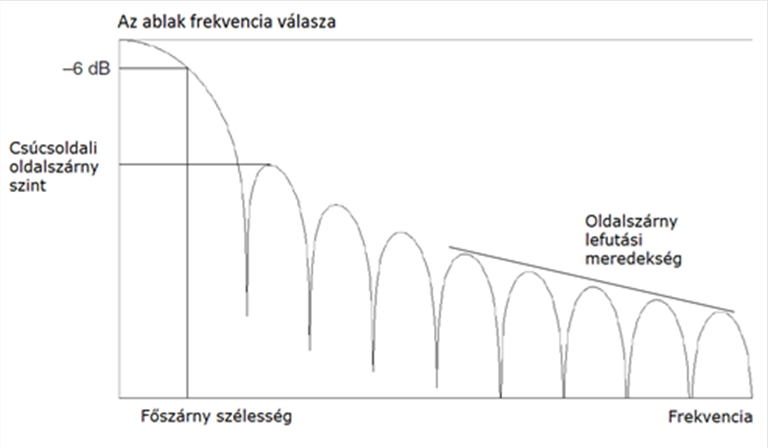
12.3.1. Fő szárny
A simító ablak fő szárnyának közepe az időtartománybeli jel minden egyes frekvencia komponensénél megjelenik. Megegyezés szerint, a fő szárny alakjának jellemzése a szélességével történik, ami alatt a csúcshoz képest -3 dB és -6 dB értékekhez tartozó frekvenciák által meghatározott szélességet értjük. A fő szárny szélességének megadása FFT tartományokban vagy frekvencia vonalakban történik.
A simító ablak spektrum fő szárnyának szélessége meghatározza az ablakozott jel frekvencia felbontását. Emiatt, két közeli frekvencia komponens megkülönböztetésének képessége növekszik a fő szárny szélességének csökkentésével. Ahogy a fő szárny keskenyebbé válik és a spektrális felbontóképesség javul, az ablak teljesítménye szétterül az oldal szárnyakba, megnövelve ezáltal a spektrum szóródást és csökkentve az amplitúdó pontosságot. Az amplitúdó pontosság és a spektrális felbontóképesség között kompromisszumot kell találni.
12.3.2. Oldalszárnyak
Oldal szárnyak a fő szárny mindkét oldalán megjelennek és a fő szárnytól fs/N többszöröseinél elérik a nulla értéket. A simító ablakok oldal szárnyainak karakterisztikái közvetlenül befolyásolják annak a mértékét, hogy a melyik szomszédos frekvenciakomponensek szóródnak a szomszédos frekvencia sávokon. Egy erős szinusz jel oldal szárny frekvenciaválasza elnyomhatja egy szomszédos gyengébb szinusz jel fő szárnyának frekvenciaválaszát!
A maximális oldal szárny szint és az oldal szárnyak csökkenésének mértéke jellemzi a simítóablak oldal szárnyát.
A maximális oldal szárny szint a legnagyobb oldal szárny szintje decibelben a főszárny csúcsához viszonyítva.
Az oldal szárny csökkenésének mértéke az oldal szárny csúcsaira fektetett egyenes meredeksége dB/dekádban megadva.
A 12.1. táblázat - A simító ablakok jellemzői táblázat megadja az egyes simító ablakok jellemzőit
|
Simító ablak |
-3 dB Főszárny szélesség (sávok) |
-6 dB Főszárny szélesség (sávok) |
Maximális Oldalszárny szint [dB] |
Oldalszárny lefutási meredekség [dB/dekád] |
|---|---|---|---|---|
|
Négyszögletes (ablakozás nélküli) |
0.88 |
1.21 |
-13 |
20 |
|
Hanning |
1.33 |
2.00 |
-32 |
60 |
|
Hamming |
1.3 |
1.81 |
-43 |
20 |
|
Backman-Harris |
1.62 |
2.27 |
-71 |
20 |
|
Exact Blackman |
1.81 |
2.25 |
-57 |
20 |
|
Blackman |
1.64 |
2.3 |
-58 |
60 |
|
Flat Top |
2.94 |
3.56 |
-44 |
20 |
12.3.3. Négyszögletes ablak (ablakozás nélküli állapot)
A négyszögletes ablak értéke 1 az egész hossza mentén. Az alábbi egyenlet írja le a négyszögletes ablakot:
|
w(n)= 1 |
(12.1) |
ahol
|
n= 0, 1, 2, .... N-1 |
Ahol N az ablak hossza és w az ablak értéke
Négyszögletes ablak alkalmazása olyan, mintha nem használnánk egyáltalán ablakot, mivel a négyszög függvény csak véges hosszúságúvá vágja a jelet.
A négyszögletes ablak alkalmazásánál a legnagyobb mértékű a spektrális szóródás.
A 12.12. ábra - Négyszögletes ablak ábra egy négyszögletes ablakot mutat N=32 értékkel.
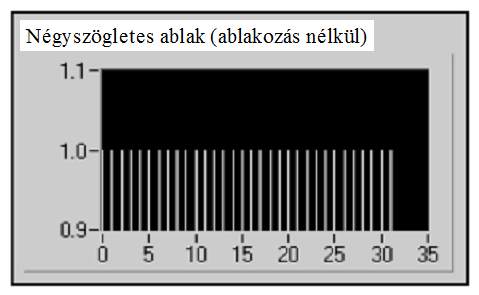
A négyszögletes ablak olyan tranziens jelek vizsgálatánál hasznos, melyek rövidebb ideig tartanak, mint az ablak. A tranziensek olyan jelek, amelyek rövid ideig állnak fenn. A négyszögletes ablak használatos még sorrendkövetésre, ahol az effektív mintavételi sebesség arányos a forgó gépek tengelyének fordulatszámával. A sorrendkövetésnél a négyszögletes ablak érzékeli a gép rezgésének saját frekvenciáját és a felharmonikusait.
12.3.4. Hanning ablak
A Hanning ablak alakja egy fél koszinusz függvényre hasonlít. Az alábbi egyenlet írja le a Hanning-ablakot:
|
|
(12.2) |
ahol
|
n= 0, 1, 2, .... N-1 |
Ahol N az ablak hossza és w az ablak értéke
A 12.13. ábra - Hanning ablak ábra egy Hanning ablakot mutat N=32 értékkel.
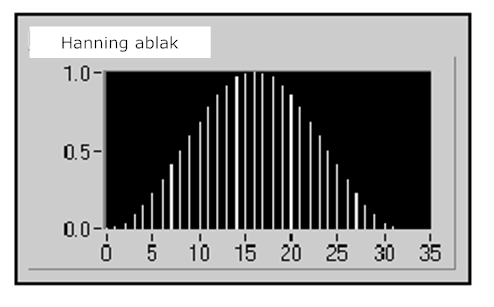
A Hanning ablak alkalmazása olyan tranziens jelek vizsgálatánál hasznos, melyek az ablak időtartamánál hosszabb ideig fennállnak, valamint általános célú alkalmazásoknál.
12.3.5. Hamming ablak
A Hamming ablak a Hanning ablak egy módosított változata. A Hamming ablak alakja hasonlít egy fél koszinusz hullámra.
Az alábbi egyenlet írja le a Hamming-ablakot:
|
|
(12.3) |
ahol
|
n= 0, 1, 2, .... N-1 |
Ahol N az ablak hossza és w az ablak értéke
A 12.14. ábra - Hamming ablak ábra egy Hamming ablakot mutat N=32 értékkel.
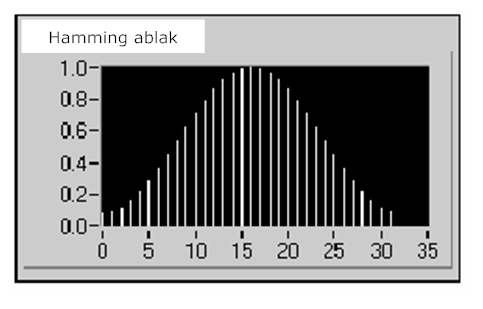
Amint az a 12.13. ábra - Hanning ablak és 12.14. ábra - Hamming ablak ábrán látható, a Hanning és a Hamming ablak hasonlít egymásra. Azonban az időtartományban a Hamming ablak nem közelít annyira nullához a széleknél, mint a Hanning ablak.
12.3.6. Kaiser-Bessel ablak
A Kaiser-Bessel ablak egy rugalmas simító ablak, melynek alakja változtatható a béta tényező értékének változtatásával. Ezért, a feladattól függően az ablak alakja megváltoztatható és így a spektrális szóródás mértéke szabályozható. Az alábbi egyenlet írja le a Kaiser-Bessel ablakot:
Kaiser függvény:
|
|
(12.4) |
a képletben I 0 (x) Bessel függvény:
|
|
(12.5) |
ahol
|
n= 0, 1, 2, .... N-1 |
Ahol N az ablak hossza és w az ablak értéke
A 12.15. ábra - Kaiser-Bessel ablak ábra a Kaiser-Bessel ablakot mutatja különböző béta értékeknél
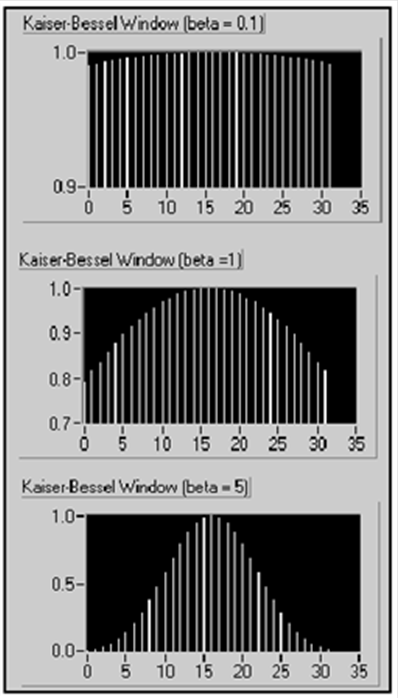
Kis béta értékeknél a négyszögletes ablakhoz hasonlít. Valójában béta=0-nál négyszögletes ablakot kapunk. Ahogy növeljük béta értékét, az ablak alakja egyre jobban elkeskenyedik mindkét oldalon. A Kaiser-Bessel ablak használható két, közel azonos frekvenciájú, de jelentősen különböző amplitúdójú jel érzékelésére.
12.3.7. Háromszög ablak
Ez az ablak a háromszög alakú. Az alábbi egyenlet írja le a háromszög ablakot:
|
|
(12.6) |
ahol
|
n= 0, 1, 2, .... N-1 |
Ahol N az ablak hossza, w az ablakfüggvény értéke.
A 12.16. ábra - Háromszög ablak ábra egy háromszög ablakot mutat N=32 értékkel.
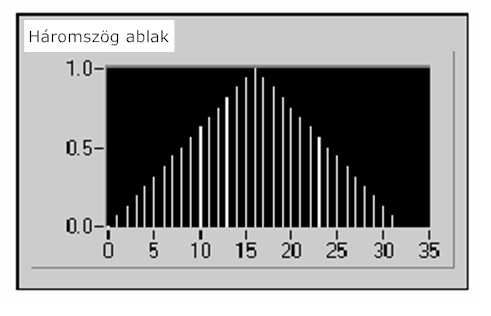
12.3.8. “Flat Top” ablak
A „flat top” ablaknak van a legnagyobb amplitúdó pontossága a simító ablakok között (±0,02 dB) az olyan jelekre, amelyek tipikusan nem egész periódusokból állnak. Mivel a „flat top” ablaknak széles fő szárnya van, ezért a frekvencia felbontóképessége gyenge. Az alábbi egyenlet írja le a „flat top” ablakot:
|
|
(12.7) |
ahol
|
| ||
|
és | ||
|
a0 = 0.215578948 | ||
|
a1 = 0.416631580 | ||
|
a2 = 0.277263158 | ||
|
a3 = 0.083578947 | ||
|
a4 = 0.006947368 |
A 12.17. ábra - Flat Top ablak ábra egy „flat top” ablakot mutat
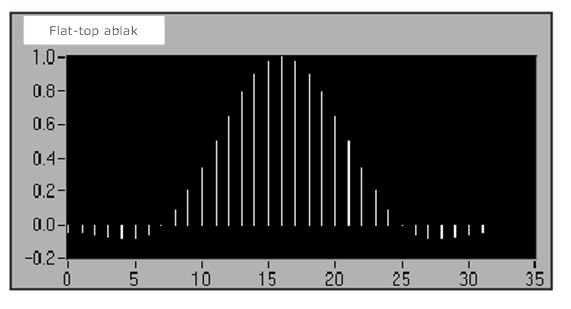
A „flat top” ablak a legalkalmasabb egy frekvencia komponens amplitúdójának pontos megmérésére, olyan jeleknél ahol alacsony szomszédos spektrális energia van a jelben.
12.3.9. Exponenciális ablak
Az ablak alakja csökkenő exponenciális függvény szerint változik. Az alábbi egyenlet írja le az exponenciális ablakot:
|
|
(12.8) |
ahol
|
n = 0, 1, 2, .... N-1 |
Ahol N az ablak hossza, w az ablak függvény értéke és fa végső érték.
Az ablakfüggvény kezdő értéke 1 és fokozatosan 0-ra csökken. Az exponenciális ablak végső értéke 0 és 1 között beállítható.
A 12.18. ábra - Exponenciális ablak ábra az exponenciális ablakot mutatja N=32 értékkel, amikor a végső érték f=0,1.
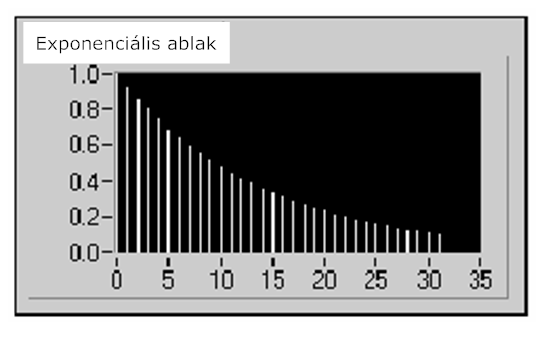
Az exponenciális ablak tranziens válaszfüggvények elemzéséhez használhatók, melyek hossza nem nagyobb, mint az ablak hossza. Az exponenciális ablak csillapítja a jel végét, ezáltal biztosítva, hogy a jel teljesen lecsengjen a minta-blokk végére. Az exponenciális ablak olyan jeleknél is használható, melyek exponenciálisan csökkennek, mint például az alak válasz enyhe csillapítással, amit egy külső hatás, mint például egy kalapácsütés gerjeszt.
12.4. Spektrális elemzéshez használt ablakok összehasonlítása az együttható tervezéshez használt ablakokkal
A spektrális analízis és a szűrők együttható tervezése különböző követelményeket támaszt az ablakokkal szemben. A spektrális analízis DFT-szerű ablakot igényel, míg a szűrő együttható tervezésnél a középpontjára szimmetrikus ablakra van szükség.
12.4.1. Spektrális analízis
A spektrális analízishez tervezett simítóablaknak DFT-szerűnek kell lenni. Egy simító ablak DFT-szerű, ha a skaláris (belső) szorzat a szinuszos jelek egész számú periódusaira azonosan egyenlő nullával. Más szavakkal, egy DFT-szerű szekvencia DFT-jének nincs képzetes összetevője.
A 12.19. ábra - Hanning ablak 8 mintavételi ponttal és a 12.20. ábra - Szinusz hullám 8 mintavételi ponttal ábra egy Hanning ablakot és egy szinusz hullám periódust mutat 8 mintavételi ponttal.
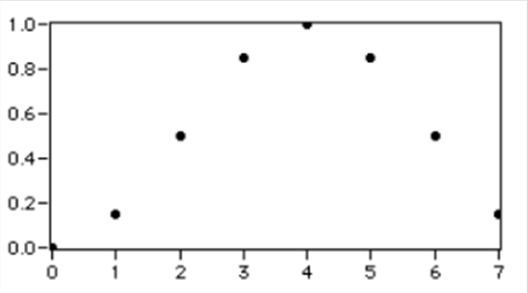
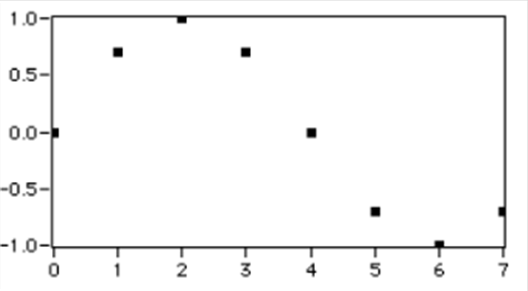
A (12.19. ábra - Hanning ablak 8 mintavételi ponttal) ábrán látható DFT-szerű Hanning ablak nem szimmetrikus a középpontjára. A ablak függvény utolsó pontja nem egyenlő az első pontjával, hasonlóan a (12.20. ábra - Szinusz hullám 8 mintavételi ponttal) ábrán látható teljes periódusnyi szinusz hullámmal.
A spektrális analízishez használt simító ablakok spektrális ablakok és a következő ablak típusokat foglalja magába:
Skálázott időtartománybeli ablak
Hanning ablak
Hamming ablak
Háromszög ablak
Blackman ablak
Egzakt Blackman ablak
Blackman-Harris ablak
Flat top ablak
Kaiser-Bessel ablak
Általános koszinusz ablak
Elkeskenyedő koszinusz ablak
12.4.2. Ablakok FIR szűrőegyütthatók tervezéshez
FIR szűrőegyütthatók tervezése olyan ablakot igényel, amely szimmetrikus a középpontjára.
A 12.9. és 12.10. egyenletek szemléltetik a különbséget a spektrális ablak és a szűrő együtthatók tervezéshez használt szimmetrikus ablak között.
A 12.9. egyenlet leírja a spektrális analízishez használt Hanning ablakot
|
|
(12.9) |
Ahol N az ablak hossza, w az ablak függvény értéke és i=0..N-1.
A 12.10. egyenlet leírja a szűrőegyüttható tervezéshez használt szimmetrikus Hanning ablakot
|
|
(12.10) |
ahol N az ablak hossza, w az ablak függvény értéke és i=0..N-1.
Egy spektrális ablak módosításával, amint azt a 12.10. egyenlet mutatja, meghatározható egy szimmetrikus ablak szűrőegyüttható tervezéséhez. A digitális szűrők tervezésével kapcsolatban további információk a Digitális szűrés című (10. fejezet - Digitális szűrés) fejezetben találhatók.
12.5. A megfelelő simító ablak kiválasztása
Egy simító ablak kiválasztása nem egyszerű feladat. Mindegyik simító ablaknak megvan a saját tulajdonsága, és különböző alkalmazásokhoz való alkalmassága. A simító ablak kiválasztásához meg kell becsülni a jel frekvencia tartalmát. Ha a jel erős egymásra hatással bíró frekvencia komponenseket tartalmaz távol a vizsgált frekvenciától, olyan simító ablakot kell kiválasztani, amelynél nagy az oldal szárnyak csökkenésének mértéke. Ha a jel erős egymásra hatással bíró frekvencia komponenseket tartalmaz a vizsgált frekvenciához közel, olyan simító ablakot kell választani, amelynél az oldal szárny maximális értéke kicsi. Lásd az 12.1. táblázat - A simító ablakok jellemzői táblázatot az oldal szárny csökkenés mértéke és a maximális oldal szárny szint értelmezéséhez a különböző simító ablakok esetén.
Ha a vizsgált frekvencia két vagy több egymáshoz nagyon közeli jelet tartalmaz, a spektrális felbontóképesség a fontos. Ebben az esetben olyan simító ablakot kell választani, amely fő szárnya nagyon keskeny.
Ha egyetlen frekvencia komponens amplitúdó pontossága fontosabb, mint a helyének pontos meghatározása egy adott frekvenciasávban, széles fő szárnyú ablakot kell választani.
Ha a jel spektruma inkább egyenletes vagy szélessávú a frekvencia tartalom tekintetében, négyszögletes ablakot kell választani, vagy nem kell ablakozni a jelet.
Általában a Hanning ablak az esetek 95%-ban megfelelő. Jó a frekvencia felbontóképessége és alacsony a spektrális szóródása. Ha nem ismerjük a jel természetét, de simító ablakot akarunk alkalmazni, Hanning ablakkal kell kezdeni!
A 12.2. táblázat - Jelek és javasolt ablakok táblázat felsorolja a különböző típusú jeleket és a hozzájuk használható ablakokat.
|
A jel típusa |
Javasolt ablak függvény |
|---|---|
|
Olyan tranziensek, melyek időtartama rövidebb, mint az ablak hossza |
Négyszögletes |
|
Olyan tranziensek, melyek időtartama hosszabb, mint az ablak hossza |
Exponenciális, Hanning |
|
Általános célú alkalmazások |
Hanning |
|
Spektrális analízis (frekvenciaválasz mérések) |
Hanning (véletlenszerű gerjesztésre), Négyszögletes (pszeudorandom gerjesztésre) |
|
Két nagyon közeli frekvenciájú, de nagyon különböző amplitúdójú jel szétválasztása |
Kaiser-Bessel |
|
Két nagyon közeli frekvenciájú, de majdnem azonos amplitúdójú jel szétválasztása |
Négyszögletes |
|
Pontos egy frekvenciájú amplitúdó mérés |
Flat top |
|
Szinusz hullám vagy szinusz hullámok kombinációja |
Hanning |
|
Szinusz hullám, az amplitúdó pontosság fontos |
Flat top |
|
Keskenysávú zavarjel (rezgés adatok) |
Hanning |
|
Szélessávú zavarjel (fehérzaj) |
Uniform |
|
Közeli térközű szinusz hullámok |
Uniform, Hamming |
|
Gerjesztő jelek (kalapács ütés) |
Exponenciális |
|
Válasz jelek |
Exponenciális |
|
Ismeretlen tartalom |
Hanning |
Kezdetben lehet, hogy nincs elegendő információ a jelről ahhoz, hogy a legjobb ablakot kiválasszuk. Lehet, hogy különböző simító ablakokkal kell próbálkozni ahhoz, hogy a legjobbat megtaláljuk. Mindig hasonlítsuk össze a különböző ablakok eredményét, hogy megtaláljuk az adott alkalmazáshoz a legmegfelelőbbet.
12.6. A simító ablakok paraméterezése
Amikor simító ablakot alkalmazunk egy időtartománybeli jelhez, az azt jelenti, hogy a jel hossza megtöbbszöröződik a simító ablak hosszára és eltorzul a simító ablak miatt. A simító ablak mindenütt megváltoztatja a jel amplitúdóját. Ha több simító ablakot alkalmazunk ugyanarra a jelre, mindegyik ablak paraméterezése úgy történik, hogy mindegyik csillapító ablakot osztjuk az ablakozott mátrixszal, amelyik az ablak eredmények egy összetartozó erősítése, minden ablakban csökkentve ugyanazt a spektrum amplitúdó eredményt az ablakok korlátozó pontossági feltételeivel. A 12.17. ábra - Flat Top ablak és 12.18. ábra - Exponenciális ablak ábrán látható rajzok méretezett simító ablakok alkalmazásának eredményei azonos időtartománybeli jelnél.
Egy FFT egyenértékű egy sorozat párhuzamos szűrő alkalmazásával, ahol mindegyik szűrő sávszélessége egyenlő Δɸ- el. A simító ablak „szétkenő” hatása miatt a simító ablak megnöveli az FFT sáv effektív sávszélességét egy ENBW-nek (equivalent noise-power bandwidth= egyenértékű zaj-energia sávszélesség) nevezett értékkel. Az adott frekvencia csúcsenergiája egyenlő a csúccsal szomszédos frekvencia sávok összegével, megnövelve egy arányossági tényezővel, ami a simítóablak ENBW-jével egyenlő. Az arányossági tényezőt figyelembe kell venni, amikor a teljesítmény spektrumon alapuló számítást hajtunk végre. Lásd a Diszkrét frekvencia analízis című (11. fejezet - Diszkrét frekvencia analízis) fejezetet az energia spektrumon végrehajtott számításokkal kapcsolatban.
A 12.3. táblázat - Simító ablakok korrekciós tényezői és a legrosszabb esetben fellépő amplitúdó hibák táblázat felsorolja az arányossági tényezőket, amelyet összetartozó erősítésnek is neveznek, az ENBW-t és a legrosszabb esetben fellépő amplitúdó pontosságot, melyet a középponton kívüli komponenseik okoznak számos simító ablaknál.
|
Ablak |
Paraméter (összetartozó erősítés) |
ENBW |
Legrosszabb esetben fellépő amplitúdó hiba [dB] |
|---|---|---|---|
|
Négyszögletes (ablakozás nélküli) |
1.00 |
1.00 |
3.92 |
|
Hanning |
0.50 |
1.50 |
1.42 |
|
Hamming |
0.54 |
1.36 |
1.75 |
|
Blackman-Harris |
0.42 |
1.71 |
1.13 |
|
Pontos Blackman |
0.43 |
1.69 |
1.15 |
|
Blackman |
0.42 |
1.73 |
1.10 |
|
Flat Top |
0.22 |
3.77 |
<0.01 |
Irodalom
[12.1.] LabVIEW Control Design User Manual. 2009.
13. fejezet - Számítógépes mérésadatgyűjtés és beavatkozás
13.1. A számítógépes mérésadatgyűjtő / feldolgozó rendszer felépítése
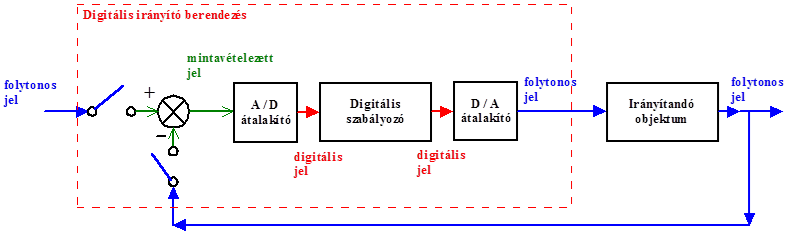
A számítógépes mérés adatgyűjtés és feldolgozás előnyei:
Digitális (mintavételes) átalakítók alkalmazásával az analóg jeleket digitálisan kódolt információvá (jellé) alakítjuk át.
Digitálisan kódolt jelek tárolása, (digitális) szűrése és a jeltovábbítás egyszerűbben valósítható meg, mint az analóg jeleknél.
A mintavételes rendszerek tervezése funkcionális modulok segítségével történik.
Intelligens szabályozók alkalmazhatók (adaptív szabályozás, fuzzy szabályozás, vagy pl. az alapjel súlyozású anti-windup szabályozás, ami egy speciális tulajdonságú (telítésgátolt) PID szabályzó).
Egyszerre több berendezést lehet működtetni egy mintavételes irányító rendszerrel, illetve egy rendszer több digitális számítógépből állhat.
A mintavételes irányító rendszerben különböző mintavételi sebességek alkalmazhatók.
A számítógépes mérés adatgyűjtés és feldolgozás hátrányai:
A mintavételes rendszer tervezéséhez matematikai analízis szükséges, amely néha nagyon komplex és bonyolult, összehasonlítva a folytonos rendszerek tervezésénél alkalmazott módszerekkel.
A mintavételes rendszerek stabilitás vizsgálata részletes hatás analízist és behangolást igényel, mint minden más szabályozási rendszeré.
A mintavételezéssel a kezelt jelek információ tartalma csökken.
Az alkalmazott algoritmusból vagy zajokból eredő programhibák befolyásolhatják a mérőrendszer helyes működését.
A mintavételezés információ késleltetést visz be a mérő körbe.
A mintavételes (digitális) berendezések működtetéséhez mindig szükséges külső energiaforrás alkalmazása.
Mindezen hátrányok mellett a digitális mérés és irányítástechnika egyre jobban kiszorítja az analóg elven működő méréstechnikát.
Egyedül a nagyfrekvenciás GHz tartományú méréseknél alkalmaznak ma is még analóg működésű mérő és beavatkozó berendezéseket a számítástechnikai rendszerek korlátozott számítási feldolgozási kapacitása miatt.
Áramköri megvalósítások (analóg áramkörök helyett) digitális mérő/irányító rendszereket illetve programozható digitális áramköröket FPGA-t (FPGA = Field Programable Gate Array) alkalmazhatunk, amelyek minden felmerülő feladatot képesek megoldani.
Digitális információ továbbítás, pl. hang/kép továbbítás (pontosság, zavarérzé-ketlenség).
Számítógépes hálózatok az információ forgalom szupersztrádái. Jeltovábbítás az Internet segítségével tetszőleges helyről tetszőleges helyre.
Az alkalmazott analízis és szintézis technikák
Idő tartományban:
Lineáris differenciál/differencia egyenlet megoldási eljárások
Impulzus válasz analízis
Állapotváltozós alakban történő analízis
Frekvencia tartományban:
Fourier transzformáció (frekvencia tartomány)
Gyökhely görbe (pólusok és zérusok analízise)
Frekvencia válasz analízis (impulzus-átviteli függvény)
Z transzformáció (mintavételes jelek elemzése)
Tervezés állapotváltozós alakban (s tartományban; z tartományban)
Megjegyzendő, hogy minden vizsgálati módszer egy
DSP (= Digital Signal Processing = Digitális Jelfolyamat Kezelés ) eljárást modellez.
A DSP-t „Digitális Jelfeldolgozásnak” nevezik a magyar szakirodalomban.
Egyéb tudományok, amelyek szerepet játszanak a mintavételes irányítástechnika alkalmazásában, mint
differenciál és differencia egyenletek,
klasszikus szabályozás elmélet,
numerikus analízis,
végeselem analízis,
mintavételes szabályozás elmélet,
számítógépes rendszer felépítése,
digitális integrált áramkörök működése,
jelátalakítók (senzorok és aktuátorok),
információs struktúrák (adatelemek felépítése, nagy mennyiségű adat tárolása),
irányítási algoritmus tervezés,
digitális jel processzálás,
program tervezés,
ellenőrző programok (önteszt).

Az mérő/feldolgozó rendszereknél jelek bejuttatása a számítógépbe és a számított értékek eljuttatása a berendezésekhez a legfontosabb feladat.
A következőkben röviden áttekintjük a számítógépbe beolvasott és abból kiadott jelek típusait. A jelek tulajdonságainak és mérésének lehetőségei az ezt követő fejezetekben jelennek meg részletesen.
13.2. Logikai (digitális) jelek
|
Jeltípus |
Ábra |
|---|---|
|
Logikai bemeneti és kimeneti jelek A logikai jelek aktuális időpillanatbeli állapota az információ. |
|
|
Logikai pulzushordozók A logikai jelek állapotváltozása, mint esemény a jelből meghatározott információ. |
|
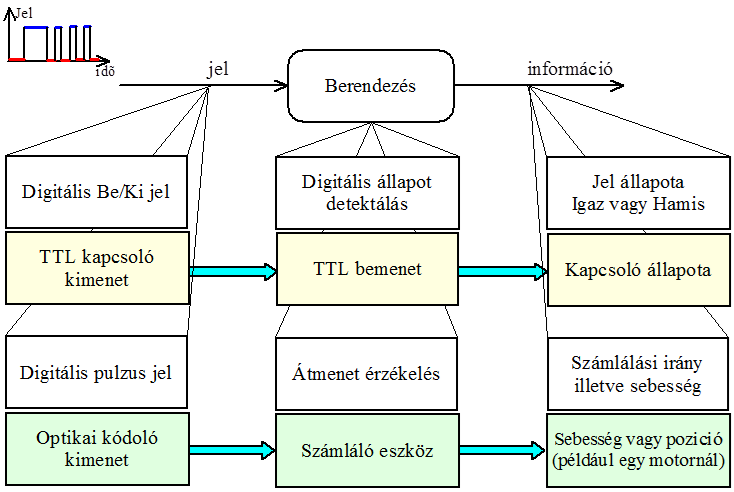
13.2.1. Digitális bemenetek
13.2.1.1. TTL bemenet
Nem biztosít galvanikus elválasztást!
A galvanikus elválasztás azt jelenti, hogy a vezérlő bemenet és a vezérelt kimenet között nincs vezetékes (galvanikus) kapcsolat.

A TTL melynek jelentése tranzisztor-tranzisztor-logika (TTL = Transistor Transistor Logic) a logikai eszköz bementi és kimeneti elektronikus elemének típusát írja le. A kis feszültségszintű tápellátás (5 Volt) mellett jó zajelnyomással rendelkezik, ennek alapján világszabvánnyá vált a logikai áramkörök területén.
Jelölések:
OL = Kimenet logikai hamis értéke (Output Low)
OH = Kimenet logikai igaz értéke (Output High)
IL = Bemenet logikai hamis értéke (Input Low)
IH = Bemenet logikai hamis értéke (Input High)
A TTL kimenetekáram és feszültség specifikációi a következők:
VOL = 0.4 V
VOH = 2.4 V
IOL = 16 mA
IOH = 400 µA
A TTL bemenetekáram és feszültség specifikációi a következők:
VIL = 0.8 V
VIH = 2.0 V
IIL = 1.6 mA
IIH = 40 µA
A maximum emelkedési/esési időtartam 50 ns a VIL és VIH között. (fmax = 20 MHz)
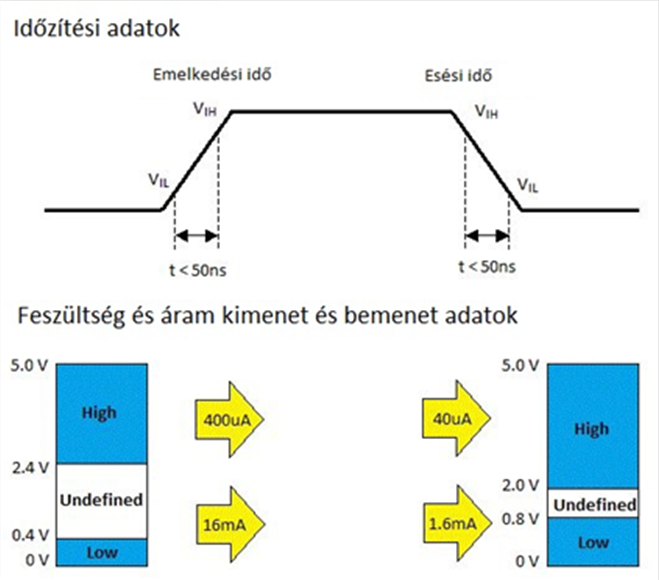
Megjegyzés: A kimeneti áram értékek a kimeneti feszültségszintek megtartása mellett 10 darab TTL bemenet kapcsolódására alkalmasak.
13.2.1.2. Relés érintkező bemenet
Galvanikus elválasztást biztosít!
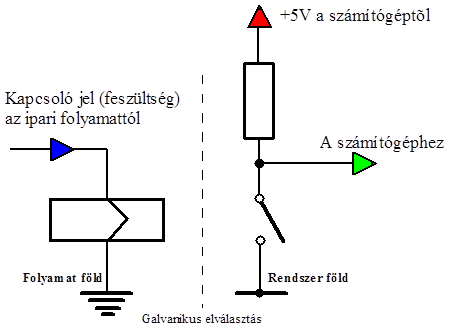
Az áramkör jelszint transzformációt (is) végez tetszőleges szintű bemeneti logikai értékről TTL szintű logikai értékre.
A késleltetés több komponensből tevődik össze
a villamos rendszer késletetése a relé tekercs induktivitásán kialakuló áram késleltetése
a relé és a kapcsolódó rugók mechanikai mozgatásához szükséges időtartam, amely a geometria méretektől (is) függ.
A relék késleltetése 10-100 msec.
Hátrányuk még a nagy (működtető) teljesítmény igény, amely a relék működtető tekercsei áramfelvételéből ered.
13.2.1.3. Digitális bemenet fotodióda segítségével
Galvanikus elválasztást biztosít!
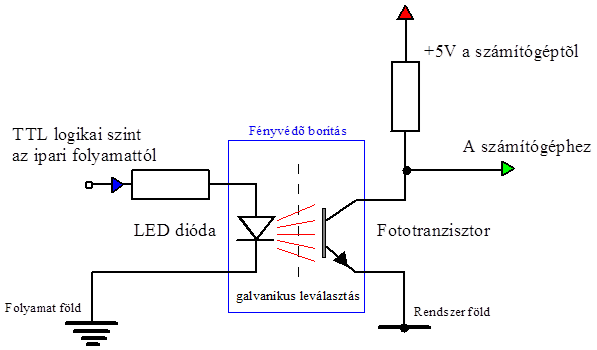
A logikai jelek galvanikus elszigetelését (elválasztását) napjainkban foto-dióda- foto-tranzisztor páros segítségével biztosítják, amely optikai elven valósítja meg a bemeneti és a kimeneti oldal villamos elszigetelését. Az eszköz kis méretű, nem tartalmaz mozgó alkatrészt, nincs karbantartás igénye és kis teljesítmény szükséges a működtetéséhez. A kapcsolási idő, amely a bemenő és a kimenő jel közötti késleltetés nano secundum (ns) nagyságrendű.
Az eszközt a galvanikus elválasztás mellett gyakran alkalmazzák elfordulás (elmozdulás), érzékelőként, amelyre példát a (13.8. ábra - Digitális bementi pozicionáló eszköz) ábrán láthatunk. Itt a fotodiódát és a foto-tranzisztort úgy helyezik el egymáshoz képest, hogy közöttük egy megszakító elem biztosítja/megszünteti a fény útját a két elem között. Ezzel biztosítható, hogy a kódtárcsán elhelyezett rések elmozdulását érzékeljük, és villamos jellé alakítsuk át. A kimeneten megjelenő impulzus sorozatot egy impulzusszámláló áramkör segítségével közvetlenül elmozdulássá tudjuk átalakítani.
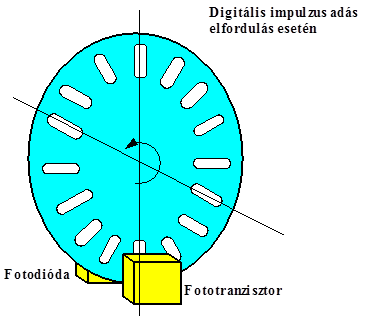
13.2.1.4. CMOS áramköri bemenetek
Galvanikus elválasztást biztosít!
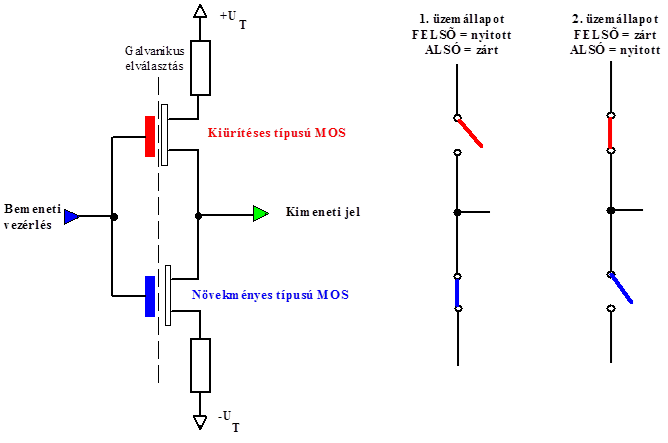
A (13.9. ábra - Digitális CMOS bemenet kapcsolása) ábrán látható CMOS elemekből felépített logikai jel elválasztó kapcsolás előnyei, hogy
galvanikus elválasztást biztosít a bemeneti és a kimeneti áramkör között
a bementi jel logikai szintjét –amely így eltérő lehet a TTL jelszintektől – TTL szintű jellé alakítja át
a két MOS tranzisztor közül az egyik mindig zárt a másik pedig mindig nyitott a két logiai szint értéknél, ezért az eszközön nagyon kicsiny áram folyik át, amely nanoAmper – pikoAmper nagyságú, ezért az eszköz működtetéséhez nagyon kis teljesítmény szükséges.
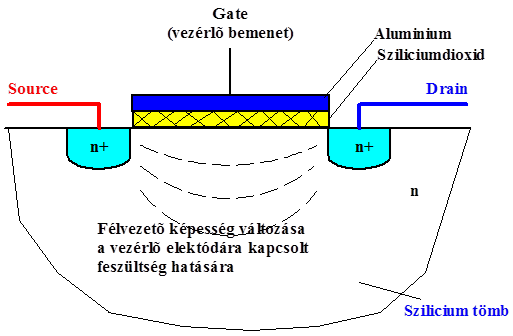
Növekményes és kiürítéses típusú FET tranzisztorok.
Az eszközben alkalmazott MOS tranzisztor típusok működési elve biztosítja, hogy ugyanazon logikai jelszint értéknél az egyik tranzisztor nyitott a másik pedig zárt állapotban legyen.
13.2.2. Digitális kimenetek
13.2.2.1. TTL kimenetek
Nem biztosít galvanikus elválasztást! (Standard 2 állapotúak)

Egy TTL kimenet a hozzá kapcsolt TTL bemenet logikai magas/igaz (High, True) állapotban tartásához nem igényel csak minimális mikroAmper nagyságú kimeneti áramot.
Jóval nagyobb viszont a TTL kimenet áramkibocsájtása, ha a logikai szintet logikai alacsony/hamis (Low, False) értékre kell beállítania. A TTL kimenethez kapcsolt TTL bementek mindegyike ~1,6 mA áramot igényel az alacsony (hamis) logikai szint megtartásához, így a TTL szabvány szerinti ~16-24 mA maximális áram kibocsájtására alkalmas logikai kimenethez véges számú TTL logikai bemenet kapcsolható.
13.2.2.2. Három állapotú kimenetek (Three State)
Nem biztosít galvanikus elválasztást! )
Ezek a logikai jelkimeneti eszközök egy további engedélyező jel segítségével a két logikai szint értéken kívül egy „harmadik állapotba” is képesek beállítani az eszköz kimentét. Ez a kimeneti állapot a nem aktív állapot , amely sem logikai alacsony, sem pedig logikai magas értékű, hanem a kimenetet szabadon hagyja ”elhúzni” egy másik kimenet által rákényszerített értékre.
A kimenet „elhúzhatósága” azt jelenti, hogy az inaktív elem kimenete úgy viselkedik, mintha egy nagy értékű ellenállással kapcsolódna a korábban általa vezérelt vezetékre, így biztosítja, hogy a vezeték arra a logikai szint értékre állhasson be, amelyet egy másik (aktív) elem kimenete rákényszerít.
Ezzel a villamos logikai elemmel úgynevezett busz áramkört hozhatunk létre, amelynél ugyanazt a villamos vezetéket időben egymás után különböző eszközök közötti logikai jeltovábbításra alkalmazhatunk. Az adott vezeték logikai jelszintjének értékét mindig csak egyetlen eszköz állíthatja be, amelyet az eszközök címzési technikájával választunk ki – ez a beszélő (talker) kimenet. A többi ugyanerre a vezetékre csatlakozó kimenet a harmadik állapotban (tree state) van, ami azt jelenti, hogy nem befolyásolják a vezeték állapotát saját kimeneti értékükkel, mert úgynevezett nagy impedanciás kimeneti állapotban szabadon „elhúzhatók”, az aktív kimenet által rájuk kényszerített értékre.
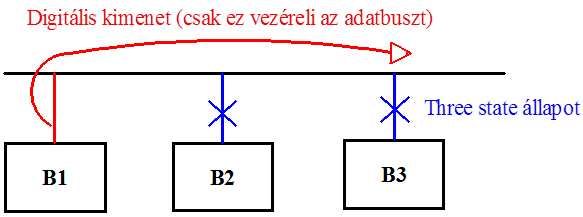
13.2.2.3. Relés kimenet
Galvanikus elválasztást biztosít!
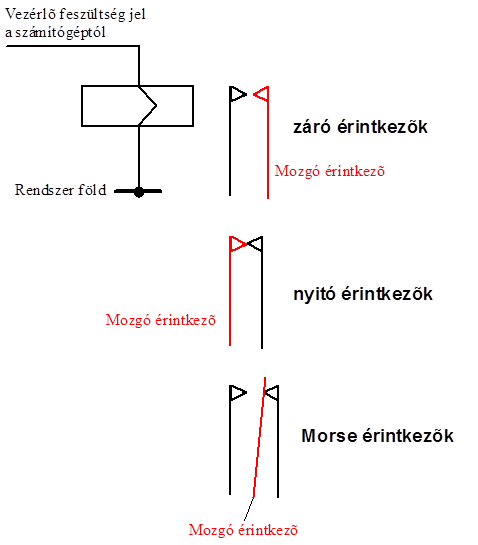
A relés kimeneteket elsősorban nagyobb teljesítmény kapcsolásának megvalósításához alkalmazzuk. A szabványos TTL jelszint kimeneti értékétől nagyobb feszültség és áramigény esetén a TTL kimenet „csak” a relés kimeneti egység vezérlő jele és a relé kapcsoló érintkezők segítségével kapcsolunk be/ki a számítógéphez kapcsolt nagyobb teljesítmény igényű berendezéseket.
A relés kimenet előnye, hogy a villamos kapcsolatot fém kontaktusok segítségével valósítjuk meg, így ezek kapcsolódás esetén minimális ellenállásúak. A kis kapcsolói ellenállás pedig azt jelenti, hogy a kontaktusokon átfolyó általában nagy értékű áram a kontaktusok nagyon kicsiny ellenállásán minimális hőmennyiséget hoz létre, és ezt a hőt is gyorsan elvezeti a jó hővezetési tényezővel rendelkező fém érintkező.
A relés kapcsolók előnye:
Nagy teljesítményű berendezések kapcsolható be/ki a segítségükkel. Meghatározott teljesítményekhez meghatározott érintkező méretek szükségesek az áramsűrűség, érintkező nyomás biztosításához ezért gyakran alkalmaznak kaszkád kapcsolású relé -ket, amelyek lehetővé teszik, hogy egy relé általánosan csak ~10-50-szer nagyobb teljesítményű jelet kapcsoljon, mint amilyen a saját bementi vezérlő jele.
A relés kapcsolók hátrányai:
A kapcsolási időtartam ~10-100 ms. Az általános vezérlési feladatok megoldásához ezek a kapcsolási idők elegendőek.
A relé mozgó mechanikai elemeket tartalmaz, amelyek karbantartást igényelnek és véges számú kapcsolás megvalósítására alkalmasak.
A relék működtetéséhez szükséges villamos teljesítmény (áram érték) jelentős mértékű többlet teljesítmény igényt jelent a logikai kapcsolat megvalósításánál.
13.2.2.4. Félvezetős kimenet (Solid State Relay)
Galvanikus elválasztást biztosít!
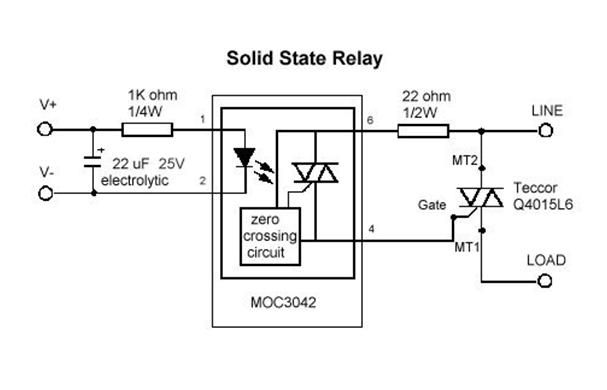
A 13.14. ábra - Digitális félvezetős kimenet ábrán egy szilárd test relé (solid state relay) kapcsolási rajza látható. Nagy teljesítményű egyen és/vagy váltakozó áramú kapcsoló. KW-os nagyságú kimeneti teljesítmény kapcsolására alkalmas. Mivel a „kapcsoló elem” félvezetőből van, melynek jóval nagyobb ellenállása van, mint a fémeknek, ezért a kapcsoló elemen átvezetett áram magát a kapcsoló elemet is fűti. Ezt a keletkezett hőmennyiséget kell megfelelő hűtő felülettel és intenzív hűtéssel eltávolítani, mert a túlmelegedés az eszköz tönkremenetelét eredményezi (13.15. ábra - Optikai vezérlésű CMOS kapcsolók).
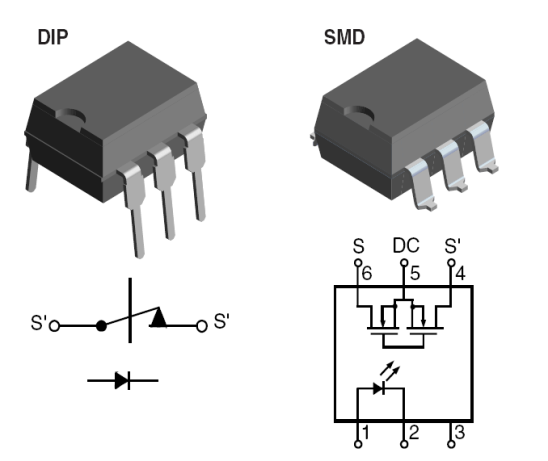

13.2.2.5. CMOS áramköri kimenetek
Galvanikus elválasztást biztosít!
CMOS = C omplementer M etal O xide S emiconductor
Áramköri megoldás szintáttevésre alkalmas ±15V nagyságú feszültség szintekre „alakítja át” a TTL feszültség szinteket, amelyek a logikai állapotokat jelentik.
Összefoglalás digitális bemenetek
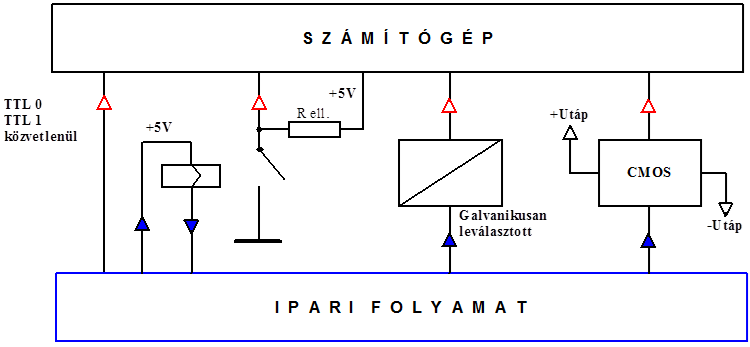
Összefoglalás digitális kimenetek
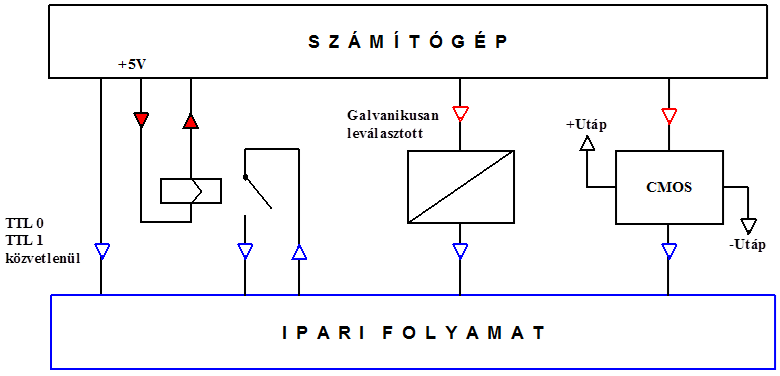
Általánosan elmondható, hogy a normál TTL szint 1-2 m távolságra vihető át megfelelő vevőoldali jelszint mellett.
A nagy jelsebesség miatt (20-60 MHz) a logikai jelet egy távvezetékhez hasonló rendszerben kell vizsgálni. Ebből a szempontból a jelvezetéket egy elosztott paraméterű hálózattal modellezzük és így vizsgáljuk meg a jeltovábbítás időbeni folyamatát.
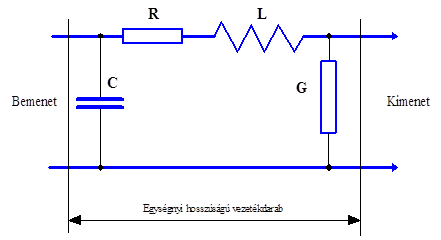
ahol
|
R |
ellenállás [Ohm] | |
|
C |
kapacitás [Farad] | |
|
L |
induktivitás [Henry] | |
|
G |
vezetés (a jelvezetékek közötti átvezetés) [Siemens] |
Ideális eset lenne, ha: R=0 [Ohm]; C=0 [Farad]; L=0 [Henry]; G=∞ [Siemens] lenne.
Elosztott paraméterű modell alapján kell azt a lezárási impedanciát meghatároznunk, amellyel túllendüléstől mentes kimeneti jelet biztosítjuk.
A kimenetet a hullámimpedanciával kell lezárni, ahhoz, hogy a kialakuló esetleges jel visszaverődésekből keletkező jelszint változás (lengés) minimális legyen. A lezáró hullámimpedancia értéket az egyes jelvezeték típusokhoz megadják illetve méréssel meghatározzák (pl. 75 Ohm). A mérés megvalósítását a (13.20. ábra - Hálózat rövidzárási és üresjárási impedanciájának mérése) ábrán láthatjuk, a mérések alapján a hullámimpedancia számítási képletét a 13.1 képlet adja meg.
Minél nagyobb a jelszint (értsd a jel feszültség szintje) annál kevésbé sérülékenyek a logikai értékek, ezért történik a kis feszültség szint értékű TTL jelszintek átalakítása nagyobb feszültség szint értékű jelekké.
Áramgenerátoros táplálással (4-20 mA) szintén nagy távolságú megbízható adatátvitelt lehet megvalósítani. A nagyobb áram értékek azonban vastagabb vezetékeket, így nagyobb a távolságra vetített fajlagos költség.

A hullám-impedancia meghatározásának képlete:
|
|
(13.1) |
ahol 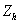 a hullámimpedancia
a hullámimpedancia
13.3. Analóg jelek
|
Jeltípus |
Ábra |
|---|---|
|
Egyenfeszültségű jel Programozott időzítés (mintavétel) beolvasás egyedi adatonként a számítógépbe. |
|
|
Időfüggvény Hardware-rel támogatott időzítés (mintavétel) blokkok formájában történő beolvasás a számítógépbe. |
|
|
Frekvenciafüggvény Az időfüggvényből határozzuk meg! Hardware-rel támogatott időzítés (mintavétel) blokkok formájában történő beolvasás a számítógépbe. |
A transzformált jel különböző frekvenciájú komponenseinek amplitúdó függvénye |
13.4. Analóg be/kimeneti jelek
13.4.1. Analóg jel / Egyenfeszültségű jel
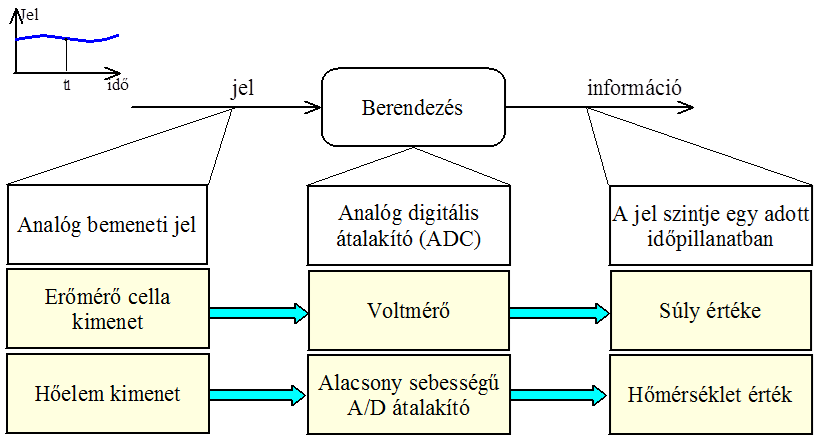
13.4.2. Analóg jel / Időfüggvény
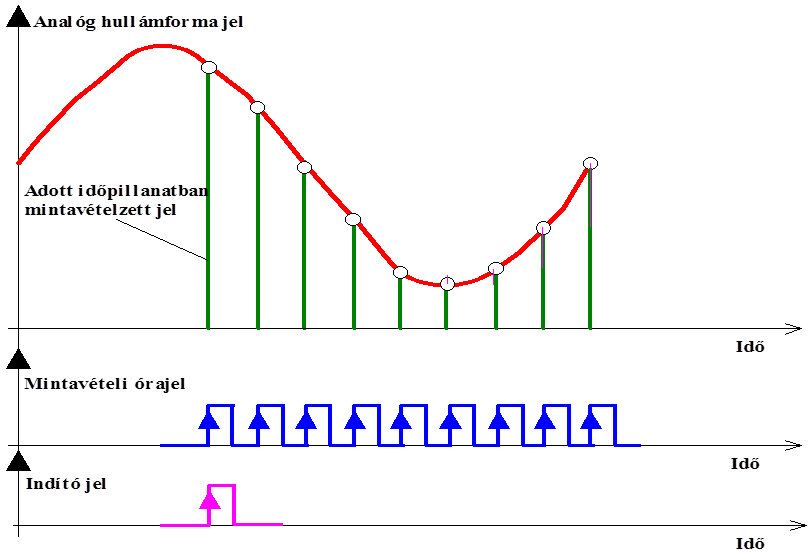
13.4.3. Frekvenciafüggvény
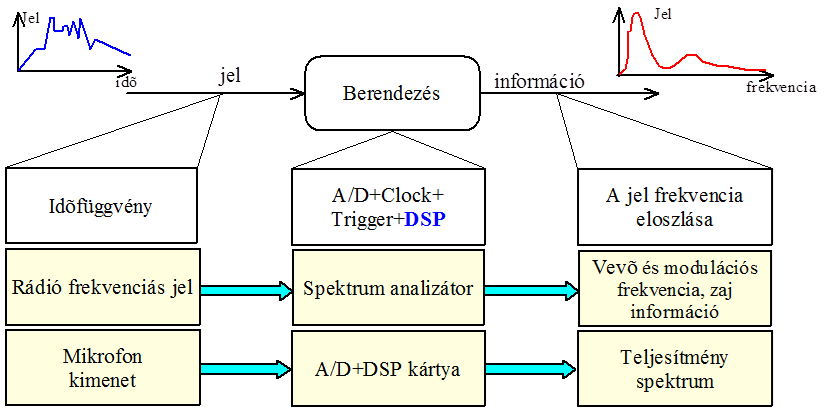
DSP = Digital Signal Processing
A frekvencia tartományban történő feldolgozáshoz alapvető a gyors Fourier transzformáció (FFT = Fast Fourier Transzformáció), amely egy alapfüggvény a DSP könyvtárban.
Inverz Fast Fourier Transzformációval visszatérhetünk a frekvencia tartományból időtartományba. Ilyen módon történik a frekvencia átviteli függvényekkel történő jelanalízis.
13.5. Időzítés mérése
|
Jeltípus |
Ábra |
|---|---|
|
Időzítések mérése Digitális impulzus időtartamának lemérése (Gate) adott nagyságú órajel alkalmazásával egy számláló áramkört kapuzunk (Gate AND Clock). |
|
Irodalmak
[13.1.] Analog And Digital Control System Design. Sounders College Publishing . 2006.
[13.2.] Linear System Theory and Design. Oxford University Press. 1999.
[13.3.] Modern Control Systems Engineering. 1996.
14. fejezet - Analóg bemenetek
- 14.1. A jelforrások típusai
- 14.2. Jelvevő áramkörök
- 14.3. Az illesztés legfontosabb szabályai
- 14.4. Zavarjelek
- 14.4.1. A csatolások típusai
- 14.4.2. A zavarjelek kiküszöbölésének általános módszerei
- 14.4.3. A zavarjelek típusai, időbeni változásuk alapján
- 14.4.4. A zavarjelek típusai áramkörökben való megjelenési formájuk szerint
- 14.4.5. A zavarjelek típusai keletkezési ok szerint és a zajcsökkentés módszerei
- 14.4.5.1. Csatlakozási potenciál
- 14.4.5.2. Termikus potenciál (termoelem)
- 14.4.5.3. Átmeneti ellenállás, átvezetés
- 14.4.5.4. Elektromágneses (induktív) zavarjel
- 14.4.5.5. Elektrosztatikus (kapacitív) zavarjel
- 14.4.5.6. Villamos áramkörök be és kikapcsolásakor keletkező zavarjel
- 14.4.5.7. Kábelhajlításból származó zavarjel
- 14.4.5.8. Rádiófrekvenciás zavarjel
- 14.4.5.9. Tápforrásból származó zavarjel
- 14.5. Földelések
- 14.6. A nemkívánatos föld áramkörök kiküszöbölésének módjai
- 14.7. Analóg bemenetek elemei
- 14.8. Analóg jel kondicionálása
- 14.9. Small Computer Extended Interface (SCXI)
- 14.10. Analóg méréspont váltók (multiplexerek)
- 14.11. Mintavevő tartó és erősítő
- 14.12. Analóg digitális (A/D) átalakítók
- 14.13. Mérés-adatgyűjtés általános áttekintése
- 14.13.1. Mérés-adatgyűjtő rendszerek komponensei
- 14.13.2. Analóg bemenet
- 14.13.3. Egy kimenetű jelek (Single-Ended Inputs)
- 14.13.4. Különbségi bemenetek (Differential Inputs)
- 14.13.5. Felbontás (Resolution)
- 14.13.6. Mérési határok (Range)
- 14.13.7. Erősítés (Gain)
- 14.13.8. Mintavételezés sebessége (Sampling Rate)
- 14.13.9. Átlagolás (Averaging)
- 14.13.10. Analóg bemenet eljárása a számítógépben
- 14.13.11. Analóg bemenet csatorna mintavételezés
- 14.13.12. Hullámforma bemenet (Waveform Input)
- 14.13.13. Analóg input hullámforma adatgyűjtő
- 14.14. Az analóg bemeneti perifériák perifériavezérlő egysége
- 14.15. Folytonos idejű mérésadatgyűjtés
- Irodalmak
A számítógépes analóg bemeneti kártyák általánosan a következő blokk diagrammal jellemezhetők:
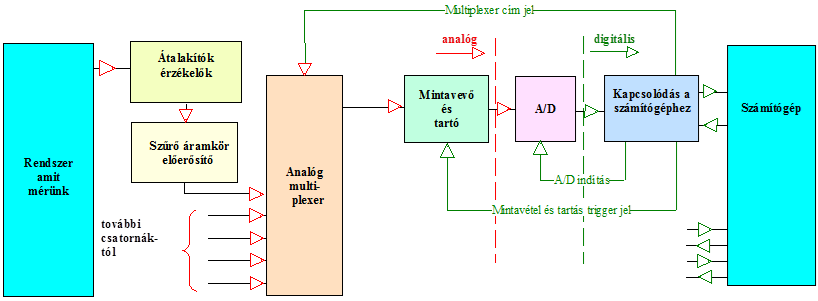
Csak analóg bemeneti jel kezelése esetén a számítógépnek a következő időtartamokra van szüksége:
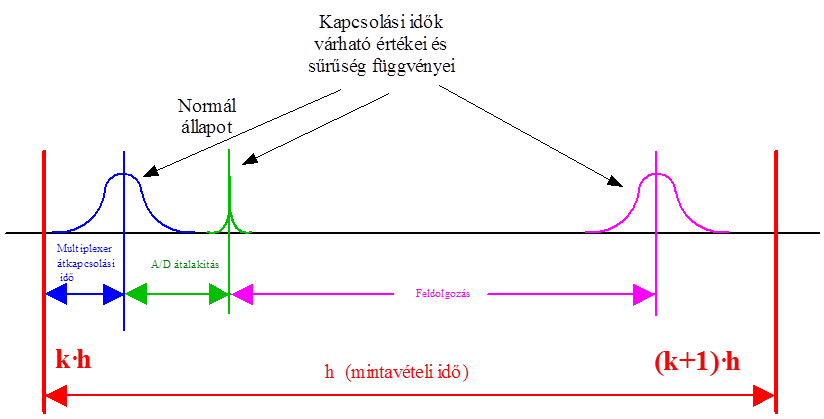
14.1. A jelforrások típusai
14.1.1. Aszimmetrikus földelt jelforrás
A kimeneti vezetékek és a föld között mérhető impedanciák nagysága különböző.
Az egyik kimeneti vezeték földelt!
14.1.2. Aszimmetrikus földfüggetlen jelforrás
A két kimeneti vezeték a földfüggetlen (például ilyen egy 1.5 Voltos ceruzaelem).
Az egyik kimeneti vezeték a folyamat oldalon leföldelhető.
14.1.3. Aszimmetrikus földelt eltolt nullszintű jelforrás
A kimeneti vezeték és a föld között különböző impedanciák mérhetők.
A kimeneti vezetékek nem földelhetők!
14.1.4. Szimmetrikus földelt jelforrás
A kimeneti pontok között mérhető impedanciák azonosak.
A kimeneti vezetékek nem földelhetők!
14.1.5. Szimmetrikus földfüggetlen jelforrás
A kimeneti pontok között mérhető impedanciák azonosak.
Az egyik kimeneti vezeték a folyamat oldalon leföldelhető.
14.2. Jelvevő áramkörök
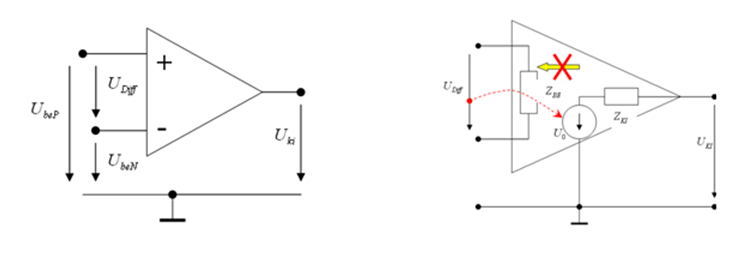
A jel fogadását a rendszer oldalon (a számítógépes mérés előtt) általánosan egy műveleti erősítős áramkörrel biztosítjuk, amely nagy bementi ellenállással rendelkezik, így nem terheli a jelforrást. A műveleti erősítő kimenete közel ideális feszültséggenerátor – nulla belső ellenállással.
A jelvevő áramkörök általánosan egy fém (lágyvas) árnyékoló dobozban elhelyezett műveleti erősítős kapcsolást tartalmaznak – beállított erősítési értékkel.
A különböző jelvevő kapcsolásoknál a háromszöggel jelzett fémdobozt illetve az ettől elszigetelten bevezetett bemeneteket és a műveleti erősítős kapcsolás legfontosabb elemeit jelöljük.
14.2.1. Aszimmetrikus földelt jelvevő
A bemeneti vezetékek és a föld között mérhető impedanciák nagysága különböző. Az egyik bemeneti és a kimeneti vezeték valamint a külső ház földelt.
14.2.2. Szimmetrikus földelt jelvevő
A bemenetek és a föld között mérhető impedanciák nagysága azonos.
Az impedanciák kivezetett közös pontja, az egyik kimeneti vezeték és a külső ház földelt .
14.2.3. Aszimmetrikus földfüggetlen jelvevő
A bemeneti vezetékek a földtől, a külső háztól és a kimeneti vezetékektől szigeteltek.
Az egyik bemeneti vezeték a földfüggetlen árnyékolásra kapcsolódik. Az egyik kimeneti vezeték és a külső ház földelt .
Ha az egyik bemeneti vezetéket leföldeljük a bemenetek és a föld között mérhető impedanciák nagysága különböző lesz.
14.2.4. Szimmetrikus földfüggetlen védőárnyékolt jelvevő
A bemeneti vezetékek és a védőárnyékoláshoz kapcsolódó közös vezeték között mérhető szórási impedanciák megegyeznek, csak a külső ház és az egyik kimeneti vezeték földelt.
Ha a védőárnyékolás kivezetését az egyik bemeneti vezetékkel összekötik a jelvevő aszimmetrikus földfüggetlen lesz.
14.2.5. Aszimmetrikus földfüggetlen védőárnyékolt jelvevő
A melegpont (high) a földhöz képest nagy szórási impedanciájú pont.
A hidegpont (low) a földhöz képest kis impedanciájú.
A védőárnyékolás (guard) pedig a jelvevő földfüggetlen lebegő bemeneti pontja.
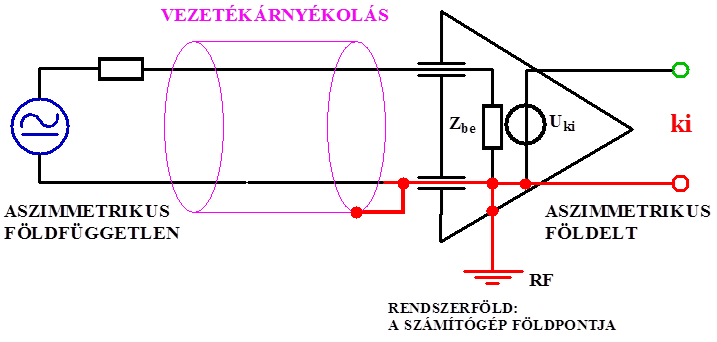
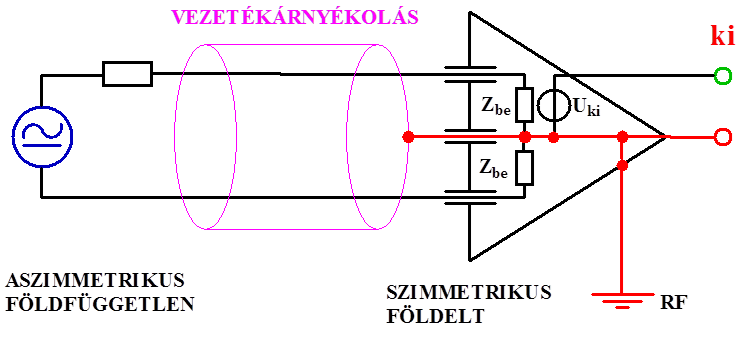
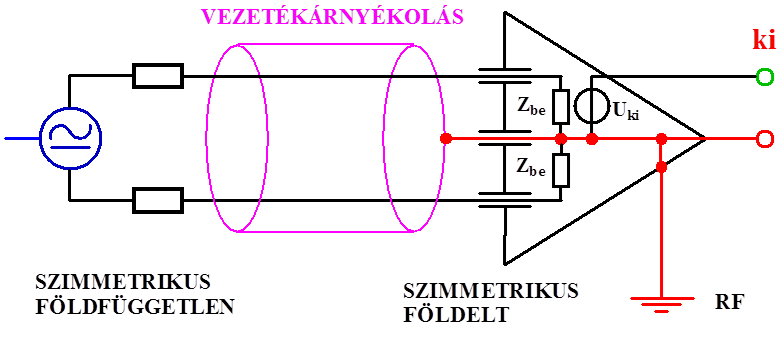
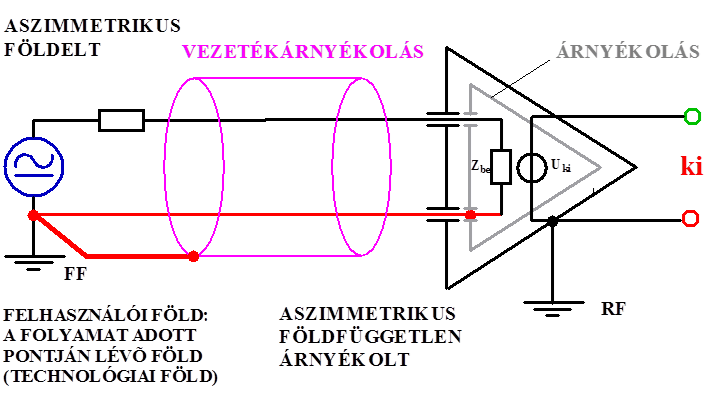
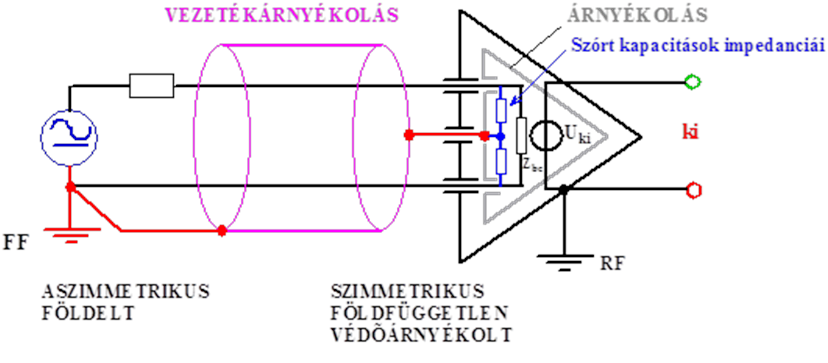
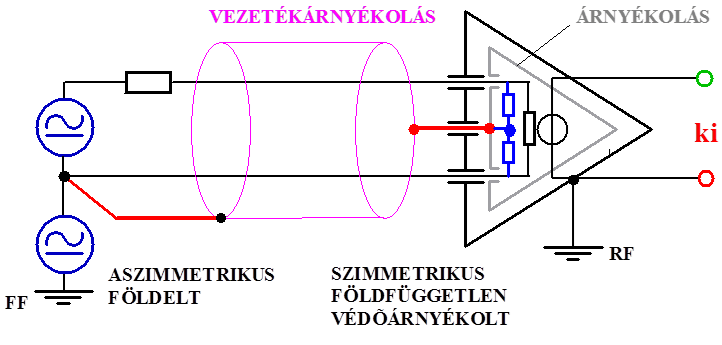
Megjegyzés:
A jelforrások és jelvevők egyes típusainak megkülönböztetése azért lényeges, mert a számítógép és a folyamat összekapcsolásában egy adott típusú jelforrás csak megfelelő jelvevővel kapcsolható össze.
HA AZ ILLESZTÉSI SZABÁLYOK NEM TARTJUK BE AZ MEGENGEDHETETLEN JELTORZULÁSOKHOZ VEZET!
Az illesztésekkel kapcsolatos problémák csak a zavarjelek hatásmechanizmusának tanulmányozásával érthetők meg.
14.3. Az illesztés legfontosabb szabályai
Egyetlen pont földelése: A jelforrást és a jelvevőt tartalmazó rendszerben CSAK EGY PONT FÖLDELHETŐ, de egy pontban le kell földelni a rendszert.
Szimmetrikus áramkör kialakítása: A nagy zavarjel elnyomás érdekében törekedni kell szimmetrikus jelforrások és jelVevők kialakítására.
A vezeték árnyékolás potenciáljának rögzítése: A vezeték árnyékolás potenciálját CSAK EGYETLEN PONTBAN szabad rögzíteni, DE EGY PONTBAN SZÜKSÉGES RÖGZÍTENI!
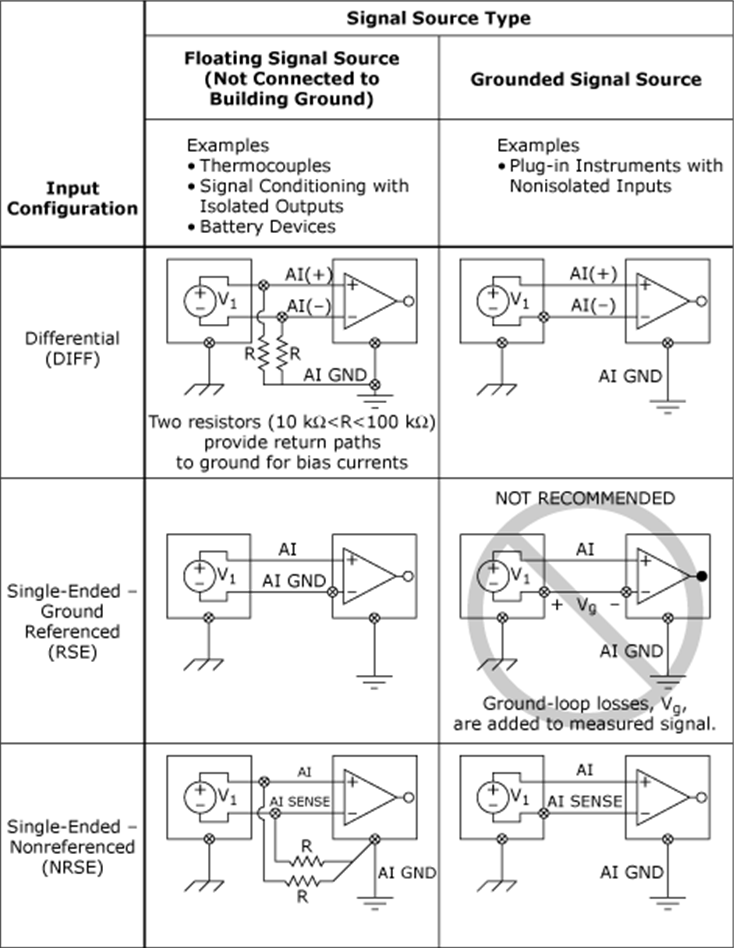
14.4. Zavarjelek
A zaj (noise) a hasznos információt hordozó jel (hasznos jel) olyan torzulása, amely információ veszteséget okoz. A torzult jel a hasznos jel és a zavarjel összegzett eredője.
A számítógépes folyamatirányításban egy nagyságrenddel szigorúbb a pontossági igény az ipari mérésekhez viszonyítva.
A számítógépes mérőrendszerek többnyire a jel pillanatértékét mérik , így nem működik például a zajok átlagolásával dolgozó szűrés.
Nagyszámú áramkör van jelen, így fokozott az áramkörök egymásra hatása.
A hasznos jel és a zaj kapcsolódásának hatásvázlata:
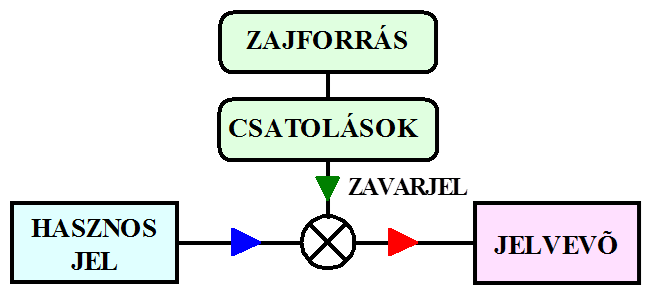
14.4.1. A csatolások típusai
Konduktív csatolás: A zajforrás és a hasznos jelet szolgáltató áramkör galvanikus kapcsolatban vannak.
Induktív csatolás: A zajforrásból származó jel a hasznos jelet elektromágneses indukció útján torzítja.
Kapacitív csatolás: A zajforrás és a hasznos jelet szolgáltató áramkör elektrosztatikus kapcsolatban van egymással.
Ezek csak a leggyakoribb zavarjel típusok és csatolások. Ezen kívül még számos zajforrás fajta jelenhet meg, ilyen például akusztikus csatolás és zavarjel.
14.4.2. A zavarjelek kiküszöbölésének általános módszerei
A zajforrás keletkezésének megakadályozása, a zajforrás megszüntetése .
A zajforrás és a hasznos jelet szolgáltató áramkör közötti csatolás megszüntetése .
A zavarjel kiszűrése a torzult jelből.
14.4.3. A zavarjelek típusai, időbeni változásuk alapján
Egyenfeszültségű zavarjel: a zavarjel időben állandó értékkel jellemezhető.
Váltakozó feszültségű zavarjel: adott frekvenciájú és amplitúdójú zavarjel.
Tranziens zavarjel: adott lefutási idejű végül teljesen megszűnő zavarjel.
14.4.4. A zavarjelek típusai áramkörökben való megjelenési formájuk szerint
Ellenfázisú zavarjel (normal mode interference): a jelforrás által szolgáltatott hasznos jellel sorosan kapcsolódik, a jelvevő bemeneti pontjait ellenfázisban vezérli.
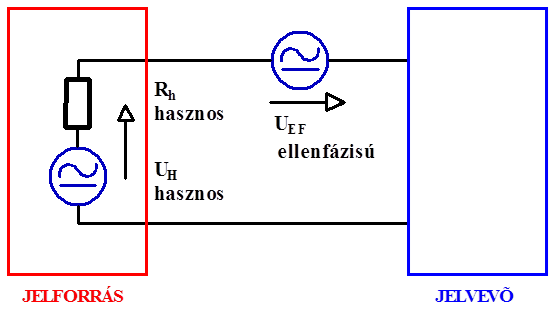
Ezt a jelet még szokás soros vagy tranzverzális zavarjelnek is nevezni.
Azonos fázisú zavarjel (common mode interference): a hasznos jelet szállító két jelvezeték közös pontja és valamilyen referencia pont – rendszerint a jelvevő föld pontja – között lép fel, a jelvevő bemeneti pontjait azonos fázisban vezérli.
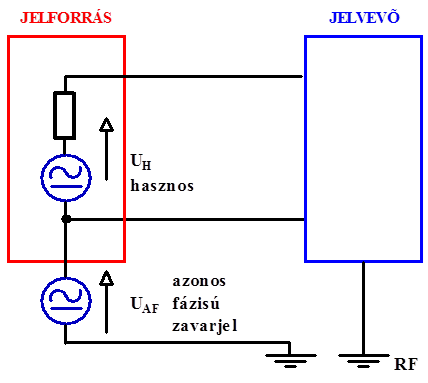
A két zavarjel típus általánosan együttesen jelentkezik, illetve az azonos fázisú zavarjelből belső ellenfázisú zavarjel keletkezhet.
Ha a rendszerben a jelforrás és a jelvevő is aszimmetrikus földelt típusú.
Tehát az áramkör két pontján van földelve! (Ami alapvető hiba) Ekkor a következő kapcsolás valósul meg:

RF (Rendszer Föld) és a FF (Folyamat Föld) potenciálja nem azonos, így egy váltakozó és egyenfeszültségű komponenseket tartalmazó zavarjel jelenik meg.
A vizsgálathoz tételezzük fel, hogy Uk=0 (szuperpozició alkalmazása!)
Az ellenállásviszonyok: r < RH < RBE
|
r |
vezeték ellenállása (~ 0,01 - 0,1 ohm) | |
|
RH |
generátor belső ellenállása (~ 0,1 – 1 ohm) | |
|
RBE |
műveleti erősítő bemeneti ellenállása (~ 1 -1000 Mohm) |
|
|
(14.1) |
ahol
|
|
az azonos fázisú zavarjelből keletkezett ellenfázisú zavarjel | |
|
|
az azonos fázisú zavarjel |
A fenti ellenállás viszonyok figyelembevételével:
|
|
(14.2) |
Tehát ilyen jelforrás jelvevő összekapcsolásnál a zavarjel teljes egészében átkerül a hasznos jelet erősítő áramkörbe.
Adott nagyságú azonos fázisú jelből létrejövő ellenfázisú zavarjel nagysága az úgynevezett azonos fázisú zavarjel elnyomással jellemezhető.
A műveleti erősítő erősítése:
|
|
(14.3) |
ahol
|
|
a műveleti erősítő kimeneti feszültsége | |
|
|
a műveleti erősítő nem invertáló bemenetére adott feszültség jel | |
|
|
a műveleti erősítő invertáló bemenetére adott feszültség jel | |
|
|
a műveleti erősítő differenciál erősítése | |
|
|
a műveleti erősítő közös modusú erősítése |
Az azonos fázisú zavarjel elnyomás (közös jel elnyomás)
(CMR = Common Mode Rejection) valamely adott azonos fázisú zavarjel és e zavarjelből keletkező ellenfázisú zavarjel abszolút értékének a hányadosa dB-ben kifejezve:
|
|
(14.4) |
Az ideális közös jel elnyomás értéke végtelen .
A gyakorlatban ez maximálisan ~100 dB nagyságrendű elnyomást jelenthet.
|
|
(14.5) |
ahol
|
|
a műveleti erősítő differenciál bemenetének erősítése | |
|
|
a műveleti erősítő közös modusú erősítése |
Adott kapcsolás CMR értékét a bemutatott eljárás segítségével lehet meghatározni!
A vizsgálatok eredménye, hogy a hálózati aszimmetria viszonyok jelentősen csökkentik a CMR értékét.
Aszimmetrikus földelt jelforrás -
Szimmetrikus földeletlen jelvevő összekapcsolása

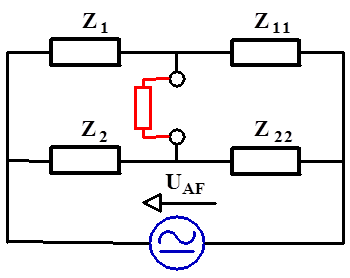
|
|
(14.6) | |
|
|
(14.7) | |
|
|
(14.8) | |
|
|
(14.9) |
A gyakorlatban (50 Hz hálózati frekvenciánál):
|
|
(14.10) |
Az összefüggés szemléletessé tétele érdekében a következő feltételezéseket tesszük:
|
|
(14.11) | |
|
|
(14.12) | |
|
|
(14.13) | |
|
|
(14.14) |
Ahol a z azonos fázisú bemeneti impedancia, Δz pedig a két információs vezeték villamos impedanciái közötti eltérés aszimmetria impedancia.
A CMR növelésére a következő lehetőségek vannak:
Szimmetrikus áramkör kialakítása: ahol: 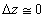
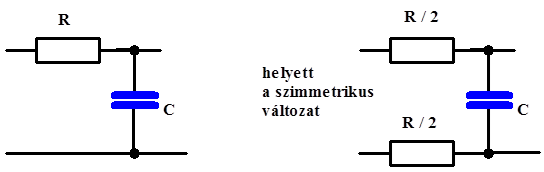
Az azonos fázisú bemeneti impedancia növelése : adott frekvenciánál (50 Hz) a szórt kapacitások határozzák meg a z értékét. Adott frekvencián ezek tehát meghatározott értékű CMR-t biztosítanak.
Védőárnyékolás alkalmazása : A védőárnyékolás (guard) a jelvevő bemeneti áramköreit magába foglaló, a külső földelt háztól villamosan elszigetelt fémdoboz.
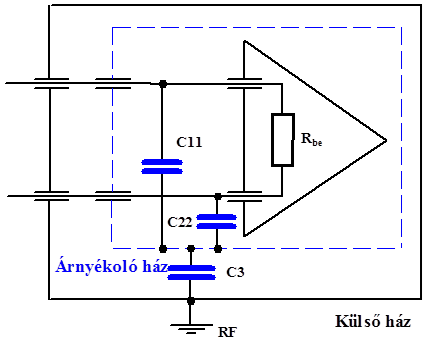
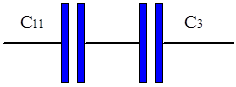
|
|
(14.15) |
ahol
|
|
(14.16) | |
|
|
(14.17) | |
|
|
(14.18) |
A védőárnyékoló fém ház alkalmazása nélkül a C 11 és C 22 kapacitások a jeltovábbító vezetékek és a berendezést tartalmazó fémdoboz (külső ház) között jönnek létre.
A z azonos fázisú bemeneti impedanciát itt úgy növeljük meg, hogy a teljes erősítő/fogadó áramkört elhelyezzük egy másik fém dobozban (árnyékoló ház), amely a berendezés fém dobozától (külső ház) el van szigetelve. A külső ház és az árnyékoló ház között létrejövő kapacitás C 3 sorba kapcsolódik a C 11 -el illetve a másik vezetékhez tartozó C 22 -vel így mind a két vezeték külső házhoz mérhető kapacitását csökkent. A kapacitív impedancia, amelyet 14.18 egyenlet szerint határozunk meg csökkenő C exx esetén impedancia növekedést eredményez.
14.4.5. A zavarjelek típusai keletkezési ok szerint és a zajcsökkentés módszerei
14.4.5.1. Csatlakozási potenciál
Nem megfelelő villamos csatlakozásnál a nedvesség, kémiai anyagok, hatására galvánelemek keletkeznek, melyek egyenfeszültségű ellenfázisú zavarjelet okoznak. Megoldás: a csatlakozások számának minimalizálása, védőbevonat a csatlakozásokra.
14.4.5.2. Termikus potenciál (termoelem)
A villamos áramkörben levő különböző anyagú fémek csatlakozási pontjánál , ha a csatlakozások hőmérséklete eltérő a környezettől, termikus potenciál keletkezik. A kialakuló termofeszültség, egyenfeszültségű ellenfázisú zavarjelet okoz.
|
forraszanyag és réz 1°C–ra |
3-10 μV, | |
|
vas-réz csatlakozás 1°C–ra |
30 μV. |
Az egyenfeszültségű ellenfázisú zavarjelet nem lehet a hasznos jeltől megkülönböztetni. A zavarjel által okozott hiba utólag semmilyen módszerrel nem csökkenthető.
Ezért az egyenfeszültségű ellenfázisú zavarjelet a zajforrásnál kell megszüntetni!
A termo feszültségből származó zavarjelek az alábbi módszerekkel csökkenthetők:
A csatlakozások számának csökkentése.
Egymáshoz közeli termo feszültségű anyagok használata (vörösréz, ezüst, arany, kadmium ötvözet).
A hőtermelő egységek és a kisfeszültségű áramkörök térbeli szétválasztása.
A környezeti hőmérséklet gyors változásaiból eredő hőmérséklet különbségek csökkentése.
Kis teljesítményű áramkörök kiöntése epoxigyantával vagy szilikonnal.
14.4.5.3. Átmeneti ellenállás, átvezetés
Néhány tipikus átmeneti ellenállás érték:
Mechanikai kapcsoló zárt érintkezője nagy rugónyomás esetén: 15 [milliOhm]
Higanyérintkezős reed relé zárt érintkezője: 20 [milliOhm]
Száraz reed relé zárt érintkezője: 200 [milliOhm]
Ilyen nagyságrendű átmeneti ellenállás elhanyagolható hibát okoz !
Bizonytalan, nagy átmeneti ellenállású érintkezők azonban jelentős zajforrást jelenthetnek.
Különösen sok problémát okoz a bizonytalan földelés , ugyanis a vezeték megszakadásakor bizonytalan potenciálra töltődik fel.
A szennyezés, por, nedvesség jelentősen lecsökkenti a szigetelési ellenállást.
A folytonos hő, a kémiai hatóanyagok, a mechanikai behatások pedig megrongálják a szigetelést és nemkívánatos átvezetések jönnek létre.
A meghibásodott szigetelés miatt az áramkör több ponton leföldelődhet!
A megengedettnél nagyobb átvezetés mind azonos fázisú mind pedig ellenfázisú zavarjel et okozhat!
14.4.5.4. Elektromágneses (induktív) zavarjel
Az induktív zavarjel a környezettel való mágneses kapcsolat miatt keletkezhet. A külső mágneses tér által keltett zavarjel nagysága az indukált feszültséggel egyezik meg.
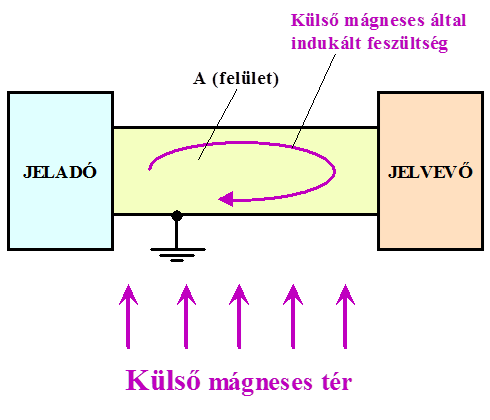
Ha nagy a távolság a jeladó ás a jelvevő között, akkor főként ellenfázisú jelek keletkeznek.
Az induktív zavarjel csökkentésére a leggyakrabban alkalmazott módszer a vezetékek megcsavarása (sodort érpárú kábelek) . Az ilyen esetben keletkező indukált feszültségeket a (14.31. ábra - A vezetékek megcsavarásakor kialakuló elektromágneses jelek) ábrán láthatjuk. A teljes vezeték hosszára eső zavarjel a vezetékek megcsavarásával a megcsavarásokra eső kisebb, és egymással ellentétes irányú feszültség komponensekre bomlik. Ha a megcsavarások száma páros érték, akkor az egymással ellentétes feszültség komponensek mindegyikének van ellentétes értékű párja. Páratlan számú megcsavarás esetén is csak az egy csavarásra eső kisebb (kisebb felületű megcsavaráson keletkező) zajfeszültség érték marad meg.
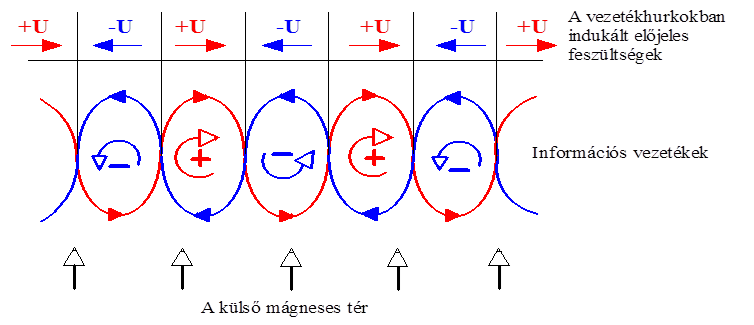
Az induktív zajfeszültség csökkentésének másik módszere, a vezetékek mágneses árnyékolása , amikor az információs vezetékeket mágneses árnyékoló rétegekkel vonják be 1-5 rétegben. A mágneses árnyékoló rétegek anyaga olyan vas ötvözet, amely könnyen alakítható és nem oxidálódik.
Az induktív zajfeszültség csökkentésének harmadik módszere a szabályos geometriájú, koaxiális elrendezésű jelvezeték-pár használata. A koaxiális kábel mágneses térre merőleges metszetén belátható, hogy a belső ér és a külső köpeny által alkotott felület normálisa a felső és alsó felületnél ellentétes, ezért a külső mágneses tér is ellentétes feszültségeket indukál ezekben a felületekben. Az ellentétes indukált feszültségek által a belső érben létrehozott zavaráramok tehát kioltják egymást.
14.4.5.5. Elektrosztatikus (kapacitív) zavarjel
A kapacitív zavarjel valamely áramkörben a környezettel való elektrosztatikus kapcsolat – szórt kapacitások - miatt keletkeznek. A kapacitív zaj ellenfázisú , és azonos fázisú is lehet. A távolság növelésével a csatoló kapacitás csökken. Az egyik módszer a zajforrás és a jelvezeték térbeli elkülönítése. Jó zajcsökkentés érhető el az elterjedten alkalmazott elektrosztatikus árnyékolással. Az elektrosztikus árnyékoláshoz általában rezet (Cu), illetve könnyű fém anyagokat alkalmaznak.
|
Elektrosztatikus árnyékolás típus |
Zajcsökkentés [dB] |
|---|---|
|
Árnyékolatlan vezeték |
0 dB |
|
Rézfonat árnyékolás, 85% fedettség |
-40 dB |
|
Spirálisan feltekercselt rézlemez, 90% fedettség |
-50 dB |
|
Aluminium Mylar szalag vezető drain szállal, 100% fedettség |
-76 dB |
Itt a dB érték egy csökkentési arányt fejez ki, melynek értékei:
-40 dB => az eredeti zaj érték 0.01-ad részre,
-76 dB közelítőleg az eredeti zaj érték 0.0001-ed részre csökkenti az zaj értékét.
14.4.5.6. Villamos áramkörök be és kikapcsolásakor keletkező zavarjel
Elsősorban tranziens zavarjeleket okoznak.
Konduktív, induktív és kapacitív úton kerülnek az áramkörbe. Elsősorban az induktív terheléseken folyó áramok megszakításakor keletkeznek zajok (Lencz törvény). Ezért kapcsolunk az induktív terhelésre a záró irányba folyó áramainak rövidre zárásához diódát .
Kapacitív terhelések rövidre zárásakor hirtelen áramlökés, és tranziens zaj keletkezik.
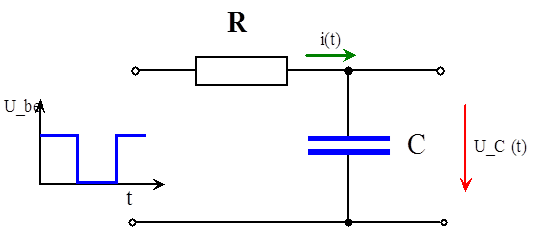
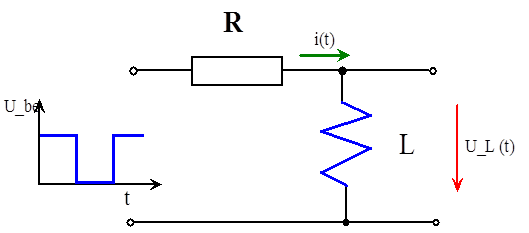
14.4.5.7. Kábelhajlításból származó zavarjel
A kábel jelvezetékei között és az árnyékolások közötti szigetelések piezoelektromos tulajdonsággal rendelkeznek, így meghajlításukkor a piezo hatás miatt váltakozó feszültségű zavarjel keletkezik, amelynek amplitúdója több Volt nagyságú is lehet.
14.4.5.8. Rádiófrekvenciás zavarjel
Közvetlen elektromágneses és elektrosztatikus zavarás hatótávolsága kicsiny (néhány méter). Nagy távolságokra az elektromágneses hullámok közvetítik a zavarjeleket. Frekvenciatartományuk 500 kHz – 1GHz, teljesítményük általában kicsiny.
14.4.5.9. Tápforrásból származó zavarjel
Fő forrása a hálózati transzformátor
Vasmag szórt mágneses tere
Elektrosztatikus szórt kapacitások
A berendezések a tápvezetéken keresztül kölcsönhatásba kerülnek (vagy egyedi tápegységeket kell alkalmazni, vagy szűrőáramkörökkel kell elválasztani a tápvezetéket az egyes berendezéseknél.
Egyenirányító, inverter (feszültségnövelő áramkör) szűrése.
14.5. Földelések
A földelés (ground) rögzített potenciálú villamos vezető, amelyet a földbe épített fémvezetőhöz (földelő lemez, földelő rúd, földelő rács) csatlakoztatnak.
A folyamatirányító számítógépekben a földelés funkciója alapján a következő földelési típusokat különböztetjük meg:
14.5.1. Védelmi föld
A villamos berendezések környezetében levő fémből, vagy nem szigetelő anyagból készült üzemszerűen feszültségmentes alkatrészekhez (műszer doboza, fém szekrény) csatlakozó vezeték.
Életvédelmi szerepe van , mivel megakadályozza, hogy az ember közelébe kerülhető szerkezeti elemek valamilyen meghibásodás következtében feszültség alá kerüljenek és balesetet okozzanak.
A védelmi földvezetéket egyéb (áramvezetési) feladatra tilos használni!
14.5.2. Gyengeáramú teljesítmény föld
Az egyenáramú tápfeszültség et szolgáltató hálózat közös vezetéke.
Áramvezetés a feladata! A számítógépes mérőrendszerekben ez az +5 V-os tápellátás föld vezetéke.
14.5.4. Digitális föld
Az információt hordozó digitális jelek referencia pontjaiként szolgáló vezeték.
A felsorolt földvezetékek többnyire egymástól független vezetékek, amelyek egy pontban, az úgynevezett fő rendszer ponthoz csatlakoznak.
A teljesítmény föld, az analóg és a digitális jelföld vezetéke összevonható, de ezt a lehetőséget
a jelszintek
a terhelések
és a zavarjelek
figyelembevételével egyedileg kell minden esetben megvizsgálni.
Kis jelszintű analóg rendszereknél ajánlatos a föld vezetékeket szétválasztani!
A számítógépes mérő rendszerekben szokás megkülönböztetni a földelést aszerint is, hogy a technológia oldali földről (Felhasználói Föld), vagy a számítógéprendszer oldali földről (Rendszer Föld)van szó.
Fontos szempont, hogy a földvezetéknek is van impedanciája, így helytelen földelés esetén a létrejövő feszültségesések miatt a készülékek eltérő potenciálra kerülnek. Ezért a soros földelés helyett sugaras földelést alkalmazunk.
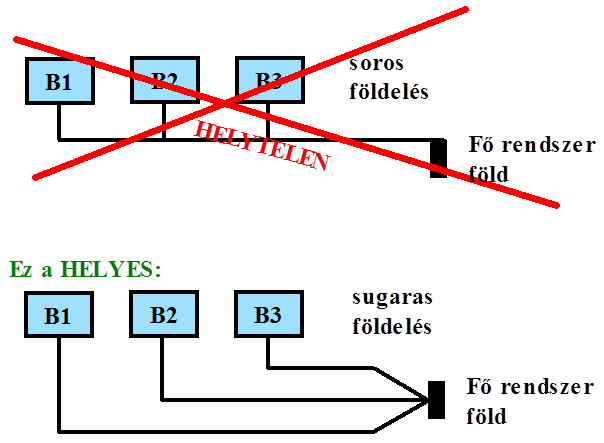
A helytelen földelés következtében két helyen történő földeléssel a földelési pontok között egy zárlati áramkör jön létre a földelési potenciálkülönbségek miatt. Ez több Volt nagyságrendű egyen és- és váltakozó áramú jel lehet.
14.6. A nemkívánatos föld áramkörök kiküszöbölésének módjai
Egyetlen pont földelésével vagy a föld áramkörök galvanikus leválasztással történő megszakításával.
14.6.1. Egyetlen pont földelése
A rendszer földelése esetén földeletlen jelvevőt, míg földelt jelvevő esetén földeletlen jelgenerátort kell alkalmaznunk. Ha nem tudjuk ezeket a feltételeket teljesíteni, akkor galvanikus le(el)választást alkalmazzunk, hogy megszüntessük a mérési elrendezés helytelen működését eredményező „földhurkot!
14.6.2. Galvanikus leválasztás
A galvanikus leválasztás megakadályozza a földáramkörök kialakulását. Galvanikus leválasztással például földelt jelforrás, és földelt jelvevő is összekapcsolható anélkül, hogy föld potenciálkülönbségből származó azonos fázisú zavarjel átalakulna ellenfázisú zavarjellé.
14.6.2.1. Repülő kondenzátoros leválasztás
Egy kondenzátor kapcsaira csatlakozó relé érintkezők nyugalmi állapotban a jelforrásra csatlakoznak, így a kondenzátor mindig a hasznos feszültség értékre töltődik fel. Átkapcsoláskor megszakítja a jelforrással a föld kapcsolatot, így a kettős földelésből származó azonos fázisú jelet nem viszi tovább . A közös jel elnyomás nagyon jó.
(Kis értékű szórt kapacitások esetén nagy közös jel elnyomás értéket valósíthatunk meg.)
14.6.2.2. Transzformátoros leválasztás
Analóg jelek galvanikus leválasztása oldható meg a segítségével. Precíziós egyen-váltó, váltó-egyen átalakítót igényel.
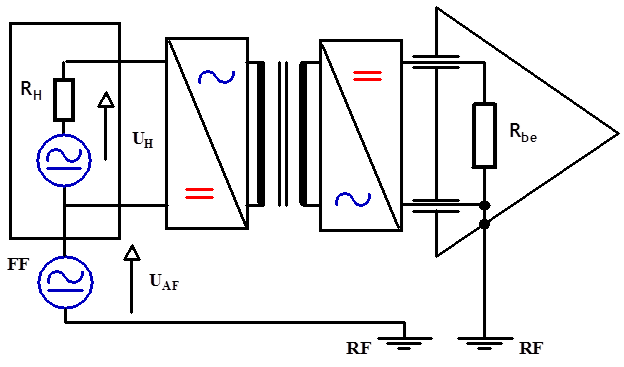
14.6.2.3. Fotodiódás optikai leválasztók
Ezek a kapcsolások kb. 100mA-el terhelhetők, és 1000-2500 V szigetelési feszültségük van, csatoló kapacitásuk kisebb, mint 1 pF.
Az optikai leválasztások jelleggörbéje lehetővé teszi a közvetlen analóg jelátvitelt , de a
nagy linearitási hiba, és
kis kivezérelhetőség
miatt speciális kapcsolásokat kell alkalmazni.
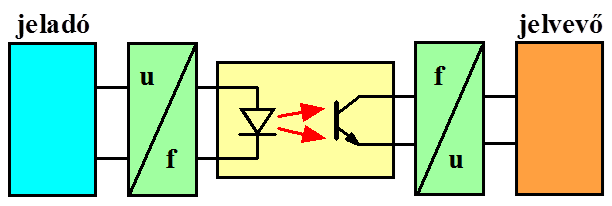
A jelforrástól érkező analóg jelet frekvenciajellé alakítjuk át, és ezt a jelet vezetjük át az optikai leválasztón . A frekvenciajellé történő átalakítás előnye, hogy a leválasztó nemlinearitása nem befolyásolja a mérési pontosságot .
14.7. Analóg bemenetek elemei
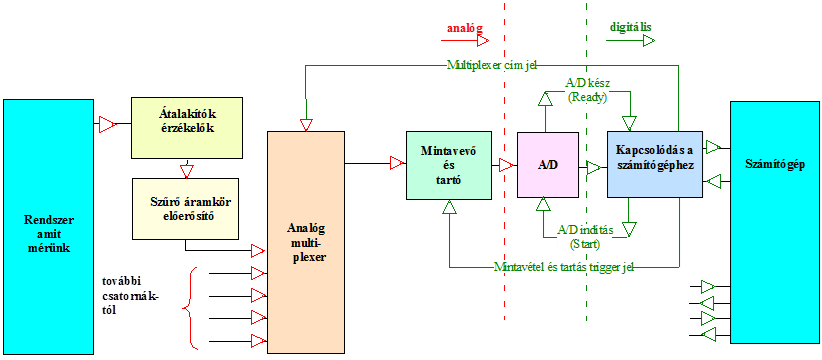
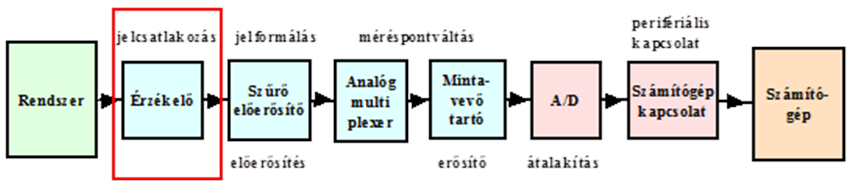
14.7.1. Érzékelő átalakítók és jeleik
Valamilyen fizikai mérési elv felhasználásával a mérendő mennyiség változásával arányos kimenő jelet szolgáltatnak. Nem villamos jelből villamos jelet állítanak elő. A lehetséges kimenetek közül a legjobb a feszültség kimenet, de az áram és ellenállás kimenet is elfogadható és feszültséggé átalakítható. Az az ideális, ha az érzékelő statikus karakterisztikája lineáris tulajdonságú , de a környezeti hatások miatt ez a valóságos statikus karakterisztika általában nemlineáris . A számítógépes mérésnél a későbbi feldolgozás miatt előnyben részesülnek a mechanikai mozgás mentes, karbantartást nem igénylő érzékelési megoldások.
14.7.1.1. Áramló gáz mennyiségének mérése: bolométer
Ceruzahegy nagyságú fűtött spirál, amelynek a gázáramban az ellenállása megváltozik az áramló gáz sebességgel arányos hűtési tulajdonsága miatt. A bolométer ellenállását Wheathstone hídba kötve az ellenállás változást feszültségváltozássá alakítjuk.
|
|
(14.19) |
A Wheathstone hídban a mérő ellenállással egy ágban szereplő ellenállás (R1) értékének növelésével csökkenthetjük a mérőhíd relatív hibáját, amely a maximális hibaérték végértékre vonatkozóan meghatározott százaléka.
Ha az üresjárati kimenő feszültséget áram táplálással írjuk fel:
|
|
(14.20) |
Másik lehetőség, hogy egy áramgenerátorral táplálva a mérő ellenállást azonnal feszültség jelet kapunk.
A híd kapcsolást sűrűn alkalmazzák nem csak ellenállás mérésre,
Elmozdulás → ellenállás helipot (többszörös körülfordulású potenciométer)
Nyúlás → nyúlásmérő bélyeg → hídkapcsolás
Erő, nyomás → mérés visszavezetése nyúlásmérő bélyeggel történő mérésre
Hőmérséklet → ellenállás változás
A Wheathstone hídkapcsolás nem csupán ellenállást tud mérni, hanem váltakozó feszültségű táplálással impedanciát is. Ezért az induktivitás és kapacitás változást is érzékelni tudjuk, és átalakíthatjuk váltakozó feszültségű villamos jellé.
Alkalmazásuk elsősorban (elmozdulás) érzékelőkben történik
Induktív és kapacitív típusú elmozdulás érzékelők
Mágneses elmozdulás érzékelők → egyenes vonalú mozgásokhoz
Elfordulás érzékelők – ellenállás, kapacitás, induktivitás változással
14.7.1.2. Áramló mennyiségek mérése
Nyomás érzékelés:
A nyomás változást átalakítjuk elmozdulássá, amelyet → ellenállás változássá → majd feszültségváltozássá alakítunk.
A nyomásérzékelés segítségével módunk van az áramló mennyiségeket mérni (fojtóelemmel történő nyomáskülönbség segítségével)
Az átáramló mennyiség és az érzékelőn eső nyomás mint bemenő jel között nemlineáris kapcsolat van:
|
|
(14.21) |
ahol
|
|
a bemeneti nyomáskülönbség, | |
|
c |
a mérőberendezás geometriája és áramlási viszanyainak megfelelő konstans, | |
|
Q |
az átáramlott térfogat értéke |
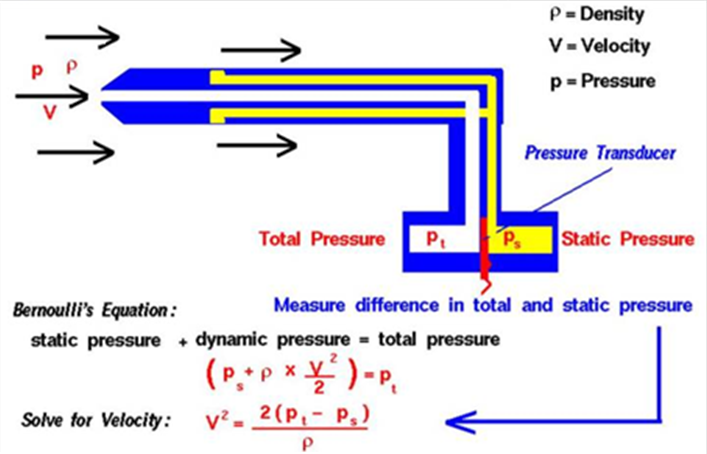
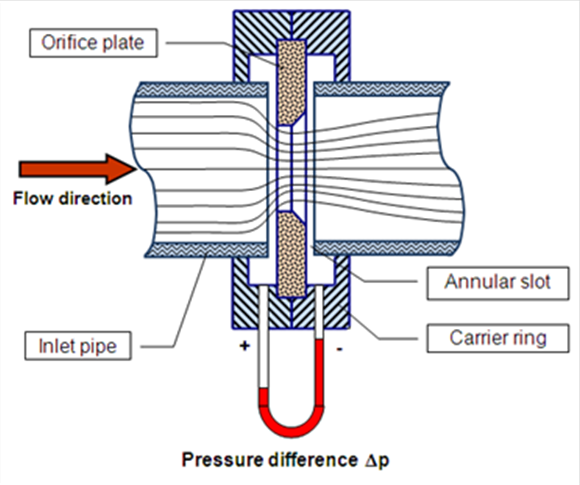
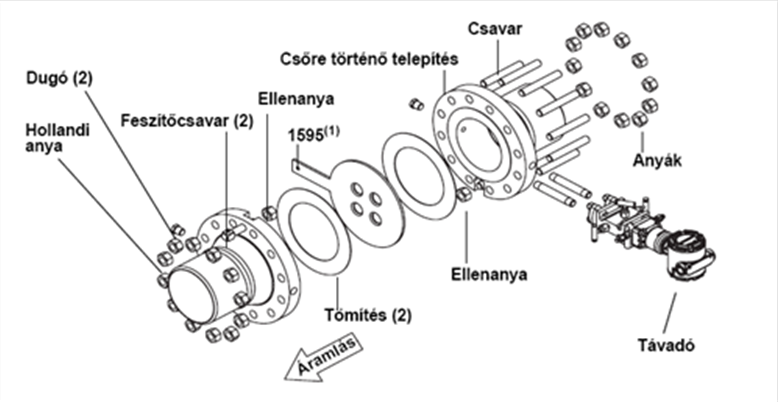
Átáramló mennyiségek szállítása (kis mennyiség érték nagy pontosságú adagolása):

Meghatározott fordulatszámhoz meghatározott szállított mennyiség tartozik
Köböző számláló (szivattyú):

Meghatározott fordulatszám megtétele után meghatározott mennyiséget szállít a berendezés.
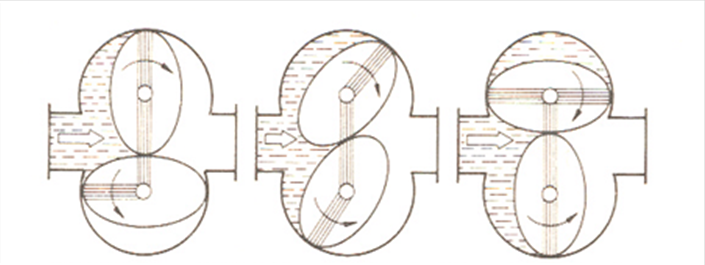
Áramló mennyiség mérési lehetősége nem nyomásesés alapján:
Az áramló közegbe elhelyezett propellerrel a sebesség forgó mozgássá alakítása. A propeller lapátjaiban kemény mágneses anyagból készített kisméretű mágneseket helyezünk el, amelyek egy külső indukciós tekercsben impulzusokat gerjesztenek. A gerjesztett impulzusok közötti időtartam arányos a propeller fordulatszámával, amely pedig a sebesség függvénye. Így a folyadék mennyiség mérését impulzus periódus méréssé alakítjuk át, amelyet a számítógépes időmérési metódussal határozunk meg.
Mesterséges fémoxid alapú hőmérséklet érzékelő
Termisztor (NTK ellenállás): a termisztorok olyan félvezetők, amelyek ellenállása a hőmérséklet emelkedésével csökken.
A termisztorok kerámia anyagú hőmérsékletfüggő félvezető ellenállások, amelyeknek erősen negatív hőmérsékleti tényezőjük van. Ezen tulajdonságaik miatt ezeket az elemeket mind kompenzációs kapcsolásokban, mind hőmérséklet-érzékelőként alkalmazzák.
14.7.1.3.2. Platina ellenállás hőmérő
|
|
(14.22) |
ahol
|
R 0 |
ellenállás 0°C-nál | |
|
|
a hőmérséklet °C-ban | |
|
A : a·10-3 B : b·10-6 |
egymáshoz viszonyított értéke. |
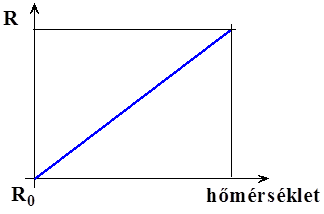
14.7.1.3.3. Félvezetős ellenállás hőmérő
|
|
(14.23) |
ahol 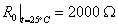
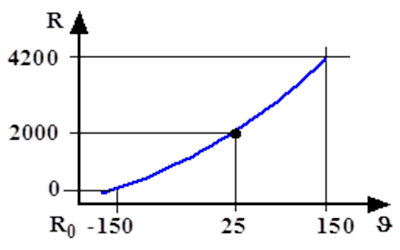
A mért ellenállás érték a hőmérséklet nemlineáris függvénye, linearizálni szükséges.
14.7.1.3.4. Hőelemek

|
|
(14.24) |
ahol
|
|
hőelem által létrehozott feszültség érték | |
|
|
a mérendő hőmérséklet | |
|
|
hőelem típustól függő konstans érték | |
|
|
a környezeti hőmérséklet, a kompenzációs hely hőmérséklete |
Áramköri megoldás segítségével (hidegponti kompenzáció) a hőelemes érzékelésnél lehetőségünk van a környezeti hőmérséklet változásától függetlenül mérni a termoelem hőmérsékletet.
Ezen kívül számos egyéb mennyiség és általános mérési elv jelenik meg, melyek mindegyikének általános jellemzője, hogy a mérendő fizikai mennyiségekkel arányos kimeneti feszültséget hoznak létre.
Az érzékelők által szolgáltatott jel szintje, energiája rendkívül kicsiny, ezért feltétlenül erősíteni kell a jelet.
Az érzékelőtől jövő analóg jelnek el kell jutnia az A/D (analóg/digitális) átalakítóhoz, amely általában a digitális számítógép környezetében van (tiszta technológia), eközben számos zavar éri, amely a környezetből ered.
14.8. Analóg jel kondicionálása

A jel zajszűrését passzív és aktív áramköri kapcsolásokkal végezzük, amelyekkel a mérési frekvenciatartomány feletti jelek jól csillapíthatók.
A leggyakrabban hálózati frekvencia ( f=50 Hz → T=20 ms ) zavaró hatását kell csükkentenünk.
14.8.1. Passzív szűrő
Szimmetrikus két tárolós aluláteresztő szűrő áramköri kapcsolása.
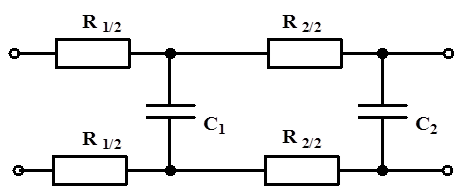
14.8.2. Időzítéses integrálás (mint zavarszűrési lehetőség)
Ha az áramkörbe a jelfeldolgozás előtt egy időzített integráló egység et iktatunk be, az integrálás időzítésétől függően bizonyos frekvenciájú váltakozó feszültségű jeleket elvileg teljesen kiszűr. (Például Ti = k.20ms os időzítéssel az 50 Hz-es hálózati zavarfeszültségeket ki lehet szűrni.)
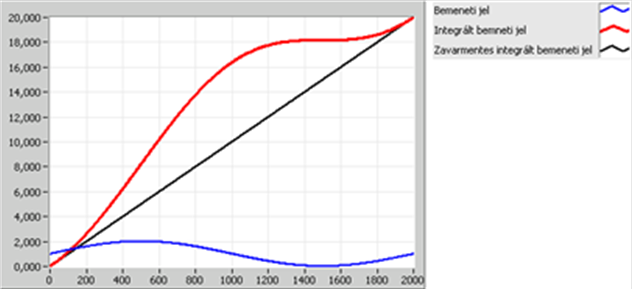
Az integráló tag a zajfeszülség pozitív és negatív amplitúdójú részének területeit előjelhelyesen összegzi, így ha az integrálási időtartam megegyezik a periódus idővel, akkor egy teljes periódus alatt a zajfeszültségből keletkezett integrál érték nulla lesz. Az egyéb frekvenciájú jelet pedig csak meghatározott mértékben csökkenti.
14.8.3. Áram feszültség átalakító
A bemeneti áram típusú jelet feszültség típusú jellé alakítja át.
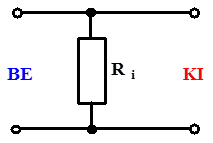
Áram távadó kimenetű érzékelőnél a 4-20 mA tartományt 1-5 V tartományra alakítja át (Ri = 250 Ohm ellenállás szükséges hozzá).
A áram távadó jelének fogadását megvalósíthatjuk műveleti erősítős megoldással is, amelynél a 250 ohmos ellenállással visszacsatoljuk a műveleti erősítő kimenetét az invertáló bemenetéhez. Ekkor a differenciális bementek értékét cca. 0 V-al közelítve a bementi áram a műveleti erősítő kimeneti feszültségeként hozza létre a 250 ohm-os ellenálláson létrejött feszültség értéket.
14.8.4. Fix és változtatható feszültségosztók
A bemeneti nagyobb feszültség tartományú jelet az átalakító mérési tartományának megfelelő nagyságú jellé alakítja át.
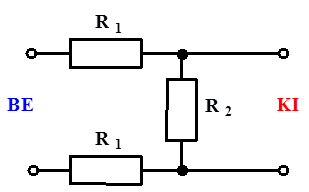
|
|
(14.25) |
14.8.5. Egyszerű RC szűrő
Szimmetrikus egytárolós aluláteresztő szűrő áramköri kapcsolása.
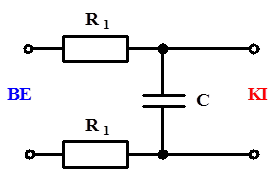
|
|
(14.26) |
A kapcsolás Bode amplitúdó jelleggörbéje:
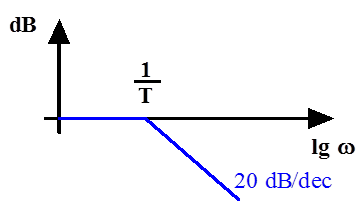
ahol T = 2·R1·C
14.8.6. Változtatható feszültség osztású bemenet
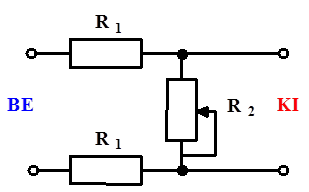
14.8.7. Feszültségosztó és szűrő
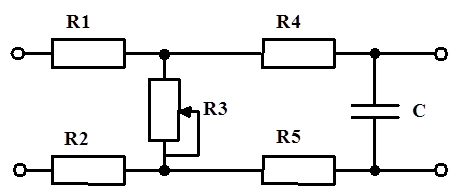
14.8.8. Kettős RC szűrő
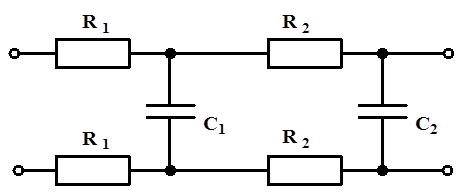
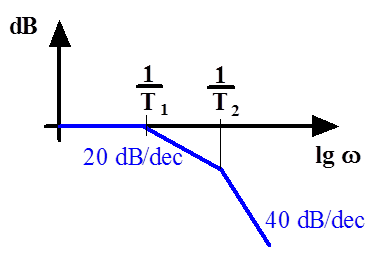
14.9. Small Computer Extended Interface (SCXI)
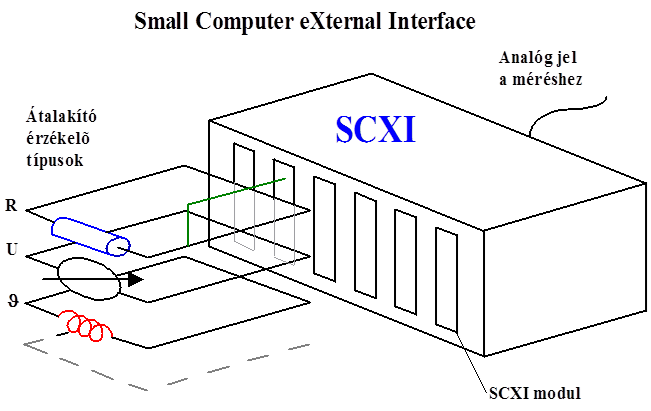
Feladatai:
a bemeneti jel kondicionálása
az alacsony szintű jelek felerősítése,
galvanikus (el)szigetelése a számítógéptől,
analóg szűrés,
áram/feszültség átalakítás.
14.10. Analóg méréspont váltók (multiplexerek)
A méréspont váltó feladata, hogy több bemeneti vonal közül egyet a kimeneti vonalra kapcsoljon. (az A/D átalakítás gyors, az A/D átalakító a legdrágább szerkezet a mérőrendszerben)
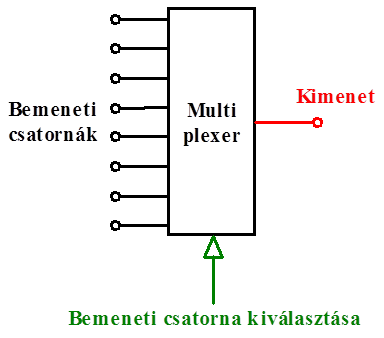
Fejlődési irány, hogy minden analóg mérővonalat külön A/D átalakítóval kezeljenek, ma azonban ez még drága eljárás.
14.10.1. Relés méréspont váltó
(Száraz és higany érintkezős relé)
Reed relay (reed relé)
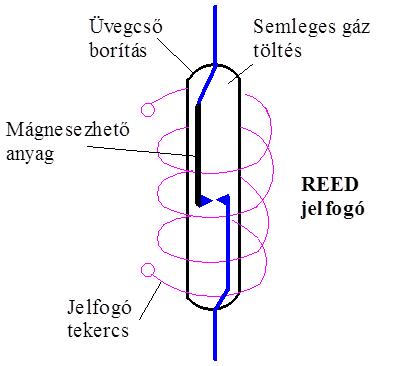
Néhány technikai adat:
Rzárt=200 mOhm (milliOhm)
Rnyitott= 1010 Ohm
Kapcsolási idő = 1-2 ms
Kapcsolási szám ≈109 (illetve véges érték)
Jó rázásállóság
A relés méréspont váltókat modulokba kapcsolva kötik össze, amelynek az az oka, hogy így nem kapcsolódik párhuzamosan az összes bemenet.

Galvanikus elválasztásra használható a repülőkondenzátoros megoldás.
14.10.2. Félvezetős méréspont váltó
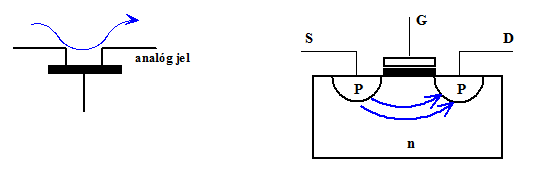
Néhány technikai adat:
Rzárt = 20 Ohm
Rnyitott = 109 Ohm
Rszigetelési = 1012 Ohm (a kapcsoló és vezérlő elektródák között)
Kapcsolási idő = 0,1 μs
Élettartam = ∞
A blokkkapcsolásra vonatkozó alapelvek itt is érvényesek. A probléma az, hogy a félvezetős méréspont váltók a felhasználói földpontokat sem egymástól sem a rendszer földtől nem választják el .
Ezért földfüggetlen jeladók szükségesek, vagy a jelfogadó oldalon kell megoldani a galvanikus leválasztást.
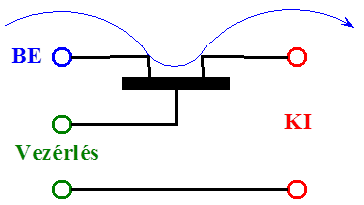
14.11. Mintavevő tartó és erősítő

Az analóg bemeneti perifériában használt mintavevő tartó + erősítő feladata:
az analóg jelszint illesztése az A/D átalakító jeltartományhoz
zajelnyomás
galvanikus leválasztás
mintavételezés és tartás
Alkalmazott erősítők
földelt vagy földfüggetlen szimmetrikus, vagy aszimmetrikus egyenfeszültség erősítők
programozható erősítésűek
mintavevő és tartó ( Sample and Hold ) áramkört tartalmaznak, amelyet az analóg jel változására érzékeny A/D átalakítók bemeneténél használnak, hogy a bemeneti jelet állandó értéken tartsák.
Működési elve:
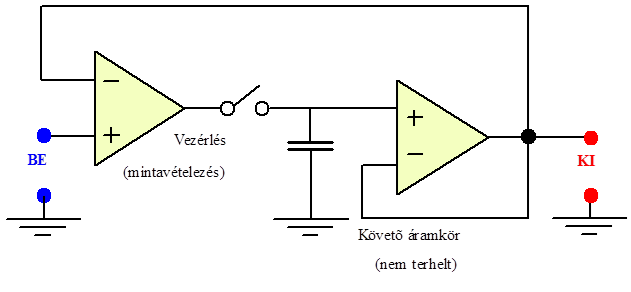
Analóg bemeneti perifériában alkalmazott erősítő főbb technikai jellemzői:
Ap=1-100 ( 1, 2, 5, 10, 20, 50, 100 ) vezérléssel változtatható
RBE = 109 Ohm
Nullpont eltolódás: 1 mV/°C , 20 μV/hónap (hosszú időtartamra vonatkozó stabilitással)
Az erősítőt általában az A/D átalakítókkal egybeépítik.
A változtatható erősítés szerepe:
A bemeneti jelet úgy erősítjük fel a változtatható előerősítéssel, hogy az A/D átalakító mérési tartományának felső felébe kerüljön. Ezzel a módszerrel az A/D átalakítóban rendelkezésre álló összes bitet alkalmazzuk az átalakításhoz. Az A/D átalakítás után a mért értéket osztjuk az előerősítésnél alkalmazott értékkel, hogy a pontos értéket kapjuk.
14.12. Analóg digitális (A/D) átalakítók

Az A/D átalakító a bemenetére kapcsolt analóg jelet kódolt digitális jellé alakítja át.
Az analóg jel polaritása szerint a következő lehet:
Egy polaritású: nincs előjel, az átalakító csak az analóg jel nagyságát adja meg.
Két polaritású: bipoláris mind pozitív, mind pedig negatív jelet képes mérni és átalakítani.
A jel kódolások:
előjel és abszolút érték,
kettes komplemens,
eltolt nullpontú,
egyes komplemens kódolás.
Az A/D átalakítók (szokásos) bemeneti jeltartománya:
0 .. +5V
±5V
0 .. 10V
±10V
Az A/D átalakítók típusai:
pillanatérték mérők:
fokozatos közelítésű A/D átalakítók
több komparátoros párhuzamos A/D
D/A visszacsatolásos A/D átalakítók
integráló típusúak:
kettős integráló típusú A/D átalakító
feszültség frekvencia átalakító típusú átalakító
14.12.1. D/A visszacsatolásos A/D átalakító
(Counter type A/D converter)
Mérés elve: az Ux mérendő feszültséget egy D/A átalakító kimeneti feszültségével hasonlítják össze, melyet egy számláló vezérel.
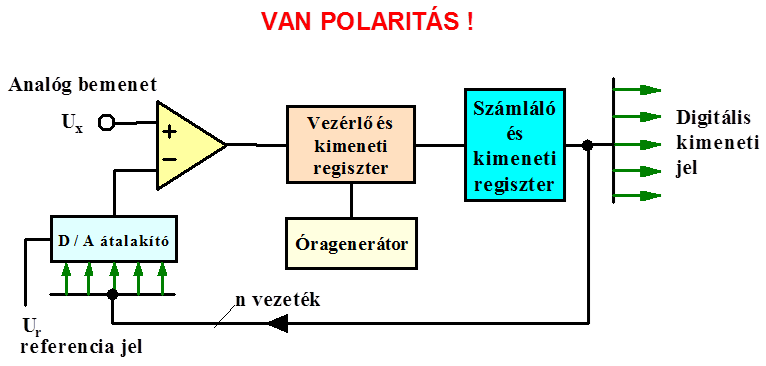
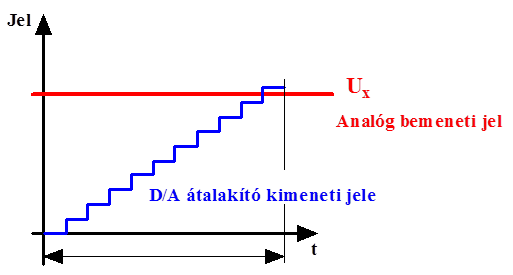
A mérés időtartama az órajel nagyságától és a bemeneti jel nagyságától függ.
10MHz órajel 10 bit felbontás ~ 100 μs mérési időt jelent. Pillanatértéket mér, ezért méréskor a hasznos jellel együtt a zavarjelet is méri.
Gyors, bár a mérési időtartam a mérendő jel nagyságától függ, mert az első beállás után követi a jel „lassú” változását.
14.12.2. Fokozatos közelítésű A/D átalakító
(Successive approximation A/D converter)
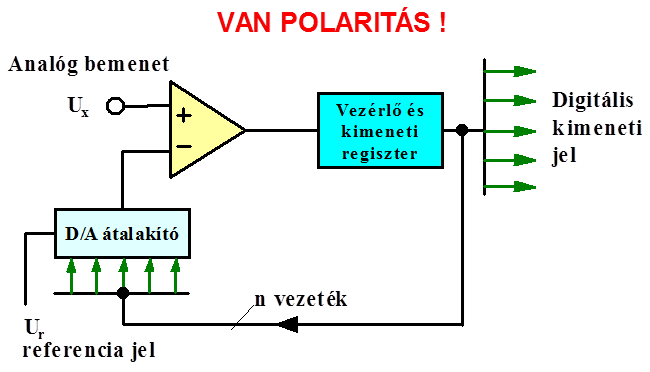
A mérés elve: kettő különböző hatványainak megfelelő feszültség értékek („súlyok”) be illetve kikapcsolásával egy kiegyenlítési stratégia segítségével határozza meg, hogy az adott bemeneti jelhez milyen bináris jel kombináció illeszkedik.
Pillanatértékeket mér (a zaj értékét együtt méri a hasznos jellel)
A mérés ideje alatt a feszültségnek állandó értékűnek kell lennie (jeltartás!)
Pontosságát a D/A átalakító, a referencia feszültség és a komparátor pontossága határozza meg.
A mérések időtartama állandó!

14.12.3. Több komparátoros A/D átalakító
(Multi comparator A/D converter)
A mérés elve: A mérendő jelet egy időben több komparátorral hasonlítjuk össze, melyeknek különböző a referencia feszültsége . A komparátorok akkor adnak kimenő jelet, ha a pozitív bemenetre kapcsolt Ux feszültség nagyobb, mint a negatív bemenetre kapcsolt referencia feszültség, vagy azzal egyenlő.
Mivel a mérés egy lépésben történik az átalakító nagy sebességű analóg/digitál átalakítást képes megvalósítani. (Ezért szimultán A/D átalakítónak is nevezik.)
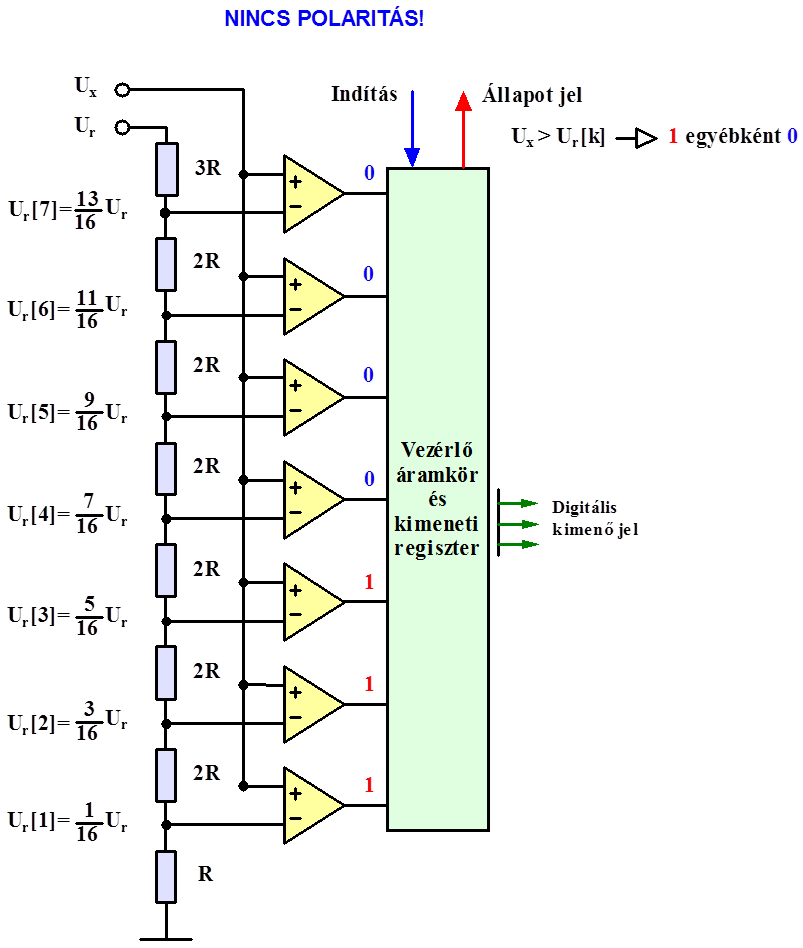
14.12.4. Kettős meredekségű (integráló) A/D átalakító
(Dual-ramp, dual-slope A/D converter)
Mérési elv: a mérendő feszültséget egy integrátor kapcsolás bemenetére vezetik, és rögzített Ti ideig (meghatározott órajel impulzus) integrálják . Ezután bekapcsolják az ellenkező előjelű referencia feszültséget és „visszaintegrálnak” a nulla kimeneti feszültség értékig. Az integrátorban lévő kondenzátor kisülése alatt óraimpulzusokkal mérik az eltelt időt, ameddig a 0 (nulla) komparálási értéket el nem érik.
Az integrátor kisülésének időtartama arányos a bemeneti jel átlagértékével!
|
|
(14.27) | |
|
|
(14.28) | |
|
|
(14.29) | |
|
|
(14.30) |
ahol
|
f 0 |
a rendszerben alkalmazott órajel generátor frekvenciája. | |
|
N x |
a Tx idő alatti impulzusok száma f0 frekvenciájú generátorral. |
|
|
(14.31) |
ahol
|
f 0 |
a rendszerben alkalmazott órajel generátor frekvenciája. | |
|
N i |
a Ti idő alatti impulzusok száma f0 frekvenciájú generátorral. |
|
|
(14.32) |
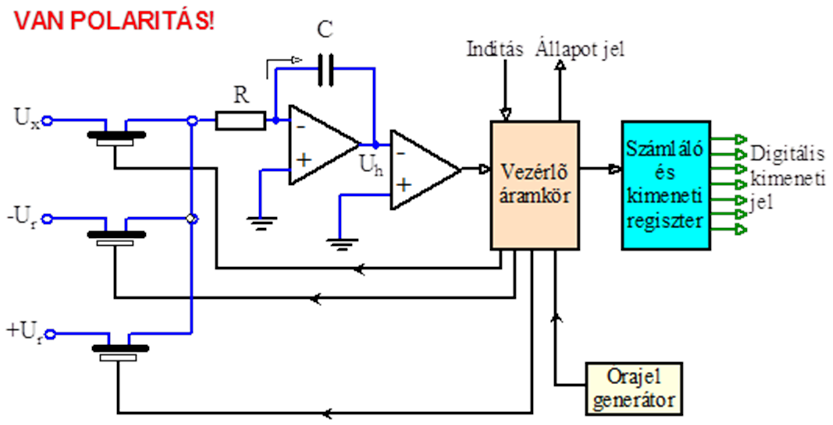
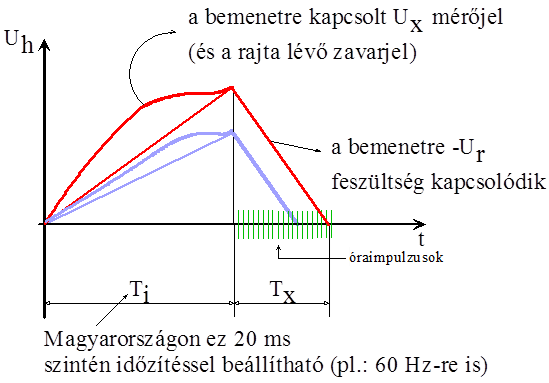
Előnyei:
Az átalakítás pontossága nem függ az R, C elemek és az órajel pontosságától, mivel a töltéshez és a kisütéshez ugyanazokat az elemeket használják.
Integrálással valósítják meg a zaj szűrést.
Mérési idő maximum 40 msec, de olcsó, ezért elterjedten alkalmazzák.
14.12.5. Feszültség frekvencia A/D átalakító
(Voltage to frequency A/D converter)
Működési elve: A bemeneti jelet integráljuk, addig, amíg el nem érünk egy komparálási szintet, azután az átalakító egy ellenkező polaritású komparáló feszültséget kapcsol ΔT ideig az integrátorra, amely azt részben kisüti. A folyamat ezután ismétlődik, és a kimenő jel frekvenciája a bemeneti feszültség nagyságával lesz arányos.
|
|
(14.33) |
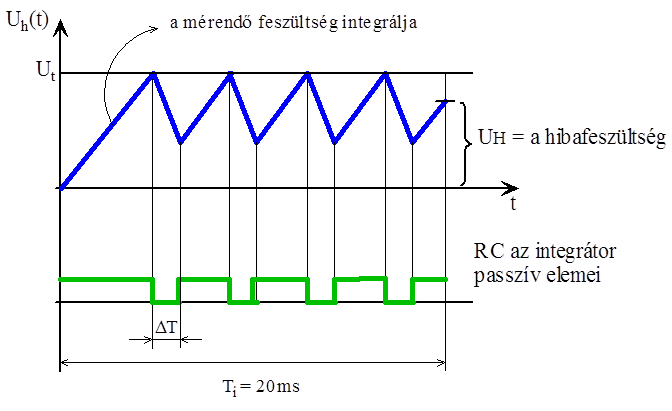
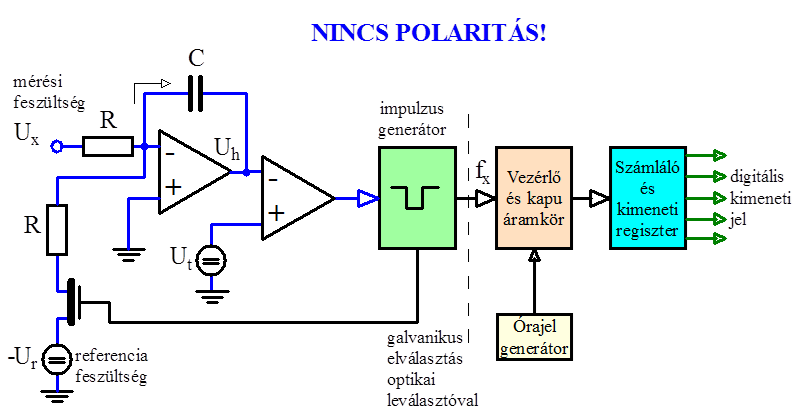
|
|
(14.34) | |
|
|
(14.35) |
Ha az RC szorzat kicsiny a 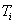 időhöz képest, akkor a második tag elhanyagolható, így:
időhöz képest, akkor a második tag elhanyagolható, így:
|
|
(14.36) |
ahol
|
|
az integrálási idő alatt „létrejött” impulzusok száma. | |
|
|
a mérendő feszültség átlagértéke. |
Ha a 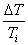 állandó, akkor az
állandó, akkor az 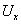 és
és 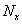 között egyenes arányosság van.
között egyenes arányosság van.
Ha a számláló kapuidejét 20 msec-ra változtatjuk, az átalakító kiszűri az 50 Hz-es zavarjeleket.
Átalakítási ideje: ~25msec (valamivel gyorsabb, mint a kettős integráló A/D)
A zajelnyomási tulajdonsága olyan jó, hogy ipari perifériákban gyakran alkalmazzák.
14.13. Mérés-adatgyűjtés általános áttekintése
Egy mérés-adatgyűjtő könyvtára olyan eljárásokat tartalmaz, amelyek vezérlik a PC-hez illeszthető DAQ (Data AcQuisition = mérés-adatgyűjtő) kártyáit. Egy kártya rendszerint számos funkciót ellát, így az analóg-digitális ( A/D ) átalakítást, a digitális bemenetek és kimenetek megvalósítását és a számláló/időzítő műveletek kezelését.
14.13.1. Mérés-adatgyűjtő rendszerek komponensei
A mérés-adatgyűjtő rendszerek alapvető feladata a valós világ fizikai jeleinek mérése illetve ilyen jelek létrehozása. Mielőtt egy számítógép alapú rendszer megmérne egy fizikai jelet, egy érzékelővel át kell alakítani a fizikai jelet villamos jellé, amely lehet áram vagy feszültség.
A számítógéphez illeszthető mérés-adatgyűjtő kártyát rendszerint úgy tekintik, mint a teljes mérés-adatgyűjtő rendszert, bár a kártya csak a rendszer egyik komponense.
A számítógéppel megvalósított automatikus műszerek mindegyike eltérő működésű és néha nem kapcsolhatjuk közvetlenül a fizikai jelet a mérés-adatgyűjtő kártya bemeneteihez. Egy jelszűrő és szint-illesztő áramkörbe (berendezésbe) kell a mérendő jelet az átalakítás előtt belevezetni, majd ezután kell elvégezni az átalakítást digitális információvá. A mérés-adatgyűjtő rendszerben programmal gyűjtjük össze a mérési adatokat, programmal analizáljuk őket és programmal jelenítjük meg a számítási eredményeket.
14.13.2. Analóg bemenet
Amikor analóg jeleket mérünk egy mérés-adatgyűjtő kártya segítségével a következő tényezőket kell figyelembe venni a digitalizált jel minősítésénél: milyen az alkalmazott mérési mód (egyszeres kimenetű és a differencia típusú mérés), milyen nagyságú a jel felbontása, (elő)erősítése, a mintavételezés sebessége és a zajok elnyomásának mértéke.
14.13.3. Egy kimenetű jelek (Single-Ended Inputs)

Az egy kimenetű jelek mindegyike ugyanarra a közös föld pontra kapcsolódik. Ezeket a bemenet típusokat akkor használjuk, ha a bemeneti jel szintje magas (nagyobb, mint 1 Volt), a jelforrástól az analóg bemenetekhez rövid összekötő huzallal (kevesebb, mint 5 méter) vezetünk minden jelet, valamint a jelek mindegyike egy közös referencia föld pontot alkalmaz. Ha a mérendő jel nem teljesíti ezeket a feltételeket, akkor különbségi (differencia) bemeneteket kell alkalmaznunk.
14.13.4. Különbségi bemenetek (Differential Inputs)
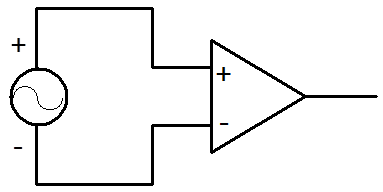
A különbségi bemenetek megengedik, hogy minden bemenetnek különböző feszültség értéke legyen, amely a földhöz képest jelenik meg. A különbségi bemenetek csökkentik a mérési zajt, mivel a vezetékekről "felvett" közös módusú zajt a bemenetek kivonják egymásból.
14.13.5. Felbontás (Resolution)
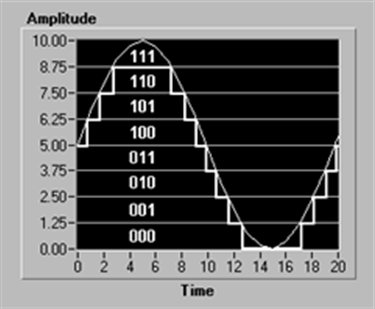
A felbontás a bitek száma, amelyet a mérés-adatgyűjtő analóg/digitális átalakító (ADC= Analog to Digital Converter) használ, hogy az analóg jelet ábrázolja. Nagyobb felbontással nagyobb az adott mérési határok közötti felosztások száma és ezért kisebb az érzékelhető legkisebb feszültségváltozás nagysága.
Vegyünk például egy szinusz hullámot és a hozzá tartozó digitális értékeket, amelyeket egy 3 bites ADC (Analog to Digital Converter = Analóg digitális átalakító) hozott létre (ilyen átalakítót ritkán alkalmazunk, de a példát nagyon szemléletessé teszi) és a mérési határt 23 azaz 8 részre osztja. Egy 000 és 111 közötti bináris számmal írjuk le az átalakító különböző értékeit. Más szóval ez a digitális jel nem megfelelő ábrázolása az eredeti jelnek, mivel nagyon sok információt veszítünk el az átalakításnál. A felbontást megnövelve 16 bitre az ADC lehetséges állapotainak számát 8-ról 65536-ra (216) növeljük és az analóg jel rendkívül pontos ábrázolását kapjuk.
14.13.6. Mérési határok (Range)
A mérési határok azok a minimális és maximális feszültség szintek, amelyek között az ADC (Analog to Digital Converter = Analóg digitális átalakító) a jel átalakítást végzi. A mérés-adatgyűjtő kártyák változtatható méréshatárokat (tipikusan 0-tól 10 Volt-ig; vagy -10 Volt-tól +10 Volt-ig) kínálnak, melyek közül megtalálhatjuk azokat a mérés határokat, amelyekkel adott felbontás mellett a legpontosabban mérhetjük meg a jelet.
14.13.7. Erősítés (Gain)
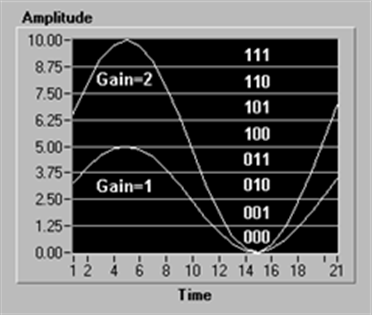
Az erősítés a mérendő jel bármilyen felerősítése vagy leosztása, amely a jel digitalizálása előtt történik. Az erősítés alkalmazásával jelentősen lecsökkenthetjük az ADC (Analog to Digital Converter = Analóg digitális átalakító) bemeneti mérési határait, így biztosítjuk, hogy az ADC a lehető legtöbb digitális osztást alkalmazza a jel ábrázolásához. Például, alkalmazzunk egy három bites ADC-t és a mérési határokat 0 és +10 Volt-ra állítsuk be, vizsgáljuk az erősítés hatását egy olyan jel esetén, amely 0 és +5 Volt között váltakozik.
Erősítés nélkül, vagy más szóval egyszeres erősítéssel az ADC csak négy osztást használ a nyolc lehetségesből az átalakításkor. A digitalizálás előtt felerősítve a jelet egy kétszeres erősítéssel az ADC most használni tudja mind a nyolc osztást és a digitális ábrázolás sokkal pontosabb. Ebben az esetben a kártya tényleges bemeneti mérési határai 0 és +5 Volt lettek, mivel bármilyen +5 Volt-nál nagyobb jel kétszeres erősítéssel az ADC bemenetén +10 Volt-nál nagyobb jelet eredményez.
A DAQ kártyán lehetséges mérési határok, a felbontás és az erősítés meghatározzák a legkisebb érzékelhető bemeneti feszültség nagyságát. Ez a feszültség az átalakított digitális érték legkisebb helyiértékű bit-jén (LSB = Less Significant Bit) ábrázolt érték Volt-ban, amelyet gyakran kód szélességnek is neveznek. A legkisebb érzékelhető feszültségváltozást (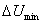 ) a következő képlettel lehet meghatározni:
) a következő képlettel lehet meghatározni:
|
|
(14.37) |
Például egy 12 bites DAQ kártya 0-tól +10 Volt-ig terjedő bemeneti mérési határokkal egyszeres erősítéssel 2.4 mVolt változást még érzékel, ugyanez a kártya -10 Volt-tól +10 Volt-ig terjedő bemeneti mérési határokkal csak 4.8 mVolt változást képes érzékelni.
14.13.8. Mintavételezés sebessége (Sampling Rate)
A mintavételezés időköze (h [sec]) megadja, hogy egy analóg-digitális átalakítás milyen gyakran történik. Nagyobb mintavételezési sebesség mellett adott idő alatt több mérési pontot gyűjthetünk össze, és ezért jobb ábrázolást valósíthatunk meg, mint kisebb mintavételi sebesség mellett. Minden bemeneti jelből a lehetséges legnagyobb mintavételi sebességgel kell mintát vennünk, hogy a legpontosabban jeleníthessük meg az analóg jelet a számítógépben. A kis sebességű mintavételezés az analóg jel egy nagyon gyenge minőségű mintavételes (digitális) megjelenését eredményezi.
A következő ábrán a felső hullámot megfelelően mintavételeztük. Az alsó hullámnál az alul-mintavételezés eredménye egy rosszul mintavételezett ( aliased = látszólagos ) jel.
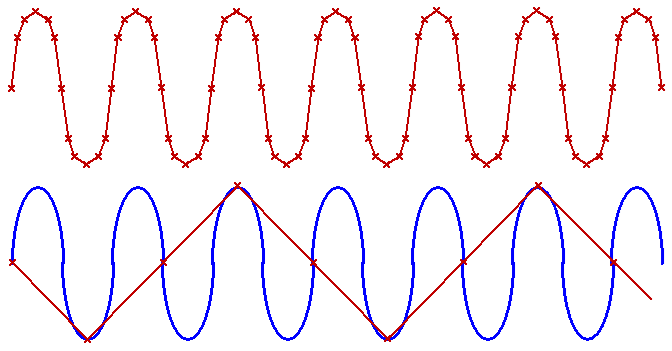
A Shannon-féle mintavételezési elv szerint a bejövő jelből a teljes visszaállíthatósághoz legalább olyan frekvenciával kell mintát venni, amely (minimálisan) kétszer nagyobb, mint a bejövő jel legmagasabb frekvenciájú komponense.
Például, ha hangfrekvenciás jeleket alakítunk át villamos jellé a bemeneti jel legmagasabb frekvenciájú komponense 20 kHz nagyságú is lehet, ezért egy olyan mérésadatgyűjtő kártyára van szükség, amely 40 kHz-nél nagyobb mintavételi sebességgel képes mintákat venni, ahhoz hogy a jelet megfelelően mintavételezzük.
A hőmérséklet átalakítók rendszerint nem kívánnak nagy mintavételi sebességet, mivel a hőmérséklet a legtöbb alkalmazásban nem változik olyan gyorsan. Ezért egy kisebb mintavételi sebességű kártya megfelelően tudja gyűjteni a hőmérsékleti adatokat.
14.13.9. Átlagolás (Averaging)
A nem kívánt zaj torzítja azt az analóg jelet, amelyet digitális jellé akarunk átalakítani. A zajforrás lehet külső zaj vagy a számítógépen belül keletkező zaj. A külső zajt megfelelően korlátozhatjuk elő-szűrő áramkör alkalmazásával. Szintén csökkenthetjük a zaj hatását, ha a szükségesnél nagyobb mintavételi frekvenciát alkalmazunk és átlagoljuk a mintavételi pontokat (digitális szűrés).
A zaj szintje átlagolás után a következő képlet szerinti csökken:
|
|
(14.38) |
Például, ha 100 pont átlagát vesszük, a zaj hatását a jelben 1/10-ed részére csökkentjük.
A méréselméletben rendszerint megkülönböztetik a zajt és a zavart ! A zavar determinisztikus , de nehéz meghatározni, korrigálni. A zavar torzítja a mérést! (Pl. a hálózati frekvenciás elektromágneses zavar.) A zaj sztochasztikus , szűréssel csökkenthető, de nem kiküszöbölhető. A zaj bizonytalanná teszi a mérést!
14.13.10. Analóg bemenet eljárása a számítógépben
A Data Acquisition (Mérés-adatgyűjtés) alpalettán lévő Analog Input (Analóg bemenet) alpaletta tartalmazza azokat a VI-ket, amelyek végrehajtják az analóg-digitális (A/D) átalakítást. (LabVIEW program)
14.13.11. Analóg bemenet csatorna mintavételezés
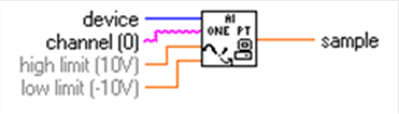
A mérés-adatgyűjtő kártya egyik bemeneti pontjáról lemérhetjük a feszültség értékét az "AI Sample Channel " (Analóg bemenet csatorna mintavételezés) eljárás alkalmazásával.
Ez az eljárás megméri a mérés-adatgyűjtő kártya megadott bemeneti csatornájához kapcsolt feszültségjel nagyságát és visszaadja a mért értéket.
Az " AI Sample Channel " (Analóg bemenet csatorna mintavételezés) eljárásnak a következő bemenetei és kimenetei vannak:
|
Bemenet/kimenet |
Leírás |
|---|---|
|
Device (Berendezés) (bemenet) |
A mérés-adatgyűjtő kártya berendezésszáma. |
|
Channel (Csatorna) (bemenet) |
Egy szöveg típusú adat, amely megadja a mérni kívánt csatorna sorszámát. |
|
High limit (Felső határ) (bemenet) |
A bemeneti jel felső méréshatára. Ha a programban nem adunk meg értéket a bemenethez, akkor értéke +10 Volt |
|
Low limit (Alsó határ) (bemenet) |
A bemeneti jel alsó méréshatára. Ha a programban nem adunk meg értéket a bemenethez, akkor értéke -10 Volt. |
|
Sample (Minta) (kimenet) |
A mért érték Volt-ban. |
Ha hiba történik az "AI Sample Channel" (Analóg bemenet csatorna mintavételezés) VI működése közben, egy dialógus ablakba írt szöveggel megkapjuk a hiba okát, ezután választási lehetőségünk van, hogy befejezzük a programot, vagy folytatjuk a végrehajtást.
14.13.12. Hullámforma bemenet (Waveform Input)
Sok alkalmazásban egy mérési pont megadott időben történő mintavételezése nem elegendően gyors. Mindezekhez még hozzájárul, hogy nehéz megvalósítani egy állandó mintavételi időközt minden mérési pont között, mivel az időköz számos tényező függvénye, amelyek a következők: a ciklusutasítás végrehajtási sebessége, a hívó program időszükséglete és további technikai tényezők. Meghatározott VI-kkel több mérési pontról végezhetünk adatgyűjtést nagyobb sebességgel, mint amit az "AI Sample Channel" (Analóg bemenet csatorna mintavételezés) VI elérhet. Mindemellett, ez a VI elfogadja a felhasználó által megadott mintavételi sebességet. Erre egy mintapélda az "AI Acquire Waveform.llb".
14.13.13. Analóg input hullámforma adatgyűjtő
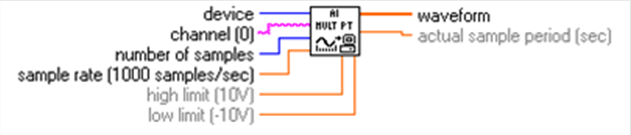
Az "Analóg input hullámforma adatgyűjtő" VI meghatározott számú minta gyűjtését végzi el meghatározott mintavételi sebességgel egy bemeneti csatornáról és visszaadja a mintavételezés eredményét, mint egy tömböt.
Az " AI Acquire Waveform " (Analóg input hullámforma adatgyűjtő) VI-nek a következő bemenetei és kimenetei vannak:
|
Bemenet/kimenet |
Leírás |
|---|---|
|
Device (Berendezés) (bemenet) |
A mérés-adatgyűjtő kártya berendezésszáma. |
|
Channel (Csatorna) (bemenet) |
Egy szöveg típusú adat, amely megadja mérni kívánt csatorna számát. |
|
Number of samples (A minták száma) (bemenet) |
Egy végrehajtással összegyűjtött minták száma. |
|
Sample rate (Mintavételi sebesség) (bemenet) |
A másodpercenként összegyűjtött minták száma. |
|
High limit (Felső határ) (bemenet) |
A bemeneti jel felső méréshatára. Ha a programban nem adunk meg értéket a bemenethez, akkor értéke +10 Volt. |
|
Low limit (Alsó határ) (bemenet) |
A bemeneti jel alsó méréshatára. Ha a programban nem adunk meg értéket a bemenethez, akkor értéke -10 Volt. |
|
Waveform (Hullámforma) (kimenet) |
Egydimenziós tömb, amely a mérés után tartalmazza az analóg bemeneti adatok mért értékeit Volt-ban. |
|
Actual sample period (Aktuális mintavételi periódusidő) (kimenet) |
Az alkalmazott mintavételi sebesség reciproka. Ez a szám egy kicsit eltér a megkívánt mintavételi sebességtől és az alkalmazott hardware-től függ (számítógép és adatgyűjtő kártya típus). |
14.14. Az analóg bemeneti perifériák perifériavezérlő egysége
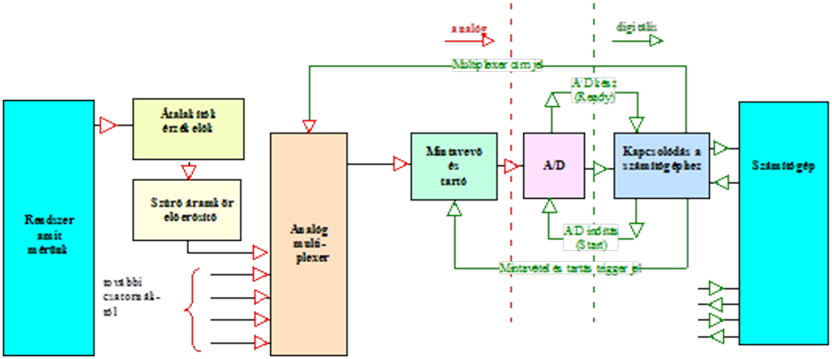
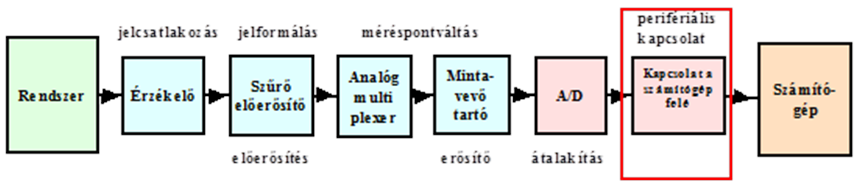
A periféria vezérlő egységnek a következő feladatokat kell ellátnia:
Periféria cím dekódolása , amely megadja, hogy a következő parancs az adott periféria számára érkezett vagy sem.
Parancs fogadása és dekódolása.
Feladatai részletesen:
Méréspont váltás vezérlése. A parancsban szereplő mérési csatorna kiválasztása.
Az A/D átalakítás késleltetése a méréspont váltás megvalósulásáig. A méréspont váltó típusától függően a méréspont váltás állandó kapcsolatának megvalósulásáig.
Erősítési tényező beállítása az A/D átalakítás előtt . A bemeneti jel érték gyors komparálásával a szükséges előerősítés mértékének meghatározása.
Integrálási idő beállítása (csak integráló A/D átalakító típus esetén).
Az A/D átalakító külső jelre történő indításának engedélyezése . Ez az úgynevezett trigger impulzus bemenet engedélyezése, amely általánosan egy másik jelcsatorna nulla átmenetének értékét alkalmazza az adott csatorna mérésének indításához.
Az A/D átalakító programmal történő indítása . A mérés elindítását kiváltó impulzus kibocsájtása.
Periféria kész (Ready) lekérdezése . A mérési folyamat befejezésének érzékelését biztosító jel.
Periféria kész (Ready) állapotjel törlése.
Megszakítás jel (Interrupt) engedélyezése.
Megszakítás jel (Interrupt) lekérdezése . A mérési folyamat végén a számítógép aktuális működő programjának megszakítása ahhoz, hogy a mérési adatokat a számítógép memóriájába bevigyük.
Megszakítás jel (Interrupt) törlése.
Az A/D átalakító kimeneti regiszterének olvasása . Az analóg/digitál átalakító mérési adatának olvasása.
Az A/D átalakító kimeneti regiszterének törlése.
Periféria önteszt végrehajtása . Az analóg/digitál átalakító helyes működését ellenőrző teszt mérési sorozat végrehajtása, amelynek az a célja, hogy mért jel felhasználhatóságát (helyességét) igazolja.
Az összegyűjtött adatok átmeneti tárolása pufferben (az átalakítás helyén). (FIFO = First In First Out alagút típusú puffer) A mérési adatokat nagyobb mintavételezési frekvenciánál, mérési egységekben (csomagokban) juttatjuk el a számítógép memóriájába. Az adatátvitel a csomag elkészülésének időpontjában megszakítással történik.
Közvetlen memória átviteli lehetőség megvalósítása a számítógéppel (DMA = Direct Memory Access). Nagyobb mennyiségű mérési adatot tartalmazó adatcsomag átviteli eljárása, amely az A/D kártya memóriájából juttatja el az adatokat a számítógép memóriájába úgy, hogy közben a számítógépet alvó (Hold) állapotba kapcsolja.
14.15. Folytonos idejű mérésadatgyűjtés
A folytonos idejű mérésadatgyűjtés alkalmazásokban néha nincs meghatározva a mintavételek száma, vagy olyan hosszú idő alatt kell megvalósítanunk a mérésadatgyűjtést, amelyhez az egyszeres blokkolt (pufferelt) adattároláshoz szükséges memória nagysága gyakorlatilag nem fér el a számítógép memóriájában.
Folytonos idejű mérésgyűjtésnél az adatokat egy ciklikus pufferben helyezi el a mérésadatgyűjtő berendezés (hardver). Ezzel párhuzamosan a program kiolvassa az összegyűjtött adatokat a tárolóból és feldolgozza azokat. Tipikus feldolgozások: matematikai műveletek, adat megjelenítés és file input/output műveletek. Amilyen gyorsan olvassa ki a program az adatokat, a hardware ugyanolyan gyorsan tölti fel az új adatokkal, így a ciklikus puffer soha nem töltődik fel és a művelet folyamatosan végezhető végtelen ideig.
14.15.1. Kettős tárolású (pufferelésű) bemeneti műveletek
Az adat tárolót a kettős pufferelésű bemeneti műveletekhez úgy konfiguráljuk, mint egy ciklikusan tárolót. További információ, hogy az operációs rendszer fizikailag felosztja a tárolót két egyenlő részre. A tároló felosztásával az operációs rendszer képes irányítani a tárolóhoz történő felhasználói hozzáférést a mérésadatgyűjtés kezelő programjának segítségével. Az irányítási séma nagyon egyszerű – az operációs rendszer átmásolja az adatokat a ciklikus tárolóból egy átmeneti (sorrendi) tárolóba, amelyből a kiolvasás valóságban megtörténik. Az átmeneti tárolóban műveletet végezhetünk az adatokkal, vagy csak tároljuk őket.
A kettős pufferelésű bemeneti művelet azzal kezdődik, hogy a mérésadatgyűjtő berendezés először a ciklikus puffer első felébe kezdi el írni az adatokat (14.92. ábra - Kettős pufferelésű bemenet, sorrendi adat átvitellel a. ábra). Miután a berendezés elkezdi a ciklikus puffer második felét írni, az operációs rendszer átmásolja a ciklikus puffer első felének tartalmát az átmeneti tárolóba (14.92. ábra - Kettős pufferelésű bemenet, sorrendi adat átvitellel b. ábra). Ezután az átmeneti tárolóban lévő adatokat kiolvashatjuk és tárolhatjuk háttértárolón vagy feldolgozhatjuk őket egy alkalmazásban. Miután a bemeneti berendezés feltöltötte a ciklikus tároló második felét is visszatér a ciklikus tároló első feléhez és felülírja az ott található adatokat az új bejövő adatokkal. Az operációs rendszer ekkor átmásolhatja a ciklikus puffer második felének tartalmát az átmeneti tárolóba (14.92. ábra - Kettős pufferelésű bemenet, sorrendi adat átvitellel c. ábra). Az átmeneti tárolóban lévő adat ismét az alkalmazás rendelkezésére áll. Az eljárás végtelen ideig ismétlődhet, hogy folytonos adatfolyamot biztosítson az alkalmazás számára. Megjegyezzük, hogy a 14.92. ábra - Kettős pufferelésű bemenet, sorrendi adat átvitellel d. ábra megegyezik a 14.92. ábra - Kettős pufferelésű bemenet, sorrendi adat átvitellel b. ábrán bemutatott lépéssel és így a két lépéses ciklus kezdetévé válik.
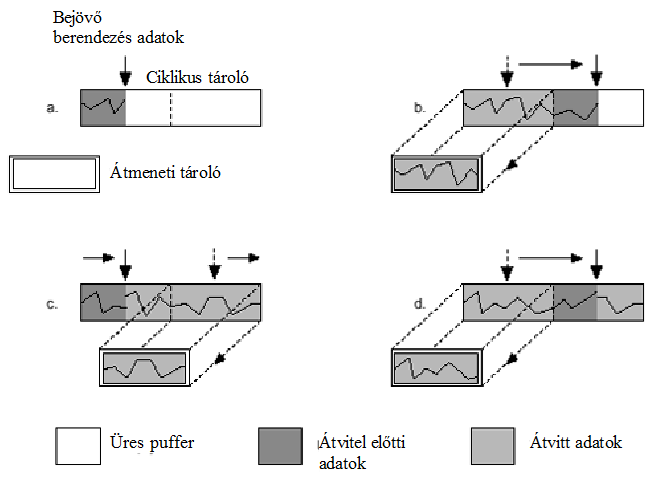
14.15.2. Az átviteli módszer meghibásodási lehetőségei
A kettős pufferelés egyes műveletei esetenként hibásan is működhetnek. Az alkalmazásokban alapvetően a következő két hibás működési szituáció fordulhat elő:
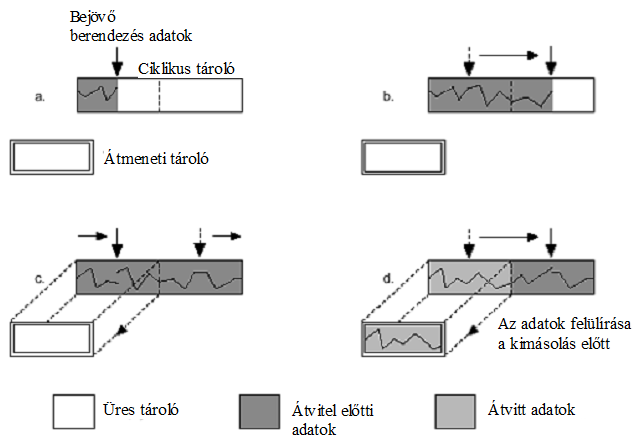
A mérésadatgyűjtő berendezés felülírja a ciklikus pufferben lévő korábbi adatokat, mielőtt azokat az átmeneti tárolóba másoltuk volna. (14.93. ábra - Kettős pufferelésű bemenet felülírása mielőtt kimásoltuk volna a tartalmát ábra )
A 14.93. ábra - Kettős pufferelésű bemenet felülírása mielőtt kimásoltuk volna a tartalmát b. ábra alapján látható, hogy az operációs rendszer lekéste azt a lehetőséget, hogy átmásolja az adatokat a ciklikus puffer első feléből az átmeneti pufferbe, mialatt a mérésadatgyűjtő berendezés az adatokat a ciklikus tároló második felébe írta. Ennek eredményeként a mérésadatgyűjtő berendezés elkezdi a ciklikus tároló első felében lévő adatok felülírását, mielőtt azokat az operációs rendszer átmásolta volna az átmeneti tárolóba (14.93. ábra - Kettős pufferelésű bemenet felülírása mielőtt kimásoltuk volna a tartalmát c. ábra ). Ahhoz, hogy az adatok hibamentes átmásolását megvalósítsuk, az operációs rendszernek várnia kell az átmásolással addig, ameddig a berendezés befejezi az adat-felülírást a ciklikus tároló első felében. Amikor a berendezés elkezdi a ciklikus tároló második felét írni, az operációs rendszer átmásolja az adatokat a ciklikus tároló első feléből az átmeneti tárolóba (14.93. ábra - Kettős pufferelésű bemenet felülírása mielőtt kimásoltuk volna a tartalmát d. ábra ).
Az előzőleg bemutatott szituáció esetén az operációs rendszer egy felülírási hibával tér vissza a kezelő programból ( overWrite Error = felülírási hiba ). Ez a figyelmeztetés azt jelzi, hogy az átmeneti tárolóban lévő tartalom érvényes, de néhány korábbi adat elveszett. A későbbi átvitelek nem térnek vissza figyelmeztetéssel addig, ameddig a mérésadatgyűjtő berendezés az átviteli sebességet megtartja, ahogy az a (14.92. ábra - Kettős pufferelésű bemenet, sorrendi adat átvitellel) ábrán látható.
A másik lehetséges probléma akkor jelenik meg, amikor egy bemeneti berendezés felülírja az adatokat, mialatt az operációs rendszer párhuzamosan másolja azokat az átmeneti tárolóba.
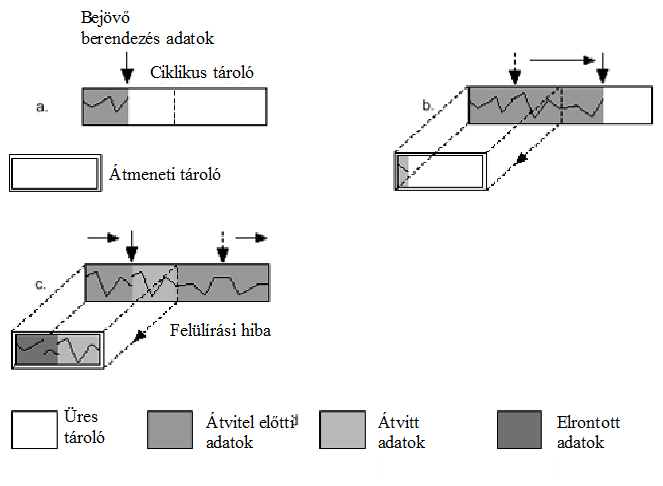
Az operációs rendszer ilyenkor egy felülírási hibával tér vissza a kezelő programból (Overwrite Error = felülírási hiba ). A szituáció a (14.94. ábra - Kettős pufferelésű bemenet egy adat felülírással) ábrán látható.
A (14.94. ábra - Kettős pufferelésű bemenet egy adat felülírással) b. ábrán az operációs rendszer elkezdi az adatok átmásolását a ciklikus tároló első feléből az átmeneti tárolóba. Azonban az operációs rendszer képtelen átmásolni a teljes fél tárolót (a ciklikus tároló első felét), mielőtt a mérésadatgyűjtő berendezés elkezdi felülírni a ciklikus puffer területét (14.94. ábra - Kettős pufferelésű bemenet egy adat felülírással c. ábra). Következésképpen azok az adatok, amelyeket az átmeneti tárolóba másoltunk nem helyes értékek és együtt tartalmazzák a megelőző, és az újonnan felülírt adatokat. Ha a további átvitelek normálisan zajlanak le, akkor az előbb leírt probléma nem jelentkezik.
A leggyakoribb probléma a folytonos mérésadatgyűjtésnél az, hogy a program elvéti az adatok gyors kiolvasását és nem képes olyan gyorsan olvasni, mint ahogy a hardware küldi azokat. Hogy megelőzzük ezt, optimalizáljuk a program hurkot, amely az adatokat gyűjti. Lehetőség szerint távolítsunk el minden, a feldolgozáshoz nem feltétlenül szükséges eljárást az adatgyűjtő hurokból. Ha ez nem lehetséges, akkor a mérésadatgyűjtés sebességét kell csökkentenünk.
Irodalmak
[14.1.] Analog And Digital Control System Design. Sounders College Publishing . 2006.
[14.2.] Linear System Theory and Design. Oxford University Press. 1999.
[14.3.] Modern Control Systems Engineering. 1996.
15. fejezet - Analóg kimenetek
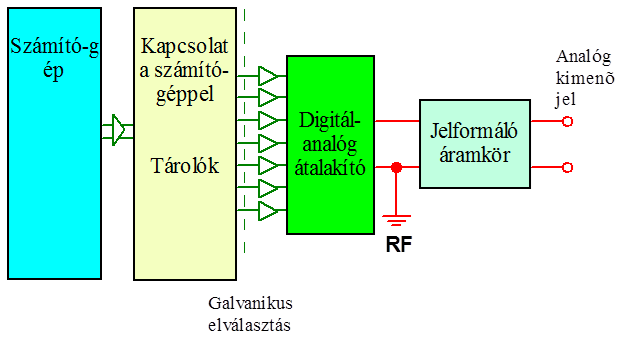
Az analóg kimeneti jelek típusai:
Egyenfeszültség és váltakozó feszültség
Egyenáram és váltakozó áram
Frekvenciajel (pulzus szélesség moduláció (PWM = Pulse Wave Modulation)
15.1. Digitál-analóg konverterek
A digitál/analóg átalakítók szokásos felbontása 8, 10, 12, 16 bites.
Kimeneti feszültség értékük:
0..+5V; (unipoláris)
0..10V; (unipoláris)
±5V; (bipoláris)
±10V; (bipoláris)
Az áramjelet megfelelő feszültségvezérelt áramgenerátor segítségével ebbe az áram-tartományba transzformálják 0..20 mA vagy 4..20 mA (élőnullás!).
Frekvencia kimenet esetén meghatározott periódusidejű (~1 kHz-es) négyszög jel magas és alacsony amplitúdójú részeinek arányát változtatjuk. Így nullától (0-tól) száz százalékig (100%) történő jel kitöltést valósíthatunk meg tetszőleges felbontás mellett.
Ezt a D/A kimeneti jelet általában egy arányos tárolós (PTn) berendezésre kapcsolják (pl. egyenáramú motorra), amely a beérkező impulzusokból – működéséből eredően - meghatározza a jel effektív értékét (egyen feszültségű megfelelő értékét) és erre a kimeneti jel értékre áll be.
15.2. D/A átalakító típusok
ahol
|
MSB |
Most Significant Bit | |
|
LSB |
Least Significant Bit |
Ehhez a digitális/analóg átalakító típushoz 1 : 2n átfogású pontos ellenállásokra van szükség. Ezért ezen drágább megoldás helyett, gyakrabban alkalmazzák az úgynevezett R-2R létrahálózatot az A/D átalakításhoz.
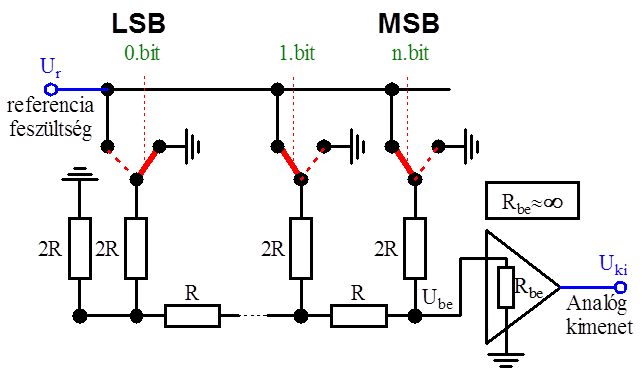
A D/A átalakító átalakítási időtartama μs nagyságrendű!
Ha több analóg kimenet szükséges, annyi D/A átalakítót alkalmaznak, ahány kimeneti csatorna szükséges. Általában jóval több bemeneti csatorna (analóg) szükséges , mint kimeneti csatorna, mert a több forrásból érkező információt általában egy kimenet jelének meghatározásához használjuk fel.
15.3. Analóg kimenet eljárása a számítógépben
15.3.1. Analóg kimenet csatorna frissítés
Az "Analóg kimenet csatorna frissítés" eljárás egy meghatározott feszültség- értéket ír ki egy kiválasztott analóg kimeneti csatornára. Az " AO Update Channel " (Analóg kimenet csatorna frissítés) eljárásnak a következő bemenetei és kimenetei vannak:
|
Bemenet/kimenet |
Leírás |
|---|---|
|
Device (Berendezés) (bemenet) |
A mérés-adatgyűjtő kártya berendezés száma. |
|
Channel (Csatorna) (bemenet) |
Egy szöveg típusú adat, amely megadja az analóg kimeneti csatorna számát. |
|
Voltage (Feszültség) (bemenet) |
A kártya kimenetre adott feszültség értéke Volt-ban. |
Ha hiba történik az "AO Update Channel" (Analóg kimenet csatorna frissítés) eljárás működése közben, egy dialógus ablakba írt szöveggel megkapjuk a hiba okát, ezután választási lehetőségünk van, hogy befejezzük a program működését, vagy folytassuk az eljárás végrehajtását.
15.3.2. Hullámforma előállítása
Sok alkalmazásban egy analóg kimeneti pont megadott időben történő beállítása nem elegendően gyors. Mindezekhez még hozzájárul, hogy nehéz megvalósítani egy állandó mintavételi időközt minden kimeneti pont értékének beállítása között, mivel az időköz számos tényező függvénye, amelyek a következők: a ciklusutasítás végrehajtási sebessége, a hívó program időszükséglete és és további technikai tényezők. Az "AO Generate Waveform" (Analóg kimenet hullámforma létrehozása) eljárással több kimeneti pont értékének beállítását végezhetjük, nagyobb sebességgel, mint ahogy az "AO Update Channel" (Analóg kimenet csatorna frissítés) eljárás elvégezheti. Mindemellett, ez az eljárás elfogadja a felhasználó által megadott adatfrissítési sebességet is.
15.3.3. Analóg kimeneti hullámforma létrehozása

Az "Analóg kimenet hullámforma létrehozása" eljárás létrehoz egy mintavételes feszültség sorozatot (hullámformát) egy kiválasztott analóg kimeneti csatornán a megadott frissítési sebességgel.
Az " AO Generate Waveform " (Analóg kimenet hullámforma létrehozása) eljárásnak a következő bemenetei és kimenetei vannak:
|
Bemenet/kimenet |
Leírás |
|---|---|
|
Device (Berendezés) (bemenet) |
A mérés-adatgyűjtő kártya berendezésszáma. |
|
Channel (Csatorna) (bemenet) |
Egy szöveg típusú adat, amely megadja az analóg kimeneti csatorna számát. |
|
Update rate (Frissítési sebesség) (bemenet) |
A másodpercenként végzett frissítések száma. |
|
Waveform (Hullámforma) (bemenet) |
Egydimenziós tömb, amely tartalmazza azokat az adatokat Volt-ban, amelyeket kiírunk az analóg kimeneti csatornára. |
Irodalmak
[15.1.] Analog And Digital Control System Design. Sounders College Publishing . 2006.
[15.2.] Linear System Theory and Design. Oxford University Press. 1999.
[15.3.] Modern Control Systems Engineering. 1996.
16. fejezet - A mérésadatgyűjtő számítógép algoritmusai
Algoritmus: valamely feladat megoldási lépéseinek leírása.
Típusi: periodikus , nem periodikus (kezelő vagy egy esemény váltja ki)
Állapot változók: a mérési folyamat állapotát leíró, vagy működését meghatározó analóg illetve mintavételes változók.
Típusai:
mért: egy bemenet mérése alapján meghatározott változó érték
számított: két vagy több mért értéke alapján képzett (számított) változó érték
16.1. Az analóg és digitális jelek mérése, és előzetes feldolgozása
A mérési feladat elemei a számítógép számára:
mintavételezés
átkódolás
méréskorrekció
digitális szűrés
átszámítás fizikai értékre
Ezeket a műveleteket a mérést irányító számítógép periódikusan hajtja végre.
16.1.1. Mintavételezés
Csak az állandó mintavételezési idejű rendszerekkel foglalkozunk.
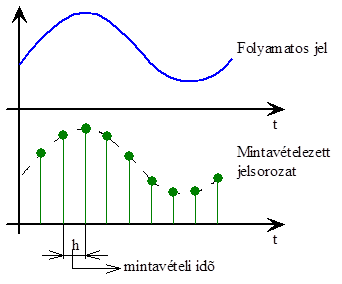
A mintavételezési törvény alkalmazása
Ha a mintavételezendő jel sáv korlátozott, vagyis megadható egy fmax frekvencia, amelynél nagyobb frekvenciájú jelet nem tartalmaz, a mintavételezendő jelet egyértelműen jellemzi az fmax frekvencia kétszeresénél nagyobb frekvenciával vett minták sorozata. A helyesen megválasztott mintavételezési frekvencia tehát:
|
f s > 2*f max |
(16.1) |
ahol
|
|
a mintavételezés frekvenciája, | |
|
|
a mérendő jelben előforduló legmagasabb frekvenciájú komponens. |
Ha csak a feltétellel megadott mintavételi frekvenciát alkalmazzuk, azaz az fmax frekvencia kétszeresével mintavételezünk, nem kapjuk meg azt a mintavételezett jelet, amelyből visszaállíthatnánk az eredeti mintavételezett jelet, mint ahogy azt a 16.2. ábra - A szinuszos jel mintavételezése ábra mutatja.
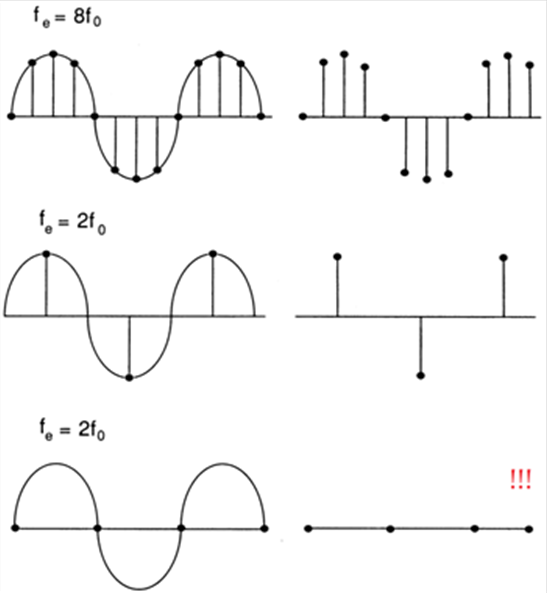
A valóság azonban az, hogy a jelek nem sávkorlátozottak, ezért gyakorlati javaslatot kell adni arra vonatkozóan, hogy milyen értékű legyen a mintavételezés frekvenciája. Ez egy közepes bonyolult matematikai formula, amelyből meghatározható, hogy az alul mintavételezéssel milyen torzítást okozunk.
A gyakorlatban az f max értékének 6-25-szeresével meghatározott mintavételi frekvenciát alkalmazunk ipari berendezésenként f sample -ként!
16.1.2. Átkódolás és kódkonverzió
Átkódolásra szükség van mind az analóg, mind a digitális bemeneti és kimeneti jeleknél egyaránt.
Az analóg bemeneteknél az analóg érték mintavételes átalakításához szükséges lépéseket kell megtennünk. Így az A/D átalakító által szolgáltatott számábrázolási formát át kell alakítani a számítógépben történő számábrázolási formára.
Mivel a digitális jelek ábrázolása a számítógépben az adatátviteli kódoktól eltérő, a megfelelő átkódolási műveleteket programmal kell végrehajtani.
Átkódolásra van szükség az analóg kimenetek és a kezelő számára a megfelelő formátumú táblázatok, naplók előállításához is.
Átkódoláshoz soroljuk a fixpontos/lebegőpontos , illetve a lebegőpontos/fixpontos átalakításokat is. Erre azért van szükség, mert az A/D átalakítók által adott adat, illetve a D/A átalakítók beállításához szükséges adat egész típusú, fixpontos , míg a számítógép általában lebegőpontos formátumban végzi a műveleteket.
Az adatátvitel biztonsága érdekében a digitális be/kimeneti jeleket is sokszor redundáns módon kódolják (a feltétlenül szükséges információn túl további kiegészítő információkat is kódolnak).
A redundáns kódok a torzult információ felismerését, illetve a hiba kijavítását teszik lehetővé.
16.1.3. Méréskorrekció
A méréskorrekció célja a mért értékek pontosságának növelése. A korrekció történhet korrekciós egyenletek alapján, vagy ezek sorba fejtésével kapott közelítő egyenletek alapján, illetve táblázatban megadott adatok felhasználásával. Gyakran alkalmazott korrekciótípus a mérőműszer referencia feltételének megváltozását figyelembe vevő méréskorrekció.
Például
hőelemes hőmérsékletmérés referencia hőmérsékletének megváltozása
|
|
(16.2) |
ahol
|
|
hőelem által adott feszültség érték | |
|
|
a mérendő hőmérséklet | |
|
|
hőelem típustól függő konstans érték | |
|
|
a környezeti hőmérséklet, kompenzáció hőmérsékleti hely |
Gázmennyiség szűkítő elemes mérésénél alkalmazható korrekciós egyenlet:
|
|
(16.3) |
ahol
|
|
mért mennyiség | |
|
|
mért sűrűség | |
|
|
mért hőmérséklet | |
|
|
mért nyomás érték | |
|
|
névleges sűrűség ([kg/m^3]) | |
|
|
névleges hőmérséklet (20 fokC) | |
|
|
névleges nyomás érték (1 bar) |
16.1.4. Digitális szűrések megvalósítása a gyakorlatban
A digitális szűrés a számítógépben levő jeleken tetszőleges algoritmussal leírható digitális jelfeldolgozási algoritmus.
16.1.4.1. Átlagoló szűrő
Az átlagoló szűrőt, amely egy FIR típusú aluláteresztő szűrő, a bemeneti mintevételes jel zajszűrésénél alkalmazzák.
|
|
(16.4) |
ahol
|
y[k] |
a kimenő jel az | |
|
u[k-i] |
a bemenő jel az |
Az n-edik időpillanatban a jel átlag-értéke (az előző N pont átlaga).
16.1.4.2. Exponenciális szűrő
Az exponenciális szűrőt, a bemeneti mintavételes jel zajszűrésénél alkalmazzák.
|
|
(16.5) |
ahol
|
y[k] |
a kimenő jel az | |
|
y[k-1] |
a kimenő jel az | |
|
u[k-1] |
a bemenő jel az |
A szűrő az 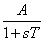 egytárolós tag mintavételes megfelelője.
egytárolós tag mintavételes megfelelője.
Az aluláteresztő szűrő mintavételes algoritmusa:
|
|
(16.6) | |
|
|
(16.7) | |
Differenciálegyenlet megoldása, amelynek a differencia egyenlettel történő helyettesítése megadott mintavételi időtartammal:
|
|
(16.8) |
Általánosan
|
|
(16.9) |
A következő időpillanatban a jel értéke rekurzív formulával adható meg (h mintavételi idő esetén.).
16.1.4.3. Logikai adaptív szűrő
A bemeneti jelen megjelenő kiugró értékű véletlenszerű zavarok hatásának kiküszöbölésére alkalmazható.
Az algoritmussal minden egyes mérésnél (mintavételezésnél) meghatározunk (D k ) értékeket, az N darab korábbi értékre vonatkozó jelváltozás gradiens értékét (D k , D k-1 ,..... D k-(N-1) ).
|
|
(16.10) | |
|
|
(16.11) |
Meghatározzuk ezek átlagértékét és szórását és ennek alapján avatkozunk be a jel szűrésébe.
Ha
|
|
(16.12) |
akkor változatlan szűrőegyenletet alkalmazunk.
Ha
|
|
(16.13) |
A bemeneti jelen nagy értékű pillanatnyi zavarjel jelenik meg, akkor a szűrő kimenetét „befagyasztják”.
|
|
(16.14) |
Ha adott mintavételi idő után a feltétel még mindig fennáll 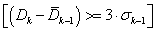 , az azt jelenti, hogy a bemeneti jel megváltozott, ekkor
, az azt jelenti, hogy a bemeneti jel megváltozott, ekkor
|
|
(16.15) |
a szűrő algoritmus a megváltozott bemeneti jel környezetében dolgozik tovább.
16.1.4.4. Másodrendű szűrő
|
|
(16.16) |
Differenciálegyenlet differencia egyenletté alakításával kapjuk.
|
|
(16.17) | |
|
|
(16.18) | |
|
|
(16.19) |
Látható, hogy a kimenet meghatározásához a k. időpillanatban a megelőző két mintavételi időpillanatban szükséges a kimenet ismerete. Ez általánosan is igaz, ahányad rendű a szűrő, annyi korábbi mintavételi időpillanatbeli kimeneti jel értékre van szükségünk a szűrési egyenlet kiszámításához.
16.1.5. Átszámítás fizikai értékekre
A fizikai értékekre való átszámítás az A/D átalakító által szolgáltatott mintavételes adatot visszaalakítja fizikai mértékegységekben kifejezett értékké annak érdekében, hogy a folyamatváltozó feldolgozásakor közvetlenül a folyamatváltozó valós értékét alkalmazhassuk.
Az átszámítás lineáris jelleggörbéjű jeladó esetén az adat lineáris transzformációját jelenti.
|
|
(16.20) |
ahol
|
m |
a folyamatváltozó fizikai mértékegységben kifejezett értéke | |
|
m kezdő |
a folyamatváltozó fizikai mértékegységben kifejezett kezdőértéke | |
|
m végső |
a folyamatváltozó maximális értéke A/D átalakítónál | |
|
p |
a folyamatváltozó A/D átalakítás utáni számértéke | |
|
p kezdő |
kezdőérték az A/D átalakításnál | |
|
p végső |
végérték az A/D átalakításnál |
|
|
(16.21) |
|
folyamatváltozó |
m kezdő = 10at |
m = 17.5 at |
m végső = 25 at |
|---|---|---|---|
|
áramtávadó |
4 mA |
12 mA |
20 mA |
|
áram-feszültség átalakító (250 ohm-mal) |
2 V |
6 V |
10 V |
|
A/D átalakító 11 bites átalakító [ ] |
pkezdő = 409 |
p = 1228 |
pvégső = 2047 |
|
|
(16.22) |
Nem lineáris jelleggörbéjű érzékelő esetén:
Szakaszonkénti lineáris (egyenesekkel) közelítéssel
Közelítő polinommal
számítjuk át az értékeket.
Általánosan alkalmazott harmadrendű polinom:
|
|
(16.23) |
ahol
|
m |
a folyamatváltozó fizikai mértékegységben kifejezett értéke | |
|
p |
a folyamatváltozó A/D átalakítás utáni számértéke |
az ak értékeket (k=0..3) az adott átalakításhoz meg kell határoznunk.
16.2. Számított állapotváltozók képzése
A számított állapotváltozókat a számítógép mért, vagy más számított állapotváltozókkal végzett aritmetikai, illetve logikai műveletek eredményeként állítja elő. Az ilyen típusú állapotváltozókat abban az esetben szokás képezni, ha
a jel méréssel történő meghatározása aránytalanul költséges,
fizikailag nem lehetséges,
célszerűen egy algoritmussal meghatározható az értéke egy adott időtartamra vonatkozó mérési adatok alapján.
Számított állapotváltozók a következők lehetnek:
A mért és számított értékek idő szerinti első deriváltja.
A mért és számított értékek idő szerinti integrálja.
Egyéb tetszőleges érték meghatározása.
16.2.2. Idő szerinti integrálási formulák
Az integrálási formulák közös tulajdonsága, hogy az adott időpillanatig meghatározott integrál értéket az y[k] kimenő változóban tárolják.
A y[k] kimenő változó értéke a k=0 mintavételi időpontban az integráló tag kezdeti értéke .
Az integrálási értékek meghatározása csak a mintavételi időpontokban történik. Ez azt jelenti, hogy az aktuális mintavételi időpontot megelőző mintavételi pontig meghatározott integrál értékhez hozzáadjuk a aktuális bemeneti jellel (és korábbi értékeivel) meghatározott adott lépéshez tartozó részintegrál értékét.
16.2.2.1. Téglány (Euler) integrálás
Az integrálási eljárás a bemenő jel nulladrendű tartós közelítését alkalmazza.
|
|
(16.25) |
16.2.2.2. Trapéz integrálás
Az integrálási eljárás a bemenő jel elsőrendű polinomiális közelítését alkalmazza.
|
|
(16.26) |
Irodalmak
[16.1.] Analog And Digital Control System Design. Sounders College Publishing . 2006.
[16.2.] Linear System Theory and Design. Oxford University Press. 1999.
[16.3.] Modern Control Systems Engineering. 1996.
Tárgymutató
A
- ablakozás, Véges impulzus válasz szűrők (FIR szűrők) tervezése ablakozással
- ablakozási vizsgálatok, Simító ablakok
- ablakozott jel, Ablakozási technika
- alul mintavételezett jel, Alul-mintavételezés (Aliasing)
- aluláteresztő szűrő, Egy ideális szűrő jellemzői
- amplitúdó arány, Áttérés logaritmikus mértékegységekre
- amplitúdó spektrum, Amplitúdó és fázis információ
- analóg bemenet, Analóg bemenetek
- analóg föld, Analóg föld
- analóg frekvencia, Normalizált frekvencia
- analóg kimenet, Analóg kimenetek
- analóg-digitális átalakító, Analóg digitális (A/D) átalakítók
- áram-feszültség átalakítók, Áram feszültség átalakító
- áramló mennyiségek mérése, Áramló mennyiségek mérése
- ARMA szűrő, Végtelen impulzus válasz (IIR) szűrők
- aszimmetrikus földelt eltolt nullszintű jelforrás, Aszimmetrikus földelt eltolt nullszintű jelforrás
- aszimmetrikus földelt jelforrás, Aszimmetrikus földelt jelforrás
- aszimmetrikus földelt jelvevő áramkör, Aszimmetrikus földelt jelvevő
- aszimmetrikus földfüggetlen jelforrás, Aszimmetrikus földfüggetlen jelforrás
- aszimmetrikus földfüggetlen jelvevő áramkör, Aszimmetrikus földfüggetlen jelvevő
- aszimmetrikus földfüggetlen védőárnyékolt jelvevő áramkör, Aszimmetrikus földfüggetlen védőárnyékolt jelvevő
- átkódolás, Átkódolás és kódkonverzió
- átlagolás, Átlagolás (Averaging)
- átlagoló szűrő, Átlagoló szűrő
- átmeneti ellenállás, Átmeneti ellenállás, átvezetés
- átmeneti sáv, Átmeneti sáv
- átvezetés, Átmeneti ellenállás, átvezetés
- átviteli sáv ingadozása, Átviteli sáv ingadozása és vágási sáv csillapítása (ripple)
- auto teljesítmény spektrum, Kereszt teljesítmény spektrum SAB(f) (Cross Power Spectrum)
- auto-spektrum, Kereszt teljesítmény spektrum SAB(f) (Cross Power Spectrum)
- autoregresszív mozgó átlag szűrő, Végtelen impulzus válasz (IIR) szűrők
- azonos fázisú zavarjel, A zavarjelek típusai áramkörökben való megjelenési formájuk szerint
- azonos fázisú zavarjel elnyomás, A zavarjelek típusai áramkörökben való megjelenési formájuk szerint
B
- Bessel-szűrő, Bessel-szűrők
- bolométer, Áramló gáz mennyiségének mérése: bolométer
- Butterworth-szűrő, Butterworth-szűrők
C
- CMOS áramköri bemenet, CMOS áramköri bemenetek
- CMR, A zavarjelek típusai áramkörökben való megjelenési formájuk szerint
- csatlakozási potenciál, Csatlakozási potenciál
- csatolások típusai, A csatolások típusai
- Csebisev II szűrő, Csebisev II - szűrők
- Csebisev szűrő, Csebisev-szűrők
- csúcsérték megtartása, A csúcsérték megtartása
- csúcshiba, Csúcshiba minimalizálása
D
- D/A átalakító típusok, D/A átalakító típusok
- dBA, Áttérés logaritmikus mértékegységekre
- dBP, Áttérés logaritmikus mértékegységekre
- decibel (dB), Áttérés logaritmikus mértékegységekre
- differencia egyenlet, Szűrők osztályozása impulzusválaszuk alapján
- differenciál bemenet, Különbségi bemenetek (Differential Inputs)
- differenciálási formula, Idő szerinti differenciálási formula
- Digital Signal Processing, Gyors FFT transzformáció számítási időszükséglete, A számítógépes mérésadatgyűjtő / feldolgozó rendszer felépítése, Frekvenciafüggvény
- digitális bemenetek, TTL bemenet
- digitális föld, Digitális föld
- digitális fotodióda bemenet, Digitális bemenet fotodióda segítségével
- digitális frekvencia, Normalizált frekvencia
- digitális jelfeldolgozás, Bevezetés a digitális jelfeldolgozásba és analízisbe
- digitális kimenetek, TTL kimenetek
- digitális szűrés, Digitális szűrések megvalósítása a gyakorlatban
- diszkrét Fourier transzformáció, Diszkrét frekvencia analízis, A kétoldalas 0(nulla) frekvencia középpontú FFT transzformáció matematikai leírása
- DSP alkalmazások, Az adatelemzés jelentősége
E
- egyenfeszültségű zavarjel, A zavarjelek típusai, időbeni változásuk alapján
- elektromágneses induktív zavarjel, Elektromágneses (induktív) zavarjel
- elektrosztatikus kapacitív zavarjel, Elektrosztatikus (kapacitív) zavarjel
- ellenfázisú zavarjel, A zavarjelek típusai áramkörökben való megjelenési formájuk szerint
- elliptikus szűrő, Elliptikus szűrők
- előreható együtthatók, Szűrő együtthatók
- eltolási tételek, A Z transzformáció legfontosabb tulajdonságai
- erősítés, Erősítés (Gain)
- erősítő, Mintavevő tartó és erősítő
- érzékelő átalakítók, Érzékelő átalakítók és jeleik
- exponenciális ablak, Exponenciális ablak
- exponenciális súlyozás, Súlyozás
- exponenciális szűrő, Exponenciális szűrő
F
- fázisjel előállítása, Fázis jel generálás
- fázistolás, Amplitúdó és fázis információ
- fehér zaj, Frekvencia átvitel mérése
- felfutási idő, Egyszerű vizsgáló jelek
- felüláteresztő szűrő, Egy ideális szűrő jellemzői
- félvezetős ellenállás hőmérő, Félvezetős ellenállás hőmérő
- félvezetős kimenet, Félvezetős kimenet (Solid State Relay)
- félvezetős méréspont váltó, Félvezetős méréspont váltó
- feszültség-frekvencia A/D átalakító, Feszültség frekvencia A/D átalakító
- FET tranzisztor, CMOS áramköri bemenetek
- FIR szűrő, Véges impulzus válasz (FIR) szűrők
- flat top ablak, “Flat Top” ablak
- fokozatos közelítésű A/D átalakító, Fokozatos közelítésű A/D átalakító
- földelések, Földelések
- földelt bemenet, Egy kimenetű jelek (Single-Ended Inputs)
- fotodiódás galvanikus leválasztás , Fotodiódás optikai leválasztók
- Fourier transzformáció, Fourier transzformáció, mint a DFT alapja
- Fourier-tétel, A frekvencia és az időtartomány közötti különbségek
- Frekvencia kimenetű D/A átalakító (PWM), Digitál-analóg konverterek
- frekvencia tartománybeli megjelenítés, A frekvencia és az időtartomány közötti különbségek
- frekvencia válasz, Egyszerű vizsgáló jelek
- frekvencia válasz függvény, Frekvencia válasz függvény H(f)
- fűrész jel, Egyszerű vizsgáló jelek
G
- galvanikus leválasztás, Galvanikus leválasztás
- Gauss-eloszlású zaj, Zavarjel generálás
- gerjesztési jel, Egyszerű vizsgáló jelek
- gyengeáramú teljesítmény föld, Gyengeáramú teljesítmény föld
- gyors Fourier transzformáció, Diszkrét frekvencia analízis
- gyors Fourier transzformáció (FFT), Gyors Fourier transzformáció alapjai (FFT= Fast Fourier Transformation)
H
- Hamming ablak, Hamming ablak
- Hanning ablak, Hanning ablak
- három állapotú kimenet, Három állapotú kimenetek (Three State)
- háromszög ablak, Háromszög ablak
- háromszög jel, Egyszerű vizsgáló jelek
- hasznos jel, Zavarjelek
- Hilbert transzformáció, Visszhang észlelése
- hőelem, Hőelemek
- hőmérséklet mérése, Hőmérséklet mérés
- homogén fehér zaj, Zavarjel generálás
- hullámosság, Véges impulzus válasz szűrők (FIR szűrők) tervezése
I
- IIR szűrő, Végtelen impulzus válasz (IIR) szűrők
- illesztési szabályok, Az illesztés legfontosabb szabályai
- impulzus, Impulzusválasz
- impulzus jel, Egyszerű vizsgáló jelek
- impulzus válasz függvény, Impulzus válasz függvény FFT1( H(f) )
- induktív csatolás, A csatolások típusai
- integrálásos zavarszűrés, Időzítéses integrálás (mint zavarszűrési lehetőség)
- intermodulációs torzítás, Egyszerű vizsgáló jelek
- Inverz Fourier transzformáció, Fourier transzformáció, mint a DFT alapja
- inverz Z transzformáció, Az inverz Z transzformációs módszerek
J
- jel-zaj viszony, Változó frekvenciájú szinusz jel, illetve többfrekvenciás jel
- jelgenerátor, Jelgenerálás
K
- kábelhajlításból származó hiba, Kábelhajlításból származó zavarjel
- Kaiser-Bessel ablak, Kaiser-Bessel ablak
- kapacitív csatolás, A csatolások típusai
- kaszkád szűrés, Az IIR szűrés kaszkádképlete
- kereszt teljesítmény spektrum, Kereszt teljesítmény spektrum SAB(f) (Cross Power Spectrum)
- kettős meredekségű (integráló) A/D átalakító, Kettős meredekségű (integráló) A/D átalakító
- kimenő jel késleltetés, Véges impulzus válasz (FIR) szűrők
- koherencia függvény, Koherencia függvény K(f)
- koherencia tényező, Koherencia függvény K(f)
- konduktív csatolás, A csatolások típusai
- konverzió, Átkódolás és kódkonverzió
- konvolúció, Véges impulzus válasz (FIR) szűrők, Ablakozott jelek
- közvetlen alakú szűrő, Az IIR szűrés kaszkádképlete
L
- látszólagos frekvencia, Alul-mintavételezés (Aliasing)
- lefutási idő, Egyszerű vizsgáló jelek
- lineáris fázis menet, Véges impulzus válasz szűrők (FIR szűrők) tervezése
- lineáris súlyozás, Súlyozás
- lineáris szűrő, Bevezetés a digitális szűrés gyakorlati alkalmazásába
- logikai adaptív szűrő, Logikai adaptív szűrő
M
- MA szűrő, Véges impulzus válasz (FIR) szűrők
- mágneses árnyékolás, Elektromágneses (induktív) zavarjel
- másodrendű szűrő, Másodrendű szűrő
- mennyiségek átszámítása, Átszámítás fizikai értékekre
- mérési eredmények átlagolása, Átlagolás a mérési eredmények ábrázolásához
- mérési felbontás, Felbontás (Resolution)
- mérési határok, Mérési határok (Range)
- méréskorrekció, Méréskorrekció
- mintavételezés, Mintavételezés sebessége (Sampling Rate)
- mintavételezési törvény, Mintavételezés
- mintavételi érték, Vizsgáló jelek
- mintavételi frekvencia, Vizsgáló jelek
- mintavételi idő, Mintavételi idő, Kapcsolat az N mintát tartalmazó időtartománybeli és frekvenciatartománybeli jel értékek között
- mintavételi intervallum, Vizsgáló jelek
- mintavételi periódus, Vizsgáló jelek
- mintavevő, Mintavevő tartó és erősítő
- mozgó átlag szűrő, Véges impulzus válasz (FIR) szűrők
- multiplexer, Analóg méréspont váltók (multiplexerek)
N
- négyszög hullám, Egyszerű vizsgáló jelek
- négyszögletes ablak, Négyszögletes ablak (ablakozás nélküli állapot)
- négyzetes (effektív) átlagolás, Négyzetes (effektív) átlagolás (RMS Averaging)
- négyzetes középérték, Csúcstényező, Az amplitúdó meghatározása Vrms-ben valamint a fázis meghatározása fokban
- nem rekurzív művelet, Szűrők osztályozása impulzusválaszuk alapján
- nemlineáris szűrő, Nemlineáris szűrők
- Nyquist frekvencia, Frekvencia lépés a DFT minták között
- Nyquist frekvencia, Alul-mintavételezés (Aliasing)
P
- Parseval tétel, A frekvencia és az időtartomány közötti különbségek
- passzív szűrő, Passzív szűrő
- platina ellenállás, Platina ellenállás hőmérő
- Probability Density Function, Zavarjel generálás
- pufferelt adatátvitel, Az analóg bemeneti perifériák perifériavezérlő egysége
R
- rádiófrekvenciás zavarjel, Rádiófrekvenciás zavarjel
- RC szűrő, Egyszerű RC szűrő
- rekurzív művelet, Szűrők osztályozása impulzusválaszuk alapján
- rekurzív szűrő, Végtelen impulzus válasz (IIR) szűrők
- relés bemenet, Relés érintkező bemenet
- relés kimenet, Relés kimenet
- relés méréspont váltó, Relés méréspont váltó
- repülő kondenzátoros leválasztás, Repülő kondenzátoros leválasztás
S
- sampling frequency, Frekvencia lépés a DFT minták között
- sáváteresztő szűrő, Egy ideális szűrő jellemzői
- sávvágó szűrő, Egy ideális szűrő jellemzői
- SCXI, Small Computer Extended Interface (SCXI)
- Shannon-féle mintavételi elv, A mintavételi frekvencia növelése az alul-mintavételezéselkerüléséhez
- simító ablak fő szárny, Fő szárny
- simító ablak kiválasztása, A megfelelő simító ablak kiválasztása
- simító ablak oldal szárny, Oldalszárnyak
- Simpson integrálás, Simpson integrálás
- Solid State Relay, Félvezetős kimenet (Solid State Relay)
- spektrális energia átszivárgás, Ablakozási technika
- spektrum amplitúdója, Amplitúdó és fázis spektrumok kiszámítása
- spektrum fázisa, Amplitúdó és fázis spektrumok kiszámítása
- spektrum szóródás, Spektrális szóródás, Nem egész számú periódus mintavételezése, Ablakozott jelek
- sugaras földelés, Digitális föld
- súlyozás, Súlyozás
- számított változók, Számított állapotváltozók képzése
- széles sávú zavarjel, Frekvencia átvitel mérése
- szimmetrikus földelt eltolt nullszintű jelforrás, Szimmetrikus földelt eltolt nullszintű jelforrás
- szimmetrikus földelt jelforrás, Szimmetrikus földelt jelforrás
- szimmetrikus földelt jelvevő áramkör, Szimmetrikus földelt jelvevő
- szimmetrikus földfüggetlen jelforrás, Szimmetrikus földfüggetlen jelforrás
- szimmetrikus földfüggetlen védőárnyékolt jelvevő áramkör, Szimmetrikus földfüggetlen védőárnyékolt jelvevő
- szinusz hullám, Egyszerű vizsgáló jelek
- szűrő átviteli sávja, Egy ideális szűrő jellemzői
- szűrő együtthatók, Szűrő együtthatók
- szűrő impulzus válasza, Impulzusválasz
- szűrő késleltetés, Átmeneti függvény
- szűrő vágási sávja, Egy ideális szűrő jellemzői
T
- tápforrásból származó hiba, Tápforrásból származó zavarjel
- tartó áramkör, Mintavevő tartó és erősítő
- téglány integrálás, Téglány (Euler) integrálás
- teljes harmonikus torzítás, Egyszerű vizsgáló jelek
- teljesítmény arány, Áttérés logaritmikus mértékegységekre
- teljesítmény spektrum, Teljesítmény Spektrum SAA(f)
- termikus potenciál, Termikus potenciál (termoelem)
- termisztor, Termisztor
- több komparátoros A/D átalakító, Több komparátoros A/D átalakító
- transzformátoros leválasztás, Transzformátoros leválasztás
- tranziens zavarjel, A zavarjelek típusai, időbeni változásuk alapján
- tranziens zavarjeleket, Villamos áramkörök be és kikapcsolásakor keletkező zavarjel
- trapéz integrálás, Trapéz integrálás
- triggerelt jel, Amplitúdó és fázis információ
- TTL bemenet, TTL bemenet
- TTL kimenet, TTL kimenetek
V
- váltakozó feszültségű zavarjel, A zavarjelek típusai, időbeni változásuk alapján
- változó frekvenciájú szinusz jel, Egyszerű vizsgáló jelek
- védelmi föld, Védelmi föld
- végérték tételek, A Z transzformáció legfontosabb tulajdonságai
- véges impulzus válasz szűrő, Digitális szűrés, Szűrők osztályozása impulzusválaszuk alapján, Véges impulzus válasz (FIR) szűrők
- végtelen impulzus válasz szűrő , Digitális szűrés, Szűrők osztályozása impulzusválaszuk alapján, Végtelen impulzus válasz (IIR) szűrők
- vektoros átlagolás, Vektoros átlagolás
- véletlenszerű periódikus zaj, Zavarjel generálás
- visszacsatolásos A/D átalakító, D/A visszacsatolásos A/D átalakító
- visszaható együtthatók, Szűrő együtthatók
- visszhang észlelése, Visszhang észlelése
- vizsgáló jel, Egyszerű vizsgáló jelek
W
- Wheathstone híd, Áramló gáz mennyiségének mérése: bolométer
Z
- Z és Laplace transzformáció kapcsolata, A Z transzformáció legfontosabb tulajdonságai
- Z transzformáció, A Z transzformáció
- Z transzformáció tulajdonságai, A Z transzformáció legfontosabb tulajdonságai
- Z transzformációs szabályok, A Z transzformáció
- zaj jel, Zavarjelek