3. fejezet - Mérési hibák
Vissza		Előre

3. fejezet - Mérési hibák

Tartalom

Közismert a méréstechnikával foglalkozók számára a szabály, hogy a mérési munka csak akkor befejezett, ha a hibaszámítást is elvégeztük. Ha tehát egy „eredmény” közlésében nem szerepel „±” előjellel egy bizonytalanságot megjelenítő tag, akkor az adott mérés „finoman szólva” nem lehetett igényesen megtervezett munka.

Az eredményben alapvetően két hiba típusnak kell tükröződnie. Az egyik a rendszeres hibák eredője, amit korrekcióként ismert előjellel és nagysággal veszünk figyelembe, és éppen ezért az eredményben az átlaggal összevonva szerepel, hacsak valamilyen okból nem tüntetik különállóan fel. A másik hibatípus a véletlen hibák eredője, ami közvetlenül nem észlelhető, mert a mérési bizonytalanságba van „beágyazva”, sok összetevőjű, és a bizonytalanság meghatározásában már a megbízhatósági szintet is figyelembe vesszük.

3.1. A mérési hibák az eredményben, a hibák rendszerezése

A mérési eredmény a mérőszám és a mértékegység szorzata, de maga a mérőszám három tagból áll:

	$y = {y} \cdot [y]$	(3.1)
	${y} = \bar{x} - H \pm U$	(3.2)

A második egyenletben szereplő 3 tag jelentése az alábbi:

„Helyes érték”, azaz a valódi érték legjobb becslése az átlaggal
„H” a korrekció, azaz a rendszeres hibák előjeles eredője
Kiterjesztett bizonytalanság, azaz a megadott konfidencia szinthez tartozó faktorral, a tapasztalati szórások eredőjével és az egyéb mérési bizonytalanságok figyelembe vételével számított konfidencia intervallum. A bizonytalanság un. „A” és „B” típusú megadásáról később még lesz szó.

Szembetűnő, hogy a mérőszám 2/3 részben hibákkal kapcsolatos adatokat tartalmaz. Ezek után jogosan merül fel az a kérdés, hogy mik a mérési hibák okozói, és főként az, miként lehet a véletlen hibákat minél jobban visszaszorítani, és ezzel a bizonytalanságot csökkenteni?

A jelen fejezet a hibák rendszerezésével, ismertetésével foglalkozik, hiszen visszaszorításuk, esetleges megszűntetésük, vagy csökkentésük attól függ, mennyire vagyunk tisztában eredetükkel. Erről a témáról részletesen a Halász G. - Huba A.: Műszaki mérések című jegyzetben [3.1.] olvashatunk.

A mérési hibákat három szempont alapján lehet vizsgálni, és csoportosítani:

eredetük,
jellegük, és
formájuk szerint.

A három csoport nem egymást kizáró, hanem egymást szinergikusan értelmező megközelítést jelent. Példaként tekintsük egy digitális műszer kijelzési bizonytalanságát, ami a legkisebb megjeleníthető (LSB=Least Significant Bit) érték 29 %-a (lásd 3.9 képlet). Véletlen jellegű hibákat a szakirodalom gyakran „bizonytalanság” kifejezéssel is illet. Ez a hiba eredete szerint a mérés kivitelezéséből adódik (digitális kijelzővel ellátott mérőeszköz miatt jelentkezik), jellegét tekintve véletlen, és forma szerint abszolút hiba.

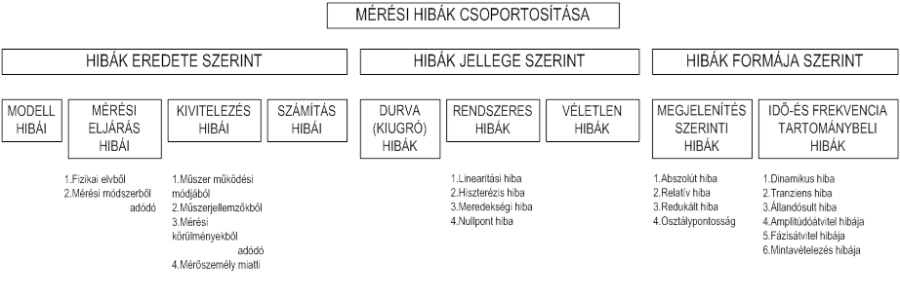
3.1. ábra - A mérési hibák rendszerező áttekintése

Látjuk az ábrán, hogy eredetük szerint a hibákat négy csoportba lehet sorolni. Ezek ismerete döntő jelentőségű a mérési munka minőségére vonatkozóan. Adott esetben ugyanis minden más, a mérési adatokkal való statisztikai „bűvészkedés” sem képes már közömbösíteni a mérési munka elején, a tervezés során elkövetett hibákat.

3.2. A mérési hibák eredete

A modell általánosságban a mérés „modellfüggvényét” jelenti, azt a matematikai összefüggést (ld.: Mérés egyenlete), amelynek alapján az eredményt a bemenő mennyiségek és az állandók segítségével ki lehet számítani.

A mérési eljárás definíciója szakirodalmanként változhat, de abban teljes az egyetértés, hogy az eljárás a mérési tevékenység „műszaki dokumentációja”. Ebben rögzítik a modellre alapozva a mérés fizikai elvét, és a mérési módszert. Néha a módszerek közé sorolják a közvetett és közvetlen mérést is, de az azért felesleges, mert az eredmény egyenlet (modellfüggvény) már önmagában jelzi, hogy melyik formáról van szó. A mérési módszerek száma nagy, a gépészetben és a mechatronikában minimum 6 módszer ismerete elengedhetetlenül fontos. Ezek a következő ábrán vannak röviden összefoglalva.

3.2. ábra - A legfontosabb mérési módszerek áttekintése

A mérés kivitelezése igen tekintélyes hibák forrása lehet. Ebbe a csoportba egyrészt a műszer, mérőrendszer működési módja, tehát a gépészetben konkrétan az, hogy a mérés során az mérőeszköz a vizsgált objektummal kontaktusba kerül-e, befolyásolja-e valamilyen módon annak energia állapotát? Köznapi megfogalmazással érintéses, vagy érintésmentes a mérőeszköz működési módja.

Ebben a csoportban a hibák további forrásait a műszerjellemzők, a mérés körülményei (nyomás, páratartalom, rezgések, stb.) és a mérést végző személyek körében kell keresnünk.

A kiértékelés, a számítások során is követhetünk el hibákat, ezek mértéke igen változó lehet. Kezdve a legdurvább „elszámolások” eseteitől, a becslési hibákig. Ez utóbbira jó példa lehet a konfidencia intervallum téves megadása. Normál eloszlást feltételezünk olyan esetben, amikor sem a mérési adatok értékei, sem a mérések száma ezt nem támasztják alá, és ennek következtében kisebb faktor alkalmazásával határozzuk meg a bizonytalansági tartományt.

3.3. A mérési hibák vizsgálata jellegük szerint

3.3.1. Rendszeres hibák

A rendszeres hibák a mérési eljárás (fizikai elv és mérési módszer) és a mérés kivitelezésének (mérőeszközök és mérési körülmények) elvi hibái, amelyek az eredményt torzítják. Ennek a torzításnak a mértéke és előjele megfelelő elméleti felkészültséggel és megfelelő mérőeszközök alkalmazásával megállapítható. Az eredményben a rendszeres hibák eredője korrekcióként jelenik meg, az eredő nagysága és előjele ismert .

A rendszeres hibák megjelenhetnek mind az időben állandó, mind pedig az időben változó mennyiségek mérése során.

A rendszeres hibák közül négyet érdemes kiemelni.

A linearitási hiba kompenzálása a modern számítástechnikai eszközök birtokában már nem jelent műszaki problémát. Ez a torzítás egy adott mérési tartomány bármely pontjában állandó, de a mérési tartományonként eltérő is lehet. Nem definiálható műszerállandó, ha a műszer jelleggörbéje négyzetes, exponenciális stb. függvénykapcsolatot mutat.
A nullpont hiba az un. regressziós egyenes és a függőleges tengely metszéspontja. Ezt a torzítást a regressziós egyenes paramétereinek meghatározásakor részben már megismertük, de természetesen felléphet nemlineáris karakterisztikájú műszer esetében is.
Hiszterézis hiba elsősorban mechanikus, vagy elektromechanikus mérőeszközöknél jelentkezik. Lényegében a fel-és leterhelés, azaz kitérítés és visszatérítés között kijelzett értékek közötti különbség formájában mutatkozik. A két karakterisztika nem esik egybe, sőt gyakran előfordul, hogy a kiinduló pont sem. A maradó eltérést a súrlódás okozza, és ezért ajánlott például tapintós mechanikus mérőeszközökkel történő mérés esetén, a mérendő felületet következetesen egy irányból megközelíteni (pl. felülről, a tapintó felemelésével).
A meredekségi hiba elektronikus és elektromechanikus műszerek esetében leginkább hőmérsékleti drift hatására jelentkezik. Ennek oka az elektronikus egységek jellemzőinek – így például az erősítésnek, hő okozta megváltozása. A műszer karakterisztikájának meredeksége változik meg. Kis mérési tartományban kisebb, a végkitérés tartományában maximális mértékű az erősítés megváltozásából eredő hiba

A fentieken kívül más rendszeres hibák is torzíthatják az eredményt, ezek részletes tárgyalása a műszertechnika témakörébe tartozik.

3.3.2. Véletlen hibákból adódó bizonytalanságok

A véletlen hibák hatása többségében a mérés bizonytalanságában, „beágyazottan” jelenik meg. A beágyazottság azt jelenti, hogy ezeket a hibákat nem „direkt” formában láthatjuk, hanem az „U” szimbólummal jelzett, un. kiterjesztett mérési bizonytalanság foglalja őket magába. A kiterjesztés az eredő mérési bizonytalanságok meghatározott faktorral való súlyozását jelenti. Ez a faktor a megbízhatósági szinttől és az eloszlás típusától függően a minta elemszámától is függhet. A kérdéssel a 4. fejezet fejezetben részletesebben foglalkozunk.

A véletlen hiba oka vagy ismeretlen, vagy a hibaokozók felderítése a mérés egészét tekintve aránytalanul nagy munkával és anyagi befektetéssel járna, ezért ésszerűtlen lenne keresésük. E hibatípus pontos értéke és előjele nem ismert, csak az alsó és felső korlátja valószínűsíthető.

Az eredmény bizonytalanságai azt tükrözik, hogy a mérendő mennyiségre vonatkozó ismereteink hiányosak. A „teljes” ismerethez „végtelen” mennyiségű információra lenne szükség. Nézzük ezek után egy-egy jellemző példán, hogy melyek azok a legfontosabb tényezők, amelyek a bemeneti mennyiségek véletlenszerű ingadozásait, bizonytalanságait okozzák:

A mérendő mennyiség hiányos meghatározása. (Nincs definiálva, hogy egy alkatrész átmérőjét mely keresztmetszetben kell mérni.)
A mérés nem tökéletes megvalósítása. (Hibás lehet a modellfüggvény, a mérési eljárás, a mérés kivitelezése és az alkalmazott számítási módszerek.)
A nem reprezentatív mintavétel. (Egy gyártóberendezés beállítási pontosságát kívánjuk ellenőrizni adott időpontban, de az ellenőrzésbe bevont munkadarabok gyártási ideje ismeretlen, vagy bizonytalan.)
A környezeti feltételek hatásának nem tökéletes ismerete. (Nincs adat a hőmérsékletről, páratartalomról, stb.)
A mérést végző személy hibájából adódó eltérések. (Annyira fontos tényező, hogy nagyobb üzemekben meghatározzák, kik azok a személyek, akik a minőségellenőrzésben egymást váltva végezhetik a méréseket. Ld.: Ismétlőképesség)
A műszer véges felbontása, küszöbérzékenysége. (A műszer nem alkalmas a felbontása alatti eltéréseket kimutatni.)
Az etalonok és anyagminták pontatlan értékei.
Az állandók és az algoritmusban alkalmazott faktorok pontatlansága
A mérési eljárásban alkalmazott közelítések. (Kúposság mérése mérőhasábokkal és görgőkkel. A módszer általában két keresztmetszet magasságában vett átmérőkkel számítja ki a kúpszöget, egyéb adatok híján nincs pontos információ a munkadarab valódi alakjáról, hiszen az alkatrész alkotói nem feltétlenül egyenesek.)
A mérés ismétlőképességéből adódó eltérések. (Az ismétlőképesség nem csupán a mérést végző személytől függ, ld.: 2. fejezet fejezet.)

A fentiek mellett nem szabad elfeledkeznünk a korszerű méréstechnika digitális kijelző eszközeinek kijelzési bizonytalanságáról sem. A közvetlen A/D konverziós (átalakítási) eljárás kvantálást, azaz értékekhez rendelést jelent mind az amplitúdókra, mind pedig az időre nézve. Az időbeli kvantálást nevezzük mintavételezésnek. A kvantálás miatt a jelszinteket egy adott tartományban azonos értékűnek vesszük, ebből következik, hogy egy kvantum teljes tartományában a sűrűségfüggvény egyenletes. Ezt mutatjuk be a következő ábrán.

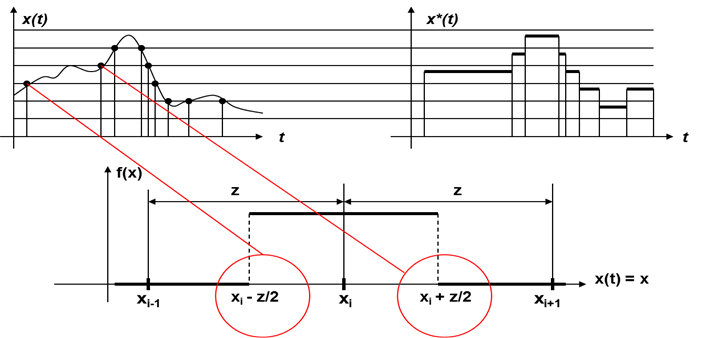
3.3. ábra - Az amplitúdó kvantálásból eredő f(x) egyenletes sűrűségfüggvény

A digitális kijelzésű műszerek esetében az abszolút hiba egy „kvantumon” belül változó, és maximális értéke a kvantum fele. Ezt látjuk a következő ábrán.

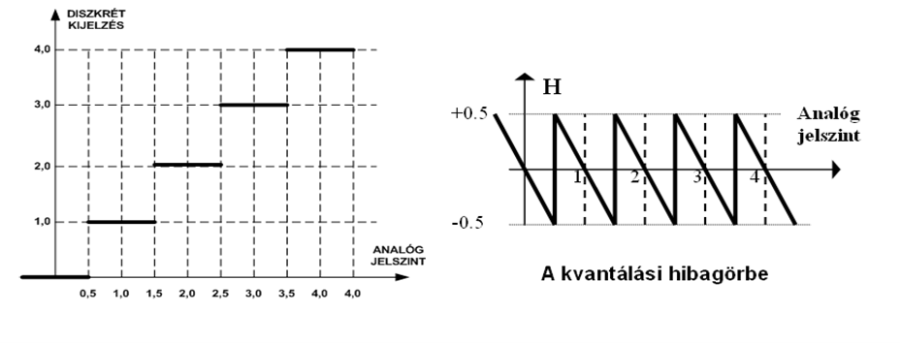
3.4. ábra - A kvantálásból származó hiba

Ez a maximum azonban nyilvánvalóan „pesszimista” becslés, hiszen a mért értékek és a kijelzett értékek között nem mindig ez az eltérés adódik. Kérdés, hogy digitális műszereknél milyen bizonytalansággal jellemezhetjük a kijelzést? A megoldást az egyenletes eloszlás sűrűségfüggvényének segítségével keressük meg.

A következő ábrán az egyenletes eloszlás függvényeit látjuk folytonos változó esetére. Az ábra a levezetés megértését igyekszik segíteni.

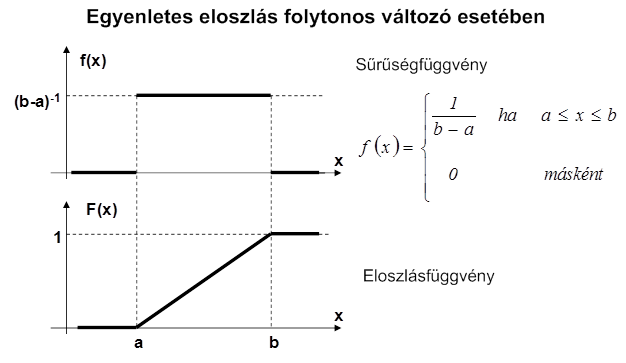
3.5. ábra - Egyenletes eloszlás függvényei

A várható érték kiszámítása az első lépés:

	$μ = \int_{a}^{b} x \cdot f (x) \cdot d x = \frac{1}{b - a} \int_{a}^{b} x \cdot d x$	(3.3)
	$μ = \frac{1}{b - a} \cdot \frac{x^{2}}{2} \| \begin{matrix} b \\ a \end{matrix} = \frac{1}{b - a} \cdot \frac{b^{2} - a^{2}}{2} = \frac{b + a}{2}$	(3.4)

Ezt követően a varianciát (szórásnégyzet) határozzuk meg úgy, hogy felhasználjuk az alábbi azonosságot is. Ez a szórás lesz a digitális kijelzés bizonytalansága, a legkisebb digitre (LSB:Least Significant Bit) vonatkoztatva:

$σ^{2} = \int_{a}^{b} f (x) {(x - μ)}^{2} d x = \int_{a}^{b} f (x) x^{2} d x - μ^{2}$

(3.5)

Az összefüggés jobb oldalán kijelölt matematikai műveleteket kibontva igazoljuk, hogy az azonosság fennáll:

$\begin{array}{l} σ^{2} = \int_{- \infty}^{\infty} f (x) [x^{2} - 2 x μ + μ^{2}] d x = \int_{- \infty}^{\infty} f (x) x^{2} d x - 2 μ \int_{- \infty}^{\infty} f (x) \cdot x \cdot d x + μ^{2} \int_{- \infty}^{\infty} f (x) d x \\ a h o l \\ \int_{- \infty}^{\infty} f (x) \cdot x \cdot d x = μ \\ \int_{- \infty}^{\infty} f (x) d x = 1 \\ t e h á t : \\ σ^{2} = \int_{- \infty}^{\infty} f (x) x^{2} d x - 2 μ \cdot μ + μ^{2} \cdot 1 = \int_{- \infty}^{\infty} f (x) x^{2} d x - μ^{2} \end{array}$

(3.6)

Felhasználva az azonosságot, a könnyebben integrálható kifejezésbe behelyettesítjük a várható értéket:

$σ^{2} = {\int_{a}^{b} \frac{1}{b - a} (x - \frac{a + b}{2})}^{2} d x = \frac{1}{b - a} \int_{a}^{b} x^{2} d x - \frac{{(a + b)}^{2}}{4}$

(3.7)

Az integrálás elvégzése után úgy alakítjuk át a kapott kifejezést, hogy az egyszerűsítés lehetővé válhasson:

$\begin{array}{l} σ^{2} = \frac{1}{b - a} \cdot \frac{x^{3}}{3} | \begin{matrix} b \\ a \end{matrix} - \frac{{(a + b)}^{2}}{4} = \frac{4 b^{3} - 4 a^{2} - 3 (b - a) {(a + b)}^{2}}{12 (b - a)} \\ σ^{2} = \frac{4 b^{3} - 4 a^{3} - 3 b^{3} + 3 a^{2} b - 3 a b^{2} + 3 a^{3}}{12 (b - a)} = \frac{b^{3} - 3 a b^{2} + 3 a^{2} b - a^{3}}{12 (b - a)} \\ σ^{2} = \frac{(b^{2} - 2 a b + a^{2}) (b - a)}{12 (b - a)} = \frac{{(b - a)}^{2}}{12} \end{array}$

(3.8)

A digitális kijelzés bizonytalansága tehát a legkisebb digitre vonatkoztatva:

$σ = u_{L S B} = \frac{b - a}{2 \sqrt{3}} ≅ 0,29 \cdot z = 0,29 \cdot L S B$

(3.9)

A kijelzés bizonytalanságaként tehát nem a legkedvezőtlenebb esetet, azaz 0,5·LSB értéket kell alkalmaznunk, hanem ennél jóval kisebbet.

3.3.3. Közvetett mérés rendszeres hibája, rendszeres hiba terjedése

Láttuk a (2.8. szakasz) fejezetben, hogy a mérés egyenletének segítségével adjuk meg a bemenő mennyiségek ismeretében a keresett kimenő mennyiséget.

$Y = f (X_{A 1}, X_{A 2},... X_{A, n - k}, X_{B 1},... X_{B k})$

(3.10)

A becslésben megjelenik a korrekció, azaz a rendszeres hibák eredője, valamint a kiterjesztett mérési bizonytalanság is:

$\bar{y} = f ({\bar{x}}_{A 1}, {\bar{x}}_{A 2},... {\bar{x}}_{A, n - k}, x_{B 1},... x_{B k}) - H_{e r e d ő} \pm U$

(3.11)

Kérdés, hogy több bemenő mennyiség esetében miként lehet az eredő rendszeres hibát meghatározni. Ezt a hibát a szakirodalom hibaterjedésnek nevezi.

A feladatunk megkeresni „y₀” azon „dy₀” változását, amely azért lép fel, mert „x_i0” helyett „x_i” volt a mérésünk eredménye. Az ilyen típusú feladatok megoldására szolgál a Taylor sor, amely fontos szerepet játszik, ha egy függvényt hatványsorral kell közelítenünk.

A méréstechnikában és a fizikai kísérletek kiértékelésénél Taylor-sorfejtést akkor alkalmaznak, ha egy mérendő mennyiség valamilyen hatás miatti megváltozása nagyságrendekkel kisebb, mint maga a mérendő mennyiség. A hangsúly a kis mértéken van, ezért elegendőek a vizsgálathoz a Taylor sor első tagjai. A hatványsor magasabb fokú tagjai ugyanis a kis változás miatt már nem befolyásolják az eredményt.

Az eredmény egyenletének (modellfüggvénynek) parciális deriválása révén lehet megállapítani az egyes változókhoz (bemeneti mennyiségekhez) tartozó súlyfaktorokat.

$d y = {\frac{\partial y}{\partial x_{1}} |}_{X_{10},... X_{n 0}} \cdot d x_{1} + ... {\frac{\partial y}{\partial x_{n}} |}_{X_{10},... X_{n 0}} \cdot d x_{n}$

(3.12)

Az eredmény (matematikai) egyenletének „x_i” változó szerinti parciális deriváltjába behelyettesítve az adott változó legvalószínűbb értékének becslésére használt átlagértéket, kapjuk az un. súlyfaktort (c_i), ami az adott változó hatásának mértékét jelzi, mind a rendszeres , mind pedig a véletlen hiba terjedésének , valamint az eredő (tapasztalati) szórásnak meghatározásában.

A rendszeres hibák terjedését a szakirodalom két alap képletforma segítségével magyarázza. Az egyiket az összeg/különbség jellegű, míg a másikat szorzás/osztás/hatványozás alakú modellfüggvényre írják fel.

Nézzük elsőként azt a modellfüggvényt, amelyben az „y” kimenet az „x” és „z” bemenő mennyiség összege vagy különbsége. Az eredő maximális abszolút hiba a fentebb ismertetett parciális deriválással határozható meg:

$Δ y = | \frac{\partial y}{\partial x} \cdot Δ x | + | \frac{\partial y}{\partial z} \cdot Δ z |$

(3.13)

A legtöbb méréstechnikai szakirodalom összeg-képlet esetére az eredő abszolút, más néven eredő maximális hiba számítását alkalmazza (például a német szakirodalomban ennek neve: Größtfehler). Ez a lehetséges legnagyobb hiba, vagyis a legkedvezőtlenebb eset.

Előfordul azonban, hogy nem az abszolút értéket, hanem a tagokat a deriválásból adódó előjellel használják a hiba meghatározására. Ez különbség esetén természetesen optimistább becslést ad. Szélsőséges esetben - különbség-jellegű modellfüggvény mellett – a hibák kompenzálhatják egymást.

Az előírásokon (szabványokon), esetleg a mérést végző, képzett személyen múlik, hogy adott esetben melyik formát alkalmazza. Egyéb előírás hiányában ajánlott az eredő abszolút hiba kiszámítása a fent látható képlettel.

Szorzat és hatványfüggvény formájú eredmény egyenlet esetében az alábbi általános formából indulunk ki, ahol „x” és „z” megint csak a bemenő mennyiségek:

$y = x^{n} \cdot z^{m}$

(3.14)

ahol „n” és „m” pozitív, vagy negatív előjelű, egynél kisebb, vagy nagyobb valós szám lehet.

Parciális deriválás révén jutunk az eredő abszolút hibához, ami a legkedvezőtlenebb eset:

$Δ y = | n x^{n - 1} \cdot z^{m} \cdot Δ x | + | x^{n} \cdot m z^{m - 1} \cdot Δ z |$

(3.15)

Mérlegelés tárgya, hogy az előjelek figyelembevétele milyen torzítást okoz, és megengedhető-e? Ha a deriválásból származó előjeleket is figyelembe vesszük, akkor a hibát csökkentheti az osztóként megjelenő bemenő mennyiség:

$Δ y = n x^{n - 1} \cdot z^{m} \cdot Δ x + x^{n} \cdot m z^{m - 1} \cdot Δ z$

(3.16)

Nézzük ezt egy egyszerű példán:

$\begin{matrix} y = \frac{x}{z} \to & Δ y = \frac{1}{z} Δ x - \frac{x}{z^{2}} Δ z \end{matrix}$

(3.17)

Csupán a teljesség kedvéért említjük meg, hogy számos szakirodalomban találkozhatunk a hibaterjedés kapcsán az eredő relatív hibákkal is. Összeg esetében két bemenő mennyiséggel (x,z) az alább látható formát kapjuk. Felhívjuk a figyelmet az összefüggésben rejlő veszélyre. Ha ugyanis a két bemenő mennyiség értéke közel esik egymáshoz, netán azonosak, akkor különbség esetén a nevező nullává is válhat. Ezért ezzel a formával óvatosan kell bánni.

$\frac{Δ y}{y} = \frac{Δ y}{x \pm z} = \frac{Δ x + Δ z}{x \pm z} = \frac{| \frac{Δ x}{x} | + | \frac{Δ z}{x} |}{1 \pm \frac{z}{x}} = \frac{| \frac{Δ x}{x} | + \frac{z}{x} | \frac{Δ z}{z} |}{1 \pm \frac{z}{x}}$

(3.18)

Szorzat és hatvány modellfüggvényeknél az abszolút relatív hiba megadását ajánlja a szakirodalom, mert a deriválásból adódó előjelek indokolatlanul csökkenthetik az eredő hiba nagyságát.

$\frac{Δ y}{y} = \frac{| n x^{n - 1} \cdot z^{m} \cdot Δ x | + | x^{n} \cdot m z^{m - 1} \cdot Δ z |}{x^{n} \cdot z^{m}} = | n \frac{Δ x}{x} | + | m \frac{Δ z}{z} |$

(3.19)

Az eredő relatív hiba, amely hibaterjedéssel, tehát több bemenő mennyiséget tartalmazó modellfüggvényre adódik, általában a legkedvezőtlenebb eset.

3.3.4. Közvetett mérés bizonytalansága, véletlen hiba terjedése

Láttuk, hogy valamennyi részeredményt a rendszeres hibák mellett véletlen hibák is terhelnek. A rendszeres hibákat a korrekcióban vesszük figyelembe, a véletlen hibákat az empirikus szórásukkal jellemezhetjük.

A leghelyesebb, ha újra a modellfüggvényt vesszük alapul, és az „U” kiterjesztett bizonytalanságban az eredő tapasztalati (korrigált) szórást vesszük figyelembe. A hibaterjedésnél azt vizsgáljuk, hogy az eredmény kismértékű változásához a részadatok milyen mértékben járulnak hozzá.

Ismeretes a valószínűség számításból, hogy ha az x₁, x₂, …x_i,…x_n valószínűségi változók egymástól függetlenek, akkor az alábbi képlettel határozható meg az eredő variancia:

$σ_{y}^{2} = V a r [f (x_{1} ... x_{n})] = {(\frac{\partial f (x_{1} ... x_{n})}{\partial x_{1}})}^{2} V a r [x_{1}] + ... {(\frac{\partial f (x_{1} ... x_{n})}{\partial x_{n}})}^{2} V a r [x_{n}]$

(3.20)

Az eredő variancia tehát független változók esetében a súlyozott varianciák összege.

Mivel x₁, x₂, … x_n valószínűségi változók, a képletben szereplő y=f(x₁, x₂, … x_n) modellfüggvény (eredményegyenlet) természetesen maga is valószínűségi változó lesz.

A közvetett mérés várható értékét a részeredmények átlagaival becsüljük. Ezért nyilvánvaló, hogy a hibaterjedés eredő szórásának becslésére használt számítási képletben, az egyes összetevőkben, az átlagok korrigált tapasztalati szórását használtuk fel.

Tehát a közvetett mérés eredő (korrigált) tapasztalati szórása jellemzi majd az átlagos érték ingadozását.

$s_{_{\bar{y}}}^{*} = + \sqrt{{(\frac{\partial f (x_{1},... x_{n})}{\partial x_{1}} \cdot s_{{\bar{X}}_{1}}^{*})}^{2} + ... {(\frac{\partial f (x_{1},... x_{n})}{\partial x_{n}} \cdot s_{{\bar{X}}_{n}}^{*})}^{2}}$

(3.21)

Az eredő korrigált tapasztalati szórás meghatározásában is láthatók a „súlyfaktorok” (c_i), amelyeket az eredményfüggvény Taylor sorának elsőrendű tagjaiból nyertünk, parciális deriválás révén.

3.4. A mérési hibák formai megjelenése

A hibák csoportosításánál látott harmadik megközelítés a hibák formájára, megadási módjára vonatkozott. Ebben az aspektusban két alcsoportot lehet megkülönböztetni: Az egyik alcsoport a hiba megadási módját jelenti, és ide tartoznak olyan fogalmak, mint az

abszolút hiba,
relatív hiba,
redukált hiba, és
osztálypontosság.

Ezek magyarázatát korábbi fejezetekben, a metrológiai és a műszertechnikai fogalmak között már megadtuk, és néhányat közülük az eddigiek során már rendszeresen alkalmaztunk is. További taglalásuk tehát nem indokolt. A hangsúlyt az időben változó mennyiségek méréstechnikájára helyezzük.

3.4.1. Időben változó mennyiségek mérésének jellegzetes hibái

Az időben változó mennyiségek mérése a gépészetben rendkívüli fontosságú, és ezért a másik alcsoporttal, az időbeli és frekvencia tartománybeli hibákkal a következőkben részletesebben foglalkozunk. A méréstechnika egyik jellegzetes ellentmondása talán éppen ezen a területen jelentkezik a legszembetűnőbben. Nevezetesen az, hogy már a mérés megtervezésekor „à priori” (előzetes) ismeretekkel kell rendelkeznünk nem csak a mérendő jelek nagyságát, hanem azok spektrumát illetően is. Magyarul: Ismernem kell a megismerni kívánt mennyiség bizonyos jellemzőit. A jelekkel és a jelanalízissel külön fejezetekben foglalkozunk.

A jelek spektrumának és az adott mérőrendszer dinamikai tulajdonságainak figyelmen kívül hagyása súlyos mérési hibákhoz vezethet, mind analóg, mind pedig a mintavételezett jelek esetében. Sajnos, gyakran találkozhatunk a mérőrendszer, mérőlánc, vagy egy-egy mérőműszer frekvenciafüggő átvitelének figyelmen kívül hagyásából származó hamis eredményekkel.

Az időben változó gépészeti mennyiségek mérésének bemutatására a nemzetközi gyakorlatban is előszeretettel alkalmazott megközelítés a „mérőlánc”. A jellegzetes villamos mérésektől ez a struktúra alapvetően különbözik, hiszen ennek igen fontos részét képezi a bemenő (mérendő) mennyiségek villamos jellé történő átalakítása. Ezt a műveletet a szakirodalom sokféle módon nevezi, de alapvetően „jelátalakítás” ami itt végbemegy. A következő ábra a mérőlánc tagjait és ezek legfontosabb feladatait mutatja be.

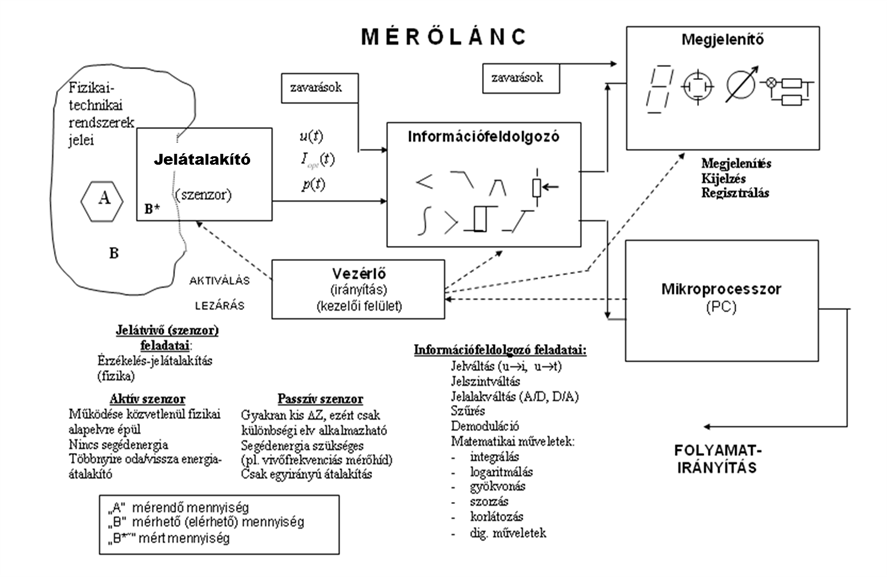
3.6. ábra - A mérőlánc felépítése és szerepe

A hibaanalízis szempontjából fontos, hogy a mérőlánc és a mérendő fizikai mennyiségek, jelek közötti kapcsolatot dinamikai szempontok figyelembe vételével megvilágítsuk.

Tehát, nagyvonalakban össze kell gyűjtenünk előzetesen minden lehetséges és fontos ismeretet arról a mennyiségről, amit meg akarunk „ismerni”. Az ok a dinamikában, rendszertechnikában és rezgéstanban járatos gépészek, mechatronikusok számára világos. A jelátalakítók (jeltovábbítók) többségében vegyes, mechanikai-villamos rendszerelemek találhatóak, és ezek között is meghatározó jelentőségűek az energiatárolók . A példákat igen hosszan lehetne sorolni, legyen elegendő ezen a helyen csak a különféle gyorsulásérzékelőkre (induktív, nyúlásmérő bélyeges, piezoelektromos, vagy a MEMS-technikában /Micro Electro Mechanics/ a kapacitív) utalni, amelyekben valamilyen formában szeizmikus tömeg csillapított rugalmassággal van felfüggesztve, és így mindegyik azonnal másodrendű lengő rendszert képez. A következő ábra egy induktív útadós szenzorral ellátott szeizmikus gyorsulásérzékelő kitöréses metszetét mutatja.

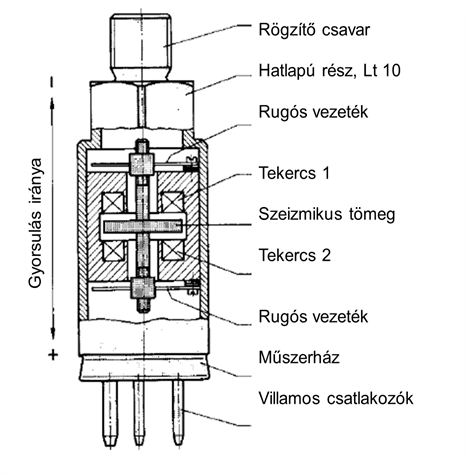
3.7. ábra - Induktív gyorsulásérzékelő felépítése (Hottinger és Baldwin)

A jelátalakító (jeltovábbító) és annak induktív útadó szenzorja nagyszerű példa annak illusztrálására, hogy a mérőlánc tagjai bizony tartalmazhatnak energiatárolókat, amelyek az eszköz dinamikus tulajdonságait – értsd alatta: jelátvitelét – alapvetően meghatározzák. A műszertechnikában szokás arányos, egytárolós és kéttárolós tagokról beszélni. Nem, mintha kettőnél több független energiatároló nem lehetne egy rendszerben. Helyesebb is lenne egytárolós helyett páratlan és kéttárolós helyett páros jellegről beszélni, mert ezek kombinációjával a gyakorlatban előforduló – magasabb rendszámú - műszertechnikai átviteli tagok „összerakhatóak”.

Ezt olvashatjuk le a következő ábrán látható diagramról, amelyet, egy valós eszköz műszerkönyvéből vettünk.

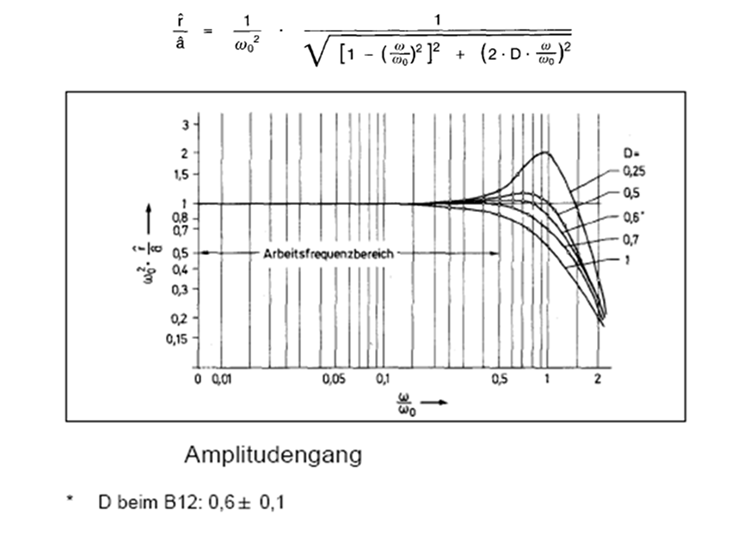
3.8. ábra - Részletek a H&B B12 gyorsulásérzékelő adatlapjából

A fenti ábrán a H&B B12 gyorsulásérzékelő „amplitúdó menete”, és felül az átviteli függvény abszolút értékének kiszámításához szükséges összefüggés látható. A diagram se nem un. Bode-diagram, se nem normalizált frekvenciamenet, ahogy a műszaki mechanika ismeri, hanem egy vegyes kép, de jól szemlélteti a dinamikai problémát. A jelátalakító másodrendű, mert rugalmas vezetéken felfüggesztett, szeizmikus tömeget tartalmaz. A csillapítást igen körülményes módon 0.6 értékre állítják be. Ez a másodrendű rendszer alul-áteresztő szűrőként működik, azaz 0.6-es csillapítási fok esetén 0≤f≤0.5f_rez frekvencia sávban arányos működésű, tehát mérésre alkalmas. Ebben a frekvencia tartományban minden harmonikus jelet - ezek a mérendő gyorsulás jel Fourier összetevői - a műszerkönyvben megadott arányossági tényezővel súlyozva alakít át elmozdulássá. Ugyanakkor f>0.5f_rez frekvenciákon egy szűk tartományt, a rezonancia sávot kivéve, csökken az arányossági tényező, frekvencia dekádonként (frekvencia megtízszereződése) 40 dB-lel, ami jelszintben 0.01-es szorzót jelent.

Mindez jól leolvasható a diagramról, és tájékoztatja a felhasználót a dinamikai szempontból fontos alkalmazhatósági feltételekről.

Összefoglalva tehát az energiatároló elemek (tömeg, rugómerevség, induktivitás, kapacitás, stb.) hatása idő tartományban dinamikai hibák , a frekvencia tartományban pedig az amplitúdó átvitel és fázis átvitel hibáknak forrása lehet.

3.4.2. Dinamikus hiba

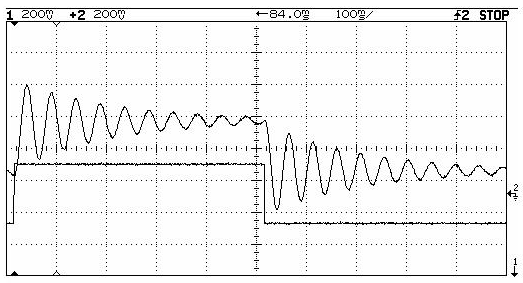
Már a dinamikus kalibrálással foglalkozó fejezetben is találkozhattunk a problémával. A lényeg tehát az, hogy a műszerek, mérőrendszerek a bennük lévő energiatárolók miatt csak időben késleltetve, esetleg amplitúdóban nagyobb eltéréssel képesek követni a mérendő bemenő jelet. A dinamikus hiba a következő ábrán látható módon, amplitúdóját tekintve időbeli késésként, vagy adott időpillanatban amplitúdó hibaként jelentkezik.

3.9. ábra - A dinamikus hiba szemléltetése

A dinamikus hiba különösen nagy problémákat okozhat másod, vagy annál magasabb rendű rendszerek esetében. A műszer, vagy mérőrendszer csillapítási fokától függően hosszabb-rövidebb ideig tartó lengésekre kell számítani, esetenként tekintélyes túllendüléssel. A kalibrálással foglalkozó fejezetben már leírtuk, hogy a leolvasás csak az állandósult állapotban lehetséges. Egy jellegzetes finommechanikai méretekkel rendelkező másodrendű műszer ugrásfüggvény bemenetre (ez is látható az oszcilloszkóp kép alsó részén) adott válaszát (un.: step response) látjuk a következő ábrán. A kép baloldalán a pozitív, a jobboldalán a negatív irányú kitérítés dinamikája figyelhető meg.

3.10. ábra - Másodrendű rendszer átmeneti függvénye (step response)

3.4.3. Mérőlánc frekvenciafüggő átviteléből adódó hibák

Az „Időben változó mennyiségek mérésének jellegzetes hibái” című fejezet bevezetőjében már jeleztük, hogy a mérendő mennyiség várható nagysága (amplitúdója) mellett ismerni kell a mérendő mennyiség (jel) időbeli alakját, és ebből következően a frekvencia spektrumát, hogy a mérőlánc minden tagjának frekvencia-átvitelét ehhez a spektrumhoz illeszthessük, hiszen a mérőlánc dinamikai tulajdonságainak figyelmen kívül hagyása a létező legdurvább hibákat eredményezheti.

A problémát frekvencia tartományban jól szemlélteti a (3.8. ábra) ábrán látható diagram, amelyet, egy valós eszköz műszerkönyvéből vettünk.

A 3.7. ábra felső részén látható frekvencia átviteli függvény (r/a, azaz a ház és a tömeg közötti relatív elmozdulás amplitúdója osztva a bemenő gyorsulás amplitúdójával) levezetése igen egyszerű, ha feltételezzük, hogy a rugós vezeték rugómerevsége (k) és a csillapítási tényező (b) lineáris és idő-invariáns rendszerelemek. Ebben az esetben a műszerház és a szeizmikus tömeg közötti relatív elmozdulás, valamint a bemenő gyorsulás közötti összefüggést, e két mennyiséggel matematikai kapcsolatban álló sebességek alkalmazásával, és impedancia módszerrel írhatjuk fel. Az általános impedancia a keresztváltozó (mechanikában sebesség) és az átmenő változó (mechanikában erő) Laplace transzformáltjának hányadosa.

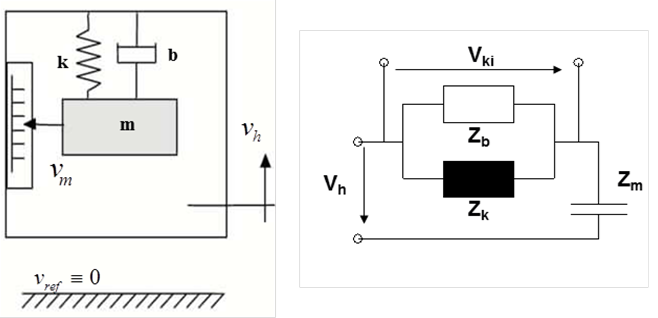
3.11. ábra - A gyorsulásérzékelő működési modellje és impedancia hálózata

A fenti ábra jobb oldalán látható impedancia kapcsolásban meghatározzuk a kimenő sebességhez tartozó impedanciák párhuzamos eredőjét és a keresztváltozó-osztó szabályt alkalmazva azonnal az implicit átviteli függvényt kapjuk:

$\frac{V_{k i}}{V_{h}} = \frac{\frac{s}{s \cdot b + k}}{\frac{s}{s \cdot b + k} + \frac{1}{s \cdot m}} = \frac{s^{2} \cdot \frac{m}{k}}{s^{2} \cdot \frac{m}{k} + s \cdot \frac{b}{k} + 1}$

(3.22)

A sebességek helyére a Laplace transzformáció szabályit figyelembe véve (integrálás, deriválás) az elmozdulás és a gyorsulás helyettesíthető:

$\frac{X_{r e l a t}}{a_{h}} (s) = \frac{X_{k i}}{a_{h}} (s) = \frac{\frac{1}{s} V_{k i}}{s \cdot V_{h}} = \frac{1}{s^{2}} \frac{s^{2} \cdot \frac{m}{k}}{s^{2} \cdot \frac{m}{k} + s \cdot \frac{b}{k} + 1} = \frac{\frac{m}{k}}{s^{2} \frac{m}{k} + s \frac{b}{k} + 1}$

(3.23)

Ha az átviteli függvényben a Laplace operátor helyére annak „jelentését” írjuk s=jω, akkor nyilvánvalóvá válik számunkra az átvitel körfrekvenciától való függése:

$\frac{X_{k i}}{a_{h}} (j ω) = \frac{\frac{m}{k}}{{(j ω)}^{2} \cdot \frac{m}{k} + j ω \cdot \frac{b}{k} + 1} = \frac{\frac{m}{k}}{(1 - ω^{2} \frac{m}{k}) + j ω \frac{b}{k}}$

(3.24)

Bevezetve a mechanikában, műszertechnikában szokásos jelöléseket azzal, hogy a nemzetközi szakirodalom a csillapítatlan rezonancia körfrekvenciát hol „α”, hol „ω₀” szimbólummal jelöli,

$\begin{matrix} \frac{m}{k} = T^{2} = \frac{1}{α^{2}} = \frac{1}{ω_{0}^{2}}; & \frac{b}{k} = 2 ξ T = \frac{2 ξ}{ω_{0}} \end{matrix}$

(3.25)

majd az átviteli függvény abszolút értékét képezve a műszer adatlapon szereplő összefüggéshez jutunk:

	$\frac{X_{k i}}{a_{h}} (j ω) = \frac{1}{ω_{0}^{2}} \cdot \frac{1}{(1 - {(\frac{ω}{ω_{0}})}^{2}) + j 2 ξ \frac{ω}{ω_{0}}}$	(3.26)
	$\| \frac{X_{k i}}{a_{h}} (j ω) \| = \frac{1}{ω_{0}^{2}} \cdot \frac{1}{\sqrt{{(1 - {(\frac{ω}{ω_{0}})}^{2})}^{2} + {(2 ξ \frac{ω}{ω_{0}})}^{2}}}$	(3.27)

Az átviteli függvény abszolút értéke „normálás”, azaz „dimenziótlanítás” után alkalmas a Bode diagram megrajzolására, hiszen a bemenő és kimenő jelek fizikai dimenziója nem azonos. A normálásra azért van szükség, mert az átviteli függvény dimenziója, a dB nem fizikai mennyiségekből adódik.

A méréstechnikában a normálás úgy történik, hogy az átviteli függvény adott körfrekvencián vett értékét osztják egy célszerűen igen alacsony körfrekvencián vett átvitel értékével, esetünkben:

$\frac{| G (ω) |}{| G_{0} (ω = ω_{r e f}) |} = \frac{| \frac{X_{k i}}{a_{b e}} (ω) |}{| \frac{X_{k i}}{a_{b e}} (ω = ω_{r e f}) |}$

(3.28)

Erre az arányra már képezhető a „lg” és az eredmény megadható dB-ben.

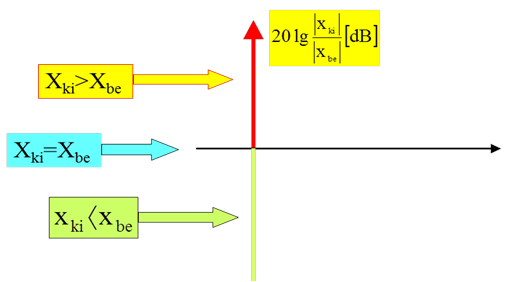
A „frekvencia-átviteli” tulajdonságok Bode diagramon történő ábrázolása elterjedt és jellemző a mérés-és szabályozástechnikai gyakorlatban. Alkalmazása több előnnyel jár. Mindkét tengely „komprimált”, azaz széles frekvencia tartományban, és nagy amplitúdó arány átfogással jeleníthetőek meg az átviteli tagok frekvencia-függő tulajdonságai. Ezen túlmenően igen szemléletes, mert „első ránézésre” megállapítható, hogy az átviteli tag egy adott körfrekvencián milyen mértékben változtatja meg a harmonikus jel (összetevő) amplitúdóját. A körfrekvencia tengely log léptéke körfrekvencia-dekádonként azonos távolságot jelent, és így nem gond számos dekád, tehát nagy frekvencia tartomány ábrázolása. Zérus körfrekvencia természetesen nem jeleníthető meg, csak valamely tetszőleges, nagyon alacsony körfrekvencia érték. A fázis-átvitelt külön diagramon ábrázolják, de a frekvencia tengely léptéke megegyezik az amplitúdó átvitelével.

A kalibrációs Bode diagramot a legtöbb dinamikus műszer esetében közlik a gyártók, de ha mégsem, akkor az arányos átviteli tartományt mindenképpen megadják.

A kimenő és bemenő harmonikus jelek amplitúdó arányának logaritmusa 20-szal szorozva adja azt a dimenzió nélküli mértékegységet, amit a mérés- és híradástechnikában decibel-nek (dB) nevezünk. A „bel” (rövidítése: B) egységet a Bell Telephone Laboratory mérnökei alkalmazták először, a szabványos telefonkábel 1 mérföld (1,6 km) hosszú darabja okozta hangerősség-csökkenés mértékének meghatározásához. Eredetileg „transmission unit” vagy TU (átviteli egység) volt az egység neve, majd az 1920-as évek közepén nevezték el a labor alapítójáról (A. G. Bell). A „bel”, mint egység, túl nagy a műszaki alkalmazásra, ezért használjuk a tizedét.

A dB mértékegységet alkalmazzák az akusztikában, az optikában is, de vigyázat, az akusztikai dB számítása egészen más alapon történik, csak a logaritmus számítás bennük a közös, nem átviteli függvényről van szó! Az akusztikai dB-t hangnyomásszint és hangteljesítményszint megadására alkalmazzák. A tört számlálójában az aktuális érték (hangnyomás, teljesítmény), míg a nevezőben egy vonatkoztatási érték szerepel!

Kétféle dB használatos a műszertechnikában, az egyik az jelszint-decibel, a másik a teljesítmény-decibel. Ez utóbbi esetében a tízes alapú logaritmus előtt azonban nem 20-as, hanem 10-es a szorzó áll. A jelek frekvencia analízise kapcsán a teljesítményre még visszatérünk. Egyébként ez az eredeti formája is a dB definíciónak, mert a kimenő és bemenő teljesítmény közötti viszony meghatározására hozták létre. Teljesítmény viszonyok esetében a szorzó tehát 10, míg a teljesítményben négyzetesen szereplő - többnyire keresztváltozó - amplitúdók arányát behelyettesítve (pl.: P=U²/ R) a szorzat a log előtt 2·10 lesz.

Érdemes néhány fontos dB értéken és a mögöttük lévő amplitúdó arányon, és ezek diagramon való megjelenésén elgondolkodni, mert a méréstechnikában a használatuk mindennapos, és ezért ezeket összefoglalva bemutatjuk.

A méréstechnikában gyakran alkalmazott 1%-os hibakorlát (amplitúdó) dB-ben kifejezett értékét is megtaláljuk a táblázatban, célszerűen kerekítve 0.1 dB-t szokás megadni.

Amplitúdó arány	dB	Amplitúdó arány	dB
1000	60	10-3	-60
100	40	10-2	-40
10	20	10-1	-20
3,3	10	0,33	-10
2	6	0,5	-6
1,4	3	0,7(=1/1,4)	-3
1	0
1.01	0.09	0.99	-0.09

3.12. ábra - Méréstechnikában fontos dB értékek és az ábrázolás előnyei

A gyorsulásérzékelő esetében a Bode diagram függőleges tengelyén ábrázolt átviteli tényező értékek normálás nélkül az alábbi összefüggéssel számíthatók ki:

$20 \lg | \frac{X_{k i}}{a_{h}} (j ω) | = 20 \lg \frac{1}{ω_{0}^{2}} + 20 \lg \frac{1}{\sqrt{{(1 - {(\frac{ω}{ω_{0}})}^{2})}^{2} + {(2 ξ \frac{ω}{ω_{0}})}^{2}}} = 20 \lg \frac{1}{ω_{0}^{2}} - 10 \lg [{(1 - {(\frac{ω}{ω_{0}})}^{2})}^{2} + {(2 ξ \frac{ω}{ω_{0}})}^{2}]$

(3.29)

Az amplitúdó átvitel hibája tehát jól leolvasható a Bode diagramról, és tájékoztatja a felhasználót a dinamikai szempontból fontos alkalmazhatósági feltételekről.

3.4.4. Mintavételezési hiba

A digitális kijelzésből származó bizonytalansággal egy korábbi fejezetben már foglalkoztunk, és láttuk, hogy ez a legkisebb kijelzett érték mintegy 30 %-a. Hiba azonban nem csak az amplitúdó léptékezés (kvantálás) során keletkezik, hanem az időben történő kvantálás, más elterjedt kifejezéssel „mintavételezés” miatt is. Ebben a fejezetben röviden arra világítunk rá, hogy adott, időben változó jel spektrumának ismeretében milyen szabályt kell figyelembe venni a jel mintavételezése során a hiba elfogadható szinten tartása érdekében.

Az első ábrán egy analóg jel amplitúdó kvantálását látjuk.

A kvantálási szabály a következő:

$N - 0,5 < A \leq N + 0,5$

(3.30)

Ahol „N” az analóg jelhez rendelt diszkrét szintet, „A” pedig az analóg jel pillanatnyi értékét jelenti az adott tartományban.

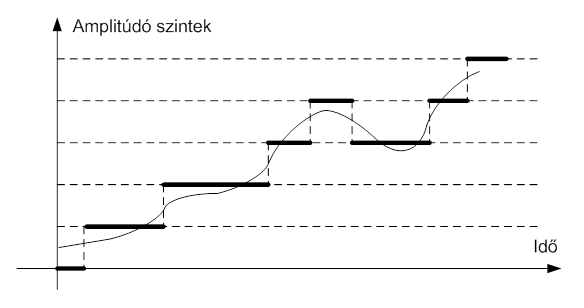
3.13. ábra - Amplitúdó kvantált jel

A fenti ábrán az eredeti analóg jelet vékony folytonos vonallal, az amplitúdó kvantáltat pedig vastagabb vonallal jelöltük. Az amplitúdó kvantálás szemmel láthatóan önmagában eléggé torzítja a jelet. A torzítás a kvantálási szinttől függ, ez a szakirodalom által emlegetett „LSB”, azaz legkisebb kijelezhető bit.

Az A/D konverzió (analóg-digitális átalakítás) sokféle módon történhet, ezek alapvetően közvetett, vagy közvetlen csoportba sorolhatók. A közvetett A/D átalakítás során az időalapra, mint köztes mennyiségre vezetik vissza az átalakítást, ilyen volt a régebben alkalmazott fűrészfog-generátoros, napjainkban pedig a dual-slope (kettős integrálás) konverzió. A közvetlen átalakítók, amint az elnevezés is mutatja, időalap igénybevétele nélkül végzik az átalakítást. Ilyen a szimultán A/D konverter és a szukcesszív approximációs átalakító. Különböznek az A/D átalakítók abban is, hogy a jel pillanatnyi értékét, vagy a jel egy meghatározott idő alatti integrálásának eredményét méri. Pillanatnyi értéket mér a szimultán és a szukcesszív approximációval dolgozó átalakító, és a régi fűrészfog-generátoros rendszer is. A szukcesszív approximációs átalakítónál szükség van a pillanatnyi jel értékének tárolására is, mert a közelítés és a kódolás több lépcsőben történik. A dual-slope átalakító viszont nem pillanatnyi értéket mér, hanem adott időállandóval és meghatározott ideig integrálja a bemenő jelet.

Az A/D átalakítás, és az ezt követő kódolás mindenképpen időt vesz igénybe. A vizsgálandó jel átalakítását ezért nem folyamatosan, hanem „idő-kvantumokban” végzik el. Az időbeli kvantálás a mintavételezés. Az előző ábrán már látott analóg jel (vékony vonal) egy lehetséges T_m idővel történő mintavételezését mutatja az alábbi ábra:

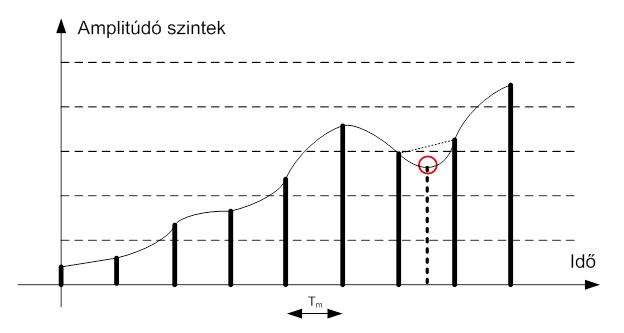
3.14. ábra - Időben mintavételezett analóg jel

A fenti ábrán érzékeltetni akartuk, hogy a mintavételi idő nagy ahhoz, hogy a jelben meglévő, pirossal körülrajzolt információ elvesszen. A mintavételi értékek csúcsait képzeletben összekötve láthatjuk, hogy az eredeti jelhez képest itt komoly eltérés lenne.

A helyzet tovább romolhat, ha a kétféle kvantálást együttesen alkalmazzák, márpedig ez a helyzet minden A/D átalakító esetében! A gyakorlatban tehát mintavételezett és amplitúdó kvantált jelekből származó információt jelenítenek meg a digitális kijelzésű eszközök. A következő ábrán az eddigiekben alkalmazott analóg jelen mutatjuk be a kettős torzító hatást:

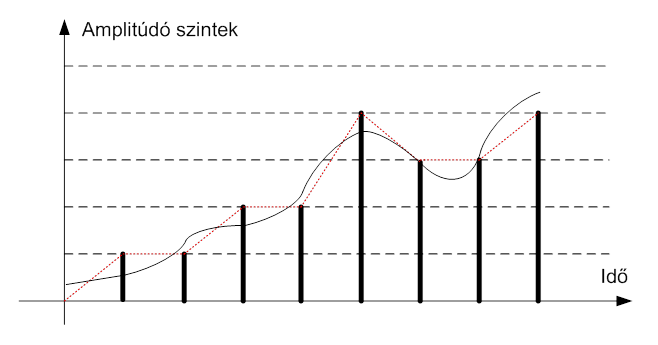
3.15. ábra - Mintavételezett és amplitúdó kvantált analóg jel

Ha szemléltetési célból most is összekötjük a mintavételezés csúcsait, amint ez az ábrán piros szaggatott vonallal megtörtént, akkor az eredeti analóg jelhez képest jól kivehető a különbség.

Mindenképpen kell tehát hibával számolnunk, a kérdés az, hogy miként lehet a mintavételezéssel járó hibát minimalizálni?

Első látásra világos, hogy a jel változásának követése csak megfelelően kis mintavételi időkkel valósítható meg. Shannon volt az, aki a mintavételezés róla elnevezett szabályát kidolgozta. Abból kell kiindulnunk, hogy minden jel harmonikus összetevőkre bontható.

Minél meredekebb a jel változása, annál több és nagyobb frekvenciájú harmonikus összetevőből épül fel a jel. Jó példája ennek a Dirac-impulzus, illetve ennek közelítése valós impulzusokkal.

A jelek Fourier analízisével a 6. fejezet fejezet részletesen foglalkozik, de a dinamikus okokra visszavezethető hibák nem tárgyalhatóak bizonyos ismeretek ismétlő áttekintése nélkül. A Fourier analízissel a BSc tanulmányok során feltehetően már mindenki találkozott, ezen a helyen csupán a hibák vizsgálatához nélkülözhetetlen ismeretekre szorítkozunk.

Az időben kétoldalasan határolt jelek spektruma folytonos, így az elméleti és a valós impulzus spektruma is. Az impulzusspektrumának abszolút értéke eredetileg |sinx/x| függvény jellegű, amelynek zérus helyei egy [-T_imp/2;+T_imp/2 ] időtartamú és „A” magasságú négyszög impulzus esetében ω_n=n2π/T_imp körfrekvenciáknál vannak. Ebből adódóan, ha minden határon túl csökkentjük a négyszög impulzus időtartamát, akkor az első zérushely a végtelen körfrekvencia irányába tolódik el, és a spektrum egyenletesen „kisimul” és az összetevők értéke is zérushoz tart.

Ezt a jelenséget érdemes nyomon követni a négyszög impulzus Fourier transzformálásának bemutatásával.

A négyszög impulzus függvény és spektruma az alábbi ábrán látható:

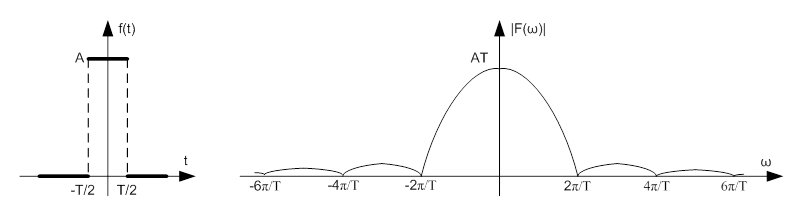
3.16. ábra - A négyszög impulzus és spektruma

Az ábra baloldalán látható időfüggvényt Fourier transzformáljuk:

$F (ω) = \int_{- T / 2}^{T / 2} A \cdot e^{- j ω t} d t = {- \frac{A}{j ω} e^{- j ω t} |}_{- T / 2}^{T / 2} = \frac{A}{j ω} (e^{j ω T / 2} - e^{- j ω T / 2})$

(3.31)

Célszerű átformálással kapjuk a fent leírt eredményt:

$| F (ω) | = | \frac{A \cdot \frac{T}{2} \cdot 2}{ω \frac{T}{2}} \cdot \frac{(e^{j ω T / 2} - e^{- j ω T / 2})}{2 j} | = | A \cdot T \frac{\sin ω \frac{T}{2}}{ω \frac{T}{2}} |$

(3.32)

A függvény értéke a ω=0⁺ helyen, valamint zérus helyei csak a L’Hospital szabállyal határozhatók meg:

$\frac{\frac{d}{d ω} N (ω)}{\frac{d}{d ω} D (ω)} = A \cdot T \frac{\frac{T}{2} \cos ω \frac{T}{2}}{\frac{T}{2}}$

(3.33)

A spektrum legfontosabb értékeit az alábbi táblázatban foglaltuk össze:

ω	0	n·2π/T
\|F(ω)\|	AT	0

Gondolati kísérletként az impulzus ”T” idejét csökkentve látjuk, hogy az első zérus hely egyre távolabb kerül az origótól, miközben a függvény értéke ω=0 helyen folyamatosan csökken. Végül - legalábbis elméletben - eljutunk az ideális Dirac impulzushoz, amelynek, mint ismeretes, az időtartama zérus, és a spektruma folytonos, a frekvencia tengellyel párhuzamos egyenes.

3.17. ábra - A Dirac impulzus spektrumának közelítése

Fontos tudni, hogy amíg egyetlen négyszög impulzus spektruma |sinx/x| jellegű addig az impulzus sorozat spektruma periodikus. A mintavételezett analóg jel a mintavételi időpillanatokban vett nagyságú impulzusok sorozata.

A jegyzet terjedelme nem teszi lehetővé, hogy bemutassuk az impulzus sorozat spektrum ának kiszámítását a Fourier transzformáció segítségével, de az érdeklődők a Fodor Gy.: Jelek és rendszerek című munkában [3.2.] részletes bemutatót találhatnak.

A későbbiek megértéséhez azt viszont tudni kell, hogy az impulzus sorozat spektrumának periódusa a körfrekvencia tengely mentén éppen ω_m, azaz a periódus éppen a mintavétel körfrekvenciája lesz.

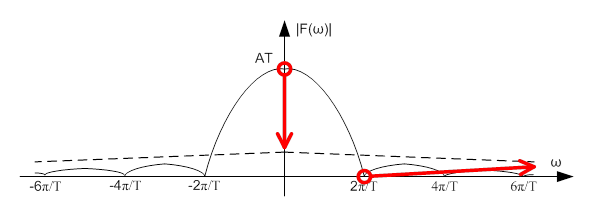
Nincs olyan műszer, mérőrendszer, amely egy impulzus, vagy egy impulzus sorozat hibátlan leírásához szükséges valamennyi, elméletben végtelen számú harmonikus összetevőt képes lenne átvinni. Nincs is gyakorlati szempontból jelentősége egy bizonyos felső határ(kör)frekvencia feletti összetevők átvitelének, mert azok a visszaállítható jel alakját érdemben már nem befolyásolják. Az elterjedt gyakorlat az, hogy az első zérus hely környékén adják meg azt a felső határ(kör)frekvenciát, amelynél az impulzus spektrumát levágják. Ezt a körfrekvenciát a következőkben „Ω”-val jelöljük. A frekvencia-korlátozást angol kifejezéssel „anti-aliasing” szűrésnek nevezik. A következő ábrán egyetlen impulzus spektrumának anti-aliasing szűrését szemléltetjük.

3.18. ábra - Anti-aliasing szűrés ábrázolása

Említettük, hogy az impulzus sorozat spektruma a mintavétel körfrekvenciájával periodikus. Az anti-aliasing szűrésen átesett impulzusokból álló sorozat spektrumát látjuk a következő ábrán:

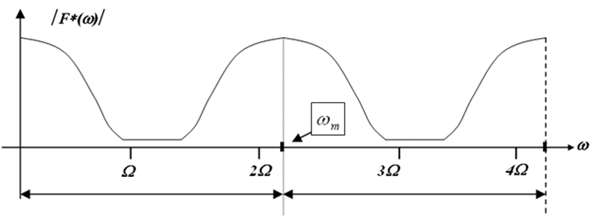
3.19. ábra - Az ω_m mintavételi körfrekvenciával mintavételezett és anti-aliasing szűrőn átengedett impulzus sorozat spektruma

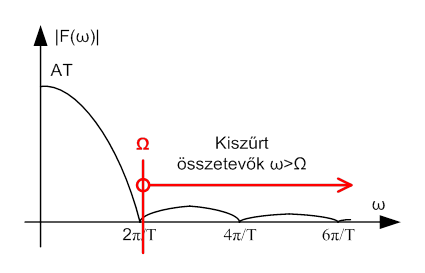
A fenti ábrán látjuk, hogy az impulzus-sorozat periodikus spektrumában, szűrés után, a 0≤ω≤Ω körfrekvencia tartományban a legfontosabb harmonikus összetevők maradtak. A görbe alakja hasonlít az egyetlen impulzus spektrumára jellemző sinx/x jellegű függvényből az első zérus helyig terjedő részhez. Az impulzus-spektrumból tehát már hiányzik az a tartomány, amelyet az anti-aliasing szűrővel vágási, vagy sávkorlátozó körfrekvencia felett kiszűrtünk.

Ha tehát nem egyetlen impulzus, hanem impulzus sorozat spektrumát vizsgáljuk, ez a sávkorlátozott spektrumkép jól láthatóan ismétlődik. Az impulzus sorozat spektruma szabályosan periodikus, a periódus körfrekvenciája éppen ω_m .

Az ábrán úgy viszonylik egymáshoz mintavételi ω_m körfrekvencia és Ω vágási körfrekvencia (antialiasing szűrő), hogy minimális mértékben, de teljesül a Shannon-szabály, mert a mintavétel körfrekvenciája nagyobb, mint a vágási körfrekvencia kétszerese.

A Shannon szabály tehát a következő módon adható meg:

$\begin{matrix} ω_{m} 〉 2 Ω & f_{m} 〉 2 f_{f e l s ő} & T {}_{m}〈 \frac{1}{2} T_{Ω} = \frac{π}{Ω} \end{matrix}$

(3.34)

A mintavétel (kör) frekvenciája legyen a mintavételezett jelben megtalálható legmagasabb (kör)frekvenciájú harmonikus összetevő kétszeresénél nagyobb. Másként fogalmazva a mintavételi idő legyen kisebb, mint a jelben található legmagasabb (kör)frekvenciájú összetevő periódusidejének fele.

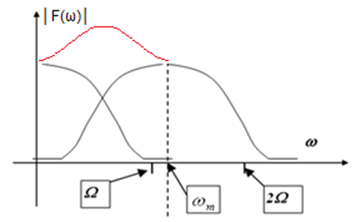
A következő ábrán látható, hogy mi történik a Shannon-szabály figyelmen kívül hagyása esetén? Ha tehát ω_m körfrekvencia kisebb, mint az Ω vágási körfrekvencia kétszerese, akkor a spektrum „összecsúszik”. Az így torzult spektrumot úgy kell elképzelni, mintha a görbék felső szakaszai felett haladnánk végig. Az összecsúszott eredő spektrumot piros vonallal jelöltük. Ha a mintavételi frekvencia még a vágási körfrekvenciánál is kisebb, akkor a spektrum közelíthet egy egyeneshez.

3.20. ábra - Impulzus sorozat túl alacsony körfrekvenciával mintavételezett „összecsúszott” spektruma

A Shannon szabály gyakorlati alkalmazásához nyújt segítséget a következő ábrán látható összeállítás. Tévedés lenne azt gondolni, hogy a mintavételezésből adódó hiba már azzal megszűntethető, ha a mintavételezési frekvencia nagyobb, mint a még átvinni (mérni) kívánt legmagasabb harmonikus összetevő kétszerese. Mekkora legyen a gyakorlatban elégséges körfrekvencia?

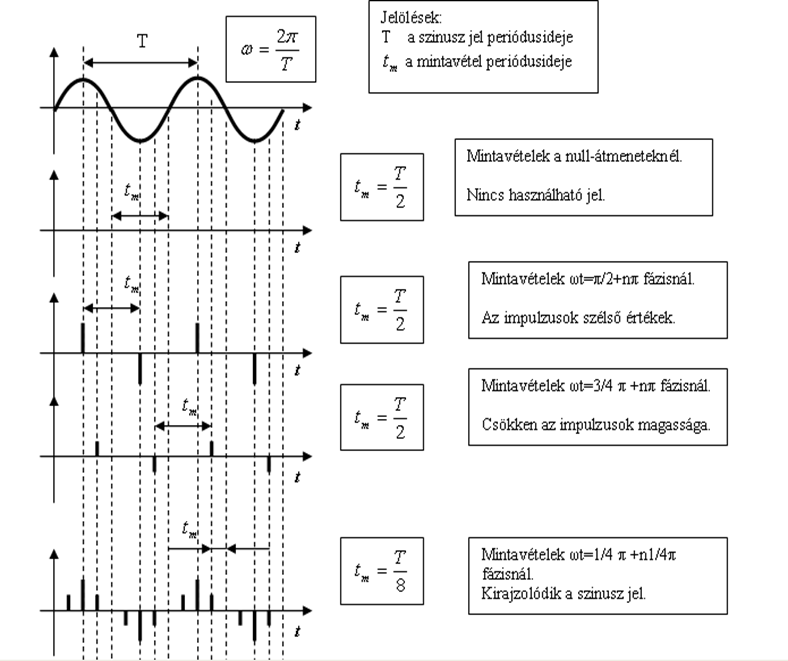
3.21. ábra - A mintavételezés szemléltetése a legmagasabb harmonikus összetevőn

A fenti ábra-soron első helyen azt az esetet látjuk, amikor a Shannon szabály nem teljesül, mert a mintavételi idő éppen a fele a legnagyobb frekvenciájú harmonikus periódusidejének. Előállhat olyan eset, hogy a mintavételezés éppen a null-átmeneteknél következik be, és ezért erről az összetevőről semmilyen információnk nem lesz. Ezért helytelen az a megfogalmazás, amelyet bizonyos internetes oldalakon is olvashatunk, miszerint a mintavételezés frekvenciája „legalább” kétszerese legyen a jelben megtalálható legnagyobb, még releváns összetevő frekvenciájának. A „legalább” kifejezésbe az „=2” is beleértendő, és ezért ez a megfogalmazás nem helyes.

Némiképp javul a helyzet, ha a mintavétel a null-átmenetekhez képest fázisban eltolt, ugyanakkor nagy képzelőerő kell a szinuszos jel rekonstrukciójához periódusonként kettő mintából. Ha a mintavétel frekvenciája már nyolcszorosa a legmagasabb frekvenciájú összetevőnek, akkor a harmonikus jel tűrhetően kirajzolódik. Gyakorlati szempontból tehát arra kell törekedni, hogy a mintavételi (kör)frekvencia legalább tízszerese legyen a legmagasabb (kör)frekvenciájú harmonikus összetevő (kör)frekvenciájának:

$\begin{matrix} ω_{m} \approx (10...20) \cdot Ω & f_{m} \approx (10...20) \cdot f_{f e l s ő} & T {}_{m}\approx (\frac{1}{20} ... \frac{1}{10}) T_{Ω} \end{matrix}$

(3.35)

A mintavételezés gyakorlati kivitelezésére a (8.3. szakasz) és (8.4. szakasz) fejezetben visszatérünk.

Irodalmak

[3.1.] Halász, G. és Huba, A.. Műszaki mérések. Műegyetemi kiadó. 2008.

[3.2.] Fodor, Gy.. Jelek és rendszerek. Műegyetemi kiadó. 2006.

Vissza		Előre
2. fejezet - Mérés-és műszertechnika	Főoldal	4. fejezet - Mérés és valószínűség számítás