6. fejezet - A közönséges differenciálegyenlet
Vissza		Előre

6. fejezet - A közönséges differenciálegyenlet

Tartalom

Az olyan egyenleteket nevezzük differenciálegyenleteknek, amelyekben deriváltak szerepelnek. Ha a differenciálegyenletben csak egy független változó van, akkor közönséges differenciálegyenletről beszélünk. Differenciálegyenlet-rendszerről van szó akkor, ha az egyenletek száma egynél több, és ugyanennyi ismeretlen függvényt kell meghatároznunk a megoldás során.

6.1. A közönséges differenciálegyenletek osztályozása

A közönséges differenciálegyenletek osztályozása rendkívül fontos, ugyanis a különböző típusokhoz kidolgozott megoldási módszerek közül csak ennek ismeretében lehet választani.

Definíciók:

A differenciálegyenlet rendje egyenlő a benne szereplő legmagasabb rendű derivált rendszámával.

Lineáris az a differenciálegyenlet, amelyben az ismeretlen függvény és annak deriváltjai csak első hatványon szerepelnek, valamint az ismeretlen függvénynek és deriváltjainak szorzata semmilyen kombinációban sem fordul elő.

Inhomogén az a differenciálegyenlet, amelynek van olyan tagja, amelyben az ismeretlen függvény, vagy annak valahányadik deriváltja nem szerepel. Ellenkező esetben a differenciálegyenlet homogén.

Állandó együtthatós az a differenciálegyenlet, amelyben a függvényt, és annak deriváltjait tartalmazó tagok együtthatói állandók. Ellenkező esetben a differenciálegyenlet függvényegyütthatós.

Példák:

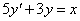
elsőrendű (mert y első deriváltja a legmagasabb rendű derivált), lineáris (mert y és deriváltja csak első hatványon szerepel, és nincs a szorzatukat tartalmazó tag sem), inhomogén (mert van olyan tagja – az x –, amelyben nem szerepel y, vagy annak deriváltja), állandó együtthatós (mert 5 és 3 állandó).
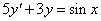
elsőrendű (mert y első deriváltja a legmagasabb rendű derivált), lineáris (mert y és deriváltja csak első hatványon szerepel, és nincs a szorzatukat tartalmazó tag sem), inhomogén (mert van olyan tagja – a sin x –, amelyben nem szerepel y, vagy annak deriváltja), állandó együtthatós (mert 5 és 3 állandó).
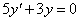
elsőrendű (mert y első deriváltja a legmagasabb rendű derivált), lineáris (mert y és deriváltja csak első hatványon szerepel, és nincs a szorzatukat tartalmazó tag sem), homogén (mert minden tagjában szerepel y, vagy annak deriváltja), állandó együtthatós (mert 5 és 3 állandó).
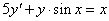
elsőrendű (mert y első deriváltja a legmagasabb rendű derivált), nemlineáris (mert van x és y szorzatát tartalmazó tag), inhomogén (mert van olyan tagja – az x –, amelyben nem szerepel y, vagy annak deriváltja), függvényegyütthatós (mert y sin(x) -ben sin(x) nem állandó).
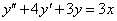
másodrendű (mert y második deriváltja a legmagasabb rendű derivált), lineáris (mert y és deriváltjai csak első hatványon szerepelnek, és nincs a szorzatukat tartalmazó tag sem), inhomogén (mert van olyan tagja – a 3x –, amelyben nem szerepel y, vagy annak deriváltja), állandó együtthatós (mert 1, 4 és 3 állandó).
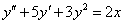
másodrendű (mert y második deriváltja a legmagasabb rendű derivált), nemlineáris (mert van benne y2), inhomogén (mert van olyan tagja – a 2x –, amelyben nem szerepel y, vagy annak deriváltja), állandó együtthatós (mert 1, 5 és 3 állandó).

A Rendszertechnikában általában állandó együtthatós-, inhomogén-, lineáris differenciálegyenletekkel fogunk foglalkozni.

6.2. A differenciálegyenletek megoldásai

A differenciálegyenlet megoldásai azok a függvények, amelyek deriváltjaikkal együtt azonosan kielégítik az adott differenciálegyenletet.

Megkülönböztetünk általános és partikuláris megoldást. Egy n-ed rendű differenciál-egyenlet általános megoldása olyan függvény, amely n számú egymástól független paramétert tartalmaz és deriváltjaival együtt azonosan kielégíti az adott differenciálegyenletet. Partikuláris megoldás esetén a paraméterek száma legfeljebb n-1. Partikuláris megoldást előállítani rendkívül egyszerű, csak valamely paraméternek (lehet többnek is) kell értéket adni. Általában az általános megoldás tartalmazza az összes partikuláris megoldást.

Példák:

Az 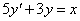egyenlet általános megoldása 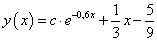, mivel azonosan kielégíti a differenciálegyenletet, hiszen

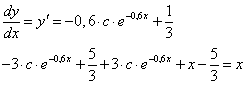
Ennek egy partikuláris megoldása c=0 esetén: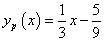

Az 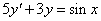egyenlet általános megoldása 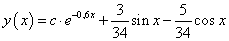, mivel azonosan kielégíti a differenciálegyenletet, hiszen

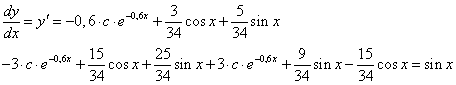
Ennek egy partikuláris megoldása c=0 esetén: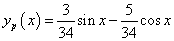

Az 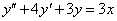egyenlet általános megoldása 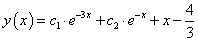, mivel azonosan kielégíti a differenciálegyenletet, hiszen

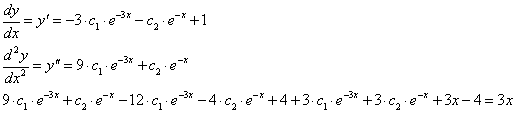
Ennek egy partikuláris megoldása c1=0 esetén: 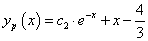, c1=c2=0 esetén pedig: .

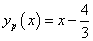6.3. Megoldás keresése próbafüggvény módszerével

Az n-ed rendű állandó együtthatós-, inhomogén-, lineáris differenciálegyenletek általános alakja:

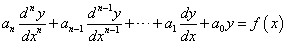
vagy tömörebb formában:

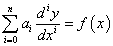
A differenciálegyenlet homogén részéhez úgy jutunk, hogy f(x) helyére nullát írunk.

A megoldás menetének ismertetése előtt két tételt kell megemlíteni.

Ha egy n-ed rendű homogén lineáris differenciálegyenletnek yn(x), yn-1(x),… y1(x) lineárisan független partikuláris megoldásai, akkor az általános megoldás:

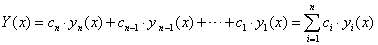
Lineárisan függetlennek akkor nevezzünk két függvényt, ha a:

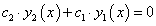
egyenlőség akkor és csak akkor teljesül, ha mindkét c paraméter zérus. Másképpen megfogalmazva: a két függvény hányadosa nem lehet állandó.

Ha egy n-ed rendű inhomogén differenciálegyenlet homogén részének általános megoldása Y(x), és az inhomogén egyenlet egy partikuláris megoldása y0(x), akkor az inhomogén egyenlet általános megoldása:

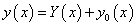
Ez a két tétel már sugallja a megoldás menetét. Először a differenciálegyenlet homogén részének általános megoldását keressük meg, majd a teljes differenciálegyenlet egy partikuláris megoldását fogjuk meghatározni.

6.3.1. Állandó együtthatós, homogén, n-ed rendű lineáris differenciálegyenletek megoldása

Az állandó együtthatós, homogén, n-ed rendű lineáris differenciálegyenlet általános alakja a következő:

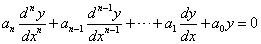
Keressük a differenciálegyenlet egy partikuláris megoldását

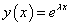
alakban, mivel az exponenciális függvény az egyetlen függvény, amely arányos a saját deriváltjaival. Behelyettesítve a differenciálegyenletbe:

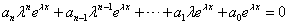
Mivel 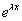sosem lehet zérus, ezért vele végigoszthatjuk az egyenletet. Így egy n-ed fokú polinomhoz jutunk, amelynek n darab gyöke van. A gyökök tulajdonságai alapján három esetet különböztethetünk meg:

egyszeres valós gyökök (K darab),

többszörös valós gyökök (P darab a multiplicitásukkal együtt),

komplex gyökök (Q darab).

Nyilvánvaló (mivel másmilyen gyökök nem lehetnek), hogy a különböző gyökök darabszámainak összege n, azaz n=K+P+Q.

6.3.1.1. Egyszeres valós gyökök

A K darab gyök mindegyike ad egy partikuláris megoldást. Kérdés már csak az, hogy ezek függetlenek-e.

Legyen K1 és K2 két ilyen gyök. Ekkor a két partikuláris megoldás hányadosa:

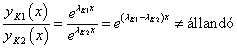
mivel a két gyök különböző. Így tehát K egymástól független partikuláris megoldásunk van.

Példa:

Oldjuk meg az 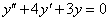differenciálegyenletet. Az 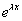helyettesítés elvégzése után a

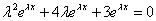
egyenlethez jutunk. Ebből a karakterisztikus polinomot 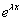-vel való osztás után kapjuk:

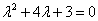
Vegyük észre, hogy ha a differenciálegyenletben y, illetve deriváltjai helyére  annyiadik hatványát írjuk, ahányadik deriváltja szerepel y-nak, akkor éppen a karakterisztikus polinomot kapjuk. Megoldva a másodfokú karakterisztikus polinomot, 1=-1 és 2=-3 gyökökhöz jutunk. A differenciálegyenlet általános megoldása tehát:

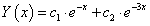
Visszahelyettesítve a differenciálegyenletbe:

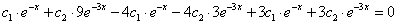
6.3.1.2. Többszörös valós gyökök

Többszörös gyökök esetén az előző módszer nem megfelelő, hiszen a gyökök között vannak azonosak. Legyen a különböző gyökök száma p, és ezek multiplicitása rendre m1, m2, …mp. Az előzőek alapján nyilvánvaló, hogy:

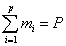
Bizonyítható, hogy ekkor a differenciálegyenlet partikuláris megoldásai az

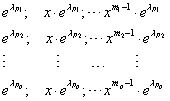
függvények. Ezen függvények páronként lineárisan függetlenek is, hiszen bármely kettő hányadosára igaz, hogy értéke nem állandó. A teljes függvényrendszer is független, de ennek igazolásával itt nem foglalkozunk. Így tehát újabb, ezúttal P egymástól független partikuláris megoldáshoz jutottunk.

Példa:

Oldjuk meg az 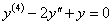differenciálegyenletet.

A karakterisztikus polinom:

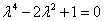
Látható, hogy az egyenlet bal oldala 2-re teljes négyzet, amiből 2=1 adódik. Ebből már könnyű meghatározni a gyököket:

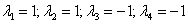
Az általános leírásban alkalmazott jelöléseket alkalmazva:

P=4, mert összesen 4 többszörös gyök van; p=2, mert kétféle gyök van (1 és –1); m1=2 és m2=2, mert mindegyik gyök kétszeres gyök. Ennek megfelelően a partikuláris megoldások:

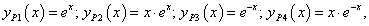
és az általános megoldás:

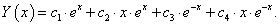
6.3.1.3. Komplex gyökök

Bizonyítható, hogy ha egy z komplex szám gyöke egy polinomnak, akkor a konjugáltja is gyök (tehát Q páros szám). Ennek megfelelően, ha 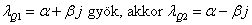is gyök. Az ezek segítségével felírható két partikuláris megoldás:

Alkalmazva a komplex számok exponenciális és trigonometrikus alakjai közötti Euler-féle összefüggést, a mindkét gyököt felhasználó partikuláris megoldás:

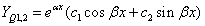
Így tehát újabb, ezúttal Q/2 egymástól független partikuláris megoldáshoz jutottunk, amelyek azonban darabonként 2-2 paramétert tartalmaznak.

Ha a komplex gyökök között van többszörös is, akkor a többszörös valós gyököknél ismertetett módszert kell alkalmazni.

Példák:

Oldjuk meg az 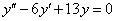differenciálegyenletet.

A karakterisztikus polinom:

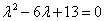
Ennek gyökei komplexek: 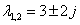. Alkalmazva az általános leírásban használt jelöléseket: α=3 és =2. Így az általános megoldás:

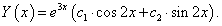
Oldjuk meg az 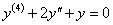differenciálegyenletet.

A karakterisztikus polinom:

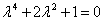
Látható, hogy az egyenlet bal oldala 2-re teljes négyzet, amiből 2=-1 adódik. Ebből már könnyű meghatározni a gyököket:

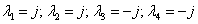
Most α=0 és =1. Mivel e0=1, így a megoldásból az e-ados rész hiányzik. Az egyik partikuláris megoldás:

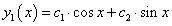
a másik pedig ennek x-el való szorzata (természetesen más c paraméterekkel). A teljes megoldás tehát:

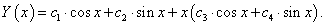
6.3.2. Állandó együtthatós, inhomogén, n-ed rendű lineáris differenciál-egyenletek megoldása próbafüggvény módszerrel

A 6.3 fejezet 2. tétele szerint a differenciálegyenlet homogén részének általános megoldását kell kiegészíteni a teljes egyenlet egy partikuláris megoldásával. Az előző pontban részletesen taglaltuk a homogén rész általános megoldásának meghatározására rendelkezésre álló legegyszerűbb módszert, így most csak a teljes egyenlet egy partikuláris megoldását kell megtalálnunk.

A következő módszer akkor alkalmazható, ha az inhomogén tag (f(x) függvény) csak olyan tagokból áll, amelyeknek csak véges számú lineárisan független deriváltjuk van. Ez másképpen azt jelenti, hogy e függvények deriváltjai egy idő után vagy arányosak lesznek az eredeti függvénnyel, vagy nullává válnak. Az első feltételnek megfelelő függvények:

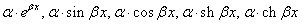
Hiperbolikus függvények esetén azok e-ados alakját kell használni.

A második feltételnek a polinomok felelnek meg.

Természetesen nem csak a felsorolt függvények megfelelőek, hanem tetszőleges lineáris kombinációjuk – azaz szorzataik, és ezek összegei – is.

Ha az f(x) függvény a fent leírtak szerinti, akkor a partikuláris megoldás hasonló lesz hozzá, azzal a kiegészítéssel, hogy minden olyan deriváltját szerepeltetni kell, amely eltér tőle:

e-ad esetén nincs ilyen, hiszen ez a függvény arányos a saját deriváltjával,
szinusz, vagy koszinusz esetén mindkettőnek szerepelni kell,
hiperbolikus függvényeknél az e-adnál leírtak szerint kell eljárni, mivel az e-ados alakjukat kell használni,
polinomoknál pedig az összes a legnagyobb kitevőnél kisebb kitevőjű tagot.

Abban az esetben, ha valamelyik tag szerepel a homogén általános megoldásban (rezonancia), ugyan úgy kell eljárni, mintha a homogén megoldásban többszörös gyök lenne, azaz x legkisebb még nem szereplő hatványával kell szorozni.

6.4. Mintapéldák

Oldjuk meg az 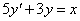egyenletet. Ennek homogén része 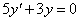, amiből a karakterisztikus polinom:

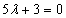
A megoldása -0.6, tehát a homogén rész általános megoldása:

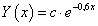
A partikuláris megoldást keressük 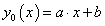alakban. Így a teljes megoldás, és annak első deriváltja:

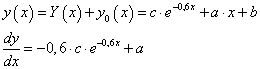
Ezt behelyettesítve a differenciálegyenletbe, majd rendezve:

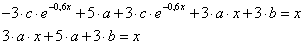
egyenletet kapjuk. Vegyük észre, hogy a homogén megoldás kiesett a rendezés során. Ez természetes is, hiszen a homogén egyenlet egyenlő nullával, ebből következően mindig ki kell esnie! A későbbi feladatoknál már csak a partikuláris részt fogjuk behelyettesíteni.

Visszatérve a rendezés után kapott egyenlethez, ez csak akkor teljesülhet, ha a jobb- és baloldalon álló x azonos fokszámú tagjait tartalmazó tagok együtthatói megegyeznek. Ennek megfelelően két egyenletet írhatunk fel a két ismeretlen meghatározására:

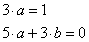
A megoldás után a differenciálegyenlet teljes megoldása:

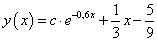
Ellenőrzés:

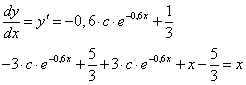
Oldjuk meg az 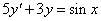egyenletet. Ennek homogén része megegyezik az előző feladat egyenletével. A partikuláris megoldást keressük 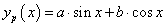alakban. Helyettesítsük be a differenciálegyenletbe, rendezzük, majd a jobb- és bal oldalak összevetésével írjuk fel az egyenleteket a paraméterek meghatározásához:

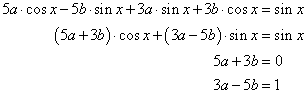
Az egyenletrendszer megoldása után az általános megoldás:

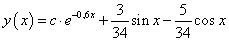
Oldjuk meg az 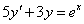egyenletet. Ennek homogén része megegyezik az előző feladat egyenletével. A partikuláris megoldást keressük 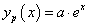alakban. Helyettesítsük be a differenciálegyenletbe, rendezzük, majd a jobb- és bal oldalak összevetésével írjuk fel az egyenletet a paraméterek meghatározásához:

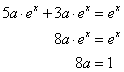
Ez után az általános megoldás:

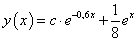
Oldjuk meg az 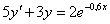egyenletet. Ennek homogén része megegyezik az előző feladat egyenletével. Most a partikuláris megoldást nem kereshetjük 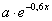alakban, mert az rezonál a homogén megoldással, így – x-el szorozva – a helyes alak: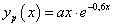. Helyettesítsük be a differenciálegyenletbe, rendezzük, majd a jobb- és bal oldalak összevetésével írjuk fel az egyenletet a paraméterek meghatározásához:

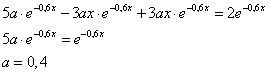
Ez után az általános megoldás:

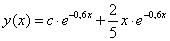
Oldjuk meg az 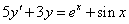egyenletet. Ennek homogén része megegyezik az előző feladat egyenletével. Ezt követően a partikuláris megoldást keressük 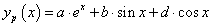alakban. Helyettesítsük be a differenciálegyenletbe, rendezzük, majd a jobb- és bal oldalak összevetésével írjuk fel az egyenleteket a paraméterek meghatározásához:

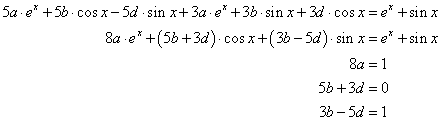
Az egyenletrendszer megoldása után az általános megoldás:

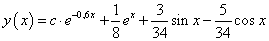
Oldjuk meg az 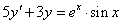egyenletet. Ennek homogén része megegyezik az előző feladat egyenletével. Ezt követően a partikuláris megoldást keressük 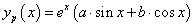alakban. Helyettesítsük be a differenciálegyenletbe, rendezzük, majd a jobb- és bal oldalak összevetésével írjuk fel az egyenleteket a paraméterek meghatározásához:

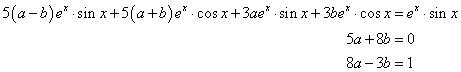
Az egyenletrendszer megoldása után az általános megoldás:

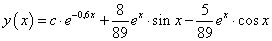
Oldjuk meg a 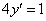egyenletet. A karakterisztikus polinom 4=0, amiből =0. Így a homogén általános megoldás Y(x)=c. Az inhomogén partikuláris megoldást keressük yp(x)=a alakban, de ez ugyan úgy konstans, mint Y(x), tehát rezonancia van. A partikuláris megoldást ezért x-el szorozva yp(x)=ax alakban kell keresnünk. Behelyettesítve a differenciálegyenletbe 4a=1 egyenlethez jutunk, amelynek megoldása: 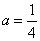. Az általános megoldás ezek után:

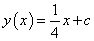
Oldjuk meg a 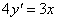egyenletet. A karakterisztikus polinom 4=0, amiből =0. Így a homogén általános megoldás Y(x)=c. Az inhomogén partikuláris megoldást keressük yp(x)=ax+b alakban, de ennek konstans része (b) rezonál Y(x)-el. A partikuláris megoldást ezért x-el szorozva yp(x)=ax2+bx alakban kell keresnünk. Behelyettesítve a differenciálegyenletbe 8ax+4b=3x egyenlethez jutunk. A paraméterek meghatározására szolgáló egyenletrendszer:

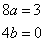
Ennek megoldása 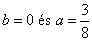. Az általános megoldás ezek után:

Oldjuk meg a 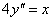egyenletet. A karakterisztikus polinom 4=0, amiből =0. Így a homogén általános megoldás Y(x)=c1e0x+c2 xe0x= c1+c2 x , mivel a 0 kétszeres gyök. Az inhomogén partikuláris megoldást keressük yp(x)=ax+b alakban, de ennek mindkét része rezonál Y(x)-el. Ha megszorozzuk x-el, akkor a bx még mindig rezonál c2 x –el, így x2-el kell szorozni. A helyes próbafüggvény tehát: yp(x)=ax3+bx2. Behelyettesítve a differenciálegyenletbe 24ax+8b=x egyenlethez jutunk. A paraméterek meghatározására szolgáló egyenletrendszer:

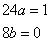
Ennek megoldása 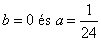. Az általános megoldás ezek után:

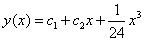
Oldjuk meg az 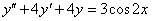egyenletet. A karakterisztikus polinom megoldásával megkapjuk a homogén általános megoldást:

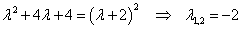
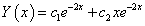
mert kettős gyökök vannak. Mivel nincs rezonancia, a próbafüggvény alakja:

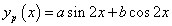
Behelyettesítve a differenciálegyenletbe, majd rendezve:

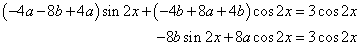
Az inhomogén egyenlet általános megoldása tehát:

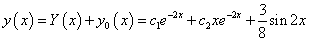
Oldjuk meg az 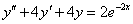egyenletet. A karakterisztikus polinom megegyezik az előző feladatéval, így a homogén általános megoldás:

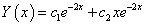
Mivel kétszeres rezonancia van, a próbafüggvény alakja:

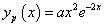
Behelyettesítve a differenciálegyenletbe, majd rendezve:

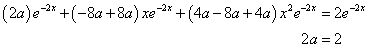
Az inhomogén egyenlet általános megoldása tehát:

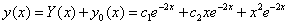
Oldjuk meg az 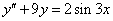egyenletet. A karakterisztikus polinom megoldásával megkapjuk a homogén általános megoldást:

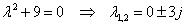
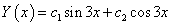
Mivel rezonancia van, a próbafüggvény alakja:

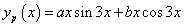
Behelyettesítve a differenciálegyenletbe, majd rendezve:

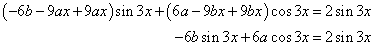
Az inhomogén egyenlet általános megoldása tehát:

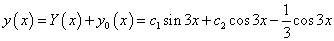
6.5. Műszaki példák

A műszaki feladatokban a független változó általában az idő (t). Ilyen esetekben a deriváltakat nem vesszővel, hanem ponttal jelöljük. A függő változó(k) pedig a fizikai jelentésüknek megfelelő megszokott jelölésüket kapják.

Határozzuk meg a folyadékszint változásának időfüggvényét egy töltés alatt álló kifolyás nélküli tartály esetében. Legyen a tartály keresztmetszete A, a kezdeti folyadékszint magasság h0, a töltő térfogatáram pedig b. t idő alatt a folyadékszint h-val változik, így a tartályban a folyadék térfogatának változása Ah. Ugyanezen idő alatt a beáramló folyadék mennyisége: bt. Az anyagmegmaradás törvénye alapján ez a két térfogat megegyezik. Az így nyert differenciaegyenlet felhasználásával felírható a rendszert leíró differenciálegyenlet (matematikai modell):

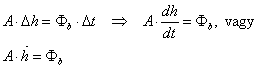
A homogén rész megoldását keressük et alakban. Behelyettesítve:

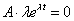
Ennek megoldása =0, így a homogén általános megoldás H(t)=c állandó.

Az inhomogén partikuláris megoldáshoz a differenciálegyenlet jobboldala alapján választott próbafüggvény hp(t)=a állandó lenne (mivel b állandó, tehát nulladfokú polinomnak tekinthetjük), de ez rezonál a homogén általános megoldással, így t-szeresét kell választani (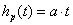). Behelyettesítve a differenciálegyenletbe:

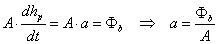
A differenciálegyenlet teljes megoldása ennek megfelelően:

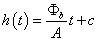
A c konstans meghatározásához használjuk fel a kezdeti feltételt, miszerint h(0)=h0. Ebből c=h0 adódik. A feladat – kezdeti feltételt is kielégítő – megoldása tehát:

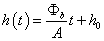
Egy m tömegű, c fajhőjű, a környezetétől hőáramlás szempontjából elzárt testtel h hőáramot közlünk. Határozzuk meg a test hőmérséklet változásának függvényét, ha a test kezdeti hőmérséklete 0.

Vissza		Előre
5. fejezet - Komplex számok	Főoldal	7. fejezet - Rendszerek és modellezési analógiák