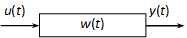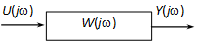4. fejezet - SISO LTI rendszerek vizsgálata a Laplace-operátoros tartományban
- 4.1. Átviteli függvény
- 4.2. Átviteli függvény meghatározása hatásvázlat segítségével
- 4.3. Átviteli függvény alkalmazása
- 4.4. Lineáris rendszerek stabilitás vizsgálata
- 4.5. Frekvencia átviteli függvény megjelenítése
- 4.6. Alaptagok átviteli függvénye, Nyquist és Bode diagramja
- 4.7. Holtidős tagok
- 4.8. Alaptagokból előállítható összetett tagok
- 4.9. Kidolgozott feladatok Bode és Nyquist diagram megrajzolására
- 4.10. Szűrő típusok Bode diagramja
Az előző fejezetben a matematikai eszköztár volt a fókuszban, ebben a fejezetben magát a rendszert vizsgáljuk.
4.1. Átviteli függvény
Definíció
Az átviteli függvény a ki- és a bemenőjel és Laplace-transzformáltjának hányadosa, ha a bemenőjel (gerjesztés) egy ugrásfüggvény és a rendszer (állapotváltozók) energiamentes kezdeti állapotából indulunk ki (ez nem zárja ki azt, hogy ), szokásos jelölése: és , de előfordul a szakirodalomban és jelölés is. A továbbiakban a jelölést használjuk.
|
|
(4.1) |
Értelmezés
Mivel a Dirac-impulzus Laplace-transzformáltja 1, ezért a Dirac-impulzusra adott válasz ( súlyfüggvény) Laplace-transzformáltja megegyezik az átviteli függvénnyel.
|
|
(4.2) |
Ha a rendszer energiamentes kezdeti állapotból indul, valamint (2.107) alakú differenciálegyenlettel írható le, továbbá a gerjesztés ugrás függvény, akkor az átviteli függvény s-re nézve valós együtthatójú racionális törtfüggvény.
|
|
(4.3) |
A megvalósíthatóság feltétele, hogy . Ha az egyenlőség áll fent, akkor (4.3) nem valódi tört, és polinom osztással átalakítható egy konstans plusz -re nézve valódi tört polinommá (kizárva azt a triviális esetet, amikor a számláló egyszerűen -szerese a nevezőnek, mert ebben az esetben nincs dinamikai összefüggés a kimenőjel és az bemenőjel között).
|
|
(4.4) |
Felhasználva az átviteli függvény definícióját
|
|
(4.5) |
Látható, hogy azt jelenti, hogy a bemenőjel közvetlenül (a dinamikát megkerülve) is megjelenik a kimeneten.
Mind a számláló, mind a nevező valós együtthatójú polinom, ezért az átviteli függvény zérusai, illetve pólusai vagy valósak, vagy komplex konjugált párok. Többszörös zérusok és pólusok is előfordulhatnak. Az átviteli függvény számlálóját és nevezőjét szokás gyöktényezős alakban felírni, mert ekkor a zérusok és pólusok közvetlenül látszanak,
|
|
(4.6) |
Az átviteli függvény (4.6) alakja minden esetben felírható, egy másik szokásos alak leginkább akkor használatos, ha az összes pólus és zérus valós, továbbá nullától különböző.
|
|
(4.7) |
A (4.7) alak előnye, hogy a rendszer erősítése és a időállandói közvetlenül látszanak. Ha egy (4.7) alakú átviteli függvénnyel rendelkező rendszerre egységugrás bemenőjelet kapcsolunk, akkor az állandósult érték a következő módon határozható meg
|
|
(4.8) |
Irányítástechnikai problémák esetén sokat segít a közelítő Bode diagram, ennek felrajzolásához célszerű a zérusokat és a pólusokat három csoportra osztani
-
nulla értékűek
-
nullától különböző valós értékűek
-
komplex konjugált párok
A nullától különböző valós értékű pólusok és zérusok esetén vezessük be a következő jelölést
|
|
( 4.9 ) |
Látható, hogy ebben az esetben is a értékek a rendszer időállandói. A komplex konjugált pár értékű pólusok és zérusok esetén vezessük be a következő jelölést
|
|
( 4.10 ) |
ahol
|
|
( 4.11 ) |
|
|
( 4.12 ) |
ahol
|
|
( 4.13 ) |
A paramétert csillapítási tényezónek nevezzük. A valós értékű pólusok esetén megegyezik az időállandóval, de komplex konjugált pár esetén nem azonos az időállandóval, hanem a közelítő Bode di agram töréspontjá nak a helyét jelöli ki körfrekvencia értékben kifejezve
|
|
( 4.14 ) |
Felhívjuk a figyelmet, hogy (4.14) kifejezésben kapott érték mértékegysége rad/sec és nem Hz.
A nem nulla értékű pólusokat és zérusokat kiemeljük, tegyük fel, hogy a számlálónak számú 0 értékű zérusa és számú 0 értékű pólusa van és ezek a zérusok és pólusok kapják a nagyobb sorszámot. Először a komplex konjugált pár értékű zérusok és pólusok kapnak sorszámot, ezekből , illetve pár van. Egy (2.107) alakú differenciálegyenlettel leírható rendszer átviteli függvénye felírható az alábbi általános alakban
|
|
( 4.15 ) |
Természetesen előfordulhat, hogy a számláló és a nevező gyökei megegyeznek és a kifejezésében szereplő racionális törtfüggvény egyszerűsíthető. Egy ilyen matematikai egyszerűsítés hátterében fizikai okokat is kell keresnünk. Később látni fogjuk, hogy bizonyos esetekben a nem megfigyelhető alrendszerekhez tartozó pólusok esnek ki ilyen egyszerűsítéssel.
4.1.1. Közönséges állandó együtthatós differenciálegyenletek megoldása átviteli függvény segítségével
Korábban láttuk, hogy bármely lineáris állandó együtthatós differenciálegyenlet-rendszer átírható (2.107) alakúra.
|
|
( 4.16 ) |
ahol az idő szerinti i-edik deriváltat jelöli. Az általánosságot nem csökkenti, ha az feltételezéssel élünk. A fizikai megvalósíthatóság feltétele .
A gerjesztés fizikailag mindig csak belépő függvényként értelmezhető ezért
|
|
( 4.17 ) |
ahol . Ennek megfelelően minden gyakorlati esetben
|
|
(4.18) |
Ugyancsak fizikai megfontolások alapján: véges gerjesztés esetén folytonos és hagyományos értelemben -szer deriválható.
|
|
(4.19) |
ahol az függvény -edik deriváltjának baloldali határértéke a helyen.
Általános esetben átviteli függvények segítségével is felírható
|
|
(4.20) |
ahol az függvény -edik deriváltjának helyen vett baloldali határértékétől a kimenetre vonatkozó átviteli függvénye. bevezetése elsősorban akkor célszerű, ha a rendszer differenciálegyenletét blokkdiagrammal szemléltetjük, ebben az esetben az átviteli függvények felírása sok esetben jelentősen leegyszerűsödik.
Energiamentes kezdeti állapot esetén
|
|
(4.21) |
inverz Laplace-transzformációjával kifejezhető.
4.1.2. Kidolgozott feladatok átviteli függvény alkalmazására
4 - 1 feladat átviteli függvény
Írja fel az átviteli függvényt
-
a 2-7 feladat alapján, ha a bemenőjel és a kimenőjel.
Megoldás
Mindhárom feladatban egy-energiatárolós tag szerepel, amelynek az átviteli függvénye általános alakban a (4.7) legegyszerűbb esete
|
|
(4.22) |
4 - 2 feladat (2.107) alakú differenciálegyenlet megold ása
A 2-16-2-17 feladatokban bemutattuk, hogy különböző rendszerek differenciálegyenletei átírhatók (2.107) alakúra. Tegyük fel, hogy egy rendszert az alábbi (2.107) alakú lineáris differenciálegyenlet ír le:
|
|
( 4.23 ) |
A rendszert az u(t) ugrás időfüggvény gerjeszti, és keressük az y(t) függvényt éskezdeti feltételekkel
Megoldás
Laplace-transzformáljuk a rendszeregyenletet:
|
|
( 4.24 ) |
Fejezzük ki a kimenőjel Laplace-transzformáltját
|
|
( 4.25 ) |
eset
Helyettesítsük be a megadott gerjesztés Laplace-transzformáltját
|
|
( 4.26 ) |
|
|
( 4.27 ) |
A nevező gyökei ( pólusai): .
A megoldás alakú lesz. A negatív hatványkitevőkből látszik, hogy „lecsengő” függvény. A pólus reciprokának valós részét időállandónak nevezzük. Esetünkben a rendszernek két időállandója van.
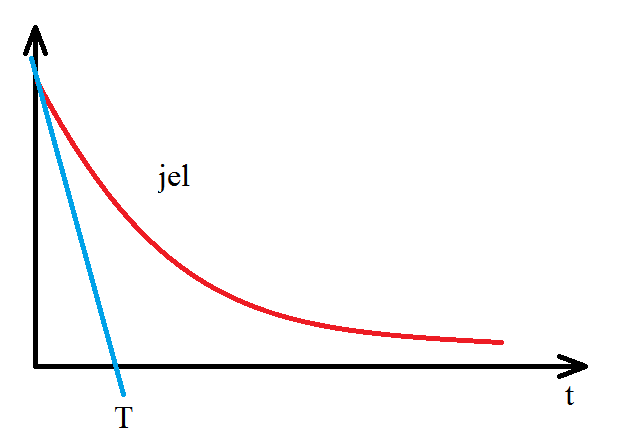
Egy-energiatároló esetén a T időállandó értékét a kezdeti érintő metszi ki. (ld. 4-2. ábra)
A feladatban keresett és együtthatók kiszámítása (egyszeres pólusokat feltételezve):
|
|
( 4.28 ) |
takarjuk le (s+2) kifejezést a nevezőből majd a letakart kifejezésben szereplő pólust helyettesítjük be a megmaradó egyenletbe. Így megkapjuk értékét
|
|
( 4.29 ) |
Hasonlóan megkapjuk értékét is, csak most (s+4)-et takarjuk le és –et helyettesítünk be.
|
|
( 4.30 ) |
tehát a keresett megoldás:
|
|
( 4.31 ) |
Ellenőrzés a végérték tételek segítségével:
|
|
( 4.32 ) |
|
|
( 4.33 ) |
|
|
( 4.34 ) |
|
|
( 4.35 ) |
eset
Helyettesítsük be az adott gerjesztést! Hasonlóan a fentiekhez, a megoldás:
|
|
( 4.36 ) |
|
|
( 4.37 ) |
4 - 3 feladat Folytonos érzelmi modell pillanatszerű eseménnyel
Képzeljük el, hogy létezik egy olyan különleges állatfaj, amelynek minden puskalövés után a félelemérzését egy lineárisdifferenciál egyenlettel írhatunk le. Minden puskalövés után két elkülöníthető hatás tapasztalható. Az első, rövidtávú hatás esetében a puskalövés eldördülése után a félelemérzet ugrásszerűen 0.9 relatív egységre nő, majd a 0.9 relatív egységről időállandóval exponenciálisan csökken nullára. A második, hosszú távú hatás esetében a puskalövés eldördülése után a félelemérzet ugrásszerűen 0.1 relatív egységre nő, majd a 0.1 relatív egységről időállandóval exponenciálisan csökken nullára. Az állat félelemérzése a két hatás összege. Ha egy puskalövés után újabb puskalövés dörren, akkor annak hatása ismét hozzáadódik az előző hatáshoz (a hozzászokás jelenséget nem modellezzük).
Írja fel a rendszert leíró lineáris differenciálegyenleteket.
-
A bemeneten milyen függvénnyel (disztribúcióval) modellezhető a puskalövés (figyelembe véve a két hatásról leírtakat)?
-
Hány állapotváltozóra van szükség a jelenség leírásához? (válaszát indokolja)
-
Írja fel a félelem alakulásának időfüggvényét egy puskalövés után.
-
Írja fel a félelemérzésre vonatkozó átviteli függvényt.
-
Milyen értékre nő az állat félelemérzete, ha periodikusan, időnként eldördül egy puskalövés?
Megoldás
Adatok:
|
|
( 4.38 ) |
Definíció alapján (ld. 161. oldal) az időállandó a pólus valós részének mínusz egyszeresének reciproka, esetünkben a két pólus értéke
|
|
( 4.39 ) |
1.
A puskalövés Dirac-delta (impulzus) disztribúcióval modellezhető, minthogy egyszeri kiugró értékű bemenetet (jelen esetben egy hangos durranást) jelent, előtte is és utána is az értéke nulla.
|
|
( 4.40 ) |
2.
Minthogy a puskalövés az állatból két különböző dinamikájú hatást vált ki, így ennek a két hatásnak a leírására két állapotváltozó bevezetésére van szükség:
|
|
( 4.41 ) |
3. A félelem alakulásának időfüggvénye a rendszer kimenőjele. A rövid és a hosszú távú hatást összegezni kell.
|
|
( 4.42 ) |
4 .
A rendszer átviteli függvénye megegyezik a Dirac-impulzusra adott válasz Laplace-transzformáltjával:
|
|
( 4.43 ) |
|
|
( 4.44 ) |
A kezdeti és az állandósult értéket meghatározhatjuk az átviteli függvényből (a várakozásainknak megfelelő eredményt kapunk)
|
|
( 4.45 ) |
|
|
( 4.46 ) |
5.
Könnyen belátható, hogy a bemenőjel egy Dirac impulzusokból álló végtelen sor
|
|
( 4.47 ) |
A bemenőjel Laplace-transzformáltja
|
|
( 4.48 ) |
A (4.48) sor akkor ad véges értéket, ha a sor kvóciensének abszolút értéke egynél kisebb, ez tetszőleges frekvencián és tetszőleges érték mellett biztosan teljesül, ha valós része pozitív
|
|
( 4.49 ) |
Ezzel a feltétellel a bemenőjel Laplace transzformáltja zárt alakban is megadható.
|
|
( 4.50 ) |
Az is megállapítható, hogy a félelemérzet nem válik végtelenné, de ebben az esetben a végérték tétel nem alkalmazható. Az állandósult állapotra jellemző középértéket a következő gondolatmenettel számíthatjuk ki. A Dirac impulzust az egységterületű impulzusból származtattuk, most az ellenkezőjét kell tenni, vagyis a Dirac-impulzust átlagoljuk egy periódusra és egy nagyságú hosszúságú impulzussal helyettesítjük, amelyek folyamatosan érkeznek egymás után, vagyis a bemenőjel a következő átlag értékkel helyettesíthető
|
|
( 4.51 ) |
Ennek alapján a kimenőjel átlagértéke
|
|
( 4.52 ) |
4 - 4 feladat Folytonos érzelmi modell nem pillanatszerű eseménnyel
Tegyük fel, hogy van egy különleges állatfaj, amelyiknek az érzelmi állapotát egyetlen változóval lehet leírni, ha e változó értéke pozitív, akkor jókedvű, ha ez negatív, akkor rosszkedvű. Ez az állat egy olyan állatkertben él, ahol csak 3 különböző esemény történhet vele. Természetesen az itt leírt minta alapján több fajta érzelem (pl, öröm, bánat, félelem és düh), továbbá több esemény is megadható. Minden eseménynek van egy kezdete és egy vége, továbbá minden esemény hat az érzelmi állapotra, amelyben két elkülöníthető hatás tapasztalható. Az első - rövidtávú érzelem- az esemény kezdetekor gyors felfutási idővel, pontosabban rövid időállandóval a táblázatban megadott értékkel növeli meg az érzelmet leíró változó értékét, majd ez az érték az esemény befejezésekor időállandóval lecseng. A második, hosszú távú hatás jellegre hasonló, de a felfutás és lecsengés időállandója nagyobb a rövid távú hatásénál, továbbá a hosszú távú érzelem csak a táblázatban megadott érték ötödére fut fel. Az események hatásai szuperponálódnak (nincs telítődés és hozzászokási jelenség). Megengedett az is, hogy egy esemény hamarabb befejeződjön, mint ahogy az eseményhez tartozó érzelmi felfutás gyakorlatilag befejeződne (elvileg minden felfutás a végtelenben fejeződik be).
|
esemény sorszáma |
esemény leírása |
állandósult érték |
|
1. |
egyedül unatkozik |
-1 |
|
2. |
gondozó közelében van |
1 |
|
3. |
a gondozóval játszik |
3 |
|
4. |
a gondozó megbünteti |
-3 |
|
5. |
látogatók kedveskednek vele |
2 |
|
6. |
látogatók bosszantják |
-2 |
-
A bemeneten milyen függvénnyel modellezhető az esemény kezdete és vége?
-
Hány állapotváltozóra van szükség a jelenség leírásához? (válaszát indokolja)
-
Írja fel az érzésre vonatkozó átviteli függvényt.
-
Tegyük fel, hogy csak egyetlen állandósult értékű esemény történik, és annak kezdete és vége ismert. Írja fel az érzelem alakulásának időfüggvényét.
Megoldás
1.
Az esemény kezdete és vége is egy-egy ugrásfüggvénnyel modellezhető. Jelölje az -dik esemény kezdetét és végét , valamint az eseményhez tartozó állandósult értéket . Célszerű az esemény kezdetét és végét mindig párban megadni, így az -dik eseményhez tartozó bemenőjel időfüggvénye és Laplace-transzformáltja
|
|
( 4.53 ) |
2.
Minthogy minden esemény az állatból két különböző dinamikájú hatást vált ki, így ennek a két hatásnak a leírására két állapotváltozó bevezetésére van szükség, amelyek hatását összegezni kell:
3 .
A rövid és hosszú távú hatást egy-egy párhuzamosan kapcsolt egységnyi, illetve 0.2 erősítésű energiatárolóval modellezhetjük
|
|
( 4.54 ) |
4 .
Az előző pontból ismert a rendszer átviteli függvénye és adott a bemenőjel
|
|
( 4.55 ) |
|
|
( 4.56 ) |
4 - 5 feladat Tömeg-rugó rendszer
Adott a 4-3. ábra látható tömeg-rugó rendszer, ahol a kimenőjel a tömeg elmozdulása, amelynek a nyugalmi állapotához rögzítjük a nulla elmozdulási szintet. A bemenőjel a második rugó végének az elmozdulása.
-
Írja fel a rendszer átviteli függvényét, és oldja meg a differenciálegyenletet egységugrás gerjesztéssel.
-
Végérték tétellel határozza meg az állandósult elmozdulás értéket.
-
Vizsgáljuk meg, hogy milyen gyorsan kell a rugó végét mozgatni, hogy az egységugrással lehessen közelíteni.
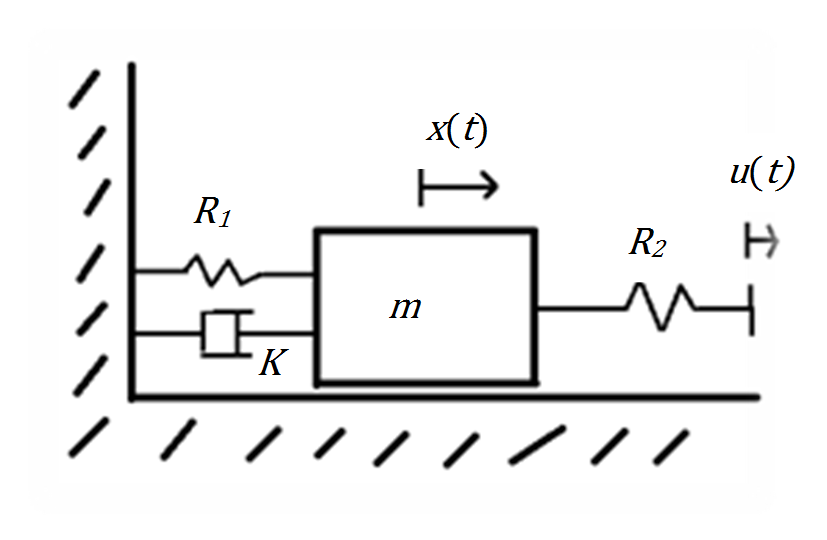
Adatok: m=10 [kg] ; R1=1000 [N/m]; R2=500 [N/m]; K=600 [Ns/m]
Megoldás
A mozgásegyenlet:
|
|
(4.57) |
ahol a gerjesztés és a kimenőjel. Nyugalmi állapotban az állapotváltozók kezdeti értéke nulla. Laplace-transzformáljuk az egyenletet:
|
|
(4.58) |
A kimenőjel Laplace-transzformáltja:
|
|
(4.59) |
A rendszer átviteli függvénye:
|
|
(4.60) |
Adatokat behelyettesítve:
|
|
(4.61) |
|
|
(4.62) |
|
|
(4.63) |
Vizsgáljuk meg a rendszer viselkedését egységugrás bemenetre.
Egységugrás függvénnyel gerjesztett rendszer
A bemenet legyen egységugrás függvény. Ez fizikailag azt jelenti, hogy nagyon gyorsan megrántjuk a második rugó végét. Fontos kérdés az is, hogy mikor tekinthetjük a rugó mozgatását nagyon gyorsnak (erre később visszatérünk).
|
|
(4.64) |
Az átviteli függvény nevezőjének szorzattá alakítása:
|
|
(4.65) |
Az elmozdulás függvény pólusai:
|
|
(4.66) |
|
|
(4.67) |
A rendszer időállandói, a pólusok valós részének reciprokának mínusz egyszerese:
|
|
(4.68) |
Az elmozdulás függvénye az időtartományban a következő alakot fogja felvenni:
|
|
(4.69) |
A konstans szorzókat meghatározzuk a letakarásos módszerrel (ld. 3.2.7 pont):
|
|
(4.70) |
|
|
(4.71) |
|
|
(4.72) |
A tömeg elmozdulásának (kimenőjelnek) időfüggvénye:
|
|
(4.73) |
Elemezzük a kapott eredményt! A két rugó együttes hosszát egy egységnyivel növeltük meg. Mivel a két rugóállandó nem egyenlő, konkrétan az 1. rugó kétszer olyan erős, mint a 2. rugó, ezért állandósult állapotban a 2. rugó megnyúlása kétszerese lesz az 1. rugó megnyúlásának. Vagyis az egységnyi megnyúlás 1/3-2/3 arányban oszlik meg a két rugó között. A tömeg elmozdulása megegyezik az első rugó megnyúlásával. Ez kiolvasható a (4.60) átviteli függvényből. Egységugrás bemenőjelre a végérték tételt alkalmazva kapjuk
|
|
(4.74) |
A tömeget a rugóerők eredője mozgatja, ebből következik, hogy a beállási időt a rugóállandók határozzák meg. Minél merevebb a rugó, a rugó végének adott elmozdulás annál nagyobb rugóerőt eredményez és annál gyorsabb lesz a beállás. A beállás idejét egy gyors fejszámolással is megbecsülhetjük. Esetünkben a kisebb pólus kb. két és fél körül van, annak reciproka kb. 0.4. Az állandósult érték 99% körüli megközelítéséhez kb. 0.4∙5=2s szükséges. Ha mindkét rugóállandót tizedére csökkentjük, akkor az átviteli függvény két pólusa . Látható, hogy a kisebb pólus kb. egy nagyságrenddel lecsökkent, így a beállási idő egy nagyságrenddel megnő.
A jelen adatok mellett a tömeg lengések nélkül áll be. Ez a kellően nagy csillapításnak köszönhető. Ha a csillapítást pl. tizedére csökkentjük, akkor az átviteli függvény pólusai konjugált komplex párrá válnak . Ez (3.99) alapján azt jelenti, hogy a tömeg 1/3s időállandóval lecsengő kb. 12 rad/sec körfrekvenciájú lengésekkel áll be az állandósult értékre. A lengések amplitúdója 5∙1/3≈1.7s környékén csökken 1% alá, ez alatt az idő alatt a periódusok száma 3-nál több, 4-nél kevesebb. Ismét csak fejben számolva a π értékét 3-mal közelítve a lengések periódusideje kb. 0.5s. Összefoglalva: a tömeg kb. három lengés (három jól kivehető lokális csúcs) után kb. 1.7s alatt áll be. A pontos számítást az olvasóra bízzuk.
Vizsgáljuk meg, hogy milyen gyorsan kell a rugó végét mozgatni, hogy az egységugrással lehessen közelíteni. Tegyük fel, hogy a rugó végét állandó sebességgel idő alatt mozgatjuk egységnyi távolságra. A rugó végének mozgását leíró egyenlet
|
|
(4.75) |
A (4.75) gerjesztés Laplace-transzformáltja
|
|
(4.76) |
|
|
(4.77) |
Az elmozdulás függvénye az időtartományban a következő alakot fogja ölteni:
|
|
(4.78) |
csak a tartományban jelenik meg, a tartományban nem játszik szerepet. kivételével a konstans szorzókat meghatározhatjuk a letakarásos módszerrel (ld. 3.2.7 pont):
Látható, hogy (4.78) a következő (4.79) egyenlet differenciahányadosa a tartományban
|
|
(4.79) |
A fentiekből következik, hogy határátmenetben, ha , akkor a (4.78) egyenlet tart a (4.69) egyenlethez. Vagyis ha a rugó végét állandó sebességgel idő alatt mozgatjuk egységnyi távolságra, akkor ez a mozgás annyira tekinthető egységugrásnak, amennyire a (4.79) egyenlet lépéssel felírt differenciahányadosa a differenciálhányadosának tekinthető.
4 - 6 feladat D ifferenciálegyenlet megoldása szinuszos gerjesztés esetén
Ha egy csillapítatlan rezgőmozgást végző tömegpontra periodikus erő hat, a pont kényszerrezgést végez. Legyen a periodikus gerjesztő erő , ekkor a mozgást leíró differenciálegyenlet:
|
|
(4.80) |
Legyenek a kezdeti feltételek: . Határozzuk meg a kitérést, mint az idő függvényét.
-
A feladatot oldjuk meg az operátoros tartományban az átviteli függvény felírásával és az időtartományban is. Hasonlítsuk össze a két megoldási módszert!
Megoldás az operátoros tartományban
A rendszer átviteli függvénye
|
|
( 4.81 ) |
Az első derivált kezdeti értékre vonatkozó átviteli függvény
|
|
( 4.82 ) |
Az operátoros tartományban a gerjesztés
|
|
( 4.83 ) |
A szuperpozíció elvének kihasználásával és a két átviteli függvény segítségével Y(s) kifejezhető:
|
|
( 4.84 ) |
A Laplace-transzformáció tulajdonságait figyelembe véve az inverz transzformációt tagonként végezhetjük el. A második tag egyszerűen inverz Laplace-transzformálható (3.91) alapján.
|
|
( 4.85 ) |
Az első tagot gyöktényezőkre bontva
|
|
( 4.86 ) |
Az első tag visszatranszformálását részlettörtekre bontással is elvégezhetjük, az együtthatók legyenek sorra , , és , amelyeket , , és helyettesítéssel kapunk
Az első tag inverz Laplace-transzformáltja komplex formában
|
|
( 4.91 ) |
Behelyettesítve
|
|
( 4.92 ) |
(4.92) átírható
|
|
( 4.93 ) |
Másképpen is eljárhatunk, hogy meghatározzuk a (4.86) inverz Laplace-transzformáltját. Felhasználhatjuk a következő kiegészítő összefüggést:
|
|
( 4.94 ) |
amellyel az első tag inverz transzformáltja a tartományban:
|
|
( 4.95 ) |
a differenciálegyenlet megoldása (továbbra is csak a a tartományban) tehát:
|
|
( 4.96 ) |
Megoldás az idő tartományban
A kapott differenciálegyenlet állandó együtthatós, inhomogén, másodrendű, közönséges, lineáris egyenlet. Általános megoldását a homogén rész általános megoldása és az inhomogén egyenlet egy partikuláris megoldása összegeként kaphatjuk meg. A megfelelő homogén egyenlet megoldását keressük alakban,
A homogén rész megoldása két egymástól lineárisan független partikuláris megoldás összegeként kapható. A differenciálegyenlet partikuláris megoldását alakban keressük, mert ez az egyetlen függvény, amely arányos deriváltjaival. Behelyettesítve a differenciálegyenletbe:
|
|
(4.97) |
Ez két lineárisan független megoldás, hiszen csak akkor áll fenn, ha . A homogén rész általános megoldása tehát:
Alkalmazva az EULER-féle formulát: .
A kezdeti feltételeket ugyan később kell csak figyelembe venni, de célszerűségi okokból ettől most eltérünk. Kihasználjuk, hogy , ezért a megoldásban cos-os tag biztosan nem lesz, így
|
|
(4.98) |
azaz B=0. Ellenőrizzük most, hogy yh valóban megoldása-e a homogén egyenletnek:
|
|
(4.99) |
Behelyettesítve:
|
|
(4.100) |
Látható tehát, hogy yh valóban a homogén egyenlet megoldása. Az inhomogén egyenlet egy partikuláris megoldását keressük
|
|
(4.101) |
próbafüggvény felhasználásával. Az kezdeti feltétel miatt most is megállapítható, hogy . Helyettesítsük be a próbafüggvényt a differenciálegyenletbe és rendezzük:
|
|
(4.102) |
Ahogy az várható is volt, a megoldás egy része (a homogén egyenlet megoldása) kiesett, így az egyik paramétert meg lehetett határozni. Az egyik (y(0)=0) kezdeti feltételt már felhasználtuk, vegyük most a másikat A meghatározásához:
|
|
( 4.103 ) |
Behelyettesítés után nyerjük a differenciálegyenlet megoldását:
|
|
( 4.104 ) |
Látható, hogy ezzel a módszerrel is ugyanazt az eredményt kaptuk.
4 - 7 feladat Domináns pólus
Adott egy olyan rendszer, amelynek nincs integráló és deriváló tagja, és az átviteli függvénye a következő alakú
|
|
(4.105) |
Az egyszerűség kedvéért tegyük fel, hogy az összes pólus negatív valós szám, nincsenek többszörös pólusok. Ugyancsak a könnyebb tárgyalási mód kedvéért tegyük fel, hogy
|
|
(4.106) |
Továbbá feltételezzük azt is, hogy az egyik pólus abszolút értéke sokkal kisebb a többi pólusnál. Ezt nevezzük domináns pólusnak, és legyen a sorszáma 1. Kapcsoljunk egységugrást a bemenetre. Lássuk be, hogy a rendszer válaszát alapvetően a domináns pólus hatása határozza meg.
Megoldás
A kimenőjel Laplace-transzformáltja a következő alakú lesz
|
|
(4.107) |
Ezt úgy is felfoghatjuk, hogy az eredeti átviteli függvényt kibővítjük egy -edik sorszámú értékű pólussal, ezért az inverz Laplace-transzformált alakja a következő
|
|
(4.108) |
A kifejtési tétel alapján és (4.106) alapján az pólushoz tartozó konstans értéke 1. Ugyancsak közelítőleg 1 az értéke konstansnak. Mivel a feltételezésünk szerint
|
|
(4.109) |
A többi együttható abszolút értéke -nél sokkal kisebb, mert azok kiszámításánál –hez képest a nevezőbe sokkal nagyobb abszolút értékű számokat helyettesítünk.
Konkrét példaként legyen az átviteli függvény
|
|
(4.110) |
A rendszer válasza egységugrás bemenőjelre
|
|
(4.111) |
Inverz Laplace-transzformálva tartományban
|
|
(4.112) |
4.2. Átviteli függvény meghatározása hatásvázlat segítségével
Az átviteli függvény felírásához alapvetően a rendszert leíró differenciálegyenletekből kell kiindulni. Az átviteli függvény meghatározásához szükség van az egyenletek Laplace-transzformálására, és megfelelő átrendezésére. Az átrendezés történhet a Laplace-transzformálás előtt vagy után a szokásos matematikai átalakításokkal (erre láttunk példát a 2-16-2-19 feladatok kapcsán). A mérnökök sokszor törekednek arra, hogy a problémákat szemléletesen, ábrák segítségével jelenítsék meg. Az átalakítást segíti az ún. hatásvázlat, amelyet tekinthetünk a rendszer differenciálegyenleteinek grafikus megjelenítésének, amelyből jól látható az egyenletek struktúrája és útmutatóként is használható a differenciálegyenletek elvi megoldására. (ld. 4-4. ábra).
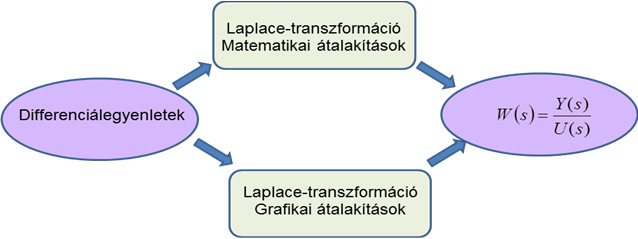
Ennek különös jelentősége volt az analóg számítógépek idején. Egy kellően részletes hatásvázlat egyben egy analóg számítógépes program. A személyi számítógépek megjelenésével (azok számítási kapacitásának növekedésével) az analóg számítógépek eltűntek, de a hatásvázlat továbbra is fontos szerepet játszik a differenciálegyenletek elvi megoldásában.
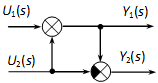
A be- és kimenőjel között kell matematikai kapcsolatot teremteni. Ebből következően a jelnek van terjedési iránya, alapvetően balról haladunk jobbra, ezt nevezzük előrevezető iránynak. Gyakran szükséges a kimenet visszacsatolása, általában a jobbról balra haladva visszacsatoló ágról beszélünk. A jelekkel végzendő matematikai műveletek: összegzés (előjelesen), szorzás egy konstans értékkel, integrálás, deriválás és konvolúció. Mivel egy jellel párhuzamosan is lehet műveletet végezni, így szükség van elágazásra is. A MATLAB Simulink legfontosabb szimbólumai a 4-5. ábran láthatók. Megjegyezzük, hogy az ábrán kétféle összegzőt látunk. Az első a klasszikus jelölésnek megfelelően egy kör, amelynek egy kimenete és legfeljebb három egymásra merőleges bemenete van. A második típusú összegző négyszögletes, ennek igazán akkor van jelentősége, ha több jelet kívánunk összegezni. Klasszikus jelöléssel több egymásután kapcsolt kör alakú összegzőt kell alkalmazni, a négyszögletes összegzőhöz könnyebb több bemenetet rajzolni (ld. 4-6. ábra).
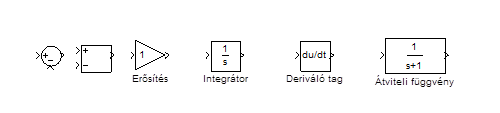
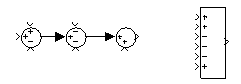
4.2.1. Hatásvázlatok
Az eddigiekben a rendszert egy egységként kezeltük, és különböző módszereket mutattunk be arra, hogyan határozható meg a rendszer válasza (Laplace transzformáció, Köz.diff egy melléklet), azaz mi lesz a hatása annak, ha a bemenetre valamilyen jelet kapcsolunk:
|
Időtartomány |
Operátoros tartomány |
Frekvenciatartomány |
|
vagy rendszer jellemző függvénnyel:
|
|
|
|
(konvolúciós integrál) |
|
|
Mint látható, a kimenet mindhárom esetben valamilyen szorzással állítható elő. Bonyolultabb esetekben célszerű a rendszert részrendszerekre bontani. Lineáris rendszerek esetén alkalmazható a szuperpozíció, de a felbontás ezt nem mindig teszi lehetővé. A következő fejezetekben azzal foglalkozunk, hogy hogyan lehet a részrendszerekből előállítani a teljes rendszert egyben leíró kapcsolatot. Ennek leírására az operátoros tartománybeli legegyszerűbb írásmódot választjuk.
4.2.2. Jelölések
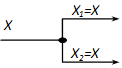
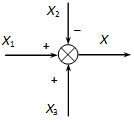
A részrendszerek között a jel haladását egy irányított szakasz jelzi, amelynek minden pontjában állandó a jel értéke. A jel értékét a szakasz fölé (mellé, alá, stb.) írhatjuk, de ha értéke egyértelmű, akkor nem kötelező kiírni. A részrendszereket téglalappal jelezzük, amelybe a rá jellemző átviteli függvényt írjuk. Ha a jel valamely pontban elágazik, akkor minden irányban gyengítetlenül terjed, azaz minden irányban azonos lesz. Az előjeles összegzés jelölésére két módszer terjedt el. Az egyik esetben kiírjuk az előjelet, a másikban pedig a negatív előjelet feketítéssel jelöljük. Mindkét esetben az összegzést körrel jelöljük.
|
jel haladása
|
elágazás
|
|
összegzés előjel kiírással
|
összegzés feketítéssel
|
4.2.3. Soros kapcsolás
Tegyük fel, hogy a rendszerünket két alrendszerre bontottuk úgy, hogy az első kimenete egyben a második bemenete:
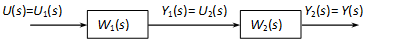
Határozzuk meg az eredő átviteli függvényt.
A számítás lépései
Az eredmény
|
|
( 4.113 ) |
Két sorba kapcsolt, átviteli függvénnyel adott rendszer eredő átviteli függvénye tehát a két átviteli függvény szorzataként állítható elő.
4.2.4. Párhuzamos kapcsolás
Párhuzamos kapcsolás esetén a két alrendszer ugyanazt a bemenőjelet kapja, kimenetük pedig összeadódik:
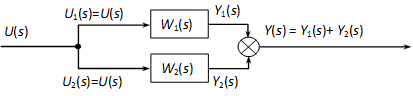
Határozzuk meg az eredő átviteli függvényt Y(s) és U(s) között.
A számítás lépései
|
|
( 4.114 ) |
Az eredmény
|
|
( 4.115 ) |
Két párhuzamosan kapcsolt, átviteli függvénnyel adott rendszer eredő átviteli függvénye tehát a két átviteli függvény összegeként állítható elő. Mint látható, ebben az esetben alkalmazható a szuperpozíció.
4.2.5. Visszacsatolás
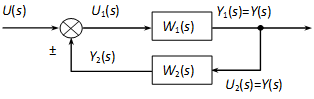
Határozzuk meg az eredő átviteli függvényt Y(s) és U(s) között.
A számítás lépései
|
|
( 4.116 ) |
Az eredmény
|
|
( 4.117 ) |
A szorzatot a felnyitott kör átviteli függvényének nevezzük, szokásos jelölése . A nevezőben a felnyitott kör átviteli függvénye előtt az előjel negatív visszacsatolás esetén pozitív, pozitív visszacsatolás esetén negatív.
4.2.6. Hatásvázlat átalakítása
Egy bonyolultabb rendszer hatásvázlata nagyon „ágas-bogas” lehet. A következőkben megnézzük, milyen átalakításokkal lehet egyszerűbb, az előző fejezetben ismertetett részeket tartalmazó blokkokra bontani. Az átalakítások során csak olyan műveleteket lehet végezni, amelyek az eredőt nem befolyásolják, de lehet például új taggal bővíteni, vagy tagokat összevonni.
4.2.6.1. Elágazási pont áthelyezése tag elől tag mögé
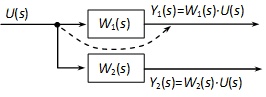
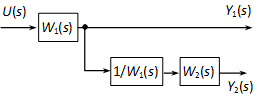
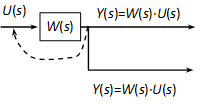
4.2.6.2. Elágazási pont áthelyezése tag elé
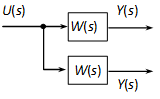
4.2.6.3. Összegzési pont áthelyezése tag mögé
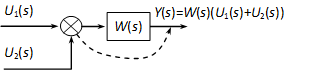
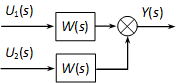
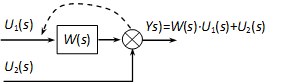
4.2.6.4. Összegzési pont áthelyezése tag elé
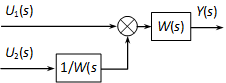
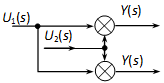
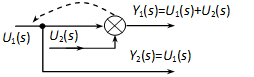
4.2.6.5. Összegzési pont és elágazási pont felcserélése
Ha lehet, ne alkalmazzuk, mert általában bonyolultabb hatásvázlatot kapunk, mint amilyenből kiindultunk!
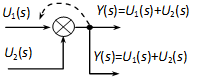
Megjegyezzük, hogy az analóg számítógépek programozása hasonló feladat, mint a hatásvázlat felírása. Általános célú analóg számítógépek használata a személyi számítógépek megjelenésekor erőteljesen háttérbe szorult. Ezt követően sokáig megmaradtak a (műveleti erősítőkre alapozott) analóg elektronikai szabályozók. Ezeket lehet célorientált analóg számítógépeknek tekinteni.
4.2.7. Kidolgozott feladatok hatásvázlat átalakításra
Az egyszerűség kedvéért a függvények s független változóját mindenhol elhagyjuk. Az átviteli függvények minden feladatban: . A megoldások eleinte minden lépést megmutatnak, a későbbiekben azonban azok, amelyek már szerepeltek, egy lépésben kerülnek végrehajtásra.
4 - 8 . feladat H atásvázlat átalakítás a
Határozzuk meg az eredő átviteli függvényt a következő ábrán látható hatásvázlat alapján:
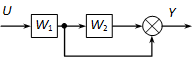
Megoldás:
Ha egy ágra semmilyen átviteli függvény sincs megadva, akkor úgy értelmezhetjük, mintha W=1 lenne. A 4-17. ábrán szaggatottal körülhatárolt rész két tag párhuzamos kapcsolását tartalmazza, ennek eredője a két átviteli függvény összege.

Az átalakítás után a két tag soros kapcsolása marad, így az eredő:
|
|
( 4.118 ) |
4 - 9 . feladat H atásvázlat átalakítás a
Határozzuk meg az eredő átviteli függvényt a következő ábrán látható hatásvázlat alapján:
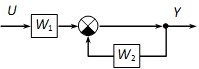
Megoldás:
A 4-19. ábrán szaggatottal körülhatárolt rész negatív visszacsatolást tartalmaz, ennek eredője (4.117) alapján meghatározható.

Az átalakítás után az két tag soros kapcsolása marad, így az eredő:
|
|
( 4.119 ) |
4 - 10 . feladat H atásvázlat átalakítás a
Határozzuk meg az eredő átviteli függvényt a következő ábrán látható hatásvázlat alapján:
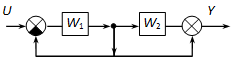
Megoldás:
A középen lévő ágat rajzoljuk két külön ágként, ekkor sorba kapcsolva egy negatív visszacsatolást és egy párhuzamos kapcsolást kapunk. Ezután az eredő az eddigiek alapján már könnyen meghatározható.

Az átalakítás után két tag soros kapcsolása marad, így az eredő:
|
|
( 4.120 ) |
4 - 11 . feladat H atásvázlat átalakítás a
Határozzuk meg az eredő átviteli függvényt a következő ábrán látható hatásvázlat alapján:
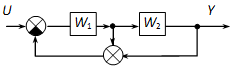
Megoldás:
A két összegzési pontot össze lehet vonni, az előjelekre azonban figyelni kell. Kis betűkkel (a, b) az ágakon levő jel értékét jelöltük.
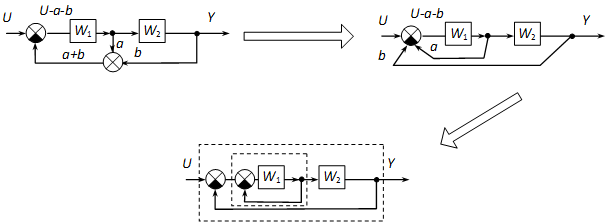
Az eredő meghatározása közben emeletes törteket kapunk. A következő eljárás javasolható ebben az esetben: határozzuk meg a számlálóban és a nevezőben levő törtek nevezőinek legkisebb közös többszörösét, majd ebből képezzünk 1/1 alakú törtet, amellyel megszorozzuk a törtet. A feladatban ezek a törtek és .
|
|
( 4.121 ) |
4 - 12 . feladat H atásvázlat átalakítás a
Határozzuk meg az eredő átviteli függvényt a következő ábrán látható hatásvázlat alapján:
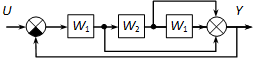
Megoldás:
Az jobboldali összegzési pontot bontsuk szét, így egymásba ágyazott párhuzamos kapcsolású részeket kapunk.
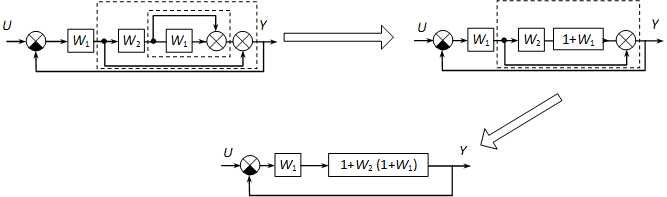
|
|
( 4.122 ) |
4 - 13 . feladat H atásvázlat átalakítás a
Határozzuk meg az eredő átviteli függvényt a következő ábrán látható hatásvázlat alapján
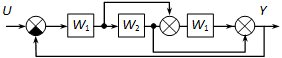
Megoldás:
Ahhoz, hogy számolható alrendszerekre váljon szét, át kell alakítani. Több lehetőségünk is van, az egyik például egy elágazási pont áthelyezés, a másik pedig egy összegzési pont áthelyezés. Mindkét módszerrel megoldjuk a feladatot, a közös bennük – ami általában célszerű is – hogy „nyújtani” fogják a hurkot. Ennek hatása látszik a következő ábra felső sorának jobb oldalán, ahol a szaggatott rész eredője könnyen számíthatóvá vált.
Csomópont áthelyezéssel:
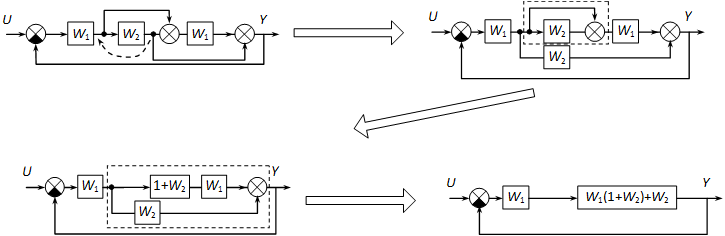
|
|
( 4.123 ) |
Összegzési pont áthelyezéssel:
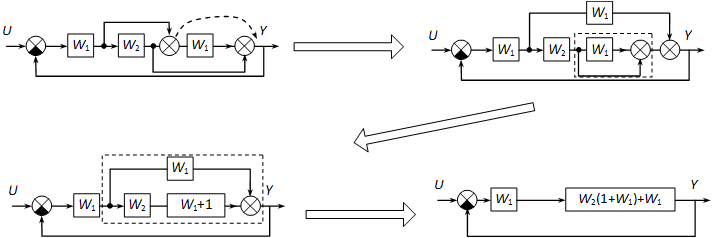
|
|
( 4.124 ) |
Mint látható, a két eredmény megegyezik.
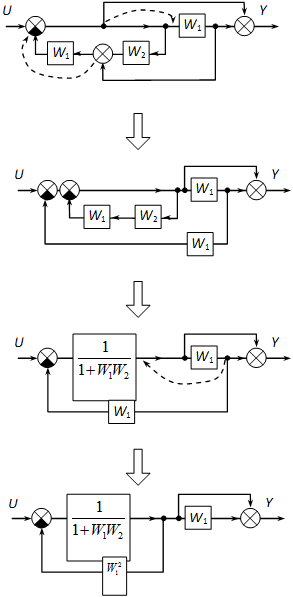
4 - 14 . feladat H atásvázlat átalakítás a
Határozzuk meg az eredő átviteli függvényt a következő ábrán látható hatásvázlat alapján:
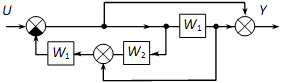
Megoldás:
Két eltérő módszerrel is megoldjuk a feladatot.
Hatásvázlat átalakítással:
|
|
( 4.125 ) |
Algebrai egyenletekkel:
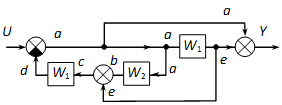
Az ábrán kis betűkkel (a,b,c,d,e) jelöltük a jelek értékét. Írjuk fel az ezeket előállító egyenleteket:
|
|
( 4.126 ) |
|
|
( 4.127 ) |
4.3. Átviteli függvény alkalmazása
Az átviteli függvény alkalmas egy lineáris időinvariáns rendszer legfontosabb tulajdonságainak leírására, de a fizikai hátterét azért nehéz közvetlenül elemezni, mert egy komplex változós komplex függvény. (4.2) alapján az átviteli függvény megegyezik a súlyfüggvény Laplace-transzformáltjával. Ez azért egy fontos megállapítás, mert a (2.107) alakú differenciálegyenlettel leírható rendszerek impulzus válasza (súlyfüggvénye) garantáltan lecsengő, ezért létezik Fourier-transzformáltja, vagyis a frekvencia átviteli függvénye (frekvencia karakterisztikája) az átviteli függvényből egyszerű helyettesítéssel megkapható. A frekvencia átviteli függvény fizikailag értelmezhető.
4.3.1. Kidolgozott feladatok átviteli függvények felírására
4 - 15 feladat Külsőgerjesztésű egyenáramú motor átviteli függvényei
Az hogy mit tekintünk bemenetnek és kimenetnek egy motor esetében, az a motor használatától is függ. A szabályozott bemenet lehet a motor armatúra feszültsége vagy lehet az armatúra árama is. Értelemszerűen, ha az egyiket szabályozzuk, akkor a másik kiadódik, vagyis az kimenetként kezelendő. Az terhelőnyomatékot a motor szempontjából minden esetben bemenetnek kell tekintenünk. (A terhelés szempontjából az természetesen kimenet). Válasszuk mellé először bemenetnek a motor armatúra feszültségét, és vizsgáljuk meg azt, hogy ezek a bemenetek miként hatnak a motor szögsebességére.
-
Írja fel egy külső gerjesztésű egyenáramú motor átviteli függvényét az bemenet és kimenet között
-
Írja fel egy külső gerjesztésű egyenáramú motor átviteli függvényét az bemenet és kimenet között.
-
Írja fel egy külső gerjesztésű egyenáramú motor átviteli függvényét az bemenet és kimenet között.
-
Írja fel egy külső gerjesztésű egyenáramú motor átviteli függvényét az bemenet és kimenet között.
-
Az átviteli függvények segítségével írja fel az szögsebesség időfüggvényét az armatúra feszültség bekapcsolása, illetve terhelésrádobás után.
-
A végérték tétel segítségével mindkét esetben adja meg az állandósult értéket (szuperpozíció elvét kihasználva, a két hatás egymástól függrtlenül számítható).
Megoldás:
A külső gerjesztésű egyenáramú motor helyettesítő vázlata két fő részre tagolódik, az armatúra körre és a gerjesztő körre (ld. 4-32. ábra).
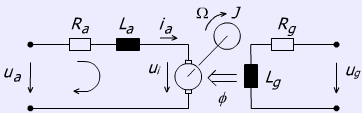
A gerjesztő tekercs egy Rg és Lg paraméterekkel jellemzett R-L körként modellezhető. Az armatúra kör egy soros R-L impedancia és indukált feszültség sorba kapcsolásával modellezhető. Az egyenáramú gép armatúra körének egyenlete:
|
|
( 4.128 ) |
nyomatékegyenlet:
|
|
( 4.129 ) |
a mozgásegyenlet:
|
|
( 4.130 ) |
ahol, a motor armatúra feszültsége, a motor armatúra árama, az armatúra kör ellenállása, az armatúra kör induktivitása, : a motor fordulatszáma, a motor indukált feszültsége, a motor villamos nyomatéka, a motor terhelő nyomatéka, a motor fluxusa, a forgórész inerciája és : a motor gyorsító nyomatéka.
A differenciál egyenleteteket átírjuk a Laplace operátoros tartományba:
|
|
( 4.131 ) |
A (4.131) egyenletek alapján felrajzolhatjuk a motor hatásvázlatát (ld. 4-33. ábra).
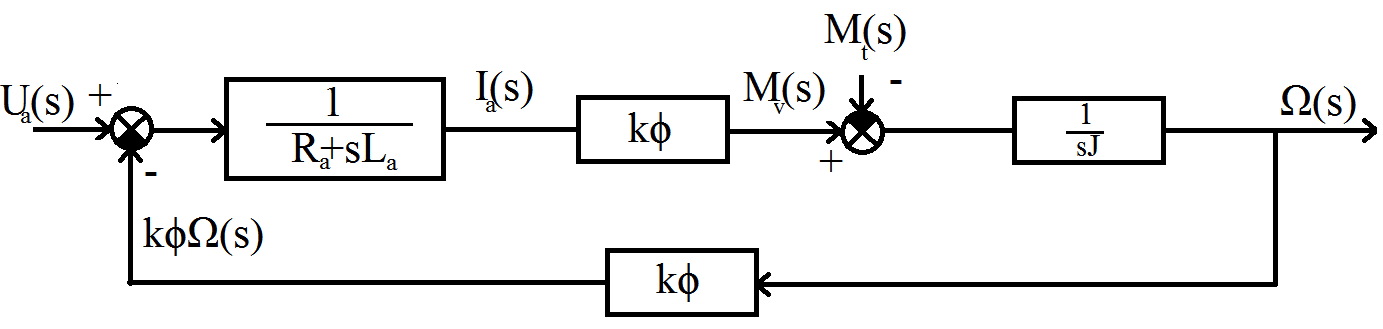
A 4-33. ábraán egy visszacsatolt kört látunk, ezért átviteli függvény felírásakor a 4.2.5 pont alapján először fel kell írnunk a teljes felnyitott kör átviteli függvényét.
|
|
( 4.132 ) |
A negatív visszacsatolás miatt tetszőlegesen választott bemenet és kimenet esetén az átviteli függvény nevezője és ezzel együtt az átviteli függvény pólusai mindig azonosak lesznek. A nevező így a következő alakot ölti
|
|
( 4.133 ) |
Ez azt plauzibilis állítást fejezik ki, hogy egy rendszer időállandói nem függnek a nézőponttól (a ki- és bemenet megválasztásától). Mivel a legtöbb motor esetén teljesül a következő egyenlőtlenség (Megjegyezzük, hogy léteznek olyan kis inerciájú szervomotorok, ahol ez nem teljesül)
|
|
( 4.134 ) |
A villamos és a mechanikai időállandó definíciója
|
|
( 4.135 ) |
Leegyszerűsítve a motoron belül a mágneses tér felépítéséhez (más megközelítésben az áram kialakulásához), a motor forgórészének felpörgetéséhez szükséges időhöz köthető. Természetesen ez a két folyamat egy visszacsatolt körben szoros kölcsönhatásban zajlik le, ezért ez a leegyszerűsítés csak értelmezhető, ha (4.134) teljesül. Jelölje és a motor két tényleges időállandóját. Ha (4.134) telesül, akkor
|
|
( 4.136 ) |
Ha (4.134) nem telesül, akkor is használjuk a (4.135) definíciót, ebben az esetben akár az is előfordulhat, hogy
|
|
( 4.137 ) |
Ez fizikailag nem jelenti azt, hogy a motoron belül a mágneses tér felépítéséhez több idő kellene, mint a motor forgórészének felpörgetéséhez. Ilyen esetekben és a motor két jól definiált paramétere, amelyek fizikai tartalma nehezen értelmezhető.
Elsőként írjuk fel az átviteli függvényt az bemenet és kimenet között. Ekkor az előrevezető ág átviteli függvénye csak abban különbözik felnyitott kör átviteli függvényétől, hogy az előbbiben a visszacsatoló ágban található tag nem szerepel
|
|
( 4.138 ) |
(4.138) átrendezése után jobban látszik az erősítés és kiolvashatók az időállandók is.
|
|
( 4.139 ) |
Látható, hogy és akkor lehetne a motor két időállandója, ha a nevezőben együtthatója lenne. Ha (4.134) telesül, akkor igaz a következő is
|
|
( 4.140 ) |
Vagyis élhetünk (4.136) közelítéssel.
Kapcsoljunk ugrás feszültséget az armatúra körre és legyen . Az átviteli függvény segítségével könnyen felírható a részlet törtekre bontáshoz célszerű alakban
|
|
( 4.141 ) |
Látható, hogy (4.141) kifejezésnek három pólusa van. A kifejtési tétel alapján
|
|
( 4.142 ) |
Átrendezve
|
|
( 4.143 ) |
(4.143) kifejezésből az is kiolvasható, ha (4.134) teljesül, akkor élve a (4.136) közelítéssel a fordulatszám időfüggvénye jól közelíthető úgy, hogy csak a domináns pólus hatását vesszük figyelembe.
|
|
( 4.144 ) |
Az egységugrás feszültségjel hatására a kialakuló fordulatszám állandósult értéke.
|
|
( 4.145 ) |
(4.145) az ún. üresjárási fordulatszámot adja meg.
Írjuk fel az átviteli függvényt az bemenet és kimenet között, ekkor az előrevezető ágban figyelembe kell venni negatív előjelét
|
|
( 4.146 ) |
(4.146) nevezője megegyzik (4.138) nevezőjével. (4.146) is átírható olyan formára, ahol az időállandók jobban láthatók
|
|
( 4.147 ) |
Az ugrás alakú terhelésrádobás hatására a kialakuló fordulatszám Laplace operátoros alakja
|
|
( 4.148 ) |
Az inverz Laplace-transzformációt elvégezve
|
|
( 4.149 ) |
Az állandósult érték létezik, ezért a végérték tétel alkalmazható.
|
|
( 4.150 ) |
Ha a két hatást a szuperpozíció elvének megfelelően összegezzük, akkor megkapjuk a jól ismert statikus fordulatszám nyomaték összefüggést
|
|
( 4.151 ) |
(4.146) alapján könnyen megkapjuk az áram és fordulatszám között felírható átviteli függvényt. Az előrevezető ág egy negatív előjellel és egy szorzóvel különbözik.
|
|
( 4.152 ) |
A motor terhelése növeli a motor aramatúra áramát. Ennek dinamikai összefüggéseit leíró átviteli függvény esetén az előrevezető ágban két -1-es szorzó szerepel. A nyomaték negatív előjele mellett figyelembe kell venni a negatív visszacsatolás negatív előjelét, így végül terhelőnyomaték és annak hatására kialakuló áram előjele megegyezik. A következő átviteli függvény írható fel
|
|
( 4.153 ) |
4 - 16 feladat Egyenáramú motor és terhelő nyomaték rugalmas tengelyen keresztül (Házi feladat megoldását nem közöljük)
A 2-16-től 2-19-ig terjedő feladatokban leírt esetre rajzolja fel a rendszer hatásvázlatát és írja fel a megfelelő átviteli függvényeket.
4.4. Lineáris rendszerek stabilitás vizsgálata
Ebben a fejezetben vizsgálatainkat kizárólag lineáris, koncentrált paraméterű, folytonos rendszereken végezzük, melyek általános matematikai modellje (2.107) alakú:
|
|
( 4.154 ) |
ahol a rendszert érő hatást írja le, pedig a rendszer válasza. A 2.13 alfejezet definíciója alapján látható, hogy a stabilitás nem függ az gerjesztéstől, ezért elegendő lesz az egyenlet homogén részét vizsgálni.
Más gondolatmenettel is ugyanerre a következtetésre juthatunk: az kitérítő hatás rövid idejű (2.13 alfejezet, aszimptotikus stabilitás), tehát -nek gyorsan nullához kell tartania. Viszont a differenciálegyenlet megoldásánál – ha a próbafüggvény módszert alkalmazzuk (lásd melléklet) – a homogén általános megoldást kiegészítő partikuláris megoldást az -hez hasonló alakban keressük. Ennek megfelelően ez is nullához tart, így a teljes megoldásban ez a rész az idő előre haladtával eltűnik. A stabilitás meglétének megállapításához elegendő csak a homogén általános megoldást vizsgálni.
Legyen a rendszer nullpontja az egyensúlyi állapot, itt tehát az kimenet értéke zérus. Ez azt jelenti, hogy stabil rendszer esetén a differenciálegyenlet homogén részének megoldása nullához tart. Az állandó együtthatós, homogén lineáris differenciálegyenletek megoldását alakban keressük. Behelyettesítve a differenciálegyenletbe és -vel egyszerűsítve a rendszer karakterisztikus egyenletét kapjuk (A karakterisztikus polinomot megtaláljuk az átviteli függvények nevezőjében is):
|
|
( 4.155 ) |
Megjegyezzük, hogy a rendszer karakterisztikus polinomja alakra megegyezik az átviteli függvény nevezőjében található polinommal, ha helyére -et írunk.
Ezen egyenlet gyökei szolgáltatják a homogén egyenlet partikuláris megoldásait. A polinom gyökei négyfélék lehetnek, ennek megfelelően a homogén partikuláris megoldások is eltérőek:
|
gyök típusa (száma) |
partikuláris megoldás |
|
egyszeres valós (K) |
|
|
többszörös (m) valós (L) |
|
|
egyszeres konjugált komplex (M) |
|
|
többszörös (m) konjugált komplex (N) |
|
A homogén általános megoldás ezen partikuláris megoldások lineáris kombinációja lesz:
|
|
( 4.156 ) |
Mint már láttuk, a rendszer akkor lesz stabil, ha:
|
|
( 4.157 ) |
Ez a határérték csak akkor lesz biztosan zérus, ha az összeg minden tagja nullához tart. Ennek megfelelően a négy esetet külön-külön vizsgáljuk:
|
egyszeres valós |
egy exponenciális függvény végtelenhez tart, ha a kitevője pozitív, de nullához, ha negatív. Ebből következik, hogy minden -nak negatívnak kell lennie |
|
többszörös valós |
az előzőekből következik, hogy csak negatív gyökök jöhetnek szóba. Kérdés, hogy is nullához tart-e. Legyen , ekkor a L’Hospital szabályt többször (-szer) alkalmazva:
|
|
egyszeres konjugált komplex |
a szorzat trigonometrikus része korlátos, az exponenciális rész viszont nullához tart, ha α<0, azaz Re()<0 |
|
többszörös konjugált komplex |
az előzőekből már következik. hogy tmeαt–nek kell nullához tartani, ez viszont αRe()<0 esetén fennáll |
Összefoglalva elmondhatjuk, hogy stabil a rendszer, ha karakterisztikus polinomjának gyökei negatívak vagy negatív valós részűek.
Napjainkban egy n-edfokú polinom gyökeinek meghatározása általában nem okoz gondot, köszönhetően a számítástechnika fejlődésének. Régebben több olyan eljárást is kifejlesztettek, amelyek segítségével a gyökök meghatározása nélkül is el lehetett dönteni egy rendszerről, hogy stabil-e. A következő fejezetben az egyik legelterjedtebb olyen módszert ismertetjük, amelyet napjainkban is használunk a tervezéshez. Az adott kritériumot paraméteresen írjuk fel, és azt vizsgáljuk, hogy az adott szabályozóköri paraméter mely értékei mellett stabilis a rendszer.
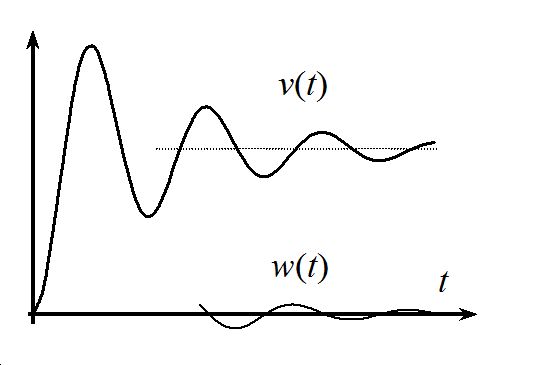
Térjünk vissza a stabilitás definíciójához és vizsgáljuk meg milyen gerjesztést alkalmazhatunk! A definíció szerint a rendszert kitérítjük, majd magára hagyjuk. Ilyen hatást például a δ(t) egységimpulzussal érhetünk el. Az erre adott válasz a w(t) súlyfüggvény, így tehát stabil rendszer súlyfüggvényének nullához kell tartania. Mivel a gyakorlatban az egységimpulzus csak pontatlan közelítéssel állítható elő, ezért helyette a következő módszer alkalmazható:
állítsuk elő az átmeneti függvényt, mivel az ehhez szükséges egységugrás () jel előállítása általában pontosabban megtehető,
-
mérjük meg a rendszer válaszát, ez lesz a közelítő átmeneti függvény,
-
amennyiben az átmeneti függvény állandósult értéket vesz fel, a rendszer stabil. Ennek oka az, hogy a súlyfüggvény az átmeneti függvény deriváltja, és az állandósult részen a függvény jó közelítéssel állandó, aminek a deriváltja zérus. Így tehát ebben az esetben a súlyfüggvény zérushoz fog tartani, és mint láttuk ez a stabilitás feltétele.
Jól szemlélteti ezt a 4-34. ábra, amelyen a súlyfüggvénynek csak azt a részét rajzoltuk meg, ahol az átmeneti függvény már közel állandó.
4.4.1. Routh-Hurwitz stabilitási kritérium
Ezen kritériumot két matematikus (Routh és Hurwitz) dolgozta ki. Tételük a (2.107) alakú differenciálegyenlettel leírható rendszerekre vonatkozik. Lineáris rendszerek akkor stabilisak, ha a karakterisztikus polinomjának csak negatív- vagy negatív valós részű gyökük van. Az ilyen feltételt kielégítő polinomokat Hurwitz polinomoknak nevezzük. Feladatunk ezek szerint az, hogy egy karakterisztikus polinomról a gyökök kiszámítása nélkül megállapítsuk, hogy Hurwitz polinom-e.
A kritérium két részből áll:
-
a polinom minden együtthatója vagy negatív, vagy pozitív. Másképpen megfogalmazva: az együtthatók azonos előjelűek és nem lehet közöttük zérus értékű
-
az együtthatókból képzett Hurwitz determináns és annak a főátlóra támaszkodó minden aldeterminánsa pozitív.
A Hurwitz determináns:
|
|
(4.158) |
A determinánsból kiolvasható, hogy egy n-ed fokú polinomhoz n × n-es determináns tartozik.
4.4.2. Kidolgozott feladatok stabilitásvizsgálatra nem visszacsatolt rendszerek esetén
4 - 17 . feladat
Adott a rendszer differenciálegyenletével: , ahol A>0. Határozzuk meg, hogy milyen A paraméterek esetén lesz stabil a rendszer.
A rendszer karakterisztikus egyenlete, és annak megoldása:
|
|
(4.159) |
Mivel A>0, így <0, tehát a rendszer minden pozitív A-ra stabil.
Az olyan rendszereket, amelyek tetszőleges paraméterértékek esetén stabilak, strukturálisan stabil rendszereknek nevezzük.
4 - 18 . feladat
Adott a rendszer differenciálegyenletével: , ahol T>0 és D>0. Határozzuk meg, hogy milyen T és D paraméterek esetén lesz stabil a rendszer.
A rendszer karakterisztikus egyenlete:
-
mivel T is és D is pozitív, 2TD is pozitív, tehát minden együttható pozitív,
-
n=2, tehát an=a2=T2, a1=2TD, a0=1, tehát a Hurwitz determináns, és aldeterminánsai:
Mivel minden aldetermináns pozitív minden pozitív paraméterre, így ez is strukturálisan stabil rendszer.
Ugyanerre az eredményre jutunk, ha a karakterisztikus egyenlet gyökeit vizsgáljuk:
Ha a diszkrimináns negatív (azaz D<1), a gyökök valós része , ami nyilvánvalóan negatív, hiszen D is és T is pozitív. Abban az esetben, ha , akkor . Ebből következően , így a pozitív T miatt a gyökök negatívak.
4 - 19 . feladat
Adott a rendszer differenciálegyenletével: Vizsgáljuk meg vajon stabil-e.
A rendszer nem stabil, mert a második derivált együtthatója zérus.
4 - 20 . feladat
Adott a rendszer differenciálegyenletével: Vizsgáljuk meg vajon stabil-e.
A rendszer karakterisztikus egyenlete:
-
minden együttható pozitív
-
a Hurwitz determináns és aldeterminánsai:
A harmadik aldetermináns meghatározására nincs is szükség, hiszen a második negatív, tehát a rendszer nem lehet stabil.
4 - 21 . feladat
Adott a rendszer differenciálegyenletével: Vizsgáljuk meg vajon stabil-e.
A rendszer karakterisztikus egyenlete:
-
minden együttható pozitív
-
a Hurwitz determináns és aldeterminánsai:
Mivel minden feltétel teljesül, a rendszer stabil.
4 - 22 . feladat
Adott a rendszer a átviteli függvényével. Vizsgáljuk meg vajon stabil-e.
A rendszer karakterisztikus polinomja az átviteli függvény nevezőjében található:
Mivel ez megegyezik az előző feladat karakterisztikus egyenletével, a rendszer stabil.
4 - 23 . feladat
Adott a rendszer a átviteli függvényével. Vizsgáljuk meg vajon stabil-e.
A rendszer karakterisztikus polinomja az átviteli függvény nevezőjében található:
-
ha T>0, akkor minden együttható pozitív
-
a Hurwitz determináns és aldeterminánsai:
Mivel az együtthatók vizsgálata alapján T>0 kell legyen, az aldeterminánsok alapján pedig T>2 szükséges, a mindkét feltételt kielégítő megoldás: T>2.
4 - 24 . feladat
A rendszer hatásvázlata az alábbi ábrán látható. Az átviteli függvények: és . Határozzuk meg, hogy milyen T értékek esetén stabil a rendszer.

Először meg kell határoznunk az eredő átviteli függvényt:
Ebből a karakterisztikus egyenlet:
-
az együtthatók akkor pozitívak, ha rendre T>-2, T>-0.5 és T>0. Ebből következően T>0 esetén lesz minden együttható pozitív,
-
a Hurwitz determináns és aldeterminánsai:
A minden feltételt kielégítő megoldás tehát: T>0.
4.5. Frekvencia átviteli függvény megjelenítése
A frekvencia átviteli függvénynek fontos fizikai tartalma van. Vissza kell utalnunk a 3-12. ábrara. A frekvenciatartománybeli vizsgálat alapja, hogy a jelek felbonthatók különböző frekvenciájú komponensekre, a komponensek hatása külön számítható, majd a hatások összegezhetőek. A frekvencia átviteli függvény azt mondja meg, hogy a rendszer miként reagál a különböző frekvenciájú szinuszos gerjesztésekre, pontosabban, ha a bemenőjel egy adott frekvenciájú szinuszos jel, akkor a bemenőjelhez képest miként változik meg a kimenőjel amplitúdója és fázisa. Így minden frekvenciához két értéket rendelünk
-
a kimenő- és bemenőjel amplitúdójának arányát
-
a kimenőjel fáziseltolódását a bemenőjelhez képest.
Ez a meghatározás egyben útmutató a frekvencia átviteli függvény mérésére is. Mivel minden frekvenciához két értéket rendelünk, egy amplitúdó és egy fázisszög értéket, így kézenfekvő, hogy a frekvencia függvényt komplex számként ábrázoljuk. Így összefoglalva a frekvencia átviteli függvény egy olyan komplex függvény, amely a nem negatív körfrekvenciákhoz egy olyan komplex számot rendel hozzá, amelynek az abszolút értéke a kimenőjel állandósult állapotbeli amplitúdójának és bemenőjel amplitúdójának aránya, a szöge megegyezik a kimenőjel állandósult állapotbeli fáziseltolódásával a bemenőjelhez képest (az adott körfrekvencián).
A fenti definíció értelmezéseként, tegyük fel, hogy egy rendszer bemenetére szinuszos jelet kapcsolunk, akkor a kimenőjel állandósult állapotban (ld. 4-36. ábra)
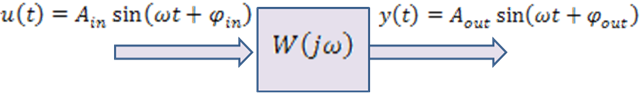
A 4-36. ábra jelöléseivel:
|
|
( 4.160 ) |
|
|
( 4.161 ) |
A fenti definícióból adódik, hogy miként mérhetjük meg a frekvencia átviteli függvényt. A bemenetre szinuszos gerjesztést kapcsolunk, megvárjuk a tranziensek lezajlását, és kvázi stacioner állapotban mérjük a kimenőjelet. Ezt a mérést több frekvencián elvégezzük.
4-25 feladat
Egy MATLAB program segítségével mutassa be a frekvencia átviteli függvény értelmezését.
Megoldás
A 4-37. ábra egy absztrakt elrendezést mutat. Szinuszos mechanikai gerjesztés előállítása és mechanikai lengések mérése, regisztrálása nehézkesebb, de több módon megvalósítható. A 2-8 és 2-10 feladatban vázolt probléma esetén még nehézkesebb lenne a szinuszos gerjesztést előállítani, de egy áramkör esetén ténylegesen használhatunk elektronikus jelgenerátort és oszcilloszkópot, így a 4-37. ábran látható elrendezés könnyen megvalósítható a gyakorlatban. Nem szabad megfeledkezni arról, hogy a 4-37. ábra látható elrendezés esetén a mérés megkezdése előtt el kell jutnunk az állandósult állapothoz.
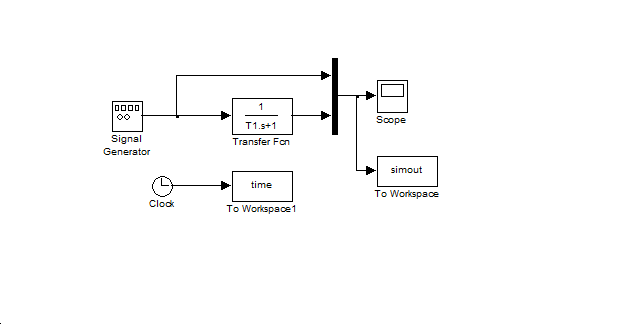
A következő szimulációkban a paramétereket úgy állítjuk be, hogy a gerjesztésnek pont 5 periódusa legyen látható, és minden periódusban legalább 100 mintát vegyünk. A mérésben szereplő egy-energiatárolós rendszer időállandója legyen 1. A gerjesztés körfrekvenciáját az időállandóhoz viszonyítva számítjuk ki. A számításhoz használt MATLAB fájl
% Adatok
T1=1;
omega=0.01*1/T1; % 1/T1 együtthatója: 0.01, 0.1, 1, 10 és 100
% Frekvencia átviteli függvény kiszámítása
abs(1/(1+omega*i))
angle(1/(1+omega*i))
% Szimulációs paraméterek, a maximális lépésközt
% és a szimuláció hosszát állítják be.
Tmax_step=2*pi/omega/100;
Tmax=5.0/omega*2*pi;
% Eredmények kirajzolása
plot(time,simout)
set(gca, 'fontsize', 19);
ylabel('y(t) u(t) [relatív egység]');
xlabel('Idő [s]');
title('Frekvencia átmeneti függvény mérése');
axis([0 Tmax -1 1]);
grid
Először egy nagyon kicsi körfrekvenciájú, más megközelítésben nagyon nagy periódus idejű gerjesztést kapcsolunk a rendszerre. A lassú változás miatt a kimenet szinte pontosan követi a gerjesztést. A 4-38. ábran a kimenő- és bemenőjelet nem lehet megkülönböztetni. A frekvencia átviteli függvény gyakorlatilag 1-nek vehető, a fáziseltolás alig fél fok.
|
|
( 4.162 ) |
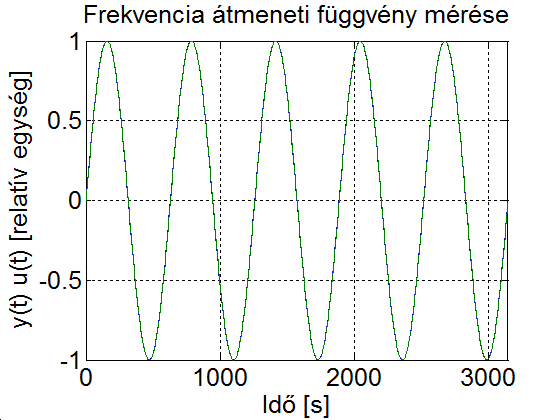
Ha egy nagyságrenddel növeljük a gerjesztés frekvenciáját, akkor a ki- és bemeneti jel között egy nagyon pici különbség van, a fázistolás -5.7̊.
|
|
( 4.163 ) |
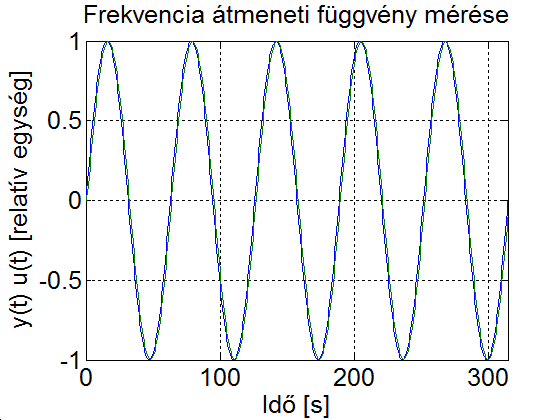
Ha ismét egy nagyságrenddel növeljük a gerjesztés frekvenciáját, akkor a ki- és bemeneti jel között már látható különbség van. A 4-40. ábra jól látható, hogy a kimenőjel amplitúdója kb. 0.7 (a pontos érték ). Az állandósult állapot kb. az első periódus után kialakul. A nagyságú fáziseltolás is kiolvasható.
|
|
( 4.164 ) |
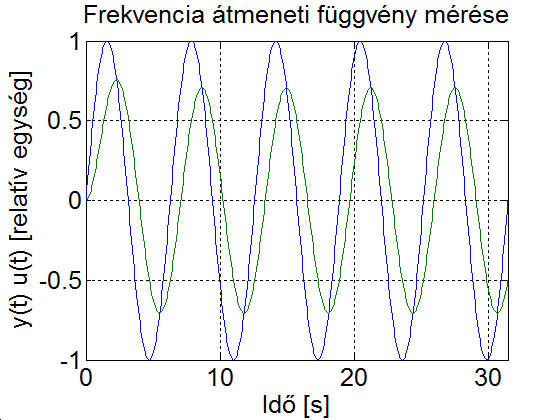
Ha ismét egy nagyságrenddel növeljük a gerjesztés frekvenciáját, akkor a kimenőjel amplitúdója alig egy tizede a bemenőjel amplitúdójának és a fázistolás -84.2894̊. Úgy látszik, hogy az állandósult állapot kb. az ötödik periódus után kialakul. Pontos számítás alapján az ötödik periódus után a tranziens összetevő a kezdeti értékének kb. 5%-ra csökken.
|
|
( 4.165 ) |
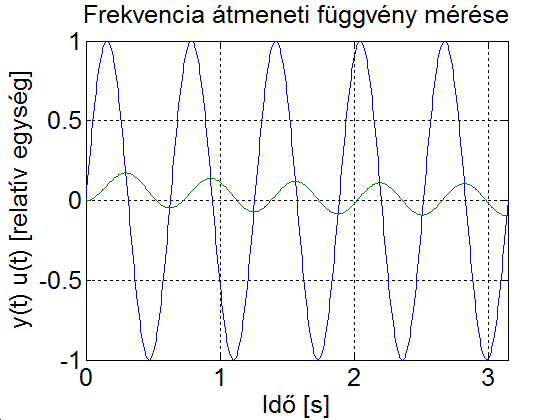
Ha ismét egy nagyságrenddel növeljük gerjesztés frekvenciáját, akkor öt periódus alatt közelítőleg sem érjük el az állandósult állapotot, de az jól látható, hogy a kimenőjel amplitúdója alig egy százaléka a bemenőjel amplitúdójának és a fázistolás közel .
|
|
( 4.166 ) |
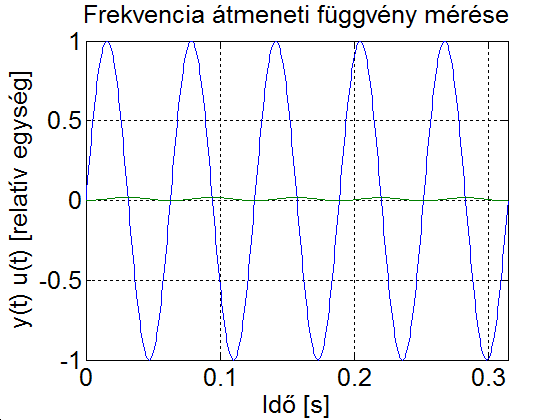
4.5.1. Az átviteli és a frekvencia átviteli függvény kapcsolata
A frekvencia átviteli függvényt gyakran az átviteli függvényből számítjuk helyettesítéssel, így a frekvencia átviteli függvény -ra nézve racionális törtfüggvény, ezért a szokásos jelölése:
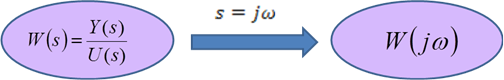
Itt fontos megjegyezni, hogy az átviteli függvény a súlyfüggvény Laplace-transzformáltja. Valóságos (veszteséges) rendszerek esetén a súlyfüggvény lecsengő, ezért általában van Fourier transzformáltja, és ezért fizikai megfontolások alapján állítjuk azt, hogy teljesül a matematikai feltétele annak, amikor az helyettesítéssel élhetünk
Kétféle grafikus ábrázolási mód terjedt el a helygörbe vagy Nyquist-diagram és a Bode-diagramok (amplitúdó és fázis).
4.5.2. Nyquist-diagram
Legyen a frekvenciaátviteli függvény a következő alakú:
|
|
( 4.167 ) |
Az =0 paraméterrel a frekvenciafüggvényt ábrázoljuk a komplex számsíkon.
Nézzük meg, hogyan fog viselkedni a függvény a két szélső helyzetben, tehát =0 és = esetben.
A, =0
Tegyük fel, hogy értéke nem zérus. Ekkor -t kapunk, tehát a diagram a valós tengelytől indul.
Ha , akkor a vizsgálatot 0 esetre végezzük el. Ekkor a számlálóban is és a nevezőben is a legkisebb kitevőjű tag lesz a domináns, tehát
|
|
( 4.168 ) |
Ez azt jelenti, hogy a diagram a „lap aljától” indul.
B, =
Ekkor a legnagyobb fokszámú tag lesz a domináns, tehát elegendő a
|
|
( 4.169 ) |
kifejezést vizsgálni.
Tegyük fel, hogy , tehát a nevező fokszáma nagyobb, mint a számlálóé. Mivel ebben az esetben a kitevő negatív, a kifejezés értéke zérushoz tart. Látszik azonban, hogy páros vagy páratlan voltának megfelelően a görbe vagy a valós, vagy a képzetes tengely mellett simul be az origóba:
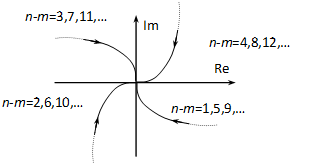
Amennyiben , a diagram a valós tengely pontjában végződik.
Ha , akkor u.n. differenciáló hatás érvényesül, és a kifejezés értéke a végtelenhez tart. Meg kell azonban jegyezni, hogy fizikai rendszerek esetében ez az eset nem valósítható meg!
4 - 26 . feladat
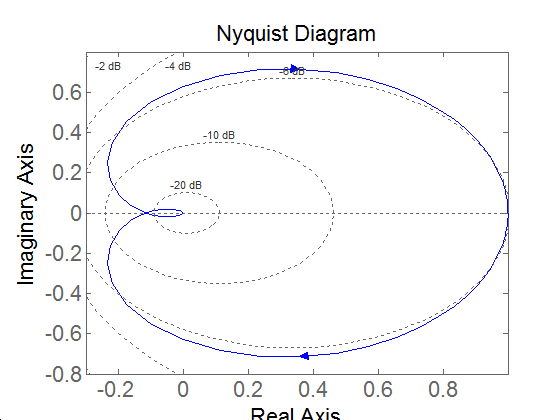
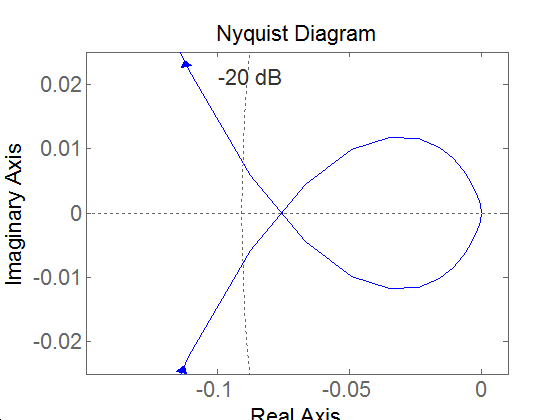
Legyen . Rajzoljuk meg a Nyquist diagramját.
Esetünkben . Mivel , ezért a diagram a pontból indul. A végpont meghatározásához szükséges a határérték vizsgálata. Most és , valamint és így
|
, |
( 4.170 ) |
ami láthatóan zérushoz tartó negatív képzetes érték. Most már csak a közbenső értékeket kell meghatározni. Ehhez állítsuk elő a valós- és a képzetes részt:
Nem negatív esetén a valós rész mindig pozitív, a képzetes pedig mindig negatív lesz, tehát a görbe egy síknegyedben marad:
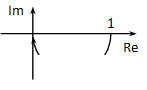
A teljes ábrázoláshoz készítsünk értéktáblázatot:
|
|
0 |
0.5 |
1 |
2 |
∞ |
|
Im |
0 |
-0.4 |
-0.5 |
-0.4 |
0 |
|
Re |
1 |
0.8 |
0.5 |
0.2 |
0 |
A későbbiekben igazolni fogjuk, hogy a diagram egy félkör, amelynek középpontja a valós tengelyen van 0.5-nél és a sugara is 0.5.
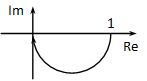
4.5.3. Bode-diagram
Tulajdonképpen két diagramról van szó, hiszen az amplitúdót és a fázisszöget külön diagramban ábrázoljuk pozitív függvényében.
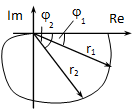
A 4-47. ábraán láthatjuk a kapcsolatot a Nyquist diagrammal. A vektorok hossza jelenti az amplitúdót, a pozitív valós tengellyel bezárt előjeles szögük pedig a fázisszöget.
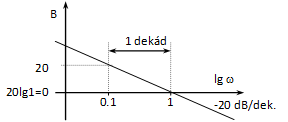
Az amplitúdó diagramon a függőleges tengelyen decibel (), a vízszintesen pedig lg skálát használunk. Ennek megfelelően a szokásos skála értékek 0.1; 1; 10 stb. Egy-egy ilyen a szokásos skálaértékekkel határolt szakaszt (ahol a frekvencia 10-szeresére nő) nevezünk 1 dekádnak. Mivel a diagramokat általában csak a tendenciákat pontosan mutató, aszimptotákkal közelítő diagramokkal szoktuk megrajzolni, a meredekség értékét is jelezzük, pl. -20 dB/dek, ami azt jelenti, hogy egy dekádon a csökkenés 20 decibelnyi.
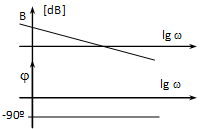
A függőleges tengely helyzete esetleges, hiszen a vízszintes tengelynek nincs zérus pontja, mivel a logaritmikus léptékezés miatt nem lehet zérus. Jelentősége van azonban annak, hogy az amplitúdó diagram hol metszi a vízszintes tengelyt. Ezt a egyenletből határozhatjuk meg. Ebből az következik (mint ahogy az a 4-48. ábrán is látszik), hogy a tengelymetszésnél az amplitúdó viszony éppen egységnyi.
A fázis diagramnál csak a vízszintes tengely esetében térünk el a megszokottól, itt is lg-t alkalmazunk.
Amplitúdó Bode diagramok esetében az ábrázolás során általában aszimptotikus közelítést alkalmazunk, ami nagymértékben megkönnyíti a dolgunkat. Gyakran előfordul, hogy az aszimptota egyik pontját ismerjük, és szükségünk lenne egy másik pont koordinátáira is. Mivel egyenesekről van szó, ez nem okozhat problémát, nehézséget csak az okozhat, hogy logaritmikus léptéket használunk. A következőkben meghatározunk egy minden, a gyakorlatban előforduló meredekségű aszimptóta esetén jól használható összefüggést.
Legyen az ismert pont (1,A1) az ismeretlen pedig (2,A2), valamint a meredekség n∙20 dekád, ahol n=0,±1,±2,…. Vegyük fel az (,A) pontot úgy, hogy 1=10 legyen, azaz a távolság éppen 1 dekád. Ekkor:
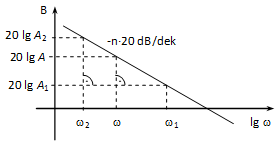
A 4-49. ábrán két hasonló derékszögű háromszög látható. A befogók arányaira felírhatjuk a következő egyenletet, amit rendezve a keresett összefüggést kapjuk:
|
|
( 4.171 ) |
Mint már tudjuk, sorba kapcsolt rendszerelemek eredő átviteli függvényét a tagok átviteli függvényének szorzataként állíthatjuk elő. Ebből következik, hogy sorba kapcsolt tagok eredő Bode diagramját a tagok diagramjainak összegzéseként kaphatjuk. Ezen állítás az amplitúdó diagram esetén nyilvánvaló, hiszen a decibel tulajdonképpen logaritmikus skálát jelent, és a szorzás logaritmusa az elemek összeadása. Nem szabad azonban elfelejtenünk, hogy itt tulajdonképpen két komplex érték szorzatáról van szó. Mint tudjuk ekkor az abszolút értékek összeszorzódnak, a szögek pedig összeadódnak (gondoljunk csak a komplex számok trigonometrikus alakjára!).
Ha nem tudjuk az eredő diagramot egyszerű, sorba kapcsolt tagok diagramjainak felhasználásával megrajzolni, akkor határozzuk meg a valós- és képzetes részeket. Ezek ismeretében az amplitúdó és a fázisszög meghatározható. Az így kapott függvények vizsgálata segítségével rajzolhatunk közelítő Bode diagramokat.
A Nyquist diagramból a minőségi tulajdonságok, a Bode diagramból a mennyiségi összefüggések olvashatók ki.
4.6. Alaptagok átviteli függvénye, Nyquist és Bode diagramja
Az alaptagok tulajdonképpen a frekvenciaátviteli függvény szorzattá bontott alakjában előforduló tagok. Legtöbbjüknek fizikai jelentése is van.
4.6.1. Arányos tag (P)
Leíró differenciálegyenlet: .
Átmeneti függvény:
Súlyfüggvény:
Átviteli függvény: W(s)=P
Frekvenciafüggvény: W(j)=P
Nyquist diagram: a frekvenciafüggvény -tól független konstans, így a komplex síkon egy a valós tengelyen lévő pontként ábrázoljuk.
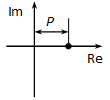
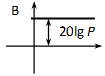
Bode diagram: az amplitúdó diagram egy 20 lg(P) ordinátájú vízszintes egyenes, a fázis pedig zérus.
Amennyiben 0<P<1 az egyenes a vízszintes tengely alatt halad, hiszen ekkor a logaritmus értéke negatív.
Abban az esetben, ha P negatív az amplitúdó diagramon az abszolút értékét ábrázoljuk, fázisszöge pedig -180°.
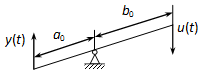
Példa: kétkarú emelő.
4.6.2. Differenciáló tag (D)
Leíró differenciálegyenlet: .
Átmeneti függvény:
Súlyfüggvény: függvényként nem értelmezhető és olyan egyszerű közelítése sincs, mint a Dirac impulzusnak
Átviteli függvény:
Frekvenciafüggvény:
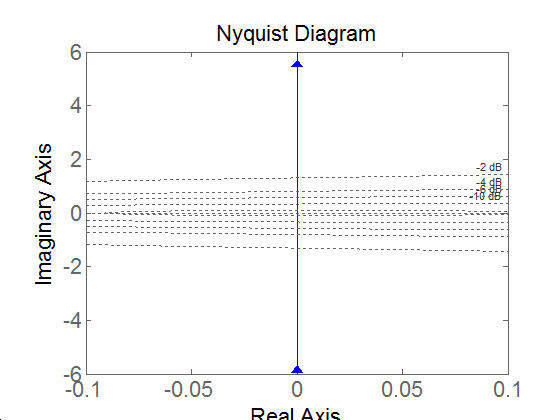
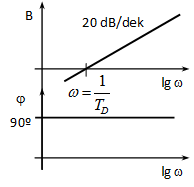
Nyquist diagram: az origóból induló, a pozitív imaginárius tengelyen végigfutó félegyenes.
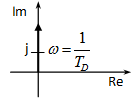
Bode diagram:
Amplitúdó: , ami lg -re egy 20 egység meredekségű egyenes egyenlete. A vízszintes tengelyt -nél metszi, hiszen a függvényérték itt 1, de a függőleges tengely decibelben (azaz logaritmikus léptékben) van skálázva.
Fázis: a Nyquist diagramról leolvasható, hogy a valós tengellyel +90°-ot zár be, tehát a fázistolás: 90°.
Példa: fizikailag nem megvalósítható.
4.6.3. Integráló tag (I)
Leíró differenciálegyenlet:
|
|
( 4.172 ) |
Átmeneti függvény:
Súlyfüggvény:.
Átviteli függvény:
Frekvenciafüggvény:
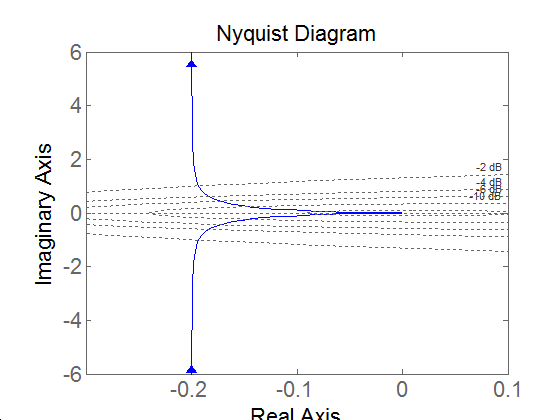
Nyquist diagram: az origóba tartó, a negatív imaginárius tengelyen végigfutó félegyenes, hiszen a frekvenciafüggvény algebrai alakja:
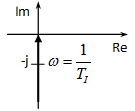
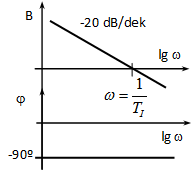
Bode diagram:
Amplitúdó: , ami lg -ra egy 20 egység meredekségű egyenes egyenlete. A vízszintes tengelyt -nél metszi, hiszen a függvényérték itt 1, és a függőleges tengely decibelben (azaz logaritmikus léptékben) van skálázva.
Fázis: a Nyquist diagramról leolvasható, hogy a valós tengellyel -90°-ot zár be, tehát a fázistolás: -90º.
Példa:
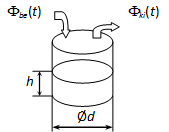
A tartályban lévő folyadék térfogatának megváltozása t időegység alatt:
|
|
( 4.173 ) |
Ezek után a rendszert leíró differenciálegyenlet:
|
|
( 4.174 ) |
4.6.4. Arányos differenciáló tag (PD)
Leíró differenciálegyenlet:
|
|
( 4.175 ) |
Átmeneti függvény:
Súlyfüggvény: függvényként nem értelmezhető és olyan egyszerű közelítése sincs, mint a Dirac impulzusnak
Átviteli függvény: W(s)=P(1+sTD)
Frekvenciafüggvény: W(j)= P(1+jTD)
Nyquist diagram: a valós tengelyről induló, a pozitív imaginárius tengellyel párhuzamosan végigfutó félegyenes.
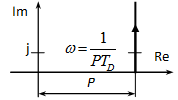
Bode diagram: Nem a valódi, hanem az aszimptotákkal közelített diagramokat határozunk meg.
Amplitúdó:
|
|
( 4.176 ) |
amely
0 esetén , tehát a vízszintes tengellyel párhuzamos egyenes,
esetén , lg -ra egy 20 dB/dekád meredekségű egyenes egyenlete.
A két egyenes metszéspontja:
|
|
( 4.177 ) |
Fázis: , ami 0 esetén 0, esetén 90º, és =1/TD esetén arctg 1 =45º.
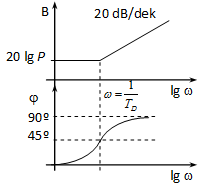
Más gondolatmenettel is ugyanerre az eredményre juthatunk! A frekvenciafüggvény alakjából látszik, hogy egy arányos (P) és egy erősítés nélküli arányos, differenciáló (PD) tag sorba kapcsolása, tehát az eredő Bode diagram a két diagram összegeként előállítható.
Legyen W1(j)=P és W2(j)=1+jTD. W1(j)-val az arányos tagnál már foglalkoztunk. W2(j) kis esetén (0) W2(j)=1-hez , azaz egy egységnyi erősítésű P taghoz tart, így a diagramjai az elején úgy néznek ki, mint az arányos tagé. Amplitúdó: lg1=0 egyenes a valós tengelyen, fázis: =0 (ld. 4-60. ábra). Nagy esetén () W2(j)=jTD, tehát egy differenciáló taghoz tart (ld. 4-60. ábra).
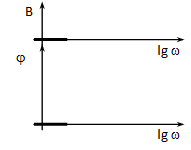
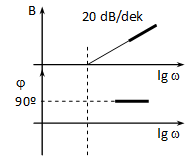
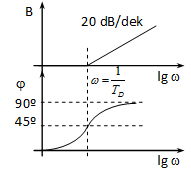
Ha ehhez még hozzávesszük W1(j)-et, akkor az amplitúdó diagram 20lgP értékkel feljebb tolódik, a fázis pedig változatlan marad, hiszen az arányos tag fázisa (amit hozzá kell adni) 0.
Nézzük meg, hogy mekkora az eltérés a pontos és a közelítő diagramok között! A legnagyobb eltérés nyilvánvalóan a két aszimptota metszéspontjánál lesz. Az ehhez a ponthoz tartozó frekvencia értéket, sarok-körfrekvenciának nevezzük és mint láttuk értéke . Az egyszerűség kedvéért tegyük fel, hogy P=1, hiszen az előzőekben megmutattuk, hogy P csak egy függőleges eltolást okoz, a közelítés mértékét nem befolyásolja, és ekkor a sarokpont a vízszintes tengelyen van. Ezután a (4.212)-be való behelyettesítéssel kapjuk az eltérést:
|
|
( 4.178 ) |
Érdemes meghatározni még a fázisgörbe érintőjének meredekségét az inflexiós pontban. A fázisgörbe egyenlete ismert, a meredekséget a differenciálhányados ismeretében tudjuk felírni. Gondot csak az okoz, hogy a vízszintes tengelyen logaritmikus léptéket alkalmaztunk. A problémát helyettesítéssel oldjuk meg:
|
|
( 4.179 ) |
Az inflexiós pont az helyen van, ezért a meredekség:
|
|
( 4.180 ) |
Ez az érték az érintő vízszintes tengellyel bezárt szögének a tangense, így a szög . A gyakorlatban elterjedt a 45º/dekádos közelítés.
Példa: fizikailag nem valósítható meg
4.6.5. Arányos tag egy tárolóval (PT1)
Leíró differenciálegyenlet: .
Átmeneti függvény:
Súlyfüggvény:
Átviteli függvény:
Frekvenciafüggvény:
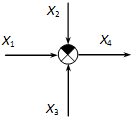
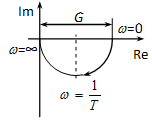
Nyquist diagram: egy középpontú sugarú félkör. Nézzük a továbbiakban ezen állítás igazolását. A koordinátageometriában tanultak szerint a kör egyenlete, ahol x=Re W, y=Im W.
Hozzuk a frekvenciafüggvényt algebrai alakra:
|
, |
( 4.181 ) |
majd helyettesítsük be a kör egyenletének bal oldalába a kiszámított valós és képzetes részt:
|
, |
( 4.182 ) |
Ezzel állításunkat részben igazoltuk. Hátra van még annak bizonyítása, hogy a diagram csak félkör. Mivel esetén a képzetes rész mindig negatív, így a diagramot csak a kör alsó fele alkotja (4-61. ábra). Keressük meg még a kör -hez tartozó pontját (az előzőekben már láttuk, hogy ennek a Bode diagramoknál kitüntetett szerepe van!).
|
, |
( 4.183 ) |
Ez a pont tehát a körív felezőpontja.
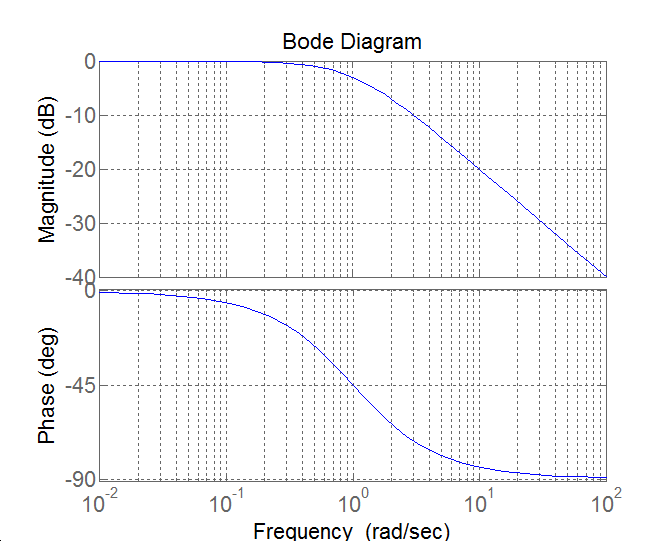
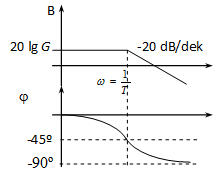
Bode diagram: A közelítő diagram meghatározásához használjuk a PD tagnál ismertetett gondolatmenetet:
ha 0 , tehát arányos viselkedésű,
ha , tehát integráló jellegű.
A két aszimptota metszéspontja:
sarokfrekvencia.
A legnagyobb eltérés (G=1 esetén) a már ismertetett módon határozható meg (értéke itt is 3 dB).
4.6.6. Arányos tag két tárolóval (PT2)
Leíró differenciálegyenlet: .
Átmeneti függvény: az átmeneti függvény a tag paramétereitől függően különböző alakú.
A differenciálegyenlet egy partikuláris megoldása G. A homogén egyenletet a próbafüggvények módszerével oldjuk meg (lásd melléklet), ekkor:
|
, |
( 4.184 ) |
egyenlet adódik. Az egyenlet megoldása:
|
, |
( 4.185 ) |
A gyökök típusa D értékétől függ.
a, D>1, aperiodikus eset
Ekkor két valós gyök van, ennek megfelelően a megoldás:
|
, |
( 4.186 ) |
Amennyiben a kezdeti feltételek ismertek, a c1, c2 konstansok meghatározhatók. Legyen most minden kezdeti feltétel zérus. Ekkor:
|
, |
( 4.187 ) |
b, D=1, aperiodikus határhelyzet
Ekkor kettősgyök van, tehát:
|
, |
( 4.188 ) |
Zérus kezdeti feltételek esetén:
|
, |
( 4.189 ) |
c, 0<D<1, periodikus eset
A gyökök ebben az esetben konjugált komplex értékek. Az Euler formula alkalmazásával juthatunk a megoldás elterjedten használt alakjához:
|
, |
( 4.190 ) |
Zérus kezdeti feltételek esetén:
|
, |
( 4.191 ) |
Súlyfüggvény: itt is három különböző eset van. Mivel a súlyfüggvény az átmeneti függvény deriváltja, ezért mindhármat könnyen előállíthatjuk.
a, D>1, aperiodikus eset
|
, |
( 4.192 ) |
b, D=1, aperiodikus határhelyzet esete
|
, |
( 4.193 ) |
c, D<1, periodikus eset
|
, |
( 4.194 ) |
Átviteli függvény:
Frekvenciafüggvény:
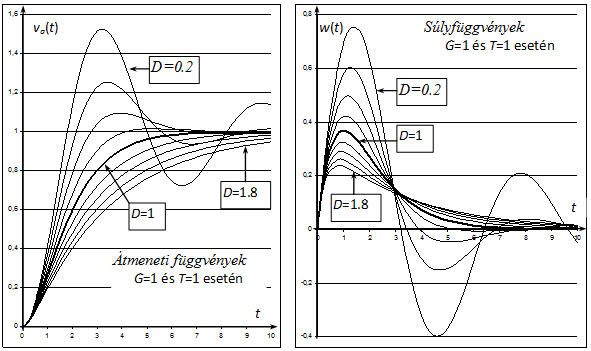
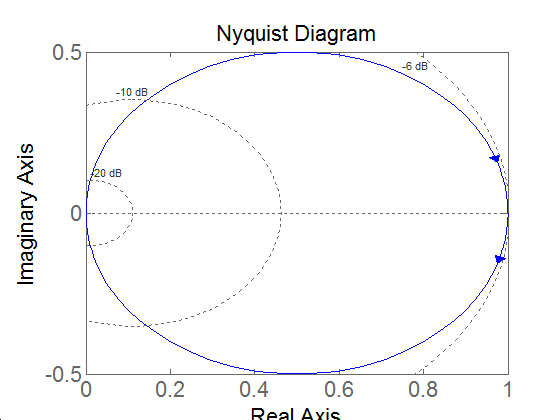
Nyquist diagram: az általános leírásnál megfogalmazottaknak megfelelően megállapítható, hogy a valós tengely G pontjából indul, és a valós tengely negatív része mellett fut be az origóba, mivel a nevező és a számláló fokszám különbsége kettő. Határozzuk meg a frekvenciaátviteli függvény valós és képzetes részét:
|
, |
( 4.195 ) |
Ebből kiolvasható, hogy a képzetes rész pozitív paraméterek esetén mindig negatív, a valós rész viszont pozitív és negatív is lehet. fázisszöge esetén 0, esetén -180°. Ennek megfelelően a diagram kezdete és vége megrajzolható (ld. 4-64. ábra).

A teljes diagramot például értéktáblázat felhasználásával tudjuk elkészíteni (ld. 4-65. ábra):
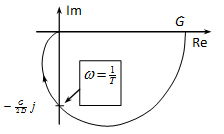
A görbe nevezetes pontja a képzetes tengellyel való metszéspontja. Ekkor a valós rész zérus, ebből viszont következik. A képzetes rész értéke: .
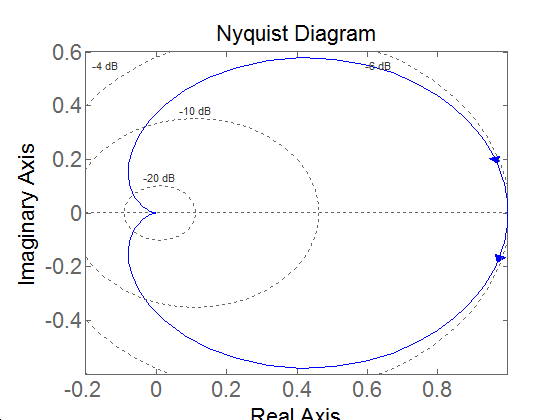
Vajon előfordulhat-e olyan eset, amikor növekvő frekvenciához növekvő amplitúdó tartozik?
Ez csak akkor lehet, ha:
|
, |
( 4.196 ) |
Mivel T22 tetszőlegesen kicsi lehet, ezért 2 > 4D2-nek kell igaznak lennie. Ebből azonban következik. A 4-66. ábrán egy ilyen esethez tartozó Nyquist diagramot látunk.
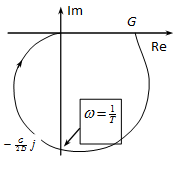
Bode diagram: három esetet kell megkülönböztetnünk, ugyanúgy, ahogy az átmeneti függvénynél tettük.
a, , aperiodikus eset
|
, |
( 4.197 ) |
Mint láthatjuk, most egy arányos és két egytárolós tag frekvenciaátviteli függvényének szorzatát kaptuk. A Bode diagramot a szokásos módon szerkeszthetjük meg (ld. ???
4-67. ábra):
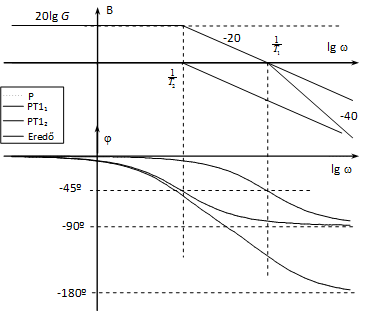
b, , aperiodikus határhelyzet eset
Tulajdonképpen az előző speciális esete, ugyanis ekkor T1=T2=T, tehát a két töréspont egybeesik. (ld.???
4-68. ábra)
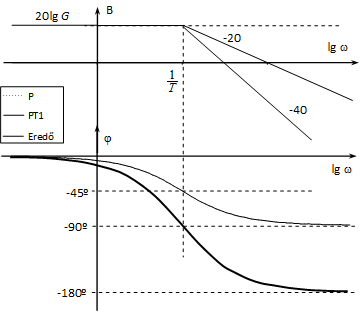
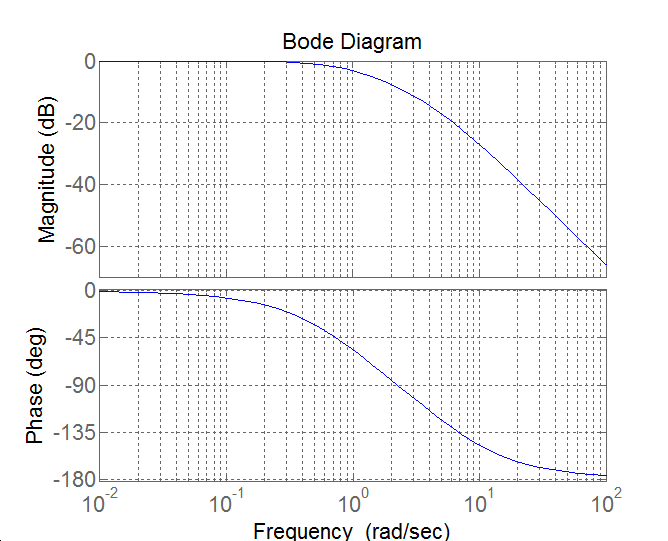
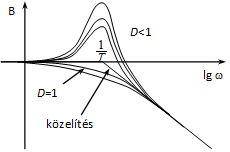
c, , periodikus eset
Ebben az esetben a rendszert nem lehet felbontani két sorba kapcsolt egytárolós arányos tagra, mert a karakterisztikus polinomnak nincsenek valós gyökei. A közelítő diagram meghatározásához alkalmazzuk itt is a jól bevált módszert:
ha 0 , tehát arányos viselkedésű,
ha , tehát kétszeresen integráló jellegű.
A két aszimptóta metszéspontja:
|
sarokfrekvencia., |
( 4.198 ) |
Vizsgáljuk meg, mekkora lesz a közelítés hibája. Természetesen ennek maximuma a töréspontnál lesz:
|
|
( 4.199 ) |
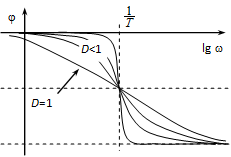
Mint látható, most a hiba nem állandó, hanem függ D –től.
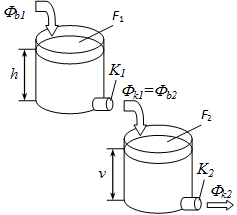
4 - 27 feladat
Határozzuk meg a 4-70. ábra látható második tartályban levő folyadék szintváltozását leíró egyenletet. Jelölések: , , ahol a tartály, pedig a kiömlési cső átmérője. A kezdeti folyadékszintek legyenek és .
Megoldás:
A 2-10 feladatban már vizsgáltunk ehhez hasonló rendszert, igaz ott csak egy tartály volt, de az ott kapott részeredményeket itt is felhasználhatjuk:
|
|
( 4.200 ) |
ezekkel:
|
|
( 4.201 ) |
Az így kapott egyenletrendszer is leírja a rendszert, de most egy egyenletet szeretnénk vizsgálni. A második egyenletből fejezzük ki h-t, majd helyettesítsük be az elsőbe:
|
|
( 4.202 ) |
A kapott egyenlet egy kéttárolós tag differenciálegyenlete.
4 - 28 feladat
Írjuk fel az ábrán látható tömeg mozgását leíró egyenletet.
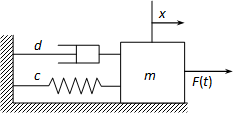
Az egyenlet a külső- és belső erők egyensúlya alapján írható fel:
Külső erő:
Belső erők:rugóerő
csillapító erő
tömeg erő.
Mint látható, most is a kéttárolós tag differenciálegyenletét kaptuk eredményül. Az előző feladatnál egyértelmű volt, hogy mi a két tároló. Itt a tömeg és a rugó lesz, hiszen mindkettő képes energia tárolásra (mozgási- illetve rugóenergia).
További műszaki jellegű példák:
-
az egytárolós tagnál ismertetett melegítési feladat tovább fejlesztve úgy, hogy a tömeget hőkapacitással és tömeggel rendelkező szigetelőanyag veszi körül, feltételezve, hogy a hőáram mindig csak a szigetelés felé terjed;
-
az elektrotechnikából ismert rezgőkörök.
Ezzel végére értünk az alaptagok ismertetésének. Szinte minden alaptagnak van egy paramétere, amely betűvel az időt szokás jelölni. Megvizsgálva a – műszaki élet különböző területeiről származó – példákat azt tapasztaljuk, hogy minden esetben idő dimenziójú értéket jelöl a .
4.7. Holtidős tagok
A holtidős tagok bizonyos szempontból nem illeszkednek az eddig tárgyalt tagokhoz, mivel átviteli függvényük nem tört alakú. Az időtartományban tulajdonképpen egy időbeli eltolást jelentenek.
Tipikus formájuk a szállításból adódó időkésés. Legegyszerűbb formája talán a futószalag, vagy egy termikus rendszer esetén a hőt szállító közeg áramlási sebességéből adódó időkésés.
4.7.1. Arányos holtidős tag (PH)
Leíró differenciálegyenlet: .
Átmeneti függvény:
Súlyfüggvény:
Átviteli függvény:
Frekvenciafüggvény:
Nyquist diagram: a frekvenciaátviteli függvényt trigonometrikus alakja:
A trigonometria egyik legfontosabb azonossága alapján (sin2α+cos2α=1) a valós rész négyzetének és a képzetes rész négyzetének összege állandó, pontosan . Ebből következik, hogy a diagram egy origó középpontú, sugarú kör:
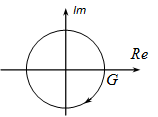
Bode diagram: az előzőekből látszik, hogy a komplex vektorok hossza mindig , tehát az amplitúdó diagram vízszintes egyenes, a fázis pedig lineárisan változik:
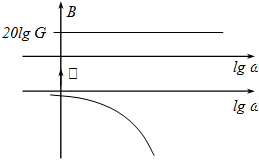
4.7.2. Holtidős integráló tag (HI)
Leíró differenciálegyenlet: .
Átmeneti függvény:
Súlyfüggvény:
Átviteli függvény: (a Laplace transzformáció eltolási szabályát alkalmazva).
Frekvenciafüggvény:
Nyquist diagram: két, már ismert tag szorzatának diagramját kell ábrázolni. Komplex számok esetén szorzáskor a szögek összeadódnak. Mivel az integráló tag fázisa mindig -90º, így a – a holtidős tag miatt – az origó körül forgó vektorokat kapunk. A vektorok hosszát (az amplitúdót) a két tag abszolút értékének szorzataként kapjuk, itt viszont a holtidősé mindig egy lesz. Ennek megfelelően az integráló tag helygörbéjének hosszváltozásával megegyező, azaz végtelenről nullára csökkenő hosszúságú vektorok lesznek:
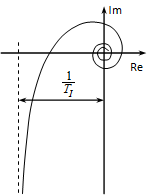
Bode diagram: mivel két, már ismert tag szorzatának diagramját kell meghatározni, egyszerűen csak össze kell adni a résztagok diagramját:
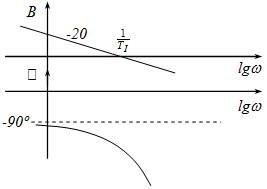
4.7.3. Holtidős tag egy tárolóval (PHT1)
Leíró differenciálegyenlet:
Átmeneti függvény:
Súlyfüggvény:
Átviteli függvény: (a Laplace transzformáció eltolási szabályát alkalmazva)
Frekvenciafüggvény:
Nyquist diagram: a holtidős tag miatt az origó körül forgó, egyre csökkenő hosszúságú vektorok végpontjai alkotják. Az első vektor hossza A.
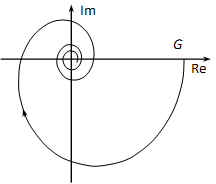
Bode diagram: két ismert tag soros eredőjét kell meghatározni:
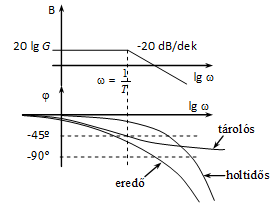
Példa: Az egytárolós tagnál közölt feladatot bővítsük ki úgy, hogy a b hőáram egy hosszúságú csövön keresztül érkezyen. Ebben a csőben az áramlás sebessége legyen w. Ekkor a holtidő: . Ennek megfelelően:
4.8. Alaptagokból előállítható összetett tagok
4.8.1. Arányos, integráló tag (PI)
A tag kapcsolása:
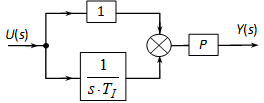
Leíró differenciálegyenlet: .
Átmeneti függvény:
Súlyfüggvény:
Átviteli függvény:
Frekvenciafüggvény:
Nyquist diagram: a valós tengelyhez tartó, az imaginárius tengellyel párhuzamosan futó félegyenes.
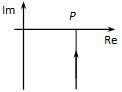
Bode diagram: hozzuk a frekvenciafüggvényt alakra. Felismerhetjük, hogy a kifejezés három már ismertetett tag (P, I, PD) szorzatából áll. Az eredőt a logaritmikus skála miatt három tag összegzéseként kapjuk a keresett Bode diagramon (ld.4-80. ábra):
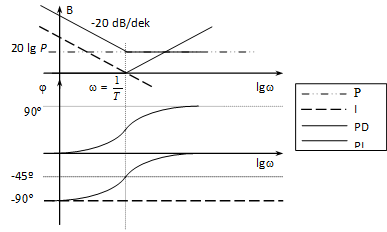
A PD tagnál leírt gondolatmenet itt is alkalmazható. Kis -nál integráló típusú, nagynál pedig arányos jellegű lesz a tag viselkedése.
4.8.2. Ideális arányos integráló differenciáló tag (PID)
A tag kapcsolása:
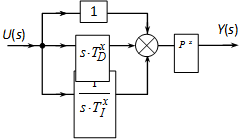
Leíró differenciálegyenlet: .
Átmeneti függvény:
Súlyfüggvény: függvényként nem értelmezhető és olyan egyszerű közelítése sincs, mint a Dirac impulzusnak
Átviteli függvény: .
Frekvenciafüggvény: .
Nyquist diagram: a valós rész minden esetben , a képzetes rész mínusz végtelentől plusz végtelen felé tart:
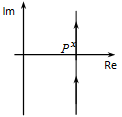
Bode diagram: állítsuk elő az átviteli függvényt tört alakban, majd írjuk fel az alaptagok szorzataként:
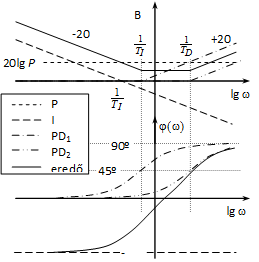
Az ideális PID tag fizikailag nem valósítható meg.
4.8.3. Arányos differenciáló tag egy tárolóval (valóságos PD)
A tag kapcsolása:
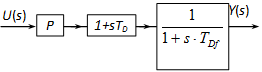
Leíró differenciálegyenlet: .
Átmeneti függvény:
Súlyfüggvény: nincs értelme
Átviteli függvény:
Frekvenciafüggvény:
Nyquist diagram: igazolható, hogy a diagram a valós tengelyről induló, és ott végződő félkör lesz. Határozzuk meg a paramétereit.
Az =0 helyen a függvény értéke P, →∞ esetén pedig . Ebből adódik, hogy a kör középpontja a valós tengely pontjában van, a sugár pedig . Azt kell még eldönteni, hogy a félkör a pozitív, vagy a negatív képzetes félsíkon van-e. Ehhez állítsuk elő a frekvenciaátviteli függvény algebrai alakját:
A képzetes részből kiolvasható, hogy TD> TDf esetén a pozitív félsíkon (ld. 4-85. ábra), ellenkező esetben pedig a negatív félsíkon (ld. 4-85. ábra) halad a félkör.
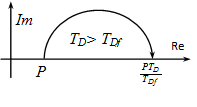
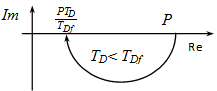
Bode diagram: a frekvenciaátviteli függvény felírható alaptagok soros eredőjeként, így nem okozhat gondot az ábrázolás.
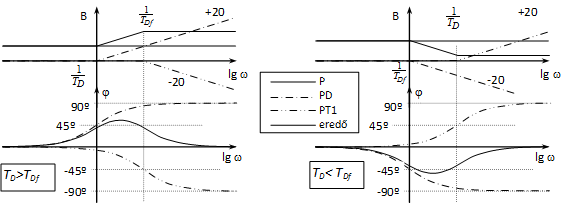
4.9. Kidolgozott feladatok Bode és Nyquist diagram megrajzolására
4 - 29 . feladat
Legyen . Rajzoljuk fel a Bode diagramját.
A feladatot kétféle módszerrel is megoldjuk. Először egyben, majd két tag soros kapcsolásaként értelmezzük.
Ez egy y=20-20x jellegű egyenes, mely a vízszintes tengelyt =10-nél metszi. Nézzük a fázist:
.
Tehát +90º vagy -90º, ha azonban egy tetszőleges -t behelyettesítünk a frekvenciaátviteli függ-vénybe, majd megvizsgáljuk a kapott értéket, a kérdés könnyen eldönthető. Legyen =1, ekkor W=-j, amiből =-90º következik.
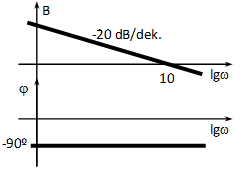
Értelmezzük most az átviteli függvényt két tag soros kapcsolásaként:
Határozzuk meg külön-külön a két tag Bode diagramját. Látható, hogy W1 esetén sem az amplitúdó, sem a fázis nem függ -tól, így mindkettő vízszintes egyenes lesz. A fázis azonosan zérus, hiszen képzetes része zérus. Mivel az amplitúdó mindig 10, ezért 20lg10=20. W2 fázisdiagramja itt is -90º lesz, hiszen () most is -∞. Az amplitúdó diagram kissé módosul:
ami szintén –20dB/dekádos meredekségű egyenes, viszont a vízszintes tengelyt =1-nél metszi. Most már csak összegezni kell a diagramokat. A fázissal semmi gondunk, hiszen az egyik azonosan zérus. Az amplitúdó diagram esetén W2 egyenese 20 decibellel feljebb tolódik, de mivel meredeksége éppen -20dB/dekád, ezért a tengely metszéspontja egy dekádnyival jobbra tolódik, azaz 1 helyett 10 lesz. Megfigyelhetjük, hogy ezzel a módszerrel is az előzővel megegyező eredményt kaptunk.
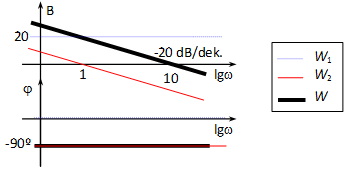
4 - 30 . feladat
Határozzuk meg, milyen értéknél metszi a vízszintes tengelyt a következő diagram:
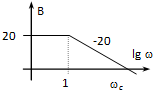
A megoldáshoz használjuk a (4.172) összefüggést. Az ábráról leolvasható, hogy: B1=20; 1=1; n=+1; B2=0. Ezek után:
Megjegyzések:
-
2-t nem véletlenül jelöltük c-vel. Azt a frekvenciát, amelynél az amplitúdó egységnyi, vágási körfrekvenciának hívjuk és a jele: c.
-
az eredményt mindenféle számítás nélkül is megkaphattuk volna, hiszen: az egyenes 20 decibelről 0 decibelre csökken az adott körfrekvencia értékek között, meredeksége -20 dB/dekád, azaz a frekvencia éppen a tízszeresére nő.
4 - 31 . feladat
Határozzuk meg, milyen értéknél metszi a vízszintes tengelyt a következő diagram:
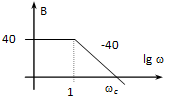
Az előző feladathoz képest annyi a változás, hogy B1=40 és n=+2. Ennek megfelelően A1=102=100, és
A megoldást most is megkaphattuk volna számítás nélkül, lásd az előző feladat második megjegyzését.
4 - 32 . feladat
Határozzuk meg a következő Bode diagram alapján a számozott pontoknál a hiányzó amplitúdó értékeket:
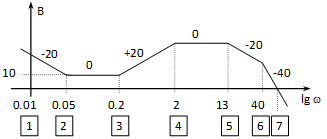
Az első dolgunk olyan pontot keresni, ahol minden értéket ismerünk. Ilyen kettő is van, a kettes és a hármas. Innen kiindulva, a megfelelő aránypárokat alkalmazva meghatározhatjuk a keresett értékeket:
4 - 33 feladat
Ábrázoljuk a (PIT1 típusú) frekvenciaátvitelifüggvényt.
4.9.1. Nyquist diagram
Állítsuk elő a frekveciafüggvény algebrai alakját:
Készítsünk értéktáblázatot néhány -hoz:
|
|
0 |
0.1 |
0.3 |
0.5 |
0.7 |
1 |
|
|
Re |
-6 |
-5.77 |
-4.412 |
-3 |
-2.027 |
-1.2 |
0 |
|
Im |
- |
-28.84 |
-7.353 |
-3 |
-1.448 |
-0.6 |
0 |
Ábrázolva:
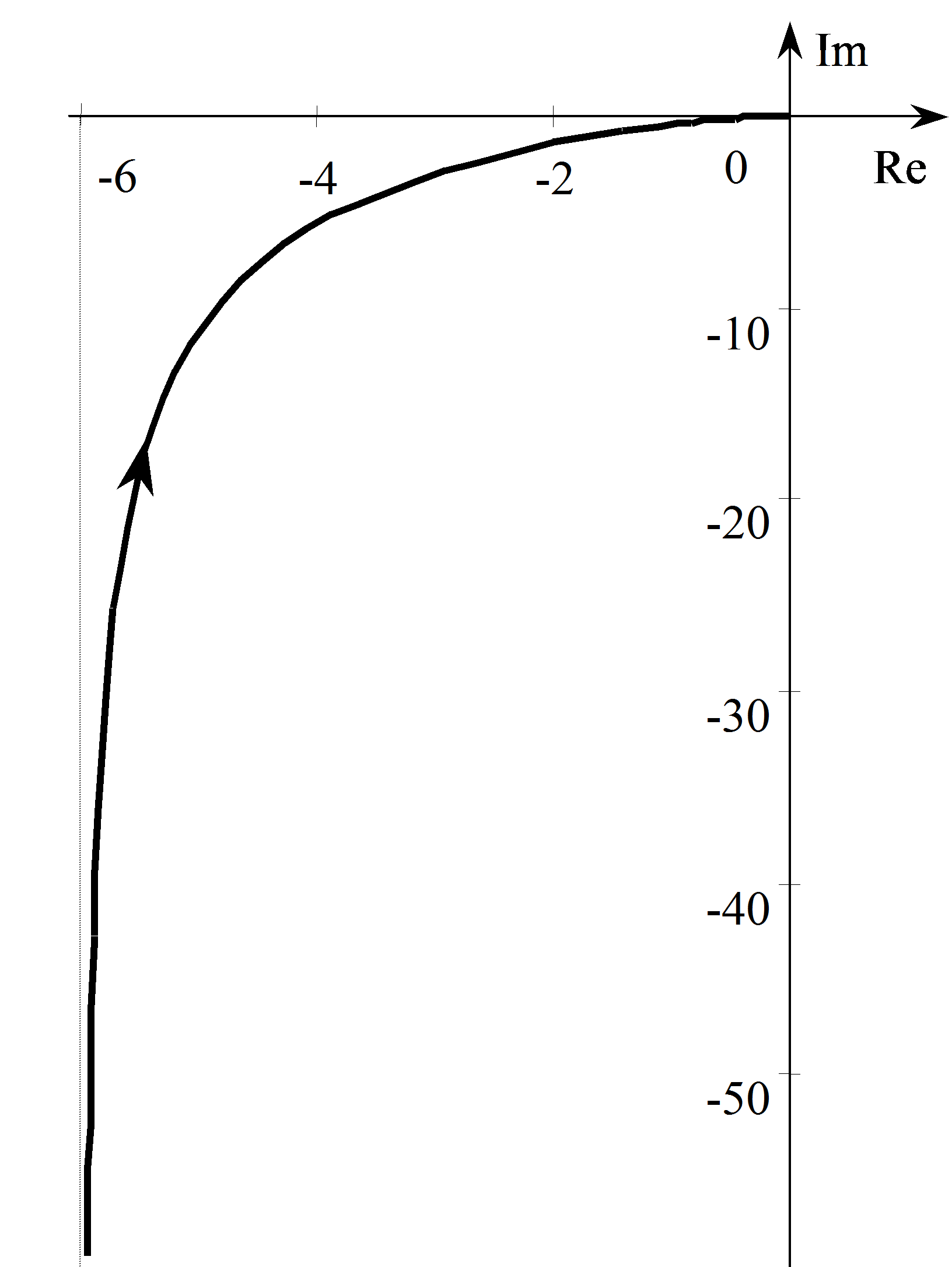
A másik (egyszerűbb esetekben alkalmazható) lehetőség kevesebb számítást, több gondolkodást igényel. Ekkor megpróbáljuk a függvény menetét kikövetkeztetni. Először meghatározzuk a függvény értékét 0 és esetén, majd megvizsgáljuk, hogy a görbe melyik síknegyedeken haladhat keresztül. Ezen számítások eredményeit tartalmazza a következő táblázat:
|
|
0 |
0< |
|
|
Re |
-6 |
0 |
negatív |
|
Im |
- |
0 |
negatív |
Látható, hogy -6-nál aszimptota van, és a görbe végig egy síknegyedben marad (Holtidő mentes egytárolós rendszer esetén mindig egy síknegyedben marad!) Azt kell már csak eldönteni, hogy hogyan fut be az origóba. A 248. oldalon közölteknek megfelelően:
,
tehát tisztán (negatív) valós, ezért a valós tengely mellett halad.
4.9.1.1. Bode diagram
Ehhez célszerű a frekvenciafüggvényt a sorba kapcsolt alaptagoknak megfelelő szorzattá bontani:
We=W1W2W3, ahol W1=3, , .
Az eredő Bode diagram ezen elemi tagok ábrázolásának összegzéseként adódik.
W1: P tag, amplitúdója 20lg39.5 [dB] magasságú egyenes, fázisa 0.
W2: PT1 tag, amplitúdója eleinte a vízszintes tengelyen fut (20lg1=0), az -nél levő törésponttól kezdve -20dB/dekád meredekségű egyenes. A fázisdiagram inflexiós pontja ugyanott van, ahol az amplitúdó diagram töréspontja.
W3: I tag, amplitúdója -20dB/dekád meredekségű egyenes, amely 1-nél metszi a vízszintes tengelyt. Fázisa -90 függetlenül a frekvenciánál.
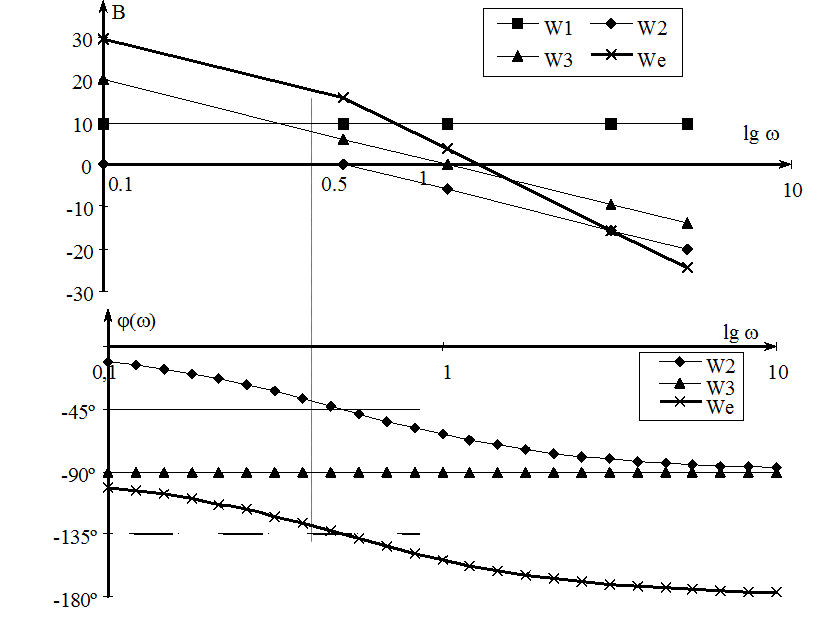
4 - 34 feladat
Ábrázoljuk az (PT2 típusú) frekvenciaátviteli függvényt.
4.9.1.2. Nyquist diagram
Állítsuk elő a frekveciaátviteli függvény algebrai alakját:
Készítsünk értéktáblázatot néhány esetén:
|
|
0 |
0.01 |
0.03 |
0.06 |
0.1 |
0.3 |
0.5 |
0.8 |
1 |
2 |
3 |
5 |
|
Re |
5 |
4.99 |
4.91 |
4.64 |
4.1 |
1.2 |
0 |
-0.42 |
-0.44 |
-0.23 |
-0.12 |
-0.05 |
|
Im |
0 |
-0.2 |
-0.74 |
-1.41 |
-2.13 |
-2.82 |
-2 |
-1.08 |
-0.74 |
-0.15 |
-0.05 |
-0.01 |
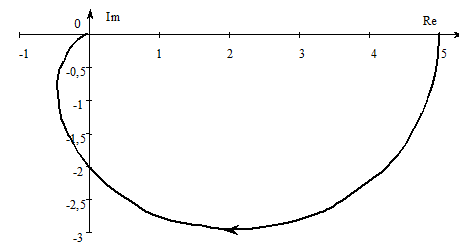
A 4-94. ábrából is látszik, hogy a görbe két síknegyeden halad keresztül, ami természetes, hiszen kéttárolós rendszerről van szó. Az origóba a negatív valós tengely mellett fut be.
Határozzuk meg, hol metszi a görbe az imaginárius tengelyt (természetesen ott, ahol Re(W(j))=0).
A táblázatból látható, hogy itt Im(W(j))=-2.
4.9.1.3. Bode diagram
Célszerű a frekvenciafüggvényt az alaptagoknak megfelelő szorzattá bontani. Esetünkben a nevezőt kell felírni gyöktényezős alakban:
Így a frekvenciafüggvény:
,
tehát egy P és két PT1 tag szorzataként írható fel, ahol a töréspontok helye 1 és 0.25.
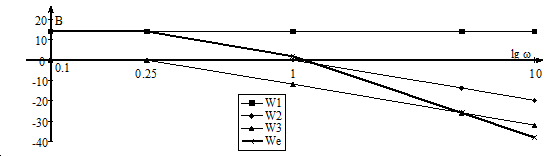
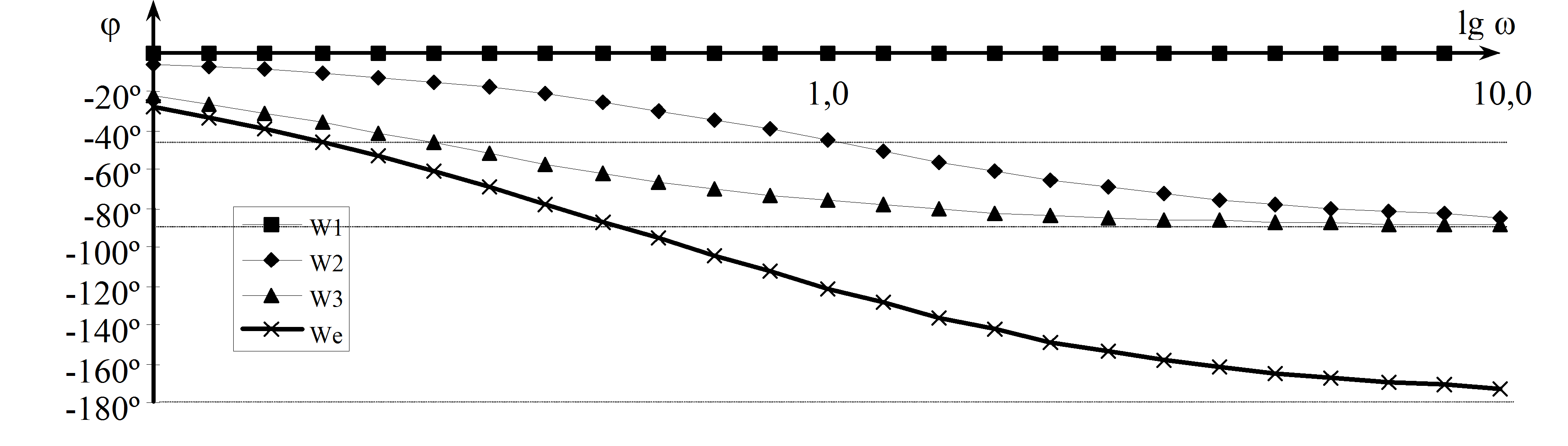
4 - 35 . feladat
Tekintsünk most egy olyan rendszert, ahol az előző két példában szereplő tagok párhuzamosan vannak kapcsolva:
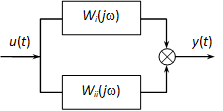
Az eredő frekvenciafüggvény:
4.9.1.4. Nyquist diagram
Állítsuk elő a frekveciafüggvény algebrai alakját (a részletszámításokat mellőzve):
Meglehetősen bonyolult. A továbbiakban két út közül választhatunk:
a, értéktáblázat és rajz (pl. valamilyen táblázatkezelő szoftverrel könnyen elvégeztethető)
b, az előző két példában kapott diagramokat vektoriálisan összegezzük (a pontos eredményhez meglehetősen sokat kell dolgozni).
a, megoldás:
Az algebrai alakból nehéz következtetéseket levonni a rendszer összetevőire nézve. Erre sokkal jobban használható a Bode diagram elkészítését segítő alak, ahol a frekvenciafüggvény számlálója és nevezője polinomok szorzataként van felírva. Az azonban most is látszik, hogy a rendszer integráló jellege megmaradt, hiszen az imaginárius rész nevezőjéből a rendezések után is ki lehetett emelni -t.
Az értéktáblázat:
|
|
0.051 |
0.06 |
0.1 |
0.15 |
0.3 |
0.35 |
0.4 |
0.5 |
0.65 |
0.8 |
1 |
5 |
|
Re |
-1.2 |
-1.27 |
-1.67 |
-2.23 |
-3.21 |
-3.26 |
-3.22 |
-3 |
-2.54 |
-2.11 |
-1.64 |
-0.11 |
|
Im |
-59.49 |
-50.7 |
-30.98 |
-21.05 |
-10.17 |
-8.39 |
-6.99 |
-5 |
-3.19 |
-2.14 |
-1.34 |
-0.02 |
A Nyquist diagram:
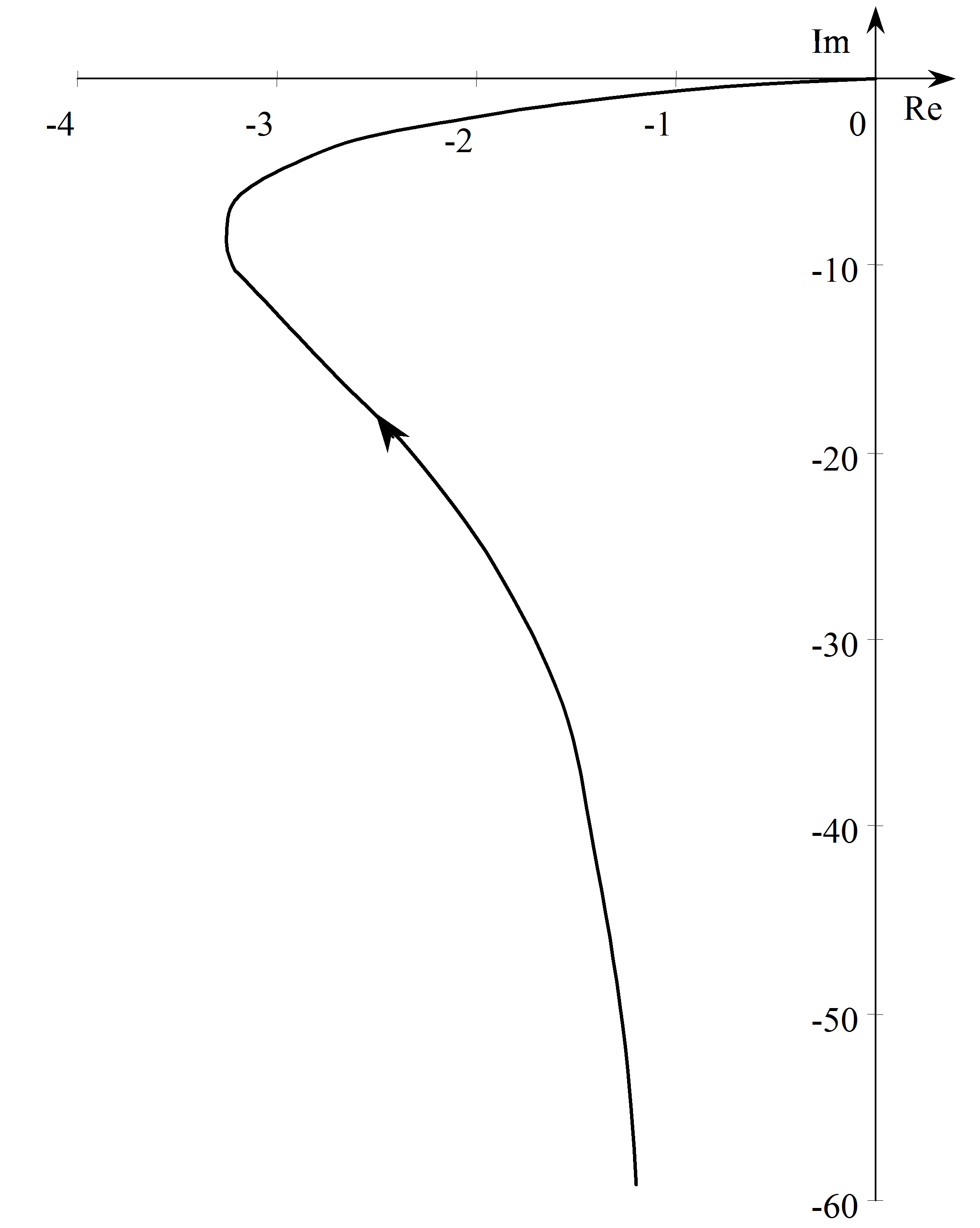
b, megoldás:
A 4-98. ábrán két különböző értékhez tartozó vektoriális összegzést láthatunk. A szaggatott vonal az =0.3 a folytonos pedig az =0.5 értékekhez tartozik. Természetesen ennyi nem elegendő a teljes diagram elkészítéséhez!
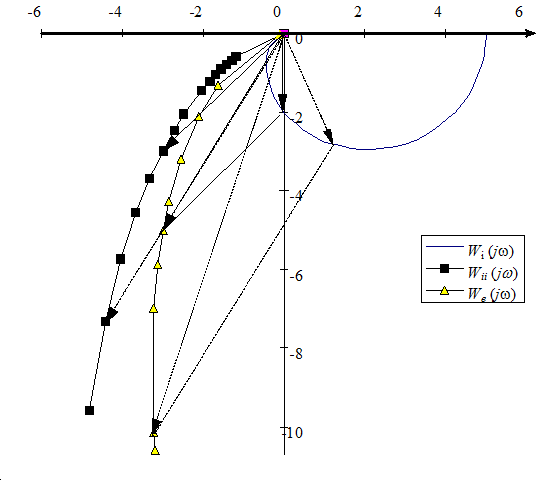
4.9.1.5. Bode diagram
A Bode diagram elkészítéséhez úgy kell átalakítani a frekvenciafüggvényt, hogy a számláló és a nevező is a lehető legalacsonyabb fokszámú polinomok szorzata legyen. Ehhez a következő alakból indulunk ki:
Rendezés után kapjuk a következő alakot:
Ebből leolvasható, hogy milyen alaptagokból tevődik össze a rendszer:
,
tehát egy P, egy I, három PT1 és két PD tagból.
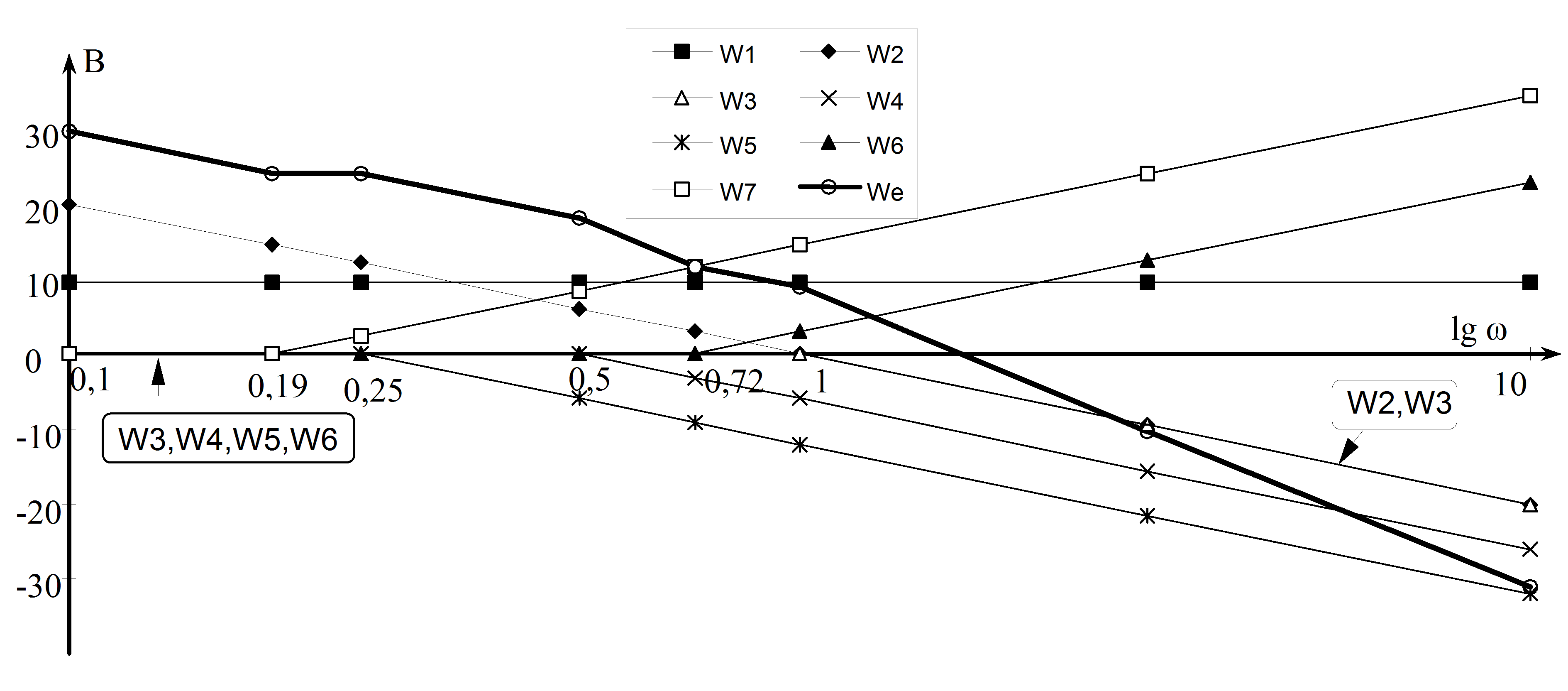
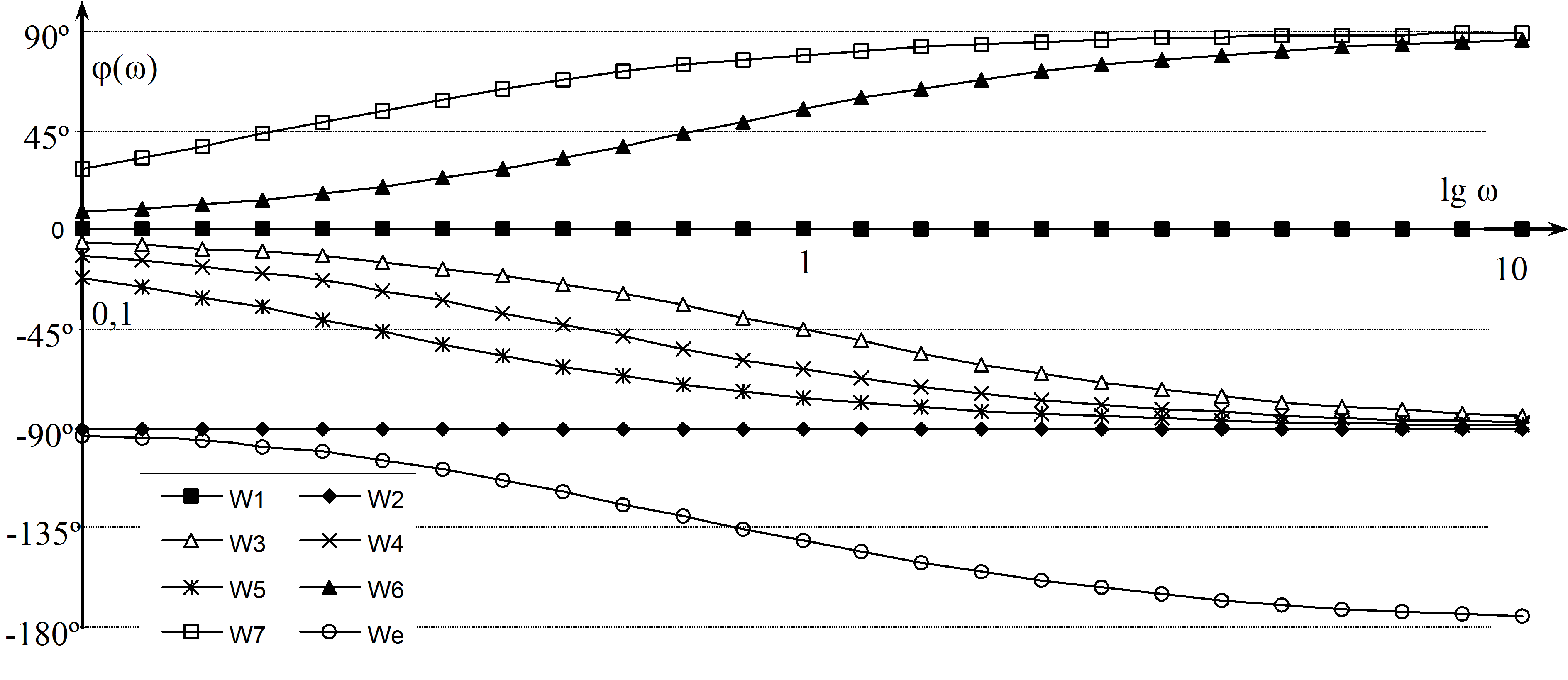
4 - 36 . feladat
Feladatunk megegyezik az előzővel, csak most a tagok sorba vannak kapcsolva.

Az eredő frekvenciafüggvény:
4.9.1.6. Nyquist diagram
Állítsuk elő a frekveciafüggvény algebrai alakját (a részletszámításokat mellőzve):
Ha valaki ezt a rendezést el akarja kerülni, akkor másik utat is választhat: az azonos paraméterű helyvektorok, mint komplex vektorok összeszorzását, azaz a fázisszögek összeadását és az abszolút értékek összeszorzását. Nem biztos, hogy ez az egyszerűbb megoldás!
Maradjunk az értéktáblázatos módszernél (ld.4-101. ábra):
|
|
0.01 |
0.02 |
0.05 |
0.1 |
0.2 |
7 |
|
Re |
-104.76 |
-104.08 |
-99.43 |
-85.19 |
-50.64 |
0.00075 |
|
Im |
-1494.76 |
-739.58 |
-274.92 |
-105.87 |
-16.68 |
0.0002 |
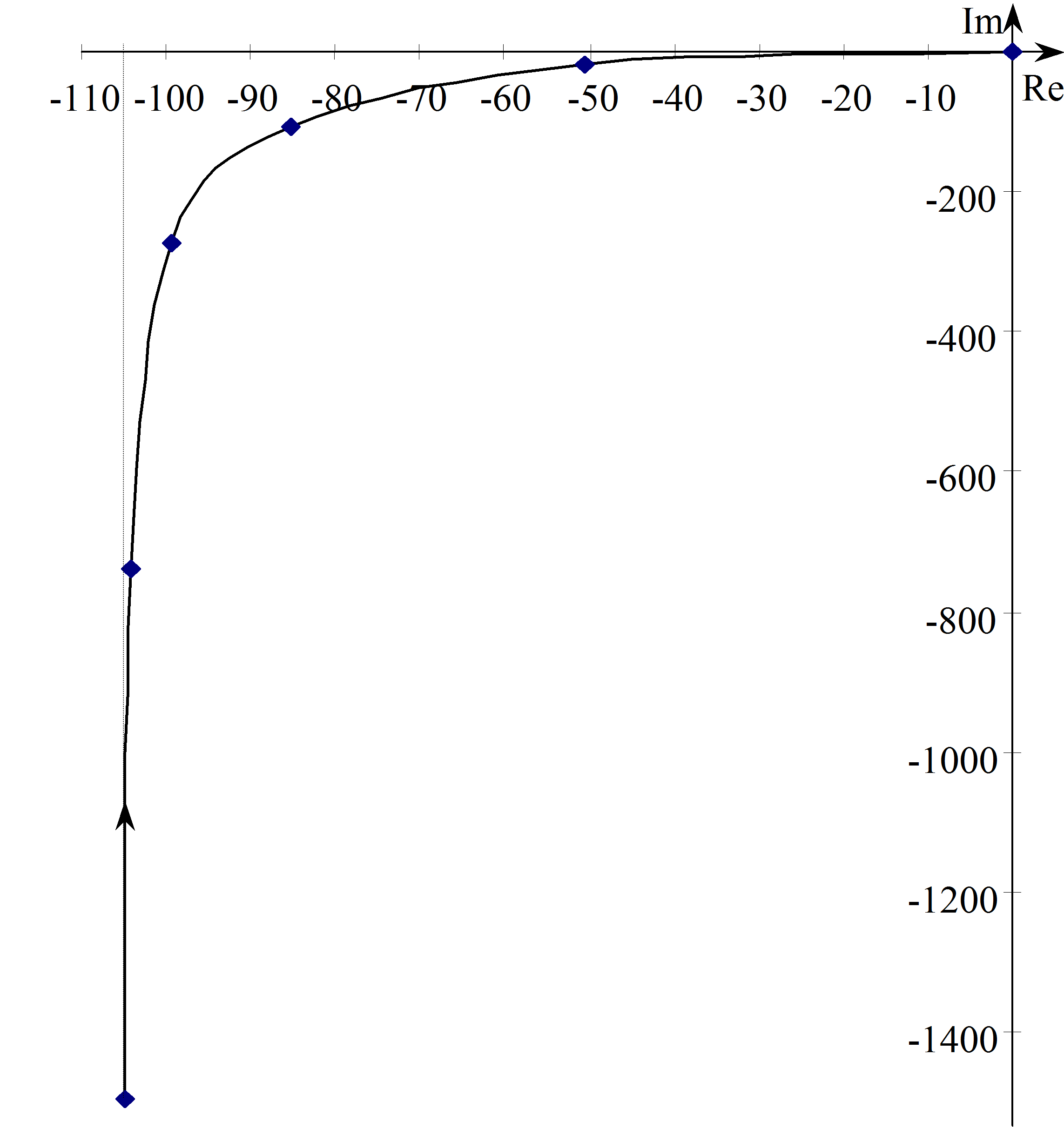
A 4-101. ábraából látszik, hogy a diagramnak 0 helyen aszimptótája van -105-nél. Az azonban nem látszik, hogy metszi-e a valós tengelyt, ezért a diagram ezen részét nagyítsuk ki (4-102. ábra):
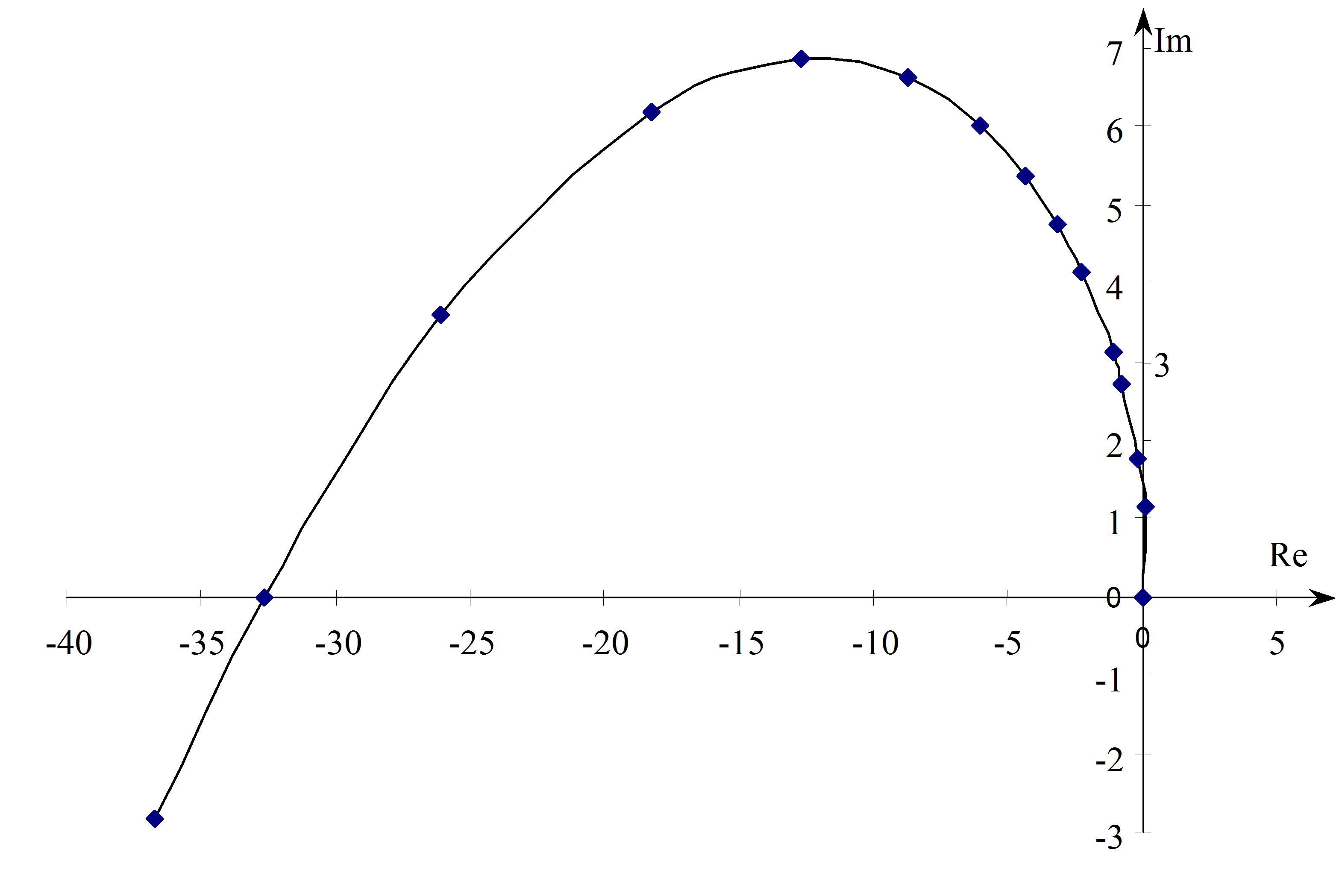
Ezek szerint a görbe metszi a valós tengelyt, de azt még mindig nem látjuk jól, hogyan fut be az origóba. Nagyítsuk ki ezt a részt is (4-103. ábra):
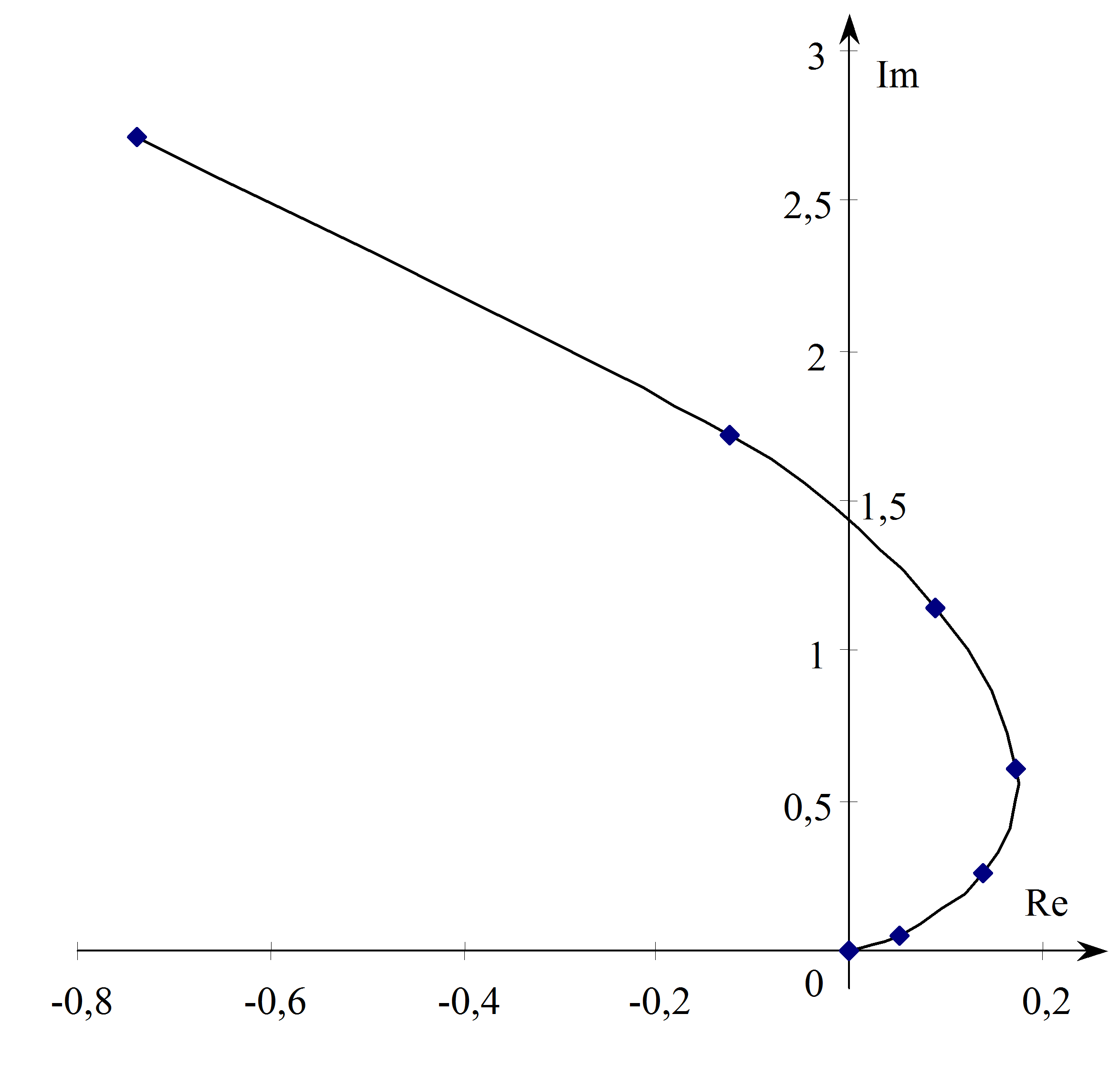
Most már azt is látjuk, hogy metszi a képzetes tengelyt is és a pozitív valós tengely mellett simul be az origóba.
Az átviteli függvényből is kiolvasható, amit a diagram is igazol (három síknegyeden halad keresztül), hogy a rendszer háromtárolós (PIT3). Az integráló jelleg pedig abból látszik, hogy Im=--ből indul.
A teljesség kedvéért határozzuk még meg a tengelymetszési értékeket.
A valós tengelyt Im=0-nál metszi, tehát a felírható egyenlet:
Ebből a megoldás , hiszen minket csak a pozitív frekvencia értékek érdekelnek! Behelyettesítve kapjuk, hogy a valós rész értéke ekkor: -32.667.
A képzetes tengely metszéspontja Re=0-nál van. Ekkor az egyenlet:
Ebből a megoldás . Behelyettesítve Im=1.425.
4.9.1.7. Bode diagram
A Bode diagram elkészítéséhez úgy kell átalakítani a frekvenciafüggvényt, hogy a számláló és a nevező is a lehető legalacsonyabb fokszámú polinomok szorzata legyen. Ehhez a következő alakból indulunk ki:
A Nyquist diagramnál már láttuk, hogy a rendszer milyen tagokból épül fel (3 tároló, integráló). A diagram elkészítésénél felhasználhatjuk, hogy két már ábrázolt elem soros kapcsolásáról van szó, tehát az eredőt grafikus összegzéssel kaphatjuk:
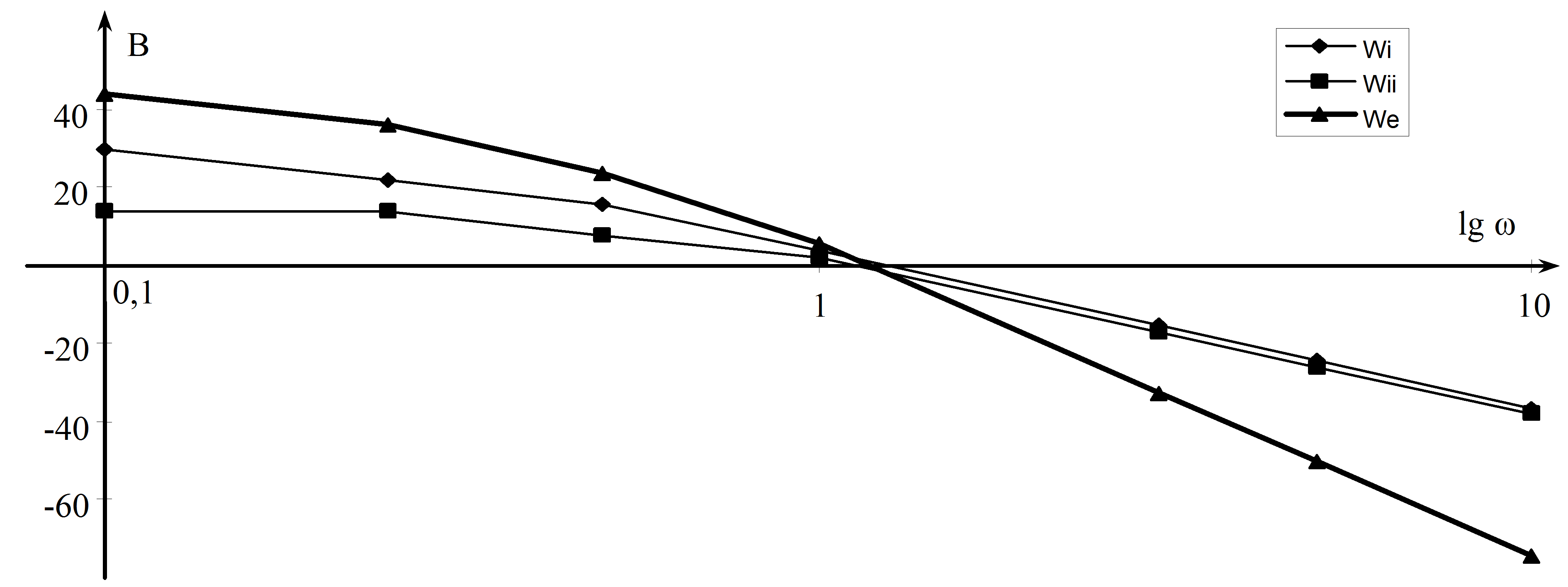
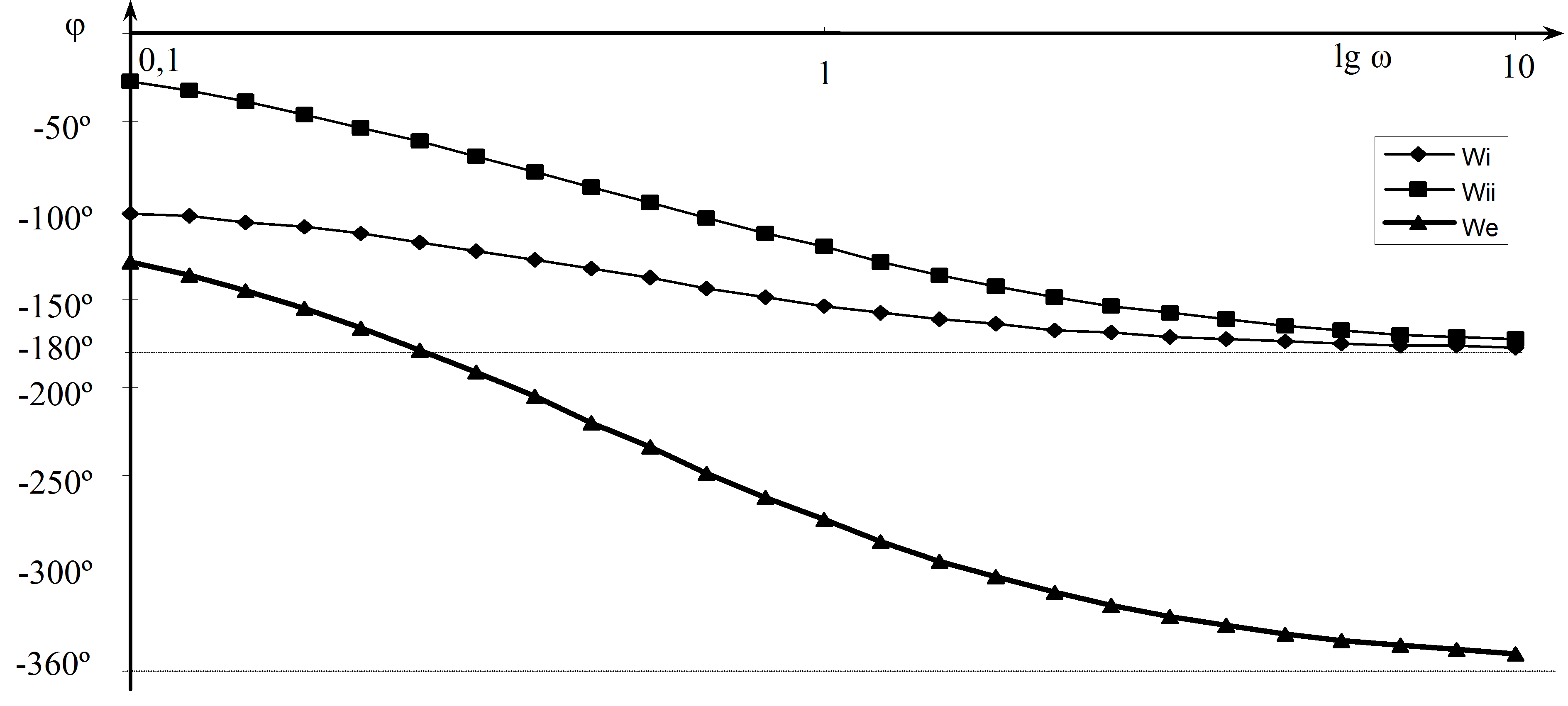
4 - 37 . feladat
Határozzuk meg az eredő Bode diagramot, ha a következő elemek vannak sorba kapcsolva:
Soros kapcsolás esetén a tagok Bode diagramjának összegzésével kapjuk az eredőt (érdemes megfigyelni, hogy mivel az arányos tag kisebb 1-nél, ezért egyenese a vízszintes tengely alatt fut):
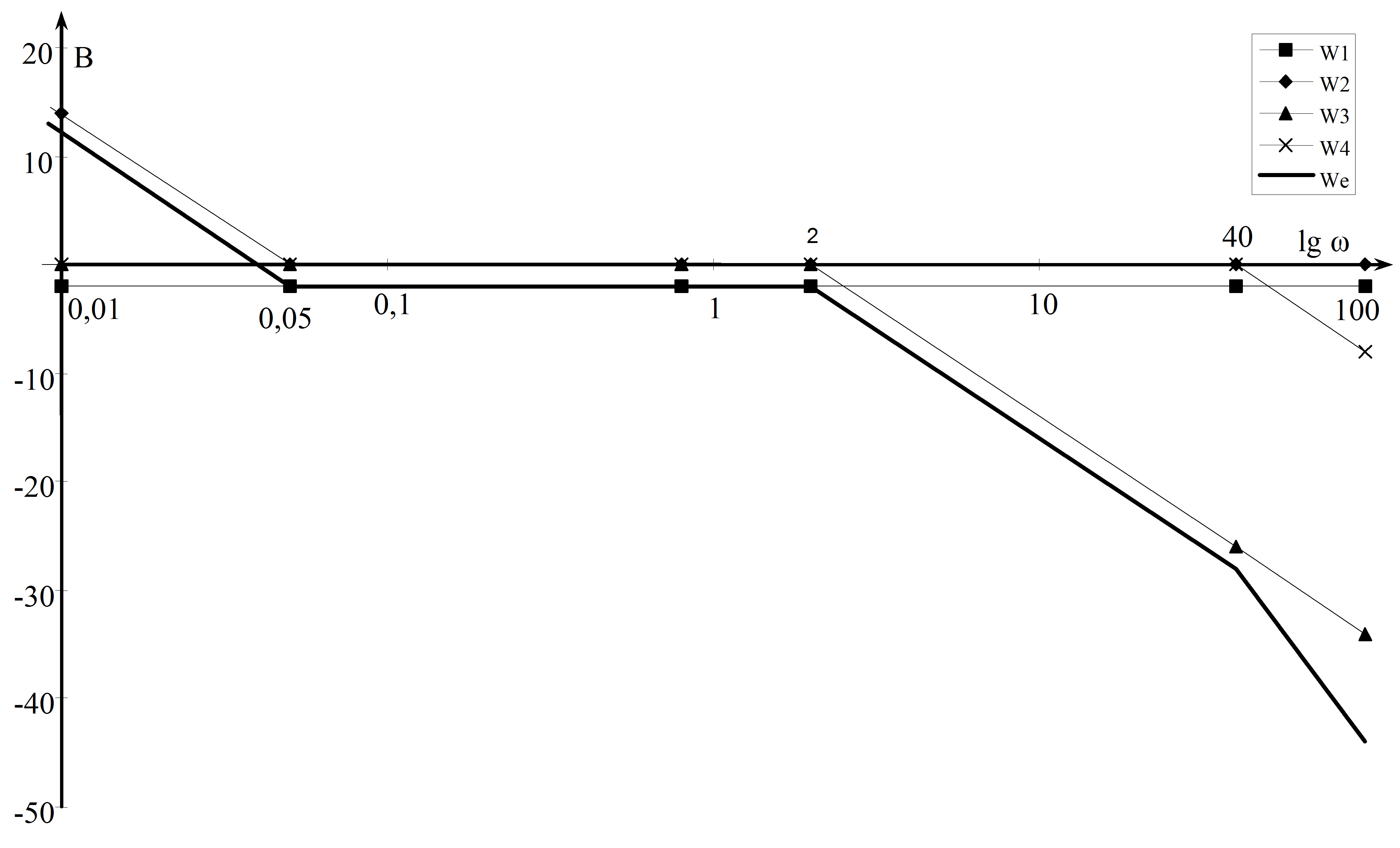
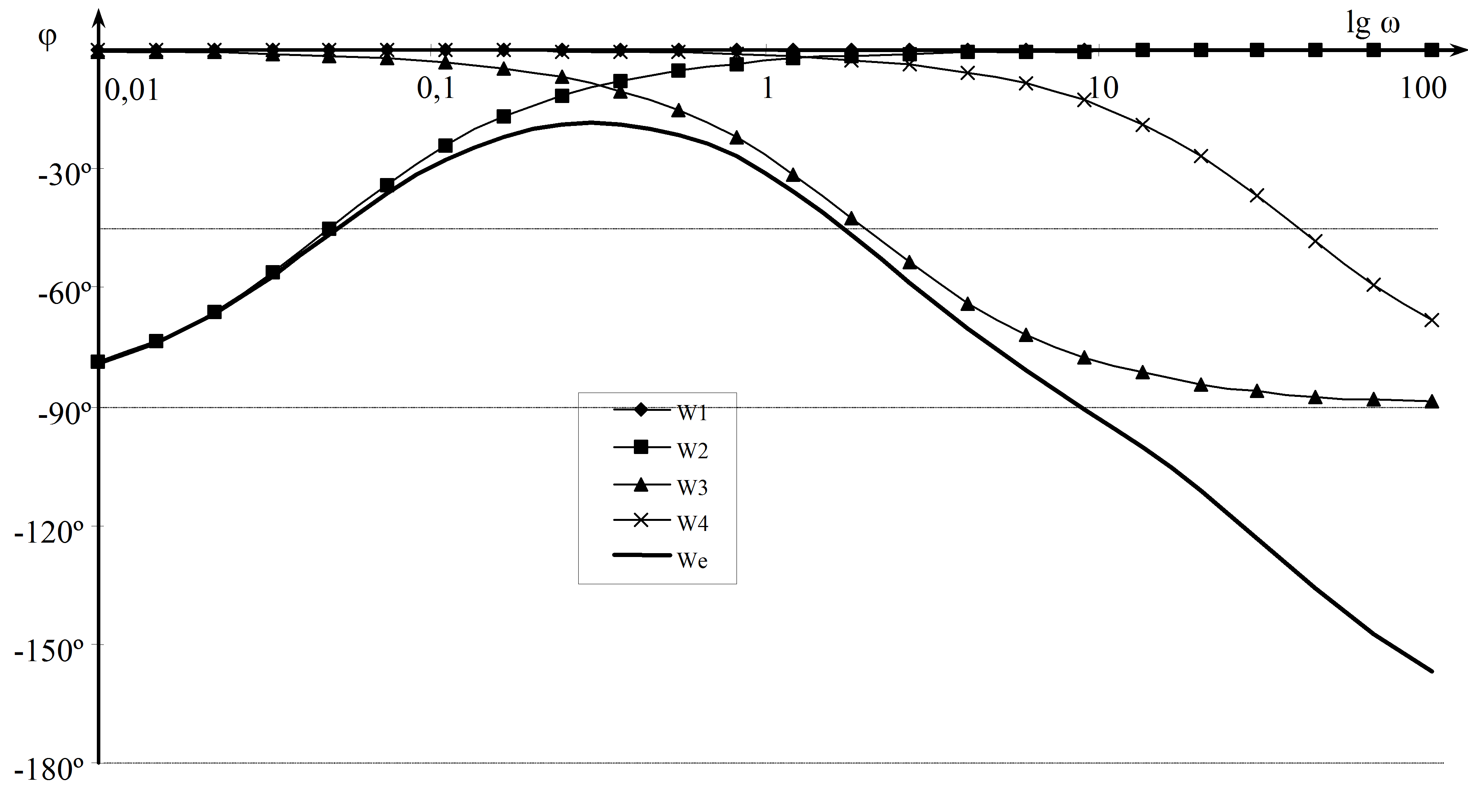
4 - 38 . feladat
Adott a következő aszimptotikus amplitúdó Bode diagram. Határozzuk meg a frekvenciaátviteli függvényt.
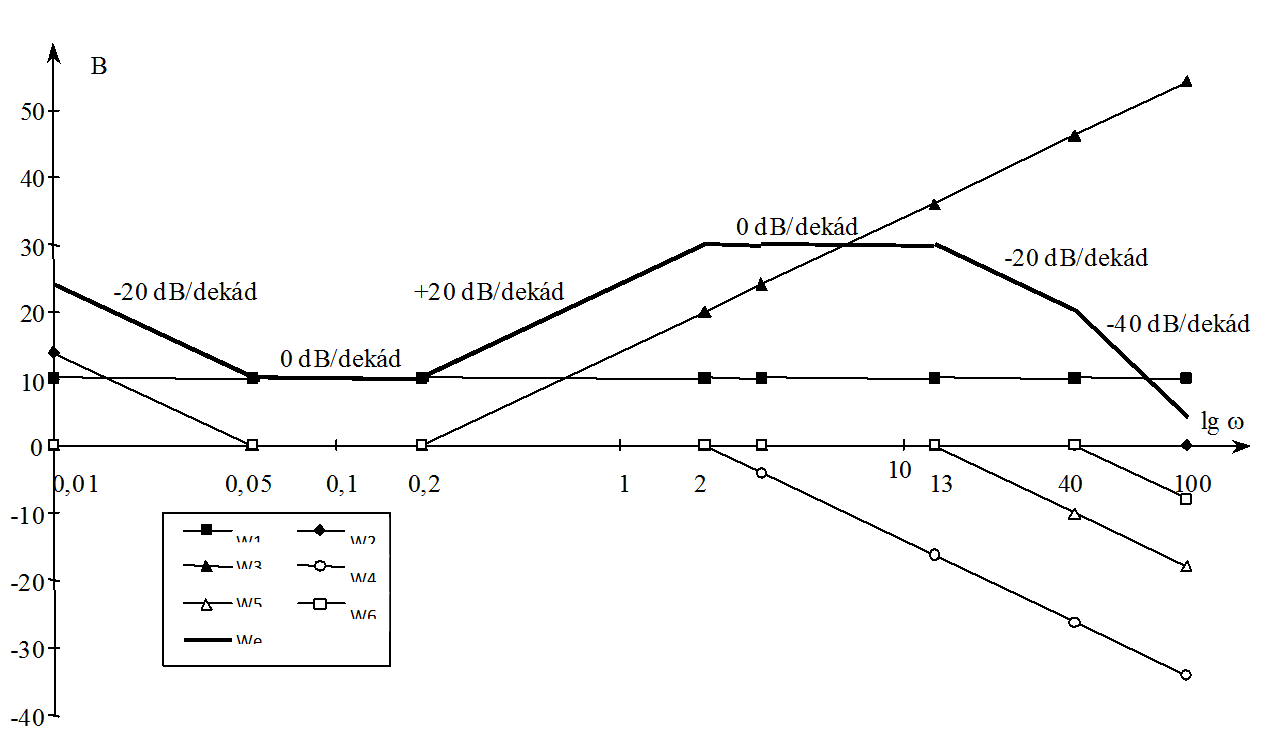
Próbáljuk az átviteli függvényt néhány egyszerűbb tag szorzataként előállítani, ugyanis ezen tagok grafikus összegzése a diagram. Ilyen tagok a következők: P, PI, PD és PT1. Az ábrában a vastag vonal mutatja az eredőt.
Először mindig megkeressük az első vízszintes szakaszt. Esetünkben ez az első és a második töréspont között van. Ez az egyenes szakasz egy arányos tag diagramjának a része:
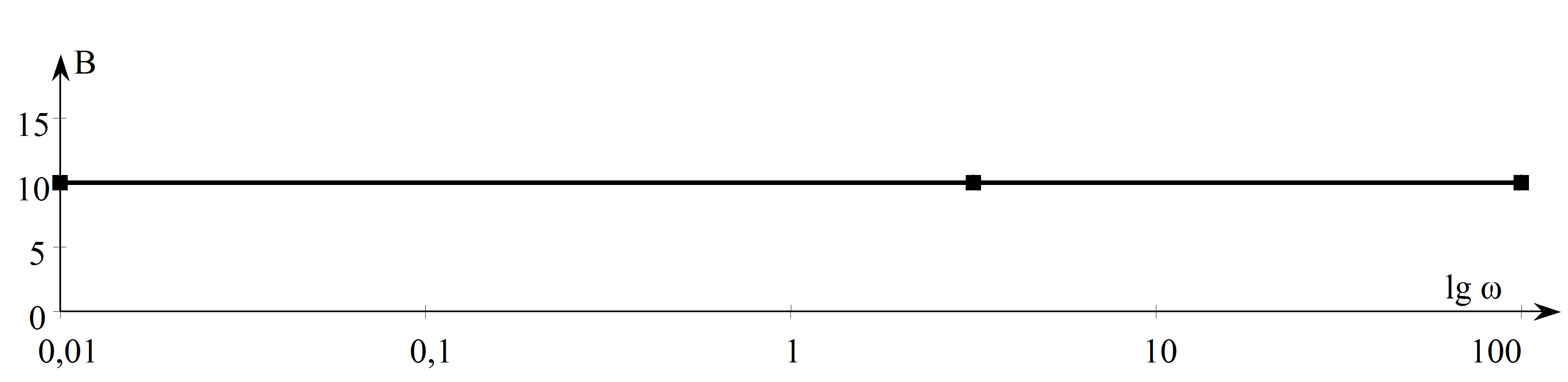
A 4-107. ábraáról leolvashatjuk, hogy 10-nél metszi a függőleges tengelyt. Figyelembe véve, hogy a skála dB, Tehát az első tag: W1=3.15.
Ezután balról jobbra haladva végigmegyünk az összes törésponton. Minden töréspontnál egy-egy újabb taggal bővül a függvények listája. Ha az első töréspont előtt a meredekség negatív, akkor az PI tagot jelent. Ilyenkor a PI tag arányos része mindig egy. Ennek két oka van. Egyrészt ekkor diagramjának vízszintes része a tengelyen halad, hiszen 20lg1=0, tehát nem szól bele az eredő további menetébe. Másrészt az összes arányos részt már összevontuk az előzőekben leírt arányos tagban.
Ha a meredekség eltér -20 dB/dekádtól, akkor annyi PI tagot veszünk ahányszoros az eltérés (pl. -40-nél 2 PI tag van). TI értékét a törésponti frekvencia reciproka adja.
A 4-108. ábra mutatja, hogy esetünkben ez hogy néz ki. Itt a meredekség -20, a töréspont 0.05-nél van, tehát a tag átviteli függvénye: .
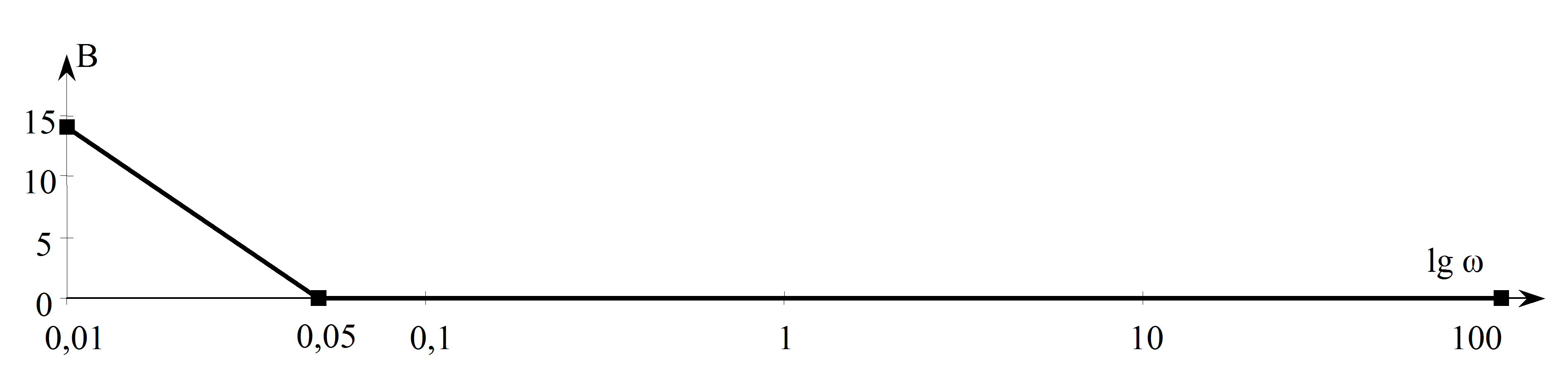
Ezt követően már csak 2 tag fordulhat elő: PD és PT1. Ha a töréspont után a meredekség változása +20 dB/dekád akkor PD, ha -20 akkor PT1 tagot kell figyelembe vennünk. Mindkét esetben az arányos rész értéke 1, az előző lábjegyzetben leírtak miatt. Ha a meredekség változása nagyobb, akkor a megfelelő tagból többet kell venni, az előzőekben a PI tagnál leírtak szerint. A függvények T paraméterét itt is a körfrekvencia reciproka adja.
A következő két ábra (4-109, 4-110) a fent leírtakat szemlélteti a példa adataival. Ennek megfelelően látszik, hogy egy PD tag és három PT1 tag van még a rendszerben. Ezek függvényei rendre a következők:
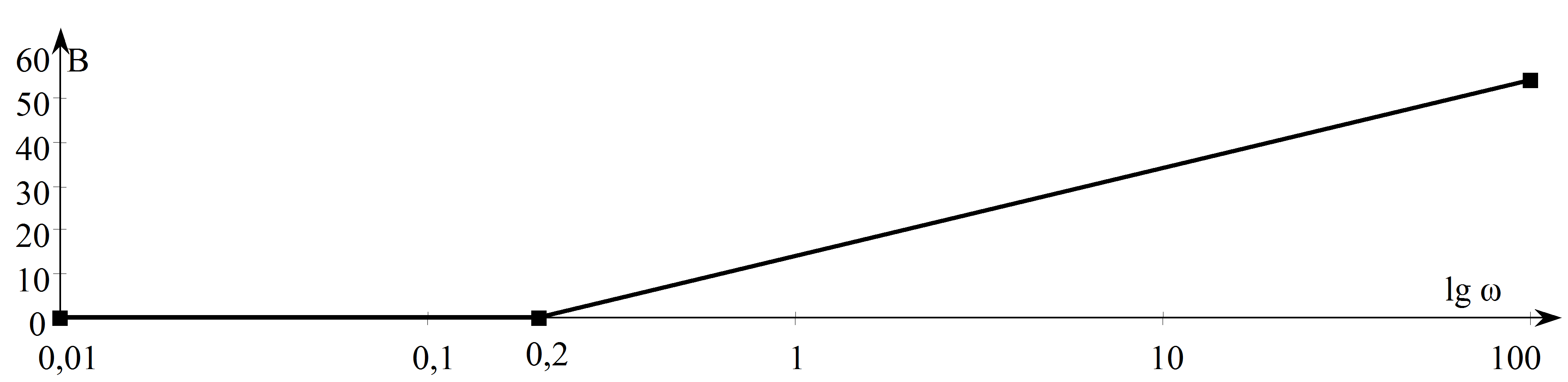
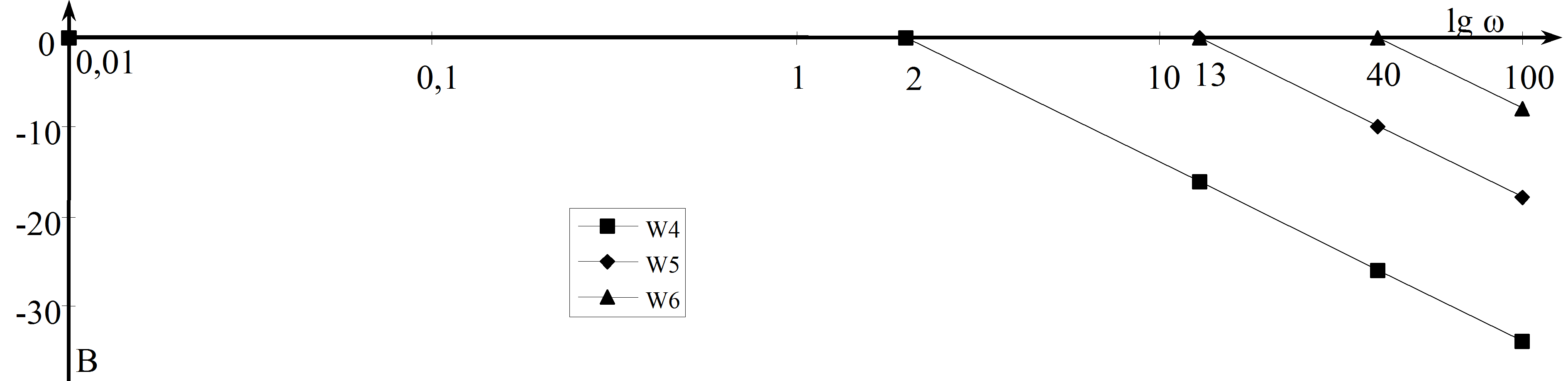
Ezek után az eredő átviteli függvény már egyszerűen előállítható, hiszen a tagok összeszorzásával kapjuk.
Figyelem: a kérdés az átviteli függvény volt, és nem a frekvenciafüggvény. Ennek megfelelően W(s)-t kell felírni. Ez azonban nem okoz nehézséget, hiszen tudjuk, hogy az s=j formális helyettesítésével megkaphatjuk.
Amennyiben a feladat kiírása külön nem tartalmazza, akkor a tagok összeszorzását nem kell elvégezni, így a megoldás:
4 - 39 . feladat
Adott a következő közelítő amplitúdó Bode diagram. Határozzuk meg az átviteli függvényt és rajzoljuk meg a fázismenetet.
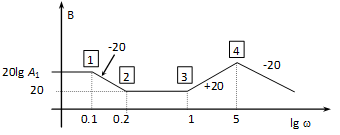
Az első vízszintes szakasz a diagram elején van, de magassága nem ismert. A következő 2 pont minden adata ismert, így A1 értékét kiszámíthatjuk:
Az első tag tehát: Y1=20. A diagram ezek után a következőképpen néz ki:
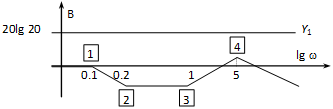
Most már csak sorra végig kell menni a töréspontokon, ahol a változás +20 decibel/dekádos ott egy PD, ahol –20 decibel/dekádos ott egy PT1 tagot kell elhelyezni:
Az utolsó tag esetén a változás –40 decibel, ezért két azonos időállandójú egytárolós taggal kell figyelembe venni. Az eredő átviteli függvény ezen tagok szorzataként állítható elő:
A frekvenciamenetet megrajzolhatjuk úgy is, hogy a tagok frekvenciamenetét összegezzük. Nézzünk azonban egy ugyan nem pontos, de jellegre helyes eredményt adó gyorsabb, közelítő módszert.
Induljunk ki az alaptagok ismert tulajdonságaiból. Arányos tag esetén a fázis zérus, jelöljük ezt az intervallumok közepén:
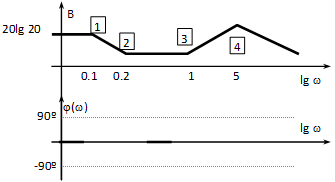
A töréspontoknál a fázismenetben inflexiós pontok vannak. Ha a változás értéke ±20 decibel/dekád, a fázis értéke ±45º, illetve többszörös meredekségnél ±45º többszöröse:
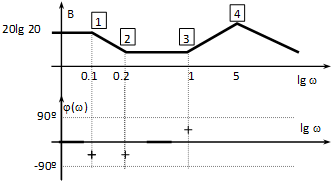
Az egytárolós, illetve az arányos-differenciáló tagok mínusz, illetve plusz 90º-hoz tartanak. Jelöljük a megfelelő intervallumok közepét egy vízszintes szakasszal:
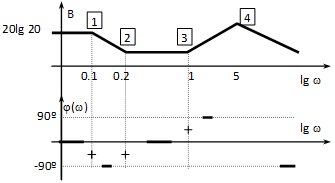
A 4 pontnál is töréspont van, de ott a változás nagyobb mértékű. A fázis ezen a részen +90º-ról -90º-ra csökken. A két szög középértéke nulla:
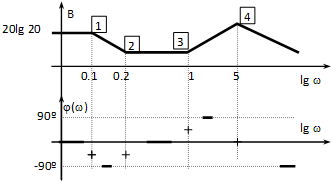
Most próbáljuk meg folytonos vonallal összekötni az így kapott jellegzetes fázisszög értékeket:
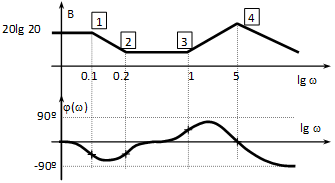
Ügyeljünk arra, hogy ahol a töréspontok közel vannak egymáshoz, ott a görbe nem fogja elérni az aszimptotát. Esetünkben ez történik az 1 és 2 , valamint a 3 és 4 pontok között.
Jól látható, hogy a görbének lokális minimum helye van =0.1 és =0.2 között, körülbelül középen. Határozzuk meg ezt a frekvencia értéket. Mivel a tengelyen logaritmikus lépték van, ezért a számtani közép számítás közvetlenül nem alkalmazható, de:
,
amiből az következik, hogy a mértani közepet kell meghatározni:
.
4 - 40 . feladat
Adott egy rendszer az amplitúdó Bode diagramjával. Határozzuk meg a rendszer válaszát, ha u1(t)=sin(0.1t); u2(t)=sin(t), u3(t) =sin(10t) és a kezdeti feltétel zérus.
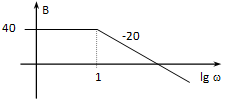
a, megoldás
Oldjuk meg a feladatot analitikusan. Állítsuk elő a rendszer átviteli függvényét. A diagram alapján megállapíthatjuk, hogy a rendszer arányos egytárolós, átviteli függvénye általános alakban: . Tudjuk, hogy a töréspont -nél van, így T értéke egy. G értékét a diagram vízszintes része adja, így: -ből G=100 adódik:
A differenciálegyenletet az átviteli függvény inverz Laplace transzformációjával állíthatjuk elő:
Természetesen egy állandó együtthatós, homogén, lineáris differenciálegyenletet kaptunk. Először állítsuk elő a homogén rész megoldását. A karakterisztikus egyenletből:
.
A partikuláris megoldást próbafüggvény módszerrel határozzuk meg. Mivel mindhárom függvényünk szinuszos és csak a körfrekvenciában tér el, ezért keressük a megoldást:
alakban. Helyettesítsünk be a differenciálegyenletbe:
A trigonometrikus függvényeket szétválogatva kapjuk a következő egyenletrendszert:
Megoldva az egyenletrendszert:
A c paramétert a kezdeti feltételből kapjuk:
a,α eset: =0.1
a, eset: =1
,
mivel azonban , így
a, eset: =10
b, megoldás
Induljunk ki a frekvenciaátviteli függvény definíciójából:
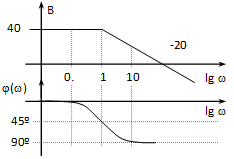
Vegyük észre, hogy U0 minden esetben egy, mivel megegyezik az ui gerjesztő függvények amplitúdójával.
b.α eset: =0.1
Láthatóan az analitikus megoldás domináns tagját kaptuk. Mint a 4-120. ábrán is látszik, az exponenciális tag hatása nagyon hamar eltűnik. A két függvény közötti különbség oka, hogy a fázist nem pontosan olvastuk le a Bode diagramról.
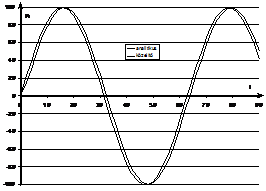
b. eset: =1
Most is az analitikus megoldás domináns tagja jelenik meg, de nem elég pontosan. Tudjuk azonban, hogy az aszimptotikus Bode diagram közelítő diagram, és a legnagyobb eltérés a pontos és a közelítő diagram között éppen a töréspontnál van. A hiba kb. 3dB, ami pontosan . Nézzük meg, mennyi lesz a pontos érték:
Ezek után a megoldás már megegyezik a domináns taggal:
A fázis leolvasása most pontos volt, ezt láthatjuk a 4-121. ábrán is. Kezdetben az eltérés jelentős, ennek oka az exponenciális tag, amit a közelítés nem vesz figyelembe.
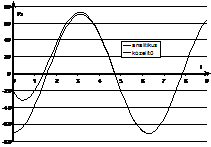
b. eset: =10
Az erősítés azért 10, mert éppen egy dekádnyira van a törésponttól. Itt is az analitikus megoldás domináns tagját kaptuk eredményül. A 4-122. ábrán látható kezdeti eltérést itt is az exponenciális rész okozza.
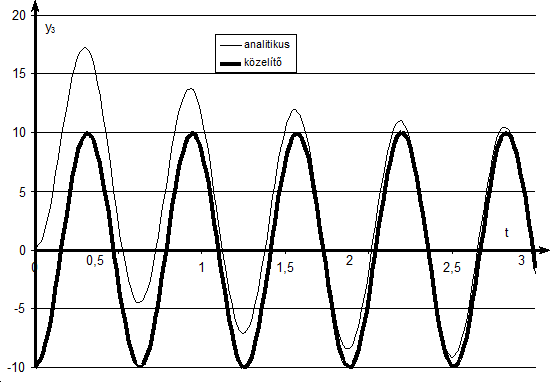
Összefoglalóan megállapíthatjuk, hogy a közelítés az indítási (tranziens) folyamatot figyelmen kívül hagyja, állandósult állapotban viszont (amikor a rendszer már a gerjesztésnek megfelelően változik) kielégítő pontosságú eredményt ad.
4 - 41 . feladat
Adott egy rendszer matematikai modellje:
.
Keressük a közelítő megoldást u1(t)=sin(0.01t) és u2(t)=sin(t) esetén, ha minden kezdeti feltétel zérus.
Első lépésként állítsuk elő az átviteli függvényt, majd rajzoljuk fel a Bode diagramot:
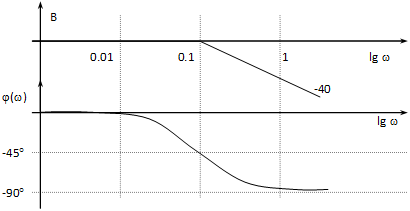
A közelítő megoldás u1(t)=sin(0.01t) esetén
a pontos megoldás:
A közelítő megoldás u2(t)=sin(t) esetén
és a pontos megoldás:
4 - 42 . feladat
Adott egy rendszer amplitúdó Bode diagramja. Keressük a közelítő megoldást u1(t)=sin(0.1t) és u2(10t)=sin(t) esetén, ha minden kezdeti feltétel zérus.
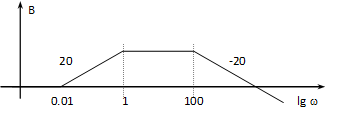
Mint már láttuk, a közelítő megoldáshoz szükségünk lesz a fázisdiagramra is. Ennek megszerkesztéséhez alkalmazhatjuk a már megismert közelítő módszert. Mivel a töréspontok messze (2 dekádnyira) vannak egymástól, a közelítés hibája elenyésző lesz.
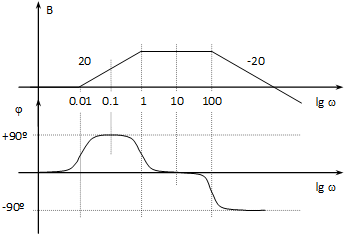
A közelítő megoldás u1(t)=sin(0.1t) esetén
a pontos megoldás:
A közelítő megoldás u2(t)=sin(10t) esetén
a pontos megoldás:
4 - 43 feladat
Adott egy többfrekvenciás feszültségforrás valamint ehhez sorban kapcsolódó ellenállás és induktivitás. A feszültségforrás feszültségét tekintjük bemeneti jelnek, és az ellenállás feszültségét tekintjük kimeneti jelnek. A feszültségforrás feszültségének az időfüggvénye: V, kΩ
-
Mekkora az alap és a felharmonikus ( első és második tagjának) frekvenciája?
-
Írja fel a fenti áramkör jel átviteli függvényét.
-
Válassza meg az induktivitás értékét, ha az a célunk, hogy a kimeneti feszültség felharmonikusának amplitúdója kb. ötödére csökkenjen a bemeneti felharmonikus értékhez képest (nem kell pontosan ötödére, csak közelítőleg).
-
Mennyire csökken ekkor az alapharmonikus?
-
Mekkora az alap és a felharmonikus fáziskésése?
-
Rajzolja fel az átviteli függvény közelítő Bode diagramját közelítőleg léptékhelyesen, közelítőleg a skálát is tüntesse fel.
4.9.2. MATLAB feladatok
4 - 44 feladat
A MATLAB program segítségével rajzolja fel a következő frekvencia átviteli függvények Nyquist diagramját
|
|
|
(4.203) |
|
|
|
(4.204) |
|
|
|
(4.205) |
|
|
(4.206) |
Megoldás:
% Időállandó adatok T11=1; T21=1; T22=0.2; T31=1; T32=0.01; T41=1; T42=1/1.5; T43=0.5; T51=1; T61=1; T62=0.2; T71=1; T72=0.2; T73=0.125; % A frekvencia átviteli függvény számláló és nevező polinomja szamlalo= 1; nevezo1=T11*poly([-1/T11]); nevezo2=T21*T22*poly([-1/T21 -1/T22]); nevezo3=T31*T32*poly([-1/T31 -1/T32]); nevezo4=T41*T42*T43*poly([-1/T41 -1/T42 -1/T43]); nevezo5=T51*poly([0]); nevezo6=T61*T62*poly([0 -1/T62]); nevezo7=T71*T72*T73*poly([0 -1/T72 -1/T73]); % A Nyquist diagram kirajzolása nyquist(szamlalo,nevezo1) axis([0 1 -0.5 0.5]) grid print -djpeg W1_Nyquist pause nyquist(szamlalo,nevezo2) axis([-0.2 1 -0.6 0.6]) grid print -djpeg W2_Nyquist pause nyquist(szamlalo,nevezo3) axis([-0.2 1 -0.6 0.6]) grid print -djpeg W3_Nyquist pause nyquist(szamlalo,nevezo4) axis([-0.3 1 -0.8 0.8]) grid print -djpeg W4_Nyquist pause nyquist(szamlalo,nevezo5) axis([-0.1 0.1 -6 6]) grid print -djpeg W5_Nyquist pause nyquist(szamlalo,nevezo6) axis([-0.3 0.1 -6 6]) grid print -djpeg W6_Nyquist pause nyquist(szamlalo,nevezo7) axis([-0.4 0.1 -6 6]) grid print -djpeg W7_Nyquist pause axis([-0.15 0.01 -0.025 0.025]) print -djpeg W7b_Nyquist
|
|
|
|
|
|
|
|
|
|
|
|
4-126. ábra MATLAB Nyquist diagramok
4 - 45 feladat
A MATLAB program segítségével rajzolja fel a következő frekvencia átviteli függvények Bode diagramját
|
|
|
(4.207) |
|
|
|
(4.208) |
|
|
|
(4.209) |
|
|
|
(4.210) |
|
(4.211) |
||
Megoldás:
% Időállandó adatok T11=1; T21=1; T22=0.2; T31=1; T32=0.01; T41=1; T42=1/1.5; T43=0.5; T51=1; T61=1; T62=0.2; T71=1; T72=0.2; T73=0.125; % A frekvencia átviteli függvény számláló és nevező polinomja szamlalo= 1; nevezo1=T11*poly([-1/T11]); nevezo2=T21*T22*poly([-1/T21 -1/T22]); nevezo3=T31*T32*poly([-1/T31 -1/T32]); nevezo4=T41*T42*T43*poly([-1/T41 -1/T42 -1/T43]); nevezo5=T51*poly([0]); nevezo6=T61*T62*poly([0 -1/T62]); nevezo7=T71*T72*T73*poly([0 -1/T72 -1/T73]); % A Bode diagram kirajzolása Bode(szamlalo,nevezo1) grid print -djpeg W1_Bode pause Bode(szamlalo,nevezo2) grid print -djpeg W2_Bode pause Bode(szamlalo,nevezo3) grid print -djpeg W3_Bode pause Bode(szamlalo,nevezo4) grid print -djpeg W4_Bode pause Bode(szamlalo,nevezo5) grid print -djpeg W5_Bode pause Bode(szamlalo,nevezo6) grid print -djpeg W6_Bode pause Bode(szamlalo,nevezo7) grid print -djpeg W7_Bode pause Bode(szamlalo,nevezo8) grid print -djpeg W8_Bode
|
|
|
|
|
|
|
|
|
|
|
|
4-127. ábra MATLAB Bode diagramok
4.10. Szűrő típusok Bode diagramja
A mért jelek (legyenek akár analógok, akár digitálisak) általában zajosak, ezért a jelfeldolgozásban az egyik legfontosabb művelet a szűrés. Olyan is előfordul, hogy egy jelre rászuperponálunk további információt és ezt az információt a fogadó oldalon szűréssel nyerjük vissza. A teljesítményelektronikában csak négyszög feszültségjeleket tudunk előállítani, ugyanakkor a berendezéseink szinuszos feszültséget igényelnek. A négyszög feszültségjelből szűréssel állítjuk elő a szinuszos feszültségjelet. Nem csak villamos jeleket szűrhetünk. Szűrőnek kell tekinteni a lengéscsillapítókat, a fényképezőgépek kézremegés csillapítóját. Rendszertechnikai megközelítésben a szűrők a jelek spektrumát módosítják. A szűrőket többféleképpen lehet csoportosítani.
-
A jel típusa szerint
-
analóg
-
digitális
-
A szűrő energia felvétele szerint
-
passzív
-
aktív
-
A jelformálás szerint
-
aluláteresztő (felülzáró)
-
felüláteresztő (alulzáró)
-
sáváteresztő (egy felül- és egy aluláteresztő részből áll)
-
sávzáró (egy alul- és egy felüláteresztő részből áll)
A szűrők további csoportosítása is lehetséges (pl. korábban említettük a kauzális és nem kauzális szűrőket). Ebben a jegyzetben elsősorban passzív analóg szűrők jelformáló tulajdonságait (frekvencia átviteli függvényét, illetve Bode diagramját) vizsgáljuk. Az ideális passzív szűrők Bode diagramja vízszintes és függőleges egyenes szakaszokból áll (ld. 4-128. ábra). Bizonyos frekvenciájú jelek áthaladnak a szűrőn, bizonyos frekvenciájú jeleket teljesen elnyel. Az aktív szűrők karakterisztikái annyiban térnek el a 4-128. ábra látottaktól, hogy a vízszintes szakasz nem az egységnyi erősítésnek megfelelő 0dB-nél van, hanem feljebb.
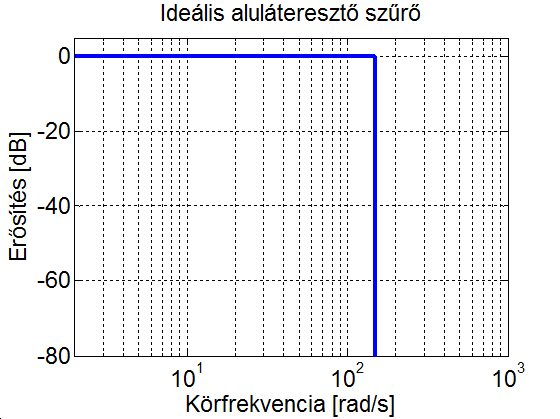
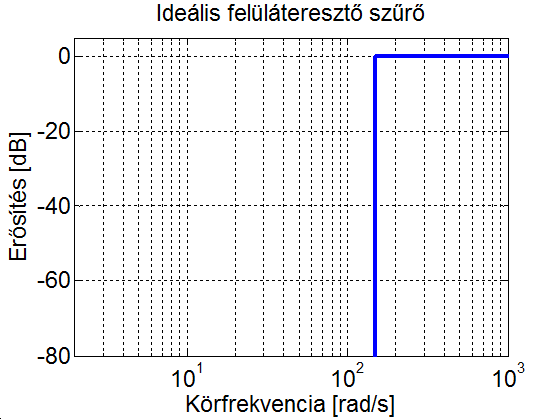
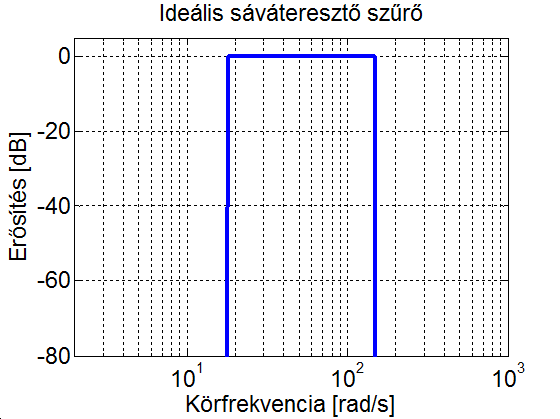
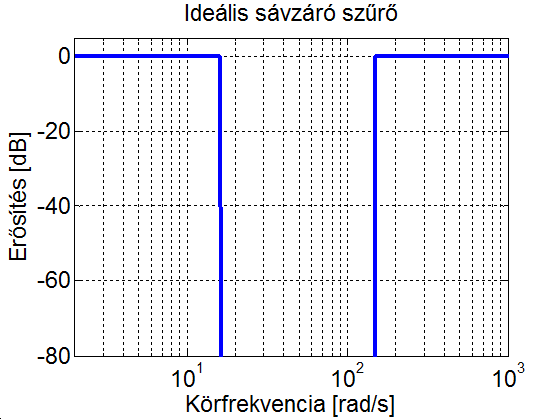
A valóságban olyan nem létezik, hogy egy bizonyos frekvenciájú bemenőjel változatlanul megjelenik a kimeneten, és pl. egy tized Hz-cel nagyobb vagy kisebb frekvenciájú bemenőjel teljesen elnyelődik. Ez a kauzalitásnak is ellentmond. Pl. egy szinuszos jel kezdeti meredeksége a nulla-átmenetnél függ a frekvenciától és a jel amplitúdójától. Ugyanolyan kezdeti meredekségű bemenőjel lehet egy kisebb frekvenciájú nagyobb amplitúdójú, vagy nagyobb frekvenciájú kisebb amplitúdójú jel. A jelnek egy bizonyos szakaszát végig kell várni, hogy utólag eldönthető legyen, hogy az adott bemenőjelet szűrni kell, vagy át kell engedni. Ez matematikailag is könnyen belátható, ha kiszámítjuk az ideális aluláteresztő szűrő súlyfüggvényét (impulzus válaszát). A Dirac-impulzus Fourier transzformáltja minden frekvencia értéknél 1. Legyen az aluláteresztő szűrő vágási körfrekvenciája . Ennek megfelelően a kimenőjel spektruma (pontosabban annak pozitív tartománya) a 4-129. ábra látható.
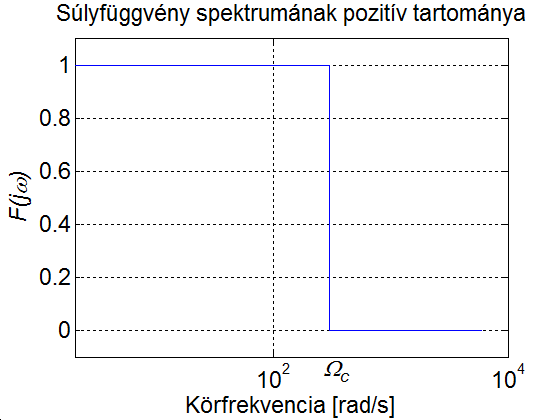
A súlyfüggvényt az időtartományban inverz Fourier-transzformációval kaphatjuk meg
|
|
(4.212) |
Az ideális aluláteresztő szűrő súlyfüggvényének (4.212) alakja tartományban nem nulla, vagyis ha az ideális aluláteresztő bemenetére a időpillanatban egy Dirac-impulzust kapcsolunk, akkor az erre adott válasz már korábban megkezdődik, mint ahogy az impulzust a bemenetre kapcsoljuk. Ez nyilvánvalóan ellentmond a kauzalitásnak.
A valóságos szűrők közelítő amplitúdó Bode diagramján a függőleges szakaszok helyett meghatározott meredekségű egyenes szakaszokat találunk. A meredekség lehet (ld. 4-130. ábra), ahol pozitív egész szám felüláteresztő jellegnél és negatív egész szám aluláteresztő jellegnél. Az abszolút értékét szokás a szűrő fokszámának nevezni.
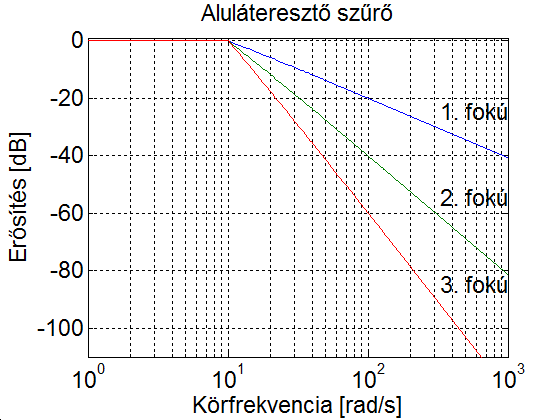
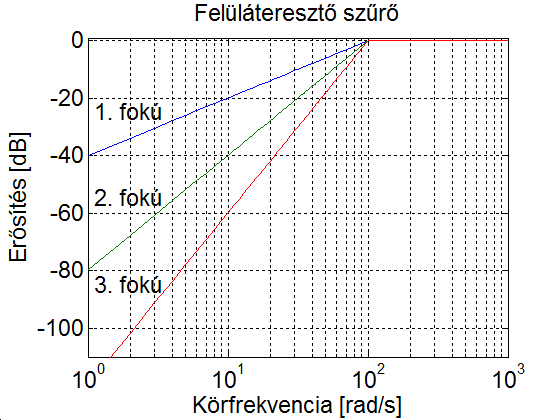
A legegyszerűbb passzív szűrő elrendezés a 4-131. ábraán látható. A szűrő jelformáló tulajdonsága a és impedancia segítségével állítható be.
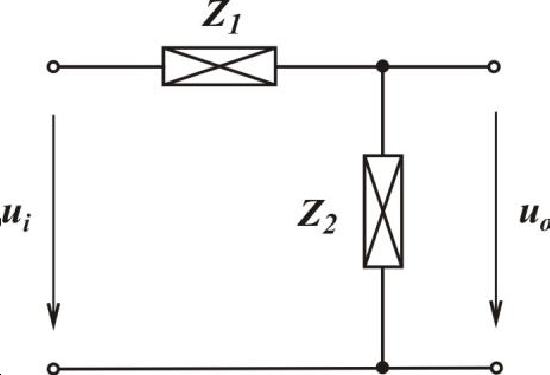
4.10.1. Aluláteresztő szűrő
Az aluláteresztő szűrők olyan rendszerek, amelyek bemenetére szinuszos gerjesztést kapcsolva a kimenetén is szinuszos jel alakul ki (lineáris rendszerek). Ha a bemenőjel frekvenciája kicsi, akkor (passzív szűrőt feltételezve) a be- és kimenőjel amplitúdója, illetve fázisa közel azonos (ideális esetben azonos). Ha a bemenőjel frekvenciája nagy, akkor a kimenőjel amplitúdója kicsi (ideális esetben nulla). Valóságos esetben minél nagyobb a bemenőjel frekvenciája, annál kisebb a kimenőjel amplitúdója és annál nagyobb a fáziskésése.
A teljesítményelektronikában a és impedancia helyén induktivitás és kapacitás található. Ha a veszteségeket is modellezni kívánjuk, akkor az induktivitással sorban, a kondenzátorral párhuzamosan szokásos egy-egy ellenállást kapcsolni. Ennek megfelelően a két operátoros impedancia
|
|
(4.213) |
|
|
(4.214) |
Az átviteli függvény operátoros feszültség osztással határozható meg
|
|
(4.215) |
|
|
(4.216) |
Adatok (A 3-6 feladat 3-18. ábraáján látható szünetmentes áramforrás szűrőjének ideális, vagyis veszteséges és induktivitását és kondenzátorát valóságos, vagyis veszteséges impedanciákkal modellezzük)
,
Behelyettesítve
|
|
(4.217) |
A két pólus
|
|
(4.218) |
Mivel a két pólus komplex konjugált párt alkot, a közelítő Bode diagramnak egy töréspontja van, ahol a -40 dB/dekád meredekségű szakasz kezdődik.
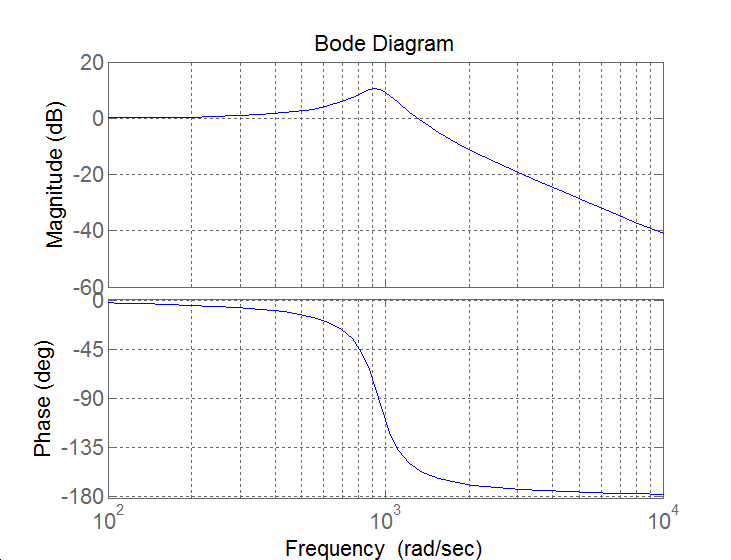
A töréspont helye (4.14) alapján
A 3-6 feladatban a 3-18. ábraán látható szünetmentes áramforrás szűrőjének az a feladata, hogy a tranzisztorkapcsolgatással előállított impulzus szélesség modulált jelből kiszűrje a szinuszos 50 Hz-es alapharmonikust. A 3-6 feladatban láttuk, hogy jól választott impulzus mintával elérhető, hogy az impulzus szélesség modulált jel spektrumában ne szerepeljenek az alacsony rendszámú felharmonikusok. Ezért lehetett a szűrő vágási frekvenciáját 150Hz-re beállítani. Egyszerű négyszögjel esetén, ahol a 150Hz-es harmadik felharmonikus amplitúdója nem hanyagolható el, e feladatban szereplő szűrő nem ad kielégítő eredményt, mivel kiemeli a harmadik felharmonikust.
Bár a szűrők esetén kevésbé van jelentősége, de vizsgáljuk meg, hogy egységugrás bemenőjel hatására miként alakul a kimenőjel.
|
|
(4.219) |
A részlettörtekre bontáshoz a MATLAB residue utasítását felhasználva (a MATLAB programot ld. később)
|
|
(4.220) |
Megjegyezzük, hogy az utolsó tag együtthatójának pontos értéke ezt egy numerikus számításnál 1-nek vehetjük.
Az inverz Laplace-transzformációhoz szükségünk van a komplex együtthatójú részlettörtek Euler alakjára (MATLAB program segítségével)
|
|
(4.221) |
(3.99) alapján
|
|
(4.222) |
Az időfüggvényt ugyancsak MATLAB segítségével lehet kirajzolni
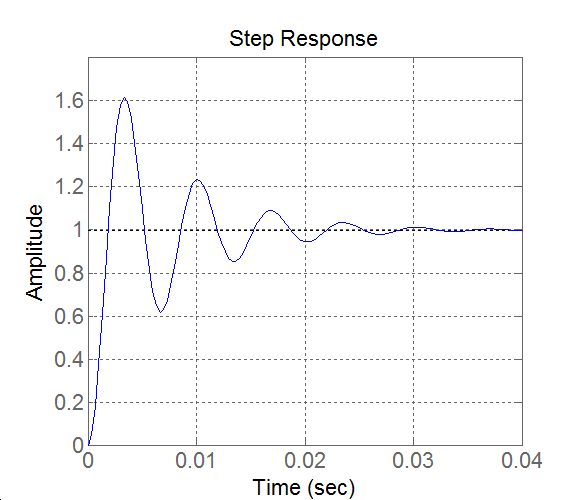
Az átmeneti függvény esetén a kezdeti és végérték tétel alkalmazható
|
|
(4.223) |
|
|
(4.224) |
Fizikai megfontolások alapján:
Ökölszabály: az induktivitás árama és a kondenzátor feszültsége ugrásszerűen nem változhat, ha mindkettő értéke bekapcsolás előtt nulla volt, akkor utána is nulla marad. Tehát a bekapcsolás pillanatában a kondenzátor feszültsége nulla, ezért a vele párhuzamosan kapcsolt ellenálláson is nulla feszültség eshet. Vagyis a kimeneten megjelenő feszültség nulla (ld. (4.223)). Ha az induktivitás árama nulla, akkor minden sorba kapcsolt elem árama is nulla, így Ohm törvény értelmében az induktivitással sorba kapcsolt ellenálláson is nulla feszültség esik. A Kirchhoff huroktörvény miatt a bemeneti feszültséget valahol egy feszültségnek ki kell egyensúlyoznia, de a körben csak az induktivitás tud feszültséget magára venni, vagyis a bekapcsolás pillanatában a teljes bemeneti feszültség az induktivitáson esik. Állandósult állapotban (konstans gerjesztés estén) az induktivitás rövidzárral, a kondenzátor szakadással helyettesíthető. Ennek megfelelően a szűrő állandósult állapotban két ellenállásból álló feszültségosztóként működik, ahol a két ellenállás értéke között nyolc nagyságrend van. Gyakorlati szempontból azt mondhatjuk, hogy állandósult állapotban a teljes bemeneti feszültség a kondenzátoron, illetve a vele párhuzamos ellenálláson esik.
A fenti számításhoz tartozó MATLAB fájl
% Adatok C2=3200e-6; R2=10e+6; R1=0.1; L1=0.35e-3; % Az átviteli függvény számláló és nevező polinomja szamlalo=[R2]; nevezo= [L1*C2*R2 C2*R2*R1+L1 R1+R2]; % A Nyquist diagram kirajzolása nyquist(szamlalo, nevezo) grid %print -djpeg AASZ_Nyguist pause % A Bode diagram kirajzolása bode(szamlalo, nevezo) grid %print -djpeg AASZ_Bode pause % A nevező gyökei roots(nevezo) % A nevező polinom megszorzása 1/s-sel nevezo_s= [L1*C2*R2 C2*R2*R1+L1 R1+R2 0]; % Részlettörtekre bontás [G, P, k]=residue(szamlalo,nevezo_s) % A komplex együttható Euler alakja abs(G(1)) angle(G(1)) % Az aluláteresztő szűrő átviteli függvénye nyitott=tf(szamlalo, nevezo) % Átmeneti függvény step(nyitott) set(gca, 'fontsize', 18); grid %print -djpeg AASZ_step
4.10.2. Felüláteresztő szűrő
Felüláteresztő szűrőt úgy kaphatunk, ha az előző példában a és impedancia szerepét felcseréljük
|
|
(4.225) |
|
|
(4.226) |
Az átviteli függvény operátoros feszültségosztással határozható meg
|
|
(4.227) |
|
|
(4.228) |
Adatok
,
Behelyettesítve
|
|
(4.229) |
A két pólus ugyanaz, mint az előző esetben. Ez azt jelenti, hogy a töréspont helye sem változott meg.
|
|
(4.230) |
Mivel a két pólus komplex konjugált párt alkot, a közelítő Bode diagramnak egy töréspontja van, ahol a +40 dB/dekád meredekségű szakasz befejeződik.
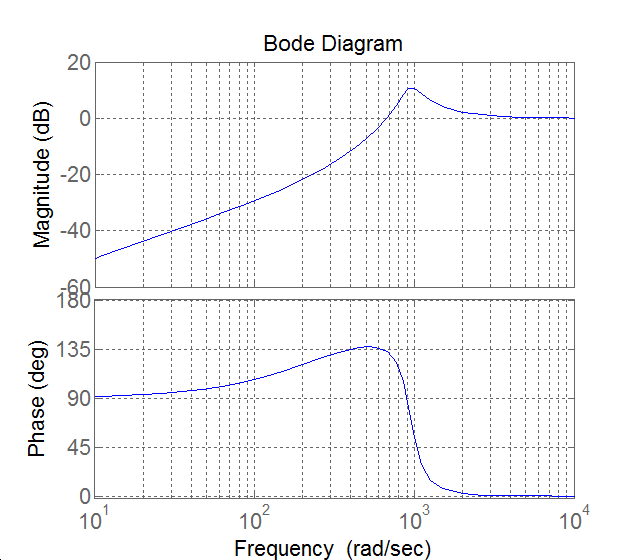
Ebben az esetben is vizsgáljuk meg, hogy egységugrás bemenőjel hatására miként alakul a kimenőjel.
|
|
(4.231) |
A részlettörtekre bontáshoz a MATLAB residue utasítását felhasználva
|
|
(4.232) |
Az inverz Laplace-transzformáció (3.99) alapján
|
|
(4.233) |
Az időfüggvényt ugyancsak MATLAB segítségével lehet kirajzolni
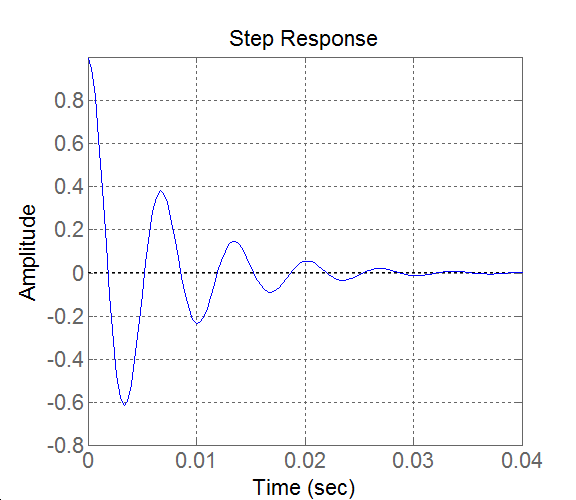
A kezdeti és végérték tétel ebben az esetben is alkalmazható
|
|
(4.234) |
|
|
(4.235) |
Fizikai megfontolásként ugyanaz mondható el, mint az első esetben, csak a szűrő belső és kimeneti feszültsége esése felcserélődik.
A fenti számításhoz tartozó MATLAB fájl
% Adatok C1=3200e-6; R1=10e+6; R2=0.1; L2=0.35e-3; % Az átviteli függvény számláló és nevező polinomja szamlalo=[L2*C1*R1 C1*R1*R2+L2 R2]; nevezo= [L2*C1*R1 C1*R1*R2+L2 R1+R2]; % A Nyquist diagram kirajzolása nyquist(szamlalo, nevezo) grid pause % A Bode diagram kirajzolása bode(szamlalo, nevezo) grid pause roots(szamlalo) roots(nevezo) nevezo_s= [L2*C1*R1 C1*R1*R2+L2 R1+R2 0]; [G, P, k]=residue(szamlalo,nevezo_s) abs(G(1)) angle(G(1)) nyitott=tf(szamlalo, nevezo) step(nyitott) set(gca, 'fontsize', 18); grid
Függelék