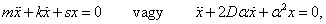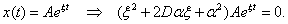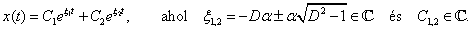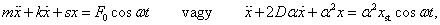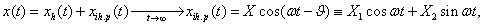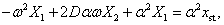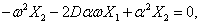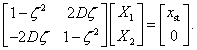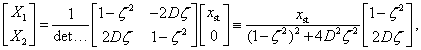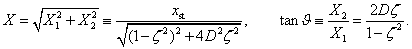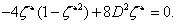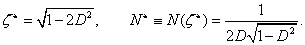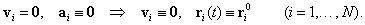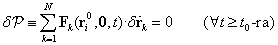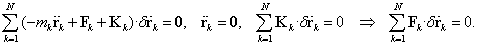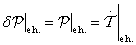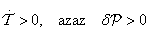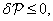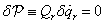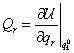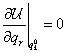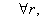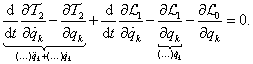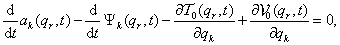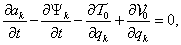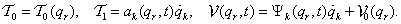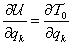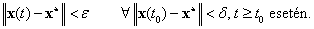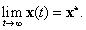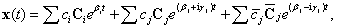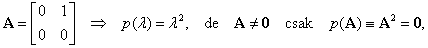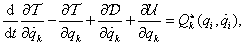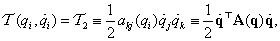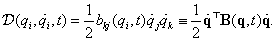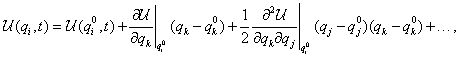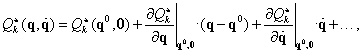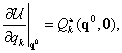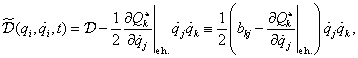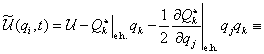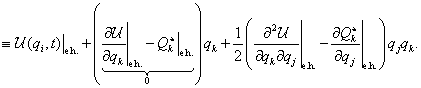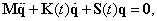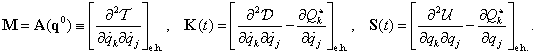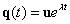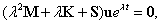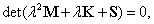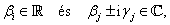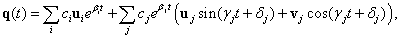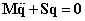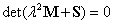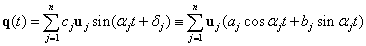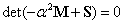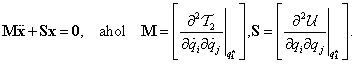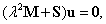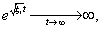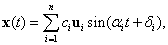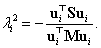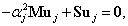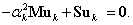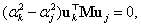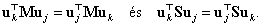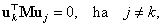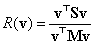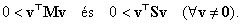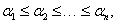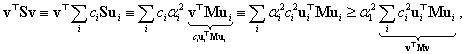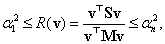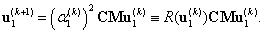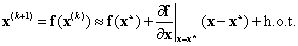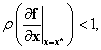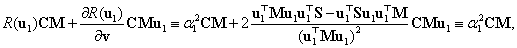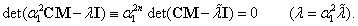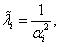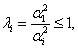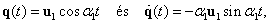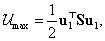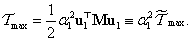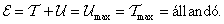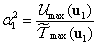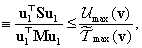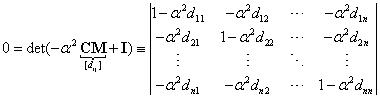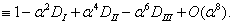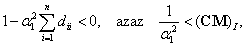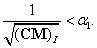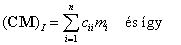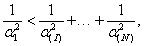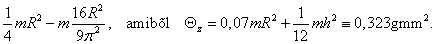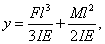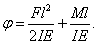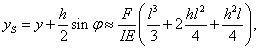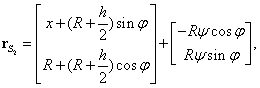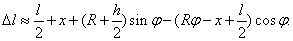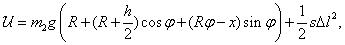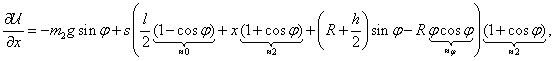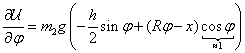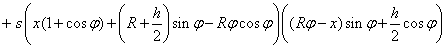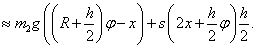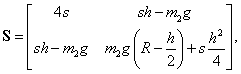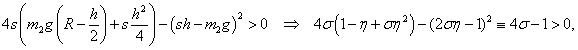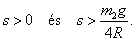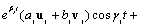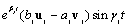3. fejezet - Mozgások jellemzése és stabilitása
3.1. Egy szabadsági fokú csillapított rezgések
3.1.1. Szabad rezgések
A legtöbb egyszabadsági fokú mechanikai rendszer viselkedését kis kitérésű mozgásokra jól leírja a lineáris elemekből álló referencia modell mozgásegyenlete:
|
|
ahol 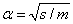 az ún. csillapítatlan sajátkörfrekvencia és
az ún. csillapítatlan sajátkörfrekvencia és 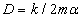 a relatív csillapítási tényező.
a relatív csillapítási tényező.
Az egyenlet megoldását a lineáris differenciálegyenletek elmélete alapján az alábbi alakban keressük:
|
|
A nem triviális megoldást a zárójelben szereplő karakterisztikus polinom gyökeivel a következőképpen írhatjuk fel (a 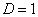 eset kivételével, ld. később):
eset kivételével, ld. később):
|
|
Vizsgáljuk meg az ún. gyökhelygörbét, ha 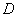 változik:
változik:
-
mivel
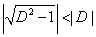 ,
, 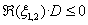 továbbá
továbbá 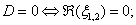 vagyis, ha
vagyis, ha 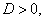 akkor a gyökök a komplex számsík baloldalán helyezkednek el, ha pedig
akkor a gyökök a komplex számsík baloldalán helyezkednek el, ha pedig 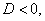 akkor a jobboldalán;
akkor a jobboldalán; -
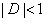 esetén komplex konjugált gyökpár a megoldás
esetén komplex konjugált gyökpár a megoldás 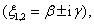 mégpedig az origó középpontú
mégpedig az origó középpontú 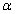 sugarú körön:
sugarú körön: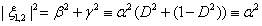 .
. -
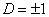 esetén
esetén 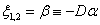 kétszeres gyökök;
kétszeres gyökök; -
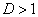 esetén
esetén 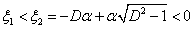 valósak;
valósak; -
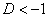 esetén
esetén 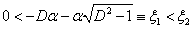 valósak.
valósak.
A továbbiakban csak a 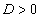 esetekhez tartozó megoldásokat vizsgáljuk:
esetekhez tartozó megoldásokat vizsgáljuk:
-
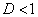 :
: 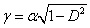 a csillapított sajátkörfrekvencia (a lengésidő
a csillapított sajátkörfrekvencia (a lengésidő 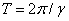 ),
),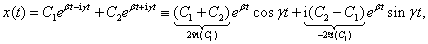
mivel
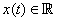 , azaz
, azaz 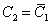 (komplex konjugáltak). A csillapodó rezgés
(komplex konjugáltak). A csillapodó rezgés 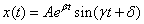 alakban is felírható, melynek segítségével értelmezhetjük a csillapodási hányados
alakban is felírható, melynek segítségével értelmezhetjük a csillapodási hányados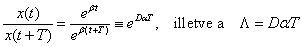
ún. logaritmikus dekrementum fogalmát.
-
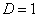 : aperiodikus határeset; a kétszeres gyök miatt a megoldás kvázipolinom alakú:
: aperiodikus határeset; a kétszeres gyök miatt a megoldás kvázipolinom alakú: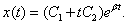
-
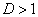 :
: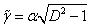 , a jelenség exponenciálisan csökkenő aperiodikus mozgás:
, a jelenség exponenciálisan csökkenő aperiodikus mozgás: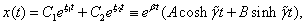
ahol
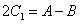 és
és 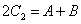 .
.
Rajzoljuk fel 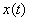 grafikonjait a
grafikonjait a 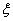 komplex számsík néhány tipikus pontjában …!
komplex számsík néhány tipikus pontjában …!
3.1.2. Gerjesztett rezgések
A referencia modellt most kiegészítjük az 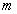 tömegre ható
tömegre ható 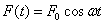 harmonikus gerjesztő erővel. Ezáltal a mozgásegyenlet új alakja:
harmonikus gerjesztő erővel. Ezáltal a mozgásegyenlet új alakja:
|
|
ahol 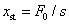 az ún. statikus kitérés vagy deformáció, ami az
az ún. statikus kitérés vagy deformáció, ami az 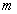 tömeg statikus elmozdulását adja meg konstans
tömeg statikus elmozdulását adja meg konstans 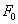 esetén (
esetén (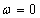 ).
).
A mozgásegyenlet most egy inhomogén közönséges differenciálegyenlet, melynek általános megoldását a homogén rész általános megoldásának és az inhomogén egyenlet partikuláris megoldásának összegeként kapjuk meg:
|
|
mivel kvázipolinomiális gerjesztő függvény esetén a partikuláris megoldást is a megfelelő fokú és frekvenciájú függvény alakjában keressük.
A 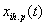 -t visszaírva a differenciálegyenletbe és
-t visszaírva a differenciálegyenletbe és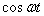 ,
, 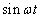 együtthatói szerint szétválasztva:
együtthatói szerint szétválasztva:
|
|
||
|
|
illetve 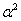 -tel való osztás után (a
-tel való osztás után (a 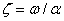 frekvenciaviszony vagy hangolás bevezetésével) mátrix alakba rendezve:
frekvenciaviszony vagy hangolás bevezetésével) mátrix alakba rendezve:
|
|
Az egyenletrendszer megoldása:
|
|
amiből kapjuk, hogy
|
|
Innen a nagyítás:
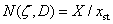 , és
, és 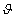 a fázisszög (vagy fáziskésés — a gerjesztéshez képest).
a fázisszög (vagy fáziskésés — a gerjesztéshez képest).
A nagyítás függvény szélsőértékhelye megegyezik a gyökjel alatti kifejezés szélsőértékhelyével (mivel a 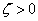 tartományon az
tartományon az 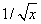 szigorúan monoton változik):
szigorúan monoton változik):
|
|
Innen a 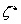 szélsőértékhely és az
szélsőértékhely és az 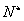 szélsőérték:
szélsőérték:
|
|
Ha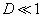 , akkor
, akkor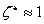 , és
, és 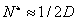 – minőségi tényező, illetve
– minőségi tényező, illetve 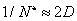 – veszteségi tényező.
– veszteségi tényező.
3.2. Mechanikai rendszerek egyensúlya
Egyensúly alatt a mechanikai rendszer tartós nyugalmi állapotát értjük, azaz ha (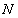 anyagi pont esetén)
anyagi pont esetén)
|
|
(3.1) |
Elnevezések: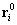 : egyensúlyi helyzet;
: egyensúlyi helyzet;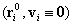 : egyensúlyi állapot.
: egyensúlyi állapot.
3.2.1. Virtuális teljesítmény elve
(Bernoulli, 1717; Galilei: „A mechanika aranyszabálya”):
Egy rendszernek az (ideális) kényszerekkel összeférő 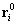 pozíciója egyensúlyi helyzet
pozíciója egyensúlyi helyzet 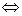 az
az 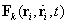 szabaderők virtuális teljesítményének összege ott tartósan zérus:
szabaderők virtuális teljesítményének összege ott tartósan zérus:
|
|
(3.2) |
Bizonyítás: 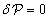 szükséges feltétel, hiszen a d'Alembert-elv alapján
szükséges feltétel, hiszen a d'Alembert-elv alapján
|
|
Másrészt, ha 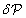 tartósan zérus egy
tartósan zérus egy 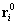 helyzetben (és itt
helyzetben (és itt 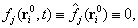 azaz
azaz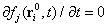 ), akkor megegyezik a ténylegesen lehetséges teljesítménnyel, mivel
), akkor megegyezik a ténylegesen lehetséges teljesítménnyel, mivel 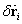 megegyezik a lehetséges sebességekkel (vagyis az ilyen helyzet szkleronom, időtől független). Tehát
megegyezik a lehetséges sebességekkel (vagyis az ilyen helyzet szkleronom, időtől független). Tehát
|
|
(3.3) |
a teljesítménytétel értelmében. Viszont ha ez az 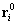 helyzet nyugalmi helyzet — azaz a
helyzet nyugalmi helyzet — azaz a 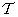 kinetikus energia zérus és egyben minimális, hiszen
kinetikus energia zérus és egyben minimális, hiszen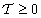 — akkor a szabaderők zérus virtuális teljesítménye esetén a kinetikus energia változatlan, azaz zérus marad, tehát az adott helyzet tartós nyugalmi, vagyis egyensúlyi helyzet.
— akkor a szabaderők zérus virtuális teljesítménye esetén a kinetikus energia változatlan, azaz zérus marad, tehát az adott helyzet tartós nyugalmi, vagyis egyensúlyi helyzet.
Általánosabban megfogalmazva: mivel a nyugalmi állapot megszűnése csak
|
|
(3.4) |
esetén következhet be, az egyensúly szükséges és elégséges feltétele, hogy
|
|
(3.5) |
ami egyenlőtlenséggel megadott kényszerfeltételek mellett is alkalmazható.
Következmény: holonom mechanikai rendszernek 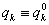 (
(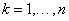 ) egyensúlyi helyzete
) egyensúlyi helyzete 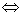 ha ott az általános erők tartósan zérusok:
ha ott az általános erők tartósan zérusok: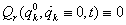 , mivel
, mivel
|
|
(3.6) |
és 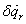 a kényszerfeltételeket kielégítik, így tetszőlegesek (függetlenek), tehát
a kényszerfeltételeket kielégítik, így tetszőlegesek (függetlenek), tehát 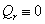
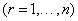 .
.
Konzervatív holonom szkleronom mechanikai rendszerekben a 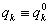 egyensúlyi helyzetben
egyensúlyi helyzetben
|
|
(3.7) |
és mivel 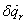 -k függetlenek és tetszőlegesek az egyensúly szükséges és elégséges feltétele, hogy
-k függetlenek és tetszőlegesek az egyensúly szükséges és elégséges feltétele, hogy
|
|
(3.8) |
vagyis, hogy az 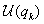 potenciál függvénynek az egyensúlyi helyzetben lokális szélsőértéke legyen.
potenciál függvénynek az egyensúlyi helyzetben lokális szélsőértéke legyen.
3.2.2. Dinamikus egyensúly
Potenciálos erőtérben mozgó holonom (reonom) mechanikai rendszer mozgásegyenlete az 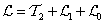 alakú kinetikus potenciállal:
alakú kinetikus potenciállal:
|
|
(3.9) |
Egyensúly esetén (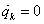 ,
,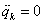 ) az első, a második és a negyedik tag eltűnik:
) az első, a második és a negyedik tag eltűnik:
|
|
(3.10) |
mivel 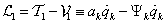 és
és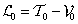 . Az idő szerinti teljes deriválás után csak a parciális derivált marad meg (mert a másik tag
. Az idő szerinti teljes deriválás után csak a parciális derivált marad meg (mert a másik tag 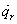 -tal szorzódna):
-tal szorzódna):
|
|
(3.11) |
és ennek az egyenletrendszernek a megoldása adja az egyensúlyi helyzetet. Ez persze nem függhet az időtől, ami tipikusan[3] akkor teljesül, ha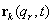 ,
, 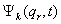 az időnek legfeljebb elsőfokú,
az időnek legfeljebb elsőfokú, 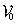 pedig nulladfokú kifejezése. Ebben az esetben
pedig nulladfokú kifejezése. Ebben az esetben
|
|
(3.12) |
Konzervatív erők (nem rendszer!) esetén 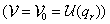 pedig a
pedig a
|
|
(3.13) |
feltétel határozza meg a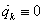 ,
, 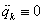 tulajdonsággal bíró
tulajdonsággal bíró 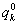 dinamikus egyensúlyi helyzetet, hiszen itt
dinamikus egyensúlyi helyzetet, hiszen itt 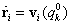 is lehetséges, ami alapján a kinetikus energia
is lehetséges, ami alapján a kinetikus energia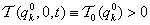 , de az időben állandó (ld. kritikus fordulatszám legegyszerűbb modellje).
, de az időben állandó (ld. kritikus fordulatszám legegyszerűbb modellje).
3.2.3. Stabilitási alapfogalmak
Azt mondjuk, hogy az 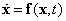 differenciálegyenlet-rendszer (
differenciálegyenlet-rendszer (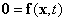 egyenletrendszert kielégítő)
egyenletrendszert kielégítő) 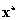 egyensúlyi helyzete vagy pontmegoldása Ljapunov-stabilis, ha
egyensúlyi helyzete vagy pontmegoldása Ljapunov-stabilis, ha 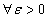 számhoz
számhoz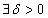 , hogy
, hogy
|
|
(3.14) |
Azaz bármilyen kis 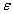 számhoz megadható az
számhoz megadható az 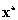 egyensúlyi helyzetnek egy valamilyen (esetleg
egyensúlyi helyzetnek egy valamilyen (esetleg 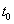 -tól függő)
-tól függő) 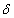 sugarú környezete, hogy az abból indított megoldások mindig az egyensúlyi helyzet
sugarú környezete, hogy az abból indított megoldások mindig az egyensúlyi helyzet 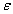 sugarú környezetében maradjanak.
sugarú környezetében maradjanak.
Azt mondjuk, hogy az 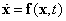 differenciálegyenlet-rendszer
differenciálegyenlet-rendszer 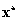 egyensúlyi helyzete vagy pontmegoldása aszimptotikusan stabilis, ha Ljapunov-stabilis és
egyensúlyi helyzete vagy pontmegoldása aszimptotikusan stabilis, ha Ljapunov-stabilis és
|
|
(3.15) |
Az 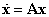 állandó, valós együtthatós, homogén lineáris differenciálegyenlet-rendszer általános megoldása:
állandó, valós együtthatós, homogén lineáris differenciálegyenlet-rendszer általános megoldása:
|
|
(3.16) |
ahol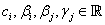 ,
, 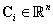 ,
, 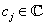 ,
, 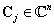 , továbbá
, továbbá 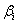 valamint
valamint 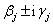 az
az 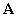 együtthatómátrix valamelyik
együtthatómátrix valamelyik 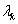 sajátértékével egyezik meg (ha az összes
sajátértékével egyezik meg (ha az összes 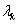 egyszeres gyök!).
egyszeres gyök!).
Az 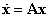 rendszer
rendszer 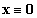 (triviális) pontmegoldása (tetszőleges valós állandó
(triviális) pontmegoldása (tetszőleges valós állandó 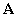 mátrix esetén is)
mátrix esetén is)
-
aszimptotikusan stabilis, ha
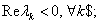
-
Ljapunov-stabilis, ha
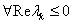 és a
és a 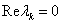 gyökök multiplicitása egyszeres
gyökök multiplicitása egyszeres 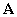 mátrix minimálpolinomjában (ellenpélda:
mátrix minimálpolinomjában (ellenpélda: -
egyébként pedig instabil.
Példa Ha
|
|
tehát 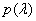 a minimálpolinom és
a minimálpolinom és 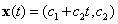 nem korlátos megoldás. Viszont
nem korlátos megoldás. Viszont 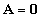 esetén bár
esetén bár 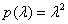 ismét, de
ismét, de 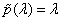 lesz a minimálpolinom és korlátosak az
lesz a minimálpolinom és korlátosak az 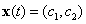 alakú megoldások.
alakú megoldások.
3.3. Holonom szkleronom rendszerek kis mozgásai
3.3.1. A mátrix differenciálegyenlet
Időtől független gerjesztés esetén a másodfajú Lagrange-egyenletek holonom szkleronom rendszernél az alábbi alakot öltik:
|
|
(3.17) |
ahol
|
|
||
|
|
Vizsgáljuk a rendszer 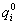 egyensúlyi helyzetének környezetében történő mozgásokat (azaz
egyensúlyi helyzetének környezetében történő mozgásokat (azaz 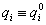
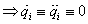 megoldása a (3.17) egyenleteknek). Ekkor az
megoldása a (3.17) egyenleteknek). Ekkor az 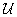 potenciálfüggvény másodfokú tagokig történő és a
potenciálfüggvény másodfokú tagokig történő és a 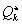 általános erők első fokig történő sorfejtése az egyensúlyi helyzet körül:
általános erők első fokig történő sorfejtése az egyensúlyi helyzet körül:
|
|
||
|
|
Tehát az egyensúlyi helyzetben (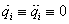 miatt)
miatt)
|
|
(3.18) |
amiből 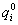 meghatározható.
meghatározható.
Bevezetve a 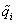 koordinátákat a
koordinátákat a 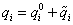 összefüggés alapján, majd átparaméterezve az egyenleteket a
összefüggés alapján, majd átparaméterezve az egyenleteket a 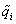 koordinátákkal kifejezve és elhagyva a ~-t formailag a (3.17) egyenlettel azonos összefüggésre jutunk, azonban a vizsgált egyensúlyi helyzet a konfigurációs tér origójába kerül:
koordinátákkal kifejezve és elhagyva a ~-t formailag a (3.17) egyenlettel azonos összefüggésre jutunk, azonban a vizsgált egyensúlyi helyzet a konfigurációs tér origójába kerül: 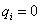 (eredetileg
(eredetileg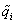 ). Azaz az általánosság megszorítása nélkül feltehetjük, hogy az általános koordináták mindig választhatók úgy, hogy egy egyensúlyi helyzetet (e.h.) a
). Azaz az általánosság megszorítása nélkül feltehetjük, hogy az általános koordináták mindig választhatók úgy, hogy egy egyensúlyi helyzetet (e.h.) a 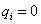 koordinátaértékek azonosítsanak.
koordinátaértékek azonosítsanak.
Módosítsuk 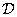 -t és
-t és 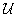 -t a következő módon:
-t a következő módon:
|
|
(3.19) |
|
|
(3.20) |
|
|
Ezzel a másodfajú Lagrange-egyenletek kis mozgások esetén egy homogén lineáris másodrendű közönséges differenciálegyenlet-rendszert alkotnak, melyek az alábbi mátrix alakba rendezhetők:
|
|
(3.21) |
ahol a tömeg-, csillapítási és merevségi mátrix rendre
|
|
(3.22) |
Időtől független esetben, vagyis állandó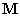 ,
, 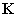 ,
, 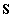 esetén a (3.21) egyenletnek a homogén általános megoldása
esetén a (3.21) egyenletnek a homogén általános megoldása
|
|
(3.23) |
próbafüggvény (Ansatz) alakjában keresendő, amit ha beírunk a (3.21) mátrix differenciálegyenletbe, akkor egy homogén lineáris egyenletrendszerhez illetve sajátérték–sajátvektor feladathoz jutunk:
|
|
(3.24) |
ami 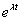 -től függetlenül kell, hogy teljesüljön. Viszont, ha
-től függetlenül kell, hogy teljesüljön. Viszont, ha 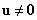 (nem triviális) megoldásokat (sajátvektorokat) keresünk, akkor az együttható mátrix determinánsának kell zérusnak lennie, azaz
(nem triviális) megoldásokat (sajátvektorokat) keresünk, akkor az együttható mátrix determinánsának kell zérusnak lennie, azaz
|
|
(3.25) |
ami a 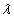 sajátértékekre vonatkozó
sajátértékekre vonatkozó 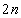 -edfokú karakterisztikus egyenlet.
-edfokú karakterisztikus egyenlet.
A karakterisztikus egyenlet gyökei között lehetnek komplex konjugált párok, hasonló komplex konjugált sajátvektorokkal, vagyis
|
|
úgy hogy
|
|
(3.26) |
ahol már 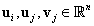 valós vektorok és
valós vektorok és 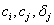 a kezdeti feltételektől függő
a kezdeti feltételektől függő 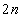 darab valós szám (amennyiben a sajátértékek egyszeresek).[4]
darab valós szám (amennyiben a sajátértékek egyszeresek).[4]
3.3.2. Csillapítatlan rezgések
3.3.2.1. Sajátkörfrekvenciák, lengésképek
Amennyiben a 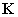 csillapítási mátrix zérus elemekből áll és az összes
csillapítási mátrix zérus elemekből áll és az összes 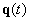 megoldás korlátos (pl. konzervatív rendszerekben), akkor az
megoldás korlátos (pl. konzervatív rendszerekben), akkor az
|
|
(3.27) |
hiányos másodrendű mátrix differenciálegyenlet sajátértékei tiszta képzetes gyökpárok lesznek, mivel a
|
|
(3.28) |
karakterisztikus egyenlet egy 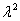 -re
-re 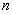 -edfokú algebrai egyenlet lesz. Belátható, hogyha ennek gyöke egy
-edfokú algebrai egyenlet lesz. Belátható, hogyha ennek gyöke egy 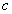 pozitív valós szám, vagy egy
pozitív valós szám, vagy egy 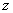 konjugált képzetes gyökpár, akkor ezekhez tartozik pozitív valós részű
konjugált képzetes gyökpár, akkor ezekhez tartozik pozitív valós részű 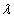 gyök (
gyök (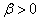 ), ami az exponenciális kitevőben
), ami az exponenciális kitevőben 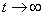 esetén a
esetén a 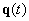 megoldások korlátosságának ellentmond.
megoldások korlátosságának ellentmond.
Viszont, ha 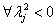 (valós szám), akkor
(valós szám), akkor 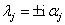 tiszta képzetes gyököket kapunk (ennek feltétele, hogy
tiszta képzetes gyököket kapunk (ennek feltétele, hogy 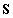 szimmetrikus pozitív definit mátrix legyen), aminek a
szimmetrikus pozitív definit mátrix legyen), aminek a
|
|
(3.29) |
homogén általános megoldás felel meg, 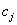 és
és 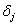 integrálási állandókkal. Tehát a megoldás harmonikus függvények lineáris kombinációja, melyeknek — azaz a magára hagyott rendszer szabad rezgéseinek — körfrekvenciája
integrálási állandókkal. Tehát a megoldás harmonikus függvények lineáris kombinációja, melyeknek — azaz a magára hagyott rendszer szabad rezgéseinek — körfrekvenciája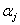 . Mivel ezek értéke csak az
. Mivel ezek értéke csak az 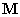 tömegmátrixtól és az
tömegmátrixtól és az 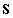 merevségi mátrixtól függ — melyeket többnyire csak a rendszer fizikai, geometriai paraméterei határoznak meg, külső hatások nem —, ezért
merevségi mátrixtól függ — melyeket többnyire csak a rendszer fizikai, geometriai paraméterei határoznak meg, külső hatások nem —, ezért 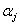 -t a csillapítatlan rendszer
-t a csillapítatlan rendszer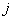 -edik sajátkörfrekvenciájának is nevezzük
-edik sajátkörfrekvenciájának is nevezzük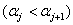 , a
, a
|
|
(3.30) |
karakterisztikus egyenletet pedig frekvenciaegyenletnek.
Megfelelő kezdeti feltételekkel elérhető, hogy a megoldás tisztán az egyik vagy másik sajátkörfrekvenciájú rezgést tartalmazza. Ilyenkor az egyes általános koordináták értékeinek egymáshoz viszonyított arányai minden időpillanatban megegyeznek a megfelelő sajátvektor elemeinek egymáshoz képesti arányaival, és a koordináták egyszerre érik el a szélsőértékeiket illetve válnak zérussá. E fizikai tartalom miatt a sajátvektorokat az egyes sajátkörfrekvenciákhoz tartozó lengésképek vektorának is nevezzük.
3.3.3. Stabilitás
A mozgásegyenletet linearizálva a 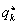 egyensúlyi helyzet körül,
egyensúlyi helyzet körül, 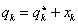 bevezetésével kapjuk a következő mátrix együtthatós differenciálegyenlet-rendszert:
bevezetésével kapjuk a következő mátrix együtthatós differenciálegyenlet-rendszert:
|
|
(3.31) |
Az 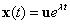 próbafüggvényt behelyettesítve egy sajátérték-sajátvektor feladat homogén lineáris algebrai egyenletrendszerét kapjuk:
próbafüggvényt behelyettesítve egy sajátérték-sajátvektor feladat homogén lineáris algebrai egyenletrendszerét kapjuk:
|
|
(3.32) |
melynek akkor létezik nemtriviális 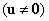 megoldása, ha
megoldása, ha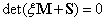 . Az utóbbi karakterisztikus egyenletnek a
. Az utóbbi karakterisztikus egyenletnek a 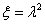 gyökei valósak, mivel mind
gyökei valósak, mivel mind 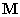 , mind
, mind 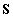 valós szimmetrikus mátrixok, továbbá a megfelelő
valós szimmetrikus mátrixok, továbbá a megfelelő 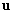 sajátvektorok is valós eleműek (vagy tiszta képzetes konjugáltak, ami persze nem jelent érdemi különbséget).
sajátvektorok is valós eleműek (vagy tiszta képzetes konjugáltak, ami persze nem jelent érdemi különbséget).
Mivel 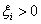 gyök esetén
gyök esetén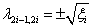 , azaz az egyik gyök mindenképpen pozitív lenne és így
, azaz az egyik gyök mindenképpen pozitív lenne és így
|
|
(3.33) |
azaz 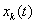 nem marad korlátos az egyensúlyi helyzet bármilyen kis mértékű megzavarása esetén, ezért csak a
nem marad korlátos az egyensúlyi helyzet bármilyen kis mértékű megzavarása esetén, ezért csak a 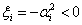 gyökök esetén lehet a
gyökök esetén lehet a 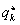 egyensúlyi helyzet stabilis. Ekkor
egyensúlyi helyzet stabilis. Ekkor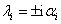 , azaz
, azaz 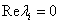 , és
, és
|
|
(3.34) |
ami eleget tesz a Ljapunov-féle stabilitási kritériumnak (de nem aszimptotikusan stabilis!).
Visszahelyettesítve az előbb karakterisztikus egyenlet 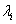 megoldását és a hozzátartozó
megoldását és a hozzátartozó 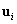 sajátvektort a homogén lineáris egyenletrendszerbe és megszorozva azt balról
sajátvektort a homogén lineáris egyenletrendszerbe és megszorozva azt balról 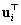 -val, átrendezés után az alábbi kifejezéshez jutunk:
-val, átrendezés után az alábbi kifejezéshez jutunk:
|
|
(3.35) |
Mivel a Ljapunov-féle stabilitáshoz 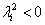 szükséges és
szükséges és 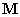 szimmetrikus pozitív definit mátrix, a számláló pozitivitásának elégséges feltételét jelenti, ha
szimmetrikus pozitív definit mátrix, a számláló pozitivitásának elégséges feltételét jelenti, ha 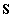 mátrix illetve az
mátrix illetve az 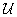 potenciálfüggvény kvadratikus alakja az egyensúlyi helyzet környezetében is pozitív definit, azaz
potenciálfüggvény kvadratikus alakja az egyensúlyi helyzet környezetében is pozitív definit, azaz 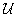 -nak az egyensúlyi helyzetben lokális minimuma van. Tehát
-nak az egyensúlyi helyzetben lokális minimuma van. Tehát 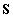 mátrix összes sajátértéke pozitív valós szám, ami a Sylvester-féle tétel értelmében igaz,
mátrix összes sajátértéke pozitív valós szám, ami a Sylvester-féle tétel értelmében igaz, 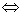 ha
ha 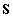 összes sarokaldeterminánsa pozitív.
összes sarokaldeterminánsa pozitív.
A pozitív definitség 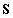 illetve
illetve 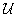 esetében szükséges feltétel is egyben: minthogy
esetében szükséges feltétel is egyben: minthogy 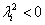 az összes gyökre értendő, ami az
az összes gyökre értendő, ami az 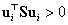 feltételt vonja maga után
feltételt vonja maga után 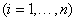 , amiből viszont az
, amiből viszont az 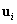 sajátvektorok
sajátvektorok 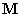 -re vonatkozó ortogonalitása miatt következik, hogy
-re vonatkozó ortogonalitása miatt következik, hogy 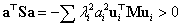
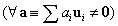 .
.
3.3.3.1. A sajátvektorok ortogonalitása
Ha a 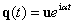 megoldásokat behelyettesítjük a (3.27) egyenletbe, akkor a
megoldásokat behelyettesítjük a (3.27) egyenletbe, akkor a 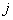 -edik illetve
-edik illetve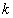 -adik sajátkörfrekvenciákhoz és
-adik sajátkörfrekvenciákhoz és 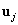 illetve
illetve 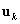 sajátvektorokhoz a következőket kapjuk:
sajátvektorokhoz a következőket kapjuk:
|
|
(3.36) |
|
|
(3.37) |
Az egyenleteket megszorozva balról 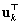 -val illetve
-val illetve 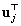 -vel majd kivonva őket egymásból:
-vel majd kivonva őket egymásból:
|
|
(3.38) |
mivel 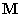 és
és 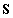 szimmetrikussága miatt
szimmetrikussága miatt
|
|
A (3.38) egyenletből következik, hogy
|
|
(3.39) |
azaz a sajátvektorok ortogonálisak az 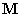 tömegmátrixra nézve.
tömegmátrixra nézve.
3.3.4. A saját-körfrekvenciák becslési módszerei
3.3.4.1. A Rayleigh-hányados
Legyen 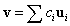 a lengésképek valamilyen lináris kombinációjaként előállított tetszőleges vektor. Ekkor az
a lengésképek valamilyen lináris kombinációjaként előállított tetszőleges vektor. Ekkor az
|
|
(3.40) |
hányadost Rayleigh-hányadosnak nevezzük.
A kinetikus energia pozitív definit kvadratikus alakjából következik a szimmetrikus 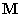 mátrix pozitív definitsége. Így a korlátos, nem csillapodó rezgések kialakulásának feltétele, hogy a szimmetrikus
mátrix pozitív definitsége. Így a korlátos, nem csillapodó rezgések kialakulásának feltétele, hogy a szimmetrikus 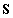 mátrix is pozitív definit legyen:
mátrix is pozitív definit legyen:
|
|
Rendezzük sorba az 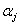 sajátkörfrekvenciákat úgy, hogy
sajátkörfrekvenciákat úgy, hogy
|
|
(3.41) |
és vizsgáljuk a Rayleigh-hányados számlálójában szereplő kifejezést:
|
|
(3.42) |
ahol 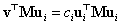 összefüggésben kihasználtuk a sajátvektorok ortogonalitását.
összefüggésben kihasználtuk a sajátvektorok ortogonalitását.
A (3.42)-ben megfogalmazott egyenlőtlenséget átrendezve kapjuk, hogy
|
|
(3.43) |
azaz az 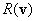 Rayleigh-hányados tetszőleges
Rayleigh-hányados tetszőleges 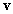 vektor esetén felülről becsli az első (legkisebb) sajátkörfrekvencia négyzetét (a legnagyobb sajátkörfrekvenciájét pedig alulról). Természetesen minél jobb közelítést adunk
vektor esetén felülről becsli az első (legkisebb) sajátkörfrekvencia négyzetét (a legnagyobb sajátkörfrekvenciájét pedig alulról). Természetesen minél jobb közelítést adunk 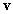 -vel
-vel 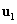 -re, az első lengésképre,
-re, az első lengésképre, 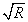 is annál jobban közelíti
is annál jobban közelíti 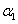 -et.
-et.
3.3.4.2. Stodola-iteráció
A (3.36) egyenletet az 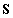 merevségi mátrix
merevségi mátrix 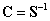 inverzével végigszorozva balról képezzük
inverzével végigszorozva balról képezzük 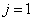 esetén az alábbi iterációs eljárást:
esetén az alábbi iterációs eljárást:
|
|
(3.44) |
Megmutatjuk, hogy ez az iteráció konvergens, és tipikusan 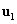 -hez, az első lengésképvektorhoz tart.
-hez, az első lengésképvektorhoz tart.
Az iterációnak több fixpontja is van, hiszen bármelyik 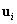 sajátvektort behelyettesítve a frekvenciaegyenlet átírt formáját kapjuk vissza, amit
sajátvektort behelyettesítve a frekvenciaegyenlet átírt formáját kapjuk vissza, amit 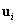 -k kielégítenek.
-k kielégítenek.
Az
|
|
(3.45) |
iterációt az 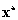 fixpont
fixpont 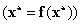 környezetében jól közelíti a
környezetében jól közelíti a 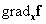 derivált tenzorral megadott lineáris leképezés, ami akkor konvergens, ha
derivált tenzorral megadott lineáris leképezés, ami akkor konvergens, ha 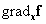 mátrixának spektrálsugara
mátrixának spektrálsugara
|
|
(3.46) |
vagyis az összes sajátértéke a komplex egységkör belsejében található.
Képezzük tehát a Stodola-iteráció jobb oldalán szereplő kifejezés gradiensét:
|
|
(3.47) |
mivel a második tagban a számláló zérus, hiszen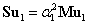 , továbbá
, továbbá 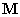 és
és 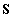 szimmetrikus mátrixok (másképpen: mivel az
szimmetrikus mátrixok (másképpen: mivel az 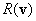 Rayleigh-hányados
Rayleigh-hányados 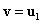 esetén minimális, ezért ott a gradiense
esetén minimális, ezért ott a gradiense ).
).
Nézzük most az 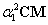 mátrix sajátértékeit:
mátrix sajátértékeit:
|
|
(3.48) |
Belátható, hogy 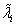 -k a
-k a 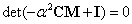 frekvenciaegyenletből számítható sajátkörfrekvenciák négyzeteinek reciprokával egyenlőek:
frekvenciaegyenletből számítható sajátkörfrekvenciák négyzeteinek reciprokával egyenlőek:
|
|
amiből viszont
|
|
(3.49) |
és az egyenlőség csak 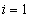 esetén áll fenn. Vagyis tetszőleges
esetén áll fenn. Vagyis tetszőleges 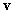 vektor esetén az
vektor esetén az 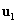 sajátvektoron kívüli altérbe eső komponensek előbb-utóbb eltűnnek, és a Stodola-iterációval
sajátvektoron kívüli altérbe eső komponensek előbb-utóbb eltűnnek, és a Stodola-iterációval 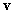 az
az 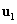 lengéskép által meghatározott első sajátirányhoz tart.
lengéskép által meghatározott első sajátirányhoz tart.
3.3.4.3. Rayleigh-elv
Ha a csillapítatlan (konzervatív) rendszer első lengésképhez tartozó megoldását nézzük, illetve ha a rendszer tisztán az első sajátrezgésével rezeg, vagyis
|
|
(3.50) |
akkor
|
|
(3.51) |
mivel a legnagyobb kitérésnél maximális az alakváltozási energia és ez egyben az 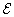 mechanikai összenergia is, hiszen a legnagyobb kitérésnél a kinetikus energia zérus
mechanikai összenergia is, hiszen a legnagyobb kitérésnél a kinetikus energia zérus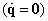 .
.
A kinetikus energia 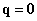 esetén lesz a legnagyobb (és ekkor
esetén lesz a legnagyobb (és ekkor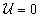 ):
):
|
|
(3.52) |
Mivel konzervatív rendszerről van szó, a mechanikai összenergia állandó:
|
|
(3.53) |
Vagyis
|
|
(3.54) |
ami a Rayleigh-hányados általánosításaként az első sajátfrekvenciára kínál becslést végtelen szabadságfokú (kontinuum) rendszerek esetén is. Azaz a legkisebb sajátfrekvenciához tartozó lengésalakot megfelelően közelítve (becsülve), a hozzá tartozó 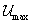 és
és 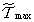 kifejezések hányadosának gyöke
kifejezések hányadosának gyöke 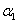 -hez közeli értéket ad eredményül.
-hez közeli értéket ad eredményül.
3.3.4.4. Dunkerley-becslés
Vizsgáljuk ismét a frekvenciaegyenletet:
|
|
(3.55) |
|
|
A 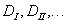 együtthatók a
együtthatók a 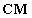 mátrix első, második, stb. skalárinvariánsait jelölik, tehát pl.
mátrix első, második, stb. skalárinvariánsait jelölik, tehát pl.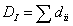 , ami a
, ami a 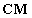 mátrix nyomának felel meg.
mátrix nyomának felel meg.
A váltakozó előjelű együtthatójú, csupa valós gyökkel bíró karakterisztikus polinom analízisével megmutatható, hogy az 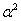 -nél magasabb fokú tagokat elhagyva az első két tag által alkotott másodfokú polinom az
-nél magasabb fokú tagokat elhagyva az első két tag által alkotott másodfokú polinom az 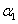 helyen negatív értéket vesz fel:
helyen negatív értéket vesz fel:
|
|
(3.56) |
vagy másképpen
|
|
(3.57) |
Olyan különleges esetekben, amikor az 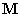 tömegmátrix diagonális, akkor
tömegmátrix diagonális, akkor
|
|
(3.58) |
ahol 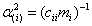 az eredeti mechanikai rendszerből képzett olyan egyszabadságfokú rendszerek sajátkörfrekvenciái, ahol csak az
az eredeti mechanikai rendszerből képzett olyan egyszabadságfokú rendszerek sajátkörfrekvenciái, ahol csak az 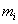 tömeget tartottuk meg és a többit elhagytuk, és az így kapott részmodell rugómerevsége
tömeget tartottuk meg és a többit elhagytuk, és az így kapott részmodell rugómerevsége 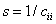 lett.
lett.
Példa Vizsgáljuk egy rezgető motor 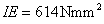 hajlítómerevségű tengelyére erősített
hajlítómerevségű tengelyére erősített 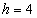 mm magasságú és
mm magasságú és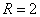 mm sugarú félhenger alakú
mm sugarú félhenger alakú 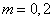 g-os rezgő tömeg alkotta rezgőrendszer sajátkörfrekvenciáit. A teljes henger tehetetlenségi nyomatéka
g-os rezgő tömeg alkotta rezgőrendszer sajátkörfrekvenciáit. A teljes henger tehetetlenségi nyomatéka 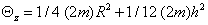 lenne, ahol az első tag a két félhengernek a henger
lenne, ahol az első tag a két félhengernek a henger 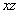 szimmetriasíkjáraszámított
szimmetriasíkjáraszámított 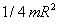 nagyságú tehetetlenségi nyomatékainak összegével egyezik meg. Ebből a félhengernek a
nagyságú tehetetlenségi nyomatékainak összegével egyezik meg. Ebből a félhengernek a 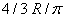 távolságra levő súlypontján átmenő
távolságra levő súlypontján átmenő 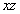 síkkal párhuzamos síkra számított tehetetlenségi nyomatéka a Steiner-tételt visszafelé alkalmazva:
síkkal párhuzamos síkra számított tehetetlenségi nyomatéka a Steiner-tételt visszafelé alkalmazva:
|
|
A továbbiakban az egyszerűség kedvéért feltesszük, hogy a tömeg súlypontja a motor tengelyén helyezkedik el, 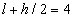 mm távolságra a tengely csapágyazásától (
mm távolságra a tengely csapágyazásától (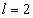 mm a szabad tengelyhossz).
mm a szabad tengelyhossz).
Az 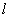 hosszúságú befogott rúd szabad végének
hosszúságú befogott rúd szabad végének 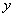 lehajlása és
lehajlása és 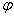 szögelfordulása a rúd végére ható
szögelfordulása a rúd végére ható 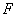 koncentrált erő és
koncentrált erő és 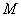 erőpár hatására:
erőpár hatására:
|
|
||
|
|
Így a szabad tengelyszakasztól 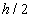 távolságra levő súlypont
távolságra levő súlypont 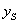 függőleges elmozdulása a ráható
függőleges elmozdulása a ráható 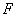 erő következtében:
erő következtében:
|
|
mivel 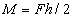 és
és 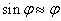 kis elmozdulások esetén.
kis elmozdulások esetén.
-
Azaz az egyenértékű rugómerevség illetve az abból számítható sajátkörfrekvencia:
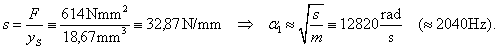
-
Ha a tehetetlenségi nyomatékot is figyelembe vesszük, akkor egy két szabadsági fokú rendszert vizsgálhatunk, melynek kinetikus illetve potenciális (alakváltozási) energiája:
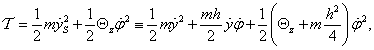
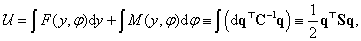
ahol
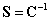 és
és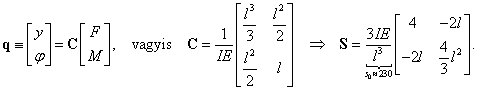
Az
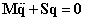 mozgásegyenlet
mozgásegyenlet 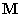 tömegmátrixa és
tömegmátrixa és 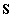 merevségi mátrixa numerikusan:
merevségi mátrixa numerikusan: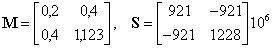
és a karakterisztikus egyenlet:
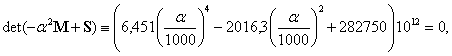
amiből
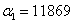 rad/s (1890 Hz) és
rad/s (1890 Hz) és 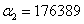 rad/s (28073 Hz).
rad/s (28073 Hz). -
Ha az első sajátfrekvenciával való rezgéshez tartozó rugalmas szál alakját a befogásnak megfelelő peremfeltételt
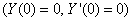 kielégítő legegyszerűbb
kielégítő legegyszerűbb 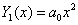 függvénnyel közelítjük, valamint
függvénnyel közelítjük, valamint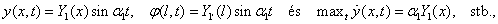
akkor
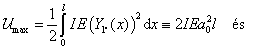
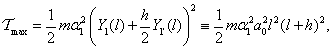
amiből a Rayleigh-hányados szerint
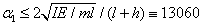 rad/s
rad/s 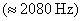 .
. -
A kinetikus energia előbbi kifejezésébe beleszámítva a tehetetlenségi nyomatékot is:
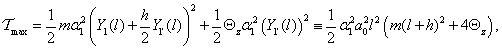
és így az első sajátkörfrekvencia javított becslése (vö. két szabadságfokú eset)
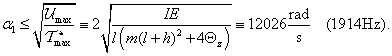
-
A rugalmas szál alakját magasabb fokszámú, több ismeretlen paramétert tartalmazó polinommal vagy más függvénnyel (pl.
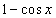 ) is közelíthetjük. Legyen most
) is közelíthetjük. Legyen most 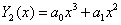 , ami továbbra is megfelel a kinematikai peremfeltételnek. Ezzel
, ami továbbra is megfelel a kinematikai peremfeltételnek. Ezzel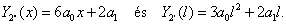
A potenciális energia maximuma most:
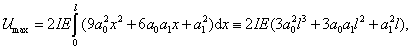
a kinetikus energia pedig
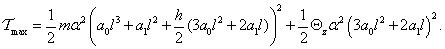
Most is feltételezhetjük, hogy a sajátrezgések során a rezgő rendszer minden (anyagi) pontja egyszerre éri el a szélsőhelyzetét, amikor is
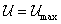 és
és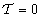 , valamint
, valamint 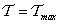 esetén
esetén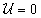 , azaz
, azaz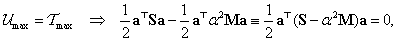
mivel
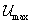 és
és 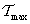 is homogén kvadratikus kifejezése az
is homogén kvadratikus kifejezése az 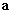 vektort alkotó
vektort alkotó 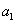 és
és 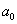 paramétereknek. Az
paramétereknek. Az 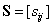 és
és 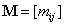 mátrixokat az
mátrixokat az 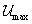 és
és 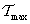 kifejezéseinek
kifejezéseinek 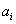 és
és 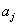 szerinti paricális deriválásából kaphatjuk meg:
szerinti paricális deriválásából kaphatjuk meg: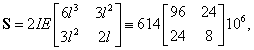
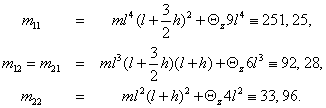
Triviálistól eltérő,
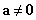 vektort úgy kaphatunk, ha
vektort úgy kaphatunk, ha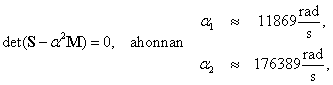
vagyis visszakapjuk két szabadságfokú esetnél kiszámított eredményeket, ami nem meglepő, hiszen a köbös közelítés már elégséges a rugalmas szál pontos alakjához. Amennyiben a tengely tömege nem lenne elhanyagolható, a tengely
 mozgási energiáját is beszámítva a
mozgási energiáját is beszámítva a  -ba az eredmények pontossága tovább javítható.
-ba az eredmények pontossága tovább javítható.
Példa Az ábrán egy  tömegű
tömegű 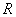 sugarú tárcsa és a tetejére helyezett
sugarú tárcsa és a tetejére helyezett 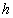 magasságú,
magasságú, 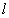 hosszúságú homogén hasáb látható, melyet a hasáb végét és a falat összekapcsoló
hosszúságú homogén hasáb látható, melyet a hasáb végét és a falat összekapcsoló 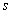 merevségű rugó tart egyensúlyban. A tárcsa gördül a talajon, és a hasáb sem csúszik meg a tárcsa felszínén a kis kitérésű mozgások alatt. Határozzuk meg, hogy milyen paraméterértékek esetén lesz stabilis az egyensúlyi helyzet!
merevségű rugó tart egyensúlyban. A tárcsa gördül a talajon, és a hasáb sem csúszik meg a tárcsa felszínén a kis kitérésű mozgások alatt. Határozzuk meg, hogy milyen paraméterértékek esetén lesz stabilis az egyensúlyi helyzet!
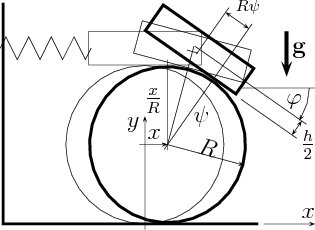
A stabilitás a rugó és a nehézségi erőtér potenciáljának pozitív definitásától függ. Mivel a tárcsa súlypontjának függőleges helyzete nem változik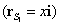 , csak a hasáb súlyponti helyvektorára van szükségünk:
, csak a hasáb súlyponti helyvektorára van szükségünk:
|
|
ahol 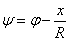 , azaz
, azaz 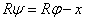
Feltéve, hogy a rugó az egyensúlyi helyzetben feszítetlen, a megnyúlása egy tetszőleges kitérés esetén:
|
|
Ezzel az 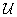 potenciálfüggvény:
potenciálfüggvény:
|
|
melynek parciális deriváltjai és egyensúlyi helyzet körüli linearizálása:
|
|
||
|
|
||
|
|
||
|
|
A linearizált rendszer 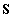 merevségi mátrixa tehát:
merevségi mátrixa tehát:
|
|
és a determinánsa:
|
|
ahol 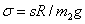 és
és 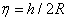 . Tehát a stabilitás feltételei (
. Tehát a stabilitás feltételei (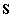 sarokaldeterminánsai alapján):
sarokaldeterminánsai alapján):
|
|