1. fejezet - Időben folytonos működésű rendszerek
- 1.1. Rendszerleírási módok
- 1.2. Alapelemek (objektumok, blokkok, műveletek)
- 1.3. Alapelemek összekapcsolása
-
- 1.3.1. Integrálást vagy differenciálást alkalmazunk a differenciálegyenlet megoldásához
- 1.3.2. Átviteli függvények számítási blokkdiagramjának meghatározása
-
- 1.3.2.1. Arányos típusú átviteli függvények számítási blokkdiagramjának meghatározása PT1, PT2
- 1.3.2.2. Integráló típusú átviteli függvények számítási blokkdiagramjának meghatározása IT1, IT2
- 1.3.2.3. Differenciáló típusú átviteli függvények számítási blokkdiagramjának meghatározása DT1, DT2
- 1.3.2.4. Előretartó-késleltető tag (Lead–lag compensator) számítási blokkdiagramjának meghatározása
- 1.3.3. Alapelemek különböző összekapcsolásából keletkező részrendszerek
- 1.4. Átviteli függvény számítási blokkdiagramjának megvalósítása
-
- 1.4.1. Átviteli függvény számítási blokkdiagramja soros kapcsolású részelemekkel
- 1.4.2. Átviteli függvény számítási blokkdiagramja párhuzamos kapcsolású részelemekkel
- 1.4.3. Átviteli függvény megvalósítása közvetlen programozással
- 1.4.4. Átviteli függvény megvalósítása M-programozással
- 1.4.5. Állapottér módszer számítási blokkdiagramjának meghatározása SISO rendszereknél
- 1.4.6. Állapottér-leírás, állapottér-reprezentációk kapcsolata
- 1.5. Rendszer-transzformációk
- 1.6. Több bemenetű és több kimenetű rendszerek (MIMO) leírása
- 1.7. Folytonos rendszerek megvalósítása műveleti erősítő áramkörökkel
- 1.8. Folytonos rendszerek szimulációja digitális számítógéppel
- 1.9. Numerikus differenciálás és integrálás
-
- 1.9.1. Numerikus differenciálás
- 1.9.2. Numerikus integrálás
-
- 1.9.2.1. Szemléletes megközelítés
- 1.9.2.2. Alapgondolat Taylor sor alkalmazására
- 1.9.2.3. Általános, hibatagot is szolgáltató eljárások - szimmetrikus formulák
- 1.9.2.4. Általános, hibatagot is szolgáltató eljárások - Adams-Bashforth formulák
- 1.9.2.5. Általános, hibatagot is szolgáltató eljárások - Adams-Moulton formulák
- 1.9.2.6. Runge-Kutta módszer
- 1.9.2.7. Az integrálformulák csoportosítása
- 1.10. Differenciálegyenletek numerikus megoldása
-
- 1.10.1. Megoldás negyedrendű Runge-Kutta módszerrel
- 1.10.2. Megoldás másodrendű Adams-Bashforth integrátorokkal
- 1.10.3. Megoldás másodrendű Adams-Moulton integrátorokkal
- 1.10.4. Megoldás másodrendű prediktor – korrektor módszerrel
- 1.10.5. Megoldás másodrendű vegyes módszerrel
- 1.10.6. Hibabecslés módszerei
- 1.10.7. Változó lépésköz alkalmazhatósága
- 1.10.8. A különböző módszerek összehasonlítása
- 1.11. Frekvenciatartománybeli vizsgálatok
-
- 1.11.1. A Bode-diagram
-
- 1.11.1.1. A közelítő Bode–diagram
-
- 1.11.1.1.1. Nulladrendű számláló, nulladrendű nevező
- 1.11.1.1.2. Nulladrendű számláló és egy zérusértékű pólus
- 1.11.1.1.3. Egy nullaértékű zérus és nulladrendű nevező
- 1.11.1.1.4. Nulladrendű számláló és egy pólus
- 1.11.1.1.5. Egy zérus és nulladrendű nevező
- 1.11.1.1.6. Nulladrendű számláló és két pólus
- 1.11.1.1.7. Két zérus és nulladrendű nevező
- 1.11.2. A Nyquist diagram
- 1.11.3. A Nichols–diagram
- 1.11.4. A pólus–zérus diagram
- 1.11.5. A gyökhelygörbe
1.1. Rendszerleírási módok
A modellek egyik legegyszerűbb csoportosítása a fizikai és matematikai modellek megkülönböztetése. A fizikai modell alatt a rendszer valamiféle fizikai megvalósítását értjük, matematikai modellnek pedig a matematika eszközkészletével – általában egyenletekkel vagy egyenletrendszerekkel – megadott leképezést nevezzük.
Az alábbiakban egy bemenetű, egy kimenetű rendszerekkel foglalkozunk, a több bemenetű, több kimenetű rendszerekről később esik szó. Az angol szakirodalomban elterjedt SISO (Single Input Single Output) rövidítéssel szokás ezekre a rendszerekre hivatkozni, ahogyan ezt a továbbiakban tesszük.
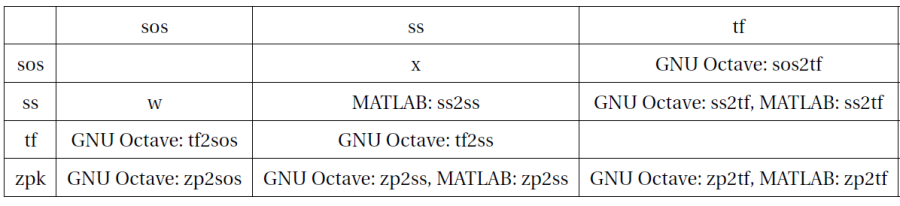
A teljesség kedvéért az összes vonatkozó rövidítést felsoroljuk:
A bemenetet u, a kimenetet y betűvel jelöljük. Attól függően, hogy milyen tartományban (idő, frekvencia vagy Laplace-operátoros), vagyis milyen független változó szerint végezzük vizsgálatainkat, kisbetűs és nagybetűs jelöléssel egyaránt találkozunk. Amennyiben a jel egykomponensű, skalárként adjuk meg, a több be- és/vagy kimenetű rendszereknél viszont vektorként kezeljük ezeket a jeleket.
A matematikai modelleket több szempont szerint csoportosíthatjuk, ezek közül néhány:
-
statikus (más szóval stacionárius, vagyis időben állandósult viselkedésű) és dinamikus (időben változó),
-
lineáris és nemlineáris,
-
koncentrált paraméterű és elosztott paraméterű, valamint a két véglet közötti, összekapcsolt, koncentrált paraméterű részmodellekből álló, feldaraboltnak nevezhető modell,
-
determinisztikus és sztochasztikus,
-
folytonos és nem folytonos (az időtől függő jel értelmezési tartománya és értékkészlete szerint egyaránt beszélhetünk folytonosságról vagy annak hiányáról).
Ebben a részben időben változó (dinamikus) és a jelek értelmezési tartománya szerint folytonos idejű rendszerekkel foglalkozunk, bár nem minden esetben időtartományban. A vizsgált rendszerek, ha külön nem említjük lineárisak és determinisztikusak. A modellalkotás módszereivel más anyag foglalkozik, ezért a modell részletességét (koncentrált, illetve elosztott paraméterű, esetleg feldarabolt) adottnak tekintjük. Amennyiben a vizsgált rendszer tartalmaz statikus matematikai modellel (algebrai egyenlettel) leírható elemeket, például nemlinearitást, azok matematikai modelljét a megfelelő helyen említjük.
1.1.1. Rendszer leírás időtartományban
Az időtartománybeli leírásban a független változó a t betűvel jelölt idő. Időtartományban a dinamikus rendszer bemenet–kimenet kapcsolatát differenciálegyenlet adja meg. Ha a modellben célunk a belső állapotok figyelembe vétele, a dinamikus rendszert állapottér modelljével írhatjuk le. Az állapottér modell felépítésénél fogva alkalmas több bemenetű, több kimenetű rendszerek leírására is. Az állapottér modell kanonikus alakját a bemenetek/kimenetek leírásából (differenciálegyenletből) formális matematikai módszerrel is előállíthatjuk.
Ebben a leképezésben nem biztos, hogy a tényleges fizikai állapotok változását követjük, lehetséges, hogy csupán a matematikai formalizmussal előállított, fizikai mennyiséggel állapotváltozó értelemben össze nem rendelhető mennyiségeket vizsgálunk. A differenciálegyenletet és az állapottér modellt nemlineáris rendszerekre is felírhatjuk, azonban sok esetben közelítésként linearizáljuk a modellt.
1.1.1.1. Differenciálegyenlet (lineáris, állandó együtthatós)
Az általános nemlineáris, ám koncentrált paraméterű és determinisztikus jelekkel leírható, időben és a jelek értékkészlete szerint is folytonos, egy bemenetű, egy kimenetű rendszer y(t) kimenete a rendszer struktúrájától, az u(t) gerjesztéstől és a kezdeti feltételektől függ. Ha egy képletben szeretnénk összefoglalni (a kezdeti feltételeket nem feltüntetve), a rendszer struktúrájának megfelelően szerepeltetnünk kell a bemenő és a kimenő jel deriváltjait is az f nemlineáris függvény független változói között
|
|
(1.1) |
A lineáris, idővariáns (LTV = Linear Time Variant), dinamikus SISO rendszereket időtartományban közönséges, időtől függő együtthatós, lineáris, inhomogén differenciálegyenlettel adhatjuk meg. A differenciálegyenlet matematikában megszokott paraméteres alakjában a bal oldalon az y(t ) kimenő jel és deriváltjai szerepelnek időtől függő együtthatókkal szorozva, a jobb oldalon az u(t ) bemenő jel szerepel hasonlóan megadva:
|
|
(1.2) |
Lineáris, időinvariáns (LTI, Linear Time Invariant), dinamikus SISO rendszerek időtartománybeli leképezése közönséges, állandó együtthatós, lineáris, inhomogén (K.Á.L.I.) differenciálegyenlettel történik. A K.Á.L.I. differenciálegyenlet matematikában megszokott paraméteres alakjában a baloldalon az y(t) kimenő jel és deriváltjai szerepelnek állandó együtthatókkal szorozva, a jobb oldalon pedig az u(t) bemenő jel szerepel hasonló formában:
|
|
(1.3) |
A műszaki gyakorlatban elterjedtebb az időállandós alak, amelyből az arányos viselkedésű rendszer állandósult állapotbeli viselkedésére (erősítésére) egyszerűen következtethetünk, mivel a kimenő és a bemenő jel közvetlenül összehasonlítható.
|
|
(1.4) |
A formálisan előállított időállandós alak a paraméteresnél kevésbé általános, hiszen a kimenő jel oldalán az integráló és a bemenő jel oldalán a differenciáló hatást nem tudjuk figyelembe venni, hiszen (y(t ) és u(t ) együtthatója egy).
Integráló jellegű rendszernél a kimenő jel együtthatója zérus.
|
|
(1.5) |
Differenciáló jellegű rendszernél a bemenő jel együtthatója zérus.
|
|
(1.6) |
A megvalósítható rendszerekre érvényes az n<=m összefüggés, vagyis a bemenő jel oldalán nem szerepelhet magasabb derivált, mint a kimenő jel oldalán.
A magasabb rendű differenciálegyenlet kezelése nehézkes, a rendszer belső állapotairól (a tárolók töltöttségéről) nem, vagy csak hosszadalmas számításokkal tájékozódhatunk.
1.1.1.2. Az állapottér-leírási mód
Az állapottér modell a differenciálegyenlettel szemben folyamatosan tájékoztat a bonyolultabb rendszerek belső állapotairól. Az állapottér modellben az állapotváltozók minden időpillanatban megadják az extenzív mennyiségekkel (pl. anyag, energia, töltés) jellemezhető tárolók töltöttségét. Az állapotváltozókat oszlopvektorként adjuk meg, esetleg tömörebb leíráshoz transzponált sorvektor formában. Az állapotváltozók száma megegyezik a rendszerben lévő különböző energiatárolók számával.
|
|
(1.7) |
Mivel a SISO rendszer a MIMO speciális esete, az általánosság érdekében először a MIMO rendszer állapottér modelljét írjuk fel. A rendszer bemeneteinek száma m, a kimenetek száma p, az állapotváltozók száma n.
Az általános MIMO állapottér modellben két alapvető összefüggést definiálunk. Az állapotegyenlet az állapotváltozók változását az állapotváltozók korábbi értéke és a bemenetek segítségével adja meg.
|
|
(1.8) |
Az állapottér modellben nem olyan közvetlen a kimenet–bemenet kapcsolat, mint a differenciálegyenlet esetén, szükségünk van tehát egy második egyenletre, ami az állapotváltozókon keresztül megadja a kimenő jelek értékét. Ezt az egyenletet kimeneti vagy kicsatolási egyenletnek nevezzük.
|
|
(1.9) |
1.1.1.2.1. Általános, lineáris MIMO állapottér modell
A fenti két egyenlet (1.8 és 1.9) az általános, nemlineáris MIMO rendszerre vonatkozik. A lineáris, időtől függő együtthatós (LTV) MIMO rendszerre vonatkozó állapottér modell két egyenlete mátrixos alakban
|
|
(1.10) |
|
|
|
(1.11) |
A lineáris, időinvariáns (LTI, azaz állandó együtthatós) MIMO rendszerre vonatkozó állapottér modell két egyenlete tömören
|
|
(1.12) |
|
|
|
(1.13) |
és kifejtve
|
|
(1.14) |
|
|
|
(1.15) |
SISO rendszerben egy bemenet (m=1) és egy kimenet (p=1) van az n állapotváltozó mellett. Emiatt a mátrix n elemű oszlopvektorrá, a mátrix n elemű sorvektorrá, a mátrix pedig skalárrá alakul, az rendszermátrix marad n x n méretű.
|
|
(1.16) |
|
|
|
(1.17) |
Mátrixos formában, az említett vektorokkal és a skalárral
|
|
(1.18) |
|
|
|
(1.19) |
1.1.1.2.2. Kanonikus alakú állapottér modell előállítása
A K.Á.L.I. differenciálegyenletből formálisan felírhatjuk a fázistér modellnek is nevezett, kanonikus alakú állapottér modellt. Ugyan a mindennapi gyakorlatban az így felírt egyenleteket is állapottér modellnek nevezzük, az elnevezés nem feltétlenül helyes, hiszen a formálisan előállított állapotváltozók (pontosabban fázisváltozók) nem feltétlenül felelnek meg a korábban állapotváltozóként definiált tárolók töltöttségnek.
Tekintsük az (1.1. ábra) ábrán látható egyszerű mechanikai rendszer, egy ütköző differenciálegyenletét és abból a fázistér modell előállítását. Az F(t) erővel gerjesztett m tömeget párhuzamosan kapcsolt k rugó és b csillapítás rögziti a falhoz. Kimenetként keressük a tömeg vízszintes x(t ) elmozdulását!
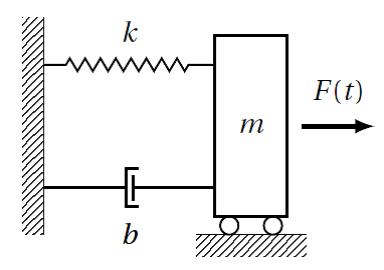
A mechanikai modellt leképező differenciálegyenlet a fizikai mennyiségekre jellemző jelölésekkel (x(t ) elmozdulás, F(t ) erő, m tömeg, b csillapítási tényező, k rugómerevség):
|
|
(1.20) |
Az állapottér (fázistér) modell előállításához fejezzük ki a differenciálegyenletből (1.20) a legmagasabb deriváltat:
|
|
(1.21) |
Az állapotváltozók (fázisváltozók) száma megegyezik a legmagasabb derivált fokszámával, jelen esetben az állapotváltozók vektora kételemű:
|
|
(1.22) |
Első állapotváltozónak a kimenő jelet választjuk, másodiknak a kimenő jel első deriváltját. (Magasabb rendű rendszernél természetesen a további deriváltak is állapotváltozók lesznek, egészen a második legnagyobb fokszámú deriváltig.)
|
|
(1.23) |
|
|
|
(1.24) |
Ezzel a választással az első állapotváltozó deriváltja megegyezik a második állapotváltozóval, ez utóbbi deriváltja pedig a differenciálegyenletből kifejezett legmagasabb (most második) deriválttal azonos. A választott kimenő jel (elmozdulás) pedig az első állapotváltozó értékével egyenlő.
|
|
(1.25) |
|
|
|
(1.26) |
|
|
|
(1.27) |
Az állapottér modell mátrixos alakja:
|
|
(1.28) |
|
|
|
(1.29) |
A fenti másodrendű differenciálegyenlet általános paraméteres alakban:
|
|
(1.30) |
Az állapottér modell a differenciálegyenletből származó általános jelölésekkel:
|
|
(1.31) |
|
|
|
(1.32) |
1.1.1.2.3. P vagy I jellegű, többtárolós SISO rendszer
A két energiatárolós ütköző állapottér modelljéhez hasonlóan állíthatjuk elő a több energiatárolós arányos (legfeljebb integráló) rendszerek állapottér modelljét. Az ilyen rendszerek differenciálegyenletében a jobb oldalon egyedül a bemenő jel együtthatója különbözik nullától.
Arányos viselkedésű rendszer esetén, a homogén oldalon a kimenő jel és a tárolók számának megfelelő derivált szerepel. Egyszeres integráló tulajdonságú rendszer egyenletéből hiányzik a kimenő jel (együtthatója nulla).
|
|
(1.33) |
Az előbb bemutatott állapotváltozó választás szerint a kimenő jelet első állapotváltozónak, az egyre magasabb deriváltjait - egészen a második legmagasabbig - a többi állapotváltozónak választva, most is ki tudjuk fejezni a legmagasabb deriváltat (az utolsó állapotváltozó deriváltját) a többi állapotváltozó és a bemenő jel lineáris kombinációjaként. Ezzel elő tudjuk állítani a rendszer állapotegyenletét
|
|
(1.34) |
A kicsatolási egyenlet rendkívül egyszerű, a kimenő jel megegyezik az elsőként választott állapotváltozóval:
|
|
(1.35) |
A megvalósítható rendszerekben érvényes, hogy a kimenő jel oldalán a deriváltak szám nem lehet kevesebb a bemenő jel oldalán lévő deriváltak számánál, m≤n. Később látunk példát megvalósítható, nem zérus együtthatójú, bemenő jel oldali deriváltakat tartalmazó differenciálegyenletű rendszer állapottér modelljének felírására.
A Laplace-operátoros tartományba átalakított differenciálegyenlet segítségével tudjuk felírni a bemenő jel egy vagy több deriváltját is tartalmazó differenciálegyenlettel modellezhető rendszerek állapottér (fázistér) modelljét.
Az állapottér modell előnye a differenciálegyenlettel szemben különösen a (számító) gépesített megoldásnál szembetűnő, hiszen elsőrendű differenciálegyenletet könnyebb megoldani a magasabb rendűnél, és a számítógépek kimondottan alkalmasak ismétlődő feladatok végrehajtására, vagyis könnyen megbirkóznak az egyenletrendszerek megoldásával.
1.1.2. Frekvenciatartomány
A frekvenciatartománybeli vizsgálatokkal a rendszer különböző frekvenciájú, harmonikus gerjesztésre adott válaszát határozzuk meg. Lineáris rendszereknél a tranziensek lecsengése után a harmonikus gerjesztő jellel azonos frekvenciájú harmonikus válaszfüggvény amplitúdójában és/vagy fázisában térhet el a gerjesztő jeltől. Nemlineáris rendszerek esetén a helyzet bonyolultabb, a probléma kezelésére később látunk módszereket, addig is lineáris rendszerekkel foglalkozunk.
Tulajdonképpen a harmonikus gerjesztő jel és az arra adott harmonikus válasz is időfüggvény, tehát alkalmazhatnánk a differenciálegyenlet-megoldás megszokott módszereit.
Célszerű azonban a frekvenciaátviteli függvény bevezetésével időtartomány helyett frekvenciatartományban vizsgálódnunk. (A differenciálegyenlet-megoldás módszerei természetesen nemlineáris rendszereknél is használhatók, bár nem feltétlenül létezik analitikus megoldás.)
Az általános ω körfrekvenciájú, U 0 amplitúdójú harmonikus gerjesztő jelet komplex függvényként adjuk meg, mégpedig Euler- vagy más néven exponenciális alakban. A gerjesztés és a válasz frekvenciatartománybeli vizsgálatoknál nem lehet akármilyen, hanem csak harmonikus függvény, ezt a jelölésben is külön érzékeltetjük. A továbbiakban a harmonikus időfüggvényeket az jelöléssel különböztetjük meg a tetszőleges u(t) időfüggvényektől.
A harmonikus gerjesztés algebrai alakjában megjelenik a két harmonikus függvény (sin és cos).
|
|
(1.36) |
Lineáris rendszer harmonikus gerjesztésre adott harmonikus válasza a gerjesztő jel ω (kör)frekvenciájától függő Y 0 (ω) amplitúdóban és az ugyancsak a gerjesztő jel körfrekvenciájától függő φ(ω) fázistolásban térhet el.
|
|
(1.37) |
1.1.2.1. Exponenciális alakú frekvenciaátviteli függvény
A lineáris rendszereknél értelmezhető G(jω) frekvenciaátviteli függvény a harmonikus gerjesztésre adott harmonikus válasz, és a harmonikus gerjesztés hányadosaként előállított komplex függvény.
|
|
(1.38) |
Bár a frekvenciaátviteli függvény formálisan két időfüggvény hányadosa, az időtől mégsem függ, csak a gerjesztő jel (kör)frekvenciájától! Erről könnyen meggyőződhetünk, ha behelyettesítünk a definiáló összefüggésbe:
|
|
(1.39) |
Az egyszerűsítésből kiderül, hogy a frekvenciaátviteli függvény két lényeges információt hordoz. A frekvenciafüggő amplitúdó viszonyt (átviteli tényezőt) és a szintén frekvenciafüggő fázistolást, amiből megtudhatjuk, hogy a tranziensek lecsengése után az adott frekvenciájú bemenő jel amplitúdója hányszorosára változik, és mekkora fáziseltérése lesz a gerjesztéshez képest.
A komplex számok terminológiája szerint a frekvenciafüggő amplitúdó viszony a frekvenciaátviteli függvény abszolút értéke, a frekvenciafüggő fázistolás pedig az argumentuma.
|
|
(1.40) |
|
|
|
(1.41) |
1.1.2.2. Polinomiális alakú frekvenciaátviteli függvény
A komplex alakú harmonikus gerjesztés és harmonikus válasz idő szerinti deriváltjait behelyettesítve a (K.Á.L.I. ) differenciálegyenletbe (1.3), a frekvenciaátviteli függvény polinomiális alakját kapjuk.
|
Bemeneti jel |
Kimeneti jel |
|---|---|
|
…… |
…… |
A fentiek alapján megállapíthatjuk, hogy a komplex alakú harmonikus jelek idő szerinti deriválása jω-val való szorzásnak felel meg. Ahányadik deriváltat kell előállítanunk, a jelet jω annyiadik hatványával kell megszoroznunk.
Ha a K.Á.L.I differenciálegyenletbe (1.3) az általános gerjesztés és válasz helyett a harmonikust írjuk
|
|
(1.42) |
majd helyettesítjük az előbb előállított deriváltakat
|
|
(1.43) |
a harmonikus jelet mindkét oldalon kiemelhetjük
|
|
(1.44) |
A frekvenciaátviteli függvény definícióját (1.38) alkalmazva
|
|
(1.45) |
1.1.2.3. Zérus–pólus–erősítés alakú frekvenciaátviteli függvény
A polinomiális frekvenciaátviteli függvényt átalakíthatjuk úgy, hogy a számlálóból és a nevezőből is kiemeljük a legmagasabb jω hatványok együtthatóját (a számlálóból b m -et, a nevezőből a n -t):
|
|
(1.46) |
A számláló és nevező polinomot felírhatjuk gyöktényezős alakban:
|
|
(1.47) |
A számláló (i = 1,2, . . . ,m) gyökeit (zérusok) és a nevező (k = 1,2, . . . ,n) gyökeit (pólusok) egyszerűen ábrázolhatjuk a komplex számsíkon, ha felírjuk a frekvenciaátviteli függvény zérus–pólus–erősítés alakját (1.48).
|
|
(1.48) |
1.1.3. Rendszerek leírása Laplace tartományban
Az időtartományból Laplace–operátoros tartományba való áttérésnek számos oka lehet. Ezek egyike, hogy a K.Á.L.I. differenciálegyenlet időtartománybeli megoldását operátoros tartományban, algebrai egyenlet megoldásával válthatjuk ki. Az algebrai egyenlet megoldása ugyan egyszerűbb, de gondoskodnunk kell az idő- és operátoros tartomány közötti oda és vissza transzformációról, ami a rendelkezésre álló Laplace–transzformációs táblázatok alkalmazásával viszonylag egyszerűen megvalósítható.
Formálisan az s = jω helyettesítéssel származtathatjuk a G(s) átviteli függvényt a G(jω) frekvenciaátviteli függvényből, azonban ez csak harmonikus gerjesztés és az arra adott harmonikus válasz esetén érvényes. Amennyiben kiterjesztjük vizsgálatainkat periodikus, majd nem periodikus (végtelen periódusidejűnek tekintett) jelek kezelésére, a Fourier–sorfejtés, a Fourier–transzformáció, valamint a Laplace–transzformáció alkalmazására kényszerülünk.
A rendszervizsgálatokban előforduló nem periodikus jelek Laplace–transzformáltja előállítható, sőt táblázatok állnak rendelkezésünkre rengeteg időfüggvény–Laplace transzformált függvény párral. Ha a Laplace–transzformációt, mint féloldalas (az integrálás alsó határa helyett 0), () függvénnyel súlyozott Fourier–transzformációt tekintjük, akár magunk is előállíthatjuk különböző időfüggvények Laplace-transzformáltját (és természetesen inverz transzformációval a megfelelő időfüggvényeket is).
A Laplace–transzformáció segítségével bevezethetjük a G(s) átviteli függvényt, ami a rendszer differenciálegyenlettel és frekvenciaátviteli függvénnyel egyenértékű matematikai modellje.
1.1.3.1. Polinomiális átviteli függvény
Az átviteli függvényt a differenciálegyenlet (1.3) mindkét oldalának zérus kezdeti feltételek melletti Laplace-transzformálásával állíthatjuk elő
|
|
(1.49) |
Ezután a baloldalról kiemelhetjük a kimenő jel Y(s), a jobb oldalról a bemenő jel U(s) Laplace-transzformáltját
|
|
(1.50) |
majd ezek hányadosaként állíthatjuk elő az átviteli függvény polinomiális alakját
|
|
(1.51) |
1.1.3.2. Zérus-pólus-erősítés alakú átviteli függvény
Ahogy a frekvenciaátviteli függvénynél már láttuk, a polinomiális átviteli függvényt átalakíthatjuk úgy, hogy a számlálóból és a nevezőből is kiemeljük a legmagasabb s hatványok együtthatóját:
|
|
(1.52) |
A számláló és nevező polinomjait felírhatjuk gyöktényezős alakban:
|
|
(1.53) |
Bevezetve a K = b m /a n erősítés, a zérus polinom és a pólus polinom jelölést, az átviteli függvény zérus–pólus–erősítés (ZPK) alakja:
|
|
(1.54) |
1.1.3.3. Differenciálegyenlet-megoldás Laplace-operátoros tartományban
A K.Á.L.I. differenciálegyenlet megoldásához az időtartománybeli differenciálás Laplace–operátoros tartománybeli megfelelőjére van szükségünk.
|
|
(1.55) |
|
|
|
(1.56) |
Zérus kezdeti feltétel esetén az időtartománybeli deriválás megfelelője Laplace–operátoros tartományban az s operátorral való szorzás.
1.1.3.4. Az állapottér modell Laplace-operátoros tartományban
Ha az állapottér modellt időtartományban írjuk fel, a fentiek értelmében bármilyen differenciálegyenlet (differenciálegyenlet–rendszer) Laplace–transzformációval algebrai egyenletté (algebrai egyenletrendszerré) alakítható, a megoldás inverz Laplace–transzformálásával pedig megkapjuk az eredeti differenciálegyenlet (differenciálegyenlet–rendszer) megoldását.
Korábban láttuk, hogy az n-ed rendű közönséges, állandó együtthatós, lineáris differenciálegyenlet formálisan átalakítható állapottér modellé, ha a jobb oldalon csak a gerjesztés szerepel, a bemenő jel deriváltjai nem. Ha a differenciálegyenlet gerjesztés oldala m-ed rendű, az átviteli függvény segítségével írjuk fel az állapottér modellt. A jobb oldali deriváltak az átviteli függvény számlálójában s hatványok formájában szerepelnek.
Bővítsük a polinomiális átviteli függvényt az alábbiak szerint, az első állapotváltozó X 1 (s) Laplace–transzformáltjának bevezetésével! A polinomok hányadosát két sorba kapcsolt rendszer átviteli függvényeként értelmezve, és felhasználva az átviteli függvény definíciójából, hogy sorba kapcsolt rendszerek eredő átviteli függvénye az egyes rendszerek átviteli függvényének szorzata, az alábbi össefüggéshez jutunk:
|
|
(1.57) |
Nézzük meg először a bal oldali átviteli függvényből a differenciálegyenlet segítségével létrehozható állapottér modellt!
|
|
(1.58) |
Keresztbe szorzással és inverz Laplace–transzformációval egy u(t ) bemenetű, x 1 (t ) kimenetű rendszer differenciálegyenletét kapjuk:
|
|
(1.59) |
|
|
|
(1.60) |
|
|
|
(1.61) |
A korábban ismertetett módon kifejezzük a differenciálegyenletből a legmagasabb deriváltat:
|
|
(1.62) |
A további állapotváltozókat a megszokott módon, a megelőző állapotváltozó deriválásával állítjuk elő
|
|
(1.63) |
majd ezeket helyettesítjük az imént kifejezett legmagasabb deriváltba:
|
|
(1.64) |
A fentiek alapján felírhatjuk a rendszer állapotegyenletét:
|
|
(1.65) |
Folytassuk a másik átviteli függvény átalakításával!
|
|
(1.66) |
Keresztbe szorzással és inverz Laplace–transzformációval egy x 1 (t ) bemenetű, y(t ) kimenetű rendszer differenciálegyenletét kapjuk:
|
|
(1.67) |
|
|
|
(1.68) |
Ebbe az egyenletbe is behelyettesíthetjük a korábban bevezetett állapotváltozókat:
|
|
(1.69) |
Az n-ed rendű differenciálegyenletből adódóan legfeljebb n állapotváltozót használhatunk a fenti egyenletben, így érvényes az n ≥ m+1 egyenlőtlenség, ami szigorúbb a megvalósítható differenciálegyenletnél említett n ≥ m feltételnél. Az n = m+1 feltétel kizárja (az egyébként nem megvalósítható) differenciáló jellegű rendszerek állapottér modelljének felírását.
Az n ≥ m+1 feltétel teljesülése esetén felírhatjuk az állapottér modell második részét, a kicsatolási egyenletet az inverz Laplace-transzformáció alkalmazásával:
|
|
(1.70) |
Az n ≥m+1 feltételt teljesítő differenciálegyenletből származtatható állapottér modell:
|
|
(1.71) |
|
|
|
(1.72) |
Az általános SISO LTI állapottér modell b és c vektora különbözik a differenciálegyenlet jobb oldalán álló, csak az u(t ) bemenő jelet tartalmazó differenciálegyenletből képzett állapottér modelltől.
Ha ismert a SISO rendszer állapottér modellje, a gerjesztés és a kezdeti feltételek, az állapottér modell Laplace–transzformálásával is kiszámíthatjuk a kimenő jelet időtartományban.
A számítás során a rendszer átviteli függvényét is előállítjuk.
Az általános SISO LTI állapottér modell két egyenlete mátrixos formában (1.71 és 1.72), Laplace–transzformálásához az állapotváltozó vektor Laplace–transzformáltja , a bemenő jel , a kimenő jel . Az állapottér modell elemei (jelen esetben mátrix, b és c vektor és d skalár) a transzformáció során nem változik. Az állapotváltozók Laplace–transzformáltját az állapotváltozókra vonatkozó kezdeti feltételek figyelembevételével írjuk fel, .
|
|
(1.73) |
|
|
|
(1.74) |
Az állapotegyenletből (1.73) kifejezhetjük az állapotváltozók vektorát. Amennyiben az állapotváltozók kezdeti értéke zérus (), a számítás valamelyest egyszerűsödik.
|
|
(1.75) |
|
|
|
(1.76) |
Az így kifejezett állapotváltozó vektort behelyettesíthetjük a kicsatolási egyenletbe, hogy megkapjuk a kimenő jel Laplace–transzformáltját:
|
|
(1.77) |
A kapott kifejezés jobb oldalán kiemelhetjük a bemenő jel Laplace–transzformáltját, és elosztjuk vele az egyenlet mindkét oldalát, hogy megkapjuk a SISO rendszer átviteli függvényét az állapottér modell segítségével:
|
|
(1.78) |
Természetesen nemcsak zérus kezdeti feltételeknél használhatjuk a Laplace-transzformációs megoldást. Ekkor a deriválás Laplace-transzformációs szabályában meghatározott módon kell figyelembe vennünk a t = 0 időpillanatbeli kezdeti értékeket.
1.1.4. Jellegzetes állapottér modell struktúrák
Külön elnevezéssel illetjük az adott struktúrájú mátrixokból felépülő állapottér modelleket.
További vizsgálatainkban, a differenciálegyenletben azonos fokszámú a kimenő jel és a bemenő jel oldala (ennek megfelelően az átviteli függvényben azonos fokszámú a számláló és a nevező), ami a korábban ismertetett n ≥ m megvalósíthatósági feltételből az egyenlőségnek felel meg.
A rendszer bemenet–kimenet leképezése maga a differenciálegyenlet, ha mindkét oldal legmagasabb deriváltja az n-edik
|
|
(1.79) |
illetve az ezzel egyenértékű átviteli függvény
|
|
(1.80) |
A kanonikus alakú állapottér modellt korábban már említettük, itt részletesen bemutatjuk, hogyan jutunk el a differenciálegyenlet együtthatóiból egyszerűen felírható fázisváltozós alakú állapottér modell mátrixaihoz.
A közvetlen és párhuzamos programozás módszerével további állapottér reprezentációkhoz juthatunk, akár a differenciálegyenletből, akár az átviteli függvényből indulva. Az így kapott állapottér modellek nem feltétlenül tartalmazzák az átviteli függvényben lévő összes pólust. Ha az átviteli függvény egy vagy több zérusa megszünteti a megfelelő pólusokat, vagyis csökken az átviteli függvény fokszáma, akkor az állapottér modellben ezek a kiejtett gyökök nem jelennek meg. Az egyszerűsítéssel megszüntetett gyökök kérdése a rendszer irányíthatóságához és megfigyelhetőségéhez kapcsolódik - ez utóbbi pedig az analóg számítógépes szimulációban kap szerepet az állapotváltozók kezdeti értékének meghatározásában.
A különböző állapottér modell struktúrák között lineáris transzformációk ( a transzformációs mátrix) teremtenek kapcsolatot.
A fázisváltozós (kanonikus) alakot a differenciálegyenletből formális módszerekkel állítjuk elő. A kísérő alakok (companion form) közé tartozik az irányíthatósági normálalak és a megfigyelhetőségi normálalak. A kísérő alakok jellemzői az rendszermátrix egy sorát vagy egy oszlopát kitöltő karakterisztikus polinom-együtthatók (vagyis a differenciálegyenlet homogén oldalán lévő kimenő jel és deriváltjai együtthatói). A modális alakban (modal form) az rendszermátrix diagonális, a főátlóban a karakterisztikus polinom egyszeres gyökei (a rendszer pólusai) szerepelnek. Amennyiben van többszörös pólus, a rendszermátrix a „majdnem diagonális” Jordan–alakot ölti.
1.1.4.1. Fázisváltozós alak
A fázistér modell korábbi formális bevezetésével (a kimenő jelet választva első állapotváltozónak, majd deriváltjait rendre a következőknek) a fázisváltozós alakot (phase variable canonical form) kapjuk.
A levezetés áttekinthetőségét segítendő, az első lépésben olyan rendszerrel foglalkozunk, ahol a bemenő jel deriváltjainak együtthatója zérus.
|
|
(1.81) |
Az állapotváltozókat és deriváltjaikat az alábbi szabályszerűség szerint írhatjuk fel
|
Állapotváltozók |
Állapotváltozók idő szerinti deriváltja |
|---|---|
|
…… |
…… |
Az állapotegyenlet
|
|
(1.82) |
A kicsatolási egyenlet rendkívül egyszerű, a kimenő jel megegyezik az elsőként választott állapotváltozóval:
|
|
(1.83) |
Ahhoz, hogy kiterjeszthessük a leírást olyan rendszerre is, ahol a bemenő jel oldalán is szerepelnek deriváltak, a már megismert módon csatoljuk szét a differenciálegyenletet, ezúttal időtartományban!
|
|
(1.84) |
A v(t ) változó bevezetésével a szétcsatolással kapott két differenciálegyenlet
|
|
(1.85) |
|
|
|
(1.86) |
Írjuk fel az állapotváltozókat (és deriváltjaikat) a megszokott módon az új v(t ) kimenő jellel
|
Állapotváltozók |
Állapotváltozók idő szerinti deriváltja |
|---|---|
|
…… |
…… |
Az n-edik állapotváltozó deriváltját a megszokott módon fejezzük ki a differenciálegyenletből
|
|
(1.87) |
A kicsatolási egyenletet az v(t) előbb kifejezett legmagasabb (n-edik) deriváltjának az eredeti differenciálegyenlet szétcsatolásával kapott második egyenletbe való helyettesítésével állítjuk elő.
|
|
(1.88) |
Mátrixos alakban
|
|
(1.89) |
|
|
|
(1.90) |
|
|
|
(1.91) |
|
|
|
(1.92) |
|
|
|
(1.93) |
Az igen gyakori b n = 0 esetben, a kicsatolási egyenlet alakja könnyen megjegyezhetővé válik.
|
|
(1.94) |
Ezzel b n = 0 (vagyis n ≥ m) esetén a SISO LTI rendszer fázisváltozós (ph a phase variable kifejezésből származó rövidítés) kanonikus alakú állapottér modell mátrixai.
|
|
(1.95) |
|
|
|
(1.96) |
|
|
|
(1.97) |
|
|
|
(1.98) |
Ha a n = 1, még egyszerűbbek a mátrixok.
1.1.4.2. Az irányíthatósági normálalak
Az irányíthatósági normálalakot (controllable canonical form) a közvetlen programozás módszerével állíthatjuk elő az átviteli függvény polinomiális alakjából (1.51) vagy az ezzel ekvivalens differenciálegyenletből (1.3). A következőkben feltételezzük, hogy a kezdeti feltételek mindegyike zérus.
|
|
(1.99) |
A rendszert szétcsatolhatjuk két sorba kapcsolt átviteli függvény eredőjére. Az egyik egységnyi számlálójú, a másik egységnyi nevezőjű, a kettő között egy V (s) kisegítő változó bevezetésével teremthetünk formálisan kapcsolatot.
|
|
(1.100) |
A két átviteli függvény:
|
|
(1.101) |
|
|
|
(1.102) |
Ezt a szétcsatolást blokkdiagramon is ábrázolhatjuk (1.2. ábra).

Az U(s) bemenetet tartalmazó átviteli függvényből keresztbe szorzással kialakuló egyenletet akár differenciálegyenletté is alakíthatnánk, de most maradunk Laplace–operátoros tartományban
|
|
(1.103) |
V(s)-t és deriváltjait választva állapotváltozóknak (és rögtön felírva az állapotváltozók deriváltját)
|
Állapotváltozók |
Az állapotváltozók idő szerinti deriváltjainak Laplace-függvénye |
|---|---|
|
…… |
…… |
A keresztbe szorzással előállított egyenletből kifejezhetjük a legmagasabb deriváltnak megfelelő s n V (s) elemet
|
|
(1.104) |
és felírhatjuk az állapotváltozók segítségével is
|
|
(1.105) |
Az állapotegyenletet mátrixos alakban, Laplace–operátoros tartományban felírva a fázisváltozós alakkal egyező struktúrát kapunk:
|
|
(1.106) |
A szétcsatolással kapott G 2 (s) második átviteli függvényt megszorozva V (s)-sel, kifejezhetjük az Y (s) kimenetet, V (s) és deriváltjai lineáris kombinációjaként
|
|
(1.107) |
V (s) és deriváltjai helyére a választott állapotváltozókat beírva
|
|
(1.108) |
Az s·X n (s) helyére az első átviteli függvényből kifejezett képletet írhatjuk
|
|
(1.109) |
Rendezés után
|
|
(1.110) |
a kicsatolási egyenletet kapjuk
|
|
(1.111) |
A közvetlen programozás módszerével előállított irányíthatósági normálalak megegyezik az előző részben ismertetett fázisváltozós alakkal.
Differenciálegyenletből (vagy átviteli függvényből) igen gyakran az egyenlet analóg számítógépes (szimulációs) megoldásának blokkvázlata (algoritmusa) alapján állítjuk elő az állapottér modellt. Az analóg számítógépekkel később részletesebben foglalkozunk, itt csupán a szükséges alapokat tekintjük át.
A szimulációs diagramnak is nevezhető ábra az analóg számítógép műveleti egységeinek (integrátor, összegző, előjelfordító, szorzó) megfelelő szimbólumokból épül fel. A bemenő jelek előállításáról függvénygenerátorokkal gondoskodhatunk, bár ez jelenleg nem lényeges, hiszen a szimulációs diagramot csupán az állapottér modell felírásához használjuk, nem pedig az analóg számítógép programozásához.
Az analóg számítógép időtől függő jelekkel dolgozik, azonban a szemléletességen nem változtat, ha Laplace–operátoros tartományban írjuk fel a jeleket és az integrálás operátoros tartománybeli megfelelőjét, 1/s-t írjuk a megfelelő blokkokba. Eltekintünk továbbá az analóg számítógépes kapcsolásokban használt műveleti erősítővel megvalósított elemek előjelfordító tulajdonságától. Szintén nem foglalkozunk az állandóval való szorzás és az összegzés analóg számítógépes megvalósításával, hanem a hatásvázlatokban előforduló jelképeket használjuk.
Példánkban (a fázisváltozós alaknál már alkalmazott b n = 0 esetre) a közvetlen programozáshoz n darab integrátort kapcsolunk sorba. Az első integrátor bemenete a legmagasabb deriváltnak megfelelő s n ·V(s), kimenete s n-1 ·V(s). A sorban utolsó integrátor kimenete V (s).
A szétcsatolásból származó első átviteli függvényből kifejezett s n ·V(s) jelet a képletben szereplő elemek összegzésével állíthatjuk el
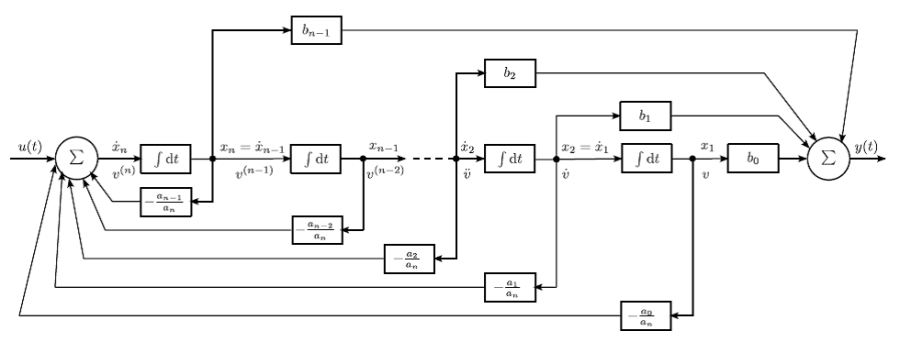
A szimulációs diagramon (1.3. ábra) szereplő integrátorok kimenetét választva állapotváltozónak, a fázisváltozós alakkal egyező irányíthatósági normálalak mátrixok könnyen felírhatók.
|
|
(1.112) |
|
|
|
(1.113) |
|
|
|
(1.114) |
|
|
|
(1.115) |
Az irányíthatósági normálalak a modern irányítástechnikában az irányíthatóság vizsgálatában és biztosításában igen fontos rendszerleírási mód.
1.1.4.3. A megfigyelhetőségi normálalak
A megfigyelhetőségi normálalak (observer canonical form) szintén igen fontos a modern irányítástechnikában. Felírásához ugyancsak az átviteli függvényből (1.51) indulunk ki. Az átviteli egyenletből kifejezzük a kimenő jel s n ·Y(s) formában megadott legmagasabb deriváltját
|
|
(1.116) |
Osszuk végig mindkét oldalt s n -el, és az a n együtthatóval az osztást vigyük be a zárójel mögé!
|
|
(1.117) |
A zárójelek feloldása után
|
|
(1.118) |
Végezzünk integrálást a Laplace–operátoros tartományban és osztást az s operátorral. Ezzel az s hatványok szerint alakíthatjuk tovább a kifejezést
|
|
(1.119) |
Az egyenletnek (b n = 0 feltételezésével) megfelelő analóg számítógépes program szimulációs diagramja (1.4. ábra) szintén n egymás után kapcsolt integrátorból épül fel.
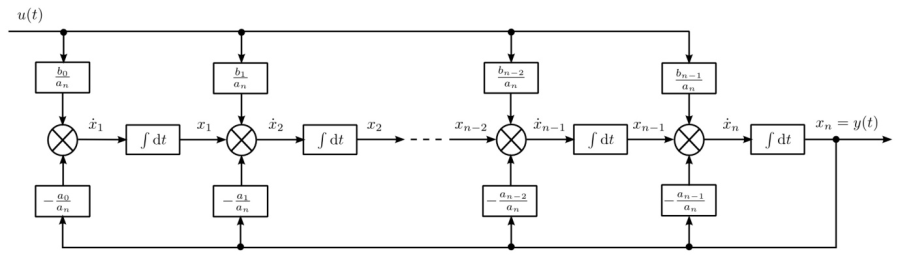
Az integrátorok kimenetét úgy választva állapotváltozóknak, hogy az első integrátor kimenete az első állapotváltozó, a második integrátor kimenete a második állapotváltozó, és így tovább, a diagramban jobbról balra haladva először a kicsatolási egyenletet kapjuk meg.
|
|
(1.120) |
majd pedig felírhatjuk az állapotváltozók differenciálegyenletét
|
|
(1.121) |
|
|
|
(1.122) |
|
|
. . . . . . . . . |
||
|
|
(1.123) |
|
|
|
(1.124) |
Most már egyszerűen felírhatjuk a megfigyelhetőségi normálalak állapottér mátrixait.
|
|
(1.125) |
|
|
|
(1.126) |
|
|
|
(1.127) |
|
|
|
(1.128) |
A megfigyelhetőségi normálalak lineáris, dinamikus rendszerek számítógépes szimulációjában is nagyon jól használható, mivel a rendszer kezdeti feltételeit is könnyen figyelembe tudjuk venni. Ez az alak a rendszer megfigyelhetőségével áll kapcsolatban, ami azt jelenti, hogy az összes állapotváltozó hatással van a rendszer kimenetére és fordítva, a rendszer kimenete és az állapotegyenlet ismeretében az állapotváltozókat bármelyik időpillanatban rekonstruálhatjuk. Ha t = 0-ban végezzük el a számításokat, a kimenő jel és deriváltjai kezdeti értékei segítségével meghatározhatjuk az állapotváltozók kezdeti értékeit.
1.1.4.4. A modális alak
A párhuzamos programozás módszerével állítjuk elő a modális kanonikus alakot (szétcsatolt alakot) és ennek speciális esetét a Jordan–féle kanonikus alakot.
Amennyiben a rendszer n-edfokú karakterisztikus egyenletének n különböző valós gyöke van, és feltételezzük, hogy n > m, az átviteli függvény zérus–pólus–erősítés alakját (1.54) résztörtekre bontással írjuk fel
|
|
(1.129) |
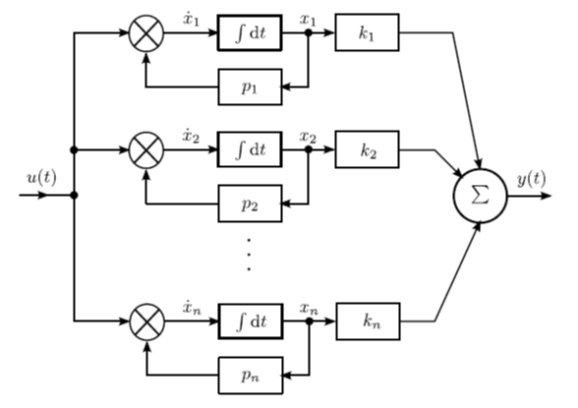
Az átviteli függvény ilyenkor n darab, párhuzamosan kapcsolt, egytárololós, arányos tag eredője. Az egyes egytárolós tagok az integrátor pólusértékkel való visszacsatolásával adják meg az állapotváltozókat, a visszacsatolás bemenő jele a rendszer u(t) bemenő jele, kimenete pedig az állapotváltozó. A résztörtekre bontásból származó k állandóval szorozva az állapotváltozót, majd összegezve ezeket a szorzatokat, megkapjuk a rendszer y(t ) kimenő jelét. A rendszer szimulációs diagramján (1.5. ábra) most is n integrátor szerepel.
|
|
(1.130) |
|
|
|
(1.131) |
|
|
|
(1.132) |
|
|
|
(1.133) |
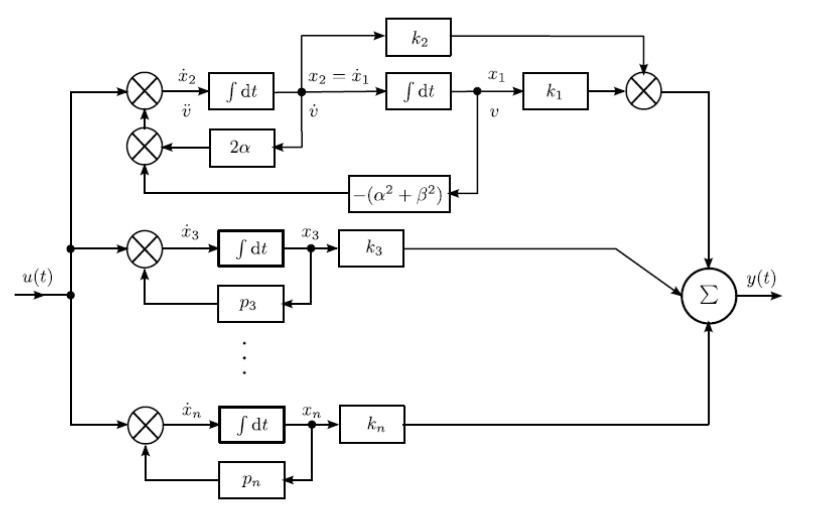
Amennyiben a rendszer n-edfokú karakterisztikus egyenletének n-2 különböző valós gyöke és egy konjugált komplex gyökpárja van, az átviteli függvény zérus–pólus–erősítés alakját (1.54) résztörtekre bontással úgy írjuk fel, hogy a konjugált komplex p1=α+j•β és p2=α-j•β gyökpárt egy másodrendű taggal helyettesítjük.
|
|
(1.134) |
Az egyszeres gyököknek megfelelő tagokat az imént bemutatott párhuzamos programozással adjuk meg. A másodrendű nevezőjű tagot a közvetlen programozás módszerével kezeljük, akár irányíthatósági, akár megfigyelhetőségi normálalakban felírva (1.6. ábra).
|
|
(1.135) |
|
|
|
(1.136) |
|
|
|
(1.137) |
|
|
|
(1.138) |
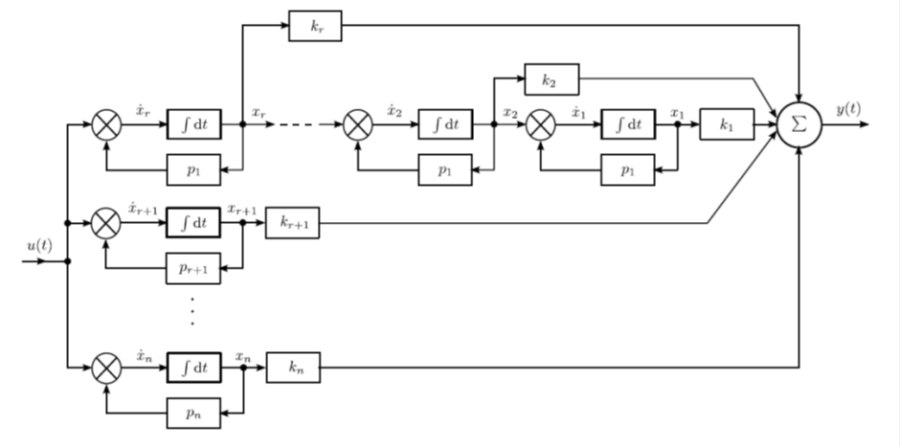
Amennyiben a rendszer n-edfokú karakterisztikus egyenletének egyik gyöke r–szeres valós, a többi n-r pedig különböző valós gyök, és feltételezzük, hogy n > m, az átviteli függvény zérus–pólus–erősítés alakját (1.54) ismét résztörtekre bontással írjuk fel.
|
|
(1.139) |
A szimulációs diagramban (1.7. ábra) a különböző valós gyökökhöz tartozó ábrarészlet megegyezik az (1.5. ábra) ábra felépítésével. Az r-szeres pólusnak megfelelő x 1 , x 2 ,…,x r állapotváltozók sorban egy–egy, a p 1 pólussal visszacsatolt integrátor kimenete. A résztörtekből számított k 1, k 2 , ,k r konstansokkal súlyozva a megfelelő állapotváltozókat, megkapjuk a többszörös gyök y(t ) kimenő jelben szereplő részét.
|
|
(1.140) |
|
|
|
(1.141) |
|
|
|
(1.142) |
|
|
|
(1.143) |
1.2. Alapelemek (objektumok, blokkok, műveletek)
A folytonos rendszerek áramköri megvalósításai napjainkban is megkülönböztetett jelentőségűek. Bár mintavételes rendszerekkel egyre egyszerűbben és olcsóbban valósíthatók meg azok a funkciók, amelyeket régebben csak analóg áramkörökkel voltak megvalósíthatók. A folytonos (analóg) rendszerek műveleti egységei olyan alapműveleteket valósítanak meg a rendszerépítésben, amelyeket hasonló funkcióval, de mintavételes interpretációban alkalmaznak a digitális rendszerekben.
A folytonos rendszer áramköri elemekkel történő megvalósításához tekintsük az (1.144) egyenlettel leírt folytonos, lineáris állandó együtthatós differenciálegyenletet:
|
|
(1.144) |
ahol
|
a 0 ..a n |
a differenciálegyenlet kimenő jelének és deriváltjainak együtthatói, |
|
|
b 0 ..b m |
a differenciálegyenlet bemenő jelének és deriváltjainak együtthatói, |
|
|
y(t) |
a rendszer kimenő jele, |
|
|
n |
a kimenő jel legmagasabb deriváltjának fokszáma, |
|
|
u(t) |
a rendszer bemenő jele, |
|
|
m |
a bemenő jel legmagasabb deriváltjának fokszáma, |
|
|
t |
időváltozó. |
A differenciálegyenletben a következő alapműveletek szerepelnek:
-
jelkomponensek összeadása (kivonása = mínusz egyszeres érték hozzáadása),
-
jelkomponensek szorzása állandó értékkel (az együtthatókkal),
-
jelkomponensek idő szerinti derivált értékének meghatározása.
Az alapelemek fizikai megvalósításánál a jelek idő szerinti derivált értékének meghatározása – a műveleti erősítő tápfeszültségei, mint jelkorlátok miatt – nehézségbe ütközik. A derivált értékek meghatározásának másik problémája, hogy mivel a bemeneti jel változásának sebességével arányos a kimeneti jel nagysága, ezért a nagyobb frekvenciájú jeleket jobban erősítik a differenciáló tagok, mint az alacsony frekvenciájú jelkomponenseket. Ez azt jelenti, hogy a differenciáló tagok nem a hasznos jelet, hanem elsősorban a hasznos jelen lévő nagyfrekvenciás zajokat erősítik. Ezen tulajdonságuk alapján nem alkalmasak a folytonos rendszerek időfüggő tagjának megvalósítására.
A folytonos rendszerek áramköri megvalósításánál a differenciálhányadosokat megadó differenciáló tagok helyett, azok inverz függvényét, a jel idő szerinti integráljainak értékét alkalmazzák.
1.2.1. Műveleti erősítő
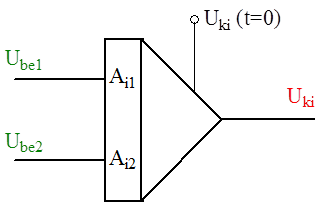
Az ideális műveleti erősítő a következő tulajdonságokkal rendelkezik (1.8. ábra):
|
ZBE = , |
|
fband = , |
|
A = , |
|
ZKI = 0, |
|
P = 0. |
A kimeneti feszültség értéke a nem invertáló (+) és az invertáló (-) bemeneteken a föld potenciálhoz képest megjelenő feszültségkülönbség értéke a differencia feszültség szorzata az erősítéssel, amelyet a műveleti erősítő a feszültségvezérelt feszültséggenerátor értékeként jelenít meg a kimeneten. Mivel a ideális műveleti erősítő bemeneti ellenállása végtelen értékű, a műveleti erősítő nem tereheli azt az áramkört, amelyhez hozzákapcsoltuk. Az ideális műveleti erősítő nulla ellenállása pedig azt jelenti, hogy a kimeneti feszültség teljes egészében a műveleti erősítőhöz kapcsolódó következő áramkörön jelenik meg.
Az ideális esetben a műveleti erősítő végtelen sávszélessége azt jelenti, hogy az erősítő a nullától (egyenfeszültség) a végtelen frekvenciáig terjedő frekvenciájú jeleket azonos mértékben erősíti.
Az ideális műveleti erősíő végtelen feszültség erősítésére (A) azt teszi lehetővé, hogy az alapelem (a műveleti erősítőt) negatív visszacsatolásos áramkörben történő alkalmazása esetén a nagy erősítés miatt alapvetően a visszacsatoló ágban szereplő impedancia határozza meg a visszacsatolás mértékét. Ezzel a lehetőséggel rendkívül egyszerűvé válik tetszőleges tulajdonsággal rendelező átviteli tulajdonságú tag előállítása, mert a frekvenciafüggő erősítés értékét a visszacsatoló ágban elhelyezett impedancia és a bemenetre kapcsolt impedancia hányadosa határozza meg.
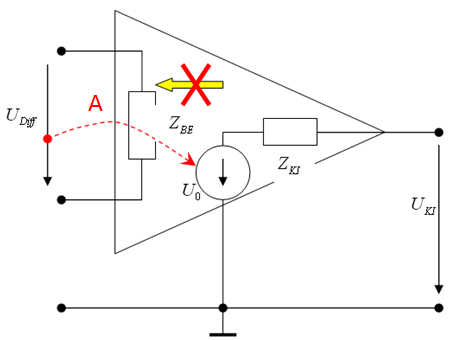
A valóságos műveleti erősítő a következő paraméterértékekkel rendelkezik (ua 741 típusú műveleti erősítő):
-
bemeneti impedancia (ZBE) a műveleti erősítő szimmetrikus bemeneti ellenállása. Jellemző értéke bipoláris tranzisztoros bemeneti fokozat esetén néhány MΩ,
FET tranzisztoros bemenet esetén néhány TΩ.
-
sávszélesség azt a frekvenciát jelenti, ahol visszacsatolatlan erősítő erősítése 3 dB-t csökken a névleges frekvencián mért erősítéshez képest. Jellemzően 5-10 Hz körüli érték.
fband =
5-10 Hz (felnyitott körerősítés esetén)
1MHz (egységnyi negatív, visszacsatolt körerősítés esetén)
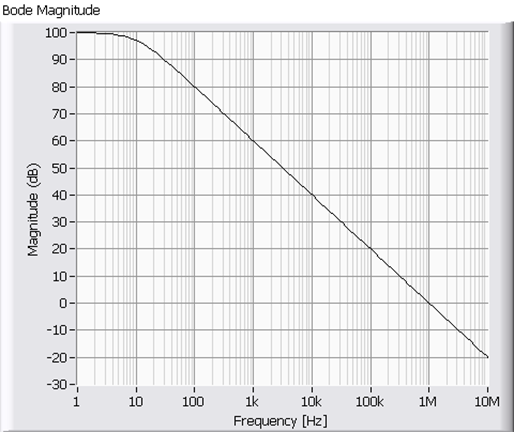 1.9. ábra - A valóságos műveleti erősítő Bode frekvencia diagramja (amplitúdó)
1.9. ábra - A valóságos műveleti erősítő Bode frekvencia diagramja (amplitúdó)
-
erősítés (A) megadja, hogy a bemenetekre kapcsolt feszültséget (az invertáló és nem invertáló bemenet feszültségének a különbségét) az erősítő külső visszacsatolás nélkül hányszorosára erősíti a kimenetén, névleges terhelés mellett. Ez az érték általában 100 dB körüli (néhány 100 000 szeres), különleges kapcsolásokkal elérhető 170 dB feletti erősítés is.
-
kimeneti impedancia (Z KI ) a műveleti erősítő aszimmetrikus kimeneti ellenállása. Visszacsatolás nélkül az értéke néhány 10 Ω és néhány 100 Ω között szokott lenni a végerősítő fokozat kivitelétől függően.
-
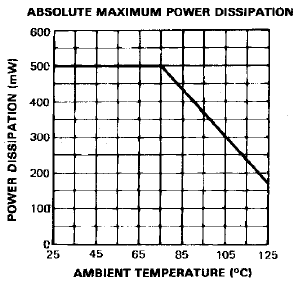
teljesítményfelvétel P = kb. 500mW (melynek az eszköz aktuális hőmérséklete a paramétere).
1.2.2. Negatív visszacsatolású műveleti erősítő
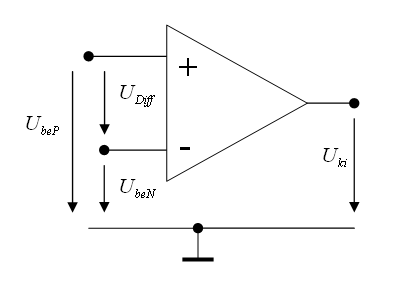
A valós műveleti erősítő műszaki paraméterei alapján a nagy értékű, nyílthurkú erősítés (A) lehetővé teszi, hogy az U diff bemeneti feszültség értéke a kivezérlés teljes tartományában közelítőeg nulla értékű legyen. Minél nagyobb értékű az A erősítés, ez a közelítés annál jobb feltételekkel valósul meg.
Az (1.12. ábra) ábrán egy negatív visszacsatolású műveleti erősítővel megvalósított kapcsolást láthatunk. Az erősítő felépítésénél a műveleti erősítő kimenete és az invertáló bemenet között egy ellenállás (R v ), a bemenet és a műveleti erősítő invertáló bemenete között szintén egy ellenállás (R b ) található. Az ellenállások számértékének kisebb a jelentősége, mint az ellenállásértékek arányának. Bemeneti és visszacsatoló ellenállásként általában 10kOhm – 1MOhm értékek közötti ellenállások szerepelhetnek.
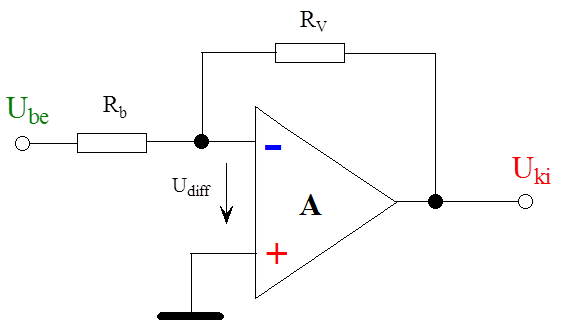
A nagy értékű, felnyitott körű erősítés eredményeként () az invertáló és a nem invertáló bemenetek közelítőleg azonos (föld)potenciálon vannak, aminek az a következménye, hogy így a műveleti erősítő invertáló bemenetére felírható a következő csomóponti egyenlet:
|
|
(1.145) |
amelyet rendezve a kimenő jelre a következő összefüggést kapjuk:
|
|
(1.146) |
Ebből a negatív visszacsatolású erősítő erősítése
|
|
(1.147) |
A negatív erősítési tényező azt jelenti, hogy az így kialakított erősítő a bemeneti jel előjelét is megfordítja az erősítés mellett.
Az erősítés értékét, mint látható, az ellenállások aránya határozza meg a nagy értékű nyilthurkú erősítés miatt.
Az ellenállások segítségével kialakított erősítő kapcsolásoknál jelentős szerepe van annak a kapcsolásnak, amelynél a visszcsatoló és a bemeneti ellenállás azonos értékű. Ez az előjel fordító kapcsolás , amely a rendszer analóg műveleti elemekből kialakított blokkdiagramjánál biztosítja a jel előjelhelyes műveletvégzését.
1.2.3. Jelek összeadása
A műveleti erősítő nem invertáló bemenetére nemcsak egy bemenettel csatlakoztathatunk, hanem a nem invertáló bemeneti csomópont befolyó áramát több bemeneti feszültség és a hozzá tartozó bemeneti ellenállás hozhatja létre. Ez biztosítja a jelek összegzését .
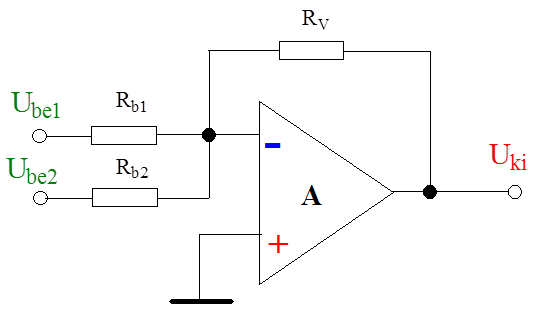
A műveleti erősítő invertáló bemenetére felírt csomóponti egyenlet ebben az esetben (1.13. ábra):
|
|
(1.148) |
amelyet rendezve a kimenő jelre a következő összefüggést kapjuk:
|
|
(1.149) |
|
|
|
(1.150) |
Az A 1 = -R v /R b1 az U be1 jelhez tartozó erősítési tényező, míg az A 2 = -R v /R b2 az U be2 jelhez tartozó erősítés értéke. Bár az erősítésértékek különbözők lehetnek az egyes bemeneteken, a kimeneten megtörténik a bemeneti jelek összegzése.
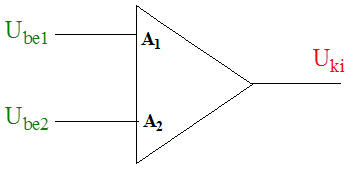
A jelek összegzését végző elem jelölése a blokkdiagramban az (1.14. ábra) ábrán látható.
1.2.4. Időfüggő jel szorzása konstanssal
Ha egy időfüggő jelet konstans értékkel szorzunk meg , akkor eredményként a jel időbeni lefutásával azonos, a jel időpillanatonkénti értékében pedig a konstans értékszerese jelenik meg kimeneti jelként. Jel konstans értékkel való szorzásához együttható-potenciométert alkalmazunk, amelynek erősítési tényezője nulla(0) és egy (1) értékekek között állítható be.
Egynél nagyobb erősítési igény esetén az együttható-potenciométer után kapcsolt negatív visszacsatolású erősítő segítségével növeljük meg az erősítés mértékét, általában 10-, 100-szoros erősítés alkalmazásával.
Az együttható-potenciométer jelölését blokkvázlatban az (1.15. ábra) ábra mutatja.

Az (1.15. ábra) ábrán látható ”a” paraméter az együttható-potenciométer leosztása.
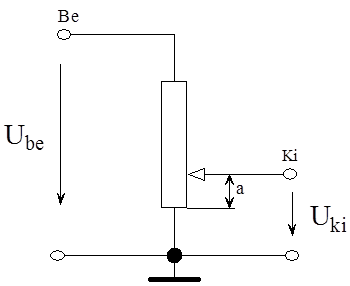
Az együttható-potenciométer bemenete és kimenete nem cserélhető fel a villamos hálózatban, mivel a bemeneti jelnek az egész ellenállásértékre, a leosztott kimenetnek pedig a potenciométer csúszkájára kell csatlakoznia. Ha fordított módon kapcsoljuk a hálózatba az együttható-potenciométert, a leosztás nagyságát másképpen kell meghatározni, illetve a csúszka nulla állapotánál rövidre zárjuk a bemeneti jelet.
1.2.5. Jel integrálása idő szerint
Az integrátor elem abban tér el a jelösszegző elemtől, hogy a visszacsatoló ágban egy C kapacitású kondenzátort helyezünk el. Az erősítő kapcsolásban ebben az esetben a visszacsatoló impedancia értéke a kondenzátor Laplace-operátoros impedanciája Z c .
|
|
(1.151) |
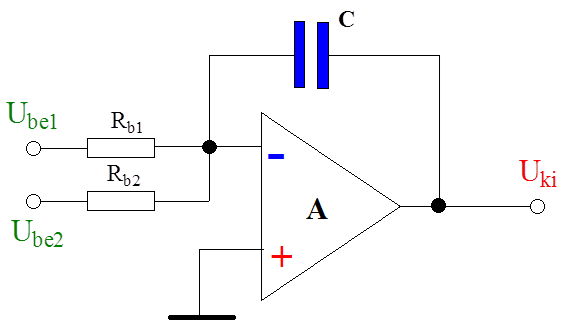
A műveleti erősítő invertáló bemenetére felírt csomóponti egyenlet Laplace-operátoros tartományban:
|
|
(1.152) |
amelyet a kimenő jelre rendezve a következő összefüggést kapjuk:
|
|
(1.153) |
Ha a következő jelöléseket bevezetjük:
|
|
(1.154) |
|
|
|
(1.155) |
Az A i1 az U be1 jelhez tartozó integrálási erősítési tényező, míg az A i2 az U be2 jelhez tartozó integrálási erősítés értéke.
A kimenő jel a fentiek alapján
|
|
(1.156) |
Az integrálási erősítésértékek különbözőek lehetnek az egyes bemeneteken, a kimeneten a bemeneti jelek összegzése történik meg.
A Laplace-operátoros alakból visszatérve időtartományba (inverz Laplace-transzformációval), felírhatjuk a kimenő jel időfüggvényét:
|
|
(1.157) |
A kétbenentű integrátor jelölése a blokkdiagramban az (1.18. ábra) ábrán látható.:
Az (1.18. ábra) ábrán az integrátor szimbólikus jelölésénél a kimenet kezdeti értéke a t=0 időpillanatban látható. Ez az érték az U ki kimeneti feszültség kezdeti értékét állítja be a t =0 időpillanatban, hogy ettől a kezdeti értéktől történjék az integrálás. A megadott kezdeti érték a visszacsatoló kondenzátoron t =0 pillanatban beállítandó feszültség értéke, amely egyben a kimenő feszültség is t =0-ban.
1.2.6. Jelkésleltetés (Padé-közelítés)
Tetszőleges nagyságú késleltetés megvalósítása villamos áramkör segítségével nagy kapacitású (Farad) tároló elemeket igényel. A jelenlegi technikai lehetőségek kb. 100 Farad nagyságú, néhány Volt maximális feszültségű kapacitív elemek alkalmazását teszik lehetővé. Nagyobb feszültség értékekhez csak néhány 1000 mikroFarad kapacitású tároló elem áll rendelkezésre.
A fenti korlátozások, illetve az áramköri magvalósítás Padé-közelítő jelege miatt, valódi jelkésleltetést nagyon ritkán alkalmaznak .
Az (1.19. ábra) ábrán egy, az irodalomban található jelkésleltető kapcsolást mutatunk be, amely lehetővé teszi kis értékű késleltetés megvalósítását, ha a műveleti erősítő erősítésének beállításával nagy sávszélességet biztosítunk (egységnyi erősítéssel).
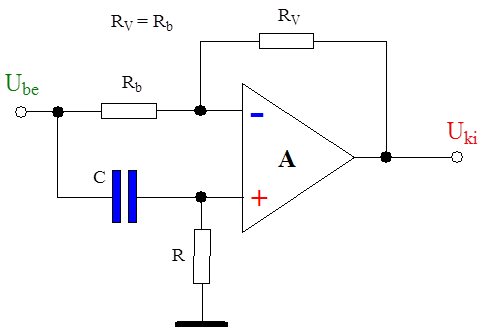
Az (1.9. ábra) ábrán látható áramkör Padé-közelítést valósít meg, és nagyon kis nagyságrendű (ns) késleltetést képes biztosítani. Az áramkör a következő operátoros átviteli függvényt valósítja meg,
|
|
(1.158) |
ahol τ = 2.R.C. A jobb oldalon álló kifejezés a következő formában írható fel:
|
|
(1.159) |
Az (1.9. ábra) ábrán látható kapcsolást a következő értékekkel megvalósították : Rb=Rv=249 Ohm
C=63pF és R=95.3 Ohm, a műveleti erősítő típusa pedig CLC428. Ezekkel az elemekkel elért késleltetés 11.9 ns értékű.
1.2.7. Nemlineáris elemek
A digitális számítógépek napjainkban történő tömeges alkalmazása mellett egyre inkább elvesztik a jelentőségüket azok az analóg áramkörökkel megvalósított nemlineáris tulajdonságú áramkörök , amelyek korábban a nemlineáris szimulációs elemek alkalmazásának egyetlen útját jelentették.
Ezen elemek alkalmazási lehetőségeit a digitális számítógéppel megvalósított időváltozós differenciálegyenlet megoldó algoritmusoknál ismertetjük.
1.3. Alapelemek összekapcsolása
A folytonos rendszerek differenciálegyenletének megoldásához a korábbi fejezetben bemutatott alapelemeket kell összekapcsolnunk, hogy így biztosítsuk a differenciálegyenlet kiszámítási algoritmusát minden időpillanatban. A folytonos, analóg alapelemek alkalmazásával valóban folytonos megoldást kapunk, míg a digitális számítógépes megvalósításnál csak a mintavételi időpillanatokban határozhatjuk meg kimenő jelet (jeleket).
1.3.1. Integrálást vagy differenciálást alkalmazunk a differenciálegyenlet megoldásához
Ha csak analitikus függvényekről lenne szó, akkor egyértelmű a válasz: differenciálást, hiszen a derivált függvény előállítására minden esetben eredményesen alkalmazható szabályok vannak. Az integrálásnál azonban könnyen találhatunk olyan, a gyakorlatban is nagy jelentőségű függvényeket, melyeknek nem létezik a primitív függvénye (pl. , ami a valószínűség számítás egyik alapfüggvénye).
A számítógépes szimuláció során általában differenciálegyenleteket kell megoldanunk közelítő módszerekkel. A későbbiekben a megoldásokról még részletesebben is lesz szó, most csak két gondolatmenetet mutatunk be. Az egyik esetben a legmagasabb rendű deriváltat, a másik esetben pedig éppen fordítva, a legalacsonyabb azaz nulladrendű deriváltat fejezzük ki a megoldandó differenciálegyenletből.
Tekintsük az egyenletet (ahol i=0…n és j=0…m), amelyből a kimenő jel legalacsonyabb deriváltjának kifejezése:
|
|
(1.160) |
ahol k=1…n,
illetve a kimenő jel legmagasabb deriváltjának kifejezése
|
|
(1.161) |
ahol l=0…n-1.
A megoldás során az első esetben sorozatos differenciálással , a második esetben pedig integrálással tudjuk az ismeretlen függvényt, illetve annak deriváltjait előállítani.
A differenciálegyenlet megoldása során általában numerikus módszereket használunk, és ekkor egészen más következtetésre juthatunk, mint analitikus esetben .
A megoldást a következőkben több oldalról is bemutatjuk.
1.3.1.1. Hibával terhelt értékű függvények esete
Az egyik esetben a döntő különbséget az okozza, hogy míg a differenciálás pontbeli műveletként értelmezhető, addig az integrálás egy intervallumon van definiálva. Amennyiben a vizsgálandó függvény nem pontosan ismert, mert például mérési hibákat vagy numerikus közelítésből adódó hibákat tartalmaz, akkor például az (1.20. ábra) ábrán látható esetek fordulhatnak elő:
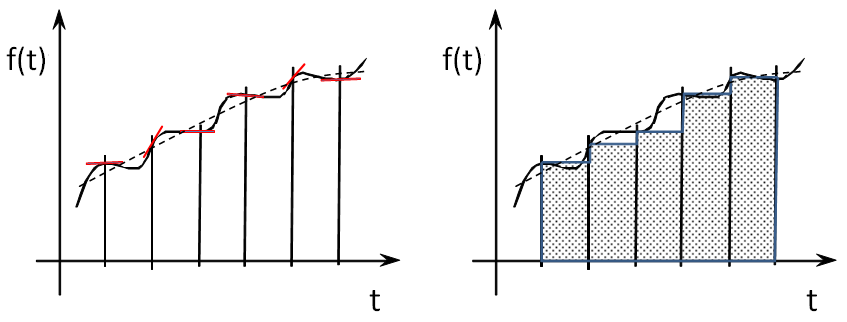
A szaggatott vonal a pontos értékek alapján rajzolt görbe, a „hullámos” pedig a közelítő adatsor felhasználásával készült. Mint látható, a differenciálás esetén a keresett érték és a közelítés eltérése olyan mértékű, hogy az eredmény használhatatlan. Az integrálás esetén vannak hibák, de ezek mértéke kezelhetővé tehető, ha a téglalapok számát növeljük. A differenciálás esetén azonban ez sem segít!
1.3.1.2. Numerikus hibák
A differenciálás esetén gondot okoz a kiegyszerűsödés jelensége [1]. Ennek a lényege, hogy közel azonos számok különbsége esetén sok értékes jegyet veszítünk. Nézzük például a szinusz függvény értékét az 1 illetve az 1+10-5 helyen, valamint a két helyettesítési érték különbségét!
Az idő szerinti differenciálhányados közelítő értékét több módszerrel is előállíthatjuk.
Közelítő formulát kaphatunk a Taylor-sorok felhasználásával is.
Ilyenek például a következők:
|
|
(1.162) |
|
|
|
(1.163) |
|
|
|
(1.164) |
|
|
|
(1.165) |
|
|
|
(1.166) |
Mindegyik formulában az a közös, hogy a számláló esetén zérushoz tart. Ekkor a kivonások miatt az értékes jegyek „elvesznek”, így tulajdonképpen a számábrázolás pontossága csökken. Egy‑egy közelítés esetén ez még nem nagy probléma, de a szimuláció során nagy ismétlésszámú ciklusokkal dolgozunk, és ekkor a hiba halmozódása fatális következményekkel jár (csak igen ritkán fordul elő olyan eset, amikor nincs belőle probléma).
Az előzőekben leírt problémák numerikus idő szerinti integrálás során nem lépnek fel. A közelítő formulák látszólag hasonlóak, de ekkor tulajdonképpen egy súlyozott átlag meghatározásáról van szó, ezért a kiegyszerűsödés sem lép fel.
Illusztrációként álljon itt három egyszerű integráló összefüggés!
1.3.1.3. Összehasonlító mintapélda megoldása differenciáló és integráló algoritmussal
Illusztrációként tekintsük az egytömegű csillapított lengőrendszert (1.21. ábra), ahol m=1[kg]; k=3 ; s=2 ; és a gerjesztés pedig: F=2[N], egységugrás alakú!
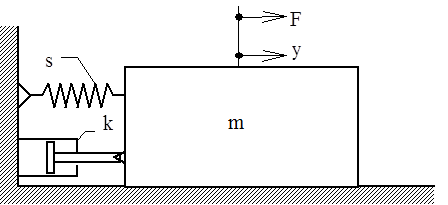
A rendszert a következő differenciálegyenlettel lehet leírni:
|
|
(1.170) |
melynek pontos megoldása:
|
|
(1.171) |
Először differenciálással oldjuk meg a feladatot. Ekkor az 1.3.1. szakasz fejezetben leírtaknak megfelelően átalakított egyenlet:
|
|
(1.172) |
Ha az explicit megközelítést választjuk, akkor az (1.166) összefüggést kell alkalmazni. A számítások elkezdése azonban nehézségekbe ütközik, hiszen a formula három különböző időpontbeli érték ismeretét kívánja meg, és ez kezdetben nem áll rendelkezésünkre. „Kegyes csalással” a pontos megoldásból számolhatók ki a hiányzó értékeket az első három lépés esetén (Ezt általában nem ismerjük, de most csak az a cél, hogy a módszer használhatatlanságát illusztráljuk!).
Ennek megfelelően az (Táblázat 1.5) táblázatban lehet az algoritmust összefoglalni (ahol a fizikai mennyiségeket paraméteresen jelöltük).
|
i |
||||
|---|---|---|---|---|
|
0 |
||||
|
1 |
||||
|
2 |
||||
|
3 |
||||
|
i |
A számításokat táblázatkezelő rendszerrel végeztük el. Az „eredményeket” az (Táblázat 1.6) táblázat tartalmazza esetén.
|
0 |
0 |
0 |
2 |
|
0,1 |
0,009056 |
0,172213 |
1,465248 |
|
0,2 |
0,032859 |
0,296821 |
1,043819 |
|
0,3 |
0,045159 |
0,459227 |
0,532002 |
|
0,4 |
-0,0212 |
-0,04954 |
2,191014 |
|
0,5 |
11,34291 |
-1,84356 |
-15,1551 |
|
0,6 |
-408,038 |
285,0984 |
-37,2193 |
|
0,7 |
12383,25 |
-10655 |
7200,46 |
|
0,8 |
-350205 |
326072,8 |
-277806 |
|
0,9 |
9593721 |
-9256578 |
8582296 |
|
1,0 |
-2,6E+08 |
2,54E+08 |
-2,4E+08 |
Az eredményekből jól látszik, hogy semmi közük nincs a valóságos értékekhez! A lépésköz változtatásával a helyzet nem javul! A táblázat első 3 sora tartalmazza a pontos értékeket.
Sokkal jobb eredményhez juthatunk, ha implicit megközelítéssel élünk. Ekkor az (1.163) összefüggés mellett szükségünk van még a második differenciálhányados közelítő képletére is:
|
|
(1.173) |
Ezeket behelyettesítve a differenciálegyenletbe, és alkalmazva az jelölést a következő alakhoz jutunk:
|
|
(1.174) |
Ebből kifejezhető az elmozdulás következő időpillanatbeli értéke:
|
|
(1.175) |
Most már összeállíthatjuk az algoritmust leíró táblázatot (Táblázat 1.7), amelyben az1.165. összefüggést fogjuk alkalmazzuk. Az első lépéseknél itt is van egy kis gond (hiányoznak értékek), de ezt az egyszerű differenciahányados alkalmazásával át lehet hidalni.
|
i |
||||
|---|---|---|---|---|
|
0 |
||||
|
1 |
||||
|
2 |
||||
|
i |
Az integrálásnál csak az egyszerűbben megvalósítható explicit eljárással foglalkozunk, így az átalakított differenciálegyenlet:
|
|
(1.176) |
Az algoritmust most is célszerű táblázatban (Táblázat 1.8) összefoglalni (az 1.167, 1.168. és 1.169. összefüggések alkalmazásával):
|
i |
||||
|---|---|---|---|---|
|
0 |
||||
|
1 |
||||
|
2 |
||||
|
i |
A számításokat most is táblázatkezelő programmal végeztük el. Az (1.22. ábra) ábrán látszik, hogy az integrálás eredménye és a pontos érték egy vonalvastagságon belül helyezkedik el, azonban helyenként eltér tőle.
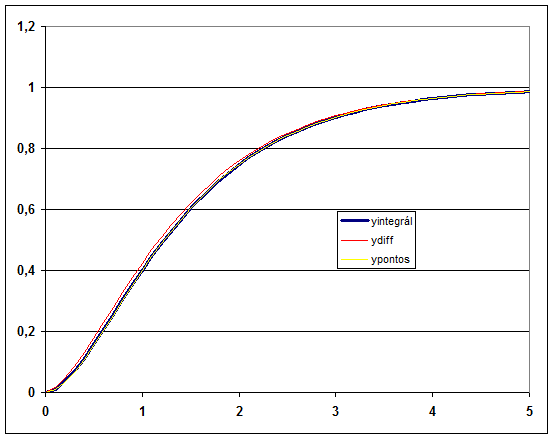
Összefoglalva megállapíthatjuk, hogy integrálással könnyebben, pontosabb eredményt értünk el. Természetesen egyetlen példából a pontosságra vonatkozóan általánosítani nem szabad. Az algoritmus előállítása azonban az implicit technika miatt sokkal munkaigényesebb. Amennyiben -et nem lehet kifejezni zárt alakban, akkor az algoritmust még ki kell egészíteni egy gyökkereső módszerrel is (lásd a 7. fejezet fejezetet)!
1.3.2. Átviteli függvények számítási blokkdiagramjának meghatározása
A differenciálegyenlettel leírt folytonos rendszer számítási blokkdiagramjának meghatározásával a rendszer megoldását biztosítjuk minden egyes mintavételi (számítási) időpontban, tetszőleges bemenő jel esetén.
Az arányos időállandóval rendelkező rendszerek jellemzője, hogy a differenciálegyenlet tartalmazza mind a bemenő jelet, mind pedig a kimenő jelet. A tároló tulajdonságot a kimenő jel derivált értékeinek darabszáma határozza meg, így első kimeneti jel deriváltat tartalmazó rendszert egytárolósnak nevezzük. A kimeneti jel magasabb deriváltjait tartalmazó rendszerek tárolóinak száma megegyezik a kimenő jel legmagasabb (idő szerinti) deriváltjának fokszámával. Más megfogalmazásban, a rendszer tárolóinak darabszámát a folytonos rendszer karakterisztikus polinomjának fokszáma határozza meg.
A differenciálhányadosok legmagasabb fokszámának meghatározásánál a nulladik (0.) derivált érték maga a jel, míg a negatív kitevőjű derivált értékek integrálási műveletet jelölnek.
|
|
(1.177) |
|
|
|
(1.178) |
|
|
|
(1.179) |
A folytonos rendszerek időfüggő differenciálegyenletének megoldásához ki kell fejeznünk a kimenő jel legmagasabb deriváltjának értékét. A megoldáshoz felhasználható alapelemek (integrátorok, összeadók és együttható-szorzóelemek) segítségével létre kell hoznunk a számításokat elvégző blokkdiagramot.
Ezzel a blokk diagrammal nemcsak egy bemenő jelhez vagy bemenő jel típushoz tartozó egyedi megoldást kapunk meg, hanem az összes bemenő jel esetén megkapjuk a rendszer válaszát az adott bemenő jelre. Más szavakkal, a differenciálegyenlet számítási blokkdiagramja a rendszer viselkedését írja le nem csak egy adott bemeneti jelhez tartozó partikuláris megoldást.
A számítási blokkdiagram meghatározásánál alapvető szempontok a folytonos rendszert leíró paraméterek ( differenciálegyenlet-együtthatók ) egyszerű változtatási lehetősége és a blokkdiagram felépítéséhez alkalmazott elemek számának minimalizálása . A felhasznált elemek minimalizálása még azokba az időkbe nyúlik vissza, amikor a számítási blokkdiagramot analóg számítógépi elemekből építették fel, és nem volt közömbös, hogy a kapcsoláshoz hány darab műveletvégző elemet alkalmaznak (teljesítményfelvétel, meghibásodás szempontjából).
Az F(y(t), u(t),t) folytonos, lineáris állandó együtthatós differenciálegyenlet általános alakja:
|
|
(1.180) |
ahol
|
a 0 ..a n |
a differenciálegyenlet kimenő jelének és deriváltjainak együtthatói, |
|
|
b 0 ..b m |
a differenciálegyenlet bemenő jelének és deriváltjainak együtthatói, |
|
|
y(t) |
a rendszer kimenő jele, |
|
|
n |
a kimenő jel legmagasabb deriváltjának fokszáma, |
|
|
u(t) |
a rendszer bemenő jele , |
|
|
m |
a bemenő jel legmagasabb deriváltjának fokszáma, |
|
|
t |
időváltozó. |
Ezt a részletesen kifejtett alakot tömörebben is felírhatjuk a következő formában
|
|
(1.181) |
|
|
|
(1.182) |
Ha ebből az alakból kifejezzük a kimenő jel legmagasabb idő szerinti deriválját, egy olyan általános számítási formulát kapunk, amely folytonos és mintavételes rendszerek esetén egyaránt alkalmazható. Mintavételes rendszeren a folytonos rendszer digitális számítógéppel történő számítását értjük.
|
|
(1.183) |
A számítási blokkdiagram létrehozásának következő lépése, hogy a kimenő jel legmagasabb deriváltjának integrálásával létrehozzuk az alacsonyabb fokszámú deriváltakat, és ezeket is felhasználjuk a legmagasabb derivált kiszámításához.
A számítási blokkdiagram analóg működésű elemekkel történő megvalósításánál az alacsonyabb fokszámú derivált értékek kiszámítását valamint a legmagasabb derivált meghatározásához szükséges jeleket az analóg működésű elemek biztosítják.
Digitális számítógépes megvalósításnál ez nem lehetséges, mert ezzel egy algebrai hurkot hozzunk létre. Az algebrai hurok olyan számítási képlet, amelynél a kiszámítandó mennyiség saját maga is részt vesz saját értékének a meghatározásában, egy bemeneti komponensként. Ezt nem lehet megvalósítani, ezért a számítási képletben egy késleltetést alkalmazunk a kiszámítandó változóra, amely így egy mintavételi időlépéssel korábbi értéket alkalmaz a számítás során. Ezzel egy kismértékű időbeni elcsúszást okozunk, hiszen a k. időpillanatbeli jelértéket egy (k-1). időpillanatbeli értékkel határozzuk meg, de másképp nem végezhetnénk el a számítást.
Analóg áramkörökkel megvalósított integráló tag a bemeneti jelen előjelfordítást végez. Hogy ezt a specialitást ne kelljen a blokkdiagramba továbbvinnünk, és folyamatosan a jelek előjelfordítását figyelnünk, a mintapéldákban olyan integráló tagot alkalmazzuk, amely nem forít előjelet. Ha a rendszer megvalósítását analóg áramkörökkel végezzük természtesen a jelek előjelfordítását is számba kell vennünk!
1.3.2.1. Arányos típusú átviteli függvények számítási blokkdiagramjának meghatározása PT1, PT2
Az arányos típusú tagok (P = Proportional) jellemző tulajdonsága, hogy rendszerleíró differenciálegyenletükben szerepelnek a bemenő és kimenő jelek valamint a kimenő jel deriváltjai. A kimenő jel deriváltjainak darabszáma alapján kapjuk meg, hogy az adott rendszer hány darab tárolóval rendelkezik.
Az egytárolós, arányos tag (PT1) átviteli függvénye :
|
|
(1.184) |
Az egytárolós, arányos tag (PT1) differenciálegyenlete:
|
|
(1.185) |
|
|
|
(1.186) |
|
|
|
(1.187) |
Az egytárolós, arányos tag (PT1) számítási blokkdiagramja:
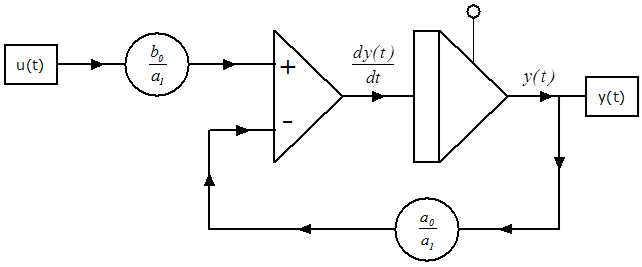
A kéttárolós, arányos tag (PT2) átviteli függvénye (1. verzió):
|
|
(1.188) |
A kéttárolós, arányos tag (PT2) differenciálegyenlete (1. verzió):
|
|
(1.189) |
|
|
|
(1.190) |
|
|
|
(1.191) |
A kéttárolós, arányos tag (PT2) számítási blokkdiagramja (1. verzió):
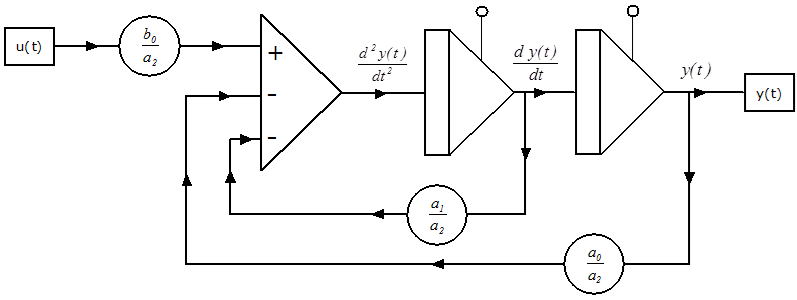
Másodrendű tag (PT2) átviteli függvénye (2. verzió):
|
|
(1.192) |
Másodrendű tag (PT2) differenciálegyenlete (2. verzió)::
|
|
(1.193) |
|
|
|
(1.194) |
|
|
|
(1.195) |
mindkét oldalt integrálva az idő szerint a következő egyenletet kapjuk:
|
|
(1.196) |
Másodrendű tag (PT2) számítási blokkdiagramja (2. verzió):
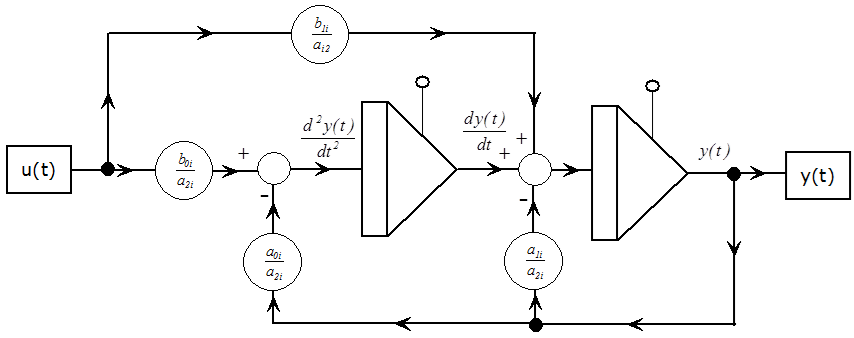
1.3.2.2. Integráló típusú átviteli függvények számítási blokkdiagramjának meghatározása IT1, IT2
Az integráló típusú tagok (I = Integrate) jellemző tulajdonsága, hogy rendszerleíró differenciálegyenletükben nem szerepel a kimenő jel. Szerepelnek viszont a kimenő jel magasabb deriváltjai. A kimenő jel deriváltjainak darabszáma alapján kapjuk meg, hogy az adott rendszer hány darab tárolóval rendelkezik.
Az egytárolós, integráló tag (IT1) átviteli függvénye :
|
|
(1.197) |
Az egytárolós, integráló tag (IT1) differenciálegyenlete:
|
|
(1.198) |
|
|
|
(1.199) |
|
|
|
(1.200) |
Az egytárolós, integráló tag (IT1) számítási blokkdiagramja:
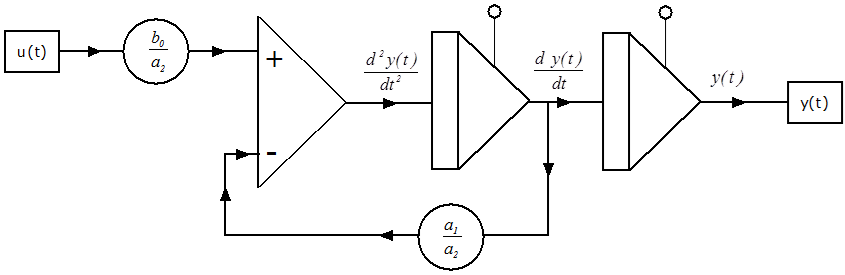
A kéttárolós, integráló tag (IT2) átviteli függvénye :
|
|
(1.201) |
A kéttárolós, integráló tag (IT2) differenciálegyenlete:
|
|
(1.202) |
|
|
|
(1.203) |
|
|
|
(1.204) |
A kéttárolós, integráló tag (IT2) számítási blokkdiagramja:
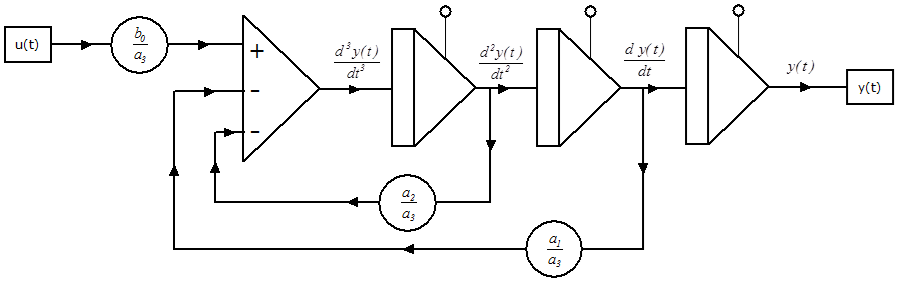
1.3.2.3. Differenciáló típusú átviteli függvények számítási blokkdiagramjának meghatározása DT1, DT2
A differenciáló típusú tagok (D = Differential) jellemző tulajdonsága, hogy rendszerleíró differenciálegyenletükben nem szerepel a bemenő jel, csak a bemeneti jel idő szerinti differenciálhányadosa. A rendszer bemenetén csak a bemeneti jelet tudjuk megadni, a differenciálhányadosát azonban nem. Ezért, a rendszert számító blokkdiagramban a bemenő jelből elő kell állítani a bemeneti jel derivált értékét, de ehhez a művelethez csak integráló tulajdonságú tagot alkalmazhatunk.
Szerepelnek még az ilyen típusú rendszerekben a kimenő jel magasabb deriváltjai is, amelyek darabszáma alapján tudjuk megállapítani, hogy az adott rendszer hány darab tárolóval rendelkezik.
Az egytárolós, differenciáló tag (DT1) átviteli függvénye:
|
|
(1.205) |
Az egytárolós, differenciáló tag (DT1) differenciálegyenlete:
|
|
(1.206) |
|
|
|
(1.207) |
|
|
|
(1.208) |
|
|
|
(1.209) |
Az egytárolós, differenciáló tag (DT1) számítási blokkdiagramja:
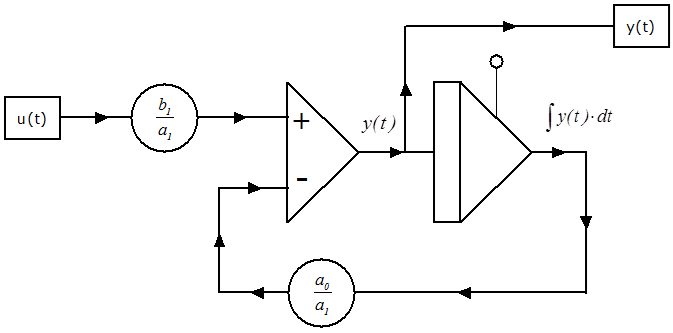
A kéttárolós, differenciáló tag (DT2) átviteli függvénye:
|
|
(1.210) |
A kéttárolós, differenciáló tag (DT2) differenciálegyenlete:
|
|
(1.211) |
|
|
|
(1.212) |
|
|
|
(1.213) |
|
|
|
(1.214) |
|
|
|
(1.215) |
A kéttárolós, differenciáló tag (DT2) számítási blokkdiagramja:
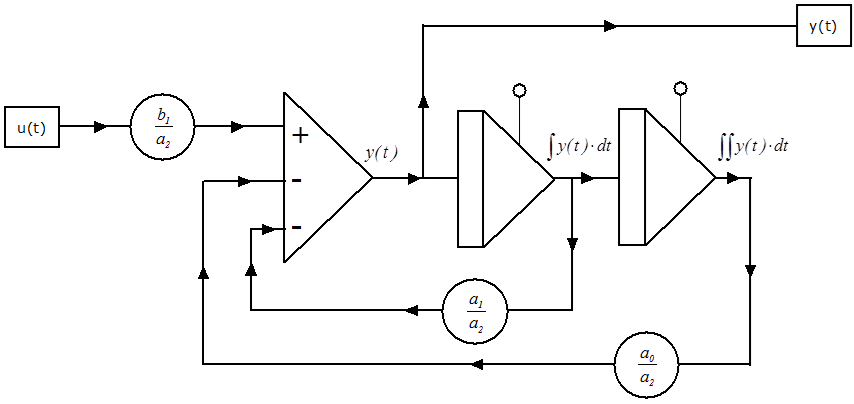
1.3.2.4. Előretartó-késleltető tag (Lead–lag compensator) számítási blokkdiagramjának meghatározása
Az előretartó-késleltető tag (Lead-Lag) átviteli függvénye:
|
|
(1.216) |
Az előretartó-késleltető tag (Lead-Lag) differenciálegyenlete:
|
|
(1.217) |
|
|
|
(1.218) |
|
|
|
(1.219) |
|
|
|
(1.220) |
Az előretartó-késleltető tag (Lead-Lag) számítási blokkdiagramja:
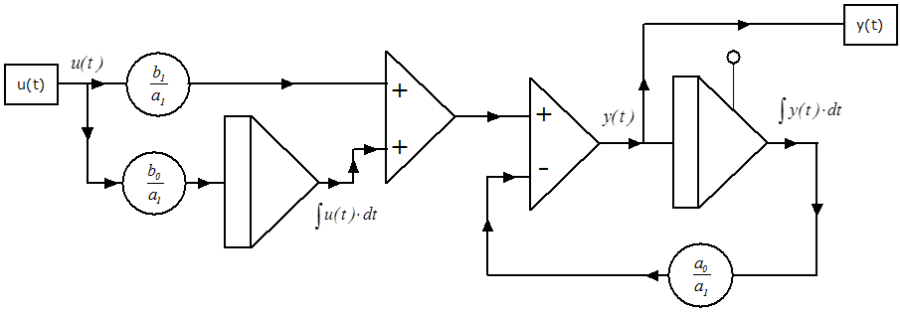
1.3.3. Alapelemek különböző összekapcsolásából keletkező részrendszerek
Nagyméretű, több blokkból álló rendszerek hálózatának megvalósításához nyújtanak segítséget a következő algoritmusok, amelyek több rendszertechnikai blokk összekapcsolásának eredményét adják meg folytonos és mintavételes rendszereknél. A mintapéldákat folytonos rendszerek esetén mutatjuk be, de az algoritmusok változatlan formában alkalmazhatók mintavételes rendszerek blokkjai esetén is.
1.3.3.1. Alapelemek összekapcsolásánál alkalmazott műveletek
A G(s) átviteli függvény számlálójával (numerator) és nevezőjével (denominator), mint polinomokkal végezhetünk műveleteket: polinomok összeadását, kivonását és szorzását. Ezeket a műveleteket a következő módon valósíthatjuk meg:
|
|
(1.221) |
ahol
|
R |
a polinomok összeadásával létrehozott eredő polinom, melynek fokszáma = max(n,m), |
|
|
i |
= 0..max(n,m) a művelet indexének értéke, |
|
|
P |
az első összeadandó polinom, |
|
|
n |
a P polinom fokszáma, |
|
|
Q |
a második összeadandó polinom, |
|
|
m |
a Q polinom fokszáma. |
A polinomok összeadásával keletkezett polinom (R) fokszáma az összeadandó polinomok fokszáma közül a nagyobb lesz.
|
|
(1.222) |
ahol
|
R |
a polinomok kivonásával létrehozott eredő polinom, melynek fokszáma = max(n,m), |
|
|
i |
= 0..max(n,m) a művelet indexének értéke, |
|
|
P |
a kisebbítendő polinom, |
|
|
n |
a P polinom fokszáma, |
|
|
Q |
a kivonandó polinom, |
|
|
m |
a Q polinom fokszáma. |
A polinomok kivonásával keletkezett polinom (R) fokszáma a kisebbítendő és kivonandó polinomok fokszáma közül a nagyobbal egyezik meg.
|
|
(1.223) |
ahol
|
R |
a polinomok szorzásával létrehozott eredő polinom, melynek fokszáma = n+m, |
|
|
P |
az első szorzandó polinom, |
|
|
i |
= 0..n a P polinom indexének értéke, |
|
|
Q |
a második szorzandó polinom, |
|
|
j |
= 0..m a Q polinom indexének értéke. |
A bemutatott polinom műveletek segítségével lehetőségünk van az átviteli függvény alakban megadott részrendszerek tetszőleges topológiával történő összekapcsolására. Minden bonyolult felépítésű rendszer topológia felbontható a részelemek soros, párhuzamos és visszacsatolt kapcsolásából kialakított részhálózatokra, amelyek a felsorolt műveletekkel ismét összekapcsolhatók. Eredményül a bonyolult felépítésű topológia megadott bemenet és kimenet közötti átviteli függvényét kapjuk.
A következő fejezetekben bemutatjuk az alapelemek három alapszintű összekapcsolásával létrejövő részrendszereket (átviteli függvényeket).
1.3.3.2. Alapelemek soros összekapcsolásából keletkező részrendszer
Két alapelem soros kapcsolását az (1.31. ábra) ábrán láthatjuk.

Az ábrán használt jelölések:
|
C(s) |
átviteli függvény, |
|
|
G(s) |
átviteli függvény, |
|
|
U(s) |
a bemenő jel Laplace-transzformáltja, |
|
|
Y(s) |
a kimenő jel Laplace-transzformáltja. |
A soros kapcsolás eredő átviteli függvénye (G serial (s))
|
|
(1.224) |
|
|
|
(1.225) |
ahol
|
G serial (s)[num] |
a soros kapcsolás eredő átviteli függvényének számlálója, |
|
|
G serial (s)[den] |
a soros kapcsolás eredő átviteli függvényének nevezője, |
|
|
C(s)[num] |
az átviteli függvény számlálója, |
|
|
C(s)[den] |
az átviteli függvény nevezője, |
|
|
G(s)[num] |
az átviteli függvény számlálója, |
|
|
G(s)[den] |
az átviteli függvény nevezője. |
1.3.3.3. Alapelemek párhuzamos összekapcsolásából keletkező részrendszer
Két alapelem párhuzamos összekapcsolását az (1.32. ábra) ábrán láthatjuk.
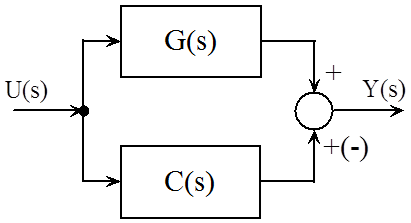
Az ábrán szereplő jelölések:
|
C(s) |
átviteli függvény, |
|
|
G(s) |
átviteli függvény, |
|
|
U(s) |
a bemenő jel Laplace-transzformáltja, |
|
|
Y(s) |
a kimenő jel Laplace-transzformáltja. |
A párhuzamos kapcsolás eredő átviteli függvénye (G parallel (s)):
|
|
(1.226) |
|
|
|
(1.227) |
|
|
|
(1.228) |
ahol
|
G parallel (s)[num] |
a párhuzamos kapcsolás eredőátviteli függvényének számlálója, |
|
|
G parallel (s)[den] |
a párhuzamos kapcsolás eredő átviteli függvényének nevezője, |
|
|
C(s)[num] |
az átviteli függvény számlálója, |
|
|
C(s)[den] |
az átviteli függvény nevezője, |
|
|
G(s)[num] |
az átviteli függvény számlálója, |
|
|
G(s)[den] |
az átviteli függvény nevezője. |
1.3.3.4. Alapelemek negatív visszacsatolt összekapcsolásából keletkező részrendszer
Két alapelem negatív visszacsatolt kapcsolását az (1.33. ábra) ábrán láthatjuk.
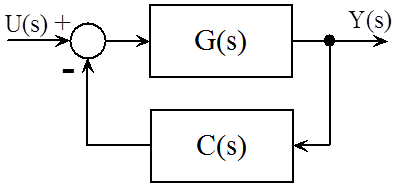
Az (1.33. ábra) ábra jelölései:
|
C(s) |
átviteli függvény, |
|
|
G(s) |
átviteli függvény, |
|
|
U(s) |
a bemenő jel Laplace-transzformáltja, |
|
|
Y(s) |
a kimenő jel Laplace-transzformáltja. |
A negatív visszacsatolt kapcsolás eredő átviteli függvénye (G closed_loop (s)):
|
|
(1.229) |
|
|
|
(1.230) |
|
|
|
(1.231) |
|
|
|
(1.232) |
ahol
|
G closed_loop (s)[num] |
a negatív visszacsatolt kapcsolás eredő átviteli függvényének számlálója, |
|
|
G closed_loop (s)[den] |
a negatív visszacsatolt kapcsolás eredő átviteli függvényének nevezője, |
|
|
C(s)[num] |
az átviteli függvény számlálója, |
|
|
C(s)[den] |
az átviteli függvény nevezője, |
|
|
G(s)[num] |
az átviteli függvény számlálója, |
|
|
G(s)[den] |
az átviteli függvény nevezője. |
1.4. Átviteli függvény számítási blokkdiagramjának megvalósítása
Átviteli függvényeket megvalósító rendszereinkben a leggyakrabban egy bemenetű és egy kimenetű (SISO) rendszereket készítünk. Ezek a következő átviteli függvényalakkal rendelkeznek:
|
|
(1.233) |
ahol
|
U(s) |
a bemenő jel Laplace-transzformáltja, |
|
|
m |
az átviteli függvény számlálójában előforduló legmagasabb s hatvány, |
|
|
Y(s) |
a kimenő jel Laplace-transzformáltja, |
|
|
n |
az átviteli függvény nevezőjében előforduló legmagasabb s hatvány. |
Az átviteli függvény megvalósíthatóságához teljesülnie kell az m<=n feltételnek!
1.4.1. Átviteli függvény számítási blokkdiagramja soros kapcsolású részelemekkel
A G(s) átviteli függvény számítási blokkdiagramjának megvalósításához létrehozhatunk olyan alakot, amelynél az egyszerűen számítható részelemek soros kapcsolásával alakítjuk ki a bonyolult felépítésű átviteli függvényt.
|
|
(1.234) |
ahol
PT1 típusú tag
|
|
(1.235) |
Előretartó-késleltető típusú tag
|
|
(1.236) |
PT2 típusú tag (2. verzió)
|
|
(1.237) |

Az egyes alaptagok számítási blokkdiagramjának kialakítását az 1.3.2. szakasz fejezetben mutattuk be.
Mintapélda:
Határozzuk meg a következő átviteli függvény számítási blokkdiagramját sorosan kapcsolt részrendszerekkel!
|
|
(1.238) |
Az átviteli függvényt sorosan kapcsolt részrendszerekre bontjuk fel, amelynek egyik lehetséges megoldása szerepel a következő függvényként.
|
|
(1.239) |
|
|
|
(1.240) |
|
|
|
(1.241) |
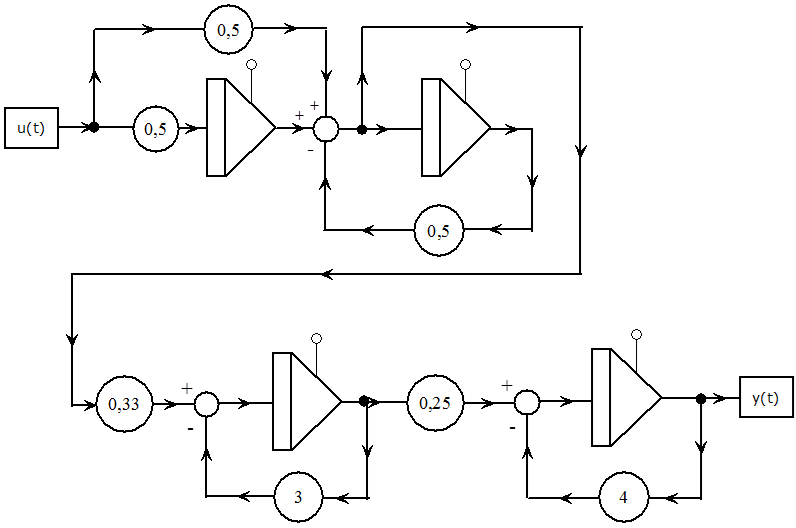
1.4.2. Átviteli függvény számítási blokkdiagramja párhuzamos kapcsolású részelemekkel
A G(s) átviteli függvény számítási blokkdiagramjának megvalósításához létrehozhatunk olyan alakot is, amelynél egyszerűen számítható részelemek párhuzamos kapcsolásával alakítjuk ki az összetett átviteli függvényt.
|
|
(1.242) |
ahol
PT1 típusú tag
|
|
(1.243) |
Előretartó-késleltető típusú tag
|
|
(1.244) |
PT2 típusú tag (2. verzió)
|
|
(1.245) |
Az egyes alaptagok számítási blokkdiagramjának kialakítását az 1.3.2. szakasz fejezetben mutattuk be.
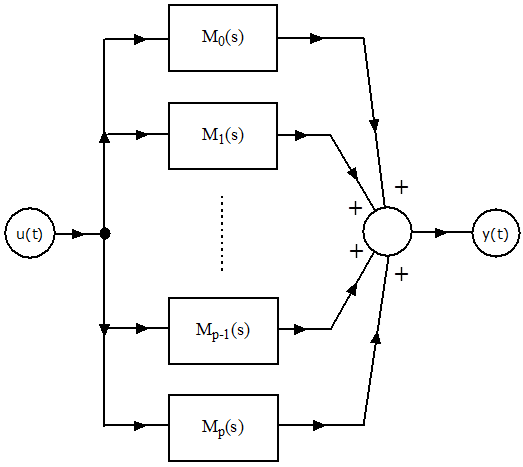
Mintapélda:
Határozzuk meg a következő átviteli függvény számítási blokkdiagramját párhuzamosan kapcsolt részrendszerekkel!
|
|
(1.246) |
Az átviteli függvényt párhuzamosan kapcsolt részrendszerekre bontjuk fel, amelynek egyik megoldása szerepel a következő összefüggésben.
|
|
(1.247) |
|
|
|
(1.248) |
|
|
|
(1.249) |
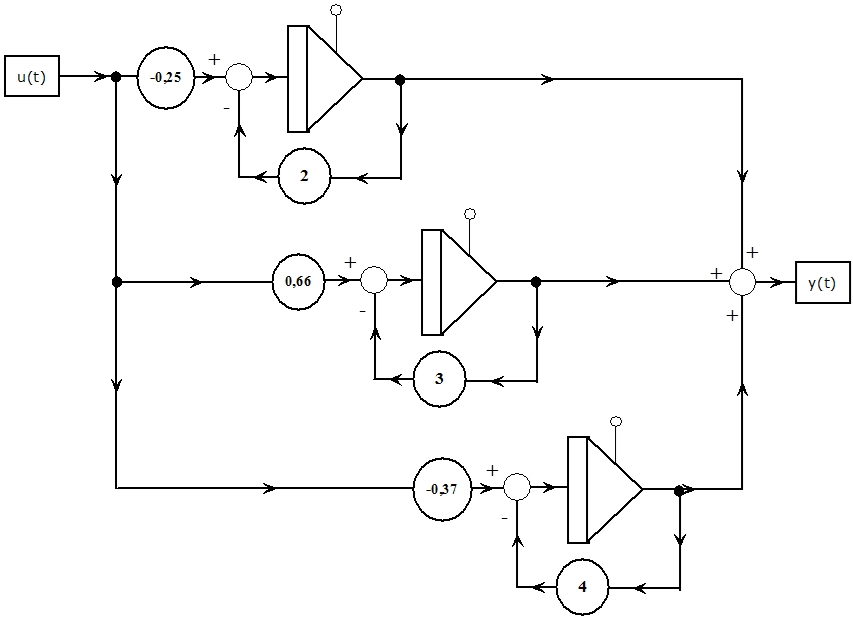
1.4.3. Átviteli függvény megvalósítása közvetlen programozással
A G(s) átviteli függvény számítási blokkdiagramját úgy is megvalósíthatjuk, hogy számlálót olyan nulla(0) értékű együtthatókkal egészítjük ki, amelyek lehetővé teszik az azonos s hatványkitevőjű számítási elemek párosítását. Az algoritmus segítségével az adott átviteli függvény megvalósításához minimális számú integráló elemet alkalmazunk.
|
|
(1.250) |
Az átviteli függvény alakból kapjuk:
|
|
(1.251) |
Mindkét oldalt -el szorozva a következő összefüggést kapjuk:
|
|
(1.252) |
ahol k = n – m.
Ha az egyenlet jobb oldalát kiegészítjük b i =0 együtthatójú tagokkal ahol i = m+1, m+2, …. n; akkor a következő egyenlet írható fel:
|
|
(1.253) |
amelyből az an-el mindkét oldalt elosztva a következő egyenlőséget kapjuk:
|
|
(1.254) |
amelyből
|
|
(1.255) |
( b n , b n-1 , ….. b n-k =0, ahol k = n-m-1)
A közvetlen programozás blokkdiagramja:
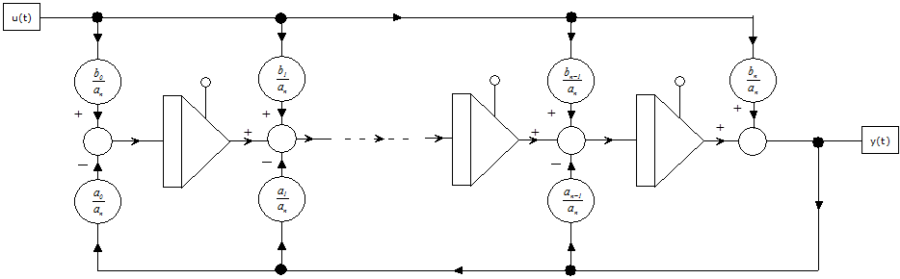
Mintapélda:
Határozzuk meg a következő átviteli függvény számítási blokkdiagramját közvetlen programozással!
|
|
(1.256) |
|
|
|
(1.257) |
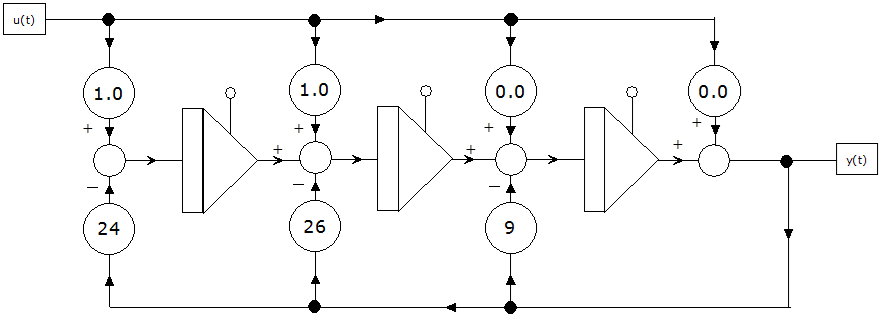
1.4.4. Átviteli függvény megvalósítása M-programozással
A G(s) átviteli függvény számítási blokkdiagramját a leggyakrabban az M-programozási alak alkalmazásával valósítjuk meg. Ezt a függvényszámítási algoritmust alkalmazzuk a digitális számítógépen megvalósított folytonos rendszerek szimulációjánál, illetve a digitális szűrők számításánál. Az algoritmus segítségével az adott átviteli függvény megvalósításához minimális számú integráló elemet alkalmazunk.
|
|
(1.258) |
Megvalósítható rendszereknél .
A számlálót és nevezőt elosztva sn-el, kapjuk a következő alakot:
|
|
(1.259) |
amelyből
|
|
(1.260) |
ahol
|
|
(1.261) |
|
|
|
(1.262) |
mivel ezért
|
|
(1.263) |
Az M-programozás blokkdiagramja:
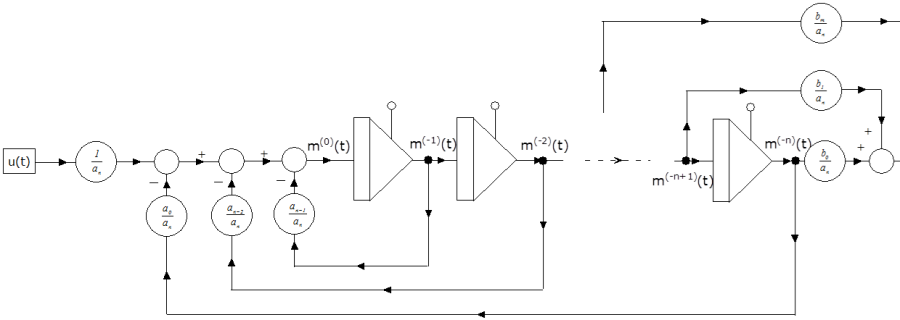
az ábrán:
|
a jel idő szerinti (k)-ik integráltjának időfüggvénye. |
Mintapélda:
Határozzuk meg a következő átviteli függvény számítási blokkdiagramját M-programozással!
|
|
(1.264) |
|
|
|
(1.265) |
|
|
|
(1.266) |
|
|
|
(1.267) |
Az M-programozás mintapélda blokkdiagramja:
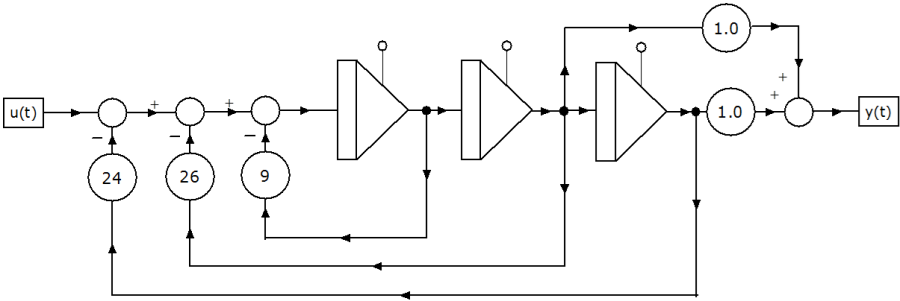
ahol
|
a jel idő szerinti (k)-ik integráltjának időfüggvénye k=1,2,3. |
1.4.5. Állapottér módszer számítási blokkdiagramjának meghatározása SISO rendszereknél
Az F(y(t), u(t),t) lineáris, állandó együtthatós differenciálegyenlet (SISO rendszer)
|
|
(1.268) |
leírása állapottér alakban a következő egyenletek segítségével valósítható meg.
|
|
(1.269) |
ahol
|
az állapottér-leírási mód mátrixai, |
||
|
u(t) |
a bemenő jel, |
|
|
y(t) |
a kimenő jel, |
|
|
az állapotváltozók vektorának idő szerinti deriváltja, |
||
|
x (t) |
az állapotváltozók vektora. |
Ebből felírhatjuk az állapottér alakkal meghatározott kimenő jel számítási blokkdiagramját az állapotmátrixok és az állapotvektor segítségével.
Az állapotvektor egyes elemeinek meghatározása a következő módon történik a rendszerleíró Az F(y(t), u(t), t) differenciálegyenlet együtthatóinak alkalmazásával:
|
|
(1.270) |
állapotváltozó választásával a többi állapotváltozót a következő módon választva,
|
|
(1.271) |
|
|
|
(1.272) |
|
|
… |
||
|
… |
||
|
|
(1.273) |
|
|
|
(1.274) |
|
|
|
(1.275) |
A rendszerleíró differenciálegyenletből meghatározhatjuk az állapottér mátrixokat.
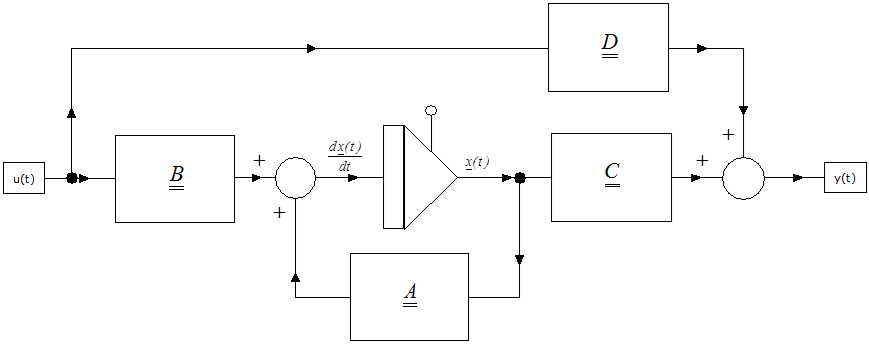
Mintapélda:
Határozzuk meg a következő átviteli függvény számítási blokkdiagramját állapottér programozással!
|
|
(1.276) |
|
|
|
(1.277) |
|
|
|
(1.278) |
|
|
|
(1.279) |
Az együtthatók értékeivel (b 3 = b 2 = 0):
|
|
(1.280) |
|
|
|
(1.281) |
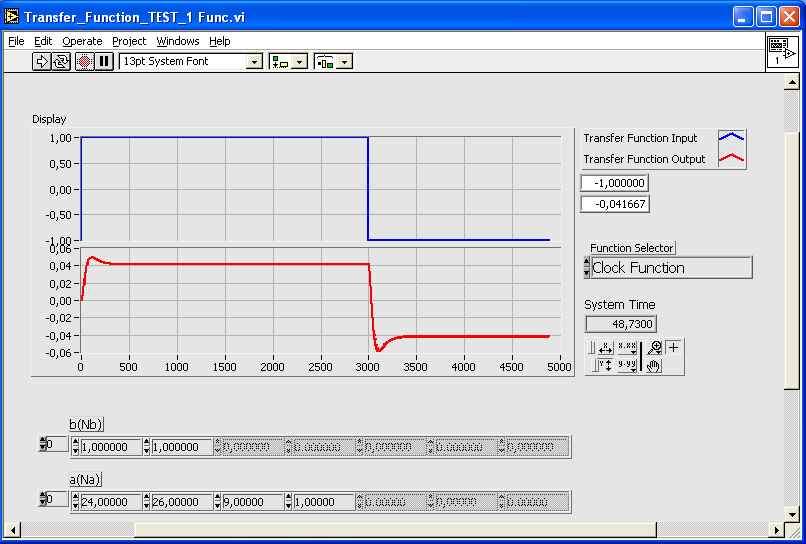
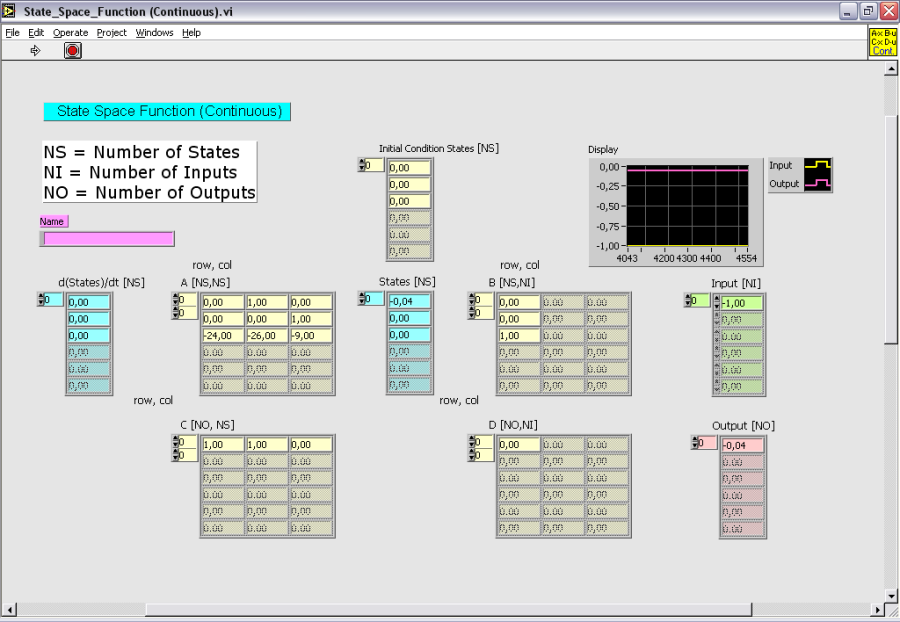
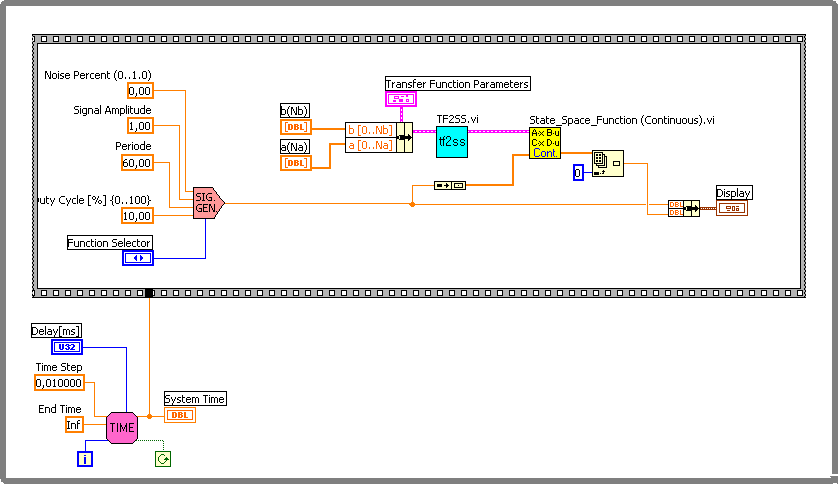
1.4.6. Állapottér-leírás, állapottér-reprezentációk kapcsolata
Az állapottér típusú rendszerleírást általánosan alkalmazzuk több-bemenetű és több kimenetű rendszerek vizsgálatához, illetve időfüggő vagy nemlineáris rendszerparaméterek esetén.
Egy rendszer leírásához szükséges állapotváltozókat egy differenciálegyenlettel leírt rendszer kimeneti jelének és deriváltjainak lineáris kombinációjából állíthatjuk elő. Ennek alapján ugyanazon rendszer leírásához végtelen sok állapottér alak tartozik, hiszen a kimenő jelből és deriváltjaiból végtelen sok kombináció állítható elő. Ez a tisztán matematikai megközelítés az állapotváltozók kiválasztásához a mérnöki gyakorlatban praktikus szempontok figyelembevételével módosul.
A legfontosabb szempont az állapotváltozók megválasztásánál, hogy mérhetők, illetve befolyásolhatók legyenek. További szempont, hogy a kiválasztott állapotváltozók segítségével meghatározott rendszerkimeneti adatok egyszerűen értelmezhetők legyenek, illetve egyszerűen lehessen őket meghatározni az állapotváltozókkal.
A modellezéskor létrehozott állapotváltozós rendszer szimulációs algoritmusának adott szempontok szerinti megvalósításához ezért szükség van arra, hogy az állapotváltozókat és ezzel együtt az egész korábbi állapotváltozókkal leírt rendszeregyenleteket (mátrixokat) egy új állapotváltozó vektorral leírt rendszer-egyenletrendszerbe transzformáljuk.
Ezt a transzformációt valósítja meg az állapotváltozós rendszerek transzformációs mátrixa ( ), amely a kiindulási rendszer állapotvektorából az áttranszformált rendszer állapotvektorába ( x trans ) viszi át az állapotmennyiségeket az alábbi módon:
|
|
(1.282) |
ahol n x n méretű nem szinguláris transzformációs mátrix, és .
Ha az x állapotvektor az mátrixokkal leírt állapottér-reprezentációhoz tartozik, azaz
|
|
(1.283) |
akkor meghatározhatjuk az állapotvektorhoz az
|
|
(1.284) |
egyenletekben szereplő mátrixokat.
Mivel , ezt behelyettesítve az 1.284 egyenletbe kapjuk, hogy
|
|
(1.285) |
azaz
|
|
(1.286) |
tehát
|
|
(1.287) |
Az és mátrixok közötti fenti kapcsolatot hasonlósági transzformációnak nevezzük. Azt mondhatjuk, hogy egy rendszer adott dimenziós állapottér-reprezentációi egymásból hasonlósági transzformációval megkaphatók. [4.]
A következőkben felírjuk az irányíthatósági alak előállítását biztosító (controllability) transzformációs mátrix összefüggését:
|
|
(1.288) |
ahol az irányíthatósági mátrix
|
|
(1.289) |
és egy n x n dimenziós Toeplitz-mátrix:
|
|
(1.290) |
amelynek elemei a karakterisztikus egyenlet együtthatói:
|
|
(1.291) |
Ekkor az irányíthatósági állapottér alak az 1.287 összefüggések alapján:
|
|
(1.292) |
Az irányíthatósági állapottér alak blokkdiagramja:

Egy állapottér-reprezentáció diagonális alakjának előállításához a következő transzformációs mátrixot kell alkalmazni:
|
|
(1.293) |
és egy n x n dimenziós Vandermonde-mátrix:
|
|
(1.294) |
ahol értékek
|
|
(1.295) |
a karakterisztikus egyenlet gyökei i = 1..n.
Ekkor a diagonális állapottér alak az 1.287 összefüggések alapján:
|
|
(1.296) |
A diagonális állapottér alak blokkdiagramja:
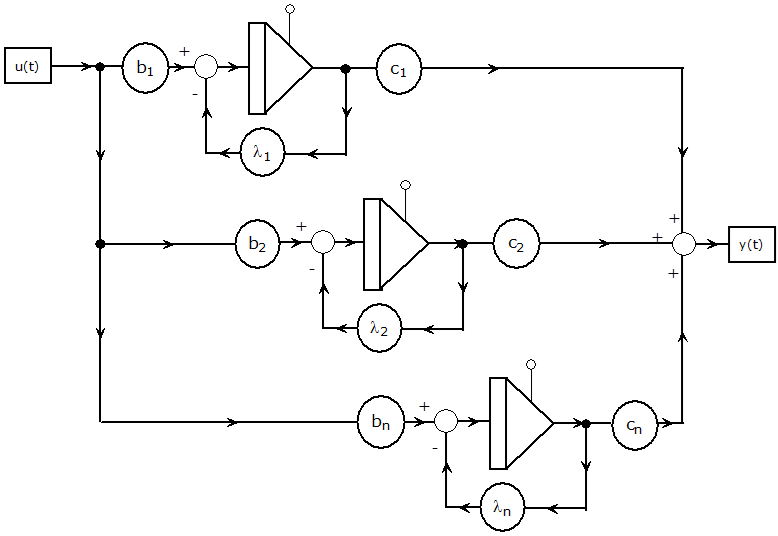
Az ábrán a b i együtthatók a (diagonális) mátrix elemei, a c i értékek pedig a (diagonális) mátrix elemei. [4.]
1.5. Rendszer-transzformációk
Ebben a fejezetben a korábban ismertetett matematikai rendszerleírások, vagyis az átviteli függvény polinomiális és zérus-pólus-erősítés alakja, valamint az állapottér-leírás közötti áttérések matematikai alapjaival foglalkozunk. Az m-script alapú programrendszerekben, így a MATLAB® programban (Control System Toolbox) és számos hasonló rendszerben (pl. GNU Octave signal csomag, NI LabVIEWMathScript, Scilab CACSD (Computer Aided Control System Design) utasításkészlet) az említett háromféle matematikai modell angol elnevezéséből származó két (esetleg három) betűs rövidítéseket használnak.
-
sos: second-order section , átviteli függvénnyel adott másodrendű rendszerek sorba kapcsolt eredője (GNU Octave,MATLAB,MathScript)
-
ss: state space , állapottér modell (GNU Octave,MATLAB,MathScript, Scilab)
-
tf: transfer function , polinomiális alakú átviteli függvény (GNU Octave, MATLAB, MathScript, Scilab)
-
zp: zero-pole(-gain), zérus-pólus-erősítés alakú átviteli függvény (GNU Octave, MATLAB)
-
zpk: zero-pole(-gain) , zérus-pólus-erősítés alakú átviteli függvény (MATLAB,Math-Script)
Az egyes modellek közötti transzformációt biztosító függvények elnevezése ezeket a rövidítéseket használja úgy, hogy először szerepel az eredeti rendszer, ezt követi az angol to (-ba, -be) helyettesítésére gyakran használt 2 (MathScript-ben _to_), végül pedig a célrendszer formátuma.
|
|
A MATLAB®-ban előforduló utasítások listája:
-
zp2tf,
-
ss2tf,
-
tf2zp,
-
ss2zp,
-
tf2ss,
-
zp2ss,
-
ss2ss (különböző struktúrájú állapottér modellek közötti áttérésre).
Természetesen a GNU Octave, MathScript és Scilab környezetben (és a nem említett többiben) nem feltétlenül szerepel az összes említett utasítás, viszont vannak a MATLAB®-ból hiányzó, azonban kifejezetten hasznosnak számító egyéb konverziós lehetőségek.
1.5.1. Átviteli függvény (tf) transzformációk {ss2tf, zp2tf}
A függvény három paramétere a zérusok Z-vel jelölt vektora, a pólusok P-vel jelölt vektora és a K skalár erősítési tényező. A függvény két visszatérési értéke a számláló polinom (num) és a nevező polinom (den). Konjugált komplex gyökpár esetén természetesen a gyökpár mindkét elemének szerepelni kell a bemenet megfelelő (zérus, pólus) polinomjában.
[num,den] = ZP2TF(Z,P,K)
MATLAB-ban SISO rendszer esetén a két bemenő polinomot oszlopvektorként kell megadni.
A függvény s csökkenő hatványai szerint adja meg a számláló és a nevező együtthatóit.
>_> zerusok = [-2; -0.4], polusok = [-1-2i; -1+2i; -5], erosites = 10 zerusok = -2.0000 -0.4000 polusok = -1.0000 - 2.0000i -1.0000 + 2.0000i -5.0000 erosites = 10 >_> [szamlalo, nevezo]=zp2tf(zerusok, polusok, erosites) szamlalo = 0 10 24 8 nevezo = 1 7 15 25 >_>
GNU Octave-ban:
>_> zerusok = [-2; -0.4], polusok = [-1-2i; -1+2i; -5], erosites = 10 zerusok = -2.00000 -0.40000 polusok = -1 - 2i -1 + 2i -5 + 0i erosites = 10 >_> [szamlalo, nevezo]=zp2tf(zerusok, polusok, erosites) szamlalo = 10 24 8 nevezo = 1 7 15 25 >_>
NI LabVIEWMathScript-ben:
>_>zerusok = [-2; -0.4], polusok = [-1-2i; -1+2i; -5], erosites = 10 zerusok = -2 -0.4 polusok = -1 - 2i -1 + 2i -5 + 0i erosites = 10 >_>[szamlalo, nevezo]=zpk_to_tf(zerusok, polusok, erosites) szamlalo = 10 24 8 nevezo = 1 7 15 25
Scilab-ban nincs zp2tf jellegű utasítás, kis kerülővel tudjuk meghatározni zérusokból, pólusokból és erősítésből a számláló és nevező polinomot, aminek együtthatói az előző példákkal ellentétben s növekvő hatványai szerint rendezettek:
-->zerusok = [-2; -0.4], polusok = [-1-2*%i; -1+2*%i; -5], erosites = 10 zerusok = - 2. - 0.4 polusok = - 1. - 2.i - 1. + 2.i - 5. erosites = 10. -->s=poly(0,"s"), szamlalo_polinom=erosites*poly(zerusok,"s","roots"), nevezo_polinom=s = s szamlalo_polinom = 2 8 + 24s + 10s nevezo_polinom = 2 3 25 + 15s + 7s + s -->szamlalo=coeff(szamlalo_polinom), nevezo=coeff(nevezo_polinom) szamlalo = 8. 24. 10. nevezo = 25. 15. 7. 1.
1.5.1.1. Átviteli függvény állandósult állapotbeli erősítése
Az átviteli függvényt s növekvő hatványai szerint felírva
|
|
(1.297) |
és a Laplace-transzformáció végérték tételét alkalmazva
|
|
(1.298) |
Ha a bemenő jel 1(t), akkor állandósult állapotban az egységnyi nagyságú bemenő jelre adott válaszfüggvényből megkapjuk A p_folytonos -t, a G(s) átviteli függvény állandósult állapotbeli erősítését.
|
|
(1.299) |
A G(s) átviteli függvényben – mind a számlálóban, mind a nevezőben – az s és s magasabb kitevős hatványai mind a nulla (0) értékhez tartanak.
|
|
(1.300) |
A G(s) átviteli függvény állandósult állapotbeli erősítése (A p_folytonos ) az s nulladfokú számláló- és nevezőbeli polinomiális együtthatóinak hányadosa.
Az állandósult állapotbeli erősítés meghatározása LabVIEW MathScript-ben:
|
dcgain (sys) |
(1.301) |
ahol
|
dcgain |
az állandósult állapotbeli erősítés meghatározása függvény elnevezése, |
|
|
sys |
a vizsgált rendszer átviteli függvénye LabVIEW Matscript-ben (átviteli függvény vagy állapotváltozós alak). |
Mintapélda:
Egy polinomiális alakú átviteli függvénnyel megadott rendszer állandósult erősítési tényezőjét szeretnénk meghatározni.
A h a mintavételi időtartam, amely folytonos rendszer esetén nulla (0.0).
NUM=[1]
DEN=[1, 5, 6, 5]
h=0.0
sys_poly=tf(NUM, DEN, h)
Ap_folytonos=dcgain(sys_poly)
>>
NUM =
1
DEN =
1 5 6 5
h =
0
Transfer Function
Input:1 Output:1
1,000
------------------------------
1,000s^3+5,000s^2+6,000s+5,000
Continuous-time model.
Ap_folytonos =
0.2
1.5.1.2. zp2tf: zérus-pólus-erősítés alakú átviteli függvény alakból transzformáció polinomiális alakú átviteli függvény alakba
A zérus-pólus-erősítés átviteli függvény a következő alakú:
|
|
(1.302) |
Az átalakításnál a gyöktényezős alakban felírt számlálóból s hatványainak megfelelő polinomiális alakot hozunk létre, majd a számláló polinom minden együtthatóját megszorozzuk a zérus-pólus-erősítés alakú átviteli függvény K erősítési tényezővel.
Hasonlóan elvégezzük a nevező s hatványainak megfelelő polinom előállítását is. Ezek után rendelkezésünkre állnak a polinomiális alakú átviteli függvény együtthatói.
|
|
(1.303) |
A zérus-pólus-erősítés alakú átviteli függvényből a polinomiális alakú átviteli függvény alakba az átalakítás LabVIEW MathScript-ben a következő függvénnyel történik:
|
[d, e] = zpk_to_tf (a, b, c) |
(1.304) |
ahol
Mintapélda:
Egy zérusaival, pólusaival és erősítési tényezőjével megadott átviteli függvényt sys_zpk-t szeretnénk átalakítani polinomiális átviteli függvény alakra sys_poly-ra.
A h a mintavételi időtartam, amely folytonos rendszer esetén nulla (0.0).
zeros=[1, 2, 1]
poles=[-1, -2, -3]
k = 3
h=0.0
sys_zpk=zpk(zeros, poles, k, h)
[NUM, DEN] = zpk_to_tf(zeros, poles, k)
sys_poly=tf(NUM, DEN, h)
>>
zeros =
1 2 1
poles =
-1 -2 -3
k =
3
h =
0
Zero-Pole-Gain Model
Input:1 Output:1
3,000(s-1)^2 (s-2)
--------------------
(s+1) (s+2) (s+3)
Continuous-time model.
NUM =
3 -12 15 -6
DEN =
1 6 11 6
Transfer Function
Input:1 Output:1
3,000s^3-12,000s^2+15,000s-6,000
--------------------------------
1,000s^3+6,000s^2+11,000s+6,000
Continuous-time model.
1.5.1.3. ss2tf: transzformáció állapottér modell alakból, polinomiális alakú átviteli függvény alakba
Az állapottér alakban felírt rendszer a Laplace-transzformáció után a következő egyenleteket eredményezi:
|
|
(1.305) |
|
|
|
(1.306) |
Az állapotegyenletből (1.305) kifejezhetjük az állapotváltozók vektorát. Amennyiben az állapotváltozók kezdeti értéke zérus (), a számítás egyszerűsödik.
|
|
(1.307) |
|
|
|
(1.308) |
Az így kifejezett állapotváltozó vektort behelyettesíthetjük a kicsatolási egyenletbe, hogy megkapjuk a kimenő jel Laplace–transzformáltját:
|
|
(1.309) |
A kapott kifejezés jobb oldalán kiemelhetjük a bemenő jelet U(s)-t, és eloszthatjuk vele az egyenlet mindkét oldalát, hogy megkapjuk a SISO rendszer átviteli függvényét az állapottér modell segítségével:
|
|
(1.310) |
A állapottér alakú rendszerfüggvényből a polinomiális alakú átviteli függvény alakba az átalakítás LabVIEW MathScript-ben a következő függvénnyel történik:
|
[e, f] = ss_to_tf (a, b, c, d) |
(1.311) |
ahol
Mintapélda:
Állapottér alakban mátrixokkal megadott rendszert szeretnénk átalakítani polinomiális átviteli függvény alakra, a sys_poly-ra (LabVIEW MathScript-ben).
A h a mintavételi időtartam, amely folytonos rendszer esetén nulla (0.0).
A=[ 0, 1, 0
0, 0, 1
-5, -6, -5]
B =[0; 0; 1]
C =[1, 0, 0]
D =[0]
h=0.0
[NUM, DEN]=ss_to_tf(A, B, C, D, h)
sys_poly=tf(NUM, DEN)
>>
A =
0 1 0
0 0 1
-5 -6 -5
B =
0
0
1
C =
1 0 0
D =
0
h =
0
NUM =
1
DEN =
1 5 6 5
Transfer Function
Input:1 Output:1
1,000
------------------------------
1,000s^3+5,000s^2+6,000s+5,000
Continuous-time model.
1.5.2. Zérus-pólus-erősítés függvény (zp) transzformációk, {tf2zp, ss2zp}
1.5.2.1. Zérus-pólus függvény erősítése (K)
Az átviteli függvényt s hatványaival felírva
|
|
(1.312) |
majd meghatározva a számláló m darab és a nevező n darab gyökét, felírhatjuk a G(s) átviteli függvény gyöktényezős alakját. Mivel a gyökök meghatározásánál a legmagasabb fokú tagok együtthatóinak mind a számlálóban mind pedig a nevezőben 1-nek kell lennie. Így a számlálóból és a nevezőből ki kell emelni a legmagasabb s hatványok együtthatóit - ezek hányadosa lesz K, az erősítés értéke.
|
|
(1.313) |
|
|
|
(1.314) |
1.5.2.2. tf2zp: transzfomáció polinomiális alakú átviteli függvényből zérus-pólus-erősítés alakú átviteli függvénybe
A polinomiális alakú átviteli függvény a következő függvénnyel írható le:
|
|
(1.315) |
Az átalakításnál kiemeljük a számlálóból és a nevezőből s legmagasabb hatványainak együtthatóit b m -et és a n -et. A pólus-zérus-erősítés átviteli függvény K erősítési tényezőjének előállítását az 1.5.2.1. szakasz pontban ismertettük. Ezután meghatározzuk a számláló és a nevező gyökeit, és felírjuk az átviteli függvény gyöktényezős alakját a K erősítési tényezővel.
|
|
(1.316) |
A polinomiális alakú átviteli függvényből zérus-pólus-erősítés átviteli függvény alakba az következő függvénnyel történik az átalakítás LabVIEW MathScript-ben:
|
[c, d, e] = tf_to_zpk (a, b) |
(1.317) |
ahol
|
tf_to_zpk |
a polinomiális alakú átviteli függvényből zérus-pólus-erősítés alakú átviteli függvény alakba az átalakítást végző függvény neve LabVIEW MatScript-ben, |
|
|
a |
a polinomiális alakú átviteli függvény számlálójában az s hatványok együtthatói, |
|
|
b |
a polinomiális alakú átviteli függvény nevezőjében az s hatványok együtthatói, |
|
|
c |
a zérus-pólus-erősítés alakú átviteli függvény zérusai, |
|
|
d |
a zérus-pólus-erősítés alakú átviteli függvény pólusai, |
|
|
e |
a zérus-pólus-erősítés alakú átviteli függvény erősítése (K), amely skalár érték. |
Mintapélda:
Egy polinomiális átviteli függvényt, sys_poly-t szeretnénk átalakítani zérusaival, pólusaival és erősítési tényezőjével megadott átviteli függvény alakra (sys_zpk) (LabVIEW MathScript-ben).
A h a mintavételi időtartam, amely folytonos rendszer esetén nulla (0.0).
NUM=[1, 2]
DEN=[1, 2, 3]
h=0.0
sys_poly=tf(NUM, DEN, h)
[zeros, poles, k] = tf_to_zpk(NUM, DEN)
sys_zpk=zpk(zeros, poles, k, h)
>>
NUM =
1 2
DEN =
1 2 3
h =
0
Transfer Function
Input:1 Output:1
1,000s+2,000
---------------------
1,000s^2+2,000s+3,000
Continuous-time model.
zeros =
-2
poles =
-1 + 1.4142i
-1 - 1.4142i
k =
1
Zero-Pole-Gain Model
Input:1 Output:1
1,000(s+2)
--------------------------
(s+1-1.4142i)(s+1+1.4142i)
Continuous-time model.
1.5.2.3. ss2zp: átalakítás állapottér modellből zérus-pólus-erősítés alakú átviteli függvénybe
Az (1.310) egyenlettel megadtuk, hogyan lehet állapottér alakból polinomiális átviteli függvény alakba átalakítani a rendszerleíró egyenletet. Ebben az esetben is ezt kell alkalmaznunk, majd az előző (1.5.2.2. szakasz) fejezetben bemutatott eljárással meghatározhatjuk a polinomiális alakból a zérus-pólus-erősítés átviteli függvény alakot.
Mintapélda:
Állapottér alakban, mátrixokkal megadott rendszert szeretnénk átalakítani zérus-pólus-erősítés alakú átviteli függvény alakra (sys_zpk-ra) (LabVIEW MathScript-ben).
A h a mintavételi időtartam, amely folytonos rendszer esetén nulla (0.0).
A=[ 0, 1, 0
0, 0, 1
-5, -6, -5]
B =[0; 0; 1]
C =[1, 0, 0]
D =[0]
h=0.0
[zeros, poles, k]=ss_to_zpk(A, B, C, D, h)
sys_zpk=zpk(zeros, poles, k, h)
>>
A =
0 1 0
0 0 1
-5 -6 -5
B =
0
0
1
C =
1 0 0
D =
0
h =
0
zeros =
empty matrix 0 by 1
poles =
-0.6214 + 0.9719i
-0.6214 - 0.9719i
-3.7573 + 0i
k =
1
Zero-Pole-Gain Model
Input:1 Output:1
1,000
-----------------------------------------------
(s+3.7573) (s+0.6214-0.9719i)(s+0.6214+0.9719i)
Continuous-time model.
1.5.3. Állapottér (ss) transzformációk, {tf2ss, zp2ss}
1.5.3.1. tf2ss: transzformáció polinomiális alakú átviteli függvényből állapottér modellbe
A polinomiális alakú átviteli függvényből a fázisváltozós alakú állapottér modell létrehozását az 1.4.5. szakasz fejezetben mutattuk be. Ezt a számítási eljárást alkalmazva állapottér meghatározáshoz, alkalmas modellt hozhatunk létre.
Mintapélda:
Polinomiális átviteli függvény alakról hozzunk létre állapottér alakú mátrixokat amellyel leírjuk a vizsgált rendszert (LabVIEW MathScript-ben)!
A h a mintavételi időtartam, amely folytonos rendszer esetén nulla (0.0).
NUM=[1]
DEN=[1, 5, 6, 5]
h=0.0
sys_poly=tf(NUM, DEN, h)
[A, B, C, D]=tf_to_ss(NUM, DEN)
>>
NUM =
1
DEN =
1 5 6 5
h =
0
Transfer Function
Input:1 Output:1
1,000
------------------------------
1,000s^3+5,000s^2+6,000s+5,000
Continuous-time model.
A =
-5 -6 -5
1 0 0
0 1 0
B =
1
0
0
C =
0 0 1
D =
0
1.5.3.2. zp2ss: átalakítás zérus-pólus-erősítés alakú átviteli függvényből állapottér modellbe
Ennél az átalakítási módszernél felhasználunk korábban bemutatott transzformációs eljárásokat. Első lépésben a zérus-pólus-erősítés alakú átviteli függvényből polinomiális átviteli függvény alakot hozunk létre, majd alkalmazzuk az 1.5.3.1. szakasz fejezetben bemutatott eljárást.
Mintapélda:
Zérus-pólus-erősítés alakú átviteli függvényből hozzunk létre állapottér alakú mátrixokat, melyekkel a vizsgált rendszert írjuk le (LabVIEW MathScript-ben)!
A h a mintavételi időtartam, amely folytonos rendszer esetén nulla (0.0).
zeros=[-1, -2, -1]
poles=[-1.4, -2.4, -3]
k = 3
h=0.0
sys_zpk=zpk(zeros, poles, k, h)
[A, B, C, D] = zpk_to_ss(zeros, poles, k)
>>
zeros =
-1 -2 -1
poles =
-1.4 -2.4 -3
k =
3
h =
0
Zero-Pole-Gain Model
Input:1 Output:1
3,000(s+1)^2 (s+2)
----------------------
(s+1.4) (s+2.4) (s+3)
Continuous-time model.
A =
-6.8 -14.76 -10.08
1 0 0
0 1 0
B =
1
0
0
C =
-8.4 -29.28 -24.24
D =
3
1.6. Több bemenetű és több kimenetű rendszerek (MIMO) leírása
A lineáris rendszerek leírásában a differenciálegyenlet és a (polinomiális) átviteli függvény egymásból formális átalakítással felírhatók, ezért a differenciálegyenletek helyett a matematikailag kényelmesebben kezelhető átviteli függvényekkel dolgozunk.
A több bemenetű, több kimenetű (MIMO = Multiple Input Multiple Output) lineáris rendszerek matematikai leírása során m–bemenetű (), p–kimenetű (), időben állandó paraméterű rendszerekre szorítkozunk. Természetesen a digitális számítógépes szimulációban az alább ismertetett levezetésekre építve, akár a paraméterek változását is könnyen kezelhetjük.
Lineáris MIMO rendszerekben az egyes bemenetek és kimenetek kapcsolatát egy–egy átviteli függvény (vagy differenciálegyenlet, illetve akár állapottér modell) segítségével adhatjuk meg.
1.6.1. Átviteli mátrix {G(s)}
A MIMO rendszerekre értelmezett átviteli mátrix bevezetéséhez a SISO rendszertől kezdve végignézzük, hogyan befolyásolja a bemenetek és kimenetek számának növekedése az átviteli tulajdonság leírását.
1.6.1.1. A SISO rendszer
SISO rendszer esetén egy u(t ) bemenet és az egy y(t ) kimenet között a korábban (1.3) paraméteres differenciálegyenlettel megadott kapcsolat:
|
|
(1.318) |
A kimenő jel és a bemenő jel Laplace–transzformáltja (Y (s) illetve U(s)) hányadosaként előállítható a G(s) átviteli függvény (1.51 egyenlet) a differenciálegyenletnél kényelmesebb, „kevesebb helyet foglaló”, ugyanakkor azzal teljesen egyenértékű rendszerleírás
|
|
(1.319) |
Az átviteli függvény polinomiális alakban rövidebben is felírható, a num(s) számláló (az angol numerator szóból) és a den(s) nevező (az angol denominator szóból) polinom hányadosaként. (A különböző matematikai programokban gyakori a num és den használata.)
|
|
(1.320) |
Ebből az alakból szorzással kifejezhetjük a kimenet Y(s) Laplace–transzformáltját:
|
|
(1.321) |
1.6.1.2. A MISO rendszer
MISO vagyis több bemenetű, egy kimenetű rendszer esetén minden egyes bemenethez felírhatunk egy átviteli függvényt ugyanazzal a kimenettel:
|
|
(1.322) |
|
|
|
(1.323) |
|
|
……… |
||
|
|
(1.324) |
Ahhoz, hogy csak egy bemenet hatását vegyük egyszerre figyelembe, az összes többi bemenő jel értékét nullára kell állítanunk. A továbbiakban ennek jelölését mellőzzük.
|
|
(1.325) |
|
|
|
(1.326) |
|
|
……… |
||
|
|
(1.327) |
Az összes bemenet hatását az egyes bemenetek hatásának egyenkénti figyelembevételével határozhatjuk meg (szuperpozíció).
|
|
(1.328) |
Mátrixos alakban kifejezve a kimenetet tovább egyszerűsíthetjük összefüggésünket
|
|
(1.329) |
1.6.1.3. A SIMO rendszer
SIMO vagyis egy bemenetű, több kimenetű rendszerben minden egyes kimenethez felírhatunk egy átviteli függvényt:
|
|
(1.330) |
|
|
|
(1.331) |
|
|
….. |
||
|
|
(1.332) |
Mátrixos alakra hozva, ismét tömöríthetjük a kifejezést.
|
|
(1.333) |
1.6.1.4. A MIMO rendszer
Az előzőek kombinációjával felírhatjuk az m–bemenetű (), p–kimenetű () rendszer átviteli függvényét (helyesebben átviteli mátrixát).
|
|
(1.334) |
Az átviteli mátrix i-edik sora az i-edik kimenet előállításáért felel. Az átviteli mátrix () k-adik oszlopa a k-adik bemenet hatását mutatja a kimeneteken.
|
|
(1.335) |
Az m–elemű oszlopvektor formában felírt bemenetek és a p–elemű oszlopvektorba foglalt kimenetek felhasználásával tovább egyszerűsödik a MIMO rendszer Laplace–operátoros tartománybeli átviteli függvénye.
|
|
(1.336) |
1.6.2. Az állapottér módszer
Az általános lineáris, időtől független, n állapotváltozót tartalmazó az m–bemenetű (), p–kimenetű () MIMO rendszer állapotér modelljét (1.12 és 1.13 egyenletekkel) sokkal egyszerűbb felírni, mint az előzőekben levezetett átviteli függvényt, hiszen az állapottér modell mátrixegyenletei önmagukban hordozzák a több bemenet és kimenet közötti kapcsolat kezelését.
|
|
(1.337) |
|
|
(1.338) |
Természetesen, ahogyan korábban láttuk a SISO rendszer állapottér modelljénél, itt is felírhatjuk mátrixegyenletként az állapotegyenletet és a kicsatolási egyenletet.
|
|
(1.339) |
|
|
|
(1.340) |
Laplace–transzformáció után
|
|
(1.341) |
|
|
|
(1.342) |
Zérus kezdeti értékek ( x (0) = 0 ) feltételezésével, az mátrix méretével egyező méretű egységmátrix felhasználásával az állapotegyenletből kifejezhetjük az állapotváltozók vektorát
|
|
(1.343) |
|
|
|
(1.344) |
Az így kifejezett állapotváltozó vektort behelyettesíthetjük a kicsatolási egyenletbe, hogy megkapjuk a kimenő jel vektor Laplace–transzformáltját:
|
|
(1.345) |
A kapott kifejezés jobb oldalán kiemelhetjük a bemenő jel vektor Laplace–transzformáltját
|
|
(1.346) |
Ebből aztán formálisan előállíthatjuk a MIMO rendszer G(s) átviteli mátrixát
|
|
(1.347) |
Az inverz mátrix számításához használhatjuk az alábbi formulát
|
|
(1.348) |
A fenti kifejezés nevezőjében szereplő kifejezésből felírhatjuk a MIMO rendszer karakterisztikus egyenletét (melynek gyökei a rendszer pólusai)
|
|
(1.349) |
Természetesen nemcsak zérus kezdeti feltételeknél használhatjuk a Laplace–transzformációs megoldást. Ekkor a deriválás Laplace–transzformációs szabályában meghatározott módon kell figyelembe vennünk a t = 0 időpillanatbeli kezdeti értékeket.
|
|
(1.350) |
|
|
|
(1.351) |
|
|
|
(1.352) |
|
|
|
(1.353) |
A helyettesítés után kapott kifejezés első része a semleges kezdeti állapotú gerjesztett rendszer válasza, a második rész a valamilyen kezdeti állapotban lévő, magára hagyott rendszer válasza.
|
|
(1.354) |
1.7. Folytonos rendszerek megvalósítása műveleti erősítő áramkörökkel
1.7.1. Átviteli függvény megvalósítása
Adott egy gépkocsi lengéscsillapítójának szerkezeti vázlata, amely egy tömegből, egy rugóból és egy csillapításból áll (1.48. ábra).
A bemenő jel a gerjesztés, a rugó szabad végének sebessége, a kimenő jel pedig a tömeg sebessége.
Mintapélda:
Írjuk fel a rendszert leíró differenciálegyenletet, készítsük el a rendszer blokkvázlatát és átviteli függvényét. Adott bemenő jel esetén készítsük el a rendszer analóg számítógépes szimulációs modelljét! (A gravitációs gyorsulást nem vesszük figyelembe!)
Az egyes elemek paramétereinek jelölése (1.48. ábra):
|
c |
a rugómerevségi együttható [N/m], |
|
|
m |
tömeg [kg], |
|
|
d |
csillapítási tényező [N*s/m]. |
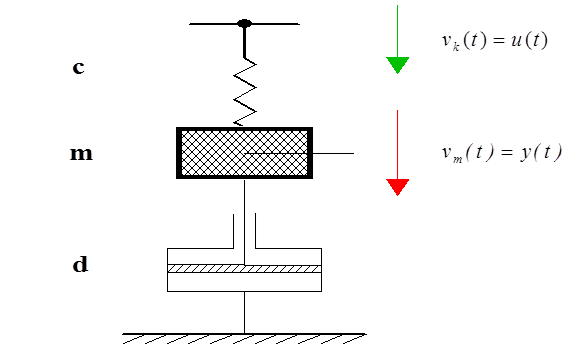
A megoldásban először a rendszert alrendszerekre bontjuk, felírjuk az egyes alrendszerek differenciálegyenleteit, és elkészítjük blokkvázlatukat.
Rugó alrendszer
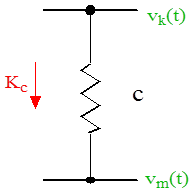
A rugóerő differenciálegyenlete az időtartományban,
|
|
(1.355) |
illetve Laplace-transzformált tartományban
|
|
(1.356) |
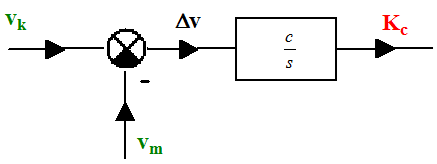
Tömeg alrendszer
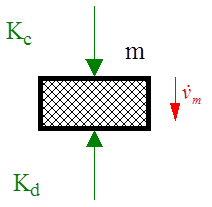
A tömegre ható erők differenciálegyenlete időtartományban
|
|
(1.357) |
|
|
|
(1.358) |
illetve a kimenő jel Laplace-transzformáltja
|
|
(1.359) |
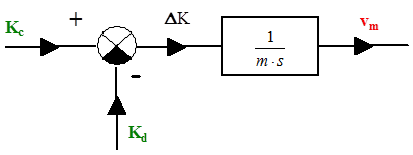
Csillapítás alrendszer
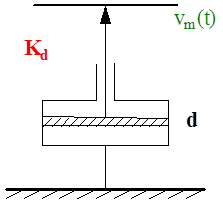
A csillapításra ható erő egyenlete időtartományban
|
|
(1.360) |
illetve Laplace-transzformált tartományban
|
|
(1.361) |

A teljes lengéscsillapitó rendszer blokkvázlatát a részrendszerek blokkvázlatainak összekapcsolásával lehet meghatározni.
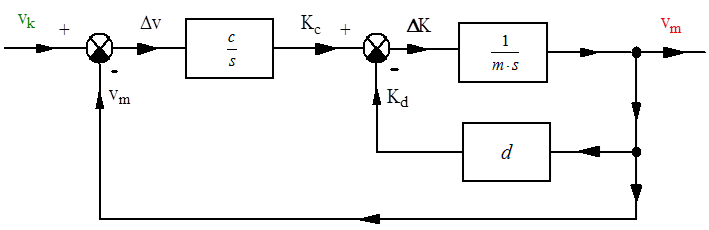
A rendszer átviteli függvénye meghatározható a rendszer blokkvázlatának egyszerűsítésével. A blokkvázlat egyszerűsítésének lépései:
A belső visszacsatolás kiküszöbölése.

Az előremenő ágban lévő soros tagok összevonása.
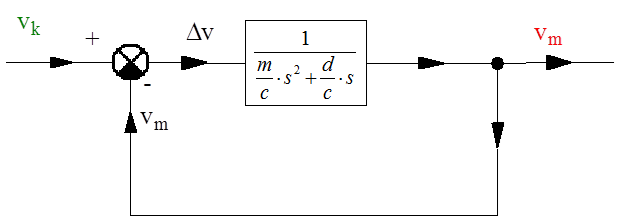
A negatív visszacsatolás kiküszöbölése.
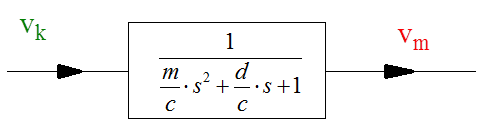
A rendszer átviteli függvénye
|
|
(1.362) |
Amely egyszerűsítés után a következő alakú lesz:
|
|
(1.363) |
A rendszert leíró differenciálegyenlet leírásának módja a következő:
-
felírjuk az alrendszerekre jellemző differenciálegyenleteket, és ezekből építjük fel az elemek összekapcsolásával a teljes rendszert.
A teljes rendszer differenciálegyenlete:
|
|
(1.364) |
|
|
|
(1.365) |
A kezdeti feltételek legyenek a következő értékek:
|
|
(1.366) |
A bemenő jel időfüggvénye legyen a következő függvény:
|
|
(1.367) |
A rendszer differenciálegyenletéből kifejezhetjük a kimenő jel legmagasabb deriváltját.
Így a kimenő jel legmagasabb deriváltját kifejező egyenlet tartalmazni fogja a bemenő jelet és deriváltjait, illetve a kimenő jel alacsonyabb rendű deriváltjait.
A következő egyenletben megadjuk az egyes változók és konstansok értékeinek elnevezését.
|
|
(1.368) |
Ezekkel a változó és konstans elnevezésekkel létrehozhatunk egy blokkdiagramot, amelynél meghatározhatjuk a kimenő jel legmagasabb deriváltértékét (D2VM).
A kimenő jel alacsonyabb deriváltjait integráló típusú blokkal valósítjuk meg, és a legmagasabb derivált értékének meghatározásánál a megfelelő együttható konstanssal történő szorzatértékeket alkalmazzuk.
Ha a differenciálegyenletben a bemenő jel idő szerinti derivált értékei is szerepelnek, akkor a teljes rendszer differenciálegyenletének mindkét oldalát integráljuk, addig amíg csak a bemeneti jel, illetve annak idő szerinti integráljai szerepelnek. Mivel ezeket elő tudjuk állítani.
Ügyeljünk arra, hogy a műveleti erősítővel megvalósított áramköröknél az erősítési és integrálási erősítési tényezők előjelet fordítanak !
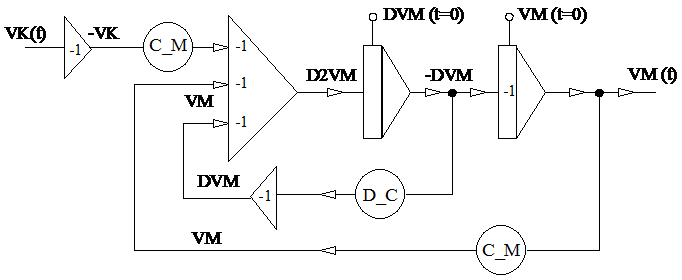
A gépkocsi lengéscsillapító rendszerében a különböző paramétereknek számértéket adva, meghatározhatjuk a rendszer viselkedését egységugrás bemeneti jel esetén.
Válasszuk a következő paraméterértékeket!
|
m = 1 kg |
||
|
d = 1 N.s/m |
||
|
c =1 N/m |
||
|
dt =0,02 s |
||
|
t_max =25 s |
Ezekkel a paraméterekkel a szimuláció eredménye az (1.60. ábra) ábrán látható.:
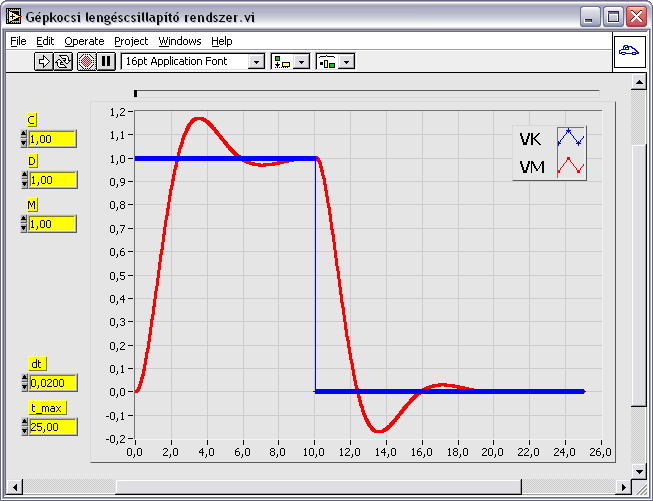
1.7.2. Analóg számítógép
A modell a valóságos rendszer - vizsgálat szempontjából - lényeges tulajdonságait kiemelő, a kevésbé fontosakat elhanyagoló, egyszerűsített mása. A modellalkotás során csak a vizsgálatban meghatározó tulajdonságokkal foglalkozunk. Természetesen a modell finomítása során új tulajdonságokat is bekapcsolhatunk a vizsgálatba, a korábbiak közül pedig elhanyagolhatjuk a „mégsem annyira fontosakat”. A modellezés folyamata a valóságos rendszer - vizsgálat szempontjából - lényeges tulajdonságainak felismerése és valamilyen formájú leképezése.
Absztrahált (elvonatkoztatott) modellnek nevezzük a vizsgált jelenség absztrakció eszközeivel előállított, legtöbbször verbális, esetleg grafikus vázlattal kiegészített leképezését. A rendszermodell az absztrahált modell alapján előállított fizikai (homológ és analóg) vagy matematikai modell.
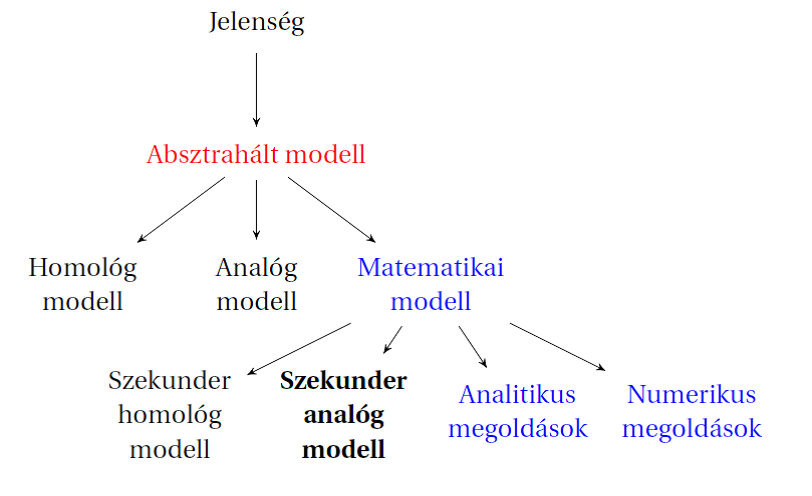
Szimulációnak nevezzük a rendszermodell működtetését, a modellen végzett kísérletsorozatot. A kísérletek során a modell struktúráját általában nem változtatjuk. Fizikai modell esetén analóg vagy homológ szimulációról beszélünk. A matematikai modellen végzett vizsgálatokat nem nevezzük „matematikai szimulációnak”, hanem a számolást végző gép jellege alapján analóg és digitális szimulációt különböztetünk meg.
A szekunder analóg modell a matematikai modell alapján elkészített, az eredeti rendszerrel csupán a bemenetek és kimenetek közötti matematikai kapcsolat szempontjából analóg fizikai modell, amelynek nincs köze a rendszer struktúrájához. Az ilyen eszközt a rendszeregyenletet (matematikai modellt) megoldó „ analóg számítógépnek ” nevezhetjük, a fizikai megvalósítástól (villamos, mechanikai, hidraulikus stb.) függetlenül. Leggyakrabban elektromos/elektronikus elemekből építik fel a rendszeregyenlet megoldása szempontjából lényeges műveleti egységeket. A modell változóit (állapotjelzőit) időben és értékkészletben egyaránt folytonos analóg villamos jelekkel valósítjuk meg. Szükségünk van a jelek összeadását (és kivonását), állandóval való szorzását, idő szerinti integrálását biztosító elemekre. Differenciáló áramkört azért nem használunk, mert a differenciálás a zajokat felerősíti, szemben a zajelnyomó hatású integrálással. A modellbeli nem-linearitások kezelésére különböző áramköröket (pl. exponenciális függvény, logaritmus függvény, jeleket szorzó), valamint függvénygenerátorokat is építhetünk. Az igazán hatékony elektronikus analóg számítógépek létrehozása a tranzisztor alapú műveleti erősítők megjelenéséhez és elterjedéséhez köthető. Az analóg számítógépek jellegzetessége a párhuzamos működés, hátránynak tekinthető a korlátozott pontosság és a holtidő elektronikus megvalósításának nehézsége. (Hidraulikus analóg számítógépeknél a holtidő megvalósítása megfelelő térfogatú, összekötő csövekkel lehetséges.)
Az elektronikus elemekből épített analóg számítási blokkok paramétereinek változtatása sokkal egyszerűbben megoldható pl. potenciométerek segítségével, mint egy transzlációs mechanikai elemeket használó analóg gépnél, ahol rugókat, csillapításokat, tömegeket kell cserélni hasonló helyzetben. Az elektronikus áramkörök általában magasabb frekvencián is működhetnek, mint a modellezett rendszer, ezért a szimulációs vizsgálatok a rendszeren végzett valós idejű kísérleteknél gyorsabban adnak eredményt. A mechanikai rendszerekkel szemben viszont hátránynak számít, hogy az elektronikus kapcsolásokban a (dinamikus) jeltartomány korlátozottabb. A jelek mellett megjelenő zajokra szintén figyelni kell, a jel–zaj viszony szempontjából szintén „érzékenyebbek” az elektronikus analóg számítógépek. Az elektronikus analóg számítógépek pontossága nemcsak számítási egységeitől függ, hanem az elektromos összeköttetésektől és a megfelelő tápellátástól is. Az analóg számítógépek által szolgáltatott eredmények pontossága nemcsak a kijelzők pontosságától függ, hanem a függvénygenerátor áramköröktől is, ami általában néhány tizedes jegy pontosságú. Mivel feszültségjelekkel egyszerűbb dolgozni, mint áramjelekkel, az analóg számítógépek leggyakrabban az előbbiekkel működnek.
Az elektronikus analóg számítógépek kiválóan használhatók differenciálegyenlettel és állapottér modellel adott rendszerek szimulációs vizsgálatára.
Azért említjük mégis az analóg számítógépeket ilyen részletesen, mert a (megfelelő számítási teljesítményű) digitális számítógépek elterjedésekor, az analóg gépek működését utánzó programozási nyelvekhez (Fortran, Algol, BASIC, stb.) kiegészítéseket, szimulációs nyelveket, majd önálló szimulációs programokat készítettek. A CSSL (Continuous System Simulation Language, folytonos rendszer szimulációs nyelv) szabványon alapuló megoldások blokkorientált (blokkdiagram–alapú) vagy egyenletalapú nyelv. Közös jellemzőjük a modell leírásához szükséges nyelvi elemkészlet, az ezeket összekapcsoló „nyelvtan”, a programhibák észlelése a felhasználó szimulációs modelljében, a modell fordítása a számítógép által végrehajtható gépi kódra. Röviden, a CSSL nyelvek szimulációs feladatok implementálására és végrehajtására alkalmasak, a szimuláció eredményeinek ábrázolásával és tárolásával. Hasonlóság, egyenletmegoldásnál az analóg számítógéphez hasonló elvek szerint. A digitális számítógépes szimulátorokból természetesen hiányoznak az analóg számítógépes megvalósítási korlátok (többek között a műveleti erősítős blokkok előjelfordító tulajdonsága). A digitális számítógépek viszont jellemzően soros működésűek, ezért az egyenletek (blokkok) összekapcsolása szigorúan meghatározza a modell számítási sorrendjét.
1.7.2.1. Az elektronikus, analóg számítógépek műveleti egységei
|
Műveleti egység |
Működési leírás |
|---|---|
|
Együttható potenciométer |
A változtatható ellenállásával a bemenő jel nulla és egy közötti osztását biztosítja. |
|
Előjelfordító |
Egyetlen egységnyi erősítésű műveleti erősítő, mínusz egyszeresre változtatja a bemenő feszültség értékét. |
|
Összegző |
A bemenetére kapcsolt jelek súlyozott összegét állítja elő. Elektronikus analóg számítógépnél a súlytényezők általában tíz hatványaival adhatók meg, és a kimenet előjelet vált. Az együttható potenciométerrel együtt tetszőleges állandó értékkel történő szorzás biztosítható. |
|
Integrátor |
Az összegzőhöz hasonlóan működik, a bemenetek súlyozott összegét integrálja és előjelet fordít. Az integrátor kezdeti értéke („kezdeti töltöttsége”) beállítható. |
|
Nemlineáris kimenet–bemenet kapcsolatok |
Alkalmazása is szükséges lehet, megvalósításukra külön áramkörök szükségesek. A teljesség igénye nélkül
|
|
Logaritmikus áramkörök |
Alkalmazhatók például két jel összeszorzására (pl. két-síknegyedes szorzó), exponenciális áramkör (pl. hatványozás megvalósítására), logaritmus számítása. |
1.7.2.2. Az analóg számítógép szerkezeti felépítése
Az analóg számítógép egy olyan, folytonos áramköröket tartalmazó berendezés, amellyel differenciálegyenletek megoldását lehet megvalósítani. A differenciálegyenlet megoldása úgy történik, hogy a differenciálegyenlet analóg műveleti elemekből elkészített blokkdiagramját felépítjük az analóg számítógép előlapjára kivezetett elemek segítségével. Erre a villamos kapcsolásra bocsájtjuk a bemeneti jel időfüggvényét, és a vizsgált kimeneteken lemérjük, és tároljuk a kimeneti jel(ek) időfüggvényét.
A berendezés nagyszámú integrátort, összegzőt és együttható potenciométert tartalmaz, amelyek segítségével a vizsgált blokkdiagram könnyen összeállítható. Az összeállított kapcsolás „tárolására” az előlap olyan kialakítású, hogy a huzalozott összeköttetéseket tartalmazó előlapot egyszerűen le lehessen venni, és a egy másik előlappal helyettesíteni.
Ez azt jelenti, hogy adott differenciálegyenlet megoldását biztosító blokkdiagramot az előlapon megvalósított fizikai összekapcsolással „programoztuk”.
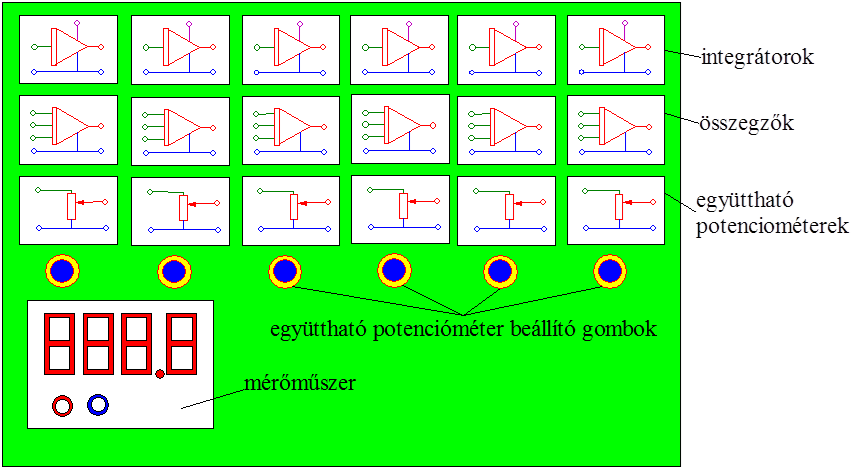
Az analóg számítógéppel történő differenciálegyenlet megoldás üzemmódjai a következők:
-
Alaphelyzetbe állítás
Ebben az üzemmódban lehetőség van az integrátorok kezdeti feltételeinek beállítására. Ezek meghatározzák, hogy a differenciálegyenletet milyen kezdeti feltételekkel oldjuk meg.
-
Számítás (vagy futtatás)
Ebben az üzemmódban a bemenő jel időbeni változása alapján a differenciálegyenletként felépített áramkör a benne lévő integrátorok töltésével (kisütésével) megvalósítja ugyanazokat, a diffenciálegyenlet megoldását jelentő, állapotváltozásokat, amelyet az analitikus megoldás időfüggvényként adna meg.
A differenciálegyenlet megoldásaként az egyik műveleti elem kimenetén egy villamos jelet kapunk, amelyet az előlapon elhelyezett műszerrel közvetlenül mérni tudunk (villamos feszültségként), vagy egy rajzoló vagy adattároló berendezésre eljuttatva rögzíteni tudjuk.
-
Tartás
Ebben az üzemmódban „befagyagyasztjuk” az analóg számítógép működését. Ezt a legegyszerűbben úgy érhetjük el, ha ebben az üzemállapotban az integrátor áramkörök bemeneteit megszakítjuk, így a műveleti erősítő kimenete és a bemenete között elhelyezkedő, adott feszültségre feltöltött kondenzátor marad csak az áramkörben, amely a nagy értékű bemeneti ellenálláson keresztül nem tud kisülni.
A differenciálegyenlet analóg számítógéppel történő megoldásánál
1.7.2.3. Az analóg számítógép programozása
A programozáshoz a matematikai modellt (differenciálegyenlet, átviteli függvény vagy állapottér modell) jelfolyam gráfon vagy tömbvázlaton (másképp hatásvázlaton) ábrázoljuk. A vázlat a jellegzetes műveleteket (állandóval szorzást, összegzést, integrálást) tünteti fel. Az integrátorok számát a rendszermodell rendszáma (legmagasabb derivált vagy a karakterisztikus egyenlet fokszáma, illetve állapotváltozók száma) határozza meg. A „szimulációs diagramok” az állapottér modell különböző alakjait bemutató fejezetben közvetlenül programozhatók.
A vázlat segíthet a fizikai megvalósításhoz szükséges számítógépelemek (pl. előjelfordítók, együttható potenciométerek) számát minimalizálni.
1.7.2.4. Amplitúdó–léptékezés
Az folytonos (analóg) áramkörökkel megvalósított differenciálegyenlet megoldásaként megjelenő villamos jel egyik problémája, hogy nem vehet fel tetszőleges értéket. A műveleti erősítőkkel megvalósított áramkörben a kimeneti jel maximális és minimális értékét az áramkör tápfeszültségei határozzák meg.
Ez azt jelenti, hogy bár a differenciálegyenlet megoldásaként jelentkező érték abszolút értéke nagyobb, mint a megfelelő előjelű tápfeszültség értéke, de az eszköz működéséből eredően ez nem lehetséges, ezért a kimenő jel a tápfeszültség értékét veszi fel és nem változik. Ez helytelen megoldást eredményez, amit el kell kerülni.
A megoldás, hogy a vizsgált kimenetre megállapítjuk a maximális kimeneti jelértéket. Majd a tápfeszültség maximális értékével egy szorzó konstanst határozunk meg, amellyel a maximális kimenő jel esetén is csak a tápfeszültség értékét érjük el.
Amplitúdó–léptékezést azért használunk, hogy az analóg számítógép maximális jeltartományát használhassuk. Tulajdonképpen normálásról van szó, az x gépi változó értékét és a hozzá tartozó U feszültséget maximális értékükhöz (x max és U max ) viszonyítva normáljuk.
|
|
(1.369) |
Ezzel a dimenziótlanítással a differenciálegyenletet mértékegységek nélküli alakra, relatív egységekre írjuk át. A kezdeti értékek beállításánál is alkalmaznunk kell a választott amplitúdó–léptéket.
Az amplitúdó–léptékezés segítségével a számítógép teljes működési feszültségtartományát ki tudjuk használni.
1.7.2.5. Időléptékezés
Az időléptékezés megfelelő értékét a rendszeregyenlet dinamikai sajátságai (időállandói és az ezekből számított vizsgálati időtartam), valamint a számítógép elemeinek frekvenciaátviteli tulajdonságai ismeretében határozhatjuk meg. A gyors (pl. 1–10 MHz frekvenciatartományban) működő integrált áramkörök miatt is sokszor lassítanunk kell a számítást az értékelhető eredmények eléréséhez. Legegyszerűbb a t független változójú differenciálegyenlet időléptékét megváltoztatni, a τ gépi idő megfelelő megválasztásával. Ehhez a rendszer valós idejű működése szempontjából megállapított t max vizsgálati időt és a számítógép választott τ max maximális futásidejét kell aránypárral összekapcsolnunk.
|
|
(1.370) |
A k t időlépték a maximális futásidő és a maximális „valós idő” hányadosa
|
|
(1.371) |
Ezzel a valós idő és a gépi idő kapcsolata
|
|
(1.372) |
|
|
|
(1.373) |
|
|
|
(1.374) |
|
|
|
(1.375) |
Az egynél nagyobb időlépték a valós időhöz képest lassítást, a kisebb pedig gyorsítást jelent. Az időlépték hatása az x(t) jel deriváltjaira
|
|
(1.376) |
|
|
|
(1.377) |
|
|
……… |
||
|
|
(1.378) |
A derivált kezdeti értékeknél is megfelelően figyelembe kell venni az időléptékezés hatását. Az időléptékezést az amplitúdó–léptékezés előtt kell elvégezni, mert az időlépték a maximális jelnagyságot (amplitúdót) megnövelheti.
1.7.2.6. Valós idejű futás (a műveleti erősítő frekvenciaátviteli korlátai)
A műveleti erősítőkből azért építjük fel az adott differenciálegyenletet megvalósító áramkört, hogy valamilyen valós jelszűrési, jelfeldolgozási műveletet valósítsunk meg a segítségével. Mivel a műveleti erősítők rendelkeznek saját frekvenciaátviteli tulajdonsággal, nem mindegy, hogy az erősítő milyen üzemmódban működik.
A műveleti erősítők nagyon alacsony (kb. 10 Hz) frekvenciáig tudják a maximális erősítésüket biztosítani, ennél nagyobb frekvenciájú bemenő jelek esetén az erősítés nagysága rohamosan csökken. Egységnyi erősítés esetén mérhetjük az úgynevezett zárthurkú határfrekvenciát, amely az μa 741-es műveleti erősítő esetén 1 MHz.
A műveleti erősítő frekvencia jelleggörbéje alapján (1.9. ábra) lehetőség van arra, hogy nagyobb erősítésű, de kisebb sávszélességű erősítőt alkalmazzunk.
Ha nagy erősítésre és nagy sávszélességre van szükség, mindenképpen ajánljuk, hogy több fokozatból álló, kisebb erősítésértékű erősítőkből építsük fel a szükséges erősítő fokozatot, amelynek erősítő elemenként megvan az előírt sávszélessége.
1.8. Folytonos rendszerek szimulációja digitális számítógéppel
Az időben folytonos differenciálegyenlettel leírt rendszerek digitális számítógéppel történő meghatározása csak úgy lehetséges, ha a folytonos bemeneti és kimeneti jel helyett mintavételezett jeleket alkalmazunk, és a mintavételezési időpontok közötti időtartamban a számításoknál gondoskodunk a jelek időbeni folytonosságáról.
Az időben folytonos differenciálegyenlet mintavételezési pontokban történő megoldására két eljárás lehetséges.
-
Az egyik megoldásnál olyan kis mintavételezési időtartamot alkalmazunk, amellyel a differenciálegyenletben, illetve a bemenő jelben szereplő legmagasabb frekvenciájú Fourier-komponens 50-100-szoros frekvenciájával mintavételezünk. Ez a nagy mintavételezési frekvencia (nagyon kicsiny mintavételezési időtartam) gyakorlatilag megteremti a digitális számítógépben a folytonos rendszer számítási feltételeit . A számításnál alkalmazott rendszerelemek az analóg áramkörökkel megvalósított programozási elemek mintavételes megfelelői (mintavételes integrátorok, összegzők, illetve szorzó elemek), a differenciálegyenletet pedig hasonló blokk diagrammal építjük fel, mint az analóg elemekből felépített differenciálegyenlet megoldásánál.
-
A második megoldás során a mintavételezési törvény alapján meghatározott (a még szükséges, de a lehető legnagyobb) mintavételezési időtartammal létrehozzuk a rendszer differenciálegyenletéből a rendszer differenciaegyenletét . Az időben folytonos differenciálegyenlet mintavételes impulzusátviteli függvényének vagy mintavételes állapottér modelljének paramétereit a Z-transzformáció segítségével határozzuk meg. A Z-transzformáció tulajdonsága, hogy különböző mintavételi időtartam alkalmazása esetén, különböző együtthatókkal rendelkező differenciaegyenletet eredményez. Ennél a számítási eljárásnál a rendszer mintavételi időpontjaiban határozzuk meg a rendszert leíró differenciaegyenlet állapotváltozóinak új értékét, az állapotváltozók és a bemenő jel korábbi mintavételi értékének a segítségével.
1.8.1. Folytonos bemeneti jelek és rendszerek mintavételezése
Az analóg, folytonos műveleti elemek költségei és felhasználásuk hátrányai miatt a kis- és középfrekvenciás alkalmazásoknál (0..1 MHz) a rendszer-differenciálegyenletek megvalósítása digitális számítógépeken, mikroprocesszorokon vagy ezekkel egyenértékű logikai-aritmetikai műveletek végzésére alkalmas áramkörökön (FPGA = Field Programmable Gate Array) történik. Ezért kiemelt jelentősége van az időben folytonos differenciálegyenletek digitális számítógépen történő megvalósításának.
A digitális számítógépek működéséből eredően ezek az eszközök csak mintavételesen képesek feldolgozni a folytonos jeleket, mivel a két mintavételezés közötti időtartamban végzik el a feldolgozási műveleteket.
A mintavételezés segítségével olyan sűrűséggel végezzük el a számításokat, hogy az eredmények szempontjából nem lehet különbséget tenni egy valóban folytonos és egy mintavételezett rendszeren meghatározott eredmény között.
1.8.1.1. A folytonos bemeneti jelek mintavételezése
A digitális számítógép működési elvéből következően folytonos jeleket nem tud közvetlenül feldolgozni, hanem a jel adott pillanatban vett értéke (mintavételezési érték) segítségével véges, a számításhoz szükséges időtartam segítségével határozza meg a vizsgált rendszer következő állapotát. A kimeneti jel nagyságát az állapotváltozók értékei alapján szintén a mintavételi időpontban számítja ki.
A bemeneti jelet tehát mintavételeznünk kell, mégpedig úgy, hogy a mintavételezett jelből a folytonos bemeneti jel a lehető kisebb torzítással legyen rekonstruálható.
A jelek mintavételezési időtartamára vonatkozóan a Shannon-tétel ad útmutatást, amely eredeti alakjában kimondja, ha egy folytonos időfüggvény u(t) nem tartalmaz egy megadott frekvenciájú komponensnél magasabb frekvenciájú komponenst, azaz a jel sávkorlátozott, akkor jel mintavételezéséhez alkalmazható mintavételezési időtartam a legmagasabb frekvenciájú komponens kétszerese.
Más szavakkal ez azt jelenti, hogy sávkorlátozott jel rekonstrukciója tökéletesen megvalósítható megszámlálható mintavételi jel értékből, ha a sávszélesség értéke nem nagyobb, mint a mintavételi sebesség fele (a másodpercenkénti minták száma).
Ha a jelhez tartozó sávkorlát túlságosan magas, (vagy végtelen értékű) akkor a mintavételezett jel értékekből történő rekonstrukciónál megjelenik az aliasing jelenség .
Az „aliasing” jelenség egy olyan ál-rekonstrukciós jel megjelenése ugyanahhoz a mintavételi jelsorozathoz, amely ugyanazokban a mintavételi pontokban jelentkezik, mint az eredeti mintavételezett jel, de annál jóval kisebb frekvenciájú.
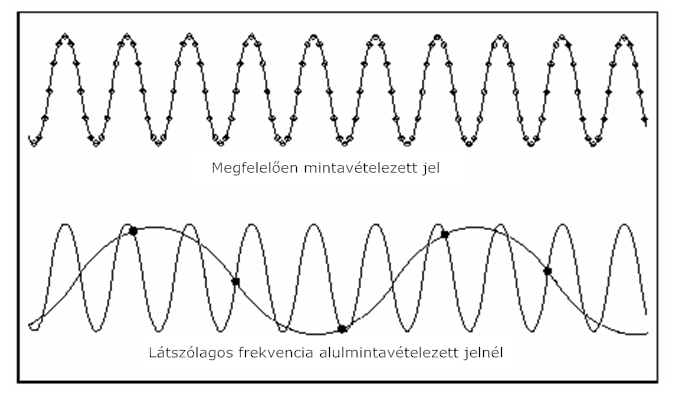
Az (1.63. ábra) ábrán jól látható, hogy az alul-mintavételezett jelnek van egy alacsonyabb frekvenciájú komponense is, ahol az eredeti tíz periódusból csak kettő látszik. Ha megnöveljük a mintavételi frekvenciát, ezzel megnöveljük a mintavételi pontok számát is az adott időtartam alatt. A nagyobb mintavételezési frekvencia az eredeti analóg jel egy jobb, több információt tartalmazó átalakítása, a kisebb frekvenciájú mintavételezéshez képest. Meg lehet adni egy olyan mintavételi frekvenciát, amellyel a mintavételezett jelben lévő maximális frekvenciát is mindig pontosan elő tudjuk állítani alulmintavételezés (aliasing) nélkül, ez az úgynevezett Nyquist-frekvencia . A Nyquist-frekvencia megegyezik az alkalmazott mintavételi frekvencia felével, amelyet a következő képlettel írhatunk le:
|
|
(1.379) |
ahol
|
f N |
a Nyquist frekvencia, |
|
|
f s |
a mintavételi frekvencia (sampling frequency). |
Az olyan jelek, amelyeknek bizonyos frekvencia-komponensei a Nyquist-frekvencia felett vannak, vonalasnak, szaggatottnak látszanak a tényleges és a Nyquist-frekvencia között. A Nyquist-frekvencia feletti komponensek Nyquist-frekvencia alatt látszanak a vonalas jelben. Például, ha egy frekvencia-komponens közé esik, akkor frekvenciaként jelentkezik.
Az 1.64. ábra és 1.65. ábra) ábra mutatja be az alulmintavételezés jelenségét.
Az (1.64. ábra) ábra a bejövő jel frekvencia-komponenseit és a mintavételi frekvenciát (f s ), amely 100 Hz, mutatja.
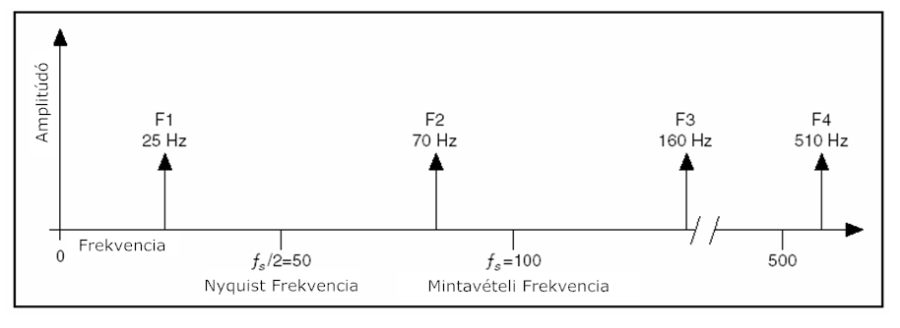
Az (1.65. ábra) ábra a bejövő jel látszólagos és a tényleges frekvencia-komponenseit mutatja.
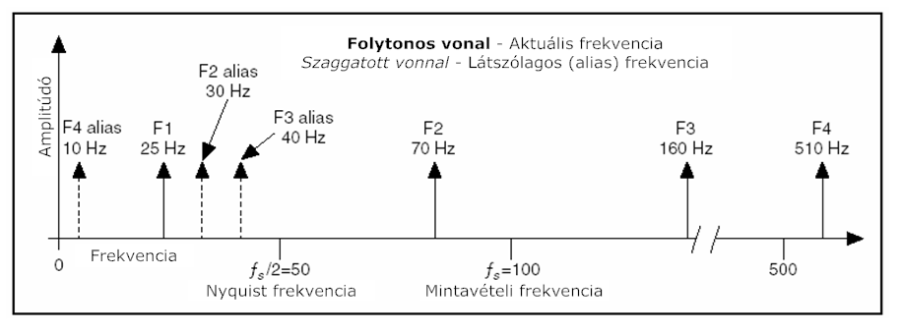
Az (1.65. ábra) ábra szerint alatti komponensek helyesen vannak mintavételezve - például, F1 jó helyen van. A Nyquist-frekvencia feletti frekvenciájú komponensek viszont máshol látszódnak. Például az F2, F3 és F4 frekvencia-komponensek 30 Hz-en, 40 Hz-en és 10 Hz-en látszanak külön-külön.
A látszólagos frekvencia értéke egyenlő a mintavételi frekvencia legközelebbi egész számú többszöröse, és a bejövő frekvencia különbségének abszolút értékével.
|
|
(1.380) |
ahol
|
AF |
a látszólagos frekvencia, ( Alias Frequency ), |
|
|
CIMSF |
a mintavételi frekvencia legközelebbi egész számú többszöröse ( Closest Integer Multiple of the Sampling Frequency ), |
|
|
IF |
a bejövő frekvencia ( Input Frequency ). |
Például, az F 2 , F 3 és F 4 -ből származó látszólagos frekvenciákat meghatározhatjuk a következő képletek szerint:
|
|
(1.381) |
A mintavételi frekvencia növelése az alulmintavételezés elkerüléséhez úgy történik, hogy a Shannon mintavételi elv szerint, a mintavételi frekvenciának a mintavételezett jel maximális frekvencia-komponensének legalább a duplájának kell lennie, hogy elkerüljük a látszólagos frekvenciák jelenségét.
Az (1.66. ábra) ábra különböző mintavételi frekvenciákkal történt mintavételezések hatását mutatja.
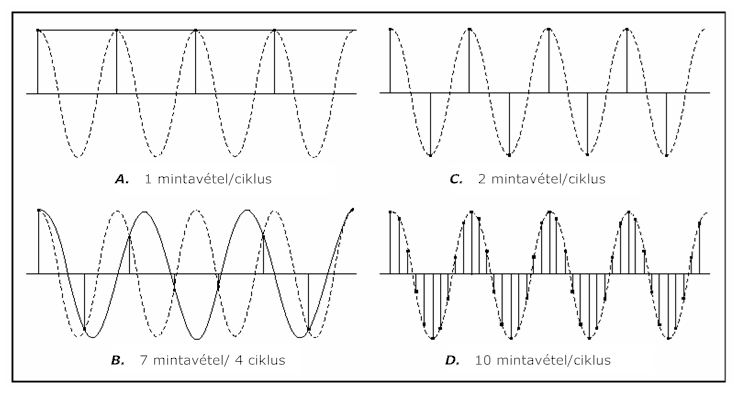
Az (1.66. ábra) ábra szerinti A esetben az mintavételi frekvencia egyenlő a mintavételezett szinusz hullám frekvenciájával. mértékegysége minta/másodperc. mértékegysége periódus/másodperc. Tehát A esetben 1 mintavételi érték 1 periódusnak felel meg. A leképezett hullámforma az eredeti jel látszólagos frekvenciáját mutatja be, amely egy egyenfeszültség (minden mintavételezésnél állandó értékű jel).
Az (1.66. ábra) ábra szerinti B esetben , azaz 7 minta esik 4 periódusra.
A B esetben tehát a mintavételi gyakoriság növelésére emelkedik a hullámfrekvencia. Azonban a látszólagos frekvencia kisebb, mint az eredeti jel frekvenciája , 4 helyett csak 3 periódus jelenik meg.
Az (1.66. ábra) ábra szerinti C esetben a mintavételi gyakoriság -re való növelésére a digitalizált hullámformát helyes frekvenciával kapjuk. A periódusok száma az eredeti jellel azonos. A C esetben az előállított hullámforma pontosabb leképezése az eredeti szinusz hullámnak, mint A vagy B esetben. Ha a mintavételi gyakoriságot kellő mértékben f fölé növeljük, például -re, azaz 10 minta/periódusra, akkor megfelelően és precízen mintavételeztük a jelet.
Az (1.66. ábra) ábra szerinti D esetben a mintavételi frekvencia tízszerese az eredeti jel frekvenciájának, amelynek eredménye látható az ábrán.
Gyakorlatban a periódusonkénti minták száma 10-től 25-ös értékig vehet fel értéket. A 10 mintavétel/periódus egy minőségileg már elfogadható mintavételi sűrűséget jelent, a 25 mintavétel/periódus egy nagyon jó minőségű mintavételezési sűrűség.
Ennél az értéknél (25) nagyobb mintavétel/periódus érték alkalmazása mintavételes rendszerek számításánál indokolatlanul megnöveli a rendszer ugyanolyan minőségű analíziséhez szükséges számításának időtartamát.
1.8.1.2. Folytonos rendszerek mintavételezése
A folytonos jelek mintavételezésénél a jelben – illetve annak Fourier-transzformáltjában – megjelenő legmagasabb frekvenciakomponens alapján határozzuk meg a jel pontos rekonstrukcióját biztosító mintavételi frekvenciát és ebből a mintavételi időtartamot.
A módszert úgy tudjuk alkalmazni a rendszert leíró differenciálegyenletek esetében, hogy a mintavételezési szabályokat, a differenciálegyenletből előállított állapottér modell sajátértékeire alkalmazzuk. Más szavakkal megállapítjuk a differenciálegyenlet időállandóit (T k k=1..n), és ezek alapján meghatározhatjuk a rendszer mintavételezéséhez szükséges időtartam nagyságát.
A szimulált rendszer időállandóit a sajátértékekből a következő képlettel állíthatjuk elő:
|
|
(1.382) |
ahol
|
T k |
a rendszer k. időállandója, |
|
|
α k |
a rendszer k. sajátértéke. |
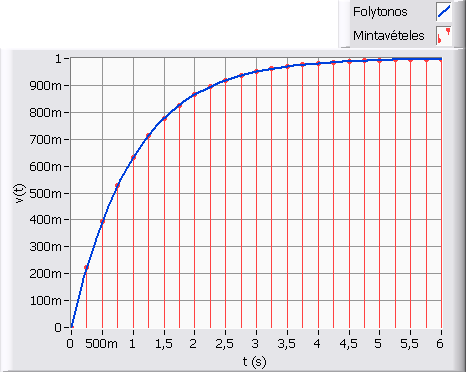
Egy rendszer helyes mintavételezéséhez a rendszer legkisebb időállandója által előállított jelértéket is az időállandó alatt 4-10-szer kell mintavételezni, hogy a legkisebb időállandóval befolyásolt jel viselkedését is rekonstruálni tudjuk.
|
|
(1.383) |
ahol
|
h |
a differenciálegyenlet mintavételezéséhez ajánlott mintavételezési időtartam, |
|
|
T min |
a differenciálegyenlet karakterisztikus egyenletének (nevező polinomjának) legkisebb időállandója. |
Az eddig bemutatott módszer jól alkalmazható, ha mintavételezendő rendszernek csak valós pólusai vannak, amelyek egyszerűen átalakíthatók valós időállandókká, és leválaszthatjuk közülük a legkisebbet.
Ha a rendszernek vannak konjugált komplex pólusai is, akkor az ezek által meghatározott kimeneti jelkomponensek helyes mintavételezéséhez a konjugált komplex pólus (p k ) abszolút értékét kell alkalmazni . A konjugált komplex pólusok polárkoordinátabeli sugarának abszolút értéke a pólus valós és képzetes részéből meghatározott Pitagoraszi távolság.
|
|
(1.384) |
ahol
|
R |
a polár koordinátabeli sugár értéke – a pólus távolsága az origótól, |
|
|
Re |
a pólus Descartes-koordinátabeli valós koordinátája, |
|
|
Im |
a pólus Descartes-koordinátabeli képzetes koordinátája. |
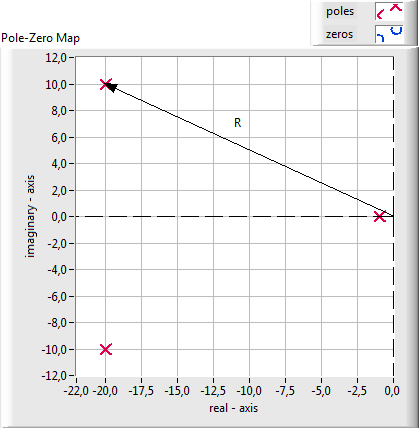
Az így meghatározott R (sugárértékeket) most már ugyanúgy alkalmazhatjuk, mint a valós pólusokat. A valós pólusok és az R sugárértékek abszolút értékeinek sorrendbe állítása alapján megállapíthatjuk a maximális abszolút értékű pólust. Ennek alkalmazásával pedig meghatározhatjuk a javasolt mintavételi időtartamot az (1.383) képlet alapján.
A mintavételi időtartam meghatározásában nem alkalmazzuk a vizsgált rendszer átviteli függvényében szereplő zérusokat, mert azok nem befolyásolják a rendszer dinamikáját.
1.8.2. Rendszerek digitális számítógépen történő futtatása
Egy folytonos rendszer digitális számítógépen történő szimulációjához meg kell határozni a számítások elvégzéséhez szükséges mintavételi időt. A mintavételi időnek figyelembe kell vennie, hogy a lehető legjobban közelítse a folytonos rendszer dinamikai tulajdonságait, valamint a bemeneti jel legmagasabb frekvenciájú komponensét is mintavételezze.
Ehhez a következő lépésekben kell a mintavételi időtartamot beállítani:
-
meg kell határozni a vizsgált bemeneti jel helyes mintavételezéséhez szükséges mintavételi időt , (dt bemeneti_jel ) valamint a
-
a vizsgált rendszer mintavételezéséhez szükséges mintavételi idő nagyságát (dt rendszer ).
A két mintavételi frekvencia értéke közül a kisebbiket kell alkalmazni a további számításokhoz (dt).
Ahhoz, hogy a digitális számítógépen a mintavételezéssel történő számítás közben megvalósítsuk a „folytonos rendszer számítási feltételeit”, a bemeneti jel, illetve a vizsgált rendszer segítségével meghatározott mintavételi frekvencia értékének többszörösét kell alkalmazni mintavételi frekvenciaként.
|
|
(1.385) |
|
|
|
(1.386) |
ahol
|
f max_bemeneti_jel |
a folytonos bemeneti jelben előforduló legmagasabb frekvenciájú komponens, |
|
|
dt bemeneti_jel |
a folytonos bemeneti jel digitális számítógépen történő számításánál javasolt mintavételi idő, |
|
|
f sample_bemeneti_jel |
a folytonos bemeneti jel vizsgálatához alkalmazott mintavételi frekvencia. |
Ugyanígy kell megállapítanunk a számított rendszer differenciálegyenletének legpontosabb számítását megvalósító mintavételi időtartam értékét is.
|
|
(1.387) |
|
|
|
(1.388) |
ahol
|
α max_rendszer |
a folytonos rendszer legnagyobb abszolút értékű pólusa, |
|
|
dt rendszer |
a folytonos rendszer digitális számítógépen történő számításánál javasolt mintavételi idő, |
|
|
f sample_rendszer |
a folytonos rendszer vizsgálatához alkalmazott mintavételi frekvencia. |
Ezekből meghatározható a javasolt mintavételi időtartam (dt) értéke, amelyet a két korábban meghatározott mintavételi érték közül a kisebb értékű, osztva egy 4-től 10-ig választott értékkel.
|
|
(1.389) |
Ennél a mintavételi frekvenciánál olyan kicsi a mintavételi időlépés (dt) nagysága, hogy a vizsgált rendszer következő állapotát, a mintavételes bemeneti jelérték valóságos impulzusközelítési értékeként számítjuk.
Általánosabb megfogalmazásban a folytonos rendszerben, illetve a bemenő jelben előforduló legmagasabb frekvenciájú komponens 40 ÷ 100-szorosát alkalmazzuk mintavételi frekvenciaként.
A mintavételes időpontokban a számított jelek értékének meghatározásánál numerikus integráló algoritmust alkalmazunk a rendszer-differenciálegyenlet megoldásánál, amelynek integrálási hibája a mintavételezési időtartam függvénye. Minél kisebb a mintavételi időtartam annál kisebb az integrálási hiba. Azoknál a szimulációs rendszereknél, amelyek automatikus lépésköz beállító algoritmussal rendelkeznek, az integrálási hiba maximálisan megengedett értéke alapján állítják be a szükséges mintavételezési időtartamot (dt) .
A vizsgált rendszer differenciálegyenletének megoldásaként (adott bemenő jelre) olyan kimeneti jeleket kapunk, amelyeknek a mintavételi időpontokban felvett értéke a numerikus integráló tagok kimeneti értékeinek kombinációjaként jelenik meg.
A vizsgált folytonos rendszer digitális számítógépen történő számításához létre kell hoznunk egy olyan struktúrát, amely a dt szimulációs időlépéssel t max időtartamig (a számítás végértékéig ) meghatározza a rendszer minden egyes időpillanatbeli állapotváltozó értékét.
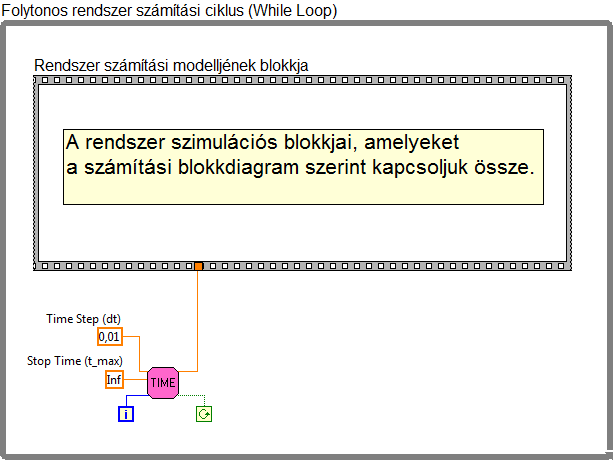
Az (1.69. ábra) ábrán látható blokkdiagram egy While Loop-ban valósítja meg a folytonos rendszer számítását (szimulációját), amelynél elsőként megtörténik a TIME blokk végrehajtása az adott mintavételi időpontban, majd ezután következik az összes többi műveletvégző blokk végrehajtása a „Rendszer számítási modelljének blokkjában”.
A TIME blokknak két bemeneti paramétere van a számítás időlépése (mintavételi időtartama = dt) és a számítás befejezésének időpontja (t max ). Ezekből, illetve a While Loop ciklusváltozójával meghatározza a számítás időpontját, azaz, hogy az adott paraméterekkel melyik számítási időpontnál tart (t). Ezt az időpontértéket globális változó segítségével az összes a „Rendszer számítási modelljének blokkjában” szereplő számítási blokkhoz eljuttatja, hogy az adott időpontra vonatkozó számításokat elvégezhessék a blokkban szereplő elemek.
A „Rendszer számítási modelljének blokkjában” a számítást végző blokkok (eljárások) végrehajtási sorrendjét az adatfolyam-programozás szabályai adják meg.
Az adatfolyam-programozás szabályai a következők:
-
Egy számítást végző blokk (eljárás) végrehajtása akkor kezdődhet el, ha minden bemeneti paramétere megérkezett a blokkhoz (eljáráshoz).
-
Egy éppen számítást végző blokk (eljárás) kimenetén csak akkor jelenhetnek meg az eredmények (kimeneti értékek), ha az éppen számítást végző blokkban már minden számítást elvégeztünk.
Ezekkel az egyszerű szabályokkal tetszőleges mélységű, egymásba ágyazott blokk (eljárás) struktúrát létrehozhatunk, amely megvalósítja a folytonos rendszer számításához szükséges feladatok (egy lehetséges) kiszámításának sorrendjét, adott mintavételi időpontban.
Abban az esetben, ha szöveges típusú programozási nyelvet alkalmaztunk a számításokhoz, az adatfolyam-programozás szerinti eljárás kiszámítási sorrendet nekünk kell biztosítani. Matlab programkörnyezetben mi adjuk meg a számítást végző program utasításainak sorrendjével a kiszámítás sorrendjét. A Simulink-ben maga a (Simulink) program határozza meg a blokkok (eljárások) kiszámítási sorrendjét, hasonlóan történik a LabVIEW-ban is az adatfolyam-programozás szabályai szerint.
1.8.3. Az alapelemek megvalósítása
Az 1.2. szakasz fejezetben bemutattuk az időben folytonos differenciálegyenlettel leírt rendszer analóg áramköri elemekkel történő megvalósításához szükséges alapelemeket. Ebben a fejezetben bemutatjuk a lineáris, állandó együtthatós (LTI= Linear Time Invariant) differenciálegyenlettel leírt rendszer digitális számítógépen történő megvalósításához szükséges számítógépes elemeket (algoritmusokat).
A folytonos rendszer áramköri elemekkel történő megvalósításához tekintsük az1.3 egyenlettel leírt időben folytonos állandó együtthatós differenciálegyenletet:
|
|
(1.390) |
ahol
|
a 0 ..a n |
a differenciálegyenlet kimenő jelének és deriváltjainak együtthatói, |
|
|
b 0 ..b m |
a differenciálegyenlet bemenő jelének és deriváltjainak együtthatói, |
|
|
y(t) |
a rendszer kimenő jele, |
|
|
n |
a kimenő jel legmagasabb deriváltjának fokszáma, |
|
|
u(t) |
a rendszer bemenő jele, |
|
|
m |
a bemenő jel legmagasabb deriváltjának fokszáma, |
|
|
t |
időváltozó. |
A differenciálegyenletben a következő alapműveletek szerepelnek:
-
a jelkomponensek összeadása, kivonása, szorzása, osztása,
-
a jelkomponensek idő szerinti derivált értékeinek meghatározása.
Az alapelemek számítógépes megvalósításánál a jelek idő szerinti derivált értékeinek meghatározása és alkalmazása helyett, azok inverz függvényét a jel idő szerinti integráljainak értékét alkalmazzák a rendszer számítási blokkjának megvalósításánál.
1.8.3.1. Jelkomponensekkel végzett aritmetikai műveletek

Az „ M ” művelet a folytonos rendszer differenciálegyenletének digitális számítógépes megoldásánál a következő lehet
-
összeadás ( + ),
-
kivonás ( - ),
-
szorzás ( * ),
-
osztás ( / ).
A két bemenet, az u1[k] és az u2[k], a rendszer differenciálegyenletében a k. mintavételi időpontokban megjelenő jelek értéke.
A műveleti elem nem hisztórikus tulajdonságú , azaz a bemeneteire érkezett adatokból egyik értéket sem tárolja a további számításokhoz.
A számítási blokkdiagramokban néhány oyan műveletvégző elem és szimbólum is megtalálható, amelyek nem az (1.70. ábra) ábrán látható általános leírási formátumúak.
Ezek a következők:

Az (1.71. ábra) ábrán látható műveletvégző egyég a következő műveletet végzi el, ahol a bemenetek jelszorzó tulajdonságát (előjelét) is megadhatjuk:
|
|
(1.391) |

Az (1.72. ábra) ábrán látható műveletvégző egyég a következő műveletet végzi el végzi el, ahol c konstans érték:
|
|
(1.392) |
1.8.3.2. A jel integrálása idő szerint az adott mintavételi időpontban
Ahogyan azt a korábbi fejezetekben bemutattuk, a rendszer differenciálegyenletének numerikus megoldása differenciáló tulajdonságú blokkok alkalmazásával számos előnytelen számítási jellemzővel rendelkezik. Ezeket úgy foglalhatjuk össze, hogy a differenciáló tulajdonságú tagok bemeneti jel zaj összetevőit jobban felerősítik a hasznos jelkomponenshez képest, illetve a differenciahányados meghatározásánál a számok számítógépbeli lebegőpontos ábrázolásából adódóan számítási pontossági problémák merülnek fel.
Ezen megfontolások alapján a rendszerek digitális számítógépes megoldásánál az idő szerinti differenciálás helyett numerikus integrálási eljárásokat alkalmazunk.
Az integráló elem hisztórikus tulajdonságú (vannak belső állapotváltozói és tárolja ezek korábbi értékeit), azaz a pillanatnyi kimeneti értéket befolyásolja, hogy milyenek voltak korábbi bemeneti mintavételi értékek.
A t=0 időpillanatban beállíthatjuk az állapotváltozók úgynevezett kezdeti értékét .
Számos numerikus integrálási algoritmus létezik, melyek közül hármat emeltünk ki, amelyek a leggyakrabban szerepelnek a szimulációs rendszerekben:
-
téglány vagy Euler integrátor,
-
trapéz vagy másodrendű Adams-Moulton integrátor,
-
másodrendű Adams-Bashforth integrátor.
A téglány (Euler) integrátort a következő függvényt valósítja meg:
|
|
(1.393) |
ahol
|
y [k] |
– az integrál értéke a mintavételi időpontban, |
|
|
y [k-1] |
– az integrál értéke az előző mintavételi időpontban, |
|
|
u[k-1] |
– az integrálandó függvény értéke az előző mintavételi időpontban, |
|
|
dt |
– az integrálási lépésköz. |
Ez az integrátor csak egyetlen állapotváltozóval rendelkezik, ezért csak egy időpillanatbeli értékről tud információt tárolni. Felépítéséből adódóan alkalmazható változó lépésközű integrálási algoritmus megvalósítására, valamint alkalmas arra, hogy a k=0 időpillanatban el tudjuk indítani a számításainkat.
Mivel hisztórikus (emlékező) tulajdonságú elem, a k=0 értékhez megadhatjuk a kimeneti érték kiindulási állapotát – a kezdeti értéket (IC = Initial Condition).
A trapéz vagy másodrendű Adams-Moulton integrátor nál a következő függvény határozza meg az integrál értékét:
|
|
(1.394) |
ahol
|
y [k] |
– az integrál értéke a mintavételi időpontban, |
|
|
y [k-1] |
– az integrál értéke az előző mintavételi időpontban, |
|
|
u [k] |
– az integrálandó függvény értéke az aktuális mintavételi időpontban, |
|
|
u [k-1] |
– az integrálandó függvény értéke az előző a mintavételi időpontban, |
|
|
dt |
– az integrálási lépésköz. |
Az Adams-Moulton integrátorok igen jó pontosságúak, egyetlen hátrányuk, hogy nem tudnak időben előre haladni, ezért vagy más integrátorokkal együtt alkalmazzuk őket, vagy kívülről kell biztosítani az időléptetést. Mivel hisztórikus (emlékező) tulajdonságú elem, a k=0 értékhez megadhatjuk a kimeneti érték kiindulási állapotát – a kezdeti értéket.
Az Adams-Bashforth integrátor számítási algoritmusát a következő összefüggést valósítja meg:
|
|
(1.395) |
ahol
|
y [k] |
– az integrál értéke a mintavételi időpontban, |
|
|
y [k-1] |
– az integrál értéke az előző mintavételi időpontban, |
|
|
u [k-1] |
– az integrálandó függvény értéke az előző mintavételi időpontban, |
|
|
u [k-2] |
– az integrálandó függvény értéke a két időlépéssel ezelőtti mintavételi időpontban, |
|
|
dt |
– az integrálási lépésköz. |
Az Adams-Bashforth integrátorok az Adams-Moulton-nal közel azonos pontosságú integrátorok. Amint az a képletből is látszik, az integrál értékét előre megjósolják a rendelkezésre álló adatokból.
A három integrálási eljárás előnyös tulajdonságait úgy használhatjuk ki, hogy a különböző számítási időlépésekben különböző integrálási algoritmust alkalmazunk.
A téglány (Euler) integrátort általában a szimuláció első lépésében (k=1) használjuk, mert önindító tulajdonságú. A második és további lépésekben már trapéz, vagy Adams-Bashforth integrátor t célszerű alkalmazni, mert pontosabbak, illetve ezektől a lépésektől áll rendelkezésükre minden szükséges, korábbi bemeneti mintavételi adat.
A numerikus integrálási algoritmus jelölése a blokkdiagramban az (1.73. ábra) ábrán látható:

Az integrátor szimbólikus jelölésénél a kimenet értéke a k=0 mintavételi időpontban az y[0] bemenettel megadott, úgynevezett kezdeti érték , egyébként pedig az integrálási algoritmussal a k. időpillanatban meghatározott érték.
A bemutatott integrálási algoritmusok mindegyikében az integrátor kimeneti jele a korábbi bemenetek által létrehozott részintegrál értékeinek összegét is tartalmazza. Tehát az integrátorok altuális kimeneti értéke „emlékszik arra”, hogy milyen korábbi bemeneti értékek voltak, amelyek létrehozták a jelenlegi kimeneti értéket.
1.8.3.3. Jelkésleltetés
Az időbeni jelkésleltetés megvalósítása digitális számítógéppel két módon lehetséges.
Az első megoldásnál mintavételi időpontonként tároljuk egy vektor típusú adatstruktúrában a bemeneti jel mintavételi értékeit. Amikor a bemeneti adaton adott késleltetést szeretnénk megvalósítani, akkor az adatok mintavételi időnként tárolt adataiból N d eltolással olvassuk ki az adatokat. Az N d értékét az aktuális mintavételi idő felhasználásával a következő összefüggés adja meg:
|
|
(1.396) |
ahol
|
T delay [k] |
– a jelkésleltetés időtartama az aktuális mintavételi időpontban, |
|
|
N d [k] |
– a késleltetés szorzószáma dt-vel a mintavételi időlépéssel a mintavételi időpontban, |
|
|
dt |
– a számítás lépésköze. |
Az ilyen típusú késleltető elem bemeneti jel értékeket tartalmazó vektor struktúrája nem lehet végtelen hosszúságú, ezért ennél az alkalmazásnál úgynevezett gyűrű típusú memóriát hozunk létre, amelynek jellemzője, hogy az elemek elérési indexe a legutolsó elem után az első elemnél folytatódik. Ezzel a memóriakezelési megoldással csak meghatározott mértékű késleltetést lehet megvalósítani, amely a vektor típusú adatstruktúra elérhető maximális memóriaindexének függvénye.
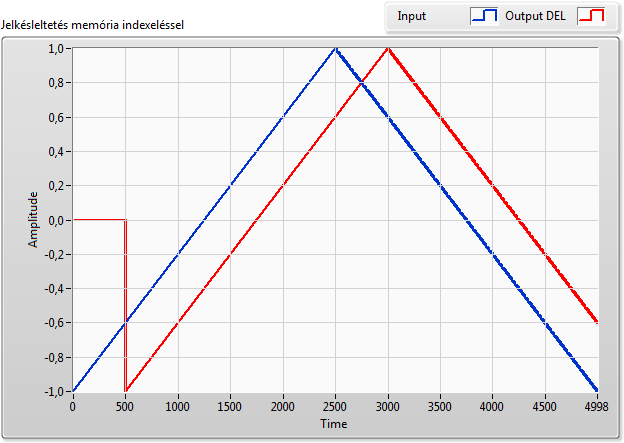
A második megoldás a – korábban már bemutatott (1.2.6. szakasz) – Padé-közelítés megvalósítása digitális számítógépes környezetben.
|
|
(1.397) |
|
|
|
(1.398) |
ahol
|
c k |
– a Padé-közelítés együtthatója, |
|
|
τ |
– a késleltetés időtartama, |
|
|
n |
– a Padé-közelítés fokszáma. |
A Padé-közelítés együtthatóit az első 5 taghoz az (Táblázat 1.11) táblázat tartalmazza.
|
Az approximáció fokszáma |
k együttható |
c együttható |
|---|---|---|
|
n=1 |
k=0 |
|
|
n=1 |
k=1 |
|
|
n=2 |
k=2 |
|
|
n=3 |
k=3 |
|
|
n=4 |
k=4 |
|
|
n=5 |
k=5 |
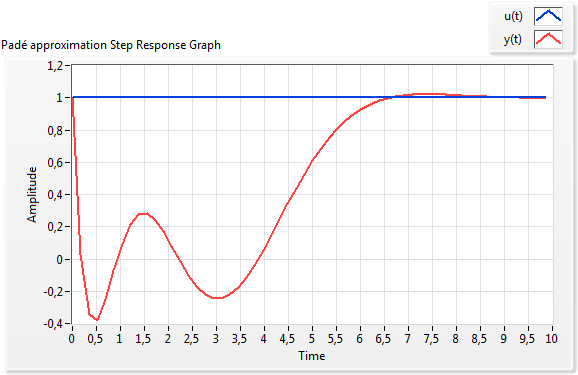
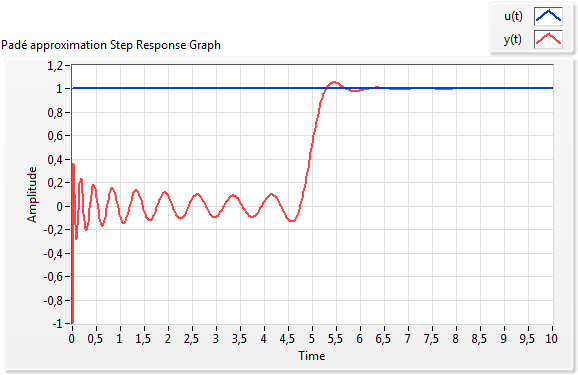
Ahogy az ábrákról látható, a Padé-közelítés a jelkésleltetés (holtidő) megvalósításában különböző nagyságú túllendülésekkel valósítja meg a bemeneti jel (u(t)) késleltetését a kimeneti jelben (y(t)), illetve a közelítés pontossága függ a Padé-közelítés fokszámától.
1.8.3.4. Nemlineáris elemek
Bár jegyzetünkben alapvetően lineáris, állandó együtthatós differenciálegyenletekkel leírható, vagy ezekre visszavezethető rendszerek számításának bemutatásával foglalkozunk, előfordul azonban, hogy a lineáris közelítést bizonyos elemeknél nem tudjuk biztosítani. Ezek a rendszerelemek olyan nemlineáris tulajdonságot valósítanak meg, amelyet nem lehet, vagy túlságosan sok számítással megvalósítható közelítéssel lehetne csak munkapontonként linearizálni.
A nemlineáris tulajdonságú rendszerelemek a műszaki gyakorlatban két nagy csoportba sorolhatók, amelyek a következők:
-
egy bemenetű, egy kimenetű nemlineáris elemek,
-
egy bemenetű, több kimenetű nemlineáris elemek.
A következő ábrákon olyan függvényeket mutatunk be, amelyek egy bemenettel és egy kimenettel, valamint több kimenettel rendelkeznek.
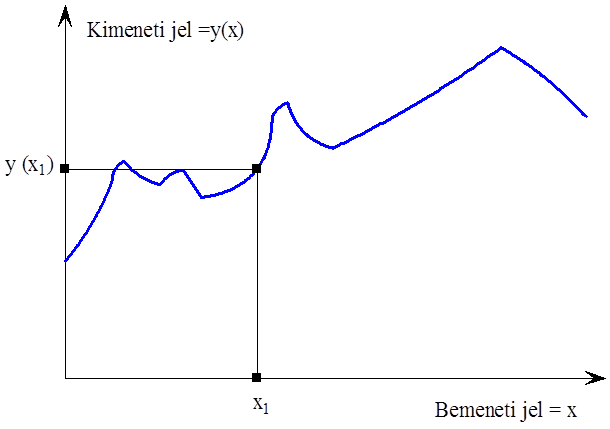
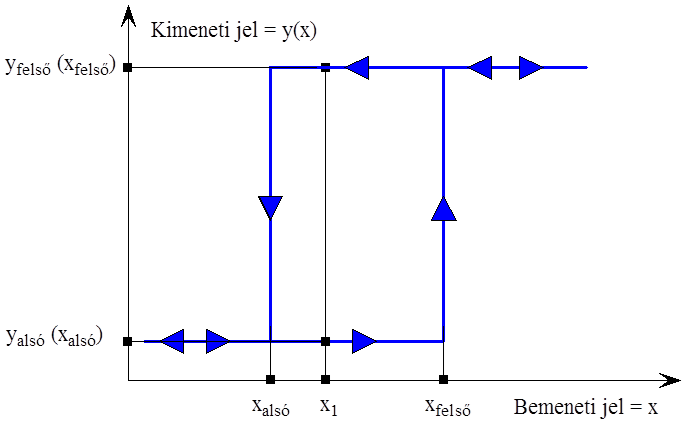
A nemlineáris elemek adott bemeneti jelértékhez tartozó kimenetét szintén két módon határozhatjuk meg. Ha ismerjük a nemlineáris viselkedést megvalósító függvényt, akkor megadhatjuk ezt a nemlinearitást meghatározó matematikai összefüggést. Ekkor a rendszeregyenlet számítása során meghatározhatjuk az adott bemeneti paraméterhez tartozó kimeneti jel értékét. Ezzel leírási móddal tetszőleges függvényt (négyzetgyökös, logaritmikus, trigonometrikus vagy más függvényt) meg lehet valósítani.
Az (1.78. ábra) ábrán egy olyan függvény látható, amely ugyanazon bemeneti értékhez több kimeneti értéket rendel. A kimeneti értékek közül az jelenik meg kimeneten, amely közelebb van az egy lépéssel korábban felvett függvényértékhez.
Megállapítható, hogy számítógépes környezetben tetszőleges függvénnyel leírható számítási elem megvalósítható, ha ismerjük a függvény leírásához szükséges algoritmust.
Nemlineáris rendszerelem megvalósításakor gyakran előfordul, hogy a függvény leírásához szükséges algoritmust nem ismerjük, csak a megvalósítandó függvény értékeit és az őket definiáló bemeneti jel értékét. A definiáló pontokkal megadott függvényt úgynevezett függvényadat-táblázat elem ( Lookup Table ) segítségével alakítjuk át a teljes alkalmazási tartományban aktuális értékkel rendelkező függvénnyé. Ezt úgy valósítjuk meg, hogy azoknál a bemeneti értékeknél, amelyeknél nem rendelkezünk függvényérték ponttal, a bemeneti érték két szomszédos függvény értékéből lineáris interpolációval határozzuk meg a szükséges függvényértéket, ahogy az a (1.79. ábra) ábrán látható.
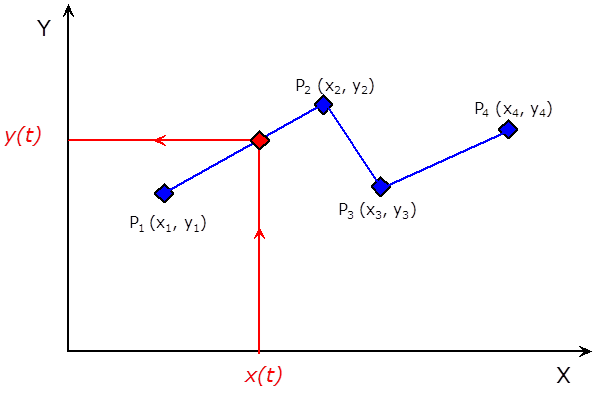
Az eljárás két vagy több bemeneti paraméter esetén is megvalósítható, ilyenkor az interpoláció és a kimeneti függvényérték meghatározása a bemeneti változók számának megfelelő dimenziójú hipersíkban történik, a rendelkezésre álló függvényértékek felhasználásával.
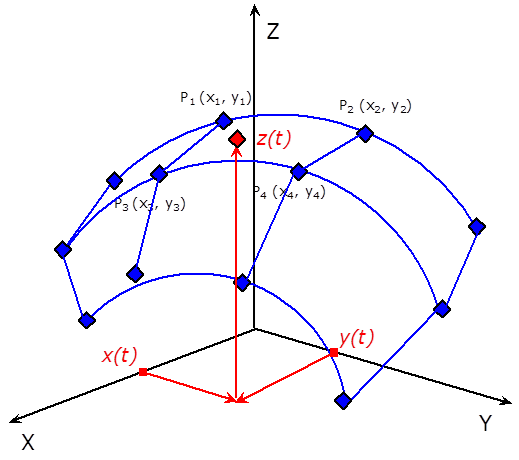
1.8.4. Alapelemek összekapcsolása
Folytonos rendszerek digitális számítógépen történő számításához az egyes alapelemeket (integrátor, összeadó, szorzó elem) megvalósító alprogramokat olyan sorrendben kell végrehajtani, hogy ezzel előállítsunk egy adatfolyam-programozás számítási sorrendet.
Az elemek összekapcsolásának művelete nem más, mint az egyes blokkok kimeneti értékének meghatározása, amelyhez más blokkok - korábban kiszámított - értékeit alkalmazzuk a blokk bemeneti paramétereként. Ezzel létrehozunk egy kapcsolatot, az egyik alkalmazott blokk kimeneti paramétere és számítási blokkunk egyik bemeneti paramétere között. Az összes kapcsolat létrehozása hasonló módon történik a számítási blokkok kimeneteinek meghatározásával.
Az egyes alapelemek programbeli leírásához meg kell adnunk, hogy az elem milyen kimeneti értéket határoz meg, és ehhez milyen bemeneti paramétereket igényel. Például, a következő definíció egy integráló típusú alapelem szöveges programozással megvalósított leírását mutatja be:
|
dy = INTEGRALAS (d2y, dy0); |
(1.399) |
ahol
|
INTEGRALAS () |
az integrálási eljárás elnevezése, |
|
|
dy |
az integráló elem kimenetének értéke a számítási időpillanatban, |
|
|
d2y |
az integráló elem bemenetének értéke a számítási időpillanatban, |
|
|
dy0 |
az integráló elem kimenetének (kezdeti) értéke t=0 időpillanatban. |
Egy differenciálegyenlet megoldását, a fentihez hasonló kimenő jel definíciók sorozata adja meg, amelyben szerepelnek a többi alapelemek is.
Minden elemtípusból tetszőleges mennyiségű elemet alkalmazhatunk a feladat leírásához.
Nem biztos, hogy az egyenletek sorozata kiszámítható lesz az adatfolyam-programozás szabályai szerint abban a sorrendben, ahogy a szimulációt végző személy megadja az egyes egyenleteket. A számítást végző programnak tehát képesnek kell lennie, hogy „átrendezze” a szövegben megadott elemek kiszámítási sorrendjét egy valóságban is kiszámítható sorrenddé.
A következő mintapéldában egy egytárolós, arányos tag differenciálegyenletének kiszámítási blokkdiagramját rajzoltuk fel. A differenciálegyenlet a következő elemekből áll:
|
|
(1.400) |
A differenciálegyenlet megoldásához a következő (elemkimeneti) értékeket kell meghatároznunk (a program készítője által definiált sorrendben):
|
Utasítás sorrend a definíciónál |
Utasítás |
|
|---|---|---|
|
1. utasítás |
b0 =KONSTANS (b0_értéke); |
(1.401) |
|
2. utasítás |
a0=KONSTANS (a0_értéke); |
(1.402) |
|
3. utasítás |
a1=KONSTANS (a1_értéke); |
(1.403) |
|
4. utasítás |
y_k=INTEGRALAS (dy_dt, y0); |
(1.404) |
|
5. utasítás |
b0u=SZORZAS (b0, u_k); |
(1.405) |
|
6. utasítás |
a0y=SZORZAS (a0, y_k-1); |
(1.406) |
|
7. utasítás |
b0u_a0y=KIVONAS (b0u, a0y); |
(1.407) |
|
8. utasítás |
dy_dt=OSZTAS (b0u_a0y, a1); |
(1.408) |
|
9. utasítás |
y_k-1=SHIFT (y_k); |
(1.409) |
Az (1.401)-től az (1.409)-ig leírt egyenletekben minden számítási blokk kimenetét meghatároztuk, de a kiszámítási sorrend nem egyezik meg az egyenletek leírási sorrendjével. Vegyük például az (1.404)-es INTAGRALAS elnevezésű elemet, amelynek a jelenlegi kiszámítási sorrendben még nincs meg a bemeneti értéke, amikor kiszámítjuk, mert azt csak a (1.408) egyenletnek megfelelő lépésben fogjuk meghatározni.
Az (Táblázat 1.13) táblázat az egyik kiszámíthatósági sorrendnek megfelelően átrendezett függvénysorrendet mutatja be.
|
Kiszámít-hatósági sorrend |
Művelet |
Eredeti sorrend |
Megjegyzés |
|---|---|---|---|
|
1. |
b0 =KONSTANS (b0_értéke); |
1. utasítás |
|
|
2. |
a0=KONSTANS (a0_értéke); |
2. utasítás |
|
|
3. |
a1=KONSTANS (a1_értéke); |
3. utasítás |
|
|
4. |
y_k_1=SHIFT (y_k); |
9. utasítás |
Az y_k_1 értéket az előző lépésben szereplő y_k érték alkalmazásával számítjuk ki. |
|
5. |
b0u=SZORZAS (b0, u_k); |
5. utasítás |
|
|
6. |
a0y=SZORZAS (a0, y_k-1); |
6. utasítás |
|
|
7. |
b0u_a0y=KIVONAS (b0u, a0y); |
7. utasítás |
|
|
8. |
dy_dt=OSZTAS (b0u_a0y, a1); |
8. utasítás |
|
|
9. |
y_k=INTEGRALAS (dy_dt, y0); |
4. utasítás |
ahol
|
u_k |
az adott számítási időlépésben a bemenő jel értéke, |
|
|
y_k |
az adott számítási időlépésben a kimenő jel értéke, |
|
|
y_k_1 |
az egy számítási időlépéssel korábbi y_k kimenő jel értéke, |
|
|
SHIFT |
művelet, amely a bemeneti paramétereként szereplő változó (y_k) egy időlépéssel korábbi értékét adja meg kimeneti értékként. |
A leírásban azért szerepel, hogy a kiszámíthatóság egyik megoldását mutattuk be , mert az egyes blokkokkal más sorrendben is létrehozhatunk teljes kiszámíthatósági sorrendet!
Az egyenletek kiszámíthatóság szerinti sorba rendezése tulajdonképpen az adatfolyam-programozás megvalósítása a számítás elvégzéséhez rendelkezésre álló blokkok kiszámítási sorrendjének kialakításával. Ez a művelet a szövegtípusú programozási nyelvekben a program sorainak „átrendezésével” történik, természetesen az egyes sorok kezdetére mutató pointerek segítségével. Grafikus programozási nyelvek, mint például a Simulink vagy a LabVIEW, alkalmazásakor a kiszámíthatósági sorrend megállapítása a program futása során automatikusan végbemegy. Ezért például a Matlab-ban helytelen sorrendben leírt műveleti sorrend, amely így helytelen eredményt ad, a Simulink-ben a felhasználó „tudta nélkül” átrendeződik, és így a helyes sorrendben történik a számítás.
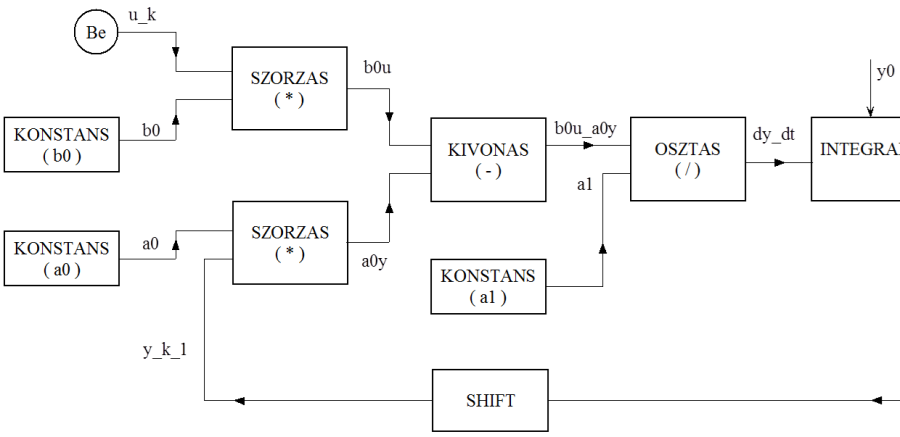
1.9. Numerikus differenciálás és integrálás
1.9.1. Numerikus differenciálás
1.9.1.1. Idő szerinti differenciálás szemléletes megközelítése
Kezdjük a legegyszerűbb esettel, egy pontban határozzuk meg a derivált közelítő értékét. Mint az olvasók nyilvánvalóan tudják, a derivált értéke a függvény adott pontjához húzott érintőjének meredekségével egyezik meg. Ezt mindkét oldalról közelíthetjük (1.82. ábra):
|
|
(1.410) |
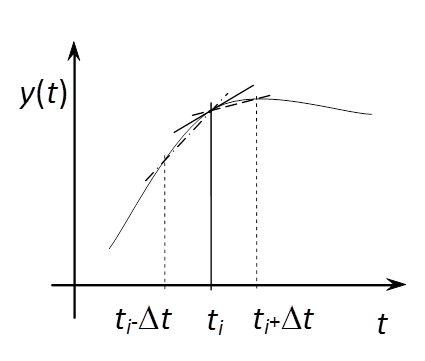
Amennyiben az y(t) függvényt ismerjük és (1.410) igaz, akkor a függvényt egyszer differenciálhatónak nevezzük. Ekkor egyszerűbb az ismert függvény deriváltját előállítani, és abba behelyettesíteni.
Más a helyzet, ha a függvényt csak pontjaiban ismerjük, például mérés eredményeként kaptuk. Ekkor interpolációs polinomot fektethetünk a pontokra, majd azt deriválhatjuk.
Nézzünk egy egyszerű esetet. Három alappontra illesszünk polinomot, ahol a pontok legyenek ekvidisztánsak (azonos lépésközűek), és a ti-re szimmetrikusan helyezkedjenek el. Ekkor a polinomot a következő egyenlettel írhatjuk le:
|
|
(1.411) |
A három ismert pontot behelyettesítve, egy lineáris egyenletrendszer kapunk, melyet megoldva az a, b és c paraméterek meghatározhatók. Nekünk csak a deriváltra lesz szükségünk, így c-t nem szükséges meghatározni, hiszen nem tartalmazza!
Az egyenletrendszer a következő:
|
|
(1.412) |
|
|
|
(1.413) |
|
|
|
(1.414) |
Adjuk össze (1.412)-t és (1.414)-t:
|
|
(1.415) |
Vonjuk ki (1.415)-ből (1.413) kétszeresét, majd fejezzük ki a-t:
|
|
(1.416) |
|
|
|
(1.417) |
Térjünk vissza a kiinduló egyenletekhez, és vonjuk ki (1.414)-ből (1.412)-t, majd helyettesítsük be (1.417)-ot azaz a-t, végül fejezzük ki b-t:
|
|
(1.418) |
|
|
|
(1.419) |
|
|
|
(1.420) |
Végül helyettesítsük be a-t és b-t a deriváltat közelítő polinomba:
|
|
(1.421) |
|
|
|
(1.422) |
Hosszas számításunk eredménye tulajdonképpen egy húr egyenlete lett (1.83. ábra).
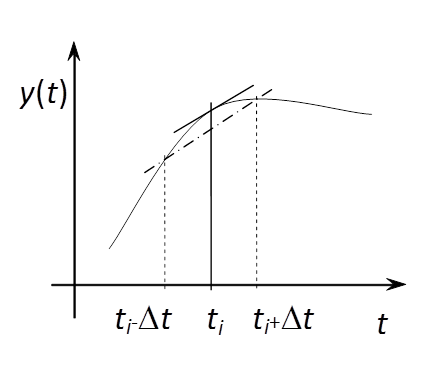
A módszert több pontra alkalmazva kapjuk a következő (nyílván pontosabb) közelítéseket:
|
|
(1.423) |
|
|
|
(1.424) |
Ezeket és az ehhez hasonló formulákat közönséges- és parciális differenciálegyenlet közelítő megoldásainak meghatározásánál is szokták alkalmazni, ilyen például a véges differenciák módszere, bár akkor a független változó általában az x, ami térbeli pozíciót jelöl. Jelen jegyzet témái közé az időben, és nem a térben lejátszódó folyamatok vizsgálata tartozik, ezért is használjuk függetlenváltozónak a t-t. Ekkor azonban – ha t i -vel az aktuális idő pillanatot jelöljük – a t i +Δt, t i +2Δt, stb. időpillanatbeli értékek még nem állnak rendelkezésünkre, hiszen az a JÖVŐ. Az interpolációs technika ekkor is alkalmazható, csak az alappontokat kell másképpen – nem t i -re szimmetrikusan – megválasztani. A következőkben ismét egy egyszerű esetet vizsgáljunk meg.
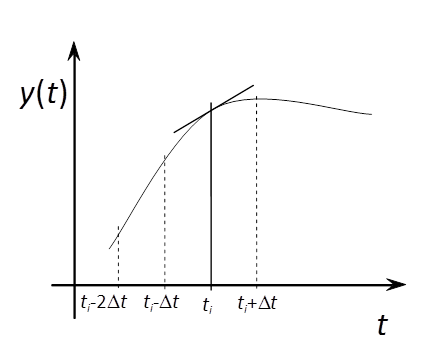
A kiinduló állapotot az (1.84. ábra) ábra mutatja. Határozzuk meg a derivált közelítő formuláját a t i és a t i +Δt pontokban. A kiinduló egyenletrendszer most:
|
|
(1.425) |
|
|
|
(1.426) |
|
|
|
(1.427) |
Vonjuk ki (1.425)-ből és (1.426)-ből (1.427)-at:
|
|
(1.428) |
|
|
|
(1.429) |
Ha (1.429) kétszeresét kivonjuk (1.428)-ből, akkor a-t könnyen kifejezhetjük:
|
|
(1.430) |
Most (1.429) négyszeresét kivonjuk (1.428)-ből, majd fejezzük ki b-t:
|
|
(1.431) |
Határozzuk meg először -t:
|
|
(1.432) |
|
|
|
(1.433) |
Ugyanebből az interpolációs polinomból kaphatunk becslést -re is:
|
|
(1.434) |
|
|
|
(1.435) |
Ezeket az összefüggéseket már használtuk az 1.3.1.3. szakasz fejezetben. Az eddig bemutatott módszer szemléletes, könnyen érthető, azonban nem biztosít lehetőséget a hiba megbecslésére. A következőkben ezt a hiányosságot is megszüntetjük a Taylor sorok felhasználásával.
1.9.1.2. Alapgondolat Taylor sor alkalmazásához
Írjuk fel y(t) t i körüli Taylor sorát a maradék taggal:
|
|
(1.436) |
Keressük -t a következő alakban:
|
|
(1.437) |
Az (1.436) alkalmazásával írjuk fel -et, -t és-et, majd helyettesítsük be (1.437)‑be:
|
|
(1.438) |
|
|
|
(1.439) |
|
|
|
(1.440) |
|
|
|
(1.441) |
Az (1.437) és (1.441) összevetéséből adódik a következő egyenletrendszer:
|
|
(1.442) |
|
|
|
(1.443) |
|
|
|
(1.444) |
A megoldás pedig és .
A közelítő összefüggés ennek megfelelően:
|
|
(1.445) |
Mivel csodák nincsenek, ez az összefüggés megegyezik (1.422)-el. Kihasználhatjuk azonban azt, hogy a számításainkhoz a Taylor sort vettük igénybe, és annak maradéktagja ismert, így becslést kaphatunk a hibára! Helyettesítsünk be most (1.445)-ba a maradéktaggal kiegészített értékeket:
|
|
(1.446) |
Az (1.446)-ből a hibatag könnyedén kiolvasható. Hozzuk könnyebben kezelhető, egyszerűbb alakra.
Állítás:
|
. |
(1.447) |
ahol
Aki ismeri a Bolzano-Darboux tételt , az a következő gondolatmenetet kihagyhatja. Vezessük be a következő függvényt:
|
|
(1.448) |
Helyettesítsünk be (1.448)-be ξ-t és ς -t, majd írjuk fel a szorzatukat:
|
|
(1.449) |
|
|
|
(1.450) |
|
|
|
(1.451) |
Bolzano tétele alapján azonban ha egy folytonos függvény valamely intervallumának két szélén ellentétes előjelű, akkor az intervallumban biztosan van legalább egy zérus hely. Esetünkben, mivel a feltétel teljesül. Legyen η a zérus hely. Ekkor -ből állításunk adódik! A differenciáló formula ezután a következő alakban írható fel:
|
|
(1.452) |
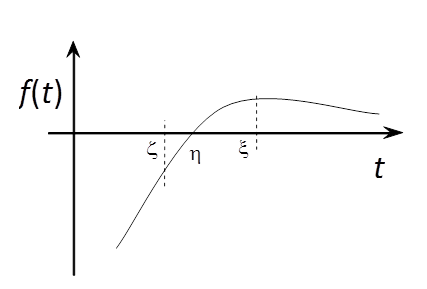
A most ismertetett módszerrel előállítható a második derivált közelítése is.
Keressük -t a következő alakban:
|
|
(1.453) |
(1.436) alkalmazásával írjuk fel -et, -t és-et, majd helyettesítsük be (1.453)‑be:
|
|
(1.454) |
|
|
|
(1.455) |
|
|
|
(1.456) |
|
|
|
(1.457) |
Az (1.453) és (1.457) összevetéséből adódik a következő egyenletrendszer:
|
|
(1.458) |
|
|
|
(1.459) |
|
|
|
(1.460) |
A megoldás pedig és . A közelítő összefüggés ennek megfelelően:
|
|
(1.461) |
Ezt az összefüggés már használtuk az 1.3.1.3. szakasz pontban. Ismét kihasználhatjuk azonban azt, hogy a számításainkhoz a Taylor sort vettük igénybe, és annak maradéktagja ismert, ezért annak felhasználásával becslést kaphatunk a hibára. Helyettesítsünk be (1.461)‑be a maradéktaggal kiegészített értékeket:
|
|
(1.462) |
Az (1.462)-ból a hibatag most is könnyedén kiolvasható. Ezt az előző példánál bemutatott levezetésben alkalmazott módszerrel tudjuk ezúttal is egyszerűbb alakra hozni, így a differenciáló formula végleges alakja:
|
|
(1.463) |
1.9.1.3. Általános, hibatagot szolgáltató eljárás
Az előző pontban bemutatott módszert általánosíthatjuk, ily módon a közelítő formulák előállítása egyszerűbbé szinte automatikussá válik.
Legyen adott a függvény az (t 0 ,y 0 ), (t 1 ,y 1 ),…(t 2m ,y 2m ) ekvidisztáns pontpárokkal, azaz t i+1 -t i =Δt, i=0,1,2…2m esetén. Keressük a közelítő formulát
|
|
(1.464) |
alakban, ahol legyen O. Fejezzük ki az itt szereplő függvényértékeket a következő Taylor sorral:
|
, |
(1.465) |
majd helyettesítsünk be:
|
|
(1.466) |
Hogy a hibára vonatkozó feltételünket teljesíteni tudjuk, válasszuk meg az első 2m+1 tagot úgy, hogy az n-ediket kivéve legyen zérus, az n. pedig legyen egyenlő a keresett deriválttal:
|
|
(1.467) |
A c r konstansokra így 2m+1 darab egyenletet kaptunk, melynél az együtthatómátrix determinánsa Vandermonde típusú, így az egyenletrendszer mindig egyértelműen megoldható:
|
⇒ |
(1.468) |
A közelítés hibájára becslést [33.] első – de az n.-nél nagyobb indexű – nem zérus értékű tagjából kapjuk, felhasználva a Taylor sorok maradéktagjára vonatkozó összefüggést, és a Bolzano-Darboux tételt:
|
|
(1.469) |
Mintapélda:
Határozzuk meg az első deriváltra vonatkozó összefüggést O nagyságrendű hiba esetén!
A kiírásnak megfelelően n=1. Mivel a hiba nagyságrendje 2, így 2m-n+1=2, amiből m=1 adódik. Ennek megfelelően az egyenletrendszer:
|
|
(1.470) |
|
|
|
(1.471) |
|
|
|
(1.472) |
Az egyenletrendszer megoldása, és a közelítő formula:
|
|
(1.473) |
|
|
|
(1.474) |
Határozzuk meg a hiba becslésére vonatkozó közelítést:
|
|
(1.475) |
Mintapélda:
Határozzuk meg a második deriváltra vonatkozó összefüggést, ha m=1!
Az előző példához hasonlóan most is három egyenletet kell felírni, és csak a jobb oldalukon térnek el:
|
|
(1.476) |
|
|
|
(1.477) |
|
|
|
(1.478) |
Az egyenletrendszer megoldása, és a közelítő formula:
|
|
(1.479) |
|
|
|
(1.480) |
Határozzuk meg a hiba becslésére vonatkozó közelítést:
|
|
(1.481) |
Természetesen le lehet vezetni az előzőekben látottaknál kisebb hibataggal rendelkező közelítéseket is, de azok nagyobb számítási igénnyel rendelkeznek:
|
; hiba becslés: |
(1.482) |
Általában a kívánt pontosságot nem egy bonyolultabb formula alkalmazásával célszerű elérni, hanem a kisebb intervallum megválasztásával.
Az itt bemutatott módszer által előállított formulák a differenciahányados helyére szimmetrikusan elhelyezkedő pontokat használnak. Természetesen lehet ettől eltérő összefüggéseket is keresni (lásd. (1.435)), ekkor azonban a kiinduló összefüggésben (1.464) kell az összegzés határait módosítani.
1.9.2. Numerikus integrálás
Egy függvény határozott integrálásakor tulajdonképpen a függvény alatti területet szeretnénk meghatározni. Ha az y(t) függvénynek ismerjük az Y(t) primitív függvényét, akkor egyszerű a dolgunk:
|
|
(1.483) |
A primitív függvény azonban nem mindig áll a rendelkezésünkre, vagy mert a matematikai ismereteink nem elégségesek a meghatározásához, vagy mert nem lehet előállítani. Ekkor numerikus módszereket alkalmazunk. Az idők során nagyon sok különböző elvű integrálási formulát állítottak fel. Hogy éppen mikor melyiket alkalmazzuk, az több dologtól függ, például az integrálandó függvény tulajdonságaitól, megadásának módjától, a megkívánt pontosságtól, stb.
A következőkben néhány elterjedten használt módszerrel és származtatásukkal ismerkedhetünk meg. A későbbiekben ez jól felhasználható annak eldöntésére is, hogy mikor melyiket alkalmazzuk.
A differenciálszámításhoz hasonlóan itt is több lépcsőre bontjuk az ismertetést. Az első rész tartalmazza a szemléletes megközelítést, a második a Taylor sorokon alapuló, de egyszerű módszert, és végül a harmadik az általános eljárást, több esetre is.
1.9.2.1. Szemléletes megközelítés
Nézzünk most néhány esetet, egyszerűbb, nem általános módon, amikor hiba becslésre nincs lehetőségünk. Legyen adott az integrálandó y függvény az ekvidisztáns t i -2 , t i -1 , t i , t i +1 pontokban rendre y i -2 , y i -1 , y i , y i +1 értékkel. Az integrált az [t i , t i +1 ] intervallumban keressük az ismert pontokra fektetett különböző fokszámú interpolációs polinomokkal.
Az első esetben csak az i és i+1 indexű pontokat használjuk:
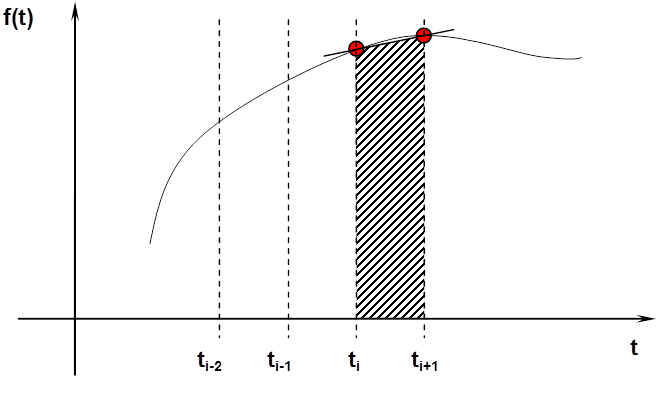
Fektessünk egyenest a két ponton keresztül, majd végezzük el az integrálást:
|
|
(1.484) |
A t i +1 -t i =Δt helyettesítés bevezetése után a jól ismert trapéz formulát kapjuk:
|
. |
(1.485) |
Ez az összefüggés sokféle módon levezethető. Az itt bemutatott előállítás – és annak általánosítása esetén – az un. interpolációs formulákat kaphatjuk. Az elnevezés magától értetődő, hiszen egy interpolációs polinom felhasználásával állítottuk elő a formulát. Ekkor a trapéz formulát másodrendű Adams-Moulton formulának is hívhatjuk.
A második esetben csak az i és i-1 indexű pontokat használjuk (1.86. ábra), fektessünk egyenest a két ponton keresztül, majd végezzük el az integrálást:
|
|
(1.486) |
Alkalmazzuk most is a t i +1-t i =Δt helyettesítést:
|
|
(1.487) |
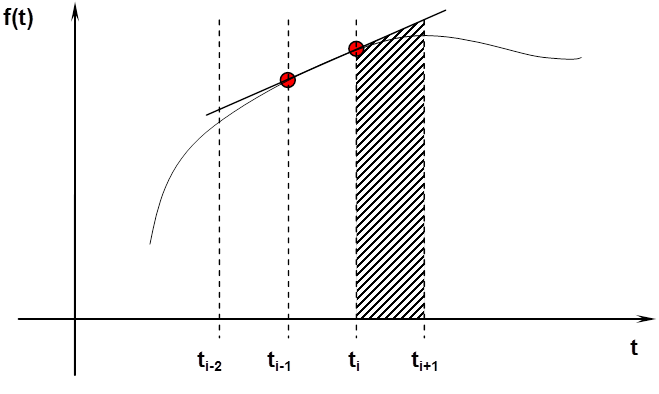
Az így kapott formulát másodrendű Adam-Bashforth integrátornak hívjuk. Az ilyen típusú integrátorokra jellemző, hogy az integrálást a tartópontokon kívüli területen végzik el, ezért az „extrapolációs” jelzőt is elterjedten használjuk.
A következő esetben csak az i-1,i és i+1 indexű pontokra támaszkodunk:
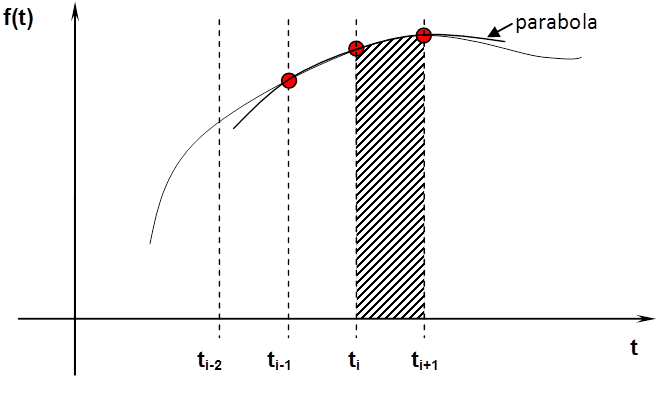
Fektessünk parabolát a pontokon keresztül, majd végezzük el az integrálást. A feladat megoldásához a Maxima nevű ingyenes programot használtuk, mellyel a következő egyenletrendszert oldottuk meg, majd az eredményeket felhasználva integráltunk:
|
|
(1.488) |
(%i1) e1:yip1=a*(ti+dt)^2+b*(ti+dt)+c$
(%i2) e2:yi=a*(ti)^2+b*(ti)+c$
(%i3) e3:yim1=a*(ti-dt)^2+b*(ti-dt)+c$
(%i4) globalsolve: true$
(i%5) solve([e1,e2,e3],[a,b,c])$
(i%6) integrate(a*t^2+b*t+c,t,ti,ti+dt)$
(i%7) radcan(%);
5 dt yip1 – dt yim1 + 8 dt yi
(o%7) --------------------------------
12
Az eredmény átírva a megszokott jelölésekre, és -t kiemelve a harmadrendű interpolációs Adams-Moulton féle formulát adja:
|
|
(1.489) |
A következő esetben mozdítsuk visszafelé a pontokat, azaz csak az i-2, i-1 és i indexűeket használjuk:
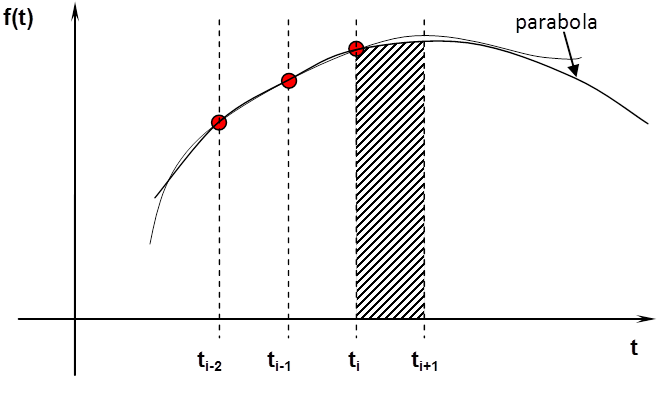
Fektessünk most is parabolát a pontokon keresztül, majd végezzük el az integrálást. A feladat megoldásához újra a Maxima nevű programot használtuk, mellyel a következő egyenletrendszert oldottuk meg, majd az eredményeket felhasználva integráltuk:
|
|
(1.490) |
(%i1) e1:yi=a*(ti)^2+b*(ti)+c$
(%i2) e2:yim1=a*(ti-dt)^2+b*(ti-dt)+c$
(%i3) e3:yim2=a*(ti-2*dt)^2+b*(ti-2*dt)+c$
(%i4) globalsolve: true$
(i%5) solve([e1,e2,e3],[a,b,c])$
(i%6) integrate(a*t^2+b*t+c,t,ti,ti+dt)$
(i%7) radcan(%);
5 dt yim2 – 16 dt yim1 + 23 dt yi
(o%7) --------------------------------
12
Az eredmény átírva a megszokott jelölésekre, és -t kiemelve a harmadrendű extrapolációs Adams-Bashforth féle formulát adja:
|
|
(1.491) |
1.9.2.2. Alapgondolat Taylor sor alkalmazására
A következőkben mindig közelítő meghatározására fogunk törekedni. Írjuk fel y(t) ti körüli Taylor sorát a maradék taggal [12.] :
|
|
(1.492) |
Legyen a közelítő formula alakja a következő:
|
, |
(1.493) |
ahol a hibatag. Írjuk fel -t és -t a Taylor sor (1.492) segítségével, majd helyettesítsük be (1.493)-ba:
|
, ahol |
(1.494) |
|
|
|
(1.495) |
Határozzuk meg -t úgy, hogy y(t)-t csak az első két tagjával vesszük figyelembe, hiszen -ben is csak ezek a tagok szerepelnek:
|
|
(1.496) |
|
|
|
(1.497) |
(1.495) és (1.497) összevetéséből a következő egyenletrendszer adódik:
|
|
(1.498) |
Ennek megoldása , így a közelítő formula alakja:
|
|
(1.499) |
A közelítés hibája pedig:
|
|
(1.500) |
Eredményül a trapéz formulát kaptuk. Végezzük el a számítást akkor is, ha
|
|
(1.501) |
A számítás menete eleinte ugyanaz mint a trapéz formulánál volt, csak a hibatagok eltérőek, mivel itt két különböző intervallum van:
|
, ahol |
(1.502) |
|
|
|
(1.503) |
|
|
, ahol |
(1.504) |
|
|
|
(1.505) |
Ennek megoldása és , így a közelítő formula alakja:
|
|
(1.506) |
A közelítés hibája most is a következőképpen írható fel:
|
|
(1.507) |
A hibatag most nem írható fel olyan egyszerűen. A numerikus deriválásnál leírt módszer azonban – kisebb módosítással – itt is alkalmazható. Állítás:
|
ahol . |
(1.508) |
Vezessük be a következő függvényt:
|
|
(1.509) |
Helyettesítsünk b e (1.509)-be ξ-t és ς -t, majd írjuk fel a szorzatukat:
|
|
(1.510) |
Bolzano tétele alapján azonban ha egy folytonos függvény valamely intervallumának két szélén ellentétes előjelű, akkor az intervallumban biztosan van legalább egy zérus hely. Esetünkben, mivel a feltétel teljesül. Legyen η a zérus hely. Ekkor -ből állításunk adódik. Vissza kell még helyettesíteni (1.507)‑ba:
|
|
(1.511) |
1.9.2.3. Általános, hibatagot is szolgáltató eljárások - szimmetrikus formulák
Ebben, és a következő három fejezetben [8.] a független változó x lesz, jelezve, hogy az itt bemutatott formulák általánosan is használhatók.
Feladatunk a következő: egy adott [a,b] intervallumon szeretnénk meghatározni egy tetszőleges függvény integrálját. Bontsuk az intervallumot q egyenlő hosszúságú részre. Bontsuk tovább ezen intervallumokat n egyenlő hosszúságú részre, így végül n*q=m darab szakaszhoz jutottunk. Olyan formulát keresünk, amely a q darab intervallumon külön-külön megadja a közelítést, felhasználva az ezen belüli n+1 függvényértéket.
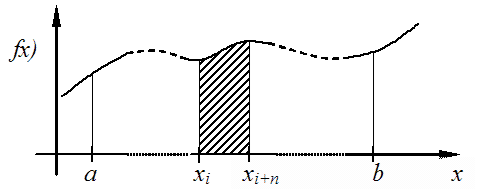
Legyen adott az integrálandó függvény explicit alakban, azaz y=f(x). Tegyük fel, hogy létezik az [a,b] intervallumon a Riemann‑integrálja, továbbá, hogy létezik az x i pontokra felírt konvergens Taylor‑sora, ahol
|
|
(1.512) |
Keressük a közelítő formulát
|
|
(1.513) |
alakban, ahol y i+k =f(x i+k ), n nem negatív egész szám. Felhasználjuk még az integrálandó függvény x i+p körül felírt Taylor‑sorát, ahol :
|
|
(1.514) |
Írjuk fel a [x i , x i+n ] intervallumon vett integrál hibáját:
|
|
(1.515) |
Helyettesítsük az f(x) függvényt mindenhol a Taylor‑sorával, kivéve a x i+p helyet:
|
|
(1.516) |
Cseréljük fel az integrált és a szummát, majd vigyünk minden x-től független tagot az integráljel elé, valamint használjuk ki, hogy x i+k -x i+p = x i +kh- x i -ph=(k-p)h, és cseréljük fel a két szummát:
|
|
(1.517) |
Végezzük el az integrálást:
|
|
(1.518) |
Vonjuk össze a két szummát, és emeljünk ki:
|
|
(1.519) |
Ezzel egy olyan összefüggéshez jutottunk, amely alkalmas mind a formulában szereplő c együtthatók meghatározására, mind a közelítés hibájának becslésére.
Az együtthatókat úgy kapjuk, hogy a felírt összefüggés első n+1 tagját nullának vesszük, így az n+1 darab c együttható meghatározásához éppen n+1 darab egyenletet írhatunk fel. A maradék, azaz az integrál közelítéssel elkövetett hiba, viszont az x i+p körül felírt Taylor‑sor maradéktagjából határozható meg:
|
|
(1.520) |
ahol .
Ebből már könnyen meghatározható a hiba formulája:
|
|
(1.521) |
Vegyük észre azonban, hogy ez a (1.519) összefüggés első nem zérus tagjával egyezik meg.
1.9.2.3.1. Trapéz formula
Legyen n=1 és p=0, valamint m=2q, ahol q pozitív egész. Ekkor az első n+1=2 tag a következő:
|
|
(1.522) |
Az egyenletek rendezése után a következő egyenletrendszert kapjuk:
|
|
(1.523) |
A két együttható tehát: . Határozzuk még meg a közelítés hibáját:
|
|
(1.524) |
Ezek után a közelítő formula egy intervallumra:
|
, |
(1.525) |
és a teljes [a,b] intervallumra:
|
|
(1.526) |
1.9.2.3.2. Simpson formula
Legyen n=2 és p=0, valamint m=2q, ahol q pozitív egész. Ekkor az első n+1=3 tag a következő:
|
|
(1.527) |
Az egyenletrendszert megoldva kapjuk: . Határozzuk még meg a közelítés hibáját. j=3 esetén zérust kapunk, ezért j=4 adja az eredményt:
|
|
(1.528) |
Ezek után a közelítő formula egy intervallumra:
|
, |
(1.529) |
és a teljes [a,b] intervallumra:
|
|
(1.530) |
1.9.2.3.3. Newton-féle 3/8-os formula
Legyen n=3 és p=0, valamint m=3q, ahol q pozitív egész. Ekkor az első n+1=4 tag a következő:
|
|
(1.531) |
Az egyenletrendszert megoldva kapjuk: . Határozzuk még meg a közelítés hibáját:
|
|
(1.532) |
Ezek után a közelítő formula egy intervallumra:
|
, |
(1.533) |
és a teljes [a,b] intervallumra:
|
|
(1.534) |
1.9.2.3.4. Szimmetrikus 4-lépéses formula
Legyen n=4 és p=0, valamint m=4q, ahol q pozitív egész. Ekkor az első n+1=5 tag a következő:
|
|
(1.535) |
Az egyenletrendszert megoldva kapjuk: . Határozzuk még meg a közelítés hibáját. j=5 esetén zérust kapunk, ezért j=6 adja az eredményt:
|
|
(1.536) |
Ezek után a közelítő formula egy intervallumra:
|
, |
(1.537) |
és a teljes [a,b] intervallumra:
|
|
(1.538) |
1.9.2.4. Általános, hibatagot is szolgáltató eljárások - Adams-Bashforth formulák
Az integrálandó függvény értékeit n darab egymástól egyenlő távolságra (Δx) lévő pontban ismerjük. Határozzuk meg az integrál közelítő értékét a következő Δx intervallumon az ismert függvényértékek segítségével. Mivel itt csak a megelőző függvényértékekre támaszkodunk, szokás ezeket a formulákat prediktor formuláknak is nevezni.
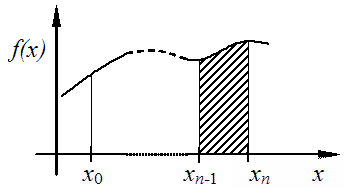
Legyenek adottak az integrálandó függvény értékei az x0, x1, ..., x n- 1 pontokban, azaz f(x0), f(x1), ... f(x n- 1). Tegyük fel, hogy létezik az [a,b] intervallumon a függvény Riemann‑integrálja, továbbá, hogy létezik az x i pontokra felírt konvergens Taylor‑sora, ahol
|
|
(1.539) |
Keressük a közelítő formulát
|
|
(1.540) |
alakban, ahol y i-k =f(x i-k ), és i=n-1. Felhasználjuk még az integrálandó függvény x i körül felírt Taylor‑sorát:
|
|
(1.541) |
Írjuk fel az [x i , x i+1 ] intervallumon vett integrál hibáját:
|
|
(1.542) |
Helyettesítsük az f(x) függvényt mindenhol a Taylor‑sorával, kivéve az x i helyet:
|
|
(1.543) |
Cseréljük fel az integrált és a szummát, majd vigyünk minden x-től független tagot az integráljel elé, valamint használjuk ki, hogy x i-k -x i = x i -kh- x i =-kh, és cseréljük fel a két szummát:
|
|
(1.544) |
Végezzük el az integrálást:
|
|
(1.545) |
Vonjuk össze a két szummát, és emeljünk ki:
|
|
(1.546) |
Ezzel egy olyan összefüggéshez jutottunk, amely alkalmas mind a formulában szereplő c együtthatók meghatározására, mind a közelítés hibájának becslésére.
Az együtthatókat úgy kapjuk, hogy a felírt összefüggés első n tagját nullának vesszük, így az n darab c együttható meghatározásához éppen n darab egyenletet írhatunk fel. A maradék, azaz az integrál közelítéssel elkövetett hiba, viszont az x i körül felírt Taylor‑sor maradéktagjából határozható meg:
|
|
(1.547) |
ahol .
Ebből már könnyen meghatározható a hiba formulája:
|
|
(1.548) |
Vegyük észre azonban, hogy ez a (1.546) összefüggés első nem zérus tagjával egyezik meg.
1.9.2.4.1. Elsőrendű Adams-Bashforth integrátor
Legyen n=1. Ekkor az első tag a következő:
|
|
(1.549) |
Az együttható tehát: c0=h. Határozzuk még meg a közelítés hibáját:
|
|
(1.550) |
Ezek után a közelítő formula:
|
. |
(1.551) |
1.9.2.4.2. Másodrendű Adams-Bashforth integrátor
Legyen n=2. Ekkor az első két tag a következő:
|
|
(1.552) |
Az egyenletrendszert megoldva kapjuk:. Határozzuk még meg a közelítés hibáját:
|
|
(1.553) |
Ezek után a közelítő formula:
|
. |
(1.554) |
1.9.2.4.3. Harmadrendű Adams-Bashforth integrátor
Legyen n=3. Ekkor az első három tag a következő:
|
|
(1.555) |
Az egyenletrendszert megoldva kapjuk:. Határozzuk még meg a közelítés hibáját:
|
|
(1.556) |
Ezek után a közelítő formula:
|
. |
(1.557) |
1.9.2.4.4. Negyedrendű Adams-Bashforth integrátor
Legyen n=4. Ekkor az első négy tag a következő:
|
|
(1.558) |
Az egyenletrendszert megoldva kapjuk:.
Határozzuk még meg a közelítés hibáját:
|
|
(1.559) |
Ezek után a közelítő formula:
|
. |
(1.560) |
1.9.2.5. Általános, hibatagot is szolgáltató eljárások - Adams-Moulton formulák
Az integrálandó függvény értékeit n darab egymástól egyenlő távolságra (Δx) lévő pontban ismerjük. Határozzuk meg az integrál közelítő értékét az utolsó Δx intervallumon az ismert függvényértékek segítségével.
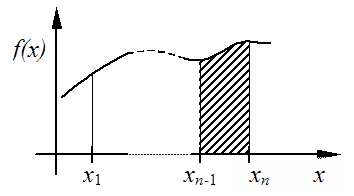
Legyenek adottak az integrálandó függvény értékei az x1, x2, ..., x n pontokban, azaz f(x1), f(x2), ... f(x n ). Tegyük fel, hogy létezik az [a,b] intervallumon a függvény Riemann‑integrálja, továbbá, hogy létezik az x i pontokra felírt konvergens Taylor‑sora, ahol
|
|
(1.561) |
Keressük a közelítő formulát
|
|
(1.562) |
alakban, ahol y i-k+ 1 =f(x i-k+ 1 ), és i=n-1. Felhasználjuk még az integrálandó függvény x i körül felírt Taylor‑sorát:
|
|
(1.563) |
Írjuk fel az [x i , x i+1 ] intervallumon vett integrál hibáját:
|
|
(1.564) |
Helyettesítsük az f(x) függvényt mindenhol a Taylor‑sorával, kivéve az x i helyet:
|
|
(1.565) |
Cseréljük fel az integrált és a szummát, majd vigyünk minden x-től független tagot az integráljel elé, valamint használjuk ki, hogy x i-k+ 1 -x i = x i +h-kh-x i =(1-k)h, és cseréljük fel a két szummát:
|
|
(1.566) |
Végezzük el az integrálást:
|
|
(1.567) |
Vonjuk össze a két szummát, és emeljünk ki:
|
|
(1.568) |
Ezzel egy olyan összefüggéshez jutottunk, amely alkalmas mind a formulában szereplő c együtthatók meghatározására, mind a közelítés hibájának becslésére.
Az együtthatókat úgy kapjuk, hogy a felírt összefüggés első n tagját nullának vesszük, így az n darab c együttható meghatározásához éppen n darab egyenletet írhatunk fel. A maradék, azaz az integrál közelítéssel elkövetett hiba, viszont az x i körül felírt Taylor‑sor maradéktagjából határozható meg:
|
|
(1.569) |
ahol .
Ebből már könnyen meghatározható a hiba formulája:
|
|
(1.570) |
Vegyük észre azonban, hogy ez az (1.568) összefüggés első nem zérus tagjával egyezik meg.
1.9.2.5.1. Elsőrendű Adams-Moulton integrátor
Legyen n=1. Ekkor az első tag a következő:
|
|
(1.571) |
Az együttható tehát: c0=h. Határozzuk még meg a közelítés hibáját:
|
|
(1.572) |
Ezek után a közelítő formula:
|
. |
(1.573) |
1.9.2.5.2. Másodrendű Adams-Moulton integrátor
Legyen n=2. Ekkor az első két tag a következő:
|
|
(1.574) |
Az egyenletrendszert megoldva kapjuk:. Határozzuk még meg a közelítés hibáját:
|
|
(1.575) |
Ezek után a közelítő formula:
|
. |
(1.576) |
1.9.2.5.3. Harmadrendű Adams-Moulton integrátor
Legyen n=3. Ekkor az első három tag a következő:
|
|
(1.577) |
Az egyenletrendszert megoldva kapjuk:. Határozzuk még meg a közelítés hibáját:
|
|
(1.578) |
Ezek után a közelítő formula:
|
. |
(1.579) |
1.9.2.5.4. Negyedrendű Adams-Moulton integrátor
Legyen n=4. Ekkor az első négy tag a következő:
|
|
(1.580) |
Az egyenletrendszert megoldva kapjuk:. Határozzuk még meg a közelítés hibáját:
|
|
(1.581) |
Ezek után a közelítő formula:
|
. |
(1.582) |
1.9.2.6. Runge-Kutta módszer
A Runge‑Kutta módszer alapvetően eltér az eddigiektől, nem elegendő az integrálandó függvény csak pontjaiban ismerni, hanem teljes egészében adottnak kell lennie. Így tulajdonképpen differenciálegyenletet oldunk meg.
Legyen az integrálandó függvény y’=f(x,y), és a kezdeti feltétel y(x0)=y0. A megoldás során h>0 lépéstávolsággal fogunk haladni, és rendre meghatározzuk az y i =y(x i ) függvényértékeket, ahol
|
|
(1.583) |
Az n-ed rendű Runge‑Kutta módszer alkalmazása során minden i-edik lépésnél a függvényérték megváltozását, azaz Δy i =y i+ 1-y i –t határozzuk meg. Ehhez felhasználjuk a k i,q korrekciós tagokat, ahol
|
|
(1.584) |
A függvényérték megváltozását ezen korrekciós tagok súlyozott számtani középértékeként állítjuk elő:
|
|
(1.585) |
Feladatunk ezután az, hogy a (1.584)–ben szereplő A, és a (1.585)–ben szereplő α konstansokat meghatározzuk. Ehhez a függvény növekményét felírjuk y(x i ) Taylor-sorával, valamint a növekmény (1.585) alakját az f(x,y) függvény kétváltozós Taylor-sorával. A kétféle alakot a h n -t tartalmazó tagokig bezárólag egyenlőnek tekintjük. Az így kapott egyenletrendszerből határozzuk meg a hiányzó konstansokat. Ebből még az is következik, hogy közelítésünk pontossága O(h n+ 1) lesz.
A továbbiakban az egyszerűség kedvéért az i indexet elhagyjuk, valamint f(x,y)-t f-el jelöljük.
Írjuk fel először a növekmény Taylor-sorát:
|
|
(1.586) |
Állítsuk elő a deriváltakat (csak a harmadikig, mert a későbbiekben csak eddig fogjuk használni):
|
|
(1.587) |
Most behelyettesítéssel a növekményre a következő alakot kapjuk:
|
|
(1.588) |
Ezután állítsuk elő a növekményben szereplő k tagokat a kétváltozós Taylor-sor
|
|
(1.589) |
alakját felhasználva, a h 3 –t tartalmazó tagokig:
|
|
(1.590) |
1.9.2.6.1. Elsőrendű Runge‑Kutta
Legyen n=1. Ekkor a növekmény két alakja:
|
|
(1.591) |
Ebből α1=1, azaz
|
|
(1.592) |
Ez az alak megegyezik az Euler‑Cauchy‑féle törtvonalmódszernél, valamint a véges differenciák módszerének legegyszerűbb változatánál használt formulával.
1.9.2.6.2. Másodrendű Runge‑Kutta
Legyen n=2. Ekkor a növekmény két alakja:
|
|
(1.593) |
Ebből a következő egyenletek adódnak:
|
. |
(1.594) |
Látható, hogy az utolsó két egyenlet megegyezik, tehát több megoldás is van. Válasszuk A2-t 1-nek, így
|
|
(1.595) |
adódik. Így a közelítő formula:
|
|
(1.596) |
Érdemes megvizsgálni milyen alakot ölt a formula akkor, ha a differenciálegyenletünk nem függ y-tól, csak x-től, azaz y’=f(x). Ekkor
|
|
(1.597) |
1.9.2.6.3. Harmadrendű Runge‑Kutta
Legyen n=3. Ekkor a növekmény két alakja (1.588) és (1.590) összefüggésekből pontosan meghatározható. Ezek alapján a következő egyenletek adódnak:
|
|
(1.598) |
Rendezés után az egyenletrendszer:
|
|
(1.599) |
Látható, hogy a 7. és a 8. egyenlet megegyezik. A 2. és a 3. egyenletből a következő új egyenletet nyerjük:
|
|
(1.600) |
Ezt behelyettesítve 5.-be és 6.-ba azt kapjuk, hogy ezek megegyeznek 4.-el. Ezek után a következő öt egyenlet marad:
|
|
(1.601) |
Mivel hét ismeretlenünk van, de csak öt egyenletünk, így két paramétert felvehetünk. Legyen A3=1. Ekkor az egyenletrendszerünk a következő alakot ölti:
|
|
(1.602) |
Végül legyen Így a megoldandó egyenletrendszer:
|
|
(1.603) |
Meghatározva a paramétereket kapjuk, hogy:
|
|
(1.604) |
A közelítő formula:
|
|
(1.605) |
1.9.2.6.4. Negyedrendű Runge‑Kutta
Már a harmadrendű Runge‑Kutta formula előállítása is meglehetősen bonyolult volt, ezért a negyedrendű előállításától tekintsünk el. Mint ahogy harmadrendűnél már láttuk, úgy itt is vannak szabadon választható paraméterek, ennek megfelelően a negyedrendű Runge‑Kutta formulának is többféle alakja állítható elő. Mivel alkalmazása igen elterjedt, ezért szerepeljen itt is a leggyakrabban alkalmazott (a legkevesebb számítást igénylő) alakja:
|
|
(1.606) |
Érdemes megvizsgálni milyen alakot ölt a formula akkor, ha a differenciálegyenletünk nem függ y-tól, csak x-től, azaz y’=f(x). Ekkor
|
|
(1.607) |
1.9.2.7. Az integrálformulák csoportosítása
Ettől a fejezettől kezdve a független változónak ismét a t-t használjuk, mert sokszor fontos lesz, hogy időben lejátszódó folyamatok vizsgálatához megfelelő formulákat keresünk, alkalmazunk.
Az előző fejezetekben néhány közelítő integrál típus származtatását láthattuk. Természetesen ezektől akár lényegesen is eltérő jellegű összefüggéseket is találhatunk különböző szakkönyvekben, de számunkra ezek lesznek később fontosak.
A csoportosítás szempontjai különbözőek lehetnek. Számunkra először az lesz lényeges, hogy hány h=Δt hosszúságú intervallumból származnak azok a pontok amelyek segítségével egy lépésnyit haladhatunk az időben! Az egyértelműség kedvéért álljanak itt sorban a harmadrendű alakok:
|
Simpson |
|
|
harmadrendű Adams-Bashforth |
|
|
harmadrendű Adams-Moulton |
|
|
harmadrendű Runge-Kutta |
A Simpson formula kilóg a sorból, mert az integrálási intervalluma kétszeres hosszúságú a többiekhez képest, de könnyedén átalakíthatjuk a következőképpen:
|
|
(1.610) |
Egylépéses formulák nak nevezzük azokat, amelyek csak egy Δt hosszúságú intervallumból veszik az értéket az integrál közelítéséhez. Ebbe természetesen beleértjük azt is, ha a jobb illesztés miatt az intervallum belső pontjait is figyelembe veszik. A fenti táblázatból könnyedén kiolvasható, hogy ilyen a Simpson, és a harmadrendű Runge-Kutta. Általánosan elmondható, hogy egylépésesek a szimmetrikus-, és a Runge-Kutta féle formulák. A másik két csoport a többlépéses integrátorok csoportjába tartozik, bár legegyszerűbb eseteik – az elsőrendű Adams-Bashforth (1.551), az elsőrendű Adams-Moulton (1.573) és a másodrendű Adams‑Moulton (1.576) – az egylépéses formulák szabályainak is megfelel!
Összefoglalva:
|
Egylépéses |
Többlépéses |
|---|---|
|
Szimmetrikus |
Adams-Bashforth |
|
Runge-Kutta |
Adams-Moulton |
A szimulációk során előfordulhatnak olyan esetek is, amikor a leíró differenciálegyenlet, vagy annak egyes részei nem állnak rendelkezésünkre analitikus formában, mert például adott mintavételezési idővel készített mérés eredményein alapulnak. Ekkor nem, vagy csak nehézkesen (pl. interpolációval kiegészítve) alkalmazhatók azok az összefüggések, amelyek az intervallumok belső pontjaira is építenek. Ennek megfelelően készült a következő táblázat:
|
Folytonos |
Mintavételes |
|---|---|
|
Szimmetrikus |
Adams-Bashforth |
|
Runge-Kutta |
Adams-Moulton |
Az időben lejátszódó folyamatok vizsgálatánál fontos szempont az is, hogy az integrálási módszer használ-e a időponthoz képest „újabb” értékeket is. Folytonos esetben ez nem szokott gondot okozni, mintavételes esetekben azonban igen, hiszen az összefüggés által megkívánt érték még nem áll a rendelkezésünkre!
|
Csak jelen és múlt |
Jövő is |
|---|---|
|
Adams-Bashforth |
Szimmetrikus |
|
Adams-Moulton |
|
|
Runge-Kutta |
1.10. Differenciálegyenletek numerikus megoldása
A következőkben példákon keresztül mutatunk be néhány megoldási lehetőséget. A közölt módszerek egyaránt alkalmazhatók lineáris és nemlineáris rendszerek esetén is. Az alkalmazott integrálási metódusoknak megfelelően lehet majd eldönteni, hogy az adott módszer alkalmas-e mintavételes rendszer esetén is, vagy csak folytonosnál használható!
A megoldások lépéseit minden esetben táblázatos formában közöljük, és ahol szükséges a számítási sorrendet nyilak fogják mutatni. Ezek a táblázatok bármilyen táblázatkezelővel létrehozhatók, és a számításokat el lehet végeztetni. Természetesen, ha sok időlépésre van szükségünk, akkor korlátokba ütközhetünk, mivel egy időlépés általában egy sornak felel meg.
Nézzük milyen eszközök, értékek állnak rendelkezésünkre a megoldás elkészítéséhez. Első lépésként minden esetben szükségünk van a leíró differenciálegyenletre, amely például a következő alakú:
|
, ahol k=0…n és j=0…m |
(1.611) |
Ezt írjuk fel úgy, hogy a legmagasabb rendű deriváltat fejezzük ki:
|
ahol l=0…n-1 |
(1.612) |
Egy differenciálegyenlet felfogható egy adott pillanatban/helyzetben igaz egyenletnek is, tehát
|
, |
(1.613) |
illetve
|
|
(1.614) |
Minden differenciálegyenletben szerepel az ismeretlen függvény deriváltja, amely és a függvény közti kapcsolatot integrálással lehet megteremteni.
A megoldáshoz tehát rendelkezésre állnak:
-
differenciálegyenlet(ek),
-
integrálási formulák,
-
kezdeti feltétel(ek).
A kezdeti feltételek olyanok, hogy egy híján megadják az ismeretlen függvény, és deriváltjai kezdeti értékeit. Ezt a differenciálegyenlet megfelelő átalakításával könnyedén meghatározhatjuk:
|
ahol l=0…,kf-1,kf+1,…,n |
(1.615) |
Általában az ismeretlen kezdeti érték a legmagasabb derivált értéke, így még külön számításra sincs szükségünk, használhatjuk (1.612)-t. Most még valami olyan kellene, ami -et, illetve ugyanezen időponthoz tartozó deriváltjait előállítja. Ha megnézzük az integrál formulákat, akkor azt látjuk, hogy éppen ilyen, vagy ilyen alakúvá tehetők (lásd (1.610)-t). Ezek segítségével tudjuk a következő időpillanathoz tartozó értékeket meghatározni. Ha ez így még nem érthető, akkor a feladatok mindenképpen segíteni fognak, csak akkor majd vissza kell ide térni, és értelmezni az egyes lépéseket.
Az első feladat modellje egy nemlineáris elsőrendű differenciálegyenlet lesz:
adva van egy nyitott tartály, amelyből az alján elhelyezett csövön keresztül folyik ki a folyadék. A tartály keresztmetszete mindenhol állandó, legyen A. Feladatunk a tartályban a folyadékszint változásának nyomon követése (az aktuális folyadékszint meghatározása) a folyamat során. Veszteségmentes szabad kifolyás esetén a kiömlő folyadék sebessége: , ahol h a folyadék szint magassága a tartályban. A kiáramló folyadék mennyisége Δt alatt:, ahol d a cső átmérője. Amennyiben a tartályt egy „nagyon vastag” csőnek tekintjük, akkor a tartályra felírható összefüggés itt is sebesség*keresztmetszet*Δt, így a tároló folyadékszintjének változása Δt alatt:, ahol a folyadékszint változásának sebessége. A felírható differenciálegyenlet tehát előjelesen:
|
, |
(1.616) |
A kezdeti feltétel pedig: h(0)=h 0 . A numerikus számításokat a következő adatokkal fogjuk elvégezni: d=5 cm= 0,05 m; A=1 m2; h 0 =10 m.
Az analitikus megoldás:
|
|
(1.617) |
azaz
|
|
(1.618) |
A második feladat modellje egy állandó-együtthatós-, másodrendű-, inhomogén-, közönséges differenciálegyenlet lesz:
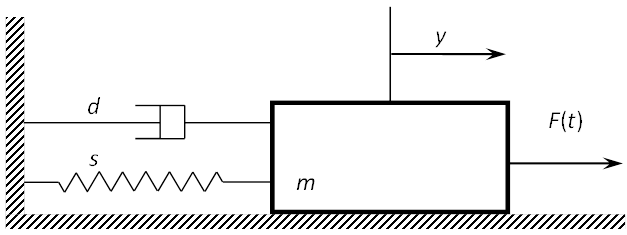
Határozzuk meg az ábrán látható egytömegű gerjesztett rendszer mozgását leíró jellemzők értékeit. A rendszert leíró differenciálegyenlet a következő:
|
|
(1.619) |
A numerikus számításokat a következő adatokkal fogjuk elvégezni:
.
Az analitikus megoldás (magyarázatok nélkül, csak a főbb lépéseket megadva):
|
|
(1.620) |
1.10.1. Megoldás negyedrendű Runge-Kutta módszerrel
1.10.1.1. Tartályos feladat megoldása (Runge-Kutta módszerrel)
A leíró egyenlet éppen olyan alakra van rendezve, ahogy nekünk szükséges, azaz a legmagasabb rendű derivált van kifejezve. Mindenféle magyarázkodás helyett álljon itt az algoritmust leíró táblázat, amely a számításokat soronként, azon belül balról jobbra kell elvégezni, és ha valamilyen érték még nem áll rendelkezésünkre (pl. k 1 h 1 meghatározásakor), akkor az előző sorban lévő értéket használjuk.
Mintapélda:
|
idő |
h |
k 1 |
k 2 |
k 3 |
k 4 |
|
|---|---|---|---|---|---|---|
Táblázatkezelővel Δt= 1 [s] esetén:
|
idő |
h |
hp |
k1 |
k2 |
k3 |
k4 |
pontos |
különbs. |
|---|---|---|---|---|---|---|---|---|
|
0 |
10 |
-0,028 |
-0,028 |
-0,027 |
-0,027 |
-0,027 |
10 |
0 |
|
1 |
9,9725 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,9725 |
0 |
|
2 |
9,9451 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,9451 |
0 |
|
3 |
9,9177 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,9177 |
0 |
|
4 |
9,8903 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,8903 |
0 |
|
5 |
9,863 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,863 |
0 |
|
6 |
9,8357 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,8357 |
-1E-14 |
|
7 |
9,8084 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,8084 |
-2E-14 |
|
8 |
9,7812 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,7812 |
-2E-14 |
|
9 |
9,754 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,754 |
-2E-14 |
|
10 |
9,7269 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,7269 |
-2E-14 |
|
11 |
9,6998 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
-0,027 |
9,6998 |
-3E-14 |
Mint látható, a közelítésünk rendkívül pontos lett. Ennek az az oka, hogy a pontos megoldás egy másodfokú polinom, a Runge-Kutta módszer pedig (a származtatása miatt) a legfeljebb harmadfokú megoldásokat pontosan követi!
1.10.1.2. Rezgő rendszer megoldása(Runge-Kutta módszerrel)
A Runge-Kutta módszerek alapvetően elsőrendű differenciálegyenletekre lettek kidolgozva, de szerencsére alkalmazhatók egyenletrendszerek esetén is. Esetünkben tehát át kell írni az egyenletet egyenletrendszerré[2].
Mintapélda:
Vezessük be a következő új változókat:
|
|
(1.621) |
Ezek felhasználásával az egyenletrendszer és a kezdeti feltételek a következőképpen írhatók fel:
|
|
(1.622) |
vagy mátrixos alakban:
|
|
(1.623) |
A könnyebb áttekinthetőség kedvéért álljon itt a negyedrendű Runge-Kutta formula időtől függő, egyenletrendszerre érvényes, az itteni jelöléseknek megfelelő változata:
|
|
(1.624) |
Foglaljuk össze a számítás menetét táblázatban is. A vektorok, és az egyenlet mérete miatt csak két részben fér el a táblázat, és ezért, valamint a könnyebb beazonosíthatóság miatt a cellákba indexelve beírtam a változókat.
Az indexek jelentése:
-
utolsó: megegyezik az idő indexével, azaz ennyiedik Δt intervallumban vagyunk,
-
utolsó előtti: a vektor index, csak 1 vagy 2 lehet
-
k esetén az első: 1, 2, 3 vagy 4.
|
idő |
||||
|
idő |
||||
A táblázat alapján a számítások most is elvégezhetők tetszőleges táblázatkezelővel. Legyen a lépésköz Δt=0,1s. Az y és yp oszlopban a pontos értékek vannak, ezeket kell összevetni x‑el és xp-vel. Az utolsó két oszlop a különbségeket mutatja a pontos és a közelítő számítás között. Mint látható, itt sokkal nagyobb (bár még mindig elfogadható) az eltérés, mint a tartályos feladatnál.
|
idő |
vektor index |
x |
xp |
k1 |
k2 |
k3 |
k4 |
y |
yp |
kül y |
kül yp |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
0 |
1 |
0 |
0 |
0 |
0,013 |
0,011 |
0,023 |
0 |
0 |
0 |
0 |
|
0 |
2 |
0 |
10 |
0,5 |
0,45 |
0,453 |
0,406 |
||||
|
0,05 |
1 |
0,012 |
0,452 |
0,023 |
0,033 |
0,032 |
0,041 |
0,012 |
0,452 |
-3,7E-07 |
-1,1E-07 |
|
0,05 |
2 |
0,452 |
8,119 |
0,406 |
0,362 |
0,365 |
0,323 |
||||
|
0,1 |
1 |
0,044 |
0,816 |
0,041 |
0,049 |
0,048 |
0,055 |
0,044 |
0,816 |
-7,4E-07 |
3,5E-08 |
|
0,1 |
2 |
0,816 |
6,464 |
0,323 |
0,285 |
0,287 |
0,251 |
||||
|
0,15 |
1 |
0,092 |
1,102 |
0,055 |
0,061 |
0,061 |
0,066 |
0,092 |
1,102 |
-1,1E-06 |
3,5E-07 |
|
0,15 |
2 |
1,102 |
5,018 |
0,251 |
0,217 |
0,22 |
0,188 |
||||
|
0,2 |
1 |
0,153 |
1,321 |
0,066 |
0,071 |
0,07 |
0,074 |
0,153 |
1,321 |
-1,4E-06 |
7,9E-07 |
|
0,2 |
2 |
1,321 |
3,763 |
0,188 |
0,159 |
0,161 |
0,134 |
||||
|
0,25 |
1 |
0,223 |
1,481 |
0,074 |
0,077 |
0,077 |
0,08 |
0,223 |
1,481 |
-1,7E-06 |
1,3E-06 |
|
0,25 |
2 |
1,481 |
2,682 |
0,134 |
0,109 |
0,111 |
0,088 |
||||
|
0,3 |
1 |
0,3 |
1,591 |
0,08 |
0,082 |
0,081 |
0,083 |
0,3 |
1,591 |
-2E-06 |
1,9E-06 |
|
0,3 |
2 |
1,591 |
1,759 |
0,088 |
0,067 |
0,068 |
0,049 |
||||
|
0,35 |
1 |
0,381 |
1,659 |
0,083 |
0,084 |
0,084 |
0,085 |
0,381 |
1,659 |
-2,2E-06 |
2,4E-06 |
|
0,35 |
2 |
1,659 |
0,978 |
0,049 |
0,031 |
0,033 |
0,016 |
||||
|
0,4 |
1 |
0,465 |
1,691 |
0,085 |
0,085 |
0,085 |
0,085 |
0,465 |
1,691 |
-2,4E-06 |
2,9E-06 |
|
0,4 |
2 |
1,691 |
0,326 |
0,016 |
0,001 |
0,003 |
-0,01 |
||||
|
0,45 |
1 |
0,55 |
1,694 |
0,085 |
0,084 |
0,084 |
0,084 |
0,55 |
1,694 |
-2,5E-06 |
3,4E-06 |
|
0,45 |
2 |
1,694 |
-0,21 |
-0,01 |
-0,02 |
-0,02 |
-0,03 |
1.10.2. Megoldás másodrendű Adams-Bashforth integrátorokkal
Ezeket a módszereket extrapolációs módszereknek is szokás nevezni.
A feladatokat a másodrendű Adams-Bashforth integrál formula felhasználásával szeretnénk megoldani. A megoldás menetéről már volt szó az 1.10. szakasz fejezet elején. Az eddigiekhez az ott leírtak elegendőek voltak, most azonban más a
helyzet, mert az extrapolációs (és az interpolációs) módszerek nem önindítók ! Mit is jelent ez? A gondot az okozza, hogy kezdetben (a számítások „elindításánál”) csak a kezdeti értéket ismerjük, a többlépéses módszerek azonban több pontra illesztett interpolációs polinomból származnak, így egynél több értékre van szükségük. A megoldás az, hogy az első időlépésnél a „legegyszerűbb” extrapolációs módszert alkalmazzuk, ez a jól ismert téglány szabály. Lépésről - lépésre emeljük az interpolációs pontok számát, hiszen mindig eggyel több pont áll rendelkezésünkre.
A módszer hátránya, hogy a kezdeti pontatlanabb közelítés miatt viszonylag nagy hibával kezdjük a közelítést. Ezen probléma megoldására több eljárás is létezik.
A teljesség igénye nélkül nézzünk néhány gyakrabban használtat [14.] :
-
az első Δt hosszú időlépést két Δt/2 hosszúságúra bontjuk, majd így kezdjük el a számítást. A hibatagokban Δt hatványai szerepelnek, így a felezéssel az un. képlethibát csökkentjük. (lehet kissebeket is lépni, de általában nem érdemes)
-
az első lépéseknél egylépéses formulát (pl. Runge-Kutta) használunk. Ha számítógép programot készítünk a szimulációs számítások elvégzésére, akkor joggal merül fel, hogyha már megírtuk az egylépéses módszerhez az eljárást, akkor számoljunk így is tovább! Az esetek többségében a programok (kényelmi okokból) így is tesznek, bár a többlépéses módszerek számítási igénye azonos pontosság esetén kisebb.
A következő példákban nem használunk ilyen finomításokat, elfogadjuk, hogy az indítás hibákkal terhelt!
Az algoritmus extrapolációs esetben a következő lépésekből áll:
-
a differenciálegyenletből kifejezzük az ismeretlen kezdeti értékű mennyiséget, és meghatározzuk (a táblázat első sora kész)
-
kifejezzük a legmagasabb rendű deriváltat, legyen ez az n.
-
közelítő integrálással meghatározzuk az n-1. deriváltat a táblázat előző soraira támaszkodva,
-
hasonlóképpen meghatározzuk az n-2. deriváltat, és így tovább, egészen a nullad rendűig
-
meghatározzuk a legmagasabb rendű derivált értékét, és ezzel kész ez a sor is, tehát léptünk az időben Δt-t
a c) ponttól folytatjuk ciklikusan, amíg a kívánt időpontig, eseményig el nem jutunk
1.10.2.1. Tartályos feladat megoldása (Adams-Bashforth integrátorokkal)
Mintapélda:
Az előzőek alapján leírt algoritmus alapján készült el a következő táblázat, ahol a nyilak a számítási sorrendet mutatják:
|
idő |
h |
|
|---|---|---|
Táblázatkezelővel Δt= 1 [s] esetén:
|
idő |
h |
hp |
pontos |
különbség |
|---|---|---|---|---|
|
0 |
10 |
-0,0275 |
10 |
0 |
|
1 |
9,9725 |
-0,02746 |
9,9725 |
1,89E-05 |
|
2 |
9,9451 |
-0,02743 |
9,9451 |
1,89E-05 |
|
3 |
9,9176 |
-0,02739 |
9,9177 |
1,88E-05 |
|
4 |
9,8903 |
-0,02735 |
9,8903 |
1,88E-05 |
|
5 |
9,8629 |
-0,02731 |
9,863 |
1,88E-05 |
|
6 |
9,8357 |
-0,02727 |
9,8357 |
1,88E-05 |
|
7 |
9,8084 |
-0,02724 |
9,8084 |
1,87E-05 |
|
8 |
9,7812 |
-0,0272 |
9,7812 |
1,87E-05 |
|
9 |
9,754 |
-0,02716 |
9,754 |
1,87E-05 |
|
10 |
9,7269 |
-0,02712 |
9,7269 |
1,87E-05 |
|
11 |
9,6998 |
-0,02708 |
9,6998 |
1,86E-05 |
A közelítésünk sokkal pontatlanabb, mint a Runge-Kutta módszer esetén volt, de ez természetes is, hiszen negyedrendű módszert hasonlítunk másodrendűhöz. Ha azonban azt vizsgáljuk, hogy elegendően pontos-e ez is, akkor arra a következtetésre juthatunk, hogy nagyon is, hiszen egy 10 m magas folyadékoszlop esetén az eltérés kisebb, mint 0,02 mm! A táblázat méretéből is látszik, hogy mindezt az eredményt sokkal kevesebb számítással értük el!
1.10.2.2. Rezgő rendszer megoldása (Adams-Bashforth integrátorokkal)
Mintapélda:
Az algoritmust most is foglaljuk táblázatba:
|
idő |
|||
|---|---|---|---|
Táblázatkezelővel Δt= 0,01 [s] esetén:
|
idő |
y |
yp |
ypp |
pontos y |
pontos yp |
pontos ypp |
kül y |
kül yp |
|---|---|---|---|---|---|---|---|---|
|
0 |
0 |
0 |
10 |
0 |
0 |
10 |
0 |
0 |
|
0,01 |
0 |
0,1 |
9,6 |
0,0005 |
0,098 |
9,6049 |
0,0005 |
-0,002 |
|
0,02 |
0,0015 |
0,194 |
9,2146 |
0,0019 |
0,1921 |
9,2193 |
0,0004 |
-0,002 |
|
0,03 |
0,0039 |
0,2842 |
8,8387 |
0,0043 |
0,2824 |
8,8432 |
0,0004 |
-0,002 |
|
0,04 |
0,0072 |
0,3707 |
8,4721 |
0,0076 |
0,369 |
8,4765 |
0,0004 |
-0,002 |
|
0,05 |
0,0113 |
0,4536 |
8,1146 |
0,0117 |
0,452 |
8,1189 |
0,0003 |
-0,002 |
|
0,06 |
0,0163 |
0,533 |
7,7663 |
0,0166 |
0,5314 |
7,7704 |
0,0003 |
-0,002 |
|
0,07 |
0,022 |
0,6089 |
7,4268 |
0,0223 |
0,6074 |
7,4308 |
0,0003 |
-0,001 |
|
0,08 |
0,0285 |
0,6815 |
7,0961 |
0,0287 |
0,6801 |
7,1 |
0,0003 |
-0,001 |
A közelítés most is pontatlanabb, még akkor is, ha a lépésközt kisebbre választottuk, mint a Runge-Kutta módszer esetén. Megállapíthatjuk azonban, hogy az eltérés nem nő, azaz a nagyobb hiba fő oka az első lépéskörüli pontatlanságokból adódott. Mint már szó volt róla, ennek a hibának a csökkentésére több lehetőség is van, ezek közül nézzük meg a kezdeti intervallum csökkentés hatását:
|
idő |
y |
yp |
ypp |
pontos y |
pontos yp |
pontos ypp |
kül y |
kül yp |
|---|---|---|---|---|---|---|---|---|
|
0 |
0 |
0 |
10 |
0 |
0 |
10 |
0 |
0 |
|
0,005 |
0 |
0,05 |
9,8 |
1E-04 |
0,05 |
9,801 |
0,0001 |
-5E-04 |
|
0,01 |
4E-04 |
0,099 |
9,604 |
5E-04 |
0,098 |
9,605 |
0,0001 |
-5E-04 |
|
0,02 |
0,002 |
0,193 |
9,218 |
0,002 |
0,192 |
9,219 |
9E-05 |
-4E-04 |
|
0,03 |
0,004 |
0,283 |
8,842 |
0,004 |
0,282 |
8,843 |
7E-05 |
-4E-04 |
|
0,04 |
0,008 |
0,369 |
8,476 |
0,008 |
0,369 |
8,477 |
6E-05 |
-3E-04 |
|
0,05 |
0,012 |
0,452 |
8,118 |
0,012 |
0,452 |
8,119 |
4E-05 |
-3E-04 |
A két táblázat összehasonlításából is látszik, hogy a hiba jelentősen csökkent.
1.10.3. Megoldás másodrendű Adams-Moulton integrátorokkal
Ezeket a módszereket interpolációs módszereknek is szokás nevezni [10.] , [14.] . A megoldás menete során itt is jelentkezik az önindítás problémája, amit az előző fejezetben leírt módszerrel (eleinte alacsonyabb rendű, majd lépésről-lépésre egyre magasabb rendű formulákat alkalmazunk) tudunk kezelni. Ennél nagyobb gondot okoz azonban az, hogy az integrál formula egy „jövőbeli” azaz i+1 indexű elemet is tartalmaz, amit még nem ismerünk. Ha az előző fejezetben leírt gondolatmenetet alkalmazzuk, akkor egy egyenletrendszert kell megoldanunk minden iterációs lépés során. Ez az egyenletrendszer a következőképpen néz ki másodrendű formulák esetén:
|
|
(1.625) |
Mint látható, n+1 darab egyenletünk van n+1 ismeretlenhez. Ha az egyenlet lineáris, akkor az egyenletrendszer lineáris, különben nem. Lineáris egyenletrendszer esetén biztosan, ellenkező esetben pedig csak ritkán tudunk általános megoldást előállítani. Ha nem sikerül zárt alakban meghatározni a megoldást, akkor csak általános, numerikus megoldások jöhetnek szóba. Ebben az esetben nem szokás ezt az interpolációs módszert alkalmazni, mert (mint majd látni is fogjuk) ugyan jóval pontosabb, mint az extrapolációs, de sokkal nagyobb a számítás igényel!
1.10.3.1. Tartályos feladat megoldása (Adams-Moulton integrátorokkal)
Mintapélda:
A feladatunk most egy nemlineáris eset vizsgálata, de szerencsére csak elsőrendű a differenciálegyenlet, így két egyenletből fog állni csak az egyenletrendszer:
|
|
(1.626) |
A következőkben nézzük a megoldást, magyarázatok nélkül:
|
|
(1.627) |
A differenciálegyenletből látszik, hogy , mivel K is és is pozitív. A gyökjel alatt négyzeténél nagyobb érték van, tehát ha a ±-ból a kivonást választjuk, az eredmény biztosan nem lesz pozitív. Ezek után következzen a szokásos táblázat:
|
idő |
h |
|
|---|---|---|
A táblázatból látszik, hogy másodrendű integrál formulák esetén az önindítás problémája nem lép fel.
A közelítő számításokat most is 1 másodperces lépésközzel végeztük el. A következő táblázat tartalmazza az eredményeket. Mint látható, a közelítés kimutatható hiba nélkül adja az analitikus megoldás alapján számított értékeket:
|
idő |
h |
hp |
pontos |
különbség. |
|---|---|---|---|---|
|
0 |
10 |
-0,0275 |
10 |
0 |
|
1 |
9,9725 |
-0,02746 |
9,9725 |
0 |
|
2 |
9,9451 |
-0,02743 |
9,9451 |
0 |
|
3 |
9,9177 |
-0,02739 |
9,9177 |
0 |
|
4 |
9,8903 |
-0,02735 |
9,8903 |
0 |
|
5 |
9,863 |
-0,02731 |
9,863 |
0 |
|
6 |
9,8357 |
-0,02727 |
9,8357 |
0 |
|
7 |
9,8084 |
-0,02724 |
9,8084 |
0 |
|
8 |
9,7812 |
-0,0272 |
9,7812 |
0 |
1.10.3.2. Rezgő rendszer megoldása (Adams-Moulton integrátorokkal)
Mintapélda:
Mivel a rendszert leíró differenciálegyenlet másodrendű, három egyenletünk lesz. A rendszer lineáris, az együtthatók állandók, így az egyenletrendszer is lineáris lesz:
|
|
(1.628) |
A megoldást a Maxima nevű programmal elvégezve:
|
|
(1.629) |
Táblázatos összefoglalásra most nincs is szükség, hiszen az eredmények pontosan egy‑egy sort jelentenek. A számításokat – hogy az összehasonlítás egyszerűbb legyen – itt is 0,01 másodperces lépésközzel végeztük el, mint az Adams-Bashforth integrál formulák esetén:
|
idő |
y |
yp |
ypp |
pontos y |
pontos yp |
pontos ypp |
kül y |
kül yp |
|---|---|---|---|---|---|---|---|---|
|
0 |
0 |
0 |
10 |
0 |
0 |
10 |
0 |
0 |
|
0,01 |
0,00049 |
0,098024 |
9,60484 |
0,000493 |
0,098016 |
9,604852 |
3,25E-06 |
-8E-06 |
|
0,02 |
0,001941 |
0,192145 |
9,21929 |
0,001947 |
0,192129 |
9,219313 |
6,35E-06 |
-1,6E-05 |
|
0,03 |
0,004314 |
0,282457 |
8,843208 |
0,004323 |
0,282434 |
8,843244 |
9,29E-06 |
-2,3E-05 |
|
0,04 |
0,007572 |
0,369056 |
8,476455 |
0,007584 |
0,369025 |
8,476502 |
1,21E-05 |
-3,1E-05 |
|
0,05 |
0,011677 |
0,452032 |
8,118889 |
0,011692 |
0,451995 |
8,118948 |
1,47E-05 |
-3,8E-05 |
|
0,06 |
0,016595 |
0,531479 |
7,770369 |
0,016612 |
0,531434 |
7,77044 |
1,72E-05 |
-4,5E-05 |
|
0,07 |
0,022289 |
0,607484 |
7,430754 |
0,022309 |
0,607433 |
7,430837 |
1,96E-05 |
-5,1E-05 |
|
0,08 |
0,028727 |
0,680138 |
7,099903 |
0,028749 |
0,68008 |
7,099997 |
2,18E-05 |
-5,7E-05 |
|
0,09 |
0,035876 |
0,749525 |
6,777675 |
0,0359 |
0,749462 |
6,77778 |
2,38E-05 |
-6,4E-05 |
|
0,1 |
0,043702 |
0,815733 |
6,463928 |
0,043728 |
0,815664 |
6,464045 |
2,58E-05 |
-7E-05 |
Az eredmények összevetéséből látható, hogy az extrapolációs módszernél sokkal pontosabb, a Runge-Kutta azonban itt is kisebb hibával dolgozik, bár ismét fel kell hívnunk a figyelmet, hogy az negyedrendű módszer!
1.10.4. Megoldás másodrendű prediktor – korrektor módszerrel
Mindkét előző módszernek vannak előnyei és hátrányai. Az extrapolációs módszer könnyen megvalósítható, csak az önindítással van gond, az interpolációs pedig pontos, csak sokkal munkaigényesebb. Próbáljuk meg a kettőt együtt használni! Az interpolációs módszernél az volt a gond, hogy a következő időpillanatbeli értékre volt szüksége (i+1), az extrapolációs pedig éppen azt állítja elő. Ha most kétszer integrálunk, azaz először az extrapolációssal megbecsüljük a következő értéket ( prediktor ), majd ezt felhasználva az interpolációssal pontosítunk ( korrektor ), és így egy jobb közelítő értéket kapunk. A módszer tovább javítható úgy, hogy a korrektorral iterációt végzünk [11.] . Ez néha abszolút pontos eredményt szolgáltat (ilyen a tartályos feladatunk), máskor azonban nem tud lényegesen javítani (ezt láthatjuk a rezgő rendszer esetében).
1.10.4.1. Tartályos feladat megoldása (másodrendű prediktor – korrektor módszerrel)
Mintapélda:
A fentiek alapján ismét összeállíthatunk egy táblázatot, ahol a p és c felsőindexek a prediktort, illetve a korrektort jelzik:
|
idő |
h |
|||||
|---|---|---|---|---|---|---|
A számításokat ismét 1 másodperces lépésközzel végeztük el, így az eredmények:
|
idő |
h |
hp |
hp |
hpp |
hc |
hcp |
pontos |
különbség |
|---|---|---|---|---|---|---|---|---|
|
0 |
10 |
-0,028 |
10 |
0 |
||||
|
1 |
9,9725 |
-0,027 |
9,972 |
-0,027 |
9,9725 |
-0,027 |
9,97252 |
-1E-08 |
|
2 |
9,9451 |
-0,027 |
9,945 |
-0,027 |
9,9451 |
-0,027 |
9,94507 |
-3E-08 |
|
3 |
9,9177 |
-0,027 |
9,918 |
-0,027 |
9,9177 |
-0,027 |
9,91767 |
-4E-08 |
|
4 |
9,8903 |
-0,027 |
9,89 |
-0,027 |
9,8903 |
-0,027 |
9,8903 |
-5E-08 |
|
5 |
9,863 |
-0,027 |
9,863 |
-0,027 |
9,863 |
-0,027 |
9,86297 |
-7E-08 |
|
6 |
9,8357 |
-0,027 |
9,836 |
-0,027 |
9,8357 |
-0,027 |
9,83568 |
-8E-08 |
|
7 |
9,8084 |
-0,027 |
9,808 |
-0,027 |
9,8084 |
-0,027 |
9,80842 |
-9E-08 |
|
8 |
9,7812 |
-0,027 |
9,781 |
-0,027 |
9,7812 |
-0,027 |
9,7812 |
-1E-07 |
|
9 |
9,754 |
-0,027 |
9,754 |
-0,027 |
9,754 |
-0,027 |
9,75402 |
-1E-07 |
Ugyanezen módszerrel, de a korrektor eredményeit újra felhasználva pontosabb eredményt kapunk:
|
idő |
h |
hp |
hp |
hpp |
hc |
hcp |
hc2 |
hc2p |
pontos |
különbs. |
|---|---|---|---|---|---|---|---|---|---|---|
|
0 |
10 |
-0,0275 |
10 |
0 |
||||||
|
1 |
9,97252 |
-0,0275 |
9,9725 |
-0,0275 |
9,97252 |
-0,0275 |
9,97252 |
-0,0275 |
9,97252 |
8,962E-12 |
|
2 |
9,94507 |
-0,0274 |
9,9451 |
-0,0274 |
9,94507 |
-0,0274 |
9,94507 |
-0,0274 |
9,94507 |
1,791E-11 |
|
3 |
9,91767 |
-0,0274 |
9,9177 |
-0,0274 |
9,91767 |
-0,0274 |
9,91767 |
-0,0274 |
9,91767 |
1,789E-11 |
|
4 |
9,8903 |
-0,0273 |
9,8903 |
-0,0273 |
9,8903 |
-0,0273 |
9,8903 |
-0,0273 |
9,8903 |
1,786E-11 |
Ez utóbbi táblázatot nem azért számoltuk ki, mert az előző pontossága nem volt elegendő, hanem csak azért, hogy igazoljuk azon állításunkat, hogy így pontosabb eredményt kapunk. Az iterációt folytatva a hiba nagyságrendje 10-16 lesz, ami megegyezik a legelterjedtebb lebegőpontos számtípus – a double – számábrázolási pontosságával.
1.10.4.2. Rezgő rendszer megoldása (másodrendű prediktor – korrektor módszerrel)
Mintapélda:
Az előzőhöz hasonlóan most is az Adams-Bashforth szerint kezdünk, majd Adams‑Molutonnal pontosítunk. A táblázat nem férne el a szokásos formájában, ezért transzponáljuk:
|
idő |
… |
|||
|---|---|---|---|---|
|
… |
||||
|
… |
||||
|
… |
||||
|
… |
||||
|
… |
||||
|
… |
||||
|
… |
||||
|
… |
||||
|
… |
A számításokat – hogy az összehasonlítás egyszerűbb legyen – itt is 0,01 másodperces lépésközzel végeztük el, mint az Adams-Bashforth integrál formulák esetén:
|
idő |
pontos |
pontos |
pontos |
kül |
kül |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
0 |
0 |
0 |
10 |
0 |
0 |
10 |
0 |
0 |
||||||
|
0,01 |
0 |
0,1 |
9,6 |
0,0005 |
0,098 |
9,605 |
0,0005 |
0,098 |
9,605 |
0,00049 |
0,098016 |
9,6048516 |
-6,6E-06 |
1,6E-05 |
|
0,02 |
0,002 |
0,192 |
9,219 |
0,002 |
0,192 |
9,219 |
0,002 |
0,192 |
9,219 |
0,00195 |
0,192129 |
9,219313 |
-3,1E-06 |
7,7E-06 |
|
0,03 |
0,0043 |
0,282 |
8,843 |
0,0043 |
0,282 |
8,843 |
0,0043 |
0,282 |
8,843 |
0,00432 |
0,282434 |
8,8432435 |
3,6E-07 |
-5E-07 |
|
0,04 |
0,0076 |
0,369 |
8,477 |
0,0076 |
0,369 |
8,476 |
0,0076 |
0,369 |
8,476 |
0,00758 |
0,369025 |
8,4765023 |
3,6E-06 |
-9E-06 |
|
0,05 |
0,0117 |
0,452 |
8,119 |
0,0117 |
0,452 |
8,119 |
0,0117 |
0,452 |
8,119 |
0,01169 |
0,451995 |
8,1189482 |
6,7E-06 |
-2E-05 |
|
0,06 |
0,0166 |
0,531 |
7,77 |
0,0166 |
0,531 |
7,77 |
0,0166 |
0,531 |
7,77 |
0,01661 |
0,531434 |
7,77044 |
9,6E-06 |
-2E-05 |
|
0,07 |
0,0223 |
0,607 |
7,431 |
0,0223 |
0,607 |
7,431 |
0,0223 |
0,607 |
7,431 |
0,02231 |
0,607433 |
7,4308367 |
1,2E-05 |
-3E-05 |
|
0,08 |
0,0288 |
0,68 |
7,1 |
0,0287 |
0,68 |
7,1 |
0,0287 |
0,68 |
7,1 |
0,02875 |
0,68008 |
7,0999969 |
1,5E-05 |
-4E-05 |
|
0,09 |
0,0359 |
0,749 |
6,778 |
0,0359 |
0,75 |
6,778 |
0,0359 |
0,75 |
6,778 |
0,0359 |
0,749462 |
6,7777799 |
1,8E-05 |
-5E-05 |
|
0,1 |
0,0437 |
0,816 |
6,464 |
0,0437 |
0,816 |
6,464 |
0,0437 |
0,816 |
6,464 |
0,04373 |
0,815664 |
6,464045 |
2E-05 |
-5E-05 |
Az eredmények összevetése után azt állapíthatjuk meg, hogy körülbelül az interpolációs módszer pontosságát hozza. Ha az iterációt tovább folytatnánk, akkor itt nem lenne olyan látványos további javulás mint a tartályos feladatnál, a hiba csak kb. feleződne.
1.10.5. Megoldás másodrendű vegyes módszerrel
Mintapélda:
A következő módszer csak másod-, vagy magasabb rendű differenciálegyenletek esetén alkalmazható, mert legalább kétszeri integrálást feltételez. Nem igényel semmilyen előkészületet hasonlóan az extrapolációs módszerhez, mivel annak továbbfejlesztett változata. Lényege, hogy az első integrálás mindig Adams-Bashforth, a második, harmadik, stb., pedig Adams-Moulton. Azért van lehetőség erre, mert az Adams-Bashforth már előállítja az Adams‑Moulton számára szükséges i+1. értéket [9.] . Nézzük mindezt táblázatos formában:
|
idő |
|||
|---|---|---|---|
Az előzőekben már láttuk, hogy az interpolációs módszereknél az indításkor viszonylag nagy hibát szedünk össze, mert csak elsőrendű formulával kezdhetünk. Vannak módszerek, amelyekkel ezen lehet javítani, de számításigényesek. Esetünkben a második integráltól kezdve már egy pontosabb, másodrendű formulát tudunk alkalmazni. Nézzük ezek után a számításokat táblázatosan is:
|
idő |
y |
yp |
ypp |
pontos y |
pontos yp |
pontos ypp |
kül y |
kül yp |
|---|---|---|---|---|---|---|---|---|
|
0 |
0 |
0 |
10 |
0 |
0 |
10 |
0 |
0 |
|
0,01 |
0,0005 |
0,1 |
9,596875 |
0,000493 |
0,098016 |
9,604852 |
-7E-06 |
-0,002 |
|
0,02 |
0,00197 |
0,194 |
9,211876 |
0,001947 |
0,192129 |
9,219313 |
-2E-05 |
-0,002 |
|
0,03 |
0,00436 |
0,284 |
8,836161 |
0,004323 |
0,282434 |
8,843244 |
-4E-05 |
-0,002 |
|
0,04 |
0,00763 |
0,371 |
8,469767 |
0,007584 |
0,369025 |
8,476502 |
-5E-05 |
-0,002 |
|
0,05 |
0,01175 |
0,453 |
8,11255 |
0,011692 |
0,451995 |
8,118948 |
-6E-05 |
-0,002 |
|
0,06 |
0,01669 |
0,533 |
7,76437 |
0,016612 |
0,531434 |
7,77044 |
-7E-05 |
-0,001 |
|
0,07 |
0,02239 |
0,609 |
7,425084 |
0,022309 |
0,607433 |
7,430837 |
-9E-05 |
-0,001 |
|
0,08 |
0,02884 |
0,681 |
7,094553 |
0,028749 |
0,68008 |
7,099997 |
-1E-04 |
-0,001 |
|
0,09 |
0,036 |
0,751 |
6,772636 |
0,0359 |
0,749462 |
6,77778 |
-0,0001 |
-0,001 |
|
0,1 |
0,04384 |
0,817 |
6,459191 |
0,043728 |
0,815664 |
6,464045 |
-0,0001 |
-0,001 |
Az összehasonlításból azt láthatjuk, hogy jobb, mint az extrapolációs, rosszabb, mint az interpolációs. Természetesen egy példa alapján merészség általános következtetést levonni, de az eredmény azt adja, amit várhattunk, hiszen egy pontosabb (kisebb hibataggal rendelkező) formulával cseréltük le az Adams-Bashforth féle összefüggést.
1.10.6. Hibabecslés módszerei
Egy közelítő módszer mindig tartalmaz hibát, ez természetes. Azonban fontos tudnunk azt is, hogy körülbelül mekkora ez a hiba (pontosan meghatározni sosem tudjuk, hiszen akkor módosítva vele a közelítést megkapnánk a pontos értékeket). Az integrál formulák levezetésnél fontos szempont volt, hogy a hibatagot is meg tudjuk határozni, mert ez szolgálhat a becslés alapjául.
Általánosságban elmondhatjuk, hogy a következő felépítésű összefüggéseket kaptunk:
|
Többlépéses n. rendű formulák: |
|
|
Egylépéses n. rendű formulák: |
A probléma többlépéses esetben a ξ-vel van, hiszen értékét nem ismerjük, az egylépéses módszereknél pedig a constans határozható meg nehézkesen [14.] .
A hiba becslésénél másképpen járunk el egylépéses-, és másképpen többlépéses módszerek esetén [14.] . Ha egylépéses formulát (Runge-Kutta) választottunk, akkor a szokásos eljárás az, hogy két különböző (általában Δt és Δt/2) lépésközzel is elvégezzük a számítást. Jelölje y l és y k a két azonos időponthoz tartozó közelítő értéket, ahol k=2l, azaz y l -t határoztuk meg Δt lépésközzel, y k -t pedig fele akkorával. Legyen továbbá Y az ehhez az időponthoz tartozó pontos érték. Feltételezve, hogy a hibatagban szereplő constans (jelöljük C-vel) közel azonos, a következő egyenletrendszert kapjuk:
|
|
(1.630) |
Látható, hogy két ismeretlen (Y,C) van, így az egyenletrendszer megoldható. Minket elsősorban a hiba érdekel, ezért azt fogjuk kifejezni. A magyarázatokat mellőzve a megoldás a következő:
|
|
(1.631) |
Vegyük azonban észre, hogy lehetőséget kaptunk egy pontosabb közelítő érték meghatározására is (Richardson ötlete alapján [8.] ):
|
|
(1.632) |
amit felhasználva negyedrendű esetben például
Ugyanez a gondolatmenet alkalmazható többlépéses esetben is, de ott elkerülhetjük azt, hogy két különböző lépésközzel számoljuk végig az egyenletet, így nyerve két közelítést. A többlépéses módszereknél mindig elő tudunk állítani két eltérő közelítést, a prediktort és a korrektort! Innentől kezdve a hibabecslést az előzőekben leírtak szerint végezhetjük el, figyelembe véve, hogy a hibatag másmilyen szerkezetű:
|
|
(1.633) |
Feltételezzük, hogy a derivált értékek közel egyenlők, és jelöljük őket D-vel. Ekkor az egyenletrendszer a következő alakú:
|
|
(1.634) |
ahol Y a pontos érték y p a közelítés prediktorral, y c pedig a közelítés korrektorral. Az ismeretlenek most Y és D. A két hiba érték közül határozzuk meg a korrektorét:
|
|
(1.635) |
A hibabecslés felhasználásával most is előállíthatunk egy pontosabb közelítést:
|
|
(1.636) |
Másodrendű esetben , így a hibatag, illetve a közelítés:
|
|
(1.637) |
1.10.7. Változó lépésköz alkalmazhatósága
A szimulációs feladatok egyik legnagyobb problémája a megfelelő lépésköz meghatározása, beállítása [14.] . A számítások előtt célszerű meghatározni egy lépésenkénti elfogadható hiba mértéket. Az előző pontban összefüggéseket határoztunk meg a hiba becslésére, így lehetőségünk van eldönteni, hogy az adott lépésköz megfelelő-e, vagy célszerű megváltoztatni. Természetesen a nagyobb lépésköz gyorsabb számítást eredményez, azonban a hiba nőni fog.
Az egylépéses módszerek esetén a lépésköz megváltoztatása nem okoz gondot, hiszen a számítások semmilyen formában sem tartalmazzák az előző lépés adatait, csak eredményét. Éppen ezen tulajdonságuk miatt önindítóak is!
Más a helyzet a többlépéses eljárásokkal. Ott a formulák levezetésénél is kihasználtuk, hogy minden intervallum azonos hosszúságú. Nincs problémánk akkor, ha csak a legegyszerűbb összefüggéseket (A-B1, A-M1, A-M2 azaz trapéz) alkalmazzuk, hiszen ezek csak egy intervallumot használnak. Változtatás során általában felezni, vagy kétszerezni szoktuk az intervallumot. A kétszerezés nem okoz gondot, mert az ekkor felhasználandó értékek rendelkezésre állnak. A felezéssel már más a helyzet, mivel ekkor két eddig használt időpont közötti értékre lenne szükségünk.
Ilyenkor több dolgot is tehetünk:
-
úgy járunk el, mint az első lépésnél, bár ekkor elveszítjük azt a tudást, amit az jelent, hogy vannak az előző időszakból értékeink,
-
interpoláció segítségével állítjuk elő a szükséges közbenső értékeket. Ekkor célszerű Hermit-féle interpolációt alkalmazni, mert az még az ismert derivált értékeket is felhasználja, így jobban közelíti a függvényt.
Abban az esetben, ha csak másodrendű közelítést alkalmazunk, akkor a következő módon is eljárhatunk [9.] (a módszer természetesen magasabb rendű esetre is általánosítható): az 1.9.1.1. szakasz fejezetben leírt módszernél ne használjuk ki, hogy a lépésköz állandó, hanem tekintsük két ismert, de eltérő értéknek. Így felírva az egyenes egyenletét, és elvégezve az integrálást egy némileg bonyolultabb összefüggést kapunk:
|
|
(1.638) |
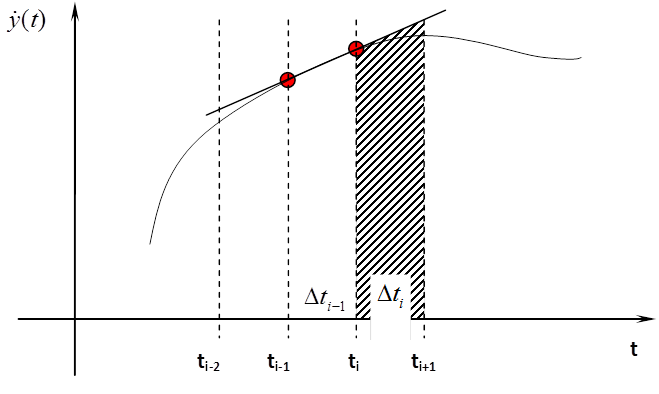
Ezt az összefüggést használva lehetőségünk nyílik tetszésszerinti új intervallum hossz alkalmazására, már csak a hibát kell valahogy megbecsülni. Az előző pontban leírt számításokat itt is elvégezhetjük, ha feltesszük, hogy hibatag a következő alakú:
|
|
(1.639) |
A részleteket mellőzve a végeredmények:
|
|
(1.640) |
Vegyük észre, hogyha az összefüggésekben a két különböző intervallumhosszt egyenlővé tesszük, akkor az előző pontban meghatározott formulákat kapjuk.
1.10.8. A különböző módszerek összehasonlítása
Amikor döntenünk kell, hogy az adott feladathoz milyen módszer válasszunk, sok szempontot kell figyelembe venni. Az elsődleges, hogy az adott eljárás alkalmas legyen a feladat kezelésére.
Alapvetően a következő esetek fordulhatnak elő:
Az ismertetésre került módszerek mindegyike alkalmas egyenletrendszerek kezelésére is, erre a Runge-Kutta esetén külön is felhívtuk a figyelmet. A többieknél csak az az egyetlen feltétel, hogy a kezdeti értékekből megtudjuk határozni a hiányzó kezdeti értékeket, másképpen mondva, a legmagasabb rendű deriváltakat úgy tudjuk kifejezni, hogy az értékeik kiszámíthatóak legyenek. A linearitás egyik módszernél sem volt feltétel, hiszen a tartályos feladat nem lineáris, és mindegyikkel megoldható volt. Az interpolációs módszer esetén okozhat nehézséget a nemlineáris rendszer, de ott is kezelhető, csak nemlineáris egyenletrendszert kell megoldanunk minden időlépés esetén. A fentiek illusztrálására nézzünk egy példát.
Mintapélda:
Legyen ez egy – az alábbi ábrán látható – kettősinga.
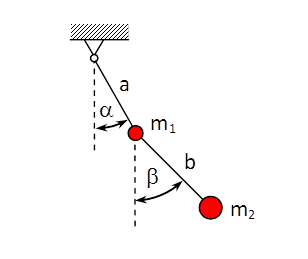
A levezetést mellőzve a leíró differenciálegyenlet-rendszer a következő[internet]:
|
|
(1.641) |
A kezdeti feltételek általában . Meg kell még határoznunk értékét. A fenti két egyenletből fejezzük ki például -t úgy, hogy ne függjön -tól, majd ‑t tetszőlegesen:
|
|
(1.642) |
az így kapott alakú egyenletek segítségével most már az összes ismertetett módszerrel megoldható a differenciálegyenlet-rendszer.
Másik fontos szempont a módszer választásánál, hogy stabil-e a közelítő módszer [11.] , [14.] . Fel kell hívnunk a figyelmet arra, hogy most nem a vizsgálandó fizikai rendszer stabilitásáról van szó, hanem a matematikai közelítő módszeréről. Többek között azért csak ezeket a módszereket mutattuk be, mert nincs stabilitási problémájuk. Praktikusan ez azt jelenti, hogyha a feladatunk megoldása során nem követtünk el hibát, és mégsem jók az eredmények („elszáll” a program), akkor csak a lépésközt választottuk túl nagyra. A számítási idő minimalizálása miatt természetesen törekszünk arra, hogy a lépésköz a lehető legnagyobb legyen. Próbáljuk úgy értelmezni az eredményt, mintha egy mérendő jel lenne. Ekkor a Shannon elv alapján szokták a mintavételezési időt meghatározni, amelyet a 1.8.1.1. szakasz fejezetben mutattunk be. Mivel a közelítésekben még sok más „zavaró hatás” is érvényesül (pl. képlet hiba), célszerű legalább a huszadát választani az elméleti mintavételezési időnek!
Ha már szóba kerültek a mintavételes rendszerek, használhatóak-e ott is ezek a módszerek? A többlépéses, állandó lépésközű módszerek mind, hiszen azok csak a Δt távolságú „pontokra” támaszkodnak, mintavételes esetben pedig nincsenek is máshol értékeink.
A számítás ideje sok mindentől függ. Fontos tudnunk, hogy az előírt hibát milyen lépésközzel tudja biztosítani a módszer, hiszen ettől függ, hogy hány időlépés alatt érünk el a kívánt időponthoz. A pontosságra nézve jó támpontot adhatnak az előzőekben közölt mintapéldák. Fel kell azonban hívnunk a figyelmet arra, hogy ilyen kevés példa alapján csak óvatos következtetéseket lehet levonni! (A Runge-Kutta és az interpolációs módszer is abszolút pontosan közelítette a tartályos feladatot, de csak azért, mert az analitikus megoldás egy másodfokú polinom.)
A szerzők rengeteg szimulációs példa vizsgálata után (csak házi feladatból volt több ezer) azonban elmondhatják, hogy a rezgő rendszernél látott arányok a tapasztalatoknak megfelelőek. A Runge-Kutta látszólagos fölényét az adja, hogy az egyetlen negyedrendű módszer. Ebből adódóan a hibatagja kisebb, tehát nagyobb lépésközzel lehet számolni, azaz összességében kevesebb pontban kell csak meghatározni az értékeket. Ezzel szemben áll azonban a lényegesen nagyobb számítási igénye [6.] . Egy program számítási igényét alapvetően a szorzások, osztások számával szokás mérni. Maguk az integrálási formulák viszonylag kevés műveletből állnak, és minél magasabb rendűek, annál több számítást igényelnek. Az igazi különbséget az okozza, hogy a megoldandó differenciálegyenlet mekkora számítási igényű, hányszor kell kiszámítani egy időlépéshez. Mint látható, míg a többlépéses módszerek csak egy új értéket várnak időlépésenként, az egylépésesnek negyedrendű esetben négy számításra van szüksége. Még inkább kiemeli ennek jelentőségét az, hogy a differenciálegyenletben lehetnek függvények (pl. négyzetgyök, szinusz, logaritmus, stb.), amelyek meghatározása sokkal időigényesebb mivel iterációval, vagy (általában Csebisev) polinommal határozzák meg az értéküket.
A már említett több ezer házi feladatban döntően (99,9%) a 1.10.5. szakasz fejezetben ismertetett vegyes módszert alkalmazták a hallgatók, mert az egyik legkönnyebben programozható, viszonylag pontos és minden esetben (nemlineáris, mintavételes) is használható.
1.11. Frekvenciatartománybeli vizsgálatok
A harmonikus analízis a harmonikus gerjesztésű rendszerek állandósult állapotú (vagy legalább a tranziensek lecsengése utáni) vizsgálatát jelenti. A korábban bevezetett rendszermodell, a frekvenciaátviteli függvény (1.38) közvetlen kapcsolatot teremt a rendszer harmonikus gerjesztésre adott válasza és a harmonikus gerjesztés között.
A frekvenciaátviteli függvény ábrázolásmódjai a harmonikus gerjesztő jel teljes körfrekvencia-tartományában leképezik a frekvenciaátviteli függvény két információját, a frekvenciafüggő átviteli tényezőt és a szintén frekvenciafüggő fázistolást. Előfordul, hogy az ábrázolásra az „negatív körfrekvencia- tartományban” is szükségünk van. Ha nem keressük a negatív körfrekvencia értelmét, matematikai formalizmussal számolhatunk vele.
A periodikus jelek közelíthetők harmonikus jelek lineáris kombinációjával. Tehát a Fourier–sor kiválasztott elemeinek megfelelő számú (és körfrekvenciájú) harmonikus gerjesztésre adott válasza meghatározható, és a válaszok összegzésével előállítható a periodikus jelre adott válasz.
1.11.1. A Bode-diagram
A Bode–diagramon (pontosabban diagram–páron) rendezett vetületben ábrázoljuk az egyes gerjesztő jel körfrekvencia értékekhez tartozó frekvenciafüggő átviteli tényezőt és fázistolást.
A gerjesztő jel teljes körfrekvencia-tartományát a vízszintes tengelyen tízes alapú logaritmikus skálán adjuk meg. A tengelyen általában a tényleges körfrekvenciaértéket tüntetjük fel, ritkábban fordul elő a körfrekvencia tízes alapú logaritmusa.
Az ábrázoláshoz a frekvenciaátviteli függvény exponenciális alakját (1.39) használjuk. A felső diagram függőleges tengelyén a frekvenciaátviteli függvény A 0 abszolút értékét, a B[dB]=20·log·A 0 összefüggéssel decibelbe átváltva ábrázoljuk. Az alsó diagramra az általában fokban, ritkábban radiánban adott fázistolást rajzoljuk. A Bode–diagram pontjainak számításánál célszerű a vízszintes tengelyen választott körfrekvencia-tartományt logaritmikusan felosztani.
A bemenet–kimenet alakú matematikai modellel (differenciálegyenlet, frekvenciaátviteli függvény, átviteli függvény) adott rendszer Nyquist–diagram ábrázolása könnyen algoritmizálható, az állapottér modellel adott rendszer esetén célszerű visszatérni a bemenet–kimenet leképezések valamelyikére.
1.11.1.1. A közelítő Bode–diagram
A gyors közelítő ábrázolására kiválóak a töréspontokban kapcsolódó, különböző meredekségű egyenesekkel megrajzolható, közelítő Bode–diagramok. Néhány alapelem segítségével bármilyen frekvenciaátviteli függvényt felírhatunk ezen „alaptagok” soros eredőjeként, és így pillanatok alatt felvázolhatjuk a frekvenciaátviteli tulajdonságokat közelítő Bode–diagramon.
A közelítő Bode amplitúdó menet alapján a frekvenciaátviteli függvény is könnyen felírható az alapelemek soros eredőjeként. Ezt a hatékony, közelítő ábrázolást soros kompenzációval történő szabályozásoknál tudjuk kihasználni.
A választott (nem feltétlenül megvalósítható, de számítás és rajzolás szempontjából praktikus) alapegységeket a frekvenciaátviteli függvény számláló- és nevezőbeli gyökei alapján, az alábbiak szerint definiálhatjuk:
-
nulladrendű (konstans) számláló és nevező (arányos vagy P tag) ,
-
konstans számláló, egy nullaértékű pólus (integráló vagy I tag),
-
egy nullaértékű zérus, konstans nevező (ideális, azaz nem megvalósítható differenciáló vagy D tag),
-
konstans számláló és egy pólus (elsőrendű késleltetésű vagy egytárolós arányos tag, P-T1),
-
egy zérus és konstans nevező (párhuzamosan kapcsolt arányos és ideális differenciáló tag, PD),
-
konstans számláló és két pólus (másodrendű késleltetésű vagy kéttárolós arányos tag, P-T2),
-
két zérus és konstans nevező.()
1.11.1.1.1. Nulladrendű számláló, nulladrendű nevező
Más néven arányos vagy P–tag.
|
|
(1.643) |
|
|
|
(1.644) |
|
|
|
(1.645) |
|
Amplitúdó-diagramja |
[dB] magasságú vízszintes, |
|
Fázisdiagramja |
0o magasságú vízszintes, |
1.11.1.1.2. Nulladrendű számláló és egy zérusértékű pólus
Más néven integráló vagy I–tag.
|
|
(1.646) |
|
|
|
(1.647) |
|
|
|
(1.648) |
|
Amplitúdó-diagramja |
-20 [dB/dekád] meredekségű egyenes, amely a 0 dB-es tengelyt az ω = 1/T i pontban metszi, |
|
Fázisdiagramja |
-90o magasságú vízszintes egyenes. |
1.11.1.1.3. Egy nullaértékű zérus és nulladrendű nevező
Más néven ideális ( nem megvalósítható ) differenciáló vagy D–tag.
Formálisan a D-tag frekvenciaátviteli függvénye az I-tag frekvenciaátviteli függvényének reciproka.
|
|
(1.649) |
|
|
|
(1.650) |
|
|
|
(1.651) |
|
Amplitúdó-diagramja |
+20 dB/dekád meredekségű egyenes, amely a 0dB-es tengelyt az ω =1/T d pontban metszi, |
|
Fázisdiagramja |
+90o magasságú vízszintes egyenes. |
1.11.1.1.4. Nulladrendű számláló és egy pólus
Egytárolós arányos vagy P–T 1 tag. A közelítő Bode–diagram felrajzolása szempontjából az egységnyi erősítésű, egytárolós, arányos tagot használjuk. Ez azt jelenti, hogy a számlálóban és a nevezőben szereplő konstans értékek egyenlőek: b 0 = a 0 . Ettől eltérő esetben, az egytől különböző A p erősítésértéket sorba kapcsolt arányos (P) tagként vesszük figyelembe. Az alábbi képletben a b 0 = a 0 feltételezéssel élünk.
|
|
(1.652) |
|
|
|
(1.653) |
|
|
|
(1.654) |
|
Amplitúdó-diagramja |
az ω = 1/T 1 töréspontig a 0 dB-es tengelyen haladó vízszintes, utána -20 dB/dekád meredekségű egyenes, |
|
Fázisdiagramja |
az ω = 1/T 1 törésponttól 1 dekáddal balra (ω = 0.1/T 1 ) ér véget a 0o-os vízszintes, ezt követi két dekádon keresztül (ω = 10/T 1 -ig) a -45o/dekád meredekségű egyenes, majd -90o magasságú vízszintes, -45o a töréspontban. |
1.11.1.1.5. Egy zérus és nulladrendű nevező
Párhuzamosan kapcsolt arányos és ideális differenciáló tag, jele PD.
A közelítő Bode–diagram felrajzolása szempontjából egységnyi erősítésű, arányos taggal használjuk.
Ez azt jelenti, hogy a számlálóban és a nevezőben lévő konstans értéke megegyezik: b 0 = a 0 . Ettől eltérő esetben, az egytől különböző A p erősítésértéket sorba kapcsolt arányos (P) tagként vesszük figyelembe. Az alábbi képletben a b 0 = a 0 feltételezéssel élünk.
Formálisan az egységnyi erősítésű PD–tag frekvenciaátviteli függvénye az egységnyi erősítésű P-T 1 tag frekvenciaátviteli függvényének reciproka.
|
|
(1.655) |
|
|
|
(1.656) |
|
|
|
(1.657) |
|
Amplitúdó-diagramja |
az ω = 1/T d töréspontig a 0 dB-es tengelyen haladó vízszintes, utána +20 dB/dekád meredekségű egyenes, |
|
Fázisdiagramja |
az ω = 1/T d törésponttól 1 dekáddal balra (ω = 0.1/T d ) ér véget a 0o -os vízszintes, ezt követi két dekádon keresztül (ω = 10/T d -ig) a +45/dekád meredekségű egyenes, majd +90o magasságú vízszintes, +45o a töréspontban. |
1.11.1.1.6. Nulladrendű számláló és két pólus
Kéttárolós, arányos vagy P–T 2 tag. A közelítő Bode–diagram felrajzolása szempontjából az egységnyi erősítésű, kéttárolós arányos tagot használjuk. Ez azt jelenti, hogy a számlálóban és a nevezőben lévő konstansok értéke azonos: b 0 = a 0 . Ettől eltérő esetben, az egytől különböző A p erősítésértéket sorba kapcsolt arányos (P) tagként vesszük figyelembe. Az alábbi képletben a b 0 = a 0 feltételezéssel élünk.
|
|
(1.658) |
|
|
|
(1.659) |
|
|
|
(1.660) |
A csillapítási tényező értéke alapján a nevező polinom gyökeloszlása háromféle lehet:
-
ha , a másodfokú egyenletnek két különböző valós gyöke van, a tag felírható két eltérő időállandójú, egytárolós, arányos tag soros eredőjeként: (1+T 1 jω)(1+T 2 jω)
-
ha , a másodfokú egyenletnek két azonos valós gyöke van, a tag felírható két azonos időállandójú, egytárolós, arányos tag soros eredőjeként: (1+T 1 jω)2
-
ha , a másodfokú egyenlet megoldása konjugált komplex gyökpár, a két energiatárolót nem tudjuk „szétválasztani”, maradnunk kell az eredeti leírásnál.
|
Amplitúdó-diagramja |
a csillapítási tényező értéke alapján háromféle lehet:
|
|
Fázisdiagramja |
a csillapítási tényező értéke alapján háromféle lehet:
|
1.11.1.1.7. Két zérus és nulladrendű nevező
Formálisan az egységnyi erősítésű P–T 2 –tag frekvenciaátviteli függvényének reciproka. Az előzőekhez hasonlóan itt is feltételezzük, hogy a számlálóban és a nevezőben lévő konstans értékek egyenlők: b 0 = a 0 . Ettől eltérő esetben, az egytől különböző A p erősítésértéket sorba kapcsolt arányos (P) tagként vesszük figyelembe.
|
|
(1.661) |
|
|
|
(1.662) |
|
|
|
(1.663) |
A „csillapítási tényező” értéke alapján a számláló polinom gyökeloszlása háromféle
lehet:
-
ha , a másodfokú egyenletnek két különböző valós gyöke van, a tag felírható két eltérő differenciálási idejű, arányos differenciáló tag soros eredőjeként: (1+T d1 j·ω) (1+T d2 j·ω)
-
ha , a másodfokú egyenletnek két azonos valós gyöke van, a tag felírható két azonos differenciálási idejű, arányos differenciáló tag soros eredőjeként: (1+T d ·jω)2
-
ha , a másodfokú egyenlet megoldása konjugált komplex gyökpár, maradnunk kell az eredeti leírásnál
|
Amplitúdó-diagramja |
a csillapítási tényező értéke alapján háromféle lehet:
|
|
Fázisdiagramja |
a csillapítási tényező értéke alapján háromféle lehet:
|
1.11.2. A Nyquist diagram
A helygörbe (Nyquist–diagram, vektordiagram) a frekvenciaátviteli függvény ω körfrekvenciával paraméterezett leképezése a komplex számsíkon, az ω értékekhez rendelhető komplex vektorok végpontjának összessége. Természetesen a komplex értékek algebrai alakban (valós és képzetes rész), valamint exponenciális (Euler–) alakban egyaránt megadhatók. A „tükörkép” diagram, vagyis az tartománybeli leképezés a „normál” tartománybeli diagram valós tengelyre való tükrözésével egyszerűen előállítható. A bemenet–kimenet alakú matematikai modellel (differenciálegyenlet, frekvenciaátviteli függvény, átviteli függvény) adott rendszer Nyquist–diagram ábrázolása könnyen algoritmizálható. Az állapottér modellel adott rendszer esetén célszerű visszatérni a bemenet–kimenet leképezések valamelyikére
-
MATLAB-ban,
-
Octave-ban,
-
Scilab-ban,
-
LabVIEW-ban az NIMathScript RT-ben,
-
LabVIEW-ban a Control Design Toolkit-tel,
-
LabVIEW-ban készített saját VI-al.
1.11.3. A Nichols–diagram
A Nichols–diagramon a frekvenciaátviteli függvény (1.39) két, a Bode–diagram két részén, a körfrekvencia függvényben ábrázolt információját jelenítjük meg. A vízszintes tengelyen a (kör)frekvenciafüggő fázistolás, a függőleges tengelyen a decibelben megadott, szintén (kör)frekvenciafüggő amplitúdó viszony szerepel. A görbe a Nyquist–diagramhoz hasonlóan az ω körfrekvencia értékével paraméterezett.
A bemenet–kimenet alakú matematikai modellel (differenciálegyenlet, frekvenciaátviteli függvény, átviteli függvény) adott rendszer Nichols–diagram ábrázolása könnyen algoritmizálható, az állapottér modellel adott rendszer esetén célszerű visszatérni a bemenet–kimenet leképezések valamelyikére.
1.11.4. A pólus–zérus diagram
A pólus–zérus diagramon a zérus–pólus(–erősítés) alakú átviteli (1.54) vagy frekvenciaátviteli függvény (1.48) számlálóbeli (zérusok) és nevezőbeli (pólusok) gyökeit ábrázoljuk a komplex számsíkon.
1.11.5. A gyökhelygörbe
A gyökhelygörbe a rendszer gyökeinek (zérusainak és pólusainak) komplex számsíkbeli elhelyezkedését ábrázolja egy paraméter értékváltozását követve. Gyakran alkalmazzák szabályozási körök vizsgálatára, a nyílt hurkú erősítést (körerősítést) használva paraméterként.