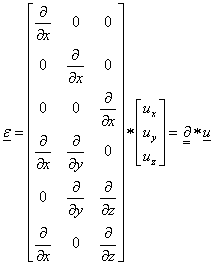
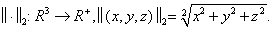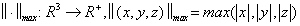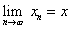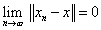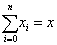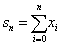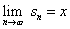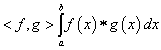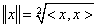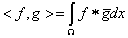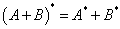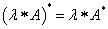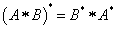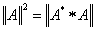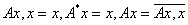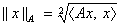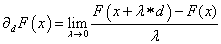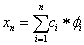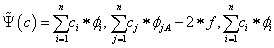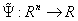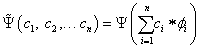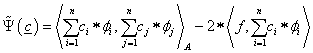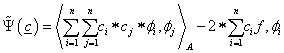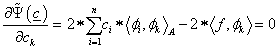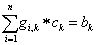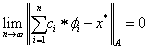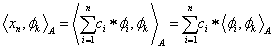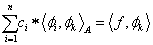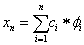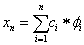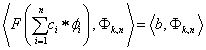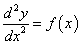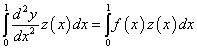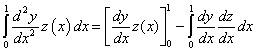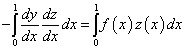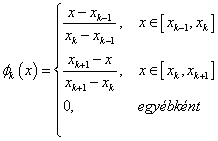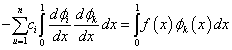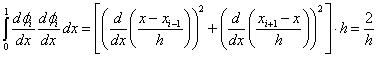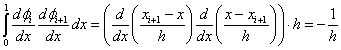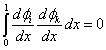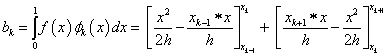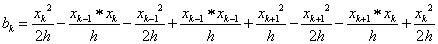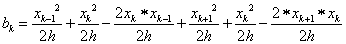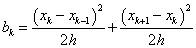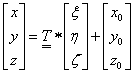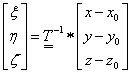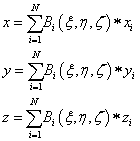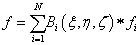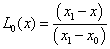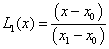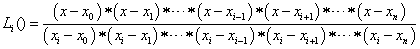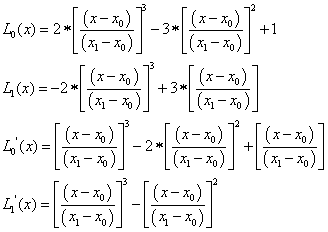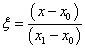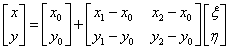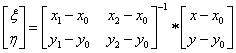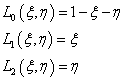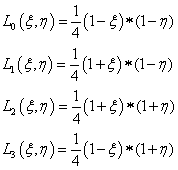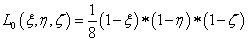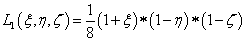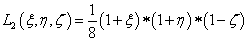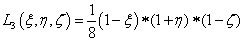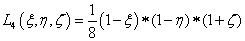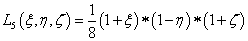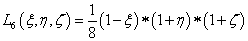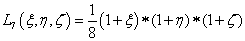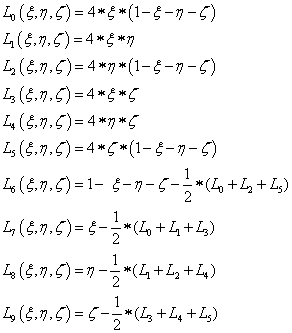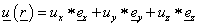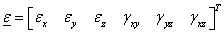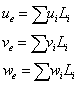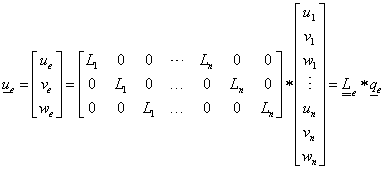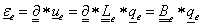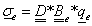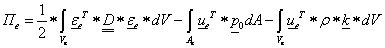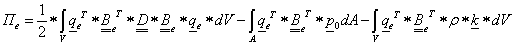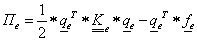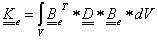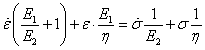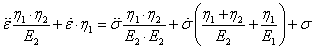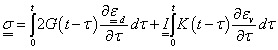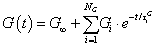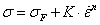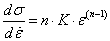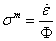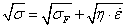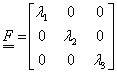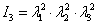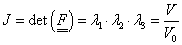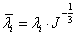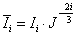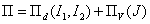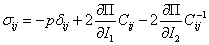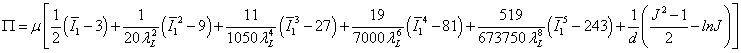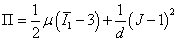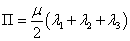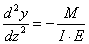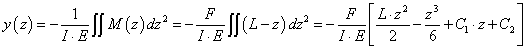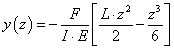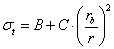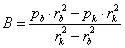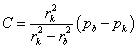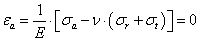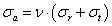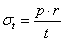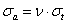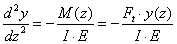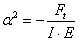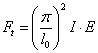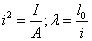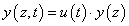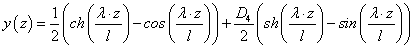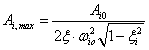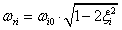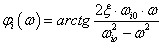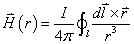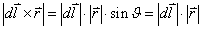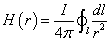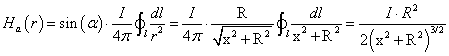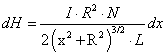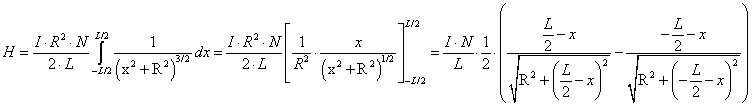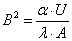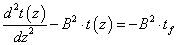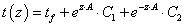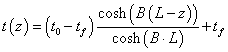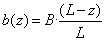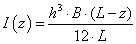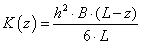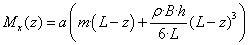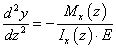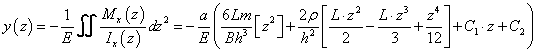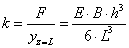Végeselem módszerek

Dr. Tamás, Péter

Bojtos, Attila

Décsei-Paróczi, Annamária

Dr. Fekete, Róbert Tamás

A tananyag a TÁMOP-4.1.2.A/1-11/1-2011-0042 azonosító számú „ Mechatronikai mérnök MSc tananyagfejlesztés ” projekt keretében készült. A tananyagfejlesztés az Európai Unió támogatásával és az Európai Szociális Alap társfinanszírozásával valósult meg.

Kézirat lezárva: 2014 február

Lektorálta: Dr. Molnár László

További közreműködők: Dr. Samu Krisztián, Knopp Ferenc

A kiadásért felel a(z): BME MOGI

Felelős szerkesztő: BME MOGI

ISBN 978-963-313-145-9

2014

Tartalom

1. A Végeselem módszer elméleti alapjai

1.1. Alapfogalmak

1.1.1. Az algebrai test
1.1.2. A vektortér
1.1.3. A metrikus tér
1.1.4. Norma, normált tér
1.1.5. Sorok és sorozatok normált térben
1.1.6. A Banach-tér
1.1.7. Lineáris leképezések, funkcionálok, korlátos leképezések
1.1.8. A skalárszorzás vektorterekben
1.1.9. A Hilbert-tér
1.1.10. Szimmetrikus operátorok
1.1.11. Adjungált és önadjungált operátorok
1.1.12. Pozítív, szigorúan pozitív, egyenletesen pozitív önadjungált operátorok, koercív operátorok
1.1.13. Monoton és Lipschitz-folytonos operátorok
1.1.14. Operátorok bihemi-folytonossága
1.1.15. Az energianorma
1.1.16. Bilineáris formák

1.2. Operátoregyenletek megoldása

1.2.1. Lineáris, korlátos operátoregyenletek

1.2.2. Lineáris nem korlátos operátoregyenletek

1.2.2.1. Szimmetrikus operátoregyenletek gyenge megoldása
1.2.2.2. Nem szimmetrikus operátoregyenletek gyenge megoldása

1.2.3. Nem lineáris operátoregyenletek

1.2.4. Gâteaux-derivált, potenciál operátor

1.2.5. A variációs elv

1.3. Variációs elven alapuló közelítő módszerek

1.3.1. Lineáris, szimmetrikus operátoregyenletek funkcionáljai
1.3.2. Nemlineáris egyenletek funkcionáljai

1.4. Ritz-Galjorkin módszer

1.4.1. A Ritz-Galjorkin módszer szimmetrikus lineáris egyenletekre
1.4.2. A Ritz-Galjorkin módszer általánosítása
1.4.3. A Ritz-Galjorkin módszer nem szimmetrikus lineáris egyenletekre
1.4.4. A Ritz-Galjorkin módszer nemlineáris egyenletekre

1.5. A végeselem-módszer háttere

1.5.1. A végeselemes technika

1.5.1.1. Koordináta-rendszerek
1.5.1.2. Bázisfüggvények

1.5.2. Egyváltozós bázisfüggvények

1.5.3. Kétváltozós bázisfüggvények

1.5.4. Háromváltozós bázisfüggvények

1.5.5. Végeselemek használata térbeli rugalmasságtani feladatokon

2. A végeselem rendszerek működésének alapjai

2.1. Bevezetés: A végeselem analízis alapvető lépései

2.2. Geometria modellezés

2.2.1. Geometriai modellek és előállításuk

2.2.1.1. Testmodell előállítása primitívekkel (Primitives)
2.2.1.2. Alaksajátosságra (Features) épülő parametrikus modell
2.2.1.3. Explicit modellezési eljárás (Explicit or Direct 3D)
2.2.1.4. Testmodell előállítása határfelületekkel (Boundary Representation)

2.2.2. Geometria importálása

2.2.3. Egyszerűsítések

2.2.3.1. Szimmetria feltételek alkalmazása

2.2.3.2. 2D-s és 3D-s modellek alkalmazása

2.2.3.2.1. Testmodell
2.2.3.2.2. Térbeli felületmodell
2.2.3.2.3. Sík felületmodellek
2.2.3.2.4. Vonalmodellek

2.3. Hálókészítés

2.3.1. Elemtípusok

2.3.1.1. Kiterjedésük szerint

2.3.1.2. Az elemek fokszámuk szerint

2.3.1.3. Az elemek szabadságfoka

2.3.1.4. Az elemtulajdonságok

2.3.1.4.1. A feszültséganalízis elemei
2.3.1.4.2. A termikus analízis elemei
2.3.1.4.3. Az elektromos és mágneses analízis elemei
2.3.1.4.4. Csatolt-tér elemek

2.3.2. A hálózás lépései

2.3.2.1. Attribútumok és kontrollok beállítása (mesh controls)

2.3.2.2. Automatikus hálózási eljárások

2.3.2.3. Strukturálatlan háló létrehozása

2.3.2.3.1. Topológia felosztása (Topology decomposition)
2.3.2.3.2. Csomópont csatlakozás (Node connection)
2.3.2.3.3. Mozaik (Advancing front, Paving)
2.3.2.3.4. Négy-fa (Octree)
2.3.2.3.5. Rács alapú (Grid-based)

2.3.2.4. Strukturált háló létrehozása

2.3.2.4.1. Minta leképezéses eljárások (Mapped element)
2.3.2.4.2. Geometria szétválasztás (Geometry decomposition, Sub-maping)
2.3.2.4.3. Söprés (Sweeping)

2.3.2.5. A háló illeszkedése

2.3.3. Konvergencia módszerek

2.3.3.1. Hálósűrítés, hálósimítás
2.3.3.2. Adaptív hálózás

2.3.4. A hálózásnál előforduló hibák

2.4. Anyagmodellek létrehozása

2.4.1. Általános anyagtulajdonságok

2.4.1.1. Linearitás

2.4.1.2. Homogenitás

2.4.1.3. Irányfüggőség

2.4.1.3.1. izotróp anyagmodell (Isotropic model)
2.4.1.3.2. Ortotróp modell (Orthotropic model)
2.4.1.3.3. izotrópAnizotróp modell (Anisotropic model)

2.4.2. Az anyagmodellek csoportosítása szabadságfokuk alapján

2.4.3. Mechanikai, vagyis elmozdulás szabadságfokú anyagmodellek

2.4.3.1. A mechanikai anyagmodellek csoportosítása fesz-nyúlás karakterisztikájuk szerint

2.4.3.2. Lineárisan rugalmas anyagmodell (Linear elastic)

2.4.3.3. Viszkoelasztikus anyagmodellek (Viscoelastic Material Model)

2.4.3.3.1. A leggyakrabban alkalmazott viszkoelasztikus anyagmodellek
2.4.3.3.2. Maxwell modell
2.4.3.3.3. Kelvin-Voigt modell
2.4.3.3.4. Standard-Solid modell
2.4.3.3.5. Burgers modell
2.4.3.3.6. Általánosított modellek
2.4.3.3.7. A viszkoelasztikus modellek VEM-es alkalmazása
2.4.3.3.8. A viszkoelasztikus anyagok hőmérsékletfüggése

2.4.3.4. Sebességfüggetlen plasztikus anyagmodellek (rate-independent plasticity)

2.4.3.4.1. A folyási feltétel
2.4.3.4.2. Keményedési szabály (hardening rule).

2.4.3.5. Viszkoplasztikus anyagmodellek

2.4.3.5.1. Bingham modell
2.4.3.5.2. Herschel-Bulkley modell
2.4.3.5.3. Hatványtörvény, (Ostwald-de Waele egyenlet)
2.4.3.5.4. Casson
2.4.3.5.5. Módosított Bingham,
2.4.3.5.6. Perzyna
2.4.3.5.7. Peirce
2.4.3.5.8. EVH (Exponential visco-hardening)
2.4.3.5.9. Anand

2.4.3.6. Összetett reológia anyagmodellek

2.4.3.7. Hiperelasztikus anyagmodellek

2.4.3.7.1. Arruda-Boyce
2.4.3.7.2. Neo-Hooke
2.4.3.7.3. Saint Venant–Kirchhoff model
2.4.3.7.4. Mooney-Rivlin
2.4.3.7.5. Ogden
2.4.3.7.6. Polinomiális
2.4.3.7.7. Yeoh
2.4.3.7.8. Marlow modell
2.4.3.7.9. Van der Waals
2.4.3.7.10. Összenyomható hiperelasztikus modellek habok modellezésére
2.4.3.7.11. Blatz-Ko habmodell
2.4.3.7.12. Varga-modell
2.4.3.7.13. További hiperelasztikus modellek biológiai szövetek modellezésére

2.4.3.8. Anyagparaméterek megadása

2.4.3.8.1. Mechanikai anyagvizsgálati adatok

2.4.3.8.1.1. A mechanikai anyagvizsgálatok főbb típusai
2.4.3.8.1.2. Az anyagvizsgálati adatok formátuma
2.4.3.8.1.3. Görbeillesztés

2.4.3.8.2. Sűrűség (Density)

2.4.3.8.3. Hőtágulási együttható (Coefficient of thermal expansion)

2.4.3.8.4. Anyagcsillapítási tényező (Material Damping Ratio)

2.4.3.8.5. Az anyag szilárdsági határa (Material Strength Limits)

2.4.4. Hőmérsékleti szabadságfokkal rendelkező anyagok

2.4.4.1. Hővezető képesség (Thermal Conductivity)
2.4.4.2. Fajhő (Specific Heat)
2.4.4.3. Sűrűség (Density)

2.4.5. Elektromágneses szabadságfokú anyagok

2.4.5.1. Az anyagok mágneses tulajdonságai

2.4.5.1.1. Mikroszkopikus modell.
2.4.5.1.2. Makroszkopikus modell.

2.4.5.2. Mágneses anyagok típusai

2.4.5.2.1. A diamágneses anyagok
2.4.5.2.2. A paramágneses anyagok
2.4.5.2.3. Ferromágneses anyagok
2.4.5.2.4. Ferrimágneses anyagok
2.4.5.2.5. Az antiferromágneses anyagok

2.4.5.3. A mágneses szimuláció során definiálható mágneses anyagtípusok

2.4.5.4. Elektromos anyagmodellek

2.4.5.4.1. Elektromos vezető
2.4.5.4.2. Dielektrikum

2.4.6. Csatolt anyagmodellek

2.4.6.1. Piezorezisztív anyag
2.4.6.2. Piezoelektromos anyagmodell

2.5. Terhelések, perem- és kezdeti feltételek

2.5.1. Kezdeti feltételek

2.5.2. Peremfeltételek

2.5.3. Terhelések

2.5.3.1. Terhelési lépések (Load steps)

2.5.4. Szimmetriafeltételek

2.5.4.1. Tengelyszimmetrikus (Axisymmetric) terhelések

2.6. Alkatrészek közötti kapcsolatok

2.7. A szimuláció főbb beállításai és futtatása

2.7.1. Az analízis típusának kiválasztása
2.7.2. A megoldó kiválasztása (Selecting a Solver)

2.8. Az eredmények lekérdezése és kiértékelése (posztprocesszálás)

2.8.1. Lekérdezett mennyiségek
2.8.2. Az eredmények megjelenítési formái

2.9. Ellenőrző kérdések a 2. fejezethez.

3. Lineáris statikai analízis

3.1. Áttekintés

3.1.1. Lineáris analízis
3.1.2. A statikai analízis esetében alkalmazható anyagmodellek
3.1.3. Alkalatrész viselkedés
3.1.4. Hálózás
3.1.5. A szimuláció fontosabb beállításai
3.1.6. Peremfeltételek / Kinematikai kényszerek
3.1.7. A statikai analízisben alkalmazható terhelések
3.1.8. Az eredmény bemutatása

3.2. Gyakorlat: Befalazott tartó lehajlása

3.2.1. A mintafeladat analitikus megoldása
3.2.2. Numerikus megoldás ANSYS Workbench-ben
3.2.3. Egyszerű statikai analízis SolidWorksben
3.2.4. Az analitikus és numerikus megoldások összehasonlítása

3.3. Alkalmazási példa: Erőmérő cella statikai analízise

3.3.1. Modellezés
3.3.2. Anyagmodell hozzárendelés
3.3.3. Hálózás
3.3.4. Megtámasztás és terhelés hozzárendelése
3.3.5. Futtatás és az eredmények lekérdezése

3.4. Ellenőrző feladatok

3.4.1. Feladat
3.4.2. Feladat

4. Nemlineáris statikai analízis

4.1. A nemlinearitás okai

4.1.1. Anyagi nemlinearitás
4.1.2. Geometrriai nemlinearitások, nagy deformációk
4.1.3. A terhelési állapot megváltozása, nemlineáris kontaktok

4.2. A nemlineáris feladat megoldása

4.2.1. Alkalmazható anyagmodellek
4.2.2. Alkatrész viselkedés
4.2.3. Hálózás
4.2.4. A szimuláció beállításai
4.2.5. Peremfeltételek / Peremfeltételek / Eredmények

4.3. Mintafeladat instabil terhelési állapotra

4.4. Mintafeladat anyagi és geometriai nemlinearitásra

5. Paraméter vizsgálatok, optimalizációs feladatok

5.1. Példa optimalizációs feladatra

6. A geometriai modellek egyszerűsítésének lehetőségei

6.1. Példa szimmetriafeltételek alkalmazására: belső nyomással terhelt cső

6.1.1. Analitikus megoldás
6.1.2. A feladat megoldása ¼ testmodell segítségével
6.1.3. A feladat megoldása negyed héjmodell segítségével
6.1.4. A feladat megoldása 2D-s sík alakváltozás (Plane Strain) típusú modellként
6.1.5. A feladat megoldása 2D-s tengelyszimmetrikus (Axisymmetric) típusú modellként
6.1.6. Összefoglalás

6.2. Példa egy oldalon befogott, hajlított tartó négyféle megoldására

6.2.1. A feladat megoldása 3D-s teljes testmodellel (3D body)
6.2.2. A feladat 3D-s megoldása felületmodell (shell) definiálásával
6.2.3. A probléma megoldása 2D-s feladatként
6.2.4. A feladat megoldása vonalmodell keresztmetszet definiálásával (gerenda elemmel)
6.2.5. Összefoglalás

6.3. Példa gerenda modell alkalmazására: Hegesztett rácsos szerkezet

6.4. Mechatronikai példa: CD fej tartó rugók

6.5. Ellenőrző feladatok

6.5.1. Feladat
6.5.2. Feladat

7. Több alkatrészes, statikai analízis

7.1. A kontaktok csoportosítása

7.2. Példa - kontaktfeladat az alkatrészek közötti alapvető kapcsolat típusok bemutatására

7.2.1. Súrlódásos kapcsolat (Frictional)
7.2.2. Súrlódásmentes kapcsolat (Frictionless)
7.2.3. Elválás nélküli kapcsolat (No separation)
7.2.4. Végtelen súrlódású kapcsolat (Rough)
7.2.5. Ragasztott-hegesztett típusú kapcsolat (Bonded)
7.2.6. Eredmények

7.3. Példa - Érintkezési feszültség és benyomódás

7.3.1. Analitikus megoldás
7.3.2. Numerikus megoldás
7.3.3. Összefoglalás

8. Kihajlás vizsgálat

8.1. Áttekintés
8.2. Kihajlás vizsgálat VEM példa
8.3. Analitikus megoldás

9. Dinamikus, tranziens mechanikai analízis

9.1. Áttekintés
9.2. Példa tranziens szimulációra

10. Modális analízis

10.1. Áttekintés

10.2. Konzolos lemez modal analízise előfeszítés nélkül és előfeszítéssel

10.2.1. Modal analízis előfeszítés nélkül
10.2.2. Modal analízis előfeszítéssel
10.2.3. Analitikus megoldás

11. Harmonikus terhelések vizsgálata

11.1. Áttekintés
11.2. Példa harmonikus analízisre
11.3. Analitikus megoldás

12. Elektromos és mágneses szimulációk

12.1. Bevezetés

12.2. Példa elektromágneses szimulációra – solenoid tekercs szimulációja

12.2.1. Analitikus megoldás
12.2.2. Összefoglalás

12.3. Alkalmazási példa elektromágneses szimulációra

13. Termikus szimuláció

13.1. Áttekintés

13.2. A termikus szimulációk beállításai

13.3. Terhelések tranziens termikus analízisek során

13.3.1. Hőmérséklet kénszer
13.3.2. Hőátadás
13.3.3. Hősugárzás
13.3.4. Hőáram
13.3.5. Hőáramsűrűség
13.3.6. Belső hőtermelés
13.3.7. Tökéletes szigetelés

13.4. Példa hőtani szimulációra –hűtőborda hőmérsékleti viszonyainak vizsgálata

13.5. Analitikus megoldás

14. Komplex mechatronikai projektfeladat

14.1. Numerikus megoldás

14.1.1. Statikai analízis
14.1.2. Modal analízis
14.1.3. Harmonikus
14.1.4. Tranziens

14.2. A komplex feladat analitikus megoldása

14.2.1. Statikus lehajlás számolása
14.2.2. Dinamikai számítás

15. Korszerű végeselelem rendszerek áttekintése

15.1. Korszerű végeselem rendszerek áttekintése
15.2. ANSYS Classic és Workbench
15.3. ABAQUS
15.4. NASTRAN
15.5. Mark
15.6. ADINA
15.7. LS-DYNA
15.8. SolidWorks Design Validation Tools (CosmosWorks)
15.9. Solid Edge
15.10. Autodesk Inventor
15.11. További kereskedelmi végeselem rendszerek
15.12. További nyílt forráskódú végeselem rendszerek

Irodalomjegyzék

Az ábrák listája

1.1. A (0,1) intervallumok szakaszonként folytonos függvény
1.2. A választott bázisfüggvények
1.3. A C0 folytonos vonali bázisfüggvények akkor az L0
1.4. A C0 folytonos vonali bázisfüggvények
1.5. Hermite-féle görbeszakasz
1.6. A C1 folytonos vonali bázisfüggvények
1.7. Lineáris függvény háromszög elemen
1.8. A kétdimenziós bázisfüggvények háromszög elemen
1.9. A négycsomópontú lineáris elem
1.10. A kétdimenziós bázisfüggvények négyszög elemen
1.11. A háromdimneziós lineárisan módosított elem
1.12. A háromdimneziós kvadratikus
2.1. A végeselem szimuláció folyamatának legfontosabb lépései, (statikai példán bemutatva).
2.2. Testmodelleken alkalmazható szimmetriák.
2.3. Térbeli testek felületmodellel történő modellezése.
2.4. Elemek csoportosítása alakjuk és fokszámuk szerint.
2.5. Gyakori mechanikai elemtípusok és a csomópontok szabadságfoka.
2.6. Automatikus és részben automatikus hálógenerálási eljárások.
2.7. 2D-s hálókialakítások.
2.8. 3D-s testek hálózása különféle eljárásokkal.
2.9. Különálló felületek vagy testek határán lévő csomópontok illeszkedése.
2.10. Konvergenciát elősegítő eljárások.
2.11. Elemátmenetek különböző mértékű növekedési arány (Growth Rate) megadásával.
2.12. Elemtulajdonságok vizuális megjelenítése.
2.13. Példa az inhomogén és anizotróp anyagokra.
2.14. Néhány gyakran alkalmazott szerkezeti anyag jellemző feszültség-nyúlás karakterisztikája.
2.15. Az anyagok mechanikai viselkedését leíró főbb anyagmodelleket jellemző feszültség - nyúlás karakterisztikák [22.] .
2.16. A reológiai anyagmodelleket alkotó alapvető modellek.
2.17. A viszkoelasztikus anyagokat jellemző jelenségek az állandó alakváltozás alatt bekövetkező feszültségrelaxáció, az állandó feszültség alatt bekövetkező kúszás, a feszültség – nyúlás karakterisztika sebességfüggése és a hiszterézis.
2.18. Viszkoelasztikus anyagmodellek és válaszfüggvényeik.
2.19. Általánosított modellek.
2.20. Az eltolási függvények értelmezése.
2.21. (a.) Lineáris elasztoplasztikus modell főbb részei I.) Lineárisan rugalmas szakasz, II.) folyási szakasz. (b.) Az elasztoplasztikus modellek főbb típusai: 2.) ideálisan képlékeny, 3.) nemlineárisan felkeményedő, 4.) nemlineárisan lágyuló, 5.) ridegen lágyuló.
2.22. A folyási felület értelmezése.
2.23. Lineáris tagokból álló egyszerű elasztoplasztikus modellek.
2.24. A kinematikus (a.) és izotróp (b.) keményedésű elasztoplasztikus anyagok feszültség-nyúlás jelleggörbéje és a folyási felület megváltozásának módja.
2.25. A viszkoplasztikus, az ideálisan viszkózus (Newtoni) és az ideálisan képlékeny (St. Venant) modellek Feszültség - alakváltozási sebesség karakterisztikája (a.). A legismertebb viszkoplasztikus anyagmodellek (b.).
2.26. Bingham modell - párhuzamosan kapcsolt viszkózus és súrlódó elem.
2.27. Hiperelasztikus anyagok jellemző feszültség-nyúlás karakterisztikája. 0 (a.), 1 (b.) ill. 2 inflexiós ponttal rendelkező húzókarakterisztika (c.).
2.28. A modellalkotáshoz leggyakrabban használt anyagvizsgálatok értelmezése.
2.29. Mágneses anyagok jellemző B-H görbéje
2.30. Szimmetria és anti-szimmetria értelmezése.
2.31. Az eredmény megjelenítésének lehetséges módjai.
2.32. Az eredmény megjelenítésének módjai.
2.33. Egyenértékű színsávok megjelenítési módjai.
2.34. Metszési módok.
3.1. Egy oldalán befogott rúd igénybevétele.
3.2. Geometria létrehozása.
3.3. Mértékegység kiválasztása.
3.4. Vázlatsík kijelölése és új vázlat létrehozása.
3.5. Vázlatrajzolás.
3.6. Szimmetria kényszer definiálása.
3.7. Vázlat méretezése.
3.8. A kihúzás paramétereinek beállítása.
3.9. A kihúzás végrehajtása.
3.10. Szimuláció kiválasztása.
3.11. Engineering Data.
3.12. Anyagparaméterek megadása.
3.13. A szimulációs környezet megnyitása.
3.14. Anyagmodell hozzárendelése az alkatrészhez.
3.15. A hálózás.
3.16. Rögzítés parancs kiadása.
3.17. A rögzítés helyének kijelölése.
3.18. A terhelőerő hozzárendelése.
3.19. A terhelőerő beállításai.
3.20. Deformáció lekérdezése.
3.21. A deformáció lekérdezésének beállítása.
3.22. Y irányú deformáció.
3.23. Z irányú fajlagos nyúlás.
3.24. Egyenértékű feszültség.
3.25. A deformáció skálázása. A valós deformáció 14 szeres (a.) és 36 szoros (b.) nagyítása.
3.26. A geometria metszése különböző felületekkel: a.) metszés nélkül, b.) nyitott, egyenfeszültségű felületekkel, c.) zárt, megadott feszültségű felülettel, d.) síkokkal.
3.27. Színsávok beállítása.
3.28. Deformálatlan test (a-c.) és a végeselem háló (d.) megjelenítése.
3.29. Cimkék.
3.30. Animáció készítése.
3.31. Deformációlekérdezés beállításai.
3.32. Egy él elmozdulásának lekérdezése.
3.33. Az él átalakítása útvonallá.
3.34. Numerikus eredmények exportálása.
3.35. Új alkatrész létrehozása.
3.36. Téglalap rajzolása.
3.37. Elölnézet beállítása.
3.38. Méretezés ikon.
3.39. Méretezés.
3.40. Kihúzás parancs kiadása.
3.41. A kihúzás paramétereinek beállítása.
3.42. Anyagmodell szerkesztése.
3.43. Új anyagmappa létrehozása.
3.44. Új anyag létrehozása.
3.45. Az anyagparaméterek megadása.
3.46. Belépés a szimulációs környezetbe.
3.47. A szimuláció típusának kiválasztása.
3.48. Rögzítési mód kiválasztása.
3.49. A rögzítés helyének megadása.
3.50. Külső terhelés kiválasztása.
3.51. Az erő megadása.
3.52. Hálózás parancs kiadása.
3.53. A hálózás paramétereinek beállítása.
3.54. A végeselemháló.
3.55. A szimuláció futtatása.
3.56. Az eredmények definíciójának beállítása.
3.57. Az eredmény típusának módosítása.
3.58. Egyenértékű feszültség.
3.59. Y irányú deformáció.
3.60. Z irányú fajlagos nyúlás.
3.61. Az eredmények megjelenítésének beállítása.
3.62. Az eredmények grafikus megjelenítésének formái.
3.63. Az eredmények numerikus megjelenítése.
3.64. Animáció készítése a szimulációról.
3.65. A konzolosan befogott rúd terhelési eredményei: a.) Z – tengely irányú normál feszültség, b.) lehajlás.
3.66. Acél mérőtest egyszerűsített, méretezett rajza.
3.67. A geometriai modell létrehozásának lépései.
3.68. ANSYS analízis indítása a SolidWorks-ből.
3.69. A projektfelületen megjelenő importált geometria és a hozz csatolt anyagmodell, és analízis.
3.70. Az anyagkönyvtár.
3.71. Anyag hozzárendelése a testmodellhez.
3.72. Az elvégzett analízis modellfája.
3.73. A háló globális paramétereinek beállítása.
3.74. A behálózott modell.
3.75. A cella megtámasztása és terhelése.
3.76. Megtámasztások.
3.77. Terhelések.
3.78. Eredmények lekérdezése a felső ikonsorból. Alakváltozási tenzor lekérdezése.
3.79. A nyúlásmérő bélyeg felragasztásának helyén ébredő alakváltozási állapot.
3.80. Az analízis eredményei: a.) von Mieses féle egyenértékű feszültség, b.) Y irányú elmozdulás, c-d.) X irányú fajlagos nyúlás.
4.1. Lineáris és nemlineáris szerkezeti analízis.
4.2. A Newton-Raphson és az Ívhossz eljárás.
4.3. Domború héjszerkezet
4.4. A végeselem háló globális beállítása.
4.5. A nemlineáris analízis beállításai.
4.6. Az átpattanás folyamata.
4.7. Anyagvizsgálatból származó Feszültség-nyúlás karakterisztika.
4.8. Váltás 2 dimenziós geometriára.
4.9. Forgásszimmetrikus test 2D-s modellje
4.10. A nemlineáris analízis időlépéseinek és nagy elmozdulásának beállítása.
4.11. Az erő konvergenciáját mutató diagram.
4.12. A membrán felfújódásának folyamata, (az X és Y irányú elmozdulásokat bemutató eredmények egy ábrára szerkesztve a szemléletesség kedvéért).
5.1. Geometria létrehozása.
5.2. Mértékegység kiválasztása.
5.3. Vázlat megrajzolása.
5.4. A vázlatrajzoláskor alkalmazható kényszerek.
5.5. Szimmetriakényszer kiadása.
5.6. Vázlat méretezése.
5.7. Méretek paraméterré alakítása.
5.8. Paraméter nevének megadása.
5.9. A kihúzás vastagságának paraméterré alakítása.
5.10. Kihúzás műveletének beállítása.
5.11. Kihúzás mélységének beállítása.
5.12. A kihúzás mélységét határoló felület kiválasztása.
5.13. A kihúzás mélységét határoló felület kijelölése.
5.14. Az alkatrészmodell a kivágott furattal.
5.15. Kiosztás létrehozása.
5.16. A kiosztás számának paraméterré alakítása.
5.17. A létrejött paraméterkészletet.
5.18. Belépés a szimulációs környezetbe (Jobb gombos menüből).
5.19. Hálósűrítés beállítása.
5.20. A hálósűrítés célfelületének kijelölése.
5.21. Sűrített háló, 1mm-es elemekkel.
5.22. Fix befogás az alkatrész szélesebb végénél.
5.23. 50N nagyságú, -Z irányú erőterhelés az alkatrész keskenyebb végénél.
5.24. Az erő értékének megadása, majd paraméterré alakítása.
5.25. Az eredmények lekérdezése.
5.26. Az eredmények kimenő paraméterré alakítása.
5.27. Az alkatrészben ébredő egyenértékű feszültség.
5.28. Z irányú deformáció.
5.29. A paramétervizsgálat különböző lehetőségei.
5.30. A kimenő paraméterekkel és a célérték optimalizációval kiegészült projektpanel.
5.31. A design konfigurációk szerkesztése (Jobbgombos menüből).
5.32. A paraméterek típusának és szélső értékeinek beállítása.
5.33. Diszkrét paraméter beállítása.
5.34. A paramétertábla futás közben.
5.35. Belépés a Response Surface felületre az eredmények megtekintéséhez.
5.36. Az eredmények megjelenítésének frissítése.
5.37. Az eredmény egy paraméterpárosának megjelenítése 2D-s diagramon.
5.38. Váltás 2 és 3 dimenziós megjelenítés között.
5.39. Az eredmény 2 bemenő és egy kimenő paraméterének megjelenítése 3D-s diagramon.
5.40. A célértékoptimalizáció megkezdése.
5.41. Az egyes paraméterekkel szemben támasztott kívánalmak beállítása.
5.42. az egyes paraméterek célértékeinek súlyozása.
5.43. Rangsorolt eredmények.
6.1. Csőszakasz modellje különböző megközelítés szerint.
6.2. ¼ testmodell.
6.3. Hengerkoordináta-rendszer beállítása a radiális elmozdulások lekérdezéséhez.
6.4. Csőszakasz negyed felületmodellje.
6.5. Hálózott modell a negyed héj esetén
6.6. Terhelés és a permfeltételek a negyed felületmodellel felépített cső esetében.
6.7. A megnyúlás és egyenértékű feszültség a csőmodell negyed héjmodellként való szimulációja során
6.8. Cső modell 2D-s negyed geometriája
6.9. Váltás 2 dimenziós geometriára.
6.10. 2D-s negyed csőmodell hálója
6.11. 2D-s negyed csőmodell terhelése és megfogásai
6.12. 2D-s negyed csőmodell egyen értékű feszültség értékei
6.13. 2D-s tengelyszimmetrikus csőmodell geometriája
6.14. 2D-s tengelyszimmetrikus csőmodell véges elemes hálója
6.15. 2D-s tengelyszimmetrikus csőmodell véglapjainak megfogása (UY=0).
6.16. 2D-s tengelyszimmetrikus csőmodell nyomásterhelése
6.17. 2D-s tengelyszimmetrikus csőmodell egyenértékű feszültség viszonyai
6.18. A cső falában ébredő (von Mieses féle) egyenértékű feszültség analitikus és végeselemes megoldása.
6.19. Egy oldalon befogott, hajlított tartó négyféle megoldása.
6.20. A hajlított rúd geometriai méretei [mm]
6.21. Terhelési modell a hajlított rúd esetében
6.22. Az elkészített 3D-s geometria
6.23. A 3D-s modell véges elemes hálója
6.24. A 3D-s modellen létrehozott konstrukciós geometria
6.25. 3D-s geometria esetén a terhelési modell megadása
6.26. 3D-s modell esetén a teljes deformáció eloszlása [mm]
6.27. 3D-s modell esetén a vonal menti, y irányú deformáció [mm]
6.28. A felületi geometria
6.29. Felületmodell létrehozása vázlat alapján (menüpont elérése)
6.30. Véges elemes háló shell modell esetén
6.31. Konstrukciós vonal shell modell esetén
6.32. Terhelési modell felületi test esetén
6.33. Teljes deformáció [mm]
6.34. Y irányú deformáció [mm] konstrukciós vonal mentén
6.35. Az elkészült vázlat és felület
6.36. A véges elemes háló (elemméret 1 [mm])
6.37. A terhelési modell
6.38. A konstrukciós vonal (path) definiálása
6.39. Teljes deformáció [mm]
6.40. Vonal menti, y irányú deformáció [mm]
6.41. A vonal test és keresztmetszet alapján definiált geometria
6.42. ANSYS WB Design Modeler moduljában a vonal testté alakításhoz használatos menüpont elérése
6.43. ANSYS WB Design Modeller moduljában a keresztmetszet definiálásához használatos menü elérése
6.44. A véges elemes háló
6.45. Konstrukciós vonal definiálása diszkrét kezdő és végpont segítségével
6.46. A terhelési modell
6.47. Y irányú deformáció [mm] a konstrukciós vonal mentén
6.48. Teljes deformáció [mm] (a minimum és maximum értékek feltüntetésével).
6.49. Gerendák igénybevételére vonatkozó eredmények is lekérdezhetőek.
6.50. Teljes hajlító nyomaték [Nmm] eredménye.
6.51. Teljes nyíróerő [N] eredménye.
6.52. A tartókonzol geometriai méretei [mm]
6.53. A konzol terhelési modellje
6.54. Az elkészült geometria (rúdmodell)
6.55. A rúdmodellhez tartozó keresztmetszet vázlata
6.56. A véges elemes háló (100 mm-es elemméret)
6.57. A terhelési modell
6.58. Teljes deformáció a konzolon [mm]
6.59. Hajlító nyomaték a konzolon [Nmm]
6.60. Tengely irányú erő a konzolon [N]
6.61. Csavaró nyomaték a konzolon [Nmm]
6.62. Megoszló erő a konzolon [N]
6.63. A CD-fej egyszerűsített geometriája.
6.64. A modellfán szereplő elemek.
6.65. A CD-fej vizsgálatának eredményei.
7.1. 2D-s Geometria.
7.2. Kontakt feladat - hálózott modell.
7.3. Kontakt feladat, terhelési modell.
7.4. Konzolos kontakt feladat geometriája a kijelölt kapcsolódó élekkel.
7.5. Súrlódásos kapcsolat beállításának részletei.
7.6. A kontaktvizsgálat eredményei.
7.7. Peremfeltételek és erőterhelés.
7.8. Kontaktbeállítások.
7.9. Globális hálóbeállítások.
7.10. Lokális hálósűrítés beállítása az érintkezés helyén.
7.11. Különböző mértékű lokális hálófinomítás.
7.12. Az analízis eredménye: a.) Y irányú elmozdulás, b.) Y irányú normálfeszültség.
7.13. Az Y irányú normál feszültség értékének vonal menti lekérdezése.
7.14. Az Y irányú normál feszültség értéke a kontaktfelülettől való távolság (r) függvényében, és az analitikus számolásból származó kontaktnyomás összehasonlítása.
7.15. Az elemméret hatása az érintkezési feszültségre és benyomódás mértékére.
8.1. A geometriai és a végeselem modell négyszög keresztmetszetű rúd esetén
8.2. Az erőterhelés (F=100N), és a megmaradt szabadságfokok a különböző megfogási esetekben. A peremfeltételektől függő működő rúdhossz: l_0,I=l, l_0,II=2l, l_0,III=0,7l, l_0,IV=0,5l.
8.3. Y irányú deformáció az első megfogási esetben.
8.4. Y irányú deformáció a második megfogási esetben.
8.5. Y irányú deformáció a harmadik megfogási esetben.
8.6. Y irányú deformáció a negyedik megfogási esetben.
8.7. A kihajlás vizsgálat analitikus és VEM eredményeinek összevetése.
9.1. A konzol megtámasztása és terhelése.
9.2. Deformáció [mm] a tranziens szimuláció 2. időpillanatának végén
9.3. A konzol véglapjának Y irányú deformációjának időbeli lefutása.
10.1. A konzol felületmodellje.
10.2. A hálózott végeselem modell.
10.3. A konstrukciós vonal helye.
10.4. A fix megfogás helye a lemezen - kék címkével jelölve.
10.5. Lengésképek lekérdezése a sajtfrekvenciák eredményei alapján.
10.6. Automatikus átnevezés a definíció alapján.
10.7. A statikus előfeszítés terhelési modellje.
10.8. A terheletlen szerkezet lengésképei és sajátfrekvenciái.
10.9. A terheletlen szerkezet Y irányú jellemző lengéssel rendelkező módusainak vonal menti eredménye.
10.10. Terheletlen rúd lengésképei különféle peremfeltételek esetén.
11.1. a.) Egyenletes eloszlású számolási pontok és b.) a pontok besűrítése a sajátfrekvenciáknál (Cluster result).
11.2. Csapágyterhelés szinuszos váltakozása ANSYS-ban, Forrás: [6.] .
11.3. A harmonikus erőterhelés helye
11.4. Harmonikus terhelés esetén a Bode-diagram
11.5. Amplitúdó és fázismenet normált diagram
11.6. Az analitikus és a numerikus eredmények összehasonlítása.
12.1. Tekercs modellezése.
12.2. A geometriai modell a környezettel.
12.3. A testek egy alkatrésszé alakítása.
12.4. Konstrukciós geometria definiálása solenoid tekercs tengelyében
12.5. Szimmetria síkok a solenoid tekercs esetében
12.6. Hálósűrítési beállítások a solenoid tekercs szimulációja során
12.7. Peremfeltételek a solenoid tekercs szimulációja során.
12.8. A mágneses térerősség alakulása a konstrukciós geometria mentén
12.9. A mágneses térerősség bemutatása a tekercs környezetében: a.)színsávokkal, b, c.) vektorokkal.
12.10. Egy felületen áthaladó fluxus lekérdezése.
12.11. Az analitikus H(x) és végeselem H (VEM) számolás eredményeinek összehasonlítása. Ho=IN/L közelítő értéket mutatja, (a tekercs széléig jelölve).
12.12. Az elektromágnes geometriai modellje.
12.13. A geometriai modell alkotói. Balról jobbra haladva: belső vasmag, tekercs, felső vasmag.
12.14. A környezetet geometriai modellje (sárga színű test)
12.15. A véges elemes háló.
12.16. A terhelési modell komponensei elektromágneses szimuláció esetén
12.17. A mágneses indukcó eredményei vektoros formában
12.18. A mágneses térerősség eredménye vektoros formában
12.19. Az áramsűrűség vektoros formában
12.20. Y irányú erőhatás a fedőlapra [N]
13.1. Konstrukciós geometria a hőmérséklet-eloszlás hossz menti lekérdezéséhez.
13.2. Véges elemes háló a hőtani példa esetén
13.3. A hőtani analízisperem feltételei.
13.4. Az állandósül hőmérsékleti viszonyok a teljes test felületén
13.5. Állandósult hőmérsékleti viszonyok a konstrukciós geometria mentén
13.6. Állandósult hőmérsékleti viszonyok a konstrukciós geometria mentén grafikon formátumban
13.7. Az analitikus és numerikus eredmények összehasonlítása.
14.1. A projektfelületen elhelyezett analízisek.
14.2. Az egyenfeszültségű tartó geometriája, Hálózása és perem, ill. terhelési feltételei.
14.3. Strukturált háló létrehozása háromszög felületen.
14.4. Az egyenfeszültségű tartó analízisének eredményei.
14.5. Megtámasztás a terheletlen modál analízis esetén.
14.6. A modellfában megjelenő előterhelés.
14.7. A jelátalakító földi gravitációval terhelt modelljének első 6 sajátfrekvenciája és lengésképe.
14.8. A harmonikus analízis beállításai.
14.9. A harmonikus analízis során alkalmazott megtámasztás, gyorsulás és tömegpont.
14.10. A jelátalakító végének elmozdulása a gerjesztő gyorsulás hatására, Bode-diagramon ábrázolva.
14.11. A jelátalakító felületén ébredő fajlagos nyúlás értéke a gerjesztés frekvenciájának függvényében (Bode).
14.12. Maximális elmozdulás lekérdezése a 20,609Hz frekvencián, 90°-os fázisnál.
14.13. A tranziens szerkezeti analízis során alkalmazott perem és kezdeti feltételek.
14.14. Az elmozdulás kezdeti feltétel beállítása, mint az 1. lépésben létrehozott elmozdulás.
14.15. Az analízis beállításai.
14.16. A végpont csillapodó lengését szemléltető eredmény.
14.17. A gyorsulásérzékelő különböző szintű absztrakciói: a.) egyszerűsített szerkezeti ábra, b.) szabadtest ábra, c.) Struktúra gráf.
14.18. Az egyenfeszültségű tartó eredményei kis lehajlás esetén (h=0,5).
14.19. Az egyenfeszültségű tartó eredményei (főfeszültség és főnyúlás) nagy lehajlás esetén (h=0,1).
14.20. Az egyenfeszültségű tartó eredményei (z irányú normál feszültség és fajlagos nyúlás) nagy lehajlás esetén (h=0,1).
14.21. A jelátalakító frekvenciadiagramja (az összehasonlíthatóság kedvéért, a szokásos Bode-diagramtól eltérően, abszolút értékekkel megadva).
14.22. A deformált és magára hagyott („megpendített”) tartó tranziens viselkedése.
15.1. [Forrás: http://www.econengineering.com/hu/szoftvereink/ansys.html]
15.2. [Forrás: http://www.3ds.com/products-services/simulia/portfolio/abaqus/overview/]
15.3. [Forrás: http://www.mscsoftware.com/product/marc]
15.4. [Forrás: http://www.adina.com/newsgH141.shtml]
15.5. [Forrás: http://upload.wikimedia.org/wikipedia/en/3/36/LS_DYNA_geo_metro.png]
15.6. [Forrás: http://www.solidworks.com]
15.7. [Forrás: http://upload.wikimedia.org/wikipedia/en/7/75/NEi_Fusion_image_servo_motor_FEA_and_CAD_1000px.JPG]
15.8. [Forrás: http://upload.wikimedia.org/wikipedia/en/4/45/Noraneng.JPG]
15.9. [Forrás: http://upload.wikimedia.org/wikipedia/commons/3/34/Lav.png]
15.10. [Forrás: http://upload.wikimedia.org/wikipedia/commons/1/19/FreeFEM%2B%2B_CS_Example_-_Dirichlet.png]
15.11. [Forrás: http://upload.wikimedia.org/wikipedia/commons/7/71/Harmonic_Wave_Propogation.png]
15.12. [Forrás: http://upload.wikimedia.org/wikipedia/commons/4/4a/FAE_visualization.jpg]
15.13. [Forrás: http://upload.wikimedia.org/wikipedia/commons/8/8c/Screenshot_OpenFOAM-2.1.x_gnome-terminal.png]

A táblázatok listája

2.1. Különböző geometriai egyszerűsítések áttekintése, mechanikai példán keresztül.
2.2. A direkt és az automatikus hálózás összehasonlítása.
2.3. Hiperelasztikus anyagmodellek csoportosítása összefoglalása [36.] , [21.] , [37.] , (nincs adat: „-”).
2.4. Az anyagok csoportosítása mágneses tulajdonságuk szerint.
2.5. Néhány analízis típushoz tartozó elsődleges és másodlagos mennyiségek.
4.1. Anyagvizsgálati adatok.
6.1. A négy különböző végeselemes módszer és az analitikus eredmények összehasonlítása.
6.2. A különféle geometriai megoldások eredményeinek összehasonlítása az analitikus megoldással.
7.1. A kontaktok csoportosítása a normális és tangenciális irányú viselkedésük alapján.
7.2. A végeselemes és az analitikus megoldás eredményeinek összehasonlítása, különböző elemméret mellett.
10.1. A terheletlen és az előfeszített szerkezet első 6 sajátfrekvenciájának összehasonlítása.
10.2. Az analitikus és numerikus eredmények összehasonlítása az első 3, Y irányú lengés esetében.
12.1. A környező levegőréteg vastagságának hatása a tekercs középpontjában számolt mágneses térerősségre.
14.1. A jelátalakító első 6 sajátfrekvenciája terheletlen és terhelt állapotban.
14.2. Az analitikus és VEM eredmények összehasonlítása.

1. fejezet - A Végeselem módszer elméleti alapjai

Tartalom

1.1. Alapfogalmak

1.1.1. Az algebrai test
1.1.2. A vektortér
1.1.3. A metrikus tér
1.1.4. Norma, normált tér
1.1.5. Sorok és sorozatok normált térben
1.1.6. A Banach-tér
1.1.7. Lineáris leképezések, funkcionálok, korlátos leképezések
1.1.8. A skalárszorzás vektorterekben
1.1.9. A Hilbert-tér
1.1.10. Szimmetrikus operátorok
1.1.11. Adjungált és önadjungált operátorok
1.1.12. Pozítív, szigorúan pozitív, egyenletesen pozitív önadjungált operátorok, koercív operátorok
1.1.13. Monoton és Lipschitz-folytonos operátorok
1.1.14. Operátorok bihemi-folytonossága
1.1.15. Az energianorma
1.1.16. Bilineáris formák

1.2. Operátoregyenletek megoldása

1.2.1. Lineáris, korlátos operátoregyenletek

1.2.2. Lineáris nem korlátos operátoregyenletek

1.2.2.1. Szimmetrikus operátoregyenletek gyenge megoldása
1.2.2.2. Nem szimmetrikus operátoregyenletek gyenge megoldása

1.2.3. Nem lineáris operátoregyenletek

1.2.4. Gâteaux-derivált, potenciál operátor

1.2.5. A variációs elv

1.3. Variációs elven alapuló közelítő módszerek

1.3.1. Lineáris, szimmetrikus operátoregyenletek funkcionáljai
1.3.2. Nemlineáris egyenletek funkcionáljai

1.4. Ritz-Galjorkin módszer

1.4.1. A Ritz-Galjorkin módszer szimmetrikus lineáris egyenletekre
1.4.2. A Ritz-Galjorkin módszer általánosítása
1.4.3. A Ritz-Galjorkin módszer nem szimmetrikus lineáris egyenletekre
1.4.4. A Ritz-Galjorkin módszer nemlineáris egyenletekre

1.5. A végeselem-módszer háttere

1.5.1. A végeselemes technika

1.5.1.1. Koordináta-rendszerek
1.5.1.2. Bázisfüggvények

1.5.2. Egyváltozós bázisfüggvények

1.5.3. Kétváltozós bázisfüggvények

1.5.4. Háromváltozós bázisfüggvények

1.5.5. Végeselemek használata térbeli rugalmasságtani feladatokon

Megfelelő matematikai apparátussal a végeselem módszer egyszerűen megfogalmazható, áttekinthető számítási metodika. Az egyszerű megfogalmazáshoz azonban szükséges néhány alapfogalom tisztázása. Az alábbiak elsősorban Karátsony János [1.] előadásaira alapozottak. Nem tartalmazzák azonban a funkcionál analízis összes rejtélyét, csak azokat az alapfogalmakat, melyek a végeselem módszerről való plasztikus – a numerikus részletek kidolgozási metódusait elfedő – kép kialakításához szükségesek.

1.1. Alapfogalmak

A módszer matematikai értelmezéséhez tekintsünk át először a fent említett néhány alapfogalmat!

1.1.1. Az algebrai test

Definíció: Az algebrai test egy olyan struktúra (alapelemek, relációk és műveletek halmaza) ahol értelmezettek + és a ∗ műveletek.

F = (T, + , ∗)

(1.1)

ahol T kommutatív csoportot alkot az összeadás (+) műveletre és a szorzás (∗) műveletre.

Létezik 0 elem, azaz

Minden a ∈ T, a+0 = a

a,b ∈ T, a+b = b+a ∈ T,

(1.2)

Létezik 1 elem, azaz

Minden a ∈ T, a∗1 = a

(1.3)

A szorzás kommutatív

a,b ∈ T, a∗b = b∗a ∈ T

(1.4)

A szorzás asszociatív

a,b,c ∈ T a ∗ (b∗c)=(a∗b)∗c∈T

(1.5)

Minden nem 0 elemnek létezik inverze (a^-1 ∈ T)

a ∈ T, a≠0 a∗a^-1 = 1

(1.6)

A ∗ szorzás disztributív az összeadásra nézve, azaz

a,b,c ∈ T (a+b) ∗c=(a∗c)+(b∗c)

(1.7)

Ha jól végiggondoljuk a definíciót, akkor láthatjuk, hogy a valós számok, a komplex számok egyaránt testet alkotnak. Szokás is beszélni a valós számtestről, illetve a komplex számtestről. A későbbiekben ez a két test alapvető szerepet játszik.

1.1.2. A vektortér

Definíció: Egy V nem üres halmazt vektortérnek nevezünk egy F test felett, ha V halmaz elmei között értelmezett az összeadás művelete, azaz bármely két elemhez értelmezett egy + függvény úgy, hogy

u,v ∈ V akkor u+v ∈V vagy másképp

+:V×V→V

(1.8)

F és V között értelmezve van a skalárral való szorzás művelete (∗) azaz

λ ∈ F és v ∈V akkor λ∗v ∈V vagy másképp

∗:F×V→V

(1.9)

úgy hogy V az összeadásra nézve kommutatív csoport, és a skalárral való szorzásra igaz, hogy

λ ∈ F és u,v ∈V akkor λ∗ (u+v)= λ∗u+λ∗v

λ,μ ∈ F és u ∈V akkor (λ+μ) ∗u= λ∗u+μ∗u

λ,μ ∈ F és u ∈V akkor λ∗ (μ∗u)=(λ∗μ) ∗u

minden u ∈V akkor 1∗u=u, ahol 1 a test egysége

(1.10)

Ha a térbeli vektorokra gondolunk, akkor könnyen meggyőződhetünk arról, hogy azok vektorteret alkotnak az összeadásra és a valós skalárral való szorzásra. De vektortér a folytonos függvények tere is, ha a függvények közötti összeadásra és a függvény skalárral való szorzására gondolunk. A függvények tere különösen fontos szerepet játszik majd, hiszen a differenciálegyenletek megoldásai függvények.

1.1.3. A metrikus tér

Metrikus térnek nevezünk egy olyan halmazt (X), melyen értelmezett egy olyan d függvény, amely a halmaz bármely két eleméhez hozzárendel egy nem negatív valós számot. Legyen

d:X×X→R^+,

(1.11)

amelyre igazak az alábbiak:

1.) d(x,y)=0 akkor és csak akkor,ha x=y,

2.) d(x,y)=d(y,x),

3.) d(x,z)≤d(x,y)+d(y,z).

(1.12)

Ez megfelel a távolság fogalmunknak, például a térben két pont távolsága csak akkor 0, ha azonos pontokról van szó (ez éppen az első feltétel), x pont távolsága y-tól ugyanannyi, mint y-nak x-től (a második feltételnek megfelelően) a távolság szimmetrikus. Végül igaz a háromszög-egyenlőtlenség (pontosan a harmadik feltétel írja le).

1.1.4. Norma, normált tér

Definíció: Legyen X vektortér K felett, ahol K = C (a komplex számok halmaza) vagy R (a valós számok halmaza). A norma X vektortéren értelmezett függvény, mely a vektortér elemeihez nem negatív egész számot rendel

‖ ⋅ ‖:X→R^+,

(1.13)

és

1.) minden x∈X-re ‖x‖≥0 és ‖x‖=0 akkor és csak akkor,ha x=0,

2.) minden λ∈K és x∈X-re ‖λ∗x‖= |λ|∗‖x‖,

3.) minden x,y∈X-re ‖x+y‖≤‖x‖+‖y‖.

(1.14)

A |λ| a komplex szám abszolút értéke

A háromdimenziós vektorok (x,y,z) ∈ R³ között értelmezett az euklideszi norma

(1.15)

Könnyen meggyőződhetünk arról, hogy norma az úgynevezett maximum-norma is

(1.16)

hiszen a definícióban megfogalmazott összes feltételt teljesíti.

Az (X, ‖⋅‖) vektorteret és az azon értelmezett normából képzett párt normált térnek hívjuk. Az R valós számok halmaza az abszolút értékkel normált tér, a háromdimenziós vektorok szintén normált teret alkotnak az euklideszi normával. A normált terek egyúttal metrikus terek is, hiszen a ρ(x,y)=‖x-y‖ metrika értelmezhető.

1.1.5. Sorok és sorozatok normált térben

Definíció: Legyen (X, ‖⋅‖) normált tér, x_n⊂X a tér elemeiből alkotott sorozat és x∈X egy vektor! Azt mondjuk, hogy a x_n sorozat határértéke x, ha az ‖x_n-x‖ számsorozat határértéke 0, azaz

, ha .

(1.17)

Azt mondjuk, hogy a 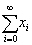sorösszeg x, ha a részösszegekből alkotott sorozat tart x-hez, azaz

, ha sorozatra

(1.18)

Tehát a normált terekben minden ugyanúgy működik, mint a valós számoknál.

Definíció: Egy vektortér elemeiből képzett sorozatot Cauchy sorozatnak hívunk, ha minden ε>0 számhoz létezik olyan – ε-tól függő – N egész, hogy minden n>m>N(ε) számra

‖x _n -x _m ‖<ε

(1.19)

Ez azt jelenti, hogy ha a sorozat elejét levágjuk, akkor a maradék tagok közel vannak egymáshoz.

A sorok és sorozatok segítségével a határérték és a Cauchy sorozat pontosan úgy definiálható normált terekben, mint a valós számok esetében.

Tétel: A norma folytonos függvény, azaz ha vektorok egy sorozata (x_n) közeledik a vektortér egy vektorához, akkor a sorozat elemeinek normái is közelítenek a határérték normájához.

1.1.6. A Banach-tér

Definíció: Egy normált teret Banach-térnek nevezünk, ha minden Cauchy sorozata konvergens, azaz a tér teljes.

Ez is azt jelenti, hogy a Banach-tér elemei úgy viselkednek, mint a valós számok. Az Rⁿaz n elemű valós vektorok is az euklideszi normával Banach teret alkotnak. Minden véges dimenziós normált tér Banach-tér. A intervallumon folytonos függvények C_[a,b] a maximum normával (‖f‖_max=max_[a,b]f) szintén Banach-teret alkotnak.

Tétel: Legyen (X, ‖⋅‖) normált tér, X₀ ⊂ X véges dimenziós altér és x ∈ X tetszőleges vektor. Ekkor létezik y₀ ∈ X₀, amelyre d = min(x, y₀ ∈X₀) =‖x-y₀ ‖=dist(x,X₀).

Ez azt jelenti, hogy egy véges-dimenziós altérnek a tér bármelyik eleméhez van legközelebbi eleme. Ezt nevezzük a vektor és az altér távolságának. Ha a háromdimenziós térben gondolkodunk, akkor annak például a sík altere. Bármely térbeli vektor sík altérre vetett merőleges vetülete a kétdimenziós sík altér legközelebbi eleme.

1.1.7. Lineáris leképezések, funkcionálok, korlátos leképezések

Azonos test felett definiált vektorterek között leképező függvényt lineárisnak nevezzük, ha

két vektor összegének képe a két vektor képének összege, és
egy vektor számszorosának képe a vektor képének ugyanezen számszorosa.

Ugyanez definíciószerűen megfogalmazva:

Definíció: Legyenek X és Y vektorterek a T számtest felett. Az

L:X→Y

(1.20)

leképezés lineáris, ha L értelmezési tartománya a H altér, és bármely u, v ∈ H valamint λ ∈T-re igaz, hogy

L(u+v)=L(u)+L(v) és

L(λ ∗ u)=λ ∗ L(u).

(1.21)

A lineáris leképezéseket szokták lineáris operátoroknak is hívni. Lineáris operátoroknál el szokták hagyni a () jeleket, és mintha mátrix-szorzás lenne Ax –szel jelölik. A definícióból egyértelmű, hogy A0=0.

A linearitás definíciója pontosan megfelel az egyváltozós lineáris függvényeknek, illetve a vektorok mátrixszal való szorzásának és eltolásának. (Ax+b).

Definíció: Legyen X vektortér a T alaptest felett! Funkcionálnak nevezzük a

F:X→T

(1.22)

leképezéseket.

A funkcionál tehát egy olyan leképezés, ami a vektortér elemeit az alaptest „számaira” képezi.

Definíció: Normált térben korlátosnak nevezünk egy L leképezést, ha létezik olyan M állandó, hogy

‖Lx‖≤M ∗ ‖x‖

(1.23)

minden L értelmezési tartományában lévő x esetén.

Tétel: Egy lineáris leképezés akkor és csak akkor folytonos, ha korlátos.

A továbbiakban legyen X normált tér. A fenti tétel funkcionálokra is érvényes, így egy

ϕ : X → K

(1.24)

lineáris funkcionál pontosan akkor folytonos, ha korlátos, azaz ha van olyan M ≥ 0 állandó, hogy minden x ∈ X esetén |ϕx| ≤ M∥x∥.

Tétel: Ha X normált tér és K az alaptest, akkor az X-n értelmezett korlátos lineáris funkcionálok halmaza Banach-tér.

1.1.8. A skalárszorzás vektorterekben

A vektorterek skaláris szorzata is általánosítható.

Definíció: Legyen X vektortér T (valós vagy komplex számok) felett! Egy olyan <,>-nal jelölt leképezést, amelyre

< ,>X×X→T

(1.25)

skalár szorzatnak nevezünk, ha

lineáris funkcionál, azaz minden x,y,z ∈ X-re és λ∈T-re, igaz, hogy
<x,λ y+z >= λ <x,y>+<x,z>
hermitikus, azaz <x,y>= 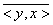, ahol a felülvonás a komplex konjugáltat jelöli. Természetesen valós számok esetén ez szimmetriát jelent.
pozitív definit, azaz <x,x>≥0, és <x,x>=0 akkor és csak akkor, ha x=0.

A térbeli valós számtest feletti vektorok skaláris szorzata ilyen értelemben is skaláris szorzat. Hasonlóan igaz ez a komplex számtest felett értelmezett vektorokra.

Például az intervallumon folytonos függvények (C_[a,b]) esetében az integrál alaptulajdonságai miatt skaláris szorzat lehet a

(1.26)

Bizonyítható, hogy az X vektortér 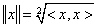skalárszorzata (x ∈ X esetén) norma.

Definíció: Az X vektortérben a skalár szorzat

(1.27)

kifejezését (x ∈ X) a skalárszorzat által indukált normának nevezzünk.

A valós vektorok körében a szokásos skaláris szorzat az euklideszi normát indukálja.

1.1.9. A Hilbert-tér

Definíció: Egy teljes (minden Cauchy sorozat konvergens) normált (Banach) teret

(H, <,>)

(1.28)

Hilbert-térnek nevezünk, ha a norma a skaláris szorzat által indukált 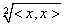norma.

A véges-dimenziós vektorterek Hilbert-terek, a szokásos skalárszorzással az euklideszi normára.

A Ω ⊂ Rⁿ négyzetesen integrálható függvények (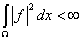) Hilbert-teret alkotnak a

(1.29)

normára.

Definíció: Azt mondjuk, hogy az x, y ∈ H (Hilbert-tér) vektorok ortogonálisak (vagy merőlegesek x ⊥ y) egymásra, ha <x,y> = 0.

A síkban és a térben jól ismert a merőleges vektorok ilyen tulajdonsága a szokásos skaláris szorzásra nézve.

Bizonyíthatók az alábbi állítások:

Tétel: Legyen H Hilbert-tér, K ⊂ H nem üres, konvex, zárt halmaz. Ekkor bármely x ∈ H esetén van egyetlen olyan y ∈ K, melyre ‖x - y‖ = min(x,y)=dist(x,K) (vagyis az x-nek K-tól vett távolsága).

Tétel: (Riesz reprezentációs tétele). Legyen H Hilbert-tér. Ekkor minden ϕ : H → C folytonos, lineáris funkcionálhoz létezik egyetlen olyan y ∈ H, hogy

ϕx = 〈 x,y 〉 minden x∈H

(1.30)

Tehát minden folytonos, lineáris funkcionál leírható a Hilbert-tér egy elemével való skalárszorzással. Más szavakkal minden folytonos lineáris funkcionál azonos a tér valamely elemével való skalárszorzással.

1.1.10. Szimmetrikus operátorok

Definíció. Legyen H Hilbert-tér, A lineáris operátor! Az

A : H → H

(1.31)

lineáris operátor szimmetrikus, ha

< Ax,y> = <x,Ay>

(1.32)

teljesül minden x, y-ra A értelmezési tartományán.

Egy mátrixot akkor nevezünk szimmetrikusnak, ha elemei a főátlóra szimmetrikusak. Bizonyítható, hogy a szimmetrikus mátrixok is definiálhatók a fenti módon.

Tétel: Ha H komplex Hilbert-tér, az A : H→H operátor akkor és csak akkor szimmetrikus ha

< Ax,x> ∈ R ∀x ∈ H

(1.33)

1.1.11. Adjungált és önadjungált operátorok

Amennyiben a skaláris szorzatokban operátorok által leképzett elemeket is használunk, szükséges néhány fogalom tisztázása.

Tétel: Ha A Hilbert-téren értelmezett korlátos lineáris operátor, akkor létezik egyetlen olyan A^∗ korlátos lineáris operátor, melyre

〈 Ax,y 〉 = 〈 x,A^ ∗ y 〉 minden x,y∈H

(1.34)

Ezt az A^∗ operátort az A adjungáltjának nevezzük.

Az adjungált operátorra bizonyíthatóak az alábbi állítások

Tétel: Ha A és B korlátos lineáris operátorok, és λ komplex szám, akkor

		(1.35)
		(1.36)
		.37)
		(1.38)

Definíció: Egy A korlátos és lineáris operátor önadjungált, ha

A ^* =A

(1.39)

Az önadjungált operátor definíciója alapján írhatjuk, hogy

〈 Ax,y 〉 = 〈 x,Ay 〉 minden x∈H

(1.40)

Ha A korlátos és lineáris operátor akkor és csak akkor önadjungált, ha

〈 Ax,x 〉 valós minden x∈H

(1.41)

Hiszen fennállnak a (1.42) egyenlőségek.

minden x∈H

(1.42)

1.1.12. Pozítív, szigorúan pozitív, egyenletesen pozitív önadjungált operátorok, koercív operátorok

Definíció. Egy H Hilbert-téren értelmezett A lineáris korlátos operátor pozitív, ha

〈 Ax,x 〉 ≥ 0 ( ∀ x ∈ H);

(1.43)

szigorúan pozitív, ha

〈 Ax,x 〉 > 0 ( ∀ x ∈ H,x≠ 0);

(1.44)

egyenletesen pozitív, ha létezik

m > 0 úgy,hogy 〈Ax,x〉≥ m∥x∥² (∀x ∈ H).

(1.45)

Definíció: Legyen A korlátos lineáris leképezés! Az A operátort koercívnek hívjuk, ha létezik m > 0, hogy

Re 〈 Ax,x 〉 ≥m ∗ ‖x‖ ², minden x∈H

(1.46)

Valós Hilbert-térben, illetve önadjungált esetben elhagyható a valós rész képzés Re operátora.

Ha H komplex Hilbert-téren értelmezett, önadjungált, egyenletesen pozitív, korlátos operátor, akkor <Ax,x> valós, így (1.41) miatt önadjungált. Ha A valós Hilbert-téren értelmezett egyenletesen pozitív operátor, akkor ugyancsak (1.41) miatt önadjungált kell, legyen, és létezik m > 0, hogy (1.46) fennáll.

Tétel: Összefoglalva tehát, egy operátor akkor és csak akkor egyenletesen pozitív, ha koercív és önadjungált.

1.1.13. Monoton és Lipschitz-folytonos operátorok

Definíció: Legyen H Hilbert-tér! Azt mondjuk, hogy F : H → H operátor

monoton operátor, ha

〈Fx-Fy,x-y〉≥0 minden x,y∈H

(1.47)

szigorúan monoton operátor, ha

〈 Fx-Fy,x-y 〉 >0 minden x,y∈H

(1.48)

egyenletesen monoton operátor, ha létezik m > 0, hogy

〈 Fx-Fy,x-y 〉 >m ∗ ‖x-y‖ ² minden x,y∈H

(1.49)

Definíció: Legyen H Hilbert-tér! Az F : H → H operátror Lipschitz-folytonos, ha létezik M > 0, hogy

〈 Fx-Fy,x-y 〉 ≤M ∗ ‖x-y‖ minden x,y∈H

(1.50)

A monotonitás és a Lipschitz feltétel is megfelel a függvényeknél megismerteknek.

1.1.14. Operátorok bihemi-folytonossága

Definíció. Legyenek X, Y és Z normált terek! Legyen A leképezés, ami a X ről, az Y-ról Z-re képező korlátos és folytonos leképezések halmazára (ez is vektortér) képez. Azt mondjuk, hogy

a kérdéses A leképezés hemi-folytonos, ha minden u, v ∈ X és minden w ∈ Y, valamint t∈R esetén a

t → A(u+tv)w

leképezés folytonos;

A bihemi-folytonos, ha minden u, v,w ∈ X, z ∈ Y valamint s,t∈R esetén az

(s, t) → A(u + tv + sw)z

leképezés folytonos.

A hemi- és a bihemi-folytonosság valami olyasmit takar, hogy ha egy egyenes mentén, vagy két paraméterrel, két egyenessel meghatározott módon változtatjuk egy leképezés független változóját, akkor a leképezések a paraméterek függvényében folytonosan változnak.

1.1.15. Az energianorma

Definíció. Legyen H Hilbert-téren értelmezett A operátor folytonos, korlátos, lineáris és szigorúan pozitív (A:H→H) . Ekkor az

〈 x,y 〉 _A = 〈 Ax,y 〉

(1.51)

skalárszorzatot az A operátorhoz tartozó energia-skalárszorzatnak, az indukált

(1.52)

normát pedig energianormának nevezzük.

Tétel: Ha A:H→H egyenletesen pozitív (1.1.12. szakasz) operátor, akkor H Hilbert-tér a < , >_A skalárszorzat által generált ∥x∥_A normával is Hilbert-tér lesz.

1.1.16. Bilineáris formák

Definíció. Egy B : H × H → K (ahol K a komplex vagy a valós számtest) leképezés

bilineáris, ha mindkét változójában lineáris;
konjugáltan bilineáris, ha első változójában lineáris, második változójában konjugáltan lineáris, azaz

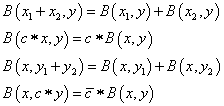
(1.53)
szimmetrikus, ha

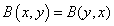
(1.54)
konjugáltan szimmetrikus, ha

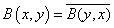
(1.55)

korlátos, ha létezik M > 0, hogy

|B(x,y)|≤M ∗ ‖x‖ ∗ ‖y‖ minden x,y ∈H

(1.56)

koercív, ha létezik m > 0, hogy

Re B(x,x)≥m ∗ ‖x‖ ² minden x ∈H

(1.57)

Tétel (korlátos formák Riesz-reprezentációja). Legyen H valós (komplex) Hilbert-tér, és B : H × H → K korlátos, (konjugáltan) bilineáris forma. Ekkor létezik pontosan egy olyan A korlátos, lineáris operátor, melyre

B(x,y)= 〈 Ax,y 〉 minden x,y ∈H

(1.58)

A tétel állítása emlékeztet a 1.1.9. szakasz fejezet (1.30) állítására. Minden korlátos, konjugált, bilineáris forma reprezentálható lesz korlátos, lineáris operátorral.

Tétel. Legyen H valós (komplex) Hilbert-tér, B : H × H → K korlátos, (konjugáltan) bilineáris forma, és A korlátos és lineáris operátor, a B forma Riesz-reprezentánsa.

B akkor és csak akkor (konjugáltan) szimmetrikus, ha A önadjungált.
B akkor és csak akkor koercív, ha A koercív.

Látható tehát, hogy a bilineáris formák az operátorokhoz hasonlóan viselkednek. Kapcsolat is teremthető köztük.

Tétel: (Lax_Milgram-lemma, koercív változat).

(1) Legyen H valós Hilbert-tér, B : H × H → R korlátos, koercív, bilineáris forma. Ekkor minden ϕ:H→R korlátos lineáris funkcionálhoz létezik egyetlen olyan x ∈ H, melyre

B(x,y)=ϕy minden y ∈H

(1.59)

(2) Legyen H komplex Hilbert-tér, B : H × H → C korlátos, koercív, konjugáltan bilineáris forma. Ekkor minden ϕ:H→C korlátos, lineáris funkcionálhoz létezik egyetlen olyan x ∈ H, melyre

B(y,x)=ϕy minden y ∈H

(1.60)

Tétel (Lax_Milgram-lemma, általános változat). Legyen H valós Hilbert-tér, B :H × H → R korlátos és létezik m>0 úgy, hogy

|B(x,x)|≥m ∗ ‖x‖ ² minden x ∈H

(1.61)

akkor a valós tér esetén minden ϕ : H → R korlátos, lineáris funkcionálhoz létezik pontosan egy olyan x ∈ H, melyre

B(x,y)=ϕy minden y ∈H

(1.62)

Illetve, ha H komplex Hilbert-tér, B :H × H → C esetén

B(y,x)=ϕy minden y ∈H

(1.63)

Az alapfogalmak eddigi tisztázása után kezdhetünk foglalkozni célunkkal az operátoregyenletek megoldásával.

1.2. Operátoregyenletek megoldása

Mielőtt a numerikus megoldásokra koncentrálnánk célszerű néhány szót ejteni az

Ax=f

(1.64)

operátoregyenlet megoldásáról, a megoldás létezéséről és egyértelműségéről.

1.2.1. Lineáris, korlátos operátoregyenletek

Tétel. Legyen A a H Hilbert-téren értelmezett, korlátos, lineáris és egyenletesen pozitív operátor, azaz A koercív és önadjungált. Ekkor bármely f ∈ H esetén az Ax = f egyenletnek létezik pontosan egy x^∗ ∈ H megoldása.

Szokás ezt az első megoldhatósági tételnek is nevezni.

Tétel. Legyen A a H Hilbert-téren értelmezett, korlátos, lineáris és koercív. Ekkor bármely f ∈ H esetén az Ax = f egyenletnek létezik pontosan egy x^∗ ∈ H megoldása.

Láthatóan ez az előző tétel kiterjesztése - nem kell, hogy az operátor önadjungált legyen, elég, ha csak koercív. Szokás ezt a tételt második megoldhatósági tételnek is nevezni.

Tétel. Legyen A a H Hilbert-téren értelmezett, korlátos, lineáris. Ha

|Ax,x|≥m ∗ ‖x‖ ² minden x∈H

(1.65)

akkor bármely f ∈ H esetén az (1.64 egyenletnek létezik pontosan egy x^∗ ∈ H megoldása.

Még a koercivitás sem feltétel, elég a pozitívságot biztosító feltétel.

1.2.2. Lineáris nem korlátos operátoregyenletek

A nem korlátos operátoregyenletekre nem mondható ki egzisztencia és unicitás jellegű állítás, ezért bevezetjük a gyenge megoldás fogalmát.

1.2.2.1. Szimmetrikus operátoregyenletek gyenge megoldása

Tekintsük a (1.64) egyenletet! Legyen A szimmetrikus operátor!

Definíció. Legyen H Hilbert-tér, f ∈ H adott vektor és A szimmetrikus operátor! Az x ∈ H vektort az Ax = f feladat gyenge megoldásának nevezzük, ha

〈 x,y 〉 _A = 〈 f,y 〉 (minden y ∈ H)

(1.66)

Ha x az A operátor értelmezési tartományában található, akkor a gyenge megoldás egyúttal megoldás is. Tehát a gyenge megoldás arra az esetre vonatkozik, ha f nincs A képterében.

Tétel. Ha A egyenletesen pozitív, nem korlátos, akkor minden f ∈ H esetén az Ax = f egyenletnek egyértelműen létezik x^* ∈ H gyenge megoldása.

〈 x ^* ,y 〉 _A = 〈 f,y 〉 (minden y ∈ H)

(1.67)

1.2.2.2. Nem szimmetrikus operátoregyenletek gyenge megoldása

Tekintsük a (1.64) egyenletet! Ha A nem szimmetrikus operátor, akkor azzal nem definiálhatunk energia-skalárszorzatot (1.52), mert nem egyenletesen pozitív, így, ha a gyenge megoldást szeretnénk értelmezni, akkor egy másik, alkalmas S szimmetrikus operátor energiaterére vezetjük vissza a feladatot.

Definíció: Legyen S : H → H egyenletesen pozitív operátor, melynek értelmezési tartománya H altere (H_s). Azt mondjuk, hogy az A : H → H lineáris operátor, melynek értelmezési tartománya szintén H altere S -korlátos és S -koercív, ha

A értelmezési tartománya részhalmaza H_S–nek, és az értelmezési tartomány sűrű H_S-ben (a lezártja H_s az energianormában)

Létezik M > 0 állandó, hogy

| 〈 Ax,y 〉 |≤M ∗ ‖x‖ _s ∗ ‖y‖ _s minden x,y∈A ért.tartományára

(1.68)

Létezik m > 0 állandó, hogy

| 〈 Ax,x 〉 |≤m ∗ ‖x‖ _s ² minden x∈A ért.tartományára

(1.69)

Ezzel az A operátort mintegy becsültük az S operátor és energianormája segítségével.

Definíció. Legyen az A : H → H leképezés S-korlátos és S-koercív, ahol az A értelmezési tartománya H altere (H_S)! Ekkor A_S a H_S-ről H_S–re képező korlátos, lineáris operátor, melyre

〈 A_S x,y 〉 _S = 〈 Ax,y 〉 minden x,y ∈A ért.tartományára

(1.70)

Tétel: Az A_S operátor jól definiált.

Ez az állítás belátható, hiszen (1.68) miatt <Ax,y> bilineáris forma folytonos a S operátorhoz tartozó normára. A bilineáris formának létezik pontosan egy reprezentánsa a Riesz-féle reprezentációs tétel miatt (1.58).

Definíció: Legyen A : H → H S-korlátos és S-koercív ahol A értelmezési tartománya H altere,. Az x∈H_S vektor a (1.64) egyenlet gyenge megoldása, ha

〈 A_S x,y 〉 _S = 〈 f,y 〉 minden y ∈H_s

(1.71)

Tétel. Nem szimmetrikus S-korlátos és S-koercív A esetén bármely f ∈ H esetén az (1.64) egyenletnek egyértelműen létezik gyenge megoldása.

Ezzel, a gyenge megoldást használva a nem szimmetrikus operátorok esetére is kimondhattunk egzisztencia és unicitás jellegű állítást. Kérdés, hogy mit tegyünk nem lineáris esetben.

1.2.3. Nem lineáris operátoregyenletek

Nemlineáris esetben F a H valós Hilbert-térről H valós Hilbert-térre képező operátorra vonatkozó

F(x)=f

(1.72)

egyenlet megoldását keressük.

Tétel. Legyen H valós Hilbert-tér és F : H → H adott operátor. Tegyük fel, hogy F egyenletesen monoton és F Lipschitz-folytonos, ekkor bármely b ∈ H esetén az F(x) = b egyenletnek létezik pontosan egy x^∗ ∈ H megoldása.

A Lipschitz-folytonosság – az implicit függvényrendszerekhez hasonlóan – ebben az esetben is biztosítja az egyértelmű megoldás létezését.

Ahhoz, hogy potenciál függvényt használva az operátoregyenlet helyett variációs elvet használjunk a megoldás keresésére szükségünk van a derivált fogalom általánosítására. Operátorok között is értelmezhető derivált jellegű kifejezés.

1.2.4. Gâteaux-derivált, potenciál operátor

Definíció: Legyenek X, Y normált terek! Egy F:X → Y (nemlineáris) operátorról azt mondjuk, hogy Gâteaux deriválható az x∈X pontban, ha

Bármely d∈X -hez létezik

(1.73)

A d→∂_d F(x) hozzárendelés folytonos, lineáris operátor, melynek jele F’(x)

F’(x)=∂ _d F(x)

(1.74)

A ∂ _dF(x) Gâteaux derivált (F’(x)) a d irányú iránymenti derivált, az operátor pedig a definíció szerint d irányhoz rendeli az iránymenti deriváltat, tehát X-ből Y-ba képező operátor

Definíció: Legyen X Banach-tér! Egy A: X → X (nemlineáris) operátort potenciáloperátornak nevezünk, ha létezik olyan J : X → R Gâteaux-deriválható funkcionál, melyre J’= A, azaz J’(x) = A(x) minden x ∈ X. Ekkor a J funkcionált A potenciáljának hívjuk.

1.2.5. A variációs elv

Ha egy A operátor potenciáloperátor, akkor az A(x) = b egyenletek megoldása helyett egy funkcionál minimalizálására vezethetjük vissza az egyenlet megoldását.

Legyen X Banach-tér és A:B→B potenciáloperátor és J:B→R a potenciálja! Azaz

J’(x)=A(x) (x ∈ B)

(1.75)

Legyen

E ∶ X→R

(1.76)

funkcionál a következő!

E(x)=J(x)- 〈 b,x 〉

(1.77)

Akkor E potenciáloperátora az x→A(x)-b leképezésnek

E'(x)=A(x)–b (x ∈ X)

(1.78)

hiszen J’=A és <b,x>’=b.

Tehát az A(x)–b=0 egyenlet megoldása megegyezik E funkcionál stacionárius értékével. Az E funkcionál sokszor energia jellegű mennyiség, és ilyenkor az energiaminimumot keressük.

1.3. Variációs elven alapuló közelítő módszerek

A következőkben variációs elven alapuló módszerekkel foglalkozunk.

1.3.1. Lineáris, szimmetrikus operátoregyenletek funkcionáljai

Legyen H komplex Hilbert-tér, A : H → H szimmetrikus, szigorúan pozitív, lineáris operátor, amelynek értelmezési tartománya altér, és f∈ H adott vektor!

Definíció. Az

Ax = f

(1.79)

egyenlethez tartozó kvadratikus funkcionál az alábbi Φ : H → R funkcionál:

Φ(x)= 〈 Ax,x 〉 - 2 ∗ Re 〈 f,x 〉

(1.80)

Tétel: Ha létezik A (szigorúan pozitív) operátor értelmezési tartományában x^∗, amelyre Ax^∗ = f, akkor Φ-nek pontosan egy minimumhelye van, és ez éppen x^∗.

Egyszerűen meggyőződhetünk a tétel igazságáról, hiszen bármely x≠ x^*esetén írjuk át a fenti egyenletet úgy, hogy „ketté írjuk” a (1.80) jobb oldalán álló kifejezés második tagját!

Φ(x)= 〈 Ax,x 〉 - 〈 f,x 〉 - 〈 x,f 〉 =

(1.81)

(1.81)-ban f helyébe írhatjuk az Ax^* kifejezést

Φ(x)= 〈 Ax,x 〉 - 〈 Ax ^* ,x 〉 - 〈 x,Ax ^* 〉

(1.82)

(1.82) első két tagját összevonva

Φ(x)= 〈 A(x-x ^* ),x 〉 - 〈 x,Ax ^* 〉

(1.83)

(1.83) egyenlet jobb oldalát bővítsük a -<A(x-x^*),x^*>+<A(x-x^*),x^*> azonosan 0 kifejezéssel!

Φ(x)= 〈 A(x-x ^* ),x 〉 - 〈 A(x-x ^* ),x ^* 〉 + 〈 A(x-x ^* ,x ^* 〉 - 〈 x,Ax ^* 〉

(1.84)

összevonva az első két tagot

Φ(x)= 〈 A(x-x ^* ),x-x ^* 〉 + 〈 A(x-x ^* ),x ^* 〉 - 〈 x,Ax ^* 〉

(1.85)

kihasználva A szimmetrikus voltát, és összevonva az utolsó két tagot

Φ(x)= 〈 A(x-x ^* ),x-x ^* 〉 - 〈 Ax ^* ,x ^* 〉

(1.86)

<Ax^*,x^*> helyébe (1.80) alapján írhatjuk,

〈 Ax ^* ,x ^* 〉 =Φ(x ^* )+2 ∗ Re 〈 f,x ^* 〉

(1.87)

Mivel x^* megoldás, így f=Ax^* és így Re(Ax^*, x^*) A szimmetriája miatt valós

Φ(x ^* )+2 ∗〈 Ax ^* ,x ^* 〉 = 〈 Ax ^* ,x ^* 〉

(1.88)

azaz

〈 Ax ^* ,x ^* 〉 =-Φ(x ^* )

(1.89)

(1.89)-t (1.86)-be helyettesítve

Φ(x)= 〈 A(x-x ^* ),x-x ^* 〉 +Φ(x ^* )>Φ(x ^* )

(1.90)

Tehát ha létezik az x^* megoldás, akkor az a Φ funkcionál stacionárius értéke. Kérdés létezik-e megoldás?

Ha A egyenletesen pozitív és korlátos, akkor 1.2.1. szakasz első tétele szerint (1.79) egyenletnek létezik pontosan egy megoldása.

Ha A egyenletesen pozitív, de nem korlátos, akkor 1.2.2. szakasz tétele szerint egyértelműen létezik az u^∗ ∈ H gyenge megoldás.

Gyenge megoldás esetén a variációs elvet úgy tudjuk használni, hogy (1.80) egyenlet helyett áttérünk az energiatérre, azaz Φ-t kiterjesztjük a H értelmezési tartományról a teljes X-re. Legyen Ψ:X→R olyan, hogy

Ψ(x)=‖x‖ _A ² -2 ∗ Re<f,x> x∈X

(1.91)

Ha H valós Hilbert-tér, A : H → H szimmetrikus, szigorúan pozitív operátor, melynek értelmezési tartománya H altere, f ∈ H adott vektor. A (1.80) egyenlethez tartozó eredeti, ill. kiterjesztett kvadratikus funkcionál ekkor az alábbi Φ és Ψ funkcionálokra is érvényes a (1.92) eredmény.

ϕ(x)= 〈 Ax,x 〉 -2 ∗ <f,x> Ψ(x)=‖x‖_A²-2∗<f,x> x∈X

(1.92)

1.3.2. Nemlineáris egyenletek funkcionáljai

Legyen H valós Hilbert-tér. Ha az A : H → H nemlineáris operátor potenciáloperátor, akkor az

A(x)=f

(1.93)

egyenlethez, mint a 1.2.4. szakasz fejezetben láttuk, bizonyos feltételek esetén van minimalizáló funkcionál

Φ:X→R, Φ(x)=J(x)-〈f,x〉

(1.94)

ahol X Banach-tér, J egy potenciálja A-nak. Itt ugyanis A(x^*) = f pontosan akkor áll fenn, ha Φ′(x^*) = 0.

Arról, hogy a nemlineáris egyenletnek létezzék megoldása a következő tétel feltételeivel gondoskodhatunk.

Legyen a (1.93) egyenlet A operátora

Gâteaux-deriválható, és A′ bihemi-folytonos,
minden u ∈ H esetén A′(u) ∈ B(H) önadjungált,
létezik m > 0, hogy

〈 A(u)h,h 〉 ≥m‖h‖ ², minden h∈H

(1.95)

Legyen J egy potenciálja A-nak! Ekkor bármely f ∈ H esetén J funkcionálnak egyértelműen létezik minimumhelye, és ez az A(u) = f egyenlet megoldása.

1.4. Ritz-Galjorkin módszer

A Ritz-Galjorkin módszer az egyik legelterjedtebben használt variációs módszer [2.] .

1.4.1. A Ritz-Galjorkin módszer szimmetrikus lineáris egyenletekre

A Ritz-Galjorkin módszer hasonlóan működik más variációs módszerekhez. Legyen H Hilbert-tér, A:H→H egyenletesen pozitív leképezés és A értelmezési tartománya altér! Ekkor az

Ax = f

(1.96)

egyenlet megoldása a

Ψ(x)=‖x‖ _A ² -2 ∗ <f,x>, x∈H

(1.97)

funkcionál minimuma, hiszen a (1.80)-(1.90) egyenletekkel jellemzett – Φ-re elvégzett bizonyítást –végigvezethetjük Ψ-re is.

Ψ(x)=‖x-x ^* _A -‖x ^* ‖ _A ² =‖x-x ^* ‖ _A +Ψ(x ^* )>Ψ(x ^* )

(1.98)

és (1.90) egyenlet helyett (1.98) adódik.

Legyenek ϕ₁, ϕ₂, . . . ∈H elemek halmaza olyan, hogy H Hilbert-tér összes belső pontja kifejezhető ϕ_i elemekből képzett, lineáris kombináló sorok összegével. Ekkor a {ϕ₁, ϕ₂,… ϕ_n } elemek a H_n altér egy bázisát adják. Ha definiálnánk is ilyen {ϕ_i} végtelen elemű halmazt, a variációs egyenletek megoldása nyilván lehetetlen végtelen számú ϕ_i-re.

Keressük a megoldás közelítését egy véges-dimenziós altéren! Legyen n rögzített egész és H_n a ϕ₁, ϕ₂,… ϕ_n elemek (vektorok) által kifeszített altér! Ritz-Galjorkin módszere szerint a közelítő megoldást, a Ψ minimumát csak a H_n altéren keressük.

Keressük a minimumot H_n altéren

(1.99)

formában!

Itt x_n egyértelműsége ugyanúgy következik, mint x^∗-é (1.3.1. szakasz)-ban, hiszen a kvadratikus funkcionálnak a H_n végesdimenziós téren is egyetlen minimumhelye van.

Mondhatjuk, hogy (1.97) egyenletbe helyettesítve a (1.99) kifejezést,

(1.100)

adódik. Ekkor

(1.101)

azaz

(1.102)

funkcionál, és ennek keressük a minimumát. Bizonyítható, hogy a minimum a parciális deriváltak 0 helyén található. Jelöljük a c_i-kből képzett vektort c-vel!

(1.103)

Átrendezve

(1.104)

A minimum feltétele tehát

(1.105)

A (1.105) lineáris egyenletrendszer az ismeretlen c_i-kre.

Jelöljük az egyenletrendszer együtthatóit g_ik-val!

g _ik = 〈 ϕ _i ,ϕ _k 〉 _A = 〈 ϕ _k ,ϕ _i 〉 _A =g _ki

(1.106)

A (1.106) egyenletek g_ik elemeiből alkotott szimmetrikus mátrixot Gram mátrixnak, a végeselem rendszerek pedig merevségi mátrixnak hívják. Vezessük be a (1.107) jelölést!

b _k = 〈 f,ϕ _k 〉

(1.107)

Az egyenlet tehát

k=1..n

(1.108)

azaz

[g _i,k ] ∗ [c _k ]=[b _k ]

(1.109)

Tétel: Az egyenletrendszer megoldásaként adódó összeg A norma szerint tart a tényleges megoldáshoz, ha n tart a végtelenhez, azaz

(1.110)

Ha egy konkrét problémát szeretnénk megoldani, azt háromféleképpen is megtehetjük az alábbi tétel szerint:

Tétel. A Ritz-Galjorkin módszerrel kapott (1.99) szerinti x_n-re az alábbi tulajdonságok teljesülnek:

(a) Közelítő minimalizálás: kereshetjük a fenti (1.108) egyenletrendszerrel a minimumot.

(b) Vetületi egyenlet:

〈 x _n ,y 〉 _A = 〈 f,y 〉, minden y∈H_n

(1.111)

〈 x _n -x ^* ,y 〉 _A =0, minden y∈H_n

(1.112)

Két utóbbi (1.111), (1.112) tulajdonság azt jelenti, hogy x_n éppen x^∗ vetülete H_n-re.

A tétel (a) állítása éppen a Ritz-Galjorkin módszer definíciója.

A (1.111) kifejezést elég, ha minden Φ_k-ra igazoljuk, hiszen akkor lineáris kombinációjukra (v) is igaz lesz.

(1.113)

a (1.113) kifejezés jobb oldala viszont (1.105) miatt éppen

(1.114)

a (1.113) és (1.114) egyenletek összevetéséből viszont (1.111) igaz minden Φ_k-ra.

A (1.112) állítást igazolhatjuk, ha az (1.111) vetületi egyenletet x_n-re és x^*-ra alkalmazva

〈 x _n ,y 〉 = 〈 f,y 〉

(1.115)

és

〈 x ^* ,y 〉 = 〈 f,y 〉

(1.116)

(1.115) és (1.116) egyenleteket egymásból kivonva

〈 x _n ,y 〉 - 〈 x ^* ,y 〉 = 〈 f,y 〉 - 〈 f,y 〉 =0

(1.117)

adódik.

Szemléletessé tehetjük a fenti tétel (b) és (c) állítását, ha a normál háromdimenziós térre és annak egy síkjára, mint kétdimenziós altérre gondolunk. Egy tetszőleges térbeli vektorhoz legközelebbi altérbeli vektor meghatározható, mint a térbeli vektor altérre vetett vetülete (b), vagy az altérbeli közelítő és a térbeli vektor távolságának minimalizálása (a merőleges az eltérés) (c).

1.4.2. A Ritz-Galjorkin módszer általánosítása

Ahogy a fenti gondolatmenetben növeltük az altér dimenzióját, a közelítő megoldás úgy közelítette a tényleges megoldást (1.110), vagyis a módszer konvergens volt. Az altér dimenziójának megnövelésekor a választott Φ_i bázishoz mindig új elemet választottunk. A módszert úgy általánosíthatjuk, hogy minden egyes lépésben az altér teljes bázisát lecseréljük.

A dimenziószám növelése során x_n (1.99) szerinti közelítésében minden egyes lépésben választhatunk az altérben új bázisfüggvényeket. Az n. lépésben a bázisfüggvények Φ_i,n, amelyek kifeszítik (span) az aktuális alteret.

H _n =span{Φ _1,n ,Φ _2,n ⋯ Φ _n,n }

(1.118)

Az x_n közelítést minden lépésben ugyanúgy állíthatjuk elő, mint a szimmetrikus esetben, az x_n együtthatóit a (1.109) lineáris algebrai egyenletrendszer megoldásával kapjuk, azonban most ezek származtatása esetén nem használhatjuk fel az eggyel kisebb dimenzióra meghatározott Gram-mátrixot. Érvényesek a (1.110), (1.111), (1.112) tulajdonságok is, és a nem használtuk ki a H_n alterek egymásba ágyazottságát.

Ebben az esetben a konvergenciához plusz feltételre van szükség a szimmetrikus esethez képest (1.110). Legyen igaz bármely x∈H_Aesetén, hogy

dist _A (x,H _n )=min{‖x-x _n ‖ _A : x _n ∈ H _n }→0,ha n→∞

(1.119)

Olyan sorozatot kell keresnünk, ahol a sorozat n. tagja H_n-ből való, azaz bármely x esetén az kifejezhető Φ_i,n lineáris kombinációjával. A (1.119) feltétel és (1.112 miatt x^*-x_n éppen merőleges H_n-re, tehát az van a legközelebb, így

‖x ^* -x _n ‖ _A =min{‖x-x _n ‖ _A : x _n ∈ H _n }→0,ha n→∞

(1.120)

azaz olyan sorozattal közelítjük x^*-t, amelynek n. tagja éppen Hn-ben van.

1.4.3. A Ritz-Galjorkin módszer nem szimmetrikus lineáris egyenletekre

Most a nem szimmetrikus operátorok esetén megvizsgáljuk a Ritz-Galjorkin módszer lehetőségeit! Legyen H valós Hilbert-tér, A: H →H, nem szimmetrikus, lineáris operátor és gϵH. Ebben az esetben a

Ax=f

(1.121)

operátoregyenlettel kell foglalkoznunk. Módszerünk szerint megvizsgáljuk, hogyan lehet a problémát visszavezetni egy szimmetrikus operátorra. Mivel az energianormához szimmetrikus operátor szükséges, mi az A helyett egy másik S szimmetrikus operátorra vezetjük vissza a feladatot.

Az 1.2.2.2. szakasz fejezet szerint ennek egyértelműen létezik gyenge megoldása, azaz x^* ∈ H_S, melyre igaz, hogy

〈 A _s x ^* ,y 〉 _s = 〈 f,y 〉, minden y∈H_s

(1.122)

Bázisfüggvényeket rögtön válasszuk az általánosított (1.118) szerint!

A (1.119)-hez hasonlóan itt is legyen feltétel, hogy bármely x∈H_sesetén

dist (x,H _n )=min{‖x-x _n ‖ _S : x _n ∈ H _n }→0,ha n→∞

(1.123)

Legyen ebben az esetben is

(1.124)

Most azonban a szimmetria hiánya miatt nem használhatunk kvadratikus funkcionált. A közelítő megoldást keressük

〈 A _s x _n ,y 〉 _s = 〈 f,y 〉 minden y∈H_s

(1.125)

alakban. Ez egyértelműen létezik 1.2.2. szakasz fejezet szerint.

Az x_n együtthatóit ugyanúgy számíthatjuk, mint szimmetrikus esetben, ha (1.124)-t (1.122) – be helyettesítjük, és az y helyett a Φ_k-kat használjuk, akkor egy lineáris algebrai egyenletrendszer adódik.

Gc=b

(1.126)

Az egyenletrendszer együtthatómátrixának elemei g_ik-k és jobb oldala b_k.

g _k i= 〈 A _s ϕ _i ,ϕ _k 〉 _s, b_k=〈f,ϕ_k〉, i,k=1,2,…n

(1.127)

(A reziduális hiba ortogonalitása.) Ez esetben a Galjorkin féle ortogonalitás nem az x_n − x^∗, hanem az A_S(x_n−x^∗) vektorra teljesül. A (1.122) és (1.125) egyenleteket kivonva egymásból

〈 A _s (x _n -x ^* ),y 〉 _s =0, minden y∈H_s

(1.128)

azaz L_Sx_n − L_Sx∗ ⊥H_n–re. Ha b ∈ H_S jelöli (1.122) jobb oldalának Riesz-reprezentánsát, azaz

〈 b,y 〉 s= 〈 f,y 〉 _s ,minden y∈H_s

(1.129)

akkor mivel Ax^*=f, (1.128) miatt

A _s x _n -b ⊥ H _n

(1.130)

Bizonyítható, hogy ha (1.123) fennáll, akkor

x _n →x ^* ‖⋅‖s normában, ha n→∞

(1.131)

azaz a módszer konvergens.

1.4.4. A Ritz-Galjorkin módszer nemlineáris egyenletekre

Tétel: Legyen tehát H valós Hilbert-tér, F : H → H adott nemlineáris operátor, amelyre fennáll, hogy létezik olyan m≥0 valós szám, hogy F egyenletesen monoton és Lipschitz-folytonos operátor, akkor létezik olyan M ≥m>0, hogy bármely x, y ∈ H esetén

〈 A(x)-A(y),x-y 〉 ≥m ∗ ‖x-y‖ ² és

‖A(x)-A(y)‖≤M ∗ ‖x-y‖ , minden x,y ∈H

(1.132)

Legyen tehát H valós Hilbert-tér, F : H → H adott nemlineáris, egyenletesen monoton, Lipschitz-folytonos operátor, akkor 1.2.3. szakasz szerint a (1.133) egyenletnek létezik pontosan egy megoldása.

F(x)=b

(1.133)

Ekkor írhatjuk, hogy

〈 F(x ^* ),y 〉 = 〈 b,y 〉, minden y∈H

(1.134)

Legyenek (1.118)-hez hasonlóan H_n Φ_i,n lineárisan független elemek által kifeszített alterek!

H _n =span{Φ _1,n ,Φ _2,n ⋯ Φ _n,n }

(1.135)

és (1.119)-hoz hasonlóan

dist _F (x,H _n )=min{‖x-x _n ‖ : x _n ∈ H _n }→0,ha n→∞

(1.136)

Most is x_n ∈ H_n közelítést keressük az (1.124) alakban

(1.137)

A (1.137) egyenletet (1.134)-be helyettesítve, és y helyett Φ_k,n-t használva adódik, hogy

, k=1,2,…n

(1.138)

A (1.138) c_i-re nézve nemlineáris egyenletrendszer megoldásával kaphatjuk a keresett közelítő megoldást.

A lineáris esethez hasonlóan a (1.134) és (1.138) egyenleteket kivonva egymásból következik, hogy

〈 F(x ^* )-F(x _n ),y 〉 =0, minden y∈H_n

(1.139)

azaz a hiba merőleges H_n-re. A lineáris esethez hasonlóan (1.131) állítás fennáll, azaz a módszer konvergens, ha n→∞

1.5. A végeselem-módszer háttere

A végeselem módszer (Finite Element Method) a fent leírt Ritz-Galjorkin módszer differenciálegyenletek megoldására szolgáló speciális alkalmazása. Általában függvények Hilbert-terén dolgozunk, ahol a független változók terét, amelyen az ismeretlen függvényt keressük, véges számú elemre bontjuk. Síkbeli esetben az elemek lehetnek háromszögek, négyszögek stb., a térben hasábok tetraéderek stb. A modellben az elemek csak sarokpontjaikon (csomópontjaikon) csatlakoznak egymáshoz. Ekkor az ismeretlen függvény az elemeken olyan a csomópontok által meghatározott polinomokkal közelíthető, hogy azok megfelelő számban folytonosan differenciálhatók legyenek.

Példaként tekintsük az alábbi egyszerűen megoldható (a rugalmas szál lehajlásának megfelelő) egydimenziós esetet!

x∈(0,1)

(1.140)

ahol f(x) ismert (rugalmas szál esetén a nyomatéki ábra által meghatározott M/I/E függvény) legyenek a peremfeltételek

y(0)=0 és y(1)=0

(1.141)

a fenti (1.140)-(1.141) peremérték probléma gyenge megoldására (1.111) egyenlet szerint igaz, hogy ha bármilyen folytonos z peremértékeket kielégítő függvényre (z(0)=z(1)=0) akkor

(1.142)

Parciális integrálással

(1.143)

mivel az z függvény a peremeken 0, (1.143) jobb oldalának első tagja eltűnik, így a (1.122) szerinti operátoregyenlet (1.143) alapján

(1.144)

Keressük a (1.144) egyenlet megoldásait a (0,1) intervallumon a peremeket kielégítő szakaszonként lineáris függvények halmazán (1.1. ábra)!

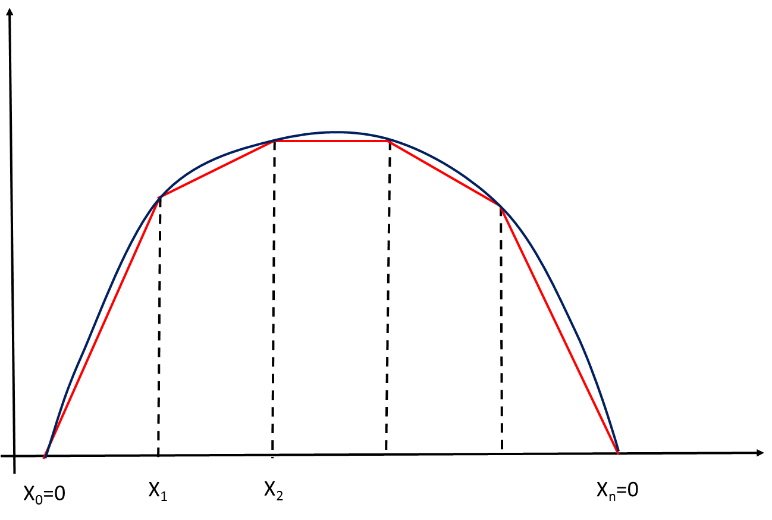
1.1. ábra - A (0,1) intervallumok szakaszonként folytonos függvény

Bontsuk fel a (0,1) intervallumot n részre, x₀=0 és x_n=1 között x_k=k/n osztópontokkal! Ki kell választanunk az szakaszosan lineáris függvények egy n-1 elemű bázisát. A folytonos bázisfüggvények legyenek olyanok, hogy minden belső osztóponthoz egy olyan függvény tartozzon, amely az osztópontban egy, az osztópontot tartalmazó két szakaszon lineáris, egyébként 0! (1.2. ábra)

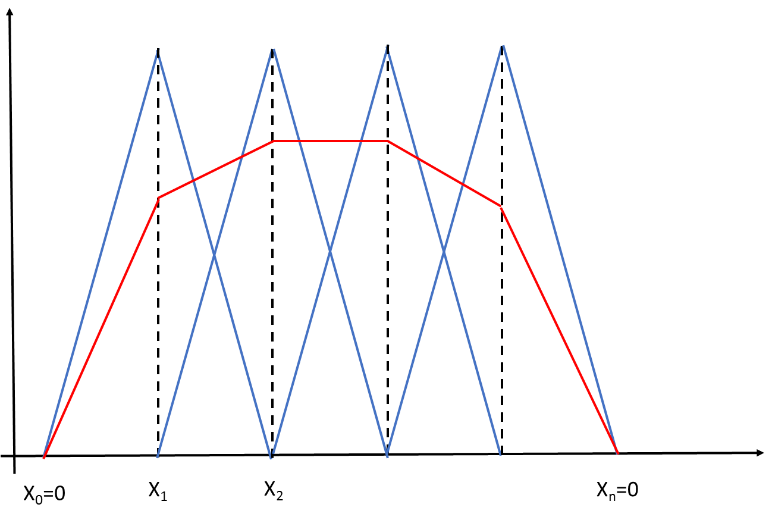
1.2. ábra - A választott bázisfüggvények

A bázisfüggvények ekkor a 1.2. ábra jelöléseivel:

(1.145)

A (1.145) bázisfüggvényeket a (1.144) operátoregyenletbe helyettesítve (1.114)-nak megfelelően a tetszőleges z függvény helyett ϕ_k-kra felírva:

, k=1,2,…n

(1.146)

Tegyük fel a példa egyszerűsítése kedvéért, hogy a vizsgált diszkrét intervallumok egyenlő hosszúak, azaz

x _k -x _k-1 =h, k=1,2,…n

(1.147)

Ha i=k, akkor a

, i=1,2,…n

(1.148)

Ha |i-k|=1, akkor a

, i=1,2,…n

(1.149)

Egyébként

i,k=1,2,…n ,|i-k|>1

(1.150)

A merevségi mátrix tehát

(1.151)

Legyen például az f(x)≡1 függvény!

, k=1,2,…n

(1.152)

azaz

(1.153)

azaz

(1.154)

azaz

(1.155)

helyettesítsük x_k+1-x_k= x_k-x_k-1 = h-val!

b _k =h

(1.156)

Amit akár a kis háromszögek területéből is kiszámíthattunk volna.

1.5.1. A végeselemes technika

Ha egy valós problémával találjuk magunkat szemben, akkor a fentiekhez hasonlóan a keresett, ismeretlen függvény értelmezési tartományát elemekre kell bontanunk. Tényleges mérnöki modellek esetén az ismeretlen függvényeink egy, két illetve háromváltozósak attól függően, hogy vonalmenti, síkbeli vagy térbeli feladatot oldunk meg. Az ismeretlen függvényt úgy keressük, hogy az elemeken kitüntetett pontokat (csomópontokat) veszünk fel. Az elem alakja a csomópontok függvényében közelíthető. A véges elemekre bontott geometriához csatlakozóan az ismeretlen függvényt sem a teljes (végtelen dimenziós) téren keressük, hanem annak egy olyan közelítésén, amelyet a csomóponti értékek határoznak meg. A csomópontjaikban egymáshoz kapcsolódó elemeken az ismeretlen függvények megfelelő rendben folytonosan csatlakoznak egymáshoz. Természetesen meg kell követelnünk azt, hogy a közelítő megoldás is a megfelelő rendben folytonos és fizikailag megvalósulható legyen. (Például, rugalmasságtani feladatoknál az ismeretlen elmozdulásmező kinematikailag lehetséges legyen.)

1.5.1.1. Koordináta-rendszerek

Az adott mérnöki probléma megfogalmazása sokszor egyszerűbb az elemhez csatlakoztatott koordináta-rendszerben. Az egyes, véges elemekre vonatkozó összefüggések levezetéséhez gyakran célszerű az elemeken lokális koordináta-rendszert használni. A lokális rendszerből a globális rendszerbe egyszerű, kölcsönösen egyértelmű koordináta-transzformációval térhetünk át. Használhatunk paraméteres – akár görbevonalú – koordináta-rendszert, melynek jellemző pontjai a -1, 0, 1 koordináta-értékek. Bármely térbeli pont globális koordinátái (x,y,z) származtathatók a lokális koordinátákból (ξ,η,ζ) egy lineáris transzformációval (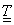) és egy eltolással.

(1.157)

illetve fordítva

(1.158)

1.5.1.2. Bázisfüggvények

Az elem alakját és az ismeretlen függvényt azonos módon bázisfüggvényekkel közelítjük, például 3D-ben az elem (ξ,η,ζ) lokális koordinátarendszerben értelmezett pontjához az (x,y,z) ontok tartoznak az alábbiak szerint:

(1.159)

ahol az elemnek N pontja van, és az i. pont globális koordinátái (x_i, y_i, z_i). Az elem egy pontjának lokális koordinátái (ξ,η,ζ), és a megfelelő pont globális koordinátái (x,y,z).

A feladat ismeretlen függvényének értékeit csak a kitüntetett pontokban határozzuk meg, úgy hogy a teljes ismeretlen mező a koordinátafüggvényekhez hasonló

(1.160)

legyen.

1.5.2. Egyváltozós bázisfüggvények

Ha vonalszerű alkatrészen egyváltozós lineáris függvénnyel közelítünk (1.3. ábra),

1.3. ábra - A C0 folytonos vonali bázisfüggvények akkor az L0

(1.161)

és az

(1.162)

súlyfüggvényeket használhatjuk az (x₀,x₁) intervallum által jellemzett kétpontos vonalelemen. Ha az (1.4. ábra) ábrát megnézzük, akkor azt látjuk, hogy az L₀(0)=1 és L₀(1)=1, illetve az L₁(0)=0 és L₁(1)=1. Ha x₀=0, és x₁=1, akkor a függvények ξ lokális változót is használhatjuk a szakasz saját koordináta-rendszerében.

Ha vonalszerű alkatrészek ismeretlen függvényét közelítjük, akkor ha n csomópontunk van az elemen, akkor az ismeretlen függvény folytonos (C⁰), így használhatjuk a Lagrange-féle interpolációs polinomokat. Ezek bázisfüggvényei n csomópont esetén (n-1)-ed fokúak

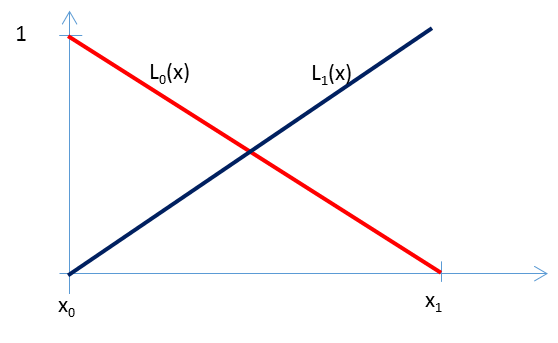
1.4. ábra - A C0 folytonos vonali bázisfüggvények

(1.163)

Ha megfigyeljük a Lagrange súlyfüggvényeket, akkor azt látjuk, hogy az L_i mindegyik csomópontban 0, kivéve az i. csomópontot, ahol az értéke 1. Ez a tulajdonság biztosítja, hogy a bázisfüggvények (1.158)-nek megfelelő lineáris kombinációja éppen a kívánt függvényértékeket veszi fel.

A fenti példában a (1.140) bázisfüggvények választásánál gyakorlatilag ezt használtuk.

Ha folytonosan deriválható függvényeket szeretnénk használni (C¹), akkor alkalmazhatjuk a (1.159) alapján felírt Hermite-féle interpolációt [3.] . Az interpoláció alapgondolata szerint az elem szélső közös pontjában a függvényértékek mellett a deriváltak azonossága is biztosított.

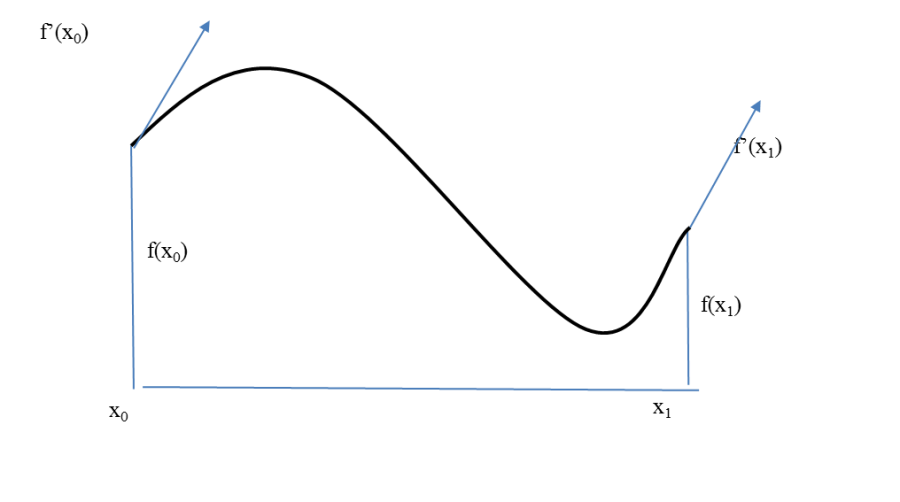
1.5. ábra - Hermite-féle görbeszakasz

Ekkor az

, x∈[x₀,x₁]

(1.164)

A ξ ∈ [0,1] intervallumra transzformált bázisfüggvények az (1.6. ábra) ábrán láthatók.

(1.165)

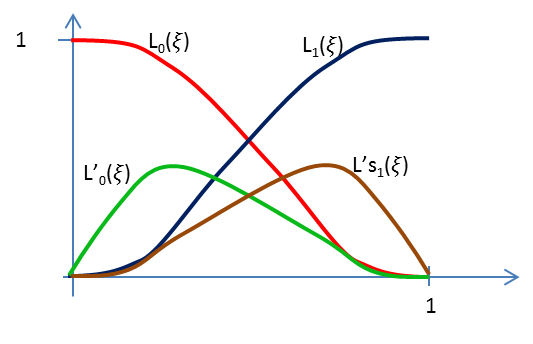
1.6. ábra - A C1 folytonos vonali bázisfüggvények

Többpontos C¹ folytonos bázisfüggvények esetén több belső pontban megadott függvényértéket (akár derivált értéket is) előírhatunk. A szélső, csatlakozó pontokban a függvényértékek és a derivált értékek azonossága biztosíthatja a folytonosságot. A bázisfüggvények felírásához meg kell határoznunk azokat a függvényeket, amelyek csak az adott pontban vesznek fel 1 értéket és az összes többi helyen 0-t, továbbá az adott pontban a derivált értéke 0, illetve a pontban, ahol derivált kényszert írunk elő, a derivált értéke 1, a függvény 0 és az összes többi pontban a függvényérték és a derivált érték egyaránt 0. A bázispolinomok fokszáma a felírt kényszerek számánál eggyel kisebb. Az együtthatókra a kényszerek alapján egyenletrendszereket írhatunk fel.

1.5.3. Kétváltozós bázisfüggvények

Legyen egy háromszög elemünk az (1.7. ábra) ábrának megfelelően a síkban! Bármely (x,y) síkbeli pont kifejezhető , mint a lokális (ξ,η) koordináták függvénye. [4.]

(1.166)

illetve

(1.167)

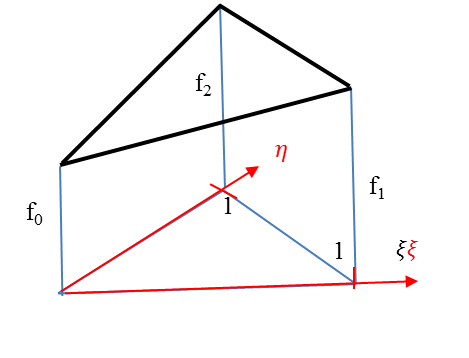
1.7. ábra - Lineáris függvény háromszög elemen

A bázisfüggvények a lokális koordináta-rendszerben (1.8. ábra)

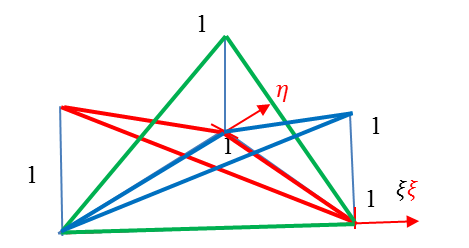
1.8. ábra - A kétdimenziós bázisfüggvények háromszög elemen

(1.168)

Négycsomópontú lineáris elemet is készíthetünk (1.9. ábra)

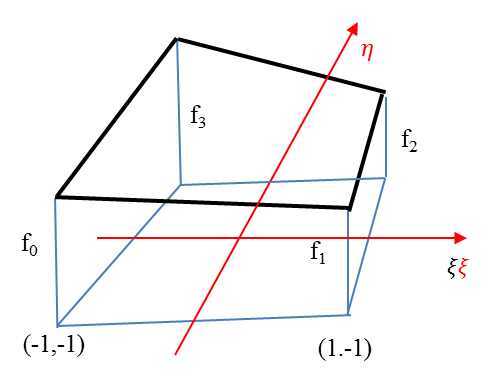
1.9. ábra - A négycsomópontú lineáris elem

A bázisfüggvények a lokális koordinátarendszerben

(1.169)

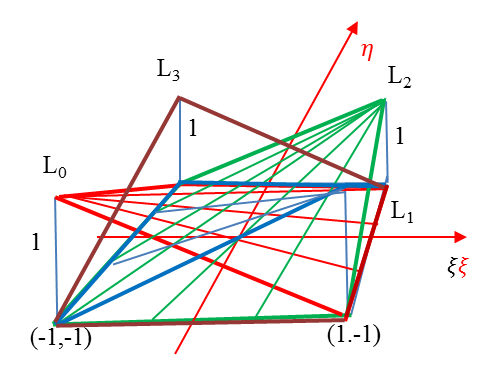
1.10. ábra - A kétdimenziós bázisfüggvények négyszög elemen

1.5.4. Háromváltozós bázisfüggvények

Az izoparametrikus térbeli elemek a tégla vagy tetraéder topológiájúak. Az élek lehetnek egyenesek ilyenkor a függvények paramétereikben lineárisak, ha a görbültek az élek, akkor a függvények legalább kvadratikusak.

Egy térbeli tégla topológiájú elem nyolc paraméterfüggvénye:

(1.170)

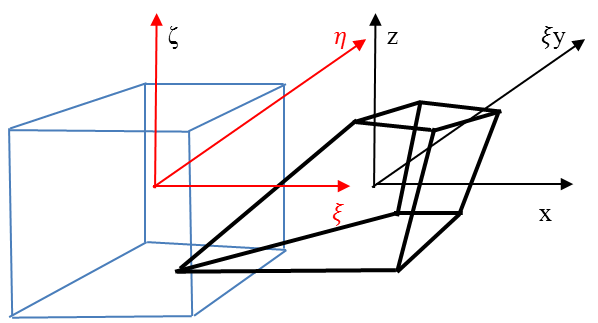
1.11. ábra - A háromdimneziós lineárisan módosított elem

hasonlóan a görbült tertraéder-forma:

(1.171)

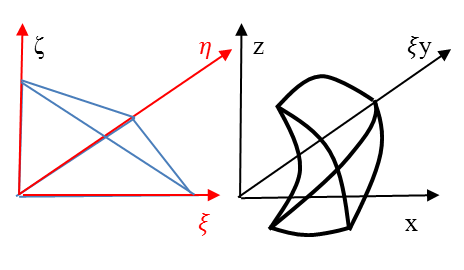
1.12. ábra - A háromdimneziós kvadratikus

1.5.5. Végeselemek használata térbeli rugalmasságtani feladatokon

Tekintsünk egy V térfogatú lineárisan rugalmas térbeli testet, melyet A határoló felület vesz körül! Az A felület egy részén (A_u) elmozdulás kényszer adott, míg másik részét (A_p) terheljük. A test bármely r pontjának elmozdulása ( u ) leírható a koordináta-rendszer e _i egységvektorainak lineáris kombinációjával.

(1.172)

Ekkor az alakváltozási tenzor

(1.173)

ennek független elemeit hatelemű vektorba szervezhetjük.

(1.174)

A hatelemű vektor és az elmozdulásmező kapcsolata operátorszimbólumokkal tehát

(1.175)

Közelítsük egyetlen elemen az elmozdulásmezőt a megismert bázisfüggvények segítségével!

(1.176)

Ekkor az n csomópont alapján egyetlen elemen

(1.177)

(1.175) és (1.176) egyenletek alapján

(1.178)

Kifejezhetjük tehát az elmozdulás tenzor független elemeit a csomóponti elmozdulásokkal.

A feszültségtenzor

(1.179)

melynek független elemeit is hatelemű vektorba szervezhetjük.

(1.180)

Rugalmas test esetén rugalmassági modulus (E) és a Poisson állandó (ν) segítségével kapcsolatot írhatunk fel a feszültségtenzor és az alakváltozási tenzor elemei között. Legyen

(1.181)

Ekkor

(1.182)

(1.178)-t felhasználva az elemen, a feszültségtenzor elemei az elemen

(1.183)

Rugalmas test esetén a csomóponti elmozdulásokkal a feszültségtenzor elemei is kifejezhetők.

Az egyensúlyi egyenlet a feszültségtenzorral és a 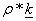megoszló terheléssel

(1.184)

Ezeket az egyenleteket egészítik ki az

az A_u peremen előírt elmozdulás,

az A_p peremen előírt terhelés

(1.185)

peremfeltételek.

A differenciálegyenlet-rendszer megoldása helyett, a (1.184) egyenletek és a kapcsolódó (1.185) peremelőírások helyett a teljes potenciális energia (Π_e) minimumát keressük az aktuális elemen (ezt választjuk skaláris szorzatnak).

(1.186)

Felhasználva a (1.178) összefüggést,

(1.187)

Írhatjuk tehát, hogy egyetlen elemre vonatkozóan

(1.188)

ahol az elemi merevségi mátrix

(1.189)

az elemi terhelés.

(1.190)

(1.189) alapján a térfogati integrálást lokális ξ,η,ζ koordinátákra transzformálva bekerül a képletbe a Jacobi mátrix determinánsa

(1.191)

A szerkezet több elemből áll, a szerkezet potenciálos energiája (1.188) alapján, az elemek (N_e darab) energiája mellett az elemektől független csomóponti erők (W) munkáját kell figyelembe venni.

(1.192)

Ha a terhelés vektorokat és az elmozdulás vektorokat összegyűjtjük, akkor az Ncs csomópontra

(1.193)

Legyen 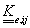az i és j csomópontot egyaránt tartalmazó elem merevségi mátrixa. Összegezzük az összes olyan elem merevségi mátrixát, amely tartalmazza az i,j pontokat!

(1.194)

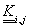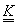Az így adódó a merevségi mátrix i,j csomópontokhoz tartozó almátrixa.

(1.192) és (1.193) és (1.194) egyenletek alapján a külső erők munkáját is csomópontra bontva

(1.195)

Ha az energiaminimumot keressük, akkor annak szükséges és elégséges feltétele

(1.196)

lineáris egyenletrendszer teljesülése.

Az egyenletrendszer ismeretlenjeinek nagy száma mellett vigasztalhat minket az, hogy az együttható mátrixnak csak azok az i,j indexű elemei különböznek zérustól, ahol egy elemen belül szerepel az i és a j indexű csomópont is. A csomópontok megfelelő számozásával elérhető, hogy az együttható mátrix sávszerkezetű legyen, hiszen a sáv szélességét az egy elemen belül lévő indexek maximális különbsége szabja meg.

2. fejezet - A végeselem rendszerek működésének alapjai

Tartalom

2.1. Bevezetés: A végeselem analízis alapvető lépései

2.2. Geometria modellezés

2.2.1. Geometriai modellek és előállításuk

2.2.1.1. Testmodell előállítása primitívekkel (Primitives)
2.2.1.2. Alaksajátosságra (Features) épülő parametrikus modell
2.2.1.3. Explicit modellezési eljárás (Explicit or Direct 3D)
2.2.1.4. Testmodell előállítása határfelületekkel (Boundary Representation)

2.2.2. Geometria importálása

2.2.3. Egyszerűsítések

2.2.3.1. Szimmetria feltételek alkalmazása

2.2.3.2. 2D-s és 3D-s modellek alkalmazása

2.2.3.2.1. Testmodell
2.2.3.2.2. Térbeli felületmodell
2.2.3.2.3. Sík felületmodellek
2.2.3.2.4. Vonalmodellek

2.3. Hálókészítés

2.3.1. Elemtípusok

2.3.1.1. Kiterjedésük szerint

2.3.1.2. Az elemek fokszámuk szerint

2.3.1.3. Az elemek szabadságfoka

2.3.1.4. Az elemtulajdonságok

2.3.1.4.1. A feszültséganalízis elemei
2.3.1.4.2. A termikus analízis elemei
2.3.1.4.3. Az elektromos és mágneses analízis elemei
2.3.1.4.4. Csatolt-tér elemek

2.3.2. A hálózás lépései

2.3.2.1. Attribútumok és kontrollok beállítása (mesh controls)

2.3.2.2. Automatikus hálózási eljárások

2.3.2.3. Strukturálatlan háló létrehozása

2.3.2.3.1. Topológia felosztása (Topology decomposition)
2.3.2.3.2. Csomópont csatlakozás (Node connection)
2.3.2.3.3. Mozaik (Advancing front, Paving)
2.3.2.3.4. Négy-fa (Octree)
2.3.2.3.5. Rács alapú (Grid-based)

2.3.2.4. Strukturált háló létrehozása

2.3.2.4.1. Minta leképezéses eljárások (Mapped element)
2.3.2.4.2. Geometria szétválasztás (Geometry decomposition, Sub-maping)
2.3.2.4.3. Söprés (Sweeping)

2.3.2.5. A háló illeszkedése

2.3.3. Konvergencia módszerek

2.3.3.1. Hálósűrítés, hálósimítás
2.3.3.2. Adaptív hálózás

2.3.4. A hálózásnál előforduló hibák

2.4. Anyagmodellek létrehozása

2.4.1. Általános anyagtulajdonságok

2.4.1.1. Linearitás

2.4.1.2. Homogenitás

2.4.1.3. Irányfüggőség

2.4.1.3.1. izotróp anyagmodell (Isotropic model)
2.4.1.3.2. Ortotróp modell (Orthotropic model)
2.4.1.3.3. izotrópAnizotróp modell (Anisotropic model)

2.4.2. Az anyagmodellek csoportosítása szabadságfokuk alapján

2.4.3. Mechanikai, vagyis elmozdulás szabadságfokú anyagmodellek

2.4.3.1. A mechanikai anyagmodellek csoportosítása fesz-nyúlás karakterisztikájuk szerint

2.4.3.2. Lineárisan rugalmas anyagmodell (Linear elastic)

2.4.3.3. Viszkoelasztikus anyagmodellek (Viscoelastic Material Model)

2.4.3.3.1. A leggyakrabban alkalmazott viszkoelasztikus anyagmodellek
2.4.3.3.2. Maxwell modell
2.4.3.3.3. Kelvin-Voigt modell
2.4.3.3.4. Standard-Solid modell
2.4.3.3.5. Burgers modell
2.4.3.3.6. Általánosított modellek
2.4.3.3.7. A viszkoelasztikus modellek VEM-es alkalmazása
2.4.3.3.8. A viszkoelasztikus anyagok hőmérsékletfüggése

2.4.3.4. Sebességfüggetlen plasztikus anyagmodellek (rate-independent plasticity)

2.4.3.4.1. A folyási feltétel
2.4.3.4.2. Keményedési szabály (hardening rule).

2.4.3.5. Viszkoplasztikus anyagmodellek

2.4.3.5.1. Bingham modell
2.4.3.5.2. Herschel-Bulkley modell
2.4.3.5.3. Hatványtörvény, (Ostwald-de Waele egyenlet)
2.4.3.5.4. Casson
2.4.3.5.5. Módosított Bingham,
2.4.3.5.6. Perzyna
2.4.3.5.7. Peirce
2.4.3.5.8. EVH (Exponential visco-hardening)
2.4.3.5.9. Anand

2.4.3.6. Összetett reológia anyagmodellek

2.4.3.7. Hiperelasztikus anyagmodellek

2.4.3.7.1. Arruda-Boyce
2.4.3.7.2. Neo-Hooke
2.4.3.7.3. Saint Venant–Kirchhoff model
2.4.3.7.4. Mooney-Rivlin
2.4.3.7.5. Ogden
2.4.3.7.6. Polinomiális
2.4.3.7.7. Yeoh
2.4.3.7.8. Marlow modell
2.4.3.7.9. Van der Waals
2.4.3.7.10. Összenyomható hiperelasztikus modellek habok modellezésére
2.4.3.7.11. Blatz-Ko habmodell
2.4.3.7.12. Varga-modell
2.4.3.7.13. További hiperelasztikus modellek biológiai szövetek modellezésére

2.4.3.8. Anyagparaméterek megadása

2.4.3.8.1. Mechanikai anyagvizsgálati adatok

2.4.3.8.1.1. A mechanikai anyagvizsgálatok főbb típusai
2.4.3.8.1.2. Az anyagvizsgálati adatok formátuma
2.4.3.8.1.3. Görbeillesztés

2.4.3.8.2. Sűrűség (Density)

2.4.3.8.3. Hőtágulási együttható (Coefficient of thermal expansion)

2.4.3.8.4. Anyagcsillapítási tényező (Material Damping Ratio)

2.4.3.8.5. Az anyag szilárdsági határa (Material Strength Limits)

2.4.4. Hőmérsékleti szabadságfokkal rendelkező anyagok

2.4.4.1. Hővezető képesség (Thermal Conductivity)
2.4.4.2. Fajhő (Specific Heat)
2.4.4.3. Sűrűség (Density)

2.4.5. Elektromágneses szabadságfokú anyagok

2.4.5.1. Az anyagok mágneses tulajdonságai

2.4.5.1.1. Mikroszkopikus modell.
2.4.5.1.2. Makroszkopikus modell.

2.4.5.2. Mágneses anyagok típusai

2.4.5.2.1. A diamágneses anyagok
2.4.5.2.2. A paramágneses anyagok
2.4.5.2.3. Ferromágneses anyagok
2.4.5.2.4. Ferrimágneses anyagok
2.4.5.2.5. Az antiferromágneses anyagok

2.4.5.3. A mágneses szimuláció során definiálható mágneses anyagtípusok

2.4.5.4. Elektromos anyagmodellek

2.4.5.4.1. Elektromos vezető
2.4.5.4.2. Dielektrikum

2.4.6. Csatolt anyagmodellek

2.4.6.1. Piezorezisztív anyag
2.4.6.2. Piezoelektromos anyagmodell

2.5. Terhelések, perem- és kezdeti feltételek

2.5.1. Kezdeti feltételek

2.5.2. Peremfeltételek

2.5.3. Terhelések

2.5.3.1. Terhelési lépések (Load steps)

2.5.4. Szimmetriafeltételek

2.5.4.1. Tengelyszimmetrikus (Axisymmetric) terhelések

2.6. Alkatrészek közötti kapcsolatok

2.7. A szimuláció főbb beállításai és futtatása

2.7.1. Az analízis típusának kiválasztása
2.7.2. A megoldó kiválasztása (Selecting a Solver)

2.8. Az eredmények lekérdezése és kiértékelése (posztprocesszálás)

2.8.1. Lekérdezett mennyiségek
2.8.2. Az eredmények megjelenítési formái

2.9. Ellenőrző kérdések a 2. fejezethez.

2.1. Bevezetés: A végeselem analízis alapvető lépései

A végeselemes analízis a fizikai szerkezet matematikai modelljét képviseli, ami magában foglalja az elemeket, anyagmodelleket, peremfeltételeket és mindazon tulajdonságokat, amelyek a fizikai valóságot modellezik. A módszer lényege a vizsgált geometria véges kis részekre (véges elemekre) bontása, és az elemeket összekapcsoló csomópontokra ható csomóponti terhelések és a hatásukra létrejövő kimenő mennyiség közötti kapcsolatot leíró egyenletrendszer megoldása. A végeselemes analízis folyamatát három jól elkülöníthető részre, előkészítés (Preprocess) , megoldás (Process) és kiértékelés (Posztprocess) szokás osztani, amit meg kell, hogy előzzön a döntési szakasz.

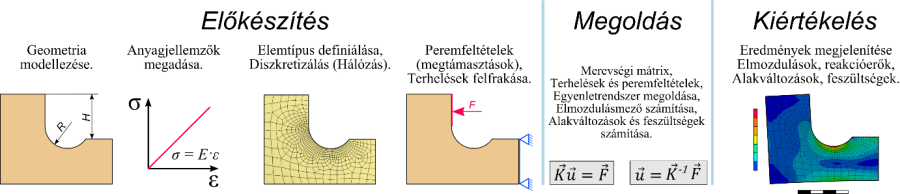
2.1. ábra - A végeselem szimuláció folyamatának legfontosabb lépései, (statikai példán bemutatva).

Döntési szakasz – a probléma jellegének meghatározása és a megoldásához használt eljárás kiválasztása.
- A fizikai probléma jellege (mechanikai, hőtani, elektromágneses, stb.)
- Az analízis típusa (statikai, modal, harmonikus, tranziens, stb.)
- Milyen közelítéssel akarjuk vizsgálni a valóságot (Lineáris/nemlineáris)?
- Az alkalmazott modell típusa (3D-s testmodell vagy egyszerűsített 2D-s, héj, rúd, stb.)
- Szimmetria feltételek alkalmazhatósága (fél, negyed modell, tengelyszimmetria, ciklikusság, stb.).
- Elemtípus (alakjuk vagy fokszámuk szerint).
- Hálósűrűség (globális elemméret), részletesség (lokális hálósűrítés mértéke).
- Peremfeltételek megfelelő alkalmazása (alkatrészek kiváltása kényszerekkel).
Előkészítés (Preprocessing) – a végeselem modell előkészítését jelenti, amely az alábbi lépéseket tartalmazza:
- Geometria létrehozása, (modellezés, importálás).
- Anyagmodell kiválasztása, (anyagparaméterek megadása, görbeillesztés anyagvizsgálati adatokra.).
- Hálózás, (elemtípus, hálózási eljárás, elemméret, stb. megadása).
- Peremfeltételek, kezdeti feltételek és terhelések definiálása, (Megtámasztások, kényszerek, alkatrészkapcsolatok, koncentrált és megoszló erők, nyomatékok, hőterhelés, inerciális terhelések, stb. definiálása).
Megoldás (Solution) – lényegében a megoldó futtatását jelenti. Ez a szakasz az, amely a felhasználó elől leginkább rejtve marad.
- Transzformációs mátrix (lineáris statikai esetben merevségi mátrix) létrehozása az egyes elemekre, majd ezekből a teljes szerkezetre.
- Csomóponti terhelések és peremfeltételek felvétele.
- Egyenletrendszer megoldása, az elemek szabadságfokának megfelelő mennyiségek (mechanikai esetben elmozdulás) kiszámolásával.
- A kívánt származtatott mennyiségek számolása a fenti eredményből (pl. mechanikai feszültség és alakváltozás számítása az elmozdulásmezőből).
Kiértékelés (Post-processing) – az eredmények lekérdezését és kiértékelését jelenti. A jelenlegi modern végeselem szoftverek számos olyan eszközzel rendelkeznek, amely segítségünkre van ebben a munkában.
- Az eredmény megjelenítése a testmodellen színsávok vagy vektormező ábrázolásával.
- A deformált test megjelenítése és testmodellként való kimentése, animálása, stb.
- Diagramok, szöveges kimenet, maximum / minimum helyek lekérdezése, stb.

[5.] , [6.]

2.2. Geometria modellezés

2.2.1. Geometriai modellek és előállításuk

A végeselem analízisben vizsgált fizikai test digitális reprezentációja a számítógépes geometriai modell. A modellt felépítő elemek lehetnek pontok, görbék (egyenes, körív, paraméteres polinomok, Spline-ok, Bezier görbék, stb.), felületek (analitikus és parametrikus felületek) és szilárd testek. A testmodellek leírása zárt felületekkel határolt, anyaggal kitöltött objektumként történik. A testmodellek előállításának legelterjedtebb megvalósítási módját az alábbiakban foglaljuk össze, a teljesség igénye nélkül. A lent leírtakhoz hasonló eljárásokkal hozhatók létre a térbeli felületmodellek is, de ez esetben nem követelmény a generálógörbe és a létrejött felületmodell zárt szerkezete.

2.2.1.1. Testmodell előállítása primitívekkel (Primitives)

Halmazműveletek segítségével (unió, különbség és metszet képzésével) elemi testekből, un. primitívekből hozható létre a teljes geometria. Primitíveknek azokat az előre definiált alaptesteket nevezzük, melyekből a kívánt geometria épül fel (kúp, gúla, henger, gömb, tórusz, ék, téglatest). A modellezés során a primitívek helyzetét, méretét és a velük végzett halmazműveleteket (boolean) definiáljuk. Az így végrehajtott műveletek sora, vagyis a primitívek kombinálása vezet a kívánt geometria kialakulásához. A primitívekkel való művelet ma már elavultnak számít, mivel nem támogatja az iteratív parametrikus alkatrész-modellezést.

2.2.1.2. Alaksajátosságra (Features) épülő parametrikus modell

Az alaksajátosságokon alapuló modellezés a primitívekhez hasonlóan szintén a modell jellemző geometriai adottságainak kombinálásával építkezik, de ebben az esetben az alaksajátosságok lényegesen szabadabb építőelemei a modellnek. Csoportosításuk sokféle szempont szerint történhet, de legcélszerűbb talán a létrehozás módja szerint osztályozni. E szerint beszélhetünk vázlatra épülő és elhelyezett alaksajátosságról.

A vázlatra épülő alaksjátosságot mint a neve is mutatja valamilyen (az alaksajátosság típusától függően tetszőleges bonyolultságú is lehet) vázlat egy pálya mentén történő elmozdításával generáljuk. A vázlat (ok) és a pálya(k) alakjától függ a létrehozott geometria. A leggyakrabban használt vázlatra épülő alaksajátosságok: kihúzás (Extrude), megforgatás (Revolve), pásztázás (Loft), söprés (Sweep), borda (Rib), spirál (Coil), domborítás (Emboss), szelés (Slice). Az elhelyezett alaksajátosságoknál éppúgy értelmezhetőek a boolean műveletek, mint a primitíveknél.

Az elhelyezett alaksajátosságok csak meglévő geometriára lehet érvényesíteni, önmagukban nem értelmezhetőek. Általában gyakran ismétlődő, szabványos technológiai lépéseket foglalnak magukban, mint a furat (Hole), lekerekítés (Fillet), letörés (Chamfer), kilökési ferdeség (Draft), menet (Thread), héj (Shell), különféle kiosztások (Pattern), tükrüzés (Mirror), stb.

A szilárdtest részét nem képező, de a megalkotásához nélkülözhetetlen elemeket munka alaksajátosságnak nevezzük, mint a munkasík (Plane), tengely (Axis), stb.

Az alaksajátosságra épülő modell jellemző tulajdonsága a modelltörténet (modellfa), vagyis, hogy a modellalkotás folyamata visszatekinthető és bármely eleme utólag módosítható, paraméterezhető. Jelenleg ez az általánosan elterjedt modellezési eljárás a korszerű CAD rendszerekben.

2.2.1.3. Explicit modellezési eljárás (Explicit or Direct 3D)

Az explicit modellezési eljárás lehetőséget biztosít a modellfa nélküli geometria létrehozására és módosítására. Közvetlen modellezésel, ha egy vázlat segítségével hozunk létre geometriát, akkor az beépül a geometriába és a továbbiakban a vázlat nélkül, közvetlenül a geometriát módosíthatjuk. A parametrikus modellezéshez hasonlóan lehetőséget ad az egyes geometriai elemek közötti kényszerek definiálására. A módszer rugalmassága nagyobb mozgásteret enged a szabad formájú organikus felületek modellezése során. A modellezési gyakorlat elkövetkező fejlődési fokát látják benne és számos fejlett modellezőrendszer már beépítette az eszköztárába a parametrikus modellezés mellett.

2.2.1.4. Testmodell előállítása határfelületekkel (Boundary Representation)

A határfelületekkel való testmodell definiálás alapkövetelménye egy térrészt elkülönítő zárt felületmodell megléte. A felületelemek normálvektora határozza meg, hogy a felület melyik oldalán van az anyag (a vektor általában kifelé mutat). A határoló felületmodell előállítása történhet a fenti módszerek bármelyikével, primitív felületek kombinálásával, alaksajátosság alapú felületmodellek definiálásával vagy a felületet leíró vezérgörbék, kontrolpontok, stb. közvetlen megadásával.

[7.] , [8.] , [9.] , [10.] .

2.2.2. Geometria importálása

A végeselem (VEM) és a geometriai modellező (CAD) szoftverek együttműködésének, integrációjának különböző szintjei vannak. A szoftverek fejlődése során a tendencia a minél nagyobb mértékű integráció felé mutat. A kezdeti teljesen különálló működés során a két szoftver együttműködése biztosította a kapcsolatot. Részleges együttműködés esetén a még mindig különálló VEM szoftver a CAD program részeként teljesíti a feladatát. Az integráció legmagasabb fokának a CAD rendszerbe szakmodulként teljesen beépülő VEM rendszert tekintjük. A két program között súlypont gyakran eltolódik valamelyik javára. Ennek megfelelően a véges elemes szoftverek között találunk olyat, amely egy főként tervezésre használt CAD rendszer beépülő modulja, de olyat is, amely függetlenül működő VEM program saját geometriai modellezővel. Az utóbbi esetben is tartalmaz a véges elemes szoftver a geometria megalkotására alkalmas modellező modult, de az képességeiben és szolgáltatásaiban általában nem éri el egy korszerű CAD rendszer tulajdonságait.

Egyszerű geometria esetén általában a véges elemes szoftver részeként működő geometriai modellezővel készítjük el a geometriát. Ebben az esetben a két rendszer közti átmenet gyorsan és dinamikusan valósul meg, nem kell a geometria importálásával külön foglalkoznunk, a paraméterek átöröklődnek a véges elemes rendszerbe/modulba.

Természetesen, ha különálló geometriai modellező és véges elemes szoftvert használunk, akkor is mód van a geometria importálására illetve legtöbbször a CAD és a VEM rendszer dinamikus együttműködésére (paraméterek, koordináta rendszerek, anyagtulajdonságok, stb. átvitelére). A geometria véges elemes szoftverbe történő importálására a szabványos file-formátumok (pl. IGES, Parasolid, ACIS, STEP, stb.) biztosítanak lehetőséget, de számos esetben a fejlettebb végeselem szoftverek kezelik a legelterjedtebb CAD rendszerek saját formátumát is. Általában test, felület, 2D-s modellek és vonalak is importálhatóak.

Ha a tervezési folyamat különböző szakaszaiban végzünk véges elemes analíziseket, akkor úgy érdemes a beállításokat megtenni, hogy a geometria változása érvényesüljön a véges elemes rendszerben is. Amennyiben optimalizációra is sor kerül a geometriai paramétereket általában abban a CAD rendszerben kell definiálni, amelyben a geometria készült. Bizonyos egyszerűsítéseket (pl. szimmetriasíkok definiálása) a véges elemes rendszerben is elvégezhetünk.

[5.] , [6.] , [11.]

2.2.3. Egyszerűsítések

Véges elemes analízisek esetében a geometriai modell előkészítése nagymértékben befolyásolja a szimuláció lefutásának időtartamát illetve a kapott eredmény helyességét, ezért különösen fontos, hogy a lehetséges egyszerűsítéseket elvégezzük, de semmiképp ne éljünk olyan geometriai modell-egyszerűsítéssel, amely az analízis szempontjából jelentősen befolyásolná a vizsgált modell viselkedését, vagy a modellezett feltételeket.

Amennyiben az analízis tárgyát képező geometria tartalmaz olyan alaksajátosságokat, amelyekről biztosan el tudjuk dönteni, hogy elhagyása nincs befolyással az analízis eredményére, azt mellőzhetjük. Ugyanígy több testből álló geometriai modellek esetén (pl. több alkatrészből álló szerelt összeállítás) elhagyhatók akár bizonyos alkatrészek is.

A legfontosabb geometriai egyszerűsítés a szimmetria feltételek alkalmazásával (fél, negyed, ciklikus, stb.) használatával és a 2D-s modellek (sík alakváltozás, sík feszültség, tengelyszimmetrikus) alkalmazásával érhető el.

2.2.3.1. Szimmetria feltételek alkalmazása

Előnyös lehet a szimmetria feltétel alkalmazása abban az esetben, ha a geometriai modell, a peremfeltételek és a terhelések, valamint az anyagmodell valamilyen szimmetriát mutat, mivel így a teljes geometria helyett csak annak egy reprezentatív részével számolunk, így csökkentve a szimuláció időigényét. Természetesen ennek az egyszerűsítésnek alapfeltétele, hogy a geometriának, a terheléseknek, a megtámasztásoknak és az anyagmodellnek egyaránt tartalmazni kell az adott szimmetriát. Csak akkor használható szimmetria, ha az anyagmodell nem tartalmaz olyan irányfüggő tulajdonságot, amely nem összeegyeztethető az adott szimmetriával. (Megjegyzés: érdemes ellenőrizni, hogy koncentrált terheléseknél a terhelés a teljes- vagy a szimmetria szerinti részterhelés megadása szükséges, mivel ez programonként eltérő lehet.) A részmodellek alkalmazása különösen fontos abban az esetben, ha optimalizációt végzünk, mert ilyenkor a sok optimalizációs lépés miatt egy kisebb időnyereség is jelentősen gyorsítja az optimalizációs folyamatot.

Hátránya lehet az esetleges megjelenési limitáltság, mely prezentációs anyagokban való felhasználásoknál nem mindig szerencsés, illetve ha nem kellő körültekintéssel alkalmazzuk az egyszerűsítéseket, akkor egy esetleges figyelembe nem vett az egyszerűsítésnek ellentmondó tényező könnyen okozhat hibás eredményt.

Alkalmazható szimmetriák:

Tengelyszimmetria (Axisymmetry) – Forgásszimmetrikus geometria jellemzi, 2D tengelyszimmetrikus, 3D-s fél és negyedmodell alkalmazható,
Ciklikus (Rotational symmetry) - A szerkezet tengelyszimmetrikus tulajdonsággal rendelkezik, melyet a tengelyvonal körül ismétlődően kiosztott szegmensek egészítenek ki (pl. turbinalapátok).
Tükörszimmetria (Planar, reflective symmetry) – fél, negyed vagy nyolcad modell alkalmazható a szimmetriasíkok számától függően.
Ismétlődés (Repetitive, translational symmetry) – egyenes mentén kiosztott ismétlődő geometriai elem jellemzi.

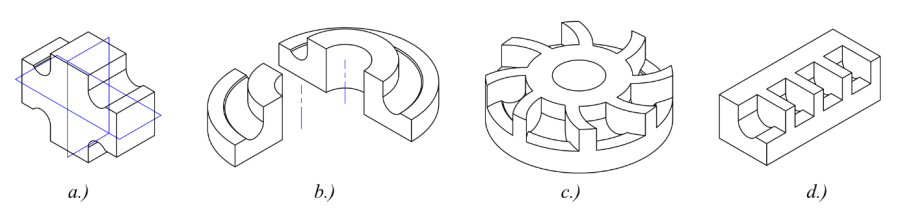
a.) Tükörszimmetria, b.) Tengelyszimmetrikus alkatrész negyed vagy félmodellel, c.) Körkörös ciklikusság, d.) Egyenes menti ismétlődés.

2.2. ábra - Testmodelleken alkalmazható szimmetriák.

2.2.3.2. 2D-s és 3D-s modellek alkalmazása

A geometria kiterjedésétől és a mechanikai feladat jellegétől függően választhatunk a térbeli vagy síkbeli analízis között, de lehetőség van térbeli analízisek elvégzésére alacsonyabb dimenziójú topológiával rendelkező elemekkel. Ezeket a lehetőségeket a legtöbb végeselemes rendszer támogatja. Az adott egyszerűsítés előfeltétele az analízis típushoz illeszkedő geometria létrehozása. A különböző geometriai típusokat és a kapcsolódó analízis típusát az Táblázat 2.1 szemlélteti.

2.1. táblázat - Különböző geometriai egyszerűsítések áttekintése, mechanikai példán keresztül.

Geometria	Analízis / Elem	Mechanikai eset	Az alkalmazás jellemzői
Testmodell	3D / 3D	Térbeli	Mindhárom irányú kiterjedése azonos nagyságrendű. Térbeli terhelés.
Térbeli Felületmodell	3D / 2D	Héj, membrán, lemez	Vékony térbeli szerkezetek. Térbeli terhelés és deformáció. (pl. lemezalkatrészek, karosszériaelemek, membránok)
Sík Felületmodell	2D / 2D	Sík feszültség	Vékony, sík szerkezetek. Csak a szerkezet síkjában fellépő feszültség. A keresztmetszet síkjába eső terhelés. (pl. Húzott lemezszerkezetek.)
	Sík alakváltozás	hosszú és állandó keresztmetszetű alkatrészek. A 2D-s geometria a szerkezet egy keresztmetszetét jelenti. Csak a keresztmeszet síkjában van alakváltozás. Keresztmetszettel párhuzamos terhelés és deformáció. (pl. Csővezetékek, zártszelvények, profilok)
	Tengely-szimmetrikus	Tengelyszimmetrikus szerkezet, melynek (fél) keresztmetszete a 2D-s modell (+XY síkon). A terhelések és a deformációk értéke állandó a kerület mentén. A kerület mentén állandó radiális és axiális komponensű terhelés. (pl. Forgástestek, nyomástartó edények.)
Térbeli vonalmodell	3D / 1D	Rúd, Gerenda	Állandó keresztmetszetű, vékony, hosszú elemekből álló térbeli szerkezetek. Vékony térbeli szerkezetek. Térbeli terhelés. (pl. Rácsos tartó, gerendaszerkezet.)

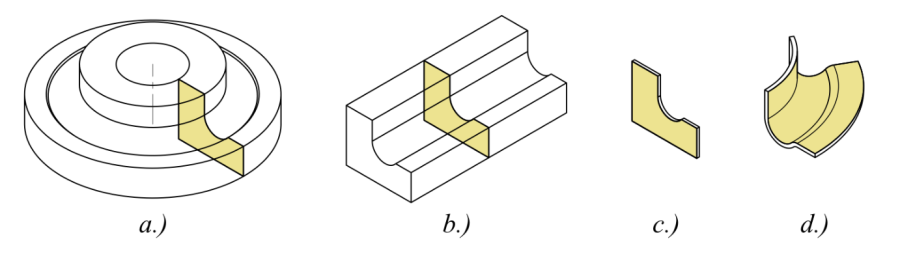
a.) Tengelyszimmetrikus, b.) Sík Alakváltozás, c.) Sík feszültség, d.) Héjmodell.

2.3. ábra - Térbeli testek felületmodellel történő modellezése.

A fenti táblázatból látható, hogy a geometriai modellek dimenzió szerinti osztályozása több szempont szerint is történhet, attól függően, hogy a vizsgált mechanikai probléma (feszültség vagy alakváltozási állapot, terhelések iránya, peremfeltételek, stb.) vagy az alkalmazott elemek, ill. a geometria topológiájának dimenzióját vesszük figyelembe. Az alábbiakban a geometriai modellek szerint soroljuk fel azok jellemzőit és alkalmazásukat.

2.2.3.2.1. Testmodell

A valós test geometriáját megközelítő tömör testmodelleket (3D-s testmodell), akkor alkalmazzuk, ha a test kiterjedése a tér minden irányába közel azonos nagyságrendű. Alkalmazásuk a legáltalánosabb és szinte minden probléma megoldásánál használható.

2.2.3.2.2. Térbeli felületmodell

Az olyan felületmodellek soroljuk ide, melyek 2 dimenziós topológiával, de 3 dimenziós kiterjedéssel vagy terhelési állapottal rendelkeznek, (pl.: héj, membrán vagy lemezmodell). A 3 dimenziós felületmodellek akkor használhatók, amikor a modellezett szerkezet vastagsága sokkal kisebb, mint a más irányú kiterjedése. Alakja lehet sík (lemezmodell) vagy térbeli kiterjedésű alakzat (héj). Fontos, hogy csak olyan igénybevételek esetén használhatók, ahol a vastagság irányában nincs olyan deformáció, amely befolyásolná a szerkezet viselkedését (pl. nyírási igénybevétel).

Modellezésük egy vastagság nélküli felület létrehozásával történik. Vastagságot a hálózáskor kapnak a megfelelő elemek hozzárendelésével. A modellezett felület általában a véges vastagságú szerkezet középfelülete, de általában lehetőség van az alsó vagy felső felületével modellezni a szerkezetet. Tipikus példa erre a fajta geometriai típusra a gépkocsik karosszériájának elemzése.

2.2.3.2.3. Sík felületmodellek

2 dimenziós modellek a 3 dimenziós modellek egyszerűsítésével hozhatóak létre a következő esetekben:

Sík feszültség - Amennyiben a tér egyik irányába fellépő feszültség elhanyagolható a másik két irányhoz képest. A geometria kiterjedése abba az irányba, amelybe a feszültség elhanyagolható sokkal kisebb, mint a másik két irányba. Tipikus példa erre az esetre egy a síkjában terhelt lemezszerű geometria vizsgálata, vagy például egy rugózó horog típusú pattanó kötés elemzése.
Sík alakváltozás - Amennyiben a tér egyik irányába fellépő deformáció elhanyagolható a másik két irányhoz képest. A geometria kiterjedése abban az irányban, amelyben a deformáció elhanyagolható sokkal nagyobb, mint a másik két irányban. Tipikus példa erre az esetre a zárszelvények bizonyos terhelési esetei, vagy például egy vonatsín terhelésének vizsgálata.
Tengelyszimmetrikus - Amennyiben a geometria és a peremfeltételek tengelyszimmetrikusak. A harmadik esetbe olyan geometriák tartoznak, amelyek tengelyszimmetrikusak, a terhelési és megfogási viszonyok is tengelyszimmetrikusak és a használt anyagmodell nem tartalmaz olyan irányfüggő tulajdonságot, amely ellentmondana a tengelyszimmetriának.

A fenti esetekben elegendő a geometriának azt a 2 dimenziós metszetét vizsgálni, amely a feszültség és deformáció szempontjából releváns (2.3. ábra). Természetesen csak akkor használhatók ezek az egyszerűsített geometriai modellek, ha a terhelések, megfogások és az esetleges irányfüggő anyagtulajdonságok ezt megengedik.

2.2.3.2.4. Vonalmodellek

Speciális eset az úgynevezett rúd, vagy gerendamodell használata, mely vonalakkal közelíti a terhelt szerkezetet. Ezt a megoldást akkor érdemes alkalmazni, amikor a geometria vonalak mentén azonos keresztmetszettel rendelkezik és az egyes geometriai szakaszok határán lévő kapcsolatot elhanyagolhatjuk, vagy későbbi vizsgálat során fogjuk annak viselkedését vizsgálni. Tipikus példa erre az esetre egy hegesztett, zártszelvényekből álló rácsszerkezet vizsgálata.

[12.]

2.3. Hálókészítés

A végeselem szimuláció alapvető lépése az adott geometria véges kis elemekre való felosztása, amit hálózásnak nevezünk. A végeselem modell létrehozásához ki kell választani a megfelelő elemtípust és a hálózás sűrűségét, figyelembe véve a kívánt pontosságot és a szükséges futásidőt. A legtöbb végeselem program a hálózást automatikus elvégzi, de lehetőség van a kézi beállításra is.

A végeselem modell elemeit (elements) és az elemeket összekapcsoló csomópontjait (nodes) a geometriai modell hálózásával (Solid modelling) vagy közvetlenül (Direct generation) hozhatjuk létre. A geometriai modell létrehozható a VEM programon belül vagy importálható külső CAD programból. A végeselemes háló közvetlen létrehozásakor (Direct generation) az egyes csomópontok helyét és az elemek tulajdonságait külön-külön kell megadni. Bár a direkt módszer több lehetőséget ad az elemek számának, eloszlásának, alakjának és más tulajdonságainak szabad befolyásolására, nagyobb elemszámnál nem hatékony és növeli a hiba lehetőségét. A két módszer tulajdonságait az alábbiak szerint foglalhatjuk össze [6.] :

2.2. táblázat - A direkt és az automatikus hálózás összehasonlítása.

	CAD modell hálózása (Solid Modelling)	Közvetlen hálógenerálás (Dirct generation)
Előnyök	Elsősorban nagy bonyolultságú, főleg 3D-s testmodellek hálózására alkalmas.	Elsősorban kis és egyszerű modellek hálózására alkalmas.
	Kisszámú paraméter kezelését teszi szükségessé.	Teljes felügyeletet biztosít a csomópontok és elemek száma, eloszlása, alakja, stb. felett.
	Az adaptív hálózáshoz ajánlott.
	Lehetővé teszi a geometria módosítását.
Hátrányok	Nagy a szimuláció futásideje.	A kis és egyszerű modelleket kivéve, időigényes az előállítása.
	Kis és egyszerű modelleknél több paraméter kezelését teszi szükségessé, mint a direkt módszer.	Nem használható adaptív hálózásra.
	Egyes esetekben a program nem tudja legenerálni a végeselemes hálót.	A háló módosítása túl bonyolult.
		A monoton művelet során könnyű hibát véteni.

2.3.1. Elemtípusok

Megjegyzendő, hogy a felsorolt elemek és azok tulajdonságának leírása közel sem teljes, mivel az meghaladná a jegyzet kereteit, csak a jegyzet témaköreiben ismertetett feladatok tárgykörébe tartozó kategóriákra szorítkozunk. Teljesebb áttekintésért és mélyebb ismeretekért érdemes használni a felhasznált és ajánlott irodalmakat és a használni kívánt végeselem szoftver súgóját, mivel azok teljes körű leírást tartalmaznak a rendelkezésre álló elemkészletről.

2.3.1.1. Kiterjedésük szerint

Bizonyos feltételek teljesülése mellett lehetőség van a 3D-s esetek síkbeli (sík feszültség, sík alakváltozás és tengelyszimmetrikus) vizsgálatára, vagy egyszerűsített térbeli, de 1 vagy 2 dimenziós topológiával rendelkező (rúd, héj, stb.) modellek alkalmazására. Mivel az 1D-s, ill. 2D-s modellek elemszáma jóval kisebb, mint ugyanannak a szerkezetnek a 3D-s modelljének, ezért futtatásuk sokkal gyorsabb és a szimuláció beállítása is egyszerűbb. Az analízisben használt elemek az alkalmazott geometriától függően kiterjedésük szerint dimenzió nélküli pont, 1D-s vonal, 2D-s felületi vagy 3D-s térfogati elemek lehet (2.3. ábra).

A pont elemeket (point element) egy csomópont (node) definiál, (pl., mint tömegpont vagy csomópont-felület kontaktelem).
A vonal elemeket (line element) két vagy három csomópontot összekötő egyenes, vagy ív definiál. A vonalelem lehet rúd (trust) , gerenda (beam) , cső (pipe) és tengelyszimmetrikus héj (axisymmetric shell) .
A felületelemek háromszög (triangular) , vagy négyszög (quadrilateral) alakúak, ill. 2D-s sík modell (2-D sík feszültség, sík alakváltozás, vagy tengelyszimmetrikus), vagy héj (shell) elemek lehetnek.
A térfogati elemek tetraéder (tetrahedral), gúla (piramid), prizma (wedge) vagy tégla (brick, hexahedron) alakú, 3D-s szilárdtest (3-D solid) elemek lehetnek.
A peremfeltételek definiálására (kontaktok, rugó elemek, tömegpont, stb.) speciális tulajdonságokkal rendelkező elemeket használunk. [6.] ).

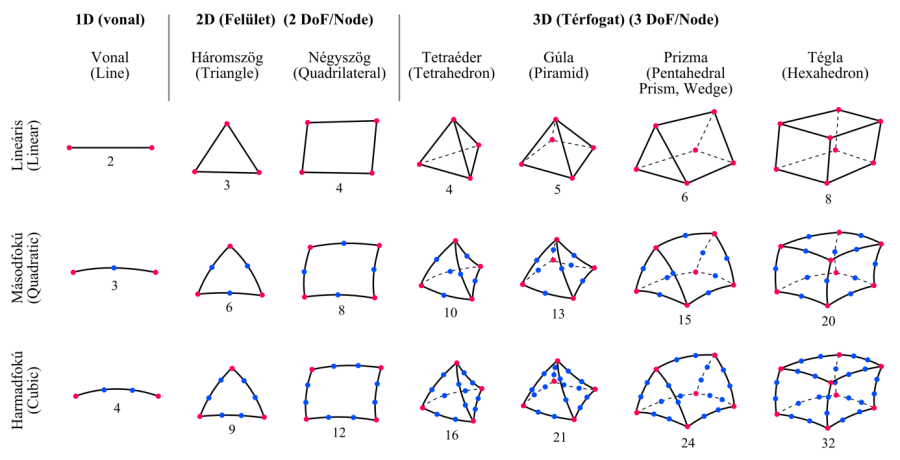
Az egyes elemek alatt a csomópontok száma van feltüntetve. (Az egy csomópontból álló és a belső csomópontokkal rendelkező elemek az ábrán nincsenek feltüntetve.)

2.4. ábra - Elemek csoportosítása alakjuk és fokszámuk szerint.

2.3.1.2. Az elemek fokszámuk szerint

A végeselem szimulációban használt elemek a geometriájuk és az alkalmazott interpolációs függvényük fokszáma szerint lineárisak (linear, first-order), másodfokúak (second-order, quadratic, parabolic) vagy harmadfokúak (third-order, cubic) lehetnek. Például egy lineáris háromszög (triangle) elem 3 csomóponttal (node) és 3 egyenes éllel van definiálva. A magasabb rendű háromszög elemnél a 3 csúcsnál lévő csomóponton felül a görbe vonalú éleken köztes csomópontok is (1 vagy 2) találhatóak.

A lineáris vagy magasabb rendű elemek választásakor az alábbiakra kell figyelemmel lenni. Alapvetően elmondható, hogy ugyanolyan hálósűrűség mellett a magasabb rendű elemek adnak pontosabb eredményt, mivel jobb matematikai közelítést használnak, és az íves élekkel / felületekkel határolt geometriát pontosabban követik. Viszont szem előtt kell tartani, hogy nagyobb teljesítményt, vagyis több számolási időt igényelnek.

Jacobi pontok (Jacobian Points). Magasabb rendű elemek esetén egy éles vagy erősen görbült perem olyan torzult elem generálását eredményezheti, melynek élei keresztezik egymást. A Jakobi vizsgálat esetén, az elem belsejében felvett pontok segítségével megállapítható a hiba, ugyanis ilyen extrém mértékben torzult elem esetén a Jakobi determináns értéke negatív lesz. (statikai feladatnál alkalmazott p-eljárás esetén célszerű a Jakobi vizsgálat elvégzése) [11.] .

2.3.1.3. Az elemek szabadságfoka

Az elemek szabadságfoka határozza meg, hogy melyik elem milyen típusú analízisre alkalmazható (pl.: szerkezeti, hő, áramlástani, elektromos, mágneses vagy kapcsolt terű analízisre.) Egy térbeli szerkezeti analízisben használt elem csomópontjainak 3 (U_x, U_y, U_z) szabadságfoka van, ezzel szemben egy hőtani szimulációban csak egy, a hőmérséklet. A megfelelő szabadságfokú elemtípus választása jellemzi a modell válaszát. Az elemek fölösleges szabadságfoka növeli a szimuláció memóriafoglalását és futási idejét. Hasonlóképpen a szükségtelen elemtulajdonságokkal rendelkező elem (pl. plasztikus tulajdonságok egy rugalmas szimulációban) alkalmazása szintén növeli a futásidőt.

2.3.1.4. Az elemtulajdonságok

Általános esetben az elemek koordinátarendszereire, bemeneteire (csomópontok, szabadságfok, anyagtulajdonságok, terhelések, stb.), és a szimuláció eredményeire (a csomópontok elmozdulása, feszültség, reakcióerő, stb.), oszthatók. Az alábbiakban nézzük meg az elemek főbb tulajdonságait a felhasználásuk szerinti csoportosításban.

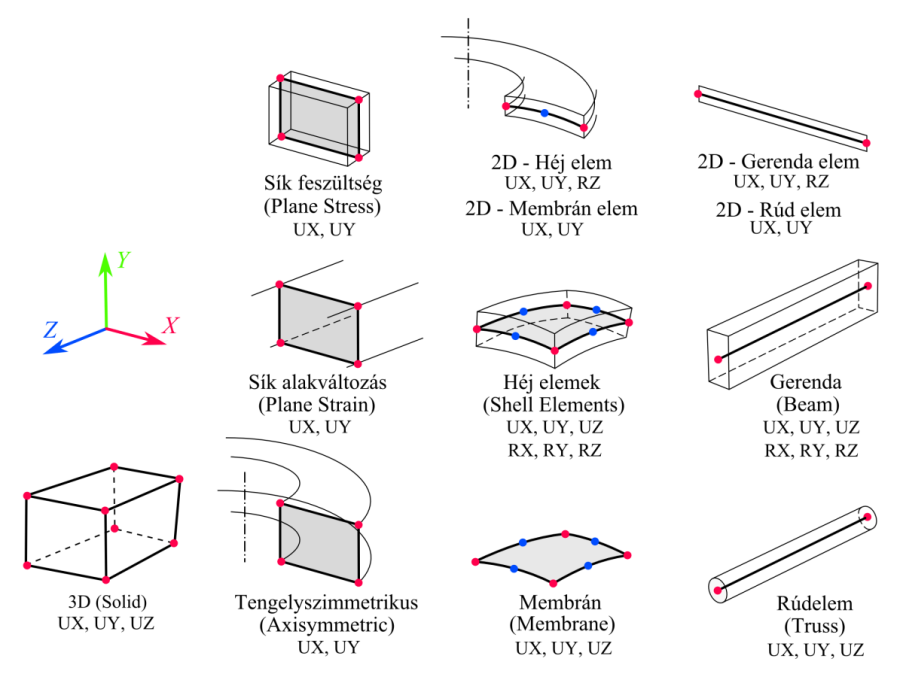
2.5. ábra - Gyakori mechanikai elemtípusok és a csomópontok szabadságfoka.

2.3.1.4.1. A feszültséganalízis elemei

az alábbiak szerint csoportosíthatók (2.5. ábra):

Kontinuum feszültségű elemek (Continuum Stress Elements) - az adott térfogatelem deformáció és feszültséganalízisére alkalmazhatóak. NEM tartoznak ide a héj, felület, kontakt, rúd és egyéb speciális elemek. Bármilyen strukturális analízishez használhatók. Nem hatékony az alkalmazása olyan esetekben, amikor a modell egy vagy két mérete sokkal kisebb a harmadiknál (pl.: membrán, lemez vagy rúdszerű modellek). Az elemek lehetnek 2, ill. 3 dimenziósak attól függően, hogy sík vagy térfogati modell hálózására használjuk. 2D-s változataik:
- Sík feszültség (Plane Stress) – olyan, csak X és Y irányokban változó feszültségi állapotoknál alkalmazzuk, amelynél a Z irányú normál, ill. az XZ és YZ nyíró feszültség nulla. Általában vékony, sík szerkezetek szimulációjára alkalmazzuk, melyeknél feltételezzük, hogy csak a szerkezet síkjában van deformáció.
- Sík alakváltozás (Plane Strain) – olyan, csak X és Y irányokban változó feszültségi állapotoknál alkalmazzuk, amelynél a Z irányú megnyúlás, ill. az XZ és YZ nyíró alakváltozás nulla. Tipikusan hosszú és állandó keresztmetszetű alkatrészek vizsgálatára alkalmazzuk, ahol a 2D-s geometria a szerkezet egy keresztmetszetét jelenti. (Az általánosított sík feszültség szimulációnál a Z irányú alakváltozás nem nulla.)
- Tengelyszimmetrikus (Axisymmetric) – A modell geometriai paraméterei, anyagjellemzői, a terhelések és a deformációk értéke állandó a kerület mentén. (Az általánosított, ill. harmonikus tengelyszimmetrikus szimulációk esetében a deformáció, ill. a terhelés lehet nem tengelyszimmetrikus.). A tengelyszimmetrikus szimulációk geometriáját az XY síkon, a +X térfélen kell elhelyezni, amely az Y forgástengelyű test keresztmetszetét jelenti [6.] vagy definiálni kell a metszősíkot és a forgástengelyt [11.] .
Héj elemek (Shell Elements) – Vékony térbeli szerkezetek szimulációjára alkalmas, melyeknél az egyik méret sokkal kisebb, mint a másik kettő. A héj elem a deformációt a felület szerinti normál és felületi irányokra bontja, ami egyszerű és hatékony szimulációt tesz lehetővé. Az elem felvehet membrán és hajlító terheléseket, ezért a csomópontok 6 szabadságfokkal (3 elmozdulás, 3 elfordulás) rendelkeznek. Az eredményként kapott eredő feszültség lekérdezhető a héj elem felső (top) ill. alsó (bottom) oldalán, továbbá a hajlító (bending) és a felület síkjába eső (membrane) feszültségkomponensek külön-külön is lekérdezhetőek. Általában lehetőség van a héj elemek membrán elemként való alkalmazására, melynél deformáció csak a felület mentén történik és a feszültség állandó a vastagság mentén.
A végeselem szoftver automatikusan héj elemeket rendel a térbeli (3D-s) felületmodellekhez vagy az olyan síkbeli felületmodellekhez, melyeknél a modell típusát 3D-re állítjuk [6.] . Egyes szoftvereknél az állandó vastagságú lemezalkatrészek (sheet metal) is héj elemekkel lesznek behálózva [11.] .
Vonal elemek (Line) – Állandó keresztmetszetű, vékony, hosszú elemekből álló szerkezetek szimulációjára alkalmas, melyeknél az egyik méret sokkal nagyobb, mint a másik kettő. A vonal elemekből álló rácsszerkezet szimulációja lényegesen egyszerűbb és gyorsabb, mint a szilárdtest-modellé. Az elemek egyenesek vagy ívek felosztásával (hálózásával) jönnek létre. A vonal elemek az alábbiak lehetnek.
- A rúdelem (Truss) csomópontjai nyomatékot nem adnak át, tehát csak tengelyirányú erőt képes átvinni, amely a rúd teljes hossza mentén állandó értékű és a keresztmetszetben egyenletesen megoszló feszültséget hoz létre. A rúdelem nulla feszültséget és alakváltozást feltételez az elem tengelyétől eltérő irányokban. Csak transzlációs mozgást enged elfordulást nem (3 DoF). Fő alkalmazási területe a rácsos tartók szimulációja. (A „link” elem a nyírófeszültséget és a feszültség gradienst szintén figyelmen kívül hagyja.)
- A gerenda (Beam) elem fel tud venni hajlító, csavaró és nyíró terhelést, ezért az elem keresztmetszetét is definiálni kell. A rúd hossza mentén és a keresztmetszet síkjában is változhat a feszültség értéke. Az elemek tengely körüli orientációja is definiálva van, tehát az elmozdulás mellett elfordulásra is képes (6 DoF), [6.] .
Speciális elemeket alkalmazunk a peremfeltételek, terhelések vagy különleges anyagtulajdonságok megadásához. Néhány példa a teljesség igénye nélkül:
- Kapcsolatot biztosító elemek - több alkatrészes összeállítás esetén az egyes alkatrészek közötti kapcsolatot lehet velük definiálni. Az alapvető kontakt elemek által biztosított kapcsolat lehet teljesen merev (Bonded), ideálisan érdes (Rough), ideálisan súrlódásmentes (frictionless), az érintkezésbenmaradó súrlódásmentes (no separation) és súrlódásos (frictional). Az alkatrészek közé lehet definiálni különböző szabadságfokokat megtestesítő csuklókat valamint rugalmas és csillapító elemeket.
- Cső (Pipe) elemek definiálására is lehetőség van egyes végeselem programokban, melyek egyenes, vékony vagy mérsékelten vastag csőszerkezetek szimulációjára alkalmas. A csőelem egy speciális rúdelem, melynek keresztmetszete tengelyszimmetrikus, külső és belső nyomás definiálható és nemlineáris anyagmodelleket is tartalmazhat [6.] .
- Felületi elemek (Surface Elements) – a szilárdtest elemek felületéhez csatlakozva lehet felruházni a modellünket speciális felületi tulajdonságokkal, mint pl. a nyomás, hidrosztatikus nyomás, sugárzás, kontakt felületek definiálása, stb.
- Erősítő elemek (Reinforcing Elements) – a kompozit anyagok vizsgálatára szolgáló elemtípus. Az erősítő szál rendszerek szimulációja egyirányú merevséggel rendelkező membrán rétegekkel történik (pl.: Szénszál erősítésű polimer kompozit). Egy rétegben lévő erősítő szálaknak egyforma keresztmetszettel, anyagtulajdonsággal, orientációval és távolsággal kell rendelkezniük. Lehetőség van az egyedi tulajdonságokkal (pl.: keresztmetszet, anyag, távolság, és a tájolás.) rendelkező ritkán elhelyezett erősítő szálak egyedi számolására (pl.: acél armatúra vasbeton szerkezetben). Alkalmazható rúd, héj vagy szilárdtest elemekhez [6.] .

2.3.1.4.2. A termikus analízis elemei

A termikus analízisekhez hőmérsékleti szabadságfokkal rendelkező elemeket használunk. A szilárd testek részeit, 2D-s vagy 3D-kontinuum elemekkel hálózhatjuk. A különböző területek közötti kapcsolat megvalósítására 1D-s elemek szolgálnak. A 0D-s pont elemet a koncentrált tömeg modellezésére lehet használni.

A szilárdtestben alkalmazható termikus elemtípusok:

3D – homogén vagy rétegezett szerkezetű szilárd testek modellezésére.
2,5D – vékony szerkezetek, mint a lemezek vagy héjak síkban történő hőmérséklet-eloszlásának vizsgálatára szolgál. A felület irányában és a vastagságon keresztüli hővezetés szimulációjára alkalmas.
2D – sík vagy tengelyszimmetrikus testek, ill. sík vagy görbe határfelületek modellezésére alkalmas.
1D - különböző területek közötti hővezetés (Conduction), hőátadás (Convection) és hősugárzás (Radiation) modellezésére szolgál.
0D – egy test hőkapacitásának (thermal capacitance) koncentrált paraméterrel történő modellezésére szolgáló termikus tömegpont. Nem rendelkezik hőmérsékleti gradienssel.

A hőterhelés közlésének két módja, a felületi hőterhelés megadásával, vagy az elem-kontaktokon keresztül történő hőátadással lehetséges.

A termikus modellben a felületi hőterhelés a konvekciót (convection), hőáramot (heat flux), vagy a hősugárzást (radiation) tartalmazhatja. A hőterhelést közvetlenül a kontinuum elemekre is lehet alkalmazni, sokkal kényelmesebb az azokat elfedő felületi elemek segítségével.

A felületi elemeken kívül a hőterhelés kontakt-elemekkel is megvalósítható. Ha két vagy több egymás közvetlen közelében lévő vagy érintkező szerkezeti régió van a modellben, kell számolni a köztük lévő hőátadással (konvekció, hővezetés, vagy a hősugárzás). Az érintkező felületek közötti súrlódási erő is lehet a hőtermelés forrása [6.] .

2.3.1.4.3. Az elektromos és mágneses analízis elemei

Az elektromágneses problémák analízisében alkalmazott elemeket a következő csoportokra bonthatjuk:

Kontinuum elemek (Continuum). Lehetnek 2, vagy 3 dimenziósak.
- Elektrosztatikus (Electrostatic) - töltés alapú, elektromos potenciál (Volt) szabadságfokú elemek.
- Elektromos (Electric) – áram alapú, elektromos potenciál (Volt) szabadságfokú elemek.
- Mágneses, elektromágneses (Magnetic, Electromagnetic) elemek – szabadságfoka mágneses skalár vagy vektor potenciál (magnetic scalar / vector potential), idő-integrált elektromos skalár potenciál (time-integrated electric scalar potential), elektromos áram (electric current) és elektromotoros erő (electromotive force) lehet.
- Végtelen tartomány (Infinite) – egy határtalan mező hatásának nyitott határfelületeken történő modellezésére szolgáló elemek. Segítségével a távoli tér (elektromos, mágneses) hatása modellezhető peremfeltételeken és testeken.
Forrás (Source) – Az elektromágneses analízisben a mágneses térerősséget létrehozó áram forrása. Az elemekben az áram iránya meghatározott, általában az áramvezető alakja is előre definiált. A vezetőben folyó áram által keltett mágneses tér (H) kiszámításához a Biot-Savart törvényt alkalmazó numerikus integrálással történik.
Áramkör (Circuit) – Az áramköri elemek modellezésére szolgál, mint az ohmnikus ellenállás (resistor), kapacitás (capacitor), induktivitás (inductor), dióda (diode) áram és feszültségforrás (current / voltage source), 2 és 3D-s tekercsek (stranded / massive coil), kölcsönös induktivitás (mutual inductor) és vezérelt forrás (controlled source), stb. Alapvetően elektromos áramkörök szimulációjára szolgál, de lehetőség van kapcsolt Elektromos-Mágneses analízis során a mágneses teret létrehozó áram közvetett megadására a segítségével.
Kontakt (Contact) – az alkatrészek közötti kapcsolatot, ill. a mágneses vektor és skalár mennyiségek kapcsolatát teremti meg.

2.3.1.4.4. Csatolt-tér elemek

A csatolt-tér (Coupled-Physics) elemek különféle fizikai jelenségek együttes vizsgálatát teszik lehetővé. Ezek az elemek mindazon szabadságfokokkal rendelkeznek, amelyek az adott típusú fizikai viselkedésre jellemzőek. A csatolt-tér elemek alkalmazásával a különböző fizikai jelenség szimulációja szimultán történik, (egyazon analízisben és egyazon végeselemes modell (háló) felhasználásával). A csatolt-tér elemek alkalmazása a szoros kapcsolatban álló fizikai jelenségek esetében ajánlott.

Főbb típusai:

Szerkezeti - termál (Structural-thermal),
Elektroelasztikus (Electroelastic),
Piezoelektromos (Piezoelectric),
Piezorezisztív (Piezoresistive),
Mágneses – szerkezeti (Magneto-structural),
Szerkezeti – elektromágneses (Structural-electromagnetic),
Elektromágneses (electromagnetic),
Termo-elektromos (thermo-electric),
Áramköri – elektromágneses (Circuit-coupled electromagnetic),
Akusztikus folyadék – szerkezeti (Acoustic fluid-structure),
Termál – folyadék (Thermal-fluid),
Porózus - nyomás (Pore-pressure),
Termál – diffúziós (Thermo-diffusion),
Szerkezeti – diffúziós (Structural-diffusion).

További általános vagy többszörösen összetett elemek is használatosak a fenti párosítások kombinációjaként [6.] .

2.3.2. A hálózás lépései

Az automatikus hálókészítés alapvetően a háló attribútumainak (attributes) beállításából, a kontrollok (mesh controls) megadásából és a hálógenerálásból áll. Lépései:

Fizikai elv kiválasztása (Mechanikai, elektromágneses, fluid, stb.),
Hálózási eljárás beállítása (Automatikus, söpréses, tetraéder/tégla, háromszög/négyszög),
Globális hálózási tulajdonságok beállítása,
Lokális hálótulajdonságok definiálása,
Előnézet és hálógenerálás,
A háló ellenőrzése.

[13.]

2.3.2.1. Attribútumok és kontrollok beállítása (mesh controls)

A hálógenerálás előtt szükség van a háló tulajdonságait meghatározó attribútumok és kontrollok beállítására. Választhatjuk az alapbeállított értékeket, ebben az esetben a program kiválasztja az adott szimulációhoz megfelelő beállításokat. A globális elemméret automatikus beállítása a modell térfogata, felülete és egyéb geometriai méretek figyelembevételével történik. Viszont lehetőség van azok egyéni, lokális beállítására is a hálógenerálás előtt. Az attribútumok és kontrollok által lehetőség van az alábbi tulajdonságok beállítására:

Attribútumok:

Elemtípus kiválasztása,
Geometriai tulajdonságok megadása (pl.: vastagság, keresztmetszet),
Anyagtulajdonságok hozzárendelése (pl.: Rugalmassági modulus, Poisson-tényező, hővezetés, stb.),
Elemkoordináta-rendszer megadása.

Kontrollok:

Az elem mérete – A globális (a teljes modellre kiterjedő) elemméret méretmegadása történhet automatikusan vagy manuálisan. A manuális elemméret megadható közvetlenül vagy a háló finomságának beállításával, valamint az elemszám, vagy az elem élhosszak minimumának és maximumának megadásával.
A háló lokális finomítása – Olyan helyeken ahol a szerkezet fizikai tulajdonságai miatt az alapértelmezett elemméret nem alkalmas (ilyenek lehetnek például a feszültséggyűjtő, vagy szinguláris helyek), szükség van a lokális hálófinomításra.
Az elem alakja - Ha olyan elemtípust kívánunk alkalmazni, amely több alakot is felvehet, akkor meg kell adnunk az alkalmazható elemalakokat. Például sok 2D-s területelem egyaránt lehet háromszög és négyszög alakú ugyanazon a behálózott területen. A térfogati elemek gyakran lehetnek hatlapú (tégla) vagy tetraéder alakúak, de a két alakzatot keverve ugyanabban a modellben nem ajánlott alkalmazni. (Kivétel ez alól átmeneti piramiselemek használata, [6.] ).
Strukturálatlan vagy rendezett háló (Free or Mapped Mesh) – A szabad vagy strukturálatlan háló esetében nincs korlátozás az elemformák tekintetében, és nincs meghatározott minta alkalmazva. A rendezett vagy strukturált háló (Mapped) esetében az elem formájára és a háló mintájára is vannak korlátozások. A rendezett felületháló csak négyszög vagy csak háromszög elemeket tartalmazhat, míg a rendezett térfogati háló csak tégla elemeket tartalmazhat. A rendezett háló mintázatát a sorbarendezett elemek alkotják, melynek előfeltétele a geometria megfelelő előkészítése [6.] .
A köztes csomópont elhelyezése (az elem fokszáma) – Kvadratikus elemekkel való hálózáskor meghatározható a köztes csomópont elhelyezése vagy annak eltávolítása. Amikor egy kvadratikus elem a határfelületen van, akkor a köztes pont követi a határfelület görbületét.

A modellépítés e szakaszának az egyik legfontosabb lépése, mivel ezek a tulajdonságok alapvetően befolyásolják az egész analízis pontosságát és munkaigényét.

[6.] , [14.] .

2.3.2.2. Automatikus hálózási eljárások

A hálógeneráló algoritmusok szempontjából a végeselem háló egyik legfontosabb tulajdonsága, az elem típusa mellett, a strukturáltsága. Vagyis, hogy a háló lehet strukturált vagy strukturálatlan. A strukturált háló lokálisan ortogonális vonalak rendezetett hálózata alkotja. A háló vonalai a geometria határához illeszkednek. A strukturálatlan hálót rendezetlen poligonok sokasága alkotja.

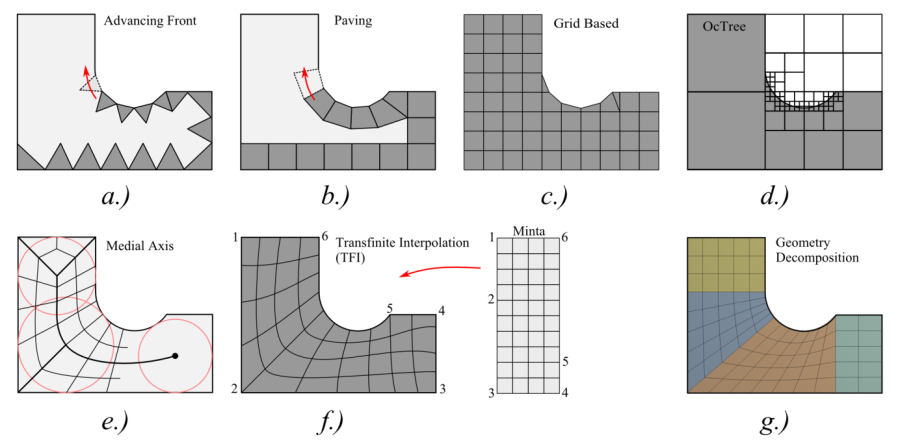
a-d.) Strukturálatlan, e-g.) strukturált háló létrehozása

2.6. ábra - Automatikus és részben automatikus hálógenerálási eljárások.

2.3.2.3. Strukturálatlan háló létrehozása

2.3.2.3.1. Topológia felosztása (Topology decomposition)

A geometriát alkotó pontok (vertex) felhasználásával a komplex geometriát minimális számú, nem átfedő háromszögekre bonjuk, az így létrejött háló torz és durva, analízisre alkalmatlan. A felosztás eredményeként létrejött háromszögek további elemekre bontásával finomítjuk a hálót.

2.3.2.3.2. Csomópont csatlakozás (Node connection)

Első lépésben a csomópontokat hozzuk létre, majd ezeket kapcsolják össze az elemek. A fenti utólagos hálósűrítés elkerülhető, ha a végső háló sűrűségének megfelelően osztjuk szét a csomópontokat. A következő lépésben az így létrejött ponthálót kell megfelelő módon összekötni, hogy a lehető legjobb elemek jöjjenek létre.

2.3.2.3.3. Mozaik (Advancing front, Paving)

A „Front” módszer háromszög elemeket a határoló éltől kiindulva befelé hozza létre (2.6. ábra, a.). A Paving eljárás a „Front” technika négyszögelemre kidolgozott változata, a háromszögelem kiváltására. (2.6. ábra, b.), (csak 2D-ben) [15.] .

2.3.2.3.4. Négy-fa (Octree)

Négyzetes háló, melynek finomítása a határvonalra eső négyzet-elem négyfelé osztásával érhető el. A kívánt felbontásig több lépcsőben ismételve a háló topológiája fa struktúrájú lesz, innen az elnevezés (2.6. ábra, d.).

2.3.2.3.5. Rács alapú (Grid-based)

Valamilyen előre generált minta adaptálásával jön létre a háló. A minta egy végtelen négyzetes vagy háromszög rács, amely a geometriára kerül ráhelyezésre. A geometria határán kívülre kerülő elemek eltávolítódnak. Azok az elemek, amelyek metszik a geometria határát elmetsződnek vagy hozzáillesztődnek a határvonalhoz. A létrejött háló belseje kitűnő tulajdonságú (2.6. ábra, c.). A 3D-s hálógenerálás egyik legelterjedtebb eljárása.

2.3.2.4. Strukturált háló létrehozása

A strukturált háló létrehozása kiváló minőségű kellően egyszerű geometriához és ezáltal hatékonyabb analízishez vezet. Jobb kontrollt biztosít a háló paraméterei felett, pl. anizotrópia esetén. Valósághű geometriák is vizsgálhatóak a „multiblock” hálózási eljárás segítségével.

2.3.2.4.1. Minta leképezéses eljárások (Mapped element)

A minta egy a paramétersíkon lévő egységoldalú elemekből álló négyszögháló, amelyet ráképezünk a hálózandó 4 oldalú felületre a minta megfelelő torzításával (2.6. ábra, f.). Ezzel a módszerrel rendezet négyszögelemmel kirakott hálót hozhatunk léte, olyan szabálytalan felületeken is, melyek topológiája visszavezethető egy 4 oldalú felületre (TFI-Transfinite Interpolation, Elliptic), vagy szétválasztható azokra (Geometry Decomposition).

2.3.2.4.2. Geometria szétválasztás (Geometry decomposition, Sub-maping)

Az eljárás a hálózás során konvex „map”-elhető részekre bonja a geometriát, majd csomópontokat helyez el ezek határán. Végül a különálló tartományokat hállózza be (2.6. ábra, g.). Az eljárás figyelembe veszi az elem alakját és méretét mialatt felosztja a geometriát. Számos eljárás rekurzív, mások iteratívak. A Multiblock-Decomposition eljárás bonyolultabb, strukturálatlan alkatrészek (négyszög oldalú) tartományokra osztása, melyek külön-külön már automatikusan „map”-elhetőek. A Medial Object Decomposition egy maximális sugarú kör / gömb végiggörbítésével jelöli ki a nyomvonalát a közép-objektumnak (középvonal, középfelület) (2.6. ábra, e.). A közép-objektum felhasználása a geometria automatikus szétválasztására, kisebb „map”-elhető részekre.

2.3.2.4.3. Söprés (Sweeping)

Prizmaszerű alaktrészek alapfelületen generált 2D-s háló végigsöprése a teljes test mentén. A véglapokon struktúrálatlan 2D-s hálót, a palást mentén struktúrált hálót generál. Követelmény, hogy a kiinduló (source) és a célfelület (target) topológiailag hasonló és az öszekötő palástfelület „map”-elhető legyen (2.8. ábra).

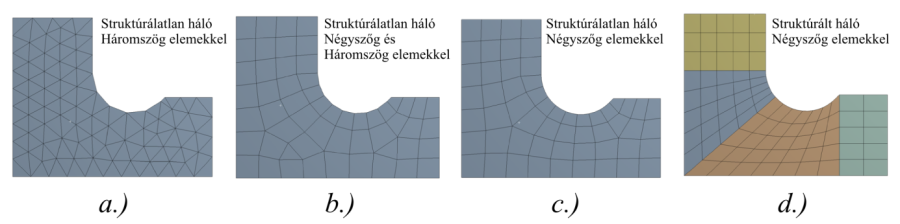
2.7. ábra - 2D-s hálókialakítások.

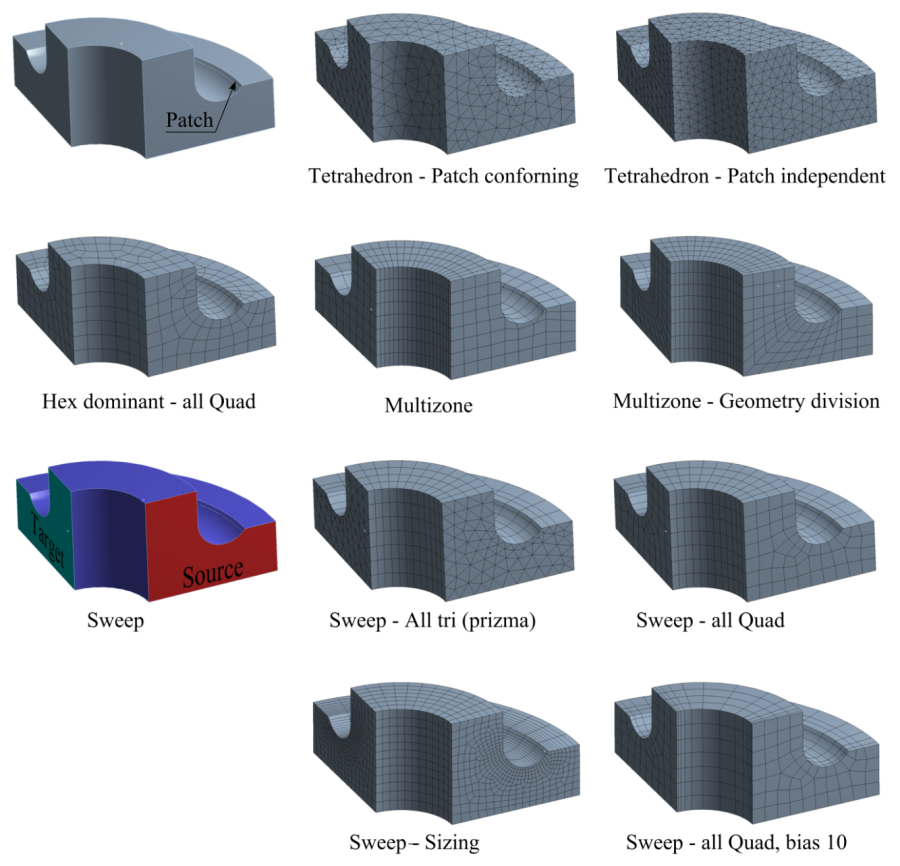
2.8. ábra - 3D-s testek hálózása különféle eljárásokkal.

[16.] , [17.] , [18.] , [19.] .

2.3.2.5. A háló illeszkedése

Több alkatrészből álló modell esetén célszerű a hálót úgy kialakítani, hogy a csomópontok illeszkedjenek, ugyanis az elemre ható terheléseket a csomópontok közvetítik.

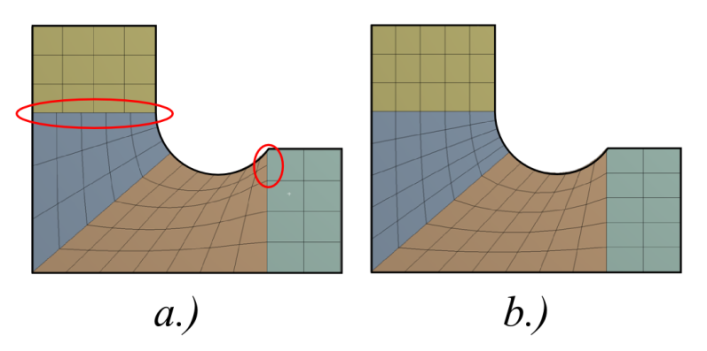
a.) Nem illeszkedő csomópontok (Non-conformal interface), b.) Illeszkedő csomópontok (Matching interface).

2.9. ábra - Különálló felületek vagy testek határán lévő csomópontok illeszkedése.

2.3.3. Konvergencia módszerek

A tervezés kezdeti stádiumában a gyors futás érdekében érdemes lehet nagyobb elemméret és lineáris elemek alkalmazása, a későbbiekben a pontosabb eredményhez pedig finomabb hálózás és vagy magasabbrendű elemek alkalmazása. A konvergencia javításának és az elérhető számítási pontosság növelésének ez a két lehetséges módját h és p konvergencia módszernek nevezik.

H – eljárás: a háló finomítás, elemméret csökkentés,

P – eljárás: az elemek fokszámának növelése,

HP – eljárás: H és P módszer együttes alkalmazása.

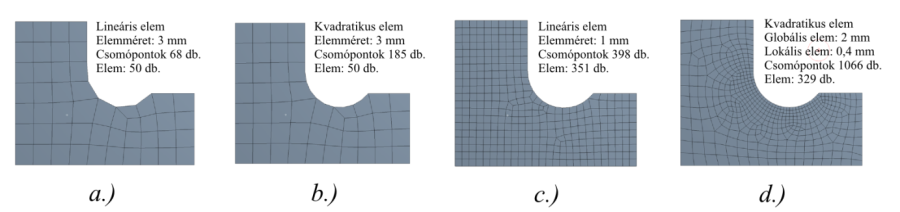
a.) Kiindulási háló, b.) P – eljárás: az elemek fokszámának növelése, c-d.) H – eljárás: elemméret csökkentés, c.) Globális elemméret beállítás, d.) Lokális hálófinomítás.

2.10. ábra - Konvergenciát elősegítő eljárások.

2.3.3.1. Hálósűrítés, hálósimítás

Az egész modellre kiterjedő globális elemparaméterek, főként az elemméret általában nem megfelelő. Olyan helyeken, ahol a vizsgált fizikai mennyiség megváltozása nagyobb (nagyobb gradiens), mint a modell többi részén (pl. feszültséggyűjtő helyek), akkor ott a háló sűrítése indokolt. A háló sűrítése történhet az adott geometria finomítási lépcsőinek megadásával (Refinement, az elemek felezési számának), adott számú elemre történő felosztásával (Number of division, éleknél alkalmazható), vagy az elemméret közvetlen megadásával (element size).

A lokális hálófinomítás során ügyelni kell az átmenet, vagyis az elemméret növekményének intenzitására, a kisméretű lokális elemek és a nagyobb globális beállítású háló között. Ugyanis túl nagy növekmény rossz minőségű, pl. nagy oldalarányú (aspect ratio) vagy torzult elemeket hozhat létre. Az átmenet mértékének (Growth Rate) kezelésére általában van lehetőség a végeselem szoftverekben.

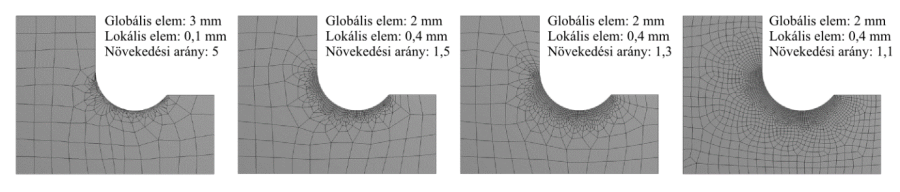
2.11. ábra - Elemátmenetek különböző mértékű növekedési arány (Growth Rate) megadásával.

További segítséget nyújt a megfelelő minőségű elemek létrehozásában a háló simítás (Mesh Smoosing) funkció. A hálósimítás egy már meglévő háló csomópontjainak eloszlását módosítja több iterációban, úgy hogy az elemek alakja minél egyenletesebb legyen. Természetesen ezt a felhasználó nem érzékeli, mert a hálógenerálás egy lépésben történik. Többféle eljárás létezik (Lapalce, Isoparametrikus, centroid, stb.), de előfordulhat, hogy a végeselem szoftverben csak a minőségre utaló értékeket tudunk kiválasztani (low, medium, high).

2.3.3.2. Adaptív hálózás

Abban az esetben, ha a nagy alakváltozások következtében a háló annyira torzul, hogy a szimuláció nem konvergál, szükséges lehet a geometria adaptív újrahálózására (adaptive remeshing). Az eljárás során, amikor a háló eltorzult, a szimuláció leáll. A torzult geometriát a szoftver újrahálózza és érvényesíti rá a korábbi hálón számolt eredményeket, perem és kontakt feltételeket és az analízis folytatódik. [20.]

2.3.4. A hálózásnál előforduló hibák

Elvékonyodó vagy túl éles geometria – a túlságosan elvékonyodó vagy éles geometria hibát okoz a tetraéderes háló generálásában a csúcsoknál (élek mentén).
Extrém elemméret átmenet – a hirtelen átmenet az elemméretben rossz minőségű tetraéder hálót eredményez.
Túl nagy elem görbület – Célszerű lineáris elemet használni, ha nincs szükség pontos feszültség meghatározásra a görbület mentén, vagy kvadratikus elem esetén növelni a háló sűrűségét, hogy egy elem ne fogjon át 15°-nál nagyobb szöget.

Tetraéderhálózási hiba – Elkerüléséhez célszerű előzetesen megvizsgálni a modellt, hogy háromszög elemmel hálózva a test egyes felületeit, tartalmazza-e a fenti hibák valamelyikét, ugyanis azok elősegíthetik a tetraéderes hálózás hibáját.

Kivonóan hálózott részek – A már hálózott elemeken végzett kivonásos boolean művelet esetében jelentkező hibát a hálózás törlésével és újra definiálásával szüntethetjük meg.

Magas és alacsonyrendű elemek szomszédos részeken – Az alacsonyabb rendű hálózást kell először létrehozni majd a magasabb rendűt [6.] .

A háló minőségének vizsgálatára többféle módszer is rendelkezésre áll a végeselemes programokban. A vizsgálatok eredményét szövegesen, statisztikai adatok formájában, hisztogramon, vagy közvetlenül a geometrián szemléltetve közli a szoftver. Az alábbiakban ez utóbbira láthatunk példát (SolidWorks), az elemek oldalarányának (Aspect ratio) és a Jakobi determináns értékének szemléltetésével [6.] , [11.] .

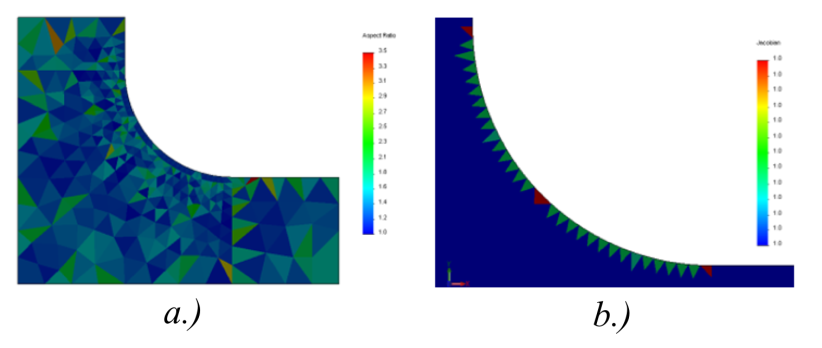
a.) Oldalarány (Aspect ratio) vizsgálata. b.) Jakobi determináns vizsgálat.

2.12. ábra - Elemtulajdonságok vizuális megjelenítése.

2.4. Anyagmodellek létrehozása

Az anyagmodell nem más, mint egy anyag az alkalmazott terhelés hatására adott válaszának matematikai ábrázolása, amely a fizikai változók (mechanikai feszültség, hőáram, villamos áram, stb.) és más fizikai mennyiségek (mint pl. alakváltozás, hőmérséklet eloszlás, villamos feszültség, stb.) között teremtenek kapcsolatot [21.] . A tipikus anyagmodell osztályok a feszültség-alakváltozás, a hőáram-hőmérsékleti gradiens, valamint a villamos áram-feszültség között teremtenek kapcsolatok, de egyéb olyan általános fizikai viselkedést, (mint például a súrlódás, hőtágulás, piezoelektromos és mágneses hatások, stb.) is az anyagmodellek segítségével írhatunk le [6.] .

2.4.1. Általános anyagtulajdonságok

a.) Nyíltcellás polimerhab, b.) szálas szerkezetű anyag, c.) koncentrikusan rétegelt struktúra, d.) szálerősítéses polimer kompozit.

2.13. ábra - Példa az inhomogén és anizotróp anyagokra.

2.4.1.1. Linearitás

Az anyagmodelleket aszerint csoportosíthatjuk, hogy miként teremtenek kapcsolatot a bemenő és kimenő mennyiségek, (vagyis mechanikai esetben a feszültség és az alakváltozás) között. Ez a kapcsolat lehet lineáris (linear), vagy nemlineáris (non-linear). Lineáris esetben a kimenő mennyiség egyenesen arányos a bemenettel és az arányossági tényező valamilyen anyagjellemző.

2.4.1.2. Homogenitás

Az anyag szerkezetét tekintve lehet homogén (homogeneous), vagy inhomogén (non-homogeneous). Az inhomogén anyagok tulajdonságainak (pl. sűrűség, szilárdsági tulajdonságok, stb.) térbeli eloszlása nem egyenletes. Mikroszkopikus szinten gyakorlatilag az összes anyag inhomogén, (kristályokra, molekulára majd atomokra tagolódik), de a szimuláció szempontjából lényeges makroszkopikus szintű inhomogenitást az anyag nagyobb strukturáltsága jelenti, amely méreteiben összevethető a teljes modell méretével (mint pl. a szivacsos csontszövet struktúrája, polimer vagy fém habok, porózus, szemcsés anyagok, stb.).

2.4.1.3. Irányfüggőség

Egy anyag iránymenti viselkedését az alábbi három modellel írhatjuk le.

2.4.1.3.1. izotróp anyagmodell (Isotropic model)

Izotróp anyagról beszélünk, ha az anyagi tulajdonságok (pl. rugalmassági modulus, Poisson-tényező, termikus tulajdonságok, stb) minden irányban megegyeznek. Mikroszerkezetük lehet homogén vagy inhomogén.

2.4.1.3.2. Ortotróp modell (Orthotropic model)

Ortotróp anyagmodell esetén az anyagtulajdonságok három, egymásra merőleges tengely mentén eltérőek és egymástól függetlenek. Tipikus példa az ortotróp anyagra a fa, melynek természetes szerkezete miatt mechanikai tulajdonságai axiális, radiális és tangenciális irányokban különböző. De további ortotrópiát okoznak a szerkezeti anyagainkban egyes technológiai lépések is, mint pl. a polimer szálak húzása, vagy az acéllemezek hengerlése, stb.

2.4.1.3.3. izotrópAnizotróp modell (Anisotropic model)

Az izotrópanizotróp anyag az irányfüggő viselkedés teljesen általános esete, melynél az anyagtulajdonságok különböző irányokban, (nem derékszögű koordináták mentén) eltérő viselkedést mutatnak.

2.4.2. Az anyagmodellek csoportosítása szabadságfokuk alapján

Az anyagmodellek a szabadságfokuk alapján az alábbiak lehetnek, amely közvetlenül vagy közvetve megadják a modell terhelési módját, vagyis az anyagmodell bemenetét:

Elmozdulás,
Hőmérséklet,
Elektromágneses,
Csatolt

2.4.3. Mechanikai, vagyis elmozdulás szabadságfokú anyagmodellek

Az elmozdulás szabadsági fokkal rendelkező elemzésekben szerepelnek, melyekben a bemenet egy deformációs függvény, mint például az alakváltozás vagy az elmozdulás, és az adott válasz valamilyen erő típusú mennyiség, mint például feszültség, vagy a normális és tangenciális erők.

2.4.3.1. A mechanikai anyagmodellek csoportosítása fesz-nyúlás karakterisztikájuk szerint

A mechanikai anyagmodelleket a feszültség-alakváltozás karakterisztikájukkal jellemezzük, amely lehet lineáris, vagy nemlineáris, ill. rugalmas, képlékeny vagy viszkoelasztikus.

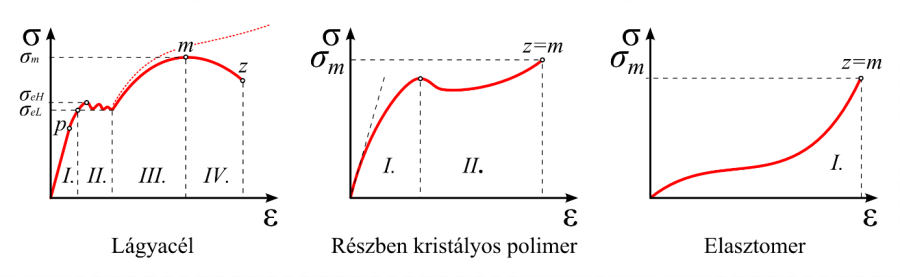
p – lineárisan rugalmas tartomány, I.- Rugalmas tartomány (reverzibilis), II.- Folyási tartomány, III.- Keményedési tartomány, IV. – Kontrakciós tartomány.

2.14. ábra - Néhány gyakran alkalmazott szerkezeti anyag jellemző feszültség-nyúlás karakterisztikája.

Az anyagok mechanikai viselkedése rendkívül változatos és rendszerint összetett (2.14. ábra). De általában kiemelhető olyan eleme, ami az adott analízis szempontjából lényeges. A felhasználástól függően ugyanannak az anyagnak különböző lehet a modellje. Például az acélt a konstruktőr egy lineárisan rugalmas anyagmodellel (2.14. ábra, I./p szakasz), a képlékeny alakítás vizsgálatához a technológus egy képlékeny anyagmodellel (2.14. ábra, I és II. szakaszok) definiálja (2.27. ábra).

2.15. ábra - Az anyagok mechanikai viselkedését leíró főbb anyagmodelleket jellemző feszültség - nyúlás karakterisztikák [22.] .

Tisztán rugalmasnak akkor nevezzük az anyagot, ha a felterhelést követő tehermentesítés során visszanyeri eredeti alakját és sem maradó sem pedig késleltetett alakváltozást nem szenved. Tehát ha a feszültség-alakváltozás diagram terhelési és a tehermentesítési görbéje egybeesik, reverzibilis és útfüggetlen. Feszültség – nyúlás karakterisztikájuk lehet lineáris, vagy nemlineáris.

Lineárisan rugalmas (Linear elastic) anyagmodellről akkor beszélünk, ha a feszültség-alakváltozás karakterisztikája egy egyenesre esik, vagyis a feszültség egyenesen arányos az alakváltozással, ellenkező esetben nemlineáris anyagmodellről beszélünk. A terhelés megszüntetésével az anyag teljes mértékben visszanyeri az eredeti alakját. Izotróp anyagok esetében a Hooke törvény, anizotróp esetben az általánosított Hooke törvény írja le az anyag viselkedését. A legtöbb szobahőmérsékletű fém viselkedésére alkalmazható kis alakváltozások esetén.

A nemlineáris anyagi viselkedés jellemzője, hogy a feszültség és fajlagos nyúlás közötti kapcsolat nem lineáris, tehát nem érvényes rá a Hook törvény. A modellezés során gyakran közelítjük a nemlineáris karakterisztikát két vagy több szakaszból álló lineáris anyagmodellel (bilinear, multilinear material models). Nemlineáris Feszültség-alakváltozás tulajdonsággal rendelkező plasztikus (plastic), multilineáris rugalmas (multilinear elastic), és a nagyrugalmas (hyperelastic) anyagmodellek különböző terhelési szinteken és hőmérsékleten a szerkezet különböző merevségét eredményezik. A kúszás (Creep), viszkoplasztikus (viscoplasticity), és viszkoelasztikus (viscoelasticity) anyagmodellek nemlinearitása lehet idő, sebesség, hőmérséklet, és a feszültségből adódó.

A nemlineáris statikus szerkezeti analízisekben leggyakrabban alkalmazott anyagmodellek az alábbiak:

Nemlineárisan rugalmas (Nonlinear Elasticity Models),
- Multilineáris rugalmas (Multilinear Elasticity Material Model),
- Hiperelasztikus vagy nagyrugalmasságú (Hyperelasticity Material Model),
Viszkoelasztikus (Viscoelasticity),
Plasztikus (Plasticity Material Model),
Viszkoplasztikus (Viscoplasticity),

Hiperelasztikus (Hyperelastic) anyagmodellek viselkedését az alkváltozási-energia potenciál, vagyis a deformált anyagban tárolt energia definiálja. A matematikai megfogalmazás lehetővé teszi a nagy alakváltozások leírását. A hiperelasztikus modelleket gyakran használják olyan anyagok esetében, amelyek nagyrugalmas alakváltozásnak vannak kitéve, mint az elasztomerek és a biológiai anyagok.

Sebesség és időfüggés (Rate effects and time dependency) olyan anyagi viselkedések, amelyek függenek a deformáció sebességétől és az eltelt időtől. Ilyenek például a viszkoelaszticitás, viszkoplaszticitás, kúszás és a csillapítás. A polimerek és magas hőmérsékletű fémötvözetek jelentős kúszást mutatnak. Az anyagmodell alkalmazható a sebesség függő fémmegmunkáló technológia, az alakváltozási sebesség-függő polimerek (tipikusan merevebbé válnak nagyobb sebességeken), és dinamikusan terhelt struktúrák frekvenciafüggő csillapításának vizsgálatára.

Viszkoelasztikus anyagmodell viszkózus és rugalmas komponenseket tartalmaz. A feszültség - nyúlás karakterisztika fel és leterhelési szakasza eltérő pályán mozog és a kezdőpontba tér vissza, vagyis visszanyeri eredeti alakját. A két görbe egy hiszterézis-hurkot ír le, és közöttük lévő terület nagysága az alakváltozás során disszipált energiával egyenlő.

A viszkoplasztikus anyagmodell egy ideálisan képlékeny, és egy ideálisan viszkózus tagból áll, így a szilárdtestek sebesség-függő rugalmatlan viselkedését írja le. A feszültség az alakváltozás sebességével arányos (a newtoni folyadékokhoz hasonlóan ideálisan viszkózus), de az alakváltozás csak egy bizonyos határfeszültség elérése után indul meg [23.] .

Plasztikus vagy elaszto-plasztikus (Plastic, elastic-plastic) anyag deformációja tartalmaz egy rugalmas és egy maradó vagy plasztikus komponenst. A terhelés megszűnésével a tehermentesítés nem a felterhelés görbéjén történik és nem tér vissza a kiindulási állapotba. Ebben az esetben a képlékeny alakváltozás nem az idő vagy a sebesség függvénye, hanem a feszültségi állapoté, a képlékeny alakváltozás egy határfeszültség elérése után indul meg. Képlékeny alakváltozás megfigyelhető a fémek, ötvözetek, a talaj, kőzetek, beton és kerámia anyagok esetében.

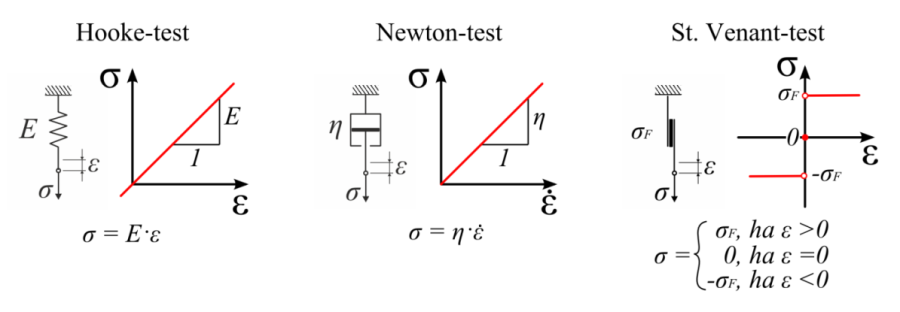
Hooke-test – ideálisan rugalmas (elasztikus), Newton-test – ideálisan viszkózus, St. Venant-test – ideálisan képlékeny (plasztikus).

2.16. ábra - A reológiai anyagmodelleket alkotó alapvető modellek.

A fenti anyagmodelleken kívül, esetleg azok kiterjesztése, vagy speciális eseteként további számos anyagmodell áll rendelkezésre a végeselemes programokban. A valós anyagi viselkedés jobb közelítésének érdekében a végeselemes szoftverekben gyakran van lehetőség ezek kombinációinak alkalmazására, (pl. viszkoelasztikus és hiperelasztikus anyagmodell). Végeselem szoftvertől függően további lehetőségek vannak a speciális anyagi tulajdonságok definiálására:

Tágulás és duzzadás (Expansion and swelling) . Némely anyag strukturális viselkedése megváltozik a fizikai környezet hatására. Ilyen például az anyag hőtágulása (térfogatváltozás a hőmérsékletváltozás hatására), vagy a duzzadás (vízmegkötés hatására), ragasztott anyagok eltérő hőtágulása, és a vizet felszívó talaj viselkedése, stb.

Kölcsönhatás (Interaction). Ennek a modellnek a válasza a struktúrák kölcsönhatásán alapul (pl.: Tömítő és ízületi anyagok, valamint ragasztott és elválasztó felületek közötti kölcsönhatások.

Alakemlékező-fém (Shape memory alloy) . Egy belső fázisátalakulással rendelkező rugalmas anyagmodell. A fázisátalakulás függ a feszültségtől és a hőmérséklettől, melyek hatására a belső átalakulási feszültség jön létre.

Kúszás (Creep), Mullin effektus (Mullins Effect). A polimerek esetében általában és gumiszerű anyagok ideális nagyrugalmas (reverzibilis) viselkedése mellett a gyakorlatban megjelennek viszkoelasztikus tulajdonságok, mint a kúszás (Creep), Mullin effektust (Mullins Effect) jelensége. A viszkoelasztikus anyag definiálásán kívül néha lehetőség van ezeket az anyagtulajdonságokat külön is definiálni.

2.4.3.2. Lineárisan rugalmas anyagmodell (Linear elastic)

Lineáris és izotróp esetben a feszültség és a fajlagos nyúlás közötti kapcsolat egyenes arányosság, és a rugalmassági (Young) modulus E az arányossági tényező, vagyis anyagmodellt a Hook törvény írja le (egytengelyű feszültségi állapot esetén: E=σ/ε). Számos anyagra jellemző a lineáris viselkedés kis alakváltozásoknál, és csak nagyobb alakváltozás után válik nemlineárissá (pl. fémek). Más anyagok egészen kis alakváltozásnál is nemlineáris tulajdonságot mutatnak (pl. polimerek). A lineáris anyagmodell lehet izotróp. ortotróp vagy izotrópanizotróp.

Izotróp esetben az anyagban ébredő feszültség és az alakváltozás közötti összefüggés megadása két paraméter megadásával lehetséges. Leggyakrabban a rugalmassági modulust (Young's modulus, E) és a Poisson-tényezőt (Poisson’s ratio, ν) alkalmazzuk, de alkalmazható a nyírási és a térfogatváltozási modulus is. Térbeli feszültségi állapot esetén az általános Hook törvény tenzoros alakja a feszültségre

(2.1)

és az alakváltozásra felírva

(2.2)

Ahol:

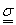– a feszültségtenzor,

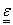– alakváltozási tenzor,

σ _I , ε _I – a megfelelő tenzorok első skalár invariánsa, (a főátló összege),

E – rugalmassági, (Young) modulus,

ν – Poisson-tényező,

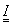– egységmátrix.

A Poisson-tényezővel adjuk meg az anyag keresztirányú alakváltozásának mértékét. A Poisson-tényező a terhelés irányára merőleges (ε_k) és azzal párhuzamos irányú fajlagos nyúlások arányát adja meg, (ν=−ε_k/ε=−ε₂₂/ε₁₁=−ε₃₃/ε₁₁). Elméleti értéke −1 és 0,5 között lehet. A 0 értéknél a terhelés hatására nincs keresztirányú méretváltozás, a negatív előjel pedig azokra az anyagokra jellemző, melyek keresztirányú nyúlása a terhelés irányába esővel azonos értelmű (pl. egyes speciális szerkezetű habok mutatják ezt viselkedést). Összenyomhatatlan anyagok esetében, amikor a deformáció hatására nem történik térfogatváltozás, csak alaktorzulás, a Poisson tényező elméleti értéke 0,5 (ezt a közelíti az elasztomerek viselkedése, a valóságban 0,49 körüli értékkel, és ilyen az emberi szervezetben lévő lágy szövetek Poisson-tényezője is [21.] ).

A nyírási modulus (Shear modulus) a tiszta nyírás (τ=σ₁₂=σ₂₁) és a hatására létrejött alaktorzulás kapcsolatát adja meg (G=τ/γ₁₂=σ₁₂/2ε₁₂). Kifejezhető a rugalmassági modulus és a Poisson-tényező segítségével(E=2G(1+ν)), ezért megadása opcionális, kiváltható vele valamelyik fenti paraméter megadása. Értéke mindig pozitív és megegyezik a második Lamé állandóval (G=µ).

A térfogat-változási modulus (Bulk modulus) a hidrosztatikus nyomás (p=σ₁₁=σ₂₂=σ₃₃=σ_I/3) hatására bekövetkezett térfogatváltozás kapcsolatát adja meg (K=p/ε_I). Ahol ε_I az alakváltozási invariáns. Kifejezhető a rugalmassági modulus és a Poisson-tényező segítségével (E=3K(1-2ν)), ezért megadása opcionális, kiváltható vele valamelyik fenti paraméter megadása. Értéke mindig pozitív.

Ha az anyagmodell izotróp akkor a fenti anyagparaméterekből elég kettőt megadni (pl. rugalmassági modulust és a Poisson tényezőt) a többi ezek lineáris kombinációjaként számítható.

További anyagállandók, az ellenállási modulus (M), és a Lamé állandók (λ, µ) leírását lásd a felhasznált irodalomban [21.] .

Ortotróp anyag esetén a rugalmassági modulus, a Poisson-tényező és a nyírási modulus együttes megadása szükséges a szimuláció dimenziója szerinti tengelyek mentén.

(3D-s szimuláció esetén: E_X, E_Y, E_Z, ν_XY, ν_YZ, ν_XZ, G_XY, G_YZ, G_XZ;

Tengelyszimmetrikus esetben, ha a tengelyek jelölése radiális (R), axiális (Z), és tangenciális irányban (θ), ekkor az anyag paraméterei: E_X = E_R, E_Y = E_Z, E_Z = E_θ. Oszlop-normalizált esetben (column-normalized) ν_XY = ν_RZ, ν_YZ = ν_Zθ = (E_θ/E_Z) ν_θZ, ν_XZ = ν_Rθ. Sor-normalizált esetben (row-normalized) ν_XY = (E_Z/E_R)ν_RZ, ν_YZ=(E_θ/E_Z)ν_θZ, ν_XZ=(E_θ/E_R)ν_Rθ.

2D-s szimuláció, pl. sík alakváltozás esetén: E_X, E_Y, ν_XY, G_XY;

Anizotróp anyag esetén a rugalmassági együttható mátrixot (elastic coefficient matrix, 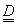) kell definiálni, mely ebben az esetben 36 ill. az ideálisan rugalmas anyagban tárolt energia reverzibilitásának figyelembevételével 21 független paraméter megadását jelenti.

Az anyagok mechanikai tulajdonságai a hőmérséklet függvényében változnak, melyek megadására különböző hőmérsékleti szinteken lehetséges a végeselemes szoftverekben. A hőmérsékletfüggő anyagmodell lineárisnak tekinthető, amennyiben a szimuláció konstans hőmérsékleten zajlik, de nemlineáris probléma megoldásról beszélhetünk ugyanakkor, ha hőtani szimulációt folytatunk ugyanezzel az anyaggal [24.] , [21.] , [25.] , [26.] .

2.4.3.3. Viszkoelasztikus anyagmodellek (Viscoelastic Material Model)

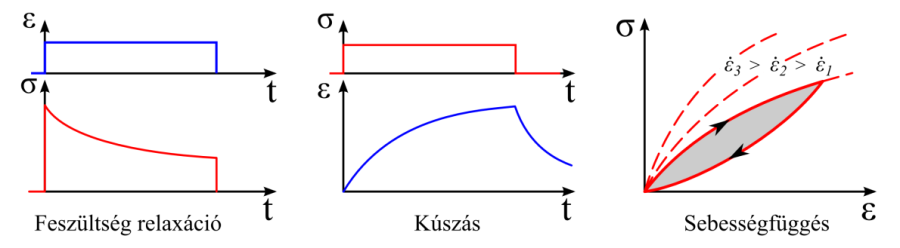
A viszkoelasztikus anyagokat jellemző jelenségek az állandó alakváltozás alatt bekövetkező feszültségrelaxáció, az állandó feszültség alatt bekövetkező kúszás, a feszültség – nyúlás karakterisztika sebességfüggése és a hiszterézis.

2.17. ábra - A viszkoelasztikus anyagokat jellemző jelenségek az állandó alakváltozás alatt bekövetkező feszültségrelaxáció, az állandó feszültség alatt bekövetkező kúszás, a feszültség – nyúlás karakterisztika sebességfüggése és a hiszterézis.

A viszkoelasztikus anyagok jellemzője, hogy a terhelés hatására az anyag válasza függ az eltelt időtől és a terhelés sebességétől. Ugrásszerűen ráadott majd állandó értéken tartott erőterhelésre az anyag időben egyre növekvő deformációval válaszol, vagyis kúszik (Creep). Ha ugrásszerűen ráadott időben állandó deformációt kényszerítünk az anyagra, akkor a reakcióerő értéke időben csökken, vagyis a feszültség relaxál (Stress relaxation). Időben változó terhelés a terhelés sebességével arányos választ produkál. Ezt a viselkedést elasztikus (rugalmas) és viszkózus elemek kombinációjával modellezzük (2.16. ábra, a, b). A modell rugalmas eleme (Hook-test) a deformáció során energiát tárol, viselkedése sebességfüggetlen és a mechanikai terhelés megszűnésével az anyag visszanyeri eredeti alakját. A viszkózus eleme (Newton-test) a deformáció folyamán energiát disszipál, viselkedése sebességfüggő és a terhelés hatására maradó deformációt okoz. Ezek különböző kombinációjaként előálló viszkoelasztikus anyagmodellek deformációját pillanatnyi rugalmas (ε_r), késleltetett rugalmas (ε_k) és maradó (plasztikus) (ε_m) alakváltozásra bonthatjuk.

A viszkoelasztikus viselkedés a polimerek jellemző tulajdonsága, de a gyakorlatban az anyagok nagy része mutat viszkoelasztikus tulajdonságot, mint az üvegszerű anyagok, a talaj, a biológiai szövetek és a textilek.

2.4.3.3.1. A leggyakrabban alkalmazott viszkoelasztikus anyagmodellek

Kis alakváltozások leírására az alábbi rugók és csillapítások segítségével felépített lineáris modelleket használják [27.] , [28.]

2.4.3.3.2. Maxwell modell

Rugó és csillapítás soros kapcsolása az un. Maxwell modell, mely a feszültségrelaxáció modellezésére szolgál (2.18. ábra, a.). Ugrásszerűen ráadott elmozdulás hatására a rugóelem szintén ugrásszerűen azonnal deformálódik, és a benne ébredő kezdeti feszültség σ₀=E·ε₀. A rugó által tárolt energiát a csillapító elem disszipálja így a Maxwell elemben ébredő feszültség idővel csökken vagyis relaxál, értéke 0-hoz konvergál. Ugrásszerűen ráadott feszültség (erő) gerjesztésre a rugóelem azonnali és a csillapító elem időben lineárisan növekvő deformációjával válaszol.

A Maxwell modellt leíró differenciálegyenlet:

(2.3)

2.4.3.3.3. Kelvin-Voigt modell

A Kelvin-Voigt modell párhuzamosan kapcsolt rugó és csillapító elemből áll. A késleltetett rugalmas deformációkomponens vagyis egy véges értékű kúszás modellezésére szolgál (2.18. ábra, b.). Ugrásszerűen ráadott feszültségterhelés hatására a nyúlás időben fokozatosan növekszik és a végtelenben a rugó merevsége által definiált értékhez konvergál, ε_∞=σ₀/E. A terhelés megszüntetésével a deformáció idővel csökken, értéke 0-hoz konvergál (az eredeti alakot veszi fel), miközben a rugó által felhalmozott energiát a csillapítóelem disszipálja. A Kelvin-Voigt modell ugrásszerű deformációval való vizsgálata nem értelmezhető, mivel ekkor végtelen nagy feszültség ébredne.

A Kelvin-Voigt modellt leíró differenciálegyenlet:

(2.4)

2.4.3.3.4. Standard-Solid modell

A Standard-Solid modell egy párhuzamosan kapcsolt rugó és Maxwell elemből áll (2.18. ábra, c.). Ezzel a modellel már modellezhető a viszkoelasztikus anyagok pillanatnyi rugalmas (ε_r), késleltetett rugalmas (ε_k) alakváltozása. Mivel az elasztomerek esetén a maradó deformációkomponens általában elhanyagolható mértékű, ezért előszeretettel alkalmazzák modellezésükre a Standard-Solid modellt.

Ugrásszerűen ráadott feszültségterhelés hatására egy azonnal bekövetkező rugalmas (ε_r), és időben fokozatosan növekvő késleltetett (ε_k) alakváltozással válaszol. A végtelenben a Maxwell testel párhuzamos rugó merevsége által definiált értékhez konvergál, (ε_∞=σ₀/E₁). A terhelés megszüntetésével a deformáció idővel csökken, értéke 0-hoz konvergál (az eredeti alakot veszi fel).

Ugrásszerűen ráadott elmozdulás hatására a rugóelemek szintén ugrásszerűen azonnal deformálódnak, a kezdeti feszültség így σ₀=(E₁+E₂)·ε₀. A Maxwell tag rugója által tárolt energiát a csillapító elem disszipálja tehát a Maxwell elemben ébredő feszültség idővel 0-hoz konvergál, így a teljes modellben a feszültség a párhuzamosan kapcsolt rugó merevsége által meghatározott szinthez közelít (σ_∞=E₁·ε₀).

A Standard-Solid modellt leíró differenciálegyenlet:

(2.5)

2.4.3.3.5. Burgers modell

A Burgers modell egy sorosan kapcsolt Kelvin-Voigt és Maxwell elemből áll (2.18. ábra, d.). Ezzel a viszkoelasztikus anyagok pillanatnyi rugalmas (ε_r), késleltetett rugalmas (ε_k) és maradó (plasztikus) (ε_m) alakváltozás egyidejű jelenléte is modellezhető (termoplasztikus polimerekre jellemző viselkedés).

Ugrásszerűen ráadott feszültségterhelés hatására egy azonnal bekövetkező rugalmas (ε_r), és időben fokozatosan növekvő késleltetett (ε_k) és maradó (ε_m) alakváltozással válaszol, ami az idő múlásával a végtelenbe tartó deformációt jelent. A terhelés megszüntetésével a deformáció idővel csökken, de a maradó alakváltozás miatt értéke nem éri el a 0-át.

Ugrásszerűen ráadott elmozdulás hatására a sorosan kapcsolt Maxwell elem, (pontosabban annak csillapítás eleme) miatt a feszültség 0-hoz konvergál.

A Burgers modellt leíró differenciálegyenlet:

(2.6)

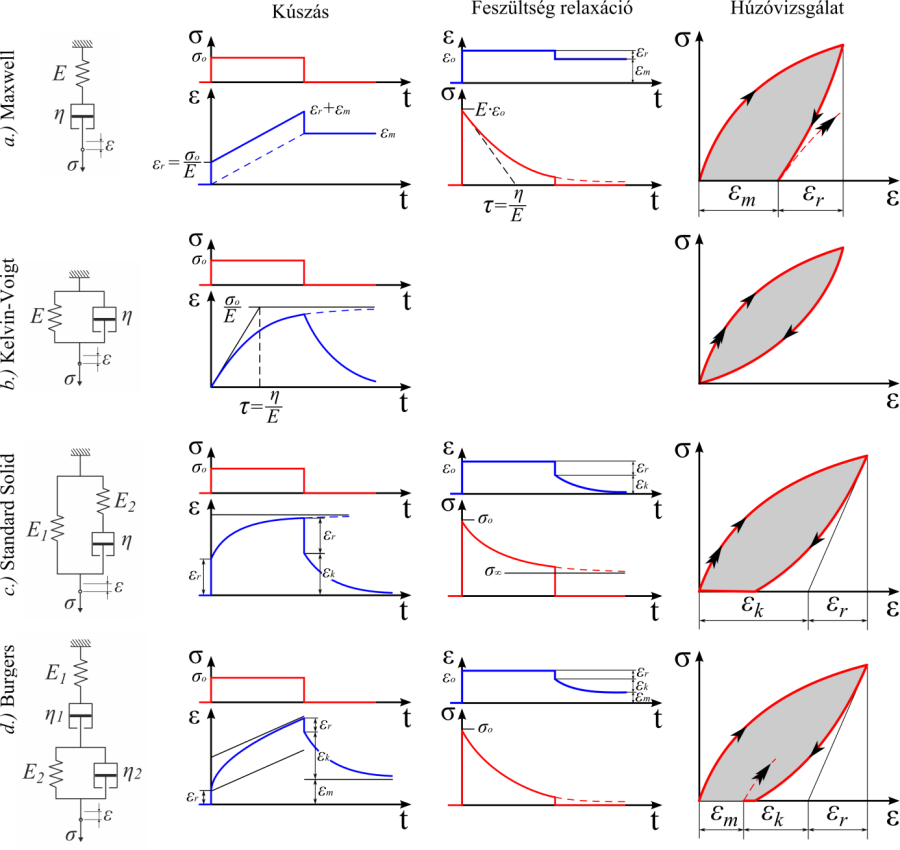
2.18. ábra - Viszkoelasztikus anyagmodellek és válaszfüggvényeik.

2.4.3.3.6. Általánosított modellek

A fenti modellek alkalmasak a viszkoelasztikus anyagok viselkedésének minőségi leírására, de mennyiségi szempontból nem megfelelőek, mivel csak durván közelítik az anyag időbeli viselkedését. A kúszás és a feszültségrelaxáció időbeli lefutásának pontos időbeli leírására az általánosított modellek szolgálnak (2.19. ábra). A kúszás leírására az Általánosított Kelvin-Voigt modellt (sorba kötött Kelvin-Voigt elemek), a feszültségrelaxáció leírására pedig az Általánosított Maxwell modellt (Párhuzamosan kapcsolt Maxwell elemek) használják. A továbbiakban ez utóbbi lesz érdekes számunkra mivel a végeselem programok többnyire ezt alkalmazzák a viszkoelasztikus anyagtulajdonságok modellezésére. Az összetett modelleke (azok időbeli viselkedését) nem csak egy időállandó (τ = E/η) jellemzi, hanem a modellt alkotó elemek számának megfelelő számú.

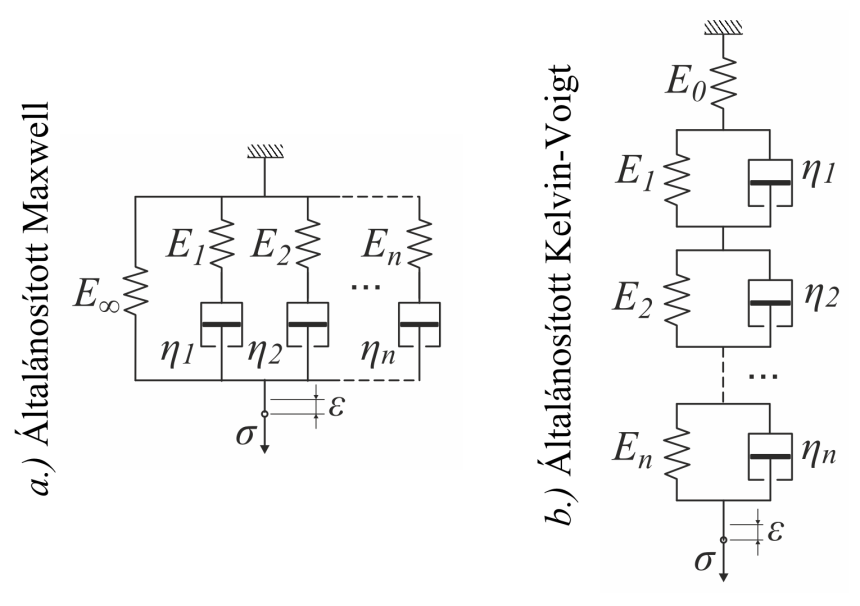
2.19. ábra - Általánosított modellek.

2.4.3.3.7. A viszkoelasztikus modellek VEM-es alkalmazása

Kis deformációk esetén az általánosított Maxwell modellel írhatjuk le az anyag viselkedését.
Nagy alakváltozás esetére az általánosított Maxwell modell, egy hiperelasztikus modellel kiegészített (a rugók helyett) változatát használjuk.

A feszültségállapot leírására az alábbi egyenletet használjuk

(2.7)

Ahol:

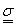= Cauchy feszültség (Cauchy stress),

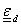= Az alakváltozás deviátoros (vagy alaktorzító) része (deviatoric part of the strain),

ε _v = Az alakváltozás hidrosztatikus (vagy gömbi) része (volumetric part of the strain),

G(t) = A nyíró modulus relaxációs függvénye (shear relaxation function),

K(t) = A térfogat-változási modulus relaxációs függvénye (bulk relaxation function),

t = jelen időpillanat (current time),

τ = az elmult idő (past time),

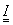= egységtenzor (unit tensor),

A relaxációs függvények az általánosított Maxwell modellel történő leírásához a modulusok Prony sorát használjuk. A nyíró és térfogat-változási moduluszok egymástól függetlenül megadhatók.

		(2.8)
		(2.9)

Ahol:

G _∞ – A teljesen relaxált anyag nyírómodulusa (t = ∞)

K _∞ – A teljesen relaxált anyag térfogat-változási modulusa (t = ∞)

		(2.10)
		(2.11)

Ahol:

G ₀ = E / 2(1+ν) – A kezdeti nyírómodulus (t = 0)

K ₀ = E / 3(1-2ν) – A kezdeti térfogat-változási modulus (t = 0)

Alkalmazva a g_i = G_i/G₀ és a k_i = K_i/K₀ relatív modulusokat, az alábbi formában írhatjuk fel

		(2.12)
		(2.13)

Így az anyagmodell merevsége csak egy paraméter a kezdeti modulus megadásával megváltoztatható, skálázható. Ezzel az anyagmodell definiálásához az időbeli viselkedést leíró k_i vagy g_i és a hozzájuk tartozó relaxációs idő τ_i mellett meg kell adnunk a merevségi tulajdonságokat leíró paramétereket is. (pl. lineárisan rugalmas anyag esetén a nyíró (G) és térfogat-változási (K) modulust vagy a rugalmassági modulust (E) és a Poisson-tényezőt (ν), ill. nagy deformációk esetén alkalmazott hiperelasztikus anyagmodell esetén pedig a megfelelő (C_ij, d, stb.) konstansokat).

Mivel a k és g konstansok relatív értékek összegük nem haladhatja meg az 1,0-et. A k_∞ és g_∞konstansok határozzák meg az anyag merevségét végtelen idő elteltével. Értéküket nem kell közvetlenül megadni ugyanis a k_∞ + Σk_i =1 és g_∞ + Σg_i =1 összefüggések szerint számolódik. Ezek szerint, ha Σk_i ill. Σg_i egyenlő 1,0-el, akkor az anyag merevsége „végtelen” idő elteltével 0-ra csökken [29.] , [6.] , [11.] .

2.4.3.3.8. A viszkoelasztikus anyagok hőmérsékletfüggése

A viszkoelasztikus anyagok lényeges tulajdonsága a hőmérsékletfüggés. Jellemzően a hőmérséklet emelkedésével csökken az anyag merevsége, vagyis a relaxáció gyorsabbá válik. A különböző hőmérsékleten felvett merevségi görbék között az eltolási (Shift) függvények teremtenek kapcsolatot. Ez lehetővé teszi, hogy csak egy hőmérsékletfüggő Proni sorral megadott relaxációs görbével definiáljuk az anyag idő és hőmérsékletfüggő viselkedését.

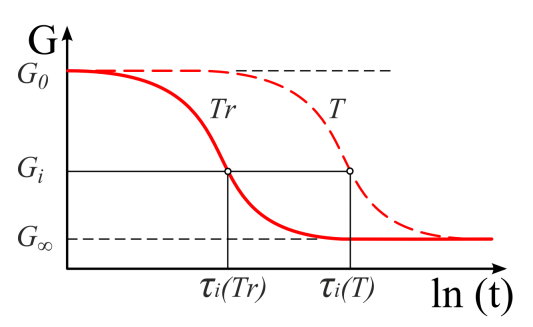
2.20. ábra - Az eltolási függvények értelmezése.

Az eltolási függvény a merevségi görbét az időtengellyel párhuzamosan tolja el. A leggyakrabban alkalmazott eltolási függvény a William-Landel-Ferry (WLF)

(2.14)

és a Tool-Narayanaswamy (TN)

(2.15)

Ahol:

T _r – a referencia hőmérséklet,

τ – a látszólagos idő (pseudo time),

c ₁ , c ₂ , d ₁ – anyagállandók.

2.4.3.4. Sebességfüggetlen plasztikus anyagmodellek (rate-independent plasticity)

Az elasztoplasztikus modellek az anyag irreverzibilis viselkedését modellezi egy bizonyos feszültségérték elérése után. A képlékeny alakváltozás jellemzője, hogy azonnal végbemegy, vagyis a modell viselkedése az időtől független, irreverzibilis (maradó alakváltozás) és útfüggő (függ a terhelési előélettől). A sebességfüggetlen képlékeny anyagmodellek elméletnek két lényeges eleme van, a folyási feltétel (yield criterion) és a felkeményedési szabály (hardening rule).

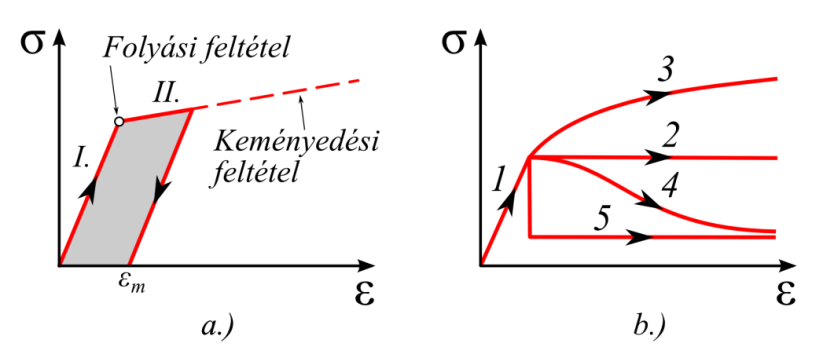
(a.) Lineáris elasztoplasztikus modell főbb részei I.) Lineárisan rugalmas szakasz, II.) folyási szakasz. (b.) Az elasztoplasztikus modellek főbb típusai: 2.) ideálisan képlékeny, 3.) nemlineárisan felkeményedő, 4.) nemlineárisan lágyuló, 5.) ridegen lágyuló.

2.21. ábra - (a.) Lineáris elasztoplasztikus modell főbb részei I.) Lineárisan rugalmas szakasz, II.) folyási szakasz. (b.) Az elasztoplasztikus modellek főbb típusai: 2.) ideálisan képlékeny, 3.) nemlineárisan felkeményedő, 4.) nemlineárisan lágyuló, 5.) ridegen lágyuló.

2.4.3.4.1. A folyási feltétel

A folyási feltétel azt a feszültségszintet (σ_y) jelenti, melynél az anyag elkezdi a plasztikus alakváltozást, ez alatt viselkedése rugalmas. Értéke többtengelyű feszültségi állapot esetén a feszültségi vektor függvénye, melyet a folyási felületdiagram segítségével ábrázolunk. A folyási felületen belüli feszültségi állapot rugalmas alakváltozáshoz tartozik, a felületen következik be a plasztikus deformáció.

Homogén és izotróp anyag esetén, amennyiben a hidrosztatikus hatás elhanyagolható (a legtöbb fém ilyen) a folyási felület a hidrosztatikus egyenessel meghatározott vezérgörbéjű mindkét végén nyitott felület. Ha a hidrosztatikus hatás nem hagyható el (Kőzetek, talaj, beton, stb.) a folyási felület legalább egyik végén zárt.

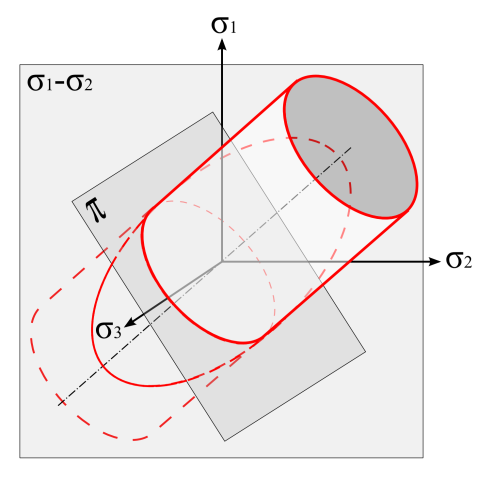
A henger alakú (HMH) folyási felület metszete a fősíkokkal (σ₁-σ₂) ellipszis, a deviátoros síkkal (π) kör alakú.

2.22. ábra - A folyási felület értelmezése.

A Huber-Mises-Hencky modellben a felület egy mindkét végén nyitott henger, melynek metszetei a deviátoros síkon kört, az egyes főfeszültségi síkokon ellipsziseket alkotnak. A fémek, kompozitok és lágy polimerek esetében leggyakrabban használt modell.
A Tresca féle modellt melyben a folyási felület egy hatszög alapú palástfelület, lágyabb fémek (pl. alumínium, rézötvözetek) még ma is alkalmazzák.
A Rankine modell geometriai megjelenése a főfeszültségi térben a hidrosztatikai hatás figyelembevételére is alkalmas, egyik csúcsa felől zárt téglatest felület. Az eredetileg talajok képlékenységi felületeként megadott modell ma inkább rideg anyagok törési feltételeként alkalmazzák.
A Mohr-Coulomb szintén figyelembe veszi a hidrosztatikus hatásokat. A felület egyik végén zárt hatoldalú gúla. A talajmechanika leírásokra előszeretettel alkalmazott.
A Prager-Drucker -modell a Huber-Mises-Hencky modell hidrosztatikai hatást is figyelembe vevő általánosításának tekinthető. A folyási felület alakja a főfeszültségi térben a húzás irányában zárt kúp.

Általános anizotróp modellt a mérési nehézségek miatt nem hoztak létre, hanem több olyan modell is van, amely valamely izotróp modell ortotróppá általánosításával kaptak, (pl.: Mises-Hill és a Kubik - Mielniczuk modell (HMH-feltétel kiterjesztése), Sawczuk - Iwlin (Tresca-feltétel általánosítása).

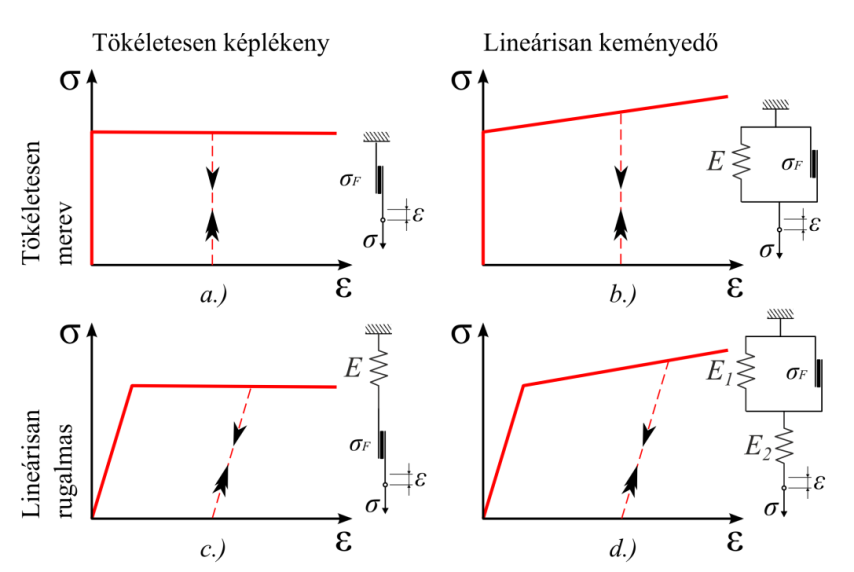
2.23. ábra - Lineáris tagokból álló egyszerű elasztoplasztikus modellek.

2.4.3.4.2. Keményedési szabály (hardening rule).

Abban az esetben, amikor a képlékenységi szakaszba lépő anyag alakváltozása a feszültség további növelése nélkül folytatódik, tökéletesen képlékeny alakváltozásnak nevezzük. Ez a modell egy erősen leegyszerűsített modellje a képlékeny anyagok valós viselkedésének. Ha a képlékeny alakváltozás szakaszában csak a feszültség további növelésével folytatódik az alakváltozás, felkeményedő anyagokról beszélünk. Tökéletesen képlékeny anyag esetén a folyási felület a feszültségi térben fix, míg felkeményedő anyagnál elmozdulhat, és/vagy az alakját változtathatja. Ezek alapján a keményedést leíró modell lehet:

izotróp (a folyási felület alakja nem, csak mérete változik minden irányban arányosan),
kinematikus (a folyási felület mérete nem, csak a helyzete változik), vagy
vegyes (a valóságot jobban modellező kombinációk, pl. izotróp-kinematikus, lokálisan változó alakú, stb.).

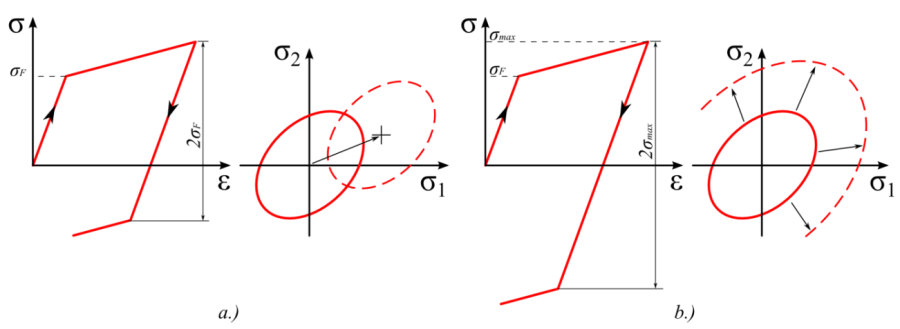
A kinematikus (a.) és izotróp (b.) keményedésű elasztoplasztikus anyagok feszültség-nyúlás jelleggörbéje és a folyási felület megváltozásának módja.

2.24. ábra - A kinematikus (a.) és izotróp (b.) keményedésű elasztoplasztikus anyagok feszültség-nyúlás jelleggörbéje és a folyási felület megváltozásának módja.

2.4.3.5. Viszkoplasztikus anyagmodellek

A viszkoplasztikus anyagmodellek a képlékeny anyagok sebességfüggő rugalmatlan viselkedését írják le. Ami azt jelenti, hogy az anyagban ébredő feszültség az alakváltozási sebesség függvénye. Az anyagmodell egy ideálisan képlékeny (St. Venant-test), és egy ideálisan viszkózus tagból (Newton-test) áll. A viszkózus elemnek köszönhetően a feszültség az alakváltozás sebességével arányos, de az alakváltozás csak egy bizonyos határfeszültség elérése után indul meg (σ_F) a plasztikus elem jóvoltából. A fő különbség a sebességfüggetlen plasztikus vagy elasztoplasztikus és a viszkoplasztikus anyagok között, hogy ez utóbbi alakváltozása nem csak maradó alakváltozást mutat, hanem a deformáció az idő elteltével folytatódik a terhelés alkalmazása után is, vagyis kúszik. Főként a rugalmatlan fémek (mint pl. a forrasztóón, ólom), kerámia szuszpenziók, Zagyok, paszták leírására alkalmazzák. [30.] , [23.] .

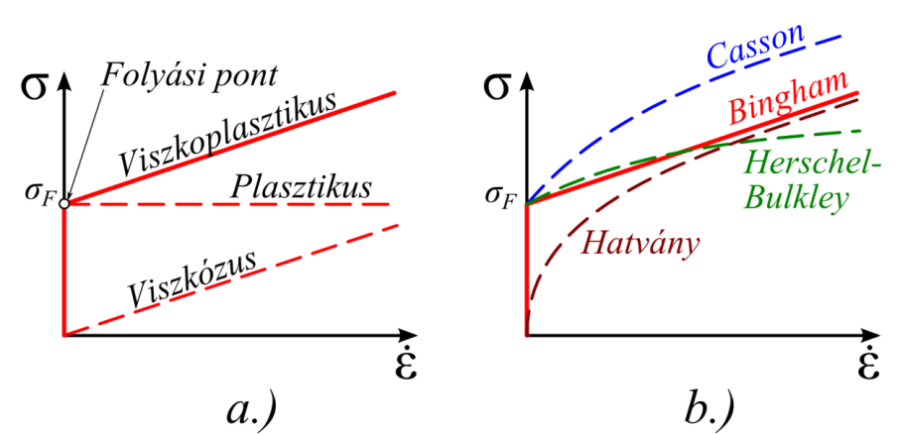
A viszkoplasztikus, az ideálisan viszkózus (Newtoni) és az ideálisan képlékeny (St. Venant) modellek Feszültség - alakváltozási sebesség karakterisztikája (a.). A legismertebb viszkoplasztikus anyagmodellek (b.).

2.25. ábra - A viszkoplasztikus, az ideálisan viszkózus (Newtoni) és az ideálisan képlékeny (St. Venant) modellek Feszültség - alakváltozási sebesség karakterisztikája (a.). A legismertebb viszkoplasztikus anyagmodellek (b.).

2.4.3.5.1. Bingham modell

A viszkoplasztikus anyagok jellemzésére szolgáló egyik legismertebb anyagmodell.

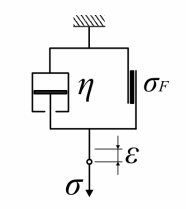
2.26. ábra - Bingham modell - párhuzamosan kapcsolt viszkózus és súrlódó elem.

A Bingham modellt leíró differenciálegyenlet:

(2.16)

Ahol:

η – viszkozitás,

σ _F – a folyási feszültség,

ֹ ε – az alakváltozási sebesség.

2.4.3.5.2. Herschel-Bulkley modell

		(2.17)
		(2.18)

Ahol:

K – a látszólagos viszkozitás,

n – a folyási szám. n=1 estén a Bingham modellt kapjuk, n<1 esetén a feszültség degresszív növekedését, (szerkezeti viszkózus; nyírásra vékonyodó - shear thinning) és n>1 esetén a feszültség progresszív növekedését (dilatáns; nyírásra vastagodó - shear thickening) eredményezi.

A nyíró-határfeszültség elhanyagolásával az Ostwald-de Waele hatványtörvényhez jutunk.

2.4.3.5.3. Hatványtörvény, (Ostwald-de Waele egyenlet)

(2.19)

Ahol:

m és Φ – anyagi függvények, Φ(T) a „fluiditás” hőmérsékletfüggő.

A fluiditás helyett gyakran alkalmazzák a K konzisztencia faktort, K = Φ ^-1/m .

2.4.3.5.4. Casson

(2.20)

[31.] .

2.4.3.5.5. Módosított Bingham,

A lineáris Bingham modell egy másodrendű taggal kiegészített változata.

(2.21)

Ahol:

c – a nemlineáris viselkedést befolyásoló állandó, c/η=0 estén a lineáris Bingham modellt kapjuk, c/η<0 esetén a feszültség degresszív növekedését (szerkezeti viszkózus; nyírásra vékonyodó – shear thinning) és c/η>0 esetén a feszültség progresszív növekedését, (dilatáns; nyírásra vastagodó – shear thickening) eredményezi.

2.4.3.5.6. Perzyna

(2.22)

2.4.3.5.7. Peirce

(2.23)

2.4.3.5.8. EVH (Exponential visco-hardening)

Az exponenciálisan viszkoelasztikus keményedő (EVH) modell lehetőséget ad nemlineáris kinematikai keményedésre a von Mises vagy Hill plaszticitás alkalmazásával.

		(2.24)
		(2.25)

Ahol:

Ko, Ro, R _∞ , b – alakváltozás-keményedési (strain hardening) paraméter,

m – alakváltozási sebesség-keményedési (strain rate hardening) anyagparaméter,

K – viszkozitási (viscosity) paraméter.

2.4.3.5.9. Anand

Az Anand plasztikus modell egy teljes értékű anyagmodell, amely nem igényli más anyagmodellekkel való kombinálását. Fémek képlékenyalakításának modellezésére hozták létre. A magas hőmérsékleten fémek fizikai viselkedése nagyban függ az alakítás sebességétől, a hőmérséklettől, az alakváltozás sebességi és hőmérsékleti előélettől, és az alakváltozási keményedéstől vagy lágyulástól. Mindezen tulajdonságokat figyelembe veszi az Anand viszkoplasztikus anyagmodell.

(2.26)

Ahol:

ֹ << eqn0033.wmf >> - az alakváltozási sebesség tenzor,

ε ֹ ˆ - a halmozott egyenértékű fajlagos nyúlás sebessége

S – a Cauchy feszültségtenzor deviátoros része,

q – egyenértékű feszültség.

[6.] , [32.] , [31.] , [23.] .

2.4.3.6. Összetett reológia anyagmodellek

A fenti kétkomponensű modellek mellett, az anyagok valós fizikai viselkedésének leírására számos összetett, mindhárom reológiai alaptestet (rugalmas, viszkózus, súrlódó) tartalmazó modellt alkottak. Dinamikai vizsgálatok leírásához ezek kiegészülnek a „tömeg-elemmel”, amely az anyag tehetetlenségét hivatott modellezni. A végeselemes anyagmodellben ez az anyag sűrűségének (fajsúly) megadásával kerül definiálásra. A teljesség igénye nélkül néhány összetett reológiai modell:

Kiterjesztett Bingham,
3 elemű modell,
BingMax modell,
Bouc-Wen modell.

[33.]

2.4.3.7. Hiperelasztikus anyagmodellek

A hiperelasztikus anyagmodell (Hyperelastic Material Model) viselkedését az alkváltozási-energia sűrűség, vagyis az egységnyi térfogatú deformált anyagban tárolt potenciális energia alapján írja le. A matematikai megfogalmazás lehetővé teszi a nagy alakváltozásokat. A hiperelasztikus, vagy Green féle anyagmodelleket gyakran használják olyan anyagok esetében, amelyek nagyrugalmas alakváltozásnak vannak kitéve, mint a gumiszerű anyagok és egyes biológiai szövetek.

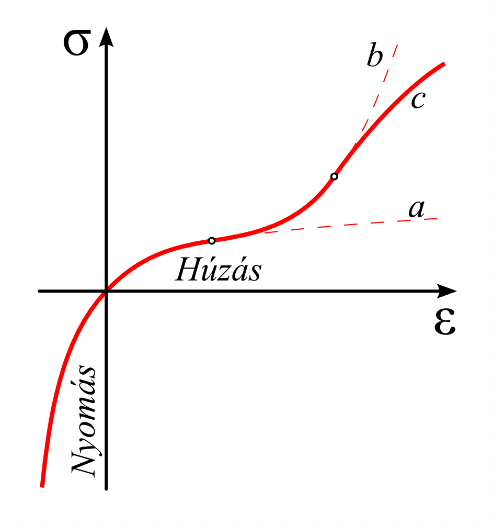
Hiperelasztikus anyagok jellemző feszültség-nyúlás karakterisztikája. 0 (a.), 1 (b.) ill. 2 inflexiós ponttal rendelkező húzókarakterisztika (c.).

2.27. ábra - Hiperelasztikus anyagok jellemző feszültség-nyúlás karakterisztikája. 0 (a.), 1 (b.) ill. 2 inflexiós ponttal rendelkező húzókarakterisztika (c.).

A gumiszerű anyagokra jellemző

a nagymértékű alakváltozási képesség, amely általában több 100% de akár 1000% fölé is emelkedhet,
a döntően rugalmas deformáció (recoverable),
erősen nemlineáris feszültség-nyúlás karakterisztika, (általában húzás esetén először lágyul, majd felkeményedik, nyomás esetén felkeményedés tapasztalható),
a deformáció során bekövetkező kis- vagy elhanyagolható mértékű térfogatváltozás (összenyomhatatlan, ν ~ 0,5.)

Az alkalmazott hiperelasztikus anyagokra nemlineárisan rugalmas, izotróp, izotermikus és teljesen, vagy közel összenyomhatatlan (térfogat-állandóságot, ν ~ 0,5) tulajdonságokat feltételezünk.

Mivel a hiperelasztikus anyagmodellek az alakváltozási energia alapján vannak felírva, ezért kielégítik a termodinamika főtételeit, reverzibilisek és útfüggetlenek. Viszont a hőmérséklet és az idő hatását nem veszik figyelembe.

(2.27)

Ahol:

Π - az anyag egységnyi térfogatára vonatkozó alakváltozási energia, alakváltozási energiasűrűség, (strain energy per unit reference volume),

σ _ij - a Cauchy (valódi) feszültség,

ε _ij – a rugalmas alakváltozás.

A megnyúlás definíciója, az i. irányba eső főnyúlás (stretch ratio / stretch):

(2.28)

Ahol:

l ₀ – a kezdeti hossz,

l – a pillanatnyi hossz,

Δl – a hosszváltozás.

A főnyúlásokkal felírt deformációgradiens tenzor, (elastic deformation gradient tensor):

(2.29)

A jobboldali Cauchy-Green alakváltozási tenzor főnyúlások segítségével felírva:

(2.30)

A Cauchy-Green féle alakváltozási tenzor invariánsai:

		(2.31)
		(2.32)
		(2.33)

A térfogatváltozás definíciója, (a deformációgradiens tenzor determinánsa):

(2.34)

Látható, hogy ha az anyag teljesen összenyomhatatlan, akkor I₃ = 1.

A térfogat-változási komponenst különválasztva a deviátoros nyúlás:

(i= 1, 2, 3)

(2.35)

A deviátoros alakváltozási invariáns:

(2.36)

A fenti mintára az alakváltozási energiafüggvényt deviátoros (Π_d) és a térfogat-változási (Π_V) komponensekre bonthatjuk, és ez utóbbit felírhatjuk a deformációgradiens tenzor determinánsával (J=det( 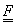)) segítségével.

(2.37)

Izotróp anyag esetén az alakváltozási energiát az alakváltozási skalár invariánsok, vagy közvetlenül a főnyúlások segítségével írjuk fel, (melyek függetlenek a koordinátarendszer megválasztásától).

Összenyomhatatlan anyag esetében az alakváltozási munka csak deviátoros vagyis alaktorzító komponensből áll, és a három alakváltozási invariánsból csak kettő független (I₃=1). Ebben az esetben a jobboldali Cauchy-Green alakváltozási tenzorral a modell az alábbi alakban írható fel [21.] , [6.] .

(2.38)

Ahol:

p - a hidrosztatikus nyomás,

δ _ij - a Kronecker delta,

[21.] , [34.] , [6.] , [35.] .

A hiperelasztikus anyagmodellek néhány széles körben használatos energiafüggvényét az alábbiakban ismertetjük. Az adott modell tárgyalásánál csak fent definiáltaktól és az alábbiakban felsorolt jelölésektől eltérőt ismertetjük.

Megjegyzés: Mivel a modellek a hőmérséklet hatását nem veszik figyelembe, hőtágulással járó vizsgálat esetén a modellekben szereplő teljes deformációgradiens tenzor determinánsa (J) helyettesítésre kerül, annak hőtágulástól megtisztított rugalmas részével (J_el=J/J_th). Ahol a J_th=(1+αΔT)³;

α – a lineáris hőtágulási együttható, J_th – a referencia hőmérséklethez viszonyított hőmérsékletkülönbség.

Alkalmazott jelölések:

μ – Az anyag kezdeti nyírómodulusa (initial shear modulus),

d – az anyag összenyomhatatlanságra jellemző paraméter, 0 ha összenyomhatatlan, mivel d=2/K, ahol K – a kezdeti térfogat-változási modulus (initial bulk modulus).

2.4.3.7.1. Arruda-Boyce

Az Arruda-Boyce (vagy eight-chain) egy statisztikus mechanikára épülő modell. Főleg polimereknél használt, nyúlási korláttal (λ_L) definiált hiperelasztikus anyagmodell, amely általában 300%-os nyúlásig alkalmazható.

A Yeoh modell N=5 fokú eseteként értelmezhető a nyúlási korlát függvényekén definiált együtthatókkal. Végtelen nyúlási korlát (λ_L = ∞) esetén a Neo-Hooke modellel egyenértékű lesz.

(2.39)

Ahol:

λ _L – nyúlási korlát, (melynél a feszültség felkeményedési szakaszba, vagyis határtalan növekedésbe kezd),

2.4.3.7.2. Neo-Hooke

Ez a legegyszerűbb hiperelasztikus modell mely konstans nyírómodulust használ. Viszont alkalmazhatósága 30-40%-os egytengelyű húzásig vagy 80-90%-os tiszta nyírásig terjed.

A Neo-Hooke modell egy mikromechanikai modell, ami az elasztomerek anyagszerkezeti vizsgálatán alapszik és a klasszikus Hooke anyagmodell kiterjesztését jelenti nagy deformációkra. A μ = 2·C₁₀; C₁₀ = 0 és N=1 esetén a polinomiális modell speciális eseteként áll elő. Eszerint az energiafüggvény:

(2.40)

2.4.3.7.3. Saint Venant–Kirchhoff model

A legegyszerűbb hiperelasztikus modell, amely a lineárisan rugalmas anyagmodell kiterjesztése a nagyrugalmasságú tartományba. Főleg kis alakváltozások és nagy elfordulások esetén alkalmazzuk (pl. horgászbot).

(2.41)

Ahol:

µ és λ – a Lamé állandók.

E – Lagrange Green nyúlás

2.4.3.7.4. Mooney-Rivlin

A Mooney-Rivlin modell nagy deformációkra jó eredményt ad. A leggyakrabban 2, 3, 5, esetleg 9 paraméteres változatát használják, A kétparaméteres változat energiafüggvénye:

(2.42)

Ahol:

C ₁₀ és C ₀₁ – anyagra jellemző konstansok, (A kezdeti nyírási modulus értéke: μ =2(C ₁₀ +C ₀₁ ).

Az anyag feszültség-nyúlás görbéjén lévő inflexiós pontok száma alapján választhatunk a megfelelő paraméterszámú anyagmodellt. A 2 paraméteres MR modell 90-100%-os nyúlásig alkalmazható. A modellnek nincs inflexiós pontja, így nem jelentkezik a felkeményedési szakasz, ezért az összenyomás modellezésére nem alkalmas (2.27. ábra, a.). Nagyobb alakváltozás modellezésére (100-200%) magasabbrendű modellek, mint az 5, ill. 9 paraméteres MR lehet alkalmas (2.27. ábra, b ill. c.).

2.4.3.7.5. Ogden

Az Ogden egy fenomenológiai megközelítésű anyagmodell, melyben közvetlenül a főnyúlások segítségével van felírva az energiafüggvény. Ebből kifolyólag pontosabb és jobban leírja a nagyobb alakváltozásokat, akár 700%-ig is.

(2.43)

Ahol:

α _i és μ _i – anyagjellemző konstansok, a kezdeti nyírómodulus μ ₀ = (Σ α _i μ _i )/2

N elvileg korlátlan, a gyakorlatban 3-nál nagyobb értéket nem szoktak használni.

2.4.3.7.6. Polinomiális

A polinomiális modellben az 1. és 2. alakváltozási invariáns segítségével van felírva az energiafüggvény. Általában ritkán használnak 3-nál magasabb fokú (N) polinomot.

(2.44)

Ahol: μ = 2(C ₁₀ +C ₀₁ ) – Az anyag kezdeti nyírómodulusa (initial shear modulus).

2.4.3.7.7. Yeoh

A Yeoh modell a polinomiális modell, csak az 1. alakváltozási invariánsra épülő, redukált változata. Közel összenyomhatatlan nemlineárisan rugalmas anyagok modellezésére alkalmazzák, pl. gumi. Általában az N=3 értékkel használatos, amivel jól modellezhetők a nagy alakváltozások.

(2.45)

Ahol:

μ = 2·C ₁₀ – Az anyag kezdeti nyírómodulusa (initial shear modulus).

Gent

Mikromechanikai alapokon nyugvó (Hibrid) modell, mely az Arruda-Boyce modellhez hasonlóan a nyúlások határértékét (J_m) alkalmazza.

(2.46)

Ahol:

J _m – a (I ₁ – 3) határértéke. J _m = ∞ esetén a Neo-Hooke modellel egyenértékű lesz.

2.4.3.7.8. Marlow modell

(2.47)

2.4.3.7.9. Van der Waals

(2.48)

Ahol:

		(2.49)
		(2.50)

λ _m – záróparaméter, (nyúlási korlát),

α - globális kölcsönhatási paraméter,

β – invariáns keverési paraméter.

2.4.3.7.10. Összenyomható hiperelasztikus modellek habok modellezésére

Ezen anyagok fő tulajdonsága az előzőekkel ellentétben, hogy nagymértékben összenyomható anyagot modelleznek, ezért az energiafüggvény deviátoros és volumetrikus része között szoros összefüggés van.

Odgen habmodell (Hiperfoam)

(2.51)

Ahol:

μ ₀ = (Σ α _i μ _i )/2 - az anyag kezdeti nyírási modulusa,

K =Σ α _i μ _i ((1/3)+ β _i ) - a kezdeti térfogat-változási modulus.

2.4.3.7.11. Blatz-Ko habmodell

Az összenyomható Poliuretán gumi hab modellezésére lett létrehozva.

(2.52)

K =µ 5/3 - a kezdeti térfogat-változási modulus.

2.4.3.7.12. Varga-modell

(2.53)

2.4.3.7.13. További hiperelasztikus modellek biológiai szövetek modellezésére

Fung energiafüggvénye

Holzapfel modellje

2.3. táblázat - Hiperelasztikus anyagmodellek csoportosítása összefoglalása [36.] , [21.] , [37.] , (nincs adat: „-”).

	Anyagmodell	Alapja	Alkalmazás, max. ε
Összenyomhatatlan vagy közel összenyomhatatlan, (ν ~ 0,5)	Arruda-Boyce	I ₁	300 %
	Neo-Hooke	I ₁	30-40 %
	Gent	I ₁	-
	Van der Waals	I ₁ , I ₂	-
	Mooney-Rivlin	I ₁ , I ₂	MR2 = 90-100 % MR5/9 = 100-200 %
	Ogden	λ ₁ , λ ₂ , λ ₃	700 %
	Polinomiális	I ₁ , I ₂	300 %
	Yeoh	I ₁	-
	Saint Venant–Kirchhoff	µ, λ (Lamé)	kis alakváltozások és nagy elmozdulás
	Marlow	I ₁ , I ₂	-
	Fung	Q(E _ij )	érfalak vizsgálatára
	Holzapfel		emberi artéria vizsg.
Összenyomható (0 < ν < 0,5)	Ogden habmodell	λ ₁ , λ ₂ , λ ₃	Összenyomható habok vizsgálatára
Összenyomható (0 < ν < 0,5)	Blatz-Ko habmodell	I ₂ , I ₃	Összenyomható habok vizsgálatára

[38.] , [21.] , [6.] , [35.] .

2.4.3.8. Anyagparaméterek megadása

Mivel az anyagmodell a matematikai kapcsolatot testesíti meg a terhelés és a válasz között, szükséges a bemenő anyagparaméterek megadása, azért hogy a modell illeszkedjen az anyag valós viselkedéséhez. Egyes esetekben a paraméterek függhetnek a fizikai környezet tulajdonságaitól, úgy mint a hőmérséklet, frekvencia vagy az idő, illetve különböző mennyiségek kölcsönhatásától, mint pl. a normál nyomás, relatív távolság, vagy relatív sebesség.

2.4.3.8.1. Mechanikai anyagvizsgálati adatok

Az anyagmodellek meghatározása történhet az anyag mikroszintű vizsgálatával (mikromechanikai modell), vagy makromechanikai vizsgálatok útján (fenomenológiai modell). A jegyzetben ez utóbbiról adunk rövid áttekintést.

Példaként nézzük a mechanikai anyagmodellek létrehozásához az egyik leggyakrabban alkalmazott anyagvizsgálati eljárását, a szakítóvizsgálatot. A vizsgálat során a próbatestre állandó sebességű egytengelyű megnyúlást kényszerítünk és mérjük a fellépő reakcióerőt. Ezeket a kiinduló paraméterekkel (keresztmetszet, hossz) fajlagos mennyiségekké konvertáljuk, így kapjuk meg a szóban forgó anyag (mérnöki) feszültség-nyúlás karakterisztikáját, melyet bemenő adatként használhatunk egy anyagmodell definiálásához. Hasonló elvek szerint végezhetünk nyomó, nyíró vagy többtengelyű vizsgálatokat. Az alábbiakban nézzük meg a leggyakrabban használt anyagvizsgálati eljárásokat.

2.4.3.8.1.1. A mechanikai anyagvizsgálatok főbb típusai

A lineáris vagy lineáris szakaszokkal közelíthető (pl. ideálisan rugalmas – tökéletesen képlékeny) anyag esetén elég megadni az anyagvizsgálatból származtatott anyagjellemzőket (pl. a rugalmassági modulus és a Poisson-tényező) vagy a karakterisztika jellemző pontjait (pl. folyási pont). Nemlineáris esetben görbe-illesztés segítségével határozzuk meg a megfelelő anyagjellemzőket, (pl. kúszás, hiperelasztikus, viszkoelasztikus, és néhány plasztikus anyagmodell esetén). Az anyagmodell felállításához és az anyagvizsgálati adatok feldolgozásához a legtöbb végeselem program beépített megoldást nyújt. Ebben az esetben az importált adatokra a kiválasztott anyagmodellnek megfelelő görbét illeszthetjük.

A mechanikai anyagmodellek felállításához általában az alábbi vizsgálati eljárásokból származó adatokat használhatjuk:

Egytengelyű (Uniaxial)
(Egyen-) Kéttengelyű (Equibiaxial)
Tiszta nyírás (Pure shear / planar tension)
Térfogati vizsgálat (Volumetric)
Egyszerű nyírás (Simple shear)
Egytengelyű húzás (Uniaxial tension)
Egytengelyű nyomóvizsgálat (Uniaxial compression)
Nyírómodulus (Shear modulus)
Térfogat-változási modulus (Bulk modulus)
Húzó (rugalmassági) modulus (Young’s / Tensile modulus)
Poisson-tényező (Poisson's ratio)

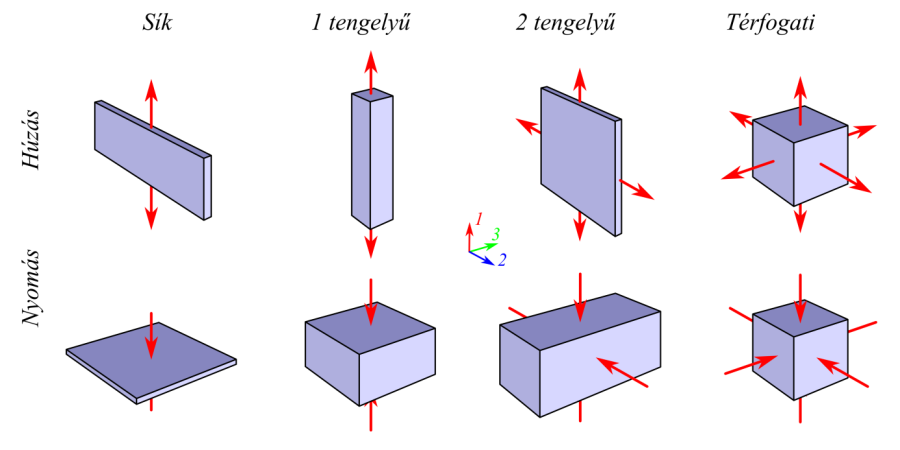
2.28. ábra - A modellalkotáshoz leggyakrabban használt anyagvizsgálatok értelmezése.

Az alábbiakban bemutatott anyagvizsgálatok alakváltozási és feszültségi állapotai homogén, izotróp és összenyomhatatlan (I₃=1) hiperelasztikus anyagmodellre vonatkoznak.

Egytengelyű (Uniaxial) anyagvizsgálat magában foglalja az egytengelyű húzás (Uniaxial tension) és/vagy az egytengelyű nyomóvizsgálat (Uniaxial compression) adatait.

Térfogatállandóságot feltételezve az alakváltozási állapot:

λ ₁ =λ – A terhelés irányába eső nyúlás,

λ ₂ =λ ₃ =λ ^-1/2 – A keresztirányú nyúlás.

Az alakváltozási invariánsok:

I ₁ =λ ² +2λ ^-1

I ₂ =2λ+2λ ^-2

A feszültségi állapot főfeszültségei:

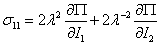
		(2.54)
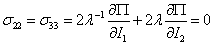
		(2.55)

A σ₁₁ – σ₂₂ egyenletek különbségét képezve a terhelés irányába eső főfeszültség:

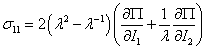
(2.56)

A terhelt keresztmetszet pillanatnyi (a) és kezdeti (A) területének viszonya, az alakváltozási állapot alapján (a/A=1/ λ). Így a terhelés irányú mérnöki (σ_E) és a valós Cauchy (σ₁₁) feszültség közötti összefüggés:

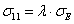
(2.57)

A Kéttengelyű (Equibiaxial) anyagvizsgálat szintén magában foglalja a húzás és/vagy a nyomóvizsgálat adatait.

Térfogatállandóságot feltételezve az alakváltozási állapot:

λ ₁ =λ ₂ =λ – A terhelés irányába eső nyúlás,

λ ₃ =λ ^-2 – A keresztirányú nyúlás.

Az alakváltozási invariánsok:

I ₁ =2λ ² +λ ^-4

I ₂ =λ ⁴ +2λ ^-2

A feszültségi állapot főfeszültségei:

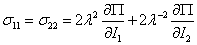
		(2.58)
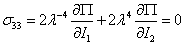
		(2.59)

A σ₁₁ – σ₃₃ egyenletek különbségét képezve a terhelés irányába eső főfeszültség:

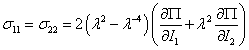
(2.60)

A fentiek alapján a terhelés irányú mérnöki és a valós feszültség közötti összefüggés:

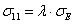
(2.61)

Tiszta nyírás (Pure shear / planar tension)

Térfogatállandóságot feltételezve az alakváltozási állapot:

λ ₁ =λ – A terhelés irányába eső nyúlás,

λ ₂ =1 – A keresztirányú nyúlás (a próbatest szélessége mentén – nincs nyúlás),

λ ₃ =λ ^-1 – A keresztirányú nyúlás (a próbatest vastagsága mentén – nem ébred feszültség).

Az alakváltozási invariánsok:

I ₁ =λ ² +λ ^-2 +1

I ₂ =λ ² +λ ^-2 +1

A feszültségi állapot főfeszültségei:

		(2.62)

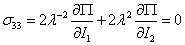
A σ₁₁ – σ₂₂ egyenletek különbségét képezve a terhelés irányába eső főfeszültség:

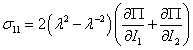
(2.63)

A fentiek alapján a terhelés irányú mérnöki és a valós feszültség közötti összefüggés:

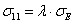
(2.64)

Térfogati vizsgálat (Volumetric test)
Az alakváltozási állapot:
λ ₁ =λ ₂ =λ ₃ =λ=J ^1/3 ,
J=V/V ₀ ;
Térfogatállandóságot feltételezve:
λ≈1;
A feszültségi állapot:

(2.65)

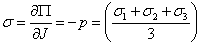
[6.] , [35.] .

2.4.3.8.1.2. Az anyagvizsgálati adatok formátuma

Fontos tisztában lenni azzal, hogy amíg a végeselem programok által kiszámított eredmények a valós feszültség (Cauchy) és a valós (logaritmikus vagy Hencky féle) nyúlás értékeit mutatják (beállítástól és szoftverről függően: ha be van kapcsolva a nagy alakváltozások opció, akkor logaritmikus nyúlás a kimenet, egyébként mérnöki nyúlás), addig az anyagmodell típusától függően a bemenetnek általában az anyagvizsgálatokból származó mérnöki (engineering, nominal) vagy az ezekből számolható valós értékeket kell betáplálni.

Például egy hiperelasztikus anyagmodell létrehozásához az ANSYS és az Abaqus végeselem programban a mérnöki (Engineering, nominal) feszültséget és fajlagos nyúlást, a SolidWorks CAD szoftver szimulációs moduljában a mérnöki feszültséget (Engineering Stress) és a megnyúlást (Stretch ratio) kell megadni. Ezért a vizsgálati adatok betáplálása előtt mindenképen szükséges informálódni az adatok elvárt formájáról, mert azok szoftverenként és anyagmodellenként változó lehet.

Anyagvizsgálatból származó adatok megadásának formátuma hiperelasztikus anyaghoz:

	ANSYS és ABAQUS:	σ _E – ε _E
	SolidWorks:	σ _E – λ

Egy anyagvizsgálat során a mérnöki feszültség és fajlagos nyúlás értéke a kezdeti geometria alapján kerül kiszámításra (σ_E=F/A₀, ε_E=ΔL/L₀), ellenben a valós érték a pillanatnyi geometria függvénye. Mivel a vizsgálat közben a pillanatnyi geometria mérése nehézkes lenne, ezért a mérnöki gyakorlatban a mérnöki feszültség alkalmazása terjedt el. Tekintve, hogy a legtöbb szerkezeti anyag normál igénybevétele során csak kis alakváltozást szenved (<5%), e két érték jó közelítéssel megegyezik. Nagy alakváltozásra képes (pl. elasztomerek) vagy képlékeny anyagok esetén viszont már jelentős különbséggel kell számolnunk. Nagyrugalmasságú elasztomerek esetén, ha a Poisson-tényezőt 0,5 közelinek feltételezzük, így a térfogatállandóság miatt a mérnöki és valós feszültség között a σ_T=λ·σ_Eösszefüggés teremt kapcsolatot. A valós fajlagos nyúlás értékét a logaritmikus (természetes vagy Hencky féle) nyúlással adjuk meg, ε_ln=ln(λ), ahol λ=L/L₀=ε_E+1 a terhelés irányába eső megnyúlás (Stretch ratio).

2.4.3.8.1.3. Görbeillesztés

A végeselem programok általában automatikusan elvégzik az anyagparaméterek meghatározását a betáplált vizsgálati adatok (pl. szakítódiagram) alapján. A görbeillesztés (curve fitting) a legkisebb négyzetek módszerével történik, mely az illesztett és a mért adatok közötti hibát minimalizálja. Választhatunk a normalizált (S=Σ(1-σ/σ_E)²) vagy az abszolút (S=Σ(σ_E-σ)²) hibaszámítás között. Ahol S - a relatívhiba, σ és σ_E– az illesztett és mért feszültségértékek [6.] .

Az alábbiakban a mechanikai analízis során alkalmazott további anyagparamétereket soroljuk fel, melyek többnyire konstans értékként szerepelnek a szimulációban.

2.4.3.8.2. Sűrűség (Density)

Az anyag sűrűsége vagy más néven fajsúlya azt adja meg, hogy egységnyi térfogatú anyagnak mennyi a tömege (ς=m/V), mértékegysége [kg/m³]. Alkalmazásának a dinamikai szimulációk (modál, harmonikus, tranziens analízis), az inerciális terhelésekkel (szögsebesség, gyorsulás, gravitáció) végzett statikai vagy kihajlás analízisekben, illetve termikus vizsgálatokban van szerepe.

2.4.3.8.3. Hőtágulási együttható (Coefficient of thermal expansion)

A lineáris hőtágulási együttható az anyag 1°C hőmérsékletváltozás hatására bekövetkező fajlagos nyúlását adja meg (α=Δl/l·ΔT), mértékegysége [1/K] vagy [1/°C].

2.4.3.8.4. Anyagcsillapítási tényező (Material Damping Ratio)

Anyagcsillapítás lehetővé teszi az anyag belső csillapításának modellezését a dinamikai szimulációkban. Az anyagfüggő tömeg és merevségi csillapítás (α, β, - Rayleigh Damping), hasznos eszköze a dinamikai analíziseknek olyan esetben, amikor az egyes alkatrészek különböző csillapítással rendelkeznek. Az anyagcsillapítási állandó (Constant material damping coefficient) egy anyagfüggő csillapítási együttható, amely a harmonikus analízis gerjesztési frekvenciáin állandó értékű és a modell egyes alkatrészei különböző értékű anyagcsillapítással rendelkezhetnek. A csillapítási együtthatók hőmérsékletfüggetlenek.

2.4.3.8.5. Az anyag szilárdsági határa (Material Strength Limits)

Az anyag szilárdsági határai azt a feszültséget vagy alakváltozást jelentik, amit az anyag még képes elviselni. Megadása történhet pl. a szakító, ill. nyomó folyáshatár (Tensile Yield Strength) vagy az anyag szakítószilárdságának (Tensile Ultimate Strength) megadásával. A megadott érték az analízis eredményében, mint tájékoztató érték (pl. a színskálán bejelölve) jelenik meg, vagy felhasználásra kerül a biztonsági tényező számításához.

2.4.4. Hőmérsékleti szabadságfokkal rendelkező anyagok

A hőmérséklet szabadsági fokkal rendelkező elemzésekben szerepelő hővezetési anyagmodellek megadják a hőmérséklet gradiens hatására kialakuló hőáramot (heat flux), valamint a testek közötti kölcsönhatásnál, a felületi hőmérséklet-különbségek hatására kialakuló sugárzásos hőátadást (radiative heat transfer). A termikus szimuláció anyagmodelljében az alábbi tulajdonságokat kell definiálni:

2.4.4.1. Hővezető képesség (Thermal Conductivity)

Egy anyag hővezetési képességét a hővezetési együtthatójával definiáljuk. Az együttható azt adja meg, hogy egységnyi vastagságú anyagon milyen hőáram keletkezik, ha a két oldalán egységnyi hőmérsékletkülönbség van (λ=q/A⋅ΔT), mértékegysége [W/mK].

2.4.4.2. Fajhő (Specific Heat)

A fajhő vagy más néven fajlagos hőkapacitás értéke azt mondja meg, hogy milyen hőmennyiségre van szükség egységnyi tömegű anyag hőmérsékletének egy fokkal való megnöveléséhez (c=dQ/dT·m), mértékegysége [J/kgK].

2.4.4.3. Sűrűség (Density)

Az anyag sűrűsége vagy más néven fajsúlya azt adja meg, hogy egységnyi térfogatú anyagnak mennyi a tömege (ς=m/V), mértékegysége [kg/m³]. Alkalmazásának a dinamikus szimulációk (modál, harmonikus, tranziens analízis), az inerciális terhelésekkel (szögsebesség, gyorsulás, gravitáció) végzett statikai, vagy kihajlás analízisekben, illetve termikus vizsgálatokban van szerepe.

A fenti anyatulajdonságok lehetnek konstansak, vagy hőmérsékletfüggőek. Ez utóbbi esetben a paraméterek megadása különböző hőmérsékleti szinteken lehetséges a végeselemes szoftverekben. Egy mechanikai analízisben a hőmérsékletfüggő anyagmodell lineárisnak tekinthető, amennyiben a szimuláció konstans hőmérsékleten zajlik, de nemlineáris probléma megoldásról beszélhetünk ugyanakkor, ha hőtani szimulációt folytatunk ugyanezzel az anyaggal.

A hővezetési tényező lehet izotróp (minden irányban azonos) vagy ortotróp (egymásra merőleges tengelyek mentén eltérő) is.

2.4.5. Elektromágneses szabadságfokú anyagok

Az elektromágneses szabadsági fokkal rendelkező elemzésekben szerepelő anyagmodellek az alábbiak lehetnek:

Mágneses, (Magnetic) - a mágneses fluxus (magnetic flux) hatására megadja a mágneses erőt (magnetomotive force).

Vezetőképesség, (Conductivity) - az elektromos és mágneses áramvezető képesség modellezi egy adott mező és annak fluxusa közötti kapcsolatot.

Permittivitás és Permeabilitás, (Permittivity, Permeability) - egy elektromágneses mező hatására megadja az anyag energiatároló képességét.

Veszteség, (Loss) - Az elektromágneses anyagok és dielektrikumok elektromágneses mező változásának hatására bekövetkező energiaveszteségét képviseli.

2.4.5.1. Az anyagok mágneses tulajdonságai

2.4.5.1.1. Mikroszkopikus modell.

Az anyagok mágneses tulajdonságait az atomszerkezetre lehet visszavezetni. Az atommag körül keringő elektron egy elemi köráramnak tekinthető, így egy mágneses dipólussal modellezhető. Az elemi dipólus dipólus-momentumát a d m =I⋅d A összefüggésből, az elektron pályája által meghatározott A felület és az I áram szorzataként kapjuk.

2.4.5.1.2. Makroszkopikus modell.

Mérnöki szempontból nem az egyes dipólusok, hanem azok sokaságának a modellezésére van szükség. Egy dV térfogatban, N darab mágneses dipólus helyezkedik el. Az egyes dipólusok mágneses dipólus-nyomatékát tekintsük közel azonosnak. Így m _i≈α⋅ H , ahol: α kölcsönhatási tényező. Az anyag mágnesezettségét az egységnyi térfogatban elhelyezkedő dipólus-momentumok sűrűsége határozza meg.

(2.66)

Ahol:

n _m = N/dV - a dipólus sűrűség,

κ=α⋅n_m - a mágneses szuszceptabilitás,

M - az anyagra jellemző mágnesezettség.

Sok esetben a µ ₀⋅ M mágneses polarizációt alkalmazzák az anyag mágneses tulajdonságainak jellemzésére.

(2.67)

Ahol az μ _r =1+κ a relatív mágneses permeabilitás.

2.4.5.2. Mágneses anyagok típusai

A tapasztalat azt mutatja, hogy ha valamilyen anyagot mágneses térbe helyezünk, akkor megváltozik a mágneses indukció értéke. Ugyanis megváltozik a tér mágneses vezetőképessége, vagyis a permeabilitása. Az anyagok, permeabilitásuk alapján, három csoportba sorolhatók. Ami tovább bontható a mikromágneses viselkedésük alapján.

Az anyagok makromágneses viselkedése alapján:

Diamágneses anyagok
Parramágneses anyagok
Ferromágneses anyagok

Az anyagok mikromágneses viselkedése alapján:

Rendezetlen mágneses anyagok
- Diamágneses anyagok
- Paramágneses anyagok
Rendezett mágneses anyagok
- Ferromágneses anyagok
- Ferrimágneses anyagok
- Antiferromágneses anyagok

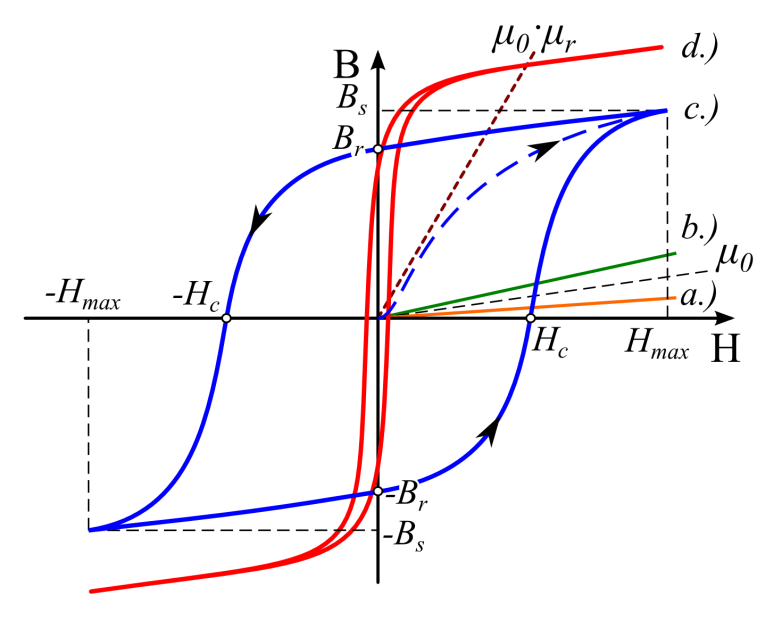
a.) Diamágneses anyag; b.) Paramágneses anyag; c.) "Kemény" ferromágneses anyag (állandómágnes); d.) "Lágy" ferromágneses anyag; µ₀ – a vákuumpermeabilitás egyenese; µ₀⋅ µ_r – lineáris mágneses anyagmodell;

2.29. ábra - Mágneses anyagok jellemző B-H görbéje

[39.] , [40.] .

2.4.5.2.1. A diamágneses anyagok

κ ≈−10^-5; μ_r=1+κ<1;

(H₂, H₂O, Si, P, S, Cu, Zn, Ge, Hg, Bi, C, Ag, Au, Pb, Zn fa, paraffin, pirolitikus grafit, gyémánt, szerves vegyületek,)

A diamágneses anyagok egynél kisebb permeabilitásuak, ami azt jelenti, hogy a mágneses vezetőképességük rosszabb a vákuuménál (2.29. ábra, a.). Szemléletesen úgy képzelhetjük el, hogy az ilyen anyagok kis mértékben taszítják a mágnest. Persze ez a taszítóerő olyan kis értékű, hogy nem tudjuk érzékelni. A diamágneses anyagok ilyen viselkedésének az az oka, hogy két ellentétes irányú mágneses momentumú vegyértékelektronnal rendelkeznek, amelyek külső mágneses tér hatására beállnak a térrel párhuzamos irányba, és a térrel ellentétes irányú mágneses momentum megnő, míg az azonos irányú lecsökken

A diamágneses anyagok mágneses szuszceptibilitása ill. permeabilitása nem függ a hőmérséklettől.

Szupravezető állapot κ=−1; μ=1+κ= 0;

A szupravezetők ideális diamágnesekként viselkednek. Úgy is szokás fogalmazni, hogy a szupravezetőből a mágneses tér "kiszorul", tehát az anyag belsejében a mágneses indukció értéke zérus [39.] .

2.4.5.2.2. A paramágneses anyagok

κ≈10^-5; μ_r=1+κ>1;

(O₂, Al, Bi, Pb, Pt, Mg, Ti, Cr, Mn, Mo,W, Cr, K, Na)

A paramágneses anyagok permeabilitása egynél kicsit nagyobb, ami azt jelenti, hogy az ilyen anyagok kis mértékben vonzzák a mágnest (2.29. ábra, b.). Persze ez a vonzóerő olyan kis értékű, hogy nem tudjuk érzékelni. A paramágneses anyagok ilyen viselkedésének az az oka, hogy egy vegyértékelektronnal rendelkeznek, amely mágneses momentuma külső mágneses tér hatására beáll a mágneses tér irányába.

Mágneses szuszceptibilitásuk fordítottan arányos hőmérséklettel. κ=C/T, ahol C anyagi minőségtől függő ún. Curie-állandó [39.] .

2.4.5.2.3. Ferromágneses anyagok

κ ≈10³-10⁶; μ_r=1+κ>>1;

(Fe, Ni, Co, Gd), doménszerkezetük: ↑↑↑↑

A ferromágneses anyagokban lévő elemi térfogatokban (doménekben) a mágneses dipólusok, külső tér nélkül is, egy irányba rendeződnek, a közöttük lévő erős kölcsönhatás miatt. A ferromágneses anyagok mágneses szuszceptibilitása nagyon nagy pozitív érték. Ha az anyag még nem volt kitéve mágneses térnek a domének statisztikus elrendeződése olyan, hogy az anyag kifelé nem mutat mágneses tulajdonságokat. Az első felmágnesezés során a B - H görbe az un. szűzgörbén halad (2.29. ábra, c.- kék szaggatott vonal), mely során a domének befordulnak a mágneses térrel párhuzamos irányába, majd a mágneses tér irányába mutató domének térfogata növekszik, az ellentétes irányúaké csökken, végül minden domén befordul a mágneses tér irányába, ahol a görbe telítési szakaszba ér. Tovább növelve a H mágneses térerősség értékét B indukció értéke nem változik.

A térerősség csökkentésével az indukció nem a szűzgörbén fog visszatérni, a domének átrendeződésére fordított energiaveszteség miatt fölötte fog haladni, a térerősség nulla értékénél marad egy B _r remanens mágneses indukció. A mágneses indukció megszüntetéséhez ellenkező irányú, - H _c koercitív mágneses térerősségre van szükség. Tovább növelve az ellenkező irányú térerősség értékét ismét eljutunk a telítési pontba. Majd megfordítva a gerjesztés irányát - B _r majd H _c pontokon keresztül záródik a hiszterézis karakterisztika.

Keskeny hiszterézis görbével (kis ± H _c érték) az un. lágy mágneses anyagok rendelkeznek (2.29. ábra, d.), ezeknél kicsi a domének átrendeződéséhez szükséges energiaveszteség. Ilyen anyag pl. a transzformátorlemez és dinamólemez.

Széles hiszterézis görbével (nagy ± H _c érték) az un. kemény mágneses anyagok rendelkeznek (2.29. ábra, c.), ezeknél nagy a domének átrendeződéséhez szükséges energiaveszteség. Ilyen anyagok pl. az állandó-mágnesként használt alnico és nipermag ötvözetek.

A ferromágneses anyagok mágneses szuszceptibilitása az ún. Curie-hőmérsékletig (T_C) rendkívül nagy, majd e hőmérséklet felett a paramágneses anyagokhoz hasonlóan csökken. A paramágneses tartományban

κ=C/(T−T _C ), ahol C a Curie-állandó, (T_C értéke vasra 768°C, kobaltra 1130°C, nikkelre 360°C).

[Sályi István: Pattantyús II.]

2.4.5.2.4. Ferrimágneses anyagok

(Fe3O4, CrO2, ErO, …), doménszerkezetük: ⇑↓⇑↓

Mágneses viselkedésű kerámiák, melyek elektromos viselkedésüket tekintve szigetelők. Telítési pontjuk alacsonyabb, mint a ferromágneses anyagoknak. Szupceptibilitás hőmérsékletfüggése a ferromágneses anyagokéhoz hasonló.

2.4.5.2.5. Az antiferromágneses anyagok

κ=0, μ_r≈1

(Cr, Mn, ausztenites acélok), doménszerkezetük: ↑↓↑↓

Az antimágneses anyagokban a mágneses tér irányába és azzal ellentétesen beálló domainek mennyisége megegyezik, ezért nem változtatják meg a mágneses teret.

Az antimágneses anyagok κ–T görbéje két szakaszra osztható: Néel-hőmérsékletig (T_N) tartó szakasz az antiferromágneses tartomány, felette pedig paramágneses hatás κ≈C/(T-T_N), érvényesül. Ahol C a Curie-állandó.

2.4. táblázat - Az anyagok csoportosítása mágneses tulajdonságuk szerint.

Anyag / állapot	Hiszterézis	B -függés	Hőmérséklet-függés	Példa (μ=1+κ)
Diamágneses anyagok	Nincs	Nincs	Nincs	Víz: κ=−9.0×10^-6
Paramágneses anyagok	Nincs	Nincs	κ=C/T	Al: κ=2.2 ×10^-5
Ferro-és ferrimágneses anyagok	Van	Van	κ=C/(T−T _C )	Vas: κ=3000
Antiferromágneses anyagok	Van	Van	κ≈C/(T−T _N )	Terbium: κ=2500

[41.] .

A mágneses anyagokat relatív permeabilitásuk ill. mágneses szuszceptibilitásuk szerint a fenti csoportokba lehet sorolni. Azonban a dia, paramágneses valamint antiferromágneses anyagok mágneses szuszceptibilitása |κ|=|μ_r−1|≈10^-5nagyságrendű, tehát gyakorlati szempontból a mágneses anyagokat ferromágneses és nem ferromágneses csoportokba sorolhatjuk [40.] .

2.4.5.3. A mágneses szimuláció során definiálható mágneses anyagtípusok

Lineáris "lágy" (soft) mágneses anyag

Ebben az esetben a permeabilitás (az indukció és a térerősség hányadosa, μ= B / H ) konstans érték, nem függ a térerősségtől és a mágnesezési előélettől (2.29. ábra, μ_o⋅μ_r). A relatív permeabilitást (μ_r) kell definiálni, μ=μ_o⋅μ_r, ahol a vákuumpermeabilitás értéke: μ₀=4π⋅10^-7 H/m. Általában a nem mágneses anyagok esetén használjuk (pl. levegő, réz), vagy olyan mágneses anyagok közelítésére, melyeknek nem ismerjük a mágnesezési (B-H) görbéjét. Előfordulhat olyan eset, hogy a permeabilitás nem izotróp, ilyenkor általában lehetséges ortotróp anyagmodell definiálása is. (Mivel ilyenkor globális vagy lokális koordináta rendszerben kell definiálni a relatív permeabilitás irányonkénti értékét célszerű az adott alkatrészhez saját, releváns koordinátarendszert meghatározni. Fontos továbbá megjegyezni, hogy ortotróp anyagmodellek estén a többi anyagtulajdonságot is irányonként kell megadni.)

Nemlineáris "lágy" (soft) mágneses anyag

Ebbe a kategóriába tartoznak azok az anyagok, amelyek nemlineáris viselkedést mutatnak. Ilyenkor a B-H görbe pontos megadásával tudjuk definiálni a fő mágneses tulajdonságokat (2.29. ábra, d.). Egyetlen B-H görbét lehet megadni ebben az esetben. A B-H görbe definiálása történhet a görbe pontjainak megadásával, vagy az adott szoftver anyag adatbázisaiból kiválasztásával (a leggyakoribb anyagok B-H görbéi általában elérhetőek). Ha az adott anyag ortotróp viselkedést mutat, akkor itt is megadható irányonként a relatív permeabilitás és a többi anyagjellemző is, így akár a B-H görbe is megadható irányonként is. Ortotróp anyagmodell esetén is érdemes az alkatrészhez saját koordinátarendszert definiálni. A B-H görbe megadásakor az alábbi alapszabályokat mindenképpen érdemes betartani:

A görbe legyen sima és folytonos.

A görbe nyúljon túl a működési tartományon, tartalmazza a telítődés szakaszát is. (A telítődési szakasz aszimptotikusan közelít a vákuumpermeabilitás egyeneséhez, tehát a program ez alapján tud extrapolálni ha szükséges.)

A szimuláció során a B-H görbe az origó közelében a 0,0 értékhez tart, egy ettől eltérő közeli pont megadása konvergencia problémát okozhat.

Lineáris "kemény" (hard) mágneses anyag

A keménymágneses anyagok, jellemző tulajdonsága a nagy koercív erővel jellemezhető (széles hiszterézishurokkal rendelkező) B-H karakterisztika (2.29. ábra, c.). Ebbe a kategóriába tartoznak pl. a permanens mágnesek. Ennél az anyagmodellnél a lemágnesezési görbét lineárisnak feltételezzük. Így két értéket kell csak megadni; ahol az egyenes metszi a B-H görbe H (mágneses térerősség) tengelyét azt nevezzük koercív erőnek (Coercive Force), mely azt a mágneses térerősség értéket jelenti, amely elégséges az adott anyag lemágnesezésére, tehát ahol B (mágneses indukció) nulla (Ansys programban ezt abszolút értékben kell megadni, tehát pozitív értékként). A második megadandó érték a lemágnesezési egyenes metszéspontja a B tengellyel, melyet remanens, vagyis maradó mágnesezettségnek vagy remanenciának nevezünk (Residual Induction). Az anyagtulajdonságok mellett definiálni kell a mágnes polaritását is. (Ansys programban mindig a globális, vagy egy alkatrészhez meghatározott lokális koordinátarendszer X tengelye mutatja meg a polaritás irányát, alapértéken az északi pólus a koordinátarendszer X tengelyének pozitív irányába mutat, ezt természetesen át lehet állítani. Mivel nem csak Descart-féle, hanem poláris koordinátarendszert is definiálhatunk akár radiális irányú mágnesezettséget is tudunk szimulálni.

Nemlineáris "kemény" (hard) mágneses anyag

A nemlineáris keménymágneses anyagot a B-H karakterisztika 2. síknegyedbe eső pontjaival adjuk meg. Az első adatpár a B=0, H=−H_c kell, hogy legyen. Az állandómágnes mágnesezése egy tengely mentén történik, amely egy célszerűen megválasztott modellkoordináta rendszer X tengelye lehet (a +X irány jelenti az állandómágnes északi pólusát). Ellenkező esetben a mágnesezettség iránya az alapértelmezett Globális Koordinátarendszer X tengelye lesz. A választott koordinátarendszer lehet derékszögű (Cartesian) vagy hengeres (cylindrical). Hengeres koordinátarendszer alkalmazásával létrehozhatunk radiálisan mágnesezett modellt is. A B-H görbe megadásakor az alábbi alapszabályokat mindenképpen érdemes betartani:

A görbe legyen sima és folytonos.

A görbe megadása a 2. síknegyedben történik, de kiterjedhet az 1. síknegyedbe is.

2.4.5.4. Elektromos anyagmodellek

2.4.5.4.1. Elektromos vezető

Az anyag elektromos vezetési tulajdonságát a fajlagos ellenállás (Resistivity) (ς [Vm/A=Ωm]) vagy a fajlagos vezetőképesség (Specific conductivity) (γ=1/ς [A/Vm=S/m]) megadásával definiálhatjuk, amely lehet izotróp vagy ortotróp. Ez utóbbi esetben célszerű lokális koordinátarendszert definiálni az adott alkatrészhez. Az ellenállás lehet a hőmérséklettől függő is melyet különböző hőmérsékleti szinteken megadott ellenállás értékekkel definiálhatunk.

2.4.5.4.2. Dielektrikum

A nagy fajlagos ellenállású (ς>10⁸ Ωm)anyagokat szigetelőknek, vagyis dielektrikumoknak hívjuk. Jellemzésükre a relatív permittivitást (ε_r) használjuk. A mágneses permeabilitás analógiájára a permittivitás vagyis a dielektromos állandó (ε=ε₀⋅ε_r) teremti meg a kapcsolatot az elektromos térerőség (E) és az eltolási vektor (D) között: D =ε E ; (ε₀=8,854⋅10−12 As/Vm).

2.4.6. Csatolt anyagmodellek

Számos modell alkalmazható csatolt termikus, elektromágneses és elmozdulás szabadsági fokokkal rendelkező elemzésekhez. Bár a modellek kapcsolva vannak, azok továbbra is önállóak és így az egyéni terhelés-válasz viselkedéssel rendelkeznek. A piezoelektromos anyagok azonban elektromechanikusan csatolt modellek, amelyek villamos feszültség bemenetre alakváltozást adnak válaszul, valamint deformáció hatására villamos feszültséget generálnak.

A csatolt tér analízisek típusai, mint már az elemtípusoknál láthattuk, rendkívül sokfélék lehetnek. Jellemzően a mechanikai, villamos, mágneses, termikus, és áramlási hatások páronkénti vagy többszörösen összetett modelljei alkotják, de léteznek akusztikus, dífúziós, stb. elemei is. Az alábbiakban az elektro-mechanikus analízis anyagaira hozunk két példaként.

2.4.6.1. Piezorezisztív anyag

A piezorezisztív anyagok fő jellegzetessége, hogy mechanikai feszültség, (vagyis közvetlenül az alakváltozás) hatására megváltozik az ellenállásuk. Egy deformált test ellenállás-változása tenzometrikus és piezorezisztív komponensekből áll. A tenzometrikus komponens csak a geometria változásától függ, így a Poisson-tényező és az alakváltozási állapot ismeretében könnyen számolható (fémekre jellemző). A piezorezisztív hatásként oka az, hogy az anyag a fajlagos ellenállása megváltozik (félvezetőkre jellemző).

Piezorezisztív anyagmodell végeselemes definiálásához az anyag fajlagos ellenállásának (ς), a rugalmassági együtthatók (pl. rugalmassági modulus E, Poisson-tényező ν) és a piezorezisztív mátrix megadása szükséges. Ez utóbbi a mechanikai feszültség, vagy alakváltozás (megadástól függ, hogy melyik) hatására bekövetkező ellenállás-változás mértékét adja meg [42.] .

2.4.6.2. Piezoelektromos anyagmodell

A piezoelektromos anyag egy elektromechanikusan csatolt anyag, melynek jellemzője, hogy villamos feszültség hatására alakváltozással válaszol, valamit fordított helyzetben deformáció (vagy mechanikai feszültség) hatására villamos feszültséggel, pontosabban töltésszétválasztással reagál.

Piezorezisztív anyagmodell az anyag permittivitásának (dielektromos állandójának), a rugalmassági együttható mátrixának (pl. rugalmassági modulus E, Poisson-tényező ν) és a piezoelektromos együttható mátrixának megadásával definiálható. A piezoelektromos együttható mátrix a mechanikai feszültség vagy alakváltozás (megadástól függ, hogy melyik) és az elektromos térerősség kapcsolatát adja meg.

2.5. Terhelések, perem- és kezdeti feltételek

A geometriai modell elemeire (térfogat, felület, él, pont) vagy közvetlenül a végeselem háló csomópontjaira peremfeltételeket és terheléseket írhatunk elő.

2.5.1. Kezdeti feltételek

Egy időben változó analízis során lehetőségünk van a szimulációt egy előre definiált kezdeti feltétellel indítani. A feltétel megadja a t₀=0 időpillanatban az adott konfiguráció valamely paraméterének értékét. Tranziens folyamatoknál ez lehet pl. egy geometriai elem sebessége, hőmérséklete, stb. Homogénnek nevezzük a peremfeltételt, ha értéke 0; inhomogénnek, ha 0-tól különböző értékű, [43.] .

Típusa az adott szimuláció típusától függ, pl. lehet egy előzőleg futtatott szimuláció eredménye, valamilyen kapcsolódó környezet vagy egy kezdeti hőmérséklet.

Kezdeti feltétel (Initial State Loading) - Statikai, tranziens, modál, harmonikus és kihajlás típusú szerkezeti analízisek esetén alkalmazható a kezdeti feltétel, melyet az első lépésben kell definiálni.

2.5.2. Peremfeltételek

A peremfeltételek a fizikai valóság azon részeinek hatását jelentik, amelyeket elhagyunk a modellezés során. Ezért rendkívül körültekintően kell eljárnunk akkor, amikor ezeket a külső hatásokat modellezzük, mivel a modell helyessége fejti ki az egyik legnagyobb hatást a teljes végeselem modell jóságára [5.] .

A peremfeltételek származhatnak közvetlenül az adott modellre definiált kényszerekből (megtámasztás, elmozdulás kényszer, szimmetriafeltétel) vagy más alkatrésszel való érintkezésből (kontaktokból). Általános esetre megfogalmazva az adott szimulációnak megfelelő szabadságfokot korlátozó feltételről beszélünk. Például mechanikai, (vagyis elmozdulás szabadságfokú) rendszer esetén, kinematikai kényszerről; termikus (hőmérséklet szabadságfokú) szimuláció esetén megadott hőmérséklet-kényszer, stb. Az alábbiakban láthatjuk a jegyzet témaköreit érintő analízistípusokban definiálható peremfeltételek:

Szerkezeti analízis (Structural) - elmozdulás, elfordulás, sebesség kényszer vagy szimmetriafeltétel.
Hőtani analízis (Thermal) - előírt hőmérséklet.
Mágneses (Magnetic) - párhuzamos-fluxus, Vektor vagy skalár potenciál.
Elektromos (Electric) – Feszültség.

Homogénnek nevezzük a peremfeltételt, ha értéke 0 (pl. fix megtámasztás); inhomogénnek, ha 0-tól különböző értékű (pl. elmozduláskényszer).

[43.] , [6.] .

A különféle típusú feladatok megoldásánál alkalmazott peremfeltételeket az adott analízis fejezetében részletesebben tárgyaljuk.

2.5.3. Terhelések

Egy végeselemes analízis elsődleges célja annak meghatározása, hogy egy szerkezet, hogyan reagál bizonyos terhelésekre. Ezért a megfelelő terhelési feltételek definiálása kulcsfontosságú a szimuláció szempontjából. A jegyzet témaköreit érintő analízistípusokban definiálható terhelések:

Szerkezeti analízis (Structural) - elmozdulás (displacements), sebesség (velocities), gyorsulás (accelerations), gravitáció (gravity), erő (forces), nyomás (pressures), hőmérséklet (temperatures) [hőtágulásnál].
Hőtani analízis (Thermal) - hőmérséklet, hőáram sűrűség (heat flow rates), konvekció (convections), belső hőtermelés (internal heat generation), végtelen felület (infinite surface).

Mágneses (Magnetic) - mágneses potenciálok (magnetic potentials),mágneses fluxus (magnetic flux), mágneses áramszegmensek (magnetic current segments), áramsűrűség (source current density), végtelen felület (infinite surface).

Elektromos (Electric) - elektromos potenciál (feszültség), (electric potentials (voltage)), elektromos áram (electric current), elektromos töltések (electric charges), töltéssűrűség (charge densities), végtelen felület (infinite surface).

A terhelés lehet a vizsgált test külső, határoló entitásaira (felület, él, pont) ható koncentrált vagy megoszló terhelés (mint az erő, nyomaték, nyomás), vagy a test teljes térfogatára ható test, vagy inerciális terhelés, (mint a gravitációs gyorsulásból eredő súlyerő, vagy a rotációs vagy transzlációs gyorsulásból származó tehetetlenségi erő). A terhelések, a terhelt testen való eloszlásuk szerint, az alábbi kategóriákba sorolhatók:

Erők (Forces / concentrated loads) – egy csomópontra (node) ható koncentrált terhelés. Például egy erő, vagy egy nyomaték a szerkezeti analízisben; hőáramsűrűség a hőtani szimulációban; vagy gerjesztőáram egy mágneses mező vizsgálatnál.
Felületi terhelés (Surface loads) – egy felület mentén megoszló erő. Például nyomás a szerkezeti analízisben; konvekció és a hőáram a termikus analízisben.
Test terhelés (body loads) – térfogati vagy mező jellegű terhelés. Pl.: a hőmérséklet a szerkezeti analízisben; belső hőtermelés sűrűség a hőtani szimulációban; áramsűrűség a mágneses vizsgálatban.
Inerciális terhelés (Inertia loads) – a test tehetetlenségének (tömeg mátrix) tulajdonítható terhelések, mint a gravitációs gyorsulás, szögsebesség és a szöggyorsulás a szerkezeti analízisben.
Csatolt tér terhelések (coupled-field loads) – a fenti terhelések speciális esete, amikor is egy szimuláció eredménye szolgál egy más típusú analízis terheléseként. Például a mágneses szimulációban kiszámolt erő, mint terhelés egy szerkezeti analízisben; vagy egy hőtani szimuláció eredménye, mint bemenet egy szerkezeti analízisben a hőtágulásból eredő deformációk számításához.

A fentiek szerint a terheléseket a geometriai modell entitásaira (pontok, élek, felületek) vagy a végeselem modell csomópontjaira lehet érvényesíteni. A terhelés megadásának módjától függetlenül, a megoldó (solver) áthelyezi a terheléseket a végeselemes modell csomópontjaira, és úgy futtatja a számolást. A terhelések alkalmazásának szempontjai:

A szilárdtest modellre alkalmazott terhelések függetlenek a végeselem hálótól, (a háló módosítható a terhelés változtatása nélkül.
A szilárdtest modell lényegesen kevesebb elemet tartalmaz, mint a végeselem modell, ezért a kijelölés egyszerűbb, (grafikus kijelölés).
A szilárdtest és a végeselem modellnek általában eltérő a koordinátarendszere, így a terhelés iránya is eltérő lehet a különböző kijelölés esetén.
Az egyszerűsített szimulációkat egyszerűvé teszik a terhelések végeselem modellre történő közvetlen alkalmazása, mivel a terheléseket közvetlenül a csomópontokra helyezhetjük.

2.5.3.1. Terhelési lépések (Load steps)

A terhelési lépés (load step) – a terhelés egy konfigurációja melyre megkapjuk a megoldást. A lineáris statikai (linear static) vagy a stacionárius (steady-state) analízisekben különböző terhelési lépésekben állíthatunk be különböző terhelési konfigurációkat (pl. erőterhelés az első lépésben, nyomás a másodikban, mindkét terhelés és megváltoztatott rögzítés a harmadik lépésben.). Tranziens analízisben több lépésben adhatjuk meg a terhelés időbeni lefutását.

Nincs szükség több időlépés beállítására akkor, ha csak a terhelés mértékét akarjuk változtatni az idő függvényében. Erre a célra a terhelési lépések allépésekre való felosztása szolgál.

Allépések (Substeps) – a terhelési lépések közötti lépések. Az allépések sűrűségét megadhatjuk a lépések számával vagy a köztük eltelt idővel (A statikai szimuláció esetén ez csak egy követési paraméter). Alkalmazásuknak az alábbi okai lehetnek:

Egy nemlineáris statikai (nonlinear static) vagy a stacionárius (steady-state) analízisben, allépések alkalmazásával, a terhelés fokozatos ráadásával pontosabb eredmény érhető el.
Egy lineáris, vagy nemlineáris tranziens analízis esetén alkalmazzuk az idő integráció feltételeinek kielégítése érdekében (ami egy minimális integrálási időt ír elő a pontos eredmény érdekében).
Harmonikus analízisben használunk allépéseket a frekvenciatartományokon belüli számos frekvencián való megoldásért.

A terhelések alkalmazása az allépésekben történhet ugrásszerűen (stepped) vagy fokozatosan emelkedő (ramped) módon. Az ugrásszerű megoldásnál az egy lépésen belüli allépések mind egyazon terhelési szinten vannak, míg az emelkedő eljárással fokozatosan változtatva, csak a lépés végén éri el a beállított szintet a terhelés [6.] .

Egyensúlyi iteráció (Equilibrium iterations) – Nemlineáris analízisek során a konvergencia elősegítése miatt, egy adott allépésen belül további iteratív megoldások számolódnak. Gyakori eljárás a nemlineáris analíziseknél, hogy a pontos eredmény érdekében a terhelést két lépésben adják rá a szerkezetre, az első lépés több (5-10) allépésre van osztva, allépésenként egy egyensúlyi iterációval; a második lépés viszont csak egy allépésből áll, ami több (10-20) egyensúlyi iterációt tartalmaz. Az első lépés a végső terhelési szint stabil elérését hivatott biztosítani, a második lépés pedig a pontos eredményeket adó konvergenciát szolgálja.

2.5.4. Szimmetriafeltételek

A 2.2.3.1. szakasz fejezetben láthattuk a geometria lehetséges szimmetriáit. Ezeket a végeselem modellen a megfelelő kényszer és terhelés felrakásával, vagy a végeselem programban előre definiált szimmetriafeltételekkel tudjuk érvényesíteni. Ez utóbbi megoldás esetén is a program a megfelelő szabadságfok kényszert (DOF constraints) hozza létre, valamint a szimmetriasíkban lévő csomópontok koordinátarendszerét befordítja a szimmetriasíkba.

Beszélhetünk szimmetrikus és antiszimmetrikus peremfeltételekről. Például egy szerkezeti analízisben a szimmetria peremfeltétel esetén a szimmetriasíkra merőleges elmozdulások és azzal párhuzamos tengelyű elfordulás értéke lesz nulla, az antiszimmetria esetén a síkban történő elmozdulás és a síkra merőleges tengelyű elfordulás lesz zérus értékű.

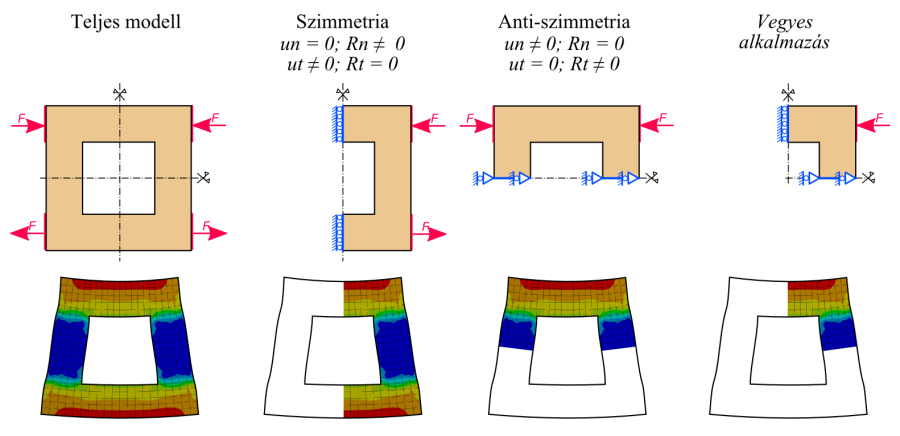
Az „u” - az elmozdulást, az „R” - az adott tengely körüli elfordulást jelenti, ahol az „n” index a normális a „t” a tangenciális irányt jelöli.

2.30. ábra - Szimmetria és anti-szimmetria értelmezése.

2.5.4.1. Tengelyszimmetrikus (Axisymmetric) terhelések

A kényszerek, felületi és volumetrikus erők, valamint a tengelyirányú gyorsulásokat úgy kell definiálni, mint egy nem tengelyszimmetrikus modell esetén. A koncentrált erőket és a számítások eredményeit a teljes kör mentén (360°) kell értelmezni, vagyis a modellen koncentrált erőként definiált terhelés a valóságban vonalmentén megoszló terhelésnek felel meg. Például egy cső végére alkalmazott tengelyirányú megoszló terhelés q [N/mm], a tengelyszimmetrikus végeselem modellen F=2Rπq [N] értékű koncentrált erőként szerepel.

2.6. Alkatrészek közötti kapcsolatok

Az egyes alkatrészek közötti kapcsolatot nevezzük kontaktoknak, melyek az alkatrészek közötti terhelés és kényszerek átadását biztosítják. Ennek a kapcsolatnak a tulajdonságai határozzák meg az egyes geometriai elemek egymáshoz képesti viselkedését. Nagyon fontos, hogy olyan kontaktot definiáljunk, amely leginkább megfelel az adott szerkezet valós viselkedésének. A kontaktok definiálása az olyan mechanikai esetekben a legfontosabb, ahol az alkatrészek elmozdulást, deformációt szenvednek. Ennél fogva a legtöbb kontaktok jelentős nemlinearitást visznek a feladatba.

a kontaktproblémák két fő nehézsége abból adódik, hogy nehéz megjósolni az analízis előtt, hogy pontosan milyen területek fognak részt venni a kontaktban. A másik probléma a kontaktokkal átadott mennyiségek (súrlódó erő, hő, elektromos áram, stb.) nemlineáris jellegében van. Olyan esetekben, ahol nem történik deformáció (pl. bizonyos elektromágneses, hőtani szimulációk) ott nem szükséges a kontaktok beállításaira különösebb figyelmet fordítani.

A mechanikai analízis kontaktproblémájának két lényeges típusa a merev – rugalmas és a rugalmas – rugalmas kapcsolat. A merev – rugalmas kapcsolat esetén a kapcsolatban lévő testek egyike rugalmas, a másik pedig merev test (vagy sokkal merevebb, mint a másik). Tipikus példa lehet erre a fém - polimer kapcsolat vagy a fémek képlékenyalakítási eljárásainak szerszámai és munkadarabja közötti kapcsolat. A rugalmas – rugalmas kapcsolat minden alkatrésze deformálható (vagy hasonló merevségű).

A kontaktok csoportosítása kapcsolódó geometria szerint a következő lehet:

Csomópont – csomóponttal (node-to-node), – a két elem egymáshoz képest csak kis elmozdulásra képes.
Csomópont – felülettel (node-to-surface),
Él – éllel kapcsolódik (line-to-line),
Él – Felülettel (line-to-surface),
Felület – felülettel (surface-to-surface).

Az analízis típusa szerint az alábbiak lehetnek a kontaktok [6.] :

Szerkezeti analízis (Structural)
- Súrlódásos (Frictional) – a valós fizikai kapcsolatot a legjobban modellező kontakt. A felületek eltávolodhatnak és a súrlódási erő ellenében elcsúszhatnak egymáson.
- Súrlódásmentes (Frictionless) – Idealizált csúszó kontakt. A felületek akadálymentesen elcsúszhatnak egymáson és eltávolodhatnak egymástól.
- Síkban maradó (No-separation) – A súrlódásmentes speciális esete, amikor a felületek akadálymentesen elcsúszhatnak egymáson, de nem eltávolodhatnak el egymástól.
- Tapadó (Rough) – Idealizált csúszásmentes kontakt. A felületek nem csúszhatnak el egymáson, de eltávolodhatnak egymástól.
- Ragasztott (Bonded) – minden szabadságot megkötő, a kapcsolódó felületeket egymáshoz fixen rögzítő kontakt.
Hőtani analízis (Thermal) – a termikus analízisben szereplő kontakt a kapcsolódó felületek közötti hőellenállást vagy hővezető képességet definiálja. Egy összeállításban a testek közötti hőátadáshoz elengedhetetlen a fenti kontaktok megléte és a testek érintkezése vagy közelsége. Nem érintkező, de közel (pinball region) lévő felületek hőátadása csak a bonded, vagy a no-separation kényszerrel valósul meg. A pinball régión kívül eső felületelemek között már nem jön létre hőátadás [44.] .
Elektromos (Electric) – az elektromos vagy elektromágneses analízisben szereplő villamos vezetők közötti elektromos ellenállást vagy vezetőképességet definiálja. A hőtani analízishez hasonlóan, két test közötti áramvezető képesség megléte a testek érintkezésének, vagy egymáshoz közel lévő felületek esetén a köztük lévő távolság függvénye, amit a pinball opcióval állíthatunk be.

2.7. A szimuláció főbb beállításai és futtatása

2.7.1. Az analízis típusának kiválasztása

A szerkezeti analízis a mechatronikai feladatok talán az egyik leggyakrabban alkalmazott végeselemes vizsgálati módszere. A kifejezés magában foglalja az építészetben előforduló szerkezetek, (úgy, mint a hidak, épületek, stb.), valamint a gépészetben előforduló mechanikus elemeket, (mint pl.: közlekedési eszközök, gépalkatrészek, stb.). A szerkezeti analízis egyre nagyobb teret nyer a bimechanikában és az orvostudományban is (biológiai szövetek, implantátumok, orvosi eszközök vizsgálatában.). A szerkezeti analízisek során az elsődlegesen kiszámolt ismeretlen az elmozdulás, az összes többi mennyiség (megnyúlás, feszültség, reakcióerők) ebből vannak származtatva. A szerkezeti analízisek főbb típusai:

Statikai analízis (Static Analysis) – Statikai (tehát időfüggetlen) terhelés hatására kialakuló állandósult deformáció, feszültség, stb. meghatározására szolgál. Figyelmen kívül hagyja a tehetetlenséget és csillapítást, vagyis az időfüggő terheléseket okozó elemeket. Tartalmazhat viszont időben állandó inerciális terheléseket, mint pl. a gravitáció vagy a szögsebesség, vagy időben lassan változó hatásokat, mint a terhelés lassú megváltozása, vagy az anyag időfüggő viselkedése (pl. kúszás). A statikai analízis lehet lineáris, vagy nemlineáris. A nemlineáris oka lehet az anyagi nemlinearitás, nagy alakváltozás (large deflection / large strain), vagy a terhelési, ill. peremfeltételek megváltozása.
Modál analízis (Modal Analysis) – A modál vagy alaki analízis az adott szerkezet rezgési karakterisztikájának meghatározására, vagyis a sajátfrekvenciáinak kiszámolására és a lengésképek bemutatására használjuk. A modál analízis kiindulási pontja lehet részletesebb dinamikai vizsgálatoknak, mint a tranziens dinamikai, harmonikus, vagy a spektrum analízis. Lehetőség van előfeszített szerkezetek modál analízisére, mint pl. nagy sebességgel forgó, rezgésre hajlamos alkatrészek (turbinalapát).
Harmonikus analízis (Harmonic Analysis) – Egy szerkezet időben ciklikusan változó, (harmonikus) gerjesztésre adott állandósult válaszának meghatározására használjuk. Tehát az eredmény nem tartalmazza a terhelés elején fellépő tranziens rezgéseket. Az analízis segítségével előrejelezhető a szerkezet hosszú távú dinamikai viselkedése harmonikus gerjesztés hatására. Ezáltal vizsgálható a szerkezet rezonanciája vagy kifáradása. A vizsgálat eredményeként, a vizsgált mennyiséget (leggyakrabban elmozdulást) kapjuk a frekvencia függvényében. A lineáris harmonikus vizsgálatban a nemlineáris elemek figyelmen kívül maradnak.
Tranziens dinamikai analízis (Transient Dynamic Analysis / Time-history Analysis) –Egy szerkezet tetszőleges, időben változó terhelésre (statikus, tranziens, harmonikus) adott válaszának meghatározására használjuk. Minden fajta nemlinearitás alkalmazható, ami a statikus szimulációban. A tranziens analízis időbeli lefolyása szempontjából a szerkezet tehetetlenségének és csillapításának van fontos szerepe. Amennyiben ezek hatása nem fontos, akkor a statikus analízis alkalmazható helyette.
Spektrum analízis (Spectrum Analysis) – A modál analízis kiterjesztett változata, amely a válaszspektrum vagy véletlenszerű rezgés bemenetre adott feszültséget vagy alakváltozást számolja ki.
Kihajlás vizsgálat (Buckling Analysis) – A kihajlást előidéző terhelés (az a kritikus terhelés, amelynél a szerkezet elveszti stabilitását) és a kihajlási alak meghatározására szolgál. Lineáris és nemlineáris kihajlás egyaránt vizsgálható.
Explicit dinamikai analízis (Explicit Dynamic Analysis) – Az explicit dinamika gyors számolást nyújt rövid idejű feladatok, nagy alakváltozások, összetett érintkezési problémák, valamint nagy alakváltozásokkal és összetett nemlinearitásokkal rendelkező kvázistatikus problémák megoldásához.
Többtest dinamikai szimuláció (Multibody simulation) – Több összekapcsolt merev vagy rugalmas testből álló rendszer dinamikai szimulációja alkotja. Az egyes testeket kinetikailag megengedett kényszerek láncolata, mint pl. csuklók kötik egymáshoz. A komponensek így nagy elmozdulásra, nagy elfordulásra és véges alakváltozásra képesek.

Termikus analízisek (Thermal Analysis)

Állandósult termikus analízis (steady-state thermal analysis) – A hőmérsékleteloszlás vagy egyéb hőtani mennyiségek meghatározására szolgál állandósult terhelési feltételek mellett. A szimuláció során a hőtároló hatás időbeli változása figyelmen kívül hagyható. Eredményül a hőtani folyamat állandósult állapotát adja.
Tranziens termikus analízis (transient thermal analysis) - A hőmérsékleteloszlás vagy egyéb hőtani mennyiségek, az idő függvényében történő meghatározására szolgál.

Elektromágneses analízis (Electromagnetic Analysis)

Nagyfrekvenciás elektromágneses analízis (High-Frequency Electromagnetic Analysis)–adott szerkezetben terjedő, nagyfrekvenciás elektromágneses tér és hullámok szimulációjára szolgál. Olyan esetekben célszerű az alkalmazása, amikor a hullámhossz hasonló nagyságrendű vagy kisebb, mint a vizsgált szerkezet mérete. A vizsgálati frekvenciatartomány néhány száz MHz-től néhány száz GHz-ig terjedhet.
Alacsony frekvenciás elektromágneses analízis (Low-Frequency Electromagnetic Analysis) – A szimuláció során a mágneses tér az elektromos áram, állandómágnes vagy külső tér hatására jöhet létre. A szimulációban résztvevő anyagokat villamos szempontból nem vezető és vezető (örvényáram vagy a nélküli) ill. mágneses tulajdonságaik szempontjából nem mágneses, lágy és kemény mágneses anyagok lehetnek.

Folyadék analízis (Fluids Analysis) [6.]

Noha a folyadékszimulációk nem tartoznak a jegyzet témakörébe, említés szinten érdemes róluk szót ejteni, mivel nagy fontossággal bírnak a végeselemes analízisek terén. Főbb típusaik:

Numerikus folyadékdinamika (Computational Fluid Dynamics (CFD))–(FLOTRAN, CFX, FLUENT, POLYFLOW). A CFD folyadékáramlást, hőátadást, kémiai reakciókat és egyéb kapcsolódó fizikai jelenségeket szimulációjára szolgáló eszköz. A szimuláció megoldása egy meghatározott régióra korlátozódik, amely a meghatározott peremfeltételekkel rendelkezik. A CFD analízisben lehetőség van Lamináris vagy turbulens, termál vagy adiabatikus, Szabad felület, Összenyomható vagy összenyomhatatlan, Newtoni vagy nem Newtoni, és többfajta áramlás szimulációkra vagy ezek kombinációjára.

Akusztikus (Acustics) – Az akusztikus analízis a rezgések, hanghullámok keletkezését (generation), terjedését (propogation), abszorpcióját (absorption) és visszaverődését (reflection) vizsgálja valamilyen fluidumban.

Vékony réteg (Thin Film) –A szimuláció mozgó felületek közötti vékony folyadékréteget vizsgálja, amely megváltoztatja a szerkezet viselkedését, merevség és csillapítás hozzáadásával. A felületek a résre merőleges elmozdulása a folyadék préselését, érintő irányú elmozdulása a folyadék csúszását eredményezi.

2.7.2. A megoldó kiválasztása (Selecting a Solver)

A szimuláció futtatása előtt az alábbi megoldók közül választhatunk a feladat elvégzésére [6.] .

Ritka közvetlen, (sparse direct solution) – Közvetlen elimináció, (direct elimination). Alkalmazása olyan esetben célszerű, ahol a robusztus megoldás és a számolási idő a követelmény (nemlineáris), és olyan lineáris számolásnál, ahol az iteratív megoldók túl lassúak a konvergáláshoz. Ideális modellméret: 0,1 - 5 millió szabadságfok.
Előkezelt konjugált gradiens, (Preconditioned Conjugate Gradient (PCG)) - Iterációs megoldó, (iterative solver). A direkt megoldóhoz képest relatíve kis I/O követelmény. Nagy szilárdtest elemeket és finom hálót tartalmazó modelleknél a legelőnyösebb az alkalmazása. [A legrobosztusabb iteratív megoldó az Ansys-ban] Ideális modellméret: 0,5 - 20 millió szabadságfok.
Jacobi-konjugált gradiens, (Jacobi Conjugate Gradient (JCG)), - Iterációs megoldó. Egyszeres terek (termikus, mágneses, akusztikus) megoldására a legalkalmasabb. Gyors és egyszerű előkészítőt (preconditioner) használ, minimális memóriaigénnyel. Nem olyan robusztus, mint a PCG. Ideális modellméret: 0,5 - 20 millió szabadságfok.
Befejezetlen Cholesky-konjugált gradiens, (Incomplete Cholesky Conjugate Gradient (ICCG)) - Iterációs megoldó. Kifinomultabb előkészítővel rendelkezik, mint a JCG. A legalkalmasabb olyan bonyolultabb problémák megoldására, melyeknél a JCG már hibázik, mint például aszimmetrikus termál analízis. Ideális modellméret: 0,05 – 1 millió szabadságfok
Kvázi-minimális maradék (QMR) megoldás,(Quasi-Minimal Residual (QMR) solution) - (Iterációs megoldó) Nagyfrekvenciás elektromágneses analízis. Ideális modellméret: 0,05 - 1 millió szabadságfok.

A Direkt megoldó speciális változata, a PCG és a JCG megoldók alkalmasak párhuzamosan (klaszterekbe) rendezett hardveren történő futtatásra is.

2.8. Az eredmények lekérdezése és kiértékelése (posztprocesszálás)

A szimuláció futtatása után választ akarunk kapni azokra a kérdésekre, amelyek információt szolgáltatnak a szerkezet működéséről, ill. működőképességéről. Például, hogy milyen feszültség ébred az adott szerkezet egyes részein, mi a szerkezet maximális alakváltozása, milyen elmozdulást végez a szerkezet egy pontja adott terhelés hatására, milyen lesz a szerkezet hőmérséklet-eloszlása, vagy hogy milyen a mágneses tér az adott szerkezetben, stb. A szimuláció eredményeinek feldolgozása és a kívánt mennyiség bemutatása (postprocessing) érdekében definiálnunk kell, hogy mire is vagyunk kíváncsiak.

2.8.1. Lekérdezett mennyiségek

A lekérdezett mennyiségek helyes értelmezése döntő fontosságú, mivel egy jól összeállított és helyes eredményeket hozó szimulációról is kiolvashatunk fals eredményeket a helytelenül értelmezett lekérdezések miatt. A helyes kiértékelés érdekében tekintsük át a legfontosabb fizikai mennyiségeket.

Elsődleges adatok – Az elsődlegesen kiszámolt mennyiségek az egyes csomópontok szabadságfokainak megoldása (nodal solution), úgy mint az elmozdulás, hőmérséklet, mágneses potenciál, stb.

Származtatott adatok – Az elsődlegesen kiszámolt adatokból számolt, úgy mint a feszültség és alakváltozás, hőmérsékleti gradiens, mágneses fluxus, stb. A származtatott mennyiségek megoldása az elemekre (element solution) vagy a csomópontokra vonatkozhat (nodal solution). Az alábbiakban táblázatosan mutatjuk be néhány analízis típushoz tartozó elsődlegesen és másodlagosan kiszámolt mennyiségeket.

2.5. táblázat - Néhány analízis típushoz tartozó elsődleges és másodlagos mennyiségek.

Analízis típus

(Discipline)

Elsődleges adat

(Primary Data)

Származtatott adatok

(Derived Data)

Szerkezeti

(Structural)

Elmozdulás (Displacement)

Feszültség, fajlagos nyúlás, reakcióerő, stb.

(Stress, strain, reaction, etc.)

Termikus

(Thermal)

Hőmérséklet (Temperature)

Hőáram, hőmérsékleti gradiens, stb.

(Thermal flux, thermal gradient, etc.)

Mágneses

(Magnetic)

Mágneses potenciál (Magnetic Potential)

Mágneses fluxus, áramsűrűség, stb.

(Magnetic flux, current density, etc.)

Elektromos

(Electric)

Elektromos potenciál (Electric Scalar Potential)

Elektromos térérősség, indukció, stb.

(Electric field, flux density, etc.)

Folyadék

(Fluid)

Sebesség, nyomás (Velocity, Pressure)

Nyomásgradiens, hő fluxus, stb.

(Pressure gradient, heat flux, etc.)

2.8.2. Az eredmények megjelenítési formái

Az eredmények megjelenítése történhet grafikus vagy szöveges formában. Az alábbiakban bemutatunk néhány általánosan használt eljárást egy statikus szerkezeti analízis példáján keresztül. A grafikus megjelenítés történhet a modellen szilárdtest vagy vektoros formában, ill. diagramon.

Valamely számolt mennyiség (pl. feszültség, alakváltozás, stb.) a szilárdtestben való eloszlását a színsávokkal ábrázoljuk. Az egyes színekhez tartozó értéket a képernyőn megjelenő színskála segítségével olvashatjuk le. Alkalmasan elhelyezett címkék segítségével a számolás lokális eredményeit, vagy annak minimum és maximum helyeit közvetlenül a testmodellen is lekérdezhetjük.

Vektormennyiségek bemutatása történhet vektoros formában is. Némely esetben ezek hossza vagy sűrűsége változtatható az adott mennyiség intenzitása szerint.

Diagramban számos mennyiség ábrázolható és lekérdezhető a végeselem programokon belül. Például statikus szerkezeti analízisnél, a lekérdezett mennyiség eloszlása egy él mentén vagy tranziens dinamikai szimulációnál az időbeli változása.

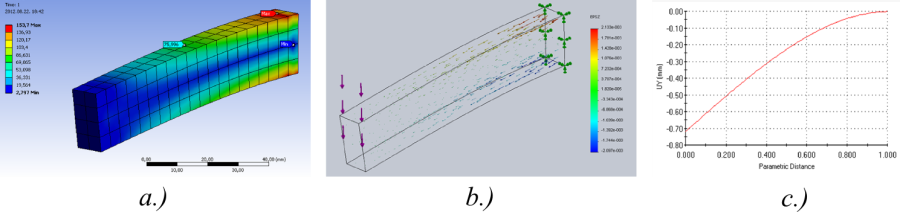
a.) testmodellen színsávok segítségével, b.) a testmodellen vektorok segítségével, c.) diagramon.

2.31. ábra - Az eredmény megjelenítésének lehetséges módjai.

A szilárdtest megjelenítése történhet a deformáció ábrázolásával, ill. a nélkül, valamint a két állapotot együttesen ábrázolva. A deformáció megjelenítés mértéke skálázható, így az esetlegesen kis valós (True scale) deformáció is látványossá tehető annak nagyításával. Természetesen ebben az esetben csak a képi megjelenítés változik, a színsávok értéke továbbra is a valós értéket mutatja. Általában lehetőség van az elemek kontúrjának kirajzolására is a látványosabb megjelenítés érdekében.

a.) deformálatlan drótváz, b.) deformálatlan átlátszó, c.) csak deformált test, d.) háló megjelenítése.

2.32. ábra - Az eredmény megjelenítésének módjai.

A színsávok megjelenítése történhet éles és lágy átmenettel, vagy csak az egyenértékű határvonalak (isolines) kirajzoltatásával a modell felületén. A színsávok nélküli deformált modell ábrázolása is lehetséges.

a.) kontrasztos, b.) "lágy" átmenet, c.) Egyenértékű vonalak, d.) csak a szilárdtest megjelenítése.

2.33. ábra - Egyenértékű színsávok megjelenítési módjai.

A belső helyeken lévő eredmények megtekintése érdekében lehetőség van a modell metszésére sík vágófelületekkel vagy az egyenértékű felületek mentén nyitott vagy zárt formában egyaránt.

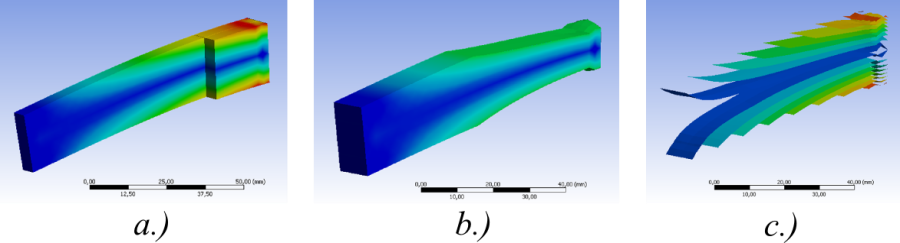
a.) Metszősíkokkal feldarabolt térfogat, b.) egyenértékű felületekkel határolt zárt térfogat, c.) egyenértékű felületek.

2.34. ábra - Metszési módok.

2.9. Ellenőrző kérdések a 2. fejezethez.

Milyen alapvető lépései vannak egy végeselemes analízisnek?
1. Hálókészítés, anyagmodell hozzárendelés, posztprocesszálás, eredmények kiértékelése.
2. Geometria elkészítése, hálózás, anyagmodell hozzárendelés, peremfeltételek és terhelések megadása, megoldás, eredmények kiértékelése.
3. Geometria elkészítése, hálózás, elemek hozzárendelése, terhelőerők definiálása, preprocesszálás, posztprocesszálás.
Hány szabadságfokkal rendelkezik egy 2D-s statikai analízisben használt lineáris háromszögelem?
1. 3,
2. 6,
3. 9,
4. 12.
Hány szabadságfokkal rendelkezik egy hőtani analízisben használt lineáris tetraéder elem?
1. 4,
2. 6,
3. 8,
4. 12.
Milyen típusú analízist alkalmazna egy kivágásokat tartalmazó sík lemez vizsgálatához, ha ismert, hogy a lemezt terhelő erők a lemez síkjában hatnak?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú analízist alkalmazna egy forgásszimmetrikus nyomástartó edény vizsgálatához?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú analízist alkalmazna egy hosszú, állandó keresztmetszetű alkatrész vizsgálatához, ha az alkatrészt a hossza mentén állandó nagyságú és a keresztmetszetével párhuzamos irányú megoszló erő terheli?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú szimulációt alkalmazna egy lemezalkatrész vizsgálatához, ha a lemezt terhelő erők a lemez síkjára merőlegesek?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Az alábbi feltételek melyike okozhatja a szimuláció nemlinearitását? (Több válasz is megjeleölhető.)
1. Nagy deformáció,
2. Változó terhelési feltételek,
3. „Ragasztott” (Bonded) kontaktok,
4. Nemlineáris anyagmodell.
Mi a különbség az ortotróp és izotróp anyagmodell között?
1. Az ortotróp anyag viselkedése nemlineáris, míg az izotrópé igen.
2. Az ortotróp anyag tulajdonságai a derékszögű vagy polár koordinátarendszer tengelyei mentén különbözőek lehetnek, míg az izotrópé minden irányban megegyezik.
3. Az ortotróp anyag tulajdonságai a tetszőleges irányban különbözőek lehetnek, míg az izotrópé csak a Descartes koordináta rendszer tengelyei mentén lehetnek eltérőek.
Lineárisan rugalmas, homogén és izotróp anyag statikus szerkezeti analízise esetén milyen anyagparaméterek megadása szükséges (elégséges)?
1. Rugalmassági modulusz és a sűrűség,
2. Rugalmassági modulusz, a Poisson-tényező és a nyíró modulusz,
3. Rugalmassági modulusz és a Poisson-tényező,
4. Rugalmassági modulusz, a Poisson-tényező és a folyáshatár.
Melyik az HAMIS állítás az alábbiak közül?
1. A Poisson-tényező az anyag összenyomhatóságát jellemzi.
2. A Poisson-tényező a terhelés irányába eső és az arra merőleges alakváltozás különbsége.
3. A Poisson-tényező elméleti értéke – 1 és 0,5 közötti lehet.
Milyen esetekben van szükség az anyag sűrűségének megadására? (Több válasz is megjelölhető.)
1. Statikus szerkezeti analízis esetén ha időben állandó inerciális jellegű terhelés van megadva.
2. Tranziens jelenségek dinamikai szimulációjánál.
3. Modás és harmonikus analízis esetén.
4. Statikus szerkezeti analízis esetén, ha terhelési lépésenként változó erő van megadva.

Megoldások

Milyen alapvető lépései vannak egy végeselemes analízisnek?
1. Hálókészítés, anyagmodell hozzárendelés, posztprocesszálás, eredmények kiértékelése.
2. Geometria elkészítése, hálózás, anyagmodell hozzárendelés, peremfeltételek és terhelések megadása, megoldás, eredmények kiértékelése.
3. Geometria elkészítése, hálózás, elemek hozzárendelése, terhelőerők definiálása, preprocesszálás, posztprocesszálás.
Hány szabadságfokkal rendelkezik egy 2D-s statikai analízisben használt lineáris háromszögelem?
1. 3,
2. 6,
3. 9,
4. 12.
Hány szabadságfokkal rendelkezik egy hőtani analízisben használt lineáris tetraéder elem?
1. 4,
2. 6,
3. 8,
4. 12.
Milyen típusú analízist alkalmazna egy kivágásokat tartalmazó sík lemez vizsgálatához, ha ismert, hogy a lemezt terhelő erők a lemez síkjában hatnak?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú analízist alkalmazna egy forgásszimmetrikus nyomástartó edény vizsgálatához?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú analízist alkalmazna egy hosszú, állandó keresztmetszetű alkatrész vizsgálatához, ha az alkatrészt a hossza mentén állandó nagyságú és a keresztmetszetével párhuzamos irányú megoszló erő terheli?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Milyen típusú szimulációt alkalmazna egy lemezalkatrész vizsgálatához, ha a lemezt terhelő erők a lemez síkjára merőlegesek?
1. 2D – Sík alakváltozás,
2. 2D – Sík feszültség,
3. 2D – tengelyszimmetrikus,
4. 3D – héj modell,
5. 3D – testmodell.
Az alábbi feltételek melyike okozhatja a szimuláció nemlinearitását? (Több válasz is megjeleölhető.)
1. Nagy deformáció,
2. Változó terhelési feltételek,
3. „Ragasztott” (Bonded) kontaktok,
4. Nemlineáris anyagmodell.
Mi a különbség az ortotróp és izotróp anyagmodell között?
1. Az ortotróp anyag viselkedése nemlineáris, míg az izotrópé igen.
2. Az ortotróp anyag tulajdonságai a derékszögű vagy polár koordinátarendszer tengelyei mentén különbözőek lehetnek, míg az izotrópé minden irányban megegyezik.
3. Az ortotróp anyag tulajdonságai a tetszőleges irányban különbözőek lehetnek, míg az izotrópé csak a Descartes koordináta rendszer tengelyei mentén lehetnek eltérőek.
Lineárisan rugalmas, homogén és izotróp anyag statikus szerkezeti analízise esetén milyen anyagparaméterek megadása szükséges (elégséges)?
1. Rugalmassági modulusz és a sűrűség,
2. Rugalmassági modulusz, a Poisson-tényező és a nyíró modulusz,
3. Rugalmassági modulusz és a Poisson-tényező,
4. Rugalmassági modulusz, a Poisson-tényező és a folyáshatár.
Melyik az HAMIS állítás az alábbiak közül?
1. A Poisson-tényező az anyag összenyomhatóságát jellemzi.
2. A Poisson-tényező a terhelés irányába eső és az arra merőleges alakváltozás különbsége.
3. A Poisson-tényező elméleti értéke – 1 és 0,5 közötti lehet.
Milyen esetekben van szükség az anyag sűrűségének megadására? (Több válasz is megjelölhető.)
1. Statikus szerkezeti analízis esetén ha időben állandó inerciális jellegű terhelés van megadva.
2. Tranziens jelenségek dinamikai szimulációjánál.
3. Modás és harmonikus analízis esetén.
4. Statikus szerkezeti analízis esetén, ha terhelési lépésenként változó erő van megadva.

3. fejezet - Lineáris statikai analízis

Tartalom

3.1. Áttekintés

3.1.1. Lineáris analízis
3.1.2. A statikai analízis esetében alkalmazható anyagmodellek
3.1.3. Alkalatrész viselkedés
3.1.4. Hálózás
3.1.5. A szimuláció fontosabb beállításai
3.1.6. Peremfeltételek / Kinematikai kényszerek
3.1.7. A statikai analízisben alkalmazható terhelések
3.1.8. Az eredmény bemutatása

3.2. Gyakorlat: Befalazott tartó lehajlása

3.2.1. A mintafeladat analitikus megoldása
3.2.2. Numerikus megoldás ANSYS Workbench-ben
3.2.3. Egyszerű statikai analízis SolidWorksben
3.2.4. Az analitikus és numerikus megoldások összehasonlítása

3.3. Alkalmazási példa: Erőmérő cella statikai analízise

3.3.1. Modellezés
3.3.2. Anyagmodell hozzárendelés
3.3.3. Hálózás
3.3.4. Megtámasztás és terhelés hozzárendelése
3.3.5. Futtatás és az eredmények lekérdezése

3.4. Ellenőrző feladatok

3.4.1. Feladat
3.4.2. Feladat

3.1. Áttekintés

A statikai analízis az egyensúlyi terhelés hatására kialakuló állandósult feszültség, alakváltozás, elmozdulás és a reakcióerők meghatározására szolgál. A terhelések és a válaszreakció tehát időben állandó, vagy az idő függvényében csak lassan változó lehet. Figyelmen kívül hagyja a tehetetlenséget és csillapítást, vagyis az időfüggő terheléseket okozó elemeket. Ugyanakkor legtöbbször lehetőség van időben állandó inerciális terhelések megadására, mint a szögsebesség, vagy a gyorsulás.

3.1.1. Lineáris analízis

A statikai analízis az alkalmazott anyagtól, geometriától és peremfeltételektől függően lehet lineáris, vagy nemlineáris. A lineáris analízisnél azzal a feltevéssel élünk, hogy a vizsgált testre ható erő és a hatására létrejött deformáció közötti kapcsolat lineáris. Például a terhelő erő mértékének megkétszerezése a modell válaszának (deformáció, fajlagos nyúlás, feszültség) szintén kétszeres növekedését eredményezi. Ehhez az alábbiaknak kell teljesülni:

a létrejött deformáció elég kicsi ahhoz, hogy a terhelés hatására létrejövő merevségváltozás elhanyagolható legyen.
a modell deformációja alatt a peremfeltételek nem változnak, a terhelés nagysága, eloszlása és iránya állandó marad.
az anyagmodellt a Hooke törvény írja le, vagyis a feszültség és a fajlagos nyúlás közötti kapcsolat lineáris, (egytengelyű feszültségi állapot esetén E a rugalmassági (Young) modulus az arányossági tényező, σ=E⋅ε). Számos anyagra jellemző a lineáris viselkedés kis alakváltozásoknál, és csak nagyobb alakváltozás után válik nemlineárissá (pl. fémek).

3.1.2. A statikai analízis esetében alkalmazható anyagmodellek

Az anyagmodell ebben az esetben lineáris, mely lehet izotróp, ortotróp, vagy anizotróp, ill. hőmérséklet független, vagy hőmérsékletfüggő.

Az anyagmodelt a merevség (rugalmassági modulus és a Poisson-tényző, vagy nyírási modulus, stb.) definiálásával adhatjuk meg. Időben állandó inerciális terhelések alkalmazása esetén a sűrűség definiálása is szükséges.

3.1.3. Alkalatrész viselkedés

Inerciális terhelések alkalmazásakor általában lehetőség van pontszerű tömeg alkalmazására, melynek nemcsak a tömegét, de a különböző tengelyekre vonatkozó tehetetlenségi nyomatékát is megadhatjuk.

A geometriai modellben szereplő testek, alkatrészek viselkedése lehet rugalmas (elastic), vagy merev (Rigid). Merev test esetén az alkatrész nem szenved deformációt csak elmozdul és az erőket közvetíti. A statikai analízisben csak inerciális terheléseket lehet rá érvényesíteni.

Nagy bonyolultságú összetett geometria esetén a nagy elemszám miatt a számolási idő csökkentése érdekében célszerű egyszerűsítéseket alkalmazni, (pl. a szimmetriafeltételeket, 2d-s, vagy héjmodelleket).

3.1.4. Hálózás

Fontos a megfelelő elemméret beállítása. Abban az esetben, ha a feszültségre, vagy a fajlagos nyúlásra, vagyunk kíváncsiak, viszonylag finomabb háló szükséges, mint az elmozdulások vizsgálatakor. Célszerű a háló helyi finomítása feszültséggyűjtő helyek környezetében (pl. belső sarkok, lekerekítések, vagy érintkezési, támasztási, vagy erőbevezetési helyek közelében), amennyiben fontos az itt ébredő feszültségek, alakváltozások ismerete.

3.1.5. A szimuláció fontosabb beállításai

Nagy lehajlások (Large Deflection) bekapcsolása nemlineáris szimulációt eredményez. Kis elmozdulás esetén nem szükséges az alkalmazása. Kis elmozdulást akkor feltételezhetünk, ha a fajlagos nyúlás elég kicsi ahhoz, hogy az eredő merevség ne változzon jelentősen.

Időlépések (Time Steps) - Statikai feladatnál nincs valós időlépés, az csupán a terhelés növekményét meghatározó paraméter. Beállításával lehet a terhelést fokozatosan ráadni a szerkezetre, a konvergencia biztosítása érdekében. Ennek főleg a nemlineáris feladatmegoldásnál van szerepe. De több lépésre akkor is szükség lehet, ha lépésenként különböző terhelési állapotot akarunk beállítani, pl. előfeszítés beállítása, elmozduláskényszer bekapcsolása / kikapcsolása, stb.

Kezdeti feltételek nem alkalmazhatók a statikai analízisben.

3.1.6. Peremfeltételek / Kinematikai kényszerek

A geometriai modell egyes elemeinek szabadságfokát befolyásoló peremfeltételek lehetnek statikus (megkötő), valamint passzív (pl. pálya mentén korlátozó) és aktív (elmozdulást kényszerítő) kinematikai kényszerek.

A kinematikai kényszerrel, vagy terheléssel ellátott pont, vagy vonal (3D-s analízis esetén) nem egy valós mechanikai eset, és szinguláris feszültséghez vezet. A rögzített pont/vonal közelében a feszültség végtelenhez közelít, ezért annak kis környezetében a feszültséget és az alakváltozás értékét figyelmen kívül kell hagyni.

A megfogás (Fix Support) statikus kényszer, melyet érvényesíthetünk felületeken, éleken és pontokon egyaránt. A kényszer az adott elem minden szabadságfokát megköti.
Elmozdulás (Displacement) segítségével kényszeríthetünk rá felületekre, élekre, vagy pontokra egy állandó, vagy időben változó elmozdulásokat egy, vagy több koordinátatengely mentén. Az elmozdulás lehet valamilyen konstans, időben változó, vagy 0 értékű, ill. szabad. Az elmozdulás során a kijelölt geometriai elem megtartja az alakját.
Külpontos elmozdulás (Remote Displacement) segítségével valamilyen geometriai elem elmozdulását és/vagy elfordulását adhatjuk meg. egy a térben tetszőlegesen megválasztott ponthoz viszonyítva.
Súrlódásmentes felület (Frictionless Face) kényszer megakadályozza a felület normális irányában történő mozgását. A felületi normálisra merőleges irányban (tehát a felület tangenciális irányában) az elmozdulás és az elfordulás kötetlen. Egy test sík felületére érvényesített súrlódásmentes kényszer egyenértékű a szimmetriafeltétellel.
Csak nyomás (Compression only) kényszer normálirányú az adott felületelemre.
Hengeres (Cylindrical Support) kényszerrel egy hengeres felület mozgását, ill. deformációját engedhetjük, vagy köthetjük meg axiális, radiális, vagy tangenciális irányban.
Egyszerű él kényszer (Simply Supported Edge) a kijelölt vonalszakasz minden irányú elmozdulását gátolja, csak az él (mint forgástengely) körüli elfordulást enged. Csak 3D-s felület, vagy rúdmodell esetén alkalmazható.
Egyszerű pont kényszer (Simply Supported Vertex) a kijelölt pont minden irányú elmozdulását gátolja, csak a pont körüli minden irányú elfordulást enged. Csak 3D-s felület, vagy rúdmodell esetén alkalmazható.
Kötött elfordulás (Fixed Rotation) kényszerrel egy felületmodell valamely felület, él, vagy pont elemének elfordulását akadályozhatjuk meg egy választott koordinátatengely körül. Az elmozdulás minden irányban szabad marad.
Rugalmas kényszer (Elastic Support) felületek, vagy élek elmozdulását, vagy deformációját engedi rugalmas támasz mellett.

3.1.7. A statikai analízisben alkalmazható terhelések

A statikai analízisben minden szerkezeti kényszer, szerkezeti és inerciális terhelés alkalmazható:

Külsőleg alkalmazott erő, vagy nyomás,
Időben állandó inerciális terheléseket (mint pl. a gyorsulás, vagy a szögsebesség),
Hőmérséklet (a hőtágulás számításához).

A terhelések és kényszerek a terhelési lépések függvényében változhatnak.

3.1.8. Az eredmény bemutatása

Az eredményeket megkaphatjuk grafikusan ábrázolva a geometriai modellen, animálva, vagy diagramon. Lekérdezhetjük a minimum - maximum helyeket és tetszőleges helyen a kiszámolt értéket. Metszeteket készíthetünk síkok, vagy szintfelületek mentén. Változtathatjuk az ábrázolt deformáció mértékét és az eredmény értékeléséhez használt színskála beosztását.

A lekérdezett mennyiségek statikai analízis esetén az alábbiak lehetnek:

Elmozdulás (Deformation) – a test egyes pontjainak elmozdulása, mely lehet teljes (Total) , vagy irány menti (Directional) . Egy adott pont teljes elmozdulása nem más, mint a pont kezdeti és végső helyzetének abszolút távolsága. Az irány menti elmozdulás az elmozdulásvektor adott koordináta-tengelyre eső vetületének hossza. Az irány menti elmozdulás lekérdezésekor tehát ki kell választanunk, hogy melyik koordinátarendszer, melyik tengelye mentén akarjuk lekérdezni. Általában lehetőség van polár koordináta rendszer használatára, ez esetben a tangenciális irányú elmozdulások is lekérdezhetőek, melyből kis deformáció esetén az elfordulás is számolható.
Reakcióerő (Reaction Force) – a megtámasztásoknál, rögzítéseknél illetve a kinematikai kénszereknél fellépő ellenerő. Lekérdezhető a teljes erő nagysága, vagy az egyes koordináta tengelyek menti komponensei.
Feszültség (Stress) – a szerkezetben ható fajlagos erő. Általában lehetőségünk van az egyenértékű (von Mises féle), a 3 főfeszültség, a feszültségintenzitás, illetve a kiválasztott koordináta-tengely mentén a normál és nyíró feszültségek lekérdezésére.
Fajlagos nyúlás (Strain) – az anyagban egymástól egységnyi távolságra lévő pontok távolságának változása. A feszültséghez hasonlóan, általában lehetőségünk van az egyenértékű és a 3 főnyúlás, illetve a kiválasztott koordináta-tengely mentén a normál és nyíró alakváltozások továbbá a teljes alakváltozási energia és az alakváltozási energia sűrűség lekérdezésére.

A megjelenített feszültség és fajlagos nyúlás a „valós” és nem pedig a „mérnöki” értéket mutatja!

További lehetőségek állnak rendelkezésünkre a szerkezet vizsgálatához, mint pl. az érintkező felületek kontakt analízise, tönkremeneteli kritériumok vizsgálata, ill. a biztonsági tényező megállapítása, alakoptimálás a szerkezet kihasználtsága alapján, stb.

3.2. Gyakorlat: Befalazott tartó lehajlása

A következőekben egy egyszerű statikai analízist fogunk bemutatni, az egyik oldalán befalazott konzolos tartó példáján keresztül.

3.2.1. A mintafeladat analitikus megoldása

A végeselemes programok eredményének ellenőrzéseként oldjunk meg egy egyszerű mechanikai esetet az elemi szilárdságtan módszereivel. Kiindulásnak adva van egy, az egyik oldalán befogott tartó melynek másik végét függőlegesen ható erővel terheljük.

Az alábbi paraméterek adottak:

A hasáb méretei – hossza: L=100mm, magassága: h = 20 mm, szélessége: b = 10 mm;

Anyaga – alumínium, Rugalmassági modulus: E = 71 GPa, Poisson-tényező: ν = 0,33;

Terhelőerő: F = 1000 N.

Vizsgáljuk meg a hajlított hasáb szélső szálaiban ébredő feszültséget, fajlagos nyúlást és a rúd lehajlását.

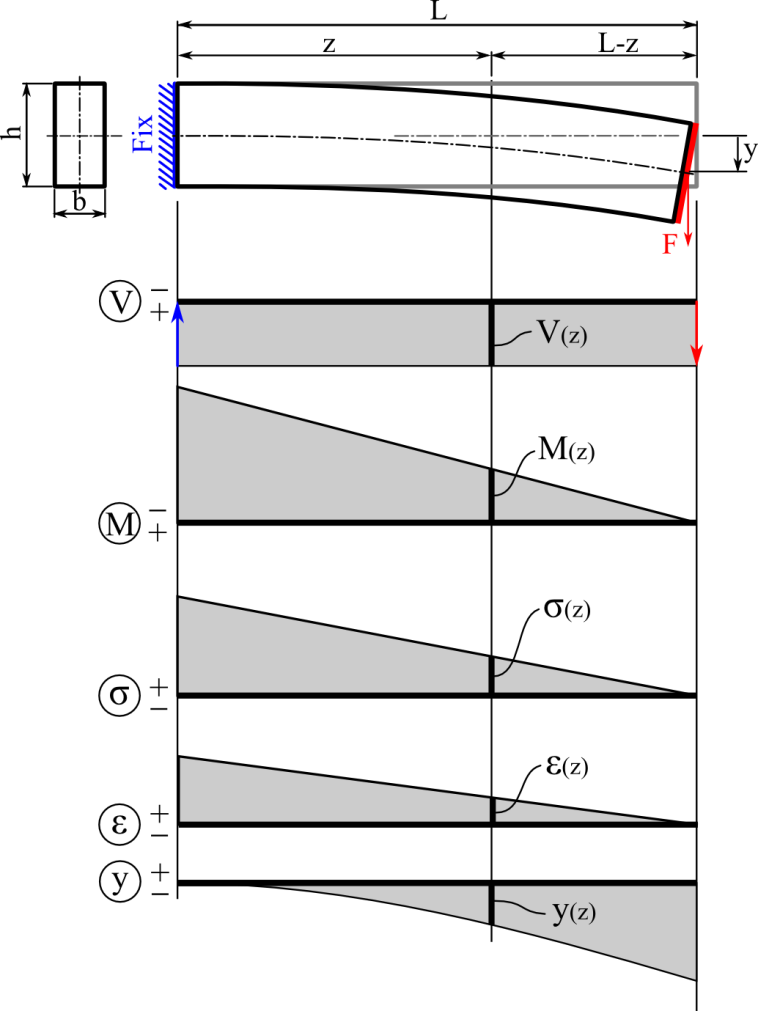
3.1. ábra - Egy oldalán befogott rúd igénybevétele.

A rudat terhelő erő hatására a befogástól számított z távolságú helyen M(z) = F ·(L-z) nyomaték hat. Ennek hatására a külső szálakban σ = M(z)/K= F ·(L-z)/K normál feszültség és lineáris anyagmodellt feltétételezve, ε=σ/E=F ·(L-z)/K·E fajlagos nyúlás ébred.

Ahol:

I – a keresztmetszeti tényező, (téglalap esetén I = b·h ³ /12),

K – a keresztmetszeti tényező, (K = 2I/h = b·h ² /6),

E – az anyag rugalmassági modulusa.

A lehajlás egyenletét a rugalmas szál differenciál egyenletéből számoljuk ki.

(3.1)

Az egyenletet z szerint kétszer integrálva kapjuk a lehajlásfüggvényt,

(3.2)

Mivel a befogás zérus elfordulás és elmozdulás peremfeltételeket jelent, ezért a C1 és C2 értéke szintén nulla. Így a lehajlás függvénye a következő alakban írható le:

(3.3)

[25.] .

✎ A fenti egyenletek alapján rajzoltassuk ki diagramban a hasáb szélső szálaiban ébredő feszültséget, fajlagos nyúlást és a rúd lehajlását. Hasonlítsuk össze a végeselemes programok eredményeivel.

A fent bemutatott feladat numerikus megoldására az ANSYS Workbench végeselem programot és a SolidWorks CAD program beépített FEM modulját fogjuk használni.

3.2.2. Numerikus megoldás ANSYS Workbench-ben

Elsőként nézzük az ANSYS Workbench használatát. A program megnyitásakor egy üres projekt felületet találunk magunk előtt, amelybe a bal oldali Toolbox paneljeiről húzhatjuk be a kívánt elemet. Egy statikai analízis indításához először a geometriát kell létrehoznunk. Ezt közvetlenül a kívánt analízis behúzásával is elérhetjük, de lehetőség van különálló geometria panel létrehozására, amely a későbbiekben tetszés szerint felhasználható további szimulációk bemeneteként. Ez utóbbit, a különálló geometriát a Toolbox / Component systems / Geometry elemének a behúzásával érhetjük el (3.2. ábra). A behúzott panel második sorára ( Geometry ) jobb gombbal kattintva, a helyi menü New Geometry… sorára bal gombbal kattintva nyithatjuk meg a geometria létrehozására szolgáló Design Modeller modult. Amint a jobb gombos menüben látható, lehetőség van számos köztes, vagy natív CAD formátumú geometria importálására is (ezt egy későbbi példánkon mutatjuk be).

3.2. ábra - Geometria létrehozása.

A geometriaszerkesztő modul elindulásakor megjelenik a mértékegység kiválasztó párbeszédablak. Válasszuk ki a megfelelő, esetünkben „ Millimeter ” mértékegységet, és kattintsunk az OK gombra (3.3. ábra). Amennyiben nem szeretnénk, hogy a későbbiekben megjelenjen ez a kérdés, értelem szerűen pipáljuk be az alsó négyzetek valamelyikét. Amennyiben a későbbiekben változtatni szeretnénk a mértékegységet, abban az esetben a Design Modeller felső menüsorában a Tools / Options / Design Modeller / Units / Length Units helyen tudjuk megtenni, vagy „use project unit” választása esetén, a Projekt felület felső menüsorában lévő Unit menüpont alatt beállított mértékegységet fogja használni.

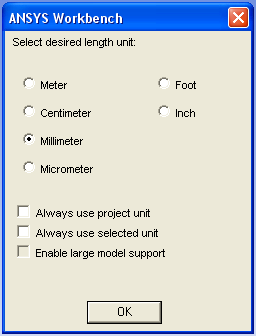
3.3. ábra - Mértékegység kiválasztása.

Az új geometria létrehozását célszerű a munkasík kiválasztásával kezdeni. Ezt legegyszerűbben a modellfában ( Tree Outline ) tehetjük meg, a megfelelő sík kijelölésével. Jelöljük ki az XY -síkot ( XYPlane ). A munkatérben a kijelölt síkon fekvő koordináta tengelyek vastag szaggatott vonallal jelennek meg, ami azt jelzi, hogy a vázlat rajzolásakor ezt, mint referenciát használhatjuk, vagyis ezekhez lehet kényszereket és mérethálót definiálni (3.4. ábra). (Ehhez hasonlóan a testmodell kijelölt felületének vastag szaggatott vonallal megjelenő határoló élei, vagy a láthatóvá tett korábbi vázlatok ugyanúgy referenciaként viselkednek).

Miután kijelöltük a megfelelő munkasíkot, a New Sketch ikonra kattintva hozhatunk létre új vázlatot (3.4. ábra). Ekkor a modellfa XYPlane eleme alatt megjelenik a vázlat neve. A későbbiekben minden egyes új vázlat létrehozásakor érdemes itt ellenőrizni, hogy az a megfelelő síkon jött-e létre. (Ugyanis ha úgy rajzolunk, hogy előzőleg egy már meglévő vázlat volt kijelölve, akkor azt fogjuk szerkeszteni és nem pedig újat létrehozni.)

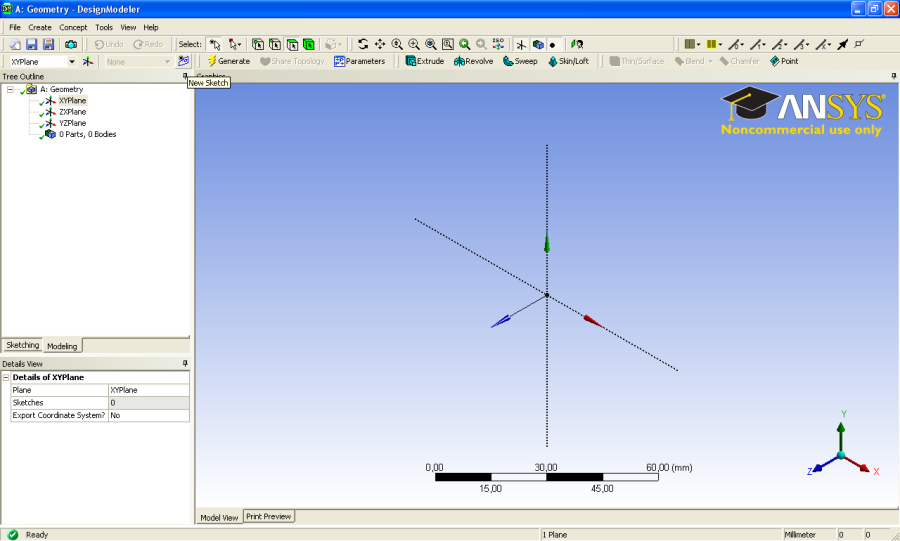
3.4. ábra - Vázlatsík kijelölése és új vázlat létrehozása.

A vázlat rajzolásához szükséges rajzeszközöket ( Sketching Toolboxes ) a modellfa alatt lévő Scetching fül kiválasztásával érjük el, amely további öt csoportra van osztva a jobb kezelhetőség érdekében (3.5. ábra). A legfelső rajz-panel ( Draw ) alatt találhatjuk a rendelkezésre álló rajzelemeket. A rajzelemek létrehozása a megfelelő ikonra/sorra való kattintással indítható, majd az ikonokon pirossal jelzett pontok lerakásával hozható létre. A folyamatot lépésről-lépésre vezetik az alsó állapotsorban megjelenő információk. Kattintsunk a téglalap ( Rectangle ) ikonra, majd a két átellenes sarokpont lerakásával helyezzük el a munkasíkunkon. (A sarokpontok lerakása történhet két bal egérgomb kattintással az 1. és 2. sarokpont helyeknél, vagy az egér húzása lenyomott bal egérgombbal majd felengedése a 2. sarokpontnál.). Helyezzük el úgy, hogy az origó a téglalap belsejében legyen. A pontos elhelyezésre nem kell ügyelni, mert azt a következő lépésekben kényszerekkel és méretezéssel oldjuk meg. A sarokpontok utólagos mozgatását a Modify / Drag parancs segítségével tehetjük meg. (A mozgatás csak a meg nem kötött szabadságfokok irányában lehetséges.)

A kényelmesebb munka érdekében forgassuk be a rajzsíkot a képernyő síkjába a jobb alsó sarokban lévő koordinátarendszer Z tengelyére való kattintással. (A főnézetek beállításához mindig a beforgatandó sík normálisának megfelelő tengelyre kell kattintani. Ha adott esetben valamelyik negatív tengelyre lenne szükségünk, akkor az megjelenik amint fölé visszük az egérkurzort. Isometrikus nézet beállításához a koordinátatengelyek közötti golyóra kell kattintani.)

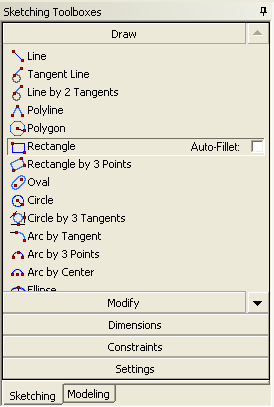
3.5. ábra - Vázlatrajzolás.

A rajzelemek lerakása után célszerű a kényszerek megadásával folytatni, hogy minél kevesebb méret definiálására legyen szükség. Esetünkben célszerű szimmetrikussá tenni a vázlatot a Constrains/Symmetry parancs kiadásával (3.6. ábra). Az elemek kiadásának sorrendjét ebben az esetben is nyomon követhetjük az alsó állapotsoron, (Szimmetriatengely; 1. él, vagy pont; 2. él, vagy pont). Adjuk meg a vízszintes vonalak szimmetriáját. Ezután a szimmetriatengelyre történő újbóli rákattintással szüntessük meg a kijelölését és jelöljük ki a függőleges tengelyvonalat a függőleges vonalak kényszerezéséhez. Az Esc billentyű segítségével lépjünk ki a parancsból, (a parancs nem szakad meg automatikusan, mivel több elempárost is hozzárendelhetnénk az elsőnek kijelölt szimmetriatengelyhez). A létrehozott kényszerek sajnos nem jelennek meg a rajzterületen így körülményesebb a szerkesztésük, vagy eltávolításuk. Egy rajzelemhez tartozó kényszerek a modellfa alatt lévő Details Wiew panelen láthatóak, amikor az adott rajzelem ki van jelölve.

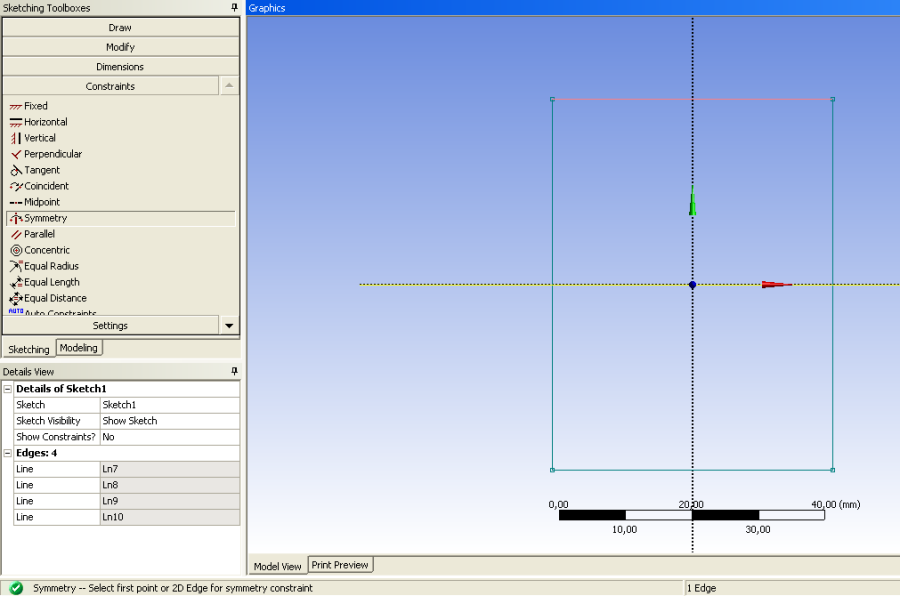
3.6. ábra - Szimmetria kényszer definiálása.

A vázlatrajzolás befejezéseként határozzuk meg a téglalap méreteit a Dimensions / General parancs segítségével (3.7. ábra). A General parancs segítségével automatikusan tudunk méretezni különböző típusú és állású rajzelemeket. Viszont a rajzelemek kijelölésének módja eltérő a specifikus méretező parancsokétól. Például vonalszakaszra történő kattintással csak az adott szakasz hosszát tudjuk méretezni, nem tudjuk két párhuzamos közötti távolságot definiálni, mert a második kattintás a méretvonal elhelyezését eredményezi. Ezzel szemben egy specifikus pl. a vízszintes ( Horizontal ) parancs kiadásával két függőleges szakasz kijelölhető és a 3. kattintással helyezzük el a méretvonalat. Adjuk ki a parancsot és jelöljük ki a felső vízszintes szakaszt, majd második kattintással helyezzük el a méretvonalat. A függőleges méret megadásánál használjuk a sarokpontokat referenciának. Ha nem léptünk ki a parancsot nem kell újra kiadni, csak kattintsunk először a bal felső, majd a bal alsó sarokpontra, majd a méretvonal helyén. Ha olyan rajzelemet méreteznénk, amely már definiálva van valamilyen kényszer, vagy méret által, akkor egy hibaüzenet ugrik fel, jelezve a túlhatározottságot. A hibaüzenet OK -ra kattintva eltűnik, de folytatódik a méretezés folyamata, ami a jobb gombos menü Cancel parancsával szakítható meg. A méretek megadása utólag történik, baloldalon a modellfa alatt lévő Details Wiew panelen. Adjunk meg vízszintes méretnek ( H1 ) 10 mm-t és függőleges méretnek ( V1 ) 20 mm-t.

Érdemes megfigyelni, hogy a rajzelemek színe, hogyan változik a szabadságfokuk függvényében. Az alulkényszerezett rajzelemek színe zöldeskék, a teljesen meghatározott rajzelemeké kék, és a túlhatározottaké piros színű. Ez segít a kényszerek és méretek definiálásánál.

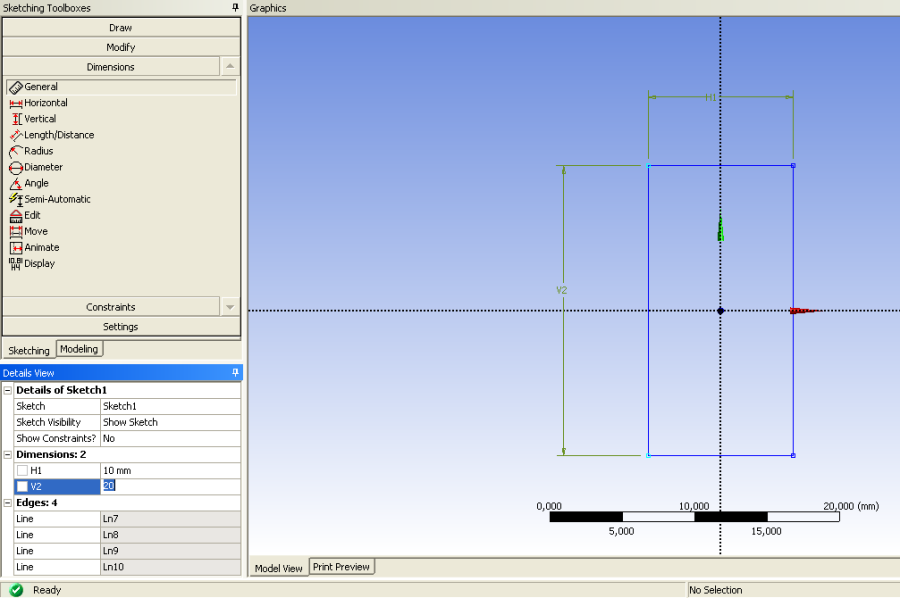
3.7. ábra - Vázlat méretezése.

A vázlat befejezése után kiadhatjuk a 3D-s testmodellt létrehozó kihúzás ( Extrude ) parancsot a felső menüsorból. A kihúzás paramétereit a Details Wiew panelen állíthatjuk be. Állítsuk be a kihúzás hosszát ( Depth ) 100 mm-re (3.8. ábra).

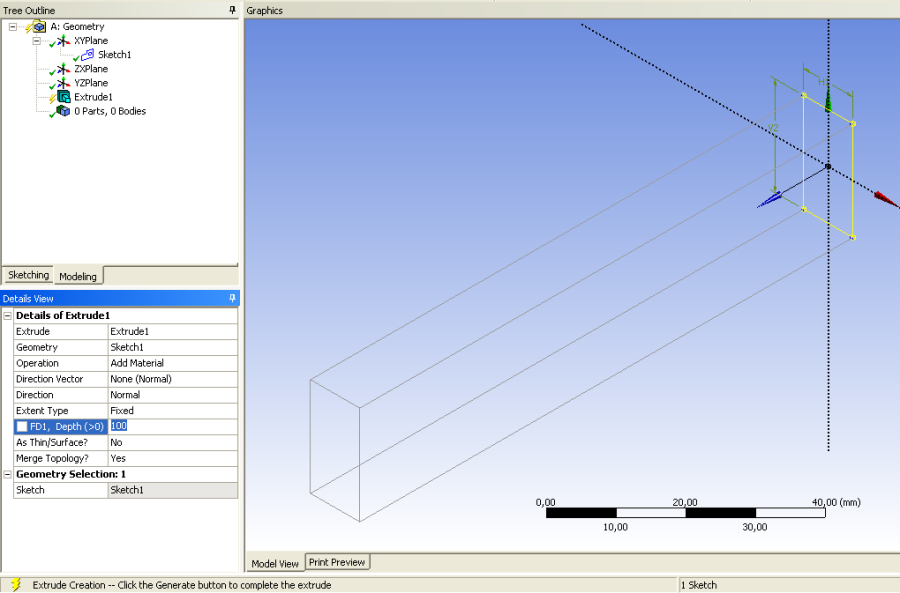
3.8. ábra - A kihúzás paramétereinek beállítása.

A kihúzást a Generate gomb segítségével hajthatjuk végre, minek eredményeként az addig drótháló megjelenítésű téglatest szilárdtest megjelenítést kap (3.9. ábra).

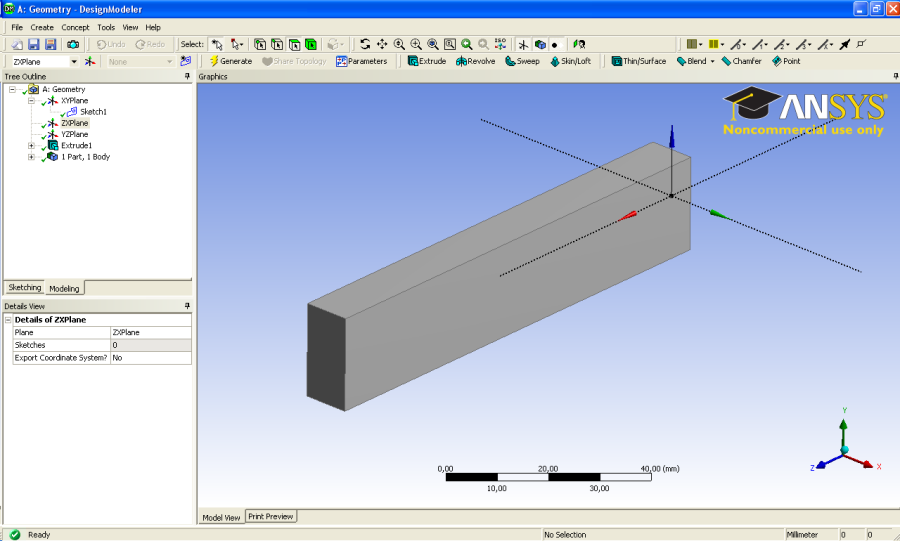
3.9. ábra - A kihúzás végrehajtása.

A kihúzás végrehajtása után visszatérhetünk a modellfához ( Tree Outline ) a rajzeszközök ( Sketching Boxes ) alatti Modeling fül kiválasztásával. A modellfa alján látható elem mutatja, hogy az aktuális modellünkben hány alkatrész és hány testmodell van. Ha helyesen jártunk el, esetünkben itt 1-1 látható.

Ezzel befejeztük a geometria modellezését. Lépjünk vissza a Projekt felületre, hogy hozzárendelhessük a megfelelő szimulációt. A választható szimulációk a bal oldali Toolbox / Analysis Systems paneljén találhatóak. Válaszuk ki a statikai ( Static Structural ) analízist és húzzuk be a geometria panelje mellé jobb oldalra. A geometria panel Geometry feliratú (második) sorát lenyomott bal egérgombbal húzzuk rá a szimulációs panel szintén Geometry feliratú sorára, aminek hatására a két sort egy görbe fogja összekötni (az analízist, behúzáskor a geometriára ráhúzva azonnal létrejön a kapcsolat). Ezzel a művelettel a szimuláció bemeneteként állítottuk be az előzőleg létrehozott geometriát. (Ezentúl a geometria bárminemű módosítása, a felső ikonsoron lévő projektfrissítés ( Refresh Project ) parancs hatására, érvényesül a szimulációban is.)

A geometriát követően az egyik legfontosabb lépés az anyagi viselkedés modellezése, melyet a mérnöki adatokat tartalmazó ( Engineering Data ) felületen találunk meg. A szimuláció paneljének második sorára, az Engineering Data -ra jobb gombbal kattintva az Edit menüpont kiválasztásával jutunk az anyagmodelleket tartalmazó felületre (3.10. ábra).

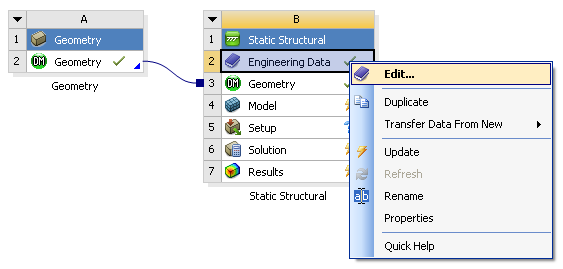
3.10. ábra - Szimuláció kiválasztása.

A bal oldali Toolboxban most a különböző anyagi viselkedéseket leíró modellek alapválasztéka található. Ezeket hozzárendelve és felparaméterezve hozhatunk létre új anyagmodellt. Az ANSYS szép számmal tartalmaz előre definiált anyagmodelleket, melyek az Engineering Data Sources panelen (a középső oszlop felső panelje) látható könyvtárakban találhatóak. Az anyagkönyvtárat a felső ikonsor jobb oldalán lévő könyveket ábrázoló ikon segítségével kapcsolhatunk be. Az itt kiválasztott könyvtár tartalma az alatta lévő Outline of … Materials panelen látható, melyben már az egyes anyagok között válogathatunk. Amennyiben egy itt szereplő anyagot hozzá akarunk rendelni a szimulációhoz, akkor az anyag neve mellett lévő + jelre kell kattintani. Ennek hatására a + jel melletti cellában megjelenik egy kis kék könyv ikon, ami annak a jele, hogy az anyag bekerült az Engineering Data könyvtárba. A kiválasztott anyag tulajdonságait a legalsó Properties of Outline … panelen láthatjuk. Itt az egyes sorok az egyes anyagi viselkedést leíró modellek, amelyeket a Toolbox-ból tudunk hozzárendelni. A kijelölt tulajdonság paraméterei a jobb oldalon található Table of Properties… és Chart of Properties … paneleken jelennek meg.

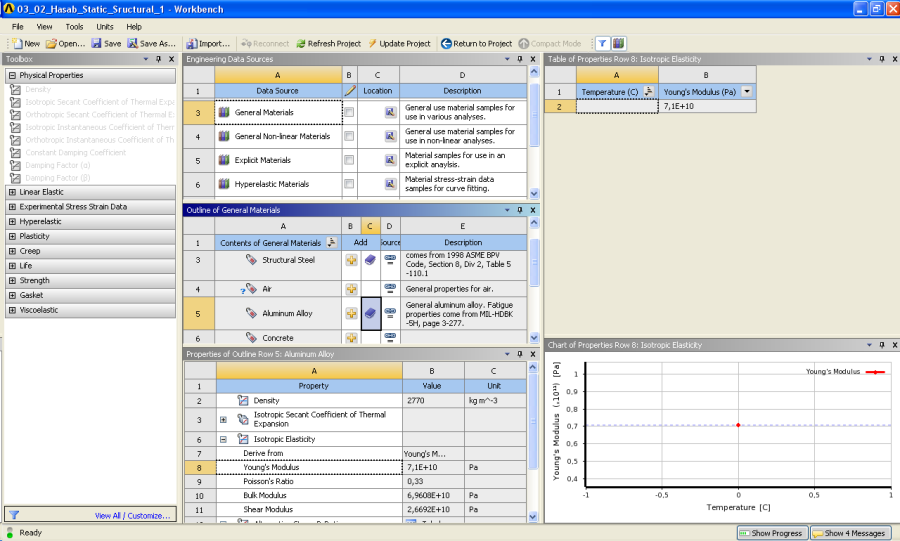
3.11. ábra - Engineering Data.

Saját magunk is létrehozhatunk anyagmodelleket a Toolboxban lévő tulajdonságok segítségével. Új anyag létrehozásához a felső ikonsor jobb oldalán lévő könyveket ábrázoló ikon segítségével ki kell kapcsolnunk az anyagkönyvtárakat (3.12. ábra). Amint kikapcsoljuk, láthatóvá válik a saját anyagkönyvtárunk tartalma, ami alapesetben a Structural Steel nevű anyag. Az alatta levő cellába kattintva hozhatunk létre új anyagot a neve beírásával („Aluminium”).

Mivel még nem definiáltunk semmilyen tulajdonságát, egy kérdőjel jelenik meg a neve mellett, ami azt jelzi, hogy hiányosak az adatok. Egy statikai analízishez, (lineárisan rugalmas, izotróp és homogén anyagmodell esetén) két paraméter, a rugalmassági modulus és a Poisson-tényező megadása elégséges. Ehhez kattintsunk duplán a Toolbox / Linear Elastic / Isotropyc Elasticity elemére, aminek hatására a Properties panelen megjelennek az anyagtulajdonságok. A sárga mezők jelzik a hiányzó paramétereket. Állítsuk át a rugalmassági modulus mértékegységet MPa-ra és adjunk meg 71 000 MPa-t (3.12. ábra). A Poisson-tényező értékét válasszuk 0,33-ra. Ezzel az anyamodellünket definiáltuk, a projektfelületre való visszatéréshez kattintsunk a Return to Project gombra.

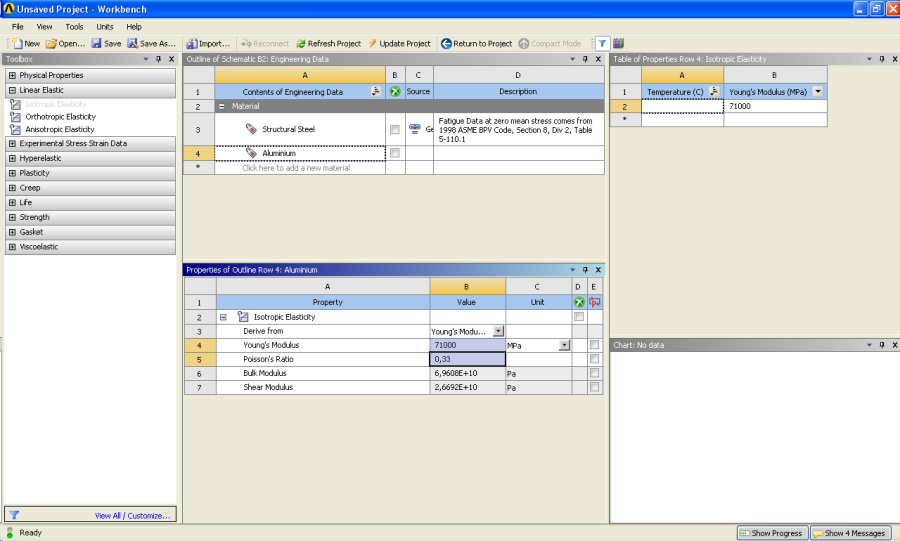
3.12. ábra - Anyagparaméterek megadása.

Miután visszatértünk a projekt felületre, a szimuláció paneljének Model sorára való jobbgombos kattintással, aztán az Edit menüpont kiválasztásával juthatunk a szimulációs felületre. (A további, 5.-7. sorok szerkesztése is a szimulációs felületre vezet.)

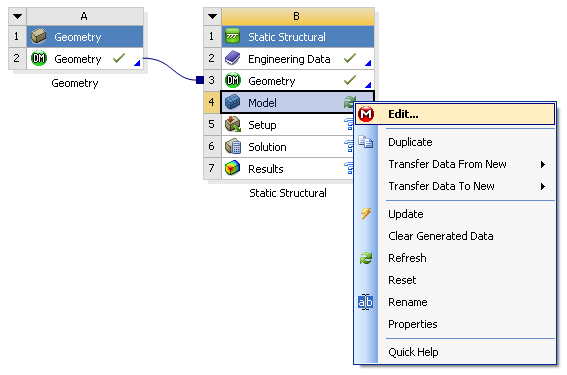
3.13. ábra - A szimulációs környezet megnyitása.

A szimulációs ablak munkaterében látható a létrehozott geometria, a bal oldalon az Outline és a Details panelek láthatóak egymás alatt. Az Outline ablakban a geometria modellfájához hasonlóan jelennek meg a szimulációban lévő geometriai modellek, peremfeltételek, hálózás, a beállítások és a lekérdező parancsok. A panel alatt lévő Details panelen jelennek meg az Outline -ban kiválasztott elem tulajdonságai, beállításai és paraméterei.

Jelöljük ki az Outline ablakban a Model / Geometry / Solid elemet és nézzük meg a Details panelen megjelenő tulajdonságait. A Material / Assigment mellett található az adott alkatrészhez hozzárendelt anyag, ami alapértelmezetten egy szerkezeti acél ( Structural Steel ). Az anyag neve melletti háromszögre kattintva, a legördülő menüből választhatjuk ki az Engineering Data könyvtárban lévő anyagaink valamelyikét. Válasszuk ki az előzőleg létrehozott Aluminium elnevezésű anyagot.

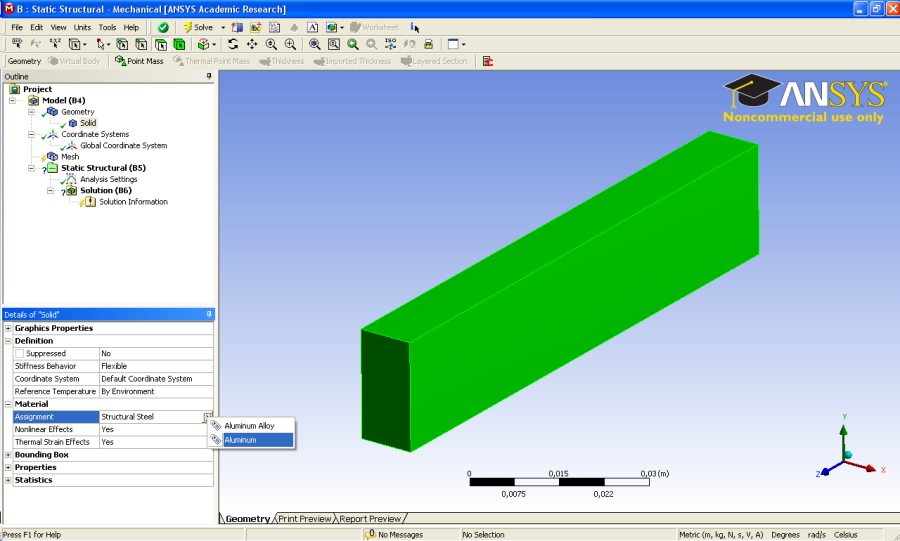
3.14. ábra - Anyagmodell hozzárendelése az alkatrészhez.

Ezután végezzük el a hasáb hálózását. Kattintsunk jobb gombbal a modellfa ( Otline ) Mesh sorára és válasszuk a Generate Mesh parancsot a hálózás végrehajtásához (3.15. ábra). Mivel esetünkben az automatikus hálózás kielégítő eredményt ad, most nem foglalkozunk a háló részletes beállításával, az a későbbi példák segítségével mutatjuk be.

Megjegyzés: a modellfa ( Otline ) elemeire való jobbgombos kattintással előhívott helyi menü Insert menüpontja alatt elérhető parancsok a felső ikonsorban is megjelennek az adott elem kijelölésekor.

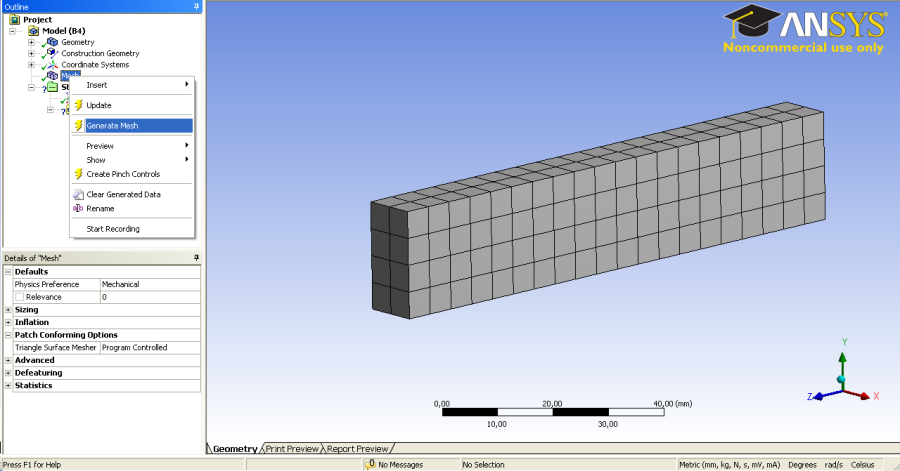
3.15. ábra - A hálózás.

A peremfeltételek hozzárendelése a felső, Environment elnevezésű menüsorból elvégezhető, de a modellfa Static Structural sorára jobb gombbal kattintva, az Insert menüpont alól szintén lehetséges. Ez utóbbi módszert alkalmazva rendeljünk a hasábunk egyik végéhez egy fix megfogást ( Fix Support ) (3.16. ábra).

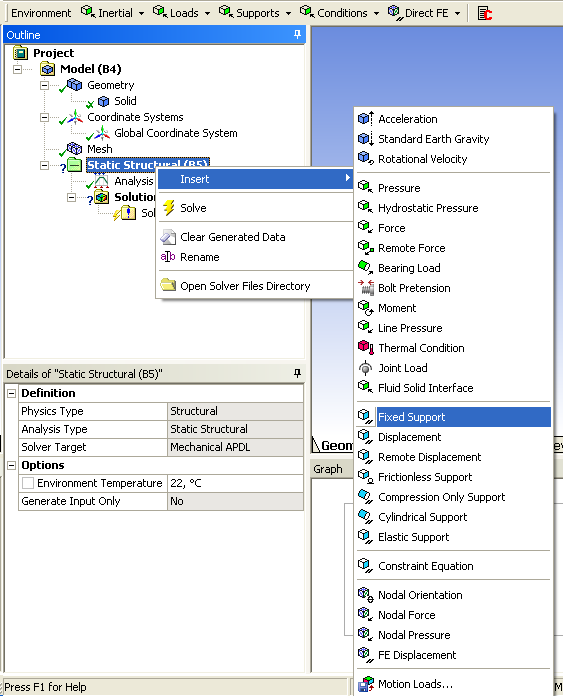
3.16. ábra - Rögzítés parancs kiadása.

A modellfában (Outline) megjelenő Fix Support tulajdonságai az alsó Details panelen jelennek meg. A parancs kiadása után a rögzítésre szánt geometriai elemet ki kell választani a modellen és az Apply gombbal jóváhagyni a Details panelen. A felső menüsorban lévő kijelölést szabályozó szűrők beállításától függően kijelölhetünk pontot, vonalat, vagy felületet, (ebben az esetben a test kijelölése nem aktív) (3.17. ábra).

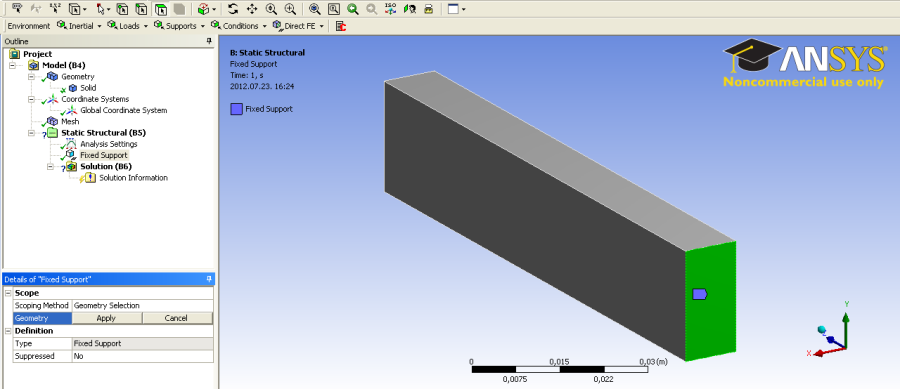
3.17. ábra - A rögzítés helyének kijelölése.

A terhelések definiálását szintén végezzük a jobbgombos menüből: Outline / Static Strutural (JG) / Insert / Force .

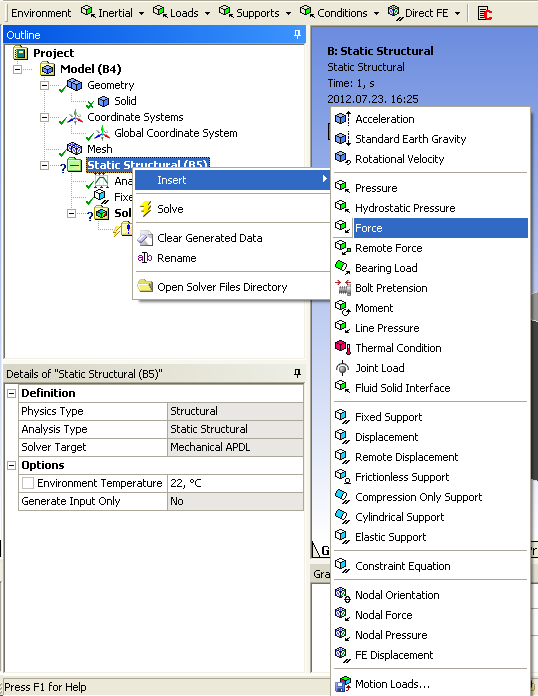
3.18. ábra - A terhelőerő hozzárendelése.

A parancs kiadása után, a rögzítéshez hasonlóan, ki kell választani az erő támadásának felületét és jóváhagyni a Details panelen lévő Apply gombbal. Válasszuk a rögzítéssel szemközti oldalt az erő támadási felületének. Alapértelmezett esetben az erő iránya kijelölt felület normálisával egy irányba esik. Az irány módosításához, vagy egy vektorként szolgáló rajzelemet, vagy az erő komponenseit kell megadni a választott koordinátarendszerben. A Details panel Defined by felirata mellett a legördülő menüből válaszuk Componets opciót, és az alatta megjelenő sorokban írjunk -1000 N-t az Y komponens mellé (3.19. ábra).

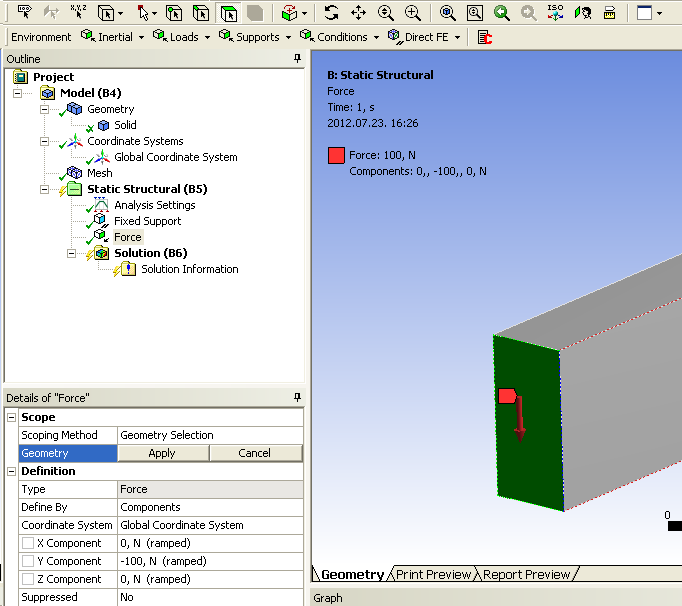
3.19. ábra - A terhelőerő beállításai.

Ezzel a lépéssel a szimuláció peremfeltételeit teljesen definiáltuk, amit az jelez, hogy a modellfából eltűntek a kis kérdőjelek. A sárga villám ikonok azt jelzik, hogy a szimuláció kész a futtatásra. De mielőtt ezt megtennénk, definiáljunk néhány lekérdező parancsot az ébredő deformáció, a fajlagos nyúlás és a feszültség bemutatására.

A lekérdező parancsokat a modellfa Solution sorára való jobbgombos kattintással majd az Insert menüpont kiválasztásával érhetjük el. A Deformation menüpont alatt további két lehetőséget találunk: a teljes ( Total ) és az irány menti ( Directional ) deformáció lekérdezését. Bármelyiket is választjuk, van lehetőségünk utólagos változtatásra a Details panelen.

Válasszuk ki az Outline /Solution (JG) / Insert / Deformation /Directional opciót (3.20. ábra) és a Details panel Orientation soránál válasszuk ki az Y tengelyt (3.21. ábra).

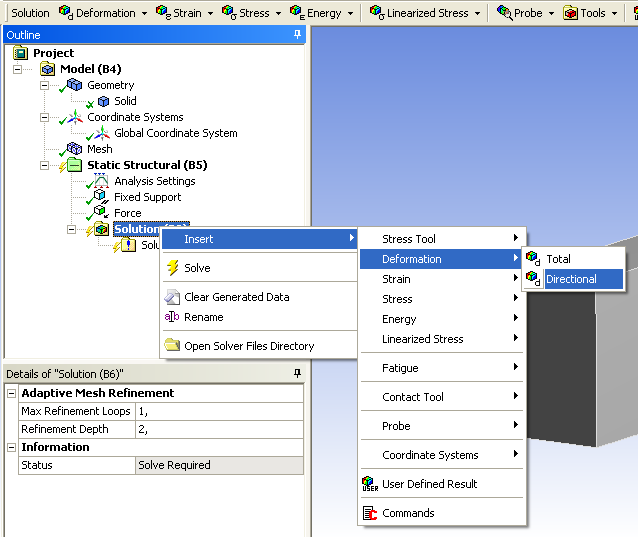
3.20. ábra - Deformáció lekérdezése.

3.21. ábra - A deformáció lekérdezésének beállítása.

Hasonlóképpen válasszuk ki az Outline /Solution (JG) / Insert / Strain / Equivalent (von-Mises) opciót az egyenértékű fajlagos nyúlás, valamint az Outline /Solution (JG) / Insert / Stress / Equivalent (von-Mises) opciót az egyenértékű feszültség lekérdezéséhez.

Végül futtassuk a szimulációt a legfelső menüsorban lévő Solve gomb segítségével. Az eredményeket az alábbi ábrákon láthatjuk. Figyeljük meg, hogy az ábra színezése előjel helyesen történik. Esetünkben a legnagyobb deformáció negatív értelmű, ezért az ábrán kék színnel jelenik meg, az oldalsó színskála értékeinek megfelelően.

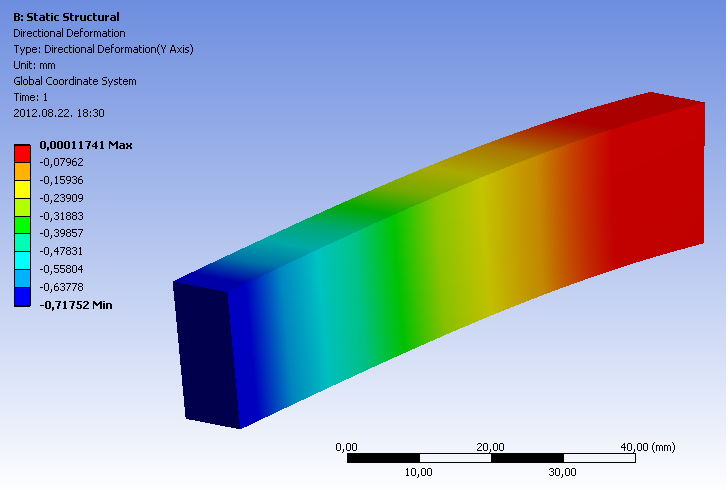
3.22. ábra - Y irányú deformáció.

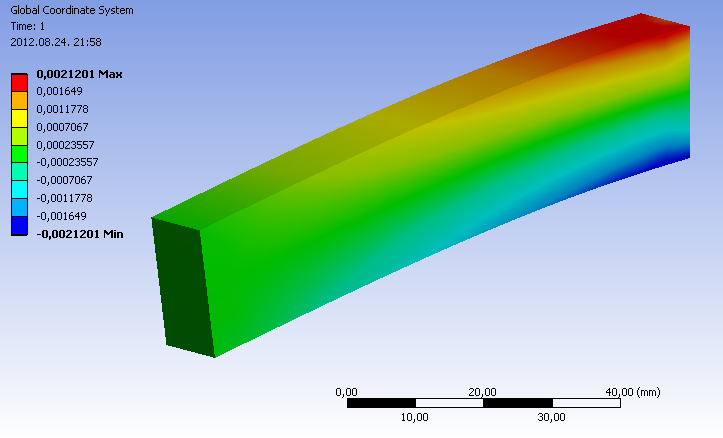
3.23. ábra - Z irányú fajlagos nyúlás.

3.24. ábra - Egyenértékű feszültség.

Az eredmények megjelenítésére és lekérdezésére a Result ikonsoron további lehetőségek állnak rendelkezésünkre.

Az ikonsor első legördülő menüje segítségével a deformáció mértékét skálázhatjuk: a szemléletesség kedvéért a valós deformáció többszörösét, vagy éppen deformálatlan állapotot is beállíthatunk (3.25. ábra).

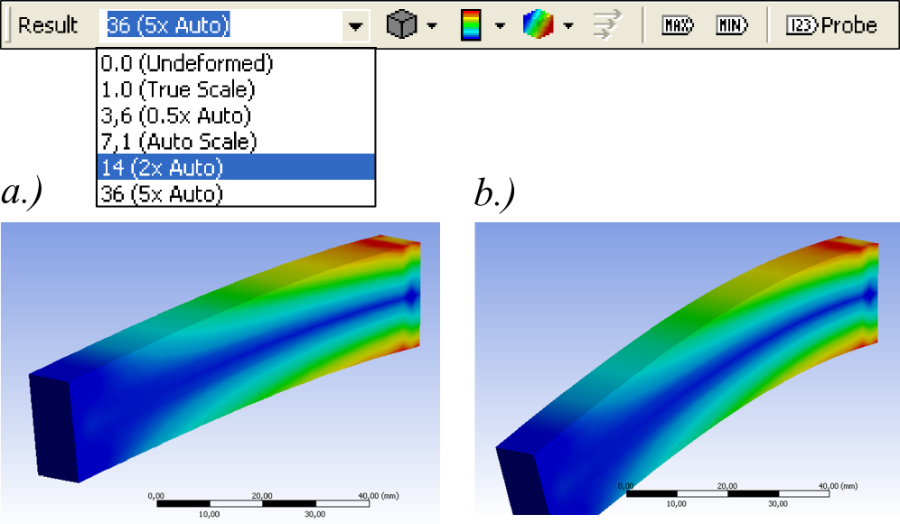
3.25. ábra - A deformáció skálázása. A valós deformáció 14 szeres (a.) és 36 szoros (b.) nagyítása.

A Result ikonsor második, Geometry elnevezésű ikonja segítségével a megjelenített geometria határfelületeinek típusát választhatjuk meg (3.26. ábra). Az Exterior opció esetén a teljes geometria látszik, míg az IsoSurfaces választása esetén az egyenértékű (az ábrán egyenfeszültségű) felületek jelennek meg. Az egyenértékű felületek száma az oldalsó színskála felosztásától függ. A Capped IsoSurfaces ellentétben az előzővel csak egy egyenértékű felületet jelenít meg, amelynek értékét mi határozzuk meg egy csúszka segítségével. Meghatározható ennél a megjelenítési módnál az is, hogy a megadott érték alatti, feletti, vagy mindkét értékű, vagyis, hogy az egyenértékű felület melyik oldalán lévő térfogatot tüntesse el a program. A Slice Planes megjelenítési mód választásához előzőleg metszősíkokat kell definiálni a legfelső ikonsor New Section Plane ikonja segítségével (3.26. ábra, d. – pirossal karikázott ikon).

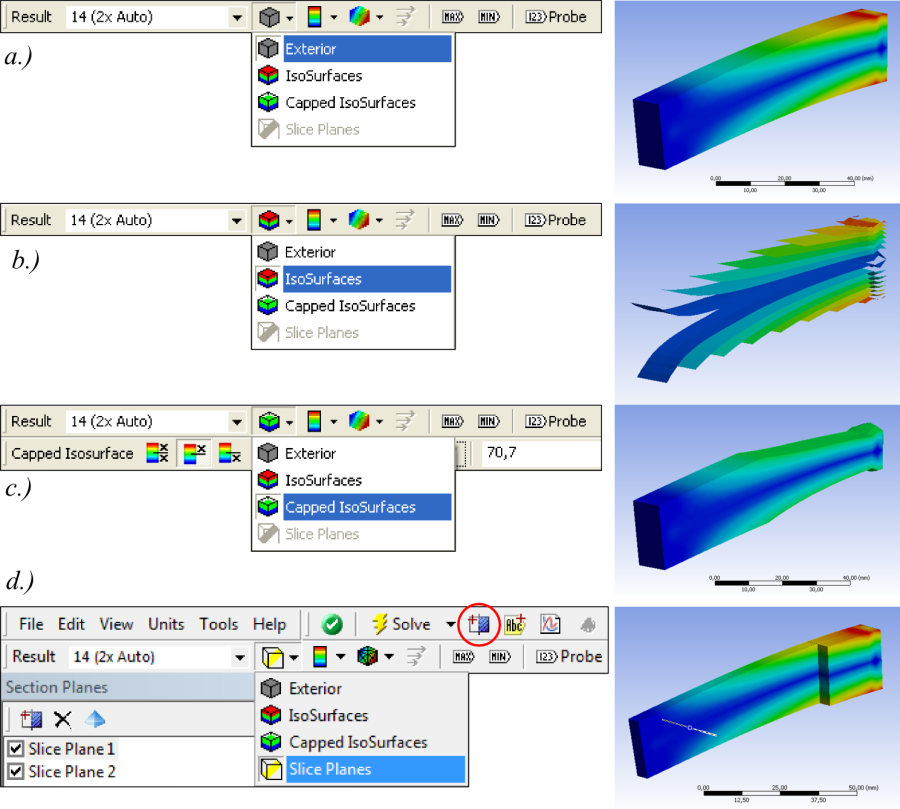
A geometria metszése különböző felületekkel: a.) metszés nélkül, b.) nyitott, egyenfeszültségű felületekkel, c.) zárt, megadott feszültségű felülettel, d.) síkokkal.

3.26. ábra - A geometria metszése különböző felületekkel: a.) metszés nélkül, b.) nyitott, egyenfeszültségű felületekkel, c.) zárt, megadott feszültségű felülettel, d.) síkokkal.

A Result ikonsor harmadik, Contours elnevezésű ikonja segítségével a színsávok megjelenítését tudjuk megváltoztatni (3.27. ábra). Az alapértelmezett Contour Bands opció az oldalsó skála szerinti színeket kontúrosan jeleníti meg, ellentétben a Smooth Contours opcióval, amelyik lágy átmenettel ábrázolja a színsávokat. Isolines opcióval csak az egyenfeszültségű kontúrok jelennek meg. Valamint lehetőség van a színsávoktól mentes deformált test megjelenítésére is a Solid Fill opció segítségével.

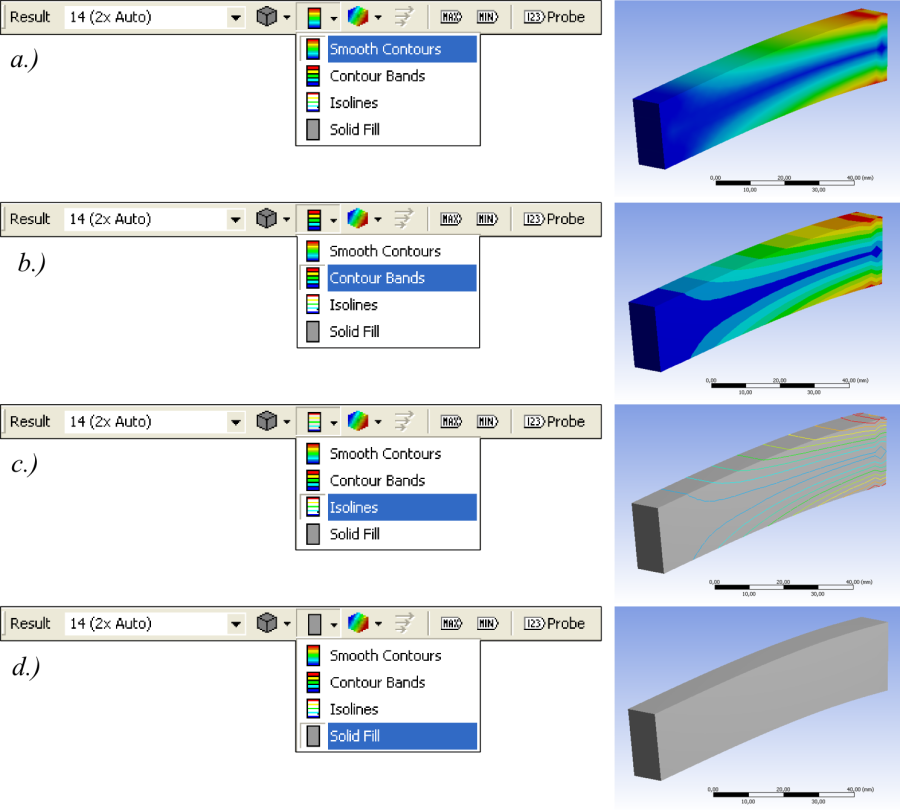
3.27. ábra - Színsávok beállítása.

A Result ikonsor negyedik, Edges elnevezésű ikonja segítségével a deformálatlan test és az elemek éleinek láthatóságát állíthatjuk be (3.28. ábra). Az alapértelmezett megjelenítési forma a No Wireframes , amely önmagában a deformált testet mutatja. A Show Undeformed Wireframe és Show Undeformed Model opciók a deformált alak mellett egyidejűleg mutatják a deformálatlant is drótvázas, vagy áttetsző testmodell formában. A Show Elements opció segítségével láthatóvá válnak a deformált test elemei is.

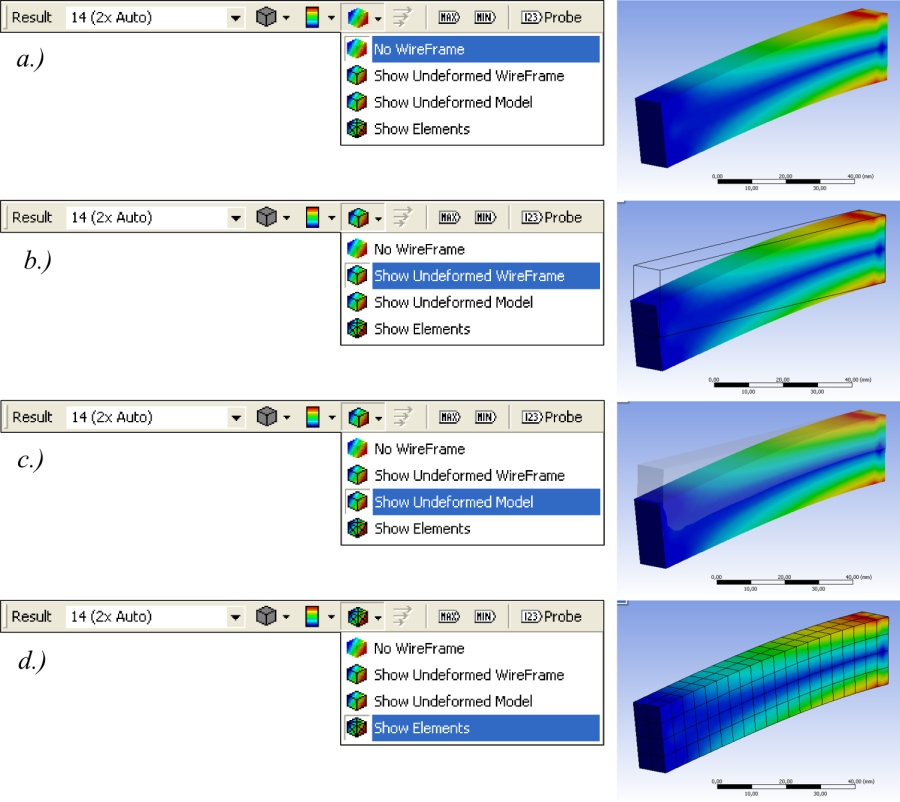
3.28. ábra - Deformálatlan test (a-c.) és a végeselem háló (d.) megjelenítése.

A Result ikonsor utolsó elemei, a Label elnevezésű eszközökkel közvetlenül a modellen tudjuk megnézni a minimum és maximum értékű helyeket. Lehetőség van a Probe eszköz segítségével tetszőleges, a modellen kijelölt helyen lekérdezni a szimuláció eredményét (3.29. ábra).

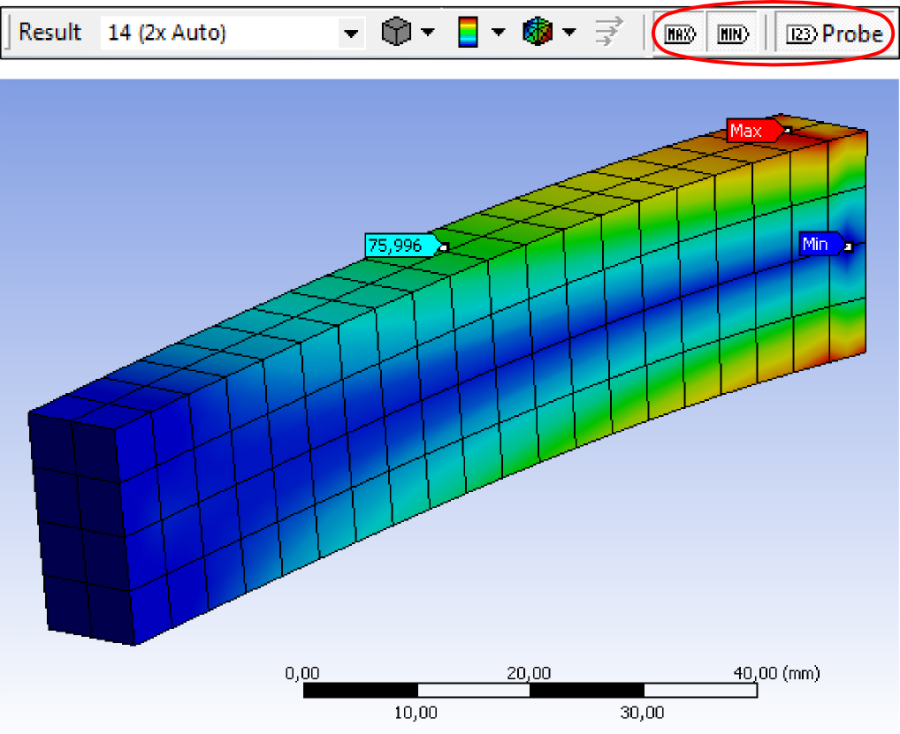
3.29. ábra - Cimkék.

A munkaterület alatti panel Graph fülén lévő eszközök segítségével lehetőség van a szimuláció animálására (3.30. ábra). Beállítható a képkockák ( Frames ) száma és elosztása valamint az animáció időtartama. A szokásos Play és Stop gombokkal lehet indítani és leállítani, valamint az Export Video File gombbal tudjuk kimenteni (AVI formátumban) az animációt.

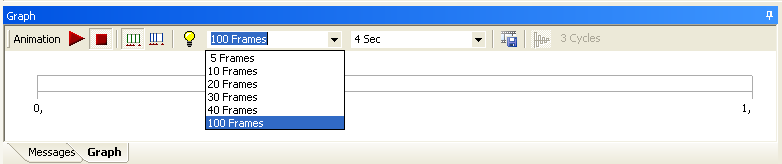
3.30. ábra - Animáció készítése.

Az eredmények lekérdezése nemcsak a teljes testmodellre vonatkozhat, hanem annak egyes elemeire is (mint pl.: felületek, élek, pontok). Továbbá a színsávos ábrázoláson túl, van lehetőség az eredmények számszerű megjelenítésére és kimentésére.

A fentiek bemutatására végezzük el a hasábunk lehajlásának lekérdezését a hely függvényében. Adjunk hozzá a szimulációhoz egy újabb deformáció lekérdezést az Outline /Solution (JG) / Insert / Deformation / Directional opció kiválasztásával és a Details panel Orientation soránál válasszuk ki az Y tengelyt. A Details panel Geometry felirata mellett alapértelmezésként az „All Bodies” szerepel (3.31. ábra).

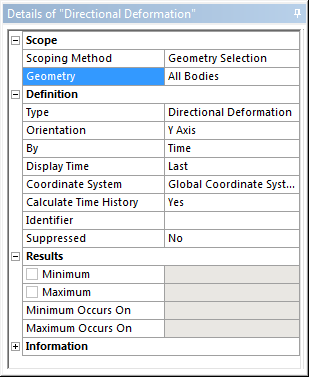
3.31. ábra - Deformációlekérdezés beállításai.

Kattintsunk a feliratra, a fenti ikonsorból a kijelölés szűrőt vonalra ( Edge ), jelöljük ki a hasáb egyik felső élét (3.32. ábra) majd kattintsunk a Details panelen megjelenő Apply gombra. Ha helyesen jártunk el, a mezőben az „1 Edge” felirat jelenik meg, ami jelzi a kijelölt elemek számát és típusát.

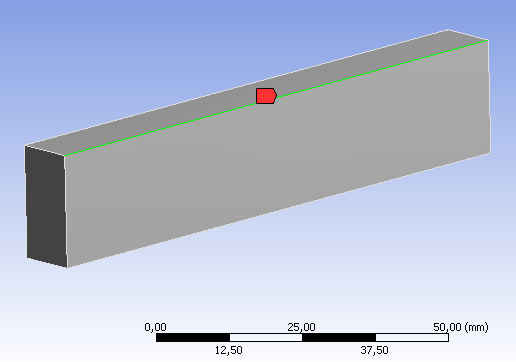
3.32. ábra - Egy él elmozdulásának lekérdezése.

Ezzel a lépéssel azt tettük lehetővé, hogy a lehajlás mértékét jelző színkép csak a kijelölt vonalon jelenjen meg. Ahhoz, hogy a lehajlás értékét a hely függvényében, numerikusan is megkapjuk, a kijelölt vonalat un. útvonallá ( Path ) kell alakítani. Ezt az Outline panelen, a deformáció eredmény sorára jobb gombbal kattintva és a Convert to Path Result választásával tudjuk megtenni (3.33. ábra). Nemcsak geometriai éleken tudunk útvonalat generálni, hanem a végpontok megadásával akár a test belsejében is.

3.33. ábra - Az él átalakítása útvonallá.

Látható, hogy a testmodell élén és a modellfában is megjelent az útvonal (3.34. ábra). A peremfeltételek elhelyezkedésének ismeretében látható, hogy a lehajló résznél kezdődik, és a rögzítettnél fejeződik be a végpontok sorszámozása. Ez lényeges lesz a kimentett adatok feldolgozásánál. (Az útvonal számozása megfordítható és a felosztások száma is beállítható.)

A Solve gombra kattintva nem a teljes szimuláció fut le újra, hanem csak az új elemeket számolja a program. A deformáció mértékét a testmodell élén is láthatjuk a megfelelő színnel, valamint diagramban ábrázolva és táblázatosan az alsó Graph és Tabular Data paneleken. A Tabular Data táblázatból közvetlenül kimásolható, vagy az Outline panelen, a deformáció eredmény sorára jobb gombbal kattintva TXT fájlba Exportálható (3.34. ábra).

✎A deformáció mintájára exportálják ki a fajlagos nyúlás és a feszültség értékeket is.

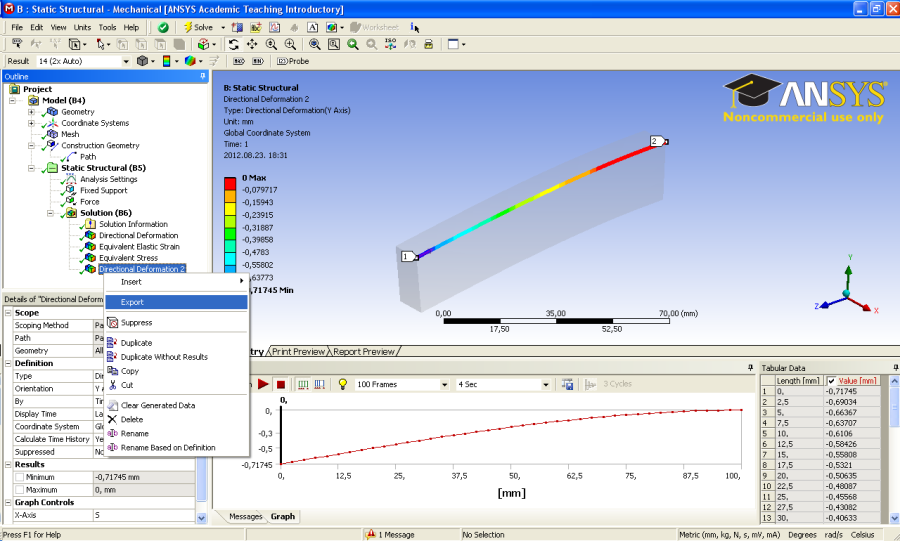
3.34. ábra - Numerikus eredmények exportálása.

3.2.3. Egyszerű statikai analízis SolidWorksben

A SolidWorks alapvetően nem FEM program, mégis a beépített végeselem modul segítségével, a mérnöki tevékenység ezen részét is remekül támogatja. Az összehasonlíthatóság kedvéért, az előző feladatot fogjuk megoldani SolidWorks-ben is. A munkát itt is a geometria modellezésével kezdjük.

A program megnyitása és az új dokumentum létrehozása ( New ) parancs kiadása után megjelenő párbeszédablakon válasszuk az alkatrész ( Part ) opciót.

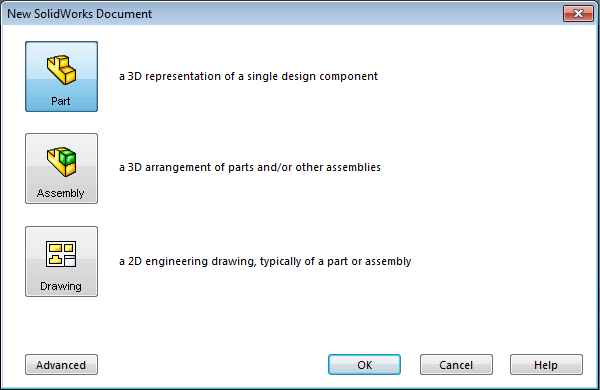
3.35. ábra - Új alkatrész létrehozása.

A geometria létrehozását kezdjük a vázlat megrajzolásával. Válasszuk a Command Manager -nek nevezett felső menüsor vázlatok ( Sketch ) fülét (3.36. ábra). Ezen a lapon találjuk a vázlatrajzolással kapcsolatos rajzelemeket és szerkesztő eszközöket. Az egyes ikonok melletti kis háromszögre kattintva az ikon legördül, és további lehetőségek tárulnak elénk, amiket a parancskiadása után is átválthatunk. Az ikonokon, az ANSYS-hoz hasonlóan, piros pontokkal vannak jelölve a rajzelem definiálására szolgáló pontok. Gördítsük le a téglalap ikont és válasszuk a középpontjával megadható téglalapot ( Center Rectangle ).

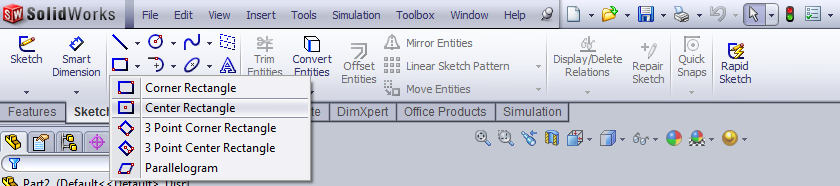
3.36. ábra - Téglalap rajzolása.

A parancs kiadása után, mielőtt megkezdhetnénk a rajzolást, ki kell választanunk a munkasíkot. Válasszuk ki a Front Plane -t, majd a munkatér felső részénél lévő nézetbeállító ( View Orientation ) ikonra kattintva forgassuk be a Front síkot a képernyő síkjába.

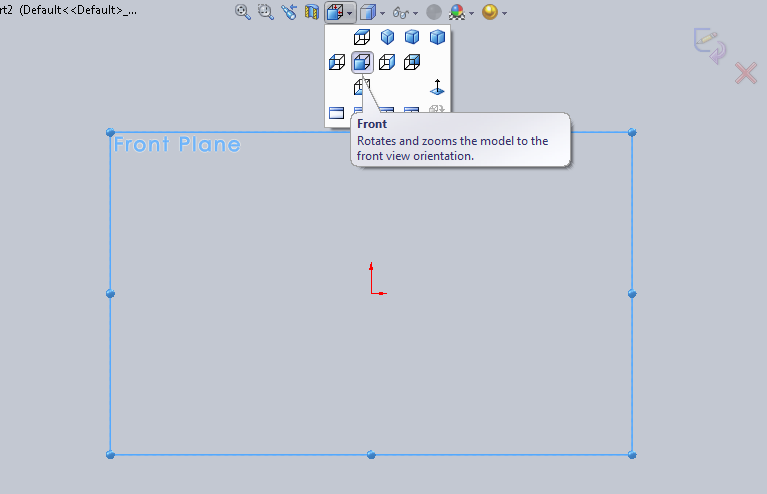
3.37. ábra - Elölnézet beállítása.

A téglalap megrajzolását a középpont elhelyezésével kell kezdeni. Ha az egérmutatót az origó fölé visszük, egy kis piros pötty megjelenése jelzi a létrejövő kapcsolatot. Ha így kattintunk, a téglalap középpontja hozzátapad az origóhoz. A második kattintással a téglalap egyik sarokpontját helyezzük el.

A vázlatot meghatározó kényszerek kis zöld hátterű négyzetek formájában jelennek meg az adott rajzelem mellett. (A kényszer ikonok és egyéb elemek megjelenítését a View menüben lehet ki- és bekapcsolni.)

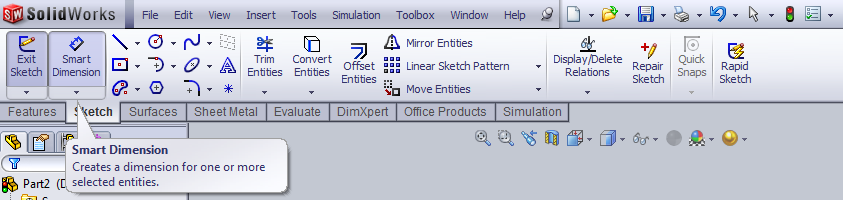
3.38. ábra - Méretezés ikon.

A téglalap méretezését a Smart Dimension gomb segítségével tudjuk indítani (3.38. ábra). A legördülő ikon a speciális méretezési lehetőségeket rejti. Adjuk ki a parancsot és kattintsunk a téglalap egyik vízszintes élére majd a megjelenő panelen (3.39. ábra) írjuk be a méretet (10 mm). (Figyeljük meg, hogy az alulkényszerezett rajzelemek színe kék, a teljesen meghatározott rajzelemeké fekete, és túlhatározottság esetén piros lesz.) Ismételjük meg a méretezést az egyik függőleges éllel írjuk be a méretet (20 mm).

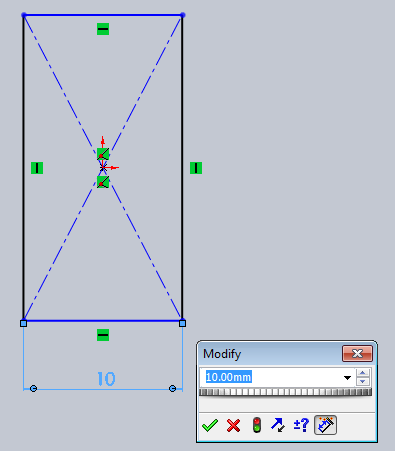
3.39. ábra - Méretezés.

A méretezés befejeztével a vázlat teljesen határozottá vált. A munkatér jobb felső sarkában lévő kék nyíl segítségével léphetünk ki a vázlatrajzolás módból.

Lépjünk át a menüsor ( Command Manager ) alaksajátosságok ( Features ) fülére és kattintsunk a kihúzás ( Extruded Boss/Base ) parancsra (3.40. ábra). A parancs kiadása után a baloldali panelen a modellfa ( Feature Manager Model Tree ) helyét egy tulajdonságok ablak ( Property Manager ) veszi át. Itt tudjuk beállítani a kihúzás paramétereit. Állítsuk be a kihúzás hosszát (100 mm), és a tulajdonságok panel tetején, vagy a munkatér jobb felső sarkában lévő zöld pipa segítségével lépjünk ki a parancsból (3.41. ábra). Ezzel a lépéssel befejeztük a geometria modellezését, most rendeljük hozzá a kívánt anyagmodellt.

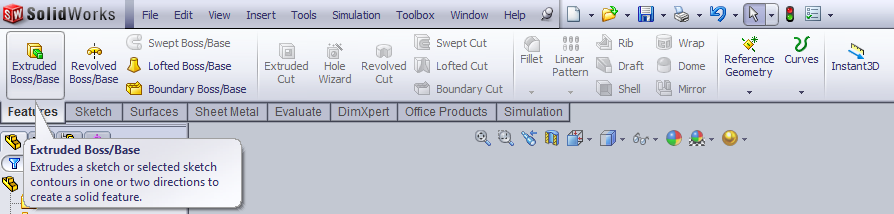
3.40. ábra - Kihúzás parancs kiadása.

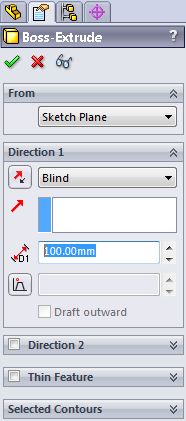
3.41. ábra - A kihúzás paramétereinek beállítása.

A modellfában található Material sorra kattintsunk jobb gombbal és a megjelenő helyi menüből válasszuk az anyag szerkesztése ( Edit Material ) lehetőséget.

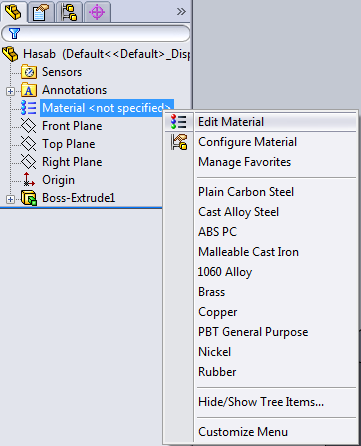
3.42. ábra - Anyagmodell szerkesztése.

A megjelenő anyag ( Material ) ablak bal oldalán böngészhetünk a meglévő anyagok között, a jobb oldali panel lapjain pedig a kiválasztott anyag tulajdonságait láthatjuk. Saját anyag létrehozására is van lehetőség, ehhez a Custom Materials mappára jobb gombbal kattintva, majd a New Category sort választva hozzunk létre egy új kategóriát (almappát) az anyag elhelyezéséhez, és nevezzük el („Metals”).

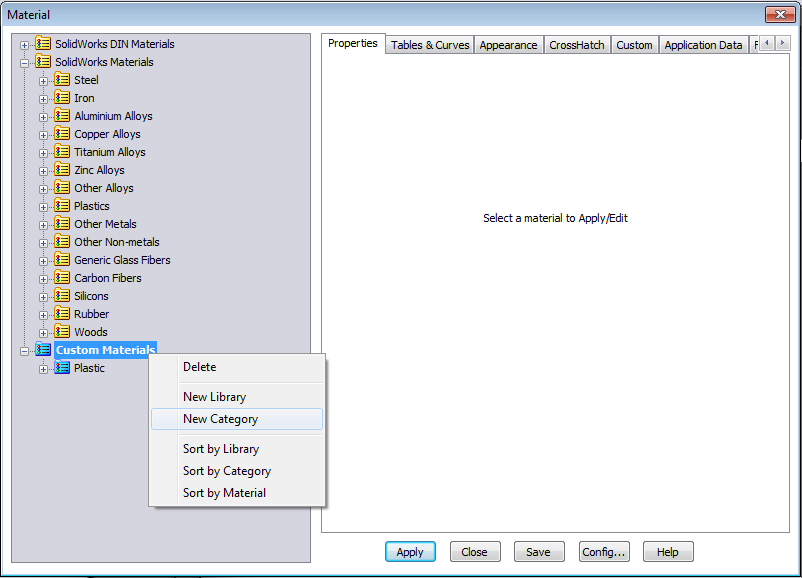
3.43. ábra - Új anyagmappa létrehozása.

Az újonnan létrehozott mappára jobb gombbal kattintva, a megjelenő helyi menüből válasszuk az New Material opciót az új anyag létrehozásához, és nevezzük el azt („Aluminium”).

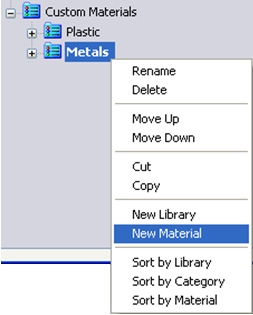
3.44. ábra - Új anyag létrehozása.

Ha a létrehozott anyag, a baloldalon, ki van jelölve, a jobboldali panel tulajdonságok ( Properties ) lapján be tudjuk állítani az anyagmodell alapvető tulajdonságait. Állítsunk be az anyagmodell paramétereit az ábrán látható módon (3.45. ábra). (A SolidWorks esetében a fajsúlyt ( Mass Density ) is meg kell adni, mivel a program CAD része ez alapján számolja a testmodell inerciális adatait.) A paraméterek megadása után mentsük az anyagmodellt a Save gombbal és rendeljük hozzá az alkatrészhez az Apply gomb segítségével. Ezután bezárhatjuk az ablakot.

3.45. ábra - Az anyagparaméterek megadása.

Ezzel előkészítettük a modellt az analízisre. A szimulációs környezetbe a Command Manager utolsó, Simulation fülére kattintva és a Study Advisor ikon legördítése után a New Study sorra való kattintással léphetünk be.

3.46. ábra - Belépés a szimulációs környezetbe.

Első lépésként ki kell választanunk a szimuláció típusát ( Static ), majd a zöld pipával hagyjuk jóvá. Ennek hatására a geometriai sajátosságokat tartalmazó modellfa ( FeatureManager Design Tree ) alatt megjelenik a szimulációs sajátosságokat tartalmazó modellfa (innentől ezt értjük modellfa alatt ebben a példában). A munkatér alján megjelenő „Study 1” fül lesz aktív, ami szintén azt jelzi, hogy a szimulációs környezetben, vagyunk. A geometria módosítása érdekében bármikor visszatérhetünk a modelltérbe a Model fülre való kattintással.

3.47. ábra - A szimuláció típusának kiválasztása.

A hálózás, peremfeltételek, terhelések és egyéb beállítások elvégzése, az ANSYS Workbench-hez hasonlóan, történhet a felső menüsorból, vagy a modellfa elemeire történő jobbgombos kattintással. Válasszuk ez utóbbi utat a parancsok kiadására, és kattintsunk jobb gombbal a modellfa rögzítések ( Fixtures ) sorára. A megjelenő rögzítési lehetőségek közül válasszuk a rögzített geometria ( Fixed Geometri ) opciót.

3.48. ábra - Rögzítési mód kiválasztása.

A parancs kiadása után a baloldalon megjelenő tulajdonságok ablak segítségével beállíthatjuk a rögzítés paramétereit. Válasszuk ki a rögzíteni kívánt felületet, (legyen az a hasáb egyik vége). Hagyjuk jóvá a beállításokat a zöld pipa segítségével (3.49. ábra).

3.49. ábra - A rögzítés helyének megadása.

Hasonlóképpen járunk el a terhelőerő megadásánál is. Kattintsunk jobb gombbal a modellfa külső erők ( ExternalLoads ) sorára, majd válasszuk ki az erő ( Force ) opciót a megjelenő menüből.

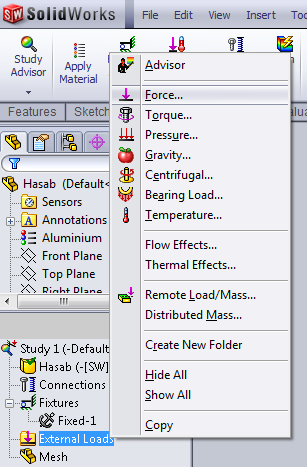
3.50. ábra - Külső terhelés kiválasztása.

Az erő támadási felületének válasszuk ki a hasáb másik végét. Az erővektor alapértelmezetten párhuzamos a felület normálisával, de iránya ellentétes értelmű. Az irány megváltoztatásához válasszuk a Selected Direction opciót és jelöljünk ki egy függőleges élt a támadási felületen. Ez fogja megadni az erővektor irányát. (figyeljük meg, hogy a baloldali tulajdonságok panelen az aktív kijelölő ablak (szövegdoboz) háttere világoskék lesz és megjelenik benne a kijelölt geometriai elem neve.) Amennyiben az erővektorok értelme ellentétes a kívánt iránnyal, a Force ablakban lévő ellentétes irány ( Reverse Direction ) bepipálásával megfordíthatjuk az erővektorokat. Ugyanezen a panelen tudjuk megadni az erő mértékét (1000 N). Végezetül a szokásos módon, a zöldpipával lépjünk ki a parancsból.

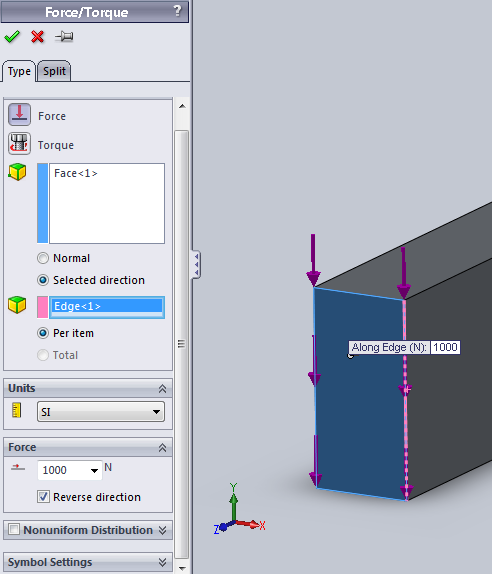
3.51. ábra - Az erő megadása.

A hálózás beállításához kattintsunk jobb gombbal a modellfa háló ( Mesh ) sorára majd válasszuk a helyi menü hálókészítés ( Creat Mesh ) sorát. A Hálóparaméterek panelen ( Mesh Parameters ) állítsuk 2,5 mm-re globális elemméretet (felső szövegablak), és zöld pipával hajtsuk végre a hálózást.

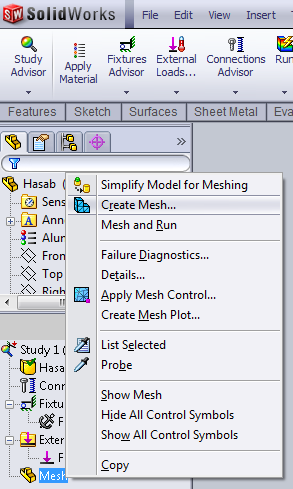
3.52. ábra - Hálózás parancs kiadása.

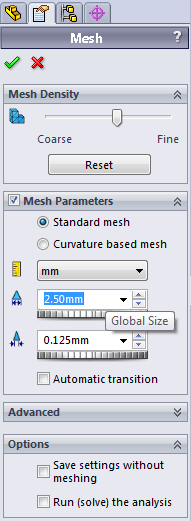
3.53. ábra - A hálózás paramétereinek beállítása.

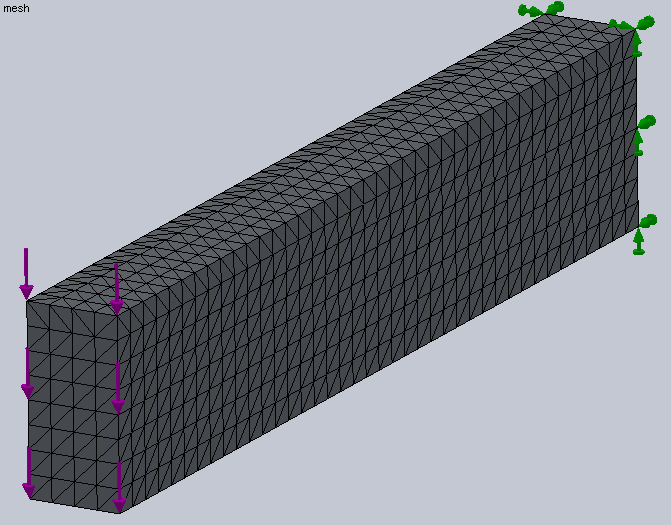
3.54. ábra - A végeselemháló.

A szimulációt a felső menüsor Run ikonjával futtathatjuk. Az alapvető eredményeket tartalmazó sorok, úgy mint a feszültség, deformáció és a fajlagos nyúlás (Stress, Displacement, Strain), automatikusan megjelennek a modellfa eredmények ( Results ) sora alatt (3.56. ábra).

3.55. ábra - A szimuláció futtatása.

Egy eredményre való jobbgombos kattintással az adott eredmény definíciója, vagy megjelenítése módosítható. Kattintsunk jobb gombbal a Strain sorra majd válasszuk az Edit Definition menüpontot (3.56. ábra).

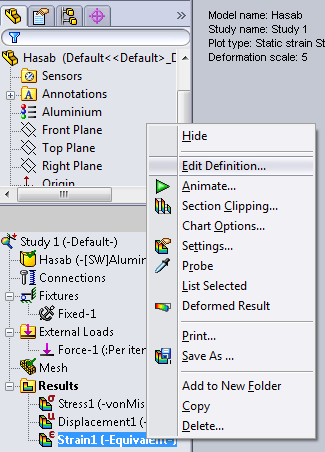
3.56. ábra - Az eredmények definíciójának beállítása.

A megjelenő baloldali tulajdonságok panelen váltsuk át az egyenértékű feszültséget Z irányú normál feszültségre (EPSZ: Z NormalStrain) .

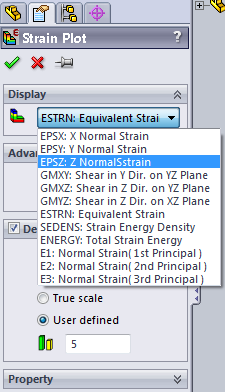
3.57. ábra - Az eredmény típusának módosítása.

Hasonló módon váltsuk át deformáció lekérdezés definícióját eredő deformációról ( URES: Resultant Displacemet ) Y irányúra. Ehhez kattintsunk a modellfában a Results / Displacemet sorra jobb gombbal, majd válasszuk az Edit Definition menüpontot. A tulajdonságok panel felső legördülő listájából válasszuk az Y irányú elmozdulást ( UY: YDisplacemet ).

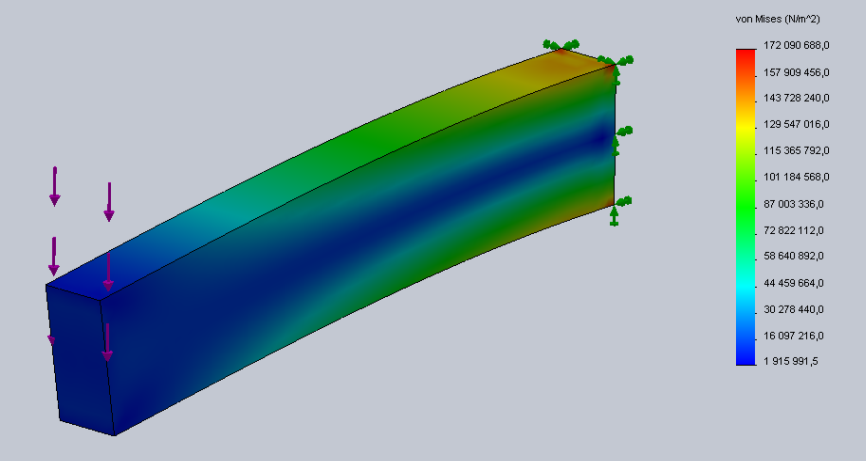
3.58. ábra - Egyenértékű feszültség.

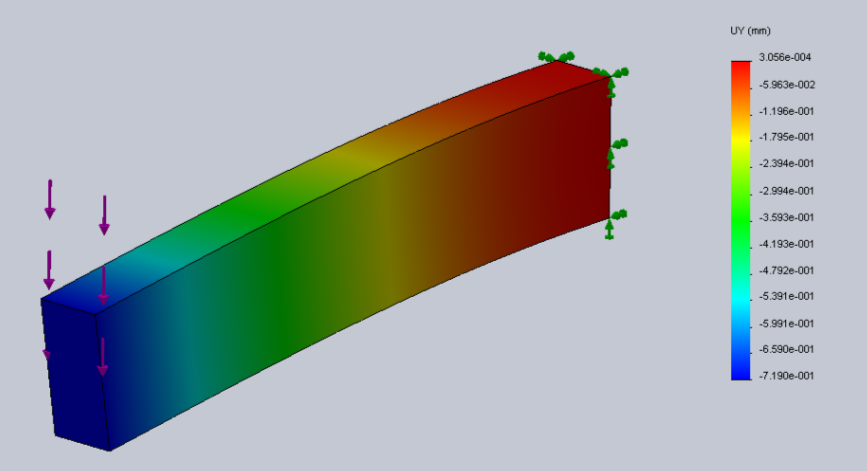
3.59. ábra - Y irányú deformáció.

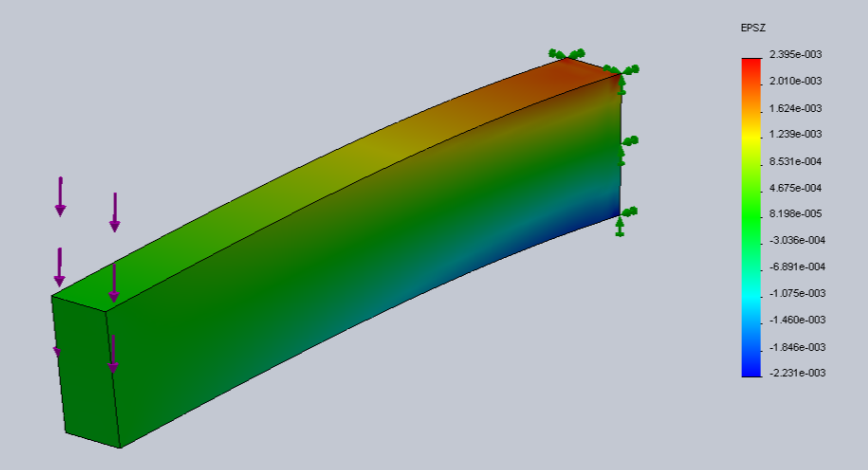
3.60. ábra - Z irányú fajlagos nyúlás.

A Result sorra való jobbgombos kattintással új lekérdezések is hozzáadhatók a listához.

Az eredmények megjelenését a Results / Strain (JG) / Settings menüpont alatt tudjuk megváltoztatni.

3.61. ábra - Az eredmények megjelenítésének beállítása.

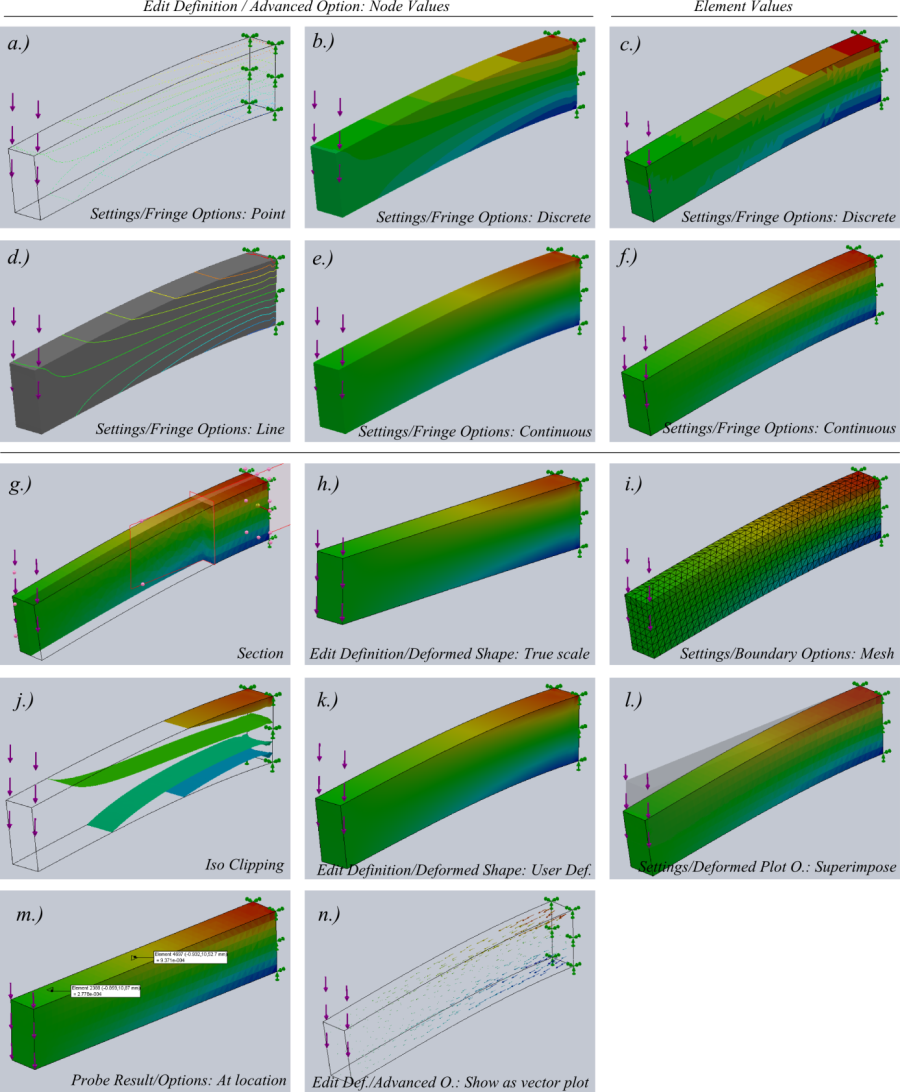
3.62. ábra - Az eredmények grafikus megjelenítésének formái.

A jobbgombos menü Edit Definition menüpontja alatt van továbbá lehetőség az elemekre vonatkozó, vagy csomóponti eredmények átváltására, a vektoros megjelenítés bekapcsolására, vagy a megjelenített deformáció mértékének nagyítására.

Amennyiben a Results / Strain (JG) / Edit Definition / Advanced Option panelen az Node Values van bekapcsolva, akkor a Settings menüpont Fringe Options panelén az Point, Line, Discrete és Continous árnyalási forma lehetséges (3.62. ábra, a, b, d, e.).

Amennyiben a Results / Strain (JG) / Edit Definition / Advanced Option panelen az Element Values van bekapcsolva, akkor a Settings menüpont Fringe Options panelén az Discrete és Continous árnyalási forma lehetséges (3.62. ábra, c, f.).

Lehetőség van a hálózás megjelenítésére a Boundary Options / Mesh opció segítségével és a deformálatlan test megjelenítésére a Deformed Plot Options panelen lévő pipa bejelölésével (3.62. ábra, i, l.).

Az eredmények megjelenítésének további beállítását a felső menüsor Plot Tools ikonja alatt lévő eszközök, vagy a jobb gombos menü erre szolgáló menüpontjaival kezdeményezhetjük. A Plot Tools / Section Clipping parancs segítségével metszősíkokat állíthatunk be (3.62. ábra, g.). A Plot Tools / Iso Clipping parancsa az egyenértékű felületeket jeleníti meg, vagy azok segítségével metszhetjük el az alkatrészünket (3.62. ábra, j.).

A Plot Tools / Probe, vagy List Selected parancsával tudjuk egyes pontokban, vagy valamilyen geometriai elem mentén lekérdezni az eredményeket. A két eljárás között a parancs kiadása után is válthatunk a tulajdonságok panelen az At Location és az On Selected Entities opciók alkalmazásával (3.62. ábra, m.; 3.63. ábra).

A lehajlás számszerű lekérdezéséhez váltsunk át a deformáció eredményére és adjuk ki a Plot Tools / List Selected parancsot . Jelöljük ki a hasáb egyik felső élét és a baloldali tulajdonságok panelen lévő Update gomb segítségével frissítsük az alatta lévő táblázat tartalmát. A tulajdonságok panel alján lévő Report Option panelen lévő Plot ikon segítségével egy diagramba rajzoltathatjuk az elmozdulások értékét a hely függvényében, ami a hasáb alakváltozásának jellegét fogja mutatni. A mellette lévő Save gomb segítségével TXT fájlba menthetjük az adatsort (3.63. ábra). Ha a diagramot fordított irányban szeretnénk felrajzolni, (úgy, hogy a befogott rész legyen az X tengely 0 értékénél) akkor a panelen jelöljük be a Flip edge plot opciót.

✎A deformáció mintájára exportálják ki a fajlagos az egyenértékű feszültség értékeket is. (A feszültség és a fajlagos nyúlás esetében át kell állítani az eredményeket csomópontira ( Results / Stress1 (JG) / Edit Definition / Advanced Option / Node Values . Ez azért szükséges, hogy él mentén is le tudjuk kérdezni az eredményeket.)

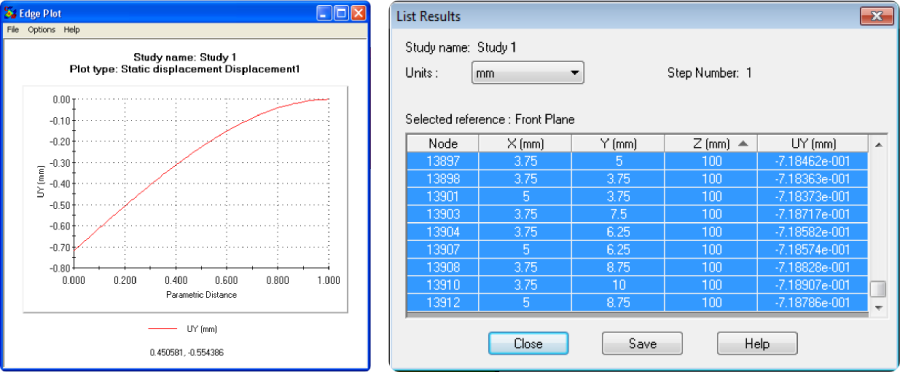
3.63. ábra - Az eredmények numerikus megjelenítése.

A Plot Tools / Save as parancsával az eredményt megjelenítő modellt tudjuk kimenteni kép, vagy 3D-s modell formátumokban. A Plot Tools / Animate parancsa segítségével animációt készíthetünk a deformáció folyamatáról, és menthetjük ki AVI formátumban. Lehetőség van a képkockák számának, az animáció sebességének és különböző végződési módok beállítására (3.64. ábra).

3.64. ábra - Animáció készítése a szimulációról.

3.2.4. Az analitikus és numerikus megoldások összehasonlítása

A feladat zárásaként hasonlítsuk össze a két végeselemes megoldást az analitikussal.

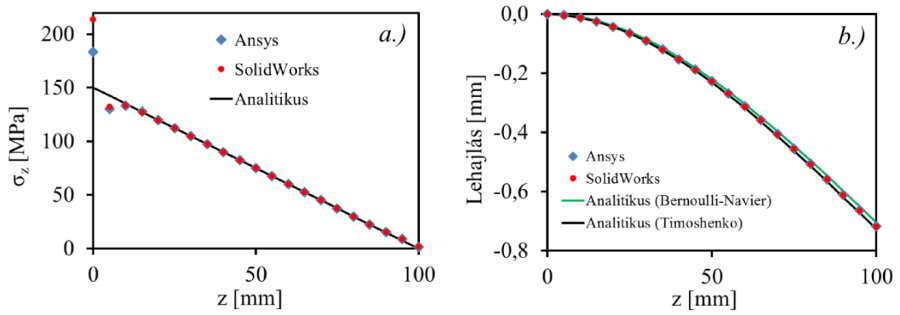
3.65. ábra - A konzolosan befogott rúd terhelési eredményei: a.) Z – tengely irányú normál feszültség, b.) lehajlás.

A feszültségi adatokból látható, hogy a fix megfogás közelében a szimuláció eredménye jelentősen eltér az elméleti értéktől. Mivel, praktikussági okokból, a lekérdezést nem a szimmetriasíkban vettük fel, hanem a hasáb szélén, ez az eltérés eléggé jelentős. Az elméleti értékhez jobban igazodó eredményeket kaphatunk, ha a lekérdezéshez használt útvonalakat középen vesszük fel. Ezt ANSYS-ban az útvonal (Path) végpontjainak koordináttákkal való megadásával, SolidWorks esetén pedig a felső felület középen való felbontásával érjük el. A további feladatokban mindkét eljárásra mutatunk példát.

3.3. Alkalmazási példa: Erőmérő cella statikai analízise

Az alábbi ábrán az iparban és a méréstechnikában gyakran alkalmazott nyúlásmérő bélyeges erőmérő cella egyszerűsített, méretezett rajzát láthatjuk (3.66. ábra). A feladat a megadott mérési tartomány és érzékenység biztosítása a mérőtest megfelelő kialakítása által.

Megadott paraméterek:

Mérési tartomány: F=10N,

Anyagminőség: acél, E=210 GPa; v=0,28,

A nyúlásmérő bélyeg ajánlott maximális üzemi nyúlása: ε_max=1-1,5⋅10^-3; (0,10-0,15%),

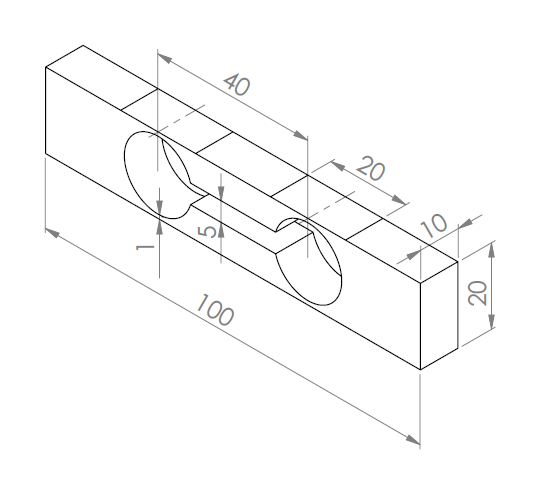
3.66. ábra - Acél mérőtest egyszerűsített, méretezett rajza.

3.3.1. Modellezés

A geometriát hozzuk létre SolidWorks-ben. Első lépésben hozzuk létre a hasáb profilját, úgy, hogy szimmetrikusan legyen elhelyezve az origóhoz képest. A vázlatrajzolás (Sketch/Sketch) parancs kiadása után válasszuk ki a Front síkot. A szimmetrikusan elhelyezett téglalap rajzolásához használhatjuk a középpontjával definiált téglalapot (Center Rectangle) , vagy az oldalélek középpontjára illesztett konstrukciós (Cenerline) vonalat használhatjuk segédvonalként. A teljesen határozott (fekete) vázlaton hajtsuk végre a kihúzás (Features/Extruded Boss) parancsot, a kihúzás mélységére használjuk a Mid Plane opciót (a Blind legördítésével érhető el). Ezzel a hasáb az XY síkra is szimmetrikus lesz.

A piskóta alakú kivágást indíthatjuk az alaksajátosság, tehát kivágásos kihúzás (Extruded Cut) parancs kiadásával is. Ekkor a program automatikusan a vázlatrajzolás módba lép, és kéri a munkasík kijelölését. A vázlatot létrehozhatjuk a hasáb oldalán, vagy szintén az XY síkon. Ez utóbbi esetben arra ügyeljünk, hogy a kivágás/ kihúzás mindkét irányban hajtsuk végre. Célszerű a mindenen keresztül (Through All) mélységi opciót választani és mindkét irányt (Direction 1, 2) bejelölni. A vázlat elkészítésénél érdemes minél több szabadságfokot kényszerekkel megkötni (pl.: a két kör sugara, a két vízszintes szakasz egyenlősége, középponthoz illesztés, szimmetria, stb.) és csak a fennmaradókat méretezni. A kör méretét ne a sugárral definiáljuk, hanem az oldaléltől való legkisebb távolságával. Ezt a méretezés közben lenyomott Shift billentyűvel, vagy a kijelölt méret tulajdonságok ablakban a középső (Leader) fülön az Arc Condition: Min opció megadásával érhetjük el.

Mivel a mérőtest végeselemes modelljét a valóságos geometria egyszerűsítésével hozzuk létre, ezért nincsenek rajta olyan geometriai elemek (pl. furatok) melyekre definiálni tudnánk a megfogást és a terhelést. Erre a célra, valamint a hálózás lokális finomítása és az eredmény lekérdezése miatt szükséges lehet a felület felosztása megfelelő méretű és elhelyezkedésű részekre. Ehhez a hasáb alsó, ill. felső felületén, vagy az XZ síkon hozzunk létre egy olyan vázlatot, amely 4 db. a hasáb egyik szélétől a másikig tartó, a Z tengellyel párhuzamos szakaszból áll. Fontos, hogy a szakaszok végpontja mindkét oldalon kapcsolódjon ( Coinciden kényszer), a hasáb széléhez. A méretezést a rajz szerint végezzük el (3.66. ábra). Az elkészült vázlat és a legördülő menüből ( Insert/Curve/SplitLine) , vagy az ikonsorból ( Features/Curve/SplitLine) elérhető vágóél parancs segítségével az alsó és felső felületeket feloszthatjuk a megrajzolt szakaszok szerint. A parancs végrehajtásakor a merőleges vetítés (Projection) opciót kell alkalmazni, és ki kell választani a vágóélként szolgáló vázlatot és a felosztani kívánt alsó és felső felületeket.

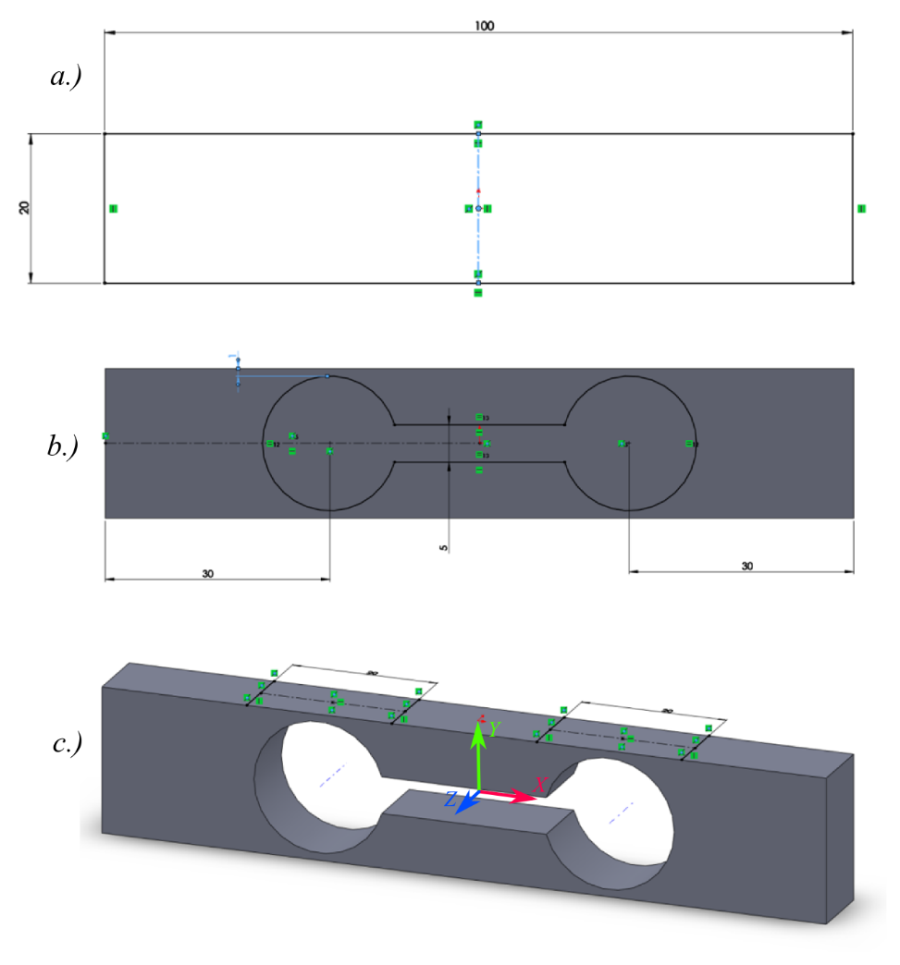
3.67. ábra - A geometriai modell létrehozásának lépései.

Az előző példákban a geometria modellezése és az analízis ugyanabban a szoftverben történt. A jelenlegi példában azonban a geometriát SolidWorks-ben az analízist pedig ANSYS-ban készítjük. A geometriai modell átviteléhez nincs szükségünk köztes formátumú fájlok manuális export/import műveletére, mivel az automatikusan megtörténik a beépülő Add-Ins segítségűével. Így az analízis indítását kezdeményezhetjük a SolidWorks legördülő menüsorából az ANSYS/Workbench sorára kattintva (3.68. ábra).

3.68. ábra - ANSYS analízis indítása a SolidWorks-ből.

A parancs hatására megnyílik az ANSYS projektfelülete az importált geometriával. Az ábrán látható módon (3.69. ábra) rendeljük hozzá egy statikai analízishez (Analysis Systems/Static Structural) , melyet dupla klikkel, vagy behúzással helyezünk el a munkatérben. Ezután hasonló módon helyezzük el és csatoljuk az analízishez az anyagmodelleket tartalmazó egységet (Componenet Systems/Engineering Data) .

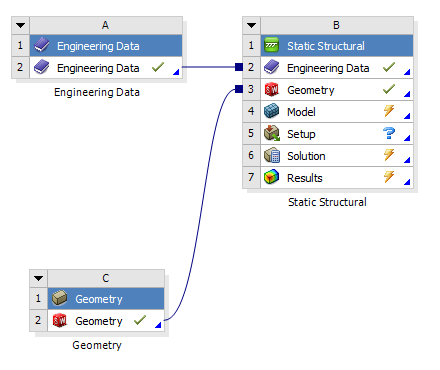
3.69. ábra - A projektfelületen megjelenő importált geometria és a hozz csatolt anyagmodell, és analízis.

3.3.2. Anyagmodell hozzárendelés

Az alsó Enginnering Data sorra duplán kattintva lépjünk be az anyagkönyvtárba, és adjuk hozzá az analízisünkhöz a General Materials könyvtárban lévő Stainless Steel-t a sárga + megnyomásával. Az ikonsor jobb szélén lévő könyveket ábrázoló ikonnal tehetjük láthatóvá a teljes anyagkönyvtárat. Az ikonsorban lévő kék visszanyíl (Return to Project) segítségével térjünk vissza projektfelületre (3.70. ábra).

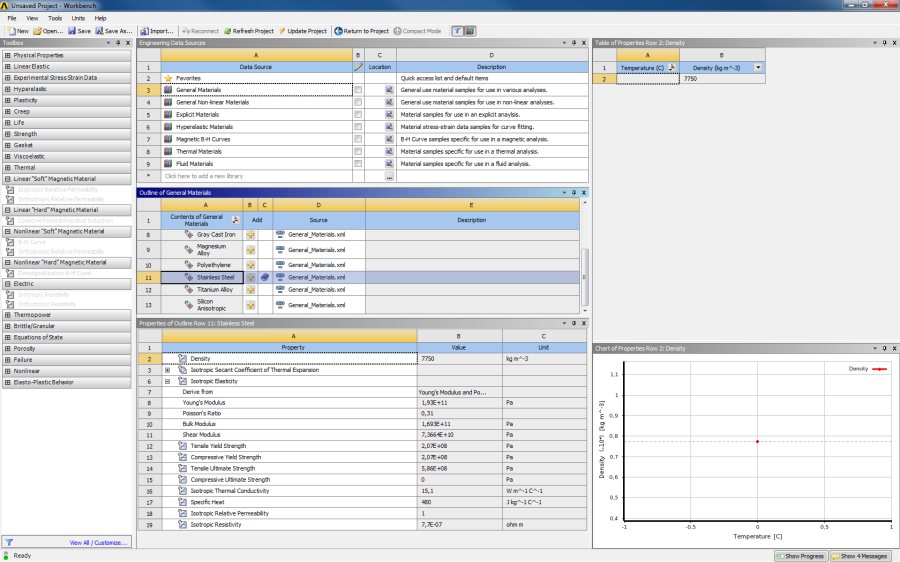
3.70. ábra - Az anyagkönyvtár.

A projektfelületen az elhelyezett Static Structural analízis Model sorára, vagy az alatta lévő sorok valamelyikére duplán kattintva, lépjünk be a mechanikai modulba az analízis elvégzéséhez. A modellfán végighaladva végezzük el a szükséges lépéseket. A modellfában lévő geometria sort legördítve jelöljük ki az alatta lévő alkatrész nevét (Outline/Project/Model/Geometry/Part) , és a modellfa alatt lévő Details of … panel Material/Assignment felirat mellett gördítsük le az anyagnevet tartalmazó cellát és rendeljük hozzá az előzőleg ki választott rozsdamentes acélt (Stainless Steel) .

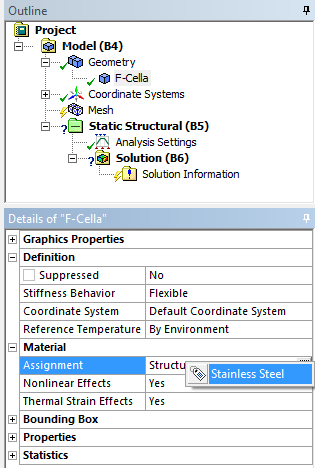
3.71. ábra - Anyag hozzárendelése a testmodellhez.

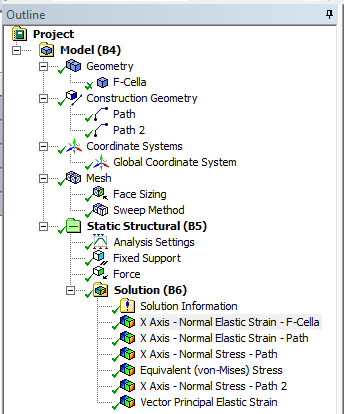
3.72. ábra - Az elvégzett analízis modellfája.

3.3.3. Hálózás

A hálókészítést kezdjük a globális paraméterek beállításával, melyek a modellfa Mesh elemének kijelölésével jelennek meg a Details panelen. Az elemméret beállításához válasszuk a Sizing/Use Advanced Size Funktion/On: Fixed lehetőséget és állítsuk be az ábrán látható paramétereket (3.73. ábra). A Max , ill. Min size értékekkel az elemméretet meghatározott határértékek közé tudjuk szorítani, és a Growth Rate paraméterrel határozzuk meg az elemméret átmenet intenzitását (lásd a 2. fejezet fejezet hálózás részét).

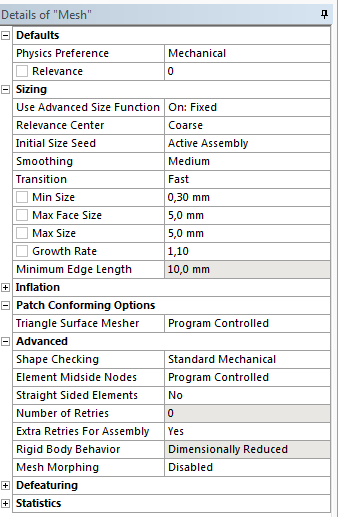
3.73. ábra - A háló globális paramétereinek beállítása.

A kikönnyített deformációs részeknél egyrészt a geometria elvékonyodása, másrészt azt itt jelentkező nagyobb mértékű feszültség és fajlagos nyúlás indokolja a háló lokális finomítását ezen a részen. Ehhez jelöljük ki a hengeres furatok palásfelületét és a furatok alatt és felett leválasztott felületelemeket, majd a modellfa Mesh sorára jobb gombbal kattintva válasszuk ki a Sizing opciót. Kattintsunk a Details panelen megjelenő Apply gombra, a kijelölt felületek elfogadásához. Ha helyesen jártunk el, a gomb helyén a „6 surfaces” felirat jelenik meg. Állítsuk az elemméretet (Element Size) 0,3 mm-re.

A következő lépésben a háló elrendezését tesszük egyenletessé a szélesség mentén. Ehhez a modellfa Mesh sorára jobb gombbal kattintva válasszuk ki a Method opciót, majd a Details panelen a Method felirat mellet válasszuk ki a Sweep azaz söprés eljárást. A CAD modellezéshez hasonlóan a Sweep parancs valamilyen generáló mintát, (esetünkben az oldalfalon lévő háló mintázatát) söpri végig egy útvonal mentén (esetünkben a szélesség). Bonyolultabb véglapok esetén szükség lehet azok manuális kijelölésére, Src/Trg Selection: Manual Source and Target . A megjelenő két sárga kijelölő ablakban jelöljük ki a cella jobb és bal oldalát. A méretezés típusát állítsuk elemméretre ( Details of Sweep Method/Type/Size) , majd állítsuk az elemméretet 1 mm-re.

Ezután generáljuk le a végeselem hálót a beállított kontrollokkal, (Outline/Mesh(JG)/Generate Mesh) .

3.74. ábra - A behálózott modell.

3.3.4. Megtámasztás és terhelés hozzárendelése

Az alábbi ábrán látható felületekre rakjuk fel a terhelőerőt (Loads/Force) és a megtámasztást (Supports/Fixed Support) (3.75. ábra). A parancsokat a modellfa aktuális szimulációt tartalmazó mappáját (Outline/Static Structural) kijelölve érjük el a felső menüsorból, vagy a jobbgombos menüből (3.76. ábra, 3.77. ábra). Az erő beállításainál a Details panelen írjunk be -10 N-t az erő nagyságához. A negatív előjelre azért van szükség, mert alapértelmezetten a kijelölt felület normális vektorának irányába esik az erővektor.

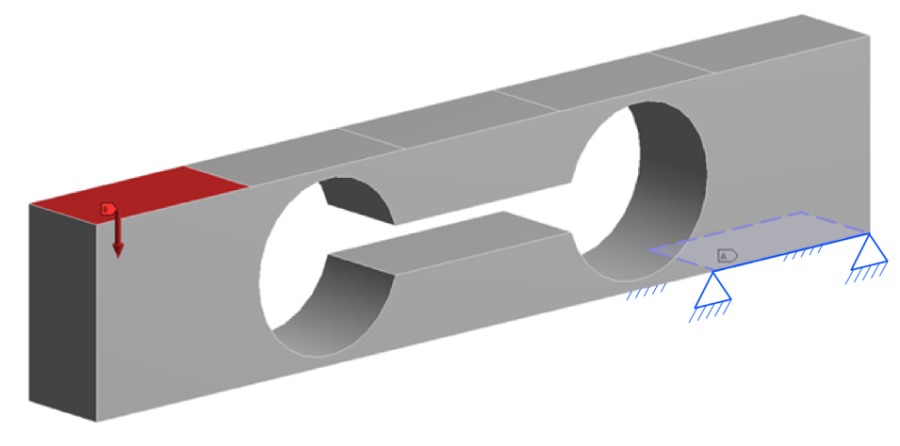
3.75. ábra - A cella megtámasztása és terhelése.

3.76. ábra - Megtámasztások.

3.77. ábra - Terhelések.

3.3.5. Futtatás és az eredmények lekérdezése

A szimuláció futtatásához kattintsunk a felső ikonsor Solve gombjára. A számolás folyamatát felugró ablakban jelzi a program. A lefuttatott analízis eredményeinek lekérdezése hasonlóan történik a terhelések beállításához. A modellfa megoldásokat tartalmazó mappáját (Outline/Solution) kijelölve, a felső menüsorból, vagy a jobbgombos menüből érhetjük el a kívánt mennyiséget lekérdező parancsot.

Első lépésben győződjünk meg arról, hogy a nyúlásmérő bélyegek helyén, az alakváltozási állapot az előzetes elvárásoknak megfelelően alakul e, (vagyis X irányú fajlagos nyúlás a domináns). Ehhez adjuk ki a felső ikonsorból a Strain/Vector Principal parancsot (3.78. ábra) és ismét nyomjuk meg a Solve gombot.

3.78. ábra - Eredmények lekérdezése a felső ikonsorból. Alakváltozási tenzor lekérdezése.

Az eredmény megmutatja a terhelés hatására kialakuló főnyúlások irányát és hozzávetőleges értékét. Az ábrán látható, hogy a várakozásoknak megfelelően, a cella deformálódó részén, a kikönnyítés feletti sík részen döntően X (hossz) irányú alakváltozás ébred (3.79. ábra). Hasonló képen lehet lekérdezni a feszültségi állapotot is.

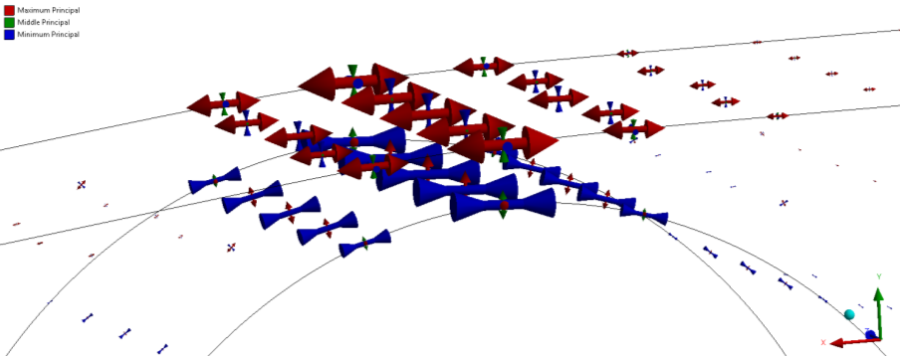
3.79. ábra - A nyúlásmérő bélyeg felragasztásának helyén ébredő alakváltozási állapot.

A továbbiakban, a már tanult módon kérdezzük le az egyenértékű feszültséget (Equivalent (von Mieses) Stress), az Y irányú elmozdulást (Directional Deformation, Y Axis), és az X irányú fajlagos nyúlást (Normal Elastic Strain, X axis). Ez utóbbit a teljes modellre, ill. csak a deformációs régiók feletti leválasztott felületelemekre is kérdezzük le.

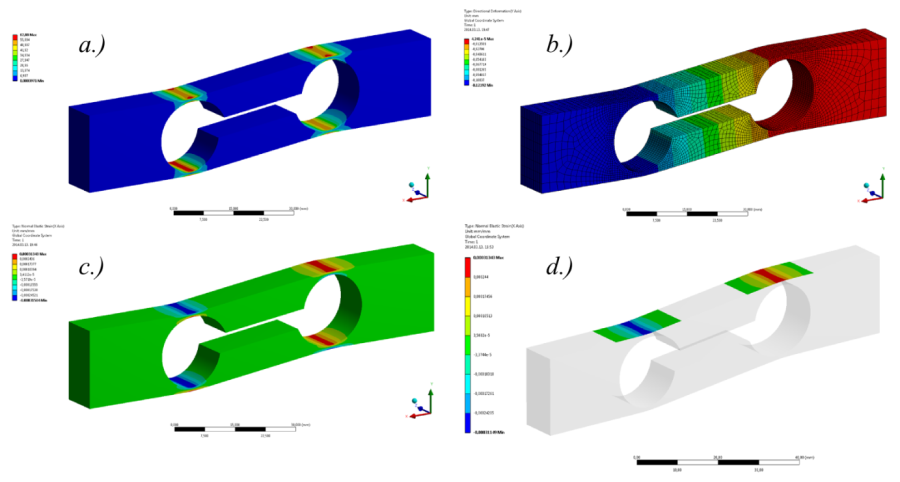
3.80. ábra - Az analízis eredményei: a.) von Mieses féle egyenértékű feszültség, b.) Y irányú elmozdulás, c-d.) X irányú fajlagos nyúlás.

3.4. Ellenőrző feladatok

3.4.1. Feladat

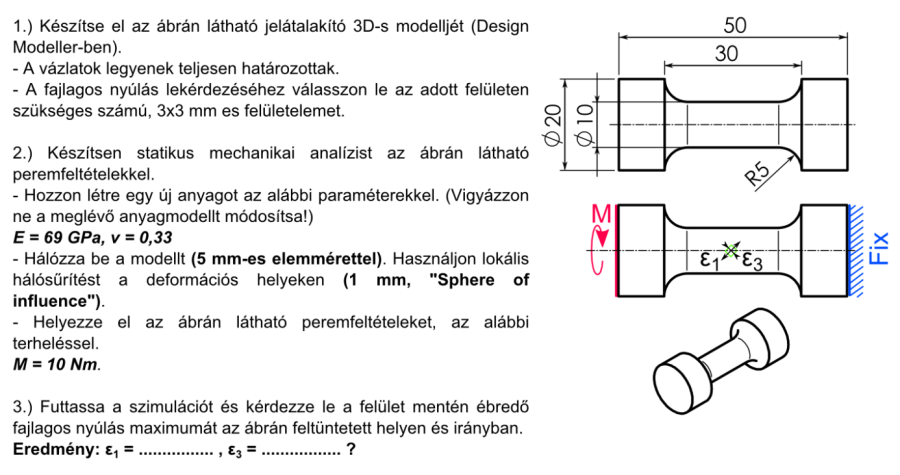
3.4.2. Feladat

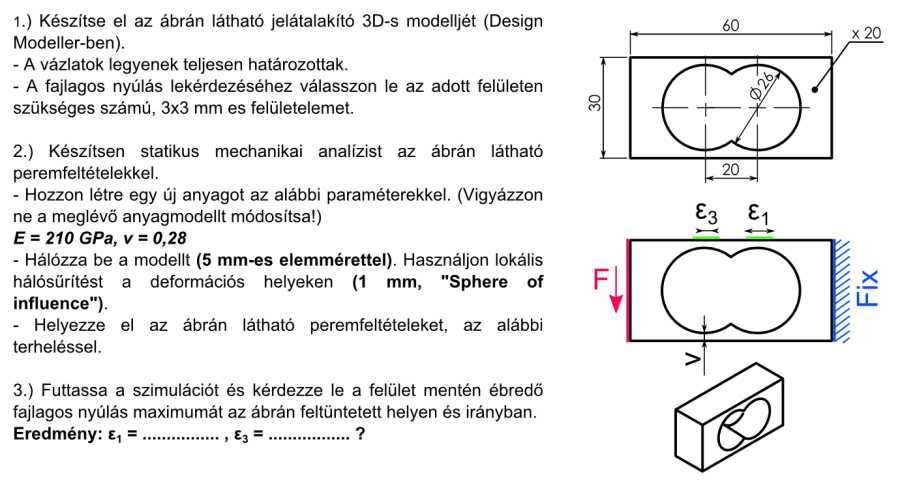
4. fejezet - Nemlineáris statikai analízis

Tartalom

4.1. A nemlinearitás okai

4.1.1. Anyagi nemlinearitás
4.1.2. Geometrriai nemlinearitások, nagy deformációk
4.1.3. A terhelési állapot megváltozása, nemlineáris kontaktok

4.2. A nemlineáris feladat megoldása

4.2.1. Alkalmazható anyagmodellek
4.2.2. Alkatrész viselkedés
4.2.3. Hálózás
4.2.4. A szimuláció beállításai
4.2.5. Peremfeltételek / Peremfeltételek / Eredmények

4.3. Mintafeladat instabil terhelési állapotra

4.4. Mintafeladat anyagi és geometriai nemlinearitásra

A valós szerkezetek viselkedése általában eltér a lineáristól. Sok esetben a lineáris szimuláció jó közelítést adhat a probléma megoldására, de számos esetben hibás eredményre vezet, mivel az alapjául szolgáló feltételezések már nem helytállóak. A nemlineáris szimuláció megoldása több terhelési lépésben történik. A konvergencia elérése érdekében, az egyes lépéseket a program iterálva oldja meg, ezért a nemlineáris feladatok sokkal idő és számításigényesebbek, mint a lineáris.

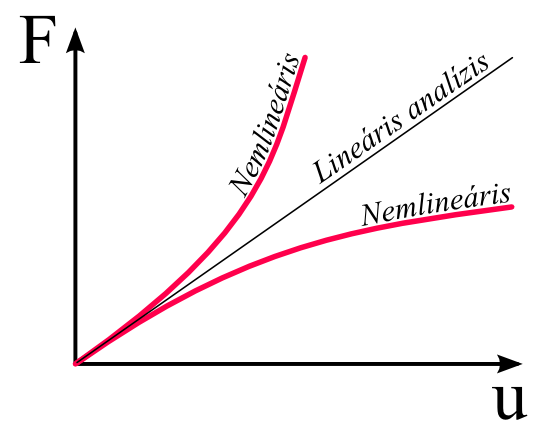
4.1. ábra - Lineáris és nemlineáris szerkezeti analízis.

4.1. A nemlinearitás okai

A nemlineáris viselkedést okozhatja az anyagi viselkedés, a nagy deformáció, vagy a nemlineáris terhelési, vagy peremfeltételek, ill. kontaktok.

4.1.1. Anyagi nemlinearitás

A nemlinearitás egyik alapvető oka a nemlineáris anyagi viselkedés. Jellemzője, hogy a feszültség és fajlagos nyúlás közötti kapcsolat nem lineáris, tehát az analízis során az anyag merevsége változik (nem érvényes rá a Hooke törvény). Nemlineáris feszültség-alakváltozás tulajdonsággal rendelkező plasztikus (plastic), multilineáris rugalmas (multilinear elastic), és a nagyrugalmas (hyperelastic) anyagmodellek a szerkezet különböző merevségét eredményezik a különböző terhelési szinteken (és hőmérsékleteken). A kúszás (Creep), viszkoplasztikus (viscoplasticity), és viszkoelasztikus (viscoelasticity) anyagmodellek nemlinearitása lehet idő, sebesség, hőmérséklet-, és a feszültség szerinti.

4.1.2. Geometrriai nemlinearitások, nagy deformációk

A végeselemes analízisekben jelentkező nemlinearitások egyik fő oka az egész szerkezetre jellemző nagy elmozdulások, amelyek egyben a terhelési konfiguráció megváltozását is jelentik, (Például egy vékony, egyik oldalán befogott rúdra ható erő és a rúd tengelye által bezárt szög a rúd nagymértékű lehajlásával jelentősen megváltozik).

Nagy deformációk esetén a terhelés hatására létrejövő merevségváltozás már nem elhanyagolható, (Például egy kábel-szerkezetet terhelő húzóerő a merevség növekedését okozza, míg egy kupola, vagy boltív szerű szerkezet terhelés hatására történő átpattanásakor (snap-through) először lágyítja, aztán merevíti a szerkezetet). A nemlineáris szimuláció során lehetőségünk van nagy alakváltozások (Large Deflections) számolására. Ilyenkor a szoftver újraszámolja a modell merevségi mátrixát minden lépés során.

4.1.3. A terhelési állapot megváltozása, nemlineáris kontaktok

Nemlineáris viselkedést okoz a vizsgált szerkezet státuszának / terhelési állapotának megváltozása a szimuláció alatt. Ennek okai a szerkezet és a terhelés együttes viselkedésében keresendő. Ilyen viselkedést mutat pl. egy megfeszített kötél, amely meglazul; két felület, amelyik egyszer érintkezik máskor nem.

Tehát a nemlineáris viselkedés egyik gyakori forrása a nemlineáris viselkedésű kontaktok. A ragasztott (Bonded) kivételével a kapcsolódó felületek elmozdulhatnak egymáson, ezért az átadódó terhelés lépésenként változó. A nemlineáris szimulációban a program lépésenként frissíti az átadott terhelés mértékét, eloszlását és irányát.

4.2. A nemlineáris feladat megoldása

Newton-Raphson közelítés az alkalmazott terhelés felosztásával és több lépésben történő közelítésével oldja meg a nemlineáris feladatot. Minden megoldás előtt a program megbecsül egy az egyensúlyi helyzetből kitérítő (out-of-balance) terhelési vektort, ami az elemfeszültségeknek megfelelő visszaható (restoring,) terhelés és az alkalmazott terhelés különbsége. Ezután a program futtat egy lineáris megoldást az out-of-balance terhelési vektor felhasználásával és vizsgálja a konvergenciát. Ha nem teljesítette a konvergencia kritériumot, akkor az out-of-balance terhelési vektort újra megbecsüli, a merevségi mátrixot frissíti, és újra futtatja a számolást. Ezen lépéseket addig futtatja, amíg nem konvergál a szimuláció. Különböző eszközök léteznek a konvergencia elősegítése érdekében úgy, mint az él keresés (line search), a terhelések automatikus felosztása (automatic load stepping), kettéosztás (bisection).

Amennyiben a számolás nem konvergál, a terhelési lépések csökkentésével lehet elősegíteni a megoldást.

A terhelési lépéseket (load steps) a felhasználó állítja be közvetlenül.
Ezek feloszthatóak al-lépésekre (substeps / time steps), mely történhet automatikusan, vagy manuálisan.
A konvergencia elérése érdekében, minden al-lépésben számos egyensúlyi iteráció (equilibrium iterations) fut le.

Egyes esetekben a Newton-Raphson egyedüli alkalmazása nem vezet eredményre a szingulárissá váló érintő merevségi mátrix (tangent stiffness matrix) miatt. Olyan esetekben következhet ez be, amikor például a szerkezet instabil lesz és átbillen (snap-through) egy másik egyensúlyi helyzetbe, pl. nemlineáris kihajlás vizsgálatkor. Ilyen esetekben célszerű az Ívhossz (arc-length) eljárás kiegészítő alkalmazása. Az ívhossz eljárás a Newton-Raphson egyensúlyi iteráció konvergenciáját eredményezi egy ív mentén, azáltal, hogy megakadályozza a divergenciát olyan esetekben, amikor a terhelés-deformáció görbe meredeksége nulla illetve negatív értékűvé válik (4.2. ábra) [45.] , [6.] .

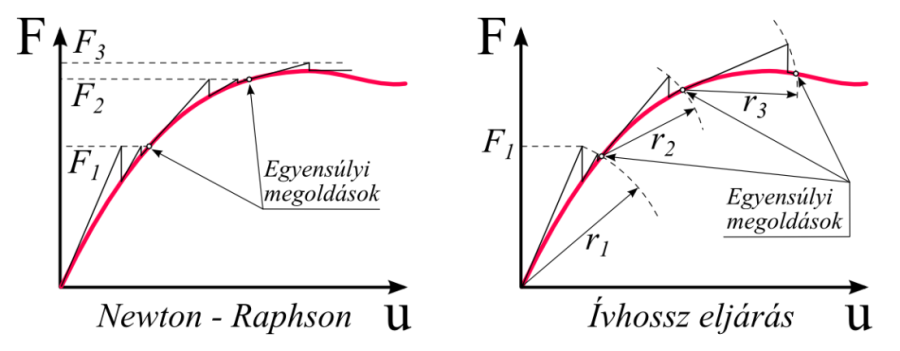
4.2. ábra - A Newton-Raphson és az Ívhossz eljárás.

4.2.1. Alkalmazható anyagmodellek

A nemlineáris mechanikai anyagmodell merevségét a feszültség-nyúlás karakterisztikájával, vagy a származtatott paramétereivel definiáljuk (pl.: hiperelasztikus anyagállandók, multilineáris karakterisztika, stb.). Időben állandó inerciális terhelések alkalmazása esetén a sűrűség definiálása is szükséges.

A nemlineáris anyagmodellek tartalmazhatnak plaszticitás (plasticity), felkeményedő (stress stiffening), nagy alakváltozás (large deflection / large strain), nagyrugalmas (hyperelasticity), és kúszás (creep), stb. viselkedésű elemeket.

4.2.2. Alkatrész viselkedés

A lineáris statikai analízishez hasonló viselkedésű alkatrészek alkalmazhatóak. Amennyiben a modell nemlinearitásokat tartalmaz, (pl. karcsú szerkezetek nagy lehajlása, instabil viselkedése, vagy hiperelasztikus anyagmodell, stb.) a számolási idő jelentősen megnövekedhet az iteratív procedúrának köszönhetően. Ilyen esetén célszerű egyszerűsítéseket alkalmazni, mint pl. a szimmetria feltételek, 2d-s, vagy héjmodell.

4.2.3. Hálózás

A lineáris statikai analízisnél alkalmazott szempontok, továbbá a nemlineáris viselkedéssel gyakran együtt járó nagy alakváltozások figyelembevétele szükséges a háló elkészítésénél. Nemlineáris vizsgálatok esetén a hálónak követnie kell az adott szimuláció tulajdonságait, megfelelően finom háló szükséges például a nagy plasztikus alakváltozást szenvedő területeken.

4.2.4. A szimuláció beállításai

Nagy lehajlások (Large Deflection) bekapcsolása szükséges, ha egy karcsú szerkezet lehajlása meghaladja a vastagsága 10%-át, hiperelasztikus anyagmodell alkalmazásakor, vagy ha instabil viselkedést (pl. kihajlást) várunk. (Kis elmozdulást akkor feltételezhetünk, ha a fajlagos nyúlás elég kicsi ahhoz, hogy az eredő merevség ne változzon jelentősen.) A nagy elmozdulások opció bekapcsolásával a merevség az elemek alakjával és orientációjával változik, ami pontosabb eredményhez vezet. A nagy lehajlások alkalmazásával a számolás iteratívvá válik, ami növelheti a számolási időt.
Időlépések – a szimuláció nemlineáris megoldása szükségessé teheti az időlépések alkalmazását, vagyis a terhelés kis lépésenkénti növelését. Több lépésre akkor is szükség lehet, ha lépésenként különböző terhelési állapotot akarunk beállítani, pl. előfeszítés beállítása, elmozdulás kényszer bekapcsolása / kikapcsolása, stb. (Részletesebben lásd a 2. fejezet fejezet ide vonatkozó részét.)
A kimenet beállításával (Output Controls) határozhatjuk meg a mentésre szánt lépéseket, mivel egy nemlineáris szimuláció sok olyan lépést tartalmazhat, amelyre nem, vagyunk kíváncsiak és fölöslegesen növelik a tárolandó adatok mennyiségét.
Nemlineáris beállítások
- Nemlineáris kontrollokkal (Nonlinear Controls) módosíthatjuk a konvergencia kritériumokat. Az adott al-lépésekben lefutó egyensúlyi iterációk akkor sikeresek, ha az out-of-balance terhelés egy meghatározott konvergencia kritérium értéke alá csökken.
- Vonalkeresés (line search) – hatásos, de energiaigényes megoldás a konvergencia elérése érdekében. Alkalmazása erő jellegű terhelések, karcsú szerkezetek alkalmazása, vagy oszcilláló konvergencia minta esetén ajánlott.
- Stabilizáció (Stabilization) – Kis erők hatására fellépő nagy deformáció instabilitást okozhat, amelyet a csomópontokhoz rendelt mesterséges csillapításokkal tudunk stabilizálni. A csillapítás értékét megadhatjuk a csillapítási fokkal (damping factor), vagy a disszipált energia aránya (energy dissipation ratio, 0-1), melyek lehetnek konstansok (Constant), vagy csökkenő (Reduce, lineárisan 0-ra csökken) értékűek.

4.2.5. Peremfeltételek / Peremfeltételek / Eredmények

A lineáris statikai analízisben alkalmazható terhelések és peremfeltételek érvényesek, valamint az eredmények lekérdezésének és kiértékelésének módja is hasonló.

4.3. Mintafeladat instabil terhelési állapotra

Az alábbi példában egy lineáris anyagmodellel definiált alkatrész terhelés hatására létrejövő nemlineáris viselkedését fogjuk bemutatni. A szerkezeti instabilitás egyik gyakran emlegetett esete a boltozatszerű geometriák átpattanása (snap-through). Egy ilyen boltozatos héjszerkezet domború felületét terhelő nyomás hatására bekövetkező átpattanását vizsgáljuk meg.

Kiinduló adatok:

Átmérő: D=20mm,

Magasság: H=3mm,

Vastagság: t=0,1mm,

Anyag: Acél: E=200GPa, v=0,3,

Terhelő nyomás: p=12MPa,

Megtámasztás: Fix megfogás körben a perem mentén.

A feladatot az ANSYS Workbench végeselem programban oldjuk meg. A modell létrehozása a Design Modeller -ben az XY síkra rajzolt körív (az alábbi ábrán piros vonallal jelölve), Y tengely (zöld pont-vonal) körüli megforgatásával történik (4.3. ábra, a.). Fontos, hogy csak felületmodellt készítsünk, melynek vastagságát a szimulációs környezetben (Mechanikal modul) adunk. Az így létrejött héjmodell kisebb számolási igénnyel bír, mint ha testmodellel hoznánk létre. A strukturált háló létrehozását elősegítendő, osszuk fel a felületetet az ábrán látható módon (4.3. ábra, b.). A felosztáshoz használjuk a már ismert (Extrude/Inprint Faces) opciót két lépésben. Első lépésben rajzoljuk meg és válasszuk le a központi íves oldalakkal definiált négyszögű régiót (zöld vonal), majd második lépésben ennek sarkaitól kifelé húzott vonalakkal (kék vonalak) válasszuk 4 részre a külső gyűrűszerű felületet. Figyeljünk arra, hogy a két rajz külön vázlaton készüljön el.

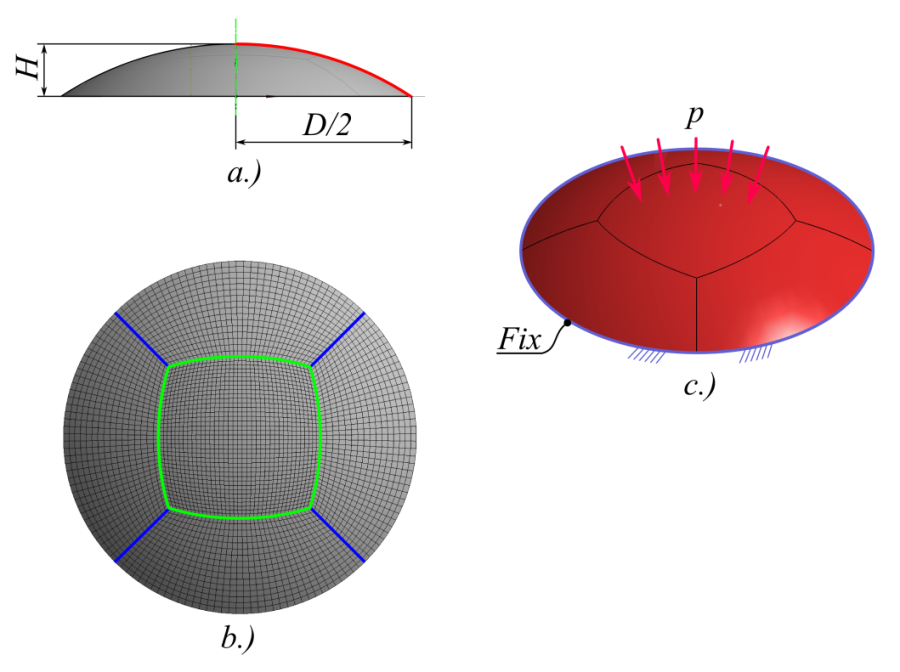
a.) geometriai modellje, b.) hálózása valamint c.) terhelése és megtámasztása

4.3. ábra - Domború héjszerkezet

A geometriához alapértelmezettként hozzárendelt szerkezeti acélt hagyjuk érvényben. A hálózásnál használjunk 0,2mm-es elemméretet, négyszögelemekkel. Ehhez a modellfában kijelölt háló (Outline/Mesh) globális elemméretét állítsuk be a Details of „Mesh” panel Sizing részén. Használjuk a Use Advanced Size Function: On: Fixed opciót az ábrán látható elemméret beállításokkal (4.4. ábra). A fenti ábrán lévő rendezett háló elérése érdekében adjuk ki az Outline/Mesh(JG)/Insert/Mapped Face Meshind parancsot és jelöljük ki mind az 5 felületelemet.

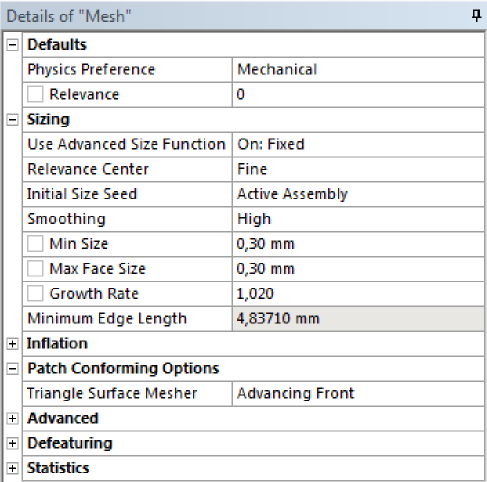
4.4. ábra - A végeselem háló globális beállítása.

Helyezzünk el egy Fix kényszert a modell pereme mentén, (él mentén), majd a nyomást (Pressure) a teljes felületre érvényesítve (4.3. ábra, c.).

A szimulációt az alapbeállításokkal futtatva azt tapasztaljuk, hogy nem fut le. A modellfa Settings sorát kijelölve a Details panelen végezzük el az alábbi ábrán látható beállításokat (4.5. ábra).

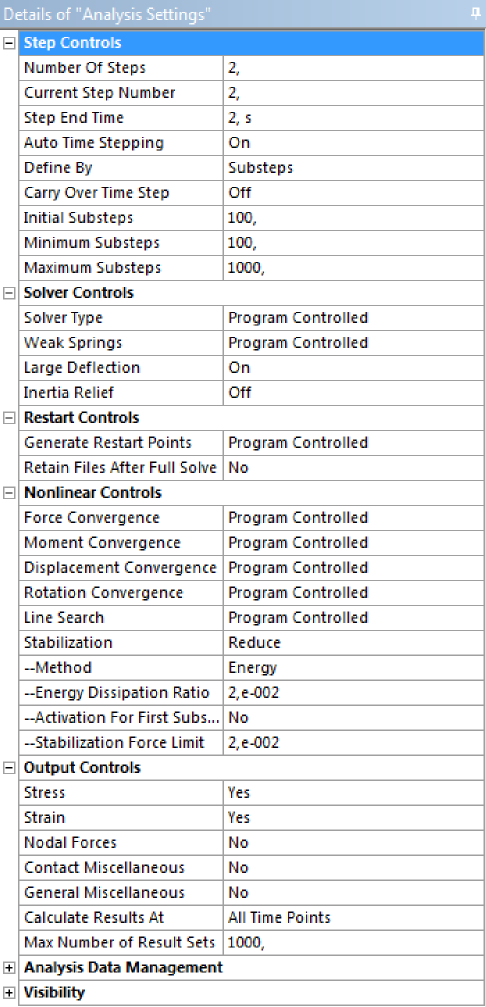
4.5. ábra - A nemlineáris analízis beállításai.

Indítsuk el az analízis számítását. A modellfa megoldási információk (Outline/Solution/Solution Information) elemére kattintva nyomon követhetjük a számolás folyamatát. A Force Convergence opció segítségével információt kaphatunk arról, hogy a számolás konvergál-e, és, hogy az egyes lépések végrehajtódtak-e. Ez főleg a nagy számolási igényű feladatoknál jelent segítséget.

A számolás lefutása után adjunk hozzá egy a deformáció lekérdező parancsot (Outline/Solution(JG)/Insert/Deformation/Total Deformation) , majd a képernyő alján lévő Graph panelen animáljuk az átpattanás folyamatát.

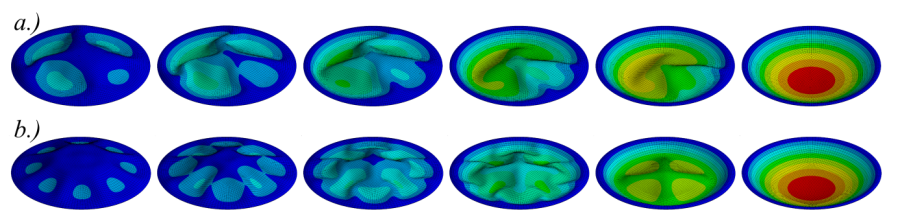
a.) strukturálatlan, és b.) strukturált háló esetén

4.6. ábra - Az átpattanás folyamata.

Futtassuk a szimulációt strukturált és strukturálatlan hálóval, és hasonlítsuk össze az eredményeket. Látható, hogy a 4 szegmensre osztott hálóstruktúrával az eredmény is 4 szegmenses mintázatot mutat (4.6. ábra).

Megjegyzés: Vegyük figyelembe, hogy az analízis során lineáris anyagmodellt alkalmaztunk, ami nem vette figyelembe azt, hogy az átpattanás során helyenként a feszültség igen magas, a valós anyag folyáshatárát és szakítószilárdságát is meghaladó értéket ért el.

4.4. Mintafeladat anyagi és geometriai nemlinearitásra

A következő feladat során szimuláljuk az egyik oldalán nyomással terhelt, elasztomer membrán felfújódását. Az analízis nemlinearitását a nemlineáris anyagi viselkedés és a rendkívül nagy elmozdulások okozzák, ez utóbbi következménye továbbá a terhelési feltételek megváltozása is.

Kiinduló adatok:

A geometria egy forgásszimmetrikus, domború membrán, melynek méretei:

Átmérő: D=50mm,

Magasság: H=7,4mm,

Vastagság: t=1mm,

Anyag: Szilikongumi (paramétereit lásd lentebb),

Terhelő nyomás: p=0,04MPa,

Megtámasztás: Fix megfogás körben a perem mentén,

Az anyagmodell létrehozásához egytengelyű húzó és nyomó, valamint kéttengelyű anyagvizsgálatokból származó adatok állnak rendelkezésre (4.7. ábra, Táblázat 4.1).

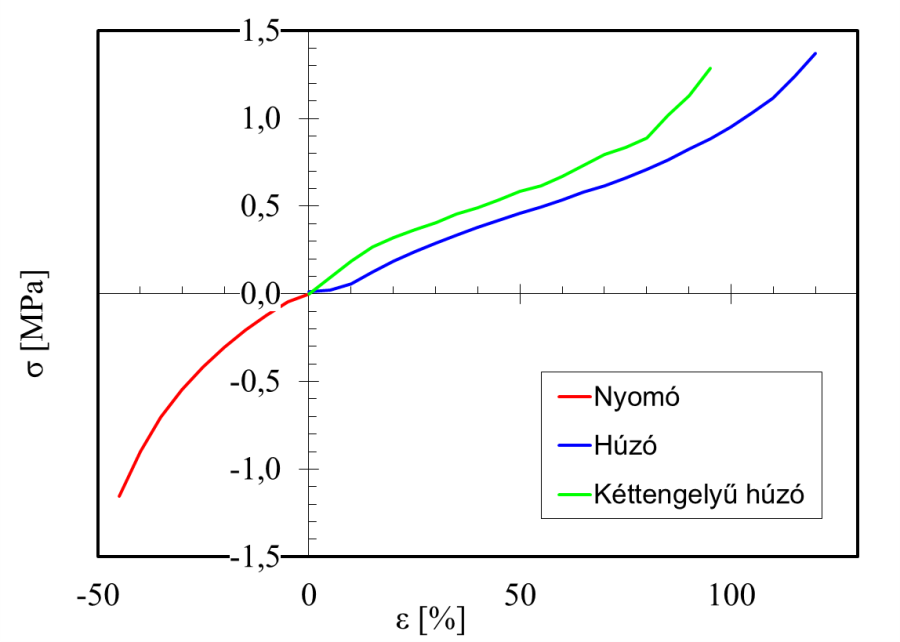
4.7. ábra - Anyagvizsgálatból származó Feszültség-nyúlás karakterisztika.

A nyomó és húzóvizsgálatokat egy táblázatba másolva egy adatsorként (Uniaxial Data) lehet bevinni a programba.

4.1. táblázat - Anyagvizsgálati adatok.

Egytengelyű		Kéttengelyű húzó
ε [-]	σ [Mpa]	ε [-]	σ [Mpa]
-0,450	-1,157	0,000	0,000
-0,400	-0,901	0,050	0,094
-0,350	-0,705	0,100	0,188
-0,300	-0,547	0,150	0,268
-0,250	-0,416	0,200	0,322
-0,200	-0,304	0,250	0,365
-0,150	-0,207	0,300	0,405
-0,100	-0,121	0,350	0,456
-0,050	-0,048	0,400	0,493
0,000	0,000	0,450	0,536
0,050	0,020	0,500	0,584
0,100	0,055	0,550	0,616
0,150	0,123	0,600	0,669
0,200	0,186	0,650	0,732
0,250	0,242	0,700	0,793
0,300	0,290	0,750	0,834
0,350	0,334	0,800	0,886
0,400	0,378	0,850	1,018
0,450	0,419	0,900	1,128
0,500	0,457	0,950	1,286
0,550	0,495
0,600	0,535
0,650	0,579
0,700	0,617
0,750	0,661
0,800	0,709
0,850	0,762
0,900	0,827
0,950	0,885
1,000	0,951
1,050	1,031
1,100	1,119
1,150	1,236
1,200	1,371

Az anyagmodell definiálásához az ANSYS Workbench projektfelületén helyezzünk el egy Engineering Data panelt, majd duplán kattintva rá, lépjünk be az analízis anyagkönyvtárába. A Structural Steel alatti sorra kattintva, és az új anyag nevét (Szilikongumi) beírva hozzunk létre egy új anyagot. Az ekkor még üres keretbe behúzással, vagy dupla kattintással, helyezzünk el a bal oldali panel Experimental Stress Strain Data részéről egy Uniaxial Test Data és egy Biaxial Test Data elemet. A jegyzet fenti táblázatából a megfelelő adatpárost másoljuk be az anyagmodell megfelelő helyére (a jobb felső, Table of Properties panelen található táblázatokba). Ügyeljünk arra, hogy a táblázat fejlécén a megfelelő mértékegységet válasszuk (mm mm^-1; MPa). Mindkét vizsgálati adat táblázata mellett lévő hőmérséklet (Temperature) cellába írjunk 22°C-ot, ami az adott anyagvizsgálat elvégzésekor mért környezeti hőmérsékletet jelenti. Ezután szintén a bal oldali panel Hyperelastic sora alatti anyagmodellek közül dupla kattintással helyezzünk el egy 5 paraméteres Mooney-Rivlin anyagmodellt. Az anyagmodellünkben megjelenő Mooney-Rivlin sort gördítsük le, majd abszolút hibavizsgálatra (Absolute Error) állítva, jobb gombos kattintással a Curve Fitting sorra, a Solve Curve Fit parancs kiadásával illesszünk görbét a vizsgálati adatokra. Miután ellenőriztük a görbe illeszkedését a jobb oldali grafikonon, jobbgombos menüből másoljuk az illesztett paramétereket az anyagmodellbe ( Curve Fitting(JG)/Copy Calculated Values to Property) . Ez után az Mooney-Rivlin modellben megjelenő paraméterek között írjunk az összenyomhatatlansági (Incompressibility Parameter, D1) paraméter cellájába 0-t, (ez jelenti az elasztomerekre jellemző térfogat-állandóságot), majd ellenőrizzük a modellt alkotó mindhárom görbét. Az anyagmodell létrehozása után térjünk vissza projektfelületre, majd adjunk hozzá egy statikai (Static Structural) analízist, melybe kössük be az Engineering Data panelt.

Az analízis típusa 2D tengelyszimmetrikus analízis lesz, amihez a 2D-s viselkedést a szimulációs környezetbe való belépés előtt be kell állítanunk, mert utólagosan már nincs lehetőség az átjárásra. Célszerű a geometria létrehozása előtt átállítani, a Static Structural/Geometry sorát kijelölve, a projektfelület jobb oldalán megjelenő tulajdonságok panelen (Properties of Schematic … : Geometry/Advanced Geometry Options/Analysis Type: 2D) , (4.8. ábra). Ha a panel nem jelenik meg akkor a statikai analízis paneljének Geometry sorára való jobb gombos kattintással, majd Properties parancs kiadásával előhozható.

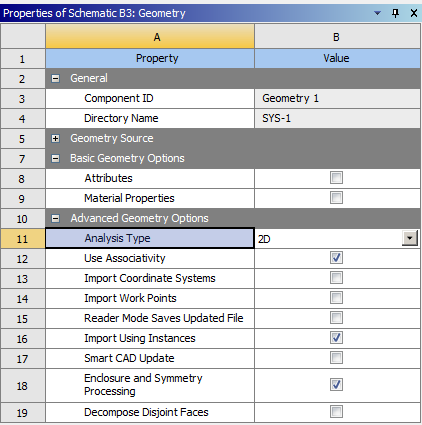
4.8. ábra - Váltás 2 dimenziós geometriára.

A szerkezeti analízis Geometry sorára duplán kattintva hozzuk létre a geometriát. A 2D-s tengelyszimmetrikus analízis előfeltétele az ANSYS-ban, hogy a forgástest félmetszetét az XY síkon helyezzük el a +X térfélen, ugyanis az Y tengely lesz a forgásszimmetrikus analízis tengelyvonala. Hozzuk létre a rajzon lévő geometria vázlatát, majd feszítsünk rá sík felületet a Tools/Surfaces From Sketches paranccsal (4.9. ábra, a.). Méretek:

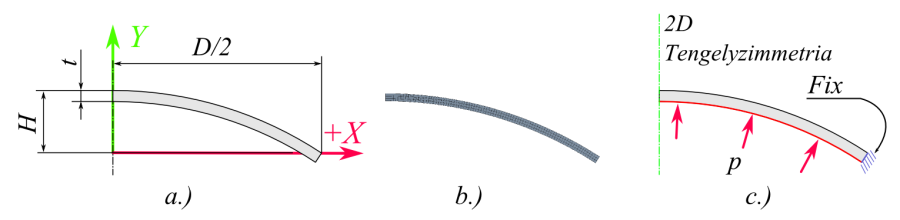
a.) Geometria, b.) hálózás, c.) Peremfeltételek és terhelés

4.9. ábra - Forgásszimmetrikus test 2D-s modellje

Ezután a Geometry alatti bármelyik sorra való dupla kattintással lépjünk be a Melchanical modulba, vagyis a szimulációs környezetbe. A modellfán a geometriát kijelölve a szimuláció típusát állítsuk tengelyszimmetrikusra (Outline/…/Geometry => Details /Definition/2D Behavior: /Axisymmetric) .

A geometriát legördítve a felületmodellhez rendeljük hozzá az általunk létrehozott „Szilikongumi” nevű anyagmodellt (Outline/…/Geometry/Surface Body => Details/Material/Assigment: Szilikongumi) .

A hálózásnál állítsunk be 0,3mm-es globális elemméretet és rendezett hálót (Mapped Face Meshing) .

Adjuk hozzá az ábrán látható megfogást és terhelést.

Az analízis beállításainál állítsunk be az időlépéseket az alábbi ábrán látható módon (Outline/…/Static Structural/Analysis Settings => Details/Step Controls) és kapcsoljuk be a nagy elmozdulásokat lehetővé tevő Details/Solver Controls Large Deflection opciót (4.10. ábra).

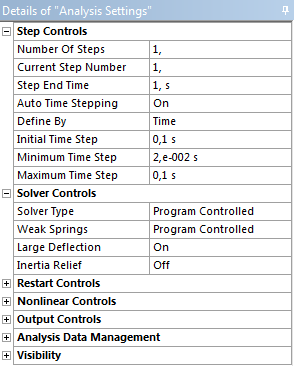
4.10. ábra - A nemlineáris analízis időlépéseinek és nagy elmozdulásának beállítása.

Ezután futtassuk a szimulációt, miközben figyeljük a megoldás konvergenciáját (4.11. ábra), (Outline/…/Solution/Solution Information=> Details/Solution Information/Solution Output/Force Convergence) .

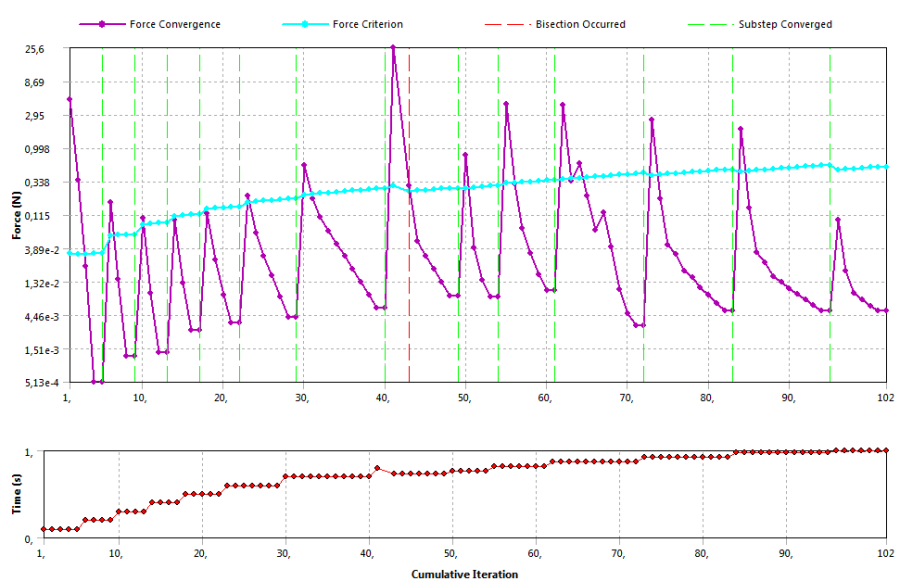
4.11. ábra - Az erő konvergenciáját mutató diagram.

Ha lefutott az analízis, kérdezzük le az 1. főfeszültség (Maximum Principal Stress) és 1. főnyúlás (Maximum Principal Strain) értékét, és a külső kontúr irány menti elmozdulását (Directional Deformation) mind X mind pedig Y irányban.

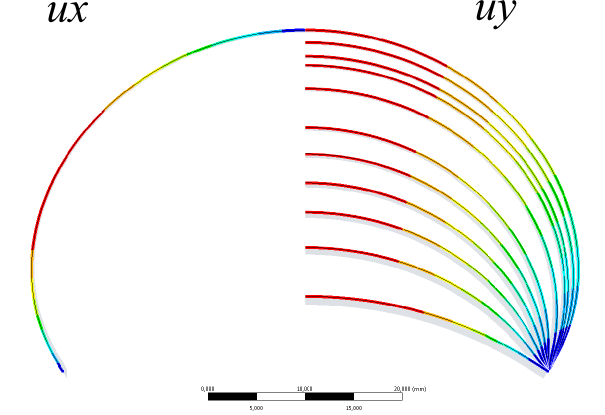
A membrán felfújódásának folyamata, (az X és Y irányú elmozdulásokat bemutató eredmények egy ábrára szerkesztve a szemléletesség kedvéért).

4.12. ábra - A membrán felfújódásának folyamata, (az X és Y irányú elmozdulásokat bemutató eredmények egy ábrára szerkesztve a szemléletesség kedvéért).

Megjegyzés: A fenti eredmények a felső felületet jelentő él mentén lettek lekérdezve. Az eredményeket a már tanult módon (jobb gombos kattintás a megfelelő lekérdezés során, majd Convert to Path Result ) átalakíthatjuk útvonal menti lekérdezéssé. Így megkaphatjuk az X és Y irányú elmozdulások értékét az útvonal menti elhelyezkedést jelző S[mm] paraméter függvényében (Lásd 3. fejezet 1. példáját). A modellfában az útvonalra jobb gombbal kattintva kiexportálhatjuk a vizsgált pontok kiinduló XY koordinátáit (Outline/Construction Geometry/Path(JG)/Export) , ezzel kiszámolhatjuk és akár diagramon is ábrázolhatjuk a deformált test alakját.

5. fejezet - Paraméter vizsgálatok, optimalizációs feladatok

Tartalom

5.1. Példa optimalizációs feladatra

Paraméternek nevezünk minden olyan változót a végeselemes szimulációk estében, amelyeknek a szimuláció folyamán változik az értéke. Bemenő paramétereket típusuk szerint a következőképpen csoportosíthatjuk:

geometriai, vagy CAD paraméter – a geometria modell egy mérete (pl. egy lemezes alkatrész vastagsága, könnyítő furatok száma stb.)
anyagtulajdonságra vonatkozó paraméter – adott anyagmodell egy tulajdonságának értéke (pl. szakító szilárdság)
terhelésre vonatkozó paraméter - a geometriára ható terhelés értéke (pl. terhelő erő mértéke).

Kimenő paraméter a szerkezet terhelésre adott válaszának egy meghatározott értéke lehet, legtöbbször egy kimenő érték szélső értéke, vagy adott geometriai helyen lévő értéke a releváns információ. (Pl. maximális feszültség, maximális deformáció adott irányban, maximális fluxus-sűrűség stb.)

Bemenő és kimenő paraméterekből is tetszőleges számút definiálhatunk.

Optimalizációs feladatok alatt azokat a feladatokat értjük, ahol a megadott bemenő paraméterek változtatásával a definiált kimenő paraméter egy adott célértékét keressük.

Ilyen feladatok esetén a véges elemes szoftverek a bemenő paramétereket folyamatosan változtatva számítja ki a különböző paraméterkombinációkhoz tartozó célértékeket. Természetesen minél több a bemenő paraméterek száma exponenciálisan annál több időt vesz igénybe a számítási folyamat.

A paraméterek változtatási módját is definiálni kell, célszerű olyan értéktartományt meghatározni, amely lefedi a lehetséges változatok egészét (amely pl. egy megadott méreten belül van). A paraméterek változtathatóak folyamatosan és diszkrét értékekkel is. Utóbbinak akkor van különös jelentősége, amikor az adott paraméter csak bizonyos értékeket vehet fel (pl. szabványos zártszelvény méretek, lemezvastagságok, csavarméretek, konkrét anyagtípusok). A folyamatos változtatás esetén is tulajdonképpen konkrét értékekre áll be az adott paraméter, azonban ebben az esetben pl. egy adott mérettartomány értékeit egyenletesen elosztva alakulnak ki ezek az értékek, függetlenül attól, hogy a valóságban használunk-e olyan méretet.

A bemenő paraméterek, de főként a geometriai paraméterek definiálásánál kell figyelni arra, hogy az adott paraméterek egyetlen kombinációja se okozzon megoldhatatlan helyzetet, tehát például egy lemezen lévő furat helyzetének paraméterezése során egyik esetben se kerüljön a furat a lemezen kívüli térbe.

Az optimalizáció futtatása közben a paraméterértékek kombinációira adott választ mutatják meg a kimenő paraméterek értékei. Ezek megjelenítése általában 2 dimenziósan grafikon formájában, vagy 3 dimenzióban egy felületen történik. Előbbi esetben a két tengely közül az egyiken a kiválasztott bemenő paraméter a másikon a kiválasztott kimenő paraméter helyezkedik el. Ez alapján könnyen eldönthető, hogy az adott bemenő és kimenő paraméter között van-e illetve ha igen, akkor milyen az összefüggés. Utóbbi esetben 3 paraméter kapcsolatát tudunk meghatározni, a 3 tengelyen legalább egy kimenő és legalább 1 bemenő paraméternek kell szerepelnie. Mikor a kiválasztott paraméterek közötti összefüggést vizsgáljuk, fontos megjegyezni, hogy ilyenkor a többi paraméter konstans értéket vesz fel. Ezt általában lehet módosítani, tehát konkrét értékekre be lehet állítani.

A paraméterek vizsgálata során számos összefüggésre fényt deríthetünk, például megfigyelhetjük, hogy az adott paraméterek milyen mértékben befolyásolják a kimenő paramétert. Ezt általában Pie chart diagrammon célszerű ábrázolni. Az ebből levont következtetések abban nyújtanak segítséget, hogy melyek azok a paraméterek, amelyeket érdemes változtatni a lehetőségekhez képest.

Az optimalizációs analízisek két legfőbb típusa az adott célértékre való optimalizálás, illetve adott kimenő paraméter szélsőértékre való optimalizálása.

Célértékre történő optimalizálás esetén a kimenő paraméter kívánatos értéke egy konkrét számérték. Tipikus példa erre a fajta feladatra egy tapintós útadó deformációjának optimalizálása. Ezekben az esetekben pl. adott terhelésre adott deformációt kell elérni, ehhez pedig a többi bemenő paramétert úgy kell meghatározni, hogy kialakuljon a kívánt deformációs érték.

Szélsőértékre történő optimalizálás esetében az adott kimenő paraméter maximuma illetve minimuma a cél. Tipikusan a feszültség maximum értékét célszerű minimalizálni, illetve a deformáció maximumát célszerű minimalizálni (általában a statikai analízisek során).

Amennyiben több célértékre, vagy több szélsőértékre szeretnénk definiálni, akkor ezeket a kívánalmakat célszerű súlyozni.

A legtöbb véges elemes szoftverben a CAD szoftverrel történő együttműködés miatt egy optimalizációs folyamat során kapott eredmény könnyen átvihető a CAD rendszerbe, és akár kiindulópontja lehet egy következő optimalizációs folyamatnak.

5.1. Példa optimalizációs feladatra

A következő példát ANSYS Workbench -ben oldjuk meg. A feladat egy statikai analízishez kapcsolódó szimuláción keresztül mutatja be a paraméterek beállítását és a geometriai optimalizációt. Mivel a korábbiakban a statikai analízis már bemutatásra került, így itt ezt a részt csak nagyvonalakban mutatjuk be.

Az optimalizáció előtt mindig el kell készíteni az alap analízist, csak utána lehet minden paramétert beállítani.

Elindítunk egy statikai analízist, majd létrehozzuk az új geometriát az ANSYS Worbench beépített Design Modeler moduljában.

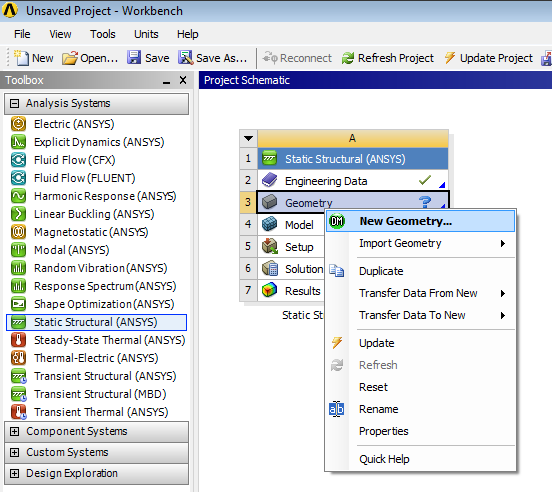
5.1. ábra - Geometria létrehozása.

A geometria nagyságrendjének megfelelően, mm-t választunk szimuláció mértékegységeként, így elegendően kis numerikus hiba terheli a szimulációnkat.

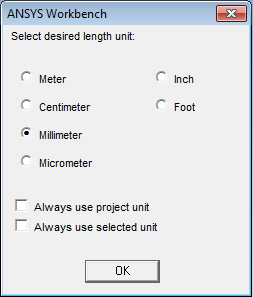
5.2. ábra - Mértékegység kiválasztása.

Ezután történik a geometriai modell megalkotása. Jelen esetben 3 dimenziós geometriát használunk. Létrehozzuk az XY síkon az első vázlatunkat, amelyre felrajzoljuk a geometria alapját.

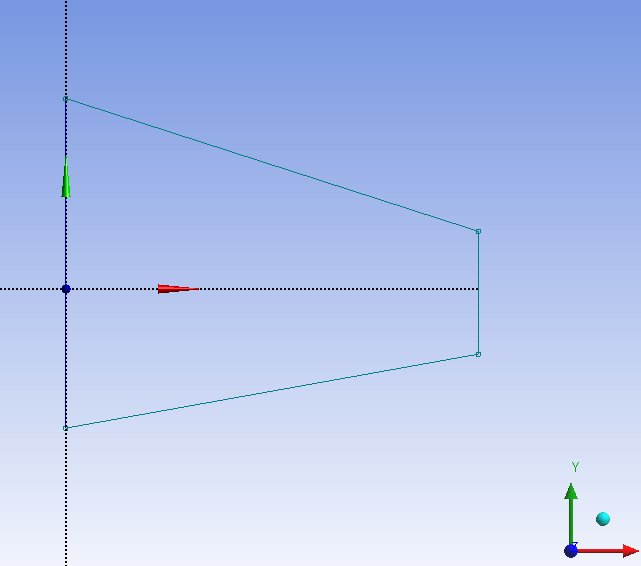
5.3. ábra - Vázlat megrajzolása.

Általában célszerű a tengelyekhez kapcsolódóan elhelyezni a geometriát, mert így az alapsíkokkal dolgozhatunk, kevesebb esetleges plusz síkot, koordinátarendszert kell létrehozni. A vázlatokat célszerű mindig teljesen határozottá tenni. Ennek eléréséhez praktikus, ha minél több kényszert és minél kevesebb méretet használunk. Egy paraméteres modell esetén mindig érdemes előre átgondolni, hogy milyen paraméterekkel kell majd dolgoznunk és annak megfelelően felépíteni a geometriai modellt. Jelen esetben egy szimmetriakényszert definiálunk, a Sketching eszköztár Constrains al-menüjéből Symmetry kiválasztásával. ( ANSYS Workbench használatakor mindig először kell kiválasztani a szimmetria tengelyét, utána pedig a szimmetrikus rajzi elemeket, erre a sorrendre a parancssorban is tájékoztatást kapunk.)

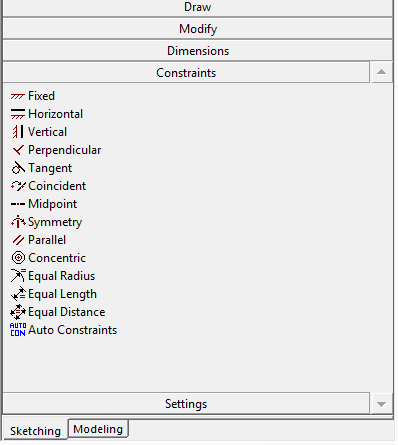
5.4. ábra - A vázlatrajzoláskor alkalmazható kényszerek.

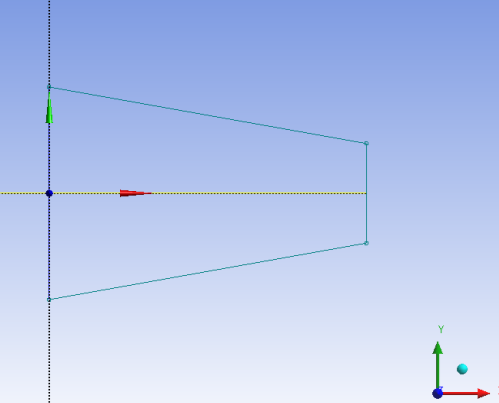
5.5. ábra - Szimmetriakényszer kiadása.

Így kialakul a már kényszerekkel ellátott körvonal. (Szerencsésebb először a geometriai kényszereket megadni és csak utána a méreteket.)

Ezután annyi méret megadása szükséges, amennyi teljesen határozottá teszi a körvonalat.

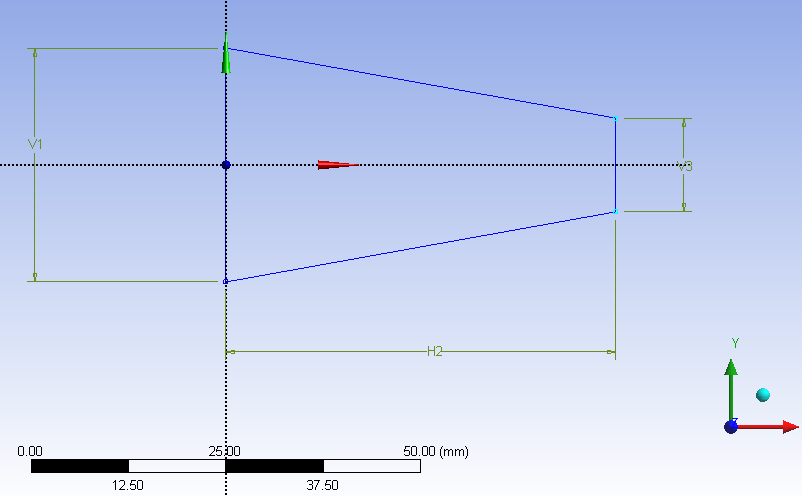
5.6. ábra - Vázlat méretezése.

A méretek elhelyezése után következik a méretek beállítása konkrét értékre, majd ezek paraméterré alakítása a Details panelen (5.7. ábra). A méret neve melletti kis fehér négyzetre kattintva (bal gombbal) lehet paraméterré tenni az adott méretet. Ilyenkor egy kék színű D betű kerül az üres négyzetbe. Ekkor megjelenik egy párbeszédablak, amelybe a paraméter nevét kell megadni (mint általában, most is kerüljük az ékezetes karakterek használatát). Amennyiben a későbbiekben szeretnénk a méretet kivenni a paraméter készletből egyszerűen újra rákattintva az immár D betűt tartalmazó négyzetre újra üressé válik és a méret kikerül a paraméterek közül.

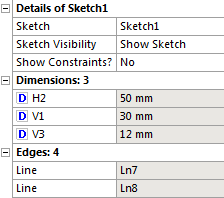
5.7. ábra - Méretek paraméterré alakítása.

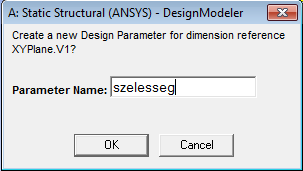
5.8. ábra - Paraméter nevének megadása.

Ezután a vázlatot az kihúzás (Extrude) paranccsal 3 dimenziós testté alakítjuk (korábbi példából már ismert módon). Látható, hogy az alaksajátosságokat létrehozó parancsoknál is megtalálható az üres négyzet a méret (jelen esetben a kihúzás mértéke) előtt, így azt is paraméterként definiálhatjuk (5.9. ábra). Minden teljesen ugyanúgy működik, mint a vázlatban meghatározott paramétereknél.

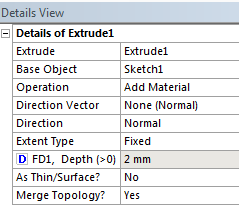
5.9. ábra - A kihúzás vastagságának paraméterré alakítása.

Az alaptest létrehozása után felrajzoljuk az első furathoz tartozó vázlatot, majd kényszerek és méretek megadásával teljesen határozottá teszünk, majd szintén az kihúzás (Extrude) parancs segítségével kivágjuk a furatot. Ilyenkor a kivágás műveletet kell választani (Details View/Operation/Cut Material) , (5.10. ábra).

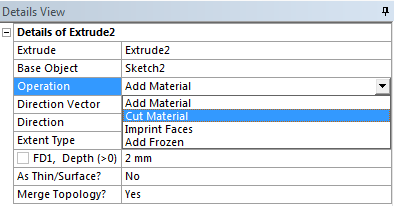
5.10. ábra - Kihúzás műveletének beállítása.

Amennyiben előre tudjuk, hogy a test vastagsága változni fog különösen fontos, hogy a kihúzás mélysége (Extent Type) lehetőségek közül olyat válasszunk, amely a megváltozott vastagság esetén is ugyanolyan alaksajátosságot hoz létre. (Ha itt figyelmetlenségből a 2 mm-es alapértelmezett távolságot nem módosítjuk, akkor a vastagság növekedésével nem átmenő furat alakul ki.) Ezért most ezt átállítjuk a felületig (To Surface) opcióra (5.11. ábra).

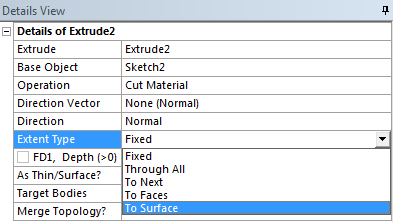
5.11. ábra - Kihúzás mélységének beállítása.

Végfelületnek (Target Face) , (5.12. ábra) a test vázlattal ellentétes oldalát határozzuk meg (5.13. ábra).

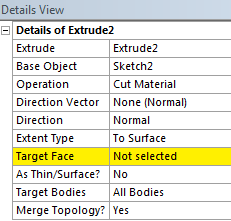
5.12. ábra - A kihúzás mélységét határoló felület kiválasztása.

A kiválasztást az elfogadás (Apply) gombbal véglegesítjük. Ha véglegesítésre kerül egy kiválasztott felület, akkor az felveszi a tulajdonságának megfelelő színt a zöld helyett. (Jelen esetben türkiz színűvé válik, 5.13. ábra)

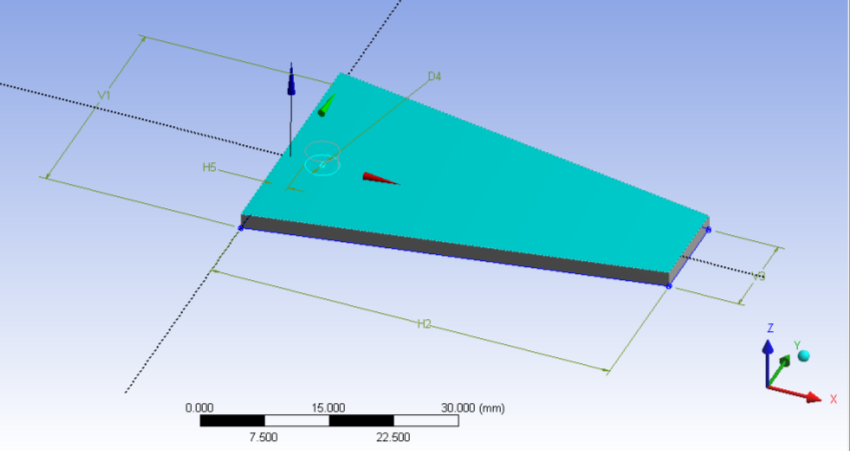
5.13. ábra - A kihúzás mélységét határoló felület kijelölése.

A szokásos létrehoz (Generate) gombbal elvégeztetjük a parancsot. Immár kialakult az egy furattal rendelkező test (5.14. ábra).

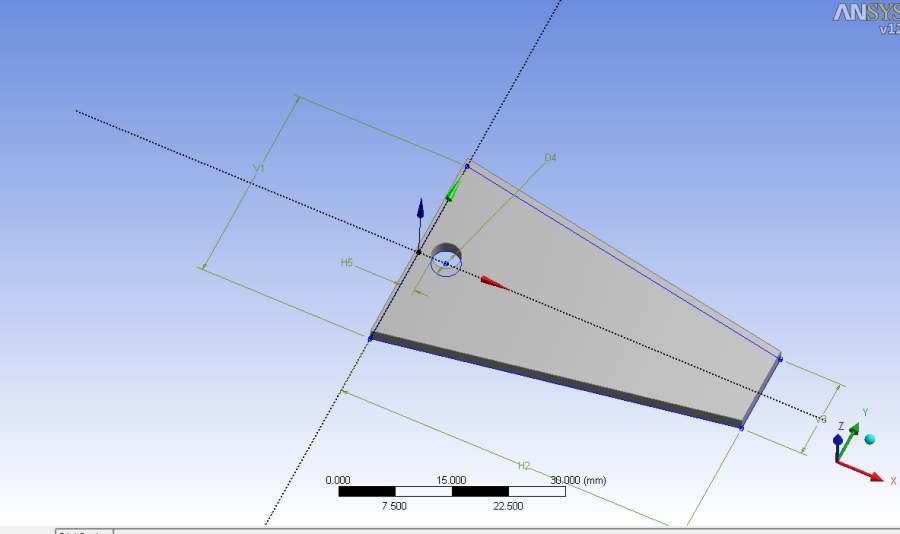
5.14. ábra - Az alkatrészmodell a kivágott furattal.

Ezután történik a furatok kiosztása. Optimalizációtól függetlenül is érdemes kiosztással létrehozni az ismétlődő alaksajátosságokat, de ilyenkor különösen is praktikus, mert diszkrét paraméterként beállítható a furatok száma is. (Diszkrét paraméternek nevezzük azokat a változókat, amelyek csak egész számokat vehetnek fel értékként.) Kiosztást a létrehozás (Create) menüpont kiosztás (Pattern) parancsával tudunk készíteni (5.15. ábra). Megvalósítható testek, felületek és akár vonal elemek kiosztása is. Amennyiben például egy furatot szeretnénk kiosztani, akkor a furat belső felületét kell kiválasztani, mint kiosztandó geometria (ebben az esetben, a felső ikonsorban a kiválasztás szűrőjét át kell állítani a felületkijelölés (Face) opcióra).

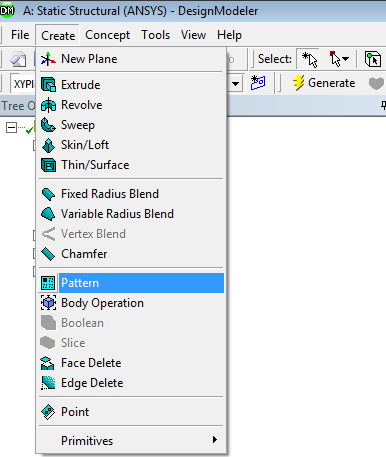
5.15. ábra - Kiosztás létrehozása.

A kiosztás részleteit tartalmazó Details panelen be kell állítani a kiosztás típusát (jelen esetben linear, tehát vonal menti egyenes kiosztásról van szó), az egyes elemek közötti távolságot, és az elemek számát. Mint látjuk akár az elemek száma, akár a köztük lévő távolság paraméternek választható. Fontos tudni, hogy a későbbiekben, az optimalizáció során az ANSYS Workbench -ben át kell állítani az elemszám paramétert diszkrét változóvá, mert alapesetben, ha folyamatos változóként van definiálva az automatikus méretváltozás során akár nem egész értéket is felvehet.

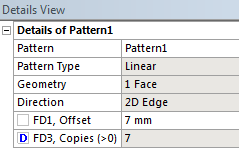
5.16. ábra - A kiosztás számának paraméterré alakítása.

Amennyiben a geometria elkészült, a projekt ablakban megjelenik a paraméter készlet (Parameter Set) . A szövegdobozból kifelé mutató nyíl jelzi, hogy egyelőre csak bemenő paramétereket tartalmaz a véges elemes projektünk (5.17. ábra). Amennyiben a szimulációt lefuttatjuk és kimenő paramétert is meghatározunk, itt megjelenik egy, az eredményekből a paraméter készletbe mutató nyíl is.

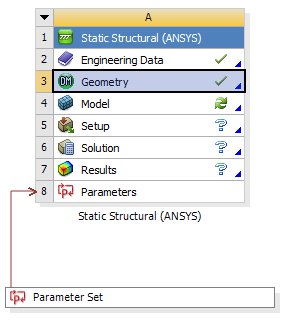
5.17. ábra - A létrejött paraméterkészletet.

Ezután következik a statikai analízis beállítása és az alap szimuláció lefuttatása. (A beállítások csak szükséges mértékben lesznek ismertetve.)

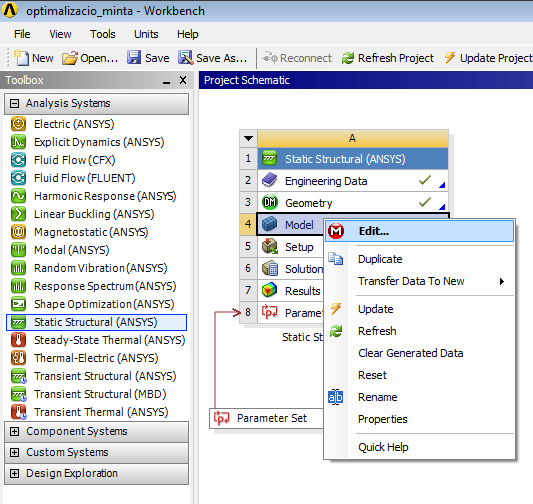
5.18. ábra - Belépés a szimulációs környezetbe (Jobb gombos menüből).

A geometria anyagtulajdonságát jelen esetben nem módosítjuk, szerkezeti acél anyagot használunk.

Az alapértelmezett háló (Mesh) túlságosan nagy elemekből áll, a geometria legkeskenyebb részén csak 1 sor elem található, ezért a hálóméretezés (Sizing) eszközzel beállíthatunk egy sűrűbb, tehát kisebb elemekből álló hálót (5.19. ábra).

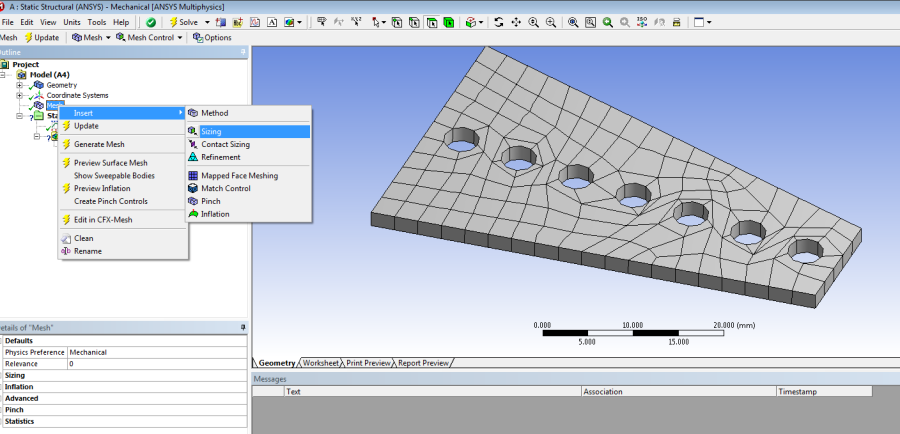
5.19. ábra - Hálósűrítés beállítása.

A háló elemméretét 1mm-re állítsuk, így már biztosan több sor elem lesz a legkisebb vastagságnál.

A hálósűrítés felületének a test felső lapját határozzuk meg (5.20. ábra).

Külön lépés helyett a mesh (háló) details ablakában is be lehet állítani a háló elemeinek méretét.

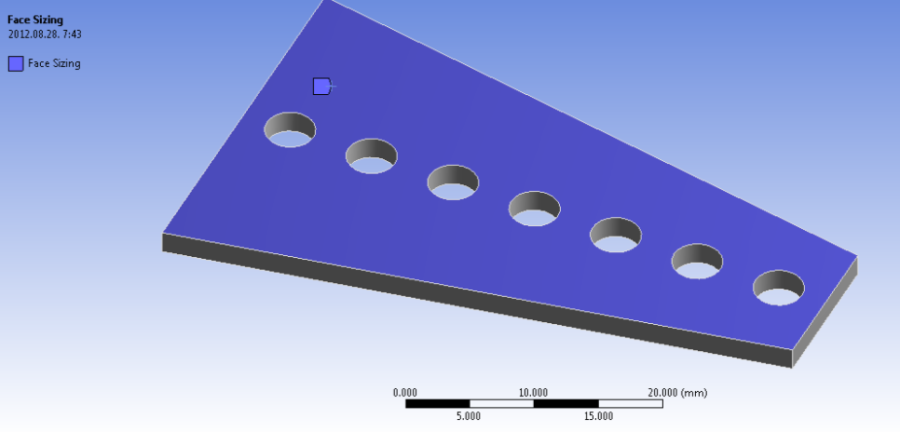
5.20. ábra - A hálósűrítés célfelületének kijelölése.

Az 1mm-es háló már elégségesnek mondható, az elemek rendezettek (5.21. ábra).

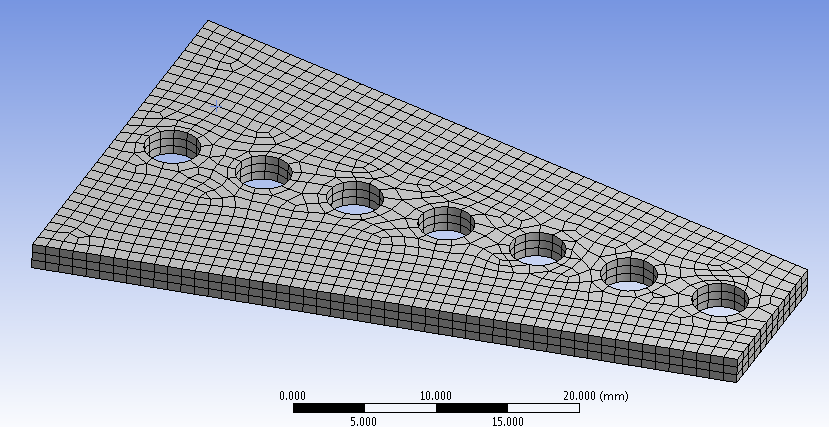
5.21. ábra - Sűrített háló, 1mm-es elemekkel.

Ha a hálóval elkészültünk beállítjuk a terheléseket és megfogásokat. Jelen esetben fix befogás (Fixed Support) típusú befogást definiálunk a test szélesebb végére (5.22. ábra).

5.22. ábra - Fix befogás az alkatrész szélesebb végénél.

A testre hat egy erőterhelés (Force) a megfogással ellentétes, rövidebb oldalon. Ennek nagysága alap esetben 50N, mely a globális -Z irányba mutat. Amennyiben a globális koordináta rendszer segítségével nem tudjuk megadni az erő hatásvonalát, akkor vektorosan is lehet definiálni, ehhez felhasználható bármilyen más koordináta rendszer tengelye, valamint a geometriához kapcsolódó élek bármelyike, vagy egy külön erre a célra létrehozott vonal elem.

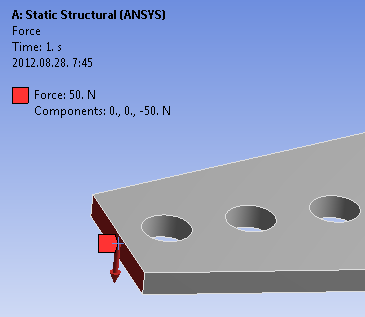
5.23. ábra - 50N nagyságú, -Z irányú erőterhelés az alkatrész keskenyebb végénél.

Ahogy itt is látjuk, az erőértékek előtt megjelenik az üres négyzet, amely jelzi, hogy paraméterként definiálhatók. Ezt meg is tesszük, ami változás a geometriai paraméterekkel szemben, hogy itt már nem lehet nevet adni a paraméternek, hanem az előre definiált nevet kapja, amely egyértelműen definiálja az adott terhelés komponenst.

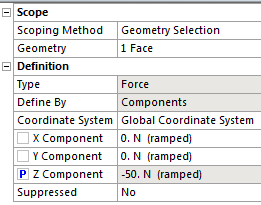
5.24. ábra - Az erő értékének megadása, majd paraméterré alakítása.

Érdemes előre meghatározni, hogy a rendszernek milyen típusú válaszára, vagyunk kíváncsiak, természetesen itt már érdemes olyan végeredményt is lekérdezni, amire optimalizálni szeretnénk. A modellfa megoldás (Outline/…/Static…/Solution) pontjában kiválasztjuk a teljes deformáció (Total Deformation) , egyenértékű feszültség (Equivalent von Mises Srtess) és az irány menti deformáció (Dierctional Deformation) opciókat. Fontos, hogy az irány menti deformációnál azt az irányt válasszuk ki, amely releváns a szimulációnk szempontjából, jelen esetben a Z irányt (Z axis) válasszuk ki. Már most is láthatjuk a Details ablakban, az eredmények (Results) felületen a paraméterek definiáláshoz szükséges jelölő négyzetet. Akár már most meg lehet adni, hogy mely eredményeket tesszük paraméterré, de ezt a szimuláció után is megtehetjük.

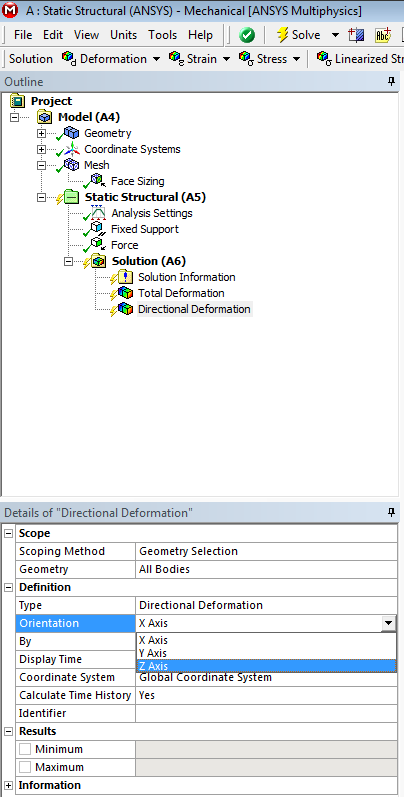
5.25. ábra - Az eredmények lekérdezése.

Futtassuk a szimulációt, majd az adott eredményképre kattintva kiválasszuk ki, hogy mely eredménytípusokat definiáljuk paraméternek. Ahogy a terhelésnél is, itt sem lehetséges a paraméter nevének változtatása. Jelen esetben a Z irányú deformáció minimumát és az egyenértékű feszültség maximumát választjuk paraméternek. Előbbinél figyelni kell, hogy mivel a terhelés –Z irányba hat, a tulajdonképpeni maximális deformáció az irány menti deformáció előjeles eredményének minimális értékeként kapjuk.

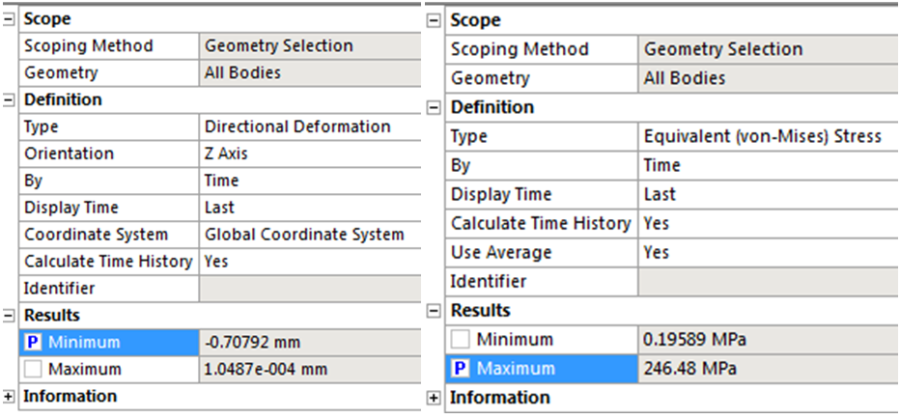
5.26. ábra - Az eredmények kimenő paraméterré alakítása.

A futtatás után, nézzük meg az eredményeket, itt még észre lehet venni esetleges hibákat, ha valami nem az előzetes várakozásnak megfelelően viselkedik érdemes ellenőrizni a beállításokat, anyagmodelleket.

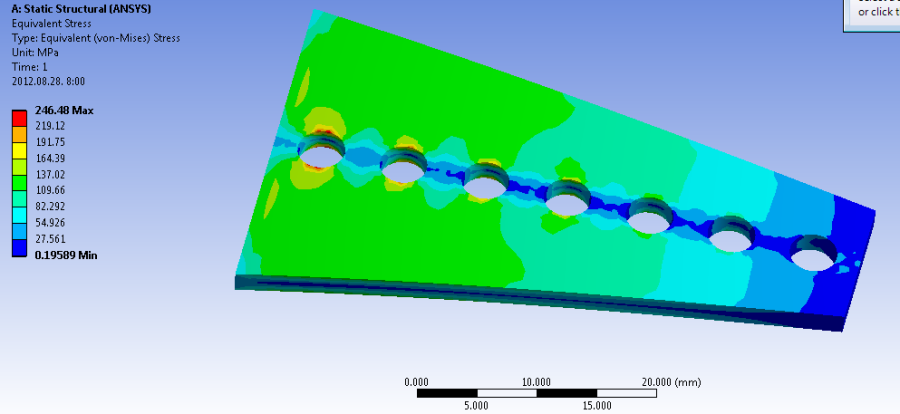
5.27. ábra - Az alkatrészben ébredő egyenértékű feszültség.

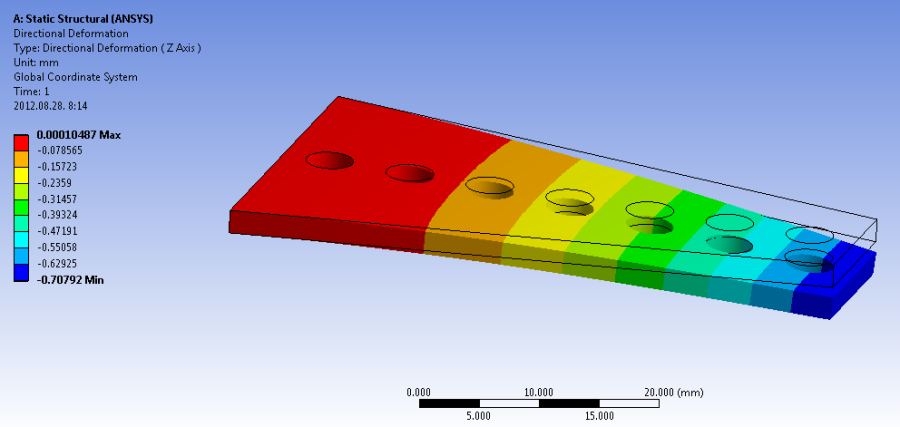
5.28. ábra - Z irányú deformáció.

Ha a szimuláció lefutott és a kimenő paraméterek is definiálásra kerültek elkezdődhet a tulajdonképpeni paramétervizsgálat és optimalizáció. A projektablakban a Design Exploration menü alpontjaiból lehet választani a kívánt feladatot, melyet a paraméterkészlet (Parameter Set) alá kell behúzni a projektünkbe. Ebben a példában válasszuk a célértékre optimalizálás (Goal Driven Optimization) lehetőséget (5.29. ábra), amely magában foglalja a válasz felület (Response Surface) menüpontot is, ezeket csak egymás után lehet elvégezni, ahogy látszik is a projektünkben (5.30. ábra).

5.29. ábra - A paramétervizsgálat különböző lehetőségei.

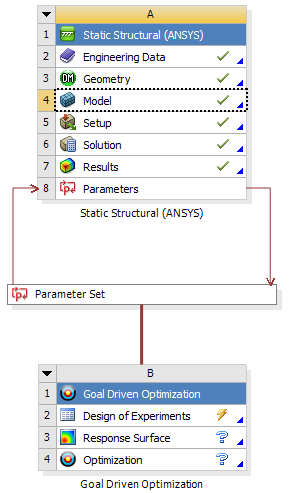
5.30. ábra - A kimenő paraméterekkel és a célérték optimalizációval kiegészült projektpanel.

Itt is célszerű felülről lefelé haladni a menüpontok között. Első lépésként a design konfigurációk (Design of Experiments) menüpontban be kell állítani az összes változó típusát és szélső értékeit (azt az értéktartományt, amelyet felvehet a megoldás során).

5.31. ábra - A design konfigurációk szerkesztése (Jobbgombos menüből).

A szokásos jobb kattintással tudjuk módosítani a paramétereket. Több táblázat segítségével lehet mindent beállítani ezen az egyetlen képernyőn.

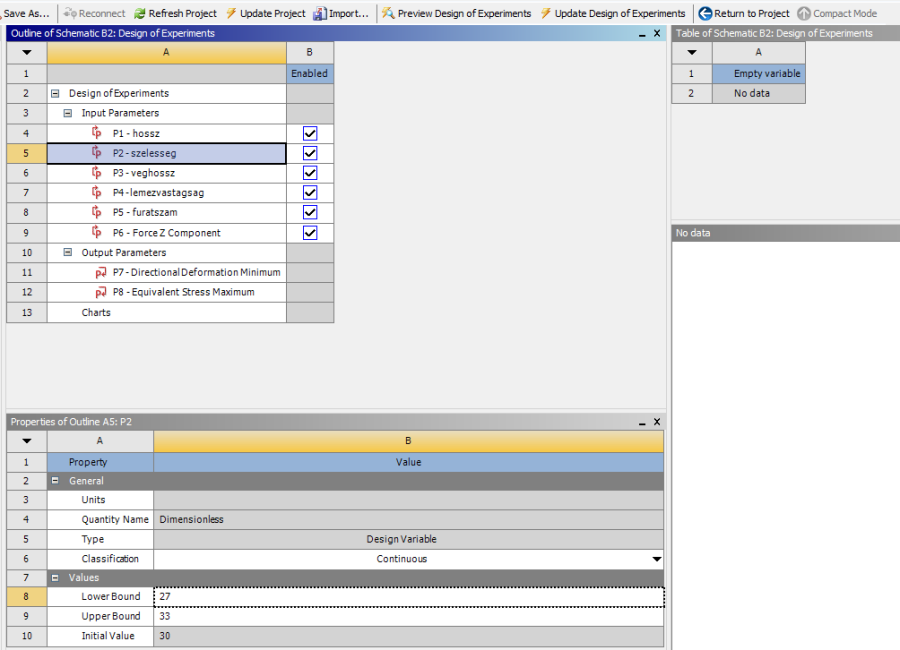
5.32. ábra - A paraméterek típusának és szélső értékeinek beállítása.

Látjuk, hogy az összes paraméter fel van sorolva a bal felső táblázatban. Ezeknek „P” előtagos sorszámozása van, a sorszám mellett van a paraméter neve. A bemenő paraméterekből nem muszáj mindegyiket használni, az engedélyezett (Enabled) oszlopban a pipák ki illetve bekapcsolásával lehet elhanyagolt, vagy aktív paraméterekké változtatni. Alapesetben minden paraméter aktív. Amennyiben egy paramétert kiveszünk az aktívak köréből, az alapértéken marad, a szimuláció további részében nem változik. A bal felső táblázatban kijelölt paraméter értékeit az alatta lévő táblázatban lehet beállítani. Itt be lehet állítani a paraméter típusát (Classification) és értékét. Alapbeállításként mindegyik folytonos (Continous) típusú változó.

A következő típusokból lehet választani:

Folytonos (continous)
Diszkrét (discrete)

Ha folyamatos típusút választunk, akkor meg kell adni a paraméter értéktartományának alsó- és felső határát (Lower és Upper Limit) . Alapbeállításként ez ±10%-os eltérésű az alapértékhez képest, amely tájékoztatásként szerepel a táblázatban, de ennek a mértéke nem módosítható. A határokat tetszőlegesen lehet változtatni (természetesen addig a határig, amíg a geometria fel tud épülni mindegyik paraméter-érték kombinációban.

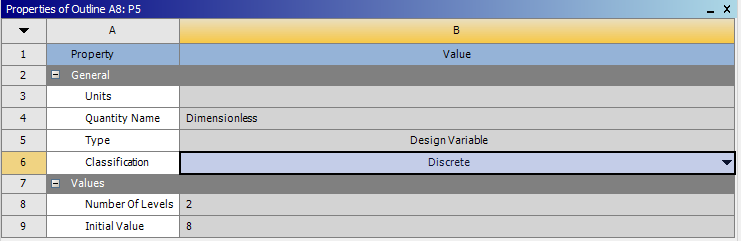
5.33. ábra - Diszkrét paraméter beállítása.

Ha mindegyik paramétert beállítottunk a kívánt típusra és a kívánt értéktartományokra, elkezdődhet az optimalizáció folyamata. Ekkor az Update of Design Experiments gombra kattintva a szoftver a paraméterek változtatásaival elkészíti azokat a design kombinációkat, amelyekre elvégzi az alap szimulációt. Ez táblázatos formában megjelenik a képernyőn és a jobb szélső oszlopba folyamatosan jelennek meg az adott sorhoz tartozó megoldott kimenő paraméterértékek.

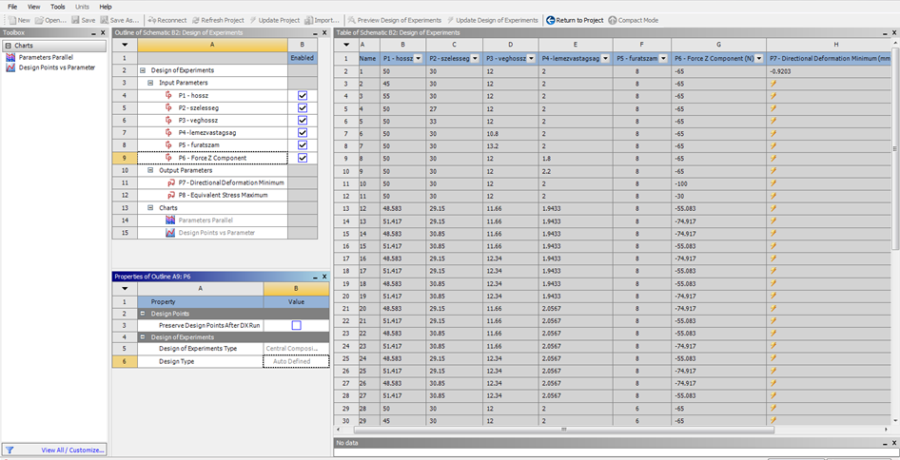
5.34. ábra - A paramétertábla futás közben.

Ha lefutott a szimuláció az összes design konfigurációra (Design Points) , akkor a Response Surface -re továbblépve (5.35. ábra), lehet megtekinteni a bemenő paraméterek hatását a kimenő paraméterekre. Ehhez az eredmények frissítése szükséges (amit a projekt ablakban megjelenő jellegzetes két zöld körkörös nyíl ikon jelez), amit az Update Response Surface gomb segítségével érünk el (5.36. ábra). Ekkor megtekinthetővé válnak az előbbi számítások eredményei (5.37. ábra).

5.35. ábra - Belépés a Response Surface felületre az eredmények megtekintéséhez.

5.36. ábra - Az eredmények megjelenítésének frissítése.

Az eredmények legtipikusabb megjelenítési formája a 2D-s diagram, melyhez ki kell választani a két paramétert, melyek közötti összefüggést meg szeretnénk tudni. Természetesen az egyik bemenő, a másik pedig kimenő paraméter. Ezeket a diagram x és y tengelyére is el lehet helyezni, tetszőleges kombinációban.

A többi paraméter értéke természetesen ebben az esetben konstans, értékét a paraméter melletti csúszkával lehet beállítani. Alapesetben a középértéknél helyezkedik el. Ha a grafikon típusa megkívánja, akkor lehet növelni a grafikonon megjelenő pontok számát (Number of Pionts on X).

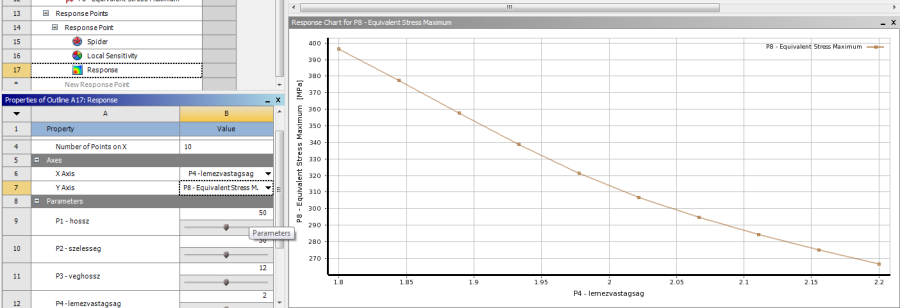
5.37. ábra - Az eredmény egy paraméterpárosának megjelenítése 2D-s diagramon.

Amennyiben egyszerre 3 paraméter közti összefüggést szeretnénk ábrázolni a megjelenítési mód (Mode) menüpontban lehet váltani a 2D-s megjelenítésről 3D-s ábrázolásra.

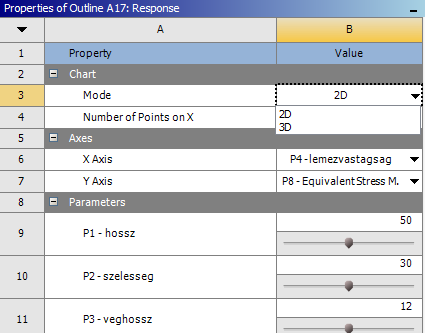
5.38. ábra - Váltás 2 és 3 dimenziós megjelenítés között.

Ebben az esetben az x, y és z tengelyek változói is kiválaszthatóak, értelem szerint legalább egy kimenő és legalább egy bemenő paraméternek kell lennie.

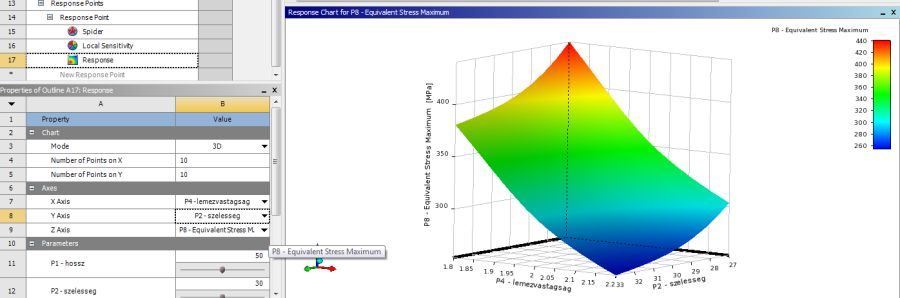
5.39. ábra - Az eredmény 2 bemenő és egy kimenő paraméterének megjelenítése 3D-s diagramon.

A 3 dimenziós grafikon az egér bal gombját lenyomva tartva forgatható, és az egér görgetőjével közelíthető és távolítható, így a leginformatívabb oldaláról nézhető. Ha kellőképpen áttekintettük a paraméterek közti összefüggéseket, akkor elkezdhetjük a célértékre való optimalizálást. Ehhez az optimalizáció (Optimization) almenüt kell kiválasztani (5.40. ábra).

5.40. ábra - A célértékoptimalizáció megkezdése.

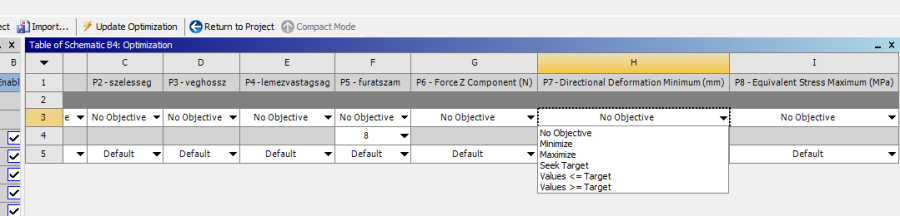
5.41. ábra - Az egyes paraméterekkel szemben támasztott kívánalmak beállítása.

Az ekkor megjelenő táblázatban az egyes paraméterekkel szemben támasztott kívánalmakat állíthatjuk be (5.41. ábra).

A következő lehetőségek közül választhatunk:

nincs célérték (No Objective) – az adott paraméter a megengedett tartományon belül szabadon változhat,
minimalizál (Minimize) – a paraméter a lehető legkisebb legyen,
maximalizál (Maximize) – a paraméter a lehető legnagyobb legyen,
célértéket elérése (Seek Target) – a paraméter értéke közelítsen meg egy magadott célértéket,
érték adott célérték alá (values <= target) – a paraméter értéke maradjon egy bizonyos célérték alatt,
érték adott célérték fölé (valuse >= target) – a paraméter értéke maradjon egy bizonyos célérték felett.

5.42. ábra - az egyes paraméterek célértékeinek súlyozása.

Ha olyan célt határozunk meg, amelyhez tartozik célérték, akkor ennek értékét a 4. sorban kell megadni. Természetesen bizonyos szintig lehet súlyozni a célok fontosságát, ezt alapértelmezett (Default) , alacsony fontosságú (Lower) és fontos (higher) lehet. Érdemes egyszerre csak 1-2 paraméterre optimalizálni. Ha a beállítások megtörténtek az Update Optimization gomb megnyomásával lehet a célértéknek megfelelő konfigurációkat keresni. Ilyenkor csak abban a paraméter tartományban keres megoldást a szoftver, amelyet előzetesen beállítottunk a Design of Experiments táblázatban. Amennyiben más tartományban is szeretnénk megoldást keresni, vagy egy-egy paraméter tartományát szeretnénk kibővíteni újra definiálni kell ezeket az értéktartományokat.

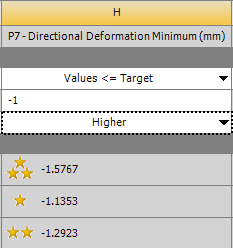
5.43. ábra - Rangsorolt eredmények.

Ha olyan kívánatos célt határoztunk meg, amelyre van megoldás az előzetesen lefutott konfigurációk között, akkor csillagokkal jelölve megjelenik 3 lehetséges verzió, melyek közül a 3 csillagos a leginkább közelíti a célértéket, az 1 csillagos a legkevésbé a felkínáltak közül. Amennyiben nincs olyan megoldás az előzetesen számoltak között, amely megfelelne a kívánt célnak, akkor csillagok helyett piros x-ek jelzik, hogy a talált (a célt leginkább megközelítő) konfigurációk valójában nem felelnek meg az elvárt követelményeknek. Ilyenkor a paraméterek tartományát módosítani kell és újra futtatni a szimulációs folyamatot.

6. fejezet - A geometriai modellek egyszerűsítésének lehetőségei

Tartalom

6.1. Példa szimmetriafeltételek alkalmazására: belső nyomással terhelt cső

6.1.1. Analitikus megoldás
6.1.2. A feladat megoldása ¼ testmodell segítségével
6.1.3. A feladat megoldása negyed héjmodell segítségével
6.1.4. A feladat megoldása 2D-s sík alakváltozás (Plane Strain) típusú modellként
6.1.5. A feladat megoldása 2D-s tengelyszimmetrikus (Axisymmetric) típusú modellként
6.1.6. Összefoglalás

6.2. Példa egy oldalon befogott, hajlított tartó négyféle megoldására

6.2.1. A feladat megoldása 3D-s teljes testmodellel (3D body)
6.2.2. A feladat 3D-s megoldása felületmodell (shell) definiálásával
6.2.3. A probléma megoldása 2D-s feladatként
6.2.4. A feladat megoldása vonalmodell keresztmetszet definiálásával (gerenda elemmel)
6.2.5. Összefoglalás

6.3. Példa gerenda modell alkalmazására: Hegesztett rácsos szerkezet

6.4. Mechatronikai példa: CD fej tartó rugók

6.5. Ellenőrző feladatok

6.5.1. Feladat
6.5.2. Feladat

Az egyszerűsítések csoportosítása többféleképen történhet, pl. szimmetriák típusa, vagy a mechanikai probléma dimenziója, ill. az alkalmazott elemtípus szerint. Ezekkel illetve az egyszerűsítések okaival, a geometriai, perem és terhelési feltételeket érintő követelményekkel, valamint az alkalmazott elemtípusokkal már foglalkoztunk a 2. fejezet fejezetben. Most nézzünk néhány egyszerű gyakorlati példát ezek alkalmazására. Az alábbiakban olyan modelleket vizsgálunk meg, amelyeken ugyanaz a terhelési eset többféle egyszerűsítéssel vizsgálható, ezért a feladatok sorrendje nem követi a fent említett csoportosítási lehetőségeket.

6.1. Példa szimmetriafeltételek alkalmazására: belső nyomással terhelt cső

Az alábbiakban egy belső nyomással terhelt cső modelljén keresztül mutatjuk be a szimmetria-feltétel alkalmazását 3D-s test, ill. héjmodell esetén és a 2D-s sík alakváltozás, ill. tengelyszimmetrikus modell használatát (6.1. ábra).

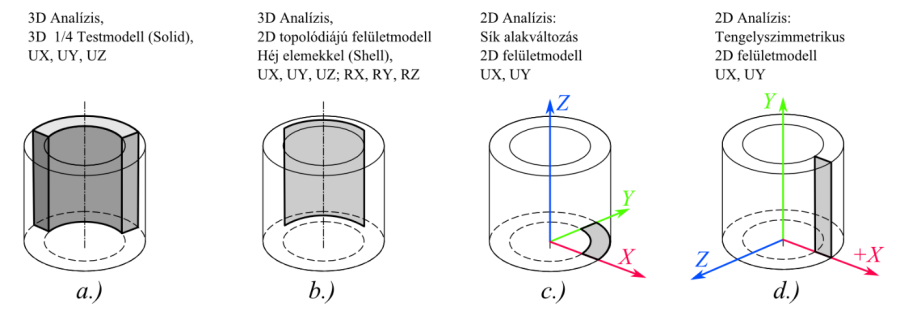
a.) ¼ testmodell, b.) ¼ héjmodell, c.) ¼ sík alakváltozás modellje, d.) tengelyszimmetrikus modell.

6.1. ábra - Csőszakasz modellje különböző megközelítés szerint.

Kiinduló adatok:

Külső átmérő: D=12mm,

Falvastagság: t=2mm,

Magasság: H=10mm,

Anyag : Acél: rugalmassági modulus: E=200GPa, Poisson-tényező: v=0,3,

Belső nyomás: p=100MPa,

Megtámasztás: Szimuláció típusától függően változó. A modellezett eset a tengelyirányú elmozdulásban gátolt cső, vagyis a kiemelt szakasz mindkét végén a tengelyirányú elmozdulást megkötő, a radiális elmozdulást engedő kényszerek szükségesek.

6.1.1. Analitikus megoldás

A fenti feladat analitikus megoldását kétféleképpen végezzük el, vékony és vastag falú csövek számítási módszere szerint [25.] .

Feltételezzük, hogy a cső anyaga lineáris, homogén és izotróp.

Méretei – belső sugár: r_b=4mm, külső sugár: r_k=6mm, a hossza pedig ebben az esetben lényegtelen.

A vastag falú csövek keresztmetszetének feszültségállapotát az alábbi egyenletekkel írhatjuk le.

A radiális irányú feszültségkomponens:

(6.1)

A tangenciális irányú feszültségkomponens:

(6.2)

Ahol:

		(6.3)
		(6.4)

r – a cső külső _(k) és belső _(b) sugara,

p – a csövet terhelő nyomás, (esetünkben p _k =0).

A tengelyirányú feszültségkomponenst a peremfeltételektől függően tudjuk számolni. Esetünkben cső mindkét vége rögzítve van axiális irányban, tehát az ilyen irányú alakváltozás nulla.

(6.5)

Ebből a tengelyirányú feszültség értéke:

(6.6)

Vékonyfalu csövek esetén azzal a feltételezéssel élünk, hogy a cső anyagában csak tangenciális és axiális feszültség ébred, tehát a cső falában ébredő radiális feszültségkomponens 0. Ekkor a belső nyomás és a geometria ismeretében a tangenciális feszültségkomponens:

(6.7)

Ahol:

r – a cső közép sugara,

t – a cső falvastagsága,

Az axiális feszültség a peremfeltételek és az (6.5) egyenlet alapján, az alábbi módon számolható:

(6.8)

✎ A fenti egyenletek alapján határozzuk meg a rúd keresztmetszete mentén ébredő feszültségkomponenseket és ábrázoljuk az egyenértékű feszültséget.

6.1.2. A feladat megoldása ¼ testmodell segítségével

Hozzuk létre a csőszakasz teljes testmodelljét Design Modellerben , és jelöljük ki a szimmetriasíkokat. Többféle lehetőség is kínálkozik a tükörszimmetria érvényesítésére, egyik az, ha a geometria modellezőben rendeljük hozzá a legördülő menüsor Tools/Symmetry parancsának kiadásával. Első lépésben meg kell határoznunk a szimmetria síkok számát (Details …/Number of Planes) , esetünkben 2, (de akár 3 is lehetne, ha a hossza mentén is kettévágnánk). Ezután a beállítottaknak megfelelő számú kijelölő ablak jelenik meg a panelen. Ha cső tengelyvonala egybeesik a globális koordinátarendszer Y tengelyével, akkor az XY és YZ síkokat kell kiválasztanunk a modellfából (6.2. ábra, b.). Állítsuk be a részleges (Partial) modellt és nyomjuk meg a Generate gombot. A parancs hatására a szimmetriasíkok feldarabolják modellt, és csak egy ¼ modell marad.

Másik lehetőség a szimmetria kényszer definiálására, ha eleve ¼ modellt hozunk létre, és a testmodell megfelelő felületeihez hozzárendeljük a kényszert akár a geometriamodellező, akár a szimulációs felületen. Ha ¼ modellünk van, akkor egyszerű kinematikai kényszerek segítségével is definiálhatjuk a szimmetriát, mégpedig olyan elmozdulás kényszer segítségével, amely csak a felület síkjában történő elmozdulást engedi, és az arra merőleges irányút nem. Ez az ANSYS -ban a Frictionless Support nevet viseli, de akár a Diplacement kényszert is alkalmazhatjuk erre a célra az egyes szabadságfokok megfelelő megkötésével.

Hasonló módon kötjük meg a két véglap axiális elmozdulását a radiális szabadságfokok engedésével. Itt is használhatjuk a Frictionless, vagy a Diplacement kényszert.

A modell belső felületére (6.2. ábra, b. – B felületre) helyezzünk el egy 100MPa nagyságú nyomást (Pressure) .

Ezután végezzük el a modell hálózását, 1mm-es méretű tégla elemeket tartalmazó rendezet struktúrájú hálóval (6.2. ábra, a.), és futtassuk a szimulációt. Az elemméret beállításához kapcsoljuk ki a Details panelen a Use Advanced Size Function -t és az Element Size sorban adjuk meg az elemméretet.

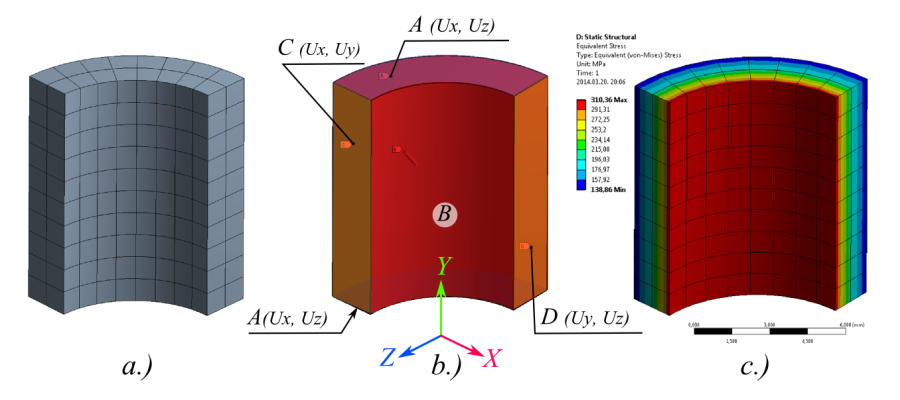
a.) Végeselemháló, b.) Peremfeltételek és terhelés, c.) A cső falában ébredő egyenértékű feszültség

6.2. ábra - ¼ testmodell.

A szimuláció futtatása után kérdezzük le az egyenértékű feszültséget, fajlagos nyúlást és a radiális deformációt. Ez utóbbihoz egy henger koordinátarendszert kell definiálnunk, amit a modellfa koordinátarendszerek sorára jobbgombbal kattintva hozhatunk létre (Outline/Coordinate Systems(JG)/Insert/Coordinate System) . Kijelölve az új elemet a modellfán, a Details panelen állítsuk át a típusát henger koordináta rendszerre (Details/Type/Cylindrical) , és az origó referenciáját a globális koordinátarendszerre (Details/Origin/Defined by/Global Coordinates: 0,0,0) . A tengelyeket forgassuk be a henger állásának megfelelően ( Principal Axis/Axis: X, Defined by: Global Z Axis; Orientation About Principal Axis/Axis: Z, Defined by: Global Y Axis) , (6.3. ábra).

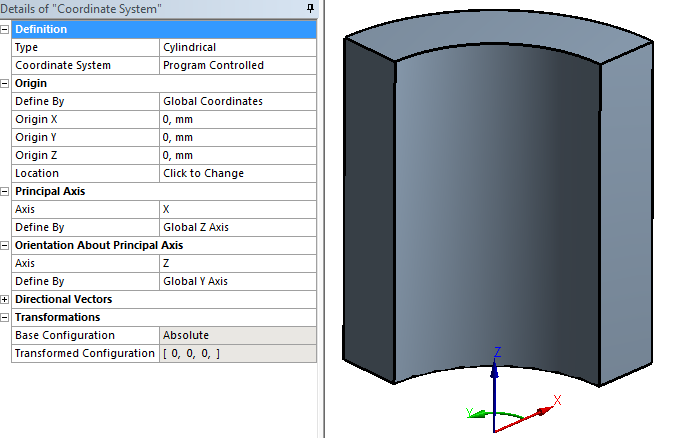
6.3. ábra - Hengerkoordináta-rendszer beállítása a radiális elmozdulások lekérdezéséhez.

Így a deformáció lekérdezését az X tengely menti elmozdulásra átállítva (Type:Directional Deformation/Orientation: X axis) , a radiális elmozdulást kapjuk eredményül.

6.1.3. A feladat megoldása negyed héjmodell segítségével

A feladat héjmodellel történő megoldásának előnye, hogy viszonylag kevés véges elem számot tartalmaz a modell, de mégis mindhárom irányú terheléseket és eredményeket is meg tudunk jeleníteni a segítségével. Szimmetria síkoknak az XY és YZ síkokat választottuk. A henger alakú héj átmérője 10mm, (6.4. ábra).

6.4. ábra - Csőszakasz negyed felületmodellje.

Az analízis típusa ebben az esetben 3D-s, így az alapbeállítások maradhatnak érvényben. A héjmodell vastagságát a szimuláció során definiáljuk (Outline/Geometry/Surface Body => Details/Definition/Thickness: 2mm.) . Héjmodell esetén definiálni kell a felülettől való eltolás irányát is. Annak függvényében, hogy a véges vastagságú héjszerkezetet annak belső, külső, vagy középfelületével modelleztük (a középfelület az alapértelmezett).

A hálózásnál 1mm-es elemméret esetén 80 elemet tartalmazó modell alakul ki (6.5. ábra).

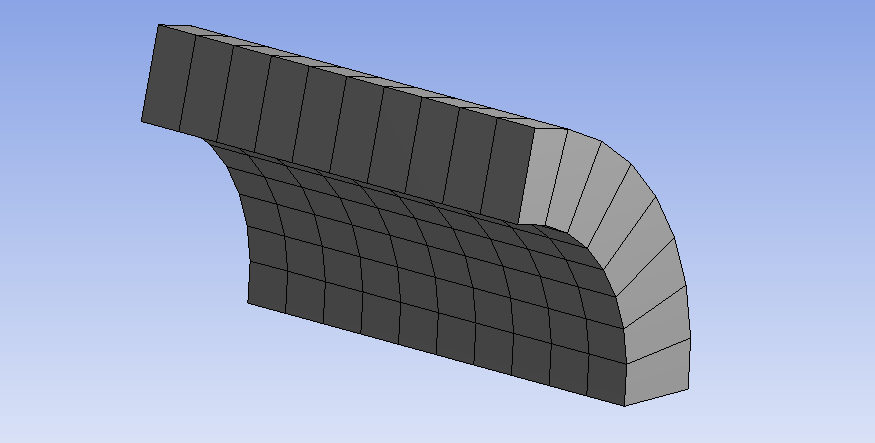
6.5. ábra - Hálózott modell a negyed héj esetén

A cső két végét elmozdulás kényszer segítségével rögzítjük, melynél az axiális (Y) irányú elmozdulást 0 értéken rögzítettük, míg a henger tengelyére merőleges (X és Z) irányokban a test szabadon elmozdulhat. A szimmetriasíkok mentén az adott síkban történő mozgást megengedő és a síkra merőleges irányú elmozdulást gátoló kényszert kell definiálnunk. Ez utóbbi peremfeltétel automatikusan létrejön, ha a geometria létrehozásánál, vagy a szimulációs felületen definiáltuk a szimmetriakényszert (Symmetry) .

A belső nyomást az egész felületre érvényesített -100MPa nagyságú nyomás típusú (Pressure) terheléssel definiáltuk (6.6. ábra). A negatív előjel azért szükséges, mert a felületre ható nyomás iránya a felületi normálissal ellentétes irányú.

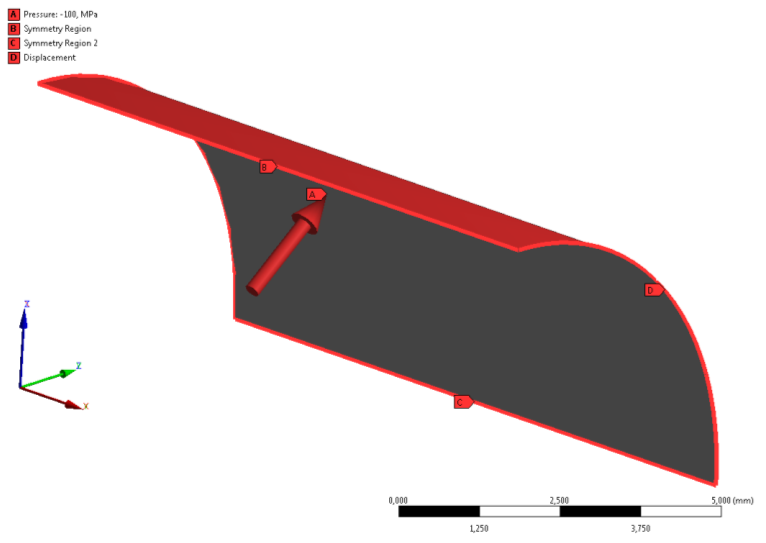
A – nyomás (p=100MPa); Szimmetriakényszerek: B (Ux, Uz), C (Ux, Uy); Kinematikai kényszer: D (Uy, Uz).

6.6. ábra - Terhelés és a permfeltételek a negyed felületmodellel felépített cső esetében.

A szimuláció lefuttatása után, az előző példához hasonlóan kérdezzük le az egyenértékű feszültséget, a fajlagos nyúlást és a radiális deformációt. Az eredményeken látható, hogy az értékek változása a vastagság mentén eltér az előző szimuláció eredményétől. Ennek oka, hogy a héjelemekkel végzett szimuláció (ellentétben a kontinuum elemekkel), nem ad információt a radiális irányú normál feszültségekről.

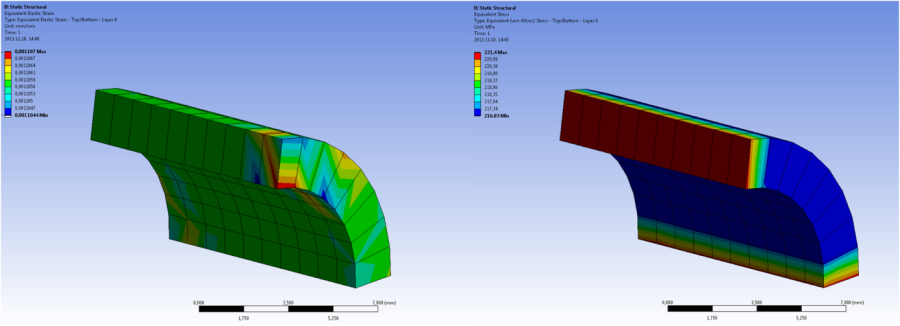
6.7. ábra - A megnyúlás és egyenértékű feszültség a csőmodell negyed héjmodellként való szimulációja során

6.1.4. A feladat megoldása 2D-s sík alakváltozás (Plane Strain) típusú modellként

A feladatot az ANSYS Workbench végeselem szoftverben oldjuk meg. Mivel feltételeztük, hogy a cső keresztmetszetéhez képest hosszú, tehát a tengelyirányú (Z) kiterjedése jelentősen nagyobb, mint a radiális irányú (X és Y) kiterjedése, valamint tengelyirányú terhelés nincs jelen, a feladat megoldható 2D-s sík alakváltozás típusú szimulációval. Emellett a cső geometriája miatt szimmetria feltételeket is alkalmazhatunk; elegendő a negyed geometria felépítése. (Megjegyzés: a nyomás típusú terhelés természetesen egy az egyben definiálható, mivel felülethez kötött, azonban például erőterheléses feladatnál figyelni kell a terhelés arányos osztására.)

A geometria tehát a cső egy negyed szelete, melyet egy sík felületmodellként (Surface Body) definiálunk a koordinátarendszer XY síkján. Az ANSYS Workbench Design Modeler moduljában létrehozott geometriát mutatja a 6.8. ábra. Az egyszerűség kedvéért a fősíkok szolgáltatják a szimmetria síkokat. Természetesen a 2D-s geometria esetén szimmetria tengelyekről beszélünk, melyek így a globális koordinátarendszer X és Y tengelyei.

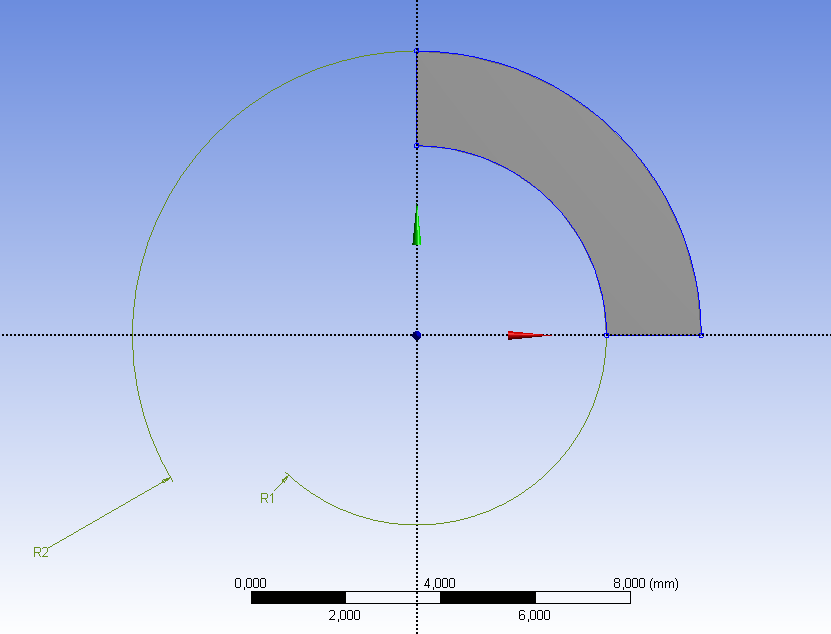
6.8. ábra - Cső modell 2D-s negyed geometriája

Mivel az analízis típusa sík alakváltozás (Plane Strain) , a 2D-s viselkedést a szimulációs környezetbe való belépés előtt be kell állítanunk, mert utólagosan már nincs lehetőség az átjárásra. Célszerű a geometria létrehozása előtt átállítani, a Static Structural/Geometry sorát kijelölve, a projektfelület jobb oldalán megjelenő tulajdonságok panelen (Properties of Schematic … : Geometry/Advanced Geometry Options/Analysis Type: 2D) , (6.10. ábra). Ha a panel nem jelenik meg akkor a statikai analízis paneljének Geometry sorára való jobb gombos kattintással, majd Properties parancs kiadásával előhozható.

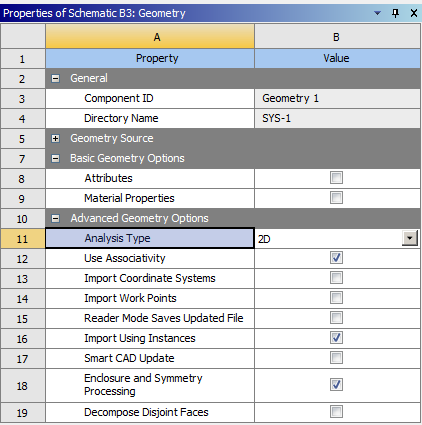
6.9. ábra - Váltás 2 dimenziós geometriára.

A szimulációs környezetbe való belépés után a modellfában a geometriát kijelölve, a Details panelen tudjuk beállítani a szimuláció típusát sík alakváltozásra (Outline/…/Geometry/ => Details…/Definition: Plane Strain) . A szimuláció során szerkezeti acél anyag került beállításra. A hálózás során strukturált hálót használunk négyszög elemekkel (Mapped Face Meshing) . A véges elemek mérete 0,5mm (6.10. ábra).

A modell így 64 elemet tartalmaz, tehát viszonylag kevés, azonban ez olyan pontos eredményt fog adni, mintha a teljes 3D-s geometriát kb. 5000 elem segítségével szimulálnánk, tehát majdnem 80-szoros sebességgel kapunk eredményt.

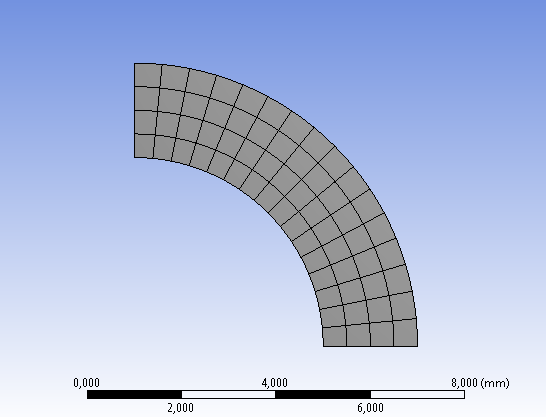
6.10. ábra - 2D-s negyed csőmodell hálója

A szimmetriafeltételeknél mindig figyelni kell arra, hogy a megfogások megfeleljenek a valóságnak. Jelen esetben a valós viselkedés modellezése az X és Y tengelyre illeszkedő 2 él adott tengelyre merőleges elmozdulásának megkötése. Ez egy-egy elmozdulás típusú kényszer segítségével oldható meg, melyek az illeszkedő tengely irányába eső elmozdulást szabadon engedik, míg a tengelyre merőlegest gátolják (6.11. ábra. A és B - címkével jelölt geometriai elemek).

A szerkezet terhelése a cső belső falán ébredő 100MPa nagyságú nyomás (6.11. ábra. C - címkével jelölt geometriai elemek).

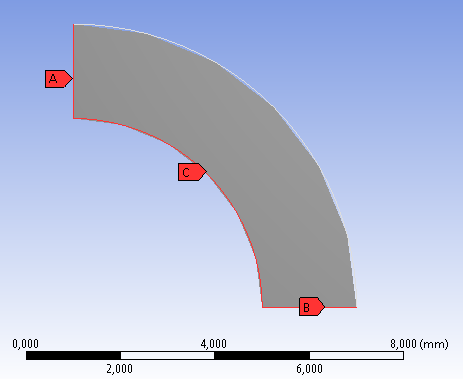
6.11. ábra - 2D-s negyed csőmodell terhelése és megfogásai

A szimuláció futtatása után kérdezzük le az egyenértékű feszültséget, fajlagos nyúlást és a radiális deformációt. Ez utóbbihoz egy polár koordináta rendszert kell definiálnunk. Az alábbi ábrán láthatjuk az ébredő egyenértékű feszültség eloszlását a cső fala mentén (6.12. ábra). A minimum és a maximum értékek mutatják a cső belső és külső falában ébredő feszültséget.

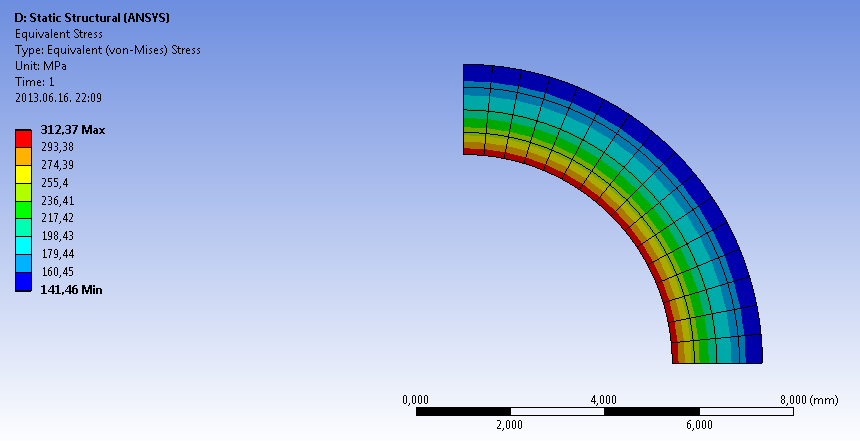
6.12. ábra - 2D-s negyed csőmodell egyen értékű feszültség értékei

6.1.5. A feladat megoldása 2D-s tengelyszimmetrikus (Axisymmetric) típusú modellként

Ugyanezt a feladatot meg lehet oldani 2D-s tengelyszimmetrikus modellként, mivel mind a geometria, mind a terhelés tengelyszimmetrikus. Ebben az esetben a geometria azt a fél hosszmetszetet jelenti, amelyet körbeforgatva megkapjuk a teljes geometriát, tehát a csövet modellező feladatnál ez egy 10mm*2mm-es téglalap a forgatási tengelytől 4mm-es minimális távolságra. Megjegyzés: ANSYS szoftverben a 2D-s tengelyszimmetrikus modelleket úgy kell felépíteni, hogy a forgástengely a globális Y tengely legyen, a geometria pedig az 1. és a 4. sík negyedben (+X) helyezkedjen el (6.13. ábra).

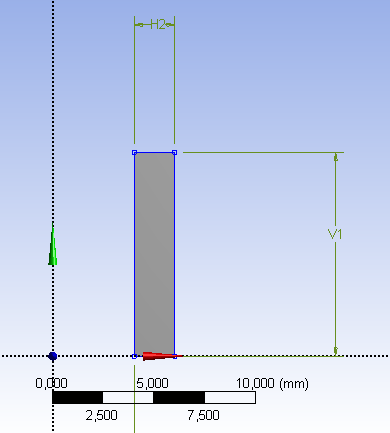
6.13. ábra - 2D-s tengelyszimmetrikus csőmodell geometriája

Mivel az analízis típusa 2D tengelyszimmetrikus, a 2D-s viselkedést, az előző feladathoz hasonlóan, a szimulációs környezetbe való belépés előtt be kell állítanunk (6.10. ábra), (S tatic Structural/Geometry => Properties of Schematic … : Geometry/Advanced Geometry Options/Analysis Type: 2D) ,

Belépve a szimuláció környezetbe, a modellfa geometria sorát kijelölve állítsuk be a szimuláció típusát tengelyszimmetrikusra, (Outline/…/Geometry => Details /Definition/2D Behavior: /Axisymmetric) .

Az anyag hozzárendelés és a szimuláció általános beállításai után készítsük el a végeselemes hálót. A háló, ahogy az előző esetben is 0,5mm nagyságú négyszög elemekből áll. Az így létrehozott háló összesen 80 elemet tartalmaz (6.14. ábra).

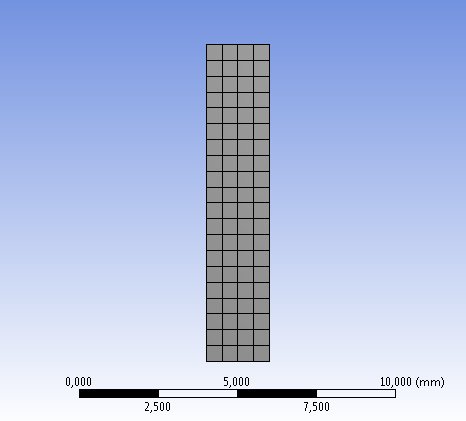
6.14. ábra - 2D-s tengelyszimmetrikus csőmodell véges elemes hálója

A megfogások definiálása itt is különös figyelmet igényel. A csőmodell két végén olyan elmozdulás típusú kényszert célszerű alkalmazni, amely megengedi a cső tágulását, tehát radiális (X) irányú elmozdulását, de leköti az axiális (Y) irányú elmozdulás lehetőségét. Mivel ebben a modellben a két véglap párhuzamos egymással, elegendő egyetlen megfogást megadni, mert mindkét oldal ugyanolyan irányban mozoghat, illetve van lekötve (6.15. ábra).

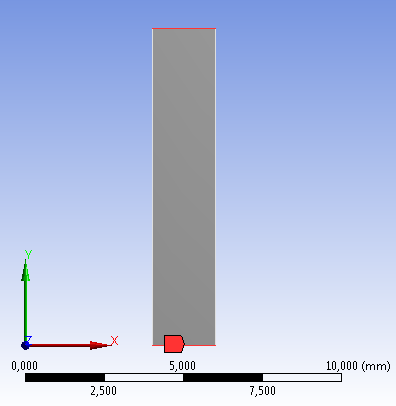
6.15. ábra - 2D-s tengelyszimmetrikus csőmodell véglapjainak megfogása (UY=0).

A 100MPa-os belső nyomás a csőfelület belső felületén, tehát itt a tengelyhez közel álló párhuzamos élen van (6.16. ábra).

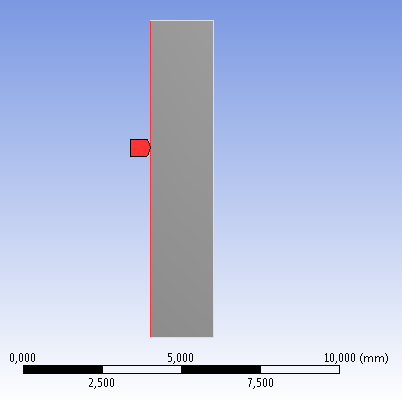
6.16. ábra - 2D-s tengelyszimmetrikus csőmodell nyomásterhelése

A szimuláció lefuttatása után, az előző példához hasonlóan kérdezzük le az egyenértékű feszültséget, a fajlagos nyúlást és a radiális deformációt. Ez utóbbihoz most nem kell poláris koordináta rendszert definiálnunk, mivel az az X tengely irányába esik. Az alábbi ábrán láthatjuk az ébredő egyenértékű feszültség eloszlását a cső fala mentén (6.17. ábra). A minimum és a maximum értékek mutatják a cső belső és külső falában ébredő feszültséget.

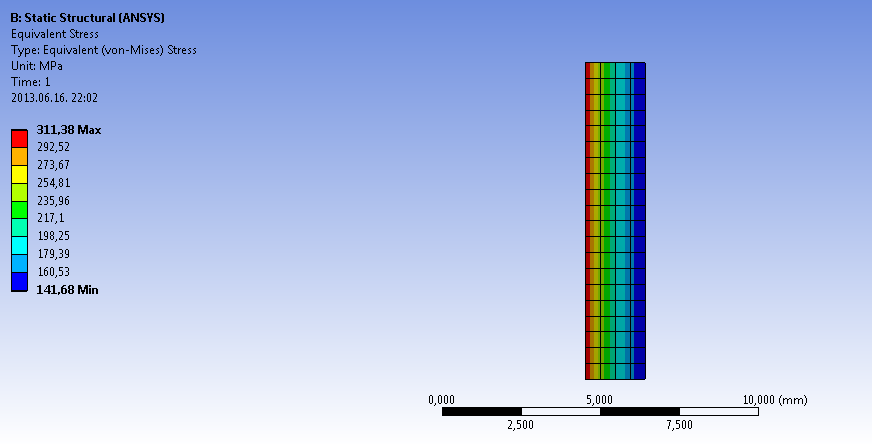
6.17. ábra - 2D-s tengelyszimmetrikus csőmodell egyenértékű feszültség viszonyai

6.1.6. Összefoglalás

Miután négy féle módon elvégeztük a szimulációt, azonos feltételekkel (azonos anyag és geometria, azonos elemméret és szimulációs beállítások) láthatjuk, hogy a héjmodell kivételével az eredmények nagymértékben egyeznek az analitikus számolással, melyet a vastag csövekre alkalmazott formulákkal végeztünk. Ugyanakkor, a vékonyfalú csövekre alkalmazott analitikus számolás eredménye jó egyezést mutat a héjmodellel végzet szimulációval. Ez nem meglepő, hisz mindkét eljárás a kiterjedéséhez (itt átmérő és hossz) mérten kis falvastagságú szerkezetek vizsgálatára szolgál.

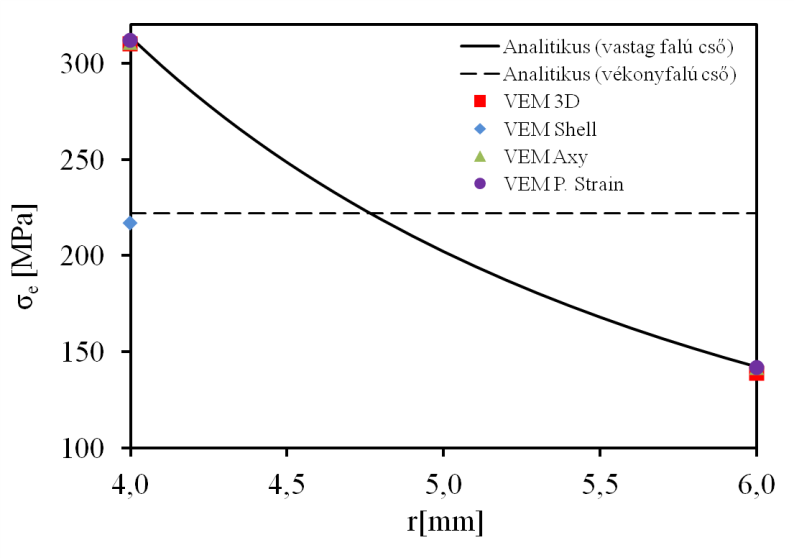
6.18. ábra - A cső falában ébredő (von Mieses féle) egyenértékű feszültség analitikus és végeselemes megoldása.

6.1. táblázat - A négy különböző végeselemes módszer és az analitikus eredmények összehasonlítása.

Egyenértékű feszültség, [MPa]

Analitikus

(vastag falú cső)

VEM

Axy

VEM

P. Strain

Analitikus

(vékonyfalú cső)

VEM

Shell

Külső oldalon

313

310

311

312

222

217

Belső oldalon

142

139

142

6.2. Példa egy oldalon befogott, hajlított tartó négyféle megoldására

Az alábbi példában egy egyik oldalon befogott, koncentrált erővel terhelt gerenda statikai analízise által fogjuk bemutatni, hogy a különböző típusú szimulációk összeállításának módját és eredményeit.

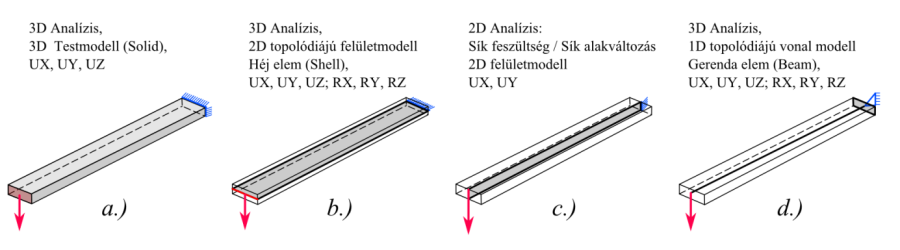
a.) Testmodell, b.) héjmodell, c.) 2D sík alakváltozási, vagy sík feszültségi modell, d.) gerendamodell.

6.19. ábra - Egy oldalon befogott, hajlított tartó négyféle megoldása.

Az alábbi ábrákon látható a geometriai modellt az adott a terhelési és permfeltételekkel a következő módokon fogjuk tudni vizsgálni (6.19. ábra):

3D-s teljes testként (3D body) .
3D-s felületmodellként (Shell body),
2D-s sík alakváltozás és sík feszültség típusú feladatként (2D Plane Strain, Plane Stress) ,
Vonalmodellként (Gerenda elemmel), keresztmetszettel definiálva (Line body, Cross section)

6.20. ábra - A hajlított rúd geometriai méretei [mm]

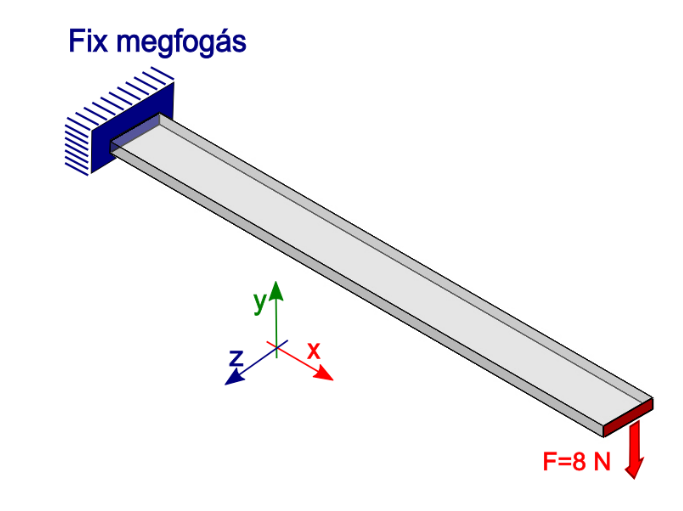
6.21. ábra - Terhelési modell a hajlított rúd esetében

Minden esetben azonos anyagtulajdonságok lesznek definiálva; az ANSYS Workbench beépített szerkezeti acél (Structural Steel) nevű anyagja. A szimulációk beállításánál a nagy alakváltozások megengedettek (Simulation Settings/Large deflection: On) .

6.2.1. A feladat megoldása 3D-s teljes testmodellel (3D body)

A 3D-s geometria használata általában a leghosszadalmasabb számítási igényű eljárás. Tehát célszerű (amennyiben lehetséges) a további példák során bemutatott egyszerűsített eljárásokat használni. A teljesség kedvéért azonban bemutatjuk a teljes 3D-s geometria szimulációját is ugyanazon a példán. A geometriai modell felépítése történhet a véges elemes szoftverben illetve akármelyik más CAD rendszerben is.

Jelen példában az ANSYS Workbench Design Modeler moduljában építettük fel a hasábot, egyetlen kihúzás (Extrude) segítségével. A vázlatot egy 100x10mm-es téglalap alkotja, a kihúzás mértéke normál irányba 2mm, (6.22. ábra).

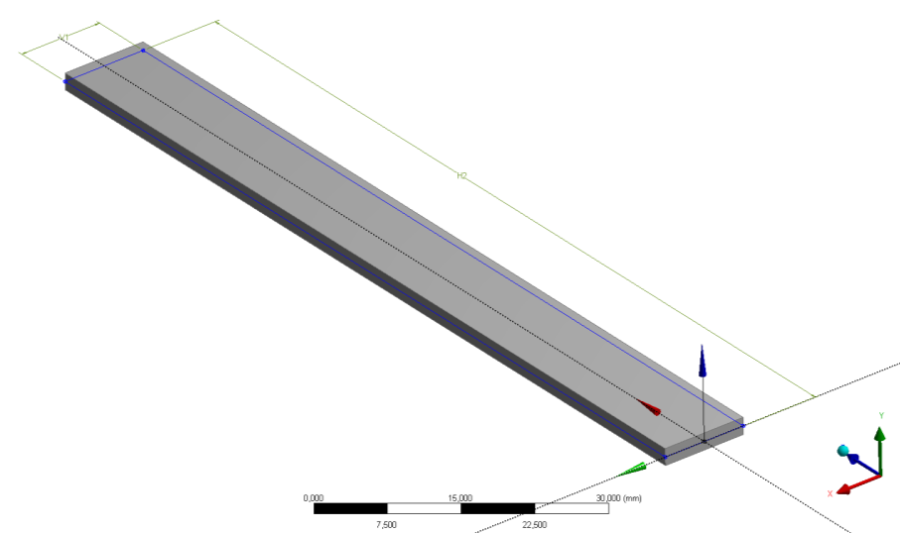
6.22. ábra - Az elkészített 3D-s geometria

Az általános beállítások után (anyag hozzárendelés, nagy elmozdulások engedélyezése stb.) készítsük el a véges elemes hálót téglaelemek felhasználásával (6.23. ábra). Az elemek mérete 1mm, így összesen 2000 elemből áll a modell.

6.23. ábra - A 3D-s modell véges elemes hálója

Az eredmények összehasonlíthatósága miatt definiáljunk azt a konstrukciós geometriát, amely segítségével a vonal menti deformáció lekérdezhető.

Konstrukciós geometrialétrehozás ANSYS Workbenchben :

A konstrukciós görbe (Path) egy olyan térbeli görbét jelent, mely mentén diszkrét pontokban lekérdezhető az eredmény, és az eredmény pontonként táblázatban és diagramon is megtekinthető. A pontokat és értékeket tartalmazó táblázat exportálható abból a célból, hogy más programok segítségével is elemezhető legyen. A diszkrét pontokhoz tartozó eredményeket idő és út függvényében is meg lehet jeleníteni, az út természetesen a vonal kezdő pontjától a végpontja felé haladva jelenik meg.

A konstrukciós vonal definiálását kétféle módon tehetjük meg; a kezdő és végpont megadásával, illetve meg lévő egyenes kijelölésével.

Első lehetőséget kétféle módon lehet megoldani. Közvetlenül a kezdő és végpont megadásával (ilyenkor létező pontok kijelölése szükséges), vagy a vonal megadható a pozitív x tengely és a háló modell metszéseként. (Ebben az esetben a kezdő és végpont helyzetét jelöli ki a háló, és e két pont közti vonal lesz a konstrukciós elemünk.) A konstrukciós pálya lehet egyenes, vagy íves, attól függően, hogy milyen típusú koordináta rendszert használunk. (Descartes-féle koordináta rendszernél egyenes, míg henger koordináta rendszernél íves.) A konstrukciós vonal diszkrét pontjainak száma definiálható, de maximum 200 lehet. (Megjegyzés: a kezdő-és végpont segítségével csak tömör test és felületmodell esetén lehet megadni a konstrukciós egyenest.)

Második lehetőség, amikor egy meglévő él kijelölésével definiáljuk a konstrukciós vonalat. Ebben az esetben a vonal alatt lévő csomópontok jelentik a vonal diszkrét pontjait. Több egyenesből álló vonalláncoknál figyelni kell arra, hogy a vonalak egymással folytonosak legyenek.

ANSYS Workbenchben mielőtt létrehoznánk egy konstrukciós geometriát egy „Path Object”- et létre kell hozni, melyet a konstrukciós eszköztárban (Construction Geometry toolbar) találhatunk meg. Ezután a fenti módszerek bármelyikével létrehozható a kívánt konstrukciós vonal.

A példában szereplő útvonalat a modellfa modell sorának kijelölésével, a felső ikonsorból hozzuk létre (Outline/Model=>Construction Geometry/Path) . Az útvonal típusa legyen élre illeszkedő, melyet a testmodellünk egyik hosszanti élének kijelölésével rendelhetünk hozzá (6.24. ábra).

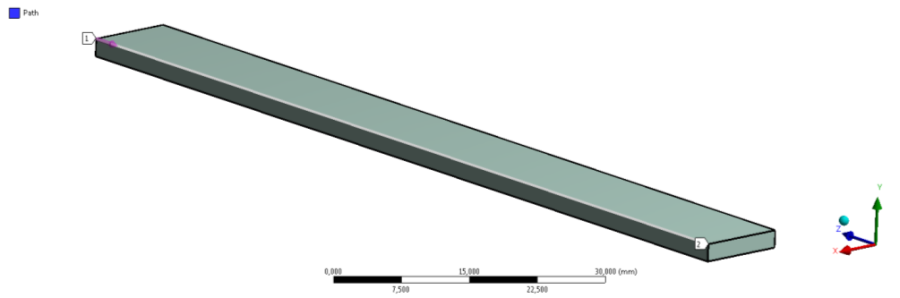
6.24. ábra - A 3D-s modellen létrehozott konstrukciós geometria

A terhelési és peremfeltételek elkészítésekor összesen két elemet használtunk; egy fix megfogást a rúd egyik véglapján (Supports/Fix support) , mely a véglap csomópontjainak minden szabadságfokát eliminálja és egy erő (Force) jellegű terhelést a rúd másik végén. Az erőt komponensenként megadva –Y irányban 8N nagyságú, míg X és Z irányba 0N nagyságú. A terhelést a 6.24. ábra mutatja, ahol piros B jelű címkével a –Y irányú, 8N nagyságú erőterhelés, és a kék A jelű címkével ellátott fix megfogás van jelölve.

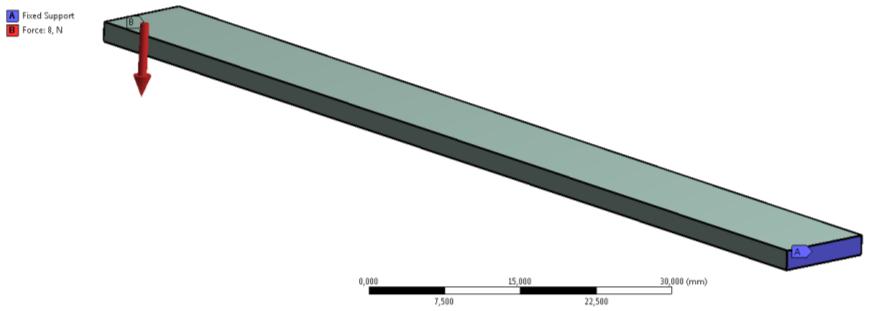
6.25. ábra - 3D-s geometria esetén a terhelési modell megadása

A szimuláció futtatása után kérdezzük le a teljes (6.26. ábra), és az Y irányú lehajlás értékét a létrehozott konstrukciós vonal (Path) mentén (6.27. ábra).

6.26. ábra - 3D-s modell esetén a teljes deformáció eloszlása [mm]

6.27. ábra - 3D-s modell esetén a vonal menti, y irányú deformáció [mm]

6.2.2. A feladat 3D-s megoldása felületmodell (shell) definiálásával

A modellt egy felületi geometriával (Surface) és a hálózáskor hozzárendelt vastagsági paraméterrel definiáljuk, amely héj (Shell) elemekkel való szimulációt jelent. Jelen esetben egy 100x10mm-es síklap és egy ehhez tartozó 2mm-es vastagság határozza meg a testet.

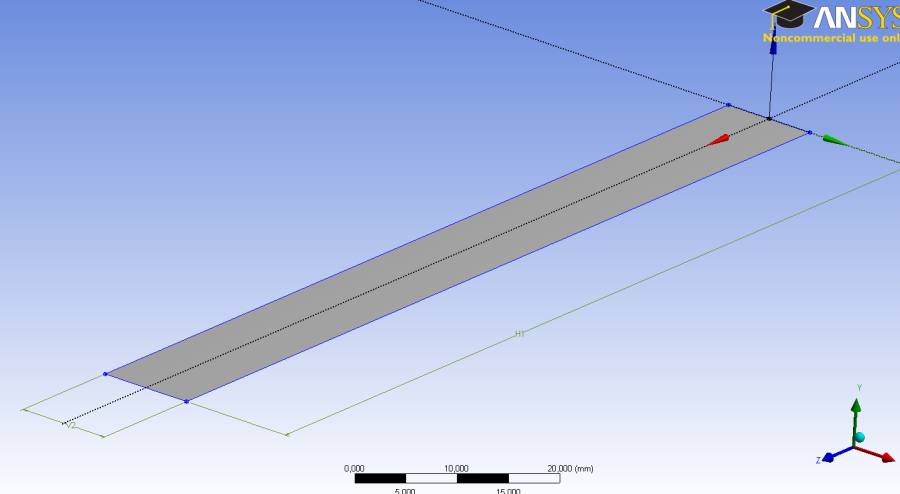
6.28. ábra - A felületi geometria

Az ANSYS Workbench Design Modeler moduljában a vázlatelemek felületté alakítása a Concept menü Surfaces From Sketches menüpontjában végezhető el (6.29. ábra).

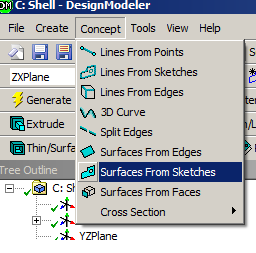
6.29. ábra - Felületmodell létrehozása vázlat alapján (menüpont elérése)

A geometria elkészülte után, lépjünk be a szimulációs környezetbe. A modellfában a geometria alatt megjelenő felületmodellt kijelölve állítsuk be a lemez vastagságát (Outline/…/Geometry/Surface Body => Details…/Definition/Thickness: 2mm) , az eltolás típusát hagyjuk „közép”-re állítva ( Offset Type: Middle ). Az anyagot hagyjuk az alapértelmezett szerkezeti acélnak (Strutural steel) .

Ezután végezzük el a hálózást. Ugyanúgy, mint az előző esetben 2mm-es elemméretet használtunk. Látható, hogy ez meglehetősen eltér az előző esettől, mivel a test vastagsága mentén csak egy elemre oszlik a geometria (6.30. ábra).

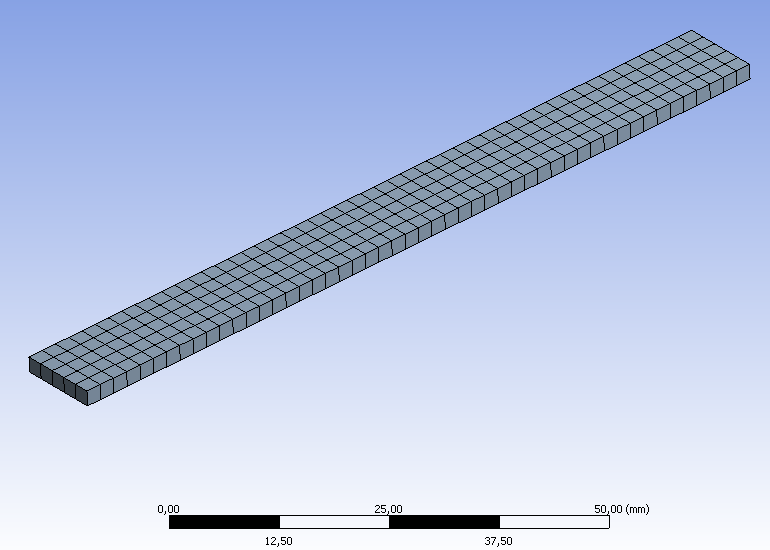
6.30. ábra - Véges elemes háló shell modell esetén

Ahogy az előbbi esetben itt is, hozzunk létre egy konstrukciós geometriát, mely segíti az eredmények értékelését. Jelen esetben az egyik hosszanti él lett a konstrukciós vonal (Path) alapja (6.31. ábra).

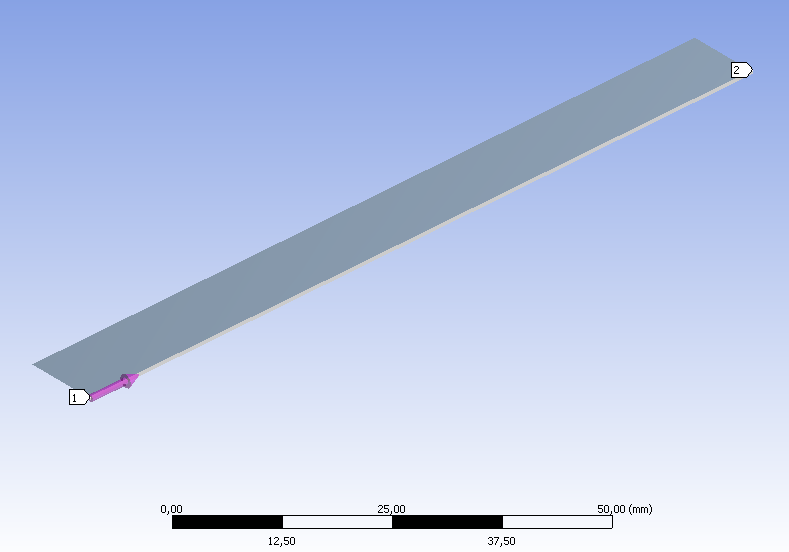
6.31. ábra - Konstrukciós vonal shell modell esetén

A terhelés ugyanaz, mint az előző esetben (Fix megfogás a test egyik véglapján, 8N erőterhelés –Y irányban a másik végén), mivel itt felületmodellről van szó, a véglapok kijelöléséhez a felületet határoló él kijelölése szükséges (6.32. ábra).

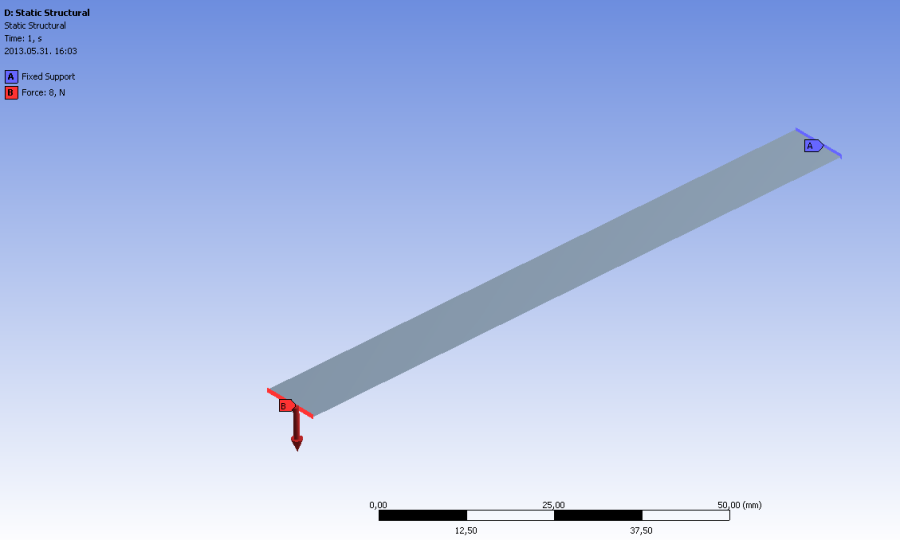
6.32. ábra - Terhelési modell felületi test esetén

A szimuláció futtatása után a kérdezzük le a teljes (6.33. ábra), és a konstrukciós vonal menti Y irányú deformációt (6.34. ábra).

6.33. ábra - Teljes deformáció [mm]

6.34. ábra - Y irányú deformáció [mm] konstrukciós vonal mentén

6.2.3. A probléma megoldása 2D-s feladatként

A fenti probléma megoldására kétféle 2 dimenziós eset áll rendelkezésünkre a sík feszültség (Plane Stress) és a sík alakváltozás (Plane Strain).

A sík feszültség (Plane Stress) analízis esetén a test vizsgált metszetére merőleges (ANSYS-ban: Z tengely) irányában nem ébred feszültség. Ez az állapot vékony (a vizsgált metszetre merőleges kiterjedése kisebb, mint a másik két irányban), és a vizsgált metszet síkjába eső terhelési és megfogásai feltételekkel rendelkező testekre jellemző.

A 2D-s sík alakváltozás (Plane Strain) típusú szimulációk lényege, hogy a test vizsgált keresztmetszetére merőleges (ANSYS-ban: Z tengely) irányában nincs alakváltozás. Ez az állapot hosszú, állandó keresztmetszetű (a vizsgált keresztmetszetre merőleges kiterjedése nagyobb, mint a másik két irányban), és a hossz mentén állandó és a keresztmetszet síkjába eső terhelési és megfogásai feltételekkel rendelkező testekre jellemző. Ennél fogva a feszültségi állapot és a keresztmetszet síkjába eső alakváltozási állapot is azonos a hossz (Z tengely) mentén, tehát elegendő egyetlen keresztmetszet 2D-s vizsgálata. A sík alakváltozásnál végtelen hosszú modellt feltételezünk fajlagos terhelésekkel, míg az általánosított változatánál (Generalized Plane Strain) a vastagságot is megadhatjuk.

Mivel ebben a példában a terhelés és megfogás is egyenletes a Z tengely mentén (és nincs Z tengely irányú komponense), mindkét eset megvalósítható. Viszont, mivel a valós geometria Z irányú mérete lényegesen kisebb, mint az X irányú hossza, és nagyobb mint az Y irányú magassága, ezért egyik eljárás geometriai feltételeit sem teljesíti., vagyis Z irányban sem a feszültség, sem pedig az alakváltozás értéke nem lesz teljesen 0. Viszont mivel elhanyagolható mértékűek a síkbeli komponensekhez képest, ezért jó közelítést jelentenek. Végezzük el az analízist mindkét esetre és vessük össze az eredményeket.

Vázlatkészítésnél a 100x2mm-es téglalp megrajzolását az XY síkon szükséges elvégezni. A 10mm-es vastagságot pedig a szimuláció során tudjuk megadni. A 6.35. ábra mutatja az elkészült vázlatot és a felületet, amelyet a vázlatból definiáltunk (Concept/ Surfaces From Sketches) . A felület létrehozásának menete ugyan az, mint a 3D-s Shell modelles példában, annyi különbséggel, hogy a felületnek mindenképp egy síkban (XY) kell lennie (6.35. ábra), és a szimuláció során 2D-s beállításokat kell alkalmazni az ott használt 3D-s helyett. A 2D-s viselkedést a szimulációs környezetbe való belépés előtt be kell állítanunk, ( Static Structural/Geometry => Properties of Schematic… : Geometry/Advanced Geometry Options/Analysis Type: 2D) .

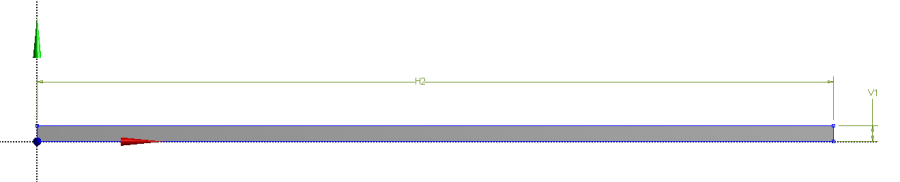
6.35. ábra - Az elkészült vázlat és felület

A szimulációs környezetbe való belépés után a modellfában a geometriát kijelölve, a Details panelen tudjuk beállítani a szimuláció típusát általánosított sík alakváltozásra (Outline/…/Geometry/ => Details…/Definition: Generalized Plane Strain) . A későbbiekben futtassuk le szimulációt a sík feszültség (Plane Strain) beállítással is.

A geometria elkészítése és a szükséges beállítások (anyagdefiniálás, nagy alakváltozás engedélyezése, vastagság beállítása stb.) után készítsük el a végeselemes hálót, mely elemméretét állítsuk 1mm-re. Mivel itt jóval kevesebb véges elem adódik, mint például a 3D- szimulációk esetén, lehetőség van a sűrűbb háló használatára (6.36. ábra).

6.36. ábra - A véges elemes háló (elemméret 1 [mm])

A terhelés hasonlóan az eddigi esetekhez egy fix megfogást és egy –Y irányú, 8N nagyságú erőterhelést jelent (6.37. ábra).

6.37. ábra - A terhelési modell

Mivel ennél az esetnél is szükség van a vonal menti deformáció értékeire, így definiáljuk a konstrukciós vonalat ( Path ) a rúd felső élén (6.38. ábra).

6.38. ábra - A konstrukciós vonal (path) definiálása

Eredményként, a bevezetésben megfogalmazott problémák ellenére, az eddigiekhez nagyon hasonló értékeket kaptunk. A teljes deformáció eredményét a 6.39. ábra, az Y irányú, vonal menti deformáció eredményét a 6.40. ábra szemlélteti.

6.39. ábra - Teljes deformáció [mm]

6.40. ábra - Vonal menti, y irányú deformáció [mm]

6.2.4. A feladat megoldása vonalmodell keresztmetszet definiálásával (gerenda elemmel)

A vonalelemek két fő csoportja a rúd (Truss) és a gerenda (Beam) elemek, melyeknek alkalmazását a szerint választhatjuk ki, hogy a vizsgált szerkezetben lévő vonal elemek felvesznek-e hajlító igénybevételt (gerenda), vagy csak tengelyirányú terhelést (rúd). Esetünkben egyértelműen a gerendamodellre van szükség mivel a konzol tengelyére merőleges terhelés hajlításra veszi igénybe a tartót. Az ANSYS Workbench használatakor a program a vonal elemeket automatikusan gerenda elemekkel hálózza be.

A geometria két részből, a tartó tengelyét képviselő vonalmodellből, és a keresztmetszet definíciójából áll. A vezérgörbe a Z tengely mentén fekvő, 100mm hosszú vonal, a keresztmetszet pedig egy 10x2mm-es téglalap (6.41. ábra).

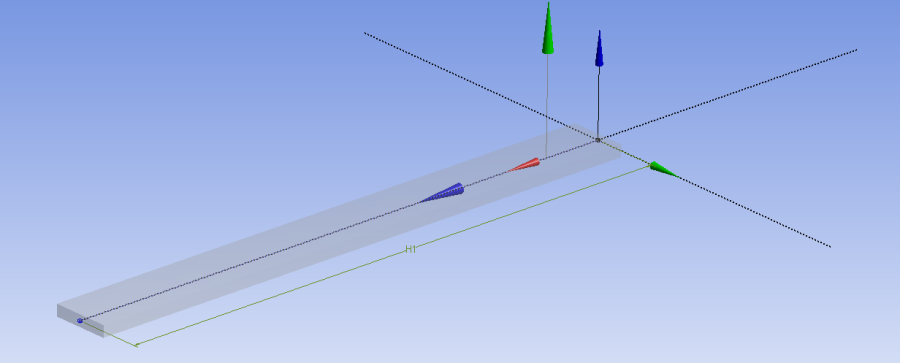
6.41. ábra - A vonal test és keresztmetszet alapján definiált geometria

Az ANSYS Workbench Design Modeler moduljában a vonal test a Concept menü Lines From Sketches parancsával hozható létre, a már előzőleg megrajzolt vonal vázlatának kijelölésével (6.42. ábra). A keresztmetszet definiálását a Concept menü Cross Section parancsával lehet elvégezni (6.43. ábra). Lehetőségünk van az előre definiált, jellegzetes keresztmetszetek kiválasztására (ilyenkor csak a méreteket kell megadni), illetve saját vázlat készítésére. Ezután a vonalmodellhez (line body) , a létrehozott keresztmetszetet hozzá kell rendelni. Ehhez a modellfa utolsó (az alkatrészek és a testek számát mutató) sorát le kell gördíteni és a vonalmodell kijelölése után a Details panel Cross Section sora mellett kiválasztani a létrehozott keresztmetszet nevét („Rect1”).

A keresztmetszet definiálásakor figyelni kell a vonalelem orientációjára (a zöld színű koordinátatengely jelöli a +Y irányt). A keresztmetszet a modellen való állásának ellenőrzésére, a View menüben bekapcsolhatjuk a testmodell (Cross Section Solids) és/vagy a vonal koordinátarendszer (Cross Section Alignments) láthatóságát (6.41. ábra).

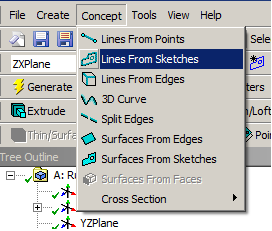
6.42. ábra - ANSYS WB Design Modeler moduljában a vonal testté alakításhoz használatos menüpont elérése

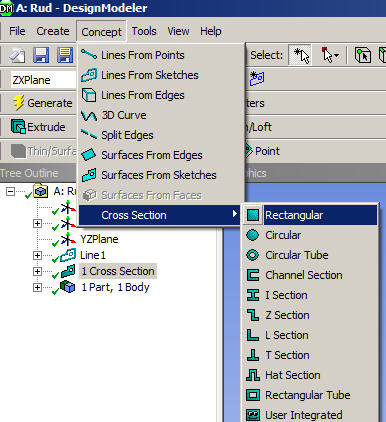
6.43. ábra - ANSYS WB Design Modeller moduljában a keresztmetszet definiálásához használatos menü elérése

Miután a szimuláció beállításai megtörténtek (pl. anyag hozzárendelés) elkészítjük a véges elemes hálót. A testet 2mm-es elemmérettel hálóztuk be. Ahogy a 6.44. ábra mutatja a vonalmodell mentén mindenhol csak 1 db elem helyezkedik el. Így a véges elemes modellünk 50 elemet tartalmaz.

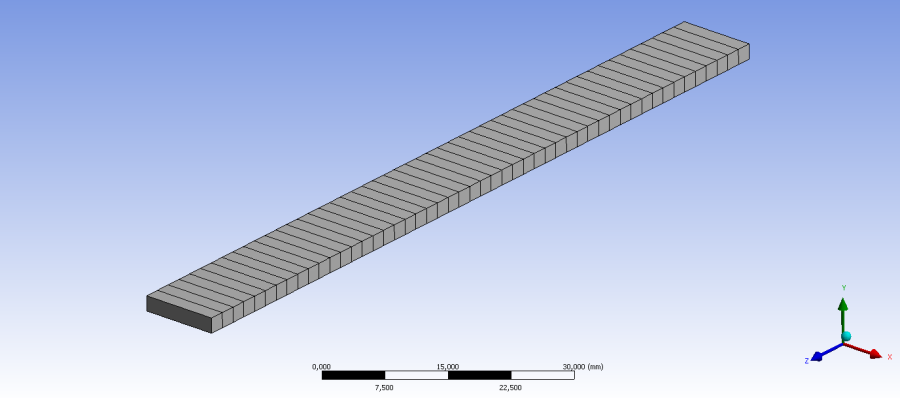
6.44. ábra - A véges elemes háló

Az eredmények lekérdezéséhez definiáljunk egy konstrukciós rajzi elemet (Construction Geometry) , melynek segítségével egy vonal (Path) mentén lekérdezhető a szimuláció eredménye. Jelen feladatban a konstrukciós segédvonalat a test közepén végigfutó vonalmodell kijelölésével definiáljuk (6.45. ábra).

6.45. ábra - Konstrukciós vonal definiálása diszkrét kezdő és végpont segítségével

A megtámasztás (Supports/Fix support) és az erő (Loads/Force) megadásakor a 2 végpontot jelöltük ki. A terhelést a 6.46. ábra mutatja, ahol piros, B jelű címkével a –Y irányú, 8N nagyságú erőterhelés, és a kék, A jelű címkével ellátott fix megfogás van jelölve. Mivel vonalmodell lett definiálva a terhelések és megfogások megadásakor, a vonalak végpontjainak kijelölésével az adott csomópontok mind a 6 szabadságfokát meghatároztuk.

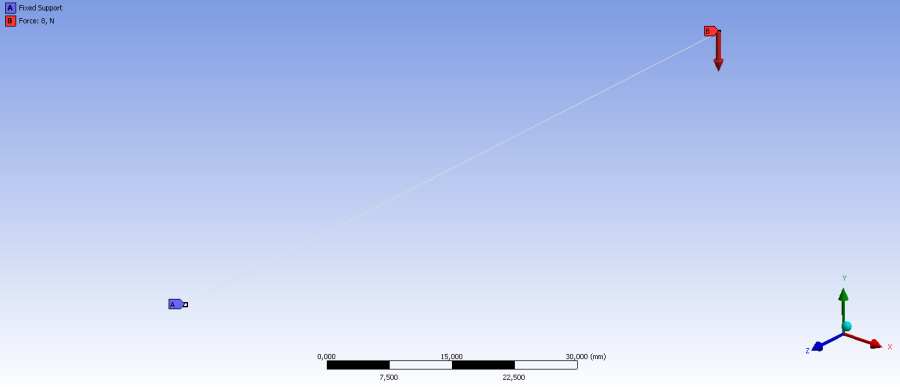
6.46. ábra - A terhelési modell

A szimuláció lefuttatása utána az alábbi eredményeket kérdeztük le:

Y irányú deformáció (Directional Deformation) a konstrukciós vonal mentén (6.47. ábra),
Teljes deformáció (Total Deformation) (6.48. ábra),

6.47. ábra - Y irányú deformáció [mm] a konstrukciós vonal mentén

6.48. ábra - Teljes deformáció [mm] (a minimum és maximum értékek feltüntetésével).

Gerendamodell esetén a Beam Result menüponttal további, specifikusan a gerendák igénybevételére vonatkozó eredmények is lekérdezhetőek (6.49. ábra). Kérdezzük le az alábbi eredményeket:

Teljes hajlító nyomaték (Total Bending Moment) (6.50. ábra),
Teljes nyíróerő (Total Shear Force) (6.51. ábra)

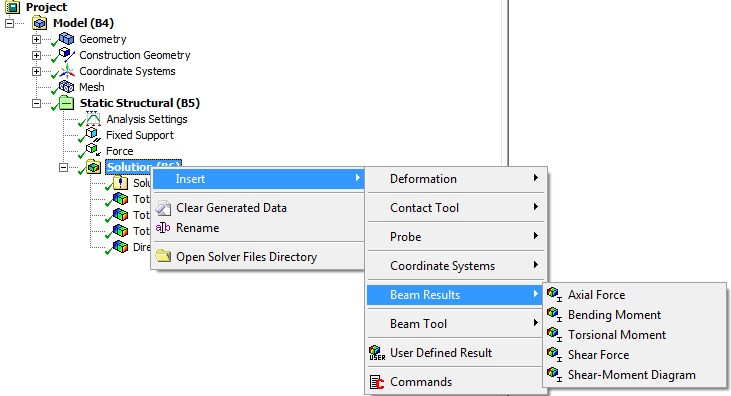
6.49. ábra - Gerendák igénybevételére vonatkozó eredmények is lekérdezhetőek.

6.50. ábra - Teljes hajlító nyomaték [Nmm] eredménye.

6.51. ábra - Teljes nyíróerő [N] eredménye.

Vegyük észre, hogy a folytonos színátmenet ellenére, a nyíróerő értéke az elvártaknak megfelelően, gyakorlatilag állandó a rúd hossza mentén.

6.2.5. Összefoglalás

A fenti példán jól látható, hogy ugyanazon feladat négyféle megoldása nagyon hasonló eredményeket hozott. A rúdvég lehajlásának mértékét a Táblázat 6.2 mutatja, a végeselemes eredmények és az analitikus számolástól való eltéréseik százalékos feltüntetésével.

6.2. táblázat - A különféle geometriai megoldások eredményeinek összehasonlítása az analitikus megoldással.

Modell (Elemtípus)	Szimuláció típusa	Uy [mm]	Eltérés [%]
3D testmodell	3D Térbeli	1,983	0,85
2D héjmodell	3D Térbeli	1,983	0,85
1D vonal elem	3D Térbeli	1,9998	0,01
2D felületmodell	2D sík feszültség	1,999	0,05
2D felületmodell	2D sík alakváltozás	1,935	3,25
	Analitikus megoldás	2,000

6.3. Példa gerenda modell alkalmazására: Hegesztett rácsos szerkezet

Rúdmodell használatát akkor célszerű megfontolni, mikor olyan feladattal állunk szembe, amelyben rácsszerkezetek, zártszelvények, csövek, azonos, vagy váltakozó keresztmetszetű idomelemekből álló szerkezetek mechanikai, vagy egyéb szimulációját kívánjuk elvégezni. Ebben az esetben a szimuláció lefutása lényegesen rövidebb időt vesz igénybe, ahhoz képest, mintha a teljes test vizsgálatát végeznénk. Hátránya azonban, hogy általában nem lehetséges a csomópontok vizsgálata. Amennyiben például egy ilyen szerkezet csomópontjában lévő hegesztett kötés szimulációjára is szükség van, célszerű először rúdmodellként analízist készíteni, majd a csomópont környezetének teljes modelljét vizsgálva a rúdmodell analízisből származó terhelési értékekkel szimulálható a csomópont mechanikai viselkedése. A módszer különösen hasznos például hídszerkezetek, rácsos tartók statikai és dinamikai ellenőrzéséhez.

Rúdmodellt (Trust) használunk abban az esetben, ha a modellezett szerkezetben szereplő, rudak csak tengelyirányú, (vagyis rúdirányú) erőt képesek felvenni. Tehát hajlító nyomaték nem ébred a csatlakozási csomópontokban (csuklóval modellezhető).

Gerendamodellt (Beam) alkalmazunk akkor, ha a csatlakozási pontokban nyomaték is átadódik, tehát a gerendamodellen hajlító igénybevétel is ébredhet. Például vékony, vagy közepesen vékony idomelemekből álló hegesztett rácsszerkezet szimulációjánál alkalmazhatjuk.

A vonalelemek egyik speciális fajtáját, a csőmodelleket (Pipe) vékony falú, vagy közepesen vékony falú főleg kör keresztmetszetű csövek vizsgálatánál alkalmazhatjuk. Ebben az esetben az ANSYS lehetőséget kínál olyan speciális terhelések definiálására, mint például a cső-nyomás.

A gerendamodell (Beam) készítéséhez egy vonalmodellt (Line body) és egy keresztmetszetet (Cross Section) kell definiálni. A vonalmodellek kizárólag egyenes, vagy görbe vonalakból állnak, nincs felületük, vagy térfogatuk, a gerendamodell nyomvonalát határozzák meg. A gerendamodell keresztmetszetének (Cross Section) megadása a felület nagyságának illetve a különböző irányú másodrendű nyomaték értékek számolásához szükséges. A keresztmetszet definiálásakor lehetőség van megadni, hogy a keresztmetszet mely pontján menjen keresztül a vezérgörbe (tehát a vonalmodell). Ez lehet például a keresztmetszet középpontja, súlypontja, nyírási középpontja, vagy egy tetszőlegesen megadott pont.

Az alábbi esetben egy négyszög keresztmetszetű zártszelvényből álló háromszög alakú hegesztett tartókonzol szimulációját vizsgáljuk meg. A feladathoz tartozó geometriát a 6.52. ábra mutatja.

6.52. ábra - A tartókonzol geometriai méretei [mm]

A terhelési model:

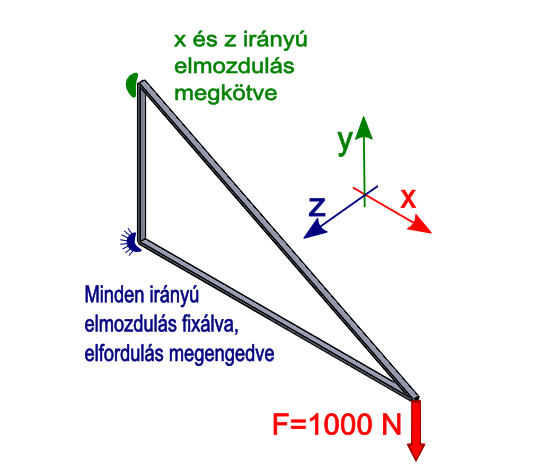
6.53. ábra - A konzol terhelési modellje

A végeselemes szoftverben elegendő a szerkezet körvonaláról vázlatot készíteni, majd ehhez a körvonalhoz hozzárendelni a megrajzolt, vagy kiválasztott keresztmetszetet (6.55. ábra). Csak abban az esetben kell a keresztmetszetet vázlat szintjén elkészíteni, amikor a szokványostól eltérő, egyedi keresztmetszetet használunk.

A keret nyomvonalának megrajzolása után a vázlatot (Sketch) vonalmodellé (line body) kell alakítani a Concept menüpont Lines From Sketches parancsával. A keresztmetszet kiválasztását és a méreteinek megadását a Concept menü Cross Section parancsával lehet elvégezni. A vonalmodell (line body) létrehozása után, a létrehozott keresztmetszetet hozzá kell rendelni. Ehhez a modellfa utolsó (az alkatrészek és a testek számát mutató) sorát le kell gördíteni és a vonalmodell kijelölése után a Details panel Cross Section sora mellett kiválasztani a létrehozott keresztmetszet nevét („Rect1”).

Megjegyzendő, hogy bár a modellen a zártszelvény darabok csatlakozási pontjában úgy látszik, mintha az egyes darabok a belső oldalon egymásba érnének, a külső oldalon meg távol lennének egymástól ez csak a megjelenítési képen ilyen, a szimuláció során itt egy pontban érintkezés valósul meg.

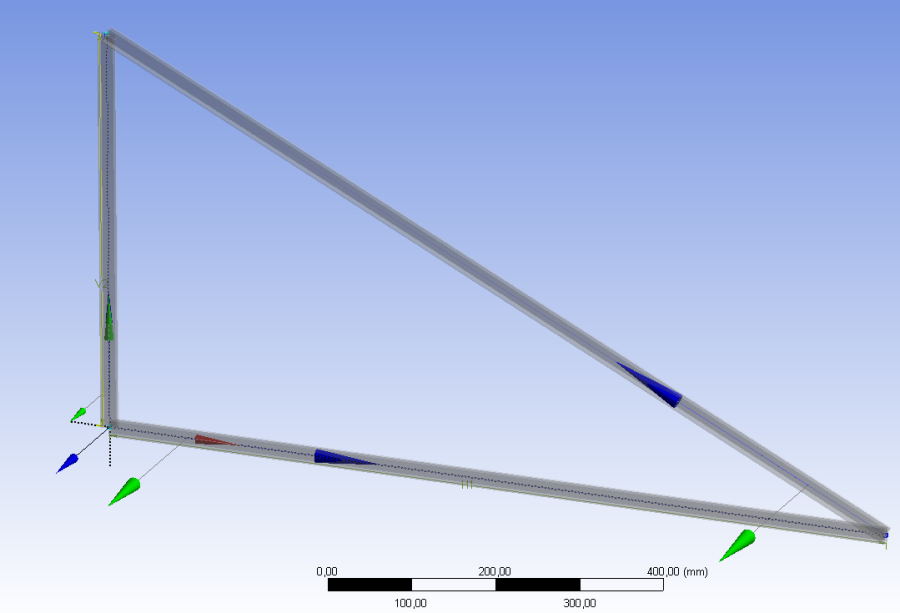
6.54. ábra - Az elkészült geometria (rúdmodell)

Ahogy láthatjuk a modellünk minden egyes vonalszakaszának az Y és Z irányokat jelző koordinátatengelyek jelennek meg. A kék színű (Z) vektor mutatja az adott vonal, vagy görbeszakasz érintő (tangent) irányát, míg a zöld színű (Y) vektor a keresztmetszet +Y irányát jelöli. Amennyiben ezek nem olyan irányban állnak alapértelmezetten, ami a feladatunkhoz megfelelő, akkor módosíthatjuk az állásukat.

6.55. ábra - A rúdmodellhez tartozó keresztmetszet vázlata

Az elkészült geometria anyaga jelen esetben az ANSYS Workbench szerkezeti acél (Structural Steel) nevű anyagja. A végeselemes háló elkészítése során 100 mm-es elemméretet használjunk (6.56. ábra). Látható, hogy a vonalmodell felosztása csak a vonal mentén történt meg, a keresztmetszetben csak egy elem található. Így látható ezzel a módszerrel, kevés elemmel, viszonylag gyors lefutású szimulációk hozhatóak létre (ebben a példában a modell mindössze 27 elemet tartalmaz.)

6.56. ábra - A véges elemes háló (100 mm-es elemméret)

A véges elemes háló elkészítése után a legfontosabb feladat a terhelési modell definiálása. Definiáljuk a következő típusú megfogásokat és terheléseket (6.57. ábra):

Erő terhelés a konzol végén: komponensenként definiált erő (Force) , a globális koordinátarendszer szerinti –Y irányban. A többi irányban az erő komponensei nulla értékűek. (6.57. ábra, piros színű, C jelű címke jelzi.)

Csuklós megtámasztás a konzol alsó részén: elmozdulás ellen biztosított, de elfordulást (minden tengely mentén) megengedő megfogás, mely egy pontra vonatkozik (Simply Supported) . (6.57. ábra, kék színű, A jelű címke jelzi.)

Görgős megtámasztás a konzol felső részén: globális X és Z irányú elmozdulás ellen biztosított, de az Y irányú elmozdulás és az elfordulás (minden tengely mentén) megengedett (Remote displacement) . (6.57. ábra, sárga színű, B jelű címke jelzi.)

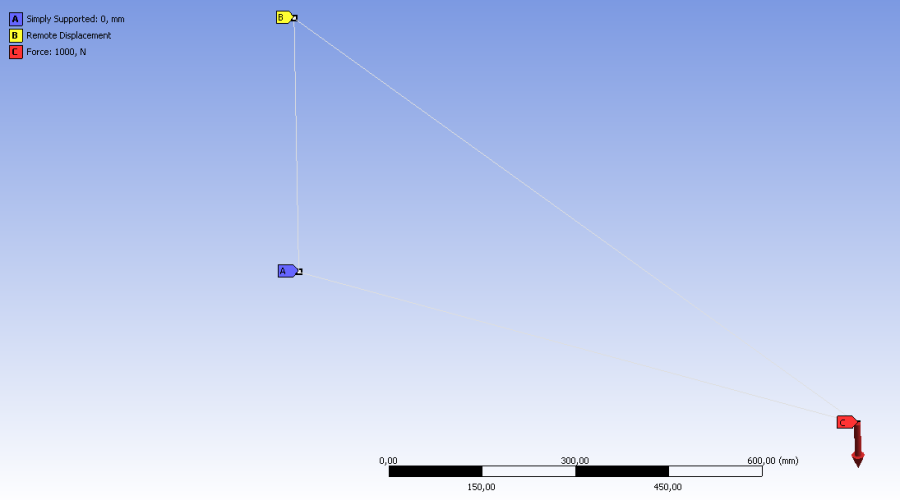
6.57. ábra - A terhelési modell

A szimuláció futtatása után kérdezzük le a számunkra fontos eredményeket. Jelen példánkban a következő jellemzőket célszerű lekérdezni:

Teljes deformáció (Total Deformation) , lásd 6.58. ábra
Teljes hajlító nyomaték (Total Bending Moment) , lásd 6.59. ábra
Axiális irányú erő (Axial Force) , lásd 6.60. ábra
Csavaró nyomaték (Torsional Moment) , lásd 6.61. ábra
Teljes nyíróerő (Total Shear Force) , lásd 6.62. ábra

Az alábbi ábrákon láthatóak az egyes eredmények.

6.58. ábra - Teljes deformáció a konzolon [mm]

6.59. ábra - Hajlító nyomaték a konzolon [Nmm]

6.60. ábra - Tengely irányú erő a konzolon [N]

6.61. ábra - Csavaró nyomaték a konzolon [Nmm]

6.62. ábra - Megoszló erő a konzolon [N]

6.4. Mechatronikai példa: CD fej tartó rugók

Az alábbi példán egy CD-fej tartó rugók analízisét végezzük el gerenda modell (rugó szálak) és testmodell (mozgó fej) alkalmazásával. A valós szerkezetben a fej egy lencserendszert tartalmazó egység, melynek a függőleges (Y) és egyik irányú vízszintes (X) elmordulását elektromágneses tekercsekkel és megfelelően lágy rugórendszerrel kell biztosítani. Ennek egyik szokásos megoldása a fej 4 db. vékony rugószálra való felfüggesztése. A rendszer csillapítását rendszerint a szálak rögzítésénél elhelyezett nagy viszkozitású anyag biztosítja, de a statikai szimuláció szempontjából ez elhagyható. Jelen analízis feladata a rugóelemek erő-elmozdulás karakterisztikájának megállapítása, vagyis, hogy a gerjesztőtekercsek által kifejtett erő hatására mennyi lesz a fej elmozdulása.

A feladat megoldásához, először hozzuk létre a geometriát az ANSYS Design Modellerében . Első lépésben célszerű a fejet jelképező testmodell vázlatát létrehozni egy, a globális koordinátarendszer XY síkjával párhuzamos munkasíkon. Így a későbbiekben a vázlaton szereplő téglalap négy sarokpontját felhasználhatjuk referenciaként a rugószálakat jelentő vonalmodellek létrehozásakor. Ehhez tehát hozzunk létre egy új síkot párhuzamosan a globális koordinátarendszer XY síkjával, és 10mm-el eltolva a +Z irányban (New Plane) . Az újonnan létrehozott síkra rajzoljunk egy az origóra szimmetrikusan elhelyezett téglalapot, 8x4mm-es méretekkel. Majd hajtsuk végre a kihúzást 8mm hosszon (6.63. ábra).

A következő lépésben hozzunk létre konstrukciós pontokat a vonalelemek túlsó végénél, a globális koordináta rendszer XY síkján. A pontok elhelyezésére használjuk a Create/Point parancsot, és a Details panelen adjuk meg a pontok koordinátáit: Point1(4,2,0); Point1(-4,2,0); Point1(-4,-2,0); Point1(4,-2,0).

Ezután páronként kössük össze a konstrukciós pontokat a testmodell a vázlatának négy sarokpontját a Concept/Lines From Points paranccsal.

A már tanult módon hozzuk létre a vonalmodellek 0,1mm átmérőjű kör keresztmetszetét a Concept/Cross Section/Circular paranccsal és rendeljük hozzá az egyes vonalmodellekhez (Line Body) .

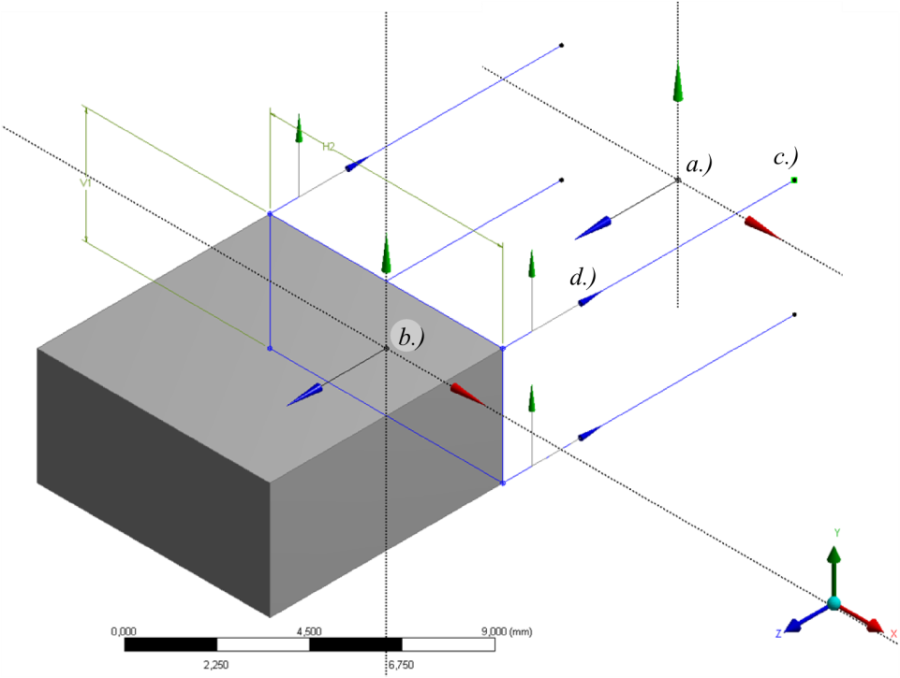
a.) Globális koordináta rendszer, b.) a testmodell vázlatának munkasíkja, d.) a vonalmodellek és a létrehozásukhoz használt c.) konstrukciós pontok

6.63. ábra - A CD-fej egyszerűsített geometriája.

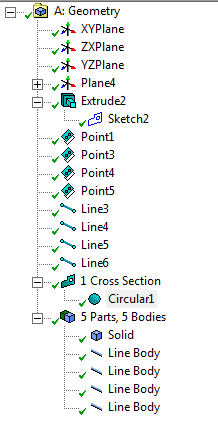
6.64. ábra - A modellfán szereplő elemek.

A fenti lépések elvégzése után a modellfa utolsó sora 5 elemet kell, hogy tartalmazzon, 1 testmodellt (Solid) és 4 vonalmodellt (Line Body), (6.64. ábra). Ha ez így jelenik meg, lépjünk ki a geometria modellezőből és szerkesszük az anyagmodelleket tartalmazó Engineering Data -t. Rendeljünk hozzá a szimulációnkhoz az ANSYS General Materials anyagkönyvtárából (jobb felső könyveket ábrázoló ikon bekapcsolásával), a Polyethylene, és a Cooper Alloy anyagokat. Ezután lépjünk át a szimulációs felületre és rendeljük hozzá az anyagmodelleket az egyes alkatrészekhez, Testmodell: Polyethylene, Vonalmodellek: Cooper Alloy.

Helyezzük el a megtámasztásokat (Fix Support) a vonalelemek szabad végeire és az –Y irányú 0,2N nagyságú erőterhelést (Force) a testmodell teljes térfogatára.

Mivel több testből áll a modellünk létre kell hozni a testmodell és a vonalmodellek közötti kapcsolatot. Ehhez a modellfa Connections pontjára való jobbgombos kattintással adjunk hozzá a modellhez 4 db. ponthegesztés nevű kapcsolatot (Outline/…/Connections(JG)/Insert/Spot Weld) , és mindegyiknél jelöljük ki a Details panelen a megfelelő pontpárokat. Az egymást elfedő elemek kijelölésénél segítséget jelent a modelltér bal alsó sarkában megjelenő lapok, a különböző alkatrészek színével. A lapokra való kattintással választhatjuk ki, hogy egy helyen lévő pontok közül, melyik legyen kijelölve.

Ezután futtassuk a szimulációt és kérdezzük le az alábbi eredményeket (6.65. ábra):

A fej Y irányú deformációja (Directional Deformation) ,
A teljes modell Y irányú deformációja (Directional Deformation) ,
A rúdban ébredő kombinált feszültség maximuma (Maximum Combined Stress) ,
A rúdban ébredő rúdirányú feszültség (Direct Stress) .

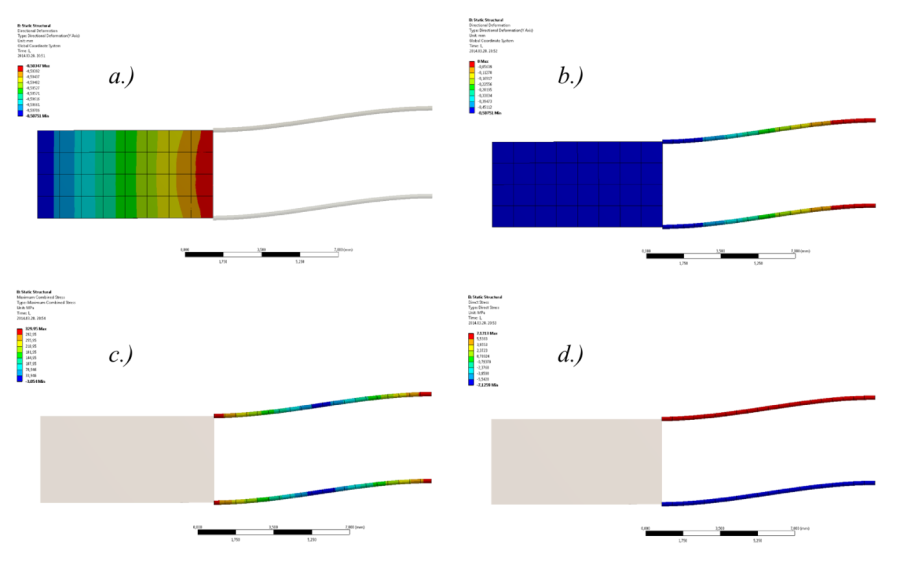
a.) a fej és, b.) a teljes modell Y irányú deformációja, c.) a rúdban ébredő kombinált feszültség maximuma, és d.) a rúdban ébredő rúdirányú feszültség

6.65. ábra - A CD-fej vizsgálatának eredményei.

6.5. Ellenőrző feladatok

6.5.1. Feladat

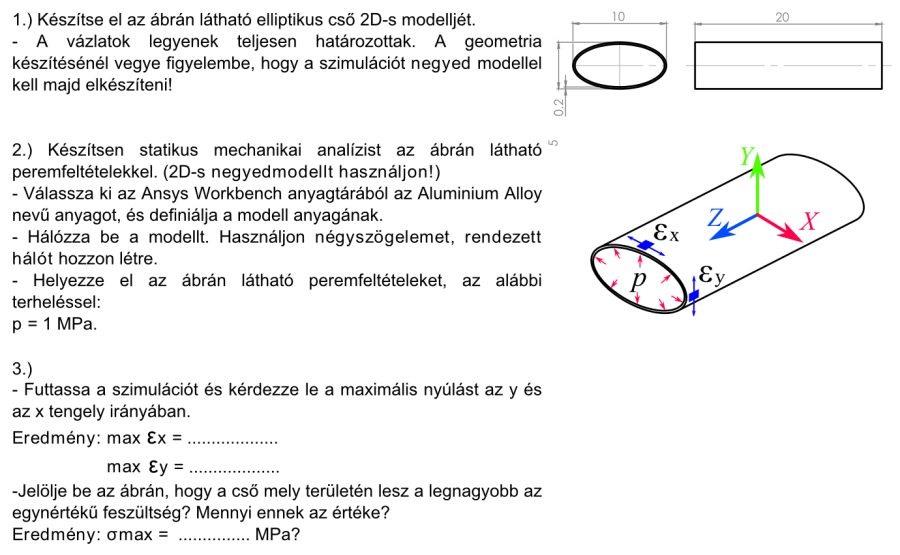
6.5.2. Feladat

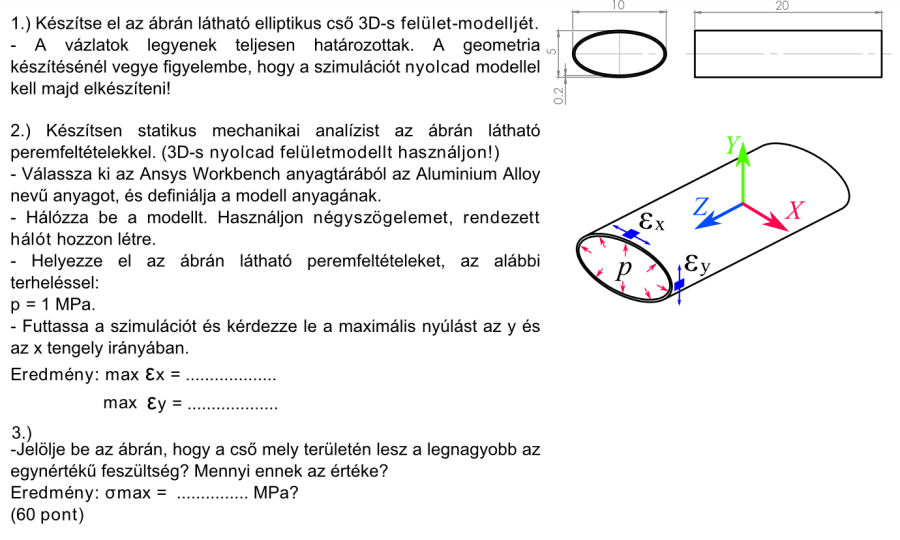
7. fejezet - Több alkatrészes, statikai analízis

Tartalom

7.1. A kontaktok csoportosítása

7.2. Példa - kontaktfeladat az alkatrészek közötti alapvető kapcsolat típusok bemutatására

7.2.1. Súrlódásos kapcsolat (Frictional)
7.2.2. Súrlódásmentes kapcsolat (Frictionless)
7.2.3. Elválás nélküli kapcsolat (No separation)
7.2.4. Végtelen súrlódású kapcsolat (Rough)
7.2.5. Ragasztott-hegesztett típusú kapcsolat (Bonded)
7.2.6. Eredmények

7.3. Példa - Érintkezési feszültség és benyomódás

7.3.1. Analitikus megoldás
7.3.2. Numerikus megoldás
7.3.3. Összefoglalás

Az összeállítások, vagyis a több alkatrészes modellek analízisénél az un. kontaktok testesítik az egyes alkatrészek közötti kapcsolatokat, vagyis a csomóponti elmozdulások és erők átadását az alkatrészek kapcsolódó felületein keresztül. Mivel így az egyes alkatrészek terhelési és peremfeltételét a kontaktok adják, nagy jelenetősséggel bírnak az analízis eredményét illetően. A valós fizikai kontaktok bonyolult viselkedésének leírására számos modellt dolgoztak ki, de a jegyzetünk csak a valóságot lényegesen leegyszerűsítő, a végeselemes programokban beépített megoldások bemutatására szorítkozik. Az alábbiakban nézzük meg a statikai analízisben használatos kontaktok csoportosítását.

7.1. A kontaktok csoportosítása

Az alap kontaktokat könnyen átláthatjuk, ha a szerint csoportosítjuk őket, hogy a két kapcsolódó alkatrész a kapcsolódó felületre (vagy élre) merőlegesen (normális irányban), és azzal párhuzamos, vagy érintő (tangenciális) irányban milyen elmozdulásokat tehet. Az előbbi jelentése, hogy a két kapcsolódó elem el tud-e távolodni, esetleg egymásba hatolni, vagy az érintkező elemek mindig egy felületbe (vonalba) esnek. A felülettel párhuzamos, vagy tangenciális elmozdulást gyakorlatilag a súrlódási tényezővel definiálhatjuk. Ez alapján a következő csoportokba sorolhatjuk az idealizált kontaktokat:

7.1. táblázat - A kontaktok csoportosítása a normális és tangenciális irányú viselkedésük alapján.

	Az érintkező felületek
A súrlódási tényező:	eltávolodhatnak egymástól	nem távolodhatnak el egymástól
µ=0	Ideális súrlódásmentes	Elválás nélküli kapcsolat
0<µ<∞	Súrlódásos	-
µ=∞	Ideálisan érdes, tapadó	Ragasztott

Súrlódásos (Frictional) – a valós fizikai kapcsolatot a legjobban modellező kontakt. A felületek eltávolodhatnak és a súrlódási erő ellenében elcsúszhatnak egymáson. A két geometria között idealizált súrlódásos kapcsolat van, ekkor definiálni kell a súrlódási tényezőt. Ebben az esetben a két felület/él között tapadás van, mely a súrlódási tényezőből adódó feszültséget elérve megszűnik és a két felület/él egymáson elcsúszik, eközben azonban súrlódási veszteség lép fel.
Súrlódásmentes (Frictionless) – Idealizált csúszó kontakt. A kacsolódó felületek/élek egymáson súrlódás nélkül, akadálymentesen (tehát veszteség nélkül) elcsúszhatnak egymáson és eltávolodhatnak egymástól. Ilyen kontakt alkalmazása esetén különös figyelmet kell fordítanunk a megfogások és terhelések definiálásánál, hogy ne jöjjön létre olyan eset, amikor a súrlódásmentes elcsúszás végtelen elmozdulást eredményezhet.
Elválás nélküli kapcsolat (No-separation) – A súrlódásmentes speciális esete, amikor a felületek/élek akadálymentesen elcsúszhatnak egymáson, de nem eltávolodhatnak el egymástól.
Tapadó (Rough) – Idealizált csúszásmentes kontakt. A súrlódási tényező végtelennek tekinthető, tehát a felületek nem csúszhatnak el egymáson, de a kontaktfelületre merőleges irányban eltávolodhatnak egymástól, (pl. egy dörzshajtás modellezése).
Ragasztott (Bonded) – minden szabadságot megkötő, a kapcsolódó felületeket egymáshoz fixen rögzítő kontakt. A súrlódási tényező végtelennek tekinthető, de a két felültet egymástól nem tud elmozdulni semmilyen irányba. Ezt nevezhetjük ragasztott, vagy hegesztett kontaktnak is. Használhatjuk abban az esetben is, mikor a két geometria külön modellezésének csak az az oka, hogy más anyagminőséggel rendelkezik, és ezt szükséges volt definiálni. Több esetben, mikor több alkatrészből álló geometriákat modellezünk és a kontaktok milyensége elhanyagolhatóan befolyásolja a szimuláció végeredményét, akkor pl. a csavarkötések helyett is lehetséges csupán ragasztott kontaktot használni. Természetesen az ilyen esetekben körültekintően meg kell vizsgálni, hogy valóban nem befolyásolja-e ez az egyszerűsítés a végeredményt.

A legtöbb véges elemes szoftver a kapcsolódó felületeket automatikusan felismeri, de általában mód van a kontaktok kézi definiálására is. Ez utóbbi esetnek akkor van kiemelt jelentősége, amikor az alkatrészek egymáshoz képesti elmozdulása viszonylag nagy, és olyan felületek is kontakt kapcsolatba kerülnek a szimuláció közben, amelyek az elején még egymástól távolabb helyezkednek el. Ilyenkor a későbbi helyzetet ismeretében mindenképp érdemes az összes szimuláció során érintkező felület közötti kontakt beállítása már a szimuláció előtt. (Természetesen, ha nem látható előre a terhelés hatására fellépő geometriai helyzet, akkor egy előzetes szimuláció után is finomíthatóak a beállítások.)

7.2. Példa - kontaktfeladat az alkatrészek közötti alapvető kapcsolat típusok bemutatására

Az alábbi példában egy egyszerű geometrián fogjuk bemutatni az alkatrészek közti kapcsolatok típusait. A két alkatrészből álló összeállítás és a terhelési és anyagmodellek minden esetben ugyanolyanok, így egyedül a két alkatrész közötti fizikai kapcsolat lesz más és más. Annak érdekében, hogy az eredmény látványosabb legyen két egymástól eléggé eltérő anyagot definiálunk az alkatrészek anyagának. A modell egy hosszú, az egyik végén befogott szerkezeti acél konzolból és egy rajta lévő lekerekített szélű polietilén téglatestből áll.

Kiinduló adatok.

A konzol méretei:

Hossz (X irányban): 50mm,

Vastagság (Y): 2mm,

Szélesség (Z – a szimulációnál kell megadni): 10mm,

A konzolon lévő test méretei:

10mm élhosszúságú kocka (a 2D-s modellben négyzet),

Saroklekerekítés sugara 2mm,

Konzol anyaga: Structural Steel,

A lévő lekerekített szélű négyzet anyaga: Polyethilene.

A feladatot 2D-s analízissel oldjuk meg, a geometriát tehát az ANSYS Design Modeller moduljában az XY síkra kell rajzolni, és a projektfelületen a geometria tulajdonságai között, a geometria típusát 2D-re kell átállítani az analízis hozzácsatolása előtt. A geometria elkészítésénél ügyeljünk arra, hogy a két alkatrész külön vázlattal legyen létrehozva. A második alkatrész vázlatának rajzolásakor a téglalap parancs kiadásakor bejelölhetjük az automatikus lekerekítés opciót (Draw/Rectangle/Auto-Fillet) , így később ezzel nem kell külön foglalkoznunk. A második felület létrehozásakor (Concept/Surfces From Sketches) , a „fagyasztott hozzáadása” művelet (Details/Operation/Add Frozen) legyen kiválasztva. Ennek hatására a két felület, mint két különálló alkatrész szerepel majd a modellfa utolsó sorában. Tehát így hozhatunk létre összeállításokat a Design Modeller –ben, (7.1. ábra).

Megjegyzés: Kontakt feladatok esetén fontos lehet az alkatrészeken található lekerekítés is, így ilyen feladatok esetén nem szabad a geometria egyszerűsítésekor a kontakt szempontjából releváns lekerekítéseket mellőzni.

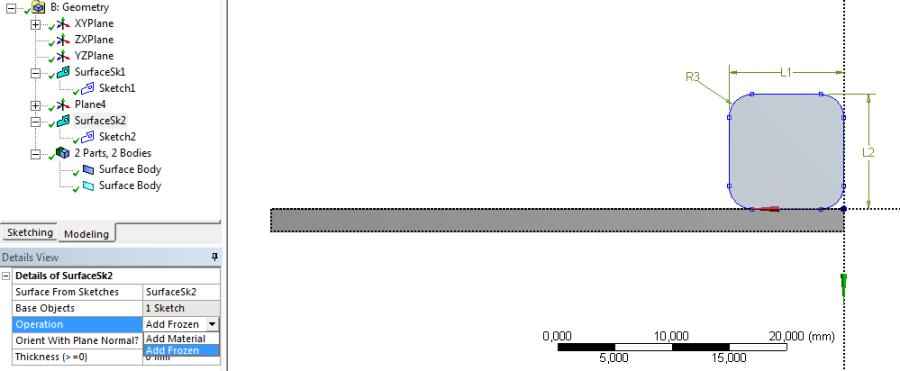
7.1. ábra - 2D-s Geometria.

A geometria elkészítése után lépjünk át az anyagkönyvtárat tartalmazó Engineering Data felületre és rendeljük hozzá az analízisünkhöz a fentebb definiált anyagmodelleket. Majd átlépve a szimulációs környezetbe rendeljük hozzá őket a megfelelő geometriához.

A hálózáskor 1mm-es elemméretet használva végezzük el, így a teljes modell 219 véges elemet tartalmaz. A hálózott modellt a következő 7.2. ábra szemlélteti.

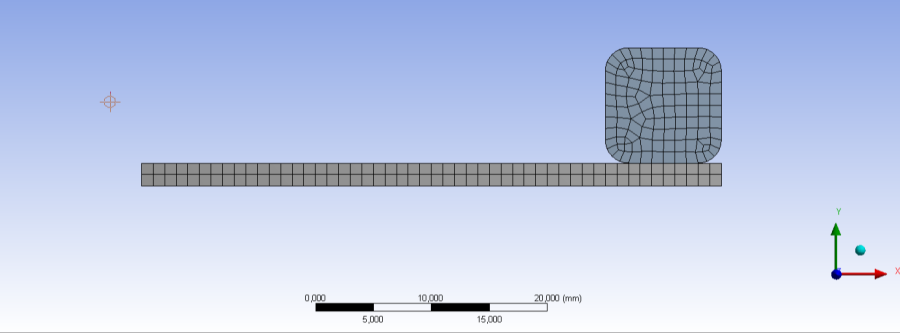
7.2. ábra - Kontakt feladat - hálózott modell.

A pontos összehasonlíthatóság miatt a konzol fix megfogása (Fix Support) a rajta lévő testre elmozdulás típusú terhelés kerül (Displacement) . Ezen terhelés nagysága irányonként definiálva: X irányban -2mm és Y irányban -3mm nagyságú. A terhelési modell az alábbi ábrán látható. Az ábrán kék jelzéssel a fix megfogás helye, míg piros jelzéssel az elmozdulás típusú terhelés helye és iránya látható (7.3. ábra).

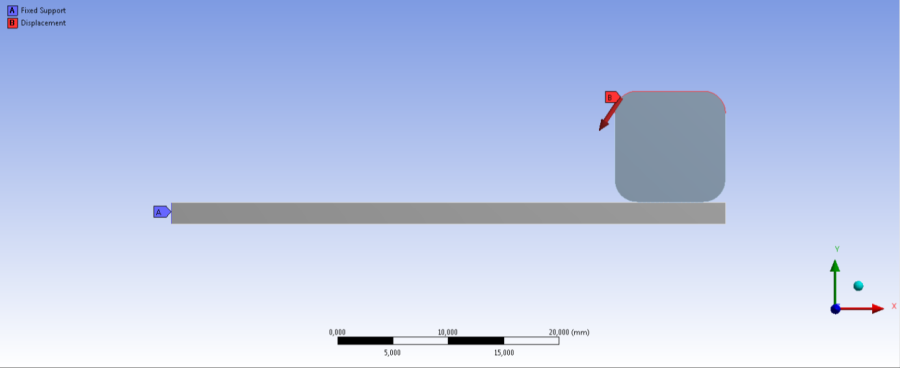
7.3. ábra - Kontakt feladat, terhelési modell.

A fenti beállítások után hozzuk létre a két alkatrész megfelelő felületei között lévő kontaktot az Add Manual Contact Region parancs alkalmazásával. Majd válaszuk ki a kapcsolatban résztvevő, a Details panelen jelzett, Contact és Target éleket (7.5. ábra). Az alábbi ábrán kék illetve piros vonallal van jelölve az érintkező felületeket jelentő kontúrvonal (7.4. ábra). Fontos, hogy a lekerekítéseket is vegyük bele a kontakt hatókörébe, mivel azok az alkatrészek deformációjakor érintkezésbe léphetnek a konzol felső élével.

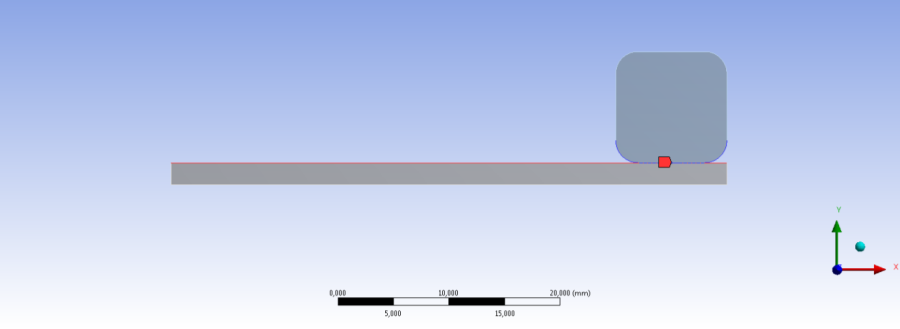
7.4. ábra - Konzolos kontakt feladat geometriája a kijelölt kapcsolódó élekkel.

A modellfában megjelenő kontaktot kijelölve, a Details panelen tudjuk átállítani a kontakt típusát (alapértelmezettként Bonded ), és egyéb tulajdonságát (7.5. ábra). A következőkben végezzük el az alábbi beállításokat és futtassuk a szimulációt mindegyik kontakt típussal, majd hasonlítsuk össze az alkatrészek viselkedését.

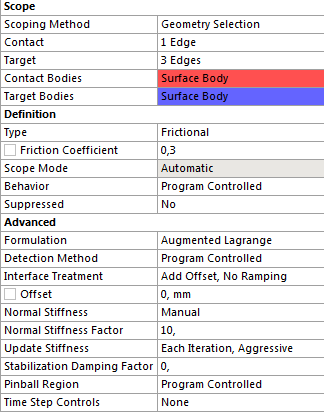
7.5. ábra - Súrlódásos kapcsolat beállításának részletei.

7.2.1. Súrlódásos kapcsolat (Frictional)

A legáltalánosabban használt kapcsolat típus a súrlódásos kapcsolat (Details/Definition/Type: Frictional) . Mivel ez áll a legközelebb az érintkező felület valós viselkedéséhez, ez a leggyakrabban használt kapcsolat-típus a több alkatrészből álló szerkezetek viselkedésének modellezésénél.

A súrlódási tényezőt (Friction Coefficient) 0,3-ra állítjuk (ez megfelel az acél és a polietilén közötti átlagos súrlódási tényezőnek).

A beállításoknál még fontos a szoftver által használt számítási formula kiválasztása, a pontosabb eredmény érdekében súrlódásos kapcsolatnál célszerű a kiterjesztett Lagrange típusú (Augmented Lagrange) számítási formulát választani, valamint a merevségi mátrix újraszámítását (Update Stiffness) minden iteráció után (Each Iteration, Agressive) . Előfordulhat, hogy a kontaktfelületek elemei közötti rugómerevséget (Normal Stiffness) is definiálni kell. Jelen példánkban ezt a merevségi értéket (Normal Stiffness Facor) 10-re választjuk. Az összes, súrlódásos kapcsolatkor használt beállítást tartalmazza a 7.5. ábra.

7.2.2. Súrlódásmentes kapcsolat (Frictionless)

Súrlódásmentes kapcsolatnál a súrlódási tényező nulla, melyre külön típus van definiálva a kontakt típusok között (Details/Definition/Type: Frictionless) . Az összes többi beállítás megegyezik a súrlódásos kapcsolatnál használt beállításokkal. Végezzük el a beállításokat és futtassuk a szimulációt.

7.2.3. Elválás nélküli kapcsolat (No separation)

Ebben az esetben a két alkatrész kontakt felülete között a súrlódási tényező nulla, azonban a két alkatrész a kontakt felületeinél nem válhat szét. Az összes többi szimulációs beállítás megegyezik az első két típusú kontaktnál használttal. Végezzük el a beállításokat és futtassuk a szimulációt.

7.2.4. Végtelen súrlódású kapcsolat (Rough)

Ebben az esetben a két alkatrész közti kontakt felületek közti súrlódási tényező végtelen, azonban a két alkatrész normál irányban elmozdulhat egymáshoz képest. Ebben a példában az előzőekhez képest annyi a különbség, hogy kiterjesztett Lagrange formula helyett Normál Lagrange formulát használjunk. Ebben az esetben nem történik meg a két alkatrész között egymásba nyomódás. Végezzük el a beállításokat és futtassuk a szimulációt.

7.2.5. Ragasztott-hegesztett típusú kapcsolat (Bonded)

Ebben az esetben a súrlódási tényező a két alkatrész mereven kapcsolódik egymáshoz. A beállításoknál ebben a példában annyiban tértünk el a súrlódásos kapcsolathoz képest, hogy a két alkatrész közti normál merevséget nem definiálunk. (Mivel itt a két alkatrész nem fog egymáshoz képest elmozdulni, így egyszerűbb ezt a szoftver által konrollált értéken hagyni a számítási idő csökkentése végett.)

7.2.6. Eredmények

Az ötféle kontakttípus viselkedésének jellegzetességeit, első lépésben vizsgáljuk meg a teljes deformáció (Total Deformation) , és az elmozdulás kényszeren eső reakcióerő (Force Reaction) lekérdezésével. A csúszás folyamatának vizsgálatakor, a felhasználói felület alján lévő Graph fülön grafikusan (és mellette táblázatos formában is) nyomon követhetjük a reakcióerő (Force reaction) komponenseinek változását az elmozdulás (idő) függvényében.

A kontaktfelületeken végbemenő folyamatok vizsgálatára a Contact Tools eszköz szolgál, melynek segítségével az alábbi eredményeket lehet lekérdezni:

Kontakt állapot (Status) – megadja, hogy a két felület milyen kapcsolatban áll egymással:
- távol van (Far), – kék színnel jelölve,
- közel van (Near), – sárga színnel jelölve,
- csúszik (Sliding), – narancs színnel jelölve,
- tapad (Sticking), – piros színnel jelölve.
Rés (Gap) - a két alkatrész közötti rés mértékét adja meg. (A piros részeken nulla a rés mértéke, míg a kék szín felé negatív értelmű rés található.)
Egymásba nyomódás (Penetration) – a két alkatrész kapcsolódó felületének (elemeinek) egymásba hatolását adja meg. (Kék színnel a nulla értékű részek, míg piros szín felé közeledve egyre nagyobb, pozitív értelmű egymásba nyomódás figyelhető meg.)
Csúszási távolság (Sliding Distance) – a két kapcsolódó felület egymáson való tangenciális irányú relatív elmozdulásának, vagyis elcsúsznak mértékét adja meg.
Kontakt nyomás (Pressure) – az érintkezési felületeken eső, a felületekre merőleges irányú normál feszültség, vagyis palástnyomás értékét adja meg.
Súrlódási feszültség (Frictional Stress) – az érintkezési felületeken eső, a felületekkel párhuzamos tangenciális, vagyis csúsztató feszültség értékét adja meg.

Az eredményeket a könnyebb átláthatóság érdekében táblázatos formában összegeztük (7.6. ábra).

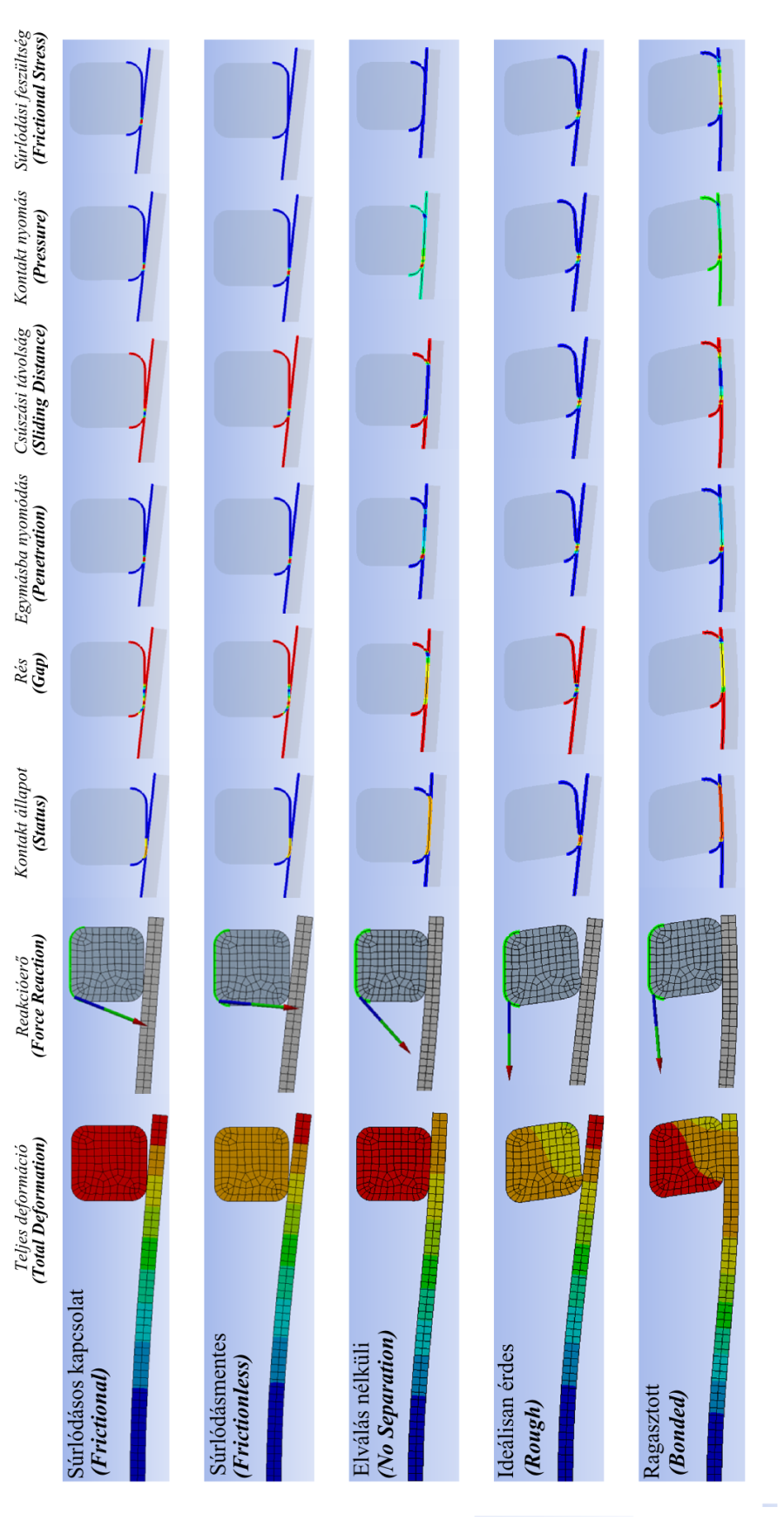
7.6. ábra - A kontaktvizsgálat eredményei.

7.3. Példa - Érintkezési feszültség és benyomódás

Az alábbi példában egy acélgolyó és egy alumínium sík lap érintkezésénél fellépő feszültséget és alakváltozást vizsgáljuk meg. A golyót a síkra merőleges irányú F erő nyomja a sík laphoz.

Kiinduló adatok:

A golyó sugara: R = 10 mm,

A terhelőerő: F = 100 N,

A sík felületű test anyaga – acél: Rugalmassági modulus: E₁ = 200 GPa, Poisson tényező: ν₁ = 0,30,

A golyó anyaga – alumínium: Rugalmassági modulus: E₂ = 71 GPa, Poisson tényező: ν₂ = 0,33.

7.3.1. Analitikus megoldás

A két érintkező test érintkezési helyén ébredő feszültséget és deformációt számoljuk ki Hertz módszerével [25.] . Kiindulásnak adva van egy végtelen félsík és a vele érintkező R sugarú gömb melyet a sík felületre merőleges F erő terhel. Feltételezzük, hogy a testek anyaga homogén, izotróp és érvényes rájuk a Hooke törvény, valamint a testek között súrlódásmentes kapcsolatot tételezünk fel.

Határozzuk meg az érintkezés helyén ébredő maximális palástnyomás és a két test közeledésének mértékét.

Gömb és sík érintkezésénél a maximális palástnyomás értéke:

(7.1)

A két test közeledésének mértéke

(7.2)

A benyomódott, (érintkező) felület sugara

(7.3)

ahol:

(7.4)

ν – az adott anyag Poisson-tényezője,

E – az adott anyag rugalmassági modulusa.

A számolás eredményei:

	Maximális palástnyomás:	p _max =871,4MPa
	A két test közeledése:	δ=0,00548mm
	A érintkező felület sugara:	a=0,23409mm

7.3.2. Numerikus megoldás

A fenti problémát ANSYS Workbench-ben, 2D-s Tengelyszimmetrikus feladatként oldjuk meg, mivel mind a geometria, mind pedig a terhelési és peremfeltételek tengelyszimmetrikusak. Ennek előfeltétele, hogy a projektfelületen (a tulajdonságok panelen) átváltsuk a geometria típusát 2D-re, és a rajzolás során az XY sík +X térfelén dolgozzunk. Készítsük el az ábrán látható geometriát, úgy, hogy a golyónak csak a „jobb” alsó (R=10mm) negyedét rajzoljuk meg. A függőleges felezés a tengelyszimmetria miatt szükséges, a vízszintes tengely menti kettévágást pedig azért tehetjük meg, mert a felső rész már nem fog érdemi hatást gyakorolni az érintkezési pontban ébredő feszültségi állapotra, és alakváltozásokra. Érdemes úgy létrehozni a vázlatot, hogy az érintkezési pont a koordinátarendszer origójába essen. Az alsó síkfelület modellezésére egy 10x10mm-es négyzetet használunk (7.7. ábra).

A geometria megrajzolása után adjuk hozzá az anyagkönyvtárunkhoz (Engineering Data) az alumínium ötvözet (Aluminium Alloy) és a szerkezeti acél (Structural Steel) anyagmodelleket, majd átlépve a szimulációs felületre, rendeljük hozzá őket a megfelelő alkatrészekhez.

A modellfában a geometriát kiválasztva, állítsuk át az analízis típusát tengelyszimmetrikusra (Outline/…/Geometry => Details /Definition/2D Behavior: /Axisymmetric) .

A terhelések és peremfeltételek megadásánál definiáljunk a golyó felső sík felületére egy (lefelé ható), –Y irányú 100N nagyságú erőt a komponenseivel megadva (Loads/Force) . A négyzet alsó élén lévő fix megtámasztás (Fix Support) már kellő mértékben meghatározza a szerkezetünk viselkedését, ugyanis a szimmetriatengelyre ható kényszer automatikusan érvényesül (7.7. ábra, a.). Viszont, mint majd később látni fogjuk, némiképp befolyásolja az eredményeket, ha manuálisan is hozzárendeljük a forgástengely oldalirányú elmozdulását megkötő kényszert (Frictionless Support) , (7.7. ábra, a.).

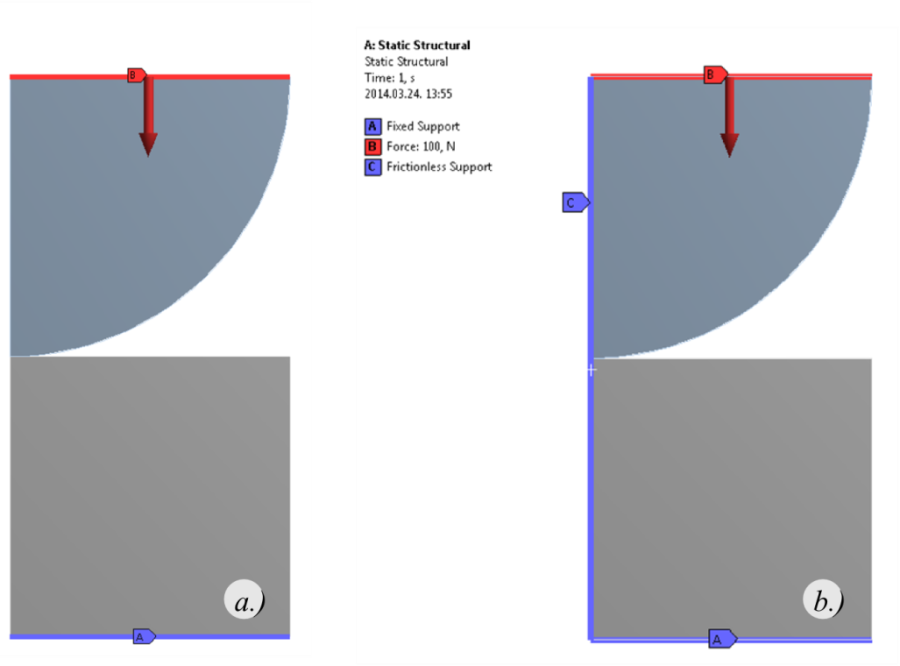
7.7. ábra - Peremfeltételek és erőterhelés.

Következő lépésben hozzuk létre a két alkatrész közötti kapcsolatot. Beállítástól függ, hogy a geometria importálásakor automatikusan felismeri-e az egymáshoz közel lévő felületeket/éleket, vagy manuálisan kell megadni azokat. Ha automatikus kontakt definíció történt akkor csak a beállításokat kell megváltoztatni (ugyanis az alapértelmezetten, mindig ragasztott, vagyis Bonded kontaktot rendel hozzá a program). Ha nem jött létre a kontakt automatikusan, akkor az Add Manual Contact Region parancsal megtehetjük. Az érintkező élek kijelölése után állítsuk át a kontakt típusát súrlódásmentesre (Details/Definition/Type:Frictionless) . Az összehasonlíthatóság kedvéért nem használunk súrlódásos kapcsolatot, ugyanis az analitikus összefüggések súrlódásmentes érintkezést feltételeznek. Használjuk a 7.8. ábra beállításait.

Megjegyzés: Ha az érintkező éleket nem egy folytonos vonallal rajzoljuk meg, hanem két folytatólagosan elhelyezett, és a megfelelő kényszerekkel ellátott vonalszakaszból, akkor lehetőség van az él lokális kijelölésére. Így nem vesznek részt a kontaktban olyan területek, amelyek biztosan nem fognak érintkezésbe lépni a szimuláció során (7.8. ábra).

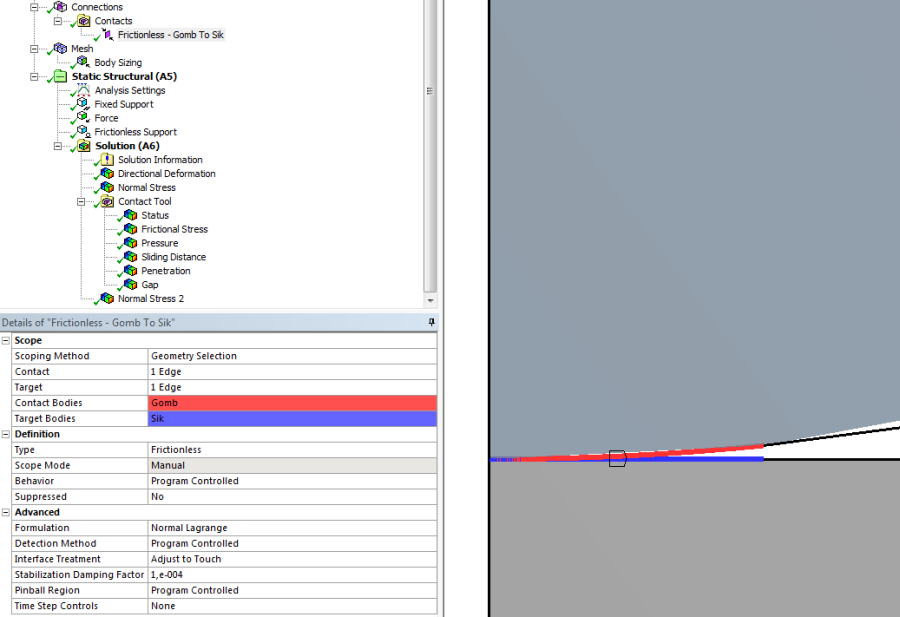
7.8. ábra - Kontaktbeállítások.

Mivel egy nemlineáris kontaktról van szó, a konvergencia elősegítése érdekében, érdemes csökkenteni az időlépéseket (Outline/…/Analisis Settings => Details/Step Controls) . Ezért végezzük el az alábbi beállításokat:

Details/Step Controls:

Auto Time Stepping: On,

Defined By: Substeps,

Initial Substeps: 10,

Minimum Substeps: 10,

Maximum Substeps: 1000.

Details/Solver Control: Large Deflection: On.

A hálózás globális beállításánál alkalmazzuk a fix méretfunkciót (Details/Sizing/Use Advanced Size Funktion: „On:Fixed”) , amellyel többek között megadhatjuk az elemek minimális (Min size: 0,01mm), maximális (Max Face Size: 2mm) méretét, és a növekmény (Growth Rate: 1,05) értékét (7.9. ábra).

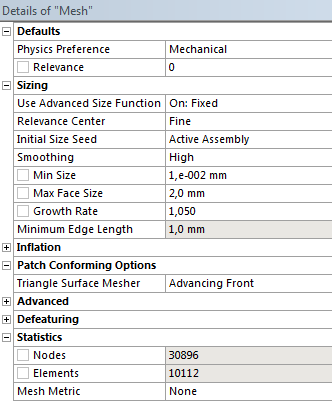
7.9. ábra - Globális hálóbeállítások.

Az érintkezés helyén történő hálósűrítést egy Sizing parancs hozzáadásával érhetünk el, melynek hatókörét a teljes modellre kivetjük (Details/Geometry: 2 Bodies) , típusát Sphere of Influence -re állítjuk, melynek középpontjául a globális koordinátarendszert választjuk. A gömb sugarát (Sphere Radius) 0,5mm-re, a gömbön belül elhelyezkedő elemek méretét (Element Size) pedig 0,01mm-re választjuk (7.10. ábra).

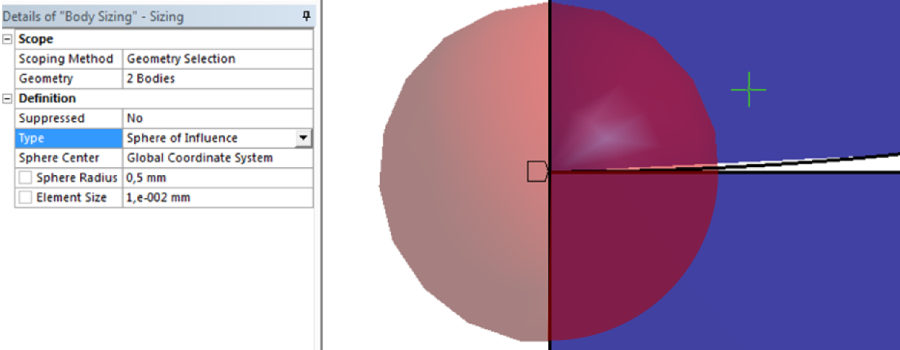
7.10. ábra - Lokális hálósűrítés beállítása az érintkezés helyén.

Az analízist elvégezhetjük a lokális hálósűrítés elemméretének változtatásával (7.11. ábra), hogy megfigyeljük az elemméret eredményre gyakorolt hatását (7.15. ábra).

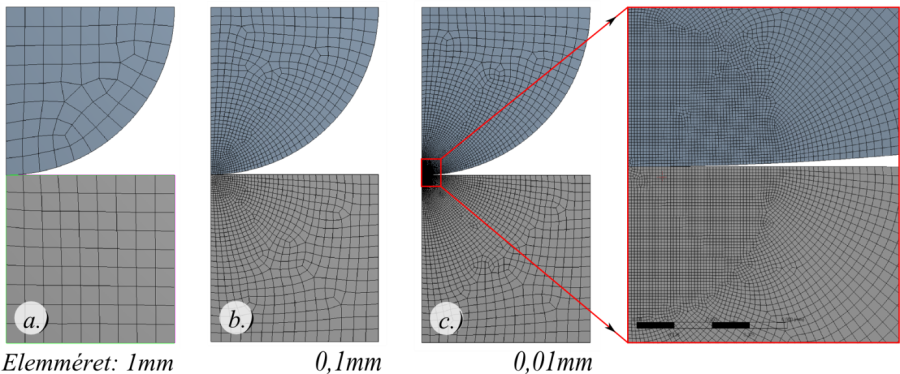
7.11. ábra - Különböző mértékű lokális hálófinomítás.

A háló beállítása után futtassuk a szimulációt, és kérdezzük le az Y irányú deformáció (Directional Deformation) , (7.12. ábra, b.), és normálfeszültség (Normal Stress) , (7.12. ábra, b.) értékét a teljes modellre, valamint az Y tengely mentén futó 2mm hosszú konstrukciós vonalra (Path) , (7.13. ábra).

7.12. ábra - Az analízis eredménye: a.) Y irányú elmozdulás, b.) Y irányú normálfeszültség.

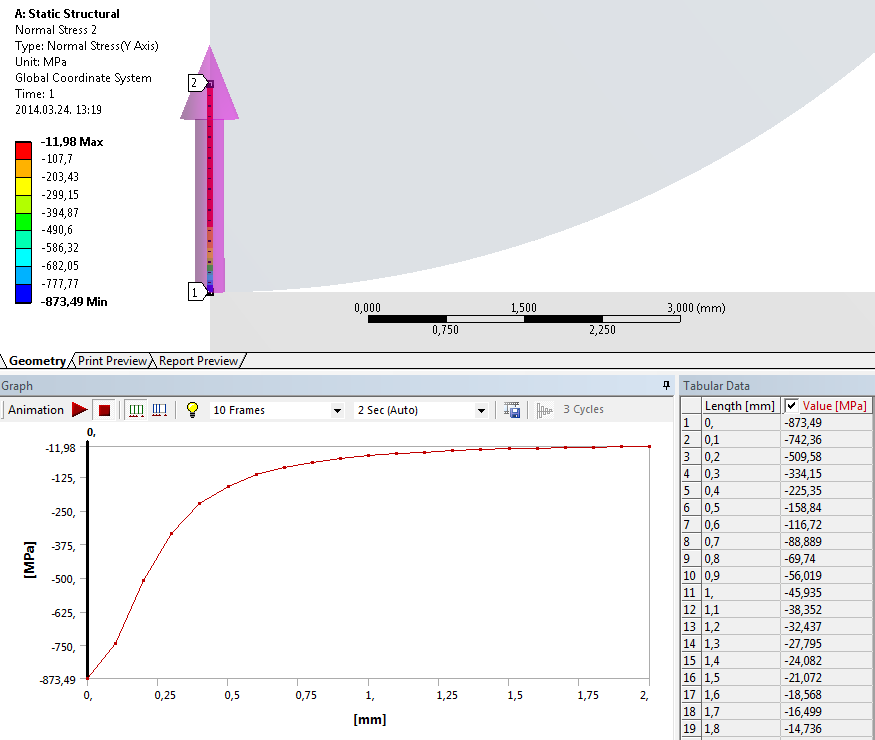
7.13. ábra - Az Y irányú normál feszültség értékének vonal menti lekérdezése.

Megjegyzés: Egy (a tengelyszimmetrikus analízisnél elvileg szükségtelen), a tengelyt oldalirányban megkötő Frictionless kényszer hozzáadásával a Normal Lagrange eljárással számolt kontaktnyomás (Contct Tool/Pressure) értéke 873,42MPa, ami 0,23%-os eltérést eredményezett az elméleti értékhez képest. A tengelyt megkötő Frictionless kényszer nélkül a Normal Lagrange kontaktnyomás (Contct Tool/Pressure) értéke teljesen fals értéket ad, az Augmented Lagrange és a Pure Penalty pedig 849 MPa-t, ami egy nagyságrenddel nagyobb (2,5%-os) hiba az előzőhöz képest, de még így is elfogadhatónak számít.

7.3.3. Összefoglalás

A numerikus analízis és az analitikus számolás eredményeit az alábbi ábrákon foglaljuk össze.

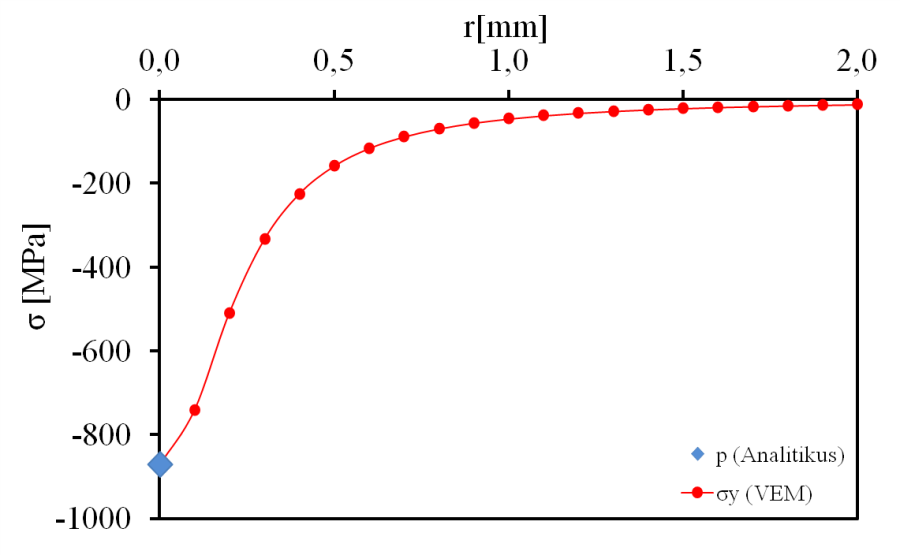
Az Y irányú normál feszültség értéke a kontaktfelülettől való távolság (r) függvényében, és az analitikus számolásból származó kontaktnyomás összehasonlítása.

a.) Az érintkezési pontban lekérdezett Y irányú normál feszültség és a kontaktnyomás értéke. b.) A két test közeledésének (benyomódás) mértéke, és a számítási idő az elemméret függvényében.

7.14. ábra - Az Y irányú normál feszültség értéke a kontaktfelülettől való távolság (r) függvényében, és az analitikus számolásból származó kontaktnyomás összehasonlítása.

Az analízis különböző elemmérettel történő futtatásának eredményeiből látható, hogy megfelelő kontaktbeállítás és hálófinomítás mellett az elméleti és a numerikus eredmény jó egyezést mutatnak.

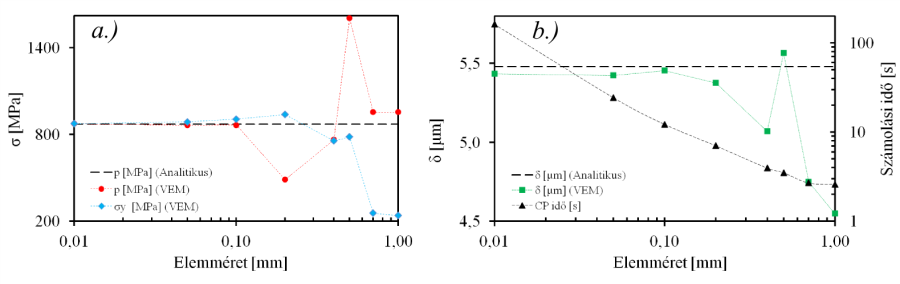
7.15. ábra - Az elemméret hatása az érintkezési feszültségre és benyomódás mértékére.

7.2. táblázat - A végeselemes és az analitikus megoldás eredményeinek összehasonlítása, különböző elemméret mellett.

Elemméret [mm]	δ [μm]	p [MPa]	σ _y [MPa]	CP idő [s]	Elemszám
0,01	5,43	873,4	873,5	160,7	10112
0,05	5,42	863,8	886,0	24,2	2486
0,10	5,45	864,2	905,9	12,2	1490
0,20	5,37	486,0	937,5	7,0	809
0,40	5,07	763,2	755,1	3,9	383
0,50	5,57	1602,9	783,3	3,5	314
0,70	4,75	954,9	254,1	2,7	194
1,00	4,55	954,8	238,8	2,6	151
Analitikus:	5,48	871,4	871,4	-	-

8. fejezet - Kihajlás vizsgálat

Tartalom

8.1. Áttekintés
8.2. Kihajlás vizsgálat VEM példa
8.3. Analitikus megoldás

8.1. Áttekintés

Az alábbiakban az ANSYS Workbench végeselem programban elvégezhető lineáris kihajlás vizsgálatot mutatjuk be. A lineáris kihajlás vizsgálat (Linear Buckling Analysis) , (vagy más néven sajátérték kihajlás (Eigenvalue Buckling) ), egy ideálisan rugalmas szerkezet elméleti kihajlási merevségét határozza meg, (pl. egy rugalmas oszlop kihajlásának Euler féle megoldását adja meg.). Bár a valóságban az anyagszerkezet hibái és nemlinearitásai megakadályozzák, hogy a szerkezet elérje az elméleti kihajlási merevségét, mégis hasznos lehet az (nem konzervatív) eredmény gyors becslésére. Az instabilitás előrejelzésére sokkal pontosabb megoldást ad a nemlineáris kihajlás vizsgálat, amely magában foglal egy statikai analízist, bekapcsolt „nagy lehajlások” (Large Deflection) effektussal. Ebben a vizsgálatban fokozatosan növekedő terhelést használunk az instabillá válás terhelési szintjének megtalálásához. Nemlineáris technika alkalmazásakor lehetőségünk van kezdeti tökéletlenségek, plasztikus viselkedés, hézagok, nagy lehajlások alkalmazására a modellben.

Anyagmodellek.
Az anyagmodell csak lineáris lehet, továbbá izotróp, vagy ortotróp, állandó, vagy hőmérsékletfüggő. Az anyag nemlineáris tulajdonságai figyelmen kívül maradnak. Meg kell adnunk az anyag merevségét (pl.: rugalmassági modulus és Poisson-tényező).
Alkatrész viselkedés, Kontaktok, Hálózás.
A statikai szimulációnál leírtak vonatkoznak rá.
A szimuláció beállításai.
Meg kell adni a módusok számát, (általában az 1., vagyis a legalacsonyabb az érdekes).
Kezdeti és Peremfeltételek / Terhelések
A lineáris kihajlás vizsgálatot egy statikai analízisnek kell megelőznie, ami a lineáris kihajlás vizsgálat kezdeti feltételét fogja jelenteni. A kihajlás vizsgálatban nem lehet terheléseket és peremfeltételeket definiálni. Ezek és a feszültségi állapotok a statikai analízisből kerülnek felhasználásra.
Nem nulla értékű kényszerek is alkalmazhatók.
Az eredmény bemutatása.
A lineáris kihajlás vizsgálat eredménye a kihajlási terhelés faktora és a hozzá tartozó kihajlási alakok. A kihajlási terhelés faktora a statikai analízisben megadott terheléssel szorozva adja meg az instabil viselkedéshez tartozó kritikus terhelést értékét. (Kihajlási terhelés = Kihajlási terhelés faktora * Statikus terhelés). A kihajlási terhelés faktora az összes alkalmazott terhelésre vonatkozik. Egy szerkezet elvileg végtelen sok kihajlási terhelési faktorral rendelkezhet, és minden faktor egy instabilitási mintához tartozik. De számunkra általában a legalacsonyabb az érdekes.
Az eredményként kapott módusok hasznos segítséget nyújtanak a kihajlás alakjának szemléltetésében, de a deformáció abszolút értéke nem ad valós eredményt. Lekérdezhető a feszültség és a fajlagos nyúlás is, de abszolút értékük nem valós, (az elmozduláshoz hasonlóan), helyes információt csak a relatív eloszlásukról ad. Az eredményt animálhatjuk, ami a relatív elmozdulások időbeni lefolyásával szemléletesen mutatja a kihajlás módját.

8.2. Kihajlás vizsgálat VEM példa

Az alábbi példában, ugyanazt a geometriai modellt felhasználva, többféle megtámasztási esettel vizsgáljuk a szerkezet kihajlását. A geometria minden esetben egy, a korábbi példákban alkalmazott, 100mm hosszú és 10x2mm-es négyszög keresztmetszetű gerendamodell (Line Body/Beam Element).

A szimuláció mindig két részből áll, először az adott befogási feltételekkel egy statikai vizsgálatból, majd egy erre épülő (kezdeti feltétel a megelőző statikai analízis) lineáris kihajlás vizsgálat (Linear Buckling) . Tehát a geometria létrehozása után egy statikai (Static Structural) analízist kell létrehoznunk, melyben definiáljuk az anyagmodellt, a hálózást, valamint a perem és terhelési feltételeket. A feladatban eltekintünk a statikai analízis eredményeinek bemutatásától, csak a kihajlási eredményeket tekintjük át az egyes befogási eseteknél.

Az anyaghoz használjunk szerkezeti acélt (E=200GPa, v=0,3). A hálózáshoz 2mm-es elemméretet használtunk, így a teljes elemszám 50 lett. A geometriát és a véges elemes hálót a 8.1. ábra szemlélteti.

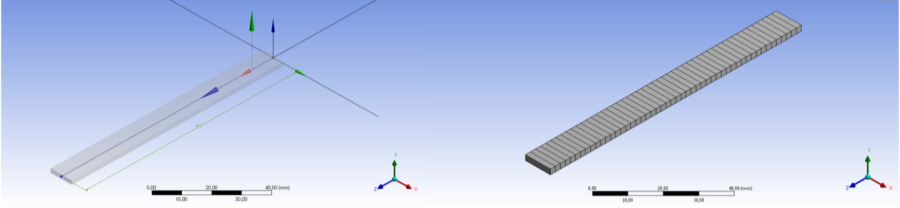
8.1. ábra - A geometriai és a végeselem modell négyszög keresztmetszetű rúd esetén

A szerkezeti analízisben egy alapterhelést kell beállítanunk, amelynek a szorzóját a kihajlás vizsgálat fogja megadni. A négyszög keresztmetszetű rudat mindegyik esetben 100N nagyságú –Z tengely irányú erővel terheljük az egyik végén, úgy, hogy a rúd nyomva legyen.

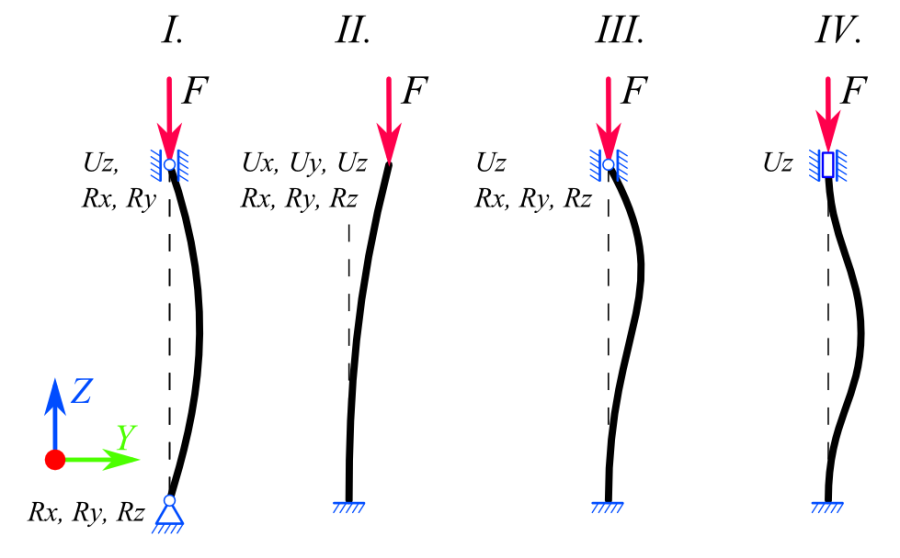
Az erőterhelés (F=100N), és a megmaradt szabadságfokok a különböző megfogási esetekben. A peremfeltételektől függő működő rúdhossz: l0,I=l, l0,II=2l, l0,III=0,7l, l0,IV=0,5l.

8.2. ábra - Az erőterhelés (F=100N), és a megmaradt szabadságfokok a különböző megfogási esetekben. A peremfeltételektől függő működő rúdhossz: l_0,I=l, l_0,II=2l, l_0,III=0,7l, l_0,IV=0,5l.

A vizsgálatot a peremfeltételek, vagyis a két rúdvég megtámasztásának különböző eseteivel végezzük el. A befogási esetek megegyeznek a karcsú rúd analitikus kihajlás vizsgálata során használt, és jól ismert 4 modellel:

befogási eset (8.2. ábra, I.):
Az első esetben az erőterhelési oldalon egy külpontos megfogás (Remote Displacement) típusú kényszerrel definiáljuk ennek a végpontnak a viselkedését. Ezzel az adott pont elmozdulását és elfordulását is beállíthatjuk. (Jelen esetben a végpont elmozdulása oldalirányban (X és Y) gátolva van, azonban tengelyirányban (Z) szabadon elmozdulhat, az elfordulás X és Y tengely körül megengedett, Z tengely körül azonban 0˚, tehát e tengely mentén nincs elfordulás.)
A terhelőerővel ellentétes oldalon egy egyszerű megtámasztás típusú (Simply Supported) befogást definiáltunk, amely azt jelenti, hogy a rögzített pont elmozdulása minden irányban gátolt, azonban az elfordulás minden tengely mentén megengedett.
Kihajlás vizsgálat eredménye az első befogási viszonyokkal:
A kihajlás nagyságát az középvonal mentén kérdeztük le, X és Y irányban megfigyelve a deformációt. Látható, hogy a kihajlás Y irányba, (vagyis a keresztmetszet kisebb másodrendű nyomatékának tengelyére merőleges irányban) történt, az X irányban a deformáció elhanyagolható. A kihajlott alak megfelel a peremfeltételek mellett várt alaknak, a konzol közepe kihajlik.

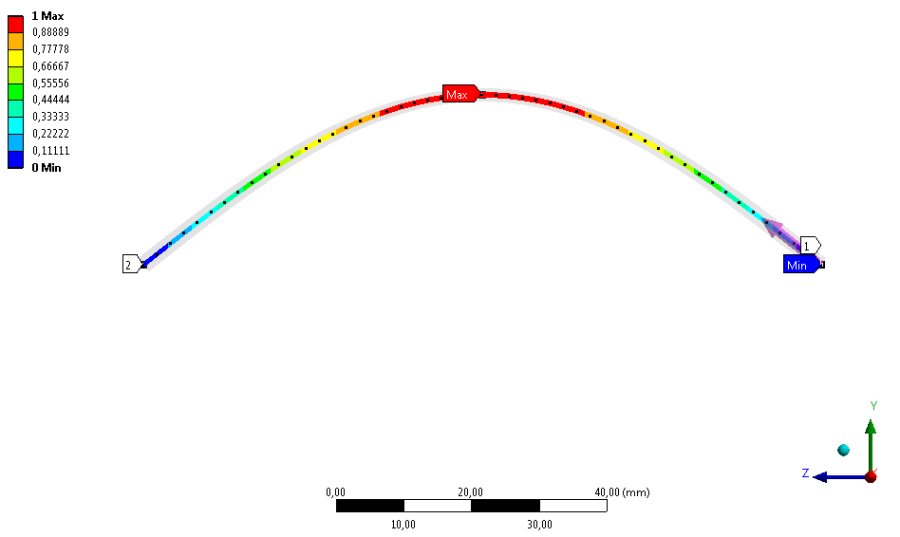8.3. ábra - Y irányú deformáció az első megfogási esetben.
befogási eset, (8.2. ábra, II.):
Ebben a megfogási esetben a terheléssel ellentétes oldalon egy fix megfogás (Fix Support) típusú megtámasztás található. Tehát ennek a pontnak minden szabadságfokát elimináltuk, se elmozdulás, se elfordulás nem lehetséges. A terhelés támadáspontjánál nem definiáltunk kényszereket, ez a pont szabadon elmozdulhat és elfordulhat minden irányban.
Kihajlás vizsgálat eredménye a második befogási esetnél:
Az deformációs eredményen jól látható, hogy a kihajlott alak megfelel az előzetes várakozásainknak, a terhelés támadáspontja az Y irányba, (vagyis a keresztmetszet kisebb másodrendű nyomatékának tengelyére merőleges irányban) mozdul el (8.4. ábra).

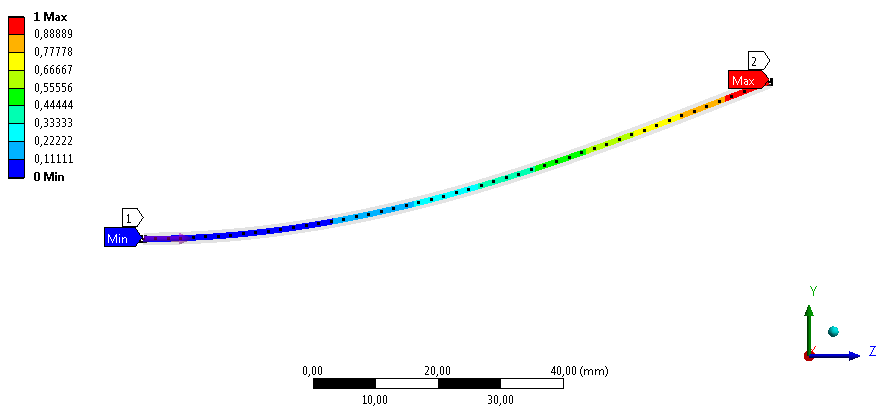8.4. ábra - Y irányú deformáció a második megfogási esetben.
befogási eset, (8.2. ábra, III.):
Ebben az esetben a konzol befogásánál fix megfogást (Fix Support) definiálunk, míg a terhelési pontnál egy külpontos megfogást (Remote Displacement) alkalmazunk, a következő beállításokkal: X és Y irányú elmozdulás megkötése, a Z irányú elmozdulás, valamint az X, Y és Z tengely körüli elfordulás szabadon hagyása. Mivel az elfordulást egyik tengely mentén sem kell megkötni, használhatunk Displacement kényszert is.
Kihajlás vizsgálat eredménye a harmadik befogási esetnél:
Az alábbi ábrán látható, hogy a kihajlott deformált alak megfelel a várakozásoknak, a konzol egy része az Y irányba kihajlik (8.5. ábra).

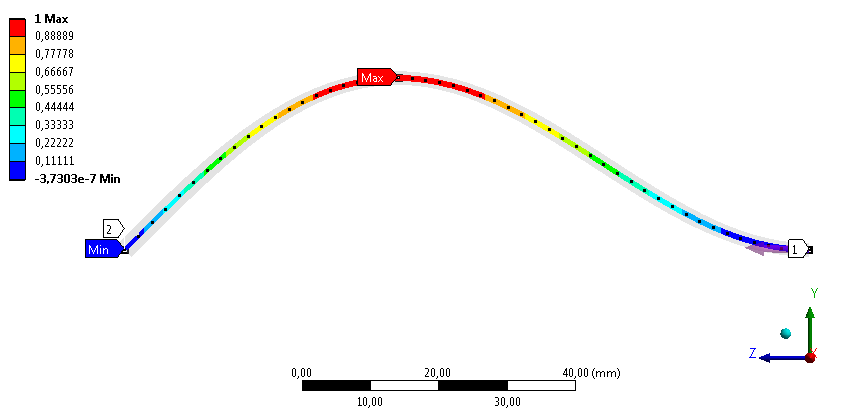8.5. ábra - Y irányú deformáció a harmadik megfogási esetben.
befogási eset, (8.2. ábra, IV.):
Utolsó esetben a terhelési oldalon egy olyan külpontos megfogást (Remote Displacement) alkalmazunk, amely csak a Z irányú elmozdulást enged meg, a többi irányú elmozdulás és minden tengely menti elfordulás gátolva van. A befogási pont fixen van rögzítve (Fix Support) . (8.2. ábra, I.)

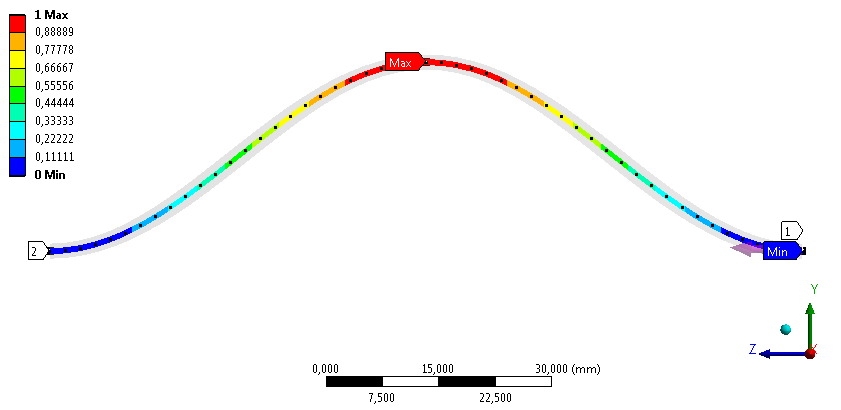8.6. ábra - Y irányú deformáció a negyedik megfogási esetben.

8.3. Analitikus megoldás

A végeselemes programok eredményének ellenőrzéseként oldjunk meg a feladatot Euler és Tetmajer módszerével. Kiindulásnak adva van egy téglalap keresztmetszetű rúd, az alábbi paraméterekkel. Feltételezzük, hogy a rúd anyaga homogén és izotróp és a terhelés a keresztmetszet súlypontjában, rúdirányban hat. [25.] .

Kiinduló adatok:

A hasáb méretei – hossza: L = 100 mm, magassága: h = 2 mm, szélessége: b = 10 mm;

Anyaga – Szénacél [25.] , Rugalmassági modulus: E = 200 GPa, Poisson tényező: ν = 0,3;

A Tetmajer egyenes állandói a = 308, b = 1,14; Folyáshatár: σ_eH = 240 MPa.

Határozzuk meg a rúd kritikus (törő) feszültségét és a meghajolt rúd alakját.

A rudat terhelő kritikus erő hatására a rúdvégtől számított (z) távolságú helyen M(z)=F_t·y(z) nyomaték hat, amely a rúd alakváltozását okozza.

Ahol:

M(z) – a rúdba ébredő hajlítónyomaték,

F _t – a kritikus terhelőerő,

y(z) – az egyenestől való kitérés mértéke.

A kihajlás egyenletét a rugalmas szál differenciál egyenletéből származtatjuk.

(8.1)

ahol:

I – a keresztmetszeti tényező, (téglalap esetén I = b·h ³ /12),

E – az anyag rugalmassági modulusa.

(8.2)

helyettesítéssel az y”+α²⋅y=0 másodrendű homogén differenciálegyenletet kapjuk, melynek általános megoldása adja a rúd alakját leíró függvény.

(8.3)

Az A és B tagok a rúdvégeken alkalmazott peremfeltételektől függő állandók. Mindkét végén csuklós megfogást választva ( y(0)=0, y(l)=0), B=0 és A⋅sin (α⋅l)=0, ebből A=0 triviális megoldás a y(z)=0 -t eredményezné ezért α=n⋅π/l adódik (n=1 -nek van gyakorlati jelentősége). Visszahelyettesítés után kapjuk a kritikus erő számításának Euler féle egyenletét, ahol az l₀ a peremfeltételektől függő működő rúdhossz (lásd: 8.2. ábra).

		(8.4)
		(8.5)

állandók bevezetésével kapjuk a gépészeti tervezésben szokásos összefüggést.

(8.6)

ahol:

σ _t – a kritikus törőfeszültség,

λ – karcsúsági tényező.

Az Euler féle összefüggés csak karcsú rudak rugalmas kihajlására érvényes. A zömök rudak képlékeny kihajlására a Tetmajer összefüggés ad megoldást.

(8.7)

ahol:

a, b– anyagtulajdonságtól függő állandók.

A képlékeny szakaszra számos más megoldás is létezik, de példánkban a Tetmajer egyenest vesszük fel mivel ez a legismertebb eljárás.

✎ A fenti egyenletek alapján rajzoltassuk ki diagramban a kritikus feszültség értékét a karcsúsági tényező függvényében és a kihajlott rúd alakját különböző peremfeltételek alkalmazása mellett. Hasonlítsuk össze a végeselemes programok eredményeivel.

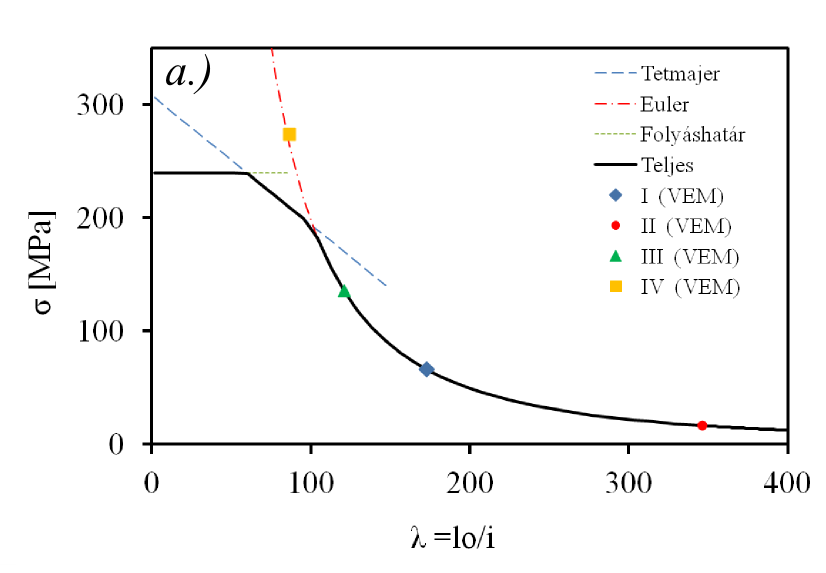
8.7. ábra - A kihajlás vizsgálat analitikus és VEM eredményeinek összevetése.

Ismét felhívnánk a figyelmet az eredmények körültekintő alkalmazására. Látható, hogy a IV. megfogási eset végeselem megoldása már a képlékeny tartományba esik, tehát a kapott eredményt felül kell bírálni az adott anyagra érvényes karcsúsági határ (λ₀) szerint.

9. fejezet - Dinamikus, tranziens mechanikai analízis

Tartalom

9.1. Áttekintés
9.2. Példa tranziens szimulációra

9.1. Áttekintés

A dinamikus, vagy más néven tranziens mechanikai analízis (Transient Structural Analysis, time-history analysis) során adott szerkezet időfüggő terhelés hatására bekövetkező dinamikus válaszát vizsgáljuk. Az analízis során meghatározhatjuk az elmozdulások, fajlagos nyúlás, feszültség, stb. időbeli változását a tranziens terhelés hatására. A szimuláció időbeli lefutását főként a szerkezet tehetetlensége és csillapítása befolyásolja. Amennyiben ezek hatása nem fontos, használhatunk statikai analízist a probléma megoldására.

( ANSYS -ban a Mode Superposition eljárás segítségével lehetőség van a tranziens analízis terhelési feltételeinek, a Modal analízis sajátvektorainak lineáris szuperpozícióval való számolására.)

A tranziens mechanikai analízis lehet lineáris, vagy nemlineáris (nagy alakváltozás, plasztikus, vagy hiperelasztikus anyagi viselkedés, nemlineáris kontaktok, stb.).

A tranziens analízis lényegesen számolásigényesebb, mint a statikai szimuláció, ezért az erőforrások gazdaságos felhasználása érdekében az alkalmazó mérnöknek tisztában kell lenni a probléma fizikai hátterével:

A szimulációban lévő nemlinearitások statikai vizsgálata segítségével eldönthetjük, hogy szükséges-e alkalmazásuk a dinamikai analízis során.
Előzetes modál analízis segítségével képet kaphatunk a szerkezet viselkedéséről adott frekvencián és a sajátfrekvenciák segítségével beállíthatjuk a megfelelő integrációs időt a tranziens analízisben.
Egy egyszerűsített modell vizsgálata gazdaságosan adhat képet a szerkezet viselkedéséről.

A tranziens szerkezeti analízis esetében alkalmazható anyagmodellek.
A statikai analízisben alkalmazott anyagmodellek itt is használhatók (lineáris, vagy nemlineáris, izotróp, vagy ortotróp, állandó, vagy hőmérsékletfüggő), de az inerciális terhelés miatt az anyag sűrűségét is meg kell adni.
Alkatrész viselkedés.
Egy összeállítás dinamikai analízisében gyakran szerepelnek olyan alkatrészek, melyek deformációjára és feszültségi állapotára nem, vagyunk kíváncsiak, csupán a terhelések átadásában van szerepük. Ezeket merevtestként (Rigid Parts) definiáljuk a szimulációban.
Lehetőség van pontszerű tömeg (Point Mass) megadására, amelynek általában a tehetetlenségi nyomatéka is megadható.
A statikai analízishez hasonlóan, itt is célszerű a modell egyszerűsítése (2D-s geometria, vagy szimmetriafeltételek alkalmazásával).
Alakatrészkapcsolatok, Kontaktok.
Némely végeselem szoftverben (pl. ANSYS) a hagyományos kontaktok mellett csukló (joint), vagy csillapítással ellátott rugóelemek (Spring) is alkalmazhatók.
Hálózás.
Egy dinamikus analízis esetében, a statikai analízisnél leírtak figyelembevételén túl, a hálónak elég finomnak kell lennie, hogy képes legyen bemutatni a vizsgált legnagyobb módushoz tartozó alakot.
A szimuláció beállításai.
A dinamikus szerkezeti analízisben (a statikaihoz hasonlóan), karcsú szerkezetek nagy lehajlásai, vagy hiperelasztikus anyagmodellek alkalmazása esetén szükség lehet a nagy lehajlások (Large Delection) funkció alkalmazására. (Bővebben lásd a „Statikai analízis” fejezetben leírtakat.)
A dinamikai szimulációnál kap igazi jelentőséget az időlépések (Time Steps) beállítása, ugyanis az időben lefutó tranziens jelenségről csak akkor kapunk megfelelő képet, ha a számolási pontok időbeni sűrűsége megfelelő. Az időlépések (Time Steps) definiálásánál több lépés is megadható, aminek segítségével lépésenként változó beállításokat, vagy terheléseket definiálhatunk. Megadható az al-lépések (Substeps) száma, vagy időintervalluma, mellyel egy lépés felosztását definiáljuk. A tranziens analízisnél beállított időlépések a valós időt jelentik (Time Integration = ON) .
Egy mechanikai szerkezet időbeni viselkedésének egyik fontos meghatározója a szerkezeti elemek csillapítása, aminek a definiálására a csillapítás beállításánál (Damping Controls) van lehetőségünk. (Az ANSYS VEM szoftverben Béta, numerikus, anyag és a rugóelemek csillapítása definiálható.)
Nemlineáris analízis esetében számolni kell a konvergencia problémák felmerülésével. A problémát okozhatják merevtest szerűen elmozduló alkatrészek, túl nagy terhelés-növekmény, anyagi instabilitások, vagy a nagy deformáció okozta elemtorzulások. A megoldást, a probléma okától függően, az elemméret, ill. az időlépések optimális megválasztása, a konvergencia kritériumok módosítása, vagy a megoldó megfelelő megválasztása jelentheti.
Kezdeti feltételek
Tranziens szerkezeti analízis során a terhelések az idő függvényei, melynek első lépésében a kezdeti feltételek (tehát a nulladik időpillanatban érvényes kondíciók) érvényesülnek. Az alapértelmezett kezdeti feltételként a szerkezet nyugalomban van, tehát mind az elmozdulások, mind pedig a kezdeti sebesség értéke nulla. A szerkezet egy, vagy több alkatrészére definiálható konstans sebesség kezdeti feltételként, a többi alkatrészen nyugalmi kezdeti feltétel marad.
Peremfeltételek / Terhelések
Alkalmazható minden, a statikai analízisnél használható szerkezeti kényszer és terhelés, valamint inerciális terhelés. A terhelések mértéke lehet állandó, vagy időben változó. Az időben változó terhelést definiálhatjuk az egyes lépések terhelésszintjének megadásával direkt módon (táblázatosan), az al-lépések növekményével (lineárisan növekvő – ramped, vagy egy lépésben stepped), vagy függvény megadásával. Az egyes terhelések, vagy peremfeltételek hatása adott lépésnél ki, ill. bekapcsolható.
Az eredmény bemutatása.
Az eredmények lekérdezése és bemutatása hasonlóan történik, mint a statikai analízisnél, de itt az eredmény az idő függvényében értelmezendő. Az eredmény animálásánál az időskála a valós időt mutatja, de a lejátszás sebessége általában ettől eltérő. Egy lengő, vagy rezgő mozgást végző szerkezet esetében a képkockák sűrűségének beállításánál (Frame/s) ügyelni kell a rezgés frekvenciájára, ugyanis a túl ritkán felvett képkockák nem a valós tranziens jelenséget fogják bemutatni.

9.2. Példa tranziens szimulációra

Ebben a tranziens dinamikus szimulációban, (a korábbi statikai feladatokból ismert) konzol adott terhelésre adott válaszának időbeni lefutását szimuláljuk. A terhelési modell egy fix befogást (Fix Support) tartalmaz a konzol egyik végén, míg a másik oldalán egy olyan elmozdulás (Displacement) típusú terhelést, melyben +Y irányban 2mm elmozdulás van definiálva, míg a másik két tengely (X és Z) irányában a szabad elmozdulás megengedett (9.1. ábra). A szimulációnál kezdeti feltételként a modál analízis eredményeit használtuk fel.

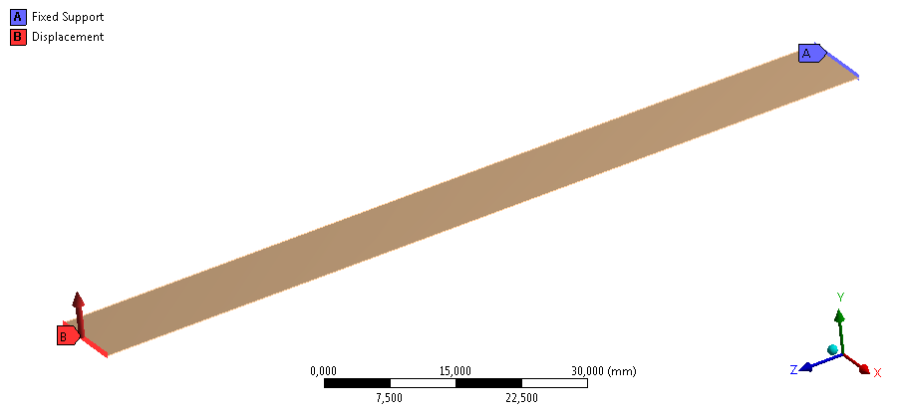
9.1. ábra - A konzol megtámasztása és terhelése.

A beállításoknál nagyon fontos a lépések és a lépések időtartamának beállítása. Ebben az esetben a szimuláció 2 lépést tartalmazott, az első lépés időtartama 0,0001s, míg a második lépés vége 0,1s. Fontos az al-lépések időtartamának helyes beállítása, ugyanis ez határozza meg a tranziens jelenség számolása során az időbeni eredménypontok sűrűségét. Ha túl ritkán vesszük fel az időlépéseket az helytelen eredményhez vezet, ha túl sűrűn, akkor nagy számolási idő és tárolókapacitás igényű lesz az analízisünk. Ezért érdemes valamilyen módszerrel (előzetes modál analízis, közelítő analitikus számolás, stb.) a rendszer vizsgálandó legnagyobb sajátfrekvenciájának, vagy becslése, mert ez jó támpontot ad az időlépések sűrűségének beállításához. Ha ez ismert, akkor az időlépéseket úgy érdemes felvenni, hogy a rezgés periódusidejétől legalább egy nagyságrenddel kisebbek legyenek az időlépések.

Mivel esetünkben a rúd 1. sajátfrekvenciája: f=163Hz, periódusideje: T≈0,006s, ezért érdemes az időlépések felosztását dt<0,0006s –ra választani.

A tranziens jelenség kialakulásának oka a rugalmasan deformált, (meghajlított) konzol elengedésekor létrejövő rezgés. Ehhez nem elég a rúd végének Y irányú 2mm-es elmozdítása, de el is kell engedni azt. Ezt úgy tehetjük meg, hogy a modellfán kijelölt elmozdulás kényszert (Displacement) , az idődiagramján, a második időlépésben ki kell kapcsolni ( Graph fülön a munkatér alatt, az elmozdulást jelképező vízszintes vonalra való jobb egérgombos kattintással, majd Deactivate ).

Megjegyzés: A kikapcsolással (Deactivate) nem egyenértékű a 0 érték megadása, mert míg az előző magára hagyja a rendszert, addig a második megoldás 0 elmozdulást kényszerít rá, vagyis rögzíti az eredeti helyzetben.

A nagy alakváltozások miatt, a Large Deflection opciót alkalmazni kell. Mivel minden tranziens szimulációnál alapvető a csillapítás definiálása, itt is adjuk meg az értékét a modellfa szimulációs beállítások elemével (Outline/…/Analysis Settings => Outline/Damping Control/…) . A csillapítást jelen esetben merevségi együttható (Stiffness Coefficient) megadásával határozzuk meg, melynek értéke 0,0001[-]. A numerikus csillapítási érték (Numerical Damping Value) 0,1 [-].

9.2. ábra - Deformáció [mm] a tranziens szimuláció 2. időpillanatának végén

A szimuláció lefutása után látható az eredményen, hogy a 2. időintervallum végén a deformáció már jóval alatta marad a megadott 2mm nagyságú elmozdulásnak. Az egy pillanatra vonatkozó deformációs értékek azonban nem sokat árulnak el a folyamat lényegéről, vagyis az időbeli lefolyásáról. Ezért a tranziens szimulációknál elengedhetetlen az időbeli eredmény grafikus megtekintése. A konzol terhelt véglapjának Y irányú deformációjának (Directional Deformation) időbeli lefutását mutatja be a 9.3. ábra. Látható, hogy a konzol a terhelés kikapcsolása után, a beállított csillapítás hatására, pár lengés után visszaáll kiinduló helyzetébe.

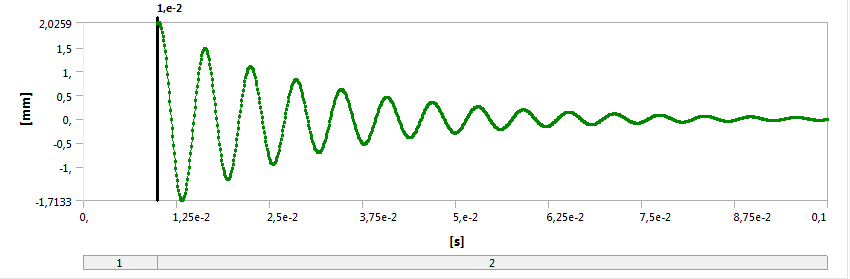
9.3. ábra - A konzol véglapjának Y irányú deformációjának időbeli lefutása.

10. fejezet - Modális analízis

Tartalom

10.1. Áttekintés

10.2. Konzolos lemez modal analízise előfeszítés nélkül és előfeszítéssel

10.2.1. Modal analízis előfeszítés nélkül
10.2.2. Modal analízis előfeszítéssel
10.2.3. Analitikus megoldás

10.1. Áttekintés

A modál (Modal) , vagy alaki analízis segítségével határozhatjuk meg egy szerkezet rezgésének karakterisztikáját, tehát a rezgési sajátfrekvenciáit és a hozzájuk tartozó lengésképeket. Ezek fontos paraméterei egy dinamikusan igénybevett szerkezet tervezésének. A modál analízis eredményeit kiindulópontként használhatjuk más, részletesebb vizsgálathoz, (mint pl.: a tranziens dinamikus, harmonikus válasz, vagy a spektrum analízis).

Előfeszített (Prestressed) szerkezetek analízisére is lehetőség van, mint pl.: nagy centripetális gyorsulásnak kitett turbinalapát, előfeszített szerkezeti elem, stb.

Csillapított szerkezeti elem esetén a szimuláció csillapított, a sajátfrekvenciák és a lengésalakok komplexek lesznek.

Forgó szerkezet esetén a szögsebességből fakadó giroszkópikus hatás bekerül a modál analízisbe, ami hatással van a rendszer csillapítására. A sajátérték változását különböző szögsebességnél a Campbell diagramon vizsgálhatjuk.

Anyagmodellek.
A modál analízis jellegéből adódóan csak a lineáris anyagtulajdonságokkal dolgozhatunk. Meg kell adnunk az anyag merevségét (pl.: rugalmassági modulus és Poisson-tényező) és a tömegét valamilyen formában (pl.: sűrűség, vagy pontszerűen megadott tömeg, stb.).
Alkatrész viselkedés, kontaktok.
A statikai szimulációnál leírtak vonatkoznak ide is. A 2D-s és szimmetriakényszerek alkalmazásánál figyelembe kell venni, hogy az aszimmetrikus módusok nem kerülnek bele az eredménybe.
Megoldótól függően csuklók, rugó és csillapító elemek valamint pontszerű tömegek alkalmazhatók [6.] .
Hálózás.
A statikai szimulációnál leírtak szerint.
A szimuláció beállításai.
Az egyik legfontosabb beállítás a módusok számának megadása, vagyis, hogy az első hány db. sajátfrekvenciát és a hozzátartozó lengésképet akarjuk kiszámoltatni (minimum 1).
Beállítható a megoldó típusa és, hogy a rendszer csillapított, vagy nem. Kétféle csillapítás, a merevségi együttható (Stiffness Coefficient) és a tömeg együttható (Mass Coefficient) segítségével adható meg.
Kezdeti feltételek
Előfeszített szerkezetek szimulációjára használhatunk statikai analízist a modál analízis bemeneteként. Olyan esetekben célszerű az alkalmazása, amikor egy szerkezet tipikus üzemi feltételei olyan mértékű deformációt, vagy feszültséget okoznak, ami jelentősen befolyásolja a rezgési karakterisztikáját, vagyis elhangolja azt. Előfeszített szerkezet szimulációjakor a modál analízis peremfeltételeit nem kell külön megadnunk, mert azt a statikus terhelési esetből (előfeszítés) származtatjuk.
Peremfeltételek / Terhelések
Terhelésként csak szögsebesség adható, egyéb mechanikai terhelést előfeszítésként kell megadni. A szabadságfokok megkötésére szolgáló kinematikai kényszerek alkalmazhatók, kivéve a nem nulla elmozdulás kényszereket (Ansysban: Non-zero Displacement, Remote Displacement, Velocity boundary condition) . Nemlineáris jellege miatt a csak nyomóhatást kifejtő kényszerek (Compression Only Supports) kerülendőek.
Az eredmény bemutatása.
A modál analízis eredménye alapvetően a szerkezet sajátfrekvenciái és a hozzájuk tartozó lengésképek. Egyes esetekben lekérdezhető a feszültség és a fajlagos nyúlás is, de abszolút értékük nem valós, (az elmozduláshoz hasonlóan), helyes információt csak a relatív eloszlásukról ad. Az eredményt animálhatjuk, ami a relatív elmozdulások időbeni lefolyásával szemléletesen mutatja a rezgés módját.
Forgó szerkezet esetén a sajátérték változását különböző szögsebességnél a Campbell diagramon vizsgálhatjuk.

10.2. Konzolos lemez modal analízise előfeszítés nélkül és előfeszítéssel

Ebben a fejezetben egy egyszerű konzol előfeszítés nélküli és előfeszített modál analízisét mutatjuk be ANSYS Workbench végeselem programmal. A következő fejezetekben pedig a harmonikus terhelésre adott válaszát és tranziens viselkedését vizsgáljuk.

A konzol geometriája mindhárom szimulációnál, a már korábban alkalmazott 100x10x2mm nagyságú hasáb, amelyet felületként modelleztünk. Ez látható a következő ábrán. (A lemez vastagságát a szimuláció során definiáltuk.)

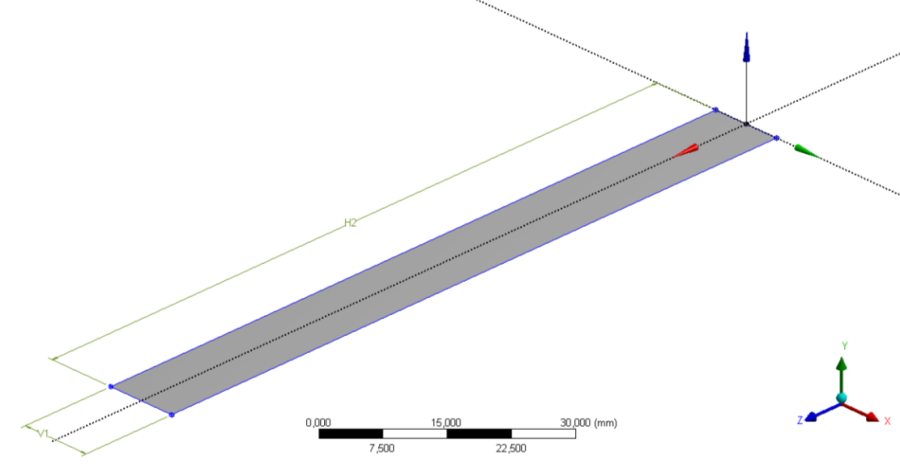
10.1. ábra - A konzol felületmodellje.

A test anyaga minden szimuláció során szerzeti acél (Structural Steel) . A modell hálózásánál 2,5mm-es hexa elemeket használjunk. Így a teljes modell 160 elemet tartalmaz (10.2. ábra).

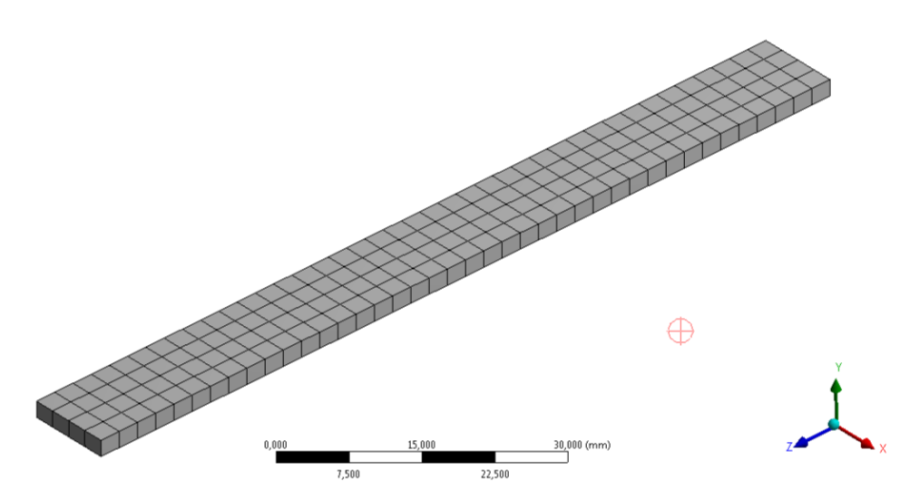
10.2. ábra - A hálózott végeselem modell.

Az eredmények lekérdezéséhez egy a lemez hosszanti irányában végig futó konstrukciós geometria (Path) is definiáljunk (10.3. ábra).

10.3. ábra - A konstrukciós vonal helye.

10.2.1. Modal analízis előfeszítés nélkül

Az előfeszítés nélküli modal analízis megmutatja a rendszer saját frekvenciáját abban az esetben, ha nincs semmilyen terhelő erő. Ekkor csak a rögzítést kell megadni. Jelen példában ez egy fix megfogás (Fix Support) a lemez egyik végén (10.4. ábra).

10.4. ábra - A fix megfogás helye a lemezen - kék címkével jelölve.

Ezután állítsuk be a keresendő sajátfrekvenciák számát (6 az alapértelmezett), (Outline/…/Analysis Settings => Details/Options/Max Modes to Find: 6).

Futtassuk a szimulációt, majd kérdezzük le a lengésképeket. A lengésalakok lekérdezésénél eljárhatunk a hagyományos módon a deformáció (Total Deformation) parancs kiadásával. Ekkor lekérdezésenként a vizsgálni kívánt módus számának manuális beállítása szükséges (Details/Definition/Mode: 1, 2, ...) . Több módus vizsgálata esetén egyszerűbb, ha az eredményeket tartalmazó táblázat (Outline/Solution => Tabular Data) , minden sorát kijelölve, a jobbgombos menüből a Creat Mode Shape Results parancsot alkalmazzuk (10.5. ábra). Ekkor minden kijelölt frekvenciához automatikusan létrejön a lengésképeket bemutató teljes deformációs eredményt. Ismételt futtatás után megjelennek a lengésképek.

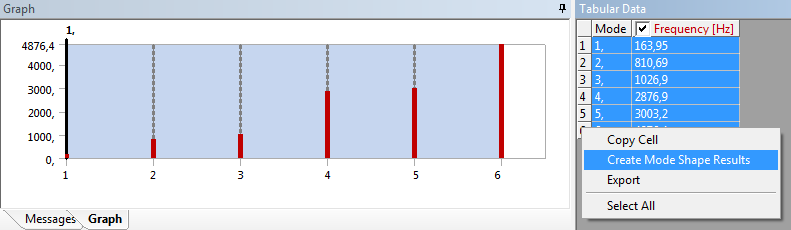
10.5. ábra - Lengésképek lekérdezése a sajtfrekvenciák eredményei alapján.

A teljes deformáció képe alapján, az eredmények nélkül duplikáljuk (Duplicate Without Results) azokat az eredményeket, amelyek csak Y irányú lengést végeznek. Majd a kijelölést (Scoping Methode) állítsuk át a konstrukciós vonalra (Path) , és a típusát pedig (Y) irány menti deformációra (Type: Directional Deformation; Orientartion: Y Axis) . Ismételt futtatás után megjelennek az eredmények, az ábra alatt grafikon és táblázatos formában is.

Az eredmények jobb áttekinthetősége végett, a modellfában átnevezhetjük az eredményeket tartalmazó sorokat, a rájuk vonatkozó sajátfrekvencia alapján. Ehhez jelöljük ki az összes eredménysort a Shift billentyű lenyomásával az elsőre és utolsóra kattintva), majd jobbgombos menüből válasszuk a Rename Based On Definition parancsot (10.6. ábra).

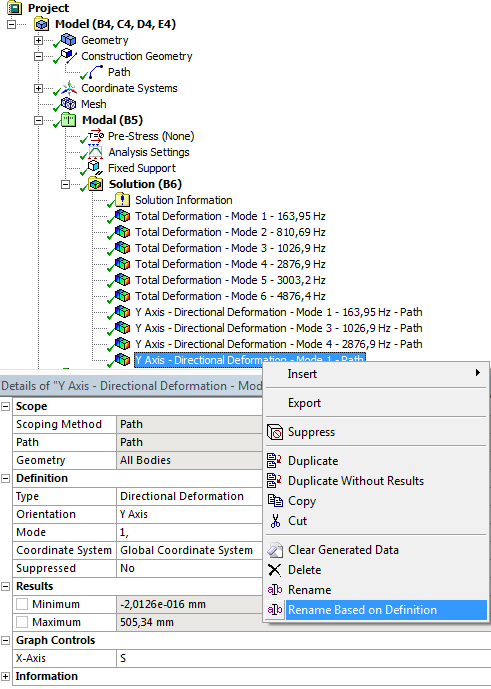
10.6. ábra - Automatikus átnevezés a definíció alapján.

10.2.2. Modal analízis előfeszítéssel

A következő példa ugyanannak a konzolnak a saját frekvenciáit keresi, mint az előző példában, annyi különbséggel, hogy itt egy statikus előfeszítést alkalmazunk. A fix befogás (jelen példában egy egyszerű megtámasztást (simply supported) használtunk 0 elmozdulással) a konzol ugyanazon oldalán található, az ellentétes oldalon pedig egy 0,5 [mm] nagyságú, pozitív z irányú elmozdulás típusú terhelés található. Jelen példában egy külpontos elmozdulást (remote displacement) alkalmaztunk. A statikus előfeszítés terhelési modellje a következő ábrán látható.

10.7. ábra - A statikus előfeszítés terhelési modellje.

Eredmények:

A terheletlen szerkezet modál analízisének eredményeit a 10.8. ábra és a 10.9. ábra tartalmazza.

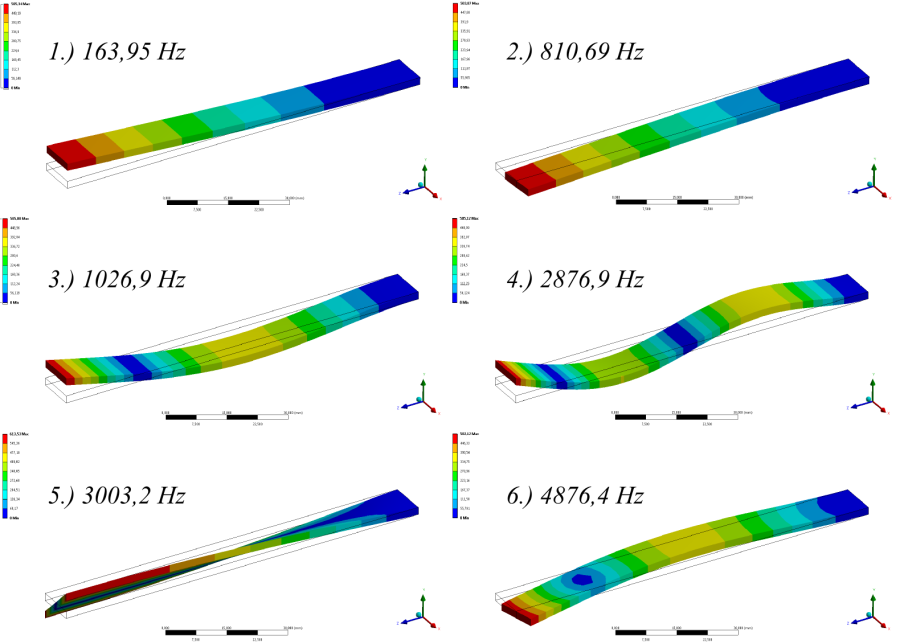
10.8. ábra - A terheletlen szerkezet lengésképei és sajátfrekvenciái.

Az Y irányú konstrukciós geometria mentén lekérdezett saját frekvenciák természetesen csak az Y irány mentén változó lengésképen mutat értelmezhető eredményt. Ezeket a következő táblázat tartalmazza.

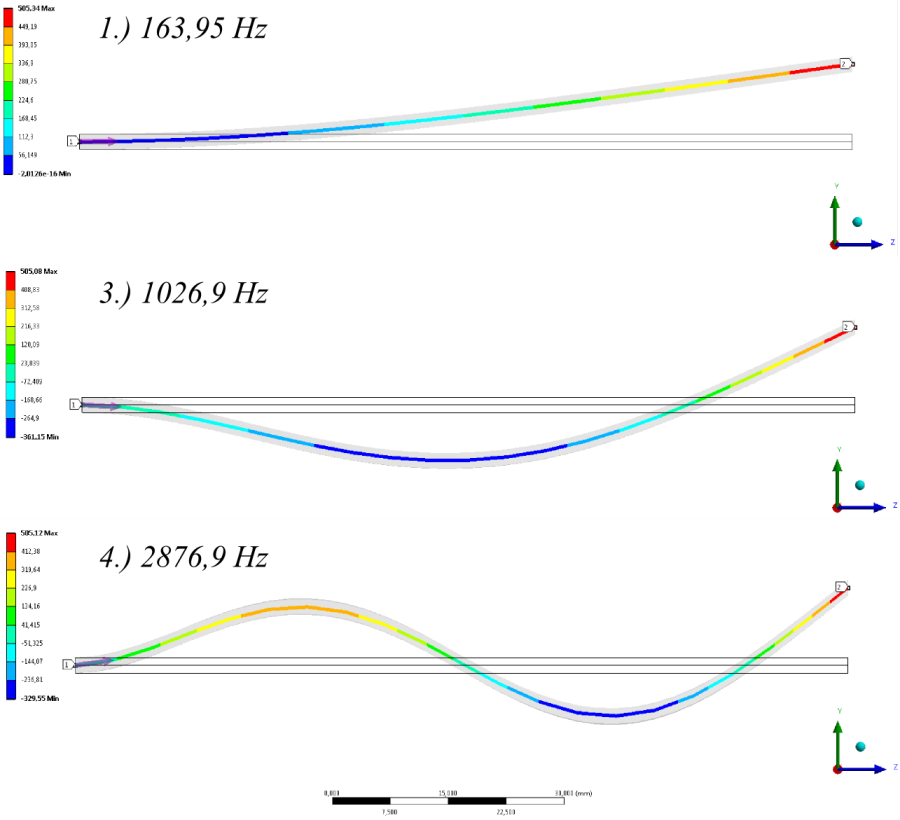
10.9. ábra - A terheletlen szerkezet Y irányú jellemző lengéssel rendelkező módusainak vonal menti eredménye.

Az előfeszített konzol saját frekvenciái, ahogy az várható volt, nőttek (Táblázat 10.1), a saját frekvenciák lengésképe lényegesen nem változott.

10.1. táblázat - A terheletlen és az előfeszített szerkezet első 6 sajátfrekvenciájának összehasonlítása.

Módus	A jellemző lengés iránya	Terheletlen f ₀ [Hz]	Terhelt f ₀ [Hz]
1.	Uy	163,95	979,87
2.	Ux	810,69	1611,1
3.	Uy	1026,9	3088,7
4.	Uy	2876,9	3130,1
5.	Rz	3003,2	5612,6
6.	Ux	4876,4	7155,9

10.2.3. Analitikus megoldás

A végeselemes eredményének ellenőrzéseként oldjunk meg a feladatot analitikusan is [25.] , [46.] . Kiindulásnak adva van egy téglalap keresztmetszetű homogén és izotróp rúd, az alábbi paraméterekkel.

A hasáb méretei – hossza: L=100mm, magassága: h = 4 mm, szélessége: b = 10 mm;

Anyaga – acél, Rugalmassági modulus: E = 200 GPa, Poisson tényező: ν = 0,3.

Határozzuk meg a rúd első sajátfrekvenciáját és a meghajolt rúd alakját.

Egy állandó keresztmetszetű prizmatikus rúd hajlító rezgéseit, idő és a keresztmetszet helye szerint az alábbi parciális differenciálegyenlet írja le:

(10.1)

Bevezetve a

(10.2)

az egyenlet megoldása az

(10.3)

alakban várható, melynek helyfüggő, v(z) tagjának általános megoldása az alábbi:

(10.4)

ahol:

y(z) – az egyenestől való kitérés mértéke,

I – a keresztmetszeti tényező, (téglalap esetén I = b·h ³ /12),

E – az anyag rugalmassági modulusa,

ρ – az anyag sűrűsége,

A – a keresztmetszet területe,

ω ₀ – a sajátkörfrekvencia.

Az A, B, C és D tagok a rúdvégeken alkalmazott peremfeltételektől függő állandók.

A mindkét végén csuklós megfogást választva (y(0)=0, y(l)=0, y”(0)=0, y”(l)=0), A=C=D=0 és B⋅sin(λ⋅z/l)=0. Ebből B=0 triviális megoldás az y(z)=0-t eredményezné, ezért λ=n⋅π adódik (n=1,2,3… a sajátfrekvenciák sorszámának megfelelően.)

Visszahelyettesítés után kapjuk a rezgő rúd sajátfrekvenciáit és a lengésképet leíró függvényt.

		(10.5)
		(10.6)

Az egyik végén befalazott rúd (y(0)=0, y’(0)=0, y”(l)=0) esetén λ értéke az első 3 sajátfrekvencia esetén rendre λ=1,875; 4,694; 7,855. A lengésképet leíró függvény (Rayleigh féle függvényekből kifejezve):

(10.7)

ahol: D4 állandó értéke az első 3 sajátfrekvencia esetén rendre: D₄=-0,734; -1,018; -0,999.

Mindkét végén befalazott rúd (y(0)=0, y’(0)=0, y(l)=0, y’(l)=0) esetén λ értéke az első 3 sajátfrekvencia esetén rendre λ = 4,7301; 7,8532; 10,9956. A D₄ állandó értéke az első 3 sajátfrekvencia esetén rendre: D4=-0,9826; -1,0008; -0,9999.

✎ A fenti egyenletek alapján határozzuk meg a rúd első 3 sajátfrekvenciáját és rajzoltassuk ki diagramban a rezgő rúd alakját különböző peremfeltételek alkalmazása mellett. Hasonlítsuk össze a végeselemes programok eredményeivel.

10.2. táblázat - Az analitikus és numerikus eredmények összehasonlítása az első 3, Y irányú lengés esetében.

Módus	fo [Hz] (Analitikus)	fo [Hz] (VEM)	Hiba [%]
1	163,95	163,06	0,55
2	810,69	-	-
3	1026,9	1021,94	0,49
4	2876,9	2861,75	0,53

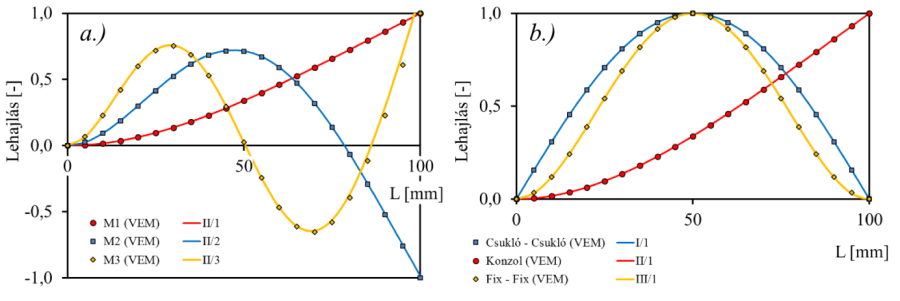
a.) Egy oldalon befogott tartó első 3, Y irányú lengésképe. b.) Mindkét végén megtámasztott tartó első lengésképe, különféle típusú megtámasztásokkal.

10.10. ábra - Terheletlen rúd lengésképei különféle peremfeltételek esetén.

11. fejezet - Harmonikus terhelések vizsgálata

Tartalom

11.1. Áttekintés
11.2. Példa harmonikus analízisre
11.3. Analitikus megoldás

11.1. Áttekintés

Mechanikai rendszereket gyakran ér tartósan ciklikus, ill. harmonikus terhelés, melynek hatására a szerkezet szintén harmonikus válasszal reagál. A harmonikus válasz analízis egy lineáris szerkezet időben szinuszosan változó terhelés(ek) hatására bekövetkező egyensúlyi válaszát adja meg (tranziens rezgések vizsgálatára nem alkalmas). Ez segít feltárni a gerjesztett rezgéseknek kitett szerkezet viselkedését (kifáradás, rezonancia, stb.). Mechatronikai rendszereknél, mérőműszereknél, szenzoroknál, a működési tartomány és az átviteli tulajdonságaik megállapításához különösen fontos, hogy vizsgálni tudjuk a szerkezet frekvenciafüggő dinamikus viselkedését. Az alábbiakban nézzük meg a harmonikus analízis speciális beállításait az ANSYS Workbench példáján keresztül.

Anyagmodellek.
Az analízis lineáris jellegéből adódóan a nemlineáris anyagtulajdonságok figyelmen kívül maradnak. Definiálnunk kell az anyag merevségét (pl.: rugalmassági modulus és Poisson-tényező) és a tömegét valamilyen formában (pl.: sűrűség, vagy ponszerűen megadott tömeg, stb.). Az anyag lehet izotróp, vagy ortotróp, állandó, vagy hőmérsékletfüggő.
Alkatrész viselkedés.
A statikai szimulációnál leírtak a mérvadóak.
Pontszerű tömeg alkalmazható. Csukló definiálására viszont nincs lehetőség a harmonikus analízisben. A rugóelemek csillapítása a csak a Teljes (Full) eljárásban használható, a módus szuperpozíciónál figyelmen kívül marad.
Alkatrészkapcsolatok, Kontaktok.
A nemlineáris kontaktok, mint pl. a súrlódásos kontakt (Frictional Contact) , a kezdeti értéküket kapják meg. A kontaktfelületek között definiált merevség a kezdeti feltételt veszi fel és a szimuláció alatt nem változik.
Hálózás.
A statikai analízisnél leírtak alkalmazhatók.
A szimuláció beállításai
A legfontosabb beállítás a vizsgált frekvenciatartomány kijelölése és a számítási pontok számának megadása. Ez utóbbi fogja meghatározni a frekvencia függvényében megadott eredménygörbe részletességét.
Az ANSYS esetében két számítási eljárást választhatunk a Teljes-et (Full) és a Módus Szuperpozíciót (Mode Superposition) . A Teljes módszer a szimultán mozgásegyenletek direkt megoldásával működik. A Módus Szuperpozíció esetében a harmonikus gerjesztésre adott válasz a modál analízisből származó sajátvektorok lineáris kombinációiból számolódik. Ez utóbbi esetben előnyös egy meglévő modál analízis eredményeinek felhasználása. (Mivel a sajátvektorok számítása a leg időigényesebb, ezért gyorsabban létrehozhatunk akár több harmonikus analízist, eltérő terhelési esetekkel, ugyanarra a modál analízisre építkezve.) A Módus Szuperpozíció általában gyorsabb eredményt ad, mint a Teljes eljárás. (Viszont nem alkalmazható akkor, ha (nem nulla) elmozdulást írunk elő.)
A fent már említett számítási pontokat egyenletes osztásközzel, vagy a rezonancia frekvenciák köré csoportosítva (Cluster Results) lehet kiosztani. Egyenletes kiosztásnál, ritkán felvett számolási pontok esetén, rezonanciacsúcsok maradhatnak ki. A rezonancia frekvenciák köré csoportosított pontok simább eredménygörbét adnak, viszont a módszer szükségessé teszi csillapítás definiálását, mivel a csillapítatlan rendszer csomópontjai a végtelenhez tartó rezonancia körül csoportosulnának. Ez utóbbi csak Módus Szuperpozíció esetén alkalmazható.

11.1. ábra - a.) Egyenletes eloszlású számolási pontok és b.) a pontok besűrítése a sajátfrekvenciáknál (Cluster result).

A vizsgált rendszer csillapításának definiálására az ANSYS végeselem rendszerben az alábbi lehetőségek állnak rendelkezésünkre: A csillapítási fok ( Constant Damping Ratio ) segítségével definiálhatjuk a legegyszerűbben a csillapítást. Béta csillapítás (Beta Damping) a merevségi mátrix szorzóját határozza meg. Segítségével közvetlenül adhatunk meg frekvenciafüggő csillapítást. Az anyagcsillapítást az anyagmodell definiálásánál kell megadnunk, ( ANSYS -ban kétféle: Material Dependent Damping, Constant Material Damping Coefficient ). Valamint alkalmazhatunk még elemcsillapítást (Element Damping), mint a rugóelem csillapítása. Többféle csillapítás definiálásakor hatásuk halmozódik.
Kezdeti és hőmérsékleti feltételek nem alkalmazhatók.
Peremfeltételek / Terhelések
A legtöbb mechanikai terhelés alkalmazható, melyek időben szinuszosan változó amplitúdójúak. Több terhelés megadásánál a jellegük, amplitúdójuk és fázisuk különböző lehet, de a frekvenciájuk azonos kell, hogy legyen. A terhelések fázisa a legtöbb esetben tetszőlegesen megadható, viszont a külpontos erő (Remote Force) , a nyomaték (Moment) és a gyorsulás (Acceleration) esetében csak nulla lehet. A terhelések szinuszos változása által csak az erővektor hossza és iránya változik támadáspontja nem ANSYS-ban. Ezért olyan terheléseket, amelyek támadáspontja irányfüggő, pl. csapágyterhelés (Bearing Loads) , nem célszerű alkalmazni.

11.2. ábra - Csapágyterhelés szinuszos váltakozása ANSYS-ban, Forrás: [6.] .

A lineáris kényszerek alkalmazhatók, viszont a nemlineáris kényszerek, mint a Csak nyomó (Compression Only) , vagy a Súrlódásmentes kényszer (Frictionless Support) viselkedése lineárissá válik a harmonikus szimuláció alatt.
Az eredmény bemutatása.
Az eredmények bemutatásának két lényeges módja lehetséges. Az egyik a modellen színsávok segítségével szemléltetett feszültség, alakváltozás, vagy elmozdulás, stb. Ebben az esetben definiálni kell, hogy az adott eredményt milyen frekvencián és fázisszög mellett szeretnénk megtudni.
A másik lehetőség az eredmények diagramon való ábrázolása, mely lehet Bode, vagy a reális és imaginárius részeket bemutató diagram.

11.2. Példa harmonikus analízisre

Harmonikus analízis esetén harmonikus gerjesztésre adott rendszerválaszt tudunk szimulálni. Ebben a példában kezdeti feltételként a korábban ismertetett modál analízis lett definiálva, mely tartalmazza a konzol megfogását az egyik végén (10.4. ábra). (Abban az esetben, ha nincs előzetes analízis, amelyben definiálva van a megtámasztás, akkor a terheléssel átellenes oldalon egy fix megfogást (Fix Support) kell alkalmaznunk.) A harmonikus terhelés a konzol másik végén, 8N nagyságú, +Y irányú erő (Force) .

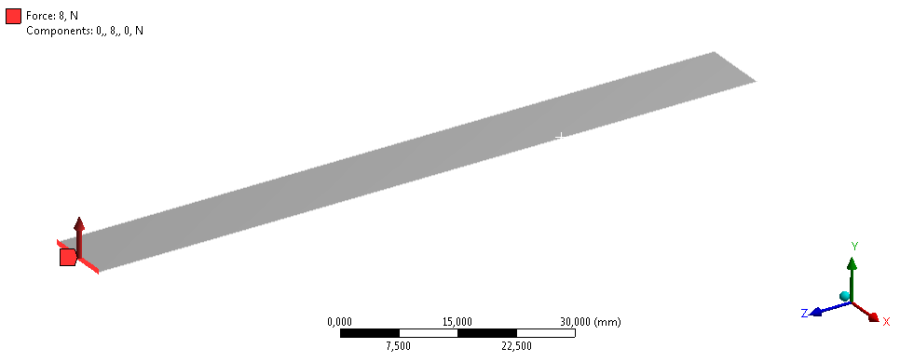
11.3. ábra - A harmonikus erőterhelés helye

A vizsgálat frekvenciatartományát 0-500Hz-re választjuk, az előzetes modál analízis alapján (1. sajátfrekvencia 164Hz), (Outline/Analysis Settings => Details/Options/Range Minimum: 0; Range Maximum: 500 Hz) .

A számolási pontok, a sajátfrekvencia környékén történő besűrítéséhez kapcsoljuk be a Cluster Result opciót, (a pontok száma: 10 (Cluster Number) ). Ehhez definiálni kell a rendszer csillapítását, amit a merevségi mátrix csillapítás (Details/Damping Control/Stiffness Coefficient) , értékének 0,0001 –re állításával adunk meg.

A szimuláció futtatása után, az eredményeket Bode-diagramon tudjuk megtekinteni, a Frequency Response/Deformation lekérdezés hozzáadásával. A lekérdezett, vagyis kimenő paraméter az erővel terhelt rúdvég Y irányú elmozdulása. A Bode diagram, így a rúdvég elmozdulásának amplitúdóját (felső, amplitúdó görbe), és a gerjesztő erőhöz viszonyított fáziskésését (alsó, fázisszög) mutatja a frekvencia függvényében.

Megjegyzés: A rendszertechnikában alkalmazott (az itt használatossal ellentétben), Bode diagram vízszintes tengelye logaritmikus osztású, melyen a körfrekvencia értékek megadása viszont lineáris. Így nagyobb tartományok átfogására is kitűnően alkalmas. Valamint az amplitúdómenettel a ki és bementi mennyiségek hányadosának hússzoros logaritmusát ábrázoljuk lineáris osztású tengelyen.

A Bode-diagramot elemezve láthatjuk, hogy a diagramon lévő rezonanciacsúcs helye megegyezik a korábbi példánál számított első sajátfrekvenciájával (10.8. ábra).

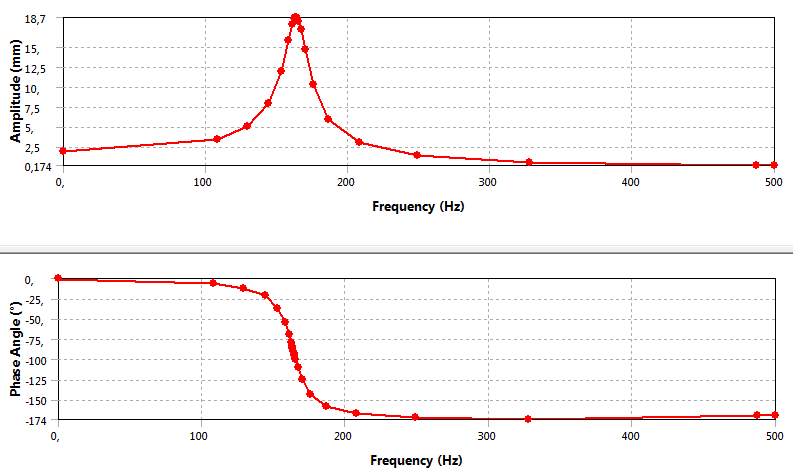
11.4. ábra - Harmonikus terhelés esetén a Bode-diagram

A normált megjelenítésnél egy diagramban láthatjuk az amplitúdó és fázismenetet. Mellette táblázatos formában találhatjuk a görbe pontjait, melyeket vágólapra másolva kimenthetünk további feldolgozás céljából (11.5. ábra).

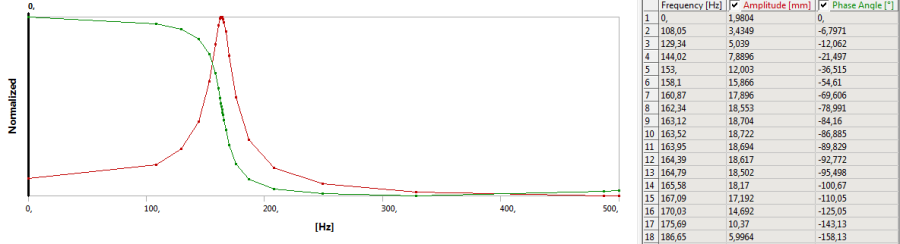
11.5. ábra - Amplitúdó és fázismenet normált diagram

11.3. Analitikus megoldás

Az előző fejezetben már vizsgáltuk a rudak szabad rezgéseit. Most vizsgáljuk meg az egyik oldalán befogott rúd gerjesztett rezgését. A végeselemes harmonikus analízis eredményének ellenőrzéseként oldjunk meg a feladatot analitikusan is [46.] . Kiindulásnak adva van egy téglalap keresztmetszetű, homogén és izotróp rúd, az alábbi paraméterekkel.

Gerjesztő erő: F ₀ = 8N.

A hasáb méretei – hossza: L=100mm, magassága: h=2mm, szélessége: b=10mm;

Anyaga – acél, Rugalmassági modulus: E=200GPa, Poisson-tényező: ν=0,3.

Határozzuk meg a rúd rezgésének nagyítási (vagy Bode) diagramját és feszültségét.

Az egyik oldalán befogott állandó keresztmetszetű prizmatikus rudat a rúd tengelyére merőleges harmonikus erő gerjeszti, amit az F=F₀⋅sin(ωt) egyenlettel írhatunk le. A rúd anyagának belső csillapítása és a levegő ellenállása csillapítják a rezgést. Így a rúd rezgését leíró (10.3) egyenlet időfüggő része (u(t)), az alábbi formában adható meg, (állandósult csillapított kényszerrezgés).

(11.1)

Az i. módus amplitúdója, (i=1,2,3…):

(11.2)

Az egyes módusokhoz tartozó saját-körfrekvencia:

(11.3)

Ahol λ az alkalmazott peremfeltételektől függő tényező. Az egyik végén befalazott rúd (y(0)=0, y’(0)=0, y”(l)=0) esetén λ értéke az első 3 sajátfrekvencia esetén rendre λ=1,875; 4,694; 7,855.

Az amplitúdó maximuma a rezonancia-körfrekvencia értékénél van:

		(11.4)
		(11.5)

A csillapítás hatására létrejövő fáziseltérést a gerjesztő erő és a rúd rezgése között a fáziskésés értékével adjuk meg:

(11.6)

Ahol:

A _0i – A gerjesztés mértékétől függő amplitúdó-állandó,

ω _0i –az egyes módusokhoz tartozó saját-körfrekvencia,

ω _ri –az egyes módusokhoz tartozó rezonancia-körfrekvencia,

φ – a fáziskésés szöge,

ξ – a csillapítási fok (0,05),

I – a keresztmetszeti tényező, (téglalap esetén I = b·h ³ /12),

E – az anyag rugalmassági modulusa,

ρ– az anyag sűrűsége,

T– a keresztmetszet területe,

A fenti egyenletek segítségével diagramon adhatjuk meg a rezgő rúd amplitúdó és fáziskésés értékét a körfrekvencia függvényében.

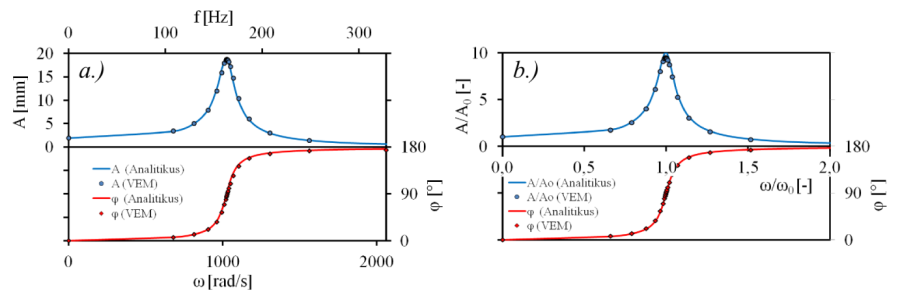
a.) abszolút értékekkel és b.) normált formában. (Csillapítási fok: 0,05)

11.6. ábra - Az analitikus és a numerikus eredmények összehasonlítása.

12. fejezet - Elektromos és mágneses szimulációk

Tartalom

12.1. Bevezetés

12.2. Példa elektromágneses szimulációra – solenoid tekercs szimulációja

12.2.1. Analitikus megoldás
12.2.2. Összefoglalás

12.3. Alkalmazási példa elektromágneses szimulációra

12.1. Bevezetés

Mágneses tér jöhet létre áramjárta vezető, vagy állandó mágnes hatására is. Mikor véges elemes szoftver segítségével mágneses szimulációról beszélünk legtöbbször egy, vagy több árammal átjárt vezető, vagy egy, vagy több állandó mágnes által létrehozott mágneses tér analízisét végezzünk. A szimuláció célja többféle lehet, pl. a szenzortechnika területén, induktív elven működő érzékelők tervezésekor a mozgó alkatrész által létrehozott induktivitás-változás detektálása, elektromágneses aktuátorok által kifejtett erő, vagy nyomaték analízise, stb. Mágneses szimulációk esetén különösen fontos szerepe van a megfelelő anyagmodellek definiálásának. Lényegi kérdés az állandó mágnesek, mágnesezhető anyagok (pl. vasmag anyaga egy tekercsben), vezetők (pl. réz kábel), valamint a rendszer elemeit körbevevő levegő modellezésének helyessége. Mágneses szimulációk során általában a kontaktok modellezése elhanyagolható tényező. A mágneses szimulációk tipikus felhasználási területei a következők:

Elektromos motorok
Transzformátorok
Indukciós hőfejlesztés
Mágnesszelep
Nagy mágneses térrel rendelkező mágnesek felhasználása
Roncsolásmentes anyagvizsgálat modellezése
Mágneses keverés
Elektrolizáló cellák
Részecske gyorsító
Orvosi és geofizikai eszközök

Mivel mágneses szimulációk során az alkatrészek közötti és körüli levegő (vagy egyéb közeg) is modellezésre kerül különösen fontos a szimmetria- feltételek használata. Ellenkező esetben a nagy elemszám meglehetősen megnöveli a számítási időt. A szimuláció során az alábbi mennyiségeket számoltathatjuk ki:

Mágneses indukció (Magnetic flux density)
Teljesítményveszteség (Power loss)
Mágneses térerősség (Magnetic field intensity)
Fluxus szivárgás (Flux leakage)
Mágneses erők és nyomatékok (Magnetic forces and torques)
S-paraméterek (S-parameters)
Impedancia (Impedance)
Minőségi tényező (Quality factor)
Induktív ellenállás (Inductance)
Visszirányú csillapítás (Return loss)
Örvényáramok (Eddy currents)
Sajátfrekvenciák (Eigenfrequencies)

12.2. Példa elektromágneses szimulációra – solenoid tekercs szimulációja

A következő példában egy árammal átjárt, vasmag nélküli, hengeres (solenoid) tekercs mágneses terét fogjuk megvizsgálni az ANSYS Workbench -ben végzett szimuláció segítségével.

A mágneses szimulációknál a testeket körülvevő környezet modellezése miatt különösen fontos a geometria egyszerűsítése, amire a legcélravezetőbb módszer a 2D-s, fél-, negyed- és nyolcad modellek alkalmazása.

A tekercset egy 19mm belső és 21mm külső átmérőjű, 50mm magasságú szilárd henger nyolcadával modelleztük.

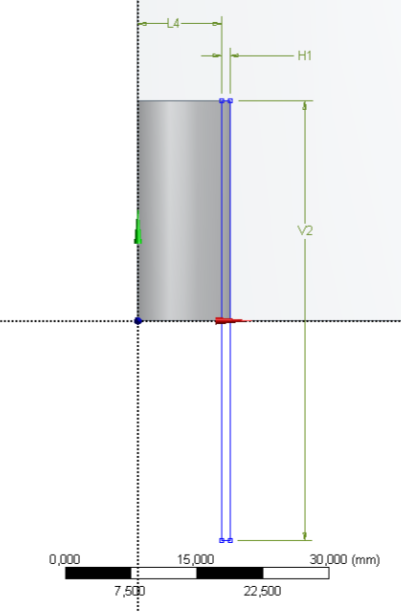
12.1. ábra - Tekercs modellezése.

A teljes tekercs megrajzolása után, a hengert körülvevő 100mm-es vastagságú környezet-modellt (levegő) kell definiálni, amelynek alakja szintén hengeres (Tools/Enclosure => Details/Shape: Cylinder) .

Ezután darabolhatjuk csak szét a modellt a szimmetriasíkok mentén. Mivel a tekercset 1/8 modellként valósítjuk meg, az elkészült teljes tekercset mindhárom fősíkkal elmetszük (Tools/Symmetry => Number of Planes: 3).

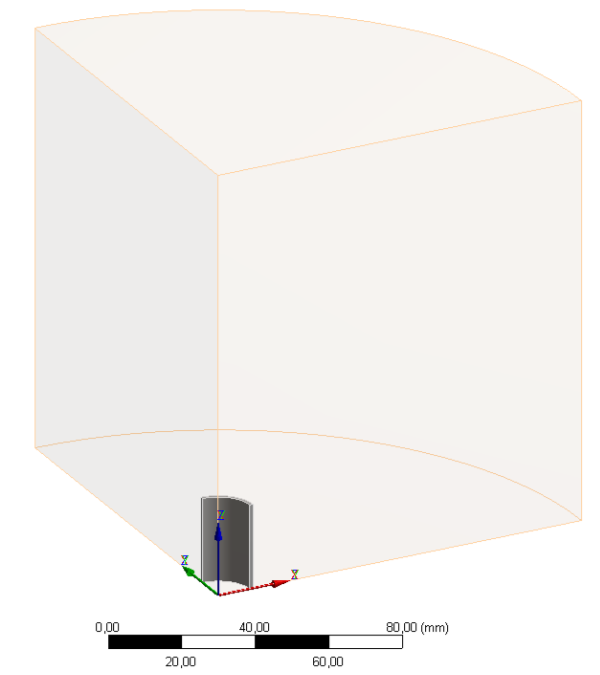
12.2. ábra - A geometriai modell a környezettel.

Mivel itt az alkatrészek közötti mechanikai kontaktok nem játszanak szerepet, a geometriában lévő alkatrészeket egybe kell kapcsolni. Ezt a modellfa utolsó, testek (Body) sorában lévő alkatrészek kijelölésével, és a jobb gombos menü egy alkatrészbe tömörítés (Form new Part) parancsával lehet elérni (12.3. ábra).

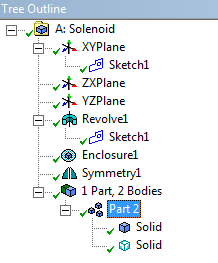
12.3. ábra - A testek egy alkatrésszé alakítása.

A geometria elkészítése után lépjünk át az anyagkönyvtárba és rendeljük hozzá a szimulációnkhoz egy Copper Alloy anyagmodellt. A levegő (Air) anyagmodell, alapértelmezetten a szimulációs könyvtár része.

A szimulációs környezetbe való belépés után rendeljük hozzá az előre definiált anyagmodelleket az egyes testmodellekhez. Ellenőrizzük, hogy a környezethez alapértelmezetten hozzá van-e rendelve a levegő.

Az eredmények megjelenítéséhez szükséges egy konstrukciós vonal (Path) definiálása. Ezt a tekercs tengelyében hozzuk létre, amely túllóg a tekercs magasságán (összesen 50mm hosszú). Az 1. és 2. címke között futó konstrukciós vonalat szemlélteti 12.4. ábra.

12.4. ábra - Konstrukciós geometria definiálása solenoid tekercs tengelyében

A 3 definiált szimmetria síkot a 12.5. ábra szemlélteti.

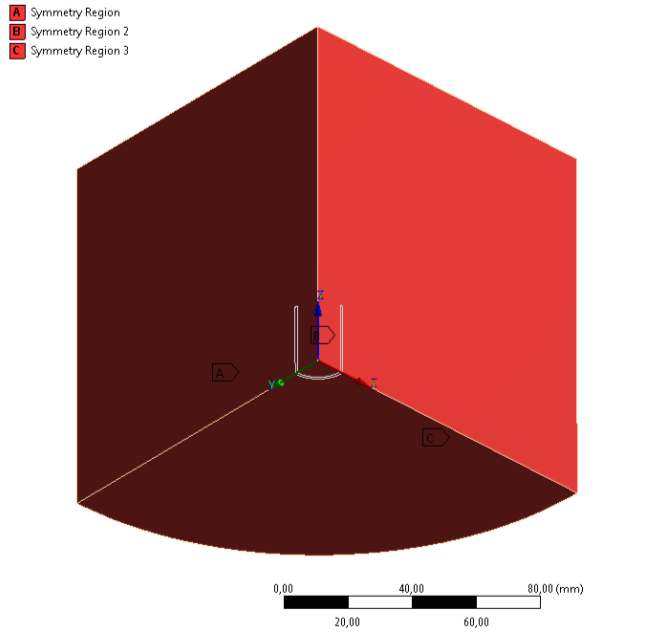
12.5. ábra - Szimmetria síkok a solenoid tekercs esetében

A hálózásnál fontos, hogy a tekercs és közvetlen környezete megfelelően kicsi elemméretet tartalmazzon a pontos eredmény érdekében. Ennél a példánál három hálósűrítési beállítást használtunk. A globális beállításokat, egy a tekercsen alkalmazott elemméret meghatározást (Sizing) és egy gömbfelületen belüli (Sphere of influence) hálósűrítést (12.6. ábra).

A globális beállításokat az (Outline/…/Mesh => Details/Sizing/Use Advanced Size Function/On:Fixed) opció bekapcsolásával, az elemméret alsó (Min Size: 0,5mm ) és felső (Max Face Size: 10mm ) korlátjával és a növekményi faktorral (Growth Rate: 1,1 ) adjuk meg.

A tekercset jelentő testmodell elemméretét, egy Sizing funkció hozzáadásával állítjuk 0,5mm-re.

A levegő modelljének lokális hálósűrítését egy újabb Sizing parancs hozzáadásával, és a Sphere of influence opció beállításával érjük el. A gömb sugarát 30mm-re, a benne található elemek méretét 1mm-re állítjuk.

12.6. ábra - Hálósűrítési beállítások a solenoid tekercs szimulációja során

A beállításoknak köszönhetően a véges elemes háló mérete egyenletesen csökken a tekercstől a környezet széle felé. A háló a környezet esetén tetra elemeket, míg a tekercsként szolgáló test esetén hexa elemekből áll.

A szimuláció során az alábbi peremfeltételek megadása szükséges (12.7. ábra):

Mágneses fluxus párhuzamossága (Magnetic Flux Prallel) - a mágneses fluxussal párhuzamos falak megadása a külső felületeken (Open Domain) és az oldalsó szimmetriasíkok mentén ( Symmetry:XYPlane , és Symmetry:YZPlane , amennyiben Y a tengelyvonal). Az alsó szimmetriasíkot nem kell kijelölni, mivel arra merőlegesek az erővonalak. Megjegyzés: a felületek kijelölésénél, használjuk a modellfában lévő előre definiált kiválasztásokat (Named Selections) .
Vezető test (Source Conductor) – az áramvezető anyag, a tekercset modellező test kijelölése.
Áramerősség (Current) - a vezető tekercsen átmenő áram (500mA) belépési felületének kijelölése a tekercs egyik végén.
Potenciál (Voltage) – A tekercs másik, (az árambevezetéssel ellentétes) végén a potenciál (föld-pont: 0mV) megadása szükséges.

12.7. ábra - Peremfeltételek a solenoid tekercs szimulációja során.

A szimuláció futtatása után, kérdezzük le a teljes mágneses térerősséget (Magnetic Field Intensity) a teljes testre vonatkoztatva (12.9. ábra), és az Y irányú (tehát tengely irányú) mágneses térerősség értékét a tekercs tengelyében definiált konstrukciós egyenes mentén, (12.8. ábra).

Ha az erővonalak irányát is szeretnénk látni a tekercs környezetében, a mágneses térerősséget vektorosan célszerű megjeleníteni (12.9. ábra, b, c). Ahogy az alábbi ábrákon látható a térerősség eloszlása és a vektorok eloszlása megfelel a várakozásainknak és előzetes ismereteinknek.

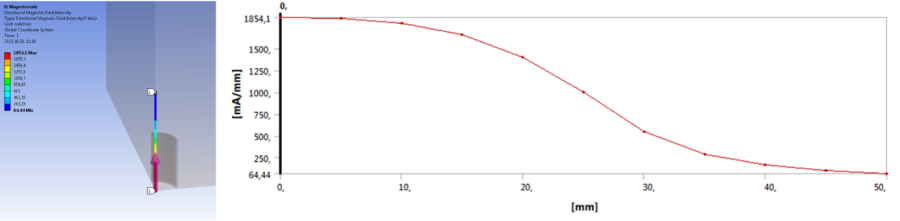
12.8. ábra - A mágneses térerősség alakulása a konstrukciós geometria mentén

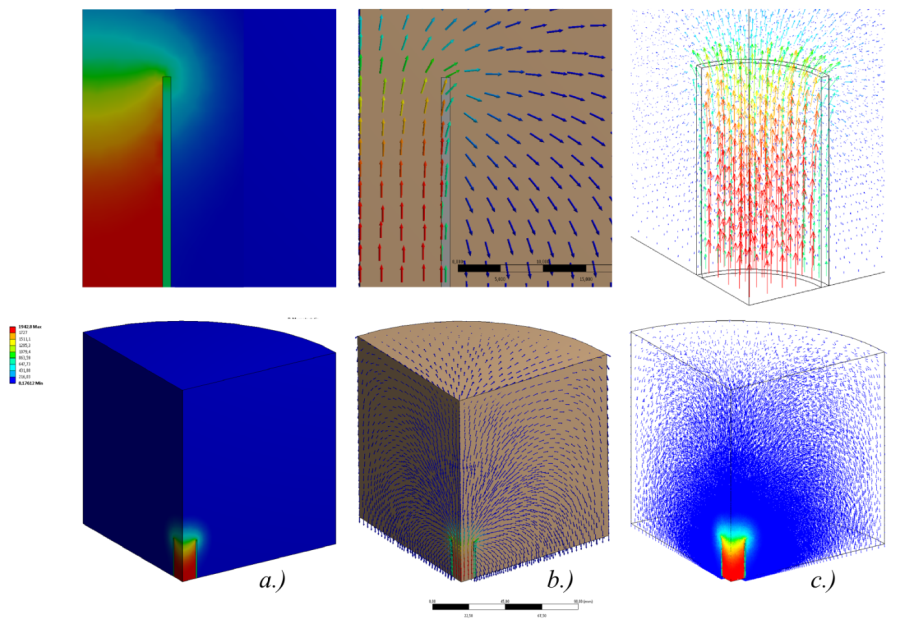
12.9. ábra - A mágneses térerősség bemutatása a tekercs környezetében: a.)színsávokkal, b, c.) vektorokkal.

Hasonló módon kérdezzük le a mágneses indukció (Magnetic Flux Density) értékét a teljes modellre és a konstrukciós vonal mentén. Látható, hogy a mágneses indukció nagysága a vonal mentén hasonló jelleggel változik, mint a mágneses térerősség esetében, mivel a légmagos tekercsben a permeabilitás értéke konstans, a két diagram csak a skálázásában tér el egymástól.

Lehetőségünk, van egy felületen áthaladó fluxus lekérdezésére (Magnetic Flux Probe) . A tekercs negyed keresztmetszetére kapott eredmény: 1,82⋅10^-4 mWb, (12.10. ábra).

A tekercs induktivitását (Inductance) egy egyszerű lekérdezéssel kapjuk meg. Ez jelen példában 0,032mH.

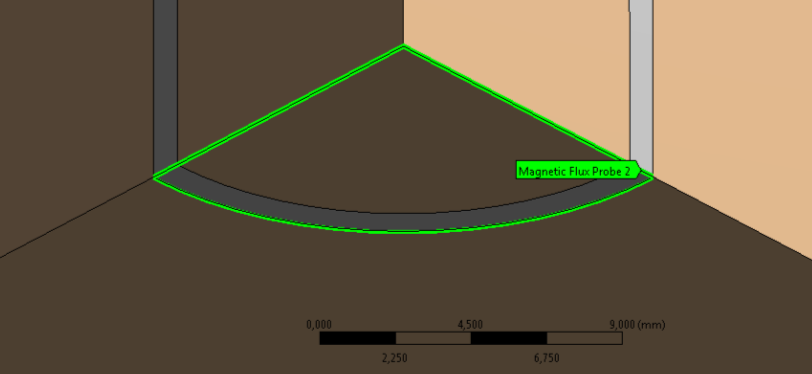
12.10. ábra - Egy felületen áthaladó fluxus lekérdezése.

12.2.1. Analitikus megoldás

Határozzuk meg egy homogén közegben lévő hengeres tekercsben (Szolenoid) folyó állandó áram által keltett mágneses térerősséget, a tér valamely P pontjában. Oldjuk meg a feladatot a tekercs tengelyére, az alábbi adatokkal.

A tekercs hossza: L = 50 mm, sugara: R = 10 mm, menetszáma: N = 100.

A tekercsen átfolyó áram erőssége: I = 1 A.

Első lépésben, határozzuk meg egy menet által keltett térerősség H értékét a tekercs tengelye mentén a menettől mért távolság függvényében a Biot-Savart törvény segítségével.

(12.1)

A tengelyvonalon fekvő ponthoz tartozó r helyvektor merőleges az elemi vezetékhossz d l érintő vektorával, tehát a szorzatuk abszolút értékére felírhatjuk:

(12.2)

Ezzel a térerősség abszolút értéke:

(12.3)

A térerősség-vektor radiális komponensei kioltják egymást, így a tengelyirányú komponens

(12.4)

Hengeres tekercs esetén ezt kell összegeznünk a tekercs teljes hosszára, ahol az elemi hosszra n = N⋅dx/L számú menet jut.

(12.5)

A tekercs tengelye mentén a mágneses térerősség abszolút értéke

(12.6)

Ahhol az I⋅N/L szorzat a szolenoid tekercsek belsejében lévő mágneses tér közelítő képlete.

[47.]

12.2.2. Összefoglalás

Az alábbi diagramon (12.11. ábra) láthatjuk a numerikus, valamint a közelítő és pontos analitikus számolás eredményét. A diagram csak a tekercs felét mutatja, amely 25mm-nél ér véget, az origó pedig a tekercs közepét jelenti.

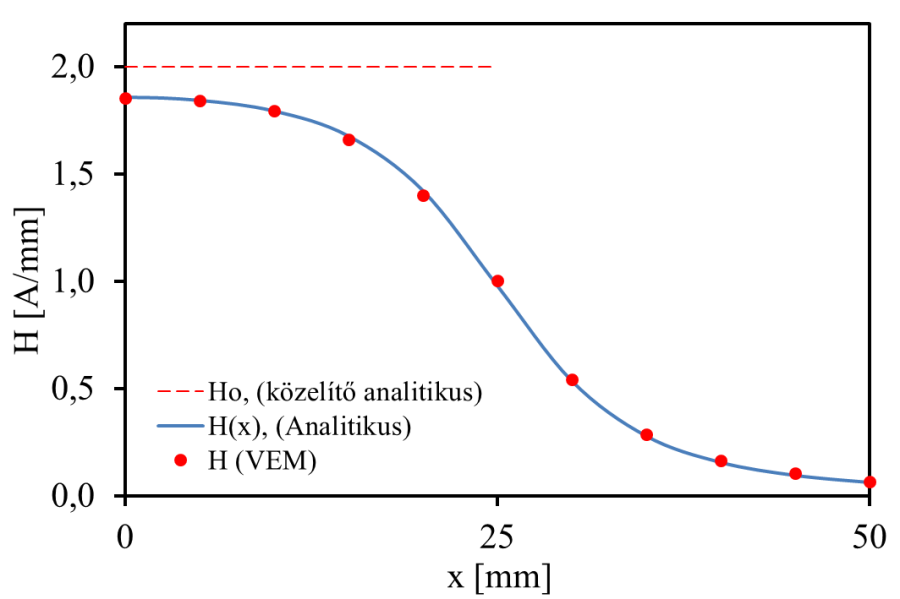
Az analitikus H(x) és végeselem H (VEM) számolás eredményeinek összehasonlítása. Ho=IN/L közelítő értéket mutatja, (a tekercs széléig jelölve).

12.11. ábra - Az analitikus H(x) és végeselem H (VEM) számolás eredményeinek összehasonlítása. Ho=IN/L közelítő értéket mutatja, (a tekercs széléig jelölve).

Az analízis elvégezve a környezet (levegő) különböző vastagságaival, azt találjuk, hogy jelentősen befolyásolja az eredményt. A tekercs sugarával azonos nagyságrendű levegőburok esetén a numerikus analízis hibája 30% feletti, (Táblázat 12.1).

12.1. táblázat - A környező levegőréteg vastagságának hatása a tekercs középpontjában számolt mágneses térerősségre.

Környezet vastagsága [mm]	H [A/mm]	Hiba [%]
5	1,166	37,2
25	1,777	4,3
40	1,839	1,0
100	1,854	0,2
Analitikus megoldás: 1,857 A/mm

12.3. Alkalmazási példa elektromágneses szimulációra

Az alábbiakban egy árammal átjárt tekercs és a benne lévő vasmag mágneses terének szimulációját mutatjuk be. A 3D-s negyed-modellként elkészített feladatban meg tudjuk majd figyelni a létrejövő mágneses tér jellemzőit, illetve a tekercs feletti tárcsára ható erő nagyságát. Az analízist az ANSYS Workbench végeselem programban végezzük el, melynek Magnetostatic szimulációját kell hozzáadnunk a projektünkhöz.

Minden elektromágneses és mágneses szimuláció estén különösen figyelni kell a geometria felépítésénél arra, hogy megfelelő méretű környezetet építsünk fel az alkotó alkatrészek köré, hogy a levegőben futó mágneses erővonalak is számításra kerüljenek.

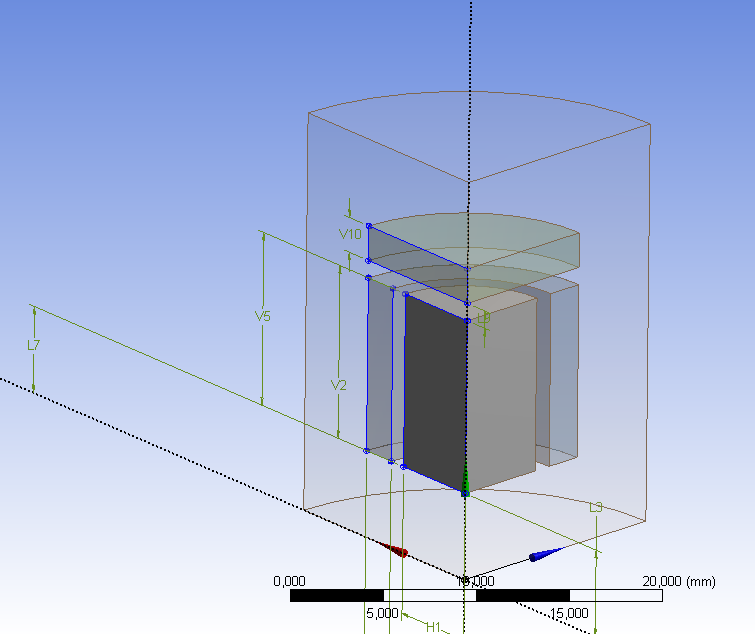
12.12. ábra - Az elektromágnes geometriai modellje.

A vasmag, tekercs és a fedőlap geometriáját 90˚-os forgatással hoztuk létre, ahogy a 12.13. ábra is mutatja, (zöld színnel jelölt testek). Így egyből negyed modellt kapunk. (Megjegyzés: mivel több testet tartalmazó geometriát modellezünk, az újonnan létrehozott testeket „fagyasztott módban” (Add Frozen) kell elkészíteni.

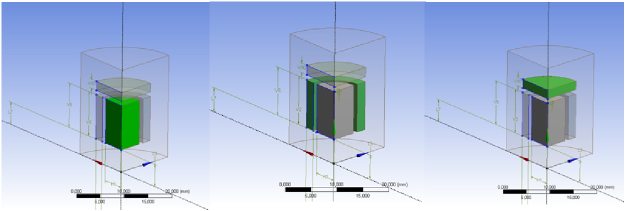
12.13. ábra - A geometriai modell alkotói. Balról jobbra haladva: belső vasmag, tekercs, felső vasmag.

A környezetet egy olyan testtel kell modellezni, amely adott (lehetőleg egyenletes) távolsággal túlnyúlik a szimulációban részt vevő többi test szélétől, nem tartalmazza a többi test térfogatát és a levegő fizikai és elektromos-mágneses jellemzőivel rendelkezik.

A tekercset körülvevő környezetet (Tools/Enclosure) a többi test szélétől 5mm-es túlnyúlással hozunk létre, ugyanazokkal a szimmetria síkokkal, amik már definiálva vannak. Természetesen a szimmetria síkok irányában nincs túlnyúlása a környezetnek. A környezetet modellező geometria alakja hengeres.

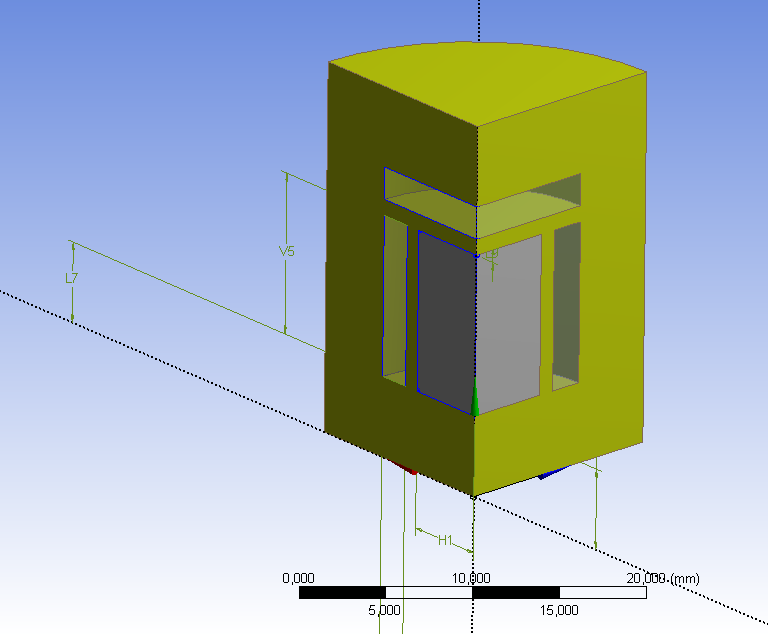
12.14. ábra - A környezetet geometriai modellje (sárga színű test)

Az elektromos-mágneses szimulációknál fontos, hogy a szilárd testek (Solid Bodies) egy alkatrészbe (Part) legyenek összefogva. Ezt a testek modellfában történő kijelölése után, a jobbgombos menüből elérhető új alkatrész készítése (Form New Part) paranccsal végezhetjük el. Ebben az esetben a testek közötti kapcsolatok (Contacts) nem kerülnek számításra.

A szimuláció során 3 féle beépített anyagot használunk, (Új anyag definiálása esetén csak az elektromágneses tulajdonságaikat kell definiálni). A felhasznált három anyag, és azok elektromágneses tulajdanoságaik a következők:

levegő (Air)
- Izotróp relatív permeabilitás (Isotropic Relative Permeability) : 1 [-],
réz ötvözet (Copper Alloy)
- Izotróp relatív permeábilitás (Isotropic Relative Permeability) : 1 [-],
- Izotróp fajlagos ellenállás (Isotropic Resistivity) : értéke hőmérséklettől függően megadva a következő:
  - 0˚C-on 1,548·10 ^-7 Ohm·m,
  - 20˚C-on 1,694·10 ^-7 Ohm·m,
  - 100˚C-on 2,277·10 ^-7 Ohm·m,
szerkezeti acél (Structural Steel)
- Izotróp relatív permeábilitás (Isotropic Relative Permeability): 10000 [-],
- Izotróp fajlagos ellenállás (Isotropic Resistivity): 1,7·10^-7 Ohm·m.

Az anyagkönyvtárba (Engineering Data) belépve, rendeljük ezeket a szimulációnkhoz, majd átlépve a szimulációs környezetbe, rendeljük hozzá őket a megfelelő testekhez. A levegő anyagot a környezethez, a szerkezeti acélt a belső vasmag és a fedőlap modellezésénél, míg a réz ötvözetet a tekercs modellezésénél használjuk.

A végeselemes háló elkészítésekor 1mm-es elemméretet alkalmaztunk, a környezet esetén tetra (tetraéder) elemeket, míg a vasmag, tekercs és fedőlap esetén hexa (tégla) elemeket használunk. A hálózott modellt a 12.15. ábra mutatja.

12.15. ábra - A véges elemes háló.

A szimuláció során alkalmazott terheléseket és peremfeltételeket a 12.16. ábra mutatja. Ezek alapján a környezeti levegő külső határaira olyan kényszert alkalmaztunk, mely definiálja, hogy a kijelölt felületekkel csak párhuzamos erővonalak húzódhatnak (Magnetic Flux Parallel) . A réz tekercset modellező testet vezető forrásként (Source Conductor) definiáltuk és 1000mA nagyságú áram (Current) átvezetését írtuk elő. (Megjegyzés, az áram be- és kivezetését nem szükséges külön definiálni.) Valamelyik pont potenciálját (Voltage) meg kell adni, esetünkben az árambevezetés helyén adjunk meg 0V-ot.

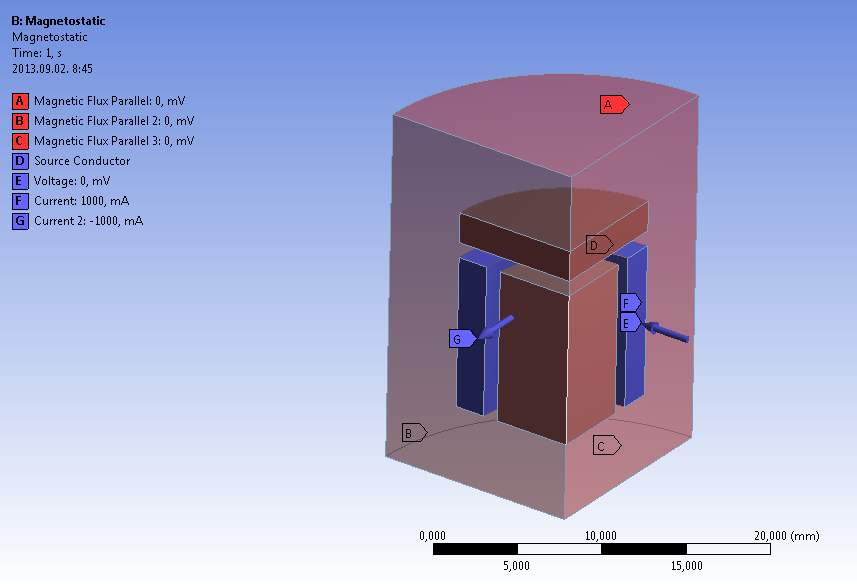
12.16. ábra - A terhelési modell komponensei elektromágneses szimuláció esetén

Az eredményeket tekintve láthatjuk, hogy a mágneses erővonalak a várakozásainknak megfelelő irányba haladnak. Ezt szemlélteti a 12.17. ábra és a 12.18. ábra, ahol a mágneses indukció (Magnetic Flux Density) és a mágneses térerősség (Magnetic Field Intensity) látható. Ebben az esetben érdemes az eredmények megjelenítését vektoros formában értékelni.

12.17. ábra - A mágneses indukcó eredményei vektoros formában

12.18. ábra - A mágneses térerősség eredménye vektoros formában

A következő, 12.19. ábra mutatja az áramsűrűséget (Current Density) szintén vektoros formában. Az eredmény mA/mm² mértékegységben látható.

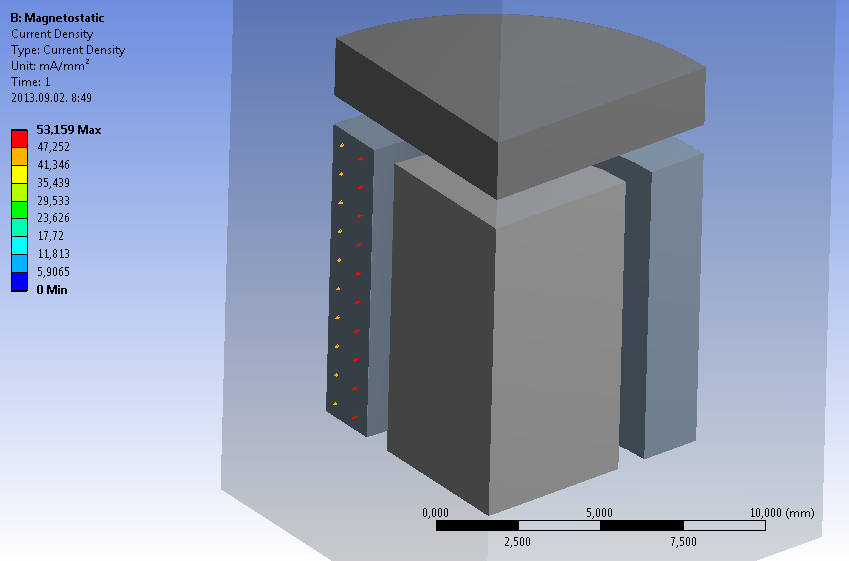
12.19. ábra - Az áramsűrűség vektoros formában

A következő ábrán megfigyelhetjük az áramjárta tekercs erőhatását a szerkezeti acél fedőlapra (12.20. ábra). Mivel a fedőlapra –Y irányú vonzóerő lép fel, az eredmény negatív előjelű, tehát a fedőlap tekercshez közelebb eső részén nagyobb az erőhatás abszolút értéke (kb. 2 nagyságrenddel), mint a fedél tekercstől távolabb lévő részén.

12.20. ábra - Y irányú erőhatás a fedőlapra [N]

13. fejezet - Termikus szimuláció

Tartalom

13.1. Áttekintés

13.2. A termikus szimulációk beállításai

13.3. Terhelések tranziens termikus analízisek során

13.3.1. Hőmérséklet kénszer
13.3.2. Hőátadás
13.3.3. Hősugárzás
13.3.4. Hőáram
13.3.5. Hőáramsűrűség
13.3.6. Belső hőtermelés
13.3.7. Tökéletes szigetelés

13.4. Példa hőtani szimulációra –hűtőborda hőmérsékleti viszonyainak vizsgálata

13.5. Analitikus megoldás

Hőtani szimulációk során a rendszerre, vagy annak egy komponensére ható hőtani terhelés hatására létrejött állapotot vizsgálunk.

13.1. Áttekintés

A hőtani szimulációknak két nagy csoportját különböztethetjük meg; az állandósult hőtani szimulációkat (Steady-state Thermal Analysis) , és az időben változó hőtani szimulációkat (Transient Thermal Analysis) . Előbbi esetében állandó értékű hőterhelés hatására (elvileg végtelen idő eltelte után) kialakuló állandósult állapot szimulálható, tehát a folyamatot nem tudjuk áttekinteni, csak az egyensúlyi végállapotot. Utóbbi esetében azonban a hőterhelés, (ami lehet időben változó is) hatására kialakuló folyamat is nyomon követhető, és a meghatározott idő múlva fennálló aktuális állapot megtekinthető. A hőtani terhelések és peremfeltételek meghatározása gyakorlatilag ugyanúgy történik, csak a végeredmény esetében van különbség abban, hogy a kialakult egyensúlyi állapot, vagy a kérdéses időpillanatban fennálló állapot kerül megjelenítésre. A két típus számítási igénye természetesen eltérő, az időben változó szimuláció hosszabb idő alatt fut le.

A két fajta szimulációt sok esetben egymás után futtatjuk le. Egyik jellemző eset, hogy egy állandósult termikus analízist felhasználunk egy utána következő tranziens hőtani szimuláció kezdeti feltételeként. Másik eset, mikor egy tranziens hőtani szimuláció utolsó lépéseként alkalmazunk egy állandósult hőtani analízist, ezzel csökkentve az összes tranziens hőtani terhelés hatását.

Az állandósult termikus analíziseket olyan hőtani terhelések hatására kialakuló állapot meghatározására használjuk, amelyek időben nem változnak. A következő típusú terheléseket használhatjuk (ha megfelelnek a fenti kritériumnak): hőmérséklet, hőáramlás, hősugárzás, hővezetés, hőáram-sűrűség illetve állandó belső hőfejlődés.

Állandósult termikus analízisek esetén használhatunk lineáris és nem lineáris hőtani anyagtulajdonságokat is. Előbbi esetében konstans anyagtulajdonságokat használunk az anyagmodell definiálásához, míg utóbbi esetben ezek a tulajdonságok hőmérsékletfüggőek. Legtöbb esetben azonban az anyagtulajdonságok függenek a hőmérséklettől, így a nemlineáris anyagmodell a jellemző.

A tranziens termikus szimulációk felhasználási területe igen széles. Elemezhető a segítségével például egy elektromos eszköz használat közbeni hő fejlődése során kialakuló hőmérsékleti eloszlása, a hűtőbordák működése, vagy akár egy oltási folyamat hatása.

A hőtani szimulációkat, de főként a tranziens termikus analíziseket nagyon jól lehet használni olyan statikai szimulációk kezdeti feltételeként, ahol a hőmérséklet, vagy a hőmérséklet változása befolyásolja a szerkezet viselkedését. Különösen fontos ez olyan esetekben, ahol a hőmérséklet változása nagy mértékű, és a használat során olyan esetek is előfordulnak, amikor extrém terhelés lép fel (pl. műszaki probléma miatt). Ahogyan az állandósult termikus analíziseknél is itt is lehet lineáris és nemlineáris anyagmodelleket alkalmazni. A termikus anyagtulajdonságok, mint pl. a hővezetési tényező (Thermal Conductivity) , fajhő (Specific Heat) , hőátadási tényező (Convection Coefficient) hőmérsékletfüggő viselkedése nemlinearitást okoz, amely esetén a pontos eredmény eléréséhez olyan iteratív megoldásra van szükség.

13.2. A termikus szimulációk beállításai

Hőtani szimuláció esetében első lépésként definiálni kell a megfelelő anyagtulajdonságokat.

Az alábbi anyagjellemzőket szükséges megadni:

hővezetési tényező (Thermal Conductivity) ,
sűrűség (Density) ,
fajhő (Specific Heat) .

A hővezetési tényező lehet izotróp (minden irányban azonos), vagy ortotróp (merőleges koordinátarendszerben irányonként eltérő), valamint minden érték lehet konstans, vagy hőmérsékletfüggő.

A geometria kialakításában nincsenek különleges kritériumok a hőtani szimulációk esetén, 3 és 2 dimenziós geometria alkalmazására is van lehetőség.

Alkatrészek közötti kapcsolatok közül csak a kontakt típusú kapcsolatok használhatók, az esetlegesen definiált csukló jellegű (Joint) és rugó típusú (Spring) kapcsolatok nem fognak részt venni a szimulációban. A hőtani szimulációk során az alkatrészek közötti kontakt nem változik, tehát a zárt érintkező felületek zártak maradnak, a nyitott felületek nyitottak maradnak. Az egymáshoz zártan illeszkedő felületek között (ha a hővezetési tényező kellően nagy) a hőtani ellenállás minimális. Amennyiben nem így van, kézzel is be lehet állítani a hővezetést a két felület között.

Termikus analíziseknél általában nem kell semmiféle specifikus hálózási módot használni, ebben az esetben ugyanis kevesebb jelentősége van a háló finomságának, mint például egy jelentősebb alakváltozással járó statikai analízisnél. Arra azonban mindenképpen érdemes figyelni, hogy ha a termikus analízisünk egy későbbi statikai analízis kezdeti feltétele lesz, akkor olyan hálót használjunk, amely megfelel a későbbi szimulációnak. (Ansys programban ugyanazt a hálót lehet csak használni.)

Tranziens termikus szimulációk esetén az Ansys programban a következő szabályozókat (Controls) érdemes beállítani:

Lépések (Step Control) – ezt a beállítást a következőkre használhatjuk:
- tranziens analízis időintervallumának beállítására,
- az egyes lépésközök nagyságának beállítására,
- több lépcsőből álló terhelések definiálásához, amennyiben erre szükség van.
A több lépcsőben megadott terhelésre abban az esetben van különösen szükség, amikor az anyagtulajdonságok hőmérsékletfüggése gyorsan változik. Ilyenkor a terhelést kis lépésekkel növelve biztosítható, hogy a szimuláció konvergens legyen. Akkor is szükséges a több lépcsős terhelés-definiálás, amikor az eredményeket kis időtartományokban szeretnénk lekérdezni.
Kimeneti beállítások (Output Controls) - ezek a beállítások lehetőséget adnak arra, hogy beállítsuk, a folyamat mely időpillanataiban szeretnénk az eredményeket vizsgálni, azonban nem lehetséges az összes közbülső időpontra lekérdezni az eredményeket. A túl sok időpontra lekérdezett eredmények irreális mértékben megnövelik az eredményfile méretét, így nehezen kezelhetővé válik a szimuláció. Ha mégis előfordul ez az eset mindenképpen érdemes a lekérdezési időpontokat jelentősen csökkenteni.
Nemlinearitás szabályozói (Nonlinear Controls) – itt van lehetőségünk változtatni a konvergencia kritériumokon (Convergence Criteria) és néhány a megoldási folyamathoz kapcsolódó beállítást.
Adatkezelési beállítások (Analysis Data Management) – lehetőséget ad arra, hogy bizonyos eredmény fájlokat kimentsünk, így más szimulációkban is felhasználhatók.
Szükséges kezdeti feltétel (Initial Condition) tranziens termikus analízisek során, hogy definiáljuk a 0. időpillanatban a hőmérséklet-eloszlást. Az ANSYS-ban a kezdeti feltétel alapértelmezetten 22°C (71.6°F) értékű egyenletes hőmérséklet. Ha nem szobahőmérséklet a kezdeti állapot, akkor ezt itt kell beállítani. Pl. ha egy felhevített tárgy hűlési folyamatát szeretnénk vizsgálni hideg vízben. Kezdeti feltételként természetesen nem csak egy egyenletes hőmérsékletet lehet megadni, hanem egy korábban elvégzett állandósult termikus analízis végeredményét is. Pl. egy öntőformában lévő olvadt fém megszilárdulási folyamatának elemzése, melyet előzetesen állandósult termikus analízissel vizsgáltunk.

13.3. Terhelések tranziens termikus analízisek során

A következő alapvető terheléseket alkalmazhatjuk az időfüggő hőtani szimulációk során:

Hőmérséklet (Temperature) ,
Hőátadás (Convection) ,
Hősugárzás (Radiation) ,
Hőáramlás (Heat Flow) ,
Hőáramsűrűség (Heat Flux) ,
Belső hőtermelés (Internal Heat Generation,)
Tökéletes szigetelés (Perfectly Insulated) .

Minden terhelés definiálható konstans értékként, időben változókként, amit akár táblázatosan akár függvény szerint is megadhatunk. Az alábbiakban bemutatjuk ezeknek a terheléseknek a lehetőségeit:

13.3.1. Hőmérséklet kénszer

Használható 3 és 2 dimenziós szimulációk során is, annyi megkötéssel, hogy 2D-ben csak síkfeszültség (Plane Stress) és tengelyszimmetrikus (Axisymmetric) típusú modelleknél alkalmazható. Hőmérsékletterhelést definiálhatunk egy, vagy több felületre, élre, pontra, vagy akár egész testekre. Ha egy hőmérsékletterhelésen belül definiáljuk a különböző területeket (akár kapcsolódnak egymáshoz akár nem) azonos és egyenletes eloszlású hőmérséklet lesz minden kijelölt területen. Lehet azonban definiálni olyan hőmérsékletterhelést is, amely helytől függően változik, ebben az esetben pl. egy koordináta rendszer tengelye mentén, akár egy függvény szerint is meghatározhatjuk a nem egyenletes eloszlást.

13.3.2. Hőátadás

Olyan hőátadást jelent, amely egy, vagy több (sík, vagy ívelt) felület és a környező közeg (levegő, folyadék) között valósul meg. Ugyanazon geometriai típusok esetében használható, mint a hőmérséklet kényszer. Meg kell határozni a közeg és a felületek hőmérsékletét, valamint a kettő közötti hőátadási tényezőt. A környezeti közeg (folyadék) hőmérséklete egyenletes eloszlású, és a kapcsolódó felülettől távolabbi pontra vonatkozik. A hőátadási tényező a külső környezetnek (folyadék) a kapcsolódó felületre vonatkozó értéke, mely függ a felület nagyságától és geometriájától, valamint a környező közeg áramlási viszonyaitól. Lehetőség van idő- és hőmérsékletfüggő hőátadási tényező definiálására is. A környezet hőmérsékletét is definiálhatjuk időfüggő tényezőként.

A hővezetés során bekövetkező hőátadást a következőképpen számíthatjuk ki (Newton törvény szerint): q/A=h(t_s-t_f), ahol q/A a hőáram sűrűség a felületen, h a hőátadási tényező, t_s a felület hőmérséklete és t_f a környezet (folyadék) hőmérséklete.

Amikor a környezet hőmérséklete meghaladja a felület hőmérsékletét, akkor a tárgy felé energia áramlás következik be, amikor a felület hőmérséklete meghaladja a környezet hőmérsékletét akkor a test energiát veszít. Egyszerre több felület és a környezet között is végbemehet a hőáramlás (függetlenül attól, hogy a felületek kapcsolódnak-e egymáshoz).

13.3.3. Hősugárzás

A hősugárzás elektromágneses hullámokkal megvalósuló energiaátvitel, melyhez nem szükséges közvetítő közeg jelenléte. Mivel a sugárzás által okozott hőáram a hőmérséklet 4. hatványának függvénye, ezért a hősugárzást tartalmazó analízis erősen nemlineáris. Az analízisben a hősugárzás vonatkozhat egy 3D-s modell felületére, vagy egy 2D-s modell élére. Ilyen terhelés esetén meg kell határozni a sugárzó képességet (Emissivity) , amely a felület által kibocsátott sugárzást az ideális fekete test azonos hőmérsékleten kibocsátott sugárzásának arányaként határozza meg. Emellett definiálni kell a környezet hőmérsékletét.

13.3.4. Hőáram

A hőáram adott geometrián időegység alatt áthaladó energiamennyiséget határoz meg. Csak 3D-s szimulációk és 2D-s tengelyszimmetrikus és síkfeszültség típusú analíziseknél használható. A geometria típusa szerint 3 csoportra oszthatjuk a hőáramlási terheléseket:

Felületen ható hőáramlás (Face Heat Flow Rate),
Élen ható hőáramlás (Edge Heat Flow Rate),
Pontszerűen ható hőáramlás (Vertex Heat Flow Rate).

Egy adott felületen áthaladó hőáramlást határoz meg. A felület lehet sík, vagy ívelt. Pozitív hőáramlásnak tekintjük a felület felé irányuló hőáramlást. Energia per időegységként definiálhatjuk. Amennyiben több felületet választunk ki, a megadott hőáramlás érték megoszlik ezek között. Amennyiben a felület a szimuláció közben növekszik a teljes terhelés változatlan marad, azonban a hőáram-sűrűség (mely tulajdonképpen a hőáramlás felületre vonatkoztatott mennyisége) természetszerűleg csökkenni fog. Ha olyan felületeket választunk ki a hőáramlás definiálásához, amely különböző testekhez tartozik, akkor az értelmezhetetlen lesz, és a véges elemes szoftver figyelmen kívül fogja hagyni.

Élen ható hőáram: Gyakorlatilag ugyanazok vonatkoznak erre a terhelésre, mint a felületre vonatkoztatott esetében, annyi különbséggel, hogy itt egy élen hat az áramlás, tehát a hőáram sűrűséget az adott hosszra kell vonatkoztatni, nem pedig a felületre.

Pontszerűen ható áramlás: Szintén ugyanazok vonatkoznak rá, mint a fenti 2 geometrián ható háramlásra, annyi különbséggel, hogy ebben az esetben a hőáram sűrűség nem definiálható a pontszerű geometria miatt.

13.3.5. Hőáramsűrűség

A hőáram-sűrűség egységnyi geometrián időegység alatt áthaladó energiamennyiséget határoz meg. 3D-s szimulációk és 2D-s tengelyszimmetrikus és síkfeszültség típusú analízisek esetében használható. Egy, vagy több sík, vagy ívelt felületre lehet definiálni. A hőáramsűrűség akkor pozitív irányú, ha a test belseje felé mutat. Ekkor a test energiát vesz fel. A hőáramsűrűséget energia per időegység per felületként adjuk meg. Ha több felületet jelölünk ki, akkor mindegyik esetében ugyanaz az érték valósul meg. Ha a meghatározott felület növekszik a szimuláció folyamán, akkor a teljes terhelés (hőáramlás) növekszik, de a hőáramsűrűség állandó marad.

13.3.6. Belső hőtermelés

Egyenletes eloszlású hőtermelést határoz meg a testben. 3D-s szimulációk és 2D-s tengelyszimmetrikus és síkfeszültség típusú analízisek esetében alkalmazható. Pozitív hőtermelésről akkor beszélünk, ha a test energiája növekszik (tehát a hőmérséklete is növekszik). A hőtermelést energia per idő per térfogatként határozhatjuk meg. Ha több testet jelölünk ki a hőtermeléshez, akkor mindegyik test ugyanazzal a hőtermelési értékkel fog rendelkezni. Amennyiben a test térfogata növekszik a szimuláció során a teljes termelt energia mennyisége is növekszik, (mivel az térfogategységre vonatkozik).

13.3.7. Tökéletes szigetelés

Ez a lehetőség gyakorlatilag a „nincs terhelés” feltételt jelenti. 3D-s szimulációk és 2D-s tengelyszimmetrikus és síkfeszültség típusú analízisek esetében alkalmazható. A kiválasztott geometriai elemekre (elsősorban felületekre) nem hatnak a szimuláció során megadott hőterhelések. A szigeteléssel ellátott felületeken 0 hőáramlás megy végbe. Akkor hasznos ez az opció, amikor egy geometriai modell adott hőterheléséből csak néhány felület van kivonva (Pl. egy földelt terület).

Ha egy geometrián belül több, akár különböző testekhez tartozó felületre van definiálva a szigetelés, természetesen mindegyik rendelkezik majd ezzel a tulajdonsággal.

13.4. Példa hőtani szimulációra –hűtőborda hőmérsékleti viszonyainak vizsgálata

Az alábbi egyszerű példában egy 100mm*10mm*2mm nagyságú hasáb, mint hűtőborda hőtani szimulációját láthatjuk. Ennél a példánál állandósult hőtani szimulációt (Steady-State Thermal) használunk.

Mivel kizárólag hőtani szimulációt végzünk nincs szükség a hűtőborda anyagának mechanikai tulajdonságira. Egyedül az izotróp hővezetési tényező (Isotropic Thermal Conductivity) megadása szükséges: 60,5W/mC°.

A geometria felépítése után egy olyan konstrukciós geometriát (Path) definiáltunk, mely hosszirányban végigfut a rúd tengelye mentén (13.1. ábra).

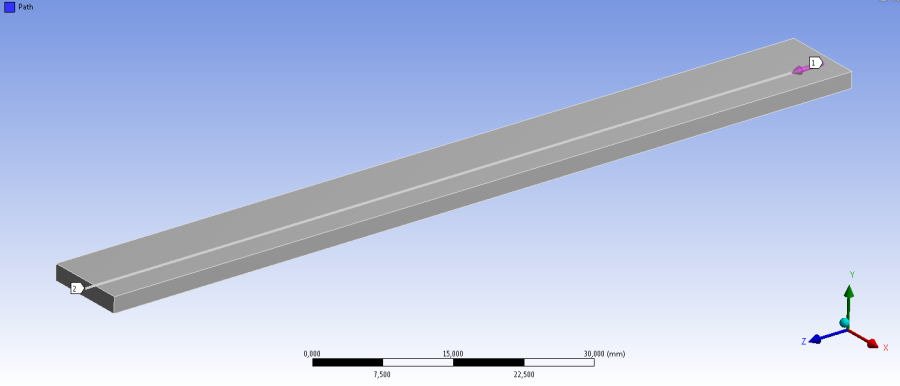
13.1. ábra - Konstrukciós geometria a hőmérséklet-eloszlás hossz menti lekérdezéséhez.

A háló elkészítésénél 4mm-es elemméretet használtunk, így a véges elemek száma összesen 40 db. A hálózott modell a 13.2. ábra mutatja.

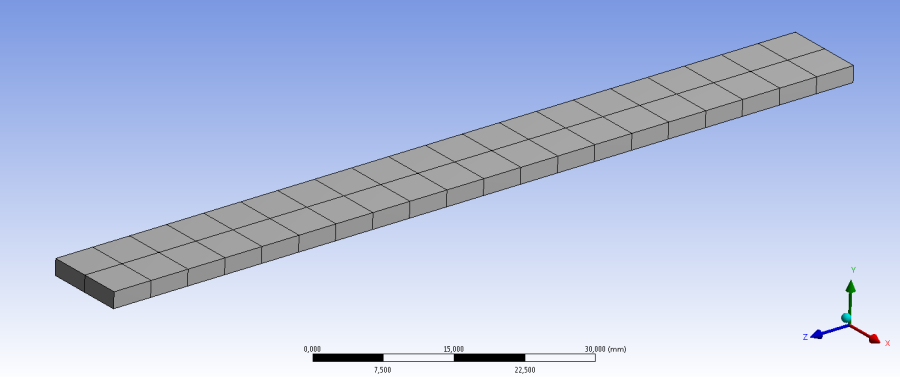
13.2. ábra - Véges elemes háló a hőtani példa esetén

Kezdeti feltételként 20˚C-os környezeti hőmérsékletet határoztunk meg. (Ez a modelltérben lévő testekre is érvényes.)

Az alkalmazott peremfeltételek: 50˚C-os hőmérséklet kényszer (Temperature) , a rúd egyik végén (13.3. ábra „A” jellel jelölt kisméretű felületen), valamint a hosszanti oldalakon (4 hosszú oldal) hőátadási tényezővel (film coefficient: 0,0002W/mm²C˚) definiált hőátadás (Convection), mely a 20˚C-os környezett felé történő hőközlést definiálja. A hőmérséklet kényszert táblázatosan adjuk meg, amiben 2 lépést definiáltunk, az első lépésben 20, a második lépésben pedig 50˚C-os a felület.

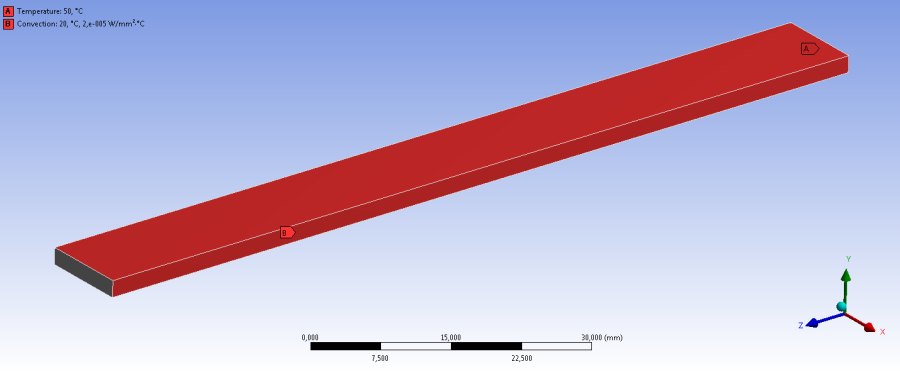
13.3. ábra - A hőtani analízisperem feltételei.

Az alábbi ábrákon láthatóak az állandósult hőmérsékleti viszonyok. A hőmérsékleti terheléssel ellentétes oldalon kialakuló hőmérséklet nagyjából 28˚C. A teljes test eredményeit bemutató 13.4. ábra is mutatja, hogy a hőmérsékleti eloszlás nem egyenletes. Ezt megerősíti a konstrukciós geometria mentén lekérdezett grafikonban ábrázolt hőmérséklet (13.5. ábra és 13.6. ábra).

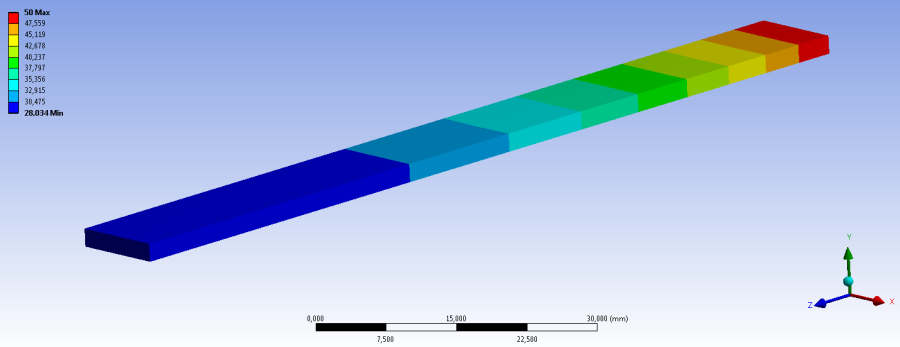
13.4. ábra - Az állandósül hőmérsékleti viszonyok a teljes test felületén

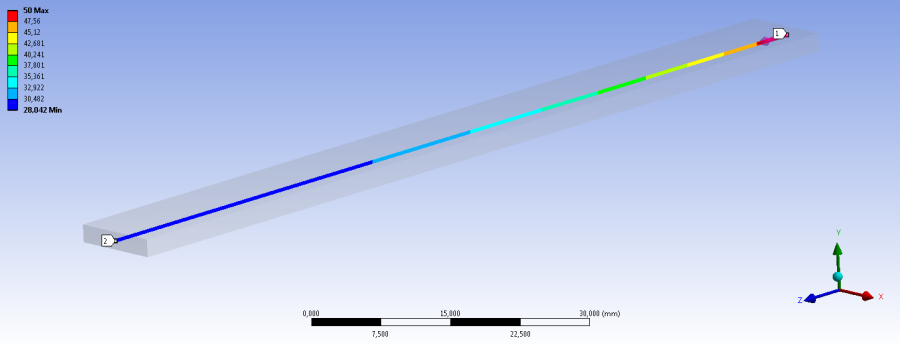
13.5. ábra - Állandósult hőmérsékleti viszonyok a konstrukciós geometria mentén

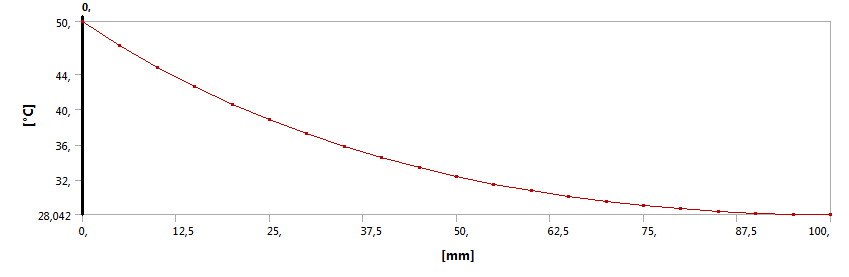
13.6. ábra - Állandósult hőmérsékleti viszonyok a konstrukciós geometria mentén grafikon formátumban

13.5. Analitikus megoldás

Egy homogén rúd (hűtőborda) hőmérsékletének állandósult állapotbeli eloszlását a hővezetés és a palástján történő hő leadás ismeretében számolhatjuk ki. Oldjuk meg a feladatot arra az esetre, ha ismerjük a rúd egyik végének hőmérsékletét és a környezeti hőmérsékletet. [48.]

A rúd hossza: L = 100 mm; keresztmetszetének méretei: a = 2 mm, b = 10mm,

Az egyik rúdvég hőmérséklete: t₀ = 50 °C, a környezeti hőmérséklet: t_f = 20 °C.

Anyaga – acél, hővezetési tényező: λ = 50 W/mm·K; a hőátadási tényező közelítő értéke (levegő közeg és természetes konvekció esetén) α= 20 W/mm²·K.

Határozzuk meg a rúd (hűtőborda) állandósult állapotbeli hőmérséklet eloszlását,

A rúdban lévő hőáram a hely függvényében írható fel, mivel a hőmérséklet eloszlás és a hőmérséklet gradiens is változik a rúd hossza mentén.

(13.1)

Felhasználva, hogy a palást elemi felületén leadott hőmennyiség megegyezik a hővezetés hőáramának ezen elemi hosszra eső növekményével, a paláston történő hőleadást a rúd hosszának elemi részére az alábbi módon írhatjuk fel.

(13.2)

Ahol: az U·dz jelenti a palást felültének elemi részét,

A – a keresztmetszet területe,

U – a keresztmetszet kerülete,

λ - hővezetési tényező,

α - a hőátadási tényező becsült értéke.

Két egyenlet rendezése után kapjuk,

(13.3)

Az egyenletet rendezve, állandó keresztmetszetű rúd esetén

(13.4)

helyettesítéssel, a

(13.5)

másodrendű differenciálegyenletet kapjuk, melynek általános megoldása

(13.6)

Ahol: C₁, C₂ – a peremfeltételektől függő állandók. t(0)=t₀ peremfeltétel esetén, ha a véglap hőleadását elhanyagoljuk

(13.7)

ahol: L – a rúd teljes hossza.

Az analitikus és numerikus eredmények összehasonlítását az alábbi ábrán láthatjuk.

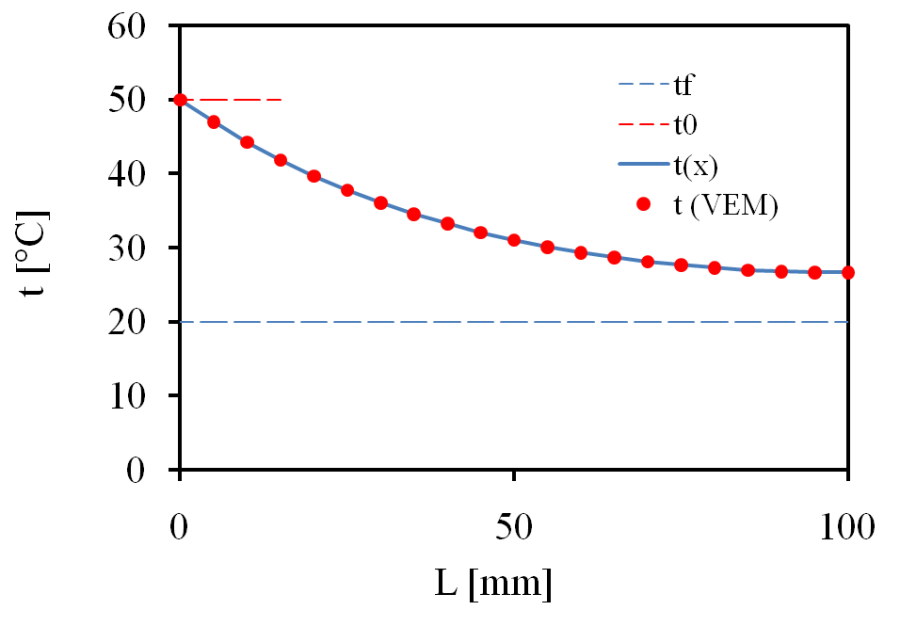
13.7. ábra - Az analitikus és numerikus eredmények összehasonlítása.

14. fejezet - Komplex mechatronikai projektfeladat

Tartalom

14.1. Numerikus megoldás

14.1.1. Statikai analízis
14.1.2. Modal analízis
14.1.3. Harmonikus
14.1.4. Tranziens

14.2. A komplex feladat analitikus megoldása

14.2.1. Statikus lehajlás számolása
14.2.2. Dinamikai számítás

A feladat egy egyszerű nyúlásmérő bélyeges gyorsulásérzékelő tervezése. A legegyszerűbb konstrukció, egy mozgó házban konzolosan rögzített lemez, melynek a befogással ellentétes végén egy tehetetlen tömeg teremti meg a gyorsulás és a rúdvégre ható erő közötti kapcsolatot. A lemez alakját egyenszilárdságúra célszerű kialakítani, hogy a fajlagos nyúlás értéke állandó legyen a deformálódó lemez hossza mentén. Így kevésbé lesz érzékeny a nyúlásmérő bélyegek elhelyezésére. Az állandó vastagságú egyenszilárdságú tartó előkövetelménye, hogy a befogás helyétől a terhelés (az elhelyezett tömeg) támadáspontjáig lineárisan csökkenjen a szélessége. Tehát egy háromszög alakú lemezre van szükség, melynek oldalai a tömeg rögzítésnek középpontjában metszik egymást. Természetesen a kész jelátalakító geometriája ettől bonyolultabb, a rögzítési helyek megfelelő kialakítása miatt, de a vizsgálat szempontjából, elég az egyszerűsített modellel dolgozni.

14.1. Numerikus megoldás

A feladat megoldására az ANSYS Workbench végeselem programot fogjuk használni. A projektszervező felületen látható, hogy statikai (jelátalakító statikus jelleggörbéjének a meghatározásához), modál, harmonikus és tranziens mechanikai analízist (a dinamikai átviteli tulajdonságok meghatározásához) fogunk végezni.

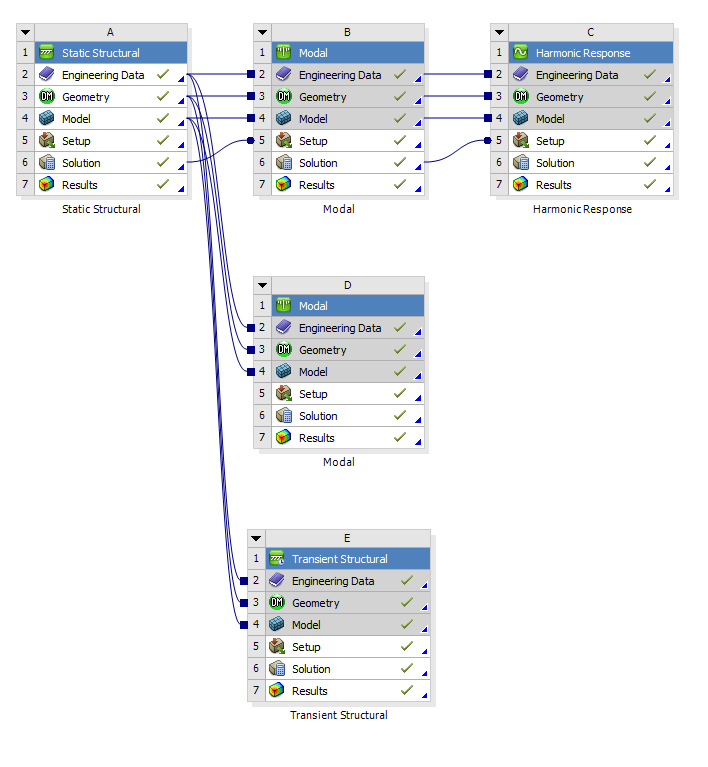
14.1. ábra - A projektfelületen elhelyezett analízisek.

14.1.1. Statikai analízis

A következőekben egy statikai analízissel vizsgáljuk, hogy az egyik oldalán befogott egyenszilárdságú tartó, mekkora Z tengely irányú lehajlást és Y tengely menti fajlagos nyúlást szenved a Z irányú gyorsulás hatására.

Kiinduló adatok:

Méretek: B=10mm, L=20mm, vastagság: h=0,2mm;

Anyag: Rugóacél – E=200GPa, ν=0,3;

Tömeg a tartó végén: m=0,02kg;

Terhelés: a=1G, (9,8066m/s ² ).

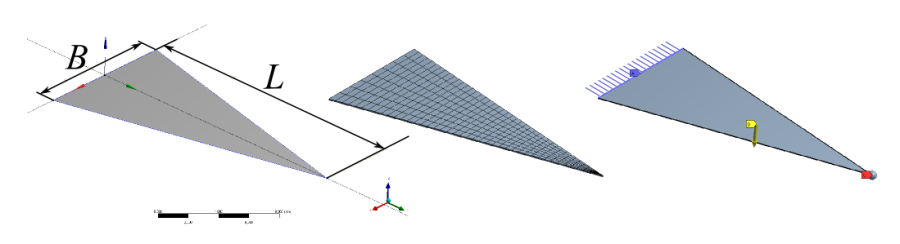
14.2. ábra - Az egyenfeszültségű tartó geometriája, Hálózása és perem, ill. terhelési feltételei.

A geometriát célszerű felületmodellként létrehozni, így héjelemeket használhatunk a hálózás során. A rendezett háló érdekében célszerű a felület felosztása (14.3. ábra).

A lemez megtámasztása a széles végénél történik egy Fix kényszerrel (Fix Support) . A háromszög csúcsánál elhelyezünk egy tömegpontot (Point Mass) , és terhelésként a földi gravitációt (Standard Earth Gravity) alkalmazzuk.

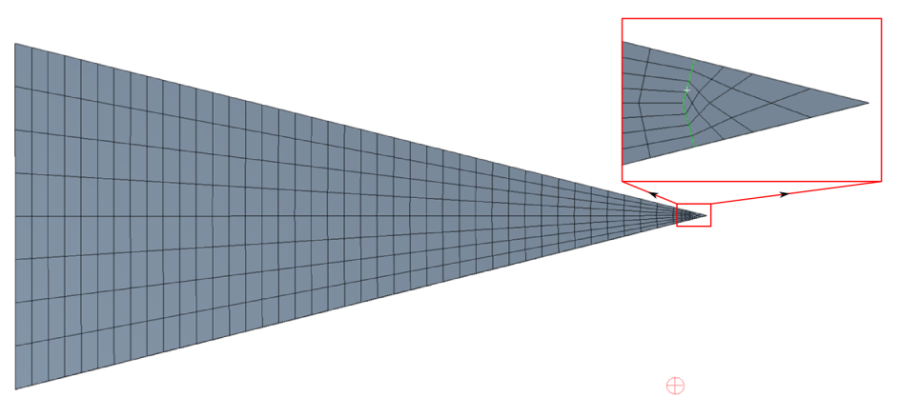
14.3. ábra - Strukturált háló létrehozása háromszög felületen.

A lehajlás számszerű lekérdezéséhez helyezzünk el egy konstrukciós vonalat (Path) , a lemez hossztengelye mentén.

A futtatás után kérdezzük le az Z irányú lehajlás (Directional Deformation), valamint a főfeszültségek (Maximum Principal Stress) és főnyúlások (Maximum Principal Strain) értékeit. És ellenőrzésképpen lekérdezhetjük a befogás helyén ébredő reakcióerő (Force Reaction) és nyomaték (Reaction Moment) értékét (14.4. ábra).

Megjegyzés: Amennyiben nem, vagyunk biztosak az alakváltozási főirányokkal, célszerű ellenőrizni a helyi tenzorok megjelenítésével ( Strain/Vector Principal ). Ennek megfelelően célszerű lehet egy alkalmasan elhelyezett koordinátarendszer, valamely tengelye szerint lekérdezni a normálfeszültségek, ill. alakváltozások értékét (Normal Elastic Strain) , (pl. esetünkben, az hossztengely irányában (Y)). Nagy alakváltozások esetén, a kezdetben párhuzamos tengely nem követi a deformált alakot, ezért célszerűbb lehet a főnyúlás lekérdezése.

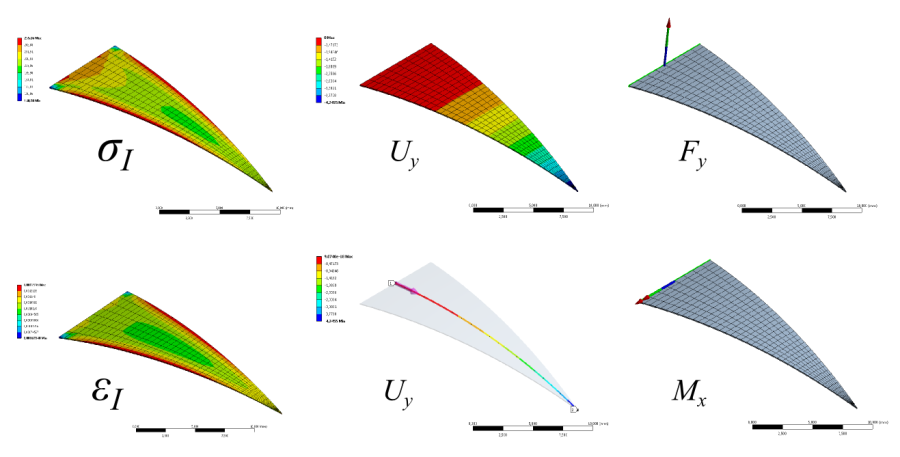
14.4. ábra - Az egyenfeszültségű tartó analízisének eredményei.

14.1.2. Modal analízis

Egy gyorsulásérzékelő esetében nélkülözhetetlen a dinamikai tulajdonságok vizsgálata. Első lépésben határozzuk meg a szerkezet sajátfrekvenciáit (első 6-ot), és a hozzájuk tartozó lengésképeket. Megjegyzés: Valójában elég lenne az első sajátfrekvencia vizsgálata, mivel a jelátalakító működési tartománya ez alatt kell, hogy legyen. A többi csak a példa kedvéért mutatjuk meg.

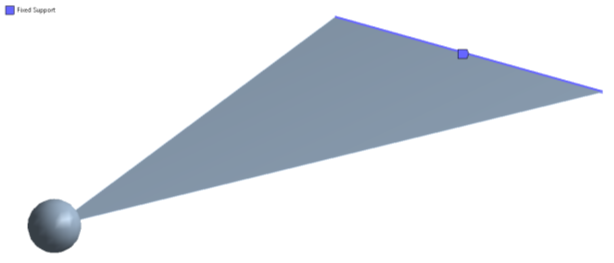
14.5. ábra - Megtámasztás a terheletlen modál analízis esetén.

A modál analízis során lehetőség van terheletlen és az előterhelt vizsgálat elvégzésére. Előfeszített, vagy előterhelt analízishez egy előzetesen lefuttatott statikai analízis jelenti terhelési és peremfeltételeket. Ehhez a projekt felületen, létrehozásakor a modál analízis panelt rá kell húzni a már meglévő statikai (Static Structural) megfelelő sorára. A megoldásra (Solution) húzva az előterhelt esetet, a végeselem modellre (Modell) húzva csak a beállításokkal ellátott terheletlen analízist hozzuk létre. A terheletlen analízisnél csupán a megfogást (Fix Suppoert) kell definiálni (14.5. ábra), a pontszerű tömeget, anyagmodellt és a hálózási beállításokat megörökli a végeselem modell a statikai analízistől. Figyeljük meg, hogy melyik analízisbe milyen elemek vannak bekötve (14.1. ábra).

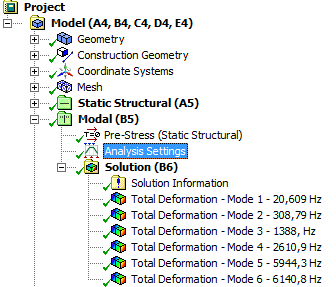
14.6. ábra - A modellfában megjelenő előterhelés.

A beállítások elvégzése után futtassuk mindkét analízist és hasonlítsuk össze az eredményeket.

14.1. táblázat - A jelátalakító első 6 sajátfrekvenciája terheletlen és terhelt állapotban.

Módus	Terheletlenül f [Hz]	Előterheléssel f [Hz]
1.	20,575	20,609
2.	315,85	308,79
3.	1877,1	1388,
4.	1937,5	2610,9
5.	5933,1	5944,3
6.	6019,1	6140,8

Mivel sem a sajátfrekvenciák értékében, sem pedig a lengésképek alakjában nincs jelentős különbség a kétfajta terhelési állapot során, itt csak a terhelt szerkezet lengésképeit mutatjuk.

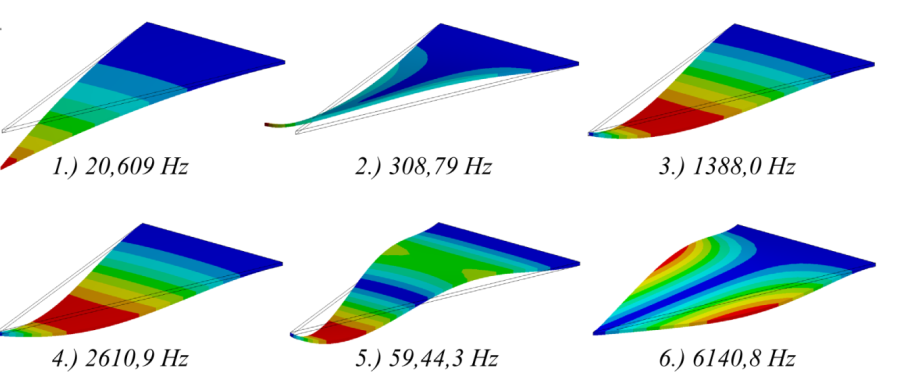
14.7. ábra - A jelátalakító földi gravitációval terhelt modelljének első 6 sajátfrekvenciája és lengésképe.

Mint már említettük számunkra az 1. sajátfrekvencia a lényeges, mert mint ahogy a hozzá tartozó lengésalak is mutatja, ez az első lengés, amelyik a mérés irányába esik.

14.1.3. Harmonikus

Hogy megvizsgáljuk a jelátalakító átviteli tulajdonságait a frekvenciatartományban, el kell végezni egy harmonikus válasz analízist (Harmonic Response) , amely a harmonikusan gerjesztett rendszer válaszát (kimeneti amplitúdóját) adja meg egy megadott frekvenciatartományon. Amint a 14.1. ábra mutatja, lehetőség van a modál analízis eredményeinek (Solution) felhasználására a harmonikus analízis során, a (Mode Superposition) beállítás alkalmazásával.

Az analízis beállításai során meg kell adni a vizsgálat frekvenciatartományát. Esetünkben az előzetes modál analízis eredményei alapján (f₀=20,6Hz), ezt 0-50Hz tartományra állítjuk. Így csak, a számunkra érdekes, 1 rezonanciahely fog szerepelni a frekvenciadiagramon.

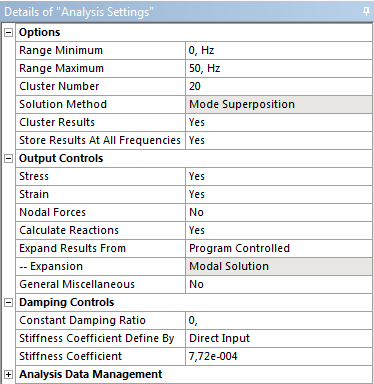
14.8. ábra - A harmonikus analízis beállításai.

Ahhoz, hogy a számolási pontok, a frekvenciatartományon ne egyenletesen, hanem a számunkra fontos helyeken, a sajátfrekvenciák környékén, sűrűbben legyenek elosztva, be kell kapcsolnunk a Cluster Result opciót. Ez szükségessé teszi csillapítás megadását, mivel e nélkül a végtelenhez tartana az amplitúdó értéke ezen a helyen.

A csillapítást (Damping) definiálhatjuk a csillapítási fok (ξ=0,05; Constant Damping Ratio ), vagy a Rayleigh féle anyagcsillapítás merevségi tagjának (β_R=2⋅ξ/ω= 0,0007746s; Stiffness Coefficient ) megadásával.

Ha a modál analízist felhasználtuk bemenetként, akkor a megtámasztást, anyagot, hálózást nem, csak a terhelést kell definiálnunk. Összességében az alábbi ábrán szereplő megtámasztásnak, gravitációs gyorsulásnak és egy koncentrált tömegpontnak kell szerepelnie a modellen (14.9. ábra). A terhelés amplitúdója megegyezik a statikai analízisnél alkalmazott földi gravitációs gyorsulás értékével (9,8066m/s²), de egy általános célú gyorsulással (Acceleration) kell megadni. Mivel a harmonikus analízis során szinuszosan változik a terhelés értéke és előjele, tehát a földi gravitáció nem jöhet szóba mint terhelés.

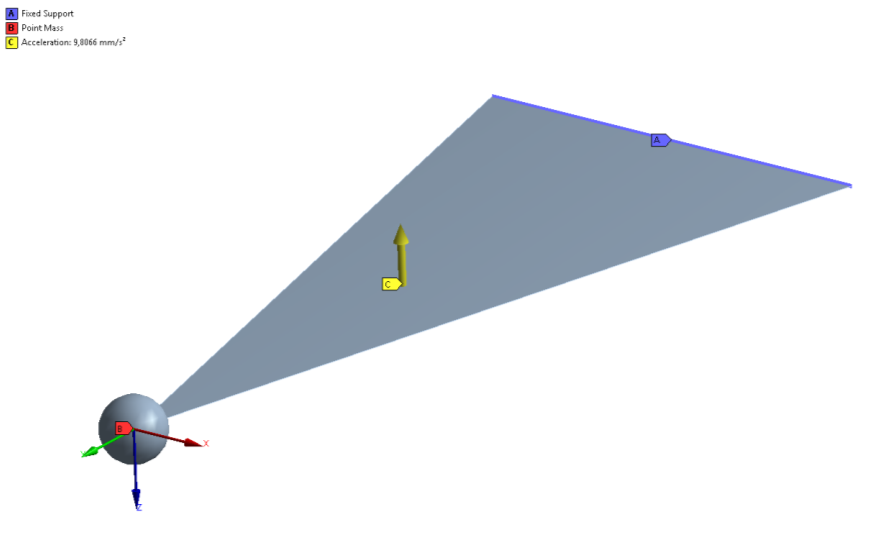
14.9. ábra - A harmonikus analízis során alkalmazott megtámasztás, gyorsulás és tömegpont.

A beállítások elvégzése után futtassuk az analízist és kérdezzük le a konzolvég lehajlásának amplitúdóját és fázisát a frekvencia függvényében, vagyis egy Bode-diagramot. Ehhez a Frequency Response/Deformation parancs kiválasztása után jelöljük ki a konzol végpontját (a tömegpont közepén), és állítsuk át Z–re az irányt. A megjelenítés típusa alapértelmezetten Bode-diagram. Az adatokat a Tabular Data táblázatból egyszerűen vágólapra helyezve átvihetünk más programba adatfeldolgozás céljából.

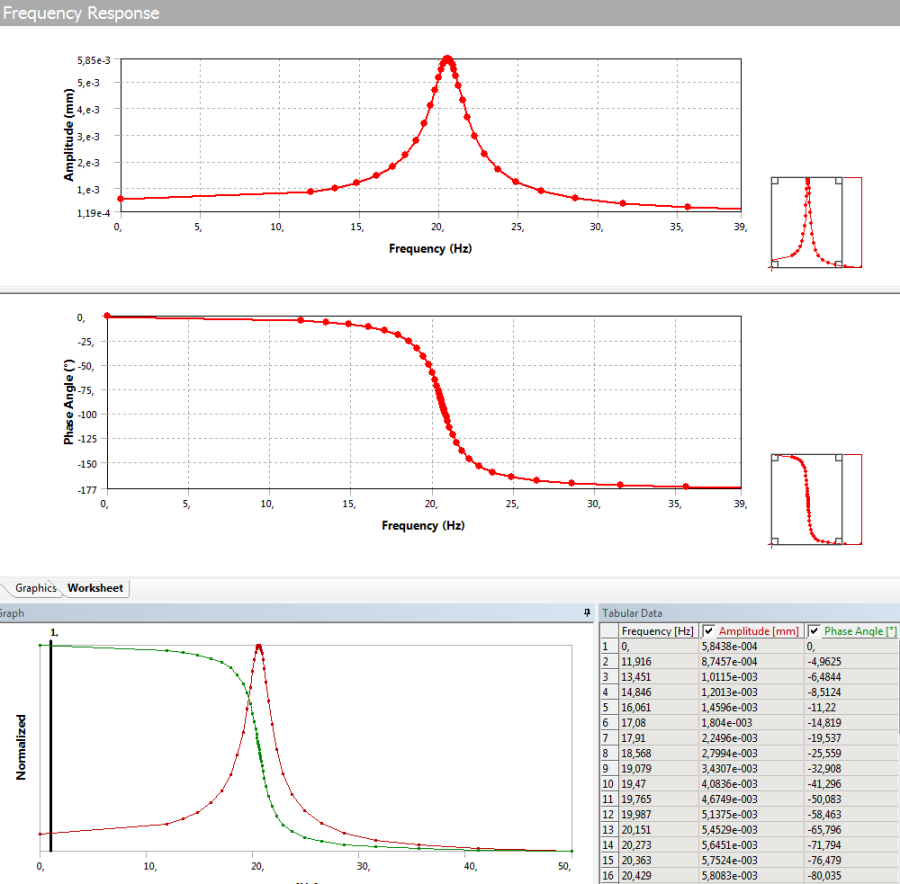
14.10. ábra - A jelátalakító végének elmozdulása a gerjesztő gyorsulás hatására, Bode-diagramon ábrázolva.

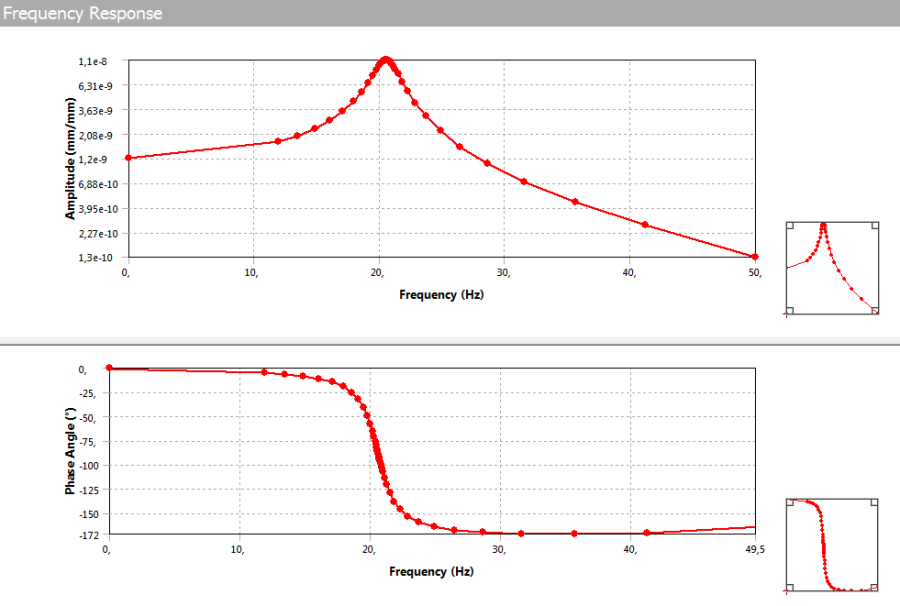
14.11. ábra - A jelátalakító felületén ébredő fajlagos nyúlás értéke a gerjesztés frekvenciájának függvényében (Bode).

A statikai analízishez hasonlóan, itt is le tudjuk kérdezni a feszültség, alakváltozás és deformáció értékeit a teljes, vagy a kiválasztott geometriára vonatkoztatva, annyi kiegészítéssel, hogy a harmonikus analízis esetén a lekérdező parancsokban definiálnunk kell, hogy melyik frekvencián és milyen fázisszögben akarjuk tudni az adott mennyiséget (14.12. ábra).

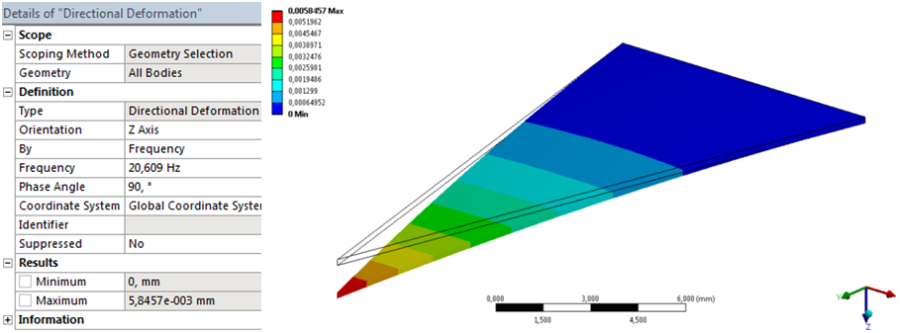
14.12. ábra - Maximális elmozdulás lekérdezése a 20,609Hz frekvencián, 90°-os fázisnál.

14.1.4. Tranziens

A műszerünk időtartománybeli viselkedését, vagyis tranziens hatásokra adott időbeni válaszát a tranziens szerkezeti analízissel (Transient Structural) vizsgálhatjuk. A harmonikushoz hasonlóan a tranziens analízisnek is lehet bemenete egy modál analízis, de példánkon csak a geometriát, anyagot és hálózást tartalmazó végeselem modellt örökítettük át a statikai analízisről (14.1. ábra). Tehát a megtámasztást és a terhelést létre kell hoznunk az analízisen belül.

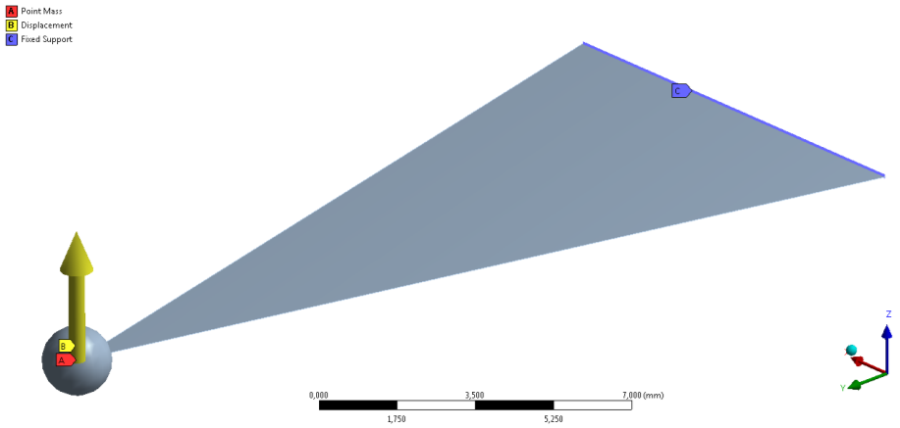
14.13. ábra - A tranziens szerkezeti analízis során alkalmazott perem és kezdeti feltételek.

A megtámasztás továbbra is a tartó széles végének fix megfogása jelenti, de a terhelés most nem a gyorsulás lesz. Azt az esetet szeretnénk szimulálni, amikor bizonyos mértékig (1mm), meghajlított tartót elengedjük, és az csillapodó lengésbe kezd., vagyis az z₀=1mm, és v₀=0m/s, kezdeti feltétellel megadott, magára hagyott rendszer viselkedését szeretnénk vizsgálni.

Ehhez definiálni kell a megtámasztást (Fix Support) és egy Z irányú, 1mm-es elmozdulás kényszert (Displacement), amit az 1mm elérésese után kikapcsolunk. Ezt 2 terhelési lépés (Step) beállításával oldjuk meg úgy, hogy az elmozdulás kezdeti értéke

az 1. lépés elején, t=0s időpillanatban z=0mm;

az 1. lépés végén t=0,5s időpillanatban z=1mm; és

a 2. lépésben kapcsoljuk ki a kényszert.

Ezt az elmozdulás mértékét jelző grafikonon (Graph), a 2. lépésben a terhelés vonalára jobb gombbal kattintva, majd az Activate/Deactivate… opciót választva tehetjük meg (14.14. ábra).

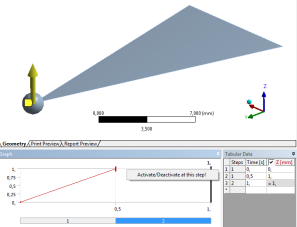
14.14. ábra - Az elmozdulás kezdeti feltétel beállítása, mint az 1. lépésben létrehozott elmozdulás.

A következő fontos lépés a lépések felosztásának, vagyis az al-lépések időtartamának (Time Step) megadása. Egy rezgő rendszernél a rezonancia periódusideje, amit az (előzetes modál analízisből megkaptunk, Tp=1/f≈0,05s) nyújt támpontot az időlépések beállításában. Az elmozdulásfüggvény alakhű reprodukálásához a periódusidőtől legalább egy nagságrendel kisebb időlépést célszerű venni, de nemlineáris problémák esetén a konvergencia elősegítése érdekében további csökkentésre is szükség lehet. Így a példánkban szereplő szerkezet analízise során az 1. lépés 0,01s-os és a 2. lépés 0,0001-0,001s-os beállítása volt szükséges (14.15. ábra).

Az analízis beállításainál a numerikus csillapítás (Numerical Damping Value) és/vagy a Rayleigh féle merevségi csillapítás (Stiffness Coefficient) értékét tudjuk megadni. Ez utóbbi értékét a harmonikus analízishez hasonlóan állítsuk β_R=2⋅ξ/ω= 0,0007746s-ra, és a numerikus csillapítást állítsuk 0-ra.

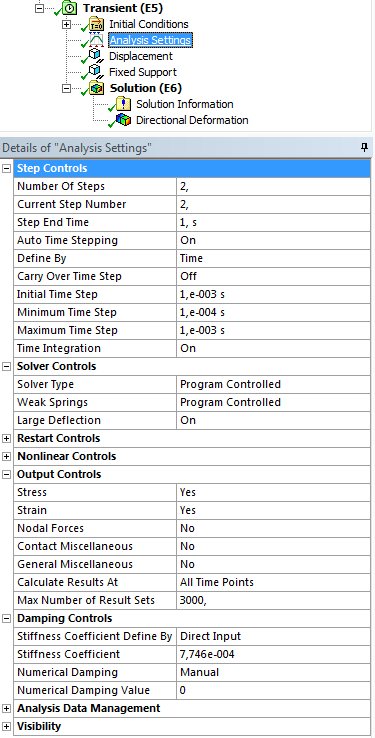
14.15. ábra - Az analízis beállításai.

A nagy lehajlások (Large Deflections) bekapcsolása után indítsuk az analízist, majd kérdezzük le a végpont Z tengely menti elmozdulását (Directonal Displacement).

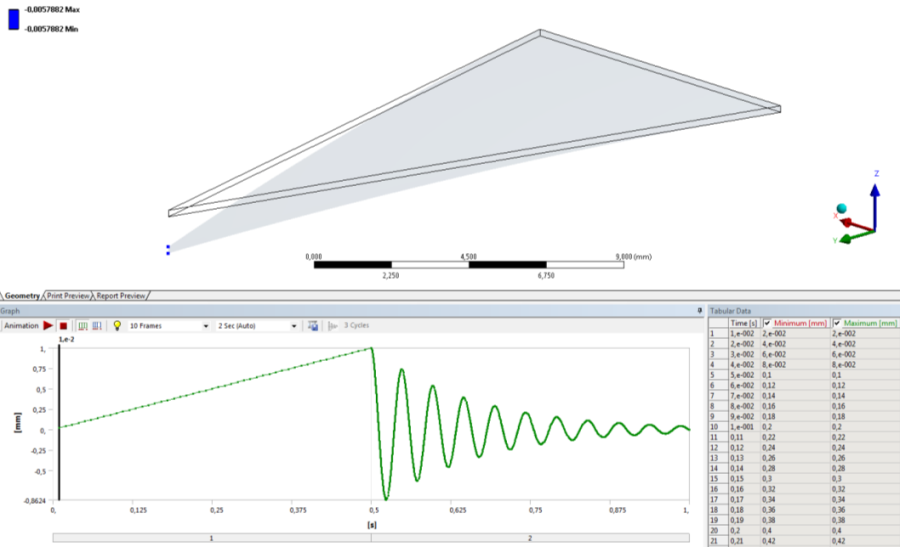
14.16. ábra - A végpont csillapodó lengését szemléltető eredmény.

14.2. A komplex feladat analitikus megoldása

A végeselemes programok eredményének ellenőrzéseként oldjunk meg a feladatot a rugalmasságtan és a dinamika módszereivel. Kiindulásnak adva van egy az egyik oldalán befogott egyenszilárdságú tartó melynek másik oldalán koncentrált tömeget helyezünk el. A lemez síkjára merőlegesen hat a gravitációs gyorsulás, melynek hatását vizsgáljuk első lépésben.

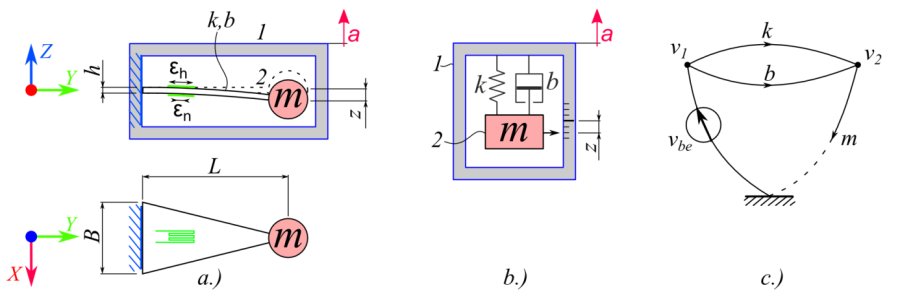
14.17. ábra - A gyorsulásérzékelő különböző szintű absztrakciói: a.) egyszerűsített szerkezeti ábra, b.) szabadtest ábra, c.) Struktúra gráf.

Kiinduló adatok:

Méretek: B=10mm, L=20mm, vastagság: h=0,2mm;

Anyag: Rugóacél – E=200GPa, ν=0,3;

Tömeg a tartó végén: m=0,02kg;

Terhelés: a _z =1G, (9,8066m/s ² ).

14.2.1. Statikus lehajlás számolása

Mivel a tartó szélessége a befogástól távolodva lineárisan csökken (14.1), ezért a keresztmetszetet jellemző mennyiségek is a hely (z) függvényei.

		(14.1)
		(14.2)
		(14.3)

Ahol:

I – a másodrendű nyomaték,

K – a keresztmetszeti tényező,

h – a tartó vastagsága,

L – a tartó teljes hossza,

B – a tartó szélessége a „z=0” helyen,

b(z) – a tartó szélessége a „z” helyen,

A tartó egész térfogatára és a végén elhelyezett koncentrált tömegre ható Y irányú gyorsulás hatására a tartót M_x(z) nyomaték terheli.

(14.4)

Ennek hatására a külső szálakban σ_z=M_x(z)/K(z) normál feszültség,

és lineáris anyagmodellt feltétételezve, ε_z=σ_z/E fajlagos nyúlás ébred.

Ahol: E – az anyag rugalmassági modulusa.

A lehajlásfüggvényt a rugalmas szál differenciál egyenletéből számoljuk ki [25.] .

(14.5)

Az egyenletet z szerint kétszer integrálva kapjuk a lehajlásfüggvényt,

(14.6)

Mivel a befogás zérus elfordulás és elmozdulás peremfeltételeket jelent, ezért a C₁ és C₂ értéke szintén nulla. Ezzel a lehajlás Értéke a z=L helyen:

(14.7)

Koncentrált tömeggel modellezve a (14.7) egyenletnek csak az 1. tagja marad meg:

(14.8)

A konzol végének lehajlása	y _z [mm]
Elosztott tömeggel számolva	-0,5892
Koncentrált tömeggel számolva	-0,5884

Látható, hogy a kétféle számolás eredménye nagy pontossággal megegyezik, ami azt jelenti, hogy a továbbiakban elegendő a koncentrált paraméterű modell alkalmazása. Persze ezt az egyszerűsítést csak akkor tehetjük meg, ha az elmozduló mérőtest tömege elhanyagolható a koncentrált tömeghez képest.

✎ A fenti egyenletek alapján rajzoltassuk ki diagramban a tartó szélső szálaiban ébredő feszültséget, fajlagos nyúlást és a rúd lehajlását. Hasonlítsuk össze a végeselemes programok eredményeivel.

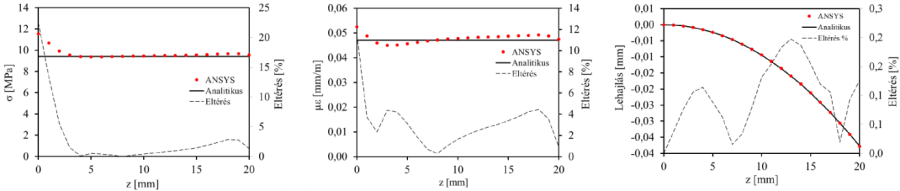
14.18. ábra - Az egyenfeszültségű tartó eredményei kis lehajlás esetén (h=0,5).

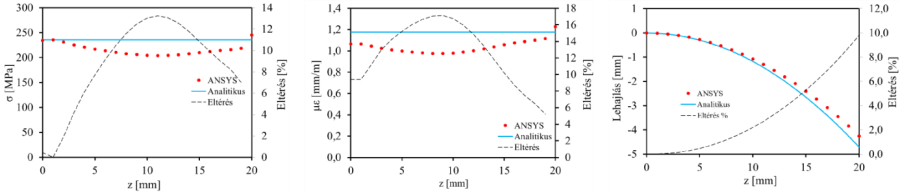
14.19. ábra - Az egyenfeszültségű tartó eredményei (főfeszültség és főnyúlás) nagy lehajlás esetén (h=0,1).

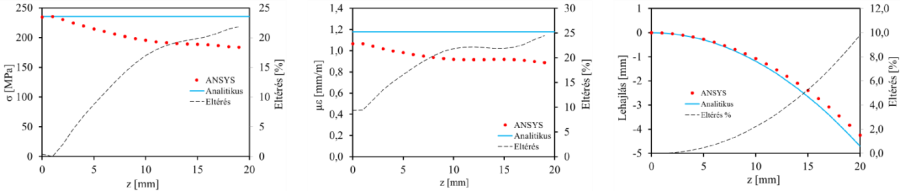
14.20. ábra - Az egyenfeszültségű tartó eredményei (z irányú normál feszültség és fajlagos nyúlás) nagy lehajlás esetén (h=0,1).

14.2.2. Dinamikai számítás

A szenzor dinamikai vizsgálatához szükségünk lesz a koncentrált paraméterű modell paramétereinek meghatározására, ami esetünkben a rugómerevséget (k [N/m]), a csillapítási tényezőt (b [Ns/m]), és a tömeget (m [kg]) jelenti.

A tömeg értéke adott, mint a fenti számolásban láthattuk, ebben az esetben elegendő a tömeg koncentrált paraméterként történő modellezése.

Ami esetünkben a pontszerű tömeg: m=0,02kg.

A rugómerevség értékét a mérőtest végén ható tehetetlenségi erő (F) és fenti számolás (14.8) eredményeként kapott lehajlás (f_y) hányadosaként áll elő.

(14.9)

A csillapítási tényező meghatározására nem mindig állnak rendelkezésére megfelelő adatok, mivel rendkívül összetett jelenség. Értékét jelen esetben az anyagcsillapítás, a terhelési állapot és a mozgó lemez körül áramló levegő által okozott csillapítás egyaránt befolyásolja, ezért pontos értékét csak kísérleti úton tudnánk meghatározni. A koncentrált paraméterű lineáris vizsgálat során a csillapítást is lineáris viszkózus csillapítással modellezzük. Jó közelítést jelent az irodalomban fellelhető csillapítási fok értéke, amely meghatározza az egész rendszer csillapítását [49.] .

Acél szerkezetre:

a csillapítási fok: ξ=0,00143; [49.] ,
a logaritmikus dekrementum: δ =0,009; [49.] ,
a csillapítási tényező: b=2 ⋅ ξ ⋅ (k ⋅ m) ^1/2 =0,007384Ns/m
a Rayleigh féle merevségi csillapítás, β_R=2⋅ξ/ω=0,00002215s; (a sajátfrekvencia értékére számolva, a Rayleigh féle tömegcsillapítás α_R figyelmen kívül hagyásával).

Megjegyzés: Az eredmény és a csillapítás hatásának szemléletes megjelenítése miatt közel egy nagyságrenddel nagyobb értékkel mutatjuk be a példát, mint az irodalmi adat:

a csillapítási fok: ξ=0,05;
a csillapítási tényező: b=2 ⋅ ξ ⋅ (k ⋅ m) ^1/2 = 0,2582Ns/m
a Rayleigh féle merevségi csillapítás, β_R=2⋅ξ/ω= 0,0007746s; (a sajátfrekvencia értékére számolva, a Rayleigh féle tömegcsillapítás α_R figyelmen kívül hagyásával).

A fenti struktúra gráf (14.17. ábra) segítségével felírhatjuk a rendszer csomóponti egyenletét. Mivel az 1-es csomópont (Ház) sebessége megegyezik a sebesség gerjesztéssel, egy ismeretlenünk marad így elég csak a 2. csomópontra (a mozgó tömegre) felírni az egyenletet. Az 1-es és a 2-es csomópont sebesség különbségéből számított elmozdulás jelenti majd a kimenő mennyiséget számunkra.

(14.10)

Amelynek Laplace transzformálásával, a t időtartományból átlépve az s operátor tartományba jutunk. Végül a fizikai paramétereket (k,b,m) megfelelően összevonva, és bevezetve a rendszertechnikában szokásos jelöléseket, a másodrendű lengő rendszer átviteli függvényét kapjuk (14.14).

		(14.11)
		(14.12)
		(14.13)
		(14.14)

ahol:

A=m/k – a rendszer erősítése,

T=(m/k) ^1/2 – a rendszer időállandója, (ω ₀ =1/T, - a rendszer saját-körfrekvenciája),

ξ= b/2(k ⋅ m) ^1/2 – a csillapítási fok, (definíció szerint: ξ=b/b _k ; ahol: b _k =2(k ⋅ m) ^1/2 – a kritikus csillapítási tényező).

Az így felírt átviteli függvény nevezőjében szereplő karakterisztikus polinom megoldásával jutunk el a rezonanciafrekvencia meghatározásához.

		(14.15)
		(14.16)

A megoldáson látható, hogy csak ξ értékétől függ, hogy valós, vagy komplex gyököt kapunk.

Ha ξ>1, tehát nagy csillapítás esetén (b>b_k), az átviteli függvény két egytárolós tag szorzataként írható fel. A túlcsillapított rendszer rezgésre nem képes.
Ha ξ=1, (b=b_k), Ez az aperiodikus határesetet jelenti. Az egyenletnek egy valós gyöke van (s₁=s₂).
Ha 0<ξ<1, tehát kis csillapítás esetén (b<b_k), Az egyenletnek egy konjugált komplex gyökpár a megoldása. A magára hagyott, alulcsillapított rendszer csillapodó rezgést végez.
Ha ξ=0, tehát nincs csillapítás. Az előző speciális esete (gyakorlatban nincs ilyen), melynél a magára hagyott, csillapítatlan rendszer, nem csillapodó rezgést végez.

Esetünkben a 3. esetnek van jelentősége, mivel 0<ξ<1értékű. Ebben az esetben az (14.16) egyenletet komplex összetevőivel felírva az alábbi összefüggést kapjuk.

(14.17)

Az s operátor definíció szerinti komplex összetevői az s=σ+jω, innen a rezonancia körfrekvencia:

(14.18)

ahol: ω ₀ =1/T=(k/m) ^1/2 – a sajátkörfrekvencia értéke, és β= ω ₀ ⋅ ξ =b/2m – a csillapítási kitevő.

A Bode diagramon, frekvenciatartományban való ábrázoláshoz végezzük el a s=jω, helyettesítést a (14.14) egyenleten, majd rendezzük át az alábbi (14.19) egyenleten látható formában, a valós és a képzetes tagok csoportosításával a nevezőben. A gerjesztés hatására a kimenet amplitúdójának (14.20) és fáziskésése (14.21) az átviteli függvény komplex vektorának abszolút értékével és állásszögével adható meg.

		(14.19)
		(14.20)
		(14.21)

✎ A fenti egyenletek alapján számítsuk ki a jelátalakító sajátfrekvenciáját, és rezonancia frekvenciáját, a gyorsulás érzékelő végén lévő tömeg minimális és maximális elmozdulását. Továbbá, rajzoltassuk ki Bode-diagramban az elmozdulás amplitúdóját és fáziskésését a körfrekvencia függvényében. Hasonlítsuk össze a végeselemes programok eredményeivel.

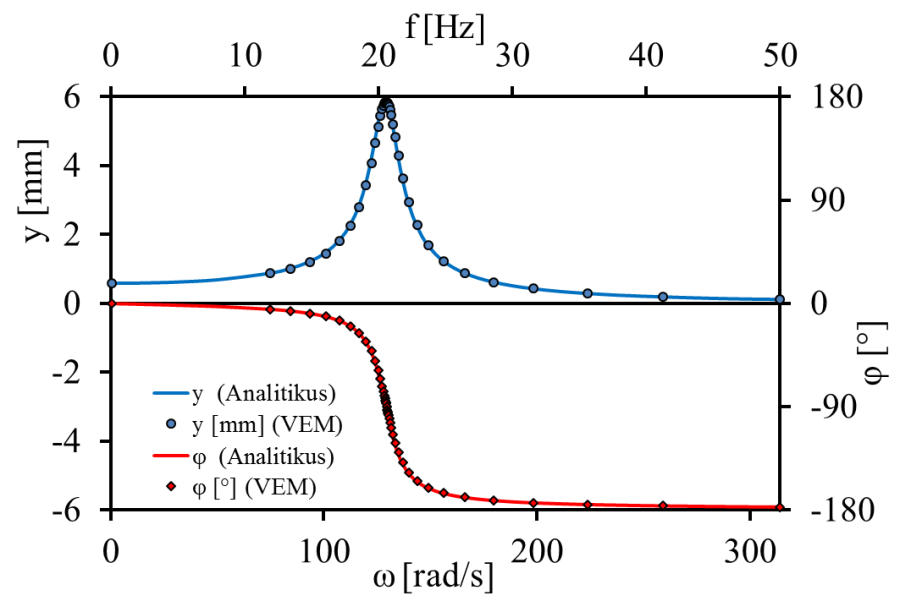
A jelátalakító frekvenciadiagramja (az összehasonlíthatóság kedvéért, a szokásos Bode-diagramtól eltérően, abszolút értékekkel megadva).

14.21. ábra - A jelátalakító frekvenciadiagramja (az összehasonlíthatóság kedvéért, a szokásos Bode-diagramtól eltérően, abszolút értékekkel megadva).

A szerkezet időtartománybeli tranziens viselkedésének vizsgálatához írjuk fel a gerjesztetlen, csillapított másodrendű rendszer differenciálegyenletének általános megoldását.

(14.22)

Melynek A és B állandóinak a t=0, időpillanatban vett y(0)=y₀, v(0)=0; kezdeti feltételekre megoldva kapjuk az alábbi alakot.

(14.23)

✎ A fenti egyenletek alapján rajzoltassuk ki az y ₀ =1, kezdeti feltételű, tranziens rezgést időtartományban. Hasonlítsuk össze a végeselemes eredménnyel.

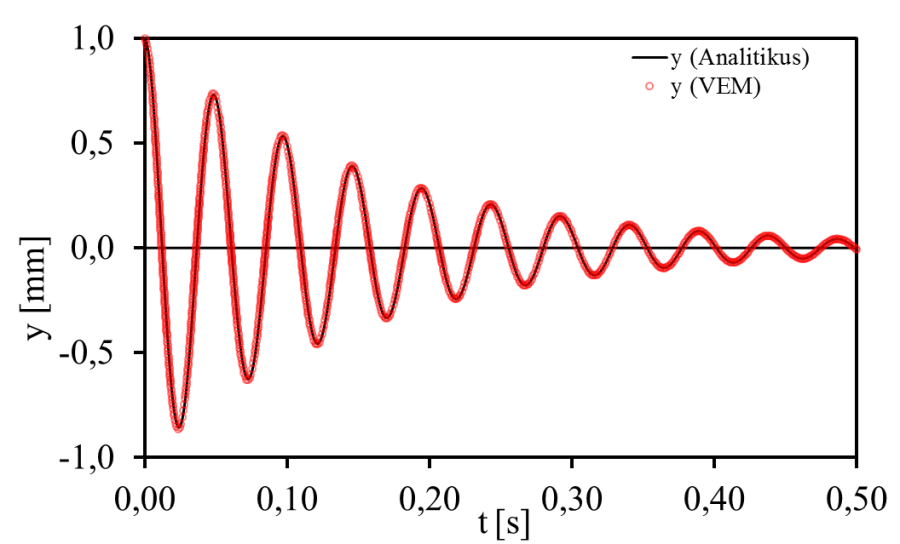
14.22. ábra - A deformált és magára hagyott („megpendített”) tartó tranziens viselkedése.

14.2. táblázat - Az analitikus és VEM eredmények összehasonlítása.

Mennyiség	Jelölés	m.e.	VEM	Analitikus, kontinuum tömeggel	Eltérés [%]	Analitikus, pontszerű tömeggel	Eltérés [%]
Hajlítónyomaték a befogásnál	M(z=0)	Nmm	3,93	3,93	0,06	3,92	0,21
Normálfeszültség a külső szálban	σ	MPa	58,09	58,88	1,53	58,84	1,27
Fajlagos nyúlás a külső szálban	ε	-	2,936E-04	2,944E-04	0,28	2,942E-04	0,22
Lehajlás a tartó végénél	y(z=L)	mm	-0,586	-0,588	0,36	-0,589	0,49
Rugómerevség	k	N/m	337	336	0,51	333	1,16
Saját-körfrekvencia	ω ₀	rad/s	129,28			129,10	0,14
Sajátfrekvencia	fo	Hz	20,58			20,55	0,14

15. fejezet - Korszerű végeselelem rendszerek áttekintése

Tartalom

15.1. Korszerű végeselem rendszerek áttekintése
15.2. ANSYS Classic és Workbench
15.3. ABAQUS
15.4. NASTRAN
15.5. Mark
15.6. ADINA
15.7. LS-DYNA
15.8. SolidWorks Design Validation Tools (CosmosWorks)
15.9. Solid Edge
15.10. Autodesk Inventor
15.11. További kereskedelmi végeselem rendszerek
15.12. További nyílt forráskódú végeselem rendszerek

15.1. Korszerű végeselem rendszerek áttekintése

Az alábbiakban szeretnénk összefoglalni azokat a fontosabb VEM rendszereket, amelyeket jelenleg el lehet érni akár szabad szoftverként, akár kereskedelmi forgalomban.

Egy VEM rendszer kiválasztásánál elsősorban azt kell mérlegelnünk, hogy mire szeretnénk használni. 3 dimenziós modelleket szeretnénk vele szimulálni, vagy elég a 2 dimenzió használata? Egyszerűbb szilárdságtani méretezéseket készítenénk, vagy folyadék, esetleg gáz szimulációra is használnánk?

A forgalomban lévő VEM rendszerek közül mi az AnSYS Workbench rendszeren mutattuk be az egyes szimulációs példákat. Ennek ellenére javasoljuk, hogy az előbbi kérdéseket válaszolja meg a választás előtt, hiszen ha egy szimulációs feladat komplexitása meglehetősen egyszerű, akkor nem érdemes egy robosztus, „mindentudó” rendszer alkalmazni, még akkor sem. Ekkor a leginkább mérlegelendő egy szabadon letölthető VEM rendszer alkalmazása a cél érdekében.

15.2. ANSYS Classic és Workbench

Az ANSYS Inc által forgalmazott program egy széleskörűen alkalmazott végeselem szoftver, amely egyre bővülő modulpalettájával lefedi a mérnöki gyakorlatban alkalmazott analízisek szinte teljes tartományát. Különféle statikai és tranziens, lineáris és nemlineáris, mechanikai, hőtani, elektromágneses, áramlástani, explicit dinamikai stb. vizsgálatok mellett, ezek bizonyos kombinációit, az un. csatolt tér analíziseket is kiválóan kezeli.

A program kétféle kezelőfelülettel rendelkezik, az ANSYS Classic jelenti az alapot, amely minden funkció elérést biztosítja, használata komolyabb szimulációkhoz célszerű. Egyszerűbb szimulációkhoz viszont érdemes a sokkalta könnyebben kezelhető Workbenc-et használni. Ez utóbbi előnye a könnyen kezelhető és átlátható kezelőfelület, ami sok automatizmussal segíti a felhasználót. Viszont ennek hátránya, hogy némely funkció közvetlenül nem érhető el benne. Ennek ellenére, mára teljes értékű végeselem programmá nőtte ki magát a Workbench is.

15.1. ábra - [Forrás: http://www.econengineering.com/hu/szoftvereink/ansys.html]

15.3. ABAQUS

A Dassault Systemes által fejlesztett végeselem rendszer, hatékony és komplett megoldást jelent az ipari feladatok széles spektrumához. Főként az autó és repülőgép iparban alkalmazzák előszeretettel, ahol egy közös modell és az integrált megoldó segítségével szinte a teljes járműterhelés analízisét képesek lefedni, (mint pl. a dinamikus rezgések, nemlineáris statikai, többtest rendszerek, üztközésvizsgálat, a mechanikaival csatolt termikus és akusztikus analízisek). Implicit és explicit mechanikai, áramlástani és elektromágneses megoldóval rendelkezik.

15.2. ábra - [Forrás: http://www.3ds.com/products-services/simulia/portfolio/abaqus/overview/]

15.4. NASTRAN

Eredetileg a NASA-nak (NASA STRucture ANalysis) az MSC által fejlesztett végeselem szoftver, mely forráskódja számos szoftverben integrálva lett. Mára a NASTRAN kódja széleskörűen alkalmazott a repülőgép, autó és a tengerészeti iparágakban. Különböző forgalomban lévő verziói: MSC Software (eredeti), MSC Nastran, NX Nastran, NEi Nastran. A program FORTRAN-ban íródott, és számos architektúrán és operációs rendszeren működik. Számos lineáris és nemlineáris szerkezeti probléma megoldására létezik modulja, melyeket egy köztes modul a Direct Matrix Abstraction Program (DMAP) vezérel.

15.5. Mark

Az MSC Software által forgalmazott általános célú végeselem program, mely fejelett nemlináris megoldóval rendelkezik. Statikus és dinamikus jellegű, különféle fizikai terhelések szimulációjára alkalmas. Sokoldalúsága az anyagi nemlinearitás, tönkremeneteli hatások, adaptív újrahálózás, kontakt feladatok és tranziens környezeti hatások kezelésében, komplex problémák megoldására teszik alkalmassá. Az MSC által forgalmazott további szoftverek: MSC Nastran (szerkezeti), Actran (akusztikai), MSC Fatigue (kifáradás), Adams (többtest dinamika), SimXpert (multidiszciplináris), stb.

15.3. ábra - [Forrás: http://www.mscsoftware.com/product/marc]

15.6. ADINA

Az ADINA név az Automatikus Dinamikus Inkrementális Nemlináris Analízist jelzi. Szerkezeti, hőtani áramlástani, elektromágneses és csatolt termo-mechanikai problémák megoldására alkalmas.

15.4. ábra - [Forrás: http://www.adina.com/newsgH141.shtml]

15.7. LS-DYNA

Az LS-DYNA egy kombinált implicit/explicit megoldó, mely erősen nemlineáris csatolt fizikai problémák megoldására alkalmas.

15.5. ábra - [Forrás: http://upload.wikimedia.org/wikipedia/en/3/36/LS_DYNA_geo_metro.png]

15.8. SolidWorks Design Validation Tools (CosmosWorks)

A SolidWorks CAD rendszer tartalmaz egy végeselem szimulációs rendszert, mely többek között lineáris és nemlineáris szerkezeti, dinamikai, kifáradás, mozgás, termikus, rezgés, áramlástani analízisre alkalmas. Nagy előnye, hogy (mivel nem kell környezetet váltani és konvertálni a modellt) rendkívül gördülékenyen lehet benne szimulálni és azonnal optimalizálni a modellt. A modell konverziós hiba valószínűsége csekély.

15.6. ábra - [Forrás: http://www.solidworks.com]

15.9. Solid Edge

A Solid Edge CAE rendszer 2009-től rendelkezik beépülő végeselem modullal, amely a Siements PLM Femap és NX Nastran technológiáján alapul.

15.10. Autodesk Inventor

Az Autodesk Inventor CAE rendszer saját végeselem modullal rendelkezik, amelyben lehetőség van mozgás és feszültség szimulációkra. Lehetőség van továbbá parametrikus optimalizációra, rezgés szimulációra és szerkezeti analízisre is.

A teljesség igénye nélkül, az alábbiakban felsorolásszerűen bemutatunk néhány kereskedelmi és ingyenes végeselem szoftvert.

15.11. További kereskedelmi végeselem rendszerek

Advance Design BIM – Végeselem strukturális analízisre, GRAITEC által fejlesztve.

Altair HyperWorks – Termékek költséghatékonyságának javítása.

ANSA – Haladó szintű CAE pre-processzor szoftver teljes modellépítésre.

COMSOL Multiphysics – Korábban Femlab-nak nevezték.

Creo Elements / Pro Mechanica – A Parametric Technology Corporation által fejlesztett, MCAD-be beépülő rendszer.

Diffpack – Végeselem rendszer parciális differenciálegyenletekkel.

Diana – Többcélú végeselem rendszer háromdimenziós és nemlineáris alkalmazásokkal.

Falcon2.0 – Pehelysúlyú FEM post-processzor.

FEFLOW – Talajvízáramlás szimuláció, tömegáramlás szimuláció és hőáramlás szimuláció porózus anyagon keresztül.

Femap – Siemens PLM pre- post-processzor Windows rendszerre.

FEM – A svéd StruSoft cég fejlesztése, szerkezeti tervezésre.

FEMtools – Eszköztár statikai és dinamikai szimulációra, szerkezeti optimalizációval.

FENSAP-ICE – Légi járművek jegesedésének szimulációja.

Flux – Elektromágneses és hőtani szimulációk.

HydroGeoSphere – Hidrológiai, hő és folyadékáramlás szimuláció.

HyperSizer – Kompozitok szimulációja.

Infolytica MagNet – Elektromágneses, elektromos és hőtani szimulációk.

JMAG – Akusztikus szimulációk.

LINKpipe – Csővezetékek nemlineáris szinmulációja.

LUSAS – UK szoftver.

MADYMO – Közlekedésbiztonsági szimulációk.

NEi Fusion, NEi Software – 3 dimenziós modellező és Nastran FEM

15.7. ábra - [Forrás: http://upload.wikimedia.org/wikipedia/en/7/75/NEi_Fusion_image_servo_motor_FEA_and_CAD_1000px.JPG]

NEi Nastran, NEi Software – Általános célú végeselem rendszer.

15.8. ábra - [Forrás: http://upload.wikimedia.org/wikipedia/en/4/45/Noraneng.JPG]

NEi Works, NEi Software – Beépülő modul SolidWorks-ben.

NISA – Indiai szoftver.

PAK – Lineáris és nem lineáris szerkezeti szimulációk, folyadék és hőtani szimulációk, mechanikai törések és biomechanikai alkalmazások.

Plaxis – Geotechnikai szimulációk, feszültségekre, deformációkra, talajvízáramlásra és dinamikára.

PZFlex – Piezoelektromos szimulációk.

Quickfield – Fizikai szimulációs szoftver.

Radioss – Lineáris és nemlineáris az Altair Engineering-től.

Range Software – Multifizikai szimulációs szoftver.

SAMCEF – Belga fejlesztésű CAE rendszer.

SAP2000 – Amerikai szoftver.

STRAND7 – Ausztrál fejlesztés.

StressCheck – Igénybevett alkatrészek pontosságának szimulációjára.

Vector Fields Concerto – Mikrohullámú és elektromágneses szimulációk.

Vector Fields Opera – Elektromágneses és multifizikai végeselem rendszer.

Vflo – Hidrológiai szimulációk.

Zébulon – Francia szoftver.

15.12. További nyílt forráskódú végeselem rendszerek

ALBERTA - Adaptív hierarchiájú végeselem eszköztár.

CalculiX - A megoldó egység részlegesen kompatibilis az ABAQUS formátummal. Számos kimeneti kompatibilitással rendelkezik VEM és CFD rendszerekhez.

15.9. ábra - [Forrás: http://upload.wikimedia.org/wikipedia/commons/3/34/Lav.png]

Code Aster -Python és Fortran alapon írt, francia nyelvű rendszer.

Deal II – Végeselem differenciálegyenlet eszköztár.

DUNE – Egy C++-ban fejlesztett elosztott és egyesített numerikus környezet.

Elmer FEM solver – c, c++ és Fortran nyelven, a Finn Oktatási Minisztérium megbízására fejlesztett multifizikai szimulációs lehetőséggel rendelkező szoftver.

FEAPpv – Általános célú végeselem rendszer.

FEBio – Végeselem rendszer biomechanikai szimulációkhoz.

FEMM – Egy Windows környezetben futó, végeselem rendszer, 2 dimenziós és tengelyszimmetrikus mágneses, elektrosztatikus, hőtani és áramköri szimulációkhoz.

FEMPACK – Végeselem rutinok.

FEniCS – Általános célú végeselem rendszer amerikai és európai kutatók által fejlesztve.

FETK – Adaptív végeselem eljárások függvénykönyvtárai nemlineáris, parciális differenciálegyenlet megoldásokkal.

FRANC2D and FRANC3D – Két- és háromdimenziós végeselem rendszer görbe vonalú törés szimulációra, tengelyszimmetrikus, sík feszültségek és deformációk mellett.

Freefem++ – Általános célú végeselem rendszer.

15.10. ábra - [Forrás: http://upload.wikimedia.org/wikipedia/commons/1/19/FreeFEM%2B%2B_CS_Example_-_Dirichlet.png]

GetFEM++ – Általános célú végeselem függvénykönyvtár.

Hermes Project – C és C++ nyelven fejlesztett függvénykönyvtár hely és hely-idő tartományban.

15.11. ábra - [Forrás: http://upload.wikimedia.org/wikipedia/commons/7/71/Harmonic_Wave_Propogation.png]

Impact – JAVA-ban fejlesztett, dinamikus végeselem programcsomag, főleg törés szimulációkra.

15.12. ábra - [Forrás: http://upload.wikimedia.org/wikipedia/commons/4/4a/FAE_visualization.jpg]

libMesh – Keretrendszer parciális differenciálegyenletek numerikus szimulációjára.

OFELI – C++ nyelven írt, többcélú végeselem rendszer.

OOF – Végeselem rendszer anyagtudományi szimulációkhoz.

OOFEM – C++ nyelven írt, objektumorientált megoldó.

OpenFOAM – Mező operáció és manipuláció.

15.13. ábra - [Forrás: http://upload.wikimedia.org/wikipedia/commons/8/8c/Screenshot_OpenFOAM-2.1.x_gnome-terminal.png]

OpenSees – Földrengés szimulációhoz.

ParaFEM – Hordozható függvénykönyvtár, párhuzamos végeselem analízissel.

WARP3D – Statikai és dinamikai, nemlineáris analízis, törés szimulációra.

Z88 – Általános célú végeselem rendszer.

Irodalomjegyzék

[1.] Karátsony, János. Numerikus funkcionálanalízis. Available [Online] : http://www.cs.elte.hu/applanal/preprints/nfa.pdf. 2010.

[2.] Gáspár, I. és Bojtár, Z.. Available [Online]: http://www.epito.bme.hu/me/htdocs/oktatas/oktatas.php. 2013.

[3.] Bajcsai, P.. Numerikus analízis. Budapest. Tankönyvkiadó . 1969.

[4.] Páczelt, István, Nándori, Frigyes, Sárközi, László, Szabó, Tamás, Dluhi, Kornél, és Baksa, Attila. A VÉGESELEMES MODELLEZÉS KONTINUUMMECHANIKAI ALAPJAI (Szakmérnöki jegyzet). Available [Online]: http://www.mech.uni-miskolc.hu/~abaksa/education/notes/VEM-HEFOP-2006.pdf.

[5.] Váradi, Károly és Horváth, Imre. Gépészeti tervezést támogató technológiák. Budapest. Műegyetemi Kiadó . 2008.

[6.] Kohnke, Peter. Ansys, Theory Reference, R5.6. ANSYS, Inc.. Southpointe . 1994.

[7.] Váradi, Károly és Molnár, László. CAD alapjai. www.tankonyvtar.hu. 2009.

[8.] Available [Online]: [http://en.wikipedia.org/wiki/Computer-aided_design]. Hozzáférés dátuma: 2014.

[9.] Várady, Tamás. 3D-s számítógépes geometria. Available [Online]: http://cg.iit.bme.hu/portal/content/3d-s-szamitogepes-geometria. 2010.

[10.] Kosztyán, Zsolt Tibor. 3D tervezés (előadásjegyzet).

[11.] SolidWorks Help.

[12.] Madenci, E. és Guven, I.. The Finite Element Method and Applications in Engineering Using ANSYS. The University of Arizona: Springer. 2006.

[13.] Available [Online]: http://deust.wordpress.com/2013/04/23/meshing-methods-ansys-meshing.

[14.] Váradi, Károly. Szerkezetanalízis, (Előadásjegyzet).

[15.] Bojtár, Imre és Gáspár, Zsolt. A végeselemmódszer matematikai alapjai. BME Tartószerkezetek Mechanikája Tanszék. Budapest . 2009.

[16.] Ho-Le, K.. Finite element mesh generation methods: a review and classification. Computer-aided design. kötet20 szám1. pp. 27-38. 1988.

[17.] Cho, W. és Patrikalakis, N. M.. COMPUTATIONAL GEOMETRY. Cambridge: Massachusetts Institute of Technology. 2003.

[18.] Schneiders, R.. Algorithms for Quadrilateral and Hexahedral Mesh Generation. Germany:MAGMA Gießereitechnologie GmbH..

[19.] Thompson, J. E., Warsi, Z., és Mastin, C. W.. Numerical Grid Generation, Foundations and Applications, http://www.hpc.msstate.edu/publications/gridbook/chap02.php.

[20.] Nonlinear Finite Element Analysis of Elastomers http://www.mscsoftware.com/sites/default/files/white-paper-nonlinear-fea-elastomers.pdf. MSC.Software.

[21.] Bojtár, Imre. Mechanikai anyagmodellek, (előadásvázlat). BME Tartószerkezetek Mechanikája Tanszék. Budapest . 2010.

[22.] Kurutzné Kovács, M B. I.. Szilárdságtan Előadások Vázlata. 2006.

[23.] Available [Online]: http://en.wikipedia.org/wiki/Bingham_plastic.

[24.] Kovács, Ádám. VÉGESELEM-MÓDSZER. Typotex Kiadó. 2011.

[25.] Muttnyánszky, Ádám. Szilárdságtan. Műszaki könyvkiadó. Budapest . 1981.

[26.] Szalai, József. A faanyag és faalapú anyagok anizotróp rugalmasság- és szilárdságtana. Erdészeti És Faipari Egyetem. Sopron . 1994.

[27.] Bodor, Géza és Vas, László Mihály. Polimer Anyagszerkezettan. Műegyetemi Kiadó. Budapest . pp. 168-178. és 230-238.. 1999.

[28.] Thamm, Frigyes. Műanyagok szilárdságtana. BME. Budapest . 1988.

[29.] Imaoka, S.. Analyzing Viscoelastic Materials. ANSYS Advantage. Volume II, Issue 4. 2008.

[30.] Tombácz, Etelka. Reológia (előadás vázlat).

[31.] Mitsoulis, E.. FLOWS OF VISCOPLASTIC MATERIALS: MODELS AND COMPUTATIONSE. Rheology Reviews. pp. 135 - 178.. 2007.

[32.] Bojtár, Imre. Mechanika MSc. (Előadásvázlat). BME Tartószerkezetek Mechanikája Tanszék. Budapest . 2010.

[33.] Butz, T. és von Stryk, O.. Modelling and Simulation of Rheological Fluid Devices. Sonderforschungsbereich. kötet438.

[34.] M., László. Szilikon anyagú finommechanikai elemek és szerkezetek modellezése, PhD értekezés. Budapest . 2001.

[35.] Abaqus help. Dassault Systemes, Available [Online]: http://abaqus.me.chalmers.se/v6.8/books/usb/default.htm. Hozzáférés dátuma: 2013.

[36.] B., Nándor. Elasztomer anyagok és csúszótömítések súrlódása és kopása, PhD értekezés. Budapest . 2011.

[37.] Available [Online]: http://en.wikipedia.org/wiki/Hyperelastic_material.

[38.] Ogden, R. W.. Non-linear Elastic Deformations. GB: Ellis Horwood Ltd. pp. 220-222.. 1984.

[39.] Sályi, István. Pattantyús II. Gépész- és villamosmérnökök kézikönyve. Műszaki Könyvkiadó. Budapest . 1961.

[40.] Fodor, György. Elméleti elektrotechnika I. Tankönyvkiadó. Budapest . 1970.

[41.] Available [Online]: http://info.ee.surrey.ac.uk/Workshop/advice/coils/mu/.

[42.] Bojtos, A. és Huba, A.. Electrical Properties of Conductive Silicone Rubber. IX International PhD Workshop, OWD’2007. 20–23 October 2007.

[43.] Páczelt, István, Szabó, Tamás, és Baksa, Attila. A végeselem-módszer alapjai. 2007.

[44.] Ruiz, M. J. G.. Thermal Analysis, Incluye material propiedad de ANSYS, Inc. Available [Online]: http://mecanica.eafit.edu.co/~mgarcia/diplomadoDM/termal/thermal.pdf.

[45.] Bojtár, Imre és Gáspár, Zsolt. Nemlineáris végeselemek.

[46.] Dr. Nagy, Zoltán. Kontinuumok rezgése, hangfrekvenciás mechanikai rezgések vizsgálata. ELTE.

[47.] Budó, Ágoston. Kísérleti fizika, II. kötet. Elektromosságtan és mágnesességtan. Tankönyvkiadó. Budapest . 1991.

[48.] Gróf, Gyula. Hőközlés. Budapest . 1999.

[49.] Makhult, M.. Gumirugók. Műszaki Könyvkiadó. Budapest . 1963.