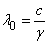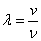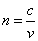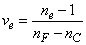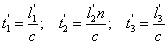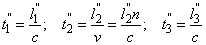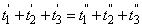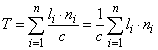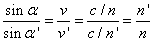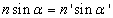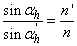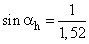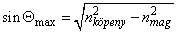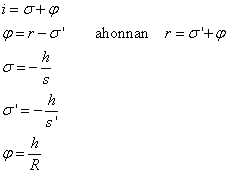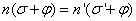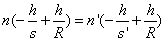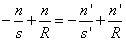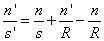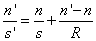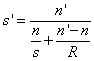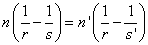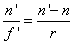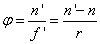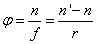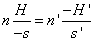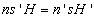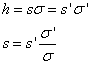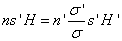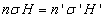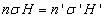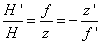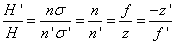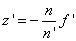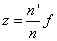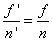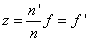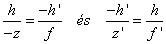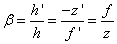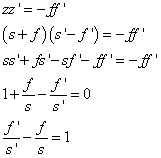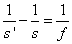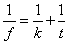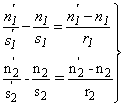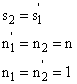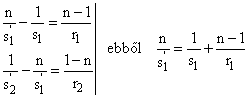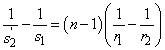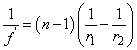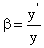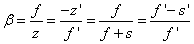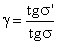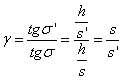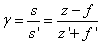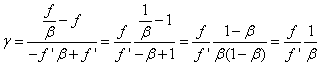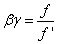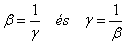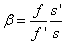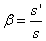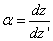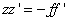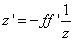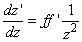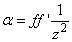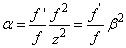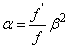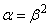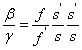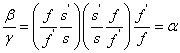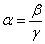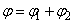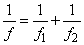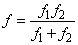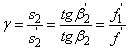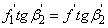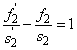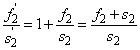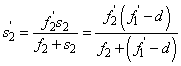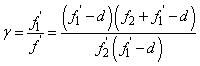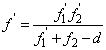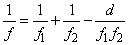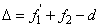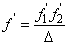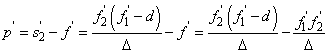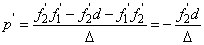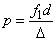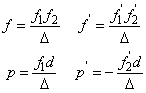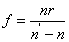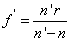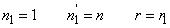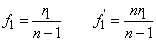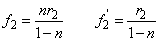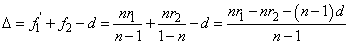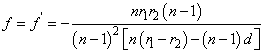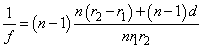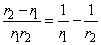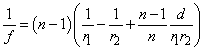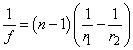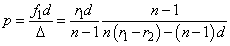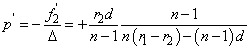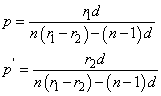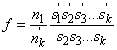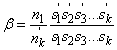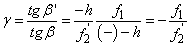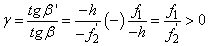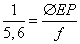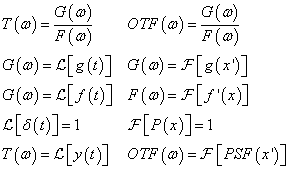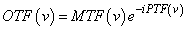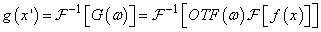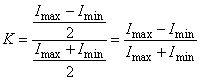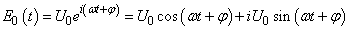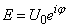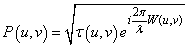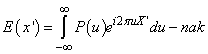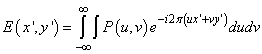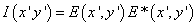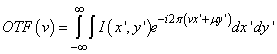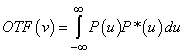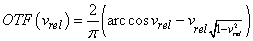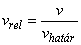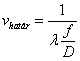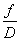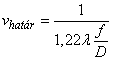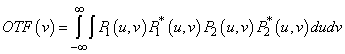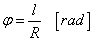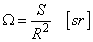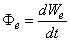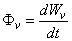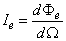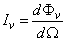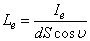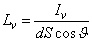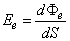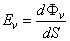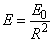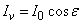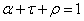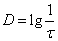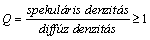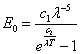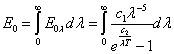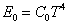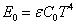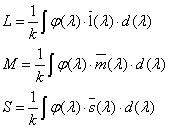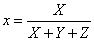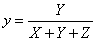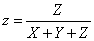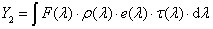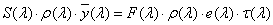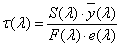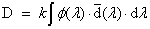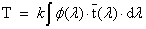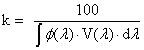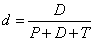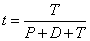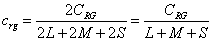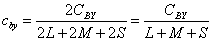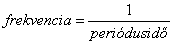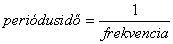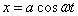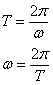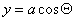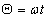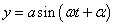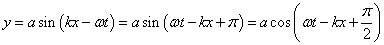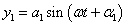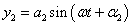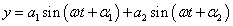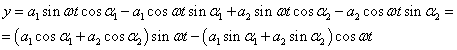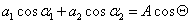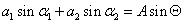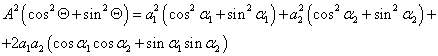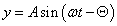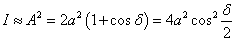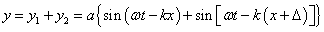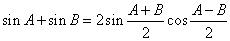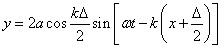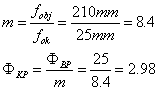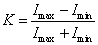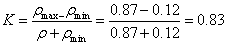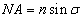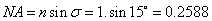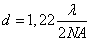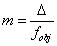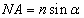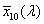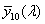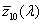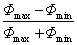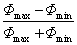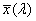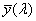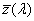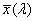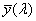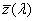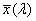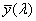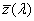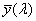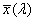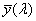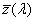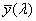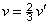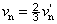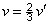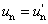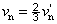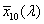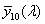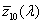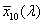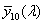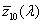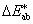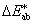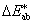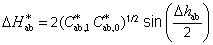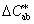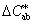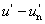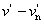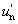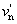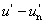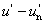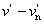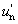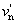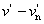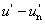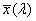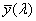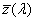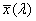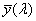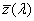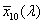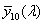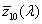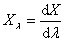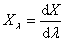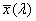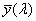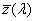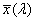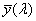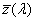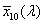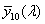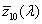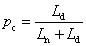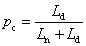Műszaki Optika
Szerzői jog © 2014 Dr. Ábrahám György, Dr. Wenzelné Gerőfy Klára, Dr. Antal Ákos, Dr. Kovács Gábor

A tananyag a TÁMOP-4.1.2.A/1-11/1-2011-0042 azonosító számú „ Mechatronikai mérnök MSc tananyagfejlesztés ” projekt keretében készült. A tananyagfejlesztés az Európai Unió támogatásával és az Európai Szociális Alap társfinanszírozásával valósult meg.

Dr. habil Ábrahám György (1. fejezet) egyetemi tanár, BME-MOGI
Dr. habil Wenzel Klára (4. fejezet és CIE szótár) egyetemi tanár
Dr. Antal Ákos (2., 3., 5., 6., 7. fejezetek ) egyetemi adjunktus, BME-MOGI
Dr. Kovács Gábor (2., 3. fejezetek ) tudományos munkatárs, BME-MOGI
Kézirat lezárva: 2014 február
Lektorálta: Dr. Kalló Péter
További közreműködő: Németh Zoltán
A kiadásért felel a(z): BME MOGI
Felelős szerkesztő: BME MOGI
2014
- 1. A képalkotás alapjai
- 1.1. Fénytani alapismeretek
- 1.2. A geometriai optika alapjai
- 1.3. Valóságos lencsék számításai
- 1.4. Teleszkopikus rendszerek
- 1.5. Rekeszek
- 1.6. Képméret, képszög, fősugár
- 1.7. Optikai átviteli függvények
- 1.7.1. Elemi alakzatok képalkotása
- 1.7.2. Az optikai átviteli függvény rendszertechnikai származtatása
- 1.7.3. Az optikai átviteli függvények szemléletes magyarázata
- 1.7.4. Az apertúrafüggvény és kapcsolata az optikai átviteli függvénnyel
- 1.7.5. Aberrációmentes optikai rendszer átviteli függvénye
- 1.7.6. Sorba kapcsolt rendszerek átviteli függvénye
- 2. Radiometria – fotometria
- 2.1. A radiometria és a fotometria jelölésrendszere
- 2.2. Optikai sugárzás
- 2.3. A térszög
- 2.4. Radiometriai és fotometriai mennyiségek és egységek
- 2.5. A távolságtörvény
- 2.6. A Lambert-féle koszinusztörvény
- 2.7. Fotometriai és radiometriai mennyiségek mérése
- 2.8. A vizuális fotometria
- 2.9. Objektív fotometria
- 2.10. A hőhatás elvén működő sugárzásmérés
- 2.11. Sugárzásmérés a fényelektromos hatás elvén
- 2.12. A fotográfiai hatáson alapuló sugárzásmérés
- 2.13. Denzitometrálás
- 2.14. Izokromatikus, és heterokromatikus fotometrálás
- 2.15. Ellenőrző kérdések
- Felhasznált irodalom
- 3. Fényforrások
- 3.1. A fényforrások működését leíró alapfogalmak és törvények
- 3.2. A sugárzás fontosabb törvényei
- 3.3. A Planck-törvény
- 3.4. A Wien-törvény
- 3.5. Rayleigh–Jeans-törvény
- 3.6. A Stefan-Boltzmann-törvény
- 3.7. Nem abszolút fekete-test jellegű sugárzók
- 3.8. A Kirchhoff törvény
- 3.9. Fényforrások hatásfoka
- 3.10. Fénykibocsátás az abszolút fekete test sugárzása alapján
- 3.11. A Nap sugárzása
- 3.12. Izzólámpák
- 3.13. Elektromos kisülés gázokban
- 3.14. Gázkisülő lámpa
- 3.15. Nagyintenzitású ívlámpák
- 3.16. Ellenőrző kérdések
- Felhasznált irodalom
- 4. Színtan
- 4.1. Történeti áttekintés
- 4.2. Mit nevezünk színnek?
- 4.3. Az emberi szem; a színes látás
- 4.4. A színtévesztés
- 4.4.1. Mi a színtévesztés?
- 4.4.2. Genetikus háttér, a színtévesztés elterjedtsége
- 4.4.3. A színtévesztés optikai magyarázata
- 4.4.4. A színtévesztés típusai
- 4.4.5. A színlátás javításának elve
- 4.4.6. A színtévesztés mérése; a diagnózis
- 4.4.6.1. A pszeudoizokromatikus tesztek
- 4.4.6.2. Az anomaloszkóp
- 4.4.6.3. Új színlátás vizsgáló műszerünk: az Anomal Tester
- 4.4.6.4. Új színlátás vizsgáló tesztünk: a színlátás vizsgáló Atlasz
- 4.4.6.5. Tapasztalatok a színlátás-javító szemüvegekkel
- 4.4.6.6. A színlátás javító szemüveg viselésének hatása a színtévesztésre
- 4.5. A színek jellemzése
- 4.5.1. A színek spektrális jellemzése (MSz 9620)
- 4.5.2. A színek tristimulusos jellemzése
- 4.5.3. A színek pszichofizikai (köznapi) jellemzése
- 4.5.4. A színek fizikai jellemzése
- 4.6. A színkeverés
- 4.7. A kiegészítő színek
- 4.8. A metameria
- 4.9. Az RGB és a CMYK színrendszer
- 4.10. A gamut
- 4.11. A színmérő rendszerek
- 4.11.1. A CIE színmérő rendszer
- 4.11.1.1. A CIE RGB-színrendszer
- 4.11.1.2. A CIE xyY színrendszer
- 4.11.1.3. A CIE L*a*b* színrendszer
- 4.11.1.4. A 20°-os és a 100°-os CIE adatok
- 4.11.1.5. A normál színmérő észlelő
- 4.11.1.6. A spektrális fényhatásfok függvény
- 4.11.1.7. A Planck-féle fekete sugárzó („fekete test”)
- 4.11.1.8. A színhőmérséklet
- 4.11.1.9. A szabványos CIE fényforrások
- 4.11.1.10. A színvisszaadás
- 4.11.2. Színminta gyűjtemények és színminta alapú szín rendszerek
- 4.11.2.1. A Munsell színminta atlasz és színrendszer (1929)
- 4.11.2.2. Az NCS (Natural Color System) színrendszer (1979)
- 4.11.2.3. Az Ostwald színrendszer (1931)
- 4.11.2.4. A Coloroid színrendszer
- 4.11.2.5. A RAL színtervezési rendszer
- 4.11.2.6. Jean Bourges digitális színrendszere
- 4.11.2.7. A színminta gyűjtemények
- 4.12. A színmérés
- 4.13. Az emberi színlátás modellezésén alapuló színrendszerek
- 4.14. Ajánlott irodalom
- 5. Interferometria
- 5.1. Bevezető gondolatok
- 5.2. Történeti előzmények
- 5.3. A fény terjedési sebességének kérdése
- 5.4. Hullámtani alapfogalmak
- 5.5. A periodikus mozgás
- 5.6. Egyszerű harmonikus rezgőmozgás
- 5.7. Transzverzális hullámok
- 5.8. Amplitúdó és intenzitás
- 5.9. Frekvencia és hullámhossz
- 5.10. Fényinterferencia
- 5.11. A szuperpozíció elve
- 5.12. Egyszerű harmonikus rezgőmozgások összeadása egy egyenes mentén
- 5.13. Lézer interferometria
- 5.14. Amplitúdóosztás. Michelson-interferométer
- 5.15. Ellenőrző kérdések
- Felhasznált irodalom
- 6. A távcső, mint látószögnövelő eszköz
- 6.1. A távcsövek csoportosítása
- 6.2. Történeti áttekintés
- 6.3. Tükrös távcsövek története
- 6.4. A Magyarországi csillagászati megfigyelések története
- 6.5. A lencsés távcsövek optikai rendszere
- 6.6. Tükrös-távcsövek
- 6.7. A Newton távcső
- 6.8. Cassegrain távcső
- 6.9. A Schmidt távcső (Schmidt kamera)
- 6.10. Maksutov távcsövek
- 6.11. Ellenőrző kérdések:
- Felhasznált irodalom
- 7. A mikroszkóp mint optikai rendszer
- 7.1. Bevezető fogalmak
- 7.1.1. A látószög növelése
- 7.1.2. A mikroszkóp és a mikroszkópos képalkotás
- 7.1.3. A mikroszkópos képalkotás értelmezésének eszköztára
- 7.1.4. A mikroszkóp, mint finommechanikai eszköz
- 7.1.5. A képrögzítés, megfigyelés és nagyítás
- 7.1.6. Válogatott fejezetek a mikroszkópia történetéből
- 7.1.7. A mikroszkópos észlelés alapfogalmai
- 7.1.8. A szem felbontóképessége
- 7.1.9. A térlátás
- 7.1.10. A kép tulajdonságai
- 7.1.11. A kép világossága és kontrasztossága
- 7.1.12. Numerikus apertúra
- 7.1.13. A mélységélesség
- 7.1.14. A kép nagyítása
- 7.1.15. A kép látómezeje
- 7.1.16. Felbontóképesség
- 7.2. Az egyszerű és összetett mikroszkóp felépítése és megvilágítása
- 7.3. A mikroszkóp képalkotást végző optikai rendszerei
- 7.3.1. A mikroszkopizálás során alkalmazott optikai rendszerek és tulajdonságaik
- 7.3.2. A mikroszkópok legfontosabb képalkotó optikai rendszerei
- 7.3.3. Az objektív
- 7.3.4. A mikroszkóp objektívek képalkotási hibái
- 7.3.5. Akromátok
- 7.3.6. Apokromátok
- 7.3.7. Speciális objektívek
- 7.3.8. Okulárok
- 7.3.9. A főbb okulártípusok
- 7.3.10. Speciális okulárok
- 7.3.11. Az okulárok szerkezeti kialakítása
- 7.3.12. Kondenzorok
- 7.4. Ellenőrző kérdések
- Felhasznált irodalom
- A. CIE szótár
- 1.1. Spektrumszínek és spektrumvonalak
- 1.2. Az optikában használatos anyagok a törésmutató és az Abbe-szám függvényében
- 1.3. Képalkotás a Fermat-elv alapján
- 1.4. Fénytörés két közeg határán
- 1.5. A totálreflexió
- 1.6. Az optikai szál működési elve
- 1.7. A síkpárhuzamos lemez
- 1.8. Gömbfelület képalkotása
- 1.9. Vázlat a Lagrange-féle invariánshoz
- 1.10. A fősíkok és a főpontok szerkesztése
- 1.11. A csomópontok származtatása
- 1.12. Vázlat a csomópontok helyének számításához
- 1.13. Vázlat a Newton-formulához
- 1.14. Vázlat a vékonylencse számításhoz
- 1.15. A lineáris nagyítás számítása
- 1.16. A szögnagyítás számítása
- 1.17. Vázlat az eredő gyújtótávolság számításához
- 1.18. Vastag lencse
- 1.19. Vázlat a vastag lencse fősíkjainak számításához
- 1.20. A Kepler-távcső
- 1.21. A Galilei-távcső
- 1.22. Az apertúrarekesz
- 1.23. Elemi alakzatok szórásképei
- 1.24. Az optikai átviteli függvény, mint a rendszertani átviteli függvény analógiája
- 1.25. A csíkos tárgy képalkotása.
- 1.26. A modulációs átviteli függvény és a fázisátviteli függvény
- 1.27. A hullámaberráció értelmezése
- 1.28. Aberrációmentes rendszer átviteli függvényének szemléltetése
- 1.29. Aberrációmentes rendszer átviteli függvénye
- 1.30. Aberrációval terhelt és aberrációmentes rendszerek átviteli függvényei a rekeszelés függvényében
- 2.1. A szem érzékenységi görbéi [2.4.]
- 2.2. A térszög értelmezése
- 2.3. A Lambert-féle koszinusztörvény [2.4.]
- 2.4. Az áteresztési, visszaverési és elnyelési tényező értelmezése
- 2.5. A fotográfiai réteg jelleggörbéje [2.4.]
- 3.1. A Planck-törvény grafikus ábrázolása
- 3.2. A Wien-féle eltolási törvény szemléltetése
- 3.3. A Wien-féle eltolási törvény ábrázolása
- 3.4. Rayleigh–Jeans-törvény és a Wien-törvény
- 3.5. Különböző hőmérsékletű abszolút fekete test sugárzási görbéi
- 3.6. A Nap sugárzásának spektrális eloszlása m=0 a légkörön kívül; m=1 a Föld felszínén; a merőleges beesésnél; m=2 Nap állása 60°; m=3 Nap állása 70°
- 3.7. Különböző hőmérsékletű volfrámszálak kibocsátó képessége
- 3.8. Különböző hőmérsékletű volfrámszálak spektrális felületi fénysűrűsége
- 3.9. 2,5 kW teljesítményű higany-xenon ív fényességeloszlása
- 3.10. Nagynyomású higanyívlámpa spektrális eloszlása
- 4.1. A spektrum
- 4.2. Az emberi szem metszete
- 4.3. Egy pálcika és egy csap metszete
- 4.4. A retina metszete
- 4.5. A vörösre, zöldre és kékre érzékeny csapok elhelyezkedése a retinán
- 4.6. A csapok és a pálcikák 1 mm2-re jutó száma a retinán
- 4.7. A szem látómezeje
- 4.8. Marks, Dobelle és Mc Nichol 1964-ben publikált mérési eredményei
- 4.9. A Marks által kiértékelt mérési eredmények
- 4.10. Szín kontraszt és világosság kontraszt jelenség
- 4.11. A színtévesztés gyakorisága a férfiak között
- 4.12. A vörös-, zöld- és kék-érzékeny csapok spektrális érzékenysége
- 4.13. A színérzékelő receptorok spektrális eltolódásai
- 4.14. Protanomália
- 4.15. Deuteranomália
- 4.16. A színlátás javításának elve
- 4.17. Az optimalizálás elve a színlátás javító szemüveg tervezésénél
- 4.18. A pszeudo-izokromatikus tesztábra
- 4.19. Heidelbergi anomaloszkóp és látómezeje
- 4.20. Az anomaloszkópi mérés kiértékelése
- 4.21. Az Anomal Tester
- 4.22. Az Anomal Tester LED-jeinek spektruma
- 4.23. A színlátás vizsgáló Atlasz 3 sorozatának kezdő ábrája
- 4.24. Az elektromágneses sugárzás tartományai
- 4.25. A spektrális eloszlás függvény
- 4.26. Egy optikailag átlátszó réteg a fényt részben reflektálja, részben átbocsátja, és részben szórja
- 4.27. A Nap spektrális energia eloszlása
- 4.28. A transzmissziós tényező
- 4.29. Színes felületek spektrális reflexiója
- 4.30. A színinger kialakulása
- 4.31. Vörös, zöld és kék alapszín additív keveréke
- 4.32. Világos telített és sötét telített zöld szín spektruma
- 4.33. Világos telítetlen és sötét telítetlen zöld szín spektruma
- 4.34. Világos és sötét telített piros szín spektruma
- 4.35. Egyenlő energiájú szürke színek
- 4.36. Az additív színkeverés alapszínei
- 4.37. A színkeverés színháromszöge
- 4.38. A színinger kialakulása
- 4.39. A szubtraktív színkeverés alapszínei
- 4.40. Az additív alapszínek
- 4.41. Az additív alapszínek additív keverése szubtraktív alapszíneket eredményez
- 4.42. A szubtraktív alapszínek szubtraktív keverékei éppen az additív alapszíneket eredményezik
- 4.43. Kiegészítő színek
- 4.44. Kiegészítő színek a CIE színezeti háromszögben
- 4.45. A színes monitoron megjeleníthető színek
- 4.46. Ideális additív és szubtraktív alapszínek spektrális eloszlása
- 4.47. CRT (képcsöves) színes monitor fényének spektrális energia eloszlása
- 4.48. Szubtraktív alapszínek színpontjai
- 4.49. Egy színes nyomtató C, M és Y alapszínének és azok szubtraktív keverésével létrehozott R, G és B színének színpontja
- 4.50. Színegyeztetési kísérletek eltűnő éles látómezőben
- 4.51. A CIE RGB színmegfeleltető függvények
- 4.52. Az R, G és B alapszínek színterének ábrázolása
- 4.53. A befoglaló háromszög
- 4.54. A CIE X, Y és Z alapszín ingerek színterének ábrázolása
- 4.55. A CIE színmegfeleltető függvények
- 4.56. A CIE színezeti diagram vagy CIE színháromszög (népszerű nevén „papucsdiagram”).
- 4.57. A MacAdam ellipszisek
- 4.58. A CIE L*a*b* színrendszer
- 4.59. A spektrális fényhatásfok függvény
- 4.60. A Planck sugárzó
- 4.61. A Planck sugárzó spektrális energia eloszlása
- 4.62. A Planck sugárzó vonala a papucs diagramban
- 4.63. A korrelált színhőmérséklet vonalai
- 4.64. Az etalon színminták színpontjai
- 4.65. A színvisszaadási index számítási módszere
- 4.66. A Munsell-színkör 10 alapszíne
- 4.67. A Munsell alapszínek jelei
- 4.68. Egy szabályos hengeres szín-test
- 4.69. Reálisan megvalósítható színek háromdimenziós képe
- 4.70. Az NCS színkör
- 4.71. Az NCS Színatlasz egyik lapja
- 4.72. Ostwald színköre. A szemben elhelyezkedő színek kiegészítő színek.
- 4.73. Ostwald Szín-Atlaszának egyik lapja
- 4.74. Ostwald színkörének alapszínei a CIE színezeti diagramban
- 4.75. Harmonikus színhármasok
- 4.76. Négyes színharmóniák
- 4.77. A COLOROID színrendszer színköre
- 4.78. A COLOROID alapszínek jellemző hullámhossza a CIE színezeti diagramban
- 4.79. A COLOROID alapszínek színkoordinátái a CIE színezeti diagramban
- 4.80. A COLOROID színtest
- 4.81. A RAL színtest
- 4.82. A RAL színkör egy színsíkkal
- 4.83. RAL színkártyák
- 4.84. Jean Burges színköre
- 4.85. Jean Burges színrendszerének alapszínei a CIE színezeti diagramban
- 4.86. Színárnyalatok 10-10 fokozatban
- 4.87. Felületek reflexiójának típusai
- 4.88. A CIE szabványos mérési geometriák
- 4.89. Diffúzor gömb
- 4.90. A GretagMachbeth Color Box
- 4.91. DATACOLOR Handy spektrofotométer, 2000
- 4.92. Az AVANTES spektrofotométer és színmérő műszer optikai vázlata
- 4.93. Konica-Minolta 2600 CM-2600d színmérő műszer
- 4.94. A BME Finommechanikai, Optikai Tanszékén (ma: MOGI Tanszék) kifejlesztett kétcsatornás tristimulusos színmérő műszer
- 4.95. A protos, a deuteros és a tritos spektrális érzékenysége
- 4.96. A színezeti diagram a PDT színrendszerben
- 4.97. Az intenzitásra normált csatorna függvény alakja, ezek az organikus színrendszer színkoordinátái
- 4.98. Az organikus színrendszer
- 4.99. Az OCS színtest
- 5.1. Pierre de Fermat (1601 – 1665)
- 5.2. Leonhard Euler (1707 – 1783)
- 5.3. Michael Faraday (1791 – 1867)
- 5.4. James Clerk Maxwell (1831 – 1879)
- 5.5. Albert Abraham Michelson (1852 – 1931) [5.11.]
- 5.6. Frits Zernike (1888 – 1966) [5.10.]
- 5.7. A Michelson interferométer
- 6.1. A Kepler-típusú távcső és sugármenete
- 6.2. A Galilei-típusú távcső és sugármenete
- 6.3. A terresztikus távcső és sugármenete
- 6.4. Lencsés képfordító rendszer
- 6.5. Prizmás képfordító rendszer
- 6.6. A mezőlencse szerepe
- 6.7. A Newton távcső
- 6.8. Cassegrain távcső
- 6.9. A Schmidt távcső
- 6.10. A Makszutov távcső
- 7.1. A látószög értelmezése
- 7.2. A mikroszkópizálás történetének meghatározó alakjai
- 7.3. A mikroszkópizálás történetének meghatározó alakjai
- 7.4. Az egyszerű mikroszkóp
- 7.5. Az összetett mikroszkóp
- 7.6. A Köhler-féle megvilágítás
- 7.7. A Köhler-féle megvilágítás vázlata
- 7.8. Objektív tartó revolver
- 7.9. A longitudinális és a transzverzális színhiba szemléltetése
- 7.10. Fedorow-asztal
- 7.11. Ramsden-okulár
- 7.12. A Huygens okulár
- 7.13. Egy szerelt mikroszkóp okulár
- 1.1. A fény terjedési sebessége különböző anyagokban
- 1.2. Optikai üveg adatok
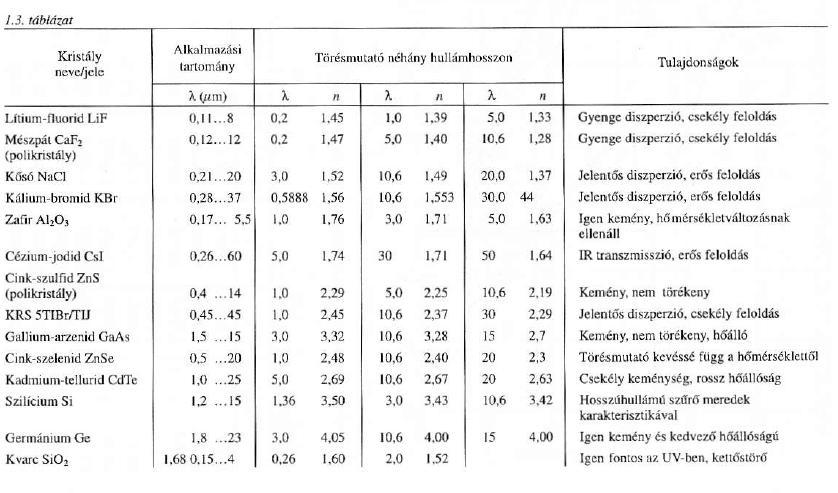
- 1.3. Optikai kristály adatok
- 2.1. Néhány fényforrás fényerőssége
- 2.2. Fontosabb fényforrások fénysűrűsége
- 2.3. Fontosabb megvilágítás értékek
- 2.4. Az emberi munkavégzéssel kapcsolatos megvilágítás szintjeinek jellegzetes értékei
- 2.5. A fontosabb radiometriai és fotometriai mennyiségek [2.4.]
- 6.1. A Cassegrain-rendszerek főé és segédtükteinek típusai
1. fejezet - A képalkotás alapjai
- 1.1. Fénytani alapismeretek
- 1.2. A geometriai optika alapjai
- 1.3. Valóságos lencsék számításai
- 1.4. Teleszkopikus rendszerek
- 1.5. Rekeszek
- 1.6. Képméret, képszög, fősugár
- 1.7. Optikai átviteli függvények
- 1.7.1. Elemi alakzatok képalkotása
- 1.7.2. Az optikai átviteli függvény rendszertechnikai származtatása
- 1.7.3. Az optikai átviteli függvények szemléletes magyarázata
- 1.7.4. Az apertúrafüggvény és kapcsolata az optikai átviteli függvénnyel
- 1.7.5. Aberrációmentes optikai rendszer átviteli függvénye
- 1.7.6. Sorba kapcsolt rendszerek átviteli függvénye
1.1. Fénytani alapismeretek
1.1.1. A fény tulajdonságai
A fény elektromágneses rezgés. Kettős, hullám-, illetve részecsketermészete van, ezért bizonyos jelenségeket hullámtani, másokat pedig kvantummechanikai tárgyalással lehet leírni.
A fény hullámhossza:
|
|
(1.1) |
ahol
|
λ 0 |
a fény hullámhossza vákuumban | |
|
c |
a fény terjedési sebessége vákuumban (közelítőleg: 3x108 m/s) | |
|
v |
a fény frekvenciája |
Általában a fény keletkezésével és elnyelésével (detektálásával) kapcsolatos esetekben kvantummechanikai leírás szükséges, míg terjedésekor a hullámtani, sőt sokszor – a még egyszerűbb – ún. geometriai optikai tárgyalásmód is elegendő.
Fénynek az elektromágneses spektrumnak az emberi szem által látott tartományát (VIS) és a mellette lévő ibolyántúli (UV), valamint infravörös (IR) tartományokat hívjuk. (Lásd. 1.1. ábra - Spektrumszínek és spektrumvonalak)
A látható fény tartománya 380 < λ 0 < 780 nm, amelynek részleteit a látott színek szerint nevezünk el.
A hullámtani tárgyalásmód használatakor hullámfelületekkel jellemezzük a fény terjedését.
A geometriai optika bevezeti a fénysugarak fogalmát, amelyeken a hullámfelületek ortogonális trajektóriáit értjük. Ezen sugároptikai leírás segítségével a legtöbb elemi optikai képalkotást megmagyarázhatjuk.
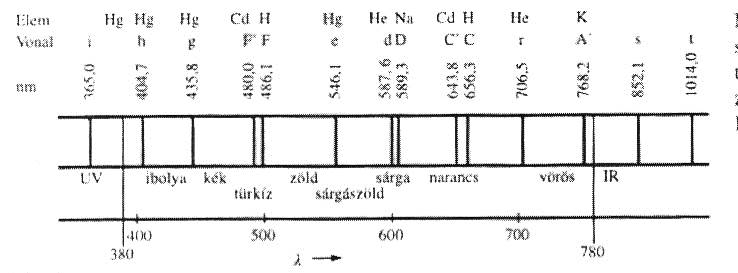
Mivel az atomok emissziós sugárzásai nagyon pontos hullámhosszakon történnek, ezért ezek jeleivel dolgozunk az optikában, ha pontos hullámhosszra akarunk hivatkozni.
1.1.2. Fény terjedése közegekben. A törésmutató és az Abbe-szám
A fény lassabban terjed anyagi közegekben, ekkor sebességét v-vel, hullámhosszát λ-val jelöljük. Frekvenciája változatlan marad.
|
|
(1.2) |
A különböző színű fények hullámhossza és terjedési sebessége más és más. (lásd 1.1. táblázat - A fény terjedési sebessége különböző anyagokban)
|
Anyag |
Sebesség km/s |
Anyag |
Sebesség km/s |
|---|---|---|---|
|
hidrogén |
299 959 |
glicerin |
204 152 |
|
oxigén |
299 918 |
koronaüveg |
197 980 |
|
levegő |
299 914 |
kanada balzsam |
194 553 |
|
nitrogén |
299 912 |
flintüveg |
186 013 |
|
víz |
225 059 |
nehézflint |
170 374 |
|
etil-alkohol |
220 312 |
gyémánt |
124 105 |
A sebesség vákumbanihoz képesti csökkenését egy viszonyszámmal, a törémutatóval fejezzük ki.
|
|
(1.3) |
A levegő törésmutatója 20 °C-on és 1013 mbar nyomáson n = 1,0003, így a továbbiakban n = 1-nek vesszük.
A víz törésmutatója: 1,33
A leggyakoribb, tradicionális optikai anyag az üveg, amelynek átlagos törésmutatója: 1,5, míg a különféle üvegek törésmutatója: 1,45 < n < 1,95 között változik.
A törésmutató is színfüggő, vagyis egy adott anyagnak nem egyetlen törésmutatója van, hanem minden színre más és más.
Az üveg törésmutatója is változik a fény színe szerint. Ernst Abbe-ról Abbe-számnak nevezzük a következő összefüggést:
|
|
(1.4) |
A nevezőben a spektrum kék, illetve vörös színeire vonatkozó törésmutatók különbsége, a számlálóban pedig egy közepes (pl. „e”, vagy „d”) színre vonatkozó törésmutató szerepel.
ν indexe a közepesnek választott színre utal. λ e = 546,1 nm, λ d = 587,6 nm. Az emberi szem legérzékenyebb a λ = 555 nm-re, így az ehhez közel álló színeket szokás alapul venni közepes hullámhosszként.
Néhány optikai üveg betű-számjelét, törésmutatóit és Abbe-számát az (1.2. táblázat - Optikai üveg adatok) táblázatban láthatjuk.
|
Az üveg jele |
nF’ |
ne |
nC’ |
νe |
|---|---|---|---|---|
|
BK7 |
1.52283 |
1.51872 |
1.51472 |
63.96 |
|
K5 |
1.52910 |
1.52458 |
1.52024 |
59.20 |
|
ZK N 7 |
1.51470 |
1.51045 |
1.50633 |
60.98 |
|
BaK 4 |
1.57648 |
1.57125 |
1.56625 |
55.85 |
|
SK 15 |
1.63108 |
1.62555 |
1.62025 |
57.79 |
|
SK 16 |
1.62814 |
1.62286 |
1.61777 |
60.08 |
|
F 2 |
1.63310 |
1.62408 |
1.61582 |
36.11 |
|
SF 2 |
1.66238 |
1.65222 |
1.64297 |
33.60 |
|
SF 6 |
1.82970 |
1.81265 |
1.79750 |
25.24 |
|
SF 10 |
1.74805 |
1.73430 |
1.72200 |
28.19 |
A törésmutató indexeként az 1.1. ábra - Spektrumszínek és spektrumvonalak szerinti spektrumvonalak jeleit használjuk pl. nd, ne, nc, nF. Ha egy törésmutató jele (n) mellett nincs index, akkor megállapodásszerűen a d vonalra kell gondolni, vagyis
Ezekről néhány jellemzőt találhatunk az (1.3. táblázat - Optikai kristály adatok) táblázatban.
|
n = nd |
Az üveg mellett különféle kristályokat is használunk az optikában.
|
|
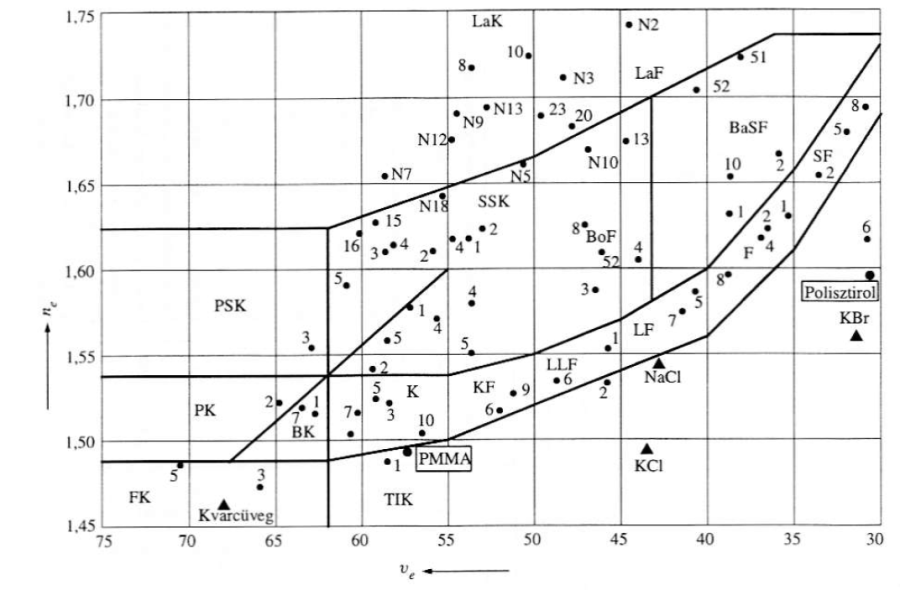
Az optikai üvegeket és kristályokat a katalógusok diagramban is meg szokták adni, a közepes törésmutató és az Abbe-szám függvényében.
Egy ilyen összeállítást mutat az 1.2. ábra - Az optikában használatos anyagok a törésmutató és az Abbe-szám függvényében.
1.1.3. A fény viselkedése közegek határfelületein
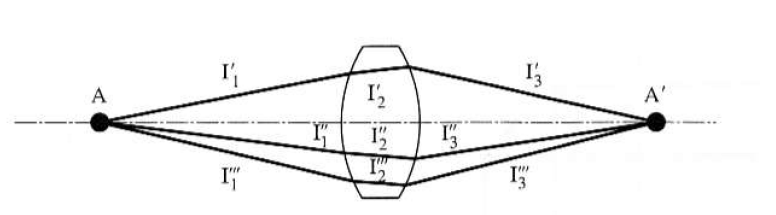
A Fermat-elv
Két pont között a fénysugár azokon az utakon halad, amelyek megtételéhez a legrövidebb időre van szükség más útvonalakkal szemben.
|
|
mivel 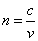
így
|
| ||
|
|
és így továbbb.
A t 2 kifejezéskor a számlálóban megjelent l 2 n szorzatot – vagyis a geometriai távolság és a közeg törésmutatójának szorzatát – optikai úthossznak nevezzük.
Eszerint egy lencse képalkotását, vagyis egy tárgypontból kiinduló több fénysugárnak a képpontban való találkozását úgy képzelhetjük el, hogy valamennyi, a lencsén keresztülhaladó fénysugár azonosan minimális időket fut, miközben más-más utakat tesz meg. Ez úgy lehetséges, hogy a lencsén belül v, a levegőben c sebességgel terjed a fény, így a részidők összege egyenlő lehet egy megfelelő alakú lencse esetén.
A tárgy és képpont közötti utak befutásához szükséges idő:
|
|
(1.5) |
Vagyis a két pont között a fénysugár olyan utakon fog haladni, hogy azok mentén az optikai úthosszak összege egyenlő legyen.
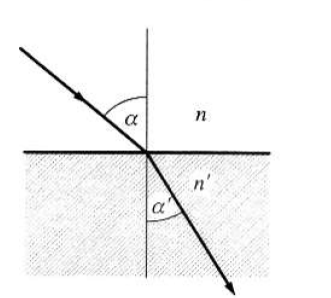
A Snellius–Descartes-törvény szerint két közeg határán a fénysugár megváltoztatja irányát, megtörik.
|
| ||
|
|
(1.6) |
Sűrűbb közegből ritkább közegbe haladó fénysugár felvehet egy olyan beesési szöget, amelynél törési szögként 90º adódik. Ekkor a fénysugár nem lép ki a sűrűbb közegből – totálreflexiót szenved. (1.5. ábra - A totálreflexió)
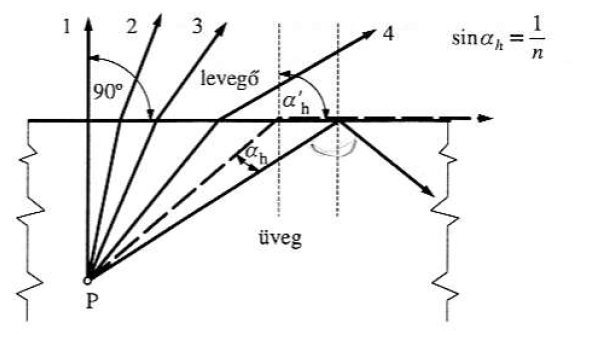
|
|
A határszögnél nagyobb beesési szöggel érkező fénysugarak nem tudnak kilépni a közegből, totálreflexiót szenvednek.
Példa
Üveg-levegő felületre:
|
n=1,52 | ||
|
n’=1 | ||
|
αh=90° | ||
|
| ||
|
αh=41,1° határszög |
45º-os prizma esetén az oldallapokra merőleges fénysugarak az átfogó felületéről úgy verődnek vissza, mintha az tükör lenne, hiszen a visszaverődéskor a 45º > 41,1º, tehát totálreflexió áll fenn.
Alkalmazási példa: optikai szálak
Optikai szálakban a mag és a köpeny határfelületén totálreflexió jön létre. (1.6. ábra - Az optikai szál működési elve)
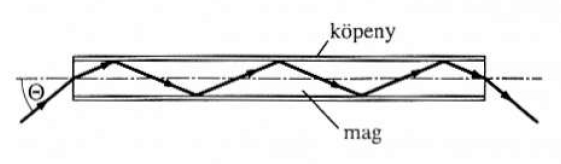
Van egy maximális Θ szög, amelynél nagyobb szöggel érkező fénysugarak nem tudnak az optikai szálba belépni.
|
|
(1.7) |
Az optikai szálakat felhasználási cél szerint három csoportra oszthatjuk:
informatikai célra egyetlen elemi szál sok, modulált információt vihet át. Ezeknél nem található külön mag és köpeny, hanem a törésmutató belülről kifelé folyamatosan csökken (gradiens szál);
fénykábelként sok elemi szálat köteggé fogunk össze, és világítási célból továbbítjuk velük a fényt;
képtovábbító szálkötegek esetében vigyázunk arra, hogy a köteg egyik végén a szálak relatív helye ugyanolyan legyen, mint a másik végén, így képet lehet továbbítani velük.
A síkpárhuzamos (planparalell) lemez
A síkpárhuzamos lemez d vastagságú átlátszó, fénytörő anyagból pl. üvegből, műanyagból készül. A határoló felületek egymással párhuzamosak. A levegőből az első felülethez érkező fénysugár az anyagba lép, sebessége csökken.
A sugár a beesési merőleges felé törik. A lemezen áthaladva az előbbi közegbe, pl. a levegőbe lép ki, és itt eredeti sebességét nyeri vissza. A sugár a beesési merőlegestől törve, eredeti irányával párhuzamosan folytatja útját. Ezen áthaladás alatt két jelenséget tapasztalunk:
fénysugár eredeti irányától t távolságban eltolódott,
P fénypont, amelyből a fénysugár eredetileg elindult, látszólag a síkpárhuzamos lemezhez k-val közelebb P’-be került.
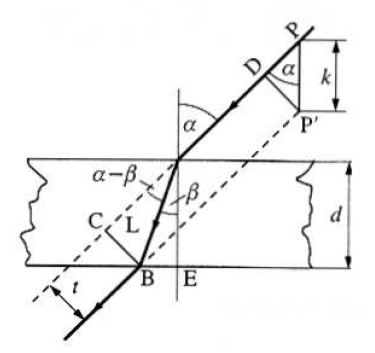
1.2. A geometriai optika alapjai
1.2.1. A geometriai optika alaptörvényei
A fény egyenes vonalban terjed. Ez természetesen homogén, izotróp közegben érvényes.
Különböző közegek határain a fénysugár megtörve folytatja útját. A fénytörést a Snellius–Descartes-törvény írja le.
Különböző közegek határán a fény egy része visszaverődik. Ezt a tükör-törvény írja le, miszerint a beeső, a visszavert fénysugár és a beesési merőleges egy síkban fekszik, valamint a beesési és visszaverődési szög egyenlő. A szögeket a beesési merőlegestől mérjük, amely a fénysugár döféspontjában a felület normálisa.
A fénysugarak függetlenségének elve kimondja, hogy a tér egy pontján keresztül akárhány fénysugár áthaladhat egymás zavarása nélkül. E törvény nyilván nem érvényes pl. koherens lézerfények találkozása esetén, amelyek egymásra hatásakor interferencia jön létre.
A fénysugarak megfordíthatóságának elve szerint ha fény a tér egyik pontjából egy bizonyos útvonalon halad a tér egy másik pontjába, akkor a visszafelé indított fénysugár ugyanazon úton fog haladni.
1.2.2. Előjelszabályok (megállapodások)
A sugármenet-rajzokat úgy vesszük fel, hogy a fénysugarak balról jobbra haladjanak (1.8. ábra - Gömbfelület képalkotása).
Az optikai tengely mentén a gömbfelülettől balra eső távolságok negatívok, a jobbra esőek pozitívok.
Az optikai tengely feletti távolságok (pl. h) pozitívok, a tengely alattiak pedig negatívok.
A távolságok előjelei olyanok, mintha egy felvett koordináta-rendszer origója az S pontban lenne.
A fénysugarak optikai tengellyel bezárt szögei (Ϭ, Ϭ’) akkor pozitívok, ha az optikai tengelyt a fénysugárba az óramutató járásával ellentétes irányban lehet 90°-nál kisebb szöggel beforgatni. Ellenkező esetben a szögek negatívok.
Eszerint az (1.8. ábra - Gömbfelület képalkotása) ábrán: s és Ϭ’ előjele negatív, h, s’, és Ϭ -é pedig pozitív.
A felület döféspontjában a fénysugarak beesési (i), illetve törési (r) szögei akkor pozitívok, ha a beesési merőlegest a fénysugárba az óramutató járásával ellenkező irányba lehet 90°-nál kisebb szöggel beforgatni. Ellenkező esetben a szögek negatívok.
Eszerint i és r pozitív.
A gömbfelületek görbületi sugarai akkor pozitívok, ha a felület balról nézve konvex, és akkor negatívok, ha balról nézve konkáv.
Eszerint R pozitív.
A fókusztávolság előjele pozitív gyűjtő-, negatív pedig szórólencse esetében.
1.2.3. Egyetlen gömbfelület képalkotása
Egy lencse (vagy tükör) leképező rendszerként használva képet alkot a tárgyról. A képalkotás akkor ideális, ha a tárgy és a képe arányos (torzulásmentes), a lencse pontot ponttá, egyenest egyenessé, síkot síkká képez le. A geometriai optikának a fényelhajlás miatt korlátja van, ezért pl. pontot egy valóságos lencse egy kis folttá tud csak leképezni. Ezzel a jelenséggel az optikai átviteli függvényekről szóló 1.7. szakasz - Optikai átviteli függvények fejezetben foglalkozunk.
Paraxiális képalkotásról beszélünk akkor, ha a leképzésben részt vevő fénysugarak az optikai tengelyhez képest csak kis szögeket zárnak be, vagyis tengelyközelben haladnak. Ilyenkor a szögfüggvények (sin, tg) helyett a szögek ívmértékben vett nagyságát használhatjuk.
Metszéki távolságoknak (s, s’) nevezzük a gömbfelület tengelypontjától a tárgy (P), illetve a képpontig (P’) terjedő mennyiségeket.
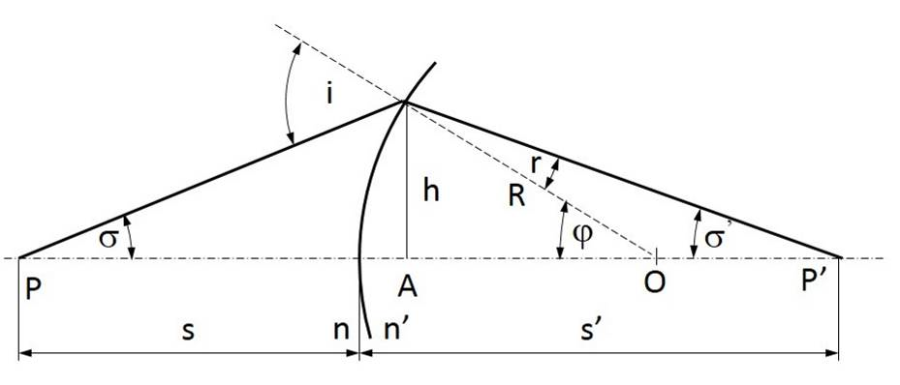
A Snellius–Descartes-törvény szerint:
|
nsini=n’sinr |
Kis szögek esetében (paraxiális eset):
|
ni=n’r |
(1.8) |
Az előjel szabályok alkalmazásával az egyes szögekre a megfelelő háromszögekből:
|
|
Ezeket az (1.8)-ba helyettesítve:
|
| ||
|
|
h-val végig osztva és beszorozva:
|
|
Az ismeretlen a képtávolság:
|
| ||
|
|
(1.9) | |
|
|
(1.10) |
Az összefüggés szerint egy r sugarú gömbfelülettől s távolságra fekvő tárgypont képe a felülettől s’ távolságra keletkezik.
A képlet átrendezésével, egy-egy oldalra gyűjtve a tárgyoldali (veszszőtlen) és a képoldali (vesszős) mennyiségeket az Abbe-féle invariánst kapjuk.
|
|
(1.11) |
Ha a gömbfelületre párhuzamos fénysugarak érkeznek (a tárgy a végtelenben van), akkor a fénysugarak a képoldalon a fókuszpontban találkoznak. (1.9) – ből s= - ∞ és s’=f’ helyettesítéssel:
|
|
(1.12) |
A jobb oldalon lévő mennyiséget törőértéknek nevezzük, és dioptriában adjuk meg:
|
|
(1.13) | |
|
|
(1.14) |
(Dioptriában való számoláskor a fókusztávolságokat méterben kell helyettesíteni!)
A Langrange-féle invariáns
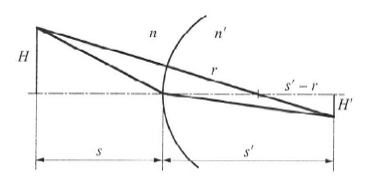
A Snellius–Descartes-törvény szerint a törési pontban kis szögek esetén:
|
|
másképpen
|
|
de az (1.8. ábra - Gömbfelület képalkotása) ábrából
|
| ||
|
|
ahonnan
|
|
Ezt nevezzük Lagrange-féle invariánsnak, ami azt fejezi ki, hogy a fénysugár paraxiális tartományban úgy törik, hogy a törésmutató, a tárgy, ill.képszög és a tárgy, ill. képnagyság szorzata állandó marad.
1.2.4. Kardinális elemek: fősíkok, főpontok, csomópontok
A fősíkok az első és utolsó felületével jellemzett optikai rendszerbe a tengellyel párhuzamosan belépő fénysugarak és a rendszert elhagyó megfelelő fénysugarak meghosszabbításainak metszéspontjai által kifeszített felületek (1.10. ábra - A fősíkok és a főpontok szerkesztése).
A főpontok a fősíkoknak és az optikai tengelynek a döféspontjai (H,H’)
Minden optikai rendszernek két fősíkja (és főpontja) van: tárgyoldali és képoldali fősíkok (főpontok).
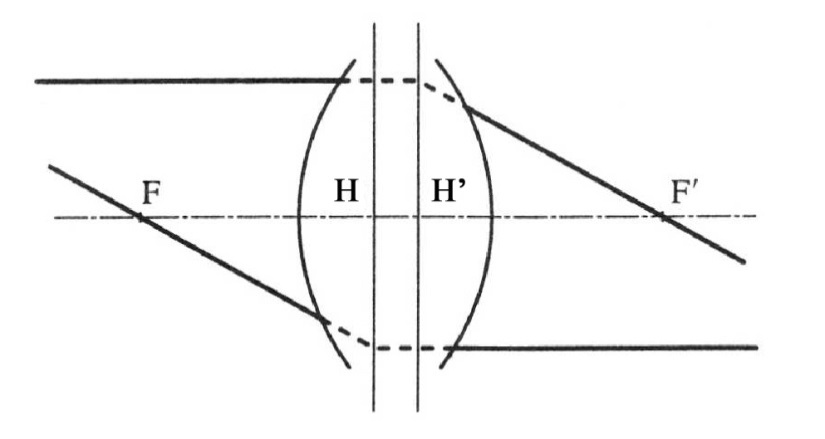
A fősíkoktól mérjük a fókusztávolságokat, a tárgytávolságot, illetve a képtávolságot.
A főpontokra nézve az optikai rendszer nagyítása 1-szeres és pozitív (egyenes állású).
A fősíkok sorrendje és helye az adott optikai rendszertől függ. Egy optikai rendszer főpontjai egymás konjugáltjai, vagyis ha az egyikbe helyezünk egy tárgyat, akkor annak képe a másikban lesz.
A csomópontok
Egy optikai rendszer egyik csomópontjába (N) irányított fénysugár a rendszert önmagával párhuzamosan hagyja el, úgy, mint ha a másik csomópontból (N’) indult volna (1.11. ábra - A csomópontok származtatása).
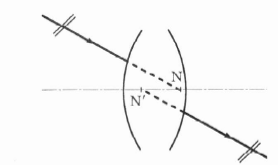
A csomópontok egymás konjugáltjai.
A Lagrange-féle invariáns szerint (lásd az (1.12. ábra - Vázlat a csomópontok helyének számításához) ábrát):
|
|
Newton-formulából: (lásd a következő pontban az 1.16 összefüggést):
|
| ||
|
|
Ugyanis a csomópontokra nézve Ϭ = Ϭ’
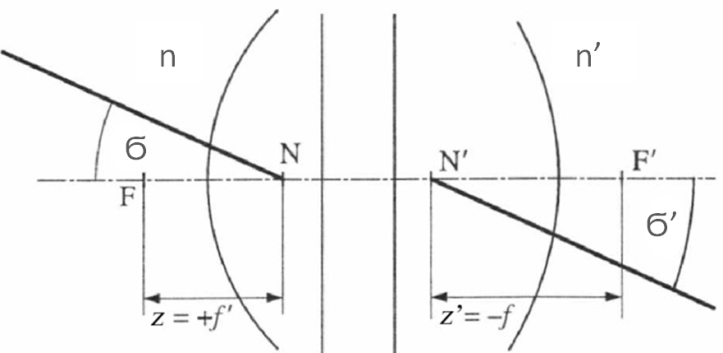
innen
|
|
De a lencse dioptriája mindkét oldalon azonos, így a reciproka is.
|
|
Értelmezés: A csomópontok helye a Newton-féle koordináta-rendszerben, tehát a fókuszpontokból számítva a következő:
A tárgyoldali csomópont a tárgyoldali fókuszponttól éppen a képoldali fókusztávolságnyira van, míg a képoldali csomópont a képoldali fókuszponttól éppen tárgyoldali fókusztávolságnyira van, és a távolságokat előjelesen kell érteni.
Ha az optikai rendszer tárgy-, és képtere azonos törésmutatójú (pl. levegő), akkor a csomópontok és a főpontok egybeesnek.
1.2.5. Newton-formula
Ábrázoljunk egy optikai rendszert a fősíkjaival és a fókuszpontjaival! Mérjük a tárgy illetve a kép távolságát a fókuszpontoktól (z illetve z’) (1.13. ábra - Vázlat a Newton-formulához).
Az (1.13. ábra - Vázlat a Newton-formulához) ábrából hasonló háromszögek felhasználásával:
|
|
(1.15) |
A nagyítás (β) felhasználásával
|
|
(1.16) |
Az utolsó egyenlőség felhasználásával a Newton-formula:
|
zz’=-ff’ |
(1.17) |
a Newton-formula segítségével írhatók az alábbiak:
|
|
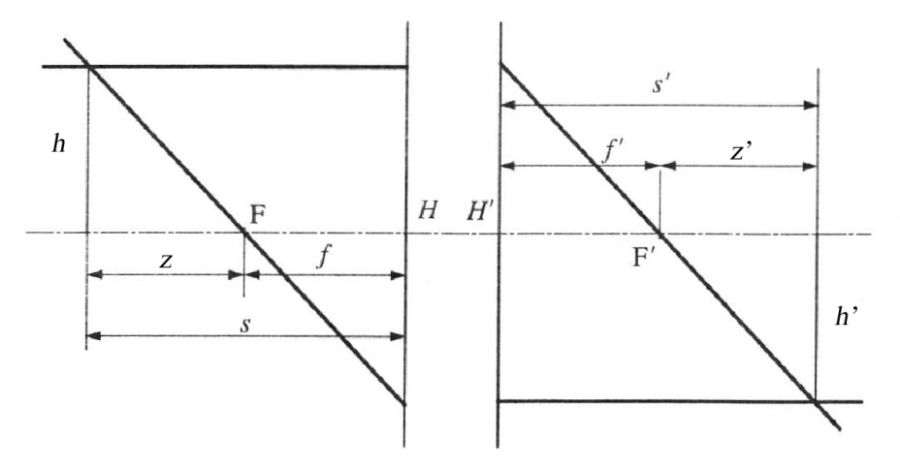
Ez az összefüggés „vékony” lencse esetén megadja a tárgy és kép távolsága közötti összefüggést. Amennyiben a tárgy- és képtér is levegő (vagy azonos közeg) akkor f’=f és így
|
|
(1.18) |
Vigyázzunk az előjelekre: s negatív esetén a középiskolás fizikában tanult
összefüggés adódik.
|
|
1.2.6. A vékony lencse
Vékony lencsénél a metszéki és a tárgy-, illetve képtávolságok azonosak.
A vékony lencse absztrahálás eredménye. Ilyenkor eltekintünk a lencse vastagságától.
Egy egyszerű lencse két gömbfelületből áll, tehát az egyetlen gömbfelület képalkotására levezetett összefüggéseinket kell kétszer alkalmazni.
|
|
mivel vékony a lencse:
|
| ||
|
|
Átalakítva:
|
|
(1.19) |
(1.18) felhasználásával a vékony lencse fókuszképlete:
|
|
(1.20) |
másképpen:
|
ha s 1 = - ∞, akkor s 2 ’=f’ |
1.2.7. A lineáris, longitudinális és szögnagyítás
A lineáris nagyítás (β)
|
|
(1.21) |
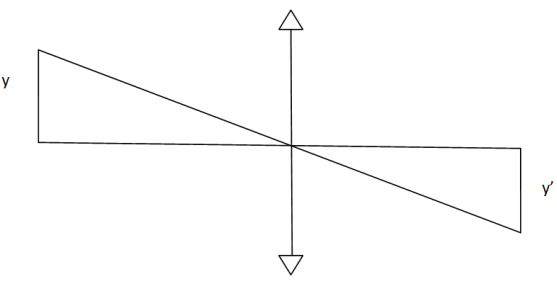
Kifejezhető még a Newton-formula segítségével:
|
|
(1.22) |
A szögnagyítás (γ) (1.16. ábra - A szögnagyítás számítása)
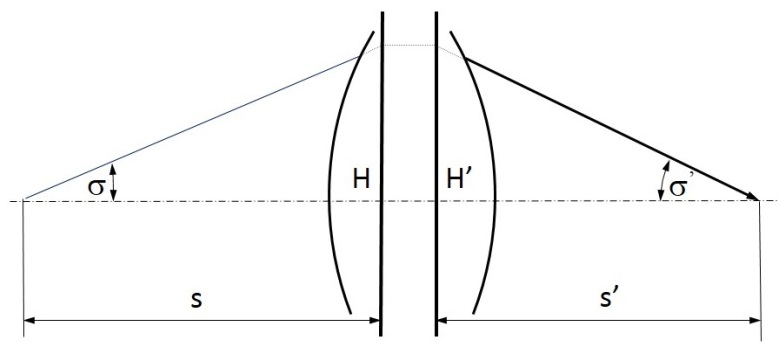
|
|
(1.23) |
Kifejezhető még a következőképpen:
|
|
(1.24) |
A csomópontokra nézve a szögnagyítás γ=1
Számítsuk ki a lineáris és a szögnagyítás szorzatát:
|
|
mivel 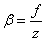 , amiből
, amiből 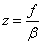
és 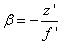 , amiből
, amiből 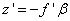
|
|
ebből
|
|
(1.25) |
ha f=f’, akkor
|
|
(1.26) |
(1.24) felhasználásával
|
|
(1.27) |
ha f=f’, akkor
|
|
(1.28) |
Longitudinális nagyítás (α)
|
|
(1.29) |
dz deriválást jelent z szerint
A Newton-formulából
|
|
ebből
|
|
deriváljunk z szerint
|
|
Tehát
|
|
(1.30) |
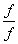 -el beszorozva
-el beszorozva
|
|
mivel 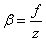 , így
, így
|
|
(1.31) |
Ha f = f’, akkor:
|
|
(1.32) |
Számítsuk ki a lineáris és a szögnagyítás hányadosát!
|
|
mivel 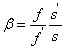 , és
, és 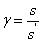
Beszorozva 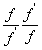 -fel
-fel
|
|
mivel a zárójeles mennyiség ß és (1.31) szerint 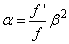
Így tehát
|
|
(1.33) |
1.3. Valóságos lencsék számításai
1.3.1. Vékony lencsék eredője
Két elemi vékony lencsét egymás mellé helyezve, dioptriáik, vagyis törőértékeik összeadódnak:
|
|
(1.34) |
mivel azonos közegekben 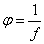 , ezért
, ezért
|
|
(1.35) |
f-re kifejezve
|
|
(1.36) |
1.3.2. Légközzel elválasztott két vékony lencse eredője
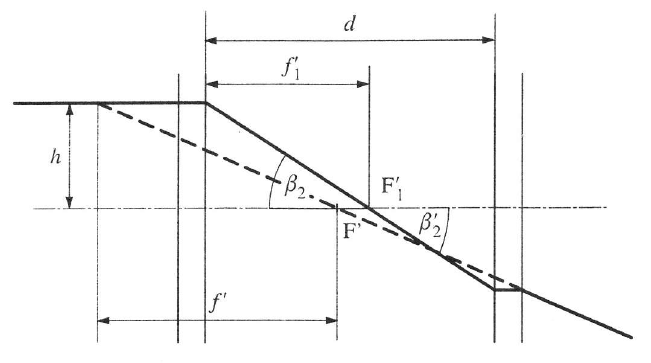
Más a helyzet akkor, ha a két vékony lencse között d távolság van (1.17. ábra - Vázlat az eredő gyújtótávolság számításához).
Eredő gyújtótávolság számításához a szögnagyítás a 2. lencsére:
|
|
(1.37) |
mivel 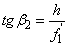 és
és 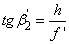
|
|
Mint ismeretes:
|
|
amiből
|
|
innen s 2 =f 1 ’-d felhasználásával
|
|
Ezt behelyettesítve (1.37)-be
|
|
és innen
|
|
(1.38) |
illetve levegőben lévő lencsék összerakásakor:
|
|
(1.39) |
A vékony lencsével ekvivalens vastag lencséről akkor beszélünk, ha a két lencsének azonos a fókusztávolsága, a törésmutatója és az első görbületi sugara. (Tehát a vastagságban és a hátsó görbületi sugárban térnek el).
Az (1.38) összefüggés nevezőjében lévő kifejezést jelöljük Δ-val.
Ezt nevezzük optikai tubushossznak.
|
|
(1.40) | |
|
|
(1.41) |
Miután az így létrejött valóságos lencse két fősíkkal kell rendelkezzen, ezek helyét is kiszámíthatjuk. Legyen p’ a képoldali fősík és a második vékony lencse távolsága és p a tárgyoldali fősík és az első vékony lencse távolsága. Ezekkel a valóságos lencse fősíkjainak helyei
|
| ||
|
|
Hasonló levezetéssel:
|
|
Összefoglalva:
|
|
(1.42) |
1.3.3. A vastag lencse
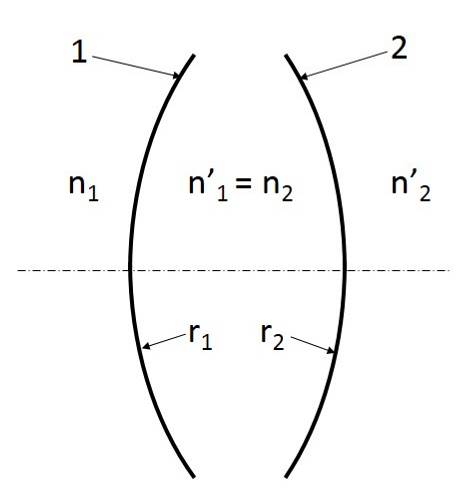
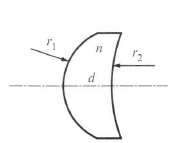
Alkalmazzuk most a görbületi sugarakat is tartalmazó (1.42) összefüggést a „vastag” lencsére, vagyis egy két (r 1 és r 2 ) görbületi sugarú gömbfelületből álló, d vastagsággal és n törésmutatóval rendelkező valóságos lencsére! (1.18. ábra - Vastag lencse)
|
| ||
|
| ||
|
| ||
|
|
majd ezt a 2. felületre:
|
| ||
|
| ||
|
| ||
|
|
Fennáll egy azonosság:
|
|
ezzel
|
|
(1.43) |
d = 0 esetében
|
|
vagyis megkapjuk a vékony lencse képletét (pl. szemüvegnél így számolhatunk).
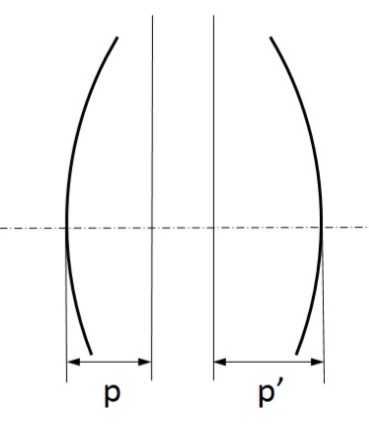
Számítsuk ki a fősíkok helyeit is a lencsegörbületek segítségével (1.43)-ből. (1.19. ábra - Vázlat a vastag lencse fősíkjainak számításához)
|
| ||
|
|
Rendezve:
|
|
(1.44) |
Ha d = 0, akkor p= p’= 0 a két fősík egybeesik.
p– t az első lencsefelülettől p’-t a hátsó lencsefelülettől kell mérni.
1.3.4. Több felületből álló lencserendszerek
A vastag lencsénél kétszer alkalmaztuk a gömbfelületre vonatkozó összefüggéseket. Ha több lencsés optikai rendszerünk van, akkor a gömbfelületre vonatkozó összefüggések sorozatos alkalmazásával a következő öszszefüggésekhez jutunk:
Eredő fókusztávolság:
|
|
(1.45) |
Eredő lineáris nagyítás:
|
|
(1.46) |
ahol
|
k |
a gömbfelületek száma | |
|
n 1 |
a tárgytér törésmutatója | |
|
n’ 2 |
a képtér törésmutatója |
Nagyításról csak véges tárgytávolság (s 1 )esetén beszélhetünk!
1.4. Teleszkopikus rendszerek
A teleszkopikus rendszerek olyan kéttagú összetett optikai rendszerek, amelyeknél Δ = 0, vagyis az egymás felé eső két fókuszpont egybeesik.
Két ilyen rendszer lehetséges:
|
f 1 > 0 f 2 > 0 |
Kepler-távcső | |
|
f 1 > 0 f 2 < 0 |
Galilei-távcső |
1.4.1. Kepler-távcső (csillagászati távcső)
A rendszer szögnagyítása
|
|
(1.47) |
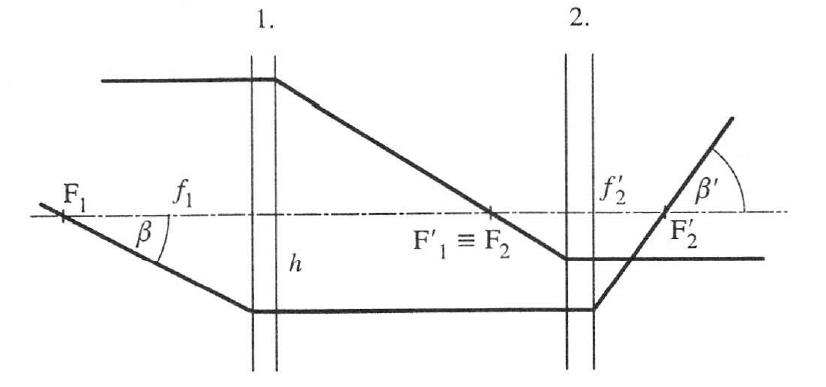
γ negatív előjele a fordított állású képet jelzi.
A rendszer akkor nagyít, ha 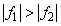
1.4.2. Galilei-távcső (színházi vagy terresztikus távcső)
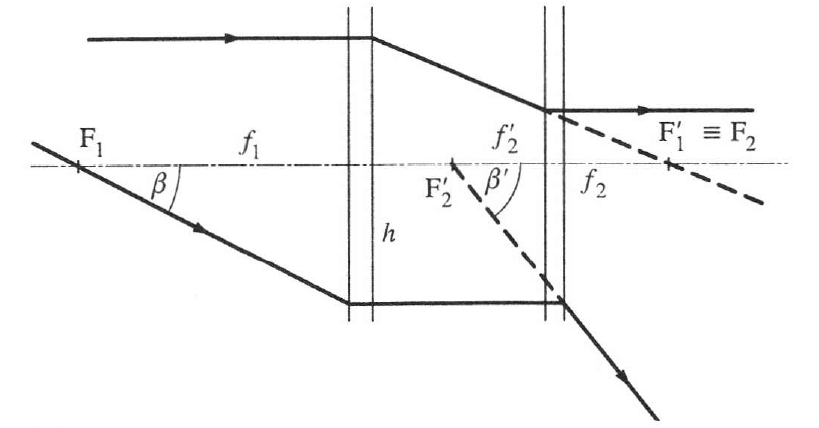
A szögnagyítás (1.21. ábra - A Galilei-távcső)
|
|
(1.48) |
Ha 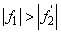 , akkor nagyít.
, akkor nagyít.
1.5. Rekeszek
A rekeszek az optikai rendszeren áthaladó fénysugarak egy részének kizárását, vagy a kép határolását végzik. Tengelyszimmetrikus rendszereknél a rekeszek általában szintén tengelyszimmetrikusak, sokszor kör alakúak.
Feladatuk szerint kétféle rekesz van: apertúrarekesz és mezőrekesz.
1.5.1. Apertúrarekesz
Az apertúrarekesz feladata a lencserendszer nyílásának határolása, vagyis a szélső sugarak kizárása (1.21. ábra - A Galilei-távcső).
A P-vel jelölt rekesznek két képét külön is használjuk: a rekesztől balra eső részrendszer által a rekeszről alkotott kép neve: belépő pupilla (EP). Az apertúrarekesztől jobbra eső részrendszer által a róla alkotott kép neve: kilépő pupilla (AP).
A belépő és kilépő pupillák egymás konjugáltjai az egész rendszerre vonatkozóan.
Ha egy sugarat a belépő pupilla közepe felé irányítunk, akkor az – miközben az apertúrarekesz közepén átmetszi az optikai tengelyt, úgy fogja elhagyni az optikai rendszert, mintha a kilépő pupilla középpontjából indult volna.
Ha a rendszer torzításmentes, akkor ezen belépő és kilépő fénysugár párhuzamos.
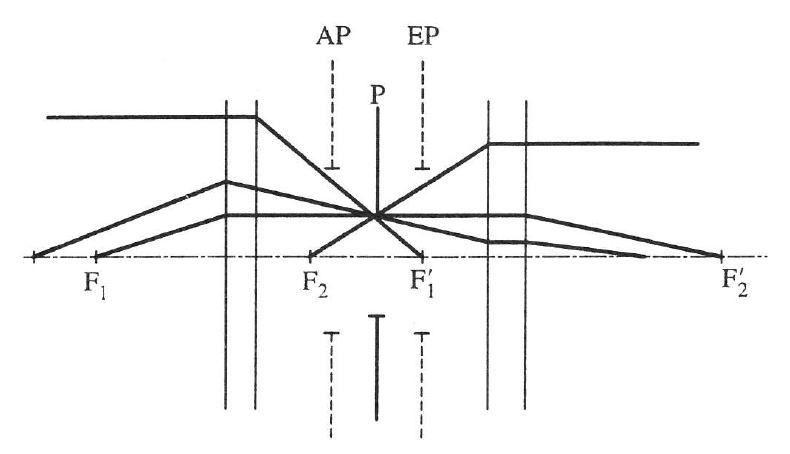
Minden olyan fénysugár, amelyik a tárgypontból a belépő pupilla széle felé halad, át fog jutni az optikai rendszeren. Ezek segítségével meg lehet határozni az egyes lencsetagok szükséges átmérőjét. Ezen sugarak a rendszerből úgy fognak kilépni, mintha a kilépő pupilla széléből indulnának.
Az apertúrarekesz helye (az optikai tengely mentén) hatással van a képminőségre, hiszen általa a szélső sugarak más-más része záródik ki a képalkotásból.
Természetes rekeszhely
Van egy ún. természetes rekeszhely, amelyet kétféleképpen definiálhatunk:
Ha az apertúrarekesz a természetes rekeszhelyen van, akkor a belépő és a kilépő pupillák éppen a fősíkokban vannak.
Megfordítva: ha egy fősugarat az egyik fősík tengelypontja felé irányítunk, akkor az a másik fősík tengelypontja felől fog eltávozni, miközben a valóságos fénysugár éppen a természetes rekeszhelyen metszi az optikai tengelyt.
Fotoobjektívek rekesze az ún. íriszblende. A fotoobjektívek fényerejének a belépő pupilla átmérőjének és a fókusztávolságnak a hányadosát nevezik.
Távcsöveknél az apertúrarekesz éppen az objektív széle, foglalata, ezért azonos a belépő pupillával.
Ennek képe – az egész rendszer által leképezve – viszont a kilépő pupilla. Az emberi szem pupillája ideális esetben a távcső kilépő pupillája helyére kerül, és nagyságuk közel egyenlő.
Így pl. ha egy objektív fényereje 1 : 5,6 az azt jelenti, hogy
|
|
ezt nevezik másképpen relatív nyílásnak.
1.5.2. Mezőrekesz, nyílások
A mezőrekesz feladata az, hogy a képnek éles széle legyen. Elhelyezése a tárgy-, vagy a képtérben történik.
A mezőrekesz az az átmérő, amelyik a belépő pupilla középpontjából a legkisebbnek látszik.
A mezőrekesz képei a nyílások: a belépő nyílás a mezőrekesznek a tárgyoldali részrendszer által alkotott képe. A kilépő nyílás a képoldali részrendszer által alkotott rekeszkép.
Mikroszkópnál a mezőrekeszt az okulár síkjában helyezzük el. Fényképezőgépnél a film síkjában lévő téglalap alakú nyílás a mezőrekesz.
1.6. Képméret, képszög, fősugár
A képméret a nem végtelenben lévő tárgyról alkotott kép nagysága.
A képszög a fősugarak átal alkotott kép félszöge.
A fősugár a tárgypontból a belépő pupilla középpontjába mutató sugár. Kiterjedt tárgy esetén több fősugár van, hiszen minden tárgypontból indul egy fősugár.
1.7. Optikai átviteli függvények
A képalkotó optikai rendszerek működését úgy is szemlélhetjük, hogy eltekintünk a rendszerek optikai jellegétől, és mindössze azt vesszük észre, hogy milyen összefüggés van a tárgyak és képeik között. Nem törődve azzal, mi hozta létre ezt a transzformációt, a kapcsolatot függvényekkel írjuk le. Hasonló feladatokat már más tudományterületek eredményesen megoldottak, pl. az elektronikai rendszerek esetében bevezették az átviteli függvényeket a bemeneti és a kimeneti jelek közötti kapcsolatok leírására. Az optikai rendszerek esetében hasonlóan járunk el, megkülönböztetésül optikai átviteli függvényekről beszélünk.
Az optikai átviteli függvények ma már széles körben elterjedtek. Az optikai rendszereket minősítők és a felhasználók számára a legfontosabb információkat adják, a tervezők számára pedig analitikus tervezőmunkájuk eredményének végső ellenőrzését jelentik. Forradalmi változást jelentettek az optikai átviteli függvények a hibaminimumra törekvő automatikus finomkorrigáló számítógépprogramok fejlődéstörténetében az 1970-es években. Ekkor ugyanis azok a programok, amelyek már „készre” korrigálták a rendszereket, eredményüket illetően elmaradtak azoktól az új programoktól, amelyeken még ezután elvégeztek egy olyan korrekciót is, amelynek célfüggvénye az optikai átviteli függvény számítása alapján került kialakításra.
Felmerült a kérdés: szükség van-e akkor más hibafüggvény-aberráció számítására, miért nem lehet közvetlenül az optikai átviteli függvényekre optimalizálni a leképző rendszerek tervezési folyamatát? A válasz az, hogy az optikai átviteli függvények annyira eredő jellemzői az egész optikai rendszer bármely eleme által okozott hibáknak, hogy visszafelé – néhány speciális esettől eltekintve – nem lehet egyértelműen megmondani, hogy mi okozta a rendszer átviteli függvényének romlását. Mivel a hagyományos aberrációk elmélete ezzel ellentétben viszont rendelkezik a hiba okokra vonatkozó következtetés lehetőségével, így mind a mai napig használjuk a klasszikus technikát, és csak a végső fázisban térünk át az optikai átviteli függvények használatára.
Tekintettel leszünk ugyanakkor a más tudományterületeken már elterjedten használt fogalmakra (pl. moduláció, frekvencia, fázis), és azokhoz igazodóan vezetjük be az optikai megfelelőiket (pl. kontraszt, térfrekvencia).
Mint látni fogjuk, a matematikai formulák nagyon hasonlóak. Ez praktikussága mellett azzal az előnnyel is jár, hogy viszonylag könnyen lehet majd vegyes rendszereket tárgyalni, amelyekben az optikai leképző rendszer pl. elektronikus detektorral csatoltan működik.
Az optikai átviteli függvények használata könnyebbé teszi a sorba kapcsolt optikai rendszerek tárgyalását is, eredő optikai átviteli függvények képzésével.
1.7.1. Elemi alakzatok képalkotása
Általános értelemben az optikai leképzést úgy tekinthetjük, mint a tárgytér fényeloszlása és a képtér fényeloszlása közötti transzformációt. A leképzendő tárgy minden egyes pontjának van valamilyen felületi fényessége, és ez a keletkezett képre is elmondható. Ideális esetben a megfelelő tárgy- és képpontok között homogén lineáris kapcsolat áll fenn.
Az optikai rendszereknél az átviteli függvény szempontjából nem foglalkozunk az időbeliséggel, vagyis állandó megvilágítású tárgyak statikus képét vizsgáljuk. A transzformációt akkor tartjuk jónak, ha a pontot ponttá, egyenes vonalat egyenes vonallá alakítja át a rendszer, miközben a szükséges nagyítás létrejön. A nagyításra vonatkozóan pedig elvárjuk, hogy az a képtér minden tartományában azonos legyen, vagyis egyenes szakaszt nagyítás szoros hosszúságú egyenes szakasszá képezze le.
Egyetlen pont képének fényeloszlás függvényét pontszórás függvénynek, egyetlen vonalét vonalszórás függvénynek, egyetlen élét pedig élszórás függvénynek nevezzük.
Az optikai rendszerek által alkotott kép minősége sokszor jelentősen változik a kép közepétől (az optikai tengelytől) távolodva. A képsík egy kis tartományában feltételezhető, hogy a képminőség azonos (izoplanatikus tartományok).
Ugyanez a detektorok esetében csak bizonyos munkaponti tartományokban igaz, nagyon kis és nagyon nagy fénymennyiségeknél nemlineáris jelenségekkel kell számolnunk. A képet akkor érezzük élesnek, ha részletgazdagságban nem marad el a tárgyétól, vagy ha a tárgyak szélei a képen kontrasztosan jelennek meg. Ez utóbbit úgy képzelhetjük el, hogy a képen az éles sötét-világos részek átmenetszerűen jönnek létre. Annál rosszabb egy kép, minél nagyobbak ezek az átmenetek (1.23. ábra - Elemi alakzatok szórásképei). Egy vékony vonal képének mindkét oldalán is megtalálhatók ezek az átmenetek (1.24. ábra - Az optikai átviteli függvény, mint a rendszertani átviteli függvény analógiája), sőt egyetlen pont képe körkörösen átmenetszerűen jön létre (1.23. ábra - Elemi alakzatok szórásképei).
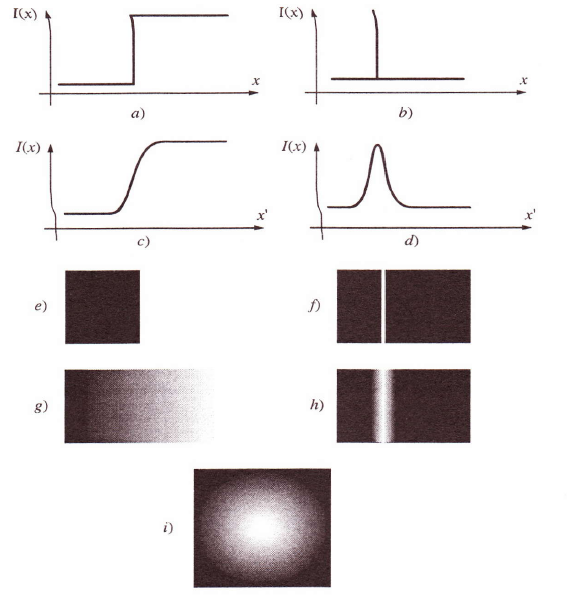
a) sötét-világos félsíkok (pl. kések) fényintenzitás-eloszlása a tárgyon. x a késélre merőleges hosszúság, I(x) a tárgy felületi fényessége vagy egyszerűen intenzitása; b) sötét háttéren lévő világos vonal fényeloszlása a tárgytérben; c) az a) szerinti tárgy képének fényeloszlása; d) a b) szerinti tárgy képének fényeloszlása (x’ az x-szel párhuzamos és annak megfelelő irány a képtérben); e) az a) szerinti tárgysík rá merőleges irányból nézve; f) a b) szerinti tárgysík rá merőleges irányból nézve; g) a c) szerinti kép rá merőleges irányból nézve; h) pontszórásfüggvény; i) egy sötét háttérben lévő világos pont képe rá merőleges irányból nézve (fényeloszlásának függvénye a d) ábráéhoz hasonlít)
1.7.2. Az optikai átviteli függvény rendszertechnikai származtatása
Az időbeli vagy dinamikai rendszerek vizsgálatával foglalkozó rendszertechnika kialakította azt az általános tárgyalásmódot, amit analógiaként felhasználhatunk az optikai átviteli függvények fogalmának bevezetésénél. A rendszertechnika általánosította azokat a villamosságtanban, mechanikában, hőtanban stb. hasonlóan tárgyalható rendszerelemeket, amelyekre egyaránt jellemző, hogy időben változó bemeneti jelekre f(t) időben változó kimeneti jeleket g(t) hoznak létre ún. válaszfüggvényként.
Definiálásra került az átviteli függvény T(ω), amely a kimeneti jelek és a bemeneti jelek Laplace-transzformáltjainak F(ω), illetve G(ω) hányadosa. (1.24. ábra - Az optikai átviteli függvény, mint a rendszertani átviteli függvény analógiája)
Mivel az ún. impulzusfüggvény, vagy Dirac-függvény speciális Laplace-transzformálttal rendelkezik
ℒ [δ (t)] = 1), így az átviteli függvény az erre adott válaszfüggvény transzformáltjával egyenlő.
Mindezek az optikai rendszerek esetében is felhasználhatók. Itt a Laplace-transzformáció helyett elegendő a Fourier-transzformációt használni:
|
|
(1.49) |
Míg az időbeli rendszereknél a vízszintes tengelyen a t szerepel, addig az optikai rendszereknél a helykoordináta x. Időbeli rendszereknél ω=2πf, ahol f a frekvencia, vagyis a másodpercenkénti periódusok száma (1.49).
Optikai rendszereknél
|
ω=2πv |
A v a térfrekvencia, vagyis a milliméterenkénti periódusok száma. Optikai rendszereknél a Dirac-bemenetnek egy fénylő csillag felel meg a sötét égbolton, amelyre 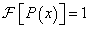 , így ennek válaszfüggvényét Fourier-transzformálva előállítjuk az optikai átviteli függvényt (OTF). A Fourier-transzformáció képletéből látható, hogy az eredmény komplex függvény lesz, amelyet Euler-alakban ábrázolva abszolút értékre és fázisra bonthatjuk.
, így ennek válaszfüggvényét Fourier-transzformálva előállítjuk az optikai átviteli függvényt (OTF). A Fourier-transzformáció képletéből látható, hogy az eredmény komplex függvény lesz, amelyet Euler-alakban ábrázolva abszolút értékre és fázisra bonthatjuk.
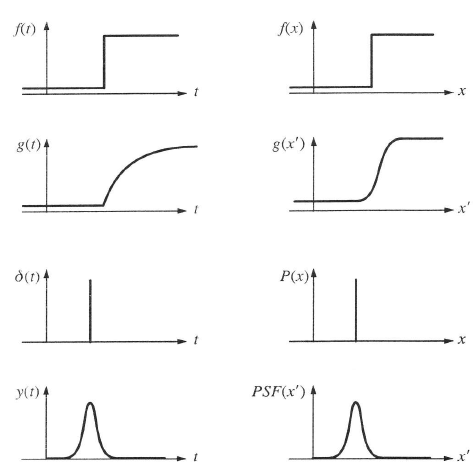
|
|
Hasonló felbontással találkozunk a rendszertechnikában, ahol az abszolút érték részét és a fázisrészt egymás alatt a frekvencia függvényében szokás ábrázolni. Az optikában is ezt tesszük.
|
|
(1.50) |
Az OTF az MTF és a PTF jelölést a nemzetközi irodalom miatt tartjuk meg (optical transfer function, modulation transfer function, illetve phases transfer function), utóbbit szokás még egyszerűen ϕ(ν)-vel jelölni.
Definicíószerűen MTF(0) = 1 vagyis nulla térfrekvencián a modulációs átviteli függvény értéke egységnyi, míg PTF(0) = 0, vagyis a fázisátviteli függvényérték ugyanott zérus.
Valamely tetszőleges tárgy f(x) leképzésekor keletkező kép g(x΄) intenzitáseloszlását a leképző optikai rendszer OTF-jének ismeretében úgy kaphatjuk meg, hogy az 1.24. ábra - Az optikai átviteli függvény, mint a rendszertani átviteli függvény analógiája szerinti összefüggésből kifejezzük. G(ω)-t és azt inverz-Fourier-transzformáljuk:
|
|
(1.51) |
Egy rendszer optikai átviteli függvényét tehát egyszer kell csak meghatározni, azután bármely tárgy képét segítségével kiszámíthatjuk. Eredményünk tartalmazni fogja a képalkotási hibák hatását is.
1.7.3. Az optikai átviteli függvények szemléletes magyarázata
Tekintsük az 1.25. ábra - A csíkos tárgy képalkotása. szerinti sűrűn csíkos tárgyat. A négyszögszerű jelsorozat mutatja a tárgy fényeloszlását. A kép fényeloszlását rárajzoltuk a tárgyéra (egységnyire normálva a nagyítást). Látható, hogy a képen a sarkos fényeloszlás helyett színusszerű jelenik meg, sőt a jelsorozat amplitudója sem olyan nagy mint a tárgyé.
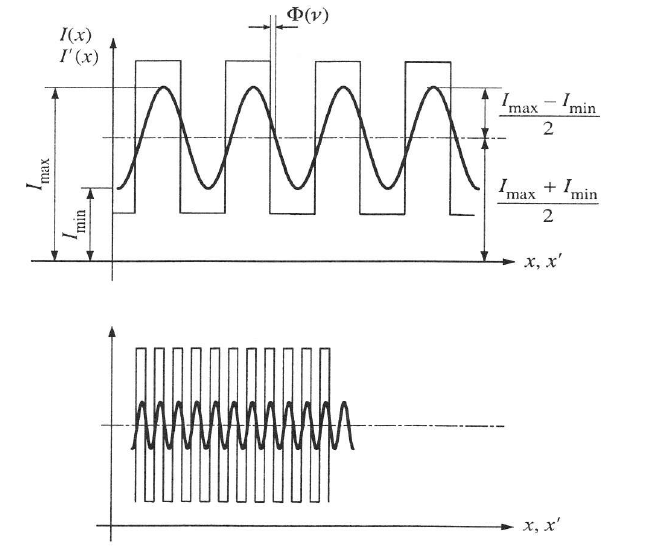
A tárgy fényeloszlássa a négyszög-, a képe pedig a szinusszerű. A térfrekvencia növelésével a képkontraszt csökken.
Megfigyelhető az is, hogy a kép- és tárgyjel között egy kis Φ(ʋ) nagyságú fáziseltolódás is van. A jel amplitúdócsökkenés és a fáziseltolódás általában annál nagyobb, minél sűrűbb, vagyis nagyobb térfrekvenciájú a tárgyfüggvény.
Kontrasztnak nevezzük a sötét és a világos részek viszonyát. E viszonyt a híradástechnikai moduláció fogalomnak megfelelően a jel középvonalától mért amplitúdó és a középvonalnak a vízszintes tengelytől mért magassága hányadosaként definiáljuk.
|
|
(1.52) |
Látható, hogy a kontraszt maximális értéke egységnyi lehet, általában pedig 0-1 közé esik. (Akkor lehetne egységnyi, vagyis 100%-os, ha az I min =0 lenne, ez pedig akkor állhat elő, ha az optikai rendszer a kép fekete területére semmilyen fényt nem juttatna).
Az (1.25. ábra - A csíkos tárgy képalkotása.) ábrából az is látható, hogy egyetlen élátmenet leképzésének hiányossága miatt áll elő a kontrasztcsökkenés, hiszen a rendszer csak bizonyos meredekséggel képes átvinni a hirtelen emelkedő négyszögjelet – így minél sűrűbb a négyszögjelsorozat, annál kisebb értékre tud felemelkedni a válaszjel, mire a négyszöggel ismét csökkenni kezd. Tehát a térfrekvencia növekedésével a kontraszt csökkenni fog.
Ha a kontraszt csökkenését a térfrekvencia függvényében ábrázoljuk, megkapjuk a kontrasztátviteli vagy modulációs átviteli függvényt.
Az 1.26. ábra - A modulációs átviteli függvény és a fázisátviteli függvény szerinti két függvény nem más, mint az OTF(ʋ) komplex optikai átviteli függvény abszolút értéke és fázisa.
Persze egy valóságos tárgy általában nem periodikus struktúrájú. Mint a függvénytanból tudjuk, felírható azonban függvénysorként, vagyis különféle frekvenciájú összetevők összességeként. Miután az egyes összetevő frekvenciák átvitele nem azonos, ezért a tárgy leképzése nem lesz ideális. Általában igaz, hogy a magasabb frekvenciákon csökken a kontraszt és növekszik a fázishiba. Ez olyan, mint a rendszertechnikában a felülvágó szűrők hatása.
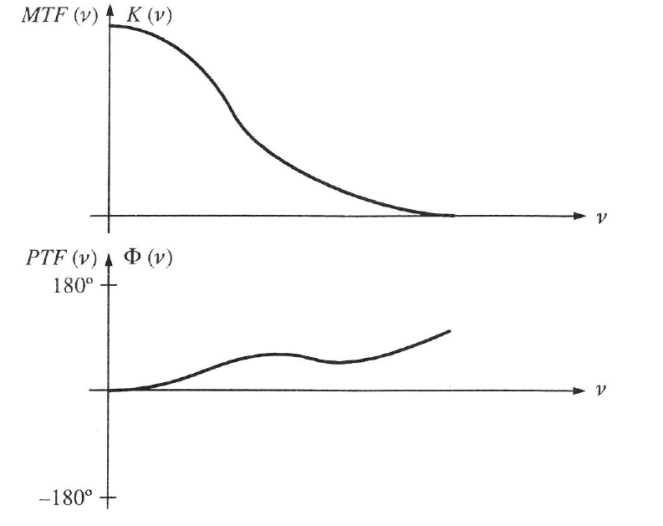
Itt a függőleges tengely léptéke szög, mivel egyetlen periódust 360º-nak tekintünk, és ehhez képest léptékezzük a fáziseltolódást.
A fázishiba jelentéséhez megjegyezzük, hogy azt úgy kell elképzelni, mintha az egyes képrészletek (pl. a négyszöggel felfutó vagy lefutó éle) nem pontosan oda kerülne a képen, ahová ideális képszerkesztés útján.
A vízszintes tengelyen a ʋ térfrekvencia található ciklus/mm egységben. Az ábra alatt szokás ábrázolni a fázishiba változását szintén a térfrekvencia függvényében.
1.7.4. Az apertúrafüggvény és kapcsolata az optikai átviteli függvénnyel
E fejezet tanulmányozását a könyv II. részének ismeretében könnyebben elvégezhetjük. Azért szerepeltetjük mégis itt, és nem a hullámoptikai részek után, mert az optikai átviteli függvények megértését teljesebbé teszi.
A fény hullámtani leírásakor elektromágneses rezgésekről, hullámokról beszélünk. Az elektromos térerőt, amelynek változásaként is leírhatjuk a fényt, a következő képlettel szemléltethetjük:
|
|
(1.53) |
Ha összevonjuk az időtől független tagokat: 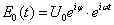 alakot kapjuk. Ebben az alakban jelöljük E-vel az időtől független részt:
alakot kapjuk. Ebben az alakban jelöljük E-vel az időtől független részt:
|
|
(1.54) |
és nevezzük ezt komplex amplitúdónak, hiszen az időbeli rezgésnek ez jelenti az amplitúdóját.
Itt U 0 a rezgés amplitúdója, t az idő, j a kezdő fázisszög, i az imaginárius egység. Az összefüggés valós része a cosinuszos terjedés leírását szemlélteti. A továbbiakban a komplex amplitúdónak lesz csak jelenősége, mert a másik tényező csak az időtől függ, mi pedig a helytől függő viszonyokat vizsgáljuk.
Tekintsük az (1.27. ábra - A hullámaberráció értelmezése) ábrát!
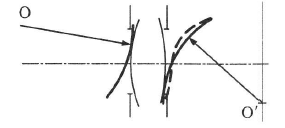
Képzeljük el az optikai leképzést úgy, mintha a lencsébe bemenő fényhullám komplex amplitúdója megszorzódna egy – a lencsére jellemző ún. pupillafüggvénnyel, és így alakulna ki a kimeneten a fényhullám komplex amplitúdója. A pupillafüggvényre vonatkozóan két dolgot kell számításba vennünk. Egyrészt lehet a lencsének τ(u,v) átbocsátási tényezője, másrészt megváltoztathatja a fényhullámok gömbszerűségét, amelyet az 0’ középponttól rajzolt referenciagömbtől való W(u,v) eltéréssel vehetünk figyelembe. Ezekkel a pupillafüggvény
|
|
(1.55) |
Itt a négyzetgyök értelme az intenzitás képzésénél látható, amikor is négyzetre emelés miatt eltűnik.
λ a fény hullámhossza, 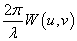 pedig a W(u,v) hatására létrejövő fáziseltolódás.
pedig a W(u,v) hatására létrejövő fáziseltolódás.
A leképzés síkjában a fényhullám komplex amplitúdója egydimenziós esetben:
|
|
(1.56) |
adódik, amely összefüggésről felismerhető, hogy az nem más, mint egy Fourier-transzformáció! Kimondható tehát, hogy a képsíkon a fényhullám komplex amplitúdója arányos a pupillafüggvény Fourier-transzformációjával.
Kétdimenziós esetre:
|
|
(1.57) |
A képsíkon egy pont képének intenzitását úgy kaphatjuk meg, ha az amplitúdót ismerjük, hogy azt négyzetre emeljük, pontosabban, a komplex amplitúdó ismeretében
|
|
E*(x’,y’) az E(x’,y’) komplex konjugáltját jelenti.
Mivel az optikai átviteli függvény a pontszórásfüggvény Fourier-transzformáltja,
|
|
A behelyettesítéseket elvégezve egydimenziósan írva:
|
|
(1.58) |
Miután az ilyen összefüggést autokorrelációnak nevezzük, kijelenthető, hogy az optikai átviteli függvényt a pupillafüggvény autokorrelációjaként is előállíthatjuk.
1.7.5. Aberrációmentes optikai rendszer átviteli függvénye
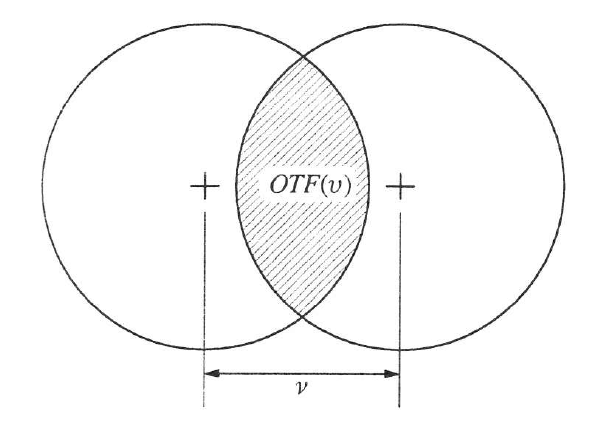
Ha az optikai rendszer aberrációmentes, akkor W(u,v) hullámaberráció zérus, az 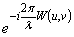 tényező egységnyi lesz, tehát P(u,v) kivihető az integrál jel elé. Az integrálandó függvény ekkor a pupilla területének és önmagával eltolt területének az 1.28. ábra - Aberrációmentes rendszer átviteli függvényének szemléltetése szerinti metszete lesz az eltolás mértékének függvényében. Az eltolás mértéke pedig arányos a térfrekvenciával. (Mindez az autokoreláció miatt van így.)
tényező egységnyi lesz, tehát P(u,v) kivihető az integrál jel elé. Az integrálandó függvény ekkor a pupilla területének és önmagával eltolt területének az 1.28. ábra - Aberrációmentes rendszer átviteli függvényének szemléltetése szerinti metszete lesz az eltolás mértékének függvényében. Az eltolás mértéke pedig arányos a térfrekvenciával. (Mindez az autokoreláció miatt van így.)
Látható, hogy ʋ = 0 esetén a terület maximális (ezt tekintjük 1-nek), amikor pedig a két kör érinti egymást, akkor a terület zérus lesz. Ekkor a u = ʋhatár. vagyis a felbontóképesség elvi határa így határozható meg.
A függvény jellegét az alábbi összefüggéssel írhatjuk le:
|
|
(1.59) |
ahol
|
| ||
|
|
Kör Alakú apertura esetén
|
|
(1.60) |
1,22 az elsőfajú Bessel-függvény miatt kerül be.
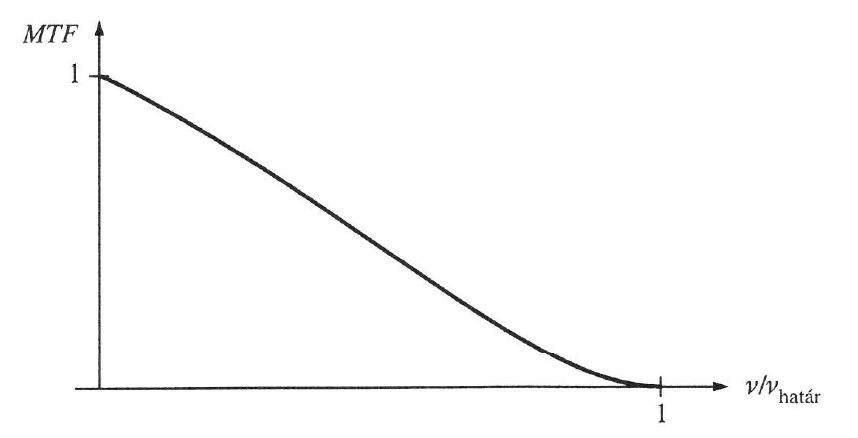
Az 1.29. ábra - Aberrációmentes rendszer átviteli függvénye az aberrációmentes optikai rendszerek átviteli függvényét mutatja. Mivel a vízszintes tengely relatív koordinátájú, ebben ábrázolva az összes tengelyszimmetrikus optikai rendszer egyetlen függvénynyel ábrázolható.
Az (1.30. ábra - Aberrációval terhelt és aberrációmentes rendszerek átviteli függvényei a rekeszelés függvényében) ábrán különböző mértékben rekeszelt optikai rendszer modulációs átviteli függvényei láthatóak.
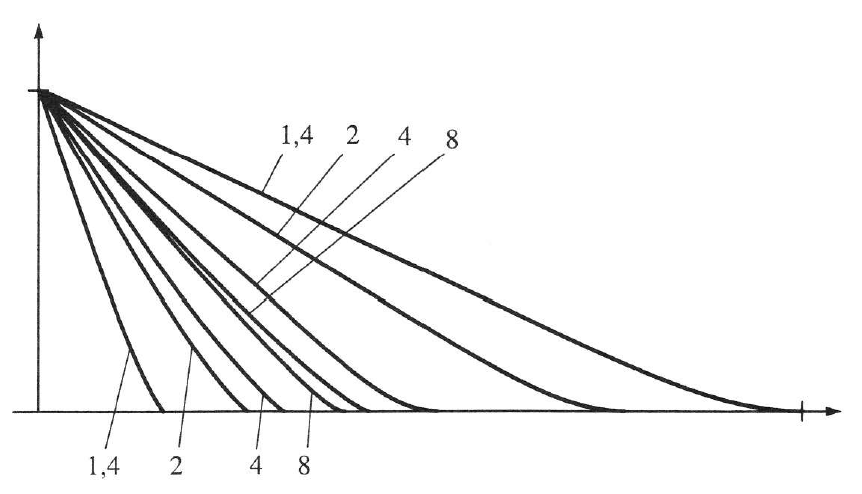
Feltüntettük az egyes rekeszállásoknak megfelelő aberrációmentes átviteli függvényeket is. Mint látható, két ellentétes folyamat játszódik le rekeszeléskor: egyrészt javult a rendszerek átviteli függvénye, hiszen kizáródnak a szélső nyalábok, csökken az abberáció, másrészt romlik az adott rekesznek megfelelő aberrációmentes átviteli függvény. Az adott objektívnél 8-os rekeszértéknél összesimul a valós és az aberrációmentes átviteli függvény. Ha tovább rekeszelünk, akkor már csak romolhat a rendszer, hiszen az aberrációmentes függvény romlik, a valós pedig nem lehet jobb nála. Minden objektívnél van egy olyan rekeszérték, amelynél előáll ez a helyzet.
Miután az aberrációmentes rendszereknél a képminőséget csak a diffrakció korlátozza, az ilyen rendszereket diffrakciókorlátozott, vagy diffrakciólimitáló rendszerekként is említi az irodalom.
1.7.6. Sorba kapcsolt rendszerek átviteli függvénye
Összetett rendszereknél az eredő átviteli függvény az integrál alatt összeszorzódik a két rendszerre:
|
|
(1.61) |
Négy esetet különböztetünk meg:
Az egyes rendszerek aberrációmentesek. Ekkor a W(u,v) hullámaberráció zérus, ezért az imaginárius tag elmarad, a határtérfrekvenciát a legkevésbé fényerős rendszer ʋ határa szabja meg, de a nagyobb fényerejű nem rontja az eredményt.
Az egyes rendszerek aberrációval terheltek, ilyenkor minden elemi rendszer hat az eredőre.
A hullámaberációk a kitevőben algebrailag összegződnek (tehát javíthatják is egymást).
Ha az egyes összetevő rendszerek között valódi kép jön létre, és azt leképezi a következő rendszer, akkor az MTF-ek összeszorzódnak, a PTF-ek pedig összeadódnak.
2. fejezet - Radiometria – fotometria
- 2.1. A radiometria és a fotometria jelölésrendszere
- 2.2. Optikai sugárzás
- 2.3. A térszög
- 2.4. Radiometriai és fotometriai mennyiségek és egységek
- 2.5. A távolságtörvény
- 2.6. A Lambert-féle koszinusztörvény
- 2.7. Fotometriai és radiometriai mennyiségek mérése
- 2.8. A vizuális fotometria
- 2.9. Objektív fotometria
- 2.10. A hőhatás elvén működő sugárzásmérés
- 2.11. Sugárzásmérés a fényelektromos hatás elvén
- 2.12. A fotográfiai hatáson alapuló sugárzásmérés
- 2.13. Denzitometrálás
- 2.14. Izokromatikus, és heterokromatikus fotometrálás
- 2.15. Ellenőrző kérdések
- Felhasznált irodalom
Az emberi szem által érzékelhető fényhatások elsősorban onnan származtathatók, hogy az elektromágneses sugárzás a szemben fényérzetet kelt [2.2.] . Bizonyított tény, hogy a fény transzverzális elektromágneses hullám, melynek frekvenciája a meghatározható és energiajellegű, azaz energia hatására keletkezik és azzá alakul át. A fény csoportosítása általában:
a frekvenciája vagy hullámhossza
a láthatósága
alapján történik
A frekvencia alapján történő csoportosításkor megkülönböztetjük:
a monokromatikus sugárzást, amely egyetlenegy frekvenciával jellemezhető. Ez azt jelenti, hogy olyan szűk a hullámhossz-tartománya, így a sávszélessége, hogy egyetlenegy hullámhosszal jellemezhető.
az összetett sugárzást, mely több frekvenciát tartalmaz.
A láthatóság alapján a sugárzásokat a következő csoportokba soroljuk:
Vizuálisan érzékelhetetlen sugárzás, mely természetesen elektromágneses sugárzás. Ide tartozik az infravörös sugárzás [2.19.] , amely 780 nm-nél nagyobb hullámhosszúságú monokromatikus sugarakból áll, tehát a látható sugárzásnál kisebb a frekvenciája; és az ultraibolya sugárzás, amelynek hullámhossza kb. 380 nm-nél kisebb, tehát nagyobb a frekvenciája mint a látható sugárzásé.
A vizuálisan érzékelhető sugárzás látásérzetet hoz létre a szemben,
hullámhossza a 380 nm és 780 nm közötti
frekvenciatartományai: 750 ezer GHz – 375 ezer GHz, ez a látható tartomány, mely az infravöröstől az ultraibolyáig tart. Az eltérő hullámhosszú, látható tartományú sugarakat az emberi szem eltérő érzékenységgel detektálja.
Az emberi látórendszer
a fénysűrűséget,
a kisugárzott teljesítményt,
a színösszetételt, azaz a detektált fény hullámhosszát érzékeli. Azonos teljesítmény mellett az 550 nm hullámhosszú fényt érzékeli az emberi szem leginkább [2.2.] .
2.1. A radiometria és a fotometria jelölésrendszere
|
λ |
hullámhossz |
[nm] |
|
φ,ν,ε |
szög |
[rad] |
|
Ω |
térszög |
[sd] |
|
S |
felület |
[m 2 ] |
|
R |
sugár |
[m] |
|
W e |
sugárzási energia |
[Ws] |
|
W v |
fényenergia |
[lm ⋅ s] |
|
Φ e |
sugárzási teljesítmény |
[W] |
|
Φ v |
fényáram |
[lm] |
|
L e |
sugársűrűség |
[W ⋅ m -2 ⋅ sr -1 ] |
|
L v |
fénysűrűség |
[lm ⋅ m -2 ⋅ sr -1 ] |
|
E v |
megvilágítás |
[lm ⋅ m -2 ] |
|
I e |
sugárerősség |
[W ⋅ sr -1 ] |
|
I v |
fényerősség |
[sd] |
|
D |
denzitás | |
|
τ |
áteresztési tényező | |
|
P |
visszaverési tényező | |
|
α |
elnyelési tényező |
2.2. Optikai sugárzás
![A szem érzékenységi görbéi [2.4.]](images/image_II_1.png)
A CIE fényerő észlelő egy olyan sugárzást érzékelő eszköz, amelynek relatív spektrális érzékenységi görbéje a V(λ) vagy V’(λ) láthatósági függvénnyel megegyezik, tehát az emberi szem spektrális érzékenységére vonatkoztatott fotometriai mennyiségek és a radiometriai mennyiségek között számszerűen kifejezhető összefüggések vannak [2.4.] . Tehát a radiometriai illetve a fotometriai mennyiségek között a kapcsolatot az emberi szem spektrális érzékenysége teremti meg.
Más szóval ez azt jelenti, ha a fényforrások által kisugárzott fényben megjelelő energia terjedésének törvényeit vizsgáljuk, akkor azt a radiometria eszközeivel tesszük. Ha figyelembe vesszük azt, hogy az emberi szem a különböző spektrális összetételű, de azonos teljesítményű fényforrásokat másképpen érzékeli, akkor a jelenségeket a fotometria fogalmaival írjuk le, tehát a fotometriában a fény energetikai jellemzőinek meghatározásakor tekintetben vesszük az emberi szem spektrális érzékenységét is, és a méréseket etalon fényforrásra vezetjük vissza [2.19.] .
2.3. A térszög
A geometria eszköztárában a szög fogalma két egymást metsző egyenes egymástól való elhajlását jelenti. E két egyenes metszéspontja körül behúzott egységnyi sugarú kör területén a két egyenes által kimetszett l hosszúságú ívdarabbal, azaz ívmértékkel magát a szöget jellemezzük [2.4.] . Nem egységnyi, hanem R sugarú kör esetén a szög
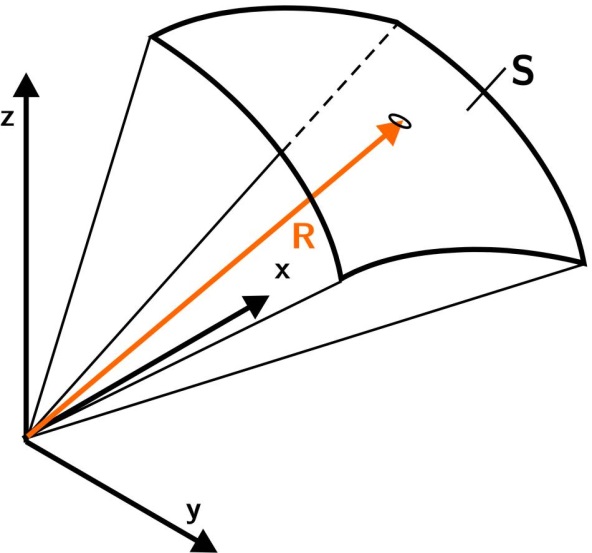
|
|
Az SI-rendszer szerint tehát a síkszög egysége a radián.
Ha az előzőek analógiájára értelmezzük egy R sugarú gömbből kimetszett S felület és egy gömb sugara négyzetének arányát, akkor eljutunk a térszög fogalmához, melynek mértékegysége a szteradián.
|
|
Egységnyi sugarú gömb esetén a lehetséges legnagyobb, az egész teret befogó térszög mértéke 4π szteradián.
2.4. Radiometriai és fotometriai mennyiségek és egységek
Tapasztalati tények alapján állítható, hogy a fénynyalábban energia áramlik, és ezen energia áramlásának irányát a fénysugarak iránya adja meg. A fényforrások által kisugárzott fény a látható összetevő mellett láthatatlan sugárzást is tartalmaz, így a teljes sugárzási energiának csak egy része a látható fény által szállított fényenergia [2.12.] .
A „fény” szót használják a látható tartományon kívül található optikai sugárzás megnevezésére is, azonban szigorú értelemben a fény a CIE fénymérő észlelő szerint súlyozott sugárzás.
Ha valamely főnyaláb adott metszetén dt idő alatt dW e sugárzási energia, illetve dW v fényenergia áramlik át, akkor a teljesítmény jellegű
|
|
sugárzási teljesítményt (energiaáramot), illetve a
|
|
fényáramot tudjuk definiálni.
A sugárzási teljesítmény mértékegysége a watt, a fényáramé a lumen.
A sugárerősség a sugárforrást elhagyó, az adott irányt tartalmazó dΩ térszögben terjedő dΦ e sugárzott teljesítmény és a dΩ térszög hányadosa:
|
|
Egysége a W⋅sr -1
Fotometriai értelemben ezzel analóg mennyiség a fényerősség, amely a fényforrást elhagyó, az adott irányt tartalmazó dΩ térszög hányadosa:
|
|
Egysége a candela = lumen⋅sr-1. A candela (cd) az SI-rendszer alapmértékegysége, és definíció szerint olyan fényforrás fényerőssége adott irányban, amely 540⋅1012 Hz frekvenciájú monokromatikus fényt bocsát ki, és sugárerőssége ebben az irányban 1/683 watt/szteradián, azaz a fekete sugárzó 1/600000 cm2–nyi felületének fényerőssége a felületre merőleges irányban, a platina dermedési hőmérsékletén, 101325 Pa nyomáson.
|
Megnevezés |
értéke [cd] |
|---|---|
|
viaszgyertya |
1 |
|
petróleumlámpa |
35 |
|
100 W-os kriptonizzó |
120 |
|
vetítőlámpa |
1.500 |
|
Nagy fényerejű ívlámpa |
9.000 |
A sugársűrűsség adott irányban az Ie sugárerősségnek és a dS felületelem látszólagos nagyságának, a dScosν vetületnek a hányadosa és mértékegysége W⋅m-2⋅sr-1.
|
|
A fénysűrűség, a fényforrás felületi fényessége vagy világossága adott irányban, az Iv fényerősségnek és a dS felületelem látszólagos nagyságának, a dScosϑ vetületének hányadosa,
|
|
Mértékegysége a cd⋅m -2 . Használatos még a stilb (sb) egység is, amely 1 cd/cm 2 , s ebben a gyertya fénysűrűsége kb. 1 sb, a Napé derűs időben kb. 105 sb.
|
Fényforrás megnevezése |
Fénysűrűség értéke [cd/m2] |
|---|---|
|
Éjszakai égbolt |
8 |
|
Hold |
0,2 |
|
Kék égbolt |
1 |
|
Gyertyafény lángja |
1 |
|
Matt búrájú izzólámpa |
40 |
|
Napfény alkonyatkor |
700 |
|
Napfény napközben |
150 000 |
|
Xenon-gáztöltésű lámpa |
80 000 |
A besugárzott teljesítmény a felület egy adott pontján az oda beeső dΦ e sugárzási teljesítmény és a felületelem dS területének a hányadosa
|
|
Egysége a W⋅m-2.
A megvilágítás a felület egy adott pontján az oda beeső dΦ e sugárzási teljesítmény és a felületelem dS területének a hányadosa
|
|
Egysége a lux = lm⋅m-2.
|
Megnevezés |
Érték [lux] |
|---|---|
|
Nyári napfény mellett |
100 000 |
|
Téli napfény mellett |
10 000 |
|
Telihold mellett |
0,3 |
|
Holdfogyatkozáskor |
0,0002 |
|
Érték [lux] |
Megnevezés |
|---|---|
|
1500-2000 |
Nagyon erős megvilágítás |
|
1000-1500 |
Erős megvilágítás |
|
500-1000 |
Normál megvilágítás |
|
200-500 |
Gyenge megvilágítás |
|
50-200 |
Tájékozódó fény |
|
|
2.5. A távolságtörvény
Azt a fény- vagy sugárforrást, melynek méretei a forrás és az érzékelő közötti távolsághoz képest kicsik, pontszerű forrásnak nevezzük. Az ilyen források fényét a geometriai optika egyenesekkel, a fénysugarakkal jellemzi. A pontszerű fényforrás által keltett árnyékok kontúrvonala éles, kemény. Ilyen forrásnak tekinthető a Nap, az ívfény, a fény szóródását biztosító, bura nélküli izzó.
Pontszerű fényforrások alkalmazása esetén a fényforrás és a felület megvilágítási viszonyaira a távolságtörvény a jellemző, mely szerint pontszerű fényforrás esetén a fényforrás megvilágítása a felülettől való távolság négyzetével arányosa csökken.
|
|
2.6. A Lambert-féle koszinusztörvény
A pontszerű sugárzók kemény fényével ellentétben definiálhatók olyan források, melyek lágy fényt sugároznak. Az ilyen típusú sugárzást nevezzük szórt vagy diffúz fénynek. Tulajdonsága, hogy az árnyékhatás jelentéktelen. Nem érvényesek rá a pontszerű fényforrások törvényszerűségei. Az ideálisan diffúz felület az ún. Lambert-féle felület, amit a Lambert-féle koszinusztörvény jellemez. E törvény kimondja, hogy a visszaverő felület fényerőssége a felület normálisával bezárt szög koszinuszával arányos.
|
|
Az ábra alapján könnyen belátható, hogy a fénysűrűség azért állandó bármely irányból tekintve, mert a csökkentett intenzitást egy szintén a szög koszinuszával arányosan csökkenőnek látszó felület sugároz ki.
![A Lambert-féle koszinusztörvény [2.4.]](images/image_II_4.png)
2.7. Fotometriai és radiometriai mennyiségek mérése
A radiometriai és fotometriai mérések célja a fény által transzportált energia, vagy a sugárzási teljesítmény számszerű kiértékelése. A sugárzásdetektorok három fő csoportra oszthatók, aszerint hogy működésük a fény melyik fizikai hatásán alapszik [2.17.] .
hőhatáson alapuló sugárzásmérők: ezek kalorikus módszert alkalmazó műszerek, termoelemek, bolométerek, hőcellák.
fényelektromos hatáson alapuló sugárzásmérés: ide tartoznak a fotocellák, fotomultiplikátorok, fényelemek, fotoellenállások, a pn átmenet eszközei.
fotográfiai hatáson alapuló sugárzásmérésnél a fényérzékeny nyersanyagban keletkező fotofizikai változás, azaz a denzitás mértéke jellemzi a sugárzási mennyiségeket.
A fotometria legfontosabb feladata különböző fotometriai mennyiségek: a fénysűrűség, a megvilágítás, a fényáram és a fényerősség mérése. Ha a mérést a szemünkkel végezzük, akkor vizuális vagy szubjektív fotometriáról, ha azonban valamilyen fényre érzékeny eszközzel, akkor fizikai vagy objektív fotometriáról beszélünk.
2.8. A vizuális fotometria
Az emberi szem a fényerősség mértékének abszolút meghatározására alkalmatlan, azonban két szomszédos felület fényerősségének összehasonlítását nagy biztonsággal tudja elvégezni. A vizuális fotométerek egy tipikus példája a Ritchie-féle fotométer. Egy derékszögű szimmetrikus gipszprizmát egyik oldalról egy ismert fényerősségű forrás világít meg adott távolságról. A prizma másik oldalán elhelyezkedő, ismeretlen fényerősségű forrásprizmától mért távolságát addig változtatjuk, míg a prizma két oldalát vizuálisan egyenlő világosnak nem találjuk. Ilyenkor a prizma éle gyakorlatilag láthatatlanná válik. Ha a források méreteikhez képest nagy távolságban helyezkednek el, akkor a távolságtörvény alapján az ismeretlen fényerősség meghatározható [2.4.] .
2.9. Objektív fotometria
Objektív fotometriáról akkor beszélünk, ha a szem helyett a sugárzásmérést egy érzékelő mérő-eszközre bízzuk, és az általa szolgáltatott jelet értékeljük. Mivel ezek az érzékelő eszközök az elektromágneses spektrum látható, infravörös és ultraibolya részében is érzékenyek, ezért itt fotometria helyett optikai sugárzásmérésről beszélhetünk. A sugárzásmérő eszközök (detektorok) a fizikai működés szempontjából három fő csoportra oszthatók – hő, fényelektromos és fotográfiai hatáson alapulókra.
2.10. A hőhatás elvén működő sugárzásmérés
Ha a sugárzás időben állandó és kellően intenzív, akkor teljesülnek a kalorimetrikus sugárzásmérési módszer feltételei. A termoelemes sugárzásmérés esetén a termoelem forrasztási pontjára ható sugárzás eredményeként keletkező termofeszültség – mely galvanométerrel mérhető – arányos a sugárzási teljesítménnyel.
A termoelem helyett elterjedtebben alkalmazzák a termooszlopokat. A termooszlop tulajdonképpen több, sorba kapcsolt termoelem, így a termoelemeken megjelenő feszültségek összege mérhető.
Egy fekete fémlapba termoelemes hőmérő illetve elektromos izzítást lehetővé tevő izzószál van beépítve. A fekete fémlap a ráeső sugárzás hatására melegedni kezd. Adott idő után a sugárzás hatására felvett, illetve a hő veszteség által leadott hő egyensúlyba kerül, a fémlap állandó hőmérsékletet vesz fel. A mérendő sugárzás kiiktatása után a fémlapot a benne elhelyezett fűtőszál segítségével az egyensúlyi hőmérsékletre hevítjük fel. A bevezetett elektromos teljesítmény egyenlő a felvett sugárzási teljesítménnyel. Így a fűtőszálba bevezetett elektromos áram erősségéből, illetve a feszültségből meghatározható a sugárzási teljesítmény abszolút mértéke. A platina- vagy félvezetőlemezkék, melyek a sugárzás hatására létrejövő felmelegedés miatt megváltoztatják vezetőképességüket a bolométeres sugárzásmérést teszik lehetővé [2.20.] .
Mivel a bolométerek a mérőáramkörökben mint ellenállások működnek, külön figyelmet kell szentelni a feszültség-áram-karakterisztikájuknak. A kis áramok tartományában a jelleggörbéjük közel lineáris, közel ohmos terhelést képviselnek. Az áram növekedésével azonban a keletkező hő visszahat az elemre, fokozatosan eltér a lineáris karakterisztikától, majd egy maximumérték után az áram növekedését csökkenő feszültség kíséri, ezt negatív ellenállású tartománynak nevezzük. A bolométereket mérési célokra általában a lineáris tartományban használják. Az érzékelő lemezeket kiegyenlíthető hídba kapcsolva alkalmazzák. A gyakorlatban három fő típusukat különböztetik meg, a fém bolométereket, a félvezető bolométereket, illetve a szupravezető bolométereket.
A Golay-cella alkalmazása esetén, a sugárzás hatására felmelegedő cella a hőjét a gáznak átadva, közvetve a gáz hőtágulása révén membrán deformációt hoz létre, mely mérhető. A Golay-cellák a legérzékenyebb sugárzásdetektorok közé tartoznak.
Gyakran nevezik pneumatikus sugárzásdetektornak, mivel a gázhőmérővel azonos elven működik. A gyakorlatban a Golay-detektorok egy kis hővezető-képességű, gázzal töltött cellából állnak. A cella egyik oldalán egy alkalmasan megválasztott abszorpciójú filmréteg van, a túloldalán pedig az ún. membrántükör helyezkedik el. A cellában elhelyezett gáz a sugárzás hatására megváltoztatja térfogatát, és a tükröt elmozdítja. A detektor részét képezi egy optikai rendszer is. A fényforrásból kilépő fényt egy kondenzor egy rácson keresztül a tükörre juttatja. A rács és a tükör között elhelyezkedő optika a fényt úgy fókuszálja, hogy a rács egyik felének a képe fedje a másik felének a képét, ha nincs membrábdeformáció. A deformáció bekövetkezte után a rács elmozdul, ez a kondenzátor túloldalán fényváltozást eredményez.
2.11. Sugárzásmérés a fényelektromos hatás elvén
A fényelektromos hatás elvén működő sugárzásmérők alapeszközei a fényelemek, a fotoellenállások, fotodiódák és a fotocellák. A fényelemek tulajdonképpen pn-n átmenetet tartalmazó fotodetektorok. A megvilágított pn-n átmenet áramforrásként szerepel, energiáját a gerjesztett töltéshordozópárok szétválasztásából és felhalmozódásából kapja. A fotoellenállás működésének alapja az, hogy a sugárzás hatására többlet-töltéshordozók keletkeznek, amelyek hatással vannak a kristály vezetőképességére. A CdS, illetve a CdSe fotoellenállások nagy előnye, hogy érzékenységi görbéjük nagyon jól megközelíti a szem érzékenységi görbéjét. Emellett azonban rendelkeznek hátrányos tulajdonságokkal is. Ezek közé tartozik a nagy időállandó és az úgynevezett drift.
A fotodiódák és a fényelemek szerkezeti kialakításukat tekintve szinte megegyezők. Alapvető különbség az üzemeltetés módjában van. A zárófeszütséges, fotodióda üzemmódban a pn-n átmenet ellenállása nagy lesz. Ebben az esetben mérhető a megvilágítás hatására fellépő fotoáram. A fotodióda-üzemre a viszonylag gyors működés a jellemző. A gáztöltésű fotocellákat szintén széles körben alkalmazzák sugárzásmérésre. A fotoáram arányos a katódra eső sugárzás teljesítményével. Az egyszerű fotocella helyett a gyakorlatban úgynevezett elektronsokszorozó fotocellákat alkalmaznak. A mérendő sugárzás hatására a katódból kilépő elektronok a pozitív feszültségű elektródból másodlagos elektronokat váltanak ki. Ez tulajdonképpen azt jelenti, hogy az elektromos válaszjel elcsúszik a megvilágítás intenzitásának függvényében, illetve annak függvényében, hogy a cella a mérést megelőzően mennyi ideig volt megvilágítva. Ha ezt több fokozaton keresztül végezzük, akkor az anódra jutó elektronok száma elérheti az elsődlegesek számának 108 szorosát is.
2.12. A fotográfiai hatáson alapuló sugárzásmérés
A fotográfiai hatáson alapuló sugárzásmérés alapgondolata az, hogy egy fotográfiai réteg expozíciója és az előhívott kép optikai denzitása között jól definiálható összefüggés van. Az expozíció a megvilágítás és az expozíciós idő szorzata [2.16.] .
Ha egy optikai közegre fényt bocsátunk, annak egy része a közegen áthatol, egy másik része elnyelődik, a maradék pedig visszaverődik. Ennek megfelelően értelmezni tudunk egy transzmissziós vagy áteresztési tényezőt, amely az áteresztett és a beeső sugárzott teljesítmények vagy fényáramok aránya. Ebből származtatott mennyiség a denzitás vagy feketeség, amely az áteresztési tényező reciprok értékének 10-es alapú logaritmusa.
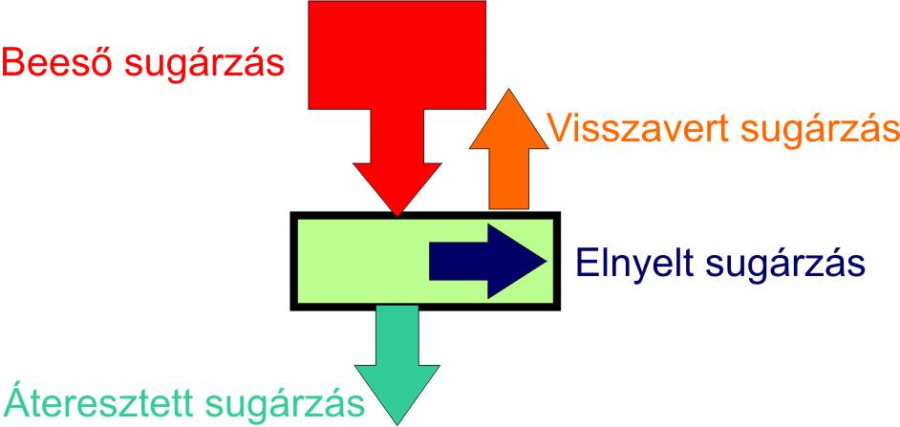
|
| ||
|
|
τ az áteresztési tényező.
![A fotográfiai réteg jelleggörbéje [2.4.]](images/image_II_6.png)
A jelleggörbe függőleges tengelyén az optikai denzitás látható, míg a vízszintes tengelyen az expozíció logaritmusa. A görbén rendre a következő szakaszok különböztethetők meg. Az alapfátyol a nyersanyagon az elérhető legkisebb denzitást jelöli. A lineáris szakasz alatt található az alsó könyök, felette pedig a felső könyök. A felső könyök után a görbe eléri a maximumát, ami azt a denzitást jelöli, amely a nyersanyaggal maximálisan elérhető. Innen az expozíció növelésével a denzitás csökken, ez a szolarizáció szakasza. A görbének egy jellemző paramétere a lineáris szakasz meredeksége, a gamma-érték. Egy ezüsthalogén alapú fekete-fehér nyersanyag kidolgozása a hívásból és a rögzítésből áll. Ha exponált és kidolgozott fotografikus nyersanyag egy adott pontjára fénynyalábot bocsátunk, megmérjük a bebocsátott illetve az áteresztett fényáramokat, ezekből kiszámíthatjuk a denzitást. Mivel a nyersanyag feketedése számos tényezőtől függ, ezért abszolút intenzitásmérésre nem alkalmas, azonban ha két azonos fénynyaláb ugyanazon a fotográfiai nyersanyagon, azonos expozíciós idők mellett azonos feketedést eredményez, akkor a két nyaláb intenzitása azonos.
2.13. Denzitometrálás
A denzitométerek segítségével lehet az áteresztési tényezőt, illetve a denzitást meghatározni. A gyakorlatban alkalmazott denzitométerek működési elv szempontjából két csoportba oszthatók. A közvetlen leolvasásúak esetében a vizsgálandó lemezen áthaladó fény az elektromos érzékelő jelét megváltoztatja, s így a változást közvetlenül leolvashatjuk. Az összehasonlító elven működők kétsugaras berendezésekben a mérendő és az összehasonlító fényáram összehasonlításából lehet következtetni az ismeretlen minta denzitására [2.16.] .
2.13.1. Denzitásmérés gyakorlata
Denzitometráláskor az eredményül kapott mérési eredmény nagymértékben függ a mérőműszer fényérzékelője és a mérendő közeg közötti távolságtól, azaz az érzékelőbe érkező fénynek a mérés normálisával bezárt szögétől. Megállapítható, hogy a legkisebb denzitásérték akkor mérhető, ha a rétegből kilépő összes szórt fény az érzékelőbe jut, azaz a nyílásszög kilencven fok; a denzitásérték akkor a legnagyobb, ha a rétegre merőlegesen beeső fénysugárnak csupán merőleges komponensét mérjük. Az első esetben diffúz denzitásról, a második esetben spekuláris denzitásról [2.16.] beszélünk. A két szélsőséges mérőfényben mért denzitás arányát Q-val jelöli:
|
|
A Q-t Callier-koeffciensnek nevezik, függ a mérőfény hullámhosszától is, mert a rövid hullámhosszúságú fény erősebben szóródik, mint a hosszú hullámú.
2.13.2. A denzitásmérés során alkalmazott fényforrások
A denzitometriai berendezések belső fényforrásai kell, hogy illeszkedjenek a vizsgálatokhoz. Elvárható, hogy a fényforrások által biztosított megvilágítás jól mérhető és reprodukálható legyen. Ez azt jelenti, hogy a fényforrás fényereje és a fényárama időben állandó. Ismert kell legyen a fényforrás által kibocsátott sugárzás spektrális energiaeloszlása is; nem megfelelő spektrális összetétel esetén, szűrők útján történő korrekcióra van szükség. Fényforrásként általában volfrámszálas izzólámpát használnak.
2.13.3. A volfrámlámpa
A denzitometriai célra használt fényforrásnak időben nagyon stabilan kell izzania. Kedvező tulajdonsága, hogy könnyen kalibrálható, pontosan szabályozható és jól kezelhető, 2360 K eloszlási hőmérsékleten sugároz.
2.13.4. A halogénlámpa
A denzitásmérés során alkalmazott fényforrások között elterjedten használják a halogén izzólámpákat is. Előnyei a hagyományos izzólámpákkal szemben, hogy viszonyítva kisebb méretűek, sokkal jobb fényhasznosításuk, magasabb a színhőmérsékletük és a teljes élettartam során közel azonos fényáramot biztosítanak [2.16.] . A halogén lámpában a töltőgáz megakadályozza az elpárolgó wolfram kicsapódását a bura belső felületén. Ilyenkor a wolfram és a halogén vegyületet alkot, mely a nagy hőmérsékletű környezetben bomlik atomokra, így a wolfram ismét visszakerül az izzószálra, a halogén pedig felszabadulva folytatja a körfolyamatot. A halogén izzók spektrális tulajdonságai hasonlítanak az izzólámpákéhoz, a feszültségesés színhőmérséklet-esést eredményez. Fényhasznosításuk 35 lm . W-1 körüli.
2.13.5. A geometriai viszonyok denzitásmérés során
A méréstechnikai gyakorlatban a vizsgálandó réteget kis nyílásszöggel világítják meg, és a közel merőlegesen kilépő fényt hasznosítják a mérésre. Ilyenkor ugyanis a spekuláris denzitás értéke alapvetően a kilépő fénysugár nyílásszögétől függ. Ritkább az a módszer, amikor a tárgyat diffúz, vagy közel párhuzamos fénnyel világítják meg, és minden kilépő fényt detektálnak [2.16.] .
2.13.6. Szabványos mérési eljárások
A diffúz fény előállítására Ulbricht-féle integrálógömböt használnak, aminek belső felülete erősen fényszóró, nagy visszaverő képességű festékkel van bevonva. Legfontosabb jellemzője, hogy ha a gömb belső felületét megvilágítják, akkor a gömb belső felülete minden pontjának a fénysűrűsége a sokszoros fényvisszaverődés sorozat következtében ugyanakkora, és az iránytól függetlenül arányos a gömbbe eső fényárammal [2.16.] . Ilyenkor fontos, hogy
a diffúz mérőfény egyenletesen essék a test felületére, és az onnan merőlegesen kilépő sugarak vesznek részt a mérésben.
a test és a mérőberendezés mérőfelülete közötti reflexió kicsi legyen,
a zavaró melléksugárzások csak elhanyagolható hatásúak lehetnek.
2.14. Izokromatikus, és heterokromatikus fotometrálás
Logikusnak tűnik, hogy a fotometriai mennyiségek tárgyalásánál azok mérésénél a fénynek az emberi szemre gyakorolt hatását vegyük alapul. Ennek azonban az a hátránya, hogy szemmel a fotometriai mennyiségeket nem tudjuk számszerűen meghatározni, mivel a szembe jutó fényáram és a detektált fényérzet nem arányos egymással. Amellett, hogy a fényérzetet még számtalan fizikai és szubjektív paramétertől függ, probléma az is, hogy a növekvő fényárammal szem érzékenysége jelentősen csökken. Kihasználható előny viszont, hogy az emberi szem nagy biztonsággal tudja meg különböztetni a megvilágításbeli különbségeket, melyekre igen érzékeny. Két azonos tulajdonságú felület azonos színű megvilágítása mellett, az ember szemmel történő megfigyeléssel képes eldönteni a megvilágítások bizonyos határon belüli egyezőségét. Ez az izokromatikus fotometria alapgondolata, és a fent leírtaknak megfelelően, úgynevezett kiegyenlítő mérési módszerek alkalmazását teszi lehetővé [2.18.] . Az eltérő szerkezeti és elvi kialakítású izokromatikus fotométerekben ezen kiegyenlítés történhet polarizációs szűrőpárokkal, fényhatároló rekeszekkel, forgótárcsákkal, szürke ékekkel, de lehetséges pusztán a távolságtörvény megfelelő alkalmazásával is. Ebben az esetben merőleges beesésnél az a távolságra levő I 1 fényerősségű és az b távolságra elhelyezett I 2 fényerősségű fényforrások akkor eredményeznek egyenlő megvilágítást, ha
|
|
Ismerve az egyik fényerősséget és a hozzá tartozó távolságot, a másik távolság megfelelő változtatásával a keresett fényerősség meghatározható.
Probléma léphet föl két különböző színű fény összehasonlításakor, mivel az izokromatikus fotometria módszerei csak nagyon kis mértékű színkülönbség esetében alkalmazhatók [2.18.] . Ilyenkor válik szükségessé a heterokromatikus fotométerek alkalmazása, mint amilyen például a gyakran alkalmazott, és széles körben elterjedt villogásos fotométer. Alkalmazása során egy felületet felváltva világítanak meg két különböző színű, és erősségű fénnyel, amit a szem érzékel. A szemet érő fény villogtatásának frekvenciájának növelésével egy keverékszín válik érzékelhetővé. Az egyik fényforrás fényáramát addig szabályozzák, míg a fényvillogás meg nem szűnik, ilyenkor a megvilágítások értékei azonosak.
2.15. Ellenőrző kérdések
Mit nevezünk optikai sugárzásnak?
Az egységsugarú gömb segítségével hogyan értelmezzük a térszöget?
Definiálja a fénysűrűséget és a megvilágítást!
Ismertesse az áteresztési, visszaverési és elnyelési tényező kapcsolatát! Magyarázza meg a denzitás fogalmát!
Pontszerű fényforrások alkalmazása esetén a fényforrás és a felület megvilágítási viszonyaira a távolságtörvény a jellemző, mely szerint pontszerű fényforrás esetén a fényforrás megvilágítása a felülettől való távolság négyzetével arányosa csökken. Hol van ennek jelentősége?
Az ideálisan diffúz felületet az úgynevezett Lambert-féle felület, amit a Lambert-féle koszinusztörvény jellemez. E törvény kimondja, hogy a visszaverő felület fényerőssége a felület normálisával bezárt szög koszinuszával arányos. Érvényesek rá a pontszerű fényforrások törvényszerűségei?
A sugárzásdetektorok három fő csoportra oszthatók, aszerint hogy működésük a fény melyik fizikai hatásán alapszik. Sorolja fel ezeket a fizikai elveket!
Mi az alapja a fotográfiai hatáson alapuló sugárzásmérésnek?
Egy ezüsthalogén alapú fekete-fehér nyersanyag karakterisztikája számos jól elkülöníthető szakaszt tartalmaz. Melyek ezek, és milyen fizikai mennyiségek találhatók a koordinátatengelyeken?
Milyen esetben beszélhetünk diffúz denzitásról, illetve spekuláris denzitásról? Mondjon példákat!
Ismertesse a halogén lámpában lejátszódó folyamatokat. Mi a szerepe a halogén vegyületnek? Mit tud a halogén izzók spektrális tulajdonságairól, a feszültség és a színhőmérséklet közötti kapcsolatról?
Az Ulbricht-féle gömb legfontosabb jellemzője, hogy ha a gömb belső felületét megvilágítják, akkor a gömb belső felülete minden pontjának a fénysűrűsége a sokszoros fényvisszaverődés sorozat következtében ugyanakkora, és az iránytól függetlenül arányos a gömbbe eső fényárammal. Milyen fotometriai mennyiségek mérésére használhat az Ulbricht-féle gömb?
Magyarázza el a különbséget az izokromatikus, és heterokromatikus fotometrálás között!
Mit jelent az, hogy neutrális szürke ék?
Hasonlítsa össze a radiometriai és a fotometriai mennyiségeket!
Felhasznált irodalom
[2.1.] A hőmérsékleti skála megvalósítása optikai pirométerrel az 1000 ºC…3000 ºC tartományban. Mérés és automatika. 48-52. o.. 1986.
[2.2.] A napsugárzás spektruma és az emberi szem érzékenysége. Fizikai Szemle. 199-203.o..
[2.3.] Modern optika mérnököknek és kutatóknak. Műszaki Könyvkiadó. Budapest . 1982.
[2.4.] Optika. Panem-McGraw-Hill. Budapest . 1997.
[2.5.] Kozmikus fizika. Egyetemi jegyzet, ELTE. Budapest . 2002.
[2.6.] Termodinamika és statisztikus mechanika. Tankönyvkiadó. Budapest . 1991.
[2.7.] Gyula. Hőközlés. BME . 1999.
[2.8.] Tables of blackbody radiation. Macmillan. New York . 1961.
[2.9.] Telesistemy dla izmerenia i kontrola ioniziruşih izlucsenij. Atomizdat. Moskva . 1978.
[2.10.] Photometry and radiometry for engineers. Wiley-Intersc.. New York . 1974.
[2.11.] Radiometria. Tankvk.. Budapest . 1991.
[2.12.] Kísérleti fizika. Nemzeti Tankvk.. Budapest . 1999.
[2.13.] Optika, Nyitott rendszerű képzés - távoktatás - oktatási segédlet. LSI Oktatóközpont. Budapest . 1992.
[2.14.] Principles of optics. Cambridge University Press. Cambridge . 1997.
[2.15.] Einführung in die Theorie der Wärme. Hirzel. Leipzig . 1930.
[2.16.] Megvilágításmérés, szenzitometria. Műszaki Kvk.. Budapest . 1978.
[2.17.] Hőtechnikai alapmérések. Tankvk.. Budapest . 1979.
[2.18.] Optika. Editura Ábel. 2008. ISBN 9789731140728.
[2.19.] MSZ 6240.
[2.20.] Félvezető fotodetektorok. Műszaki Könyvkiadó. Budapest . 1977.
3. fejezet - Fényforrások
- 3.1. A fényforrások működését leíró alapfogalmak és törvények
- 3.2. A sugárzás fontosabb törvényei
- 3.3. A Planck-törvény
- 3.4. A Wien-törvény
- 3.5. Rayleigh–Jeans-törvény
- 3.6. A Stefan-Boltzmann-törvény
- 3.7. Nem abszolút fekete-test jellegű sugárzók
- 3.8. A Kirchhoff törvény
- 3.9. Fényforrások hatásfoka
- 3.10. Fénykibocsátás az abszolút fekete test sugárzása alapján
- 3.11. A Nap sugárzása
- 3.12. Izzólámpák
- 3.13. Elektromos kisülés gázokban
- 3.14. Gázkisülő lámpa
- 3.15. Nagyintenzitású ívlámpák
- 3.16. Ellenőrző kérdések
- Felhasznált irodalom
Optikai rendszerek tervezésekor alapos vizsgálat alá kell venni a rendszerben alkalmazott fényforrásokat is, hiszen az optikai rendszer többi elemének tervezése nagymértékben függ az alkalmazott elektromágneses sugárzás hullámhosszától és intenzitásától. A fény keletkezését, elektromágneses hullám lévén, az elektromos töltések sebességváltozása okozza. A mindennapi életben fellelhető fényforrások nagyobbik részénél több-kevesebb pontossággal alkalmazhatók is az elektronok rezgésére és keringésére vonatkozó elméletek, azonban a fénykibocsátás leírásának pontosabb elméleteinél figyelembe kell vennünk a fény részecsketermészetét és a kvantummechanika törvényszerűségeit is.
A leggyakrabban előforduló fényforrások általában az alábbi két nagy csoport egyikébe sorolhatók, bár a csoportok között nincs éles határvonal:
Termikus fényforrások esetében a fénykibocsátás a magas hőmérséklet eredménye.
Elektromos kisülés gáztéren keresztül, amikor a fénykibocsátás a feszültség hatására létrejövő ionizációk és ütközések eredménye.
A fényforrások egy speciális típusával, a lézerrel egy másik fejezet foglalkozik.
3.1. A fényforrások működését leíró alapfogalmak és törvények
A testeket sugárzáshoz való viszonyulásuk alapján a következőképpen csoportosíthatjuk [3.1.] :
Ha α = 1, akkor ρ = 0 és τ = 0.
Ez esetben a test a ráeső sugárzó energiát teljesen elnyeli. Az ilyen testeket abszolút fekete testnek, vagy egyszerűen fekete testnek nevezik.
Ha ρ = 1, akkor α = 0 és τ = 0.
Ez azt jelenti, hogy a test a ráeső sugárzó energiát teljesen visszaveri. Ha a visszaverődés szabályos, akkor a test tükröző. Ha a visszaverődés diffúz, a testet abszolút fehér testnek nevezzük.
Ha τ =1, akkor α = 0 és ρ = 0.
Ilyenkor a teljes sugárzó energia áthalad a testen, az ilyen test átlátszó.
Az abszolút fekete test viselkedését jól modellezi a falán kis nyílással ellátott üreges test. Az üreg nyílásánál az abszorpciós tényező közel egységnyi, azaz a nyílásra eső, és azon belépni szándékozó sugárzás energiája az üregbe bejutva, azon belül szinte teljesen elnyelődik [3.1.] .
3.2. A sugárzás fontosabb törvényei
A fizikai törvényszerűségeiről a legrégebbi ismereteink természetesen azokról a területekről származnak, ahonnan a legkönnyebb volt pontos mérési eredményeket szerezni. Ezek közé tartozik a tér, idő, a mozgás és a hő. Az is könnyen belátható, hogy törvényszerű összefüggések megkonstruálása legelőször azoknál a jelenségeknél sikerült, amelyek megfigyelhető lefolyása gyakran a külső, kísérő körülményektől és beavatkozásoktól függetlenül folyt. A megfigyelt fizikai törvényt, már a kezdeti időktől rendszerint egy matematikai formulában próbálták kifejezni. Ez biztosította, és tette lehetővé, hogy az általunk választott feltételek mellett végbemenő folyamatokat, adott körülmények között előre tudjuk meghatározni, időbeli lefolyásukat pedig a lehető legpontosabban kiszámítani. Az érvényes a sugárzást leíró törvényszerűségekre is, melyek összefüggéseit sok spontán megfigyeléssel, tervezett kísérleti vizsgálattal igyekeztek leírni. Megjegyzendő, hogy az alábbiakban ismertetésre kerülő általános törvényszerűségeket természetesen csak az abszolút fekete test által kibocsátott vagy elnyelt sugárzásra lehet értelmezni, érvényességük pontosan csak légüres térben végbemenő sugárzásokra vonatkozik, más, például gáznemű közegekben végbemenő sugárzás esetében csak jó közelítésnek tekinthetők [3.4.] .
3.3. A Planck-törvény
|
Max Karl Ernst Ludwig Planck (1858 –1947) Nobel-díjas német fizikus, a kvantummechanika megalapítója. Gyermekkorát Kielben és Münchenbe töltötte, egyetemi tanulmányai során a kor hírességeinek előadásait hallgathatta, olyanokét, mint Hermann von Helmholtz, Gustav Kirchhoff, valamint Karl Weierstraß. Magánúton tanulmányozta Rudolf Clausius feljegyzéseit, ennek a köszönhető, hogy érdeklődése a hőtan felé fordult. 1879-ben nyújtotta be doktori disszertációját „A mechanikai hőtan második főtétele” címmel, majd 1880-ban a habilitációs értekezését „Izotróp testek egyensúlyi állapota különböző hőmérsékleteken” címmel. 1889-ben Helmholtz közbenjárásával Berlinbe hívták, hogy Kirchhoff utóda legyen, ahonnan 1926-ban vonult nyugdíjba; az ő utóda Erwin Schrödinger lett. 1894-ben kezdett a Kirchhoff által már 1859-ben megfogalmazott feketetest-sugárzás problémájával foglalkozni. A klasszikus fizikára alapozva levezetett Rayleigh-Jeans-törvény a magas frekvenciákon nem illeszkedett a mérési eredményekhez. A Wilhelm Wien által, és róla elnevezett törvény sem volt kielégítő, hiszen az a magas frekvenciájú eredményeket igazolta, de alacsony frekvenciákon nem egyezett a mérésekkel. Plancknak sikerült tisztán matematikai megfontolásokra alapozva e két törvényt egyetlen összefüggéssel helyettesítenie. 1918-ban elnyerte a Nobel-díjat a plancki hatáskvantum felfedezéséért, amit csak 1919-ben vehetett át. Minden idők egyik legnagyobb fizikusa 1947-ben halt meg; a göttingeni városi temetőben nyugszik. |
Az E emisszióképesség azt az energiamennyiséget jelenti, amelyet a test egységnyi felülete egységnyi idő alatt a teljes hullámhossz tartományban kisugároz. Emellett azonban rendkívüli jelentőséggel bír annak ismerete, hogy különböző testhőmérsékleteken hogyan változik a kisugárzott energia hullámhossz függvényében.
A Planck törvény segítségével kiszámítható a sugárzás intenzitásának nagysága fekete test esetén, adott sugárzó testre vonatkozó abszolút hőmérséklet és a sugárzási hullámhossz esetén.
|
|
ahol a λ a hullámhossz, T a sugárzó test abszolút hőmérséklete, c 1 és c 2 állandók. A c 1 állandó a h=6,626068⋅10 -34 m 2 kgs -1 Planck-állandó és a c=299792458ms -1 fénysebesség négyzetének szorzata.
c 2 állandó az alábbiak szerint határozható meg:
|
|
ahol c=299792458ms -1 , h=6,626068⋅10 -34 m 2 kgs -1 és k=1,3806503⋅10 -23 m 2 kgs -2 K -1 az úgynevezett Boltzmann-állandó.
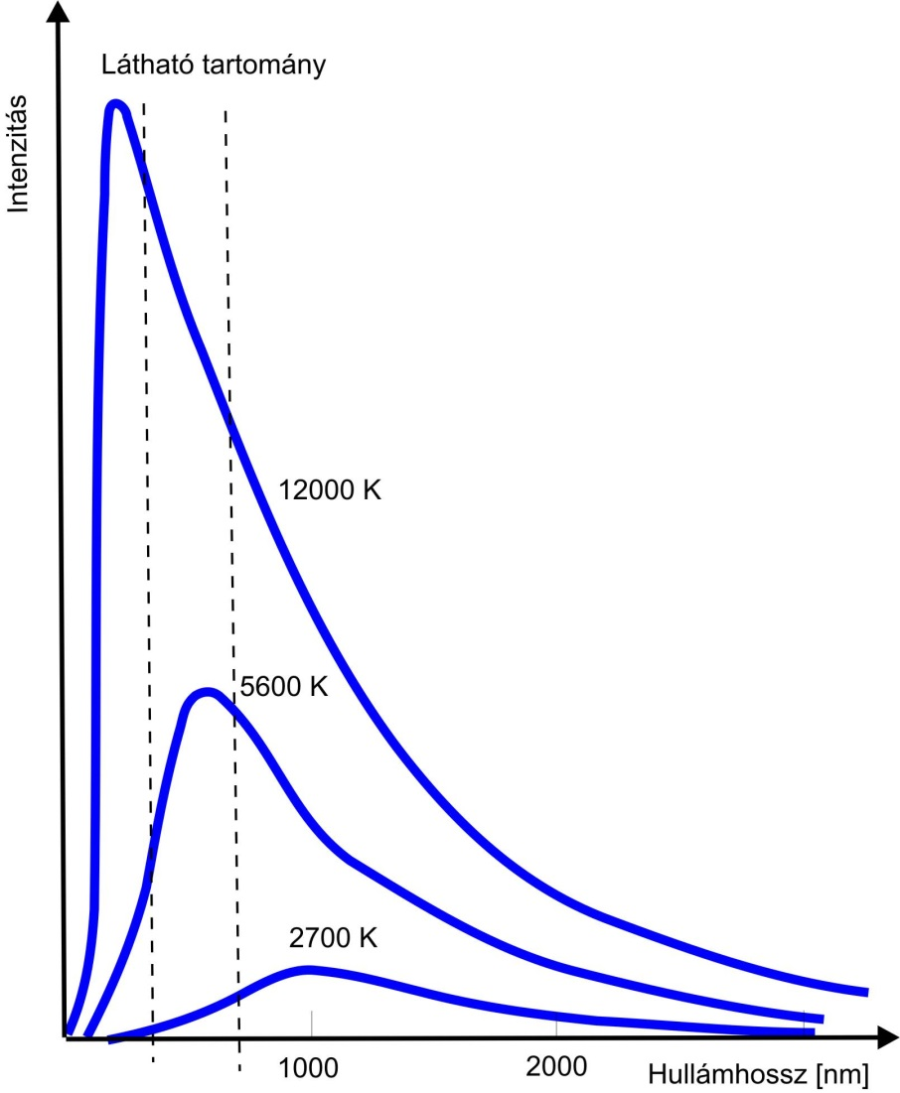
A Planck-törvény ábrájából következtethető, hogy a sugárzás intenzitása a hőmérséklettel nagyon határozottan nő. Az egyes hőmérséklethez tartozó intenzitás-görbék maximumai, növekvő hőmérséklettel csökkenő hullámhosszakat adnak.
3.4. A Wien-törvény
|
Wilhelm Wien (1864–1928) német fizikus. Munkásságának legjelentősebb része az elektromágnesesség és a hőtan elméletéhez kapcsolódik. A legismertebb, nevéhez fűződő megállapítás a Wien-féle eltolódási törvény, mely a fekete test sugárzásának számítására vonatkozik. A hősugárzás területén végzett munkásságáért 1911-ben Nobel-díjat kapott. Általános iskolai tanulmányait Rastenburgban és Heidelbergben végezte. Egyetemi tanulmányait a göttingeni, majd a berlini egyetemen folytatta. 1883-85 között Hermann von Helmholtz mellett, annak laboratóriumában dolgozott, 1886-ban szerezte meg doktori fokozatát a fémek környezetében bekövetkező fényelhajlási jelenségek vizsgálatával. 1896-1899 között Aachen-i egyetemen adott elő, majd 1900-ban a würzburgi egyetemre került, ahol Wilhelm Conrad Röntgen utóda lett. 1896-ban tapasztalati úton meghatározta a fekete test sugárzási törvényét, ezt róla nevezik Wien törvénynek. Hőtani eredményi csoportjába tartozik továbbá a Wien-féle eltolódási törvény, vagy más néven Wien I. törvénye, mely segítségével egy test emisszióképességének maximális értéke határozható meg. A törvény szerint az abszolút fekete test emisszióképességének hullámhossz szerinti maximumhelye fordítva arányos a termodinamikai hőmérséklettel. Az eltolódási törvény a gyakorlatban is megfigyelhető, egy test fokozatos hevítéséhez tartozó színváltozásával. Alacsony hőmérsékleten a hevített test vöröses színű. A hevítés fokozásával, azaz a hőmérséklet emelésével a test színe fokozatosan változik a világos vöröstől, sárgásfehéren keresztül egészen, a magas hőmérsékleten tapasztalható kékes színig. Wien II. törvénye kevésbé ismert ugyan, azonban jelentősége szintén nagy. A törvény a maximális intenzitásérték hőmérsékletfüggését adja meg, mely szerint annak maximális értéke a hőmérséklet ötödik hatványával arányos. |
A Planck-törvény segítségével számszerűen meghatározható a sugárzás nagysága, ha ismeretes a sugárzó test abszolút hőmérséklete és a sugárzás hullámhosszúsága. Wien-törvény kapcsolatot teremt a sugárzó test abszolút hőmérséklete és a sugárzás hullámhosszúsága között, és megmutatja, hogy mekkora a fekete test sugárzás intenzitásának nagysága, adott sugárzó testre vonatkozó abszolút hőmérséklet és a sugárzási hullámhossz esetén.
A Wien-törvényt grafikusan ábrázolva látható, hogy azok a hullámhosszak, amelyeknél E 0 maximális értéket ér el, növekvő hőmérséklettel egyre kisebb λ értékek felé tolódnak el. A Wien-törvényből kiadódik a T=állandó görbék szélső értékeinek helye a λ függvényében
|
|
vagyis az intenzitás-maximumokhoz tartozó hullámhosszak és a megfelelő abszolút hőmérsékletek szorzata állandó [3.2.] . Ezt nevezik Wien-féle eltolódási törvénynek.
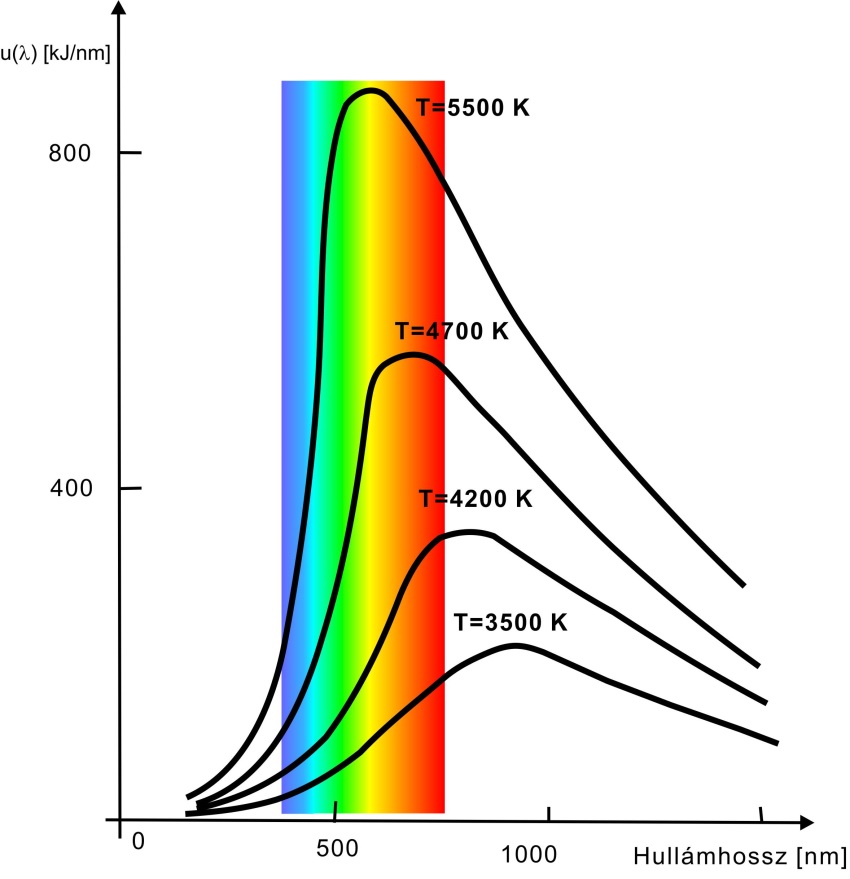
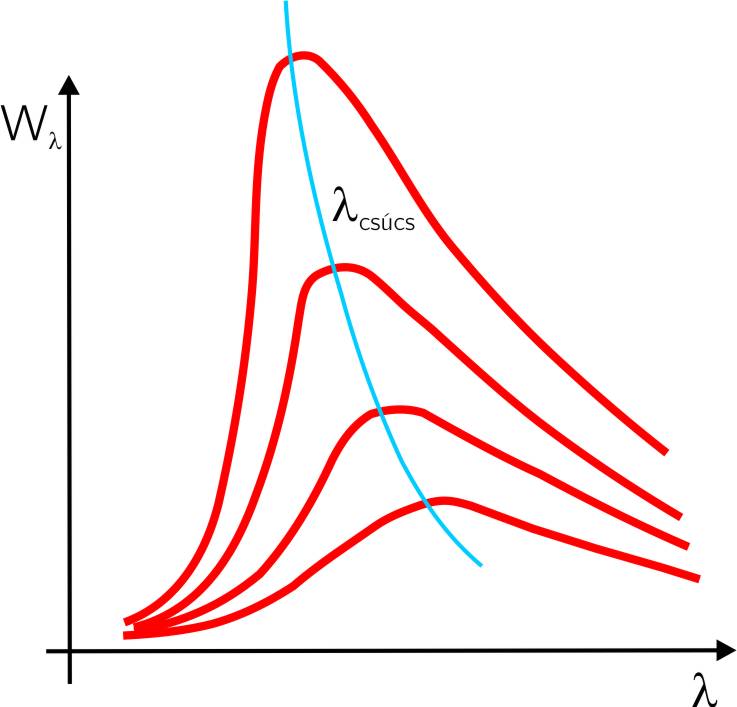
3.5. Rayleigh–Jeans-törvény
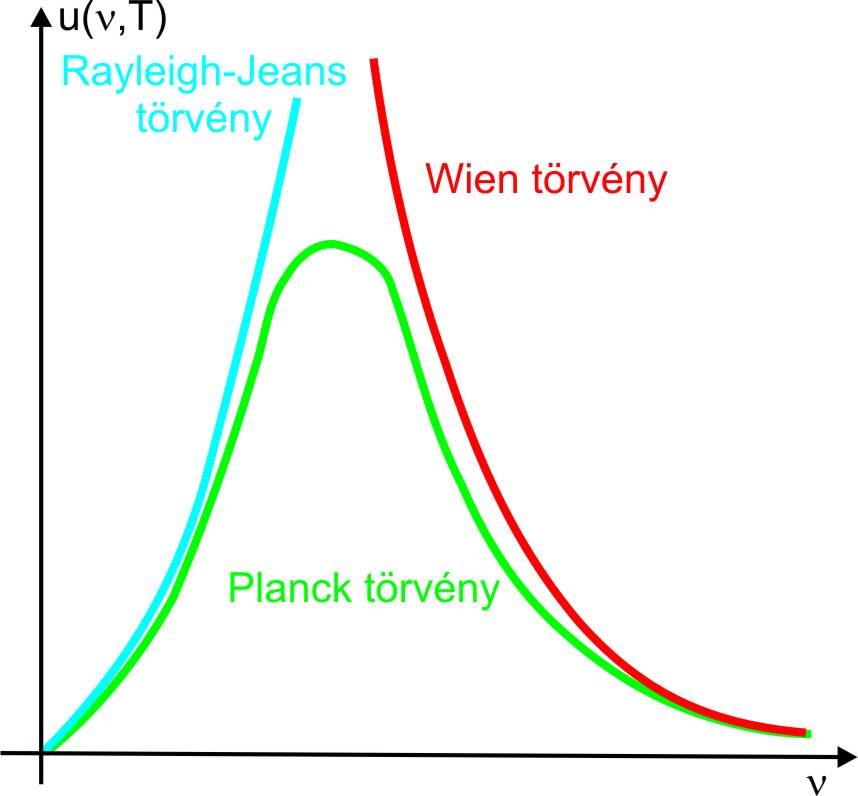
A Wien-törvény csak a sugárzás nagy frekvenciáin írja le helyesen a tapasztalati eloszlást, a frekvenciát csökkentve bekövetkezne az úgynevezett infravörös katasztrófa. Ezzel szemben a Rayleigh–Jeans-törvény csak az alacsony frekvencián követi helyesen a tapasztalati eloszlást; a frekvenciát növelve itt az úgynevezett ultraibolya-katasztrófa következne be. Tehát sem a Wien- törvény, sem a Rayleigh–Jeans-törvény nem adja vissza a tapasztalati intenzitáseloszlást a teljes frekvencia tartományon. Max Planck vizsgálta az energiaeloszlás és az entrópia közti kapcsolatot. A Wien-féle és a Rayleigh–Jeans-féle alakot az entrópia második deriváltja segítségével kombinálta össze, és a Boltzmann-féle termodinamikai valószínűséget alkalmazta, mely eredményeként az ismert, Planck-féle sugárzási formulát kapta, mely a kis frekvenciákra a Rayleigh–Jeans-törvényt, míg a nagyfrekvenciákra a Wien-törvényt adta, és belőle a Stefan–Boltzmann-törvény is levezethető.
3.6. A Stefan-Boltzmann-törvény
|
Ludwig Eduard Boltzmann (1844–1906) osztrák fizikus. Számos tudományos eredménye közül az egyik legjelentősebb a feketetest-sugárzásra vonatkozó Stefan- Boltzmann -féle törvény megalkotása. Róla nevezték el többek között a Boltzmann-állandót, és a Boltzmann-féle transzportegyenletet. 1863-ban iratkozott a Bécsi Egyetemre, fizikát hallgatott. Külön érdekesség, hogy tanára volt a magyar származású, az optika terén is maradandót alkotó Petzval József is, valamint Josef Stefan, aki irányítása mellett 1866-ban a Bécsi Egyetemen doktori fokozatot szerzett a kinetikus gázelmélet terén végzett vizsgálataival, majd 1867-től az ő asszisztense lett. Josef Stefan (1835 – 1893) szlovén fizikus mérte meg először a feketetest által az összes hullámhosszon kisugárzott energiát. Azt tapasztalta, hogy egy abszolút fekete test kisugárzott összes energiája a hőmérséklet negyedik hatványával arányos. Ezt Boltzmann 1879-ben elméletileg is megalapozta, ezért nevezik az eredményt Stefan-Boltzmann-törvénynek. Számos ismert és nagyhírű egyetemen töltött esztendő után 1893-ban visszatért Bécsbe, hogy egykori mentora, Josef Stefan után az Elméleti Fizikai Intézetének vezetője legyen. |
Az abszolút fekete test felületének területegysége által időegység alatt kisugárzott teljes energiamennyiség értéke a Planck-törvény és az összsugárzásra vonatkozó összefüggés felhasználásával:
|
|
Az integrálás után
|
|
ahol a C 0 =5,67⋅10 -8 Wm -2 K -4 állandó az abszolút fekete test sugárzási együtthatója. A Stefan-Boltzmann-törvény tehát kimondja, hogy a test egységnyi felületéről időegység alatt kisugárzó összes energia a sugárzó test abszolút hőmérsékletének negyedik hatványával arányos.
3.7. Nem abszolút fekete-test jellegű sugárzók
A Stefan-Boltzmann-törvény csak abszolút fekete testre vonatkozik, de átalakítással szürke testekre is alkalmazható. Ebben az esetben:
|
|
A ε < 1 relatív emisszióképesség, vagy más néven a test feketeségi foka mindig kisebb, mint a fekete testé. Nyilvánvaló, hogy egy valós test viselkedése eltér az abszolút fekete testétől.
3.8. A Kirchhoff törvény
|
Gustav Robert Kirchhoff (1824–1887) német fizikus. Egyetemi előadói karrierjét1847-ben kezdte a Berlini Egyetemen, majd három évvel később már a fizika rendkívüli tanára a Breslaui Egyetemen. A Heidelbergi Egyetemre fizikaprofesszorrá1855-ben nevezték ki, itt született Bunsennel közösen a színképelemzés módszere. 1845-ben közölte a róla elnevezett Kirchhoff-törvényeket, melyek segítségével lehetséges villamos hálózatokban az áram, a feszültség és az ellenállások számítása. 1859-ből származik a sugárzási törvénye, mely szerint bármely testnél egy adott hullámhosszon és hőmérsékleten a spektrális emisszióképesség és az abszorpcióképesség hányadosa állandó. 1875-től a Berlini Egyetem matematikai fizika professzora. |
Kirchhoff törvénye a test emisszióképessége és abszorpcióképessége, azaz elnyelőképessége között állapít meg összefüggést [3.2.] . Kirchhoff törvénye a fentiek alapján tehát a következőképpen is megfogalmazható: Az emisszióképesség és abszorpcióképesség viszonya minden testre vonatkozóan ugyanakkora és csak az abszolút hőmérséklet függvénye egyben egyenlő az abszolút fekete test ezen hőmérsékletéhez tartozó emisszióképességével. Kirchhoff törvénye nem csak a teljes sugárzásra vonatkozólag adható meg, hanem a részsugárzásra is alkalmazható, s ez esetben az alábbi formában fogalmazható meg: Egy adott hullámhosszhoz tartozó emisszóképességnek és az ugyanazon hullámhosszhoz tartozó abszorpcióképességhez az aránya valamennyi testre nézve azonos, és ez az arány csak a hullámhossz és a hőmérséklet függvénye.
3.9. Fényforrások hatásfoka
A fényforrások jelentős részénél a kisugárzott energiának csak kis része esik a látható fény tartományába. A nagyobbik rész a világítás szempontjából elvész, így a hatásfok alacsony marad. A fénykibocsátás gazdaságosságának megítélésekor figyelembe kell venni az emberi szem spektrális érzékenységét is. A fotometriával, illetve radiometriával fogalakozó fejezetben megismert összefüggések alapján a szem legnagyobb érzékenységének megfelelő zöld színnél azt találjuk, hogy a fény teljesítmény-egyenértéke 680 lumen/watt. Vagyis ennyi lenne az elérhető legnagyobb fényhasznosítás, ha a forrás csak ezen az egy hullámhosszon sugározna. A valós helyzet ennél sokkal rosszabb, pl. egy 30 wattos izzó fényhasznosítása csak kb. 2%. A világítástechnika fejlődésében a fentiek alapján a nagyobb hatásfok elérése érdekében egyre nagyobb hőmérsékletű termikus sugárzókat használunk, amelyek energiájuk jelentős részét a látható tartományban bocsátják ki. Ezek többnyire gázkisüléseken, illetve lumineszcencián alapulnak.
3.10. Fénykibocsátás az abszolút fekete test sugárzása alapján
A folyamatos spektrális eloszlású fényforrások legáltalánosabb példája a magas hőmérsékleten izzó szilárd test. Tapasztalataink azt mutatják, hogy a sugárzás erőssége a növekvő hőmérséklettel szintén nő, és a sugárzás intenzitásának maximuma, spektrálisan a hőmérséklet növekedésével a rövidebb hullámhosszak felé tolódik el. A termikus fényforrások vizsgálata során használt modell az abszolút fekete test, amely minden hullámhosszon minden sugárzást egyformán elnyel. A különböző hőmérsékletű abszolút fekete testek sugárzási görbéit az ábra mutatja.
Abszolút fekete test a valóságban természetesen nem létezik. Gyakorlati megvalósításakor, egy a sugárzást át nem eresztő, belül kormozott falú edényen kis lyukat fúrnak. A lyukon át behatoló sugárzás az alacsony reflexiójú falakon való többszörös diffúz visszaverődések következtében gyakorlatilag abszorbeálódik, mielőtt a lyukból kijutna.
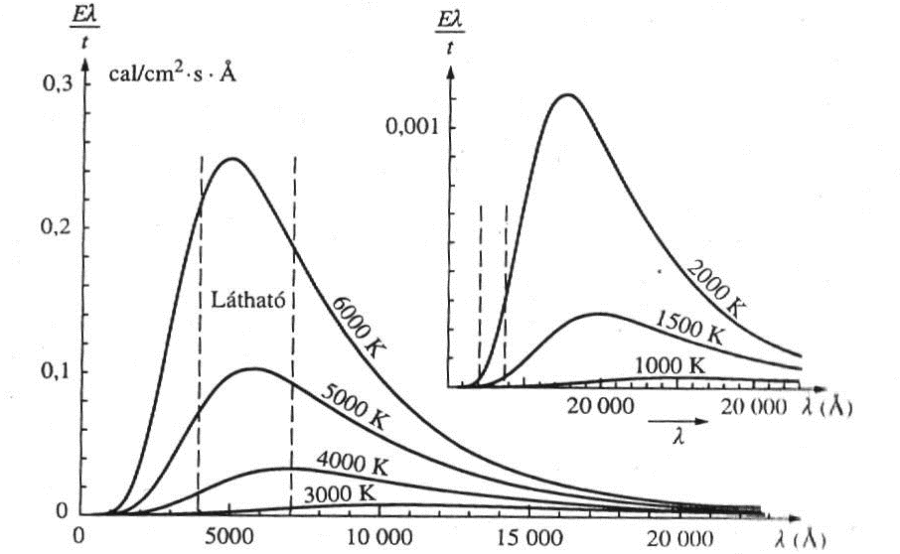
A Planck-féle sugárzási törvény elméleti megalapozásakor érdemes megemlíteni, hogyan képzelték a termikus fényforrások keletkezését. A molekulák rendezetlen hőmozgásának energiája bizonyos mértékben az elektronoknak illetve az atomoknak adódik át, és ezeket rendszertelen rezgésekre gerjeszti. A rezgő töltések elektromágneses hullámokat bocsátanak ki, ami mindenféle frekvenciát tartalmaz. Megfordítva, a beeső sugárzás hatására, a részecskék rezgésbe jönnek, tehát a sugárzásból energiát nyernek el, amely vagy kibocsátódik, vagy az ütközések miatt hővé alakul. A törvény megalkotásakor Planck arra a klasszikus fizika által megoldatlan problémára igyekezett választ adni, hogy az adott frekvenciával rezgő elemi oszcillátorok nem vehetnek fel tetszőleges, folytonosan változó értéket, hanem csak egy legkisebb energiakvantumnak, az egész számú többszöröseit.
3.11. A Nap sugárzása
A hőmérsékleti sugárzók legalapvetőbb példája központi csillagunk, a Nap. Sugárzásának döntő többségét felületének egy viszonylag vékony rétege, a fotoszféra bocsátja ki. Sugárzásenergia-eloszlása a 600 K hőmérsékletű feketetest sugárzásához hasonlít a legjobban. A Nap folytonos spektrális eloszlású színképében diszkrét helyeken sötét, ún. Fraunhoffer-féle vonalak figyelhetők meg. Ennek oka a nap légkörében keresendő: a napkorona, vagy kromoszféra lényegesen alacsonyabb hőmérsékletű gázokból áll, mint a fotoszféra, és így elnyeli azoknak a hullámhosszaknak egy részét, amelyek megegyeznek a gázok gerjesztési energiaszint-különbségeivel.
A Föld légköre szintén elnyel a sugárzásból bizonyos hullámhosszakat, és bizonyos tartományokban jelentős szóródást is okoz. Így a Nap sugárzásának spektrális eloszlása jelentős mértékben eltér a Föld felszínén és a légkörön kívül.
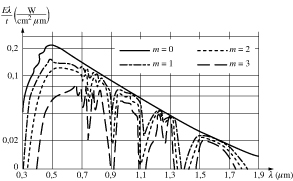
A Naphoz hasonlóan keletkezik a többi csillag fénye is, így fénykibocsátásuk spektrális eloszlása elsősorban az adott égitest felületi hőmérsékletétől függ, ami általában a 3500-5000K tartományba esik.
A csillagok színképét az alábbiak szerint osztályozzák:
|
Q |
Újonnan fellángolt csillagok, szupernóvák | |
|
W |
Rendkívül forró, 50000K felszíni hőmérsékletű csillagok | |
|
B |
20000K felszíni hőmérsékletű ún. héliumcsillagok | |
|
A |
Kb. 10000K felszíni hőmérsékletű ún. hidrogéncsillagok, a színképben már megjelennek a fém- és hidrogénvonalak | |
|
F |
6000-8000K felszíni hőmérsékletű csillagok, a színképben egyre több fémvonallal | |
|
G |
6000K hőmérsékletű csillagok nagyszámú sötét abszorpciós vonallal, ilyen a Nap is | |
|
K |
A színképet a fémek sötét abszorpciós vonalai jellemzik, megjelennek a molekulák vonalai is, a hőmérséklet kb. 4500K | |
|
M |
3500K hőmérsékletű vöröses csillagok, molekulaabszorpciós sávokkal | |
|
RN |
Hidegebb ún. széncsillagok | |
|
S |
Ritkán előforduló hideg csillagok színképtípusa |
3.12. Izzólámpák
A mesterséges hőmérsékleti sugárzók leggyakoribb típusát a különféle izzólámpák alkotják. Ezekben villamos árammal 1000-3000K környékére felmelegített áramvezető izzószál atomjai világítanak folytonos spektrális eloszlással. Az izzószál általában spirál, vagy dupla spirál alakúra húzott volfrámszál, amelyet üveg- vagy kvarcburában helyeznek el. A volfrámszál méretei (hossz, keresztmetszet) az izzó teljesítményét határozzák meg, míg hőmérséklete és felületének nagysága a kisugárzott energiát [3.3.] .
A lámpa élettartamát a wolframszálnak a magas hőmérséklet miatti, párolgása határozza meg. A párolgás hatása kettős: egyrészt a szál átmérőjét csökkentve végül is meghibásodáshoz vezet, másrészt a burán lecsapódó anyag a lámpa hatásfokát csökkenti. Ez a fényáram csökkenés a lámpa élettartama során elérheti a 20%-ot. A párolgás csökkentésére a burát semleges gázzal (pl. nitrogén vagy argon) töltik fel, ez azonban a hővezetés miatt veszteséget is okoz. Ha az izzószálas lámpán a feszültséget növeljük, a fényáram jelentősen növelhető, viszont az élettartam ugrásszerűen csökken. Hasonló módon az alulfűtött izzók élettartama jelentősen növelhető.
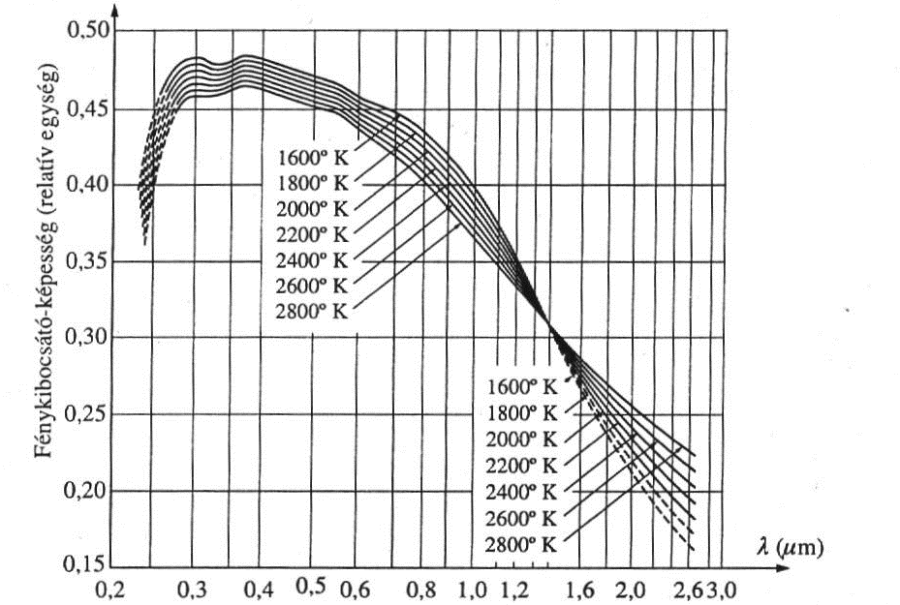
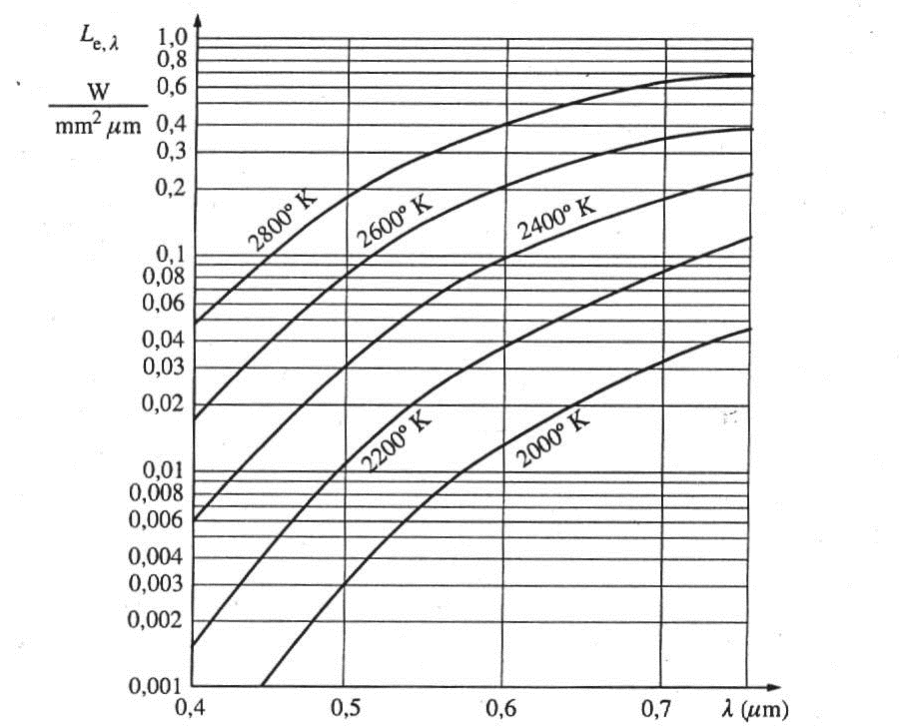
Az izzólámpák egy speciális csoportját alkotják a halogénizzók. Itt az élettartam növelése céljából a lámpát halogénelem-tartalmú gázzal töltik fel. A halogén anyaggal az elpárolgó volfrámrészecskék reakcióba lépnek, a burára kicsapódó fémhalogén visszadiffundál az izzószálba. A burában így kialakuló ciklus, jelentősen megnöveli az élettartamot, és a lámpa fényáram csökkenését is megakadályozza, egyúttal lehetővé teszi a magasabb izzószál-hőmérsékletek elérését, és így a nagyobb fényhasznosítást és fényáramot.
Az izzószál az abszolút fekete test sugárzásával szemben ún. szürke testnek tekinthető. Ennek sugárzási eloszlása a látható tartományban megközelítőleg olyan, mint a hasonló hőmérsékletű fekete testé, de a kisugárzott összes intenzitás kevesebb.
3.13. Elektromos kisülés gázokban
Ha egy semleges részecskéket tartalmazó gáztérre feszültséget kapcsolunk, alaphelyzetben nem jön létre megfigyelhető változás. Ha azonban a térben szabad elektronok is jelen vannak, ezek a feszültség hatására felgyorsulva, és az atomokkal illetve molekulákkal ütközve, gerjesztett állapotot hoznak létre, és sugárzást bocsátanak ki. Ez az alapelve a gázkisüléses lámpáknak.
A gázcsőben a hőmozgás és a külső sugárzás hatására létrejövő szabad töltések száma viszonylag kevés, így a szabad elektronok forrása elsősorban a katód, ahonnan az alábbi jelenségek hatására léphetnek ki a töltések:
hő hatására létrejövő emisszió a katód fűtésének segítségével
megfelelő nagy térerő hatására létrejövő emisszió
másodlagos emisszió, amit a katódba becsapó pozitív ionok hoznak létre.
Ha a gáztérben a feszültség nagyobb, mint az első gerjesztett állapothoz tartozó minimális gerjesztési feszültség, monokromatikus fénykibocsátás jön létre ω frekvenciával.
|
|
h a Planck-féle állandó, és az e az elektron töltése.
A feszültséget növelve magasabb gerjesztési állapotok is létrejönnek, és további hullámhosszokon is energia sugárzódik ki. Amikor a feszültség nagyobb, mint az ionizációs potenciál, a részecskék ionizálódnak az ütközések következtében, és az így keletkező pozitív és negatív töltések az anód és a katód felé gyorsulva tovább növelik az áramot. Alacsony nyomáson az elektronok és az ionok rekombinációjának valószínűsége kicsi, és a katódba csapódó ionok további elektronok kiválását okozzák. Amikor ez a másodlagos emisszió elegendően nagy a kisülési áram fenntartásához, parázskisülésről, vagy más néven glimmkisülésről beszélünk. A parázskisülést állandó áramsűrűség jellemzi. Ha növekszik az áram, növekszik a kisülési keresztmetszet, míg a feszültség állandó marad. Ha a feszültséget tovább növeljük, a glimmkisülés átmegy ívkisülésbe, ami hirtelen feszültségcsökkenéssel jár, jelezve egy másfajta elektronemissziós jelenség kialakulását. Ívkisülés esetén a katódba csapódó pozitív ionok annyira felhevítik az elektródát, hogy a hő hatására kilépő elektronok tartják fenn a folyamatos kisülést. Az energiát egyrészt a nagy hőmérsékletű elektródok, másrészt az ív 4000-8000K hőmérsékletű plazmája sugározza ki.
3.14. Gázkisülő lámpa
A gázkisülő lámpák, vagy közismert nevükön a neoncsövek, alacsony nyomású gázzal töltött, hideg elektródás fényforrások. A neontöltésű cső piros, a héliumtöltésű narancsos fénnyel világít. Higany hozzáadásával a neon fénye kékesfehérré tehető. Színes üvegcsövet alkalmazva, szinte tetszőleges színű fény hozható létre. A csőben a gáz nyomása 0,5 és 10Hgmm között van. A gyújtási feszültség 3000V.
3.15. Nagyintenzitású ívlámpák
A folyamatos fényű mesterséges fényforrások közül az ívlámpák szolgáltatják a legnagyobb teljesítményt. A szén-, és a nagynyomású higany és xenonív fénye megközelíti, illetve néha meg is haladhatja a Nap fényességét (1500 cd/mm 2 ).
A nagynyomású higanyívlámpák zárt térben hozzák létre a kisülést, rendkívül nagy fényerőt biztosítva. A nagy teljesítmény miatt folyamatos hűtést igényelnek. További hátrányuk, hogy robbanásveszélyesek, így csak megfelelő mechanikai foglalással, védőházban használhatóak. Spektrális eloszlásuk erősen vonalas karakterisztikájú.
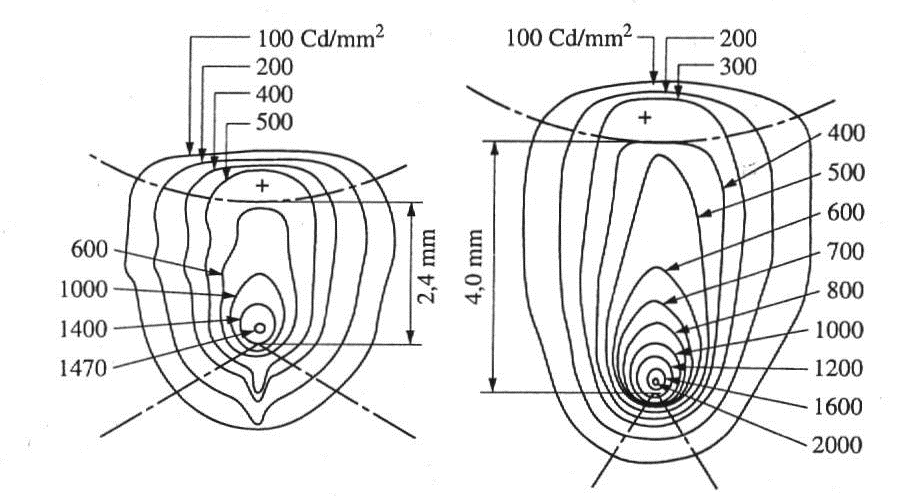
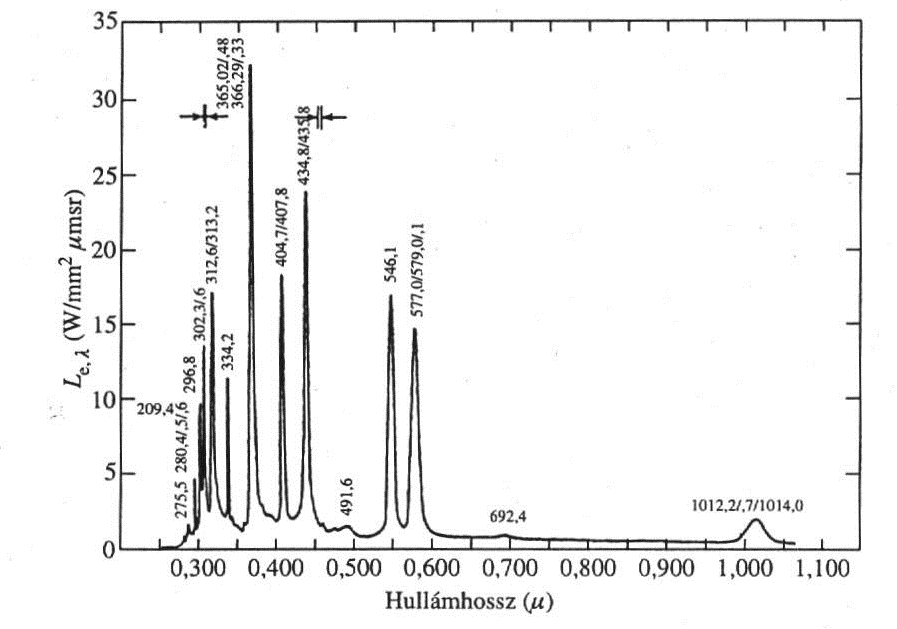
A nagy intenzitású ívfénylámpák legrégebben használt típusa szénelektródával működött. Vetítőgépekben, színpad megvilágításnál, légvédelmi reflektorokban alkalmazták. Az ívet szabad térben, levegőn hozták létre. Az elektródák fogyása miatt a szénrudakat folyamatos előtolással mozgatni kellett, hogy az elektródatávolság állandó maradjon. A higanyív vonalas spektrumának javítására jó eredménnyel használhatók bizonyos semleges gázok. Ezek alapján fejlesztették ki a nagynyomású gázívlámpák családját, amelyek a látható tartományban egyenletesnek tűnő spektrális eloszlást mutatnak.
3.16. Ellenőrző kérdések
A leggyakrabban előforduló fényforrások általában az alábbi két nagy csoport egyikébe sorolhatók: a termikus fényforrások esetében a fénykibocsátás a magas hőmérséklet eredménye, elektromos kisülés gáztéren keresztül történő fénykibocsátás során a feszültség hatására létrejövő ionizációk és ütközések az okok. Világítson rá e két fénykibocsátás típus közötti alapvető különbségre és mutasson példákat mindkét típusra!
A testeket sugárzáshoz való viszonyulásuk alapján az abszorpciós, reflexiós és transzmissziós tényezőjük alapján hogyan csoportosíthatók? Mondjon példákat ezen csoportosításra!
Az abszolút fekete test viselkedését jól modellezi a falán kis nyílással ellátott üreges test. Az üreg nyílásánál az abszorpciós tényező közel egységnyi, azaz a nyílásra eső, és azon belépni szándékozó sugárzás energiája az üregbe bejutva, azon belül szinte teljesen elnyelődik. Hogyan magyarázza ez a fekete sugárzással jól közelíthető viselkedést?
A Planck-törvény segítségével kiszámítható a sugárzás intenzitásának nagysága fekete test esetén, adott sugárzó testre vonatkozó abszolút hőmérséklet és a sugárzási hullámhossz esetén. Ismertesse az összefüggést és magyarázza el az egyes tényezők jelentését, szerepét!
Wien-törvény kapcsolatot teremt a sugárzó test abszolút hőmérséklete és a sugárzás hullámhosszúsága között. Megmutatja, hogy mekkora a sugárzás intenzitásának nagysága fekete test esetén, adott sugárzó testre vonatkozó abszolút hőmérséklet és a sugárzási hullámhossz esetén. Ábrázolja a Wien-törvényt grafikusan Planck-törvény segítségével, adjon magyarázatot arra, hogy az intenzitás-maximumokhoz tartozó hullámhosszak és a megfelelő abszolút hőmérsékletek szorzata miért állandó!
A Stefan-Boltzmann-törvény kimondja, hogy a test egységnyi felületéről időegység alatt kisugárzó összes energia a sugárzó test abszolút hőmérsékletének negyedik hatványával arányos. Hol van jelentősége ennek a megállapításnak?
Kirchhoff törvénye a test emisszióképessége és abszorpcióképessége, azaz elnyelőképessége között állapít meg összefüggést. Mit mond ki?
A fényforrások jelentős részénél a kisugárzott energiának csak kis része esik a látható fény tartományába. A nagyobbik rész a világítás szempontjából elvész, milyen hatással van ez a fényforrás hatásfokára?
Abszolút fekete test a valóságban természetesen nem létezik. Gyakorlati megvalósításakor, egy a sugárzást át nem eresztő, belül kormozott falú edényen kis lyukat fúrnak. A lyukon át behatoló sugárzás az alacsony reflexiójú falakon való többszörös diffúz visszaverődések következtében gyakorlatilag abszorbeálódik, mielőtt a lyukból kijutna. Magyarázza meg, hogy ez a modell miért helyettesítheti a fekete sugárzót?
A Nap folytonos spektrális eloszlású színképében diszkrét helyeken sötét, úgynevezett Fraunhoffer-féle vonalak figyelhetők meg. Mi ennek az oka?
A mesterséges hőmérsékleti sugárzók leggyakoribb típusát a különféle izzólámpák alkotják. Ezekben villamos árammal felmelegített áramvezető izzószál atomjai világítanak folytonos spektrális eloszlással. Milyen szerkezetű egy ilyen fényforrás, mik a jellemzői?
A lámpa élettartamát a wolframszálnak a magas hőmérséklet miatti, párolgása határozza meg. Milyen hatásai vannak a párolgásnak?
Mi történik, ha az izzószálas lámpán a feszültséget növeljük? Hogyan viselkednek az alulfűtött izzók, hogyan növelhetők élettartamuk jelentősen?
Mi az alapelve a gázkisüléses lámpáknak?
A nagynyomású higanyívlámpák zárt térben hozzák létre a kisülést, rendkívül nagy fényerőt biztosítva. Mik az előnyeik és a hátrányaik?
Felhasznált irodalom
[3.1.] Hőtechnikai alapmérések. Tankvk.. Budapest . 1979.
[3.2.] Optika. Editura Ábel. 2008. ISBN 9789731140728.
[3.3.] Kísérleti fizika. Nemzeti Tankvk.. Budapest . 1999.
[3.4.] Optika. Panem-McGraw-Hill. Budapest . 1997.
[3.5.] Gyula. Hőközlés. BME . 1999.
4. fejezet - Színtan
- 4.1. Történeti áttekintés
- 4.2. Mit nevezünk színnek?
- 4.3. Az emberi szem; a színes látás
- 4.4. A színtévesztés
- 4.4.1. Mi a színtévesztés?
- 4.4.2. Genetikus háttér, a színtévesztés elterjedtsége
- 4.4.3. A színtévesztés optikai magyarázata
- 4.4.4. A színtévesztés típusai
- 4.4.5. A színlátás javításának elve
- 4.4.6. A színtévesztés mérése; a diagnózis
- 4.4.6.1. A pszeudoizokromatikus tesztek
- 4.4.6.2. Az anomaloszkóp
- 4.4.6.3. Új színlátás vizsgáló műszerünk: az Anomal Tester
- 4.4.6.4. Új színlátás vizsgáló tesztünk: a színlátás vizsgáló Atlasz
- 4.4.6.5. Tapasztalatok a színlátás-javító szemüvegekkel
- 4.4.6.6. A színlátás javító szemüveg viselésének hatása a színtévesztésre
- 4.5. A színek jellemzése
- 4.5.1. A színek spektrális jellemzése (MSz 9620)
- 4.5.2. A színek tristimulusos jellemzése
- 4.5.3. A színek pszichofizikai (köznapi) jellemzése
- 4.5.4. A színek fizikai jellemzése
- 4.6. A színkeverés
- 4.7. A kiegészítő színek
- 4.8. A metameria
- 4.9. Az RGB és a CMYK színrendszer
- 4.10. A gamut
- 4.11. A színmérő rendszerek
- 4.11.1. A CIE színmérő rendszer
- 4.11.1.1. A CIE RGB-színrendszer
- 4.11.1.2. A CIE xyY színrendszer
- 4.11.1.3. A CIE L*a*b* színrendszer
- 4.11.1.4. A 20°-os és a 100°-os CIE adatok
- 4.11.1.5. A normál színmérő észlelő
- 4.11.1.6. A spektrális fényhatásfok függvény
- 4.11.1.7. A Planck-féle fekete sugárzó („fekete test”)
- 4.11.1.8. A színhőmérséklet
- 4.11.1.9. A szabványos CIE fényforrások
- 4.11.1.10. A színvisszaadás
- 4.11.2. Színminta gyűjtemények és színminta alapú szín rendszerek
- 4.11.2.1. A Munsell színminta atlasz és színrendszer (1929)
- 4.11.2.2. Az NCS (Natural Color System) színrendszer (1979)
- 4.11.2.3. Az Ostwald színrendszer (1931)
- 4.11.2.4. A Coloroid színrendszer
- 4.11.2.5. A RAL színtervezési rendszer
- 4.11.2.6. Jean Bourges digitális színrendszere
- 4.11.2.7. A színminta gyűjtemények
- 4.12. A színmérés
- 4.13. Az emberi színlátás modellezésén alapuló színrendszerek
- 4.14. Ajánlott irodalom
4.1. Történeti áttekintés
Az ember a külvilágról érzékszerveivel vesz tudomást. Öt érzékszervünk közül (látó-, halló-, tapintó-, ízlelő- és szaglószerv) a legfontosabb a látás szerve, a szemünk. Az összes információ több mint 90 %-át ez továbbítja számunkra a környezetünkből.
Szemünk a nappali fényben színesen látja a világot. Bár az emberi szem alapvetően a látható spektrumnak csak három tartományát: a vöröset, a zöldet és a kéket tudja megkülönböztetni, ebből a három színélményből a látási információt feldolgozó emberi agy több milliónyi színárnyalatot varázsol elénk.
A színek több szempontból is fontosak számunkra. Hangulatunkat befolyásoló hatásukat a festő művészek, a belső építészek vagy a reklám szakemberek tudatosan fel is használják. A vörös szín pl. élénkít, a zöld nyugtat, míg a kék segíti a logikus gondolkodást. A fény és a színek hiánya valósággal búskomorrá teszi a sarkkörön túl élőket a hosszú tél folyamán, de még a mi rövidebb teleink után is bámulatosan jó hatásúak az első tavaszi fények és színek. Modern korunkban termékeink színét a minőség egyik fontos jellemzőjének tartjuk. Nemcsak a nyomdai, kozmetikai, textilipari termékek, de az élelmiszerek, konzervek, gyümölcsök, húsok színétől is elvárjuk, hogy pont a megfelelő legyen; s ha nem olyan, nem lesz eladható az igényes külföldi piacokon. A színek fontos információkat is hordozhatnak. A közlekedésben a piros a tiltás, a zöld a szabad haladás jele, míg a sárga színnek figyelemfelkeltő szerepe van. Európában a fekete szín a gyászt, a fehér az ártatlanságot jelképezi. A színszimbolika különösen fontos a népművészetben. A színeknek különböző kultúrákban eltérő jelentése van.
Mindaz, ami a színekkel kapcsolatban igaz egy ép színlátó számára, egészen másként igaz egy színtévesztő, vagy egy színvak számára, aki a színeket nem olyan szemmel nézi, mint az ép színlátó. Minthogy a színtévesztők száma jelentős (Magyarországon kb. 400 000 színtévesztő ember él), érdemes azzal is foglalkozni, hogyan látják ők a színeket.
Hogy milyen fontosak életünkben a színek, az is mutatja, hogy hány és hány tudós, fizikus, orvos, matematikus, festő, fiziológus, költő és filozófus kutatta az elmúlt évszázadok során a színek, a színes látás titkait.
4.1.1. A színtan kutatói
Leonardo da Vinci, a híres reneszánsz festő és tudós, a 15. – 16. század fordulóján talán az első volt, aki tudományos alapossággal, a jelenségek gondos megfigyelésével kereste a színek, a fények és az árnyékok törvényszerűségeit. Az volt a terve, hogy könyvet ír a művészetről, és ebben egy színelméleti fejezetet is szándékozott írni.
Isaac Newtont, a 17. – 18. század fordulóján egészen más szempontból érdekelték a színek. Fizikusként üvegprizmával kísérletezve felfedezte, hogy a fehér fény a szivárvány színeire bontható, majd ismét fehér fénnyé egyesíthető. Newton a szivárvány színeit kiegészítette az abban nem található, de a festőanyagok között akkor már létező bíbor (vagy lila) színnel, és a színeket egy kör mentén helyezte el.
Színkörében 7 szín szerepel: vörös, narancs, sárga, zöld, indigó, kék és ibolya.
Le Blond frankfurti rézmetsző művész a 18. század közepén rájött, hogy három színnel, a sárga, vörös és kék színek egymásra nyomásával a színkör minden színét, sőt azok finom átmeneteit is meg tudja valósítani. Ő tekinthető tehát a háromszínnyomás feltalálójának, bár vele egy időben hasonló megoldásra jött rá egy vetélytársa, a párizsi Gautier is.
Mayer Tóbiás, a kiváló göttingeni matematikus a 18. század közepén a színárnyalatok rendszerbe foglalásában ért el jelentős eredményt. Három alapszínt, vöröset, zöldet és kéket egy háromszög egy-egy sarkába állította. A háromszög oldalain a mellette fekvő csúcsokon ábrázolt színek keverékeit helyezte el, míg a háromszög belsejébe a mindhárom alapszínt felhasználó keverékszíneket.
A színvakság első pontos leírását a kémikus Dalton hagyta ránk, aki saját magán végezte megfigyeléseit a 18. század végén. Róla nevezik a színvakságot daltonizmusnak.
A „költőfejedelem”, Goethe, a 18. -19. század fordulóján igen elmélyült színtani kutatást folytatott. Főleg a színek fiziológiai-lélektani vonatkozásai érdekelték. A kiegészítő színekkel, a színes utóképekkel, a színek pszichológiai hatásaival kapcsolatos megfigyelései és megállapításai ma is helytállóak. „Mindazt, amit költőként alkottam, nem sokra tartom. Kiváló költők éltek koromban, még kiválóbbak előttem, s hasonlóan kiválóak fognak élni utánam. De hogy századomban a színtan bonyolult tudományában én vagyok az egyetlen, aki tudja az igazat, erre büszke vagyok.” – írja Színtan című művében. Tanítványát, Schopenhauert, maga Goethe oktatta színelméletre. Schopenhauer volt az első, aki szerint a színérzet létrejöttében az agyműködésnek igen jelentős szerepe van.
Helmholtz a 19. században a spektrum hullámhosszai és az általuk kiváltott színérzet kapcsolatát vizsgálta. A mai színelmélet alapját a Young-Helmholtz-féle három-szín elmélet képezi. Lényege, hogy az emberi szem a színeket három különböző típusú receptorral érzékeli, a vörösre érzékenyt protossal, a zöldre érzékenyt deuterossal, és a kékre érzékenyt tritossal.
A 19. századi tudós, Maxwell, az elektromágneses fényelmélet megalkotója, a színtant is fontos felfedezésekkel gazdagította. Elsőnek dolgozott ki egy színmérő eljárást, amelyhez forgó színtárcsát alkalmazott.
A színvakság és a színtévesztés mérésére Lord Rayleigh dolgozott ki először egy módszert a 19. század végén. Ezt a módszert, és az általa tervezett műszert, az anomaloszkópot napjainkban is használják.
A 20. században felgyorsult a színekkel kapcsolatos ismeretek bővülése. A három színérzékelő receptor spektrális érzékenységének mérésére parányi intenzitású fényt vetítettek az élő emberi szembe, és a visszavert még csekélyebb intenzitású fény spektrumát bravúros méréstechnikával detektálták. Az első méréseket Wald végezte 1945-ben, majd Crawford 1949-ben, Rushton 1959-ben, Marks, Dobelle és Mac Nichol 1964-ben, végül Estevez 1979-ben. A mérések egyre finomodtak, de a mérési eredmények az egyes szerzőknél jelentős különbségeket mutattak. Ennek oka feltehetőleg az, hogy a vizsgált emberek színérzékenysége sem volt azonos, de még inkább az, hogy a mérési körülmények is eltérőek voltak. Különösen nagy nehézséget okozott az, hogy a három receptor spektrális érzékenységi tartománya a spektrum jelentős részében átfedi egymást.
Walraven és Bouman 1966-ban úgy találta, hogy a három receptor érzékenysége nem csak spektrálisan tér el, hanem nagyságuk sem azonos. Szerintük legérzékenyebb a protos, legkevésbé érzékeny a tritos.
Walraven szerint az érzékenységek aránya a következő: protos : deuteros: tritos = 40 : 20 : 1
A 20. században megfogalmazódott az igény a színek számszerűsítésére, mérésére is. 1905-ben Munsel amerikai festőművész egy mintegy 4000 tagból álló közel egyenközű színminta gyűjteményt és egy színrendszerezést dolgozott ki. Ezt a színrendszert igen elterjedten alkalmazzák ma is. A másik fontos színrendszert és színminta gyűjteményt a német kémikus-fizikus Ostwald hozta létre 1939-ben. Ez a rendszer a színharmóniákon alapul.
Az építészek számára dolgozta ki a Coloroid színrendszert és színmintákat a magyar Nemcsics professzor 1980-ban. Ez a színrendszer a színpreferencián alapul.
Ezeken kívül még számtalan színminta gyűjtemény és színrendszer ismeretes, szinte minden szakma kidolgozta a maga színmérési rendszerét.
4.1.2. A színekkel foglalkozó szervezetek
A Nemzetközi Világítástechnikai Bizottság (Commission Internationale de l’Eclairage, CIE) 1931-ben kezdte meg a színekkel kapcsolatos terminológia és a színmérés szabványosítását
1964-ben egy „kiegészítő” színmérő rendszert is bevezettek. Ezek a nemzetközi szabványok a magyar szabványokban is helyet kaptak (MSz 9620).
A CIE az egész világra kiterjedő nonprofit szervezet. Minden 4. évben nemzetközi konferenciát, és azt követően szekciótalálkozókat tart. A konferenciát követő 2. évben pedig egy kisebb konferenciát (Interim Meeting) tartanak.
A másik nagy nemzetközi színbizottság az AIC (Association Internationale de la Couleur). Míg a CIE elsősorban a világítással kapcsolatos méréstechnikai kérdésekkel foglalkozik, és ezen belül a színek méréstechnikájával, addig az AIC fő célja a színekkel kapcsolatos tudományos, művészeti és oktatási munka koordinálása. Az AIC is négyévenként tartja nemzetközi konferenciáját, de a CIE-hez képest két év eltolással.
Magyarország a színekkel kapcsolatos kutatásban élen jár. A CIE és az AIC magyar szekcióin kívül a MTESZ-ben a kémikusok egyesületének is van egy jól működő Kolorisztikai Bizottsága, amely kétévenként nemzetközi részvételű Kolorisztikai Szimpóziumot szervez.
4.2. Mit nevezünk színnek?
A fény elektromágneses sugárzás, melynek az emberi szem által érzékelhető tartományát nevezzük fénynek (4.1. ábra - A spektrum).
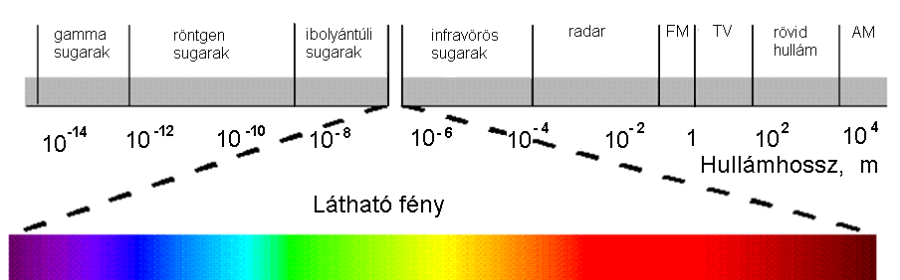
Színesnek nevezzük a fényt, ha különböző hullámhosszúságokon eltérő intenzitása van. Színesnek nevezzük a felületeket, ha különböző hullámhosszokon más-más mértékben verik vissza a fényt. Színesnek mondjuk az átlátszó anyagokat is, ha különböző hullámhosszakon más-más mértékben bocsátják át a fényt. Azt mondhatjuk tehát, hogy a szín a szemünkbe érkező fénynek azon tulajdonsága, hogy különböző hullámhosszúságú összetevői nem azonos intenzitásúak.
A magyar szabvány (MSz 9620) definíciója szerint a szín „A látható sugárzásnak az a jellemzője, amelynek alapján a megfigyelő a látótér két azonos méretű, alakú és szerkezetű, egymáshoz csatlakozó része között különbséget tud tenni, és ezt a különbséget a megfigyelt sugárzások spektrális eloszlásának eltérése okozhatja.”
A fény színességét nem csak az ember képes érzékelni, hanem az állatok is, pl. a kutyák, a macskák és a lepkék, a rovarok és a madarak. Mindegyik kicsit másképpen, a saját spektrális érzékenységének megfelelően. Köznapi értelemben ezek az állatok is mind színesen látnak.
A színtan tudományterületén azonban a szín fogalmát teljesen az emberi szem látásához kapcsoljuk. Színnek csak azt a spektrális élményt nevezzük, amelyet az emberből (méghozzá az átlagos, ép színlátású emberből) vált ki a színes fény.
Színmérésről is csak akkor beszélünk, ha olyan mérőműszert, illetve mérési eljárást sikerül alkalmaznunk, amely modellezi az ember színlátását, és számokkal azt írja le, amit az ember érzékel.
A színes látás összetett, bonyolult működés eredménye. Azt szoktuk mondani, hogy a szemünkkel nézünk, de az agyunkkal látunk. Ez az összetettség lehet az oka annak, hogy a szín fogalomnak a CIE és a magyar szabvány szerint is 3 definíciója van:
Fizikai szempontból: a szín meghatározott hullámhosszúságú (380 nm-től 780 nm-ig terjedő) fény.(„Inger”)
Fiziológiai szempontból: a szín a látás érzékszervében (a szemben) egy vagy több fénysugár által kiváltott ingerület.(„Ingerület”)
Pszichológiai szempontból: a szín a látószerv idegpályáin továbbított ingerületek által az agykérgi látóközpontban létrejött érzet. („Színérzet”)
4.3. Az emberi szem; a színes látás
A színek, a színes látás megértéséhez meg kell ismerkednünk a színes látás folyamatával, és az emberi szemmel, amely (az aggyal együttműködve) a színes látást biztosítja számunkra.
4.3.1. Az emberi szem szerkezete
A 4.2. ábra - Az emberi szem metszete a jobb oldali emberi szem egyszerűsített vízszintes metszetét ábrázolja. Szemünk gömb alakú, kb. 25 mm átmérőjű szerv. Falát három, egymástól különálló, de egymásra simuló réteg alkotja. A legkülső a rugalmas rostos szövetű ínhártya. Elülső része a szaruhártyába megy át. A középső réteg hátsó kétharmadát az erekkel dúsan átszőtt érhártya alkotja. Első egyharmadát a sugártest képezi, és az alkalmazkodáshoz szükséges izmokban végződik. Legbelső, megvékonyult, kerek része a szivárványhártya (írisz), amelyet egyénenként különböző színűnek látunk. Az írisz közepén találjuk a kör keresztmetszetű látólyukat (pupilla).
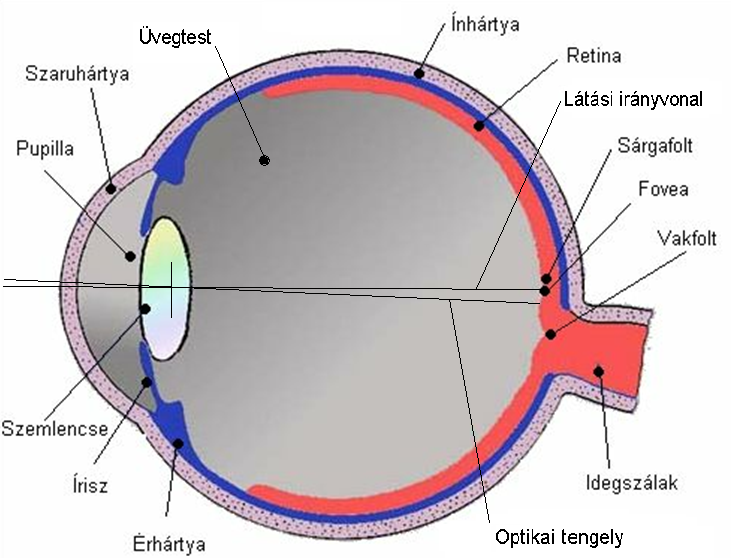
A szivárványhártya és a szaruhártya közötti üreget, az elülső csarnokot a csarnokvíz tölti ki. A belső réteget a természet különleges alkotása, az ideghártya (retina) alkotja. Az ideghártya vastagsága csak néhány század milliméter. A pupillával szemben fekvő ellipszis alakú sárgafolt közepén kis mélyedés, a látógödör (fovea centralis) a legélesebb látás helye.
A tárgyakról alkotott éles kép látásához szemgolyóinkat úgy forgatjuk, hogy a kép a látógödör területére essék.
A látógödörtől az orr felé mintegy négy milliméter távolságban találjuk a látóideg belépései helyét, a vakfoltot, ahol érzékelő idegvégződésekkel nem találkozunk, tehát ezzel a résszel nem látunk. A vakfolt területe 1,5 – 2,1 négyzetmilliméter között ingadozik.
Az üvegtestet kocsonyás, átlátszó anyag alkotja. Ez biztosítja a szemgolyó csaknem tökéletes gömb-alakját, amely egy hasonlóan tökéletes gömb alakú üregben foglal helyet.
A szemlencse keresztmetszete nem homogén, hanem egymást burkoló, a hagyma keresztmetszetére emlékeztető rétegekből áll. Ezeket egy külső rugalmas tok fogja össze.
A szemlencse átlátszó, színtelen, kétszer domború rugalmas test. Hátsó görbülete erősebb.
A szemlencsét rostos szövetű, gyűrű alakú izom veszi körül. Nyugalmi állapotban ez az izom el van ernyedve. A lencse hátsó fősíkjára merőleges és a csomópontokon átmenő egyenes, a fénytani, vagy optikai tengely nem megy át az éleslátás területén. Az éleslátás helyét a csomóponttal összekötő egyenes, a szem irányvonalával, a fénytani tengellyel kb. 5 fokos szöget zár be.
Végtelenbe néző szem esetén a szemgolyók tengelyei párhuzamosak, míg a végtelennél közelebb álló tárgyak figyelésénél az irányvonalak összetartók. Ezt a szemgolyókat működtető izmok biztosítják, és ezen alapul – bár csak kisebb távolságokra – a tapasztalatok alapján nyert távolságbecslési készség.
A megfigyelt tárgyról a szem képalkotó rendszere a retina síkjában fordított állású, kicsinyített, reális, éles képet hoz létre. A képalkotó elemek: a szaruhártya, a csarnok és a szemlencse háromtagú, rendkívül nagy látószögű objektívhez hasonlóan működik. Az általa alkotott kép ugyan sok képalkotási hibával terhelt: csak a közepe éles, a széleken nemcsak az élesség, hanem a megvilágítottság is csökken, és hordós torzítású. Mindezeket a képhibákat azonban az agyunk korrigálja.
4.3.2. Az ideghártya (a retina)
Az ideghártya (a retina) a szem legfontosabb és legérdekesebb része. Itt a fényre érzékeny idegvégződéseket, a látás receptorait. A néhány századmilliméter vastag hártya vázlatos keresztmetszetét a (4.4. ábra - A retina metszete) ábrán látjuk.
A több rétegből felépített hártya legbelső részében találjuk a henger alakú, 0,063 – 0,081 mm hosszú, és 0,0018 mm vastag pálcikákat és a vastagabb, 0,0045 – 0,0065 mm átmérőjű, de rövidebb csapokat. Ezek végeikkel a pigment rétegbe nyúlnak. A csapok a nappali látás, a pálcikák az esti látás receptorai.
A látóideg végződések (pálcikák és csapok) a retinarétegben keverten helyezkednek el. A sárgafolton és annak környékén a legsűrűbbek, a retina felé erősen ritkulnak. A sárgafolt területén kizárólag színekre érzékeny, egymáshoz simuló csapokat találunk. Számuk a retina széle felé fokozatosan csökken. Itt már csak színekre érzékeny csapokat nem, csupán a fényerősség-különbségre érzékeny pálcikákat találjuk (4.3. ábra - Egy pálcika és egy csap metszete).
A (4.3. ábra - Egy pálcika és egy csap metszete) ábrán látható pálcika és csap felépítése hasonló. Mindkettő egyetlen idegsejt, amelynek belső szegmentumában található a sejtmag, míg külső szegmentumában a fényre érzékeny anyag. A pálcika fényérzékeny anyaga a rhodopsin, míg a csapokban fényérzékeny pigmentek találhatók. A csapok három félék: van, amelyikben vörös színre, van amelyikben zöld színre, és van amelyikben kék színre érzékeny pigment található. A fényérzékeny anyagok a külső szegment membrán rendszerét töltik ki, amely megnöveli a fényelnyelés valószínűségét. A szinaptikus végződés az ingerületet továbbító sejtek csatlakozását biztosítja.
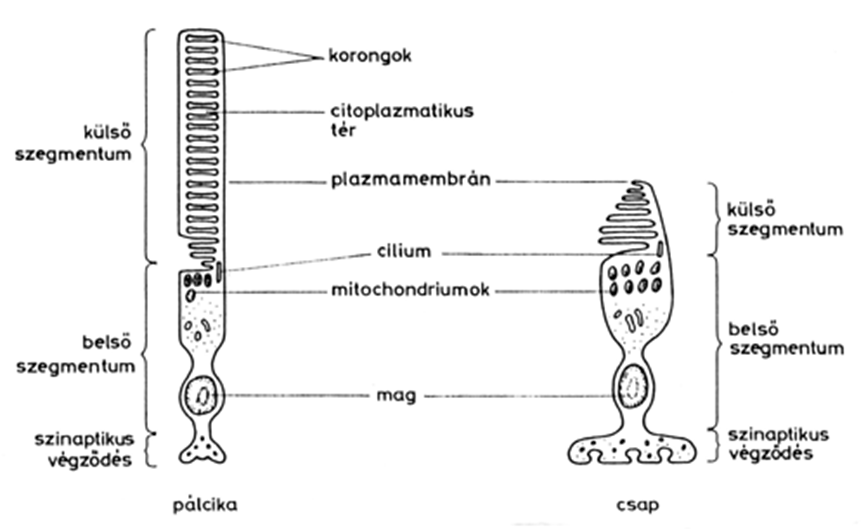
A csapok vége az éleslátás helyén sokkal keskenyebb, mint másutt (4.4. ábra - A retina metszete). Közéjük pigmentes testek nyúlnak be, és az idegeket fényhatás ellen és egymástól elszigetelik. Az idegszálak keresztmetszete szigetelt kábelvezetékre emlékeztet.
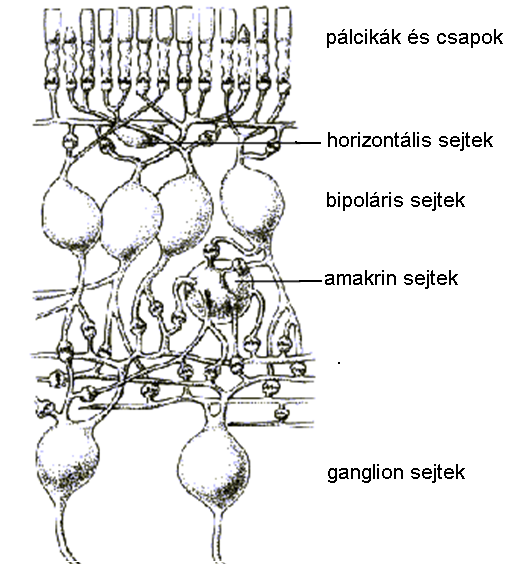
A pálcikák és csapok információi között kereszt-kapcsolatok jönnek létre a horizontális sejteken keresztül és ezzel valószínűleg elkezdődik a látási információ feldolgozása. Itt összehasonlításra kerül a különböző színekre érzékeny csapok ingerülete, és valószínűleg itt jön létre a világosság- és színkontraszt fokozó hatás.
A horizontális sejtek után a bipoláris sejtek továbbítják a látási információt, majd az amacrine sejteken ismét keresztkapcsolatok jönnek létre.
A ganglion sejtek továbbítják a pálcikák, ill. a csapok által felvett látási információt az agyba.
Pálcikákat a sárgafolt területén nem találunk, viszont a szem széle felé fokozatosan sűrűsödnek, így a retinának ezen a részén 20 pálcikára már csak egy csap jut (4.5. ábra - A vörösre, zöldre és kékre érzékeny csapok elhelyezkedése a retinán).

A pálcikák száma közel 130 millió, míg a csapok száma 7 millió. A retina belső felületét, a szemfeneket idegek és vérerek gazdag hálózata borítja.
A kereken 1 fok 20 perc szögnagyságú látógödör (fovea centralis) területének nagysága mintegy 0,4 milliméter átmérőjű, ahol kb. 3400 csapot találunk. Ennek egy jelentős része, kb. 2500 csap egy mindössze 0,1 mm átmérőjű 20 ívperc látószög alatt fekvő területen, a foveolán oszlik szét, és csak ezek állnak egyenként a kapcsoló sejtrendszeren keresztül egy-egy látóideg rosttal összeköttetésben. Ez a terület az általunk „legélesebb” látásnak nevezett hely. A látógödörtől az ideghártya széle felé haladva a csapok fokozatosan vastagodnak, és mindinkább növekvő csoporttal csatlakoznak egy látóidegrosthoz, és majdnem kivétel nélkül pálcikákkal vannak összekeverve. A csoportos elosztás a pálcikák és a csapok között a retinaszélek felé, a csapok hátrányára történik. Azonban a retina legkülső részén is találunk csapot, nem úgy, mint a látógödörben, ahol csapokon kívül pálcikák egyáltalán nincsenek (4.6. ábra - A csapok és a pálcikák 1 mm2-re jutó száma a retinán).
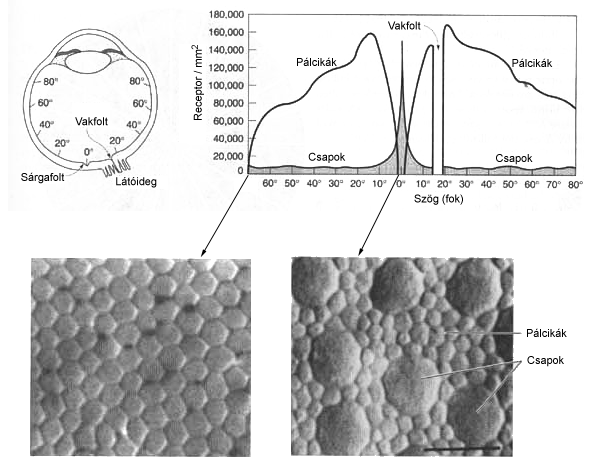
A pálcikák belsejében található festékanyag – a retinabíbor – fényhatásra elhalványul, elsárgul, míg sötétben rövid idő múlva ismét visszanyeri eredeti színét. A vizsgálatot a gyorsan bomló festékanyag pusztulása, valamint a halott szem egyéb elváltozása megnehezíti. A retina belső részét, a fovea centralist „sárga folt”-nak szokás nevezni, mivel itt a látó idegeket tápláló narancssárga színű karotinoidok nagy mennyiségben vannak jelen.
A csapok között nem találunk retinabíbort, ellenben a pálcikák ebbe vannak beágyazva. A retinabíbor a sötétlátásnál (adaptáció) játszik szerepet, világosban viszont gyorsan lebomlik.
A szem fényérzékenysége rendkívül nagy. Sötétben 10 km távolságban álló gyertyaláng fényét is észrevesszük. Wien kísérletei szerint a még érzékelhető fényenergia másodpercenként 4 – 10-8 erg. Ez átlagérték, mert a retina különböző részeinek érzékenysége különböző. A széleken az ingerkiváltáshoz 15-ször kevesebb fénymennyiség szükséges, mint az éleslátás környékén.
Ha erős világításból sötét helyiségbe lépünk, az első pillanatban semmit sem látunk, mert a pálcikák a gyenge fényre még nem elég érzékenyek. Idővel a retinabíbor újból képződik, a pálcikák érzékenysége lassan növekedik, végül huzamosabb idő múlva sötétben is látjuk a tárgyakat. Idős korban vagy vitaminhiányos állapotban a retinabíbor képződés lassú. Ilyenkor a sötét adaptáció is lassan alakul ki. Ezt az állapotot nevezik „farkasvakság”-nak. Sok karotint tartalmazó ételek (sárgarépa, cékla, paradicsom) fogyasztásával illetve A-vitamin szedéssel védekezhetünk ellene.
4.3.3. A szem látómezeje
A pálcikák száma az „éleslátás” helyétől kiindulva a csapok rovására növekedik, de a retina széle felé minden irányban rohamosan csökken, ezért az éleslátást észrevehetően befolyásolja. Élesen csak a nézési irányba eső tárgyakat látjuk. Környéke már életlen. Ezt a hátrányt a szemgolyó forgatásával kiküszöböljük.
Az éleslátás helyét a figyelt pontra irányítjuk. A szemgolyó forgatásával az egész teret végigtapogatjuk. A sorozatosan felvett képekből mozaikszerűen összerakjuk a tárgytér képét. A látó rendszer mintegy 30 millisec-onként vesz fel új információt.
A mozdulatlan szem vízszintes látómezeje kereken 180 fok, sőt, esetenként nagyobb. A függőleges látómező kb. 130 fok. A teljes látómező az arc felépítésétől, a szemgolyók fekvésétől stb. is függ.
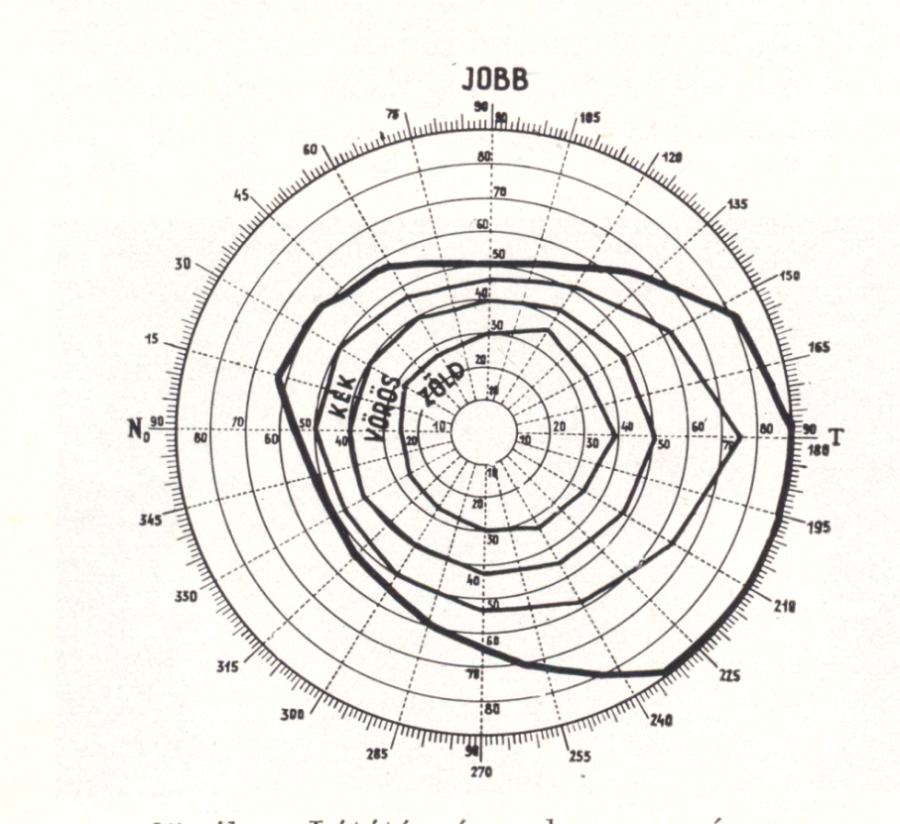
A látómező meghatározása fontos, mert alakja orvosi szempontból sok mindenre enged következtetni. A színes látómezők egyénileg egymástól eltérők (5. ábra).
A 4.7. ábra - A szem látómezeje a jobb szem látómezejét mutatja. Az orr felőli oldalon a látómező terjedelme kisebb, mint a halántékfelőli oldalon. A mérések azt mutatják, hogy a zöld színre kb. 30 fokos, a vörösre 40 – 50 fokos, a kékre 50 – 80 fokos látómezőben vagyunk érzékenyek. Ezen kívül már színeket nem látunk, csak egy sötét-világos ábrát – viszont a mozgásokra rendkívül érzékenyek vagyunk.
4.3.4. A színérzékelő receptorok
A Jung (1802) - Helmholtz (1866) színlátási modell szerint a retinán elhelyezkedő érzékelő elemek egy része – a nappali látást biztosító csapok – spektrális érzékenységük alapján háromfélék. A protosnak nevezett csapok főleg a spektrum hosszú hullámú (vörös) részére érzékenyek. A deuteros a középhullámú (zöld), a tritos a rövidhullámú (kék) spektrumtartományban érzékeny a fényre. Angol nevük alapján („long, middle és short wave sensitive receptors”) a szakirodalom L, M és S receptoroknak nevezi őket. A Joung-Helmholtz elmélet szerint tehát a színes látás három alapszínen alapul.
A receptorok spektrális érzékenységének megmérése nem egyszerű: A legtudományosabb mérés fundusreflectometriával, azaz az élő ember szemébe bevetített parányi intenzitású monokromatikus fény segítségével történt. A bevetített és a visszavert fény intenzitását megmérték, és a kettő különbségét úgy tekintették, hogy az nyelődött el a szemben, tehát az hasznosult a látás számára. A mérést 10 nm-enként elvégezték az egész látható tartományban, és így alakultak ki a spektrális abszorpciós görbék, amelyeket azonosnak tekintenek a spektrális érzékenységi görbékkel. Az átfedő spektrumtartományok a szelektív mérést lehetetlenné teszik, ezért a méréseket színvakokon végezték. A 4.8. ábra - Marks, Dobelle és Mc Nichol 1964-ben publikált mérési eredményei Marks, Dobelle és Mc Nichol 1964-ben publikált mérési eredményeit mutatja az eredeti formában, míg a 4.9. ábra - A Marks által kiértékelt mérési eredmények a Marks által kiértékelt mérési eredményeket tartalmazza.
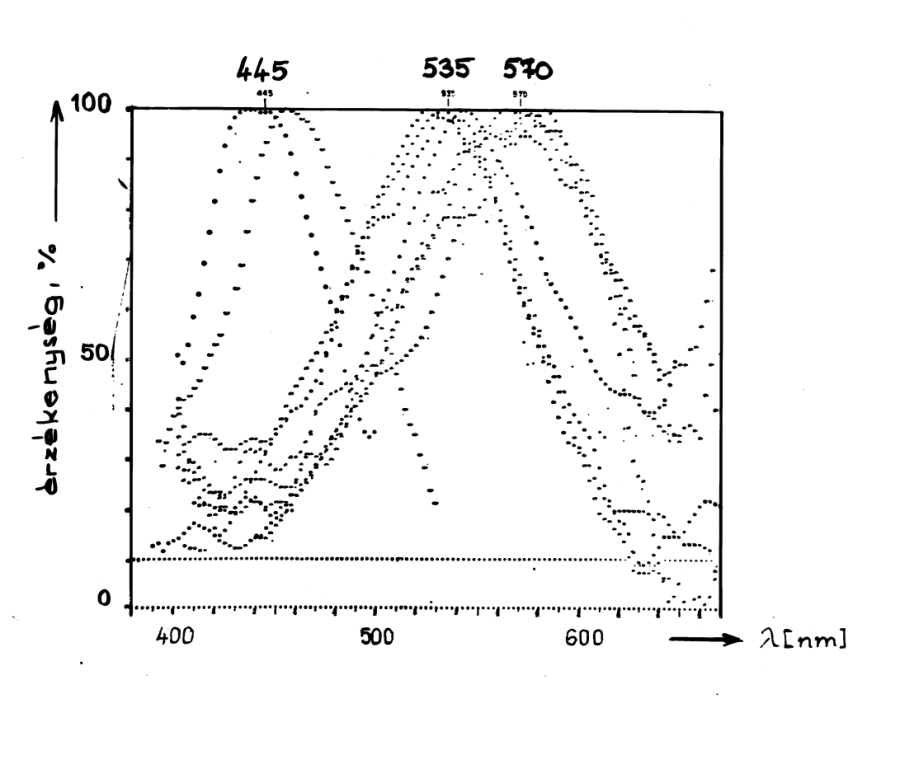
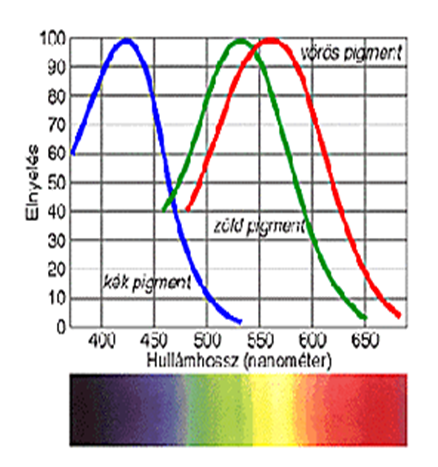
Az érzékenységi tartományok jelentős részben átfedik egymást. Az érzékelő elemek spektrális érzékenységi függvényei nagy egyéni eltéréseket mutatnak.
A csapok működése három, egymástól független fényérzékelő detektor működéséhez hasonló. Minden egyes csap saját spektrális érzékenységének megfelelően ad egy-egy kimenő jelet, az őt ért megvilágítás hatására:
|
|
Itt λ a fény hullámhossza, az L, M és S a protos, deuteros illetve tritos típusú csapok kimenőjele, φ(λ) a szín-inger függvény, azaz a csapokat megvilágító fény spektrális teljesítmény eloszlása, l(λ), m(λ) és s(λ) a protos, deuteros, illetve tritos típusú csapok spektrális érzékenysége, és k az ingerek nagyságát befolyásoló erősítési tényező.
A csapok az őket érő fényt spektrális érzékenységüknek megfelelő mértékben elnyelik, és az elnyelt energia a csapok fényérzékeny pigmentjét lebontja. A bomlástermékek a csapokhoz csatlakozó idegvégződéseket ingerlik; az inger frekvenciakódolással továbbítódik az agyba.
A P, D, T ingerek egymáshoz viszonyított értékei alapján alakul ki a színérzet, amely a színárnyalatok szinte végtelen sorát jelenti a harsány, rikító színektől a halvány, finom árnyalatokig; a sötét, tompa színektől a világos, csillogó színekig.
Minthogy mindhárom érzékelő (más néven receptor) kb. 100-120 világosságfokozat megkülönböztetésére képes, a megkülönböztethető színárnyalatok száma mintegy 100-120 a köbön, azaz 1 – 2 millió!
A csapok fényérzékeny pigment anyaga nem csak bomlik, hanem folyamatosan újra is termelődik.
A bomlás és az újratermelődés a megvilágítás szintjétől függő egyensúlyi állapot kialakulásához vezet, ezt nevezik adaptációnak.
4.3.5. A kontrasztfokozás
Szemünknek egyik igen fontos funkciója a kontrasztnövelő képesség. A szem leképező rendszere a háromdimenziós világról egy kétdimenziós képet hoz létre a retinán, amely sötétebb és világosabb, illetve különböző színű (hullámhosszúságú) foltokból áll. Ezekből a foltokból kell összeraknunk és felismernünk a környezetünket. Ha a foltok sötétsége illetve színe között nincs elegendően nagy különbség, a világ felismerése csak bizonytalanul sikerül. A retina kontrasztfokozó működése azonban ezeket a különbségeket felerősíti.
A kontrasztfokozó mechanizmus működésének alapja a retina szomszédos érzékelő elemei közötti kölcsönhatás. Ha egy fényérzékeny csapot fényhatás ér, a benne levő fényérzékeny pigmentek bomlásnak indulnak. Ez a folyamat kismértékben abban a szomszédos csapban is beindul, amelyik esetleg nem is kap fényt, mert az inger átadódik a szomszédos sejteknek is. Ezért ez a sötétben lévő sejt a csökkenő pigment mennyisége miatt a sötétet még sötétebbnek „látja”, mint távolabbi szomszédjai.
De nemcsak az inger adódik át, hanem a gátlás is, ezért egy sötétben lévő receptor, amelyben intenzív a pigmentek termelődése, ezt a hatást átadja a szomszédos sejteknek is, amelyek esetleg világosban vannak, ezért a világosságot még világosabbnak „látják”, mint a távolabbi sejtek. Így alakul ki a 4.10. ábra - Szín kontraszt és világosság kontraszt jelenség, amelyen egy sötét-világos határvonal mentén a sötét sötétebbnek, a világos világosabbnak látszik, mint a határvonaltól távolabb.
A kontraszt jelenség nemcsak sötét-világos határvonalak mentén alakul ki, hanem különböző színű felületek határvonala mentén is. Ez a színkontraszt a legerősebben a kiegészítő (komplementer) színek határvonalán alakul ki.
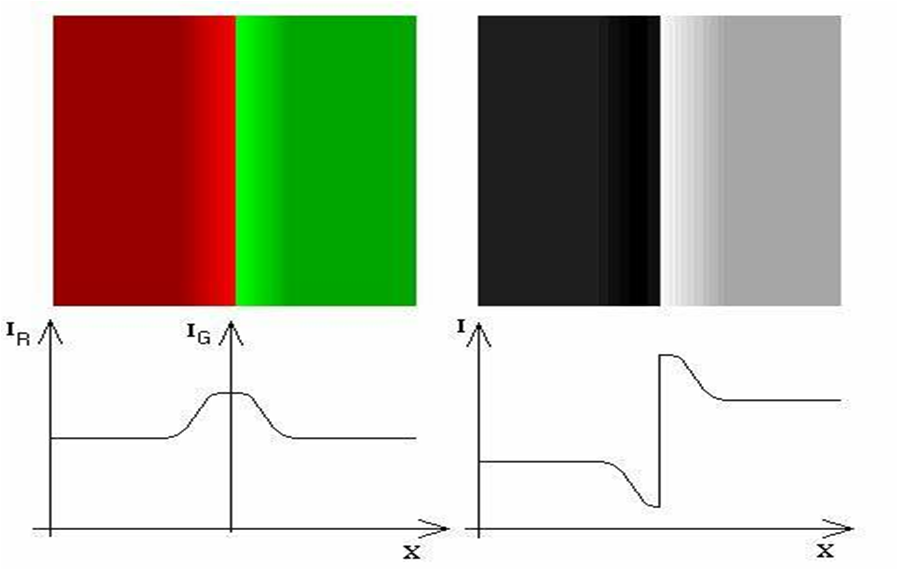
4.3.5.1. A káprázás
A kontraszt tehát segíti a látást a körvonalak kiemelése által. Azonban zavarhatja is a látást, ha túlságosan erős. Ilyenkor káprázásról beszélünk.
A káprázás különösen zavaró lehet az esti vezetésnél, amikor a szemből jövő kocsik reflektora valósággal elvakíthatja az embert egy rövid időre. Az idős emberek kontraszt érzékenysége nagyobb, mint a fiataloké. A CIE kétféle káprázást különböztet meg:
A zavaró káprázás kellemetlen érzést okoz, de nem zavarja a látást.
A rontó káprázás a látási teljesítményt rontja.
4.4. A színtévesztés
4.4.1. Mi a színtévesztés?
A legelterjedtebb színlátási hiba a vörös-zöld színtévesztés. A vörös-zöld színtévesztés nemhez kötött öröklődő látási rendellenesség. A színtévesztés anyai ágon öröklődik, és többnyire a férfiaknál jelentkezik. Európában a férfiak 8 %-a, míg a nőknek mindössze 0.5 %-a színtévesztő. Magyarországon tehát közel 400 000 színtévesztő él.
A színes látás két legfontosabb jellemzője:
A színárnyalat megkülönböztető képesség (szín diszkrimináció) az a képesség, amellyel két, egymástól csekély mértékben eltérő szín között különbséget tudunk tenni
A szín felismerési képesség (szín identifikáció) az a képesség, amellyel az egyes színeket és színárnyalatokat helyesen meg tudjuk nevezni
A színtévesztőknél mindkét jellemző gyengébb, mint az ép színlátóknál.
A színtévesztés több mint 100 foglalkozás esetében korlátozó, vagy kizáró tényező lehet. Korunkban a legtöbb munkatevékenységnél szükség van a jó színlátásra. Egyébként teljesen egészséges fiatalokat kényszeríthet a színtévesztés arra, hogy további tanulmányait – megálmodott hivatását – esetleg a meglévő foglalkozását feladja.
A színtévesztést egészen napjainkig gyógyíthatatlan rendellenességnek tekintették, mivel genetikai oka van. Egy új magyar találmány alapján azonban a színtévesztés tünetei - éppen úgy, mint a dioptria hibák - egy speciális szemüveggel csaknem teljesen korrigálhatók.
A rendelkezésre álló diagnosztikai eszközök nem elegendőek arra, hogy az egyes személyek látási képességéről reális képet alkothassunk. A színtévesztés korrekciójához új diagnosztikai eszközökre, és új tesztvizsgálatokra is szükség van.
A továbbiakban áttekintjük a színtévesztés mechanizmusát, a napjainkban elterjedten alkalmazott diagnosztikai módszereket, továbbá a színtévesztés korrekciójára kifejlesztett módszereinket és az ehhez szükséges új diagnosztikai módszereket.
4.4.2. Genetikus háttér, a színtévesztés elterjedtsége
A 4.11. ábra - A színtévesztés gyakorisága a férfiak között azt mutatja, hogy a Föld különböző területein 1000 ember közül hány színtévesztő. Az ábrán látható, hogy a színtévesztők részaránya elsősorban az iparilag fejlett régiókban magas (8 %), míg azokon a vidékeken, ahol az emberek még természethez közeli életmódot folytatnak, ez az arány alacsonyabb.
Ezt a jelenséget valószínűleg az okozza, hogy az őserdőben vagy a sivatagban nagyobb jelentősége van annak, hogy valaki megtalálja a táplálékát, vagy észrevegye az életére törő ellenfeleit, mint civilizált körülmények között. Ezért a természeti népek színtévesztői nagyobb valószínűséggel halnak meg még mielőtt gyermekük születhetne, míg civilizált körülmények között a színtévesztők is életben maradnak.
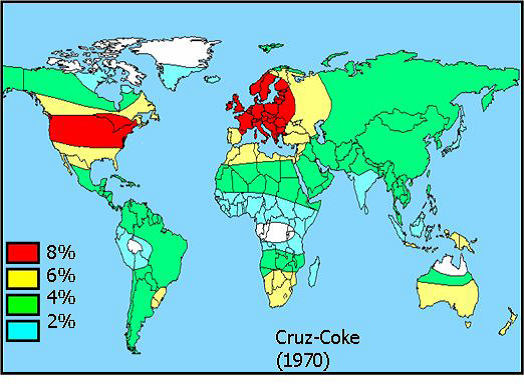
4.4.3. A színtévesztés optikai magyarázata
Amint azt az előző fejezetben láttuk, a színes látást a szemfenéken, a retinán található kb. 6,8 millió érzékelő elem, csap (más néven receptor) biztosítja. Ezek egy része a vörös, másik része a zöld, és egy harmadik része a kék színre érzékeny. A jó színlátású emberek három fajta receptorának spektrális érzékenysége a hullámhossz függvényében a (4.12. ábra - A vörös-, zöld- és kék-érzékeny csapok spektrális érzékenysége) ábrán látható.
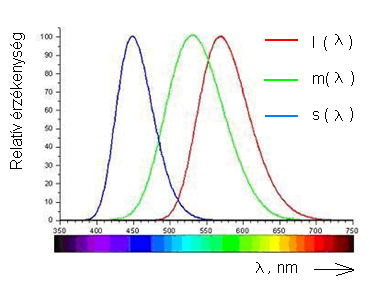
A színtévesztést az okozza, hogy a színtévesztők spektrális érzékenységi görbéi a (4.13. ábra - A színérzékelő receptorok spektrális eltolódásai) ábrán látható módon kisebb-nagyobb mértékben eltérnek a normál megfigyelőkétől.
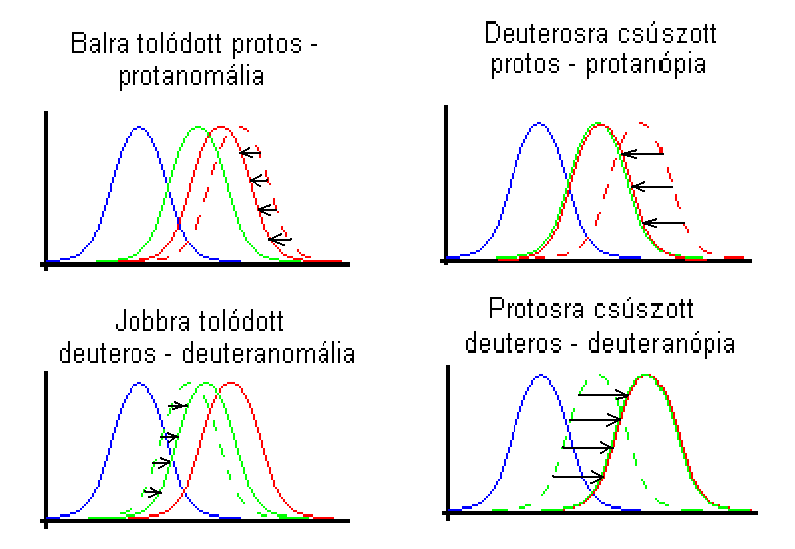
Az esti/éjszakai látást egy másik receptor típus elemei, a pálcikák biztosítják. A pálcikák nem három, hanem csak egyféle spektrális érzékenységűek, ezért ezekkel nem látunk színeket.
4.4.4. A színtévesztés típusai
A színtévesztés ismert típusai a következők:
Rendellenes színlátás (anomális trikromázia)
protanomália (zavar a vörös színek érzékelésében)
deuteranomália (zavar a zöld színek érzékelésében)
tritanomália (zavar a kék színek érzékelésében)
Részleges színvakság (dikromázia)
protanopia (a vörös színekre érzékeny receptorok funkcióképtelensége, illetve nagymértékű hasonlósága a zöldre érzékeny receptorokhoz
deuteranopia (a zöld színekre érzékeny receptorok funkcióképtelensége, illetve nagymértékű hasonlósága a vörösre érzékeny receptorokhoz
tritanopia (a kék színekre érzékeny receptorok hiánya illetve hibája)
Monochromazia
Csak egyetlen csap típus működik.
Teljes színvakság
Egyetlen csap típus sem működik, csupán az éjszakai pálcikalátás áll rendelkezésre
Az öröklődő színtévesztés leggyakoribb formája a deuteranomália és a protanomália, A 4.14. ábra - Protanomália diagramja a protanomália spektrális érzékenységének rendellenességét ábrázolja. Látható, hogy a színérzékelési problémát az okozza, hogy a protos spektrális érzékenysége a deuteros spektrális érzékenységéhez közelebb található, mint a normális színlátók esetében. Ennek következtében csökken a különbség a vörös és zöld színek között, és ez azt eredményezi, hogy romlik a szín- megkülönböztető képesség. Ugyanakkor a szín-azonosító képesség is gyengül, mivel a protos receptor nem a vörös színekre, hanem inkább a narancssárga, esetleg a sárga színekre érzékeny.
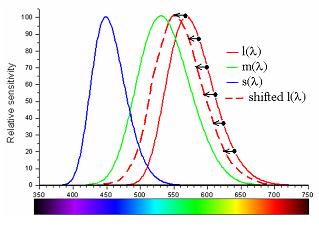
A 4.15. ábra - Deuteranomália a deuteranomália spektrális érzékenységét ábrázolja. Ebben az esetben a deuteros spektrális érzékenysége található közelebb a protos spektrális érzékenységéhez, mint a normál színlátók esetében. Az eredmény azonos az előző esettel: a vörös és zöld színek közti különbség csökken, azaz a szín megkülönböztetési képesség most is romlik. Romlik a színazonosítási képesség is, mivel most a deuteros nem a zöld színre, inkább a sárgászöld, esetleg a sárgás színekre érzékeny.
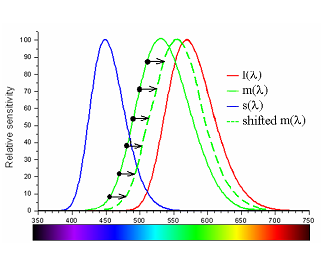
Tehát mindkét esetben a vörös és zöld színek megkülönböztetési képessége gyengébb, mint a normál színlátóké, ezért mindkét esetben vörös-zöld színtévesztésről beszélhetünk.
A színtévesztőknek méréseink szerint kb. 23 %-a protanomál, 73 %-a deuteranomál, a súlyos színtévesztők (protanópok és deuteranópok) pedig az eseteknek kb. 4 %-át adják.
A színlátási hibák legsúlyosabbika, a monokromázia és a teljes színvakság szerencsére azonban csak nagyon ritkán fordul elő.
A kék érzékeny receptor, a tritos igen ritkán hibás érzékenységű. Hibáját általában betegségek illetve mérgezések okozzák, és a kiváltó ok megszűnésével a színlátás ismét normálissá válik. Ezért a következőkben csak az öröklött vörös-zöld színtévesztés: a protanomalia és a deuteranomália vizsgálatával és korrigálásával fogunk foglalkozni.
A protanomalia és a deuteranomalia az általunk kidolgozott módszer segítségével sikeresen javítható.
4.4.5. A színlátás javításának elve
A feladat elvben egyszerűnek tűnik. Ha a hibás receptor egy másik színre érzékeny, mint normális esetben, egy jól megtervezett színszűrő alkalmazásával a receptor érzékelése spektrálisan a helyes irányba eltolható, mivel egy színszűrő hatása egy detektor spektrális érzékenységére:
|
S 1 (λ) * τ(λ) = S 2 (λ) |
Ahol
|
S1(λ) |
a detektor spektrális érzékenysége színszűrő nélkül | |
|
S2(λ) |
a detektor spektrális érzékenysége a színszűrővel együtt, és | |
|
τ(l) |
a színszűrő spektrális transzmissziója |
Innen:
|
τ(λ) = S 2 (λ) / S 1 (λ) |
Ha a színszűrő spektrális transzmissziója a hosszabb hullámhosszak felé növekszik, akkor a szűrő hatására a detektor érzékenységének maximuma is jobbra tolódik (4.16. ábra - A színlátás javításának elve).
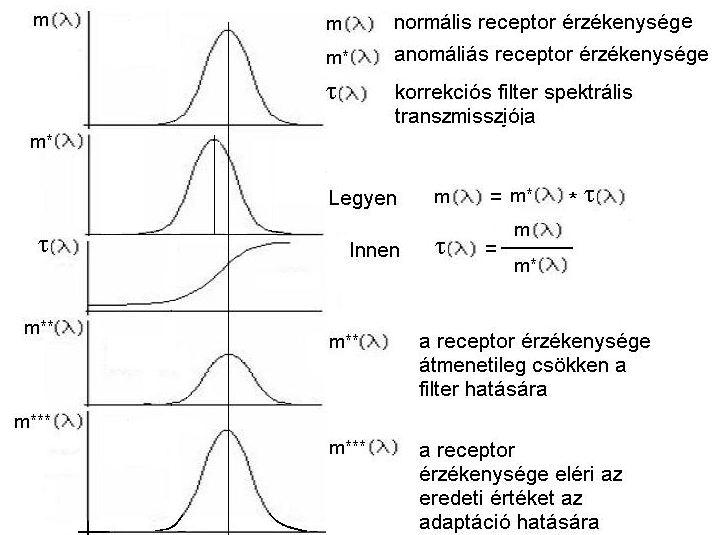
Ebben az eljárásban az a jó, hogy nem avatkozunk be a szervezetbe, és mégis valami olyat teszünk, mintha a hibás receptor érzékenységét megjavítottuk volna. Felismertük ugyanis, hogy a szembe jutó fény színképe (spektruma) a megfelelő színszűrő alkalmazásával annyira megváltoztatható, hogy hatása a hibás receptor érzékenységének kívánt módosításával egyenértékű lesz.
Az eljárás még egy fontos tényezőn alapul. A színes szűrő hullámhosszról-hullámhosszra különböző mértékben csökkenti a szembe jutó fény intenzitását, ezért a receptorok érzékenysége látszólag lecsökken. Szerencsére az emberi szem alkalmazkodási (adaptációs) képessége kompenzálni tudja ezt a mellékhatást, sőt ennél nagyságrendekkel nagyobb adaptációs képessége is van. A 4.16. ábra - A színlátás javításának elve utolsó lépése ezt az állapotot mutatja.
Itt persze nemcsak egyszerűen a pupilla kitágulására kell gondolni, azaz nemcsak a csökkent fénymennyiséget kell kompenzálni, hanem az egyes receptorok érzékenységének arányait kell újra helyreállítani. Az emberi szemnek meg van ez a képessége is. Ezt a képességet szín-adaptációnak nevezzük, és rendszeresen használjuk a színlátás javító szemüveg nélkül is. Ha például a fehér színű napfényről egy sárgás fényű lámpával megvilágított helyiségbe lépünk, a fehér felületeket, sőt a többi színt is először sárgásnak látjuk, a szín-adaptáció következtében azonban a színek rövidesen ismét természetesnek hatnak. Ezt a jelenséget nevezik szín konstanciának. Videokameránál ezt a „white balance” beállítással oldják meg, szemünkben viszont automatikusan következik be. Ez a szín-adaptáció a színlátás javító szemüveg felhelyezése után néhány percen belül bekövetkezik, és éppen ez kell ahhoz, hogy a korrekciós szemüveg kifejtse a javító hatását. A szín-adaptáció teljes kialakulásának az a jele, hogy a fehér felületeket a korrekciós szemüvegen keresztül ismét fehérnek látjuk.
A színtévesztés korrekciójának elve tehát két lépésből áll: egyrészt a hibás receptor érzékenységi területének színszűréssel történő eltolása, másrészt a receptorok közötti viszonynak a színadaptáció általi helyreállítása.
Az elv egyszerű és érthető. A gyakorlatban azonban bonyolultabb a helyzet, mivel nemcsak egy receptorunk van. A hibás receptor spektrális érzékenységét úgy kell korrigálni, hogy közben a másik két receptort „megkíméljük”. Ezt viszont nehéz elérni, mivel – különösen a zöld és vörös receptorok – spektrális érzékenységi tartománya egymáshoz közel helyezkedik el, sőt át is fedi egymást egy viszonylag széles hullámhossz tartományban. Ezt a problémát úgy oldottuk meg, hogy a színszűrő tervezését három spektrumtartományban külön-külön végeztük el, majd a három szűrőgörbét egyesítettük. A (4.17. ábra - Az optimalizálás elve a színlátás javító szemüveg tervezésénél) ábrán bemutatott példán például az egyik tartományban a protost kívántuk jobbra tolni, a másikban a deuterost balra tolni, és a harmadik tartományban a tritost nem toltuk egyik irányban sem.
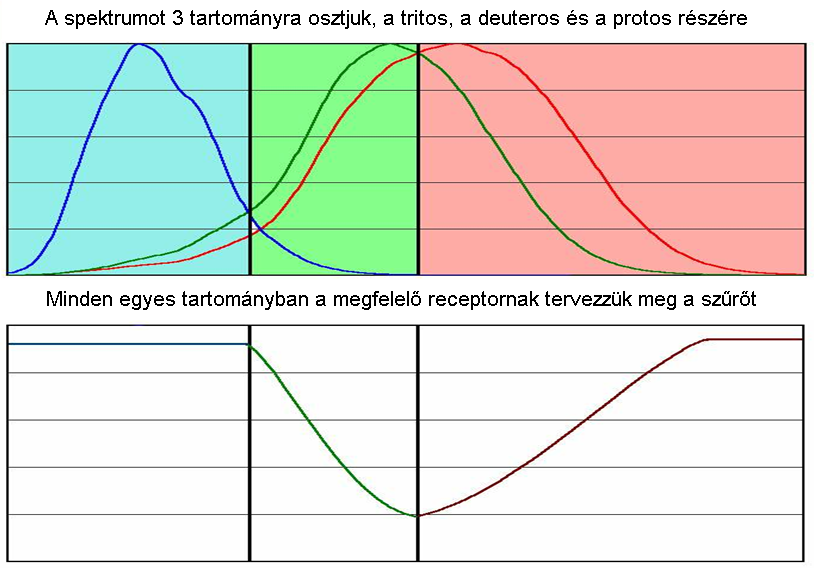
4.4.6. A színtévesztés mérése; a diagnózis
A színtévesztés felismerése, típusának és súlyosságának meghatározása nehéz feladatot jelent. Ugyanis nem egyszerű fizikai mennyiséget – mint pl. a hosszúság, a súly, vagy a hullámhossz - kell megmérni, hanem a szem színérzékenységét, amely pszichofizikai mennyiség. Bizonyára ezért van az, hogy az elmúlt 200 év folyamán több mint száz mérési módszert és eszközt dolgoztak ki a színtévesztés mérésére. A más- és más módszerekkel kapott mérési eredmények a színlátást különböző szempontokból jellemzik. Sok esetben ezek az eredmények egymásnak ellentmondhatnak. Ezért a színtévesztést legalább két különböző módszerrel kell megvizsgálni.
A színtévesztés mérésére leggyakrabban a pszeudoizokromatikus teszteket és az anomaloszkópot alkalmazzák.
4.4.6.1. A pszeudoizokromatikus tesztek
A pszeudo-izokromatikus teszt-könyvek olyan képgyűjtemények, amelyeket színes, kerek vagy szabálytalan alakú pontokból állítottak össze („pöttyös könyvek" vagy "babos könyvek”). Ezeken a képeken az átlag-megfigyelő bizonyos betűket, valamilyen számokat, vagy más alakokat lát kirajzolódni, míg ezek az ábrák a színtévesztők számára felismerhetetlenek maradnak. A pontok színei, amelyekből az alakot, illetve a hátteret kirakják, pszeudokromatikus párokat alkotnak. Ez azt jelenti, hogy világosságuk és szín telítettségük azonos, csak színárnyalatban különböznek egymástól (4.18. ábra - A pszeudo-izokromatikus tesztábra). A vörös-zöld színtévesztés felismerésére szolgáló képeken általában narancssárga és sárga pontok alkotják a figurát, míg a háttér sárga és sárgászöld pontokból áll – vagy megfordítva. A tesztlapokat olyan festékkel nyomtatják, amelyeket speciális festékanyagból, direkt keveréssel állítanak elő, ezért ezeket az ábrákat nem lehet színes nyomtatással tökéletesen reprodukálni.
Nagyon fontos a tesztnél a megfelelő megvilágítás biztosítása. A legjobb megoldás halogén lámpa vagy kompakt fénycső alkalmazása. Azok a fénycsövek viszont, amelyek vonalas spektrumú fényt bocsátanak ki, ("neon-cső"), nem használhatók színlátás vizsgálatra. A megvilágítás diffúz, szórt fényű legyen, sem túl sötét, sem vakítóan világos. Ne legyen a vizsgált személlyel szemben vakító fényforrás, és ne világítsunk úgy, hogy a teszt-ábra csillogása zavarja a látást.

A vizsgálatok folyamán a kísérletben résztvevő személy lehetőleg 15-20 képet azonosítson. Ha a vizsgálat során kettőnél több hibát követ el, színtévesztőnek tekinthetjük. A pszeudoizokromatikus teszt csak egy a színtévesztés kiszűrésére alkalmas módszerek közül. A teszt alapján nem lehet a színtévesztés típusára és súlyosságára következtetni, bár fel lehet tételezni, hogy valaki, aki több képet is elvét, rosszabb színlátással rendelkezik, mint az, aki kevesebbet hibázott. A pszeudoizokromatikus tesztek elsősorban a színek közötti különbségtétel képességét ellenőrzik.
Legismertebb az Ishishara- (Japán), Velhagen- (Németország), Rabkin- (Oroszország) és Dvorine- (Amerika) pszeudoizokromatikus teszt-könyv.
A pszeudoizokromatikus teszt-könyv viszonylag olcsó és kezelése egyszerű. Segítségével mégis csak az állapítható meg, hogy valakinek a színlátása gyenge, vagy sem. A színtévesztés súlyosságának és típusának meghatározására azonban nem alkalmas.
4.4.6.2. Az anomaloszkóp
A színtévesztés vizsgálatára a legismertebb és a legpontosabbnak tartott készülék az anomaloszkóp. A készülék elvét Lord Rayleigh dolgozta ki. Ismert típusa a Nagel-anomaloszkóp. A Nagel-anomaloszkóp látóterében a vizsgált személynek egy köralakú, kettéosztott látómező felső térfelére vetített vörös (R) és zöld (G) monokromatikus fényt kell összekeverni, mindaddig, míg a kevert szín a látómező alsó térfelére vetített "cél-színnel", azaz sárga monokromatikus fénnyel (Y) azonosnak tűnik (4.19. ábra - Heidelbergi anomaloszkóp és látómezeje). Ha a látómező felső és alsó felét azonos színűnek és azonosan világosnak látjuk, a mérőműszer kijelzőjén a színtévesztés az R/G vörös-zöld viszony, és a sárga cél-szín Y intenzitása olvasható le. A keveréshez alkalmazott színek mennyiségéből következtetni lehet a színlátásra, illetve a vizsgált személy színtévesztésének fokára. Normális színlátású résztvevők esetén a műszer R/G = 45 és Y=15 értéket mutat.

A legidősebb anomaloszkópok egyike a Schmidt-Haensch gyár Nagel-anomaloszkópja. Ennél egy izzólámpa gondoskodik a megvilágításról, amelynek fényét vörös, zöld és sárga színszűrőn keresztül vetítik be a látómezőbe.
Egy modernebb variációt jelent a Heidelbergi anomaloszkóp, amelynek mérési adatai számítógépre vihetők, de a műszer számítógép nélkül is üzemeltethető. Fényforrásként vörös, zöld és sárga LED szolgál (4.19. ábra - Heidelbergi anomaloszkóp és látómezeje).
Ma a legmodernebb változat az OCULUS cég HMC anomaloszkópja. Csak számítógéppel üzemeltethető.
A japán Tomey anomaloszkóp nemcsak a Rayleigh színkeverést (vörös + zöld = sárga), hanem a Moreland színkeverést (kék + zöld = türkiz-zöld) is lehetővé teszi, ezáltal több információt szolgáltat a színtévesztésről mint a normál anomaloszkóp.
Az anomaloszkóp mérési eredményét a diagnózis meghatározásához ki kell értékelni. Egyetlen színegyeztetés alapján nem lehet megbízható diagnózist felállítani. Meg kell határozni, hogy milyen R/G értékeknél tudja a vizsgált személy egyformára beállítani az alsó és a felső mező színét. A súlyos színtévesztők (protanópok és deuteranópok) minden R/G mellett be tudják állítani a színegyezést.
A kiértékelés a vizsgált személy által beállított vörös-zöld arány és a sárga mező világossága alapján történik. A diagnózis adatai a (4.20. ábra - Az anomaloszkópi mérés kiértékelése) ábrán láthatók.
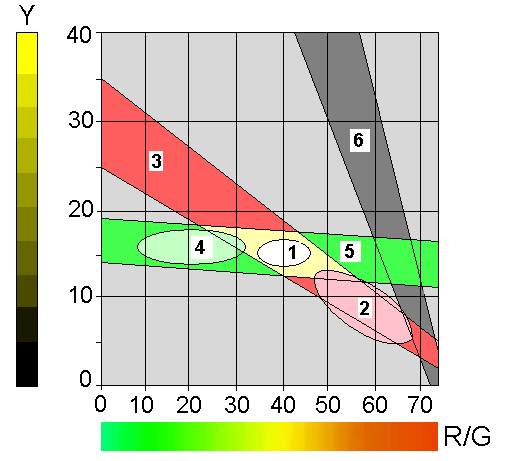
Az anomaloszkóp kezelése és a mérési adatok kiértékelése komplikált, viszont pontos, számszerű mérési eredményt ad a színtévesztés fokáról és típusáról. Ára igen magas, az egyéb igényes látásvizsgáló műszerekéhez hasonlóan.
4.4.6.3. Új színlátás vizsgáló műszerünk: az Anomal Tester
Az Anomal Tester műszer három szín-egyensúly megkeresése alapján működik. A műszerben 3 LED van: vörös, kék és zöld. A vizsgált személynek három szín-egyensúlyt kell meghatározni:
meg kell határozni azt a beállítást, amelynél a vörösből és zöldből kikevert sárga szín nem narancsos és nem zöldes
meg kell határozni azt a beállítást, amelynél a vörösből és kékből kikevert lila szín nem vöröses és nem kékes
meg kell határozni azt a beállítást, amelynél a kékből és zöldből kikevert türkiz szín nem kékes és nem zöldes
A műszerrel még egy vizsgálatot lehet végezni: sárga háttérszín közepén észre kell venni egy vörös pöttyöt. A protanomáliás vagy protanóp személyek sokkal nehezebben fedezik fel a vörös pöttyöt, mint a normál színlátók.
A beállított adatok alapján számítógépi programmal lehet meghatározni a színtévesztés típusát és súlyosságát. A műszer a (4.21. ábra - Az Anomal Tester) ábrán látható.

A műszer LED-jeinek spektrális emissziója a (4.22. ábra - Az Anomal Tester LED-jeinek spektruma) ábrán látható. Érdekes megfigyelni, hogy a LED-ek teljesítményének csökkentése során a spektrális maximum hely kismértékben megváltozik, de még 10 % teljesítmény alatt sem nagyobb ez a változás, mint 4 nm.
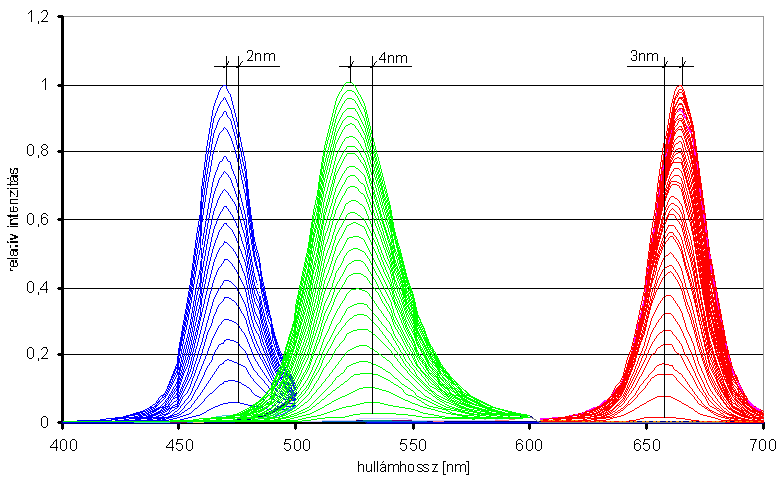
4.4.6.4. Új színlátás vizsgáló tesztünk: a színlátás vizsgáló Atlasz
A kutatás évei alatt a színlátás vizsgálatára számos új módszert és műszert fejlesztettünk ki. Ezek közül a gyakorlatban a Színlátás Vizsgáló Atlasz vált be legjobban. A színlátás képesség vizsgálatára szolgáló Atlasz egy sor pszeodoizokromatikus tesztképet tartalmaz. Ezek az Ishihara könyvhöz hasonlóan színes pöttyökből vannak összeállítva. A tesztképeken a páciensnek nem számokat vagy betűket kell felismerni, hanem "Landolt C" képeket. A C betűk nyílása véletlenszerűen 8 különböző irányban helyezkedhet el, és a vizsgált személynek csak azt kell megmondani, hogy merre látja a nyílást. Így kiküszöböljük a pszeudoizokromatikus teszteknek azt a hibáját, hogy gyakran a színtévesztőkhöz sorolják a diszlexiában szenvedő, de egyébként jó színlátású pácienseket. Ezeknél a személyeknél a számok vagy betűk felismerési hibája nem a színlátás gyengeségéből, hanem az olvasási nehézségből adódik.
A Színlátás Vizsgáló Atlasz három sorozat képet tartalmaz. A sorozatok egyre nehezebbé váló sorrendben tartalmaznak pszeudokromatikusan kidolgozott képeket. Az első képeken a pontok színe nagymértékben különbözik a háttérben lévő pontokétól, a kép könnyen felismerhető. Ezután képről-képre csökken a színkülönbség, és az utolsó képen a színkülönbség olyan csekély, hogy ezt a képet már csak rendkívül jó színérzékkel megáldott személyek képesek felismerni.
Az első sorozat a vörös-zöld szín megkülönböztetési hiba súlyosságának meghatározására szolgál. A második sorozat a vörös érzékeny receptor (Protos) és a harmadik sorozat a zöld színre érzékeny receptor (Deuteros) hibájának kimutatására szolgál. (4.23. ábra - A színlátás vizsgáló Atlasz 3 sorozatának kezdő ábrája). Aki a második sorban hamarabb hibázik, mint a harmadikban, az protanomal vagy protanop, aki a harmadik sorban hibázik hamarabb, mint a másodikban, az deuteranomál, vagy deuteranop.
Az Atlasz ezzel a három sorozattal lehetővé teszi a vörös-zöld szín megkülönböztetési hiba súlyosságának, és a színtévesztés típusának megállapítását is. Az Atlasszal tehát teljes diagnózist állíthatunk fel, és ennek alapján ki tudjuk választani a megfelelő korrekciós szemüveget is. Az eredmények az esetek 96 %-ában azonosak az anomaloszkopos mérési eredményekkel. Az Atlasz segítségével a korrekciós szemüveg által elért javulás is kimutatható. A mérés kb. 10 percet vesz igénybe, és a színtévesztők játéknak tekintik és szórakoztatónak tartják.

4.4.6.5. Tapasztalatok a színlátás-javító szemüvegekkel
A korrekciós szemüveg javító hatása már a vizsgálatok folyamán, a lencsék próbájánál beigazolódik.
Az esetek 95 %-ánál (főleg a deuteranomália eseteknél) a színmegkülönböztetés képesség a korrekciós szemüveg hatására javul. Míg a javító-szemüveg nélküli színtévesztők már az első (a legkönnyebben felismerhető) képeknél is bizonytalanok lesznek, a szemüveggel korrigált színtévesztők, az egészséges színlátásúakkal azonosan, csaknem az utolsó (legnehezebben azonosítható) képig felismerik a tesztképeket.
Az Ishihara-tesztnél a vizsgált személyeknek átlag 20 számjegyet mutatunk be. A korrigálás nélküli színtévesztők ezekből általában csak 4-5 számot ismernek föl, míg azok, akik viselik a színtévesztést korrigáló szemüveget, általában 20, de legalább 19 számot képesek felismerni.
A színazonosítás-képesség javulása általában nem következik be látványos gyorsasággal. Először meg kell tanulni az új színárnyalatokat – amelyeket eddig a színtévesztő még sohasem látott – a javító-szemüveggel nézni és felismerni.
A színtévesztőknek mindössze kb. 4 %-át kitevő gyenge-színlátók (főleg protanópok) állapota nehezen javul, de a megfelelő korrekciós szemüveg alkalmazásával még ezeknél a pácienseknél is jelentős javulás érhető el.
4.4.6.6. A színlátás javító szemüveg viselésének hatása a színtévesztésre
A színtévesztés típusától és súlyosságától függően már a szemüveg felvétele pillanatában azonnal jelentős javulás mutatható ki. Azoknál a személyeknél, akik csak kicsit vagy közepesen színtévesztők, a szín megkülönböztetés gyorsan javul, míg azoknál, akik súlyosabb mértékben színtévesztők, csak később várhatunk eredményt, bizonyos szín-tanulási gyakorlat után. A rendszeres szemüvegviselés a korrekció eredményességét tovább fokozza, ezért célszerű a szemüveget minél többet viselni és közben figyelni a színeket - gyakorlással segíteni a színek megkülönböztetését és felismerését. Rossz megvilágítású helyiségekben, vagy éjszakai vezetésnél viszont nem ajánljuk a szemüveg viselését, mivel a beeső fényt a színszűrő némileg csökkenti. Egyéb esetekben - a TV-nézéstől a számítógépes munkáig – előnyös a viselése, mindenütt, ahol a színes látás fontos.
4.5. A színek jellemzése
A színeket a köznapi életben három jellemzővel szoktuk meghatározni: világosság, színezet, telítettség. Ezeket a jellemzőket pszichofizikai jellemzőknek nevezzük.
A színek pontosabban számszerűsíthető, matematikai leírásához pedig két, egymástól eltérő módszert alkalmazhatunk. Az egyik a spektrális módszer; ha ezt alkalmazzuk, a színingert, a szembe bejutó színes fényt kell fizikai jellemzőjével, spektrális energia- vagy teljesítményelosztásával leírni. A másik módszer tristimulusos módszer; a szem három alapérzetét, a vörös-, a zöld- és a kékérzetet, vagy másképpen színösszetevőt adjuk meg, és ezzel, illetve ezek additív keverékeivel jellemezzük a színérzetet. Ezt a színleírási módot tristimulusos színjellemzésnek nevezzük.
4.5.1. A színek spektrális jellemzése (MSz 9620)
A fény az elektromágneses sugárzásnak egy nagyon keskeny tartománya (4.24. ábra - Az elektromágneses sugárzás tartományai).
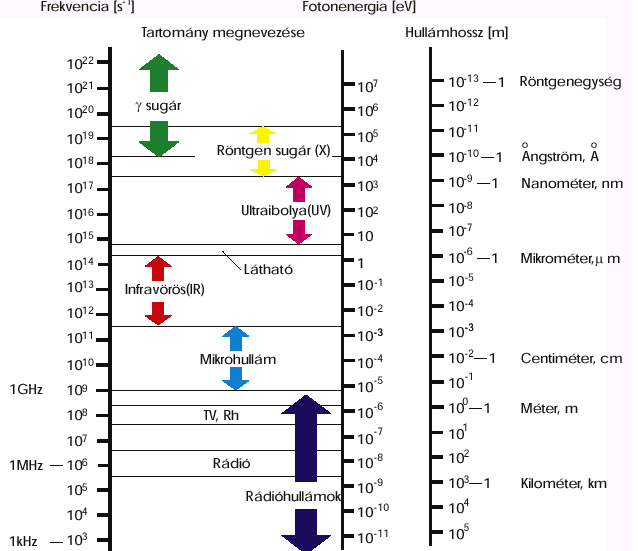
4.5.1.1. A spektrális eloszlás és a spektrális sűrűség
A sugárzott mennyiség Φ e (λ) spektrális sűrűsége: a spektrális eloszlásnak egy megadott hullámhosszat tartalmazó elemi sávba eső része és a sáv szélességének hányadosa:
|
Φ e (λ) = d Φ e (λ) / dλ |
, ahol λ a fény hullámhossza
A Φ e (λ) spektrális eloszlás: a sugárzást jellemző mennyiség spektrális sűrűség értékei a hullámhossz függvényében (4.25. ábra - A spektrális eloszlás függvény).
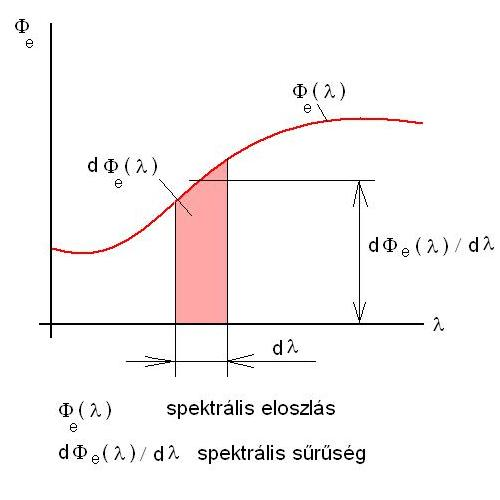
4.5.1.2. A spektrális emisszió, a spektrális transzmisszió, a spektrális reflexió és a spektrális abszorpció
Ha egy anyag fényt bocsát ki, Φ(λ) spektrális emisszióról, ha fényt bocsát át, τ(λ) spektrális transzmisszióról, ha fényt ver vissza, ρ(λ) spektrális reflexióról és ha fényt nyel el, α(λ) spektrális abszorpcióról beszélünk.
Ha egy felületre Φ fény mennyiség esik, annak egy részét az anyag átereszti (Φ τ ), egy másik részét visszaveri (Φ ρ ), és egy részét elnyeli (Φ α ). (4.26. ábra - Egy optikailag átlátszó réteg a fényt részben reflektálja, részben átbocsátja, és részben szórja)
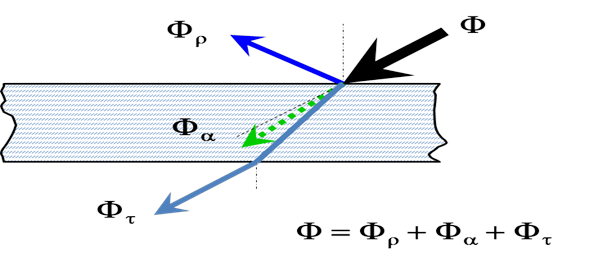
4.5.1.2.1. A spektrális emisszió, Φ(λ)
A Φ(λ) spektrális emisszió egy fényforrás által kibocsátott teljesítmény illetve
energia (4.27. ábra - A Nap spektrális energia eloszlása).
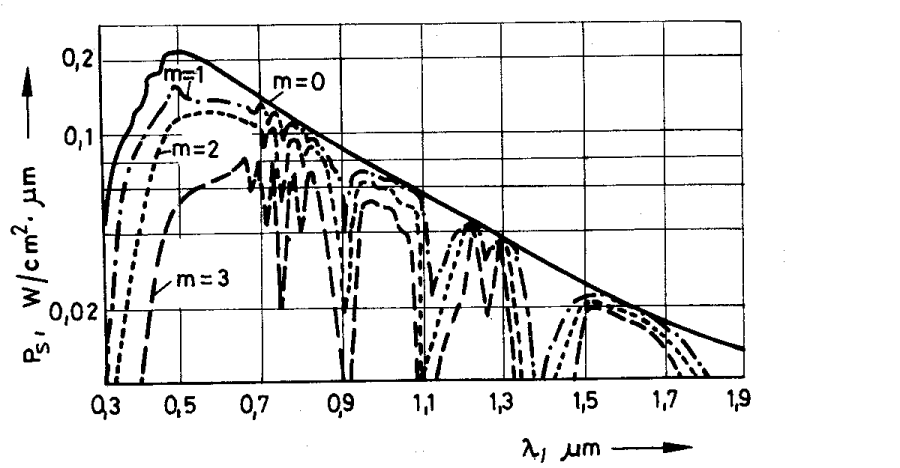
(m=0 →a világűrből,m=1→ 8000 m magasban, m=3→ 4000 m magasban; m=4→ a Föld felszínén)
A Φ e (λ) sugárzott teljesítmény a sugárzás formájában kibocsátott, átvitt vagy
felfogott teljesítmény (Φ e (λ),watt/nm)
A Q e (λ) sugárzott energia a sugárzás formájában kibocsátott, átvitt vagy felfogott energia (Q e (λ), joule/nm).
Összefüggés Φ e (λ) és Q e (λ) között:
|
d Φ e (λ) = d Q e (λ) / dt |
4.5.1.2.2. A spektrális transzmisszió, τ(λ)
A τ(λ) áteresztési v. transzmissziós tényező az áteresztett (Φ τ (λ)) és a beeső
(Φ e0 (λ)) sugárzott teljesítmények aránya:
|
τ (λ) = Φ τ (λ) / Φ e0 (λ) |
A színes közegek τ(λ) spektrális transzmissziója a transzmissziós tényező
spektrális sűrűség értékei a hullámhossz függvényében.
A színes szűrő olyan szűrő, amelynek spektrális áteresztési tényezője a
hullámhossz függvényében változó (4.28. ábra - A transzmissziós tényező).
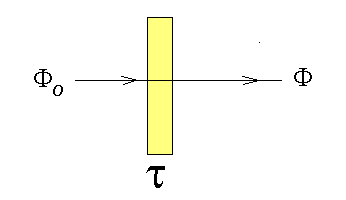
4.5.1.2.3. A spektrális reflexió, ρ(λ)
A ρ(λ) áteresztési v. transzmissziós tényező a visszavert (Φ ρ (λ)) és a beeső
(Φ e0 (λ)) sugárzott teljesítmények aránya:
ρ(λ) = Φ ρ (λ) / Φ e0 (λ)
A színes felületek spektrális reflexiójára néhány példa a (4.29. ábra - Színes felületek spektrális reflexiója) ábrán látható.
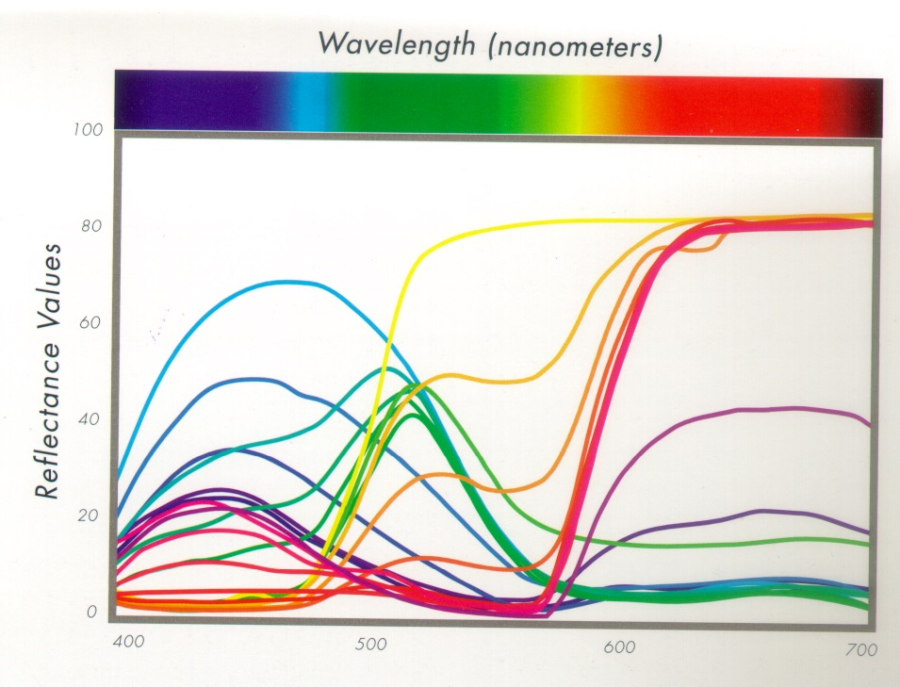
Az olyan felületet, amelynek visszaverési tényezője minden hullámhosszon a maximális 1-gyel egyenlő, ideális fehér felületnek nevezzük.
Az olyan felületet, amelynek visszaverési tényezője minden hullámhosszon 0, abszolút fekete felületnek nevezzük.
A valóságban sem ideális fehér, sem abszolút fekete felület nem létezik.
4.5.1.2.4. A spektrális abszorpció, α(λ)
Az α(λ) elnyelési v. abszorpciós tényező az elnyelt (Φ α (λ)) és a beeső
(Φ e0 (λ)) sugárzott teljesítmények aránya:
|
α(λ) = Φ α (λ) / Φ e0 (λ) |
4.5.1.2.5. A spektrális emisszió, a spektrális transzmisszió és a spektrális reflexió összefüggése
A 4.26. ábra - Egy optikailag átlátszó réteg a fényt részben reflektálja, részben átbocsátja, és részben szórja szerint az áteresztett, a visszavert és a szórt fény mennyisége megegyezik a beérkező fény mennyiségével:
|
Φ 0 = Φ τ + Φ ρ + Φ α |
Ha az egyenlet minden tagját osztjuk Φ 0 -val, a következő összefüggést kapjuk:
|
1 = τ (λ) + ρ(λ) + α(λ) |
4.5.1.2.6. A szín inger függvény (φ(λ))
A színes felületek színét csak akkor látjuk, ha valamilyen fényforrás megvilágítja őket. A fényforrás és a megvilágított színes felület között színes, fényáteresztő közegek (pl. napszemüveg) helyezkedhet el (4.30. ábra - A színinger kialakulása).
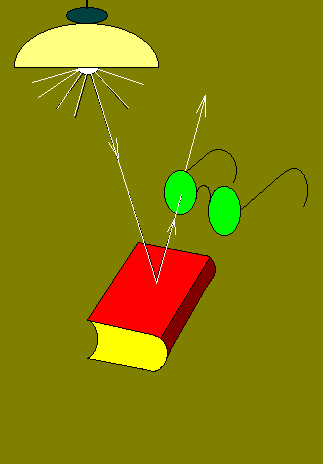
A színinger függvény annak a színes fénynek a spektrális energia eloszlását írja le, amely ezek után a színes felületről a szemünkbe jut:
|
φ(λ) = Φ e (λ) * τ (λ) * ρ(λ) |
4.5.2. A színek tristimulusos jellemzése
Grassmann törvénye szerint (4.6.2. szakasz - A szubtraktív színkeverés fejezet) az additív színkeverés törvényszerűségei lehetővé teszik, hogy bármely tetszés szerinti színnel azonos színt kikeverjünk három alapszínből. Ha vörös (R), zöld (G) és kék (B) alapszínt (stimulust) használunk, a Q színt így jellemezhetjük:
|
Q = rR + gG + bB |
Ezt az összefüggést a 4.31. ábra - Vörös, zöld és kék alapszín additív keveréke szerint ábrázolhatjuk.
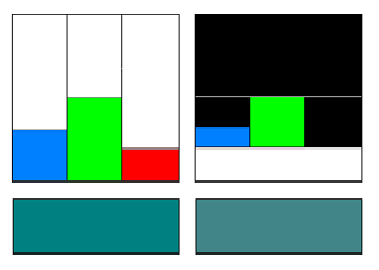
A 4.31. ábra - Vörös, zöld és kék alapszín additív keveréke baloldali képén látható szín egy zöldes árnyalatú szín, mivel a G (zöld) mennyisége a legnagyobb benne. Jelentős mennyiségű R (vörös) és valamivel több B (kék) is látható a színben.
Ugyanezt a színt úgy is előállíthatjuk, hogy az R-rel azonos mennyiségű szürkéhez adunk (b - r) mennyiségű kéket, és (g – r) mennyiségű zöldet, a (4.31. ábra - Vörös, zöld és kék alapszín additív keveréke) ábrának megfelelően.
A 4.31. ábra - Vörös, zöld és kék alapszín additív keveréke meggyőzően bizonyítja, hogy az R, G és B alapszínek közül az, amelyik a legkisebb mennyiségben van jelen, (adott esetben az R vörös), az additív színkeverék telítettségét határozza meg. A másik két alapszínnek a szürke feletti mennyisége, (G – r) mennyiségű G (zöld) és (B – r) mennyiségű B (kék), határozza meg az additív színkeverék színezetét. Ez adott esetben kékeszöld színt jelent.
A színek additív jellemzésénél nincs fogalmunk a spektrális összetételről, hiszen Grassmann törvényének értelmében az additív színkeverés független az alapszínek spektrális jellemzőitől.
4.5.3. A színek pszichofizikai (köznapi) jellemzése
Az emberiség a színeket háromdimenziós mennyiségként érzékeli. Minden nyelvben három jellemzője van a színeknek: a világosság, a telítettség, és a színezet.
A szín világossága a színes fénynek a környezethez viszonyított relatív intenzitásától függ. A (4.32. ábra - Világos telített és sötét telített zöld szín spektruma) ábrán azonos zöldes színárnyalatú, világos és sötét szín relatív spektrális energiaelosztása látható.
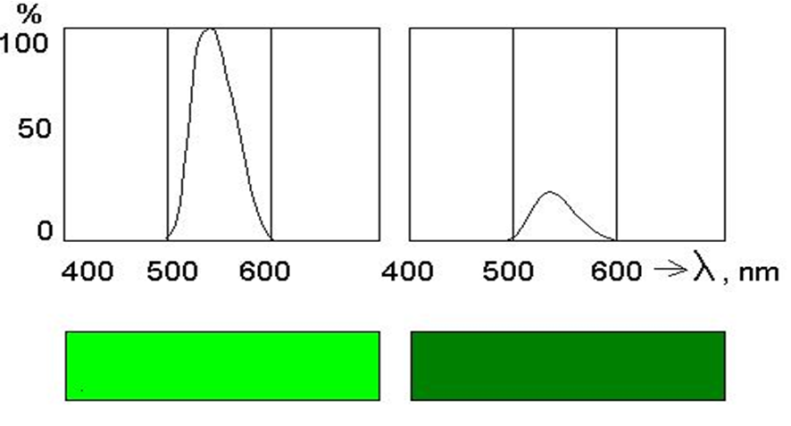
A szín telítettsége attól függ, hogy sok vagy kevés fehér, ill. szürke színt tartalmaz. A fehér, ill. szürke szín jelenléte ugyanis telítetlenséget okoz. (4.33. ábra - Világos telítetlen és sötét telítetlen zöld szín spektruma).
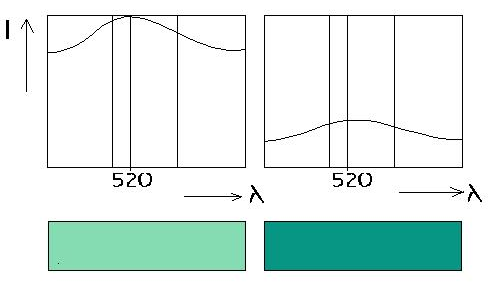
A színezetet Helmholtz annak a spektrális tiszta (monokromatikus) fénynek a hullámhosszával jellemezte, amely azonos színűnek látszik az adott színnel. Ezt a hullámhosszat „jellemző hullámhossz”-nak nevezzük. A (4.33. ábra - Világos telítetlen és sötét telítetlen zöld szín spektruma) ábrán bemutatott szín jellemző hullámhossza pl. körülbelül 520 nm.
A φ(λ) spektrális teljesítmény eloszlással jellemzett fényt pirosnak látjuk, ha nagyrészt a spektrum vörös tartományát tartalmazza (4.34. ábra - Világos és sötét telített piros szín spektruma), hasonlóképpen zöldnek, vagy kéknek, ha nagyrészt a spektrum zöld vagy kék tartományát tartalmazza (4.32. ábra - Világos telített és sötét telített zöld szín spektruma és 4.33. ábra - Világos telítetlen és sötét telítetlen zöld szín spektruma).
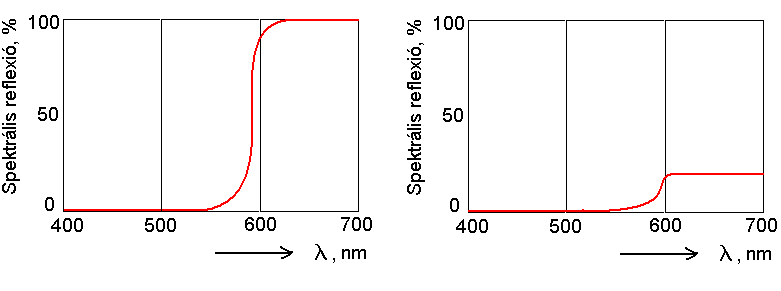
Az egyenlő energiájú spektrumú fény mindhárom receptort azonos mértékben ingerli, ezért az ilyen fényt az intenzitástól függően fehérnek, szürkének, vagy feketének látjuk (4.35. ábra - Egyenlő energiájú szürke színek).
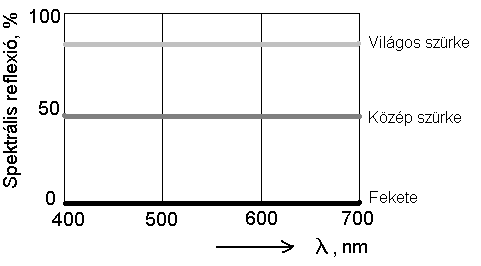
Szokták még a színeket természeti jelenségekkel vagy összehasonlítással is jellemezni: cseresznyepiros, borostyán sárga, tengerkék, stb.
4.5.4. A színek fizikai jellemzése
A szemünkbe jutó szín-inger forrása lehet egy fényforrás színes fénye („fény-színek), és lehet egy színes felületről visszaverődő színes fény is (felület-színek). Bár mindkét szín esetében szín-ingerről van szó, és spektrálisan lehetnek teljesen egyformák is, a pszichofizikai jellemzők nem egészen azonosak.
4.5.4.1. A fény-színek
A fény-színek intenzitása a fényforrás fényerejétől függ. Mivel a szemünk fényadaptációs képessége gyors és 10..16 nagyságrend nagyságú, a fény színek világosságát csak egymáshoz viszonyítva, relatív világosságként tudjuk értelmezni. A spektrálisan tiszta színek nagyon élénkek, telítettek, a széles spektrális reflexiós görbéjű színek fakóbbak, telítetlenebbek.
4.5.4.2. A festék-színek (felület-színek)
A festék-színek előállításánál valamilyen színező anyagot (színezéket) szoktak összekeverni fehér színezékkel, ha világosítani akarják a színt, és fekete színezékkel, ha sötétíteni akarják. Mindkét esetben csökken a szín élénksége, tisztasága, telítettsége. Itt tehát a világosság és a telítettség között szoros összefüggés van.
4.6. A színkeverés
A színtannak egy nagyon fontos fejezete a színkeverés. Alapvetően két módszere ismert: a szubtraktív színkeverés, amely az emberi szemtől függetlenül, a fények természetes spektrális módosulása útján jön létre, és az additív színkeverés, amely az emberi látórendszerben alakul ki. A kétféle színkeverés természetesen egyidejűleg is felléphet, és talán ennek a folyamatnak a bonyolultsága okozhatja, hogy gyakran még színekkel foglalkozó szakemberek is tévesen alkalmazzák a kétféle színkeverés szabályait.
4.6.1. Az additív színkeverés
Az additív színkeverés az emberi szemben játszódik le. Többféleképpen is létrehozhatunk additív színkeverést:
egyidejűleg egy reflexiós felületre (pl. vetítővászonra) több színű fényt vetítünk
a szembe gyors egymásutánban (a fúziós frekvenciánál, azaz 50 Hz-nél nagyobb frekvenciával) vetítjük be az összekeverendő színeket. Például így működik a Maxwell-féle színkeverő: a legyezőszerűen elrendezett, különböző színű színmintákat olyan fordulatszámmal forgatjuk meg, hogy a színminták színe összeolvadni látszik;
az összekeverendő színeket olyan kicsi pontok formájában helyezzük el sűrűn egymás mellett, hogy a szem ne tudja felbontani. Például így működik a színes TV, amelynek minden elemi pontja egy piros, egy zöld, és egy kék pontból áll. Ezek intenzitásának arányától függ, hogy az elemi pontot pirosnak, zöldnek, kéknek, vagy éppen fehérnek látjuk.
Az additív színkeverésnél tehát elvileg három alapszínt alkalmazunk. Ez lehet egy élénk, telített vörös, zöld és kék; ezekre legérzékenyebbek szemünk nappali receptorai. és ezekből elméletileg minden színárnyalat kikeverhető (4.36. ábra - Az additív színkeverés alapszínei).
Ha az alapszínekből kettőt-kettőt additívan összekeverünk, akkor vörösből és zöldből sárga színt, zöldből és kékből türkizt, míg kékből és vörösből lilát (más néven bíbort vagy pinket vagy magentát) kapunk. Mint a következőkben látni fogjuk, ezek a színek éppen a szubtraktív színkeverés alapszínei. Ha pedig mindhárom additív alapszínt additívan összekeverjük, fehér színt kapunk.
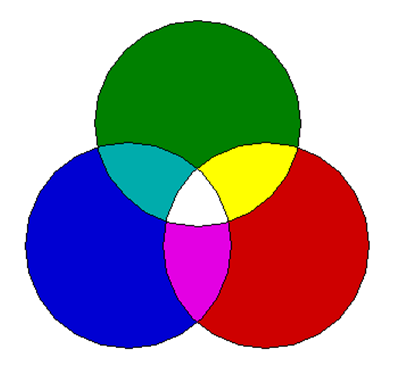
Gyakorlatban szokás még fehér és fekete színt is alkalmazni a három alapszínen kívül; ezekkel lehet egyszerűen beállítani a keverékszín világosságát és telítettségét.
Az additív színkeverés szabályait Grassmann törvényei foglalják össze:
Az additív színkeverék csak az alapszínek színösszetevőitől függ, azok spektrális jellemzőitől nem.
Egy szín additív kikeveréséhez 3 független alapszín szükséges, és elegendő.
Az additív színkeverés folytonos.
Az additív színkeverést egy háromszögben is szokták ábrázolni. (4.37. ábra - A színkeverés színháromszöge). A háromszög csúcspontjain a három alapszínt, a vörös (R, red), a zöld (G, green), és a kék (B, blue) alapszínt helyezzük el. A vörös és a zöld szín additív keveréke a sárga (Y, yellow), az (R) és (G) pontot összekötő vonalra kerül. A vörös és kék additív keverékét, a lilát (P, purple), ill. a kék és zöld additív keverékét, a türkizt (T, turquoise), hasonlóképpen, a megfelelő pontokat összekötő vonalakon helyezzük el. A háromszög belsejében középen található a fehér szín (W, white).
Ha igen finom lépésekben akarjuk a színkeverést elvégezni, a kikeverendő színtől csak kismértékben eltérő színeket alkalmazzunk alapszínként. Például paradicsompüré színének kikeveréséhez sötétpirosat, narancssárgát, és feketét választhatunk.
Az additív színkeverés segítségével bármely színpont (színárnyalat) helye megadható a 4.37. ábra - A színkeverés színháromszöge színháromszögében.
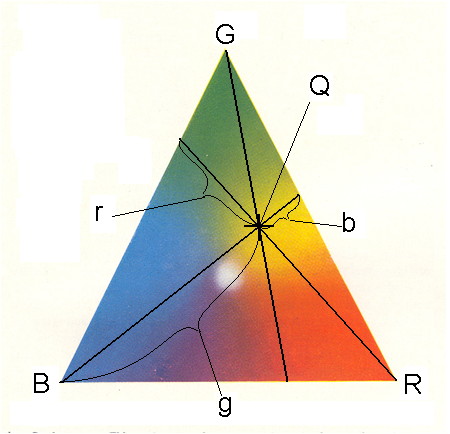
A színpont helyét az R, G, B alappontokhoz való közelséggel jellemezzük. A Q színpont helyét pl. az alábbi módon adhatjuk meg:
|
Q = rR + gG + bB |
Mivel pedig
|
r + g + b = 1 |
ahonnan r = 1 – g – b.
Ezért
|
Q = (1 – g – b)R + gG + bB |
4.6.2. A szubtraktív színkeverés
Az alábbi egyenletben a szemünkbe jutó színes fény spektrális teljesítményelosztását φ(λ)-val jelöltük. Ez a fény úgy jön létre, hogy egy színes Ф(λ) spektrális teljesítmény eloszlású fényforrás fénye színes τ(λ) spektrális transzmissziójú közegeken halad át, amelyek megváltoztatják spektrális jellemzőit; majd ezután színes ρ(λ) spektrális reflexiójú felületről visszaverődve, ismét színváltozáson esik át. Ezt a folyamatot nevezzük szubtraktív színkeverésnek. A folyamatot a következő összefüggés írja le:
|
φ(λ) = Ф(λ) * τ(λ) * ρ(λ) |
A képletben a fényt spektrálisan módosító τ(λ) és ρ(λ) függvény szorzat-kapcsolatban áll a fényforrást jellemző Ф(λ) - val. A szorzótényezők sorrendje tetszés szerinti, éppen úgy, mint ahogy mindegy az is, hogy a színszűrő van előbb, vagy a színes felület. Természetesen a képlet a körülményeknek megfelelően bővíthető (ha több színszűrő, vagy reflektáló felület vesz részt a szín kialakulásában), illetve szűkíthető, ha pl. nincs színszűrő a sugármenetben (4.38. ábra - A színinger kialakulása).
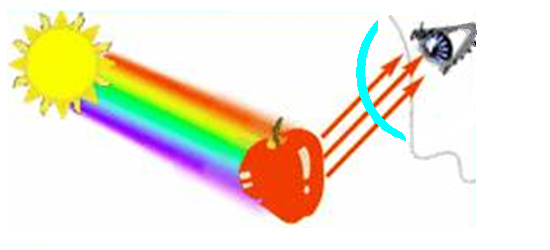
A színt a fényforrás, a fény útjába helyezett színszűrők, és a fényt visszaverő színes felületek együttesen hozzák létre.
A színes fény színezete attól függ, hogy melyik spektrumtartomány jut túlsúlyba a fény relatív teljesítmény eloszlásában.
A szubtraktív színkeverés alapszíne a sárga, a türkiz és a lila. Ha ezeket szubtraktíven akarjuk keverni, pl. úgy járhatunk el, hogy különböző sötétségű sárga, türkiz és lila színszűrőket veszünk, és ezeket egymás mögé helyezzük. Az egymás mögé helyezett szűrőkön a fénynek csak az a része jut át, amelyet mindegyik szűrő átereszt (4.39. ábra - A szubtraktív színkeverés alapszínei). Ez a szubtraktív színkeverék.
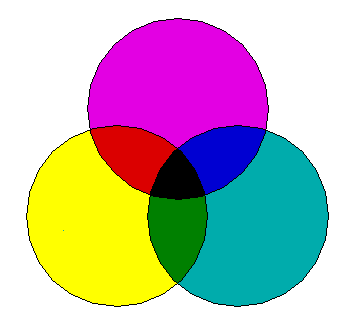
A (4.39. ábra - A szubtraktív színkeverés alapszínei) ábrán látható, hogy a sárga és a türkiz szín szubtraktív keveréke zöld, a sárga és lila szín szubtraktív keveréke vörös, a türkiz és lila szín szubtraktív keveréke pedig kék. Mindhárom szubtraktív alapszín szubtraktív keveréke fekete színt eredményez.
4.6.3. Összefüggés az additív és a szubtraktív színkeverés alapszínei között
Az additív és a szubtraktív színkeverés alapszínei közötti összefüggést a színek spektrális jellemzőiben találhatjuk meg. A (4.40. ábra - Az additív alapszínek) ábrán az additív alapszíneket a tristimulusos ábrázolási módszerrel mutatjuk be. Az ábrán a vörös alapszín a spektrum hosszúhullámú részén ábrázolható, a zöld a középhullámú, míg a kék a rövidhullámú részen.
Ha az additív alapszínekből kettőt-kettőt additíven összekeverünk, azaz összeadunk, akkor éppen a szubtraktív alapszíneket kapjuk meg (4.41. ábra - Az additív alapszínek additív keverése szubtraktív alapszíneket eredményez). A sárga szín a vörös és zöld additív keveréke, tehát a spektrum hosszú- és középhullámú részét foglalja el. A türkiz a kék és zöld additív keveréke, ezért a spektrum rövid- és középhullámú részén található. A bíbor szín pedig a kék és vörös szín keveréke, ezért a spektrum rövid- és hosszúhullámú részén helyezkedik el.
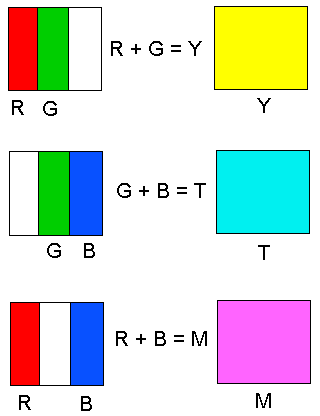
Két-két szubtraktív alapszín szubtraktív összekeverése pedig éppen az additív alapszíneket eredményezi, mivel két szín szubtraktív színkeverése két színszűrő egymás után helyezésével valósítható meg, vagyis a fénynek mindkét színszűrőn át kell menni (4.42. ábra - A szubtraktív alapszínek szubtraktív keverékei éppen az additív alapszíneket eredményezik)
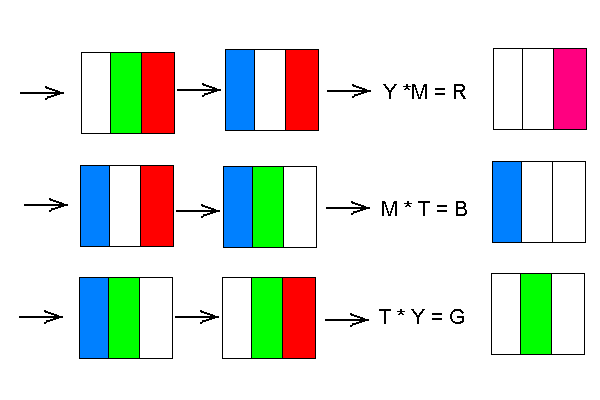
4.7. A kiegészítő színek
A kiegészítő színek (színpárok) olyan színek, melyeknek additív keveréke fehér színérzetet eredményez.
Kiegészítő színeket úgy hozhatunk létre, hogy a fehér érzetet kiváltó spektrumot tetszés szerinti arányban kettéválasztjuk (4.43. ábra - Kiegészítő színek).
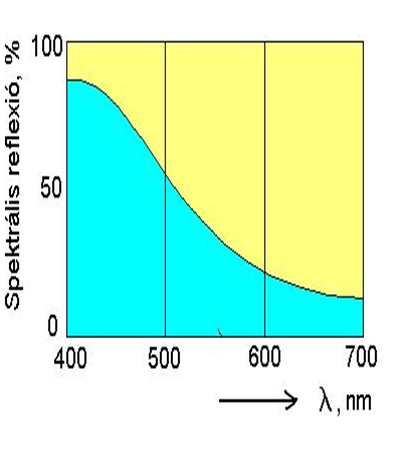
A kettéválasztást pl. prizma által szétbontott spektrumon végezhetjük el, tükörrel két nyalábra választva a fényt.
Kiegészítő szín lehet két tetszés szerinti monokromatikus fény is, amelyek additív keveréke fehér színérzetet vált ki.
Az additív és szubtraktív alapszínek egymásnak kiegészítő színei (sárga-kék, türkiz-vörös, bíbor-zöld).
Mivel a kiegészítő színek definíciója alapján kiegészítő színekből additív színkeveréssel mindig létrehozható fehér (vagy szürke) szín, ezért a kiegészítő színek színpontjainak mindig a CIE színezeti diagram fehér pontján átmenő egyenesen kell lenni (4.44. ábra - Kiegészítő színek a CIE színezeti háromszögben)
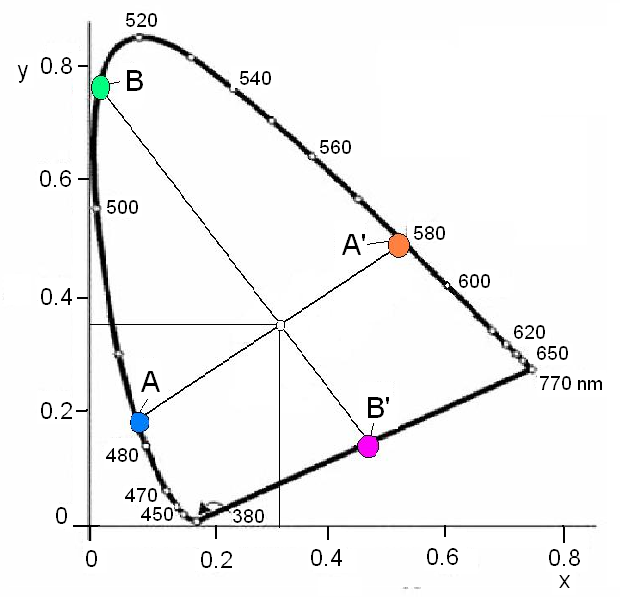
4.8. A metameria
Mivel szemünk mindössze három, széles sávban érzékeny receptor típussal rendelkezik, spektrálisan eltérő színek is kiválthatnak azonos színérzetet. Ennek feltétele mindössze az, hogy a protos L, a deuteros M, és a tritos S ingere azonos legyen. Ez pedig végtelen sokféle φ(λ) színinger esetében megvalósulhat.
Azokat a φ 1 (λ) és φ 2 (λ) színpárokat, amelyeknek spektrális energia eloszlása eltérő, de bizonyos körülmények között azonosnak látszanak, metamer színpároknak nevezzük. A látszólagos azonosság az ilyen színpároknál megszűnik, amint a körülmények (pl. megvilágítás) megváltoznak.
Jó példa a metameria jelenségre a metamer fehér színpár. A 4.5.3. szakasz - A színek pszichofizikai (köznapi) jellemzése fejezet szerint az egyenlő energiájú spektrummal megvilágított ideális fehér felületet fehér színűnek látjuk, mivel mind a három receptort azonos mértékben ingerli. De mindhárom receptort azonos mértékben ingerelhetjük akkor is, ha az ideálisan fehér felületet három olyan monokromatikus fénnyel világítjuk meg, amelyek a három receptor típust éppen azonos mértékben ingerlik. Tehát ez a két, egymástól tökéletesen eltérő spektrális energia eloszlású fény teljesen egyformának tűnhet.
Az egyformaság azonban nem jön létre egy olyan színlátó személy esetében, akinek a receptor érzékenységi függvényei kicsit eltérnek az előzőétől. Ez az érzékelő metameriája.
Az egyformaság akkor is megszűnik, ha a fehér felületet nem egészen egyenlő energiájú fehér fénnyel világítjuk meg. Ez a fényforrás metameriája.
4.9. Az RGB és a CMYK színrendszer
A nyomdaiparban két féle technikát szoktak alkalmazni: az additív és a szubtraktív technikát (és gyakran ennek a kettőnek a keverékét is).
4.9.1. A színes monitorok RGB színrendszere
A színes ábrák megtervezése általában színes monitoron történik. A színes monitorok additív színkeveréssel működnek: a szemünk által nem megkülönböztethetően kicsi vörös, zöld és kék pontok hozzák létre a mintegy 16 millió színárnyalatot. A monitor alapszíne a vörös (Red azaz R), zöld (Green azaz G) és kék (Blue azaz B) .Mind a három alapszín 256 különböző intenzitás fokozatot tud létrehozni, ezek összes lehetséges arányú keveréke 256*256*256=16 777 216 különböző színárnyalatot jelent. A CIE színezeti diagramban a színes monitoron megjeleníthető színek a monitor vörös, zöld és kék alapszínének színpontja között elhelyezhető háromszögön belül találhatók (4.45. ábra - A színes monitoron megjeleníthető színek).
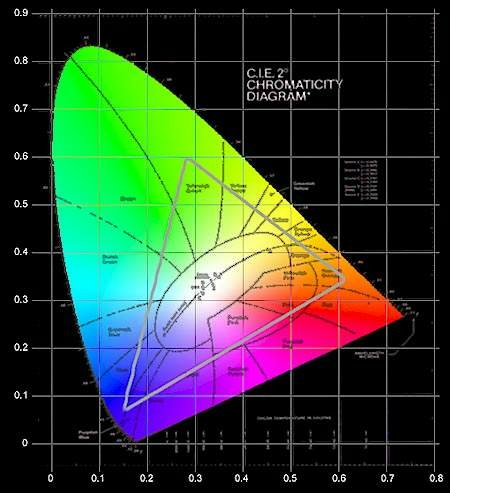
Ez a háromszög elméletileg lehetne nagyobb is, ha az R, G és B alapszín spektrálisan tiszta, monokromatikus szín (adott esetben fény) lenne. Ekkor az alapszínek színpontjai a „papucs” határoló vonalain lennének. Akkor is jobb lenne az eredmény, ha széles sávúak lennének, a (4.46. ábra - Ideális additív és szubtraktív alapszínek spektrális eloszlása) ábrán látható spektrális energia eloszlással. A széles sávú színek ugyan mindig fakóbbak, mint a monokromatikus színek, de a (4.46. ábra - Ideális additív és szubtraktív alapszínek spektrális eloszlása) ábrán látható színek spektrum-tartományai legalább nem fedik át egymást, ezért additív színkeverékeik ideális szubtraktív alapszíneket hoznának létre (4.46. ábra - Ideális additív és szubtraktív alapszínek spektrális eloszlása).
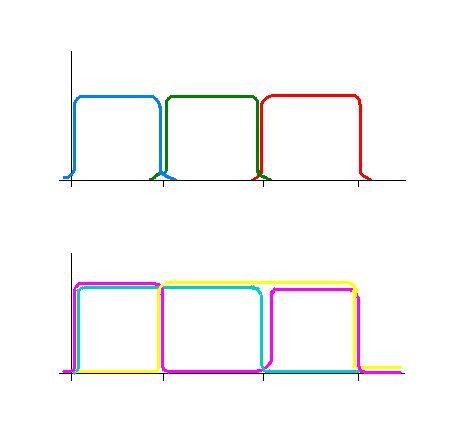
A valóságban az R, G és B additív alapszín spektrális energia eloszlása CRT (képcsöves) színes monitor esetén a (4.47. ábra - CRT (képcsöves) színes monitor fényének spektrális energia eloszlása) ábrán látható. Az LCD színes monitorok spektrális energia eloszlása még ennél is inkább vonalas jelleget mutat. Az R, G és B alapszín spektrumtartománya széles és jelentősen átfedi egymást. Tehát ezek az alapszínek meglehetősen fakók, és az alapszínek additív keverékei is kissé „piszkosak”.
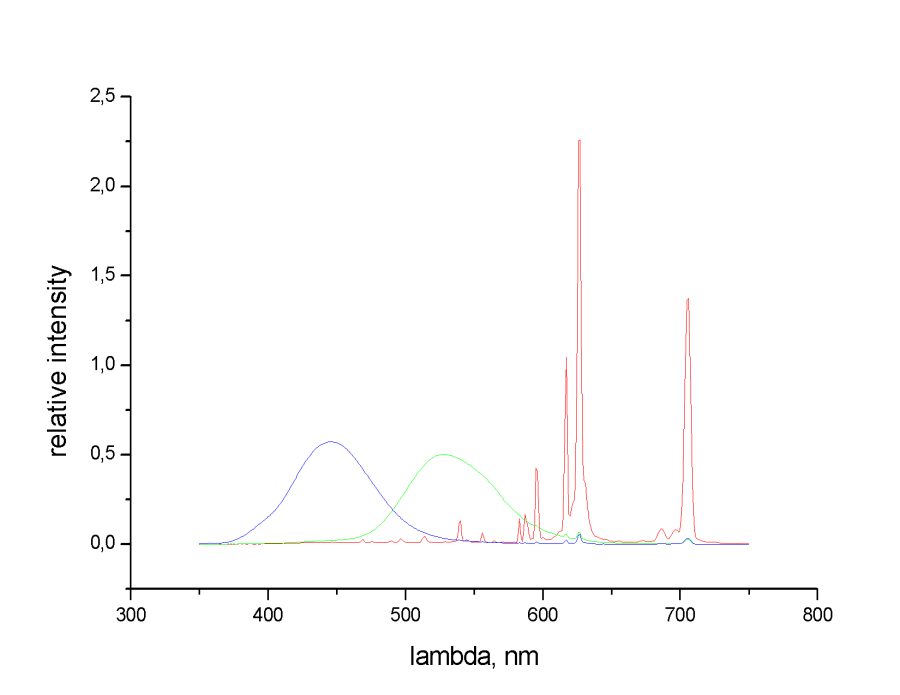
4.9.2. A színes nyomtatás CMYK színrendszere
A színes nyomtatók általában a szubtraktív színkeverés alapszíneivel (Cyan azaz C, Magenta azaz M és Yellow azaz Y) dolgoznak (4.48. ábra - Szubtraktív alapszínek színpontjai). Ha ezeket a színeket tisztán, önmagukban (nagyobb foltban vagy raszteres pöttyök formájában) alkalmazzuk, akkor ragyogó tisztán megjelenik a sárga, türkiz és lilás (pink vagy magenta) alapszín (4.48. ábra - Szubtraktív alapszínek színpontjai). Ha az alapszínek áttetszőek, és egymással fedésbe kerülnek, kijönnek a szubtraktív színkeverékek, a vörös, a zöld és a kék, azaz az additív alapszínek is. Azonban nem biztos, hogy ez a vörös, zöld és kék megegyezik a monitoron megjelenő vörös, zöld és kék színnel. Ez már a C, M és Y alapszín spektrális jellemzőitől függ. Sajnos ezek az alapszínek sem olyanok, mint a (4.46. ábra - Ideális additív és szubtraktív alapszínek spektrális eloszlása) ábrán bemutatott ideális szubtraktív alapszínek. Additív keverékeik többé-kevésbé eltérnek a monitorok additív alapszíneitől.
Ha a nyomtató mindhárom alapszínét egymás fölé nyomtatjuk, elméletileg fekete színt kellene kapnunk. A valóságban - az alapszínek fogyatékossága miatt - ez a fekete sem lesz eléggé fekete. Ezért kell a nyomtatókban egy negyedik alapszínt, a feketét is alkalmazni. Ezt K betűvel jelölik, innen ered a CMYK színrendszer nevében a K betű.
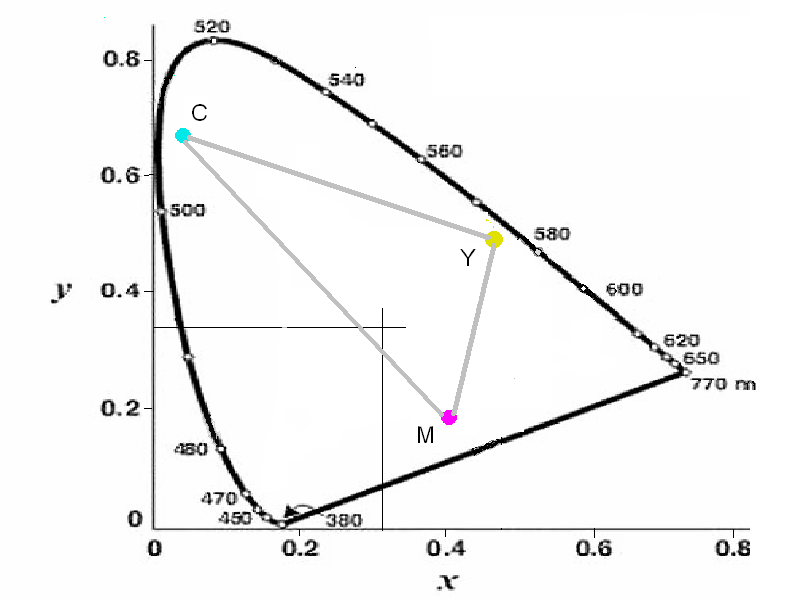
4.10. A gamut
Gamutnak nevezzük egy adott technikával megjeleníthető színek tartományát.
A különböző színrendszerekben különböző mennyiségű színárnyalat ábrázolható. Az ábrázolható színárnyalatok száma alapvetően az alapszínek tisztaságától és egymástól való távolságától, tehát a színpontjaikra fektethető háromszög területének nagyságától függ. A színes monitoron pl a (4.45. ábra - A színes monitoron megjeleníthető színek) ábrán berajzolt háromszög csúcspontjai (a monitor R, G és B alapszíneinek színpontjai) által bezárt háromszögön belüli színek keverhetők ki. A színes nyomtatókon pedig a (4.48. ábra - Szubtraktív alapszínek színpontjai) ábrán látható C, M és Y jeleníthető meg. Ha valaki színes monitoron tervez meg egy látványt, az RGB háromszögön belüli színeket tudja alkalmazni a terven (a (4.49. ábra - Egy színes nyomtató C, M és Y alapszínének és azok szubtraktív keverésével létrehozott R, G és B színének színpontja) ábrán a piros színnel jelzett színtartományt). Ha viszont színes nyomtatón akarja kinyomtatni a tervet, akkor csak a CMY háromszögön belüli színeket tudja kinyomtatni (a (4.49. ábra - Egy színes nyomtató C, M és Y alapszínének és azok szubtraktív keverésével létrehozott R, G és B színének színpontja) ábrán a zöld színnel jelzett tartományt).
Mivel a nyomtató gamutja nem egyezik meg a monitor gamutjával, lesznek olyan színek, amelyek a monitoron megjeleníthetők, de a nyomtatóval nem, és lesznek olyanok, amelyeket a nyomtató meg tudna jeleníteni, de a monitor nem, így végül is csak a sárga színel jelölt közös rész lesz használható.
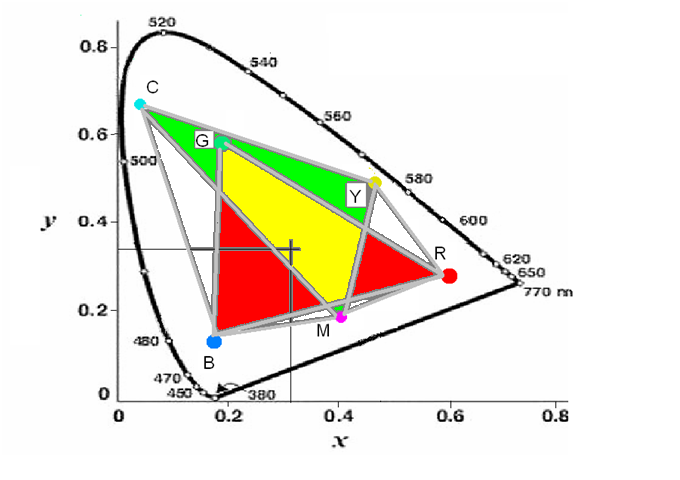
4.11. A színmérő rendszerek
4.11.1. A CIE színmérő rendszer
A színek egyértelmű, objektív leírására és meghatározására a Nemzetközi Világítástechnikai Bizottság (Commission Internationale de L’Eclairage, C.I.E.) 1931-ben elfogadta az additív színkeverésen alapuló trikromatikus színmérő rendszert, majd 1962-ben ezt kiegészítette egy újabb módosulattal. Azóta ezt a szín meghatározási rendszert mindenütt elfogadták, és alkalmazása egyre nagyobb teret nyer.
A CIE színrendszer minden színhez egy-egy színhármast rendel. A megfigyelések ugyanis azt mutatják, hogy a szín háromdimenziós mennyiség. Ez minden bizonnyal azért van, mert a szemünk három receptorral: a vörösre érzékeny protossal, a zöldre érzékeny deuterossal, és a kékre érzékeny tritossal érzékeli a színeket, amint erről már korábban szó volt.
4.11.1.1. A CIE RGB-színrendszer
A CIE additív színkeverési kísérletek alapján meghatározott függvények segítségével írja le a színeket.
Grassmann törvényei alapján három független alapszínből (pontosabban alapszín ingerből) bármely szín additív módon kikeverhető. A három alapszín tetszőlegesen választható, csak függetlenek legyenek, vagyis egyiket se lehessen a másik kettőből kikeverni. A legfüggetlenebb három alapszín az a három szín lenne, amelynek egyike csak a vörös-, másik csak a zöld- és a harmadik csak a kékérzékeny receptort ingerelné.
A CIE által választott alapszínek a λ 1 =700 nm hullámhosszúságú vörös (R), az λ 2 =546,1 nm-es zöld (G) és a λ 3 =435,8 nm-es kék (B) spektrumszín volt.
Kísérletekkel megállapították, hogy ha a választott piros, zöld és kék alapszíneket rendre
|
1 : 4,5907 : 0,0601 |
arányban keverik, akkor olyan fehér szín adódik, amely azonosnak tűnik az egyenlő energiájú fehér fényforrás színével. (Egyenlő energiájú fényforrásnak azt a fényforrást nevezzük, amelynek spektrális teljesítmény-eloszlása állandó, azaz 380-tól 780 nm-ig egyenlő hullámhossztartományokban a kisugárzott teljesítmény ugyanakkora.)
Ezeket az arányszámokat tekintjük az alapszín ingerek egységnyi (R), (G) és (B) mennyiségének.
Az alapszínek egységei:
|
(R) = 0,17697 lm | ||
|
(G) = 0,81240 lm | ||
|
(B) = 0,01063 lm. |
Ilyen megállapodással 1 egységnyi piros + 1 egységnyi zöld + 1 egységnyi kék keveréke 1 egységnyi (1 lm) fehér. Ezek a számok éppen az előbbi arányban állnak egymással, és összegük éppen 1.
Általában pedig, ha egy szín kikeveréséhez r, g, ill. b egységnyi kell az alapszín ingerekből, akkor a kapott szín világossága
|
L = r R + g G + b B |
Az itt szereplő r, g és b együtthatók az L világosságú szín trikromatikus jellemzői.
Miután ismertek az alapszín ingerek egységei, kísérletileg meg lehetett határozni, hogy ezekből milyen arányban lehet kikeverni a spektrumszíneket. Ezeket a méréseket Wright és Guild el is végezte 1928-1931-ben. Jó színlátású kísérleti személyekkel végezték a méréseket. Olyan mérőműszert alkalmaztak, amelynek eltűnő éles látómezejének egyik felébe felváltva, 5 nm-enként egymás után λ m hullámhosszúságú monokromatikus fényt vetítettek be („cél-fény”), míg a másik felébe a három monokromatikus alap-színt („keverő fények”). A kísérleti személynek a három alapszín mennyiségét úgy kellett beállítani, hogy összegük színe megegyezőnek látsszon a cél-fény színével. Ilyenkor a látómező két felét elválasztó vonal eltűnni látszik (4.50. ábra - Színegyeztetési kísérletek eltűnő éles látómezőben).
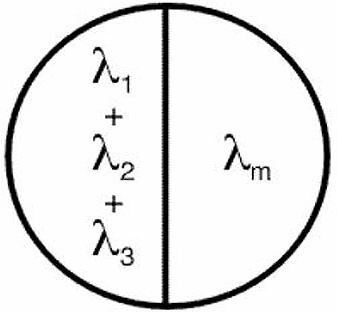
Legyen a jobb oldali változó hullámhosszúságú fény mennyisége (intenzitása) a mérések során állandóan egységnyi. Jelöljük ezt a fényt Q(λ)-val. A bal oldalon r mennyiségű vöröset, g mennyiségű zöldet (G) és b mennyiségű kéket (B) kell összekeverni, hogy azonos színűnek tűnjön Q(λ)-val.
|
Q(λ) = rR(700,0) + gG(546,1) + bB(435,8) |
Azonban a három alapszín keveréke mindig fakóbbnak tűnt a monokromatikus cél-fénynél. Ezt a problémát úgy oldották meg, hogy a három keverő fény egyikét mindig a célfényhez vetítették be, és ez által ez az oldal is fakóbb lett.
A folyamatot most az alábbi egyenletek írják le annak megfelelően, hogy melyik alapszínt kellett a másik oldalra vetíteni be az egyezés létrehozásához.
|
Q(λ) + rR(700,0) = gG(546,1) + bB | ||
|
Q(λ) + gG(546,1) = rR(700,0) + bB | ||
|
Q(λ) + bB (435,8) = rR(700,0) + gG |
A fenti egyenleteket Q(λ) –ra rendezve a keverő fények egyike minden esetben negatív lesz.
A spektrum minden hullámhosszához három érték tartozik: r, g és b. Ilyen arányban kell az R, G és B alapszín ingereket keverni ahhoz, hogy a tetszés szerinti λ hullámhosszúságú Q(λ) spektrumszínnel azonosnak tűnő színt megkapjuk.
A színkeveréshez felhasznált alapszínek mennyiségét diagramban ábrázolták, és a diagram görbéit CIE RGB rendszerbeli szín megfeleltető függvényeknek nevezték. A szín megfeleltető függvények jele:
|
|
Az RGB rendszerben a szín megfeleltető függvények a (4.51. ábra - A CIE RGB színmegfeleltető függvények) ábrán láthatók.
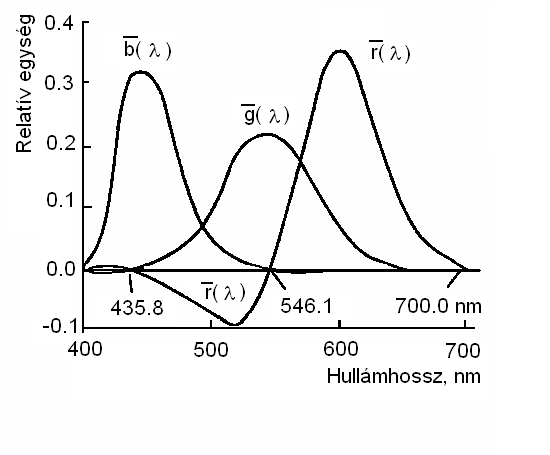
A (4.51. ábra - A CIE RGB színmegfeleltető függvények) ábrán ugyan nem jól látható, de a három koordináta valamelyike valóban mindig negatív előjelű. Negatív fénymennyiséget viszont nem lehet egy másik fényhez hozzákeverni. Ez azt jelenti, hogy egyetlen spektrumszínt sem lehet az alapszínekül választott három spektrumszínből additív módon, közvetlenül kikeverni.
Ha az alapszíneket egy háromszög sarkain helyezzük el, az additív színkeverékek színpontjai a háromszög területén belül helyezkednek el. A negatív színek a háromszögön kívül találhatók (4.52. ábra - Az R, G és B alapszínek színterének ábrázolása)
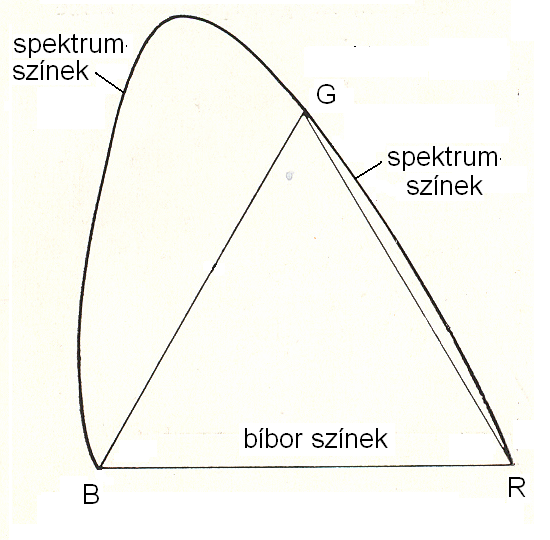
4.11.1.2. A CIE xyY színrendszer
Az R, G és B alap színingerek pontjait összekötő egyenesek által körülzárt területen belül azoknak a színeknek a színpontjai vannak, amelyek kikeverhetők ezen alapszín ingerek pozitív értékeiből. Az ezen területen lévő színek színpontjai negatív értékeket is tartalmaznak.
Számítástechnikai szempontból a CIE célszerűnek találta, hogy az (R), (G) és (B) alapszín ingerek helyett minden valóságos színre kizárólag pozitív értékeket adó alapszín ingereket válasszanak. Ez csak abban az esetben valósulhat meg, ha olyan új alap szín ingereket választanak, amelyek az R, G és B alapszín ingereken kívül található spektrum-vonalon kívül esnek. Az új (X), (Y), (Z) alapszíneket úgy kell megválasztani, hogy az általuk alkotott háromszög teljesen körülzárja a spektrumszínek vonalát, és a bíborvonalat. Így az RGB rendszerhez hasonlóan alkotott új XYZ rendszerben minden valóságos szín jellemző értékei pozitívak lesznek.
Ilyen befoglaló háromszöget sokféleképpen lehet választani. Ezért még az alábbi követelményeket állították fel:
Az egyenlő energiájú fehér W szín X, Y és Z színösszetevője legyen egymással egyenlő.
Minden szín Y színösszetevője adja meg a szín világosságát.
Az X, Y, Z alappontok essenek minél közelebb a spektrumvonalhoz.
Az egymástól minimálisan, de szemmel észrevehetően különböző színeket ábrázoló pontok távolsága az egész színtartományban lehetőleg egyforma legyen.
Azok a pontok, amelyek az RGB színtérben egy egyenes mentén fekszenek, az új színtérben is egy egyenesre essenek.
A 3. követelményt úgy elégítjük ki, hogy a háromszög másik két oldalául a spektrumvonal egy-egy érintőjét vesszük. A spektrumvonal vörös része majdnem egyenes, ezért a végén, a 700 nm- es pontban rajzolt érintőt választották. A spektrumvonal másik oldalán D.B. Judd javaslatára, a 4. követelmény minél jobb megközelítéséhez azt az érintőt választották, amely az 504 nm-s pontban érinti a spektrumvonalat. Ez a befoglaló háromszög kielégíti az összes követelményt. (4.53. ábra - A befoglaló háromszög).
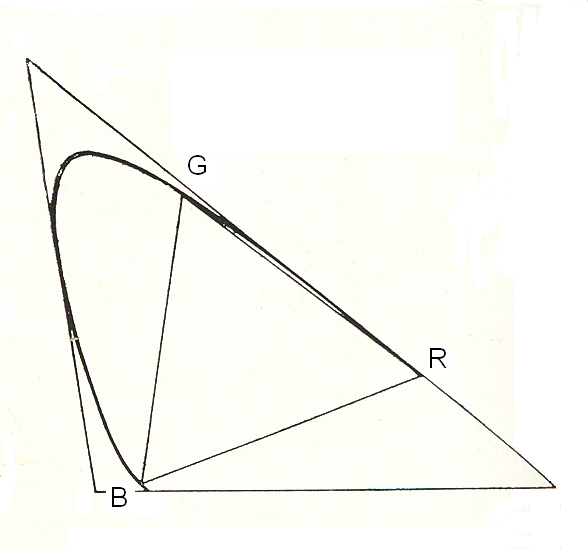
Annak érdekében, hogy az X, Y és Z tengelyek derékszögű koordináta rendszerben legyenek ábrázolhatók, még egy transzformációt hajtottak végre (4.54. ábra - A CIE X, Y és Z alapszín ingerek színterének ábrázolása).
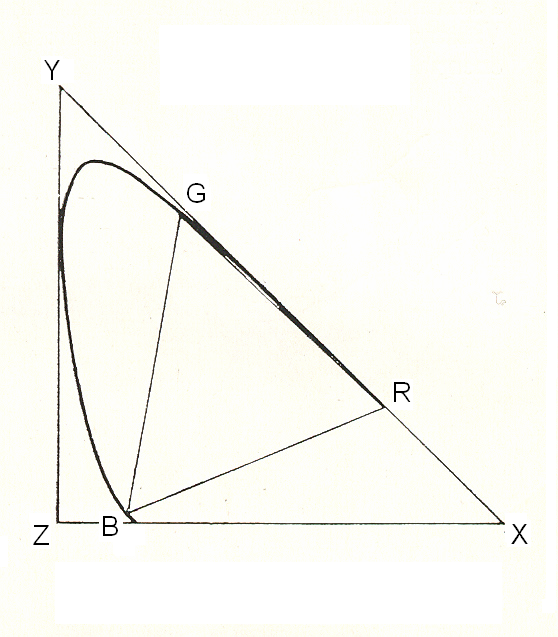
Az X, Y és Z új, virtuális alapszín ingereket az R, G és B alapszínekből a CIE az alábbi képlet szerint egy lineáris transzformációval a hozta létre:
|
X = 0.49000 R + 0.31000 G + 0.20000 B | ||
|
Y = 0.17697 R + 0.81240 G + 0.01063 B | ||
|
Z = 0.00000 R + 0.01000 G + 0.99000 B |
Megjegyezzük, hogy a fenti értékekből számított egyenes nem érinti szigorúan a spektrumvonalat 504 nm –nél, de hozzá nagyon közel halad el.
Az X, Y, Z alapszínek a spektrumvonal területén kívülre esnek. Ezek tehát nem valóságos színek, hanem képzetesek. Belőlük ténylegesen nem lehet színeket kikeverni. Ha azonban az R, G, B alapszínekből kikevertünk egy színt, amelynek komponensei R, G, és B, akkor a transzformációs egyenletrendszerrel kiszámíthatjuk ennek a színnek az X, Y és Z összetevőit.
A transzformáció természetesen visszafelé is elvégezhető. Az X, Y és Z értékekből a következő képen meghatározható R, G és B.
|
R = + 2,36460 X – 0.89653 Y – 0.46807 Z | ||
|
G = - 0.51515 X + 1,42640 Y + 0.08875 Z | ||
|
B = + 0.00520 X – 0.01441 Y + 1. 00921 Z |
Az új, nem valóságos (képzetes) X, Y és Z alapszín ingerek alkalmazása esetén a színmegfeleltető függvények csak pozitív értékekből állnak (4.55. ábra - A CIE színmegfeleltető függvények).
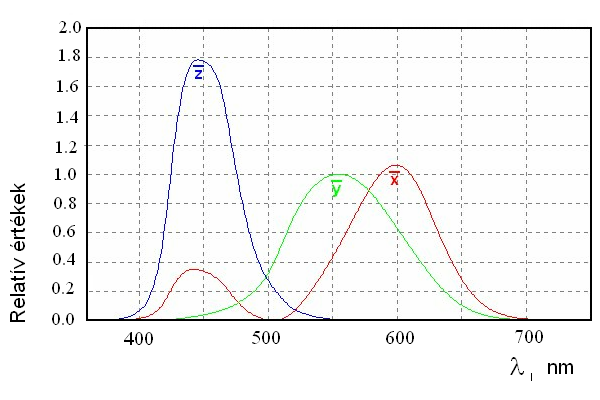
A CIE színmérő számokat – a színösszetevőket – a színmegfeleltető függvények segítségével a már korábban definiált φ(λ) szín-ingerfüggvény ismeretében az alábbi összefüggések szerint határozhatjuk meg.
A φ(λ) szín-inger függvény – a szemünkbe jutó, a szín-élményt kiváltó fény – elsősorban a fényforrás színétől függ, de ha színes felületről visszaverődve vagy színes közegeken áthaladva jut a szembe, akkor spektrális összetétele módosulhat: Emlékeztetőül felidézzük a korábban ismertetett színinger függvényt:
φ(λ) = Ф(λ) * ρ(λ) * τ(λ)
ahol
|
φ(λ) |
a szín-inger függvény, | |
|
Ф(λ) |
a fényforrás spektrális teljesítmény eloszlása, | |
|
ρ(λ) |
a színes felület spektrális reflexiója, és | |
|
τ(λ) |
a színes közeg spektrális transzmissziója. |
A φ(λ) szín-inger függvény alapján határozhatjuk meg a szín X, Y és Z színösszetevőjét:
|
|
Ahol k egy normalizáló tényező. A normalizáló tényező biztosítja azt, hogy az egyenlő energiájú fehér fény, vagy pedig az ideálisan fehér felület esetén X = Y = Z = 100 legyen.
|
|
Az X, Y, Z színösszetevőkből az x, y, z színkoordinátákat az alábbi módon határozhatjuk meg:
|
| ||
|
| ||
|
|
A (4.56. ábra - A CIE színezeti diagram vagy CIE színháromszög (népszerű nevén „papucsdiagram”).) ábrán látható az xyY színháromszög, azaz a CIE színezeti diagram (népszerű nevén „papucsdiagram”). Ez a diagram a CIE x, y, z színkoordináták kétdimenziós ábrázolása. Vízszintes tengelyén az x, függőleges tengelyén az y koordináta található. A z koordináta ábrázolására nincs szükség, mivel a három színkoordináta nem független egymástól, hiszen:
|
x + y + z = 1 |
Valamely szín helyét a koordináta rendszerben az x, y színkoordinátákkal, világosságát az Y színösszetevővel adják meg.
A színezeti diagram határoló vonalán a 780 nm-s vöröstől a 380 nm-s ibolyáig a spektrumszínek láthatók („spektrum-vonal”). A vörös és a kék határpontot összekötő egyenes a „bíbor-vonal”. Az x = 0,33, y = 0,33 pontban van a fehér szín. A fehér szín pontján átfektetett egyenesek végpontjain helyezkednek el a kiegészítő színek, amelyekből mindig kikeverhető a fehér (vagy szürke) szín. A fehér pont környezetében találhatók a fakó, telítetlen színek, míg a spektrum-vonal közelében az élénk, telített színek.
A CIE színezeti diagram világossága az egész diagram területén Y=100.
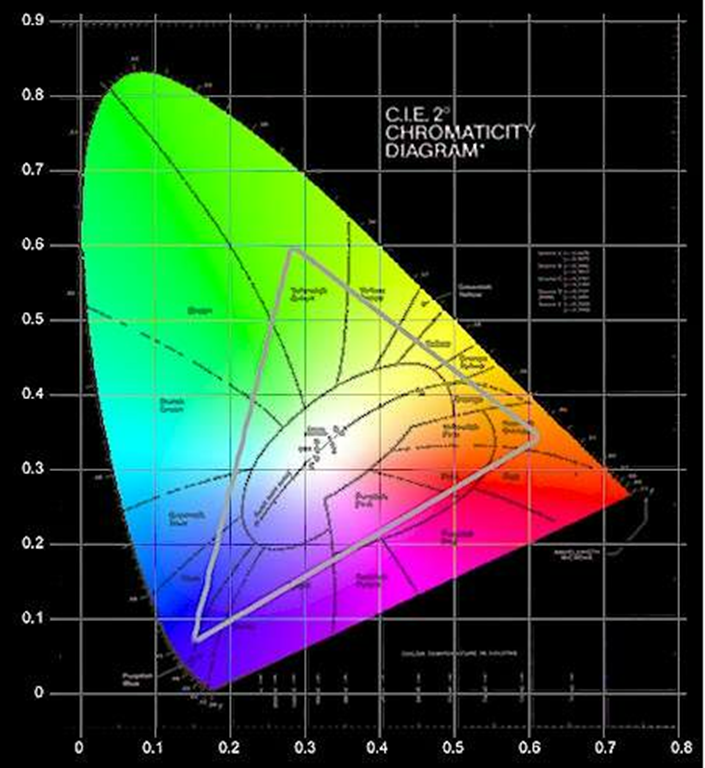
A CIE xyY szín rendszer sok szempontból jónak bizonyult:
A CIE színezeti diagram minden egyes pontja az x és y színkoordináta által definiál egy színárnyalatot, amelynek mindig meg kell adni az Y világossági tényezőjét is. Vagyis a színeket az xyY számhármassal definiáljuk, és így a színek továbbra is háromdimenziósak maradnak.
Az új szín megfeleltető függvények nem tartalmaznak negatív értéket (4.55. ábra - A CIE színmegfeleltető függvények).
Azonban van ennek a rendszernek egy hibája, amelyre MacAdam mutatott rá. Ő újabb színkeverési méréseket folytatott a szín-tér 25 pontjában. A színeket különböző monokromatikus szín-párokból kevertette ki a kísérletben résztvevő jó színlátású személyekkel. Azt tapasztalta, hogy a mérési bizonytalanságból eredő szórási ellipszisek a színtér különböző területein egymástól nagymértékben eltérnek, vagyis a szín-tér nem egyenletes. Ennek pedig kellemetlen következménye az, hogy ebben a rendszerben a színek tűrésezése (a megengedett hibák definiálása) nehéz és bonyolult. Minden színnek minden irányban más a megengedett hibája (4.57. ábra - A MacAdam ellipszisek)
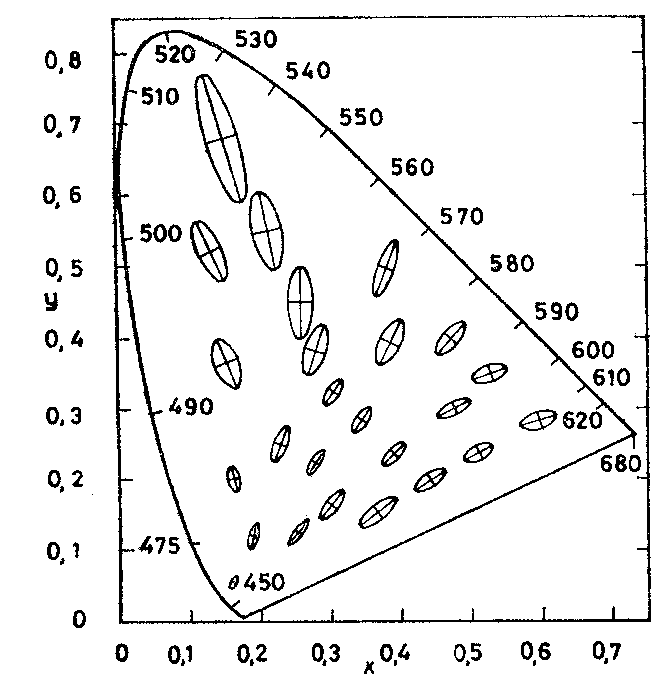
Ezért az xyY színtér új meg új transzformációjával próbálták egyenletesebbé tenni a CIE színrendszert. Több mint 20 új szín-rendszert vezetett be a CIE (Pl. FMC2, CIE LAB, CIE LUV, CIE L*a*b*, CIE L*u*v*, stb). Ezek közül jelenleg a CIE L*a*b* színrendszer a szabványos.
4.11.1.3. A CIE L*a*b* színrendszer
A CIE L*a*b* színrendszer alapja a CIE X, Y és Z szín összetevő. Ezek alapján definiálják a CIE L, a* és b* színkoordinátát:
|
L* = 116 (Y/Yn)1/3 – 16 | ||
|
a* = 500 [(X/Xn)1/3 – (Y/Yn)1/3] | ||
|
b* = 200 [Y/Yn)1/3 – (Z/Zn)1/3] |
Ahol
|
X, Y, Z |
a vizsgált színminta színösszetevője | |
|
Xn, Yn, Zn |
a fehér etalon felület színösszetevője az adott megvilágítás mellett | |
|
X/Xn, Y/Yn, Z/Zn > 0,01 kell legyen |
Mivel ez a színtér érzet szerint egyenletesnek tekinthető, a szín különbségeket (és a színek megengedett eltéréseit) az egész színtérben azonos módon, a térbeli Pythagoras tétel alkalmazásával határozhatjuk meg.
|
ΔEab* = [(ΔL*)2 + (Δa*)2 + (Δb*)2]1/2 |
Ahol az érzékelt színkülönbségek nagysága:
0,0 ~ 0,5 nem vehető észre
0,5 ~ 1,5 alig vehető észre
1,5 ~ 3,0 észrevehető
3,0 ~ 6,0 jól látható
6,0 ~ 12,0 nagy
A CIE L*a*b* színrendszer – mint minden szín rendszer – továbbra is három dimenziós. Ábrázolása a (4.58. ábra - A CIE L*a*b* színrendszer) ábrán látható.
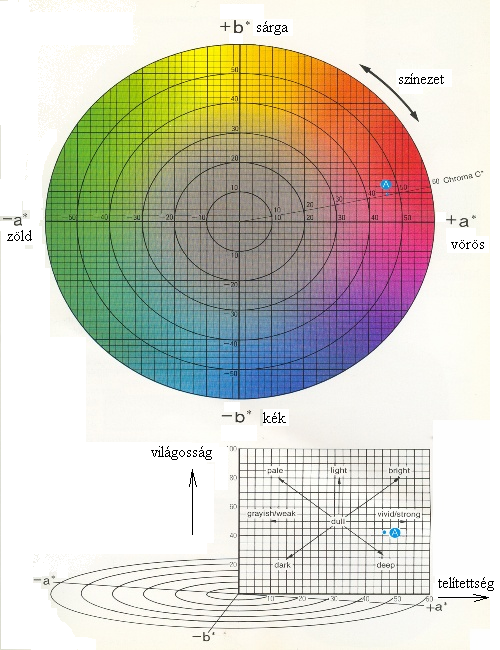
4.11.1.4. A 20°-os és a 100°-os CIE adatok
Az első színegyeztető méréseket a CIE szakemberei 2°-os látómezőben végezték, mivel a retinán 2°-on belül nem találhatók pálcikák, csak csapok, és így a színlátás 2°-on belül egyenletesnek tekinthető. A CIE 1931-es adatok tehát 2° látómezőre vonatkoznak.
1962-ben a CIE újabb mérések alapján újabb adatokat szabványosított. Ezeket az adatokat 10°-ban végzett mérések alapján hozták létre. Igaz, hogy 10°-ban a retinán a középrésztől kifelé fokozatosan egyre több pálcikát találunk, de a 10°-os látómező a gyakorlatban mégis jobban bevált, mert a színeket inkább 10°-ban és nem 2°-ban figyeljük meg. Ezek az adatok a CIE 1962-es néven ismeretesek.
4.11.1.5. A normál színmérő észlelő
Normál színmérő észlelőnek nevezzük azt a képzeletbeli személyt, akinek a színlátása kielégíti a CIE színmegfeleltető függvényeket.
4.11.1.6. A spektrális fényhatásfok függvény
A CIE színmérő rendszer egyik alap pillére a spektrális fényhatásfok függvény (relatív világossági vagy luminozitási függvény). Jele V(λ), de gyakran V λ – val is szokták jelölni. A V(λ) függvény a látórendszerünk által a spektrum színekhez (monokromatikus színekhez) rendelt világosság érzetet írja le. A nappali látó rendszer (a csapok) V(λ) függvénye eltér az esti látó rendszer (a pálcikák) V’(λ) függvényétől (4.59. ábra - A spektrális fényhatásfok függvény).
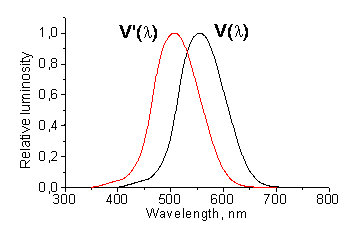
A nappali fotopicus látás V(λ) függvényének maximuma 555 nm-nél van, éppen ott, ahol a napsugárzás energia eloszlásának maximumát találjuk, Az esti scotopicus látás V’(λ) függvényének maximuma pedig a Hold fényének maximuma közelében, 507 nm-nél található. A szürkületi mezopikus látásnál a V(λ) és a V’(λ) függvény különböző arányú keverékeivel számolhatunk.
Az esti látás ~ 1600-szor érzékenyebb, mint a nappali látás
4.11.1.7. A Planck-féle fekete sugárzó („fekete test”)
A fényforrások színének mérésénél fontos szerepe van a Planck-féle fekete sugárzónak (fekete testnek). A fekete test sugárzása ugyanis a sugárzások spektrális teljesítmény eloszlásának etalonja. A Planck által létrehozott fekete test egyetlen példánya a National Physical Laboratory-ban, Párizsban található.
A fekete test olyan hőmérsékleti sugárzó, amely minden ráeső sugárzást teljesen elnyel, függetlenül a sugárzás hullámhosszától, beesésének irányától vagy polarizációs állapotától.
Megvalósítása: gondosan hőszigetelt, fekete belső felületű platina cső, indukciós fűtéssel.
A (4.60. ábra - A Planck sugárzó) ábrán a fekete test sematikus ábrája látható.
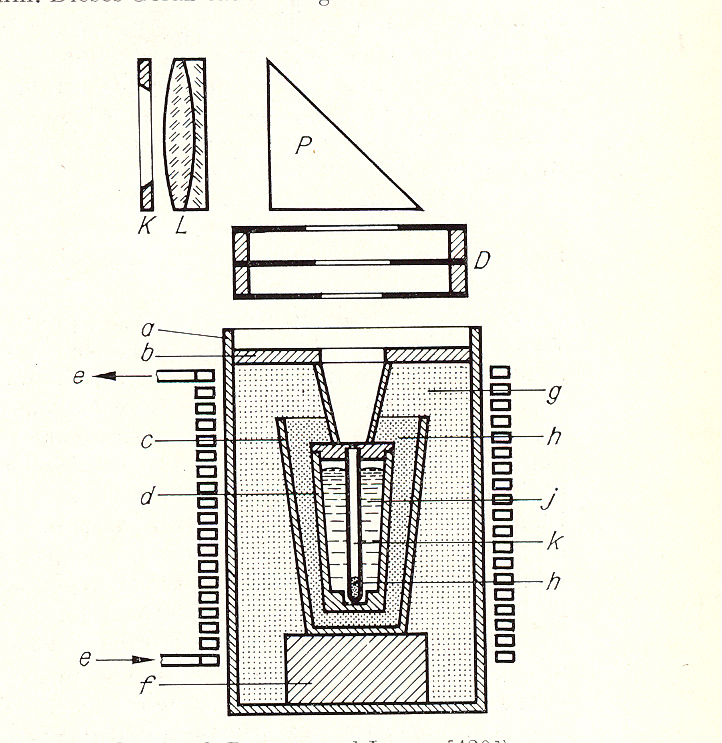
Az ábra jelölései:
|
a, b |
védőburkolat | |
|
c, d |
thorium tégely | |
|
e |
indukciós fűtés | |
|
f |
thorium tömb | |
|
h,g |
thorium zúzalék | |
|
j |
platina őrlemény | |
|
k |
sugárzó thorium-cső, F 2.5x45 mm | |
|
D |
blende rendszer | |
|
P |
optikai prizma | |
|
L |
leképező objektív | |
|
K |
blende |
A fekete test sugárzásának spektrális teljesítmény eloszlása a test T hőmérsékletétől függ az alábbi összefüggés („Planck-formula”) szerint:
|
M e,λ (λ,T) = c 1 λ -5 [exp (c 2 / λT) - 1] -1 |
Ahol
|
λ |
a hullámhossz | |
|
T |
a hőmérséklet, K fok | |
|
c 1 |
= 3,74150 * 10 -16 W*m2 | |
|
c 2 |
= 1,43879 * 10 -2 m*K |
A sugárzás spektrális teljesítmény eloszlása a hullámhossz függvényében különböző hőmérsékletek mellett a (4.61. ábra - A Planck sugárzó spektrális energia eloszlása) ábrán látható.
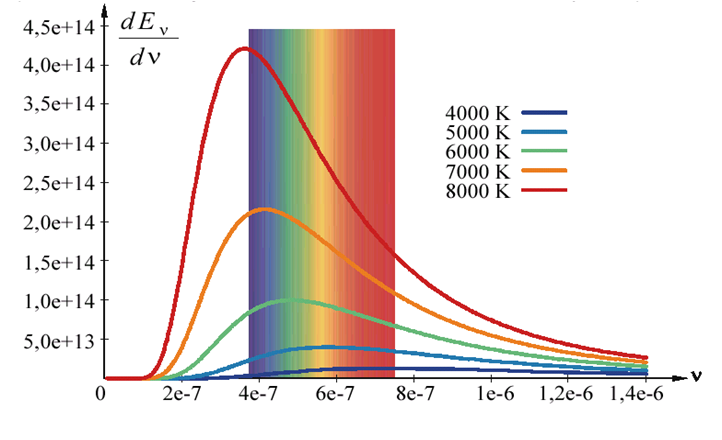
A fekete test színe a CIE színezeti diagramban is ábrázolható. A hőmérséklet függvényében a fekete test színe változó; alacsony hőmérsékleten (kb 1000 K° mellett) narancssárga, 3000 K°-nál sárga, 6000 K°-nál fehér, majd a még magasabb hőmérsékleteken kékes színű. A különböző színű pontokat a Planck sugárzó vonala köti össze (4.62. ábra - A Planck sugárzó vonala a papucs diagramban).
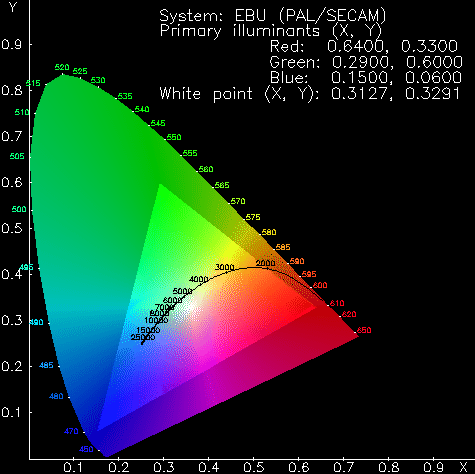
4.11.1.8. A színhőmérséklet
A fényforrások színének meghatározása a fekete sugárzóval való összehasonlítás alapján történik.
A színhőmérséklet a fekete sugárzó azon hőmérséklete, amelyen sugárzásának színessége azonos a jellemzett sugárzás színességével. (Figyelem! Csak folyamatos, a fekete sugárzóéhoz hasonló spektrumú sugárzó jellemezhető a színhőmérséklettel!) Ha az adott sugárzó színpontja a Planck sugárzó vonalára esik, a színhőmérsékletet a Planck sugárzó vonalán feltűntetett hőmérséklettel jellemezzük. A színhőmérséklet mértékegysége: K (Kelvin) – Vigyázat! Nem fok, csak Kelvin!
A különböző színhőmérsékletekhez tartozó színek a CIE színességi diagramban ábrázolhatók. Ezek a színek a Planck sugárzó vonalán találhatók.
Korrelált színhőmérséklet a fekete sugárzó azon hőmérséklete, amelynek színpontja a CIE színezeti háromszögben legközelebb található a jellemzendő sugárzás színpontjához. Ha az adott sugárzó színpontja nem a Planck sugárzó vonalára esik, akkor a Planck sugárzó vonaláig a megfelelő korrelációs egyenesen haladunk, és ahol a korrelációs egyenes metszi a Planck sugárzó vonalát, ott olvassuk le a korrelált színhőmérséklet értékét (4.63. ábra - A korrelált színhőmérséklet vonalai).
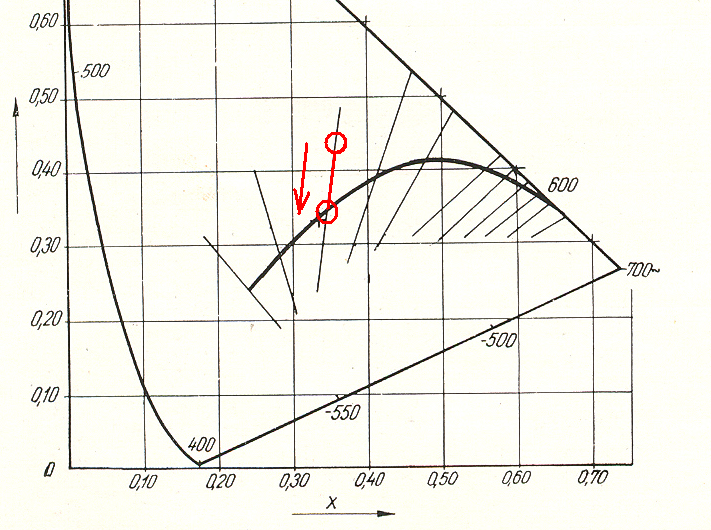
4.11.1.9. A szabványos CIE fényforrások
A színes felületet megvilágító fényforrás színe jelentősen befolyásolja a színes felületek színét. Ezért a CIE meghatározott néhány sugárzás eloszlást, amelyek mellett a méréseket végezni kell. Ezek a következők:
|
CIE A |
A 2855,6 K° hőmérsékletű fekete sugárzó megfelelője | |
|
CIE B |
A 4874 K korrelált színhőmérsékletű közvetlen napfény megfelelője | |
|
CIE C |
A 6774 K korrelált színhőmérsékletű nappali fény megfelelője | |
|
CIE D65 |
A 6504 K korrelált színhőmérsékletű nappali fény megfelelője |
4.11.1.10. A színvisszaadás
A színvisszaadás a fényforrások egyik fontos jellemző tulajdonsága, amely azt mutatja meg, hogy az adott fényforrás fényével megvilágított színes felület színei mennyire helyesen jelennek meg. Helyesnek tekintjük az egyenlő energia eloszlású fényforrással megvilágított felület színeit, és a fekete test fényével megvilágított felület színeit (függetlenül a Napfény pillanatnyi színhőmérsékletétől).
Definició szerűen a színvisszaadás az adott fényforrás és egy tökéletes színvisszaadású referencia fényforrás által megvilágított azonos színes felület színingereinek összehasonlításával jellemezhető. A színingerek képzésénél figyelembe kell venni a szem színadaptációját az adott fényforráshoz. A színvisszaadás jellemzője:
Egyedi színvisszaadási index, ez egyetlen színes felületre vonatkozik (Ri)
Általános szín visszaadási index, ez több színes felület egyedi színvisszaadási indexének átlaga (Ra)
Az általános színvisszaadási indexet tehát több színmintára meg kell határozni ahhoz, hogy ezekből egy általánosan jó értéket képezhessünk, a CIE 8 halványabb és 6 rikítóbb színmintát szabványosított.. Ezeket a színmintákat régebben zománc színetalonok formájában elküldték a fényforrás gyártóhoz, hogy minősíthesse a fényforrását. A szabványos CIE színminták:
|
CIE sorszám |
Munsell jelölés |
Szín |
|---|---|---|
|
1 |
7.5 R 6/4 |
fáradt rózsaszín |
|
2 |
5 Y 6/4 |
mustársárga |
|
3 |
5 GY 6/8 |
erős sárgászöld |
|
4 |
2.5 G 6/6 |
közepes sárgászöld |
|
5 |
10 BG 6/4 |
türkiz |
|
6 |
5 PB 6/8 |
világos piros |
|
7 |
2.5 P 6/8 |
világos ibolya |
|
8 |
10 P 6/8 |
orgonaszín |
Speciális igények esetére szolgál a további 6 színminta.
A szabványos CIE színminták színpontjai a CIE színezeti diagramban a (4.64. ábra - Az etalon színminták színpontjai) ábrán láthatók.
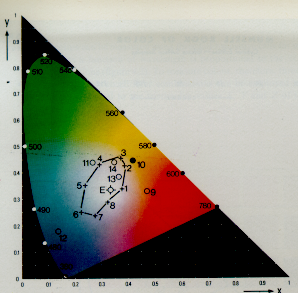
A (4.64. ábra - Az etalon színminták színpontjai) ábrán látható, hogy a színminták színpontjai a fehér-pont közelében vannak, tehát meglehetősen telítetlenek, fakók. A fakó színek spektrális reflexió görbéi lankásak, tehát a fényforrásnak a referencia-fényforrástól való eltéréseit nem mutatják ki érzékenyen, A hat speciális színminta már élénkebb színekből áll, ezért a fényforrásokat ezekkel szigorúbban lehet minősíteni.
Az Ra általános színvisszaadási indexet az Ri egyedi színvisszaadási index átlagaként lehet meghatározni:
|
Ra = 1/n (Σ Ri) |
Az Ra színvisszaadási index számítással történő meghatározása az alábbi folyamatábra szerint történik (4.65. ábra - A színvisszaadási index számítási módszere):
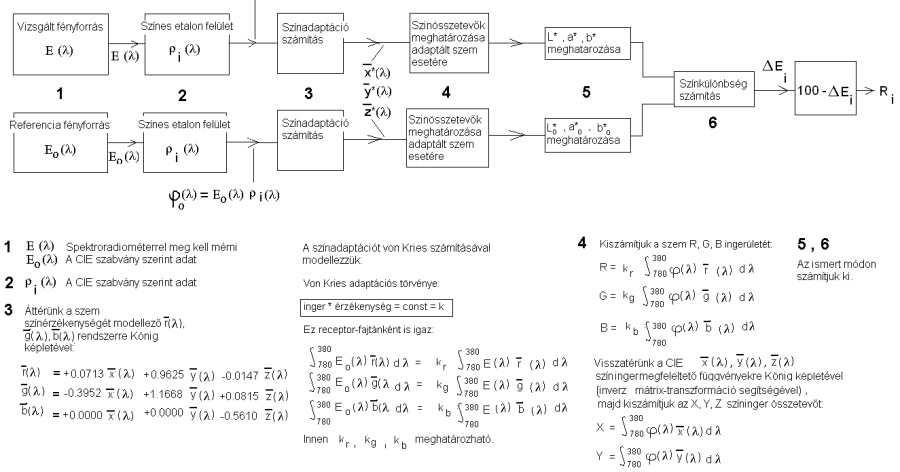
Az Ri meghatározásához nincs is szükség magukra a színmintákra, csupán spektrális reflexiójukra. A vizsgált fényforrás spektrális teljesítményeloszlásából és a referencia fényforrás spektrális teljesítményeloszlásából, továbbá a vizsgált színminta spektrális reflexiójából számítástechnikailag meghatározhatjuk a színkülönbségre jellemző ΔE értékeket.
Az egyes színmintákra vonatkozó ΔE értékeket 100-ból levonva kapjuk meg az (Ri) értékeket.
Az (Ri) értékek átlagaként meghatározható az Ra értéke.
|
Ra = 1/8 ΣRi | ||
|
i = 1…8 |
4.11.2. Színminta gyűjtemények és színminta alapú szín rendszerek
A gyakorlati élet igen sok területén, például a festék-,textil- és konzerviparban, az építészetben és az iparművészetekben elterjedten alkalmazzák a színminta alapú szín meghatározási, színmérési módszereket. Ezeknek a módszereknek nagy előnye, hogy a színeket közvetlenül, vizuálisan minősíteni lehet.
Különbséget kell tennünk a színminta gyűjtemény és a színrendszer fogalma között.
Színminta gyűjteménynek nevezzük a különböző festék-, textil-, porcellán és egyéb színes termékeket gyártó cégek tájékoztató jellegű színmintáinak gyűjteményét. Ezeket a mintákat valamilyen kódrendszerrel vagy megnevezéssel is meg szokták jelölni. A minták közötti színezet-, világosság- és telítettség közötti különbség nincs tudományos rendszerességgel beállítva, hanem a minták színe többé-kevésbé esetleges.
Színmintákon alapuló színrendszernek azokat a rendszereket nevezzük, amelyek alapját néhány jól definiált, reprodukálhatóan előállítható és stabil színű színminta képezi (ezek a színrendszer etalonjai), és a színrendszer többi színe ezekből szintén reprodukálható módon és érzet szerint lehetőleg egyenletes különbségekkel előállítható.
A továbbiakban a legismertebb színminta gyűjteményeket illetve színmintákon alapuló színrendszereket ismertetjük.
4.11.2.1. A Munsell színminta atlasz és színrendszer (1929)
Albert H. Munsell egy több ezer színmintából álló gyűjteményt hozott létre.
Munsell (1859-1918) amerikai festőművész volt, rajzot, művészi kompozíciót és anatómiát tanított a Massachusetts Normal Art School-on. Színminta gyűjteményének tagjait kézzel festették, és kézzel ragasztották kartonlapokra. Ez utóbbi műveletet mind a mai napig kézzel végzik. A Munsell színminta atlasz a legpontosabb, legmagasabb minőségű (és legdrágább) színminta gyűjtemény. Színmintáinak színét több mint egy évszázadon keresztül változatlanul elő tudják állítani. Természetesen, mint minden festett színes felület, ezek a színminták is fakulhatnak, piszkolódhatnak magas hőmérséklet, nedvesség vagy fény hatására, ezért lehetőleg légkondicionált helyen, sötétben kell tárolni azokat.
A Munsell színminta atlasz szín észleleten alapul, így három szín-jellemzője a Munsell-világosság, a Munsell-színezet és a Munsell-króma, ez utóbbi a telítettség megfelelője.
A Munsell-világosság a felület-színek fényvisszaverő képessége olyan skálán, amely 0-tól 10-ig terjed. A tökéletesen elnyelő (ideális fekete) felület Munsell-világossága 0, míg a tökéletesen szórtan visszaverő (ideális fehér) felületé 10. A két szélsőérték között a skála vizuálisan egyenközűnek látszik. A Munsell világossági skála az egész világon elfogadott legegyenközűbb világossági skála! A világosság jele az angol Value szóból V. Az akromatikus (szürke) színeket a Munsell Atlaszban N betűvel jelölik, a Munsell-világossági skála közepén lévő akromatikus színminta jele N 5,0.
Általában a szürke színek nem teljesen neutrálisak, hanem van valamilyen enyhe színességük, vagyis Munsell-krómájuk nem teljesen 0,0. Ha egy színminta Munsell-krómája kisebb 0,5-nél, akkor N szürke besorolást kap, de jelzésében egy / jel után zárójelbe írják a 0,0-tól eltérő Munsell-króma értékét és színét. Például N = 8,7/(B0,3) egy kicsikét kékes tónusú szürke színt jelent.
A Munsell-króma a felület-színek jellemzője. Definíciója szerint a Munsell-króma az ugyanolyan Munsell-világosságú akromatikus (0 krómájú) színtől mért távolság olyan skálán, amelynek osztása ( a Munsell-színezettől függetlenül) érzékelés szerint közel egyenletes. Jele az angol Chroma szóból Ch. Bizonyos mértékben a Munsell-króma a telítettséggel korrelációban van. A telítettség legnagyobb értéke mindig 100 %, de ezt az értéket a gyakaorlatban egyetlen festett színminta sem éri el, mert a festékek szinezékeinek mindig van egy kis szennyezettsége. A Munsell-króma elérhető maximuma mindig függ a színezettől és a világosságtól is.
A Munsell-színezet a színészleletnek megfelelő tulajdonságot jellemzi. Jele az angol Hue szóból H.
A Munsell színminták színei szigorú rendszer szerint követik egymást. A Munsell-színezeti skála 5 alapszínből és 5 keverék-színből áll. Az alapszínek és a keverék-színek között még további 10-10 színárnyalat helyezkedik el, így a Munsell-színezet összesen 100 színárnyalatot különböztet meg. Az alapszíneket és a keverék-színeket a következő képen jelölik:
|
R |
vörös |
(red) |
|
YR |
sárgáspiros |
(yellow-red) |
|
Y |
sárga |
(yellow) |
|
GY |
zöldessárga |
(green-yellow) |
|
G |
zöld |
(green) |
|
BG |
kékeszöld |
(blue-green) |
|
B |
kék |
(blue) |
|
PB |
liláskék |
(purple-blue) |
|
P |
bíbor |
(purple) |
|
RP |
pirosaslila |
(red-purple) |
A Munsell-színeket egy szín-kör mentén szokták elhelyezni (4.66. ábra - A Munsell-színkör 10 alapszíne és 4.67. ábra - A Munsell alapszínek jelei).

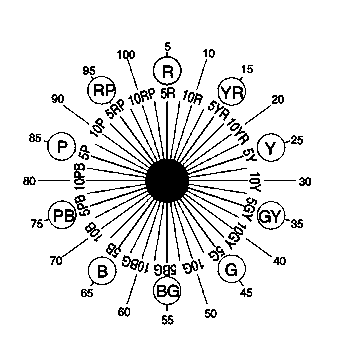
A Munsell színminta gyűjtemény teljes ábrázolása azonban csak három dimenziósan lehetséges, mivel három színjellemző szerint kell rendezni a színeket. Ha a szín-körre merőlegesen ábrázoljuk a színminták világosságát, akkor egy hengeres szín-testhez jutunk. Ennek külső palástján helyezkednek el a legtelítettebb színek, lent a sötét, fent a világos árnyalatok és körben a különböző színezetek. A henger tengelyén helyezkednek el az akromatikus (szürke) színek a feketétől a fehérig, a henger belsejében pedig belülről kifelé az egyre telítettebb színek (4.68. ábra - Egy szabályos hengeres szín-test).
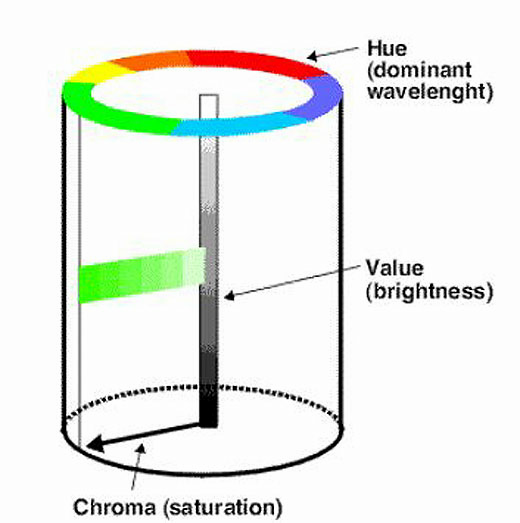
A valóságos Munsell szín-test viszont nem lesz olyan szabályos, mint a 4.68. ábra - Egy szabályos hengeres szín-test, mert teljesen telített árnyalatokat nem tartalmaz. Nem is tartalmazhat, mert ilyeneket nem lehet előállítani. Teljesen tiszta pigmenteket ugyanis nem lehet gyártani, mindig van bennük több-kevesebb szennyezés, ami telítetlenebbé teszi a festéket (4.69. ábra - Reálisan megvalósítható színek háromdimenziós képe).
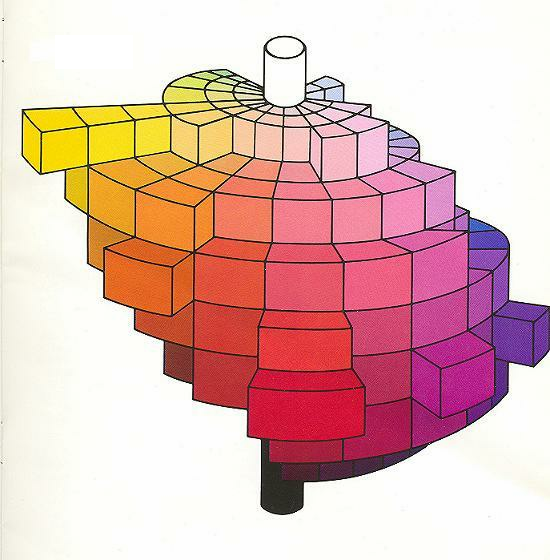
4.11.2.2. Az NCS (Natural Color System) színrendszer (1979)
Ezt a színrendszert elsőként a német fiziológus, Ewald Hering dolgozta ki, és Svédországban vezették be 1979-ben. Alapja a három opponens szín-pár: fekete-fehér, vörös-zöld és kék-sárga. Ezek alapján 40 színárnyalatot és azon belül 10-10 fokozatot, tehát összesen 400 színt definiáltak. Az NCS színkör a (4.70. ábra - Az NCS színkör) ábrán látható.
Az NCS színrendszert 4 alap-színre építették fel, ez az érzet szerinti 2-2 ellentétpár, vagyis a vörös és a zöld, valamint a sárga és a kék. Ezek közé 9-9 átmeneti színárnyalatot helyeztek el, így az NCS színkörön összesen 40 alapszínt találhatunk. Ezeknek fehérrel vagy feketével kevert árnyalatai alapján az NCS színminta gyűjtemény több ezer színárnyalatból áll.
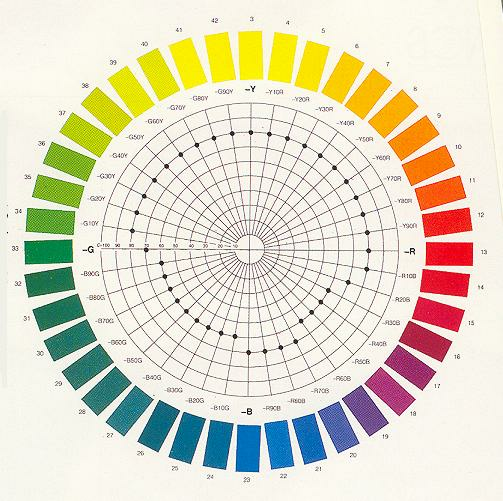
A színminta gyüjtemény festett színmintáit egy album lapjain helyezték el. Minden színárnyalat külön lapra került, amelyen a minták világossága alulról felfelé 100 fokozatban változik, míg telítettsége a bal oldali függőleges világossági tengelytől kifelé fokozatosan növekszik. Ezen a tengelyen találhatók a neutrális (szürke) színek (4.71. ábra - Az NCS Színatlasz egyik lapja).
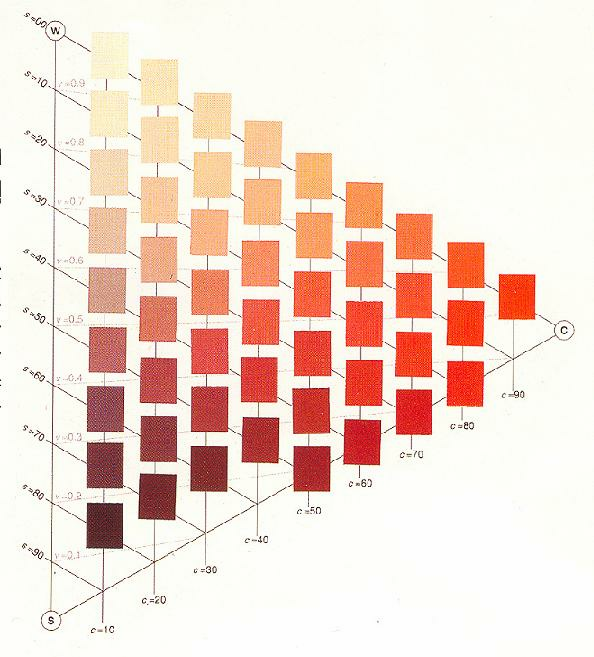
Az NCS szín-test a világossági tengelyre felfűzött színes lapok összessége, tehát egy kúpos forgástest
A színeket az NCS-ben is színezetükkel, világosságukkal és telitettségükkel jellemzik. Például:
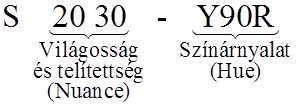
Ahol
S a telítettséget jelenti. Ezt a függőleges világossági tengelytől való távolsággal jellemzik,
A 2030 szám azt jelenti, hogy az adott színminta világossága a felülről lefelé növekvő számozású világossági tengely 20-as számánál található, míg telítettsége a függőleges világossági tengelytől kifelé növekvő számozás szerint a 30-as számnál van,
Az Y90R pedig azt jelenti, hogy a színminta színezete a sárga és vörös színminta között, a sárgától 90 egységre (míg a vöröstől 10 egységre) található, tehát erősen vörösessárga színárnyalatú).
4.11.2.3. Az Ostwald színrendszer (1931)
Ostwald színrendszere az első tudományos igényű, harmóniákon alapuló színrendszer.
Wilhelm Friedrich Ostwald (1853-1932) - német származású, Nobel-díjas kémikus - nyugdíjas éveiben sok egyéb között színtannal is foglalkozott. Az Ostwald-féle színatlasz 1917-ben jelent meg.
A színrendszer 24 tiszta, a lehető legszínezet-dúsabb festékkel festett alapszínre épül fel. Ezek 1:4, 2:4 ill. 3:4 arányú keverékeiből további 3-3- színárnyalat hozható létre. Így a teljes színkör összesen 96 tiszta (azaz maximálisan színezet dús) alapszínből áll. Ebben a színkörben egymással szemben találhatók a kiegészítő színek, amelyeknek additív keveréke fehér vagy szürke színt eredményez (4.72. ábra - Ostwald színköre. A szemben elhelyezkedő színek kiegészítő színek.). Például az 1. szín a 13-nak, a 3. szín a 15-nek kiegészítő színe. A kiegészítő színek harmonikus színpárt alkotnak.
A tiszta színekből fehér és fekete hozzáadásával hozhatók létre a világosabb illetve a telítetlenebb színek. Az Ostwald Szín-Atlasz egy-egy lapján az egyik alapszínhez tartozó, fehérrel illetve feketével kevert színárnyalatok találhatók. Ezek – éppen úgy, mint az NCS színrendszerben - a függőleges világossági tengelyre támaszkodó háromszögben helyezkednek el. A tengelytől kifelé haladva itt is az egyre telítettebb színek találhatók, az alsó részen a feketével kevert sötétebb, a felső részen a fehérrel kevert világosabb színárnyalatok helyezkednek el. A kiegészítő színek gyűjtőlapjai egymással szembe kerülnek (4.72. ábra - Ostwald színköre. A szemben elhelyezkedő színek kiegészítő színek.).
A színkör színei a CIE színezeti diagramban a (4.74. ábra - Ostwald színkörének alapszínei a CIE színezeti diagramban) ábrán láthatók. Az ábra alapján úgy tűnik, mintha az alapszínek közötti különbség helyenként nagyon kicsi, máshol nagyon nagy volna. Ez azonban a CIE színezeti diagram nem-linearitásából ered (l. MacAdam ellipszisei, 4.11.1.2. szakasz - A CIE xyY színrendszer fejezet).
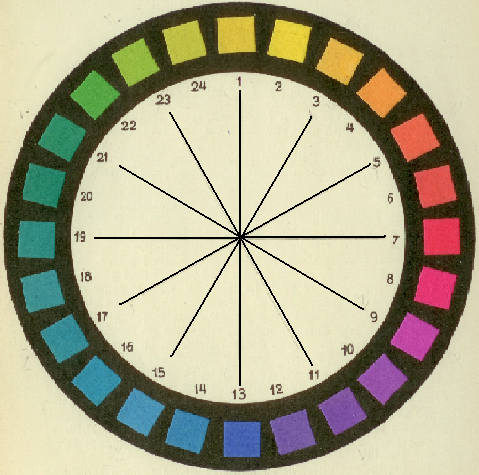

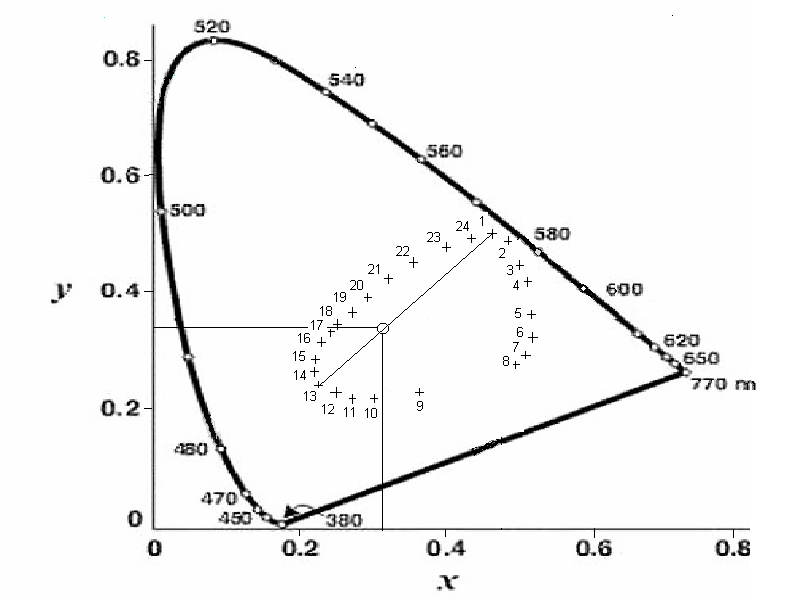
Ostwald színköre alapján egyszerűen választhatunk ki egymással harmonikus összeállítást alkotó színeket. A harmonikus színpárok a kiegészítő színek, ezek a (4.72. ábra - Ostwald színköre. A szemben elhelyezkedő színek kiegészítő színek.) ábrán láthatók. Egymással harmonizáló 3 - 3 színt a 4.75. ábra - Harmonikus színhármasok alapján, egymással harmóniában álló 4 - 4 színt a 4.76. ábra - Négyes színharmóniák alapján választhatunk ki.
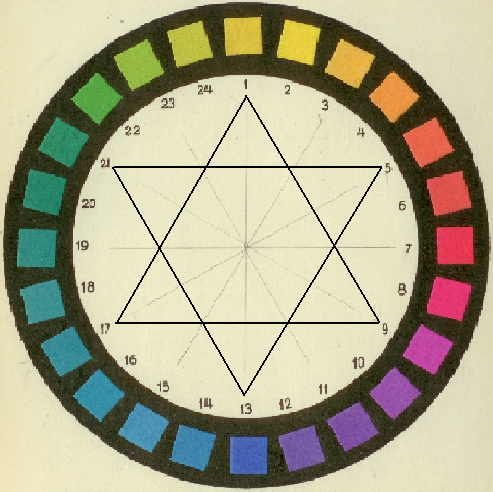
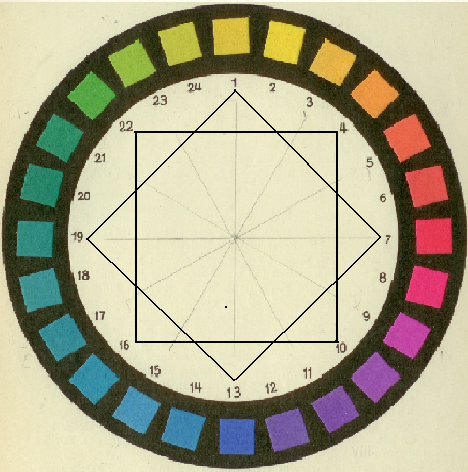
4.11.2.4. A Coloroid színrendszer
A Coloroid színrendszert a magyar Nemcsics Antal fejlesztette ki - elsősorban építészeti alkalmazás céljára. Dr. Nemcsics Antal festőművész, a Budapesti Műszaki Egyetem emeritus professzora. Színdinamika című könyvét 9 országban adták ki. A Coloroid színrendszert az egész világon ismerik és alkalmazzák.
A Coloroid színrendszer az additív színkeverésen alapul. A színeket a határszínből (az adott alapszínből elérhető legtelítettebb színből) valamit fehérből és feketéből kevert színként kezeli. Ezen összetevők arányából határozhatók meg a Coloroid színrendszer színkoordinátái. A Coloroid színrendszer háromdimenziós színeit (színezet, fehér tartalom, fekete tartalom) a Munsell színrendszerhez hasonlóan henger-kordináta rendszerben lehet ábrázolni.
A színezetek a henger kerülete mentén körben helyezkednek el. A Coloroid 48, egymástól esztétikailag egyenlő, de ábrázolás technikailag nem egyenlő távolságban lévő alapszíne a 4.9.2.4.1. ábrán látható. A 8 alapszín jele 10 sárga, 20 narancs, 30 vörös, 40 bíbor, 50 viola, 60 kék, 70 hideg zöld, 80 meleg zöld. Ezek között 6-6 átmeneti színárnyalat található, egymástól esztétikailag megközelítően egyenlő távolságban. Így az alapszínek száma összesen 48.
A szürke színek a COLOROID színrendszer hengeres színterének hossztengelyében helyezkednek el.
A szürke skála Coloroid jelzőszáma egész szám 1-től 100-ig.
A szürke skála bármely tagjának Coloroid jelzőszámát tízzel osztva, majd az eredményt négyzetre emelve megkapjuk az adott szín CIE Y színösszetevőjét (CIE világosságát).
A fekete jele 0, a fehéré 100.
A COLOROID színrendszer alapszínei a CIE színezeti diagramban a 4.78. ábra - A COLOROID alapszínek jellemző hullámhossza a CIE színezeti diagramban és a 4.79. ábra - A COLOROID alapszínek színkoordinátái a CIE színezeti diagramban ábrán láthatók. A (4.78. ábra - A COLOROID alapszínek jellemző hullámhossza a CIE színezeti diagramban) ábrán a jellemző hullámhosszak, a (4.79. ábra - A COLOROID alapszínek színkoordinátái a CIE színezeti diagramban) ábrán az x és y színkoordináták vannak feltűntetve.
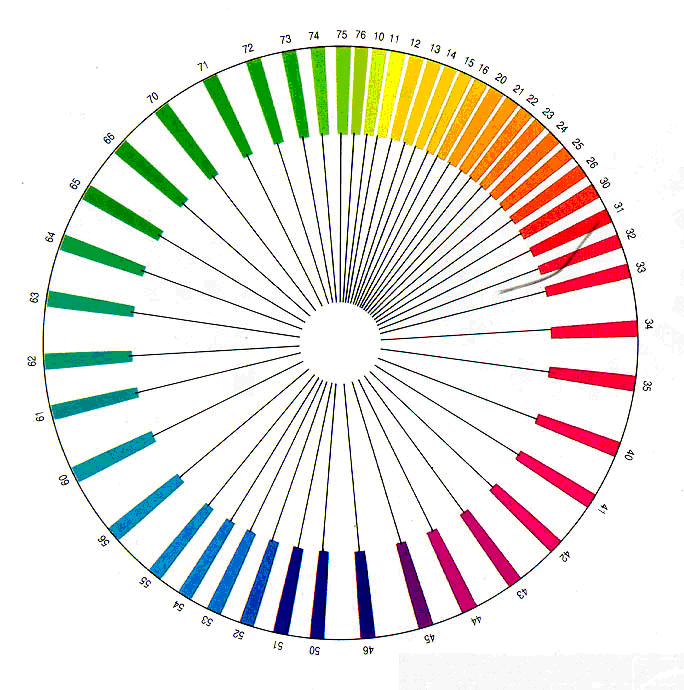
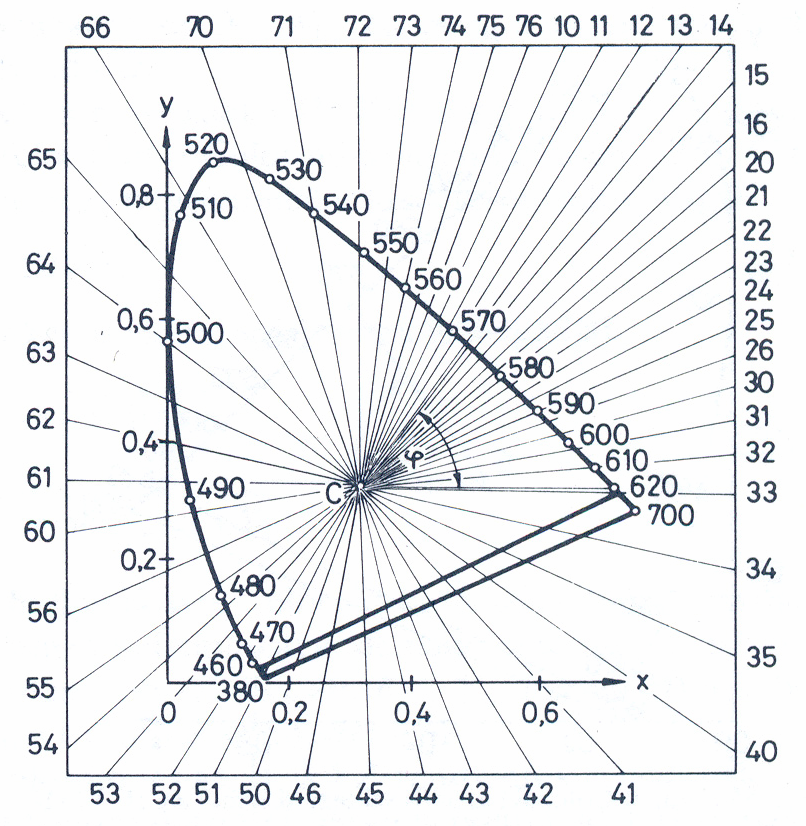
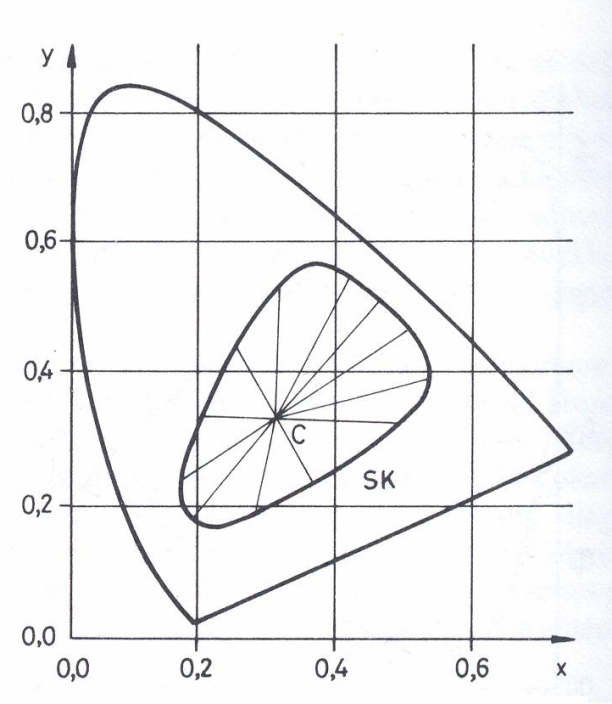
A telítettség a henger belsejében a sugarak mentén, belülről kifelé növekvő értékekkel találhatók. A telítettségi fokozatok száma 100.
A világosság változása a függőleges tengely mentén, alulról felfelé növekvő értékekkel ábrázolható (4.78. ábra - A COLOROID alapszínek jellemző hullámhossza a CIE színezeti diagramban). A színtelen (akromatikus) tengely egyik végpontján, legfelül, a tökéletesen fehér, másik végpontján, legalul, a tökéletesen fekete szín helyezkedik el.
A Coloroid színrendszer határszínei nem érik el a színteste elméletileg határoló (100 egység telítettségű) hengerpalást pontjait. A tökéletesen fehér és a tökéletesen fekete színnél e színtest a vízszintes metszetben egyetlen ponttá zsugorodik (4.80. ábra - A COLOROID színtest).

A Coloroid színkörön a kiegészítő (komplementer) színek egymáshoz képest 180° -ban találhatók. A színrendszer segítségével különböző harmonikus színösszeállítások tervezhetők, ezért ezt a színrendszert az építészek, belső építészek, iparművészek széles körben alkalmazzák.
A keverék színek szín-atlaszát nyomdatechnikai úton is előállították. Digitális változata is elkészült.
A Coloroid színrendszer színmintái közül csak a 48 határszín készült el festett formában. A keverék-színeket egy additív színkeverő berendezéssel lehet előállítani. A színkeverő berendezés a 48 határ-színmintán kívül fehér és fekete határ-színt is tartalmaz. A színes minták egy kör alakú tárcsán helyezkednek el, és egyenként beforgathatók a fény-útba. A színkeverő berendezés egy szabványos fényforrást is tartalmaz. A beállított additív keverékszín egy osztott éles látómező egyik oldalán jelenik meg, míg másik oldalán az azonos fényforrással megvilágított mérendő minta látható, amelyre a műszert rá kell helyezni.
4.11.2.5. A RAL színtervezési rendszer
A RAL Tervezési Rendszert 1976-ban a CIE (Comission International d'Eclairage) dolgozta ki. Ez a rendszer szakmai színtervezéshez lett kifejlesztve. 1688 színt tartalmaz, rendszerbe szervezve. Mindegyik 7 számjegyű színárnyalat különálló RAL színként van definiálva. Ezek jelzik a technológiailag mért színárnyalati, fényességi és színtelítettségi értékeket.
A RAL színkör 360 színárnyalatot tartalmaz. A RAL Tervezési Rendszerben a színek színárnyalat, fényesség és színesség szerint vannak rendszerbe foglalva. A 4.81. ábra - A RAL színtest mutatja a RAL Tervezési Rendszer térbeli felépítését. Ebben a színárnyalatok a spektrális színek sorrendjében körben vannak elrendezve, az elnevezés a szög-nagyságok alapján történik. Így a piros 00-nál (=3600) indul, a sárga 900-nál, a zöld 1800-nál és a kék 2700-nál.
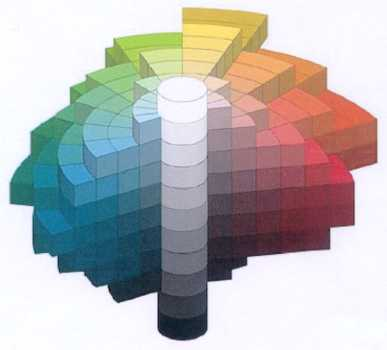
A különböző világossági értékek, amelyeknél még meg lehet egy-egy árnyalatot különböztetni, a különböző szintekhez síkokon kerülnek elhelyezésre. A 4.82. ábra - A RAL színkör egy színsíkkal mutat egy ilyen síkot. A központokon keresztül fut a színtelen tengely (4.82. ábra - A RAL színkör egy színsíkkal), amely egyúttal a világosságot is megadja. Ez a 0-nál feketével kezdődik, amely folyamatosan világosodva vált a szürke árnyalataira, majd végül 100-nál a fehérben végződik.
Az egyes színárnyalatok közti eltérést a CIELAB színárnyalat standard formái révén definiálták, amely a DIN 6174-ben is rögzítésre került.
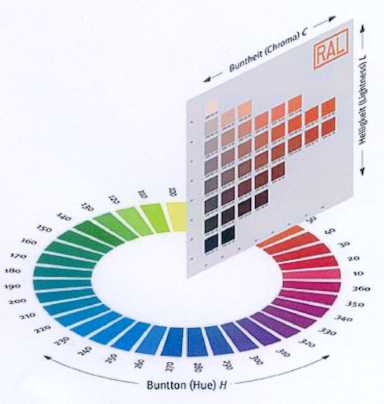
Egy 210 60 30-as RAL szín jelenti például a 210-es színárnyalatot, 60-as fényességgel és 30-as színtelítettséggel. Ha például ezt a színárnyalatot világosabbal szeretnénk kombinálni, akkor választhatjuk a RAL 210 70 30-ast. Ezáltal egy 70-es fényességű szintet kapunk. A színárnyalat másik két paramétere változatlan marad.
A RAL színmintákat az egyszerű gyakorlati alkalmazás kedvéért legyezőszerűen kinyitható kártyák formájában szokták gyártani (4.83. ábra - RAL színkártyák).

4.11.2.6. Jean Bourges digitális színrendszere
Jean Burges amerikai designer, reklámgrafikus. Színrendszerének alapgondolata a monitoron történő színtervezés és nyomdaipari színmegjelenítés összehangolása volt.
Ez a színrendszer a színes nyomtató három alapszínére (C, M, Y) épül fel. Ezáltal a színes nyomtató teljes gamutját kihasználja.
Jean Bourges színrendszerében a színeket 4 csoportba sorolja (vörösek, sárgák, zöldek és kékek). Minden csoportban 5-5 színátmenet található, így az alapszínek száma 20.
A kiegészítő színek Jean Bourges színkörében is egymással szemben találhatók (4.84. ábra - Jean Burges színköre).
Jean Burges szín-terének gamutja nagyobb, mint a többi színminta gyűjteményen alapuló színrendszeré. Ennek oka az, hogy Jean Bourges szín-terét a monitoron megjeleníthető és a színes nyomtatókon kinyomtatható színek határolják, míg az összes többinek az alapszínei festékekkel festett színminták. Ezek színei soha nem olyan színezet dúsak, mint a monitor vagy a nyomtatók alapszínei, (például az Ostwald színrendszer gamutja a (4.74. ábra - Ostwald színkörének alapszínei a CIE színezeti diagramban) ábrán, vagy a Coloroid színrendszer gamutja a (4.79. ábra - A COLOROID alapszínek színkoordinátái a CIE színezeti diagramban) ábrán).
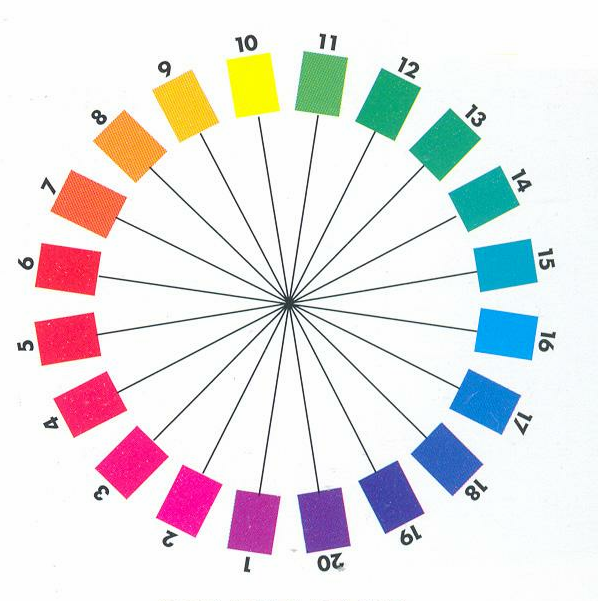
A színkör színei a CIE színezeti diagramban a (4.85. ábra - Jean Burges színrendszerének alapszínei a CIE színezeti diagramban) ábrán láthatók. Ennek a színrendszernek a gamutja valóban nagyobb az előzőekben ismertetett színrendszerekénél.
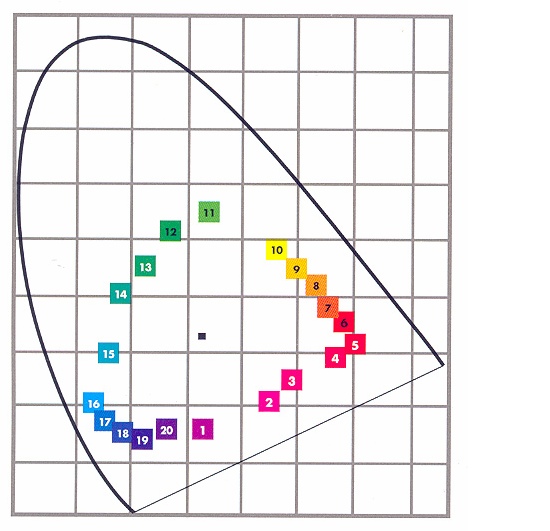
A 20 színárnyalatot 10 fokozatban világosítja. Minden szín C, M, Y és K színjellemzőjét megadja (4.86. ábra - Színárnyalatok 10-10 fokozatban). A számadatok alkalmazásához a nyomtató alapszíneit be kell kalibrálni.
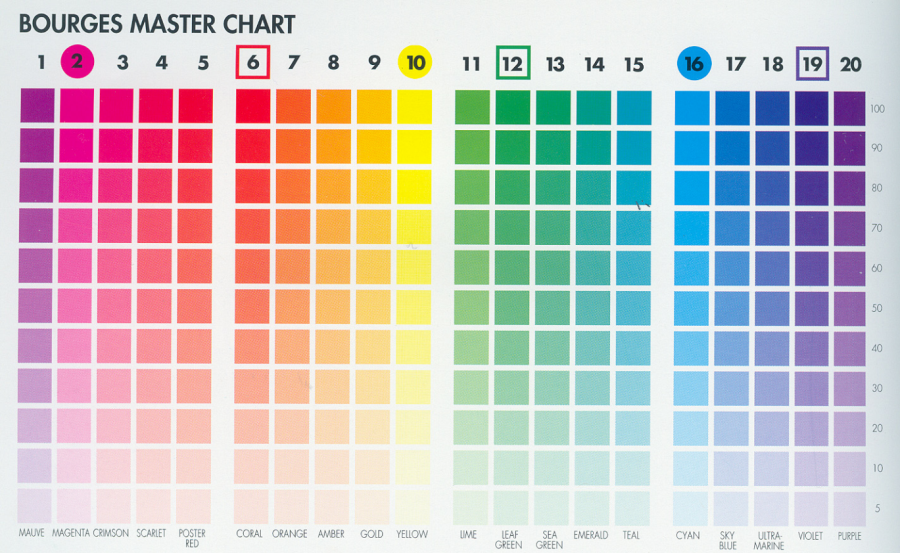
Jean Bourges azt javasolja, hogy négy kiegészítő színből állítsunk össze színharmóniákat, mindig az azonos világosságú illetve fekete tartalmú fokozatokat
4.11.2.7. A színminta gyűjtemények
Pantone szín táblázat
A Pantone szín táblázatot a számítógépi grafikai tervezésnél használják.
Ez egy referencia táblázat. A színek a különböző számítógépeken másként jelenek meg. Ez függ a grafikus kártyától, a monitortól és az operációs rendszertől és annak
beállításától, így a monitoron megjelenő PANTONE táblázat is csak tájékoztató jellegü.
Egyéb színminták.
A színes termékek gyártói általában elkészítik a saját termékeik színválasztékát bemutató színminta gyűjteményüket (Pl. Tikkurila). Ezek a színminták akkor hitelesek és használhatók, ha ugyanabból az anyagból készülnek, mint az adott színes termék. Így ismertek bőrből, textilből, falfestékből, fából, stb. készült színminták. A teljesen meggyőző színbemutatáshoz az is fontos, hogy a színminta felülete, érdessége és a hordozó anyaga is olyan legyen, mint amilyen a felhasználónál lesz.
4.12. A színmérés
A színek mérése megoldhatatlan feladatnak tűnhet, hiszen – mint láttuk – a szín pszichofizikai mennyiség, tehát valami, amit mai tudásunk szerint közvetlenül nem, csupán közvetve lehet mérni.
Galileo Galilei (1564-1642) tanácsa az ilyen megoldhatatlannak tűnő feladat megoldására a következő volt:
|
“Ami számítható, azt számítsd ki; ami mérhető, azt mérd meg; és ami nem mérhető, azt tedd mérhetővé!” |
Éppen ezért a műszeres mérési módszerekkel nem a pszichofizikai színt mérjük meg, hanem az azt kiváltó φ(λ) szín ingert, és ebből számítástechnikai úton határozzuk meg, hogy milyen szín észleletet válthat az ki az átlagos („normál”) színlátóból.
4.12.1. A szín inger függvény
Amint azt korábban láttuk, a ɸ(λ) színinger függvényt
a fényforrás színe (Φ e (λ) spektrális teljesítmény eloszlása),
a fényforrás által megvilágított színes felületek színe (ρ(λ) spektrális reflexiója) és
a fény útjába kerülő színszűrők színe (τ(λ) spektrális transzmissziója) együttesen alakítja ki:
|
φ (λ) = Φ e (λ) * ρ(λ) * τ (λ) |
A ɸ(λ) színinger váltja ki a szemben a szín érzetet és végül agyunkban a szín észleletet:
4.12.2. A színmérés elve és műszerei
A színek mérésére három mérési elv ismeretes:
Színmintákkal történő összehasonlítás
Spektrális mérés
Tristimulusos mérés
A színek mérésére színmérő műszereket alkalmazunk. Az alkalmazott mérési elv szerint ezek is három félék lehetnek:
Vízuális színmérő műszerek
Spektrofotométeres színmérő műszerek
Tristimulusos színmérő műszerek
A színmérő műszereket a mérendő mennyiség alapján is meg szokták különböztetni:
Színes felületek színének mérése (reflexiós színmérő műszerek)
Színes, átlátszó közegek (színes folyadékok, színszűrők, színes szemüvegek) színének mérése (Transzmissziós színmérő műszerek)
Színes fények színének mérése (spektroradiométerek)
A leggyakoribb feladat a színes felületek színének mérése.
4.12.3. A felületek reflexiójának térbeli eloszlása
A felületek színét spektrális reflexiójuk és a megvilágító fényforrás színe határozza meg.
A felületek felszínének struktúrájától nagymértékben függ a reflexió térbeli eloszlása. Elméletileg kétféle reflexió létezik: a tükrös és a diffúz reflexió. A gyakorlatban azonban mindig a kettő kombinációjával találkozunk (4.87. ábra - Felületek reflexiójának típusai).
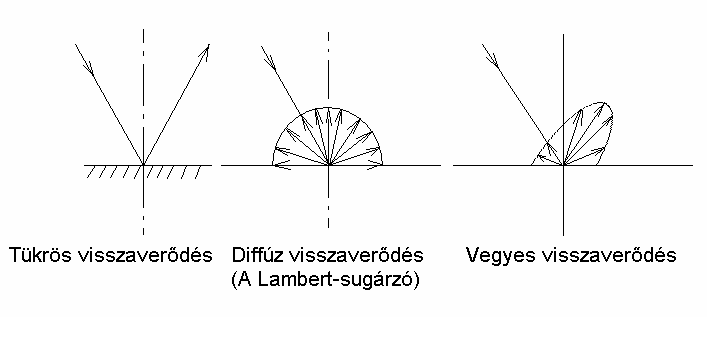
A tükrös reflexió csak a fényforrás fényét továbbítja, míg a felület színének információja csak a diffúz részben található meg. Ezért színmérésnél mindig törekedni kell arra, hogy a tükrös hányad ne jusson a detektorra, és valóban kizárólag a diffúz reflexiót mérjük..
A színmérés szabványos mérési geometriái a (4.87. ábra - Felületek reflexiójának típusai) ábrán láthatók.
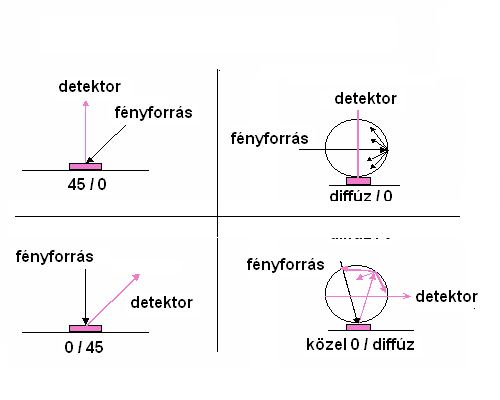
|
45 / 0 |
a megvilágítás 45°-os, a mérés a felületre merőleges irányú | |
|
0 / 45 |
a megvilágítás a felületre merőleges irányú, a mérés 45°-ban történik | |
|
diffúz / 0 |
a megvilágítás egy diffúz felületről történik, a mérés a felületre merőleges irányú | |
|
0 / diffúz |
a megvilágítás a felületre merőleges irányú, a mérés egy diffúziós felületről történik. |
A diffúz megvilágítást matt fehér belső felületű gömbbel, ún. Ulbricht gömbbel hozzák létre (4.89. ábra - Diffúzor gömb).
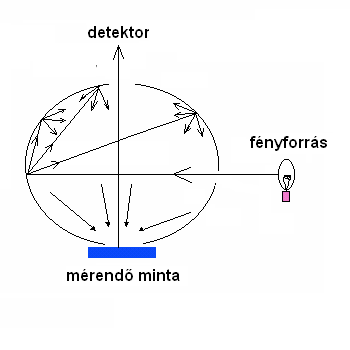
A geometriai optika egyik alaptörvénye szerint a fénysugár útja mindig megfordítható. Ezért azt gondolhatnánk, hogy a szabványos mérési geometriák közül pl. a D/0 alkalmazása teljesen ugyanolyan mérési eredményt ad, mint a 0/D. Ez azonban nem így van; egy kis különbség mindig adódik. Egy színmérési adat mellett ezért mindig meg kell adni, hogy milyen mérési geometriával készült.
4.12.4. A látómező látószöge
Nem mindegy az, hogy a felület diffuz reflexiójából mekkora rész jut be a mérőműszerbe. Ezért meg kell adni, hogy a mérés milyen látószögben történt. Általában 2°-os vagy 10°-os látómezővel mérünk, és ennek megfelelően a mérési adatok kiértékelésénél a CIE 2°-os vagy a CIE 10°-os adataival kell számolni.
4.12.5. Színmérési módszerek
4.12.5.1. Színmintákkal történő összehasonlítás
A színmintákkal történő összehasonlítást jó színlátású emberek végzik, tehát ez vizuális mérési módszer.
Az emberi szem rendkívüli fényérzékenysége a legjobb fénymérő műszerekkel vetekszik. A legérzékenyebb fényérzékelő, a photomultiplier elméletileg már egyetlen fotont is érzékelni tud. Dr. Bárány Nándor véleménye szerint szemünk pedig 2 foton érzékelésére képes. Ez a biológiai érzékelők gazdaságosságát is mutatja: egy foton beérkezése lehet véletlen, de ha ugyanarra a receptorra két foton érkezik be egyidejűleg, akkor ez már valószínűleg nem véletlen, tehát érdemes érzékelni.
Az emberi szem a színérzékelésben is nagyon jó. Azonban igazán jó teljesítményt csak a színkülönbségek érzékelésében tud nyújtani, abszolút értékeket nem tud mérni. A színkülönbséget akkor tudja legérzékenyebben észre venni, ha a két szín egymás közelében, lehetőleg egymás mellett van.
A színes felületek színét a felület spektrális reflexiója és a megvilágító fényforrás spektrális emissziója együtt határozza meg (32). A színmintával történő összehasonlítást ezért egyik oldalán nyitott, egyenletes, szabványos megvilágítású dobozban („color boksz”) kell végezni (4.90. ábra - A GretagMachbeth Color Box).

A GretagMachbeth Color Box színszűrőkkel kombinált halogén lámpákkal szimulálja a különböző szabványos ill. szokásos megvilágításokat:
CIE „A”
Napfény (D75, D65 vagy D50 választható)
Hideg fehér
Meleg fehér
A color box tetején homályos üveglap fölött helyezkednek el a szabványos fényforrások (halogén lámpák és fénycsövek), megfelelő színszűrőkkel kiegészítve. A color box belső felülete matt és világosszürke, hogy színes reflexiók ne színezzék el a mintákat. Az elülső fal nyitott, itt áll a szín összehasonlítást végző jó színlátású, képzett mérő személy.
A színminták a mérés etalonjai, a 4.9.2. szakasz - A színes nyomtatás CMYK színrendszere fejezetben ismertetett színminta gyűjtemények egyikének tagjai.
A vizuális színmérést általában gyártás közbeni ellenőrzésnél alkalmazzák. Előnye, hogy nem igényel érzékeny, laboratóriumi környezetben üzemeltethető műszereket. Másik előnye, hogy a mérés azonnal, személyesen érzékelhető eredményt ad. Hátránya, hogy a véletlen hiba eshetősége nagyobb, mint a műszeres színmérésnél.
4.12.5.2. A spektrális színmérés
A leggyakrabban alkalmazott színmérő műszerek spektrális módszerrel működnek. Megmérik a színes felület spektrális reflexióját, és abból számolják ki a CIE színjellemzőket. A mérést a műszerbe beépített spektrofotométer végzi. A mérendő mintát a műszerbe beépített fényforrás világítja meg. A CIE színösszetevőket és színkoordinátákat a műszerbe beépített miniszámítógép határozza meg.
A műszerek általában meghatározzák az X, Y, Z színösszetevőket, az x, y, z színkoordinátákat és az L*, a*, b* színkoordinátákat, és meg tudják jeleníteni a színes felület spektrális reflexiós görbéjét is. Két különböző színű felület egymás utáni mérése alapján meg tudják határozni a színkülönbséget is.
A kereskedelemben kapható kis kézi műszerek általában 10 nm lépésközzel működnek a 400 nm…700 nm spektrumtartományban. Ha ez a lépésköz a nagyon élénk, színezet dús (tehát meredek spektrális reflexiós görbével rendelkező) színminták mérésénél nem ad elegendően pontos eredményt, akkor célszerű egy komolyabb spektrofotométerrel végezni el a mérést és a spektrum alapján külön számítógéppel végezni el a kiértékelést.
A műszereken általában be lehet állítani azt is, hogy melyik szabványos fényforrással mérjen. Ezt szellemes módon nem úgy oldják meg, hogy több szabványos fényforrást építenek be, hanem egyetlen fényforrást (Általában villanó fényt, hogy a fényforrás által termelt hő ne melegítse fel se a műszert, se a mérendő mintát), és ennek a fényével a mérés elején meg kell világítani a műszerhez adott etalon fehér felületet. A műszer megméri ennek a spektrális reflexióját az adott fényforrás fényében, és a számításnál ezekből az adatokból meghatározzák, hogy mi lenne az eredmény, ha valamelyik szabványos fényforrást alkalmazták volna.
Ha a műszer detektora φ(λ) színinger függvényt érzékel a műszerbe beépített Φ e (λ) fényforrás fényében a ρ(λ) felület mérésekor, viszont φ CIE (λ) színingert kellene érzékelnie, ha a szabványos Φ CIE (λ) fényforrás lenne beépítve, akkor írható, hogy
|
φ (λ) = Φ e (λ) * ρ(λ) | ||
|
φ CIE (λ) = Φ CIE (λ) * ρ(λ) | ||
|
φ (λ) / Φ e (λ) = φ CIE (λ) / Φ CIE (λ) |
és innen
|
φ CIE (λ) = φ (λ) * [Φ CIE (λ) / Φ e (λ)] |
A (4.91. ábra - DATACOLOR Handy spektrofotométer, 2000) ábrán egy spektrofotométeres kézi színmérő műszert láthatunk. A műszer olyan kicsi, hogy elfér egy ember kezében.

A kis kézi színmérő műszerekbe egy teljes spektrofotométer van beépítve (4.92. ábra - Az AVANTES spektrofotométer és színmérő műszer optikai vázlata és 4.93. ábra - Konica-Minolta 2600 CM-2600d színmérő műszer).
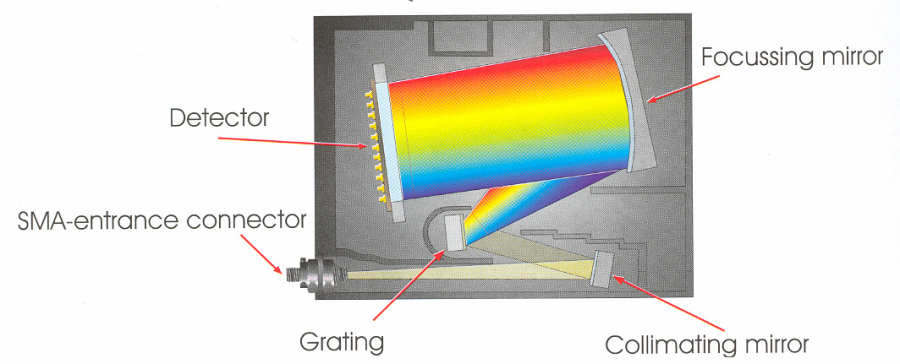
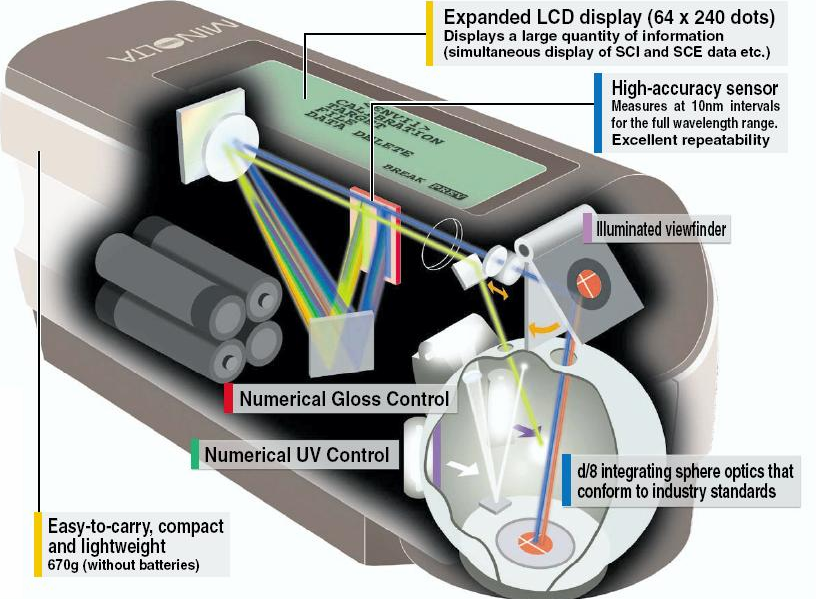
4.12.5.3. A tristimulusos színmérés
A mérésnél 4 speciális színszűrőt alkalmazunk, amely közvetlenül az X1, X2, Y és Z színösszetevő értékét méri meg. (Itt X1 és X2 az x szín-megfeleltető függvény két maximuma körül különválasztott két rész alapján meghatározott színösszetevőt jelenti.)
A műszer fényforrása egyszerű autó-izzó, amelynek előnye, hogy spektrális energia eloszlása folytonos, és ezen kívül hosszú élettartamú és jól bírja a mechanikus igénybevételt. Az érzékelő általában szelén-fényelem, amelynek spektrális érzékenysége hasonló a V(λ) függvényhez.
A műszerben speciális színszűrőket alkalmaznak, amelyek biztosítják, hogy minden csatorna mért értéke olyan legyen, mintha szabványos megvilágítással és a CIE színmegfeleltető függvényekkel azonos spektrális érzékenységű detektorokkal történt volna a mérés.
Az alábbiakban ismertetjük a tristimulusos színmérő műszerek színszűrőinek tervezési elvét:
|
Y 1 legyen a ρ(λ) felületnek egy szabványos S(λ) megvilágításra vonatkozó Y színösszetevője:
Azonban a műszerben egy F(λ) spektrális teljesítmény eloszlású izzót és egy e(λ) érzékenységű detektort szeretnénk alkalmazni. Ezért a műszerbe behelyezzük a τ(λ) spektrális transzmissziójú színszűrőt:
Ha a feladat az, hogy Y 1 =Y 2 legyen, akkor a színszűrő τ(λ) spektrális transzmisszióját az alábbi módon kell meghatározni:
|
A tristimulusos színmérő műszerek előnye, hogy közvetlenül a CIE színösszetevőket mérik. További előny, hogy nem 10 vagy ritkább esetben 5 nm-es lépésközzel mérnek, mint a spektrofotométeres műszerek, hanem a hullámhossz függvényében folyamatos érzékenységű színszűrőkkel, ezért a rikító (gyorsan változó spektrális transzmissziójú) színeket pontosabban mérik, mint a spektrofotométeres színmérők. Előnyük még, hogy a hullámhossz kalibrációjuk nem állítódik el, mint némely esetben a spektrális műszereké.
Hátrányuk, hogy amennyiben a leírt módon megtervezett színszűrők spektrális illesztése nem megfelelő, ez egy rendszeres hibát okoz. Ennek a hibának csökkentésére azt a módszert alkalmazzák, hogy nem teljes spektrumtartományban, egyetlen fehér etalonnal kalibrálják a műszert, hanem szín-tartományonként más-más színű etalonnal. A kalibráló etalon színét aszerint határozzák meg, hogy milyen színű felületet akarnak mérni. Ilyen módon minden színtartományban külön-külön csökkenteni lehet a rendszeres hibákat.
Magyarországon a MOM optikai gyár gyártott világszínvonalú tristimulusos színmérő műszereket. Ehhez a műszerhez 15 tagú színes zománc etalon készletet fejlesztettek ki a LAMPART zománc-edény gyárral, amelyet az OMH (Országos Mérésügyi Hivatal) hitelesített nagypontosságú spektrofotométeres mérésekkel.
Ennek a műszernek a továbbfejlesztésével készült a BME MOGI Tanszékén a KONTAKTA villamossági Gyár megrendelésére egy olyan tristimulusos kétcsatornás színmérő műszer, amely egyidejűleg két alkatrész színösszetevőit mérte. Az egyik csatorna a megrendelt színű alkatrész (az etalon színminta), a másik a megrendelés alapján elkészült színminta színét. A műszer ki tudta külön-külön is jelezni az egyes csatornákon mért értékeket, tehát egycsatornás műszerként is működött, de alkalmas volt a színösszetevők különbségének kijelzésére is.
A (4.94. ábra - A BME Finommechanikai, Optikai Tanszékén (ma: MOGI Tanszék) kifejlesztett kétcsatornás tristimulusos színmérő műszer) ábrán a BME MOGI Tanszéken kifejlesztett kétcsatornás tristimulusos színmérő műszer kísérleti példánya látható az OMH zománc etalonokkal együtt.

4.12.5.4. A színmérés etalonjai
A színmérő műszerek kalibrálására szín etalonokat alkalmaznak.
4.12.5.4.1. A spektrális reflexió mérés etalonjai
Vegytiszta magnézium oxid por kötőanyag nélkül sajtolva (fehér)
Vegytiszta bárium szulfát por kötőanyag nélkül sajtolva (fehér)
Halon (fehér)
Égetett zománc (lehet fehér és színes is)
4.12.5.4.2. A spektrális transzmisszió mérés etalonjai
Spektrál lámpák. Ezeknek ismert hullámhosszakon vékony vonalai vannak. Leggyakrabban a higany- és a nátrium lámpát használják
Holmium szűrő. Ez ismert spektrális transzmissziójú üveg színszűrő, melynek ismert hullámhosszakon vannak áteresztési csúcsai.
Didimium szűrő. Ez is ismert spektrális transzmissziójú üveg színszűrő.
Interferenciaszűrők is alkalmazhatók etalonként, de ezeknek csúcsai nem olyan élesek, mint az előzőek.
4.12.5.4.3. A spektrális emisszió mérés etalonjai
A spektrális emisszió mérés elsődleges etalonja a fekete sugárzó.
A másodlagos etalon wolfram szalagos izzó
A harmadlagos etalonok általában halogén izzók, amelyeket a másodlagos etalonhoz hitelesítenek. Élettartamuk (ameddig etalonnak tekinthetők) általában 8 óra égetés.
4.13. Az emberi színlátás modellezésén alapuló színrendszerek
A CIE, mint azt a 4.9.1. szakasz - A színes monitorok RGB színrendszere fejezetben láttuk, színegyeztetési mérésekre alapozott színrendszert dolgozott ki. Véleményünk szerint helyesebb lenne, ha a színeket a protosra, a deuterosra és a tritosra ható fény által kiváltott ingerek erősségével jellemeznénk. Erre azonban 1931-ben még nem volt mód, mert nem volt ismeretes a receptorok spektrális érzékenysége. Mai ismereteink alapján azonban erre már lehetőség nyílik. Tanszékünk oktatói ezért kidolgozták az emberi színlátást jobban modellező színrendszer alapjait.
4.13.1. A PDT színrendszer (Wenzel, 1991)
A PDT színrendszer kidolgozásának célja az volt, hogy egy olyan színrendszert hozzak létre, amely a CIE alapjául szolgáló színmegfeleltető függvények (amelyek nem mások, mint színkeverési „ recept könyvek”) helyett az emberi színes látás receptorainak színérzékenységi függvényeire épül. Ugyanakkor a PDT színrendszer legyen összhangban a CIE színrendszerrel, vagyis a CIE felépítése, számítási képletei legyenek azonosak, sőt a CIE színmérő észlelő is legyen azonos a CIE által 1932-ben definiált színmérő észlelővel, azaz annak színegyeztető függvényeivel.
4.13.1.1. Az emberi szem spektrális érzékenységi függvényeinek meghatározása
A PDT színrendszer kidolgozása idején még nem voltak ismeretesek az emberi szem Stockmann és Sharpe által meghatározott l(λ), m(λ) és s(λ) spektrális érzékenységi függvényei. Több mint 10 szerző ismertetett ilyen függvényeket (Pl. König, Fick, Hunt, Thomson és Wright, Schmidt és Pokorny, Mac Leod és Boynton, Judd, és mások). Ezek a függvények azonban a CIE színmegfeleltető függvények különböző együtthatókkal meghatározott lineáris transzformációi voltak. A színkeverési „receptkönyv” egyszerű lineáris transzformációja csak többé-kevésbé jó közelítést adhat a színérzékenységi függvényekre, hiszen alapvetően más célú méréseken alapul. Természetesen mindegyik közelítés más alakú és más maximum helyekkel rendelkező színérzékenységi függvényeket eredményezett.
Más szerzők (Pl. Estevez, Marks, Dobelle és Mac Nichol) különböző mérések alapján közöltek színérzékenységi függvényeket. Ezek szintén egymástól különbözőek voltak. Ezért célszerűnek tűnt újra gondolva a kérdést újra meghatározni ezeket a függvényeket.
A protos, deuteros és tritos (azaz L, M és S) színérzékelő receptor spektrális érzékenységi függvényét Weibull-eloszlás alakú háromparaméteres függvények alakjában a CIE színmegfeleltető függvények alapján határoztuk meg Dr. Szász Gábor kollégámmal:
|
f(λ) = a * b * c ( λ max - λ ) (b-1) * exp [ - c ( λ max – λ ) b ] |
Itt f(λ) a keresett l(λ), m(λ) és s(λ) színérzékenységi függvény közelítő függvénye, λ a fény hullámhossza, és a, b, c, és λ max konstans értékek.
A λ max paramétert a függvények várható alakjának ismeretében vettük fel és konstansnak tekintettük, 3x3 további paraméterét (a, b és c) pedig úgy határoztuk meg, hogy az így kapott érzékenységi függvényekkel felruházott színmérő észlelő a színmegfeleltető méréseket éppen a CIE színmegfeleltető függvényekkel azonos eredménnyel végezze el. A megoldást a keresett p(λ), d(λ), t(λ) és egy kiinduló paraméterekkel felvett p(λ), d(λ), t(λ) érzékenységi függvényből meghatározott hibafüggvény minimalizálásával hoztuk létre, komplex tanuló algoritmus alkalmazásával.
Kiinduló feltételünk volt még, hogy a kapott színérzékenységi függvények összege megegyezzen a V(λ) spektrális fényhatásfok függvénnyel:
|
p(λ) + d(λ) + t(λ) = V(λ) |
Az ily módon létrehozott virtuális CIE színmérő észlelő spektrális érzékenységét P, D és T betűvel jelöltük, az érzékenységi függvényeiket pedig p(λ), d(λ) és t(λ)-val.
A függvények az alábbiak:
|
p(λ) = 5.72 * 10 -14 (780 – λ) 5.78 * exp [ - 1.32 * 10 -16 (780- λ) 6.78 ] | ||
|
d(λ) = 2.02 * 10 -90 (700 – λ) 3.85 * exp [ - 1.21 * 10 -11 (700- λ) 4.85 ] | ||
|
t(λ) = 2.20 * 10 -15 (660 – λ) 5.70 * exp [ - 2.19 * 10 -16 (660- λ) 6.70 ] |
A (4.95. ábra - A protos, a deuteros és a tritos spektrális érzékenysége) ábrán látható a függvények alakja akkor, ha mindegyik színérzékenységi függvény maximumát 100 %-nak tekintjük.
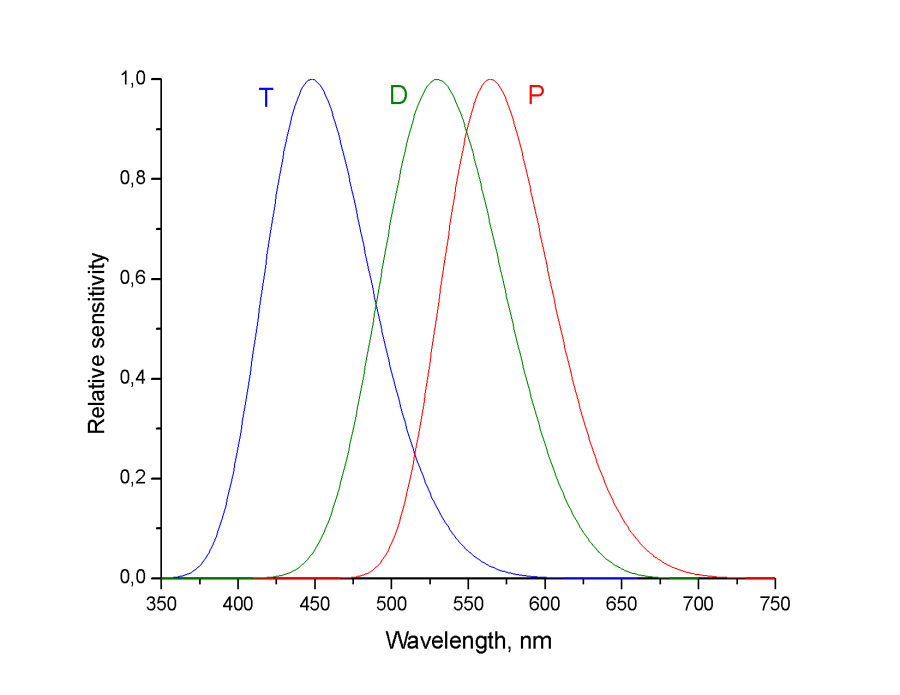
4.13.1.2. A PDT színrendszer felépítése
A PDT színrendszer felépítése teljes mértékben megegyezik a CIE xyY színrendszerrel. Ez biztosítja azt, hogy az új színrendszerre való esetleges áttérés zökkenőmentes legyen. Az áttérésnél mindössze a CIE színmegfeleltető függvényeket kell kicserélni a p(λ), d(λ) és t(λ) spektrális érzékenységi függvényekre.
A P, D és T színösszetevők ezek után a CIE formulákhoz hasonlóan
|
| ||
|
| ||
|
|
Ahol a k értéke:
|
|
A p, d és t színkoordináták pedig:
|
| ||
|
| ||
|
|
A PDT színrendszer színezeti diagramja a (4.96. ábra - A színezeti diagram a PDT színrendszerben) ábrán látható. Ebben éppen úgy, mint a CIE xyY színrendszerben, a papucs alakú görbe vonalon helyezkednek el a spektrumszínek, és ennek a vonalnak a két végpontját összekötő egyenesen a bíbor (vagy lila) színek. A neutrális pont helye is – a CIE xyY színezeti diagramhoz hasonlóan - a p = d = 1/3 pontban van.
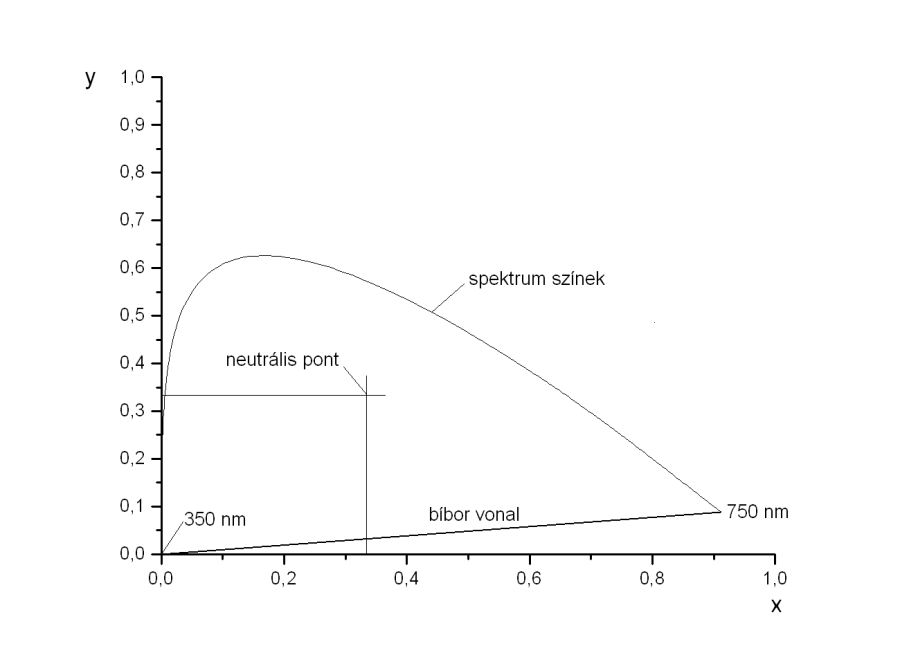
Ennek a színrendszernek előnye a CIE xyY színrendszerhez képest, hogy a színtévesztők színlátásának modellezésére (bemutatására, elemzésére) is alkalmas. Ehhez egyszerűen a normál színlátók spektrális érzékenységi függvényei helyett a színtévesztő személy spektrális érzékenységi függvényeit kell behelyezni a P, D és T színösszetevő képletébe.
4.13.2. Az OCS színrendszer
Kézenfekvő, hogy kíséreljünk meg egy olyan színrendszert szerkeszteni, ami a szem látórendszerében valójában létrejövő jelekkel dolgozik. Már Rodieck, (1998) is megpróbálta a két csatornajelet, mint koordinátatengelyt használva ábrázolni a színeket, azonban ahhoz, hogy használható színdiagramot kapjunk, a színek mindenkori intenzitását le kell választani a csatornajelekről. Vezessük be intenzitásként a három receptorjel átlagát 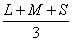 -at, majd a nevezőben lévő 3-at elhagyva normáljuk L+M+S-sel a csatorna jeleket, és jelöljük kisbetűkkel az így kapott színkoordinátákat a
-at, majd a nevezőben lévő 3-at elhagyva normáljuk L+M+S-sel a csatorna jeleket, és jelöljük kisbetűkkel az így kapott színkoordinátákat a
|
C RG = L-M és a | ||
|
C BY = S-(L+M) csatorna jeleket |
ahol L, M, S jelenti a három színérzékelő csap receptor kimenetét, továbbá
|
| ||
|
|
Erre a normálásra azért van szükség, hogy a különböző intenzitású színingerek összehasonlíthatók legyenek.
Ha egy Φ(λ) spektrális fénysűrűség eloszlású fény éri a szemet, akkor hatására a szemben L, M, S jelek jönnek létre, amelyek segítségével keletkeznek a C RG és a C BY kromatikus csatorna jelek.
A korábbi egyenletek alapján:
|
| ||
|
|
adódik. (A kis és nagybetűk jobb megkülönböztethetősége miatt az indexben álló r, g, b, y -t is kisbetűkkel írjuk.) Ezek az összefüggések a normálás következtében biztosítják az intenzitástól való függetlenséget. (Természetesen a mondottak csak a fényérzékelés lineáris modelljének érvényességi körén belül igazak.)
Ábrázolva az összefüggéseket a (4.97. ábra - Az intenzitásra normált csatorna függvény alakja, ezek az organikus színrendszer színkoordinátái) ábrát kapjuk.
Az ábrázoláskor a c rg és a c by függvényeket egyaránt +1-es maximális értékre normáltuk.
Ha most ezeket az összefüggéseket mint egymás függvényeit ábrázoljuk, akkor a (4.98. ábra - Az organikus színrendszer) ábrát kapjuk.
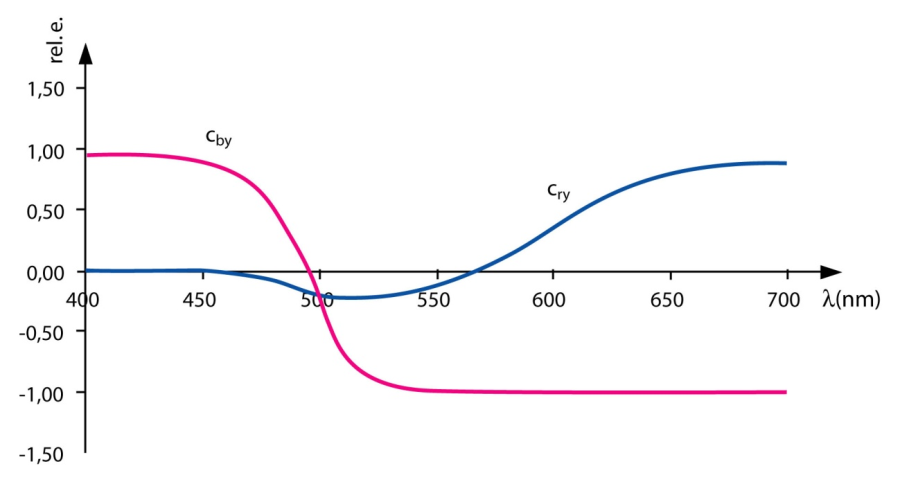
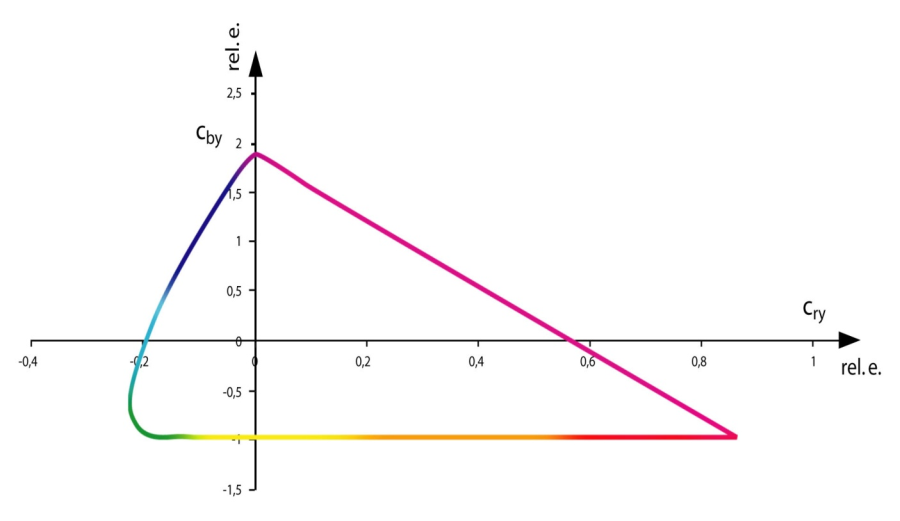
Nevezzük az így adódó színrendszert organikus színrendszernek (Organic Color System, OCS), utalva arra, hogy a látószervben ténylegesen létrejövő jelekből állítottuk elő.(Ábrahám, Nagy, 2003; Ábrahám, 2004)
Az organikus színrendszer (OCS) az emberi látórendszerben létrejövő jelek felhasználásával állítható elő, benne a színezetet a 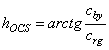
a színezet-dússágot a 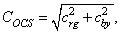 míg
míg
a világosságot az L OCS = L+M+S jelenti,
ahol L, M, S rendre a protos, deuteros és tritos receptor ingerülete, 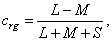 és
és 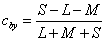
Az OCS színrendszerben a spektrális színek a „színháromszög” körvonalán, míg a telítetlen (alacsonyabb színezet dússágú) színek a háromszög belsejében helyezkednek el. Az origóban az akromatikus „fehér” pont található, koordinátái tehát (0,0).
A világosság megfogalmazása nem azonos az akromatikus csatornajel alakjával (C V =1,7L+M), amely a szem relatív világosságérzékenységi függvényének leírására alkalmas. Az LOCS-ben a „kék” receptor is szerepet játszik a színtani súlyának megfelelően. A kétféle világosságot tehát célszerű megkülönböztetni egymástól.
A pupillánk összehúzódását vezérlő világosságjelet időben gyorsabb, un. magnocellurális sejtek továbbítják (Fonyó, 1999), míg a színtani jeleket a nagyobb térbeli felbontású un. parvocellurális sejtek.
A színkoordináták tehát függetlenek a világosságtól, így a három adat együtt jeleníti meg az emberi szem által érzékelt színeket. A három színkoordináta az OCS színtestet alkotja, amelynek azonos világosságú metszetei a 4.98. ábra - Az organikus színrendszer szerintiek. Maga a színtest a (4.99. ábra - Az OCS színtest) ábrán látható nem kör alapú, hengerszerű alakzat, melyek metszetei azonosak, de más-más világossághoz tartoznak.
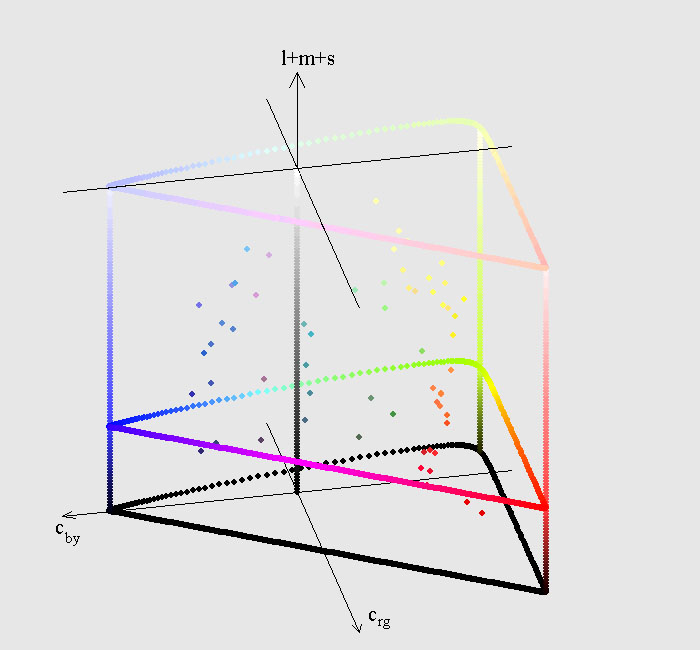
4.14. Ajánlott irodalom
Commission Internationale de l¢Eclairage: Colorimetry, 2000
MSz 9620 Világítástechnika, Színtechnika
Ábrahám: Optika, McGraw Hill, 1998
Király: Általános színtan és látáselmélet, Nemzeti Tankönyvkiadó, 1994
Nemcsics: Színtan, Színdinamika, Tankönyvkiadó, 1988
Bernolák: A fény, Műszaki Könyvkiadó, 1981
Julesz: Dialógusok az észlelésről, Typotex, 2000
Lukács: Színmérés, Műszaki Könyvkiadó, 1982
Hruska: Általános színtan és színmérés, Közgazdasági és Jogi Könyvkiadó, 1956
Ferenczy: Video- és hangrendszerek, Tankönyvkiadó, 1986
Cole: Szemtanú művészet, A szín, Dorling Kindersley, 1993
Gegenfurtner-Sharpe: Color Vision from Genes to Perception, Cambridge University Press, 1999
Bourges: Color Bytes,Chromatics Press, New York, 1997
Kaiser-Boynton: Human Color Vision, OSA, 1996
Watermann: Lakberendezési színtanácsadó, Hajja & Fiai, 1993
Buscher: Farb Beratung, Falken-Verlag, 1991
Goethe: Színtan, Corvina, 1983
Kardos: Tárgy és árnyék, Akadémiai Kiadó, 1984
Hurvich: Color Vision, Sinauer, 1981
Schober: Das Sehen, Verlag für Fachliteratur, 1950
Itten: Kunst der Farbe, Otto Menge Verlage, Ravensburg, 1970
Itten: A színek művészete, Corvina, 1978
Gregory: The Intelligent Eye, McGraw Hill, 1971
Leonardo: A festészetről, Corvina, 1967
Németh: Seurat, Corvina, 1966
Wyszecki-Stiles: Color Science, Wiley, 1966
Gulyás: Színdinamika és színharmónia, GTE Műszaki kiadványsorozat, 1963
Nathans, J., Piantanida, T.P., Eddy, R.L. et al.: Molecular genetics of inherited variation in human colour vision. Science 1986; 232:203-210.
Fletcher, R., Voke, J.: Defective Colour Vision, Adam Hilger Ltd., Bristol and Boston, 1985
Mollon, J.D., Pokorny, J., Knoblauch, K.: Normal & Defective Colour Vision, Oxford University Press, 2003
Gegenfurtner, K.R., Sharpe L.T.: Color Vision from Genes to Perception (Cambridge University Press, 1999)
Ábrahám, Gy., Szappanos, J., Wenzel, K.: Method and optical means for improving or modifying colour vision and method for making said optical means. Patent No. 0770 6-PCT
Birch, J.: Diagnosis of Defective Colour Vision, Butterworth- Heineman, 1993
Ábrahám, Gy., Wenzel, K. : Method and apparatus for determining spectral sensitivity parameters of colour/sensitive receptors in the eye, PCT/HU95/00009
Wenzel, K., Szász, G.: Numerische Methode zur Ermittlung von Simultanen Funktionen, die mit indirekter Methode gemessen wurden (Periodica Polytechnika Vol. 32. Nos.3-4. 1988. P.213-222)
Wenzel, K., Ábrahám, G., Szappanos, J.: New Anomaloscope (Image&Sound Technology Vol XXXVI. 1990/1)
Wenzel, K., Szász, G.: Examination of Spectral Sensitivity Functions of the Retinal Receptors (Die Farbe vol.39, Heft 1-6, 1994)
Ábrahám, G., Körösi, H., Schanda, J., Wenzel, K. Anomalies in additive colour matches (Colour research and Application Volume 20, Number 4, August 1995.)
Kovacs, G., Abraham, Gy., Kucsera, I., Wenzel, K.:: Improving color vision for color deficient patients on video displays, OSA Trends in Optics and Photonics, Vol. 35 Vision Science
Kovacs, G., Kucsera, I., Abraham, Gy., Wenzel, K.: Enhancing Color Representation for Anomalous Trichromats on CRT Monitors, COLOR research and Application, Supplement ,Volume 26, 2001, S273-S276.
Wenzel, K., Ladunga, k., Samu, K.: Measurement of color defective and normal color vision subject’s color and luminance contrast treshold functions on CRT,monitors, Periodica Polytechnica, Vol. 45. No. 1., PP. 103-108, 2001
5. fejezet - Interferometria
- 5.1. Bevezető gondolatok
- 5.2. Történeti előzmények
- 5.3. A fény terjedési sebességének kérdése
- 5.4. Hullámtani alapfogalmak
- 5.5. A periodikus mozgás
- 5.6. Egyszerű harmonikus rezgőmozgás
- 5.7. Transzverzális hullámok
- 5.8. Amplitúdó és intenzitás
- 5.9. Frekvencia és hullámhossz
- 5.10. Fényinterferencia
- 5.11. A szuperpozíció elve
- 5.12. Egyszerű harmonikus rezgőmozgások összeadása egy egyenes mentén
- 5.13. Lézer interferometria
- 5.14. Amplitúdóosztás. Michelson-interferométer
- 5.15. Ellenőrző kérdések
- Felhasznált irodalom
5.1. Bevezető gondolatok
A mérnöki optika, amely elsősorban az optikai jelenségek gyakorlati implementálásával foglalkozik, az optikai alapismeretek mellett műszertechnikai, finommechanikai, mechatronikai elvekre építve szintetizál. Az ilyen jellegű rendszerszintézis alkalmazott optikai eszköztára jellemzően a geometriai optikát fedi le. Azonban nem egy műszer, berendezés működése olyan elvekre épül, mely tárgyalásához a geometriai optika eszköztára már nem elegendő, hullámoptikai megközelítés szüksége. Ez két esetben nagyon markánsan érhető tetten. Egyrészt, amikor a képalkotás során a képalkotás minőségét már csak a diffrakció korlátozza, ilyenkor a geometriai optikai elvekre épülő analízis, illetve szintézis érvényességét veszti. Másrészt, amikor a geometriai optika alaptörvényei közül az, mely kimondja, hogy számtalan sugár vezethető át egyetlen ponton anélkül, hogy azok egymásra hatást gyakorolnának, bizonyos esetekben nem alkalmazható elv. Hiszen az interferometrikus berendezések pont azt a jelenséget használják ki, hogy a bennük terjedő hullámfrontok találkozásukkor egymásra hatva egy újabb jelenséget hoznak létre.
Az optikai jelenségek magyarázata az idők folyamán sokat változott, fejlődött. A nagy elődöknek sok hibás megközelítésen, téves elméleten át kellet verekedniük magukat, hogy a kérdéseikre tiszta, megállapodott válaszokat kapjanak. Mivel a hullámoptika és az általa magyarázható interferencia és diffrakció, mint jelenség ma már a korszerű méréstechnika egyik alapköve; alapfogalmainak ismerete a mérnöki optikát művelők számára elengedhetetlen. Ezért a következő fejezetekben a hullámoptikai megközelítés történeti fejlődését és annak alapfogalmait és jelenségeit tárgyaljuk.
5.2. Történeti előzmények
Az fénytan, mint diszciplína, a fizika egyik legrégibbi területe; fejlődése rendkívül érdekes és tanulságos. Az iránta tanúsított érdeklődés egyrészt visszavezethető arra, hogy az emberek nagy többsége környezetéből az ingerek szinte elsöprő hányadát látása útján szerzi úgy, hogy a forrásokból, tárgyakról érkező fény a szembe kerülve, onnan az agyba jutva egy nagyon bonyolult fiziológiai és kognitív pszichológiai folyamat útján válik hasznosítható információvá. A fokozott érdeklődés másik oka talán az lehetett, hogy a fénytani jelenségek hordozója és okozója, maga a fény mint jelenség sokáig maradt nehezen magyarázható.
Optikai ismeretekkel már a régi görögöknek is rendelkeztek [5.2.] . Időszámításunk előtt mintegy háromszáz esztendővel Euklidesz foglalta össze – mai tudásunkkal többé kevésbe általános érvényűnek tekinthető – megállapításait tapasztalati úton szerzett eredményei alapján. Platonra hivatkozva kifejti, hogy tárgyak láthatóságának oka az, hogy a szemből kiinduló látósugarak gyakorlatilag letapogatják a tárgyakat. Az Optika és Katoptrika című műveiben megmagyarázza, hogy ezen látósugarak érintői a vizsgált tárgynak, azok leírják annak körvonalát és az így keletkező látószögtől függ a tárgy látszólagos nagysága. Szintén ad magyarázatot a tárgyak látszólagos nagyságának annak helyzetétől és távolságától való függésére. Kimondja a geometriai optika alaptörvényét, mely szerint a fény egyenesvonal mentén terjed, és helyesen írja le a visszaverődés törvényét. Tudjuk, hogy foglakozott a sík- és gömbtükrökkel, az optikai lencsékkel. Igazi különlegesség, hogy egy rendkívül előremutató gondolatot tudott időszámításunk előtt százhúsz körül megfogalmazni Herón, aki szerint a fénysugár által megtett út időminimumot elégít ki. Ennek szabatosabb formáját csak mintegy ezerhétszáz évvel később tudta megfogalmazni Pierre de Fermat (1601 – 1665). Herónnal szinte egy időben tanulmányozat a fénytörés jelenségét Ptolemaiosz, aki erre – ugyan nem teljesen helyes, de egészen Keplerig érvényes – matematikai összefüggés írt fel. A modern – hullámoptikai és korpuszkuláris – fényelméletek kezdetleges megfogalmazásai a görögöknél már szintén megjelentek. Arisztotelész az euklideszi látósugarak helyett egy hullámelmélet szerű magyarázatot adott, míg Epikurosz szerint a fényérzet a forrásból kilépő részecskék hatásával magyarázható, ami tulajdonképpen – az akkori kor ismereteinek szintjén – egy fajta korpuszkuláris fényelméletnek tekinthető.

A középkori arab optikai megfigyelések után az első igazán meghatározó eredmények Robert Bacon nevéhez fűződnek, aki az ezerkétszázas években meg tudta mérni a homorú tükrök fókusztávolságát, és leírta a szférikus aberráció, azaz a nyíláshiba jelenségét. Tőle származik a sötétkamra – camara obscura – gondolata, melyet Giovanni Battista della Porta egészített ki azzal, hogy, annak hatékonyságát egy a nyílásban elhelyezett lencsével lehet fokozni.
Az optikai műszerek építésének első jelentős korszakára meghatározó hatással volt az optikai üvegek előállításának és megmunkálási eljárásainak tökéletesedése. A tizenhetedik században járunk, ekkor találja fel Hans és Zacharias Jansen (egyes szakirodalmak Janssen-nek írják nevüket) a mikroszkópot [5.26.] , és készíti el Galileo Galilei (1564 – 1642) első távcsövét.
A fejlődés ekkorra érte el azt a szintet, ami világossá tette, hogy az optikai eszközök tervezésének, előállításának nagyobb tömegben történő gyártásának elengedhetetlen kelléke az, hogy az optikai jelenségek megértéséhez és alkalmazásához szabatos elméleti megközelítések szükségesek. E téren szerzett elévülhetetlen érdemeket Johannes Kepler (1571 – 1630) prágai csillagász, akit elsősorban a bolygómozgásokat leíró, róla elnevezett Kepler-törvények miatt ismerünk. Kepler egyik legjelentősebb munkája az 1611-ben megjelent Dioptrice volt, melyben lefektette az optika tudományos szintű tárgyalásának alapjait. Könyvében az általa szerkesztett Kepler-távcső mellett foglakozik a fénytöréssel és az optikai leképezéssel kapcsolatos eredményeivel. A kor színvonalának megfelelően írta le a szem működését, elemezte a látáshibákat, valamint magyarázatot adott a szemüveglencsék működésére vonatkozóan is [5.4.] . Eredménye a fénytörés tekintetében kimagasló jelentőségű, megállapítja az üvegre a teljes visszaverődés szögét. A róla elnevezett távcső szintén jelentős lépés az égi jelenségek megfigyelésének történetében.
A fénytörés törvényéhez érdekes tudománytörténeti adalék az, hogy ugyan az 1626-han elhunyt Willebrord Snel van Royen (1580 – 1626) holland matematikus – aki a Ledeni Egytem oktatója volt – hallgatói feljegyzései közt megtalálták azt a tanulmányt, amely már tartalmazta a fénytörés helyesen megfogalmazott törvényét. Az nem ismert, hogy René Descartes (1596 – 1650) olvasta-e ezt a tanulmányt, azonban tény, hogy a fénytörés törvényét elsőként ő közölte nyomtatásban. A mai szakirodalom is Snellius– Descartes törvényként jegyzi. Descartes további jelentős, optikai téren szerzett érdeme a szivárvány elméletének pontos megfogalmazása. A fénytörés jelenségének pontos megfogalmazása úttörő jelentőségű az optikai műszertervezés fejlődése szempontjából, hiszen ez által vált lehetővé az optikai rendszerekkel kapcsolatos számítások pontos elvégzése. Először 1693-ban Edmond Halley angol csillagász és matematikus végzett a lencsékre vonatkozóan általános – még mai szemmel is elfogadhatónak tűnő alaposságú – számításokat [5.2.] .
A hullámoptika, vagy más néven a fizikai optika igazi kezdete 1665-re tehető. Ebben az évben felfedezte fel Francesco Maria Grimaldi (1618 – 1663) olasz jezsuita szerzetes a fény diffrakcióját, és Robert Hooke (1635 – 1703) az interferencia jelenségét, megállapítva, hogy a fény egy rezgés.
1666-ban Sir Isaac Newton (1642– 1710) kísérletileg valósítja meg a fehér fény spektrálisan felbontását, és kidolgozza a fény korpuszkuláris elméletét. 1672-ben Olaf Römer, (1644 – 1710) a Jupiter holdjainak fogyatkozását felhasználva megmérte a fény terjedési sebességét. 1669-ben dolgozta ki Christiaan Huygens (1629 – 1695) a fény hullámelméletét, szemben a newtoni korpuszkuláris elmélettel.
Ezen időszakkal bezárólag, gyakorlatilag tehát a tizenhetedik század végéig felfedezték azokat az alapvető és kiemelten fontos optikai jelenségeket, amelyek a fizikai fénytan, azaz a hullámoptika alapját jelentik, és egyben kísérleti úton ismertté váltak azok a fényjelenségek, amelyek a fény hullámtermészetét alátámasztották és igazolták.
Annak ellenére, hogy ezen század második felének optikai jellegű eredményei a fény hullámtermészetét voltak hivatottak igazolni, a kor meghatározó és nagy tekintélyű fizikusa, Newton nem értett egyet ezzel az elmélettel. Mivel az általa ismert longitudinális hullámokkal nem tudta magyarázni a fény terjedését, ezért 1717-ben ismét felelevenítette fény részecske természetére vonatkozó, úgynevezett korpuszkuláris fényelméletét [5.27.] . Ekkor az optikai eredmények születésének üteme hanyatlani kezdett, a tizennyolcadik században a korpuszkuláris elmélet dominált, annak ellenére, hogy például Leonhard Euler (1707 – 1783) Szentpétervárott dolgozó svájci matematikus, és Mihail Vasziljevics Lomonoszov (1711 – 1765), szintén Szentpétervárott dolgozó orosz fizikus és vegyész ismét előtérbe helyezték a fényjelenségek magyarázatára a hullámelméletet.

1793-ban nagy fontosságú megállapításokat tett a látás fiziológiájának értelmezésében Thomas Young (1773 – 1829) angol orvos és fizikus, aki 1801– 1804 között kidolgozta az interferencia elméletét a hullámelméletre alapozva.
Egy 1801-ben kiadott publikációjában részletesen és szabatosan leírta a fény hullámelméletének alapfeltevéseit [5.2.] :
Létezik egy az egész világegyetemet betöltő ritka és rugalmas fényközvetítő közeg; az éter.
Egy forrás fénykibocsátása során ebben az éterben rezgőmozgások keletkeznek.
A különböző színérzetek a szem ideghártyáját elérő különböző frekvenciájú rezgésektől függnek.
Minden anyagi test vonzza az éterközeget, ezért az éter koncentrálódik a test anyagában és tőle kis távolságra nagyobb sűrűségre, de nem nagyobb rugalmasságra tesz szert.
Young ezirányú munkásságának talán legértékesebb eredménye, hogy elsőként utal a diffrakció jelenségére. Sikerül cáfolnia Huygens azon gondolatát, miszerint a hullámfelület oldalpontjaiból kiinduló, úgynevezett oldalhullámok fizikailag nem észlelhetők, így a fényhatároló elem széléről éles képet kapunk. Mint fogalmakat, Young bevezeti a hullámoptikát, a fényhullámhosszt, és elsõként kísérleti úton azt meg is méri [5.2.] . Kimondja, hogy fényinterferenciára csak koherens fényhullámok képesek.
A tizennyolcadik század végén, Étienne-Louis Malus (1775 – 1812) hadmérnök, fizikus és matematikus elévülhetetlen érdemeket szerez a kettőstörés jelenségének magyarázatával. Ismert tudománytörténeti érdekesség, hogy az ötlet Malus fejében akkor fogalmazódott meg, amikor egy este a Luxemburg-palota ablakainál egy kettőstörésű izlandi páton keresztül tanulmányozta a lenyugvó nap visszaverődő fényét, és meglepetésére két kép helyett csupán egyet látott [5.2.] .
Erre az időszakra esik Augustin-Jean Fresnel (1788 – 1824) francia fizikus meghatározó munkáinak megjelenése is [5.5.] , 1815-ben lefektette a diffrakció jelenségének új magyarázatát.

Michael Faraday (1791 – 1867) angol fizikus és kémikus, az elektrotechnika nagy alakja 1846-ban felfedezte – az optika történetében döntő fontosságú –, róla elnevezett effektust, amely szerint az elektromágneses tér az anyagokon való áthaladás közben elforgatja az áthaladó fény polarizációs síkját. Ahogy a Faraday-effektus, úgy az 1873-ban megjelent – a modern elektromágneses fényelmélet alapjait lefektető – James Clerk Maxwell (1831 – 1879) skót matematikus-fizikus által írt tanulmány mérföldkövet jelent a korszerű optika történetében.

Még mai is igaz, hogy az elektrodinamika az elméleti fizika egyik legfontosabb, gyakorlati szempontból is meghatározó, rendkívül érdekes fejezete. Joggal mondhatjuk, hogy a Maxwell által kidolgozott elektromágneses térelmélet a tizenkilencedik század fizikájának is az egyik legmeghatározóbb és legfontosabb eredménye, amely egyben utat nyitott a relativitáselmélet és a kvantumelmélet előtt. Maxwell nagy érdeme, hogy felismerte a közeg elektromos és mágneses jelenségekre gyakorolt befolyását. Az egzakt matematikai formába öntött törvényszerűségek egyértelművé teszik, hogy az elektromágneses – és ezen belül természetesen az optikai – jelenségek helye a tér, teljesen függetlenül attól, hogy azt mi tölti ki.
![Albert Abraham Michelson (1852 – 1931) [5.11.]](images/image_V_5.png)
A fizikusokat már régóta foglalkoztató éter-elv kísérleti vizsgálatához kapcsolódik az úgynevezett Michelson–Morley-kísérlet, melyet 1887-ben végeztek el Albert Abraham Michelson (1852 – 1931) és Edward Williams Morley (1838 – 1923) amerikai fizikusok a mai Case Western Reserve University-n. A kísérlet jelentőségét bizonyítja, hogy Albert Abraham Michelson 1907-ben Nobel-díjat kapott a Michelson–Morley-kísérletért. A kísérlet célja az volt, hogy megmérjék a Föld éterhez viszonyított sebességét. A lebonyolításhoz a Michelson által kifejlesztett Michelson-interferométert használták, amely a méréstechnikában mai is az egyik leggyakrabban alkalmazott interferometrikus elrendezés. E kísérlet – melyet az év folyamán többször is megismételtek, és döntő lökést adott a relativitáselmélet fejlődésének – eredményeként azt nyerték, hogy a keresett sebesség mindig nullával volt egyenlő.
![Frits Zernike (1888 – 1966) [5.10.]](images/image_V_6.jpeg)
A holográfia elvét a magyar, Gábor Dénes publikálta 1947-ben, módszerével teljes hullámfront rekonstrukció valósítható meg, kidolgozásáért 1971-ben fizikai Nobel-díjat kapott [5.28.] . Hullámoptika huszadik századi történetében fontos lépés volt Frits Zernike (1888 – 1966) holland Nobel-díjas fizikus és matematikus 1953-ban felfedezett fáziskontraszt mikroszkópja és a lézerek, azaz a fénykibocsátáshoz indukált emissziót használó fényforrások 1960-as fedezése, mely az amerikai Theodore Harold Maiman (1927 – 2007) nevéhez köthető. 1963-ban Yuri Nikolaevich Denisyuk (1927 – 2006) szovjet fizikus a Lippmann-emulzióra alapozva fehér fényben rekonstruálható hologramot készített. A kvantumelektronika területén a lézerelven működő oszcillátorok és erősítők létrehozásához vezető úton kifejtett tevékenységükért Charles Townes, Nikolay Basov és Aleksandr Prokhorov 1964-ben Nobel-díjat kaptak.
5.3. A fény terjedési sebességének kérdése
Az optika alapvető kérdéseire magyarázatot kereső természettudósokat az idők során folyamatosan foglalkoztatták a fény terjedésének körülményeire vonatkozó kérdések, de ezek között is kiemelt szerepet töltött be annak terjedési sebessége. Hosszú ideig tartotta magát az a nézet, mely szerint a fény esetében nem lehet beszélni terjedési sebességről, azaz ahhoz, hogy a tér egyik pontjából a másikba jusson, nincs szüksége időre. A fénysebesség mérésére már a kezdetekben is számos kísérlet történt, Galileo Galilei például két távoli hegycsúcson helyezett el fényforrásokat [5.3.] . A kísérlet során először Galilei nyitotta fel a fényforrás fedőlemezét, és mikor a másik hegycsúcson elhelyezkedő személy ezt észlelte, ő is felnyitotta a nála lévő fényforrás fedőlemezét. A kísérletet több különböző távolság esetén is megismételték, de az eltérést észlelni nem voltak képesek, sőt azt is megállapította Galilei, hogy a mérésben az idő jelentős részét az észlelő reakcióideje teszi ki. Csupán annyit következtetést tudott levonni, hogy a fénynek van terjedési sebessége, az igen jelentős. Később a kísérletet éjszaka elsütött ágyúk torkolattüze fényének egy tükörről történő visszaverődésének megfigyelésével próbálták pontosítani, azonban ezek a vizsgálatok sem vezettek használható eredményre. Galilei kísérletének igazi eredménye az a megállapítás volt, miszerint a fény sebessége igen nagy.
Első olyan kísérletet, amely a fény – rendkívül nagy –, de véges terjedési sebességére engedett következtetni 1672-ben Olaf Römer (Ole Christensen Rømer (1644 – 1710)) dán csillagász végezte el, nem földi objektumok felhasználásával. A Jupiter egyik holdját, az Iót figyelte meg távcsővel, és eltéréseket vett észre annak keringési periódusában; vizsgálta azt az időközt, amely a megfigyelt égitestnek a Jupiter árnyékából történő két egymás utáni kilépése között telik el [5.12.] . Megmérte tehát a keringési időt, és ebből kiszámította az árnyékból való kilépések feltételezett időpontjait. A Jupiter földközelben lévő állapotához tartozó számított eredmények és a fél évvel későbbiek között tizenhat perc és negyven másodpercet eltérést tapasztalt. Tehát egy félév múlva, amikor a Jupiter földtávolba került, holdjának kilépése az előre kiszámított időponthoz képest késett. Römer arra a következtetésre jutott, hogy e jelentős késés okát csak a fény terjedési sebessége okozhatja, mert a Földhöz képest a legtávolabbi és a legközelebbi Jupiter helyzet esetén az érkező fényeknek mintegy háromszáz millió kilométerrel – a földpálya átmérőjével – több utat kellett megtenniük. A távolság és a mért idő segítségével Römer kiszámította a fény sebességét, amire másodpercenként kettőszázhuszonhétezer kilométert kapott.
Römer okoskodása helyes volt, ugyanis az igen nagy terjedési sebességet csillagászati viszonyok mellett könnyebb meghatározni, mint a Földi körülmények között. Az utóbbira, azaz földi fényforrás segítségével történő fény terjedési sebesség meghatározásra első ízben Armand Hippolyte Louis Fizeau (1819 – 1896) francia fizikus tett javaslatot [5.12.] .
Fizeau, fénysebesség mérésére kifejlesztett berendezésében két, egymástól adott és ismert távolságokban elhelyezkedő mérőhelyeken egy – fókuszsíkjában tükröt tartalmazó – kollimátor és egy speciális távcső volt elhelyezve úgy, hogy egymás felé irányzottak és optikai tengelyeik egy közös tengelyre voltak felfűzve. A speciális távcsőben elhelyezett nagy fényerejű fényforrás fényét egy féligáteresztő tükör segítségével a kollimátor irányába terelte úgy, hogy a speciális távcső féligáteresztő tükre előtt egy vezérelhető fordulatszámú fogazott tárcsa helyezkedett el úgy, hogy annak fogai, illetve a fogak közötti nyílások a fénysugár útját kitakarták, vagy szabadon hagyták. A tárcsa fordulatszámának növelésével elérhető volt az az állapot, amikor a fényforrás fénye észlelhető volt a megfigyelő által, azaz ekkor az egyik fogaskerék nyílásnak a másik helyzetébe való befordulásához tartozó idő megegyezik a fénysugár teljes útjával. Ismerve a távcső és a kollimátor távolságát, a tárcsa fordulatszámát és a fogak számát; a fény sebessége maghatározható. Fizeau vizsgálatainak eredményeképpen a fény sebességére másodpercenként háromszáztizenháromezer kilométert kapott. Ő volt tehát az első, aki a fény sebességét (1849. július 23-án) földi, laboratóriumi körülmények között mérte meg. Az eljárás során a két opikai rendszer közötti távolság a nyolc kilométer volt.
Fizeau kísérletét később Jean Bernard Léon Foucault (1819 – 1868) a róla elnevezett – a Föld tengelye körüli forgását kimutató – ingáról híres francia fizikus tökéletesített formában megismételte, s 1862-ben már a fény által egy másodperc alatt megtett útra kettőszázkilencvennyolcezer kilométert kapott. Ez az érték igen közel áll a mai ismereteink szerint elfogadott 299 792 kilométerhez. Érdekesség, hogy Albert Abraham Michelson (1852 – 1931) 1926-ban, forgó tükrök használatával, és a kaliforniai Wilson-hegy és a San Antonio-hegy távolságát használva korrigálta a mérését, és a fény által egy másodperc alatt megtett útra 299 796 kilométert kapott [5.7.] .
5.4. Hullámtani alapfogalmak
A hullámoptika tárgya azon fényjelenséget vizsgálata [5.1.] , amelyek csak a fény hullámtermészetével értelmezhetőek és magyarázhatóak. A tárgyalásmód kívánalmainak megfelelően a terjedő fényt hullámként, az esetek jelentős részében periodikus hullámként értelmezzük, melyben egy vagy több fizikai mennyiség időben és térben periodikusan változik. A hullámoptikában előforduló jelenségek magyarázhatók az általános hullámtan fogalmai és törvényszerűségei alapján.
5.5. A periodikus mozgás
Azon mozgásokat, amelyek azonos időközönként ismétlik önmagukat, periodikus mozgásoknak nevezünk. Szemléletes példaként egy spirálrugóra kötött tömeg mozgását lehet tárgyalni, mely során fellépő sajátos mozgást nevezzük egyszerű harmonikus mozgásnak vagy más szavakkal rezgőmozgásnak.
5.6. Egyszerű harmonikus rezgőmozgás
Definíció szerint az egyszerű harmonikus rezgőmozgást egy kör kerületén állandó sebességgel mozgó pontnak a kör átmérőjére vetített mozgásával határozzuk meg. A maximális elmozdulást amplitúdónak, az egy teljes rezgés megtételéhez szükséges időt pedig periódusidőnek nevezzük. A rezgő test frekvenciáján a másodpercenkénti teljes rezgések számát értjük. A rezgés frekvenciája a periódusidő reciproka. Ha egy test rezgését a körmozgást végző pont segítségével írjuk le, akkor a frekvenciát a másodpercenkénti fordulatok száma adja meg, mértékegysége a Hertz (Hz).
|
| ||
|
|
A rezgőmozgást végző pont x irányú elmozdulását a következő összefüggés adja meg:
|
|
Felhasználva azt a mechanikai összefüggést, miszerint az idő a megtett út és a haladási sebesség hányadosa, a pont ω szögsebességét a periódusidő függvényében az alábbi összefüggésekből kapjuk
|
|
A rezgőforrások demonstrálására szellemes példaként egy megnyújtott spirálrugót alkalmaznak, amely a feszítőerő hirtelen megszűnése után egyszerű harmonikus rezgőmozgással mozog tovább. Ilyen esetben a két egymást követő hullámforma azonos pontjainak távolsága a hullámhossz, melyet a görög lambda λ betűvel jelölunk. Egy hullámhossznyi a távolság két hullámhegy vagy két hullámvölgy között található. Egy időpontban a hullám bármelyik pontjának elmozdulását az egyensúlyi helyzettől való távolsága adja meg. Ennek előjele megállapodás kérdése, de folyton változik pozitív és negatív értékek között. A hullám amplitúdója az előbb definiált elmozdulás maximális értéke.
5.7. Transzverzális hullámok
Minden fényhullám transzverzális hullám, amely az a hullám, amelynek minden kis eleme a hullám terjedésének irányára merőleges mozgást végez. A legegyszerűbb hullámmozgások azok, amelyek hullámpontjainak elmozdulását valamilyen egyenletesen változó mennyiség szinusza vagy koszinusza írja le. Hullámmozgás során a mindenkori elmozdulást és annak irányát az egységkörön mozgó pont helyzetével is jellemezhetjük, meghatározhatjuk. Az adott helyzetű pontot az origóval összekötő egyenes vízszintes tengellyel bezárt, az óramutató járásával ellentétes irányban mért szöge, meghatározza azt a pozíciót, amit általánosan fázisszögnek nevezünk.
A tömegpont helyzetét annak függőleges tengelyű vetülete határozza meg. Ez és a fentiek alapján
|
|
Ha pont állandó sebességgel halad, akkor az ω szögsebesség is állandó, és a Θ szögre érvényes
|
|
Behelyettesítve és kiegészítve a fázisszöggel:
|
|
Az α szöget kezdeti fázisszögnek nevezzük és állandó. Az egyszerű harmonikus hullámok egyenleteiben az elmozdulásokat a körfrekvencia 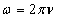 és a hullámszám
és a hullámszám 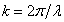 függvényében ábrázoljuk.
függvényében ábrázoljuk.
|
|
A hullámcsúcs sebességére vonatkozóan gyakran alkalmazzák a hullámsebesség, vagy fázissebesség kifejezést.
5.8. Amplitúdó és intenzitás
A hullámok, terjedésük során energia hordozói, így definíció szerint az időegység alatt a mozgásra merőleges egységnyi felületen áthaladó energiamennyiséget nevezzük a hullám intenzitásának. Ha a hullám állandó sebességgel terjed, akkor adott az egységnyi térfogatra eső teljes energia, azaz az energiasűrűség [5.18.] . A terjedést biztosító közegben az egységnyi területen időegység alatt áthaladó energia egy adott hosszúságú és egységnyi alapfelületű hasábban található. Így az intenzitást a hasáb hossza és az energiasűrűség szorzata adja, amely energiasűrűség, és az intenzitás arányos az amplitúdó, illetve a frekvencia négyzetével [5.16.] .
5.9. Frekvencia és hullámhossz
Rendkívül fontos tény, hogy minden hullámmozgást, amit valamilyen rezgő forrás hoz létre, a frekvenciája jellemez, és a kibocsátott hullámok frekvenciája megegyezik a forráséval. Egy adott közegben a hullámhosszt a terjedési sebesség határozza meg, ami a sebesség és a frekvencia hányadosa. Az egyik közegből a másikba történő áthaladáskor a frekvencia változatlan marad, így a hullámhossz a sebesség változásával azonos arányban változik meg.
5.10. Fényinterferencia
A hullámok egymásrahatásának egyik legismertebb megjelenési formája az interferencia, mely csak koherens interferáló hullámok esetén figyelhető meg. Mivel a fényforrások jelentős részénél a fénykibocsátás atomi folyamat, amely során az egyes atomok véletlenszerűen bocsátanak ki véges hosszúságú hullámvonulatokat, így azok nem koherensek. Ezért két, hagyományos fénykibocsátás elvén működő pontszerű fényforrás segítségével interferenciára jellemző térbeli intenzitáseloszlást létrehozni nem tudunk. Az ilyen, hagyományos fényforrások segítségével fényinterferenciát csak úgy tudunk megfigyelni, ha a fényforrás által kibocsátott hullámfrontokat osztjuk, majd újra egyesítünk, így tulajdonképpen a fényhullámot önmagával interferáltatjuk [5.17.] .
Ha az interferencia létrejöttének feltételei teljesülnek, akkor az interferáló hullámok találkozásakor megfigyelhetjük az interferencia jelenségét. Ilyenkor a hullámok teljesen kiolthatják vagy erősíthetik egymást. Az interferencia jelensége akkor lesz folytonosan megfigyelhető, ha huzamos idő alatt nem változik meg az interferáló hullámok fáziskülönbsége [5.19.] .
5.11. A szuperpozíció elve
A szuperpozíció elve egy olyan törvényszerűség, mely kimondja, hogy bármely pont elmozdulása azon elmozdulások összege, amelyeket az egyes hullámok külön-külön keltettek. Az ilyen formában megfogalmazott szuperpozíciós elvet, először Thomas Young (1773 – 1829) angol orvos és fizikus mondott ki először 1802-ben [5.8.] .
5.12. Egyszerű harmonikus rezgőmozgások összeadása egy egyenes mentén
Két, azonos frekvenciájú szinuszhullám egymásra hatásának vizsgálata esetén a megoldandó feladat úgy is megfogalmazható, hogy milyen az az eredő mozgás, amely akkor keletkezik, amikor egy részecske két harmonikus rezgőmozgást végez egy időben. A két hullám által okozott elmozdulásokat egy egyenes mentén ábrázolva jelöljük az amplitúdókat a 1 és a 2 -vel, ezek lesznek tehát a részecskére illesztett két periodikus mozgás amplitúdói [5.1.] .
|
| ||
|
|
A szuperpozíció elve alapján – mely kimondja, hogy bármely pont elmozdulása azon elmozdulások összege, amelyeket az egyes hullámok külön-külön keltettek – a bekövetkező y elmozdulás egyszerűen az egyes elmozdulások összege, így írható, hogy:
|
|
A két szög különbségének szinuszára érvényes kifejezés segítségével:
|
|
Bevezetve az alábbi konstansokat:
|
| ||
|
|
Négyzetre emelve és összeadva:
|
|
Egyszerűsített alakban
|
|
Arányként felírva:
|
|
A fenti összefüggések alapján
|
|
amely a két szög különbségének szinuszát kifejező képlet alapján:
|
|
Ez az egyenlet megegyezik az egyszerű harmonikus rezgőmozgás egyenletével, de módosított A amplitúdót és Θ fázisállandót tartalmaz. Mindezek alapján megállapítható, hogy két, azonos frekvenciájú, egyszerű harmonikus rezgőmozgás összege egy egyenes mentén egy velük azonos frekvenciájú, egyszerű harmonikus rezgőmozgás lesz. Az új rezgőmozgás amplitúdója és fázisállandója számítható a komponensek amplitúdójából és fázisállandójából.
Az eredő amplitúdó, az a
1
és a
2
amplitúdóktól és 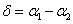 fáziskülönbségtől függ. Két fénysugár találkozásakor a fény intenzitása bármely pontban arányos az eredő amplitúdó négyzetével.
fáziskülönbségtől függ. Két fénysugár találkozásakor a fény intenzitása bármely pontban arányos az eredő amplitúdó négyzetével.
|
|
Ha a fáziskülönbség 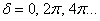 akkor 4a
2
-et kapunk, azaz bármelyik fénysugár intenzitásának 4-szeresét. Ha
akkor 4a
2
-et kapunk, azaz bármelyik fénysugár intenzitásának 4-szeresét. Ha 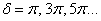 az intenzitás nulla.
az intenzitás nulla.
5.12.1. Két azonos frekvenciájú hullám szuperpozíciója
Ha feladatként meghatározandó két egyenlő frekvenciájú és amplitúdójú, x irányba haladó hullám eredője úgy, hogy köztük Δ távolság van.
|
| ||
|
|
A szuperpozíció elve alapján határozható meg az eredő hullámmozgás, amely az egyes hullámmozgások összege [5.1.] :
|
|
Az ismert matematikai összefüggés:
|
|
Alapján egyszerű matematikai átalakítások után:
|
|
Ez lényegében egy új hullámot jelent, 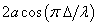 amplitúdóval. Amikor Δ a hullámhosszhoz képest kicsi, az amplitúdó közel 2a lesz, míg ha Δ az hullámhossz felével összevethető, akkor gyakorlatilag nulla. A különböző műszaki tartalmú rezgési példákon a csomópontok és az erősítések formája az állóhullámok keletkezésének szemléletes bizonyítéka két azonos frekvenciájú és amplitúdójú, de különböző irányba mozgó hullámvonulat szuperpozíciójának.
amplitúdóval. Amikor Δ a hullámhosszhoz képest kicsi, az amplitúdó közel 2a lesz, míg ha Δ az hullámhossz felével összevethető, akkor gyakorlatilag nulla. A különböző műszaki tartalmú rezgési példákon a csomópontok és az erősítések formája az állóhullámok keletkezésének szemléletes bizonyítéka két azonos frekvenciájú és amplitúdójú, de különböző irányba mozgó hullámvonulat szuperpozíciójának.
A számtalan helyen megfigyelhető, egyszerű interferenciajelenségekhez képest, a fényhullámok interferenciájának kimutatása lényegesen nehezebb feladat, hiszen a fényhullámok jellemzése sokkal bonyolultabb, ezek nem írhatók le egyetlen folytonos hullámvonulattal. A fénykibocsátás klasszikus forrásaiban, azaz a fényforrások egy jelentős részében a fénykibocsátás jelensége különálló részecskékből, egymástól függetlenül és viszonylag rendkívül rövid ideig, mintegy százmilliomod másodperc alatt zajlik le.
Ezen időintervallum alatt a fény az elemi részecskéből, a tér minden irányába, összefüggő szinuszos jelegű hullámvonulat formájában terjed tova. A hullámvonulat hossza a forrás interferenciaképességével, azaz koherenciahosszával függ össze.
A természetben sajnos ritkán tapasztalunk közvetlenül interferencia jelenséget, hiszen azt az interferenciában részt vevő, szuperponálódó két hullámvonulat közötti fáziseltolódás mértéke határozza meg. A jelenség megfigyelhetősége szempontjából ez pedig azt jelenti, hogy a két találkozó és interferáló hullám erősíti vagy gyengíti egymást. A jelenség létrejötte szempontjából kulcsfontosságú fáziseltolódás csak a két hullámvonulat által megtett utak különbségétől függhet. Ha az adott megfigyelési pont felé tartó két hullámvonulat által megtett út különbsége meghaladja a kibocsátás jellege által meghatározott hullámvonulat hosszát, azaz a koherenciahosszt, akkor a hullámfrontok nem tudnak találkozni, hiszen egyszerre nem tudnak elérni a találkozási ponthoz. Ezért, az a jelenség, miszerint az egyszerű estekben nem tapasztalunk fényinterferenciát arra vezethető vissza, hogy a hétköznapi gyakorlatban alkalmazott fényforrások koherenciahossza kicsi.
Ahhoz, hogy jól detektálható interferencia jelenséget kapjunk jelentős úthossz különbségek esetén is, nagy, több méteres koherencia-hosszú fényforrásokra van szükségünk [5.13.] .
5.13. Lézer interferometria
Az interferencia feltételeinek meglétekor [5.6.] fényhullámok találkozásakor interferencia jelenséget figyelhetünk meg. Alkalmasan megválasztott körülmények között a hullámok teljesen kiolthatják, és maximálisan erősíthetik egymást. Ahogy a fentiekben már kifejtésre került, az interferencia jelensége akkor lesz huzamosan megfigyelhető, ha e megfigyelés teljes időtartama alatt nem változik meg az interferáló hullámok fázisa, fáziskülönbsége. Az interferencia jelenségének méréstechnika alkalmazásához elengedhetetlen a nagy koherenciahosszú forrás alkalmazása. Ennek a feltételnek elsősorban a lézerek felelnek meg [5.14.] .
5.14. Amplitúdóosztás. Michelson-interferométer
A fény igen sok tulajdonsága megmagyarázható, ha feltesszük, hogy a fényhullám önmagával vagy akár egy másik hullámmal képes interferálni. Az interferencia létrehozásának két lehetséges megvalósítási formája ismert; az egyiket hullámfrontosztással hozzuk létre, ahol a hullámfrontot oldalirányban tükrökkel vagy diafragmákkal szegmensekre osztjuk. A másik osztási mód megtartja eredeti hullám méretét, de csökkenti annak amplitúdóját. Michelson-Morley kísérlethez [5.8.] kidolgozott mérési elrendezés annyira sikeresnek bizonyult, hogy jelenleg is az egyik leggyakrabban alkalmazott [5.20.] az interferometrikus mérések során [5.23.] [5.24.] .
A Michelson-interferométer [5.21.] jó példája az amplitúdóosztás elvén működő interferometrikus eszközöknek. A amplitúdóosztás segítségével létrehozott két nyaláb különböző utakat jár be addig, míg elérik a síktükröket, melyekről reflektálódva újra egyesülnek. Számtalan mérési feladat ellátására alkalmasak, például hullámhossz, fizikai hosszúság, vagy egy anyag törésmutatójának mérésére alkalmas [5.15.] . Természetesen segítségével a forrás koherenciahossza is meghatározható [5.22.] .
Amennyiben a két tükör és a nyalábosztó között a fény útja azonos, ilyenkor a kilépő fényhullámok azonos fázisban találkoznak, azaz az interferometrikusa erősítik egymást. Ha valamelyik kar hosszúsága megváltozik, akkor az interferáló hullámok fáziskülönbsége is módosul, így a detektálható intenzitás is megváltozik. Ha a két tükör egymásra nem merőleges, akkor az interferáló hullámfrontok egymással szöget zárnak be, ami hatására az intenzitásmaximumok helyén világos csíkok figyelhetők meg, melyek távolságából a két hullámfront szöge, a hullámhossz ismeretében számolható.
A Michelson-interferométer felépítését tekintve tartalmaz egy monokromatikus fényforrást. Az innen kilépő – és esetleg kitágított – hullámfront eléri az osztóelemet, melyet elhagyva a keletkező hullámok egyrészt referencia, másrészt a mozgatható tükör irányába haladnak tovább. Ezekről reflektálódva az osztóelem túloldalán találkozva hozzák létre az interferencia jelenségét. Az egyik sugárútban található lemez az üveganyagban megtett sugárutak azonosságát hivatott biztosítani [5.25.] .
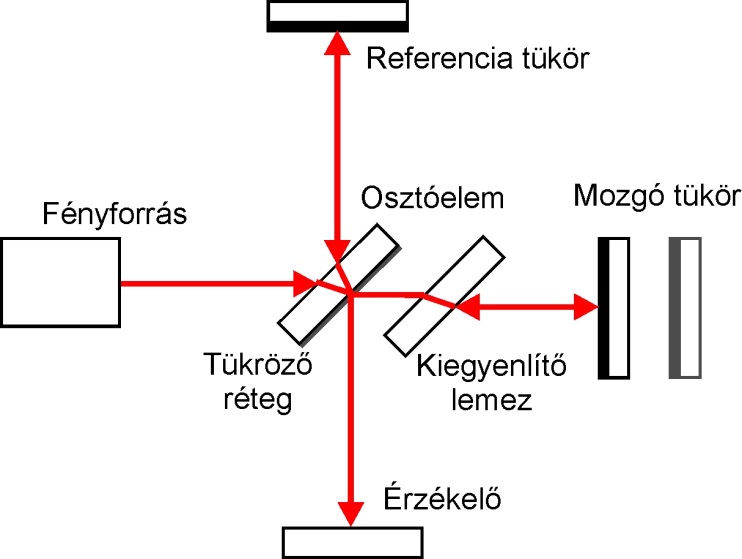
5.15. Ellenőrző kérdések
Amikor a képalkotás során a képalkotás minőségét már csak a diffrakció korlátozza, ilyenkor a geometriai optikai elvekre épülő analízis, illetve szintézis érvényességét veszti. Magyarázza el, hogy miért!
Hullámoptikai tárgyalásmód esetén a geometriai optika alaptörvényei közül az, mely kimondja, hogy számtalan sugár vezethető át egyetlen ponton anélkül, hogy azok egymásra hatást gyakorolnának, nem alkalmazható. Mondjon rá példát és magyarázza el!
Miben különbözött Galilei és Olaf Römer fénysebesség meghatározására irányuló kísérlete?
Fizeau, fénysebesség mérésére kifejlesztett berendezésében két, a fókuszsíkjában tükröt tartalmazó kollimátor, egy speciális távcső és egy vezérelhető fordulatszámú fogazott tárcsa volt megtalálható. Magyarázza el, hogy ezen berendezés segítségével hogyan volt meghatározható a fény sebessége!
Definiálja a periodikus mozgást, és jellemezze a egyszerű harmonikus rezgőmozgást!
A hullámok, terjedésük során energia hordozói, így definíció szerint az időegység alatt a mozgásra merőleges egységnyi felületen áthaladó energiamennyiséget nevezzük a hullám intenzitásának. Ez a fogalom milyen kapcsolatban áll az amplitúdóval?
Az egyik közegből a másikba történő áthaladáskor hogyan viselkedik a frekvencia és a hullámhossz?
Ha az interferencia létrejöttének feltételei teljesülnek, akkor az interferáló hullámok találkozásakor megfigyelhetjük az interferencia jelenségét. Sorolja fel ezeket a feltételeket!
Mit mond ki a szuperpozíció elve, és hogyan alkalmazható egyszerű harmonikus rezgőmozgások egy egyenes mentén történő összeadása és két azonos frekvenciájú hullám szuperpozíciója esetén?
Magyarázza el, hogy hogyan működik az amplitudóosztásos interferométer?
Milyen műszaki feladatok megoldására használják a Michelson típusú interferométert?
Az interferencia létrehozásának egy lehetséges megvalósítási formája; a hullámfrontosztás. Magyarázza el a működést a hullámfrontok oldaláról megközelítve!
Felhasznált irodalom
[5.1.] Optika. Panem-McGraw-Hill. Budapest . 1998.
[5.2.] Elméleti optika. Műszaki Könyvkiadó. Budapest . 1956.
[5.3.] The Handy Astronomy Answer Book. Visible Ink Press. 2008.
[5.4.] Einfürung in die theoretische Optik. B. G. Teubner. Berlin . 1907.
[5.5.] Optika elektromágneses fényelmélet. Tankönyvkiadó. Budapest . 1966.
[5.6.] Principles of Optics. Pergamon Press. 1975.
[5.7.] Fizika II. rész. Tankönyvkiadó. Budapest . 1951.
[5.8.] Pergamon Press. 1975.
[5.9.] Fizika II. rész. Tankönyvkiadó. Budapest . 1951.
[5.10.] http://nobelprize.org/.
[5.11.] http://astro-canada.ca/_en/photo690.php?a4313_michelson1.
[5.12.] Kísérleti Fizika III. Tankönyvkiadó. Budapest . 1985.
[5.13.] Modern optika mérnököknek és kutatóknak. Műszaki Könyvkiadó. Budapest . 1982.
[5.14.] Modern Optics. J. Wiley & Sons Inc. 1990.
[5.15.] Optical Methods of Engineering Analysis. Cambridge University Press. 1998.
[5.16.] Basics of Interferometry. Academic Press. 2006.
[5.17.] Optical Interferometry. Academic Press. 2003.
[5.18.] Selected Papers on Interferometry. Milestone Series MS28. SPIE. 1991.
[5.19.] Selected Papers on Interference, Interferometry, and Interferometric Metrology. Milestone Series MS110/HC. Society of Photo Optical. 1995.
[5.20.] Current Research on Holography and Interferometricmethods for Measurement of Object Properties 2000-2002 SPIE. 2003.
[5.21.] nterferometry VII. techniques and analysis. SPIE - the International Society for Optical Engineering. 1995.
[5.22.] Interferometry as a measuring tool. Machinery Publ.. 1970.
[5.23.] Interferometry. Cambridge University Press. 1986.
[5.24.] Interferometry. SPIE. Bellingham . 1979.
[5.25.] Hosszméréstechnikai zsebkönyv. Műszaki Könyvkiadó. Budapest . 1960.
[5.26.] Mikroszkóp-mikrokozmosz. Gondolat Kiadó. 1984.
[5.27.] Isaac Newton. Szikra Könyvkiadó. Budapest . 1948.
[5.28.] Válogatott tanulmányok. Gondolat Könyvkiadó. Budapest . 1976.
6. fejezet - A távcső, mint látószögnövelő eszköz
- 6.1. A távcsövek csoportosítása
- 6.2. Történeti áttekintés
- 6.3. Tükrös távcsövek története
- 6.4. A Magyarországi csillagászati megfigyelések története
- 6.5. A lencsés távcsövek optikai rendszere
- 6.6. Tükrös-távcsövek
- 6.7. A Newton távcső
- 6.8. Cassegrain távcső
- 6.9. A Schmidt távcső (Schmidt kamera)
- 6.10. Maksutov távcsövek
- 6.11. Ellenőrző kérdések:
- Felhasznált irodalom
A távcső kifejezés alatt azokat az eszközöket értjük, melyek távolban lévő tárgyak nagyobb látószög alatti megfigyelésére alkalmasak. Alapvető funkciójuk tehát a látószög növelése, és optikai rendszerüket tekintve pedig afokális rendszerek. Számtalan csoportosításuk ismert. Fontos ismérvük, hogy mely hullámhossz tartományban működnek; léteznek a látható tartományon kívül működő típusaik is, például röntgentávcsövek, infratávcsövek, rádiótávcsövek. A továbbiakban csak a látható tartományban működő, elsősorban vizuális megfigyelések céljára alkalmazott eszközökkel foglalkozunk.
6.1. A távcsövek csoportosítása
A távcsöveket szerkezeti felépítésük, illetve funkciójuk alapján csoportosítják. A szerkezeti kialakítás tekintetében megkülönböztetik a
lencsés, illetve a
tükrös távcsöveket, illetve a közöttük átmenetet képező, vegyes, azaz
lencsés-tükrös távcsöveket.
A lencsés távcsövek [6.4.] , [6.5.] a
Galilei típusú, úgynevezett színházi távcső, illetve a
Kepler típusú, úgynevezett csillagászati távcső.
Ha a kényelmesebb észlelés céljából a csillagászati távcsövet képfordító optikai rendszerrel egészítik ki, azt terresztikus, vagy más néven földi távcsőnek nevezik. A csillagászati távcsőben a képfordítást végző elem, lehet prizmás felépítésű, vagy lencsés is, függően a felhasználás típusától. A földi távcsővel – ahogyan azt az elnevezése is sugallja – földi körülmények között végzünk megfigyeléseket. Ilyenkor fontos, hogy a kép egyenes állású legyen és a megfigyeléshez szükséges nagyítás és fényerő is rendelkezésre álljon.
Az elnevezéstől függetlenül csillagászati megfigyelések céljára általában tükrös, vagy katadioptrikus rendszereket alkalmaznak, ezek alapvetően a bennül alkalmazott tükörfelületek típusától, egymáshoz képesti helyzetétől, illetve a lencsés tagok funkciójától függően különböznek.
A távcsövek felhasználása rendkívül széleskörű: a színházi, szabadidőstől, űrtechnikai, katonai, csillagászati, méréstechnikai, geodéziai felhasználásokig terjed [6.6.] , [6.7.] . A polgári mellett jelentős a katonai felhasználás is; a fegyvertávcsöveket egészen speciális kialakítás, és különleges optikai rendszer jellemezi.
6.2. Történeti áttekintés
Ugyan a lencsék készítését már az asszírok, az arabok és a perzsák is ismerték, azonban arról nincsenek ismereteink, hogy azokat távcsőként funkcionáló optikai rendszerbe lettek volna képesek integrálni [6.8.] . A 13. századból, Roger Bacontől származik az első följegyzés, miszerint optikai elemek felhasználásával a távoli tárgyak közelebbinek látszanak. Az első és dokumentált távcsövet Németalföldön készítették az 1600-as évek elején; előállítóik között Hans Lipperheyt, Jacob Adriaanszont, Zacharias Janssent említik. Galileo Galilei, a hozzá eljutó információk alapján építette meg saját távcsövét, és ezt használta is csillagászati megfigyeléseihez. Ezzel sikerült a Jupiter négy holdját, a Vénusz fázisváltozásait és a Hold hegyeit megfigyelnie és azokról feljegyzéseket készítenie. Az általa készített, domború és homorú lencsékből álló, egyenes állású képet adó távcsövet hollandi, vagy Galilei-féle távcsőnek nevezik, napjainkban is használják például színházi célokra, de ez az optikai elrendezés ismerhető fel egyes lézeres berendezések egyszerűbb feladatokat ellátó nyalábtágító távcsöveiben is [6.18.] .
Johannes Kepler a Német Római császár udvari csillagásza volt az, aki elsőként figyelte meg tudományos alapossággal, és jegyezte le az optikai lencsék viselkedését. Csillagászati megfigyeléseihez két domború lencsét tartalmazó – úgynevezett Kepler-féle, vagy csillagászati távcsövet – épített, amely ellentétben Galilei konstrukciójával fordított állású képet adott, de köszönhetően nagyobb nagyításának, csillagászati célokra jobban megfelelt [6.11.] .
A távcsövek képalkotási tulajdonságainak tökéletesítése útján fontos törekvés volt színhiba kiküszöbölése. Chester Moor Hall 1729-ben felismerte, hogy egy koronaüvegből készült gyűjtő és egy flintüvegből készült szórólencséből összeállított, úgynevezett akromatikus – két kitüntetett hullámhosszra egybeeső fókuszpontú – optikai rendszer generálható. A 1750-as évek végén John Dollond cége már jelentős mennyiségben és minőségben tudott akromatikus rendszereket gyártani, a különböző optikai berendezésekhez. Sajnos a minőségi fejlesztéseknek gátat szabott a szerény üvegválaszték, mely csak a 19. század második felére ért olyan szintre, hogy a színhiba mellett a többi hiba is jó minőségben vált korrigálhatóvá. Köszönhetően az egyre szélesebb üveganyag választéknak, és az egyre inkább tökéletesedő optikai gyártásnak és ellenőrzésnek, egyre nagyobb és egyre jobb képalkotású lencséket tudtak gyártani, aminek a csúcsát a pulkovói 75 cm-es (1883), a Lick 93 cm-es (1887) és a Yerkes 102 cm-es (1897) lencsék legyártása jelentette. Lényegében ezeknél nagyobb méretű lencséket távcsövekbe jelenleg sem gyártanak.
6.3. Tükrös távcsövek története
A tükrös távcsövek fejlődésének Sir Isaac Newton adott döntő lökést [6.16.] . Ugyanis a különböző anyagok színbontó képessége vizsgálata során arra a téves megállapításra jutott, hogy az egyes anyagok színbontó képessége megegyezik, így színhiba mentes lencsés optikai rendszer előállítása nem lehetséges; tehát távcsövet csak tükrös rendszerekből érdemes építeni. Meg is építette az első – róla elnevezett és ma is széles körben használt – tükrös távcsövet, ezzel elindítva a tükrös és katadioptrikus távcsövek fejlesztésének egy eredményekben igen gazdag korszakát [6.8.] . Tény, hogy a tükröket olcsóbb és egyszerűbb előállítani, továbbá a nagy méretű lencsék gyártása és szerelése számtalan technológiai nehézséget vet fel. Manapság is több méter körüli tükörátmérőjű csillagászati tükrös távcső létezik, és teszi lehetővé igen távoli objektumok hatékony és nagy felbontású megfigyelését.
A tükrös rendszerek alkalmazás melletti másik érv, hogy az egyszerűbb lencsés távcsövek másik hibája, a szférikus aberráció felületük speciális kialakításával korrigálható. Szférikus aberráció jelenléte esetén szférikus felületekből álló lencse széléhez közel belépő fénysugarak más pontban metszik az optikai tengelyt, mint a lencse közepéhez közel haladó fénysugarak [6.18.] . Ezt a rendkívül zavaró hibát nevezik még gömbi eltérésnek vagy nyíláshibának is.
Kezdetben a csillagászati fényképezés is igen komoly problémákkal küzdött, elsősorban a távcsövek üstökös hibája, vagy más néven komája miatt. Erre kínált megoldást a Ritchey és Chrétien által javasolt optikai elrendezés, amely parabola alakú főtükröt, hiperbolikus segédtükröt és konkáv felületű fotográfiai érzékelőt alkalmaz [6.1.] [6.2.] . Bernhard Woldemar Schmidt 1930-ban lencsét és tükröt tartalmazó katadioptrikus rendszert tervezett, amely egy hagyományos, és nagy fényerejű szférikus főtükröt, valamint egy speciális alakra csiszolt korrekciós lemezt használ. Ez a rendszer, az üveg anyagú tag miatt színhibát ugyan tartalmaz, de mentes az üstökös- és a nyíláshibától. A felület, amelyikre a fényérzékeny emulziót kifeszítik szintén görbült. A Schmidt típusú rendszerek szinte egy új fejezetet nyitottak az égi megfigyelések történetében. 1944-ben, az orosz Dmitrij Dmitrijevics Makszutov egy szintén a szférikus aberrációtól mentes rendszert javasolt [6.15.] ; a Makszutov-távcsőben a szférikus főtükör előtt egy erősen meniszkusz biztosítja a korrekciót.
6.4. A Magyarországi csillagászati megfigyelések története
Magyarországon az első, már csillagászati megfigyelésekre is alkalmas megfigyelő állomás a Hell Miksa által alapított nagyszombati obszervatórium. 1781-ben kezdte meg működését az egri csillagvizsgáló Specula elnevezésű tornyában, műszereivel európai színvonalat képviselt [6.3.] . A 18. század végén, Magyarországon már öt csillagvizsgáló működött (Nagyszombat, Buda, Eger, Kolozsvár és Gyulafehérvár). Az igazi fellendülés a gellérthegyi Urania obszervatórium megnyitásával, 1815-ben kezdődött. A 19. században még néhány magánkézben levő csillagvizsgáló alakult: Ógyallán Konkoly-Thege Miklós (1871), Kalocsán Haynald Lajos (1878), Herényben Gothard Jenő (1881) és Kiskartalban Podmaniczky Géza hozott létre obszervatóriumot. Ezek közül talán a legjelentősebb a magyar államra hagyományozott ógyallai csillagvizsgáló. A második világháború után az Akadémiai Csillagvizsgáló fő megfigyelőállomását a Mátrában levő Piszkéstetőre helyezte át. Fő büszkesége a Schmidt-távcső [6.9.] .
Akkorra ez a távcső már világszerte megmutatta rendkívüli hatékonyságát. A piszkéstetőihez hasonló méretű vagy nem sokkal nagyobb Schmidt-távcsövek látványosan eredményesek voltak a világ számos obszervatóriumában. A többfokos látómező nagy formátumú fotólemezekkel homogén minőségű adatok egyidejű rögzítését tette lehetővé nagy égterületekről. A Schmidt-távcsővel leginkább két területen [6.9.] vizsgálódtak:
a különleges vagy változó színképű, színű, fényességű objektumok keresése a kiterjedt látómezőben további részletes vizsgálat céljából,
a Tejútrendszer és extragalaxisok, galaxishalmazok, valamint csillaghalmazok és, -társulások szerkezetének vizsgálata fotografikus többszín-fotometria és objektívprizmás színképosztályozás alapján.
A magyar amatőrcsillagászok első szervezete az 1920-as években alapított Stella Csillagászati Egyesület volt. Ennek utóda lett a Magyar Csillagászati Egyesület. A Budapesti Uránia 1947-ben létesült. Fő műszere egy 20 centiméter átmérőjű Merz-Heyde távcső, amely egykor az ógyallai csillagvizsgálóban állt.
6.5. A lencsés távcsövek optikai rendszere
A hétköznapi értelembe vett távcső általában lencserendszer képfordítóval kiegészített változatban. Optikai képalkotásuk alapja a fénytörés, elrendezésüket tekintve afokális rendszerek [6.13.] , [6.14.] , [6.18.] . A tárgylencse, vagy más néven az objektív a végtelenből párhuzamosan érkező fénysugarakat megtöri és azokat – mivel ez minden esetben gyűjtő típusú rendszer – a mögötte elhelyezkedő fókuszpontban egyesíti. A kép az okuláron keresztül, felnagyítva szemlélhető. Ha a végtelenből, adott szög alatt érkező fősugarat vizsgáljuk, akkor az az objektíven áthaladva metszi az objektív fókuszsíkját, majd tovahaladva eléri az okulárt, melyen szögeltérést szenved. Így a vizsgált fősugár, eredeti szögéhez képest – általában – nagyobb szöggel lép ki az okulárból és lép be a megfigyelő személy szemébe. A távcsőből kilépő és az abba belépő sugár szögei tangensének aránya a távcső szögnagyítása, mely megegyezik a belépő és a kilépő pupilla átmérőjének arányával. Ez igaz a Kepler és a Galilei típusú távcsőre is, azzal, hogy a Kepler típusú esetén a kilépő fősugár szögének előjele eltér a belépő fősugár szögének előjelétől, így fordított kép keletkezik. A Galilei típusú távcsőben az okulár szóró típusú rendszer, így egyenes állású kép keletkezik.
A lencsés távcsövek előnyei:
megbízhatóak, egyszerű felépítésűek
jó képminőség érhető el
hátrányai:
a színhiba korrekciója miatt a lencsés rendszerek összetettebbek
szerényebb nagyítás érhető el velük, korlátozott fényerővel
A Galilei-típusú távcső előnye a viszonylag kicsi szerkezeti hossz, ami az objektív és az okulár fókusztávolságának különbségével egyenlő. A legnagyobb hátránya, hogy a kilépő pupilla a szerkezeten belül keletkezik, így az nem illeszthető a szem belépő pupillájához, attól jelentős távolságban helyezkedik el. Ez akadálya a nagyítás növelésének, ami általában 2-3-szoros.
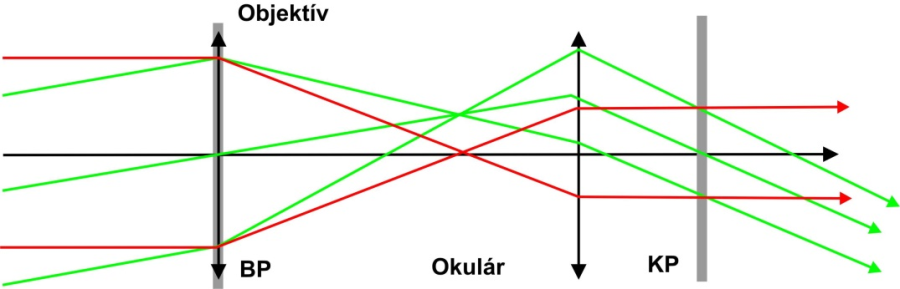
A Kepler típusú távcső előnye, hogy a kilépő pupilla az okulár után helyezkedik el, így az könnyen illeszthető a megfigyelő személy szeméhez. A belépő pupilla átmérőjének növelésével jelentős nagyítások érhetők el. A szerkezeti hossz az objektív és az okulár fókusztávolságának összege, így az lényegen nagyobb, mint a színházi távcső esetében.
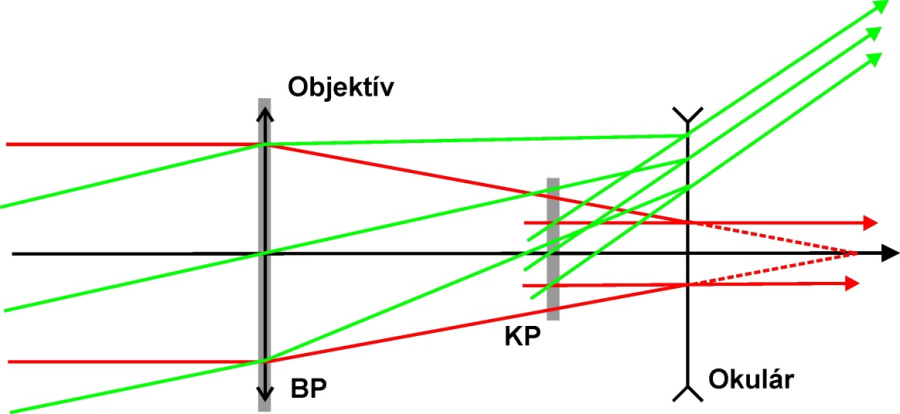
Ha a csillagászati távcsövet földi (terresztikus) célokra kívánjuk alkalmazni, képfordítóval kell kiegészíteni. Lencsés képfordítás esetén – ami általában egy -1-szeres nagyítású gyűjtő rendszernek az objektív és okulár közé illesztését jelenti – a szerkezeti hossz jelentős megnövekedésével kell számolni.
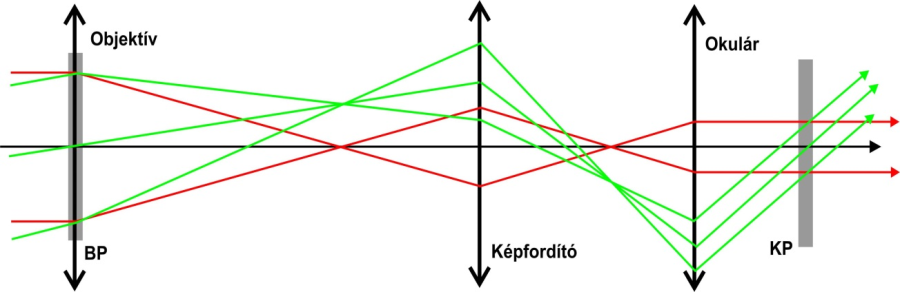
Fegyvertávcsövek esetén például ez nem akadály, azonban a kézből történő megfigyelést a jelentős méretnövekedés nehezítheti.
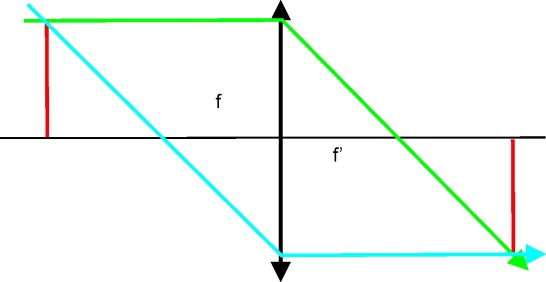
Ilyenkor alkalmaznak prizmás képfordítókat, melyek ismertebb típusai a
Porro-rendszerek, illetve a
Pechan-prizma.
Az előbbi tört sugármenetet jelent, amelynek a beszabályozása nehézkesebb. A távcsőben lévő optikai elemek átmérőinek korlátozása céljából gyakran úgynevezett mezőlencséket alkalmaznak, melyek a képhely környezetében a sugarak irányának megváltoztatására szolgálnak. Hátrányuk, hogy ilyen elrendezésben a rajtuk lévő esteleges szennyeződések a megfigyelt képen is láthatóvá válnak.
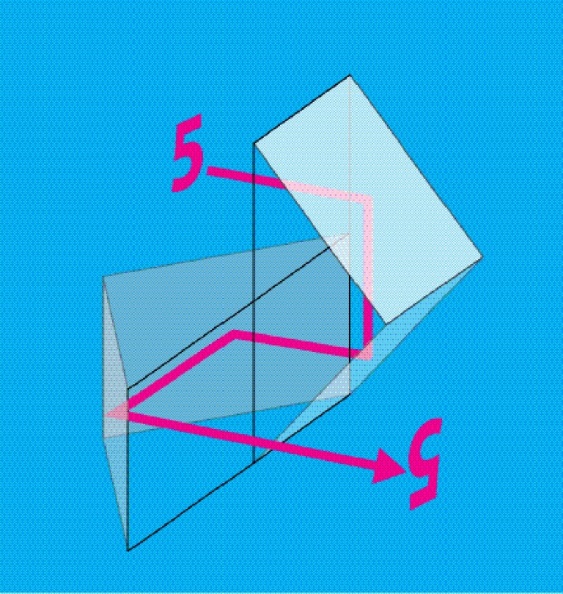
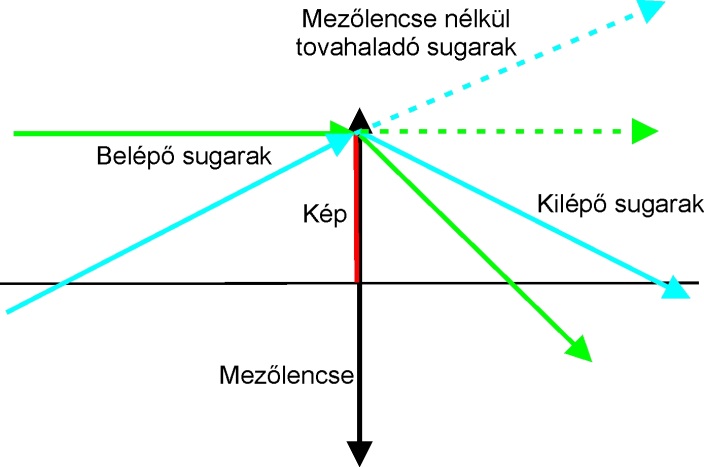
Példa:
Egy csillagászati távcső okulárja cserélhető. Az eredeti elrendezésben az objektív gyújtótávolsága 210 mm, az okulár gyújtótávolsága 35 mm. A belépő pupilla átmérője 25 mm. Határozza meg a kilépő pupilla méretét és a nagyítás változásának mértékét, ha kicseréljük az okulárt egy 25 mm fókusztávolságúra!
Megoldás:
Tudjuk, hogy a nagyítás a belépő és a kilépő pupilla átmérőjének arányával, illetve az objektív és az okulár átmérője arányával egyezik meg. Az eredet elrendezésben a nagyítás
|
|
Az új elrendezésben
|
|
Tehát a nagyítás változás mértéke 1.4-szeres, a kilépő pupilla átmérője pedig 2.98 mm.
6.6. Tükrös-távcsövek
Az égi objektumok megfigyelésére szinte kizárólag tükrös távcsöveket használnak. Természetesen a tükrös rendszerek más területeken is alkalmazást nyernek. Nem ritkák a tükrös mikroszkóp objektívek és kondenzorok [6.19.] , de a fotográfiában is gyakran alkalmaznak tükrös teleobjektíveket [6.20.] .
Tükrökként alakra és felületi minőségre csiszolt és polírozott [6.10.] , tükröző réteggel ellátott üvegkorongokat használnak. Ha a méret és az alkalmazás szempontjából az üveg mechanikai és hőtani tulajdonságai nem megfelelők, speciális anyagokat, vagy kerámiákat használnak (Pirex, Zerodur). Az objektívek általában egy főtükörből és egy segédtükörből állnak. A rendszerbe belépő, és a főtükörről visszaverődő sugarakat a segédtükör az okulár irányába tereli, ahol a létrejövő kép megfigyelhető, illetve okulár nélküli alkalmazás esetén a kép detektoron rögzíthető a későbbi feldolgozás és archiválás céljából. A fejlődés során számtalan tükrös távcső típus alakult ki. Megegyező optikai elv mellett, a fő- és segédtükör alakjában és egymáshoz viszonyított pozíciójában lelhető fel különbözőség. A legelterjedtebb tükrös-távcsöveket az alábbiakban jellemezzük.
6.7. A Newton távcső
A Newton távcsövet elsősorban az amatőrök használják, ezért igen elterjedt típus. A főtükre kis fényerőnél szférikus, nagyobb fényerő estén parabolikus [6.3.] . Az erről visszaverődő sugarakat egy ferdén elhelyezett sík felületű segédtükör téríti el, és juttatja el az okulárhoz. Tipikus hibájuk az üstököshiba, amikor a látómező szélén lévő pontszerű objektumok leképezve nem pontszerűek, hanem rendkívül zavaróan, üstökös formájúak, a fényes mag és az elmosódott csóva igen jelentősen befolyásolja a kép értékelhetőségét. Ez a hiba a fényerő és a látószög növekedésével fokozottan jelenik meg. A segédtükör méretét a látómező határozza meg, azonban a látómező növekedésével nagyobb lesz a központi kitakarás, így csökken a fényhasznosítás.
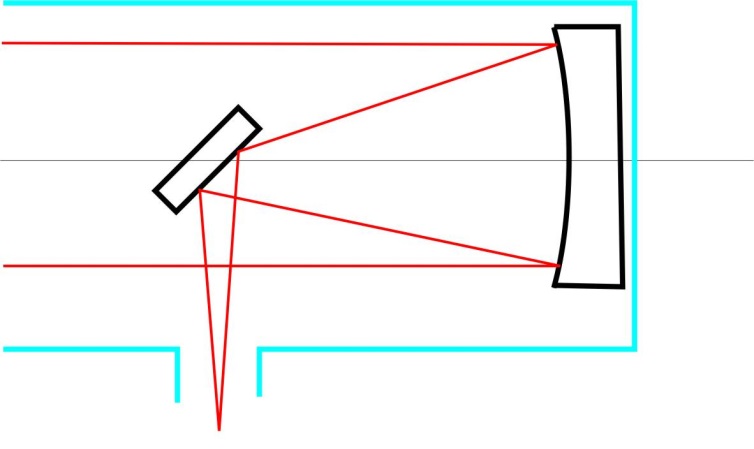
6.8. Cassegrain távcső
A Cassegrain távcső olyan előnyös tulajdonságokkal rendelkezik, amelyek miatt elterjedése igen jelentős. A legfontosabb előnyük a hosszú fókusztávolság melletti rövid tubushossz, ami elsősorban a segédtükörnek köszönhető. Alapkiépítésben a főtükörről visszaverődő sugarak egy domború felületű segédtükörről megnyújtva, a főtükör furatán keresztül jutnak el a megfigyelő okulárhoz. Sajnos a főtükör nagy fényereje miatt a segédtükör is jelentős méretű, a nagy központi kitakarás miatt a szemlélt képre jellemző jelentős mértékű a fényveszteség.
Az optikai rendszer jellege miatt a képalkotási hibák közül itt is jelentős az üstökös hiba. A Cassegrain-rendszernek több változata létezik, melyekben az egyes felületek alakja eltérő.
|
A távcső elnevezése |
A főtükör geometriája |
A segédtükör geometriája |
|---|---|---|
|
Cassegrain |
paraboloid |
hiperboloid |
|
Dall-Kirkham |
ellipszoid |
gömb |
|
Ritchey-Creatien |
hiperboloid |
hiperboloid |
|
Pressman-Camichel |
gömb |
ellipszoid |
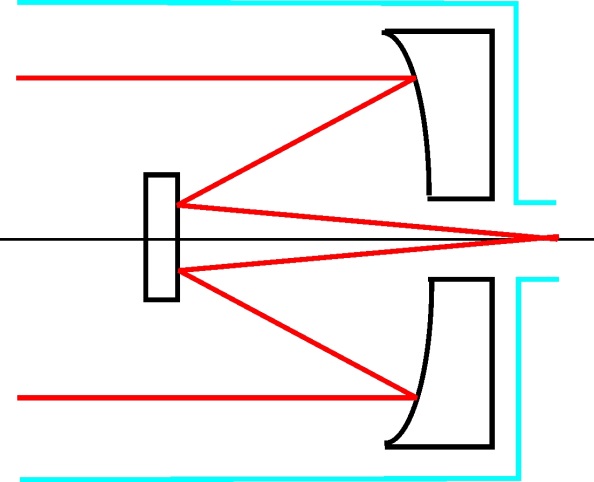
6.9. A Schmidt távcső (Schmidt kamera)
A Schmidt-féle katadioptrikus távcső objektívje, a főtükör egy homorú tükör, amely egyszerűen és pontosan, jó minőségben előállítható szférikus felület. A szférikus felület által mutatott nyíláshibát hivatott korrigálni a főtükör elé helyezett speciális optikai elem – egy korrekciós tag –, ami nagy mértékben mérsékli a főtükör hibáját [6.17.] . A Schmidt távcsőbe belépő fény a korrekciós lemezen áthaladva éri el a gömb felületű főtükröt. A sugarak innen reflektálódva alkotnak képet. A Schmidt távcsövet Schmidt kamerának is nevezik, ugyanis elsősorban nem vizuális megfigyelésekre használják, hanem rögzíthető felvételek készítésére. A fényérzékeny anyag egy szférikus felületre feszül az eredeti elrendezésben. A Schmidt kamera korrekciós lemeze egy magasabb rendű függvénnyel írható le. Bernhard Schmidt az általa tervezett rendszerek korrekciós lemezét sík üveglemezből készítette. Ritkított levegő segítségével egy speciális, szigetelt tartály peremén alátámasztva meggörbítette, majd ebbe az alakba egy szférikus felületet csiszolt bele. A nyomás helyreállta után a korrekciós lemez kó közelítéssel vette fel a kívánt alakot.
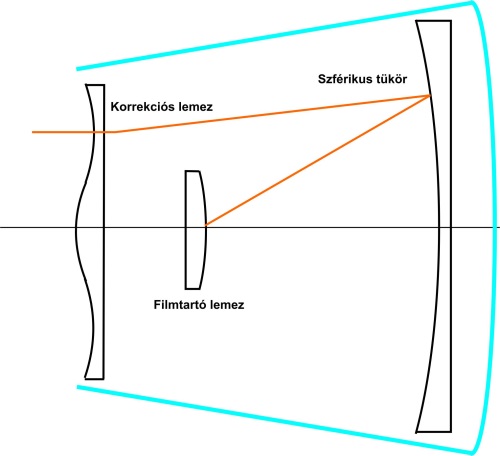
6.10. Maksutov távcsövek
A Maksutov távcső is katadioptrikus rendszer, megalkotása a Szentpétervár melletti Pulkovói Csillagvizsgáló optikai mérnökének, Dimitri Dimitrievics Maksutov (1896-1964) nevéhez fűződik. Itt a reflektáló és a reflektáló felületek is részt vesznek a kép létrehozásában [6.15.] . Ebben a távcsőtípusban felismerhetők a Schmidt távcső előnyei, de a korrekciós lemez egy könnyebben, és egyszerűbben elkészíthető, a főtükörhöz képest ellenkező előjelű szférikus aberrációjú meniszkusz. A színhibák korrekciója céljából szükség esetén akromatikus meniszkuszt alkalmaznak.
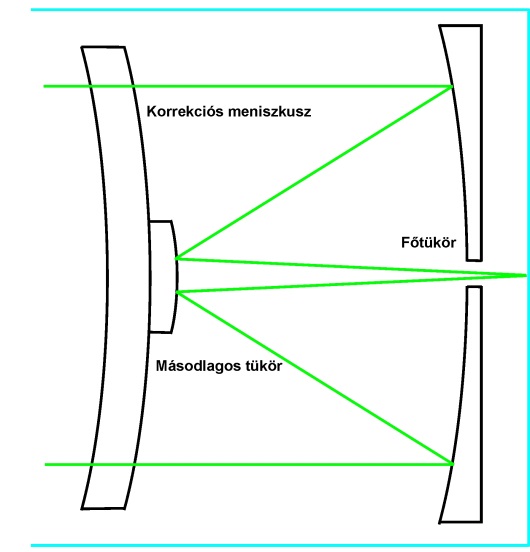
6.11. Ellenőrző kérdések:
Mit értünk a távcső kifejezés alatt?
Mit jelent a látószög?
Mit jelent az afokális rendszer?
A távcsöveket szerkezeti felépítésük, illetve funkciójuk alapján csoportosítják. Ismertesse ezen csoportosítások tagjait!
A szerkezeti kialakítás tekintetében megkülönböztetik a lencsés, illetve a tükrös távcsöveket, illetve a közöttük átmenetet képező, vegyes, azaz lencsés-tükrös távcsöveket. Mi jellemzi ezeket a rendszereket?
Hogyan jellemezhetők a katadioptrikus rendszerek.
A refraktor elnevezés a képalkotásban alapvető funkciót betöltő fénytörés, azaz a refrakció jelenségéből származik, míg a tükrös távcsöveket, azaz a reflektorokat fényvisszaverődés, tükröződés reflexió jellemzik. Mia kapcsolat e két jelenség között?
Jellemezze a Galilei típusú, úgynevezett színházi távcsövet!
Jellemezze a Kepler típusú, úgynevezett csillagászati távcsövet!
Jellemezze a kényelmesebb észlelés céljából képfordító optikai rendszerrel kiegészített, terresztikus, vagy más néven földi távcsövet!
Ismertesse a csillagászati távcsőben a képfordítást végző elem, a prizmás felépítésű, vagy a lencsés felépítésű képfordítót!
Jellemezze az afokális rendszereket!
A tárgylencse, vagy más néven az objektív a végtelenből párhuzamosan érkező fénysugarakat megtöri és azokat – mivel ez minden esetben gyűjtő típusú rendszer – a mögötte elhelyezkedő fókuszpontban egyesíti. A kép az okuláron keresztül, felnagyítva szemlélhető. Vázolja fel az ennek megfelelő sugármenetet!
A vizsgált fősugár, eredeti szögéhez képest – általában – nagyobb szöggel lép ki az okulárból és lép be a megfigyelő személy szemébe. A távcsőből kilépő és az abba belépő sugár szögei tangensének aránya a távcső szögnagyítása, mely megegyezik a belépő és a kilépő pupilla átmérőjének arányával. Igazolja ezt grafikusan és analitikusan is!
Igazolja, hogy a Kepler típusú távcső esetén a kilépő sugár szögének előjele eltér a belépő sugár szögének előjelétől, így fordított kép keletkezik!
Igazolja, hogy mivel a Galilei típusú távcsőben az okulár szóró típusú rendszer, így egyenes állású kép keletkezik.
Ismertesse a lencsés távcsövek előnyeit!
Ismertesse a lencsés távcsövek hátrányait!
A Galilei-típusú távcső egyszerű felépítése mellett számtalan előnnyel és hátránnyal rendelkezik. Melyek ezek?
Igazolja, hogy a Galilei távcső legnagyobb hátránya, hogy a kilépő pupilla a szerkezeten belül keletkezik, így az nem illeszthető a szem belépő pupillájához!
Ismertesse a alkalmaznak képfordítókat, ismertebb típusaikat: a Porro-rendszereket, illetve a Schmidt-Pechan-prizmát.
Rajzolja meg a lencsés képfordító sugármenetét!
Illesszen egy lencsés képfordítót egy csillagászati távcsőve! Rajzolja meg a sugármenetet! Szerkessze meg a kilépő pupilla helyét és méretét!
A Newton távcső főtükre kis fényerőnél szférikus, nagyobb fényerő estén parabolikus. Az erről visszaverődő sugarakat egy ferdén elhelyezett sík felületű segédtükör téríti el, és juttatja el az okulárhoz. Rajzolja meg a sugármenetet és indokolja hogy miért kell nagyobb fényerő esetén parabolikus felületet alkalmazni!
A Newton távcső tipikus hibája az üstököshiba, ami a látómező szélén lévő pontszerű objektumok leképezésekor nem pontszerű, hanem rendkívül zavaróan, üstökös formájú képet eredményez. Jellemezze az üstökös hibát!
Hasonlítsa össze a Makszutov és a Schmidt távcsövet!
Rajzolja meg a Makszutov távcső sugármenetét!
Felhasznált irodalom
[6.1.] The History of the Telescope (Dover Books on Astronomy). Dover Publications. 2011.
[6.2.] The Telescope: Its History, Technology, and Future. Princeton University Press. 2007.
[6.3.] A távcső világa. Gondolat Kiadó. 1975.
[6.4.] Optikai műszerek. Műszaki Könyvkiadó. 1963.
[6.5.] Alkalmazott optika I. rész. Felsőoktatási Jegyzetellátó Vállalat. 1957.
[6.6.] Optikai képkeresők, élességállító és vetítőberendezések. Felsőoktatási Jegyzetellátó Vállalat. 1954.
[6.7.] Finommechanikai kézikönyv. Műszaki Könyvkiadó. 1974.
[6.8.] Ki készítette az első távcsövet?. Meteor. pp.39-43..
[6.9.] A piszkéstetői Schmidt-távcső ötven éve. Magyar Tudomány. pp. 130-139..
[6.10.] Das Spiegelteleskop in der Astronomie. Barth. Leipzig . 1930.
[6.11.] Optikai műszerek elmélete és gyakorlata - Távcső általános története, kézi prizmás- és színházi távcsövek. Nehézipari Könyvkiadó. 1954.
[6.12.] Optics. Addison-Wesley. 2002.
[6.13.] Mastering optics, An applications guide to optical engineering. McGraw-Hill. 1996.
[6.14.] Geometrical optics and optical design. Oxford University Press. 1997.
[6.15.] New Catadioptric Meniscus Systems. JOSA. pp. 270-283. 1944.
[6.16.] Isaac Newton. Szikra. Budapest . 1948.
[6.17.] Elementare Theorie des Spiegeltelescops von B. Schmidt. Leipzig and Berlin. 1940.
[6.18.] Modern Optical Engineering. McGraw-Hill. 2000. ISBN 0-07-136360-2.
[6.19.] A mikroszkóp. Könyvkiadó. Budapest . 1979.
[6.20.] Das photographische Objektiv. Springer. Wien . 1955.
7. fejezet - A mikroszkóp mint optikai rendszer
- 7.1. Bevezető fogalmak
- 7.1.1. A látószög növelése
- 7.1.2. A mikroszkóp és a mikroszkópos képalkotás
- 7.1.3. A mikroszkópos képalkotás értelmezésének eszköztára
- 7.1.4. A mikroszkóp, mint finommechanikai eszköz
- 7.1.5. A képrögzítés, megfigyelés és nagyítás
- 7.1.6. Válogatott fejezetek a mikroszkópia történetéből
- 7.1.7. A mikroszkópos észlelés alapfogalmai
- 7.1.8. A szem felbontóképessége
- 7.1.9. A térlátás
- 7.1.10. A kép tulajdonságai
- 7.1.11. A kép világossága és kontrasztossága
- 7.1.12. Numerikus apertúra
- 7.1.13. A mélységélesség
- 7.1.14. A kép nagyítása
- 7.1.15. A kép látómezeje
- 7.1.16. Felbontóképesség
- 7.2. Az egyszerű és összetett mikroszkóp felépítése és megvilágítása
- 7.3. A mikroszkóp képalkotást végző optikai rendszerei
- 7.3.1. A mikroszkopizálás során alkalmazott optikai rendszerek és tulajdonságaik
- 7.3.2. A mikroszkópok legfontosabb képalkotó optikai rendszerei
- 7.3.3. Az objektív
- 7.3.4. A mikroszkóp objektívek képalkotási hibái
- 7.3.5. Akromátok
- 7.3.6. Apokromátok
- 7.3.7. Speciális objektívek
- 7.3.8. Okulárok
- 7.3.9. A főbb okulártípusok
- 7.3.10. Speciális okulárok
- 7.3.11. Az okulárok szerkezeti kialakítása
- 7.3.12. Kondenzorok
- 7.4. Ellenőrző kérdések
- Felhasznált irodalom
7.1. Bevezető fogalmak
7.1.1. A látószög növelése
A környezetünkről nyerhető információ jelentős részének megszerzésében különleges és kiemelt szerepe van látásunknak. A látás útján történő érzékelés eszköze, a vizuális detektálást végző érzékszervünk teljesítménye rendkívül behatárolt [7.36.] , e határok kiterjesztésének hatékony eszközei optikaiak, e célra speciális műszereket használunk.
Szinte lehetetlen egy vizuálisan megfigyelt tárgy két szomszédos elemi pontját egymástól megkülönböztetni, ha a belőlük szemünkbe jövő fénysugarak két szögpercnél kisebb szöget zárnak be egymással [7.8.] . Ezen érték felénél kisebb látószögnél a részletek megkülönböztetése teljesen lehetetlen, azaz a tárgyrészleteket nem vagyunk képesek megkülönböztetni, szemünkkel feloldani [7.26.] . Ebben az esetben olyan speciális optikai rendszert vagyunk kénytelenek alkalmazni, amely megnöveli a látószöget, azaz olyan képalkotási elrendezést hoz létre, amelyben a vizsgált – és vizuálisan fel nem bontható – részleteket nagyobb látószög alatt látjuk, és így már azokat felbontani vagyunk képesek. Az ilyen – látószögnövelő – optikai berendezések a távcsövek, lupék, vagy mikroszkópok.
Ha a vizsgálandó (esetleg önmagában nagy) tárgy túl messze van, a rajta lévő – a vizsgálat tárgyát képező – részletek a szem felbontóképességének határszöge alatt vannak, tehát kicsi a részletek látószöge; ilyenkor úgynevezett távcsövet kell alkalmazunk. Fordított esetben, amikor a megfigyelést végző szemünkhöz közel lévő rendkívül kisméretű tárgyak részleteit nem látjuk, azaz ebben az esetben is azok a szem felbontóképességének megfelelő hátárszög alatt látszanak csak; lupét, vagy másképpen egyszerű nagyítót alkalmazunk, melynek feladat szintén a látószög növelése. Egyszerű megfontolások alapján beláthatjuk, hogy minél közelebb kerül szemünkhöz a megfigyelés tárgyát képező objektum vizsgált két részletpontja, annál nagyobb lesz azok látószöge. Azonban szemünk fontos paramétere a közelpont [7.8.] , amelynél közelebb levő térrészben megjelenő tárgypontokat már nem vagyunk képesek felbontani. Az ilyen esetben alkalmazott lupe szerepe az, hogy a közellevő – felbontott formában megfigyelendő – tárgypontok képét a tiszta látás távolságában hozza létre úgy, hogy a képpontoknak megegyezik a látószöge azzal, mint amikor közvetlenül szemlélnénk az élesen nem látható nagyon közeli pontokat.
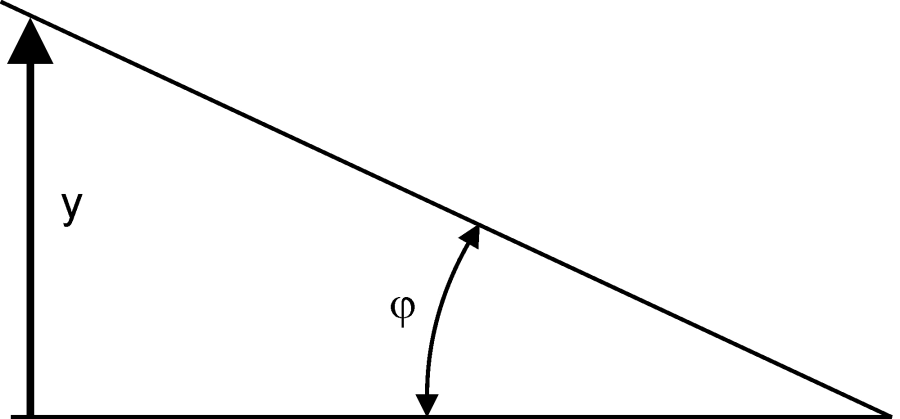
7.1.2. A mikroszkóp és a mikroszkópos képalkotás
Sajnos a lupék látószög növelő képessége igen korlátozott, a vizsgált tárgyat még ilyen eszközzel sem szemlélhetjük nagyon kicsi, a gyakorlatban tapasztalt körülbelül tíz milliméternél kisebb távolságból. Ha a vizsgált képpontok pozíciójából adódó látószög biztosításához ennél is kisebb szemlélési távolságra van igény, akkor összetett lupét, vagy más néven mikroszkópot kell alkalmazni. Ezt tükrözi az elnevezés is, hiszen az egy görög eredetű összetett szó; a mikrosz kicsit, míg a szkopein rnegfigyelést jelent [7.8.] . Tehát az elnevezés egyértelműen utal az ember képességeinek kibővítésére abban, hogy behatoljon a parányok világába, és onnan információt szerezzen.
A berendezés összetett jellege abban nyilvánul meg, hogy a megfigyelő szeme a tárgynak nem az objektív – a tárgylencse – által alkotott nagy nagyítású valós képét szemléli, hanem erről a valós képéről még egy különleges optikai rendszer, az okulár – vagy más néven szemlencse – által alkotott nagyított, egyenes állású, virtuális képet látja [7.24.] [7.25.] . Ilyen módon detektálni csak azt az információt tudjuk, amit tartalmaz a tárgyról az objektív által alkotott kép, ezért a mikroszkóppal alkotott kép minőségére döntő hatással van az objektív által alkotott kép minősége, azt az okulárral már tovább csak nagyítani, de javítani nem tudjuk.
A mikroszkópokat a tudomány, az ipar, a méréstechnika számos területén alkalmazzák. A feladat az esetek jelentős részében, elsősorban
a felbontóképesség,
a nagyítás,
a mélységélesség, illetve
a látómező mérete
tekintetében igen kiélezett, így ahhoz, hogy a mikroszkóp teljesítményét sikeresen tudjuk kihasználni, igen körültekintően kell eljárni. Másrészt azt is tudnia kell a felhasználónak, hogy a mikroszkóp egy igen összetett, speciális feladatoknak megfelelni képes, komoly technológiát maga mögött tudó eszköz, így a vele való bánásmód szintén nagy odafigyelést igényel az optimális élettartam elérése vonatkozásában. Ehhez elengedhetetlen a mikroszkóp felépítésének, működésének, kezelésének alaposan ismerete. A modern célmikroszkópok nagyon igényes műszerek, a finommechanika és az optika, mint tudomány és iparág legfejlettebb technológiáinak megtestesítői. Különösen igaz ez a megfelelő optikák kiválasztása és a megvilágítás helyes beállítása vonatkozásában [7.6.] [7.16.] [7.17.] .
7.1.3. A mikroszkópos képalkotás értelmezésének eszköztára
Az optika egyéb fejezeteiből ismert, miszerint a fény transzverzális, elektromágneses hullám formájában terjed, amely a mikroszkópban a – speciális követelményeknek megfelelően kialakított megvilágító egységgel – helyesen kivilágított tárgypontból kilépve, áthalad a tubusban elhelyezett mikroszkópos képalkotó optikai rendszereken – az objektíven és az okuláron –, majd a megfigyelő szemébe jut, átadva a megfigyelt tárgypontokról a szükséges vizuális információt. Mindezen optikai, optimechanikai és finommechanikai elemeknek ad keretet a mikroszkóp állványa.
Ahogy azt a fentiekben már tisztáztuk; a tárgyról érkező fénysugarak az objektív által a tubusban egy elsődleges képet alkotnak, amiről az okulár által nagyított képet alkotunk a tárgyról. Ezt az objektív által alkotott képet az okuláron, mint egy lupén keresztül még jobban megnagyítva látjuk. Az objektív kiválasztása és helyes alkalmazása a továbbiak szempontjából meghatározó, mivel ez van döntő hatással a mikroszkópos kép minőségére.
A képalkotás folyamatának hullámoptikai alapokon történő vizsgálata ad választ számos olyan kérdésre, amely a mikroszkópok alkalmazhatóságát, paramétereik határait jelenti.
Ez a gyakorlatban azt jelenti, hogy a képalkotás folyamatának vizsgálata során a sugároptika által nyújtott lehetőségeken túl a hullámoptika eszköztárát is igénybe vesszük, azaz nem csak a geometriai optika alaptörvényeire építve követjük végig a rendszerben a fénysugár útját a tárgytértől a képtérig [7.11.] [7.19.] , hanem – az optikai képalkotás folyamatának finomabb részletei megismerésének céljából – figyeljük a tárgyból kilépő fényhullámok formájának és pozíciójának változását, alakulását a képalkotó optikán való áthaladása során. Ez a tárgyalásmód a szakirodalomban részletesen tárgyalt, felöleli az optikai rendszerek képalkotásának általános elméletét és az optikai rendszerek analízisének módszereit is [7.27.] [7.37.] . Ezzel a hullámoptikai leírásmóddal meg tudjuk állapítani, hogy milyen alsó határméret esetén képes a mikroszkóp tárgyrészleteket különválasztani vagy más szóval feloldani [7.27.] . Ezzel a hullámkövetési eljárással egyúttal magyarázatot kapunk azokra a jelenségekre, amelyeket az egyes mikroszkópos megfigyelési módszerek esetén előállnak. Ezek rendre:
centrális világos látóterű megvilágítással,
ferde megvilágítással,
sötét látóterű megvilágítással,
fáziskontraszt eljárással,
interferencia mikroszkóppal,
polarizációs mikroszkóppal vagy
fluoreszcenciás módszerekkel állnak elő.
7.1.4. A mikroszkóp, mint finommechanikai eszköz
Az a tény sem hagyható figyelmen kívül, mely szerint a mikroszkópnak, mint egy komplex mérőberendezésnek – optikai szempontból igényes korrekciójú – eleme az optikai leképző rendszere, megvilágító és fényterelő rendszere, és ugyancsak eleme egy igényes, precíziós kivitelű, fejlett technológiát képviselő finommechanikai szerkezet. Ennek ékes bizonyítéka az a tény is, hogy ezen eszközök előállítását végző iparágak vállalatai szorosan kapcsolódnak, együttműködnek és nem ritkán szerves egységet alkotnak.
A mikroszkópon belül a mechanikai szerkezeti elemek egymáshoz képesti pozíciójának állítási lehetőségei az ezredmilliméteres elmozdulási tartományban vannak, az ezekhez kapcsolódó vezetékek pontosságára vonatkozóan szintén hasonlóak az elvárások. A legkorszerűbb mikroszkópokban széles körben alkalmazzák a finommechanika, az optomechanika legújabb szerkesztési elveit, szerkezeti megoldásait és ezek gyártásához a legfejlettebb technológiákat és szerkezeti anyagokat. E tekintetben igen gazdag irodalom áll rendelkezésre [7.1.] [7.2.] [7.3.] [7.4.]
A mikroszkóp, mint finommechanika-optikai felépítésű, műszertechnikai szerkezet, minden eleme, alkatrésze, funkcionális egysége precíziós technikai hátterű tervezői munkát igényel. Így a finommechanikai gyártás szigorú tűrései itt fokozottan érvényesülnek, ugyanis a műszeripari tűrésezés során azok méretére vonatkozóan igen szigorú megfontolások, és előírások szerint kell eljárni. A mikroszkópos technikában a tűrés, mint egy mérnöki-tervezési filozófiai alap, az elterjedt és ismert fogalom jól szemléltethető iskolapéldája. A mikroszkópos technikában, és általában a finommechanikában a tűrések nagyságrendje leggyakrabban a század vagy az ezredmilliméter környékére esik [7.1.] [7.6.] [7.8.] .
7.1.5. A képrögzítés, megfigyelés és nagyítás
A mikroszkópban előálló kép észlelése általában vizuális úton történik. Ilyenkor lehet elvégezni a legalapvetőbb beállításokat, a helyes képkivágást, az élesre állást, a nagyítást. Természetesen a mikroszkópos kép szemlélése történhet megjelenítő eszközön keresztül is, ilyenkor a képet egy érzékelő detektálja, amit mintavételezés és kvantálás után, illesztve a megjelenítő bemenetéhez arra csatlakoztatni lehet. A látott objektum dokumentálása, vagy későbbi újravizsgálata céljából a mikroszkópban látható képet elektronikusan vagy hagyományos módon rögzíthetjük, lefényképezhetjük. A mikroszkópos kép rögzítése által a képből történő újabb és mélyebb információk kinyerése céljából a rendszereket általában célorientált képfeldolgozó egységekkel egészítik ki, amelyek igen nagy számban tartalmazhatnak automatikus képjavító, rekonstruáló, szűrő, transzformáló, szegmentáló, alakfelismerő algoritmusokat. A mikroszkópos képek feldolgozásának algoritmusai és módszerei az utóbbi időben igen dinamikus fejlődésen mentek keresztül, ennek irodalma igen szerteágazó és gazdag [7.28.] .
Lehetőség van a térbeli információkat időbeli információkkal bővíteni a mikrokinematográfia, a mozgófényképezés, gyorsfilmezés eszközeivel a tárgy változásai, mozgásai, dinamikus viselkedései megörökítése útján. A fénymikroszkópok nagyítása a rendkívül szerény értékektől a mintegy kétezres értékig terjed [7.9.] . A nagyítások alsó határán a sztereomikroszkópok és mérőmikroszkópok működnek, itt egyrészt a nagyítás fokozására nincs is szükség, másrészt a nagyítással csökkenő mélységélesség is korlátot jelent. Szintén fontos tény, hogy a nagyítás növekedése és a szabad tárgytávolság közötti kapcsolat is határt jelenthet az alkalmazhatóság tekintetében. A mérőmikroszkópoknál gyakran nem a nagyítás a fontos, hanem az, hogy a tárgy képe egy – az okulár részét képező – beosztásos szállemezen keletkezik a tárgy méreteinek könnyű megmérése céljából. A nagyítások felső határán a biológiai vizsgálatokban alkalmazott mikroszkópok dolgoznak. A biológiai vizsgálatok során elsősorban az élő szervezetek alkotóelemeinek egyre kisebb és kisebb alkatrészeit analizálják, ami nagyobb nagyítást és jobb feloldóképességet igényel. Sajnos a látható fénnyel működő mikroszkópok a hullámoptikai korlátok miatt nem képesek az egymáshoz két tizedmikronnál közelebb levő tárgypontok feloldására. Könnyű belátni, hogy ilyen mértékű feloldáshoz mintegy ezerötszáz-kétezerszeres nagyítás szükséges. A két tizedmikronos tárgypont távolság ezerötszázszoros nagyításánál a kétszázötven milliméteres, tisztánlátási távolságból négy szögperc alatt látszik a két tárgypont, ami a szem feloldóképesség gyakorlati határértékének felel meg [7.8.] .
A mikroszkóp feloldóképessége növelésének eszköze – ahogy a későbbiekben látni fogjuk – az objektív numerikus apertúrájának növelése, a hullámhossz csökkentése, illetve az elektronmikroszkóp alkalmazása. Itt a képalkotást nem fénysugarak, hanem nagy sebességgel mozgó negatív töltésű elektronok, elektronsugarak végzik. Az elektronsugarak pályáját külsőleg vezérelt elektronlencsékkel, elektromos és mágneses erőterekkel úgy lehet irányítani, mint a fénysugarakat a hagyományos optikai elemekkel. A képalkotás is a hagyományos optikai mikroszkóphoz hasonlóan történik [7.8.] . Az elektronok egy elektronforrásból az úgynevezett katódból lépnek ki, nagyfeszültségű téren haladnak át úgy, hogy közben felgyorsulnak, áthaladnak a tárgyon, majd az objektívnek és az okulárnak megfelelő két elektronlencse segítségével képet alkotnak. Az ernyő fluoreszkáló anyaggal van bevonva, a becsapódó elektronok mennyisége függvényében a kép, azon erősen vagy gyengén világít, ami szemmel látható, vizsgálható. Detektort helyezve a fluoreszkáló ernyő helyére, azon ugyanúgy fényképet kapunk, mint a hagyományos fénysugarakkal.
Mivel sajnos az elektronsugarak csak nagyon vékony rétegeken tudnak csak áthatolni, az elektronmikroszkópos minták előkészítése, kidolgozása jelentősen eltér az optikai mikroszkópnál megszokottaktól. Hatalmas nagy előny viszont, hogy az elektronmikroszkóppal el lehet érni a több százezerszeres nagyítást és a fénymikroszkópnál három nagyságrenddel nagyobb feloldóképességet.
A mikroszkópos megfigyelések nemcsak kvalitatív adatok megállapítására szolgálnak, hanem egyre inkább terjednek a mikroszkópos alapú kvantitatív vizsgálatok, mérések. Az ilyen jellegű mérések a tárgyak méreteinek meghatározásán túl, mennyiségi vizsgálatokra is kiterjednek. Mérhető például a törésmutató, az abszorpció, az extinkció, a fluoreszcencia, a reflexió, a remisszió és a koncentráció, de a fáziskontraszt és a polarizációs mikroszkópia egyéb paraméterek kavalitatív és kvantitatív mérését is lehetővé teszi.
7.1.6. Válogatott fejezetek a mikroszkópia történetéből
Az optikai mikroszkópok története szorosan összefügg az optika történetével, hiszen számos felfedezés gazdagította a mikroszkopizálás gyakorlatát, de fordítva is igaz, hiszen a mikroszkópok fejlesztése során megjelenő kihívások számtalan új, az optika szempontjából fontos felfedezés ösztönzői voltak. A mikroszkópok fejlődével kapcsolatos történelmi tények az irodalomban számtalan helyen [7.8.] fellehetők, az alábbiakban csak egy rövid kivonatot adunk ebből a nagyszerű tudománytörténeti fejezetből [7.20.] [7.29.] [7.30.] .
Az egyszerű mikroszkóp használatára vonatkozó első feljegyzések csak a 16. század végére tehetők annak ellenére, hogy a fénnyel kapcsolatok alapvető jelenségét már az ókorban is ismertek voltak. Szintén a tizenhatodik századra tehető az első összetett, objektívből és okulárból álló mikroszkópok megjelenése is.
Az összetett mikroszkóp alkalmazásának elterjedését a színhibák korrekciója tette lehetővé. A mikroszkópia története nem választható el az egyetemes optika fejlődésétől, melynek lényegesebb momentumai – a teljesség igénye nélkül – az alábbiak.
Az optikai jellegű kísérletek kivitelezését és műszerek építését sokáig hátráltatta a megfelelő üvegválaszték, e tekintetben az első említésre méltó esemény a muranói üveggyár 1291-es alapítása. Természetesen az optikai tervezés vonatkozásában nagy jelentőséggel bíró és nagy szabadságfokot jelentő, gazdag üvegválasztékot előállító Schott üveggyár megalapítására még sokat kellet várni. A első összetett mikroszkópot Hans Janssen és fia Zacharias készítette el valamikor a tizenhatodik, illetve a tizenhetedik század fordulóján.
1623-ban Mansell flintüveget készített és két évre rá Faber alkalmazta először a mikroszkóp elnevezést. Az elméleti munkák tekintetében kimagasló jelentőségű az 1626-os esztendő, amikor Willebrord Snell a Leideni Egyetem tanáraként kimondta a fénytörés törvényét, amely egyik legfontosabb alapösszefüggése a geometriai optikának. Tőle talán függetlenül ugyanerre az eredményre jutott 1637-ben René Descartes. Az 1700-as évek elején Leeuwenhoek számtalan, különböző gyújtótávolságú lencsét csiszolt, elsősorban biológiai megfigyeléseihez.
Az egész optika szempontjából hatalmas jelentőségű Pierre Fermat 1657-ben kimondott elve az optikai úthosszak stacionáriusságáról. 1650-ban Francesco Grimaldi a fény diffrakciójáról írt, majd 1665-ben Robert Hook állványos mikroszkópot készített mesterséges megvilágítással. Ez az időszak az optikai megfigyelések szempontjából különös jelentőséggel bír, hiszen Sir Isaac Newton ekkor foglalkozott fénytani megfigyelésekkel, melyek elsősorban a fénytörésre, a színbontás jelentőségére és a diszperzióra (1666) vonatkoztak.
A következő esztendőben Christian Huygens összeállította a róla elnevezett okulárt, melyet ma is széles körben alkalmaznak. Erre az időszakra tehetők a mikroszkóppal kapcsolatos fontosabb fejlesztések; 1685-ben Tortoni átvilágításos mikroszkópja, 1691-ben Bonanni mikroszkópos megvilágítása fókuszálható kondenzorral, 1704-ben Marshall billenthető mikroszkópállványa, 1730-ból Culpeper mozgatható megvilágítótükre.
A mikroszkóp objektívek fejlődése tekintetében a nagy áttörés 1757-ben következett be, ugyanis a Dollond fívérek akromatikus lencsepárt készítettek sikerrel, cáfolva Newton ezirányú megállapításait. A színhibákkal terhelt optikai rendszerek korrekciója vonatkozásában a Dollond fívérek gyakorlati eredményeit Leonhard Euler szentpétervári matematikus 1762 és 1764 között végzett elméleti munkája zárta le, megoldva azaz akromatizálás kérdését. 1776-ban Adams a gyors objektívváltáshoz revolverszerkezetet tervezett.
Ramsden a geodéziában ma is széles körben alkalmazott teodolit feltalálója 1783-ban elkészítette a később róla elnevezett okulár típust. A modern mikroszkópia szempontjából nagy jelentőségű polarizáció jelenségére 1808-ben adott magyarázatot Etienne Malus, vizsgálva a fény polarizációját visszaverődés útján. 1818-ban Amici speciális, félgömb alakú objektív frontlencsét és katadioptrikus mikroszkópobjektívet készített.
1829-ben Talbot elkészítette az első polarizációs mikroszkópot. 1837-ben Ross korrekciós foglalatot tervezett a fedőlemez vastagság által okozott eltérések kiegyenlítésére. Szintén ugyanebben az esztendőben Reade sötét látóterű mikroszkópot készített.
A 1839-es esztendővel kezdődően komoly eredmények születtek, melyek meghatározó hatással voltak a fotográfia további fejlődésére. Jacques Daguerre kidolgozta a róla elnevezett Daguerrotypiát és a későbbiekben számtalan felvételt készített, melyek jelentősége kultúrtörténeti szempontból is kimagasló.
A bécsi Voigtlander cég megbízásából, a magyar származású bécsi matematikus Petzvál József 1841-ben fényerős objketívet tervezett, mellyel az addigi nagy expozíciós idők jelentősen csökkentek kimagasló képminőség mellett. Ez, az úgynevezett Petzvál-objektív volt az első olyan optikai rendszer, amelyet módszeresen terveztek, így tulajdonképpen Petzvál tekinthető a modern optikai tervezés, azaz a rendszerszintézis megalapítójának. Objektívje nagy távolságban elhelyezett légréses és ragasztott kéttag kombinációja, ma is számtalan rendszer kiindulási szerkezete. 1843-ban fogalmazat meg a képmezőhajlás és az asztigmatizmus korrekciójára vonatkozó feltételét; a Petzvál-összeg pedig a korszerű optikai tervezés egyik kiinduló feltétele még mai is. Petzvál megállapította, hogy egy leképző optikai rendszer esetén a képfelület akkor sík, ha a törésmutatók, és a lencsefelületek görbületi sugarainak kombinációja eleget tesz a róla elnevezett formulának. Petzvál szepességi német családban született, de mindig magyarnak vallotta magát. Pesten az Institutum Geometricum tanulója volt, itt szerzett mérnöki oklevelet, de később felsőbb matematikát tanított. 1837-ben Bécsben az egyetemen tanárrá nevezték ki. A Petzval-féle objektív szférikus aberrációja és longitudinális színhibája kicsi, ezért például vetítésre is alkalmas. Tőle származik a képmezőhajlásra vonatkozó általános összefüggés, melyet 1843-ban publikált. Optika mellett foglakozott ballisztikával és a hangtannal is, ezek körében is írt tanulmányokat. Saját szerkesztésű műszerével fotogrammetriai méréseket is végzett. Ő volt az első, aki kiterjedt közelítő számítások végzett optikai rendszerekre vonatkozóan méretezés céljából. Számításait nem publikálta, azért a harmadrendű hibaelmélet megalkotása Ludwig von Seidel nevéhez fűződik. A képmezőhajlás korrigálását biztosító feltétel felismerése azonban az ő érdeme, mely szerint a képmező görbületi sugara és az optikai rendszert alkotó lencsék fókusztávolságai, valamint törésmutatói között összefüggés áll fenn. Ugyanis az egy síkban fekvő, tengelyen kívüli tárgypontok képei görbült felületet alkotnak. A rendszer képmezeje általában görbült, amelyet Petzvál-görbületnek nevezünk. Ha nincs asztigmatizmus, akkor a szagittális és a meridionális képmezők egymásba egyesülnek. Ekkor csak képmezőhajlásról beszélünk. A Petzvál görbületet összefüggésében a lencsék vastagsága nem szerepel, tehát az összefüggés vékony rendszerre is alkalmazható.
1844-ben a felbontóképesség növelése céljából Amici kísérleteket végzett vízimmerziós objektívekkel. 1845-ben Chevalier alkalmazta először az elektromos ívlámpát mikroszkópos megvilágítás céljából fényforrásként. 1847-ben készítette el Carl Zeiss az első mikroszkópját.
1849-ben készítette el Kellner a ma is alkalmazott Kellner-féle és ortoszkopikus okulárt. A szem, mint optikai rendszer szintén az érdeklődés középpontjában állt, megfigyelésére Helmholtz 1850-ben szemtükröt szerkesztett. Ugyanebben az évben Porro olasz tüzértiszt elkészítette az első prizmás képfordító rendszert, és azt alkalmazta távcsövében.
A színtan területén végzett megfigyeléseket Helmholtz, a tudományterület szempontjából rendkívül fontos törvényeket 1853-ban Grassmann fogalmazta meg. Magyarázatot adott az additív színkeverés jelenségére. Ebben az évben publikálta az anyagi részecskéken végbemenő fényszóródással kapcsolatos eredményeit Tyndall.
A Petzvál József kapcsán említett harmadrendű aberrációk elméletét (a képmezőhajlás esetében Petzvál Józsefre hivatkozva) Ludwig von Seidel publikálta 1856-ban, megalapozva ezzel korszerű optikai tervezés módszertanát. James Clerk Maxwell 1864-ben ismertette az elektromos és mágneses mezők kölcsönhatását leíró elméletét. Eredményei meghatározó befolyással voltak a huszadik századi fizikára. Maxwell legfontosabb érdeme az, hogy kiterjesztette a korábbi eredményeket az elektromos és mágneses térre, azt egységes matematikai formulába öntötte. Ezek az – úgynevezett Maxwell-egyenletek – megmutatják az elektromos és mágneses mező a térben terjedésének mikéntjét.
1871-ben Lord Rayleigh kimutatta a fényszóródás hullámhossz-függését, amelyért 1904-ben Nobel-díjjal jutalmazták. 1873-ban Ernst Abbe megalkotta a mikroszkópos képalkotás elméletét, illetve levezette a mikroszkóp feloldóképességének függését a fény hullámhosszától és bevezette a numerikus apertúra fogalmát. 1884 meghatározó az optikai rendszerek tervezése és gyártása terén, ugyanis ebben az esztendőben alapította Otto Schott a jénai üveggyárat, mely széles üvegválasztékkal állt a tervezők rendelkezésére a törésmutató és a színbontó képesség tekintetében. A jénai Zeiss műveknél Ernst Abbe 1886-ban alkotta meg az első, gyakorlatban is sikerrel alkalmazott apokromátot. 1888-ban Henrich Hertz kísérleti úton is kimutatta az elektromágneses hullámokat. Ugyanebben az évben alkalmazott először monobrómnaftalin immerziós objektívet Ernst Abbe. 1893-ban a mikroszkópos megvilágítás ma is alkalmazott elvét dolgozta ki August Köhler.
1930-ban kidolgozta a vákuumgőzölés módszerét Burch. 1933 az elektronmikroszkóp felfedezésének éve. 1934-ben Chrétien változtatható gyújtótávolságú (zoom) objektívet tervezett. Szintén ebben az évben publikálta a fáziskontraszt-eljárást Frits Zernike, aki ezért 1953-ban Nobel-díjat kapott. A jénai Zeiss műveknél alkalmaztak először 1935-ben reflexiócsökkentő bevonatot. 1938-ban mutatott be Boegehold plánakromát mikroszkópobjektívet. 1942-ben Zernike tanítványa Nijboer módszert mutatott a képhibák általános osztályozására, majd a következő esztendőben értelmezést adott a hullámaberráció fogalmának. 1947-ben Max Herzberger bevezette a pontszórás függvény, azaz a spot-diagram fogalmát.
1948-ban matematikai módszerekkel alapozta meg Shannon az információelméletet, és alkotta meg Gábor Dénes a holográfia elméletét. 1950-ben Maréchal alkalmazta a térfrekvenciaszűrést, 1960-ban vezették be a kandelát a fényerősség alapegységeként, és alkotta meg Maiman az első rubin-lézert. Azóta napjainkig az optika fejlődése szinte töretlen, nem található olyan területe az életnek, a tudománynak és az iparnak, ahol ne alkalmaznák eredményeit széles körben. Szerepe a méréstechnikában szinte megkerülhetetlen.

(Balról jobbra, fentről lefelé). Johannes Kepler (1571–1630), Pierre de Fermat (1601 – 1665), Christiaan Huygens (1629 – 1695), Joseph von Fraunhofer (1787 – 1826), Leonhard Euler (1707 – 1783), Ludwig Wilhelm Seidel (1802 – 1894), Lord Rayleigh, (1842 – 1919), Ernst Karl Abbe (1840 – 1905), Petzval József (1807 – 1891)

(Balról jobbra, fentről lefelé) James Clerk Maxwell (1831 – 1879), Carl Zeiss (1816 – 1888), Friedrich Otto Schott (1851 – 1935), Frits Zernike (1888 – 1966), Gábor Dénes (1900 – 1979)
7.1.7. A mikroszkópos észlelés alapfogalmai
A mikroszkóp alkalmazásának alapgondolata az emberi szem viselkedésében keresendő. Annak anatómiai és fiziológiai tulajdonságai teszik a szemet képessé arra, hogy az érzékelést végző idegvégződésein a megfigyelt tárgy éles képét hozza létre, függetlenül attól, hogy a szemlélt tárgy hol helyezkedik el. Ez a folyamat, azaz a tárgy távolságához való illeszkedés az első képalkotás céljából az úgynevezett akkommodáció. A távolpont a legnagyobb tárgytávolság, amelyre akkommodálni kell a szemnek [7.8.] . A közelpont helye viszont attól függ, hogy a szem, szerkezetéből adódóan mennyire közeli tárgyra képes akkomodálni.
Ha erre valamilyen ok miatt nem képes, a közelpont szemléléséhez szemüveget kell alkalmazni.
Egy tárgy akkor látszik nagyobbnak, ha közelebb van a szemhez. Ha ezt minden határon túl folytatjuk, akkor a tárgy a közelpontnál is közelebb kerülhet a szemhez. Ekkor azonban az már nem látható élesen, ilyenkor kerül sor lupe vagy összetett mikroszkóp alkalmazására.
7.1.8. A szem felbontóképessége
A pupilla átmérője a környezeti világosságszintnek megfelelően változik, ez lényegében egy átmérőre történő szabályozást jelent, azaz szem fényérzékelő képessége és érzékenysége is ehhez a világosságszinthez igazodik. A szemlencse a tárgy távolságának megfelelő alakot vesz fel [7.36.] .
Ismert és kísérleti úton igazolható tény, hogy a teljes adaptáció és akkommodáció állapotában a szem feloldóképessége optimális, amin azt a legkisebb látószög értéket értjük, amely mellett sötét alapon levő két egyenlően világos, megfelelően kicsiny pont jól érzékelhetően szétválik (azaz a két pont együttes képe kellően „piskótásodott”). Az igen széleskörben elterjed egy szögperces érték különleges esetben előforduló maximumnak tekinthető, az átlag amivel a kísérletek, illetve a tervezés során számolni lehet valahol a két és a négy szögperc között található. Konkrét alkalmazásoknál célszerű a legrosszabb estet figyelembe venni [7.8.] , mivel az egyéni különbségek mellett a tárgyrészletek megkülönböztethetősége számtalan tényező függvénye. Ezek közé sorolható a világosság, a színezet, a kontraszt, a kontúrok alakja, összefüggősége, a textúra.
A körülmények miatti felbontóképesség ingadozást jól jellemzi az a tény is, hogy például két egyirányú vonaldarab esetén egymás folytatódásakor sokkal jobban meg tudjuk ítélni, hogy azok egybe esnek-e, vagy sem.
7.1.9. A térlátás
Kísérleti és tapasztalati úton is igazolt tény, hogy a perspektivikus elemeket tartalmazó vizuális ingerstruktúrák megfelelő értelmezése kulturális tényezőkre és tanulási folyamatra vezethető vissza. A térérzékelés tehát bizonyos tekintetben tanult folyamatnak tekinthető. Mivel vizuális érzékelés esetén az egyes szemek detektáló felületein keletkező képek kétdimenziósak, a harmadik dimenzióhoz kapcsolható információk előállításának e kétdimenziós képek bonyolult agyi tevékenységen alapuló értékelésén kell alapulniuk. A kognitív pszichológia szerint a térlátás, amely a két szemből érkező – és eltérő - képek agyi feldolgozásán nyugszik, a vizuális észlelés legmagasabb szintjének tekinthető. A térlátás elemei öt csoportba sorolhatók: a konvergencia, a retinális eltérés, az akkomodáció, a mozgás-parallaxis és a perspektivikus hatás.
A konvergencia a két szem látótengelye által bezárt szöggel áll kapcsolatban. E szög értéke a távolság növekedésével csökken, nagyságából az agy a tárgy távolságára következtet. A retinális eltérés oka, hogy a két retinán megjelenő, egymástól némileg eltérő kép értékelése alapján mélységérzet alakul ki. E jelenségen alapszik a sztereoszkóp, amelyben a két eltérő pozícióból készített két képet az agy egyetlen, térhatású képpé egyesíti. Az akkomodáció is hozzájárul a térlátás kialakulásához azáltal, hogy a szem közelebbi, vagy távolabbi tárgyra tekintés esetén alakot változtat, ezt értékeli az agy. A mozgási parallaxis azt jelenti, hogy az elmozdulás mértéke és a megfigyelő távolsága fordítottan arányos, így ismét egy agyi funkcióval a mozgási parallaxisból a tárgy távolságára is lehet következtetni. A perspektivikus hatást jelentik azok a mélységi információk, amelyek részei a képi tartalomnak;
a perspektívára utaló képzelt szerkesztési vonalak,
a textúra képen belüli lokális változása,
a felületelemek közötti átfedések,
a részletgazdaság csökkenése a távolság növekedésével,
az árnyékok iránya, vetülete, mérete és
a színek perspektívára gyakorolt hatása.
Döntő fontosságú a térlátás kialakulása szempontjából az, hogy a szemlélt tárgyat és környezetét a jobb szemünkkel jobbról, a ballal balról látjuk, tehát a két szem retináján eltérő képek keletkeznek, amit az agy egyetlen térbeli látvánnyá köt össze [7.8.] .
A mikroszkopikus tartományok tárgyainak térbeli érzékeléséhez sztereomikroszkópokat célszerű használni, mely lényegében két független mikroszkóp egyesítve úgy, hogy azok a megfigyelő szemeinek tengelyei meghosszabbításában helyezkednek el. A tárgy egyik szemmel balról, a másikkal jobbról látható, azok képei a tisztánlátás távolságában jönnek létre, de eltérőek, így az érzékelés térbeli, sztereoszkopikus. A sztereomikroszkópot a biológiában és a szerelési technikában használják, azzal a mikroszkóp alá helyezett tárgyakon megfigyeléseket, műveleteket, beavatkozásokat lehet végezni. A szetereomikroszkóp nem összekeverendő a binokuláris mikroszkóppal, melybe szintén két szemmel lehet betekinteni, azonban mindkét kép ugyanaz, ezért a térbeli hatás létre nem jön. A binokuláris mikroszkóp alkalmazásának nagy előnye, hogy az észlelés nem fárasztó, a kétszemű nézés a fiziológiai egyensúlyt megtartja [7.8.] .
7.1.10. A kép tulajdonságai
A tárgytér leképzéséből keletkező képtérbeli intenzitás-eloszlásban egy részlet felismerhetőségének kritériuma, hogy az a környezetétől világosság vagy szín tekintetében az érzékelhetőség határán túli mértékben különbözzön. A részletek elkülönülésének ezt a tulajdonságát és az ebből származtatható képi tulajdonságot kontrasztbeli eltérésnek nevezzük. A kisméretű folt pontnak tűnik. Pszichológiai okok miatt eltérést mutat a sötét foltnak egy világos alapon való érzékelhetősége és világos foltnak sötét környezetben való érzékelhetősége [7.8.] . Kísérleti úton igazolható, hogy a világos pont érzékelhetősége a pont világosságától függ, de független a pont nagyságától, viszont a sötét folt érzékelhetősége függ a folt kiterjedésétől is. Természetesen az érzékelhetőség mértékét jelentős mértékben befolyásolják az észlelés emberi vonatkozásai, például a szem fáradtsága és az észlelésre fordított idő hossza is, a külső zavaró hatások, figyelemelterelő ingerek, azok gyakorisága.
Az érzékelhetőség szempontjából a kontrasztosság mellett szintén rendkívül fontos tulajdonság; a gradáció. A gradáció feltétele a képtulajdonságra vonatkozóan az, mely szerint a képen két szomszédos, érintkező elemi méretű ingert akkor látunk szétválasztottnak, ha egymás között is kontrasztosak. Ennek mértéke a kép gradációja. Más megfogalmazásban a képrészleteknek akkor van megfogalmazható alakjuk és méretük, ha világosságuk és a háttér világossága közötti átmenet gyors és határozott. Természetesen, ha színingerekről van szó, a helyzet hasonló módon és formában értelmezhető úgy. Az információt hordozó képrészlet és a háttér közötti átmenetek dinamikája, annak képbeni jelenléte jellemzi az egyik legfontosabb vizuális képtulajdonságot; a kép élességét. Szintén pszichológiai és neurológiai okokra vezethető vissza az a tény, hogy a vizsgált képen ugyan az előbb tárgyalt átmenetek szinte sohasem meredekek, de a látásunk ezeket a nem ugrásszerű, tehát akár folytonosnak tekinthető átmeneteket is értékeli. A képtérben megjelenő tárgyrészletek széleit nevezzük kontúroknak. Mivel ezek a kontúrok közvetlen kapcsolatban állnak az információt hordozó képrészlet és a háttér közötti átmenetek dinamikájával, az értékelt kép élességét elsősorban a kontúrélesség határozza meg.
Speciális hatását gyakorol az érzékelt kép tulajdonságaira a mélységélesség. Jelenti ez a gyakorlatban azt az esetet, amikor a tárgy a tárgytérben térbeli kiterjedésű, viszont a kép csak síkbeli. Tehát a tárgynak csak egy síkmetszete lesz ideálishoz közeli viszonyok mellett leképezve, az attól eltérők ugyanabban a képsíkban, de életlenül kerülnek ábrázolásra. A sztereómikroszkópok alkalmazása során a kellő mélységélesség biztosítására kellő hangsúlyt kell fektetni, ugyanis ebben az esetben a kis mélységélesség rendkívül zavaró [7.21.] [7.22.] [7.8.]
Az emberi szem tulajdonsága az is, hogy látómezőnknek csak egy kicsi részét képes élesen leképezni. Ezért az agy a szemet mindig a megfigyelni kívánt tárgyrészletre fordítja, és ekkor akkommodál, természetesen ilyenkor a többi leképzett tárgyrészlet életlen. A megbízható és jó észlelésnek feltétele továbbá, hogy a világosság és kontraszt is megfelelő legyen. Emiatt kulcsfontosságú a világosság-, kontrasztosság-és élesség képmezőn belüli eloszlása. A szemmel való jó leképzéshez az is szükséges, hogy a leképzendő tárgyrészlet elég nagy méretű legyen [7.11.] [7.20.] .
Megfelelő nagyítás esetén a részletek ugyan jól azonosíthatók, de esetleg éppen emiatt az átfogó tulajdonságok már nem érzékelhetők, ezért elengedhetetlen a kép megfelelő nagyításának biztosítása mellett a kép szükséges látómező mérete is.
A látás agyi szintű megvalósulása esetén egy integráló és differenciáló tevékenység valósul meg [7.8.] , melynél az integráló tevékenység a szomszédos képfoltok együttesének egy-egy nagyobb tárgyrészlet képének formájában történő láttatását biztosítja, míg a differenciáló tevékenység eredményeként az agy egyes képrészleteket és képrészlet csoportokat más részletektől és más részletcsoportoktól elválasztva egy-egy tárgyrészlet képeként láttatja. Ezek mellett jelentkezik az agy kiegészítő tevékenysége, amely azt jelenti, hogy ha valamely tárgyrészlet képe nem látszik, azt bizonyos kritériumokon belül oda lehet képzelni. Ezzel magyarázható például a kép rendezettsége. Az agy kiválasztó tevékenysége pedig a kiegészítő tevékenység ellentéte, amikor is egy tárgy képében megjelenő, oda nem illő tárgyrészletet agyi szinten le lehet a tárgytól választani. Ezzel a jelenséggel magyarázzák a kép tisztaságát.
7.1.11. A kép világossága és kontrasztossága
A kép világosságának és kontrasztosságának értelmezéséhez elengedhetetlen a radiometria és fotometria fogalmainak helyes értelmezése. Radiometria-fotometria közötti összefüggés megértéséhez definiáljuk először a radiometriát, mely hullámhossz független érzékelést, tárgyalást jelent a szokásos energetikai egységekben.
A fotometria egy hullámhossz-függő érzékelés, melyet a világosra adaptált emberi szem láthatósági függvénye révén ír le. Az emberi szem érzékelése vonatkozásában megkülönböztetünk fotopikus látást, mely normális megvilágítás esetén érvényes; maximuma 555 nm-nél található. A szkotopikus látás gyenge megvilágítás esetén lép fel; maximuma 507 nm-nél van. A két előbbi között átmenetet jelenti a mezopos látás, melynél először a vörös színei tűnnek el, legtovább a kék színek maradnak meg. A fotometriai mennyiségek között alapmennyiség a fényerősség, mely egysége a kandela. A kandela annak az 540 THz (λ = ~555 nm) frekvenciájú monokromatikus sugárzást kibocsátó fényforrásnak adott irányban kibocsátott fényerőssége, amelynek sugárzáserőssége ebben az irányban 1/683 W/sr (Nemzetközi Súly- és Mértékügyi Bizottság 1979).
A fénysűrűség az a mérték, mely az emberi szemben a világító vagy a megvilágított felületek által keltett fényérzetet határozza meg, azaz a felületegységre jutó fényerősség. Mértékegysége a kandela/négyzetméter. A kép fénysűrűsége függ a tárgy fénysűrűségétől. A megvilágítás a megvilágított felületre eső fényáram és a megvilágított felület nagyságának hányadosa, nemzetközi egysége lux.
Lényegében a megvilágítás erőssége és a mikroszkóp objektív numerikus apertúrája tekinthethető a mikroszkópos kép világosságát leíró mértéknek [7.20.] [7.8.] .
A képvilágosság helyi változása meghatározó jelentőségű a mikroszkópos képek kontrasztjának értékelése szempontjából. A kontraszt definíciója [7.35.] :
|
|
A mikroszkópiában jelentőséggel bíró képtulajdonságok között a kontrasztosság talán az egyik legfontosabb. A jól értékelhető képhez nem elegendő, hogy a világos és éles legyen, ha alacsony a kontraszt, a képrészletek nem válnak el egymástól, nehezen megkülönböztethetőek. A kontrasztosság növelésnek célját szolgálja az összes festési eljárás. Ide tartozik továbbá a fáziskontraszt eljárás, az interferenciamikroszkóp, valamint a ferde és sötét látóterű megvilágítás is, hiszen ezen eljárásokkal a kontrasztnélküli, vagy fázistárgyakról jól megfigyelhető, kontrasztos képet tudunk előállítani.
A kép kontraszthűségén a kép tárgyéhoz viszonyított kontrasztosságát értjük, amely jelentős mértékben függ tárgy részleteinek méretétől és a tártérben található részletek térfrekvenciájától. Hiszen minél sűrűbb ráccsal modellezhető tárgyrészletet képezünk le, annál rosszabb lesz a kép kontrasztja. Ezt az összefüggést ábrázolja lényegében a kontrasztátviteli függvény [7.31.] [7.35.] is, mely a térfrekvencia függvényében ábrázolja a képtéri kontrasztot. A térfrekvencia pedig a leképzett periodikus struktúra egységnyi hosszra eső periodikus struktúráinak számát jelenti.
A mikroszkópos képalkotás, illetve a mikroszkópos kép használhatósága és értékelhetősége szempontjából kiemelten fontos a kép élessége, illetve a képélesség helyi változása. A kép élessége szempontjából fontos, hogy a képrészletek alakját meghatározó szélvonalakra, a kontúrokra merőlegesen a képvilágosság gyorsan változik. Az élességet lényegében az jelenti, hogy az átmenet mekkora út mentén történik. Gyakran a kontúrátmenetet leíró függvény emelkedő részét az inflexiós érintővel helyettesítik, és azt adják meg, hogy ez az egyenes mekkora utat tesz meg a legalacsonyabb és a legmagasabb világosságszintek között [7.8.] .
A képélesség helyi változásának okai az optikai rendszer aberrációi. Képi rögzítés esetén azonban az objektívnek a detektor egész felületére éles képet kell leképeznie. Ilyen célt szolgálnak a plánobjektívek: plánakromátok és plánapokromátok. A mikroszkópos kép mélységélessége alatt a képen élesnek látszó legközelebbi és legtávolabbi tárgyrészlet távolságát értjük az optikai tengely mentén mérve [7.8.] .
Példa:
Egy felületi struktúra átmeneténél a legsötétebb helyen 0,12 a legvilágosabb helyen pedig 0,87 értékű reflexiós tényezőt mértünk. Határozzuk meg a kontrasztot!
Megoldás:
|
|
Tehát a struktúra átmenet 83%-os kontraszt értékű.
7.1.12. Numerikus apertúra
A a mikroszkópobjektív numerikus apertúrájának fogalmát [7.20.] Ernst Abbe vezette be, és azóta is fontos szerepet tölt be. Mértéke;
|
|
ahol, n a tárgy és az objektív frontlencséje között levő közeg törésmutatója; 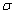 pedig az apertúrasugár optikai tengellyel bezárt szöge a vizsgált térrészben.
pedig az apertúrasugár optikai tengellyel bezárt szöge a vizsgált térrészben.
Példa:
Határozzuk meg egy rendszer tárgyoldali numerikus apertúráját, ha a rendszer levegőben helyezkedik el, a tárgytávolság 20 mm és az apertúrasugár félkúpszöge 15 fok.
Megoldás:
|
|
Tehát a vizsgált rendszer numerikus apertúrája 0.2588.
7.1.13. A mélységélesség
A mélységélesség fogalmát már tisztáztuk, azonban mértékének kézben tartását befolyásoló paramétereket még nem tárgyaltuk. Megállapítható, hogy a mélységélesség növekvő apertúrával és nagyítással csökken. Ahogy azt már fentebb írtuk, a sztereomikroszkópikus megfigyelések esetén rendkívül zavaró – gyakran a térbeliség hatását gátló tényező – a kis mélységélesség, ezért sztereomikroszkópokat kis apertúrával és kis nagyítással készítik. Hasonló a helyzet a szerelő, illetve az orvosi alkalmazású mikroszkópok esetén is.
7.1.14. A kép nagyítása
A mikroszkópos kép nagyításán a képnagyság és a tárgynagyság hányadosát értjük.
7.1.15. A kép látómezeje
A kép látómezeje alatt a tárgyról alkotott kép azon részét értjük, ami a mikroszkóp okulárja által szemlélhető [7.8.] .
7.1.16. Felbontóképesség
Felbontóképesség az optikai műszer képességeinek egyik legfontosabb mutatója, azt mutatja, hogy két különálló, tárgyrészletről készült képben azok különállónak tekinthetők-e. Fontos tudatosítani, hogy felbontóképesség nemcsak az optikai berendezéstől függ, hanem a leképzett tárgy tulajdonságaitól is. Különböző jellegű tárgyak eltérő felbontóképesség-értékeket adnak úgy, hogy a felbontóképesség függ a kép világosságától, kontrasztosságától és élességétől [7.8.] .
Az adott optikai rendszer felbontóképességét a képalkotás hullámoptikai elmélete alapján lehet számítani.
A Rayleigh-féle kritérium alapján [7.35.] egy objektív felbontóképessége két egyenlően fényes világos inkoherens pont esetén,
|
|
ahol 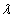 , a használt fény hullámhossza,
, a használt fény hullámhossza,
NA az objektív Abbe szerint értelmezett numerikus apertúrája.
Az összefüggés matematikailag azt fejezi ki, hogy az egyik pont Airy-féle elhajlási képének első sötét gyűrűje fedi a másik pont Airy-féle elhajlási képét annak intenzitásmaximumot képviselő középpontján. Lényegében megállapítható tehát, hogy egy optikai rendszer – fenti összefüggés szerint értelmezett – felbontóképességének elméleti határa korlátos, függ a hullámhossztól és a numerikus apertúrától. A hullámhossz csökkentésével, illetve a numerikus apertúra növelésével javul az elméleti felbontóképesség. A valóságos felbontóképesség kisebb a fenti értéknél, hiszen azt a geometriai aberrációk rontják.
7.2. Az egyszerű és összetett mikroszkóp felépítése és megvilágítása
7.2.1. Az átviteli függvény
A mikroszkópos képalkotás tulajdonságait alapvetően meghatározó rendszerek minősítésére az optikai átviteli függvényt használják.
A képalkotó optikai rendszerek felbontó-képességét régebben egyetlen értékkel, a határfelbontással adták meg. A határfelbontás szubjektív jellege miatt jelenleg a komplexebb és rendszerszemléleti eszközökkel kezelt úgynevezett kontrasztátviteli függvénnyel jellemzik a képalkotó optikai rendszereket. Előnyük, hogy geometriai optikai módszerekkel, tehát valós sugárátvezetéssel számíthatók, a valóságos rendszereken jól mérhetők, és nem utolsó sorban szemléletesen jellemzik a rendszer képalkotási viselkedését.
Trigonometrikus alakjának abszolút értéke a modulációs átviteli függvény, melyet MTF-fel jelölnek, argumentuma pedig fázisátviteli függvény (PTF), melynek esetünkben jelentősége nem számottevő.
A legelterjedtebb ábrázolásban az MTF a térfrekvencia függvényében ábrázolja a kontraszt változását [7.35.] . A valóságos rendszerek kontrasztátviteli függvénye az ideális, azaz csupán a fényelhajlás jelensége által korlátozott rendszer kontrasztátviteli függvénye alatt helyezkedik el. Lefolyása jól jellemzi a rendszert. Természetesen a kontrasztátviteli függvény a kiterjedt képmezőben értelmezhető [7.31.] .
Egyszerű megfogalmazásban az optikai rendszer az adott térfrekvenciájú szinuszos eloszlású rácsot ugyanolyan frekvenciájú szinuszos eloszlású rácsba viszi át, azonban a különböző térfrekvenciájú szinuszos eloszlású rácsokat eltérő amplitúdóval képezi le. Mérése általában közvetlenül a rendszertechnikai modell, illetve periodikus teszttárgyak képeinek értékelése alapján történik.
7.2.2. Az egyszerű mikroszkóp nagyítása
A geometriai optikai megfontolások alapján könnyen belátható, hogy egyetlen gyűjtő típusú rendszer, vagy akár egyetlen lencse a tárgyról képet alkot. Szabad szemmel történő megfigyelés esetén nagyított virtuális képre van szükségünk. Ehhez a geometriai elrendezés vonatkozásában arra van szükség, hogy a tárgy a tárgyoldali fókusz és a leképző rendszer között helyezkedjen el. Ismert tény, hogy ilyen esetben csak látszólagos nagyításról lehet beszélni, hiszen az optikai rendszeren keresztül szemlélt tárgy és az anélkül szemlélt tárgy látószögének eltérését tapasztaljuk. Ha az így kapott látószög a szabad szemmel történő szemlélés esetén fellépő látószögnél nagyobb, akkor látószög-növelésről, nagyításról beszélünk. Ilyen virtuális kép szerkesztése esetén a szerkesztő sugarak nem találkoznak, csupán azok virtuális meghosszabbításai. Az optikai eszközt nagyítónak, vagy lupénak nevezzük, és olyan műszerekben alkalmazzuk, ahol közvetlenül a tárgyat, vagy az arról létrehozott valós képet nagyobb látószög alatt kívánjuk szemlélni. Alkalmazása esetén a tárgyat a lencse tárgyoldali fókuszába helyezzük, ilyenkor a tárgyat 250 mm távolságban, a tisztánlátás távolságában adott szög alatt látjuk, ami nagyobb a lencse nélküli szemlélés esetén tapasztalható látószögnél. A szögnagyítás, azaz a lencse lupenagyítása e két szög tangensének aránya:
|
|
Az összefüggésből jól látható, hogy a lupe nagyítása a fókusztávolsággal fordítottan arányos. Az ilyen módon látószög-növelést végző lupe, vagy más néven egyszerű mikroszkóp alkalmazását korlátozza az, hogy a fókusztávolság csökkentésével a vizuális megfigyelés során technikai nehézségek lépnek föl, illetve az alkalmazhatóságot jelentős mértékben rontja az is, hogy a növekvő nagyítást a képminőség romlása és fényerő csökkenése kíséri. Ezért, ha látószög növelésének nagyobb mértékére van szükség, nagyobb nagyítású, jobb képalkotási tulajdonságokkal rendelkező, úgynevezett összetett mikroszkópot célszerű alkalmazni [7.16.] [7.17.] .
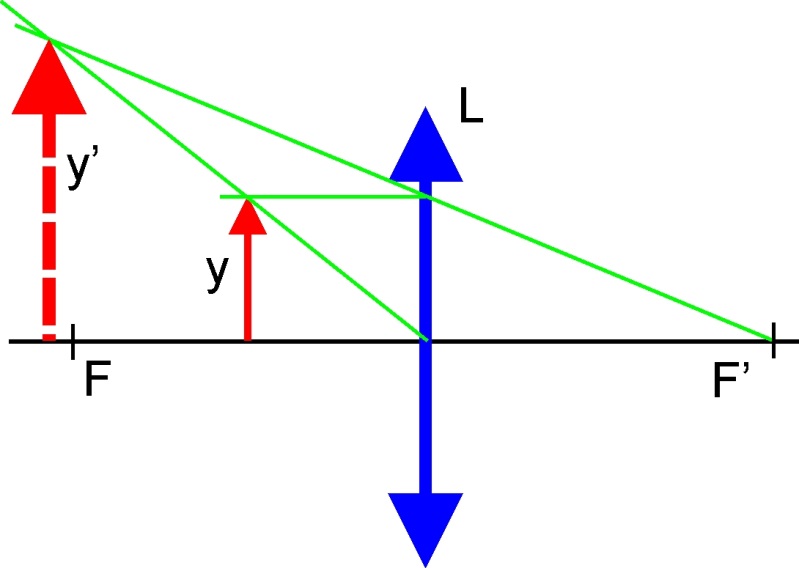
7.2.3. Az összetett mikroszkóp felépítése és nagyítása
Az összetett mikroszkóp alkalmazása során a tárgy leképezése és nagyítása két egymástól elkülönítetten is kezelhető nagyítási folyamatnak tekinthető. Egyrészt a tárgyhoz viszonylag közel lévő, rövid fókusztávolságú leképző rendszer, az úgynevezett objektív, vagy tárgylencse a leképzendő tárgyról a képalkotás tulajdonságainak megfelelő, véges távolságban valós, fordított és nagyított képet alkot [7.12.] [7.18.] . Ezt a képet nevezzük közbenső képnek. Megjegyzendő, hogy nem vizuális megfigyelés esetén, ezt a belső, közbenső képet detektálják és értékelik. Vizuális megfigyelés esetén ezt a valós fordított és nagyított képet egy következő optikai rendszeren, az úgynevezett okuláron, vagy szemlencsén keresztül szemléljük; megnagyítva a valós kép szemlélésének látószögét. Ezért a szemmel történő megfigyelés esetén a végső kép nagyított és virtuális, az eredeti tárgyhoz képest fordított állású [7.8.] .
Az objektívből és okulárból álló összetett mikroszkóp nagyításának meghatározása során ismerni kell az objektív és az okulár nagyítását, melyek szorzata az összetett mikroszkóp eredő nagyítása [7.11.] [7.12.] [7.13.] .
Gyakori feladat, hogy a mikroszkópizálás tárgyát képező objektumról valós képet kell alkotnunk, például mikroszkópos fényképezés vagy projekció esetén, ilyenkor a végső kép valós. Szerkezeti okok miatt ezt a valós képet úgy állítják elő, hogy a szemmel történő leképzéshez élesre állított mikroszkópot a tárgyhoz képest elmozdítják, így az új helyen keletkező képet az adott helyen elhelyezett fényérzékeny réteg, vagy elektronikus detektor síkjában felfogják.
Definíció szerint az objektív képoldali és az okulár tárgyoldali fókuszpontjai között mérhető távolság az optikai tubushossz, amit Δ-val jelölnek [7.8.] .
Mindezek alapján az összetett mikroszkóp nagyítása:
|
|
Az első hányados jelenti az alkalmazott okulár lupenagyítását, míg a második hányados az objektív nagyítását, ami az optikai tubushossz és az objektív fókusztávolságának aránya. Maga az optikai tubushossz egy előre meghatározott érték, ezáltal egy objektív tervezése során a képalkotási hibák korrekcióját mindig egy meghatározott távolságra, történetesen az optikai tubushosszra számítják.
Az okulárnak az a feladata, hogy az objektív által létrehozott nagyított, fordított állású, valós képet lupeszerűen tovább nagyítsa [7.13.] . Fontos szerkezeti eleme a mikroszkópnak a tubus, mely helyet ad az objektívnek és az okulárnak, biztosítja közöttük a távolság állandóságát [7.14.] . A valóságos objektívek és okulárok, a képalkotási hibák korrekciója miatt kiterjedt, több elemből álló összetett rendszerek, melyek közös foglalatban helyezkednek el. Az objektív és okulár közötti állandó távolságot egy meghatározott méretű mechanikai elem, a mikroszkóp mechanikai tubusa biztosítja. Az objektív illesztett peremes csavarmenettel foglalható a tubus végébe, az okulár pedig illesztett hüvelyen keresztül csatlakozik a tubushoz, pozícióját felfekvő váll jelöli ki [7.8.] .
Az objektív és okulár kapcsolatát biztosító mechanikus szerkezet hosszának, a mechanikai tubushossznak a mérete állandó, így az objektívek foglalatát úgy kell kialakítani, hogy a rájuk jellemző, és nagyításukat meghatározó fókusztávolságuktól függetlenül a közbenső képe a tubusban mindig ugyanazon a helyen jöjjön létre. Az objektívek felfekvő felületének a tárgytól való távolsága állandó, ez a távolságot a szakirodalom az objektív illesztési hosszának nevezi.
Az okulár tubussal való mechanikai kapcsolatát is úgy kell kialakítani, hogy annak tárgyoldali fókuszpontja mindig belessen a közbenső kép síkjába. Az okulárok foglalata tehát olyan, hogy annak felfekvő karimája és a tárgyoldali fókuszpontja közötti távolság, az úgynevezett okulár illesztési hossz állandó legyen. Mindezek alapján tehát az objektív építési hossza megegyezik az objektív illesztési hossza és a mechanikai tubushossz okulár illesztési hosszal csökkentett értékével [7.15.] .
Ez a megkötés biztosítja azt, hogy az összetett mikroszkóp nagyításának változtatásakor a képélesség nem változik meg. Tehát az objektív nagyításának mértéke
|
|
és az okulár lupenagyítása
|
|
Példa:
Egy mikroszkópos megfigyelés esetén 25 szörös nagyítású objektívet és 5 szörös nagyítású okulárt alkalmaztunk. Milyen nagyítású okulárt kell alkalmaznunk, hogy a nagyításunk 250 szeres legyen?
Megoldás:
Az eredő nagyítás az objektív és az okulár nagyításának szorzata:
|
|
Az új okulár nagyítása:
|
|
Tehát a 250 szeres nagyítás eléréséhez 10 szeres nagyítású okulárra van szükségünk.
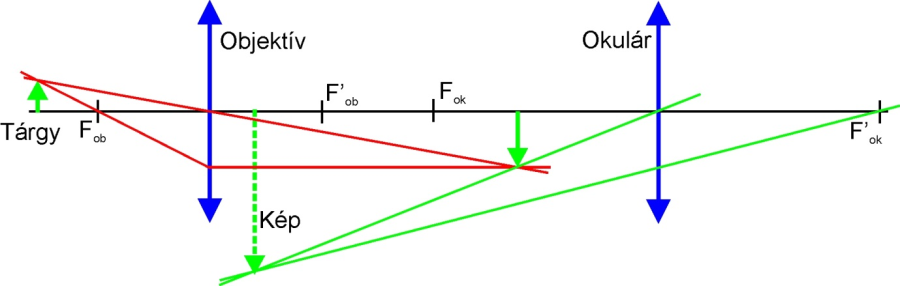
7.2.4. A tárgy megvilágítása
A mikroszkópizálás során vizsgált tárgyakat, objektumokat, melyek nem önálló fényforrások a következő képen csoportosítjuk [7.8.] :
Azok, melyek a fénysugarakat még jelentéktelen vastagság esetében sem engedik át. Az ilyen vizsgált objektumoknál a megvilágító fényt a tárgy felületére kell irányítani. Ezt a fénymennyiséget a megvilágított tárgy visszaverve az optikai rendszerbe irányítja. Ebben a megfigyelési módban tehát a fénysugarak a tárgyat a megfigyelés irányából érik, ezt felső megvilágításnak nevezzük.
Azok, melyek a belépő sugarat teljes mértékben elnyelik. Itt a tárgyakat átvilágítjuk és a sugarak a tárgy részletei optikai tulajdonságainak függvényében lépnek be az optikai rendszerbe és alkotnak képet. Ebben az esetben a fényforrás sugarai a megfigyelés irányával ellentétesen érkeznek. A megvilágítást a tárgyak optikai tulajdonságainak megfelelően megtervezni.
Azok, melyek, a megvilágító fénysugarakat kisebb, vagy nagyobb arányban áteresztik. Ez a módozat az előző kettő kombinációjának tekinthető.
Ismert tény, hogy a tárgypontban a megvilágítás erőssége négyzetesen növekszik a megvilágító sugárkúp apertúrájával, ez pedig annál nagyobb, minél nagyobb a fényforrás felülete és minél közelebb van a tárgyhoz. Ez alapvetően határozza meg a mikroszkópos megvilágítás tervezésének szempontjait.
Mivel a fényforrás által kisugárzott hő miatt a csekély fókusztávolságú optikai rendszer fókuszsíkjában azt elhelyezni gyakorlatilag nem lehet, ezért ilyen esetben a fényforrás képét egy újabb optikai rendszer, a kollektor a kondenzor első fókuszsíkjába képezi. Az ilyen felépítésű megvilágító rendszer előnyei a következők:
A fényforrás és annak képei a mikroszkópizálás tárgyát képező objektumtól távol esnek
A fényforrás és annak képei a mikroszkópizálás tárgyát képező objektumról és az objektív által leképezett képétől távol esnek
A fényforrás struktúrájából adódó egyenletlenségek sem a tárgy síkjában, sem a tárgyról az objketív által alkotott képeiben nem jelentkezne
Homogén sugárzást adó fényforrás képe bárhol elhelyezhető a mikroszkóp optikai sugárútjában (kritikus megvilágítás).
7.2.5. Köhler-féle megvilágítás
Ahogy az előzőekben láttuk a minőségi mikroszkópos képalkotás fontos feltétele a kép optimális tulajdonságokkal rendelkező megvilágítása. Ennek legfontosabb szempontjai a következők [7.8.] :
A tárgy megvilágítását végző optikai rendszer biztosítsa, hogy a vizsgálandó tárgy legyen egyenletesen és homogén megvilágítva.
A tárgy megvilágítását végző sugárkúpok apertúrája egyezzék meg az objektív apertúrájával.
A tárgy megvilágítását végző sugárkúpok fősugarai a mikroszkópos tárgyra közel merőlegesen essenek be.
E három rendkívül fontos feltétel körültekintő tervezést és beállítást igényel. Ilyen rendszert először 1893-ban A. Köhler, a Carl Zeiss művek munkatársa dolgozott ki. Ezt, a fenti feltételeknek eleget tevő megvilágítási elvet Köhler-féle megvilágításnak nevezik, és azóta a vizuális mikroszkópiában, és a mikroszkópos felvétel készítésben széles körben használják a megvilágítás módjától függetlenül [7.8.] [7.9.] [7.10.] .
A Köhler-féle megvilágítás optikai rendszerében a fényforrást egy gyűjtő típusú optikai rendszer, a kollektor a kondenzor első fókuszsíkjában fekvő szabályozható méretű apertúrarekeszre képezi, le úgy, hogy a fényforrás képe a teljesen nyitott apertúrarekesz nyílását kitölti.
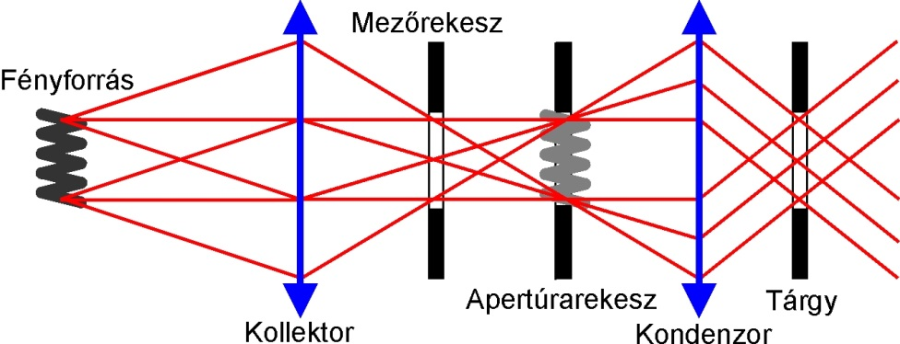
Könnyen belátható tehát, hogy a Köhler-féle megvilágítás egyik legfontosabb tulajdonsága, hogy alkalmazása esetén a tárgy és képhelyei, valamint a fényforrás és világító felületének képei soha nem esnek ugyanazon helyre.
Az optikai rendszerek tervezésének elméletéből ismert, hogy egyetlen tagból álló optikai rendszer nem képes teljesíteni az elvárt képminőséggel szembeni elvárásokat, kívánalmakat. Ezt a gyakorlatban több tagból álló rendszerek generálásával oldják meg, több lencséből álló rendszert kell építeni. Az ilyen, összetett rendszerek elemei közös foglalatban helyezkednek el úgy, hogy optikai tengelyeik egybeesnek. Ez a gyártás során külön technológiai lépéssel biztosított. A teljes mikroszkópra vonatkozóan ezt a követelményt a mikroszkóp állvány biztosítja. A modern, nagy teljesítményű mikroszkópoknál a megvilágító egység, a kiegészítő optikai elemekkel az állványba van beépítve, így a munkaasztalon való elmozdításakor nem kell a teljes megvilágítást újból beállítani.
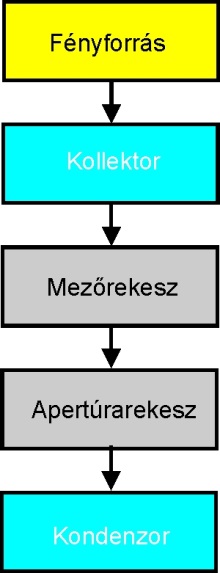
7.3. A mikroszkóp képalkotást végző optikai rendszerei
7.3.1. A mikroszkopizálás során alkalmazott optikai rendszerek és tulajdonságaik
A mikroszkópban használt optikai rendszerek csoportosításukat tekintve lefedik az általános osztályozást, mely szerint az optikai rendszerek, optikai elemek két nagy osztályba sorolhatók. Ez a csoportosítás alkalmazás szerinti, és tartalmazza a képalkotó optikai rendszereket és a nem-képalkotó optikai rendszereket.
A képalkotó optikai rendszerek a tárgy felületén tapasztalható intenzitáseloszlás módosított változatát hozzák létre a képsíkban, ahol elhelyezhető a detektor. A képalkotó rendszerek által alkotott kép legfontosabb tulajdonsága a felbontás, a kontraszt, és a geometriai aberrációk. A nem-képalkotó optikai rendszerek funkciói közé sorolható a fény gyűjtése, fénysugarak irányítása, stb. Mikroszkópos alkalmazások esetén mindkét optikai rendszer típus részt vesz a folyamatban, egyrész a képalkotás, másrészt az energetikai viszonyok megfelelő biztosításában. A mikroszkópos képalkotás minőségére elsősorban a képalkotó rendszerek képalkotási hibái, illetve azok korlátozására van hatással. Ezek két nagy csoportra oszthatók, a monokromatikus és a kromatikus aberrációkéra [7.37.] . Az előbbi csoportba tartozik a szférikus aberráció, mely lényegében a metszéki távolság változását mutatja a belépő sugár magasságának függvényében. Jelenléte foltot eredményez, aminek nagysága hatással van a kép minőségére. A fénysugarak nem az elméleti pontban metszik az optikai tengelyt, hanem szóródási kört hoznak létre. Az üstököshiba, vagy koma ferde sugárköteg esetén hoz létre egy aszimmetrikus foltot, függ a rekesz helyétől is. Képmező elhajlás jelenléte esetén a tárgyról készült kép egy görbült felületre képződik le. Ezzel függ össze az asztigmatizmus, amely a meridionális és a szagittális síkban bekövetkező képmezőhajlások eredménye. A torzítás oka az, hogy az optikai rendszer nagyítása az optikai tengelyre merőleges irányban változik [7.32.] .
A kromatikus aberrációk oka eredendően az, hogy az alkalmazott üveganyagok törésmutatója a hullámhossz függvényében változik, így a különböző színű képek máshol és más méretben keletkeznek. Ezen hibák korrekciója különös jelentőséggel bír a mikroszkópos képalkotás során. A jó minőségű optikai rendszerek tervezése és gyártása időigényes és költséges folyamat eredménye, ami a termék árát a darabszám függvényében jelentősen meghatározza [7.32.] .
Az optikai rendszerek képalkotási hibáinak mértéke az őket alkotó elemek egymáshoz illesztésével, úgynevezett összetett lencserendszerek kialakításával kézben tartható, tehát az egyes tagok képesek egymás hibáit bizonyos határok között kiegyenlíteni. A szférikus aberráció korrekciójának lehetséges módja egy, például domború és egy homorú tag illesztése, ugyanis a gyűjtő és a szóró elem szférikus aberrációja ellentétes jelleget mutat. A kromatikus aberrációk kézben tartására, az üveganyagok eltérő színbontó képességét használják ki.
7.3.2. A mikroszkópok legfontosabb képalkotó optikai rendszerei
A mikroszkopizálás során a képalkotás folyamatában közvetlenül részt vevő optikai rendszerek közül kiemelt szerepet töltenek be az objektívek és az okulárok [7.8.] . Szerepük ismert; az összetett mikroszkópban a tárgy leképezése és a nagyítása két képalkotási folyamatnak tekinthető. Egyrészt a tárgyhoz viszonylag közel lévő, rövid fókusztávolságú leképző rendszer (objektív) a leképzendő tárgyról véges távolságban valós fordított és nagyított képet alkot. Ezt a képet nevezzük közbenső képnek. Szemmel történő megfigyelés esetén ezt a valós fordított és nagyított képet egy következő optikai rendszeren (okulár) keresztül szemléljük; megnagyítva a valós kép szemlélésének látószögét. Ezért a szemmel történő megfigyelés esetén a végső kép nagyított és virtuális, az eredeti tárgyhoz képest fordított állású.
7.3.3. Az objektív
Az összetett mikroszkóp egyik legfontosabb optikai rendszere az objektív, hiszen tulajdonságai alapvetően határozzák meg a kép minőségét. Ez az elem az, amely az elsődleges, közbenső képet hozza létre. Az objektívek csoportosításukat tekintve lehetnek lencsékből, tükrökből építettek. A tükrös rendszerek nagy előnye, hogy mentesek a kromatikus aberrációktól, így a színhiba mentesítésére nem kell erőforrásokat átcsoportosítani. Hátrányuk viszont, hogy alkalmazásuk esetén a korrekció szabadságfoka igen korlátozott.
A fénytörésen alapuló mikroszkóp objektíveket elsősorban felépítésük és korrekciós állapotuk szerint szokás csoportosítani. Ezen tulajdonságaik azonban jelölésükben is megjelennek. Szokásos csoportosítás kapcsolódik a felhasználásukhoz, itt elsősorban az áteső és ráeső fényben használt mikroszkóp objektíveket érdemes kiemelni, de természetesen önálló csoportot alkotnak például a polarizációs mikroszkópia objektívjei is.

7.3.4. A mikroszkóp objektívek képalkotási hibái
A mikroszkóp optikai viszonyainak tanulmányozása alapján könnyen kikövetkeztethető, hogy az objektív a szerény méretű tárgyat nagy nyílásszögű sugarakkal, az okulár viszont az így keletkezett nagy méretű közbenső képet kis nyílásszögű sugarakkal képezi le. Mindezek alapján megállapítható, hogy az objektíveknél és az okulároknál más és más típusú sugarak képalkotási hibáinak vizsgálata az elsődleges [7.8.] . Az objektíveknél figyelembe veendő [7.32.] :
a tengely közelében haladó sugarak képalkotási hibája
a szferikus aberráció
a szinuszfeltételtől való eltérés
összetett fény alkalmazása esetén a színhibák korrekciója.
Ha a képmező kitejedt tartományára vonatkozóan is korrigált állapotot írunk elő:
kezelni kell a ferde sugarak átvezetése során fellépő aberrációkat [7.37.] azaz
az asztigmatizmust
a komát
a képmezőhajlást
a torzítást
a színnagyítási hibát.
Ezek közül is jelentős az asztigmatizmus és a koma. Szemmel történő mikroszkópos megfigyelések esetén a képmezőhajlás és a torzítás nem okoz jelentős hibát, a tárgyrészletet a látómező közepére állítva, de a mikroszkópos kép rögzítése esetén ezekre is oda kell figyelni, korrekciós állapotukat kézben kell tartani.
Külön gondot okoz, hogy a longitudinális és a transzverzális színhiba egyszerre nehezen korrigálható, az egyik színhiba javításával ugyanis a másik színhiba romolhat. Segítséget jelenthet az okulár, melyben az ellentétes maradék hiba az objektív hibáját kompenzálja.
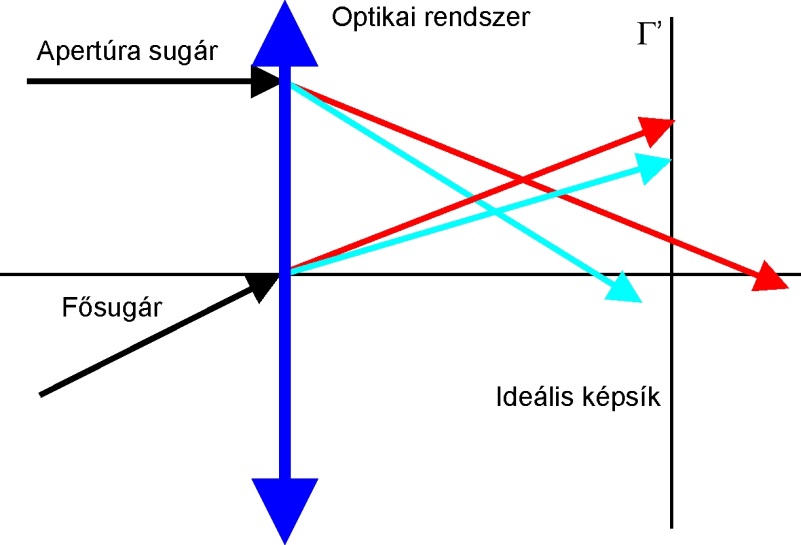
A mikroszkóp objektíveket színhibák korrekciója alapján a következők szerint csoportosítjuk:
akromátok,
apokromátok,
ha a színhibák korrekcióján túl a képrnezőhajlás is szerény mértékre van leszorítva, azaz a kép szinte síkban fekszik, akkor az ilyen tulajdonságokkal rendelkező optikai rendszereket plánobjektíveknek nevezzük. A színhibák korrekciójának figyelembe vételével ezek lehetnek plánakromátok,
plánapokromátok.
Ez utóbbiak tekinthetők a legjobban korrigált mikroszkópobjektíveknek.
Annak függvényében, hogy a tárgy és a fedőlemez illetve az objektív első felülete közötti teret milyen közeg tölti ki, beszélhetünk:
száraz
immerziós objektívekről.
Ha a vizsgálat során a tárgy nincsen fedőlemezzel lefedve, akkor a fénysugarak a levegőn keresztül jutnak az objektívbe, és a növekvő apertúrával alulkorrigáltság lép fel, amit az objektív tervezése során túlkorrigálással lehet kompenzálni. A fordított eset is okozhat problémát, a 0,3 numerikus apertúra felett a fedőlemez okozta hiba olyan mértékű lesz, hogy hatása az objektív használatára már nem hagyható figyelmen kívül. Ezért a fedőlemez vastagságát és anyagának törésmutatóját előre meg szokták határozni. A kialakult szokás szerint,
vastagságát 0,17 mm-nek
törésmutatóját n = 1,52-nek
veszik a mikroszkóp objektívek gyártói.
Előnyös a korrekciós állapot szempontjából, ha a fénysugarak a tárgytól az objektív felületéig közel azonos törésmutatójú közegben futnak. Ez úgy valósítható meg, hogy a fedőlemez és a frontlencse üveganyagával azonos törésmutatójú folyadékkal – úgynevezett immerziós folyadékkal – töltik ki a fedőlemez és frontlencse közötti teret [7.8.] . Az immerziós folyadék alkalmazása azonban további előnyt jelent, hiszen általa jelentősen növelhető az objektív numerikus apertúrája, ami közvetlen hatással van a felbontóképességre. A feloldóképességet az
|
|
numerikus apertúra jelentősen befolyásolja. Levegő (n = 1) esetén, a numerikus apertúra maximális elméleti értéke egy lehet, a gyakorlatban ez azonban a 0,95 értéket szinte sohasem haladja meg. Immerziós folyadék alkalmazása esetén a numerikus apertúra értéke az egynél is nagyobb lehet.
7.3.5. Akromátok
Az akromátok, minden hiányosságuk ellenére a széles körben alkalmazott mikroszkópobjektívek közé tartoznak. Az akromatizálás alapgondolata az, hogy a gyűjtő tag színhibáját az eltérő üveganyagú szóró lencse korrigálni tudja úgy, hogy az eredő rendszer gyújtótávolsága a kívánt értékű. Sajnos az akromátok színkorrekciója csak az ideális képhely két kitüntetett színre való egyezését biztosítja. Az akromatizálást vizuális rendszereknél általában a Fraunhofer-féle vonalak közül a C (656,3 nm) és az F (486,1 nm) színekre biztosítják. Ennek előnye az, hogy a két hullámhossz közötti színekre esik az emberi szem érzékenységi görbéjének a maximuma is [7.8.] .
A gyakorlati alkalmazásokhoz ebben a tartományban a szferikus aberrációt is korrigálják a ragasztott, vagy légréses kéttag elemeinek alakfaktorai segítségével. Ha sikerül a színuszfeltétel megsértését is alacsony szinten tartani, akkor egy színre az aplanatizmus is biztosítottnak tekinthető. Sajnos, ahogy ezt már korábban említettük a longitudinális színhiba javításával a transzverzális színhiba értéke romlik. A színnagyítási hibát a mikroszkópiában a megfelelő nagyságú, de ellentétes hibával terhes okulár, az úgynevezett kompenzációs okulár tudja javítani. Az akromatikus mikroszkóp objektívek bizonyos mértékig az asztigmatizmusra és komára korrigáltaknak tekinthetők, sajnos azonban a szagittális és meridionális képmezőhajlás mértéke jelentős marad. Vizuálisan is jól felismerhető az akromát arról, hogy mivel azok színhibájának korrekciója csak két színre vonatkozik, a tárgy széleiről érkező ferde sugarak zavaró szekunder spektrumot mutatnak, azaz színesek.
7.3.6. Apokromátok
Az apokromátok az akromátoktól abban különböznek, hogy a longitudinális színhiba három, a Fraunhofer-féle C(656,3 nm), D(589,3 nm) és F(486,1 nm) vonalra van korrigálva, azaz ezen színekre esnek egybe a paraxiális képpontok [7.33.] [7.34.] . Az ilyen rendszerek általában két színre egyben aplanatikusak is. A három színre megvalósított színkorrekció miatt a szekunder spektrum helyett ferde megvilágításnál egy annál jelentéktelenebb színhiba, a tercier spektrum jelenik meg, ennek mértéke azonban már nem zavaró [7.8.] . Sajnos ennek a jobb színkorrekciónak ára van, csak speciális üvegek és kristályok alkalmazásával valósítható meg. Az apokromátoknál a színhiba az objektív központ részén és a széleken egyaránt kiegyenlített. Az ilyen típusú mikroszkóp objektívek általában öt, vagy több tagból épülnek fel.
Az apokromátokhoz vizuális megfigyelésnél és képrögzítéses esetben is kompenzációs okulárokat kell illeszteni. Az adott esetben fellépő képmezőhajlás ebben az esetben is speciálisan az objektívhez tervezett okulárral korrigálható.
7.3.7. Speciális objektívek
Külön csoportot képeznek a tükörobjektívek, melyek ugyan széles körben nincsenek igazán elterjedve, azonban jelentőségük még így is nagy. Két általános típusuk ismert szélesebb körben; a Schwarzschild-típusú rendszerben tisztán reflexió, míg Maksutov-típusú rendszereknél vegyesen, azaz reflexió és refrakció útján keletkezik a mikroszkópos kép [7.8.] . A Schwarzschild-típusú rendszerek előnye, hogy kierjedtebb hullámhossz tartományban is alkalmazhatók, színhiba nem terheli. A használhatóságukat növeli, hogy az objektív és a tárgy közötti szabad tárgytávolság lényegesen nagyobb, mint egy hasonló paraméterekkel rendelkező lencsés objektívnél, azonban a korrekció lényegesen nehézkesebb, hiszen az alkalmazható felületek száma igen korlátozott. Tükörobjektívhez áltlában hasonló felépítésű kondenzort használnak [7.32.] .
A mikroszkópos alkalmazásokhoz különlegesnek számítanak az úgynevezett a polarizációs objektívek, melyeket külön jelöléssel látnak el. Elvárás velük szemben, hogy ne tartalmazzanak belső feszültséget, ne legyen saját kettőstörésük, amely megzavarná a keletkezett polarizációs képet. Ez különösen érvényes a fluorit tagot tartalmazó objektívekre.
Külön csoportot képeznek a polarizációs mikroszkópia objektívjei, amelyekkel például a Fedorow-asztalon lehet méréseket végezni.

A fáziskontraszt objektíveknél a hátsó fókuszsíkba illesztik a fáziseltolást biztosító rétegeket.
7.3.8. Okulárok
Az összetett mikroszkóp másik legfontosabb optikai rendszere az okulár, amely alapesetben kétféle funkciót tud ellátni.
Szemmel történő megfigyelés esetén a közbenső valós képet tovább nagyítja úgy, hogy annak virtuális képét hozza létre, a szembe a nagyításnak megfelelő szögben érkeznek a sugarak.
Detektoron való rögzítés esetén egy nagyított valós végső képet alkot távol az okulár után.
A helyesen alkalmazott okulár az objektív kilépőpupillájáról képet alkot, amely a rendszer kilépő pupillája. Vizuális megfigyelés esetén a szem pupilláját ebbe a kilépőpupillájába kell helyezni. Jelentősége van ezért a kilépő pupilla utolsó felülettől való távolságának, hiszen ez a kényelmes szemlélés szempontjából rendkívül fontos. Az okulár jellemzője a korábban definiált és leírt lupenagyitás, amit mikroszkóp okulár esetén belegravíroznak, vagy rányomtatnak annak foglalatára. A felhasználás szempontjából a nagyítás mellett legalább ilyen jelentőségű a tárgyból látott tárgymező nagysága is. A mikroszkóp közbenső képét az okulárban található úgynevezett látómezőrekesz határolja, annak milliméterben kifejezett nagysága látómezőszám [7.8.] .
Mivel az okulárok nyílásszöge viszonylag kicsi
a szferikus aberrációt,
a longitudinális színhibát
szinte nem kell korrigálni. Viszont komoly hangsúlyt kell fektetni
a színnagyítás
az asztigmatizmus
a képmezőhajlás
torzítás
kielégítő mértékű korrekciójára.
7.3.9. A főbb okulártípusok
Az egyik legismertebb egyszerű okulár az úgynevezett Huygens-féle okulár. Nincs transzverzális színhibájuk, ezért szerény paraméterekkel rendelkező akromát objektívekhez célszerű használni. Az okulár, szerkezeti felépítését tekintve két síkdomború lencséből épül fel, mindkét lencse sík felülete a vizsgáló személy szeme felé áll. A közbenső kép a két síkdomború lencse között jön létre, ahol elhelyezkedik az okulár látómezőrekesze is.
A másik ismert, és széles körben használt egyszerű kéttagú okulár a Ramsden-féle okulár, mely a Huygens-féle okulárhoz hasonlóan két síkdomború lencséből áll, azonban ezek domború felükkel egymás felé fordítottak. A mezőlencse és szemlencse fókusztávolságai egyenlők egymással és a két tag közötti távolsággal. Legnagyobb hátránya, hogy a közbenső kép az egyik lencse sík felületére képződik, így az esetleges szennyeződésekre rendkívül érzékeny, azok a képpel együtt látszanak, zavaróak. A szerkezetből adódó alkalmazástechnikai hiányossága az, hogy a kilépő pupilla zavaróan közel esik a második lencsetaghoz.
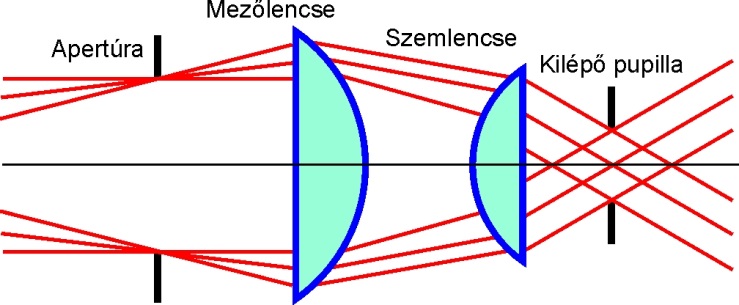
Ennek az okulár típusnak egy továbbfejlesztett változatának tekinthető a Kellner-okulár, amely abban különbözik, hogy a két lencse itt közelebb kerül egymáshoz, a kilépő pupilla távolabb kerül a szemlencsétől, és a fellépő színnagyítási hiba egy ragasztott kéttaggal korrigálva van.
A transzverzális színhiba az, amely az okulárok használata esetén a legtöbb problémát okozza. E hibát egyenlíti ki a kompenzációs okulár, mely az objektíven tapasztalható transzverzális színhibával azonos mértékű, de ellentétes irányú. Ezek lényegében a Huygens-féle okulárok továbbfejlesztett változatai, általában mindkét eleme ragasztott kéttag. A közepes és nagy nagyítású kompenzációs okulárok az úgynevezett ortoszkopikus okulárok. Minden kedvező tulajdonságuk mellet bennük még a torzítás is korrigálva van, mérőokulárok céljára is sikeresen alkalmazhatók.
Ahogy azt már korábban említettük a mikroszkóp okulárokon feltüntetik a lupenagyítást, ellentétben a távcső okulárokkal, melyekre gyújtótávolságuk a jellemző.
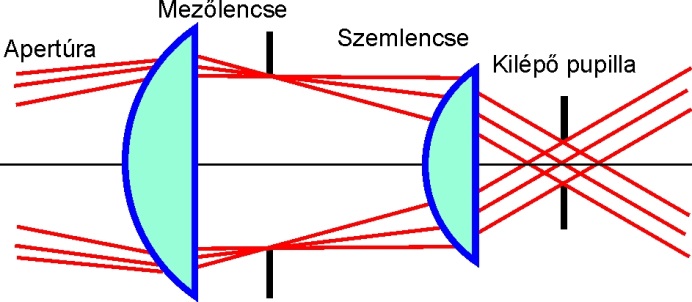
7.3.10. Speciális okulárok
Egyre nagyobb a jelentőségük a változtatható nagyítású, úgynevezett pankratikus okulároknak, melyek kényelmes és gyors megfigyelést tesznek lehetővé.
A méréstechnikai célokra fejlesztett okulárok látómezejében, pontosabb a látómezőrekesz síkjában egy úgynevezett okulármikrorméter-lemezt helyeznek el [7.8.] . Ez a lemez tartalmazza a feladathoz illesztett speciális osztást. Ezekben a szerkezetekben biztosítani kell, hogy az osztásvonalak képét, a szemlencsefoglalat menetes elmozdításával élesre lehessen állítani. Erre a célra általában az ortoszkopikus okulárt alkalmazzák, melyben – ahogy azt már fentebb részletesen kifejtettük – a torzítás ki van egyenlítve, látómezőrekesz a rendszer előtt fekszik, így a speciálisan tervezett és illesztett okulármikrométer a közbenső kép nagyságának a mérését közvetlenül teszi lehetővé. Ezek továbbfejlesztett változatai az úgynevezett mozgószálas okulármikrométerek, melyekben a szálkereszt helyzete mikrométercsavarral állítható, aktuális pozíciója a mikrométercsavar osztásai segítségével olvasható le.
7.3.11. Az okulárok szerkezeti kialakítása
Az okulárok foglalására általában egy hüvelyt használnak, melynek külső átmérője az esetek döntő többségében 23,2 mm, de kivételesen előfordul a 30 mm is. A lencsetagok pozíciója a foglalatban általában menetes gyűrűk segítségével biztosított. A foglalt optikai elemek a mikroszkóp tubusába becsúsztathatók. Az okulárok foglalatain feltüntetik a gyártót, a lupenagyitást és az okulár típusát. A komperzációs okulárokat K vagy C jelzéssel, a plán-objektívekhez használt kompenzációs okulárokat Pk jelzéssel látják el.

7.3.12. Kondenzorok
A kondenzor ugyan nem tartozik a mikroszkóp közvetlen képalkotó rendszerei közé, viszont a megvilágításban és így közvetve az egész folyamatban betöltött fontos szerep miatt tárgyalásra érdemes. Az apertúrarekeszt és egy lencserendszert alkalmazó kondenzor feladata, biztosítani, hogy a tárgyat alkalmas apertúrájú sugárkúp világítsa meg. A kondenzorok korrigáltsági állapota azok felhasználhatósága szempontjából kulcsfontosságú. A Köhler-féle megvilágítás kellemes tulajdonságainak maradéktalan kihasználhatósága megköveteli a kondenzorokkal szemben, hogy a nagy apertúra mellett a szférikus aberráció is korrigálva legyen úgy, hogy amellett a színhibák is kézben legyenek tartva. A legjobb eredmény általában aplanatikus kondenzorokkal érhető el [7.8.] .
7.4. Ellenőrző kérdések
A környezetünkről nyerhető információ jelentős részének megszerzésében a látás kiemelt szerepet tölt be. A vizuális detektálást végző érzékszervünk teljesítménye rendkívül behatárolt. Számtalan esetben van szükség látószög növelésére. Magyarázza el ennek az indokát, hozzon fel példákat ilyen esetekre! Ismertesse a látószög növelő optikai rendszerek kialakításának alapgondolatát!
Ha a vizsgálandó tárgy túl messze van, a rajta lévő – a vizsgálat tárgyát képező – részletek a szem felbontóképességének határszöge alatt vannak, tehát kicsi a részletek látószöge; ilyenkor úgynevezett távcsövet kell alkalmazunk. Fordított esetben, amikor a megfigyelést végző szemünkhöz közel lévő rendkívül kisméretű tárgyak részleteit nem látjuk, azaz ebben az esetben is a szem felbontóképességének megfelelő hátárszög alatt látszanak csak; lupét. Magyarázza meg a két eset közötti különbséget!
A mikroszkópokat a tudomány, az ipar, a méréstechnika számos területén alkalmazzák. A feladat az esetek jelentős részében, elsősorban a felbontóképesség, a nagyítás, a mélységélesség, illetve a látómező mérete vonatkozásában lépnek fel fokozott elvárások. Magyarázza meg ezeket a fogalmakat, mondjon rájuk gyakorlati példákat és magyarázza el, hogy ezeket hogyan alkalmazzuk a mikroszkóp teljesítményének növelése során!
Magyarázza el a képi tartalom perspektivikus hatást befolyásoló mélységi információit. Ismertesse a textúra képen belüli lokális változását, a felületelemek közötti átfedéseket, a részletgazdaság csökkenését, az árnyékok iránya, vetülete, mérete és a színek perspektívára gyakorolt hatását. Mondjon példákat ezekre!
Ismertesse az egyes mikroszkópos megfigyelési módszereket, a centrális világos látóterű megvilágítást, ferde megvilágítást, a sötét látóterű megvilágítást, a fáziskontraszt eljárást, az interferencia mikroszkópos eljárást, a polarizációs mikroszkópos eljárást és a fluoreszcenciás módszereket!
Hogyan értelmezzük a szem felbontó képességét?
Mi az egyszerű mikroszkóp és hogyan határozzuk meg a nagyítását?
Mi az összetett mikroszkóp, mitől függ az eredő nagyítása, mi az üres nagyítás fogalma?
Mik az optimális mikroszkópos megvilágításnál megfogalmazható követelmények?
Ismertesse a Köhler-féle megvilágítást és annak működését! Magyarázza el a kollektor és a kondenzor szerepét!
Mik azok a képalkotási hibák, melyeket a mikroszkóp objektívek kiválasztásánál szem előtt kell tartani?
Mik az előnyeik a tükrös mikroszkóp objektíveknek?
Ismertesse a fontosabb mikroszkóp okulár típusokat!
Mi a kondenzor szerepe a Köhler-féle megvlágításban?
Hogyan definiáljuk az objektív illesztési hosszát?
Hogyan definiáljuk az optikai tubushosszt? Mi a szerepe a mikroszkóp eredő nagyításában?
Miért adják meg a mikroszkóp objektívekhez a fedőlemez vastagságát?
Egy optikai rendszer numerikus apertúráját az
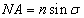 összefüggéssel határozzuk meg. Hogyan növelhető a numerikus apertúra értéke egy fölé? Van- ennek jelentősége a mikroszkóp objektívek felbontóképessége szempontjából?
összefüggéssel határozzuk meg. Hogyan növelhető a numerikus apertúra értéke egy fölé? Van- ennek jelentősége a mikroszkóp objektívek felbontóképessége szempontjából?A Köhler-féle megvilágítás kellemes tulajdonságainak maradéktalan kihasználhatósága megköveteli a kondenzorokkal szemben, hogy a nagy apertúra mellett a szférikus aberráció is korrigálva legyen úgy, hogy amellett a színhibák is kézben legyenek tartva. A legjobb eredmény általában aplanatikus kondenzorokkal érhető el. Indokolja fenti állítást!
A mikroszkóp optikai viszonyainak tanulmányozása alapján könnyen kikövetkeztethető, hogy az objektív a szerény méretű tárgyat nagy nyílásszögű sugarakkal, az okulár viszont az így keletkezett nagy méretű közbenső képet kis nyílásszögű sugarakkal képezi le. Ábrázolja grafikusan a fenti állítást!
Magyarázza meg és szemléletesen ábrázolja az alábbi képalkotási hibákat: az asztigmatizmust, a komát, a képmezőhajlást és a torzítást!
Szemmel történő mikroszkópos megfigyelések esetén a képmezőhajlás és a torzítás nem okoz jelentős hibát, ugyanis a tárgyrészletet a látómező közepén ezt kiküszöböli, de a mikroszkópos kép rögzítése esetén ezekre is oda kell figyelni, korrekciós állapotukat kézben kell tartani. Minden esetben igaz ez?
Közismert tény, hogy a longitudinális és a transzverzális színhiba egyszerre nehezen korrigálható, az egyik színhiba javításával ugyanis a másik színhiba hiba romlik. Az objektív korrigálásánál melyik színhibát kell inkább kompenzálni?
Miben különböznek az alábbi okulár típusok? Akromátok, apokromátok.
A száraz objektívekhez képest nagyobb numerikus apertúrával rendelkeznek az immerziós objektívek, azonban ezek kezelése nehézkesebb. Miért?
Ha a vizsgálat során a tárgy nincsen fedőlemezzel lefedve, akkor a fénysugarak a levegőn keresztül jutnak az objektívbe, és a növekvő apertúrával alulkorrigáltság lép fel, amit az objektív tervezése során túlkorrigálással lehet kompenzálni. Mit jelent ez a gyakorlatban?
Miben különbözik a Huygens és a Ramsden okulár? Jellemezze mindkét típust!
Mondjon példát speciális mikroszkóp objektív típusokra!
A kondenzor nem tartozik a mikroszkóp közvetlen képalkotó rendszerei közé, viszont részt vesz a minta megvilágításban. Ismertesse a kondenzor Köhler-féle megvilágításban betöltött szerepét, ismertesse a sugármenetet!
Az okulárok foglalatának felfekvő karimája és a tárgyoldali fókuszpontja közötti távolság, az úgynevezett okulár illesztési hossza állandó. Szemléltesse grafikusan!
Felhasznált irodalom
[7.1.] Gerätekonstruktion in Feinwerktechnik und Elektronik. Hanser. München . 2000. ISBN 3-446-19608-0.
[7.2.] Konstruktionselemente der Feinmechanik. Hanser. München . 1993. ISBN 3-446-16530-4.
[7.3.] Fertigungsgerechtes Gestalten in der Feingerätetechnik. Verl. Technik. Berlin . 1977.
[7.4.] Electromechanical design handbook. McGraw-Hill. New York . 1995. ISBN 0-07-068035-3.
[7.5.] Finommechanika. Műszaki Kvk.. Budapest . 1977. ISBN 963-10-1576-9.
[7.6.] Finommechanikai kézikönyv. Műszaki Kvk.. Budapest . 1974.
[7.7.] Microscopy of textile fibres. BIOS Scientific Pub.. Oxford . 1995. ISBN 1-872748-24-4.
[7.8.] A mikroszkóp: zsebkönyv. Műszaki Kvk.. Budapest . 1979.
[7.9.] Mihály. Mikroszkóp és mikrofotografálás. Könnyűipari K . 1954.
[7.10.] Mikroszkópos ásvány- és kőzethatározás. Tankvk.. Budapest . 1988.
[7.11.] Fundamentals of Light Microscopy. CUP. 1982.
[7.12.] Introduction to Modern Microscopy. Wykeham Publications. 1975.
[7.13.] Light microscopy, Bios Scientific Publishers in association with the Biochemical Society. 1992.
[7.14.] Light microscopy in biology: a practical approach. IRL Press. 1989.
[7.15.] Modern Methods of Microscopy. Butterworths Scientific Publication. 1956.
[7.16.] Selected papers on optical microscopy. SPIE Optical Engineering Press. 2000.
[7.17.] Advanced light microscopy 1-2. PWN. 1988.
[7.18.] Handbook for the light microscope: a user's guide. Noyes Publications. 1991.
[7.19.] Biomedical light microscopy. Kluwer Academic Publishers. 1991.
[7.20.] Der Theorie Der Optischen Instrumente. Johann Ambrosius Barth. Leipzig . 1924.
[7.21.] Mikroskopie für Anfänger und Fortgeschrittene. Eckart Hillenkamp Verlag. ISBN 3-9808589-0-1.
[7.22.] Das große Kosmos-Buch der Mikroskopie. Franckh-Kosmos Verlags-GmbH & Co. KG. Stuttgart . ISBN 978-3-440-12533-5.
[7.23.] Mikroskopieren: Geräte, Objekte, Praxis, BLV Verlagsgesellschaft. ISBN 3-405-14592-9.
[7.24.] Schöpfer der ersten Leica-Objektive. Pionier der Mikroskopie. 2009. ISBN: 978-3895062841.
[7.25.] Mikroskopieren ganz einfach. KOSMOS Verlag. Stuttgart . 2008. ISBN 978 963 87835 6 1.
[7.26.] Geometrical and Visual Optics. McGraw-Hill Medical. 2013.
[7.27.] Geometrická Optika I-II. Nakladatelství Ceskoslovenské Akademie Vied. Prha . 1955.
[7.28.] Microscope Image Processing. Academic Press. 2008.
[7.29.] Under the Microscope: A Brief History of Microscopy. World Scientific. 2006.
[7.30.] The Microscope and the Eye: A History of Reflections, 1740-1870. University Of Chicago Press. 2007. ISBN 978-0226737843.
[7.31.] Introduction to the optical transfer function. Wiley-Intersc.. New York . 1989.
[7.32.] Modern Optical Engineering. McGraw-Hill Professional. 2007. SBN 978-0071476874.
[7.33.] The Design of Superachromatic Lenses. Applied Optics. pp. 553-560. 1963.
[7.34.] Modern Geometrical Optics. Krieger Pub Co.. 1980. ISBN 978-0882755854.
[7.35.] Modern optika mérnököknek és kutatóknak. Műszaki Könyvkiadó. Budapest . 1982.
[7.36.]
[7.37.] Optika. Panem McGraw Hill. Budapest . 1998.
A. függelék - CIE szótár
A CIE színekkel és látással kapcsolatos kifejezéseinek megnevezései és definíciói angol és magyar nyelven
|
Angol fogalom |
Angol definíció |
Magyar fogalom |
Magyar definíció |
|---|---|---|---|
|
CIE |
acronym of the International Commission on Illumination, derived from the French name: Commission Internationale de l’Eclairage |
Nemzetközi Világítástechnikai Bizottság, CIE |
A Nemzetközi Világítástechnikai Bizottság francia nevéből (Commission Internationale de l’Eclairage) képezett betűszó |
|
background, single stimulus |
region surrounding the stimulus subtending approximately 10º |
háttér, elsődleges inger |
Az ingert körülvevő, mintegy 100 kiterjedésű környezet |
|
CIE 1964 standard colorimetric observer |
ideal observer whose colour-matching properties correspond to the CIE colour-matching functions See also ISO 11664-1:2007(E)/CIE S 014-1/E:2006 Colorimetry - Part 1: CIE Standard Colorimetric Observers |
CIE 1964 szabványos színmérő észlelő |
Az az ideális észlelő, amelynek színinger-megfeleltető tulajdonságai megegyeznek az
Lásd még az ISO 11664-1:2007(E)/CIE S 014-1/E:2006 Colorimetry - Part 1: CIE Standard Colorimetric Observers szabványban. |
|
CIE 1976 uniform-chromaticity-scale diagram |
uniform chromaticity scale diagram produced by plotting in rectangular coordinates v′ against u′, quantities defined by the equations: u′ = 4 X / (X + 15Y + 3Z) = 4x / (-2x + 12y + 3) v′ = 9 Y / (X + 15Y + 3Z) = 9y / (-2x +12y + 3) where X, Y, Z are the tristimulus values in the CIE 1931 or 1964 standard colorimetric systems, and x, y are the corresponding chromaticity coordinates of the colour stimulus considered Equivalent term: “CIE 1976 UCS diagram” NOTE This diagram is a modification of, and supersedes, the CIE 1960 UCS diagram in which v was plotted against u in rectangular coordinates. The relationships between the 2 pairs of coordinates are: u′ = u; v′ = 1,5 v. |
CIE 1976 szabványos színességi skálájú diagram |
Az alábbi összefüggések szerint számított u' és v' derékszögű koordinátákkal értelmezett egyenletes színességi skálájú diagram: u¢ = 4 X / (X + 15Y + 3Z) = 4x / (-2x + 12y + 3) v¢ = 9 Y / (X + 15Y + 3Z) = 9y / (-2x +12y + 3) ahol X, Y, Z a kiválasztott színinger színinger-összetevői a CIE 1931 vagy a CIE 1964 kiegészítő rendszerben és x, y a megfelelő színességi koordináták. Egyenértékű fogalom: CIE 1976 UCS diagram. MEGJEGYZÉS: A korábban használt u és v és az új u' és v' koordinátapár közötti összefüggés: u¢ = u; v¢ = 1,5 v. |
|
CRI (abbreviation) |
See “colour rendering index” |
CRI (rövidítés) |
Lásd „színvisszaadási index” |
|
fovea centralis |
See “fovea” |
fovea centralis |
lásd “fovea” |
|
GRL (abbreviation) |
See “glare rating limit” |
GRL (rövidítés) |
lásd „Káprázási határ” |
|
object colour |
colour perceived as belonging to an object |
tárgy szín |
egy tárgyhoz tartozó színészlelet |
|
object mode (of colour appearance) |
colour seen as ascribed to an object |
tárgyszín szemlélet (színészlelet) |
tárgyszín szemléletű színmegjelenés |
|
spectral chromaticity coordinates [r(λ), g(λ), b(λ); x(λ), y(λ), z(λ); r10(λ), g10(λ), b10(λ); x10(λ), y10(λ), z10(λ)] |
chromaticity coordinates of monochromatic stimuli |
Spektrumszín koordináták[r(λ), g(λ), b(λ); x(λ), y(λ), z(λ); r10(λ), g10(λ), b10(λ); x10(λ), y10(λ), z10(λ)] |
Monokromatikus színingerek színinger koordinátái |
|
visual field |
See “field of vision” |
Látótér |
lásd „látómező” |
|
psychophysical colour |
specification of a colour stimulus in terms of operationally defined values, such as the tristimulus values NOTE 1 When the meaning is clear from the context the term “colour” can be used alone. NOTE 2 In German, “Farbe” is often used instead of “Farbempfindung”. The use of “Farbe” in the sense of “Farbvalenz” should be avoided. It is only when the sense is obvious from the context, or when “Farbempfindung” and “Farbvalenz” are equally suitable, that “Farbe” may be used in the sense of “Farbvalenz”. See also “colour” |
(pszihofizikai) szín |
színingerek meghatározása a színészlelés mechanizmusa alapján, pl tristimulusos módon 1. MEGJEGYZÉS: amennyiben a „szín” szó a szövegkörnyezet alapján világosan érthető, önmagában is alkalmazható. 2. MEGJEGYZÉS: A német nyelvben gyakran használják a „Farbe” szót a „Farbempfindung” helyett. A “szín” szó használata “Farbvalenz” értelemben viszont kerülendő. Ez csak akkor elfogadott, ha a szövegkörnyezet alapján teljesen egyértelmű a jelentése, vagy ha a “Farbempfindung” és a “Farbvalenz” egyformán megfelelő, akkor használható a “Farbe” szó “Farbvalenz“értelemben. Lásd még “colour”, azaz “szín” |
|
lightness (of a related colour) |
brightness of an area judged relative to the brightness of a similarly illuminated area that appears to be white or highly transmitting NOTE Only related colours exhibit lightness. |
viszonylagos világosság, relatív világosság |
adott felület világossága egy hozzá hasonlóan megvilágított, fehérnek vagy nagyon fényáteresztőnek látszó felületnek a világosságához képest. MEGJEGYZÉS: Csak viszonyított színnek lehet „világosság”-a |
|
CIE 1976 u′, v′ chromaticity difference [Δc] |
difference between 2 colour stimuli, defined as the Euclidean distance between the points representing them nt he u′, v′ chromaticity diagram and calculated as equation: Δc = [(Δu′)2 + (Δv′)2]1/2 |
CIE 1976 u′, v′ szerinti színkülönbség [ Δ c] |
két színinger különbsége a színingerek színpontjainak Euclidesi távolságaként értelmezve az u’, v’ színezeti diagramban a következő formula szerint: Δc = [(Δu′)2 + (Δv′)2]1/2 |
|
eight degree geometry |
irradiation or measurement of reflecting materials at 8° to the normal, at one azimuth angle NOTE 1 This geometry is used to substitute the 0° directional geometry in many practical applications of reflection measurements, as it permits differentiation between specular component included and excluded measurements NOTE 2 This geometry is restricted to measurements using an integrating sphere as described in CIE 15 Colorimetry See also CIE 15 Colorimetry (section 5) |
8°-os geometria |
Fényvisszaverő anyagok sugárzása vagy mérése a felület normálisához képest 80-os szögben, egy bizonyos azimutszög irányában 1. MEGJEGYZÉS: Ez a geometria helyettesítheti a 0 °-os geometriát reflexiós mérések esetén, mivel lehetővé teszi a tükrös komponens kizárását. 2. MEGJEGYZÉS: Ez a geometria nem alkalmazható a CIE 15 Kolorimetria című fejezetben leírt integráló gömbbel történő mérésnél Lásd még: CIE 15 Colorimetry (5. rész) |
|
amplitude of fluctuation of the luminous flux (of a source run on alternating current) |
relative amplitude of the periodic fluctuation of the luminous flux as measured by the ratio of the difference between the maximum and the minimum instantaneous luminous flux, Φ max and Φ min respectively, to the sum of both of these values:
Unit: 1 NOTE 1 This ratio is usually expressed in % and is then known under the expression “percent flicker” which, however, should be deprecated. NOTE 2 Another means sometimes used by the lighting industry to characterize the fluctuation in light output is “flicker index”, which is defined by the ratio of 2 areas deduced from the diagram representing the variation of the instantaneous flux over a period of time; the area of the diagram above the average value is divided by the total area under the curve (this total area is the product of the average value and the given period of time). |
a fényáram ingadozás amplitudója (változóárammal táplált fényforrás) |
periodikus fényáram ingadozás relatív amplitudója a fényáram maximális és minimális értéke különbségeként mérve, (Φ max and Φ min ), és viszonyítva ugyanezen értékek összegéhez:
Egysége: 1 1. MEGJEGYZÉS: Ezt az értéket gyakran %-ban szokták megadni, és “fikker százalék”-nak szokták nevezni, de ez már elavult elnevezés. 2. MEGJEGYZÉS: Másrészt a világítástechnikai szakmában “flicker index” néven gyakran a fény fluktuációjának két terület arányával történő jellemzésére használják olymódon, hogy a fényáram változások diagramján az átlagértéket osztják a teljes görbe alatti területtel (a teljes görbe alatti terület az átlag és az adott időtartam szorzata). |
|
Abney phenomenon |
change of hue produced by decreasing the purity of a colour stimulus while keeping its dominant wavelength and luminance constant |
Abney jelenség |
A színezet megváltozása, ha a színérzékelési inger színinger-tisztasága csökken, míg ez alatt domináns hullámhossza és fénysűrűssége állandó. |
|
Abney's law |
empirical law stating that if 2 colour stimuli, A and B, are perceived to be of equal brightness and 2 other colour stimuli, C and D, are perceived to be of equal brightness, then the additive mixtures of A with C and B with D will also be perceived to be of equal brightness NOTE The validity of Abney's law depends strongly on the observing conditions. |
Abney- törvénye |
Az a tapasztalati törvény, amely szerint, ha az A és B színinger egyforma világosságú, valamint a C és a D színinger is egyforma világosságú, akkor az A és a C, valamint a B és a D additív színinger keveréke is egyforma világosságú. MEGJEGYZÉS: Az Abney törvény érvényessége jentősen függ a megfigyelési körülményektől. |
|
adaptation |
process by which the state of the visual system is modified by previous and present exposure to stimuli that may have various luminance values, spectral distributions and angular subtenses NOTE Adaptation to specific spatial frequencies, orientations, sizes, etc. is recognized as being included in this definition. |
adaptáció |
Az a folyamat, amely során a látórendszer tulajdonságai alkalmazkodnak az egymást követő — fénysűrűségben, spektrális eloszlásban és látószögben különböző — fényingerekhez. MEGJEGYZÉSEK: Használatosak a világosra adaptált és sötétre adaptált kifejezések, az elsőt mondják, ha a fénysűrűség legalább néhány kandela per négyzetméter, a másodikat pedig; ha a fénysűrűség néhány század kandela per négyzetméternél kisebb. A térbeli frekvenciákra, irányítottságokra, méretekre stb. való adaptáció beletartozik ebbe a definícióba. |
|
adaptation, state of |
state of the visual system after an adaptation process has been completed NOTE The terms “light adaptation” and “dark adaptation” are also used, the former when the luminances of the stimuli are of at least 10 cd·m-2, and the latter when the luminances are of less than some hundredths of a cd·m-2. |
adaptációs állapot |
a látórendszer állapota, amikor egy adaptációs folyamat teljesen befejeződött MEGJEGYZÉS: Használatos a „világos adaptáció” és a „sötét adaptáció” kifejezés is, az előbbi akkor, ha az inger világossága legalább 10 cd·m-2, és az utóbbi akkor, ha kevesebb, mint néhány század CD·m-2. |
|
white, adapted |
colour stimulus that an observer who is adapted to the viewing environment would judge to be perfectly achromatic and to have a luminance factor of unity NOTE The colour stimulus that is considered to be the adapted white may be different at different locations within a scene. |
fehér adaptációs színészlelet |
olyan színinger, amelyet egy, a környezethez adaptált megfigyelő tökéletesen fehérnek és a világossági tényezőjét egységnyinek ítél meg. MEGJEGYZÉS az adaptációs fehérnek tekintett színinger a látvány különböző területein különböző lehet. |
|
adapted white |
See “white, adapted” |
Fehér adaptációs pont |
Lásd „fehérpont,adaptációs (színmegjelenítési modellnél)” |
|
adaptive colour shift |
change in the perceived colour of an object caused solely by change of chromatic adaptation |
adaptációs színeltolódás |
Egy tárgy színének csak a kromatikus adaptáció megváltozása által okozott változása. |
|
adaptive colorimetric shift |
mathematical adjustment in chromaticity and luminance factor of an object colour stimulus to correct for a change in chromatic adaptation |
adaptációs színeltolódás |
A szín inger színének vagy világosságának matematikai korrekciója a szín adaptáció megváltoztatása céljából |
|
accommodation |
adjustment of the dioptric power of the crystalline lens by which the image of an object, at a given distance, is focused on the retina |
akkomodáció |
A szemlencse törőerejének megváltozása, aminek következtében egy adott távolságban lévő tárgy képe a retinán képződik le. |
|
achromatic colour |
1. in the perceptual sense: perceived colour devoid of hue NOTE The colour names white, grey and black are commonly used or, for transmitting objects, colourless and neutral. 2. in the psychophysical sense: see “achromatic stimulus” |
akromatikus szín |
Észlelet értelemben: színészlelet, amelynek nincs színezete. Megnevezésében általában a fehér, szürke és fekete vagy fényáteresztő tárgyakra vonatkozóan a színtelen és semleges neveket használják. |
|
achromatic stimulus |
stimulus that, under the prevailing conditions of adaptation, gives rise to an achromatic perceived colour NOTE In the colorimetry of object colours, the colour stimulus produced by the perfect reflecting or transmitting diffuser is usually considered to be an achromatic stimulus for all illuminants, except for those whose light sources appear to be highly chromatic. |
akromatikus színinger |
Olyan színinger, amely — általános adaptációs feltételek mellett — akromatikus színészleletet hoz létre. MEGJEGYZÉS: A tárgy színének észlelésében a tökéletesen visszaverő vagy áteresztő testet minősítik akromatikusnak minden sugárzáseloszlásra, kivéve, ha a sugárzás eloszlás nagyon kromatikusnak látszik. |
|
reference colour stimuli |
set of 3 colour stimuli on which a trichromatic system is based NOTE 1 These stimuli are either real colour stimuli or theoretical stimuli which are defined by linear combinations of real colour stimuli; the magnitude of each of these 3 reference colour stimuli is expressed in terms of either photometric or radiometric units, or more commonly by specifying the ratios of their magnitudes or by stating that a specified additive mixture of these stimuli matches a specified achromatic stimulus. NOTE 2 In the CIE standard colorimetric systems, the reference colour stimuli are represented by the symbols [R], [G], [B]; [X], [Y], [Z]; [R10], [G10], [B10] and [X10], [Y10], [Z10]. |
szín észlelési alap ingerek |
Az a három színinger, amelyen a trikromatikus rendszer alapul. 1. MEGJEGYZÉS: Ezek valós vagy elméleti színingerek, az elmélet i színingereket valós színingerek lineáris kombinációjával értelmezik; a három alapszíningert fotometriai vagy radiometriai egységekben fejezik ki; szokásos csak értékeik arányát megadni, vagy úgy értel mezni azokat, hogy a három alapszíninger meghatározott additív keveréke egy adott akromatikus színinger legyen. 2. MEGJEGYZÉS: Az alapszíningerek jelei a CIE színmérő rendszerekben [R], [G], [B]; [X], [Y], [Z] és [X10], [Y10], [Z10]. |
|
basic colour names |
group of eleven colour names found in anthropological surveys to be in wide use in fully developed languages: white, black, red, green, yellow, blue, brown, grey, orange, purple, pink |
alapszínek neve |
antropológiai megfigyelések alapján meghatározott 11 szín megnevezés, amelyeket a legfejlettebb nyelvekben széles körben alkalmaznak: fehér, fekete, vörös, zöld, sárga, kék, barna, szürke, narancs , lila, rózsaszín |
|
unique hue |
hue that cannot be further described by the use of hue names other than its own Equivalent term: “unitary hue” NOTE There are 4 unique hues: red, green, yellow and blue forming 2 pairs of opponent hues: red and green, yellow and blue. |
alapszínezet |
Színezet, amelyet csak a saját színezetének megfelelő névvel szabad leírni. azonos értelemben: „ős szín” MEGJEGYZÉS: 4 „ős szín” van: vörös, zöld, sárga, kék, melyek két kiegészítő színpárt alkotnak: vörös és zöld, sárga és kék. |
|
unitary hue |
See “unique hue” |
alapszínezet | |
|
alychne |
surface in tristimulus space that represents the locus of colour stimuli of zero luminance NOTE This surface passes through the origin of the space. It intersects any chromaticity diagram in a straight line which is also called the alychne; this line lies wholly outside the domain of chromaticities bounded by the spectrum locus and the purple boundary. |
alychne |
A nulla fénysűrűségű színingereket tartalmazó felület a trikromatikus színtérben. MEGJEGYZÉS: Ez a felület átmegy a trikromatikus tér kezdőpontján. Bármely színinger-diagrammal való metszete egyenes vonal, ennek szintén alychne a neve; ez a vonal teljesen kívül fekszik a spektrumgörbe és a btborvonal által értelmezett színesség tartományán. |
|
anomalous trichromatism |
See NOTE 1 to “defective colour vision” |
anomális trichromatizmus |
Lásd az „anomális trichromatizmus” címszónál az 1. MEGJEGYZÉS-t. |
|
aperture colour |
perceived colour for which there is no definite spatial localisation in depth, such as that perceived as filling a hole in a screen |
apertura színészlelet |
Színészlelet, amelynek nincs a térben mélységbeli kiterjedése, amint ez például egy ernyőn lévő nyílás esetében érzékelhető. |
|
Bezold-Brücke phenomenon |
change of hue produced by changing the luminance (within the range of photopic vision) of a colour stimulus while keeping its chromaticity constant NOTE 1 With certain monochromatic stimuli, hue remains constant over a wide range of luminances (for a given condition of adaptation). The wavelengths of these stimuli are sometimes referred to as “invariant wavelengths”. NOTE 2 With increasing intensity, below 500 nm hues shift more toward blue, and above 500 nm hues shift more toward yellow (reds become yellower with increasing brightness). |
Bezold-Brücke jelenség |
A színezet megváltozása, ha a színérzékelési inger fénysűrűsége megváltozik (a fotopos látási tartományban), míg a színessége állandó. 1. MEGJEGYZÉS: Vannak monokromatikus szín ingerek, amelyek színezete állandó marad széles fénysűrűségi tartományban (egy adott adaptációs állapotban). Ezeknek a színérzékelési ingereknek a hullámhosszait invariáns hullámhosszaknak nevezik. 2. MEGJEGYZÉS: Növekvő intenzitás esetén, 500 nm hullámhossz alatti színeknél a kék felé tolódik, 500 nm-en túl a sárga felé tolódik (a vörösek sárgásabbá válnak növekvő világosság esetén). |
|
purple stimulus |
stimulus that is represented in a chromaticity diagram by a point lying within the triangle defined by the point representing the specified achromatic stimulus and the 2 ends of the spectrum locus which correspond approximately to the wavelengths 380 nm and 780 nm NOTE Purple is a hue which is not represented in the hues of the spectrum. |
bíbor színinger |
olyan színinger, amelynek színpontja a színességi diagram monokromatikus színeket ábrázoló vonalának 380 nm-nél és 780 nm-nél található végpontjait összekötő egyenesen található. MEGJEGYZÉS: a bíbor szín nem található meg a spektrum színek (monokromatikus színek) között. |
|
purple boundary |
line in a chromaticity diagram, or the plane surface in a tristimulus space, that represents additive mixtures of monochromatic stimuli of wavelengths approximately 380 nm and 780 nm |
bíborvonal |
olyan vonal a színességi diagramban illetőleg a tristimulusos színtér egy sík felületén, amely a közelítőleg 380 nm-es és a 780 nm-es monokromatikus ingerek additív keverésével áll elő. |
|
CIE 1931 standard colorimetric observer |
ideal observer whose colour-matching properties correspond to the CIE colour-matching functions |
CIE 1931 szabványos színmérő észlelő |
Az az ideális észlelő, amelynek színinger- megfelel tető tulajdonságai megegyeznek az |
|
CIE 1931 standard colorimetric system [X, Y, Z] |
system for determining the tristimulus values of any spectral power distribution using the set of reference colour stimuli [X], [Y], [Z] and the 3 CIE colour-matching functions NOTE 1 NOTE 2 This standard colorimetric system is applicable to centrally-viewed fields of angular subtense between about 1° and about 4° (0,017 rad and 0,07 rad). NOTE 3 The CIE 1931 standard colorimetric system can be derived from the CIE 1931 RGB colorimetric system using a transformation based on a set of 3 linear equations. The CIE 1931 RGB system is based on 3 real monochromatic reference stimuli. See also CIE 15 Colorimetry |
CIE 1931 szabványos színmérő rendszer [X, Y, Z] |
Olyan trikromatikus rendszer, amely a CIE által elfogadott [X], [Y], [Z] alapszíningereken és az 1. MEGJEGYZÉS: Az 2. MEGJEGYZÉS: Ezt a színmérő rendszert kell használni a központi látásra a látómező 1° és kb. 4° (0,017 és 0,07 rad) között területén. 3. MEGJEGYZÉS: A CIE 1931 szabványos színmérő rendszer a CIE 1931 RGB színmérő rendszerből származtatható, 3 lineáris egyenleten alapuló transzformáció által. A CIE 1931 RGB színmérő rendszer 3 tényleges monokromatikus referencia színingeren alapul. Lásd még CIE 15 Colorimetry. |
|
CIE 1964 uniform colour space |
3-dimensional, approximately uniform colour space produced by plotting in rectangular coordinates U*, V*, W* quantities defined by the equations: W* = 25 Y1/3 - 17 U* = 13 W* (u - un) V* = 13 W* (v - vn) NOTE 1 Y, u, v describe the colour stimulus considered, and un, vn describe a specified white achromatic stimulus, where u = u′, See also “CIE 1976 uniform chromaticity scale diagram” NOTE 2 The difference between 2 stimuli, ΔE*, is defined as the Euclidean distance between the points representing them in U*V*W* space and calculated as: ΔE* = [(ΔU*)2 + (ΔV*)2 + (ΔW*)2]1/2. NOTE 3 This colour space is obsolete (except that it is still used in the calculation of colour rendering index). The currently recommended object colour spaces are CIELAB and CIELUV. |
CIE 1964 egyenletes színtér |
3-dimenziós, közelítőleg egyenletes színtér, amely a z U*, V*, W* mennyiségek derékszögű koordinátarendszerében az alábbi egyenletekkel definiálható: W* = 25 Y1/3 - 17 U* = 13 W* (u - un) V* = 13 W* (v - vn) 1. MEGJEGYZÉS: Y, u, v a megfelelő színingert, míg
a fehér akromatikus ingert írja le. Lásd még “CIE 1976 egyenletes skálázású színességi diagram”. 2. MEGJEGYZÉS: Két inger ΔE* különbsége az U*V*W* térben Euklidesi különbségként értelmezhető az alábbiak szerint: ΔE* = [(ΔU*)2 + (ΔV*)2 + (ΔW*)2]1/2. 3. MEGJEGYZÉS: Ez a színtér már elavult, (kivéve a színvisszaadási index számítására alkalmazzák). A jelenleg ajánlott színtér a CIELAB és a CIELUV. |
|
CIE 1964 standard colorimetric system [X10, Y10, Z10] |
system for determining the tristimulus values of any spectral power distribution using the set of reference colour stimuli [X10], [Y10], [Z10] and the 3 CIE colour-matching functions NOTE 1 This standard colorimetric system is applicable to centrally-viewed fields of angular subtense greater than about 4° (0,07 rad). NOTE 2 When this system is used, all symbols that represent colorimetric measures are distinguished by use of the subscript 10. See also CIE 15 Colorimetry |
CIE 1964 szabványos színmérő rendszer [X10, Y10, Z10] |
Olyan trikromatikus rendszer, amely a CIE által elfogadott [X10], [Y10], [Z10] alap színingereken és az 1. MEGJEGYZÉS: Ezt a CIE színmérő rendszert kell használni, ha a centrális látás látómezeje nagyobb, mint kb, 4° (0,07 rad). 2 MEGJEGYZÉS: Ha ezt a rendszert használják a színmérésben, minden mennyiséghez ki kell írni a 10 indexet. A Y10 értékek nem arányosak a fénysűrűséggel. Lásd még CIE 15 Colorimetry |
|
CIE 1974 special colour rendering index [Ri] |
measure of the degree to which the psychophysical colour of a CIE test colour sample illuminated by the test illuminant conforms to that of the same sample illuminated by the reference illuminant, suitable allowance having been made for the state of chromatic adaptation See also CIE 13 Method of Measuring and Specifying Colour Rendering of Light Sources |
CIE 1974 egyedi színvisszaadási index [Ri] |
Mérőszám annak jellemzésére, hogy egy adott CIE tesztelő színmintának a vizsgált fényforrással kapott színe hogyan egyezik meg ugyanazon mintának referencia sugárzáseloszlással történő megvilágítás hatására kapott színével, figyelembe véve a kromatikus adaptációt. Lásd még CIE 13 Method of Measuring and Specifying Colour Rendering of Light Sources |
|
CIE 1974 general colour rendering index [Ra] |
mean of the CIE 1974 special colour rendering indices for a specified set of 8 test colour samples See also CIE 13 Method of Measuring and Specifying Colour Rendering of Light Sources |
CIE 1974 általános színvisszaadási index |
Nyolc meghatározott CIE 1974 tesztelő színmintára számított CIE 1974 egyedi színvisszaadási index átlaga. |
|
CIE 1976 L*a*b* colour difference [
|
difference between 2 colour stimuli defined as the Euclidean distance between the points representing them in the L*a*b* space and calculated as:
Equivalent term: “CIELAB colour difference” See also CIE 15 Colorimetry See also ISO 11664-4:2008(E)/CIE S 014-4/E:2007 Colorimetry - Part 4: CIE 1976 L*a*b* Colour Space |
CIE 1976 L*a*b* színkülönbség |
Két színinger közötti különbség, amely az L*, a*, b* koordinátarendszerben értelmezett térbeli távolság és amelyet a következő egyenlet szerint lehet számítani:
MEGJEGYZÉS: A CIE 1976 a, b színezeti különbséget a következőképpen lehet számítani; CIE 1976 a,b színezeti különbség;
Lásd még: CIE 15 Colorimetry Lásd még: ISO 11664-4:2008(E)/CIE S 014-4/E:2007 Colorimetry - Part 4: CIE 1976 L*a*b* Colour Space |
|
CIE 1976 L*a*b* colour space |
3-dimensional, approximately uniform colour space produced by plotting in rectangular coordinates L*, a*, b* quantities defined by the equations: L* = 116 f (Y/Yn) - 16 a* = 500 [f (X/Xn) - f (Y/Yn)] b* = 200 [f (Y/Yn) - f (Z/Zn)] where f (X/Xn) = (X/Xn)1/3 if (X/Xn) > (6/29)3 f (X/Xn) = (841/108) (X/Xn) + 4/29 if (X/Xn) ≤ (6/29)3 and f (Y/Yn) = (Y/Yn)1/3 if (Y/Yn) > (6/29)3 f (Y/Yn) = (841/108) (Y/Yn) + 4/29 if (Y/Yn) ≤ (6/29)3 and f (Z/Zn) = (Z/Zn)1/3 if (Z/Zn) > (6/29)3 f (Z/Zn) = (841/108) (Z/Zn) + 4/29 if (Z/Zn) ≤ (6/29)3 and X, Y, Z describe the colour stimulus considered and Xn, Yn, Zn describe a specified white achromatic stimulus. Equivalent term: “CIELAB colour space” NOTE Approximate correlates of lightness, chroma and hue may be calculated as follows: CIE 1976 lightness L* = 116 f (Y/Yn) - 16 where f (Y/Yn) = (Y/Yn)1/3 if (Y/Yn) > (6/29)3 f (Y/Yn) = (841/108) (Y/Yn) + 4/29 if (Y/Yn) ≤ (6/29)3 CIE 1976 a, b chroma
CIE 1976 a, b hue angle hab = arctan (b*/a*) See also CIE 15 Colorimetry See also ISO 11664-4:2008(E)/CIE S 014-4/E:2007 Colorimetry - Part 4: CIE 1976 L*a*b* Colour Space |
CIE 1976 L*a*b* színtér |
Megközelítően egyenletes, háromdimenziós színtér, amelynek L*a*b* derékszögű koordinátáit a köv. egyenletek határozzák meg: L* = 116 f (Y/Yn) - 16 a* = 500 [f (X/Xn) - f (Y/Yn)] b* = 200 [f (Y/Yn) - f (Z/Zn)] ahol f (X/Xn) = (X/Xn)1/3 ha (X/Xn) > (6/29)3 f (X/Xn) = (841/108) (X/Xn) – 4/29 ha (X/Xn) ≤ (6/29)3 és f (Y/Yn) = (Y/Yn)1/3 ha (Y/Yn) > (6/29)3 f (Y/Yn) = (841/108) (Y/Yn) + 4/29 ha (Y/Yn) ≤ (6/29)3 és f (Z/Zn) = (Z/Zn)1/3 ha (Z/Zn) > (6/29)3 f (Z/Zn) = (841/108) (Z/Zn) + 4/29 ha (Z/Zn) ≤ (6/29)3 és X, Y, Z a választott színingert határozza meg és Xn, Yn, Zn a meghatározott fehér akromatikus színingert határozza meg MEGJEGYZÉS: A világossági tényezővel, krómával és színezettel megközelítően megfelelő mennyiségek: CIE 1976 világossági tényező: L* = 116 f (Y/Yn) - 16 ahol f (Y/Yn) = (Y/Yn)1/3 ha (Y/Yn) > (6/29)3 f (Y/Yn) = (841/108) (Y/Yn) +4/29 ha (Y/Yn) ≤ (6/29)3 CIE 1976 a, b króma
CIE 1976 a, b színezeti szög hab = arctan (b*/a*) Lásd még: CIE 15 Colorimetry Lásd még: ISO 11664-4:2008(E)/CIE S 014-4/E:2007 Colorimetry - Part 4: CIE 1976 L*a*b* Colour Space |
|
CIE 1976 L*u*v* colour difference [
|
difference between 2 colour stimuli, defined as the Euclidean distance between the points representing them in the L*u*v* space and calculated as equation:
Equivalent term: “CIELUV colour difference” See also CIE 15 Colorimetry See also ISO 11664-5:2009(E)/CIE S 014-5/E:2009 Colorimetry - Part 5: CIE 1976 L*u*v* Colour Space and u', v' Uniform Chromaticity Scale Diagram |
CIE 1976 L*u*v* színkülönbség |
Két színinger közötti különbség, amely az L*u*v* koordinátarendszerben értelmezett térbeli távolság és amelyet a (3) egyenlet szerint kell számítani:
Azonos meghatározás a CIE 1976 u,v színezeti különbség, amelyet a következőképpen lehet számítani: CIE 1976 u,v színezeti különbség:
Dhuv = huv,1 - huv,0. L. a CIE 15.2 sz. kiadványát.) |
|
CIE 1976 L*u*v* colour space |
3-dimensional, approximately uniform colour space produced by plotting in rectangular coordinates L*, u*, v* quantities defined by the equations: L* = 116 f (Y/Yn) - 16 u* = 13 L* ( v* = 13 L* ( where f (Y/Yn) = (Y/Yn)1/3 if (Y/Yn) > (6/29)3 f (Y/Yn) = (841/108) (Y/Yn) + 4/29 if (Y/Yn) ≤ (6/29)3 and Y, u′, v′ describe the colour stimulus considered and Yn, Equivalent term: “CIELUV colour space” NOTE Approximate correlates of lightness, saturation, chroma, and hue may be calculated as follows: CIE 1976 lightness L* = 116 f (Y/Yn) - 16 where f (Y/Yn) = (Y/Yn)1/3 if (Y/Yn) > (6/29)3 f (Y/Yn) = (841/108) (Y/Yn) + 4/29 if (Y/Yn) ≤ (6/29)3 CIE 1976 u, v saturation suv = 13 [( CIE 1976 u, v chroma CIE 1976 u, v hue angle huv = arctan [( See also CIE 15 Colorimetry See also ISO 11664-5:2009(E)/CIE S 014-5/E:2009 Colorimetry - Part 5: CIE 1976 L*u*v* Colour Space and u', v' Uniform Chromaticity Scale Diagram |
CIE 1976 L*u*v* színtér |
Megközelítően egyenletes, három dimenziós színinger tér, amelynek L*, u*, v* derékszögű koordinátáit a következő egyenletek határozzák meg: L* = 116 f (Y/Yn) - 16 u* = 13 L* ( v* = 13 L* ( ahol f (Y/Yn) = (Y/Yn) 1/3 ha (Y/Yn) > (6/29)3 f (Y/Yn) = (841/108) (Y/Yn) + 16/116 ha (Y/Yn) ≤ (6/29)3 és Y, u¢, v¢ a kiválasztott színinger és Yn, Egyenértékű definició: „CIELUV színtér” MEGJEGYZÉS: A világossági tényezőnek, a telítettségnek, krómának és színezetnek megközelítően megfelelő mennyiségek a következők: CIE 1976 világossági tényező: L* = 116 f (Y/Yn) - 16 , ahol f (Y/Yn) = (Y/Yn)1/3 ha (Y/Yn) > (6/29)3 f (Y/Yn) = (841/108) (Y/Yn) + 4/29 ha (Y/Yn) ≤ (6/29)3 CIE 1976 u,v telítettség: suv = 13 [( CIE 1976 u,v króma: CIE 1976 u,v színezeti szög: huv = arctan [( Lásd még a CIE 15.2 sz. kiadványát Lásd még ISO 11664-5:2009(E)/CIE S 014-5/E:2009 Colorimetry - Part 5: CIE 1976 L*u*v* Colour Space and u', v' Uniform Chromaticity Scale Diagram |
|
CIE colour-matching functions |
functions See also “CIE standard colorimetric observer”, “CIE 1931 standard colorimetric observer” and “CIE 1964 standard colorimetric observer” See also CIE 15 Colorimetry See also ISO 11664-1:2007(E)/CIE S 014-1/E:2006 Colorimetry - Part 1: CIE Standard Colorimetric Observers |
CIE 1976 színegyeztető függvény |
A CIE 193 1 színmérő rendszerében a Lásd még „CIE szabványos színmérő észlelő”, „CIE 1931 szabványos színmérő észlelő”, „CIE 1964 szabványos színmérő észlelő”. Lásd még a CIE 15. sz. kiadványát). Lásd még az ISO 11664-1:2007(E)/CIE S 014-1/E:2006 Colorimetry – 1 Rész:CIE Szabványos színmérő észlelő |
|
CIE 1976 UCS diagram |
See “CIE 1976 uniform chromaticity scale diagram” |
CIE 1976 UCS diagram |
Lásd „CIE 1976 szabványos színességi skálájú diagram” |
|
CIE standard deviate observer |
standard observer whose colour-matching functions deviate from those of the CIE standard colorimetric observer in a defined manner NOTE 1 The defined deviations can be applied to the CIE 1931 standard colorimetric observer or the CIE 1964 standard colorimetric observer. NOTE 2 The use of the standard deviate observer is intended to generate differences that are typical of those that occur when colour matches are made by different real observers whose colour vision is classified as normal. See also CIE 80-1989 |
CIE szabványostól eltérő észlelő |
Olyan színmérő észlelő, akinek a színmegfeleltető függvényei eltérnek a CIE szabványos színmérő észlelő színmegfeleltető függvényeitől. 1. MEGJEGYZÉS: Az adott eltérést a CIE 1931 szabványos színmérő észlelőhöz vagy a CIE 1964 szabványos színmérő észlelőhöz képest lehet értelmezni. 2. MEGJEGYZÉS: A CIE szabványostól eltérő észlelő fogalom alkalmazásához célszerű a szabványos színmérő észlelő és az adott különböző normál színmérő észlelők különbségét képezni. |
|
CIE standard colorimetric observer |
standard colorimetric observer defined by the CIE colour-matching functions See also “CIE colour-matching functions” |
CIE szabványos színmérő észlelő |
Az a CIE szabványos színmérő észlelő, akinek színlátása a CIE színmegfeleltető függvények alapján van meghatározva. Lásd még „CIE színmegfeleltető függvények”. |
|
CIELAB colour space |
See “CIE 1976 L*a*b* colour space” |
CIELAB színinger |
Lásd „CIE 1976 L*a*b* színtér” |
|
CIELAB colour difference [
|
See “CIE 1976 L*a*b* colour difference” |
CIELAB színinger különbség |
Lásd „CIE 1976 L*a*b* színkülönbség” |
|
CIELUV colour space |
See “CIE 1976 L*u*v* colour space” |
CIELUV színinger |
Lásd „CIE 1976 L*u*v* színtér” |
|
CIELUV colour difference [
|
See “CIE 1976 L*u*v* colour difference” |
CIELUV színinger különbség |
Lásd „CIE 1976 L*u*v* színkülönbség” |
|
cones |
photoreceptors in the retina containing light-sensitive pigments capable of initiating the process of photopic vision |
csapok |
Azok a retinában lévő, fényérzékeny pigmenteket tartalmazó fényérzékelő receptorok, amelyek lehetővé teszik a világosban (fotopos) látást. |
|
D illuminant |
See “daylight illuminant” |
D megvilágítás szabványos nappali fény |
Lásd „nappali fény” |
|
deutan |
See NOTE 2 to “defective colour vision” |
deután |
Lásd 2. MEGJEGYZÉS a „színtévesztés”-nél |
|
deuteranomaly |
See NOTE 3 to “defective colour vision” |
deuteranomál |
Lásd 3. MEGJEGYZÉS a „színtévesztés”-nél |
|
deuteranopia |
See NOTE 4 to “defective colour vision” |
deuteranópia |
Lásd 4. MEGJEGYZÉS a „színtévesztés”-nél |
|
dichromatism |
See NOTE 5 to “defective colour vision” |
dikromatizmus |
Lásd 5. MEGJEGYZÉS a „színtévesztés”-nél |
|
equivalent veiling luminance (for disability glare) |
luminance that, when added by superposition to the luminance of both the adapting background and the object, makes the luminance threshold or the luminance difference threshold the same under the two following conditions: (1) glare present, but no additional luminance; (2) additional luminance present, but no glare |
egyenértékű fátyol fénysűrűség |
Az a fénysűrűség, amelyet mind az adaptáció állapotát meghatározó háttér fénysűrűségéhez, mind a tárgy fénysűrűségéhez hozzá kell adni, hogy a rontó káprázás nélküli fénysűrűség-különbség küszöbértéke megegyezzék a rontó káprázás állapotát jellemző tényleges küszöbértékkel. |
|
equivalent contrast (of a task) |
luminance contrast of a visibility reference task having equal visibility at the same luminance level as that of the task considered See also “contrast” |
Egyenértékű kontraszt |
Egy olyan referencia látványnak a kontrasztja, amely ugyanolyan kontrasztúnak látszik, mint az adott látvány. Lásd még: „kontraszt” |
|
uniform point source |
See NOTE to “point source” |
egyenletes fénysűrűségű égbolt |
Lásd a MEGJEGYZÉS-t a „Pontszerű fényforrás”-nál |
|
UCS diagram |
See “uniform chromaticity scale diagram” |
UCS diagram |
Lásd „egyenletes színességi skálájú diagram” |
|
uniform chromaticity scale diagram |
2-dimensional diagram in which the coordinates are defined with the intention of making equal distances represent as nearly as possible equal steps of colour discrimination of colour stimuli of the same luminance throughout the diagram Equivalent term: “UCS diagram” |
egyenletes színinger tér |
olyan 2-dimenziós diagram, amelynek koordinátáit úgy definiálják, hogy azokon azonos megvilágítás mellett egyenlő távolságokhoz lehetőség szerint azonos színkülönbségi lépések tartozzanak az egész diagramban Egyenértékű definició: „UCS diagram” |
|
conventional retinal illuminance |
product of the luminance in a specified direction and the apparent area of the pupil (natural or artificial) seen from that direction Unit: cd, cd⋅m-2⋅mm2, troland |
Egyezményes retina megvilágítás |
Adott irányból és a természetes vagy mesterséges pupilla adott területén át érkező megvilágítás. Mértékegysége: cd, cd⋅m-2⋅mm2, troland |
|
primary light source |
surface or object emitting light by a transformation of energy |
elsődleges fényforrás |
Olyan felület vagy test, amely energia átalakulás eredményeként fényt bocsát ki. |
|
resultant colour shift |
combined illuminant colour shift and adaptive colour shift |
eredő színérzéklet eltolódás |
A sugárzáseloszlás és a kromatikus adaptáció okozta szín eltolódás kombinációja. |
|
resultant colorimetric shift |
combined illuminant colorimetric shift and adaptive colorimetric shift |
eredő színmérési eltolódás |
A sugárzás eloszlás okozta és az adaptációs színmérési eltolódás eredője (vektora). |
|
perceptual attribute correlate |
fundamental uni-variate colour description or metric |
érzékelés szerinti jellemző |
alapvetően egyváltozós színmeghatározás vagy mértékegység |
|
hemeralopia |
anomaly of vision in which there is a pronounced inadequacy or complete absence of scotopic vision Equivalent term: “night blindness” |
Farkasvakság, hemeralópia |
Látási rendellenesség; a szkotopos látás nagyon gyenge vagy teljesen hiányzik. |
|
veiling luminance (for disability glare) |
luminance that superimposes on the retinal image and reduces the contrast by stray light in the eye Unit: cd·m-2 |
fátyol fénysűrűség |
Megvilágítás, amely hozzáadódik a retinális képhez, és ez által csökkenti a szembe érkező fény kontrasztját. Mértékegysége: cd·m-2 |
|
veiling glare (imaging) |
light, reflected from an imaging medium, that has not been modulated by the means used to produce the image NOTE 1 Veiling glare lightens and reduces the contrast of the darker parts of an image. NOTE 2 The veiling glare is sometimes referred to as “ambient flare”. |
fátyolkáprázás (képalkotó rendszeré) |
reflektált fény, amely nem hordozza a képi információt 1. MEGJEGYZÉS: A fátyolkáprázás megvilágítja a kép sötét részeit és ezáltal csökkenti a kép kontrasztját. 2. MEGJEGYZÉS: A fátyolkáprázást szokták háttér fátyolnak is nevezni. |
|
veiling reflections |
specular reflections that appear on the object viewed and that partially or wholly obscure the details by reducing contrast |
fátyolreflexió |
Olyan tükrös reflexió, amely a szemlélt tárgyon jelenik meg és részben vagy teljesen elhomályosítja a részleteket, lecsökkentve a kontrasztot. |
|
white point, adopted (colour appearance model) |
computational reference white point (the white point used in the computation, e.g. the adopted white point or the display illuminant white point) used by a colour appearance model NOTE 1 A white point used by a colour appearance model is an adopted white point. NOTE 2 The adopted white point may or may not be the adapted white point, and one of the most common applications of an adopted white point is to achieve an optimally reproduced device white. For example, an adopted white point corresponding to a given medium may be used in place of an adapted white point in order that no colorants are used to create a white. NOTE 3 The concept of adopted white point applies to both colour appearance models and reproduction models. |
fehérpont, adaptációs (színmegjelenítési modellnél) |
számítástechnikai referencia-fehér pont (A számításokhoz alkalmazott fehér pont, például a képen kijelölt fehér pont, vagy a képernyő egy világos, fehér pontja) amelyet a színmegjelenítési modellhez használunk. 1. MEGJEGYZÉS: Felvett vagy névleges fehér pont egy fehér pont, amelyet a színmegjelenítési modellnél használunk. 2. MEGJEGYZÉS: A felvett vagy névleges fehér pont lehet az a fehér pont, amelyhez adaptálunk, és a felvett vagy névleges fehér pont leginkább szokásos alkalmazása az optimális reprodukciós fehér pont elérése. 3. MEGJEGYZÉS: A felvett vagy névleges fehér pontot egyaránt alkalmazzák a szín megjelenítési modellnél és a reprodukciós modellnél. |
|
conspicuity |
1. quality of an object or a light source to appear prominent in its surroundings 2. quality of a sign to attract (attention conspicuity) or gain (search conspicuity) the driver’s attention |
feltűnőség |
1. Olyan felület vagy fényforrás, amelynek megjelenése kiemelkedik a háttérből 2. Egy olyan jel minőségét jellemzi, amelynek fel kell kelteni a gépkocsi vezető figyelmét, vagy amely segíti, hogy megkeressen valamit. |
|
surface colour |
colour perceived as belonging to a surface from which the light appears to be diffusely reflected or radiated |
felület szín |
Színészlelet, amely egy olyan felülethez tartozik, amely a fényt diffúzan veri vissza, vagy diffúzan bocsátja ki. |
|
light |
1. characteristic of all sensations and perceptions that is specific to vision 2. radiation that is considered from the point of view of its ability to excite the human visual system NOTE 1 This term has 2 meanings that should be clearly distinguished. When necessary to avoid confusion between these 2 meanings the term “perceived light” may be used in the first sense. NOTE 2 Light is normally, but not always, perceived as a result of the action of a light stimulus on the visual system. |
Fény(észlelet) |
1. A látási rendszerrel kapcsolatos minden észlelésnek és érzékelésnek univerzális és alapvető jellemzője. 2. minden olyan elektromágneses sugárzás, amely az emberi látó rendszerrel érzékelhető 1. MEGJEGYZÉS: Ez a definició két gondolatot tartalmaz, amelyeket világosan meg kell különböztetni. Ha szükséges, az első értelemben az "érzékelt fény" kifejezést lehet használni. 2. MEGJEGYZÉS: A fény általában – bár nem mindig - a fényinger hatása a látási rendszerre. |
|
flicker index |
See NOTE 2 to “amplitude of fluctuation of the luminous flux” |
Fényáram ingadozási index |
Lásd 2. MEGJEGYZÉS „a fényáram ingadozásának amplitudója”-nál |
|
source |
object that produces light or other radiant flux |
fényforrás, sugárforrás |
felület, amely fényt vagy más sugárzást bocsát ki. |
|
luminance threshold |
lowest luminance of a stimulus which enables it to be perceived Unit: cd·m-2 NOTE The value depends on field size, surround, state of adaptation, methodology, and other viewing conditions. |
Fénysűrűség küszöb |
A legkisebb érzékelhető fénysűrűség. Mértékegysége: cd·m-2 MEGJEGYZÉS: Ez az érték függ a látómező méretétől, a környezettől, az adaptációs állapottól és a látás más körülményeitől, |
|
light pollution |
generic term indicating the sum total of all adverse effects of artificial light |
fényszennyezés |
általános kifejezés amely a mesterséges fény káros hatásainak összegét jelenti |
|
photopic vision |
vision by the normal eye in which cones are the principle active photoreceptors NOTE 1 Photopic vision normally occurs when the eye is adapted to levels of luminance of at least 5 cd·m-2. NOTE 2 Colour perception is typical of photopic vision. |
fotopikus látás (nappali látás) |
a normál szem látása, amely szemben alapvetően a csapok vannak aktív állapotban 1. MEGJEGYZÉS: A nappali látás akkor áll fenn, ha a szem a legalább 5 cd·m-2 megvilágításhoz alkalmazkodik 2. MEGJEGYZÉS: A színes látás a nappali látásra jellemző |
|
man-made sky glow |
that part of the sky glow which is attributable to man-made sources of radiation (e.g. artificial outdoor lighting) NOTE Man-made sky glow includes radiation that is emitted directly upwards and radiation that is reflected from the surface of the Earth. |
Fényszennyezés |
Az égbolt sugárzásának azon része, amelyet az ember által létrehozott fényforrások okoznak (például mesterségs kültéri világítás). MEGJEGYZÉS: Fényszennyezésnek nevezzük azt a sugárzást, amely egyenesen felfelé irányul, és azt is, amelyet a Föld felszíne ver vissza. |
|
foveola |
central region of the fovea which contains no blood vessels NOTE 1 The foveola subtends an angle of about 0,017 rad (1º) in the visual field. NOTE 2 The central area of the foveola, subtending an angle of about 0,003 rad (0,2º), contains no blue cones. |
foveola |
A látógödör középső, legmélyebb része, amelyben csak csapok vannak. 1. MEGJEGYZÉS: A foveola a látótérnek kb. 0,017 rad (1°) látószögnyi része. 2. MEGJEGYZÉS: A foveola középső részén mintegy 0,003 rad (0,2º) területen nem találhatók kékérzékeny receptorok. |
|
vertical illuminance [Ev,v; Ev] |
illuminance on a vertical plane Unit: lx = lm·m-2 |
függőleges megvilágítás [Ev,v; Ev] |
Megvilágítás a függőleges síkban Mértékegysége: lx = lm·m-2 |
|
fusion frequency |
See “critical flicker frequency” |
Fúziós frekvencia |
A fényinger változásának az a frekvenciája, amely fölött villogás nem érzékelhető. |
|
Grassmann’s laws |
3 empirical laws that describe colour-matching properties of additive colour mixtures of colour stimuli: to specify a colour match, 3 independent variables are necessary and sufficient, for an additive mixture of colour stimuli, only their tristimulus values are relevant, not their spectral compositions, in an additive mixture of colour stimuli, if one or more components of the mixture are gradually changed, the resulting tristimulus values also change gradually NOTE Grassman’s laws do not hold for all observing conditions. |
Grassmann törvények |
Az additív színinger keverés színinger-megfeleltető tulajdonságait leíró három tapasztalati törvény. Ezek a következők:
MEGJEGYZÉS: A Grassmann törvények nem érvényesek tetszőleges megfigyelési feltételek mellett. |
|
threshold increment (disability glare) |
measure of disability glare expressed as the percentage increase in contrast required between an object and its background for it to be seen equally well with a source of glare present Unit: 1 NOTE Increasing values of threshold increment correspond to increasing disability glare. |
határnövekmény (rontó káprázás) |
A rontó káprázás mértéke, egy tárgy (amely a káprázás forrása) és a háttér közötti kontraszt növekedésének százalékában kifejezve, Mértékegysége: 1 MEGJEGYZÉS: A határnövekmény növekedésének nagysága megfelel a rontó káprázás növekedésének |
|
Helmholtz-Kohlrausch phenomenon |
change in brightness of perceived colour produced by increasing the purity of a colour stimulus while keeping its luminance constant within the range of photopic vision NOTE For related perceived colours, a change in lightness can also occur when the purity is increased while keeping the luminance factor of the colour stimulus constant. |
Helmholtz-Kohlrausch jelenség |
A színészlelet világosságának megváltozása, állandó fénysűrűség mellett, a fotopos látás tartományában, ha a színinger tisztasága növekszik. MEGJEGYZÉS: A nem izolált színészlelet relatív világossága megváltozhat, ha a színinger tisztaság megnövekedik, míg a színérzékleti inger fénysűrűségi tényezője állandó. |
|
defective colour vision |
anomaly of vision in which there is a reduced ability to discriminate between some or all colours NOTE 1 Anomalous trichromatism: Form of trichromatism in which colour discrimination is less than normal. NOTE 2 Deutan: Adjective denoting deuteranopia or deuteranomaly. NOTE 3 Deuteranomaly: Defective colour vision in which discrimination of the reddish and greenish contents of colours is reduced, without any colours appearing abnormally dim. NOTE 4 Deuteranopia: Defective colour vision in which discrimination of the reddish and greenish contents of colours is absent, without any colours appearing abnormally dim. NOTE 5 Dichromatism: Defective colour vision in which all colours can be matched using additive mixtures of only 2 matching stimuli. NOTE 6 Monochromatism: Defective colour vision in which all colours can be matched using only a single matching stimulus. NOTE 7 Protan: Adjective denoting protanopia or protanomaly. NOTE 8 Protanomaly: Defective colour vision in which discrimination of the reddish and greenish contents of colours is reduced, with reddish colours appearing abnormally dim. NOTE 9 Protanopia: Defective colour vision in which discrimination of the reddish and greenish contents of colours is absent, with reddish colours appearing abnormally dim. NOTE 10 Tritan: Adjective denoting tritanopia or tritanomaly. NOTE 11 Tritanomaly: Defective colour vision in which discrimination of the bluish and yellowish contents of colours is reduced. NOTE 12 Tritanopia: Defective colour vision in which discrimination of the bluish and yellowish contents of colours is absent. |
Színtévesztés, színvakság, (hibás színlátás) |
Látási rendellenesség, amikor bizonyos színekre vagy valamennyi színre csökken az egyén megkülönböztető képessége. 1. MEGJEGZÉS: Anomális trikromatizmus, (anomális trichromázia), színtévesztés: A trikromatizmus egyik változata, amelynél a szín megkülönböztető képesség a normál színlátóénál kisebb. 2. MEGJEGZÉS: Deuteranomália: színtévesztés amelyben a színek vöröses és a zöldes tartalma közötti különbség csökkent, anélkül, hogy a többi szín fakóbbnak látszana, és ezt a zöld színre érzékeny receptor (deuteros) hibája okozza. 3. MEGJEGZÉS: Deuteranópia, színvakság: Színlátási hiba, amelyben a színek vöröses és zöldes tartalma hiányzik, helyettük sárga szín látható, anélkül, hogy bármelyik szín abnormálisan fakónak tűnne, és ezt a zöld színre érzékeny receptor (deuteros) hibája okozza. 4. MEGJEGZÉS: Protanomália: Színtévesztés amelyben a színek vöröses és a zöldes tartalma közötti különbség csökkent, anélkül, hogy a többi szín fakóbbnak látszana, és ezt a vörösre érzékeny receptor (protos) hibája okozza. 5. MEGJEGZÉS: Protanópia: Színlátási hiba, amelyben a színek vöröses és zöldes tartalma hiányzik, helyettük sárga szín látható, anélkül, hogy bármelyik szín abnormálisan fakónak tűnne, és ezt a vörösre érzékeny receptor (protos) hibája okozza. 6. MEGJEGZÉS: Tritanomália: Színtévesztés amelyben a színek kékes és a zöldes tartalma közötti különbség csökkent, anélkül, hogy a többi szín fakóbbnak látszana, és ezt a kékre érzékeny receptor (tritos) hibája okozza. 7. MEGJEGZÉS: Tritanópia: Színlátási hiba, amelyben a színek kékes és zöldes tartalma hiányzik, helyettük türkiz szín látható, anélkül, hogy bármelyik szín abnormálisan fakónak tűnne, és ezt a kékre érzékeny receptor (tritos) hibája okozza. 8. MEGJEGZÉS: A tritanomália és a tritanópia rendkívül ritka. 9. MEGJEGZÉS: Deutan: közös kifejezés a deuteranópia és a deuteranomália megnevezésére. 10. MEGJEGYZÉS: Protan: közös kifejezés a protanópia és a protanomália megnevezésére. 11. MEGJEGZÉS: Tritan: közös kifejezés a tritanópia és a tritanomália megnevezésére. 12. MEGJEGZÉS: Dikromatizmus, dikromázia: Színlátási hiba, amelyben bármely szín egyeztethető mindössze két alapszín additív keverékével (l. Színvakság, 3., 5., 7. MEGJEGYZÉS). 13. MEGJEGZÉS: Monokromatizmus: Színlátási hiba, amelyben bármely szín egyeztethető egyetlen alapszínnel. |
|
monochromatism |
See NOTE 6 to “defective colour vision” |
Színvakság (hibás színlátás) |
l. Színvakság Lásd13. MEGJEGYZÉS a „Színtévesztés, színvakság” címszónál |
|
invariant wavelengths |
See NOTE 1 to “Bezold-Brücke phenomenon” |
Invariáns hullámhossz |
Lásd 1. MEGJEGYZÉS. a „Bezold-Brücke jelenség” címszónál |
|
directional effect |
See “Stiles-Crawford effect (of the first kind)” |
Irányított emissziós tényező |
Lásd “Stiles-Crawford effektus” első esete” |
|
unrelated colour |
colour perceived to belong to an area seen in isolation from other colours |
izolált színészlelet |
Más színektől elkülönített felület által kiváltott színészlelet, |
|
field of vision |
extent of space in which objects are visible to an eye in a given position Equivalent term: “visual field” NOTE 1 In the horizontal plane meridian the field of vision extends to nearly 190° with both eyes open, the area seen binocularly is about 120°, and the area seen by one eye only is about 154°. NOTE 2 The extent of the field of vision tends to diminish with age. |
Látótér |
Az a térrész, amely egy szem számára egy adott pozícióban látható 1. MEGJEGYZÉS: A horizontális síkban a látótér két nyitott szemmel eléri a közel 190 fokot, binokulárisan pedig közel 120 fok, míg egy szem látótere csak körülbelül 154 fok. 2. MEGJEGYZÉS: A látótér nagysága a korral kismértékben csökken |
|
glare |
condition of vision in which there is discomfort or a reduction in the ability to see details or objects, caused by an unsuitable distribution or range of luminance, or by extreme contrasts See also “disability glare”, “discomfort glare” |
káprázás |
A látás kényelmetlensége és/vagy a tárgyak felismerhetőségének a csökkenése, a fénysűrűség szokatlan eloszlásának vagy szokatlan értékének, illetve a térben vagy időben fellépő igen erős kontrasztnak a következtében. |
|
glare rating limit [RG,L] |
maximum allowed value given by the CIE Glare Rating system Unit: 1 See also CIE 112-1994 Glare Evaluation System for Use within Outdoor Sports- and Area Lighting Abbreviation: “GRL” |
Káprázás korlátozási határ |
A CIE által meghatározott megengedett káprázási határérték Mértékegysége: 1 Lásd még: CIE 112-1994 „Káprázás kiértékelési rendszer” kültéri és sport megvilágítás esetére Rövidítés: [RG, L] |
|
dim (adjective) |
adjective used to describe low levels of brightness |
kisfényű |
a világosság alacsony szintjére használatos megnevezés |
|
binary hue |
hue that can be described as a combination of 2 unitary hues NOTE For example: orange is a yellowish-red or reddish-yellow; violet is reddish-blue, etc. |
kombinált színezet, kombinált szín |
Színezet észlelete, amelyet két-két alapszínezet nevének felhasználásával lehet leírni. Például: a narancs sárgás-piros vagy pirosas-sárga; az ibolya pirosas-kék stb. |
|
complementary wavelength (of a colour stimulus) [λc] |
wavelength of the monochromatic stimulus that, when additively mixed in suitable proportions with the colour stimulus considered, matches the specified achromatic stimulus |
Komplementer hullámhossz (szín ingeré) |
Annak a monokromatikus színingernek a hullámhossza, amely megfelelő arányban additívan keverve a kiválasztott színingerrel a meghatározott akromatikus színingernek felel meg. |
|
complementary colour stimuli |
set of 2 colour stimuli for which it is possible to reproduce the tristimulus values of a specified achromatic stimulus by a suitable additive mixture of these 2 stimuli |
Komplementer színinger |
Két olyan színinger, amelynek additív keverésével elő lehet állítani egy meghatározott, akromatikus színinger összetevőit. |
|
contrast |
1. in the perceptual sense: assessment of the difference in appearance of 2 or more parts of a field seen simultaneously or successively (hence: brightness contrast, lightness contrast, colour contrast, simultaneous contrast, successive contrast, etc.) 2. in the physical sense: quantity intended to correlate with the perceived brightness contrast, usually defined by one of a number of formulae which involve the luminances of the stimuli considered: for example by the proportional variation in contrast near the luminance threshold, or by the ratio of luminances for much higher luminances |
kontraszt |
1. Szubjektív: a látómezőkét vagy több, egyidejűleg vagy egymás után látott része közötti megjelenésbéli különbség értékelése (így van: világosságkontraszt, relatív világosságkontraszt, színkontraszt, szimultán kontraszt, szukcesszív kontraszt stb.). 2. Objektív: a világosságkontraszt objektív megfelelője a fénysűrűségkontraszt, amely például a fénysűrűség-küszöb közelében a DL/ L, sokkal nagyobb fénysűrűségek esetében az L1/L2 képlettel határozható meg. |
|
contrast sensitivity [Sc] |
reciprocal of the least perceptible (physical) contrast, usually expressed as L/DL, where L is the average luminance and DL is the luminance difference threshold Unit: 1 NOTE The value of Sc depends on a number of factors including the luminance, the viewing conditions and the state of adaptation. |
Kontraszt érzékenység [Sc] |
A még észlelhető (objektív) kontraszt reciproka, általában L/DL alakban kifejezve, ahol L az átlagos fénysűrűség és DL a fénysűrűség-különbség küszöbértéke. Mértékegysége: 1 MEGJEGYZÉS: Sc értéke függ a fénysűrűségtől és a látási körülményektől, beleértve az adaptációs állapotot is. |
|
visual contrast threshold |
smallest contrast, produced at the eye of an observer by a given object, which renders the object perceptible against a given background NOTE For meteorological observations, the object must be rendered recognizable, and hence a higher threshold is to be expected. The value of 0,05 has been adopted as the basis for the measurement of meteorological optical range. |
kontraszt küszöbértéke |
az a legkisebb kontraszt, amelyet egy megfigyelő észlel egy adott tárgyon, adott háttér mellett |
|
proximal field |
immediate environment of the colour stimulus considered, extending typically for about 2º from the edge of the colour stimulus considered in all, or most, directions |
közvetlen környezet |
egy szín inger közvetlen környezete, amely általában a szín inger szélétől 2 fokon belül tetszőleges irányban értendő |
|
critical flicker frequency |
for a given set of conditions, the frequency of alternation of stimuli above which flicker is not perceptible Equivalent term: “fusion frequency” |
Kritikus flikker frekvencia |
egy inger változásának frekvenciája adott körülmények között, amikor a villózás (flicker) már éppen nem észlelhető Azonos értelmű meghatározás: „fúziós frekvencia” |
|
chroma |
colourfulness of an area judged as a proportion of the brightness of a similarly illuminated area that appears white or highly transmitting NOTE For given viewing conditions and at luminance levels within the range of photopic vision, a colour stimulus perceived as a related colour, of a given chromaticity and from a surface having a given luminance factor, exhibits approximately constant chroma for all levels of illuminance except when the brightness is very high. In the same circumstances, at a given level of illuminance, if the luminance factor is increased, the chroma usually increases. |
kroma |
Egy felület színezetdússága egy hasonlóan megvilágított fehérnek vagy nagyon fényáteresztőnek látszó felületnek a világosságához képest. MEGJEGYZÉS: Adott látási körülmények és a fotopos látáshoz tartozó fénysűrűségek mellett egy viszonyított színészleletnek érzékelt, adott színességű és adott fénysűrűségi tényezőjű felülethez tartozó színészlelet krómája minden megvilágítás mellett megközelítően állandó, kivéve ha a világosság igen nagy. Ugyanezen feltételek mellett, adott megvilágítási szinten, ha a fénysűrűségi tényező nő, akkor általában a króma is nő. |
|
chromatic adaptation |
visual process whereby approximate compensation is made for changes in the colours of stimuli, especially in the case of changes in illuminants |
kromatikus adaptáció |
Adaptáció olyan fényingerek következtében, amelyekben azok relativ spektrális eloszlásai okozzák a jellemző hatást, különösen megvilágítás esetén. |
|
chromatic colour |
in the perceptual sense: perceived colour possessing hue NOTE 1.In everyday speech, the word colour is often used in this sense in contradistinction to white, grey or black. The adjective coloured usually refers to chromatic colour. NOTE 2. in the psychophysical sense: see “chromatic stimulus” |
kromatikus színészlelet |
Észlelet értelemben: színészlelet, amelynek van színezete. 1. MEGJEGYZÉS: A mindennapi szóhasználatban a szín szót gyakran ebben az értelemben használják, szembeállítva a fehérrel, szürkével és feketével. A színes jelző általában kromatikus színészleletre utal. 2. MEGJEGYZÉS: Pszihofizikai értelemben: lásd „szín inger” |
|
visual acuity |
1. qualitatively: capacity for seeing distinctly fine details that have very small angular separation 2. quantitatively: any of a number of measures of spatial discrimination such as the reciprocal of the value of the angular separation in minutes of arc of 2 neighbouring objects (points or lines or other specified stimuli) which the observer can just perceive to be separate Equivalent term: “visual resolution” |
látásélesség |
1. Minőségileg: a szemnek az a tulajdonsága, hogy képes egymástól igen kis látószögre lévő finom részletek megkülönböztetésére. 2. Mennyiségileg: annak a legkisebb, ívpercben mért látószögnek a reciprok éneke, amely alatt látott két szomszédos tárgyat (pontot vagy vonalat) a szem még elkülönítve képes észlelni. Azonos értelmű definíció: „a látás feloldása” |
|
visual sensation |
response of the visual system to stimulation |
látási érzéklet |
a látórendszer válasza a látási ingerre |
|
visual task |
visual elements of the work being done NOTE The main visual elements are the size of the structure, its luminance, its contrast against the background and its duration. |
látási feladat |
Az elvégzendő feladat látással kapcsolatos elemei MEGJEGYZÉS: A legfontosabb látási elemek egy struktúra mérete, annak világossága vagy kontrasztja a háttérhez képest, és annak időtartama |
|
visual resolution |
See “visual acuity” |
látóélesség |
Lásd: „látás élesség” |
|
fovea |
central part of the retina, thin and depressed, which contains almost exclusively cones and forming the site of most distinct vision Equivalent term: “fovea centralis” NOTE The fovea subtends an angle of about 0,087 rad (5º) in the visual field. |
Látógödör, fovea |
A retina középső, vékony és benyomódott része, amely majdnem kizárólag csapokat tartalmaz és a legélesebb látás helye. MEGJEGYZÉS: A látógödőr a látótérnek kb. 0,087 rad (5°) látószögnyi része. |
|
visual angle |
angle subtended by an object or detail at the point of observation NOTE The SI unit for the angle is rad although it may also be measured in milliradians, degrees, or minutes of arc. See also “angular subtense” |
látószög |
egy tárgy láthatóságának kiterjedése a megfigyelési pont körül MEGJEGYZÉS: A szög SI mértékegység radián, és milliradban vagy szögpercben mérhető |
|
visibility (of a sign) |
range of visual perception, normally measured in terms of the threshold distance at which a sign becomes visible |
látótávolság (meteorológiai) |
a látási észlelés mértéke, amely azon távolságban mérhető, amelyben egy tárgy láthatóvá válik |
|
viewing flare |
veiling glare that is observed in a viewing environment but not accounted for in measurements made using a prescribed measurement geometry NOTE The viewing flare is expressed as a percentage of the luminance of adapted white. |
látszólagos fátyolfény |
fátyol tükröződés amely egy megjelenítési környezetben figyelhető meg, de nem mutatható ki méréssel az előírt mérési geometria alkalmazásával MEGJEGYZÉS A látszólagos fátyolfény az adaptációs fehér százalékában van kifejezve |
|
macula lutea |
layer of photostable pigment covering parts of the retina in the foveal region Equivalent term: “yellow spot” |
macula lutea |
a retina fényérzékeny pigmentekkel borított rétege a foveális régióban |
|
secondary light source |
surface or object which is not self-emitting but receives light and re-directs it, at least in part, by reflection or transmission |
másodlagos fényforrás |
Olyan felület vagy test, amely maga nem bocsát ki fényt, csupán a ráeső fényt vagy annak egy részét áteresztéssel vagy visszaveréssel sugározza tovább. |
|
corresponding colour stimuli |
pairs of colour stimuli that have same colour appearance when one is seen in one set of adaptation conditions and the other is seen in a different set |
Megfeleltetett színingerek |
olyan szín-inger pár, amely azonos színezetűnek látszik, miközben az egyik egy adott adaptációs környezetben, a másik egy attól eltérő adaptációs környezetben látható |
|
appearance |
1. aspect of visual perception by which things are recognized 2. in psychophysical studies, visual perception in which the spectral and geometric aspects of a visual stimulus are integrated with its illuminating and viewing environment |
megjelenés |
1. a vizuális észlelésnek egy formája, amely mellett megfigyeljük a tárgyakat 2. pszichofizikai szempontból olyan vizuális észlelés, amelyben a vizuális inger tulajdonságai spektrális és geometriai jellemzői együtt hatnak a megvilágító és látszó környezettel |
|
appearance model, single-stimulus |
mathematical model which uses information about viewing conditions to estimate the subjective appearance of a coloured patch from colorimetric measurements of that patch and its surround NOTE The information about viewing conditions includes the adopted white point. |
megjelenési modell (egyetlen inger esetén) |
matematikai modell, amely a látvány körülményeinek információját dolgozza fel annak érdekében, hogy színmérés segítségével becslést adjon egy színes foltnak és környezetének a szubjektív színmegjelenéséről MEGJEGYZÉS a látvány körülményeinek információja tartalmazza az elfogadott fehér pontot. |
|
uniformity ratio of illuminance (on a given plane) |
See “illuminance uniformity” |
megvilágítás egyenletessége (egy adott síkban) |
Lásd „Megvilágítás egyenletessége” |
|
threshold of illuminance |
smallest illuminance (point brilliance), produced at the eye of an observer by a light source seen in point vision, which renders the source perceptible against a background of given luminance, where the illuminance is considered on a surface element that is normal to the incident rays at the eye Equivalent term: “visual threshold” NOTE For visual signalling, the light source must be rendered recognizable, and hence a higher threshold of illuminance is to be expected. |
megvilágítás küszöbértéke |
az a legkisebb megvilágítás (pontfény), amelyet egy megfigyelő szeme észlel egy olyan fényforrás esetén amely a látótér egy pontjában egy olyan felületeleme, amely merőlegesnek tekinthető a szembe érkező fénysugárra egy adott megvilágítású hatter előtt Egyenértékű meghatározás: “láthatósági küszöb” MEGJEGYZÉS: A fényjelzőberendezéseknél a fényforrásnak kell felismerhetőnek lenni, és így egy magasabb megvilágítási küszöböt kell elfogadni |
|
visual threshold (in point vision) |
See “threshold of illuminance” |
megvilágítási küszöb |
Lásd „megvilágítás küszöbértéke” |
|
illuminant mode (of colour appearance) |
colour seen as ascribed to a source of illumination |
megvilágítás mód (a megvilágítás színe) |
a fényforrás színének tulajdonított szín |
|
illuminant |
radiation with a relative spectral power distribution defined over the wavelength range that influences object colour perception NOTE In everyday English this term is not restricted to this sense, but is also used for any kind of light falling on a body or scene. |
Megvilágító (sugárzáseloszlás) |
sugárzás, amelynek relatív spektrális teljesítmény eloszlása befolyásolja a tárgyak szín észleletét MEGJEGYZÉS: A köznapi szóhasználatban ez a fogalom nem korlátozódik erre az egyetlen esetre, hanem minden olyan esetre alkalmazzák, amikor fény esik egy testre vagy egy látványra |
|
metameric colour stimuli |
spectrally different colour stimuli that have the same tristimulus values in a specified colorimetric system Equivalent term: “metamers” NOTE 1 The corresponding property is called “metamerism”. NOTE 2 In German, colours (“Farbvalenzen”) consisting of spectrally identical colour stimuli are described as “unbedingt-gleich”. |
metamer színinger, metamer |
Olyan spektrálisan különböző színingerek, amelyeknek ugyanazok a színinger-összetevői. 1. MEGJEGYZÉS: Ezt a tulajdonságot metameriának nevezik. 2. MEGJEGYZÉS: A németben azokat a színingereket („Farbvalenzen”), amelyek spektrálisan megegyező szín ingerekből állnak, Unbedingt-gleichnek nevezik. |
|
metamers |
See “metameric colour stimuli” |
metamerek |
Lásd „metamer színinger” |
|
metamerism |
See NOTE 1 to “metameric colour stimuli” |
metamerizmus |
Lásd 1. MEGJEGYZÉS a „metamer színinger” -nél |
|
metamerism index |
degree of colour mismatch, calculated in the form of a colour difference, caused by substituting a test illuminant (observer) of different relative spectral composition (responsivity) for the reference illuminant (observer) NOTE The colour difference is evaluated using a CIE colour difference formula and it must be clearly stated which formula has been used. |
metameria index |
A szín eltérés mértéke, amelyet azon színkülönbségként számolunk ki, amely egy referencia megvilágítás (vagy referencia megfigyelő) és az adott megvilágítás (adott megfigyelő) különbségéből ered MEGJEGYZÉS: A színkülönbséget a CIE színkülönbségi formulából kell meghatározni, és világosan meg kell adni, hogy melyik formulát használtuk. |
|
mesopic vision |
vision by the normal eye intermediate between photopic and scotopic vision NOTE In mesopic vision, both the cones and the rods are active. See also CIE 191:2010 Recommended System for Mesopic Photometry based on Visual Performance |
mezopos látás |
A fotopos és a szkotopos látás tartományai közötti látás. MEGJEGYZÉS: A mezopos látásban a csapok és a pálcikák egyaránt működnek. |
|
daylight locus |
locus of points in a chromaticity diagram that represents the chromaticities of phases of daylight given by the CIE formulae for daylight illuminants (D illuminants) with different correlated colour temperatures |
A nappali fény színességi pontjának helye a színességi diagramban |
A különböző korrelált színhőmérsékletű természetes fény fázisai színességének a helye egy színinger diagramban. A CIE által meghatározott D65 természetes fény színességének helye különböző korrelált színhőmérsékletek mellett a színességi diagramban. |
|
daylight illuminant |
illuminant having the same or nearly the same relative spectral power distribution as a phase of daylight |
nappali megvilágítás |
Olyan sugárzáseloszlás, amelynek spektrális teljesítmény eloszlása megegyezik, vagy majdnem megegyezik a természetes nappali fény sugárzáseloszlásával |
|
related colour |
colour perceived to belong to an area seen in relation to other colours |
nem izolált színészlelet |
Más színekhez viszonyított felület által kiváltott színészlelet. |
|
non-selective radiator |
thermal radiator whose spectral emissivity is constant with respect to wavelength over the spectral range considered |
nem szelektív sugárzás |
Olyan hőmérsékleti sugárzó, amelynek spektrális emissziós tényezője konstans egy adott hullámhossz tartományban |
|
readability |
measure to characterize the ease of reading |
olvashatóság |
Olyan mérőszám, amely a könnyű olvashatóságot jellemzi |
|
optimal colour stimuli |
object colour stimuli corresponding to objects whose luminance factors have maximum possible values for each chromaticity when their spectral luminance factors do not exceed 1 for any wavelength NOTE 1 These stimuli correspond, in general, to objects whose spectral luminance factors have values of either unity or 0, with not more than 2 transitions between them. NOTE 2 The luminance factors and chromaticity coordinates of these stimuli define the boundaries of a colour solid corresponding to non-fluorescent objects. NOTE 3 For a given luminance factor, these colour stimuli define the maximum purity possible for non-fluorescent objects. |
optimális színingerek |
Olyan tárgy-színingerek, amelyeket létrehozó spektrális fénysűrűségi tényezők minden színességhez a legnagyobbak, de értékük egyetlen hullámhosszon sem nagyobb, mint 1. MEGJEGYZÉS: Ezek az optimális színingerek olyan tárgyakhoz tartoznak, amelyek spektrális fénysűrűségi tényezője vagy 0, vagy 2-nél nem nagyobb. 2. MEGJEGYZÉS: Ezeknek az optimális szín ingereknek a fénysűrűségi tényezői és szín inger-koordinátái határozzák meg a nem fluoreszkáló tárgyakhoz tartozó színtest határait. 3. MEGJEGYZÉS: Egy meghatározott fénysűrűségi tényezőhöz ezek az optimális színingerek értelmezik a nem fluoreszkáló tárgyak legnagyobb színinger- tisztaságát. |
|
rods |
photoreceptors in the retina containing a light-sensitive pigment capable of initiating the process of scotopic vision |
pálcikák |
Azok a retinában lévő, fényérzékeny pigmenteket tartalmazó fényérzékelők, amelyek lehetővé teszik a sötétben (szkotopos) látást |
|
Planckian locus |
locus of points in a chromaticity diagram that represents chromaticities of the radiation of Planckian radiators at different temperatures |
Planck sugárzók görbéje |
A különböző hőmérsékletű Planck sugárzó színességének pontjai a színességi diagramban |
|
point vision |
mode of vision, of an apparently small source of light, in which the luminous sensation is determined only by the illuminance that is produced by the source at the eye of the observer |
pontlátás |
Olyan látás, melyet egy kicsiny fényforrás vált ki, amelynek fényességét csupán az észlelőben kiváltott fény észlelet alapján határozzuk meg. |
|
uniform colour space |
colour space in which equal distances are intended to represent threshold or suprathreshold perceived colour differences of equal size |
egyenletes színtér |
Olyan színtér, amelyben azonos színkülönbségekhez azonos távolságok tartoznak |
|
protan |
See NOTE 7 to “defective colour vision” |
protan |
Lásd 10. MEGJEGYZÉS a „Színtévesztés, Színvakság, (hibás színlátás)” témánál |
|
protanomaly |
See NOTE 8 to “defective colour vision” |
protanomália |
Lásd 4. MEGJEGYZÉS a „Színtévesztés, színvakság, (hibás színlátás)” témánál |
|
protanopia |
See NOTE 9 to “defective colour vision” |
protanopia |
Lásd 5. MEGJEGYZÉS a „Színtévesztés, színvakság, (hibás színlátás)” témánál |
|
Purkinje phenomenon |
reduction in the brightness of a predominantly long-wavelength colour stimulus relative to that of a predominantly short-wavelength colour stimulus when the luminances are reduced in the same proportion from photopic to mesopic or scotopic levels without changing the respective relative spectral distributions of the stimuli involved NOTE In passing from photopic to mesopic or scotopic vision, the spectral luminous efficiencies change, the wavelength of maximum efficiency being displaced towards the shorter wavelengths. |
Purkinje jelenség |
A világosság észlelet csökkenése a főleg hosszú hullámú tartományba eső színingereknél a főleg rövid hullámú tartományba eső színingerekhez viszonyítva akkor, amikor a megvilágítás csökken, és a fotopikus tartományból a mezopikus tartományba ér, miközben a színinger relatív spektrális eloszlása nem változik. MEGJEGYZÉS: A fotopikus látásról mezopikusra vagy a scotopikusra történő áttérés során a spektrális fényhatásfok függvény megváltozik, maximumának hullámhossza rövidebb hullámhosszra kerül át. |
|
basic law of radiometry and photometry |
See NOTE 7 to “radiance” |
radiometria és fotometria alaptörvénye |
Lásd a 7. MEGJEGYZÉS-t a „sugárzás”címszónál |
|
relative colour stimulus function [ɸ(λ)] |
relative spectral power distribution of the colour stimulus function |
relatív színészlelési függvény |
A színinger függvény relatív spektrális teljesítmény eloszlása. |
|
adaptation, incomplete |
phenomenon in which the adopted (computational) white in a given viewing environment does not actually appear white to an observer NOTE Familiar instances include colour images on newsprint or displays that appear “too yellow or too blue”. |
részleges adaptáció |
Jelenség, amelynél az adaptációs (számított) fehér egy adott megfigyelési környezetben nem tűnik teljesen fehérnek egy megfigyelő számára MEGJEGYZÉS: hasonló az az eset, amikor a nyomdatechnikában, vagy az újságok színes képein a fehér szín „túl sárgásnak vagy túl kékesnek” tűnik. |
|
retina |
membrane situated inside the back of the eye that is sensitive to light stimuli NOTE The retina contains photoreceptors and nerve cells that interconnect and transmit to the optic nerve the signals resulting from stimulation of the photoreceptors. The photoreceptors in the human retina are of 3 types: rods and cones, which are responsible for vision, and intrinsically photosensitive retinal ganglion cells (ipRGCs), which play a role in controlling circadian and neuro-endocrine systems. |
retina |
A szemgolyó belsejének hátsó felületén lévő, fényingerekre érzékeny hártya MEGJEGYZÉS: a retina fényérzékelőket (csapokat és idegvégződéseket) tartalmaz, amelyek a fényérzékelőkben az őket ingerlő fény hatására keletkezett jeleket a látóidegbe vezetik. A humán retina fotoreceptorai 3 félék: pálcikák és csapok, amelyek a látást biztosítják, továbbá olyan fényérzékeny retinális ganglion sejtek (ipRGCs), amelyek szerepet játszanak a circadian és a neuro endokrin rendszer működtetésében. |
|
sRGB colour space |
colour space defined by IEC See also IEC 61966-2-1 |
RGB színtér |
Az IEC által definiált színtér. Lásd még IEC 61966-2-1 |
|
disability glare |
glare that impairs the vision of objects without necessarily causing discomfort |
Rontó káprázás |
Olyan káprázás, amely rontja a tárgyak látását anélkül, hogy szükségképpen kényelmetlenséget okozna. |
|
yellow spot |
See “macula lutea” |
sárgafolt, macula lutea |
A látógödör fényérzékeny, sárgán pigmentált rétege. |
|
dark |
adjective used to describe low levels of lightness |
sötét |
Melléknév, a világosság alacsony szintjének a megjelölésére. |
|
spectral |
adjective that, when applied to a quantity X pertaining to electromagnetic radiation, indicates: either that X is a function of the wavelength λ, symbol: X(λ), or that the quantity referred to is the spectral concentration of X, symbol: NOTE 1 In the latter case, in French, “spectrique” is preferred to “spectral”. NOTE 2 Xλ is also a function of λ and in order to stress this, may be written Xλ(λ) without any change of meaning. NOTE 3 The quantity X can also be expressed as a function of frequency ν, wave number σ, etc.; the corresponding symbols are X(ν), X(σ), etc. and Xν, Xσ, etc. |
spektrális; spektral |
Az elektromágneses sugárzásra vonatkozó valamely X mennyiség jelzője, jelentheti, hogy — vagy az X a λ, hullámhossz függvénye, jelölése: X(λ), — vagy az X mennyiség spektrális sűrűsége, jelölése:
1. MEGJEGYZÉS: A „spektrális” szó helyett ajánlható a „spektral” szó alkalmazása 2. MEGJEGYZÉS: Xλ azt jelenti, hogy X a λ függvénye. és az Xλ(λ) írásmód még jobban kiemeli ezt. 3. MEGJEGYZÉS: Az X mennyiség lehet a ν frekvencia vagy a σ hullámszám függvénye is, ebben az esetben megfelelő jelölések X(ν), X(σ), stb lesznek. |
|
chromaticity coordinates, spectral |
See “spectral chromaticity coordinates” |
spektrális színességi koordináták | |
|
spectral stimulus |
See “monochromatic stimulus” |
monokromatikus szín inger |
lásd “monochromatic stimulus” |
|
spectrum locus |
locus, in a chromaticity diagram or in a tristimulus space, of points that represent monochromatic stimuli NOTE In tristimulus space, the spectrum locus is a cone that is called in German “Spektralkegel” (“spectral cone”) or, when including the vectors that represent the purple boundary, “Farbtüte”. |
spektrumgörbe |
Monokromatikus színingerekhez tartozó pontok helye a színességi-diagramban vagy a trikromatikus színingertérben. MEGJEGYZÉS: A spektrum görbéje egy kúp a tristimulusos színingertérben, neve a németben Spektralkegel (spectral cone), vagy ha magába foglalja a bíborvonal által reprezentált vektorokat is németül Farbtüte. |
|
Stiles-Crawford effect (of the first kind) |
decrease of the brightness of a light stimulus with increasing eccentricity of the position of entry of the light pencil through the pupil Equivalent term: “directional effect” NOTE If the variation is in hue and saturation instead of in brightness, the effect is called “Stiles-Crawford effect of the second kind”. |
Stiles-Crawford effektus (első esete) |
A színinger világosságának csökkenése, ha a pupillán belépő fénynyaláb excentricitása növekszik. MEGJEGYZÉS: Ha a változás színezetben és telítettségben van és nem világosságban, akkor ez a második Stiles-Crawford hatás. |
|
illuminant colorimetric shift |
change in chromaticity and luminance factor of an object colour stimulus caused by a change in illuminant |
Sugárzáseloszlás okozta színmérési eltolódás |
Egy színinger színezetének és világosságának megváltozása a megvilágítás megváltozásának hatására |
|
illuminant colour shift |
change in the perceived colour of an object caused solely by change of illuminant in the absence of any change in the observer’s state of chromatic adaptation |
Sugárzáseloszlás okozta színészlelet eltolódás |
Tárgy észlelt színességében és fénysűrűségi tényezőjében bekövetkező változás, amelyet a megvilágítás megváltozása okoz, miközben a megfigyelő színadaptációs állapota változatlan |
|
field colour |
colour perceived as not belonging to any object |
Szabad színészlelet |
Olyan szín észlelet, amelyet semmi nem befolyásol |
|
color (US) |
1. (perceived) colour: see “colour (perceived)” 2. (psychophysical) colour: specification of a colour stimulus in terms of operationally defined values, such as 3 tristimulus values Equivalent term used outside US: “colour” NOTE 1 When the meaning is clear from the context the term “colour” can be used alone. NOTE 2 In German “Farbe” is often used instead of “Farbempfindung”. The use of “Farbe” in the sense of “Farbvalenz” should be avoided. It is only when the sense is obvious from the context, or when “Farbempfindung” and “Farbvalenz” are equally suitable, that “Farbe” may be used in the sense of “Farbvalenz”. |
szín |
1. lásd “szín észlelet” 2. lásd „pszihofizikai szín”: egy szín inger definiciója 3 tristimulus érték által 1. MEGJEGYZÉS: Ha a fogalom egyértelmű, akkor a „szín” szó magában alkalmazható 2. MEGJEGYZÉS: A német nyelvben gyakran a „Farbe” szót alkalmazzák a “Farbempfindung” helyett. A “Farbvalenz” szó kerülendő. |
|
colour |
szín |
A vizuális észlelés (látás) jellemző tulajdonsága, amely a kromatikus vagy akromatikus tartalom bármilyen kombinációjából tevődhet össze. Ez a jellemző tulajdonság leírható a kromatikus színek neveivel (sárga, narancs, barna, piros, rózsaszín, zöld, kék, bíbor stb.), az akromatikus színek neveivel (fehér, szürke, fekete stb.)> a színeket minősítve úgy, hogy világos, sötét, viszonylag világos, viszonylag sötét stb. vagy a színek neveinek kombinációjával. A színészlelet függ a színinger spektrális eloszlásától, a színingerhez tartozó terület méretétől, alakjától, szerkezetétől és környezetétől, a személy látási rendszerének adaptációjától, jártasságától a megfigyelés általános és a hasonló feltételei között. MEGJEGYZÉSEK: Ha a szövegből a jelentés egyértelmű, akkor a szín szó önmagában használható. A színészlelet a színes megjelenés különböző módjai szerint jelentkezhet. A színes megjelenés különböző nevei arra valók, hogy jellemezzék a színész leletek közötti kvalitatív és geometriai különbségeket. A színes megjelenés néhány legfontosabb módjának a neveit a 845-02-19, 20, 21 szakaszok ismertetik. A színes megjelenés további módjai: a vékonyréteg-színészlelet, a térfogat-színészlelet, a sugárzáseloszlás-színészlelet, a test-színészlelet és a Ganzfeld-színészlelet. A színes megjelenésnek ezek a módjai tovább bővíthetők melléknevekkel, amelyek leírják a színek kombinációját vagy azok tér-, vagy időbeli kapcsolatait. A színészleletek közötti, a különböző színes megjelenéskor keletkező, kvalitatív különbségekre vonatkozó fogalmak a 845-02-22, 23, 24, 25 szakaszokban találhatók. | |
|
chromaticity |
property of a colour stimulus defined by its chromaticity coordinates, or by its dominant or complementary wavelength and purity taken together |
szín(esség) |
A színingernek az a tulajdonsága, amelyet vagy a színinger koordinátáival, vagy jellemző hullámhosszával és a színinger tisztaságával lehet jellemezni. |
|
colour difference (perceived) |
perceived dissimilarity between 2 colour elements See also “CIE 1976 L*a*b* colour difference”, "CIE 1976 L*u*v* colour difference”, "CIELAB colour difference”, "CIELUV colour difference” |
színkülönbség |
2 szín észlelet eltérése Lásd még: “CIE 1976 L*a*b* színkülönbség”, "CIE 1976 L*u*v* színkülönbség”, "CIELAB színkülönbség”, "CIELUV színkülönbség” |
|
colour atlas |
collection of colour samples arranged and identified according to specified rules |
színatlasz |
Meghatározott szabályok szerint rendezett és megjelölt színes minták gyűjteménye. |
|
chromaticity diagram |
plane diagram in which points specified by chromaticity coordinates represent the chromaticities of colour stimuli NOTE In the CIE standard colorimetric systems y is normally plotted as ordinate and x as abscissa, to obtain an x, y chromaticity diagram. |
színdiagram |
Síkban értelmezett diagram, amelyen a színességi koordinátákkal meghatározott pontok képviselik a színingerek színességét. MEGJEGYZÉS: A CIE szín ingermérő rendszer x, y színességi diagramjában általában az y az ordinátatengely és az x az abszcisszatengely. |
|
colourfulness |
attribute of a visual perception according to which the perceived colour of an area appears to be more or less chromatic NOTE For a colour stimulus of a given chromaticity and, in the case of related colours, of a given luminance factor, this attribute usually increases as the luminance is raised except when the brightness is very high. |
színezetdússág |
A vizuális érzékelés jellemző tulajdonsága, amely szerint egy felület színészlelete többé vagy kevésbé kromatikusnak tűnik. 1. MEGJEGYZÉS: Egy adott kromatikus színészlelési ingernek, ha adott fénysűrűségi tényezőjű viszonyított színészleletről van szó, ez a jellemző tulajdonsága megnő a fénysűrűségi tényező növekedésével, kivéve, ha a világosság nagyon nagy. 2. MEGJEGYZÉS: A francia „cromie" és az angol „chromaticness" kifejezéseket korábban a színezet és a telítettség együttes észlelésének, vagyis az észlelettel korrelált színezetnek a megnevezésére használták. |
|
colour equation |
algebraic or vector representation of the match of 2 colour stimuli, of which, for instance, one may be an additive mixture of 3 reference colour stimuli Example: [C] ≡ X[X] + Y[Y] + Z[Z] NOTE 1 In this equation, the sign ≡ indicates a colour match and is read as “matches”. The unbracketed symbols represent the amounts of the stimuli indicated by the bracketed symbols: thus R[R] means R units of stimulus [R], and the sign + means an additive mixture of colour stimuli. In such an equation, a minus sign means that the stimulus is added to those on the other side of the equation when the colour match is made. NOTE 2 The reference stimuli are represented as [R], [G] and [B] in which case the sign ‘≡’, pronounced “matches” should be used. As an alternative the colour equation can be written using boldface Roman letters when the equal sign ‘=’, pronounced “equals” should be used: C = XX + YY + ZZ. |
színegyenlet, színingeregyenlet |
Két színinger megfeleltetésének algebrai vagy vektoros leírása, ahol az egyik színinger például három alapszín-inger additív keverésének az eredménye lehet. Például: C[C] º X[X\ + Y[Y] + Z[Z] 1. MEGJEGYZÉS: A º jel a színinger megfeleltetését jelenti; jelentése: „megfelel”. A zárójelben lévő mennyiség előtti betű a zárójelesen megadott színinger mennyiségét mutatja, vagyis az R[R] kifejezésben R-nyit kell venni az [R] színingerből; és a + jel itt a színingerek additív keverését jelenti. Az ilyen egyenletben a minusz jel azt jelenti, hogy az azt követő színingert az egyenlet másik oldalához kell adni a színingerrel való megfeleltetéskor. 2. MEGJEGYZÉS: A referencia ingereket [R], [G] és [B] jelöli, és ebben az esetben a ‘≡’ jelen a “megfelel” kifejezést kell érteni. Másik lehetőségként a színinger egyenletet bold görög betűkkel kell írni, és az “=” jelet “egyenlő”-ként kell használni: C=XX+YY+ZZ |
|
colour-matching |
action of making a colour stimulus appear the same in colour as a given colour stimulus NOTE The French term applies mainly to the adjustment of equality of the fields of a visual colorimeter, whereas the English and German terms apply equally well to the selection of 2 material specimens having the same colour under a given illuminant. |
Szín megfeleltető |
eljárás, melyben létrehozunk egy színingert, amely színben azonosnak látszik egy adott másik színingerrel MEGJEGYZÉS: a francia meghatározás kifejezetten egy vizuális koloriméter mezőinek egyeztetését alkalmazza, míg az angol és a német meghatározás egyaránt 2 anyag féleség összehasonlításáról beszél, amelyek egyforma színűnek látszanak adott megvilágítás mellett. |
|
colour-matching coefficients |
3 values of a set of colour-matching functions at a given wavelength Formerly: “spectral tristimulus values”. |
Szín megfeleltető együtthatók |
A 3 szín megfeleltető függvény értéke egy adott hullámhosszon |
|
colour-matching functions (of a trichromatic system) |
tristimulus values of monochromatic stimuli of equal radiant power NOTE 1 The 3 values of a set of colour-matching functions at a given wavelength are called “colour-matching coefficients” (formerly: “spectral tristimulus values”). NOTE 2 The colour-matching functions may be used to calculate the tristimulus values of a colour stimulus from its colour stimulus functions ɸλ(λ). See also CIE 15 Colorimetry See also ISO 11664-1:2007(E)/CIE S 014-1/E:2006 Colorimetry - Part 1: CIE Standard Colorimetric Observers NOTE 3 In the CIE standard colorimetric systems, the colour-matching functions are represented by the symbols |
Szín megfeleltető függvények (egy trikromatikus rendszerben) |
Az egyenlő sugárzott teljesítményű monokromatikus színingerek színinger-összetevöi. 1. MEGJEGYZÉS: Az egy adott hullámhosszhoz tartozó három színinger- megfeleltető függvényt színinger megfeleltető együtthatóknak nevezik (régebben spektrális színinger-összetevőknek hívták). 2. MEGJEGYZÉS: A színinger- megfeleltető függvényekkel ki lehet számítani egy színinger szín inger-összetevőit a ɸλ(λ). színinger függvényből (lásd a CIE 15. sz. kiadványát). 3. MEGJEGYZÉS: A színinger- megfeleltető függvények jelei a CIE színinger mérő rendszerekben |
|
chromaticity coordinates |
ratio of each of a set of 3 tristimulus values to their sum Unit: 1 NOTE 1 As the sum of the 3 chromaticity coordinates is equal to 1, 2 of them are sufficient to define a chromaticity. NOTE 2 In the CIE standard colorimetric systems, the chromaticity coordinates are represented by the symbols x, y, z and x10, y10, z10. |
szinességi koordináták |
A három összetartozó színinger-összetevő mindegyikének és ugyanazon színinger-összetevők összegének a hányadosa. Megjegyzés : Mivel a három színességi koordináta összege1, kettő közülük elegendő a színesség jellemzésére. A színességi koordináták jelei a CIE színinger mérő rendszerekben x, y, z és x10, y10, z10. |
|
colour (perceived) |
characteristic of visual perception that can be described by attributes of hue, brightness (or lightness) and colourfulness (or saturation or chroma) NOTE 1 When necessary, to avoid confusion between other meanings of the word, the term “perceived colour” may be used. NOTE 2 Perceived colour depends on the spectral distribution of the colour stimulus, on the size, shape, structure and surround of the stimulus area, on the state of adaptation of the observer’s visual system, and on the observer’s experience of the prevailing and similar situations of observation. NOTE 3 See NOTE 1 and NOTE 2 to “colour”. NOTE 4 Perceived colour may appear in several modes of colour appearance. The names for various modes of appearance are intended to distinguish among qualitative and geometric differences of colour perceptions. Some of the more important terms of the modes of colour appearance are given in “object colour”, “surface colour” and “aperture colour”. Other modes of colour appearance include film colour, volume colour, illuminant colour, body colour, and Ganzfeld colour. Each of these modes of colour appearance may be further qualified by adjectives to describe combinations of colour or their spatial and temporal relationships. Other terms that relate to qualitative differences among colours perceived in various modes of colour appearance are given in “luminous colour”, “non-luminous colour”, “related colour” and “unrelated colour”. |
színészlelet |
A színészlelet 3 jellemzővel írható le: színezet, világosság és színezetdússág. 1. MEGJEGYZÉS: Szükség esetén annak érdekében, hogy elkerüljük a szó téves értelmezését, alkalmazzuk a színészlelet szót. 2. MEGJEGYZÉS: A színészlelet függ a színinger spektrális eloszlásától, méretétől, alakjától, struktúrájától és környezetétől, továbbá a megfigyelő vizuális rendszerének adaptációs állapotától, és a megfigyelőnek a hasonló helyzetekben szerzett tapasztalatától. 3. MEGJEGYZÉS: Lásd az 1. és 2. MEGJEGYZÉS-t a colour címszónál 4. MEGJEGYZÉS: A színészlelet kifejezés a szín megjelenésének különböző lehetőségeit világítja meg. Az eltérő kifejezések igyekeznek különbséget tenni a színészlelet általános és geometriai sajátságai között. A színmegjelenés legfontosabb tulajdonságait fejezik ki a „tárgy szín”, a „felület-szín”, és az „apertura színészlelet”. A színes megjelenés további módjai: a vékonyréteg-színészlelet, a térfogat-színészlelet, a sugárzáseloszlás-színészlelet, a test-színészlelet és a Ganzfeld-színészlelet. A színes megjelenésnek ezek a módjai tovább bővíthetők melléknevekkel, amelyek leírják a színek kombinációját vagy azok tér-,vagy időbeli kapcsolatait. A színészleletek közötti, a különböző színes megjelenéskor keletkező, kvalitatív különbségekre vonatkozó fogalmak a 845-02-22, 23, 24, 25 szakaszokban találhatók.
|
|
spot colour |
single colorant, identified by name, and specified independently from the colour values specified in a trichromatic (colour coordinate) system |
színezék megnevezése |
egyszerű szín meghatározás, a trikromatikus (szín koordinátás) színrendszertől függetlenül, a szín nevével határozva meg a színt |
|
hue |
attribute of a visual perception according to which an area appears to be similar to one of the colours: red, yellow, green, and blue, or to a combination of adjacent pairs of these colours considered in a closed ring NOTE Formerly “Farbton” in German. New term is “Buntton”. |
Színezet |
A vizuális érzékelés jellemző tulajdonsága, amely szerint úgy tűnik, hogy egy felület hasonlít a piros, sárga, zöld és kék színészlelet egyikéhez vagy közülük a kettő kombinációjához. MEGJEGYZÉS: A németben régebben; Farbton. |
|
hue quadrature |
correlate of hue expressed in terms of the proportions of the unique hues perceived to be present |
Színezet arányok |
A színészlelet körülírása az alapszínezetek arányával kifejezve. |
|
colour temperature [Tc] |
temperature of a Planckian radiator whose radiation has the same chromaticity as that of a given stimulus Unit: K NOTE The reciprocal colour temperature is also used with unit K-1 or MK-1 (where 1 MK-1 = 10-6 K-1) whose previous name “mired” is now obsolete. |
Színhőmérséklet (korrelált) |
Egy olyan Planck-sugárzónak a hőmérséklete, amely sugárzásának ugyanaz a színessége, mint a kiválasztott színingeré. Egysége: K EGJEGYZÉS: A reciprok színhőmérséklet megnevezést is használják, egysége K-1. |
|
colour stimulus |
visible radiation entering the eye and producing a sensation of colour, either chromatic or achromatic |
színinger |
A szembe behatoló és kromatikus vagy akromatikus színészlelést létrehozó látható sugárzás. |
|
chromatic stimulus |
stimulus that, under the prevailing conditions of adaptation, gives rise to a chromatic perceived colour NOTE In the colorimetry of object colours, stimuli having values of purity greater than 0 are usually considered to be chromatic stimuli. |
színinger (kromatikus) |
Olyan színinger, amely — általános adaptációs feltételek mellett — kromatikus színészleletet hoz létre. MEGJEGYZÉS: A tárgy-színészleletek színmérésében, a nullánál nagyobb tisztaságú színingereket általában kromatikus színingereknek minősítik. |
|
tristimulus values (of a colour stimulus) |
amounts of the 3 reference colour stimuli, in a given trichromatic system, required to match the colour of the stimulus considered NOTE In the CIE standard colorimetric systems, the tristimulus values are represented by the symbols R, G, B; X, Y, Z; R10, G10, B10 and X10, Y10, Z10. |
színinger összetevők |
Valamely színinger megfeleltetéséhez adott trikromatikus rendszerben szükséges alapszíningerek mennyisége. MEGJEGYZÉS: A színinger-összetevők jele a CIE színinger méro" rendszerekben: R, G, B; X, Y, Z and X10, Y10, Z10. |
|
additive mixture of colour stimuli |
stimulation that combines on the retina the actions of various colour stimuli in such a manner that they cannot be perceived individually |
színingerek additív keveréke |
A retina ingerlése több színingerrel úgy, hogy azokat nem lehet külön-külön észlelni. |
|
colour stimulus function [ɸλ(λ)] |
description of a colour stimulus by the spectral concentration of a radiometric quantity, such as radiance or radiant power, as a function of wavelength |
Színinger-függvény |
A színinger megadása valamelyik radiometriai mennyiség — például a sugársűrűség vagy a sugárzott teljesítmény — spektrális sűrűségének függvényében. |
|
colour appearance |
1. aspect of visual perception by which things are recognized by their colour 2. in psychophysical studies: visual perception in which the spectral aspects of a visual stimulus are integrated with its illuminating and viewing environment |
színmegjelenés |
1. a látási észlelés egyik fajtája, amelynél a tárgyak a színük által válnak felismerhetővé 2. pszichofizikai tanulmányokban: látási észlelés, amelyben a színinger spektrális jellemzőjét a megvilágítással és a látott környezettel együtt adják meg |
|
aperture mode (of colour appearance) |
colour seen through an aperture which prevents its association with a specific object or source |
apertúra szín észlelés |
Szín, amely egy apertúrán keresztül látható, amely megakadályozza valamely tárgy vagy fényforrás hatását |
|
colour appearance model |
model describing colour appearance, built from descriptors of colour stimuli NOTE In image processing the following definition is also used: equations and methodologies for transforming physically measurable quantities to and from viewing condition specific perceptual attribute correlates. |
színmegjelenési modell |
a színmegjelenés matematikai modellje a színingert leíró tényezők alapján MEGJEGYZÉS: A képfeldolgozásban az alábbi definíció is használatos: egyenletek és számítási algoritmusok, a fizikailag mérhető mennyiségek és a látás speciális észlelési jellemzői közötti transzformáció céljára |
|
colorimetry |
measurement of colour stimuli based on a set of conventions |
színmérés |
Színek mérése meghatározott megállapodások szerint. |
|
colour space |
geometric representation of colour in space, usually of 3 dimensions |
színtér |
A színingerek geometriai szemléltetése, általában háromdimenziós térben. MEGJEGYZÉS: A németben a Vektorraum der Farben olyan színinger teret jelent, amelyben a színingereket reprezentáló vektorok kezdőpontjai az akromatikus színérzékelési ingerhez tartozó pontban vannak. |
|
white point, colour space |
colour stimulus to which colour space values are normalized NOTE The colour space white point may or may not correspond to the adapted white point and/or the reference medium white point for a colour image encoding. |
színtér fehér pontja |
Szín inger, amelyhez a színtér értékeit normalizálják. MEGJEGYZÉS: A színtér fehér pontja nem esik egybe az adaptációs fehér ponttal, vagy színes kép referencia felületének fehér pontjával. |
|
colour solid |
part of a colour space which contains surface colours |
színtest |
A színinger térnek az a része, amely a felületszíneket tartalmazza. |
|
colorimetric purity [pc] |
quantity defined by the relation:
where Ld and Ln are the respective luminances of the monochromatic stimulus and of the specified achromatic stimulus that match the colour stimulus considered in an additive mixture NOTE 1 In the case of purple stimuli, see NOTE 1 to “purity”. NOTE 2 In the CIE 1931 standard colorimetric system, colorimetric purity, pc, is related to excitation purity, pe, by the equation pc = pe yd/y where yd and y are the y chromaticity coordinates respectively, of the monochromatic stimulus and the colour stimulus considered. NOTE 3 In the CIE 1964 standard colorimetric system, a measure, pc,10, is defined by the relation given in NOTE 2, but using pe,10, yd,10 and y10 instead of pe, yd, and y respectively. |
színtisztaság |
A következő összefüggéssel értelmezett mennyiség:
ahol Ld annak a monokromatikus és Ln annak a meghatározott akromatikus színingernek a fénysűrűsége, amely additív színinger keveréssel a kiválasztott színingerrel megfeleltethető. 1. MEGJEGYZÉS: A bíbor színingerekre vonatkozóan 1. a 845-03-46 szakasz 1. megjegyzését. 2. MEGJEGYZÉS: A CIE 1931 színmérő rendszerben a pc, fénysűrűségi tisztaság és a pe, telítettségi tisztaság között a következő összefüggés van: pc = pe yd/y ahol yd és y a monokromatikus színinger, illetve a kiválasztott színinger y színességi koordinátái. 3. MEGJEGYZÉS:
A CIE 1964 kiegészítő színmérő rendszerben a pc,10 fénysűrűségi tisztaság a 2. megjegyzésben leírt módon van értelmezve, csak a pe, yd, és y helyébe a pe,10, yd,10 értékeket kell írni. |
|
colour rendering (of a light source) |
effect of an illuminant on the colour appearance of objects by conscious or subconscious comparison with their colour appearance under a reference illuminant |
színvisszaadás |
A sugárzás spektrális eloszlásának a hatása a tárgyak színes megjelenésére; a tárgyak egy referencia-eloszláshoz tartozó színes megjelenésével való tudatos vagy tudatalatti összehasonlítása. MEGJEGYZÉS: A német nyelv a színvisszaadásra a „Farbwiedergabe" kifejezést használja. |
|
colour rendering index [R] |
measure of the degree to which the psychophysical colour of an object illuminated by the test illuminant conforms to that of the same object illuminated by the reference illuminant, suitable allowance having been made for the state of chromatic adaptation See also CIE 13 Method of Measuring and Specifying Colour Rendering of Light Sources Abbreviation: “CRI” |
színvisszaadási index [R] |
Mérőszám annak jellemzésére, hogy egy vizsgált sugárzáseloszlással megvilágított tárgy színe hogyan egyezik meg ugyanazon tárgynak referencia sugárzáseloszlással történő megvilágításakor kapott színével, figyelembe véve a kromatikus adaptációt. 1. MEGJEGYZÉS: Lásd még a „Színvisszaadás” címszót 2. MEGJEGYZÉS: Lásd még: CIE 13 Method of Measuring and Specifying Colour Rendering of Light Sources Abbreviation: “CRI” 3. MEGJEGYZÉS: A német nyelv a színvisszaadási indexre a „Farbwiedergabe-Index" kifejezést használja. |
|
scotopic vision |
vision by the normal eye in which rods are the principle active photoreceptors NOTE 1 Scotopic vision normally occurs when the eye is adapted to levels of luminance of less than ~10-3 cd·m-2. NOTE 2 In comparison to photopic vision, scotopic vision is characterized by the lack of colour perception and by a shift of the visual sensitivity towards shorter wavelengths. |
esti látás |
A néhány század kandela per négyzetméternél kisebb fény sűrűségre adaptált normális szem látása. 1. MEGJEGYZÉS: A szkotopikus látás akkor jön létre, ha a szem kisebb, mint ~10-3 cd.m-2 megvilágításra adaptált állapotban van. 2. MEGJEGYZÉS: A nappali látással összehasonlítva az esti látásra az jellemző, hogy nincs színérzékelés, és a spektrális érzékenység a rövidebb hullámhosszak felé tolódik. |
|
dispersion |
1. phenomenon of change in the velocity of propagation of monochromatic radiation in a medium as a function of the frequency of this radiation 2. property of a medium giving rise to this phenomenon 3. property of an optical system resulting in the separation of the monochromatic components of the radiation, obtained for example by means of prisms or gratings |
szórás |
1. A monokromatikus sugárzás terjedési sebességének változása valamilyen közegben, a frekvencia függvényében. 2. Valamilyen közegnek az a tulajdonsága, amely az említett jelenséget létrehozza. 3. Valamilyen optikai rendszernek az a tulajdonsága, hogy a sugárzás monokromatikus összetevőit képes elkülöníteni, például prizmákkal vagy rácsokkal. |
|
Talbot’s law |
if a point on the retina is excited by a light stimulus that undergoes periodic variations in magnitude at a frequency that exceeds the fusion frequency, the visual perception produced is identical with that produced by a steady stimulus whose magnitude is equal to the mean magnitude of the variable stimulus taken over 1 period |
Talbot törvény |
Ha a retina egy részét olyan periodikusan váltakozó fény inger éri, amelynek frekvenciája a fúziós frekvenciánál nagyobb, a létrehozott vizuális észlelés azonos azzal az észleléssel, amelyet a váltakozó fényinger időbeli átlagával meghatározott állandó fény vált ki. |
|
inherent colour |
colour perceived to belong to an object irrespective of the illumination and viewing conditions |
Saját szín |
Egy tárgyhoz tartozó színészlelet amely független a megvilágítástól és a megfigyelés körülményeitől |
|
saturation |
colourfulness of an area judged in proportion to its brightness NOTE For given viewing conditions and at luminance levels within the range of photopic vision, a colour stimulus of a given chromaticity exhibits approximately constant saturation for all luminance levels, except when the brightness is very high. |
telítettség |
Egy felület színdússága a világosságához viszonyítva. MEGJEGYZÉS: Adott látási körülmények között és a nappali látási tartományon belüli fénysűrűségi szinteken egy adott színességű színérzékelési inger minden fénysűrűségi szintre állandó telítettségű, kivéve, ha a világosság nagyon nagy. |
|
volume colour |
colour perceived as belonging to the bulk of the substance |
térfogati szín |
Nagymennyiségű anyaghoz tartozó színészlelet |
|
natural sky glow |
that part of the sky glow which is attributable to radiation from celestial sources and luminescent processes in the Earth’s upper atmosphere |
természetes égbolt sugárzás |
Az égbolt azon részének sugárzása, amelynek az égbolt ragyogása tulajdonítható, és a Föld felső légköri lumineszcens folyamatainak sugárzása |
|
natural pupil luminance |
luminance of a light source (primary or secondary) which, when viewed with the natural pupil, produces the same conventional retinal illuminance, in trolands, as that source viewed with a specified artificial pupil Unit: cd, cd⋅m-2⋅mm2, troland |
természetes pupilla fénysűrűség |
Egy fényforrás sugárzása (elsődleges vagy másodlagos), amelyet egy természetes pupillán át megfigyelve azonos általános retina megvilágítást kapunk, trolandban, mint egy adott fényforrás egy adott mesterséges pupillán keresztül nézve. Mértékegysége: cd, cd⋅m-2⋅mm2, troland |
|
purity (of a colour stimulus) |
measure of the proportions of the amounts of the monochromatic stimulus and of the specified achromatic stimulus that, when additively mixed, match the colour stimulus considered NOTE 1 In the case of purple stimuli, the monochromatic stimulus is replaced by a stimulus whose chromaticity is represented by a point on the purple boundary. NOTE 2 The proportions can be measured in various ways (see “colorimetric purity” and “excitation purity”). |
tisztaság (színingeré) |
egy monokromatikus színinger mennyiségének aránya egy meghatározott akromatikus színingerhez, amelyeknek additív keveréke egyező színűnek látszik az adott színingerrel 1. MEGJEGYZÉS: Bíbor színinger esetén a monokromatikus inger helyett egy olyan ingert veszünk amelynek a színessége a bíbor vonal megfelelő pontján van. 2. MEGJEGYZÉS: A mennyiségek különbözőképpen mérhetők, lásd „színtisztaság”, „színinger tisztaság” |
|
perfect transmitting diffuser |
diffuser exhibiting isotropic diffuse transmission with a transmittance equal to 1 |
tökéletesen áteresztő diffúzor |
Ideális egyenletesen szóró közeg, amelynek áteresztési tényezője 1. |
|
perfect reflecting diffuser |
diffuser exhibiting isotropic diffuse reflection with a reflectance equal to 1 |
tökéletesen visszaverő diffúzor |
Ideális egyenletesen szóró közeg, amelynek visszaverési tényezője 1. |
|
trichromatic system |
system for specifying colour stimuli in terms of tristimulus values, based on matching colours by additive mixture of 3 suitably chosen reference colour stimuli |
trikromatikus rendszer |
Rendszer, amely a színingereket a színinger-összetevőkkel értelmezi; három alkalmasan választott alapszíninger additív színingerkeverésén alapul. |
|
tritanomaly |
See NOTE 11 to “defective colour vision” |
tritanomália |
Lásd 6. MEGJEGYZÉS a színtévesztés címszónál |
|
tritanopia |
See NOTE 12 to “defective colour vision” |
tritanopia |
Lásd 7. MEGJEGYZÉS a színtévesztés címszónál |
|
glare by reflection |
glare produced by reflections, particularly when the reflected images appear in the same or nearly the same direction as the object viewed NOTE Formerly: “reflected glare”. |
Tükröző káprázás |
Olyan káprázás, amelyet a reflexiók okoznak főként akkor, ha a visszavert képek ugyanabban vagy közel ugyanabban az irányban jelennek meg, mint a szemlélt tárgy. MEGJEGYZÉS: Korábban reflected glare. |
|
chromatic induction |
modification of the visual response that occurs when 2 colour stimuli (of any spectral irradiance distribution) are viewed side-by-side in which each stimulus alters the appearance of the other NOTE 1 It is often referred to as simultaneous or spatial contrast because the effect is one of enhancement of colour difference. NOTE 2 The effect is virtually instantaneous, in contrast to chromatic adaptation which is considered to develop slowly in the visual system. |
szín kölcsönhatás |
A szín észlelet módosulása annak következtében, hogy 2 színinger (tetszőleges sugárzás eloszlással) látható közvetlenül egymás mellett, és így mindkét inger módosítja a másik hatását 1. MEGJEGYZÉS: Ezt gyakran nevezik szimultán vagy térbeli kontrasztnak, mivel ez a jelenség egyike a színkülönbség növekedésének. 2. MEGJEGYZÉS: Ez a hatás gyakorlatilag azonnali, ellentétben a kromatikus adaptációs hatással, amely lassan alakul ki |
|
colorimetric colour space |
colour space defined by 3 colorimetric coordinates NOTE CIE XYZ tristimulus values are colorimetric coordinates, as are RGB values that have an exact and invertible mathematical relationship to CIE XYZ tristimulus values. |
kolorimetrikus színtér |
3 színösszetevővel definiált színtér MEGJEGYZÉS: A CIE XYZ tristimulus értékek kolorimetriai színösszetevők, éppen úgy mint a CIE RGB értékek, mivel ezek matematikailag átszámítható mennyiségek. |
|
colorimetric neutral |
having the same chromaticity as the adopted white NOTE 1 When stating that an image area is a colorimetric neutral, it is necessary to designate the adopted white. For reflection hardcopy images, the adopted white is typically considered to be either the media white or a perfectly diffuse reflecting surface illuminated by the illumination source. NOTE 2 The adopted white of colorimetric neutral may or may not correspond to the adapted white according to an observer. |
kolorimetrikus semleges szín |
A kolorimetrikus semleges szín adaptációs fehér színe lehet a megfigyelő adaptációs fehér színe is. |
|
colour boundaries |
borders of an area in a chromaticity diagram bounded by segments of straight lines NOTE The area is given either by the equations of the straight lines or by the coordinates of their crossing points between themselves or with the spectrum locus. |
Szín határok |
A színességi diagram egy területének egyenes vonalakkal körülzárt határai MEGJEGYZÉS: A terület vagy a határvonalak egyenlete által határozható meg, vagy azok egymással vagy a spektrumvonallal létrejövő metszéspontjainak koordinátái által |
|
colour correction factor |
no longer in use: see “spectral mismatch correction factor” |
színkorrekciós faktor |
A továbbiakban nem használható: lásd „spektrális illesztési korrekció” |
|
colour element (of a colour appearance model) |
defined area within which the colour appearance is uniform |
elemi szín (egy színmegjelenési modellben) |
Egy adott terület egy egyenközű színmegjelenési modellben |
|
colour gamut |
volume, area, or solid in a colour space, consisting of all those colours that are either: (a) present in a specific scene, artwork, photograph, photomechanical, or other reproduction; (b) capable of being created using a particular output device and/or medium NOTE In reproduction and media applications only the volume or solid in a colour space is regarded as colour gamut. In applications such as signal lighting the colour gamut is an area. |
színtartomány |
Mennyiség, terület vagy tér rész egy színtérben, amelynek színei vagy: (a) egy adott színhely, műalkotás, fénykép, fénymásolat vagy egyéb reprodukció részei (b) alkalmasak arra, hogy létrejőjjenek egy adott kimeneti eszközön és / vagy közegen MEGJEGYZÉS: A reprodukciós és média alkalmazások esetében a színtérnek csak a területe vagy térfogata tartozik a színtartományhoz. Egy adott terület szín tartománya olyan alkalmazásoknál, mint például a fényjelek és a megvilágítás. |
|
colour gamut boundary |
outer surface of a colour gamut |
a színtartomány határa |
A színtartományt körülzáró vonal |
|
colour order system |
arrangement of samples according to a set of principles for the ordering and denotation of their colour, usually according to defined scales NOTE A colour order system is usually exemplified by a set of physical samples, sometimes known as a colour atlas. This facilitates the communication of colour but is not a prerequisite for defining a colour order system. See also “colour atlas” |
szín rendszer |
Minták rendszerezése bizonyos törvényszerűségek alapján, a színük szerint megjelölve őket egy meghatározott skálán MEGJEGYZÉS: Egy színrendszert általában egy színminta gyűjteménnyel mutatnak be, amelyet általában Szín Atlasznak neveznek. Ez megkönnyíti a szín-kommunikációt, de nem előfeltétele a színrendszerbeli meghatározásnak. Lásd még: "szín atlasz" |
|
colour patch, test area |
colour image from an output device or a reflective or transparent hardcopy to be measured, in which the device control values are kept constant within the image area |
szín minta |
Egy színes nyomtató kimeneti képe vagy egy reflexiós vagy transzmissziós színes felület, amelynek mért értéke a teljes képmezőben állandó kell legyen. |
|
afterglow |
slowly decaying luminescence persisting after the excitation of the luminescent material has ceased, the duration of which may be from about 100 ms to several minutes |
után-világítás |
A lumineszkáló anyag gerjesztésének befejezése után lassan lecsengő lumineszkálás, lecsengési ideje 100 ms-tól több percig tarthat. |
|
illumination |
application of light to a scene, objects, or their surroundings Equivalent term: “lighting” NOTE This term is also used colloquially with the meaning “lighting system” or “lighting installation”. |
Megvilágítás |
Fény alkalmazása egy jelenet, tárgy vagy tárgy környezetének megvilágítására. Egyenértékű kifejezés: "világítás" MEGJEGYZÉS: Ezt a kifejezést a köznyelvben is alkalmazzák. A jelentése "világítási rendszer" vagy "megvilágítás". |
|
lighting |
See “illumination” |
világítás |
Lásd „megvilágítás” |
|
illumination colour |
colour perceived as belonging to the light falling on objects |
megvilágítás színe |
Szín észlelet amely a tárgyra eső fényre vonatkozik |
|
illuminating engineering |
art, science and design of lighting in general, and development of systems for producing, directing, controlling or applying light in particular |
világítástechnikai tevékenység, fénytechnikai tevékenység |
Általában a fény művészete, tudománya vagy dekoratív alkalmazása, továbbá olyan rendszerek kifejlesztése, amelyek kimondottan a fény előállítására, irányítására, mérésére vagy alkalmazására szolgálnak |
|
lighting technology |
equipment for lighting or its control See also “illuminating engineering” |
világítástechnika, fénytechnika |
Világításra vagy annak mérésére szolgáló berendezés Lásd még: világítástechnikai tevékenység, fénytechnikai tevékenység |
|
bright |
adjective used to describe high levels of brightness |
világos |
Melléknév, a világosság magas szintjének a megjelölésére. |
|
light (adjective) |
adjective used to describe high levels of lightness |
világos |
Melléknév, a relatív világosság nagy szintjének a megjelölésére. |
|
brightness |
attribute of a visual perception according to which an area appears to emit, or reflect, more or less light NOTE The use of this term is not restricted to primary light sources. |
világosság |
A vizuális érzékelés jellemző tulajdonsága, amely szerint úgy tűnik, hogy egy felület több vagy kevesebb fényt bocsát ki. |
|
flicker |
impression of unsteadiness of visual perception induced by a light stimulus whose luminance or spectral distribution fluctuates with time |
Villogás |
A vizuális észlelés ingadozásáról keletkezett benyomás, a fényinger fénysűrűségének vagy spektrális összetételének az időbeni gyors ingadozása által keltett benyomás, ha a változás frekvenciája néhány hertznél nagyobb, de a fúziós frekvencia értékét még nem éri el. MEGJEGYZÉS: A magyar szakirodalomban erre a fogalomra az angol flicker illetve a német Flimniem megnevezés is használatos. |
|
visual perception |
interpretation of visual sensation |
látási érzéklet |
érzékelés a látószerv által |
|
visual colorimetry |
colorimetry in which the eye is used to make quantitative comparisons between colour stimuli |
vizuális kolorimetria |
olyan kolorimetriai eljárás, amelynek során a színingerek kvantitatív összehasonlítását a szem végzi. |
|
visual performance |
quality of performance of the visual system of an observer related to central and peripheral vision |
vizuális teljesítmény |
egy megfigyelő látórendszerének teljesítménye a centrális vagy a perifériás látásban |
|
persistence law, von Kries’ |
See “von Kries’ persistence law” |
állandósági törvénye, von Kries
|
Lásd: „von Kries állandósági törvénye” MEGJEGYZÉS: „szín konstancia” néven is ismert |
|
von Kries’ persistence law |
empirical law stating that colour stimuli that match in one set of adaptation conditions continue to do so in any other set NOTE von Kries’ persistence law does not apply to all conditions. |
von Kries állandósági törvénye |
Empirikus törvény, mely kimondja, hogy bizonyos adaptációs körülmények között egyező színingerek tetszőlegesen más adaptációs körülmények között is egyezni fognak MEGJEGYZÉS: von Kries állandósági törvénye nem alkalmazható bármely körülmények között |
|
discomfort glare |
glare that causes discomfort without necessarily impairing the vision of objects |
Zavaró káprázás |
Olyan káprázás, amely kényelmetlenséget okoz anélkül, hogy szükségképpen rontaná a tárgy látását. |
|
white point |
achromatic reference stimulus in a chromaticity diagram that corresponds to the stimulus that produces an image area that has the perception of white |
fehérpont |
akromatikus referencia inger színpontja egy színességi diagramban, amely egy olyan ingerhez tartozik, amely a fehér szín benyomását kelti |
|
colour component transfer function |
single variable, monotonic mathematical function applied individually to one or more colour channels NOTE 1 Colour component transfer functions are frequently used to account for the non-linear response of a reference device and/or to improve the visual uniformity of a colour space. NOTE 2 Generally, colour component transfer functions will be non-linear functions such as a power-law (i.e., “gamma”) function or a logarithmic function. However, in some cases a linear colour component transfer function may be used. NOTE 3 For more information on “colour channels” see NOTE 2 to “colour space encoding”. |
szín átviteli függvény |
Egyváltozós, monoton matematikai függvény amelyet egyedileg alkalmazhatunk egy vagy több színcsatornára 1. MEGJEGYZÉS: A szín átviteli függvény legtöbbször egy referencia eszköz nemlineáris válaszának meghatározására és/vagy egy színtér vízuális egyenletességének javítására alkalmazható. 2. MEGJEGYZÉS: Alapjában véve a szín átviteli függvény egy nemlineáris függvény, mint például a „gamma-függvény”, vagy egy logaritmikus függvény. Viszont sok esetben lineáris szín átviteli függvényt alkalmaznak. 3. MEGJEGYZÉS: További információ a szín átviteli függvényről a „Színtér kódolása” címszó 2. MEGJEGYZÉS-ben található |
|
contrast rendering factor (of a lighting system, for a task) |
ratio of the contrast of a task under the lighting system considered, to the contrast of the same task under reference lighting Unit: 1 |
Kontrasztvisszaadási tényező (egy megvilágító rendszer esetén) |
Egy tárgynak egy adott megvilágítás mellett észlelhető kontrasztjának és ugyanezen tárgynak egy referencia megvilágítás mellett észlelhető kontrasztjának a hányadosa Mértékegység: 1 |