3. fejezet - FAKTORIÁLIS KÍSÉRLETI TERVEK

A Box-Wilson módszer alkalmazása esetén egy kísérlet-sorozat lebonyolítása során minden faktor értékét egyetlen „lépéssel” változtatjuk meg. Ez azt jelenti, hogy a kísérlet sorozatban minden faktor egyszer az egyik, és egyszer a másik szintre (értékre) lesz beállítva. Vagyis minden faktornak csak 2 szintje lesz. Amint láttuk, k számú faktor összes lehetséges szintkombinációját realizáló kísérleti beállítások száma:

N = 2k

Legyen a kísérleti terv összeállításánál a faktorok egyik szintjének jele +1, másik szintjének jele -1. Mindegy, hogy az alsó, vagy a felső szintet jelöljük +1-gyel illetve -1-gyel. Ezek a szintek a kísérlet lebonyolítása során konkrét fizikai mennyiségeket fognak jelenteni, attól függően, hogy az adott faktor milyen mennyiség.

A kísérletet úgy kell megtervezni, hogy minden faktor ugyanannyiszor szerepeljen +1 szinten, mint -1 szinten, és a faktor-kombinációk is egyforma sokszor szerepeljenek +1 szinten, mint -1 szinten. Ehhez nyújt segítséget a kísérleti mátrix.

Az I. táblázat egy kísérleti mátrixot mutat be.

I.táblázat Kísérleti mátrix

Kísérleti mátrix

.

A kísérleti mátrix az összes lehetséges kísérleti beállítás és a kísérletek eredményének szisztematikus táblázatos ábrázolása. A kísérleti mátrix egy-egy sora („sor vektor”) egy-egy kísérletet jelent, vagyis megmutatja a kísérletsorozat egyik kísérletében a faktorok beállítási szintjeit. A kísérleti mátrix egyes oszlopai („oszlop vektor”) az egyes faktorok hatásának kiszámításához ad segítséget.

Az oszlopok szisztematikus kitöltésének több módszere is ismert. Ezek közül legegyszerűbb az előjel-váltogatás módszere. Alkalmazzuk az x1, x2, stb faktorok oszlopaiban az előjel-váltogatás módszerét, azaz az első faktornál egyenként, a második faktornál kettesével, a harmadik faktornál négyesével, stb váltogatjuk az előjeleket. A kereszthatás oszlopokban a kereszthatásban résztvevő faktorok oszlopainak összeszorzásával állapítjuk meg az előjelet. Legyen két azonos előjel szorzata mindig „+” és két különböző előjel szorzata mindig „-”.

${\displaystyle \sum }_{\text{i=1}}^{\text{N}}\text{x ji}=0$

Ahol j a faktor sorszáma,

Na kísérleti beállítások száma

${\displaystyle \sum }_{\text{i=1}}^{\text{N}}\text{xji2}=\text{N }$

${\displaystyle \sum }_{\text{i=1}}^{\text{N}}\text{xji xui=0}$

ahol

j ≠ u

j, u = 0, 1, 2, …,k

Az olyan kísérletet, amelyben a faktorok összes lehetséges szintkombinációját realizáljuk, teljes faktoriális kísérletnek nevezik. Az ilyen kísérletet kétszintű kísérletterv esetén 2k típusúkísérletnek nevezik.

A 3.2. táblázat a legegyszerűbb esetet mutatja be: csak egyetlen faktorunk van, és annak a két különböző szintjén végzünk 1-1 kísérletet. A kísérlet geometriai ábrázolása a 3.1. ábrán látható.

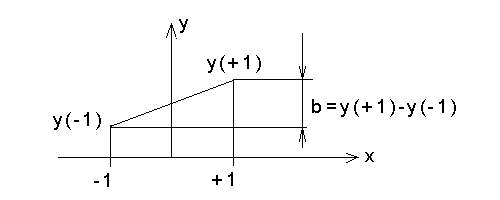
A 3.1. ábrán látható, hogy az x faktor hatása a faktor -1 jelű alsó és +1 jelű felső szintjén nyert kísérleti eredmények különbségével jellemezhető. Ha ez a különbség nagy, akkor a faktor hatása erős.

A kísérleti mátrix a II. táblázatban látható.

II.táblázat Egyfaktoros kísérleti terv mátrixa

Egyfaktoros kísérleti terv mátrixa

A II. táblázat x0 oszlopa csupa +1 értéket tartalmaz. Erre az oszlopra a kísérletek kiértékelésénél lesz szükség. Az x oszlop az egyetlen faktor beállítási értékeit tartalmazza, és az y jelű oszlopba kerülnek a kísérleti eredmények.

A táblázat legalsó sora a kísérletek alapján meghatározható b együtthatókat, azaz a válaszfüggvénynek az egyes faktorok által okozott meredekségét tartalmazza, míg a b0 a kísérletek kezdő értékét jelenti.

22 típusú (kétfaktoros kétszintű teljes) kísérleti terv tervezési mátrixa látható a III.táblázatban, a IV.táblázatban pedig 23 típusú kísérleti terv mátrixát mutatjuk be.

III. táblázat 22 kétfaktoros teljes faktoriális kísérleti terv mátrixa

22 típusú kétfaktoros teljes faktoriális kísérleti terv mátrixa

IV. táblázat 23 háromfaktoros teljes faktoriális kísérleti terv mátrixa

23 háromfaktoros teljes faktoriális kísérleti terv mátrixa

A IV. táblázatban a 2-2 faktor közötti („kétfaktoros”) kölcsönhatásokon kívül megjelent a három faktor közötti („háromfaktoros”) kölcsönhatás is. Az oszlopvektor előjeleit most is a szorzási szabály alkalmazásával határozhatjuk meg.

Bizonyos rendű interakiók lehetséges számának meghatározásához a kombinációk számának meghatározására vonatkozó ismert képletet használhatjuk föl:

$$c_k^m=\left(\begin{array}{c}k\\ m\end{array}\right)=\frac{k!}{m!(k-m)!}$$

ahol k:a faktorok száma,

m:az interakciókban szereplő elemek száma

A lehetséges hatások száma, beleértve b0-t, a lineáris hatásokat és az összes lehetséges interakciót, egyenlő a teljes faktoriális kísérlet beállításainak számával, az ismert képlet szerint:

$$2^N={\displaystyle {\sum }_{l=1}^N\left(\begin{array}{c}N\\ l\end{array}\right)}$$

aholN:a faktorok összes lehetséges szintkombinációját realizáló kísérleti beállítások száma,

l:a vizsgált hatások sorszáma

Általában a teljes faktoriális kísérletben a legmagasabb rendű interakció rendje eggyel kisebb, mint a faktorok száma.

A teljes faktoriális kísérletben a kísérleti beállítások száma jelentősen meghaladja a faktorok által okozott változások meghatározásához szükséges együtthatók számát. Például a IV. táblázatban látható kísérleti mátrixban az x1, x2 és x3 faktor hatását a b1, b2 és b3 együttható kellő mértékben jellemzi. A kereszthatások irányában (pl az x1 és x2 faktorok közös irányában) történő változások a következő lépés megtervezéséhez már kevésbé fontosak (bár megtörténhet, hogy két faktor együttes hatása lényegesen eltér a külön-külön hatástól, pl egy betegség gyógyításánál két gyógyszer együttes alkalmazása akár ronthatja is a beteg állapotát!).

Felmerül a gondolat, hogy csökkentsük úgy a kísérleti beállítások számát, hogy ezáltal csak olyan információt veszítsünk, amely nem túlságosan lényeges a válasz-függvény megismeréséhez.

A IV. táblázatban például a b12, b23 és b13 irányú meredekség ismerete csak abban a nem túl valószínű esetben lényeges számunkra, ha valamely jelentős kölcsönhatásra kell számítanunk. A b123 együttható pedig a faktorhatások nagy keveredése miatt már alig használható a válasz-függvény megismerése szempontjából. Mód van tehát arra, hogy a háromszoros kölcsönhatás oszlopvektorát egy újabb, x4 faktornak adjuk át (V. táblázat). Ezt nyugodtan megtehetjük, hiszen a tervezési mátrix nem veszíti el ezáltal kedvező tulajdonságait (ortogonalitás, elforgathatóság, stb.).

Az ilyen kísérleti tervet feles replikációnak is szokták nevezni, mivel fele annyi kísérletet kell elvégezni általa, mint a teljes kísérleti terv esetén.

V. táblázat 23-1 frakcionális faktoriális kísérleti terv mátrixa

23-1 frakcionális faktoriális kísérleti terv mátrixa

Az V. táblázat tervezési mátrixának alkalmazásával ugyanazzal a 8 kísérlettel, amellyel teljes faktoriális kísérlet esetén 3 faktor hatását vizsgálhattuk meg, most már 4 faktor hatását ismerjük meg. Ehhez teljes faktoriális kísérleti terv alkalmazása esetén 16 kísérletre lett volna szükség!

Ha pedig előzetes információk alapján biztosan tudjuk, hogy valamelyik két faktor között nem lehetséges kölcsönhatás, akkor ezt a kölcsönhatás oszlopot további, most már ötödik faktor vizsgálatára fordíthatjuk. Például egy termés mennyiség javítására irányuló kísérletben a vizsgált faktorok a vetőmag fajtája, az egy m2 területre vetett vetőmag mennyisége, a vetés időpontja, az öntözés gyakorisága, a műtrágya fajtája, az 1 m2 területre kijuttatott műtrágya mennyisége, az előzetes szántás mélysége és a talaj minősége. Ebben az esetben majdnem biztos, hogy nincs kölcsönhatás pl. vetőmag fajtája és az előzetes szántás mélysége között.

A VI. táblázat kísérleti mátrixa egy olyan 23 teljes faktoriális kísérleti tervből indult ki, amelyben a háromszoros kölcsönhatás oszlopvektorát egy újabb, x4 faktornak, az x1 és x2 faktor kölcsönhatás oszlopvektorát pedig egy további x5 faktornak adtuk át.

VI.táblázat 25-2 frakcionális faktoriális kísérleti terv mátrixa

25-2 frakcionális faktoriális kísérleti terv mátrixa

A VI. táblázatban látható kísérletet egynegyedes replikációnak is szokás nevezni, mert a teljes kísérleti terv esetében szükséges 25 = 32 kísérlet helyett mindössze egynegyedrésznyi, azaz 8 kísérletre van szükség.

A telített kísétleti terv abban az esetben alkalmazható, ha minden kétszeres és magasabb kölcsönhatásról feltételezhetjük, hogy elhanyagolható. Ekkor minden kölcsönhatás oszlopába egy-egy új faktort írhatunk be. A VII. táblázatban egy 27-4 telített frakcionált faktoriális kísérleti terv mátrixa látható. Most a 27 = 128 kísérlet helyett is csak 23 = 8 kísérletre van szükség 7 faktor vizsgálatához.

VII.táblázat 27-4 frakcionált faktoriális kísérleti terv mátrixa

27-4 frakcionált faktoriális kísérleti terv mátrixa

A generáló összefüggés azt a lépést önti matematikai formába, amelynek alapján a frakcionált kísérleti tervet létrehoztuk a teljes kísérleti tervből. A 7. táblázat frakcionált kísérleti tervét például a 4. táblázat teljes kísérleti tervéből úgy alakítottuk ki, hogy az x4 faktort az x1x2 kölcsönhatás, az x5 faktort az x2x3 kölcsönhatás, az x6 faktort az x1x3 kölcsönhatás és az x7 faktort az x1x2x3 kölcsönhatás oszlopába írtuk be. Matematikailag:

x4=x1x2; x5=x2x3;x6=x1x3; x7=x1x2x3

Tehát a generáló összefüggést ebben az esetben ez az összefüggés adja meg.

Nem mindegy, hogy a generáló összefüggést hogyan alkalmazzuk, vagyis melyik újabb faktort melyik korábbi kölcsönhatás oszlopába írjuk be. Számolnunk kell a hatások különböző keveredésével. A fontos hatásokat olyan oszlopokba célszerű helyezni, amelyekben nagyon sok hatás van kölcsönhatásban, ezért a zavaró információk nagyfokú keveredése miatt ezek a hatások valószínűleg elnyomják, kompenzálják egymást, és nem keverednek (konfundálódnak) be túl nagymértékben a fontos faktor hatásába. Vagy olyan oszlopot válasszunk a fontos faktor számára, amelyben olyan faktorok kölcsönhatása szerepel, amelyek az adott faktorral feltehetőleg nincsenek erős kölcsönhatásban.

Azt, hogy jól választottuk-e meg a generáló összefüggéseket, igazán csak a kísérletek lefolytatása után, a kiértékelés alapján végzett hibaszámításból tudhatjuk meg.

Oszlopok olyan szorzatát, amelynek minden eleme +1, vagy minden eleme -1, meghatározó kontrasztnak, más néven definiáló kontrasztnak nevezzük. A kontraszt segítséget nyújt a keveredő hatások meghatározásában. Annak megállapítása céljából, hogy egy adott hatással mely hatás keveredik, a meghatározó kontraszt mindkét oldalát meg kell szoroznunk az adott hatásnak megfelelő oszloppal.

Ha például a VII. táblázat x1, x2 és x5 oszlopában levő faktorok szorzatát képezzük, akkor az eredményként kapott oszlopvektor minden tagja 1 lesz, tehát meghatározó kontraszthoz jutottunk, és írható, hogy

x1x2x5=1minden beállításra.

Ez az összefüggés tehát a meghatározó kontraszt definiciója.

Ha most azt akarjuk megvizsgálni, hogy az x5 faktor mely hatásokkal keveredik, akkor a meghatározó kontraszt mindkét oldalát megszorozzuk x5-tel:

x5=x1x2x5x5

Mivel a kísérleti terv mátrixára vonatkozó normalitási tétel szerint x5x5=1, ezért

x5=x1x2

Tehát az x5 faktorhatásban az x1 és x2 faktor hatása keveredik.

Ez az eredmény tulajdonképpen várható is volt, mert a VII. táblázat kísérleti mátrixát a IV. táblázatban található 23 kísérleti terv mátrixából hoztuk létre, annak az oszlopvektorait adtuk át az új faktoroknak, és az x5 faktor éppen az x1x2 kölcsönhatás oszlopát kapta. Ilyen viszonylag egyszerű és áttekinthető esetben úgy tűnik, nincs is szükség a meghatározó kontraszt fogalmára, de sok faktor és sok kölcsönhatás esetén nagy segítséget jelent.

Mint már megállapítottuk, a Box-Wilson módszer alkalmazása esetén minden faktor szintjét egyszerre, egyetlen lépéssel változtatjuk meg az első kísérletsorozatban. Ezután megvizsgáljuk, melyik faktor módosítása milyen mértékben javította vagy rontotta az optimalizációs paraméter értékét, és ennek alapján tervezzük meg a következő kísérletsorozatot. Az egyes faktorok hatásának meghatározásánál elegendő a változás irányát és nagyságát (tulajdonképpen a válasz-függvény meredekségét az adott faktor irányában) megtudnunk ahhoz, hogy megtervezzük a következő lépést. A meredekséget a faktor két értékének ismeretében határozhatjuk meg, amint az a 3.1. ábrán látható

Mivel az n-dimenziós kísérleti térben egy-egy faktor irányában egy lépésben csak két adatunk van, erre a 2 pontra csak egyenes fektethető, magasabb rendű görbe nem. Ezért a mérési adatok alapján meghatározandó kísérleti felületet, azaz az összes faktor együttes hatását az előzőek értelmében egy lineáris modellel (regressziós függvénnyel) írhatjuk le:

y = b0x0+b1x1 + b2x2 + b3x3 + … +bnxn

A b együtthatók meghatározása a kísérleti mátrix segítségével nagyon egyszerű. Minden faktor előjelei a saját oszlopvektorában találhatók. Az y kísérleti eredmények oszlopvektorát skalárisan össze kell szorozni az adott faktor oszlop-vektorával, majd képezni kell az oszlopvektor elemeinek összegét. Az összeget osztani kell az oszlop elemeinek számával. Matematikailag az előzőek szerint az alábbi kifejezéssel fogalmazhatjuk meg:

bj = $\frac{{{\displaystyle \sum }}_{\text{i=1}}^{\text{N}}\text{xji yi}}{\text{N}}$

i=1, 2, 3…, Na kísérleti beállítások sorszáma

j= 0, 1, 2…, ka faktor sorszáma

Nem biztos azonban, hogy a kísérleti felületet valóban jól lehet közelíteni lineáris modellel. A kísérleti felület nemlinearitása gyakran abból ered, hogy két faktor között kölcsönhatás, interakció van (az egyik faktor változása magával vonja valamelyik másik faktor változását is).

A kölcsönhatásban álló két faktor közötti kapcsolat megfogalmazására alkalmazhatjuk pl. a két faktor szorzatát! (Természetesen ez is közelítés, de a tapasztalat szerint általában nem rossz közelítés.) Két faktor esetében ekkor a modell a következő képen alakul:

y = b0x0+b1x1 + b2x2 + b12x1x2 + b3x3 + … +bnxn

A három faktor összes lehetséges kölcsönhatásának leírásával pedig az alábbi függvénykapcsolathoz (regressziós függvényhez) jutunk:

y=b0+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b12x1x2+b123x1x2x3

A teljes faktoriális kísérlet lehetővé teszi a b12, b13, b23, b123, stb. együttható numerikus becslését is. A becsléshez az oszlopok összeszorzásának szabálya szerint előállítjuk a két faktor szorzatának oszlopvektorát. Ez lesz az interakció oszlopvektora. Az interakciónak megfelelő együttható kiszámításában ezt az új oszlopvektort ugyanúgy használjuk, mint bármelyik oszlopvektort. Ezáltal lehetővé válik a kölcsönhatások súlyának, fontosságának meghatározása.

Mindez viszont csak akkor lenne igaz, ha végtelen sok mérés (kísérlet) alapján határoznánk meg a b együtthatók értékeit. Azonban a kísérletből, amely véges számú beállítást tartalmaz, csupán becsléseket kaphatunk a b együtthatókra, és ezért helyesebb lett volna a modellt „körülbelül egyenlő” jellel, az alábbi alakban írni fel:

y ≈ b0x0 + b1x1 + b2x2 + b12x12 + b3x3 +... +bnxn

A pontos értékeket, amelyeket végtelen sok mérés alapján kapnánk meg, görög betűkkel szokás írni:

μ = β0x0 + β1x1 + β2x2 + β12x12 + β3x3 … + βnxn

A b „tapasztalati” együtthatók a β „elméleti” együtthatóknak valamilyen hibával terhelt becslései. A b0 együtthatóra nézve

$$\text{b0}\to \text{β0}+{\displaystyle \sum _{\text{j}=\text{1}}^{\text{k}}\text{βjj}}$$

ahol β0 a b0 becsült értéke, és

$${\displaystyle \sum _{\text{j}=\text{1}}^{\text{k}}\text{βjj}}$$

a hiba, amely abból ered, hogy egyszerű lineáris modellt alkalmaztunk, és a négyzetes tagokat elhanyagoltuk. Ez a hiba végtelen sok mérés estén is megmarad, tehát a b0 együttható becslése pontatlan, vagyis „torzított”. A többi együttható becslése viszont torzítatlan, azaz írható:

β1→b1, β2→b2, β12→b12, …

A kísérletek elvégzése során számtalan hiba terheli a mérési eredményt. Ezért a kísérleti beállítások változatlan körülmények közötti megismétlése esetén sem kapunk azonos értéket az előző kísérleti eredménnyel. Másrészt a kísérleti terv különbözőbeállításaival a különböző faktorhatások miatt is eltérő mérési eredményeket kapunk az optimalizációs paraméterre nézve.

Szükség van tehát egy olyan módszerre, amellyel meghatározhatjuk, hogy az optimalizációs paraméter eltéréseit véletlen hibák, vagy a faktorhatások okozzák.

A véletlen hibák kiszűréséhez ismételt kísérleteket kell végezni. Megtehetjük, hogy csak egyes beállításokat ismétlünk meg, de megismételhetjük a teljes kísérletsorozatot is. Az ismétlések száma lehet egy, de lehet több is. Minél több ismétlést végzünk, annál nagyobb biztonsággal kapunk választ a kérdéseinkre.

Ha a teljes kísérletsorozatot ismételjük meg egyszer vagy többször, a kísérletek kiértékelése egyszerűbb, mint akkor, ha csak egyes beállításokat ismétlünk meg. A továbbiakban azt a módszert ismertetjük, amikor a teljes kísérletsorozatot ismételjük meg.

Az ismételt mérések alapján a következő vizsgálatokat végezhetjük el.

A legfontosabb kérdés, hogy maga a modell megfelelően írja-e le a vizsgált folyamatot, azaz azonos körülmények között közel azonos eredménnyel megismételhető-e a kísérlet. Ezt a kérdést úgy szokták feltenni, hogy a modell adekvát-e. Ha adekvát, akkor érdemes tovább folytatni a kísérleteket, és új meg új beállítás-sorozatokkal egyre jobban megközelíteni az optimumot.

A kísérletek megismételhetőségét az optimalizációs paraméter szórásnégyzetének vagy más néven reprodukálhatósági szórásnégyzetének meghatározása alapján lehet megítélni.

Az optimalizációs paraméter szórásnégyzetét az alábbi módon határozhatjuk meg:

Ha a kísérletet j=1…n –szer ismételjük meg, akkor képezni kell az n párhuzamos megfigyelést tartalmazó kísérleti beállításhoz tartozó korrigált tapasztalati szórásnégyzetet:

$$s^2=\frac{{\displaystyle \sum _{j=1}^n{(y_j-\overline{y})}^2}}{n-1}$$

majd ezeknek meg kell határozni az átlagát, és ez lesz az optimalizációs paraméter szórásnégyzete:

$$s_{(y)}{}^2=\frac{{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^n{{\text{(y}}_{\text{ij}}\text{-}{\overline{\text{y}}}_{\text{i}}\text{)}}^{\text{2}}}}}{\text{N(n-1)}}$$

Ha meghatároztuk az optimalizációs paraméter szórásnégyzetét, el kell dönteni, hogy ennek alapján meghatározható-e az optimalizációs paraméter legjobb értéke, vagyis a jel (a faktorok hatása) kiemelkedik-e a zajból (a véletlen hibákból).

Az együtthatók meghatározása után meg kell vizsgálni, hogy az együtthatók szignifikánsak-e, azaz a kapott regressziós függvény meredeksége minden irányban jelentős-e.

Minden egyes együttható szignifikancia vizsgálatát egymástól függetlenül el kell végezni. Az együtthatók szignifikanciáját a Student-féle t-próbán alapuló megbízhatósági intervallummeghatározása alapján döntjük el.

Először meg kell határozni az együtthatók szórásnégyzetét:

$$s_{(b_j)}^2=\frac{s^2{}_{(y)}}{N}$$

A képletből látható, hogy valamennyi együttható szórásnégyzete megegyezik egymással, minthogy ez csak a kísérleti hibától és a kísérleti beállítások számától függ. Innen a regressziós együtthatók szórása:

$$s_{(b_j)}^{}=+\sqrt{s_{(b_j)}^2}$$

Innen pedig az együtthatók megbízhatósági intervallumának fél szélessége:

$$\Delta b_j=t{s}_{(b_j)}^{}$$

Ahol t a Student-féle t-próba táblázati értéke olyan szabadságfok mellett, amilyennel az együtthatók szórásnégyzetét meghatároztuk, és a megválasztott szignifikancia-szint mellett (ez általában 0,05).

Az együttható szignifikáns, ha abszolút értéke nagyobb a megbízhatósági intervallum fél szélességénél.

Az átlag és a szórásnégyzet azonban csak akkor alkalmazható a legvalószínűbb y érték és a legvalószínűbb y eltérések jellemzésére, ha az y optimalizációs paraméter normál eloszlású. Ha nincs lehetőség normalitás vizsgálatra pl. χ2 próbával, amihez elegendő számú (legalább 10) ismétlésre volna szükség, akkor azt kell megvizsgálni, hogy a tapasztalati szórásnégyzetek azonos elméleti szórásnégyzethez tartoznak-e. Ebben az esetben a tapasztalati szórásnégyzetek azonosnak tekinthetők. Tehát voltaképpen azt kell ellenőrizni, hogy a tapasztalati szórásnégyzetek azonosak. Ennek a vizsgálatára a következő számításokat lehet végezni:

Minden kísérletnél vagy mérésnél előfordulhatnak véletlenszerűen durva hibák (például hibás leolvasás, áramkimaradás, műszerhiba vagy emberi figyelmetlenség miatt). Ha ezeket már a kísérlet közben észrevesszük, azonnal ki kell hagyni az eredmények közül. Azonban sokszor elkerüli a figyelmet a durva hiba oka, és csak a mérési eredmények vizsgálata során válik gyanússá némelyik adat. Az ilyen adatok kiszűrésére egy egyszerű módszer javasolható.

Képezzük az alábbi számértéket:

$$v=\frac{(y-\overline{y})}{\text{s}}$$

Itt most y a „gyanús” kísérleti eredmény,

$$\overline{y}$$a többi eredmény átlaga, a kiugró értéket figyelmen kívül hagyva

sa többi eredmény szórása, a kiugró értéket figyelmen kívül hagyva

A „v” értéket össze kell hasonlítani egy táblázati értékkel (l. Függelék).

Ahhoz, hogy a külső körülmények (hőmérséklet, nyersanyag, évszakok változása, a kísérletet végző személyek változása, stb) által okozott szisztematikus hibák hatását kiszűrjük, javasolható a mátrix kísérleti beállításaiból véletlen sorozatok képzése: a kísérleti beállítások végrehajtási sorrendjét véletlenszerűen kell kialakítani, vagyis a kísérletek időpontjait randomizálni kell (l. Függelék).

A tovább lépéshez, vagyis a kísérleti beállítások optimalizációjához el kell dönteni, hogy melyik faktor irányában érdemes tovább lépni. Ennek érdekében meg kell vizsgálni, hogy az egyes faktorhatások (b meredekségek) szignifikánsak-e, vagyis valóban hatásosak-e. A nem szignifikáns faktorokat a további vizsgálatból általában ki lehet hagyni, és ez által a továbblépéshez szükséges kísérletek száma csökkenhet. Gondolni kell azonban arra is, hogy előfordulhat olyan eset, amikor a kísérleti mező egyik területén nem szignifikáns faktor más területen szignifikáns lehet. Ez főleg olyankor fordulhat elő, amikor a kísérleteket az optimumtól nagyon távoli beállításokkal kezdjük el.

Az együtthatók szignifikanciáját több módszerrel is vizsgálhatjuk. Az egyik lehetséges módszer, hogy először szórás analízissel megvizsgáljuk, hogy az együtthatók között van-e szignifikáns eltérés.

Ha a vizsgálat azt mutatja, hogy nincs az együtthatók között szignifikáns eltérés, akkor ebből az alábbi következtetések vonhatók le:

Ha a vizsgálat azt mutatja, hogy van az együtthatók között szignifikáns eltérés, akkor a Student-féle t-próbával egyenként megvizsgálhatjuk a 0-tól eltérő b együtthatók szignifikanciáját, és amelyik nem bizonyul szignifikánsnak, azt (esetleg csak átmenetileg) kihagyhatjuk a következő lépés megtervezésénél.