8. fejezet - Holográfia a háromdimenziós megjelenítésben és a méréstechnikában
A holográfia a megjelenítésben és a méréstechnikában egyaránt fontos szerepet tölt be, alkalmazása elterjedt. A továbbiakban a holográfiához kapcsolódó alapfogalmakat és alkalmazásokat tárgyaljuk.
8.1. A holográfia alapelvei
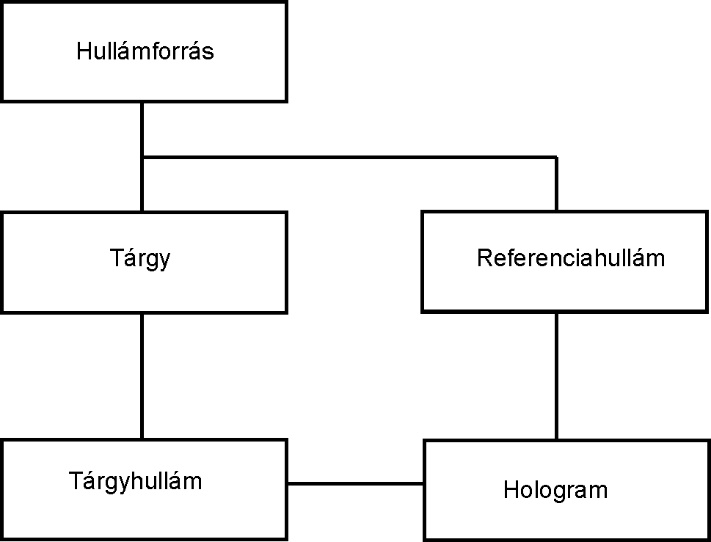
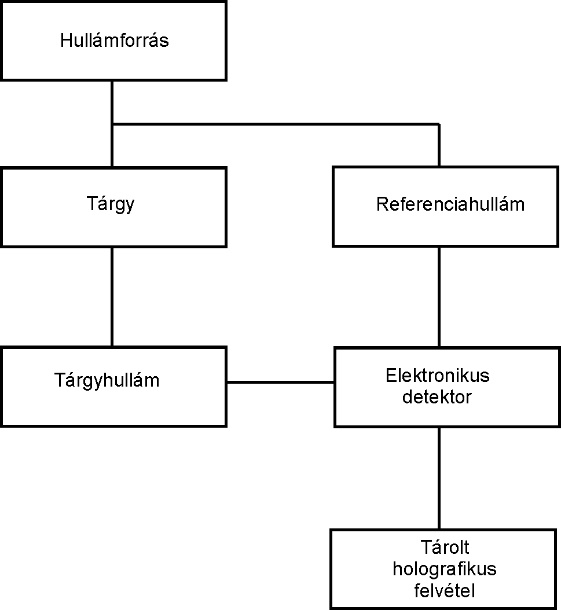
Gábor Dénes által kidolgozott, és elméleti úton megalapozott módszerben eredetileg egy koherens forrásból a tárgyra érkező fényhullám szóródott, és ezt a szóródó hullámot, amely már információt hordozott a tárgy felületéről interferáltatták egy referenciahullámmal. Ez a hullám – a tárgyhullám –, amely tulajdonképpen egy külső behatás nélkül terjedő koherens nyaláb, a lényes információt tartalmazó hullámfront. A tárgyhullám, és a vele interferáló referenciahullám az a két hullámcsomag, amelyek a találkozási helyükön elhelyezett érzékelőn – amely a fejlesztések kezdeti időszakában klasszikus értelemben vett, ezüsthalogén alapú fotólemezen volt –, találkozik, és interferenciajelenséget hoz létre. A keletkező hatás az interferenciacsíkok változó elrendezésében ölt alakot.
Egy holografikus mérőelrendezés létrehozása előtt célszerű áttekinteni a jelenség megértéséhez szükséges fizikai alapokat, elsősorban a hullámoptika eszköztárát alkalmazva. Egy, a tárgypontra érkező hullám visszaverődve egy hullámfrontot alkot, mivel a diffrakció jelensége miatt a tárgy minden egyes pontja egy-egy elemi gömbhullám forrása. Ezen – a tárgy bevilágított felületéről érkező – gömbhullámok szuperpozíciója alkotja a tárgyhullámot, amely tartalmazza a forrásként szolgáló tárgy teljes képi információját. Ez a hullám két paraméterrel jellemezhető:
-
az amplitúdóval, amely a fény energetikai paramétereivel áll kapcsolatban, valamint
-
a fázissal, amely a tárgy formájáról árulkodik.
A klasszikus fotográfia esetén, amikor a fényérzékeny réteget ezüsthalogén kristályok alkotják, a felvételkor a fázisinformáció elvész.. Így a tárgyhullám nem állítható vissza teljes egészében, még refrakción alapuló, vagy egyéb speciális optikai elem alkalmazásával sem. A fázisinformáció rögzítéséhez és tárolásához szükség van egy kiegészítő hullámra, az úgynevezett referenciahullámra, mely hullámtani értelemben vett tulajdonságaiban megegyezik a tárgyat megvilágító fényforrás által keltett hullámmal, azaz vele koherens. A hullámoknak tehát koherenseknek, vagyis állandónak és korlátosnak kell lenniük. A koherens hullámok egymásra hatása a szuperpozíció elve alapján valósul meg - ez a jelenség az interferencia. A koherencia, mint jelenség jellemzésénél megkülönböztetünk térbeli és időbeli koherenciát. Térbeli koherencia alatt egy hullámfront különböző részeinek korrelációját értjük, míg az időbeli koherencia a hullám saját magával való korrelációja különböző időpillanatokban. Holografikus alkalmazás esetén a hullámnak térben és időben is koherensnek kell lennie. Mivel a kísérletekben egyetlen koherens fényforrást alkalmaznak, így a hullámok önmagukkal és egymással való koherenciája is biztosított. [8.47.]
8.2. A holografikus felvétel
Felvételkor a koherens fényforrást egy nyalábosztó vagy részben áteresztő tükör segítségével több részre osztják, és a tárgyat egy vagy több hullámfronttal világítják meg. A visszaverődő tárgyhullám egyesül a referenciahullámmal, és létrehoz egy interferencia jelenséget. [8.27.] , [8.48.] Tehát a két beérkező hullám – a tárgy- és a referenciahullám - interferál, síkhullámok esetén interferenciacsíkok, sík- és gömbhullám találkozása esetén interferenciagyűrűk alakulnak ki. Ezek a csíkrendszerek általában mikrométeres nagyságrendűek, tehát összevethetők a fényforrás hullámhosszával. Statikus esetben az interferenciacsíkok alakja a kialakuláskor és a regisztrálás folyamán független az időtől, így kialakul egy diffrakciós rács [8.47.] .
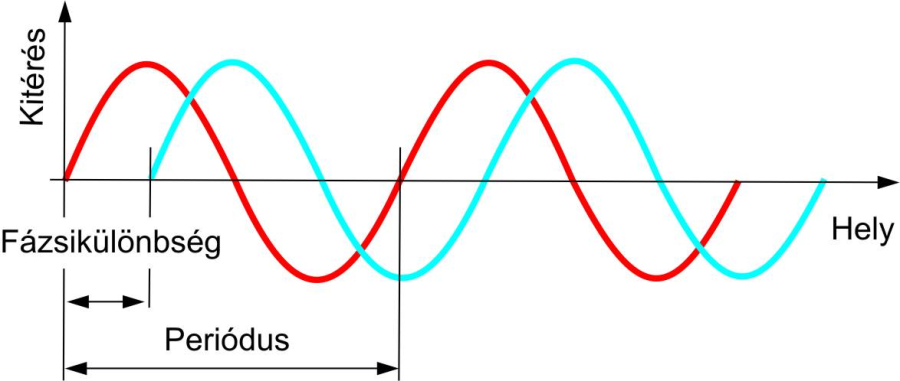
A hullám megfelel egy térben terjedő rezgésnek, ami a kiindulási pontban:
Ahol A a hullám amplitúdója, φ a hullám fázisa t=0 esetére,
a hullám körfrekvenciája. A T periódusidő alatt teszi meg a c sebességgel haladó hullám a λ hullámhossznyi távolságot, ennek reciprokjaként kapjuk meg a fázist:
Egy adott z pontban az oszcilláció:
Ahol:
A holográfiában használt lézerek fontos tulajdonsága, hogy lineárisan polarizáltak, vagyis a rezgés iránya állandó.
Az előző egyenlet Euler-féle átalakítása után:
Itt az egyenlet a valós része fontos. Mivel a hullám frekvenciája igen magas tartományba esik, ezért közvetlenül nem figyelhető meg. Mérésenként több oszcillációs periódusidőbeli átlagát kapjuk meg, így az ωt rész elhagyható. A megmaradt rész a komplex amplitúdó [8.47.] :
A Gábor Dénes által leírt, és a róla elnevezett Gábor-féle on-axis hologram alapelve igen egyszerű, és rendkívül látványos formában demonstrálja a holografikus hatást. Azonban – ahogy ezt már írtuk – a forrásra vonatkozó megkötés komoly problémát jelentett. A lézerek megjelenése rendkívül jó hatással volt a holográfiára, dinamikus fejlődését indította el világszerte. Leith és Upatnieks 1962-ben alkalmazták először lézeres forrással az úgynevezett off-axis hologramot [8.45.] , [8.22.] .
Az általuk választott megoldás egyrészt elválasztotta a valós képet a virtuális képtől, és lehetővé tette, hogy a referenciasugár és a tárgyról érkező sugarak külön legyenek kezelhetők. Így tulajdonképpen a tárgy tetszőleges irányból és oldalról meg lehetett világítva, egy alkalmasan megválasztott hullámfronttal. Az általuk javasolt elrendezésben a beeső lézernyalábot kettéosztották, és irányváltoztatásra kényszerítve ezek közül az egyiket, közvetlenül a tárgyra vetítették azt. Az érzékelő lemezen a két sugár interferenciaképe rögzült. A nagyobb hullámfrontszögek miatt, az igényelt nagy térfrekvenciához nagy felbontású holografikus filmre volt szükség, és biztosítani kellett a rezgésmentes beállítást is.
8.2.1. A vastag hologram
Az korábban alkalmazott hologramoknál a nyersanyagon a fényérzékeny réteg vastagsága nem volt számottevő, a jelenséget eredményező hullámok hullámhosszához képest. Az ilyen típusú hologramokat síkhologramoknak vagy vékony hologramoknak nevezzük. Ha az érzékelő fényérzékeny, rögzítő rétege, azaz az emulzió vastag a hullámhosszhoz képest (annak többszöröse), az interferenciacsíkok sorozata a vastagság mentén is létrejöhet. A rekonstrukció során a hullámfront visszaállítását generáló referencia-hullámfront ezeken az emulzió menti interferenciacsík-sorozatokon hatol keresztül [8.7.] , [8.8.] , [8.9.] .
Az ilyen típusú hologramoknak, a vastag emulziónak az egyik kiemelkedő tulajdonsága, hogy képes ugyanazon fotoemulzióból többszörös holografikus látványt előállítani. Ez egyben azt is jelenti, hogy sok hologram készítése válik lehetővé ugyanazon a fényérzékeny rétegben, az ezeket előállító referencianyalábok pedig különböző szögűek lehetnek [8.54.] . A későbbi rekonstrukció során a referencianyaláb szögét változtatva, mindegyik rekonstruált hullámfront külön-külön jelenik meg, és egyenként vizsgálható. Ez az alapgondolata a holografikus mozgókép létrehozásának. Egy ilyen, vastag emulziójú, többszörös hologram rekonstrukciója során a referencianyaláb szögét megfelelő időben, megfelelő módon változtatjuk.
A holográfia mozgó filmhez hasonló alkalmazásához, például egy tükör forgásával a szinkronizált lézersugár egymás utáni impulzusai segítségével kísérelték meg, hogy a hologramok rekonstruálásával filmszerű képek sorozatát állítsák elő. Ez úgy is magyarázható, hogy a vastag hologramot vékony hologramok rendezett halmazának foghatjuk fel. Ilyenkor bármilyen eltérés a felvételkor használt referenciasugár irányától a kép elvesztéséhez vezethet. Ezt a jelenséget a szakirodalom irányszelektivitásnak nevezi. Ennek az elvnek a segítségével ugyanarra a holografikus emulzióra több hologramot lehet felvenni. A felvételkor a különböző referencianyalábok más és más irányból érik a holografikus emulziót, és ez érvényesül a rekonstrukció során is. A vastag emulziójú hologramok egy másik rendkívül fontos tulajdonsága az úgynevezett színszelektivitás, ami azt jelenti, hogy összetett (például fehér) fénnyel rekonstruálva egy vastag hologramot, a hullámfront színe megegyezik a felvételkori forrás színével. Vastag hologramot először Jurij Nyikolajevics Denisjuk (1927-2006) készített 1962-ben, felhasználva a színes fotográfiai nyersanyagok történetéből jól ismert Lippmann emulziót.
8.2.2. A rekonstrukció
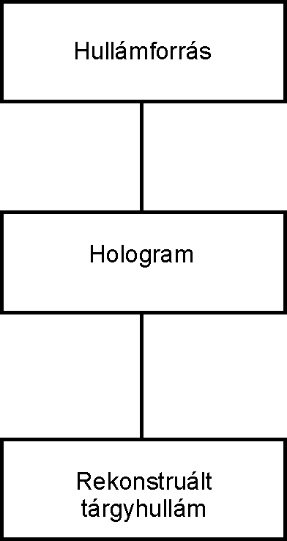
Az ezüsthalogén alapú nyersanyag feldolgozásához szükséges fotokémiai eljárásokat követően lehetőség nyílik az eredeti tárgyról szóródó hullámfront visszaállítására. A holografikus lemezen rögzített interferenciakép diffraktálja a beérkező hullámfrontot, és visszaállítja az eredeti tárgyhullámot. Ilyenkor nemcsak az eredeti hullám jelenik meg, hanem más kísérő jelenségek is tapasztalhatók.
8.2.3. A felvétel és rekonstrukció
A holografikus rögzítés során nem alkalmazunk lencsés vagy tükrös leképezést. A tárgyról érkező hullámfrontot egy másik, az úgynevezett referencia-hullámfronttal interferáltatjuk, a kölcsönhatásukat így kódoljuk, és rögzítjük. Ennek feltétele, hogy mindkét hullámfront koherens legyen, ezért a gyakorlatban lézert alkalmazunk. A hologramlemez síkjában az interferenciakép kerül rögzítésre. Amikor a rekonstrukció során a hologramot a változatlan referencia-hullámfronttal megvilágítjuk, ezen az interferenciás csíkrendszeren – amely információt tartalmaz a tárgyhullámról, tehát a tárgyról – elhajlik, azaz diffraktálódik a hullámfront.
Gábor Dénes érdeme, hogy elméleti úton levezette, és kísérleti módszerekkel igazolta, hogy a rekonstrukció során diffrakcióval keletkező hullámfrontok egyike megegyezik azzal a hullámfronttal, amely felvételkor a hologramlemezre érkezett a tárgyról. Ezért a rekonstrukció során a megfigyelő érzékelőjére ugyanaz a hullámfront érkezik, mint amilyen a tárgyról érkezett volna. A hologramot szemlélve a rekonstruált kép tulajdonságai megegyeznek a valósággal úgy a perspektíva, mint a takarások tekintetében.
8.2.4. Holografikus optikai elemek
A hologramból álló optikai eszköz, amely könnyen előállítható, lencseként, tükörként, rácsként, nyalábosztóként működik. A holografikus optikai elemek készítésének alapgondolata, hogy az egyes optikai elemek speciális hullámfrontot hoznak létre. Ha ezt a hullámfrontot használjuk a hologram készítése során tárgyhullámként, akkor a rekonstrukciókor ezt a hullámfrontot újra előállíthatjuk. Tehát a hologramunk úgy fog viselkedni, mint az eredeti optikai elem.
8.2.5. Digitális holográfia
A hagyományos holografikus eljárások használatának egyik fő hátránya, hogy az exponált holografikus lemezt fotokémiai eljárással kell kidolgozni. Ehhez laboratóriumi körülmények szükségesek, és a felvételt rögzítő nyersanyag is viszonylag drága. A hagyományos holografikus nyersanyagok speciális spektrális érzékenységgel rendelkeznek, és szenzitometriai szempontból is viszonylag alacsony érzékenységűek.
E problémákra kínál alternatívát a digitális holográfia, ami azt jelenti, hogy a hologram lemez helyett általában elektronikus detektorral rögzítik a tárgyhullám és a referenciahullám által előállított interferenciaképet. A rögzített hologramra jellemző:
-
számítógépen tárolják,
-
a rekonstrukció, azaz a kép megjelenítése numerikus feldolgozás segítségével történik.
A módszer hátrányai:
-
a jelenlegi, kereskedelmi forgalomban kapható digitális kamerák felbontása jóval kisebb, mint a holografikus lemezeké,
-
a pixelméret legalább egy nagyságrenddel haladja meg a hagyományos holografikus lemez felbontását.
Mivel a pixelek mérete meghatározza a maximális térfrekvenciát,
-
a tárgynyaláb és a referencianyaláb csaknem azonos irányból kell, hogy a kamera félvezető lapkájára essen.
-
a rekonstruált kép felbontása jóval kisebb, mint egy hagyományos hologram által rekonstruált képé.
8.3. Hullámoptikai tárgyalásmód
A hologram készítésének és megjelenítésének hullámoptikai tárgyalása szempontjából két, jól elkülöníthető fázist különböztetünk meg: a holografikus felvétel készítését és a rekonstrukciót.
8.3.1. A holografikus felvétel
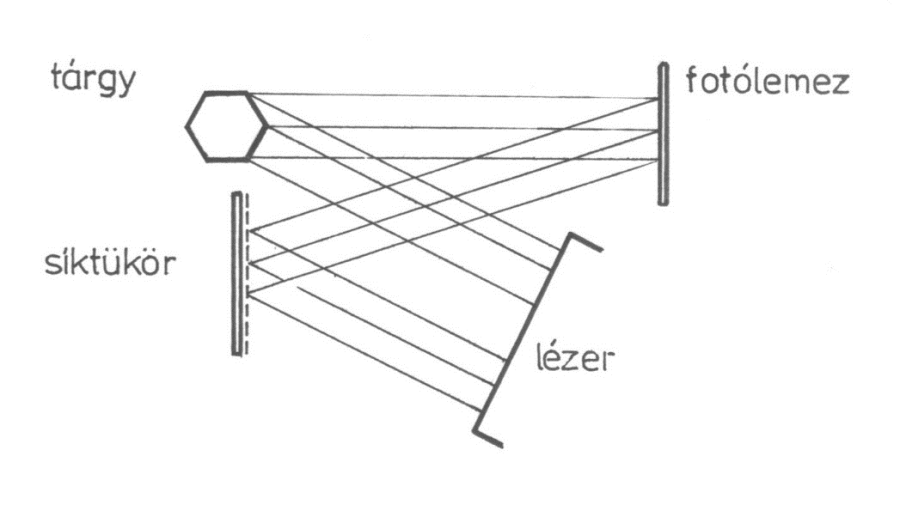
A (8.6. ábra) ábrán látható elrendezésben a koherens fényforrásból kilépő hullámok egyrészt a vizsgálandó tárgyra, másrészt a síktükörre vetülnek. A tárgyról visszaverődő – arról információt hordozó – tárgyhullámok a holografikus lemez síkjában találkoznak a síktükörről visszaverődő, úgynevezett referenciahullámokkal, és ott egy sajátságos, intenzitáseloszlást hoznak létre. Ennek fotofizikai, illetve fotokémia úton történő rögzítésével áll elő a hologram. A tárgy felületéről a holografikus lemez síkjába érkező hullám időfüggvénye:
ahol (x,y) a holografikus lemez egy pontjának koordinátája,
az amplitúdó, és
pedig a fáziseloszlás. A holografikus lemezt azonban eléri a síktükörről visszaverődő referenciahullám is, melynek időfüggvénye:
A
és a
egymással koherens hullámok, így a holografikus lemez síkjában az eredő hullám időfüggvénye a szuperpozíció elve alapján:
A lemez fotokémia kidolgozását követően, a létrejövő feketedés arányos az expozíció során a lemezt érő fényenergia eloszlásával:
Behelyettesítve:
Az egyszerűbb kezelhetőség érdekében térjünk át a trigonometrikus alakra:
Ezután
Átalakítva és rendezve
Lineáris jellegű rögzítést feltételezve – ami kissé eltér a valóságos nyersanyag tulajdonságaitól, azonban ez a közelítés a jelenség leírását nem zavarja – a holografikus lemez transzmissziója a kidolgozás után:
Vezessük be a következő jelölést:
így
Tehát ez az összefüggés írja le a hologram transzmisszió-eloszlását, tartalmazza a tárgy- és a referenciahullám amplitúdó- és fázisadatait.
8.3.2. A rekonstrukció
A 8.7. ábra szerinti elrendezésben, a már kidolgozott holografikus lemezen, azaz a hologramon bocsátjuk keresztül a felvétel készítésénél használt referenciahullámot. Az így létrejövő hullámfront időfüggvénye:
Behelyettesítve:
Rendezve, átalakítva és exponenciális alakra hozva:
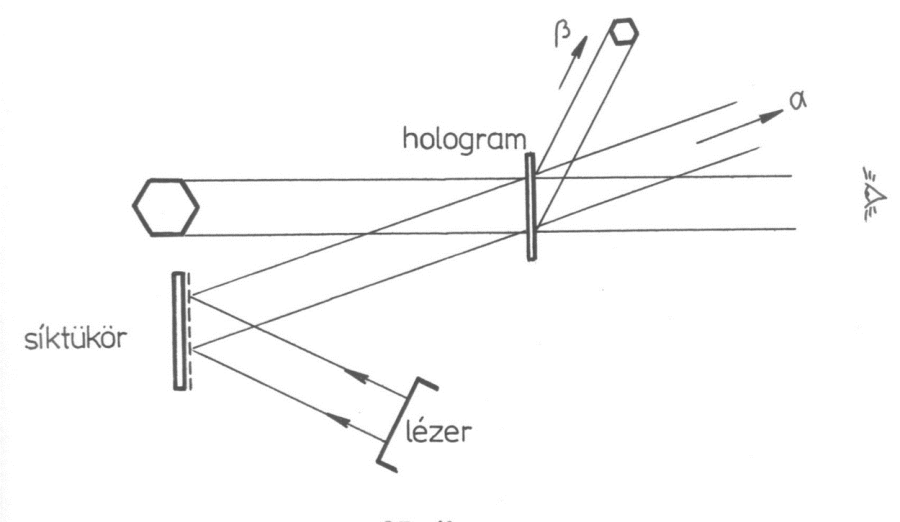
A fenti összefüggés első tagja egy tovahaladó, láthatatlan referenciahullámot jelöl. A második tagja egy amplitúdómodulált, és a referenciahullám fázisával megváltoztatott fáziseloszlású, és továbbhaladó hullámot jelent, mely a tárgy elhajlási képének keletkezésére utal, és a szemlélő számára láthatatlan marad. A harmadik tag az eredeti tárgyhullámmal arányos amplitúdójú hullámot jelent, amely a szemlélő számára megjeleníti a tárgy virtuális képét. Ha a rekonstrukció során lehetővé válik a keletkező hullámfrontok terjedési irány szerinti szétválasztása, akkor egyben lehetséges lesz azok független megfigyelése is. Ez azt is jelenti, hogy elő lehet állítani azt a hullámfrontot, amely eredetileg a felületről érkezett.
8.4. Holografikus interferometria
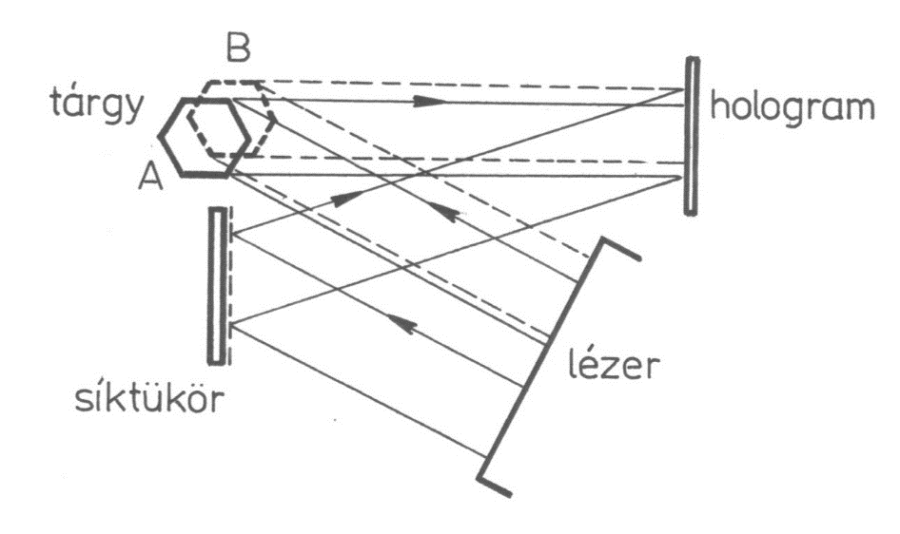
Ha a 8.8. ábra szerinti elrendezésben a tárgyról az A helyen hologram készül, majd áthelyezve a tárgyat a B helyre, és róla ismét egy hologramot készítünk ugyanarra a holografikus lemezre, majd ezt kidolgozva és rekonstruálva a referenciahullámmal, előáll a holografikus interferogram. A hologramon átnéző megfigyelő a tárgy háromdimenziós képén csíkokat lát. A csíkok a tárgy A és B állapota közötti elmozdulásról, vagy deformációról szolgáltatnak információt.
8.4.1. A holografikus interferométer
A holografikus interferométer segítségével két hullámfront hasonlítható össze interfereometrikusan. Az egyik hullámfrontot a már korábban részletesen tárgyalt, rekonstruált hullámfront képezi - ennek neve referens hullámfront. A másik hullámfront, amely a referens hullámfronttal interferál, többféle módon is előállítható, és ez az előállítási mód határozza meg a holografikus interferometria technikáját.
A technikák csoportosítása:
-
Valós idejű, vagy úgynevezett real-time holografikus interferometria. Itt a referens hullámfrontot közvetlenül a felületről szóródó hullámfronttal hasonlítjuk össze interferometrikusan. Előnye, hogy folyamatosan követhető a tárgy időbeni elmozdulása és deformációja.
-
A kétexpozíciós technika azt jelenti, hogy ugyanazon a lemezen található a két felvétel, egyiket a deformáció előtt a másik pedig utána készült. A rekonstrukció során a tárgy képén megjelennek az interferenciacsíkok.
-
A sandwich technika. Itt a vizsgálandó és a referens hullámfront két különböző holografikus lemezen, azonos referenciasugárral kerül rögzítésre. Ezek szimultán rekonstrukciójával állítható elő a holografikus interferogram.
A következő részben a kétexpozíciós technikával foglalkozunk részletesebben.
8.4.2. A kétexpozíciós holografikus interferometria technika
A (8.9. ábra) ábrán látható elrendezés segítségével készíthető kétexpozíciós holografikus interferogram. A két hullámfront rögzítése egyazon fotólemezre, egyazon referencianyalábbal történik.
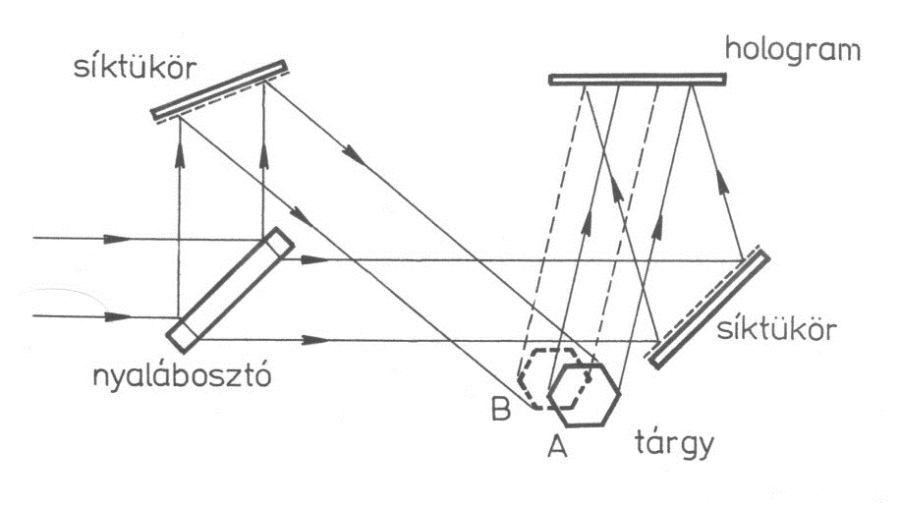
A fotólemez (x,y) pontjában legyen a tárgy A helyzetbeli felületéről a holografikus lemezre érkező hullámfront amplitúdója A1. Hasonlóan a tárgy B helyzetbeli felületéről érkező hullámfronté A2. Így a hullámfrontok komplex időfüggvényei
Illetve
A referencianyaláb időfüggvénye
Lineáris rögzítést és azonos expozíciós időket feltételezve, a holografikus lemez (x,y) pontjának feketedése arányos lesz a fényintenzitások összegével.
Kifejtve, áttérve a trigonometrikus jelölésekre, és elhagyva az (x,y) jelölést:
Előhívás után az optikai lemez transzmissziója:
Bevezetve:
Így
Ha ezt a lemezt a felvételkor használt referenciahullámmal rekonstruáljuk, akkor a keletkező hullámfront időfüggvénye a következő alakú lesz
Behelyettesítve τ értékét
A műveleteket elvégezve, és exponenciális alakra hozva a kifejezést
A fenti összefüggés leírja a kétexpozíciós technikával készített hologram rekonstruálása során keletkezett hullámfrontokat. Az összefüggés második tagjában felismerhető a két különböző időpontban rögzített hullámfront összege. A rekonstrukció után, ott ahol a tárgy A és B helyzete között eltérés volt, inteferenciacsíkok lesznek láthatók.
A kétexpozíciós holografikus interferometria előnyei és hátrányai a következőkben foglalhatók össze:
Előnyök:
-
Egyszerű és megbízható a holografikus interferogram elkészítése, és az interferométer kezelése.
-
A kétexpozíciós holografikus interferometria holografikus lemezének kidolgozása utáni deformációja nem jelentkezik az interferenciaképen.
Hátrányai:
-
A kétexpozíciós holografikus interferometria során keletkező interferenciakép csak a felület két állapota közötti eltérésekre vonatkozóan tartalmaz információkat.
-
A holografikus nyersanyag kidolgozása vegyszerigényes, a vegyszerek kezelésénél szigorú környezetvédelmi előírásokat kell betartani.
-
A nyersanyag felbontóképessége hatással van a méréstechnikai alkalmazhatóságra.
8.4.3. A holografikus interferogramok kiértékelése
A holografikus interferogramon megjelenő interferenciacsíkok a tárgy alakváltozásáról, illetve elmozdulásáról hordoznak információt. Ahhoz, hogy ezek az információk konkrét mérési adatokká, eredményekké válhassanak, olyan módszerekre van szükség, amelyek segítségével az interferogramok kiértékelhetők, tehát az alakváltozások és a deformációk mértéke számszerűsíthető. A gyakorlatban elsősorban a csíklokalizációs, a csíkszámlálásos, a kompenzációs és a fázistolásos módszert alkalmazzák.
8.5. Holografikus felvételi nyersanyagok
Cél a spektrálisan illesztett, nagyfelbontású és viszonylag nagy érzékenységű felvételi nyersanyag biztosítása. Erre kiválóan alkalmas az ezüsthalogén alapú emulzió (1873 Vogel).
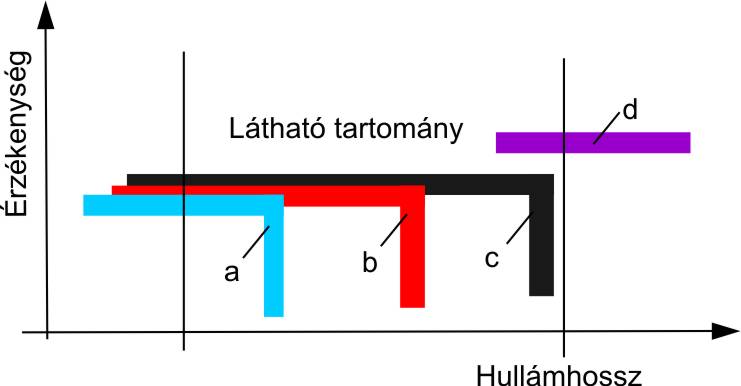
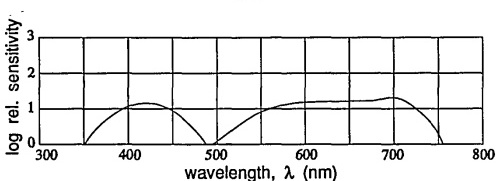
A holografikus felvételi nyersanyagok, melyek jellemzőit a 8.12. ábra szemlélteti:
-
Érzékenyítetlen ezüsthalogén (a görbe).
-
Ortokromatikus nyersanyag (b görbe).
-
(Szuper)Pánkromatikus nyersanyag (c görbe).
-
Infravörös nyersanyag (d görbe).
Holografikus nyersanyag céljára elsősorban a vörös, illetve a kékeszöld tartományban érzékeny nyersanyagot alkalmaznak, a holografikus technikákban használt lézertípusok miatt.
8.5.1. A nyersanyagok karakterisztikája
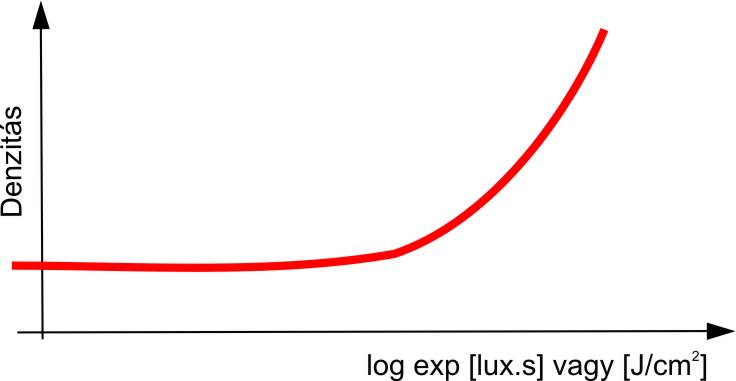
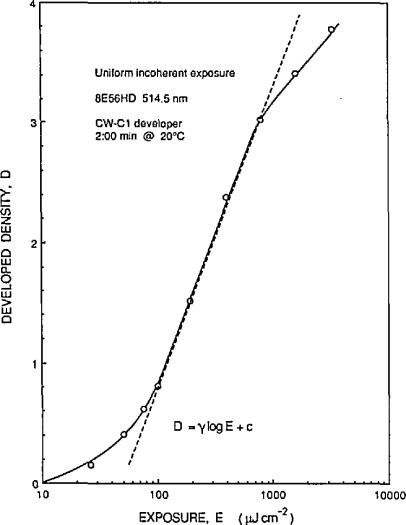
A 8.13. ábra függőleges tengelyén a denzitás található, amely a transzmissziós tényező reciprokának tízes alapú logaritmusa.
A vízszintes tengelyen a nyersanyaggal területegységenként közölt energiát, vagy az expozíció logaritmusát ábrázoljuk.
8.5.2. A nyersanyag felépítése
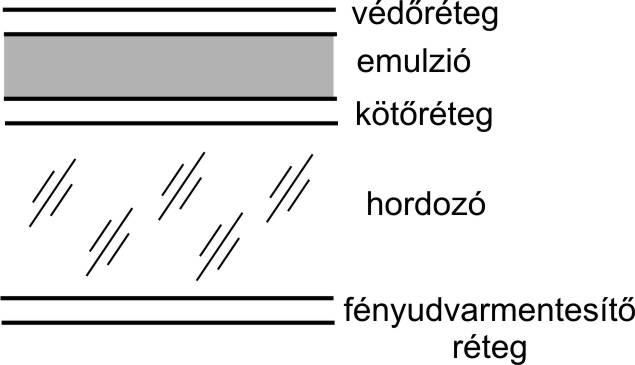
A klasszikus, ezüsthalogén alapú holografikus nyersanyag felépítése sokban hasonlít a fekete-fehér fotográfia nyersanyagéra. Felépítése a (8.15. ábra) ábrán látható.
8.5.3. Az ezüst halogén alapú holografikus nyersanyagok kidolgozása
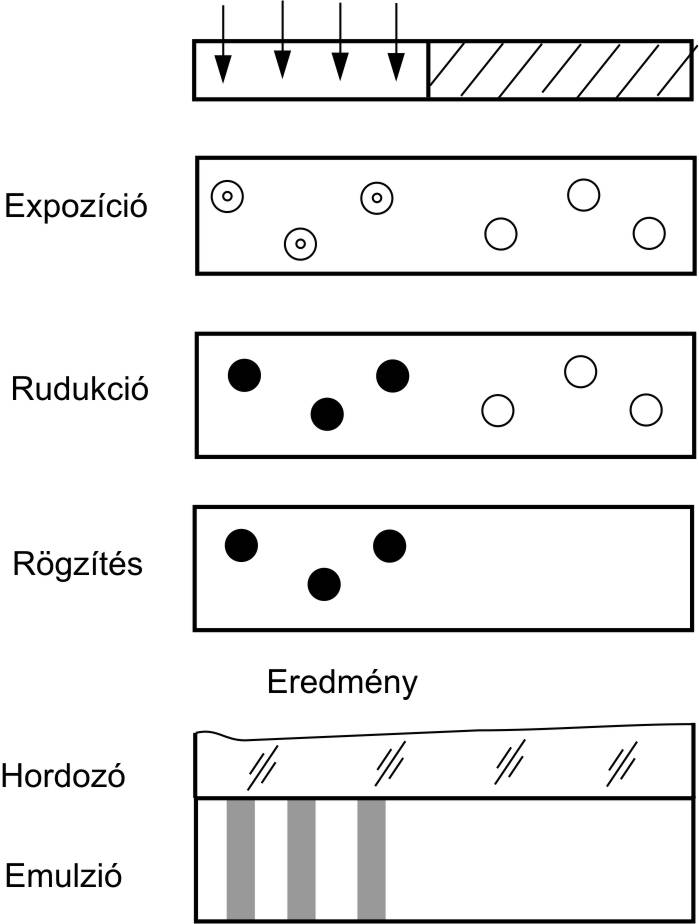
Amplitúdó hologram készítése során egyes ezüsthalogén kristályok exponálódnak, azaz fény éri őket, míg mások nem. Az így keletkezett, úgynevezett látens képben tehát jelen vannak a még nem exponált ezüsthalogén kristályok, illetve az exponáltak, amelyekben megtalálhatók az úgynevezett elemi ezüstcsíragócok. Ezt a látens képet kell egy fotokémiai folyamatnak alávetni, amely során első lépésben egy redukciós folyamat alatt az exponált ezüsthalogén kristályokban lévő elemi ezüstcsíragócok mentén megindul a redukció. Ennek során színezüst kristályok keletkeznek. A következő lépésben a rétegben maradt, nem exponált ezüsthalogént rögzítő oldat segítségével oldható sóvá kell alakítani, ami távozik a rétegből. A mosás és szárítás után megfigyelhető, hogy a fény érte helyeken fekete ezüstkristályok találhatók, míg a többi helyen csak az átlátszó emulzió látható, így lesz a kidolgozott nyersanyag az eredeti fényviszonyok negatívja. Az ilyen holografikus nyersanyag a rajta áthaladó referenciahullám intenzitását, azaz a vele kapcsolatban álló amplitúdót változtatja, modulálja a rekonstrukció során.
Fázis hologram kidolgozásának első lépése teljes mértékben megegyezik az amplitúdóhologram esetén leírtakkal. A következő lépésben azonban a réteget egy halványító-rögzítő fürdőnek kell alávetni. A fürdőben a nem exponált ezüsthalogén a rögzítő oldat segítségével oldható sóvá alakul, és távozik a rétegből, míg a kiredukált ezüst a halványítás hatására átlátszó, de az emulziótól eltérő törésmutatójú anyaggá válik. Így a rétegben a megvilágítástól függően különböző törésmutatójú helyek keletkeznek, ami azt eredményezi, hogy a rekonstrukció során, az azonos fázissal belépő refrenciahullám különböző fázisokkal fog kilépni, tehát az ilyen holografikus nyersanyag a rekonstrukció során a rajta áthaladó referenciahullám fázisát változtatja, modulálja.
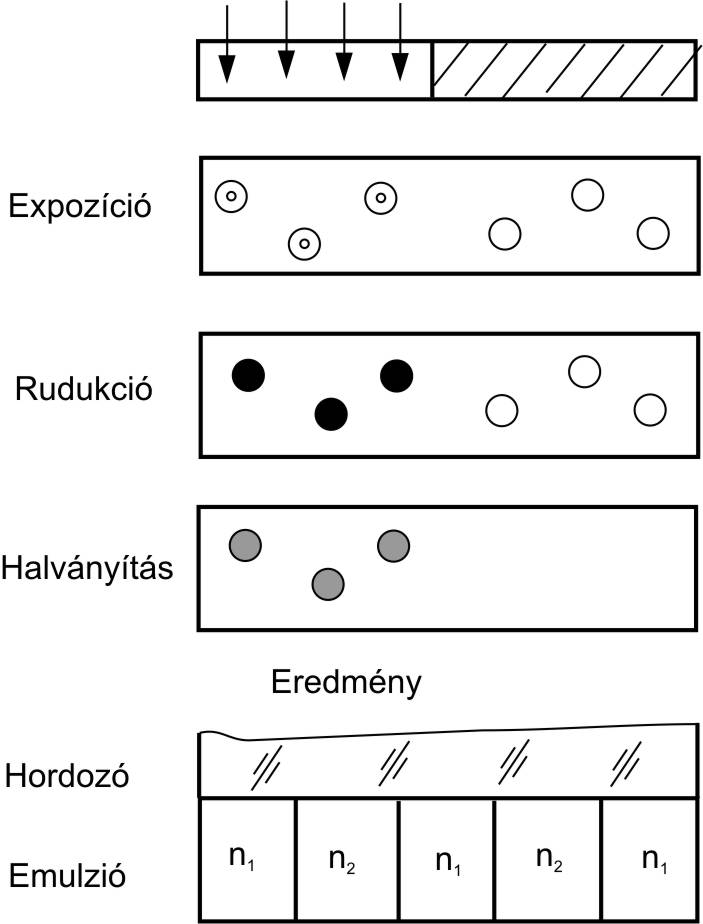
Vezessük be a hologramok jellemzésére az úgynevezett fényességet, ami a rekonstrukció során a diffraktált és a belépő hullámfrontok intenzitásának százalékos arányát jelenti! Ekkor az amplitúdó hologramok néhány százalékával szemben a fázis hologramok fényessége akár a harmincöt százalékot is elérheti.
8.5.4. Egyéb nyersanyagok
Az ezüsthalogén alapúak mellet más nyersanyagtípusok is elterjedtek, az alábbiakban ezeket ismertetjük.
8.5.4.1. Fotoreziszt emulzió
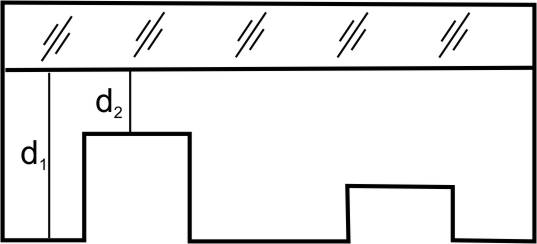
Az emulzió működésének alapja, hogy a megvilágított helyeken az úgynevezett „hívó oldatban” a réteg jobban megduzzad, mint a megvilágítatlan helyeken. Így ugyanolyan törésmutatójú, de különböző vastagságú helyek keletkeznek az emulzióban, tehát fázisrácsként viselkedik.
8.5.4.2. Termoplasztikus emulzió
Ebben az esetben három réteget alkalmazunk. Az üveg vagy polimer hordozón egy átlátszó, vékony SnO2 vezető réteg található. Ezt követi egy fényvezető és maga a termoplasztikus réteg. Az emulziót sötétben úgy érzékenyítik, hogy a vezető réteget földelik, a termoplasztikus réteget pedig körülbelül 15kV feszültség mellett feltöltik negatív töltésekkel. Ez a vezető rétegben pozitív töltést indukál. Az expozíció hatására a pozitív töltések a fényvezető réteg határára a negatív töltések közelébe vándorolnak. Egy rövid melegítés hatására a termoplasztikus réteg meglágyul, és felveszi a töltéseloszlás alakját. Lehűtéssel aztán rögzítik ezt az állapotot.
8.6. Ellenőrző kérdések
-
A holográfia egy háromdimenziós képrögzítési és rekonstruálási eljárás. Magyarázza el, mit értünk ebben az esetben a képrögzítés és a képrekonstruálás alatt! Mutassa be, hogy a folyamat miben különbözik a hagyományos értelemben vett képalkotástól!
-
Magyarázza meg, mit értünk térbeli és időbeli koherencia alatt!
-
A koherens hullámok egymásra hatása a szuperpozíció elve alapján valósul meg. Mi ez a jelenség, mi a hatása az interferencia kialakulására?
-
Ismertesse a holografikus felvétel és rekonstrukció folyamatát!
-
Mi a különbség az on-axis és az off-axis holografikus elrendezés között?
-
A holografikus optikai elemek készítésének alapgondolata, hogy az egyes optikai elemek speciális hullámfrontot állítanak elő. Ha ezt a hullámfrontot használjuk a hologram készítése során tárgyhullámként, akkor a rekonstrukció során azt újra előállíthatjuk. Mondjon példát holografikus optikai elem alkalmazására!
-
Melyek az előnyei és a hátrányai a digitális holográfiának?
-
Ismertesse a holografikus interferogramok típusait!
-
Magyarázza meg az ezüsthalogén alapú holografikus nyersanyag karakterisztikáját!
-
Az ezüsthalogén kristályok által alkotott látens kép szempontjából miben különbözik az amplitúdó és a fázis hologram?
-
Fázis hologram esetén a rekonstrukció alatt milyen fizikai-optikai jelenség játszódik le?
-
Ismertesse a fotoreziszt emulziót!
-
Ismertesse a termoplasztikus emulziót!
Hivatkozások
[8.1.] Optical holography. Univ. Press. 1984.
[8.2.] Holography technics and applications. proc. ECO1. Hamburg . 1988.
[8.3.] Holography and deformation analysis. Springer. 1985.
[8.4.] Handbook of holographic interferometry. Wiley. 2005.
[8.5.] Digital holography. Springer. 2005.
[8.6.] Modern optika mérnököknek és kutatóknak. Műszaki Könyvkiadó. Budapest . 1982.
[8.7.] Kísérleti fizika III. Tankönyvkiadó. Budapest . 1980.
[8.8.] Optika. Panem_McGraw-Hill. Budapest . 1998.
[8.9.] Holográfia optikai alkalmazásokkal. Műszaki Könyvkiadó. Budapest . 1973.
[8.10.] Methods of Digital Holography. Springer. 1980.
[8.11.] Digital Holography and Digital Image Processing : Principles, Methods, Algorithms. Kluwer Academic Publishers. 2005.
[8.12.] Digital Holography, Digital Hologram Recording, Numerical Reconstruction, and Related Techniques. Springer Verlag. 2005.
[8.13.] The Art and Science of Holography. Press Monograph. 2004.
[8.14.] Basics of Holography. Cambridge University Press. 2002.
[8.15.] Optical Holography. Cambridge University Press. 1996.
[8.16.] Látványholográfia, holografikus méréstechnika és digitális holográfa. Magyar Tudomány. pp. 1517-1520.. 2005.
[8.17.] A koherens optikai méréstechnika legújabb eredményei és hasznosítási lehetőségük a közúti közlekedésben. Innováció és fenntartható felszíni közlekedés konferencia. 2007.
[8.18.] Holographic Memory. Allerton Press. 1997.
[8.19.] Practical Holography. XII. SPIE. 1998.
[8.20.] Selected Papers on Fundamental Techniques in Holography. Milestone Series MS171. SPIE. 2001.
[8.21.] Selected Papers on Holographic Recording Materials. Milestone Series MS 130. SPIE. 1996.
[8.22.] The Art and Science of Holography. Press Monograph. 2004.
[8.23.] Optical Pattern Recognition: Using Holographic Techniques. Electronic Systems Engineering Series. Addison-Wesley. 1988.
[8.24.] Speckle Photography for Fluid Mechanics Measurements. Springer. 2005.
[8.25.] Basics of Interferometry. Academic Press. 2006.
[8.26.] Optical Interferometry. Academic Press. 2003.
[8.27.] Basics of Holography. Cambridge University Press. 2002.
[8.28.] Optical Holography. Cambridge University Press. 1996.
[8.29.] Hographic Visions: A history of New Science. Science and Computing Series. Oxford University Press. 2006.
[8.30.] The Complete Book of Holograms: How They Work and How to Make Them. John Wiley & Sons. 1987.
[8.31.] Holographic Interferometry: Principles and Methods. Vch Pub. 1996.
[8.32.] Three-Dimensional Holographic Imaging. Wiley-Interscience. 2002.
[8.33.] Holography for the New Millennium. Springer. 2002.
[8.34.] Digital Speckle Pattern Interferometry & Related Techniques. John Wiley & Sons. 2001.
[8.35.] Holographic Interferometry: Principles and Methods. Springer Series in Optical Sciences. Springer. 1994.
[8.36.] Practical Holography. Taylor & Francis. 2003.
[8.37.] Digital Holography: Digital Hologram Recording, Numerical Reconstruction, and Related Techniques. Springer. 2004.
[8.38.] Selected Papers on Holographic Interferometry: Applications. Milestone Series MS170. SPIE. 2001.
[8.39.] Electron Holography. Springer Series in Optical Sciences. Springer. 1999.
[8.40.] Holographic Interferometry. Wiley Series in Pure and Applied Optics. Wiley-Interscience. 1979.
[8.41.] Particle Field Holography. Cambridge Studies in Modern Optics. Cambridge University Press. 2005.
[8.42.] Selected Papers on Interferometry. Milestone Series MS28. SPIE. 1991.
[8.43.] Selected Papers on Interference, Interferometry, and Interferometric Metrology. Milestone Series MS110/HC. Society of Photo Optical. 1995.
[8.44.] Current Research on Holography and Interferometricmethods for Measurement of Object Properties 2000-2002. SPIE. 2003.
[8.45.] Holográfia. Gábor Dénes előszava alapján. Műszaki könyvkiadó. Budapest . 1973.
[8.46.] Digital Holography. Springer-Verlag Berlin Heidelberg. 2005.
[8.47.] Holography. A Practicalapproach. Wiley-Wch. 2007.
[8.48.] Holographyhandbook. 1982.
[8.49.] Modern optika mérnököknek és kutatóknak. Műszaki Könyvkiadó. Budapest . 1982.
[8.50.] Optika. Panem. Budapest . 1997.
[8.51.] Kozmikus fizika. Egyetemi jegyzet, ELTE. Budapest . 2002.
[8.52.] Holographic Data Storage. Springer-Verlang. Berlin . 2000.
[8.53.] Új modellek és eszközök a holografikus adattároló rendszerek kutatásában. Kézirat, BME. 2005.
[8.54.] Fotonika optikai alapjai I. Műegyetemi Kiadó. 1997.