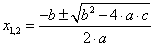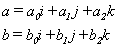Chapter I. Basics and data management of C++
- I.1. Creation of C++ programs
- I.2. Basic data types, variables and constants
- I.3. Basic operations and expressions
- I.4. Control program structures
- I.5. Exception handling
- I.6. Pointers, references and dynamic memory management
- I.7. Arrays and strings
- I.8. User-defined data types
Knowledge necessary for program development in language C++ is detailed divided into three large categories. Category one (Chapter I) presents basic elements and program structures most of which can be found both in language C and C++. A program containing one single main() function is enough to practice the curriculum.
The next chapter (Chapter II) assists in creating well-structured C and C++ programs according to algorithmic thinking using the presented solutions. Functions play the main role in this part.
The third chapter (Chapter III) presents the means of the nowadays more and more dominant object-oriented program building. Here classes that encapsulate data and the operations to be carried out on them into one single unit are in focus.
I.1. Creation of C++ programs
Before the elements of language C++ are detailed, issues on the creation and running of C++ programs are to be overviewed. A few rules that are to be applied when writing C++ source codes, program structures and steps needed for running in Microsoft Visual C++ system are described.
I.1.1. Some important rules
Standard C++ language belongs to conventional programming languages in case of which the creation of the program involves typing the whole text of the program, as well. When typing the text (source code) of the program a few restrictions have to be considered:
-
The basic elements of the program can only contain the characters of the 7 bit ASCII code table (see in Appendix Section A.1), however character and text constants, as well as remarks may contain characters of any coding (ANSI, UTF-8, Unicode). A few examples:
/* Value is given for an integer, a character and a text (string) variable (multiline remark) */ int variable = 12.23; // value giving (remark until the // end of the line) char sign = 'Á'; string header = "Programming is fun" -
C++ compiler differentiates small and capital letters in the words (names) used in the program. Most of names that make up the language contain only small letters.
-
Certain (English) words cannot be used as own names since these are keywords of the compiler (see in Appendix Section A.2).
-
In case of creating own names please note that they have to start with a letter (or underscore sign), and should contain letters, numbers or underscore signs in their other positions. (Please note that it is not recommended to use the underscore sign.)
-
One last rule before writing the first C++ program is that we should not too long however so called talkative names define such as: ElementSum, measurementlimit, piece, RootFinder.
I.1.2. The first C++ program in two versions
Since language C++ is compatible from the top with the standard (1995) C language, in case of creating simple programs C programming knowledge can also result in success. Let’s take the example of perimeter and area calculation of a circle in plane. The algorithm is very simple, since after the radius is entered, only a few formulas have to be calculated.
The two solutions below only differ from each other in the input/output operations basically. In style C case printf() and scanf() functions are used, while in the second C++ type case objects cout and cin are applied. (In case of further examples the latter solution is used.) The source code has to be placed into a .CPP extension text file in both cases.
Style C solution with a slight modification can also be compiled with a C compiler:
// Circle1.cpp
#include "cstdio"
#include "cmath"
using namespace std;
int main()
{
const double pi = 3.14159265359;
double radius, area, perimeter;
// Reading radius
printf("Radius = ");
scanf("%lf", &radius);
// Calculations
perimeter = 2*radius*pi;
area = pow(radius,2)*pi;
printf("Perimeter: %7.3f\n", perimeter);
printf("Area: %7.3f\n", area);
// Waiting for pressing Enter
getchar();
getchar();
return 0;
}
The solution that uses C++ objects is a little easier to understand:
// Circle2.cpp
#include "iostream"
#include "cmath"
using namespace std;
int main()
{
const double pi = 3.14159265359;
// Reading radius
double radius;
cout << "Radius = ";
cin >> radius;
// Calculations
double perimeter = 2*radius*pi;
double area = pow(radius,2)*pi;
cout << "Perimeter: " << perimeter << endl;
cout << "Area: " << area << endl;
// Waiting for pressing Enter
cin.get();
cin.get();
return 0;
}
Both solutions use C++ and own names as well (radius, area, perimeter, pi). It is an essential rule that all names have to be declared for the C++ compiler before first usage. In the example lines that start with double and constdouble not only declare the names but also create (define) their related storages in the memory. However, similar descriptions are not found for names printf(), scanf(), pow(), cin and cout. The declarations of these names can be found in the (#include) files (cstdio, cmath and iostream, respectively) included at the beginning of the program. The names are closed in the namespace std.
Function printf() presents data in a formatted way. If data are directed (<<) to object cout, formatting is more complicated, but in that case format elements belonging to different data types does not have to be dealt with. The same is true for scanf() and cin elements used for data entry. Another important difference is the security of the applied solution. In case scanf() is called, the beginning address (&) of the memory space for data storage has to be entered, and this way several errors may arise in the program. Oppositely, application of cin is completely safe.
Another remark to getchar() and cin.get() calls at the end of programs. After the last call of scanf() and cin the data entry buffer maintains data correspondent to key Enter. Since both functions that read characters carry out processing after key Enter is pressed, the first calls only remove Enter that remained in the buffer, and only the second call is waiting for another Enter pressing.
In both cases an integer (int) type function, named main() , contains the main part of the program, closed between the curly brackets that include body the of the function. Functions – as in mathematics – have values that are defined after statement return in language C++. The explanation of values comes from the ancient versions of language C, and accordingly 0 means that everything was all right. In case of main() this function value is received by the operation system since, which calls the function as well (starts the program running this way).
I.1.3. Compilation and running of C++ programs
In most development systems the basis of program creation is the generation of a so called project. Firstly, the type of the application has to be chosen, and then the source files have to be added to the project. From the several possibilities offered by system Visual C++ the Win32 console application is the simple C++ application type with text interface. Let’s see the necessary steps!
After selections File / New / Project… Win32 / Win32 Console Application the name of the project has to be entered:
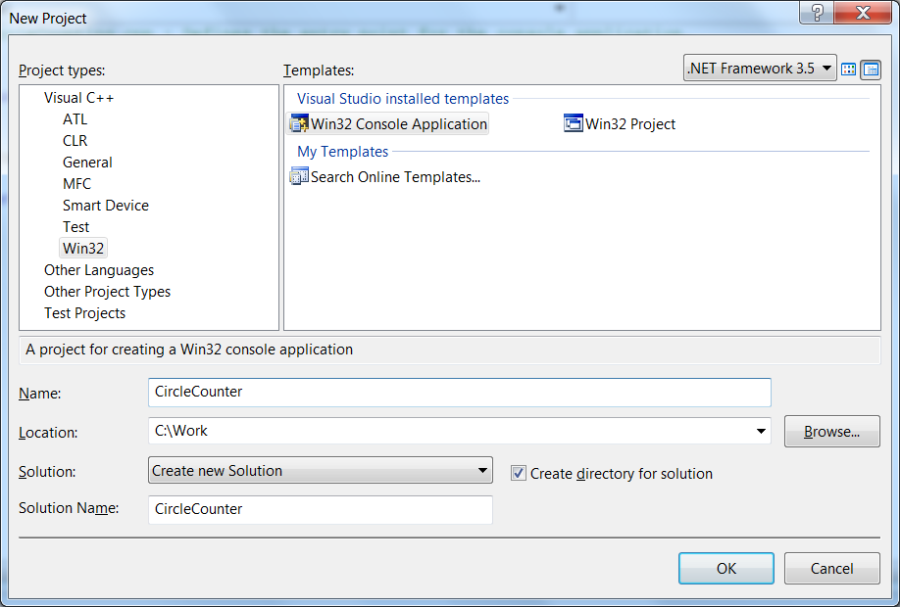
After key OK is pressed, the Console application wizard starts, and using its settings an empty project can be created:
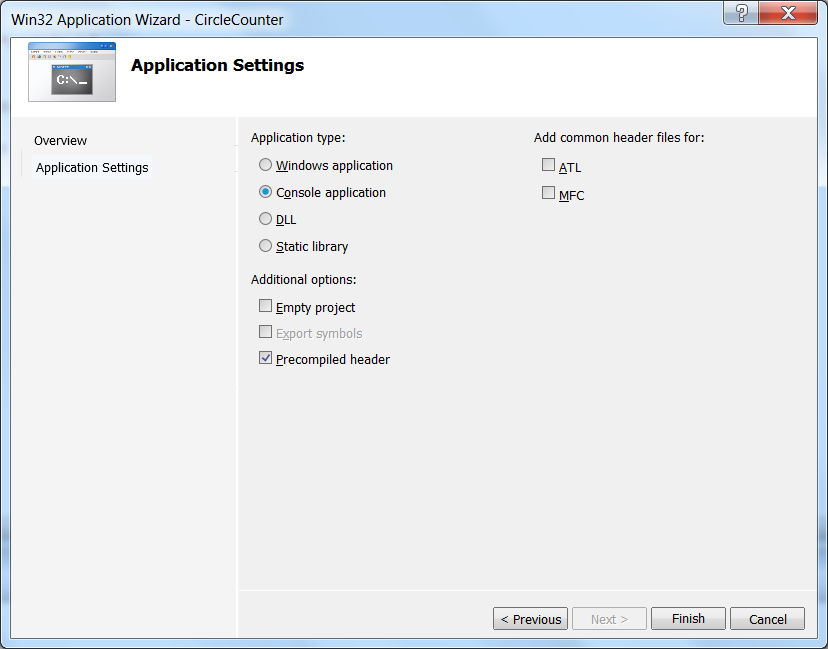
After pressing key Finish the solution window (Solution Explorer) appears, where a new source can be added to the project ( Add / New Item… ) using mouse right click on Source Files .
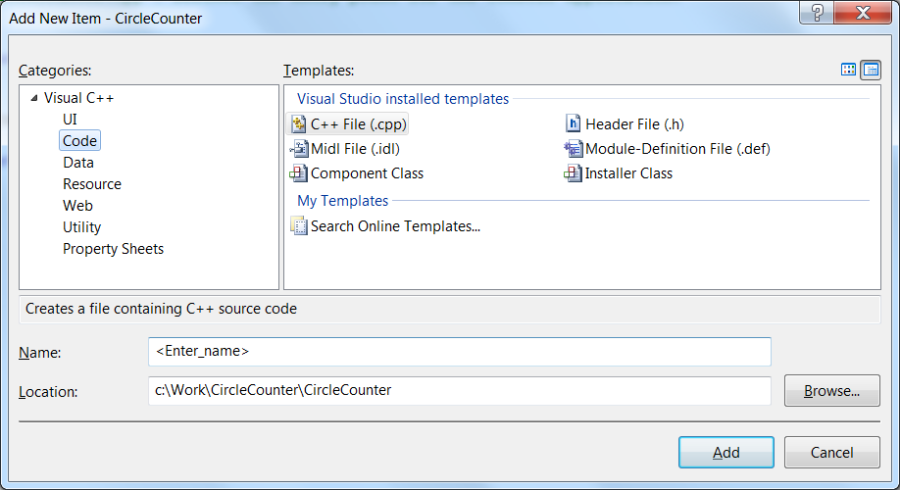
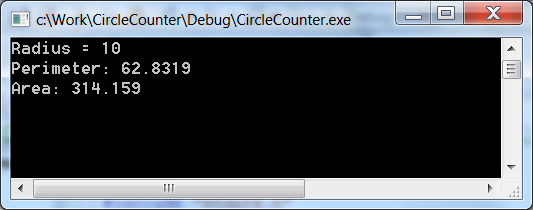
After the text of the program is typed, compilation can done through menu points Build / Build Solution or Build / Rebuild Solution . In case of successful compilation (CircleCalculation - 0 error(s), 0 warning(s)) the program can be started by choosing menuitem Debug / Start Debugging (F5) or Debug / Start Without Debugging (Ctrl+F5).
After menu Build / Configuration Manager... is selected a window pops up where either the debug ( Debug ) or final ( Release ) version can be chosen to be compiled. (This selection determines the content of the file to be run and its place on the disk.)
In case of any Build , compilation is carried out in several steps. Figure I.5 shows these steps.
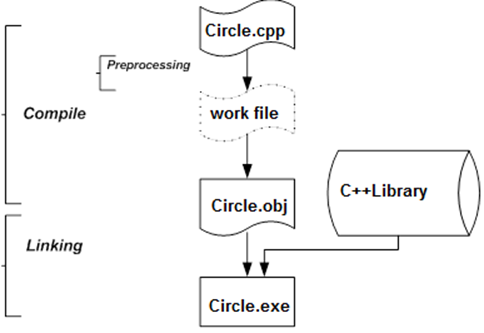
The preprocessor interprets lines starting with hash mark sign (#) and as a result source code in language C++ is created. C++ compiler compiles this code to an object code that misses the machine code that realizes library elements. As the last step the linker fills this gap and transforms the complete machine (native) code to an executable application.
It is to be noted that in case of projects that contain more source files (modules) preprocessor and compiler carry out compilation module by module and the object modules created this way are built together into one single executable file by the linker.
After running the program has to be saved so that we can work with it later. There are several possible solutions, however the next, already proven steps can help us: first all files are saved onto the disk ( File / SaveAll ), then the project is closed together with the solution ( File / Close Solution ). (Solution denotes the set of linked projects that can be recompiled in one single step if necessary.)
Finally let’s take a look at the directory structure that is created on the hard disk when the project is compiled.
C:\Work\CircleCalculation\CircleCalculation.sln C:\Work\CircleCalculation\CircleCalculation.ncb C:\Work\CircleCalculation\Debug\CircleCalculation.exe C:\Work\CircleCalculation\Release\CircleCalculation.exe C:\Work\CircleCalculation\CircleCalculation\CircleCalculation.vcproj C:\Work\CircleCalculation\CircleCalculation\Circle1.cpp C:\Work\CircleCalculation\CircleCalculation\Debug\Circle1.obj C:\Work\CircleCalculation\CircleCalculation\Release\ Circle1.obj
Debug and Release directories that can be found above this level contain the executable application, while directories below with the same names contain work files. These four folders can be deleted since they will be created again during compilation. It is also recommended to delete file Circle calculation.ncb that assists the intellisense services of development environment since its size can be quite large. The solution (project) can be reopened with the Circle calculation.sln file ( File / Open / Project / Solution ).
I.1.4. Structure of C++ programs
As the previous part revealed, all programs written in language C++ can be found in one or more source files (compilation unit, module), the extension of which is .CPP. C++ modules can be compiled to object codes independently.
So called declaration (include, header) files usually belong to the program as well and they can be integrated in the source files using precompilation statement #include. Include files cannot be compiled independently, however most development environments support their precompilation, accelerating the processing of C++ modules this way.
The structure of C++ modules follows that of C language programs. The program code – according to the principle of procedural programming – is placed in functions. Data (declarations/definitions) can be found both outside (globally, at file level) and within (on local level) the functions. The former are called external (extern) while the latter are classified in the automatic (auto) storage class by the compiler. The example program below illustrates this:
// C++ preprocessor directives
#include <iostream>
#define MAX 2012
// in order to reach the standard library names
using namespace std;
// global declarations and definitions
double fv1(int, long); // function prototype
const double pi = 3.14159265; // definition
// the main() function
int main()
{
/* local declarations and definitions
statements */
return 0; // exit the program
}
// function definition
double fv1(int a, long b)
{
/* local declarations and definitions
statements */
return a+b; // return from the functions
}
In language C++ object-oriented (OO) approach may also be used when creating programs. According to this principle, the basic unit of our program is the class that encapsulates functions and data definitions (for details see Chapter III). In this case function main() defines the entry point of our program. Classes are usually placed between global declarations, either directly in the C++ module or by the including of a declaration file. „Knowledge” placed in a class can be reached through the instances (variables) of the class.
Let’s take the example of circle calculation task defined with object-oriented approach.
/// Circle3.cpp
#include "iostream"
#include "cmath"
using namespace std;
// Class definition
class Circle
{
double radius;
static const double pi;
public:
Circle(double r) { radius = r; }
double Perimeter() { return 2*radius*pi; }
double Area() { return pow(radius,2)*pi; }
};
const double Circle::pi = 3.14159265359;
int main()
{
// Reading radius
double radius;
cout << "Radius = ";
cin >> radius;
// Creation and usage of object Circle
Circle circle(radius);
cout << "Perimeter: " << circle.Perimeter() << endl;
cout << "Area: " << circle.Area() << endl;
// Waiting for pressing Enter
cin.get();
cin.get();
return 0;
}
I.2. Basic data types, variables and constants
When programming, we attempt to make our activities comprehensible for computers in order that they could help us do those tasks or that they do those tasks for us. When we work, we receive data that we store in general to process them and to extract information from them later. Data are really diverse but most of them consist of numbers or texts in everyday life.
In this chapter, we deal with describing and storing data in C++. We also learn how to receive data (from an input) and how to visualize them.
On the basis of the Neumann principle, data are stored in a uniform way in computer memory, that is why programmers have to provide the type and the features of the data in a C++ program.
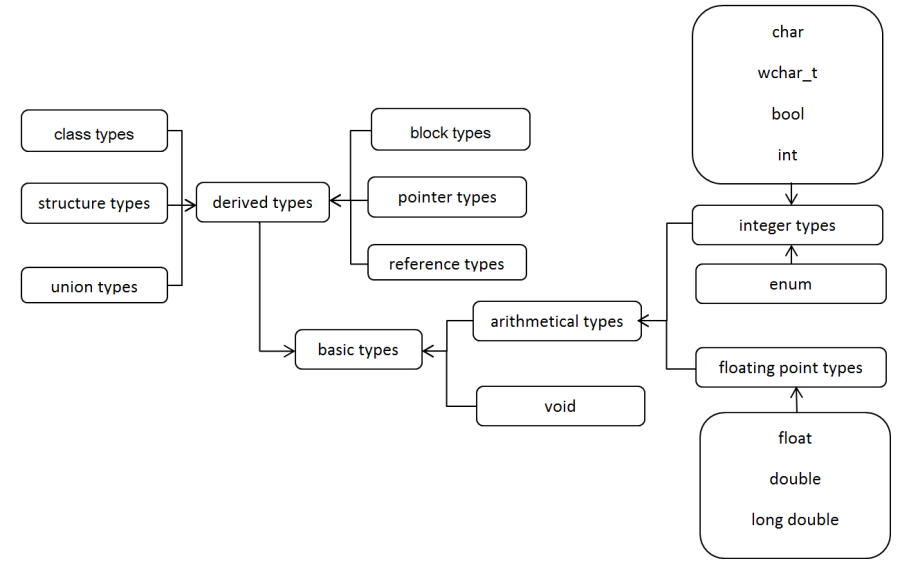
I.2.1. Classification of C++ data types
The data type determines the number of bits they occupy in memory and their interpretation (variable). It also affects the way data are processed since C++ is a strongly typed language, therefore compilers check many things.
C++ data types (shortened as types) can be classified in several ways. Let's use the classification of Microsoft VC++ language (Figure I.6). According to it, there are basic data types that can store one value (integer, character, real number). However, there are also derived data types that are based on basic types, but they allow the creation of data structures that may store more values.
I.2.1.1. Type modifiers
In C++ language the meaning of basic integer types can be altered by type modifiers . The signed/unsigned modifier pair determines whether the stored bits can be interpreted as negative numbers or not. With the short/long pair size of the storage can be fixed to 16 or 32 bits. Most C++ compilers support 64 bits storage with the long long modifier, therefore it will also be dealt with in this book. Type modifiers can also be used as type definitions alone. Possible type modifiers are summarized in the following table. Elements in each row designate the same data type.
|
char |
signed char |
||
|
short int |
short |
signed short int |
signed short |
|
int |
signed |
signed int |
|
|
long int |
long |
signed long int |
signed long |
|
long long int |
long long |
signed long long int |
signed long long |
|
unsigned char |
|||
|
unsigned short int |
unsigned short |
||
|
unsigned int |
unsigned |
||
|
unsigned long int |
unsigned long |
||
|
unsigned long long int |
unsigned long long |
The required memory of arithmetical types with type modifiers and the value range of stored data are summarized in Appendix Section A.4.
Basic types are detailed in the present subchapter, while derived types are treated in the following parts of Chapter I.
I.2.2. Defining variables
Storing data in memory and accessing them is vital for every C++ computer program. That is why, we start with getting to know memory spaces to which names are assigned, i.e. variables. In most cases, variables are defined, i.e. their type is provided (they are declared), and memory space is allocated for them. (In the beginning, we rely on compilers for memory allocation.)
The total definition row of a variable is very complex at first sight; however, it is done in a much simpler way in practice.
〈storage class〉 〈type qualifier〉 〈type modifier ... 〉 typevariable name 〈= initial value〉 〈, … 〉;
〈storage class〉 〈type qualifier〉 〈type modifier ... 〉 typevariable name 〈(initial value〉 〈, … 〉;
(In the previous generalized forms, the 〈 〉 signs indicate optional elements while the three points show that a definition element can be repeated.)
The storage classes – auto, register, staticand extern – of C++ determine the lifetime and visibility of variables. At first, storage classes are not defined explicitly, therefore the default case of C++ is used, in which variables defined outside functions have extern (global), while variables defined within a function have auto (local) storage classes. Extern variables are created when the program is started, exist until its end and can be accessed from anywhere during execution. On the contrary, auto variables are born when a function is entered and they are deleted when the function is exited. Therefore they can be accessed within the function.
With type qualifiers further information can be assigned to variables.
-
Variables with const keyword cannot be modified (they are read-only, i.e. constants).
-
The volatile type qualifier indicates that the value of the variable can be modified by a code independent of our program (e.g. by another running process or thread). The word volatile tells the compiler that it is not known in advance what will happen to that variable. (That is why, compilers get the value of the variable from the memory each time a volatile variable is referenced.)
int const const double volatile char float volatile const volatile bool
I.2.2.1. Initial values of variables
Variable definition ends with giving an initial value. Initial values can be provided after an equal sign or between parentheses:
using namespace std;
int sum, product(1);
int main()
{
int a, b=2012, c(2004);
double d=12.23, e(b);
}
In this example, there is no initial value for two variables (sum and a), which leads in general to a program error. However, the variable sum has the initial value of 0, since global variables are always initialized (to zero) by compilers. But the local a is a different case since its initial value is provided by the actual content of the memory allocated for the variable and that can be anything. In these cases, the value of these variables can be set by assignment before their usage. During assignment, the value of the expression on the right of the equal sign is assigned to the variable on the left:
a = 1004;
In C++ language the initial values can be provided by any compile-time and run-time expressions.:
#include <cmath>
#include <cstdlib>
using namespace std;
double pi = 4.0*atan(1.0); // π
int randomnumber(rand() % 1000);
int main()
{
double alimit = sin(pi/2);
}
It is important that definition and value assignment statements end with a semicolon.
I.2.3. Basic data types
Basic data types are the equivalents of digits or letters in human language. A PhD dissertation in Mathematics or Winnie the Pooh can be created with the help of them. In the following overview, integer types are divided into smaller groups.
I.2.3.1. Character types
The char type has a double role. On one hand, it makes it possible to store ASCII (American Standard Code for Information Interchange) characters (Appendix Section A.1), on the other hand, it can be used as one byte signed integer.
char lettera = 'A'; cout << lettera << endl; char response; cout << "Yes or No? "; cin>>response; // or response = cin.get();
The double nature of char type is well represented by the possibilities how constant values (literals) can be assigned to them. Characters can be provided between apostrophes or by their integer code. Besides decimal numbers, character codes can be given in octal format (starting with zero) or in a hexadecimal format (starting with 0x). As an example, let's see what the equivalents of capital letter C are.
’C’ 67 0103 0x43
Certain standard control and special characters can be given by the so-called escape sequences. In an escape sequence, character backslash (\) is followed by special characters or numbers, as it can be seen in the table of Appendix Section A.3: ’\n’, ’\t’, ’\’’, ’\”’, ’\\’.
If we want to work with characters of the 8-bit ANSI code table or with a one-byte integer value, it is recommended to use the unsigned char type.
In order to process a character of the Unicode table, the variable should be the two-byte wchar_t type, and constant character values should be preceded by capital letter L.
wchar_t uch1 = L'\u221E'; wchar_t uch2 = L'K'; wcout<<uch1; wcin>>uch1; uch1 = wcin.get();
We should always make sure not to confuse apostrophes (’) with quotation marks ("). Quotation marks are used for string constants (string literals) in the computer program.
"This is an ANSI string constant."
or
L"This is a Unicode string constant."
I.2.3.2. Logical Boolean type
Bool type variables can have two values: logical false is 0, while logical true is 1. In Input/Output (I/O) operations logical values are represented by integer values:
bool start=true, end(false); cout << start; cin >>end; This default operation can be overridden by boolalpha and noboolalpha I/O manipulators: bool start=true, end(false); cout << boolalpha << start << noboolalpha; // true cout << start; // 1 cin >> boolalpha>> end; // false cout << end; // 0
I.2.3.3. Integer types
Probably the most frequently used basic data type of the C++ language is int together with its type modifiers. When an integer value is provided in the program, compilers attempt to assign automatically the int type. If the value is out of the value range of the int type, it uses an integer type with a broader range or it gives an error message in case of a too big constant.
The type of constant integer values can be provided by the U and L postfixes. U means unsigned, L means long:
|
2012 |
int |
|
2012U |
unsigned int |
|
2012L |
long int |
|
2012UL |
unsigned long int |
|
2012LL |
long long int |
|
2012ULL |
unsigned long long int |
Of course, integer values can be given not only in decimal format (2012) but also in octal (03724) or hexadecimal (0x7DC) number system. The choice of these number systems can be expressed in I/O operations by stream manipulators ( dec , oct , hex ), the effects of which last until the next manipulator:
#include <iostream>
using namespace std;
int main()
{
int x=20121004;
cout << hex << x << endl;
cout << oct << x << endl;
cout << dec << x << endl;
cin>> hex >> x;
}
It is not needed to provide the prefixes indicating number systems in case of data entering. There are some manipulators that ensure simple formatting possibilities. With parameterized manipulator setw () the width of the field to be used in printing operations can be set; and within that the content can be aligned to the ( left ) or to the right ( right ), which is the default value. setw () effects only the next data element, while alignment manipulators keep their effect until the next alignment manipulator.
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
unsigned int number = 123456;
cout<<'|' << setw(10) << number << '|' << endl;
cout<<'|' << right << setw(10) << number << '|' << endl;
cout<<'|' << left << setw(10) << number << '|' << endl;
cout<<'|' << setw(10) << number << '|' << endl;
}
The output reflects the effects of these manipulators well:
| 123456| | 123456| |123456 | |123456 |
I.2.3.4. Floating point types
Mathematical and technical calculations require the use of real numbers containing fractions as well. Since the place of the decimal point is not fixed in these values, these numbers can be stored by floating point types: float, double, long double. These types are only different from one another concerning the necessary memory size, the range of values and the number of exact decimal places (see Appendix Section A.4). (Contrary to the standard recommendation, Visual C++ treats the long double type as double.)
It has to be noted already at the very beginning that floating point types do not make it possible to represent fractions precisely, because the numbers are stored in the scientific form (mantissa, exponent), in the binary number system.
double d =0.01; float f = d; cout<<setprecision(12)<<d*d<< endl; // 0.0001 cout<<setprecision(12)<<f*f<< endl; // 9.99999974738e-005
There is only one value the value of which is surely exact: 0. Therefore if floating point variables are set to 0, their value is 0.0.
Floating point constants can be provided in two ways. In case of smaller numbers decimal representation is used generally, where the decimal point separates the integer part from the fraction part, e.g. 3.141592653, 100., 3.0. In case of bigger numbers, the computerized version of scientific form, well known from mathematics is applied, where letter e or E is followed by the exponent (the power of 10): 12.34E-4, 1e6.
Floating point constant values are double type by default. Postfix F designates a float type variable, whereas L designates a long double variable: 12.3F, 1.2345E-10L. (It is a frequent programming error that if the constant contains neither decimal point nor exponent, the constant value will be treated as an integer and not as a floating point type as expected.)
During printing the value of floating point variables, the already mentioned field width ( setw ()), as well as the number of digits after the decimal point - setprecision () can be set (see Appendix Section A.10). If this value cannot be printed in the set format the default visualization is used. Manipulator fixed is used for decimal representation whereas scientific is applied for scientific representation.
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
double a = 2E2, b=12.345, c=1.;
cout << fixed;
cout << setw(10)<< setprecision(4) << a << endl;
cout << setw(10)<< setprecision(4) << b << endl;
cout << setw(10)<< setprecision(4) << c << endl;
}
The results of program running are:
200.0000
12.3450
1.0000
Before getting on, it is worth having a look at automatic type conversion between C++ arithmetical types. It is evident that a type with a smaller value range can be converted into a type with a wider range without data loss. However, in the reverse direction, the conversion generally provokes data loss for which compilers do not alert, and one part of the bigger number may appear in the "smaller" type variable.
short int s;
double d;
float f;
unsigned char b;
s = 0x1234;
b = s; // 0x34 ↯
// ------------------------
f = 1234567.0F;
b = f; // 135 ↯
s = f; // -10617 ↯
// ------------------------
d = 123456789012345.0;
b = d; // 0 ↯
s = d; // 0 ↯
f = d; // f=1.23457e+014 – precision loss ↯
I.2.3.5. enum type
In computer programs integer type constant values that are logically in connection with one another are often used. The readability of our programs is much better if these values are replaced by names. For that purpose, it is worth defining a new type (enum) with its range of values:
enum 〈type identifier〉 { enumeration };
If type identifier is not given, the type is not created only the constants. Let's see the following example with an enumeration that contains the days of the week.
enum workdays {Monday, Tuesday, Wednesday, Thursday, Friday};
A separate integer value is associated to the names in this enumeration. By default, the value of the first element (Monday) is 0, that of the next one (Tuesday) is 1, and so on (the value of Friday is 4).
In enumerations, we can directly assign values to their elements. In that case, automatic incrementation continues from the given value. It is not a problem if the same values are repeated or if we assign negative values to the elements. However, we have to make sure that in the definitions there are not two enum elements with the same name within a given visibility scope (namespace).
enum consolecolours {black,blue,green,red=4,yellow=14,white};
In the enumeration named consolecolours the value of white is 15.
In enumerations that do not contain direct value assignment, the number of elements can be obtained by adding an extra element:
enum stateofmatter { ice, water, vapour, numberofstates};
The value of element numberofstates equals to the number of states, i.e. 3.
In the following example the usage of enum types and enum constants are demonstrated:
#include <iostream>
using namespace std;
int main()
{
enum card { clubs, diamonds, hearts, spades };
enum card cardcolour1 = diamonds;
card cardcolour2 = spades;
cout << cardcolour2 << endl;
int colour = spades;
cin >> colour;
cardcolour1 = card(colour);
}
Enumeration type variables can be defined according to the rules of both C and C++ languages. In C language enum types are defined by keyword enum and type identifiers together. In C++ language type identifiers represent alone enum types.
When we print an enumeration type variable or an enumeration constant, by default we get the integer corresponding to the given element. However, when the input is read in, the situation is completely different. Since enum is not a predefined type of C++ language, contrary to the above mentioned types, cin does not know it. As it can be seen in the example, reading in can be realized by using an int type variable. However, the typedness of C++ language may cause problems here since it only does certain conversions if it is "asked" to do so with type conversion (cast) operation: typename(value). (The programmers have to check the values since C++ does not deal with them.)
I.2.3.6. sizeof operation
C++ language contains an operator that is evaluated during compilation and that determines the size of any type or any variable and expression type in bytes.
sizeof(typename)
sizeofvariable/expression
sizeof(variable/expression)
From that, we can infer the type of the result of a given expression:
cout << sizeof('A' + 'B') <<endl; // 4 - int
cout << sizeof(10 + 5) << endl; // 4 - int
cout << sizeof(10 + 5.0) << endl; // 8 - double
cout << sizeof(10 + 5.0F) << endl; // 4 - float
I.2.4. Creation of alias type names
When variables are defined, their types are composed of more keywords in general because of type qualifiers and type modifiers. These declaration instructions are difficult to read and they can often be misleading.
volatile unsigned short intsign;
In fact, we would like to store unsigned 16-bit integers in variable sign. Keyword volatile only gives complementary information to the compiler, we do not deal with it during programming. Declaration typedef makes the above mentioned definition more readable:
typedef volatile unsigned short intuint16;
This declaration creates type name uint16, therefore the definition of variable sign is:
uint16 sign;
typedef can also be useful in case of enumerations:
typedef enum {falsevalue = -1, unknown, truevalue} bool3;
bool3 start = unknown;
Creating type names is always successful if we respect the following empiric rule:
-
Give a variable definition without an initial value and with the type for which we would like to create an alias name.
-
Give the keyword typedef before the definition, because of which the given name will not designate a variable but a type.
It is particularly useful to use typedef in case of complex types, where type definition is not always simple.
Finally, let's see some frequently used alias type names.
typedef unsigned charbyte, uint8;
typedef unsigned shortword, uint16;
typedef long long intint64;
I.2.5. Constants in language C++
Using names instead of constant values makes program codes more readable. In C++ language we can choose from many possibilities, following the traditions of the C language.
Let's start with constants (macros) #define that should be avoided in C++ language. Preprocessor directive #define is followed by two texts, separated from each other by a space. The preprocessor reads the whole C++ source code and replaces the defined first word with the second one. It should be noted that all characters of the names used by preprocessor are always written in capital letters and that preprocessor stastements should not be terminated by semicolons.
#define ON 1
#define OFF 0
#define PI 3.14159265
int main()
{
int switched = ON;
double rad90 = 90*PI/180;
switched = OFF;
}
The compiler gets the following C++ computer program from the prepocessor:
int main()
{
int switched = 1;
double rad90 = 90*3.14159265/180;
switched = 0;
}
The big advantage and disadvantage of this solution is untypedness.
Constant solutions supported by C++ language are based on const type qualifiers and the enum type. Keyword const can transform any variable with an initial value to a constant. C++ compilers do not allow the value modification of these constants at all. The previous example code can be rewritten in the following way:
const int on = 1;
const int off = 0;
const double pi = 3.14159265;
int main()
{
int switched = on;
double rad90 = 90*pi/180;
switch = off;
}
The third possibility is to use an enum type, which can only be applied in case of integer (int) type constants. The swiching constants in the preceding example are now created as elements of an enumeration:
enum onoff { off, on };
int switched = on;
switch = off;
enum and const constants are real constants since they are not stored in the memory by compilers. While #define constants have their effects from the place of their definition until the end of the file, enum and const constants observe the traditional C++ visibility and lifetime rules.
I.3. Basic operations and expressions
After data storage is solved we can move on in the direction of obtaining information. Information is usually created as a result of a data processing that means the execution of a series of instructions in C++ language. The simplest data processing method is when different operations (arithmetic, logical, bitwise by bit etc.) are performed on our data as operands. The result of these operations is new data or the information itself that is necessary for us. (Aimed data becomes information.) Operands linked with operators are called expression s. In language C++ the most frequent instruction group consists of expressions (assignment, function call, …) closed with a semicolon.
Evaluation of an expression usually results in the calculation of a value, generates a function call or causes a side effect. In most cases a combination of these three effects occurs during processing (evaluating) the expressions.
Operations have impact on operands . The operands that require no further evaluation are called primary expressions. Identifiers, constant values and expressions in brackets are this kind.
I.3.1. Classification of operators based on the number of operands
Operators can be classified based on more criteria. Classification – for instance – can be carried out based on the number of operands. In case of operators with one operand (unary) the general form of the expression is:
op operand or operand op
In the first case, where the operator (op) precedes the operand is called a prefix form, while the second case is called postfix form:
|
|
sign change, |
|
|
incrementing the value of n (postfix), |
|
|
decrementing the value of n (prefix), |
|
|
transformation of the value of n to real. |
Most operations have two operands – these are called two operand (binary) operators:
operand1 op operand2
In this group bitwise operations are also present besides the traditional arithmetic and relational operations:
|
|
obtaining the low byte of n, |
|
|
calculation of n + 2, |
|
|
shift the bits of n to the left with 3 positions, |
|
|
increasing the value of n with 5. |
The C++ language has one three operand operation, this is the conditional operator:
operand1 ? operand2 : operand3
I.3.2. Precedence and grouping rules
As in mathematics, the evaluation of expressions is carried out according to the rules of precedence. These rules determine the execution sequence of different precedence operations in an expression. In case of identical precedence operators grouping from left to right or from right to left (associativity) provides guidance. Operations of the C++ language can be found in Appendix Section A.7, listed starting from the highest precedence. The right side of the table shows the execution direction of identical precedence operations, as well.
I.3.2.1. Rule of precedence
If different precedence operations are found in one expression, then always the part that contains an operator of higher precedence is evaluated first.
The sequence of evaluation can be confirmed or changed using brackets, already known from mathematics. In C++ language only round brackets () can be used, no matter how deep bracketing is needed. As an empirical rule if there are two or more different operations in one expression, brackets should be used in order to make sure that operations are carried out in the desired sequence. We should rather have one pair of redundant brackets than a wrong expression.
The evaluation sequence of expressions a+b*c-d*e and a+(b*c)-(d*e) is the same therefore the steps of evaluation are (* denotes the operation of multiplication):
int a = 6, b = 5, c = 4, d = 2, e = 3; b * c ⇒ 20 d * e ⇒ 6 a + b * c ⇒ a + 20 ⇒ 26 a + b * c - d * e ⇒ 26 - 6 ⇒ 20
The steps of processing expression (a+b)*(c-d)*e are:
int a = 6, b = 5, c = 4, d = 2, e = 3; (a + b) ⇒ 11 (c - d) ⇒ 2 (a + b) * (c - d) ⇒ 11 * 2 ⇒ 22 22 * e ⇒ 22 * 3 ⇒ 66
I.3.2.2. Rule of associativity
Associativity determines whether the operation of the same precedence level is carried out form left to right or from right to left.
For example, in the group of assignment statements evaluation is carried out from the right to the left and this way more variables can obtain values at the same time:
a = b = c = 0; identical with a = (b = (c = 0));
In case operations of the same precedence level can be found in one arithmetic expression, the rule from left to right is applied. The evaluation of expression a+b*c/d*e starts with the execution of three identical precedence operations. Due to associativity the evaluation sequence is:
int a = 6, b = 5, c = 4, d = 2, e = 3; b * c ⇒ 20 b * c / d ⇒ 20 / d ⇒ 10 b * c / d * e ⇒ 10 * e ⇒ 30 a + b * c / d * e ⇒ a + 30 ⇒ 36
The sequence of operations is well visible if transformed into a mathematical formula:
If the task is to program formula 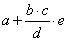 , it can be solved in two ways:
, it can be solved in two ways:
-
the denominator is put into brackets, therefore the term is divided by a product:
a+b*c/(d*e), -
division with both terms of the product in the denominator:
a+b*c/d/e.
I.3.3. Mathematical expressions
The simplest programs are usually used for the solution of mathematical tasks. In mathematical expressions different functions are also used besides basic operations (arithmetic operators in the wording of C++).
I.3.3.1. Arithmetical operators
The group of arithmetical operators includes the operator of modulo (%) besides the conventional four basic operations. Addition (+), subtraction (-), multiplication (*) and division (/) can be carried out both in case of integer and floating point numbers. Division denotes integer division in case of integer type operands:
29 / 7 value of the expression (quotient) 4
29 % 7 value of the expression (remainder) 1
In case of integers a and b that are not equal to zero, the following formula is always valid:
(a / b) * b + (a % b) ⇒ a
One operand minus (-) and plus (+) operators also belong to this group. Sign minus changes the value of the operand that stands behind it to the opposite sign (negation).
I.3.3.2. Mathematical functions
In case we need further mathematical operations besides the basic ones mentioned above, the mathematical functions of the standard C++ library have to be used. Declaration file cmath should be included into our program in order to reach the functions. The most frequently used mathematical functions are summarized in Appendix Section A.8. The library provides us all functions in three versions according to the three floating point types (float, double, long double).
Let’s take the example of the well-known solution formula of a quadratic equation with one unknown where a, b and c are the coefficients of the equation.
|
|
The solution formula program in C++:
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
double a = 1, b = -5, c =6, x1, x2;
x1 = (-b + sqrt(b*b-4*a*c))/(2*a);
x2 = (-b - sqrt(b*b-4*a*c))/(2*a);
cout << x1 << endl;
cout << x2 << endl;
}
I.3.4. Assignment
Variables obtain value usually during assignment (value giving), the general form which is:
variable = value;
In C++ language assignment operation (=) is an expression in fact that is evaluated by the compiler program, and its value is the value on its right side. Both sides of the assignment operator can contain expressions, however they differ basically. The expression on the left side denotes the memory space where the value of the expression on the right side should be stored.
I.3.4.1. Left value and right value
The C++ language has different names for the expressions on the two sides of assignment . The value of the expression on the left side of the equation sign is called left value (lvalue), while the expression on the right side is called right value (rvalue). Let’s take an example of two simple assignments.
int x;
x = 12;
x = x + 11;
During the first assignment variable x is present as left value, meaning that the address of the variable denotes the storage where the constant value given in the right side has to be copied into. During the second assignment variable x can be found on both sides of the assignment. x on the left side again denotes the storage in the memory (lvalue), while x on the right side is a right value expression, the value (23) of which is determined by the compiler before executing the assignment. (It is to be noted that the value of the whole expression is a right value that is not used for anything.)
I.3.4.2. Side effects in evaluation
As it was already mentioned the basic aim of the evaluation of all expressions is to calculate the value of them. However, during processing certain operations – assignment, function call and increment, decrement (++, --) presented later – the value of operands may also change besides the value of the expression. This phenomenon is called side effect.
The C++ standard does not defines the evaluation sequence of side effects, therefore all solutions that result of which depend on the sequence of side effect evaluation should be avoided, e.g.:
a[i] = i++; // ↯ y = y++ + ++y; // ↯ cout<<++n<<pow(2,n)<<endl; // ↯
I.3.4.3. I.3.4.3 Assignment operators
As it was already mentioned assignment in language C++ is an expression that gives the value entered on the right side to the storage denoted by the left side operand, and this value is also the value of the assignment expression. Consequently, assignment may occur in any expression. In the example below the result of expressions on the left side is the same as that of the right side:
|
|
|
|
|
|
A frequently used form of the assignment is when the value of a variable is modified with any operation and the value created this way is stored in the variable:
a = a + 2;
This kind of expressions can be written in a shorter form as well:
a += 2;
In general, it can be stated that
expression1 = expression 1 op expression 2
form expressions can also be written using the so called compound assignment operation:
expression 1 op= expression 2
The two forms are equal except that in the second case the evaluation of the left side expression is carried out only once. Two operand arithmetic and bitwise operations can be used as operator (op). (It is to be noted that no space can be entered among the characters in the operators.)
The compound assignment usually results in a faster code, and therefore the source program can be interpreted easier.
I.3.5. Increment and decrement operations
The C++ language provides an efficient possibility to increase the value of numerical variables with one ++ (increment), and to decrease those with one -- (decrement). The operators can be used only with left value operands, however both prefix and postfix forms can be applied:
int a; // prefix forms: ++a; --a; // postfix forms: a++; a--;
In case operators are used in the way presented above, there is no difference between the prefix and postfix form, since the value of the variable is incremented/decremented in both cases. In case the operator is applied in a more complex expression, using the prefix form increment or decrement takes place before processing the expression and the operand takes part in the evaluation of the expression with its new value:
int n, m = 5; m = ++n; // m ⇒ 6, n ⇒ 6
In case of postfix form increment or decrement follows the evaluation of the expression; therefore the operand has its original value in processing the expression:
double x, y = 5.0; x = y++; // x ⇒ 5.0, y ⇒ 6.0
The operation of increment and decrement operators can be understood more easily if the more complex expressions are decomposed to part expressions. Expression
int a = 2, b = 3, c; c = ++a + b--; // a will be 3, b 2 and c 6
provides the same result as the expressions (containing one or more statements) below (comma operation will be mentioned later):
a++, c=a+b, b--; a++; c=a+b; b--;
Instead of the conventional forms of increasing and decreasing by one
a = a + 1; a += 1; a = a - 1; a -= 1;
it is always recommended to use the adequate increment or decrement operator
++a; or a++; --a; or a--;
that provides faster code generation and becomes easier to overview.
It is to be noted that a variable should not be the operand of an increment or decrement operation more times within one expression. The value of such expression depends on the compiler completely.
a += a++ * ++a; // ↯
I.3.6. Phrasing of conditions
Some satetements of the C++ language work depending on a condition. The conditions in the statemnets can be any expression the zero or not zero value of which provide the logical false or true results. Comparative (relation) and logical operations can be used when conditions are created.
I.3.6.1. Relational and equalityoperations
Two operand, relational operators are available for carrying out comparisons, according to the table below:
|
Mathematical form |
C++ expression |
Meaning |
|---|---|---|
|
|
|
a is less than b |
|
|
|
a is less than or equal to b |
|
|
|
a is greater than b |
|
|
|
a is greater than or equal to b |
|
|
|
a is equal to b |
|
|
|
a is not equal to b |
All C++ expressions above are int type. The value of expressions is true (1) if the examined relation is true and false (0) if not.
Let’s take the example of some true expressions that contain different type operands.
int i = 3, k = 2, n = -3; i > k n <= 0 i+k > n i != k char first = 'A', last = 'Z'; first <= last first == 65 'N' > first double x = 1.2, y = -1.23E-7; -1.0 < y 3 * x >= (2 + y) fabs(x-y)>1E-5
It is to be noted that due to the computational and representation inaccuracy the identity of two floating point variables cannot be checked with operator ==. The absolute value of the difference of the two variables should be checked instead within the given error limit:
double x = log(sin(3.1415926/2)); double y = exp(x); cout << setprecision(15)<<scientific<< x<< endl; // x ⇒ -3.330669073875470e-016 cout << setprecision(15)<<scientific<< y<< endl; // y ⇒ .999999999999997e-001 cout << (x == 0) << endl; // false cout << (y == 1) << endl; // false cout << (fabs(x)<1e-6) << endl; // true cout << (fabs(y-1.0)<1e-6)<< endl; // true
Frequent program error is to confuse the operations of assignmnet (=) and identity testing (==). Comparison of a variable with a constant can be made safer if the left side operand is a constant, since the compiler expects a left value during assignment in this case:
2004 == dt instead of dt == 2004
I.3.6.2. Logical operations
In order to be able to word more complex conditions logical operators are also needed besides relational operators. In language C++ the operation of logical AND (conjunction, &&), logical OR (disjunction, //) and negation (!) can be used when phrasing conditions.
The operation of logical operators can be described with a so called truth table:

The condition below is true if the value of variable x is between -1 and +1. Parentheses only confirm precedence.
-1 < x && x < 1
(-1 < x) && (x < 1)
There are cases when it is simpler to phrase the opposite condition instead of the condition itself, and apply a logical negation (NO) operator (!) on it. The condition of the previous example is identical with the condition below:
!(-1 >= x || x >= 1)
During logical negation all relations are changed to their opposite relation, while operator AND to operator OR (and vice versa).
In C++ programs numerical variable ok is frequently used in expressions
!ok instead of ok == 0
ok instead of ok != 0
Right side expressions are recommended to be used mainly with bool type variable ok.
I.3.6.3. Short circuit evaluation
The table of operations reveals that the evaluation of logical expressions is carried out from left to right. In case of certain operations, it is not necessary to process the whole expression in order to make the value of expression unambiguous.
Let’s take the example of operation logical AND (&&) during the usage of which the false (0) value of the left side operand makes the processing of the right side operand unnecessary. This evaluation method is called short circuit evaluation.
If there is a side effect expression on the right side of the logical operator during the evaluation, the
x || y++
result is not always what we expect. In the example above if the value of x is not zero y is not incremented. Short circuit evaluation takes place even if the operands of the logical operations are put in parentheses:
(x) || (y++)
I.3.6.4. Conditional operator
Conditional operator (?:) has three operands:
condition ? true_expression : false_expression
If the condition is true, the value of true_expression provides the value of the conditional expression, otherwise the false_expression after the colon (:). This way only one expression is evaluated out of the two expressions on the two sides of the colon. The type of the conditional expression is the same as that of the part with higher accuracy. The type of expression
(n > 0) ? 3.141534 : 54321L;
is always double independent of the value of n.
Let’s take a typical example for the application of the conditional operator. With the help of the expression below the values between 0 and 15 of variable n are transformed into hexadecimal numbers:
ch = n >= 0 && n <= 9 ? '0' + n : 'A' + n - 10;
It is to be noted that the precedence of conditional operation is relatively low, slightly precedes that of assignment, therefore parentheses should be used in more complex expressions:
c = 1 > 2 ? 4 : 7 * 2 < 3 ? 4 : 7 ; // 7 ↯
c = (1 > 2 ? 4 : (7 * 2)) < 3 ? 4 : 7 ; // 7 ↯
c = (1 > 2 ? 4 : 7) * (2 < 3 ? 4 : 7) ; //28
I.3.7. Bit operations
Computers had quite small memory in the past therefore solutions that made it possible to store and process more data within one byte, the smallest unit that can be addressed, were quite worthy. Using bit operations even 8 logical values can be stored within one byte. Nowadays this aspect is only considered rarely, easily understandable programs are in focus instead.
However, there is a field where bit operations are still used, and that is programming different hardware elements, microcontrollers. The C++ language contains six operators with the help of which different bitwise operations can be carried out on signed and unsigned integer data.
I.3.7.1. Bitwise logical operations
The first group of operations, the bitwise logical operations make it possible to test, delete or set bits:
|
Operator |
Operation |
|---|---|
|
|
Unary complement, bitwise negation |
|
|
bitwise AND |
|
|
bitwise OR |
|
|
bitwise exclusive OR |
The description of bitwise logical operations can be found in the table below, where 0 and 1 numerals denote deleted and set bit status, respectively.
|
a |
b |
a & b |
a | b |
a ^ b |
~a |
|---|---|---|---|---|---|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
The low level control of the computer hardware elements requires setting, deletion and switching of certain bits. All these operations are called “masking” since an adequate bitmask should be prepared for every single operation, and then should also be linked logically with the value desired to be changed, and this way the desired bit operation takes place.
Before all conventional bit operations are described one after the other, bit numbering in integer data elements has to be discussed. Bit numbering in a byte starts from the smallest order bit from 0 and increases from right to left. In case of integers composed of more bytes the byte sequence applied by the processor of the computer should also be discussed.
In case “big-endian” byte sequence supported by Motorola 68000, SPARC, PowerPC etc. processors the most significant byte (MSB) is stored in the lowest memory address, while an order smaller byte in the next address and so on.
However, the members of the most widespread Intel x86 based processor family use “little-endian” byte sequence according to which the least significant byte (LSB) is stored in the lowest memory address.
In order to avoid long bit series unsigned short int type data elements are used in our examples. Let’s take a look at the structure and storing of these data according to both byte sequences. The stored data is 2012 that is 0x07DC in hexadecimal numbering.
big-endian byte sequence:

little-endian byte sequence:

(Memory addresses increase from left to right in the example.) The figure shows clearly that when the hexadecimal constant values are entered the first big-endian form is used that corresponds to the mathematical interpretation of the hexadecimal number system. This is not an issue since storing in the memory is the task of the compiler. However, if the integer variables are processed bytewise, byte sequence should be known. Hereinafter our example programs are prepared in little-endian form but they can be adapted to the first storage method, as well based on the above mentioned facts.
In the example below bits 4 and 13 of the unsigned shortint type number 2525 are handled: unsigned short int x = 2525; // 0x09dd
|
Operation |
Mask |
C++ instruction |
Result |
|---|---|---|---|
|
Bit setting |
0010 0000 0001 0000 |
x = x | 0x2010; |
0x29dd |
|
Bit deletion |
1101 1111 1110 1111 |
x = x & 0xdfef; |
0x09cd |
|
Bit negation (switching) |
0010 0000 0001 0000 |
x = x ^ 0x2010; x = x ^ 0x2010; |
0x29cd (10701) 0x09dd (2525) |
|
Negation of all bits |
1111 1111 1111 1111 |
x = x ^ 0xFFFF; |
0xf622 |
|
Negation of all bits |
x = ~x; |
0xf622 |
Attention should be drawn to the strange behavior of exclusive or operator (^). If the exclusive or operation is carried out twice using the same mask the original value is returned, in this case 2525. This operation can be used for exchanging the values of two integer variables without the use of an auxiliary variable:
int m = 2, n = 7; m = m ^ n; n = m ^ n; m = m ^ n;
A program error difficult to find is the result if the logical operators (!, &&, ||) used in conditions are interchanged with the bitwise operators (~, &, |).
I.3.7.2. Bit shift operations
Bit shift operators belong to another group of bit operations. Shift can be carried out either to the left (<<) or to the right (>>). During shifting the bits of the left side operand move to the left (right) as many times as the value of the right side operand shows.
In case of shifting to the left bit 0 is placed into the free bit positions, while the exiting bits are lost. However, shift to the right takes into consideration whether the number is signed or not. In case of unsigned types bit 0 enters from the left, while in case of signed numbers bit 1 comes in. This means that bit shift to the right keeps the sign.
short int x;
|
Value giving |
Binary value |
Operation |
Result decimal (hexadecimal) binary |
|---|---|---|---|
|
x = 2525; |
0000 1001 1101 1101 |
x = x << 2; |
10100 (0x2774) 0010 0111 0111 0100 |
|
x = 2525; |
0000 1001 1101 1101 |
x = x >> 3; |
315 (0x013b) 0000 0001 0011 1011 |
|
x = -2525; |
1111 0110 0010 0011 |
x = x >> 3; |
-316 (0xfec4) 1111 1110 1100 0100 |
If the results are examined it can be seen that due to shift to the left with 2 bits the value of variable x increased four (22) times, while shift to the right with three steps resulted in a value decrease of x to its eighth (23). It can be stated generally that if the bits of an integer number is shifted to the left by n steps, the result is the multiplication of that number with 2n. Shift to the right by m bits means integer division by 2m. It is to be noted that this is the fastest way to multiply/divide an integer number with/by 2n.
In the example below the 16-bit integer number is divided into two bytes:
short int num;
unsigned char lo, hi;
// Reading the number
cout<<"\nPlease enter an integer number [-32768,32767] : ";
cin>>num;
// Determination of the lower byte by masking
lo=num & 0x00FFU;
// Determination of the upper byte by bit shift
hi=num >> 8;
In the last example the byte sequence of the 4 byte int type variable is reversed:
int n =0x12345678U;
n = (n >> 24) | // first byte is moved to the end,
((n << 8) & 0x00FF0000U) | // 2nd byte into the 3rd
byte,
((n >> 8) & 0x0000FF00U) | // 3rd byte into the 2nd byte,
(n << 24); // the last byte to the beginning.
cout <<hex << n <<endl; // 78563412
I.3.7.3. Bit operations in compound assigment
In language C++ a compound assignmnet operation also belongs to all the five two-operand bit operations, and this way the value of variables can be modified more easily.
|
Operator |
Relation sign |
Usage |
Operation |
|---|---|---|---|
|
Assignmnet by shift left |
|
|
shift of bits of x to the left with y bits, |
|
Assignmnet by shift right |
|
|
shift of bits of x to the right with y bits, |
|
Assignmnet by bitwise OR |
|
|
new value of x: x | y, |
|
Assignmnet by bitwise AND |
|
|
new value of x: x & y, |
|
Assignmnet by bitwise exclusive OR |
|
|
new value of x: x ^ y, |
It is important to note that the type of the result of bit operations is an integer type, at least int or larger than int, depending on the left side operand type. In case of bit shift any number of steps can be entered but the compiler uses the remainder created with the bit size of the type for shifting. For example, the phenomenon listed below is experienced in case of 32 bit int type variables.
unsigned z;
z = 0xFFFFFFFF, z <<= 31; // z ⇒ 80000000 z = 0xFFFFFFFF, z <<= 32; // z ⇒ ffffffff z = 0xFFFFFFFF, z <<= 33; // z ⇒ fffffffe
I.3.8. Comma operator
In one expression more, even independent expressions can be placed, using the lowest precedence comma operator. Expressions containing comma operator is evaluated from left to right, and the value and type of the expression is the same as that of the right side operand. Let’s take the example of expression
x = (y = 4 , y + 3);
Evaluation starts with the comma operator in the parentheses, first variable y obtains a value (4), then the expression in parentheses (4+3=7). Finally variable x obtains 7 as its value.
Comma operator is frequently used when setting different initial values for variables in one single statement (expression):
x = 2, y = 7, z = 1.2345 ;
Comma operator should be used also when the values of two variables should be changed within one statement (using a third variable):
c = a, a = b, b = c;
It is to be noted that commas that separate variable names in declarations and arguments in function calls are not comma operators.
I.3.9. Type conversions
It happens frequently during expression evaluation that a two-operand operation has to be carried out with different type operands. However, in order to be able to carry out the operation, the compiler has to transform the two operands to the same type, i.e. type conversion takes place.
In C++ some type conversions are carried out automatically without the intervention of the programmer, based on the rules laid in the definition of the language. These conversions are called implicit or automatic conversions.
In a C++ program the programmer may also request type conversion using type converter operators (cast) – explicit type conversion.
I.3.9.1. Implicit type conversions
It can be stated in general that during automatic conversions the operand with “narrower value range” is converted to the operand type with “wider value range” without data loss. In the example below during the evaluation of expression m+dint type m operand is converted to double type and that is the type of the expression as well:
int m=4, n; double d=3.75; n = m + d;
Implicit conversions do not always take place without data loss. During assigment and function call conversion among any types may happen. For instance in the example above when the sum is filled into variable n data loss occurs since the fraction part of the sum is lost, and 7 will be the value of the variable. (It is to be noted that no rounding was done during value giving.)
Automatically carried out conversions during evaluation of x op y form expressions are summarized briefly below.
-
char, wchar_t, short, bool, enum type data are automatically converted to int type. If the int type is not capable of storing the value, the aim type of conversion will be unsigned int. This type conversion rule is called “integer conversion” (integral promotion). The above mentioned conversions are value keeping ones, since they provide correct results regarding value and sign.
-
If there are different types in the expression after the first step, conversion according to type hierarchy starts. During type conversion the “smaller” type operand is converted to the “larger” type. The rules used during conversion are called “common arithmetical conversions”.
int < unsigned < long < unsignedlong < longlong < unsignedlonglong < float < double < long double
I.3.9.2. Explicit type conversions
The aim of type conversions commanded explicitly by the user is to carry out conversions that do not take place implicitly. Now only conversions that can be used with the basic types are dealt with, while operations const_cast, dynamic_cast and reinterpret_cast are detailed in Section I.6.
The (static) type conversions below are all carried out during the compilation of the C++ program. A possible grouping of type conversions:
|
type conversion (C/C++) |
(type name) expression |
|
|
function-like form |
type name (expression) |
|
|
checked type conversions |
static_cast< type name >(expression) |
|
In case of writing any expression implicit and the maybe necessary explicit conversions have to be considered always. The program part below aims to determine the average of two long integer variables and store it as a double type variable:
long a =12, b=7; double d = (a+b)/2; cout << d << endl; // 9
The result is false since due to integer conversions the right side of value giving has a long type result and this is placed into variable d. The result will only be right (9.5) if any operand of the division is converted to type double using any of the methods shown below:
d = (a+b)/2.0; d = (double)(a+b)/2; d = double(a+b)/2; d = static_cast<double>(a+b)/2;
I.4. Control program structures
On the basis of what we have learnt so far, we can only make program codes in the main () function of which only contains expressions ending with semicolon (data input, value assignment, printing, etc.). In order to realize more complex algorithms, this program structure is insufficient. We have to get to know the control structures of the C++ language that make possible the execution of certain program code lines repeatedly or depending on certain conditions. (For a summary of all C++ statements, see Appendix Section A.5.)
I.4.1. Empty statements and statement blocks
Control statements of C++ "control" the execution of other statements. If we would not like to control any activity, we should provide an empty statement. However, if several statements need control, then the so-called compound statements, i.e. statement blocks should be used.
Empty statements consist only of a semicolon (;). They should be used if no activity has to be performed logically, but there has to be a statement at the given point of the code according to syntax rules.
Curly brace brackets ( { and } ) enclose declarations and statements that make up a coherent unit together within a compound statement or block . Compound statements can be used at any place where only one statement is allowed in C++. Compound statements, the general representation of which is:
{
local definitions, declarations
statements
}
are used in the following three cases:
-
when more statements forming together a logical unit should be treated as one (in these cases, blocks only contain statements in general),
-
in the body of functions,
-
to localize the validity of definitions and declarations.
In the statement blocks statements and definitions/declarations can be typed in any order we want. (It should be noted that blocks do not end with a semicolon.)
In the following example, the quadratic equation with one unknown is solved if and only if the discriminant (the number appearing under the square root) of the equation is not negative. In order that the code would function correctly, the following if control structure is used:
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
double a, b, c;
cout << "a = "; cin >> a;
cout << "b = "; cin >> b;
cout << "c = "; cin >> c;
if (b*b-4*a*c>=0) {
double x1, x2;
x1 = (-b + sqrt(b*b-4*a*c))/(2*a);
x2 = (-b - sqrt(b*b-4*a*c))/(2*a);
cout << x1 << endl;
cout << x2 << endl;
}
}
I.4.2. Selective structures
Selective structures (if, switch) decide on the following steps to be executed by a program on the basis of certain conditions. These structures allow for one-way, two-way or multiple-way branches. Selections can be nested in one another, too. Conditions are expressed by comparison (relational) and logical operations.
I.4.2.1. if statements
In the case of an if statement, the execution of an activity (statement) depends on the value of an expression (condition). if statements have three forms
One-way branch
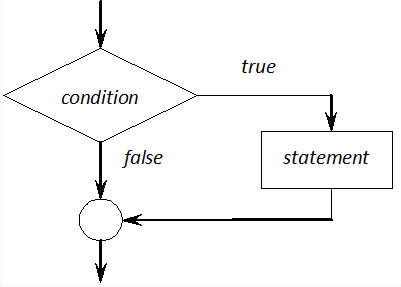
In the following form of if, the statement is only executed if the value of condition is not zero (i.e. true). (It should be noted that conditions should always be within brackets.)
if (condition)
statement
The functioning of the different control structures can be demonstrated by the following block diagram. The simple if statement is represented in Figure I.7.
In the following example, the square root of the number read from the keyboard is only calculated if it is not negative:
#include <iostream>
#include <cmath>
using namespace std;
int main() {
double x = 0;
cout << "x = "; cin >> x;
if (x >= 0) {
cout<<sqrt(x)<<endl;
}
}
Two-way branches
In the complete version of an if statement, an activity can be provided (statement2) when the value of the condition is zero (i.e. false) (Figure I.8). (If statement1 and statement2 are not compound statements, they should end with a semicolon.)
if (condition)
statement1
else
statement2
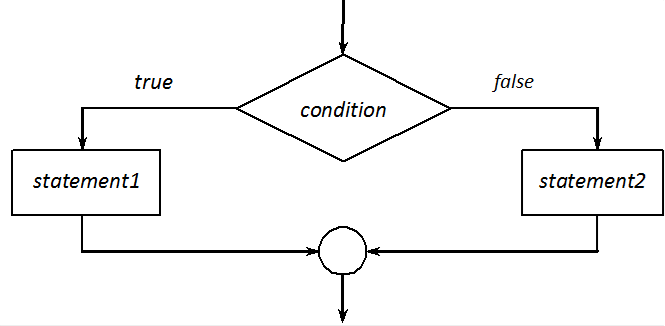
In the following example, the if statement decides whether the number read from the keyboard is even or odd:
#include <iostream>
using namespace std;
int main()
{
int n;
cout<<"Type an integer number: "; cin>>n;
if (n % 2 == 0)
cout<<"The number is even!"<<endl;
else
cout<<"The number is odd!"<<endl;
}
if statements can be nested in one another. However, in such cases, we have to be careful when using else branches. Compilers connect else branches to the closest preceding if statement.
The following example decides whether a given integer number is a positive and even number or whether it is a non-positive number. The correct solution can be realized in two different ways. One possibility is to attach an else branch containing an empty statement (;) to the internal if statement:
if (n > 0)
if (n % 2 == 1)
cout<<"Positive odd number."<< endl;
else ;
else
cout<<"Not a positive number."<<endl;
Another possibility is to enclose the internal if statement in braces, that is to place it in a statement block:
if (n > 0) {
if (n % 2 == 1)
cout<<"Positive odd number."<< endl;
} else
cout<<"Not a positive number."<<endl;
This problem does not arise if statement blocks are used in the case of both if, which is by the way required by safe programming:
if (n > 0) {
if (n % 2 == 1) {
cout<<"Positive odd number."<< endl;
}
}
else {
cout<<"Not a positive number."<<endl;
}
In this case, both branches can be safely expanded by further statements.
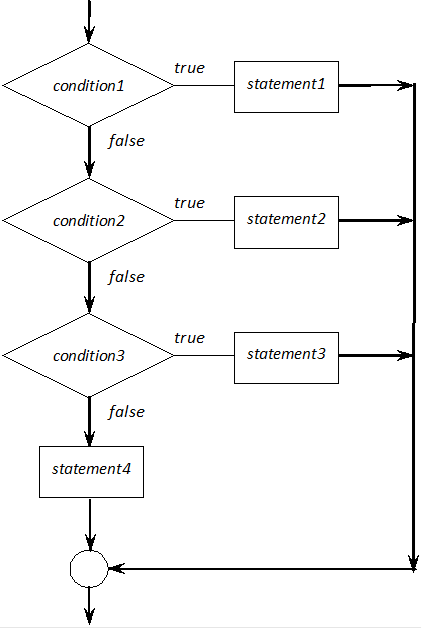
Multi-way branches
A frequent case of nested if statements is to use further if statements in else branches (Figure I.9).
This structure realizes multi-way branches. If any condition is true, the corresponding statement is executed. If no condition is fulfilled, only the last else statement is executed.
if (condition1)
statement1
else if (condition2)
statement2
else if (condition3)
statement3
else
statement4
The following example decides whether number n is negative, 0 or positive:
if (n > 0)
cout<<"Positive number"<<endl;
else if (n==0)
cout<<"0"<<endl;
else
cout<<"Negative number"<<endl;
A special case of else-if structures is when we check whether two elements are equal or not (==). The following example demonstrates a calculator counting the result of a simple addition and subtraction:
#include <iostream>
using namespace std;
int main()
{
char op;
double a, b, c;
cout<<"expression : ";
cin >>a>>op>>b; // reading from keyboard: 4+10 <Enter>
if (op == '+')
c = a + b;
else if (op == '-')
c = a - b;
else {
cout << "Not a valid operator: " << op <<endl;
return -1;
}
cout <<a<<op<<b<<'='<<c<<endl;
return 0;
}
The following example counts the grades to be given to students on the basis of the achieved points in C++ programming:
#include <iostream>
using namespace std;
int main()
{
int points
char grade = 0;
cout << "Points: "; cin >> points;
if (points >= 0 && points <= 100)
{
if (points < 40)
grade = 'A';
else if (points >= 40 && points < 55)
grade = 'B';
else if (points >= 55 && points < 70)
grade = 'C';
else if (points >= 70 && points < 85)
grade = 'D';
else if (points >= 86)
grade = 'F';
cout << "Grade: " << grade << endl;
}
else
cout <<"Not a valid number!" << endl;
}
I.4.2.2. switch statements
In fact, switch statements are statement blocks that we can enter into depending on the value of a given integer expression. The parts of the code to be executed are determined by the so-called case labels (caseconstant expressions).
switch (expression)
{
caseconstant_expression1 :
statements1
caseconstant_expression2 :
statements2
caseconstant_expression3 :
statements3
default :
statements4
}
First, switch statements evaluate the expression, then transfer control to the case label in which the value of the constant_expression equals to the value of the evaluated expression. After that, all statements are executed from the entering point until the end of the block. If none of the case constants are equal to the value of the expression, control passes to the statement with label default. If no default label is provided, control passes to the statement following the brace closing the block of the switch statement.
This little bit weird functioning is demonstrated by an exceptional example code. The following switch statement is able to count the factorial of all integer numbers between 0 and 5. (In this case, the adjective exceptional means 'not to be followed'.)
int n = 4, f(1);
switch (n) {
case 5: f *= 5;
case 4: f *= 4;
case 3: f *= 3;
case 2: f *= 2;
case 1: f *= 1;
case 0: f *= 1;
}
In most cases switch statements are used, similarly to else-if structures, to realize multi-way branches. For that purpose, all statement blocks that correspond to a case have to end with a jump statement (break, goto or return). break statements transfer control to the statement immediately following the switch block, goto to the statement with the specified label within the function block and finally return exits the function.
Since our aim is to create well functioning and easily comprehensible source codes, the number of jump statements should be reduced to a minimum level. However, the usage of break is completely allowed in switch statements. In general, statements even at the end of the default label is followed by a break since the default case can be placed anywhere within switch statements.
On the basis of the above, the calculator program of the previous subsection can be rewritten by switch in the following way:
#include <iostream>
using namespace std;
int main()
{
char op;
double a, b, c;
cout<<"expression :";
cin >>a>>op>>b;
switch (op) {
case '+':
c = a + b;
break;
case '-':
c = a - b;
break;
default:
cout << "Not a valid operator: " << op <<endl;
return -1;
}
cout <<a<<op<<b<<'='<<c<<endl;
return 0;
}
The next example demonstrates how to associate the same code part to more cases. In the source code, the case labels corresponding to cases 'y' and 'Y', as well as 'n' and 'N' were placed one after the other in the switch statement processing the response character.
#include <iostream>
using namespace std;
int main()
{
cout<<"The response [Y/N]?";
char response=cin.get();
switch (response) {
case 'y': case 'Y':
cout<<"The answer is YES."<<endl;
break;
case 'n':
case 'N':
cout<<"The answer is NO."<<endl;
break;
default:
cout<<"Wrong response!"<<endl;
break;
}
}
I.4.3. Iteration structures (loops)
In programming, program structures ensuring automatic repetitions of statements are called iterations or loops. In C++, loop statements repeat a given statement in the function of the repetition condition until the condition is true.
while (condition) statement
for (initialisation opt ; condition opt ; increment_expression opt ) statement
dostatementwhile (condition)
In the case of for statement, opt means that the corresponding expressions are optional.
Loops can be classified on the basis of the place where control conditions are processed. Loops in which the control condition is evaluated before statements are executed are called pre-test loops. Any statement in the loop is executed if and only if the condition is true. Pre-test loops of C++ are while and for.
On the contrary, the statements of do loops are always executed at least once since control condition is evaluated after the execution of the statement – post-test loops.
In all three cases, correctly organized loops terminate if the control condition becomes false (0). However, there are times we create intentionally loops the control condition of which never becomes false. These loops are called infinite loops :
for (;;) statement; while (true) statement; do statement while (true);
Loops (even infinite loops) can be exited before the control condition becomes false. For that purpose, C++ offers statements like break, return or goto, which points to a place outside the body of the loop. Certain statements of the body of the loop can be bypass by using continue. The continue makes the program continue with executing the next iteration of the loop.
I.4.3.1. while loops
while loops repeat statements belonging to them (the body of the loop), while the value of the examined condition is true (not 0). Evaluation of the condition always precedes the execution of the statement. The process of the functioning of while loops can be traced in Figure I.10.
while (condition)
statement
The next example code determines the sum of the first n natural numbers:
#include <iostream>
using namespace std;
int main()
{
int n = 2012;
cout<<"The sum of the first "<<n<<" natural number ";
unsigned long sum = 0;
while (n>0) {
sum += n;
n--;
}
cout<<"is: "<<sum<<endl;
}
Of course, the while loop of the previous example can be simplified but this step decreases its readability:
|
|
|
|
C++ makes it possible to place variable declarations anywhere in a program code. The only condition is that all variables have to be declared (defined) before they are used. In certain cases, variables can be defined in loop statement header in case they are immediately initialized, e.g. by random numbers.
The while loop of the following example code does not terminate until it reaches the first number, divisible by 10. In the code, statement
srand((unsigned)time(NULL));
initializes the random number generator with the actual time, therefore every execution result in a new number sequence. Random numbers are provided by function rand () in the value range between 0 and RAND_MAX (32767).
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
int main()
{
srand((unsigned)time(NULL));
while (int n = rand()%10)
cout<< n<< endl;
}
It should be noted that variable n defined in that way can be accessed within the while loop, thus it is local only with respect to the while loop.
I.4.3.2. for loops
In general, for statements are used if the statements within its body should be executed in a given number of times (Figure I.11). In the general form of for statements, the role of each expression is also mentioned:
for (initialization; condition; increment)
statement
In reality, for statements are the specialized versions of while statements, so the above for loop can perfectly be transformed into a while loop:
initialization;
while (condition) {
statement;
increment;
}
The following program represents a for loop and does the same as the above one: determines the sum of natural numbers. It is obvious at first sight that this solution of the problem is much more readable and simpler:
#include <iostream>
using namespace std;
int main()
{
unsigned long sum;
int i, n = 2012;
cout<<"The sum of the first "<<n<<" natural number ";
for (i=1, sum=0 ; i<=n ; i++)
sum += i;
cout<<"is: "<<sum<<endl;
}
There is only one expression-statement in the body of the loop in the example, so the for loop can be condensed in the following way:
for (i=1, sum=0 ; i<=n ; sum += i, i++) ;
or
for (i=1, sum=0 ; i<=n ; sum += i++) ;
Loops can be nested in one another, since their body can contain other loop statements. The following example uses nested loops to print a pyramid of a given size. In all three loops, loop variable is made local:
#include <iostream>
using namespace std;
int main ()
{
const int maxn = 12;
for (int i=0; i<maxn; i++) {
for (int j=0; j<maxn-i; j++) {
cout <<" ";
}
for (int j=0; j<i; j++) {
cout <<"* ";
}
cout << endl;
}
}
|
*
* *
* * *
* * * *
* * * * *
* * * * * *
* * * * * * *
* * * * * * * *
* * * * * * * * *
* * * * * * * * * *
* * * * * * * * * * *
|
I.4.3.3. do-while loops
In do-while loops, evaluation of the condition takes place after the first execution of the body of the loop (Figure I.12), so the loop body is always executed at least once.
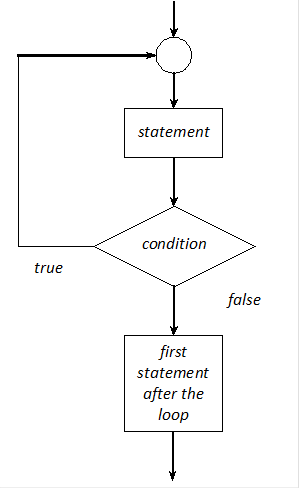
do
statement
while (condition);
As a first step, let's create the version of the program computing the sum of natural numbers with a do-while loop.
#include <iostream>
using namespace std;
int main()
{
int n = 2012;
cout<<"The sum of the first "<<n<<" natural number ";
unsigned long sum = 0;
do {
sum += n;
n--;
} while (n>0);
cout<<"is: "<<sum<<endl;
}
With the help of the following loop, let's read an integer number between 2 and 100 from the input and verify it:
int m =0;
do {
cout<<"Enter an integer number betwwen 2 and 100: ";
cin >> m;
} while (m < 2 || m > 100);
The last example calculates the power of a number with an integer exponent:
#include <iostream>
#include <cstdlib>
using namespace std;
int main()
{
double base;
int exponent;
cout << "base: "; cin >> base;
cout << "exponent: "; cin >> exponent;
double power = 1;
if (exponent != 0)
{
int i = 1;
do
{
power *= base;
i++;
} while (i <= abs(exponent));
power = exponent < 0 ? 1.0 / power : power;
}
cout <<"The power is : " << power << endl;
}
A frequent programming error is to terminate loop headers with a semicolon. Let's see some attempts to print odd integer numbers between 1 and 10.
|
|
|
|
In the case of while, the empty statement is repeated endlessly in the loop. The for loop repeats the empty statement and then prints the value of the loop variable after the loop is exited, i.e. 11. In the case of the do-while loop, the compiler gives an error message if do is followed by a semicolon, so the example code is a perfect solution.
I.4.3.4. break statements in loops
There are cases when the regular functioning of a loop has to be directly intervened into. For example, if a loop has to be exited if a given condition is fulfilled. A simple solution for that is the break statement, which interrupts the execution of the nearest while, for and do-while statements and control passes to the first statement following the interrupted loop.
The following while loop is interrupted if the lowest common multiple of two integer numbers is found:
#include <iostream>
#include <cstdlib>
using namespace std;
int main()
{
int a, b, lcm;
cout << "a = "; cin >> a;
cout << "b = "; cin >> b;
lcm = min(a,b);
while (lcm<=a*b) {
if (lcm % a == 0 && lcm % b == 0)
break;
lcm++;
}
cout << "The lowest common multiple is: " << lcm << endl;
}
The usage of break can be avoided if the condition of the if statement corresponding to it can be integrated into the condition of the loop, that will become more complicated by that step:
while (lcm<=a*b && !(lcm % a == 0 && lcm % b == 0)) {
lcm++;
}
If break statement is used in nested loops in an inner loop, it is only that inner loop that is exited. The following example prints prime numbers between 2 and maxn. The reason for exiting the loop is provided by a logical flag, by the variable (prime), to the outer loop:
#include <iostream>
using namespace std;
int main () {
const int maxn =2012;
int divisor;
bool prime;
for(int num=2; num<=maxn; num++) {
prime = true;
for(divisor = 2; divisor <= (num/divisor); divisor++) {
if (num % divisor == 0) {
prime = false;
break; // has a divisor, not a prime
}
}
if (prime)
cout << num << " is a prime number" << endl;
}
}
If the task is to find the first Pythagorean triple in a given interval, two for loops have to be exited if a match is found. Then the simplest solution is to use the flag (found):
#include <iostream>
#include<cmath>
using namespace std;
int main () {
int left, right;
cout <<"left = "; cin >> left;
cout <<"right = "; cin >> right;
bool found = false;
for(int a = left, c, c2; a<=right && !found; a++) {
for(int b = left; b<=right && !found; b++) {
c2 = a*a + b*b;
c = static_cast<int>(sqrt(float(c2)));
if (c*c == c2) {
found = true;
cout << a << ", " << b << ", " << c << endl;
} // if
} // for
} // for
} // main()
I.4.3.5. continue statements
continue statements start the next iteration of while, for and do-while loops. In the body of these loops, the statements placed after continue are not executed.
In the case of while and do-while loops, the next iteration begins with evaluating again the condition. However, in for loops, the processing of the condition is preceded by the increment.
In the following example, with the help of continue, it was realized that only the numbers divisible by 7 or 12 are printed out in the loop incrementing from 1 to maxn by one:
#include <iostream>
using namespace std;
int main(){
const int maxn = 123;
for (int i = 1; i <= maxn; i++) {
if ((i % 7 != 0) && (i % 12 != 0))
continue;
cout<<i<<endl;
}
}
It is a bad practice in programming to use often break and continue statements. It has to be always rethought if given program structures can be solved without jump statements. In the preceding example, this can easily be done by inverting the condition of the if statement:
for (int i = 1; i <= maxn; i++) {
if ((i % 7 == 0) || (i % 12 == 0))
cout<<i<<endl;
}
I.4.4. goto statements
To close the present chapter, let's see one jump statement of C++ not presented yet. We should already be careful when using break and continue statements, but this is even truer for goto statements.
goto statements that can be used to jump within functions have a bad reputation because they make program codes less understandable and more unstructured. Not to mention the tragic consequences of jumping into a loop. So, it should be stated that goto statements are to be avoided if a structured and a clearly understandable code is to be written. In most software developer companies, it is even forbidden.
In order to use goto statements, the statement to which we want to jump has to be labeled. A label is an identifier which is separated by a colon from the following statement:
label: statement
The goto statement with which control can be transferred to the line marked with the label above:
goto label;
In some and only justified cases, e.g. jumping out from a very complicated program structure, goto provides a simple alternative.
I.5. Exception handling
An anomalous state or event that hinders the normal flow of the execution of a program is called an exception.
In C language, errors were handled locally at every eventual anomalous point of a program. In general, this meant printing out an error message ( cerr ) and then interrupting the execution of that program ( exit ()). For example, when all coefficients of a quadratic equation have been read from the keyboard and the quadratic coefficient is 0, then the quadratic formula cannot be applied to solve the equation:
#include <iostream>
#include <cstdlib>
using namespace std;
int main()
{
double a, b, c;
cout<<" coefficients (separated from each"
"other by a space) :";
cin >> a >> b >> c;
if (0 == a) {
cerr << "The equation is not quadratic!" << endl;
exit(-1);
}
cout <<a<<"x^2+"<<b<<"x+"<<c<<"=0"<< endl;
}
C++ makes it possible to assign types to exceptions (errors) and to carry out all exception handling tasks at the same place. Exception handling takes place on the basis of the termination model, which means that the execution of the code part (function) that provoked an exception is interrupted when that exception arises.
Standard C++ language contains relatively few integrated exceptions; however, different class libraries prefer exceptions to signal erroneous states. Exceptions can be triggered manually by "throwing" a value of a given type. Exceptions are transferred (thrown) to the nearest exception handlers that either catch or transfer them.
This above mentioned process functions only if the code part susceptible to trigger an error is enclosed in a statement block that attempts (try) to execute that.
So, the three elements that are needed for the type-oriented exception handling of C are the following:
-
selecting the code part under exception inspection (try-block),
-
transferring exceptions (throw),
-
catching and handling exceptions (catch).
I.5.1. The try – catch program structure
In general, a try-catch program structure contains only one try block and any number of catch blocks:
try
{
// statements under exception inspection
statements
}
catch (exception1 declaration) {
// the handler of exception1
statements1
}
catch (exception2 declaration) {
// the handler of exception2
statements2
}
catch (...) {
// the handler of any other exception
statements3
}
// statements that are executed after successful handling
statements4
In case any statement of a try block causes an exception, the execution of statements is interrupted and control is passed to the catch block (that follows that try block) of the given type (if there is one). If there is no handler with the given type, then the exception is transferred to a handler belonging to an external try block. Exceptions without any type match are finally transferred to the execution environment (as unhandled exceptions). This situation is signalled by the following message: "This application has requested the Runtime to terminate it in an unusual way. Please contact the application's support team for more information.”
The exception declarations that follow the keyword catch can be provided in many ways. These declarations may contain a type , a variable declaration (type identifier) or three dots . The thrown exception can only be accessed by using the second form. The three dots means that that block catches any exception. Since exceptions are identified in the order catch blocks are provided, the three dotted version should be the last in the catch-block list.
As an example, let's transform the error inspection of the introduction part into an exception handling.
#include <iostream>
#include <cstdlib>
using namespace std;
int main()
{
try {
double a, b, c;
cout << " coefficients (separated from each"
"other by a space) :";
cin >> a >> b >> c;
if (0 == a) throw false;
cout <<a<<"x^2+"<<b<<"x+"<<c<<"=0"<< endl;
}
catch (bool) {
cerr << "The equation is not quadratic!" << endl;
exit(-1);
}
catch (...) {
cerr << "An error occurred..." << endl;
exit(-1);
}
}
I.5.2. Provoking exceptions - the throw statement
Exceptions have to be handled locally within the given part of a code with the keywords try, throw and catch. Exception handling only takes place in case the code in the catch block (and the code called from there) is executed. From the selected code portion, a throw statement
throwexpression;
passes control to the handler that corresponds to the type of the expression, which should be provided after the keyword catch.
When an exception is transferred by a throw statement, then the value of the expression given in the statement is copied into the parameter figuring in the header of the catch block, so this value can be processed in that specific handler. For that purpose, the type also has to have an identifier in that catch statement.
If a catch block contains a throw statement, the caught exception can be transferred as another exception, either transformed to another or not. If the exception is not intended to be transformed, the empty throw statement has to be used: throw;
Exception handling can be made more complete by defining exception classes. The header file named exception contains the description of the exception class, which is the base class of different logical and run-time exceptions. The function named what () of these classes returns the string identifying that exception. The following table summarises the exceptions thrown by the classes defined in the C++ standard library. All exceptions have the exception class as their base class.
|
Exception classes |
Header file |
||
|---|---|---|---|
|
exception |
<exception> |
||
|
bad_alloc |
<new> |
||
|
bad_cast |
<typeinfo> |
||
|
bad_typeid |
<typeinfo> |
||
|
logic_failure |
<stdexcept> |
||
|
domain_error |
<stdexcept> |
||
|
invalid_argument |
<stdexcept> |
||
|
length_error |
<stdexcept> |
||
|
out_of_range |
<stdexcept> |
||
|
runtime_error |
<stdexcept> |
||
|
range_error |
<stdexcept> |
||
|
overflow_error |
<stdexcept> |
||
|
underflow_error |
<stdexcept> |
||
|
ios_base::failure |
<ios> |
||
|
bad_exception |
<exception> |
||
Exception classes make it possible to pass "smart" objects as exceptions instead of simple values. The knowledge necessary for that process is only treated in Chapter III of the present book.
A comfortable way of exception handling is when a string is passed as exception. In that way, the users of a computer program will always receive meaningful messages during their work. (String constants will be declared as of type const char *, which will be treated in the next chapter.)
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
int main() {
int number;
srand(unsigned(time(NULL)));
try {
while (true) {
number = rand();
if (number>1000)
throw "The number is too big";
else if (number<10)
throw "The number is too small";
cout << 10*number << endl;
} // while
} // try
catch (const char * s) {
cerr << s << endl;
} // catch
} // main()
I.5.3. Filtering exceptions
Functions in C++ have an important role in exception handling. An exception arising in a function is generally processed within that function since related data are only available from there. However, there are some exceptions that indicate an unsuccessful working of the function back to the element that called the latter. Of course, these exceptions are transferred outside the function.
In the header of a function definition, the keyword throw can be used in a specific way, so the type of the exception to be thrown to the handler can also be defined. By default, all exceptions are transferred.
// all exceptions are transferred. int funct1(); // only exceptions of type char and bool are transferred int funct2() throw(char, bool); // only exceptions of type bool are transferred int funct3() throw(bool); // no exceptions are transferred int funct4() throw();
When a program throws an exception that does not have a handler in that program, the execution environment activates the function named terminate (), which makes the program abort ( abort ()). If a function body throws an exception that is not listed in the exceptions of the given function to be thrown, then the unexpected () system call terminates the program. Programmers can intervene in both terminating process by defining their own handlers that can be registered with the help of the functions set_terminate () or set_unexpected () declared in the header file named except.
I.5.4. Nested exceptions
A try-catch exception handling structure can be placed within another try-block, either directly or indirectly (i.e. in the function called from that try-block).
As an example, a string exception is thrown from an inner try-block. This is then processed in the inner structure and then transferred by using the empty throw; statement. The outer structure treats that exception finally.
#include <iostream>
using namespace std;
int main()
{
try {
try {
throw "exception";
}
catch (bool) {
cerr << "bool error" << endl;
}
catch(const char * s) {
cout << "inner " << s << endl;
throw;
}
}
catch(const char * s) {
cout << "outer " << s << endl;
}
catch(...) {
cout << "unknown exception" << endl;
}
}
As the final example of the present section, let's have a look at the following calculator program. Our own exceptions are stored in enumerations. The program can be exited by using the operator x.
#include <iostream>
using namespace std;
enum zerodiv {DividingWithZero};
enum wrongoperation {WrongOperation};
int main()
{
double a, b, e=0;
char op;
while (true) // exiting if op is x or X
{
cout << ':';
cin >>a>>op>>b;
try {
switch (op) {
case '+': e = a + b;
break;
case '-': e = a - b;
break;
case '*': e = a * b;
break;
case '/': if (b==0)
throw DividingWithZero;
else
e = a / b;
break;
case 'x': case 'X' :
throw true;
default: throw WrongOperation;
}
cout << e <<endl;
} // try
catch (zerodiv) {
cout <<" Dividing with zero" <<endl;
}
catch (wrongoperation) {
cout <<" Wrong operation" <<endl;
}
catch (bool) {
cout<<"Off"<<endl;
break; // while
}
catch(...) {
cout<<" Something is bad "<< endl;
}
} // while
}
I.6. Pointers, references and dynamic memory management
The most important resource of every program is computer memory since all directly accessible (on-line) data is stored there along with executed program code. In our previous examples, it is compiler that was entrusted with memory management.
|
Based on the storage class, compiler places global (extern) data grouped together on a memory place which is always accessible while the program is running. Local (auto) data are stored in a stack memory block when the corresponding functions are entered into and they are deleted when these functions are exited (Figure I.13). However, there is a space named heap, where programmers can place variables and delete those that are not needed anymore. These dynamically managed variables are different from those used so far since they have no name. They can be referenced by variables storing their address (pointers). C++ has a couple of operators that make dynamic memory management possible: *, &, new, delete. |
 Figure I.13. C++ program memory usage
|
Besides the above mentioned areas, there are many domains where pointers are used in C/C++ programs: function parameter passing, linked data structure management, etc. C++ attempts to counterbalance the exclusive usage of pointers with the help of a safer type, namely with the help of references.
I.6.1. Pointers
When defining a variable, compilers reserve the quantity of memory space that corresponds to the type of the given variable and associate to the latter the name used in its definition. In most cases, we assign values to variables and read their content by using their names. There are cases where this approach is insufficient and the address of a variable in the memory should be used directly (for example when calling the Standard Library function scanf ()).
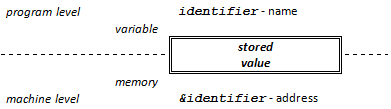
With the help of pointers, the address of variables (data stored in memory) and functions can be stored and managed. A pointer does not only store address but also have information how to interpret how many bytes from that given address. And this is the type of the referenced data, which is provided in the definition of pointers (variables).
I.6.1.1. Single indirection pointers
First, let's start with the most frequently used and the simplest form of pointers, that is with single indirection pointers the general definition of which is:
type *identifier;
The asterisk indicates that now a pointer is defined, and the type before the asterisk indicates the referenced data type. The default automatic initial value of pointers is determined by the usual rules: it is 0, if it is created outside functions and undefined when created within a function. It is a safe solution to initialize always pointers after they are created with NULL value, which can be found in most header files:
type *identifier = NULL;
If more pointers are created within a single statement, all identifier names should be preceded by an asterisk:
type *identifier1, *identifier2;
Many operations can be carried out for pointers; however, there are three operators that can exclusively be used with pointers:
|
*ptr |
Accessing the object ptr points to. |
|
ptr->member |
The access of the given member of the structure ptr points to (Section I.8). |
|
&leftvalue |
Getting the address of leftvalue. |
The two levels presented in the introduction become more understandable if they are demonstrated by an example. Let's create an integer type variable.
int x = 2;
When the variable is defined, an (int type) space is created in memory (e.g. with the address of 2004) into which the initial value is copied:

The definition of
int *p;
creates a variable (e.g. at the address of 2008), the type of which is int*. C++ generally considers p as an int* type variable or p can also be considered as an int type pointer. This pointer can be used for storing address of int type variables, that can be accessed by the "address of" & operation, e.g.
p = &x;
After that operation, the x name and *p value reference the same memory space. (the expression *p designate the storage place „p points to”.)
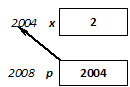
As a consequence, after the processing of
*p = x +10;
the value of x becomes 12.
An alternative pointer type can also be created by using the keyword typedef:
int x = 2; typedef int *tpi; tpi p = &x;
A single variable can be referenced by many pointers and its value can be modified by any of them:
int x = 2; int * p, *pp; p = &x; pp = p; *pp += 10; // the value of x is 12 again
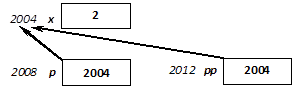
If a pointer is initialized with an address of a variable of a different type, a compiler error message is sent.
long y = 0; char *p = &y; // error! ↯
If it is not an error and the long type data is to be accessed by bytes, compilers can be asked to do value assignment by type cast:
long y = 0; char *p = (char *)&y;
or
char *p = reinterpret_cast<char *>(&y);
It is a frequent error to use a pointer without initialization. In general, this results in the interruption of the execution of the program:
int *p; *p = 1002; // ↯ ↯ ↯
I.6.1.2. Pointer arithmetic
Besides the already presented operators (* and &), other ones can also be used. These operations together are covered by pointer arithmetic. Every other operation results in an undefined result, so they are to be avoided.
The allowed pointer arithmetic operations are summarised in a table where q and p are pointers (not of void* type), n is an integer number (int or long):
|
Operation |
Expression |
Result |
|---|---|---|
|
two pointers of the same type can be subtracted from each other |
q - p |
integer number |
|
an integer number can be added to a pointer |
p + n, p++,++p, p += n, |
pointer |
|
an integer number can be subtracted from a pointer |
p – n, p--, --p, p -= n |
pointer |
|
two pointers can be compared |
p == q, p > q, etc. |
bool (false or true) |
When an integer number is added to or subtracted from a pointer, compilers automatically scale the integer number according to the type of the pointer, therefore the stored address is not modified by n bytes but by
n * sizeof(pointer_type)
bytes, so the pointer "steps" by the size of n elements in memory.
Accordingly, increment and decrement operators can also be used for pointers and not only for arithmetic types, but in the former case it means going to the neighbouring element and not an increment or decrement by one byte.
Incrementing a pointer to the neighbouring element can be carried out in many ways:
int *p, *q; p = p + 1; p += 1; p++; ++p;
Decrementing to the preceding element can also be done in many ways:
p = p - 1; p -= 1; p--; --p;
Scaling also works when the difference of two pointers is counted, so we get the number of elements between the two pointers as a result:
int h = p - q;
I.6.1.3. void * type general pointers
C++ also allows for using general pointers without a type (void types),
int x; void * ptr = &x;
which only store addresses, so they are not associated to any variable.
C++ ensures two implicit conversions for pointers. A pointer with any type can be transformed into a general (void) type pointer, and all pointers can be initialized by zero (0). For a conversion in the other direction, explicit type cast should be used.
That is why, if a value is to be given to variable referenced by ptr, the address should be associated with a type by a manual type cast. Type cast can be done in many ways:
int x; void *ptr = &x; *(int *)ptr = 1002; typedef int * iptr; *iptr(ptr) = 1002; *static_cast<int *>(ptr) = 1002; *reinterpret_cast<int *>(ptr) = 1002;
After any of these indirect value assignments, the value of x becomes 1002.
It should be noted that most of the functions in the Standard Library that return pointer are of void* type.
I.6.1.4. Multiple indirection pointers
Pointers can also be used in the case of multiple indirection relations. In these cases, the definition of pointers contains more asterisks (*):
type * *pointer;
The asterisk standing immediately before the pointer indicates that a pointer is defined, and what can be found before this asterisk is the type of the pointer (type *). Similarly to that, any number of asterisks can be interpreted to but in order to ease our readers, we note that the elements of C++ Standard Library use double indirection pointers at most.
Let's have a look at some definitions and let's find out what the created variable is.
|
int x; |
x is an int type variable, |
|
int *p; |
p is an int type pointer (that can point to an int variable), |
|
int * *q; |
q is an int* type pointer (that may point to an int* variable, that is to a pointer pointing to an integer). |
The above detailed definitions can be rewritten in a more understandable way by alternative (typedef) type names:
// iptr - pointer type pointing to an integer typedef int *iptr; iptr p, *q;
or
// iptr - pointer type pointing to an integer typedef int *iptr; // type of a pointer pointing to an iptr type variable typedef iptr *ipptr; iptr p; ipptr q;
|
When these definitions are provided, and when the statements x = 2; p = &x; q = &p; x = x + *p + **q; are executed, the value of x will be 6. |
|
It should be noted that when interpreting more complex pointer relations, graphical representations provide a useful help.
I.6.1.5. Constant pointers
C++ compilers strictly verify the usage of const type constants, for example a constant can be referenced by an appropriate pointer:
const double pi = 3.141592565; // pointer pointing to a double type data double *ppi = π // error! ↯
The assignment can be carried out by a pointer pointing to the constant:
// pointer pointing to a double constant const double *pdc; const double dc = 10.2; double d = 2012; pdc = &dc; // pdc pointer points to dc cout <<*pdc<<endl; // 10.2 pdc = &d; // pdc pointer is set to d cout <<*pdc<<endl; // 2012
By using the pdc pointer, we cannot modify the value of the d variable:
*pdc = 7.29; // error! ↯
It is a pointer with a constant value, so the value of the pointer cannot be changed:
int month; // constant pointer pointing to an int type data int *const actmonth = &month; //
The value of the actmonth pointer cannot be changed only that of *actmonth.
*actmonth = 9; cout<< month << endl; // 9 actmonth = &month; // error! ↯
Pointer with a constant value pointing to a constant:
const int month = 10; const int amonth = 8; // constant pointer pointing to an int type constant const int *const actmonth = &month; cout << *actmonth << endl; // 10
Neither the pointer, nor the referenced data can be changed.
actmonth = &amonth; // error! ↯ *actmonth = 12; // error! ↯
I.6.2. References
Reference types make it possible to reference already existing variables while defining an alternative name. The general form of their definition:
type &identifier = variable;
& indicates that a reference is defined, while the type before the & designates the type of the referenced data that have to be the same as that of the variable set as its initial value. When defining many references with the same type, the sign & should be typed before all references:
type &identifier1 = variable1, &identifier2 = variable2 ;
When a reference is defined, initialisation has to be done with a left value. Let's make a reference to the int type x variable as an example.
int x = 2; int &r = x;
Contrary to pointers, no variable is created to store references in general. Compilers just give a new name as a second name to the variable x (r).

As a consequence, the value of x becomes 12 when the following statement is evaluated:
r = x + 10;
While the value of a pointer, and the referenced storage place as a consequence, can be modified at any time, the reference r is bound to a variable.
int x = 2, y = 4; int &r = x; r = y; // normal value assignment cout << x << endl; // 4
If a reference is initialized by a constant value or a variable of a different type, a compiler error message is sent. It does not even help if type cast is used in the latter case. These cases are treated by compilers if a so-called constant (read-only) reference is created. In that case, the compiler creates first the storage place of the same type as that of the reference, then it initializes it with the right value standing after the equal sign.
const char &lf = '\n'; |
unsigned int b = 2004; const int &r = b; b = 2012; cout << r << endl; // 2004 |
Synonymous reference types can also be created by the keyword typedef:
typedef int &rint; int x = 2; rint r = x;
References can be created to pointers just like for other variable types:
int n = 10; int *p = &n; // p points to the variable n int* &rp = p; // rp is a reference to the pointer p *rp = 4; cout << n << endl; // 4
The same can be done with typedef:
typedef int *tpi; // type of a pointer pointing to an integer typedef tpi &rtpi; // reference to a pointer pointing to an integer int n = 10; tpi p = &n; rtpi rp = p;
It should be noted that a reference or a pointer cannot be defined for a reference.
int n = 10; int &r = n; int& *pr = &r; // error! ↯ int& &rr =r; // error! ↯ int *p = &r; // pointer p points to n via the reference r
Reference cannot be created for bitfields (Section I.8), and we cannot even define an array consisting of reference elements (Section I.7).
We will experience the real significance of reference types when creating functions.
I.6.3. Dynamic memory management
In general, pointers are not used to point to other variables but it can also happen (e.g. when parameters are passed). Pointers are the key to one of the most important facilities of C++, namely to dynamic memory management. With pointers, it is programmer who allocates memory space necessary for the execution of a program and it is him who frees it if they are not needed anymore.
The dynamic management of free memory (heap) is a vital part of all programs. C ensures Standard Library functions for the needed memory allocation ( malloc (),...) and deallocation ( free ()) operations. In C++, the operators new and delete replace the above mentioned library functions (although the latter are also available).
Dynamic memory management consists of the following three steps:
-
allocating a free memory block while verifying the success of the allocation,
-
accessing the memory space with a pointer,
-
freeing (deallocating) the previously allocated memory space.
I.6.3.1. Allocating and accessing heap memory
The first step of dynamic memory management is allocating a memory space of the necessary size from the heap memory. For that purpose, the operator new can be used. The operator new allocates a memory space in the heap of the size corresponding to the type provided in its operand and returns a pointer pointing to the beginning of that memory space. If needed, an initial value can also be provided in the parentheses following the type.
pointer = newtype;
pointer = newtype(initial value);
new cannot only allocate memory space for one element but also for many elements standing one after the other. The data structure created in this way is called a dynamic array (Section I.7).
pointer = newtype[number_of_elements];
Let's see some examples for the operation new.
int main() {
int *p1;
double *p2;
p1 = new int(2);
p2 = new double;
}
The above mentioned definitions result in the creation of the pointer variables p1 and p2 in the stack. After value assignment, two dynamic variables are born in the stack memory. Their address appear in the corresponding pointers (Figure I.14).
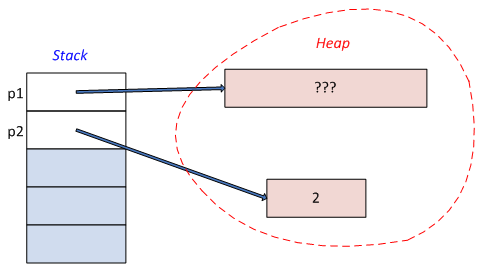
When memory space is allocated, especially for a big sized dynamic array, it may happen that there is no enough contiguous free memory at our disposal. C++ run-time system signals this issue by throwing a bad_alloc exception (exception header file). Program codes can be therefore made safe by using exception handling methods.
#include <iostream>
#include <exception>
using namespace std;
int main() {
long * pdata;
// Memory allocation
try {
pdata = new long;
}
catch (bad_alloc) {
// Unsuccessful allocation
cerr << "\nThere is no enough memory!" << endl;
return -1; // Program is exited
}
// ...
// Deallocating (freeing) allocated memory space
delete pdata;
return 0;
}
If we do not benefit from exception handling opportunities, the nothrow constant should be used as an argument for the new operator (new header file). As a result, the new operator returns a 0 value instead of throwing an exception when memory allocation is unsuccessful.
#include <iostream>
#include <new>
using namespace std;
int main() {
long * pdata;
// Memory allocation
pdata = new (nothrow)long;
if (0 == pdata) {
// Unsuccessful allocation
cerr << "\nThere is no enough memory!" << endl;
return -1; // Program is exited
}
// ...
// Deallocating (freeing) allocated memory space
delete pdata;
return 0;
}
Finally, we should not forget about another possibility of the new operator. new can also be followed directly by a pointer in parenthesis, which makes the operator return the value of the pointer (thus it does not allocate memory):
int *p=new int(10); int *q=new(p) int(2); cout <<*p << endl; // 2
In the examples above, the pointer q reference the memory space p points to. Pointers can be of a different type:
long a = 0x20042012; short *p = new(&a) short; cout << hex <<*p << endl; // 2012
I.6.3.2. Deallocating allocated memory
Memory blocks allocated by the operator new can be deallocated by the operator delete:
delete pointer;
delete[] pointer;
The first form of the operation is used to deallocate one single dynamic variable, whereas the second one is used in the case of dynamic arrays.
delete operation also works correctly with pointers of 0 value. In every other case where the value was not assigned by new, the result of delete is unpredictable.
The introductory example of the previous section can be made complete if memory space is deallocated:
int main() {
int *p1;
double *p2;
p1 = new int(2);
p2 = new double;
delete p1;
delete p2;
p1 = 0;
p2 = 0;
}
I.7. Arrays and strings
The variables in our previous examples were only able to store one (scalar) value at a time. Programming work often requires to store data sets comprising many similar or different elements in memory and to do operations on them. In C++, these tasks can efficiently be realised with the help of arrays and user-defined types (struct, class, union, see Section I.8), that is derived types.
I.7.1. C++ array types
An array is a set of data of the same type (elements) that are placed in memory in a linear sequence. In order to access its elements, we should use the name of the array followed by the indexing operator(s) ( [] ) that enclose the index(es) of the given element in the array. The first element has always the index(es) 0.
The most frequently used array type has only one dimension: one-dimensional array (vector). If the elements of an array are intended to be identified by more integer numbers, storage should be realised by multi-dimensional arrays. From among these, we only detail the second most frequent array type, the two-dimensional array, i.e. (matrix), the elements of which are stored in a linear sequence by rows.
Before detailing the two array types, let's see how to use arrays in general. The definition of n-dimensional arrays:
element_typearray_name[size 1 ][size 2 ][size 3 ]…[size n-1 ][size n ]
where size i determines the size of the ith dimension. In order to access the array elements, an index should be provided for every dimension in the closed interval between 0,size i -1:
array_name[index 1 ][index 2 ][index 3 ]…[index n-1 ][index n ]
Presented in that way, arrays might seem frightening but in many cases, it is a useful, easy and comfortable solution to store data.
I.7.1.1. One-dimensional arrays
Definition of one-dimensional arrays:
element_typearray_name[size];
The element_type determining the type of the stored elements can be of any type with the exception of void and function types. The size provided between square brackets has to be a constant expression that compilers can calculate. The size defines the number of elements that can be stored in the array. Elements are indexed between 0 and (size-1).
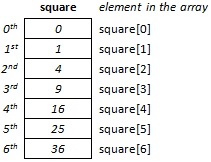
As an example, let's have a look at an integer array having 7 elements. The integer type elements of the array will all have the value of the square of their indexes (Figure I.15). It is a good solution to store the size of an array as a constant. According to what has been said so far, the definition of the array square is the following:
const int maxn =7; int square[maxn];
In order to access the elements of the array in a linear order from its beginning to its end, we use in general a for loop, the variable of which stores the index of the array. (Normally, a correct for-loop runs from 0 to size minus one). Array elements are accessed by the indexing operator ([]).
for (int i = 0; i< maxn; i++)
square[i] = i * i;
The size of memory in bytes allocated for the array square is returned by the expression sizeof (square), whereas the expression sizeof (square[0]) returns the size of one element. The number of elements of an array can therefore always be calculated by dividing the two elements by integer division:
int number_of_elements = sizeof(square) / sizeof(square[0]);
It should be noted that C++ carry out no check on array indexing. Trying to access an element at an index that is outside the array bounds can lead to runtime errors, and tracing back these errors can take too much time.
double october [31]; october [-1] = 0; // error ↯ october [31] = 0; // error ↯
In the following example, we calculate the average of float numbers read from the keyboard to an array of five elements, and then print out this average and the difference between each element and this average.
#include <iostream>
using namespace std;
const int maxn = 5 ;
int main()
{
float numbers[maxn], average = 0.0;
for (int i = 0; i <maxn; i++)
{
cout<<"numbers["<< i <<"] = ";
cin>>numbers[i]; // reading from keyboard
average += numbers[i]; // sum of all elements
}
cin.get();
average /= maxn; // counting the average
cout<< endl << "The average is " << average << endl;
// printing out differences
for (int i = 0; i <maxn; i++) {
cout<< i << ".\t" << numbers[i];
cout<< '\t' << average-numbers[i] << endl;
}
}
We should pay attention to how elements of an array are read from the keyboard. Array elements can only be accessed and set (from the keyboard) one by one.
numbers[0] = 12.23 numbers[1] = 10.2 numbers[2] = 7.29 numbers[3] = 11.3 numbers[4] = 12.7 The average is 10.744 0. 12.23 -1.486 1. 10.2 0.544001 2. 7.29 3.454 3. 11.3 -0.556 4. 12.7 -1.956 |
I.7.1.1.1. Initializing and assigning values to one-dimensional arrays
C++ language makes possible to give an initial value to array elements. When arrays are defined, the equal sign is followed by the values of the initialization list that are enclosed within curly brackets. These values are associated with the indexes of the array in that order:
element_typearray_name[size] = { initialization list delimited by commas };
Let's see some examples how to initialize vectors:
int primes[10] = { 2, 3, 5, 7, 11, 13, 17, 19, 23, 27 };
char name[8] = { 'I', 'v', 'a', 'n'};
double numbers[] = { 1.23, 2.34, 3.45, 4.56, 5.67 };
In the case of the array primes, we made sure that the number of elements in the list is equal to the size of the array. If the list contained more initial values than needed, compilers would send us an error message.
In the second example, the initialisation list contains less elements than the size of the array. In that case, the first four elements of the array name will have the given values, while the others will be 0. If we benefit from this possibility, we can easily set 0 for all elements of any array by:
int big[2012] = {0};
In the last example, the compiler sets the number of elements of the array numbers based on the number of constants provided in the initialisation list (5). This is a good solution if the number of elements is often changed between different compilations. In that case, the number of the elements can be obtained by the above mentioned method:
double numbers[] = { 1.23, 2.34, 3.45, 4.56, 5.67 };
const int numbers = sizeof(numbers) / sizeof(numbers[0]);
Initialisation lists may contain expressions the values of which are calculated runtime:
double eh[3]= { sqrt(2.3), exp(1.2), sin(3.14159265/4) };
For a more rapid but less secure management of arrays, the Standard Library functions declared in the cstring header file and beginning with ”mem” can also be used. The function memset () makes possible to set all elements of a char array to the same character or to set all elements of an array of any type to bytes with value 0:
char line[80]; memset( line, '=', 80 ); double balance[365]; memset( balance, 0, 365*sizeof(double) ); //or memset( balance, 0, sizeof(balance) );
The latest example gives rise to the question what operations can be used in C++ for arrays besides the indexing and the sizeof operators. The response is easy: nothing. The reason for that is that C/C++ languages treat array names as constant value pointers that are set by compilers. We benefitted from that when we called memset () since the first parameter of the function should be a pointer.
There are two methods for value assignment between two arrays of the same type and size. In the first case, elements are copied from one to another in a for loop, in the second one, the Library function memcpy () is called.
#include <iostream>
#include <cstring>
using namespace std;
int main()
{
const int maxn = 8 ;
int source[maxn]= { 2, 10, 29, 7, 30, 11, 7, 12 };
int destination[maxn];
for (int i=0; i<maxn; i++) {
destination[i] = source[i]; // copying elements
}
// or
memcpy(destination, source, sizeof(destination));
}
memcpy () does not always function correctly if there is an overlap between source and destination, for example if only one part of an array has to be copied to free space for a new element. In that case as well, there are two possibilities: a for loop or the memmove () Standard Library function. In the following example, a new element is intended to be inserted in the array ordered at the position with index 1:
#include <iostream>
#include <cstring>
using namespace std;
int main()
{
const int maxn = 10 ;
int ordered[maxn]= { 2, 7, 12, 23, 29 };
for (int i=5; i>1; i--) {
ordered[i] = ordered[i-1]; // copying elements
}
ordered[1] = 3;
// or
memmove(ordered+2, ordered+1, 4*sizeof(int));
ordered[1] = 3;
}
It should be noted that the address of the destination and source area is provided by using pointer arithmetic: ordered+2, ordered+1.
I.7.1.1.2. One-dimensional arrays and the typedef
As we have already mentioned, the readability of program code is increased if more complex type names are replaced by synonymous names. For that reason, typedef should be used for derived types.
Let's look an example where we aim at calculating the vector multiplication of two vectors of 3 integer elements and to place the new vector in a third vector. The general definition of vector multiplication:
|
|
||
|
|
The arrays necessary to solve the problem can be created in two ways:
int a[3], b[3], c[3];
or
typedef int vector3[3]; vector3 a, b, c;
The vectors a and b are initialized with constants:
typedef int vector3[3];
vector3 a = {1, 0, 0}, b = {0, 1, 0}, c;
c[0] = a[1]*b[2] - a[2]*b[1];
c[1] = -(a[0]*b[2] - a[2]*b[0]);
c[2] = a[0]*b[1] - a[1]*b[0];
typedef is also useful to reference an array containing 12 elements of type double with a pointer. The first idea should be to type
double *xp[12];
to create the type. When interpreting type expressions, the priority table of operators is useful (Appendix Section A.7). On the basis of that, xp is an array of 12 elements and the array name is preceded by the type of its elements. That is why, xp is a pointer array with 12 elements. The order of the interpretation can be modified by parentheses:
double (*xp)[12];
In that case, xp is a pointer and the type of the referenced data is double[12], that is a double array of 12 elements. Now we are done! However, it is more rapid and safe to use the keyword typedef:
typedef double dvect12[12]; dvect12 *xp; double a[12]; xp = &a; (*xp)[0]=12.3; cout << a[0]; // 12.3
I.7.1.2. Two-dimensional arrays
When scientific tasks are to be solved, it is often needed to store matrices in memory. For that purpose, the simplest form of multi-dimensional arrays has to be used, namely two-dimensional arrays:
element_typearray_name[size1][size2];
where sizes have to be specified by dimensions. As an example, let's store the following 3x4 matrix containing integers in a two-dimensional array.
|
|
In the definition, matrix elements can be given in many ways, we only have to make sure that the initialization list should contain the elements in the correct sequence.
int matrix[3][4] = { { 12, 23, 7, 29 },
{ 11, 30, 12, 7 },
{ 10, 2, 20, 12 } };
In order to access the elements of the array, we should use the indexing operator twice. The expression
matrix[1][2]
refers to the 2nd element of the 1st row (12). (It should be kept in mind that the first index is 0 in every dimension.)
On Figure I.16, the two-dimensional matrix array is represented with their row and column indexes (r/c).
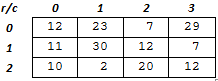
The next program code searches for the biggest (maxe) and smallest (mine) element of the matrix above. In the solution there are nested for loops, generally used for the processing of two-dimensional arrays:
int maxe, mine;
maxe = mine = matrix[0][0];
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
if (matrix[i][j] > maxe )
maxe = matrix[i][j];
if (matrix[i][j] < mine )
mine = matrix[i][j];
}
}
Printing out two-dimensional arrays as a matrix is done by the following source code:
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++)
cout<<'\t'<<matrix[i][j];
cout<<endl;
}
I.7.1.3. Variable-length arrays
According to the previous C++ standard, arrays are created during compilation and for that purpose constant expressions defining their size are made use of. The C++11 standard (Visual C++ 2012) introduces the notion of variable-length arrays and therefore it extends the number of areas where they can be used. The variable-length array created during compilation can only have automatic lifetime, can only be local and cannot be defined with an initial value. Since these arrays can only be used in functions, it is possible that the size of these arrays are different each time the function is called - that is why they are called variable-length arrays.
The size of variable-length arrays can be provided by any integer type expression; however, the size cannot be modified after creation. Compilers apply the runtime version of the sizeof operator for variable-length arrays.
In the following example, the array is created only after its size is read from the keyboard:
#include <iostream>
using namespace std;
int main() {
int size;
cout << "The number of elements of the vector: ";
cin >> size;
int vector[size];
for (int i=0; i<size; i++) {
vector[i] = i*i;
}
}
I.7.1.4. The relationship between pointers and arrays
In C++, there is a strong relation between pointers and arrays. Every operation that can be used with array indexing can also be carried out with pointers. One-dimensional arrays (vectors) and single indirection (”one-asterisked”) pointers are completely analogous with respect to form and content. The relationship between multi-dimensional arrays and multiple indirection pointers (having more asterisks) is only formal.
Let's see from where this strong relation between vectors and single indirection pointers comes from. Let's define a vector of five integer elements.
int a[5];
The elements of a vector are placed in memory in a linear sequence from a given address. All elements can be referenced by the form a[i] (Figure I.17). Let's define a pointer p pointing to an integer, and then set it to point to the first element (to the 0th element) of the array, by the "address of" operator.
int *p; p = &a[0]; or p = a;
A pointer can be set by the name of the array since this is an int * type pointer that cannot be modified. (However, the statement p = &a; leads to a compilation error since the type of the right-hand side is int (*)[5].)
After these, if the variable *p - to which the pointer p points - is referenced, then it is actually the element a[0] that is accessed.
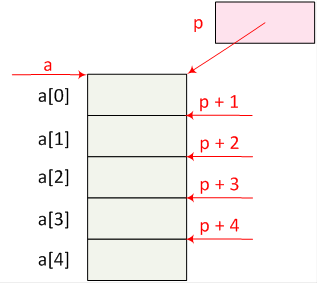
On the basis of the rules of pointer arithmetic, the addresses p+1, p+2 etc. refer the elements that follow the element to which p points. (It should be noted that elements preceding the variable can be adressed using negative numbers.) On the basis of that, every element of the array can be accessed by the expression *(p+i).
The role of the pointer p equals completely with that of the name of the array, since both define the beginning of the sequence of the elements. However, there is an important difference between the two pointers: pointer p is a variable (its value can therefore be modified any time), while a is a constant value pointer that the compiler fixes in memory.
Using the expressions of Figure I.17 the references figuring in the same row of the following table are identical:
|
|
The address of the ith element: |
|||||
|
|
|
|
|
|||
|
The 0th element of the array: |
||||||
|
|
|
|
|
|
|
|
|
The ith element of the array: |
||||||
|
|
|
|
|
|||
Most of C++ compilers transform all a[i] references automatically into *(a+i) and compiles this latter pointer form. However, this analogy is true in the inverse direction too, so instead of the indirection (*) operator, the indexing operator ([]) can always be used.
In the case of multi-dimensions, analogy is only formal; however, it can often help using correctly more complex data structures. Let's see the following double type matrix:
double m[2][3] = { { 10, 2, 4 },
{ 7, 2, 9 } };
The rows of the array are placed in memory in a linear sequence. If the last dimension is left out, the pointer of the selected row is accessed: m[0], m[1], whereas the name of the array m points to the whole array (Figure I.18). It can be concluded from the above that two-dimensional arrays are actually vectors (one-dimensional arrays), the elements of which are vectors (pointers). Nevertheless, multi-dimensional arrays are always stored in a linear sequence in memory. In the previous example, the rows of the matrix given as initial value constitute the vectors from which the vector m is built up of.
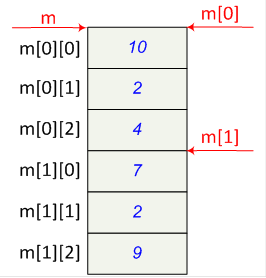
The formal analogy between vectors and pointers makes it possible to rewrite indexing operators into indirection operators without a problem. All of the following expressions refer the same element of the two-dimensional array m (precisely 9):
m[1][2] *(m[1] + 2) *(*(m+1)+2)
I.7.2. Dynamically allocated arrays
A big quantity of data can be stored and processed easily and effectively with the help of arrays. However, the big disadvantage of traditional arrays is that their size is fixed during compilation and it is only during execution that we learn if too much memory was allocated. It is especially true for local arrays created within functions.
It is a general rule that only arrays of little size can be defined within functions. If a bigger quantity of data has to be stored, the methods for dynamic memory allocation should be used since there is much more space in the heap than in stack memory.
We should not forget that memory space can be allocated by the new operator not only for one but also for more elements standing one after the other. In that case, the allocated memory space can be freed by the delete[] operator.
Methods for dynamic memory allocation and deallocation are present in the form of functions in the Standard Library of C/C++. To access these functions, the cstdlib header file should be included in the source code. The malloc () function allocates a memory space of a given byte size and returns a pointer to the beginning of the block. The calloc () works in a similar way; however, the size of the memory block should be given in number of elements and element size, and it initializes the allocated memory block to zero. The realloc () resizes the already allocated memory block while keeping its original content (if a bigger is allocated). The free () deallocates the reserved memory block.
In case of objects, the new and delete operators should be used to access all relating operations.
I.7.2.1. One-dimensional dynamic arrays
It is one-dimensional dynamic arrays that are the most frequently used in programming.
type *pointer;
pointer = newtype [number_of_elements];
or
pointer = new (nothrow) type [number_of_elements];
The difference between the two methods can only be perceived if allocation has not been successful. In the first case, the compiler throws an exception ( bad_alloc ) if there is not enough available contiguous memory, and in the second case, a pointer with the value of 0 is returned.
In case of arrays, it is extremely important not to forget about deleting allocated memory:
delete [] pointer;
In the following example, the user is asked to enter the array size. Then a memory block is allocated for the array and finally it is filled up with random numbers.
#include <iostream>
#include <exception>
#include <ctime>
#include <cstdlib>
using namespace std;
int main() {
long *data, size;
cout << "\nEnter the array size: ";
cin >> size;
cin.get();
// Memory allocation
try {
data = new long [size];
}
catch (bad_alloc) {
// Unsuccessful allocation
cerr << "\nThere is not enough memory!\n" << endl;
return -1; // Program is exited
}
// Filling up the array with random numbers
srand(unsigned(time(0)));
for (int i=0; i<size; i++) {
data[i] = rand() % 2012;
// or *(data+i) = rand() %2012;
}
// Deleting (freeing) allocated memory space
delete[] data;
return 0;
}
I.7.2.2. Two-dimensional dynamic arrays
We have already mentioned in the previous subchapters that two-dimensional arrays are actually vectors of one-dimensional vectors (rows). As a consequence, a two-dimensional array of any size cannot be created at runtime since compiler has to know the type (the size) of the elements (the row vectors). However, the number of the elements (the rows) can be provided later. The new in the following example returns a pointer to the created two-dimensional array.
const int rowlength = 4; int number_of_rows; cout<<"Number of rows: "; cin >> number_of_rows; int (*mp)[rowlength] = new int [number_of_rows][rowlength];
The solution becomes much more understandable if the keyword typedef is used:
const int rowlength = 4; int number_of_rows; cout<<"Number of rows: "; cin >> number_of_rows; typedef int rowtype[rowlength]; rowtype *mp = new rowtype [number_of_rows];
For both solutions, setting all elements to zero can be carried out by the following loops:
for (int i=0; i<number_of_rows; i++)
for (int j=0; j<rowlength; j++)
mp[i][j]=0;
where mp[i] refers to the ith row, and mp[i][j] refers to the jth element of the ith row. If the former statements are placed within the main () function, the mp pointer is placed in stack while the whole two-dimensional array in the heap. This solution has two drawbacks: arrays need memory space on the first hand, and it is annoying to provide the length of rows compile-time on the other hand.
Let's see how to avoid the constraints of memory and those of fixed row length. The next two solutions are based on the idea that arrays can be made from pointers.
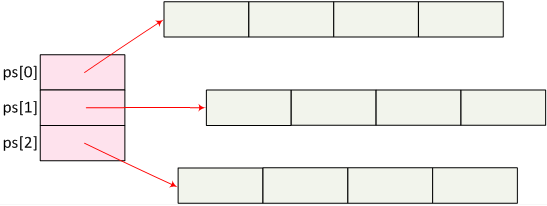
In the first case, the pointer array fixing the number of rows is created in the stack and it is only row vectors that are created dynamically (Figure I.19).
-
The pointer vector of 3 elements that selects the rows:
int* ps[3]= {0}; -
The dynamic creation of rows, if rows have 4 elements:
for (int i=0; i<3; i++) ps[i] = new int[4]; -
Elements can be accessed by the operators * and []:
*(ps[1] + 2) = 123; cout << ps[1][2];
-
Finally, we should not forget about freeing the dynamically allocated memory blocks.
for (int i=0; i<3; i++) delete[] ps[i];
If the number of rows and columns are to be set runtime, the pointer array of the previous example should be defined dynamically. In that case, stack only contains one pointer of type int * (Figure I.20).
Memory allocation, access and deallocation can easily be traced in the following example code:
#include <iostream>
using namespace std;
int main() {
int number_of_rows, rowlength;
cout<<"Number of rows: "; cin >> number_of_rows;
cout<<"The length of rows: "; cin >> rowlength;
// Memory allocation
int* *pps;
// Defining the pointer vector
pps = new int* [number_of_rows];
// Allocating rows
for (int i=0; i<number_of_rows; i++)
pps[i] = new int [rowlength];
// Accessing the array
for (int i=0; i<number_of_rows; i++)
for (int j=0; j<rowlength; j++)
pps[i][j]=0;
// Deleting (freeing) allocated memory space
for (int i=0; i<number_of_rows; i++)
delete pps[i];
delete pps;
}
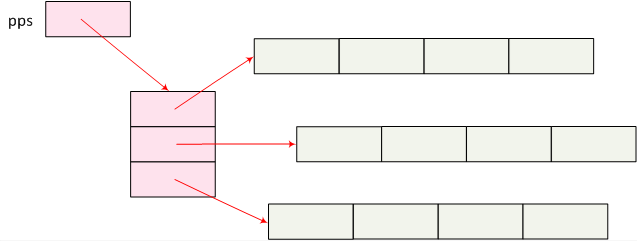
I.7.3. The usage of the vector type
Nowadays, C++ source codes use more and more frequently the vector type of C++ Standard Library (STL) instead of traditional one- or two-dimensional arrays. This type has all the features (resizing, checking that the provided index is within boundaries, automatic memory deallocation) needed for a secure usage of arrays.
Contrary to the already discussed types, vector type is parameterizable, which means that the type of stored elements should be provided within <> signs after the word vector . The created vectors, similarly to the cout and cin objects, are also objects that have their own operations and functions.
I.7.3.1. One-dimensional arrays in vectors
As its name suggests, vector type replaces one-dimensional arrays. Instead of presenting all features of that type, we will only concentrate on some basic useful information.
Let's see a solution for defining vectors, which needs that the vector header file be included in the source code.
vector<int> ivector; ivector.resize(10); vector<long> lvector(12); vector<float> fvector(7, 1.0);
ivector is an empty vector, the size of which is set by the function resize () to 10. lvector contains 12 elements of type long. In both cases, all elements are initialized to 0. fvector is created with 7 elements of type float, the values of which are all initialized to 1.0.
The actual number of elements can be obtained by the function size (), accessing elements is possible by the traditional indexing operator. An important feature of vector type is the function push_back () that adds an element to the vector.
#include <iostream>
#include <vector>
using namespace std;
int main() {
vector<int> ivector(10, 5);
ivector.push_back(10);
ivector.push_back(2);
for (unsigned index=0; index<ivector.size(); index++) {
cout << ivector[index] << endl;
}
}
It should be noted that STL data containers can be managed completely with predefined algorithms ( algorithm header file).
I.7.3.2. Two-dimensional arrays in vectors
Two-dimensional, dynamic arrays can be created by nesting vector types, and it is much easier than the methods mentioned before.
#include <iostream>
#include <vector>
using namespace std;
int main() {
int number_of_rows, rowlength;
cout<<"Number of rows: "; cin >> number_of_rows;
cout<<"The length of rows: "; cin >> rowlength;
vector< vector<int> > m (number_of_rows, rowlength);
// Accessing the array
for (int i=0; i<number_of_rows; i++)
for (int j=0; j<rowlength; j++)
m[i][j]= i+j;
}
I.7.4. Handling C-style strings
The primitive types of C/C++ do not contain the string type appropriate for storing character sequences. But since it is indispensable to store and to process strings in C/C++ programs, storage can be realised by one-dimensional character arrays. For string processing, it is also needed that valuable characters are always closed by a byte with value 0. There are no operators for managing strings; however, there are many functions for that purpose (in the cstring header file).

In program codes, we often use texts enclosed within quotation marks (string literals), that compilers store among the initialized data according to the things said before.
cout << "C++ language";
When interpreting the statement above, the string is copied into memory, (Figure I.21) and as a right operand of the operation << , an address of type const char * is compiled. When the program is executed, the cout object prints out character by character the content of the selected memory block until it reaches the byte with value 0.
Strings composed of wide characters are also stored in that way but in this case the type of the elements of the array is wchar_t.
wcout << L"C++ language";
In C++, the types string and wstring can also be used to process texts, so we give an overview of these types, too.
I.7.4.1. Strings in one-dimensional arrays
When memory space is allocated for a character string, the byte indicating the end of the string should also be taken into consideration. If a text of at most 80 characters is intended to be stored in the array named str then its size should be 80+1=81:
char line[81];
In programming tasks, we often use strings having an initial value. In order to provide an initial value, we can use the solutions already presented in relation with arrays; however, we should not forget about the final '\0' character:
char st1[10] = { 'O', 'm', 'e', 'g', 'a', '\0' };
wchar_t wst1[10] = { L'O', L'm', L'e', L'g', L'a', L'\0' };
char st2[] = { 'O', 'm', 'e', 'g', 'a', '\0' };
wchar_t wst2[] = { L'O', L'm', L'e', L'g', L'a', L'\0' };
Compiler allocates 10 bytes of memory for the string st1 and the given characters are copied into the first 6 bytes. However, st2 will be of a size of as many bytes as many characters are provided in the initialization list. For the wst1 and wst2 wide character strings, compilers allocate a memory space twice as much (in bytes) as in the previous ones.
Initializing character arrays is much safer by using string literals (string constants):
char st1[10] = "Omega"; wchar_t wst1[10] = L"Omega"; char st2[] = "Omega"; wchar_t wst2[] = L"Omega";
Whereas the initialization have the same results in both cases (i.e. with characters and with string constants), using string constants is easier to understand. Not to mention the fact that the 0 byte closing strings is placed in memory by the compiler.
The result of the storage in arrays is that there is no operation available in C++ for strings either (value assignment, comparison etc.). However, there are many Library functions for processing character sequences. Let's see some basic functions processing character sequences.
|
Operation |
Function (char) |
Function (wchar_t) |
|---|---|---|
|
reading text from the keyboard |
cin >>, cin . get (), cin . getline () |
wcin >>, wcin . get (), wcin . getline () |
|
printing out a text |
cout << |
wcout << |
|
value assignment |
strcpy (), strncpy () |
wcscpy(), wcsncpy() |
|
concatenation |
strcat (), strncat () |
wcscat(), wcsncat() |
|
getting the length of a string |
strlen () |
wcslen() |
|
comparison of strings |
strcmp (), strcnmp () |
wcscmp(), wcsncmp() |
|
searching for a character in a string |
strchr () |
wcschr() |
In order to manage strings with char type characters, we need to include the iostream and cstring header files, whereas wide character functions are found in cwchar .
The following example code transforms the text read from the keyboard and prints out all its characters in capital letters and in reverse order. It can clearly be seen from the example that we should use both Library functions and character array notion to efficiently manage strings.
#include <iostream>
#include <cstring>
#include <cctype>
using namespace std;
int main() {
char s[80];
cout <<"Type in a text: ";
cin.get(s, 80);
cout<<"The read text: "<< s << endl;
for (int i = strlen(s)-1; i >= 0; i--)
cout<<(char)toupper(s[i]);
cout<<endl;
}
The wide character version of the previous solution is:
#include <iostream>
#include <cwchar>
#include <cwctype>
using namespace std;
int main() {
wchar_t s[80];
wcout <<L"Type a text: ";
wcin.get(s, 80);
wcout<<L"The read text: "<< s << endl;
for (int i = wcslen(s)-1; i >= 0; i--)
wcout<<(wchar_t)towupper(s[i]);
wcout<<endl;
}
In both examples, we used the secure cin . get () function to read a text from the input. The function reads all characters until <Enter> is pressed. However, the given array can only have a number of characters same as or less than size-1, which is provided as one of its argument.
I.7.4.2. Strings and pointers
Character arrays and character pointers can both be used to manage strings but pointers should be used more carefully. Let's see the following frequent definitions.
char str[16] = "alfa"; char *pstr = "gamma";
In the first case, the compiler creates the array str of 16 elements and then it copies in the characters of the provided initial value and the byte with value 0. In the second case, the compiler stores the initial text in the area reserved for string literals, then it initializes the pointer pstr to the beginning address of the string.
The value of the pointer pstr can be modified later (which causes the loss of the string "gamma"):
pstr = "iota";
A pointer value assignment takes place here since pstr now points to the address of the new string literal. On the contrary, if it is the name of the array str to which a value is assigned, an error message is obtained:
str = "iota"; // error! ↯
If a string has to be processed character by character, then we can choose from the array and the pointer approach. In the following example code, the read character sequence is first encrypted with the exclusive-or operation and then its content will be replaced again by its original content. (During encryption the string is treated as an array, and during decryption the pointer approach is used.) In both cases, the loop ends if the string closing zero byte is reached.
#include <iostream>
using namespace std;
const unsigned char key = 0xCD;
int main() {
char s[80], *p;
cout <<"Type in a text: ";
cin.get(s, 80);
for (int i = 0; s[i]; i++) // encryption
s[i] ^= key;
cout << "The encrypted text: "<< s << endl;
p = s;
while (*p) // decryption
*p++ ^= key;
cout << "The original text: "<< s << endl;
}
In the following example, the increment and indirection operators are used together, which requires more carefulness. In the following example, the pointer sp points to a dynamically stored character sequence. (It should be noted that most C++ implementations do not allow modifications of string literals.)
char *sp = new char [33]; strcpy(sp, "C++"); cout << ++*sp << endl; // D cout << sp << endl; // D++ cout << *sp++ << endl; // D cout << sp << endl; // ++
In the first case (++*sp), the compiler interprets first the indirection operator and then increments the referred charater. In the second case (*sp++), the compiler first steps the pointer to the next character but since it is a post-increment operator, increment takes place after processing the whole expression. The value of the expression is the referenced character.
I.7.4.3. Using string arrays
Most C++ programs contain texts (e.g. error messages) that are printed on the basis of a certain index (error code). The simplest solution for storing such texts is defining string arrays.
When string arrays are planned, it should be decided whether they will be two-dimensional or pointer arrays. For beginners in C++ programming, it is often difficult to differentiate between the two. Let's see the following two definitions.
int a[4][6]; int* b[4];
a is a "real” two-dimensional array for which the compiler allocates a continuous memory block for 24 (4x6) elements of type int. On the contrary, b is a pointer vector of 4 elements. The compiler allocates space for only four pointers based on this definition. The other parts of initialization is done later in the code. Let's initialize the pointer array so that it would be able to store 5x10 integer elements.
int s1[6], s2[6], s3[6], s4[6];
int* b[4] = { s1, s2, s3, s4 };
It is clear that besides the memory block needed for 24 int elements, further memory space was also used (for the pointers). At this point, it would be logical to ask what the advantages are of using pointer arrays. The response can be found in the length of rows. While in a two-dimensional array every row contains the same number of elements,
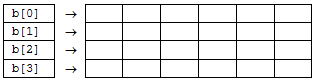
the size of each row can be different in pointer arrays.
int s1[1], s2[3], s3[2], s4[6];
int* b[4] = { s1, s2, s3, s4 };
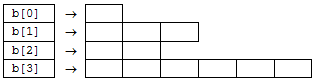
The other advantage of pointer arrays is that their structure is in line with the possibilities of dynamic memory allocation, thus it has an important role when dynamically allocated arrays are to be created.
After this short introduction, let's see the subject of the present subchapter: the creation of string arrays. In general, string arrays are defined by providing them initial values. In the first example, a two-dimensional array is defined with the following statement:
static char names1[][10] = { "Ivan",
"Olesya",
"Anna",
"Adrienn" };
This definition results in the creation of a 4x10 character array: the number of the rows is determined by the compiler on the basis of the initialization list. The rows of the two-dimensional character array are placed in a linear sequence in memory (Figure I.22).

In the second case, a pointer array is used to store the addresses of the names:
static char* names2[] = { "Ivan",
"Olesya",
"Anna",
"Adrienn" };
The compiler allocates four blocks of different size in memory, as it is shown on Figure I.23:
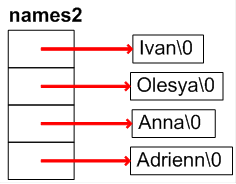
It is worth comparing the two solutions with respect to definition and memory access.
cout << names1[0] << endl; // Ivan cout << names1[1][4] << endl; // y cout << names2[0] << endl; // Ivan cout << names2[1][4] << endl; // y
I.7.5. The string type
In the C++ Standard Template Library (STL), there are classes that support string management. The solutions presented above are useful for C-style character sequences. Now let's learn the features of the types string and wstring.
In order to access C++ style character sequence management, it is necessary to include the string header file in the source code. If string objects are defined as type string, many comfortable string processing operations can be carried out with the help of operators and member functions. Let's see some of them. (In the table, member functions are preceded by a point. The name of a member function is provided after the name of the object and is separated from that by a dot.) In order to process wide character strings, we need not only the string header file but also the cwchar file.
|
Operation |
C++ solution - string |
C++ solution - wstring |
|---|---|---|
|
reading text from the keyboard |
cin>> , getline () |
wcin>> , getline () |
|
printing out a text |
cout<< |
wcout<< |
|
value assignment |
= , .assign () |
= , .assign () |
|
concatenation |
+ , += |
+ , += |
|
accessing the characters of a string |
[] |
[] |
|
getting the length of a string |
.size () |
.size () |
|
comparison of strings |
.compare (), == , != , < , <= , > , >= |
.compare (), == , != , < , <= , > , >= |
|
conversion into C-style character sequence |
.c_str (), .data () |
.c_str (), .data () |
Let's rewrite our encrypting program by using C++ style string processing.
#include <string>
#include <iostream>
using namespace std;
const unsigned char key = 0xCD;
int main() {
string s;
char *p;
cout <<"Type in a text : ";
getline(cin, s);
for (int i = 0; s[i]; i++) // encryption
s[i] ^= key;
cout << "The encrypted text: "<< s << endl;
p=(char *)s.c_str();
while (*p) // decryption
*p++ ^= key;
cout << "The original text: "<< s << endl;
}
The solution of the task with wide character strings (wstring) can be found in the following code:
#include <string>
#include <iostream>
#include <cwchar>
using namespace std;
const unsigned wchar_t key = 0xCD;
int main()
{
wstring s;
wchar_t *p;
wcout <<L"Type a text : ";
getline(wcin, s);
for (int i = 0; s[i]; i++) // encryption
s[i] ^= key;
wcout<<L"The encrypted text: "<< s << endl;
p=(wchar_t *)s.c_str();
while (*p) // decryption
*p++ ^= key;
wcout<<L"The original text: "<<s<<endl;
}
I.8. User-defined data types
Arrays can store and process easily a set of data of the same type. However, most programming tasks require treating data of different types logically as one unit. In C++, there are many possibilities for that among which the most important ones are structures and classes since they provide the basis for the object-oriented solutions discussed in Chapter III of the present book.
In the following, we will learn more about structure, class, bit fields and union types from among the aggregate types. In this chapter, stress will be laid more on structures (structs). The reason for that is that all notions and solutions related to structures can be used for other user-defined types without exception.
I.8.1. The structure type
In C++, a structure (struct) is a type that is a set of many data of any type (except for void and function types). These data members that are traditionally called structure elements or data members, have names that are only valid within their structure. (In other languages, the notion field is used for these elements; however, in C++, this name is attached to bit structures.)
I.8.1.1. Structure type and structure variables
A variable of a structure type can be created in two steps. First, a structure type has to be declared and then variables can be defined. The general declaration of structures is as follows:
struct structure_type {
type 1 member 1 ; // without an initial value!
type 2 member 2 ;
. . .
type n member n ;
};
It should be noted that the curly brackets enclosing structure declarations have to be followed by a semicolon. Data members should be declared according to the standard variable declaration rules of C++; however, initial values cannot be given for them. A structure variable (a structure) of the type above can be created by the already known method:
struct structure_type structure_variable; // C/C++
structure_type structure_variable; // only in C++
In C++, the name standing after the keywords struct, union and class can be used as type names without using the keywords. When typedef is used, the difference between the two programming languages disappears:
typedef struct {
type 1 member 1 ;
type 2 member 2 ;
. . .
type n member n ;
} structure_type;
structure_type structure_variable; // C/C++
Similarly to those of arrays, the definitions of structure variables may contain initial values. The lists of the expressions, separated from one another by commas, initializing the data members should be enclosed within curly brackets.
structure_type structure_variable= {initial_value_list}; // C/C++
It should be noted that most software development companies support structure definitions with typedef in order that confusions be avoided.
It should be noted that the visibility of member names within a struct is limited to the structure. This means that the same name can be used within the given visibility level (module, block), in other structures or as independent variable names:
struct s1 {
int a;
double b;
};
struct s2 {
char a[7];
s1 b;
};
long a;
double b[12];
Let's see an example for defining a structure type. The following data structure can be useful for a software cataloguing music CDs:
struct musicCD {
// the performer and the title of the CD
string performer, title;
int year; // year of publication
int price; // price of the CD
};
Variables can be defined with the type musicCD:
musicCD classic = {"Vivaldi","The Four Seasons", 2009, 2590};
musicCD *pmusic = 0, rock, tale = {};
From the structure type variables above, rock is not initialised whereas all members of the structure tale will have the default initial value corresponding to their type. The pointer pmusic does not refer to any structure.
We created a new user-defined type by having declared the structure. The data members of the variable of a structure type are stored in memory in the order of their declaration. On Figure I.24 , we can see the graphical layout of the data structure created by the definition
musicCD relax;
It can be clearly seen from the figure that the names of the data members indicate their distance from the beginning of the structure. In general, the size of a structure is equal to the sum of the sizes of its data members. However, in some cases, "holes" may appear between the members of a structure (when speed is optimized or when members are aligned to memory boundaries etc.). But it is always the punctual value that is obtained by the sizeof operator.
In most cases, the compiler is entrusted with the alignment of data members to memory boundaries. For a rapid access, it places the data by optimizing storage to the given hardware. However, if structures are exchanged by files between different platforms, the alignment used for saving has to be set in the reader program.
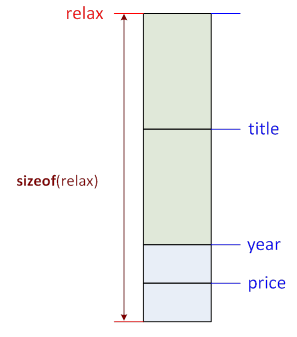
In order to control the C++ compilers, we use the preprocessor directive #pragma, the features of which are completely implementation-dependent. For example, in Visual C++, the alignment to a byte boundary is done by the following directive, which has to be placed before the structure definition:
#pragma pack(1)
The argument of pack can be 1, 2, 4, 8 or 16. Without arguments, Visual C++ uses the default value for 32-bit systems: 4. Let's see the effects of the directive in the case of the following structure type.
#pragma pack(alignment)
struct mix {
char ch1, ch2, ch3;
short sh1, sh2;
int n;
double d;
};
#pragma pack()
I.8.1.2. Accessing the data members of structures
The word structure is often used alone but in that case it means a variable created by a given structure type and not the type. Let's define some variables by using the type musicCD declared before.
musicCD s1, s2, *ps;
The memory space necessary for storing the variables s1 and s2 of type musicCD is allocated by the compiler. In order to be able to access the structure with the pointer ps of type musicCD, we have two possibilities. In the first case, ps is simply redirected to the structure s1:
ps = &s1;
The other possibility is to use dynamic memory allocation. In the following example code, memory is reserved for the structure musicCD, than it is deallocated:
ps = new (nothrow) musicCD; if (!ps) exit(-1); // ... delete ps;
After providing the appropriate definitions, we have three structures: s1, s2 and *ps. Let's see how to give values to data members. In C++, it is done by the dot ( . ) operator. The left-hand side operand of dot operators is a structure variable, the right-hand side operand selects a data member within the structure.
s1.performer = "Vivaldi"; s1.title = "The Four Seasons"; s1.year = 2005; s1.price = 2560;
If the dot operator is used on a structure to which ps points, precedence rules make it obligatory to enclose within parentheses the expression *ps:
(*ps).performer = "Vivaldi"; (*ps).title = "The Four Seasons"; (*ps).year = 2005; (*ps).price = 2560;
Since in C++, we often use structures to which a pointer points, this programming language reserves an independent operator, more precisely the arrow operator (->), for referencing data members. (The arrow operator consists of two characters: a minus and a greater than sign.) Arrow operators make more readable value assignments for data members of a structure to which ps points to:
ps->performer = "Vivaldi"; ps->title = "The Four Seasons"; ps->year = 2005; ps->price = 2560;
The left-hand operand of arrow operators is the pointer to a structure variable, whereas the right-hand operand selects the data member within that structure, similarly to dot operators. Accordingly, the meaning of the expression ps->price is: "the data member named price within the structure to which the pointer ps points".
We recommend that dot operators should be used only for direct references (accessing a data member of a variable of structure type) while arrow operators should be used only for indirect references (accessing a data member of the structure to which a pointer points).
A special case of structure value assignment is when the content of a structure type variable is intended to be assigned to another variable of the same type. This operation can even be carried out by data members:
s2.performer = s1.performer; s2.title = s1.title; s2.year = s1.year; s2.price = s1.price;
however, C++ can also interpret the assignment operator (=), so it can be used for structure variables:
s2 = s1 ; // this corresponds to the 4 assignments above *ps = s2 ; s1 = *ps = s2 ;
This way of value assignment simply means copying the memory block occupied by the structure. However, this operation results in a problem if the structure contains a pointer that refers to an external memory space. In that case, it is programmers that have to solve this problem by assigning values for each data member one by one or the other possibility is to overload the copy operation (operator overloading) by creating an assignment operator (see Chapter III) for the structure.
Structures are accessed by data members during data input/output operations. The following example code reads the structure musicCD by asking the user to type them in and then prints out the entered data:
#include <iostream>
#include <string>
using namespace std;
struct musicCD {
string performer, title;
int year, price;
};
int main() {
musicCD cd;
// reading the data from the keyboard
cout<<"Please type in the data of the music CD." << endl;
cout<<"Performer : "; getline(cin, cd.performer);
cout<<"Title : "; getline(cin, cd.title);
cout<<"Year of publication : "; cin>>cd.year;
cout<<"Price : "; cin>>cd.price;
cin.get();
// printing out the data
cout<<"\nData of the music CD:" << endl;
cout<<"Performer : "; cout << cd.performer << endl;
cout<<"Title : "; cout << cd.title << endl;
cout<<"Year of publication : "; cout << cd.year << endl;
cout<<"Price : "; cout << cd.price << endl;
}
I.8.1.3. Nested structures
As we have already said, structures can have data members of any type. If a structure has one or more data members that are also structures, it is a nested structure.
Let's suppose that some personal data are intended to be stored in a structure. Among personal data, a separate structure is defined for dates:
struct date {
int year, month, day;
};
struct person {
string name;
date birthday;
};
Let's create two persons in the following way: the first one will be initialized by an initialization list, and let's assign values separately to the members for the other one.
person brother = { "Ivan", {2004, 10, 2} };
person student;
student.name = "Bill King";
student.birthday.year = 1990;
student.birthday.month = 10;
student.birthday.day = 20;
In the initialization list, constants initializing inner structure do not necessarily have to be enclosed within curly brackets. In the second case, student.birthday refers the structure birthday of the structure student. This is followed by the dot operator (.) and the name of a data member of the inner structure.
If the structure of type date is not used anywhere else then it can be integrated directly as an anonymous structure in the structure person:
struct person {
string name;
struct {
int year, month day;
} birthday;
};
When creating more complex dynamic data structures (e.g. linear lists), elements of a given type have to be concatenated into a chain. Elements of this kind contain some kind of data and a pointer in general. C++ makes it possible to define a pointer with the type of the structure to be declared. These structures, which contain a pointer to themselves as a data member, are called self-referential structures. As an example, let's see the declaration of list_element.
struct list_element {
double data_member;
list_element *link;
};
This recursive declaration makes it possible that the pointer link points to the structure of type list_element. The declaration above does not nest the two structures in each other since the structure which we will reference later with the pointer will be placed somewhere else in memory. However, C++ compilers need this declaration in order to be able to allocate memory in compliance with the declaration, that is to get to know the size of the variable to be created. The declaration above makes compilers allocate for the pointer memory space the size of which is independent of that of the structure.
I.8.1.4. Structures and arrays
Programming can be made much more efficient if arrays and structures are used together in one data type. In the following simple codes, we first place a one-dimensional array within a structure then we create a one-dimensional array of structure type elements.
I.8.1.4.1. Arrays as data members of a structure
In the following example, besides an integer vector (v), we also store the number of valuable elements (n) in the structure svector:
const int maxn = 10;
struct svector {
int v[maxn];
int n;
};
svector a = {{23, 7, 12}, 3};
svector b = {{0}, maxn};
svector c = {};
int sum=0;
for (int i=0; i<a.n; i++) {
sum += a.v[i];
}
c = a;
In the expression a.v[i], there is no need to use parentheses since the two operations has the same precedence so the expression is evaluated from left to right. So first the member v is selected from the structure a, then the ith element of the array a.v is accessed. Another interesting part of the solution is that the elements of the vector are also copied from one of the structures to another when value assignment takes place between the two structures.
The structure of type svector can also be created dynamically. However, in that case, the structure should be accessed by an arrow operator.
svector *p = new svector; p->v[0] = 2; p->v[1] = 10; p->n = 2; delete p;
I.8.1.4.2. Structures as array elements
A structure array has to be defined exactly in the same way as arrays of any other type. As an example, let's make use of the type musicCD declared above to create a CD-catalogue of 100 elements and let's give initial values for the first two elements of CDcatalog.
musicCD CDcatalog[100]={{"Vivaldi","The Four Seasons",2004,1002},{} };
In order to reference the data members of structures as array elements, we have to first select the array element and then the structure member:
CDcatalog[10].price = 2004;
If the CD-catalogue is intended to be created dynamically, identification has to be done with a pointer:
musicCD *pCDcatalog;
Memory space for structure elements can be allocated by the operator new in the dynamically managed memory space:
pCDcatalog = new musicCD[100];
The structure stored in an array element can be accessed by using the dot operator:
pCDcatalog[10].price = 2004;
If array elements are not needed anymore, then the allocated memory space should be freed by the operator delete []:
delete[] pCDcatalog;
Certain operations (like sorting) can be carried out more efficiently if the pointers of the dynamically created CDs are stored in a pointer array:
musicCD* dCDcatalog[100];
The following loop allocates space for the structures in the dynamically managed memory:
for (int i=0; i<100; i++) dCDcatalog[i] = new musicCD;
Then, the structures selected by the array elements can be referenced by the arrow operator:
dCDcatalog[10]->price = 2004;
If these structures are not needed anymore, then we should iterate through the elements and delete them from the memory space:
for (int i = 0; i < 100; i++) delete dCDcatalog[i];
The following example searches for all CDs published between 2010 and 2012 in a dynamically created CD catalogue containing a fix number of CDs.
#include <iostream>
#include <string>
using namespace std;
struct musicCD {
string performer, title;
int year, price;
};
int main() {
cout<<"The number of CDs:";
int num;
cin>>num;
cin.ignore(80, '\n');
// Memory allocation with checking
musicCD *pCDcatalog = new (nothrow) musicCD[num];
if (!pCDcatalog) {
cerr<<"\a\nThere is not enough memory!\n";
return -1;
}
// Reading the data of CDs from the keyboard
for (int i=0; i<num; i++) {
cout<<endl<<"The data of the "<<i<<"th CD:"<<endl;
cout<<"Performer: ";
getline(cin, pCDcatalog[i].performer);
cout<<"Title: "; getline(cin, pCDcatalog[i].title);
cout<<"Year: "; cin>>pCDcatalog[i].year;
cout<<"Price: "; cin>>pCDcatalog[i].price;
cin.ignore(80, '\n');
}
// Searching for the requested CDs
int found = 0;
for (int i = 0; i < num; i++) {
if (pCDcatalog[i].year >= 2010 &&
pCDcatalog[i].year <= 2012) {
cout<<endl<<pCDcatalog[i].performer<<endl;
cout<<pCDcatalog[i].title<<endl;
cout<<pCDcatalog[i].year<<endl;
found++;
}
}
// Printing out the results
if (found)
cout<<"\nThe number of found elements: "<<found<<endl;
else
cout<<"There is no CD that matches the criteria!"<<endl;
// Deallocating memory space
delete [] pCDcatalog;
}
This program is interactive, that is data should be provided by a user, and prints out results on the screen. Testing with a bigger amount of data is more difficult in that way.
However, most operating systems make it possible to redirect the standard input and output of a program to a file. For that purpose, the input data should be typed in a file exactly in the same way the program expects them (e.g. CDs.txt), and this file name should be provided after a lower than sign when the program (CDCatalogue) is executed from the command line:
CDCatalogue <CDs.txt CDCatalogue <CDs.txt >Results.txt
The second command writes the results to a separate file (Figure I.25). (In the development environment of Visual C++ , the redirection properties can be set in the window Project /project Properties , on the tab named Debugging , in the line of Command Arguments .)

I.8.1.5. Creating singly linked lists
The simplest forms of linked lists are singly linked lists in which all elements possess a reference to the next list element. The reference in the last element has the value null (Figure I.26).
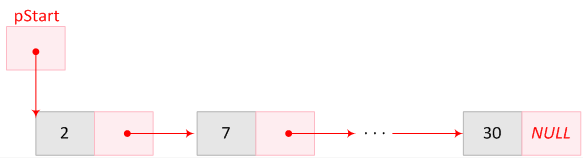
The list is selected in the memory by the pointer pStart so the value of the latter should always be kept. If the value of pStart is set to another value, the list becomes inaccessible.
Let's see what advantages the usage of a linear list has as compared with vectors (one-dimensional arrays). The size of a vector is fixed when it is defined; however, the size of a list can be increased or decreased dynamically. There is also an important difference between the two how elements are inserted in or removed from them. Whereas these operations only require the copy of some pointers in the case of lists, these operations require moving a big amount of data in vectors. There is also a significant difference between the two with respect to the structure of the storage unit, that is that of the element:
Vector elements only contain the stored data whereas list elements also contain a reference (a pointer) to (an)other element(s). C++ list elements can be created by the already presented self-referential structure.
As an example, let's store integer numbers in a linear list, the elements of which have the following type:
struct list_element {
int data;
list_element *pnext;
};
Since we allocate memory for each new list element in this example, this operation is carried out by a function to be presented in the next chapter of the present book:
list_element *NewElement(int data) {
list_element *p = new (nothrow) list_element;
assert(p);
p->data = data;
p->pnext = NULL;
return p;
}
That function returns the pointer of the new list element and initializes it if this function has run with success. We should not forget about calling the function assert (). This macro interrupts running the program and prints out the message "Assertion failed: p, file c:\temp\list.cpp, line 16” if its argument has the value of 0.
When created, the list is filled up by the elements of the following array:
int data [] = {2, 7, 10, 12, 23, 29, 30};
const int num_of_elements = sizeof(data)/sizeof(data[0]);
For a successful management of the list, we need additional variables and the pointer pStart to the beginning of the list:
list_element *pStart = NULL, *pActual, *pPrev, *pNext;
When we are dealing with a given element (pActual) of the list, we might need to know where the preceding element (pPrev) and the next one (pNext) are. In this example, in order to facilitate our task we hypothesise that the list always exists when it has been created, that is the pointer pStart is never null.
Creating the list and filling up it from the array data. When a list is created, there are three separate tasks to carry out with each element:
-
memory allocation (with checking if it has taken place) for a new list element (NewElement()),
-
assigning data to the list element (NewElement()),
-
adding the list element to (the end of) the list. When an element is added to a list, the things to be done are different in the case of first and non-first elements.
for (int index = 0; index<num_of_elements; index++) { pNext = NewElement(data[index]); if (pStart==NULL) pActual = pStart = pNext ; // first element else pActual = pActual->pnext = pNext; // not a first element } pActual->pnext = NULL; // closing the list // list: pStart ➝ 2 ➝ 7 ➝ 10 ➝ 12 ➝ 23 ➝ 29 ➝ 30
When printing out the elements of the list, we start from the pointer pStart and step to the next element in a loop until the null pointer indicating the end of the list is reached:
pActual = pStart;
while (pActual != NULL) {
cout<< pActual->data << endl;
// stepping to the next element
pActual = pActual->pnext;
}
It is often needed to remove an element from a list. In the following example, the list element to be removed is identified by its index (Indexing starts with 0 from the element to which the pointer pStart points to. This example code is not able to remove the 0th and the last element!) The removal operation also consists of three steps:
// identifying the place of the element having the index 4 (23)
pActual = pStart;
for (int index = 0; index<4; index++) {
pPrev = pActual;
pActual = pActual->pnext;
}
// removing the element of the linked list
pPrev->pnext = pActual->pnext;
// deallocating memory space
delete pActual;
// the list: pStart ➝ 2 ➝ 7 ➝ 10 ➝ 12 ➝ 29 ➝ 30
When the 0th element is removed, the pointer pStart has to be set to pStart->pnext before removal. When it is the last element that is removed, the member pnext of the element immediately before the last one has to be set to null.
Another operation is inserting a new element to a list between two already existing elements. The place of the insertion is identified by the index of the element after which the new element is to be inserted. In the example, a new list element is inserted after the element having the index 3:
// determining the place of the preceding element of index 3 (12)
pActual = pStart;
for (int index = 0; index<3; index++)
pActual = pActual->pnext;
// allocating memory for the new element
pNext = NewElement(23);
// inserting the new element in the linked list
pNext->pnext = pActual->pnext;
pActual->pnext = pNext;
// list: pStart ➝ 2 ➝ 7 ➝ 10 ➝ 12 ➝ 23 ➝ 29 ➝ 30
The code part above can even insert a new list element to the end of the list.
It is also frequent to add a new element to (the end of) the list.
// searching for the last element pActual = pStart; while (pActual->pnext!=NULL && (pActual = pActual->pnext)); // allocating memory for the new element pNext = NewElement(80); // adding the new element to the end of the list pActual->pnext = pNext; // the list: pStart ➝ 2 ➝ 7 ➝ 10 ➝ 12 ➝ 23 ➝ 29 ➝ 30 ➝ 80
We might also need to search for an element of a given value (sdata) in the list.
int sdata = 29;
pActual = pStart;
while (pActual->data!=sdata && (pActual = pActual->pnext));
if (pActual!=NULL)
cout<<"Found: "<<pActual->data<< endl;
else
cout<<" Not found!"<<endl;
Before exiting the program, the dynamically allocated memory space has to be freed. In order to delete the elements of a list, we have to iterate through the list while making sure to read the next element before deleting the actual list element:
pActual = pStart;
while (pActual != NULL) {
pNext = pActual->pnext;
delete pActual;
pActual = pNext;
}
pStart = NULL; // there is no list element!
I.8.2. The class type
Chapter III of our book will discuss object-oriented programming. For that purpose, C++ use the extended version of the type struct and introduces a new notion named class. Both types can be used to define classes. (A class can contain member functions besides its data members.) All that we have said about structures before is valid for the class type but there is a little but important difference. The difference is in the default accessibility of data members.
In order to remain compatible with C, C++ had to keep the access without restrictions (public access) of structure members. However, the basic principles of object-oriented programming require data structures, the members of which cannot be accessed by default. In order that both requirements would be met, the new keyword class was introduced in C++. With the help of class, we can define "structures", the members of which cannot be accessed from the outside (private) by default.
In order that the access of data members would be regulated, the keywords public, private and protected can be placed in structure and class declarations. If accessibility is not given for a member, the default case is private for the members of a class (that is they cannot be accessed from the outside), whereas the default is public for the data members of a class of type struct.
On the basis of these facts, the type definitions of the following table are the same in each line with respect to the accessibility of their members:
|
struct time { int hour; int minute; int second; }; |
class time { public: int hour; int minute; int second; }; |
|
struct time { private: int hour; int minute; int second; }; |
class time { int hour; int minute; int second; }; |
The definitions of variables of a struct or class type can only contain initial values, if the given class type only has public data members.
class time {
public:
int hour;
int minute;
int second;
};
int main() {
time beginning ={7, 10, 2};
}
I.8.3. The union type
When C language was created, in order that memory usage would be more economical, features were integrated in the language. These features have less importance than for example dynamic memory management. Let's see the essentials of the solutions presented in the next two subchapters.
-
Memory place is spared if more variables use mutually the same memory space (but not at the same time). These variables can be grouped together by the union type.
-
Another possibility is to place, in one byte, variables, the values of which occupy a space less than 1 byte. For that, we can use the bit fields of C++. When a bit structure (which is analogous to the struct type) is declared, it is also decided what data (of how many bits) are grouped.
We cannot economize much on memory by using unions and bit structures and also, the portability of our program decreases a lot. The portable version of the methods aiming at decreasing memory need is dynamic memory management. It should be noted that the public access of the members of a union cannot be restricted.
Nowadays, unions are mainly used for rapid and machine-dependent data conversions, whereas bit structures are used to generate command words controlling the different elements of a hardware device.
The solutions said about the struct type can be used for the union type as well: from declaration to the creation of structure arrays, including point and arrow operators. The only and important difference between the two types is the relative position of data members. Whereas the data members of a structure are placed in a linear sequence in memory, those of a union start all on the same address (they overlap). The size of a struct type is the total size of all of its data members (the size corrected after alignments), whereas the size of a union is equal to the size of its "longest" member.
In the following example, a data member of type unsignedlong can be accessed by bytes or by words. The position of the data members of the union conversion in memory is demonstrated by Figure I.27.
#include <iostream>
using namespace std;
union conversion {
unsigned long l;
struct {
unsigned short lo;
unsigned short hi;
} s;
unsigned char c[4];
};
int main()
{
conversion data = { 0xABCD1234 };
cout<<hex<<data.s.lo<<endl; // 1234
cout<<data.s.hi<<endl; // ABCD
for (int i=0; i<4; i++)
cout<<(int)data.c[i]<<endl; // 34 12 CD AB
data.c[0]++;
data.s.hi+=2;
cout <<data.l<<endl; // ABCF1235
}
I.8.3.1. Anonymous unions
The standard of C++ makes it possible that a definition of a union only contains data members. The members of these anonymous unions appear as the variables of the environment containing the union. This environment can be a module, a function, a structure or a class.
In the following example, a and b, as well as c and f can be accessed as normal variables; however, they are stored overlapped in memory, as it is required by the union type.
static union {
long a;
double b;
};
int main() {
union {
char c[4];
float f;
};
a = 2012;
b = 1.2; // the value of a changed!
f = 0;
c[0] = 1; // the value of f changed!
}
If an anonymous union is nested within a structure (a class), its data members become the members of the structure (the class) but they will remain overlapped.
The next example illustrates how to use struct and union types together. It is often necessary that the data stored in the records of a file would have different structure for every record. Let's suppose that every record contains a name and a value, the value of which is sometimes a string sometimes a number. Memory space is spared if the two possible values are combined into a union within a structure ( variant record ):
#include <iostream>
using namespace std;
struct vrecord {
char type;
char name[25];
union {
char address[50];
unsigned long ID;
}; // <---- there is no member name!
};
int main() {
vrecord vr1={0,"BME","Budapest, Muegyetem rkpt 3-11."};
vrecord vr2={1, "National Bank"};
vr2.ID=3751564U;
for (int i=0; i<2; i++) {
cout<<"Name : "<<vr1.name<<endl;
switch (vr1.type) {
case 1 :
cout<<"ID : "<<vr1.ID<<endl;
break;
case 0 :
cout<<"Address : "<<vr1.address<<endl;
break;
default :
cout<<"Not a valid data type!"<<endl;
}
vr1 = vr2;
}
}
The results:
Name : BME Address : Budapest, Muegyetem rkpt 3-11. Name : National Bank ID : 3751564 |
I.8.4. Bit fields
Classes and structures may contain members for which compilers use a space less than for integer types. Since the storage space is determined by number of bits for these members, they are called bit fields. The general declaration of bit fields:
type name_of_bitfield : bitlength;
A type can be of an integral type (enum is also). If no name is given for a bit field, an anonymous bit field is created, the function of which is to fill up the non-used bit positions. The length of a bit field has to be provided with a constant expression. The maximal value of bitlength is decided on the basis of the bit size of the biggest integer type on the given computer.
Bit fields and data members may figure in a mixed way in structure and class types:
#include <iostream>
using namespace std;
#pragma pack(1)
struct date {
unsigned char holiday : 1; // 0..1
unsigned char day : 6; // 0..31
unsigned char month : 5; // 0..16
unsigned short year;
};
int main() {
date today = { 0, 2, 10, 2012 };
date holiday = {1};
holiday.year = 2012;
holiday.month = 12;
holiday .day = 25;
}

If a bit field is not given a name in its declaration, then the space of the given bit length cannot be accessed (they are used for padding). If the length of an anonymous bit field is set to 0, then the compiler forces alignment of the following data member (or bitfield) to the next int boundary.
The following example makes more comfortable the access of the line control register (LCR) of RS232 ports by using bit fields:
#include <iostream>
#include <conio.h>
using namespace std;
union LCR {
struct {
unsigned char datalength : 2;
unsigned char stopbits : 1;
unsigned char parity : 3;
unsigned char : 2;
} bsLCR;
unsigned char byLCR;
};
enum RS232port {eCOM1=0x3f8, eCOM2=0x2f8 };
int main() {
LCR reg = {};
reg.bsLCR.datalength = 3; // 8 data bits
reg.bsLCR.stopbits = 0; // 1 stopbit
reg.bsLCR.parity = 0; // no parity
outport(eCOM1+3, reg.byLCR);
}
The necessary operations can also be carried out with the already detailed bitwise operations; however, using bit fields make the source code more structured.
The end of the present chapter also enumerates the disadvantages of using bit fields:
-
The source code becomes non-portable since the position of bits within bytes or words may be different in different systems.
-
The address of bit fields cannot be obtained (&), since it is not sure whether they are positioned on a byte boundary.
-
If more variables are placed in a storage unit used together with bit fields as well, compilers generate a complementary code to manage the variables (therefore programs run slower and the size of the code increases).