Chapter II. Modular programming in C++
- II.1. The basics of functions
-
- II.1.1. Defining, calling and declaring functions
- II.1.2. The return value of functions
- II.1.3. Parametrizing functions
-
- II.1.3.1. Parameter passing methods
- II.1.3.2. Using parameters of different types
-
- II.1.3.2.1. Arithmetic type parameters
- II.1.3.2.2. User-defined type parameters
- II.1.3.2.3. Passing arrays to functions
- II.1.3.2.4. String arguments
- II.1.3.2.5. Functions as arguments
- II.1.3.2.6. Default arguments
- II.1.3.2.7. Variable length argument list
- II.1.3.2.8. Parameters and return value of the main() function
- II.1.4. Programming with functions
- II.2. How to use functions on a more professional level?
- II.3. Namespaces and storage classes
-
- II.3.1. Storage classes of variables
- II.3.2. Storage classes of functions
- II.3.3. Modular programs in C++
- II.3.4. Namespaces
- II.4. Preprocessor directives of C++
C++ supports many programming techniques. The previous part of this book focussed on structured programming , which is based on the fact that computer programs have the following three components: sequences (the statements of which are provided in the order of their execution), decisions (if, switch) and loops (while, for, do). As it can be seen, the statement goto is not included in the previous list because its usage is to be avoided.
Structured programming relies on top-down design, which consists of dividing programming tasks into smaller units until program blocks easy to handle and to test are achieved. In C and C++ languages, the smallest structural unit having independent functionality is called function .
If functions or a group of functions belonging together are put in a separate module (source file), modular programming is realised. Modules can be compiled and tested separately, and they can be imported into other projects as well. The contents of modules (compiled or source code version) can be made available for other modules by interfaces (header files in C/C++). And certain parts of these modules are hidden from the outside (data hiding). Structural programming also contributes to creating new programs from achieved modules (components) by bottom-up design.
The next parts aim at introducing our readers into modular and procedural programming in C++. Procedural programming means solving a task by subprograms (functions) that are more or less independent from one another. These subprograms call one another directly or indirectly from the main program (main()) and communicate with each other by parameters. Procedural programming can be well combined with structural and modular programming.
II.1. The basics of functions
In C++, a function is a unit (a subprogram) that has a name and that can be called from the other parts of a program as many times as it is needed. A traditional C++ program has small size and easy to handle functions. Compiled functions can be put in libraries, from which the development kit integrates the code of the referenced functions in our programs.
In order to use a function efficiently, some of its inner variables are assigned a value when the function is called. These storage units called parameters should be declared in parentheses in the function definition after the function name. When a function is called (activated), the values (arguments) to be assigned to each parameter have to be passed in a similar way.
When a function is called, arguments (if there are) are passed to the called function and control passes to the activated function. After the algorithm of a function is executed by a return statement, or the physical end of the function is reached, the called function passes control back to the place where it was called by a return statement. The value of the expression in the return statement is the return value returned back by the function, which is the result of the function call expression.
II.1.1. Defining, calling and declaring functions
C++ Standard Library provides us many useful predefined functions. We only have to declare these functions before using them. For that purpose, the corresponding header file should be included in the source code. The following table enumerates some frequently used functions and the corresponding include files:
|
function |
header file |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contrary to Library functions, our own functions should always be defined as well. This function definition can be placed anywhere in a C++ program, but only once. If the definition of a function precedes the place where it is called (used), then it is also a declaration.
The general form of a function definition is the following (the signs 〈 〉 indicate optional parts): A parameter declaration list in the function header enumerates each parameter separated by each other by a comma, and every parameter is preceded by its type.

A storage class can also be given before the return type in the definition of functions. In the case of functions, the default storage class is extern, which indicates that the function can be accessed from other modules. If the accessibility of a function needs to be restricted to a given module, the static storage class should be used. (When parameters are declared, only the register storage class can be specified). If a function is intended to be placed within our own namespace, then the definition and the prototype of that function have to be put in the chosen namespace block. (Storage classes and namespaces are detailed later in this book.)
The next example contains a function that calculates the sum of the first n positive integer numbers. The function isum() expects an int type value and returns an int type result.
int isum(int n)
{
int s = 0;
for (int i=1; i<=n; i++)
s += i;
return s;
}
Suppose that in the source code, the definition of isum() is before the main () function from where the function isum() is called:
int main()
{
cout << isum(10) << endl;
int s = isum(7) * isum(10) + 2;
}
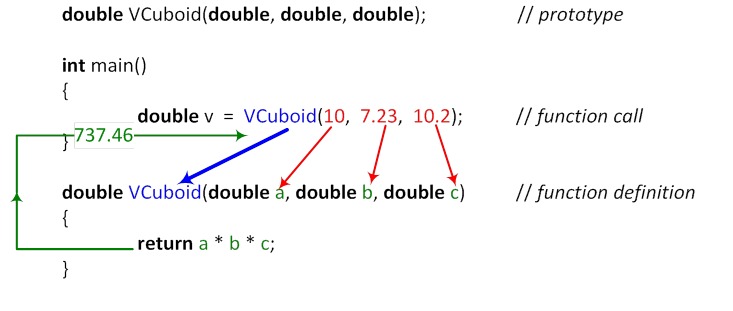
When a function is called , the name of the function is followed by a list of arguments separated from each other by a comma. The steps of calling a function can be traced on Figure II.2.
function_name (〈argument 1 , argument 2 , … argument n 〉)
Parentheses should be used even if a function does not have any parameters. A function can be called from anywhere where a statement can be given.
The order in which arguments are evaluated is not defined by the language C++. Function call operators guarantee only one thing: by the time control is passed to a called function, the argument list has completely been evaluated (together with all of its side-effects).
C++ standards require that functions have to be declared before they are called. Defining a function is therefore declaring a function. Then it may be logical to ask how we can make sure that the called function would always precede the place where it is called. Of course, this cannot be ensured because there are functions calling each other. In case the functions main () and isum() are swapped in the previous example, we get compilation errors until the prototype containing the whole description of the function is placed before the function is called:
int isum(int); // prototype
int main() {
cout << isum(10) << endl;
int s = isum(7) * isum(10) + 2;
}
int isum(int n)
{
int s = 0;
for (int i=1; i<=n; i++)
s += i;
return s;
}
The complete declaration of a function (its prototype ) contains the name and the type of the function and provides information about the number and the type of the parameters:
return_value function_name(〈parameter declaration list〉);
return_value function_name(〈type_list〉);
C++ compilers compile function calls if the prototype is already known:
-
checks the compatibility of the number and the types of parameters by comparing these parameters with the argument list,
-
converts arguments according to the types defined in the prototype and not according to the rules of automatic conversion.
(It should be noted that function definitions replace prototypes.) In most cases, a function header is used as a prototype, and it ends with a semicolon. In prototypes, parameter names do not have any importance, they can be left out or any other name can be used. The following prototypes are completely equal for compilers:
int isum(int); int isum(int n); int isum(int lots);
The prototype of a function can figure many times in the source code; however, they have to be the same, only parameter names can be different.
It should be noted that the prototype of functions without parameters is interpreted differently by C and C++ languages:
|
declaration |
C interpretation |
C++ interpretation |
|---|---|---|
|
type funct(); |
type funct(...); |
type funct(void); |
|
type funct(...); |
type funct(...); |
type funct(...); |
|
type funct(void); |
type funct(void); |
type funct(void); |
C++ makes it possible that a parameter list containing at least one parameter should end with three dots (...). A function defined in that way can be called with at least one parameter but also with any number or type of arguments. Let's look at the prototype of the function sscanf ().
int sscanf ( const char * str, const char * format, ...);
Chapter (Section I.5) dealing with exceptions also mentioned that the transferring (throw) of exceptions to the caller function can be enabled or disabled in function header. When the keyword throw is used, the definition of functions is modified in the following way:
return_type function_name (〈parameterlist〉) 〈throw(〈type_list〉)〉
{
〈local definitions and declarations〉
〈statements〉
return 〈expression〉;
}
The prototype corresponding to the definition also has to contain the keyword throw:
return_type function _ name (〈parameterlist〉) 〈throw(〈type_list〉)〉;
Let's see some prototypes mentioning the type of the thrown exceptions:
int funct() throw(int, const char*); // int and const char* int funct(); // all int funct() throw(); // not any
II.1.2. The return value of functions
The return_type figuring in the definition/declaration of a function determines the return type of the function, which can be of any C++ type with the exception of arrays and functions. Functions cannot return data with volatile or const type qualifiers; however, they can return a reference or a pointer to such data.
When the return statement is processed, the function passes control back to the caller, and the return value of type return_type can be used in the place where the function has been called.
return expression;
Within a function, many return statements may be placed; however, structured programming requires that if it is possible, only one exit point should be used.
The following prime number checker function can be exited at three points because there are three return statements, which results in a program structure more difficult to understand globally.
bool IsPrime(unsigned n)
{
if (n<2) // 0, 1
return false;
else {
unsigned limit = (unsigned)sqrt(1.0*n);
for (unsigned d=2; d<=limit; d++)
if ((n % d) == 0)
return false;
}
return true;
}
If an additional variable (result) is introduced, the code becomes much clearer:
bool IsPrime(unsigned n)
{
bool result = true;
if (n<2) // 0, 1
result = false;
else {
unsigned limit = (unsigned)sqrt(1.0*n);
for (unsigned d=2; d<=limit && result; d++)
if ((n % d) == 0)
result = false;
}
return result;
}
By using the type void, we can create functions that do not return any value. (Other programming languages call these procedures.) In that case, exiting the function is carried out by a return statement without a return value. Functions of type void are mostly exited when the closing curly bracket is reached.
The following function prints out all perfect numbers within a given interval. (A positive integer number is perfect if the sum of its positive divisors is equal to the given number. The smallest perfect number is 6 because 6 = 1+2+3, but 28 is also perfect because 28 = 1+2+4+7+14.)
void PerfectNumbers(int from, int to)
{
int sum = 0;
for(int i=from; i<=to; i++) {
sum = 0;
for(int j=1; j<i; j++) {
if(i%j == 0)
sum += j;
}
if(sum == i)
cout<< i <<endl;
}
}
Functions can return pointers or references; however, it is forbidden to return local variables or the address of local variables since they are deleted when the function is exited. Let's see some good solutions.
#include <cassert>
#include <new>
using namespace std;
double * Allocate(int size) {
double *p = new (nothrow) double[size];
assert(p);
return p;
}
int & DinInt() {
int *p = new (nothrow) int;
assert(p);
return *p;
}
int main() {
double *pd = Allocate(2012);
pd[2] = 8;
delete []pd;
int &x = DinInt();
x = 10;
delete &x;
}
The function named Allocate() allocates an array of type double with a given number of elements and returns the beginning address of the dynamic array. The function DinInt() allocates space on the heap for only one integer variable and returns the reference of the dynamic variable. This value can be accessed by a variable of reference type, the dynamic variable can be accessed without the * operator.
II.1.3. Parametrizing functions
When we create functions we have to tend to use the algorithm in the function in a range as wide as possible. This is needed because the input values (parameters) of an algorithm are assigned when the function is called. The following function without a parameter prints out a greeting:
void Greeting(void) {
cout << "Welcome on board!" << endl;
}
Every time this function is called, we always get the same message:
Greeting();
What should we do to greet users according to the part of the day? Then, the function should be parametrized:
#include <iostream>
#include <string>
using namespace std;
void Greeting(string greeting) {
cout << greeting << endl;
}
int main() {
Greeting("Good morning");
Greeting("Good evening!");
}
In a C++ function definition, each parameter is preceded by its type, no simplification is allowed. A declared parameter can be used as a local variable within a function; however, it is only accessible from the outside when they are passed as arguments. A parameter can be scalar (bool, char, wchar_t, short, int, long, long long, float, double, enumeration, reference and pointer) or structure, union, class or array.
In order to demonstrate these different types of parameters, let's make the function calculating the value of a polynomial on the basis of Horner's method.
The general form of polynomials:
Horner's scheme
The input parameters of the function are: the value of x, the degree of the polynomial and an array of the coefficients of the polynomial (having degree+1 elements). (The type qualifier const forbids the modification of the elements of the array within the function.)
double Polynomial(double x, int n, const double c[]) {
double y = 0;
for (int i = n; i > 0; i--)
y = (y + c[i]) * x;
return y + c[0];
}
int main(){
const int degree = 3;
double coefficients[degree + 1] = { 5, 2, 3, 1};
cout << Polynomial(2,degree,coefficients)<< endl; // 29
}
II.1.3.1. Parameter passing methods
In the language C++ parameters can be grouped in two categories on the basis of how they are passed. There are input parameters passed by value and variable parameters passed by reference.
II.1.3.1.1. Passing parameters by value
If parameters are passed by value , it is their value that is passed to the called function. The parameters of the function are initialised to the passed values, and after, the relation between these arguments and parameters ends. As a consequence, the operations carried out on parameters have no effect on the arguments with which the function is called.
Arguments can only be expressions, the type of which can be converted into the type of the corresponding parameters of the called function.
The function enumber() returns the approximate value of e by summing up the first n+1 elements of the sequence:
double enumber(int n) {
double f = 1;
double eseq = 1;
for (int i=2; i<=n; i++) {
eseq += 1.0 / f;
f *= i;
}
return eseq;
}
The function enumber() can be called by any numeric expression:
int main(){
long x =1000;
cout << enumber(x)<< endl;
cout << enumber(123) << endl;
cout << enumber(x + 12.34) << endl;
cout << enumber(&x) << endl;
}
When it is first called, the value of the variable x of type long is passed to the function converted to type int. In the second case, the value of the parameter becomes a constant of type int. The argument of the third call is an expression of type double, the value of which is converted to an integer before it is passed. This conversion may provoke data loss - that is why the compiler sends us an alert message. The last case is an odd-one-out in the list of the calls since in that case, the compiler rejects to convert the address of the variable x to an integer. Since type conversions of this type can lead to run-time errors, conversions have to be asked for separately:
cout << enumber((int)&x) << endl;
If the value of an external variable is intended to be modified within the function, it is the address of the variable that have to be passed and the address has to be received as a parameter of pointer type. As an example, let's have a look at the classical function swapping the values of two variables:
void pswap(double *p, double *q) {
double c = *p;
*p = *q;
*q = c;
}
int main(){
double a = 12, b =23;
pswap(&a, &b);
cout << a << ", " << b<< endl; // 23, 12
}
Arguments may also be expressions, but in that case these expressions have to be left value expressions. It should be noted that arrays are passed to functions by their beginning address.
If the type qualifier const is placed in the parameter list, we can restrict the modification of the memory space to which a pointer points ( const double *p) and restrict the modification of the value of the pointer ( double * const p) within a function.
II.1.3.1.2. Passing parameters by reference
Parameters passed by value are used as local variables in functions. However, reference parameters are not independent variables; they are only alternative names for the arguments provided in a function call.
Reference parameters are marked with a & character placed between the type and the parameter name in the function header. When the function is called, the argument variables have to have the same type as that of parameters. The function swapping the value of variables becomes simpler if we use parameters passed by reference:
void rswap(double & a, double & b) {
double c = a;
a = b;
b = c;
}
int main(){
double x = 12, y =23;
rswap(x, y);
cout << x << ", " << y << endl; // 23, 12
}
The value (right-value) and the address (left-value) of a reference parameter equals with the value and the address of the referenced variable, so it completely replaces the latter.
It should be noted that the compiled code of the functions pswap() and rswap() are completely the same in Visual Studio. That is why it is not more efficient to use pswap() in C++ program codes.
Independently of the parameter passing method, compilers allocate memory space for parameters in the stack. In the case of value parameters, the size of the allocated memory depends on the type of the parameter; therefore it can be really big, while in the case of reference parameters it is the pointer size used in the given system that counts. In the case of a bigger structure or object, we should not only consider the increased memory need but also the longer time a function call requires.
In the following example, a reference to a structure is passed to a function but we would like to prevent the modification of the structure within the function. For that purpose, the most efficient method is to use a parameter of constant reference type :
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
struct svector {
int size;
int a[1000];
};
void MinMax(const svector & sv, int & mi, int & ma) {
mi = ma = sv.a[0];
for (int i=1; i<sv.size; i++) {
if (sv.a[i]>ma)
ma = sv.a[i];
if (sv.a[i]<mi)
mi = sv.a[i];
}
}
int main() {
const int maxn = 1000;
srand(unsigned(time(0)));
svector v;
v.size=maxn;
for (int i=0; i<maxn; i++) {
v.a[i]=rand() % 102 + (rand() % 2012);
}
int min, max;
MinMax(v, min, max);
cout << min << endl;
cout << max << endl;
}
It should be noted that while in the solution above calling the function MinMax() is faster and less memory space is required in the stack, however accessing parameters within the function is more efficient by using value type parameters.
Constant reference parameters completely replace constant value parameters, so any expression (not only variables) can be used as arguments. This fact is demonstrated by the example determining the greatest common divisor of two numbers:
int Gcd(const int & a, const int & b ) {
int min = a<b ? a : b, gcd = 0;
for (int n=min; n>0; n--)
if ( (a % n == 0) && (b % n) == 0) {
gcd = n;
break;
}
return gcd;
}
int main() {
cout << Gcd(24, 32) <<endl; // 8
}
II.1.3.2. Using parameters of different types
The following subchapters will broaden our knowledge about parameters for different types with the help of examples. In the examples of this subchapter, the definition of functions is followed by the presentation of the function call after a dotted line. Of course, we give the whole program code for more complicated cases.
II.1.3.2.1. Arithmetic type parameters
Parameters can be declared by the types bool, char, wchar_t, int, enum, float and double and these types can also be function types.
In general, we do not have to hesitate much when deciding what the used parameters and the returned value will be. If a function does not return any value, i.e. it only carries out an operation, then we use the return type void and value parameters:
void PrintOutF(double data, int field, int precision) {
cout.width(field);
cout.precision(precision);
cout << fixed << data << endl;
}
...
PrintOutF(123.456789, 10, 4); // 123.4568
We also have an easy task when a function returns one value from the input values:
long Product(int a, int b) {
return long(a) * b;
}
...
cout << Product(12, 23) <<endl; // 276
However, if we want a function to return more values, then the solution should be based on reference (or pointer) parameters. In that case, the function is of type void or of a type that indicates the successfulness of an operation, for example bool. The following function Cube() calculates the surface area, the volume and the length of the body diagonal of the cube on the basis of its edge length:
void Cube(double a, double & surface_area, double & volume,
double & diagonal) {
surface_area = 6 * a * a;
volume = a * a * a;
diagonal = a * sqrt(3.0);
}
...
double f, v, d;
Cube(10, f, v, d);
II.1.3.2.2. User-defined type parameters
If user-defined types (struct, class, union) are used in parameter lists or a return value, then the solutions presented for arithmetic types can be used. The basis of that is provided by the fact that C++ defines value assignment between objects and unions of the same type.
Arguments of user-defined types can be passed to functions by value, by reference or by a pointer. In the standard C++, the return value of functions can be of a user-defined type. Therefore there are many possibilities. We only have to decide which one is the best for the given task.
As an example, let's see a structure appropriate for storing complex numbers.
struct complex {
double re, im;
};
Let's create a function to add two complex numbers. Its members and the structure that stores the result are passed to the function with a pointer to them (CSum1()). Since input parameters are not intended to be modified within the function, the type qualifier const is used.
void CSum1(const complex*pa, const complex*pb, complex *pc){
pc->re = pa->re + pb->re;
pc->im = pa->im + pb->im;
}
The second function returns the sum of the two complex numbers passed by value (CSum2()). Addition is carried out in a local structure, and it is only its value that is passed by the return statement.
complex CSum2(complex a, complex b) {
complex c;
c.re = a.re + b.re;
c.im = a.im + b.im;
return c;
}
The second solution is of course much safer and expresses more the essential of this operation than the first one. In any other aspect (memory need, speed), we have to choose the first function. However, if a reference type is used, the solution we get realises the advantages of the function CSum2() and is also able to beat the function CSum1().
complex Csum3(const complex & a, const complex & b) {
complex c;
c.re = a.re + b.re;
c.im = a.im + b.im;
return c;
}
The three different solutions require two different function calls. The following main() function contains a call for all the three adding function:
int main() {
complex c1 = {10, 2}, c2 = {7, 12}, c3;
// all the three arguments are pointers
CSum1(&c1, &c2, &c3);
c3 = CSum2(c1, c2); // arguments are structures
// arguments are structure references
c3 = CSum3(c1, c2);
}
II.1.3.2.3. Passing arrays to functions
Now let's see how we can pass arrays to functions in C++. We have already mentioned that arrays cannot be passed or returned by value (by copying their values). There is even a difference between passing one-dimensional arrays (vectors) and multi-dimensional ones as arguments.
If one-dimensional arrays (vectors) are passed as function arguments, it is a pointer to their first value that is passed. That is why, the modifications carried out on the elements of the vector within the function will remain even after the function is exited.
Parameters of a vector type can be declared either as pointers or with empty indexing operators . Since C++ arrays do not contain any information about the number of their elements, the latter information should also be passed as a separate parameter. Within functions, accessing their elements can be done by any of the already presented two methods (indexing, pointer). A function calculating the sum of the first n elements of a vector of type int can be realised in many ways. The parameters of the vector should be qualified as const because that ensures that the vector elements could not be modified within the function.
long VectorSum1 (const int vector[], int n) {
long sum = 0;
for (int i = 0; i < n; i++) {
sum+=vector[i]; // or sum+=*(vector+i);
}
return sum;
}
...
int v[7] = { 10, 2, 11, 30, 12, 7, 23};
cout <<VectorSum1(v, 7)<< endl; // 95
cout <<VectorSum1(v, 3)<< endl; // 23
However, there is a solution that is completely equal to the solution above: if the address of the vector is received in a pointer. (The second const qualifier makes it impossible to modify the pointer value.)
long VectorSum2 (const int * const vector, int n) {
long sum = 0;
for (int i = 0; i < n; i++) {
sum+=vector[i]; // or sum+=*(vector+i);
}
return sum;
}
In case the elements of a passed vector have to be modified, for example, they have to be sorted, the first const type qualifier has to be left out:
void Sort(double v[], int n) {
double temp;
for (int i = 0; i < n-1; i++)
for (int j=i+1; j<n; j++)
if (v[i]>v[j]) {
temp = v[i];
v[i] = v[j];
v[j] = temp;
}
}
int main() {
const int size=7;
double v[size]={10.2, 2.10, 11, 30, 12.23, 7.29, 23.};
Sort(v, size);
for (int i = 0; i < size; i++)
cout << v[i]<< '\t';
cout << endl;
}
One-dimensional arrays can be passed by reference , too. However, in that case, the size of the vector to be processed has to be fixed.
long VectorSum3 (const int (&vector)[6]) {
long sum = 0;
for (int i = 0; i < 6; i++) {
sum+=vector[i]; // or sum+=*(vector+i);
}
return sum;
}
...
int v[6] = { 10, 2, 11, 30, 12, 7};
cout << VectorSum3(v) << endl;
When two-dimensional array arguments are presented, we mean by the notion of two-dimensional arrays the arrays that are created (in a static way) by the compiler:
int m[2][3];
A reference to the elements of the array (m[i][j]) can also be expressed in the form *(( int *)m+(i*3)+j) (in fact, that is what compilers also do). From that expression, it can be clearly seen that the second dimension of two-dimensional arrays (3) has a vital importance for compilers, while the number of rows can be anything.
Our aim is to make a function that prints out the elements of a two-dimensional integer array of any size in a matrix form. As a first step, let's create the version of this function that is able to print out arrays of size 2x3.
void PrintMatrix23(const int matrix[2][3]) {
for (int i=0; i<2; i++) {
for (int j=0; j<3; j++)
cout <<matrix[i][j] <<'\t';
cout<<endl;
}
}
...
int m[2][3] = { {10, 2, 12}, {23, 7, 29} };
PrintMatrix23(m);
10 2 12 23 7 29 |
The two-dimensional array is passed to the function as a pointer to the start of the used memory space. When accessing array elements, the compiler makes use of the fact that rows contain 3 elements. In that way, the function above can simply be transformed into another function that prints out an array of any nx3 size, we only have to pass the number of rows as a second argument:
void PrintMatrixN3(const int matrix[][3], int n) {
for (int i=0; i<n; i++) {
for (int j=0; j<3; j++)
cout <<matrix[i][j] <<'\t';
cout<<endl;
}
}
...
int m[2][3] = { {10, 2, 12}, {23, 7, 29} };
PrintMatrixN3(m, 2);
cout << endl;
int m2[3][3] = { {1}, {0, 1}, {0, 0, 1} };
PrintMatrixN3(m2, 3);
10 2 12 23 7 29 1 0 0 0 1 0 0 0 1 |
However, there is no possibility to leave out the second dimension because in that case the compiler is not able to identify the rows of the array. We can only do one thing to get a general solution: we take over the task of accessing the memory space of the array from the compiler by using the above mentioned expression:
void PrintMatrixNM(const void *pm, int n, int m) {
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++)
cout <<*((int *)pm+i*m+j) <<'\t';
cout<<endl;
}
}
...
int m[2][3] = { {10, 2, 12}, {23, 7, 29} };
PrintMatrixNM(m, 2, 3);
cout << endl;
int m2[4][4] = { {0,0,0,1}, {0,0,1}, {0,1}, {1} };
PrintMatrixNM(m2, 4, 4);
10 2 12 23 7 29 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 |
II.1.3.2.4. String arguments
When creating functions, we can also choose between C-style (char vector) or user-defined type ( string ) string processing. Since we have already presented both parameter types, we only show here some examples.
Processing character sequences can be done in three ways. First, strings are treated as vectors (with the help of indexes), or we can carry out the necessary operations by pointers or finally we can use the member functions of the type string .
It should be noted that modifying the content of string literals (character sequence constants) leads in general to a run-time error, therefore they can only be passed to functions as constants or a value parameter of type string .
In the first example, we only iterate through the elements of a character sequence while counting the number of occurrence of a given character.
If a string is processed as a vector , we need an index variable (i) to index its characters. The condition that stops counting is fulfilled if the 0 byte closing the character sequence is reached. In the meanwhile, the index variable is incremented continuously by one.
unsigned CountChC1(const char s[], char ch) {
unsigned cnt = 0;
for (int i=0; s[i]; i++) {
if (s[i] == ch)
cnt++;
}
return cnt;
}
If we use a pointer , we go through all characters by incrementing the pointer pointing first to the beginning of the character sequence until we reach the final '\0' character (byte 0).
unsigned CountChC2(const char *s, char ch) {
unsigned cnt = 0;
while (*s) {
if (*s++ == ch)
cnt++;
}
return cnt;
}
If the string has the type string , its member functions can also be used besides indexing:
unsigned CountChCpp(const string & s, char ch) {
int cnt = -1, position = -1;
do {
cnt++;
position = s.find(ch, position+1);
} while (position != string::npos);
return cnt;
}
The corresponding function calls are demonstrated with a string constant, a character array and a string type argument. All the three functions can be called with a string literal or a character array argument:
char s1[] = "C, C++, Java, C++/CLI / C#";
string s2 = s1;
cout<<CountChC1("C, C++, Java, C++/CLI / C#", 'C')<<endl;
cout<<CountChC2(s1, 'C')<<endl;
However, if we use arguments of type string , the first two functions need a little manipulation:
cout << CountChC2(s2.c_str(), 'C') << endl; cout << CountChCpp(s2, 'C') << endl;
Conditions become more strict if the declaration const is left out before the parameters. The next example reverses the string passed to the function, and returns a pointer to the new string. The solution is carried out on all the three cases presented above:
char * StrReverseC1(char s[]) {
char ch;
int length = -1;
while(s[++length]); // determining the string length
for (int i = 0; i < length / 2; i++) {
ch = s[i];
s[i] = s[length-i-1];
s[length-i-1] = ch;
}
return s;
}
char * StrReverseC2(char *s) {
char *q, *p, ch;
p = q = s;
while (*q) q++; // going through the elements until byte 0 closing the string
p--; // p points to the first character of the string
while (++p <= --q) {
ch = *p;
*p = *q;
*q = ch;
}
return s;
}
string& StrReverseCpp(string &s) {
char ch;
int length = s.size();
for (int i = 0; i < length / 2; i++) {
ch = s[i];
s[i] = s[length-i-1];
s[length-i-1] = ch;
}
return s;
}
The functions have to be called by arguments having the same type as the parameters:
int main() {
char s1[] = "C++ programming";
cout << StrReverseC1(s1) << endl; // gnimmargorp ++C
cout << StrReverseC2(s1) << endl; // C++ programming
string s2 = s1;
cout << StrReverseCpp(s2) << endl; // gnimmargorp ++C
cout << StrReverseCpp(string(s1)); // gnimmargorp ++C
}
II.1.3.2.5. Functions as arguments
When developing mathematical applications, it is normal to expect that a well elaborated algorithm could be used in many functions. For that purpose, the function has to be passed as an argument to the function executing the algorithm.
II.1.3.2.5.1. Function types and typedef
With typedef, the type of a function can be indicated by a synonymous name. The function type declares the function that has the given number and type of parameters and returns the given data type. Let's have a look at the following example function that calculates the value of the third degree polynomial if x is given. The prototype and the definition of the function are:
double poly3(double); // prototype
double poly3(double x) // definition
{
return x*x*x - 6*x*x - x + 30;
}
Let's have a look at the prototype of the function and let's type typedef before it and replace the name poly3 with mathfunction.
typedef double mathfunction(double);
If the type mathfunction is used, the prototype of the function poly3() is:
mathfunction poly3;
II.1.3.2.5.2. Pointers to functions
In C++, function names can be used in two ways. A function name can be the left operand of a function call operator: in this case, it is a function call expression
poly3(12.3)
the value of which is the value returned by the function. However, if the function name is used alone
poly3
we get a pointer, the value of which is a memory address where the code of the function is (code pointer) and the type of which is that of the function.
Let's define a pointer to the function poly3(). This pointer can be assigned the address of the function poly3() as a value. The definition can be obtained easily if the name in the header of the function poly3 is replaced by the expression (*functionptr):
double (*functionptr)(double);
functionptr is a pointer to a function that returns a double value and that has a parameter of type double.
However, this definition can be provided in a much more legible way if we use the type mathfunction created with typedef:
mathfunction *functionptr;
When the pointer functionptr is initialised, the function poly3 can be called indirectly:
functionptr = poly3;
double y = (*functionptr)(12.3);
or
double y = functionptr(12.3);
If we want to create a reference to this function, we have to follow the same steps. But in this case, the initial value has to be given already in the definition:
double (&functionref)(double) = poly3;
or
mathfunction &functionref = poly3;
Calling the function by using the reference:
double y = functionref(12.3);
II.1.3.2.5.3. Examples for pointers to functions
On the basis of the things said above, the prototype of the Library function qsort () becomes more comprehensible:
void qsort(void *base, size_t n, size_t width,
int (*fcmp)(const void *, const void *));
With qsort (), we can sort data stored in an array by using the Quicksort algorithm. This function makes it possible to sort an array starting at the address base, having n number of elements and each element being allocated width bytes. The comparator function called during sorting has to be provided by ourselves as the parameter fcmp.
The following example uses the function qsort () to sort integer and string arrays:
#include <iostream>
#include <cstdlib>
#include <cstring>
using namespace std;
int icmp(const void *p, const void *q) {
return *(int *)p-*(int *)q;
}
int scmp(const void *p, const void *q) {
return strcmp((char *)p,(char *)q);
}
int main() {
int m[8]={2, 10, 7, 12, 23, 29, 11, 30};
char names[6][20]={"Dennis Ritchie", "Bjarne Stroustrup",
"Anders Hejlsberg","Patrick Naughton",
"James Gosling", "Mike Sheridan"};
qsort(m, 8, sizeof(int), icmp);
for (int i=0; i<8; i++)
cout<<m[i]<<endl;
qsort(names, 6, 20, scmp);
for (int i=0; i<6; i++)
cout<<names[i]<<endl;
}
The function named tabulate() in the following example codes can be used to print out in tabular form the values of any function having a parameter of type double and returning a double value. The parameters of the function tabulate() contains the two interval boundaries and the step value.
#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;
// Prototypes
void tabulate(double (*)(double), double, double, double);
double sqr(double);
int main() {
cout<<"\n\nThe values of the function sqr() ([-2,2] dx=0.5)"<<endl;
tabulate(sqr, -2, 2, 0.5);
cout<<"\n\nThe values of the function sqrt() ([0,2] dx=0.2)"<<endl;
tabulate(sqrt, 0, 2, 0.2);
}
// The definition of the function tabulate()
void tabulate(double (*fp)(double), double a, double b,
double step){
for (double x=a; x<=b; x+=step) {
cout.precision(4);
cout<<setw(12)<<fixed<<x<< '\t';
cout.precision(7);
cout<<setw(12)<<fixed<<(*fp)(x)<< endl;
}
}
// The definition of the function sqr()
double sqr(double x) {
return x * x;
}
The results:
The values of the function sqr() ([-2,2] dx=0.5)
-2.0000 4.0000000
-1.5000 2.2500000
-1.0000 1.0000000
-0.5000 0.2500000
0.0000 0.0000000
0.5000 0.2500000
1.0000 1.0000000
1.5000 2.2500000
2.0000 4.0000000
The values of the function sqrt() ([0,2] dx=0.2)
0.0000 0.0000000
0.2000 0.4472136
0.4000 0.6324555
0.6000 0.7745967
0.8000 0.8944272
1.0000 1.0000000
1.2000 1.0954451
1.4000 1.1832160
1.6000 1.2649111
1.8000 1.3416408
2.0000 1.4142136
|
II.1.3.2.6. Default arguments
In the prototype of C++ functions, certain parameters can be assigned a so-called default value. Compilers use these values if there is no argument corresponding to the given parameter when the function is called:
// prototype
long SeqSum(int n = 10, int d = 1, int a0 = 1);
long SeqSum(int n, int d, int a0) { // definition
long sum = 0, ai;
for(int i = 0; i < n; i++) {
ai = a0 + d * i;
cout << setw(5) << ai;
sum += ai;
}
return sum;
}
The function named SeqSum() creates an arithmetic sequence of n elements. The first element is a0, the difference between elements is d. The function returns the sum of the elements of the sequence.
It should be noted that parameters having a default value are placed one after another continuously from right to left, while arguments have to be provided continuously from left to right when the function is called. If a prototype is used, default values can only be provided in the prototype.
Now let's have a look at the value of the parameters after some possible calls of the function above.
|
Call |
Parameters |
||
|---|---|---|---|
|
n |
d |
a0 |
|
|
SeqSum() |
10 |
1 |
1 |
|
SeqSum(12) |
12 |
1 |
1 |
|
SeqSum(12,3) |
12 |
3 |
1 |
|
SeqSum(12, 3, 7) |
12 |
3 |
7' |
Default arguments make functions more flexible. For example, if a function is often called with the same argument list, it is worth making frequently used parameters default and calling the function without those arguments.
II.1.3.2.7. Variable length argument list
There are cases when the number and the type of the parameters of a function are not known in advance. In the declaration of these functions, the parameter list ends with an ellipsis (three dots):
int printf(const char * format, ... );
The ellipsis indicates to the compiler that further arguments can be expected. The function printf () (cstdio) has to be called by at least one argument but this can be followed by other arguments the number of which is not specified:
char name[] = "Bjarne Stroustrup";
double a=12.3, b=23.4, c=a+b;
printf("C++ language\n");
printf("Name: %s \n", name);
printf("Result: %5.3f + %5.3f = %8.4f\n", a, b, c);
The function printf () processes the next argument on the basis of format.
When functions with similar declaration are called, compilers only check the type of the parameters and that of the arguments until they reach the "..." element. After that, passing the arguments to the function is carried out on the basis of the type of the given (or eventually converted) arguments.
C++ makes it possible to use the ellipsis in our own functions, i.e. variable length argument lists. In order that the value of the passed arguments be found in the memory space containing the parameters, the first parameter always has to be provided.
C++ standard contains some macros with the help of which a variable length argument list can be processed. The macros defined in the header file cstdarg use pointers of type va_list to access arguments:
|
|
returns the following element in the argument list. |
|
|
cleaning up after all arguments are processed. |
|
|
initializes the pointer used to access the arguments. |
As an example, let's look at the function Average(), which calculates the average of any number of values of type double. The number of the elements has to be provided as the first argument.
#include<iostream>
#include<cstdarg>
using namespace std;
double Average(int num, ... ) {
va_list numbers;
// passing through the first (num) arguments
va_start(numbers, num);
double sum = 0;
for(int i = 0; i < num; ++i ) {
// accessing the double arguments
sum += va_arg(numbers, double);
}
va_end(numbers);
return (sum/num);
}
int main() {
double avg = Average(7,1.2,2.3,3.4,4.5,5.6,6.7,7.8);
cout << avg << endl;
}
II.1.3.2.8. Parameters and return value of the main() function
The interesting thing about the main () function is not only that program execution starts here but also that it can have many parameterizing options:
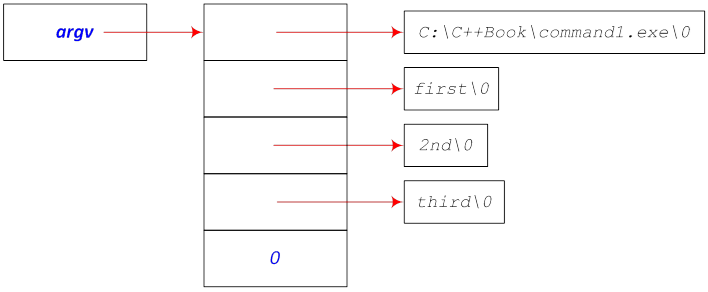
int main( ) int main( int argc) ( ) int main( int argc, char *argv[]) ( )
argv points to an array (a vector) of character pointers, argc gives the number of strings in the array. (The value of argc is at least 1 since argv[0] refers to the character sequence containing the name of the program.)
The return value of main (), which is of an int type according to the standard, can be provided within the main () function in a return statement or as an argument of the Standard Library function exit () that can be placed anywhere in a program. The header file cstdlib contains standard constants:
#define EXIT_SUCCESS 0 #define EXIT_FAILURE 1
These can be used as an exit code signalling whether the execution of the program was successful or not.
The main () function differs from other normal C++ functions in many ways: it cannot be declared as a static or inline function, it is not obligatory to use return in it and it cannot be overloaded. On the basis of the recommendations of C++ standards, it cannot be called within a program and its address cannot be obtained.
The following command1.cpp program prints out the number of arguments and then all of its arguments:
#include <iostream>
using namespace std;
int main(int argc, char *argv[]) {
cout << "number of arguments: " << argc << endl;
for (int narg=0; narg < argc; narg++)
cout << narg << " " << argv[narg] << endl;
return 0;
}
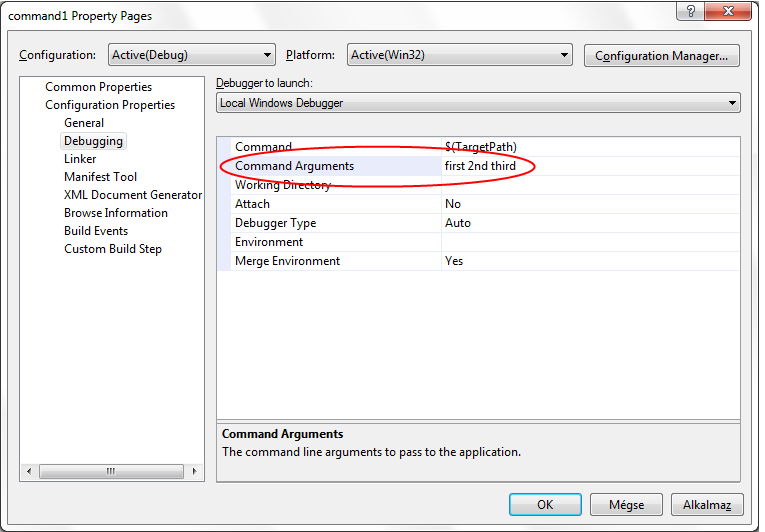
Command line arguments can be provided in the console window
C:\C++Book>command1 first 2nd third
or in the Visual Studio development environment (Figure II.5).
The results of executing command1.exe:
|
In a console window |
In a development environment |
|---|---|
C:\C++Book>command1 first 2nd third number of arguments: 4 0 command1 1 first 2 2nd 3 third C:\C++Book> |
C:\C++Book>command1 first 2nd third number of arguments: 4 0 C:\C++Book\command1.exe 1 first 2 2nd 3 third C:\C++Book> |
The next example code (command2.cpp) demonstrates a solution easy to use when creating utility software to test whether input arguments are well provided or not. The program only starts if it is called with two arguments. Otherwise, it sends an error message and prints out how to start the program from the command line properly.
#include <iostream>
#include <cstdlib>
using namespace std;
int main(int argc, char *argv[]) {
if (argc !=3 ) {
cerr<<"Wrong number of parameters!"<<endl;
cerr<<"Usage: command2 arg1 arg2"<<endl;
return EXIT_FAILURE;
}
cout<<"Correct number of parameters:"<<endl;
cout<<"1. argument: "<<argv[1]<<endl;
cout<<"2. argument: "<<argv[2]<<endl;
return EXIT_SUCCESS;
}
The results of the execution of command2.exe:
|
Wrong number of parameters: command2 |
Correct number of parameters: command2 alfa beta |
|---|---|
Wrong number of parameters! Usage: command2 arg1 arg2 |
Correct number of parameters: 1. argument: alfa 2. argument: beta |
II.1.4. Programming with functions
Procedural programming requires that separate functions be created for each subtask and that these functions could be tested separately. Solving the original task is achieved by calling these already tested functions. It is important to arrange communication between these functions. As we have already seen in some functions, parameterizing and return values represent this communication. However, in the case of functions being in a logical relationship with one another, there are more possibilities that can even increase the efficiency of the solution.
As an example, let's have a look at a task everybody knows: determining the area and the perimeter of a triangle. Calculating the area is carried out with Heron's formula , the prerequisite of which is the fulfilment of triangle inequality. This states that every side of a triangle is smaller that the sum of the two other sides.
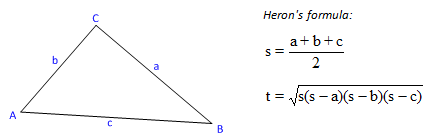
The solution consisting of only the main () function can be realised easily even if we have read only the first some chapters of this book:
#include <iostream>
#include <cmath>
using namespace std;
int main() {
double a, b, c;
do {
cout <<"a side: "; cin>>a;
cout <<"b side: "; cin>>b;
cout <<"c side: "; cin>>c;
} while(!((a<b+c) && (b<a+c) && (c<a+b)));
double p = a + b + c;
double s = p/2;
double area = sqrt(s*(s-a)*(s-b)*(s-c));
cout << "perimeter: " << p <<endl;
cout << "area: " << area <<endl;
}
This program is very simple but it has some drawbacks because it cannot be reused and its structure is not easy to understand.
II.1.4.1. Exchanging data between functions using global variables
The solution of the problem above can be divided into parts that are logically independent of each other, more precisely:
-
reading the three side lengths of the triangle,
-
checking Triangle inequality,
-
calculating the perimeter,
-
calculating the area
-
and printing out calculated data.
The first four of the above mentioned activities will be realized by independent functions that communicate with each other and the main() function by shared (global) variables. Global variables should be provided outside function blocks and before the functions. (We should not forget about providing the prototypes!)
#include <iostream>
#include <cmath>
using namespace std;
// global variables
double a, b, c;
// prototypes
void ReadData();
bool TriangleInequality();
double Perimeter();
double Area();
int main() {
ReadData();
cout << "perimeter: " << Perimeter()<<endl;
cout << "area: " << Area()<<endl;
}
void ReadData() {
do {
cout <<"a side: "; cin>>a;
cout <<"b side: "; cin>>b;
cout <<"c side: "; cin>>c;
} while(!TriangleInequality() );
}
bool TriangleInequality() {
if ((a<b+c) && (b<a+c) && (c<a+b))
return true;
else
return false;
}
double Perimeter() {
return a + b + c;
}
double Area() {
double s = Perimeter()/2;
return sqrt(s*(s-a)*(s-b)*(s-c));
}
It's clear that the code has become more legible; however, it still cannot benefit from a broader use. For example, if we want to store the data of other triangles as well and to reuse them later in other tasks, we have to make sure to set appropriately the global variables a, b and c.
int main() {
double a1, b1, c1, a2, b2, c2;
ReadData();
a1 = a, b1 = b, c1 = c;
ReadData();
a2 = a, b2 = b, c2 = c;
a = a1, b = b1, c = c1;
cout << "perimeter: " << Perimeter()<<endl;
cout << "area: " << Area()<<endl;
a = a2, b = b2, c = c2;
cout << "perimeter: " << Perimeter()<<endl;
cout << "area: " << Area()<<endl;
}
Therefore, the solution would be better if the data of triangles are passed to the concerned functions as arguments.
II.1.4.2. Exchanging data between functions using parameters
Now we will not detail the following solutions since we have already presented the things to know about that in the previous sections.
#include <iostream>
#include <cmath>
using namespace std;
void ReadData(double &a, double &b, double &c);
bool TriangleInequality(double a, double b, double c);
double Perimeter(double a, double b, double c);
double Area(double a, double b, double c);
int main() {
double x, y, z;
ReadData(x , y , z);
cout << "perimeter: " << Perimeter(x, y, z)<<endl;
cout << "area: " << Area(x, y, z) <<endl;
}
void ReadData(double &a, double &b, double &c) {
do {
cout <<"a side: "; cin>>a;
cout <<"b side: "; cin>>b;
cout <<"c side: "; cin>>c;
} while(!TriangleInequality(a, b, c) );
}
bool TriangleInequality(double a, double b, double c) {
if ((a<b+c) && (b<a+c) && (c<a+b))
return true;
else
return false;
}
double Perimeter(double a, double b, double c) {
return a + b + c;
}
double Area(double a, double b, double c) {
double s = Perimeter(a, b, c)/2;
return sqrt(s*(s-a)*(s-b)*(s-c));
}
Now let's see the main () function if two triangles are to be dealt with.
int main() {
double a1, b1, c1, a2, b2, c2;
ReadData(a1, b1, c1);
ReadData(a2, b2, c2);
cout << "perimeter: " << Perimeter(a1, b1, c1)<<endl;
cout << "area: " << Area(a1, b1, c1)<<endl;
cout << "perimeter: " << Perimeter(a2, b2, c2)<<endl;
cout << "area: " << Area(a2, b2, c2)<<endl;
}
When the two methods are compared with respect to speed, we could observe that global variables make programs run faster (and therefore they become more efficient) since arguments are not copied to the stack before a function is called. We have also seen the drawbacks of the solution, which do strongly prevent the reusability of the program code. How could we decrease the inconvenience of using a lot of arguments and of using long argument lists?
The following solution is much better and is more recommended than using global variables. Global variables and the parameters corresponding to them have to be collected in a structure or have to be passed to functions by reference or by constant reference.
#include <iostream>
#include <cmath>
using namespace std;
struct triangle {
double a, b, c;
};
void ReadData(triangle &h);
bool TriangleInequality(const triangle &h);
double Perimeter(const triangle &h);
double Area(const triangle &h);
int main() {
triangle h1, h2;
ReadData(h1);
ReadData(h2);
cout << "perimeter: " << Perimeter(h1)<<endl;
cout << "area: " << Area(h1)<<endl;
cout << "perimeter: " << Perimeter(h2)<<endl;
cout << "area: " << Area(h2)<<endl;
}
void ReadData(triangle &h) {
do {
cout <<"a side: "; cin>>h.a;
cout <<"b side: "; cin>>h.b;
cout <<"c side: "; cin>>h.c;
} while(!TriangleInequality(h) );
}
bool TriangleInequality(const triangle &h) {
if ((h.a<h.b+h.c) && (h.b<h.a+h.c) && (h.c<h.a+h.b))
return true;
else
return false;
}
double Perimeter(const triangle &h) {
return h.a + h.b + h.c;
}
double Area(const triangle &h) {
double s = Perimeter(h)/2;
return sqrt(s*(s-h.a)*(s-h.b)*(s-h.c));
}
II.1.4.3. Implementing a simple menu driven program structure
Softwares with a text-based user interface can be controlled much better if it has a simple menu. To solve this problem, the menu entries are stored in a string array:
// Defintion of the menu
char * menu[] = {"\n1. Sides",
"2. Perimeter",
"3. Area",
"----------",
"0. Exit" , NULL };
Now let's transform the main () function of the previous example to handle the user’s menu selections:
int main() {
triangle h = {3,4,5};
char ch;
do {
// printing out the menu
for (int i=0; menu[i]; i++)
cout<<menu[i]<< endl;
// Processing the answer
cin>>ch; cin.get();
switch (ch) {
case '0': break;
case '1': ReadData(h);
break;
case '2': cout << "perimeter: ";
cout << Perimeter(h)<<endl;
break;
case '3': cout << "area: " << Area(h)<<endl;
break;
default: cout<<'\a';
}
} while (ch != '0');
}
The window when the program runs
1. Sides 2. Perimeter 3. Area ---------- 0. Exit 1 a side: 3 b side: 4 c side: 5 1. Sides 2. Perimeter 3. Area ---------- 0. Exit 2 perimeter: 12 1. Sides 2. Perimeter 3. Area ---------- 0. Exit 3 area: 6 |
II.1.4.4. Recursive functions
In mathematics, there might be tasks that can be solved by producing certain data and states in a recursive way. In this case, we define data and states by providing a start state then a general state is determined with the help of the previous states of a finite set.
Now let's have a look at some well-known recursive definitions.
factorial:
Fibonacci numbers:
greatest common divisor (gcd):
binomial numbers:
In programming, recursion means that an algorithm calls itself either directly (direct recursion) or via other functions it calls (indirect recursion). A classic example of recursion is calculating factorials.
On the basis of the recursive definition of calculating a factorial, 5! can be calculated in the following way:
5! = 5 * 4!
4 * 3!
3 * 2!
2 * 1!
1 * 0!
1 = 5 * 4 * 3 * 2 * 1 * 1 = 120
The C++ function that realizes the calculating above:
unsigned long long Factorial(int n)
{
if (n == 0)
return 1;
else
return n * Factorial(n-1);
}
Recursive functions solve problems elegantly but they are not efficient enough. Until a start state is reached, the allocated memory space (stack) can have a significant size because of multiple function calls, and the function call mechanism can take a lot of time.
That is why it is important to know that all recursive problems can be transformed into an iterative one (i. e. that uses loops), which is more difficult to elaborate but is more efficient. The non-recursive version of the function calculating factorials:
unsigned long long Factorial(int n)
{
unsigned long long f=1;
while (n != 0)
f *= n--;
return f;
}
Now, let's see how we can determine the nth element of a Fibonacci sequence.
0, 1, 1, 2, 3, 5, 8, 13, 21, ...
The following recursive rule can be used to calculate the nth element of the sequence :
|
a0 = 0 |
|
|
a1 = 1 |
|
|
an = an-1 + an-2, n = 2 ,3, 4,… |
Based on the recursive rule, we can now create the function that has completely the same structure as that of the mathematical definition:
unsigned long Fibonacci( int n ) {
if (n<2)
return n;
else
return Fibonacci(n-1) + Fibonacci(n-2);
}
Like in the preceding case, we recommend here using iterative structures in order to save time and memory:
unsigned long Fibonacci( int n ) {
unsigned long f0 = 0, f1 = 1, f2 = n;
while (n-- > 1) {
f2 = f0 + f1;
f0 = f1;
f1 = f2;
}
return f2;
}
While the running time of the iterative solution increases linearly with n, that of the recursive solution increases exponentially ().
The last part of this subchapter details only the recursive solution of the problems, so we entrust our readers with the iterative solutions.
The greatest common divisors of two natural numbers can be easily determined recursively:
int Gcd(int p, int q) {
if (q == 0)
return p;
else
return Gcd(q, p % q);
}
If binomial coefficients have to be calculated, we can choose between two recursive functions:
int Binom1(int n, int k)
{
if (k == 0 || k == n)
return 1;
else
return Binom1(n-1,k-1) + Binom1(n-1,k);
}
int Binom2(int n, int k)
{
if (k==0)
return 1;
else
return Binom2(n, k-1) * (n-k+1) / k;
}
From the two solutions, Binom2() is more efficient.
In the last example, we calculate a determinant recursively. The essential of the solution is that the calculation of a determinant of degree N is reduced to the problem of calculating N determinants of degree (N-1). And we do that until second degree determinants are reached. The solution is elegant and easy to understand but it is not very efficient. Function calls are stored in tree structures chained into each other, which require a lot of time and memory.
For example, if we want to calculate a determinant of size 4x4, the function Determinant() is called 17 times (once for a 4x4 matrix, four times for a 3x3 matrix and for 4 times 3 matrices of size 2x2) and the number of times the function is called increases to 5·17+1 = 86 for a fifth degree determinant. (It should be noted that in the case of a 12x12 matrix, the function Determinant() is called more than 300 million times, which may require many minutes.)
#include <iostream>
#include <iomanip>
using namespace std;
typedef double Matrix[12][12];
double Determinant(Matrix m, int n);
void PrintOutMatrix(Matrix m, int n);
int main() {
Matrix m2 = {{1, 2},
{2, 3}};
Matrix m3 = {{1, 2, 3},
{2, 1, 1},
{1, 0, 1}};
Matrix m4 = {{ 2, 0, 4, 3},
{-1, 2, 6, 1},
{10, 3, 4,-2},
{ 2, 1, 4, 0}};
PrintOutMatrix(m2,2);
cout << "Determinant(m2) = " << Determinant(m2,2) << endl;
PrintOutMatrix(m3,3);
cout << "Determinant(m3) = " << Determinant(m3,3) << endl;
PrintOutMatrix(m4,4);
cout << "Determinant(m4) = " << Determinant(m4,4) << endl;
cin.get();
return 0;
}
void PrintOutMatrix(Matrix m, int n)
{
for (int i=0; i<n; i++) {
for (int j=0; j<n; j++) {
cout << setw(6) << setprecision(0) << fixed;
cout << m[i][j];
}
cout << endl;
}
}
double Determinant(Matrix m, int n)
{
int q;
Matrix x;
if (n==2)
return m[0][0]*m[1][1]-m[1][0]*m[0][1];
double s = 0;
for (int k=0; k<n; k++) // n subdeterminants
{
// creating submatrices
for (int i=1; i<n; i++) // rows
{
q = -1;
for (int j=0; j<n; j++) // columns
if (j!=k)
x[i-1][++q] = m[i][j];
}
s+=(k % 2 ? -1 : 1) * m[0][k] * Determinant(x, n-1);
}
return s;
}
The results:
1 2
2 3
Determinant(m2) = -1
1 2 3
2 1 1
1 0 1
Determinant(m3) = -4
2 0 4 3
-1 2 6 1
10 3 4 -2
2 1 4 0
Determinant(m4) = 144
|
II.2. How to use functions on a more professional level?
The previous chapter has given us enough knowledge to solve programming tasks with functions. Using functions leads to a structured code that is easier to test and to a decrease in the time spent for searching for program errors.
In the following, we will review the solutions that can make function usage more efficient, in the sense that code execution becomes faster, developing and algorithmization becomes more comfortable.
II.2.1. Inline functions
Calling a function takes more time and memory than those that result from the algorithm contained within that function. Passing parameters, passing control to the function and returning from the function all take time.
C++ compilers decrease the time spent on calling the functions marked with the keyword inline by compiling the statements of these functions into the place from where they are called. (This means that the compiler replaces function calls in a program code with a code sequence made on the basis of the definition and arguments of the given functions instead of passing arguments and control to a separate code compiled from the body of these functions.)
This solution is recommended to be used for small-sized and frequently called functions.
inline double Max(double a, double b) {
return a > b ? a : b;
}
inline char LowerCase( char ch ) {
return ((ch >= 'A' && ch <= 'Z') ? ch + ('a'-'A') : ch );
}
Contrary to macros that will be presented later in this book, the advantage of using inline functions is that arguments are processed with complete type checking when these functions is called. In the following example, one function, which finds an element in a sorted vector by binary search, is marked as inline:
#include <iostream>
using namespace std;
inline int BinarySearch(int vector[], int size, int key) {
int result = -1; // not found
int lower = 0;
int upper = size - 1, middle;
while (upper >= lower) {
middle = (lower + upper) / 2;
if (key < vector[middle])
upper = middle - 1;
else if (key == vector[middle]) {
result = middle;
break;
}
else
lower = middle + 1;
} // while
return result;
}
int main() {
int v[8] = {2, 7, 10, 11, 12, 23, 29, 30};
cout << BinarySearch(v, 8, 23)<< endl; // 5
cout << BinarySearch(v, 8, 4)<< endl; // -1
}
Some further remarks about inline functions:
-
In general, the keyword inline can be used efficiently for small-sized, not complicated functions.
-
inline functions should be placed in a header file in case they are called in more compilation units; however, they can only be integrated in a source file only once.
-
Inline functions result in a faster code but lead to a bigger compiled code and compilation takes longer.
-
The keyword inline is only a recommendation for compilers which may take it into consideration under certain circumstances (but not always!). Most compilers do not take into consideration the keyword inline in case of functions containing a loop or a recursive call.
II.2.2. Overloading (redefining) function names
At first sight, the usage of functions in a broader range seems to be impeded by strict type checking of parameters. From among value parameters, this obstacle only concerns pointers, arrays and user-defined types. The following function that returns the absolute value of the argument, can be called with any numeric arguments but it always returns a result of type int:
inline int Absolute(int x) {
return x < 0 ? -x : x;
}
Some example function calls and the returned values:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In the second and third cases, the compiler warns us about the data loss, but it creates an executable code.
In case of non-constant reference parameters, there are more strict constraints since the function ValueAssignment() has to be called with parameters among which the first two variables must be of type int:
void ValueAssignment(int & a, int & b, int c) {
a = b + c;
b = c;
}
The algorithm realised by a function would be more useful if the latter could be executed with parameters of different types and if the same function name could be used for that purpose. The same function name is useful because the name of a function normally reflects the activity and algorithm that that function carries out. This need is satisfied by C++ language by supporting function name overloading.
Overloading a function means that different functions can be defined with the same name and within the same scope (the meaning of which is to be explained later) but with a different parameter list (parameter signature). (Parameter signature means the number and the type order of parameters.)
Having considered the things mentioned above, let's create two versions of the function Absolute()!
#include <iostream>
using namespace std;
inline int Absolute(int x) {
return x < 0 ? -x : x;
}
inline double Absolute(double x) {
return x < 0 ? -x : x;
}
int main() {
cout << Absolute(-7) << endl; // int
cout << Absolute(-1.2) << endl; // double
cout << Absolute(2.3F) << endl; // double
cout << Absolute('I') << endl; // int
cout << Absolute(L'\x807F') << endl; // int
}
Now we will not receive any message indicating a data loss from the compiler so it is the function of type double that is called with floating point values.
In that case, the function name itself does not determine unequivocally which function will be executed. The compiler matches the signature of the arguments in function calls with that of the parameters of each function having the same name. While a compiler is trying to match a function call with a function, the following cases may occur:
-
There is only one function that completely matches the call with respect to the types of its arguments - then it is that function that is chosen by the compiler.
-
There is only one function that matches the argument list of the function call when the type of the arguments has been automatically converted - it is evident in this case as well which one to choose.
-
There are not any functions that would match the argument list - the compiler sends an error message.
-
There are more functions that match the argument list to the same extent - the compiler sends an error message.
It should be noted that the return type of a function does not have any role when a compiler chooses the appropriate function variant.
If it is needed, for example if there are more functions that would match the given argument list to the same extent, programmers can help compilers choose the appropriate function by using a type-cast:
int main() {
cout << Absolute((double)-7) << endl; // double
cout << Absolute(-1.2) << endl; // double
cout << Absolute((int)2.3F) << endl; // int
cout << Absolute((float)'I') << endl; // double
cout << Absolute(L'\x807F') << endl; // int
}
In the following example, the function named VectorSum() has two redefined forms to calculate the sum of the elements in an array: one for arrays of type unsigned int and one for arrays of type double:
#include <iostream>
using namespace std;
unsigned int VectorSum(unsigned int a[], int n) {
int sum=0;
for (int i=0; i<n; i++)
sum += a[i];
return sum;
}
double VectorSum(double a[], int n) {
double sum = 0;
for (int i=0; i<n; i++)
sum += a[i];
return sum;
}
int main() {
unsigned int vu[]={1,1,2,3,5,8,13};
const int nu=sizeof(vu) / sizeof(vu[0]);
cout <<"\nThe sum of the elements of the unsigned array: "
<<VectorSum(vu, nu);
double vd[]={1.2,2.3,3.4,4.5,5.6};
const int nd=sizeof(vd) / sizeof(vd[0]);
cout << "\nThe sum of the elements of the double array: "
<< VectorSum(vd, nd);
}
In the first case, the compiler finds appropriate the signature of the function VectorSum(unsigned int*, int), in the second case, that of the function VectorSum(double*, int). For arrays of other types (like int and float), the compiler sends an error message, since the automatic conversion of pointers is very restricted in C++.
It should not be forgotten that operator overloading can be used in a similar way than function overloading. However, operators can only be overloaded in the case of user-defined types (struct, class), so this method will only be treated in the next part of the present book.
From the examples above, it can be clearly seen that the task of creating new function variants with new types and realising the same algorithms will become a word processing task with this method (copying blocks and replacing text). In order to avoid this, C++ compilers can be entrusted with the creation of redefined function variants with the usage of function templates.
II.2.3. Function templates
In the previous parts of this chapter, we have provided an overview of functions which make program codes safer and easier to maintain. Although functions make possible efficient and flexible code development, they have some disadvantages since all parameters have to be assigned a type. Overloading, which was presented in the previous section, helps us make functions independent of types but only to a certain extent. However, function overloading can treat only a finite number of types and also, it is not so efficient to update or to correct repeated codes in the overloaded functions.
So there should be a possibility to create a function only once and to use it as many times as possible with as many types as possible. Nowadays, most programming languages offer the method called generic programming for solving this problem.
Generic programming is a general programming model. This technique means developing a code that is independent of types. So source codes use so-called generic or parameterized types. This principle increases a lot the extent to which a code can be reused since containers and algorithms independent of types can be created with this method. C++ offers templates in order that generic programming could be realised at compilation time. However, there are languages and systems that realise generic programming at run-time (for example Java and С#).
II.2.3.1. Creating and using function templates
A template declaration starts with the keyword template, followed by the parameters of the template enclosed within the signs < and >. In most cases, these parameters are generic type names but they can contain variables as well. Generic type names should be preceded by the keyword class or typename.
When we create a function template, we should start from a working function in which the certain types should be replaced by generic types (TYPE). Afterwards, the compiler should be told which types should be replaced in the function template (template<class TYPE>). The first step to take in our function named Absolute():
inline TYPE Absolute(TYPE x) {
return x < 0 ? -x : x;
}
Then the final version should be provided in two ways:
template <class TYPE>
inline TYPE Absolute(TYPE x) {
return x < 0 ? -x : x;
}
template <typename TYPE>
inline TYPE Absolute(TYPE x) {
return x < 0 ? -x : x;
}
From the function template that is now done, the compiler will create the needed function variant when the function is called. It should be noted that the template named Absolute() can only be used with numeric types among which the operations 'lower than' and 'changing the sign' can be interpreted.
When the function is called in a traditional way, the compiler determines, based on the type of the argument, which version of the function Absolute() it will create and compile.
cout << Absolute(123)<< endl; // TYPE = int cout << Absolute(123.45)<< endl; // TYPE = double
Programmers themselves can carry out a function variant using the type-cast manually in the call:
cout << Absolute((float)123.45)<< endl; // TYPE = float cout << Absolute((int)123.45)<< endl; // TYPE = int
The same result is achieved if the type name is provided within the signs < and > after the name of the function:
cout << Absolute<float>(123.45)<< endl; // TYPE = float cout << Absolute<int>(123.45)<< endl; // TYPE = int
In a function template, more types can be replaced, as it can be seen in the following example:
template <typename T>
inline T Maximum(T a, T b) {
return (a>b ? a : b);
}
int main() {
int a = 12, b=23;
float c = 7.29, d = 10.2;
cout<<Maximum(a, b); // Maximum(int, int)
cout<<Maximum(c, d); // Maximum(float, float)
↯ cout<<Maximum(a, c); // there is no Maximum(int, float)
cout<<Maximum<int>(a,c);
// it is the function Maximum(int, int) that is called with type conversion
}
In order to use different types, more generic types should be provided in the function template header:
template <typename T1, typename T2>
inline T1 Maximum(T1 a, T2 b) {
return (a>b ? a : b);
}
int main() {
cout<<Maximum(5,4); // Maximum(int, int)
cout<<Maximum(5.6,4); // Maximum(double, int)
cout<<Maximum('A',66L); // Maximum(char, long)
cout<<Maximum<float, double>(5.6,4);
// Maximum(float, double)
cout<<Maximum<int, char>('A',66L);
// Maximum(int, char)
}
II.2.3.2. Function template instantiation
When a C++ compiler first encounters a function template call, it creates an instance of the function with the given type(s). Each function instance is a specialised version of the function template with the given types. In the compiled program code, exactly one function instance belongs to each used type. The calls above were examples of the so-called implicit instantiation.
A function template can be instantiated in an explicit way as well if concrete types are provided in the template line containing the header of the function:
template inline int Absolute<int>(int); template inline float Absolute(float); template inline double Maximum(double, long); template inline char Maximum<char, float>(char, float);
It should be noted that only one explicit instantiation can figure in the source code for (a) given type(s).
Since a C++ compiler processes function templates at compilation time, templates have to be available in the form of a source code in order that function variants could be created. It is recommended to place function templates in a header file to make sure that the header file can only be included once in C++ modules.
II.2.3.3. Function template specialization
There are cases when it is not precisely the algorithm defined in the generic function template that has to be used for some types or type groups. In this case, the function template itself has to be overloaded (specialized) – explicit specialization.
The function template Swap() of the following example code exchanges the values of the passed arguments. In the case of pointers, the specialised version does not exchange pointers but the referenced values. The second specialised version can be used to swap strictly C-styled strings.
#include <iostream>
#include <cstring>
using namespace std;
// The basic template
template< typename T > void Swap(T& a, T& b) {
T c(a);
a = b;
b = c;
}
// Template specialised for pointers
template<typename T> void Swap(T* a, T* b) {
T c(*a);
*a = *b;
*b = c;
}
// Template specialised for C strings
template<> void Swap(char *a, char *b) {
char buffer[123];
strcpy(buffer, a);
strcpy(a, b);
strcpy(b, buffer);
}
int main() {
int a=12, b=23;
Swap(a, b);
cout << a << "," << b << endl; // 23,12
Swap(&a, &b);
cout << a << "," << b << endl; // 12,23
char *px = new char[32]; strcpy(px, "First");
char *py = new char[32]; strcpy(py, "Second");
Swap(px, py);
cout << px << ", " << py << endl; // Second, First
delete px;
delete py;
}
From among the different specialised versions, compilers first choose always the most specialised (concrete) template to compile the function call.
II.2.3.4. Some further function template examples
In order to sum up function templates, let's see some more complex examples. Let's start with making a generic version of the function VectorSum() of Section II.2.2. The function template can determine the sum of the elements of any one-dimensional numeric array:
#include <iostream>
using namespace std;
template<class TYPE>
TYPE VectorSum(TYPE a[], int n) {
TYPE sum = 0;
for (int i=0; i<n; i++)
sum += a[i];
return sum;
}
int main() {
int ai[]={1,1,2,3,5,8,13};
const int ni=sizeof(ai) / sizeof(ai[0]);
cout << "\nThe sum of the elements of the int array: "
<<VectorSum(ai,ni);
double ad[]={1.2,2.3,3.4,4.5,5.6};
const int nd=sizeof(ad) / sizeof(ad[0]);
cout << "\nThe sum of the elements of the double array: "
<<VectorSum(ad,nd);
float af[]={3, 2, 4, 5};
const int nf=sizeof(af) / sizeof(af[0]);
cout << "\nThe sum of the elements of the float array: "
<<VectorSum(af,nf);
long al[]={1223, 19800729, 2004102};
const int nl=sizeof(al) / sizeof(al[0]);
cout << "\nThe sum of the elements of the long array: "
<<VectorSum(al,nl);
}
The function template Sort() sorts the elements of any one-dimensional array of type Typ and of size Size in an ascending order. The function moves the elements within the array and the result is stored in the same array as well. Since this declaration contains an integer parameter (Size) besides the type parameter (Typ), the function has to be called in the extended version:
Sort<int, size>(array);
The example code also calls the Swap() template from the the template Sort():
#include <iostream>
using namespace std;
template< typename T > void Swap(T& a, T& b) {
T c(a);
a = b;
b = c;
}
template<class Typ, int Size> void Sort(Typ vector[]) {
int j;
for(int i = 1; i < Size; i++){
j = i;
while(0 < j && vector[j] < vector[j-1]){
Swap<Typ>(vector[j], vector[j-1]);
j--;
}
}
}
int main() {
const int size = 6;
int array[size] = {12, 29, 23, 2, 10, 7};
Sort<int, size>(array);
for (int i = 0; i < size; i++)
cout << array[i] << " ";
cout << endl;
}
Our last example also prints out the different variants of the function Function() used by the compiler when these functions are called. From the specialised variants, it is the generic template that is activated which prints out the elements of the complete function call with the help of the template PrintOut(). The name of the types is returned by the member name () of the object returned by the typeid operator. The function template Character() is used to print out characters enclosed in apostrophes. This little example code presents some ways function templates can be used.
#include <iostream>
#include <sstream>
#include <string>
#include <typeinfo>
#include <cctype>
using namespace std;
template <typename T> T Character(T a) {
return a;
}
string Character(char c) {
stringstream ss;
if (isprint((unsigned char)c))
ss << "'" << c << "'";
else
ss << (int)c;
return ss.str();
}
template <typename TA, typename TB>
void PrintOut(TA a, TB b){
cout << "Function<" << typeid(TA).name() << ","
<< typeid(TB).name();
cout << ">(" << Character(a) << ", " << Character(b)
<< ")\n";
}
template <typename TA, typename TB>
void Function(TA a = 0, TB b = 0){
PrintOut<TA, TB>(a,b);
}
template <typename TA>
void Function(TA a = 0, double b = 0) {
Function<TA, double>(a, b);
}
void Function(int a = 12, int b = 23) {
Function<int, int>(a, b);
}
int main() {
Function(1, 'c');
Function(1.5);
Function<int>();
Function<int, char>();
Function('A', 'X');
Function();
}
The results:
Function<int,char>(1, 'c')
Function<double,double>(1.5, 0)
Function<int,double>(0, 0)
Function<int,char>(0, 0)
Function<char,char>('A', 'X')
Function<int,int>(12, 23)
|
II.3. Namespaces and storage classes
In C++, it is easy to create an unstructured source code. In order that a bigger program code remains structured, we have to respect many rules that the syntax of C++ does not require; however, these rules have to be observed for usability purposes. Most of these rules to be applied are the direct consequence of modular programming.
In order to keep code visibility efficiently, we should divide a program in many parts which have independent functionality and which are therefore realized (implemented) in different source files or modules (.cpp). The relation between modules is ensured by interface (declaration) files (.h). In each module, the principle of data hiding should always be respected: this means that from the variables and functions defined in each module, we only share with the others those that are really necessary while hiding other definitions from the outside.
The aim of the second part of the present book is to present the C++ tools that aim at implementing well-structured modular programming. The most important element of that is constituted by the already presented functions; however, but other solutions are also needed:
-
Storage classes determine explicitly for every C++ variable its lifetime, accessibility and the place of memory where it is stored. They also determine the visibility of functions from other functions.
-
Namespaces ensure that the identifiers used in programs consisting of more modules be used securely.
II.3.1. Storage classes of variables
When a variable is created in a C++ code, its storage class can also be defined besides its type. A storage class
-
defines the lifetime or storage duration of a variable, that is the time when it is created and deleted from memory,
-
determines the place from where the name of a variable can be accessed directly – visibility, scope – and also determines which name designates which variable – linkage.
As it is already known, variables can be used after they have been declared in their respective compilation unit (module). (We should not forget that a definition is also a declaration!) We mean by compilation units all C++ source files (.cpp) together with their integrated (included) header files.
A storage class (auto, register, static, extern) can be assigned to variables when they are defined. If it lacks from the definition, compilers assign them automatically a storage class on the basis of the place where the definition is placed.
The following example that converts an integer number into a hexadecimal string demonstrates the usage of storage classes:
#include <iostream> using namespace std; static int bufferpointer; // module level definition // n and first are block level definitions void IntToHex(register unsigned n, auto bool first = true) { extern char buffer[]; // program level declaration auto int digit; // block level definition // hex is block level definition static const char hex[] = "0123456789ABCDEF"; if (first) bufferpointer=0; if ((digit = n / 16) != 0) IntToHex(digit, false); // recursive call buffer[bufferpointer++] = hex[n % 16]; } extern char buffer[]; // program level declaration int main() { auto unsigned n; // block level definition for (n=0; n<123456; n+=9876) { IntToHex(n); buffer[bufferpointer]=0; // closing the string cout << buffer << endl; } } extern char buffer [123] = {0}; // program level definition
In blocks, the default storage class is auto and, as it can be seen in the example, we stroke that word through because we practically never use that modifier. The storage class of variables defined outside function blocks are external by default; however, the keyword extern only has to be provided when we declare (not define!) external variables.
II.3.1.1. Accessibility (scope) and linkage of variables
The notion of storage class is strongly related to that of variable accessibility and scope. Every identifier is visible only within its scope. There are three basic scope types: block level (local), file level and program level (global) scope (Figure II.7).
The accessibility of variables is determined by default by the place where they are defined in the source code. We can only create block level and program level variables in that way. However, we can also assign variables a storage class directly.
The notion of scope is similar to that of linkage but it is not completely equal to that. The same identifiers can be used to designate different variables in different scopes. However, the identifiers declared in different scopes or the identifiers declared more than once in the same scope can reference the same variable because of linkage. In C++, there are three types of linkage: internal, external and no linkage.
In a C++ source code, variables can have one of the following scopes:
|
block level |
A variable of this type is only visible in the block (function block) where it has been defined so its accessibility is local, that is its accessibility is determined by the place where it is defined. When program control reaches the block closing curly bracket, a block level identifier is not going to be accessible any more. If a variable is defined on a block level without the storage classes extern and static, it does not have any linkage. |
|
file level |
A file level variable is only visible in the module containing its declaration. These variables can only be referenced from the functions of the module but not from other modules. Identifiers having file level scope are those that are declared outside the functions of the module and that are declared with internal linkage using the static storage class. (It should be noted that the C++ standard declared deprecated the usage of the keyword static for that purpose, and it recommends using anonymous namespaces for selecting internal linkage variables). |
|
program level |
A program level variable is accessible from the functions of all the modules (all compilation units) of a program. Global variables that are declared outside the functions of a module (that is with external linkage) have program level scope. For that purpose, global variables should be declared without a storage class or with the extern storage class. |
File and program level scopes can be divided furthermore by namespaces presented later which introduce the notion of qualified identifiers.
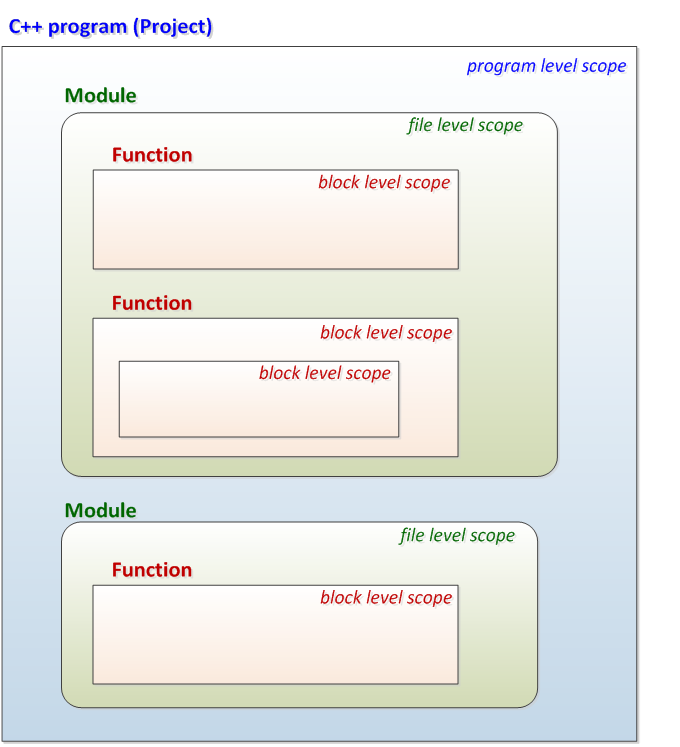
II.3.1.2. Lifetime of variables
A lifetime is a period of program execution where the given variable exists. On the basis of lifetime, identifiers can be divided into three groups: names of static, automatic and dynamic lifetime.
|
static lifetime |
Identifiers having a static or extern storage class have a static lifetime. The memory space allocated for static variables (and the data contained within it) remains until the end of program execution. A variable of this type is initialised once: when the program is launched. |
|
automatic lifetime |
Within blocks, variables defined without the static storage class and the parameters of functions have automatic (local) lifetime. The memory space of automatic lifetime variables (and the data contained within it) exist only in the block where they are defined. Variables with local lifetime are created on a new segment of memory each time their block is entered, and they are deleted when the block is exited (their content becomes lost). If a variable of this type is assigned an initial value, this initialization takes place every time the variable is created. |
|
dynamic lifetime |
Independently of their storage classes, memory blocks that are allocated by the operator new and deallocated by the operator delete have dynamic lifetime. |
II.3.1.3. Storage classes of block level variables
Variables that are defined within a function/program block or in the parameter list of functions are automatic (auto) by default. The keyword auto is not used in general. In addition, in the latest C++11 standard, this keyword has a new interpretation. Block level variables are often called local variables.
II.3.1.3.1. Automatic variables
Automatic variables are created when control is passed to their block and they are deleted when that block is exited.
As we have already said in previous chapters, compound statements (blocks) can be nested into each other. Each block can contain definitions (declarations) and statements in any order:
{
definitions, declarations and
statements
}
An automatic variable becomes temporarily inaccessible if another variable with the same name is defined in an inner block. So it is hidden until the end of that inner block and there is not any possibility to access the hidden (existing) variable:
int main()
{
double limit = 123.729;
// the value of the double type variable limit is 123.729
{
long limit = 41002L;
// the value of the long type variable limit is 41002L
}
// the value of the double type variable limit is 123.729
}
Since automatic variables cease to exist when the function containing them is exited, it is forbidden to create a function that returns the address or reference to a local variable. If we want to allocate space within a function for a variable that is used outside the function, then we should allocate that memory space dynamically.
In C++, loop variables defined in the header of a for loop are also automatic:
for (int i=12; i<23; i+=2) cout << i << endl; ↯ cout << i << endl; // compilation error: i is not defined
The initialization of automatic variables always takes place if control is passed to their block. However, it is only the variables defined with an initial value that receive an initial value. (The value of the other variables is undefined!).
II.3.1.3.2. The register storage class
The register storage class can only be used for automatic local variables and function parameters. If we provide the keyword register for a variable, we ask the compiler to create that variable in the register of the processor, if possible. In that way, the compiled code may be executed faster. If there is no free register for that purpose, the variable is created as an automatic variable. However, register variables are created in memory if the address operator (&) is used with them.
It should be noted that C++ compilers are able to optimize the compiled code, which results in general in a more efficient program code than if the keyword register was used. So it is not surely more efficient to use register storage classes.
The following Swap() function can be executed much faster than its previously presented version. (We use the word "can" because it is not known in advance how much register storage class specification takes into consideration the compiler.)
void Swap(register int &a, register int &b) {
register int c = a;
a = b;
b = c;
}
The function StrToLong() of the following example converts a decimal number stored in a string into a value of type long:
long StrToLong(const string& str)
{
register int index = 0;
register long sign = 1, num = 0;
// leaving out leading blanks
for(index=0; index < str.size()
&& isspace(str[index]); ++index);
// sign?
if( index < str.size()) {
if( str[index] == '+' ) { sign = 1; ++index; }
if( str[index] == '-' ) { sign = -1; ++index; }
}
// digits
for(; index < str.size() && isdigit(str[index]); ++index)
num = num * 10 + (str[index] - '0');
return sign * num;
}
The lifetime, visibility of register variables and the method of their initialization equal with those of variables having an automatic storage class.
II.3.1.3.3. Local variables with static lifetime
By using static storage classes instead of auto, we can create block level variables with static lifetime. The visibility of a variable like this is restricted to the block containing its definition; however, the variable exists from the time the program is launched until the program is exited. Since the initialization of static local variables takes place only once (when they are created), these variables keep their value even after the block is exited (between function calls).
The function Fibo() of the following example determines the next element of a Fibonacci sequence from the 3th element. Within the function, the static local variables a0 and a1 keep the value of the last two elements even after the block is exited.
#include <iostream>
using namespace std;
unsigned Fibo() {
static unsigned a0 = 0, a1 = 1;
unsigned a2 = a0 + a1;
a0 = a1;
a1 = a2;
return a2;
}
int main() {
for (register int i=2; i<10; i++)
cout << Fibo() << endl;
}
II.3.1.4. Storage classes of file level variables
Variables defined outside functions automatically have extern, i.e. program level scope. When software is developed from many modules (source files), it is not sufficient to use global variables in order that the principles of modular programming be observed. We might also need variables defined on module level: the access of these variables can be restricted to the source file (data hiding). This can be achieved by assigning extern variables a static storage class. If constants are defined outside functions, they have also internal linkage by default.
In the following program generating a Fibonacci sequence, the variables a0 and a1 were defined on a module level in order that their content remain accessible from another function (FiboInit()).
#include <iostream>
using namespace std;
const unsigned first = 0, second = 1;
static unsigned a0 = first, a1 = second;
void FiboInit() {
a0 = first;
a1 = second;
}
unsigned Fibo() {
unsigned register a2 = a0 + a1;
a0 = a1;
a1 = a2;
return a2;
}
int main() {
for (register int i=2; i<5; i++)
cout << Fibo() << endl;
FiboInit();
for (register int i=2; i<8; i++)
cout << Fibo() << endl;
}
The initialization of static variables takes place only once: when the program is launched. In case we do not provide an initial value for them in their definition, then the compiler initializes these variables automatically to 0 (by filling up its memory space with 0 bytes). In C++, static variables can be initialized by any expression.
C++ standards recommend using anonymous namespaces instead of static external variables (see later).
II.3.1.5. Storage classes of program level variables
Variables that are defined outside functions and to which a storage class is not assigned have an extern storage class by default. (Of course, the keyword extern can be used here, even if that is the default case.)
The lifetime of extern (global) variables begins with the launching and ends with the end of the program. However, there might be problems with visibility. A variable defined in a given module can only be accessed from another module, if the latter contains the declaration of that variable (for example by including its declaration file).
When using program level global variables, we have to pay attention whether we define or declare them. If a variable is used without a storage class specification outside functions, this means defining this variable (independently of the fact that it is provided an explicit initial value or not). On the contrary, assigning them extern explicitly can have two consequences: without initial value, they are declared , with initial value, they are defined . The following examples demonstrate what we have said so far:
|
Same definitions (only one of them can be used) |
Declarations |
|---|---|
|
double sum; double sum = 0; extern double sum = 0; |
extern double sum;
|
|
int vector[12]; extern int vector[12] = {0}; |
extern int vector[]; extern int vector[12]; |
|
extern const int size = 7; |
extern const int size; |
It should be kept in mind that global variables can be declared anywhere in a program but the effects of these declarations start from the place of the declaration until the end of the given scope (block or module). It is a frequent solution to store declarations in header files for each module and to include them at the beginning of every source file.
The initialization of global variables takes place only once when the program starts. In case we do not provide any initial value to them, then the compiler initializes these variables automatically to 0. In C++, global variables can be initialised by any expression.
It should be kept in mind that global variables should only be used with caution and only if they are really needed. Even in the case of a bigger program, only some central extern variables are allowed.
II.3.2. Storage classes of functions
Functions can only have two storage classes. Functions cannot be defined in a block; therefore a function cannot be created within another function!
The storage class of a function determines its accessibility. Therefore functions without a storage class or those defined with the extern storage class have program level scope. On the contrary, functions having a static storage class have file level scope.
We mean by the definition of a function the function itself, whereas a declaration of a function means its prototype. The following table summarizes the definitions and declarations of the function calculating the geometric mean of two numbers, in the case of both storage class.
|
Definitions (only one of them can be used) |
Prototypes |
|---|---|
double GeomMean(double a, double b)
{
return sqrt(a*b);
}
extern double GeomMean(double a, double b)
{
return sqrt(a*b);
}
|
double GeomMean(double, double); extern double GeomMean(double, double); |
static double GeomMean(double a, double b)
{
return sqrt(a*b);
}
|
static double GeomMean(double, double); |
Prototypes can be placed anywhere in a program code but their effects start from the place of declaration and ends at the end of the given scope (block or module). It is common to store prototypes for each module in separate header files that have to be included at the beginning of each concerned source file.
File and program level declarations and definitions are demonstrated by the following example code made up of two modules. The mathematical module provides the program with the mathematical constants, an "intelligent" Random() function and a function Sin() capable of calculating in degrees.
|
// |
// |
|
#include <iostream>
using namespace std;
extern int Random(int);
double Sin(double);
int main() {
for (int i=0; i<5; i++)
cout << Random(12)<< endl;
cout << Sin(45) << endl;
extern const double e;
cout << e << endl;
}
|
#include <ctime>
#include <cstdlib>
#include <cmath>
using namespace std;
extern const double pi = asin(1)*2;
extern const double e = exp(1);
static double Degree2Radian(double);
static bool firstrnd = true;
int Random(int n) {
if (firstrnd) {
srand((unsigned)time(0));
firstrnd = false;
}
return rand() % n;
}
double Sin(double degree) {
return sin(Degree2Radian(degree));
}
static double Degree2Radian(double degree) {
return degree/180*pi;
}
|
II.3.2.1. Accessing the compiled C functions from within C++ source
C++ compilers complete the name we have given for a function in the object code with the letters of the types from the parameter list of the function. This solution named C++ linkage makes possible the possibilities presented earlier in this chapter (overloading, function template).
When C++ was born, C language had already existed for nearly ten years. It was rightful to claim that the algorithms of compiled object modules and Library functions developed for C programs would also be accessible from C++ programs. (Programs in C source code could therefore be implemented in C++ with slight modifications.) C compilers place function names without any modification in the object code (C linkage), so they are not accessible by the C++ declarations presented above.
To handle this problem, C++ contains the type modifier extern "C". If a function sqrt() coded in C is intended to be used from C++ source code, it should be declared as
extern "C" double sqrt(double a);
This modifier makes C++ compilers to use the habitual C name generation for the function sqrt(). As a consequence, C functions cannot be redefined (overloaded)!
In case more C functions are needed to be accessed from a C++ code, these functions should be grouped under one extern "C" :
extern "C" {
double sin(double a);
double cos(double a);
}
If the descriptions of the functions of a C library are contained in a separated declaration file, it should be worth the following method:
extern "C" {
#include <rs232.h>
}
We should also use the extern "C" declaration if functions written and compiled in C++ are intended to be accessed from a C program code.
It is also worth mentioning here that the main () function also has extern "C" linkage.
II.3.3. Modular programs in C++
The structure of the example code of the preceding part becomes more structured if we create for the MatModule.cpp file a header file named MatModule.h that describes the interface of the module. Using constants becomes also simpler if they are placed in the file level scope (static). According to what has been said so far, the content of the MatModule.h header file:
// MatModule.h
#ifndef _MATMODULE_H_
#define _MATMODULE_H_
#include <cmath>
using namespace std;
// file level definitions/declarations
const double pi = asin(1)*2;
const double e = exp(1);
static double Degree2Radian(double);
// program level declarations
int Random(int n);
double Sin(double degree);
#endif
Lines with green and bold characters contain preprocessing statements that guarantee that the content of the MatModule.h header file would be included exactly once in the module containing the line
#include "MatModule.h"
(The Section II.4 provides readers with more information on the usage of preprocessors.)
Including the header file results in modifying the C++ modules:
|
// |
// |
|
#include <iostream>
using namespace std;
#include "MatModul.h"
int main() {
for (int i=0; i<5; i++)
cout << Random(12)<< endl;
cout << Sin(45) << endl;
cout << e << endl;
}
|
#include <ctime>
#include <cstdlib>
using namespace std;
#include "MatModul.h"
static bool firstrnd = true;
int Random(int n) {
if (firstrnd) {
srand((unsigned)time(0));
firstrnd = false;
}
return rand() % n;
}
double Sin(double degree) {
return sin(Degree2Radian(degree));
}
static double Degree2Radian(double degree) {
return degree/180*pi;
}
|
C++ compilers compile each module separately and create separate object modules for them because all the identifiers of each module have to be known in advance by compilers. This can be realized by placing declarations/prototypes and definitions adequately. After compilation, it is the task of the linker software to build one executable program from the object modules by resolving extern linkages from the object modules themselves or from standard libraries.
Integrated development environments automatize compilation and linking by creating projects. The only task of programmers is to add to the project the already existing C++ source files. In general, if we use the Build command from the menu, the whole compilation process takes place.
The
GNU C++
compiler can be activated for compilation and for linking with the following command line command. It also makes the compiler create the Project.exe executable file:
g++ -o Project MainModul.cpp MatModul.cpp
II.3.4. Namespaces
Names (identifiers) used in the program are stored by C++ compilers in different places (on the basis of how they are used) that are called namespaces. Within a given namespace, stored names have to be unique but there may be identical names in different namespaces. Two identical names that are situated in the same scope but not in the same namespace designate different identifiers. C++ compilers differentiate between the following namespaces:
II.3.4.1. The default namespaces of C++ and the scope operator
In C language, variables and functions defined on the file level (as well as Standard library functions) can be found in the same common namespace. C++ enclose Standard library elements in the namespace called std whereas the other elements defined on a file level are contained within the global namespace.
In order to be able to refer the elements of a namespace, we have to know how to use the scope operator (::). We will talk more about the scope operator later in that book, so now we only show examples for two of its possible usages.
With the help of :: operator, we can refer names having file and program level scope (that is identifiers of the global namespace) from any block of a program.
#include <iostream>
using namespace std;
long a = 12;
static int b = 23;
int main() {
double a = 3.14159265;
double b = 2.71828182;
{
long a = 7, b;
b = a * (::a + ::b);
// the value of b is 7*(12+23) = 245
::a = 7;
::b = 29;
}
}
We also use the scope operator to access directly names defined in the namespace std :
#include <iostream>
int main() {
std::cout<<"C++ language"<<std::endl;
std::cin.get();
}
II.3.4.2. Creating and using user-defined namespaces
Bigger C++ source codes are in general developed by numerous programmers. The functionalities of C++ presented so far are not enough to avoid collision or conflict of global (program level) names. Introducing namespaces having a user-defined name gives a good solution for these problems.
II.3.4.2.1. Creating namespaces
In source files, namespaces can be created either outside function blocks or in header files. In case a compiler find more namespaces with the same name, it unifies their contents, thus it extends the namespace defined earlier. To select a namespace, we have to use the keyword namespace:
namespace myOwnNamespace {
definitions and declarations
}
When planning program level namespaces, it is worth differentiating the namespaces containing definitions from those which can be placed in header files and which contain only declarations.
#include <iostream>
#include <string>
// declarations
namespace nsexample {
extern int value;
extern std::string name;
void ReadData(int & a, std::string & s);
void PrintData();
}
// definitions
namespace nsexample {
int value;
std::string name;
void PrintData() {
std::cout << name << " = " << value << std::endl;
}
}
void nsexample::ReadData(int & a, std::string & s) {
std::cout << "name: "; getline(std::cin, s);
std::cout << "value: "; std::cin >> a;
}
If a function declared in a namespace is created outside that namespace, the name of the function has to be qualified by the name of its namespace (in our example nsexample::).
II.3.4.2.2. Accessing the identifiers of a namespace
The identifiers provided in the namespace called nsexample can be accessed from every module to which the version of that namespace containing the declarations is included. Identifiers of a namespace can be accessed in many ways.
Directly by using the scope operator:
int main() {
nsexample::name = "Sum";
nsexample::value = 123;
nsexample::PrintData();
nsexample::ReadData(nsexample::value, nsexample::name);
nsexample::PrintData();
std::cin.get();
}
Or by using the directive using namespace :
It is of course more comfortable to make accessible all names for the whole program with the directive using namespace:
using namespace nsexample;
int main() {
name = "Sum";
value = 123;
PrintData();
ReadData(value, name);
PrintData();
std::cin.get();
}
Or by providing using -declarations:
With the help of using-declarations, we make available only the necessary elements from those of the namespace. This is the solution to choose if there is a name conflict between certain identifiers of a namespace.
int PrintData() {
std::cout << "Name conflict" << std::endl;
return 1;
}
int main() {
using nsexample::name;
using nsexample::value;
using nsexample::ReadData;
name = "Sum";
value = 123;
nsexample::PrintData();
ReadData(value, name);
PrintData();
std::cin.get();
}
II.3.4.2.3. Nested namespaces, namespace aliases
C++ makes it possible to create new namespaces within namespaces, that is to nest them in each other (nested namespaces). This procedure makes it possible to organize global names into a structured system. As an example, let's see the namespace called Project in which we define separate functions for every processor family!
namespace Project {
typedef unsigned char byte;
typedef unsigned short word;
namespace Intel {
word ToWord(byte lo, byte hi) {
return lo + (hi<<8);
}
}
namespace Motorola {
word ToWord(byte lo, byte hi) {
return hi + (lo<<8);
}
}
}
The elements of the namespace Project can be accessed in many ways:
using namespace Project::Intel;
int main() {
cout << hex;
cout << ToWord(0xab,0x12)<< endl; // 12ab
}
// -------------------------------------------------------
int main() {
using Project::Motorola::ToWord;
cout << hex;
cout << ToWord(0xab,0x12)<< endl; // ab12
}
// -------------------------------------------------------
using namespace Project;
int main() {
cout << hex;
cout << Intel::ToWord(0xab,0x12)<< endl; // 12ab
cout << Motorola::ToWord(0xab,0x12)<< endl; // ab12
}
// -------------------------------------------------------
int main() {
cout<<hex;
cout<<Project::Intel::ToWord(0xab,0x12)<< endl; // 12ab
cout<<Project::Motorola::ToWord(0xab,0x12)<<endl; // ab12
}
Accessing the elements of complex and multiple nested namespaces with long complex names (the elements of which are separated from each other by the namespace operator) makes program codes less legible. In order to solve this problem, C++ introduced the notion of namespace aliases:
namespace alias =externalNS::internalNS … ::most_internal_NS;
If we use aliases, the example above becomes much simpler:
int main() {
namespace ProcI = Project::Intel;
namespace ProcM = Project::Motorola;
cout << hex;
cout << ProcI::ToWord(0xab,0x12)<< endl; // 12ab
cout << ProcM::ToWord(0xab,0x12)<< endl; // ab12
}
II.3.4.2.4. Anonymous namespaces
C++ standards do not support the usage of the keyword static either in file level scopes or in namespaces. In module level scopes, we can create variables and functions in anonymous namespaces that are not accessible from outside of the compilation unit. However, the identifiers of anonymous namespaces can be used without restrictions within a module.
Within the same module, many anonymous namespaces can be created:
#include <iostream>
#include <string>
using namespace std;
namespace {
string password;
}
namespace {
bool ChangePassword() {
bool success = false;
string old, new1, new2;
cout << "Previous password: "; getline(cin, old);
if (password == old) {
cout << "New Password: "; getline(cin, new1);
cout << "New Password: "; getline(cin, new2);
if (new1==new2) {
password = new1;
success = true;
}
}
return success;
} // ChangePassword()
}
int main() {
password = "qwerty";
if (ChangePassword())
cout << "Successful password change!" << endl;
else
cout << "Not a successful password change!" << endl;
}
II.4. Preprocessor directives of C++
All C and C++ compilers contain a so-called preprocessor, which do not know anything about C++ language. Its only task is to create a program module completely in C++ from the source files of a computer program by carrying out word-processing operations. Consequently, a C++ compiler does not compile the source code programmers write but it processes the text the preprocessor creates (see Figure II.8). It can clearly be deduced from that that finding program errors that result from the statements of the preprocessor is not an easy task.
In most C++ compilers, preprocessing and real compilation are not separated from each other, that is the output of the preprocessor is not stored in any text file. (It should not be forgotten that the g++ compiler of C++ carries out only preprocessing if it is used by the switch –E .)
Actually, a preprocessor is a text processing software that is line-oriented and that can be programmed in a macro language. The rules of C++ language do not applied to the preprocessor:
-
the directives of the preprocessor are based on stricter rules than C++ statements (a single line can only contain one directive and directives cannot extend across more than one line unless this extension is not marked at the end of the line),
-
all operations carried out by the preprocessor are proper text processing tasks (independently of the fact that they may contain C++ keywords, expressions or variables).
The directives of the preprocessor start with a hash sign (#) at the beginning of the line. The most frequent operations that they carry out are: text replacement ( #define ), including a text file ( #include ) or keeping certain parts of the code under certain conditions ( #if ).
C++ relies completely on the features of the preprocessor directives of C. Since preprocessing is out of the scope of compilers of the strictly typed C++ language, C++ attempts to reduce the need of using preprocessors to a minimal level by introducing new solutions. In a C++ code, some preprocessor directives can be replaced with C++ solutions: instead of using #define constants, one can use constants of type const; instead of using #define macros , one can write inline function templates.
II.4.1. Including files
When the preprocessor encounters an #include directive, the content of the file figuring in the directive is integrated (inserted) in the code in the place of the directive. Generally, it is header files containing declarations and preprocessor directives that are integrated in the beginning of the code; however, inclusion can be applied to any text file.
#include <header> #include "filepath"
The first form is used to include the standard header files of C++ from the folder named include of the development kit:
#include <iostream> #include <cmath> #include <cstdlib> #include <ctime> using namespace std;
The second form is used to include non-standard files from the folder storing the actual C++ module or from any other folder:
#include "Module.h" #include "..\Common.h"
The following table sums up the keywords and language elements that can be used in header files:
|
C++ elements |
Example |
|---|---|
|
Comments |
|
|
Conditional directives |
|
|
Macro definitions |
|
|
#include directives |
|
|
Enumerations |
|
|
Constant definitions |
|
|
Namespaces having an identifier |
|
|
Name declarations |
|
|
Type definitions |
|
|
Variable declarations |
|
|
Function prototypes |
|
|
inline function definitions |
|
|
template declarations |
|
|
template definitions |
|
The following elements should never be placed in include files:
-
definitions of non-inline functions,
-
variable definitions,
-
definitions of anonymous namespaces.
One part of the elements that can be placed in a header file have to be included only once in a code. That is why, all header files have to have a special preprocessing structure based on conditional directives:
// Module.h
#ifndef _MODULE_H_
#define _MODULE_H_
the content of the header file
#endif
II.4.2. Conditional compilation
By using conditional directives, one can achieve that certain parts of a source code would be inserted into the C++ program created by the preprocessor only if given conditions are fulfilled. The code parts to be compiled under conditions can be selected in many ways, by using the following preprocessor directives: #if, #ifdef, #ifndef, #elif, #else and #endif.
In an #if statement, the condition can be expressed by a constant expression. If the value of the latter is zero, it means false; if the latter has a value other than 0, that means true. In an expression, only the following elements are allowed: integer and character constants, operations of type defined.
#if 'O' + 29 == VALUE
In a condition, we can check whether a symbol is defined or not with the help of the operator named defined. This operator returns 1, if its operand exists. Otherwise it returns 0:
#if defined symbol #if defined(symbol)
Since checkings of this kind are often used, we can test whether a symbol exists or not with separate preprocessing statements:
#ifdef symbol #if defined(symbol) #ifndef symbol #if !defined(symbol)
More complex conditions can be checked by #if:
#if 'O' + 29 == VALUE && (!defined(NAME) || defined(NUMBER))
The following simple text makes the code part enclosed within the #if and #endif lines integrated in the compilation unit:
#if constant_expression
code part
#endif
This structure can well be used to integrate information into a source code in order that debugging become simpler. In that example, if the value of the symbol TEST is 1, this complementary information gets compiled in the code, and if it is 0, this information is not enabled:
#define TEST 1
int main() {
const int size = 5;
int array[size] = { 12, 23, 34, 45, 56 };
int i;
for (int i = 0; i < size; i++) {
array[i] *= 2;
#if TEST != 0
cout << "i = " << i << endl;
cout << "\tarray[i] = " << array[i] << endl;
#endif
}
}
Instead of the structure above, it is better to use a solution that examines the definition of the symbol TEST. For that purpose, TEST can be defined without a value, which can be assigned to it from a parameter of the compiler:
#define TEST
int main() {
const int size = 5;
int array[size] = { 12, 23, 34, 45, 56 };
int i;
for (int i = 0; i < size; i++) {
array[i] *= 2;
#if defined(TEST)
cout << "i = " << i << endl;
cout << "\tarray[i] = " << array[i] << endl;
#endif
}
}
Each pair of the following checkings return the same results:
#if defined(TEST) ... // defined #endif |
#ifdef TEST ... // defined #endif |
|
#if !defined(TEST) ... // not defined #endif |
#ifndef TEST ... // not defined #endif |
If the following structure is used, we can choose between two code parts:
#if constant_expression
codepart1
#else
codepart2
#endif
The following example creates the two-dimensional array named array depending on the value of the symbol SIZE:
#define SIZE 5
int main() {
#if SIZE <= 2
int array[2][2];
const int size = 2;
#else
int array[SIZE][SIZE];
const int size = SIZE;
#endif
}
For more complex structures, it is recommended to use multi-way branches.
#if constant_expression1
codepart1
#elif constant_expression2
codepart2
#else
codepart3
#endif
The following example integrates the declaration file on the basis of the manufacturer:
#define IBM 1
#define HP 2
#define DEVICE IBM
#if DEVICE == IBM
#define DEVICE_H "ibm.h"
#elif DEVICE == HP
#define DEVICE_H "hp.h"
#else
#define DEVICE_H "other.h"
#endif
#include DEVICE_H
II.4.3. Using macros
The most controversial domain about using preprocessors is the usage of #define macros in C++ programs. The reason for that is that the result of processing the macro may not always correspond to the expectations of programmers. Macros are widely used in codes written in C, but they have less importance in C++. The definition of the C++ programming language prefers const and inline function templates to macros. In the present section, we will always prefer a secure macro usage.
The #define directive is used to assign an identifier to C++ constants, keywords and frequently used statements and expressions. The symbols defined for preprocessors are called macros. In a C++ source code, it is recommended that macro names should be completely written in upper-case letters in order that they become visibly separated from C++ identifiers used in the code.
Preprocessors check the source code line by line whether it contains an already defined macro name. If yes, they replace it with the appropriate replacement text and then they check again the line for further macros, which may be followed by further replacements. This process is called macro replacement or macro substitution. Macros are created by a #define statement and deleted by the directive named #undef .
II.4.3.1. Symbolic constants
Symbolic constants can be created by using the simple form of the #define directive:
#define identifier #define identifier replacement_text
Let's see some examples how to define and use symbolic constants.
#define SIZE 4
#define DEBUG
#define AND &&
#define VERSION "v1.2.3"
#define BYTE unsigned char
#define EOS '\0'
int main() {
int v[SIZE];
BYTE m = SIZE;
if (m > 2 AND m < 5)
cout << "2 < m < 5" << endl;
#ifdef DEBUG
cout << VERSION << endl;
#endif
}
The source file after the preprocessing (replacements) is the following:
int main() {
int v[4];
unsigned char m = 4;
if (m > 2 && m < 5)
cout << "2 < m < 5" << endl;
cout << "v1.2.3" << endl;
}
In the previous example, some symbolic constants can be replaced by identifiers of types const and typedef in C++:
#define DEBUG
#define AND &&
const int size = 4;
const string version = "v1.2.3";
const char eos = '\0';
typedef unsigned char byte;
int main() {
int v[size];
byte m = size;
if (m > 2 AND m < 5)
cout << "2 < m < 5" << endl;
#ifdef DEBUG
cout << version << endl;
#endif
}
II.4.3.2. Parameterized macros
The macros can be efficiently used in much more cases if they are parameterized. The general form of a function-like parameterized macro:
#define identifier(parameter_list) replacement_text
Using (calling) a macro:
identifier(argument_list)
The number of the arguments in a macro call has to be identical with that of the parameters in the definition.
In order that parameterized macros work securely, the following two rules have to observed:
-
The parameters of a macro always have to be enclosed within parentheses in the body of the macro (in the replacement text).
-
Increment (++) and decrement (--) operators should not be used in the argument list when the macro is called.
The following example code demonstrates some frequently used macro definitions and the way they can be called:
// determining the absolute value of x
#define ABS(x) ( (x) < 0 ? (-(x)) : (x) )
// calculating the maximum value of a and b
#define MAX(a,b) ( (a) > (b) ? (a) : (b) )
// calculating the square of X
#define SQR(X) ( (X) * (X) )
// generating a random number within a given interval
#define RANDOM(min, max) \
((rand()%(int)(((max) + 1)-(min)))+ (min))
int main() {
int x = -5;
x = ABS(x);
cout << SQR(ABS(x));
int a = RANDOM(0,100);
cout << MAX(a, RANDOM(12,23));
}
The backslash (\) character at the end of the first line of the macro named RANDOM() indicates that the definition of that macro is continued in the next line. The content of the main () function cannot be qualified as legible at all after the preprocessing process:
int main() {
int x = -5;
x = ( (x) < 0 ? (-(x)) : (x) );
cout << ( (( (x) < 0 ? (-(x)) : (x) )) *
(( (x) < 0 ? (-(x)) : (x) )) );
int a = ((rand()%(int)(((100) + 1)-(0)))+ (0));
cout << ( (a) > (((rand()%(int)(((23) + 1)-(12)))+ (12)))
? (a) : (((rand()%(int)(((23) + 1)-(12)))+ (12))) );
}
All advantages of macros (type-independence, faster code) can be achieved by using inline functions/function templates (instead of macros) while keeping the C++ code legible:
template <class tip> inline tip Abs(tip x) {
return x < 0 ? -x : x;
}
template <class tip> inline tip Max(tip a, tip b) {
return a > b ? a : b;
}
template <class tip> inline tip Sqr(tip x) {
return x * x;
}
inline int Random(int min, int max) {
return rand() % (max + 1 - min) + min;
}
int main() {
int x = -5;
x = Abs(x);
cout << Sqr(Abs(x));
int a = Random(0,100);
cout << Max(a, Random(12,23));
}
II.4.3.3. Undefining a macro
A macro can be undefined anytime and can be redefined again, even with a different content. It can be undefined by using the #undef directive. Before redefining a macro with a new content, the old definition always has to be undefined. The #undef statement does not signal an error if the macro to be undefined does not exist:
#undef identifier
The following example code traces the functioning of #define and #undef statements:
|
Original source code |
Substituted code |
|---|---|
int main() {
#define MACRO(x) (x) + 7
int a = MACRO(12);
#undef MACRO
a = MACRO(12);
#define MACRO 123
a = MACRO
}
|
int main() {
int a = (12) + 7;
a = MACRO(12);
a = 123
}
|
II.4.3.4. Macro operators
In our previous examples, replacement was carried out by the preprocessor only in case of separate parameters. There are cases where a parameter is a part of an identifier or where the value of an argument is to be reused as a string. If replacement has to be done in these cases as well, then the macro operators ## and # have to be used.
If the # character is placed before the parameter in a macro, the value of the parameter is replaced as enclosed within quotation marks (i.e. as a string). With this method, replacement can be carried out on strings as well, since the compiler will concatenate the string literals standing one after another into one string constant. The following code prints out the name and value of any variable by using the macro named INFO():
#include <iostream>
using namespace std;
#define INFO(variable) \
cout << #variable " = " << variable <<endl;
int main() {
unsigned x = 23;
double pi = 3.14259265;
string s = "C++ language";
INFO(x);
INFO(s);
INFO(pi);
}
x = 23 s = C++ language pi = 3.14259 |
By using the ## operator, two syntactic units (tokens) can be concatenated. To achieve this, the ## operator has to be inserted between the parameters in the body of a macro.
In the following example, the macro named PERSON() populates the array named people with values of structure type:
#include <string>
using namespace std;
struct person {
string name;
string info;
};
string Ivan_Info ="K. Ivan, Budapest, 9";
string Alice_Info ="O. Alice, Budapest, 33";
#define PERSON(NAME) { #NAME, NAME ## _Info }
int main(){
person people[] = {
PERSON (Ivan),
PERSON (Alice)
};
}
The content of the main () function after preprocessing:
int main(){
person people[] = {
{ "Ivan", Ivan_Info },
{ "Alice", Alice_Info }
};
}
There are cases when one macro is not sufficient for a given purpose. In the following example, the version number is created by concatenating the given symbolic constants:
#define MAJOR 7 #define MINOR 29 #define VERSION(major, minor) VERSION_MINOR(major, minor) #define VERSION_MINOR(major, minor) #major "." #minor static char VERSION1[] = VERSION(MAJOR,MINOR); // "7.29" static char VERSION2[] = VERSION_MINOR(MAJOR,MINOR); //"MAJOR.MINOR"
II.4.3.5. Predefined macros
ANSI C++ standard contains the following predefined macros. (Almost all identifiers start and end with a double underscore character.) The name of predefined macros cannot be used in #define and #undef statements. The value of predefined macros can be integrated into the text of a code but can also be used as a condition in conditional directives.
|
Macro |
Description |
Example |
|---|---|---|
|
|
String constant containing the date of the compilation. |
|
|
|
String constant containing the time of the compilation. |
|
|
|
The date and time of the last modification of the source file in a string constant" |
|
|
|
String constant containing the name of the source file. |
|
|
|
A numeric constant, containing the number of the actual line of the source file (numbering starts from 1). |
|
|
|
Its value is 1 if the compiler works as an ANSI C++, otherwise it is not defined. |
|
|
|
Its value is 1, if its value is tested in a C++ source file, otherwise it is not defined. |
II.4.3.6. #line, #error and #pragma directives
There are a lot of utility software that transforms a code written in a special programming language to a C++ source file (program generators).
The #line directive forces C++ compilers not to signal the error code in the C++ source text but in the original source file written in another special language. (The code and file name set by a #line statement are also present in the value of the symbols __LINE__ and __FILE__ .)
#line beginning_number #line beginning_number "filename"
If it is inserted in a code, an #error directive can be used to print out a compilation error message which contains the text provided in the statement:
#error error_message
In the following example, compilation ends with an error message if we do not use the C++ mode:
#if !defined(__cplusplus)
#error Compilation can only be carried out in C++ mode!
#endif
#pragma directives are used to control the compilation process in an implementation-dependent way. (There are not any standard solution for this directive.)
#pragma instruction
If the compiler encounters an unknown #pragma instruction, it does not consider that. Therefore the portability of computer programs is not endangered by this directive. For example, the alignment of structure members to different boundaries and disabling the printing out of warning compilation messages having a specific index can be done in the following way:
#pragma pack(8) // aligned to 8 byte boundary #pragma pack(push, 1) // aligned to 1 byte boundary #pragma pack(pop) // aligned again to 8 byte boundary #pragma warning( disable : 2312 79 )
The empty directive (#) can also be used, but it does not affect preprocessing:
#