Chapter IV. Programming Microsoft Windows in C++
- IV.1. Specialties of CLI, standard C++ and C++/CLI
-
- IV.1.1. Compiling and running native code under Windows
- IV.1.2. Problems during developing and using programs in native code
- IV.1.3. Platform independence
- IV.1.4. Running MSIL code
- IV.1.5. Integrated development environment
- IV.1.6. Controllers, visual programming
- IV.1.7. The .NET framework
- IV.1.8. C#
- IV.1.9. Extension of C++ to CLI
- IV.1.10. Extended data types of C++/CLI
- IV.1.11. The predefined reference class: String
- IV.1.12. The System::Convert static class
- IV.1.13. The reference class of the array implemented with the CLI array template
- IV.1.14. C++/CLI: Practical realization in e.g. in the Visual Studio 2008
- IV.1.15. The Intellisense embedded help
- IV.1.16. Setting the type of a CLR program.
- IV.2. The window model and the basic controls
-
- IV.2.1. The Form basic controller
- IV.2.2. Often used properties of the Form control
- IV.2.3. Events of the Form control
- IV.2.4. Updating the status of controls
- IV.2.5. Basic controls: Label control
- IV.2.6. Basic controls: TextBox control
- IV.2.7. Basic controls: Button control
- IV.2.8. Controls used for logical values: CheckBox
- IV.2.9. Controls used for logical values: RadioButton
- IV.2.10. Container object control: GroupBox
- IV.2.11. Controls inputting discrete values: HscrollBar and VscrollBar
- IV.2.12. Control inputting integer numbers: NumericUpDown
- IV.2.13. Controls with the ability to choose from several objects: ListBox and ComboBox
- IV.2.14. Control showing the status of progressing: ProgressBar
- IV.2.15. Control with the ability to visualize PixelGrapic images: PictureBox
- IV.2.16. Menu bar at the top of our window: MenuStrip control
- IV.2.17. The ContextMenuStrip control which is invisible in basic mode
- IV.2.18. The menu bar of the toolkit: the control ToolStrip
- IV.2.19. The status bar appearing at the bottom of the window, the StatusStrip control
- IV.2.20. Dialog windows helping file usage: OpenFileDialog, SaveFileDialog and FolderBrowserDialog
- IV.2.21. The predefined message window: MessageBox
- IV.2.22. Control used for timing: Timer
- IV.2.23. SerialPort
- IV.3. Text and binary files, data streams
-
- IV.3.1. Preparing to handling files
- IV.3.2. Methods of the File static class
- IV.3.3. The FileStream reference class
- IV.3.4. The BinaryReader reference class
- IV.3.5. The BinaryWriter reference class
- IV.3.6. Processing text files: the StreamReader and StreamWriter reference classes
- IV.3.7. The MemoryStream reference class
- IV.4. The GDI+
-
- IV.4.1. The usage of GDI+
- IV.4.2. Drawing features of GDI
- IV.4.3. The Graphics class
- IV.4.4. Coordinate systems
- IV.4.5. Coordinate transformation
- IV.4.6. Color handling of GDI+ (Color)
- IV.4.7. Geometric data (Point, Size, Rectangle, GraphicsPath)
- IV.4.8. Regions
- IV.4.9. Image handling (Image, Bitmap, MetaFile, Icon)
- IV.4.10. Brushes
- IV.4.11. Pens
- IV.4.12. Font, FontFamily
- IV.4.13. Drawing routines
- IV.4.14. Printing
- References:
In this chapter we will present how to use the C++ for developing Windows-specific applications.
IV.1. Specialties of CLI, standard C++ and C++/CLI
There are several ways to develop applications for a computer running the Windows operating system:
-
We implement the application with the help of a development kit and it will operate within this run-time environment. The file cannot be run directly by the operating system (e.g. MatLab, LabView) because it contains commands for the run-time environment and not for the CPU of the computer. Sometimes there is a pure run-time environment also available beside the development kit for the use of the application developed, or an executable (exe) file is created from our program, which includes the run-time needed for running the program.
-
The development kit prepares a stand-alone executable application file (exe), which contains the commands written in machine code runnable on the given operating system and processor (native code). This file is run while developing and testing the program. Such tools are e.g. Borland Delphi and Microsoft Visual Studio, frequently used in industry.
Both ways of development are characterized by the fact that if the application has a graphical user interface the applied elements are created by a graphical editor, and the state of the element during operation is visible during the development as well. This principle is called RAD (rapid application development). Developing in C++ belongs to the second group while both ways of development are present in C++/CLI.
IV.1.1. Compiling and running native code under Windows
When we create a so-called console application under Windows, Visual Studio applies a syntax that corresponds to standard C++. In this way, programs and parts of programs made for Unix, Mac or other systems can be compiled (e.g. WinSock from the sockets toolkit or the database manager MySql). The process of compliation is the following:
-
C++ sources are stored in files with the extension
.cpp, headers in files with the extension.h. There can be more than one of them, if the program parts that logically belong together are placed separately in files, or the program has been developed by more than one person. -
Preprocessor: resolving #define macros, inserting #include files into the source.
-
Preprocessed C source: it contains all the necessary function definitions.
-
C compiler: it creates an
.OBJobject file from the preprocessed sources. -
OBJ files: they contain machine code parts (making their names public – export) and external references to parts in other files.
-
Linker: after having resolved references in OBJ files and files with the extension
.LIBthat contain precompiled functions (e.g. printf()), having cleaned the unnecessary functions and having specified the entry point (function main()), the runnable file with the extension.EXEis created, which contains the statements in machine code runnable on the given processor.
IV.1.2. Problems during developing and using programs in native code
As we saw in the pervious chapters, in programs in native code, the programmer can use dynamic memory allocation for the data/objects if necessary. These variables have only an address; we cannot refer to them with names only with pointers, loading their addresses into the pointer. For instance, the output of the function malloc() and the operator new is such a memory allocation, which allocates a contiguous space and returns its address, which we put into a pointer with a value assignment operator. After this, we can use the variable (through the pointer) and the space can be deallocated. The pointer is an effective but dangerous tool: its value can be changed by pointer arithmetics so that it does not point to the memory space allocated by us but farther. A typical example of this occurs for beginners in the case of arrays: they create an array of 5 elements (there is 5 in the definition), and they refer to the element with the index 5, which is most probably in the memory space of their program but not in the array (indexes of the elements can be understood from 0 to 4). Using an assignment statement, the given value is added to the memory next to the array in an almost blind way, changing the other variable located there “by chance”. This kind of error may be hidden from us since the change of the value of the the other variable is not recognized but “the program sometimes returns strange results”. The error is easier to recognize if the pointer does not point to our own memory space but to e.g. that of the operating system. In this case we get an error message and the operating system rejects our program from the memory.
If we pay much attention to our pointers, change by accident can be avoided. However, we cannot avoid fragmentation of the memory. When memory blocks are not deallocated exactly in the reverse order compared to allocation, “holes” are created in the memory – a free block between two occupied blocks. In the case of a multitask operating system other programs also use the memory, so holes are created even if the memory is deallocated exactly in the reverse order. Allocation must be always contiguous so if the user needs more space than the free block, it can not be allocated, and the small-sized memory block will remain unused. In other words, the memory will be “fragmented”. This is the same phenomenon as the fragmentation of storages after deletion and overwriting of files.
For the storage there is a tool program which puts the files onto a contiguous area, but this takes long time, and there is no defragmenter for the memory of native code programs. It is because the operating system cannot know which pointer contains the address of which memory block and if the block is moved, it should load the new address of the block into the pointer.
Thus, there are two needs for the memory: the first is to avoid the random change of variables or the programs stopped by the operating system (everyone has seen already the blue screen) with the help of managing the variables of the program, moreover, cleaning and garbage collection. The figure below from MSDN illustrates how garbage collection works, before cleaning (Figure IV.1) and after cleaning (GC::Collect()) (Figure IV.2)
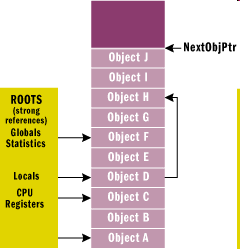
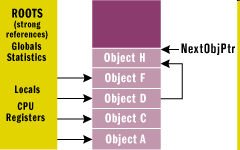
.
It can be seen that memory areas (objects) which were not referred to have disappeared, and the references now point to the new addresses and the pointer that identifies the location of the free area has moved to a lower address (that is, the free contiguous memory has grown).
IV.1.3. Platform independence
Some computers have already left their initial metal box, now we take them with us everywhere in our pockets or we wear them as clothing or accessories. In the case of such computers (which are not called computer anymore: telephone, e-book reader, tablet, media player, glasses, car), manufacturers aim at minimizing consumption besides the relatively smaller computational capacity, since the power of some 100 W necessary for their functioning is not available. The processors made by Intel (and their secondary manufacturers) rather focused on computational capacity and thus mobile devices with batteries are assigned with CPUs made by other manufacturers (ARM, MIPS, etc.). The task of program developers has become more complex: for each CPU (and platform) the application should (have been) developed. It seemed appropriate to create one run-time environment for each platform and then to create applications only once and to compile them to some intermediate code in order to protect intellectual products. This was correctly realized by Sun Microsystems when they created from the languages C and C++ the Java language, which has a simple object model and has no pointers. From Java the application is compiled to bytecode, which is run on a virtual machine (Java VM) or it is translated into native code and is runnable. Nowadays many well-known platforms use the language which has now become the property of Oracle: such an example is the Android operating system supported by Google. Obviously where there is a trademark, there is suing as weel: Oracle did not agree to use the name Java because “its intellectual rights were consciously violated”. The same happened to Microsoft in the case of Java integrated to Windows: current Windows editions do not contain Java support, JRE (the run-time environment) or JDK (the development kit) must be downloaded from the website of Oracle. In the PC world, there is an intermediate stage even without this: the 32 bit operating system cannot handle 4 GB memory. AMD developed the 64 bit instruction set extension, which was later integrated by Intel too. Since XP, Windows can be bought with two types of memory handling: 32 bit for earlier PCs with less than 4 GB memory and 64 bit for PCs with newer CPU and at least 4 GB memory. The 64 bit version runs the earlier, 32 bit applications with the help of emulation (WoW64 – Windows on Windows). When a program is complied with Visual Studio 2005 or a newer (2008, 2010, 2013) version under a 64 bit operating system, we can choose mode x64, then we get a 64 bit application. Thus, there was a need for the ability of running a program on both configurations (x86, x64) and all Windows operating system versions (XP,Vista, 7,8) even if it is not known at the moment of compiling which environment we will have later but we do not want to make more exe files. This requirement can only be fulfilled with the insertion of an intermediate running/compiling level. For bigger programs, it might be necessary that more people be involved in the development, probably with different programming languages. Given the intermediate level, it is also possible: each language compiler (C++, C#, Basic, F# etc.) compiles to this intermediate language, then the application is compiled from this to a runnable one. The intermediate language is called MSIL, which is a stack-oriented language similar to machine code. The first two letters of MSIL refers to the name of the manufacturer and later it was changed to CIL (Common Intermediate Language), which can be seen as the solution of Microsoft for the basic idea of Java.
IV.1.4. Running MSIL code
The CIL code presented in the previous paragraph is transformed into a file with .EXE extension, where it is runable. But this code is not the native code of the processor, so the operating system must recognize that one more step is necessary. This step can be done in two ways, according to the principles used in Java system:
-
interpreting and running the statements one by one. This method is called JIT (Just In Time) execution. Its use is recommended for the step by step running of the source code and for debug including break points.
-
generating native code from all statements at the same time and starting it. This method is called AOT (Ahead of Time), and it can be created by the Native Image Generator (NGEN). We use it in the case of well functioning, tested, ready programs (release).
IV.1.5. Integrated development environment
We have not mentioned yet the applied program tools in the development process of the native code that was discussed in the previous paragraph. Initially all the steps were performed by one or more (command line) programs: the developer created/extended/fixed the .C and .H source files with an optional text editor, then the preprocessor, the C compiler and the linker came. When the developer ran the application in debug mode then it meant a new program (the debugger). In case the program contained more source files then only the amended ones had to be recompiled. This was the purpose of the make utility program. When searching among the sources (e.g. searching for in which .H file can a function definition be found) then we could use the grep utility program. Batch files were created for the compiling and those files parametrized the compiler accordingly. In case of a compiling error, the number of the erroneous line was listed on the console then we reloaded the editor, navigated to the erroneous line, we fixed the error and then we restarted the compiler. Once the compiling was completed and the program was started then sometimes it gave erroneous results. In this case we ran it with the debugger then after having the erroneous part found we used the text editor again. This procedure was not effective because of the several needs for restarting the program and the manual information input (line number). On the other hand products with text editor, compiler and runner were developed already in the 70s, 80s, before the PC era. This principal tool was called the integrated development environment (IDE). This IDE type environment was also the Turbo Pascal developed by Borland Inc. that already included a text editor, a compiler and a runner in one program on an 8 bit computer (debugger was not included yet). The program was developed by a certain Anders Hejlsberg who later worked for Microsoft on the development of programming languages. Such languages are J++ and C#. IDE tool for a character screen was created at Microsoft as well: BASIC in DOS was replaced by Quick Basic that already contained an editor and a debugger.
IV.1.6. Controllers, visual programming
Applications that run on operating systems with a graphical user interface (GUI) consist of two parts at least: the code part that contains the algorithm of the program and the interface that implements the user interface (UI). The two parts are logically linked: events (event) happening in the user interface trigger the run of the defined subprograms of the algorithm part (these subprograms are called functions in C type languages). Hence these functions are called “event handler functions” and in the development kit of the operating system (SDK) we can find definitions (in the header files) that are necessary to write them. Initially, programs with a user interface contained also the program parts necessary for the UI: a C language program with 50-100 lines was capable of displaying an empty window in Windows and to manage the “window closing” event (that is, the window could be closed). This time the main part of the development consisted of developing the UI, programming the algorithm could come only after it. In the UI program all coordinates were placed as numbers and after modifying those we could check how the interface looked like. The first similar product of Microsoft (and the recent development tool was named after this) was Visual basic. In the first version of it we could place predefined controls to our form with a GUI (that was basically the user interface of our program that we were developing). A text format code was created from the controls drawn by the user and once needed it could be modified with the embedded text editor then it was compiled before running was initiated. For running the program there was needed a library, consisting the runable parts of the controls. Characteristically because of this small size exe files were created but for the completed program that version of the run-time environment had to be installed in which the program was developed. Visual Basic was later followed by Visual C++ (VC++) and other similar programs, then – based on the example of Office – instead of separate products the development tools were integrated into one product; this was called Visual Studio.
IV.1.7. The .NET framework
The programs that implement the principles discussed till this point were collected by Microsoft into one common software package that could be installed from one file only and they called it .net. During its development several versions of it were published, now at the time when this book is being written version 4.0 is the stable one and 4.5 is the pilot test version. In order to install it we need to know the type of Windows. Different versions have to be installed for each Windows, each CPU and different versions are needed for 32 and 64 bit (see the “Platform independency” chapter).
Parts of the framework:
-
Common Language Infrastructure (CLI), and its realization the Common Language Runtime (CLR): the common language compiler and run-time environment. MSIL contains a compiler, a debugger and a run-time. It is capable of collecting garbages in the memory (Garbage Collection, GC) and handling exceptions (Exception Handling).
-
Base Class Library: the library of the basic classes. GUIs can be programmed comfortably in OOP only with well prepared base classes. These cannot be instantiated directly (in most of the cases it is impossible since they are abstract classes). As an example it contains an interface class called “Object” (see later in Section IV.1.10).
-
WinForms: contols preprepared for the Windows applications, inherited from the Base Class Library. We put these to the form during development and the user interface of our program will be consisted of these. They are language independent contorls and we can use them from any applications according to the syntax of the given language. It is worth mentioning that our program will use not only those controls that were put on the form during development but the program can also create instances from these when running. That is, once putting those controls to the form a piece of the program code is created that runs when the program is initiated. This automatically created source code can be written by us (we can copy it) and it can be run at a later point as well.
-
Additional parts: these could be the ASP.NET system that supports application development on the web, the ADO.NET that allows access to databases and Task Parallel Library that supports multiprocessor systems. We do not discuss these here because of space restrictions.
IV.1.8. C#
The .NET framework and the pure managed code can be programmed with C# easily. The developer of the language is Anders Hejlsberg. He derived it from the C++ and Pascal languages, kept their advantages, made it simpler and made the usage of more difficult elements (e.g. pointers) optional. It is recommended to amateurs and students in higher education (not for programmers – their universal tools are the languages K&R C and C++). The .NET framework contains a command line C# compiler and we can also download freely the Visual C# Express Edition from Microsoft. Their goal with this is to spread C# (and .NET). Similarly, we can find free books for C# in Hungarian language on the internet.
IV.1.9. Extension of C++ to CLI
The C++ compiler developed by Microsoft can be considered as a standard C++ as long as it is used to compile a native win32 application. However, in order to reach CLI new data types and operations were needed. The statements necessary to handle the managed code (MC) appeared first in the 2002 version of Visual Studio.NET then these were simplified in version 2005. The defined language cannot be considered as C++ because the statements and data types of MC do not fit in C++ standard definition (ISO/IEC 14882:2003). The language was called C++/CLI and it was standardized (ECMA-372). Let us make a note here that usually the goal of standardization is to allow the 3rd party manufacturers to go to the market with the related product, however, in this case it did not happen: C++/CLI can be compiled only by Visual Studio.
IV.1.10. Extended data types of C++/CLI
Variables on the managed heap have to be declared differently than the variables of the native code. The allocation is not automatic because the compiler cannot make a decision instead of us: the native and the managed code can be mixed within one program (only C++/CLI is capable of doing so, the other compilers compile managed code only, e.g. there is no native int type in C#, the Int32 (its abbreviation is int) is already a class). In C++ the class on the managed heap is called reference class (ref class). It can be declared with this keyword the same way as for the native class. E.g. the .NET system contains an embedded “ref class String” type to store and manage accentuated character chains. If we create a "CLR/Windows Forms Application" with Visual Studio, the window of our program will be (Form1) a reference class. A native class cannot be defined within the reference class. The reference class behaves differently compared to the C++ class:
-
Static samples do not exist, only dynamic ones (that is, its sample has to be created from the program code). The following declaration is wrong: String text;
-
It is not pointer that points to it but handle (handler) and its sign is ^. Handle has pointer like features, for instance the sign of a reference to a member function is ->. Correct declaration is String ^text; in this case the text does not have any content yet given that its default constructor creates an empty, string with length of 0 (“”).
-
When creating we do not use the new operator but the gcnew. An example: text=gcnew String(""); creation of a string with length of 0 with a constructor. Here we do not have to use the ^ sign, its usage would be wrong.
-
Its deletion is not handled by using the delete operator but by giving a value of handle nullptr. After a while the garbage collector will free up the used space automatically. An example: text=nullptr; delete can be used as well, it will call the destructor but the object will stay in the memory.
-
It can be inherited only publicly and only from one parent (multiple inheritances are possible only with an interface class).
-
There is the option to create an interior pointer to the reference class that is initiated by the garbage collector. This way, however, we loose the security advantages of the managed code (e.g preventing memory overrun).
-
The reference class – similarly to the native one – can have data members, methods, constructors (with overloading). We can create properties (property) that contain the data in themselves (trivial property) or contain functions (scalar property) to reach the data after checking (e.g. the age cannot be set as to be a negative number). Property can be virtual as well or multidimensional, in the latest case it will have an index as well. Big advantage of property is that it does not have parenthesis, compared to a native C++ function that is used to reach member data. An example: int length=text->Length; the Length a read only property gives the number of the characters in the string.
-
Beside the destructor that runs when deleting the class (and for this it can be called deterministic) can contain a finalizer() method which is called by the GC (garbage collector) when cleaning the object from the memory. We do not know when GC calls the finalizer that is why we can call it non-deterministic.
-
The abstract and the override keywords must be specified in each case when the parent contains virtual method or property.
-
All data and methods will be private if we do not specify any access modifier.
-
If the virtual function does not have phrasing, it has to be declared as abstract: virtual type functionname() abstract; or virtual type functionname() =0; (the =0 is the standard C++. the abstract is defined as =0). It is mandatory to override it in the child. If we do not want to override the (not purely) virtual method, then we can create a new one with the new keyword.
-
It can be set at the reference class that no new class could be created from it with inheritance (with overriding the methods), and it could be only instantiated. In this case the class is defined as sealed. The compiler contains a lot of predefined classes that could not be modified e.g. the already mentioned String class.
-
We can create an Interface class type for multiple inheritances. Instead of reference we can write an interface class/struct (their meaning is the same at the interface). The access to all the members of the interface (data members, methods, events, properties) is automatically public. Methods and properties cannot be expanded (mandatorily abstract), while data can only be static. Constructors cannot be defined either. The interface cannot be instantiated, only ref/value class/struct can be created from it with inheritance. Another interface can be inherited from an interface. A derived reference class (ref class) can have any interface as base class. The interface class is usually used on the top of the class hierarchy, for example the Object class that is inherited by almost all.
-
We can use value class to store data. What refers to it is not a handle but it is a static class type (that is, a simple unspecified variable). It can be derived from an interface class (or it can be defined locally without inheritance).
-
Beside function pointers we can define a delegate also to the methods of a (reference) class that appears as a procedure that can be used independently. This procedure is secured, and errors are not faced that cause a mix up of the types and is possible with pointers of a native code. Delegate is applied by the .NET system to set and call the event handler methods, that belong to the events of the controls.
In the next table we sum up the operations of memory allocation and unallocation:
|
Operation |
K&R C |
C++ |
Managed C++ (VS 2002) |
C++/CLI (VS 2005-) |
|---|---|---|---|---|
|
Memory allocation for the object (dynamic variable) |
|
|
|
|
|
Memory unallocation |
|
|
Automatic, after |
<- similarly as in 2002 |
|
Referring to an object |
Pointer ( |
Pointer ( |
|
Pointer ( Handle ( |
IV.1.11. The predefined reference class: String
The System::String class was created on the basis of C++ string type in order to store text. Its definition is: public sealed ref class String. The text is stored with the series of Unicode characters (wchar_t) (there is no problem with accentuated characters, it is not mandatory to put an L letter in front of the constant, the compiler “imagines” that it is there: L”cat” and “cat” can be used as well). Its default constructor creates a 0 length (“”) text. Its other constructors allow that we create it from char*, native string, wchar_t* or from an array that consists of strings. Since the String is a reference class, we create a handle (^) to it and we can reach its properties and methods with ->. Properties and methods that are often used:
-
String->Length length. An example: s=”ittykitty”; int i=s->Length; after the value of i will be 9
-
String[ordinal number] character (0.. as by arrays). An example: value of s[1] will be the ‘t’ character.
-
String->Substring(from which ordinal number, how many) copying a part. An example: the value of s->Substring(1,3) will be ”tty”.
-
String->Split(delimiter) : it separates the string with the delimiter to the array of words that are contained in it. An example: s=”12;34”; t=s->Split(‘;’); after t a 2 element array that contains strings (the string array has to be declared). The 0. its element is “12”, and the 1. its elements is “34”.
-
in what -> IndexOf(what) search. We get a number, the initiating position of the what parameter in the original string (starting with 0 as an array index). If the part was not found, it returns -1. Note that it will not be 0 because 0 is a valid character position. As an example: with the s is “ittykitty”, the value of s->IndexOf(“ki”) will be 4, but the value of s->IndexOf(“dog”) will be -1.
-
Standard operators are defined: ==, !=, +, +=. By native (char*) strings the comparing operator (==) checks whether the two pointers are equal, and it does not check the equality of their content. When using String type the == operator checks the equality of the contents using operator overloading. Similarly, the addition operator means concatenation. As an example: the value of s+”, hey” will be “ittykitty, hey”.
-
String->ToString() exists as well because of inheritance. It does not have any pratical importance since it returns the original string. On the other hand, there is no method that converts to a native string (char*). Let us see a function as an example that performs this conversion:
char * Managed2char(String ^s) { int i, size=s->Length; char *result=(char *)malloc(size+1); // place for the converted string memset(result,0,size+1); // we fill the converted with end signs for (i=0; i<size;i++) // we go through the characters result[i]=(char)s[i]; // here we will got a warning: s[i] //stored on 2 bytes unicode wchar_t type character. //Converting ASCII from this the accents will disappear return result; // we will return the pointer to the result }
IV.1.12. The System::Convert static class
We store our data in variables with a type that was chosen for their purpose. For example in case we have to count the number of vehicles passing a certain point of the road per hour, we usually use the int type even if we are aware that its value will never be negative. The negative value (that can be given to the variable because it is signed) can be used in this example to mark an exception (no measuring happened yet, an error occurred etc.). The int (and the other numeric types also) stores the numbers in the memory in binary format, allowing this way performing arithmetic operations (for instance addition, substraction) and calling mathematical functions (e.g. sqrt, sin).
When the user input happens (our program asks for a number), the user will type characters. Number 10 is typed with a ‘1’ and ‘0’ character and from this a string is created: “10”. If we would like to add 20 to this and it was also entered as a string then the result will be “1020” because the “+” operator of the String class copies strings after each other. When using the scanf function of the native Win32 code and the cin standard input stream, if the input was put into numeric type, conversion will happen when reading to the type that is specified in the scanf format argument or after the cin >> operator. In case of the predefined input controls of windows it does not work like this: their output is always String type. Similarly, we always have to create String type for the output because on our controls we can display only this type. Also text files that are used to establish communication between programs (export/import) consist of strings in which numbers or other data types (date, logical, currency) can be as well. The System namespace contains a class called Convert. The Convert class has numerous overloaded static methods, which help the data conversion tasks. For performing the most common text <-> number conversions the Convert::ToString(NumericType) and the Convert::ToNumericType(String) methods are defined. For example, if in the above example s1=”10” and s2=”20”, then we add them considered as integers in the following way:
int total=Convert::ToInt32(s1)+Convert::ToInt32(s2);
In case s1 or s2 cannot be converted to a number (for example one of them is of 0 length or it contains an illegal character) an exception arises. The exception can be handled with a try/catch block. In case of real numbers we have to pay attention to one more thing: these are the region and language settings. As known, in Hungary the decimal part of numbers are separated from the integer with a comma: 1,5. On the other hand, in English speaking countries point is used for this purpose:1.5. In the source code of the C++/CLI program we always use points in case of real numbers. The Convert class, however, performs the real <-> string conversion according to the region and language settings (CultureInfo). The CultureInfo can be set for the current program, if for example we got a text file that contains real numbers in English format. The next program part sets its own culture information so that it could handle such a file:
// c is the instance of the CultureInfor reference class
System::Globalization::CultureInfo^ c;
// Like we were in the USA
c = gcnew System::Globalization::CultureInfo("en-US");
System::Threading::Thread::CurrentThread->CurrentCulture = c;
// from now onwards in the program the decimal separator is the point, the list delimiter is the comma
The methods of the Convert class can appear also in the methods of the data class. For example the instance created by the Int32 class has a ToString() method to convert to a string and a Parse() method to convert from a string. These methods can be parameterized in several ways. We often use hexadecimal numbers in computer/hardware related programs. The next example communicates with an external hardware with the use of strings containing hexadecimal numbers through a serial port:
if (checkBox7->Checked) c|=0x40;
if (checkBox8->Checked) c|=0x80;
sc="C"+String::Format("{0:X2}",c);// A 2 character hex number is created from the byte type c. C is the command;
//if the value of c was 8: “C08” will be the output, if c was 255 "CFF”.
serialPort1->Write(sc); // we sent it to the hardware
s=serialPort1->ReadLine(); // the answer was returned
// let us convert the answer to an integer
status = Int32::Parse(s, System::Globalization::NumberStyles::AllowHexSpecifier);
IV.1.13. The reference class of the array implemented with the CLI array template
In programming the array is an often used data structure with basic algorithms. Developers of .NET developed a generic array definition class template. With help of this – like a producer tool - the user can define a reference class from the required basic data type using the (<>) sign introduced in C++ to mark templates. It can be used for multidimensional arrays as well. Accessing the elements in the array can happen with the integer number (index) put into the traditional square brackets, that is with the [ ] operator.
Declaration: cli::array<type, dimension=1>^ arrayname, the dimension is optional; in this case its value is 1. The ^ is the sign of the ref class, the cli:: is also omissible, if we use at the beginning of our file the using namespace cli; statement.
We have to allocate space for the array with the gcnew operator before using – since it is a reference class when declaring a variable only the handle is created, and it is not pointing to anywhere. We can make the allocation in the declaration statement as well: we can list the elements of the array between { } as used in C++.
Array’s property: Length gives the number of elements of the onedimensional array. For arrays passed to a function we do not have to pass the size, like in the basic C. The size can be used in the loop statement, which does not address out from the array:
for (i=0; i<arrayname->Length; i++)….
For the basic array algorithms static methods were created, and those are stored in the System::Array class:
Clear(array, from where, how many) deletion. The value of the array elements will be 0, false, null, nullptr (depending on the base type of the array),
Resize(array, new size) in case of resizing (expanding) after the old elements it fills the array with the values used with Clear().
Sort(array) sorting the elements of the array. It can be used by default to order numerical data in ascendant order. We can set keys and a comparing function to sort any type data.
CopyTo(target array, starting index) copying elements. Note: the = operator duplicates the reference only. If an element of the array is changed, this changed element is reached using the other reference as well. Similarly, the == oparetor that the two references are the same but it does not compare the elements themselves.
If the type from which we create the array is another reference class (e.g. String^) then we have to set it in the definition. After creating the array we have to create each element one after the other because by default it would contain nullptrs. An example: String^ like an array element with initial value setting. If we do not list the 0 length strings, the array elements would have been nullptrs
array<String^>^ sn= gcnew array<String^>(4){"","","",""};
In the next example we create lottery numbers in an array then we check them whether they can be used in the game: not to have two identical ones. In order to do this we sort them so that we had to check only the neighbouring elements and we could list the result in ascendent order:
array<int>^ numbers; // managed array type, reference
Random ^r = gcnew Random();// random number generator instance
int piece=5, max=90,i; // we set how many numbers we need and the highest number.
//It could be set as an input after conversion.
numbers = gcnew array<int>(piece); // managed array on the heap created
for(i=0;i<numbers->Length;i++)
numbers[i]=r->Next(max)+1;// the raw random numbers are in the array
Array::Sort(numbers); // with the embedded method we set the numbers in order
// check: two identical next to each other?
bool rightnumber=true;
for (i=0;i<numbers->Length-2;i++)
if (numbers[i]==numbers[i+1]) rightnumber=false;
IV.1.14. C++/CLI: Practical realization in e.g. in the Visual Studio 2008
If we would like to create a program with CLR (that is, in .NET with windows) in Visual Studio we have to choose one of the “Application” elements of the CLR category in the new element wizard. The CLR console looks like the ”Win32 console app”, that is, it has a command line interface. Therefore we should not choose the console but the ”Windows Forms Application”. In this case the window of our program that is the container object called Form1 will be created and its code will be in the Form1.h header file. The Form Designer will place the code of the drawn controls here (and it puts a comment ahead of it saying that we should not modify the code, of course in certain cases the amendment is necessary). In the attached figure you can see the element to be selected:
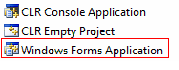
After making our selection, the folder structure of our project is created with the necessary files in it. Now we can already place controls on the form. In the “Solution Explorer” window we can find for the source files and we can modify all of them. In the next figure you can see a project that has just been started:
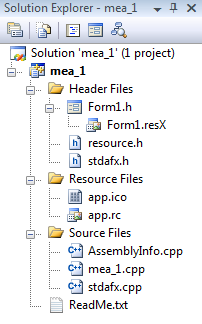
Our program is in Form1.h (it has a form icon). Usually there is code placed into stdafx.h too. In the main program (mea_1.cpp) we should not modify anything. Using the “View/Designer” menuitem, we can select the graphical editor, while with the “View/Code” menuitem the source program. After selecting the “View/Designer” menuitem our window will look like this:
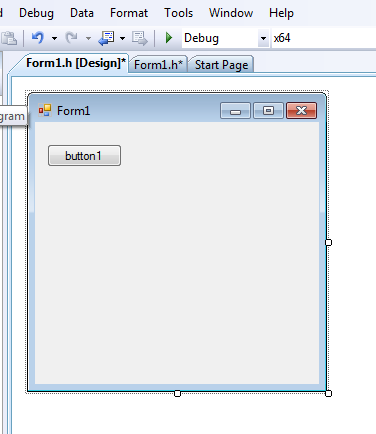
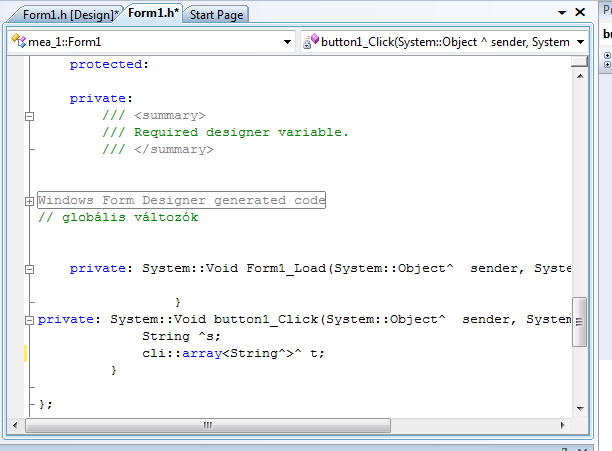
After selecting the “View/Code” menuitem our window will look like this:
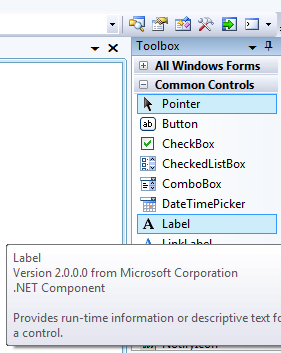
Selecting the “View/Designer” menuitem we will need the Toolbox where the additional controls can be found (the toolbox contains additional elements only in designer state). In case it is not visible we can set it back with the “View/Toolbox” menuitem. The toolbox contains a case-sensitive help as well: leaving the cursor on top of the controls we will get a short summary of the use of the control. See the next figure where we selected the label control:
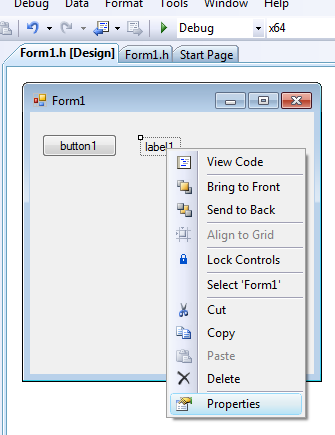
Selection of the control happens with the usual left mouse button. After this the bounding rectangle of the control will be drawn on the form if we chose a visible control. The non-visible controls (e.g. timer) can be placed in a separated band at the bottom of the form. When the drawing is done an instance of the control is put to on the form with an automatically given name. In the figure we selected the “Label” control (upper case: type), if we draw the first of this control, the developing environment will name it “label1” (lower case: instance). After drawing the controls if needed, we can set their properties and the functions that are related to their events. After selecting the control and with right mouse click we can achieve the setting in the window, opened with the “Properties” menuitem. It is important to note that these settings refer to the currently selected control and the properties windows of the certain controls differ from each other. On the next figure we select the “Properties” window of the label1 control:
After this we can set the properties in a separate window:
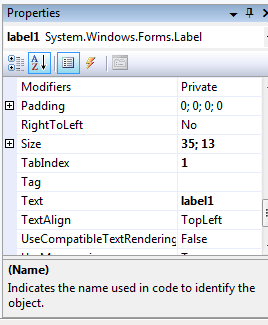
The same window serves for selecting the event handlers. We have to click on the blitz icon ( ) to define the event handlers. In this case all the reacting options will appear that are possible for all the events of the given control. In case the right side of the list is empty then the control will not react to that event.
) to define the event handlers. In this case all the reacting options will appear that are possible for all the events of the given control. In case the right side of the list is empty then the control will not react to that event.
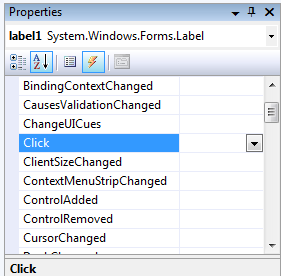
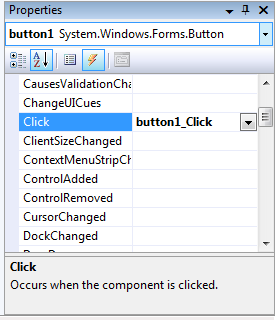
In the example the label1 control does not react when clicking on it (the label control can handle the click event but it is not common to use the control this way). A function can be added to the list in two ways: if we would like to run an already existing function when the event of the control happens (and its parameters equal to the event parameters), then we can choose the function name from the drop down list. If it does not exist then clicking on the empty area the header of a new function is created and we will reach the code editor. Each control has a default event (for example click is the default event of the button), clicking twice on the control in the designer window we will reach the code editor of the event. If such a function does not exist yet its header and an association are created. We have to be aware that the control does not work without its association! It is a typical problem to write the button1_Click function, setting the parameters correctly but without associating them. In this case – after compiling without errors – the button does not react when clicking on it. The button1 will react only if the “Click” row in the events window contains the button1_Click name.
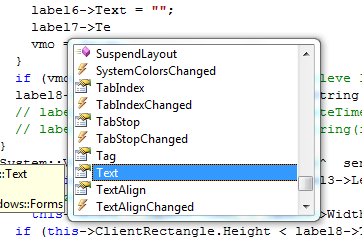
IV.1.15. The Intellisense embedded help
As we saw it in the previous figures, a control can have a lot of properties. We can use the property names in the text of the program, but since they are considered as identifiers they have to equal from character to character to the property name as set in the definition, considering case sensitivity as well. The names of the properties are often very long (for example UseCompatibleTextRendering). The programmer has to type these without mistake. The text editor contains some help: after the name of the object (button1) typing the operator that refers to the data member (->) it creates a list from the possible properties. It displays them in a short menu, we can select the ones we need with the cursor control arrows or with the mouse, then it adds the chosen name to the text of our program pushing the tab key. The help list will appear also if we start to type the name of the property. Visual Studio stores these control properties in a big size .NCB extension file and if we delete it (e.g we transfer a source file to another computer via pen drive), once opening it, it will be regenerated. Intellisense does not work in certain cases: if our program has syntax errors, and the number of opening curly brackets does not equal to the closing curly brackets, then it will stop. Similar to this it does not work in Visual Studio 2010, if we write a CLR code. In the next figure we would like to change the label7->Text property, because of the high number of properties we type the T letter then we select Text with the mouse.
IV.1.16. Setting the type of a CLR program.
As we already mentioned previously, C++/CLR is capable of developing mixed mode programs (native+managed). In case we use settings described in the previous section, our program will have purely managed code, the native code cannot be compiled. At the beginning it is worth to start with these settings because this way the window and the controls of our program will be usable. We can make these settings in the project properties (we select the project then right click and “Properties”). Be aware that it does not refer to the top level solution but to the properties of the project that is below the solution.
In the "Property Pages" window in the line “Common Language Runtime Support" we can set whether it should be native/mixed/purely managed code. We can choose from 5 setting types:

The meanings of the settings are as follows:
-
"No common Language Runtime Support" – there is no managed code. It is the same if we create a Win32 console application or a native Win32 project. With this setting it is not capable of compiling the parts of the .NET system (handles, garbage collector, reference classes, assemblies).
-
"Common Language Runtime Support" – there is native and managed code compiling as well. With this setting we can create mixed mode programs, that is, if we started to develop our program with the default window settings and we would like to use native code data and functions, then we have to set the drop down menu to this item.
-
"Pure MSIL Common Language Runtime Support" – purely managed code compiling. The default setting of programs created from the “Windows Form Application”. This is the only possible setting of C# compiler. Note: this code type can contain native code data that we can reach through managed code programs.
-
"Safe MSIL Common Language Runtime Support" – it is similar to the previous one but it cannot contain native code data either and it allows the security check of the CRL code with a tool created for this purpose (
peverify.exe). -
"Common Language Runtime Support, Old Syntax" – this also creates a mixed code program but with Visual Studio 2002 syntax. (_gc new instead of gcnew). This setting was kept to ensure compatibility with older versions, however, it is not recommended to be used.
IV.2. The window model and the basic controls
IV.2.1. The Form basic controller
Form could not be added from the toolbox, it is created with a new project. By default it creates an empty, rectangle shape window. Its settings can be found in the properties, e.g. Text is its header and by default the name of the control (if this is the first form then it will be Form1) will be added into it. We can reach it from here or from the program as well ((this->Text=…) because in the Form1.h can be used the instance of the reference class of our form (inherited from the Form class), and we can refer to this instance with this pointer within our program. From the property settings (as well) a program part is created at the beginning of form1.h in a separate section:
#pragma region Windows Form Designer generated code
/// <summary>
/// Required method for Designer support - do not modify
/// the contents of this method with the code editor.
/// </summary>
// button1
this->button1->Location = System::Drawing::Point(16, 214);
this->button1->Name = L"button1";
this->button1->Size = System::Drawing::Size(75, 23);
this->button1->TabIndex = 0;
this->button1->Text = L"button1";
this->button1->UseVisualStyleBackColor = true;
this->button1->Click += gcnew System::EventHandler(this, &Form1::button1_Click);
IV.2.2. Often used properties of the Form control
-
Text – title of the form. This property can be found at each control that contains text (as well).
-
Size – the size of the form, by default in pixels. It contains the Width and Height properties that are directly accessible. Also the visible controls have these properties.
-
BackColor – color of the background. By default it has the same color as the background of the controls defined in the system (System::Drawing::SystemColors::Control). This property will be important if we would like to delete the graphics on the form because deletion means filling with a color.
-
ControlBox – the system menu of the window (minimalizer, maximalizer buttons and windows menu on the left side). It can be enabled (by default) and disabled.
-
FormBorderStyle – We can set here whether our window can be resized or it should have a fix size or whether it had a frame or not.
-
Locked – we can prohibit resizing and movement of the window with the help of this.
-
AutoSize – the window is able to change its size aligning to its content
-
StartPosition – when starting the program where should the form appear on the Windows desktop. Its application: if we use a multiscreen environment, then we can set the x,y coordinates of the second screen, our program will be lunched there then. It is useful to set this property in a conditional statement because in case the program is lunched in one screen only the form will not be visible.
-
WindowState – we can set here whether our program would be a window (Normal), whether it would run full screen (Maximized) or whether it would run in the background (Minimized). Of course, like any of the other properties, it is reachable during run-time as well, that is, if the program lunched in the small window would like to maximalize itself (for example because it would like to show many things) then we have an option for this setting as well: this->WindowState=FormWindowState::Maximized;
IV.2.3. Events of the Form control
Load – a program part that appears when starting the program before displaying it. Load is the default event of the Form control, that is, when double clicking on its header in the Designer its handler function is placed in the editor. This function as usual can fill in the role of an initializer since it runs once when launching the program. We can set values to the variables, we can create the necessary dynamic variables, and we can change title on our other controls (if we have not already done ), we can also set the size of the form dynamically etc.
As an example let us see the Load event handler of the program of the quadratic equation:
private: System::Void Form1_Load(System::Object^ sender, System::EventArgs^ e) {
this->Text = "quadratic";
textBox1->Text = "1"; textBox2->Text = "-2"; textBox3->Text = "1";
label1->Text = "x^2+"; label2->Text = "x+"; label3->Text = "=0";
label4->Text = "x1="; label5->Text = "x2="; label6->Text = "";
label7->Text = ""; label8->Text = "";
button1->Text = "Solve it";
if (this->ClientRectangle.Width < label3->Left + label3->Width) // the form is not wide enough
this->Width = label3->Left + label3->Width + 24;
if (this->ClientRectangle.Height < label8->Top + label8->Height)
this->Height = label8->Top + label8->Height + 48; // it is not high enough
button1->Left = this->ClientRectangle.Width - button1->Width-10; // pixel
button1->Top = this->ClientRectangle.Height - button1->Height - 10;
}
In the above example after setting the initial values we set the titles then we set the size of the form to a value that the whole equation and the results (label3 was the right-most control and label8 was at the bottom of the form) were visible.
In case we find in this function that running of the program does not make sense (we would process a file but we could not find it, we would like to communicate with a hardware but we could not find it, we would like to use the Internet but we do not have connection etc.) then after displaying a window of an error message we can leave the program. Here comes a hardware example:
if (!controller_exist) {
MessageBox::Show("No iCorset controller.",
"Error",MessageBoxButtons::OK);
Application::Exit();
} else {
// controller exist, initialize the controller.
}
Let us pay attention to a thing: the Application::Exit() does not leave the program immediately, it puts a message to the Windows message queue for us to warn about leaving the program. That is, the program part after if… will run also, moreover the window of our program will show up for a second before closing it. If we would like to avoid the run of the further program part (we would communicate with the hardware that does not exist), then let us do it in the else branch of the if statement and the else branch should reach the end of the Load function. This way we can guarantee that the program part that supposedly caused the error will not run.
Resize – An event handler that runs when resizing our form (minimalizing, maximalizing, setting it to its normal size could be also considered here). It runs when loading the program, this way the increase of the form size from the previous example could have been mentioned here as well, and in this case the form could not be resized to smaller in order to ensure the visibility of our controls. In case we have a graphic which size depens on the window size, then we can resize it here.
Paint – the form has to be repainted. See the examples in the “The usage of GDI+” chapter (Section IV.4.1).
MouseClick, MouseDoubleClick – we click once or we double click on the Form with the mouse. In case we have other controls on the form then this event runs if we do not click on neither of the controls just on the empty area. In one of the arguments of the event handler we got the handle to the reference class
System::Windows::Forms::MouseEventArgs^ e
The referenced object contains the coordinates (X,Y) of the click beside others.
MouseDown, MouseUp – we clicked or released one of the mouse buttons on the Form.The Button propety of the MouseEventArgs contains which button was clicked or released. The next program part saves the coordinates of the clicks into a file, this way for example we can create a very basic drawing program:
// if save is set and we pushed the left button
if (toolStripMenuItem2->Checked && (e->Button == System::Windows::Forms::MouseButtons::Left)) {
// we write the two coordinates into the file, x and y as int32
bw->Write(e->X); // we write int32
bw->Write(e->Y); // that is 2*4 byte/point
}
MouseMove: - the function running when moving the mouse. It works independently from the buttons of the mouse. In case our mouse is moved over the form, its coordinates can be read. The next program part displays these coordinates in the title of the window (that is, in the Text property), of course after the needed conversions:
private: System::Void Form1_MouseMove(System::Object^ sender, System::Windows::Forms::MouseEventArgs^ e) {
// coordinates into the header, nobody looks at those ever
this->Text = "x:" + Convert::ToString(e->X) + " y=" + Convert::ToString(e->Y);
}
FormClosing – our program got a Terminate() Windows message for some reason. The source of the message could be anything: the program itself with Application::Exit(), the user with clicking on the “close window”, or the user with the Alt+F4 key combination, we are before stopping the operating system etc. When this function runs the Form is closed, its window disappears, resources used by it will be unallocated. In case our program decides that this is not possible yet, the program stop can be avoided by setting the Cancel member of the event’s parameter to true, and the program will run further. The operating system however, if we would like to prevent it from stopping, it will close our program after a while. In the next example the program let itself to be closed only after a question appearing in a dialog window:
void Form1_FormClosing(System::Object^ sender, System::Windows::Forms::FormClosingEventArgs^ e) {
System::Windows::Forms::DialogResult d;
d=MessageBox::Show("Are you sure that you would like to use the airbag?”,
" Important security warning ", MessageBoxButtons::YesNo);
if (d == System::Windows::Forms::DialogResult::No) e->Cancel=true;
}
FormClosed – our program is already in the last step of closure process, the window do not exist anymore. There is no way back from here, this is the last event.
IV.2.4. Updating the status of controls
After the running of the event handlers (Load, Click) the system updates the status of controls so that they are already in the new, updated state for the next event. However, let’s have a look at the following sample program part that writes increasing numbers into the form’s title bar. It can be placed for example into the button_click event handler:
int i;
for (i=0;i<100;i++)
{
this->Text=Convert::ToString(i);
}
During the running of the program (apart from the speed problem) there is no change in the form’s title. Though Text property was rewritten, the control still shows the old content. It will be changed only once, when the given event handler function terminates. But then „99” will appear in the control. In case of longer operations (image processing, large text files) it would be good to somehow inform the user about how the program proceeds, showing the current status, otherwise one might suppose that the program has stopped responding. Function call Application::DoEvents() serves exactly this purpose. It updates the current status of the controls: in our example this function will replace the form’s title. Unfortunately, from this we cannot see anything, we can read the numbers only if we build an awaiting time (Sleep) as well into the loop:
int i;
for (i=0;i<100;i++)
{
this->Text=Convert::ToString(i);
Application::DoEvents();
Threading::Thread::Sleep(500);
}
The parameter of the Sleep() function is the waiting time in milliseconds. The slow process was simulated by this. In case we need algorithm components recurring periodically, Timer control should be used (see Section IV.2.22).
IV.2.5. Basic controls: Label control
The simplest control is the Label which displays text. It’s String ^ type property called Text includes the text to be displayed. By default its width aligns to the text to be displayed (AutoSize=true). In case we display text with the help of it, its events (eg. Click) are normally not used. By default the Label has no border (BorderStyle=None), but it can be framed (FixedSingle). The background color can be found in BackColor property, the text color in ForeColor property. In case we would like to remove the displayed text, we have two choices: we either set the logical type property called Visible to false, in this case the Text property does not change, but the control is not visible, or we set the Text property to an empty string with length 0 (””).
All visible controls have this property called Visible. By setting the property to false, the control disappears, by setting it to true, the control will be visible again. In case we are sure that the control’s label will be different at the next display, it is practical to use the ‘empty string’ version, since in this case the new value appears immediately after the assignment; while in case of the other version ‘Visible property’ a new allowing program line is needed as well.
IV.2.6. Basic controls: TextBox control
TextBox control can be used for entering text (String^) (in case we need to enter numbers, we use the same control, but in this case the processing starts with a conversion). The Text property contains the text, which can be rewritten from the program and the user can also change it while the program is running. The already mentioned Visible property appears here as well as the Enabled property is available too. By setting Enabled to false, the control is visible on the form, however appears in gray and cannot be used by the user: one can neither change nor click on it. For example, the command button “Next” in an installation process has the same state until the license agreement is not accepted.
TextBox has a default event as well: it is TextChanged, which runs after each and every change (per character). In case of multi-digit numbers, data with more than one characters or in case of more input data (in several TextBoxes) we usually do not use it, since it would be pointless. For example, the user has to enter his name into the TextBox and the program stores it in a file. It would be unnecessary to write all the current content into a file in case each of the characters, since we do not know what the last character will be. Instead, we wait until editing is over, data entry is ready (maybe there are more TextBoxes in our form), and the user can give a signal by pressing a properly named (ready, save, processing) command button meaning that text boxes include the program’s input data.
Unlike the other controls that have Text property, where the Designer writes the control’s name into the Text property, it does not happen here, Text property remains empty. It can be set to multiline by switching the MultiLine property to true. Then line feeds appear in the Text, and the lines can be found in the Lines property just like the elements of a string array. Some programmers use TextBox control for output as well by setting ReadOnly property to true. In case we do not want to write back the entered characters, we can switch the TextBox to password input mode by setting UseSystemPasswordChar property to true. We have already seen the function running when starting the quadratic equation program; now let’s have a look at the calculation part. The user has written in the TextBoxes the coefficients (a,b,c) and clicked on the “solve” button. Our first job is to get data from the TextBoxes by using conversion. Then the next step is the calculation and the displaying of results.
double a, b, c, d, x1, x2, e1, e2; // local variables
// in case we forget to give values to any of the variables -> error
a = Convert::ToDouble(textBox1->Text); // String -> double
b = Convert::ToDouble(textBox2->Text);
c = Convert::ToDouble(textBox3->Text);
d = Math::Pow(b,2) - 4 * a * c; // the method for exponentiation exists as well
if (d >= 0) // real roots
{
x1=(-b+Math::Sqrt(d))/(2*a);
x2=(-b-Math::Sqrt(d))/(2*a);
label4->Text = "x1=" + Convert::ToString(x1);
label5->Text = "x2=" + Convert::ToString(x2);
// checking
e1 = a * x1 * x1 + b * x1 + c; // this way we typed less than in Pow
e2 = a * x2 * x2 + b * x2 + c;
label6->Text = "...=" + Convert::ToString(e1);
label7->Text = "...=" + Convert::ToString(e2);
}
IV.2.7. Basic controls: Button control
Button control denotes a command button that “sags” when clicking on it. We use command button(s) if the number of currently selectable functions are low. The function can be complicated as well, in this case a long function belongs to it. Button control supports the usual properties of visible controls: its caption is Text, its event is Click, which runs when clicking on the button. This is its default and commonly used event. From the event handler’s parameters the coordinates of the click cannot be told. The header of the event handler is:
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
}
Button control gives an opportunity to apply the nowadays so fashionable shortcut icon operation by using small graphics instead of captions. To do this, the following steps are needed: we load the small graphic to a Bitmap type variable, we set the Button’s sizes to the sizes of Bitmap, finally, we store the reference of the Bitmap type variable in the Image property of the button as it happened in the example below: the image called “service.png” appears in the command button called “button2”.
Bitmap^ bm;
bm=gcnew Bitmap("service.png");
button2->Width=bm->Width;
button2->Height=bm->Height;
button2->Image=bm;
IV.2.8. Controls used for logical values: CheckBox
Text property of the CheckBox control is the text (String^ type), written next to it. Its bool type property is the Checked, which is true in case it is checked. CheckedState property can take up three values: apart from ‘on’ and ‘off’ it has a third, middle value as well, which can be set up only from the program, when it is running, however it is considered to be checked. In case there are more CheckBoxes in a Form, these are independent of each other: we can set any of them checked or unchecked. Its event: CheckedChanged occurs when the value of the Checked property changes.
The sample program below is a part of an interval bisection program: when switching on the checkbox called “Stepwise”, one step will be completed from the algorithm, when switching it off, the result is provided within one loop. If we started to make the program running stepwise, the checkbox cannot be unchecked: further counting has to be performed stepwise.
switch (checkBox1->Checked)
{
case true:
checkBox1->Enabled = false;
step();
break;
case false:
while (Math::Abs(f(xko)) > eps) step();
break;
}
write();
IV.2.9. Controls used for logical values: RadioButton
RadioButton is a circular option button. It is similar to the CheckBox, but within one container object (such as Form: we put other objects in it) only one of them can be checked at the same time. It was named after the old radio containing waveband switch: when one of the buttons was pressed, all the others were deactivated. When one of the buttons is marked/activated by the circle (either by the program: Checked = true, or by the user clicking on it), the previous button (and all the others) becomes deactivated (its Checked property changes to false). We store the text, which is next to the circle in the control’s Text property. A question might be raised: if only one RadioButton can be active at the same time, then what if we have to choose from two option lists at the same time using RadioButtons? The answer is simple: we can have one active RadioButton per one container object, therefore, we have to place some container objects on the form.
IV.2.10. Container object control: GroupBox
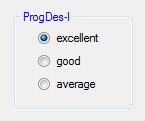
GroupBox is a rectangular frame with text (Text, String^ type) on its top left line. We placed controls in it, which are framed. On the one hand, it is aesthetic, as the logically related controls appear within one frame, on the other hand it is useful for RadioButton type controls. Furthermore, controls appearing here can be moved and removed with a single command by customizing the appropriate property of GroupBox. The example below shows marking: we can see the entry and processing of a small number of discrete elements:
groupBox1->Text="ProgDes-I"; radioButton1->Text="excellent"; radioButton2->Text="good"; radioButton3->Text="average";// no other marks can be received here … int mark; if (radioButton1->Checked) mark = 5; if (radioButton2->Checked) mark = 4;
IV.2.11. Controls inputting discrete values: HscrollBar and VscrollBar
The two controls that are called scrollbars differ only in direction. They do not have labels. In case we would like to indicate their end positions or their current status, we can do this by using separate label controls. The current value, where the scrollbar is standing, is the integer numerical value found in Value property. This value is located between the values of Minimum and Maximum properties. The scrollbar can be set to the Minimum property, this is its left/upper end position. However, for its right/lower end position we have a formula, which includes the quick-change unit of the scrollbar, called LargeChange property (the value changes this much, when we click on the empty space with the mouse): Value_max=1+Maximum-LargeChange. LargeChange and SmallChange are property values set by us. When moving the scrollbar a Change event is running with the updated value. In the example below we would like to generate 1 byte values (0..255) with the help of three equally sized horizontal scrollbars. The program part for setting the scrollbar properties in the Form_Load event are the following:
int mx; mx=254 + hScrollBar1->LargeChange; // We would like to have 255 in the right position hScrollBar1->Maximum = mx; // max. 1 byte hScrollBar2->Maximum = mx; hScrollBar3->Maximum = mx;
When the scrollbars are changing, we read their value, convert them to a color and write the values to the labels next to the scrollbars as a check:
System::Drawing::Color c; // color variable r = hScrollBar1->Value ; // from 0 to 255 g = hScrollBar2->Value; b = hScrollBar3->Value; c = Color::FromArgb(Convert::ToByte(r),Convert::ToByte(g),Convert::ToByte(b)); label1->Text = "R=" + Convert::ToString(r); //we can also have them written label2->Text = "G=" + Convert::ToString(g); label3->Text = "B=" + Convert::ToString(b);
IV.2.12. Control inputting integer numbers: NumericUpDown
With the help of NumericUpDown control we can enter an integer number. It will appear in Value property, between the Minimum and Maximum values. The user can increase and decrease the Value by 1, when clicking on the up and down arrows. All the integer numbers between the Minimum and Maximum values appear among the values to choose from. Event: ValueChanged is running after every change.
IV.2.13. Controls with the ability to choose from several objects: ListBox and ComboBox
ListBox control offers an arbitrary list to be uploaded, from which the user can choose. Beyond the list, ComboBox contains a TextBox as well, which can get the selected item as well and the user is also free to type a string. This is the Text property of ComboBox. The control’s list property is called Items, which can be upgraded by using Add() method and can be read indexed. SelectedIndex points the current item. Whenever selection changes, SelectedIndexChanged event is running. ComboBox control is used by several controls implementing more complex functions: for example OpenFileDialog. In the example below we fill up the list of ComboBox with elements. When the selection is changed, we put the new selected item in label4.
comboBox1->Items->Add("Excellent");
comboBox1->Items->Add("Good");
comboBox1->Items->Add("Average");
comboBox1->Items->Add("Pass");
comboBox1->Items->Add("Fail");
private: System::Void comboBox1_SelectedIndexChanged(System::Object^ sender, System::EventArgs^ e) {
if (comboBox1->SelectedIndex>=0)
label4->Text=comboBox1->Items[comboBox1->SelectedIndex]->ToString();
}
IV.2.14. Control showing the status of progressing: ProgressBar
With the help of ProgressBar we can give information about the status of the process, how much is still left, the program has not frozen, it is working. We have to know in advance when the process will be ready, when it should reach the maximum. The control’s properties are similar to HScrollBar, however the values cannot be modified with the help of the mouse. Certain Windows versions animate the control even if it shows a constant value. Practically, this control used to be placed in the StatusStrip in the bottom left corner of our window. When clicking on it, its Click event is running, however, it is something we normally do not deal with.
IV.2.15. Control with the ability to visualize PixelGrapic images: PictureBox

This control has the ability to visualize an image. Its Image property contains the reference of the Bitmap to be visualized. Height and Width properties show its size, while Left and Top properties give its distance from the left side and top of the window measured in pixels. It is practical to have the size of the PictureBox exactly the same as the size of the Bitmap to be visualized (which can be loaded from almost all kinds of image files) in order to avoid resizing.
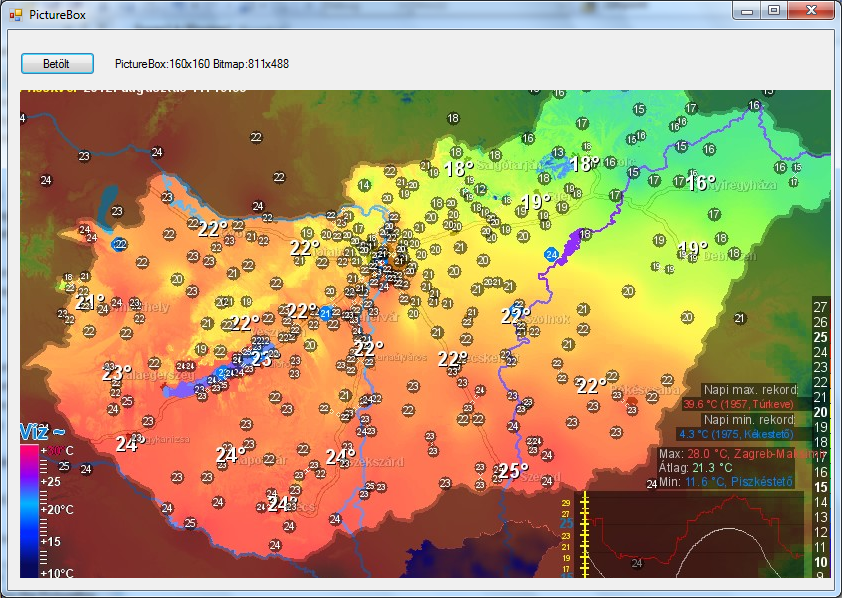
The SizeMode property contains the info about what to do if you need to resize the image: in case of Normal value, there is no resizing, the image is placed to the left top corner. If Bitmap is larger, the extra part will not be displayed. In case of StretchImage value, Bitmap is resized to be as large as the PictureBox. In case of AutoSize option, the size of the PictureBox is resized according to the size of the Bitmap. In the program below we display a temperature map (found in idokep.hu) in the PictureBox control. SizeMode property is preset in the Designer, the size parameters of the images are shown in the label:
Bitmap ^ bm=gcnew Bitmap("mo.png");
label1->Text="PictureBox:"+Convert::ToString(pictureBox1->Width)+"x"+
Convert::ToString(pictureBox1->Height)+" Bitmap:"+
Convert::ToString(bm->Width)+"x"+Convert::ToString(bm->Height);
pictureBox1->Image=bm;
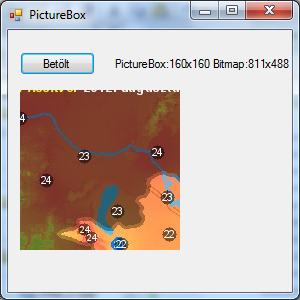
The result of the program above in case SizeMode=Normal is the following:
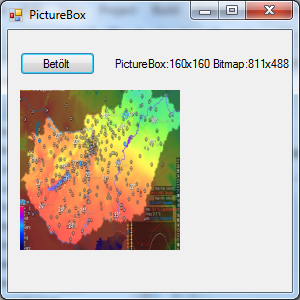
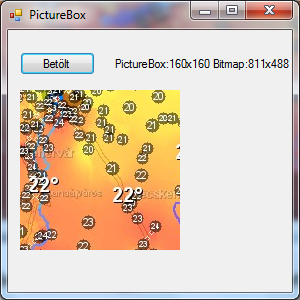
With SizeMode=StretchImage setting the scales do not match either: the map is rectangular, the PictureBox is a square:
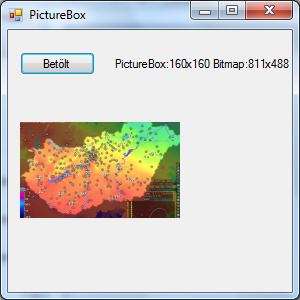
In case of SizeMode=AutoSize the PictureBox has increased, but the Form has not. The Form had to be resized manually to reach the following size:
With SizeMode=CenterImage setting: there is no resize, the centre of Bitmap was set into the PictureBox
With SizeMode=Zoom Bitmap is resized by keeping its scales so that it fits into the PictureBox:
IV.2.16. Menu bar at the top of our window: MenuStrip control
In case our program implements so many functions that we would require a large number of command buttons in order to start them, it is practical to group functions hierarchically and settle them into a menu. Imagine for example that if all the functions of Visual Studio could be operated with command buttons, editor window could not fit because of the large number of buttons. The menu starts from the main menu, this is always visible at the top of the program’s window and every menu item can have submenus. The traditional menu includes labels (Text), but newer menu items can show bitmaps as well, or there can be TextBoxes and ComboBoxes used for editing too. We can put a separator among menu items (being not in the main menu) and we can also put a checkbox in front of the menu items. Menu items similarly to command buttons get a unique identifier. The identifier can be typed by us, or similarly to the other controls, it can be named automatically. MenuStrip control appears under the form, but in the meanwhile we can write the name of the menu item in the top corner of our program, or we can choose the automatic name by using the “MenuItem” label. In the figure below we can see the start of menu editing, when we included MenuStrip:
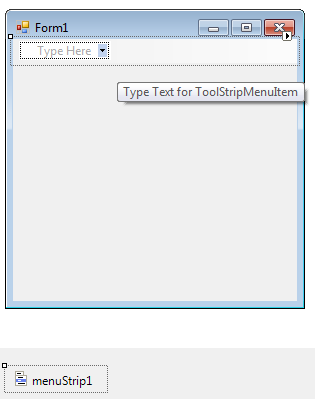
Let’s select a menu item in the menu above:
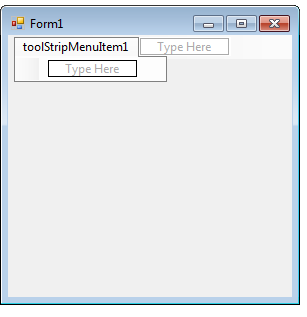
The name of the menu item in the main menu is now toolStripMenuItem1. To the place of the menu item being next to it (in the main menu) let’s type: Help.
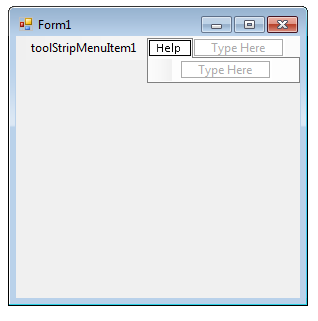
The name of the new menu item is now helpToolStripMenuItem, however its Text property does not have to be set: it is already done. Let’s create three submenu items under MenuItem1 using a separator before the third one:
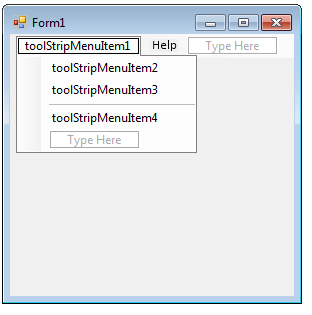
From now programming is the same as in case of buttons: in form_load function we set their labels (Text), then we write the Click event handler methods by clicking on the menuitems in the editor:
private: System::Void toolStripMenuItem2_Click(System::Object^ sender, System::EventArgs^ e) {
// We have to write here what should happen after we have selected the menu item.
}
IV.2.17. The ContextMenuStrip control which is invisible in basic mode
The main menu of the MenuStrip control is always visible. The ContextMenuStrip can only be seen while designing, during running it is only visible if it is visualized from the program. It is recommended to use it with the local menu appearing at the mouse cursor after clicking the right mouse button. We create the items of the menu in Designer, we write the Click event hanler of the menu items in the editor then in the MouseDown or MouseClick event handler of the Form (they have a coordinate parameter) we visualize the ContextMenu.
The program part below contains a ContextMenu with three menuitems:
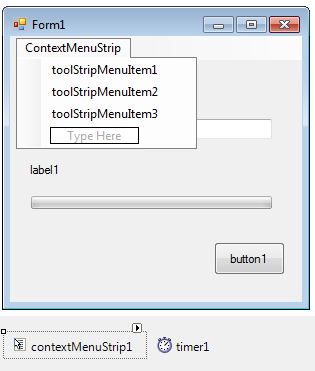
The event control Form_MouseClick looks like this:
private: System::Void Form1_MouseClick(System::Object^ sender, System::Windows::Forms::MouseEventArgs^ e) {
if (e->Button == Windows::Forms::MouseButtons::Right) // only for the right button
contextMenuStrip1->Show(this->ActiveForm, e->X, e->Y); // we show the menu to the Form
}
IV.2.18. The menu bar of the toolkit: the control ToolStrip
The toolkit contains graphical command buttons next to each other. The Image property of the buttons contains the visualized image. Since they are command buttons, they run the Click event when clicking on them. The figure below shows the elements of the toolstrip, with the button contatining the image at the top, which will bear a name starting with toolStripButton:
IV.2.19. The status bar appearing at the bottom of the window, the StatusStrip control
A status bar visualises status information, therefore it is useful to create a label and a progressbar for it. The name of the label placed over it starts with toolStripLabel, that of the progressbar will start with toolStripProgressBar. It is not clicked in general, so Click event handlers are not written for it.
IV.2.20. Dialog windows helping file usage: OpenFileDialog, SaveFileDialog and FolderBrowserDialog

Almost all computer programs in which modifications carried out can be saved contain the Open file and Save file functions. Selecting a file to be saved or to be opened is done with the same window type in each software because the developers of .NET created a uniform control for these windows.
When program is designed, controls are placed under the form, while they are only visible if they are activated from the software. Activating them is carried out by a method (function) of the control object, the output is the result of the dialog (DialogResult: OK, Cancel etc). In the next code portion, a file with the extension .CSV is selected and opened with the help of the OpenFileDialog control in case the user has not clicked the Cancel button instead of Open:
System::Windows::Forms::DialogResult dr; openFileDialog1->FileName = ""; openFileDialog1->Filter = "CSV files (*.csv)|*.csv"; dr=openFileDialog1->ShowDialog(); // open dialog window for a csv file filename = openFileDialog1->FileName; // getting the file name. if (dr==System::Windows::Forms::DialogResult::OK ) // if it is not the Cancel button that was clicked sr = gcnew StreamReader(filename); // opened for reading
The SaveFileDialog can be used in the same way but that one can be used to save a new file. The FolderBrowserDialog can be used to select a folder, in which for example we process all the images.
IV.2.21. The predefined message window: MessageBox
A MessageBox is a dialog window containing a message and is provided by the Windows. In a message box, the user can choose one of the command buttons. The combinations of the buttons are predefined constants and are provided as argumnets when the window is activated. This control cannot be found in the ToolBox, it is not necessay to put it on the Form because it was defined as a static class. It can be made appear by calling its Show() method the return value of which is the button the user clicked. In case we are sure that only one button can be chosen (because MessageBox only contains the OK button), the method can be called as a statement.
The execution of the program is suspended by the MessageBox: its controls do not function at that time, the event handler does not continue to run until one of the command buttons is chosen. The syntax of calling the Show() method: result=MessageBox::Show(the message in the window, the header of the window, buttons);, where the data type of each element is as follows:
-
result: variable of type System::Windows::Forms::DialogResult
-
The message in the window and the header of the window: data of type String^
-
buttons: a data member of the MessageBoxButtons static class, from the following:
MessageBox::Show() can be called with one string argument: in that case, it will not have a header, and will have only the "OK” button. It is not a beautiful solution, is it?
The following example was already mentioned, now we will be able to interpret it:
System::Windows::Forms::DialogResult d;
d=MessageBox::Show("Are you sure that you would like to use the airbag?”, "Important security warning", MessageBoxButtons::YesNo);
if (d == System::Windows::Forms::DialogResult::No) e->Cancel=true;
The result of executing the code portion:
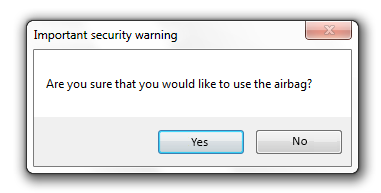
IV.2.22. Control used for timing: Timer
The Timer control makes it possible to run a code portion at given time intervals. It should be put under the form in the Designer, because it is not visible during execution. Its property named Interval contains the interval in milliseconds, and if the Enabled property is set to false, the timer can be disabled. If it is enabled and Interval contains a useful value (>=20 ms), the Timer executes its default event handler, the Tick. Progammers have to make sure that the code portion finish before the next event is occured (that is when time is out). The following code portion sets up the timer1 to run in every second:
timer1->Interval=1000; // every second timer1->Enabled=true; // go !
The programmed timer of the next code prints out the current time in seconds into the title of the form:
DateTime^ now=gcnew DateTime(); // variable of type time. now=now->Now; // what's the time? this->Text=Convert::ToString(now); // show in the title of the form.
This code portion can further be developed in order that it would play the cuckoo.wav sound file which is longer than one second: if (now->Minute==0) && (now->Second==0). If we think that the timer has already run enough times, int the Tick event handler the Enabled property can be set to false: at that case, the current event was the last.
IV.2.23. SerialPort
The SerialPort control makes possible the communication between a serial port of rs-232 standard and the peripherial devices connected to it (modem, SOC, microcontroller, Bluetooth device). The port has to be parameterized then opened. Then, textual information (Write, WriteLine, Read, ReadLine) and binary data (WriteByte, ReadByte) can be sent and received. It also has an event handler function: if data arrive, the DataReceived event is run. The following code portion checks all available serial ports, and searches the hardware named "iCorset" by sending a "?" character. If it is not found, it exits with an error message. In the case of virtual serial ports (USBs), the value of the BaudRate parameter can be anything.
array<String^>^ portnames;
bool there_is_a_controller=false;
int i;
portnames=Ports::SerialPort::GetPortNames();
i=0;
while (i<portnames->Length && (!there_is_a_controller))
{
if (serialPort1->IsOpen) serialPort1->Close();
serialPort1->PortName=portnames[i];
serialPort1->BaudRate=9600;
serialPort1->DataBits=8;
serialPort1->StopBits=Ports::StopBits::One;
serialPort1->Parity = Ports::Parity::None;
serialPort1->Handshake = Ports::Handshake::None;
serialPort1->RtsEnable = true;
serialPort1->DtrEnable = false;
serialPort1->ReadTimeout=200; // 0.2 s
serialPort1->NewLine="\r\n";
try {
serialPort1->Open();
serialPort1->DiscardInBuffer();// usb !
serialPort1->Write("?");
s=serialPort1->ReadLine();
serialPort1->Close();
} catch (Exception^ ex) {
s="Timeout";
}
if (s=="iCorset") there_is_a_controller=true;
i++;
}
if (! there_is_a_controller) {
MessageBox::Show("No iCorset Controller.",
"Error",MessageBoxButtons::OK);
Application::Exit();
}
IV.3. Text and binary files, data streams
The operative memory of a PC has a small size (as compared to the quantity of data to be stored) and forgets data easily: PC does not even have to be turned off, it is enough to exit a program, and the values of the variables stored in the memory are lost. That is why, even the first computers, manufactured after the ferrite-ring memory period, contained a data storage device that stored the software currently not in use or the data currently not used. The storage unit is the file which is a set of logically related data. It is the task of the operating system to connect a logical file to the physical organisation of the disk and to make them available for computer programs and to create and manage the file system. The programs using these files refer to them by their name. There are operations that process the content of the files and those that do not. For example, renaming or deleting a file does not require processing its content, it only requires its name. The name of the file may contain its path. If it does not contain it, the default path is the folder of the project during software development. When the .exe file, ready to be used, is run, the default folder is that of the .exe file.
IV.3.1. Preparing to handling files
Contrary to graphics or to controls, file handling namespace is not inserted in the form when a new project is created. This is the task of programmers to insert it at the beginning of the form1.h, where the other namespaces are:
using namespace System::IO;
Another thing to do is to decide what the file to be handled contains and what we would like to do with it:
-
Only deleting, renaming, copying it or checking whether it exists.
-
We would like to handle it by bytes (as a block containing bytes) if we are brave enough: virus detection, character encoding etc.
-
It is a binary file with fixed-length record structure.
-
If it is a text file with variable-length lines (Strings), and the lines end with line feed.
The file name can be given in two ways:
-
The file name is given in the code, therefore it is hard coded. If the file is only for the usage of programmer and it is always the same file, than this is a simple and rapid way of providing the name of the file.
-
Users can select the file by using OpenFileDialog or SaveFileDialog (see section Section IV.2.20). In this case, the name of the file is stored in the FileName property of these dialog boxes.
IV.3.2. Methods of the File static class
bool File::Exists(String^ filename) It examines the existence of the file given in filename, if it exists, the output is true if not, it is false. By using it we can avoid some errors: opening a non-existing file, overwriting an important data file by mistake.
void File::Delete(String^ filename) It deletes the file given in filename. As opposed to current operating systems, deletion does not mean moving to a recycle bin but a real deletion.
void File::Move(String^ oldname, String^ newname) It renames the disk file named oldname to newname. If there are different paths in the filenames, the file moves into the other directory.
void File::Copy(String^ sourcefile, String^ targetfile) This method is similar to Move, except that the source file does not disappear but the file is duplicated. A new file is created on the disk, with the content of the source file.
FileStream^ File::Open(String^ filename, FileMode mode) Opening the given file. The FileStream^ does not get its value with gcnew but with this method. It does not have to be used for text files but for all the other files (containing bytes or binary files containing records) opening should be used. The values of mode:
-
FileMode::Appendwe go to the end of the text file and switch to write mode. If the file does not exist, a new file is created. -
FileMode::Createthis mode creates a new file. If the file already exists, it is overwritten. In the directory of the path, the current user should have a right for writing. -
FileMode::CreateNewthis mode also creates a new file but if the file already exists, we get an exception. -
FileMode::Openopening an existing file for reading/writing. This mode is generally used after creating the file, e.g. after using the FileOpenDialog. -
FileMode::OpenOrCreatewe open an existing file, if it does not exist, a file with the given name is created. -
FileMode::Truncatewe open an existing file and delete its content. The length of the file will be 0 byte.
IV.3.3. The FileStream reference class
If files are processed by bytes or they are binary, we need to create a FileStream^ object for the file. The class instance of FileStream is not created by gcnew but by File::Open(), so the physical disk file and FileStream are assigned to each other. With the help of FileStream the actual file pointer is accessable, and it can be moved. The measure unit of the position and the movement is byte; its data type is 64 bit integer so that it should manage files bigger than 2GB. Its most frequently used properties and methods:
-
Length: read-only property, the actual size of the file in bytes.
-
Name: the name of the disk file that we opened.
-
Position: writable/readable property, the current file position in bytes. The next writing operation will write into this position, the next reading will read from here.
-
Seek(how much, with regard to what) method for movng the file pointer. With regard to the Position property, it can be given how we understand movement: from the beginning of the file (
SeekOrigin::Begin), from the current position (SeekOrigin::Current), from the end of the file (SeekOrigin::End). This operation must be used also when we attach BinaryReader or BinaryWriter to FileStream since they do not have aSeek()method. -
int ReadByte(),WriteByte(unsigned char)methods for reading and writing data of one byte. Reading and writing happens in the current position. At the level of the operating system, file reading is carried out into a byte array; these functions are realized as reading an array with one element. -
int Read(array<unsigned char>, offset, count): a method for reading bytes into a byte array. The bytes will be placed from the array’s element with the index offset and the count is maximum number of bytes to read. Its return value is: how many bytes could be read. -
Write(array<unsigned char>,offset, count): a method for writing a block of bytes from a byte array. Writing begins at at the element with the index offset and it writes maximum count elements. -
Flush(void): clears buffers for this stream and causes any buffered data to be written to the file. -
Close(): closing FileStream. Files should be closed after use in order to avoid data loss and running out of resources.
IV.3.4. The BinaryReader reference class
If we want to read non-byte type binary data from a file, we use BinaryReader. In the BinaryReader ‘s constructor we give the opened FileStream handle as an argument. BinaryReader is created with a regular gcnew operator. It is important to note that BinaryReader is not able to open the disk file and to assign it to a FileStream. BinaryReader contains methods for the basic data types: ReadBool(), ReadChar(), ReadDouble(), ReadInt16(), ReadInt32(), ReadInt64(), ReadUInt16(), ReadString(), ReadSingle() etc. The file pointer is incremented with the length of the read data. BinaryReader also should be closed after use with the method Close() before closing the FileStream.
IV.3.5. The BinaryWriter reference class
If we want to write binary data into FileStream, we use BinaryWriter. It is created similarly to BinaryReader, with the operator gcnew. The difference is that Reader contained methods with a given return data type but Writer contains a method with a given parameter and without a return value, with a number of overloaded versions. The name of the method is Write and it can be used with several data types: from Bool to cli::Array^ in the order of complexity. The overview of binary file processing can be seen below:
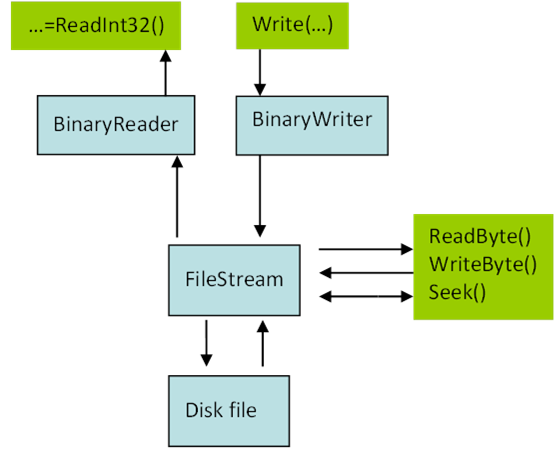
IV.3.6. Processing text files: the StreamReader and StreamWriter reference classes
Binary files that have been treated in the previous subsections are composed of fixed-length records. So a program can easily to calculate by a simple multiplication at which byte position the data to be searched for is and it can move the pointer to that position by the Seek() operation. For example if data are stored as 32-bit integers, each element occupies 4 bytes, the element having the index 10 (which actually is the 11th element) starts at the 10*4=40th byte position. In that case, as the file pointer can be moved anywhere, we speak about random access. Binary files can only be processed by a program which knows their record structure, which is in general, the program that created them.
Text files are composed of variable-length lines that are legible for human beings as well. In these files, characters are stored in ASCII, Unicode, UTF-8 etc. encoding, one line of a text file corresponds to the data type String^ of the compiler. Lines end with CR/LF (two characters) under DOS/Windows-based systems. Because of variable-length lines, text files can only be processed sequentially: reading the 10th line can be done by reading the first 9 lines and finally the requested 10th line. When the file is opened, it cannot be calculated at which byte the 10th line starts in the file, only after all preceding lines have been read.
Text files have an important role in realizing communication between different computer programs. Since they can be read for example in NotePad, humans can also modify their content. Text files are used, among other things, to save databases (in that case, a text file is called dump and it contains SQL statements that create the saved database on an empty system), to communicate with Excel (comma or tabulator separated files with CSV extension) and even e-mails are transferred as text files between incoming and outgoing e-mail servers. Measuring devices also create text files containing the measurement results. In these files, each line contains one measurement data in order that these data could be processed or visualized with any software (even with Excel) by a user carrying out the measurement.
Text files can be processed by reference variables of type StreamReader and StreamWriter classes. For that purpose, the gcnew operator should be used, and the name of the file should be specified in its constructor. A FileStream is not needed to be defined because StreamReader and StreamWriter use exclusively disk files; therefore they can create for themselves their own FileStream (BaseStream) with which programmers do not have to deal. The most frequently used method of StreamReader is ReadLine(), which reads the next line of the text file and its most frequently used property is EndOfStream, which becomes true accessing the end of the file. Attention: EndOfStream shows the state of the latest reading operation, ReadLine() returns a zero-length string at the end of the file, and the value of EndOfStream will be true. Thus, the ordinary pre-test loops can be used (while (! StreamReader->EndOfStream) …). One only has to examine if the length of the currently read line is greater than 0. The most frequently used method of StreamWriter is WriteLine(String), which writes the string passed as a parameter and `the newline character in the text file. Write(String) is the same but it does not write the newline character. The newline character(s) (CR,LF,CR/LF) can be set by the NewLine property.
The following code portion that does not function independently (i.e. without the helper functions and the initialisation parts) processes text files of CSV extension composed of semi-colon separated lines. The user is asked to select the file to be processed, the program reads the data line by line, calculates something from the read data and prints out the result at the end of the read line. After a file is processed, a total value is also calculated. Th program writes all outputs into a temporary file since the original text file is opened for reading. If data processing is done, the original file is deleted and the temporary file will receive the name of the original file. The result: the original text files will contain the results that have been calculated.
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
int m, credits, grade, creditsum = 0, gradesum = 0;
System::Windows::Forms::DialogResult dr;
String^ subject, ^line, ^outputstring = "";
openFileDialog1->FileName = "";
openFileDialog1->Filter = "CSV files (*.csv)|*.csv";
dr=openFileDialog1->ShowDialog(); // file open dialogbox, csv file
filename = openFileDialog1->FileName; // getting the file name
if (dr==System::Windows::Forms::DialogResult::OK ) // if it is not the Cancel button that was clicked
{
sr = gcnew StreamReader(filename); // open for reading
sw = gcnew StreamWriter(tmpname); // open the file for writing
while (!sr->EndOfStream) // always using a pre-test loop
{
line = sr->ReadLine(); // a line is read
if ((line->Substring(0,1) != csch) && (line->Length > 0))
// if it is not a separating character, it is processed
{
m = 0; // all lines are read from the first character
subject = newdata(line, m); // lines are split
credits = Convert::ToInt32(newdata(line, m)); // into 3 parts
grade = Convert::ToInt32(newdata(line, m));
// composing the output string
outputstring = outputstring + "subject:"+subject + " credits:" +
Convert::ToString(credits) +" grade:" +
Convert::ToString(grade) + "\n";
// and a weighted average is counted
creditsum = creditsum + credits;
gradesum = gradesum + credits * grade;
sw->WriteLine(line+csch+Convert::ToString(credits*grade));
} else { // is not processed but written back to the file.
sw->WriteLine(line);
} // if
} // while
sr->Close(); // do not forget to close the file
wa = (double) gradesum / creditsum; // otherwise the result is integer
// the previous line contained \n at its end, the result is written in a new line
outputstring = outputstring + "weighted average:" + Convert::ToString(sa);
label1->Text = outputstring;
sw->WriteLine(csch + "weighted average"+ csch + Convert::ToString(wa));
sw->Close(); // output file is also closed,
File::Delete(filename); // the old data file is deleted
// and the temporary file is renamed to the original data file.
File::Move(tmpname, filename);
}
}
IV.3.7. The MemoryStream reference class
One can also create sequential files, composed of bytes that are not stored on a disk but in the memory. A great advantage of streams created in the memory is the speed (a memory is at least two times faster than a storage device), its disadvantage is its smaller size and that its content is lost if the program is exited. MemoryStream has the same methods as FileStream: it reads/writes a byte or an array of bytes. It can be created by the gcnew operator. The maximal size of a MemoryStream can be set in the parameter of the constructor. If no parameter is given, MemoryStream will allocate memory dynamically for writing. Using that class has two advantages as compared to arrays: on one hand, automatic allocation and on the other hand, a MemoryStream can easily be transformed into a FileStream if memory runs out by using File::Open() instead of gcnew.
IV.4. The GDI+
The GDI Graphics Device Interface is a device independent (printer, screen) module of Windows systems used to develop and visualize 2D graphics (gdi.dll, gdi32.dll). The GDI+ is the improved version of this module that is also 2D and was introduced first in Windows XP and Windows Server 2003 operating systems (GdiPlus.dll). Newer Windows systems ensure the compatibility with programs developed with older versions, however, programmers can also use the optimized, inherited and new features of GDI+.
IV.4.1. The usage of GDI+
GDI+ was developed with object-oriented approach, that is, a 32/64 bit graphical programming interface which offers classes of C++ to draw in managed (.NET) as well as non-managed (native) programs. The GDI is not directly connected to the graphical hardware but to its driver. The GDI is capable of visualizing 2D vector-graphic illustrations, handling images and displaying textual information of publications in a flexible manner:
-
2D vector graphics: when making drawings, lines, curves and shapes bounded by these are defined by points given in coordinate system, and can be drawn with pens and painted with brushes..
-
Storing and displaying images: besides the flexible image storing and manipulating features, it offers the possibility to read and save a variety of image formats (BMP, GIF, JPEG, Exif, PNG, TIFF, ICON, WMF, EMFll).
-
Displaying texts: it is the task of GDI+ to visualize plenty of fonts on the screen as well as on the printer device.
The basic functions of GDI+ are contained in the System::Drawing namespace. Further options of 2D drawing can be reached using the elements of the
System::Drawing::Drawing2D
namespace.
The
System::Drawing::Imaging
namespace contains classes for handling images in an advanced level, whereas the
System::Drawing::Text
namespace ensures the special options of textual visualization
[4.1.]
.
IV.4.2. Drawing features of GDI
In order to use the basic functions of GDI+ in our program we have to use the System::Drawing namespace. (So that it can be reached the System.Drawing DLL file should be listed among the references Project / Properties / References: ).
using namespace System::Drawing;
The System::Drawing namespace contains the classes required for drawing (Figure IV.27). It is worth to highlight the Graphics class which is modelling the drawing area like it was a drawing paper. In order to draw on the drawing paper some data structures are required that are defined in the System::Drawing namespace. We can define on the drawing paper which coordinate system to use. The color model used by GDI+ is the alfa-r-g-b model (the Color structure), that is, colors can be mixed not only with the primary colors of red, green and blue but the level of transparency of the color can be set by the alfa parameter.
The integer type x and y coordinates of points can be stored in the Point structure, in case of real (float) coordinates PointF can be used. Similarly to the points the Rectangle and RectangleF structures can be used to store and access the corners of rectangles in a variety of ways. The Size and SizeF structures can be used to store the vertical and horizontal size of shapes.
Real drawing tools are modeled by classes. Our basic drawing tool is the pen (Pen class that cannot be inherited). We can set its color, width and pattern. The tool for painting planar shapes is the brush (Brush parent class). The derived classes of Brush are the SolidBrush that are modeling a brush dipped into a single color and the TextureBrush that leaves marks of a bitmap pattern. The HatchBrush paints a hatched pattern, whereas the LinearGradientBrush and PathGradientBrush leaves gradient marks. In order to use these latest classes the
System::Drawing::Drawing2D
namespace is required, too. The derived brushes cannot be inherited further. The Image abstract class has properties and member functions used to store and handle bitmaps and metafiles. The Font class contains various character forms, that is fonts. The FontFamily is the model of font families. Neither the Font nor the FontFamily classes cannot be inherited further. The Region class (cannot be inherited) is modelling an area of the graphic tool bounded by the sides of rectangles and paths. The Icon class serves to handle Windows icons (small size bitmaps).
IV.4.3. The Graphics class
Before getting familiar with the Graphics class, let’s have a few words about the Paint event of the controls. The graphic objects appearing in the windows have to be often redrawn for example when being repainted. This happens in a way that the Windows automatically invalidates the area that we would like to repaint and calls the handler function of the objects’ Paint event. In case we would like to refresh our drawing on top of the objects popup from the hiding, then we have to place the drawing methods of the Graphic class in the handler functions of the Paint event. The event handler of the Paint event has a PaintEventArgs type reference parameter that are defined by Windows when calling
[4.2.]
.
private: System::Void Form1_Paint(
System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e){ }
The PaintEventArgs class have two properties, the Rectangle type ClipRectangle that contains data of the area that we would like to repaint and the Graphics type read-only Graphics that identifies the drawing paper as a drawing tool when repainting.
Later, we will show in more details how to create Pen type pen for drawing with the gcnew operator and how to define its color by the constructor argument using the Color::Red constant of the System::Drawing namespace. Once we have our pen, then the Line() method of the Graphics class can draw lines with it (Figure IV.28).
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e){
Pen ^ p= gcnew Pen(Color::Red);
e->Graphics->DrawLine(p,10,10,100,100);
}
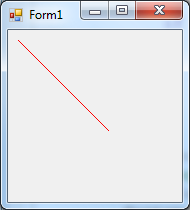
We can also initiate the repainting of windows and controls anywhere in the program. The Invalidate(), Invalidate(Rectangle) and Invalidate(Region) methods of the Control class invalidate the entire window / control or the selected area of them and activate the Paint event. The Refresh() method of the Control class invalidates the area of the window / control and initiates the repainting immediately.
We can draw on the window anywhere from the program if we create an instance of the drawing paper from the Graphics class with the CreateGraphics() method of the control / window. This time, however, the line drawn with the blue pen appears only once and will not be redrawn after hiding.
Pen ^ p= gcnew Pen(Color::Blue);
Graphics ^ g=this->CreateGraphics();
g->DrawLine(p,100,10,10,100);
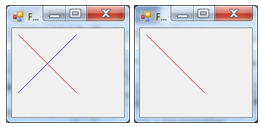
We can clear the given drawing paper with the defined background color by the
Clear(Color & Color);
method of the Graphics class.
IV.4.4. Coordinate systems
With the help of GDI+ we can think in three coordinate systems. We can create our model that we like to draw in 2D in the world coordinate system. It is useful to use such mapping that we could give these world coordinates to the drawing methods. Since the drawing methods of the Graphics class are able to receive the integer numbers (int) and floatingpoint real numbers (float) as parameters, that is why it is useful to store the world coordinates as int or float type too. We have to do ourselves the projection of 3D world to plane. The drawing paper modeled by the Graphics type reference uses the page coordinate system and it can be a form, an image storage or even a printer. It is the device coordinate system that a given tool uses (for example the left upper corner of the screen is the origin and the pixels are the units). Thus when drawing two mapping should happen:
world_coordinate → page_coordinate → device_coordinate
The first mapping have to be done by ourselves. We have more choices to obtain this. Spatial points can be projected to the plane in two ways, with parallel or central projection rays.
Projection with parallel ray is called axonometry. We can set up the mathematical model of projection by drawing the parallely projected image of x-y-z three-dimensional coordinate system to the planar sheet of the ξ-η coordinate system, assuming that the image of the three-dimensional coordinate system’s origin is the origin of the planar coordinate system. The image of x-y-z three-dimensional coordinate system appears with dashed lines in the ξ-η coordinate system drawn with solid lines (Figure IV.30). According to Figure IV.30 let’s mark the angle between ξ- and x-axes with α, the angle between ξ- and y-axes with β and the angle between η- and z-axes with γ! As the x-y-z coordinate axes are not parallel with the plane ξ-η, the image of coordinate units projected to the planar coordinate system seems to be shorter. The x-direction seems to be q x (≤1) long, the y-direction unit q y (≤1) and the z-direction unit q z (≤1) long.
Therefore, if we are looking for the planar, mapped coordinates (ξ,η) of a point with coordinates (x,y,z), then the pair of functions (f ξ , f η ) implements the mapping according to (IV.4.1).
|
|
(IV.4.1) |
Mapping can be described simply, if we consider that starting from the origin we are moving units x, y and z parallel to the images of the axes according to the shortenings, thus getting to the image (ξ, η) of point (x, y, z) (Figure IV.30). It follows that summarizing the projections of ξ and η with the red arrow, we get the coordinates as follows (IV.4.2).
|
|
(IV.4.2) |
A special type of axonometry is the isometric axonometry, when there is a 120° angle between the projections of x-y-z axes, the projection of z-axis coincides with η-axis (α=30, β=30, γ=0) and the shortenings are q x =q y =q z =1 (Figure IV.31).
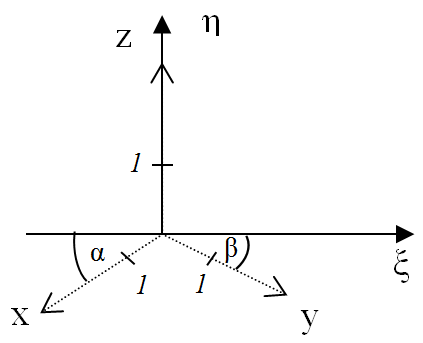
Another widely used axonometry is the Cavalier or military axonometry, where the horizontal y- axis coincides with the ξ-axis, the vertical z-axis coincides with the η-axis and there is a 135° angle between the projection of the x-axis and the other two axes (α=45, β=0, γ=0). The shortenings are q x =0,5, q y =q z =1.
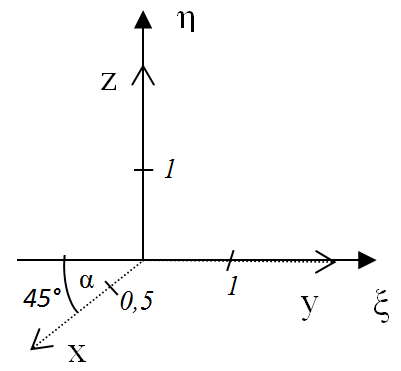
By default, the origin of the sheet’s 2D coordinate system – in case of form – is in the top left corner of the form’s active area, the x-axis is pointing to the right, while the y-axis is pointing down and the units are pixels in both axes (Figure IV.33).
Therefore, until any further actions are taken, the arguments of the already-known DrawLine() method of the Graphics class are values in this coordinate system.
As an example, let’s create the function producing the mapping of Cavalier axonometry. The input parameters of this function are the spatial coordinates (x, y, z), by substituting the constants of the Cavalier axonometry (IV.4.2) the function returns a PointF type sheet point.
PointF Cavalier(float x, float y, float z) {
float X = 0;
float Y = 0;
X=(-x*(float)Math::Sqrt(2)/2/2+y);
Y=(-x*(float)Math::Sqrt(2)/2/2+z);
return PointF(X, Y);
}
As an example, using the Cavalier() function and the DrawLine() method of the Graphics class, let’s draw in the Paint event handler a 100 units sided cube centred at point (250,250,250) illustrated in axonometry.
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
// the centre and the half side
float ox=250;
float oy=250;
float oz=250;
float d=50;
// The red pen
Pen ^p=gcnew Pen(Color::Red);
// The upper side
e->Graphics->DrawLine(p,Cavalier(ox-d,oy-d,oz-d),
Cavalier(ox+d,oy-d,oz-d));
e->Graphics->DrawLine(p,Cavalier(ox+d,oy-d,oz-d),
Cavalier(ox+d,oy+d,oz-d));
e->Graphics->DrawLine(p,Cavalier(ox+d,oy+d,oz-d),
Cavalier(ox-d,oy+d,oz-d));
e->Graphics->DrawLine(p,Cavalier(ox-d,oy+d,oz-d),
Cavalier(ox-d,oy-d,oz-d));
// The lower side
e->Graphics->DrawLine(p,Cavalier(ox-d,oy-d,oz+d),
Cavalier(ox+d,oy-d,oz+d));
e->Graphics->DrawLine(p,Cavalier(ox+d,oy-d,oz+d),
Cavalier(ox+d,oy+d,oz+d));
e->Graphics->DrawLine(p,Cavalier(ox+d,oy+d,oz+d),
Cavalier(ox-d,oy+d,oz+d));
e->Graphics->DrawLine(p,Cavalier(ox-d,oy+d,oz+d),
Cavalier(ox-d,oy-d,oz+d));
// The lateral edges
e->Graphics->DrawLine(p,Cavalier(ox-d,oy-d,oz-d),
Cavalier(ox-d,oy-d,oz+d));
e->Graphics->DrawLine(p,Cavalier(ox+d,oy-d,oz-d),
Cavalier(ox+d,oy-d,oz+d));
e->Graphics->DrawLine(p,Cavalier(ox+d,oy+d,oz-d),
Cavalier(ox+d,oy+d,oz+d));
e->Graphics->DrawLine(p,Cavalier(ox-d,oy+d,oz-d),
Cavalier(ox-d,oy+d,oz+d));
}
It is clearly shown in Figure IV.34 that axonometric mapping keeps distance in the given coordinate direction. Therefore, the back edge of the cube seems to have the same length as the front edge. However, using our eyes, we do not get this very same image. Our eyes perform central projection.
Central projection projects spatial points to the picture plane with the help of rays arriving at a certain point. In order to get the simple formulas of central projection, let’s suppose that we project the points of the spatial x-y-z coordinate system to the picture plane S parallel with x-y plane. Let’s mark the origin of the spatial x-y-z coordinate system with C. C will be the centre of projection. The orogin of ξ-η coordinate system in plane S should be O, and let it to be of d distance from C on the z-axis of the spatial coordinate system. The axes of ξ-η coordinate system of plane S are parallel with x- and y-axes (Figure IV.35). Let’s find the mapping of the central projection corresponding to (IV.4.1).

As shown in the graphic, let the distance of the origin and centre be d. Let x, y, z be the coordinates of a spatial point P and let the projection of this point be P * in the plane with coordinates ξ, η. The projection of point P to x-z plane is Pxz (of which distance from z-axis is coordinate x exactly), to y-z plane it is P yz (of which distance from z axis is coordinate y exactly). The projection of P xz in plane S is P * ξ , of which distance from the origin of the planar coordinate-system is coordinate ξ exactly, the projection of P yz in plane S is P * η of which distance from the zero point of the planar coordinate-system is coordinate η exactly. As triangle COP * ξ is similar to triangle CTP xz , therefore
|
|
(IV.4.3) |
that is
|
|
(IV.4.4) |
Similarly, in plane yz triangle CTP yz is similar to triangle COP η , therefore
|
|
(IV.4.5) |
that is
|
|
(IV.4.6) |
With this we generated (IV.4.1) mapping, as after rearranging we get
|
|
(IV.4.7) |
The problem with formulas in (IV.4.7) is that the mapping is not linear. We can make it linear by increasing the number of dimensions (from two to three), and we introduce homogeneous coordinates. Let’s have a four-dimensional point [x, y, z, 1] instead of the spatial point [x, y, z]. That is we are thinking in the w=1 three-dimensional subspace within the four-dimensional space of [x, y, z, w]. In this space the mapping of (IV.4.7) is
|
|
(IV.4.8) |
which is linear since it can be rewritten to form (IV.4.9).
|
|
(IV.4.9) |
As an example, let’s make the Perspective function performing the mapping of central projection. Input parameters are spatial coordinates (x, y, z). By giving the focal length d and using formulas (IV.4.4, IV.4.6), the function gives a PointF type sheet point.
PointF Perspective(float d, float x, float y, float z) {
float X = 0;
float Y = 0;
X = d * x / z;
Y = d * y / z;
return PointF(X, Y);
}
As an example, using the Perspective() function and the well-known DrawLine() method of the Graphics class, let’s draw in the Paint event handler a 100 units sided cube centred at point (150,150,150) illustrated in perspectiveaxonometry with f=150, f=450 and f=1050 focal lengths (Figure IV.36).
private: System::Void Form1_Paint(
System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
// the centre and the half side
float ox=150;
float oy=150;
float oz=150;
float d=50;
float f=350;
// The red pen
Pen ^p=gcnew Pen(Color::Red);
// The upper side
e->Graphics->DrawLine(p,Perspective(f,ox-d,oy-d,oz-d),
Perspective(f,ox+d,oy-d,oz-d));
e->Graphics->DrawLine(p,Perspective(f,ox+d,oy-d,oz-d),
Perspective(f,ox+d,oy+d,oz-d));
e->Graphics->DrawLine(p,Perspective(f,ox+d,oy+d,oz-d),
Perspective(f,ox-d,oy+d,oz-d));
e->Graphics->DrawLine(p,Perspective(f,ox-d,oy+d,oz-d),
Perspective(f,ox-d,oy-d,oz-d));
// The lower side
e->Graphics->DrawLine(p,Perspective(f,ox-d,oy-d,oz+d),
Perspective(f,ox+d,oy-d,oz+d));
e->Graphics->DrawLine(p,Perspective(f,ox+d,oy-d,oz+d),
Perspective(f,ox+d,oy+d,oz+d));
e->Graphics->DrawLine(p,Perspective(f,ox+d,oy+d,oz+d),
Perspective(f,ox-d,oy+d,oz+d));
e->Graphics->DrawLine(p,Perspective(f,ox-d,oy+d,oz+d),
Perspective(f,ox-d,oy-d,oz+d));
// The lateral edges
e->Graphics->DrawLine(p,Perspective(f,ox-d,oy-d,oz-d),
Perspective(f,ox-d,oy-d,oz+d));
e->Graphics->DrawLine(p,Perspective(f,ox+d,oy-d,oz-d),
Perspective(f,ox+d,oy-d,oz+d));
e->Graphics->DrawLine(p,Perspective(f,ox+d,oy+d,oz-d),
Perspective(f,ox+d,oy+d,oz+d));
e->Graphics->DrawLine(p,Perspective(f,ox-d,oy+d,oz-d),
Perspective(f,ox-d,oy+d,oz+d));
}
We can see the effect of focal length. Focal length-change behaves exactly the same as the objective of cameras. In case of small focal length there is a large viewing angle and strong perspective, in case of large focal length there is a small viewing angle and weak perspective.
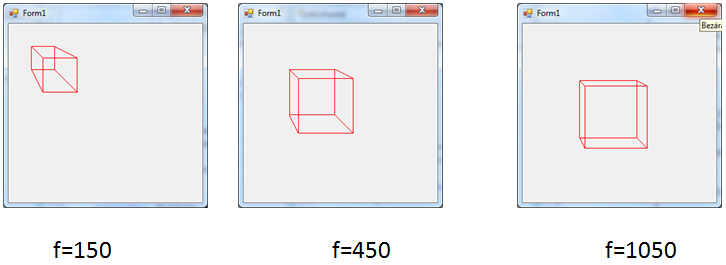
In the examples above we ensured that spatial coordinates are always projected to the plane, and we chose the centre and size of the cube in a way that it surely gets to the picture. The units of the cube’s data can be given either in mm, m or km. By drawing the cube to the form, the centres and the length of the edges were all given in pixels. However, by this we implicitly performed a zoon in/zoom out (mm->pixel, m->pixel or km->pixel). Based on the window sizes and the geometry to be displayed this should always be defined (Window-Viewport transformation
[4.3.]
). In GDI+ we can use the Transform property of the Graphics class to create coordinate transformation, thereby a Window-Viewport transformation can also be easily performed.
IV.4.5. Coordinate transformation
As we have seen the origin of the page coordinate system is the top left corner of the active area of the window, the x-axis points to the right, the y-axis points down and the units are pixels (Figure IV.33). The Transform property of the Graphics class is a reference pointing to an instance of the Matrix class. The Matrix class is defined on the System::Drawing::Drawing2D; namespace.
The Matrix class is the model of a transformation matrix of the 2D plane with homogeneous coordinates that contain 3x3 elements and its third column [0,0,1]T. The m
11
, m
12
, m
21
, m
22
mean the rotation and the scaling along the axes of the coordinate transformation, whereas d
x
, d
y
mean the translation (IV.4.10).
|
|
(IV.4.10) |
Transformation matrixes implement geometric transformations
[4.4.]
. Processing the geometric transformations one after the other results in one single geometric transformation. The transformation matrix of this is the first transformation matrix multiplied by the second transformation matrix from the left. Applying the geometric transformation matrixes one after the other is a non-commutative operation similarly to multiplying matrixes which is also non- commutative. We have to pay attention to this when assigning the Transform property. For defining the transformation we can use the methods of the Matrix class.
We can create a transformation matrix instance with the constructors of the Mátrix class. The
Matrix()
constructor activated without a parameter creates a three dimensional identity matrix. For example if we create an E identity matrix and we assign it to the Graphics->Trasform property, it will keep the coordinate system shown on Figure IV.33.
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Matrix ^ E=Matrix();
e->Graphics->Transform=E;
Pen ^ p= gcnew Pen(Color::Red);
e->Graphics->DrawLine(p,10,10,100,100);
}
We can achieve the same result with the void type Reset() method of the Matrix class:
Matrix ^ E=Matrix();
E->Reset();
We can define any transformation (that is linear in homogeneous coordinates) if we use one of the parametric constructors. As a definition of the transformation we can distort a rectangle into a parallelogram while moving it at the same time (Figure IV.37). In order to achieve this we can create the transformation with the following parametric constructor:
Matrix(Rectangle rect, array<Point>^ points)
The constructor creates such a geometric transformation that distorts the rect rectangle set as the parameter to a parallelogram (Figure IV.37). The points array contains three points. Respectively the first element is the upper left corner point of the parallelogram (ul), the second element is the upper right corner point (ur) and the lower left corner point is the third one (ll) (the place of the fourth point will be derived).
The DrawRectangle() method of the Graphics class draws a rectangle on the form with setting the pen, the starting coordinates, the width and the height. In the next example we will draw a rectangle of (10,10) starting points, 100 width and 100 height size values in red. With setting a transformation we modified the rectangle in a way that it was placed into (20,20) starting points, its height to be 200 and to be inclined 45 degrees. After this we drew the same rectangle in blue, and we can see the translation, the scaling and the shearing were applied.
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Pen ^ pen= gcnew Pen(Color::Red);
e->Graphics->DrawRectangle(pen,10,10,100,100);
array< PointF >^ p = {PointF(120,220), PointF(220,220),
PointF(20,20)};
Matrix ^ m = gcnew Matrix(RectangleF(10,10,100,100),p);
e->Graphics->Transform=m;
pen= gcnew Pen(Color::Blue);
e->Graphics->DrawRectangle(pen,10,10,100,100);
}
The transformation matrix can be set by elements (formula IV.4.7) as well using the other parametric constructor:
Matrix(float m11, float m12, float m21, float m22, float dx, float dy);
The next example uses a translaion (10, 10), double scaling in x-direction and 1.5x scaling in y-direction:
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Pen ^ pen= gcnew Pen(Color::Red);
e->Graphics->DrawRectangle(pen,0,0,100,100);
Matrix ^ m = gcnew Matrix(2,0,0,1.5,50,50);
e->Graphics->Transform=m;
pen= gcnew Pen(Color::Blue);
e->Graphics->DrawRectangle(pen,0,0,100,100);
}
Of course we can access the elements of the matrix using the (Array<float> type) Elements read only property of the Matrix class.
Fortunately we can create a transformation not only with setting the coordinates in the matrix but with the transformational methods of the Matrix class as well. We can apply the transformational functions to the instaces of the Matrix class as we multiplied the matrix of the current instance from the right or from the left by the matrix of the transformational method. The MatrixOrder type enumeration helps to control this and its members are MatrixOrder::Prepend (0, from the right) and MatrixOrder::Append (1, from the left).
We can directly multiply the instance of the class that contains the matrix by the given Matrix transformation matrix:
Multiply(Matrix matrix [,MatrixOrder order])
The square bracket means that it is not mandatory to set the MatrixOrder type order parameter. The default value of the order parameter is MatrixOrder::Prepend. We skip the explanation of the square brackets in case of the next methods.
We can define a translation and apply it on the matrix instance with the method:
Translate(float offsetX, float offsetY
[,MatrixOrder order]);
We can perform rotation transformation around the origin of the coordinate system with angle alfa
Rotate(float alfa [, MatrixOrder order])
or around a given point with alfa angle (set in degrees!);
RotateAt(float alfa, PointF point [,MatrixOrder order]);
Both methods are void methods.
The next example rotates a line around the midpoint of the form. In order to achieve this we have to know that the Size tpye ClientSize property of the form contains the dimensions of the client area.
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Matrix ^ m = gcnew Matrix();
Pen ^ p = gcnew Pen(Color::Red);
float x=this->ClientSize.Width/2;
float y=this->ClientSize.Width/2;
for (int i=0; i<360; i+=5) {
m->Reset();
m->Translate(x,y);
m->Rotate(i);
e->Graphics->Transform=m;
e->Graphics->DrawLine(p,0.0F,0.0F,
(float)Math::Min(this->ClientSize.Width/2,
this->ClientSize.Height/2),0.0F);
}
}
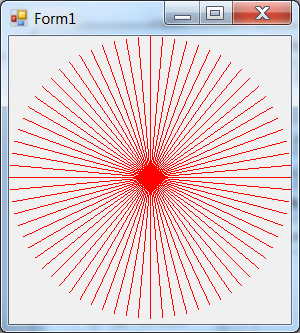
We can apply scaling (scaleX, scaleY) along the coordinate axes with a similar function:
Scale(float scaleX, float scaleY[, MatrixOrder order]);
Shearing along one of the coordinate direction means that the axis remains in place and as we move away from the axis parallel translation of the points along the fixed axis is proportional with the distance from the axis.
The transformation matrix contaning homogeneous coordinate of the shearing is:
|
|
(IV.4.11) |
We also have a function to define the shearing, where we can set the shearing coordinates of the matrix:
Shear(float mX, float mY, [, MatrixOrder order]);
In the next example we translate and shear a rectangle in both directions:
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Pen ^ pen= gcnew Pen(Color::Red);
e->Graphics->DrawRectangle(pen,0,0,100,100);
Matrix ^m=gcnew Matrix();
m->Translate(10,10);
m->Shear(2,1.5);
e->Graphics->Transform=m;
pen= gcnew Pen(Color::Blue);
e->Graphics->DrawRectangle(pen,0,0,100,100);
}
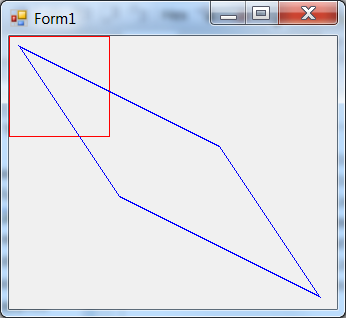
We can calculate the inverse of the transformation matrix with the void tpye method of the Matrix class:
Invert();
If we do not want to use the Transform property of the Graphics class then we can use directly the following methods of the Graphics class that directly modify the Transform property:
ResetTransform()
MultiplyTransform(Matrix m, [, MatrixOrder order]);
RotateTransform(float szog , [, MatrixOrder order])
ScaleTransform(float sx, float sy[, MatrixOrder order])
TranslateTransform Method(float dx, float dy
[, MatrixOrder order])
The Sheet transformation that maps sheets to a device can use the PageUnit and PageScale properties of the Graphics class in order to define the mapping. The PageUnit property can take a value of the System::Drawing::GraphicsUnit enumeration (UnitPixel=2, UnitInch=4, UnitMillimeter=6…).
For the example we set millimeter as a sheet unit. If the length of side of the square is 20 mm, then it will be also around 20 mm on the screen. If we set the float type PageScale property of the Graphics class then it will set our scaling on the sheet. For example if PageScale = 0.5 then the 20 mm sided square will become 10 mm (Figure IV.39).
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
e->Graphics->PageUnit=GraphicsUnit::Millimeter;
Pen ^ pen= gcnew Pen(Color::Red);
e->Graphics->DrawRectangle(pen,10,10,30,30);
e->Graphics->PageScale=0.5;
pen= gcnew Pen(Color::Blue);
e->Graphics->DrawRectangle(pen,10,10,30,30);
}
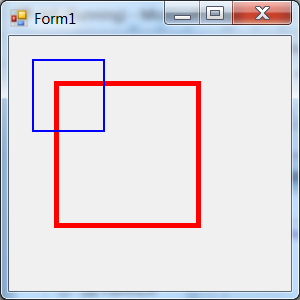
The GDI+ receives the screen resolution information from the driver and it can set the data of the mapping from here. The DpiX and DpiY read only properties contain the dot/inch resolution for the given device.
IV.4.6. Color handling of GDI+ (Color)
We use the Color structure to store GDI+ colors. This is nothing more than a 32-bit integer which each byte has a meaning (compared to traditional GDI colors where only 24 bits from the 32 coded colors). The 32-bit information is called ARGB color, the most significant byte (Alpha) shows the transparency, the rest 24 bits code the intensity of the GDI related Red, Green and Blue color components. (Alpha=0 is fully transparent, 255 is not transparent, the values for the color componenets indicate the intensity of them.) We can create a color structure with the FromArgb() method of the System::Drawing::Color structure. Calling the overloaded versions of the FromArgb() we can pass 3 integer (r, g and b) or 4 integer (a, r, g and b) arguments. In addition we can use more predefined normal colors Color::Red, Color::Blue etc. and system colors SystemColors::Control, SystemColors::ControlText etc.
The well-known application used to set the background color of the window shows well the usage/applicability of RGB colors. The background color of the window can be only an RGB color. Let us put three vertical sliders (scrollbars) to the form. The names (Name) should be red, green and blue respectively.
Let’s set their upper limit to 255 (not caring about the fact that the slider cannot go up to 255). The Scroll event of each should be the evet handler of the red, as it is apparent in the code generated by the Designer.
//
// red
//
this->red->Location = System::Drawing::Point(68, 30);
this->red->Maximum = 255;
this->red->Name = L"red";
this->red->Size = System::Drawing::Size(48, 247);
this->red->TabIndex = 0;
this->red->Scroll += gcnew
System::Windows::Forms::ScrollEventHandler(
this, &Form1::red_Scroll);
//
// green
//
this->green->Location = System::Drawing::Point(187, 30);
this->green ->Maximum = 255;
this->green ->Name = L"green";
this->green ->Size = System::Drawing::Size(48, 247);
this->green ld->TabIndex = 1;
this->green ->Scroll += gcnew
System::Windows::Forms::ScrollEventHandler(
this, &Form1::red_Scroll);
//
// blue
//
this->blue->Location = System::Drawing::Point(303, 30);
this->blue->Maximum = 255;
this->blue->Name = L"blue";
this->blue->Size = System::Drawing::Size(48, 247);
this->blue->TabIndex = 2;
this->blue->Scroll += gcnew
System::Windows::Forms::ScrollEventHandler(
this, &Form1::red_Scroll);
The event handler of the red slider’s Scroll event uses the position of all the three sliders to set the background color (Value property):
private: System::Void red_Scroll(System::Object^ sender,
System::Windows::Forms::ScrollEventArgs^ e) {
this->BackColor = Color::FromArgb(
red->Value, green->Value, blue->Value);
}
We will get familiar with the usage of transparent colors with the pen and brush drawing tools. The read only property of the Color structure, that is, the R, G and B (Byte type) properties contain the color components.
Byte r = this->BackColor.R;
IV.4.7. Geometric data (Point, Size, Rectangle, GraphicsPath)
We can create geometric objects with the Point, PointF and the Rectangle, RectangleF structures, and we can store the dimensions of rectangles within the Size, SizeF structures. The closing F letter refers to the float type of the structure’s data members. If the letter F is missing, then the data members are of type int.
IV.4.7.1. Storing dimensions
We can create Size structures with the
Size(Int32,Int32)
Size(Point)
SizeF(float,float)
SizeF(PointF)
constructors. The Height and Width properties of the Size and the SizeF structures (int and float) contain the height and width values of rectangles. The logical type IsEmpty property informs about if both size properties are set to 0 (true) or not (false).
With the size data we can perform operations with the methods of Size(F) structures. The Add() method adds the Width and Height values of Size type parameters, whereas Subtract() subtracts them.
static Size Add(Size sz1, Size sz2);
static Size Subtract(Size sz1, Size sz2);
We can compare the equality of two size structures with
bool Equals(Object^ obj)
According to the above methods there are defined the overloaded +, - and == operators of the Size(F) structures.
SizeF type values are rounded up to Size type with the Ceiling(), whereas the Round() method rounds in the usual way.
static Size Ceiling(SizeF value);
static Size Round(SizeF value);
The ToString() method converts the Size(F) structure to the form of a {Width=xxx, Height=yyy} string.
It is important to note that since the forms have a Size property, the Size type structure can be used only by defining the namespace. The following example writes the size values of the generated Size to the header of the form:
System::Drawing::Size ^ x= gcnew System::Drawing::Size(100,100); this->Text=x->ToString();
IV.4.7.2. Storing planar points
The Point, PointF structures are very similar to the Size structures with aspect their purpose, however they are defined to store point coordinates. Points can be created with the foolowing contructors:
Point(int dw);
Point(Size sz);
Point(int x, int y);
PointF(float x, float y);
In the first case the coordinate x is defined by the lower 16 bits of the parameter and the coordinate y is defined by the upper. In the second case x is defined by the Width property of the Size type parameter and y is defined by the Height property. The basic properties of the point structures are the X, Y coordinate values and the IsEmpty analysis.
We can perform point operations with the methods of the Point(F) structures. The Add() method adds the Width and Height values of the Size structure that was received also as a parameter, whereas Subtract() subtracts them.
static Point Add(Point pt, Size sz);
static Size Subtract(Point pt, Size sz);
We can investigate the equality of two Point type structures with the Equals() method:
virtual bool Equals(Object^ obj) override;
According to the above methods there are defined the overloaded +, - and == operators of the Point(F) structures.
A PointF type value rounds up to Point type the Ceiling() method, whereas the Round() method rounds in the usual way.
static Size Ceiling(SizeF value);
static Size Round(SizeF value);
The ToString() method converts the Point(F) structures to the form of a {X=xxx, Y=yyy} string.
IV.4.7.3. Storing planar rectangles
The Rectangle and the RectangleF structures are used to store the data of rectangles. Rectangles can be created with the
Rectangle(Point pt, Size sz);
Rectangle(Int32 x, Int32 y, Int32 width, Int32 height);
RectangleF (PointF pt, SizeF sz);
RectangleF(Single x, Single y, Single width, Single height);
constructors. The X, Y, the Left, Top and the Location properties of the Rectangle(F) structure contain the coordinates of the upper-left corner. The Height, Width and Size are the latitude and elevation dimensions of the rectangles, the Right and Bottom properties are the coordinates of the lower-right corner. The IsEmpty informs about whether our rectangle is real or not. The Empty is a rectangle with undefined data:
Rectagle Empty;
Empty.X=12;
We can create a rectangle (Rectangle, RectangleF) with the specified upper-left and lower-right corner coordinates:
static Rectangle FromLTRB(int left,int top,
int right,int bottom);
static RectangleF FromLTRB(float left, float top,
float right, float bottom)
The Rectangle structure offers a lot of methods to be used. From the RectanleF structure creates a Rectangle structure by rounding up the Ceiling() method, by normal rounding the Round() method and by cutting the decimal part the Truncate() method.
We can decide if the rectangle contains a point or a rectangle. With the methods of the Rectangle structure:
bool Contains(Point p);
bool Contains(Rectangle r);
bool Contains(int x, int y);
or the methods of the RectangleF structure:
bool Contains(PointF p);
bool Contains(RectangleF r);
bool Contains(single x, single y);
We can increase the area of the current Rectangle(F) by specifying the width and height data:
void Inflate(Size size);
void Inflate(SizeF size);
void Inflate(int width, int height);
void Inflate(single width, single height);
The following methods produce new, increased Rectangle(F) instances from existing rectangles:
static Rectangle Inflate(Rectangle rect, int x, int y);
static RectangleF Inflate(RectangleF rect, single x, single y);
We can move the top left corners of rectangles with the
void Offset(Point pos);
void Offset(PointF pos);
void Offset(int x, int y);
void Offset(single x, single y);
methods.
The
void Intersect(Rectangle rect);
void Intersect(RectangleF rect);
methods replace the current rectangle with the intersection of itself and the specified rectangle parameter. The static methods below produce new instance from the intersection of the Rectangle(F) type parameters:
static Rectangle Intersect(Rectangle a, Rectangle b);
static RectangleF Intersect(RectangleF a, RectangleF b);
We can also investigate if the currecnt rectangle intersects with an another with the
bool IntersectsWith(Rectangle rect);
bool IntersectsWith(RectangleF rect);
methods.
The methods
static Rectangle Union(Rectangle a, Rectangle b);
static RectangleF Union(RectangleF a, RectangleF b);
produce a new rectangle that bounds the union of two Rectangle(F) type parameters.
We can also apply for rectangles the
virtual bool Equals(Object^ obj) override
virtual String^ ToString() override
methods.
For the Rectangle(F) type elements can be used the == and != operators as well.
IV.4.7.4. Geometric shapes
The instances of the System::Drawing::Drawing2D::GraphicsPath class model an open or closed geometric shape (figure) constituted by a series of connected lines,curves and texts. This class cannot be inherited. A GraphicsPath object may be composed of any number connected graphic elements even of GraphicsPath objects (subpaths). The shapes have a starting point (the first point) and an ending point (the last point), their direction is typical. The shapes are not closed curves, even if their starting and the ending points are overlapped. We can create a closed shape with the CloseFigure() method. We can also fill the interior of shapes with the FillPath() method of the Graphics class. In this case a line connecting the start and endpoints closes the eventually unclosed shapes. The way of painting can be set for the self-intersecting figures. We can create shapes in a several ways using the constructors of the GraphicsPath class. The
GraphicsPath()
constructor creates an empty shape. We can cater for the future painting with the contructor:
GraphicsPath(FillMode fillMode)
The elements of the System::Drawing::Drawing2D::FillMode enumeration are Alternate and Winding as shown on the Figure IV.44. If the default Alternate element is set, the closed shape changes at each intersection, but with the Winding does not.

The figure defined by Point(F) type array (pts) can be created by the contructors:
GraphicsPath(array<Point>^ pts, array<unsigned char>^ types
[,FillMode fillmode]);
GraphicsPath(array<PointF>^ pts, array<unsigned char>^ types
[,FillMode fillmode]);
The types array is an array of PathPointType type elements, that defines a curvetype to every pts point . Its possible values are for example: Start, Line, Bezier, Bezier3, DashMode.
The properties of the GraphicsPath class are the PathPoints and PathType arrays, the PointCounts number of elements and the FillMode filling type. The PathData class is the encapsulation of PathPoints and PathType arrays, and its properties are the Points and Types.
We can append line sections and arrays of line sections to the figure with the methods:
void AddLine(Point pt1, Point pt2);
void AddLine(PointF pt1, PointF pt2);
void AddLine(int x1, int y1, int x2, int y2);
void AddLine(float x1, float y1, float x2, float y2);
void AddLines(array<Point>^ points);
void AddLines(array<PointF>^ points);
Polygons defined by the Point(F) type arrays can join the figure with the methods:
void AddPolygon(array<Point>^ points);
void AddPolygon(array<PointF>^ points);
We can add rectangles and array of rectangles to the figure with the methods:
void AddRectangle(Rectangle rect);
void AddRectangle(RectangleF rect);
void AddRectangles(array<Rectangle>^ rects);
void AddRectangles(array<RectangleF>^ rects);
We can add ellipses to the figure with the data of their bounding rectangles:
void AddEllipse(Rectangle rect);
void AddEllipse( RectangleF rect);
void AddEllipse(int x, int y, int width, int height);
void AddEllipse(float x, float y, float width, float height);
Elliptical arcs and the arrays of elliptical arcs can be added to the figures with the methods:
void AddArc(Rectangle rect, float startAngle, float sweepAngle);
void AddArc(RectangleF rect,
float startAngle, float sweepAngle);
void AddArc(int x, int y, int width, int height,
float startAngle, float sweepAngle);
void AddArc(float x, float y, float width, float height,
float startAngle, float sweepAngle);
An elliptical arc is always defined by the bounding rectangle, the start angle and the sweep angle.
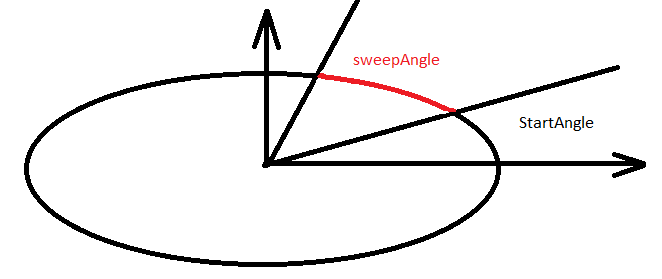
Pie is a shape defined by an arc of an ellipse and the two radial lines that intersect with the endpoints of the arc. These can be also added to the current figure with the methods:
void AddPie(Rectangle rect, float startAngle, float sweepAngle);
void AddPie(int x, int y, int width, int height,
float startAngle, float sweepAngle);
void AddPie(float x, float y, float width, float height,
float startAngle, float sweepAngle);
We can append Bezier curves to the figures.A Bezier curve of degree 3 is described by four points in the plane. The starting point is the first one, the ending point is the fourth one. The starting tangent is defined by the first and second point, the closing tangent is defined by the third and the fourth point in a way that the vector between the points is exactly three times of its derivative (Figure IV.46). The parametric equation [4.4.] contains the parametric description of the curve (IV.4.12).
|
|
(IV.4.12) |
The following methods can be used for adding cubic Bezier curves:
void AddBezier(Point pt1, Point pt2, Point pt3, Point pt4);
void AddBezier(PointF pt1, PointF pt2, PointF pt3, PointF pt4);
void AddBezier(int x1, int y1, int x2, int y2,
int x3, int y3, int x4, int y4);
void AddBezier(float x1, float y1, float x2, float y2,
float x3, float y3, float x4, float y4);
The following methods add a sequence of connected cubic Bezier curves to the current figure:
void AddBeziers(array<Point>^ points);
void AddBeziers(array<PointF>^ points);
The Points arrays contain the endpoints and the control points in a way that the first curve is defined by the first four points (Figure IV.46, equations IV.4.12), whereas each additional curve is defined by three additional points. The endpoint of the curve prior to the current curve is the startpoint. The two control points and one endpoint are the three points belonging to the current curve. If the previous curve was another one then its endpoint might also be the first point (order 0 continuous join). The DrawPath() method of the Graphics class draw the figure (Figure IV.47).
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
array<Point>^ pontok = {Point(20,100), Point(40,75),
Point(60,125), Point(80,100),
Point(100,150), Point(120,250),
Point(140,200)};
GraphicsPath^ bPath = gcnew GraphicsPath;
bPath->AddBeziers( pontok );
Pen^ bToll = gcnew Pen( Color::Red);
e->Graphics->DrawPath( bToll, bPath );
}
We can lay an interpolation curve to the series of points in a way that the curve passes through the points and in each point the tangent of the curve is proportional to the vector defined by the two neighbouring points, in this case the curve is called cardinal spline. Looking at the parametric description of the curve according to time we can say that at the time t k the curve passes through the point of P k (Figure IV.48). If the tangent of the curve is V k , at the time t k then the tangent is defined by the equation (IV.4.13).
|
|
(IV.4.13) |
where f(<1) is the tension of the curve. If f=0, then it is just the Catmull-Rom spline [4.4.] .
The (IV.4.14) equations contain the parametric description of the cardinal spline:
|
|
(IV.4.14) |
Az usual, at the edges the tangent is calculated by the one-sided difference and this way the curve passes through every point. The advantage of using cardinal splines is that there is no need to solve the system of equations, the curve passes through all the points. Its disadvantage however is that they can be derived continously only once.
The
void AddCurve(array<Point>^ points,
[[int offset, int numberOfSegments],
float tension]);
void AddCurve(array<PointF>^ points,
[[int offset, int numberOfSegments],
loat tension]);
methods add a cardinal spline to the figure. The points array contains the support points, the optional tension parameter contains the tension; and the optional offset parameter defines from which point we would like to consider the points in the points array. We can also set with the numberOfSegments parameter the number of the curve sections we want (that is, how long shall we consider the elements of the points array). By omitting the tension parameter (or setting it to 0), we can define a Catmull-Rom curve.
A closed cardinal spline is added to the figure with the methods:
void AddClosedCurve(array<Point>^ points, float tension);
void AddClosedCurve(array<PointF>^ points, float tension);
The following example lays a (Catmull-Rom) cardinal spline to the points of the previous example (Figure IV.49).
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
array<Point>^ pontok = {Point(20,100), Point(40,75),
Point(60,125), Point(80,100),
Point(100,150), Point(120,250),
Point(140,200)};
GraphicsPath^ cPath = gcnew GraphicsPath;
cPath->AddCurve( pontok);
Pen^ cToll = gcnew Pen( Color::Blue );
e->Graphics->DrawPath( cToll, cPath );
}
We can add text to the figure with the methods:
void AddString(String^ s, FontFamily^ family, int style,
float emSize, Point origin, StringFormat^ format);
void AddString(String^ s, FontFamily^ family, int style,
float emSize, PointF origin, StringFormat^ format);
void AddString(String^ s, FontFamily^ family, int style,
float emSize, Rectangle layoutRect,
StringFormat^ format);
void AddString(String^ s, FontFamily^ family, int style,
float emSize, RectangleF layoutRect,
StringFormat^ format);
The s parameter is the reference to the string to be printed out. We will talk about the features of letters and fonts later, for now we just share information that are necessary for our current example. The family reference contains the font family of the print out. We can create a similar one using the name of an already existing font family (see the next example). The style parameter is an element of the FontStyle enumeration (FontStyle::Italic, FontStyle::Bold …), the emSize is the vertical size of the rectangle enclosing the letter. We can define the location of the print out either with the Point(F) type origin parameter or with the Rectangle(F) layoutRect parameter. The format parameter is a reference to the instance of the StringFormat class, we can use the StringFormat::GenericDefault property.
The next example fits the GDI+ and Drawing words into a figure and draws it:
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
GraphicsPath^ sPath = gcnew GraphicsPath;
FontFamily^ family = gcnew FontFamily( "Arial" );
sPath->AddString("GDI+", family, (int)FontStyle::Italic,
20, Point(100,100),
StringFormat::GenericDefault);
sPath->AddString("drawing", family, (int)FontStyle::Italic,
20, Point(160,100),
StringFormat::GenericDefault);
Pen^ cToll = gcnew Pen( Color::Blue );
e->Graphics->DrawPath( cToll, sPath );
}
We can add a figure (addingPath) to the current figure instance with the method:
void AddPath(GraphicsPath^ addingPath, bool connect);
The connect parameter caters for making the two elements connected. The following exaple connects two wedges.
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
array<Point>^ tomb1 = {Point(100,100), Point(200,200),
Point(300,100)};
GraphicsPath^ Path1 = gcnew GraphicsPath;
Path1->AddLines( tomb1 );
array<Point>^ Tomb2 = {Point(400,100), Point(500,200),
Point(600,100)};
GraphicsPath^ Path2 = gcnew GraphicsPath;
Path2->AddLines( Tomb2 );
Path1->AddPath( Path2, true ); // false
Pen^ Toll = gcnew Pen( Color::Green);
e->Graphics->DrawPath( Toll, Path1 );
}
We can widen the figure creating an outline around the original lines (the same applies to the lines of the string characters) possibly at a given distance and after a given geometric transformation. This can be achieved with the method:
void Widen(Pen^ pen[, Matrix^ matrix[, float flatness]]);
The width of the pen parameter gives the distance between the existing lines and the new outline, and the optional matrix parameter defines a transformation before widening. The flatness parameter defines how accurately the outline follows the original curve (this can transform a circle into a polygon). The next example widens two circles while translating (Figure IV.52):
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
GraphicsPath^ Path = gcnew GraphicsPath;
Path->AddEllipse( 0, 0, 100, 100 );
Path->AddEllipse( 100, 0, 100, 100 );
e->Graphics->DrawPath( gcnew Pen(Color::Black), Path );
Pen^ widenPen = gcnew Pen( Color::Black,10.0f );
Matrix^ widenMatrix = gcnew Matrix;
widenMatrix->Translate( 50, 50 );
Path->Widen( widenPen, widenMatrix, 10.0f );
e->Graphics->DrawPath( gcnew Pen( Color::Red ), Path );
}
If we do not want to get a parallel outline but want to replace the figure with a sequence of connected line segments, then we can use the method:
void Flatten([Matrix^ matrix[, float flatness]]);
The interpretation of the parameters is the same as mentioned already when explaining the Widen() method.
We can apply transformations to the current figure with the method:
void Transform(Matrix^ matrix);
We can also distort the figure with the method:
void Warp(array<PointF>^ destPoints, RectangleF srcRect[,
Matrix^ matrix[, WarpMode warpMode[,
float flatness]]]);
In this case the srcRect rectangle is transformed to a quadrangle defined by the destPoints point array as if the plane were made from rubber. Moreover we can apply any geometric transformation using the optional matrix parameter. The warpMode optional parameter can be WarpMode::Perspective (this is the default one) and WarpMode::Bilinear as shown in the equation IV.4.15. We can also define the accuracy of the splitting into segments with the flatness optional parameter.
|
|
(IV.4.15) |
In the next example a text is distorted as defined by the related rectangle (black) and quadrangle (red) in a perspective method and translated.
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
GraphicsPath^ myPath = gcnew GraphicsPath;
RectangleF srcRect = RectangleF(10,10,100,200);
myPath->AddRectangle( srcRect );
FontFamily^ family = gcnew FontFamily( "Arial" );
myPath->AddString("Distortion", family, (int)FontStyle::Italic,
30,Point(100,100),StringFormat::GenericDefault);
e->Graphics->DrawPath( Pens::Black, myPath );
PointF point1 = PointF(200,200);
PointF point2 = PointF(400,250);
PointF point3 = PointF(220,400);
PointF point4 = PointF(500,350);
array<PointF>^ destPoints = {point1,point2,point3,point4};
Matrix^ translateMatrix = gcnew Matrix;
translateMatrix->Translate( 20, 0 );
myPath->Warp(destPoints, srcRect, translateMatrix,
WarpMode::Perspective, 0.5f );
e->Graphics->DrawPath( gcnew Pen( Color::Red ), myPath );
}
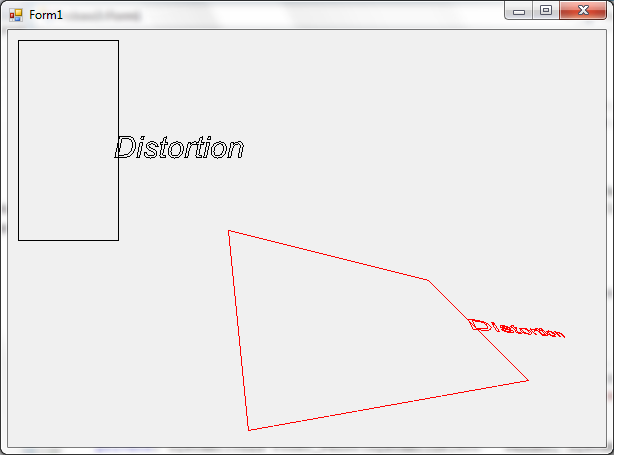
With the help of the GraphicsPathIterator class we can go through the points of the figure, we can set markers with the a SetMarker() method and we can slice the figure with the NextMarker() method. The ClearMarker() method removes the markers.
Within one figure we can define more subfigures that can be opened with the method:
void StartFigure();
We can make the figure closed by connecting the last and the first point by a line using the method:
void CloseFigure();
Each figure that is currently opened will be closed by the method:
void CloseAllFigures();
These last two methods start a new subfigure automatically.
The GetBounds() method gives back the bounding rectangle of the figure:
RectangleF GetBounds([Matrix^ matrix[, Pen^ pen]]);
The optional matrix parameter specifies a transformation to be applied to this path before the bounding rectangle is calculated. The width of the optional pen parameter will raise the size of the bounding rectangle on each side.
The
bool IsVisible(Point point[, Graphics ^ graph]);
bool IsVisible(PointF point[, Graphics ^ graph]);
bool IsVisible(int x, int y[, Graphics ^ graph]);
bool IsVisible(float x, float y[, Graphics ^ graph]);
methods will return true values, if the point of x and y coordinates or defined by the point parameter is contained within this figure. The optional graph parameter defines a drawing paper with a current clipping area, where we test the visibility (the concept of ClipRegion will be described in the next chapter).
The
bool IsOutlineVisible(Point point, Pen^ pen);
bool IsOutlineVisible(PointF point, Pen^ pen);
bool IsOutlineVisible(int x, int y, Pen^ pen);
bool IsOutlineVisible(float x, float y, Pen^ pen);
bool IsOutlineVisible(Point point, Pen^ pen
[, Graphics ^ graph]);
bool IsOutlineVisible(PointF point, Pen^ pen
[, Graphics ^ graph]);
bool IsOutlineVisible(int x, int y, Pen^ pen
[, Graphics ^ graph]);
bool IsOutlineVisible(float x, float y, Pen^ pen
[, Graphics ^ graph]);
methods will return true values if the point of x and y coordinates or defined by the point parameter is contained within (under) the outline of this figure. The optional graph parameter defines a drawing paper with a current clipping area, where we test the visibility
The
void Reverse();
method reverses the order of the points of the figure (in the PathPoints array property).
The
void Reset();
method deletes all the data of the figure.
IV.4.8. Regions
The region class (System::Drawing::Region) models the interior area of a graphics shape composed of rectangles and closed paths (contour), this way the area of the region might be of a complex shape.
We can create instances of the region using the following constructors:
Region();
Region(GraphicsPath^ path);
Region(Rectangle rect);
Region(RectangleF rect);
Region(RegionData^ rgnData);
If we do not define any parameter, then an empty region will be created. The path and the rect parameters define the initial shape of the region.
We can set the clipping region with the methods of the Graphics class:
void SetClip(Graphics^ g[, CombineMode combineMode]);
void SetClip(GraphicsPath^ path[, CombineMode combineMode]);
void SetClip(Rectangle rect[, CombineMode combineMode]);
void SetClip(RectangleF rect[, CombineMode combineMode]);
void SetClip(Region^ region, CombineMode combineMode);
This way our shape can be used as a special picture-frame. The geometry of the picture-frame is defined by the picture-frame of another drawing paper (parameter g), the figure (path), the rectangle (rect) or the region (region). The combineMode parameter (optional for all methods except for the last) may have the values of the of the CombineMode enumeration:
-
The
Replace(the currecnt clipping region (picture-frame) is replaced by the given geometry parameter G), -
Intersect(the current picture-frame – R – intersects with the given geometry – G: ), -
Union(union with the given geometry ), -
Xor(symmetric difference with the given geometry ), -
Exclude(the difference between the existing and the given region ) and -
Complement(the difference between the given and the existing region ).
Windows can use a region to refresh the drawing.
The RegionData class contains a byte array in the Data property and this array describes the data of the region.
The
RegionData^ GetRegionData()
method returns an instance of the RegionData class, which describes to the current region. The
array<RectangleF>^ GetRegionScans(Matrix^ matrix)
method approximates the selected region with the array of rectangles. The matrix parameter contains the matrix of a previous transformation.
The
void MakeEmpty()
method turns the current region into an empty one, whereas the
void MakeInfinite()
method turns the current region to an infinite one.
We can perform operations with the regions. As the result of the query of the following methods
void Complement(Region^ region);
void Complement(RectangleF rect);
void Complement(Rectangle rect);
void Complement(GraphicsPath^ path);
the current region will be the intersection of the geometry defined as parameter and the complementer of the current region. That is, the current region will be the difference of the geometry and the current region. (Let’s have R as the set of the points of the current region, and G to be the set of the given geometry, then we can describe this operation as ).
With the
void Exclude(Region^ region);
void Exclude(RectangleF rect);
void Exclude(Rectangle rect);
void Exclude(GraphicsPath^ path);
methods the current region will be the intersection of the current region and the complementer of the shape defined as parameter, that is, the result will be the difference of the current region and the given geometry ().
With the
void Intersect(Region^ region);
void Intersect(RectangleF rect);
void Intersect(Rectangle rect);
void Intersect(GraphicsPath^ path);
methods the current region will be the intersection of itself and the geometry defined as parameter ().
With the
void Union(Region^ region);
void Union(RectangleF rect);
void Union(Rectangle rect);
void Union(GraphicsPath^ path);
methods the current region will be the union of itself and the geometry defined as parameter ().
With the
void Xor(Region^ region);
void Xor(RectangleF rect);
void Xor(Rectangle rect);
void Xor(GraphicsPath^ path);
methods the current region will contain only those points that were only in one of the geometries. That geometry can be achieved by removing the intersection of the current region and the given geometry from the union of the current region and the given geometry (symmetric difference ).
We can transform the region with a transformation matrix or with given translation coordinates:
void Transform(Matrix^ matrix);
void Translate(int dx, int dy);
void Translate(float dx, float dy);
We can examine if a point is included in the current region with the methods:
bool IsVisible(Point point[, Graphics gr]);
bool IsVisible(PointF point[, Graphics gr]);
bool IsVisible(float x, float y);
bool IsVisible(int x, int y[, Graphics gr]);
We can decide if rectangles intersect with the current region using the methods:
bool IsVisible(Rectangle rect[, Graphics gr]);
bool IsVisible(RectangleF rect[, Graphics gr]);
bool IsVisible(int x, int y, int width, int height
[, Graphics gr]);
bool IsVisible(float x, float y, float width, float height
[, Graphics gr]);
In both cases the we can define the drawing paper with the optional Graphics type parameter.
The
bool IsEmpty(Graphics^ g);
method tests if the current region is empty or not, whereas the
bool IsInfinite(Graphics^ g);
method tests if it is infinite or not.
The following example creates a figure using text and defines a clipping region before to draw the figure:
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
GraphicsPath^ sPath = gcnew GraphicsPath;
FontFamily^ family = gcnew FontFamily( "Arial" );
sPath->AddString("Clipped text", family, (int)FontStyle::Italic,
40,Point(0,0),StringFormat::GenericDefault);
System::Drawing::Region ^ clip = gcnew System::Drawing::Region(
Rectangle(20,20,340,15));
e->Graphics->SetClip(clip, CombineMode::Replace);
e->Graphics->DrawPath( gcnew Pen(Color::Red), sPath );
}
IV.4.9. Image handling (Image, Bitmap, MetaFile, Icon)
There are two basic strategies to store images. In the first case the image is stored in a way like it was drawn with a pencil. In this case the storage of the image data happens in a way that the data of the line segments needed to draw the image (vectors) are stored and based on these we can draw the picture. This method of storage is called vector image storage. Figure IV.55 shows the vectorial drawing of capital A.

We also have the possibility to divide the image into pixels (raster points) and to store the color of each and every pixel. This rasterized picture is called bitmap considering its similarity to maps. Figure IV.56 shows the black and white bitmap of the capital A.
The Image is an abstract image storing class. It is the parent of the rasterized System::Drawing::Bitmap and vectorial System::Drawing::Imaging::MetaFile classes that contain Windows drawings. In order to create Image objects we can use the static methods of the Image class and with these we can load images from the given files (filename).
static Image^ FromFile(String^ filename
[, bool useEmbeddedColorManagement]);
static Image^ FromStream(Stream^ stream
[, bool useEmbeddedColorManagement
[, bool validateImageData]]);
If the useEmbeddedColorManagement logical variable is true then the color handling information of the file is used by the method, otherwise not (the true value is the default one). In case of stream the validateImageData logical variable controls the data check of the image. Data check works by default. We can also use the old GDI bitmaps with the FromHbitmap() method.
We can draw the loaded bitmaps with the Graphics::DrawImage(Image,Point) method. The next example loads the image of the Visual Studio development environment to the form (Figure IV.57).
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Image^ kep = Image::FromFile( "C:\\VC++.png" );
e->Graphics->DrawImage( kep, Point(10,10) );
}
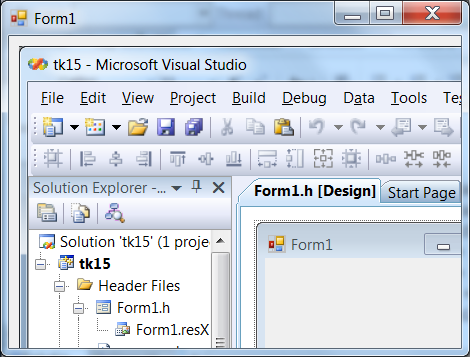
Properties of the Image class store the data of the image. The int type Width and Height read only properties define the width and the height of the image in pixels. The Size structure type Size ready only property also stores the size data. The float type HorizontalResolution and VerticalResolution properties define the resolution of the image in pixel/inch dimension. The SizeF structure type PhisicalDimension read only property defines the real size of the image, in case of bitmap it is defined in pixels whereas in case of metafile picture it is defined in 0.01 mm units.
With the ImageFormat class type RawFormat property we can specify the file format of the image, which can be used when storing the image. The Bmp property of the
ImageFormat
class specifies a bitmap, the Emf specifies an extended metafile, the Exif specifies an exchangeable image file. We can use the Gif property for the standard image format (Graphics Interchange Format). The Guid property contains the global object identifier applied by Microsoft. We can use the Icon property for the Windows icons. The Jpeg property specifies the format of the JPEG (Joint Photographic Experts Group) standard, the MemoryBmp property specifies the format of the memory bitmaps and the Png property belongs to PNG format of W3C (World Wide Web Consortium
[4.5.]
) for transmission of graphical elements through the network (Portable Network Graphics). The Tiff property specifies the format of the TIFF (Tagged Image File Format) standard, whereas the Wmf property specifies the format of the Windows metafiles.
The bits of the int type Flags property specifies the attributes of the pixel data stored in the image (color handling, transparency, enlargement etc.). Some constants adequate for a typical bit state are the ImageFlagsNone (0), the ImageFlagsScalable (1), the ImageFlagsHasAlpha (2) and the ImageFlagsColorSpaceRGB (16).
Images can store their colors in the color palette related to the image. The ColorPaletteClass type Palette property is nothing but a color array (array<Color>^ Entries) that contain the colors. The ColorPaletteClass also has a Flags property. The interpretation of this by bits is as follows: the color contains alpha information (1), the color defines a grayscale (2), the color gives the so called halftone
[4.6.]
information when the colors percieved by human eyes as grayscale are built from black and white elements (Figure IV.58).
The bounds of the picture defined in the given graphical units returns the method:
RectangleF GetBounds(GraphicsUnit pageUnit);
The
static int GetPixelFormatSize(PixelFormat pixfmt);
method defines how the image is stored, this can be a palette index or the value of the color itself. Some possible values: Gdi – the pixel contains GDI color code (rgb), Alpha – the pixel contains trasnparency information too, Format8bppIndexed – index, 8 bits per pixel color(256 colors).
With the following methods we can query if the image is transparent
static bool IsAlphaPixelFormat(PixelFormat pixfmt);
if the pixel format of the image is 32 bits
static bool IsCanonicalPixelFormat(PixelFormat pixfmt);
if the pixel format of the image is 64 bits
static bool IsExtendedPixelFormat(PixelFormat pixfmt);
With the
void RotateFlip(RotateFlipType rotateFlipType);
method we can rotate and flip the image according to the elements of the RotateFlipType enumeration (e.g Rotate90FlipNone rotates with 90 degrees and does not do flipping, RotateNoneFlipX flips to the y axis, Rotate90FlipXY rotates with 90 degrees and flips centrally).
The next example displays the image of Figure IV.57 form flipping it to the y axis:
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Image^ kep = Image::FromFile( "C:\\VC++.png" );
kep->RotateFlip(RotateFlipType::RotateNoneFlipX);
e->Graphics->DrawImage( kep, Point(10,10) );
}
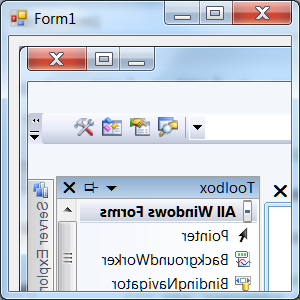
We can save the images into files with the
void Save(String^ filename[,ImageFormat^ format]);
method. The filename parameter contains the name of the file, the file extension depends on the extension in the filename. We can define the saving format with the optional format parameter. If there is no coding information defined for the file formats (like e.g. Wmf) then the method saves into Png format.
We can also save the data of the image into a stream with the method:
void Save(Stream^ stream, ImageFormat^ format);
While the Bitmap is the descendant of the Image class, it inherits all the properties and functions of the Image, however the data structure of the Bitmap corresponds to method of storing data in the memory, which gives the possibility to use a set of special methods as well. The Bitmap class have constructors and with their help we can create a bitmap from Image, from Stream, from a file, moreover from any graphics or from pixel data stored in the memory.
The following constructor creates an empty bitmap with given size (width, height parameters):
Bitmap(int width, int height[,, PixelFormat format]);
if we use the PixelFormat type format parameter, then we can specify the color depth as we could see it at the Image::GepPixelFormat() method.
The
Bitmap(Image^ original);
Bitmap(Image^ original, Size newSize);
Bitmap(Image^ original, int width, int height);
constructors create a bitmap from the Image defined as parameter. If we define the newSize parameter or the width and height parameters, then the bitmap is created with the rescaling of the image to the new size.
With the
Bitmap(Stream^ stream[, bool useIcm]);
overloaded constructor we can create a bitmap from a stream, and with the
Bitmap(String^ filename[, bool useIcm]);
overloaded constructor we can create it from a file. If we use the useIcm logical parameter, then we can specify whether to use color correction or not.
We can create a bitmap of any Graphics instance, for example of the screen with the
Bitmap(int width, int height, Graphics^ g);
constructor. The integers of width and height define the size, the g parameter define the instance of the drawing paper, the DpiX and DpiY properties of this define the bitmap resolution. We can also create a bitmap from the memory referenced by the scan0 pointer that points to the integer, if we set the width, the height and the stride (difference between two bitmap rows) in bytes:
Bitmap(int width, int height, int stride,
PixelFormat format, IntPtr scan0);
The resolution of a newly created bitmap can be set with the method:
void SetResolution(float xDpi, float yDpi);
The xDpi and yDpi parameters are in dot per inch units.
Some methods not inhereted from the Image class can supplement the opportunities offered by bitmaps. We can reach one point of the bitmap directly. The color of the given pixel (x, y) is returned by the method:
Color GetPixel(int x, int y);
We can set the color of the specified pixel with the method:
void SetPixel(int x, int y, Color color);
The
void MakeTransparent([Color transparentColor]);
function makes the default transparent color transparent for this Bitmap. If we also define the transparentColor parameter, then this color will be transparent.
The next example loads a bitmap and draws it. After it the points of the bitmap colored to a color that is close to white will be painted green and then the program draws the modified bitmap. In the next step it makes the green color transparent and draws the bitmap again moved with half of the size (Figure IV.60).
private: System::Void Form1_Click(System::Object^ sender,
System::EventArgs^ e) {
Bitmap ^ bm = gcnew Bitmap("C:\\D\\X.png");
Graphics ^ g = this->CreateGraphics();
g->DrawImage( bm, Point(0,0) );
Color c;
for (int i=0; i<bm->Width; i++) {
for (int j=0; j<bm->Height; j++) {
Color c=bm->GetPixel(i,j);
if ((c.R>200)&&(c.G>200)&&(c.B>200))
bm->SetPixel(i,j,Color::Green); }
}
g->DrawImage( bm, Point(bm->Width,bm->Height) );
}
Bitmap handling with the GetPixel() and SetPixel() methods is not effective enough. We have the option to load the bits of the bitmap into the memory and to modify them, then we can pump the bits back to the bitmap. In this case we need to ensure that the operating system does not disturb our actions. In order to store the bitmaps in the memory we can use the function:
BitmapData^ LockBits(Rectangle rect, ImageLockMode flags,
PixelFormat format[, BitmapData^ bitmapData]);
void UnlockBits(BitmapData^ bitmapdata);
Where the rect parameter selects the part of the bitmap we would like to store, the enumeration type ImageLockMode flags parameter defines the way of data handling (ReadOnly, WriteOnly, ReadWrite, UserInputBuffer). We are already familiar with the PixelFormat enumeration. The BitmapData class type bitmapdata optional parameter has the properties: Height and Width are the size of the bitmap, the Stride is the width of the scanline, whereas scan0 is the address of the first pixel. The returned value contains the data of the bitmap in an isntance of the BitmapData reference class.
After calling the function the bitmapdata is locked and it can be manipulated with the methods of the
System::Runtime::InteropServices
::Marshal class. With the methods of the Marshal class we can allocate a non-managed memory block, we can copy the non-managed memory blocks, or we can copy managed memory objects to a non-managed memory area. For example the
static void Copy(IntPtr source,
array<unsigned char>^ destination,
int startIndex, int length);
method of the Marshal class copies length bytes from the startIndex position of the memory area pointed by the source pointer to the destination managed array, whereas the
static void Copy(array<unsigned char>^ source,
int startIndex,
IntPtr destination, int length);
method copies length bytes in reverse order from the source managed array from the startindex position to the destination non-managed area.
Once we copied the parts from the bitmap that we intended to modify, we modified them and copied them back, then we can unlock the locked memory with the method:
void UnlockBits(BitmapData^ bitmapdata);
The following example draws a managed bitmap that was loaded to the memory when clicking on the form. After it locks it, copies the bytes of the image, erases the middle third of the image, stores the data back into the bitmap, unlocks the memory and draws the bitmap.
private: System::Void Form1_Click(System::Object^ sender,
System::EventArgs^ e) {
Bitmap ^ bm = gcnew Bitmap("C:\\D\\X.png");
Graphics ^ g = this->CreateGraphics();
g->DrawImage( bm, Point(0,0) );
Rectangle rect = Rectangle(0,0,bm->Width,bm->Height);
System::Drawing::Imaging::BitmapData^ bmpData = bm->LockBits(
rect, System::Drawing::Imaging::ImageLockMode::ReadWrite,
bm->PixelFormat );
IntPtr ptr = bmpData->Scan0;
int bytes = Math::Abs(bmpData->Stride) * bm->Height;
array<Byte>^Values = gcnew array<Byte>(bytes);
System::Runtime::InteropServices::Marshal::Copy( ptr, Values, 0, bytes );
for ( int counter = Values->Length/3; counter < 2*Values->Length/3; counter ++ )
{
Values[ counter ] = 255;
}
System::Runtime::InteropServices::Marshal::Copy( Values, 0,
ptr, bytes );
bm->UnlockBits( bmpData );
g->DrawImage( bm, bm->Width, 0 );}
We can also work with metafiles because we can use the methods of the Image class. The next example loads a Png file into a bitmap and saves it as a Wmf metafile.
private: System::Void Form1_Click(System::Object^ sender,
System::EventArgs^ e) {
Bitmap ^ bm = gcnew Bitmap("C:\\D\\X.png");
Graphics ^ g = this->CreateGraphics();
g->DrawImage( bm, bm->Width, 0 );
bm->Save("C:\\D\\X.wmf");
}
IV.4.10. Brushes
Brushes can be used to paint areas in GDI+
[4.1.]
. Each brush type is a descendant of the System::Drawing::Brush class (Figure IV.27). The simplest brush is of a single color (SolidBrush). The constructor of this creates a brush from the given color. Accordingly the Color property of the class picks up the color of the brush.
SolidBrush(Color color);
The following example paints a red rectangle on the form with the FillRectangle() method of the Graphics class (Figure IV.62).
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
SolidBrush ^ sb = gcnew SolidBrush(Color::Red);
e->Graphics->FillRectangle(sb,200,20,150,50);
}
HatchBrush, the patterned brush is also a descendant of the Brush class and it is defined in the System::Drawing::Drawing2D namespace, that is why it is necessary to specify:
using namespace System::Drawing::Drawing2D;
The constructor of the patterned brush defines the pattern of the brush, the color of the pattern and the background. If we omit the last parameter (squared brackets mark the optional parameters), then the background color will be black:
HatchBrush(HatchStyle hatchstyle, Color foreColor,
[Color backColor])
The HatchStyle enumeration of the Drawing2D namespace contains a lot of predefined patterns. The horizontal one is the HatchStyle::Horizontal, the vertical one is Vertical, the diagonal one (leaning to the left) is the ForwardDiagonal etc. The next example paints a yellow rectangle with a red diagonal-hatched brush (Figure IV.62).
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
HatchBrush ^ hb = gcnew HatchBrush(HatchStyle::ForwardDiagonal,
Color::Red,Color::Yellow);
e->Graphics->FillRectangle(hb,200,80,150,50);
}
The characteristic properties of the patterned brushes are the BackGroundColor for the color of the background, the ForegroundColor for the color of the foreground and HatchStyle for the pattern type.
We can create brushes painting with images using the instances of the TextureBrush class. These are its constructors:
TextureBrush(Image^ image);
TextureBrush(Image^ image, WrapMode wrapMode);
TextureBrush(Image^ image, Rectangle dstRect);
TextureBrush(Image^ image, RectangleF dstRect);
TextureBrush(Image^ image, WrapMode wrapMode,
Rectangle dstRect);
TextureBrush(Image^ image, WrapMode wrapMode,
RectangleF dstRect);
TextureBrush(Image^ image, Rectangle dstRect,
ImageAttributes^ imageAttr);
TextureBrush(Image^ image, RectangleF dstRect,
ImageAttributes^ imageAttr);
The image defines the picture used for painting, the dstRect defines the distortion of the picture when painting. The wrapMode parameter specifies how the images used for painting are tiled. (The members of the WrapMode enumeration: Tile – as if it was built from tiles, TileFlipX – built from tiles mirrored to the y axis, TileFlipY - built from tiles mirrored to the x axis, TileFlipXY – built from centrally mirrored tiles, Clamped – the texture is not built from tiles). The
System::Drawing::Imaging
::ImageAttributes^ type imageAttr contains additional information about the image (colors, color corrections, painting methods etc).
The Image (Image^ type) property of the TextureBrush class defines the graphics of the painting, the Transform^ type Transform property and its methods can be used similarly to their usage already discussed for transformations. The WrapMode property contains the arrangement.
The following example paints a rectangle with images (Figure IV.62).
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Image ^ im = Image::FromFile("c:\\M\\mogi.png");
TextureBrush ^ tb = gcnew TextureBrush(im);
Matrix ^ m= gcnew Matrix();
m->Translate(5,5);
tb->Transform->Reset();
tb->Transform=m;
Graphics ^ g = this->CreateGraphics();
g->FillRectangle(tb, 200, 140, 150, 50);
}
The Drawing2D namespace contains the LinearGradientBrush class. With its constructors we can create gradient brushes. With the various constructors we can set different gradient types. The System::Windows::Media::BrushMappingMode enumeration defines a coordinate systems for the gradient effect. The elements of this enumertion are Absolute and RelativeToBoudingBox. The Absolute means the points are interpreted in the current coordinate system. When the RelativeToBoudingBox is set, the top left corner of the bounding rectangle of the given painting will be (0,0), whereas the bottom right corner will be (1,1).
The linear gradient brushes can be created with different constructor calls. Using the constructors
LinearGradientBrush(Rectangle rect,
Color startColor, Color endColor,
double angle, [isAgleScaleable]);
LinearGradientBrush(RectangleF rect,
Color startColor, Color endColor,
double angle, [isAgleScaleable]);
we can set the starting color (startColor) and the ending color (endColor). In the RelativeToBoudingBox brush coordinate system the angle of the gradient is given in degrees (0 is a horizontal gradient, 90 is vertical).
Using the following constructors
LinearGradientBrush(Point startPoint, Point endPoint,
Color startColor, Color endColor);
LinearGradientBrush(PointF startPoint, PointF endPoint,
Color startColor, Color endColor);
LinearGradientBrush(Rectangle rect,
Color startColor, Color endColor
LinearGradientMode lgm);
LinearGradientBrush(RectangleF rect,
Color startColor, Color endColor,
LinearGradientMode lgm);
we can set the starting color (startColor) and the ending color (endColor) too. In the RelativeToBoudingBox brush coordinate system we can set the angle of the gradient with the points startPoint and endPoint or with the corners of rect in the units of %. The elements of the LinearGradientMode enumeration (Horizontal, Vertical, ForwardDiagonal, BackwardDiagonal) define the direction of the color transition.
With the
PathGradientBrush(GraphicsPath path);
PathGradientBrush(Point[] points);
PathGradientBrush(PointF[] points);
PathGradientBrush(Point[] points, WrapMode wrapMode);
constructors we can create a brush which changes its color along a curve. We can define the curve with the path and the points parameters. We already got familiar with the wrapMode WrapMode type parameter when discussing the texture brushes.
Both gradient brushes have a WrapMode property that defines the method how to repeat the painting and they also have a Transform feature that contains local transformation. Both gradient brushes contain Blend^ type Blend property. The Factors and Positions properties of the Blend class are float arrays with elements between 0 and 1, which define the intensity of the color in % and the length position in %. Both gradient brushes have an InterpolationColors (ColorBlend class type) property where we can set the colors besides the positions in % instead of the color intensity. Both gradient brushes have a bounding Rectangle property.
The Color array type SurroundColors property of the PathGradientBrush contains the applied colors.
A brush can be transparent, if we use ARGB colors. The following example draws a transparent rectangle on the top of the rectangles painted differently.
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
SolidBrush ^ sb = gcnew SolidBrush(Color::Red);
e->Graphics->FillRectangle(sb,200,20,150,50);
HatchBrush ^ hb = gcnew HatchBrush(
HatchStyle::ForwardDiagonal,
Color::Red,Color::Yellow);
e->Graphics->FillRectangle(hb,200,80,150,50);
Image ^ im = Image::FromFile("c:\\M\\mogi.png");
TextureBrush ^ tb = gcnew TextureBrush(im);
Matrix ^ m= gcnew Matrix();
m->Translate(5,5);
tb->Transform->Reset();
tb->Transform=m;
e->Graphics->FillRectangle(tb, 200, 140, 150, 50);
LinearGradientBrush ^ lgb = gcnew LinearGradientBrush(
PointF(0,0), PointF(100,100), Color::Blue, Color::Red);
e->Graphics->FillRectangle(lgb, 200, 200, 150, 50);
SolidBrush ^ at = gcnew SolidBrush(
Color::FromArgb(127,Color::Red));
e->Graphics->FillRectangle(at, 250, 10, 200, 270);
}
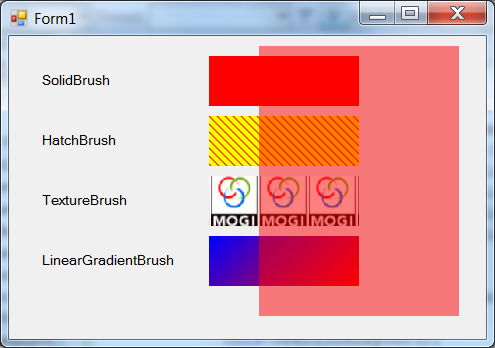
IV.4.11. Pens
We can draw line pictures with pens. The pens have color and width. With the
Pen(Brush brush [, float width]);
Pen(Color color [, float width]);
constructors of the Pen class we can create a pen defined by its color or its brush. We can also specify the width of the pen. The Brush, Color and Width properties store the mentioned features of the pen.
The DashStyle property can set with one of the elements of the DashStyle enumeration (
System::Drawing::Drawing2D
namespace). We can set this way the pattern of the pen (Solid – continuous, Dash – dashed, Dot – dotted, DashDot – dashes and dots, DashDotDot – dashes and double dots, and Custom). In case of the the last dash style we can define the pattern, with the consecutive elements of the DashPattern float array consisting the length of dashes and spaces.
With the float type DashOffset property we can set the distance between the starting point of the line and starting point of the dash. In case of dashed lines we can also set the cap style used at the end of the dashes with the DashCap (
System::Drawing::Drawing2D
). The elements of the DashCap enumeration are: Flat – flat, Round - rounded, Triangle – triangular.
The Alignment property can be a value of the PenAligment type enumeration (
System::Drawing::Drawing2D
namespace), and it specify where to put the line concerning the edge of the shape (Center – centered over the line, Inset – in the inside of a closed shape, OutSet – outside of a closed shape, Left – to the left of the line, Right – to the right of the line).
In order to achieve a joint geometry of the consecutive lines of the shapes we can use the LineJoin property of the LineJoin enumeration type (Bevel – a corner clipped in a certain angle, Round – rounded, Miter and MiterClipped also mean a clipped connection, if the length of the miter exceeds the float type MiterLimit value).
In order to control the drawing of the line endings the StartCap and the EndCap
System::Drawing::Drawing2D::LineCap
enumeration type properties can be used (Flat – flat, Square - square, Round – rounded, ArrowAnchor – ending with an arrow, RoundAnchor – ending with a circle etc). The CustomStartCap and the CustomEndCap properties can be interesting and those are instances of the CustomLineCap class. The instance can be created with the
CustomLineCap(GraphicsPath fillPath, GraphicsPath strokePath
[, LineCap baseCap[, float baseInset]]);
constructor. We can define the filling with a figure (fillPath) and the outline (strokePath). We can use an existing line cap (baseCap), or we can insert a gap into the cap and the line (baseInset). The BaseCap property of the CustomLineCap class identifies the parent line cap and the BaseInset contains the gap. We can determine the mode how lines are joined to each other (StrokeJoin), or we can set a scale for their width (WidthScale property). By default this is the width of the line.
The ready only PenType enumeration type PenType property of the Pen class tells us the type of the pen (SolidColor, HatchFill, TextureFill, LinearGradient, PathGradient)
Of course, pens also have a Transform property that defines the local transformation.
The following example draws a line with a red solid pen, then with a pen defined with a linear gradient brush. After this it draws a line on one of the end with an arrow, then on the other end with a rounded cap. Then two dashed lines come, the first with a predefined pattern, whereas the second one with an pattern array. This is followed by two rectangle shapes, one of them with a clipped and default OutSet Alignment property, then the other with the InSet property without clipping (Figure IV.63).
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Pen ^ ps = gcnew Pen(Color::Red,5);
e->Graphics->DrawLine(ps,10,25,100,25);
LinearGradientBrush ^ gb = gcnew LinearGradientBrush(
PointF(10, 10), PointF(110, 10),
Color::Red, Color::Blue);
Pen ^ pg = gcnew Pen(gb,5);
e->Graphics->DrawLine(pg,10,50,100,50);
ps->StartCap=LineCap::ArrowAnchor;
pg->EndCap=LineCap::Round;
e->Graphics->DrawLine(pg,10,75,100,75);
pg->DashStyle=DashStyle::DashDot;
e->Graphics->DrawLine(pg,10,100,100,100);
array <float> ^ dp= {1.0f,0.1f,2.0f,0.2f,3.0f,0.3f};
pg->DashPattern=dp;
e->Graphics->DrawLine(pg, 10, 125, 100, 125);
GraphicsPath^ mp = gcnew GraphicsPath;
RectangleF srcRect = RectangleF(10,150,100,20);
mp->AddRectangle( srcRect );
ps->LineJoin=LineJoin::Bevel;
e->Graphics->DrawPath( ps , mp );
Matrix ^ em = gcnew Matrix();
em->Reset();
em->Translate(0,25);
mp->Transform(em);
pg->Alignment=PenAlignment::Inset;
e->Graphics->DrawPath( pg , mp );
}
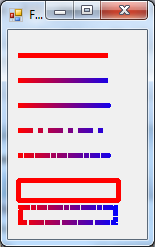
IV.4.12. Font, FontFamily
We can differentiate three basic types of character sets in Windows. In the first case the information that is necessary to display a character is stored in a bitmap. In the second case the vector based fonts define which lines should be taken to draw the character. In the third case the so called TrueType character set is used which means that the definition of characters consists of the set of points and special algorithms and those are able to define the characters for any type of resolutions.
When using the TrueType character set, then the so called TrueType rasterizer creates a bitmap character set from the points and algorithms according to the requirements. The result of this is that if we plan the page to be printed with a publishing software, then the printout will be the same what was visible on the screen (WYSIWYG - What You See Is What You Get). Microsoft bought the right of using the TrueType fonts from Apple Computer [4.7.] . It is obvious that the first two character representation methods have their advantages and disadvantages as well. It is possible to resize the vector based fonts as wished, however, in a lot of cases their visualization is not aesthetic enough and is not readable. On the other hand, bitmap fonts are well readable but they cannot be deform freely. The usage of the TrueType type character set guarantees the above benefits and eliminates disadvantages.
Let us get familiar with some notions that help us to navigate in the world of fonts. It is a basic question whether the width of the line of the letter can be changed when displaying the character. Is it possible to use a thinner or a thicker letter drawing? The line of the letter is called „stroke” in the English terminology.
There are more character sets that uses small crossing lines to close the line of the letters when drawing them. The letters will have small soles and hat. These small crossing lines are called serif. This way that character set that do not use these closing serifsis called sanserif, that is, without serif.
The rectangular area that bounds the character is called character cell. The size of this can be characterized by the emSize parameter, which shows the size of the character in points (1/72 inch). The em prefix comes from pronounciation of the M letter because it is used to sizing the font. Characters do not fully fill in their cells. The cell is characterized by its width, height and its starting point which is usually the top left corner. The character cell is devided into two parts by a horizontal line. Characters are sitting on this line, that is, the base line. The part above the base line is called ascent and the part below the base line is called descent. The distance of two base lines that are in two character cells placed below each other is called leading. Capital letters written on he base line do not reach the top of the character cell either.
The internal leading is the area between the top edge of the character cell and the top edge of capital letters. If the top and bottom edge of the character cells placed below each other do not touch, then the distance between these two is called the externalleading.

A given size of a character type is called typeface. Windows is capable of creating typefaces with distortion in the given size. Italic letters (italic) are created in a way that the points of the character remain unchanged on the base line, whereas the other parts of the character are slipped depending on their distance from the base line (the character leans). The bold letters (bold) can be easily derived from making the stroke thicker. Obviously it is easy to create underlined and lined strikeout characters with adding a horizontal line to a specific place. The notion of pitch is also in use which is specifying how many characters have to be written next to each other from a given font so that the width of the written text is one inch (~2.54 cm). It is worth mentioning that the logical inch is used for displaying characters on the screen. The size of the logical inch is defined in a way that the text is as well readable on screen as on paper. Two basic font type exist. One is non-proportional – fix sized – in which each character is placed in a cell with the same size, being either an „i” or an „m”. Recently these font types are called monospace fonts. The other is proportional in which case the width of the cell depends on the given letter. In this latest case the average character widths and the average and maximum pitch sizes can be used.
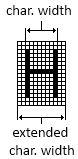
It is worth dealing with the with the aspect ratio of the characters, given that not all the fonts could be displayed on all output devices (e.g dot matrix printer). Windows can perform aspect ratio conversion in order to display successfully. The uses font families depending on the appearance of the characters.
Traditional character sets use the data shown on Figure IV.65 to descript the dimensions of the characters. Instead of this traditional interpretation the TrueType character sets use the so called ABC data. As it is visible on Figure IV.66 the A and C values can be negative as well.
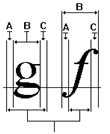
Font families contain fonts that have similar characteristics. The .Net defines the FontFamily class to model font families (this class cannot be inherited). We can create FontFamily instances with the
FontFamily(GenericFontFamilies genericFamily);
FontFamily(String^ name[, FontCollection^ fontCollection]);
constructors. We can choose the value of the genericFamily parameter from the elements of the GenericFontFamilies enumeration in order to create a family. The possible values of the enumeration (Serif, SansSerif and Monospace) cover already known notions. The name parameter contain the name of the new font family. It can be an empty string or the name of a font family that has not been installed on the computer or a name of a non TrueType font. We can also create collections from font families. We can define the collection with the fontCollection parameterwhere we can place the new font family.
We can get information opportunities from the properties of the FontFamily class. With the static Families property we can query the font families of the current drawing paper into a FontFamily type array. The FontFamily type, static GenericMonospace, GenericSansSerif and GenericSerif properties give a non proportional, a sansserif and a serif font family. The string type Name property contains the name of the font family.
The static
FontFamily[] GetFamilies(Graphics graphics);
method returns all family font names that can be found on the given drawing paper.
The following example collects the names of all font families of the drawing paper to the listbox when clicking on the form.
private: System::Void Form1_Click(System::Object^ sender,
System::EventArgs^ e) {
Graphics ^ g = this->CreateGraphics();
array <FontFamily ^> ^ f = gcnew array<FontFamily^>(100);
f=FontFamily::GetFamilies(g);
for (int i=0; i<f->GetLength(0); i++) {
listBox1->Items->Add(f[i]->Name);
}
}
The
int GetCellAscent(FontStyle style);
int GetCellDescent(FontStyle style);
int GetEmHeight(FontStyle style);
int GetLineSpacing(FontStyle style);
String^ GetName(int language);
method queries the data defined by the style parameter of the given font family.
The
bool IsStyleAvailable(FontStyle style);
method indicates if the given font family has the given style. The values of the FontStyle enumeration are: Bold, Italic, Underline and Strikeout.
The GDI+ uses the Font class to model the font types. We can create the instances of the class with the constructors:
Font(FontFamily^ family, float emSize[, FontStyle style
[, GraphicsUnit unit [, unsigned char gdiCharSet
[, bool gdiVerticalFont]]]]);
Font(FontFamily^ family, float emSize, GraphicsUnit unit);
Font(String^ familyName, float emSize[, FontStyle style
[, GraphicsUnit unit[, unsigned char gdiCharSet
[, bool gdiVerticalFont]]]]);
Font(String^ familyName, float emSize, GraphicsUnit unit);
Font(Font^ prototype, FontStyle newStyle);
The family parameter defines the familiy of the new font, the familyName defines the name of this family. The emSize is the size of the font in points, the style is the font type (italic, bold etc.). The unit parameter defines the units (Pixel, Inch, Millimeter etc.) used by the font
The gdiCharset indentifies the character set provided by GDI+. The gdiVerticalFont regulates vertical writing. We can define a new font from an existing font and with the new newStyle style.
All properties of the Font class are read-only. If we would like to make changes, then we need to create a new font. The FontFamily^ type FontFamily property identifies the font family. The Name string defines the name of the font, whereas the OriginalFontName string defines the original name of the font. If the IsSystemFont logical property is true then we work with a system font. In this case the SystemFontName string property defines the name of the system font. The GdiVerticalFont logical property defines whether the font is vertical. The GdiCharSet byte type property identifies the GDI character set. The Size (emSize) and the SizeInPonts define the font size in points. The Style logical property indentifies the font style with the elements of the FontStyle type enumeration (Italic, Bold, Underline and Strikeout). The Unit property defines the unit of measure for this font.
The
float GetHeight();
method returns the distance that can be measured between lines in pixels. The
float GetHeight(Graphics^ graphics);
method returns the distance that can be measured between lines in GraphicsUnit type units. The
float GetHeight(float dpi);
method defines the distance that can be measured between lines in pixels on a device with a given dpi (dot per inch – pont per inch) resolution.
The next example shows the distortion of a font chosen by clicking on the Type button with the Bold, Italic and Underline checkboxes. (Figure IV.68).
IV.4.13. Drawing routines
The Graphics class offers a set of drawing routines. We can erase the whole drawing paper with a given color (color)
void Clear(Color color);
In the next drawing routines the first parameter identifies the pen of the drawing. We can draw straight line sections with the methods:
void DrawLine(Pen^ pen, Point pt1, Point pt2);
void DrawLine(Pen^ pen, PointF pt1, PointF pt2);
void DrawLine(Pen^ pen, int x1, int y1, int x2, int y2);
void DrawLine(Pen^ pen, float x1, float y1, float x2, float y2);
The pt1, pt2, (x1,y1) and (x2,y2) are the endpoints.
The following methods draw a series of line segments:
void DrawLines(Pen^ pen, array<Point>^ points);
void DrawLines(Pen^ pen, array<PointF>^ points);
The points array defines the cornerpoints.
We can draw rectangles with the helpt of the methods:
void DrawRectangle(Pen^ pen, Rectangle rect);
void DrawRectangle(Pen^ pen, int x, int y,
int width, int height);
void DrawRectangle(Pen^ pen, float x, float y,
float width, float height);
The data of the rectangle are defined by the rect structure or the (x,y) upper-left corner, the width and the height parameters.
We can draw a set of rectangles defined by the rects array at once with the method:
void DrawRectangles(Pen^ pen, array<Rectangle>^ rects);
void DrawRectangles(Pen^ pen, array<RectangleF>^ rects);
The following methods draw polygons defined by the points structure array:
void DrawPolygon(Pen^ pen, array<Point>^ points);
void DrawPolygon(Pen^ pen, array<PointF>^ points);
The following methods draw an ellipse defined by the bounding rectangle specified by the rect structure or the (x,y) and (height, width) data:
void DrawEllipse(Pen^ pen, Rectangle rect);
void DrawEllipse(Pen^ pen, RectangleF rect);
void DrawEllipse(Pen^ pen, int x, int y, int width, int height);
void DrawEllipse(Pen^ pen, float x, float y,
float width, float height);
We can draw an arc representing a portion of an ellipse (as visible on Figure IV.45) with the methods:
void DrawArc(Pen^ pen, Rectangle rect,
float startAngle, float sweepAngle);
void DrawArc(Pen^ pen, RectangleF rect,
float startAngle, float sweepAngle);
void DrawArc(Pen^ pen, int x, int y, int width, int height,
int startAngle,int sweepAngle);
void DrawArc(Pen^ pen, float x, float y,
float width, float height,
float startAngle, float sweepAngle);
The
void DrawPie(Pen^ pen, Rectangle rect,
float startAngle, float sweepAngle);
void DrawPie(Pen^ pen, RectangleF rect,
float startAngle, float sweepAngle);
void DrawPie(Pen^ pen, int x, int y, int width, int height,
int startAngle,int sweepAngle);
void DrawPie(Pen^ pen, float x, float y,
float width, float height,
float startAngle, float sweepAngle);
methods draw pie slices from the arcs (straight lines go to the center point).
The following methods draw a Bezier curve according to Figure IV.46:
void DrawBezier(Pen^ pen, Point pt1, Point pt2,
Point pt3, Point pt4);
void DrawBezier(Pen^ pen, PointF pt1, PointF pt2,
PointF pt3, PointF pt4);
void DrawBezier(Pen^ pen, float x1, float y1,
float x2, float y2,
float x3, float y3,
float x4, float y4);
The control points can be defined with the pt i structures or with the x i , y i coordinates.
A given Bezier curve chain is drawn by the methods:
void DrawBeziers(Pen^ pen, array<Point>^ points);
void DrawBeziers(Pen^ pen, array<PointF>^ points);
After the first 4 points each upcoming three points define the next curve segment.
The
void DrawCurve(Pen^ pen, array<Point>^ points
[, float tension]);
void DrawCurve(Pen^ pen, array<PointF>^ points
[, float tension]);
void DrawCurve(Pen^ pen, array<PointF>^ points,
int offset, int numberOfSegments
[, float tension]);
methods draw a cardinal spline (Figure IV.49) with the given pen (pen) through the points of the points array. We can set the tension and the number of the considered curve segments (numberOfSegments).
We can draw closed cardinal splines with the method:
void DrawClosedCurve(Pen^ pen, array<Point>^ points[,
FillMode fillmode]);
void DrawClosedCurve(Pen^ pen, array<PointF>^ points[,
FillMode fillmode]);
through the points of the points array with the fillmode, which can be an element (Alternate or Winding) of the – already known - FillMode enumeration type (Figure IV.44).
The following method draws a shape (path) with the given pen:
void DrawPath(Pen^ pen, GraphicsPath^ path);
The
void DrawString(String^ s, Font^ font, Brush^ brush,
PointF point[, StringFormat^ format]);
void DrawString(String^ s, Font^ font, Brush^ brush,
float x, float y[, StringFormat^ format]);
void DrawString(String^ s, Font^ font, Brush^ brush,
RectangleF layoutRectangle[,
StringFormat^ format]);
methods draws the specified text string s on the drawing paper with the given font and brush. The place of the writing can be set with the point or the x and y parameters or with the layoutRectangle bounding rectangle. An instance of the StringFormat class defines the format of the appearance. (For example with the values (DirectionRightToLeft, DirectionVertical, NoWrap etc.) of the StringFormatFlags enumeration type FormatFlags property or in the Alignment property with the Near, Center and Far elements of the Alignment enumeration.)
We can draw the Icon type icon with the method
void DrawIcon(Icon^ icon, int x, int y);
into point x, y on the drawing paper. We can scale the icon to the targetRectangle rectangle:
void DrawIcon(Icon^ icon, Rectangle targetRect);
The icon is drawn in the rectangle without scaling with the method:
void DrawIconUnstretched(Icon^ icon, Rectangle targetRect);
We can draw the picture defined by the image or a chosen part of it (srcRect in the given srcUnit units) to the point or to the (x,y) point with the methods:
void DrawImage(Image^ image, Point point);
void DrawImage(Image^ image, PointF point);
void DrawImage(Image^ image, int x, int y [, Rectangle srcRect,
GraphicsUnit srcUnit]);
void DrawImage(Image^ image, float x, float y
[, RectangleF srcRect, GraphicsUnit srcUnit]);
The
void DrawImage(Image^ image, Rectangle rect);
void DrawImage(Image^ image, RectangleF rect);
void DrawImage(Image^ image, int x, int y,
int width, int height);
void DrawImage(Image^ image, float x, float y,
float width, float height);
methods stretch the image to the rect or the (x, y, width, height) rectangle
One rectangle (srcRect) portion of the picture (image) can be drawn to another rectangle of the drawing (destRect) with the methods:
void DrawImage(Image^ image, Rectangle destRect,
Rectangle srcRect, GraphicsUnit srcUnit);
void DrawImage(Image^ image, RectangleF destRect,
RectangleF srcRect, GraphicsUnit srcUnit);
We have to define the graphical units on the source rectangle (srcUnit).
If we would like to achieve something similar to the above, setting the source rectangle with int or float cornerpoint data (srcX, srcY) and int or float width and height data (srcWidth, srcHeight) will not be enough but we also have to define the graphical units of the source (srcUnit). In this case we can also use an instance of the ImageAttributes class to recolor (imageAttr) , morevover we can also define an error handling callback function and we can send data to the callback function (callbackData):
void DrawImage(Image^ image, Rectangle destRect,
int srcX, int srcY, int srcWidth, int srcHeight,
GraphicsUnit srcUnit
[, ImageAttributes^ imageAttr
[,Graphics::DrawImageAbort^ callback
[,IntPtr callbackData]]]);
void DrawImage(Image^ image, Rectangle destRect,
float srcX, float srcY,
float srcWidth, float srcHeight,
GraphicsUnit srcUnit[,
ImageAttributes^ imageAttrs
[,Graphics::DrawImageAbort^ callback
[,IntPtr callbackData]]]);
We can put the scaled and sheared image in a parallelogram with the method:
void DrawImage(Image^ image, array<Point>^ destPoints
[, Rectangle srcRect, GraphicsUnit srcUnit
[, ImageAttributes^ imageAttr[,
Graphics::DrawImageAbort^ callback
[,int callbackData]]]]);
The image is the picture we would like to draw, the destPoints array is three points of the parallelogram of the scaled image. Further parameters are the same as the parameters of those functions that were mentioned lately. The following example draws an image straight and distorted as well.
private: System::Void Form1_Paint(System::Object^ sender,
System::Windows::Forms::PaintEventArgs^ e) {
Image^ mogi = Image::FromFile( "C:\\M\\Mogi.png" );
int x = 100;
int y = 100;
int width = 250;
int height = 150;
e->Graphics->DrawImage( mogi, x, y, width, height );
Point l_u_corner = Point(100,100); // left-upper corner
Point r_u_corner = Point(550,100); // right-upper corner
Point l_l_corner = Point(150,250); // left-lower corner
array<Point>^ dest = {l_u_corner, r_u_corner, l_l_corner};
e->Graphics->DrawImage( mogi, dest);
}

We can draw painted shapes with the Graphics class Fillxxx()methods. The
void FillRectangle(Brush^ brush, Rectangle rect);
void FillRectangle(Brush^ brush, RectangleF rect);
void FillRectangle(Brush^ brush, int x, int y,
int width, int height);
void FillRectangle(Brush^ brush, float x, float y,
float width, float height);
methods fill the interior of a rectangle defined by the rect structure or with the x,y, and height, width data with the brush.
The rectangles specified in the rects array are filled by the methods:
void FillRectangles(Brush^ brush, array<Rectangle>^ rects);
void FillRectangles(Brush^ brush, array<RectangleF>^ rects);
Closed polygons defined by the points array parameter are filled by the brush:
void FillPolygon(Brush^ brush, array<Point>^ points
[, FillMode fillMode]);
void FillPolygon(Brush^ brush, array<PointF>^ points,
[FillMode fillMode]);
Using the optional fillMode parameter (Alternate, Winding – Graphics2D) we can define the fill mode.
The
void FillEllipse(Brush^ brush, Rectangle rect);
void FillEllipse(Brush^ brush, RectangleF rect);
void FillEllipse(Brush^ brush, int x, int y,
int width, int height);
void FillEllipse(Brush^ brush, float x, float y,
float width, float height);
methods fill the interior of an ellipse defined by the rect structure or with the x,y, and height, width data with the brush.
The interior of a pie section of an ellipse defined by the rect structure or with the x,y, and height, width data is can be filled with the brush using the following methods:
void FillPie(Brush^ brush, Rectangle rect,
float startAngle, float sweepAngle);
void FillPie(Brush^ brush, int x, int y,
int width, int height,
int startAngle, int sweepAngle);
void FillPie(Brush^ brush, float x, float y,
float width, float height,
float startAngle, float sweepAngle);
The area bounded by a closed cardinal curve defined by the control points of the points array can be filled with the brush using the following methods. We can set the optional filling mode (fillmode) and the tension of the curve (tension) parameters.
void FillClosedCurve(Brush^ brush, array<Point>^ points, [
FillMode fillmode, [float tension]]);
void FillClosedCurve(Brush^ brush, array<PointF>^ points, [
FillMode fillmode, [float tension]]);
The path shape can be filled with the brush using the method:
void FillPath(Brush^ brush, GraphicsPath^ path);
A region can be filled with the brush using the method:
void FillRegion(Brush^ brush, Region^ region);
We can copy a blocskRegionSize size rectangle from the given point (upperLeftSource or sourceX, sourceY) of the screen to a rectangle placed in the point (upperLeftDestination)of the drawing paper. We can set with the copypixelOperation parameter what to happen with the points that originally stand in the target place (the elements of the CopyPixelOperation enumeration that define the logical operations). Its elements are SourceCopy, SourceAnd, SourceInvert, MergeCopy etc.).
void CopyFromScreen(Point upperLeftSource,
Point upperLeftDestination,
Size blockRegionSize, [
CopyPixelOperation copyPixelOperation]);
void CopyFromScreen(int sourceX, int sourceY,
int destinationX, int destinationY,
Size blockRegionSize, [
CopyPixelOperation copyPixelOperation]);
We can save the state of the graphical settings, the transformations and the setting of the clippings with the
GraphicsState^ Save()
method. Later we can restore the saved settings using the gstate parameter, which is returned by the Save() method:
void Restore(GraphicsState^ gstate);
Similarly the
GraphicsContainer^ BeginContainer();
method saves a graphics container with the current state of the Graphics and opens and uses a new graphics container.
The
void EndContainer(GraphicsContainer^ container);
method closes the current graphics container and restores the state of the Graphics to the state saved (container) previously by a call of the BeginContainer() method.
IV.4.14. Printing
Printing options are defined in the System::Drawing::Printing namespace.
The printing can be done with the help of the PrintDocument class. We can either place one instance of the class from the Toolbox to the formor we can create it with the constructor:
PrintDocument()
We can print documents with an instance of the PrintDocument class. We can set the name of the document with the String type read and write property:
DocumentName
The
PrinterSettings
property of the PrintDocument class refers to an instance of the PrinterSettings class.
The static InstalledPrinters property of this is a collection of strings that contains the name of the printers installed into the system. We can use the PrinterName string property to set where we would like to print. If we do not do anything then we will use the default printer. The IsValid property tells us whether the right printer was set.
The PrinterSettings class contains a set of properties that help to query the options and the settings of the printer. For example the CanDuplex logical property informs about the option to make two-sided printouts, the Duplex - another logical property - controls the usage of this. The Collate informs about the collateral options, Copies gets the number of printouts and sets it up to the value of the MaximumCopies property. The logical IsDefaultPrinter tells if we work with the default printer, IsPlotter another logical property indicates a plotter is used whereas the SupportColor property informs about the color printer. The PaperSizes collection depends on the properties of the printer and it contains the available paper sizes, PaperSources contains the available paper sources while PrinterResolution contains the available resolutions. LandScapeAngle tells the angle between portrait and landscape settings.
The DefaultPageSettings property is an instance of the PageSetting class that contains all the settings of the page (colors, margin sizes, resolutions).
We can select a part of the document using the PrintRange property (AllPages, SomePages, Selection, CurrentPage etc. values). We can also set the first page (FromPage) and the last page (ToPage) of the printing. We can also cater for printing into a file with setting the PrintToFile logical property to true. In this case the name of the file can be given in the PrintFileName string property.
We can start the printing process with the
void Print()
method of the PrintDocument class. When printing the events of the class can be raised: BeginPrint (the beginning of printing), EndPrint (the end of printing) and PrintPage (printing of a page). Each event has a PrintEventArgs reference class type parameter. The properties of this parameter are the instance of the PageSettings class (with properties: Bounds – bounding rectagle of the page, Color – color printing, LandsCape - landscape, Margins - margins, PaperSize - the size of the paper, PrinterResolution – printer resolution), the margin and page settings and the already known Graphics type printer drawing paper as well. The HasMorePages read and write logical property indicates if there are more pages to be printed.
The following example draws a line on the default printer (in our case it is the Microsoft Office OneNote program) when clicking on the form:
private: System::Void printDocument1_PrintPage(
System::Object^ sender,
System::Drawing::Printing::PrintPageEventArgs^ e) {
e->Graphics->DrawLine(gcnew Pen(Color::Red,2),10,10,100,100);
}
private: System::Void Form1_Click(System::Object^ sender,
System::EventArgs^ e) {
printDocument1->Print();
}
References:
[4.1.] MicroSoft Developer Network http://msdn.microsoft.com/. 2012.07.
[4.2.] Könnyű a Windowst programozni!? . ComputerBooks . Budapest . 1998.
[4.3.] Lineáris algebra. Műszaki könyvkiadó . Budapest . 1974.
[4.4.] Háromdimenziós Grafika, animáció és játékfejlesztés. ComputerBooks . Budapest . 2003.
[4.5.] World Wide Web Consortium - www.w3c.org. 2012.
[4.6.] Image Quantization,Halftoning, and Dithering. Előadásanyag Princeton University www.cs.princeton.edu/courses/archive/.../dither.pdf.
[4.7.] „www.apple.com"[Online]. 2012.