II. fejezet - Moduláris programozás C++ nyelven
- II.1. Függvények - alapismeretek
-
- II.1.1. Függvények definíciója, hívása és deklarációja
- II.1.2. Függvények visszatérési értéke
- II.1.3. A függvények paraméterezése
-
- II.1.3.1. A paraméterátadás módjai
- II.1.3.2. Különböző típusú paraméterek használata
-
- II.1.3.2.1. Aritmetikai típusú paraméterek
- II.1.3.2.2. Felhasználói típusú paraméterek
- II.1.3.2.3. Tömbök átadása függvénynek
- II.1.3.2.4. Sztring argumentumok
- II.1.3.2.5. A függvény, mint argumentum
- II.1.3.2.6. Alapértelmezés szerinti (default) argumentumok
- II.1.3.2.7. Változó hosszúságú argumentumlista
- II.1.3.2.8. A main() függvény paraméterei és visszatérési értéke
- II.1.4. Programozás függvényekkel
- II.2. A függvényekről magasabb szinten
- II.3. Névterek és tárolási osztályok
-
- II.3.1. A változók tárolási osztályai
- II.3.2. A függvények tárolási osztályai
- II.3.3. Több modulból felépülő C++ programok
- II.3.4. Névterek
- II.4. A C++ előfeldolgozó utasításai
A C++ nyelv különböző programozási technikákat támogat. Könyvünk előző részében a strukturált programozás került előtérbe, melynek egyik alapelve szerint a programok háromféle építőelemből állnak: utasítássorok (ezek tagjait a végrehajtás sorrendjében adjuk meg), döntési szerkezetek (if, switch) és ismétlődő részek (while, for, do). Mint látható, ebből a felsorolásból a goto utasítás teljesen hiányzik, ennek használatát kerüljük.
Ugyancsak a strukturált programozás eszköztárába tartozik a felülről-lefelé haladó (top-down) tervezés, melynek lényege, hogy a programozási feladat megoldása során egyre kisebb részekre osztjuk a feladatot, egészen addig haladva, míg jól kézben tartható, tesztelhető programelemekig nem jutunk. A C/C++ nyelvekben a legkisebb, önálló funkcionalitással rendelkező programstruktúra a függvény .
Amennyiben az elkészült függvényt, vagy a rokon függvények csoportját külön modulban (forrásfájlban) helyezzük el, eljutunk a moduláris programozás hoz. A modulok önállóan fordíthatók, tesztelhetők, és akár más projektekbe is átvihetők. A (forrásnyelvű vagy lefordított) modulok tartalmát interfészek (esetünkben fejállományok) segítségével tesszük elérhetővé más modulok számára. A modulok bizonyos részeit pedig elzárjuk a külvilág elől (data hiding). A kész modulokból (komponensekből) való programépítéshez is ad segítséget a strukturált programozás, az alulról-felfelé való (bottom-up) tervezéssel.
A következő fejezetekben a moduláris és a procedurális programozás C++ nyelven való megvalósításával ismertetjük meg az Olvasót. Procedurális programozásról beszélünk, ha egy feladat megoldását egymástól többé-kevésbé független alprogramokból (függvényekből) építjük fel. Ezek az alprogramok a főprogramból (main()) kiindulva egymást hívják, és paramétereken keresztül kommunikálnak. A procedurális programozás jól ötvözhető a strukturált és a moduláris programozás eszközeivel.
II.1. Függvények - alapismeretek
A függvény a C++ program olyan névvel ellátott egysége (alprogram), amely a program más részeiből annyiszor hívható, ahányszor csak szükség van a függvényben definiált tevékenységre. A hagyományos C++ program kisméretű, jól kézben tartható függvényekből épül fel. A lefordított függvényeket könyvtárakba rendezhetjük, amelyekből a szerkesztő program a hivatkozott függvények kódját beépíti a programunkba.
A függvények hatékony felhasználása érdekében a függvény bizonyos belső változóinak a függvényhívás során adunk értéket. Ezek a paraméterek nek hívott tárolókat függvény definíciójában a függvény neve után zárójelben kell deklarálnunk. A függvény hívásánál (aktiválásánál) pedig hasonló formában kell felsorolnunk az egyes paramétereknek átadni kívánt értékeket, az argumentumokat.
A függvényhívás során az argumentumok (amennyiben vannak) átkerülnek a hívott függvényhez, és a vezérlés a hívó függvénytől átkerül az aktivizált függvényhez. A függvényben megvalósított algoritmus végrehajtását követően egy return utasítással, illetve a függvény fizikai végének elérésével a hívott függvény visszatér a hívás helyére. A return utasításban szereplő kifejezés értéke, mint függvényérték (visszatérési érték) jelenik meg a függvényhívás kifejezés kiértékelésének eredményeként.
II.1.1. Függvények definíciója, hívása és deklarációja
A C++ szabványos könyvtára egy sor előre elkészített függvényt bocsájt a rendelkezésünkre. Az ilyen függvényeket csupán deklarálnunk kell a felhasználást megelőzően. Ebben hatékony segítséget nyújt a megfelelő fejállomány beépítése a programunkba. Az alábbi táblázatban összeszedtünk néhány gyakran használt függvényt és a hozzájuk tartozó include fájlokat:
|
függvény |
fejállomány |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A könyvtári függvényekkel ellentétben a saját késztésű függvényeket mindig definiálni is kell. A definíció, amit csak egyszer lehet megadni, a C++ programon belül bárhol elhelyezkedhet. Amennyiben a függvény definíciója megelőzi a felhasználás (hívás) helyét akkor, ez egyben a függvény deklarációja is.
A függvény-definíció általános formájában a 〈 〉 jelek az opcionális részeket jelölik. A függvény fejsorában elhelyezkedő paraméter-deklarációs lista az egyes paramétereket vesszővel elválasztva tartalmazza, és minden egyes paraméter előtt szerepel a típusa.

A függvények definíciójában a visszatérési típus előtt megadhatjuk a tárolási osztályt is. Függvények esetén az alapértelmezés szerinti tárolási osztály az extern, ami azt jelöli, hogy a függvény más modulból is elérhető. Amennyiben a függvény elérhetőségét az adott modulra kívánjuk korlátozni, a static tárolási osztályt kell használnunk. (A paraméterek deklarációjában csak a register tárolási osztály specifikálható). Ha a függvényt saját névterületen szeretnénk elhelyezni, úgy a függvény definícióját, illetve a prototípusát a kiválasztott névterület (namespace) blokkjába kell vinnünk. (A tárolási osztályok és a névterületek részletes ismertetését későbbi fejezetek tartalmazzák.)
Példaként készítsük el az első n pozitív egész szám összegét meghatározó függvényt! Az isum() függvény egy int típusú értéket vár, és egy int típusú eredményt ad vissza.
int isum(int n)
{
int s = 0;
for (int i=1; i<=n; i++)
s += i;
return s;
}
Tételezzük fel, hogy a forrásfájlban az isum() függvény definíciója után helyezkedik el a main () függvény, amelyből hívjuk az isum() függvényt:
int main()
{
cout << isum(10) << endl;
int s = isum(7) * isum(10) + 2;
}
A függvényhívás általános formájában a függvény nevét zárójelben követi az argumentumok veszővel tagolt listája. A hívás lépéseit a II.2. ábra követhetjük nyomon.
függvénynév (〈argumentum 1 , argumentum 2 , … argumentum n 〉)
A zárójelpárt akkor is meg kell adnunk, ha nincs paramétere a függvénynek. A függvényhívást bárhol szerepeltethetjük, ahol kifejezés állhat a programban.
Az argumentumok kiértékelésének sorrendjét nem definiálja a C++ nyelv. Egyetlen dolgot garantál mindössze a függvényhívás operátora, hogy mire a vezérlés átadódik a hívott függvénynek, az argumentumlista teljes kiértékelése (a mellékhatásokkal együtt) végbemegy.
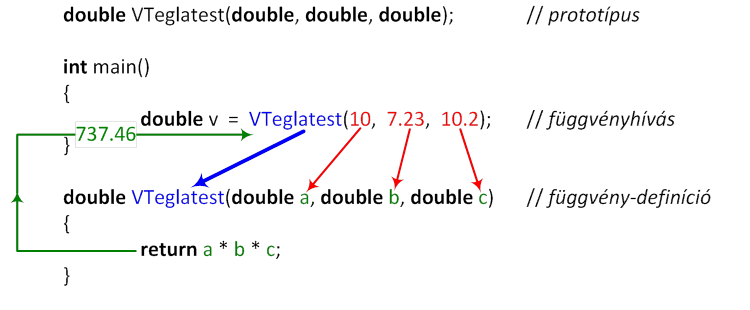
A szokásos C++ szabályok szerint a függvényeket deklarálni kell a függvényhívás helyéig. A függvény definíciója egyben a függvény deklarációja is lehet. Felvetődik a kérdés, hogyan tudjuk biztosítani, hogy a hívott függvény mindig megelőzze a hívó függvény. Természetesen ez nem biztosítható, gondoljunk csak az egymást hívó függvényekre! Amennyiben a fenti példában felcseréljük a main () és az isum() függvényeket a forrásfájlban, mindaddig fordítási hibát kapunk, míg el nem helyezzük a függvény teljes leírását tartalmazó prototípus t a hívás előtt:
int isum(int); // prototípus
int main() {
cout << isum(10) << endl;
int s = isum(7) * isum(10) + 2;
}
int isum(int n)
{
int s = 0;
for (int i=1; i<=n; i++)
s += i;
return s;
}
A függvény teljes deklarációja ( prototípusa ) tartalmazza a függvény nevét, típusát valamint információt szolgáltat a paraméterek számáról és típusáról:
visszatérési típus függvénynév (〈paraméter-deklarációs lista〉);
visszatérési típus függvénynév (〈típuslista〉);
A C++ fordító csak a prototípus ismeretében fordítja le a függvényhívást:
-
a paraméterlista és az argumentumlista összevetésével ellenőrzi a paraméterek számának és típusainak összeférhetőségét,
-
az argumentumokat a prototípusban definiált típusoknak megfelelően konvertálja, nem pedig az automatikus konverziók szerint.
(Megjegyezzük, hogy a függvény definíciója helyettesíti a prototípust.) Az esetek többségében prototípusként a függvényfejet használjuk pontosvesszővel lezárva. A prototípusban nincs jelentősége a paraméterneveknek, elhagyhatjuk őket, vagy bármilyen nevet alkalmazhatunk. Az alábbi prototípusok a fordító szempontjából teljesen azonosak:
int isum(int); int isum(int n); int isum(int sok);
Valamely függvény prototípusa többször is szerepelhet a programban, azonban a paraméternevektől eltekintve azonosaknak kell lenniük.
A C++ nyelv lehetővé teszi, hogy a legalább egy paramétert tartalmazó paraméterlistát három pont (...) zárja. Az így definiált függvény legalább egy, de különben tetszőleges számú és típusú argumentummal hívható. Példaként tekintsük a sscanf () függvény prototípusát!
int sscanf ( const char * str, const char * format, ...);
Felhívjuk a figyelmet arra, hogy a paraméterrel nem rendelkező függvények prototípusát eltérő módon értelmezi a C és a C++ nyelv:
|
deklaráció |
C értelmezés |
C++ értelmezés |
|---|---|---|
|
típus fv(); |
típus fv(...); |
típus fv(void); |
|
típus fv(...); |
típus fv(...); |
típus fv(...); |
|
típus fv(void); |
típus fv(void); |
típus fv(void); |
A kivételeket tárgyaló (I.5. szakasz) fejezetben volt róla szó, hogy a függvények fejsorában engedélyezhetjük, vagy tilthatjuk a kivételek továbbítását a hívó függvény felé. A throw kulcsszó felhasználásával a függvénydefiníció a következőképpen módosul:
visszatérési típus függvénynév (〈paraméterlista〉) 〈throw(〈típuslista〉)〉
{
〈lokális definíciók és deklarációk〉
〈utasítások〉
return 〈kifejezés〉;
}
A definíciónak megfelelő prototípusban is fel kell tüntetni a throw kiegészítést:
visszatérési típus függvénynév (〈paraméterlista〉) 〈throw(〈típuslista〉)〉;
Nézzünk néhány prototípust a továbbított kivételek típusának feltüntetésével:
int fv() throw(int, const char*); // csak int és const char * int fv(); // minden int fv() throw(); // egyetlen egyet sem
II.1.2. Függvények visszatérési értéke
A függvények definíciójában/deklarációjában szereplő visszatérési típus határozza meg a függvényérték típusát, amely tetszőleges C++ típus lehet, a tömbtípus és a függvénytípus kivételével. A függvények nem adhatnak vissza volatile vagy const típusminősítővel ellátott adatokat, azonban ilyen adatra mutató pointert vagy hivatkozó referenciát igen.
A függvény a return utasítás feldolgozását követően visszatér a hívóhoz, és függvényértékként megjelenik az utasításban szereplő kifejezés értéke, melynek típusa a visszatérési típus:
return kifejezés;
A függvényen belül tetszőleges számú return utasítás elhelyezhető, azonban a strukturált programozás elveinek megfelelően törekednünk kell egyetlen kilépési pont használatára.
Az alábbi prímszámellenőrző függvényből a három return utasítással, három ponton is kiléphetünk, ami nehezen áttekinthető programszerkezetet eredményez.
bool Prime(unsigned n)
{
if (n<2) // 0, 1
return false;
else {
unsigned hatar = (unsigned)sqrt(1.0*n);
for (unsigned d=2; d<=hatar; d++)
if ((n % d) == 0)
return false;
}
return true;
}
Egy segédváltozó (eredmeny) bevezetésével elkésztett megoldás sokkal áttekinthetőbb kódot tartalmaz:
bool Prime(unsigned n)
{
bool eredmeny = true;
if (n<2) // 0, 1
eredmeny = false;
else {
unsigned hatar = (unsigned)sqrt(1.0*n);
for (unsigned d=2; d<=hatar && eredmeny; d++)
if ((n % d) == 0)
eredmeny = false;
}
return eredmeny;
}
A void típus felhasználásával olyan függvényeket is készíthetünk, amelyek nem adnak vissza értéket. (Más programozási nyelveken ezeket az alprogramokat eljárásoknak nevezzük.) Ebben az esetben a függvényből való visszatérésre a return utasítás kifejezés nélküli alakját használhatjuk. Ebben az esetben azonban nem kötelező a return használata, a void függvények gyakran a függvény törzsét záró kapcsos zárójel elérésével térnek vissza.
Az alábbi függvény a tökéletes számokat jeleníti meg egy megadott intervallumon belül. (Valamely pozitív egész szám tökéletes, ha a nála kisebb pozitív osztóinak összege egyenlő magával a számmal. A legkisebb tökéletes szám a 6, mert 6 = 1+2+3, de tökéletes szám a 28 is, mert 28 = 1+2+4+7+14.)
void TokeletesSzamok(int tol, int ig)
{
int osszeg = 0;
for(int i=tol; i<=ig; i++) {
osszeg = 0;
for(int j=1; j<i; j++) {
if(i%j == 0)
osszeg += j;
}
if(osszeg == i)
cout<< i <<endl;
}
}
A függvények mutatóval és referenciával is visszatérhetnek, azonban nem szabad lokális változó címét, illetve magát a változót visszaadni, hiszen az megszűnik a függvényből való kilépést követően. Nézzünk néhány helyes megoldást!
#include <cassert>
using namespace std;
double * Foglalas(int meret) {
double *p = new (nothrow) double[meret];
assert(p);
return p;
}
int & DinInt() {
int *p = new (nothrow) int;
assert(p);
return *p;
}
int main() {
double *pd = Foglalas(2012);
pd[2] = 8;
delete []pd;
int &x = DinInt();
x = 10;
delete &x;
}
A Foglalas() függvény megadott elemszámú, double típusú tömböt foglal, és visszatér a lefoglalt dinamikus tömb kezdőcímével. A DinInt() függvény mindössze egyetlen egész változónak foglal tárterületet a halmon, és visszaadja a dinamikus változó referenciáját. Ezt az értéket egy hivatkozás típusú változóba töltve, a dinamikus változót a * operátor nélkül érhetjük el.
II.1.3. A függvények paraméterezése
A függvények készítése során arra törekszünk, hogy minél szélesebb körben használjuk a függvényben megvalósított algoritmust. Ehhez arra van szükség, hogy az algoritmus bemenő értékeit (paramétereit) a függvény hívásakor adjuk meg. Az alábbi paraméter nélküli függvény egy üdvözlést jelenít meg:
void Udvozles(void) {
cout << "Üdvözöllek dícső lovag..." << endl;
}
A függvény minden hívásakor ugyanazt a szöveget látjuk a képernyőn:
Udvozles();
Mit kell tennünk ahhoz, hogy például a napszaknak megfelelően üdvözöljük a felhasználót? A választ a függvény paraméterezése adja:
#include <iostream>
#include <string>
using namespace std;
void Udvozles(string udv) {
cout << udv << endl;
}
int main() {
Udvozles("Jó reggelt");
Udvozles("Good evening!");
}
A C++ függvény-definícióban szereplő paraméterlistában minden paraméter előtt ott áll a paraméter típusa, semmilyen összevonás sem lehetséges. A deklarált paramétereket a függvényen belül a függvény lokális változóiként használhatjuk, azonban a függvényen kívülről csak a paraméterátadás során érhetők el. A paraméterek típusa a skalár (bool, char, wchar_t, short, int, long, long long, float, double, felsorolási, referencia és mutató), valamint a struktúra, unió, osztály és tömb típusok közül kerülhet ki.
A különböző típusú paraméterek szemléltetésére készítsük el egy polinom helyettesítési értékét a Horner-elrendezés alapján számító függvényt!
a polinom általános alakja: 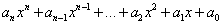
a Horner-elrendezés: 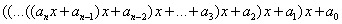
A függvény bemenő paraméterei az x értéke, a polinom fokszáma és a polinom együtthatóinak (fokszám+1 elemű) tömbje. (A const típusminősítő megakadályozza a tömb elemeinek módosítását a függvényen belül.)
double Polinom(double x, int n, const double c[]) {
double y = 0;
for (int i = n; i > 0; i--)
y = (y + c[i]) * x;
return y + c[0];
}
int main(){
const int fok = 3;
double egyutthatok[fok + 1] = { 5, 2, 3, 1};
cout << Polinom(2, fok, egyutthatok)<< endl; // 29
}
II.1.3.1. A paraméterátadás módjai
A C++ nyelvben a paramétereket - az átadásuk módja szerint - két csoportra oszthatjuk. Megkülönböztetünk érték szerint átadott, bemenő paramétereket és hivatkozással átadott (változó) paramétereket.
II.1.3.1.1. Érték szerinti paraméterátadás
Az érték szerinti paraméterátadás során az argumentumok értéke adódik át a hívott függvénynek. A függvény paraméterei az átadott értékekkel inicializálódnak, és ezzel meg is szűnik a kapcsolat az argumentumok és a paraméterek között. Ennek következtében a paramétereken végzett műveleteknek nincs hatása a híváskor megadott argumentumokra.
Az argumentumok csak olyan kifejezések lehetnek, melyek típusai konvertálhatók a hívott függvény megfelelő paramétereinek típusára.
Az eszam() függvény az e szám közelítő értékét szolgáltatja a
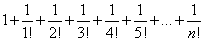
sor első n+1 elemének összegzésével:
double eszam(int n) {
double f = 1;
double esor = 1;
for (int i=2; i<=n; i++) {
esor += 1.0 / f;
f *= i;
}
return esor;
}
Az eszam() függvény tetszőleges numerikus kifejezéssel hívhatjuk:
int main(){
long x =1000;
cout << eszam(x)<< endl;
cout << eszam(123) << endl;
cout << eszam(x + 12.34) << endl;
cout << eszam(&x) << endl; // hiba
}
Az első híváskor a long típusú x változó értéke int típusúvá alakítva adódik át a függvénynek. A második esetben az int típusú konstans lesz a paraméter értéke. A harmadik hívás argumentuma egy double típusú kifejezés, melynek értéke egésszé alakítva adódik át. Ez az átalakítás adatvesztéssel járhat, ezért erre a fordító figyelmeztet. Az utolsó eset kakukktojásként szerepel a hívások listájában, mivel ebben az esetben az x változó címének számmá alakítását visszautasítja a fordító. Mivel a hasonló típus-átalakítások futás közbeni hibához vezethetnek, az átalakítást külön kérnünk kell:
cout << eszam((int)&x) << endl;
Amennyiben függvényen belül szeretnénk módosítani egy külső változó értékét, a változó címét kell argumentumként átadni, és a címet mutató típusú paraméterben kell fogadni. Példaként tekintsük a klasszikusnak számító, változók értékét felcserélő függvényt:
void pcsere(double *p, double *q) {
double c = *p;
*p = *q;
*q = c;
}
int main(){
double a = 12, b =23;
pcsere(&a, &b);
cout << a << ", " << b<< endl; // 23, 12
}
Ebben az esetben is szerelhetnek kifejezések argumentumként, azonban csak balérték kifejezések. Megjegyezzük, hogy a tömbök a kezdőcímükkel adódnak át a függvényeknek.
A const típusminősítő paraméterlistában való elhelyezésével korlátozhatjuk a mutató által kijelölt terület módosítását ( const double *p), illetve a mutató értékének megváltoztatását ( double * const p) a függvényen belül.
II.1.3.1.2. Referencia szerinti paraméterátadás
Az érték szerint átadott paramétereket a függvény lokális változóiként használjuk. Ezzel szemben a referencia paraméterek nem önálló változók, csupán alternatív nevei a híváskor megadott argumentumoknak.
A referencia paramétereket a függvény fejlécében a típus és a paraméternév közé helyezett & karakterrel jelöljük, híváskor pedig a paraméterekkel azonos típusú változókat használunk argumentumként. Referenciával átadott paraméterekkel a változók értékét felcserélő függvény sokkal egyszerűbb formát ölt:
void rcsere(double & a, double & b) {
double c = a;
a = b;
b = c;
}
int main(){
double x = 12, y =23;
rcsere(x, y);
cout << x << ", " << y << endl; // 23, 12
}
A referencia paraméter értéke (jobbértéke) és címe (balértéke) megegyezik a hivatkozott változó értékével és címével, így minden szempontból helyettesíti azt.
Megjegyezzük, hogy a pcsere() és rcsere() függvények lefordított kódja Visual Studio rendszerben teljes mértékben megegyezik. Ezért semmilyen hatékonysági megfontolás nem indokolja a pcsere() használatát a C++ nyelven készített programokban.
Mindkét féle paraméterátadás során a paramétereknek a veremben foglal helyet a fordító. Érték paramétereknél a lefoglalt terület mérete függ a paraméter típusától, tehát igen nagy is lehet, míg referencia paraméterek esetén mindig az adott rendszerben használt mutatóméret a mérvadó. Egy nagyobb struktúra vagy objektum esetén a megnövekedett memóriaigény mellett a hívásidő növekedése sem elhanyagolható.
Az alábbi példában egy struktúrát adunk át a függvénynek hivatkozással, azonban szeretnénk megakadályozni a struktúra megváltoztatását függvényen belül. Erre a célra a leghatékonyabb megoldás a konstans referencia típusú paraméter alkalmazása:
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
struct svektor {
int meret;
int a[1000];
};
void MinMax(const svektor & sv, int & mi, int & ma) {
mi = ma = sv.a[0];
for (int i=1; i<sv.meret; i++) {
if (sv.a[i]>ma)
ma = sv.a[i];
if (sv.a[i]<mi)
mi = sv.a[i];
}
}
int main() {
const int maxn = 1000;
srand(unsigned(time(0)));
svektor v;
v.meret=maxn;
for (int i=0; i<maxn; i++) {
v.a[i]=rand() % 102 + (rand() % 2012);
}
int min, max;
MinMax(v, min, max);
cout << min << endl;
cout << max << endl;
}
Megjegyezzük, hogy a fenti megoldásban ugyan gyorsabb a MinMax() függvény hívása, és kisebb helyre van szükség a veremben, azonban a paraméterek függvényen belüli elérése hatékonyabb az érték típusú paraméterek használata eseten.
A konstans referencia paraméterek teljes mértékben helyettesítik a konstans érték paramétereket, így tetszőleges kifejezést (nemcsak változót) használhatunk argumentumként. A két szám legnagyobb közös osztóját meghatározó példa szemlélteti ezt:
int Lnko(const int & a, const int & b ) {
int min = a<b ? a : b, lnko = 0;
for (int n=min; n>0; n--)
if ( (a % n == 0) && (b % n) == 0) {
lnko = n;
break;
}
return lnko;
}
int main() {
cout << Lnko(24, 32) <<endl; // 8
}
II.1.3.2. Különböző típusú paraméterek használata
A következő alfejezetekben különböző típusok esetén, példák segítségével mélyítjük el a paraméterek használatával kapcsolatos ismereteket. Az alfejezet példáiban a függvények definícióját - kipontozott sor után - követi a hívás bemutatása. Természetesen bonyolultabb esetekben teljes programlistát is közlünk.
II.1.3.2.1. Aritmetikai típusú paraméterek
A bool, char, wchar_t, int, enum, float és double típusokkal paramétereket deklarálhatunk, illetve függvények típusaként is megadhatjuk őket.
Általában rövid megfontolásra van szükség ahhoz, hogy eldöntsük, milyen paramétereket használjunk, és mi legyen a függvény értéke. Ha egy függvény nem ad vissza semmilyen értéket, csupán elvégez egy tevékenységet, akkor void visszatérési típust és érték paramétereket alkalmazunk:
void KiirF(double adat, int mezo, int pontossag) {
cout.width(mezo);
cout.precision(pontossag);
cout << fixed << adat << endl;
}
...
KiirF(123.456789, 10, 4); // 123.4568
Ugyancsak egyszerű a dolgunk, ha egy függvény a bemenő értékekből egyetlen értéket állít elő:
long Szorzat(int a, int b) {
return long(a) * b;
}
...
cout << Szorzat(12, 23) <<endl; // 276
Ha azonban egy függvénytől több értéket szeretnénk visszakapni, akkor referencia (vagy pointer) paraméterekre építjük a megoldást. Ekkor a függvényérték void vagy pedig a működés eredményességét jelző típusú, például bool. Az alábbi Kocka() függvény az élhossz felhasználásával kiszámítja a kocka felszínét, térfogatát és testátlójának hosszát:
void Kocka(double a, double & felszin, double & terfogat,
double & atlo) {
felszin = 6 * a * a;
terfogat = a * a * a;
atlo = a * sqrt(3.0);
}
...
double f, v, d;
Kocka(10, f, v, d);
II.1.3.2.2. Felhasználói típusú paraméterek
A felhasználói típusok (struct, class, union) paraméterlistában, illetve függvényértékként való felhasználására az aritmetikai típusoknál bemutatott megoldások érvényesek. Ennek alapja, hogy a C++ nyelv definiálja az azonos típusú objektumok, illetve uniók közötti értékadást.
A felhasználói típusú argumentumokat érték szerint, referenciával, illetve mutató segítségével egyaránt átadhatjuk a függvényeknek. A szabványos C++ nyelvben a függvény visszatérési értéke felhasználói típusú is lehet. A lehetőségek közül általában ki kell választanunk az adott feladathoz legjobban illeszkedő megoldást.
Példaként tekintsük a komplex számok tárolására alkalmas struktúrát!
struct komplex {
double re, im;
};
Készítsünk függvényt két komplex szám összeadására, amelyben a tagok és az eredmény tárolására szolgáló struktúrát mutatójuk segítségével adjuk át a függvénynek (KOsszeg1())! Mivel a bemenő paramétereket nem kívánjuk a függvényen belül megváltoztatni, const típusminősítőt használunk.
void KOsszeg1(const komplex*pa,const komplex*pb,komplex *pc){
pc->re = pa->re + pb->re;
pc->im = pa->im + pb->im;
}
A második függvény visszatérési értékként szolgáltatja a két érték szerint átadott komplex szám összegét (KOsszeg2()). Az összegzést egy lokális struktúrában végezzük el, melynek csupán értékét adjuk vissza a return utasítással.
komplex KOsszeg2(komplex a, komplex b) {
komplex c;
c.re = a.re + b.re;
c.im = a.im + b.im;
return c;
}
A második megoldás természetesen sokkal biztonságosabb, és sokkal jobban kifejezi a művelet lényegét, mint az első. Minden más szempontból (memóriaigény, sebesség) az első függvényt kell választanunk. A referenciatípus használatával azonban olyan megoldáshoz juthatunk, amely magában hordozza a KOsszeg2() függvény előnyös tulajdonságait, azonban az KOsszeg1() függvénnyel is felveszi a versenyt (memóriaigény, sebesség).
komplex KOsszeg3(const komplex & a, const komplex & b) {
komplex c;
c.re = a.re + b.re;
c.im = a.im + b.im;
return c;
}
A három különböző megoldáshoz két különböző hívási mód tartozik. Az alábbi main() függvény mindhárom összegző függvény hívását tartalmazza:
int main() {
komplex c1 = {10, 2}, c2 = {7, 12}, c3;
KOsszeg1(&c1, &c2, &c3); // mindhárom argumentum pointer
c3 = KOsszeg2(c1, c2); // két struktúra az argumentum
// két struktúra referencia az argumentum
c3 = KOsszeg3(c1, c2);
}
II.1.3.2.3. Tömbök átadása függvénynek
Az alábbiakban áttekintjük, hogy milyen lehetőségeket biztosít a C++ nyelv tömbök függvénynek való átadására. Már szóltunk róla, hogy tömböt nem lehet érték szerint (a teljes tömb átmásolásával) függvénynek átadni, illetve függvényértékként megkapni. Sőt különbség van az egydimenziós (vektorok) és a többdimenziós tömbök argumentumként való átadása között is.
Egydimenziós tömbök (vektorok) függvényargumentumként való megadása esetén a tömb első elemére mutató pointer adódik át. Ebből következik, hogy a függvényen belül a vektor elemein végrehajtott változtatások a függvényből való visszatérés után is érvényben maradnak.
A vektor típusú paramétert mutatóként , illetve az üres indexelés operátorával egyaránt deklarálhatjuk. Mivel a C++ tömbök semmilyen információt sem tartalmaznak az elemek számáról, ezt az adatot külön paraméterben kell átadnunk. A függvényen belül az elemek eléréséhez a már megismert két módszer (index, pointer) bármelyikét alkalmazhatjuk. Egy int vektor első n elemének összegét meghatározó függvényt többféleképpen is megfogalmazhatjuk. A vektor paraméterében a const típusminősítővel, azt biztosítjuk, hogy a függvényen belül a vektor elemeit nem lehet megváltoztatni.
long VektorOsszeg1 (const int vektor[], int n) {
long osszeg = 0;
for (int i = 0; i < n; i++) {
osszeg+=vektor[i]; // vagy osszeg+=*(vektor+i);
}
return osszeg;
}
...
int v[7] = { 10, 2, 11, 30, 12, 7, 23};
cout <<VektorOsszeg1(v, 7)<< endl; // 95
cout <<VektorOsszeg1(v, 3)<< endl; // 23
A fentivel teljes mértékben megegyező megoldást kapunk, ha mutatóban fogadjuk a vektor kezdőcímét. (A második const minősítővel biztosítjuk, hogy ne lehessen a mutató értéket módosítani.)
long VektorOsszeg2 (const int * const vektor, int n) {
long osszeg = 0;
for (int i = 0; i < n; i++) {
osszeg+=vektor[i]; // vagy osszeg+=*(vektor+i);
}
return osszeg;
}
Amennyiben módosítanunk kell az átadott vektor elemeit, például rendezni, az első const típusminősítőt el kell hagynunk:
void Rendez(double v[], int n) {
double temp;
for (int i = 0; i < n-1; i++)
for (int j=i+1; j<n; j++)
if (v[i]>v[j]) {
temp = v[i];
v[i] = v[j];
v[j] = temp;
}
}
int main() {
const int meret=7;
double v[meret]={10.2, 2.10, 11, 30, 12.23, 7.29, 23.};
Rendez(v, meret);
for (int i = 0; i < meret; i++)
cout << v[i]<< '\t';
cout << endl;
}
Az egydimenziós tömböket referenciával is átadhatjuk, azonban ekkor rögzítenünk kell a feldolgozni kívánt vektor méretét.
long VektorOsszeg3 (const int (&vektor)[6]) {
long osszeg = 0;
for (int i = 0; i < 6; i++) {
osszeg+=vektor[i]; // vagy osszeg+=*(vektor+i);
}
return osszeg;
}
...
int v[6] = { 10, 2, 11, 30, 12, 7};
cout << VektorOsszeg3(v) << endl;
A kétdimenziós tömb argumentumok bemutatása során a kétdimenziós tömb elnevezés alatt csak a fordító által (statikusan) létrehozott tömböket értjük:
int m[2][3];
A tömb elemeire való hivatkozás (m[i][j]) mindig felírható a *(( int *)m+(i*3)+j) formában (ezt teszik a fordítók is). Ebből a kifejezésből jól látható, hogy a kétdimenziós tömb második dimenziója (3) alapvető fontossággal bír a fordító számára, míg a sorok száma tetszőleges lehet.
Célunk olyan függvény készítése, amely tetszőleges méretű, kétdimenziós egész tömb elemeit mátrixos formában megjeleníti. Első lépésként írjuk meg a függvény 2x3-as tömbök megjelenítésére alkalmas változatát!
void PrintMatrix23(const int matrix[2][3]) {
for (int i=0; i<2; i++) {
for (int j=0; j<3; j++)
cout <<matrix[i][j] <<'\t';
cout<<endl;
}
}
...
int m[2][3] = { {10, 2, 12}, {23, 7, 29} };
PrintMatrix23(m);
10 2 12 23 7 29 |
A kétdimenziós tömb is a terület kezdőcímét kijelölő mutatóként adódik át a függvénynek. A fordító az elemek elérése során kihasználja, hogy a sorok 3 elemet tartalmaznak. Ennek figyelembevételével a fenti függvény egyszerűen átalakítható tetszőleges nx3-as tömb kiírására alkalmas alprogrammá, csak a sorok számát kell átadni második argumentumként:
void PrintMatrixN3(const int matrix[][3], int n) {
for (int i=0; i<n; i++) {
for (int j=0; j<3; j++)
cout <<matrix[i][j] <<'\t';
cout<<endl;
}
}
...
int m[2][3] = { {10, 2, 12}, {23, 7, 29} };
PrintMatrixN3(m, 2);
cout << endl;
int m2[3][3] = { {1}, {0, 1}, {0, 0, 1} };
PrintMatrixN3(m2, 3);
10 2 12 23 7 29 1 0 0 0 1 0 0 0 1 |
Arra azonban nincs lehetőség, hogy a második dimenziót is elhagyjuk, hiszen akkor a fordító nem képes a tömb sorait azonosítani. Egyetlen dolgot tehetünk az általános megoldás megvalósításának érdekében, hogy a fenti kifejezés felhasználásával átvesszük a tömbterület elérésének feladatát a fordítótól:
void PrintMatrixNM(const void *pm, int n, int m) {
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++)
cout <<*((int *)pm+i*m+j) <<'\t';
cout<<endl;
}
}
...
int m[2][3] = { {10, 2, 12}, {23, 7, 29} };
PrintMatrixNM(m, 2, 3);
cout << endl;
int m2[4][4] = { {0,0,0,1}, {0,0,1}, {0,1}, {1} };
PrintMatrixNM(m2, 4, 4);
10 2 12 23 7 29 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 |
II.1.3.2.4. Sztring argumentumok
Függvények készítése során szintén választhatunk a karaktersorozatok C-stílusú (char vektor) vagy felhasználói típusú ( string ) feldolgozása között. Mivel az előzőekben már mindkét paramétertípust ismertettük, most csak néhány példa bemutatására szorítkozunk.
A karaktersorozatok kezelése során három megközelítési módot használunk. Az első esetben, mint vektort kezeljük a sztringet (indexelve), a második megközelítés szerint mutató segítségével végezzük el a szükséges műveleteket, míg harmadik esetben a string típus tagfüggvényeit használjuk.
Felhívjuk a figyelmet arra, hogy a sztring literálok (karaktersorozat konstansok) tartalmának módosítása általában futás közbeni hibához vezet, így azokat csak konstans vagy pedig string típusú érték paraméternek lehet közvetlenül átadni.
Az első példában csupán olvassuk a karaktersorozat elemeit, így megszámlálva egy megadott karakter előfordulásainak számát.
Amennyiben vektorként dolgozzuk fel a sztringet, szükségünk van egy indexváltozóra (i), amellyel a karaktereket indexeljük. A számlálást leállító feltétel a karaktersorozatot záró 0-ás bájt elérése, amihez az indexváltozó léptetésével jutunk el.
unsigned SzamolChC1(const char s[], char ch) {
unsigned db = 0;
for (int i=0; s[i]; i++) {
if (s[i] == ch)
db++;
}
return db;
}
A pointeres megközelítés során a karaktersorozat elejére hivatkozó mutató léptetésével megyünk végig a karaktereken, egészen a sztringet záró '\0' karakter (0-ás bájt) eléréséig
unsigned SzamolChC2(const char *s, char ch) {
unsigned db = 0;
while (*s) {
if (*s++ == ch)
db++;
}
return db;
}
A string típus alkalmazásakor az indexelés mellett tagfüggvényeket is használhatunk:
unsigned SzamolChCpp(const string & s, char ch) {
int db = -1, pozicio = -1;
do {
db++;
pozicio = s.find(ch, pozicio+1);
} while (pozicio != string::npos);
return db;
}
A függvények hívását konstans sztring, karakter tömb és string típusú argumentummal szemléltetjük. Mindhárom függvény hívható sztring literál, illetve karakter tömb argumentummal:
char s1[] = "C, C++, Java, C++/CLI / C#";
string s2 = s1;
cout<<SzamolChC1("C, C++, Java, C++/CLI / C#", 'C')<<endl;
cout<<SzamolChC2(s1, 'C')<<endl;
A string típusú argumentum alkalmazása azonban, már beavatkozást igényel az első két függvénynél:
cout << SzamolChC2(s2.c_str(), 'C') << endl; cout << SzamolChCpp(s2, 'C') << endl;
Sokkal szigorúbb feltételek érvényesülnek, ha elhagyjuk a const deklarációt a paraméterek elől. A következő példában a függvénynek átadott sztringet helyben „megfordítjuk”, és a sztringre való hivatkozással térünk vissza. A megoldást mindhárom fent tárgyalt esetre elkészítettük:
char * StrForditC1(char s[]) {
char ch;
int hossz = -1;
while(s[++hossz]); // a sztring hosszának meghatározása
for (int i = 0; i < hossz / 2; i++) {
ch = s[i];
s[i] = s[hossz-i-1];
s[hossz-i-1] = ch;
}
return s;
}
char * StrForditC2(char *s) {
char *q, *p, ch;
p = q = s;
while (*q) q++; // lépkedés a sztringet záró 0 bájtra
p--; // p sztring első karaktere elé mutat
while (++p <= --q) {
ch = *p;
*p = *q;
*q = ch;
}
return s;
}
string& StrForditCpp(string &s) {
char ch;
int hossz = s.size();
for (int i = 0; i < hossz / 2; i++) {
ch = s[i];
s[i] = s[hossz-i-1];
s[hossz-i-1] = ch;
}
return s;
}
A függvényeket a paraméter típusával egyező típusú argumentummal kell hívni:
int main() {
char s1[] = "C++ programozas";
cout << StrForditC1(s1) << endl; // sazomargorp ++C
cout << StrForditC2(s1) << endl; // C++ programozas
string s2 = s1;
cout << StrForditCpp(s2) << endl; // sazomargorp ++C
cout << StrForditCpp(string(s1)); // sazomargorp ++C
}
II.1.3.2.5. A függvény, mint argumentum
Matematikai alkalmazások készítése során jogos az igény, hogy egy jól megvalósított algoritmust különböző függvények esetén tudjunk használni. Ehhez a függvényt argumentumként kell átadni az algoritmust megvalósító függvénynek.
II.1.3.2.5.1. A függvénytípus és a typedef
A typedef segítségével a függvény típusát egyetlen szinonim névvel jelölhetjük. A függvénytípus deklarálja azt a függvényt, amely az adott számú és típusú paraméterkészlettel rendelkezik, és a megadott adattípussal tér vissza. Tekintsük például a 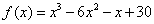 harmadfokú polinom helyettesítési értékeit számító függvényt, melynek prototípusa és definíciója:
harmadfokú polinom helyettesítési értékeit számító függvényt, melynek prototípusa és definíciója:
double poli3(double); // prototípus
double poli3(double x) // definíció
{
return x*x*x - 6*x*x - x + 30;
}
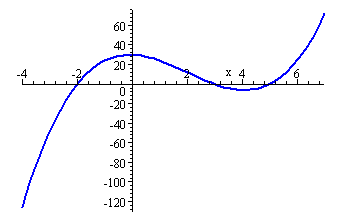
Vegyük a függvény prototípusát, tegyük elé a typedef kulcsszót, végül cseréljük le a poli3 nevet mathfv-re!
typedef double matfv(double);
A mathfv típus felhasználásával a poli3() függvény prototípusa:
matfv poli3;
II.1.3.2.5.2. Függvényre mutató pointerek
A C++ nyelvben a függvényneveket kétféle módon használhatjuk. A függvénynevet a függvényhívás operátor bal oldali operandusaként megadva, függvényhívás kifejezést kapunk
poli3(12.3)
melynek értéke a függvény által visszaadott érték. Ha azonban a függvénynevet önállóan használjuk
poli3
akkor egy mutatóhoz jutunk, melynek értéke az a memóriacím, ahol a függvény kódja elhelyezkedik (kódpointer), típusa pedig a függvény típusa.
Definiáljunk egy olyan mutatót, amellyel a poli3() függvényre mutathatunk, vagyis értékként felveheti a poli3() függvény címét! A definíciót egyszerűen megkapjuk, ha a poli3 függvény fejsorában szereplő nevet a (*fvptr) kifejezésre cseréljük:
double (*fvptr)(double);
Az fvptr olyan pointer, amely double visszatérési értékkel és egy double típusú paraméterrel rendelkező függvényre mutathat.
A definíció azonban sokkal olvashatóbb formában is megadható, ha használjuk a typedef segítségével előállított matfv típust:
matfv *fvptr;
Az fvptr mutató inicializálása után a poli3 függvényt indirekt módon hívhatjuk:
fvptr = poli3;
double y = (*fvptr)(12.3); vagy doubley = fvptr(12.3);
Hasonló módon kell eljárnunk, ha a függvényhez referenciát akarunk készíteni. Ebben az esetben a kezdőértéket már a definíció során meg kell adni:
double (&fvref)(double) = poli3;
vagy
matfv &fvref = poli3;
A függvényhívás a referencia felhasználásával:
double y = fvref(12.3);
II.1.3.2.5.3. Függvényre mutató pointer példák
A fentiek alapján érthetővé válik a qsort () könyvtári függvény prototípusa:
void qsort(void *base, size_t nelem, size_t width,
int (*fcmp)(const void *, const void *));
A qsort () segítségével tömbben tárolt adatokat rendezhetünk a gyorsrendezés algoritmusának felhasználásával. A függvénnyel a base címen kezdődő, nelem elemszámú, elemenként width bájtot foglaló tömböt rendezhetünk. A rendezés során hívott összehasonlító függvényt magunknak kell megadni az fcmp paraméterben.
Az alábbi példában a qsort () függvényt egy egész, illetve egy sztringtömb rendezésére használjuk:
#include <iostream>
#include <cstdlib>
#include <cstring>
using namespace std;
int icmp(const void *p, const void *q) {
return *(int *)p-*(int *)q;
}
int scmp(const void *p, const void *q) {
return strcmp((char *)p,(char *)q);
}
void main() {
int m[8]={2, 10, 7, 12, 23, 29, 11, 30};
char nevek[6][20]={"Dennis Ritchie", "Bjarne Stroustrup",
"Anders Hejlsberg","Patrick Naughton",
"James Gosling", "Mike Sheridan"};
qsort(m, 8, sizeof(int), icmp);
for (int i=0; i<8; i++)
cout<<m[i]<<endl;
qsort(nevek, 6, 20, scmp);
for (int i=0; i<6; i++)
cout<<nevek[i]<<endl;
}
A következő példaprogramokban szereplő tabellaz() függvény tetszőleges double típusú paraméterrel és double visszatérési értékkel rendelkező függvény értékeinek táblázatos megjelenítésére alkalmas. A tabellaz() függvény paraméterei között szerepel még az intervallum két határa és a lépésköz.
#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;
// Prototípusok
void tabellaz(double (*)(double), double, double, double);
double sqr(double);
int main() {
cout<<"\n\nAz sqr() fuggveny ertekei ([-2,2] dx=0.5)"<<endl;
tabellaz(sqr, -2, 2, 0.5);
cout<<"\n\nAz sqrt() fuggveny ertekei ([0,2] dx=0.2)"<<endl;
tabellaz(sqrt, 0, 2, 0.2);
}
// A tabellaz() függvény definíciója
void tabellaz(double (*fp)(double), double a, double b,
double lepes){
for (double x=a; x<=b; x+=lepes) {
cout.precision(4);
cout<<setw(12)<<fixed<<x<< '\t';
cout.precision(7);
cout<<setw(12)<<fixed<<(*fp)(x)<< endl;
}
}
// Az sqr() függvény definíciója
double sqr(double x) {
return x * x;
}
A program futásának eredménye:
Az sqr() fuggveny ertekei ([-2,2] dx=0.5)
-2.0000 4.0000000
-1.5000 2.2500000
-1.0000 1.0000000
-0.5000 0.2500000
0.0000 0.0000000
0.5000 0.2500000
1.0000 1.0000000
1.5000 2.2500000
2.0000 4.0000000
Az sqrt() fuggveny ertekei ([0,2] dx=0.2)
0.0000 0.0000000
0.2000 0.4472136
0.4000 0.6324555
0.6000 0.7745967
0.8000 0.8944272
1.0000 1.0000000
1.2000 1.0954451
1.4000 1.1832160
1.6000 1.2649111
1.8000 1.3416408
2.0000 1.4142136
|
II.1.3.2.6. Alapértelmezés szerinti (default) argumentumok
A C++ függvények prototípusában bizonyos paraméterekhez ún. alapértelmezés szerinti értéket rendelhetünk. A fordító ezeket az értékeket használja fel a függvény hívásakor, ha a paraméternek megfelelő argumentum nem szerepel a hívási listában:
// prototípus
long SorOsszeg(int n = 10, int d = 1, int a0 = 1);
long SorOsszeg(int n, int d, int a0) { // definíció
long osszeg = 0, ai;
for(int i = 0; i < n; i++) {
ai = a0 + d * i;
cout << setw(5) << ai;
osszeg += ai;
}
return osszeg;
}
A SorOsszeg() függvény n elemű számtani sorozatot készít, amelynek az első eleme a0, differenciája pedig d. A függvény visszatérési értéke a sorozat elemeinek összege.
Felhívjuk a figyelmet arra, hogy az alapértelmezés szerinti értékkel ellátott paraméterek jobbról-balra haladva folytonosan helyezkednek el, míg híváskor az argumentumokat balról jobbra haladva folytonosan kell megadni. Prototípus használata esetén, az alapértelmezés szerinti értékeket csak a prototípusban adhatjuk meg.
A fenti függvény lehetséges hívásait felsorolva, nézzük meg a paraméterek értékét!
|
Hívás |
Paraméterek |
||
|---|---|---|---|
|
n |
d |
a0 |
|
|
SorOsszeg() |
10 |
1 |
1 |
|
SorOsszeg(12) |
12 |
1 |
1 |
|
SorOsszeg(12, 3) |
12 |
3 |
1 |
|
SorOsszeg(12, 3, 7) |
12 |
3 |
7' |
Az alapértelmezés szerinti argumentumok rugalmasabbá teszik a függvények használatát. Például, ha valamely függvényt sokszor hívunk egyazon argumentumlistával, érdemes a gyakran használt argumentumokat alapértelmezés szerintivé tenni, és a hívást az argumentumok megadása nélkül elvégezni.
II.1.3.2.7. Változó hosszúságú argumentumlista
Vannak esetek, amikor nem lehet pontosan megadni a függvény paramétereinek számát és típusát. Az ilyen függvények deklarációjában a paraméterlistát három pont zárja:
int printf(const char * formatum, ... );
A három pont azt jelzi a fordítóprogramnak, hogy még lehetnek további argumentumok. A printf () (cstdio) függvény esetén az első argumentumnak mindig szerepelnie kell, amelyet tetszőleges számú további argumentum követhet:
char nev[] = "Bjarne Stroustrup";
double a=12.3, b=23.4, c=a+b;
printf("C++ nyelv\n");
printf("Nev: %s \n", nev);
printf("Eredmeny: %5.3f + %5.3f = %8.4f\n", a, b, c);
A printf () függvény a formatum alapján dolgozza fel a függvény a soron következő argumentumot.
A hasonló deklarációjú függvények hívásakor a fordító csak a „...” listaelemig egyezteti az argumentumok és a paraméterek típusát. Ezt követően a megadott argumentumok (esetleg konvertált) típusa szerint megy végbe az argumentumok átadása a függvénynek.
A C++ nyelv lehetővé teszi, hogy saját függvényeinkben is használjuk a három pontot – az ún. változó hosszúságú argumentumlistát. Ahhoz, hogy a paramétereket tartalmazó memóriaterületen megtaláljuk az átadott argumentumok értékét, legalább az első paramétert mindig meg kell adnunk.
A C++ szabvány tartalmaz néhány olyan makrót, amelyek segítségével a változó hosszúságú argumentumlista feldolgozható. A cstdarg fejállományban definiált makrók a va_list típusú mutatót használják az argumentumok eléréséhez:
|
|
Megadja az argumentumlista következő elemét. |
|
|
Takarítás az argumentumok feldolgozása után. |
|
|
Inicializálja az argumentumok eléréséhez használt mutatót. |
Példaként tekintsük a tetszőleges számú double érték átlagát számító Atlag() függvényt, melynek hívásakor az átlagolandó számsor elemeinek számát az első argumentumban kell átadni!
#include<iostream>
#include<cstdarg>
using namespace std;
double Atlag(int darab, ... ) {
va_list szamok;
// az első (darab) argumentum átlépése
va_start(szamok, darab);
double osszeg = 0;
for(int i = 0; i < darab; ++i ) {
// double argumentumok elérése
osszeg += va_arg(szamok, double);
}
va_end(szamok);
return (osszeg/darab);
}
int main() {
double avg = Atlag(7,1.2,2.3,3.4,4.5,5.6,6.7,7.8);
cout << avg << endl;
}
II.1.3.2.8. A main() függvény paraméterei és visszatérési értéke
A main () függvény különlegességét nemcsak az adja, hogy a program végrehajtása azzal kezdődik, hanem az is, hogy többféle paraméterezéssel rendelkezik:
int main( ) int main( int argc) ( ) int main( int argc, char *argv[]) ( )
Az argv egy karakter mutatókat tartalmazó tömbre (vektorra) mutat, az argc pedig a tömbben található sztringek számát adja meg. (Az argc értéke legalább 1, mivel az argv[0] mindig a program nevét tartalmazó karaktersorozatra hivatkozik.)
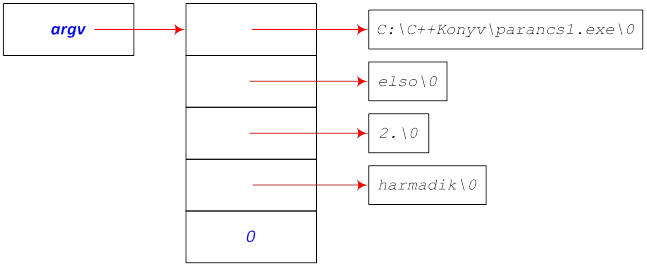
A main () visszatérési értékét, amely a szabvány ajánlása alapján int típusú, a main () függvényen belüli return utasításban, vagy a program tetszőleges pontján elhelyezett exit () könyvtári függvény argumentumaként adhatjuk meg. Az cstdlib fejállomány szabványos konstansokat is tartalmaz,
#define EXIT_SUCCESS 0 #define EXIT_FAILURE 1
amelyeket kilépési kódként használva jelezhetjük a program sikeres, illetve sikertelen végrehajtását.
A main () sok mindenben különbözik a normál C++ függvényektől: nem deklarálhatjuk static vagy inline függvényként, nem kötelező benne a return használata, és nem lehet túlterhelni. A szabvány ajánlása alapján, a programon belülről nem hívható, és nem kérdezhető le a címe sem.
Az alábbi parancs1.cpp program kiírja a parancssor argumentumok számát, és megjeleníti az argumentumokat:
#include <iostream>
using namespace std;
int main(int argc, char *argv[]) {
cout << "az argumentumok szama: " << argc << endl;
for (int narg=0; narg < argc; narg++)
cout << narg << " " << argv[narg] << endl;
return 0;
}
A parancssor argumentumokat a konzol ablakban
C:\C++Konyv>parancs1 elso 2. harmadik
és a Visual Studio fejlesztői környezetben (II.5. ábra) egyaránt megadhatjuk.
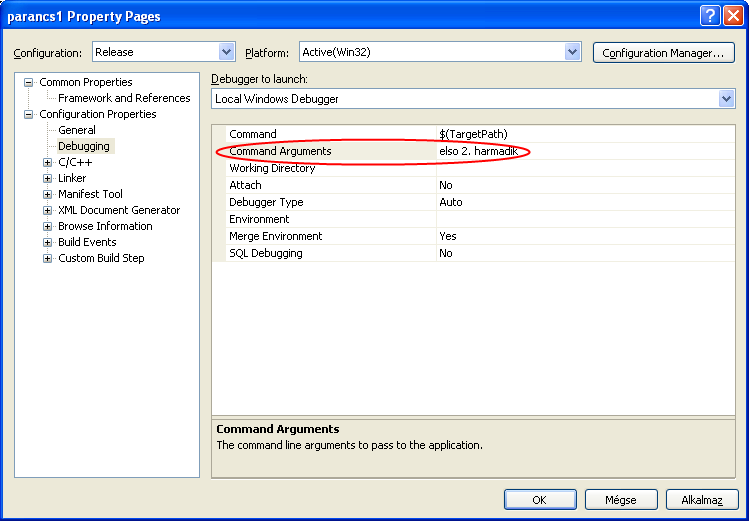
A parancs1.exe program futtatásának eredményei:
|
Konzol ablakban |
Fejlesztői környezetben |
|---|---|
C:\C++Konyv>parancs1 elso 2. harmadik az argumentumok szama: 4 0 parancs1 1 elso 2 2. 3 harmadik C:\C++Konyv> |
C:\C++Konyv>parancs1 elso 2. harmadik az argumentumok szama: 4 0 C:\C++Konyv\parancs1.exe 1 elso 2 2. 3 harmadik C:\C++Konyv> |
A következő példaprogram (parancs2.cpp) a segédprogramok írásánál jól felhasználható megoldást mutat be, az indítási argumentumok helyes megadásának tesztelésére. A program csak akkor indul el, ha pontosan két argumentummal indítjuk. Ellenkező esetben hibajelzést ad, és kiírja az indítási parancssor formáját bemutató üzenetet.
#include <iostream>
#include <cstdlib>
using namespace std;
int main(int argc, char *argv[]) {
if (argc !=3 ) {
cerr<<"Hibas parameterezes!"<<endl;
cerr<<"A program inditasa: parancs2 arg1 arg2"<<endl;
return EXIT_FAILURE;
}
cout<<"Helyes parameterezes:"<<endl;
cout<<"1. argumentum: "<<argv[1]<<endl;
cout<<"2. argumentum: "<<argv[2]<<endl;
return EXIT_SUCCESS;
}
A parancs2.exe program futtatásának eredményei:
|
Hibás indítás: parancs2 |
Helyes indítás: parancs2 alfa beta |
|---|---|
Hibas parameterezes! A program inditasa: parancs2 arg1 arg2 |
Helyes parameterezes: 1. argumentum: alfa 2. argumentum: beta |
II.1.4. Programozás függvényekkel
A procedurális programépítés során az egyes részfeladatok megoldására függvényeket készítünk, amelyek önállóan tesztelhetők. Az eredeti feladat megoldásához ezek után a már tesztelt függvények megfelelő hívásával jutunk el. Fontos kérdés a függvények közötti kommunikáció megszervezése. Mint láttuk egy-egy függvény példáján, a paraméterezés és függvényérték képezik a kapcsolatot a külvilággal. Több, egymással logikai kapcsolatban álló függvény esetén azonban más megoldások is szóba jöhetnek, növelve a megoldás hatékonyságát.
Vegyünk példaként egy mindenki által jól ismert feladatot, a síkbeli háromszög kerületének és területének meghatározását! A területszámítást Hérón képletének felhasználásával végezzük, amely alkalmazásának előfeltétele a háromszög-egyenlőtlenség teljesülése. Ez kimondja, hogy a háromszög minden oldalának hossza kisebb a másik két oldal hosszának összegénél.
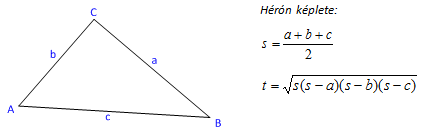
Az egyetlen main () függvényből álló megoldás könyvünk első néhány fejezetének áttanulmányozása után minden további nélkül elkészíthető:
#include <iostream>
#include <cmath>
using namespace std;
int main() {
double a, b, c;
do {
cout <<"a oldal: "; cin>>a;
cout <<"b oldal: "; cin>>b;
cout <<"c oldal: "; cin>>c;
} while(!((a<b+c) && (b<a+c) && (c<a+b)));
double k = a + b + c;
double s = k/2;
double t = sqrt(s*(s-a)*(s-b)*(s-c));
cout << "kerulet: " << k <<endl;
cout << "terulet: " << t <<endl;
}
A program igen egyszerű, azonban kívánnivalókat hagy maga után az áttekinthetősége és az újrafelhasználhatósága.
II.1.4.1. Függvények közötti adatcsere globális változókkal
A fenti probléma megoldását logikailag jól elkülöníthető részekre tagolhatjuk, nevezetesen:
-
a háromszög oldalhosszainak beolvasása,
-
a háromszög-egyenlőtlenség ellenőrzése,
-
a kerület kiszámítása,
-
a terület kiszámítása
-
és a számított adatok megjelenítése.
A felsorol tevékenységek közül az első négyet önálló függvények formájában valósítjuk meg, amelyek közös elérésű (globális) változókon keresztül kommunikálnak egymással és a main() függvénnyel. A globális változókat a függvényeken kívül, a függvények definíciója előtt kell megadnunk. (Ne feledkezzünk meg a prototípusok megadásáról sem!)
#include <iostream>
#include <cmath>
using namespace std;
// globális változók
double a, b, c;
// prototípusok
void AdatBeolvasas();
bool HaromszogEgyenlotlenseg();
double Kerulet();
double Terulet();
int main() {
AdatBeolvasas();
cout << "kerulet: " << Kerulet()<<endl;
cout << "terulet: " << Terulet()<<endl;
}
void AdatBeolvasas() {
do {
cout <<"a oldal: "; cin>>a;
cout <<"b oldal: "; cin>>b;
cout <<"c oldal: "; cin>>c;
} while(!HaromszogEgyenlotlenseg() );
}
bool HaromszogEgyenlotlenseg() {
if ((a<b+c) && (b<a+c) && (c<a+b))
return true;
else
return false;
}
double Kerulet() {
return a + b + c;
}
double Terulet() {
double s = Kerulet()/2;
return sqrt(s*(s-a)*(s-b)*(s-c));
}
A program jobb olvashatósága nem tagadható, azonban a széles körben való használhatósága akadályokba ütközik. Például, ha több háromszög adatait szeretnénk eltárolni, majd pedig a számításokban felhasználni, ügyelnünk kell a globális a, b és c változók értékének megfelelő beállítására.
int main() {
double a1, b1, c1, a2, b2, c2;
AdatBeolvasas();
a1 = a, b1 = b, c1 = c;
AdatBeolvasas();
a2 = a, b2 = b, c2 = c;
a = a1, b = b1, c = c1;
cout << "kerulet: " << Kerulet()<<endl;
cout << "terulet: " << Terulet()<<endl;
a = a2, b = b2, c = c2;
cout << "kerulet: " << Kerulet()<<endl;
cout << "terulet: " << Terulet()<<endl;
}
Ebből a szempontból jobb megoldáshoz jutunk, ha a háromszög oldalait paraméterként adjuk át az érintett függvényeknek.
II.1.4.2. Függvények közötti adatcsere paraméterekkel
Nem merülünk el a megoldás részletezésében, hiszen a szükséges ismereteket már az Olvasó elé tártuk az előző részekben.
#include <iostream>
#include <cmath>
using namespace std;
void AdatBeolvasas(double &a, double &b, double &c);
bool HaromszogEgyenlotlenseg(double a, double b, double c);
double Kerulet(double a, double b, double c);
double Terulet(double a, double b, double c);
int main() {
double x, y, z;
AdatBeolvasas(x , y , z);
cout << "kerulet: " << Kerulet(x, y, z) <<endl;
cout << "terulet: " << Terulet(x, y, z) <<endl;
}
void AdatBeolvasas(double &a, double &b, double &c) {
do {
cout <<"a oldal: "; cin>>a;
cout <<"b oldal: "; cin>>b;
cout <<"c oldal: "; cin>>c;
} while(!HaromszogEgyenlotlenseg(a, b, c) );
}
bool HaromszogEgyenlotlenseg(double a, double b, double c) {
if ((a<b+c) && (b<a+c) && (c<a+b))
return true;
else
return false;
}
double Kerulet(double a, double b, double c) {
return a + b + c;
}
double Terulet(double a, double b, double c) {
double s = Kerulet(a, b, c)/2;
return sqrt(s*(s-a)*(s-b)*(s-c));
}
Nézzük meg a main () függvényt, ha két háromszöget kívánunk kezelni!
int main() {
double a1, b1, c1, a2, b2, c2;
AdatBeolvasas(a1, b1, c1);
AdatBeolvasas(a2, b2, c2);
cout << "kerulet: " << Kerulet(a1, b1, c1)<<endl;
cout << "terulet: " << Terulet(a1, b1, c1)<<endl;
cout << "kerulet: " << Kerulet(a2, b2, c2)<<endl;
cout << "terulet: " << Terulet(a2, b2, c2)<<endl;
}
Összehasonlításképpen elmondhatjuk, hogy a globális változókkal hatékonyabb (gyorsabb) programkódot kapunk, hiszen elmarad az argumentumok hívás előtti verembe másolása. Láttuk a megoldás negatív következményeit is, melyek erősen korlátozzák a kód újrahasznosítását. Hogyan lehetne csökkenti a sok paraméterrel járó kényelmetlenségeket, és elkerülni a hosszú argumentumlistákat?
Az alábbi megoldás általánosan javasolt a globális változók használata helyett. A globális változókat, illetve a nekik megfelelő paramétereket struktúrába kell gyűjteni, melyet aztán referenciával, vagy konstans referenciával adunk át a függvényeknek.
#include <iostream>
#include <cmath>
using namespace std;
struct haromszog {
double a, b, c;
};
void AdatBeolvasas(haromszog &h);
bool HaromszogEgyenlotlenseg(const haromszog &h);
double Kerulet(const haromszog &h);
double Terulet(const haromszog &h);
int main() {
haromszog h1, h2;
AdatBeolvasas(h1);
AdatBeolvasas(h2);
cout << "kerulet: " << Kerulet(h1)<<endl;
cout << "terulet: " << Terulet(h1)<<endl;
cout << "kerulet: " << Kerulet(h2)<<endl;
cout << "terulet: " << Terulet(h2)<<endl;
}
void AdatBeolvasas(haromszog &h) {
do {
cout <<"a oldal: "; cin>>h.a;
cout <<"b oldal: "; cin>>h.b;
cout <<"c oldal: "; cin>>h.c;
} while(!HaromszogEgyenlotlenseg(h) );
}
bool HaromszogEgyenlotlenseg(const haromszog &h) {
if ((h.a<h.b+h.c) && (h.b<h.a+h.c) && (h.c<h.a+h.b))
return true;
else
return false;
}
double Kerulet(const haromszog &h) {
return h.a + h.b + h.c;
}
double Terulet(const haromszog &h) {
double s = Kerulet(h)/2;
return sqrt(s*(s-h.a)*(s-h.b)*(s-h.c));
}
II.1.4.3. Egyszerű menüvezérelt programstruktúra
A szöveges felületű programjaink vezérlését egyszerű menü segítségével kényelmesebbé tehetjük. A megoldáshoz a menüpontokat egy sztring tömbben tároljuk:
// A menü definíciója
char * menu[] = {"\n1. Oldalak",
"2. Kerulet",
"3. Terulet",
"----------",
"0. Kilep" , NULL };
Az előző példa main () függvényében pedig kezeljük a menüválasztásokat:
int main() {
haromszog h = {3,4,5};
char ch;
do {
// a menü kiírása
for (int i=0; menu[i]; i++)
cout<<menu[i]<< endl;
// A választás feldolgozása
cin>>ch; cin.get();
switch (ch) {
case '0': break;
case '1': AdatBeolvasas(h);
break;
case '2': cout << "kerulet: " << Kerulet(h)<<endl;
break;
case '3': cout << "terulet: " << Terulet(h)<<endl;
break;
default: cout<<'\a';
}
} while (ch != '0');
}
A program futásának ablaka
1. Oldalak 2. Kerulet 3. Terulet ---------- 0. Kilep 1 a oldal: 3 b oldal: 4 c oldal: 5 1. Oldalak 2. Kerulet 3. Terulet ---------- 0. Kilep 2 kerulet: 12 1. Oldalak 2. Kerulet 3. Terulet ---------- 0. Kilep 3 terulet: 6 |
II.1.4.4. Rekurzív függvények használata
A matematikában lehetőség van bizonyos adatok és állapotok rekurzív módon történő előállítására. Ekkor az adatot vagy az állapotot úgy definiáljuk, hogy megadjuk a kezdőállapoto(ka)t, majd pedig egy általános állapotot az előző(, véges számú állapot) segítségével határozunk meg.
Tekintsünk néhány jól ismert rekurzív definíciót!
faktoriális:
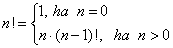
Fibonacci-számok:
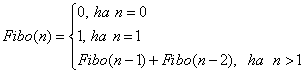
legnagyobb közös osztó (lnko):
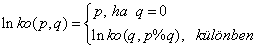
binomiális számok:
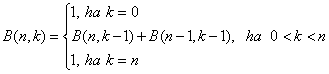
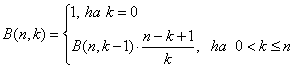
Programozás szempontjából rekurzív algoritmusnak azt tekintjük, ami közvetlenül (közvetlen rekurzió) vagy más függvények közbeiktatásával (közvetett rekurzió) hívja önmagát. Klasszikus példaként tekintsük először a faktoriális számítását!
A faktoriális számítás fenti, rekurzív definíciója alapján 5! meghatározásának lépései az alábbi szemléletes formában ábrázolhatók:
5! = 5 * 4!
4 * 3!
3 * 2!
2 * 1!
1 * 0!
1 = 5 * 4 * 3 * 2 * 1 * 1 = 120
A fenti számítási menetet megvalósító C++ függvény:
unsigned long long Faktorialis(int n)
{
if (n == 0)
return 1;
else
return n * Faktorialis(n-1);
}
A rekurzív függvények általában elegáns megoldást adnak a problémákra, azonban nem elég hatékonyak. A kezdőállapot eléréséig a függvények hívási láncolata által lefoglalt memóriaterület (veremterület) elég jelentős méretű is lehet, és a függvényhívási mechanizmus is igen sok időt vehet igénybe.
Ezért fontos az a megállapítás, hogy minden rekurzív problémának létezik iteratív (ciklust használó) megoldása is, amely általában nehezebben programozható, azonban hatékonyabban működik. Ennek fényében a faktoriális számítást végző nem rekurzív függvény:
unsigned long long Faktorialis(int n)
{
unsigned long long f=1;
while (n != 0)
f *= n--;
return f;
}
A következőkben tekintsük a Fibonacci számsorozat n-edik elemének meghatározását! A
0, 1, 1, 2, 3, 5, 8, 13, 21, ...
sorozat n-edik elemének számítására az alábbi rekurziós szabály alkalmazható:
|
a0 = 0 |
|
|
a1 = 1 |
|
|
an = an-1 + an-2, n = 2 ,3, 4,… |
A rekurziós szabály alapján elkészített függvény szerkezete teljes mértékben követi a matematikai definíciót:
unsigned long Fibonacci( int n ) {
if (n<2)
return n;
else
return Fibonacci(n-1) + Fibonacci(n-2);
}
A számítási idő és a memóriaigény jelentős mértéke miatt itt is az iteratív megoldás használatát javasoljuk:
unsigned long Fibonacci( int n ) {
unsigned long f0 = 0, f1 = 1, f2 = n;
while (n-- > 1) {
f2 = f0 + f1;
f0 = f1;
f1 = f2;
}
return f2;
}
Amíg az iteratív megoldás futásideje az n függvényében lineárisan nő, addig a rekurzív függvényhívás ideje hatványozottan növekszik (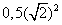 ).
).
Fejezetünk befejező részében a felvetett feladatoknak csak a rekurzív megoldását közöljük, az iteratív megközelítés programozását az Olvasóra bízzuk.
Két természetes szám legnagyobb közös osztóját rekurzív módon igen egyszerűen meghatározhatjuk:
int Lnko(int p, int q) {
if (q == 0)
return p;
else
return Lnko(q, p % q);
}
A binomiális együtthatók számításhoz kétféle rekurzív függvény közül is választhatunk:
int Binom1(int n, int k)
{
if (k == 0 || k == n)
return 1;
else
return Binom1(n-1,k-1) + Binom1(n-1,k);
}
int Binom2(int n, int k)
{
if (k==0)
return 1;
else
return Binom2(n, k-1) * (n-k+1) / k;
}
A két megoldás közül a Binom2() a hatékonyabb.
Az utolsó példában determináns kiszámításához használjuk a rekurziót. A megoldás lényege, hogy az N-ed rendű determináns meghatározását N darab (N-1)-ed rendű determináns számítására vezetjük vissza. Tesszük ezt mindaddig, míg el nem jutunk a másodrendű determinánsokig. A megoldás szép és áttekinthető, azonban nem elég hatékony. A számítás során a hívások fastruktúrában láncolódnak, ami sok futásidőt és memóriát igényel.
Például, a 4x4-es determináns számításakor 17-szer (1 darab 4x4-es, 4 darab 3x3-as és 4·3 darab 2x2-es mátrixszal) hívódik meg a Determinans() függvény, a hívások száma azonban az 5-öd rendű esetben 5·17+1 = 86-ra emelkedik. (Megjegyezzük, hogy 12x12-es mátrix esetén a Determinans() függvény, több mint 300 milliószor hívódik meg, ami perceket is igénybe vehet.)
#include <iostream>
#include <iomanip>
using namespace std;
typedef double Matrix[12][12];
double Determinans(Matrix m, int n);
void MatrixKiir(Matrix m, int n);
int main() {
Matrix m2 = {{1, 2},
{2, 3}};
Matrix m3 = {{1, 2, 3},
{2, 1, 1},
{1, 0, 1}};
Matrix m4 = {{ 2, 0, 4, 3},
{-1, 2, 6, 1},
{10, 3, 4,-2},
{ 2, 1, 4, 0}};
MatrixKiir(m2,2);
cout << "Determinans(m2) = " << Determinans(m2,2) << endl;
MatrixKiir(m3,3);
cout << "Determinans(m3) = " << Determinans(m3,3) << endl;
MatrixKiir(m4,4);
cout << "Determinans(m4) = " << Determinans(m4,4) << endl;
cin.get();
return 0;
}
void MatrixKiir(Matrix m, int n)
{
for (int i=0; i<n; i++) {
for (int j=0; j<n; j++) {
cout << setw(6) << setprecision(0) << fixed;
cout << m[i][j];
}
cout << endl;
}
}
double Determinans(Matrix m, int n)
{
int q;
Matrix x;
if (n==2)
return m[0][0]*m[1][1]-m[1][0]*m[0][1];
double s = 0;
for (int k=0; k<n; k++) // n darab aldetermináns
{
// az almátrixok létrehozása
for (int i=1; i<n; i++) // sorok
{
q = -1;
for (int j=0; j<n; j++) // oszlopok
if (j!=k)
x[i-1][++q] = m[i][j];
}
s+=(k % 2 ? -1 : 1) * m[0][k] * Determinans(x, n-1);
}
return s;
}
A program futásának eredménye:
1 2
2 3
Determinans(m2) = -1
1 2 3
2 1 1
1 0 1
Determinans(m3) = -4
2 0 4 3
-1 2 6 1
10 3 4 -2
2 1 4 0
Determinans(m4) = 144
|
II.2. A függvényekről magasabb szinten
Az előző fejezet elengedő ismeretet nyújt ahhoz, hogy programozási feladatainkat függvények segítségével oldjuk meg. Az áttekinthetőbb programszerkezet, a jobb tesztelhetőség sok programhiba keresésre fordított időt takaríthat nekünk.
A következőkben áttekintjük azokat a megoldásokat, amelyek a függvények használatát valamilyen szempont szerint hatékonyabbá tehetik. Ezek a szempontok a gyorsabb kódvégrehajtás, a kényelmesebb fejlesztés és algoritmizálás.
II.2.1. Beágyazott (inline) függvények
A függvényhívás a függvényben megadott algoritmus végrehatásán túlmenően további időt és memóriát igényel. Idő megy el a paraméterek átadására, a függvény kódjára való ugrásra és a függvényből való visszatérésre.
A C++ fordító az inline (beágyazott) kulcsszóval megjelölt függvények hívását azzal gyorsítja, hogy a hívás helyére befordítja a függvény utasításait. (Ez azt jelenti, hogy a fordító a paraméterátadás előkészítése, majd a függvény törzséből előállított, elkülönített kódra való ugrás helyett a függvény definíciójából és az argumentumaiból készített kódsorozattal helyettesíti függvényhívást a programunkban.)
Általában kisméretű, gyakran hívott függvények esetén ajánlott alkalmazni ezt a megoldást.
inline double Max(double a, double b) {
return a > b ? a : b;
}
inline char Kisbetu( char ch ) {
return ((ch >= 'A' && ch <= 'Z') ? ch + ('a'-'A') : ch );
}
Az beágyazott függvények használatának előnye a későbbiekben bemutatásra kerülő makrókkal szemben, hogy a függvényhívás során az argumentumok feldolgozása teljes körű típusellenőrzés mellett megy végbe. Az alábbi példában egy rendezett vektorban, bináris keresést végző függvényt jelöltünk meg az inline kulcsszóval:
#include <iostream>
using namespace std;
inline int BinarisKereses(int vektor[], int meret, int kulcs) {
int eredmeny = -1; // nem talált
int also = 0;
int felso = meret - 1, kozepso;
while (felso >= also) {
kozepso = (also + felso) / 2;
if (kulcs < vektor[kozepso])
felso = kozepso - 1;
else if (kulcs == vektor[kozepso]) {
eredmeny = kozepso;
break;
}
else
also = kozepso + 1;
} // while
return eredmeny;
}
int main() {
int v[8] = {2, 7, 10, 11, 12, 23, 29, 30};
cout << BinarisKereses(v, 8, 23)<< endl; // 5
cout << BinarisKereses(v, 8, 4)<< endl; // -1
}
Néhány további megjegyzés az beágyazott függvények használatával kapcsolatban:
-
Az inline megoldás általában kisméretű, nem bonyolult függvények esetén használható hatékonyan.
-
Az inline függvényeket fejállományba kell helyeznünk, amennyiben több fordítási egységben is hívjuk őket, azonban egyetlen forrásfájlba csak egyszer építhetők be.
-
A beágyazott függvények ugyan gyorsabb-, azonban legtöbbször nagyobb lefordított kódot eredményeznek, hosszabb fordítási folyamat során.
-
Az inline előírás csupán egy javaslat a fordítóprogram számára, amelyet az bizonyos feltételek esetén (de nem mindig!) figyelembe is vesz. A legtöbb fordító a ciklust vagy rekurzív függvényhívást tartalmazó függvények esetén figyelmen kívül hagyja az inline előírást.
II.2.2. Függvénynevek átdefiniálása (túlterhelése)
Első látásra úgy tűnhet, hogy a függvények széles körben való alkalmazásának útjában áll a paraméterek szigorú típusellenőrzése. Értékparaméterek esetén ez csak a mutatók, tömbök és a felhasználói típusok esetén akadály. Az alábbi abszolút értéket meghatározó függvény tetszőleges numerikus argumentummal hívható, azonban az eredményt mindig int típusúként adja vissza:
inline int Abszolut(int x) {
return x < 0 ? -x : x;
}
Néhány függvényhívás és visszaadott érték:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A fordító a 2. és 3. esetben figyelmeztet ugyan az adatvesztésre, azonban a futtatható program elkészíthető.
Nem konstans, referencia paraméterek esetén azonban sokkal erősebbek a megkötések, hiszen az Ertekadas() függvény hívásakor az első két paramétert int változóként kell megadnunk:
void Ertekadas(int & a, int & b, int c) {
a = b + c;
b = c;
}
Jogos az igény, hogy egy függvényben megvalósított algoritmust különböző típusú paraméterekkel tudjuk futatni, méghozzá ugyanazt a függvénynevet használva. A névazonossághoz azért ragaszkodunk, mert általában a függvénynév utal a függvényben megvalósított tevékenységre, algoritmusra. Ezt az igényünket a C++ nyelv a függvénynevek túlterhelésével (overloading) támogatja.
A függvénynevek túlterhelése azt jelenti, hogy azonos hatókörben (ennek pontos jelentését később tisztázzuk) azonos névvel, de eltérő paraméterlistával (paraméterszignatúrával) különböző függvényeket definiálhatunk. (A paraméterszignatúra alatt a paraméterek számát és és a peramétersor elemeinek típusait.)
Az elmondottakat figyelembe véve állítsuk elő az Abszolut() függvényünk két változatát!
#include <iostream>
using namespace std;
inline int Abszolut(int x) {
return x < 0 ? -x : x;
}
inline double Abszolut(double x) {
return x < 0 ? -x : x;
}
int main() {
cout << Abszolut(-7) << endl; // int
cout << Abszolut(-1.2) << endl; // double
cout << Abszolut(2.3F) << endl; // double
cout << Abszolut('I') << endl; // int
cout << Abszolut(L'\x807F') << endl; // int
}
Fordításkor nem jelentkezik az adatvesztésre utaló üzenet, tehát a lebegőpontos értékekkel a double típusú függvény aktivizálódik.
Ebben az esetben a függvény neve önmagában nem határozza meg egyértelműen, hogy melyik függvény fut. A fordítóprogram a hívási argumentumok szignatúráját sorban egyezteti az összes azonos nevű függvény paramétereinek szignatúrájával. Az egyeztetés eredményeként az alábbi esetek fordulhatnak elő:
-
Pontosan egy illeszkedőt talál, teljes típusegyezéssel – ekkor az ennek megfelelő függvény hívását fordítja be.
-
Pontosan egy illeszkedőt talál, automatikus konverziók utáni típusegyezéssel - ilyenkor is egyértelmű a megfelelő függvény kiválasztása.
-
Egyetlen illeszkedőt sem talál - hibajelzést ad.
-
Több egyformán illeszkedőt talál - hibajelzést ad.
Felhívjuk a figyelmet arra, hogy a megfelelő függvényváltozat kiválasztásában a függvény visszatérési értékének típusa nem játszik szerepet.
Amennyiben szükséges, például több egyformán illeszkedő függvény esetén, típuskonverziós előírással magunk is segíthetjük a megfelelő függvény kiválasztását:
int main() {
cout << Abszolut((double)-7) << endl; // double
cout << Abszolut(-1.2) << endl; // double
cout << Abszolut((int)2.3F) << endl; // int
cout << Abszolut((float)'I') << endl; // double
cout << Abszolut(L'\x807F') << endl; // int
}
A következő példában a VektorOsszeg() függvénynek két átdefiniált formája létezik, az unsigned int és a double típusú tömbök elemösszegének meghatározására:
#include <iostream>
using namespace std;
unsigned int VektorOsszeg(unsigned int a[], int n) {
int osszeg=0;
for (int i=0; i<n; i++)
osszeg += a[i];
return osszeg;
}
double VektorOsszeg(double a[], int n) {
double osszeg=0;
for (int i=0; i<n; i++)
osszeg += a[i];
return osszeg;
}
int main() {
unsigned int vu[]={1,1,2,3,5,8,13};
const int nu=sizeof(vu) / sizeof(vu[0]);
cout << "\nAz unsigned tomb elemosszege: "
<<VektorOsszeg(vu, nu);
double vd[]={1.2,2.3,3.4,4.5,5.6};
const int nd=sizeof(vd) / sizeof(vd[0]);
cout << "\nA double tomb elemosszege: "
<< VektorOsszeg(vd, nd);
}
A fordítóprogram az első híváskor a VektorOsszeg(unsigned int*, int), míg a második esetében VektorOsszeg(double*, int) szignatúrát találja illeszkedőnek. Más típusú (például int és float) tömbök esetén fordítási hibát kapunk, hiszen C++-ban erősen korlátozott a mutatók automatikus konverziója.
Felhívjuk a figyelmet arra, hogy a függvényekhez hasonló módon használható a műveletek átdefiniálásának mechanizmusa (operator overloading). Az operátorokat azonban csak felhasználó által definiált típusokkal (struct, class) lehet túlterhelni, ezért ezzel a lehetőséggel könyvünk következő részében foglalkozunk részletesen.
A fenti példákból látható, hogy további típusok bevezetése esetén szövegszerkesztési feladattá válik az újabb, ugyanazt az algoritmust megvalósító, függvényváltozatok elkészítése (blokkmásolás, szövegcsere). Ennek elkerülése érdekében az átdefiniált függvényváltozatok előállítását a C++ fordítóprogramra is rábízhatjuk, a függvénysablonok (function templates) bevezetésével.
II.2.3. Függvénysablonok
Az előző részekben megismerkedtünk a függvényekkel, amelyek segítenek abban, hogy biztonságosabb, jól karbantartható programokat készítsünk. Bár a függvények igen hatékony és rugalmas programépítést tesznek lehetővé, bizonyos esetekben nehézségekbe ütközünk, hiszen minden paraméterhez típust kell rendelnünk. Az előző alfejezetben bemutatott túlterheléses megoldás segít a típusoktól bizonyos mértékig függetleníteni a függvényeinek. Ott azonban csak véges számú típusban gondolkodhatunk, és fejlesztői szempontból igencsak nagy problémát jelent a megismételt forráskód javítása, naprakésszé tétele.
Jogosan merül fel az igény, hogy csak egyszer kelljen elkészíteni a függvényünket, azonban akárhányszor felhasználhassuk, tetszőleges típusú argumentumokkal. A legtöbb, napjainkban használatos programozási nyelv a generikus programozás eszközeivel ad megoldást a problémánkra.
A generikus (generic) programozás egy általános programozási modell. Maga a technika olyan programkód fejlesztését jelenti, amely nem függ a program típusaitól. A forráskódban úgynevezett általánosított vagy paraméterezett típusokat használunk. Ez az elv nagyban növeli az újrafelhasználás mértékét, hiszen típusoktól független tárolókat és algoritmusokat készíthetünk segítségével. A C++ nyelv a sablonok (templates) bevezetésével, fordítási időben valósítja meg a generikus programozást. Léteznek azonban olyan nyelvek és rendszerek is, amelyeknél ez futási időben történik (ilyenek például a Java és a С#).
II.2.3.1. Függvénysablonok készítése és használata
A sablonok deklarációja a template kulcsszóval indul, mely után a < és > jelek között adjuk meg a sablon paramétereit. Ezek a paraméterek elsősorban általánosított típusnevek azonban változók is szerepelhetnek közöttük. Az általánosított típusnevek előtt a class vagy a typename kulcsszavakat kell használnunk.
A függvénysablon előállításakor egy működő függvényből érdemes kiindulni, amelyben a lecserélendő típusokat általános típusokkal (TIPUS) helyettesítjük. Ezek után közölnünk kell a fordítóval, hogy mely típusokat kell majd lecserélni a függvénymintában (template<class TIPUS>). Tekintsük például az első a lépést az Abszolut() függvényünk esetén
inline TIPUS Abszolut(TIPUS x) {
return x < 0 ? -x : x;
}
majd pedig a végleges forma kétféleképpen megadva:
template <class TIPUS>
inline TIPUS Abszolut(TIPUS x) {
return x < 0 ? -x : x;
}
template <typename TIPUS>
inline TIPUS Abszolut(TIPUS x) {
return x < 0 ? -x : x;
}
Az elkészült függvénysablonból a fordító állítja elő a szükséges függvényváltozatot, amikor először találkozik egy hívással. Felhívjuk a figyelmet arra, hogy az Abszolut() sablon csak numerikus típusokkal használható, amelyek körében értelmezettek az kisebb és az előjelváltás műveletek.
A szokásos függvényhívás esetén a fordítóprogram az argumentum típusából dönti el, hogy az Abszolut() függvény mely változatát állítja elő, és fordítja le.
cout << Abszolut(123)<< endl; // TIPUS = int cout << Abszolut(123.45)<< endl; // TIPUS = double
Típus-átalakítás segítségével az automatikus típusválasztás eredményéről magunk is gondoskodhatunk:
cout << Abszolut((float)123.45)<< endl; // TIPUS = float cout << Abszolut((int)123.45)<< endl; // TIPUS = int
Ugyanerre az eredményre jutunk, ha a függvény neve után, a < és > jelek között megadjuk a típusnevet:
cout << Abszolut<float>(123.45)<< endl; // TIPUS = float cout << Abszolut<int>(123.45)<< endl; // TIPUS = int
A függvénysablonban természetesen több, azonos típus helyettesítése is megoldható, mint ahogy azt a következő példában láthatjuk:
template <typename T>
inline T Maximum(T a, T b) {
return (a>b ? a : b);
}
int main() {
int a = 12, b=23;
float c = 7.29, d = 10.2;
cout<<Maximum(a, b); // Maximum(int, int)
cout<<Maximum(c, d); // Maximum(float, float)
↯ cout<<Maximum(a, c); // nem található Maximum(int, float)
cout<<Maximum<int>(a,c);
// a Maximum(int, int) függvény hívódik meg konverzióval
}
A különböző típusok alkalmazásához több általánosított típust kell a sablonfejben megadnunk:
template <typename T1, typename T2>
inline T1 Maximum(T1 a, T2 b) {
return (a>b ? a : b);
}
int main() {
cout<<Maximum(5,4); // Maximum(int, int)
cout<<Maximum(5.6,4); // Maximum(double, int)
cout<<Maximum('A',66L); // Maximum(char, long)
cout<<Maximum<float, double>(5.6,4);
// Maximum(float, double)
cout<<Maximum<int, char>('A',66L);
// Maximum(int, char)
}
II.2.3.2. A függvénysablon példányosítása
Amikor a C++ fordítóprogram először találkozik egy függvénysablon hívásával, az adott típussal/típusokkal elkészíti a függvény egy példányát. Minden függvénypéldány az adott függvénysablon, adott típusokkal specializált változata. A lefordított programkódban minden felhasznált típushoz pontosan egy függvénypéldány tartozik. A fenti hívásokban erre az ún. implicit példányosításra láttunk példát.
A függvénysablont explicit módon is példányosíthatjuk, amennyiben a függvény fejlécét magában foglaló template sorban konkrét típusokat adunk meg:
template inline int Abszolut<int>(int); template inline float Abszolut(float); template inline double Maximum(double, long); template inline char Maximum<char, float>(char, float);
Fontos megjegyeznünk, hogy adott típus(ok)ra vonatkozó explicit példányosítás csak egyszer szerepelhet a programkódban.
Mivel a C++ fordító a függvénysablonokat fordítási időben dolgozza fel, a függvényváltozatok elkészítéséhez a sablonoknak forrásnyelven kell rendelkezésre állniuk. Ajánlott a függvénysablonokat a fejállományban elhelyezni, biztosítva azt, hogy a fejállományt csak egyszer lehessen beépíteni a C++ modulokba.
II.2.3.3. A függvénysablon specializálása
Vannak esetek, amikor az elkészített általános függvénysablonban definiált algoritmustól eltérő működésre van szükségünk bizonyos típusok vagy típuscsoportok esetén. Ebben az esetben magát a függvénysablont kell túlterhelnünk (specializálnunk) – explicit specializáció.
Az alábbi példában a Csere() függvénysablon a hivatkozással átadott argumentumok értékét felcseréli. Az első specializált változat a mutató argumentumok esetén nem a mutatókat, hanem a hivatkozott értékeket cseréli fel. A másik, tovább specializált változat kimondottan C-stílusú sztringek cseréjére használható.
#include <iostream>
#include <cstring>
using namespace std;
// Az alap sablon
template< typename T > void Csere(T& a, T& b) {
T c(a);
a = b;
b = c;
}
// A mutatókra specializált sablon
template<typename T> void Csere(T* a, T* b) {
T c(*a);
*a = *b;
*b = c;
}
// C-sztringekre specializált sablon
template<> void Csere(char *a, char *b) {
char puffer[123];
strcpy(puffer, a);
strcpy(a, b);
strcpy(b, puffer);
}
int main() {
int a=12, b=23;
Csere(a, b);
cout << a << "," << b << endl; // 23,12
Csere(&a, &b);
cout << a << "," << b << endl; // 12,23
char *px = new char[32]; strcpy(px, "Elso");
char *py = new char[32]; strcpy(py, "Masodik");
Csere(px, py);
cout << px << ", " << py << endl; // Masodik, Elso
delete px;
delete py;
}
Fordító a különböző specializált változatok közül mindig a leginkább specializált (konkrét) sablont alkalmazza először a függvényhívás fordításához.
II.2.3.4. Néhány további függvénysablon példa
A függvénysablonok összefoglalásaként nézzünk meg néhány összetettebb példát! Kezdjük a sort a II.2.2. szakasz VektorOsszeg() függvényének általánosításával! A sablon segítségével tetszőleges típusú, egydimenziós, numerikus tömb elemösszegét meg tudjuk határozni:
#include <iostream>
using namespace std;
template<class TIPUS>
TIPUS VektorOsszeg(TIPUS a[], int n) {
TIPUS sum = 0;
for (int i=0; i<n; i++)
sum += a[i];
return sum;
}
int main() {
int ai[]={1,1,2,3,5,8,13};
const int ni=sizeof(ai) / sizeof(ai[0]);
cout << "\nAz int tomb elemosszege: "
<<VektorOsszeg(ai,ni);
double ad[]={1.2,2.3,3.4,4.5,5.6};
const int nd=sizeof(ad) / sizeof(ad[0]);
cout << "\nA double tomb elemosszege: "
<<VektorOsszeg(ad,nd);
float af[]={3, 2, 4, 5};
const int nf=sizeof(af) / sizeof(af[0]);
cout << "\nA float tomb elemosszege: "
<<VektorOsszeg(af,nf);
long al[]={1223, 19800729, 2004102};
const int nl=sizeof(al) / sizeof(al[0]);
cout << "\nA long tomb elemosszege: "
<<VektorOsszeg(al,nl);
}
A Rendez() függvénysablon egy Tip típusú és Meret méretű egydimenziós tömb elemeit rendezi növekvő sorrendbe. A függvény a tömbön belül mozgatja az elemeket, és az eredmény is ugyanabban a tömbben áll elő. Mivel ebben az esetben a típus paraméter (Tip) mellett egy egész értéket fogadó paraméter (Meret) is helyet kapott a deklarációban, a hívás bővített formáját kell használnunk:
Rendez<int, meret>(tomb);
A példaprogramban a Rendez() sablonból a Csere() sablont is hívjuk:
#include <iostream>
using namespace std;
template< typename T > void Csere(T& a, T& b) {
T c(a);
a = b;
b = c;
}
template<class Tip, int Meret> void Rendez(Tip vektor[]) {
int j;
for(int i = 1; i < Meret; i++){
j = i;
while(0 < j && vektor[j] < vektor[j-1]){
Csere<Tip>(vektor[j], vektor[j-1]);
j--;
}
}
}
int main() {
const int meret = 6;
int tomb[meret] = {12, 29, 23, 2, 10, 7};
Rendez<int, meret>(tomb);
for (int i = 0; i < meret; i++)
cout << tomb[i] << " ";
cout << endl;
}
Az utolsó példánkban a Fuggveny() különböző változatainak hívásakor megjelenítjük a fordító által használt függvényváltozatokat. A specializált változatokból az általános sablont aktivizáljuk, amely a Kiir() sablon segítségével megjelenti a teljes hívás elemeit. A típusok nevét a typeid operátor által visszaadott objektum name () tagja adja vissza. A Karakter() függvénysablonnal a megjeleníthető karaktereket aposztrófok között másoljuk a kiírt szövegbe. Ez a kis példa betekintést enged a függvénysablonok használatának boszorkánykonyhájába.
#include <iostream>
#include <sstream>
#include <string>
#include <typeinfo>
#include <cctype>
using namespace std;
template <typename T> T Karakter(T a) {
return a;
}
string Karakter(char c) {
stringstream ss;
if (isprint((unsigned char)c))
ss << "'" << c << "'";
else
ss << (int)c;
return ss.str();
}
template <typename TA, typename TB>
void Kiir(TA a, TB b){
cout << "Fuggveny<" << typeid(TA).name() << ","
<< typeid(TB).name();
cout << ">(" << Karakter(a) << ", " << Karakter(b)
<< ")\n";
}
template <typename TA, typename TB>
void Fuggveny(TA a = 0, TB b = 0){
Kiir<TA, TB>(a,b);
}
template <typename TA>
void Fuggveny(TA a = 0, double b = 0) {
Fuggveny<TA, double>(a, b);
}
void Fuggveny(int a = 12, int b = 23) {
Fuggveny<int, int>(a, b);
}
int main() {
Fuggveny(1, 'c');
Fuggveny(1.5);
Fuggveny<int>();
Fuggveny<int, char>();
Fuggveny('A', 'X');
Fuggveny();
}
A program futásának eredménye:
Fuggveny<int,char>(1, 'c')
Fuggveny<double,double>(1.5, 0)
Fuggveny<int,double>(0, 0)
Fuggveny<int,char>(0, 0)
Fuggveny<char,char>('A', 'X')
Fuggveny<int,int>(12, 23)
|
II.3. Névterek és tárolási osztályok
A C++ nyelvű program gyakran áttekinthetetlen. Ahhoz, hogy egy nagyobb program átlátható maradjon, több olyan szabályt is be kell tartanunk, amit ugyan a C++ nyelv szintaktikája nem követel meg, azonban a használhatóság igen. Az alkalmazott szabályok többsége a moduláris programozás területéről származik.
Az átláthatóság megtartásának egyik hatékony módja, ha a programunkat működési szempontból részekre bontjuk, és az egyes részeket különálló forrásfájlokban, modulokban (.cpp) valósítjuk meg (implementáljuk). A modulok közötti kapcsolatot interfész (deklarációs) állományok (.h) biztosítják. Minden modul esetén alkalmazzuk az adatrejtés elvét, mely szerint a modulokban definiált változók és függvények közül csak azokat osztjuk meg más modulokkal, amelyekre feltétlenül szükség van, míg a többi definíciót elrejtjük a külvilág elől.
A könyvünk második fejezetének célja a jól strukturált, moduláris programozást segítő C++ eszközök bemutatása. Egyik legfontosabb elemmel, a függvényekkel már megismerkedtünk, azonban még további megoldásokra is szükségünk van:
-
A tárolási osztályok minden C++ változó esetén egyértelműen meghatározzák a változó élettartamát, elérhetőségét és tárolási helyét a memóriában, míg függvények esetén a függvény láthatóságát más függvényekből.
-
A névterek (namespace) segítséget nyújtanak a több modulból felépülő programokban használt azonosító nevek biztonságos használatához.
II.3.1. A változók tárolási osztályai
Amikor létrehozunk egy változót a C++ programban, a típus mellett a tárolási osztályt is megadjuk. A tárolási osztály
-
definiálja a változó élettartamát (lifetime, storage duration), vagyis azt, hogy változó mikor jön létre és mikor törlődik a memóriából,
-
meghatározza, hogy a változó neve hol érhető el közvetlenül – láthatóság (visibility), hatókör (scope), valamint azt, hogy mely nevek jelölnek azonos változókat – kapcsolódás (linkage).
Mint ismeretes, a változókat csak a fordítási egységben (modulban) való deklarálásuk után használhatjuk. (Ne feledjük el, hogy a definíció egyben deklaráció is!) Fordítási egység alatt a C++ forrásállományt (.cpp) értjük, a beépített fejállományokkal együtt.
A tárolási osztályt (auto, register, static, extern) a változó-definíciók elején adhatjuk meg. Amennyiben onnan hiányzik, akkor maga a fordító határozza meg tárolási osztályt a definíció elhelyezkedése alapján.
Az alábbi, egész számot hexadecimális sztringgé alakító példában a tárolási osztályok használatát szemléltetjük:
#include <iostream> using namespace std; static int puffermutato; // modul szintű definíció // az n és elso blokk szintű definíciók void IntToHex(register unsigned n, auto bool elso = true) { extern char puffer[]; // program szintű deklaráció auto int szamjegy; // blokk szintű definíció // hex blokk szintű definíció static const char hex[] = "0123456789ABCDEF"; if (elso) puffermutato=0; if ((szamjegy = n / 16) != 0) IntToHex(szamjegy, false); // rekurzív hívás puffer[puffermutato++] = hex[n % 16]; } extern char puffer[]; // program szintű deklaráció int main() { auto unsigned n; // blokk szintű definíció for (n=0; n<123456; n+=9876) { IntToHex(n); puffer[puffermutato]=0; // sztring lezárása cout << puffer << endl; } } extern char puffer [123] = {0}; // program szintű definíció
Az blokkok szintjén alapértelmezés szerinti auto tárolási osztályt gyakorlatilag sohasem adjuk meg, ezért a példában is áthúzva szerepeltetjük. A függvényeken kívül definiált változók alapértelmezés szerint külső (external) tárolási osztályúak, azonban az extern kulcsszót csak a külső változók deklarálása (nem definíció!!) kell megadnunk.
II.3.1.1. A változók elérhetősége (hatóköre) és kapcsolódása
A tárolási osztállyal szoros kapcsolatban álló fogalom a változók elérhetősége, hatóköre (scope). Minden azonosító csak a hatókörén belül látható. A hatókörök több fajtáját különböztetjük meg: blokk szintű (lokális), fájl szintű és program szintű (globális) (II.7. ábra).
A változók elérhetőségét alapértelmezés szerint a definíció programban elfoglalt helye határozza meg. Így csak blokk szintű és program szintű elérhetőséggel rendelkező változókat hozhatunk létre. A tárolási osztályok közvetlen megadásával árnyalhatjuk a képet.
A hatókör fogalma hasonló a kapcsolódás (linkage) fogalmához, azonban nem teljesen egyezik meg azzal. Azonos nevekkel különböző hatókörökben, különböző változókat jelölhetünk. Azonban a különböző hatókörben deklarált, illetve az azonos hatókörben egynél többször deklarált azonosítók a kapcsolódás felhasználásával ugyanarra a változóra hivatkozhatnak. A C++ nyelvben háromféle kapcsolódásról beszélhetünk: belső, külső, és amikor nincs kapcsolódás.
C++ programban a változók az alábbi hatókörök valamelyikével rendelkezhetnek:
|
blokk szintű |
A változó csak abban a blokkban (függvényblokkban) látható, amelyben definiáltuk, így elérése helyhez kötött, vagyis lokális. Amikor a program eléri a blokkot záró kapcsos zárójelet, a blokk szintű azonosító többé nem lesz elérhető. A blokk szintjén extern és static tárolási osztályok nélkül definiált változók nem rendelkeznek kapcsolódással. |
|
fájl szintű |
A változó csak abban a modulban látható, amely a deklarációját tartalmazza. Kizárólag a modul függvényeiből hivatkozhatunk az ilyen változókra, más modulokból nem. Azok az azonosítók rendelkeznek fájl szintű hatókörrel, amelyeket a modul függvényein kívül, belső kapcsolódással deklarálunk a static tárolási osztály segítségével. (Megjegyezzük, hogy a C++ szabvány a static kulcsszó ilyen módon történő felhasználását elavultnak nyilvánította, helyette a névtelen névterek alkalmazását javasolja a belső kapcsolódású azonosítók kijelölésére). |
|
program szintű |
A változó a program minden moduljának (fordítási egységének) függvényeiből elérhető. Azok az ún. globális azonosítók rendelkeznek program szintű hatókörrel, amelyeket a modulok függvényein kívül, külső kapcsolódással deklarálunk. Ehhez a globális változókat tárolási osztály nélkül vagy az extern tárolási osztállyal kell leírnunk. |
A fájl és a program szintű hatóköröket a később ismertetett névterek (namespace) tovább bontják a minősített azonosítók bevezetésével.
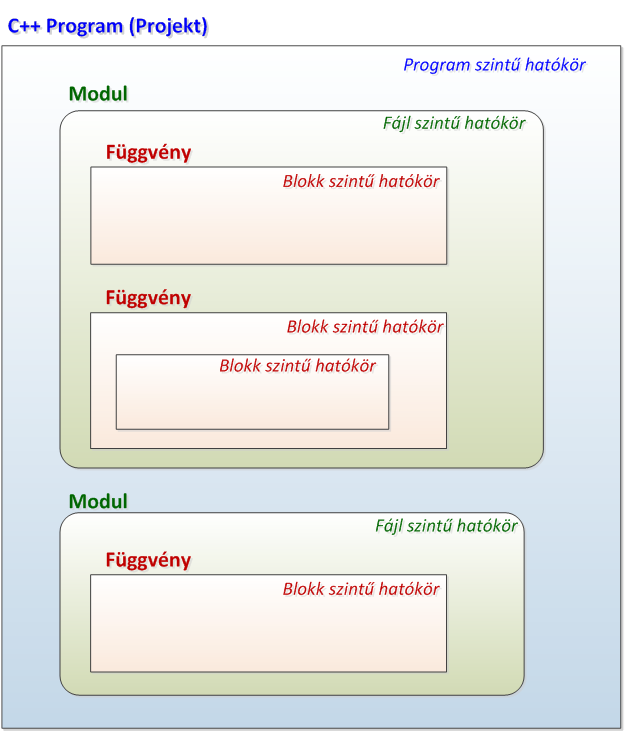
II.3.1.2. A változók élettartama
Az élettartam (lifetime) a program végrehajtásának azon időszaka, amelyben az adott változó létezik. Az élettartam szempontjából az azonosítókat három csoportra oszthatjuk: statikus, automatikus és dinamikus élettartamú nevek.
|
statikus élettartam |
Azok az azonosítók, amelyek a static vagy extern tárolási osztállyal rendelkeznek, statikus élettartamúak. A statikus élettartamú változók számára kijelölt memóriaterület (és a benne tárolt adat) a program futásának teljes időtartama alatt megmarad. Az ilyen változók inicializálása egyetlen egyszer, a program indításakor megy végbe. |
|
automatikus élettartam |
Blokkon belül a static tárolási osztály nélkül definiált változók és a függvények paraméterei automatikus (lokális) élettartammal rendelkeznek. Az automatikus élettartamú azonosítók memóriaterülete (és a benne tárolt adat) csak abban a blokkban létezik, amelyben az azonosítót definiáltuk. A lokális élettartamú változók a blokkba történő minden egyes belépéskor új területen jönnek létre, ami blokkból való kilépés során megszűnik (tartalma elvész). Amennyiben egy ilyen változót kezdőértékkel látunk el, akkor az inicializálás mindig újra megtörténik, amikor a változó létrejön. |
|
dinamikus élettartam |
A tárolási osztályoktól függetlenül dinamikus élettartammal rendelkeznek azok a memóriaterületek, amelyeket a new operátorral foglalunk le, illetve a delete operátorral szabadítunk fel. |
II.3.1.3. A blokk szintű változók tárolási osztályai
Azok a változók, amelyeket programblokkon/függvényblokkon belül, illetve a függvények paraméterlistájában definiálunk alapértelmezés szerint automatikus (auto) változók. Az auto kulcsszót általában nem használjuk, sőt a legújabb C++11 verzióban új értelmezéssel látták el a nyelv fejlesztői. A blokk szintű változókat gyakran lokális változóknak hívjuk.
II.3.1.3.1. Az automatikus változók
Az automatikus változók a blokkba való belépéskor jönnek létre, és blokkból való kilépés során megszűnnek.
A korábbi fejezetekben láttuk, hogy az összetett utasítások (a blokkok) egymásba is ágyazhatók. Mindegyik blokk tetszőleges sorrendben tartalmazhat definíciókat (deklarációkat) és utasításokat:
{
definíciók, deklarációk és
utasítások
}
Valamely automatikus azonosító ideiglenesen elérhetetlenné válik, ha egy belső blokkban ugyanolyan névvel egy másik változót definiálunk. Ez az elfedés a belső blokk végéig terjed, és nincs mód arra, hogy az elfedett (létező) változóra hivatkozzunk:
int main()
{
double hatar = 123.729;
// a double típusú hatar értéke 123.729
{
long hatar = 41002L;
// a long típusú hatar értéke 41002L
}
// a double típusú hatar értéke 123.729
}
Mivel az automatikus tárolók a blokkból kilépve megszűnnek, ezért nem szabad olyan függvényt írni, amely egy lokális változó címével vagy referenciájával tér vissza. Ha egy függvényen belül kívánunk helyet foglalni olyan tároló számára, amelyet a függvényen kívül használunk, akkor a dinamikus memóriafoglalás eszközeit kell alkalmaznunk.
A C++ szabvány szerint ugyancsak automatikus változó a for ciklus fejében definiált ciklusváltozó:
for (int i=12; i<23; i+=2) cout << i << endl; ↯ cout << i << endl; // fordítási hiba, nem definiált az i
Az automatikus változók inicializálása minden esetben végbemegy, amikor a vezérlés a blokkhoz kerül. Azonban csak azok a változók kapnak kezdőértéket, amelyek definíciójában szerepel kezdőértékadás. (A többi változó értéke határozatlan!).
II.3.1.3.2. A register tárolási osztály
A register tárolási osztály csak automatikus lokális változókhoz és függvényparaméterekhez használhatjuk. A register kulcsszó megadásával kérjük a fordítót, hogy az adott változót - lehetőség szerint - a processzor regiszterében hozza létre. Ily módon gyorsabb végrehajtható kódot fordíthatunk. Amennyiben nincs szabad felhasználható regiszter, a tároló automatikus változóként jön létre. Ugyancsak a memóriában jön létre a regiszter változó, ha a címe operátort (&) alkalmazzuk hozzá.
Fontos megjegyeznünk, hogy a regiszter tárolási osztály alkalmazása ellen szól, hogy a C++ fordítóprogramok képesek a kód optimalizálására, ami általában hatékonyabb kódot eredményez, mint amit mi a register előírással elérhetünk.
Az alábbi Csere() függvény a korábban bemutatott megoldásnál potenciálisan gyorsabb működésű. (A potenciális szót azért használjuk, mivel nem ismert, hogy a register előírások közül hányat érvényesít a fordító.)
void Csere(register int &a, register int &b) {
register int c = a;
a = b;
b = c;
}
A következő példa StrToLong() függvénye a sztringben tárolt decimális számot long típusú értékké alakítja:
long StrToLong(const string& str)
{
register int index = 0;
register long elojel = 1, szam = 0;
// a bevezető szóközök átlépése
for(index=0; index < str.size()
&& isspace(str[index]); ++index);
// előjel?
if( index < str.size()) {
if( str[index] == '+' ) { elojel = 1; ++index; }
if( str[index] == '-' ) { elojel = -1; ++index; }
}
// számjegyek
for(; index < str.size() && isdigit(str[index]); ++index)
szam = szam * 10 + (str[index] - '0');
return elojel * szam;
}
A register változók élettartama, láthatósága és inicializálásának módja megegyezik az automatikus tárolási osztályú változókéval.
II.3.1.3.3. Statikus élettartamú lokális változók
A static tárolási osztályt az auto helyett alkalmazva, statikus élettartamú, blokk szintű változókat hozhatunk létre. Az ilyen változók láthatósága a definíciót tartalmazó blokkra korlátozódik, azonban a változó a program indításától, a programból való kilépésig létezik. Mivel a statikus lokális változók inicializálása egyetlen egyszer, a változó létrehozásakor megy végbe, a változók a blokkból való kilépés után (a függvényhívások között) is megőrzik értéküket.
Az alábbi példában a Fibo() függvény a Fibonacci-számok soron következő elemét szolgáltatja a 3. elemtől kezdve. A függvényen belül a statikus lokális a0 és a1 változókban a kilépés után is megőrizzük az előző két elem értékét.
#include <iostream>
using namespace std;
unsigned Fibo() {
static unsigned a0 = 0, a1 = 1;
unsigned a2 = a0 + a1;
a0 = a1;
a1 = a2;
return a2;
}
int main() {
for (register int i=2; i<10; i++)
cout << Fibo() << endl;
}
II.3.1.4. A fájl szintű változók tárolási osztálya
A függvényeken kívül definiált változók automatikusan külső, vagyis program szintű hatókörrel rendelkeznek. Amikor több modulból (forrásfájlból) álló programot fejlesztünk, a moduláris programozás elveinek megvalósításához nem elegendő, hogy vannak globális változóink. Szükségünk lehet olyan modul szinten definiált változókra is, amelyek elérését a forrásállományra korlátozhatjuk (adatrejtés). Ezt a static tárolási osztály külső változók előtti megadásával érhetjük el. A függvényeken kívüli konstans definíciók alapértelmezés szerint szintén belső kapcsolódásúak.
Az alábbi Fibonacci-számokat előállító programban az a0 és a1 változókat modulszinten definiáltuk annak érdekében, hogy egy másik függvénnyel (FiboInit()) is elérjük a tartalmukat.
#include <iostream>
using namespace std;
const unsigned elso = 0, masodik = 1;
static unsigned a0 = elso, a1 = masodik;
void FiboInit() {
a0 = elso;
a1 = masodik;
}
unsigned Fibo() {
unsigned register a2 = a0 + a1;
a0 = a1;
a1 = a2;
return a2;
}
int main() {
for (register int i=2; i<5; i++)
cout << Fibo() << endl;
FiboInit();
for (register int i=2; i<8; i++)
cout << Fibo() << endl;
}
A statikus változók inicializálása a programba való belépés során egyszer megy végbe. Amennyiben nem adunk meg kezdőértéket a definícióban, úgy a fordító automatikusan 0-val inicializálja a változót (feltöltve annak területét nullás bájtokkal). C++-ban a statikus változók kezdőértékeként tetszőleges kifejezést használhatunk.
A C++ szabvány a statikus külső változók helyett a névtelen névterek használatát javasolja (lásd később).
II.3.1.5. A program szintű változók tárolási osztálya
A függvényeken kívül definiált változók, amelyeknél nem adunk meg tárolási osztályt, alapértelmezés szerint extern tárolási osztállyal rendelkeznek. (Természetesen az extern kulcsszó közvetlenül is megadható.)
Az extern (globális) változók élettartama a programba való belépéstől a program befejezésig terjed. Azonban a láthatósággal lehetnek problémák. Egy adott modulban definiált változó csak akkor érhető el egy másik modulból, ha abban szerepeltetjük a változó deklarációját (például deklarációs állomány beépítésével).
A program szintű globális változók használata esetén mindig tudnunk kell, hogy a változót definiáljuk , vagy deklaráljuk . Ha a függvényeken kívül tárolási osztály nélkül szerepeltetünk egy változót, akkor ez a változó definícióját jelenti (függetlenül attól, hogy adunk-e explicit kezdőértéket vagy sem). Ezzel szemben az extern explicit megadása kétféle eredményre vezethet: kezdőérték megadás nélkül a változót deklaráljuk , míg kezdőértékkel definiáljuk . Az elmondottakat jól szemléltetik az alábbi példák:
|
Azonos defíniciók (csak egyikük adható meg) |
Deklarációk |
|---|---|
|
double osszeg; double osszeg = 0; extern double osszeg = 0; |
extern double oszeg;
|
|
int vektor[12]; extern int vektor[12] = {0}; |
extern int vektor[]; extern int vektor[12]; |
|
extern const int meret = 7; |
extern const int meret; |
Felhívjuk a figyelmet arra, hogy a globális változók deklarációi a programon belül bárhova elhelyezhetők, azonban hatásuk a deklaráció helyétől az adott hatókör (blokk vagy modul) határáig terjed. Szokásos megoldás, hogy a deklarációkat modulonként fejállományokban tároljuk, és azt minden forrásfájl elején beépítjük a kódba.
A globális változók inicializálása a programba való belépés során egyszer megy végbe. Amennyiben nem adunk meg kezdőértéket, úgy a fordító automatikusan 0-val inicializálja a változót. C++-ban a globális változók kezdőértékeként tetszőleges kifejezést használhatunk.
Fontos megjegyeznünk, hogy a globális változókat csak indokolt esetben, átgondolt módon szabad használni. Egy nagyobb program esetén is csak néhány, központi extern változó alkalmazása a megengedett.
II.3.2. A függvények tárolási osztályai
Függvények esetén csupán két tárolási osztályt használhatunk. Függvényt nem definiálhatunk a blokk hatókörben, tehát függvény nem készíthető egy másik függvényen belül!
A függvények tárolási osztályai meghatározzák a függvények elérhetőségét. E szerint a tárolási osztály nélküli függvények, illetve az extern tárolási osztállyal definiáltak program szintű hatókörrel rendelkeznek. Ezzel szemben a static tárolási osztállyal rendelkező függvények állomány szintű hatókörűek.
A függvény definíciója alatt magát a függvényt értjük, míg a függvény deklarációja a prototípust jelenti. Az alábbi táblázatban két szám mértani közepét meghatározó függvény definícióit és deklarációit foglaltuk össze, mindkét tárolási osztály esetén.
|
Definíciók (csak egyikük adható meg) |
Prototípusok |
|---|---|
double Mertani(double a, double b)
{
return sqrt(a*b);
}
extern double Mertani(double a, double b)
{
return sqrt(a*b);
}
|
double Mertani(double, double); extern double Mertani(double, double); |
static double Mertani(double a, double b)
{
return sqrt(a*b);
}
|
static double Mertani(double, double); |
A prototípusokat a programon belül bárhova elhelyezhetjük, azonban hatásuk a megadás helyétől az adott hatókör (blokk vagy modul) határáig terjed. A prototípusokat is modulonként fejállományokban szokás tárolni, amit minden érintett forrásfájl elején be kell építeni a programba.
A fájl- és a program szintű deklarációk és definíciók alkalmazását szemlélteti a következő két modulból felépülő példaprogram. A matematikai modul biztosítja a program számára a matematikai állandókat, valamint egy „okos” Random() és egy fokokban számoló Sin() függvényt.
|
|
|
|
#include <iostream>
using namespace std;
extern int Random(int);
double Sin(double);
int main() {
for (int i=0; i<5; i++)
cout << Random(12)<< endl;
cout << Sin(45) << endl;
extern const double e;
cout << e << endl;
}
|
#include <ctime>
#include <cstdlib>
#include <cmath>
using namespace std;
extern const double pi = asin(1)*2;
extern const double e = exp(1);
static double Fok2Radian(double);
static bool elsornd = true;
int Random(int n) {
if (elsornd) {
srand((unsigned)time(0));
elsornd = false;
}
return rand() % n;
}
double Sin(double fok) {
return sin(Fok2Radian(fok));
}
static double Fok2Radian(double fok) {
return fok/180*pi;
}
|
II.3.2.1. A lefordított C függvények elérése C++ programból
A C++ fordító a függvények általunk megadott nevét a tárgykódban kiegészíti a függvény paraméterlistáját leíró betűkkel. Ez a C++ kapcsolódásnak (linkage) hívott megoldás teszi lehetővé a fejezet korábbi részeiben bemutatott lehetőségeket (túlterhelés, függvénysablon).
A C++ nyelv születésekor a C nyelv már közel tízéves múltra tekintett vissza. Jogos volt az igény, hogy a C nyelvű programokhoz kifejlesztett, lefordított tárgymodulok és függvénykönyvtárak algoritmusait C++ programokból is elérjük. (A C forráskódú programok felhasználása - kisebb módosításokkal - megoldottnak volt tekinthető.) A C fordító a függvényneveket változtatás nélkül helyezi el a tárgykódban (C kapcsolódás), így azok az eddig megismert C++ deklarációkkal nem érhetők el.
A probléma leküzdésére a C++ nyelv tartalmazza az extern "C" típusmódosítót. Ha például a C nyelven megírt sqrt() függvényt szeretnénk használni a C++ programból, szükséges az
extern "C" double sqrt(double a);
deklaráció megadása. Ennek hatására a C++ fordító a szokásos C névképzést alkalmazza az sqrt() függvényre. Ebből persze az is következik, hogy a C függvényeket nem lehet átdefiniálni (túlterhelni)!
Amennyiben több C függvényt kívánunk elérni a C++ programból, akkor az extern "C" deklaráció csoportos formáját használhatjuk:
extern "C" {
double sin(double a);
double cos(double a);
}
Ha egy C-könyvtár függvényeinek leírását külön deklarációs állomány tartalmazza, akkor az alábbi megoldás a célravezető:
extern "C" {
#include <rs232.h>
}
Ugyancsak az extern "C" deklarációt kell alkalmaznunk akkor is, ha C++ nyelven megírt és lefordított függvényeket C programból kívánjuk elérni.
Megjegyezzük, hogy a main () fügvény szintén extern "C" kapcsolódású.
II.3.3. Több modulból felépülő C++ programok
Az előző rész példaprogramjának szerkezete sokkal áttekinthetőbbé válik, ha a MatModul.cpp fájlhoz elkészítjük a modul interfészét leíró MatModul.h fejállományt. Ugyancsak egyszerűbbé válik a konstansok alkalmazása, ha fájl szintű hatókörbe (static) helyezzük őket. Az elmondottak alapján a MatModul.h állomány tartalma:
// MatModul.h
#ifndef _MATMODUL_H_
#define _MATMODUL_H_
#include <cmath>
using namespace std;
// fájl szintű definíciók/deklarációk
const double pi = asin(1)*2;
const double e = exp(1);
static double Fok2Radian(double);
// program szintű deklarációk
int Random(int n);
double Sin(double fok);
#endif
A zöld színnel megvastagított sorok olyan előfeldolgozó utasításokat tartalmaznak, amelyek garantálják, hogy a MatModul.h állomány tartalma pontosan egyszer épül be az
#include "MatModul.h"
utasítást tartalmazó modulba. (A II.4. szakasz további információkat tár az Olvasó elé az előfeldolgozó használatáról.)
A fejállomány alkalmazásával a C++ modulok tartalma is megváltozott:
|
|
|
|
#include <iostream>
using namespace std;
#include "MatModul.h"
int main() {
for (int i=0; i<5; i++)
cout << Random(12)<< endl;
cout << Sin(45) << endl;
cout << e << endl;
}
|
#include <ctime>
#include <cstdlib>
using namespace std;
#include "MatModul.h"
static bool elsornd = true;
int Random(int n) {
if (elsornd) {
srand((unsigned)time(0));
elsornd = false;
}
return rand() % n;
}
double Sin(double fok) {
return sin(Fok2Radian(fok));
}
static double Fok2Radian(double fok) {
return fok/180*pi;
}
|
A C++ fordítóprogram minden programmodult önállóan fordít, külön tárgymodulokat előállítva. Ezért szükséges, hogy minden modulban szereplő azonosító ismert legyen a fordító számára. Ezt a deklarációk/prototípusok és a definíciók megfelelő elhelyezésével biztosíthatjuk. A fordítást követően a szerkesztőprogram feladata a tárgymodulok összeépítése egyetlen futtatható programmá, a külső kapcsolódások feloldásával magukból a tárgymodulokból vagy a szabványos könyvtárakból.
Az integrált fejlesztői környezetek projektek létrehozásával automatizálják a fordítás és a szerkesztés menetét. A programozó egyetlen feladata: a projekthez hozzáadni az elkészített C++ forrásfájlokat. Általában a Build menüparancs kiválasztásával a teljes fordítási folyamat végbe megy.
A
GNU C++
fordítót az alábbi parancssorral aktivizálhatjuk a fordítás és a szerkesztés elvégzésére, valamint a Projekt.exe futtatható állomány létrehozására:
g++ -o Projekt FoModul.cpp MatModul.cpp
II.3.4. Névterek
A C++ fordító a programban használt neveket (azok felhasználási módjától függően) különböző területeken (névtér, névterület – namespace) tárolja. Egy adott névtéren belül tárolt neveknek egyedieknek kell lenniük, azonban a különböző névterekben azonos nevek is szerepelhetnek. Két azonos név, amelyek azonos hatókörben helyezkednek el, de nincsenek azonos névterületen, különböző azonosítókat jelölnek. A C++ fordító az alábbi névterületeket különbözteti meg:
II.3.4.1. A C++ nyelv alapértelmezett névterei és a hatókör operátor
A C nyelven a fájl szinten definiált változók és függvények (a szabványos könyvtár függvényei is) egyetlen közös névtérben helyezkednek el. A C++ nyelv a szabványos könyvtár elemeit az std névtérbe zárja, míg a többi fájl szinten definiált elemet a globális névtér tartalmazza.
A névterek elemeire való hivatkozáshoz meg kell ismerkednünk a hatókör operátorral (::). A hatókör operátor többször is előfordul könyvünk további fejezeteiben, most csak kétféle alkalmazására mutatunk példát.
A :: operátor segítségével a program tetszőleges blokkjából hivatkozhatunk a fájl- és program szintű hatókörrel rendelkező nevekre, vagyis a globális névtér azonosítóira.
#include <iostream>
using namespace std;
long a = 12;
static int b = 23;
int main() {
double a = 3.14159265;
double b = 2.71828182;
{
long a = 7, b;
b = a * (::a + ::b);
// a b változó értéke 7*(12+23) = 245
::a = 7;
::b = 29;
}
}
Ugyancsak a hatókör operátort alkalmazzuk, ha az std névtérben definiált neveket közvetlenül kívánjuk elérni:
#include <iostream>
int main() {
std::cout<<"C++ nyelv"<<std::endl;
std::cin.get();
}
II.3.4.2. Saját névterek kialakítása és használata
A nagyobb C++ programokat általában több programozó fejleszti. A C++ nyelv eddig bemutatott eszközeivel elkerülhetetlen a globális (program szintű) nevek ütközése, keveredése. A saját névvel ellátott névterek bevezetése megoldást kínál az ilyen problémákra.
II.3.4.2.1. Névterek készítése
A névtereket a forrásfájlokban a függvényeken kívül, illetve a fejállományokban egyaránt létrehozhatjuk. Amennyiben a fordító több azonos nevű névteret talál, azok tartalmát egyesíti, mintegy kiterjesztve a már korábban definiált névteret. A névtér kijelöléséhez a namespace kulcsszót használjuk:
namespace nevter {
deklarációk és definíciók
}
Program szintű névterek tervezése során érdemes különválasztani a fejállományba helyezhető, csak deklarációkat tartalmazó névteret, a definíciók névterétől.
#include <iostream>
#include <string>
// deklarációk
namespace nspelda {
extern int ertek;
extern std::string nev;
void Beolvas(int & a, std::string & s);
void Kiir();
}
// definíciók
namespace nspelda {
int ertek;
std::string nev;
void Kiir() {
std::cout << nev << " = " << ertek << std::endl;
}
}
void nspelda::Beolvas(int & a, std::string & s) {
std::cout << "nev: "; getline(std::cin, s);
std::cout << "ertek: "; std::cin >> a;
}
Amennyiben egy névtérben deklarált függvényt a névtéren kívül hozunk létre, a függvény nevét minősíteni kell a névtér nevével (példánkban nspelda::).
II.3.4.2.2. Névtér azonosítóinak elérése
Az nspelda névtérben megadott azonosítók minden olyan modulból elérhetők, amelybe beépítjük a névtér deklarációkat tartalmazó változatát. A névtér azonosítóit többféleképpen is elérhetjük.
Közvetlenül a hatókör operátor felhasználásával:
int main() {
nspelda::nev = "Osszeg";
nspelda::ertek = 123;
nspelda::Kiir();
nspelda::Beolvas(nspelda::ertek, nspelda::nev);
nspelda::Kiir();
std::cin.get();
}
A using namespace direktíva alkalmazásával:
Természetesen sokkal kényelmesebb megoldáshoz jutunk, ha az összes nevet elérhetővé tesszük a programunk számára a using namespace direktívával:
using namespace nspelda;
int main() {
nev = "Osszeg";
ertek = 123;
Kiir();
Beolvas(ertek, nev);
Kiir();
std::cin.get();
}
A using deklarációk megadásával
A using deklarációk segítségével a névtér elemei közül csak a számunkra szükségeseket tesszük egyszerűen elérhetővé. Ezt a megoldást kell használnunk akkor is, ha a névtér bizonyos azonosítóval névütközés áll fent.
int Kiir() {
std::cout << "Nevutkozes" << std::endl;
return 1;
}
int main() {
using nspelda::nev;
using nspelda::ertek;
using nspelda::Beolvas;
nev = "Osszeg";
ertek = 123;
nspelda::Kiir();
Beolvas(ertek, nev);
Kiir();
std::cin.get();
}
II.3.4.2.3. Névterek egymásba ágyazása, névtér álnevek
A C++ lehetőséget ad arra, hogy a névterekben újabb névtereket hozzunk létre, vagyis egymásba ágyazzuk őket (nested namespaces). Ezzel a megoldással a globális neveinket strukturált rendszerbe szervezhetjük. Példaként tekintsük a Projekt névteret, amelyben processzorcsaládonként különböző függvényeket definiálunk!
namespace Projekt {
typedef unsigned char byte;
typedef unsigned short word;
namespace Intel {
word ToWord(byte lo, byte hi) {
return lo + (hi<<8);
}
}
namespace Motorola {
word ToWord(byte lo, byte hi) {
return hi + (lo<<8);
}
}
}
Az Projekt névtér elemeit többféleképpen is elérhetjük:
using namespace Projekt::Intel;
int main() {
cout << hex;
cout << ToWord(0xab,0x12)<< endl; // 12ab
}
// -------------------------------------------------------
int main() {
using Projekt::Motorola::ToWord;
cout << hex;
cout << ToWord(0xab,0x12)<< endl; // ab12
}
// -------------------------------------------------------
using namespace Projekt;
int main() {
cout << hex;
cout << Intel::ToWord(0xab,0x12)<< endl; // 12ab
cout << Motorola::ToWord(0xab,0x12)<< endl; // ab12
}
// -------------------------------------------------------
int main() {
cout<<hex;
cout<<Projekt::Intel::ToWord(0xab,0x12)<< endl; // 12ab
cout<<Projekt::Motorola::ToWord(0xab,0x12)<<endl; // ab12
}
A bonyolult, sokszorosan egymásba ágyazott névterek elemeinek elérésékor használt névtérnevek hatókör operátorral összekapcsolt láncolata igencsak rontja a forráskód olvashatóságát. Erre a problémára megoldást ad a névtér álnevek (alias) bevezetése:
namespace alnev =kulsoNS::belsoNS … ::legbelsoNS;
Az álnevek segítségével a fenti példa sokkal egyszerűbb formát ölt:
int main() {
namespace ProcI = Projekt::Intel;
namespace ProcM = Projekt::Motorola;
cout << hex;
cout << ProcI::ToWord(0xab,0x12)<< endl; // 12ab
cout << ProcM::ToWord(0xab,0x12)<< endl; // ab12
}
II.3.4.2.4. Névtelen névterek
A C++ szabvány sem a fájl szintű hatókörben, sem pedig a névterekben nem támogatja a static kulcsszó használatát. A modul szintű hatókörben a névtelen névterekben hozhatunk létre olyan változókat és függvényeket, amelyek a fordítási egységen kívülről nem érhetők el. Azonban a modulon belül minden korlátozás nélkül felhasználhatók névtelen névterek azonosítói.
Egyetlen modulon belül több névtelen névteret is megadhatunk:
#include <iostream>
#include <string>
using namespace std;
namespace {
string jelszo;
}
namespace {
bool JelszoCsere() {
bool sikeres = false;
string regi, uj1, uj2;
cout << "Regi jelszo: "; getline(cin, regi);
if (jelszo == regi) {
cout << "Uj jelszo: "; getline(cin, uj1);
cout << "Uj jelszo: "; getline(cin, uj2);
if (uj1==uj2) {
jelszo = uj1;
sikeres = true;
}
}
return sikeres;
} // JelszoCsere()
}
int main() {
jelszo = "qwerty";
if (JelszoCsere())
cout << "Sikeres jelszocsere!" << endl;
else
cout << "Sikertelen jelszocsere!" << endl;
}
II.4. A C++ előfeldolgozó utasításai
Minden C és C++ fordítóprogram szerves részét képezi az ún. előfeldolgozó (preprocessor), amely semmit nem tud a C++ nyelvről. Egyedüli feladata a program forrásállományaiból a tiszta C++ kódú programmodul előállítása szövegkezelési műveletekkel. Ebből következik, hogy a C++ fordító nem azt a forráskódot fordítja, amit mi előállítunk, hanem az előfeldolgozó működésének eredményeként megjelenő szöveget dolgozza fel (lásd II.8. ábra). Könnyen beláthatjuk, hogy az előfeldolgozó utasításaiból származó C++ programhibák kiderítése nem egyszerű feladat.
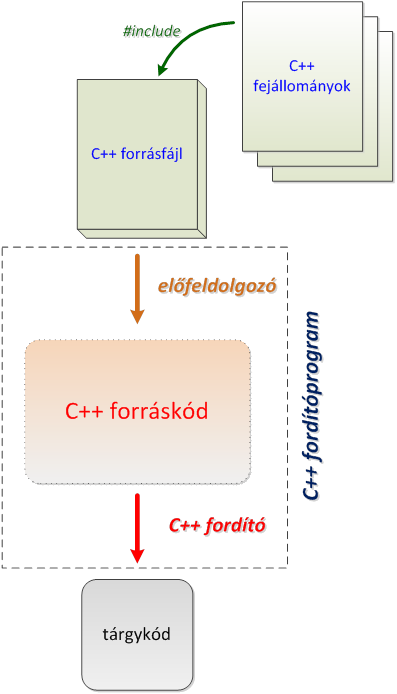
A C++ fordítóprogramok többségében az előfeldolgozás és a tényleges fordítás nem válik külön, azaz nem jelenik meg az előfordító kimenete valamilyen szöveges állományban. (Megjegyezzük, hogy GNU C++ nyelv g++ fordítója a –E kapcsoló hatására csak előfordítást végez.)
Az előfeldolgozó valójában egy makrónyelven programozható, sororientált szövegkezelő program, amelyre nem vonatkoznak a C++ nyelv szabályai:
-
az előfeldolgozó utasításait nem írhatjuk olyan kötetlen formában, mint a C++ utasításokat (tehát egy sorba csak egy utasítás kerülhet, és a parancsok nem csúszhatnak át másik sorba, hacsak nem jelölünk ki folytató sort),
-
az előfeldolgozó által elvégzett minden művelet egyszerű szövegkezelés (függetlenül attól, hogy a C++ nyelv kulcsszavai, kifejezései vagy változói szerepelnek benne).
A előfeldolgozó utasításai (direktívái) a sor elején kettős kereszt (#) karakterrel kezdődnek. A leggyakoribb műveletei a szöveghelyettesítés ( #define ), a szöveges állomány beépítése ( #include ) valamint a program részeinek feltételtől függő megtartása ( #if ).
A C++ nyelv teljes mértékben a C nyelv előfeldolgozási lehetőségeire támaszkodik. Mivel az előfeldolgozás kívül esik a szigorúan típusos C++ fordító hatáskörén, a C++ nyelv az újonnan bevezetett megoldásaival igyekszik minimálisra csökkenteni az előfeldolgozó használatának szükségességét. A C++ programban az előfeldolgozó bizonyos utasításait C++ megoldásokkal helyettesíthetjük: a #define konstansok helyett const állandókat használhatunk, a #define makrók helyett pedig inline függvénysablonokat készíthetünk.
II.4.1. Állományok beépítése
Az előfeldolgozó az #include direktíva hatására az utasításban szereplő szöveges fájl tartalmát beépíti (beszúrja) a programunkba, a direktíva helyére. Általában a deklarációkat és előfeldolgozó utasításokat tartalmazó fejállományokat (header fájlokat) szoktuk beépíteni a programunk elejére, azonban tetszőleges szöveges fájlra is alkalmazható a művelet.
#include <elérési út> #include "elérési út"
Az első formát a C++ rendszer szabványos fejállományainak beépítésére használjuk a fejlesztői környezet include mappájából:
#include <iostream> #include <cmath> #include <cstdlib> #include <ctime> using namespace std;
A második pedig a nem szabványos fájlok beépítését segíti a C++ modult tároló mappából, illetve a megadott helyről:
#include "Modul.h" #include "..\Kozos.h"
Az alábbi táblázatban összefoglaltuk azokat a nyelvi elemeket, amelyeket fejállományban szerepeltethetünk:
|
C++ nyelvi elem |
Példa |
|---|---|
|
Megjegyzések |
|
|
Feltételes fordítási direktívák |
|
|
Makró-definíciók |
|
|
#include direktívák |
|
|
Felsorolások |
|
|
Konstansdefiníciók |
|
|
Névvel ellátott névterületek |
|
|
Névdeklarációk |
|
|
Típusdefiníciók |
|
|
Változó-deklarációk |
|
|
Függvény prototípusok |
|
|
inline függvény-definíciók |
|
|
sablon deklarációk |
|
|
sablon definíciók |
|
Az alábbi nyelvi elemeket semmilyen körülmények között ne helyezzük include állományokba!
-
a nem inline függvények definícióját,
-
változó-definíciókat,
-
a névtelen névtér definícióját.
A fejállományba helyezhető nyelvi konstrukciók egy részét csak egyetlen egyszer szabad beépíteni a programunkba. Ennek érdekében minden header fájlban egy speciális előfeldolgozó szerkezetet kell kialakítunk, a feltételes fordítás eszköztárát használva:
// Modul.h
#ifndef _MODUL_H_
#define _MODUL_H_
a fejállomány tartalma
#endif
II.4.2. Feltételes fordítás
A feltételes fordítás lehetőségeinek alkalmazásával elérhetjük, hogy a forrásprogram bizonyos részei csak adott feltételek teljesülése esetén kerüljenek be az előfeldolgozó által előállított C++ programba. A feltételesen fordítandó programrészeket többféleképpen is kijelölhetjük, a különböző előfeldolgozó direktívák felhasználásával: #if, #ifdef, #ifndef, #elif, #else és #endif.
Az #if utasításban a feltétel megadására konstans kifejezést használunk, melyek nem nulla értéke jelöli az igaz, míg a 0 a hamis feltételt. A kifejezésben csak egész és karakter konstansok valamint a defined művelet szerepelhetnek.
#if 'O' + 29 == ERTEK
A feltételben a defined operátorral ellenőrizhetjük, hogy egy szimbólum definiált-e vagy sem. Az operátor 1 értékkel tér vissza, ha az operandusa létezik, ellenkező esetben 0-át ad:
#if defined szimbólum #if defined(szimbólum)
Mivel gyakran használunk ehhez hasonló vizsgálatokat, ezért valamely szimbólum létezésének tesztelésre külön előfeldolgozó utasítások állnak a rendelkezésünkre:
#ifdef szimbólum #if defined(szimbólum) #ifndef szimbólum #if !defined(szimbólum)
Az #if segítségével bonyolultabb feltételek is megfogalmazhatunk:
#if 'O' + 29 == ERTEK && (!defined(NEV) || defined(SZAM))
Az alábbi egyszerű szerkezettel az #if és az #endif sorok közé zárt programrész fordítási egységben való maradásáról dönthetünk:
#if konstans_kifejezés
programrész
#endif
Ez a szerkezet jól használható hibakeresést segítő információk beépítésére a programba. Ekkor egyetlen szimbólum (TESZT) 1 értékével elérhetjük a kiegészítő információkat megjelenítő programsorok befordítását a kódba, 0 értékkel pedig letilthatjuk azt:
#define TESZT 1
int main() {
const int meret = 5;
int tomb[meret] = { 12, 23, 34, 45, 56 };
int i;
for (int i = 0; i < meret; i++) {
tomb[i] *= 2;
#if TESZT != 0
cout << "i = " << i << endl;
cout << "\ttomb[i] = " << tomb[i] << endl;
#endif
}
}
A fenti szerkezet helyett szerencsésebb a TESZT szimbólum definiáltságát vizsgáló megoldást használni, melyhez a TESZT érték nélkül is definiálható, akár a kívülről, a fordítóprogram paramétereként megadva:
#define TESZT
int main() {
const int meret = 5;
int tomb[meret] = { 12, 23, 34, 45, 56 };
int i;
for (int i = 0; i < meret; i++) {
tomb[i] *= 2;
#if defined(TESZT)
cout << "i = " << i << endl;
cout << "\ttomb[i] = " << tomb[i] << endl;
#endif
}
}
Az alábbi vizsgálatok páronként ugyanazt az eredményt szolgáltatják:
#if defined(TESZT) ... // definiált #endif |
#ifdef TESZT ... // definiált #endif |
|
#if !defined(TESZT) ... // nem definiált #endif |
#ifndef TESZT ... // nem definiált #endif |
A következő szerkezet segítségével két programrész közül választhatunk:
#if konstans_kifejezés
programrész1
#else
programrész2
#endif
A példában a tomb kétdimenziós tömböt a MERET szimbólum értékétől függően különbözőképpen hozzuk létre:
#define MERET 5
int main() {
#if MERET <= 2
int tomb[2][2];
const int meret = 2;
#else
int tomb[MERET][MERET];
const int meret = MERET;
#endif
}
Bonyolultabb szerkezetek kialakításához a többirányú elágaztatás megvalósító előfordító utasítást ajánlott használni
#if konstans_kifejezés1
programrész1
#elif konstans_kifejezés2
programrész2
#else
programrész3
#endif
Az alábbi példában a gyártótól függően építünk be deklarációs állományt a programunkba:
#define IBM 1
#define HP 2
#define ESZKOZ IBM
#if ESZKOZ == IBM
#define ESZKOZ_H "ibm.h"
#elif ESZKOZ == HP
#define ESZKOZ_H "hp.h"
#else
#define ESZKOZ_H "mas.h"
#endif
#include ESZKOZ_H
II.4.3. Makrók használata
Az előfordító használatának legvitatottabb területe a #define makrók alkalmazása a C++ programokban. Ennek oka, hogy a makrók feldolgozásának eredménye nem mindig találkozik a programozó elvárásaival. A makrókat igen széleskörűen alkalmazzák a C nyelven készült programokban, azonban C++ nyelven a jelentőségük csökkent. A C++ nyelv definíciója előnyben részesíti a const és az inline függvénysablonokat a makrókkal szemben. Az alábbi áttekintésben a biztonságos makró-használatot tartjuk szem előtt.
A #define direktívát arra használjuk, hogy azonosítókkal lássuk el a C++ konstans értékeket, a kulcsszavakat, illetve a gyakran használt utasításokat és kifejezéseket. Az előfordító számára definiált szimbólumokat makróknak nevezzük. A C++ forráskódban a makróneveket csupa nagybetűvel ajánlott írni, hogy jól elkülönüljenek a programban használt C++ nevektől.
Az előfeldolgozó soronként megvizsgálja a forrásprogramot, hogy azok tartalmaznak-e valamilyen korábban definiált makrónevet. Ha igen, akkor azt lecseréli a megfelelő helyettesítő szövegre, majd újból megvizsgálja a sort, további makrókat keresve, amit ismételt helyettesítés követhet. Ezt a folyamatot makróhelyettesítésnek vagy makrókifejtésnek nevezzük. A makrókat a #define utasítással hozzuk létre, és az #undef direktíva segítségével semmisítjük meg.
II.4.3.1. Szimbolikus konstansok
Szimbolikus konstansok készítéséhez a #define direktíva egyszerű alakját alkalmazzuk:
#define azonosító #define azonosító helyettesítő_szöveg
Nézzünk néhány példát a szimbolikus konstansok definiálására és használatára!
#define MERET 4
#define DEBUG
#define AND &&
#define VERZIO "v1.2.3"
#define BYTE unsigned char
#define EOS '\0'
int main() {
int v[MERET];
BYTE m = MERET;
if (m > 2 AND m < 5)
cout << "2 < m < 5" << endl;
#ifdef DEBUG
cout << VERZIO << endl;
#endif
}
Az előfeldolgozás (helyettesítések) eredményeként keletkező forrásfájl:
int main() {
int v[4];
unsigned char m = 4;
if (m > 2 && m < 5)
cout << "2 < m < 5" << endl;
cout << "v1.2.3" << endl;
}
C++-ban a fenti szimbolikus konstansok egy része helyett const és typedef azonosítókat is használhatunk:
#define DEBUG
#define AND &&
const int meret = 4;
const string verzio = "v1.2.3";
const char eos = '\0';
typedef unsigned char byte;
int main() {
int v[meret];
byte m = meret;
if (m > 2 AND m < 5)
cout << "2 < m < 5" << endl;
#ifdef DEBUG
cout << verzio << endl;
#endif
}
II.4.3.2. Paraméteres makrók
A makrók felhasználási területét lényegesen bővíti a makrók paraméterezésének lehetősége. A függvényszerű, paraméteres makrók definíciójának általános formája:
#define azonosító(paraméterlista) helyettesítő_szöveg
A makró használata (hívása):
azonosító(argumentumlista)
A makróhívásban szereplő argumentumok számának meg kell egyeznie a definícióban szereplő paraméterek számával.
Annak érdekében, hogy a paraméteres makróink biztonságosan működjenek, be kell tartanunk a következő két szabály:
-
A makró paramétereit a makró törzsében (a helyettesítő szövegben) mindig tegyük zárójelek közé!
-
Ne használjunk léptető (++, --) operátort a makró hívásakor az argumentumlistában!
Az alábbi példaprogramban bemutatunk néhány gyakran használt makró-definíciót és a hívásukat:
// x abszolút értékének meghatározása
#define ABS(x) ( (x) < 0 ? (-(x)) : (x) )
// a és b maximumának kiszámítása
#define MAX(a,b) ( (a) > (b) ? (a) : (b) )
// négyzetre emelés
#define SQR(X) ( (X) * (X) )
// véletlen szám a megadott intervallumban
#define RANDOM(min, max) \
((rand()%(int)(((max) + 1)-(min)))+ (min))
int main() {
int x = -5;
x = ABS(x);
cout << SQR(ABS(x));
int a = RANDOM(0,100);
cout << MAX(a, RANDOM(12,23));
}
A RANDOM() makró első sorának végén álló fordított perjel azt jelzi, hogy a makró-definíció a következő sorban folytatódik. A main () függvény tartalma az előfordítást követően egyáltalán nem nevezhető jól olvashatónak:
int main() {
int x = -5;
x = ( (x) < 0 ? (-(x)) : (x) );
cout << ( (( (x) < 0 ? (-(x)) : (x) )) *
(( (x) < 0 ? (-(x)) : (x) )) );
int a = ((rand()%(int)(((100) + 1)-(0)))+ (0));
cout << ( (a) > (((rand()%(int)(((23) + 1)-(12)))+ (12)))
? (a) : (((rand()%(int)(((23) + 1)-(12)))+ (12))) );
}
A C++ program olvashatóságának megtartásával elérhetjük a makróhasználat összes előnyét (típusfüggetlenség, gyorsabb kód), ha a makrók helyett inline függvényt/függvénysablont használunk:
template <class tip> inline tip Abs(tip x) {
return x < 0 ? -x : x;
}
template <class tip> inline tip Max(tip a, tip b) {
return a > b ? a : b;
}
template <class tip> inline tip Sqr(tip x) {
return x * x;
}
inline int Random(int min, int max) {
return rand() % (max + 1 - min) + min;
}
int main() {
int x = -5;
x = Abs(x);
cout << Sqr(Abs(x));
int a = Random(0,100);
cout << Max(a, Random(12,23));
}
II.4.3.3. Makrók törlése
Egy makró bármikor törölhető, illetve újra létrehozható akár más tartalommal is. A törléshez az #undef direktívát kell használnunk. Egy makró új tartalommal történő átdefiniálása előtt mindig meg kell szüntetnünk a régi definíciót. Az #undef utasítás nem jelez hibát, ha a törölni kívánt makró nem létezik:
#undef azonosító
Az alábbi példában nyomon követhetjük a #define és az #undef utasítások működését:
|
Eredeti forráskód |
Kifejtett programkód |
|---|---|
int main() {
#define MAKRO(x) (x) + 7
int a = MAKRO(12);
#undef MAKRO
a = MAKRO(12);
#define MAKRO 123
a = MAKRO
}
|
int main() {
int a = (12) + 7;
a = MAKRO(12);
a = 123
}
|
II.4.3.4. Makróoperátorok
Az eddigi példáinkban a helyettesítést csak különálló paraméterek esetén végezte el az előfeldolgozó. Vannak esetek, amikor a paraméter valamely azonosítónak a része, vagy az argumentum értékét sztringként kívánjuk felhasználni. Ha a helyettesítést ekkor is el kell végezni, akkor a ## , illetve a # makróoperátorokat kell használnunk.
A # karaktert a makróban a paraméter elé helyezve, a paraméter értéke idézőjelek között (sztringként) helyettesítődik be. Ezzel a megoldással sztringben is lehetséges a behelyettesítés, hisz a fordító az egymás mellett álló sztringliterálokat egyetlen sztring konstanssá kapcsolja össze. Az alábbi példában az INFO() makró segítségével tetszőleges változó neve és értéke megjeleníthető:
#include <iostream>
using namespace std;
#define INFO(valtozo) \
cout << #valtozo " = " << valtozo <<endl;
int main() {
unsigned x = 23;
double pi = 3.14259265;
string s = "C++ nyelv";
INFO(x);
INFO(s);
INFO(pi);
}
x = 23 s = C++ nyelv pi = 3.14259 |
A ## operátor megadásával két szintaktikai egységet (tokent) lehet összeforrasztani oly módon, hogy a makró törzsében a ## operátort helyezzük a paraméterek közé.
A alábbi példában szereplő SZEMELY() makró segít feltölteni a szemelyek tömb struktúra típusú elemeit:
#include <string>
using namespace std;
struct szemely {
string nev;
string info;
};
string Ivan_Info ="K. Ivan, Budapest, 9";
string Aliz_Info ="O. Aliz, Budapest, 33";
#define SZEMELY(NEV) { #NEV, NEV ## _Info }
int main(){
szemely szemelyek[] = {
SZEMELY (Ivan),
SZEMELY (Aliz)
};
}
A main () függvény tartalma az előfeldolgozás után:
int main(){
szemely szemelyek[] = {
{ "Ivan", Ivan_Info },
{ "Aliz", Aliz_Info }
};
}
Vannak esetek, amikor egyetlen makró megírásával nem érünk célt. Az alábbi példában a verziószámot sztringben rakjuk össze a megadott szimbolikus konstansokból:
#define FO 7 #define MELLEK 29 #define VERZIO(fo, mellek) VERZIO_SEGED(fo, mellek) #define VERZIO_SEGED(fo, mellek) #fo "." #mellek static char VERZIO1[]=VERZIO(FO,MELLEK); // "7.29" static char VERZIO2[]=VERZIO_SEGED(FO,MELLEK); // "FO.MELLEK"
II.4.3.5. Előre definiált makrók
Az ANSI C++ szabvány az alábbi, előre definiált makrókat tartalmazza. (Az azonosítók majd mindegyike két aláhúzás jellel kezdődik és végződik.) Az előre definiált makrók nevét nem lehet sem a #define sem pedig az #undef utasításokban szerepeltetni. Az előre definiált makrók értékét beépíthetjük a program szövegébe, de feltételes fordítás feltételeként is felhasználhatjuk.
|
Makró |
Leírás |
Példa |
|---|---|---|
|
|
A fordítás dátumát tartalmazó sztring konstans. |
|
|
|
A fordítás időpontját tartalmazó sztring konstans. |
|
|
|
A forrásfájl utolsó módosításának dátuma és ideje sztring konstansban" |
|
|
|
A forrásfájl nevét tartalmazó sztring konstans. |
|
|
|
A forrásállomány aktuális sorának sorszámát tartalmazó szám konstans (1-től sorszámoz). |
|
|
|
Az értéke 1, ha a fordító ANSI C++ fordítóként működik, különben nem definiált. |
|
|
|
Az értéke 1, ha C++ forrásállományban teszteljük az értékét, különben nem definiált. |
II.4.4. A #line, az #error és a #pragma direktívák
Több olyan segédprogram is létezik, amely valamilyen speciális nyelven megírt programot C++ forrásállománnyá alakít át (programgenerátor).
A #line direktíva segítségével elérhető, hogy a C++ fordító ne a C++ forrásszövegben jelezze a hiba sorszámát, hanem az eredeti speciális nyelven megírt forrásfájlban. (A #line utasítással beállított sorszám és állománynév a __LINE__ illetve a __FILE__ szimbólumok értékében is megjelennek.)
#line kezdősorszám #line kezdősorszám "fájlnév"
Az #error direktívát a programba elhelyezve fordítási hibaüzenet jeleníthetünk meg, amely az utasításban megadott szöveget tartalmazza:
#error hibaüzenet
Az alábbi példában a fordítás hibaüzenettel zárul, ha nem C++ módban dolgozunk:
#if !defined(__cplusplus)
#error A fordítás csak C++ módban végezhető el!
#endif
A #pragma direktíva a fordítási folyamat implementációfüggő vezérlésére szolgál. (A direktívához nem kapcsolódik semmilyen szabványos megoldás.)
#pragma parancs
Ha a fordító valamilyen ismeretlen #pragma utasítást talál, akkor azt figyelmen kívül hagyja. Ennek következtében a programok hordozhatóságát nem veszélyezteti ez a direktíva. Például, a struktúratagok különböző határra igazítása, illetve a megadott sorszámú figyelmeztető fordítási üzenetek megjelenítésének tiltása az alábbi formában végezhető el:
#pragma pack(8) // 8 bájtos határra igazít #pragma pack(push, 1) // bájthatárra igazít #pragma pack(pop) // ismét 8 bájtos határra igazít #pragma warning( disable : 2312 79 )
Létezik még az üres direktíva is (#), amelynek semmilyen hatása sincs az előfeldolgozásra:
#