5. fejezet - Szervomotor szabályozási körének internetes távmérése (Laboratóriumi mérési gyakorlatok leírása)
- 5.1. A mérés célja
- 5.2. Bevezetés
- 5.3. Rendszer áttekintés
- 5.4. A mérésnél használt eszközök bemutatása
- 5.5. Általános utasítások a mérésekhez
- 5.6. A PCI-1720 D/A kártya használata -- Motion control/Exercise 1 menüpont alatt található laboratóriumi mérési gyakorlat
- 5.7. Valós idejű óra használata a PCI 1720 D/A kártyával -- Motion control/Exercise 2 menüpont alatt található laboratóriumi mérési gyakorlat
- 5.8. A PCI 1784 számláló használata -- Motion control/Exercise 3 menüpont alatt található laboratóriumi mérési gyakorlat
-
- 5.8.1. A PCI 1784-es kártya inicializálása a DRV_DeviceOpen függvénnyel
- 5.8.2. A számláló értékek visszaállítása a PCI 1784-es kártyán a DRV_CounterReset függvénnyel
- 5.8.3. A számlálás elindítása a PCI-1784 a kártyán a DRV_CounterEventStart függvénnyel
- 5.8.4. A számláló értékeinek olvasása PCI-1784 kártyán a DRV_CounterEventRead függvénnyel
- 5.8.5. Mintaprogram számlálási műveletekre a PCI-1784 kártyán
- 5.9. Nyílt szabályozó kör mérése -- Motion control/Exercise 4 menüpont alatt található laboratóriumi mérési gyakorlat
- 5.10. Visszacsatolt kör mérések -- Motion control/Exercise 5 menüpont alatt található laboratóriumi mérési gyakorlat
5.1. A mérés célja
A mérés a felhasználót megtanítja egy szervo hajtás, illetve egy robot számítógép általi vezérlésére. Első lépésben a felhasználó megismerkedik a számítógép és a mozgó robot egyik fontos elemével, a szervo hajtás és a számítógép közti kommunikációval, majd a robot beágyazott rendszere kerül vizsgálatra (a robot kezeléséhez külön útmutató áll rendelkezésre).
Digitális - analóg átalakítón keresztül juttatjuk el az információt a számítógépből a szervo hajtáshoz, mivel a szervo hajtás referencia jele az esetek többségében analóg feszültség. A motor mozgását egy encoder méri, amely egy impulzus sort küld a számítógépnek. Egy számláló számlálja az encoder által küldött impulzusokat, és a számítógép az encoder által küldött értékekből tudja meghatározni a motor pozícióját. A motor sebessége az előző és a jelenlegi pozíció adataiból számolható. Ez viszont zajos jelet eredményez. A mérés egy diszkrét idő-filtert tartalmaz ennek a zajnak a csökkentésére. A felhasználó megtanulhatja annak a szervomotornak PI vezérlőjének írását és hangolását.
A kezelőnek nem szükséges haladó szintű programozási ismeretekkel rendelkeznie, de az alapok szükségesek. A felhasználónak csak nagyon egyszerű C ill. Visual Basic programokat kell tudni megírni. A rendelkezésre adott példák alapján a felhasználó akkor is el tudja készíteni a programot, ha ez az első neki.
A kísérletek a http://dind.mogi.bme.hu/experiment/ címen érhetők el (a használathoz regisztráció szükséges).
5.2. Bevezetés
Az automatizálás és a robotizáció vált vezető trenddé az iparban a versenyhelyzet és a környezeti követelmények változásának hatására. A munkaerő költsége megnőtt, ezért az ismétlődő, kreativitást nem igénylő munkahelyeken célszerűbbé vált az automatizálás, a mozdulatok robotokkal történő elvégeztetése. Ugyanakkor ez a bonyolultabb, több kreativitást és ismeretet igénylő munkahelyek számának növekedésével járt, ami azt eredményezte, hogy a munkahelyek száma lényegesen nem csökkent, viszont a munkaerő szükséglet inkább a technikusok, mérnökök irányába tolódott el. Az EU kiemelt direktívákat fogalmazott meg a magas hozzáadott értéket tartalmazó termékek előállítása során kialakítandó munkakörnyezetre, valamint a kis- és középvállalkozások felsőfokú végzettségű fejlesztő műszaki szakemberek iránti igényeinek kielégítésére. Ez mind az egyre bonyolultabb termékeknek és az EU fejlettebb munkakörnyezetre fektetett hangsúlyának tulajdonítható. A fejlettebb robotrendszerek működtetésére viszont magasabb fokú végzettség szükséges, amely a kis- és középvállalkozásoknál nem áll mindig rendelkezésre. Egy emelt szintű mozgásszabályozás tárgynál az előadó hivatkozhat az internetre, mint forrásra. Ebben a speciális kurzusban új technológiákat és tanulási módszereket vegyítünk. Az interaktív multimédia alkalmazások (animációk, szimulációk, táv feladatok) és a webalapú laboratóriumi tesztek egy személyi tanulói környezetet tudnak alkotni, mely az év minden napján, bármikor rendelkezésre tud állni.
A DC motoroknak különleges helyük van az ipari elektronika történetében, mivel minden ipari szervohajtás DC motorokat használt, és az első mikroprocesszoros hajtás is DC motoros volt [36]. Számos hátrányuk ellenére jelenleg is alkalmazzák azokat [37][38]. Fő előnyük mégis, hogy a szabályozás szempontjából egyszerűek. A mikrovezérlők térnyerése előtt csak ezeket lehetett szervohajtásokban használni. Alkalmazásuk különféle DC-szervo rendszerek szabályozásához egyszerű. Érthető, miért is először DC szervo rendszerekhez használnak egyes új szabályozási módszereket. Bár a trend az, hogy a legkülönfélébb típusú motorral működő hajtásokat (indukciós mezőorientált [39], és kefe nélkülit [40]) DC szervohoz hasonlóan kezeljenek. A PID szabályozó még mindig az egyik iparilag legelterjedtebb szabályozó[41]. A másik népszerű módszer a csúszómód szabályozás, amelyet először a ’70-es évek végén mutattak be [42], és a precíziós mozgásszabályozási rendszerekre csak a közelmúltban kezdték el használni.[43]. Az újabb alkalmazásokban a csúszómód szabályozást különböző lágy számítási módszerekkel együtt alkalmazzák [44][45]. A csúszómód szabályozás változó struktúrájú rendszerekben speciális szerepet tölt be, mint robusztus szabályozás. Először is a csúszómód tulajdonság pontos leírása komoly matematikai hátteret igényel, melyet [46][47] fogalmazott meg, a ’60-as évek elején. Másodszor elég egyszerű a beillesztése a legtöbb mérnöki alkalmazásban, mivel legtöbb esetben csak egy relé szükséges. A használati útmutatóban bemutatott példákban nem szükséges az olvasó jártassága a felsorolt hivatkozásokban.
5.3. Rendszer áttekintés
A webalapú kísérletek fontos szerepet játszanak a következő generációjú laborokban. A kísérletek egész nap végezhetők. A regisztrációt követően biztosított a laborhoz való hozzáférés. Ez a fejezet a DC motor vezérlésével foglalkozik és minden más ehhez szükséges elméleti és kísérleti hátteret tartalmaz, vagy hivatkozik arra.
A használati útmutató utasításait követve a felhasználó jártasságra tesz szert elektromos rendszerek és jelen specifikus esetben, a DC szervo hajtás vezérlésére. (ld. 5-1. ábra).
A PC-re kötött DC motor elemi szintű működtetéséhez a következő rendszerelemek szükségesek:
-
Egy kártya, ami az analóg jelet generálja a hajtás be- ill. kikapcsolásához és a referenciajel előállításához (pl. D/A kártya)
-
Egy kártya, ami bemenetén az enkóder jelet veszi és továbbítja a PC-nek (pl. A/D kártya vagy számláló kártya)
-
Egy valós idejű óra, ami időzíti a mintavételezést, vagy a feladatok végrehajtását.
A használók megtanulják a modern irányítási elméletek valós körülmények közti beiktatásával a fentebb felsorolt kártyák programozási alapjait.
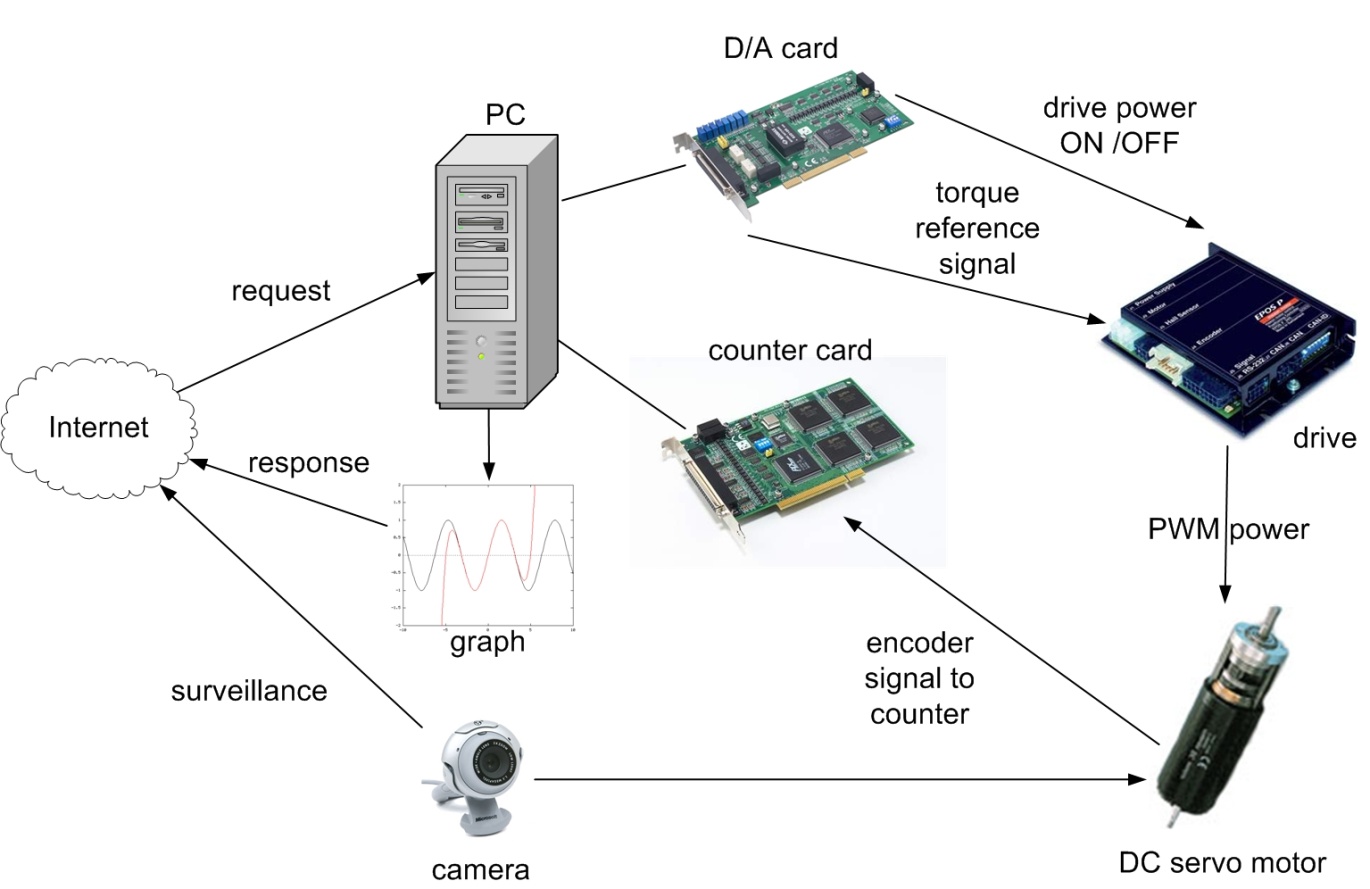
A rendszer kulcs eleme i , amiket használunk:
-
Ipari Siemens PC Pentium 4, 2.8 GHz processzorral
-
Advantec PCI-1720 D/A kimeneti kártya az 1-es funkcióhoz
-
Advantec PCI-1784 számláló bemeneti kártya a 2-es funkcióhoz
-
Szervo hajtás:
-
Szervoerősítővel
-
Maxon A-max 26(110961) DC motorral
-
Maxon Digital Encoder HP HEDL 5540
-
Maxon bolygómű GP 26(110395)
-
WebCam a labor megjelenítésére a monitoron
-
MATLAB program
5.4. A mérésnél használt eszközök bemutatása
5.4.1. Egyenáramú szervohajtás
Ebben a fejezetben a méréshez használt hajtást mutatjuk be. Mivel a méréseknél finom mozgásokat akarunk közvetíteni, ezért egy precíziós méretű motort választottunk. Szabályozástechnikai szempontból az állandó mágnessel gerjesztett egyenáramú motor egy kedvező beavatkozó szerv.
5.4.2. Állandó mágnessel gerjesztett egyenáramú motor
Egy állandó mágnessel gerjesztett egyenáramú motort választottunk. Maxon A-max sorozatú, 26 mm tengelyátmérőjű, 11 W teljesítményű, grafitkefés motort használtuk fel. A motor névleges tápfeszültsége 15V. 1999. évi Maxon katalógus 97. oldal, motor rendelési száma: 110961. A motor szögelfordulását, és forgásirányát egy optikai útadóval (enkóder) érzékeljük. A motorra a Maxon HEDL-5540-es digitális enkódert szereltük fel.

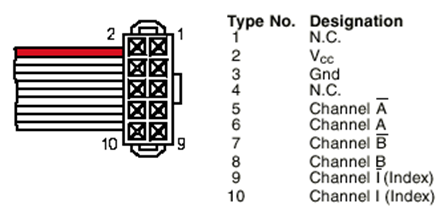
A digitális enkóder kimenetei a következők:
Az enkóder kimenetein digitális jel jelenik meg. Az enkóderben a DS26LS31C típusú vonali meghajtóáramkört helyezték el. Az 1, 3 lábakon az enkóder tápfeszültségét lehet bekötni, amely 5 V egyenfeszültség. Az 5-6 lábakon az A csatorna (0 fokos fázisszög), a 7-8. lábakon a B csatorna (90 fokos fázisszög), a 9-10. lábakon pedig az Index csatorna kivezetései találhatóak. Az Index jel nagyon fontos, főleg pozíciószabályozásnál, ugyanis a szabályozás kezdetekor a motor tengelyének helyzete nem ismert, és ez a szabályozás során állandó hiba forrása lehet. Ezért a szabályozás indítása előtt a motort egy előre meghatározott helyzetbe, ún. index pozícióba kell állítani. Az enkóder is rendelkezik ilyen index pozícióval, és ha a motor tengelye áthaladt az index pozíción, akkor az index csatorna 1-es jelet ad ki.
|
Jele |
Értéke |
Mértékegység |
Megjegyzés |
|
P |
11 |
Watt |
névleges tengelyteljesítmény |
|
Ukn |
15 |
Volt |
Névleges feszültség |
|
N |
7950 |
min^-1 |
Üresjárási fordulatszám |
|
Mt |
73.9 |
mNm |
Tartónyomaték |
|
M |
110 |
min^-1/mNm |
Jelleggörbe meredekség |
|
I |
34 |
mA |
Üresjárati áram |
|
I max |
4190 |
mA |
Tartóáram |
|
Ran |
3.58 |
ohm |
Armatura ellenállás |
|
nmax |
10400 |
min^-1 |
Határfordulatszám |
|
Inmax |
1070 |
mA |
Maximális tartós terhelőáram |
|
Mnmax |
18.9 |
mNm |
Max. tartós nyomaték |
|
Pmax |
14.6 |
W |
Max. Felvett teljesítmény |
|
Etamax |
80.3 |
% |
max. hatásfok |
|
Km |
17.6 |
mNm/A |
Nyomaték konstans |
|
Ke |
541 |
min^-1/V |
= 9.01 sec^-1/V = 56.65 rad/sec/V feszültség konstans |
|
Tm |
14.5 |
msec |
Mechanikai időállandó |
|
Jm |
12.6 |
gcm^2 |
= 12.6E-7 kgm^2 rotor tehetetlenségi nyomatéka |
|
Lan |
0.33 |
mH |
Armatura induktivitás |
|
Rt1 |
13.20 |
K/W |
Thermodinamikai ellenállás a ház és a környezet(levegő) között |
|
Rt2 |
3.20 |
K/W |
Thermodinamikai ellenállás a rotor és a ház között |
5.4.3. Motorvezérlő elektronika
A motorvezérlésnél a Maxon 4QD- 50V/5A típusú szervoerősítőt használtuk fel.
A berendezés paraméterei:
Teljes négynegyedes hajtásvezérlés motor és generátoros üzemmódban egyaránt, gyorsítás, fékezés, a motor irányváltása. Az üzemi feszültség 12-50 V egyenfeszültség, rövid ideig 10 A áramot is képes szolgáltatni, de az üzemi kimenő árama 5 A, és így a maximális üzemi teljesítménye 250 W. A szervoerősítő a 5-4 ábrán látható. A szervoerősítő bemeneteire enkóder, és tachogenerátor kapcsolható, áram és fordulatszám kimenetekkel rendelkezik, valamint PWM üzemmódban is működtethető.

A szervoerősítő elsődleges feladata a motor tengelyének terheléstől független, megadott sebességű forgatása. A szervoerősítőben található vezérlőelektronika folyamatosan figyeli a motor sebességét, és összehasonlítja a beállított értékkel. Ha eltérést észlel, akkor módosítja a szervoerősítő kimenetének értékét, és ezzel vezérli a motort. A végeredmény egy zárt sebességvezérlő hurok. Természetesen a sebesség vezérlését többféle módon végezhetjük:
Tachogenerátorral
Digitális enkóderrel
I x R kompenzációval
Tachogenerátoros sebességvezérlés:
A motorra egy tachogenerátor felszerelve, az a fordulatszámmal arányos egyenfeszültséget ad. Előnye, hogy nagyon pontos, hátránya hogy a tachogenerátor, mivel mechanikus alkatrész, egy idő után cserére szorul.
Sebességvezérlés digitális enkóderrel:
A motorra egy digitális enkódert felszerelve, az egy körülfordulás alatt bizonyos számú jelet küld. Az enkóderek kétfajta jelet állítanak elő, a két jel között 90 fok a fáziseltérés. Ez teszi lehetővé az elfordulás irányának érzékelését. Mivel az enkóder nem mechanikus, ezért élettartama nagyon hosszú. Hátránya, hogy drága.
Sebsességvezérlés I x R kompenzációval:
A motor tápfeszültsége arányos a motor előírt sebességével. Ha megnő a motor terhelése, akkor a fordulatszám lecsökken. A szabályozó áramkör megemeli a motor feszültségét, (ezzel áramát is), hogy az előírt fordulatszámot tartani tudja. A kompenzációnak azonban figyelembe kell venni a motor ellenállását, ami a hőmérséklet és terhelésfüggő. Ezért ez a szabályozási mód kevésbé pontos. A módszer előnye, hogy nincs szükség külső segédberendezésre, tehát olcsó, hátránya a pontatlanság.
A szervoerősítőbe áramkorlátozó áramkör van beépítve. A szabályozó a motor áramát állítja, ami arányos a fordulatszámmal, és a nyomatékkal. A szervoerősító kétféle üzemmódban képes működni:
lineáris
PWM
A lineáris szabályozási mód esetében a motor feszültségét ( ) a szabályozó áramkör állítja be úgy, hogy egy előtét a potenciaméter értékét állítja. A potenciaméteren eső feszültség (
) a szabályozó áramkör állítja be úgy, hogy egy előtét a potenciaméter értékét állítja. A potenciaméteren eső feszültség ( ) a potenciaméteren hővé alakul, emiatt jelentősen romlik a hatásfok.
) a potenciaméteren hővé alakul, emiatt jelentősen romlik a hatásfok.
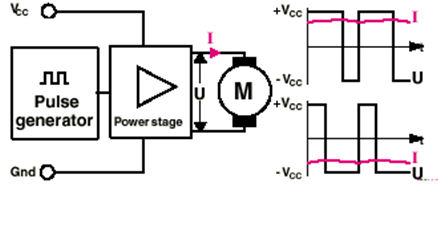
A PWM szabályozási mód esetében a motort nagyon gyorsan ki/be kapcsolgatjuk, ezzel állítva be a kívánt fordulatszámot. A motor átlagfeszültsége arányos a ki/bekapcsolt állapot idejével. A hő miatti hatásfokveszteségek alacsonyak. Jó hatásfokú, de viszonylag bonyolult kiegészítő áramköröket kíván.
A kiválasztott szabályozási mód a szervoerősítőn DIP kapcsolókkal állítható be. A maximális fordulatszám, az áram, valamint az erősítés a P1-P5 potenciaméterekkel szabályozható.
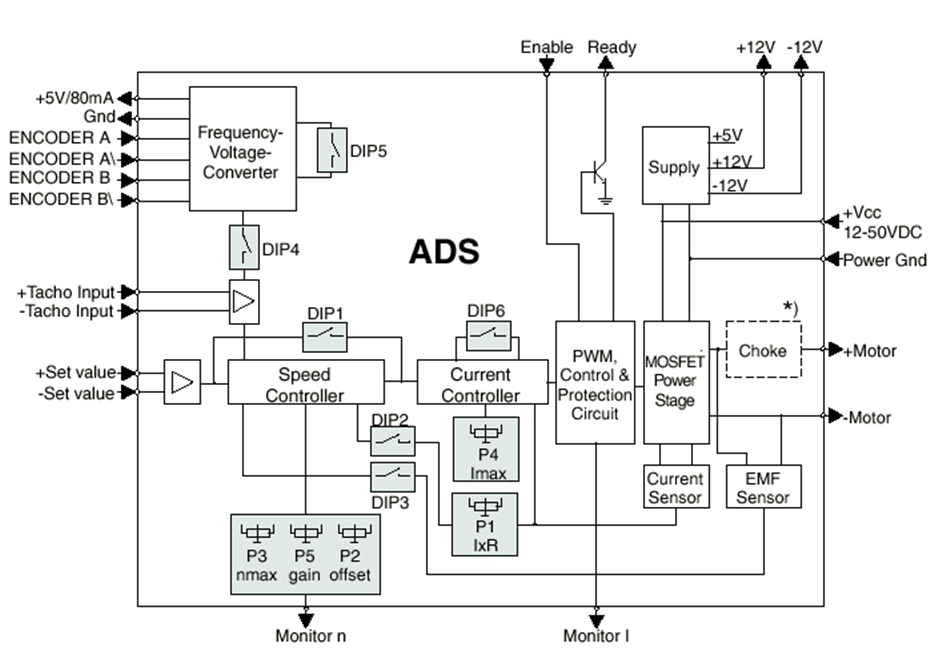
A rendszer előnye nagyfokú integráltságában rejlik. Ha a felügyelő PC (Host PC) egy számítógéphálózatra kapcsolódik, pl. az internetre, akkor megfelelő programok segítségével, tetszőlegesen távoli helyről felügyelni lehet a rendszert, és szükség esetén be lehet avatkozni. Ehhez a gondolathoz megjegyezzük, hogy a Matlab RTW része tartalmaz olyan függvényeket, amelyek segítségével a két tetszőlegesen távol lévő modell adatokat tud cserélni az interneten keresztül. Így a Matlab szoftver segítségével a probléma megoldható.
E mérésnél az áramvezérlést (Current Controller) használtuk fel, a fordulatszámvezérlést (Speed Controller) az 1-es DIP kapcsoló rövidre zárásával iktattuk ki. A maximális áram beállítása nagyon fontos, ugyanis, ha a motor terhelése annyira megnő, hogy forgása lelassul, ebben az esetben olyan áram is keletkezhet, amely már káros a motor tekercselésének.
5.5. Általános utasítások a mérésekhez
Egy feladat megnyitásához, válasszuk ki azt a menüből vagy a legördülő listából, ahogy az alábbi ábra mutatja.

Minden gyakorlat elérhető a kísérletek honlapjáról. A feladatok sorrendileg egymásra épülnek, avagy az előzőek megoldásából lehet a következőket felépíteni. Az első feladatot az ábra mutatja.
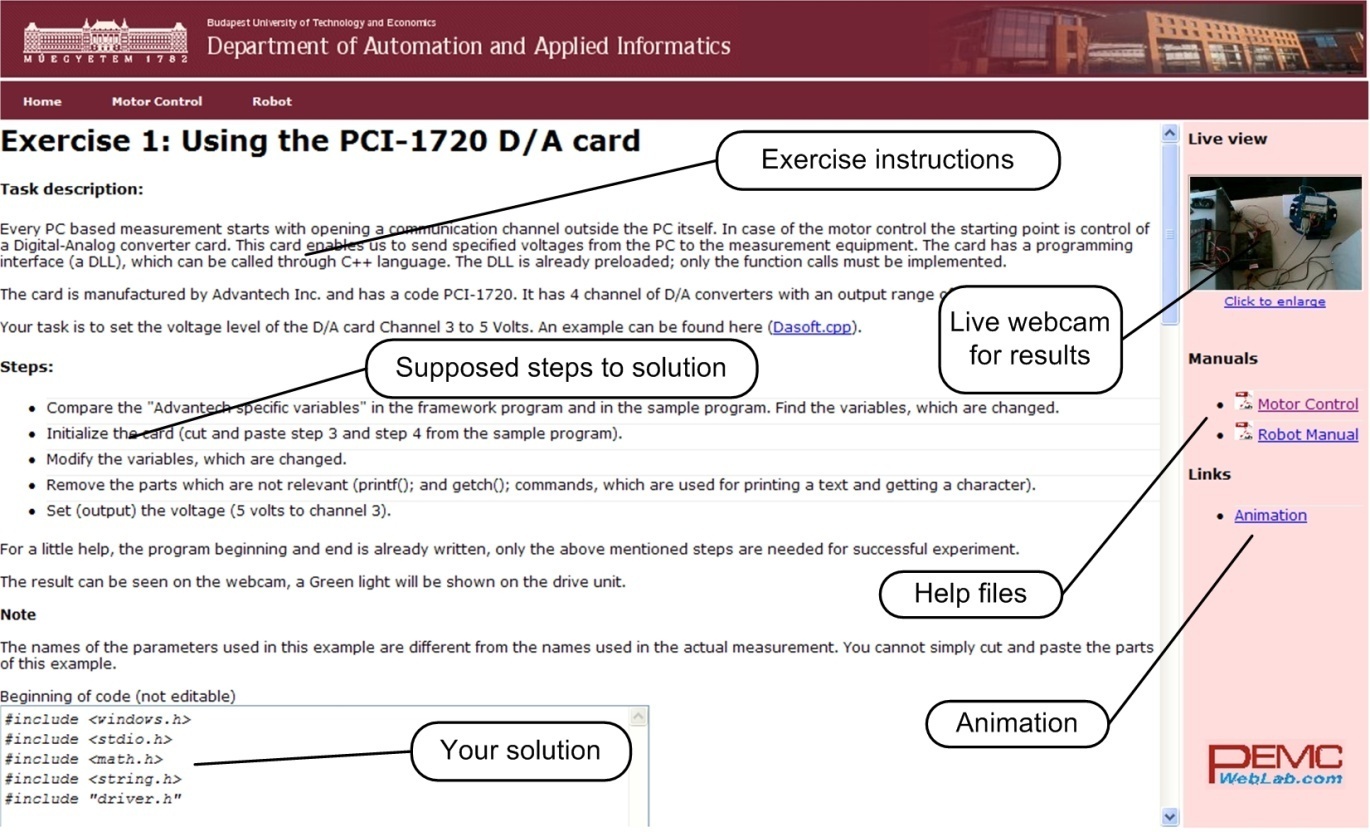
A feladat utasításainak és a rendelkezésre álló súgó fájloknak és forrásoknak elolvasása után a rendszert irányító program az adott mezők kitöltésével megírható. A keretprogram C++ nyelven íródott, a saját változókat és a kódot két beviteli mezőben lehet bevinni, ahogy azt az alábbi ábra mutatja.
|
|
|
5-10. ábra: A változó deklaráció és programkód beviteli ablaka
A kísérlet végrehajtásához nyomjuk meg a honlap alján található Upload gombot.
Ha a fordítás sikeres, a gyakorlat eredménye letölthető/megnézhető.
Minden feladat eltérő eredményt ad. Ezek megtekinthetők ill. kiszámíthatók a számítógépen
-
kameráról (pl. video kép)
-
matlab fájlokból (pl. pozíció, feszültség, sebesség, idő)
-
grafikonokból (pl. . pozíció, feszültség, sebesség-idő)
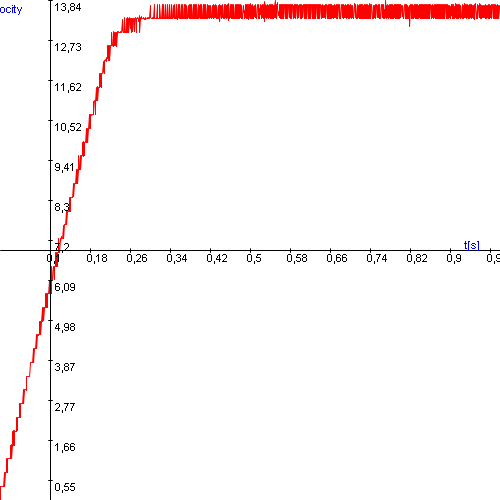
A kimenetre példát az ábra mutat, ahol épp a sebesség időfüggvényt tekintjük meg. Ha a ![]() (fel) nyílra klikkelünk, akkor a sebesség-időfüggvény eltűnik, ha egy
(fel) nyílra klikkelünk, akkor a sebesség-időfüggvény eltűnik, ha egy ![]() (le) nyílra klikkelünk, akkor az aktuális ábra megjelenik. A mérési eredményeket és az aktuális szabályozó programot elmenthetjük.
(le) nyílra klikkelünk, akkor az aktuális ábra megjelenik. A mérési eredményeket és az aktuális szabályozó programot elmenthetjük.
Experiment is complete!
Click to show time-time graph![]()
Click to show time-position graph![]()
Click to hide time-velocity graph![]()
Click to show time-torque graph![]() Select item to download:
Select item to download: 
5.6. A PCI-1720 D/A kártya használata -- Motion control/Exercise 1 menüpont alatt található laboratóriumi mérési gyakorlat
Minden PC alapú mérés egy PC-n kívüli kommunikációs csatorna megnyitásával kezdődik. A motor vezérlése esetében a kezdő pont a digitál-analóg átalakító kártya vezérlése. Ez a kártya lehetővé teszi, hogy meghatározott feszültségértékeket küldjünk a PC-ről a vizsgált rendszerre. A kártyához egy programozó felület tartozik (DLL, Dynamic Link Library), amelyet C++ nyelven meg tudunk hívni. A DLL előre betöltött, csak a függvények meghívását kell bevezetni.
A kártya az Adventech cég PCI-1720-as modellje, 4 D/A kimeneti csatornával rendelkezik, amelyek -5V és 5V közti feszültséget tudnak kivezetni.
5.6.1. A PCI 1720 kártya beállítása a „DRV_DeviceOpen” függvény segítségével
A függvény meghívása: status = DRV_DeviceOpen(DeviceNum, DriverHandle)
Rendeltetése: a registry vagy konfigurációs fájlból kinyeri az eszköz működtetéséhez szükséges paramétereket, és a gyors elérhetőség érdekében megcímzi a memóriát. Ezt a függvényt minden más függvény előtt meg kell hívni.
|
Név |
Iránya |
Típus |
Tartomány |
Leírás |
|
DeviceNum |
Input |
címzetlen long |
alapértelmezett |
berendezés szám |
|
DriverHandle |
Output |
Long pointer |
alapértelmezett |
pointer a berendezés konfigurációs adataihoz |
Eredmények:
-
SUCCESS, ha sikeres;
-
MemoryAllocateFailed, ha a memória lefoglalása sikertelen;
-
ConfigDataLost, ha a konfigurációs adat elvész;
-
CreateFileFailed, ha az alsó szintű meghajtónál megnyitási hibák vannak.
Megjegyzések:
-
Minden további függvény a DriverHandle paraméter által megszerzett konfigurációs adatok alapján hajtja végre az I/O műveletet;
-
A műveletek után meg kell hívni a DRV_DeviceClose-t a DRV_DeviceOpen által lefoglalt memória felszabadítása érdekében.
5.6.2. A feszültségszint beállítása a PCI 1720-as kártyán a DRV_AOVoltageOut függvénnyel
A függvény meghívása: status = DRV_AOVoltageOut(DriverHandle, lpAOVoltageOut)
Rendeltetése: beolvas egy lebegőpontos értéket, átalakítja a megfelelő bináris értékké, majd beírja a számot egy analóg kimeneti csatornába, hogy azon megváltozzon a feszültség.
|
Név |
Iránya |
Típus |
Tartomány |
Leírás |
|
DriverHandle |
Input |
long |
alapértelmezett |
a DRV_DeviceOpen határozza meg |
|
lpAOVoltageOut |
Input/Output |
long pointere PT_AOVoltageOut -nak |
alapértelmezett |
chan és OutputValue tárolási címe |
Eredmények:
-
SUCCESS, ha sikeres;
-
InvalidDriverHandle, ha DriverHandle = NULL;
-
InvalidChan, ha a bemeneti csatorna tartományon kívülre esik;
-
BoardIDNotSupported, ha ezt a függvényt nem támogatja az eszköz.
5.6.3. Mintaprogram a PCI 1720 kártya feszültség szintjének inicializálására és beállítására
Megjegyzés:
A paraméterek nevei ebben a példában eltérnek a mérésben valóban használtaktól. Nem lehet egyszerűen másolni és beilleszteni ezt a példát.
/*
****************************************************************************
* Program : DASOFT.CPP *
* Description : Demo program for analog output function *
* Boards Supp. : PCL-818 series/818HG/1800/816/812PG/711B/726/727/728, *
* PCI-1710/1720, MIC-2728, ADAM-4021/5024 *
* APIs used : DRV_DeviceOpen,DRV_DeviceClose, DRV_GetErrorMessage *
* DRV_AOVoltageOut *
* Revision : 1.00 *
* Date : 7/8/1999 Advantech Co., Ltd. *
****************************************************************************
*/
#include <windows.h>
#include <windef.h>
#include <stdio.h>
#include <conio.h>
#include "..\..\..\include\driver.h"
/******************************
* Local function declaration *
******************************/
void ErrorHandler(DWORD dwErrCde);
void ErrorStop(long*, DWORD);
void main()
{
DWORD dwErrCde;
ULONG lDevNum;
long lDriverHandle;
USHORT usChan;
float fOutValue;
PT_AOVoltageOut tAOVoltageOut;
//Step 1: Display hardware and software settings for running this example
printf("Before running this example, please\n");
printf("use the device installation utility to add the device.\n");
//Step 2: Input parameters
printf("\nPlease input parameters:");
printf("\nDevice Number (check the device installation utility): ");
scanf("%d", &lDevNum);
printf("\nOutput Channel: ");
scanf("%d", &usChan);
printf("\nOutput Value: ");
scanf("%f", &fOutValue);
//Step 3: Open device
dwErrCde = DRV_DeviceOpen(lDevNum, &lDriverHandle);
if (dwErrCde != SUCCESS)
{
ErrorHandler(dwErrCde);
printf("Program terminated!\n");
printf("Press any key to exit....");
getch();
exit(1);
}
// Step 4: Output value to the specified channel
tAOVoltageOut.chan = usChan;
tAOVoltageOut.OutputValue = fOutValue;
dwErrCde = DRV_AOVoltageOut(lDriverHandle, &tAOVoltageOut);
if (dwErrCde != SUCCESS)
{
ErrorStop(&lDriverHandle, dwErrCde);
printf("Press any key to exit....");
getch();
return;
}
// Step 5: Display ouptut data
printf("\nOutput data = %f\n", fOutValue);
// Step 6: Close device
dwErrCde = DRV_DeviceClose(&lDriverHandle);
printf("\nPress any key to exit....");
getch();
}//main
/***********************************************************************
* Function: ErrorHandler *
* Show the error message for the corresponding error code *
* input: dwErrCde, IN, Error code *
* return: none *
**********************************************************************/
void ErrorHandler(DWORD dwErrCde)
{
char szErrMsg[180];
DRV_GetErrorMessage(dwErrCde, szErrMsg);
printf("\nError(%d): %s\n", dwErrCde & 0xffff, szErrMsg);
}//ErrorHandler
/*
***************************************************************************
* Function: ErrorStop *
* Release all resource and terminate program if error occurs *
* Paramaters: pDrvHandle, IN/OUT, pointer to Driver handle *
* dwErrCde, IN, Error code. *
* return: none *
***************************************************************************
*/
void ErrorStop(long *pDrvHandle, DWORD dwErrCde)
{
//Error message
ErrorHandler(dwErrCde);
printf("Program terminated!\n");
//Close device
DRV_DeviceClose(pDrvHandle);
}//ErrorStop
5 . 4 mérési feladat : PCI-1720 D/A kártya használata
A feladat a kártya 3-as csatornájának 5 Volt értékre való beállítása. Tulajdonképpen ez az 5 Volt teszi lehetővé a szervohajtás működését.
Szükséges lépések:
-
Hasonlítsuk össze az „Adventech specifikus változókat” a keretrendszer programban és a mintaprogramban. Találjuk meg a megváltozott változókat.
-
Állítsuk be a kártyát (vágjuk ki és illesszük be a 3. és 4. lépést a mintaprogramból).
-
Módosítsuk a megváltozott változókat.
-
Távolítsuk el az érdektelen részeket (printf(); és getch(); utasításokat, amelyek szöveg kiírására és karakter beolvasásra szolgálnak).
-
Állítsuk be a (kimeneti) feszültséget (5 Voltra a 3-as csatornán).
5.7. Valós idejű óra használata a PCI 1720 D/A kártyával -- Motion control/Exercise 2 menüpont alatt található laboratóriumi mérési gyakorlat
A második fontos feladat egy PC alapú mérésnél a mintavételezés. Ezért szükségünk van egy valós idejű órára, ami bármikor, tetszőleges frekvencián el tudja kezdeni a számlálást. Különböző valós idejű operációs rendszerek érhetők el szinkronizálható valós idejű órajellel. A több feladat egyszerre kezelésére alkalmas Windows operációs rendszer nem támogatja a valós idejű alkalmazásokat, de a Real Time eXtension (RTX) for Control of Windows megoldást nyújt a kérdésre. Leírása lentebb olvasható, de működési módjának megértése nem szükséges a mérésekhez. A valós idejű órajel alkalmazását kell ebben a laboratóriumi gyakorlatban elvégezni. Egy óra ketyeg (milliszekundumonként) a gyakorlatban megadott programban.
5.7.1. Hogy valósul meg a valós idő nem valós idejű operációs rendszer alatt?
(olvasmány)
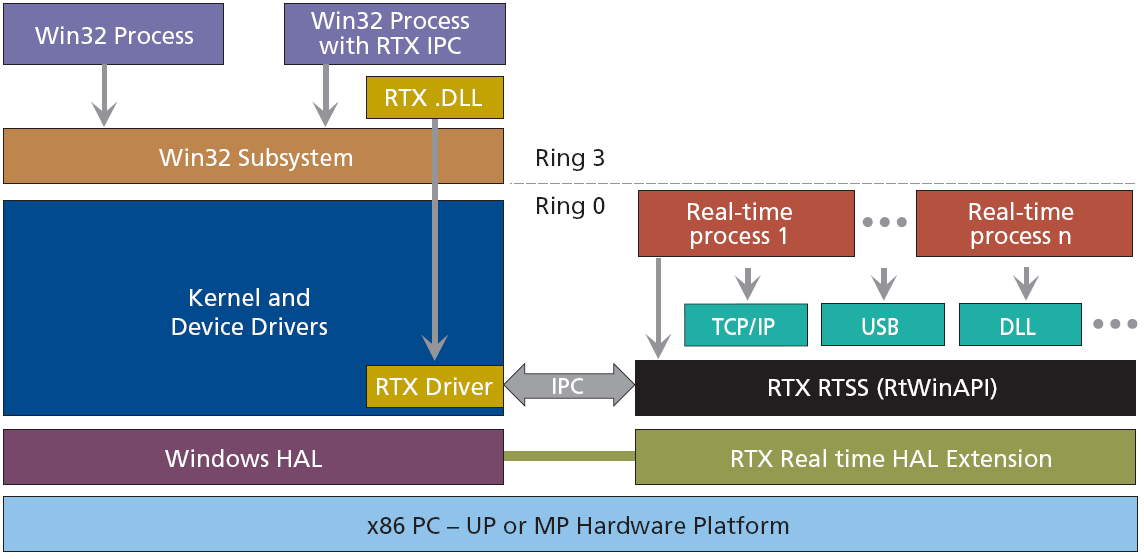
Real Time eXtension (RTX) for Control of Windows egy optimalizált bővítmény a Windows operációs rendszerhez. Nem egy valós idejű operációs rendszer ( Real Time Operating System) amit Windowsra portoltak. Az RTX precíz irányítást enged IRQ-k (Interrupt Request: megszakítási kérések), I/O, és memória felett, hogy biztosítsa az egyes feladatok megfelelő sorrendben és 100% biztossággal való végrehajtását. A Ring 0-ban való működtetés alatt az RTX biztosítja a legmagasabb teljesítményt és csak minimális beállítást igényel, biztosítva a 30Khz-es interruptokat 1 mikroszekundomos IST késési átlaggal. RTX egy igazi Windows bővítmény, alkalmazza az összes standard Windows szabványt, az API-kat, memória kezelést, SRI-ket, mutexeket, és a Windows fejlesztők számára ismert szemafórokat. Az RTX alkalmazás ki tudja használni a Windows és a Ring 3-ban lévő Intel architektúra által biztosított memóriavédelmi mechanizmusokat. Amint a fejlesztő kész a hibakereséssel és megbizonyosodik arról, hogy a memória mutatók és tömbök helyesek, az RTX alkalmazást azonnal újra lehet fordítani, hogy Ring 0-ban fusson az optimális teljesítményért. Ez a fő architektúra, amely az 5-12. ábrán látható.
Az RTX architektúra egy valódi kiegészítés, ami nem foglalja magába a Windows-t és nem avatkozik bele, vagy módosítja bármely elemét. Az elkülönítéssel az RTX valós idejű szub-rendszer (RTSS) biztosítja, hogy az RTX alapú alkalmazások túléljék a Windows összeomlásait, vagy „kék halálait”. Az RTX RTSS kernel egy nagy sebességű időzítőre lett tervezve, amik mind preemptikus, mind körbenforgó (round-robin) algoritmust használnak. Az RTX 1000 független folyamatot tud támogatni, amelyben minden folyamat korlátlan szálat támogat. Az alkalmazások finom vezérlését a 256 szintes szálprioritás beállítása biztosítja. Az ütemező azt garantálja, hogy a kritikus szál 500 nanoszekundumos prioritással vegye át a vezérlést. Az RTX folyamatok és Win32 alkalmazások közötti adatkommunikáció megkönnyítésére az RTX egy nagy teljesítményű üzenetküldő és szinkronizációs IPC mechanizmust használ. Egy megosztott memória modell használatával az IPC nagy mennyiségű adat átadására képes anélkül, hogy a teljesítmény csökkenne. Valós idejű rendszerben az esemény pontos végrehajtása kritikus. A pontosság elérése érdekében az RTX három órát használ, amelyekre alapozza az esemény időzítését. Az óra felbontása, a használt órától függően, akár 0,001 nanoszekundumos is lehet, anélkül, hogy bármilyen elcsúszás adódna.
5 . 5 mérési feladat : Egy szinuszos feszültség-idő függvény megjelenítése a PCI 1720 A/D kártya kimenetén
Meg kell határozni az összefüggést a mintavételi idő és a szinusz hullám között (3 Voltos amplitúdóval 1HZ-es frekvencián). A mintavételezés 0-tól kezdődik és a CurrentTime változón keresztül érhető el a programból. Ezt a váltózót a time_array[tickCount] változóval lehet elérni, ami 100 nanoszekundumos egységű adatot ad vissza.
Szükséges lépések:
-
Áttanulmányozni a megadott keret programot;
-
Beírni a hiányzó kódokat;
-
deklarálni a paramétereket és változókat;
-
Out=Amlitude * sin (Angular Frequency *time)(megjegyzés: ez nem egy C kód, és a time-ot a TimerHandler függvénnyel kell beolvasni).
5.8. A PCI 1784 számláló használata -- Motion control/Exercise 3 menüpont alatt található laboratóriumi mérési gyakorlat
A számlálót az enkóderből jövő jel beolvasására használjuk, amit aztán numerikusan megjelenítünk. A számláló értékét a TimerHandler függvény olvassa be, ami a valós óra minden jelére végrehajtódik.
5.8.1. A PCI 1784-es kártya inicializálása a DRV_DeviceOpen függvénnyel
Függvény hívása: status = DRV_DeviceOpen(DeviceNum, DriverHandle)
Rendeltetése: megszerzi az eszköz működtetéséhez szükséges paramétereket a regiszter ill. konfigurációs fájlból, és lefoglalja a memóriát a gyors hivatkozáshoz. Ezt a függvényt minden más függvény előtt meg kell hívni.
|
Név |
Irány |
Típus |
Tartomány |
Leírás |
|
DeviceNum |
Input |
határozatlan hosszú |
alapértelmezett |
eszköz száma |
|
DriverHandle |
Output |
long pointer |
alapértelmezett |
pointer a az eszközhöz való konfigurációs adatokhoz |
Eredmény:
-
SUCCESS, ha sikeres;
-
MemoryAllocateFailed, ha a memória allokáció hibás;
-
ConfigDataLost, ha a konfigurációs adat elveszett,
-
CreateFileFailed, ha egy alacsonyabb szintű drivert nem lehet megnyitni.
Megjegyzések:
-
Minden további függvény a DriverHandle által beszerzett konfigurációs adatok alapján hajtja végre az I/O műveleteket.
-
Az I/O műveletek után a felhasználónak meg kell hívni a DRV_DeviceClose, hogy szabaddá tegye a DRV_DeviceOpen által allokált memóriát.
5.8.2. A számláló értékek visszaállítása a PCI 1784-es kártyán a DRV_CounterReset függvénnyel
Függvény meghívása: status = DRV_CounterReset(DriverHandle, counter)
Rendeltetése: Kikapcsolja az adott számláló műveletet.
|
Név |
Irány |
Típus |
Tartomány |
Leírás |
|
DriverHandle |
Input |
long |
alapértelmezett |
DRV_DeviceOpen rendeli el |
|
counter |
Input |
long |
alapértelmezett |
számláló csatorna |
Eredmény:
-
SUCCESS, ha sikeres;
-
InvalidDriverHandle, ha DriverHandle = NULL;
-
BoardIDNotSupported, ha a függvényt nem támogatja az eszköz;
-
InvalidChannel, ha a port száma az értelmezési tartományon kívül van.
5.8.3. A számlálás elindítása a PCI-1784 a kártyán a DRV_CounterEventStart függvénnyel
Függvény meghívása: status = DRV_CounterEventStart(DriverHandle, lpCounterEventStart)
Rendeltetése: Konfigurálja a kiválasztott számlálót a feladatra és elindítja azt.
|
Név |
Irány |
Típus |
Tartomány |
Leírás |
|
DriverHandle |
Input |
long |
alapértelmezett |
DRV_DeviceOpen rendeli el |
|
LpCounterEventStart |
Input/Output |
long pointer a PT_CounterEventStart-hoz |
alapértelmezett |
a tárolási címe counter-nek és GateMode-nak |
Eredmény:
-
SUCCESS, ha sikeres;
-
InvalidDriverHandle, ha DriverHandle = NULL;
-
BoardIDNotSupported, ha a függvény nem támogatott az eszközön,
-
InvalidChannel, ha a port száma tartományon kívül esik.
Műveletek:
-
A programozás módszere a lapon található számláló/időzítő chiptől függ. Két fajta chipet szoktak használni az A/D kártyákon: Intel 8254 és AMD Am9513A. Az Am9513A-nél, a 0-9 es csatornák felmenő él számlálóként is tudnak működni. Csatlakoztassa a külsőjel generátorát a használni kívánt bemenő órajel csatornára. Ha a hardveres ”kapuzás”, amelyben a számlálót egy külső eszköz indíthatja egy másik bemenetről, előírt, válasszon egy kapuzás típust és használjon külső eszközt a számláló bemenetének triggereléséhez.
-
Mindkét előbb említett időzítő/számláló chip 16 bites, de a függvény 32 biteset támogat, vagy 232-ig számol. Leellenőrzi, hogy a számláló nem csordult-e túl, és átszámolja 32 bitre.
-
Intel 8254 hardware 2 ciklusidőt igényel a számláló beállításainak visszaállításához, tehát a számláló programnak 2 külsőjelet (ciklusidőt) meg kell várnia, hogy pontos számláló értéket olvasson be. A ”DRV_CounterEventStart” első meghívásakor, az Intel 8254 hardware alapértékeket használ a számláló beállításainak inicializálásához. Ez az inicializálás két külsőjelig (ciklusideig) tart. Ha a ”DRV_CounterEventRead” az inicializálás befejezése előtt hívódik meg, a program helytelen értéket kap. Tehát 2 külsőjelet (ciklusidőt) kell késleltetni a programban, mielőtt meghívjuk a ”DRV_CounterEventRead”-et, hogy a visszakapott érték pontos legyen. A késleltetés ideje függ a külső jelek közti időtől.
5.8.4. A számláló értékeinek olvasása PCI-1784 kártyán a DRV_CounterEventRead függvénnyel
Függvény meghívása: status = DRV_CounterEventRead(DriverHandle, lpCounterEventRead)
Rendeltetése:Kiolvassa a jelenlegi számláló összeget anélkül, hogy a számlálást megzavarná és visszaadja a számláló és túlcsordulás feltételeit.
|
Név |
Irány |
Típus |
Tartomány |
Leírás |
|
DriverHandle |
Input |
long |
alapértelmezett |
aDRV_DeviceOpen rendeli el |
|
lpCounterEventRead |
Input/Output |
long pointer a PT_CounterEventRead-hez |
alapértelmezett |
a tárolási cím counter, overflow-hoz és count-hoz |
Eredmény:
-
SUCCESS, ha sikeres;
-
InvalidDriverHandle, ha DriverHandle = NULL;
-
BoardIDNotSupported, ha a függvényt az eszköz nem támogatja;
-
InvalidChannel, ha a port száma tartományon kívülre esik.
5.8.5. Mintaprogram számlálási műveletekre a PCI-1784 kártyán
Megjegyzés:
A paraméterek nevei a bemutatott példában eltérnek a mérésben valójában használt nevektől. Nem szabad egyszerűen kivágni és beilleszteni a részeket a példából.
/*
*****************************************************************************
* Program : COUNTER.CPP *
* Description : Demo program for counter function *
* Boards Supp. : *
* APIs used : DRV_DeviceOpen,DRV_DeviceClose, DRV_GetErrorMessage, *
* DRV_CounterReset, DRV_CounterEventStart, DRV_CounterEventRead *
* Revision : 1.00 *
* Date : 7/8/1999 Advantech Co., Ltd. *
****************************************************************************
*/
#include <windows.h>
#include <windef.h>
#include <stdio.h>
#include <conio.h>
#include "..\..\..\..\include\driver.h"
/******************************
* Local function declaration *
******************************/
void ErrorHandler(DWORD dwErrCde);
void ErrorStop(long*, DWORD);
void main()
{
DWORD dwErrCde;
ULONG lDevNum;
long lDriverHandle;
USHORT wChannel = 0;
USHORT wOverflow = 0; // counter over 32 bit flag
ULONG dwReading = 0;
PT_CounterEventStart tCounterEventStart;
PT_CounterEventRead tCounterEventRead;
//Step 1: Display hardware and software settings for running this example
printf("Before running this example, please\n");
printf("use the device installation utility to add the device.\n");
//Step 2: Input parameters
printf("\nPlease input parameters:");
printf("\nDevice Number (check the device installation utility): ");
scanf("%d", &lDevNum);
printf("\nInput Channel: ");
scanf("\n%d", &wChannel);
//Step 3: Open device
dwErrCde = DRV_DeviceOpen(lDevNum, &lDriverHandle);
if (dwErrCde != SUCCESS)
{
ErrorHandler(dwErrCde);
printf("Program terminated!\n");
printf("Press any key to exit....");
getch();
exit(1);
}
// Step 4: Reset counter by DRV_CounterReset
dwErrCde = DRV_CounterReset(lDriverHandle, wChannel);
if (dwErrCde != SUCCESS)
{
ErrorHandler(dwErrCde);
printf("Program terminated!\n");
printf("Press any key to exit....");
getch();
exit(1);
}
// Step 5: Start counting operation by DRV_CounterEventStart
tCounterEventStart.counter = wChannel;
dwErrCde = DRV_CounterEventStart(lDriverHandle, &tCounterEventStart);
if (dwErrCde != SUCCESS)
{
ErrorHandler(dwErrCde);
printf("Program terminated!\n");
printf("Press any key to exit....");
getch();
exit(1);
}
// Step 6: Read counter values by DRV_CounterEventRead in while loop
// and display counter value, exit when pressing any key
tCounterEventRead.counter = wChannel;
tCounterEventRead.overflow = &wOverflow;
tCounterEventRead.count = &dwReading;
while( !kbhit() )
{
dwErrCde = DRV_CounterEventRead(lDriverHandle, &tCounterEventRead);
if (dwErrCde != SUCCESS)
{
ErrorStop(&lDriverHandle, dwErrCde);
return;
}
printf("\nCounter value = %lu", dwReading);
Sleep(1000);
}
// Step 7: Stop counter by DRV_CounterReset
dwErrCde = DRV_CounterReset(lDriverHandle, wChannel);
if (dwErrCde != SUCCESS)
{
ErrorHandler(dwErrCde);
printf("Program terminated!\n");
printf("Press any key to exit....");
getch();
exit(1);
}
// Step 8: Close device
dwErrCde = DRV_DeviceClose(&lDriverHandle);
getch();
printf("\nPress any key to exit....");
getch();
}//main
/*
***********************************************************************
* Function: ErrorHandler *
* Show the error message for the corresponding error code *
* input: dwErrCde, IN, Error code *
* return: none *
**********************************************************************
*/
void ErrorHandler(DWORD dwErrCde)
{
char szErrMsg[180];
DRV_GetErrorMessage(dwErrCde, szErrMsg);
printf("\nError(%d): %s\n", dwErrCde & 0xffff, szErrMsg);
}//ErrorHandler
/*
****************************************************************************
* Function: ErrorStop *
* Release all resource and terminate program if error occurs *
* Paramaters: pDrvHandle, IN/OUT, pointer to Driver handle *
* dwErrCde, IN, Error code. *
* return: none *
****************************************************************************
*/
void ErrorStop(long *pDrvHandle, DWORD dwErrCde)
{
//Error message
ErrorHandler(dwErrCde);
printf("Program terminated!\n");
//Close device
DRV_DeviceClose(pDrvHandle);
printf("Press any key to exit....");
getch();
exit(1);
}//ErrorStop
5 . 10 mérési feladat a PCI 1784-es kártya használata
A feladat a számláló értékének beolvasása a PCI 1784-es kártya 3-as csatornájáról.
Szükséges lépések:
-
Kártya inicializálása.
-
Számláló értékek visszaállítása.
-
A számláló művelet elindítása.
-
A számláló érték beolvasása a művelet elején.
-
A számláló értékének minden egyes órajelre való beolvasása.
5.9. Nyílt szabályozó kör mérése -- Motion control/Exercise 4 menüpont alatt található laboratóriumi mérési gyakorlat
A PC alapú mérőrendszer bemutatása után itt az ideje megírni az első szabályozót egy DC motorra. Ebben a mérésben visszacsatolás nélküli nyílt hurkú méréseket végzünk a DC motorral. Kérjük, tanumányozza a következő fejezetben a DC motorról írt „A DC motor elméleti háttere” című szöveget.
5.9.1. A DC szervomotorok elméleti háttere
Az elméleti hátteret számos animált dián mutatjuk be. Ez egy rövidített ismétlés a DC motor tárgykörnek a “INETELE Interactive and Unified E-Based Education and Training for Electrical Engineering” című számítógépes tananyagból.
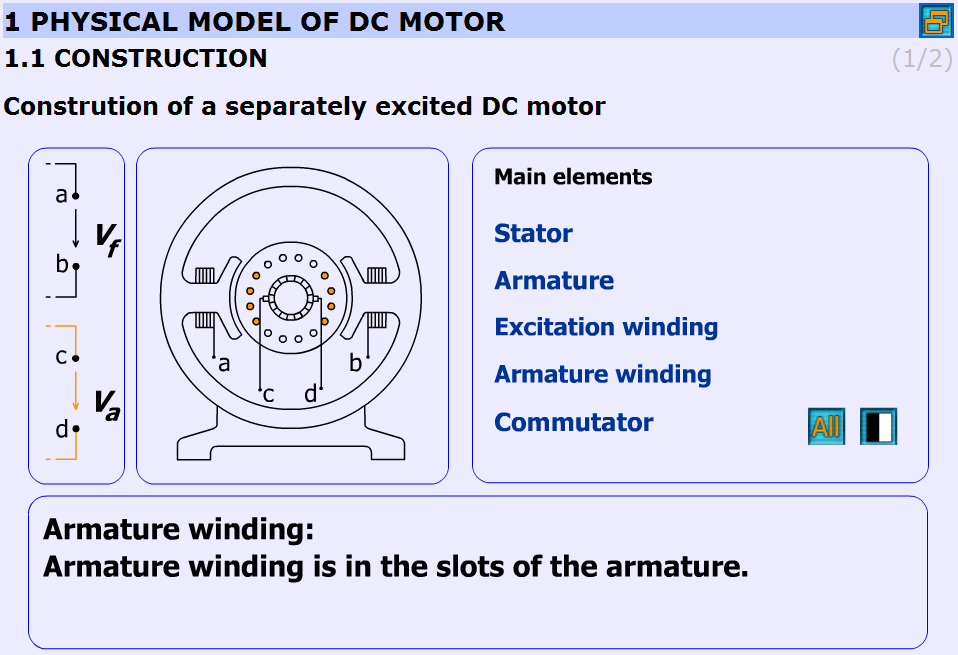
5.9.2. A DC szervomotor felépítése és leíró áramköre
-
Stator (angolul): A gép állórésze.
-
Armatura: A gép forgórésze.
-
Gerjesztő huzalozás: Az állórész pólusai köré tekert huzal.
-
Armatúra huzalozás: Huzalozás az armatúra vájataiban.
-
Kommutátor: Periódikusan megfordítja az áram irányát (az armatúrában). Egy forgó réz anyagú részből és az álló szénkefékből áll.
5.9.2.1. Egyenértékű áramkör
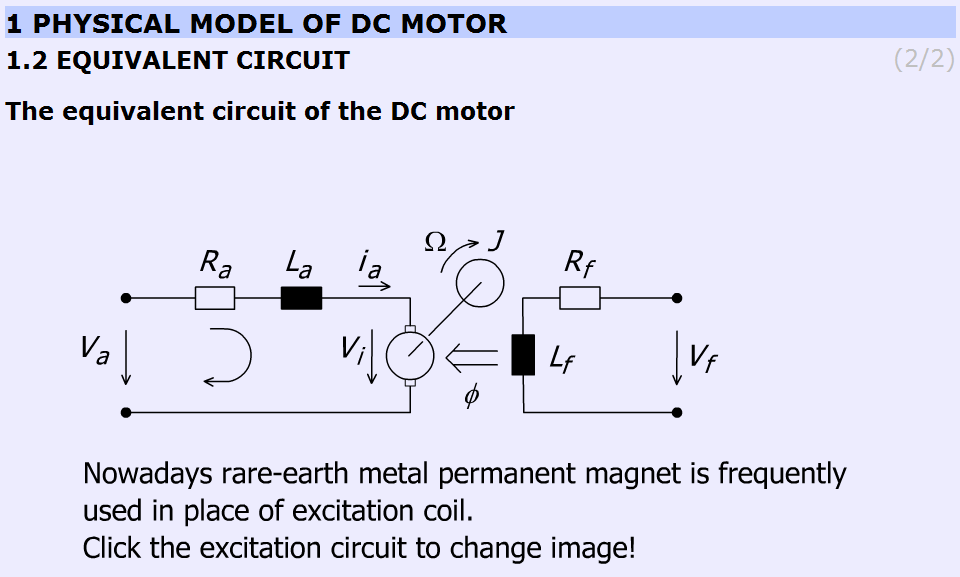
A DC motor paraméterei és változói:
-
Ra– Armatúra ellenállás [ohm];
-
La – Armatúra induktancia [henry];
-
J – Tehetetlenségi nyomaték [kgm2];
-
va – Armatúra feszültség [volt];
-
vi – visszaható indukált feszültség az armatúra menetei által [volt];
-
ia – Armatúra áram [amper];
-
Ω – A motor tengelysebessége [rad/s].
Vf, Rf, Lf, Ф a gerjesztő áramkörhöz tartoznak.
Ez a fejezet a motor gerjesztésével foglalkozik. A legtöbb esetben a kis DC motorban permanens mágnest használnak.
5.9.3. Matematikai modell
Ez a fejezet a DC motor matematikai modelljét ismerteti 3 fő fejezetben:
-
Időtartomány egyenletek
-
Frekvenciatartomány egyenletek
-
Átviteli függvények
5.9.3.1. Időtartomány egyenletek
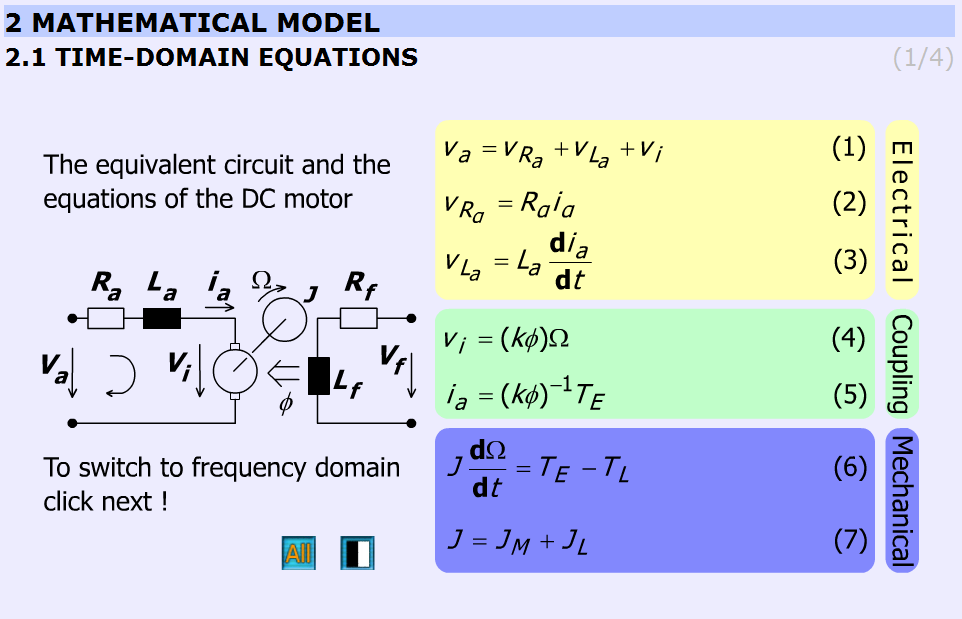
Ez a fejezet mutatja be az időtartomány egyenleteket. A diák az alábbi egyenleteket emelik ki:

, ahol  a motor elektromos nyomatéka;
a motor elektromos nyomatéka;

, ahol  a terhelés nyomatéka;
a terhelés nyomatéka;

, ahol  a terhelés tehetetlenségi nyomatéka.
a terhelés tehetetlenségi nyomatéka.
A magyarázatok az “INETELE Interactive and Unified E-Based Education and Training for Electrical Engineering”-ben találhatók. Az 5-16. ábra elnevezésében látható linkről érhető el. Tartalmazza a linket a frekvencia tartományt magyarázó tartalomhoz is.
5.9.3.2. Frekvencia tartomány egyenletek

Ez a fejezet a frekvencia tartomány egyenleteket tárgyalja. A változók komplex mennyiségek (s = jω).
|
|
(5.5) |
5.9.3.3. Átviteli függvények
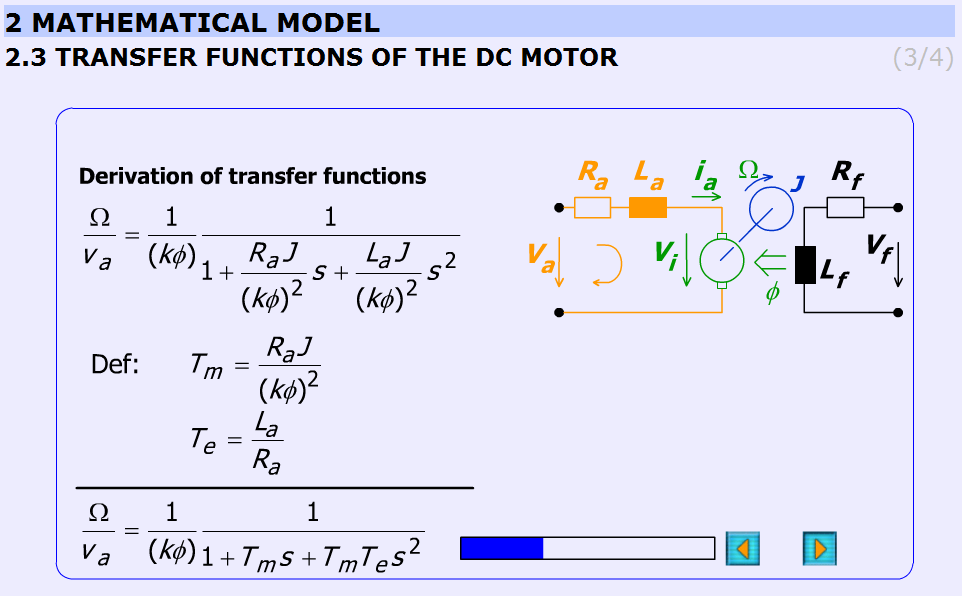
Ez a fejezet a DC-motor átviteli függvényének levezetését veszi át lépésről lépésre.
A kezdeti egyenletek az előző fejezetekből adottak (frekvencia tartomány egyenletek) és a végső egyenletek:
|
|
(5.12) |
|
|
(5.13) |
Az elektromos: Te és a mechanikus: Tm időállandók:
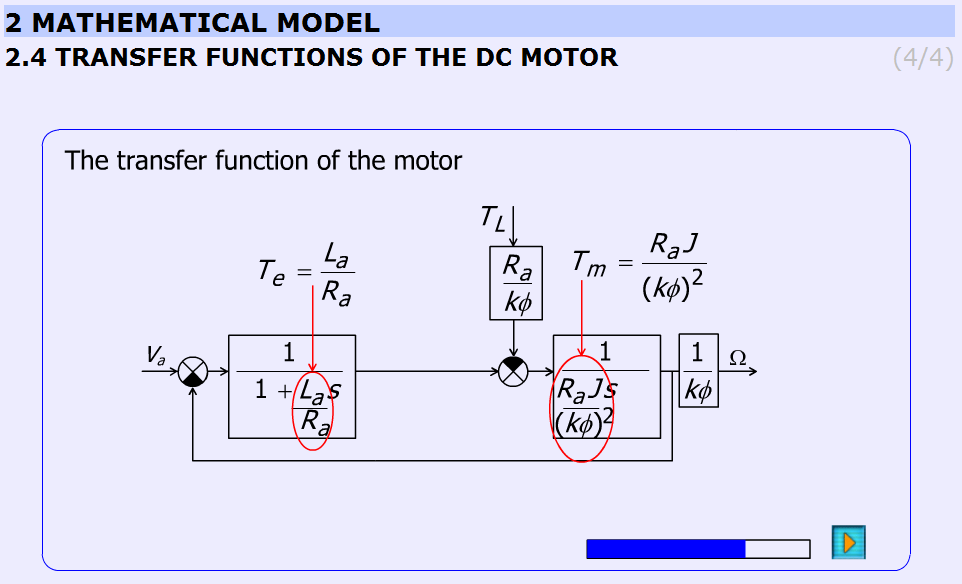
Az animáció magyarázó képeket is tartalmaz. A képek a levezetés szerint változnak. A folyamatsáv grafikusan mutatja a levezetés „helyzetét”.
A levezetéseket az 5-18. ábra mutatja.
5.9.4. A modell elemzése
5.9.4.1. Állapottér reprezentáció

Ez a fejezet az Átviteli függvények című fejezethez hasonlóan, levezeti az állapotteres felírás lépéseit. A kezdeti feltételek az időtartománybeli feltételekkel megegyeznek. Ezek szerint:
|
|
(5.16) |
vektorok és mátrixok alkalmazásával az állapottér felírva:
|
|
(5.17) |
5.9.4.2. Állandósult állapot

Ez a fejezet levezeti a DC motor stabil működési módjának a statikus karakterisztikus egyenletét. Ez alapján a következő fejezetben a statikus karakterisztika kerül bemutatásra.
A levezetés a következő felvetéssel kezdődik:
|
|
(5.18) |
és ezzel végződik ( )
)
|
|
(5.19) |
5.9.4.3. Statikus karakterisztika, munkapont
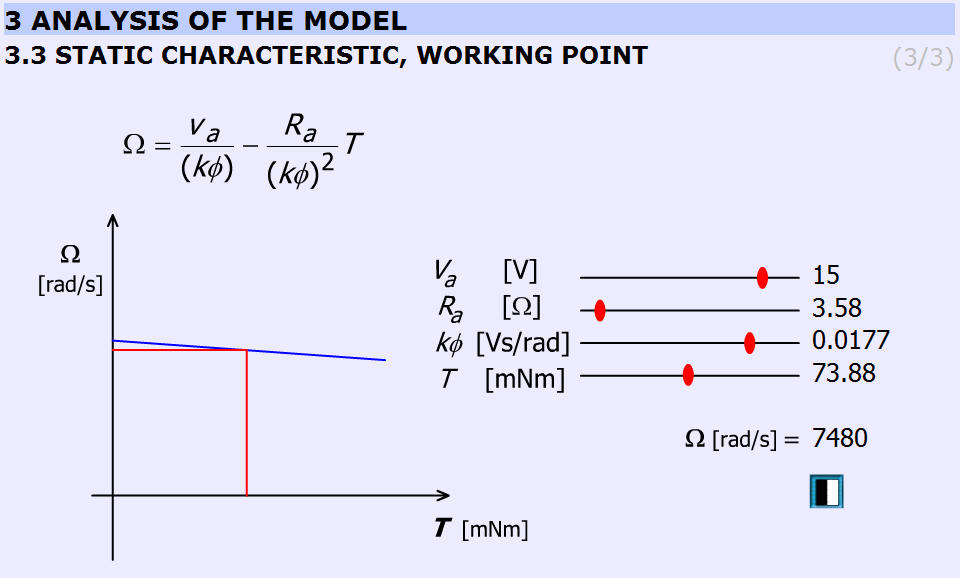
Ez a fejezet a statikus karakterisztikát, és a munkapontot magyarázza el.
Az animáció alapegyenlete:
|
|
(5.20) |
A Maxon motor kísérletben használt Simulink modellje az osztály értékei alapján a következők:
|
|
(5.21) |
Áttét: 33/1
A kék görbe a statikus karakterisztikája a motornak. A piros vonallal adott metszéspont adja meg a munkapontot. Az osztályértékeket függőleges vonalak jelölik a csúszkán (ld. 5-22. ábra).
5.9.4.4. Átviteli függvény elemzése
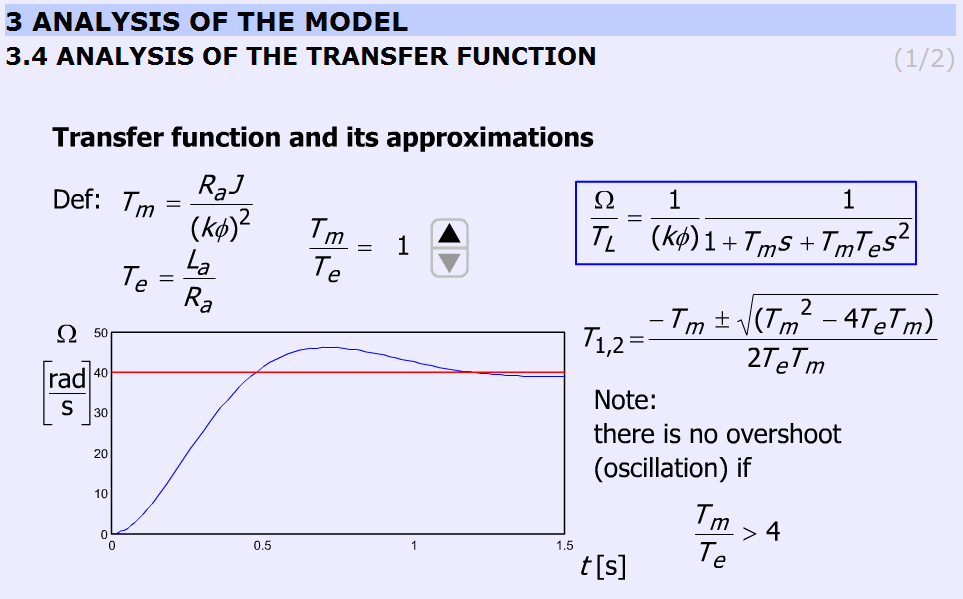
A DC motor tranziens válasza lépésszerű terhelő nyomaték változtatásokra különböző  arányt használva vizsgáljuk. A túllövés lehetőségére van magyarázat. A
arányt használva vizsgáljuk. A túllövés lehetőségére van magyarázat. A  megváltoztatásával a válasz is változik. Az időfüggvényeket kiszámítja és behelyettesíti. A
megváltoztatásával a válasz is változik. Az időfüggvényeket kiszámítja és behelyettesíti. A  arányt csak diszkrét előre definiált lépésekben változtatható.
arányt csak diszkrét előre definiált lépésekben változtatható.
A megoldandó egyenlet:
|
|
(5.22) |
A arány a következő lépésekben változtatható: 1; 2; 4; 8; 16; 33; 66.
arány a következő lépésekben változtatható: 1; 2; 4; 8; 16; 33; 66.
A magyarázat a karakterisztikus egyenlet gyökeiben keresendő:
|
|
(5.23) |
Két valós gyök létezik, ha  . Határeset:
. Határeset:
|
|
(5.24) |
akkor
|
|
(5.25) |
|
|
(5.26) |
Ha  , konjugált komplex gyököket kapunk.
, konjugált komplex gyököket kapunk.
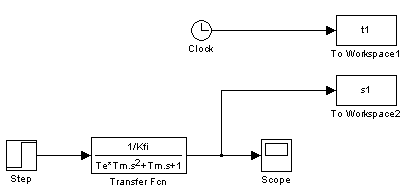
A szimulációt MatLab Simulink segítségével készítettük. A szimulációs beállításokat a 5-1. ábra: A rendszer áttekintő ábrája mutatja:
5.9.4.5. Az átviteli függvény vizsgálata
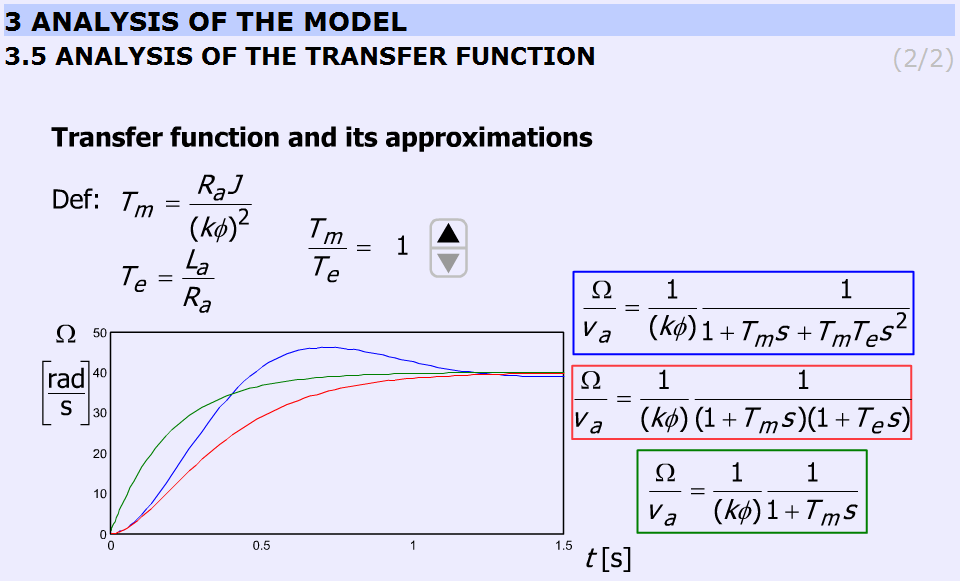
A fejezet megmagyarázza a közelítések közti különbségeket az arány megválasztásakor.Az animáció az előző fejezthez hasonlóan épül fel. A
megválasztásakor.Az animáció az előző fejezthez hasonlóan épül fel. A  arány a következő lépésekben változtatható: 1; 2; 4; 8; 16; 33; 66. Az előző fejezettel való összehasonlítás is lehetséges.
arány a következő lépésekben változtatható: 1; 2; 4; 8; 16; 33; 66. Az előző fejezettel való összehasonlítás is lehetséges.
5.9.4.6. A pontos és közelítő egyenlet:
A szimulációt MatLab Simulink segítségével készítettük. A szimulációs beállításokat az 5-25. ábra mutatja.
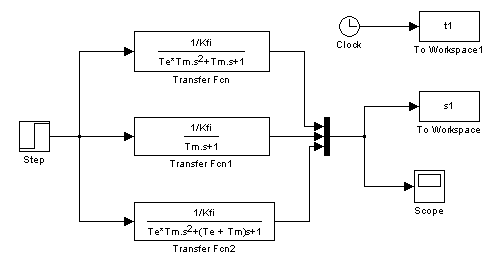
További részletekért látogasson el az alábbi animációs oldalra:
http://dind.mogi.bme.hu/animation/
5.9.5. A zajos fordulatszámjel szűrése
Az szögsebesség-idő függvénye nagyon zajos, mert a pozíciójelből digitális deriválási művelettel kapjuk. A deriválás általában kiemeli a zajokat, és ezt a méréseknél a gyakorlatban is tapasztalni fogjuk. Általában, ha lehet, akkor a deriválást kerülni szoktuk. pl. kevésbé zajos jelet kapnánk, ha a fordulatszámot közvetlenül érzékelnénk. Ha erre nincs mód, akkor a zajos jelet célszerű szűrni egy aluláteresztő szűrővel, például a következő módon.
Tekintsük a rendszer bemenetének a mért  , kimenetének a szűrt
, kimenetének a szűrt  szögsebességet.
szögsebességet.
|
|
(5.30) |
Tegyük fel, hogy sorba kapcsolunk 3 db elsőfokú aluláteresztő szűrűt, azonos  időállandóval. A szűrő átviteli függvénye
időállandóval. A szűrő átviteli függvénye
|
|
(5.31) |
Átrendezve
|
|
(5.32) |
Inverz Laplace-transzformálva
|
|
( 5.33 ) |
ahol Tc a vágási körfrekvencia reciproka és a pont jelöli (  ) az idő szerinti deriváltat. A szűrő állapottér egyenlete (5.33) alapján:
) az idő szerinti deriváltat. A szűrő állapottér egyenlete (5.33) alapján:
|
|
( 5.34 ) |
Az állapottér egyenlet (5.34) leírható diszkrét alakban.
|
|
(5.35) |
Ahol k a k-dik mintavételezés rövidítése és a rendszermátrix elemei (ai és bi) kiszámíthatók a MATLAB “c2d” függvényével, ami “continuous to discrete”, vagy folytonos-diszkrét rövidítése.
[Ad, Bd] = c2d(A, B, tsample);
ahol tsample a mintavételezési periódus és Tc szűrő időállandója
|
|
(5.36) |
|
|
(5.37) |
A  értékének meghatározásához abból indulhatunk ki, hogy a fordulatszám jelhez adódó zaj abból adódik, hogy két pozíciójel különbségéből számítjuk. A pozíciójelet a számlálóból olvassuk ki, ami az enkóderből érkező impulzusokat számlálja. Az enkóderből érkező jelek értelemszerűen nincsenek szinkronizálva a számláló értékének beolvasásával. Ezért előfordulhat, hogy egyszer pont egy enkóderből származó impulzus érkezése előtt, egyszer pont utána olvassuk ki a számláló értékét, így állandó szögsebesség esetén is két különböző értéket fogunk kiszámítani. Elképzelhető, hogy minden beolvasásánál a hiba előjelet vált, így a zaj periódus idejét jól közelíthetjük a mintavételi idő kétszeresével. Ebből már meghatározhatjuk a zaj frekvenciáját, illetve
értékének meghatározásához abból indulhatunk ki, hogy a fordulatszám jelhez adódó zaj abból adódik, hogy két pozíciójel különbségéből számítjuk. A pozíciójelet a számlálóból olvassuk ki, ami az enkóderből érkező impulzusokat számlálja. Az enkóderből érkező jelek értelemszerűen nincsenek szinkronizálva a számláló értékének beolvasásával. Ezért előfordulhat, hogy egyszer pont egy enkóderből származó impulzus érkezése előtt, egyszer pont utána olvassuk ki a számláló értékét, így állandó szögsebesség esetén is két különböző értéket fogunk kiszámítani. Elképzelhető, hogy minden beolvasásánál a hiba előjelet vált, így a zaj periódus idejét jól közelíthetjük a mintavételi idő kétszeresével. Ebből már meghatározhatjuk a zaj frekvenciáját, illetve  körfrekvenciáját, mivel a szűrő tervezéséhez ez utóbbira van szükség. Esetünkben
körfrekvenciáját, mivel a szűrő tervezéséhez ez utóbbira van szükség. Esetünkben
|
|
(5.38) |
Az aluláteresztő szűrő vágási frekvenciáját ennél kisebbre kell beállítani. Ha egy dekáddal kisebbre állítjuk be, akkor az egy harmadjajú szűrő esetén kb. ezred részére képes csökkenti a zajt.  a vágási körfrekvencia reciproka, ezért legyen a választásunk a következő
a vágási körfrekvencia reciproka, ezért legyen a választásunk a következő
|
|
(5.39) |
A diszkrét idejű szűrő együtthatóit meghatározó és a C kódot generáló MATLAB program
Ts = 0.001;
Tc = 1/(2*pi*1/(2*Ts)/10);
A = [0, 1, 0;
0, 0, 1;
-1/Tc^3, -3/Tc^2, -3/Tc];
B = [0;0;1/Tc^3];
[Ad,Bd] = c2d(A,B,Ts);
for i = 1:3
for j = 1:3
disp(['float ad',num2str(i),num2str(j),' = ', num2str(Ad(i,j)),';']);
end
end
for i = 1:3
disp(['float bd',num2str(i),' = ', num2str(Bd(i)),';']);
end
Eredmény
float ad11 = 0.99591;
float ad12 = 0.00095987;
float ad13 = 3.652e-007;
float ad21 = -11.3235;
float ad22 = 0.88778;
float ad23 = 0.00061567;
float ad31 = -19089.6748;
float ad32 = -193.6165;
float ad33 = 0.30752;
float bd1 = 0.0040906;
float bd2 = 11.3235;
float bd3 = 19089.6748;
A szűrő mellékhatása, hogy növeli a rendszer fáziseltolását. E problémán javíthatunk, ha egy más típusú szűrőt alkalmazunk.
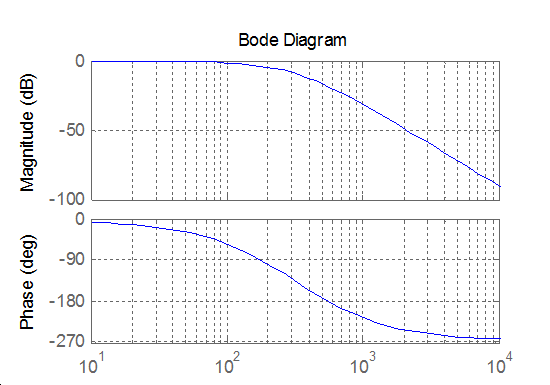
Vizsgáljunk meg egy harmadrendű Bessel szűrőt. A harmadrendű Bessel szűrő átviteli függvénye:
|
|
(5.40) |
Ts = 0.001;
Tc = 1/(2*pi*1/(2*Ts)/10);
A = [0, 1, 0;
0, 0, 1;
-15/Tc^3, -15/Tc^2, -6/Tc];
B = [0;0;15/Tc^3];
[Ad,Bd] = c2d(A,B,Ts);
for i = 1:3
for j = 1:3
disp(['float ad',num2str(i),num2str(j),' = ',num2str(Ad(i,j)),';'])
end
end
for i = 1:3
disp(['float bd',num2str(i),' = ', num2str(Bd(i)),';']);
end
Eredmény
float ad11 = 0.95193; float ad12 = 0.00083371; float ad13 = 2.6009e-007; float ad21 = -120.9668; float ad22 = 0.56688; float ad23 = 0.00034345; float ad31 = -159737.83; float ad32 = -629.4281; float ad33 = -0.080513; float bd1 = 0.048071; float bd2 = 120.9668; float bd3 = 159737.83;
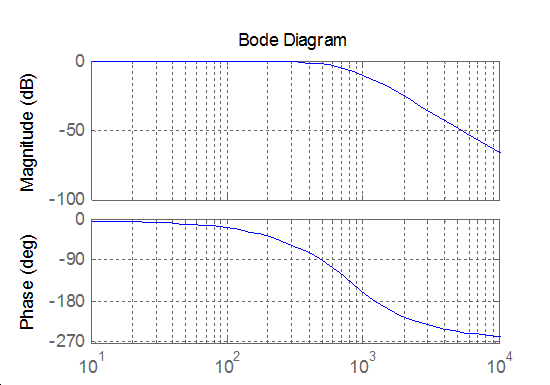
Vizsgáljunk meg egy ötödrendű Bessel szűrőt. Az ötödrendű Bessel szűrő átviteli függvénye:
|
|
(5.41) |
A diszkrét idejű szűrő együtthatóit meghatározó és a C kódot generáló MATLAB program
Ts = 0.001;
Tc = 1/(2*pi*1/(2*Ts)/10);
A = [0, 1, 0, 0, 0;
0, 0, 1, 0, 0;
0, 0, 0, 1, 0;
0, 0, 0, 0, 1;
-945/Tc^5, -945/Tc^4, -420/Tc^3, -105/Tc^2, -15/Tc];
B = [0;0;0;0;945/Tc^5];
[Ad,Bd] = c2d(A,B,Ts);
for i = 1:5
for j = 1:5
disp(['float ad',num2str(i),num2str(j),' = ',num2str(Ad(i,j)),';'])
end
end
for i = 1:5
disp(['float bd',num2str(i),' = ', num2str(Bd(i)),';']);
end
Eredmény
float ad11 = 2.3749; float ad12 = 0.0060369; float ad13 = 8.9952e-006; float ad14 = 8.7509e-009; float ad15 = -2.4834e-013; float ad21 = -55.9541; float ad22 = 0.80926; float ad23 = 0.00070548; float ad24 = 2.3492e-007; float ad25 = 6.3994e-011; float ad31 = -185062.4462; float ad32 = -645.0082; float ad33 = -0.024158; float ad34 = 4.2341e-005; float ad35 = 1.3387e-007; float ad41 = -387151871.8085; float ad42 = -1417349.3637; float ad43 = -2388.3942; float ad44 = -1.4113; float ad45 = 7.4665e-005; float ad51 = -215947384065.4345; float ad52 = -1074421228.8149; float ad53 = -2389749.1508; float ad54 = -3161.8599; float ad55 = -0.37582; float bd1 = -1.3925e-005; float bd2 = 0.00056689; float bd3 = 1.8749; float bd4 = 3922.0853; float bd5 = 2186784.2468;
5.9.6. A mérés leírása
A CalculateController függvényt a valós idejű óra minden jelére meghívja a keretprogram. A saját szabályozó algoritmusát a következő programba írhatja bele:
#include <windows.h>
#include <stdio.h>
#include <rtapi.h>
#include <math.h>
#include <string.h>
#define PI 3.14159265358979323846
typedef struct
{
float Position;
float Velocity;
float Torque;
float StateVariable_5;
float StateVariable_6;
float StateVariable_7;
float StateVariable_8;
float StateVariable_9;
float StateVariable_10;
} NewControllerData;
NewControllerData CalculateController(
const float CurrentPosition,
const float OldPosition,
const float OldVelocity,
const float CurrentTime,
const float OldTime,
const float Old_StateVariable_5,
const float Old_StateVariable_6,
const float Old_StateVariable_7,
const float Old_StateVariable_8,
const float Old_StateVariable_9,
const float Old_StateVariable_10
)
{
NewControllerData ResultData; // result
//Declaration of your controller
// Position is saved automatically
ResultData.Position = CurrentPosition;
// Angular velocity is saved automatically
if (CurrentTime != 0.0f){
ResultData.Velocity = (1000.0f * (float)(CurrentPosition - OldPosition)/(float)(CurrentTime - OldTime));
}
else {
ResultData.Velocity = 0.0f;
}
//Calculation of your controller
return ResultData;
}
A pirossal írt részek helyére kell a saját programot elhelyezni. A változók új értékeit és minden számítást ezen a függvényen belül kell megadni. A motor állapotát a keretprogram kiszámítja és a következő változókban tárolja:
ResultData.Position: pozíció
ResultData.Velocity: szögsebesség
ResultData.Time: az aktuális idő
Biztonsági okokból a motor bemeneti feszültségét nem lehet direkt módon állítani. Az irányítóprogram kimenete, amely a kimenő jel a D/A kártyán a referencia áram-jel. Ez referencia nyomaték-jelnek is tekinthető. A saját programunkban kell, hogy legyen a következő értékadás:
ResultData.Torque = …
A felhasználónak az értéket a “your controller program” végén kell beállítania. Például:
ResultData.Torque = 1;
azt jelenti, hogy a tengelyen a nyomaték (a fogaskerék után) 1 Nm-re lett állítva. Mivel a D/A kártya kimenete feszültség, a keretprogram kiszámolja a megfelelő feszültség értéket a ResultData.Torque-ból, amely a kimeneti jel lesz.
Ebben a feladatban nyílt hurkú méréseket végzünk a DC motoron. Maximum 10 állapotváltozó választható ki Matlab formátumban történő mentésre. A 10-ből 4 állapotváltozó kötött: az idő, a pozíció, a szögsebesség és a motor nyomatéka.
Ha az állapotváltozó hibát kívánja menteni, az alábbiakat kell tennie:
Írja be az állapotváltozó nevét vel_filt (szűrt sebesség) az ötödik sorba a következő formában:
5. vel_filt
Írja be a változó deklarációját:
float vel_filt;
Írja be a következőt a parancs dobozba:
Vel_filt = (ki kell számítani a szűrt sebesség értékét)
ResultData.StateVariable_5 = vel_filt;
A mérés után a vel_filt állapotváltozó is letölthető.
Hajtsa végre a feladatokat nyílt körre és hasonlítsa össze őket a P, és PI szabályozókkal.
Az eredményfájlok, amelyek a mérés végén letölthetők, MATLAB-ban kiértékelhetők. Erre a feladatra már írtunk egy programot, amely kirajzolja a tengelysebesség-idő, feszültség-idő és pozíció-idő diagramjait. Ezek a diagramok .jpg formátumban menthetők el további dokumentációkhoz.
MEGJEGYZÉS:
A szabályozó programot minden egyes mintavételező periódusban meghívja a keretprogram. A függvény végrehajtása után minden változó (kivéve a ResultData.Time, ResultData.Velocity,ResultData.Position ResultData.Torque és ResultData.StateVariable_5-10) felszabadul (avagy az értékek elvesznek). Ha szükséges egy változó a következő mintavételező periódusban is, akkor statikus típusú változóként kell deklarálni. Például:
static float vel_filt;
Általános lépések szükségesek:
-
Tanumányozza az ebben a fejezetben a DC motorról írt „A DC motor elméleti háttere” című szövegrészt.
-
Beállíthatja a mérés idejét milliszekundumban (az alapérték 1000).
-
A mérések alapján határozza meg a tranziens válaszokat és a DC szervomotor stabil-állapot karakterisztikáit.
Segítségképp az első három laboratóriumi gyakorlaton megismert két kártyát a keretprogram inicializálja. Csak a fentebb leírt lépések szükségesek a sikeres laboratóriumi mérés végrehajtásához.
5.9.7. Mérési feladatok
5 . 11 mérési feladat : K onstans nyomaték kiadása
Az első feladatban az elektromos nyomaték értéke:
-
ResultData.Torque = 0.1;
-
ResultData.Torque = 0.5;
-
ResultData.Torque =1.0;
Ezúton a különböző motor-változók különböző nyomatékjel lépés-változásaira kapott lépés válaszai kaphatók meg. Az eredmény fájlok, amelyek a mérés végén letölthetők, Matlabban kiszámíthatók. Erre a feladatra már van egy program. A program futtatásával az eredményeket megkapjuk tengelysebesség-idő, feszültség-idő és pozíció-idő diagramokon. Ezeket a diagramokat .jpg formátumban lehet elmenteni a további dokumentáció érdekében.
5 . 12 mérési feladat : K onstans nyomaték kiadása és a fordulatszám szűrése
Az előző feladathoz hasonlóan a nyomaték legyen a következő:
-
ResultData.Torque = 0.1;
-
ResultData.Torque = 0.5;
-
ResultData.Torque =1.0;
Alkalmazza az 5.9.5 pontban leírt digitális szűrőket. Legyen a töréspont helye
|
|
(5.42) |
5 . 13 mérési feladat : A motor válasza szinuszos nyomatékra és a szervoerősítő offset kompenzációja
A szervoerősítőnek (mint minden műveleti erősítőnek) van egy offset feszültsége. Ez akkor a legszembetűnőbb, ha szinuszos feszültséget alkalmazunk. Ebben az esetben a motortól azt várjuk, hogy szinuszos legyen a tengely szögsebessége és ebből adódóan, szinuszos pozícióváltozása. Az offset feszültséget célszerű hardveresen kompenzálni, de kompenzálhatjuk szoftveresen is.
-
Változtassa a motor nyomatékát szinuszosan. A szinuszos nyomatékjel amplitúdója legyen 0.6 mNm és a periódusideje legyen 0.1s és 0.5s. Vizsgálja meg a motor fordulatszámát és pozícióját.
-
Változtassa meg a szinuszos nyomatékjel offszetjét úgy, hogy a pozíciójel középértéke is nulla legyen.
5 . 14 mérési feladat : Digitális szűrő
5.10. Visszacsatolt kör mérések -- Motion control/Exercise 5 menüpont alatt található laboratóriumi mérési gyakorlat
Az előző laboratóriumi mérési gyakorlat során megismertük a szervomotoros hajtás elemeit. A mostani laboratóriumi mérési gyakorlaton konkrét szabályozókat kell tervezni.
5.10.1. Az irányításelmélet elméleti háttere
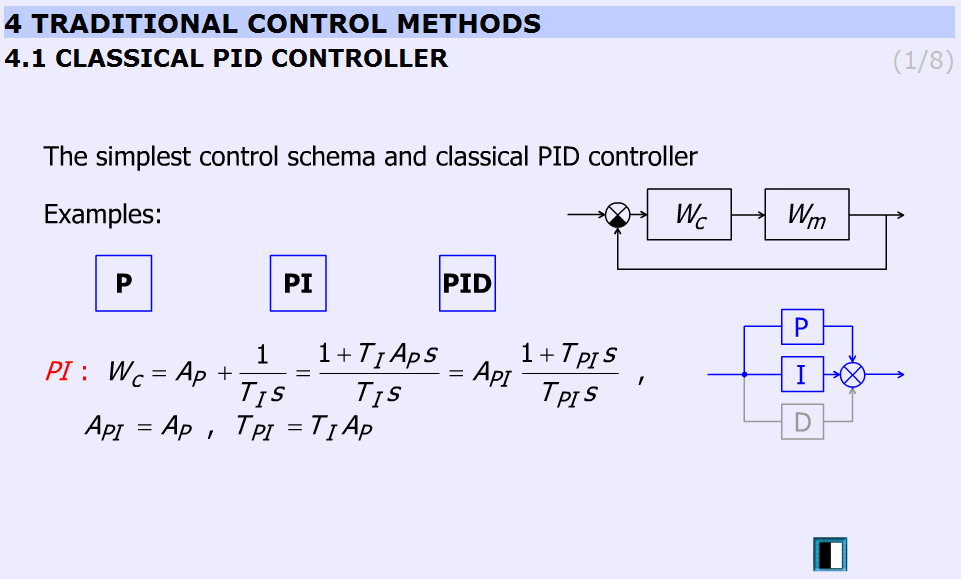
Az animáció bemutatja a P, PI, PID szabályozókat és az egymás közötti különbségeket.
“P”:
|
|
(5.43) |
“PI”:
“PID”:
|
|
(5.46) |
|
|
(5.47) |
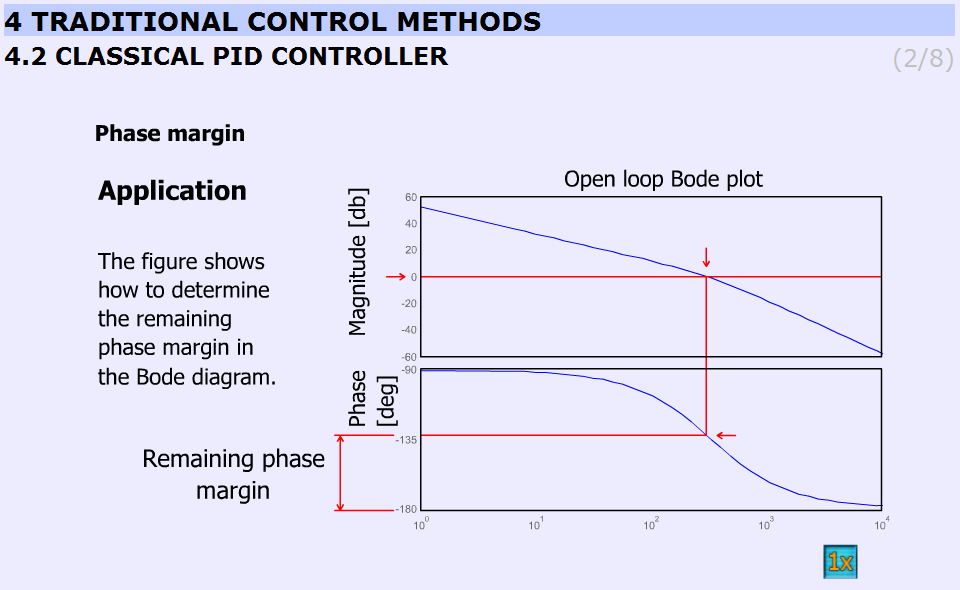
Animált magyarázat a fázistartalék meghatározására: Az amplitúdó diagramon a 0 szinten, egy piros vízszintes vonal jelenik meg. Azon a ponton, ahol a piros vonal keresztezi az amplitúdó görbéjét, egy függőleges vonal megy le a fázisdiagramig. Abban a pontban, ahol ez a vonal keresztezi a fázisgörbét, egy vízszintes vonal mutatja a pillanatnyi fázis értékét. A végén megjelenik a fázistartalék, amit az alábbiak szerint számolhatunk:
|
180o –az adott fázis = fázistartalék |
(5.48) |
Ezt a dimenzióvonal mutatja a fázis tengelyen.

A dia elmagyarázza a PI szabályozó használatát. A motor és a szabályozó átviteli függvénye 1 közelítéssel:
|
|
(5.49) |
Megválasztva, hogy  legyen: az átviteli függvény:
legyen: az átviteli függvény:
|
|
(5.50) |
Végül  és AP meghatározása a fázistartalék megválasztásával.
és AP meghatározása a fázistartalék megválasztásával.
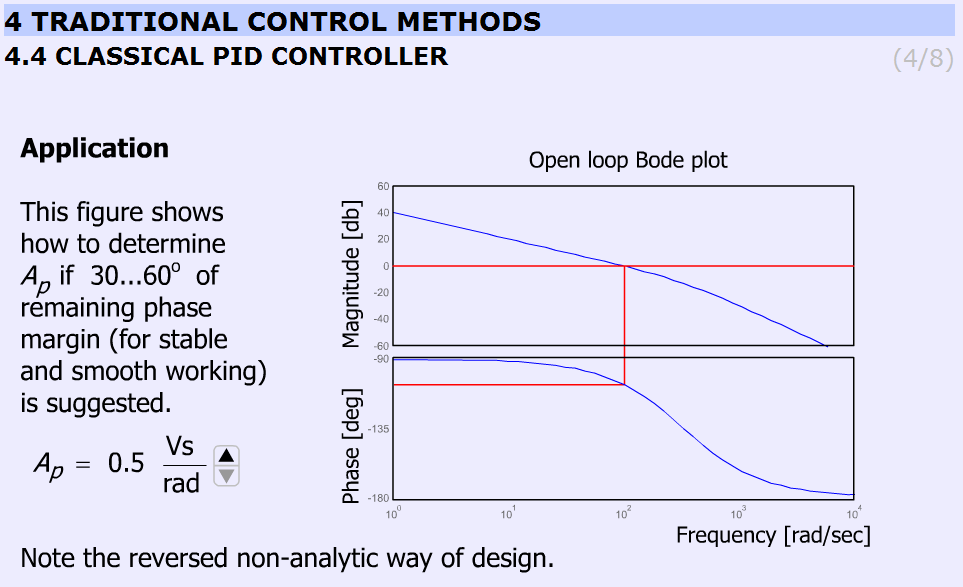
Az animáció mutatja Ap meghatározását, 30...60o fázistartalékát (stabil, sima működésnél) egy fordított, nem analitikus módon, ahol a Bode diagramokon látszik a fázistartalék. A felhasználó 0.5 és 3.5 között változtathatja Ap –t és megfigyelhetőek a különböző fáziseltolások hatásai a fázistartalékon. Az animáció az előzetesen bemutatott példa alapján rajzolja ki a grafikonokat. Ap 0.5 és 3.5 között 7 fokozatban állítható (0.5; 1.0; 1.5; 2.0; 2.5; 3.0; 3.5).
A szimuláció során használt paraméterek:
-
Tpi= 0.2 s;
-
Api= változtatható;
-
Kfi = 0.025 Vs/rad;
-
Te = 0.003 s;
-
Tm=Tpi;
MatLab utasítások:
g = tf([Api/Kfi],[Tpi*Te Tpi 0]);
bode(g);

A dia a nyílt és visszacsatolt hurkú átviteli függvényeket mutatja be ismét. PI szabályozót használ és TPI= Tm.
Az egyenletek (levezetések nélkül) az alábbiak:
-
Nyílt hurok
|
|
(5.51) |
-
Visszacsatolt hurok
|
|
(5.52) |
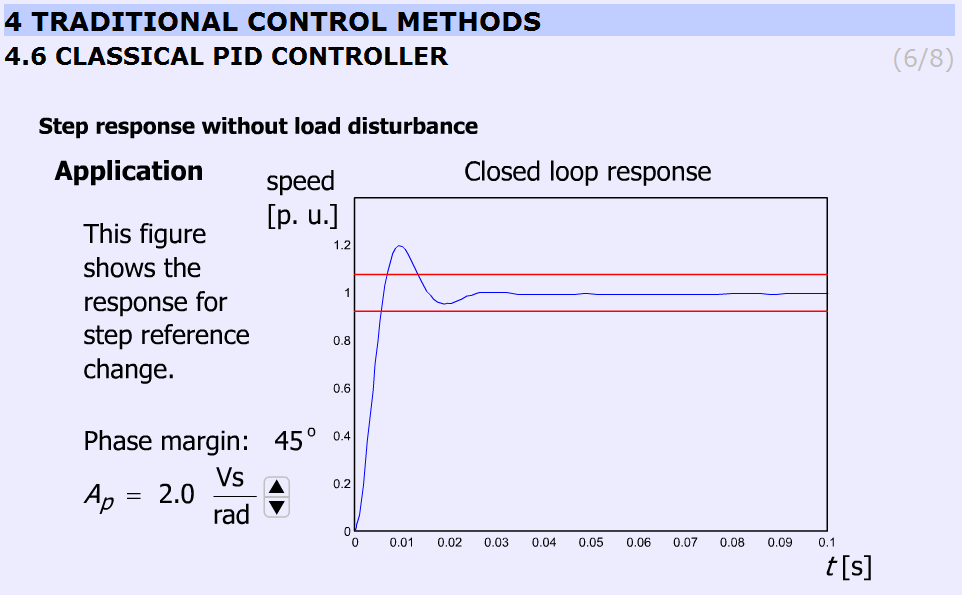
Az animáció a sebesség referencia-jel lépésszerű változására a rendszer által adott választ mutatja be.
Megjegyzendő, hogy növekvő Ap nem eredményez túllendülést. Az animáció az előzetesen használt grafikonokat és eredményeket használja. Ap 0.5 és 3.5 közt 7 fokozatban változtatható (0.5; 1.0; 1.5; 2.0; 2.5; 3.0; 3.5).
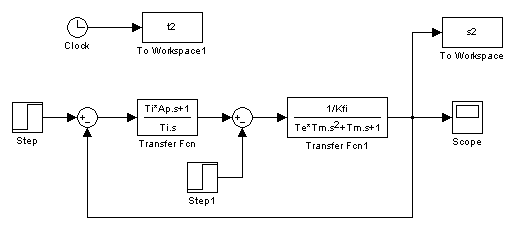
A szimuláció MatLab Simulink segítségével készült, a szimulációs beállítást az 5-35. ábra mutatja.
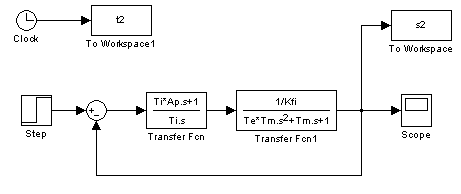
A motor és PI szabályozó elrendezése egy feedback hurokban látható az 5-37. ábra alapján.
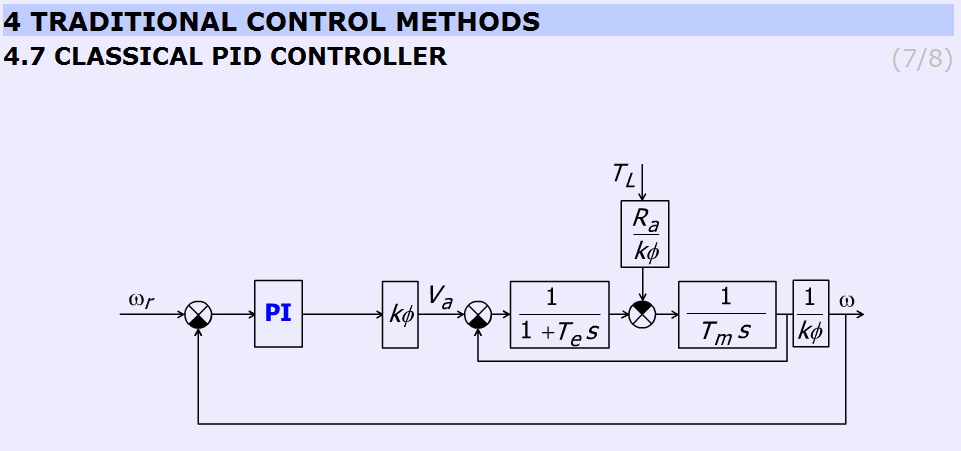
A felhasználó megfigyelheti, hogy AP növelésével a rendszer túllendülése is nő.
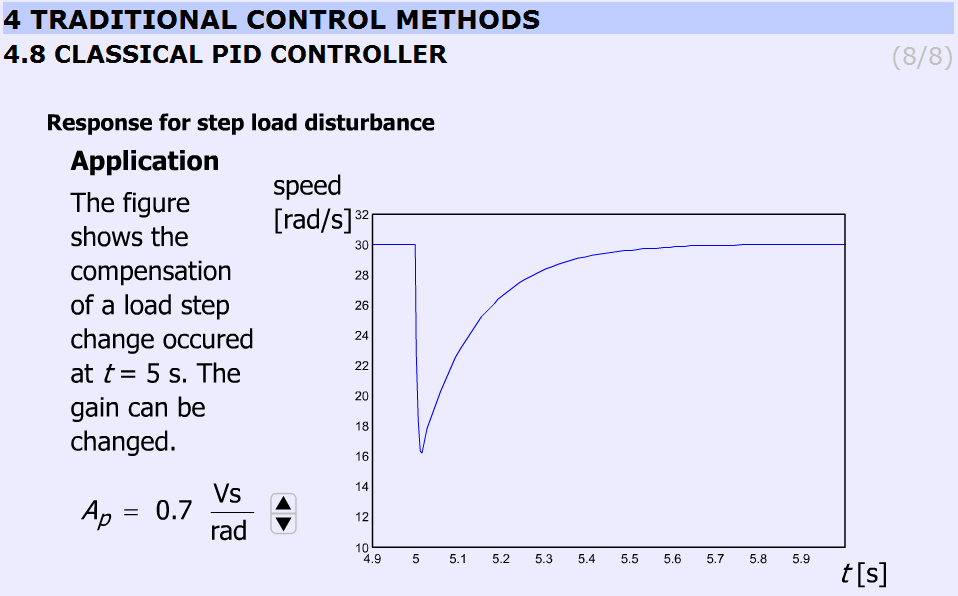
A dia a zavarérzéketlenség hatását mutatja. Egy lépésszerű nyomatékterhelést kapcsolunk t = 5s időpillanatban a bemenetre. Az animáció összehasonlítja a szabályozó sebesség értékét különböző Ap értékeknél. Ap 0.5 és 3.5 között 8 fokozatban változtatható (0.5; 0.7; 1.0; 1.5; 2.0; 2.5; 3.0; 3.5). AP = 0.7 azért adódik, mert a különbség 0.5 és 1.0 között túl nagy.
5.10.2. Áram szabályozó
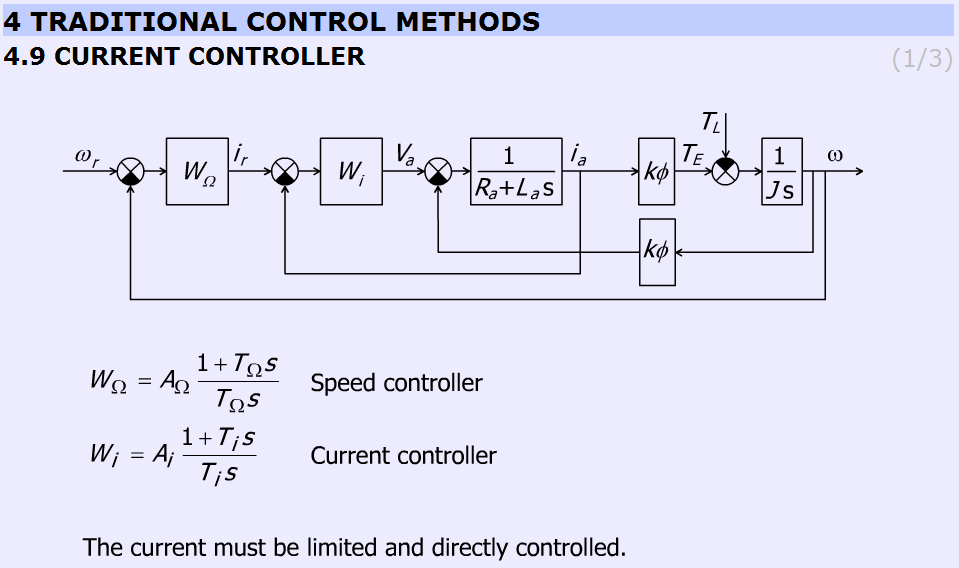
Ez a fejezet röviden ismerteti az áramszabályozó működését. Részletes blokkdiagramot tartalmaz a motorról és szabályozókról (sebesség és áram), valamint a szabályozók egyenleteiről.
Sebességszabályozó:
|
|
(5.53) |
Áramszabályozó:
|
|
(5.54) |
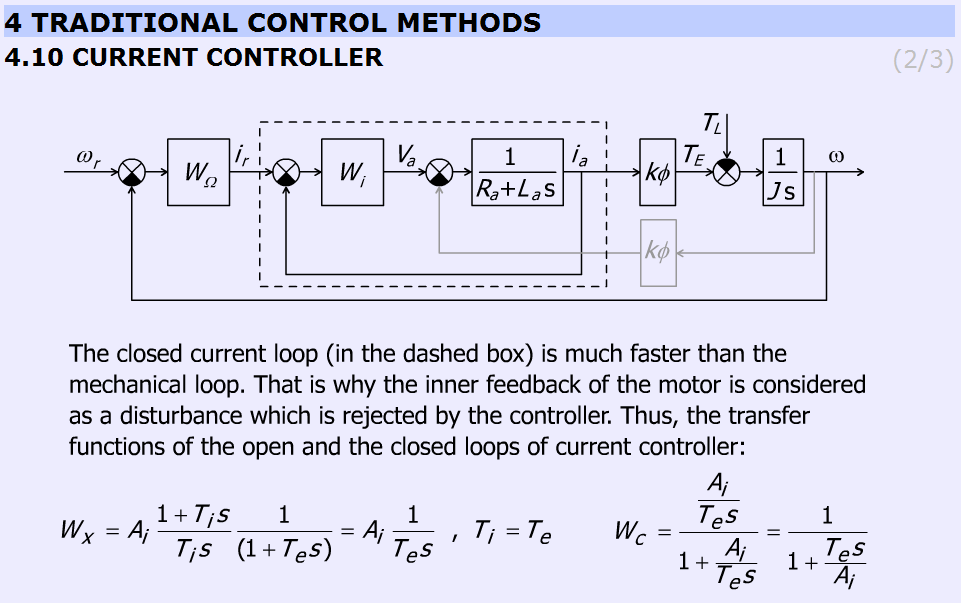
A dia azt mutatja, miért hanyagolható el a motor visszahatása. Segít azonosítani a lényeges és nem lényeges elemeket. A motor belső visszahatása elhanyagolható, mert az áramszabályozó sokkal gyorsabb működésű, mint a mechanikus szabályozó. Ezért a belső visszahatás zavarként kezelhető, amely lassan változik, a szabályozó kiküszöböli a hibát, amit a D motor pontatlan modellje okoz.
A dia a szabályozó működéséhez szüksége egyenleteket mutatja.
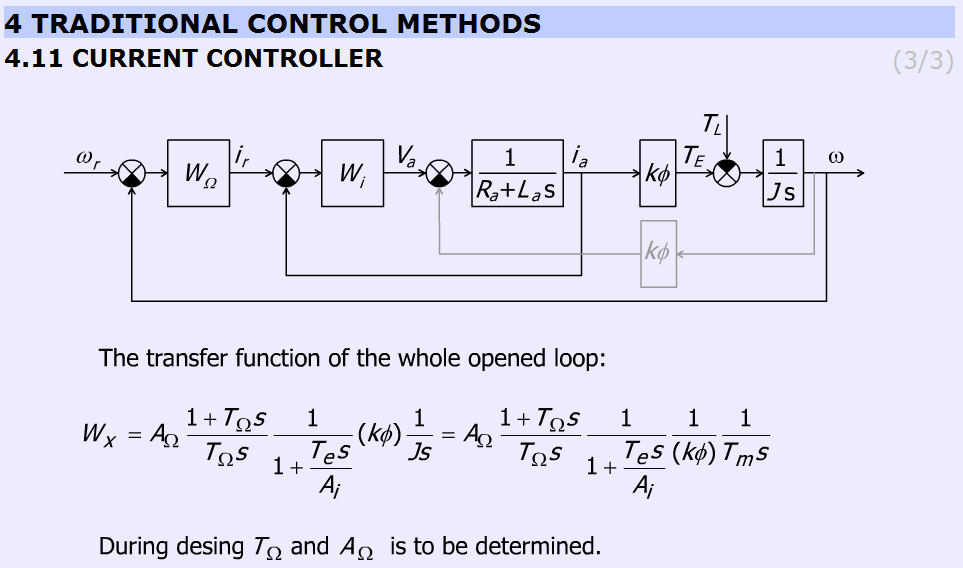
A fenti dia leírja a rendszer nyílt hurkú átviteli függvényét.
|
|
(5.55) |
|||
|
ahol ωe = ωr – ω. |
||||
További részletekért látogasson el az alábbi animációs oldalra:
http://dind.mogi.bme.hu/animation/
5.10.3. Módszerek a PID szabályozó paramétereinek megválasztásához Ziegler-Nichols módszer
A módszer célja, hogy a PID szabályozó paramétereit egy egyszerű teszttel választhassuk meg. Vannak esetek, amikor a szabályozott szakasz paraméterei nem ismertek, ezért a PID szabályozót próbálgatással, kísérletileg kell behangolni. Több olyan módszer ismert, amely a próbálgatások hatékonyságát növeli. Az egyik legnépszerűbb módszert Ziegler és Nichols dolgozta ki [48]. Elsősorban időkésleltetéssel rendelkező rendszerekhez alkalmazható, de gyakorlatilag minden szabályozó gyártó használta a módszert kisebb módosításokkal beállítási ajánlásaik elkészítéséhez. Népszerűségének oka az, hogy egyszerű megtanulni és elmagyarázni. A módszert egy egyenáramú szervomotor fordulatszám szabályozó körének kísérleti behangolásán keresztül mutatjuk be. A példában egy fordulatszám szabályozó behangolását mutatjuk be. A szabályozó algoritmus a motor armatúra áramának az alapjelét határozza meg. A program kiszámítja és kiadja a motor áramreferencia jelét, a motor áramszabályozóhurkához (amely az áramkorlátozást is megvalósítja) biztonsági okokból nem férünk hozzá. A motor tényleges árama a szabályozási idő leteltével éri el a referencia értéket. Maga a rendszer két energiatárolós szakasznak tekinthető, ezért a motor önmagában strukturálisan stabilis (így a Ziegler-Nichols módszer nem lenne alkalmazható), de a fordulatszám jelet digitális szűréssel állítjuk elő, így a motor az alkalmazott harmadfokú szűrő algoritmussal együtt már egy öt energiatárolós rendszernek tekinthető. Természetesen ez csak akkor igaz, ha a szűrt jelet használjuk fel a hiba előállításához.
Feladatok a hangolás során:
Először teszteljük, hogy a szükséges P tag negatív vagy pozitív. Kapcsoljuk a szabályozót csak P módra, avagy kapcsoljuk ki az I és D funkciókat. A bemeneti feszültséget kapcsoljuk nyílt körbe (hibajel), növeljük kicsit manuális vezérléssel, hogy lássuk az állandósult állapotú rendszer kimenetének értéke is növekedett. Ha ez így van, akkor az állandósult rendszer erősítése pozitív, avagy a P szabályozó AP-értékének is pozitívnak kell lennie, különben (ha csökkent), AP negatív lesz.
Változtassuk a szabályozó erősítését, AP –t lassan (növeljük, ha AP pozitív volt, és csökkentsük, ha AP negatív volt) és figyeljük a kimeneten adott választ. Megjegyezzük, hogy ez AP lépésenkénti változtatásával jár majd, a lépések után meg kell várni az állandósult állapotot, mielőtt AP –t újból megváltoztatnánk.
Legyen az AP kritikus (ultimate) értéke AU, amikor a kimeneten állandósult lengőjel alakul ki. Mérjük meg ennek a periódusidejét is, és nevezzük el TU-nak, (ld. 5-44. ábra). TU a határperiódusidő.
Az AU határerősítést és a TU határperiódusidőt felhasználva Ziegler és Nichols módszere a következő AP, TI és TD, értékeket javasolja a szabályozó típusától függően:
|
AP |
TI |
TD |
|
|
P szabályozó |
AU/2 |
||
|
PI szabályozó |
AU/2.2 |
TU/1.2 |
|
|
PID szabályozó |
AU/1.7 |
TU/2 |
TU/8 |
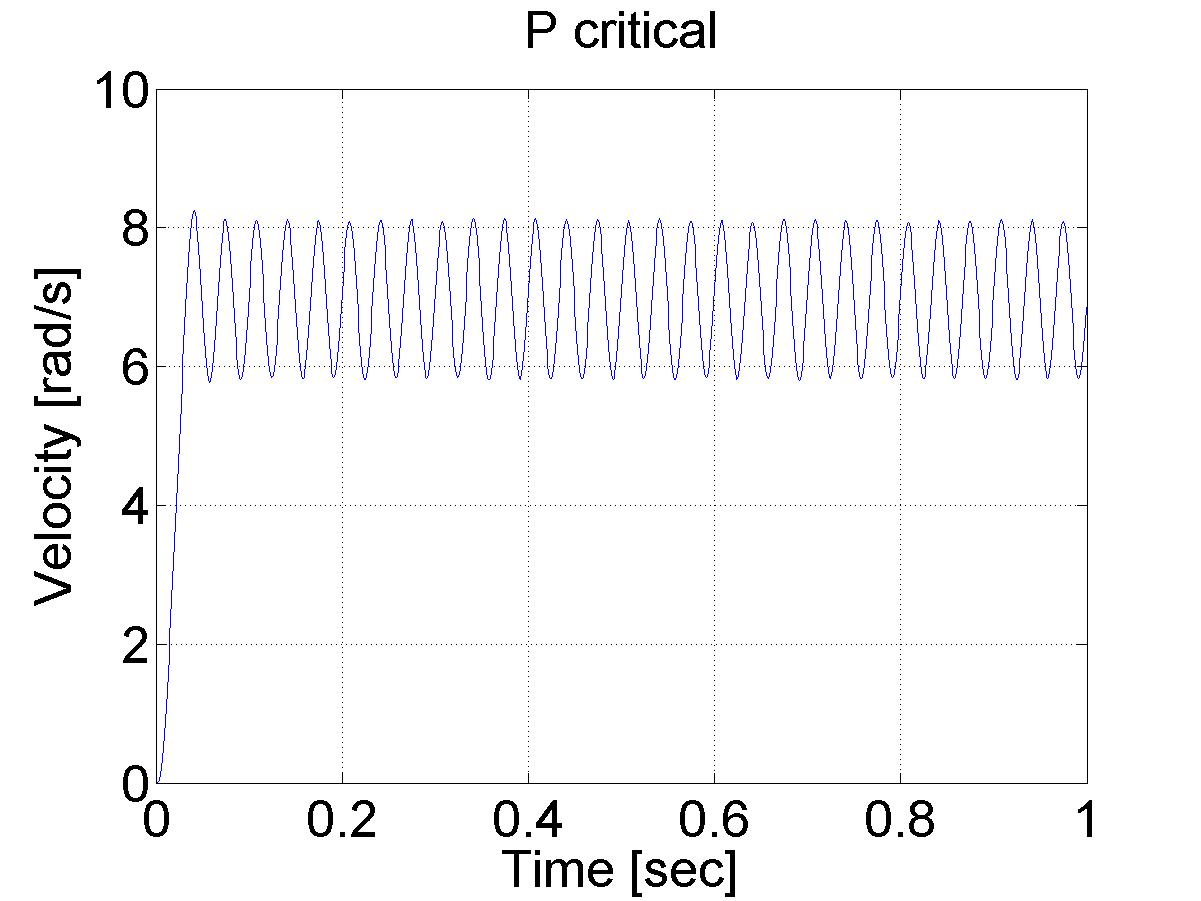
A következőkben különböző vezérlés típusokat vizsgálunk.
Ebben a gyakorlatban először P, majd PI és a legvégén PID sebességszabályozót állítunk be a DC motornak.
Lépések:
-
Tanulmányozza az irányításelméletről szóló “Az irányításelmélet elméleti háttere” című 5.10.1 fejezetet.
-
Állítsa be a szabályozókat (P, PI, PID, stb.).
5.10.4. Mérési feladatok: fordulatszám szabályozás
5 . 16 mérési feladat : A Ziegler-Nichols módszer ún. ultimate körerősítésének meghatározása
Készítsen egy P szabályozót és fokozatosan növelje a P értékét a stabilitás határáig, amikor a fordulatszám jelben közel állandó amplitúdójú lengések ki nem alakulnak. Fontos megjegyzés, hogy az ultimate körerősítés erősen függ az alkalmazott szűrő típusától és annak vágási frekvenciájától. Ezt a feladatot végezze el különböző szűrőkkel.
5 . 17 mérési feladat : P szabályozó
Vizsgálja meg a P szabályozó működését Ω = 7 rad/s tengelysebesség mellett.
5 . 18 mérési feladat : P szabályozó v áltozó alapjel lel
Az 5.17 kibővítése, azzal a különbséggel, hogy először Ω = 4 rad/s t = 0 s-mál, majd Ω = 2 rad/s t = 2 s-mál és végül Ω = 6 rad/s t = 4 s-nál.
5 . 19 mérési feladat : P szabályozó t erhelésrádobás sal
Vizsgálja meg a P szabályozó zavarérzéketlenségét. A zavart t = 0.5 s-ban adjuk a rendszerre, mint negatív nyomatékot T_load= -0.5, amely kivonódik a szabályozó által számolt kimeneti feszültségből.
ResultData.Torque = (kérjük, írja ide a szabályozóját)
ResultData.Torque = ResultData.Torque + T_load; /* ez a virtuális terhelés sora*/
5 . 20 mérési feladat : PI szabályozó
Vizsgálja meg a PI szabályozó működését Ω = 7 rad/s tengelysebesség mellett.
5 . 21 mérési feladat : PI szabályozó változó alapjel lel
Legyen először Ω = 4 rad/s t = 0 s-nál, majd Ω = 2 rad/s t = 2 s-nál, és végül Ω = 6 rad/s t = 4 s-nál.
5 . 22 mérési feladat : PI szabályozó terhelésrádobás sal
Vizsgálja meg a PI szabályozó zavarérzéketlenségét. A zavart t = 0.5 s-ban adjuk a rendszerre, mint negatív nyomatékot T_load= -0.5, amely kivonódik a szabályozó által számolt kimeneti feszültségből.
ResultData.Torque = (kérjük, írja ide a szabályozóját)
ResultData.Torque = ResultData.Torque + T_load; /* ez a virtuális terhelés sora*/
5 . 23 mérési feladat : A nti windup PI szabályozó
A PI szabályozó hibatoleranciája (maradó hiba mentes PI szabályozó)
Szimuláljunk hibát, amikor a motor megakad, vagy az elektromos egység meghibásodik és a nyomaték 0, miközben a PI szabályozó működik. Az integrál tag növekszik. A hiba után az a integráló tag értékét le kell csökkenteni (a pozitív hiba közben integráló tag értéke nagyon megnövekedhet, amelyet egy negatív hibával lehet csökkenteni).
Először hangoljuk be a PI szabályozót (állítsuk be a mérés hosszát 1000 ms-ra), és adjuk a következő sort a szabályozóhoz:
if ( CurrentTime < 0.3*1e3) {ResultData.Torque = 0.0;}
Az integrálótag értékének növekedését alapvetően két módon korlátozhatjuk. Egyrészt közvetlen korláttal, másrészt az integrátort célszerű kikapcsolni akkor, amikor a szabályozó telítésben működik. Hasonlítsa össze normál PI és az anti windup funkcióval kiegészített PI szabályozó működését.
5 . 24 mérési feladat : Ziegler-Nichols módszer időkésleltetés beiktatással
Készítsen egy P szabályozót, de a kiszámított nyomaték jelet őrizze meg 10 időlépésen keresztül, és csak azt követően adja ki a motorra. Használjon normál harmadfokú szűrőt  paraméterrel. Fokozatosan növelje a P értékét a stabilitás határáig, amikor a fordulatszám jelben közel állandó amplitúdójú lengések ki nem alakulnak. A Ziegler-Nichols módszerrel határozza meg egy PI típusú szabályozó P és I paraméterét.
paraméterrel. Fokozatosan növelje a P értékét a stabilitás határáig, amikor a fordulatszám jelben közel állandó amplitúdójú lengések ki nem alakulnak. A Ziegler-Nichols módszerrel határozza meg egy PI típusú szabályozó P és I paraméterét.
5.10.5. Mérési feladatok: pozíció szabályozás
5 . 25 mérési feladat : E gy-hurkos P és PI szabályozó ugrás függvény válasza
Legyen a referencia pozíció jel 10 rad. A nyomatékot közvetlenül a pozíció hibából számolja, P illetve PI szabályozót alkalmazva.
5 . 26 mérési feladat : Stick-slip jelenség vizsgálata
Válassza meg a P és I paramétert úgy, hogy a motor ragadjon be a referencia pozíció előtt, és az integrátor lendítse túl a hibán.
5 . 27 mérési feladat : K aszkád sz abályozás
Az előző feladatban túllövés tapasztalható, aminek oka az, hogy idő szükséges a motor lelassításához, ha az elérte a referenciaértéket. Ezt a hatást megszüntethetjük, ha egy belső szögsebesség szabályozót is beiktatunk a rendszerbe. A szögsebesség referencia értéke a motor pozíció hibájából adódik. Ez azt jelenti, amint a motor közelít a referenciapozícióhoz, a referencia sebesség is elkezd csökkeni. Ez a nullához közelít már a véghelyzet közelében. A szabályozás hatásvázlata az alábbi ábrán látható. A pozíció szabályozó P és a sebességszabályozó PI típusú.
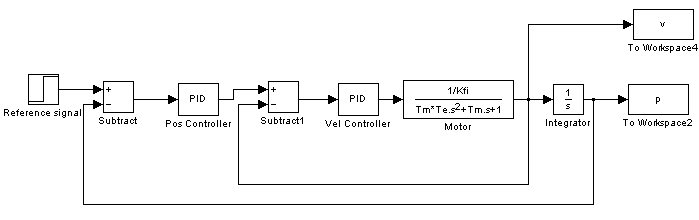
A fordulatszám szabályozó körében PI a pozíció szabályozó körben P szabályozót alkalmazzon.
5 . 28 mérési feladat : C súszómód szabályozó
Tervezzen csúszómód szabályozót a motor pozíciójához.
Ennek két fő lépése:
a csúszási felület megválasztása;
vezérlési törvény megválasztása.
A konstans referencia pozíció:
αref= 10 rad.
A pozíció és sebesség hibát
αe= αref – αmotor
Ωe= 0-Ωmotor .
értékekként deklaráljuk.
A csúszó felületet
σ=αe+λΩe
alapján választjuk.
A vezérlési törvény:
torque=0.1 sign σ.
Természetesen ezeket C kódban kell megírni. További részletes információért és új szabályozási módszerekért látogasson el az alábbi animációs oldalra:
http://dind.mogi.bme.hu/animation/
5 . 29 mérési feladat : Modellreferenc i ás adaptív szabályozó
Tervezzen modellreferenciás adaptív szabályozót a motor pozíciójához.






































































