6. fejezet - Mintamérések, néhány mérési feladat megoldása
Vissza		Előre

6. fejezet - Mintamérések, néhány mérési feladat megoldása

Tartalom

6.1. A mérés célja

A felhasználó ennek a mérésnek a segítségével elsajátíthatja egy szervomotor és robot vezérlését számítógépen keresztül. Először a felhasználó megismerkedik a szervo és a számítógép közti kommunikációval, ami lényeges eleme a mobilrobotnak. Következőleg a robot belső rendszere kerül bemutatásra. (Egy külön használati útmutató áll a robot kísérletekhez rendelkezésre).

Egy DAC segítségével küldünk információt a gépről a szervonak, mivel a legtöbb szervo esetében a referenciajelek analóg feszültség jelek. A motor mozgását egy enkóder méri, amely impulzussort küld a számítógépnek. Ezeket egy számláló számolja és a számítógép olvassa ki, így szerezve információt a motor pozíciójáról. A sebességet az előző és pillanatnyi pozíciókból számítjuk. Ez egy nagyon zajos sebességjelet eredményez. A mérésben egy diszkrét idejű szűrőt használunk, hogy csökkentsük a mérés zaját. A felhasználó megtanulhatja, hogyan kell megírni és behangolni a PI szabályozóját egy szervo egységnek.

A felhasználónak nem kell kitűnő programozónak lennie, de az alapokkal tisztában kell lennie. A felhasználó néhány nagyon egyszerű programot ír C-ben, illetve Visual Basic-ben. Példák bemutatásával segítjük a sajár program megírását, és remélhetőleg a mérést bárki úgy is el tudja majd végezni, ha ez lesz majd az első olyan C vagy Visual Basic programja, pontosabban program részlete, melyet sajár maga írt.

A kísérletek a következő helyen érhetőek el: http://dind.mogi.bme.hu/experiment/

6.2. A PCI-1720 D/A kártya használata- 5.4 mérési feladat megoldása

A megoldandó kód, és amit a kódmezőbe kell írni:

motorDA = 3;
new_voltage = 5.0;
//Első lépés: Eszköz megnyitása
dwErrCde = DRV_DeviceOpen(lDevNumDA, &lDriverHandleDA);   
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    exit(1);
}
// Második lépés: Kimeneti érték a meghatározott csatornára
tAOVoltageOut.chan = motorDA;
tAOVoltageOut.OutputValue = new_voltage;
dwErrCde = DRV_AOVoltageOut(lDriverHandleDA, &tAOVoltageOut);
if (dwErrCde != SUCCESS)
{
    ErrorStop(&lDriverHandleDA, dwErrCde);
    return;
}

Ez a kód bekapcsolja a szervot. Ilyenkor egy zöld LED világít az egységen.

A LED lekapcsolásához a következő sort kell módosítani: new_voltage = 0.0;

6.2.1. A mintafájlból (Dasoft.cpp) a következőt kell átmásolni a szövegmezőbe:

//Harmadik lépés: eszköz megnyitása
dwErrCde = DRV_DeviceOpen(lDevNum, &lDriverHandle);   
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    printf("Program terminated!\n");
    printf("Press any key to exit....");
    getch();
    exit(1);
}
// Negyedik lépés: Kimeneti jelet meghatározott csatornára
tAOVoltageOut.chan = usChan;
tAOVoltageOut.OutputValue = fOutValue;
dwErrCde = DRV_AOVoltageOut(lDriverHandle, &tAOVoltageOut);
if (dwErrCde != SUCCESS)
{
    ErrorStop(&lDriverHandle, dwErrCde);
    printf("Press any key to exit....");
    getch();
    return;
}

6.2.2. A pirossal jelölt részeket töröljük ki.

//Harmadik lépés: Eszköz megynitása
dwErrCde = DRV_DeviceOpen(lDevNum, &lDriverHandle);   
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
printf("Program terminated!\n");
    printf("Press any key to exit....");
    getch();
    exit(1);
}
// Negyedik lépés: Kimeneti értéket a meghatározott csatornára
tAOVoltageOut.chan = usChan;
tAOVoltageOut.OutputValue = fOutValue;
dwErrCde = DRV_AOVoltageOut(lDriverHandle, &tAOVoltageOut);
if (dwErrCde != SUCCESS)
{
    ErrorStop(&lDriverHandle, dwErrCde);
printf("Press any key to exit....");
    getch();
    return;
}

6.2.3. Változtassuk meg, ahogy az zölddel van jelölve.

motorDA = 3;
new_voltage = 5.0;
//Első lépés: Eszköz megnyitása
dwErrCde = DRV_DeviceOpen(lDevNumDA, &lDriverHandleDA);   
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    exit(1);
}
// Második lépés: Kimeneti érték a meghatározott csatornára
tAOVoltageOut.chan = motorDA;
tAOVoltageOut.OutputValue = new_voltage;
dwErrCde = DRV_AOVoltageOut(lDriverHandleDA, &tAOVoltageOut);
if (dwErrCde != SUCCESS)
{
    ErrorStop(&lDriverHandleDA, dwErrCde);
    return;
}
Alternatív megoldás adható az előre definiált változók nélkül (motorDAésnew_votlage). Ebben az esetben a kód a következő:
//Első lépés: Eszköz megnyitása
dwErrCde = DRV_DeviceOpen(lDevNumDA, &lDriverHandleDA);   
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    exit(1);
}
// Második lépés: Kimeneti érték a meghatározott csatornára
tAOVoltageOut.chan = 3;
tAOVoltageOut.OutputValue = 5.0f;
dwErrCde = DRV_AOVoltageOut(lDriverHandleDA, &tAOVoltageOut);
if (dwErrCde != SUCCESS)
{
    ErrorStop(&lDriverHandleDA, dwErrCde);
    return;
}

6.3. Valós idejű óra használata a PCI 1720 D/A kártyán - 5.5 feladat megoldása

A váltózó mezőbe írandó kód:

float sin_amp = 3.0;

float sin_ang_freq = 0.25;

A kódmezőbe írandó kód:

new_voltage = sin_amp * sin(sin_ang_freq * (time_array[tickCount] / 10000000.0));

A 10000-rel való osztás szükséges, hogy milliszekundumot és 1000-rel, hogy szekundumot kapjunk.

A sin()függvény benne van a C++-ban, ami a Math.h header fájlban található. Ez kiszámolja a megadott érték szinuszát.

Ha más változót használunk a new_voltage helyett, a program nem fog működni.

Az eredmény:

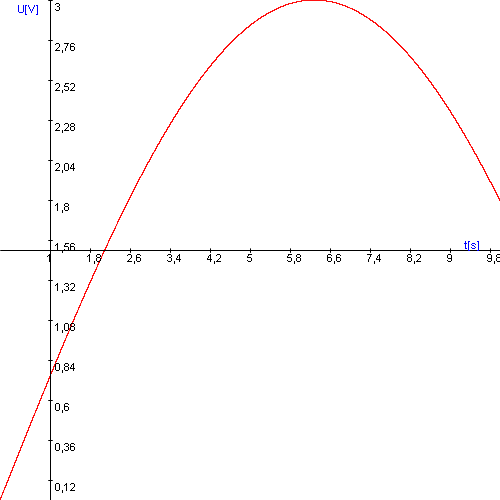
6.1. ábra - Szinuszos kimeneti feszültség

Közvetlenül lehet írni a változókba, változók létrehozása nélkül. Ebben az esetben a kód a következő:

new_voltage = 3.0 * sin(0.25 * (time_array[tickCount] / 10000000.0));

6.4. A PCI-1784 számláló használata - 5.4 mérési feladat megoldása

A kód ami az első szöveg mezőbe másolandó (inicializáció):

//Első lépés: Eszköz megnyitása
dwErrCde = DRV_DeviceOpen(lDevNumCounter, &lDriverHandleCounter);   
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    exit(1);
}
// Második lépés: Számláló visszaállítása DRV_CounterReset
dwErrCde = DRV_CounterReset(lDriverHandleCounter, wChannelCounter);
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    exit(1);
}
// Harmadik lépés: Számlálás elindítása DRV_CounterEventStart
tCounterEventStart.counter = wChannelCounter;
dwErrCde = DRV_CounterEventStart(lDriverHandleCounter, &tCounterEventStart);
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    exit(1);
}
// Negyedik lépés: Számláló érték kiolvasása DRV_CounterEventRead
tCounterEventRead.counter = wChannelCounter;
tCounterEventRead.overflow = &wOverflow;
tCounterEventRead.count = &dwReading;
dwErrCde = DRV_CounterEventRead(lDriverHandleCounter, &tCounterEventRead);
if (dwErrCde != SUCCESS)
{
     ErrorStop(&lDriverHandleCounter, dwErrCde);
     return;
}

A kód, ami a második szövegmezőbe kerül(cikluson belül):

dwErrCde = DRV_CounterEventRead(lDriverHandleCounter, &tCounterEventRead);
if (dwErrCde != SUCCESS)
{
     ErrorStop(&lDriverHandleCounter, dwErrCde);
     return;
}

Az eredmény a szinuszos nyomaték hatására kialakuló pozíció és sebesség grafikon.

6.4.1. A(Dasoft.cpp) mintafájlból a következők másolandók a szövegmezőbe:

//Harmadik lépés: Eszköz megnyitása
dwErrCde = DRV_DeviceOpen(lDevNum, &lDriverHandle);   
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    printf("Program terminated!\n");
    printf("Press any key to exit....");
    getch();
    exit(1);
}
// Negyedik lépés: Számláló visszaállítása DRV_CounterReset
dwErrCde = DRV_CounterReset(lDriverHandle, wChannel);
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    printf("Program terminated!\n");
    printf("Press any key to exit....");
    getch();
    exit(1);
}
// Ötödik lépés: Számláló elindítása DRV_CounterEventStart
tCounterEventStart.counter = wChannel;
dwErrCde = DRV_CounterEventStart(lDriverHandle, &tCounterEventStart);
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    printf("Program terminated!\n");
    printf("Press any key to exit....");
    getch();
    exit(1);
}
// Hatodik lépés: Számláló kiolvasása DRV_CounterEventRead while ciklusban
//         and display counter value, exit when pressing any key
tCounterEventRead.counter = wChannel;
tCounterEventRead.overflow = &wOverflow;
tCounterEventRead.count = &dwReading;
while( !kbhit() )
{
   dwErrCde = DRV_CounterEventRead(lDriverHandle, &tCounterEventRead);
   if (dwErrCde != SUCCESS)
   {
      ErrorStop(&lDriverHandle, dwErrCde);
      return;
   }
   printf("\nCounter value = %lu", dwReading);
   Sleep(1000);
}

6.4.2. Töröljük a pirossal jelölt részeket.

//Harmadik lépés: Eszköz megnyitása
dwErrCde = DRV_DeviceOpen(lDevNum, &lDriverHandle);   
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
printf("Program terminated!\n");
    printf("Press any key to exit....");
    getch();
    exit(1);
}
// Negyedik lépés: Számláló visszaállítása DRV_CounterReset
dwErrCde = DRV_CounterReset(lDriverHandle, wChannel);
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
printf("Program terminated!\n");
    printf("Press any key to exit....");
    getch();
    exit(1);
}
// Ötödik lépés: Számláló elindításaDRV_CounterEventStart
tCounterEventStart.counter = wChannel;
dwErrCde = DRV_CounterEventStart(lDriverHandle, &tCounterEventStart);
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
printf("Program terminated!\n");
    printf("Press any key to exit....");
    getch();
    exit(1);
}
// Hatodik lépés: Számláló kiolvasása DRV_CounterEventReadwhile ciklusban
//         and display counter value, exit when pressing any key
tCounterEventRead.counter = wChannel;
tCounterEventRead.overflow = &wOverflow;
tCounterEventRead.count = &dwReading;
while( !kbhit() )
{
   dwErrCde = DRV_CounterEventRead(lDriverHandle, &tCounterEventRead);
   if (dwErrCde != SUCCESS)
   {
      ErrorStop(&lDriverHandle, dwErrCde);
      return;
   }
   printf("\nCounter value = %lu", dwReading);
Sleep(1000);
}

6.4.3. Cseréljük a kódot a zöld szerint.

//Első lépés: Eszköz megnyitása
dwErrCde = DRV_DeviceOpen(lDevNumCounter, &lDriverHandleCounter);   
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    exit(1);
}
// Második lépés: Számláló visszaállítása DRV_CounterReset
dwErrCde = DRV_CounterReset(lDriverHandleCounter, wChannelCounter);
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    exit(1);
}
// Harmadik lépés: Számláló indítása DRV_CounterEventStart
tCounterEventStart.counter = wChannelCounter;
dwErrCde = DRV_CounterEventStart(lDriverHandleCounter, &tCounterEventStart);
if (dwErrCde != SUCCESS)
{
    ErrorHandler(dwErrCde);
    exit(1);
}
// Step 4: Számláló kiolvasása DRV_CounterEventRead
tCounterEventRead.counter = wChannelCounter;
tCounterEventRead.overflow = &wOverflow;
tCounterEventRead.count = &dwReading;
dwErrCde = DRV_CounterEventRead(lDriverHandleCounter, &tCounterEventRead);
if (dwErrCde != SUCCESS)
{
     ErrorStop(&lDriverHandleCounter, dwErrCde);
     return;
}

Hurkon belül:

dwErrCde = DRV_CounterEventRead(lDriverHandleCounter, &tCounterEventRead);
if (dwErrCde != SUCCESS)
{
     ErrorStop(&lDriverHandleCounter, dwErrCde);
     return;
}

6.5. Nyílt szabályozó kör mérése - Motion control/Exercise 4 menüpont alatt található laboratóriumi mérési gyakorlat megoldása

A nyílt hurkú tesztre több lehetőségünk van. A kimeneti feszültség kiszámítható a motor paramétereiből. Mivel itt nincs visszacsatolás, nincs pontos ismeretünk a motor pontos tengelysebességéről és a zavaró hatások teljes mértékben hatnak.

6.5.1. A motor válasza állandó nyomatékra - 5.11 feladat megoldása

A motort egy eltérő kimeneti nyomatékkal teszteltük. Először 0.1-t alkalmaztunk és másodszor 1-t. A kontrollernek deklarációk nélkül az alábbi értékei adottak:

A mérés hossza milliszekundumban : 1000

Az állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adott) - sebesség
torque (adott) - nyomaték

Deklaráció:

Szabályozó kód:

ResultData.Torque = 1;

vagy

ResultData.Torque = 0.1;

Az eredmények az alábbi ábrákon láthatók. Látható, hogy a tengelypozíció és sebesség diagramja állandó gyorsulással éri el a maximális sebességet. A nyílt hurkú rendszer nagyon lassú, mivel állandó feszültséget használ.

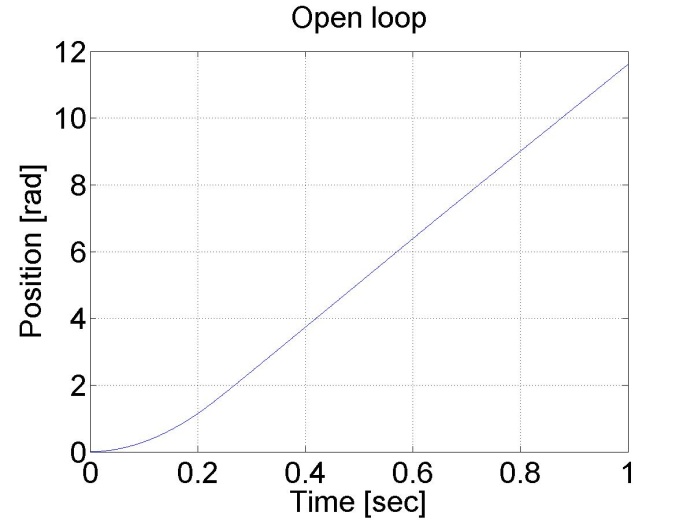
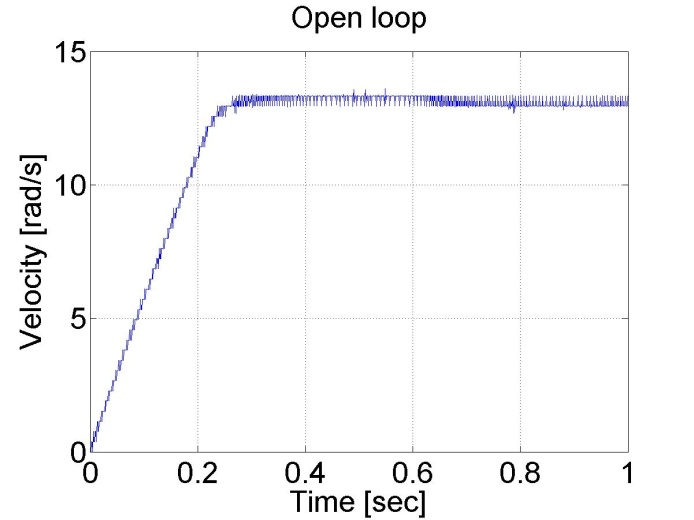
6.2. ábra - Nyílt hurkú vezérlés, nyomaték=1

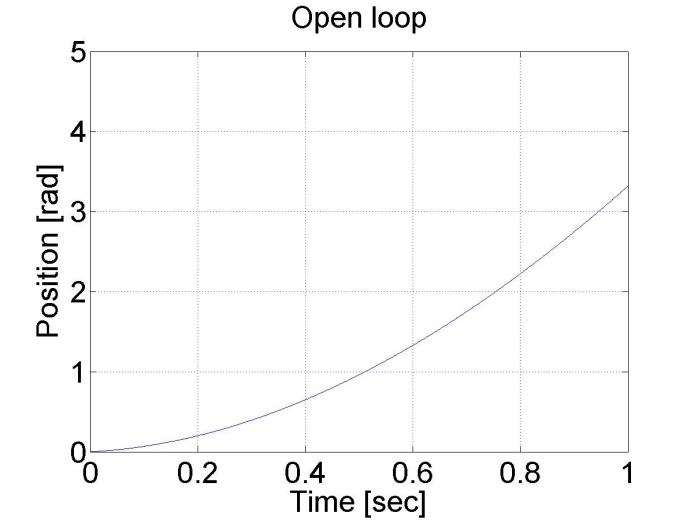
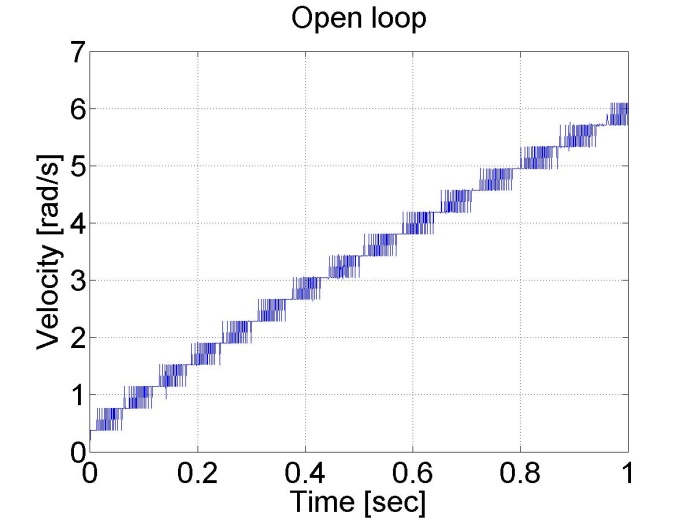
6.3. ábra - Nyílt hurkú vezérlés, nyomaték=0.1

6.5.2. Konstans nyomaték és digitális szűrő - 5.12 feladat megoldása

A motort különböző kimeneti nyomatékokkal teszteltük ebben az esetben. 0.1 az első és 1 a második esetben.

A mérés hossza milliszekundumban : 1000

Az állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adott) - sebesség
torque (adott) - nyomaték

Deklarációk:

/* velocity filter variables */
static float  z_1=0.0, z_2=0.0, z_3=0.0;
static float ztmp_1=0.0, ztmp_2=0.0;
/* velocity filter parameters */
/* Tsample=1e-3 and Tc=0.007 */   
float ad11= 0.9996, ad12= 9.9072e-004, ad13= 4.3344e-007;
float ad21= -1.2637, ad22= 0.9730, ad23= 8.0496e-004;
float ad31= -2.3468e+003, ad32= -50.5468, ad33= 0.6280;
float bd1= 4.3671e-004, bd2= 1.2637, bd3= 2.3468e+003;

Szabályozó kód:

/* Velocity filter  */
    ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;
    ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;
    z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;
           z_1  = ztmp_1;
           z_2  = ztmp_2;
ResultData.Velocity =z_1;
ResultData.Torque = 1;

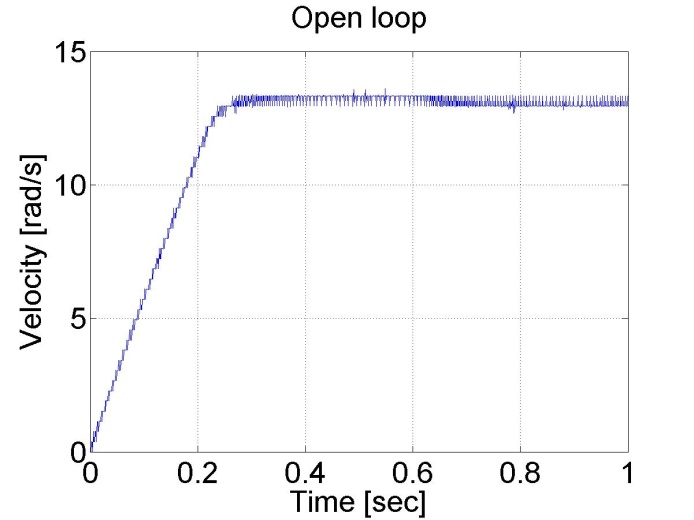
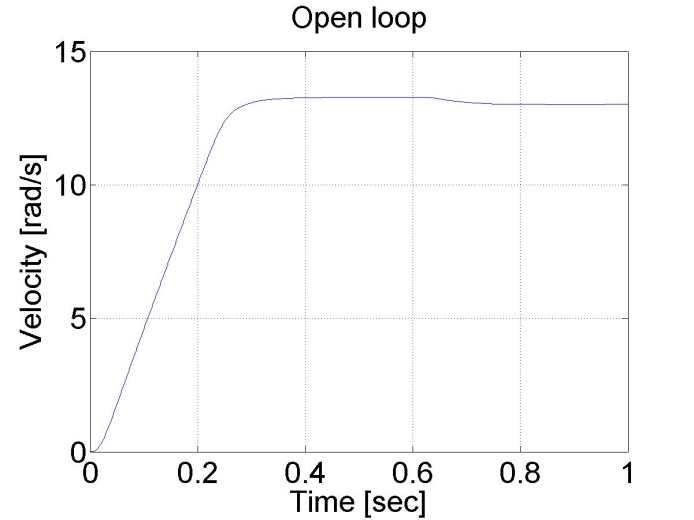
6.4. ábra - A szűrt és szűretlen sebességek összehasonlítása

6.5. ábra - Különböző szűrők összehasonlítása

6.5.3. A motor válasza a szinuszos feszültségre és a szervoerősítő offsetjének kompenzálása - 5.13 feladat megoldása

A szervoerősítő offset feszültséggel rendelkezik. Ez akkor a legszembetűnőbb, ha szinuszos feszültséget alkalmazunk. Ebben az esetben azt várnánk, hogy a motor tengelyének sebessége és pozíciója is egyaránt szinuszosan változik.

A mérés hossza milliszekundumban : 4000

Az állapot változók nevei:

time (adott) - idő
position (adott)- pozíció
velocity (adott) - sebesség
torque (adott) - nyomaték
sin_torque (választott) – sin_nyomaték

Deklaráció:

doubleparam = 0;
doublesinperiod = 1;
doublesinamplitude = 2;
doubleoffset = 0;  
// változtassuk az offset tartományát -0.3 és -0.2 közt

Szabályozó kód:

// Pillanatnyi idő millisekundumban
param = CurrentTime;
// Pillanatnyi idő másodpercben
param /= 1000;
// Eredmény
param = param * 2 * PI / sinperiod;
//
// Szabályozó kezdete
//
// Sinuszos feszültség
ResultData.Torque = sinamplitude * sin(param) + offset;
ResultData.StateVariable_5 = sinamplitude * sin(param);
//
// Szabályozó vége

Az eredmények lentebb az ábrán láthatók. A pozíció diagram nem teljesen szinuszos, hanem van egy lineáris komponense is. Ez a szervoerősítő offsetjének hatása. Ezt ki lehet vonni az alkalmazott feszültségből és ezáltal a lineáris komponens megszüntethető, csak a deklarációt kell megváltoztatni a vezérlőben:

doubleoffset = -0.27; 
A Matlab program az eredmények megjelenítéséhez
% módosítani a fájlneveknek megfelelően
sv_1_14axc255hnyzli55axowlm55
sv_2_14axc255hnyzli55axowlm55
sv_3_14axc255hnyzli55axowlm55
sv_4_14axc255hnyzli55axowlm55
sv_5_14axc255hnyzli55axowlm55
time=time/1000;
plot(time,position)
set(gca, 'fontsize', [25]);
xlabel('Time [sec]');
ylabel('Position [rad]');
title('Open loop');
% itt állítható a tengely
axis([0 4 0 12]);
grid
pause;
print -djpegopen_poz
plot(time,velocity)
set(gca, 'fontsize', [25]);
xlabel('Time [sec]');
ylabel('Velocity [rad/s]');
title('Open loop');
% itt állítható a tengely
axis([0 4 -15 15]);
grid
print -djpegopen_vel
pause;
plot(time,torque)
set(gca, 'fontsize', [25]);
xlabel('Time [sec]');
ylabel('Torque [mNm]');
title('Open loop');
% itt állítható a tengely
axis([0 4 -2.5 2.5]);
grid
print -djpegopen_torque
pause;
plot(time,sin_torque)
set(gca, 'fontsize', [25]);
xlabel('Time [sec]');
ylabel('Torque without offset');
title('Open loop');
% itt állítható a tengely
axis([0 4 -2.5 2.5]);
grid
print -djpegopen_sin

(a)

(b)

6.5.4. Digitális szűrők összehasonlítása - 5.14 mérési feladat megoldása

A mérés hossza milliszekundumban: 1000

Az állapotváltozók nevei:

time (adott)
position (adott)
velocity (adott)
torque (adott)

ref
filt
filtb

Deklarációk:

doubleparam = 0;
doublesinperiod = 0.1;
doublesinamplitude = 0.6;
doubleoffset = -0.217; 
/* sebesseg szuro valtozoi */
static float  z_1=0.0, z_2=0.0, z_3=0.0;
static float ztmp_1=0.0, ztmp_2=0.0;
/* Tsample=1e-3  Tc=0.0032*/
float ad11 = 0.99591;
float ad12 = 0.00095987;
float ad13 = 3.652e-007;
float ad21 = -11.3235;
float ad22 = 0.88778;
float ad23 = 0.00061567;
float ad31 = -19089.6748;
float ad32 = -193.6165;
float ad33 = 0.30752;
float bd1  = 0.0040906;
float bd2  = 11.3235;
float bd3  = 19089.6748; 
/* Bessel sebesseg szuro valtozoi */
static float  z_1b=0.0, z_2b=0.0, z_3b=0.0;
static float ztmp_1b=0.0, ztmp_2b=0.0;
/* Bessel Tsample=1e-3  Tc=0.0032*/
float ad11b = 0.95193;
float ad12b = 0.00083371;
float ad13b = 2.6009e-007;
float ad21b = -120.9668;
float ad22b = 0.56688;
float ad23b = 0.00034345;
float ad31b = -159737.83;
float ad32b = -629.4281;
float ad33b = -0.080513;
float bd1b  = 0.048071;
float bd2b  = 120.9668;
float bd3b  = 159737.83;

Szabályozó kód:

// Current time
param = CurrentTime;
// Only miliseconds
param /= 1000;
// Result
param = param * 2 * PI / sinperiod;
//
// Controller part begin
//
// Sinusoidal voltage
ResultData.Torque = sinamplitude * sin(param) + offset;
ResultData.StateVariable_5 = sinamplitude * sin(param);
/* Velocity filter  */
ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;
ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;
z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;
z_1  = ztmp_1;
z_2  = ztmp_2;
ResultData.StateVariable_6=z_1; 
/* Bessel velocity filter  */
ztmp_1b=ad11b* z_1b+ad12b* z_2b+ad13b* z_3b + bd1b* ResultData.Velocity;
ztmp_2b=ad21b* z_1b+ad22b* z_2b+ad23b* z_3b + bd2b* ResultData.Velocity;
z_3b=ad31b* z_1b+ad32b* z_2b+ad33b* z_3b + bd3b* ResultData.Velocity;
z_1b  = ztmp_1b;
z_2b  = ztmp_2b;
ResultData.StateVariable_7=z_1b;

A mérést két különböző periódusidővel végeztük el

doublesinperiod = 0.1;

és

doublesinperiod = 0.5;

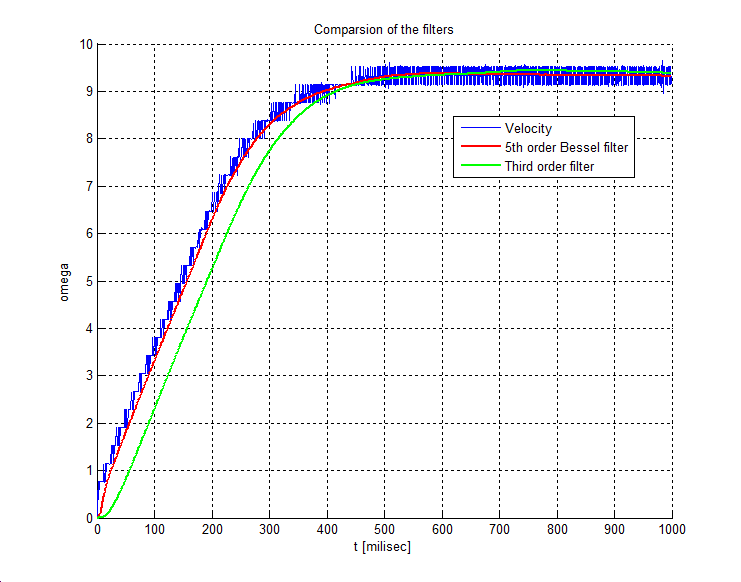
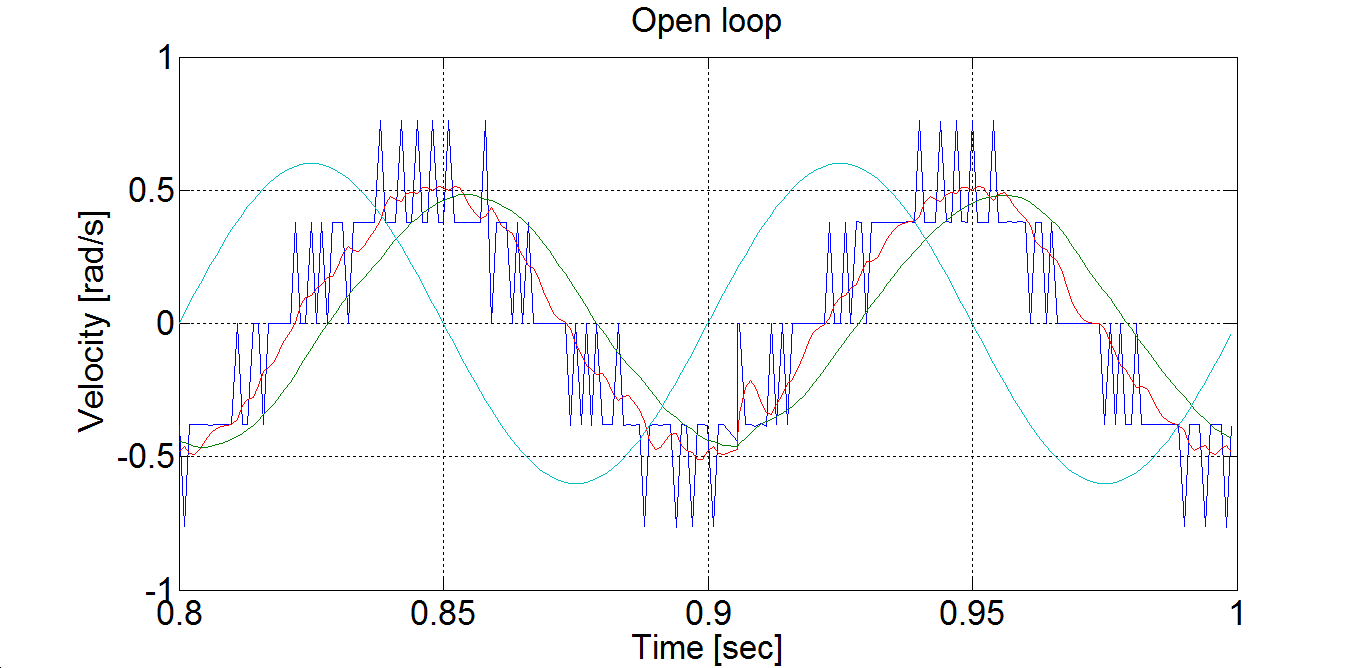
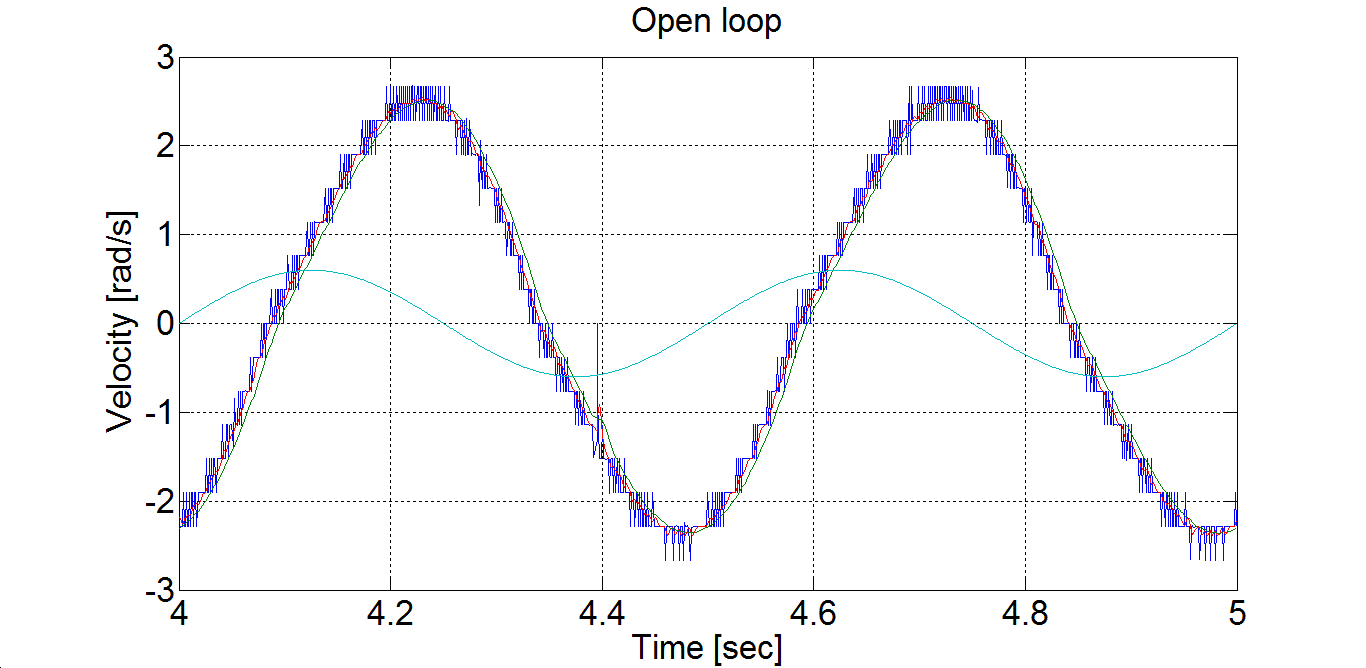
Az utóbbi esetben a mérés időtartamát 5000 ms hosszúságúra állítottuk, így mindkét esetben 10 periódust vizsgáltunk. A tranziensek lezajlása után az állandósultnak tekinthető utolsó két periódust rajzoltuk ki (ld. 6-8. és 6-9. ábra). Jól látható, hogy a gerjesztés frekvenciáját növelve a válasz amplitúdója csökken és a fáziskésése növekszik.

A 6-8. és 6-9. ábra elkésszítéséhez használt MatLab program:

sv_1_zlwzmf45pqyn1c45p31cvve4
sv_2_zlwzmf45pqyn1c45p31cvve4
sv_3_zlwzmf45pqyn1c45p31cvve4
sv_4_zlwzmf45pqyn1c45p31cvve4
sv_5_zlwzmf45pqyn1c45p31cvve4
sv_6_zlwzmf45pqyn1c45p31cvve4
sv_7_zlwzmf45pqyn1c45p31cvve4
 
plot(time,velocity,time,filt,time,filtb,time,ref)
set(gca, 'fontsize', [25]);
xlabel('Time [sec]');
ylabel('Velocity [rad/s]');
title('Open loop');
% you can adjust your axis
% axis([0.8 1 -1 1]);
axis([4 5 -3 3]);
grid
print -djpeg open_vel

Digitális szűrők összehasonlítása (periódusidő 0.1 s) Színkódolás nyomaték jel: világos kék, szűrés nélküli fordulatszám jel: kék, fordulatszám jel normál szűrővel: zöld, fordulatszám jel Bessel szűrővel: piros

6.6. ábra - Digitális szűrők összehasonlítása (periódusidő 0.1 s) Színkódolás nyomaték jel: világos kék, szűrés nélküli fordulatszám jel: kék, fordulatszám jel normál szűrővel: zöld, fordulatszám jel Bessel szűrővel: piros

Digitális szűrők összehasonlítása (periódusidő 0.4 s) Színkódolás nyomaték jel:világoskék, szűrés nélküli fordulatszám jel: kék, fordulatszám jel normál szűrővel: zöld, fordulatszám jel Bessel szűrővel: piros

6.7. ábra - Digitális szűrők összehasonlítása (periódusidő 0.4 s) Színkódolás nyomaték jel:világoskék, szűrés nélküli fordulatszám jel: kék, fordulatszám jel normál szűrővel: zöld, fordulatszám jel Bessel szűrővel: piros

6.6. Visszacsatolt kör mérések - Motion control/Exercise 5 menüpont alatt található laboratóriumi mérési gyakorlat megoldásai

6.6.1. A P szabályozó hangolása - 5.16 mérési feladat megoldása

Az első feladat a PID szabályozásnál a tagok hangolása. Ehhez a Ziegler-Nichols módszert használjuk, ami tapasztalati úton, könnyen alkalmazható a rendszerre még egy kezdő számára is. A PI szabályozó digitális megvalósításakor nem a TI paraméterre van szükség, hanem az I paraméterre. Ezért a Ziegler-Nichols hangolási táblázatot át kell írnunk.

	AP	I	TD
P szabályozó	AU/2
PI szabályozó	AU/2.2	1.2AP/Tu
PID szabályozó	AU/1.7	2AP/Tu	AP Tu/8

A hangolás első lépésében szükségünk van egy P szabályozóra (I=0, D=0), a körerősítést növelve AU értét kell meghatározni. A kontroller alakja a következő:

A mérés hossza milliszekundumban: 1000

Az állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adott) - sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba

Deklarálás:

doubleP = 4.75;

doubleref_vel = 7;

doubleerror_vel= 0;

/* sebesség szűrő változók */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* sebesség szűrő paraméterei */

/* Tsample=1e-3 and Tc=0.005 */

float ad11= 0.9989, ad12= 9.8248e-004, ad13= 4.0937e-007;

float ad21= -3.2749, ad22= 0.9497, ad23= 7.3686e-004;

float ad31= -5.8949e+003, ad32= -91.6978, ad33= 0.5076;

float bd1= 0.0011, bd2= 3.2749, bd3= 5.8949e+003;

Szabályozó kód:

/* sebesség szűrő */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//hibaszámítás a sebesség szabályozáshoz

error_vel=ref_vel- ResultData.Velocity;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.Torque = P*error_vel;

if (ResultData.Torque > 5)

{

ResultData.Torque = 5;

}

if (ResultData.Torque < -5)

{

ResultData.Torque = -5;

}

A szabályozó beállítja a kimenő feszültség minimális és maximális értékeit -5 és 5 V közötti tartományban. Az eredmények az ábrákon láthatók:

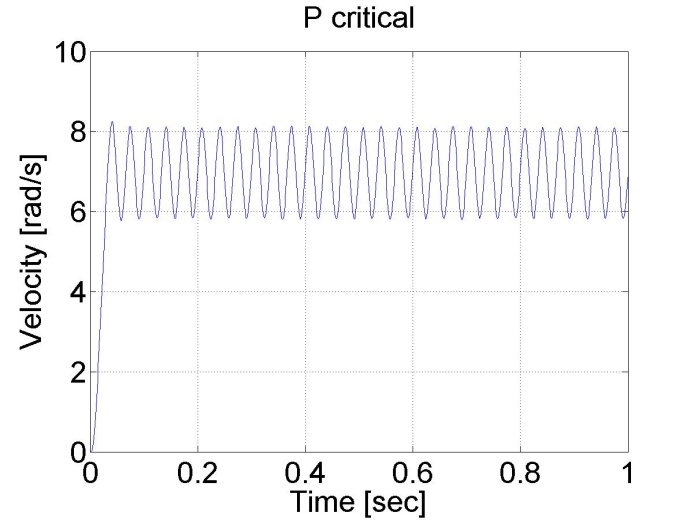
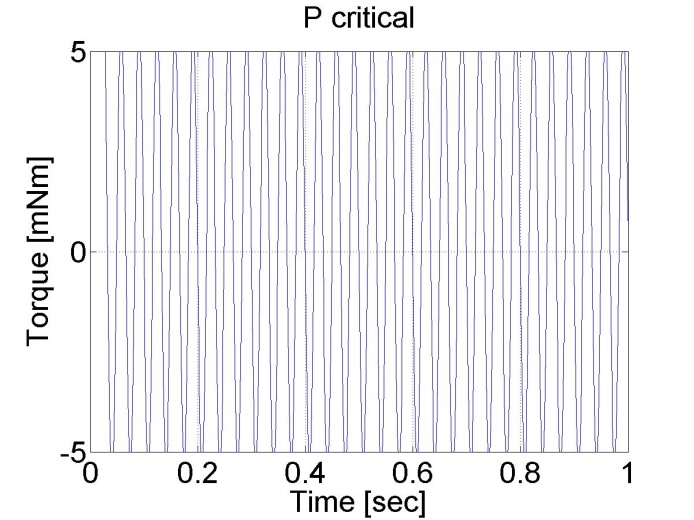
6.8. ábra - P szabályozó eredményei paraméter hangolásra

Következtetés: AU = 4.75 és TU≈0.2/6. A táblázat szerint PPI=2.1 és IPI=75.

Megjegyzés: AU és TU értékei függenek a szűrő paramétereitől.

6.6.2. A P szabályozó ugrásfüggvény válasza - 5.17 mérési feladat megoldása

Ehhez a teszthez a referencia tengely szögsebességet 1 rad/s-ra állítjuk. A szabályozó az alábbi formájú:

A mérés hossza milliszekundumban : 1000

Az állapotváltozók nevei :

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklaráció:

doubleP_par = 2.3;

doubleI_par = 0.0;

doubleref_vel = 7;

doubleerror_vel;

static doubleerror_vel_int=0.0;

double load = 0;

/* sebesség szűrő változói */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 és Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

Szabályozó kód:

/* sebesség szűrő */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Sebesség szabályozó hibaszámítása

error_vel=ref_vel- ResultData.Velocity;

error_vel_int = error_vel_int + error_vel*(CurrentTime - OldTime)/1000;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.StateVariable_7 = error_vel_int;

ResultData.Torque = P_par*error_vel + I_par*error_vel_int - load;

if (ResultData.Torque > 5) { ResultData.Torque = 5; }

if (ResultData.Torque < -5) { ResultData.Torque = -5; }

Az eredményeket az alábbi ábrák mutatják. Látható a P szabályozó állandósult hibája.

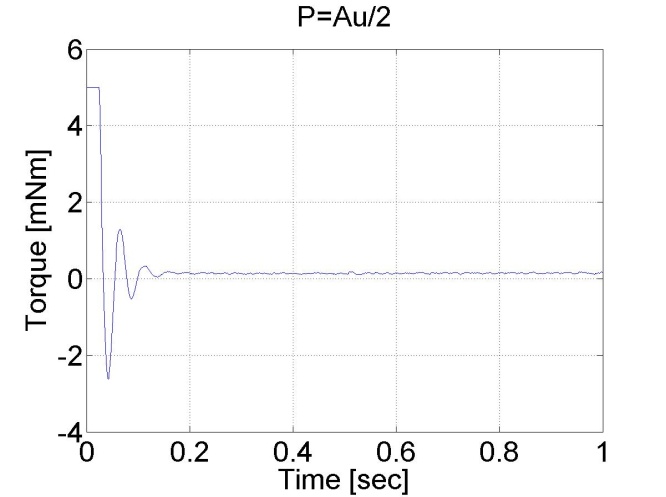
6.9. ábra - P szabályozó Ziegler-Nichols hangolása (P = 2.3)

6.6.3. A P szabályozó változó referenciajellel - 5.18 feladat megoldása

Ebben a tesztben a referencia szögsebességet két időpontban változtatjuk: t = 0.2 s és t = 0.4 s. A P szabályozó állandósult hibája itt is látható. A szabályozó a következő alakú:

A mérés ideje milliszekundumban : 1000

Állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklarációk:

doubleP_par = 2.3;

doubleI_par = 0.0;

doubleref_vel = 7;

doubleerror_vel;

static doubleerror_vel_int=0.0;

double load = 0;

/* sebesség szűrő változói */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 és Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

Szabályozó kód:

//Ugrások a referencia sebességben

if (CurrentTime > 0*1e3 && CurrentTime < 0.2*1e3)

{

ref_vel = 4;

}

if (CurrentTime >= 0.2*1e3 && CurrentTime < 0.4*1e3)

{

ref_vel = 8;

}

if (CurrentTime >= 0.4*1e3 && CurrentTime < 0.6*1e3)

{

ref_vel = 2;

}

/* Velocity filter */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//sebesség szabályozás hibaszámítása

error_vel=ref_vel- ResultData.Velocity;

error_vel_int = error_vel_int + error_vel*(CurrentTime - OldTime)/1000;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.StateVariable_7 = error_vel_int;

ResultData.Torque = P_par*error_vel + I_par*error_vel_int - load;

if (ResultData.Torque > 5) { ResultData.Torque = 5; }

if (ResultData.Torque < -5) { ResultData.Torque = -5; }

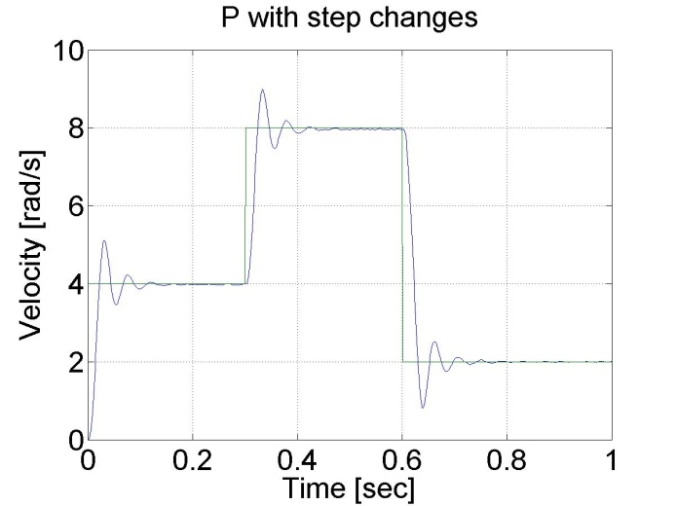
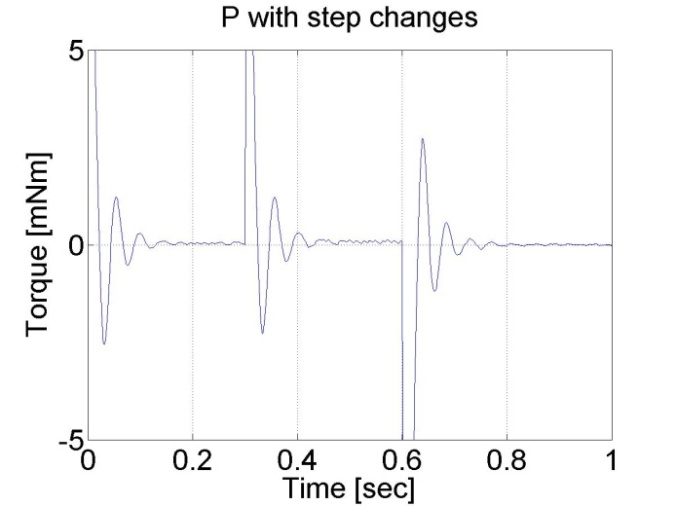
6.10. ábra - P szabályozó válaszai a referencia sebesség 3 ugrásszerű változására

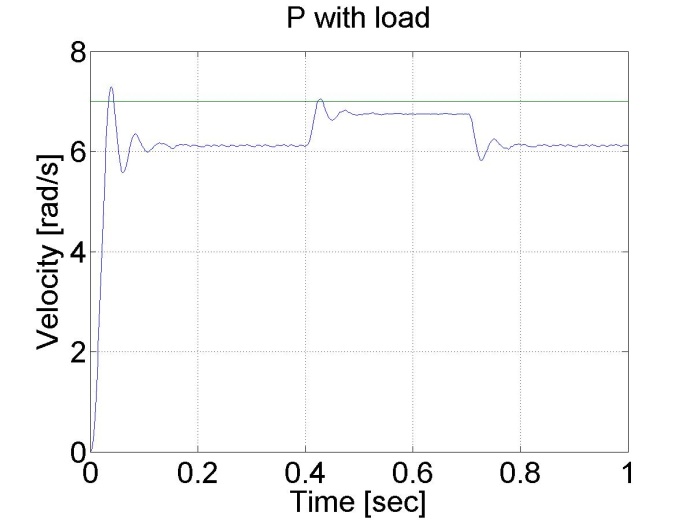
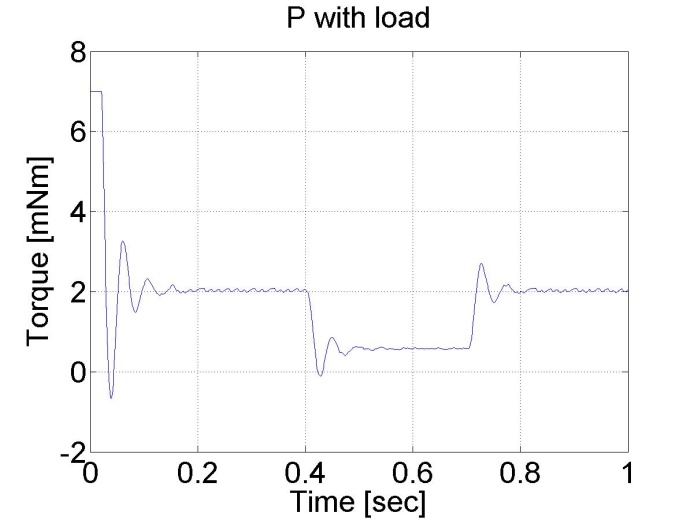
6.6.4. A P szabályozó válasza a terhelés ugrásszerű változásaira - 5.19 mérési feladat megoldása

Látható, hogy a P szabályozó legnagyobb hátránya az állandósult hibája és a zavarok bennhagyása.

A mérés hossza milliszekundumban : 1000

Az állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklaráció:

doubleP_par = 2.3;

doubleI_par = 0.0;

doubleref_vel = 7;

doubleerror_vel;

static doubleerror_vel_int=0.0;

double load = 2;

/* sebesség szűrő változók */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 és Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

Szabályozó kód:

if (CurrentTime >= 0.4*1e3 && CurrentTime < 0.7*1e3)

{

load = 0.5;

}

/* Sebesség szűrő */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Sebesség szabályozás hibaszámítása

error_vel=ref_vel- ResultData.Velocity;

error_vel_int = error_vel_int + error_vel*(CurrentTime - OldTime)/1000;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.StateVariable_7 = error_vel_int;

ResultData.Torque = P_par*error_vel + I_par*error_vel_int - load;

if (ResultData.Torque > 5) { ResultData.Torque = 5; }

if (ResultData.Torque < -5) { ResultData.Torque = -5; }

6.11. ábra - P szabályozó eredményei ugrásszerű terhelésre

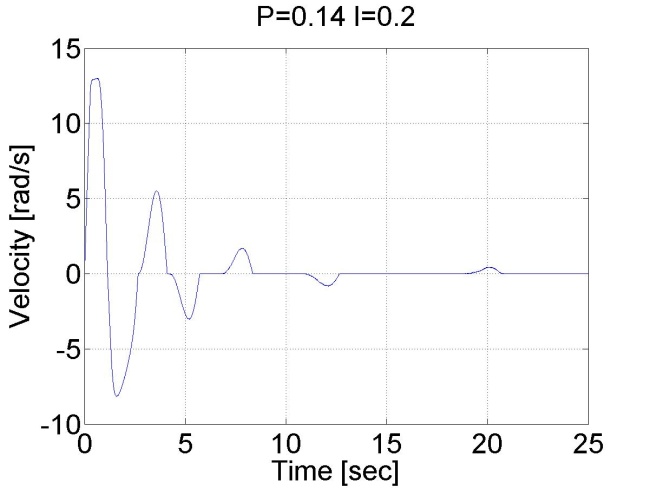
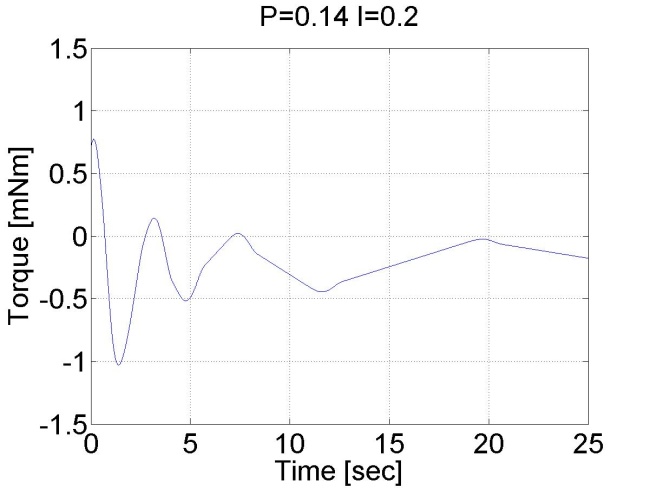
6.6.5. A PI szabályozó ugrás függvényre adott válasza - 5.20 mérési feladat megoldása

Ennél a tesztnél a referencia szögsebesség 1 rad/s. A szabályozó az alábbi alakú:

Mérés ideje milliszekundumokban : 1000

Állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklaráció:

doubleP = 0.6;

doubleI = 7;

doubleref_vel = 8;

doubleerror_vel;

static doubleerror_vel_int=0.0;

double load = 0;

/* sebesség szűrő változói */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* sebesség szűrő paraméterei */

/* Tsample=1e-3 and Tc=0.007 */

float ad11= 0.9996, ad12= 9.9072e-004, ad13= 4.3344e-007;

float ad21= -1.2637, ad22= 0.9730, ad23= 8.0496e-004;

float ad31= -2.3468e+003, ad32= -50.5468, ad33= 0.6280;

float bd1= 4.3671e-004, bd2= 1.2637, bd3= 2.3468e+003;

Szabályozó kód:

/* Sebesség szűrő */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Sebesség szabályozó hibaszámítása

error_vel=ref_vel- ResultData.Velocity;

error_vel_int = error_vel_int + error_vel*(CurrentTime - OldTime)/1000.0;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.StateVariable_7 = error_vel_int;

ResultData.StateVariable_8 = CurrentTime;

ResultData.Torque = P*error_vel + I*error_vel_int - load;

if (ResultData.Torque > 5)

{

ResultData.Torque = 5;

}

if (ResultData.Torque < -5)

{

ResultData.Torque = -5;

}

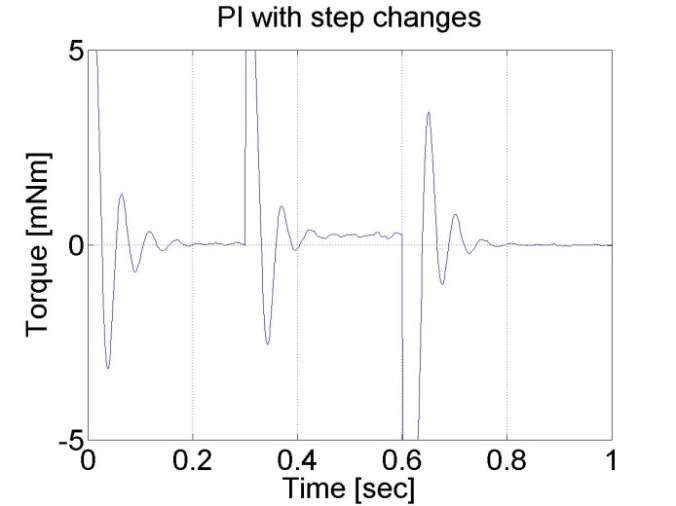
Alapvető különbség P és PI vezérkő között, hogy utóbbinak nincs állandósult hibája. Ez az integráló tag hatása, amely összegzi a hibát. Az integrálási hiba is megjelenik, ami kezdetben túllövést eredményez, majd később lecseng. Ugyanakkor a PI szabályozó gyorsabb is. Hátránya, hogy túl nagy túllövést vagy instabilitást okozhat. A jelentős túllövés oka a szabályozó telítődése (ld. 5-14. ábra). Ez egy hozzáadott D taggal csökkenthető, de lásd még a 5.23 mérési feladatot.

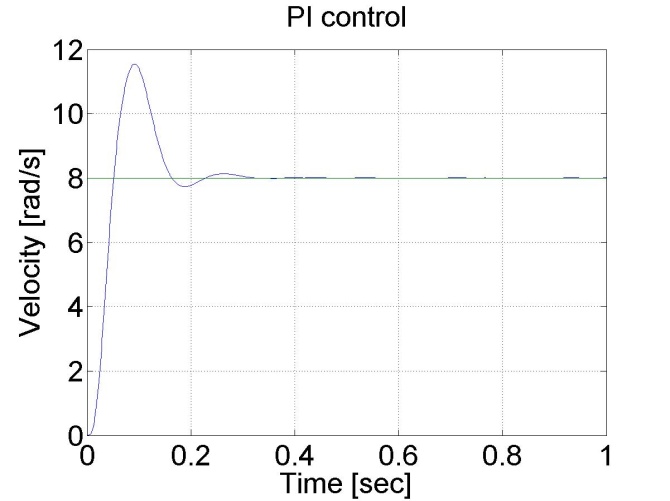
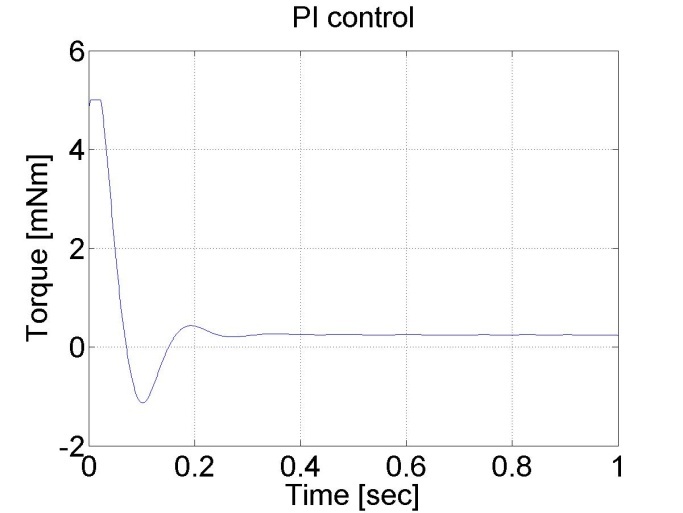
6.12. ábra - PI szabályozó eredményei ugrásszerű referencia sebesség értékre

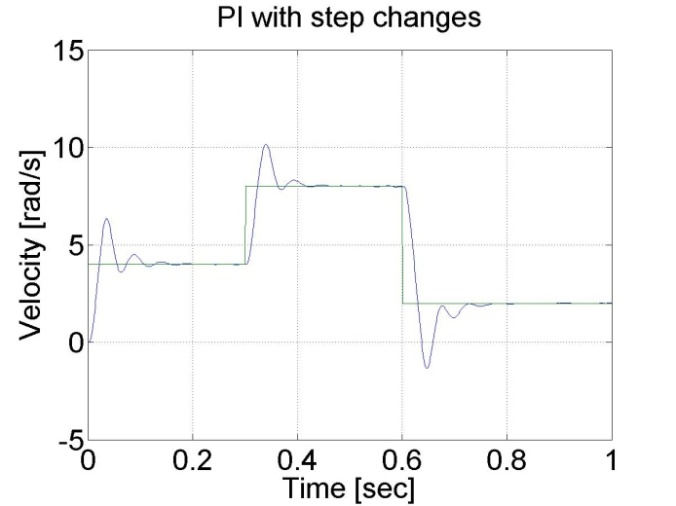
6.6.6. A PI szabályozó változó referenciajellel - 5.21 mérési feladat megoldása

Ebben a tesztben a referencia tengely szögsebességét két időpillanatban változtatjuk: t = 0.3 s és t = 0.6 s. A PI szabályozó gyorsabb a P-hez képest és a motor állandósult hiba nélkül működik. A szabályozó az alábbi alakú:

A mérés hossza milliszekundumban : 1000

Állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklaráció:

doubleP_par = 2;

doubleI_par = 50.0;

doubleref_vel = 7;

doubleerror_vel;

static doubleerror_vel_int=0.0;

double load = 0;

/* sebesség szűrő változók */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 és Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

Szabályozó kód:

//Ugrás változások referencia sebességben

if (CurrentTime > 0*1e3 && CurrentTime < 0.3*1e3)

{

ref_vel = 4;

}

if (CurrentTime >= 0.3*1e3 && CurrentTime < 0.6*1e3)

{

ref_vel = 8;

}

if (CurrentTime >= 0.6*1e3 && CurrentTime < 1.6*1e3)

{

ref_vel = 2;

}

/* Sebességszűrő */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Sebesség szabályozás hbaszámítása

error_vel=ref_vel- ResultData.Velocity;

error_vel_int = error_vel_int + error_vel*(CurrentTime - OldTime)/1000;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.StateVariable_7 = error_vel_int;

ResultData.Torque = P_par*error_vel + I_par*error_vel_int - load;

if (ResultData.Torque > 5) { ResultData.Torque = 5; }

if (ResultData.Torque < -5) { ResultData.Torque = -5; }

6.13. ábra - PI szabályozó eredménye 3 ugrásszerű változásra a referencia sebesség értékben

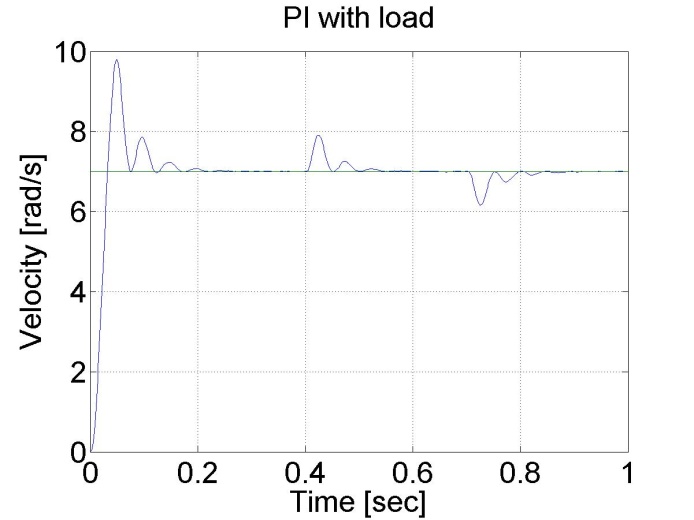
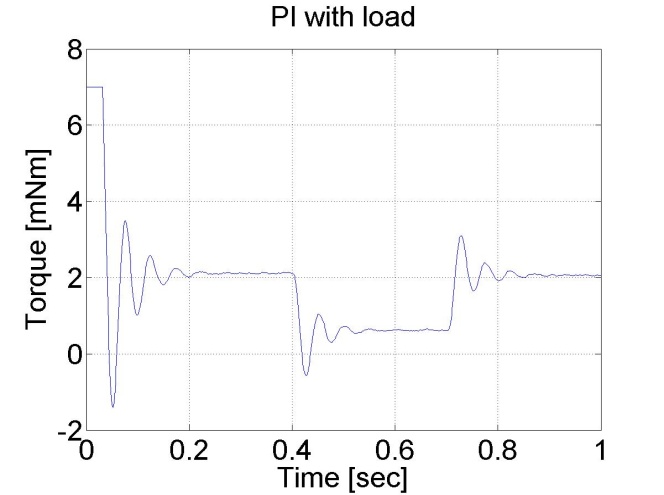
6.6.7. A PI szabályozó válasza a terhelés ugrásszerű változásaira - 5.22 mérési feladat megoldása

Ebben a tesztben virtuális terhelést alkalmazunk. Ha t< 0.3 s, akkor load=2.0 load, ha 0.3 s<t< 0.7 s, akkor load=0.5, végül, ha t>0.7 s, akkor load=2.0 ismét.

Mérés hossza milliszekundumban : 1000

Állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklarálás:

doubleP_par = 2.3;

doubleI_par = 50;

doubleref_vel = 7;

doubleerror_vel;

static doubleerror_vel_int=0.0;

double load = 2;

/* sebesség szűrő változói */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 és Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

Szabályozó kód:

/* Sebesség szűrő */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

if (CurrentTime >= 0.4*1e3 && CurrentTime < 0.7*1e3)

{

load = 0.5;

}

//Sebesség szabályozó hibaszámítása

error_vel=ref_vel- ResultData.Velocity;

error_vel_int = error_vel_int + error_vel*(CurrentTime - OldTime)/1000.0;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.StateVariable_7 = error_vel_int;

ResultData.Torque = P_par*error_vel + I_par*error_vel_int - load;

if (ResultData.Torque > 5)

{

ResultData.Torque = 5;

}

if (ResultData.Torque < -5)

{

ResultData.Torque = -5;

}

Észrevehető a PI szabályozó jó zavarszűrése a P vezérlőjével szemben.

6.14. ábra - PI szabályozó eredményei ugrásszerű terhelés változásra

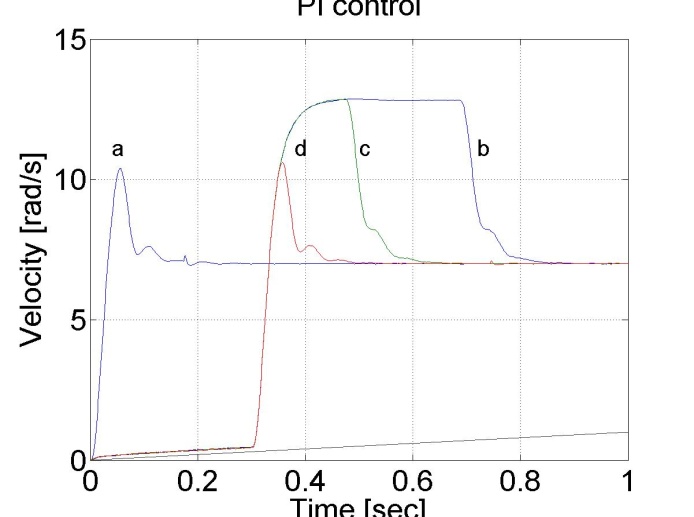
6.6.8. Hibatolerációs mérések - 5.23 mérési feladat megoldása

Először az integráló tag értékét közvetlenül korlátozzuk.

A mérés hossza mil l iszekundumban: 12000

Az állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklarációk:

doubleP_par = 2;

doubleI_par = 50;

doubleref_vel = 7;

doubleerror_vel;

static doubleerror_vel_int=0.0;

double load = 0;

// a esetben

doubleint_lim = 100;

doubleTf = -0.3*1e3;

// besetben

doubleint_lim = 100;

doubleTf = 0.3*1e3;

// c esetben

doubleint_lim = 0.9;

doubleTf = 0.3*1e3;

// d esetben

doubleint_lim = 0.15;

doubleTf = 0.3*1e3;

// kérem másolja be az egyik pár paramétert

doubleint_lim = 0.15;

doubleTf = 0.3*1e3;

/* sebesség szűrő változói */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 és Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

Szabályozó kód:

/* Sebesség szűrő */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Sebesség szabályozó hibaszámítása

error_vel=ref_vel- ResultData.Velocity;

error_vel_int = error_vel_int + error_vel*(CurrentTime - OldTime)/1000.0;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.StateVariable_7 = error_vel_int;

if (error_vel_int > int_lim)

{

error_vel_int = int_lim;

}

ResultData.Torque = P_par*error_vel + I_par*error_vel_int - load;

if ( CurrentTime < Tf)

{

ResultData.Torque = 0.0;

}

if (ResultData.Torque > 5)

{

ResultData.Torque = 5;

}

if (ResultData.Torque < -5)

{

ResultData.Torque = -5;

}

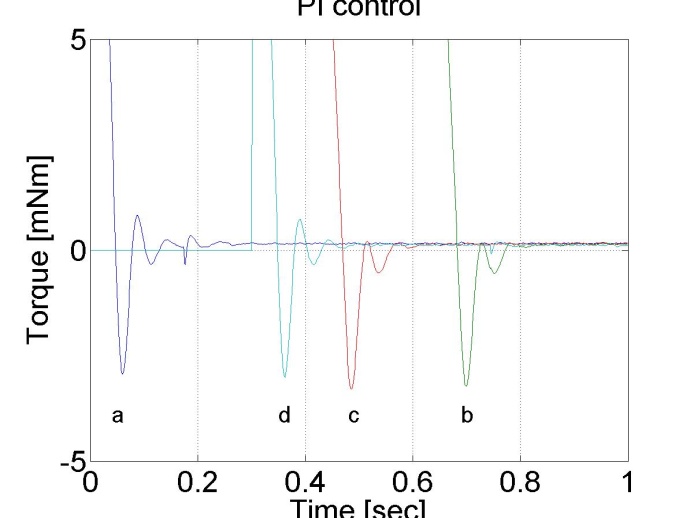
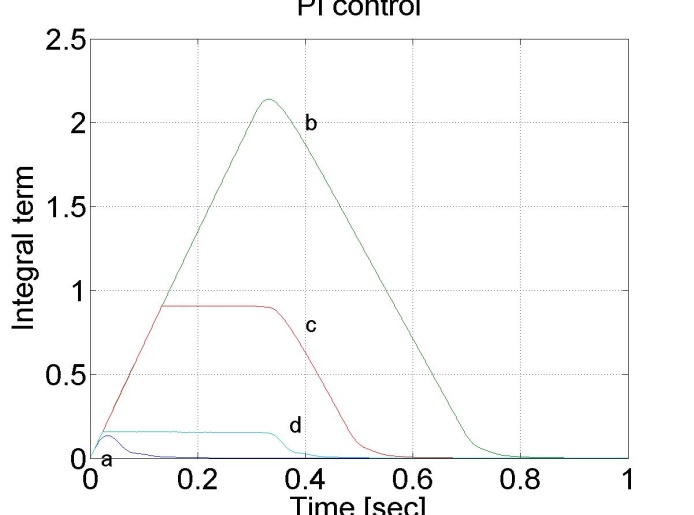
6.15. ábra - Integrátor telítődése

Hasonló eredményt érhetünk el, ha a szabályozó telítődésénél az integrálótagot kikapcsoljuk.

A mérés hossza mil l iszekundumban: 1000

Az állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklarációk:

doubleP_par = 2.1;

doubleI_par = 75.0;

doubleref_vel = 7;

doubleerror_vel;

static doubleerror_vel_int=0.0;

double load = 2;

double delta = 0;

/* velocity filter variables */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 and Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

Szabályozó kód:

/* Velocity filter */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Error calculation for velocity control

error_vel=ref_vel- ResultData.Velocity;

delta=error_vel*(CurrentTime - OldTime)/1000;

error_vel_int = error_vel_int + delta;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.Torque = P_par*error_vel + I_par*error_vel_int - load;

if (ResultData.Torque > 5) { ResultData.Torque = 5; error_vel_int = error_vel_int - delta*0; }

if (ResultData.Torque < -5) { ResultData.Torque = -5; error_vel_int = error_vel_int - delta*0;}

ResultData.StateVariable_7 = error_vel_int;

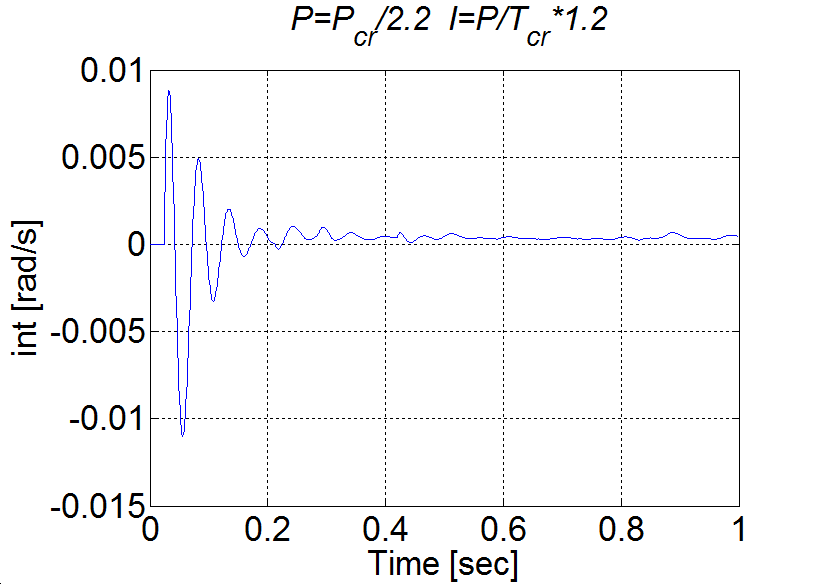
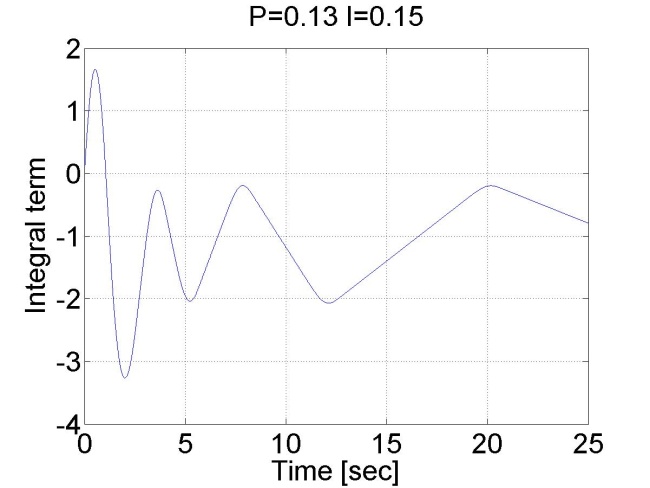
A 6-14. ábrán látható túllövést csökkenthetjük azzal, ha az integrátort kikapcsoljuk a telítődés időtartamára.

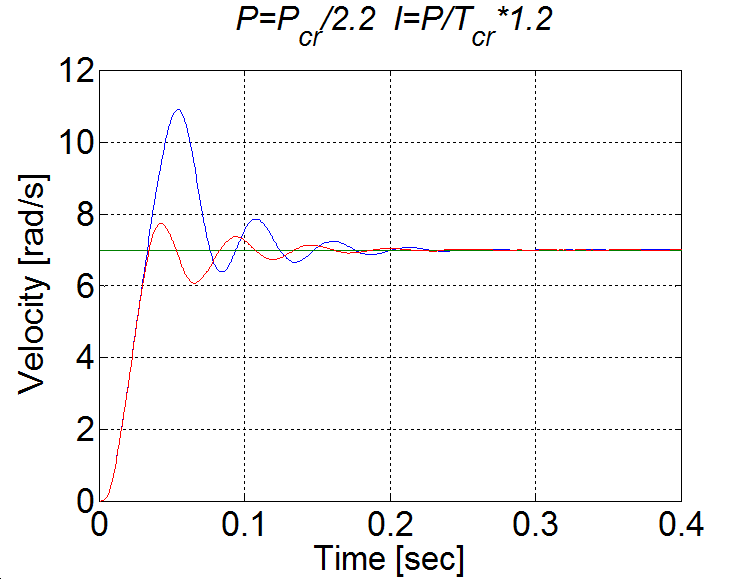
6.16. ábra - PI szabályozó telítődésének hatása

Hasonlítsuk össze a két esetben az integráló tag értékét:

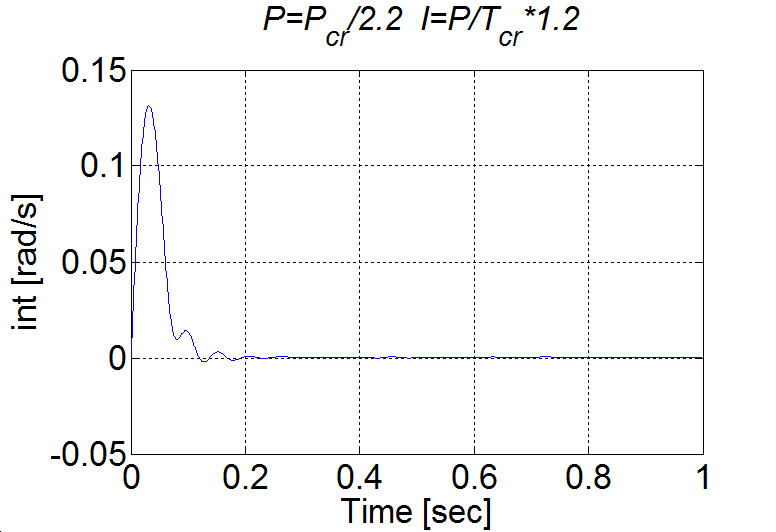
6.17. ábra - A hibaintegrál időfüggvénye PI szabályozás esetén

6.18. ábra - A hibaintegrál időfüggvénye PI szabályozás anti windup funkcióval

6.6.9. Időkésleltetett rendszer PI szabályozása - 5.24 mérési feladat megoldása

A mérés hossza mil l iszekundumban: 1000

Az állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklarációk:

doubleP_par = 0.85;

doubleI_par = 12.0;

doubleref_vel = 7;

doubleerror_vel;

static doubleerror_vel_int=0.0;

double load = 0;

/* Time delay pipe */

static float T_1=0.0, T_2=0.0, T_3=0.0;

static float T_4=0.0, T_5=0.0, T_6=0.0;

static float T_7=0.0, T_8=0.0, T_9=0.0;

/* velocity filter variables */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 and Tc=0.0032 */

float ad11 = 0.99591, ad12 = 0.00095987, ad13 = 3.652e-007;

float ad21 = -11.3235, ad22 = 0.88778, ad23 = 0.00061567;

float ad31 = -19089.6748, ad32 = -193.6165, ad33 = 0.30752;

float bd1 = 0.0040906, bd2 = 11.3235, bd3 = 19089.6748;

Szabályozó kód:

//Step changes in reference speed

/* Velocity filter */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Error calculation for velocity control

error_vel=ref_vel- ResultData.Velocity;

error_vel_int = error_vel_int + error_vel*(CurrentTime - OldTime)/1000;

ResultData.StateVariable_5 = ref_vel;

ResultData.StateVariable_6 = error_vel;

ResultData.StateVariable_7 = error_vel_int;

ResultData.Torque = T_1;

T_1=T_2;

T_2=T_3;

T_3=T_4;

T_4=T_5;

T_5=T_6;

T_6=T_7;

T_7=T_8;

T_8=T_9;

T_9= P_par*error_vel + I_par*error_vel_int - load;

if (T_9 > 5) { T_9 = 5;

error_vel_int = error_vel_int - error_vel*(CurrentTime - OldTime)/1000;}

if (T_9 < -5) { T_9 = -5;

error_vel_int = error_vel_int - error_vel*(CurrentTime - OldTime)/1000;}

Az eredményeket megjelenítő MatLab program:

% please, modify it according to you file names

sv_1_hwztupv131qjbi55l3k5oi45

sv_2_hwztupv131qjbi55l3k5oi45

sv_3_hwztupv131qjbi55l3k5oi45

sv_4_hwztupv131qjbi55l3k5oi45

sv_5_hwztupv131qjbi55l3k5oi45

sv_6_hwztupv131qjbi55l3k5oi45

sv_7_hwztupv131qjbi55l3k5oi45

time=time/1000;

plot(time,position)

set(gca, 'fontsize', [25]);

xlabel('Time [sec]');

ylabel('Position [rad]');

title('Delyed system with PI controller');

% you can adjust your axis

axis([0 1 0 12]);

grid

pause;

print -djpeg Delay_poz

plot(time,velocity)

set(gca, 'fontsize', [25]);

xlabel('Time [sec]');

ylabel('Velocity [rad/s]');

title('Delyed system with PI controller');

% you can adjust your axis

axis([0 1 0 12]);

grid

print -djpeg Delay_vel

pause;

plot(time,torque)

set(gca, 'fontsize', [25]);

xlabel('Time [sec]');

ylabel('Torque [mNm]');

title('Delyed system with PI controller');

% you can adjust your axis

%axis([0 1 -1 1]);

grid

print -djpeg Delay_torque

pause;

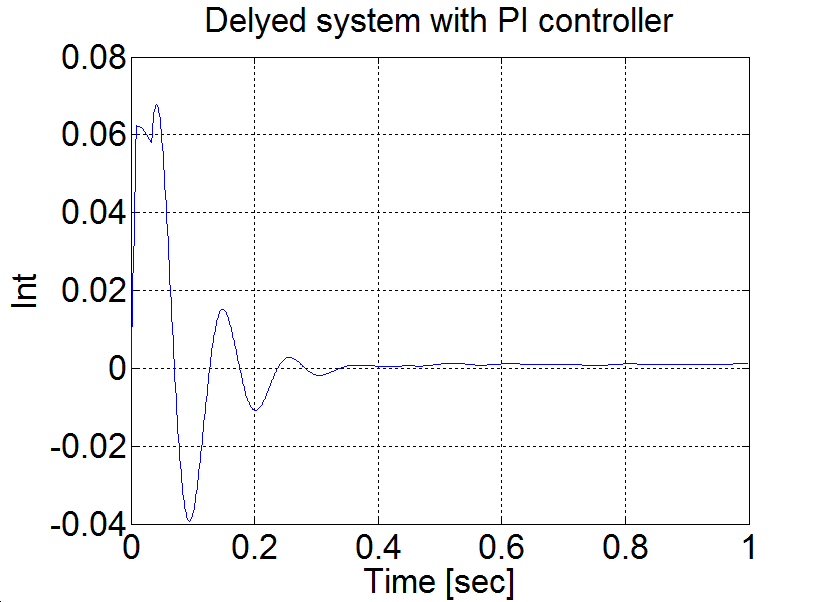
plot(time,int)

set(gca, 'fontsize', [25]);

xlabel('Time [sec]');

ylabel('Int');

title('Delyed system with PI controller');

% you can adjust your axis

%axis([0 1 -1 1]);

grid

print -djpeg Delay_int

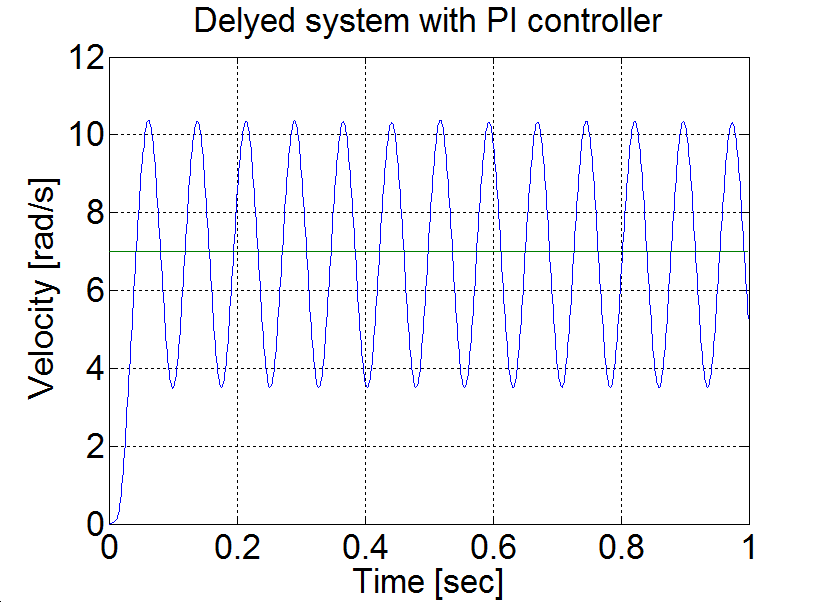
6.19. ábra - A stabilitás határa

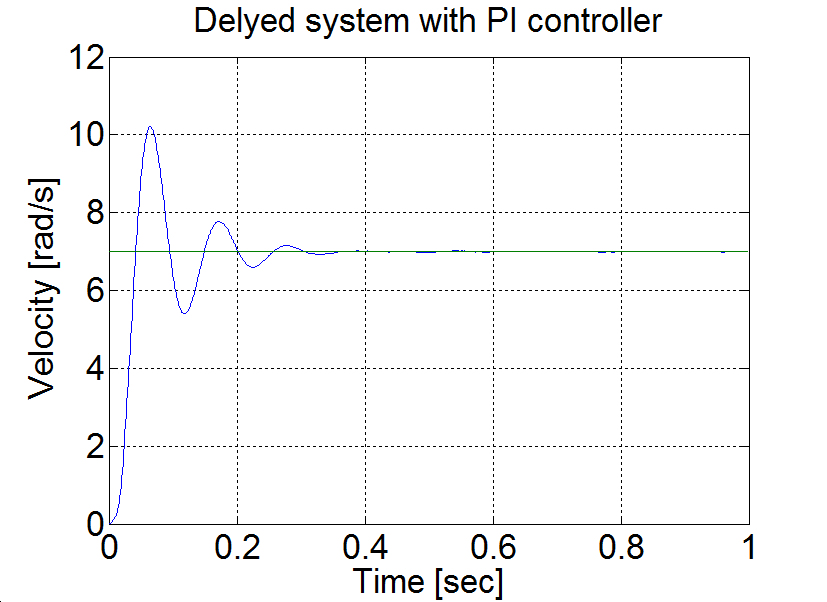
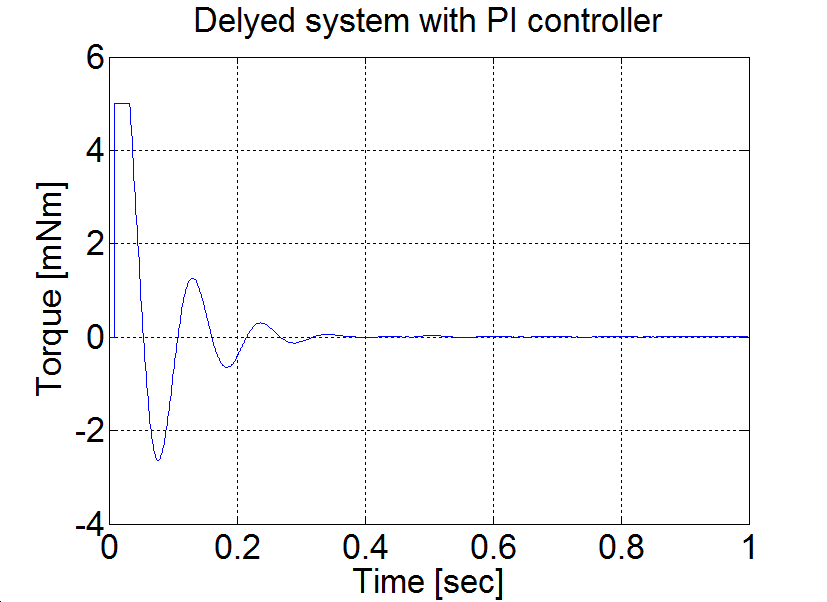
Következtetés: AU = 1.7 és TU≈0.08. A táblázat szerint PPI=0.85 és IPI=12. E paraméterekkel behangolt PI szabályozóval végzett mérés eredménye a 6-22. ábrán látható.

PI szabályozás időkésleltetett rendszer esetén

6.20. ábra - PI szabályozás időkésleltetett rendszer esetén

6.6.10. P és PI szabályozó ugrás függvény pozíció refereciajel válasza - 5.25 mérési feladat megoldása

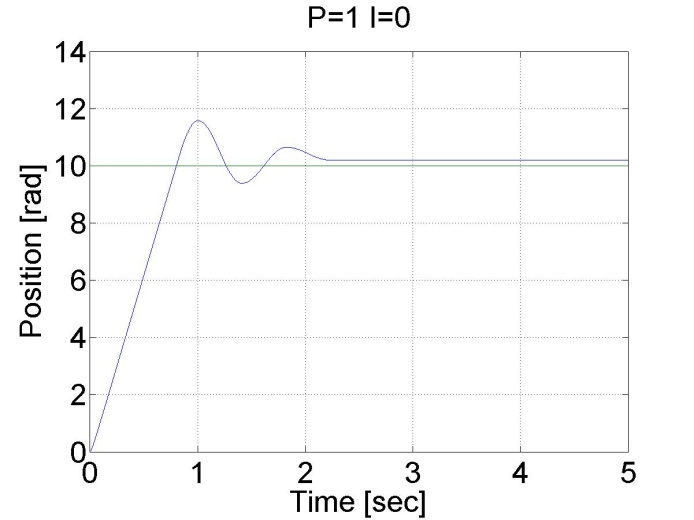
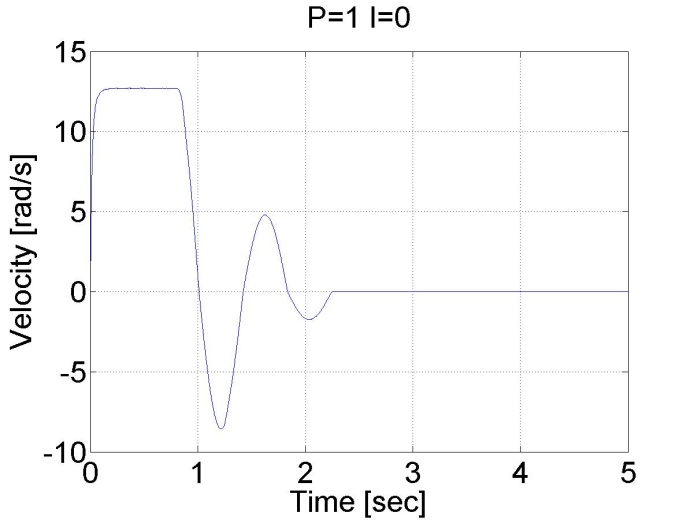
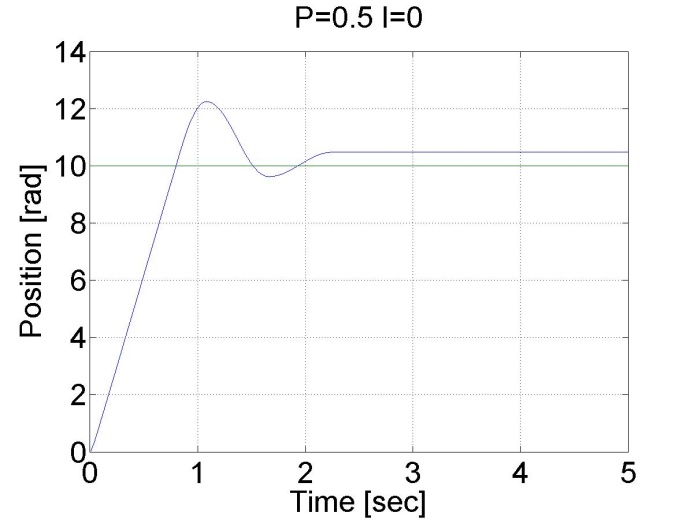
Ehhez a teszthez a referencia tengely-pozíciót 10 rad-ra állítjuk. A szabályozó a következő alakú:

A mérés hossza milliszekundumban : 1000

Az állapot változók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklarálás:

doubleP_par = 1;

doubleI_par = 0;

doubleref_pos = 10;

doubleerror_pos;

static doubleerror_pos_int=0.0;

double load = 0;

/* sebesség szűrő változói */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 és Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

static double ini_0 = 0;

static double ini_1 = -10;

Szabályozó kód:

if (ini_1 < 0)

{

ini_0 = ResultData.Position;

}

ini_1 = 5;

/* Velocity filter */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Sebesség szabályozó hibaszámítása

error_pos=ref_pos- ResultData.Position + ini_0;

error_pos_int = error_pos_int + error_pos*(CurrentTime - OldTime)/1000.0;

ResultData.StateVariable_5 = ref_pos;

ResultData.StateVariable_6 = error_pos;

ResultData.StateVariable_7 = error_pos_int;

ResultData.StateVariable_8 = ResultData.Position - ini_0;

ResultData.Torque = P_par*error_pos + I_par*error_pos_int - load;

if (ResultData.Torque > 5)

{

ResultData.Torque = 5;

}

if (ResultData.Torque < -5)

{

ResultData.Torque = -5;

}

Látható a nagy túllövés a vezérlőben, és az állandósult hiba is jelen van. Viszont most a pozíciót mértük, és nem deriválásból számoltuk, a pozíció görbe sima az előző esetekhez képest.

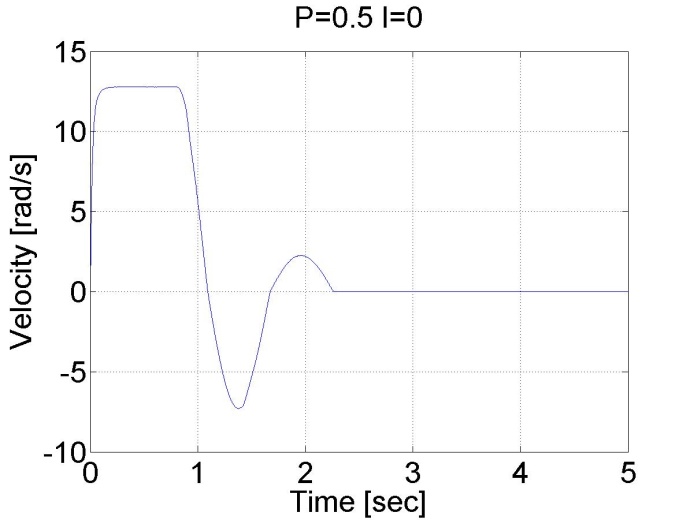
6.21. ábra - P szabályozó eredményei a referencia pozíció ugrásszerű változására

6.22. ábra - P szabályozó eredményei a referencia pozíció ugrásszerű változására

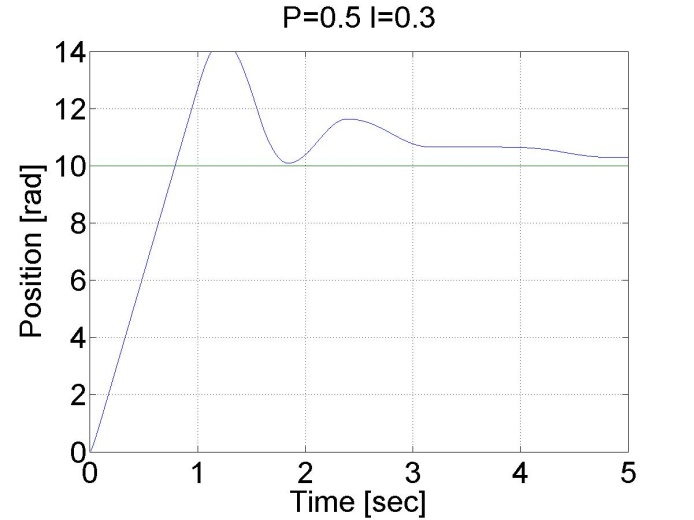
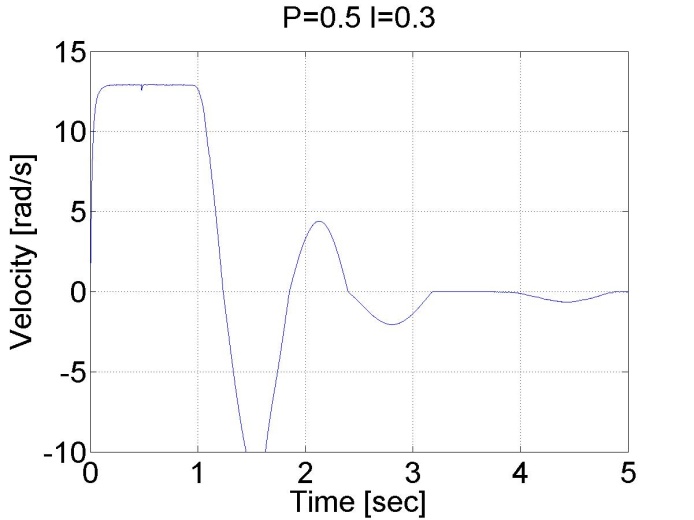
6.23. ábra - PI szabályozó eredményei a referencia pozíció ugrásszerű változására

6.6.11. Stick-slip jelenség - 5.26 mérési feladat megoldása

Mérés ideje milliszekundumban : 10000

Az állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adot) -sebesség
torque (adott) - nyomaték
ref (választott) - ref
error (választott) - hiba
integral (választott) - integrál

Deklarációk:

doubleP_par = 0.1;

doubleI_par = 0.1;

doubleref_pos = 5;

doubleerror_pos;

static doubleerror_pos_int=0.0;

double load = 0;

/* sebesség szűrő változói */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 és Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

static double ini_0 = 0;

static double ini_1 = -10;

Szabályozó kód:

if (ini_1 < 0)

{

ini_0 = ResultData.Position;

}

ini_1 = 5;

/* Sebesség szűrő */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Sebesség szabályozó hibaszámítása

error_pos=ref_pos- CurrentPosition;

error_pos_int = error_pos_int + error_pos*(CurrentTime - OldTime)/1000.0;

ResultData.StateVariable_5 = ref_pos;

ResultData.StateVariable_6 = error_pos;

ResultData.StateVariable_7 = error_pos_int;

ResultData.Torque = P_par*error_pos + I_par*error_pos_int - load;

if (ResultData.Torque > 5)

{

ResultData.Torque = 5;

}

if (ResultData.Torque < -5)

{

ResultData.Torque = -5;

}

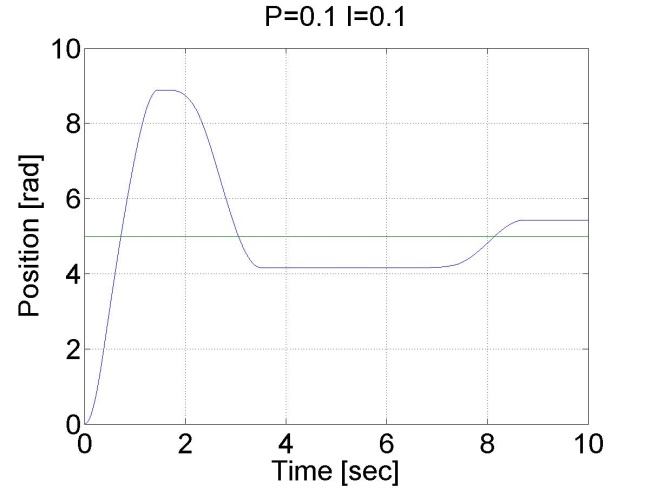
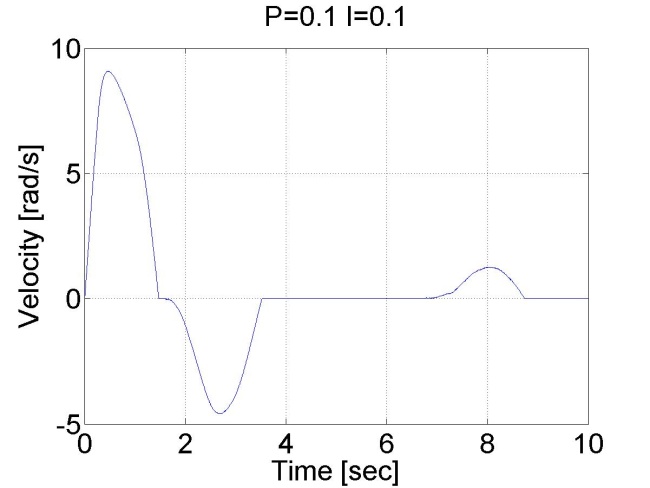
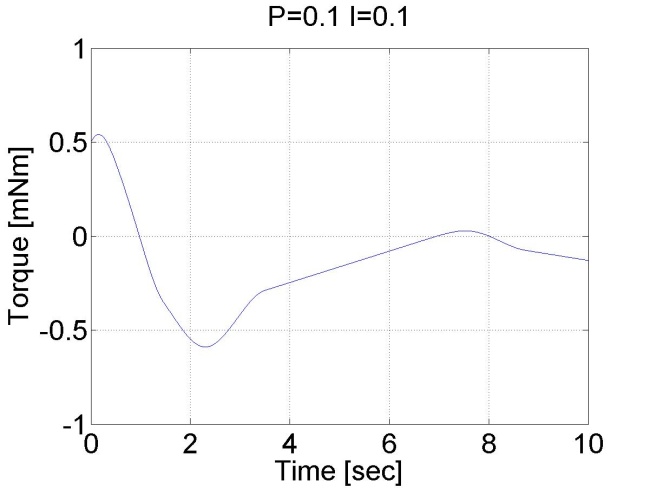
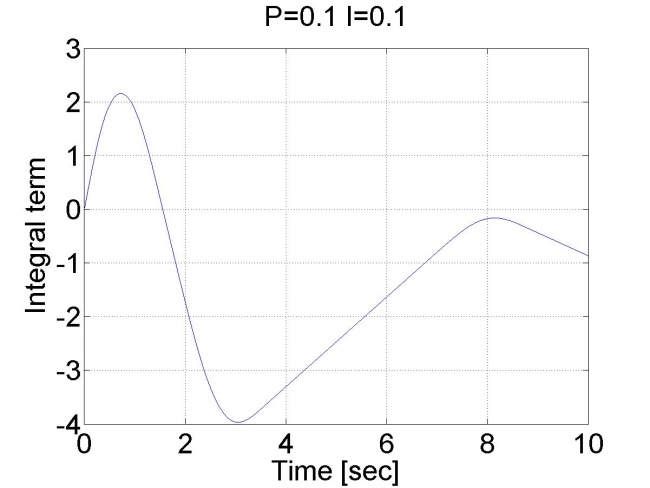
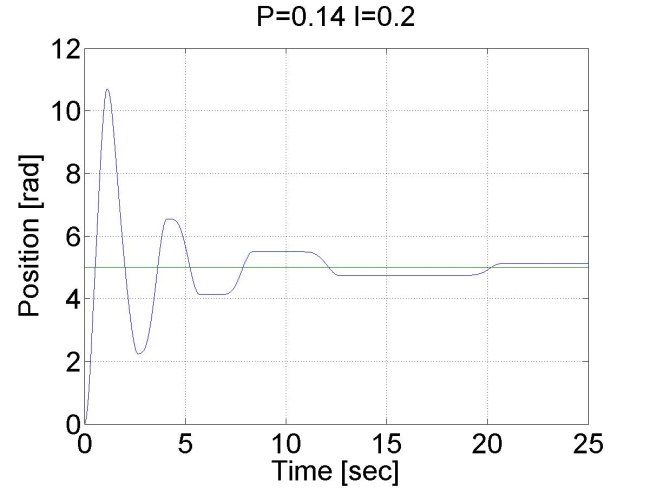
6.24. ábra - Stick-slip jelenség

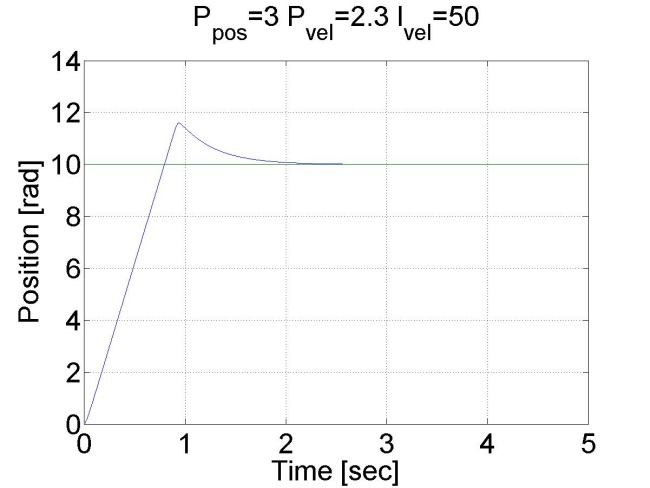
6.6.12. Pozíció szabályozás belső sebesség szabályozóval - 5.27 mérési feladat megoldása

A szabályozó kódja a következő:

Az állapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adott) - sebesség
torque (adott) - nyomaték
ref_poz (választott)
ref_vel (választott)
err_pos (választott)
err_vel (választott)
int_vel (választott)
poz (választott)

Deklaráció:

doubleP_pos = 3;

doubleP_vel = 3;

doubleI_vel = 30;

doubleref_pos = 10;

double ref_vel = 0;

doubleerror_pos = 0;

double error_vel = 0;

static double error_vel_int = 0;

static double ini_0 = 0;

static double ini_1 = -10;

/* sebesség szabályozó változói */

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/* Tsample=1e-3 és Tc=0.0027 */

float ad11= 0.9936, ad12= 9.4621e-004, ad13= 3.4524e-007;

float ad21= - 17.5400, ad22= 0.8515, ad23= 5.6261e-004;

float ad31= -2.8584e+004, ad32= -249.0676, ad33= 0.2264;

float bd1= 0.0064, bd2= 17.5400, bd3= 2.8584e+004;

Szabályozó kód:

if (ini_1 < 0)

{

ini_0 = ResultData.Position;

}

ini_1 = 5;

/* Sebesség szűrő */

ztmp_1=ad11* z_1+ad12* z_2+ad13* z_3 + bd1* ResultData.Velocity;

ztmp_2=ad21* z_1+ad22* z_2+ad23* z_3 + bd2* ResultData.Velocity;

z_3=ad31* z_1+ad32* z_2+ad33* z_3 + bd3* ResultData.Velocity;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

//Pozíció szabályozás hibaszámítása

error_pos = ref_pos- ResultData.Position + ini_0;

// Sebesség szabályozás hibaszámítása

ref_vel = error_pos*P_pos;

error_vel = ref_vel - ResultData.Velocity;

error_vel_int = error_vel_int + error_vel*(CurrentTime - OldTime)/1000;

ResultData.StateVariable_5 = ref_pos;

ResultData.StateVariable_6 = ref_vel;

ResultData.StateVariable_7 = error_pos;

ResultData.StateVariable_8 = error_vel;

ResultData.StateVariable_9 = error_vel_int;

ResultData.StateVariable_10 = ResultData.Position - ini_0;

//Szabályozó

ResultData.Torque = P_vel*error_vel + I_vel*error_vel_int;

if (ResultData.Torque > 5)

{

ResultData.Torque = 5;

}

if (ResultData.Torque < -5)

{

ResultData.Torque = -5;

}

Látható, hogy ez esetben nincs túllövés, mert a tengely sebessége idővel csökkeni kezd. Megállapíthatjuk, hogy a pozíció szabályozó belső sebességszabályozóval sokkal jobb eredményeket ad, mint a sima P szabályozó.

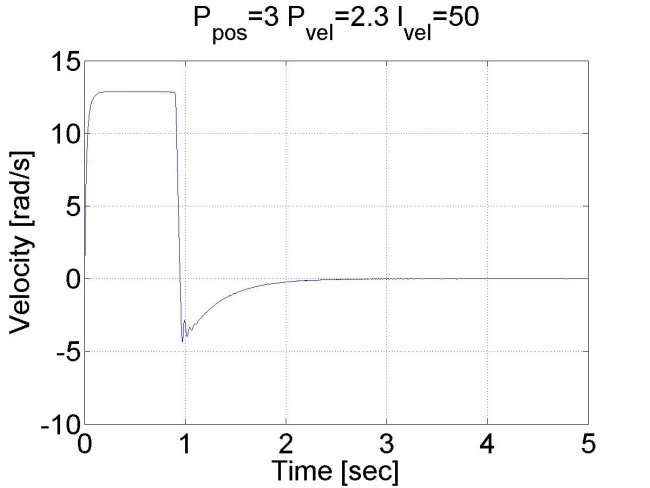
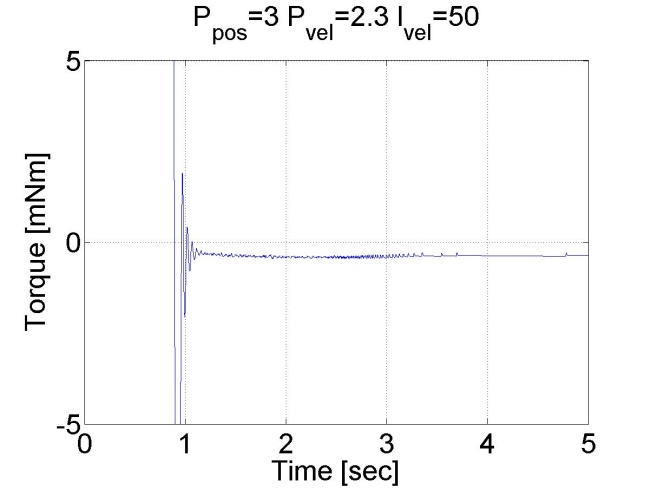
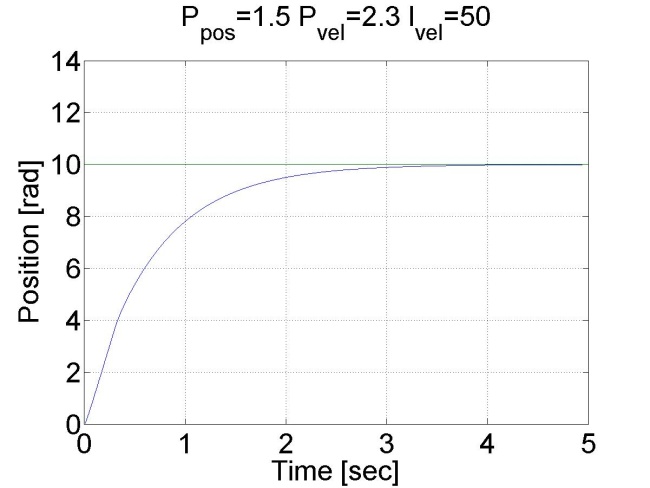
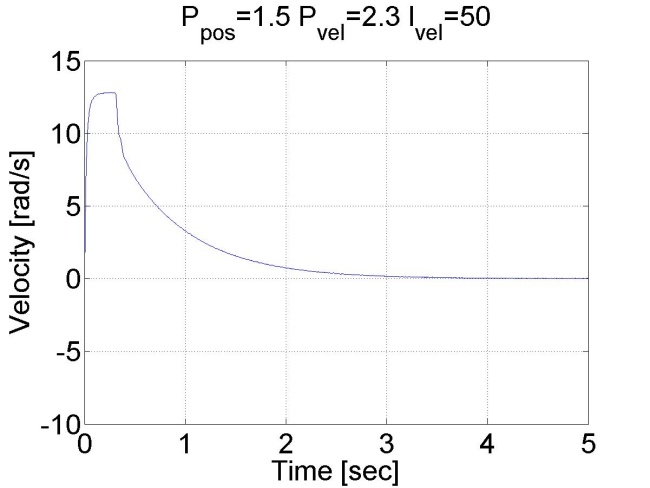
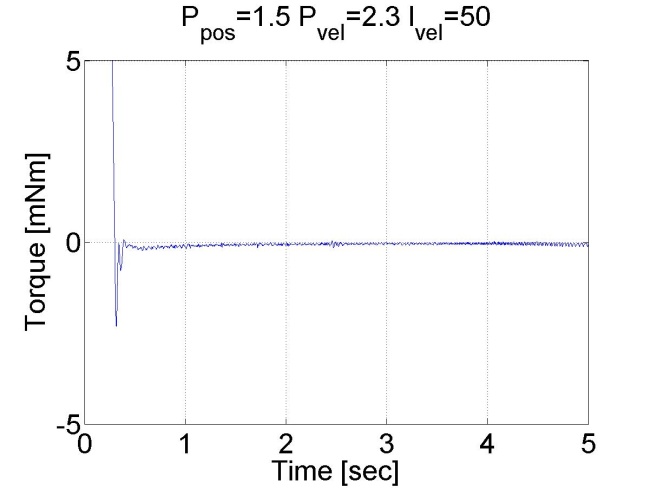
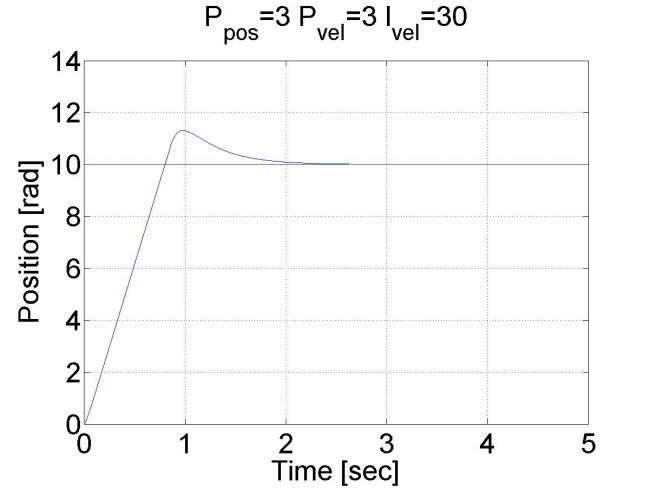
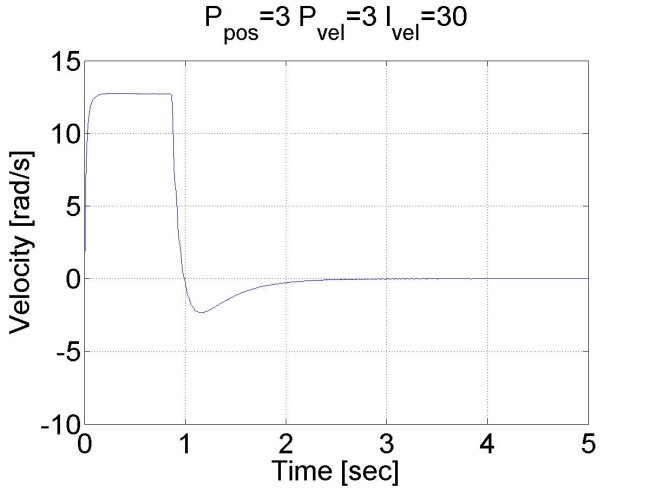
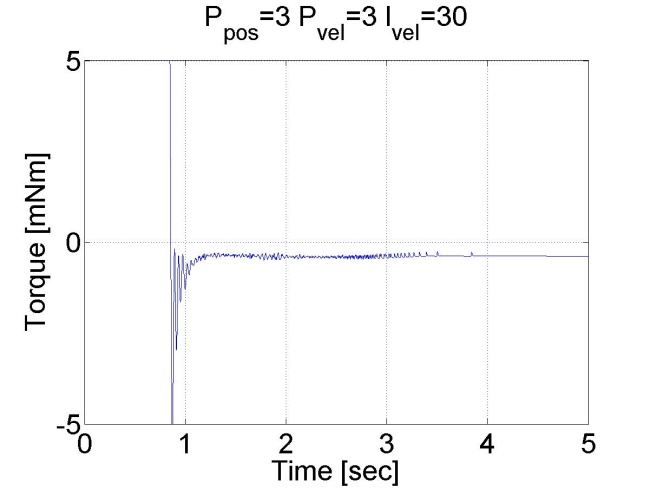
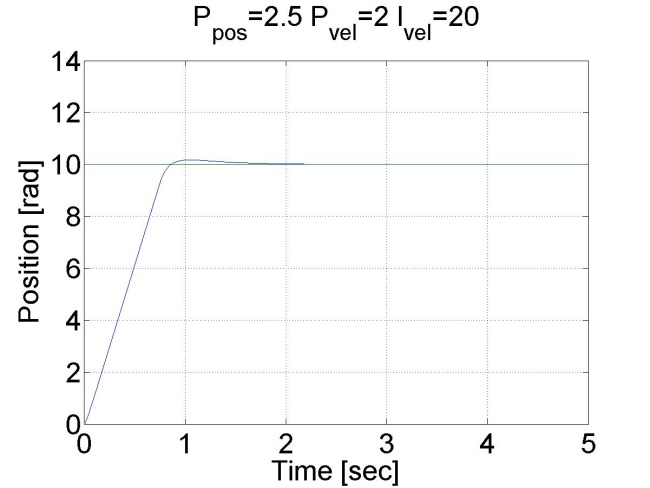
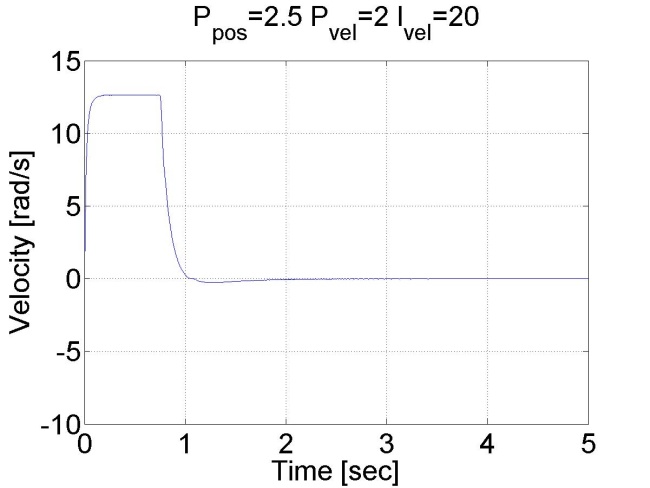
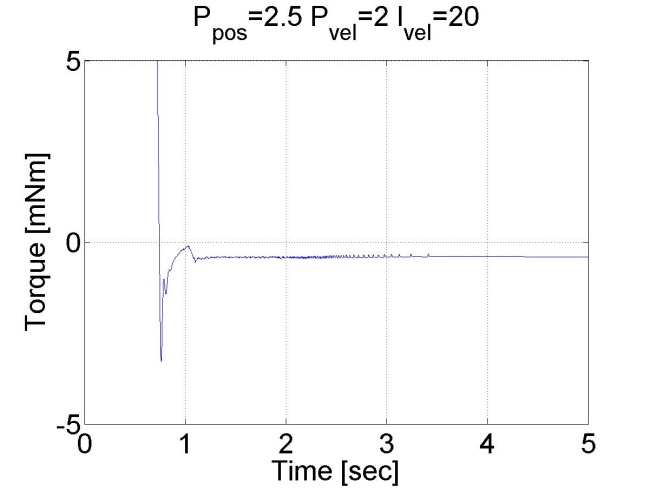
6.25. ábra - Kaszkád szabályozás eredményei

6.6.13. Csúszómód szabályozó eredmények - 5.28 mérési feladat megoldása

Csúszómód szabályozót is lehet használni. Ekkor két különböző mérést vizsgálunk, amelyek szabályozó részeik megegyeznek, de mivel a sebességet a motor pozíciójából számoljuk, így az zajossá teszi a sebesség diagramot. A sebesség értékeket szűrve a zajok kiküszöbölhetőek.

Mérés hossza milliszekundumban : 12000

Az á llapotváltozók nevei:

time (adott) - idő
position (adott) - pozíció
velocity (adott) - sebesség
torque (adott) - nyomaték
sigma (választott) - szigma

A szabályozó kódja a következő:

Deklarációk:

float sigma;

float error;

float error_dot;

float ref=5.0;

float lambda=2;

static double ini_0 = 0;

static double ini_1 = -10;

Szabályozó kód:

if (ini_1 < 0)

{

ini_0 = ResultData.Position;

}

ini_1 = 5;

error=ref-ResultData.Position+ ini_0;

error_dot=- ResultData.Velocity;

sigma= error+ lambda*error_dot;

ResultData.StateVariable_5 = sigma;

if (sigma>0)

{ ResultData.Torque=0.1;

}

if (sigma<0)

{ ResultData.Torque =-0.1;

}

if (sigma=0)

{ ResultData.Torque=0;

}

Válassza kia a letöltendő elemet: Minden fájl

Kérem, töltse le a DOWNLOAD gombra kattintva

Az eredmények a következő MATLAB fájlba plottolódnak:

% módosítani a fájlnevek szerint

sv_1_n0ktqaui51tw5hrtvpypxu45

sv_2_n0ktqaui51tw5hrtvpypxu45

sv_3_n0ktqaui51tw5hrtvpypxu45

sv_4_n0ktqaui51tw5hrtvpypxu45

sv_5_n0ktqaui51tw5hrtvpypxu45

time=time/1000;

plot(time,position)

set(gca, 'fontsize', [25]);

xlabel('Time [sec]');

ylabel('Position [rad]');

title('Sliding mode controller');

% tengely beállítása

axis([0 12 0 6]);

grid

pause;

print -djpegsmc_poz

plot(time,velocity)

set(gca, 'fontsize', [25]);

xlabel('Time [sec]');

ylabel('Velocity [rad/s]');

title('Sliding mode controller');

% tengely beállítása

axis([0 12 0 3]);

grid

print -djpegsmc_vel

pause;

plot(5-position,-velocity)

set(gca, 'fontsize', [25]);

xlabel('Position error [rad]');

ylabel('Velocity error [rad/s]');

title('Sliding mode controller');

% tengely beállítása

axis([0 5 -3 0]);

grid

print -djpegsmc_traj

pause;

plot(time,torque)

set(gca, 'fontsize', [25]);

xlabel('Time [sec]');

ylabel('Torque [mNm]');

title('Sliding mode controller');

% tengely beállítása

axis([0 12 -0.15 0.15]);

grid

print -djpegsmc_torque

pause;

plot(time,sigma)

set(gca, 'fontsize', [25]);

xlabel('Time [sec]');

ylabel('Sigma');

title('Sliding mode controller');

% tengely beállítása

axis([0 12 -2.5 2.5]);

grid

print -djpegsmc_sigm

6-28. ábra: A pozíció szabályozó eredményei csúszómódban

Csúszómód szabályozó sebesség szűrővel a következő alakú:

Deklaráció:

float sigma;

float error;

float error_dot;

float ref=5.0;

float lambda=2;

/* filter variables*/

static float z_1=0.0, z_2=0.0, z_3=0.0;

static float ztmp_1=0.0, ztmp_2=0.0;

/*omega_c=10 a modellezetlen dinamika nagy kotyogást okoz */

float Azd11= 1, Azd12= 0.0010, Azd13= 0.0000;

float Azd21= -0.0005, Azd22= 0.9999, Azd23= 0.0010;

float Azd31= -0.9851, Azd32= -0.2960, Azd33= 0.9703;

float Bzd1= 0.0000, Bzd2= 0.0005, Bzd3= 0.9851;

/* omega_c=1/0.007 a modellezetlen dinamika nem okoz nagy kotyogást

float Azd11= 0.9996, Azd12= 9.9072e-004, Azd13= 4.3344e-007;

float Azd21= -1.2637, Azd22= 0.9730, Azd23= 8.0496e-004;

float Azd31= -2.3468e+003, Azd32= -50.5468, Azd33= 0.6280;

float Bzd1= 4.3671e-004, Bzd2= 1.2637, Bzd3= 2.3468e+003;

static double ini_0 = 0;

static double ini_1 = -10;

Szabályozó kód:

if (ini_1 < 0)

{

ini_0 = ResultData.Position;

}

ini_1 = 5;

error=ref-ResultData.Position+ ini_0;

/* filter */

ztmp_1 = Azd11* z_1 +Azd12* z_2 +Azd13* z_3 + Bzd1*ResultData.Velocity ;

ztmp_2 = Azd21* z_1 +Azd22* z_2 +Azd23* z_3 + Bzd2*ResultData.Velocity ;

z_3 = Azd31*z_1 +Azd32*z_2 +Azd33* z_3 + Bzd3*ResultData.Velocity ;

z_1 = ztmp_1;

z_2 = ztmp_2;

ResultData.Velocity =z_1;

error_dot=- z_1;

sigma=error+ lambda*error_dot;

ResultData.StateVariable_5 = sigma;

if (sigma>0)

{ ResultData.Torque=0.1;}

if (sigma<0)

{ ResultData.Torque =-0.1;

}

if (sigma=0)

{ ResultData.Torque=0;}

Az eredmények az alábbi ábrákon láthatók:

6-29. ábra: Csúszómód szabályozó sebesség szűrővel

6-30. ábra: A csúszómód sebesség szabályozóval ellátott pozíció szabályozó eredményei

6.7. Komplex tervezési és mérési feladat

Ebben a fejezetben áttekintjük a DC motor szabályozásánál alkalmazott állapot-visszacsatolásos szabályozás elméleti alapjait. Mivel a motor szabályozását egy számítógép segítségével végezzük el, így diszkrét idejű modellt fogunk használni, hiszen a szabályozás implementációja is ezt kívánja. Az itt bemutatott módszerek gyakorlati megvalósítását majd később MatLab segítségével el is végezzük. Az elméleti áttekintés során csak azokat a dolgokat emeljük ki, amelyek a később elvégzett motorszabályozás során hasznosításra is kerülnek, például nem lesz szó a folytonos idejű megvalósításról, illetve nem kerül minden felhasznált matematikai eljárás részletes bemutatásra, bizonyításra, ezekhez a leírás végén az ajánlott irodalom részben helyeztünk el forrásokat.

6.7.1. Az állapot-visszacsatolás és tervezése

Tekintsük az alábbi időinvariáns diszkrét idejű állapottér modellt:

$x [k + 1] = A_{d} x [k] + B_{d} u [k]$

$y [k] = C x [k] + D u [k]$

( 6.1 )

Ahol

$x [k] \in ℝ^{n}$ : az állapotváltozók oszlop vektora $k$ -adik időpontban;
$u [k] \in ℝ^{r}$ : a bemeneti jel oszlopvektora $k$ -adik időpontban;
$y [k] \in ℝ^{m}$ : a kimeneti jel vektora $k$ -adik időpontban;
$A_{d} \in ℝ^{n \times n}$ : a rendszer/állapot mátrix;
$B_{d} \in ℝ^{n \times r}$ : a bemeneti mátrix;
$C \in ℝ^{m \times n}$ : a kimeneti mátrix;
$D \in ℝ^{m \times r}$ : a segédmátrix (ez általában 0).

Az állapot-visszacsatolás célja az, hogy a rendszermátrixot olyan módon változtassuk meg, hogy a rendszer viselkedése számunkra kedvező legyen. Mivel $A_{d}$ sajátértékei a rendszer pólusai, így jól látható, hogy ezek megváltoztatásával a rendszer viselkedését – bizonyos korlátok mellett – szabadon választhatjuk meg. Az állapotegyenletekre ránézve észrevehetjük, hogy – $u [k]$ -t a következőképpen választva – $A_{d}$ értéke megváltoztatható:

$u [k] = K x [k] + u_{r} [k]$

( 6.2 )

ahol az $u_{r} [k]$ a rendszer referenciajele. Így a következőt kapjuk:

$x [k + 1] = A_{d} x [k] + B_{d} (K x [k] + u_{r} [k]) = (A_{d} + B_{d} K) x [k] + B_{d} u_{r} [k]$

( 6.3 )

ahol:

$K \in ℝ^{r \times n}$ : az állapot-visszacsatolást definiáló mátrix;
$u_{r} [k] \in ℝ^{r}$ : a rendszer új bemeneti jele.

Az új rendszermátrix $A_{d} + B_{d} K$ lesz, amelynek értékét a $K$ mátrixszal állíthatjuk be. Mivel $K$ nem közvetlenül hat a rendszermátrixra, hanem csak $B_{d}$ -vel való szorzás után, így tetszőleges eredményt nem érhetünk el.

Ezért az állapot-visszacsatolás tervezésének, megfelelő működésének feltétele a rendszer állapot irányíthatósága, azaz, hogy a rendszer tetszőleges állapotából véges idő alatt eljuthatunk egy megfelelő bemeneti jel segítségével bármely másik állapotba. Diszkrét idejű rendszer esetén a teljes állapotirányíthatóság feltétele, hogy a rendszer irányíthatósági mátrixa ( $M_{c}$ ) maximális rangú legyen, azaz rangja megegyezzen az állapotváltozók számával ( $n$ ):

$rank M_{c} = rank [\begin{matrix} B_{d} & A_{d} B_{d} & A_{d}^{2} B_{d} & ... & A_{d}^{n - 1} B_{d} \end{matrix}] = n$

( 6.4 )

Az állapot-visszacsatolás tervezése azon alapul, hogy felírjuk, milyen karakterisztikus egyenletet szeretnénk elérni ( $φ_{c} (z)$ ), azaz hova kerüljenek a rendszer pólusai (természetesen a pólusok száma nem változhat az eredeti rendszerhez képest). Ez a felírás általában két domináns pólus megválasztására épül, amelyekkel definiáljuk, hogyan is viselkedjen az adott rendszer, és további segédpólusokat is megadunk, amelyek az előbbieknél nagyobbak (ezekre azért van szükség, hogy az eredeti rendszerrel egyező fokszámot nyerjünk).

A pólusok megadása diszkrét szabályozó esetén is folytonos időben történik, hiszen a szabályozott szakasz általában folytonos idejű. Stabil rendszert kívánva az összes pólus negatív valós résszel kell rendelkezzen. A domináns póluspárt a csillapítás ( $ξ$ ) és a szabályozási idő ( $T$ ) segítségével is megadhatjuk. Tekintsük a következő kéttárolós lengőtagot:

$W (s) = \frac{1}{1 + 2 ξ T s + T^{2} s^{2}}$

( 6.5 )

Ha $0 \leq ξ \leq 1$ , akkor az átviteli függvény pólusai:

$p_{1, 2} = - ξ ω_{0} \pm j ω_{0} \sqrt{1 - ξ^{2}} = - σ_{e} \pm j ω_{e}$

( 6.6 )

ahol:

$ω_{0} = \frac{1}{T} = \sqrt{σ_{e}^{2} + ω_{e}^{2}}$

( 6.7 )

$ξ = \frac{σ_{e}}{ω_{0}}$

( 6.8 )

Az ugrásválasz burkológörbéjéből levezethető, hogy az $α$ százalékos szabályozási idő:

$T_{α %} = \frac{ln \frac{100}{α}}{σ_{e}}$

( 6.9 )

Ha tehát megadjuk $ξ$ és $T_{α %}$ értékét, akkor:

$ω_{0} = \frac{ln \frac{100}{α}}{ξ T_{α %}}$

( 6.10 )

Innen pedig a domináns póluspár számítható. A további pólusokat, hogy hatásuk ne legyen mérvadó, sokkal nagyobbra választjuk. Ha megvannak a folytonos idejű pólusok ( $p_{i}$ ), azok diszkrét idejű megfelelői ( $z_{i}$ ) a következőképpen számíthatóak:

$z_{i} = e^{p_{i} T_{s}}$

( 6.11 )

ahol $T_{s}$ az alkalmazott mintavételezési idő.

Ezután a feladat az, hogy kiszámítsuk azt a $K$ értéket, amivel ez a cél elérhető. Egybemenetű, egykimenetű (SISO) rendszerek esetében ez könnyen megoldható: felírjuk $A_{d} + B_{d} K$ rendszermátrix pólusait $K$ paraméterrel, majd ezeket összevetve a kitűzött pólusokkal $K$ értéke meghatározható. Ezt a módszert foglalja össze az úgynevezett Ackermann formula:

$K = [\begin{matrix} 0 & ... & 0 & 1 \end{matrix}] M_{c}^{- 1} φ_{c} (A_{d})$

( 6.12 )

ahol $φ_{c} (A_{d})$ a cél karakterisztikus egyenletbe behelyettesített eredeti rendszermátrixot jelöli. Több bemenetű, több kimenetű (MIMO) rendszerek esetében $K$ meghatározása összetettebb probléma, és általában csak közelítő megoldások érhetőek el, azaz a pólusok pozíciója eltérhet a tervezettől.

6.7.2. Alapjel korrekció alkalmazása

Az előbbi eljárással egy olyan rendszert nyertünk, amely az általunk választott pólusokkal rendelkezik. Szabályozó tervezés esetén azonban azt is elvárjuk, hogy a teljes rendszer kimenete olyan értéket vegyen fel állandósult állapotban, amelyet annak alapjelként megadunk. Ehhez szükségünk van az úgynevezett alapjel korrekcióra. Az alapjel korrekcióval ellátott állapot-visszacsatolás a következő felépítésű:

6.26. ábra - Diszkrét idejű alapjel korrekció

$z^{- 1}$ $A_{d}$ $C$ $B_{d}$ $K$ $N_{x}$ $N_{u}$ $u_{r}$ $x$ $y$ $u_{\infty}$ $u$ $x_{\infty}$

Az $x_{\infty}$ az állapotvektor állandósult értéke, az $u_{\infty}$ pedig a beavatkozó jel értéke állandósult állapotban. Az $N_{u}$ -t tartalmazó előrecsatoló ág azért szükséges, mert nélküle nem lenne beavatkozó jel állandósult állapotban (tulajdonképpen egy integrátort helyettesít). Az $N_{x}$ ág kiszámítja az állapotváltozók célértékeit a kimenet célértékének megfelelően, így biztosítja, hogy $K$ bemenetére a hibajel érkezzen. Érdemes megjegyezni, hogy ha csak az előrecsatolást alkalmaznánk visszacsatolás nélkül, akkor is a véghelyzetbe kerülne egy idő után a rendszer (csak nem az általunk tervezett módon).

A cél tehát:

$y_{\infty} = u_{r}$

( 6.13 )

Ehhez:

$N_{x} u_{r} = x_{\infty}$

$N_{u} u_{r} = u_{\infty}$

( 6.14 )

$N_{x}$ meghatározása:

$y_{\infty} = C x_{\infty} = C N_{x} u_{r} = u_{r}$

$C N_{x} = I_{m}$

( 6.15 )

$N_{u}$ meghatározása:

$x_{\infty} = A_{d} x_{\infty} + B_{d} u_{\infty}$

$N_{x} u_{r} = A_{d} N_{x} u_{r} + B_{d} N_{u} u_{r}$

$(A_{d} - I) N_{x} + B_{d} N_{u} = 0_{n \times m}$

( 6.16 )

Összefoglalva:

$[\begin{matrix} N_{x} \\ N_{u} \end{matrix}] = {[\begin{matrix} A_{d} - I & B_{d} \\ C & 0 \end{matrix}]}^{- 1} [\begin{matrix} 0_{n \times m} \\ I_{m} \end{matrix}]$

( 6.17 )

ahol $0_{n \times m}$ egy n x m méretű csupa nullából álló mátrix, míg $I_{m}$ egy m méretű egységmátrix.

6.7.3. Állapot-megfigyelő tervezése

A valóságban sok esetben nem oldható meg, hogy az összes állapotváltozót megmérjük. Ennek oka lehet az, hogy az adott állapotváltozó mérésére nincs technikai lehetőség vagy nem mérhető elég pontosan, a mérés nem gazdaságos, vagy az állapotváltozó fizikai jelentése ismeretlen (például mesterségesen létrehozott, identifikációból kapott állapottér modellek esetén). Ilyenkor szükségünk lesz egy állapot-megfigyelőre, melynek feladata nevéből is jól érzékelhetően a rendszer állapotának meghatározása a kimenő- és bemenőjelek ismeretében, melyek mérése a legtöbb esetben jól megoldható. Az állapot-megfigyelőnek tehát két bemenete lesz: a szakasz be- ( $u$ ) és kimenete ( $y$ ), a kimenete pedig a megfigyelt állapotváltozók vektora lesz ( $x_{e s t}$ ).

Állapot-megfigyelő csak akkor alkalmazható, ha a vizsgált rendszer megfigyelhető. Megfigyelhetőség alatt azt értjük, hogy a rendszer véges időintervallumbeli bemenetének és kimenetének ismeretében meghatározható a rendszer kezdő időpontbeli állapota. Diszkrét időinvariáns rendszerek esetén ez akkor teljesül, ha a rendszer megfigyelhetőségi mátrixa maximális rangú, azaz rangja $n$ :

$rank M_{o} = rank [\begin{matrix} C \\ C A_{d} \\ \dots \\ C A_{d}^{n - 1} \end{matrix}] = n$

( 6.18 )

Az állapot-megfigyelő alakja diszkrét időben:

$x_{e s t} [k] = F x_{e s t} [k - 1] + G y [k] + H u [k - 1]$

( 6.19 )

A becslési hiba:

$x_{e r r} [k] = x [k] - x_{e s t} [k]$

( 6.20 )

Célunk az, hogy a becslési hiba nullához tartson ( $x_{e r r} [k] \to 0$ ). Helyettesítsük be az állapot-megfigyelő egyenletébe a becslési hibát és fejezzük azt ki:

$x_{e s t} [k] = x [k] - x_{e r r} [k] = F (x [k - 1] - x_{e r r} [k - 1]) + G y [k] + H u [k - 1]$

( 6.21 )

Mivel:

$x [k] = A_{d} x [k - 1] + B_{d} u [k - 1]$

$y [k] = C x [k] = C A_{d} x [k - 1] + C B_{d} u [k - 1]$

( 6.22 )

Így:

$x_{e r r} [k] = A_{d} x [k - 1] + B_{d} u [k - 1]$

$- (F (x [k - 1] - x_{e r r} [k - 1]) + G C A_{d} x [k - 1] + G C B_{d} u [k - 1] + H u [k - 1])$

( 6.23 )

Ebből:

$x_{e r r} [k] = F x_{e r r} [k - 1] + (A_{d} - F - G C A_{d}) x [k - 1] + (B_{d} - G C B_{d} - H) u [k - 1]$

( 6.24 )

A második két tag mindig nulla, ha:

$F = A_{d} - G C A_{d}$

$H = B_{d} - G C B_{d}$

( 6.25 )

Célunk továbbra is az, hogy $x_{e r r} [k] \to 0$ minél gyorsabban, ez akkor teljesül, ha a következő rendszer stabil és gyors:

$x_{e r r} [k] = F x_{e r r} [k - 1]$

( 6.26 )

Ezt $G$ megfelelő választásával biztosíthatjuk. Ehhez helyettesítsük be a becslési hiba egyenletébe $F$ -t és $H$ -t:

$x_{e r r} [k] = (A_{d} - G C A_{d}) x_{e r r} [k - 1]$

( 6.27 )

Transzponáljuk az egyenletet:

$x_{e r r}^{T} [k] = x_{e r r}^{T} [k - 1] (A_{d}^{T} - A_{d}^{T} C^{T} G^{T})$

( 6.28 )

Vessük ezt össze az állapot-visszacsatolás egyenletével:

$x [k] = (A_{d} + B_{d} K) x [k - 1]$

( 6.29 )

Láthatjuk, hogy a két egyenlet igen hasonló szerkezetű, és ezt felhasználhatjuk ahhoz, hogy $G$ értékét meghatározzuk az állapot-visszacsatolás esetén alkalmazott módszerekkel. Tekintsük a következő rendszert:

$A_{d I I} = A_{d}^{T}$

$B_{d I I} = A_{d}^{T} C^{T}$

( 6.30 )

Erre a rendszerre állapot-visszacsatolást tervezve $G$ értéke kiadódik:

$K_{I I} = G^{T}$

( 6.31 )

Még az a fontos kérdés marad, hogy hova helyezzük a pólusokat. Ennek eldöntéséhez induljunk ki az eredeti állapot-visszacsatolás tervezése során megadott legnagyobb abszolút értékű folytonos idejű pólusból, és annál válasszunk több nagyságrenddel nagyobbat. Ez utóbbinak különösen nagy szerepe lesz akkor, ha a szabályozott rendszerünk eltér a tervezéskor használt modellünktől, ugyanis ilyenkor a lassú megfigyelő instabil rendszert eredményez. Tehát alapvető követelmény, hogy a megfigyelő gyorsabb legyen, mint a megfigyelt rendszer. Ezzel az alábbi szabályozót nyerjük:

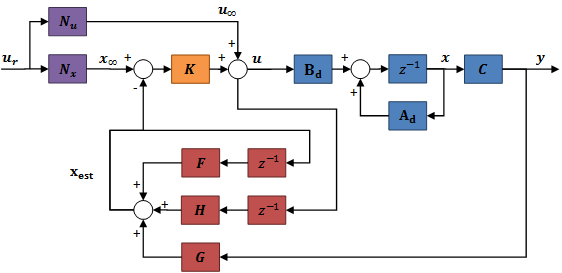
6.27. ábra - Megfigyelőre alapozott állapot-visszacsatolás

$z^{- 1}$ $A_{d}$ $C$ $B_{d}$ $K$ $N_{x}$ $N_{u}$ $u_{r}$ $x$ $y$ $u_{\infty}$ $u$ $x_{\infty}$ $F$ $G$ $H$ $z^{- 1}$ $z^{- 1}$ $x_{e s t}$

6.7.4. Integráló szabályozás

Az eddig tervezett szabályozónk nagyon jól működik elméletben: mi határozzuk meg a rendszer pólusait, megadjuk hogyan, milyen gyorsan álljon be a rendszer és nincs maradó hiba sem. Igen ám, de mi történik akkor, ha a szakasz eltér a tervezésnél használttól? Ebben az esetben egyrészt az állapot-visszacsatolásunk már nem fogja tökéletesen mozgatni a pólusokat, hiszen azok máshol vannak, mint vártuk őket, ami akár instabil rendszerhez is vezethet, és biztosan maradó hibához, hiszen az alapjel korrekció az állapot-egyenleteken alapul. Ráadásul állapot-megfigyelőnk se a valós állapotokat fogja figyelni, továbbá a zavarójel elnyomása sem megfelelő.

A maradó hibára megoldást jelent, ha a rendszerbe egy integrátort helyezünk, ezzel egyben kiválthatjuk az alapjel korrekció $N_{u} u_{r}$ részét is, hiszen az integrátor nulla hiba esetén is tud kimenetet biztosítani. Az integrátor elhelyezéséhez egy új állapotváltozó bevezetése válik szükségessé:

$x_{i} [k + 1] = x_{i} [k] + T_{s} y [k] = x_{i} [k] + T_{s} C x [k] x_{i} [k] \in ℝ^{m}$

( 6.32 )

Itt a bal oldali téglalapszabály alapján valósult meg a diszkrét idejű integrátor. Ezzel bővítsük ki a szakasz állapot-egyenletét:

$[\begin{matrix} x [k + 1] \\ x_{i} [k + 1] \end{matrix}] = [\begin{matrix} A_{d} & 0_{n \times m} \\ T_{s} C & I_{m} \end{matrix}] [\begin{matrix} x [k] \\ x_{i} [k] \end{matrix}] + [\begin{matrix} B_{d} \\ 0_{m \times r} \end{matrix}] u [k]$

$y [k] = [\begin{matrix} C & 0_{m \times m} \end{matrix}] [\begin{matrix} x [k] \\ x_{i} [k] \end{matrix}]$

( 6.33 )

Ilyenkor az állapot-visszacsatolás alakja a következő lesz:

$u [k] = - [\begin{matrix} K & K_{i} \end{matrix}] [\begin{matrix} x [k] \\ x_{i} [k] \end{matrix}]$

( 6.34 )

Ebben az esetben tehát az állapot-visszacsatolást ehhez a bővített rendszerhez tervezzük meg, majd az így kapott $K$ és $K_{i}$ mátrixokat a következőképpen alkalmazzuk:

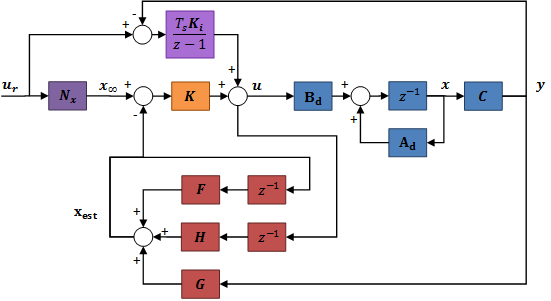
6.28. ábra - Megfigyelőre alapozott állapo-tvisszacsatolás integrátorral

$z^{- 1}$ $A_{d}$ $C$ $B_{d}$ $K$ $N_{x}$ $u_{r}$ $x$ $y$ $u$ $x_{\infty}$ $F$ $G$ $H$ $z^{- 1}$ $z^{- 1}$ $\frac{T_{s} K_{i}}{z - 1}$ $x_{e s t}$

Amint látható, az előrecsatoló $N_{u}$ -t tartalmazó ág helyét az integrátor vette át, hiszen így az integrátor biztosítja a nulla maradó hibát. Az integráló tag elhelyezése sem az alapjel-korrekció, sem az állapot-megfigyelő tervezését nem érinti.

6.7.5. A rendszer identifikációja

A szabályozó megtervezéséhez először meg kell határoznunk az irányítandó szakasz modelljét. Ennek előállítását ebben az esetben a MATLAB System Identification Toolbox segítségével végezzük el. Ez lehetőséget ad rendszerek modelljeinek mérési eredményekből való meghatározására, amelyet felhasználhatunk például szabályozó tervezéséhez is. Ennek fontos feltétele, hogy készítsünk valamilyen, a rendszert jól jellemző mérést, hiszen a program a be- és kimeneti jelek értékeiből fogja előállítani a modellt, így ha valamilyen speciális jelenség abban nem jelentkezik, az valószínűleg a modellben sem fog.

A mérés megkezdése előtt célszerű kiválasztani, hogy milyen modellt fogunk használni. Ebben az esetben a szabályozó megtervezéséhez egy diszkrét idejű állapottér modellre lenne szükség. Ez könnyen előállítható egy átviteli függvényből is. Erre a MATLAB több lehetőséget is ad, mi az úgynevezett ARMAX modellt fogjuk használni. A betűszó az „autoregressive moving-average model with exogeneous inputs” kifejezésre utal, aminek magyar jelentése: autoregresszív mozgóátlag modell külső bemenetekkel. Felmerülhet a kérdés, ha hangsúlyt kap, hogy külső bemenetek is vannak, akkor mire szolgálható anélkül a modell. Az ARMAX modell bemutatása előtt tekintsük meg két komponensét, az AR és MA modelleket. Az autoregresszív (AR) modell:

$A (z) y [k] = e [k]$

( 6.35 )

ahol:

$y [k]$ a kimenet értéke $k$ -adik időlépésben
$e [k]$ a belső bemenet, fehér zaj értéke $k$ -adik időlépésben
$A (z) = 1 + a_{1} z^{- 1} + a_{2} z^{- 2} + ... + a_{n_{a}} z^{- n_{a}}$

Ahogy az látható, egy sztochasztikus folyamat kerül leírásra. Hasonló szerkezetű a mozgóátlag (MA) modell is:

$y [k] = C (z) e [k]$

( 6.36 )

ahol $C (z) = 1 + c_{1} z^{- 1} + c_{2} z^{- 2} + ... + c_{n_{c}} z^{- n_{c}}$ . Mivel ezek a modellek nem rendelkeznek külső bemenettel, így nem alkalmasak a motor leírására, azonban a kettőt összerakva és külső bemenetekkel kibővített ARMAX modell már igen. Ennek szerkezete:

$A (z) y [k] = B (z) u [k - n_{k}] + C (z) e [k]$

( 6.37 )

ahol:

$u [k]$ a külső bemenet
$n_{k}$ a rendszer holtideje
$B (z) = b_{0} + b_{1} z^{- 1} + b_{2} z^{- 2} + ... + b_{n_{b}} z^{- n_{b}}$ , itt az első együttható nem 1, erre azért van szükség, hogy a rendszer erősítése tetszőleges lehessen

A modellben lévő fehér zaj bemenetet tartalmazó $C (z) e [k]$ tag célja a mérési hiba leképezése, ez tulajdonképpen az egyenlethiba:

$A (z) y [k] - B (z) u [k - n_{k}] = C (z) e [k]$

( 6.38 )

Ha nincs mérési hiba, akkor $e [k] = 0$ :

$A (z) y [k] = B (z) u [k - n_{k}]$

( 6.39 )

Innen az impulzusátviteli függvény:

$\frac{y [k]}{u [k - n_{k}]} = \frac{B (z)}{A (z)} = \frac{b_{0} + b_{1} z^{- 1} + b_{2} z^{- 2} + ... + b_{n_{b}} z^{- n_{b}}}{1 + a_{1} z^{- 1} + a_{2} z^{- 2} + ... + a_{n_{a}} z^{- n_{a}}}$

( 6.40 )

Az átviteli függvény felírását a MatLab elvégzi nekünk, ugyanakkor hasznos lehet a működési módjának alapszintű ismerete. Az ARMAX egyenletbe behelyettesítve az egyes értékeket paraméteresen adódik a hiba nagysága a polinomok együtthatóinak függvényében. A polinomok értéke és így az átviteli függvény úgy határozható meg, hogy a hiba négyzetét minimalizáljuk. A MatLab a holtidő értékét nem határozza meg, hanem azt nekünk kell megadni.

Az átviteli függvényből több fajta módon is létrehozhatunk állapottér modellt, például a megfigyelhetőségi vagy az irányíthatósági alakban való felírással. Ezeknél a módszereknél természetesen az állapotváltozók fizikai jelentése nem ismert, ez azonban most nem jelent hátrányt, hiszen az identifikáció miatt ez egyébként sem lenne elvárható. Alapesetben az állapottér modell felírását az alábbi átviteli függvényből kell elvégezni:

$\frac{y [k]}{u [k - 1]} = \frac{B (z)}{A (z)} = \frac{b_{0} + b_{1} z^{- 1} + b_{2} z^{- 2} + ... + b_{n - 1} z^{- n + 1}}{1 + a_{1} z^{- 1} + a_{2} z^{- 2} + ... + a_{n} z^{- n}}$

( 6.41 )

Legyen:

$x [k] = \frac{y [k]}{B (z)} = \frac{u [k - 1]}{A (z)}$

( 6.42 )

Ilyenkor:

$y [k] = B (z) x [k] = (b_{0} + b_{1} z^{- 1} + b_{2} z^{- 2} + ... + b_{n - 1} z^{- n + 1}) x [k]$

$u [k - 1] = A (z) x [k] = (1 + a_{1} z^{- 1} + a_{2} z^{- 2} + ... + a_{n} z^{- n}) x [k]$

( 6.43 )

Legyenek az állapotváltozók a következők:

$x_{1} [k] = x [k]$

$x_{2} [k] = x_{1} [k] z^{- 1}$

$\dots$

$x_{i} [k] = x_{1} [k] z^{- i} = x_{i - 1} [k] z^{- 1}$

( 6.44 )

Így:

$x [k] = u [k - 1] - a_{1} z^{- 1} x [k] - a_{2} z^{- 2} x [k] - \dots - a_{n} z^{- n} x [k]$

$x_{1} [k + 1] = u [k] - a_{1} x_{1} [k] - a_{2} x_{2} [k] - ... - a_{n} x_{n} [k]$

( 6.45 )

Tehát az állapottér modell:

$[\begin{matrix} x_{1} [k + 1] \\ x_{2} [k + 1] \\ x_{3} [k + 1] \\ \dots \\ x_{n} [k + 1] \end{matrix}] = [\begin{matrix} - a_{1} & - a_{2} & - a_{3} & \dots & - a_{n} \\ 1 & 0 & 0 & \dots & 0 \\ 0 & 1 & 0 & \dots & 0 \\ \dots & \dots & \dots & \dots \\ 0 & 0 & 0 & \dots & 0 \end{matrix}] [\begin{matrix} x_{1} [k] \\ x_{2} [k] \\ x_{3} [k] \\ \dots \\ x_{n} [k] \end{matrix}] + [\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}] u [k]$

$y [k] = [\begin{matrix} b_{0} & b_{1} & b_{2} & \dots & b_{n - 1} \end{matrix}] [\begin{matrix} x_{1} [k] \\ x_{2} [k] \\ x_{3} [k] \\ \dots \\ x_{n} [k] \end{matrix}]$

( 6.46 )

Az állapottér modell birtokában a szabályozótervezés elvégezhető.

6.7.6. A szabályozás megtervezése

Az elméleti alapok áttekintése után sor kerülhet a szabályozó megtervezésre. Ez három részre bontható fel:

Rendszer identifikációja

a szabályozó tervezés és szimuláció;
a szabályozó implementálása és tesztelése;

a motor identifikációja.

Ezek bemutatására kerül sor a következő fejezetben.

6.7.7. A motor identifikációja

6.7.7.1. A karakterisztika előzetes vizsgálata

Mielőtt az identifikációt elkezdenénk, először vizsgáljuk meg magát a szabályozandó rendszert. Az általunk alkalmazott DC motort az interneten keresztül tudjuk elérni. A rendszer segítségével C nyelven elkészíthetjük a motor bemeneti jeleit megadó szabályozót, majd ennek kódját a távoli mérőállomásra elküldve, az lefuttatja a programot, és visszaküldi a mérési eredményeket. A motor bemenete ebben az esetben az elérni kívánt nyomaték, amelyből ezután egy áramszabályozó kör számítja ki a kiadott feszültséget, így a motorra nem adhatunk a motort károsítóan nagy bemenőjelet. Az általunk szabályozott kimenőjel pedig a sebesség lesz.

Nézzük először, hogy reagál a motor konstans bemenőjel esetén, amelyet most szándékosan nagyra választva vizsgáljuk meg a maximális elérhető forgási sebességet. Legyen tehát az előírt nyomaték 100mNm:

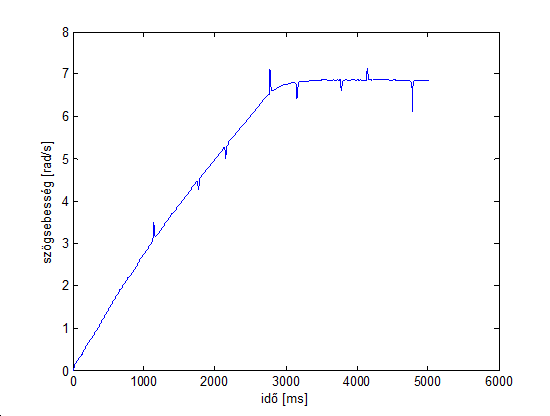
6.29. ábra - Megfigyelőre alapozott állapotvisszacsatolás integrátorral

Megjegyezzük, hogy a sebesség számítása a pozícióból numerikus deriválással és szűréssel történik. Ezért marad néhány tüske a mérési eredményben. A szűrő tervezésére majd a későbbiekben visszatérünk.

Ugyanez 3mNm esetén:

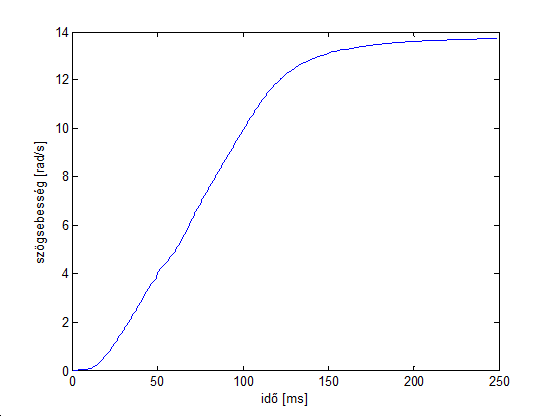
6.30. ábra - A szöbsebesség időfüggvénye

Több méréssel megállapítható, hogy kb. 14 rad/s a szögsebesség felső maximuma. Jól láthatjuk, hogy kisebb nyomaték esetén a rendszer nagyobb választ adott, ami arra utal, hogy nagy nyomatékok esetén a nyomatékszabályozás helytelenül működik.

Most nézzük ugyanezt a másik forgási irányba is (-3mNm nyomaték esetén):

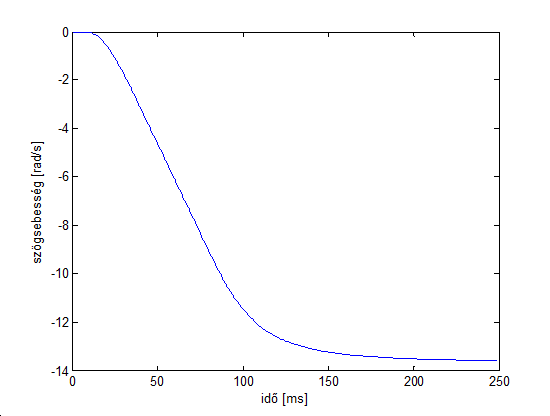
6.31. ábra - A szöbesebesség időfüggvénye

Jól látható, hogy a szögsebesség végértéke közel azonos. Hogy a rendszerről több információt nyerjünk, elvégeztünk egy kvázistatikus mérést, hogy megvizsgáljuk a nyomaték és a kimeneti sebesség közti összefüggést. A mérés során lassan, először -3mNm nyomatékot adtunk ki, és megvártuk, míg a kimenet ennek megfelelően beállt, ezután lassan növeltük a nyomatékot +3mNm eléréséig:

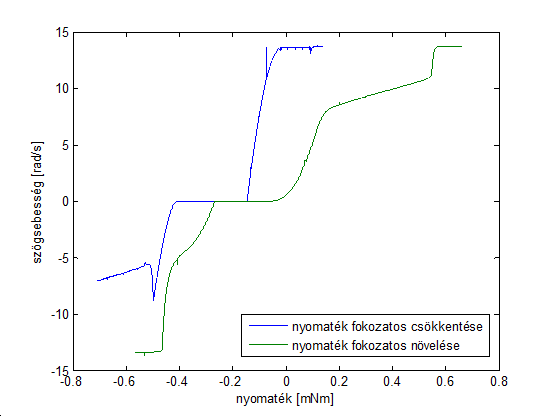
6.32. ábra - Szögsebesség nyomaték karakterisztika

Amint látható, rendszerünk igen távol áll a lineáristól:

Holtsáv: a tapadási súrlódás miatt.
Több töréspont is látható.
Hiszterézis: az is befolyásolja az eredményt, hogy milyen irányban kezdjük a mérést.

6.7.7.2. Gerjesztés megtervezése az identifikációhoz

Ahhoz, hogy szabályozónk működni tudjon, minél lineárisabb rendszerre kell törekednünk. Ennek eléréséhez használjuk fel azt, hogy a nemlineáris rendszerek adott munkapont körül általában jól linearizálhatóak. Így a szabályozó működésének bemutatása során egy precíziós sebességszabályozót készítünk. Először egy egyszerű szabályozóval a munkapont közelébe visszük a rendszert, majd onnan átadjuk azt a precíziós szabályozónknak.

Hogy a rendszer identifikációját elvégezzük, a rendszert először a kívánt munkapont közelébe visszük, majd ott adunk rá négyszögjelet, amelyre adott válasz lesz az identifikáció alapja. A kiválasztott lineáris szakasz a 0.2..0.5mNm-es lineáris szakasz. Ennek identifikációjához egy 4s periódus idejű, 0.35mNm középnyomatékú, 0.15mNm amplitúdójú négyszögjelet használtunk. A munkapontba való beállásra 2s időt hagytunk.

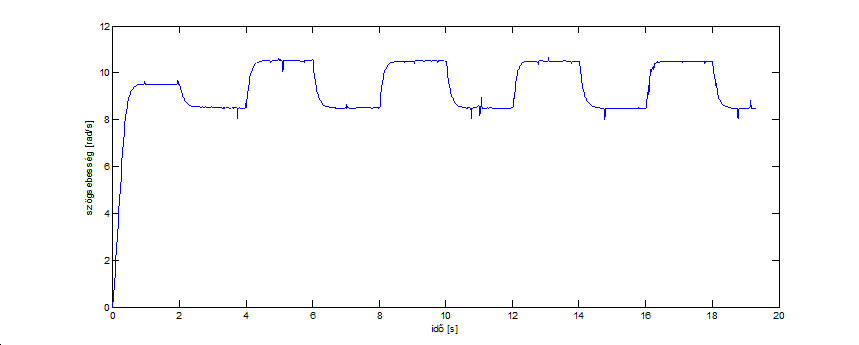
6.33. ábra - A szögsebesség változása

Amint látható, ez a kimenet már lineáris rendszer eredményének mutatkozik. A méréshez szükséges vezérlés C kódja:

typedef struct
{   
float Position;
float Velocity;
float Torque;
float StateVariable_5;
float StateVariable_6;
float StateVariable_7;
float StateVariable_8;
float StateVariable_9;
float StateVariable_10;
} NewControllerData;
NewControllerData CalculateController(
const float CurrentPosition,
const float OldPosition,
const float OldVelocity,
const float CurrentTime,
const float OldTime,
const float Old_StateVariable_5,
const float Old_StateVariable_6,
const float Old_StateVariable_7,
const float Old_StateVariable_8,
const float Old_StateVariable_9,
const float Old_StateVariable_10
)
{
NewControllerData ResultData; // result
//Szűrőegyütthatók
static float filB0 = 0, filB1 = 0.00013337, filB2 = 0.0012028, filB3 = 0.0009847099, filB4 = 7.3193E-05;
static float filA0 = 1, filA1 = -3.1152, filA2 = 3.6392, filA3 = -1.8895, filA4 = 0.36788;
//Bemeneti értékek
static float input0 = 0, input1 = 0, input2 = 0, input3 = 0, input4 = 0;
//Szűrt értékek
static float filter0 = 0, filter1 = 0, filter2 = 0, filter3 = 0, filter4 = 0;
float u;
//Nyomaték középérték
float bias = 0.35;
//Várakozás a munkapontba beállásra
int start = 2000;
//Periódusidő
int period = 4000;
//Amplitúdó
float amplitude = 0.15;
// Position is saved automatically
ResultData.Position = CurrentPosition;
// Angular velocity is saved automatically
if (CurrentTime != 0.0f){
ResultData.Velocity = (1000.0f * (float)(CurrentPosition - OldPosition)/(float)(CurrentTime - OldTime));
}
else {
ResultData.Velocity = 0.0f;
}

//Sebesség szűrése
input0 = ResultData.Velocity;
filter0 = (filB0 * input0 + filB1 * input1 + filB2 * input2 + filB3 * input3 + filB4 * input4 - (filA1 * filter1 + filA2 * filter2 + filA3 * filter3 + filA4 * filter4)) / filA0;
input4 = input3; input3 = input2; input2 = input1; input1 = input0; 
filter4 = filter3; filter3 = filter2; filter2 = filter1; filter1 = filter0; 
ResultData.StateVariable_5 = filter0; 
//Nyomaték megadása
if(CurrentTime < start)
{
u = 0; 
}
else
{
u = (((int)CurrentTime - start) % period - period / 2 > 0 ? amplitude : -amplitude);
}
ResultData.Torque = u + bias;
ResultData.StateVariable_6 = u;
return ResultData;
}

A szűrő tervezési módját a későbbiekben tárgyaljuk.

6.7.7.3. Identifikáció MATLAB segítségével

Először be kell töltenünk a mérési eredményeket a MATLAB környezetbe. A beállási szakaszt levágjuk, hiszen arra nem lesz szükség. Az identifikáció során a valódi sebesség és nyomaték helyett azok munkaponttól való különbségét használjuk, így ezek kezdő időpontban – a munkapontban – mért értékét a mérési eredményekből levonjuk. Az identifikációhoz meg kell adnunk a mintavételezési időt, ami ebben az esetben 1ms. Ezután létrehozzuk a mérést leíró adatszerkezetet a System Identification Toolbox számára az iddata parancs segítségével, amelynek meg kell adni a bemeneti és kimeneti jelek mérésének eredményét és a mintavételezési időt. Ezután következhet a polinomok fokszámának megadása az ARMAX modellhez, ezt egy sorvektorban kell megtennünk, amelynek elemei sorban: $n_{a}, n_{b} + 1, n_{c}, n_{k}$ . Az első elem adja meg az $A (z)$ polinom fokszámát, azaz az állapotváltozók számát, a második a $B (z)$ fokszámánál eggyel nagyobb, a harmadik elem $C (z)$ fokszáma, míg a negyedik a holtidő. A megadás során ügyeljünk arra, hogy $n_{a} \geq n_{b}$ és $n_{k} \geq 1$ . Bár az identifikáció igen sok polinomfokszám variáció mellett lefut, legyünk figyelemmel arra is, hogy az identifikáció bizonytalansága nő a fokszámmal, ilyenkor a MATLAB a „Warning: Pole locations are more than 10% in error.” üzenetet jeleníti meg. Ez azért fontos, mert később ezeket a pólusokat át akarjuk helyezni, ehhez pedig ki kellene ejteni őket, ami nem fog sikerülni, ha nem ott vannak, mint azt terveztük. Mivel az identifikáció csak pár másodpercig tart, így számos beállítást kipróbálhatunk. Az identifikációt az armax parancs segítségével, a mérési adatok és a polinomfokszámok megadása után végezhetjük el. A függvény eredménye az identifikált rendszert leíró struktúra, amelyből a th2poly függvénnyel megkaphatjuk a polinomokat leíró sorvektorokat. Ezekben az együtthatók csökkenő kitevőjű $z^{i}$ tagok mellett értendőek, az utolsó elem így $z^{0} = 1$ taghoz tartozik, és az eredményben lehetnek 0 együtthatók is. Mivel ezzel tulajdonképpen megkapjuk a diszkrét átviteli függvény számlálóját és nevezőjét, így az a tf függvénnyel elő is állítható. Az identifikációt elvégző MATLAB kód így:

start=1800;                                 %kezdőidőpont
y=velocity2(start:end)-velocity2(start);    %szögsebesség-mérések vektora
u=torque2(start:end)-torque2(start);        %nyomatékmérések vektora
n=3;                                        %állapotváltozók száma
Ts=0.001;                                   %mintavételezési idő megadása
z=iddata(y,u,Ts);                           %mérési adatok megadása
nn=[n,1,1,1];                               %fokszámok megadása
tharmax=armax(z,nn);                        %identifikáció
[A,B,C]=th2poly(tharmax);                   %polinomok kiolvasása
sys=tf(B,A,Ts);                             %átviteli függvény előállítása

A diszkrét idejű átviteli függvény így:

$W (z) = \frac{0.00264}{z^{3} - 2.79 z^{2} + 2.639 z - 0.8486}$

( 6.47 )

Ez persze így nem sokat mond számunkra arról, hogy ez tényleg jól leírja-e a rendszert, ezért számoljuk ki az identifikált rendszer válaszát az általunk a valós rendszernek megadott bemenetre (a nyomaték már a MATLAB importálás előtt a munkapont körül volt):

yid=idsim(tharmax,u,zeros(n,1)); %identifikált rendszer válasza

t=0:Ts:(size(y)-1)*Ts; %idővektor az ábrázoláshoz

figure(1);                                  %új grafikon

plot(t,y,t,yid); %grafikon megjelenítése

legend('mért','identifikált'); %jelmagyarázat

xlabel('idő [s]'); %vízszintes tengelycím

ylabel('szögsebesség [rad/s]'); %függőleges tengelycím

Az identifikált rendszer működését az idsim függvény segítségével ellenőrizzük, amely meghatározza a bemenetek sorvektorának és a kezdeti állapotnak megfelelő kimeneti értékeket. Ezután ezt grafikonon is könnyen ábrázolhatjuk, de ehhez szükség van egy idő sorvektorra is, amelyet a szokásos módon előállíthatunk:

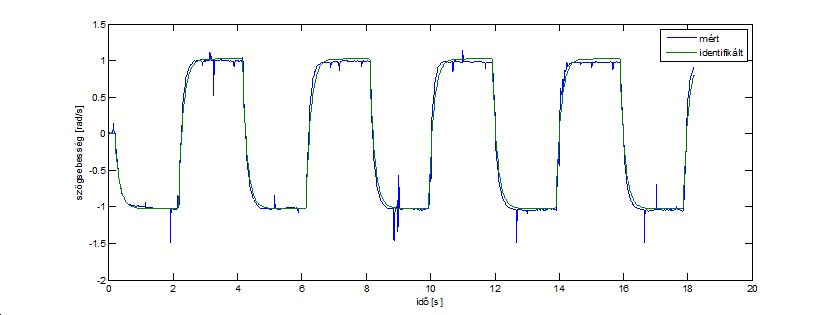
6.34. ábra - A modell és a mérés összehasonlítása

Amint az látható, az identifikált rendszer és eredeti viselkedése jól közelíti egymást. Fontos figyelembe venni, hogy az identifikációhoz használt gerjesztés ugyan tetszőleges lehet, de fontos, hogy olyan legyen, amelynek kimenete alkalmas a rendszerjellemzők megjelenítésére. Az identifikációs algoritmus a legtöbb esetben adni fog eredményt, azonban azt semmi sem garantálja, hogy ez az eredmény jól írja le a kívánt rendszert, ez ugyanis csak az adott gerjesztés esetén jelenthető ki nagyobb biztonsággal.

A szabályozó megtervezéséhez szükségünk van a rendszer diszkrét idejű állapottér modelljére, ezt az ss parancs segítségével könnyen megkaphatjuk:

sysd=ss(sys);                               %állapottér modell
[Phi Gamma C D]=ssdata(sysd);               %mátrixok kiolvasása

Ezzel készen állunk a szabályozó megtervezésére.

6.7.8. Szabályozó tervezése

6.7.8.1. Integrátor nélküli szabályozó

A szabályozó megtervezéséhez először az elméleti bevezetőnek megfelelően definiáljuk a célrendszer paramétereit, és ezekből meghatározzuk a folytonos idejű pólusokat. A jobb érthetőség kedvéért meg is jeleníthetjük a célrendszer ugrásválaszát:

a=2;                                        %hány százalékra álljunk be
Tap=0.2;                                    %szabályozási idő
xi=0.8;                                     %csillapítás
w0=log(100/a)/Tap/xi;                       %sajátfrekvencia
 
sdom1=-w0*xi+1i*w0*sqrt(1-xi^2);            %domináns pólusok
sdom2=conj(sdom1);
scinf=-4*w0;                                %segédpólusok a szabályozóhoz
soinf=scinf*5;                              %segédpólusok a megfigyelőhöz
if(-soinf>0.5/Ts)                           %Shannon-elv ellenőrzése
    display('Túl kicsi a mintavételezési idő!');
end;
 
%Célrendszer modellje egységnyi erősítéssel
tcsys=zpk([],[sdom1, sdom2, scinf*ones(1,n-2)],-w0^2*scinf^(n-2));
figure(2);                                  %új grafikon
step(tcsys);                                %ugrásválasz számítása

Az ugrásválasz:

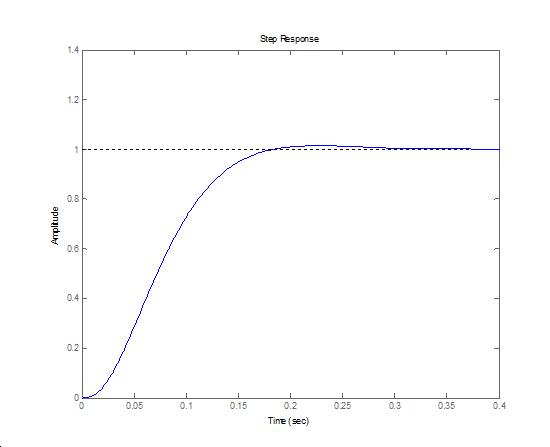
6.35. ábra - Ugrásválasz

Ezután átszámítjuk a pólusokat diszkrét időre:

%Pólusok átszámítása diszkrét időre
zdom1=exp(sdom1*Ts);                        
zdom2=exp(sdom2*Ts);
zcinf=exp(scinf*Ts);
zoinf=exp(soinf*Ts);

Ezt követően az állapot-visszacsatolás, az alapjel-korrekció és az állapot-megfigyelő az elméleti bevezető alapján már gyorsan megtervezhető:

%Az irányíthatóság ellenőrzése

Mc=ctrb(Phi,Gamma);

if rank(Mc)~=n

disp('A rendszer nem irányítható!');

end

%Állapot-visszacsatolás tervezése

phic=[zdom1 zdom2 zcinf*ones(1,n-2)]; %pólusok új helye

K=acker(Phi,Gamma,phic); %pólusáthelyezés

%Alapjel-korrekció számítása

NxNu=inv([Phi-eye(n) Gamma;C 0])*[zeros(n,1);1];

Nx=NxNu(1:n);

Nu=NxNu(n+1);

%A megfigyelhetőség ellenőrzése

Mo=obsv(Phi,C);

if rank(Mo)~=n

disp('A rendszer nem megfigyelhető!');

end

%Állapot-megfigyelő tervezése

phio=ones(1,n)*zoinf; %megfigyelő pólusai

G=acker(Phi',Phi'*C',phio)'; %pólusáthelyezés duális rsz.-en

F=Phi-G*C*Phi;

H=Gamma-G*C*Gamma;

Ezzel meg is terveztük a szabályozót. A tervezés ellenőrzéséhez végezzünk szimulációt Simulink segítségével. Építsük fel a következő modellt az elméleti bevezető alapján:

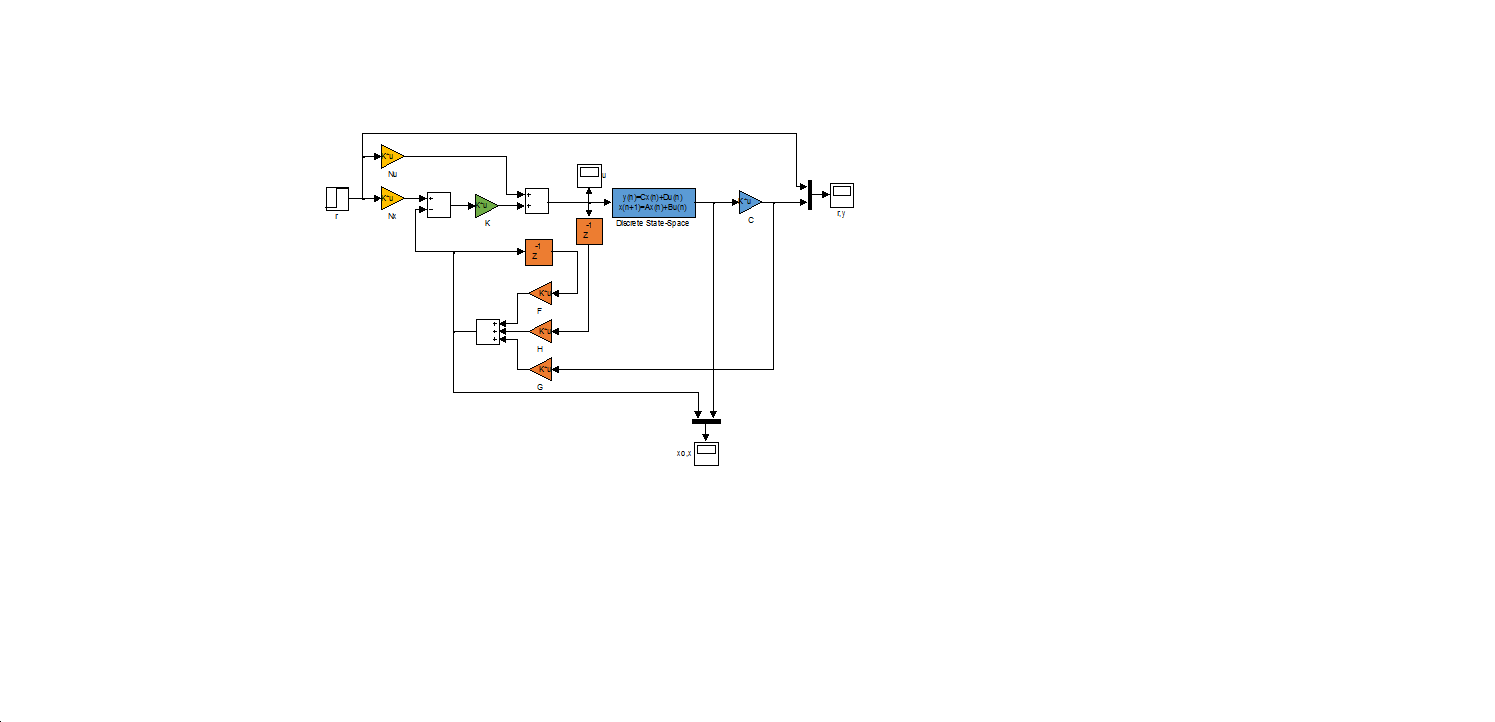
6.36. ábra - Szimulációs modell

Amint látható, a szakaszt két részre bontottuk, a diszkrét idejű állapottér modell minden állapotváltozót kivezet, ami felhasználható az állapotbecslő működésének ellenőrzésére, míg a C-t tartalmazó erősítés adja a kimeneti jelet. Ügyeljünk arra, hogy minden elem esetében megadjuk a mintavételezési idő értékét! Ezután lássuk milyen eredmények jelentek meg:

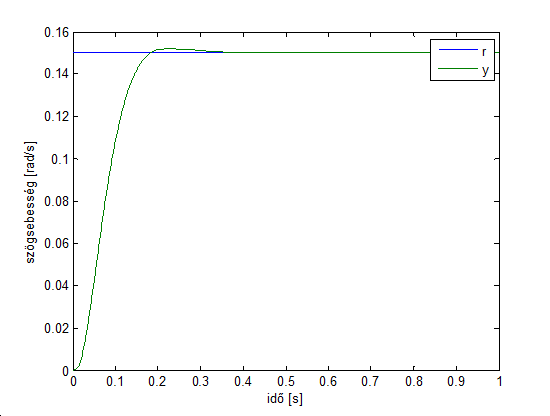
6.37. ábra - Szimulációs eredmény

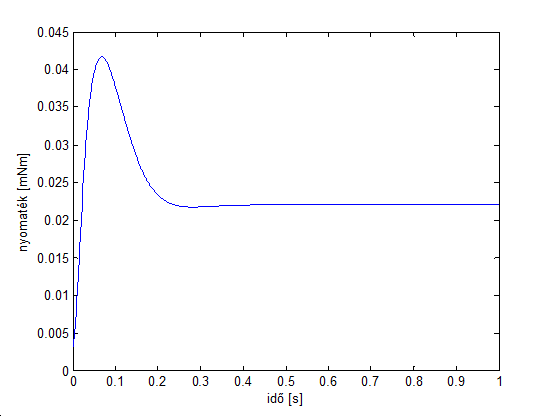
6.38. ábra - Nyomaték

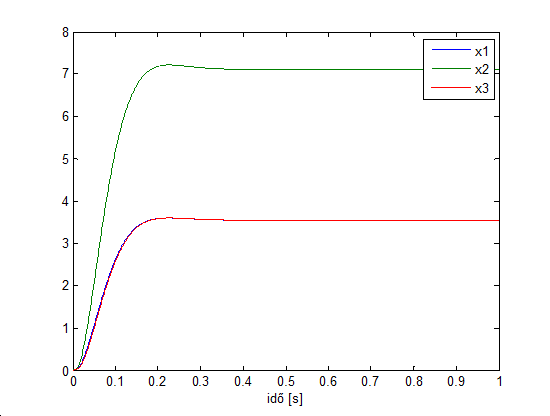
6.39. ábra - Állapotváltozók

Amint látjuk, a szabályozónk megfelelően működik. A beavatkozójel nem fut ki a lineáris tartományból.

6.7.9. Integrátoros szabályozás

Az integrátorral ellátott szabályozó megtervezése csak minimális módosításokat igényel. Először elő kell állítanunk az integrátorral bővített állapotegyenletet:

iPhi=[Phi, zeros(n,1); Ts*C, 1];
iGamma=[Gamma; 0];
iC=[C 0];

Ezenkívül szükségünk lesz még egy pólusra az állapot-visszacsatolás tervezéséhez:

siinf=scinf;                                %segédpólus integrátorhoz
ziinf=exp(siinf*Ts);
if(-min([siinf soinf])>0.5/Ts)              %Shannon-elv ellenőrzése
    display('Túl kicsi a mintavételezési idő!');
end;

Így már meg is tudjuk tervezni az állapotvisszacsatolást:

iPhic=[zdom1 zdom2 zcinf*ones(1,n-2) ziinf];%pólusok új helye
iK=acker(iPhi,iGamma,iPhic);                %pólusáthelyezés
K=iK(1:n);                                  %állapot-visszacsatolás
Ki=iK(n+1);                                 %integrátor visszacsatolása

Ezután módosítanunk kell a Simulink modellt is:

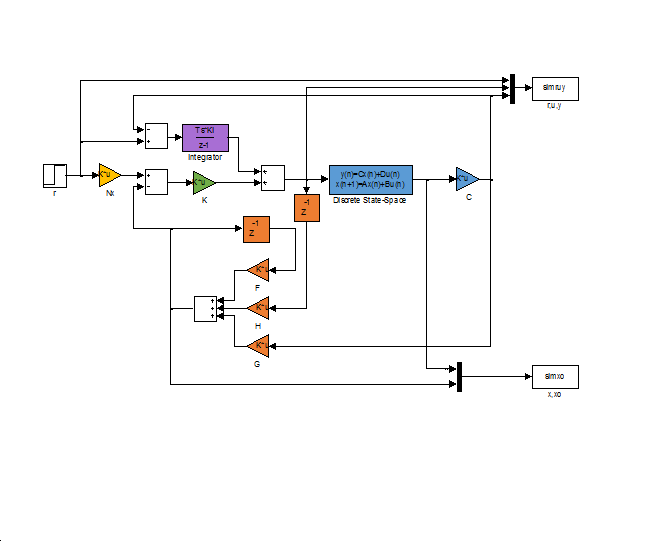
6.40. ábra - Szimulációs modell integrátorral

Ebben az esetben a szimuláció eredményeit változókban tároltuk el, hogy az eredményeket kódból ábrázolhassuk. Tekintsük meg ezeket:

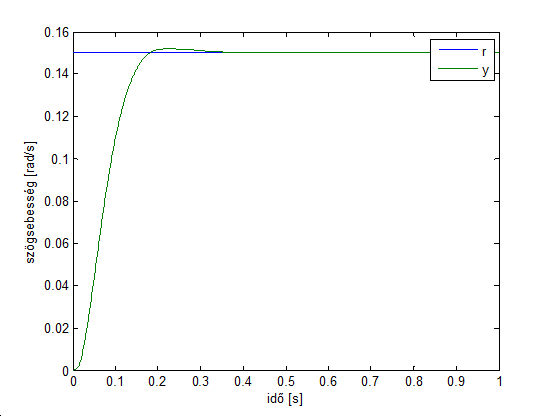
6.41. ábra - Szimulációs eredmény

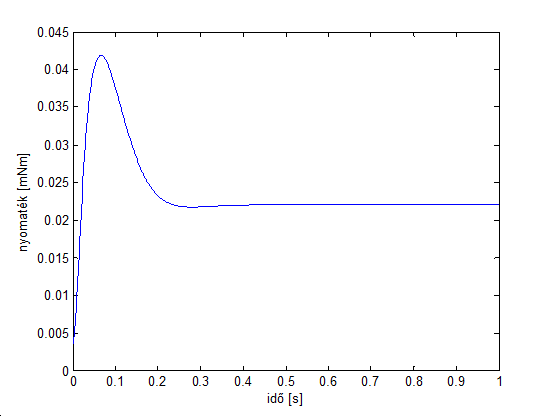
6.42. ábra - Nyomaték

Látható, hogy a rendszer válasza nem igazán változott meg. A különbség akkor jelenik meg, ha pl. feltesszük, hogy 0.01mNm-al elmértük a munkapont helyét, ilyenkor az integrátor nélküli változat válasza:

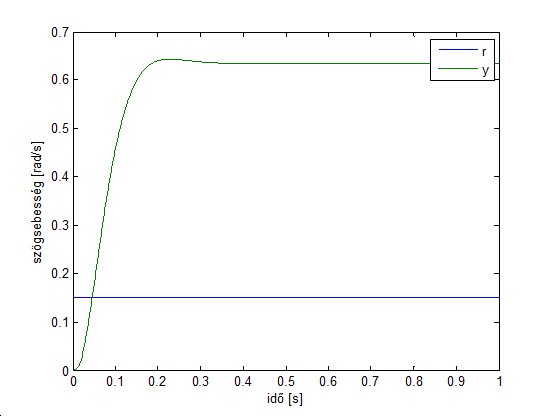
6.43. ábra - Szögsebesség

Míg az integrátoros verzióé:

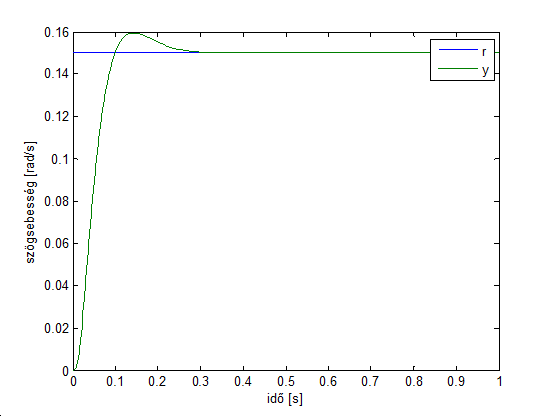
6.44. ábra - Egységugrás válasz

Látható, hogy az integrátorral már nem marad maradó hiba, a rendszer válasza közel van az ideálishoz. Ez egyben azt is mutatja, hogy az integrátor nélküli változat csak ideális esetben alkalmazható.

6.7.10. Szűrő tervezése a sebességméréshez

Mivel az általunk vizsgált rendszernél a szögsebesség a szöghelyzetből kerül meghatározásra numerikus deriválással, ezért ez mint bemenet nagyon zajos lesz. Így célszerű ezen egy szűrést is elvégezni mielőtt az állapot-megfigyelő kezébe adjuk. A szűrő megtervezése egymással ellentmondó követelmények kielégítését igényli: egyrészt minél gyorsabb szűrőre van szükség, hiszen a szűrővel bevitt késleltetés a rendszer stabilitását csökkenti, másrészt minél jobb zajszűrés kell, hiszen a zaj torzítja az állapot-megfigyelőnk működését. A legegyszerűbb szűrőt talán úgy kapjuk, hogyha sorba kapcsolunk néhány egytárolós tagot, hiszen mint ismeretes a tag pólusa után -20dB/dekád erősítésváltozással rendelkezik. Egy ilyen szűrő megtervezése egyszerűen megoldható MATLAB segítségével: mindössze a fokszámra és a pólus helyére van szükségünk. Ebből a folytonos és diszkrét átviteli függvények már könnyen előállíthatóak:

filT=0.001;                                 %Szűrő időállandója
filN=3;                                     %Szűrő fokszáma
 
%Folytonos idejű szűrő
filsys=tf(zpk([],-ones(1,filN)/filT,(1/filT)^filN));
dfilsys=c2d(filsys,Ts,'zoh');               %Diszkrét idejű verzió

A diszkrét átviteli függvény birtokában már implementálhatjuk is a szűrőt, de előtte érdemes annak működését megvizsgálni. Erre mi a szűrő Bode-diagramját, ugrásválaszát és a méréssel nyert zajos bemenetre adott válaszát használtuk:

figure(1);                                  
dbode(dfilsys.num{1},dfilsys.den{1},Ts)     %Dode diagram
 
figure(2);
step(dfilsys);                              %Ugrásválasz
 
figure(3);
v=velocity(start:end)-velocity(start);      %Zajos jel
lsim(dfilsys,v,t);                          %Zajos jel szűrése

Az eredmények:

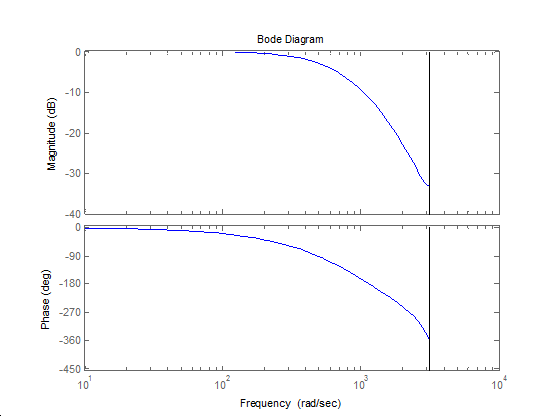
6.45. ábra - Bode-diagram

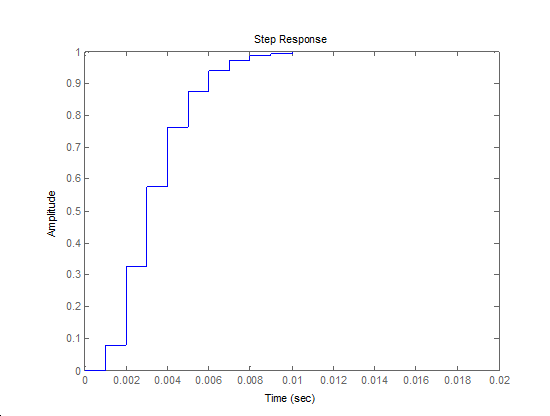
6.46. ábra - Ugrás válasz

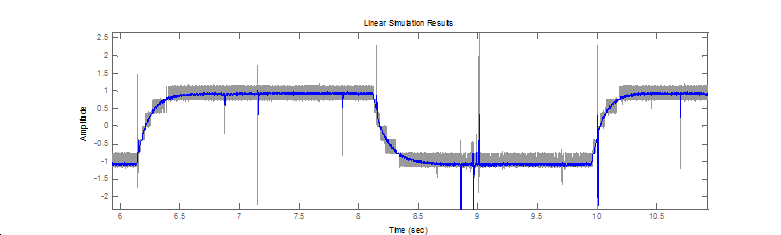
6.47. ábra - Szűrés

6.7.11. Implementáció

A szabályozó integrálása C nyelven nem különösebben nehéz feladat, az egyetlen komolyabb probléma, hogy az internetes tesztkörnyezet számos korlátozást alkalmaz. Többek között nincs lehetőségünk tömbök használatára, nem definiálhatunk saját függvényeket és globális változókat sem. Ezért erősen javasolt egy program elkészítése, amely a MATLAB kódokat átalakítja C kóddá, így könnyebben tesztelhetjük munkánkat. Ezt kívánja bemutatni a függelékben bemutatott segédprogram.

Az implementáció módját különösebben nem részletezzük, amennyiben az olvasó rendelkezik alapvető C programozási tudással, úgy a szabályozók implementálása nem okozhat gondot a Simulink modellek alapján.

6.7.12. Integrátor nélküli szabályozó

6.7.12.1. C kód

#include <windows.h>
#include <stdio.h>
#include <rtapi.h>
#include <math.h>
#include <string.h>
#define PI 3.14159265358979323846
typedef struct
{   
float Position;
float Velocity;
float Torque;
float StateVariable_5;
float StateVariable_6;
float StateVariable_7;
float StateVariable_8;
float StateVariable_9;
float StateVariable_10;
} NewControllerData;
NewControllerData CalculateController(
const float CurrentPosition,
const float OldPosition,
const float OldVelocity,
const float CurrentTime,
const float OldTime,
const float Old_StateVariable_5,
const float Old_StateVariable_6,
const float Old_StateVariable_7,
const float Old_StateVariable_8,
const float Old_StateVariable_9,
const float Old_StateVariable_10
)
{
NewControllerData ResultData; // result
static float filB0 = 0, filB1 = 0.080301, filB2 = 0.1544, filB3 = 0.017881;
static float filA0 = 1, filA1 = -1.1036, filA2 = 0.40601, filA3 = -0.049787;
static float input0 = 0, input1 = 0, input2 = 0, input3 = 0;
static float filter0 = 0, filter1 = 0, filter2 = 0, filter3 = 0;
static float Nu0_0 = 0.14662;
static float Nx0_0 = 23.677, Nx1_0 = 47.353, Nx2_0 = 23.677;
static float K0_0 = -1.2522, K0_1 = 0.81068, K0_2 = -0.37451;
static float F0_0 = 2.7896, F0_1 = -1.889, F0_2 = 0.84863, F1_0 = 2, F1_1 = -0.94991, F1_2 = 0, F2_0 = 0, F2_1 = 0.13587, F2_2 = 0;
static float G0_0 = 26.977, G1_0 = 44.981, G2_0 = 17.242;
static float H0_0 = 0.0625, H1_0 = 0, H2_0 = 0;
static float Gamma0_0 = 0.0625, Gamma1_0 = 0, Gamma2_0 = 0;
static float Phi0_0 = 2.7896, Phi0_1 = -1.3193, Phi0_2 = 0.84863, Phi1_0 = 2, Phi1_1 = 0, Phi1_2 = 0, Phi2_0 = 0, Phi2_1 = 0.5, Phi2_2 = 0;
static float C0_0 = 0, C0_1 = 0, C0_2 = 0.042236;
static float r = 0;
static float xu = 0;
static float xuL = 0;
static float xk0 = 0, xk1 = 0, xk2 = 0;
static float xkL0 = 0, xkL1 = 0, xkL2 = 0;
static float y = 0;
// Position is saved automatically
ResultData.Position = CurrentPosition;
// Angular velocity is saved automatically
if (CurrentTime != 0.0f){
ResultData.Velocity = (1000.0f * (float)(CurrentPosition - OldPosition)/(float)(CurrentTime - OldTime));
}
else {
ResultData.Velocity = 0.0f;
}
                    
r=sin(CurrentTime/1000)/2-1;
input0 = ResultData.Velocity;
filter0 = (filB0 * input0 + filB1 * input1 + filB2 * input2 + filB3 * input3 - (filA1 * filter1 + filA2 * filter2 + filA3 * filter3)) / filA0;
input3 = input2; input2 = input1; input1 = input0; 
filter3 = filter2; filter2 = filter1; filter1 = filter0; 
if(CurrentTime < 2000) ResultData.Torque =   3.5000e-001;
else 
{
y = filter0 +   -9.5218e+000;
xk0 = F0_0 * xkL0 + F0_1 * xkL1 + F0_2 * xkL2 + H0_0 * xuL + G0_0 * y;
xk1 = F1_0 * xkL0 + F1_1 * xkL1 + F1_2 * xkL2 + H1_0 * xuL + G1_0 * y;
xk2 = F2_0 * xkL0 + F2_1 * xkL1 + F2_2 * xkL2 + H2_0 * xuL + G2_0 * y;
xu = Nu0_0 * r + K0_0 * (Nx0_0 * r - xk0) + K0_1 * (Nx1_0 * r - xk1) + K0_2 * (Nx2_0 * r - xk2);
if(xu > 1) xu = 1;
if(xu < -1) xu = -1;
ResultData.Torque = xu +   3.5000e-001;
xuL = xu;
xkL0 = xk0;
xkL1 = xk1;
xkL2 = xk2;
}
ResultData.StateVariable_5 = r;
ResultData.StateVariable_6 = y;  
return ResultData;
}

6.7.13. Eredmények

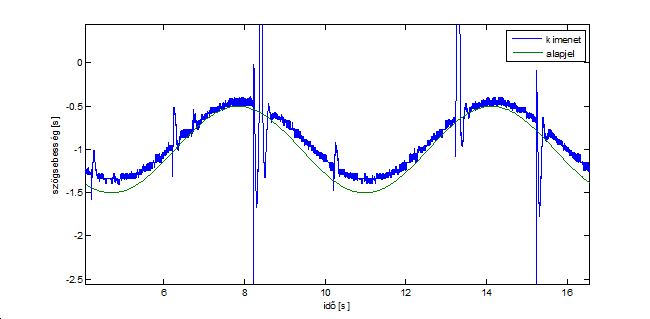
6.48. ábra - Mérési eredmény integrátor nélkül

Amint az látható, a szabályozó jól követi a referenciajelet annak ellenére is, hogy nincs integrátor a körben, és a valós rendszer is eltér a tervezettől. Az is észlelhető, hogy távolodva a munkaponttól az alapjel és a kimenet eltérése nő.

6.7.14. Integrátoros szabályozó

6.7.14.1. C kód

#include <windows.h>
#include <stdio.h>
#include <rtapi.h>
#include <math.h>
#include <string.h>
#define PI 3.14159265358979323846
typedef struct
{   
float Position;
float Velocity;
float Torque;
float StateVariable_5;
float StateVariable_6;
float StateVariable_7;
float StateVariable_8;
float StateVariable_9;
float StateVariable_10;
} NewControllerData;
NewControllerData CalculateController(
const float CurrentPosition,
const float OldPosition,
const float OldVelocity,
const float CurrentTime,
const float OldTime,
const float Old_StateVariable_5,
const float Old_StateVariable_6,
const float Old_StateVariable_7,
const float Old_StateVariable_8,
const float Old_StateVariable_9,
const float Old_StateVariable_10
)
{
NewControllerData ResultData; // result
static float filB0 = 0, filB1 = 0.080301, filB2 = 0.1544, filB3 = 0.017881;
static float filA0 = 1, filA1 = -1.1036, filA2 = 0.40601, filA3 = -0.049787;
static float input0 = 0, input1 = 0, input2 = 0, input3 = 0;
static float filter0 = 0, filter1 = 0, filter2 = 0, filter3 = 0;
static float Nu0_0 = 0.14662;
static float Nx0_0 = 23.677, Nx1_0 = 47.353, Nx2_0 = 23.677;
static float K0_0 = 0.2386, K0_1 = -0.5816, K0_2 = 0.9255, K0_3 = 1.9278;
static float F0_0 = 2.7896, F0_1 = -1.889, F0_2 = 0.84863, F1_0 = 2, F1_1 = -0.94991, F1_2 = 0, F2_0 = 0, F2_1 = 0.13587, F2_2 = 0;
static float G0_0 = 26.977, G1_0 = 44.981, G2_0 = 17.242;
static float H0_0 = 0.0625, H1_0 = 0, H2_0 = 0;
static float Gamma0_0 = 0.0625, Gamma1_0 = 0, Gamma2_0 = 0;
static float Phi0_0 = 2.7896, Phi0_1 = -1.3193, Phi0_2 = 0.84863, Phi1_0 = 2, Phi1_1 = 0, Phi1_2 = 0, Phi2_0 = 0, Phi2_1 = 0.5, Phi2_2 = 0;
static float C0_0 = 0, C0_1 = 0, C0_2 = 0.042236;
static float r = 0;
static float xu = 0;
static float xuL = 0;
static float xk0 = 0, xk1 = 0, xk2 = 0;
static float xkL0 = 0, xkL1 = 0, xkL2 = 0;
static float y = 0;
static float i = 0;
// Position is saved automatically
ResultData.Position = CurrentPosition;
// Angular velocity is saved automatically
if (CurrentTime != 0.0f){
ResultData.Velocity = (1000.0f * (float)(CurrentPosition - OldPosition)/(float)(CurrentTime - OldTime));
}
else {
ResultData.Velocity = 0.0f;
}
                    
r=sin(CurrentTime/1000)/2-1;
input0 = ResultData.Velocity;
filter0 = (filB0 * input0 + filB1 * input1 + filB2 * input2 + filB3 * input3 - (filA1 * filter1 + filA2 * filter2 + filA3 * filter3)) / filA0;
input3 = input2; input2 = input1; input1 = input0; 
filter3 = filter2; filter2 = filter1; filter1 = filter0; 
if(CurrentTime < 2000) ResultData.Torque =   3.5000e-001;
else {
y = filter0 +   -9.5218e+000;
xk0 = F0_0 * xkL0 + F0_1 * xkL1 + F0_2 * xkL2 + H0_0 * xuL + G0_0 * y;
xk1 = F1_0 * xkL0 + F1_1 * xkL1 + F1_2 * xkL2 + H1_0 * xuL + G1_0 * y;
xk2 = F2_0 * xkL0 + F2_1 * xkL1 + F2_2 * xkL2 + H2_0 * xuL + G2_0 * y;
i += 0.0019278 * (r - y);
xu = i + K0_0 * (Nx0_0 * r - xk0) + K0_1 * (Nx1_0 * r - xk1) + K0_2 * (Nx2_0 * r - xk2);
if(xu > 1) xu = 1;
if(xu < -1) xu = -1;
ResultData.Torque = xu +   3.5000e-001;
xuL = xu;
xkL0 = xk0;
xkL1 = xk1;
xkL2 = xk2;
}
ResultData.StateVariable_5 = r;
ResultData.StateVariable_6 = y;  
return ResultData;
}

6.7.15. Eredmények

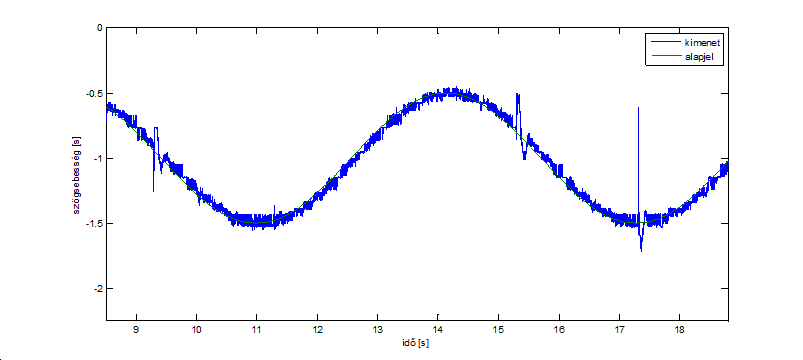
6.49. ábra - Mérési eredmény integrátorral

Ez a szabályozó is helyesen működik, az alapjelet jól követi a kimeneti jel. Az ábrán jól látható, hogy az integrátor hatására megszűnt az eltérés az alapjeltől.

6.7.16. Program kód

6.7.16.1. A szabályozótervezés teljes MATLAB kódja

%% Beállítások
integrator=true;
idplots=true;
stateplots=true;
outplots=true;
filterdesign=true;
%% Identifikáció
start=1800;                                 %kezdőidőpont
y=velocity2(start:end)-velocity2(start);    %szögsebesség-mérések vektora
u=torque2(start:end)-torque2(start);        %nyomatékmérések vektora
 
n=3;                                        %állapotváltozók száma
Ts=0.001;                                   %mintavételezési idő
z=iddata(y,u,Ts);                           %mérési adatok megadása
nn=[n,1,1,1];                               %fokszámok megadása
tharmax=armax(z,nn);                        %identifikáció
[A,B,C]=th2poly(tharmax);                   %polinomok kiolvasása
sys=tf(B,A,Ts);                             %átviteli függvény előállítása
 
yid=idsim(tharmax,u,zeros(n,1));            %identifikált rendszer válasza
t=0:Ts:(size(y)-1)*Ts;                      %idővektor az ábrázoláshoz
if(idplots)
figure(1);                                  %új grafikon
plot(t,y,t,yid);                            %grafikon megjelenítése
legend('mért','identifikált');              %jelmagyarázat
xlabel('idő [s]');                          %vízszintes tengelycím
ylabel('szögsebesség [rad/s]');             %függőleges tengelycím
end;
sys
 
%% Szűrő tervezése
if(filterdesign)
filT=0.001;                                 %Szűrő időállandója
filN=3;                                     %Szűrő fokszáma
 
%Folytonos idejű szűrő
filsys=tf(zpk([],-ones(1,filN)/filT,(1/filT)^filN));
dfilsys=c2d(filsys,Ts,'zoh');               %Diszkrét idejű verzió
 
figure(1);                                  
dbode(dfilsys.num{1},dfilsys.den{1},Ts)     %Bode-diagram
 
figure(2);
step(dfilsys);                              %Ugrásválasz
 
figure(3);
v=velocity(start:end)-velocity(start);      %Zajos jel
lsim(dfilsys,v,t);                          %Zajos jel szűrése
end;
%% Szabályozó tervezés
sysd=ss(sys);                               %állapottér modell
[Phi Gamma C D]=ssdata(sysd);               %mátrixok kiolvasása
 
a=2;                                        %hány százalékra álljunk be
Tap=0.2;                                    %szabályozási idő
xi=0.8;                                     %csillapítás
w0=log(100/a)/Tap/xi;                       %sajátfrekvencia
 
sdom1=-w0*xi+1i*w0*sqrt(1-xi^2);            %domináns pólusok
sdom2=conj(sdom1);
scinf=-4*w0;                                %segédpólusok a szabályozóhoz
soinf=scinf*5;                              %segédpólusok a megfigyelőhöz
siinf=scinf;                                %segédpólus integrátorhoz
%Shannon-elv ellenőrzése
if(-soinf>0.5/Ts || (integrator && -min([siinf soinf])>0.5/Ts))                          
    display('Túl kicsi a mintavételezési idő!');
end;
 
%Célrendszer modellje egységnyi erősítéssel
if(idplots)
tcsys=zpk([],[sdom1, sdom2, scinf*ones(1,n-2)],-w0^2*scinf^(n-2));
figure(2);                                  %új grafikon
step(tcsys);                                %ugrásválasz számítása
end;
 
%Pólusok átszámítása diszkrét időre
zdom1=exp(sdom1*Ts);                        
zdom2=exp(sdom2*Ts);
zcinf=exp(scinf*Ts);
zoinf=exp(soinf*Ts);
ziinf=exp(siinf*Ts);
 
%Az irányíthatóság ellenőrzése
Mc=ctrb(Phi,Gamma);
if rank(Mc)~=n
   disp('A rendszer nem irányítható!');
end
 
%Állapot-visszacsatolás tervezése
if(integrator)
iPhi=[Phi, zeros(n,1); Ts*C, 1];
iGamma=[Gamma; 0];
iC=[C 0];
iPhic=[zdom1 zdom2 zcinf*ones(1,n-2) ziinf];%pólusok új helye
iK=acker(iPhi,iGamma,iPhic);                %pólusáthelyezés
K=iK(1:n);                                  %állapot-visszacsatolás
Ki=iK(n+1);                                 %integrátor visszacsatolása
else
phic=[zdom1 zdom2 zcinf*ones(1,n-2)];       %pólusok új helye
K=acker(Phi,Gamma,phic);                    %pólusáthelyezés
end
 
%Alapjel-korrekció számítása
NxNu=inv([Phi-eye(n) Gamma;C 0])*[zeros(n,1);1];
Nx=NxNu(1:n);
Nu=NxNu(n+1);
 
%A megfigyelhetőség ellenőrzése
Mo=obsv(Phi,C);
if rank(Mo)~=n
   disp('A rendszer nem megfigyelhető!');
end
 
%Állapot-megfigyelő tervezése
phio=ones(1,n)*zoinf;                       %megfigyelő pólusai
G=acker(Phi',Phi'*C',phio)';                %pólusáthelyezés duális rsz.-en
F=Phi-G*C*Phi;
H=Gamma-G*C*Gamma;
 
 
%% Szimuláció
if(integrator)
    open('szabint');
    sim('szabint');
else
    open('szab');
    sim('szab');
end;
rout=simruy(:,1);
uout=simruy(:,2);
yout=simruy(:,3);
tout=[0; tout];
 
if(outplots)
figure(3);
plot(tout,rout,tout,yout);
xlabel('idő [s]');
ylabel('szögsebesség [rad/s]');
legend('r','y');
 
figure(4);
plot(tout,uout);
xlabel('idő [s]');
ylabel('nyomaték [mNm]');
end;
 
if(stateplots)
figure(5);
plot(tout,simxo(:,1:n));
xlabel('idő [s]');
ylabel('');
legend('x1','x2','x3');
 
figure(6);
plot(tout,simxo(:,n+1:2*n));
xlabel('idő [s]');
ylabel('');
legend('x1','x2','x3');
end;

Vissza		Előre
5. fejezet - Szervomotor szabályozási körének internetes távmérése (Laboratóriumi mérési gyakorlatok leírása)	Főoldal	7. fejezet - Csővezeték hálózatban használt frekvenciaváltóval ellátott aszinkron motoros hajtások gazdasági számítása