8. fejezet - Háromfázisú aszinkron motor matematikai modellezése
Vissza		Előre

8. fejezet - Háromfázisú aszinkron motor matematikai modellezése

Tartalom

A motor matematikai modellje, azaz a motor működését és jellemző tulajdonságait reprezentáló egyenletrendszer a térfazor-elmélet alapján alkotható meg, amely a váltakozó áramú villamos gépek matematikai modellezésében és mezőorientált vektoriális szabályozásukban használatos módszer[49].

Az elmélet kialakulásához az vezetett, hogy az egyenáramú gépek vizsgálata és szabályozása során nem okoz gondot a motor főmezőt alkotó fluxusáért és nyomatékáért felelős áramok szétcsatolása és külön történő kezelése, mivel a mennyiségek közti szétcsatolás a motortípus konstrukciójának köszönhetően természetesen létrejön. A váltakozó áramú motoroknál azonban a fluxust és a nyomatékot előidéző áramok nincsenek természetes úton szétválasztva, így mind a szabályozás, mind a modell meglehetősen bonyolulttá válik, hiszen háromfázisú, nemlineáris, többváltozós differenciálegyenlet rendszerrel írható le. A szétcsatolás a térfazor-elméletnek köszönhetően a váltakozó áramú motorok esetében is megtehető, így a motor vizsgálata és üzemeltetése leegyszerűsödik.

A háromfázisú váltakozó áramú gépek térfazor-elméleten alapuló, általános jelleggel rendelkező, tranziens üzemmódra is érvényes, merőleges kétfázisú matematikai modellezésének az alapja fázis- és koordináta-transzformáció. A fázis transzformáció komplex, kétfázisú rendszert, a koordináta-transzformáció pedig mezőorientáció útján egyenáramú matematikai modellt eredményez az áramok közti szétcsatolást mesterségesen létrehozva.

A matematikai modellezés első lépése a háromfázisú gép összefüggéseinek megadása egyetlen eredő vektormennyiséggel, az úgynevezett Park-vektorral vagy térfazorral, amely tartalmazza mindhárom fázisösszetevő pillanatnyi értékét[50].

A fázisfeszültségek egyenletei, az a fázist szögreferenciának, azaz 0°-nak vett koordináta-rendszerben felírva:

$u_{s a} (t) = U_{a} \cdot \sin (ω t) = i_{s a} \cdot R_{s a} + \frac{d Ψ_{s a}}{d t}$

(8.1)

$u_{s b} (t) = U_{b} \cdot \sin (ω t - 120 °) = i_{s b} \cdot R_{s b} + \frac{d Ψ_{s b}}{d t}$

(8.2)

$u_{s c} (t) = U_{c} \cdot \sin (ω t - 240 °) = i_{s c} \cdot R_{s c} + \frac{d Ψ_{s c}}{d t}$

(8.3)

ahol az usa, usb, usc időfüggvények a térbeli helyzetet nem írják le. Mindhárom feszültségegyenlet egy-egy tekercset ír le, emiatt a leírt fázis rezisztív részén eső feszültség, valamint a fázistekercs fluxusának változása által indukált feszültség szerepel bennük. A fázisok ohmos ellenállásait egyenlőnek tekintjük.

8.1. ábra - Aszinkron motor felépítésének egyszerűsített, elvi rajza

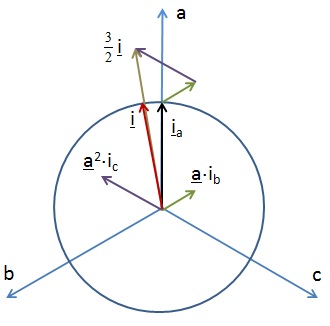
A feszültség Park-vektora a fázismennyiségek felhasználásával:

${\underline{u}}_{s} = \frac{2}{3} (\underline{1} \cdot u_{s a} + \underline{a} \cdot u_{s b} + {\underline{a}}^{2} \cdot u_{s c})$

(8.4)

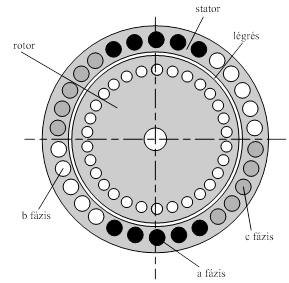
ahol 1 a háromfázisú koordináta-rendszer a fázistengelyének, a=ej120° és a2=ej240° a b és c fázistengelyeinek irányába eső egységvektorok (8-2. ábra).

A háromfázisú váltakozó áramú gépek egyik leggyakrabban használt típusa az aszinkron motor, melynek általános összefüggései felírhatók térfazoriális formában. A motor állórész egyenlete állórészhez, a forgórész egyenlete pedig forgórészhez rögzített koordináta rendszerben értelmezendő.

${\underline{u}}_{s} = R_{s} {\underline{i}}_{s} + \frac{d {\underline{Ψ}}_{s}}{d t}$

(8.5)

Az (8.5) összefüggés az (8.1)–(8.3) összefüggések (8.4) feszültség Park-vektorba történő behelyettesítésüket követően kapható meg.

8.2. ábra - A háromfázisú eredővektor képzése

A három állórész áram és csatolt fluxus szintén Park-vektor alakban felírható, így az (8.5)-ben azoknak szintén háromfázisú eredő vektoruk szerepel. A forgórész feszültség egyenlete szintén megadható egyetlen eredő vektormennyiséggel (8.6).

${\underline{u}}_{r} = R_{r} {\underline{i}}_{r} + \frac{d {\underline{Ψ}}_{r}}{d t}$

(8.6)

Hasonlóképpen a feszültség egyenletekhez a csatolt fluxus is felírható eredővektoros formában felhasználva az állórész és forgórész áramok Park-vektor alakját. A forgórész áramvektort tartalmazó tag az állórész és a forgórész között értelmezett kölcsönös induktivitások miatt jelentkezik az állórész fluxusban, míg ugyanezen okból jelentkezik az állórész áramvektort tartalmazó tag a forgórész fluxusban [51].

${\underline{ψ}}_{s} = {\underline{i}}_{s} \cdot L_{s} + {\underline{i}}_{r} \cdot e^{j θ} \cdot L_{m}$

(8.7)

${\underline{ψ}}_{r} = {\underline{i}}_{r} \cdot L_{r} + {\underline{i}}_{s} \cdot e^{- j θ} \cdot L_{m}$

(8.8)

Az állórészbe betáplált háromfázisú, időben és térben egymáshoz képest 120°-kal eltolt áram az állórészben Ψs, a forgórészben pedig indukció útján Ψr csatolt fluxust hoz létre. Mind az állórészben, mind a forgórészben létrejövő fluxusoknak záródnak erővonalai úgy, hogy nem metszik a forgórészt illetve az állórészt, azaz csak az állórész vagy csak a forgórész tekercseléshez kapcsolódnak (8-3. ábra). A légrés jelenléte miatt természetes, hogy tökéletes csatolás nem jöhet létre. Ezek a csupán saját tekercselésükhöz kapcsolódó mennyiségek az úgynevezett szórt fluxusok. Ebből következően a szakirodalomban Ψm -ként bevezetett légrés fluxus értéke kisebb lesz az állórész és a forgórész fluxusoknál. A definíció szerint a forgórész fluxusa megegyezik a légrés fluxus és a forgórész szórt fluxusának összegével (8.9), ugyanígy az állórész fluxusa megegyezik a légrés fluxus és az állórész szórt fluxusának összegével (8.10).

${\underline{ψ}}_{r} = {\underline{ψ}}_{m} + {\underline{ψ}}_{σ r}$

(8.9)

${\underline{ψ}}_{s} = {\underline{ψ}}_{m} + {\underline{ψ}}_{σ s}$

(8.10)

8.3. ábra - Fluxus eloszlás az aszinkron motorban

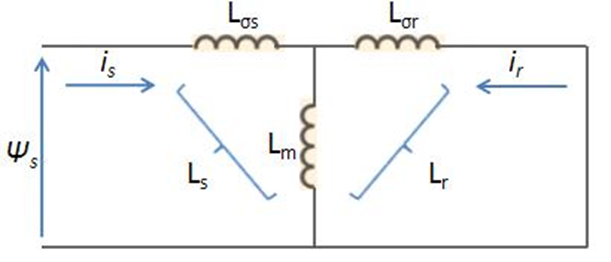
A fluxusok a hozzájuk tartozó induktivitások és az induktivitásokon átfolyó áramok kapcsolatával írhatók fel. Ez alapján megkülönböztethető állórész (Ls), forgórész (Lr) és légrés induktivitás (Lm).

A fluxusoknál tapasztalt és bevezetésre került szórt értékek természetesen az induktivitásokban jelennek meg, így létezik az állórésznek és a forgórésznek szórt induktivitása, melyeket rendre Lσs és Lσr jelölnek (8-4. ábra). Ezek alapján az induktivitások a következőképpen kerülnek bevezetésre:

$L_{r} = L_{σ r} + L_{m}$

(8.11)

$L_{s} = L_{σ s} + L_{m}$

(8.12)

Az induktivitások bevezetésének köszönhetően az (8.9) és (8.10) fluxusok a következők szerint írhatók fel:

${\underline{ψ}}_{m} = L_{m} {\underline{i}}_{m}$

(8.13)

${\underline{ψ}}_{s} = {\underline{ψ}}_{m} + L_{σ s} {\underline{i}}_{s}$

(8.14)

${\underline{ψ}}_{s} = {\underline{ψ}}_{m} + L_{σ r} {\underline{i}}_{r}$

(8.15)

Az induktivitások arányára a szakirodalomban bevezetésre került egy mennyiség, amelynek neve szivárgási tényező. A σ teljes szivárgási tényező értéke (8.16) alapján számolható.

$σ = 1 - \frac{L_{m}^{2}}{L_{r} L_{s}}$

(8.16)

A teljes szivárgási tényező megadja, hogy az állórész induktivitás és a forgórész induktivitás együttesen miként aránylik a légrés induktivitáshoz. Az (8.16) kifejezésben látható törtben szerepel az Lm/Lr és az Lm/Ls aránya is. Ezek az arányszámok azt fejezik ki, hogy a légrésben létrejövő csatolt fluxus az állórészben és a forgórészben kialakuló csatolt fluxusoknál mennyivel kisebb érték. A teljes szivárgási tényezőn kívül az állórésznek és a forgórésznek külön-külön is felírható a szivárgási tényezője, méghozzá (8.17) és (8.18) kifejezések szerint.

$σ_{r} = \frac{L_{σ r}}{L_{m}}$

(8.17)

$σ_{s} = \frac{L_{σ s}}{L_{m}}$

(8.18)

8.4. ábra - Induktivitások modellezése

8.1. A villamos modell közös koordináta-rendszer reprezentációja

A felírt Park-vektorok felbonthatók két, egymásra merőleges összetevőre, így létrejön a háromfázisú rendszerből az α - β kétfázisú rendszerbe történő áttérés (fázistranszformáció).

$[\begin{matrix} u_{α} \\ u_{β} \\ u_{γ} \end{matrix}] = \frac{2}{3} [\begin{matrix} 1 & - \frac{1}{2} & - \frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & - \frac{\sqrt{3}}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}] \cdot [\begin{matrix} u_{s a} \\ u_{s b} \\ u_{s c} \end{matrix}]$

(8.19)

Az uγ a háromfázisú rendszer aszimmetriájából adódó zérusrendű összetevő, amely csillagkapcsolású motor esetén a csillagponton megjelenő zérusrendű feszültség a földpotenciálhoz képest viszonyítva.

A kétfázisú, álló koordinátarendszerben a térfazoriális formában felírt összefüggések α illetve β komponensekre bontva felírhatók, de célszerű a fázistranszformációt követően azonnal elvégezni a koordináta-rendszer transzformációját is [52], így a motor állórészébe táplált forgó mezővel szinkron forgó kétfázisú koordináta-rendszerbe transzformálva az egymásra merőleges összetevőket (8-5. ábra).

$[\begin{matrix} u_{s d} \\ u_{s q} \\ u_{0} \end{matrix}] = [\begin{matrix} \cos (ϑ) & \sin (ϑ) & 0 \\ - \sin (ϑ) & \cos (ϑ) & 0 \\ 0 & 0 & 1 \end{matrix}] \cdot [\begin{matrix} u_{α} \\ u_{β} \\ u_{γ} \end{matrix}]$

(8.20)

ahol $ϑ$ a villamos szög, kapcsolata a $ϑ_{m}$ mechanikus szöggel:

$ϑ = z_{p} ϑ_{m}$

(8.21)

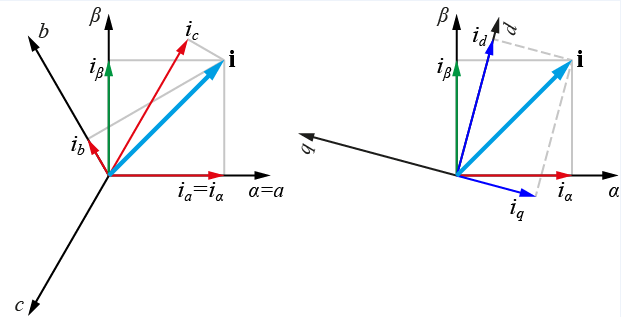
8.5. ábra - Fázis- és rendszertranszformáció

A váltakozó áramú gépek általános összefüggései a bevezetett átalakításoknak köszönhetően felírhatók d - q összetevőkkel megadva, de ezek a transzformációs mátrixok használata helyett a térfazoriális formában megadott összefüggés segítségével kerülnek bemutatásra, mivel a mátrixokkal történő transzformációkat konkrét számítások esetén célszerű alkalmazni.

Közös, a betáplált mező szinkron körfrekvenciájával forgó koordináta-rendszerbe áttérve az áram vektorok transzformációja útján felírhatók a csatolt állórész és forgórész fluxusokra érvényes összefüggések (8-6. ábra).

${\underline{i}}_{s}^{*} = {\underline{i}}_{s} \cdot e^{- j ϑ}$

(8.22)

${\underline{i}}_{r}^{*} = {\underline{i}}_{r} \cdot e^{- j (ϑ - ϑ r)}$

(8.23)

Az (8.7)–(8.8) kifejezésekkel megadott fluxusok saját koordináta rendszerükben értelmezett összefüggések. Az (8.22) és (8.23) jelöléseket bevezetve felírhatók a közös koordináta-rendszerbe forgató tagokkal való szorzást követően:

${\underline{ψ}}_{r}^{*} = {\underline{ψ}}_{r} \cdot e^{- j (ϑ - ϑ r)} = {\underline{i}}_{s} \cdot e^{- j (ϑ - ϑ r)} \cdot e^{- j ϑ} \cdot L_{m} + {\underline{i}}_{r} \cdot e^{- j (ϑ - ϑ r)} \cdot L_{r} = {\underline{i}}_{s}^{*} \cdot L_{m} + {\underline{i}}_{r}^{*} \cdot L_{r}$

(8.24)

${\underline{ψ}}_{s}^{*} = {\underline{ψ}}_{s} \cdot e^{- j ϑ} = {\underline{i}}_{s} \cdot e^{- j ϑ} \cdot L_{s} + {\underline{i}}_{r} \cdot e^{- j ϑ} \cdot e^{j ϑ r} \cdot L_{m} = {\underline{i}}_{s}^{*} \cdot L_{s} + {\underline{i}}_{r}^{*} \cdot L_{m}$

(8.25)

Az állórész feszültségegyenlet térfazoriális alakja szinkron forgó koordináta-rendszerben kibővül egy úgynevezett forgási feszültség taggal, ami fizikai oldalról a forgó állandó mágnes teréhez képest történő elmozdulását reprezentálja az állórésznek, matematikai aspektusból tekintve pedig a feszültségegyenlet $e^{j ϑ}$ forgási taggal történő beszorzása eredményezi létrejöttét.

${\underline{u}}_{s} = R_{s} {\underline{i}}_{s}^{*} + \frac{d {\underline{Ψ}}_{s}^{*}}{d t} + j ω {\underline{Ψ}}_{s}^{*}$

(8.26)

A forgórész feszültség egyenlet a szinkron forgó koordináta rendszerbe transzformálva szintén kibővül a forgási feszültséget reprezentáló taggal, hiszen a forgórész saját viszonyítási rendszeréből tekintve szlip frekvenciával rendelkeznek a forgórész mennyiségek.

${\underline{u}}_{r} = {\underline{i}}_{r}^{*} \cdot R_{r} + \frac{d {\underline{ψ}}_{r}^{*}}{d t} + j (ω - ω_{r}) {\underline{ψ}}_{r}^{*} = 0$

(8.27)

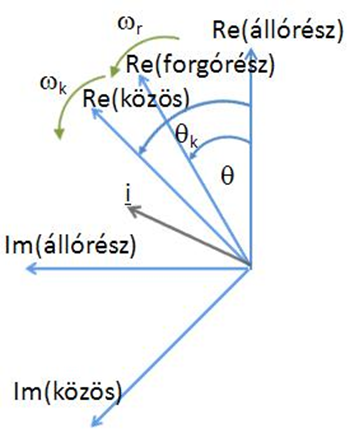
8.6. ábra - Szinkron forgó koordináta-rendszer

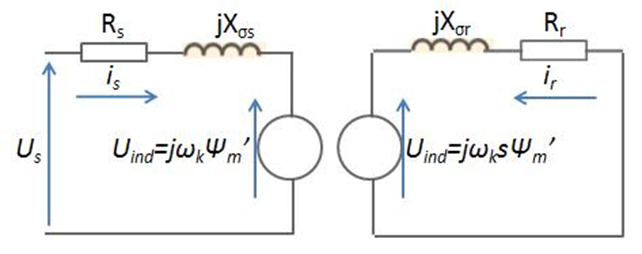
Az aszinkron motor matematikai modelljét leíró összefüggések csak akkor értelmezhetők, ha a helyettesítő kapcsolási rajzban – a transzformátorhoz hasonlóan – az állórész és a forgórész tekercselés egyesítésre kerül (8-7. ábra). A forgórész feszültségegyenlet módosításra szorul, mivel az aszinkron motor helyettesítő kapcsolási rajza alapján megállapítható, hogy az álló- és a forgórész köri helyettesítő kapcsolásban nem egyezik meg a légrés fluxussal felírt indukált feszültség. Ennek oka, hogy a forgórészen a forgási indukált feszültség szlip frekvenciás (8.27). Az állandósult állapotra vonatkozó helyettesítő kapcsolás alapján felírható, hogy:

${\underline{u}}_{r} = {\underline{i}}_{r}^{*} \cdot R_{r} + j ω \cdot s \cdot {\underline{ψ}}_{r}^{*} = 0$

(8.28)

Az (8.27) összefüggés forgási indukált feszültsége az állórészre redukálható, ha az indukált feszültségek megegyeznek (8.29).

$\frac{{\underline{u}}_{r}}{s} = {\underline{i}}_{r}^{*} \cdot \frac{R_{r}}{s} + j ω {\underline{ψ}}_{r}^{*} = 0$

(8.29)

A módosított forgórész feszültség egyenletből megállapítható, hogy a forgórész ellenállása szlip függő. A valóságban természetesen mindig a reaktancia függ a szliptől.

8.7. ábra - Az álló- és forgórész egyesítése komplex, forgó transzformátorrá

Az állórész és forgórész tekercselés menetszám áttételéből adódóan el kell végezni a forgórész-mennyiségek redukálását az állórészre egy fiktív a redukálási tényező segítségével [53]. Ennek bevezetése a következőképpen történik:

${\underline{ψ^{'}}}_{r} = a \cdot {\underline{ψ}}_{r}$

${\underline{i^{'}}}_{r} = \frac{{\underline{i}}_{r}}{a}$

${\underline{u^{'}}}_{r} = a \cdot {\underline{u}}_{r}$

${R^{'}}_{r} = a^{2} \cdot R_{r}$

Az induktivitások a következőképpen módosulnak miután a fluxus egyenletekbe behelyettesítésre kerül a forgórész fluxus és áram redukált alakja:

${\underline{L^{'}}}_{r} = a^{2} \cdot {\underline{L}}_{r}$

${\underline{L^{'}}}_{m} = a \cdot {\underline{L}}_{m}$

Az (8.24) és (8.25) fluxus egyenletekbe behelyettesítve az (8.11) és (8.12) összefüggéseket, továbbá felhasználva a redukált alakját a légrés és forgórész induktivitásoknak

${\underline{ψ}}_{s} = (L_{s} - a \cdot L_{m}) {\underline{i}}_{s} + a \cdot L_{m} ({\underline{i}}_{s} + {\underline{i}}_{R})$

(8.30)

${\underline{ψ}}_{R} = (a^{2} \cdot L_{r} - a \cdot L_{m}) {\underline{i}}_{s} + a \cdot L_{m} ({\underline{i}}_{s} + {\underline{i}}_{R})$

(8.31)

A zárójeles kifejezéseket elnevezve az (8.30)–(8.31) fluxusegyenletek a következő formában írhatók:

${\underline{ψ}}_{s} = L_{σ S} {\underline{i}}_{s} + L_{M} ({\underline{i}}_{s} + {\underline{i}}_{R})$

(8.32)

${\underline{ψ}}_{R} = L_{σ R} {\underline{i}}_{r} + L_{M} ({\underline{i}}_{s} + {\underline{i}}_{R})$

(8.33)

amely összefüggésekben szereplő új induktivitások írhatók a következőképpen is:

$L_{σ S} = L_{m} (\frac{L_{s}}{L_{m}} - a)$

(8.34)

$L_{σ R} = a \cdot L_{r} (a - \frac{L_{m}}{L_{r}})$

(8.35)

Az a redukálási tényezőt többféleképpen meg lehet választani, melyek közül három különböző érték terjedt el leginkább. Ezek közül két esetben a olyan értékű, hogy vagy az állórész vagy a forgórész szórási induktivitása eliminálható a helyettesítő kapcsolási rajzból, amelynek előnye, hogy a számítások gyorsabban elvégezhetők (8-8. ábra).

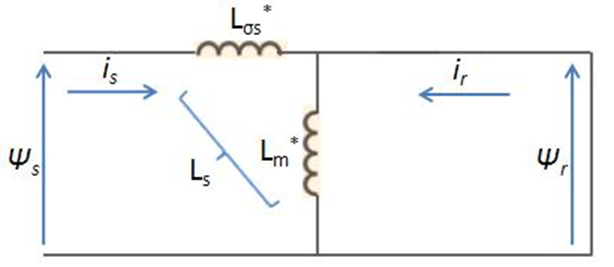
8.8. ábra - Forgórész szórt induktivitása nélküli fluxusmodell

A harmadik esetben az a értéke a legegyszerűbben egynek kerül kiválasztásra, így a forgórész összefüggések változtatás nélkül kerülnek felhasználásra a motor matematikai modelljében. Ekkor az áttételi arány az álló- és a forgórész között 1:1. Az (8.34)–(8.35) egyenletek alapján látható, hogy a értéke miként választandó meg annak érdekében, hogy az állórész vagy forgórész szórási induktivitás eliminálásra kerüljön. Ennek megfelelően a értékei a következőkképpen választhatók meg [54]:

a = 1 esetén a motor villamos matematikai modelljét leíró egyenletek (8.36)–(8.39) formában maradnak, melyek megegyeznek a korábban megállapított összefüggésekkel
$a = \frac{L_{m}}{L_{r}}$ esetén az (8.36)–(8.39) összefüggésekben LσR = 0, melynek következtében ΨM = ΨR
$a = \frac{L_{s}}{L_{m}}$ esetén az (8.36)–(8.39) összefüggésekben LσS = 0, melynek következtében ΨM = Ψs

${\underline{u}}_{s} = R_{s} {\underline{i}}_{s}^{*} + \frac{d {\underline{Ψ}}_{s}^{*}}{d t} + j ω {\underline{Ψ}}_{s}^{*}$

(8.36)

$0 = {\underline{i}}_{R}^{*} \cdot R_{R} + \frac{d {\underline{ψ}}_{R}^{*}}{d t} + j (ω - ω_{r}) {\underline{ψ}}_{R}^{*}$

(8.37)

${\underline{ψ}}_{s} = L_{σ S} {\underline{i}}_{s} + L_{M} ({\underline{i}}_{s} + {\underline{i}}_{R})$

(8.38)

${\underline{ψ}}_{R} = L_{σ R} {\underline{i}}_{r} + L_{M} ({\underline{i}}_{s} + {\underline{i}}_{R})$

(8.39)

Az egyszerűség kedvéért a = 1 - nek választva a redukálási tényezőt a villamos modellt leíró egyenletek az (8.24), (8.25), (8.26), (8.27) formában tovább vizsgálhatók. A szinkron forgó koordinátarendszerben a térfazoriális formában megadott feszültség és fluxus összefüggések felbonthatók két összetevőre. A d és q merőleges tengelyű komplex, kétfázisú forgó koordináta-rendszerben a d tengely irányába esik a valós, a q tengely irányába esik a képzetes összetevője a vektoroknak. Az összefüggések felírhatók d és q irányú feszültségekkel, áramokkal és fluxusokkal – amelyek a transzformációk alkalmazásával jönnek létre, de a forgási feszültség esetében a komplex egységvektor miatt szükséges külön megállapítani a forgási tag d és q irányú komponensét.

$j ω {\underline{Ψ}}_{s}^{*} = j ω (Ψ_{s d} + j Ψ_{s q}) = \underset{q irány}{\underset{︸}{j ω Ψ_{s d}}} - \underset{d irány}{\underset{︸}{ω Ψ_{s q}}}$

(8.40)

A felbontásnak köszönhetően felírható a két transzformált feszültség egyenlet, amelynek d irányú összetevője fogja tartalmazni a forgási feszültség -ωΨsq, míg q irányú összetevője a jωΨsd tagját.

$u_{s d} = R_{s} i_{s d} + \frac{d Ψ_{s d}}{d t} - ω Ψ_{s q}$

(8.41)

$u_{s q} = R_{s} i_{s q} + \frac{d Ψ_{s q}}{d t} + ω Ψ_{s d}$

(8.42)

Észrevehető, hogy mind a d, mind a q irányú összefüggés tartalmaz a másik komplex, kétfázisú koordináta-rendszer tengelyének irányába eső vetületet. Ez a jelenség írja le az elektromechanikus kereszthatást a motorban.

$u_{r d} = i_{r d} \cdot R_{r} + \frac{d ψ_{r d}}{d t} - (ω - ω_{r}) ψ_{r q}$

(8.43)

$u_{r q} = i_{r q} \cdot R_{r} + \frac{d ψ_{r q}}{d t} + (ω - ω_{r}) ψ_{r d}$

(8.44)

8.2. A motor mechanikai modellje

A mechanikai modell alapja a vizsgált motor nyomatékképzését leíró összefüggés megadása. A háromfázisú aszinkron motor tranziens jelenségekre is érvényes nyomatékképletét az energiaátvitelt leíró munkatétel alapján lehet levezetni. A pontos levezetés ismertetése nélkül kerül meghatározásra a motor elektromágneses nyomatékát megadó összefüggés.

A nyomaték az állórész áramának és a motorban létrejövő mágneses térnek a kölcsönhatásaként jön létre.

${\underline{M}}_{e} = k \cdot {\underline{Ψ}}_{s} \times {\underline{i}}_{s} = \frac{3}{2} z_{p} ({\underline{Ψ}}_{s} \times {\underline{i}}_{s})$

(8.45)

Mivel azonos síkban levő vektorok vektoriális szorzata adja a nyomatékot, így annak csak erre a síkra merőleges komponense lesz, amely a vektoriális szorzás szabálya értelmében

$M_{e} = \frac{3}{2} z_{p} (Ψ_{s d} i_{s q} - Ψ_{s q} i_{s d})$

(8.46)

Az elektromágneses nyomaték megadható a forgórész fluxusának és az állórész áramának ismeretében (8.47) szerint [55].

${\underline{M}}_{e} = \frac{3}{2} z_{p} \frac{L_{m}}{L_{r}} ({\underline{Ψ}}_{r} \times {\underline{i}}_{s})$

(8.47)

A vektoriális szorzás szabálya szerint az (8.47) nyomatékegyenlet (8.48) összefüggés formájában számítható ki.

$M_{e} = \frac{3}{2} z_{p} \frac{L_{m}}{L_{r}} (Ψ_{r d} i_{s q} - Ψ_{r q} i_{s d})$

(8.48)

A háromfázisú, kalickás forgórészű aszinkron motor mozgásegyenlete megegyezik bármely forgó gép nyomatéki egyensúlyát megadó összefüggésével, amely kifejezi, hogy annyi elektromágneses nyomaték jön létre a motorban, ami elegendő ahhoz, hogy a terhelő nyomatékot, a súrlódási nyomatékot és a sebességváltozás alatt fellépő tehetetlenségi nyomatékot ellensúlyozza és a motort forgásban tartsa.

A mozgásegyenletbe behelyettesítve a hengeres forgórészű motorra jellemző elektromágneses nyomatéki összefüggést, a motor mechanikai modellje a villamos modellhez hasonlóan kanonikus formára hozható és megoldható.

$\frac{3}{2} z_{p} (Ψ_{s d} i_{s q} - Ψ_{s q} i_{s d}) = M_{t} + J \frac{d ω}{d t} + B ω$

(8.49)

8.3. Motormodell álló koordináta rendszerben

A motor matematikai modelljét érdemes álló koordináta-rendszerben is felállítani, mivel a modellezés során csupán a szabályozatlan, hálózatról üzemelő motor viselkedésére irányuló vizsgálatok könnyen elvégezhetők az álló koordináta rendszerben. A mezőorientált szabályozás vizsgálatához szintúgy megfelel az álló koordináta-rendszerben felállított modell, hiszen a szabályozókörben előállított, mezőhöz orientált rendszerben értelmezett mennyiségek visszatranszformálás útján a motormodellel megegyező rendszerbe kerülnek.

A motor állórészének feszültségegyenlete az állórészhez rögzített koordináta rendszerben megegyezik az (8.5) összefüggéssel. A forgórész feszültség egyenletét az álló koordináta-rendszerbe transzformálva:

${\underline{u}}_{r} = {\underline{i}}_{r}^{*} \cdot R_{r} + \frac{d {\underline{ψ}}_{r}^{*}}{d t} - j ω_{r} {\underline{ψ}}_{r}^{*} = 0$

(8.50)

amelyben a forgórész fluxus és forgórész áram szintén az állórészhez rögzített koordináta-rendszerben értelmezendő (8.51) és (8.52) szerint.

${\underline{ψ}}_{r}^{*} = {\underline{ψ}}_{r} \cdot e^{j ϑ r}$

(8.51)

${\underline{i}}_{r}^{*} = {\underline{i}}_{r} \cdot e^{j ϑ r}$

(8.52)

A forgórész feszültség egyenletét fel lehet bontani a forgórész egyenletben megjelent forgási feszültség d - q összetevőkre bontásával (8.53).

$- j ω_{r} ψ_{r}^{*} = - j ω_{r} (ψ_{r d} + j ψ_{r q}) = \underset{d}{\underset{︸}{ω_{r} ψ_{r q}}} - \underset{q}{\underset{︸}{j ω_{r} ψ_{r d}}}$

(8.53)

Az állórész koordináta-rendszerben a két forgórész feszültségegyenlet transzformálása után az állórész és forgórész feszültséget leíró összefüggések a következőképpen írhatók d és q irányú összetevőikre való felbontást követően.

$u_{s d} = i_{s d} \cdot R_{s} + \frac{d ψ_{s d}}{d t}$

(8.54)

$u_{s q} = i_{s q} \cdot R_{s} + \frac{d ψ_{s q}}{d t}$

(8.55)

$u_{r d} = 0 = i_{r d} \cdot R_{r} + \frac{d ψ_{r d}}{d t} + ω_{r} ψ_{r q}$

(8.56)

$u_{r q} = 0 = i_{r q} \cdot R_{r} + \frac{d ψ_{r q}}{d t} - ω_{r} ψ_{r d}$

(8.57)

A villamos modell a feszültség egyenletek differenciálhányadosokra történő átrendezésével megoldható, azonban ehhez az áramok meghatározására szolgáló összefüggések ismerete szükséges. Az állórész és forgórész áramokat leíró egyenletek az (8.24) és (8.25) alapján írhatók fel. A forgórész fluxus egyenletéből a forgórész áramot kifejezve, majd azt az állórész fluxus egyenletébe visszahelyettesítve

${\underline{ψ}}_{s} = (L_{s} - \frac{L_{m}^{2}}{L_{r}}) {\underline{i}}_{s} + \frac{L_{m}}{L_{r}} {\underline{ψ}}_{r}$

(8.58)

Az (8.58)-hez hasonlóan a forgórész áram számításához szükséges összefüggés az állórész fluxus egyenletéből az állórész áramot kifejezve, majd azt a forgórész fluxus egyenletébe visszahelyettesítve kapható meg.

${\underline{ψ}}_{r} = (L_{r} - \frac{L_{m}^{2}}{L_{s}}) {\underline{i}}_{r} + \frac{L_{m}}{L_{s}} {\underline{ψ}}_{s}$

(8.59)

A zárójelekben szereplő kifejezéseket a szakirodalom úgynevezett tranziens induktivitásokként hivatkozza meg. Ezeket mind az (8.58), mind az (8.59) egyenletben elnevezve és mindkét összefüggésből az áramokat kifejezve a villamos modell megoldásához szükséges állórész és forgórész áramra vonatkozó egyenletek megállapíthatók.

${\underline{i}}_{s} = \frac{1}{σ L_{s}} ({\underline{ψ}}_{s} - \frac{L_{m}}{L_{r}} {\underline{ψ}}_{r})$

(8.60)

${\underline{i}}_{r} = \frac{1}{σ L_{r}} ({\underline{ψ}}_{r} - \frac{L_{m}}{L_{s}} {\underline{ψ}}_{s})$

(8.61)

Az (8.60) és (8.61) összefüggések d és q irányú összetevőikre történő felbontása szimplán megtehető a bennük szereplő mennyiségek felbontásával.

8.4. Motormodell állapotegyenlet reprezentációja forgó és álló koordináta-rendszerben

Az aszinkron motor modelljének ismerete forgó koordináta-rendszerben szintén nélkülözhetetlen, mivel legtöbbször a szabályozó hurkokban a szabályozáshoz szükséges számítások szinkron forgó rendszerben értelmezett mennyiségekkel kell, hogy történjenek. Így például ha fluxus szabályozást valósít meg a hajtás, akkor a hibajel a fluxus referenciaértékének a pillanatnyi fluxussal történő összehasonlítása alapján képződik. A pillanatnyilag a motorban jelen lévő állórész, forgórész vagy légrés fluxus értékéről ugyan Hall-szenzorokkal megvalósított mérés útján lehet közvetlenül is információt szerezni, de ennél jóval elterjedtebb megoldás becslő algoritmusok használata. Ha a becslő algoritmusnak forgó koordináta-rendszerben értelmezett mennyiségek a bemenetei, akkor az algoritmus a motor forgó koordináta-rendszerben felírt matematikai modellje alapján működik.

Az (8.24), (8.25), (8.26), (8.27) egyenletekből is, Ψs, ir, Ψr térfazorok bármelyikét állapotváltozónak lehet választani a modell alkotás során. Az aszinkron motor modellezéséhez érdemes az állórész áramot és a forgórész fluxust állapotváltozóknak kijelölni és így felállítani a modellt, hiszen a szabályozási hurkokban a forgórész fluxus és az áramszabályozás a cél. Az is és Ψr térfazorokat állapotváltozónak kijelölve a motor modelljének egyenletei csak ezeket az állapotváltozókat fogják tartalmazni, ennek érdekében tehát átalakításra szorulnak a villamos modellt leíró összefüggések. Az (8.27) összefüggést a forgórész fluxus differenciálhányadosára kifejezve:

$\frac{d {\underline{ψ}}_{r}^{*}}{d t} = - {\underline{i}}_{r}^{*} \cdot R_{r} - j (ω - ω_{r}) {\underline{ψ}}_{r}^{*}$

(8.62)

A forgórész áram helyett írható az (8.24) kifejezés alapján, hogy

${\underline{i}}_{r}^{*} = \frac{1}{L_{r}} ({\underline{ψ}}_{r}^{*} - {\underline{i}}_{s}^{*} \cdot L_{m})$

(8.63)

Az (8.62) összefüggésbe a forgórész áram helyett az (8.63) összefüggést behelyettesítve

$\frac{d {\underline{ψ}}_{r}^{*}}{d t} = \frac{L_{m} R_{r}}{L_{r}} {\underline{i}}_{s}^{*} - (\frac{R_{r}}{L_{r}} + j (ω - ω_{r})) {\underline{ψ}}_{r}^{*}$

(8.64)

Az (8.26) összefüggést az állórész fluxus differenciálhányadosára kifejezve

$\frac{d {\underline{Ψ}}_{s}^{*}}{d t} = {\underline{u}}_{s} - R_{s} {\underline{i}}_{s}^{*} - j ω {\underline{Ψ}}_{s}^{*}$

(8.65)

Az (8.58) összefüggés deriváltja (8.66) formában írható fel.

$\frac{d {\underline{ψ}}_{s}}{d t} = (L_{s} - \frac{L_{m}^{2}}{L_{r}}) \frac{d {\underline{i}}_{s}}{d t} + \frac{L_{m}}{L_{r}} \frac{d {\underline{ψ}}_{r}}{d t}$

(8.66)

Az (8.66)-ban látható, hogy megjelenik a forgórész fluxus, mint differenciálhányados. Annak helyére (8.64)-ot behelyettesítve, majd az egész kifejezést – amely immár csak az állórész áram és a forgórész fluxus térfazorját tartalmazza – (8.65)-be, az állórész fluxus differenciálhányadosának helyére behelyettesítve:

$(L_{s} - \frac{L_{m}^{2}}{L_{r}}) \frac{d {\underline{i}}_{s}}{d t} = {\underline{u}}_{s} - [(\frac{L_{m}^{2}}{L_{r}^{2}} R_{r} + R_{s}) + j ω (L_{s} - \frac{L_{m}^{2}}{L_{r}})] {\underline{i}}_{s} + (\frac{L_{m}}{L_{r}^{2}} R_{r} - j ω_{r} \frac{L_{m}}{L_{r}}) {\underline{ψ}}_{r}$

(8.67)

Az (8.64) és (8.67) kifejezések adják a forgórész fluxusra és állórész áramra vonatkozó állapotegyenleteket, amelyek alapján lineáris modell felírható, amely az ω és ωr szögsebességek időbeli változásának köszönhetően idővariáns (LTV). A forgórész ellenállás az üzemeltetés során a hőmérséklet-változás hatására nem állandó értékű, így sokszor Rr(t) szintén időfüggő mennyiségként kerül bevezetésre. A matematikai modellben természetesen az állapotváltozóként felvett mennyiségek d és q irányú, kétfázisú komponensei szerepelnek, így az állapotegyenletek felbontását a mátrixok megadása előtt meg kell tenni.

Az egymásra merőleges összetevőkre történő felbontás után az általános referenciájú orientációra érvényes állapot-egyenletrendszer (8.68) formájában írható fel. Az általános referenciájú orientációra érvényes felírás azt jelenti, hogy bármilyen ωk szögsebességgel forgó koordináta-rendszerhez orientált modell megadható az állapot egyenletrendszerrel. A választott koordináta-rendszer lehet akár a szinkron mezővel, akár a forgórésszel együttforgó, de ha ωk = 0 - nak kerül megválasztásra, akkor az álló koordináta-rendszer reprezentációját adja meg az egyenletrendszer.

$\frac{d}{d t} [\begin{matrix} ψ_{r d} \\ ψ_{r q} \\ i_{s d} \\ i_{s q} \end{matrix}] = [\begin{matrix} - \frac{R_{r}}{L_{r}} & ω_{k} - ω_{r} & \frac{L_{m} R_{r}}{L_{r}} & 0 \\ - (ω_{k} - ω_{r}) & - \frac{R_{r}}{L_{r}} & 0 & \frac{L_{m} R_{r}}{L_{r}} \\ \frac{L_{m} R_{r}}{L_{r}^{2} σ L_{s}} & ω_{r} \frac{L_{m}}{L_{r} σ L_{s}} & - \frac{R^{″}}{σ L_{s}} & ω_{k} \\ - ω_{r} \frac{L_{m}}{L_{r} σ L_{s}} & \frac{L_{m} R_{r}}{L_{r}^{2} σ L_{s}} & - ω_{k} & - \frac{R^{″}}{σ L_{s}} \end{matrix}] \cdot [\begin{matrix} ψ_{r d} \\ ψ_{r q} \\ i_{s d} \\ i_{s q} \end{matrix}] + [\begin{matrix} 0 & 0 \\ 0 & 0 \\ \frac{1}{σ L_{s}} & 0 \\ 0 & \frac{1}{σ L_{s}} \end{matrix}] \cdot [\begin{matrix} u_{s d} \\ u_{s q} \end{matrix}]$

(8.68)

amelyben

$σ L_{s} = (L_{s} - \frac{L_{m}^{2}}{L_{r}})$

(8.69)

$R^{″} = (\frac{L_{m}^{2}}{L_{r}^{2}} R_{r} + R_{s})$

(8.70)

Az (8.68) egyenletrendszer az aszinkron motor villamos modelljét írja le. A modell teljessé tehető és megoldható a mechanikai mozgásegyenlettel történő kibővítést követően. Ehhez a forgórész fluxusokkal és állórész áramokkal kifejezett (8.48) nyomaték egyenlet felhasználása szükséges, hiszen ezek a mennyiségek kerültek állapotváltozóként kiválasztásra.

Mivel (8.68) általános referenciájú orientációban írja le a motor villamos modelljét, így az állapot egyenleteket tartalmazó modell ωk = 0 esetén átalakítható az álló, azaz az állórészhez rögzített koordináta-rendszer reprezentációba. Ebben az esetben szintén a forgórész fluxust és az állórész áramot állapotváltozóknak választva ugyancsak megállapítható az aszinkron motor villamos matematikai modellje, amelyet álló koordináta rendszerben (8.71) egyenletrendszer ír le. A mechanikai modelljét az aszinkron motornak változatlan formában (8.48) nyomaték összefüggés adja meg.

$\frac{d}{d t} [\begin{matrix} ψ_{r α} \\ ψ_{r β} \\ i_{s α} \\ i_{s β} \end{matrix}] = [\begin{matrix} - \frac{R_{r}}{L_{r}} & - ω_{r} & \frac{L_{m} R_{r}}{L_{r}} & 0 \\ ω_{r} & - \frac{R_{r}}{L_{r}} & 0 & \frac{L_{m} R_{r}}{L_{r}} \\ \frac{L_{m} R_{r}}{L_{r}^{2} σ L_{s}} & ω_{r} \frac{L_{m}}{L_{r} σ L_{s}} & - \frac{R^{″}}{σ L_{s}} & 0 \\ - ω_{r} \frac{L_{m}}{L_{r} σ L_{s}} & \frac{L_{m} R_{r}}{L_{r}^{2} σ L_{s}} & 0 & - \frac{R^{″}}{σ L_{s}} \end{matrix}] \cdot [\begin{matrix} ψ_{r α} \\ ψ_{r β} \\ i_{s α} \\ i_{s β} \end{matrix}] + [\begin{matrix} 0 & 0 \\ 0 & 0 \\ \frac{1}{σ L_{s}} & 0 \\ 0 & \frac{1}{σ L_{s}} \end{matrix}] \cdot [\begin{matrix} u_{s α} \\ u_{s β} \end{matrix}]$

(8.71)

Az (8.71) állapot egyenletrendszerben a d és q irányú összetevők helyett α–val és β–val jelölt komponensek találhatók, mivel ez a jelölésrendszer terjedt el az álló koordináta-rendszerre érvényes egyenletekben, megkülönböztetendő a modellt a forgó rendszerben felírt változatoktól.

8.5. Mezőorientáció – forgórész fluxus orientáció

A szinkron forgó rendszerbe áttérve mező, feszültség és áram orientáció alkalmazható, hiszen a motor valamennyi változójának vektora szinkron sebességgel forog, azaz ezek közül akármelyikhez hozzá lehet rendelni a forgó, kétfázisú koordináta-rendszer valamely tengelyét. Ennek előnye az adott mennyiség könnyű szabályozhatósága, mivel d és q irányú komponense az orientált mennyiségnek a többi vektor ugyanazon irányba eső vetületével egyenesen arányos lesz.

A háromfázisú, váltakozó áramú hajtások modellezéséhez a forgórészfluxus-orientációt célszerű választani, mivel az aszinkron motor vektoriális szabályozása során a forgórész fluxus állandó értéken tartása így könnyen megvalósítható (8-9. ábra).

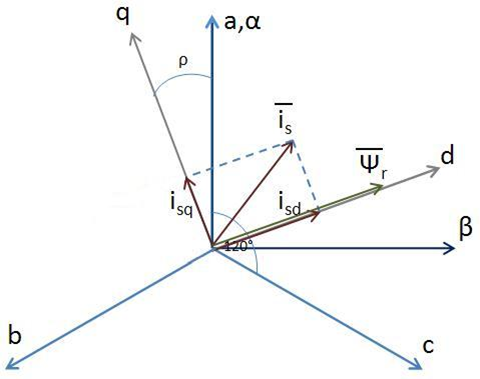
8.9. ábra - Forgórész fluxushoz történő orientáció

A rotor fluxushoz rögzített koordináta rendszerbeli modellel leírva a motor viselkedését minden vektor szinkron sebességgel forog, ezért állandósult állapotban minden mennyiség konstans. Abban az esetben, amikor a koordináta-rendszer valós tengelye együtt forog a Ψr vektorral, annak nincs képzetes komponense, így a Ψrq állapotváltozó kiesik a rendszerből. A d, valós tengelyhez rögzített forgórész fluxus a forgórésszel megegyező körfrekvenciával forog (8.72).

$ω_{ψ_{r}} = ω$

(8.72)

Az (8.68) általános referenciájú orientációt kifejező egyenletrendszer a forgórész mezőhöz történő orientációt követően (8.73) formájában írható fel a három állapotváltozóval.

$\frac{d}{d t} [\begin{matrix} ψ_{r d} \\ i_{s d} \\ i_{s q} \end{matrix}] = [\begin{matrix} - \frac{R_{r}}{L_{r}} & \frac{L_{m} R_{r}}{L_{r}} & 0 \\ \frac{L_{m} R_{r}}{L_{r}^{2} σ L_{s}} & - \frac{R^{″}}{σ L_{s}} & ω \\ - ω_{r} \frac{L_{m}}{L_{r} σ L_{s}} & - ω & - \frac{R^{″}}{σ L_{s}} \end{matrix}] \cdot [\begin{matrix} ψ_{r d} \\ i_{s d} \\ i_{s q} \end{matrix}] + [\begin{matrix} 0 & 0 \\ \frac{1}{σ L_{s}} & 0 \\ 0 & \frac{1}{σ L_{s}} \end{matrix}] \cdot [\begin{matrix} u_{s d} \\ u_{s q} \end{matrix}]$

(8.73)

A motor elektromágneses nyomatékának egyenlete szintén módosul (8.74), hiszen a q irányú forgórész fluxus eliminálásra került.

$M_{e} = \frac{3}{2} z_{p} \frac{L_{m}}{L_{r}} Ψ_{r d} i_{s q}$

(8.74)

Az (8.73) és (8.74) kifejezések alapján látható, hogy a forgórész fluxus orientáció eredményeként a szabályozás egyszerűen kivitelezhető. A forgórész fluxusa megegyezik Ψrd fluxus komponenssel, amely isd árammal arányos, míg isq áramtól független. A nyomaték kifejezésből pedig látható, hogy az elektromágneses nyomaték isd áramtól független, így a sebességhurok szabályozása isq árammal kivitelezhető.

A forgórész fluxushoz történő orientáció megvalósításához szükséges a forgórész fluxusvektor pozíciójának ismerete minden időpillanatban. Az (8.73) egyenletrendszerből megállapítható, hogy

$\frac{d ρ}{d t} = ω = ω_{r} + \frac{L_{m}}{L_{r}} \frac{R_{r} i_{s q}}{Ψ_{r d}}$

(8.75)

A forgórész fluxus nagyságának becslésére szintén szükség van a szabályozókörök kialakításánál, hiszen a fluxus szabályozó hibajelképzése a referencia és a pillanatnyi fluxus ismeretét követeli meg. Az (8.73) egyenletrendszer felső sorából következően a fluxus becslése (8.76) alapján történhet.

$\frac{d Ψ_{r d}}{d t} = \frac{R_{r}}{L_{r}} (L_{m} i_{s d} {-Ψ}_{r d})$

(8.76)

8.5.1. Motormodell mágnesezési áram bevezetésével

A forgórész fluxushoz orientált rendszer felírása megtörténhet a motort leíró egyenletekbe bevezetve a forgórész fluxust reprezentáló mágnesezési áramot, amely (8.77) szerint definiálható.

${\underline{i}}_{m r} = \frac{{\underline{ψ}}_{r}}{L_{m}}$

(8.77)

A mágnesezési áram bevezetésével a forgórész fluxus motormodellből történő eliminálása a cél. Az (8.39) kifejezés alapján egy másik mennyiség, az úgynevezett im mágnesezési áram szintén megadható:

${\underline{ψ}}_{r} = L_{σ r} {\underline{i}}_{r} + L_{m} {\underline{i}}_{m}$

(8.78)

amelyben a mágnesezési áram (8.79) szerint került bevezetésre.

${\underline{i}}_{m} = {\underline{i}}_{s} + {\underline{i}}_{r}$

(8.79)

Az (8.77) és (8.78) kifejezések alapján megállapítható az imr forgórész fluxust reprezentáló mágnesezési áram és az im mágnesezési áram kapcsolata (8.80).

${\underline{i}}_{m r} = {\underline{i}}_{m} + \frac{L_{σ r}}{L_{m}} {\underline{i}}_{r} = {\underline{i}}_{m} + σ_{r} {\underline{i}}_{r}$

(8.80)

Az imr áramot bevezetve a motor modellje felírható az állórész áramot és a mágnesezési áramot állapotváltozóknak választva. Az imr mágnesezési áram nem két komponensre bontva kerül bevezetésre, ellentétben az állórész árammal. A forgórész fluxus helyére behelyettesítve az aszinkron motor forgó koordináta-rendszerben állórész áramokkal és forgórész fluxusokkal ismertetett villamos modellje (8.81)–(8.84) egyenletekkel írható fel.

$u_{s d} = R_{s} i_{s d} + σ L_{s} \frac{d}{d t} i_{s d} - σ L_{s} ω_{1} i_{s q} + (1 - σ) L_{s} \frac{d}{d t} i_{m r}$

(8.81)

$u_{s q} = R_{s} i_{s q} + σ L_{s} \frac{d}{d t} i_{s q} + σ L_{s} ω_{1} i_{s d} + (1 - σ) L_{s} ω_{1} i_{m r}$

(8.82)

$i_{s d} = i_{m r} + τ_{r} \frac{d}{d t} i_{m r}$

(8.83)

$i_{s q} (t) = (ω - ω_{r}) \cdot τ_{r} i_{m r}$

(8.84)

Az állórész feszültség és áram összefüggések felírásával a villamos modell állapot egyenletrendszere mátrixos formában a következőképpen adható meg:

$\frac{d}{d t} [\begin{matrix} i_{s d} \\ i_{m r} \\ i_{s q} \end{matrix}] = [\begin{matrix} - \frac{1}{σ} \frac{1}{τ_{s}} & - \frac{1 - σ}{σ} & ω \\ \frac{1}{τ_{r}} & - \frac{1}{τ_{r}} & 0 \\ - ω & - \frac{1 - σ}{σ} ω & - \frac{1}{σ} \frac{1}{τ_{s}} \end{matrix}] [\begin{matrix} i_{s d} \\ i_{m r} \\ i_{s q} \end{matrix}] + \frac{1}{σ τ_{s} R_{s}} [\begin{matrix} u_{s d} \\ u_{s q} \end{matrix}]$

(8.85)

Az (8.81)–(8.82) feszültség egyenletekben található σ az (8.16)-ban került bevezetésre. Az (8.83) összefüggésből látható, hogy amikor az imr áram időbeli változása nulla – azaz a forgórész fluxus állandósult állapotban, konstans értékű – akkor az állórész áram d irányú komponensével megegyezik imr értéke.

$i_{s d} = i_{m r}$

(8.86)

Az elektromágneses nyomatékot leíró kifejezés (8.87) formában adható meg a mágnesezési áramot tartalmazó modellben az (8.77) alapján, a forgórész fluxus helyére behelyettesítve a mágnesezési áram és a légrés induktivitás szorzatát.

$M_{e} = \frac{3}{2} z_{p} \frac{L_{m}^{2}}{L_{r}} i_{s q} i_{m r}$

(8.87)

8.5.2. Feszültségforrás jellegű feszültség inverteres szabályozott hajtás

Az (8.67) összefüggésből az állórész feszültséget kifejezve, (8.88) egyenlet alapján lehetőség van feszültségforrás jellegű feszültség inverteres, azaz a feszültségjel alapján történő modulációval működő inverteres hajtás implementálására. Az egyszerűség kedvéért a gyakran használt (8.69) formában kerül a tranziens induktivitás felhasználásra (8.88)-ban.

${\underline{u}}_{s} = σ L_{s} \frac{d {\underline{i}}_{s}}{d t} + \frac{L_{m}^{2}}{L_{r}^{2}} R_{r} {\underline{i}}_{s} - \frac{L_{m}}{L_{r}^{2}} R_{r} {\underline{ψ}}_{r} - j (ω - ω_{r}) \frac{L_{m}}{L_{r}} {\underline{ψ}}_{r} + R_{s} {\underline{i}}_{s} + σ L_{s} j ω {\underline{i}}_{s} + j ω \frac{L_{m}}{L_{r}} {\underline{ψ}}_{r}$

(8.88)

Észrevehető, hogy az (8.67) kifejezésben látott formához hasonlóan a forgórész fluxust és a körfrekvenciát együttesen tartalmazó tagok összevonhatók, így a feszültség egyenlet némileg egyszerűbb formában:

${\underline{u}}_{s} = σ L_{s} \frac{d {\underline{i}}_{s}}{d t} + \frac{L_{m}^{2}}{L_{r}^{2}} R_{r} {\underline{i}}_{s} - \frac{L_{m}}{L_{r}^{2}} R_{r} {\underline{ψ}}_{r} + R_{s} {\underline{i}}_{s} + σ L_{s} j ω {\underline{i}}_{s} + j ω_{r} \frac{L_{m}}{L_{r}} {\underline{ψ}}_{r}$

(8.89)

Látható, hogy (8.89)-ben az állórész árammal arányos tagok között szerepel idővariáns kifejezés is, ahol ω és is állapotváltozó szorzata szerepel. Áramszabályozó tervezése áram hibajel alapján csak az árammal arányos tagok alapján történhet, így azok a tagjai az összefüggésnek, amelyekben szerepel az állórész áram a szabályozótervezéshez használandók fel, míg az további tagjai az egyenletnek a szabályozó kimenetén létrejövő feszültségértékhez hozzáadandók. Utóbb említett megoldást feszültség-kompenzációnak nevezik. A jobb átláthatóság érdekében (8.89) felírható a szabályozott és a kompenzációs feszültségek csoportosítását követően (8.90) formájában.

${\underline{u}}_{s} = [σ L_{s} \frac{d {\underline{i}}_{s}}{d t} + \frac{L_{m}^{2}}{L_{r}^{2}} R_{r} {\underline{i}}_{s} + R_{s} {\underline{i}}_{s}] + [- \frac{L_{m}}{L_{r}^{2}} R_{r} {\underline{ψ}}_{r} + σ L_{s} j ω {\underline{i}}_{s} + j ω_{r} \frac{L_{m}}{L_{r}} {\underline{ψ}}_{r}]$

(8.90)

Az áramszabályozók tervezéséhez szükséges összefüggések és a kompenzációs részek a feszültség egyenletek felbontását követően kerülnek végleges formába. Ennek érdekében a feszültség egyenletek (8.91)–(8.92) formában való felírása a cél.

$u_{s d} = v_{s d} + Δ u_{s d}$

(8.91)

$u_{s q} = v_{s q} + Δ u_{s q}$

(8.92)

A d és q irányú összetevőkre történő felbontást elvégezve:

$u_{s d} = [σ L_{s} \frac{d i_{s d}}{d t} + \frac{L_{m}^{2}}{L_{r}^{2}} R_{r} i_{s d} + R_{s} i_{s d}] + [- \frac{L_{m}}{L_{r}^{2}} R_{r} ψ_{r d} - σ L_{s} ω i_{s q} - ω_{r} \frac{L_{m}}{L_{r}} ψ_{r q}]$

(8.93)

$u_{s q} = [σ L_{s} \frac{d i_{s q}}{d t} + \frac{L_{m}^{2}}{L_{r}^{2}} R_{r} i_{s q} + R_{s} i_{s q}] + [- \frac{L_{m}}{L_{r}^{2}} R_{r} ψ_{r q} + σ L_{s} ω i_{s d} + ω_{r} \frac{L_{m}}{L_{r}} ψ_{r d}]$

(8.94)

Az (8.93)–(8.94) feszültségegyenletek alapján a kéthurkos szabályozott hajtás implementálható. A gyakorlatban a hajtás megfelelően működik abban az esetben is, ha a kompenzációs részből csak az árammal arányos tagokkal történik kompenzáció.

Az (8.85) és (8.87) egyenletrendszerrel megadott rendszer alapján szintén tervezhető szabályozott hajtás. Ebben az esetben szerepel az összefüggések között nemlineáris kifejezés is, hiszen állapotváltozók szorzatai is szerepelnek a differenciálegyenletekben, úgy mint az elektromágneses nyomatékot megadó (8.87) összefüggésben. A cél egy olyan modell levezetése, amely az isd, isq, imr, ωr, ϑr állapotváltozók alapján írja le a rendszert. A szabályozás implementálásához szétcsatolásra kerülnek a d irányú egyenletekben az isd és az egyéb állapotváltozókkal arányos tagok, míg a q irányú egyenletekben az isq és az egyéb állapotváltozókkal arányos tagok. A mágnesezési áramot tartalmazó, (8.81)–(8.84) egyenletekkel felírt modell alapján a két egymásra merőleges állórész feszültség komponens az alábbi alakban áll elő:

$u_{s d} = v_{s d} + Δ u_{s d} = [R_{s} i_{s d} + σ L_{s} \frac{d}{d t} i_{s d}] + [- σ L_{s} ω i_{s q} + (1 - σ) L_{s} \frac{d}{d t} i_{m s}]$

(8.95)

$u_{s q} = v_{s q} + Δ u_{s q} = [R_{s} i_{s q} + σ L_{s} \frac{d}{d t} i_{s q}] + [σ L_{s} ω i_{s d} + (1 - σ) L_{s} ω i_{m r}]$

(8.96)

A nemlinearitás a rendszerben a motor nyomatékegyenletében található az isq imr szorzat miatt. A motor folyamatos működése során elvárás a mágnesezési munkapont megfelelő beállítása és állandó értéken tartása. Az (8.77) összefüggés alapján ezért a $\frac{d}{d t} i_{m r}$ = 0 feltételezés jogosan megtehető, így $i_{m r} = i_{m r}^{r e f}$ konstans és így az elektromágneses nyomaték egyenletben állapotváltozóként csak szerepel, azaz linearizálásra került az összefüggés. A villamos modell mátrix formában (8.97)-tel adható meg.

$\frac{d}{d t} [\begin{matrix} i_{s d} \\ i_{m r} \\ i_{s q} \\ ω_{r} \\ ϑ_{r} \end{matrix}] = [\begin{matrix} - \frac{1}{σ τ_{s}} & 0 & 0 & 0 & 0 \\ \frac{1}{τ_{r}} & - \frac{1}{τ_{r}} & 0 & 0 & 0 \\ 0 & 0 & - \frac{1}{σ τ_{s}} & 0 & 0 \\ 0 & 0 & K_{J} & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{matrix}] [\begin{matrix} i_{s d} \\ i_{m r} \\ i_{s q} \\ ω_{r} \\ ϑ_{r} \end{matrix}] + [\begin{matrix} \frac{1}{σ L_{s}} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & \frac{1}{σ L_{s}} & 0 \\ 0 & 0 & - \frac{z_{p}}{J} \\ 0 & 0 & 0 \end{matrix}] [\begin{matrix} u_{s d} \\ u_{s q} \\ M_{l o a d} \end{matrix}]$

(8.97)

Az újonnan állapotváltozóként felvett mennyiségek (8.98) és (8.99) alapján kerülnek bevezetésre.

$\frac{d ϑ_{r}}{d t} = ω_{r}$

(8.98)

$\frac{d ω_{r}}{d t} = \frac{z_{p}}{J} (M_{e} (t) - M_{l o a d} (t))$

(8.99)

A villamos modellt leíró egyenletrendszer első mátrixában a mágnesezési áramot tartalmazó

$K_{J} = \frac{3}{2} \frac{z_{p}^{2}}{J} \frac{L_{m}^{2}}{L_{r}} i_{m r}^{r e f}$ (8.100)

állandó értékű paraméter. A rendszert leíró mátrix egyenletrendszer láthatóan két részrendszerre bomlik, hiszen az az isd, imr állapotváltozókkal megadott, illetve isq, ωr, ϑr részrendszerek egymástól teljesen függetlenek, így mindegyik részrendszerhez külön-külön tervezhető szabályozó. A két részrendszer a következő:

$\frac{d}{d t} [\begin{matrix} i_{s d} \\ i_{m r} \end{matrix}] = [\begin{matrix} - \frac{1}{σ τ_{s}} & 0 \\ \frac{1}{τ_{r}} & - \frac{1}{τ_{r}} \end{matrix}] [\begin{matrix} i_{s d} \\ i_{m r} \end{matrix}] + [\begin{matrix} \frac{1}{σ L_{s}} \\ 0 \end{matrix}] u_{s d}$

(8.101)

$\frac{d}{d t} [\begin{matrix} i_{s q} \\ ω_{r} \\ ϑ_{r} \end{matrix}] = [\begin{matrix} - \frac{1}{σ τ_{s}} & 0 & 0 \\ K_{J} & 0 & 0 \\ 0 & 1 & 0 \end{matrix}] [\begin{matrix} i_{s q} \\ ω_{r} \\ ϑ_{r} \end{matrix}] + [\begin{matrix} \frac{1}{σ L_{s}} & 0 \\ 0 & - \frac{z_{p}}{J} \\ 0 & 0 \end{matrix}] [\begin{matrix} u_{s q} \\ M_{l o a d} \end{matrix}]$

(8.102)

Az (8.101) rendszerhez készített szabályozó feladata a fluxus állandó értéken tartása a lehető legjobb dinamika biztosítása érdekében. A feladat megegyezik a mágnesezési áram konstans értéken tartásával, ami az usd feszültség szabályozásával valósítható meg. A sebesség szabályozása az (8.102) rendszerhez tervezett szabályozóval történik, vagyis usq lesz a szabályozó kimenete, hiszen nem lehetséges a terhelő nyomaték változtatása szabályozási célból. A sebesség szabályozása (8.87) alapján történhetne akár imr által is, azonban isq jóval gyorsabb tranziens viselkedése és a konstans fluxus biztosítása erősen indokolttá teszi a q áramkomponens általi szabályozást. A fentebb korábban ismertetésre került szabályozási elv szerint az állórész feszültségek megfelelő állórész áramokkal arányos komponensei kerülnek szabályozásra, ezért az (8.95) és (8.96) egyenletekben a második szögletes zárójelben megjelenő tagoknak az előállított szabályozó jelekhez történő hozzáadásával kapható meg a végeleges szabályozó jel (8-10. ábra).

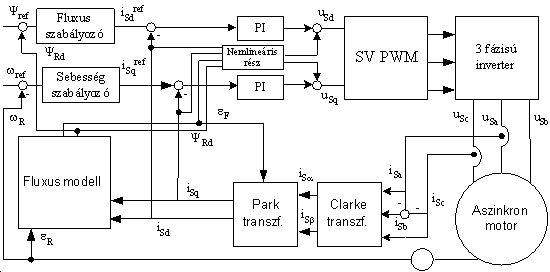
8.10. ábra - Feszültségforrás jellegű feszültség inverteres szabályozott hajtás

Valós rendszerekben az állórész áramok és a forgórész sebesség mérésére nyílik mód, így ezeknek a mennyiségeknek a felhasználásával kell a szabályozó bemeneteket előállítani. A szabályozó a forgó koordinátarendszerben valósítja meg a szabályozást, ezért szükséges a mért áramok ebbe a rendszerbe történő áttranszformálása. A transzformációhoz szükséges a forgórész fluxusvektor szögének kiszámítása érdekében elengedhetetlen a fluxus modell használata, amely a forgórész szögelfordulásából és az $α, β$ áramkomponensekből kiszámítja az elforgatáshoz szükséges szöget. A 8-10. ábrán látható külső (fluxus és sebesség) szabályozók feladata a referenciának megfelelő munkapont beállítása, ennek függvényében a két PI szabályozó egység végzi a szabályozó jelek előállítását, majd ezekhez adódnak hozzá a nem arányos tagokból eredő feszültségkomponenseket előállító blokkok által szolgáltatott jelek. A jelek egy feszültség jellegű feszültség inverter bemenetére kerülnek, amelynek alapján a vezérlő logika ellátja a félvezető kapcsolóelemek megfelelően időzített kapcsolását, például vivőhullámos inverter vezérlési stratégia alapján.

8.6. Háromfázisú aszinkron motor folytonos és diszkrét idejű állapottér-modellje

Az aszinkron motor villamos modelljét leíró állapotegyenlet-rendszer bemutatásra került a korábbi fejezetekben, azonban a szabályozott hajtás megvalósítása sok esetben valamilyen állapotbecslő segítségével kerül kivitelezésre. A szabályozó hurkok és a koordináta-transzformációs blokkok igénylik a forgórész sebességének, a forgórész fluxusnak, a forgórész fluxus szöghelyzetének ismeretét. Ezen kívül sok esetben a forgórész kör ellenállásának becslése is az állapotbecslő feladatai közé tartozik, mivel annak értéke nagymértékben változhat az üzemeltetés során a hőmérsékletváltozás következtében. Az (8.75) és (8.76) egyenletek alapján ugyan lehetséges a fluxus és a fluxus vektor szöghelyzetének számítása, de éppen a számítás során felhasznált paraméterek értékének pontatlansága miatt sokkal jobb eredmény érhető el állapotmegfigyelők alkalmazásával. Az állapotváltozók becslésére szolgáló algoritmusok alkalmazásához a rendszer állapottér-reprezentációjának ismerete szükséges. Ebből kifolyólag elengedhetetlen az állapot megfigyelő alkalmazásához az aszinkron motor állapottér-modelljének felállítása.

Az lineáris, időinvariáns rendszert jellemző állapottér-modell általános alakja (8.103)–(8.104) egyenletrendszer formájában írható fel.

$\frac{d \underline{x} (t)}{d t} = \underline{\underline{A}} \cdot \underline{x} (t) + \underline{\underline{B}} \cdot \underline{u} (t)$

(8.103)

$\underline{y} (t) = \underline{\underline{C}} \cdot \underline{x} (t) + \underline{\underline{D}} \cdot \underline{u} (t)$

(8.104)

ahol

$x = [x_{1}, x_{2}, ..., x_{n}]$ n×1 dimenziós állapotvektor,

$u = [u_{1}, u_{2}, ..., u_{m}]$ m×1 dimenziós bemeneti vektor,

$y = [y_{1}, y_{2}, ..., y_{p}]$ p×1 dimenziós kimeneti vektor,

A, B, C, D a rendszer, a bemeneti, kimeneti és az előrecsatolási mátrixok, rendre n×n, n×m, p×n és p×m méretekkel.

A rendszer állapotdinamikáját elsőrendű differenciálegyenlet írja le (8.103), míg az állapot- és kimeneti változókat a kimeneti egyenlet lineárisan köti össze (8.104). Ha a rendszerben nem található előrecsatolás, akkor a kimeneti egyenletben a második tag nem szerepel, mivel D = [0]. A fenti állapottér-modell mátrixai állandó paraméterekkel rendelkeznek, azaz egy lineáris időinvariáns rendszert írnak le.

Az aszinkron motor villamos modellje az 8.4 és 8.5 fejezetekben célszerűen állapotváltozókkal került felírásra, így az állapotdinamikai egyenletben szereplő A mátrix megfeleltethető a korábban felírt mátrixoknak, függően a reprezentáció fajtájától, azaz, hogy álló vagy szinkron forgó koordináta-rendszerre érvényes alakjában kerül felírásra az állapottér-modell. A bemeneti mátrix a d és q irányú feszültségek együtthatóit tartalmazó mátrix felhasználásával írható fel. Az 8.5 fejezetben a motor modell forgórész fluxushoz rögzített koordináta rendszerben került meghatározásra, az állórész áram ezen koordináta rendszerben lévő isd, isq komponensei változóként szerepelnek az állapotváltozók között. Ebből következően a be- és kimeneti mátrixok célszerűen úgy választandók meg, hogy a forgó rendszerből a kétfázisú álló koordináta-rendszerbe történő transzformációt hajtsák végre. Az állapottér modell elnyeréséhez az (8.73) egyenletrendszerben a bemeneti mátrix alapjául szolgáló usd és usq feszültségek együtthatóit tartalmazó mátrix kibővül tehát a visszatranszformálást megvalósító tagokkal, míg a kimeneti mátrix csak a forgatáshoz szükséges kifejezéseket tartalmazza. A megállapítások következtében az aszinkron motor folytonos idejű állapottér modellje az (8.105)–(8.106) alakban írható fel.

$\frac{d}{d t} [\begin{matrix} ψ_{r d} \\ i_{s d} \\ i_{s q} \end{matrix}] = [\begin{matrix} - \frac{R_{r}}{L_{r}} & \frac{L_{m} R_{r}}{L_{r}} & 0 \\ \frac{L_{m} R_{r}}{L_{r}^{2} σ L_{s}} & - \frac{R^{″}}{σ L_{s}} & ω \\ - ω_{r} \frac{L_{m}}{L_{r} σ L_{s}} & - ω & - \frac{R^{″}}{σ L_{s}} \end{matrix}] \cdot [\begin{matrix} ψ_{r d} \\ i_{s d} \\ i_{s q} \end{matrix}] + \frac{1}{σ L_{s}} [\begin{matrix} 0 & 0 \\ \cos (ϑ) & \sin (ϑ) \\ - \sin (ϑ) & \cos (ϑ) \end{matrix}] \cdot [\begin{matrix} u_{s α} \\ u_{s β} \end{matrix}]$

(8.105)

$[\begin{matrix} i_{s α} \\ i_{s β} \end{matrix}] = [\begin{matrix} 0 & \cos (ϑ) & - \sin (ϑ) \\ 0 & \sin (ϑ) & \cos (ϑ) \end{matrix}] \cdot [\begin{matrix} ψ_{r d} \\ i_{s d} \\ i_{s q} \end{matrix}]$

(8.106)

A gyakorlati implementációhoz illetve a valósághű, időkésleltetést tartalmazó szimulációs vizsgálatok elvégzéséhez szükséges a motor diszkrét idejű rendszermodelljének ismerete. Diszkrét idejű, lineáris időinvariáns (LTI) rendszer állapottér-modellje (8.107)–(8.108) formában adható meg, ahol a rendszer állapotdinamikáját kifejező egyenlet differenciaegyenlettel írható le.

$\underline{x} (k + 1) = {\underline{\underline{A}}}_{d} \cdot \underline{x} (k) + {\underline{\underline{B}}}_{d} \cdot \underline{u} (k)$

(8.107)

$\underline{y} (k) = {\underline{\underline{C}}}_{d} \cdot \underline{x} (k) + {\underline{\underline{D}}}_{d} \cdot \underline{u} (k)$

(8.108)

A diszkrét idejű állapottér-modell mátrixai (8.109)–(8.112) alapján határozhatók meg. A kimeneti egyenlet, így a kimeneti egyenletben szereplő mátrixok nem változnak a diszkretizálás során.

${\underline{\underline{A}}}_{d} = ℒ^{- 1} {{(s \underline{\underline{I}} - \underline{\underline{A}})}^{- 1}}_{t = T}$

(8.109)

${\underline{\underline{B}}}_{d} = {\underline{\underline{A}}}^{- 1} ({\underline{\underline{A}}}_{d} - \underline{\underline{I}}) \underline{\underline{B}}$

(8.110)

${\underline{\underline{C}}}_{d} = \underline{\underline{C}}$

(8.111)

${\underline{\underline{D}}}_{d} = \underline{\underline{D}}$

(8.112)

A rendszer és a bemeneti mátrixok számítása könnyebben kivitelezhető, ha az (8.109) és (8.110) kifejezések helyett (8.113) és (8.114) szerint megadott, sorba fejtett alakjukban kerülnek meghatározásra.

${\underline{\underline{A}}}_{d} = \underline{\underline{I}} + \underline{\underline{A}} T + \frac{1}{2!} ({\underline{\underline{A}}}^{2} T^{2}) + \dots$

(8.113)

${\underline{\underline{B}}}_{d} = \underline{\underline{B}} T + \frac{\underline{\underline{A}} \underline{\underline{B}} T^{2}}{2} = (I T + \frac{A T^{2}}{2!} + \frac{A^{2} T^{3}}{3!} + \dots) B$

(8.114)

Vissza		Előre
7. fejezet - Csővezeték hálózatban használt frekvenciaváltóval ellátott aszinkron motoros hajtások gazdasági számítása	Főoldal	9. fejezet - Aszinkronmotor érzékelő nélküli fordulatszám becslése