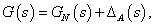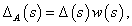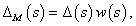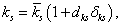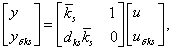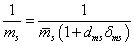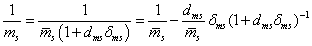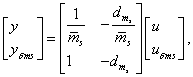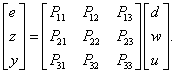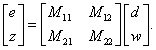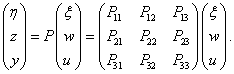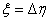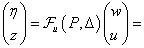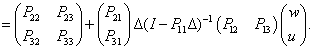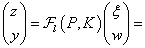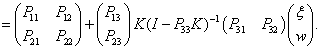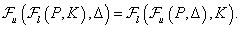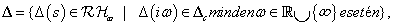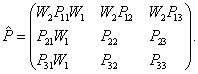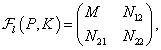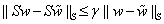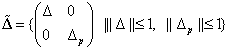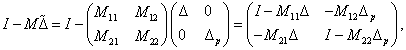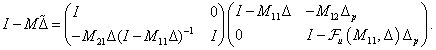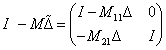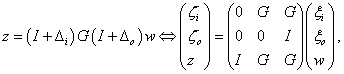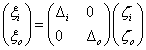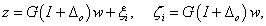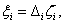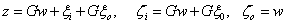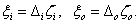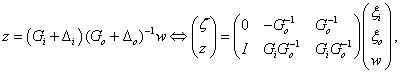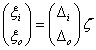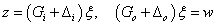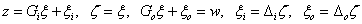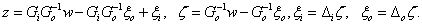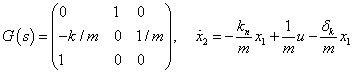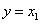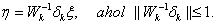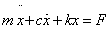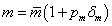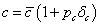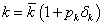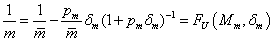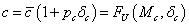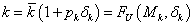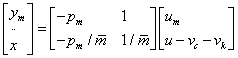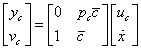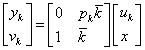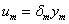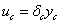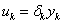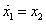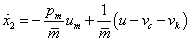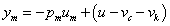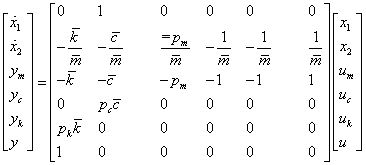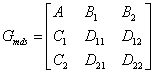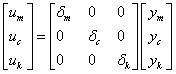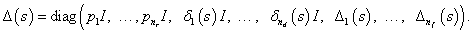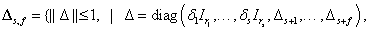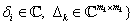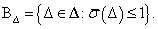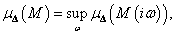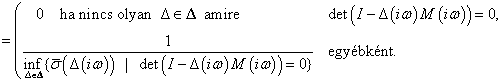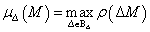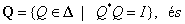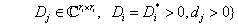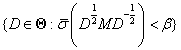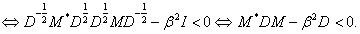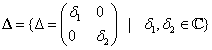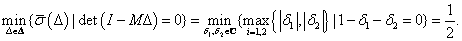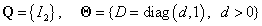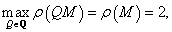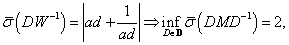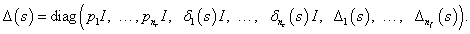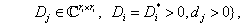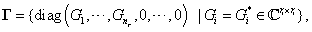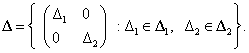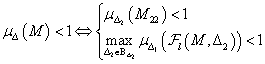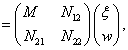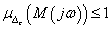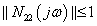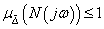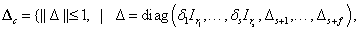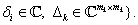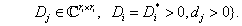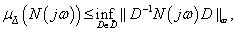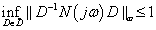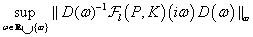3. fejezet - Bizonytalanságok modellezése
- 3.1. Bizonytalansági modellek
-
3.2. M-
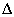 struktúra
struktúra
- 3.3. Robusztus stabilitás, robusztus performancia
- 3.4. Robusztus stabilitás vizsgálat
- 3.5. Kis erősítések tétele
- 3.6. Robusztus performancia analízis
- 3.7. Struktúrált bizonytalanság
- 3.8. Struktúrált szinguláris érték
- 3.9. Struktúrált szinguláris érték analízise
- 3.10. Struktúrált szinguláris érték: szintézis
A dinamikus jelenségek leírására közönséges vagy parciális differenciál-egyenleteket használunk. Az egyenletek alakja és struktúrája, a bennük szereplő paraméterek általában nem ismertek teljesen pontosan vagy ha azok időben változnak, a változásuk általában nem ismert.
Mivel a valódi rendszer modelljének pontos alakja a gyakorlati feladatokban nem ismert, s emiatt helyette annak közelítő, úgynevezett névleges (nominális) modelljét használjuk. A modell és a valós rendszer közötti eltérést okozzó hatások modellezésekor célszerű megkülönböztetni az állandóan jelen levő modell bizonytalanságot a külső zavarástól. Zavarások (disturbances) körébe tartozik tipikusan a rendszerre ható külső zavarás, az irányítójel hibája, a mérési zaj. Az irányítás célja, hogy a zavarások hatását csökkentse a mérnöki szempontból érdekes (esetleg fiktív) kimenő jelekre -- ez egy tipikus performancia követelmény.
Modell bizonytalanság (uncertainty) a modellben meglevő parametrikus bizonytalanságok és a nem modellezett dinamika hatása. Egy speciális eset a qLPV modellek ütemezési változói, amik ismertek a végrehajtás során de nem ismertek tervezéskor: a tervezés számára bizonyos szempontból bizonytalan paraméterként viselkednek. Az irányítás célja stabilitás és performancia garantálása adott nagyságú feltételezett modell bizonytalanság mellett.
Kétféle modell-bizonytalanságot különböztethetünk meg: strukturális és strukturálatlan modell-bizonytalanságot. A struktúrált bizonytalanság modellezésekor a bizonytalansági blokk struktúrálása (például blokk-diagonális) növelheti a modell pontosságát és használhatóságát az irányítás-tervezés szempontjából. Tipikusan struktúrált a grey-box modellezés során kapott modellben előforduló paramétereknek a bizonytalansága: a paraméter értéke pontosan nem ismert, de a bizonytalanság mértéke általában jól becsülhető.
3.1. Bizonytalansági modellek
Nemmodellezett dinamika
A mechanikai rendszerek irányítására alkalmazott lineáris vagy folytonos nemlineáris irányítási algoritmusokkal megvalósított szabályozási rendszer tulajdonságait nagymértékben leronthatják a mechanikai rendszerben jelenlevő (nemfolytonos) nemlinearitások. Tipikus nemlinearitások a szaturáció, surlódás,holtsáv, kotyogás, hiszterézis.
Számos irányítási alkalmazásnál az irányított rendszerben a nemlinearitás pontatlanul ismert vagy akár ismeretlen. Ha a linearizáláson alapuló technika kevésbé alkalmazható, a nemlinearitás hatásának kompenzálásához a szabályozót módosítani kell. Az alkalmazott technika alapján ez lehet robusztus szabályozás, amikor a szabályozót úgy tervezzük meg, hogy pontatlanul ismert nemlinearitás esetén is garantálja a zárt rendszer stabilitását és a szabályozási pontosságot, performanciát, vagy adaptív szabályozás, amikor a szabályozót kibővítjük olyan formában, hogy irányítás közben becsülje meg az ismeretlen nemlinearitást, paramétert.
A modell és a rendszer közötti hiba meghatározására általános megoldás nincs, különböző szerkezetű lehetőségek közül az additív, illetve a multiplikatív hiba struktúra a legismertebb.
A 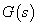 aktuális rendszer és a
aktuális rendszer és a 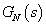 névleges rendszer közötti eltérést additív hiba struktúrának nevezzük, ha a következő összefüggés teljesül:
névleges rendszer közötti eltérést additív hiba struktúrának nevezzük, ha a következő összefüggés teljesül:
|
|
(51) |
ahol 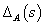 az additív hiba átviteli függvénye. Az additív hiba ismeretlen.
az additív hiba átviteli függvénye. Az additív hiba ismeretlen.
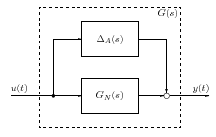
A 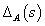 ismeretlen méretű additív hiba átviteli függvényt egy ismert korláttal rendelkező
ismeretlen méretű additív hiba átviteli függvényt egy ismert korláttal rendelkező 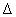 bizonytalansággal kifejezhetjük és frekvencia függvényét Nyquist diagramon ábrázolhatjuk:
bizonytalansággal kifejezhetjük és frekvencia függvényét Nyquist diagramon ábrázolhatjuk:
|
|
(52) |
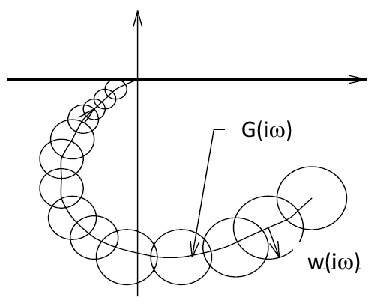
ahol 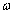 skalár függvény. Az aktuális
skalár függvény. Az aktuális 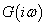 rendszer Nyquist diagramja a névleges
rendszer Nyquist diagramja a névleges 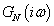 rendszer Nyquist diagramjával és a bizonytalanságot leíró
rendszer Nyquist diagramjával és a bizonytalanságot leíró 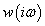 függvénynyel illusztrálható.
függvénynyel illusztrálható.
A 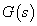 aktuális rendszer és a
aktuális rendszer és a 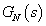 névleges rendszer közötti eltérést multiplikatív hiba struktúrájúnak nevezzük, ha a következő összefüggés teljesül:
névleges rendszer közötti eltérést multiplikatív hiba struktúrájúnak nevezzük, ha a következő összefüggés teljesül:
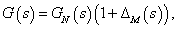
ahol 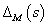 a multiplikatív hiba átviteli függvénye.
a multiplikatív hiba átviteli függvénye.
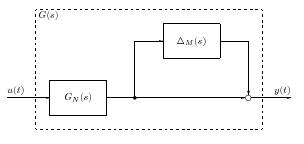
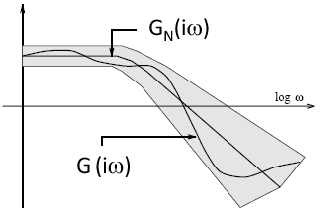
A 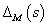 ismeretlen méretű additív hiba átviteli függvényt egy ismert korláttal rendelkező
ismeretlen méretű additív hiba átviteli függvényt egy ismert korláttal rendelkező 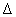 bizonytalansággal kifejezhetjük és frekvencia függvényét Bode diagramon ábrázolhatjuk:
bizonytalansággal kifejezhetjük és frekvencia függvényét Bode diagramon ábrázolhatjuk:
|
|
(53) |
ahol 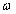 skalár függvény. Az aktuális
skalár függvény. Az aktuális 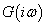 rendszer Bode diagramja a névleges
rendszer Bode diagramja a névleges 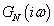 rendszer Bode diagramjával és a bizonytalanságot leíró
rendszer Bode diagramjával és a bizonytalanságot leíró 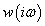 függvénnyel illusztrálható.
függvénnyel illusztrálható.
Parametrikus bizonytalanság
Gyakran a bizonytalanságok egy része a rendszert leíró modell paramétereinek változásával is megfogalmazható.
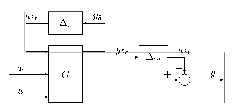
Például az 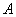 rendszermátrixban lévő
rendszermátrixban lévő 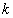 rugóállandó és
rugóállandó és 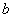 csillapítási együtthatók változnak. Ezek a paraméterek a mátrix több elemében is előfordulhatnak.
csillapítási együtthatók változnak. Ezek a paraméterek a mátrix több elemében is előfordulhatnak.
A bizonytalan rugóállandó paramétere a következőképpen modellezhető:
|
|
(54) |
ahol 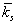 a névleges rugóállandó,
a névleges rugóállandó, 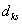 a névleges értéktől való eltérést mutatja, míg
a névleges értéktől való eltérést mutatja, míg 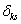 paraméterről azt tudjuk, hogy a
paraméterről azt tudjuk, hogy a 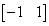 intervallumba esik. A bizonytalan rugóállandó
intervallumba esik. A bizonytalan rugóállandó 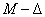 struktúrája a 11. ábrán látható.
struktúrája a 11. ábrán látható.
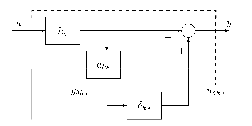
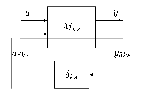
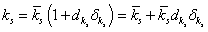
A jelek közötti kapcsolatok:
|
|
(55) |
ahol 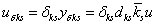 . Emiatt
. Emiatt 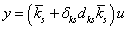 . Az ismert komponenseket tartalmazó blokk:
. Az ismert komponenseket tartalmazó blokk: 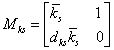
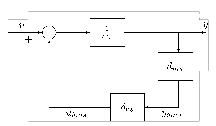
Ha egy bizonytalan paraméter a nevezőben van, akkor a következőképpen járunk el.
|
|
(56) |
ahol 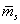 a névleges tömeg,
a névleges tömeg, 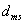 a névleges értéktől való eltérést mutatja, míg
a névleges értéktől való eltérést mutatja, míg 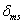 paraméterről azt tudjuk, hogy a
paraméterről azt tudjuk, hogy a 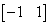 intervallumba esik. A bizonytalan rugóállandó
intervallumba esik. A bizonytalan rugóállandó 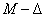 struktúrája a 12. ábrán látható.
struktúrája a 12. ábrán látható.
|
|
(57) |
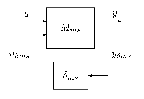
A jelek közötti kapcsolatok:
|
|
(58) |
ahol 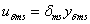 . Mivel
. Mivel 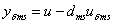 , ezért
, ezért 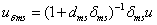 .
.
Emiatt 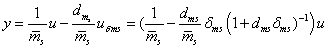 . Az ismert komponenseket tartalmazó blokk:
. Az ismert komponenseket tartalmazó blokk: 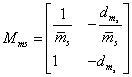 .
.
3.2. M-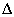 struktúra
struktúra
A szabályozott rendszer komponensei az előzőek alapján a modell és a szabályozó, valamint a minőségi specifikációkkal és bizonytalanságokkal kapcsolatos információk. A 13. ábrán látható úgynevezett 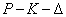 struktúrájú modellt használjuk a szabályozó tervezéséhez.
struktúrájú modellt használjuk a szabályozó tervezéséhez.
|
|
(59) |
Ha figyelembe vesszük a szabályozó hatását, azaz az irányítójel és a mért jel közötti kapcsolatot 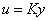 , akkor az úgynevezett M-
, akkor az úgynevezett M-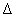 struktúrához jutunk.
struktúrához jutunk.
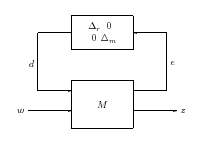
A 14 ábrán látható 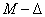 modellt a szabályozott rendszer elemzéséhez használjuk.
modellt a szabályozott rendszer elemzéséhez használjuk.
|
|
(60) |
3.3. Robusztus stabilitás, robusztus performancia
Mivel a rendszerre ható külső körülmények változhatnak, valamint az érzékelők és beavatkozó szervek tulajdonságai is módosulhatnak, kisebb hibák léphetnek fel, stb. szükség van rekonfiguráló és hibatűrő irányítások tervezése. Ezen a tulajdonságok az elérésének egy módja lehet növelni a szabályozó robusztusságát ezekre a tényezőkre és a modellezési hibákra. Az alábbiakban a feladat megoldásának ezt a stratégiáját fejtjük ki részletesebben.
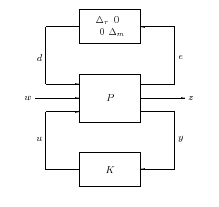
A szabályozási feladatot az 15 ábrán bemutatott 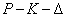 struktúrában fogalmazzuk meg amit az alábbi egyenletek írnak le
struktúrában fogalmazzuk meg amit az alábbi egyenletek írnak le
|
|
(61) |
ahol 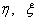 jelek a bizonytalanságok leírására szolgálnak,
jelek a bizonytalanságok leírására szolgálnak, 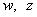 az általánosított rendszerstruktúra zavarás és performancia jelei,
az általánosított rendszerstruktúra zavarás és performancia jelei, 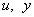 a szabályozó bemenet és a mért kimenet.
a szabályozó bemenet és a mért kimenet.
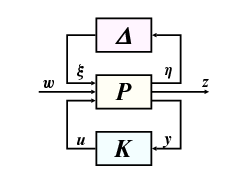
A bizonytalansági halmaz, 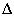 , stabil átmenetfüggvényekből áll. A perturbált kör a
, stabil átmenetfüggvényekből áll. A perturbált kör a
|
|
(62) |
bizonytalanság hatására lakul ki, ahol 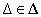 és alakja a következő:
és alakja a következő:
|
|
(63) |
|
|
(64) |
Az 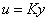 szabályozót a nominális (perturbálatlan) rendszerre kötve kapjuk, hogy
szabályozót a nominális (perturbálatlan) rendszerre kötve kapjuk, hogy
|
|
(65) |
|
|
(66) |
A szabályozott, 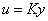 , és perturbált,
, és perturbált, 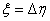 , kör alakja
, kör alakja
|
|
(67) |
Mivel a zárt körök jól definiáltak kell, hogy legyenek és nem függhetnek 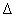 és
és 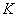 sorrendjétől, néhány feltételezéssel kell élnünk:
sorrendjétől, néhány feltételezéssel kell élnünk:
1. Létezik 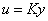 szabályozó, ami stabilizálja a nominális (
szabályozó, ami stabilizálja a nominális (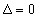 ) rendszert (
) rendszert (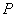 ).
).
2. A bizonytalansági halmaz
|
|
(68) |
ahol 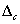 komplex mátrixok egy halmaza, ami tartalmazza
komplex mátrixok egy halmaza, ami tartalmazza 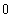 -t, ami meghatározza a bizonytalanságok méretét és struktúráját. Feltesszük, hogy ez a halmaz csillag alakú, vagyis
-t, ami meghatározza a bizonytalanságok méretét és struktúráját. Feltesszük, hogy ez a halmaz csillag alakú, vagyis 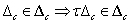 minden
minden 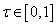 esetén.
esetén.
3. A bizonytalanságok és az általánosított rendszerstruktúra kötése jól definiált, vagyis 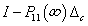 invertálható minden
invertálható minden 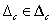 esetén.
esetén.
Ezek a feltételek jórészt automatikusan teljesülnek a szokásos, intervallum, gömb, stb. típusú bizonytalansági halmazokra.
Általában normalizáló súlyozásokat alkalmazunk, amit azután figyelembe veszünk 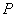 összeállításánál: ha
összeállításánál: ha 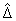 bizonytalansággal akarunk dolgozni, ahol
bizonytalansággal akarunk dolgozni, ahol 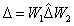 valós racionális
valós racionális 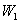 és
és 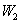 súlyokkal, akkor
súlyokkal, akkor 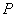 helyett
helyett 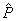 rendszert kell tekintenünk, ahol
rendszert kell tekintenünk, ahol
|
|
(69) |
3.4. Robusztus stabilitás vizsgálat
Vezessük be a
|
|
(70) |
jelölést, ahol 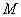 a bizonytalanság által látott átviteli függvény.
a bizonytalanság által látott átviteli függvény.
Tétel 4.1
Ha
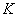 stabilizálja
stabilizálja
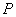 -t és ha
-t és ha
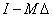 minden
minden
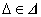 esetén stabilan invertálható akkor
esetén stabilan invertálható akkor
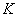 robusztusan stabilizálja
robusztusan stabilizálja
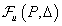 -t a
-t a
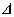 bizonytalanságra nézve.
bizonytalanságra nézve.
A gyakorlatban azt kell leelenőrizni, hogy 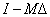 stabilisan invertálható, vagyis
stabilisan invertálható, vagyis 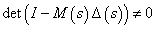 minden
minden 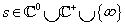 esetén. Ez a feladat bonyolult, mivel az egész jobb fél síkon kell a feltételt ellenőrizni.
esetén. Ez a feladat bonyolult, mivel az egész jobb fél síkon kell a feltételt ellenőrizni.
A következő állítás megmutatja, hogy általában elég 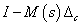 invertálhatóságát a komplex tengelyen (
invertálhatóságát a komplex tengelyen (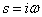 , ahol
, ahol 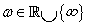 ) ellenőrizni és elegendő csak a
) ellenőrizni és elegendő csak a 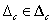 halmazra.
halmazra.
Tétel 4.2
Tegyük fel, hogy
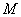 egy stabil átviteli mátrix.
egy stabil átviteli mátrix.
Ha 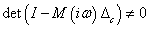 minden
minden 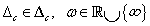 esetén, akkor
esetén, akkor 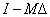 stabilisan invertálható minden
stabilisan invertálható minden 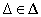 esetén.
esetén.
A fenti két állítást összegezve kapjuk a következő robusztus stabilitási eredményt:
Következmény 4.1
Ha
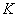 stabilizálja
stabilizálja
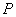 -t és
-t és
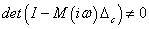 minden
minden
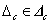 és minden
és minden
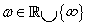 esetén, akkor
esetén, akkor
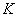 robusztusan stabilizálja
robusztusan stabilizálja
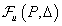 -t a
-t a
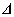 bizonytalansági halmazra nézve.
bizonytalansági halmazra nézve.
A fordított állítás általában nem igaz. Egy konkrét esetben a teszt nem konzervatív voltát megpróbálhatjuk úgy igazolni, hogy egy destabilizáló 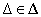 perturbációt keresünk.
perturbációt keresünk.
3.5. Kis erősítések tétele
A robusztus stabilitási analízis egy alapvető eszköze a kis erősítések tétele, ami kimondja, hogy ha a hurokátviteli szorzat normája egynél kisebb, akkor a visszacsatolás stabilis. Ez az eredmény a fixpont tétel egy következménye.
Egy 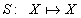 rendszert, ahol
rendszert, ahol 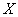 egy Banach tér (például
egy Banach tér (például 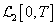 vagy
vagy 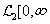 )) kontraktív, ha a (Lipschitz) indukált normája
)) kontraktív, ha a (Lipschitz) indukált normája 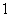 -nél kisebb, azaz létezik
-nél kisebb, azaz létezik 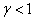 úgy, hogy
úgy, hogy
|
|
(71) |
minden 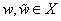 esetén. A fixpont tétel alapján egy kontraktív
esetén. A fixpont tétel alapján egy kontraktív 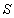 rendszerhez létezik és egyértelmű
rendszerhez létezik és egyértelmű 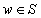 amire
amire 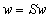 .
.
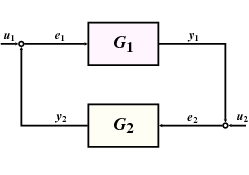
Tétel 4.3 (Kis erősítések tétele)
Tegyük fel, hogy a
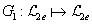 valamint a
valamint a
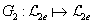 rendszereknek véges erősítése van, amire
rendszereknek véges erősítése van, amire
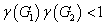 .
.
Ekkor a visszacsatolt kapcsolat stabilis, azaz minden 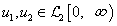 esetén létezik es egyértelmű
esetén létezik es egyértelmű 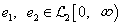 , lásd a 16 ábrát.
, lásd a 16 ábrát.
A gyakorlatban sokszor az eredeti visszacsatolás nem teljesíti a tétel feltételeit. Ilyenkor a zárt kör stabilitását megkaphatjuk a kis erősítések tételének alkalmazásával egy módosított elrendezésre, aminek a stabilitási tulajdonságai viszont azonosak az eredeti rendszerével.
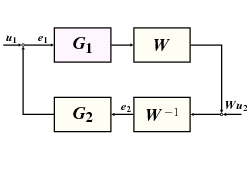
A leggyakrabban alkalmazott transzformáció stabilan invertálható súlyfüggvényeket alkalmazva módosítja a kapcsolást az 17 ábrán látható módon.
Következmény 4.2
Legyen
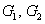 stabil rendszer. Ekkor a visszacsatolt rendszer stabilis ha létezik egy
stabil rendszer. Ekkor a visszacsatolt rendszer stabilis ha létezik egy
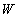 ,
,
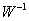 stabilis rendszer úgy, hogy
stabilis rendszer úgy, hogy
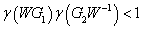 .
.
3.6. Robusztus performancia analízis
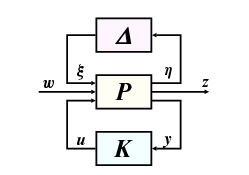
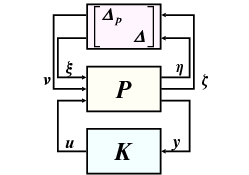
Definiáljuk a
|
|
(72) |
halmazt. A kis erősítések tételét alkalmazva megkaphatjuk a 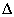 -ra vonatkozó robusztus performancia eredményt:
-ra vonatkozó robusztus performancia eredményt:
• 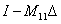 invertálható és
invertálható és 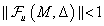 minden
minden 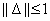 esetén,
esetén,
akkor és csak akkor ha a robusztus stabilitási feltétel minden 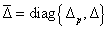 -ra fennáll, ahol
-ra fennáll, ahol 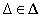 és
és 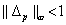 , lásd az 17 ábrát, azaz
, lásd az 17 ábrát, azaz
• 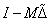 invertálható minden
invertálható minden 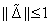 esetén,
esetén,
ahol 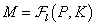 .
.
Megvizsgálva, hogy
|
|
(73) |
adódik, hogy
|
|
(74) |
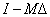 invertálható ha
invertálható ha 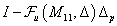 invertálható. Feltevéseink szerint
invertálható. Feltevéseink szerint 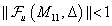 .
.
válasszuk 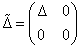 -t. Ekkor
-t. Ekkor
|
|
(75) |
invertálható, tehát 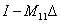 invertálható minden
invertálható minden 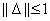 esetén.
esetén.
Mivel 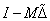 invertálható, a kis erősítések tételéből következik, hogy
invertálható, a kis erősítések tételéből következik, hogy 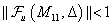 minden
minden 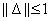 esetén.
esetén.
Összefoglalva: a robusztus performancia ekvivalens egy robusztus stabilitási feladattal, ami egy nomináis 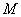 zárt körre és struktúrált bizonytalanságra vonatkozik, lásd a 19, ábrát. Mivel a bizonytalansági halmaz struktúrált, a kis erősítések tételénél kevésbé konzervatív eredmények keresése válik szükségessé.
zárt körre és struktúrált bizonytalanságra vonatkozik, lásd a 19, ábrát. Mivel a bizonytalansági halmaz struktúrált, a kis erősítések tételénél kevésbé konzervatív eredmények keresése válik szükségessé.
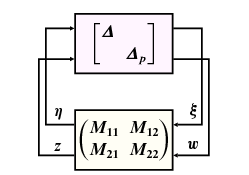
3.7. Struktúrált bizonytalanság
A bizonytalan rendszereket egy nominális LTI rendszer és egy visszacsatolt bizonytalan blokk együttesével modellezzük, ahol először a 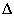 bizonytalansági halmazra az operátor egységgömböt választottuk. Ez az eset jól kezelhető a kis erősítések tételével. A továbbiakban ezt a technikát terjesztjük ki más szerkezetű bizonytalansági halmazok esetére.
bizonytalansági halmazra az operátor egységgömböt választottuk. Ez az eset jól kezelhető a kis erősítések tételével. A továbbiakban ezt a technikát terjesztjük ki más szerkezetű bizonytalansági halmazok esetére.
Egy igen fontos struktúrált bizonytalansági osztály a blokk diagonális bizonytalanságok halmaza. Blokk diagonális bizonytalansági struktúrák létrehozásának egyik módja az egyes 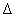 bizonytalanságok kiemelése a rendszerből és az így kapott összekötés LFT alakra való hozása.
bizonytalanságok kiemelése a rendszerből és az így kapott összekötés LFT alakra való hozása.
A továbbiakban azt az elvet illusztráljuk egy néhány konkrét példán keresztül.
Példa 4.1 Input-output multiplikatív bizonytalanság:
|
|
(76) |
|
|
(77) |
A 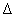 kiemelésének menete:
kiemelésének menete:
• 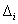 elkülönítése:
elkülönítése:
|
|
(78) |
|
|
(79) |
• 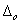 elkülönítése:
elkülönítése:
|
|
(80) |
|
|
(81) |
Példa 4.2: Faktorizált bizonytalanság (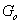 invertálható):
invertálható):
|
|
(82) |
|
|
(83) |
Az alábbi relációk
|
|
(84) |
felírhatók mint
|
|
(85) |
amiből 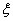 -t eliminálva és figyelembe véve, hogy
-t eliminálva és figyelembe véve, hogy 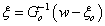 adódik
adódik
|
|
(86) |
Parametrikus bizonytalanságokra tekintsük az alábbi példákat:
Példa 4.3: Tekintsük a rugózott tömeg moddeljét: 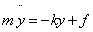 .
.
|
|
(87) |
A bizonytalan rugóállandó 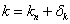 (additív bizonytalansági modell).
(additív bizonytalansági modell).
Ekkor az állapotegyenletek
|
|
(88) |
|
|
(89) |
|
|
(90) |
|
|
(91) |
|
|
(92) |
Példa 4.4: Tekintsük az 4.4 ábrán látható tömeg-csillapító-rugó rendszert (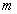 tömeg,
tömeg, 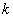 csillapítási együttható,
csillapítási együttható, 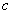 rugóállandó).
rugóállandó).
Differenciálegyenlete:
|
|
(93) |
ahol 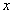 a tömeg elmozdulása,
a tömeg elmozdulása, 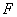 erő a rendszer gerjesztése.
erő a rendszer gerjesztése.
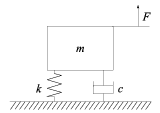
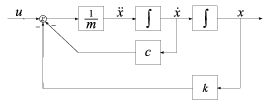
A blokkdiagram a rendszer névleges modelljét illusztrálja. A valós rendszerben a fizikai paraméterek egyrészt nem ismertek pontosan, másrészt üzem közben változnak. Ismerjük viszont ezek átlagos értékét és becslésünk van az átlagos értéktől való eltérésükre.
|
|
(94) |
|
|
(95) |
|
|
(96) |
A példában legyenek 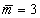 ,
, 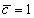 ,
, 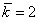 a névleges értékek,
a névleges értékek, 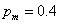 ,
, 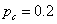 ,
, 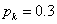 és
és 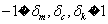 reprezentálja, hogy a rendszer modellje, csillapítása és rugóállandója rendre
reprezentálja, hogy a rendszer modellje, csillapítása és rugóállandója rendre 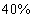 ,
, 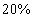 ,
, 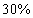 bizonytalanságú.
bizonytalanságú.
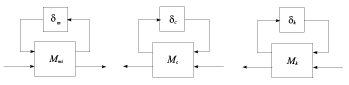
A parametrikus bizonytalanságok a következőképpen írhatók fel:
|
|
(97) |
|
|
(98) |
|
|
(99) |
ahol 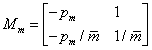 ,
, 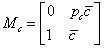 ,
, 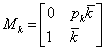 Megjegyzés: A kapcsolatokat felső bizonytalanság blokkal vettük figyelembe. A rendszer jelei közötti összefüggések ezek szerint a következőképpen alakulnak:
Megjegyzés: A kapcsolatokat felső bizonytalanság blokkal vettük figyelembe. A rendszer jelei közötti összefüggések ezek szerint a következőképpen alakulnak:
|
|
(100) |
ahol
|
|
(101) |
|
|
(102) |
|
|
(103) |
|
|
(104) |
|
|
(105) |
továbbá 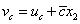 és
és 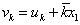 .
.
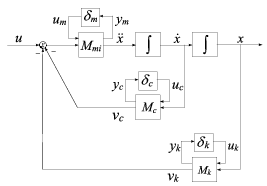
Válasszuk az állapotokat a következőképpen:
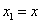
, 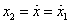 ,
, 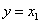 , azaz
, azaz 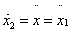 .
.
|
|
(106) |
|
|
(107) |
|
|
(108) |
Ezek után felírhatjuk a parametrikus bizonytalanságokat tartalmazó rendszer modelljét:
|
|
(109) |
A lengőrendszer modellje 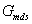 kizárólag az ismert
kizárólag az ismert 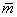 ,
, 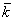 ,
, 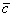 névleges paraméterektől és az ismert
névleges paraméterektől és az ismert 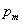 ,
, 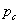 ,
, 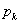 bizonytalnsági felső becslésektől függ. Így
bizonytalnsági felső becslésektől függ. Így 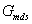 ismert és nem tartalmaz bizonytalanságokat.
ismert és nem tartalmaz bizonytalanságokat.
|
|
(110) |
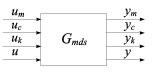
ahol 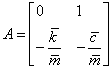 ,
, 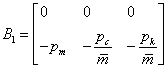 ,
, 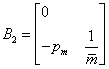 ,
,
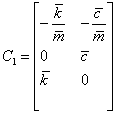
, 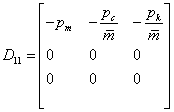 ,
, 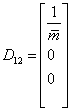 ,
,
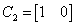
, 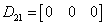 ,
, 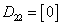 .
.
A bizonytalanságokat tartalmazó 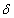 paramétereket egy külön blokk tartalmazza.
paramétereket egy külön blokk tartalmazza.
|
|
(111) |
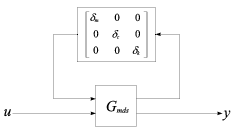
A bizonytalan paraméterek hatása a 4.4 ábrán látható Bode diagramokon jól láthatók.

A modellezés célja, hogy megkapjuk az általánosított rendszer struktúrát, ahol az összes súlyfüggvény a 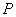 általánosított rendszerbe van beillesztve, míg a bizonytalanságokat a blokk-diagonális
általánosított rendszerbe van beillesztve, míg a bizonytalanságokat a blokk-diagonális 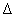 tartalmazza, ami egy
tartalmazza, ami egy 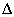 halmaz eleme, ahol:
halmaz eleme, ahol:
|
|
(112) |
és ahol minden bokk normalizált.
3.8. Struktúrált szinguláris érték
Az 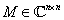 mátrixok esetén a
mátrixok esetén a 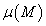 struktúrált szinguláris érték definíciójában figyelembe veszünk egy feladatfüggő
struktúrált szinguláris érték definíciójában figyelembe veszünk egy feladatfüggő 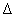 bizonytalansági struktúrát, ami az adott probléma sajátosságaitól és performancia követelményeitől függ. A vizsgált struktúrák az egységgömb megszorítását jelentik valamely
bizonytalansági struktúrát, ami az adott probléma sajátosságaitól és performancia követelményeitől függ. A vizsgált struktúrák az egységgömb megszorítását jelentik valamely 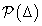 tulajdonságok mentén, amikre feltesszük, hogy ha
tulajdonságok mentén, amikre feltesszük, hogy ha 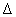 -ra teljesül
-ra teljesül 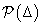 , akkor
, akkor 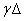 -ra is teljesülni fog minden
-ra is teljesülni fog minden 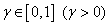 esetén, azaz
esetén, azaz 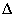 csillag szerkezetű (kúp).
csillag szerkezetű (kúp).
Tipikus példa a 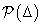 tulajdonságra a blokk-diagonális struktúra, aminek két típusát tekintjük át: az ismédlődő skalár és teljes blokkú,
tulajdonságra a blokk-diagonális struktúra, aminek két típusát tekintjük át: az ismédlődő skalár és teljes blokkú,
vagyis
|
|
(113) |
|
|
(114) |
ahol a nemnegatív 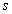 és
és 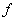 egészek az ismétlődő skalár blokkok számát illetve a teljes blokkok számát jelentik.
egészek az ismétlődő skalár blokkok számát illetve a teljes blokkok számát jelentik.
Értelemszerűen fenn kell állnia az 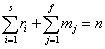 összefüggésnek. Az egyszerűség kedvéért a jelölésből elhagyjuk
összefüggésnek. Az egyszerűség kedvéért a jelölésből elhagyjuk 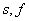 -t.
-t.
Gyakran normakorlátos 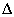 halmazzal van dolgunk
halmazzal van dolgunk
|
|
(115) |
Definíció 4.1 Az 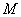 LTI operátorhoz rendelt és a
LTI operátorhoz rendelt és a 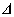 halmazra vonatkoztatott
halmazra vonatkoztatott 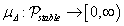 struktúrált szinguláris érték
struktúrált szinguláris érték
|
|
(116) |
ahol
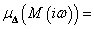
|
|
(117) |
A definíció jelentése a 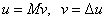 visszacsatolt kör esetén kézenfekvő:
visszacsatolt kör esetén kézenfekvő: 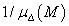 annak a struktúrált
annak a struktúrált 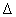 bizonytalanságnak a normája ami destabilizálja a zárt kört.
bizonytalanságnak a normája ami destabilizálja a zárt kört.
A definíció egyenes következménye, hogy minden 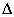 és
és 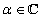 esetén
esetén 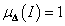 valamint
valamint 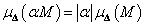 . Azonban, ha a blokkstruktúra nem triviális akkor
. Azonban, ha a blokkstruktúra nem triviális akkor 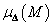 nem normája
nem normája 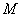 -nek, mivel a háromszög egyenlőtlenség nem teljesül.
-nek, mivel a háromszög egyenlőtlenség nem teljesül.
Bebizonyítható az alábbi egyenlőség:
|
|
(118) |
Valóban, minden 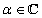 esetén
esetén 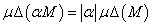 , így csak két esetet kell vizsgálnunk:
, így csak két esetet kell vizsgálnunk: 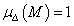 akkor és csak akkor, ha
akkor és csak akkor, ha 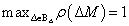 valamint
valamint 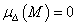 akkor és csak akkor, ha
akkor és csak akkor, ha 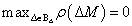 . Ezek az esetek a definíció egyszerű következményei.
. Ezek az esetek a definíció egyszerű következményei.
Ebből az egyenlőségből, a spektrálsugár és a 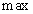 függvények folytonosságából valamint
függvények folytonosságából valamint 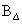 kompaktságából következik, hogy a
kompaktságából következik, hogy a 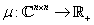 függvény folytonos.
függvény folytonos.
Általában nem könnyű a 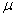 értékét kiszámítani. A továbbiakban a
értékét kiszámítani. A továbbiakban a 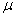 függvény néhány olyan tulajdonságát soroljuk fel, amit haszonnal lehet a számításokban és becslésekben felhasználni.
függvény néhány olyan tulajdonságát soroljuk fel, amit haszonnal lehet a számításokban és becslésekben felhasználni.
-
ha
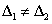 , általában
, általában 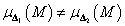 .
. -
ha
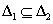 akkor
akkor 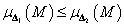 .
. -
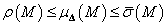
. (
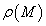 az
az 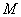 spektrál sugara)
spektrál sugara)
Valóban, ha 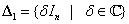 akkor
akkor 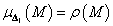 és
és 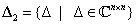 esetén
esetén 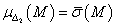 , míg tetszőleges
, míg tetszőleges 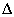 esetén
esetén 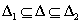 .
.
Sajnos ezek a becslések általában nagyon durvák,mivel 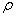 valamint
valamint 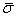 közti különbség tetszőlegesen nagy lehet. A becsléseket szűkíteni lehet
közti különbség tetszőlegesen nagy lehet. A becsléseket szűkíteni lehet 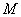 olyan transzformációinak a felhasználásával amik nem befolyásolják
olyan transzformációinak a felhasználásával amik nem befolyásolják 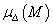 értékét, azonban hatással vannak
értékét, azonban hatással vannak 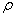 és
és 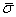 értékére.
értékére.
-
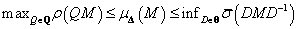
ahol
|
|
(119) |
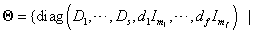
|
|
(120) |
Valóban: mivel 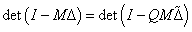 ahol
ahol 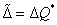 adódik, hogy
adódik, hogy 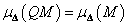 minden
minden 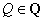 -ra. Másrészt
-ra. Másrészt 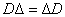 ha
ha 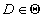 így
így 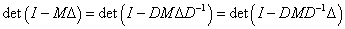 .
.
Ezért 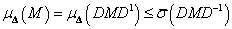 , vagyis
, vagyis 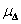 invariáns a diagonális skálázásra.
invariáns a diagonális skálázásra.
-
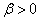
esetén a
|
|
(121) |
halmaz konvex.
Valóban:
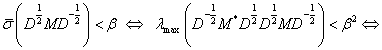
|
|
(122) |
Az utolsó feltétel egy lineáris mátrixegyenlőtlenség (LMI), ami egy konvex feltétel 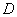 -ben.
-ben.
-
azon
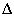 struktúrák esetén, amikre
struktúrák esetén, amikre 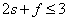 :
: 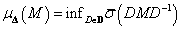 .
.
Ha 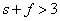 akkor az egyenlőség általában nem teljesül.
akkor az egyenlőség általában nem teljesül.
A leírtakat az alábbi példa szemlélteti: legyen 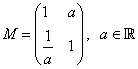 és tekintsünk egy
és tekintsünk egy
|
|
(123) |
bizonytalansági halmazt. Mivel 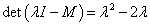 és
és 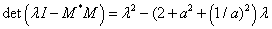 akkor
akkor 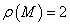 valamint
valamint 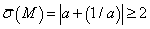 .
.
Mivel 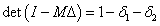 és
és 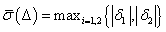 :
:
|
|
(124) |
Így 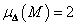 .
.
Másrészt:
|
|
(125) |
ezért
|
|
(126) |
|
|
(127) |
ami ebben a speciális esetben igazolja az állítás helyességét.
Eddig komplex skaláris blokkokat tekintettünk. Azonban a parametrikus bizonytalanságok tipikusan valós értékűek, amit figyelembe kell vennünk.
|
|
(128) |
Ez a struktúra elvezet a kevert (valós/komplex) 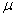 fogalmához. Ekkor a
fogalmához. Ekkor a 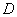 skálázás alkalmazása helyett felső becslést kaphatunk a kevert
skálázás alkalmazása helyett felső becslést kaphatunk a kevert 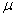 -re, ha az úgynevezett
-re, ha az úgynevezett 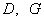 skálázást használjuk:
skálázást használjuk:
-
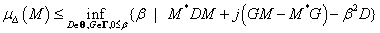
(129)
ahol
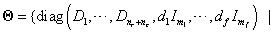
|
|
(130) |
|
|
(131) |
és 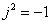 .
.
Ez általában egy kvázi-konvex problémára vezet. Ha 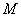 egy-rangú mátrix, akkor
egy-rangú mátrix, akkor 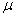 megegyezik a felső becslésével.
megegyezik a felső becslésével.
3.9. Struktúrált szinguláris érték analízise
A következő állítás alapvető szerepet játszik a 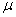 alapú robusztussági analízisben. Tekintsük a
alapú robusztussági analízisben. Tekintsük a 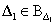 és
és 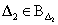 bizonytalanságokat valamint a következő blokk-diagonális
bizonytalanságokat valamint a következő blokk-diagonális 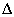 struktúrát:
struktúrát:
|
|
(132) |
Tétel 4.4 (Fő hurok tétel)
|
|
(133) |
Tekintsünk most egy általánosított 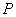 rendszerstruktúrát és egy stabilizáló
rendszerstruktúrát és egy stabilizáló 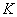 szabályozót, azaz
szabályozót, azaz
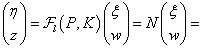
|
|
(134) |
és 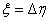 ahol
ahol 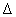 stabil bizonytalanság, amire
stabil bizonytalanság, amire 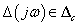 minden
minden 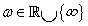 esetén.
esetén.
Ekkor a 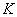 robusztusan stabilizál, ha
robusztusan stabilizál, ha
|
|
(135) |
minden 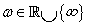 esetén.
esetén.
A 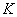 szabályozó teljesíti a nominális performancia kritériumot,ha
szabályozó teljesíti a nominális performancia kritériumot,ha
|
|
(136) |
minden 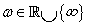 esetén.
esetén.
A Fő hurok tétel alapján a performancia robusztus, ha
|
|
(137) |
minden 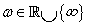 esetén, ahol
esetén, ahol 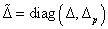 .
.
3.10. Struktúrált szinguláris érték: szintézis
Az analízis feltételek fényében egy robusztus stabilitást és performanciát garantáló szabályozó tervezéséhez minimalizálni kell egy struktúrált szinguláris értéket egy adott struktúrált bizonytalansági halmazon és minden frekvencián. Ez egy nemkonvex nemlineáris feladat, amire még nem született minden igényt kielégítő megoldó algoritmus. Egy, a gyakorlatban számos feladat esetében hatékonynak bizonyult heurisztikus algoritmus az úgynevezett 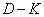 -iteráció (vagy
-iteráció (vagy 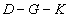 iteráció, valós bizonytalanságok kezelése esetén).
iteráció, valós bizonytalanságok kezelése esetén).
Tekintsük az alábbi bizonytalansági struktúrát:
|
|
(138) |
|
|
(139) |
A 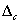 -nek megfelelő
-nek megfelelő 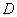 skálázó mátrixok halmaza
skálázó mátrixok halmaza
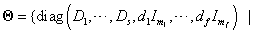
|
|
(140) |
Ekkor a 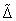 -hoz rendelt skálázó mátrixok halmaza
-hoz rendelt skálázó mátrixok halmaza
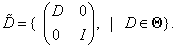
Ezekkel a skálázó szűrőkkel
|
|
(141) |
így minden stabilizáló szabályozóra, ami teljesíti a
|
|
(142) |
feltételt minden 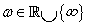 esetén, garantált a robusztus performancia. Ezért a
esetén, garantált a robusztus performancia. Ezért a 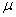 -t direktbe optimalizáló szabályozó tervezése helyett a felső becslést minimalizáljuk a
-t direktbe optimalizáló szabályozó tervezése helyett a felső becslést minimalizáljuk a 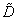 segítségével.
segítségével.
Ezt a feladatot az alábbi kritérium fogalmazza meg: minimizáljuk
|
|
(143) |
minden 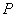 -t stabilizáló
-t stabilizáló 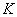 szabályozóra, és minden frekvencián a
szabályozóra, és minden frekvencián a 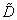 -beli
-beli 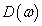 skálázó mátrixokra. Ha ez a minimum kisebb mint egy, akkor a tervezés sikeres.
skálázó mátrixokra. Ha ez a minimum kisebb mint egy, akkor a tervezés sikeres.
3.10.1. A 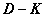 iteráció
iteráció
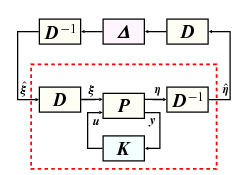
Sajnos az (143) feladatban nem tudunk egyszerre minimalizálni a 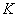 szabályozó és frekvenciafüggő
szabályozó és frekvenciafüggő 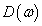 skálázó mátrixok függvényében. Ezért egy iterációt alkalmazunk: fixen tartjuk a
skálázó mátrixok függvényében. Ezért egy iterációt alkalmazunk: fixen tartjuk a 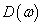 skálát és (143) minimumát keressük a stabilizáló szabályozók halmazán. A második lépésben a
skálát és (143) minimumát keressük a stabilizáló szabályozók halmazán. A második lépésben a 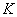 szabályozót tratjuk fixen és (143) minimumát keressük a
szabályozót tratjuk fixen és (143) minimumát keressük a 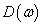 skálák függvényében. Ezt az eljárást nevezzük
skálák függvényében. Ezt az eljárást nevezzük 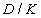 -iterációnak, lásd még a 26 ábrát.
-iterációnak, lásd még a 26 ábrát.
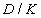
-iteráció algoritmusa:
Rögzítjük az iterációk maximális számát, MAXIT, és egy 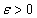 tolerancia szintet. Választunk egy
tolerancia szintet. Választunk egy 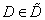 skálafüggvényt.
skálafüggvényt.
A rögzített 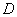 -vel megkeressük
-vel megkeressük 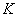 -t, az optimális
-t, az optimális 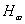 szabályozót amire
szabályozót amire 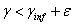 úgy, hogy fennáll a
úgy, hogy fennáll a 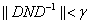
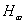 becslés. Ha
becslés. Ha 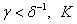 a keresett robusztus szabályozó, ha nem, akkor tovább megyünk a
a keresett robusztus szabályozó, ha nem, akkor tovább megyünk a 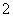 . lépésre.
. lépésre.
Rögzített 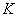 szabályozóval egy új
szabályozóval egy új 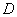 skálázó szűrőt számolunk ki, minimalizálva
skálázó szűrőt számolunk ki, minimalizálva 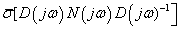 értékét
értékét 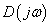 függvényében.
függvényében.
Amennyiben minden 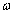 frekvencián
frekvencián 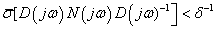 akkor
akkor 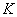 a keresett robusztus szabályozó, ha nem, tovább megyünk a
a keresett robusztus szabályozó, ha nem, tovább megyünk a 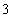 . lépésre.
. lépésre.
Ha elértük MAXIT-et, akkor az algoritmus nem szolgáltatott megoldást. Ellenkező esetben tovább megyünk az 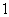 . lépésre.
. lépésre.
Az első lépés egy standard 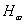 optimális szabályozási feladat megoldása. A második lépésben minimalizálni kell
optimális szabályozási feladat megoldása. A második lépésben minimalizálni kell 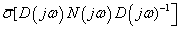 értékét, amit egy numerikus optimalizálással érünk el egy
értékét, amit egy numerikus optimalizálással érünk el egy 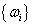 rácson, ahol a racionális
rácson, ahol a racionális 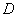 skálázó szűrőt közelítjük. A közelítés pontossága általában növeli a szűrő rendjét, így a keletkező szabályozó rendjét is. Ezért gyakran szükséges a
skálázó szűrőt közelítjük. A közelítés pontossága általában növeli a szűrő rendjét, így a keletkező szabályozó rendjét is. Ezért gyakran szükséges a 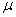 -optimális szabályozókat helyettesíteni egy redukált rendű szub-optimális szabályozóval.
-optimális szabályozókat helyettesíteni egy redukált rendű szub-optimális szabályozóval.