7. fejezet - Integrált irányítások tervezése
7.1. Bevezetés és motiváció
A hagyományos eljárások során a jármű különböző funkcióinak vezérlését és irányítását külön tervezik. Ezzel a stratégiával az egyik probléma az, hogy a különböző, de egymással kapcsolatban álló, minőségi követelmények független irányításokkal való kielégítése néha nem lehetséges konfliktusok nélkül. Például a fékezési művelet befolyásolja a hosszirányú dinamikát, a sebességet és a dőlési szöget. A jármű geometriai adottságai miatt azonban a fékezés hatására megváltozik a legyezési sebesség és a dőlési dinamika. Hasonlóképpen, a kormányzási szög is hatással van a legyezési szögre. Mivel a súlypont magasan helyezkedik el, a kormányzási manőver következtében a dőlési szög és a rugózott tömeg bólintási szöge szintén megváltozik. A független tervezési stratégia egy másik problémája az, hogy az egyes szabályozók különálló implementálása felesleges hardver redundanciához vezethet.
Az integrált járműirányítás legfőbb célja, hogy ötvözze és felügyelje a gépjármű dinamikáját befolyásoló alrendszerek működését. Ez azt jelenti, hogy a különálló performanciákat javítani kell, a rendelkezésre álló érzékelőket és beavatkozókat több irányítási feladatban kell használni, a független szabályozási körök számát csökkenteni kell, ugyanakkor az irányítási rendszerek rugalmasságát növelni kell. A beépített irányítási rendszer úgy van kialakítva, hogy az egyes vezérlő rendszereknek a jármű egyéb funkcióira való hatását is figyelembe veszik a tervezés során a különböző irányítási jellemzők, performanciák segítségével. A járműipar elvárásainak megfelelően számos irányítási kritérium áll a kutatás középpontjában: például az úttartás, az utazási kényelem javítása, a dőlési és bólintási stabilitás fejlesztése, hibatűrő ás rekonfiguráló megoldások, lásd [42], [99].
Az itt bemutatott megoldásban a decentralizált irányítási rendszert még kiegészíti egy felügyelő (supervisor) szabályozási séma. A felügyelő séma szerepe az előírt performancia garantálása és az egyes komponensek közötti áthallások és konfliktusok kiküszöbölése. A felügyelő alrendszer információval rendelkezik a jármű aktuális működési módjáról, azaz a jármű különböző manővereiről, vagy a különböző komponensek megfigyelése során gyűjtött információkról, amiket például a hibadetektáló (FDI) szűrők szolgáltatnak. A felügyelő képes a jármű alrendszereibe történő szükséges beavatkozások elvégzésére és garantálja az újrakonfigurálható és hibatűrő működést. Ezek a döntések az alacsonyabb szintek felé megfelelően választott ütemezési változók révén, előre definiált interfészeken keresztül, terjednek.
7.2. A járműdinamika irányítás-orientált modellezése
A járműirányítás tervezésének célja egy előre meghatározott útvonal követése, az úttartás és a menetstabilitás növelése. Több szabályozót alkalmazunk a rendszerben: az aktív fék, kormány és a felfüggesztési rendszert. A pályakövetési feladatot aktív kormányzással oldjuk meg, míg az úttartás és az utaskényelem érdekében aktív felfüggesztést használunk. Ha közvetlen a borulás veszélye akkor a biztonság növelése érdekében működésbe lép a fékrendszer. A fék alkalmazása viszont befolyásolja a legyező mozgást és így a valós útvonal jelentősen eltérhet a kívánt útvonaltól. Annak érdekében, hogy kiegyenlítse a legyező mozgás fékezés által okozott változását, a kormányzást szabályozó alrendszernek módosítani kell a követési parancsot, hogy elkerüljük a jármű alul- vagy túlkormányzottságát.
7.2.1. Jármű modellezés
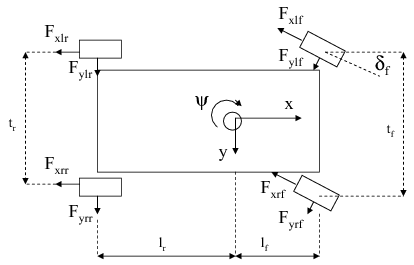


Az egyes gumiabroncsok által létrehozott hosszirányú és oldalirányú erők az egyes kerekek normális irányú terhelésének és a kerék csúszási szögének következményei. A jármű az első kerekeknél van kormányozva, ahol a kormánykerék szöghelyzete (kormányszög) . Az aktív felfüggesztés által keltett bal és a jobb oldali első és hátsó erőket jelöli.
A váz (chassis) függőleges (), longitudinális (), oldalirányú (), dőlési (), bólintási () és legyezési () dinamikája a következő egyenletek segítségével van megadva:
|
|
(499) |
|
|
(500) |
|
|
(501) |
|
|
(502) |
|
|
(503) |
|
|
(504) |
|
|
(505) |
Itt és a váz sebessége az és -irányban, és a rugózott tömeg és a rugózatlan tömeg elmozdulása a -irányban
A legyezési dinamika és a súlypont oldalkúszási szögének dinamikája közötti kapcsolat
|
|
(506) |
Kis kormányzási szögek mellett a következő közelítésekkel élünk: és .
A lokális szabályozók a különböző összetettségű jármű modellek alapján vannak megtervezve. Az 111 ábra egy komplex járműmodell hosszirányú, keresztirányú és függőleges irányú dinamikáját szemlélteti. A tervezés alapjául az alábbi állpottér-modell áll:
|
|
(507) |
ahol , és az állapot, a zavaró bemenet és az irányító bemenet. A vektor tartalmazza az ütemezési változókat. Először az állapot változót határozzuk meg, majd a performancia változók és a mért kimenetek a feladatot figyelembe véve kerülnek megválasztásra.
A fékrendszer elsődleges szerepe, hogy csökkentse a jármű haladási sebességét illetve, hogy megállítsa azt. Ugyanakkor egyoldalú fékerőt is tud generálni az első és a hátsó kerekeken mindkét oldalon. Így a fékrendszer képes arra, hogy kanyarodáskor módosítsa a jármű legyezési szögét és csökkentse az oldalirányú gyorsulás hatását. Így a fék képes helyettesíteni egyéb más komponenseket, ha azok meghibásodnak illetve csökken a hatásosságuk. A kormányzást a kívánt pálya követésére használjuk. A vezérlő bemenet a kormányzási szög. A gyakorlatban a mért jelek ezeknél a feladatoknál az oldalirányú gyorsulás és a legyezési sebesség.
Az aktív felfüggesztés biztosítja a menetstabilitást és a megfelelő kényelmet mialatt a közúti egyenetlenségek által okozott káros rezgések hatnak a járműre. A felfüggesztési rendszer képes javítani a bólintási és dőlési stabilitást, bólintó nyomatékot generálva hirtelen fékezés alkalmával vagy forgató nyomatékot hirtelen manőverek során. A
|
|
(508) |
vezérlő bemenetek a felfüggesztési beavatkozók által vannak létrehozva. Általában a mért jelek a rugózott és rugózatlan tömeg közötti relatív elmozdulások.
A sebesség, az oldalirányú tapadási együttható, a felfüggesztési rugók és csillapító elemek nemlineáris hatásait a
|
|
(509) |
ütemezési változók segítségével vesszük figyelembe, ahol és relatív elmozdulások és a hozzátartozó sebességek. A feltételezés az, hogy a megfelelően kiválasztott ütemezés változók segítségével a nemlineárisokat át lehet alakítani affin paraméter-függő elemekké. A nemlineáris modellek így átalakíthatók lineáris változó paraméterű (LPV) modellekké, ahol a nemlineáris kifejezések alkalmasan kiválasztott ütemezési változókba lesznek elrejtve. Az átalakítás feltétele, hogy a vektort mérni, illetve becsülni lehessen, lásd például [39].
7.2.2. Performancia specifikációk és szabályozótervezés
A lokális komponenseknek is tartalmazniuk kell olyan egységeket amik felügyelik és monitorozzák a jármű működését valamint FDI szűrőket. Ezek az alkatrészek képesek érzékelni a jármű kritikus manővereit, különböző hibajelenségeket vagy performancia degradációkat. Ezek az egységek üzeneteket küldenek a felügyelő rendszerhez. A lokális komponensek újrakonfigurálható és hibatűrő szabályozása során számos jelet kell monitorozni, és új ütemezési változókat kell az ütemezési vektorhoz adni annak érdekében, hogy javuljon a jármű biztonsága (pl. változók kellenek a borulási veszélyét jelzésére, a hirtelen fékezés káros hatásainak észlelésére, az aktív komponensek esetleges meghibásodásának figyelembe vételére.
A hatékony működéshez a felügyelő rendszernek és a helyi vezérlőknek megbízható és pontos információkra van szüksége. Ennek a követelménynek a kielégítésére redundáns érzékelőkre, különböző számítások elvégzésére és hiba észlelésére alkalmas szűrőkre van szükség. A hatékony és optimális beavatkozás érdekében nagyon fontos a hibás érzékelők detektálása, mivel ezeket, az általuk szolgáltatott információt, helyettesíteni kell azokban a műveletekben ahol szerepet játszanak. A jármű ipar az alacsony költségű megoldásokat részesíti előnyben, így egyszerű érzékelőket és lehetőleg szoftver alapú redundanciát kell alkalmazni.
A helyi vezérlés tervezése során kidolgozott zárt rendszer magában foglalja a modellt, a szabályozót és a minőségi követelményekkel kapcsolatos tényezők visszacsatolási struktúráját:
|
|
(510) |
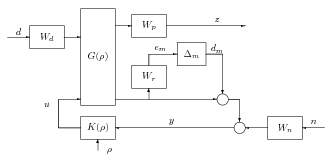
ahol magában foglalja mind a külső zavarokat, mind a zajokat. Egy tipikus összekapcsolási struktúra látható a 112 ábrán. Ezekből a tényezőkből áll össze a paraméterfüggő általánosított rendszer. A szabályozó alkalmazásával kapjuk az zárt rendszert egy lineáris tört transzformáció (LFT) által leírt struktúrában.
A javasolt eljárás keretében a minőségi követelmények a súlyozások megfelelő választása által specifikálódnak a tervezési folyamat során. A súlyozás célja általában büntető függvények meghatározása, például a súly nagy ha kis jeleket akarunk és kisebb ha nagyobb performancia kimenetek megengedettek. A bemutatott megközelítés a performanciák rekonfigurációját a súlyozás megfelelő változtatásával, ütemezésével oldja meg.
A blokk tartalmazza a rendszerben jelenlevő bizonytalanságot, mint például a nem modellezett bizonytalanságot és a parametrikus bizonytalanságokat. Ebben a kiegészített rendszermodellben a nem modellezett bizonytalanság egy súllyal és egy normált bizonytalansági blokkal van jelen. A és súlyok célja a zavarások és a szenzor zajok megjelenítése a modellben.
A javasolt megoldásban a lokális irányítási algoritmusok tervezése az LPV módszer segítségével történik. Az LPV tervezési módszerek jól kidolgozott és sikeresen alkalmazott eljárások a különböző ipari problémák megoldására. Az LPV megközelítés teszi lehetővé számunkra, hogy figyelembe tudjuk venni a nemlineáris hatásokat az állapotteres leírás során. A javasolt megközelítés kulcsfontosságú eleme az, hogy a lokális komponensek tervezésében a felügyelőtől származó ütemezési változókat használjuk az integráció kikényszerítésére. Ezen a módon a lokális irányítást ki lehet bővíteni újrakonfigurálható és hibatűrő funkciókkal.
A kvadratikus LPV performancia probléma célja,hogy egy paraméter-változós vezérlést tervezzünk úgy, hogy az zárt rendszer kvadratikus stabilis legyen és a -ről -re vett indukált norma (erősítés) legyen -nál kisebb, azaz
|
|
(511) |
Strukturálatlan bizonytalanságot feltételezve és a súlyozott kis erősítések tételét alkalmazva az LPV -performancia probléma megoldása visszavezethető egy lineáris mátrix egyenlőtlenségeket (LMI) tartalmazó feladatra, ami numerikusan kezelhető, lásd például [128]. A stabilitás és az elvárt performancia megléte a tervezési folyamat által garantált, lásd [10], [130].
Ha a paraméter-függő Lyapunov függvényt használunk, a tervezett szabályozó általában explicit módon függ a deriváltaktól. Ezek nem mérhetek a gyakorlatban, így megfelelően közelítő numerikus algoritmust kell használni ezeknek a paramétereknek a becslésére. A -tól való függés kiküszöbölésére egy függő változócserét javasolt [10].
7.3. A lokális irányítási rendszerek trervezése
7.3.1. A fékrendszer
A járműre ható nyomatékokat leíró egyensúlyi kifejezés:
|
|
(512) |
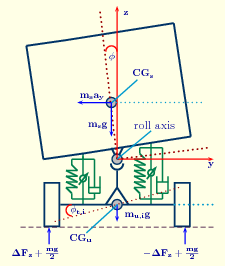
A dőlési (roll) stabilitás azáltal érhető el, hogy mindkét tengelyen csökkentjük az oldalirányú kerékterhelést egy olyan szint alá, ami biztosítja a jármű úttartását a különböző manőverek során. Az oldalirányú kerékterhelést tengelyenként megadó kifejezés: . A kerekek elemelkedését megakadályozó feltétel a jármű mindkét oldalán. Az oldalirányú kerékterhelés normalizált értékeit és a tengelyeket terhelő a tömegek aránya:
|
|
(513) |
A tervezés célja, hogy csökkentse a normalizált oldalirányú kerékterhelés maximális értékét, ha az meghalad egy előre meghatározott kritikus értéket.
A fékrendszer tervezésekor az irányító jel a fékerők különbsége, míg a performancia jel az oldalirányú gyorsulás:
|
|
(514) |
Az oldalirányú gyorsulás súlyozására
lett választva, ahol alkalmasan választott időállandók. Itt az az erősítés, amely tükrözi az oldalirányú gyorsulás relatív fontosságát és amit paraméter-függőnek választunk, azaz függvényének.
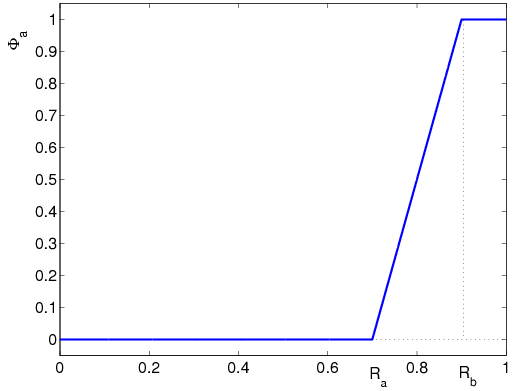
Amikor kicsi (), vagyis a jármű nincs vészhelyzetben, akkor is kicsi, ami azt jelzi, hogy a LPV irányításnak nem kell csökkenteni a gyorsulást. Amikor megközelíti a kritikus értéket, azaz, amikor , akkor nagy. Ez azt jelenti, hogy a szabályozás arra összpontosít, hogy a borulást megelőzze. Itt határozza meg azt a kritikus állapotot amikor a jármű vészhelyzetben, azaz borulás közeli helyzetben, van. Megjegyezzük, hogy a használt súlyok PD (arányos/differnciáló) tipusúak. Az időállandók és az erősítések értékei a különböző performancia jelek elvárt egyensúlyi helyzetét, valamint tranziens viselkedését tükrözik.
Ha a felfüggesztési rendszer rendszer hibát észlel, a dőlési stabilitási szerepét a fék rendszer fogja helyettesíteni. A fékrendszer egy kisebb kritikus értéken aktiválódik, mint a hibamentes esetben, azaz, ha . Ebből következően, a fékrendszer viselkedése módosul és a fékezés által gerjesztett nyomaték átveszi a meghibásodott felfüggesztés szerepét. A módosított kritikus érték az alábbi:
|
|
(515) |
ahol egy előre meghatározott állandó.
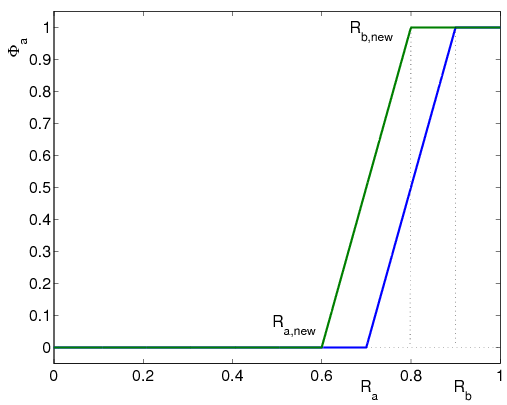
A kormány rendszer hibája esetén () a fékrendszernek a jármű legyezési dinamikájára kell koncentrálni annak érdekében, hogy csökkentse a követési hibát. Így a fékrendszer szabályozásának tervezése során a kormány rendszerre vonatkozó performancia specifikációt is figyelembe kell venni:
|
|
(516) |
ahol választása
|
(517) |
szerint történik.
A fékrendszer performancia csökkenése esetén az nem tud megfelelő nyomatékot generálni a dőlési stabilitás növelése érdekében. Ebben az esetben a helyébe lép a kormány rendszer, ami megkapja a hiba üzenetet és módosítja a működését oly módon, hogy az oldalirányú terhelést csökkentse. Ennek a megoldásnak a nehézsége az, hogy a követési feladat performancia romlása elkerülhetetlen, ezért a kormány rendszer feladata egyensúlyt keresni a követési feladat és a borulásgátlás között.
7.3.2. A kormányzó rendszer tervezése
A keresztirányú stabilitás azáltal érhető el, hogy csökkentjük az oldalirányú kerék terhelést. A tervezés célja, hogy a szabályozó minimalizálja a keresztirányú gyorsulást, amit egy performancia jellel monitoroz. Az egyik megoldás az egyoldalú fékezés, mely fékerőket generál annak érdekében, hogy stabilizáló legyezési nyomatékot hozzon létre. A másik megoldás során további kormányzási szög keletkezik annak érdekében, hogy csökkentsük a keresztirányú kerék terhelést. Ez a megoldás azonban aktív vezetői beavatkozást feltételez a járművezető részéről, annak érdekében, hogy a járművet a szándékolt pályán tartsa.
Egy másik irányítási feladat, hogy kövessünk egy előre megadott legyezési dinamikát (sebesség, szög). Ebben az esetben az aktuális legyezési szögsebességet folyamatosan ellenőrizni kell és a referencia- és az aktuális sebesség közötti különbséget meg kell határozni. A cél a lehető legkisebbre csökkentik a követési hibát.
Annak érdekében, hogy a kormányrendszer szabályozója megoldja a legyezési szögsebesség követését, a vezérlő jelet át kell adni a szabályozónak. A vezérlő jel egy előre meghatározott referencia elmozdulás és a performancia jel pedig a követési hiba, ami a tényleges legyezési szögsebesség és a referencia jel közötti különbség. A nyomkövetési hibát súlyozó függvény alakja
|
|
(518) |
ahol időállandók és ahol a követési hiba állandósult értékét kell az szint alatt tartani.
7.3.3. A felfüggesztési rendszer tervezése
Road holding is achieved by reducing the normalized suspension deflections between the sprung and unsprung masses at the four corner points of the vehicle. Since increasing road holding reduces the passenger comfort in the design of the suspension system its desired level is subject of a design decision.
Az úttartást a felfüggesztés a négy sarkokpontján levő rugózott és rugózatlan tömegek közötti normalizált relatív elmozdulásának csökkentésével érjük el. Mivel az úttartás növelése egy szint után csökkenti az utaskényelmet, a felfüggesztési rendszer tervezésekor a kívánt szintek meghatározása egy tervezési döntés eredménye.
A felfüggesztési szabályozás alapjául szolgáló jelek:
|
|
(519) |
A cél az, hogy a vertikális gyorsulások, az relatív elmozdulások, a kerékelmozdulások és a szabályozó jelek a teljes működési tartományon kicsik legyenek. A megfelelő performancia súlyokat az alábbi módon választjuk meg:
|
|
(520) |
|
|
(521) |
|
|
(522) |
ahol és időállandók, míg paraméterfüggő erősítések, amik a relatív elmozdulások függvényei.
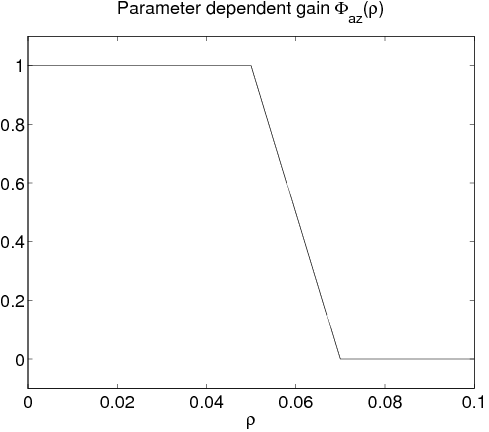
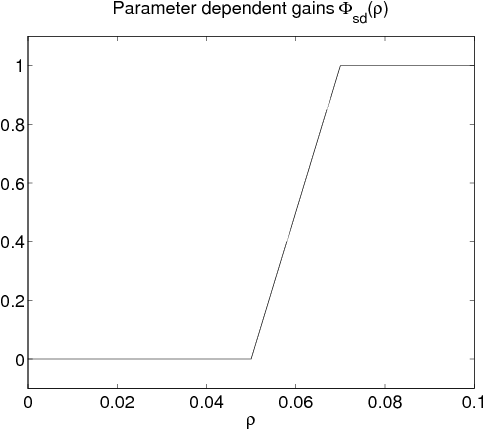
Normális körülmények közt a felfüggesztési rendszer a hagyományos performanciák szerint működik a paraméter-függő erősítések szerint, amelyek a relatív elmozdulások függvényei. Az utaskényelem és úttartás közötti konfliktus annak köszönhető, hogy nem lehet őket egyszerre kielégíteni. Egy nagy és egy kis erősítés felel meg egy olyan konfigurációnak, amely hangsúlyozza az utasok kényelmét, míg kis és nagy az úttartásra koncentrál.
Az újrakonfigurálható felfüggesztési rendszer tervezésének alapja az a tény, hogy az aktív felfüggesztés rendszer nem csak az út egyenetlenségei által okozott hatás kiküszöbölésére alkalmas, hanem dőlési nyomatékokat is létrehozhat a dőlési stabilitás javítása érdekében illetve bólintó nyomatékot a bólintó stabilitás javítása érdekében. Az újrakonfigurálható rendszer
|
|
(523) |
|
|
(524) |
paraméter függő súlyait a normalizált oldalirányú kerék terhelés és a normalizált bólintási szög függvényeként választjuk. Ha meghalad egy előre meghatározott kritikus értéket, azaz amikor , akkor a szabályozónak a bólintási stabilitásra kell fókuszálni. Vészhelyzet esetén azonban, azaz, ha , akkor a felfüggesztési rendszernek csökkentenie kell a dőlési kockázatot, azonban ezzel egy időben az utasokkényelem és előírt bólintási szögtartás már nem prioritás.
7.3.4. Beavatkozók megválasztása
A tervezés során a kerék erőket is figyelembe kell venni. Elsőkerék-hajtású jármű esetén a vonóerő a differenciálmű segítségével oszlik meg az első kerekek között. A maximális kormányzási szögnek konstrukciós korlátozása van, tehát ha elértük a maximális kormányzási szöget akkor kívánt keresztirányú jármű dinamikát fékezéssel kell elérni. Fékezés közben a kerékterhelés módosul jármű bólintási dinamikája miatt. Az első kerekek erősebb fékezése közben a hátsó kereken csökkenteni kell a fékerőt. A megcsúszás elkerülése végett folyamatosan figyelni kell a pillanatnyi fékerőket. Ehhez a súrlódási együttható becslése szükséges ami szintén kell a maximális kanyarodási sebesség kiszámításához.
A kerekeken ható maximális hosszirányú erőket meg kell határozni és összehasonlítani az pillanatnyi hosszanti erőkkel. Fontos megjegyezni, hogy a maximális hosszirányú erő függ a maximális tapadási együtthatótól és a kerék erő függőleges statikus és a dinamikus komponensétől, vagyis a kereszt és hosszirányú dinamikától. az erők arányainak maximális értéke az összes kereket igyelembe véve, pedig egy tervezési paraméter.
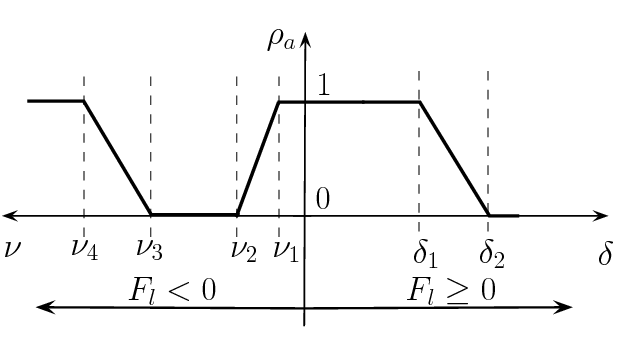
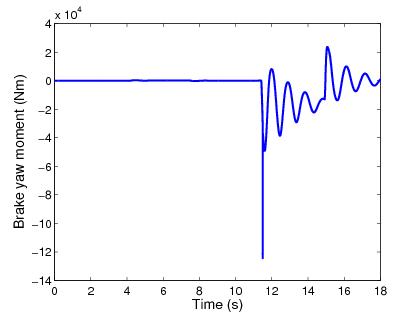
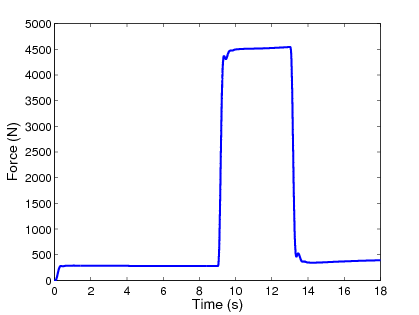
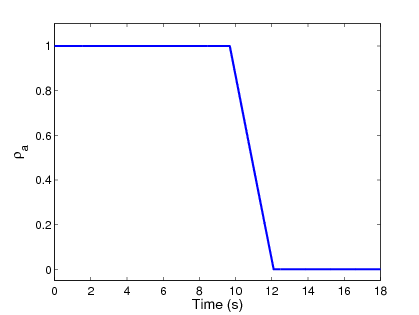
A tervezési stratégiában a súlyozási paraméter, ami a jármű állapotától függ, vagyis a vonóerőtől és a fékerőktől, kapő fontos szerepet, lásd az 118 ábrát.
7.4. Hibatűrő rendszer tervezése
A lokális hibatűrő szabályozásoknak szükségük van a detektált hiba információra. Itt egy adott szűrő FDI által szolgáltatott normalizált hibajel
|
|
(525) |
ahol az aktuális hiba nagyságának becsült értéke (az FDI szűrő kimenete) és a potenciális hibahatás várható maximális értéke (végzetes hiba). egy aktív komponens performanciájának romlását becsli.
A kapcsolási struktúra magában foglalja a függőleges járműmodellt, az FDI szűrőt és a performancia célokkal összefüggő elemeket (súlyokat).
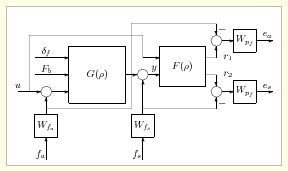
A súly a hiba jel relatív fontosságát tükrözi. Ez a súly nagy ahol kicsi hibák és kisebb ahol nagyobb hibák megengedettek. A súly meghatározza a lehetséges hiba mértékét az adott beavatkozó csatornában, míg a súly meghatározza a lehetséges hiba mértékét az adott érzékelő csatornában.
A hibajelre vonatkozó tervezési követelmény a lehető legnagyobb hiba hatást elérni a szűrő kimenetén és ezzel egy időben minimálisra csökkenteni az exogén jelek () hatását, azaz
|
(526) |
A nyitott hurokban tervezett szűrő FDI használható a zárt rendszerben is. A szűrő megkapja a mért kimeneteket és a vezérlő bemenetek és ennek alapján szolgáltatja a hibajelet.
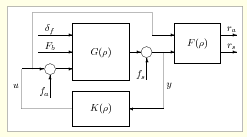
The fault-tolerant control requires fault information in order to guarantee performances and modify its operation. Thus, FDI filters are also designed for the operation of the actuators. As an example the fault information provided by a fault detection filter is given by , where is an estimation of the failure (output of the FDI filter) and is an estimation of the maximum value of the potential failure (fatal error). The value of a possible fault is normalized into the interval . The estimated value means the rate of the performance degradation of an active component.
A hibatűrő szabályozónak szüksége van a hibainformációra annak érdekében, hogy módosítsa a működését és garantáljon egy előírt performanciát. Így FDI szűrőket kell tervezni a beavatkozó elemekhez is. Az érzékelő meghibásodását a lehető legpontosabban kell detektálni, mert a szabályozás mérések alapján történik. Szenzor hiba megakadályozhatja egyes beavatkozók felhasználását; így az érzékelő meghibásodása beavatkozó rekonfigurációt eredményezhet.
7.5. Szimulációs példák
7.5.1. A hibadetektálás illusztrálása
Az FDI szűrő működését egy manőver során mutatjuk be. Az a szimulációban alkalmazott kormányzási szög egy egységugrás, a jármű sebessége . A manőver közben a fékrendszert a jármű lassítására használjuk.
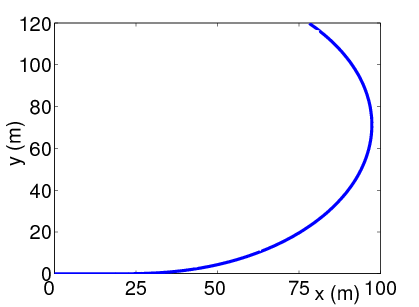
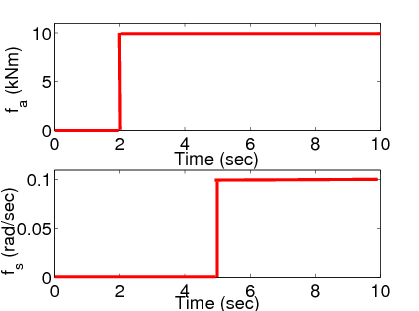
A zárt kör szimulációs forgatókönyvének adatai: destabilizáló nyomaték a második másodperctől és szenzorhiba az ötödik másodperctől. Az érzékelő hibája azt jelenti, hogy a érzékelő egy állandó additív hibával terhelt jelet mér.
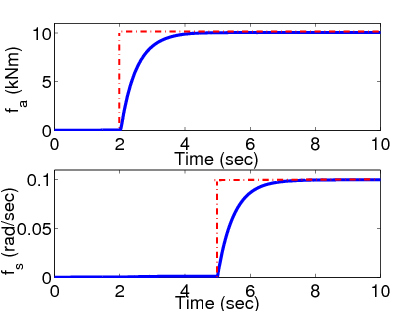
Az első hibajelek az aktuátor hibát míg a többi az érzékelő hibát mutatja. A a két hiba hatása szétcsatolódik és a becsült hibajelek elfogadható információt adnak a ténylegesen bekövetkező hibákról.
7.5.2. Hibatűrő szabályozás illusztrálása
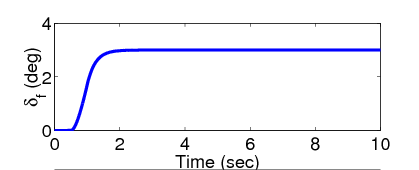
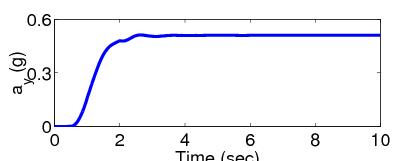
A kanyarodási manőver az első másodpercben indul és a negyedik másodpercben egy hatalmas bukkanó zavarja meg a jármű mozgását.
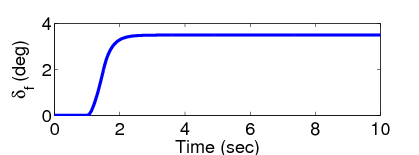
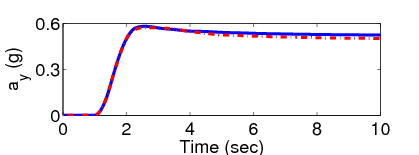
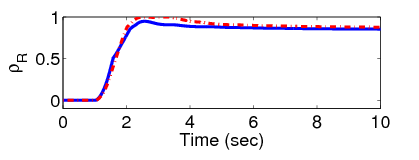
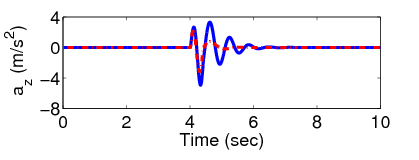
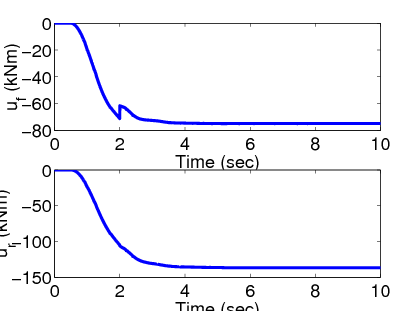
Az újrakonfigurálható manőver során a jármű potenciális felborulása kritikus helyzetet hoz létre és a felfüggesztési rendszer nyomatékot generál a dőlési nyomatékok kiegyensúlyozásának érdekében, így a szabályozó csak a normalizált oldalirányú kerék terhelés csökkentésére fókuszál.
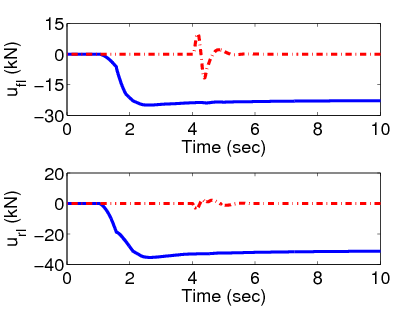
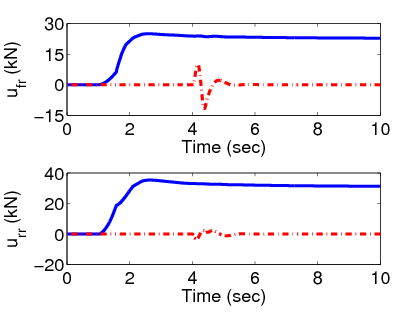
Azt feltételezzük, hogy a felfüggesztési beavatkozó hibáját már detektáltuk. Az észlelt hibának megfelelően a fékrendszer a kritikus normalizált oldalirányú terhelés kisebb értéke esetén lép működésbe. Sőt, a felfüggesztés hibája esetén a szükséges fékerőt hosszabb ideig működtetjük.
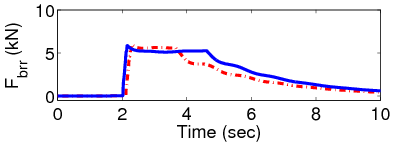
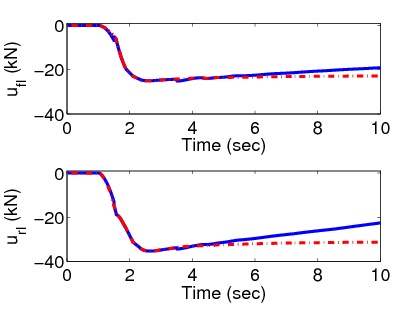
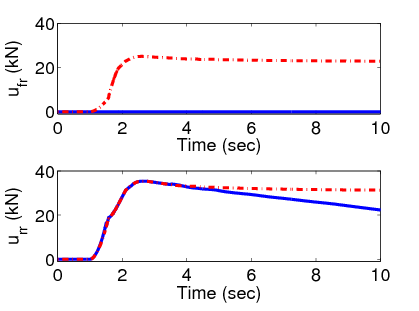
7.5.3. A beavatkozók kiválasztásának szemléltetése
A kanyarodási manőver során a sebességkövetés és az oldalirányú elmozdulás minimalizálása nagy fékerőt igényel a kerekeken. A értéke csökken a nagyobb sebesség miatt. Ez azt jelenti, hogy a gyorsítás során a differenciális fékezést kell előnyben részesíteni, mivel az gyorsabb dinamikájú.
Irodalomjegyzék
[1] E. Abdellahi, D. Mehdi, and M. M'Saad. On the design of active suspension system by and mixed : An LMI approach. Proc. of the American Control Conference, 1:21--25, 1992.
[2] A. Alleyne and J.K. Hedrick. Nonlinear control of a quarter car active suspension. Proc. of the American Control Conference, 1:21--25, 1992.
[3] A. Alleyne and J.K. Hedrick. Nonlinear adaptive control of active suspensions. IEEE Transactions on Control Systems Technology, pages 94--101, 1995.
[4] A. Alleyne and R. Liu. A simplified approach to force control for electro-hydraulic systems. Control Engineering Practice, 8:1347--1356, 2000.
[5] A. A. Alonso, J. R. Banga, and I. Sanchez. Passive control design for distributed process systems: Theory and applications. AIChE Journal, 46:1593--1606, 2000.
[6] V. I. Arnold. Ordinary Differential Equations (in Russian). Nauka, Moscow, 1984.
[7] V.I. Arnold. Mathematical methods of classical mechanics. Springer-Verlag, 1988.
[8] Karl J. Aström and Björn Wittenmark. Computer Controlled Systems. Prentice Hall, New Jersey, 1990.
[9] G. Balas, J.C. Doyle, K. Glover, A. Packard, and R. Smith. -analysis and synthesis toolbox. The Mathworks Inc., 1993.
[10] G. Balas, I. Fialho, L. Lee, V. Nalbantoglu, A. Packard, W. Tan, G. Wolodkin, and F. Wu. Theory and application of linear parameter varying control techniques. Proc. of the American Control Conference, 1997.
[11] M. Basseville and I.V. Nikiforov. Detection of Abrupt Changes. Theory and Practice. Prentice Hall, London, 1993.
[12] G. Becker and A. Packard. Robust performance of linear parametrically varying systems using parametrically-dependent linear feedback. System Control Letters, 23:205--215, 1994.
[13] Ludwig Bieberbach. Theorie der differentialgleichungen. Springer Verlag, Berlin, 1930.
[14] M. Blanke, M. Kinnaert, J. Lunze, and M. Staroswiecki. Diagnosis and fault-tolerant control. Springer, 2003.
[15] J. Bokor and G. Balas. Linear parameter varying systems: A geometric theory and applications. 16th IFAC World Congress, Prague, 2005.
[16] J. Bokor and P. Gáspár. Irányítástechnika járműdinamikai alkalmazásokkal. TypoTex Kiadó, 2008.
[17] C. Briat, O. Sename, and J.F. Lafay. Delay-scheduled state-feedback design for time-delay systems with time-varying delays: A LPV approach. Systems and Control Letters, 58:664--671, 2009.
[18] G.D. Buckner, K.T. Schuetze, and J.H. Beno. Active vehicle suspension control using intelligent feedback linearization. Proc. of the American Control Conference, pages 4014--4018, 2000.
[19] C. I. Byrnes and A. Isidori. A frequency domain philosophy for nonlinear systems. IEEE Conf. Dec. Contr., 23:1569--1573, 1984.
[20] C. I. Byrnes and A. Isidori. Local stabilization of minimum-phase nonlinear systems. Syst. Contr. Lett., 11:9--17, 1988.
[21] C. I. Byrnes and A. Isidori. Asymptotic stabilization of minimum-phase nonlinear systems. IEEE Trans. Aut. Contr., AC-36:1122--1137, 1991.
[22] C. I. Byrnes, A. Isidori, and J. C. Willems. Passivity, feedback equivalence and the global stabilization of minimum-phase nonlinear systems. IEEE Trans. Aut. Contr., AC-36:1228--1240, 1991.
[23] M. Canale, M. Milanese, C. Novara, and Z. Ahmad. Semi-active suspension control using fast model predictive techniques. IEEE, Control System Technology, 2006.
[24] Y.Y. Cao and K. Fang. Parameter-dependent Lyapunov function approach to stability analysis and design for polytopic systems with input saturation. Asian Journal of Control, 9(1):1--10, 2007.
[25] D. Cebon. Interaction between heavy vehicles and roads. SAE-SP 951, 1993.
[26] D.J. Cole. Fundamental issues in suspension design for heavy road vehicles. Vehicle System Dynamics, 35:319--360, 2001.
[27] D.A. Crolla. Active suspension control algorithms for a four-wheel vehicle model. International Journal of Vehicle Design, 13(2):144--158, 1992.
[28] F. J. D'Amato and D.E. Viassolo. Fuzzy control for active suspensions. Mechatronics, 10:897--920, 2000.
[29] B. de Jager. Multiobjective suspension control problem. Proc. of the Conference on Decision and Control, New Orleans, 4:3652--3657, 1995.
[30] H. Nijmeijer A. J. Van der Schaft. Nonlinear dynamical control systems. Springer, New York, Berlin, 1990.
[31] C. A. Desoer and M. Vidyasagar. Feed-back systems: Input-output properties. Academic Press, New York, 1975.
[32] S. Diop, J. W. Grizzle, and F. Chaplais. On numerical differentiation algorithms for nonlinear estimation. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, pages 1133--1138. 2000.
[33] H. Du and N. Zhang. control of active vehicle suspensions with actuator time delay. Journal of Sound and Vibration, 301:236--252, 2007.
[34] I.J. Fialho and G.J. Balas. Design of nonlinear controllers for active vehicle suspensions using parameter-varying control synthesis. Vehicle System Dynamics, 33:351--370, 2000.
[35] I.J. Fialho and G.J. Balas. Road adaptive active suspension design using linear parameter-varying gain-scheduling. IEEE TRANSACTIONS ON CONTROL SYSTEMS TECHNOLOGY,, 10(1):43--54, 2002.
[36] T. Fukao, A. Yamawaki, and N. Adachi. Adaptive control of partially known systems and application to active suspensions. Asian Journal of Control, 4(2):199--205, 2002.
[37] P. Gahinet and P. Apkarian. A linear matrix inequality approach to control. International Journal of Robust and Nonlinear Control, 4:421--448, 1994.
[38] P. Gahinet and P. Apkarian. Explicit controller formulas for LMI-based synthesis. Automatica, 32:1007--1014, 1996.
[39] P. Gaspar, Z. Szabo, and J. Bokor. Estimation of the friction coefficient for road vehicles. American Control Conference, 2005.
[40] T.D. Gillespie. Fundamentals of vehicle dynamics. Society of Automotive Engineers Inc., 1992.
[41] T. Gordon. An integrated strategy for the control of a full vehicle active suspension system. Vehicle System Dynamics, 25:229--242, 1996.
[42] T. Gordon, M. Howell, and F. Brandao. Integrated control methodologies for road vehicles. Vehicle System Dynamics, 40:157--190, 2003.
[43] V.E. Gough and G.R. Shearer. Front suspension and tyre wear. The Institution of Mechanical Engineers, Proceedings of the Automobile Division, pages 171--216, 1955-1956.
[44] E. Guglielmino, T. Sireteanu, C. W. Stammers., G. Ghita, and M.Giuclea. Semi-active suspension control. Springer, 2008.
[45] P. Gáspár, Z. Szabó, and J. Bokor. Design of reconfigurable and fault-tolerant suspension systems based on lpv methods. Conference on Decision and Control, Cancun, Mexico, 2008.
[46] P. Gáspár, Z. Szabó, and J. Bokor. LPV design of reconfigurable and integrated control for road vehicles. Proc. of the Conference on Decision and Control, Orlando, Fl, 2011.
[47] P. Gáspár, Z. Szabó, and J. Bokor. LPV design of fault-tolerant control for road vehicles. International Journal of Applied Mathematics and Computer Science, 22(1), 2012.
[48] P. Gáspár, I. Szászi, and J. Bokor. Active suspension design using linear parameter varying control. International Journal of Vehicle Autonomous Systems, 1(2):206--221, 2003.
[49] P. Gáspár, I. Szászi, and J. Bokor. Active suspension design using the mixed synthesis. Vehicle System Dynamics, 40(4):193--228, 2003.
[50] P. Gáspár, I. Szászi, and J. Bokor. Design of robust controllers for active vehicle suspension using the mixed synthesis. Vehicle System Dynamics, 40:193--228, 2003.
[51] P. Gáspár, I. Szászi, and J. Bokor. Active suspension design using linear parameter varying control. IFAC Symposium on Advances in Automotive Control, Salerno, 2004.
[52] A. Hac. Adaptive control of vehicle suspension. Vehicle System Dynamics, 16:57--74, 1987.
[53] J.K. Hedrick and T. Butsuen. Invariant properties of automotive suspensions. Proc. of the Institution of Mechanical Engineers, 204:21--27, 1990.
[54] R. Hermann and A. J. Krener. Nonlinear controllability and observability. IEEE Trans. Aut. Cont., 22:728--740, 1977.
[55] D. Hill and P. Moylan. Connections between finite gain and asymptotic stability. IEEE Tr. Aut. Cont., AC-25:931--936, 1980.
[56] D. J. Hill and P. J. Moylan. Stability results for nonlinear feedback-systems. Automatica, 13:377--382, 1977.
[57] D. J. Hill and P. J. Moylan. Connections between finite-gain and asymptotic stability. IEEE Transactions On Automatic Control, 25:931--936, 1980.
[58] D. J. Hill and P. J. Moylan. General instability results for interconnected systems. Siam Journal On Control And Optimization, 21:256--279, 1983.
[59] D. Hrovat. A class of active LQG optimal actuators. Automatica, 18(1):117--119, 1982.
[60] D. Hrovat. Optimal active suspension structures for quarter car vehicle models. Automatica, 26(5):845--860, 1990.
[61] D. Hrovat. Survey of advanced suspension developments and related optimal control applications. Automatica, 33:1781--1817, 1997.
[62] Rolf Isermann. Process Fault Diagnosis Based On Dynamic Models and Parameter Estimation Methods. Prentice Hall, 1989.
[63] A. Isidori. Nonlinear Control Systems. Springer, Berlin, 1995.
[64] A. Isidori. Nonlinear control systems II. Springer, 1999.
[65] A. Isidori, A. J. Krener, C. Gori Giorgi, and S. Monaco. Nonlinear decoupling via feedback: a differential geometric approach. IEEE Trans. Aut. Contr., AC-26:331--345, 1981.
[66] T. Iwasaki and R.E. Skelton. All controllers for the general control problem: LMI existence conditions and state space formulas. Automatica, 30:1307--1317, 1994.
[67] T. Iwasaki and R.E. Skelton. Parametrization of all stabilizing controllers via quadratic Lyapunov functions. Journal of Optimization Theory and Applications, 85:291--307, 1995.
[68] Z. P. Jiang and D. J. Hill. Passivity and disturbance attenuation via output feedback for uncertain nonlinear systems. IEEE Transactions On Automatic Control, 43:992--997, 1998.
[69] Z. P. Jiang, D. J. Hill, and A. L. Fradkov. A passification approach to adaptive nonlinear stabilization. Systems & Control Letters, 28:73--84, 1996.
[70] S.M. Joshi. Control of flexible space structures. Lecture Notes in Control and Information Sciences, Springer-Verlag, 1990.
[71] V. Jurdjevic and J. P. Quinn. Controllability and stability. J. Diff. Eqs., 28:381--389, 1978.
[72] V. Jurdjevic and G. Sallet. Controllability properties of affine systems. SIAM Journal On Control And Optimization, 22:501--508, 1984.
[73] T. Kailath. Linear Systems. Prentice Hall, Englewood Cliffs, 1980.
[74] N. Karlsson, M. Ricci, D. Hrovat, and M. Dahleh. A suboptimal nonlinear active suspension. Proc. of the American Control Conference, 3:4036--4040, 2000.
[75] L. Keviczky, R. Bars, J. Hetthéssy, and Cs. Bányász. Szabályozástechnika. Műegyetemi Kiadó, Budapest, 2006.
[76] U. Kiencke. A view of automotive control systems. IEEE Control Systems, 8, 1988.
[77] U. Kiencke and L. Nielsen. Automotive control systems. For engine, driveline and vehicle. Springer, 2000.
[78] A. J. Krener. Decomposition theory for differentiable systems. SIAM J. Control Optim., 15:813--829, 1977.
[79] C. Langbort, R. S. Chandra, and R. D'Andrea. Distributed control design for systems interconnected over an arbitrary graph. IEEE Transactions on Automatic Control, 49(9):1502--1519, 2004.
[80] D.J. Leith and W.E. Leithead. Survey of gain-scheduling analysis and design. International Journal of Control, 73:1001--1025, 2000.
[81] A. Levant. Higher-order sliding modes, differentiation and output feedback control. International Journal of Control, 76(9/10):924--941, 2003.
[82] J.S. Lin and T. Kanellakopoulos. Nonlinear design of active suspensions. Proc. of the Conference on Decision and Control, New Orleans, 3:3567--3569, 1995.
[83] Y. Lin and W. Kortüm. Identification of system physical parameters for vehicle systems with nonlinear components. Vehicle System Dynamics, 20:354--365, 1991.
[84] L. Ljung. System identification: Theory for the user. Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1987.
[85] L. Ljung and T. Söderström. Theory and Practice of Recursive Identification. The MIT Press, Massachusetts, 1983.
[86] X.Y. Lu and J.K. Hedrick. Impact of combined longitudinal, lateral and vertical control of autonomous road vehicle design. Int. J. Vehicle Autonomous Systems, 2(1/2):40--70, 2004.
[87] R. G. L. Luus. Application of iterative dynamic-programming to state constrained optimal-control problems. Hungarian Journal Of Industrial Chemistry, 19:245--254, 1991.
[88] Mohammad-Ali Massoumnia, George C. Verghese, and Alan S. Willsky. Failure detection and identification. IEEE Transactions on Automatic Control, 34:316--321, 1989.
[89] H.E. Merritt. Hydraulic control systems. Wiley and Sons, 1967.
[90] P. Michelberger, J. Bokor, A. Keresztes, and P. Várlaki. Design of active suspension system for road vehicles: An eigenstructure assignment approach. Proc. of the 23th Fisita Congress, pages 213--218, 1990.
[91] P. Michelberger, J. Bokor, and L. Palkovics. Robust design of active suspension system. International Journal of Vehicle Design, 14:145--165, 1994.
[92] R.H. Middleton and G.C. Goodwin. Digital Control and Estimation. A Unified Approach. Prentice Hall, London, 1990.
[93] M. Mitschke. Dynamik der kraftfahrzeuge. Springer Verlag, Berlin, 1995.
[94] A. Moran and M. Nagai. Performance analysis of vehicle active suspension with robust control. Proc. of the International Conference on Motion and Vibration Control, Yokohama, pages 756--761, 1992.
[95] P. J. Moylan and D. J. Hill. Tests for stability and instability of interconnected systems. IEEE Transactions On Automatic Control, 24:574--575, 1979.
[96] P. J. Moylan, A. J. Vannelli, and M. J. Vidyasagar. On the stability and well-posedness of interconnected non- linear dynamical-systems. IEEE Transactions On Circuits And Systems, 27:1097--1101, 1980.
[97] Alan V. Oppenheim and Ronald W. Schafer. Digital Signal Processing. Prentice Hall, New Jersey, 1975.
[98] R. Ortega and M. W. Spong. Adaptive motion control of rigid robots: A tutorial. Automatica, 25:877--888, 1989.
[99] L. Palkovics and Fries. Intelligent electronic systems in commercial vehicles for enhanced traffic safety. Vehicle System Dynamics, 35:227--289, 2001.
[100] I. G. Polushin, A. L. Fradkov, and D. J. Hill. Passivity and passification of nonlinear systems. Automation And Remote Control, 61:355--388, 2000.
[101] R. Rajamani. Vehicle dynamics and control. Springer, 2005.
[102] R. Rajamani and J.K. Hedrick. Adaptive observer for active automotive suspensons: theory and experiment. IEEE Trans. on Control Systems Technology, 3(1):86--93, 1995.
[103] W.J. Rough and J.S. Shamma. Research on gain scheduling. Automatica, 36:1401--1425, 2000.
[104] J. La Salle and S. Lefschetz. Stability by Liapunov's direct method. Academic Press, New York, London, 1961.
[105] Y.M. Sam and J.H. Shah. Modeling and control of the active suspension system using proportional integral sliding mode approach. Asian Journal of Control, 7(2):91--98, 2005.
[106] C. Scherer and S. Weiland. Linear Matrix Inequalities in Control. Lecture notes on DISC course, 2000.
[107] László Schnell. Jelek ées rendszerek Méréstechnikája. Tankönyvkiadó, Budapest, 1991.
[108] R. Sepulchre, M. Jankovic, and P. Kokotovic. Constructive Nonlinear Control. Springer-Verlag, 1997.
[109] R.S. Sharp and D.A. Crolla. Road vehicle suspension system design: A review. Vehicle System Dynamics, 16:167--192, 1987.
[110] S. L. Shishkin, R. L. Ortega, D. L. Hill, and A. L. Loria. On output feedback stabilization of Euler-Lagrange systems with nondissipative forces. Systems & Control Letters, 27:315--324, 1996.
[111] S. Skogestad and I. Postlethwaite. Multivariable Feedback Control. John Wiley & Sons, Chichester, New York, Toronto, Singapore, 1996.
[112] G. Stépán. Chaotic motion of wheels. Vehicle System Dynamics, 20:341--351, 1991.
[113] D.J. Stilwell and W.J. Rugh. Stability and l2 gain properties of LPV systems. Automatica, 38:1601--1606, 2002.
[114] M.R. Stone and A. Demetriou. Modeling and simulation of vehicle ride and handling performance. Proc. of the 15th IEEE Int. Symposium on Intelligent Control, 2000.
[115] H. Sussmann and V. Jurdjevic. Controllability of nonlinear systems. J. Diff. Eqs., 12:95--116, 1972.
[116] I. Szászi, P. Gáspár, and J. Bokor. Nonlinear active suspension modelling using linear parameter varying approach. Proc. of the 10th Mediterranean Conference on Control and Automation, Lisbon, Portugal, 2002.
[117] A.G. Thompson and B.R. Davis. Optimal linear active suspensions with derivative constraints and output feedback control. Vehicle System Dynamics, 17:179--192, 1988.
[118] R. Tuschák. Szabályozástechnika. Műegyetemi KiadŰ, Budapest, 1994.
[119] A. J. van der Schaft. L2-Gain and Passivity Techniques in Nonlinear Control. Springer-Verlag, Berlin, 2000.
[120] L. K. Vasiljevic and H.K. Khalil. Differentiation with high-gain oservers the presence of measurement noise. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, pages 4717--4722. 2006.
[121] M. A. Vidyasagar. New directions of research in nonlinear-system theory. Proceedings Of The IEEE, 74:1060--1091, 1986.
[122] M. A. Vidyasagar, H. A. Schneider, and B. A. Francis. Algebraic and topological aspects of feedback stabilization. IEEE Transactions On Automatic Control, 27:880--894, 1982.
[123] M. A. Vidyasagar and A. A. Vannelli. New relationships between input-output and Lyapunov stability. IEEE Transactions On Automatic Control, 27:481--483, 1982.
[124] H. Wang, M. Krstic, and G. Bastin. Optimizing bioreactors by extremum seeking. International Journal of Adaptive Control and Signal Processing, 13:651--669, 1999.
[125] J. Wang, N. Chen, and G. Yin. Multi-agent based vehicle integrated control framework for coordination of active steering, driveline and braking systems. International Conference on Computer Science and Software Engineering, 2008.
[126] J. Wang and M. Xin. Multi-agent consensus algorithm with obstacle avoidance via optimal control approach. International Journal of Control, 83:2606--2621, 2010.
[127] A.S. Willsky. A survey of design methods for failure detection in dynamic systems. Automatica, 12:601--611, 1976.
[128] F. Wu. A generalized LPV system analysis and control synthesis framework. International Journal of Control, 74:745--759, 2001.
[129] F. Wu, X. H. Yang, A. Packard, and G. Becker. Induced -norm control for LPV systems with bounded parameter variation rates. International Journal of Nonlinear and Robust Control, 6:983--998, 1996.
[130] F. Wu, X.H. Yang, A. Packard, and G. Becker. Induced norm controller for LPV systems with bounded parameter variation rates. International Journal of Robust and Nonlinear Control, 6:983--988, 1996.
[131] M. Yamashita, K. Fujimori, K. Hayakawa, and H. Kimura. Application of control to active suspension system. Automatica, 30:1717--1729, 1994.
[132] MATLAB (V4.2c1) User's Guide, 1994.
[133] SIMULINK (V1.3c) User's Guide, 1994.
[134] Documentation for The Fault Detection and Isolation Matlab Toolbox, EU-Copernicus Project CT94-0237, 1998.
[135] Y. Zhang and A. Alleyne. A practical and effective approach to active suspension control. Proc. of the International Symposium on Advanced Vehicle Control, Hiroshima, 2002.
[136] K. Zhou, J.C. Doyle, and K. Glover. Robust and Optimal Control. Prentice Hall, 1996.