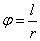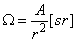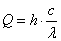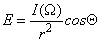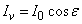3. fejezet - Világítástechnikai alapismeretek
3.1. A térszög
A geometria eszköztárában a szög fogalma két egymást metsző egyenes egymástól való elhajlását jelenti. E két egyenes metszéspontja körül behúzott egységnyi sugarú kör területén a két egyenes által kimetszett l hosszúságú ívdarabbal, azaz ívmértékkel magát a szöget jellemezzük. Nem egységnyi, hanem r sugarú kör esetén a szög
|
|
(3.1) |
Az SI-rendszer szerint tehát a síkszög egysége a radián [rad].
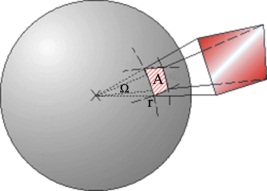
Ha az előzőek analógiájára értelmezzük egy r sugarú gömbből kimetszett A felület és egy gömb sugara négyzetének arányát, akkor eljutunk a térszög fogalmához (3.1. ábra), melynek mértékegysége a szteradián.
|
|
(3.2) |
Egységnyi sugarú gömb esetén a lehetséges legnagyobb, az egész teret befogó térszög mértéke 4π⋅sr .
3.2. Optikai sugárzás
Az optikai sugárzástartomány alatt az ultraibolya (UV) sugárzástól az infravörös (IR) tartományig terjedő elektromágneses sugárzás tartományt értjük (3.2. ábra). A sugárzás hullámhossza λ, mely két hullámhegy csúcspontja között megtett úthossz [m].
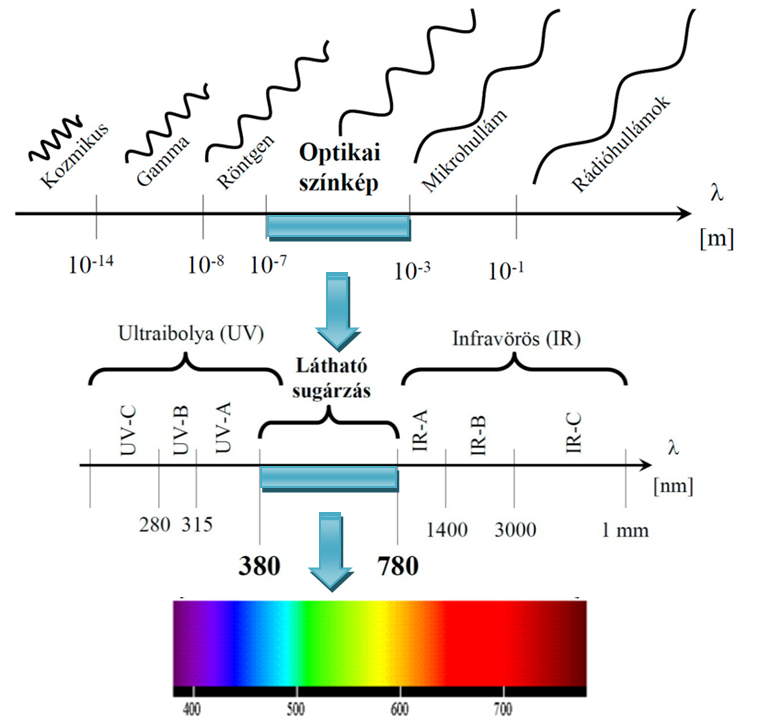
A fény az elektromágneses sugárzás szemünk által érzékelhető hányada. A látható hullámhossz tartomány (VIS) hozzávetőlegesen 380-780 nm-ig terjed, ezen belül szemünk a hullámhossztól függően képes a sugárzást fényérzetté alakítani.
3.2.1. A fény kettős természete
A rövidebb hullámhosszú, azaz nagy energiájú elektromágneses sugárzások, mint a Röntgen vagy a gamma-sugárzás inkább részecsketulajdonságokat mutatnak, míg hosszú hullámhossznál, mint a mikrohullám, inkább hullámtulajdonságok jellemzők. A látható fény a két tartomány között helyezkedik el, ezért kettős természete figyelhető meg. Egyrészt vizsgálható elektromágneses hullámként, mely a terjedésre és a hullámjelenségekre (interferencia, diffrakció, polarizáltság) ad magyarázatot, másrészt részecskeként (kvantumként), mellyel a keletkezés és a detektálás értelmezhető.
A részecske vagy kvantumelmélet szerint a fény a sugárzó energia egy formája, energia által keletkezik és energiává alakul át. Kvantumokban, azaz fotonokban továbbít energiát. A Planck-összefüggés szerint az optikai sugárzásokra érvényes teljesítmény a fotonok számának és a hullámhossznak a függvénye, mértékegysége a watt (W). A foton energiáját az alábbi összefüggés írja le,
|
|
(3.3) |
ahol
|
Q |
a foton energiája [J], |
|
|
h |
a Planck állandó - 6,63⋅10-34 [J·s], |
|
|
c |
a fénysebesség - 2.998 x 108 [m/s], |
A fenti összefüggés alapján a foton energiája hullámhossztól függ:
![Az optikai sugárzások energiája [28.]](images/image_III_3.png)
Ezért minél rövidebb hullámhosszúságú egy adott elektromágneses sugárzás, a benne továbbított energia annál nagyobb. Ezzel magyarázható az UV sugárzás számos biológiai hatása, de egyben ez alapozza meg a fluoreszcens fényforrások működési elvét is.
A nagyobb energiájú UV-B sugárzás káros biológiai hatásával gyakran szembesülünk, ez okozza ugyanis bőrünk leégését (Erythem), ezt az ózonréteg vastagságától függően képes elnyelni. Az UV-C sugárzás baktériumölő (Baktericid) hatása ismert, de kötőhártya gyulladást (Conjuctivitis) is képes okozni, mindemellett ózonképző hatású. Szerencsére az atmoszférában teljes egészében elnyelődik.
A higanykisüléses fényforrások által gerjesztett nagy energiájú fotonok UV-A tartományba esnek, melyek elnyelődnek a fénycsövek felültén található fénypor rétegben. A fénypor olyan kémiai anyag, mely fotolumineszcenciára képes, gerjesztés hatására a látható tartományban emittál (kisebb energiájú) fotonokat.
A fény detektálásakor az érzékelőre eső fotonok energiája érzékelhető, ezért IR tartományban nagyjából 1100 nm-ig képesek mérni a hagyományos kvantum-detektorok.
3.3. Fotometriai és radiometriai mennyiségek
A fotometriai és radiometriai mennyiségek tárgyalásához, és a köztük lévő különbségek megértéséhez vissza kell utalnunk szemünk érzékenységi függvényére, a V(λ) görbére (lásd Emberi látás fejezet), amely alapján az emberi látórendszer nem egyformán érzékeny a különböző hullámhosszúságú sugárzásokra, és körülbelül 380 nm és 780 nm között érzékeli az optikai sugárzásokat. Ezen törvényszerűségeket szem előtt tartva lehet megérteni a két megközelítés létjogosultságát. A különböző fényforrások működési elvüktől függően emittálhatnak olyan tartományokban is fotonokban, melyeket szemünkkel nem érzékelünk (pl. UV, IR), de azok hatása élettani vagy energetikai szempontból elhanyagolhatatlan.
A radiometria a teljes optikai színképet vizsgálja, annak energiáját fizikai mennyiségek formájában határozza meg. Tehát az emberi szem érzékenységétől független. A radiometriában a sugárzási jelenségek tárgyalására a teljesítmény, az energia idő szerinti deriváltja alkalmas. Alapmértékegysége a Watt (W). A radiometriában használatos energetikai mennyiségek spektrális mennyiségek.
Ezzel szemben a fotometria az optikai sugárzást az átlagos emberi megfigyelő látására jellemző V(λ) színképi függvény alapján értékeli, azaz kizárólag a 380 nm-től 780 nm-ig terjedő tartományt veszi alapul. Ezek nem spektrális, hanem integrált mennyiségek. Tehát a radiometriai illetve a fotometriai mennyiségek között a kapcsolatot az emberi szem spektrális érzékenysége teremti meg.
A különböző energetikai mennyiségeket ezért általánosságban radiometriailag lehet elsőként definiálni, majd minden radiometriai mennyiségnek a látható tartományon vett integrálásával és V(λ)-val történő súlyozásával előállítható fotometriai megfelelője.
Ezek alapján a világítástechnikában alkalmazott mennyiség-párok az MSZ 9620 szabvány szerint:
-
Sugárzási teljesítmény – energiaáram (radiant flux/power)
A sugárzás formájában kibocsátott, átvitt vagy felfogott teljesítmény. Definíciója szerint dWe [J] sugárzott energia idő szerinti deriváltja
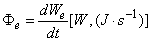
(3.4)
A sugárzási teljesítmény hullámhossz szerinti eloszlását spektrális teljesítmény-eloszlásnak (spectral power distribution) nevezzük:
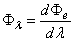
(3.5)
-
Fényáram (luminous flux)
A sugárzott teljesítményből a szabványosított spektrális fényhatásfok szerint származtatott mennyiség.
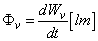
(3.6)
Mértékegysége: [lm - lumen ; cd·sr].
Definíció alapján 1 lm az a fényáram, amelyet az 1 cd fényerősségű, minden irányban egyenletesen sugárzó, pontszerű fényforrás 1 sr térszögben sugároz. Azaz a fényáram a fényerősség és a sugárzás térszögének szorzata. Másképpen a fényáram a fényforrás által emittált összes sugárzott teljesítmény látható tartományba eső hányada, ezért a kisugárzott energiát képes karakterizálni.
A fényáram és a sugárzott teljesítmény – és egyúttal a radiometriai és fotometriai mennyiségek – kapcsolatát az alábbi egyenlet segítségével definiáljuk:
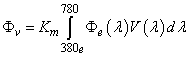
(3.7)
ahol K m = 683 lm/W a V(λ) függvény 555 nm-en lehetséges maximális fényhasznosítása. Fotometriai mennyiségek esetén az egyértelmű megkülönböztethetőség miatt az indexbe minden esetben kis „v”-t írunk, ami az adott mennyiség vizuális megközelítésére utal.
-
Sugárerősség (radiant intensity)
A sugárerősség a sugárforrást elhagyó, az adott irányt tartalmazó dΩ térszögben terjedő dΦ e sugárzott teljesítmény és a dΩ térszög hányadosa:
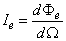
(3.8)
Egysége a W⋅sr -1
-
Fényerősség (light intensity)
Fotometriai értelemben ezzel analóg mennyiség a fényerősség, amely a fényforrást elhagyó, az adott irányt tartalmazó dΩ térszög hányadosa:
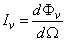
(3.9)
Egysége a candella=lumen⋅sr -1 . A candella (cd) az SI-rendszer alapmértékegysége, és definíció szerint olyan fényforrás fényerőssége adott irányban, amely 540⋅10 12 Hz frekvenciájú monokromatikus fényt bocsát ki, és sugárerőssége ebben az irányban 1/683 watt/szteradián, azaz a fekete sugárzó 1/600000 cm 2 -nyi felületének fényerőssége a felületre merőleges irányban, a platina dermedési hőmérsékletén, 101325Pa nyomáson.
-
Sugársűrűsség
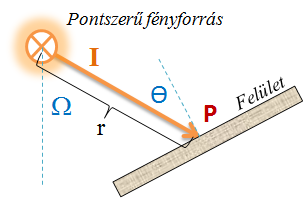
A sugársűrűsség adott irányban az dI e sugárerősségnek és a dA felületelem látszólagos nagyságának, a dAcosΘ vetületnek a hányadosa és mértékegysége W⋅m -2 ⋅sr -1 .
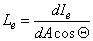
(3.10)
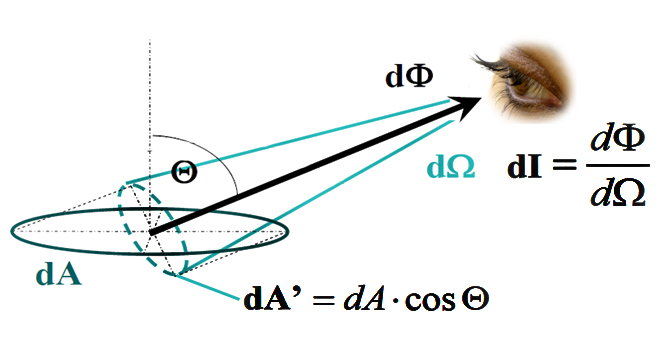3.4. ábra - Sugársűrűség szemléltetése
-
Fénysűrűség
A fénysűrűség, a fényforrás felületi fényessége vagy világossága adott irányban, az dI v fényerősségnek és a dA felületelem látszólagos nagyságának, a dAcosΘ vetületének hányadosa,
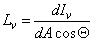
(3.11)
Mértékegysége a cdm -2 . Használatos még a stilb (sb) egység is, amely 1cd/cm 2 .
Nem csak világítástechnikában fontos mennyiség, hiszen az emberi szem fénysűrűség különbségre érzékeny, ez alapján érzékeli a kontrasztot, de ezzel írható le a káprázás vagy a vakítás jelensége is.
3.1. táblázat - Jellegzetes fénysűrűség értékekÉjszakai égbolt
10-7 cd/m2
Telihold
0.5 cd/m2
Napfény délben
100.000 cd/m2
Gyertya lángja
1 cd/m2
Izzószál
180.000 cd/m2
Xenon lámpa
150.000 cd/m2
-
Besugárzott teljesítmény (irradiance)
A besugárzott teljesítmény (3.5. ) a felület egy adott pontján az oda beeső dΦ e sugárzási teljesítmény és a felületelem dA területének a hányadosa
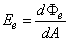
(3.12)
Egysége a W⋅m -2 .
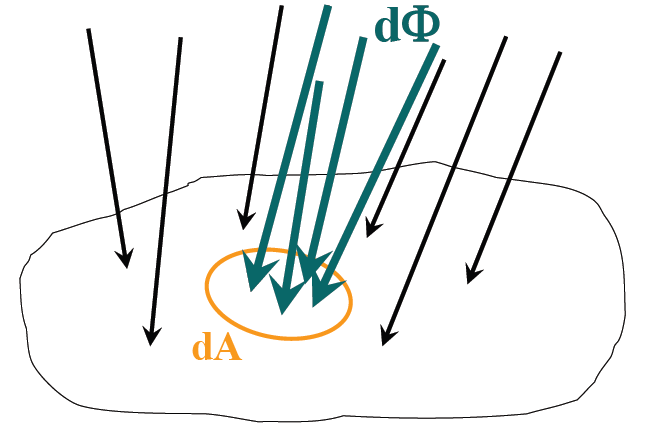3.5. ábra - Besugárzott teljesítmény szemléltetése
-
Megvilágítás (illuminance)
A megvilágítás a felület egy adott pontján az oda beeső dΦ e sugárzási teljesítmény és a felületelem dA területének a hányadosa
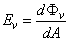
(3.13)
Egysége a lux=lm⋅m -2 .
A megvilágítás a világítástechnikában egyik leggyakrabban megadott mennyiség. A szabványok igen gyakran megvilágításban definiálják a gyakorlati követelményeket (Táblázat 3.2). Ennek egyik oka egyszerű és könnyen érthető definíció, másrészt az a tény, hogy ezt a mennyiséget könnyen, és szélesebb körben lehet mérni, nem igényel bonyolult és drága berendezéseket. Egy megvilágításmérő vagy a köznyelvben gyakran előforduló luxmérő a benne található érzékelő (fotodióda) segítségével számszerűsíti a felületére beérkező fotonok (azaz a fényáram) által kiváltott töltéshordozókkal arányos jelet. A megvilágítás kifejezéséhez szükséges másik mennyiség az érzékelő aktív felülete.
3.2. táblázat - Jellegzetes megvilágítás értékekIrodavilágítás munkasíkon, min.
300 lx
Számítógépes munkahely, min.
500 lx
Telihold fénye
0,2 lx
Szükségvilágítás
1 lx
Napfény nyáron
100.000 lx
Napfény télen
10.000 lx
3.3. táblázat - A fontosabb radiometriai és fotometriai mennyiségek összefoglalásaNév
Jel
Mértékegység
Radiometriai mennyiségek
Sugárzási teljesítmény
Φ e
[W]
Sugárzott energia
W e
[Ws]
Besugárzott teljesítmény
E e
[W ⋅ m -2 ]
Sugárerősség
I e
[W ⋅ sr -1 ]
Sugársűrűség
L e
[W ⋅ m -2 ⋅ sr -1 ]
Fotometriai mennyiségek
Fényáram
Φ v
[lm]
Fényenergia
W v
[lm ⋅ s]
Megvilágítás
E v
[lm ⋅ m -2 ]
Fényerősség
I v
[sd]
Fénysűrűség
L v
[lm ⋅ m -2 ⋅ sr -1 ]
3.4. A távolságtörvény
A megvilágításhoz kapcsolódó fontos törvényszerűség az úgynevezett távolságtörvény (Photometric distance law) amely leírja, hogy pontszerű fényforrás által létrehozott megvilágítás hogyan függ a megvilágított felület és a sugárzó közti távolságtól.
|
|
(3.14) |
Azt a fény- vagy sugárforrást, melynek mérete az érzékelőtől való távolsághoz képest kicsi, pontszerű forrásnak nevezzük. Egy elméleti pontszerű fényforrás a tér minden irányában sugároz. A fényforrás pontszerűségéből adódóan az árnyékok (amiket a testek vetnek egymásra) borotvaélesek lesznek, átmenet nélkül.
Tehát pontszerű fényforrás esetén a megvilágítás a felülettől való távolság négyzetével arányosan csökken. Vagyis ha egy a munkasíktól merőlegesen 1 méter távolságra lévő fényforrás 100 lx megvilágítást produkál, akkor azt 1 méterrel távolabbra helyezve a megvilágítás 25 lx-ra csökken majd. Véges méretű fényforrás esetében ez az összefüggés közelítőleg érvényes. Azt a távolságot, amelynél nagyobb távolság esetében a megvilágítás értéke adott hibánál kisebb eltéréssel közelíti meg az így számított értéket, fotometriai határtávolságnak nevezzük. Ha a megvilágító fényforrás nem rendelkezik külön gyűjtő optikával, ez a távolság a fényforrás legnagyobb méretének legalább ötszöröse (ökölszabály) – de inkább tízszerese – 1% nagyságrendű hiba esetében. A fotometriai határtávolságon túl minden sugárzót pontszerűnek lehet tekinteni.
3.5. A Lambert-féle koszinusztörvény
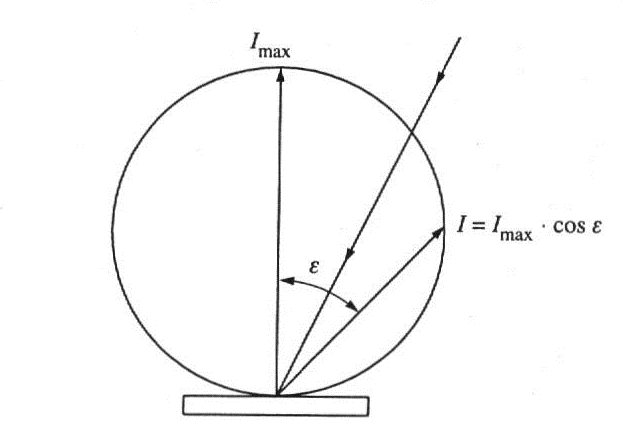
A pontszerű sugárzók kemény fényével ellentétben definiálhatók olyan források, melyek lágy fényt sugároznak. Az ilyen típusú sugárzást nevezzük szórt vagy diffúz fénynek. Tulajdonsága, hogy az árnyékhatás jelentéktelen. Nem érvényesek rá a pontszerű fényforrások törvényszerűségei. Az ideálisan diffúz felületet az ún. Lambert-féle felület, amit a Lambert-féle koszinusztörvény jellemez. E törvény kimondja, hogy a visszaverő felület fényerőssége a felület normálisával bezárt szög koszinuszával arányos.
|
|
(3.15) |
A (3.15) alapján könnyen belátható, hogy a fénysűrűség azért állandó bármely irányból tekintve, mert a csökkentett intenzitást egy szintén a szög koszinuszával arányosan csökkenőnek látszó felület sugároz ki.
