1. fejezet - Optikai alapfogalmak
Vissza		Előre

1. fejezet - Optikai alapfogalmak

A fény tulajdonságai

A fény elektromágneses rezgés. Kettős, hullám-, illetve részecsketermészete van, ezért bizonyos jelenségeket hullámtani, másokat pedig kvantummechanikai tárgyalással lehet leírni.

A fény hullámhossza:

$λ = \frac{c}{v}$

(1.1)

ahol

	λ	a fény hullámhossza vákuumban
	c	a fény terjedési sebessége vákuumban (közelítőleg: 3⋅10⁸ m/s)
	v	a fény frekvenciája

A törésmutató és az Abbe-szám

A sebesség vákuumbelihez képesti csökkenését egy viszonyszámmal, a törésmutatóval fejezzük ki.

$n = \frac{c}{v}$

(1.2)

ahol

	c	a fény terjedési sebessége vákuumban
	v	a fény terjedési sebessége az adott közegben

Az üveg törésmutatója is változik a fény színe szerint. Ernst Abbe-ról Abbe-számnak nevezzük a következő összefüggést:

$v = \frac{n_{d} - 1}{n_{F} - n_{C}}$

(1.3)

ahol

	v	az Abbe-szám
	n _d	törésmutató sárga színre
	n _F	törésmutató kék színre
	n _C	törésmutató vörös színre

Fermat-elv

Két pont között a fénysugár azokon az utakon halad, amelyek megtételéhez a legrövidebb időre van szükség más útvonalakkal szemben.

A geometriai távolság és a közeg törésmutatójának szorzatát – optikai úthossznak nevezzük.

Vagyis a két pont között a fénysugár olyan utakon fog haladni, hogy azok mentén az optikai úthosszak összege egyenlő legyen.

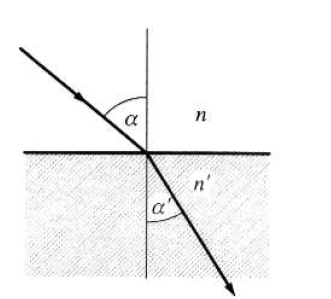
1.1. ábra - Fénytörés két közeg határán

A Snellius–Descartes-törvény

$n \sin α = n' \sin α'$

(1.4)

A totálreflexió

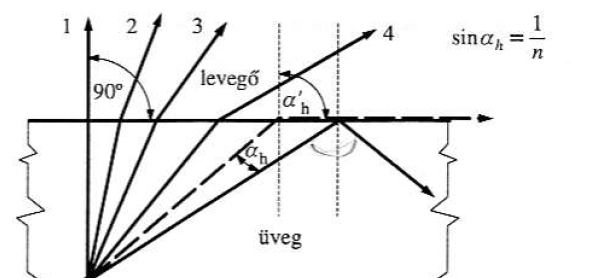
1.2. ábra - A totálreflexió

A határszögnél nagyobb beesési szöggel érkező fénysugarak nem tudnak kilépni a közegből, totálreflexiót szenvednek.

A geometriai optika alaptörvényei

A fény egyenes vonalban terjed. Ez természetesen homogén, izotróp közegben érvényes.
Különböző közegek határain a fénysugár megtörve folytatja útját. A fénytörést a Snellius–Descartes-törvény írja le.
Különböző közegek határán a fény egy része visszaverődik. Ezt a tükör-törvény írja le, miszerint a beeső, a visszavert fénysugár és a beesési merőleges egy síkban fekszik, valamint a beesési és visszaverődési szög egyenlő. A szögeket a beesési merőlegestől mérjük, amely a fénysugár döféspontjában a felület normálisa.
A fénysugarak függetlenségének elve kimondja, hogy a tér egy pontján keresztül akárhány fénysugár haladhat egymás zavarása nélkül. E törvény nyilván nem érvényes pl. koherens lézerfények találkozása esetén, amelyek egymásra hatásakor interferencia jön létre.
A fénysugarak megfordíthatóságának elve szerint ha fény a tér egyik pontjából egy bizonyos útvonalon halad a tér egy másik pontjába, akkor a visszafelé indított fénysugár ugyanazon úton fog haladni.

Előjelszabályok (megállapodások)

A sugármenet-rajzokat úgy vesszük fel, hogy a fénysugarak balról jobbra haladjanak.

Az optikai tengely mentén a gömbfelülettől balra eső távolságok negatívok, a jobbra esőek pozitívok.
Az optikai tengely feletti távolságok (pl. h) pozitívok, a tengely alattiak pedig negatívok.
A fénysugarak optikai tengellyel bezárt szögei (Ϭ, Ϭ’) akkor pozitívok, ha az optikai tengelyt a fénysugárba az óramutató járásával ellentétes irányban lehet 90°-nál kisebb szöggel beforgatni. Ellenkező esetben a szögek negatívok.
A felület döféspontjában a fénysugarak beesési (i), illetve törési (r) szögei akkor pozitívok, ha a beesési merőlegest a fénysugárba az óramutató járásával ellenkező irányba lehet 90°-nál kisebb szöggel beforgatni. Ellenkező esetben a szögek negatívok.
A gömbfelületek görbületi sugarai akkor pozitívok, ha a felület balról nézve konvex, és akkor negatívok, ha balról nézve konkáv.
A fókusztávolság előjele pozitív gyűjtő-, negatív pedig szórólencse esetében.

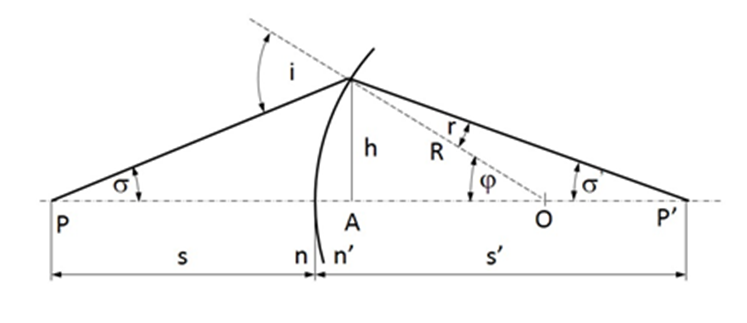
1.3. ábra - Egyetlen gömbfelület képalkotása

$s' = \frac{n'}{\frac{n}{s} + \frac{n' - n}{R}}$

(1.5)

Ha a gömbfelületre párhuzamos fénysugarak érkeznek (a tárgy a végtelenben van), akkor a fénysugarak a képoldalon a fókuszpontban találkoznak. s= - ∞ és s’=f’ helyettesítéssel:

$\frac{n'}{f'} = \frac{n' - n}{R}$

(1.6)

Ezt a mennyiséget törőértéknek nevezzük, és dioptriában adjuk meg:

$φ = \frac{n'}{f'} = \frac{n' - n}{R}$

(1.7)

Kardinális elemek: fősíkok, főpontok, csomópontok

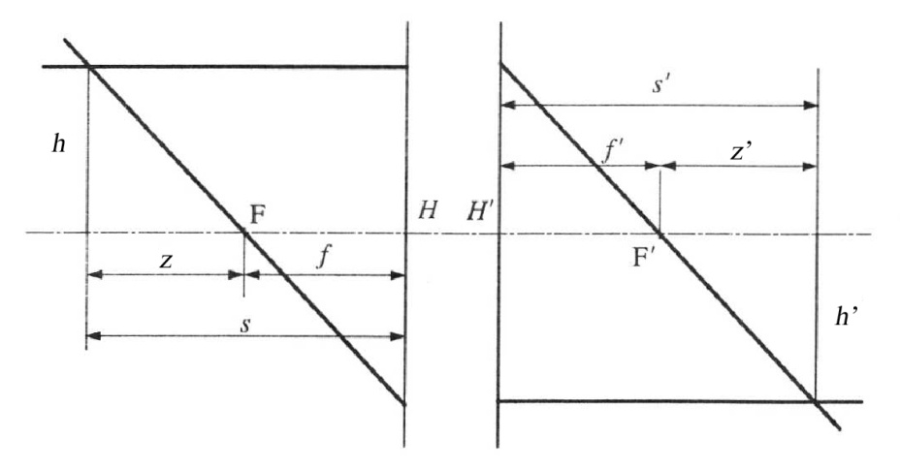
A fősíkok az optikai rendszerbe a tengellyel párhuzamosan belépő fénysugarak és a rendszert elhagyó megfelelő fénysugarak meghosszabbításainak metszéspontjai által kifeszített felületek. (1.4. ábra)

A főpontok a fősíkoknak és az optikai tengelynek a döféspontjai (H, H’).

Minden optikai rendszernek két fősíkja (és főpontja) van: tárgyoldali és képoldali fősíkok (főpontok).

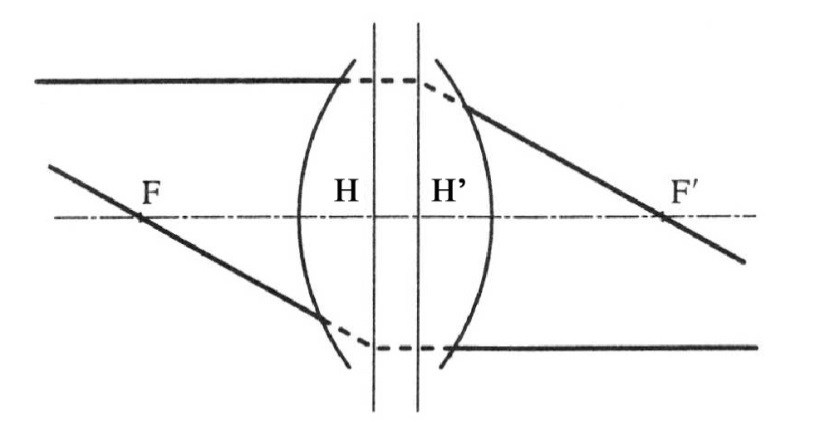
1.4. ábra - A fősíkok és a főpontok szerkesztése

A fősíktól mérjük a fókusztávolságokat, a tárgytávolságot, illetve a képtávolságot.

A csomópontok

Egy optikai rendszer egyik csomópontjába (N) irányított fénysugár a rendszert önmagával párhuzamosan hagyja el, úgy, mint ha a másik csomópontból (N’) indult volna (1.5. ábra).

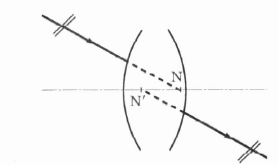
1.5. ábra - A csomópontok származtatása

Ha az optikai rendszer tárgy-, és képtere azonos törésmutatójú (pl. levegő), akkor a csomópontok és a főpontok egybeesnek.

A Newton-formula

Mérjük a tárgy illetve a kép távolságát a fókuszpontoktól (z illetve z’

Newton-formula:

$z z' = - f f'$

(1.8)

a Newton-formula segítségével írhatók az alábbiak:

$\frac{f'}{s'} - \frac{f}{s} = 1$

(1.9)

1.6. ábra - Vázlat a Newton-formulához

Amennyiben a tárgy- és képtér is levegő (vagy azonos közeg) akkor f’=f és így

$\frac{1}{s'} - \frac{1}{s} = \frac{1}{f}$

(1.10)

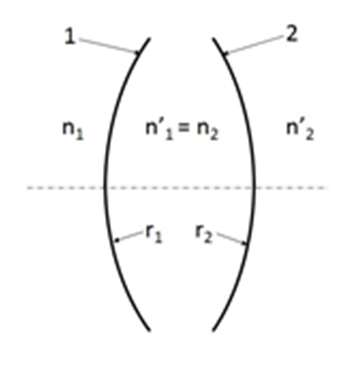
1.7. ábra - Vázlat a vékonylencse számításhoz

A vékony lencse egyenlete:

$\frac{1}{s_{2}^{'}} - \frac{1}{s_{1}} = (n - 1) (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

(1.11)

a vékony lencse fókuszképlete:

$\frac{1}{f^{'}} = (n - 1) (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

(1.12)

Nagyítások

Lineáris nagyítás (β)

$β = \frac{y^{'}}{y}$

(1.13)

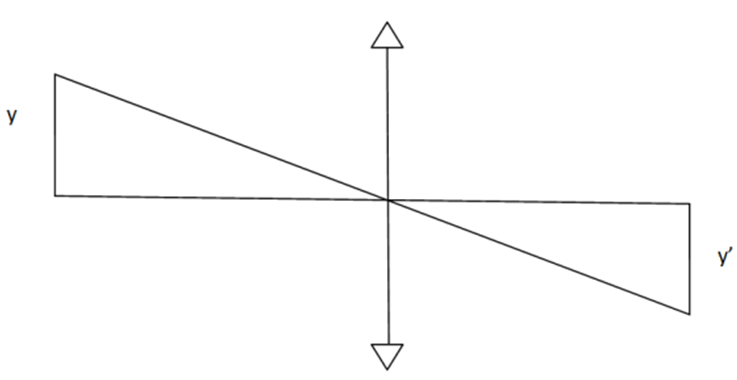1.8. ábra - A lineáris nagyítás számítása

Kifejezhető még a Newton-formula segítségével:

$β = \frac{f}{z} = \frac{z'}{f'} = \frac{f}{f + s} = \frac{f' - s'}{f'}$

(1.14)

Szögnagyítás (γ)

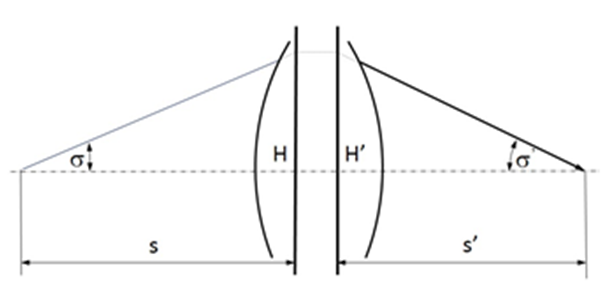1.9. ábra - A szögnagyítás számítása

	$γ = \frac{t g σ^{'}}{t g σ}$	(1.15)
	$γ = \frac{t g σ'}{t g σ} = \frac{\frac{h}{s'}}{\frac{h}{s}} = \frac{s}{s'}$	(1.16)

Számítsuk ki a lineáris és a szögnagyítás szorzatát:

$β = \frac{f}{f'} \frac{s'}{s}$

(1.17)

Ha f = f’, akkor $β = \frac{s'}{s}$

$β γ = \frac{f}{f'}$

(1.18)

Ha f = f’, akkor

$β = \frac{1}{γ} é s γ = \frac{1}{β}$

(1.19)

Longitudinális nagyítás (α)

	$α = \frac{d z}{d z'}$	(1.20)
	$α = \frac{f^{'}}{f} β^{2}$	(1.21)

Ha f = f’, akkor:

$α = β^{2}$

(1.22)

a lineáris és a szögnagyítás hányadosa

$α = \frac{β}{γ}$

(1.23)

Vékony lencsék eredője

Két elemi vékony lencsét egymás mellé helyezve, dioptriáik, vagyis törőértékeik összeadódnak:

$φ = φ_{1} + φ_{2}$

(1.24)

mivel azonos közegekben $φ = \frac{1}{f}$ , ezért

$\frac{1}{f} = \frac{1}{f_{1}} + \frac{1}{f_{2}}$

(1.25)

f-re kifejezve

$f = \frac{f_{1} f_{2}}{f_{1} + f_{2}}$

(1.26)

„vastag” lencsék eredője

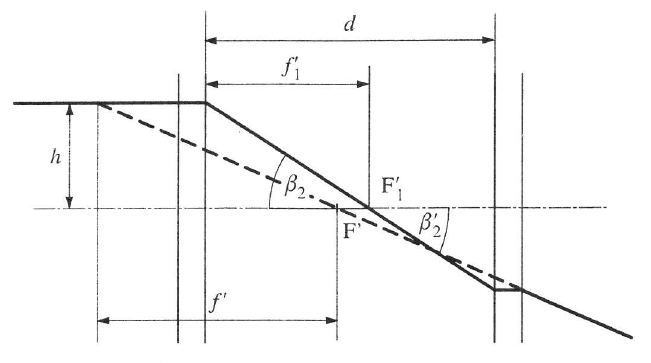
1.10. ábra - Vastag lencse eredője

$f^{'} = \frac{f_{1}^{'} f_{2}^{'}}{f_{1}^{'} + f_{2} - d}$

(1.27)

illetve levegőben lévő lencsék összerakásakor:

$\frac{1}{f} = \frac{1}{f_{1}} + \frac{1}{f_{2}} - \frac{d}{f_{1} f_{2}}$

(1.28)

Az (1.27) összefüggés nevezőjében lévő kifejezést jelöljük Δ-val.

Ezt nevezzük optikai tubushossznak.

	$Δ = f_{1}^{'} + f_{2} - d$	(1.29)
	$f^{'} = \frac{f_{1}^{'} f_{2}^{'}}{Δ}$	(1.30)

Összefoglalva:

$\begin{matrix} f = \frac{f_{1} f_{2}}{Δ} & f^{'} = \frac{f_{1}^{'} f_{2}^{'}}{Δ} \\ p = \frac{f_{1} d}{Δ} & p^{'} = - \frac{f_{2}^{'} d}{Δ} \end{matrix}$

(1.31)

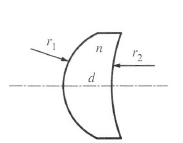
1.11. ábra - Vastag lencse fókusza és fősíkjainak helye

$\frac{1}{f} = (n - 1) \frac{n (r_{2} - r_{1}) + (n - 1) d}{n r_{1} r_{2}}$

(1.32)

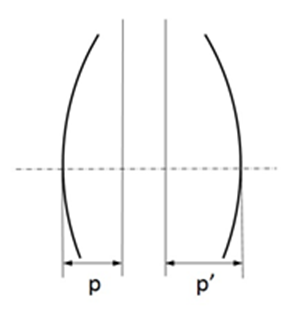
1.12. ábra - Vázlat a vastag lencse fősíkjainak számításához

Több felületből álló lencserendszerek

Eredő fókusztávolság:

$f = \frac{n_{1}}{n_{k}^{'}} \frac{s_{1}^{'} s_{2}^{'} s_{3}^{'} ... s_{k}^{'}}{s_{2} s_{3} ... s_{k}}$

(1.33)

Eredő lineáris nagyítás:

$β = \frac{n_{1}}{n_{k}^{'}} \frac{s_{1}^{'} s_{2}^{'} s_{3}^{'} ... s_{k}^{'}}{s_{1} s_{2} s_{3} ... s_{k}}$

(1.34)

ahol

	k	a gömbfelületek száma
	n ₁	a tárgytér törésmutatója
	n’ _k	a képtér törésmutatója

Kepler-távcső

A rendszer szögnagyítása

$γ = \frac{t g β'}{t g β} = \frac{- h}{f_{2}^{'}} \frac{- f_{1}}{- h} = - \frac{f_{1}}{f_{2}^{'}}$

(1.35)

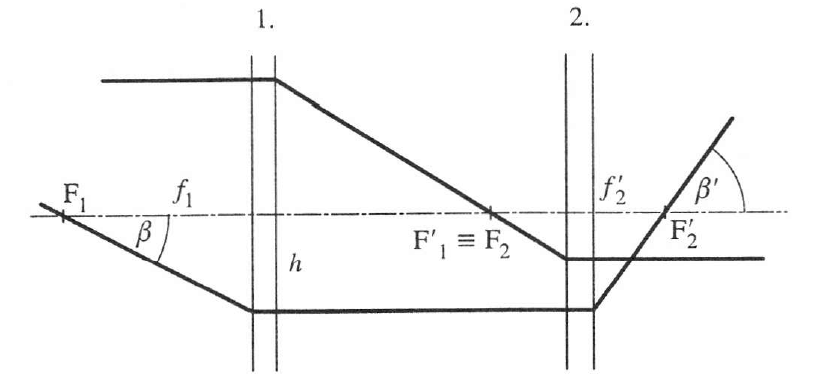
1.13. ábra - A Kepler-távcső

γ negatív előjele a fordított állású képet jelzi

Galilei-távcső (színházi vagy terresztikus távcső)

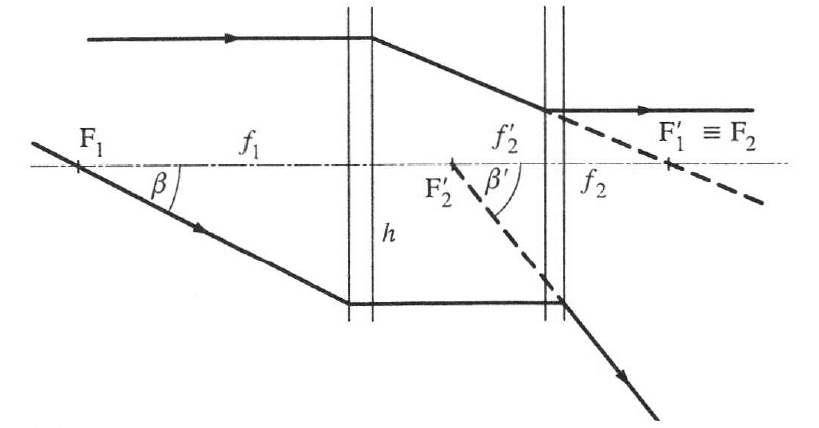
1.14. ábra - A Galilei-távcső

A szögnagyítás (1.9. ábra)

$γ = \frac{t g β'}{t g β} = \frac{- h}{- f_{2}^{'}} \frac{- f_{1}}{- h} = + \frac{f_{1}}{f_{2}^{'}} > 0$

(1.36)

A Galilei távcső egyenes állású képet alkot.

Optikai átviteli függvények

Optikai rendszereknél ω=2πv.

A v a térfrekvencia, vagyis a milliméterenkénti periódusok száma.

$O T F (v) = M T F (v) e^{- i P T F (v)}$

(1.37)

Az OTF az MTF és a PTF jelölést a nemzetközi irodalom miatt tartjuk meg (optical transfer function, modulation transfer function, illetve phases transfer function), utóbbit szokás még egyszerűen ϕ(ν)-vel jelölni.

Definicíószerűen MTF(0) = 1 vagyis nulla térfrekvencián a modulációs átviteli függvény értéke egységnyi, míg PTF(0) = 0, vagyis a fázisátviteli függvényérték ugyanott zérus.

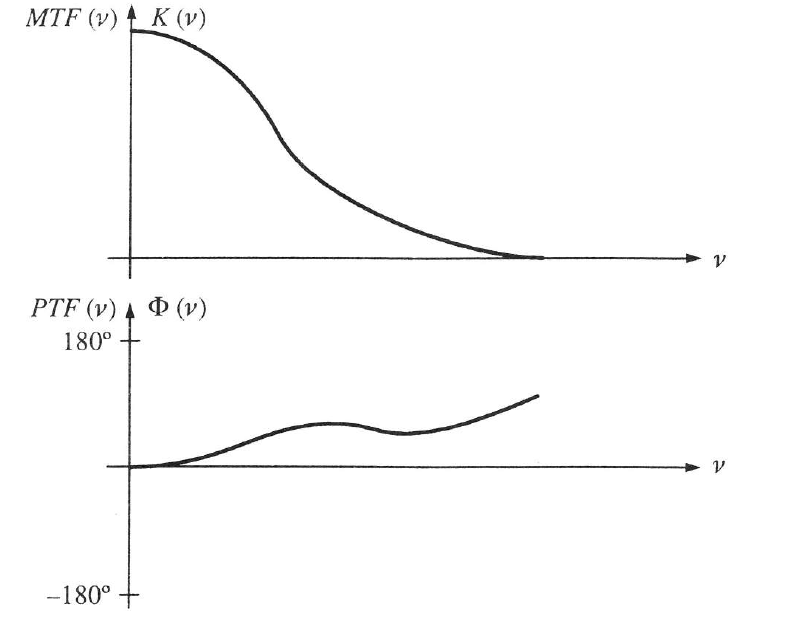
1.15. ábra - A modulációs átviteli függvény és a fázisátviteli függvény

Aberrációmentes optikai rendszer átviteli függvénye

$v_{h a t á r} = \frac{1}{1,22 λ \frac{f}{D}}$

(1.38)

Vissza		Előre
Jármű optika	Főoldal	2. fejezet - Az emberi látással kapcsolatos alapismeretek