3. fejezet - Futóművek általános feladatai, követelményrendszere
A futóműveknek az alábbi funkciókat, illetve feladatokat kell ellátni:
-
Közvetíteni az erőhatásokat az út és a jármű között
-
kellő tapadási képességgel kell rendelkezni hossz - és keresztirányban
-
maximális dinamikus kerék-, ill. tengelyterhelést kell szolgáltatni
-
-
Megfelelő lengéskényelmet nyújtani az utasok, illetve az áruk számára
-
optimális önlengési jellemzőkkel kell rendelkezni
-
megfelelő lengésátviteli karakterisztikája legyen
-
-
Csökkenteni a járműalkatrészek dinamikus igénybevételét
-
Aktívan elősegíteni a jármű menetstabilitását
-
fékezéskor kedvezően befolyásolni a jármű irányítását
-
kanyarodáskor önkormányzással csökkenteni a jármű sodródását
-
3.1. Erőhatások az út és a jármű között:
A jármű kerekeire menet közben különböző erők hatnak. Ilyenek:
-
a jármű tömegéből adódó súlyerő (Gi)
-
a járműre ható légellenállásból adódó függőleges leszorító vagy felhajtó erő (FWZ)
-
a jármű lassításához, megállításához szükséges fékezőerő (FF)
-
a jármű haladásához, gyorsulásához szükséges vonóerő (F)
-
a jármú kanyarodásakor fellépő oldalerő (FS)
Ezek az erők a gumiabroncs érintkezési felületén koncentrálódnak és a gumiabroncs és az útfelület közti tapadási viszonyoktól függően adódnak át az útra (3.1. ábra). Ha a tapadásból adódó erők nagyobbak a jelentkező aktív erőknél, akkor a jármű fékezhető, gyorsítható, kormányozható, vagyis a jármű menetstabilitása megfelelő. Ellenkező esetben a kerekek megcsúsznak, blokkolnak, kipörögnek, vagyis a jármű elveszti stabilitását. Tehát a gumiabroncs és az útfelület közti tapadási erők természetes korlátai a jármű dinamikus mozgásának.
A tapadási erő meghatározható a kereket az útra szorító erő és a tapadási viszonyokat minősítő tényező ismeretében.
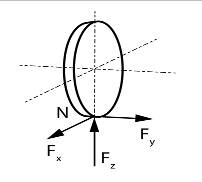
ahol:
|
Fz |
– a kereket leszorító tényleges erő; |
|
|
Fx |
– a jármű menetirányába eső tapadási erő (itt hat F és FF); |
|
|
Fy |
– a jármű oldalirányába eső tapadási erő (itt lép fel Fs); |
|
|
φx |
– a hosszirányú tapadási tényező; |
|
|
φy |
– a keresztirányú tapadási tényező; |
|
|
N |
– a kerék talppontja. |
3.2. A kerekeket leszorító erő
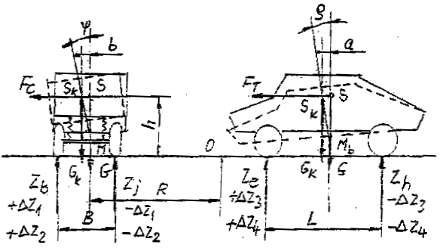
A látszólag egyszerű egyenlet a jármű dinamikus mozgása során igen bonyolulttá válik. A kereket az út felületéhez szorító erő állandóan változik a rugózás, a felépítmény billegő, bólintó mozgása, a menet és az oldalszél következtében fellépő átterhelődések miatt (3.2. ábra):
|
Fzi = Zsti ± ΔZR ± ΔZW ± ΔZ1 ±ΔZ2±ΔZ3 ± ΔZ4 |
ahol
|
Fzi |
–az egy kerékre ható tényleges, dinamikus leszorító erő; |
|
|
Zsti |
– egy kerék statikus terhelése a jármű álló helyzetében; |
|
|
ΔZR |
– a kerék és a felépítmény rugózásaiból adódó kerékterhelés változás; |
|
|
ΔZW |
– a menet – és oldalszél hatására fellépő kerékterhelés változás; |
|
|
ΔZ1 |
– a járműre ható oldalerő hatására bekövetkező kerékterhelés változás: |
|
ΔZ2 |
– a felépítmény oldalbillenése következtében fellépő súlypont eltolódás (b) hatására fellépő kerékterhelés változás: (Gk-felépítmény súlyereje) |
|
ΔZ3 |
– a fékezéskor vagy gyorsuláskor fellépő hosszirányú tehetetlenségi erő hatására bekövetkező kerékterhelés változás: |
|
ΔZ4 |
– a felépítmény bólintó mozgása következtében fellépő súlypont eltolódás (a) hatására jelentkező kerékterhelés változás: |
Az átterhelődések következtében a kereket az útfelülethez szorító erő nulla és akár ötszörös értékek között változhat.
3.3. Tapadási tényező
A tapadási tényező a gumiabroncs és az útfelület közötti tapadás minőségét fejezi ki. Nagysága nulla és egy közötti értékek között változik. Így többek közt a gumiabroncs és az út közötti fajlagos csúszástól (slip), a gumiabroncs mintázatától, anyagától, légnyomásától, az útfelület érdességétől, hőmérsékletétől, szennyezettségétől, vizességétől függ. Járműdinamikai szempontból a slip alakulása alapvetően kihat a tapadási tényezőre.
A slip a kerék és az útfelület közötti csúszás mértékére utal.
Értelmezése:
-
fékezés esetén:
-
hajtás esetén:
ahol:
|
Vgk |
– a gépkocsi haladási sebessége, |
|
|
Vk |
– a kerék kerületi sebessége. |
A slip érték 0-1 között változik. Fékezéskor blokkolás esetén a kerék megáll, a jármű tovább halad, a slip értéke 1. Hajtáskor a kipörgő kerék esetén a slip értéke 1. A különböző blokkolás – vagy kipörgésgátló rendszerek éppen ezt a fajlagos sebességkülönbséget ellenőrzik és szabályozzák.
A korszerű járműdinamikai elméletek szerint a hosszirányú és a keresztirányú tapadási tényező eltérően változik a slip függvényében. A slip is tágabb értelmezést kap. Keresztirányú csúszás esetén is változik a hosszirányú tapadási tényező (3.3. ábra).
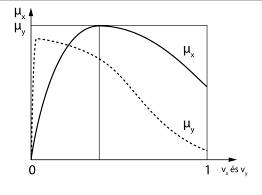
Ezzel az elmélettel megmagyarázható a jármű fékezhetőségének és gyorsíthatóságának csökkenése, amennyiben a hibás futóműgeometria vagy túl nagy oldalerő miatt a jármű kereke oldalirányba megcsúszik.
3.4. Lengéskényelem
A közúti járművek olyan úton haladnak, amelynek makroprofilja (függőleges vonalvezetése) és mikroprofilja (felületi egyenetlenségei) is véletlenszerű (sztochasztikus) függvény szerint változik. A futómű rugózási rendszerének kell gondoskodnia arról, hogy a mozgás közben az utasok és az áruk lengései megfelelő méretűek legyenek. Ennek egzakt minősítésére szolgálnak a különböző lengéskényelmi mutatók.
Ezek közül a leggyakrabban használatosak:
-
Önlengésszám:
Az álló és lengésbe kényszerített jármű percenkénti lengésszáma, melynek kedvező értéke 60 lengés/perc.
-
Saját frekvencia:
A másodpercenkénti lengésszám, melynek kedvező értéke:
f0=0,75-1,45 Hz.
-
A VDI 2057. számú ajánlás szerinti lengéskényelmi mutató:
Ez a mutató már figyelembe veszi a lengés frekvenciája mellett a lengésgyorsulásokat és az emberi érzékenység különböző tartományait. A redukált mutató értéke 1-63 érték között változhat. A kényelmes érzet 1-20 értékek tartományába esik.
-
ISO 2631. számú szabvány szerinti lengéskényelmi mutató:
Ez a legkorszerűbb, legösszetettebb és a legpontosabb lengéskényelmi mutató. Kiszámításához országúti lengésvizsgálatot és számítógépes frekvencia analízist kell végezni., ki kell számítani a redukált lengésgyorsulás szórás értékét. A kényelmes jármű ISO mutatója 0,1-0,3 m/s2 értékek közé esik.
3.5. A dinamikus tényező
A járműalkatrészek igénybevétele az álló helyzetben mért statikus terhelésen túl menet közben dinamikus többletterheléssel megnövekszik (3.4. ábra). A növekedés mértékét az ún. dinamikus tényező (d) fejezi ki.
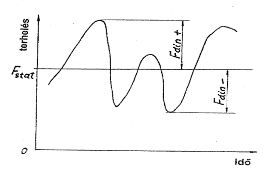
ahol:
|
a |
– a terhelő tömeg függőleges lengésgyorsulása (m/s2) |
|
|
Fö |
– az összes igénybevétel (N); |
|
|
Fst |
– statikus terhelés (N); |
|
|
Fdin |
– dinamikus többletterhelés (N); |
|
|
m |
– terhelő tömeg (kg); |
|
|
g |
– nehézségi gyorsulás (9,81 m/s2) |
A dinamikus tényező értéke 2-3 között változik. Csökkenteni lehet megfelelő lengéscsillapítókkal, helyesen megválasztott gumiabroncsokkal, gumiperselyekkel (szilentblokkokkal).
3.6. Futóművek aktivitása, önszabályozása
A gépjárművek menetstabilitását a különböző futóműparaméterek megfelelő szabályozásával lehet növelni.
A szabályozás történhet:
-
számítógépes külső szabályozással;
-
önszabályozással (pl. intelligens futóművek).
A számítógépes külső szabályozós futóművek jelenleg még fejlesztés alatt állnak, szélesebb körű alkalmazásukat egyelőre műszaki, jogi és gazdasági problémák akadályozzák.
Az intelligens futóműveknél a megfelelő paraméterek szabályozása történhet:
-
elmozdulás szabályozással;
-
erőszabályozással;
-
integrált szabályozással.
Az önszabályozás megvalósítható különböző hosszirányú (R) és beépítési szögű (κ) lengő rudakkal, lengő karokkal és nagy térfogatú önbeálló gumiágyazásokkal (elasztométerekkel).
Az elmozdulás szabályozása:
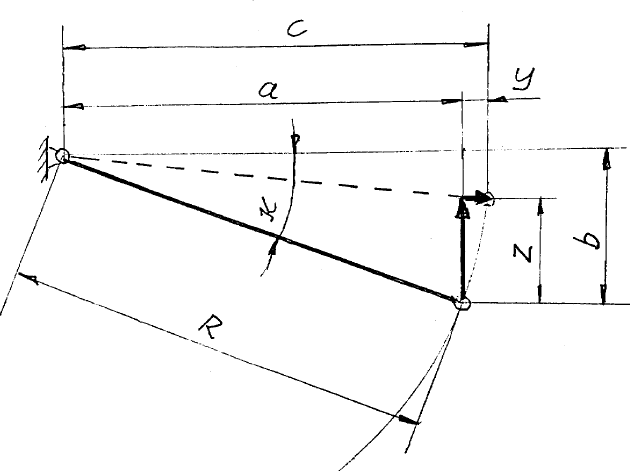
Ahol:
Fő- és mellékmozgás összefüggése a kikötőrúd helyzetétől függően:
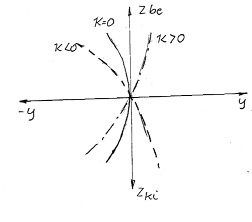
A főmozgás lehet például a tengelycsonkon lévő gömbcsukló függőleges elmozdulása (3.6. ábra), a mellékmozgás keresztirányú elmozdulása, amely a kerékdőlést vagy a kerékösszetartást változtatja meg.
Erőszabályozás
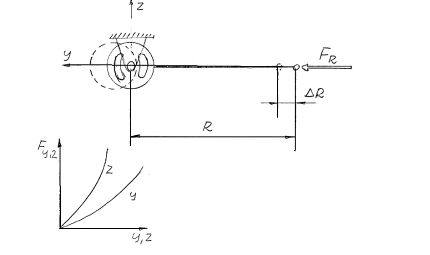
A tengelycsonk gömbcsuklójára ható erő deformálja a lengőrúdhoz kapcsolódó elasztométert (3.7. ábra), a gömbcsukló elmozdul, ami a kerékdőlést vagy kerékösszetartást változtatja.
Kettős elmozdulás szabályozás
A BMW gépkocsikhoz alkalmazott megoldás. A tengelycsonkhoz rögzített gömbcsukló R sugarú köríven tud elmozdulni, de a két rúdrész által bezárt szög változtatásával az R sugár is változtatható, így a gömbcsukló keresztirányú elmozdulása degresszív vagy progresszív pályán is történhet (3.8. ábra).
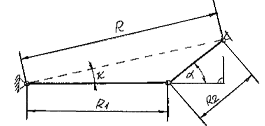
Integrált szabályozás
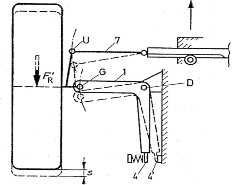
A kerékösszetartás a fékerő és a kormánymechanizmus elmozdulása hatására változik a menetstabilitás igényéből meghatározott célfüggvény szerint. A korszerű első futóműveknél arra törekednek, hogy fékezéskor az összetartás ne változzék vagy kissé a széttartás felé módosuljon (3.9. ábra).
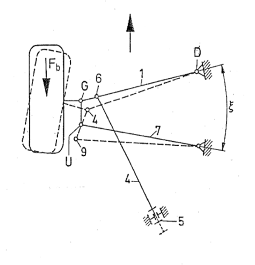
A fékerő és a rudak elmozdulása együttesen alakítja ki a kerékösszetartás megfelelő értékét. A hátsó futóműveknél leggyakrabban a változás az összetartás irányába mutat (3.10. ábra).