13. fejezet - Fékrendszer járműdinamikai elemzése
13.1. A fékezés folyamata
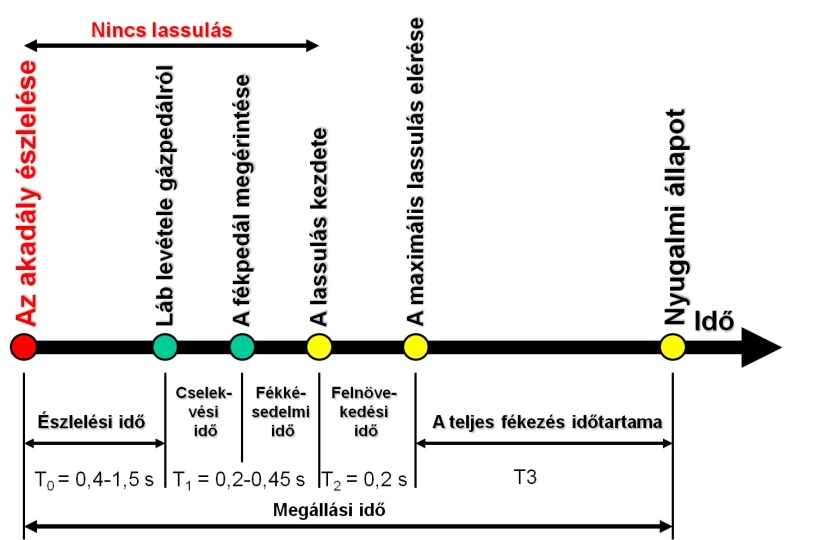
A fékezési folyamat lassulásmérővel vizsgálható, melyben a fékezés alatt az ún. szenzitív tömegen ébredő tehetetlenségi erőt alakítják át elektromos jellé, vagy elmozdulássá. Ezeket a jellemzőket az idő függvényében rögzíti és tárolja. A fékezési folyamat szakaszai:
13.1.1. Reakció idő (tr)
A felbukkanó akadály, vagy a veszélyhelyzet észlelése és a fékpedál érintése között eltelt idő. Ez további két szakaszra, a „döntési” és a „cselekvési” időre bontható. Értéke 0,5 - 2 s között változik, a vezető figyelmétől és az őt befolyásoló tényezőktől, a pillanatnyi képességétől, gyakorlatától, és az akadály felbukkanásának váratlanságától függően. A cselekvési időre hatást gyakorol a gépkocsi kialakítása is (pl. pedálok elhelyezése). Mivel a reakcióidő a vezetőtől is jelentősen függ, a fékrendszer minősítésekor figyelmen kívül hagyjuk.
13.1.2. Fékkésedelmi idő (t1)
A fékpedál érintésétől a lassulás növekedésének kezdetéig tart. Ezt befolyásolják a fékrendszerben szükséges holtjátékok (fékpedálnál, működtető egységeknél, fékpofa és a féktárcsa között stb.), továbbá a legyőzendő rugóerők és az alkalmazott közvetítő közeg összenyomhatósága. Értéke hidraulikus féknél 0,2 s, légféknél pedig 0,3 - 0,4 s.
13.1.3. A felnövekedési idő (t2)
Ez alatt az idő alatt alakul ki a maximális lassulás. Befolyásolja a beépített csövek, fékpofák, fékbetétek, fékdobok, illetve féktárcsák rugalmas deformációja. A vezető is van rá hatása, mert egy bizonyos idő szükséges ahhoz, hogy beállítsa az általa kívánatosnak tartott lassulást. Értéke 0,2 - 0,5 s.
13.1.4. A hatásos fékezés ideje (t3)
Eközben a fékezési lassulás hozzávetőleg állandó értékű.
13.2. A fékrendszer minősítése
A (13.2. ábra) ábrán egy lassulásdiagram látható. Kezdőpontja a fékpedál érintésének pillanata.
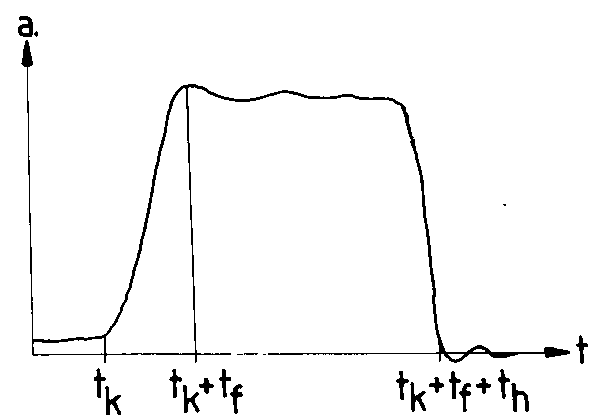
A lassulás diagram görbe alatti területe adja a sebesség mindenkori változását, tehát abból a sebesség-idő függvény meghatározható.
Ha ezt a függvényt integráljuk, akkor kapjuk a fékezési folyamat út-idő függvényét.
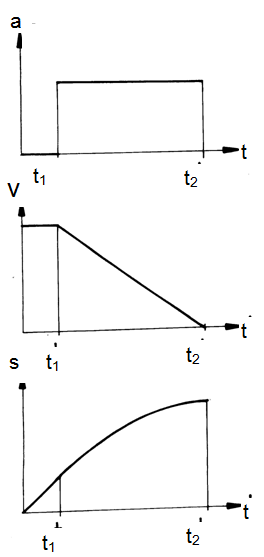
A számítások megkönnyítése érdekében az úgynevezett „egyszerűsített lassulásdiagramot” használjuk, melyben a bonyolult a(t) függvényt egy nulla-, és egy állandó értékű szakasz helyettesíti. A nulla lassulású szakasz időtartama:
Így a valóságnál néhány százalékkal hosszabb fékutat kapunk, ami a biztonság irányába jelent eltolódást.
A fékszerkezet hatásosságának minősítése három módon történhet:
-
fékút méréssel,
-
lassulás méréssel,
-
fékerő méréssel.
A nemzetközi fékelőírások alapján lefolytatott jóváhagyási vizsgálat során, ellenőrizni lehet az előírt feltételekkel végzett fékezések során, a fékutat, vagy az úgynevezett „átlagos maximális lassulást” (Mean Fully Developed Deceleration – MFDD) értékét.
Az MFDD számításának módja:
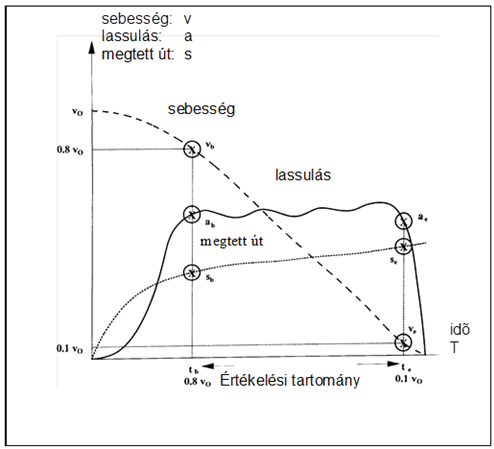
A fenti összefüggés paramétereinek értelmezését szemlélteti a 13.3. ábra, melyben a sebesség értékeket km/h-ban az utakat pedig méterben kell behelyettesíteni, így a végeredményt m/s2-ben kapjuk.
A fékrendszer gyors minősítése elvégezhető egyszerűsített fékút, vagy lassulás méréssel (Motometer, XL Méter). A hatósági műszaki felülvizsgálaton, vagy olyankor, amikor szükséges a kerékfékszerkezetek egyenkénti minősítése is, görgős fékpadon erőmérést végeznek.
13.3. A gumiabroncs tapadása és a tapadás kihasználása
A közúti járművek fékezhetőségére, fékezés közbeni viselkedésére fontos hatást gyakorol a gumiabroncs és az útburkolat között létrejövő erő nagysága. A gumiabroncs kerületén csak akkor jöhet létre fékerő, ha kialakul egy bizonyos mértékű kerékcsúszás (szlip).
|
A kerékcsúszás: |
ahol:
|
vk |
- kerék kerületi sebessége, |
|
|
v |
- gépkocsi sebessége. |
A kerékcsúszás függvényében a gumiabroncs tapadási tényezőjét (μ) a 13.5. ábra szemlélteti. Az ábrázolt görbét a legnagyobb tapadási tényező (μmax) két, stabil és instabil részre osztja. A görbe alakja, a maximális érték helye és nagysága, a blokkoláshoz (100%-os szlip) tartozó tapadási tényező értéke széles határok között változik az útburkolat fajtájának és állapotának függvényében. Ezen kívül befolyásolja még a gumiabroncs anyaga, szerkezete, mintázata, terhelése és a haladási sebesség is.
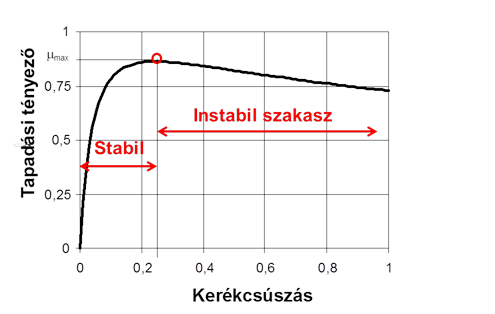
13.4. A fékezett kerék mozgásegyenlete
ahol:
|
Fx |
- fékerő, |
|
|
Mfék |
- fékezőnyomaték, |
|
|
Θ |
- a kerék és a kapcsolódó forgó tömegek tehetetlenségi nyomatéka, |
|
|
ε |
- a kerék szöglassulása, |
|
|
rdin |
- a kerék dinamikus gördülési sugara. |
A tapadási függvényből adódóan:
ahol:
|
Fz |
- a kerék függőleges, az útfelületre merőleges terhelése. |
A fenti összefüggésekből látható, hogy a fékszerkezet által kifejtett fékezőnyomaték a fékerőt nem közvetlenül, hanem a kerék mozgásállapotán és a tapadási függvényen keresztül határozza meg.
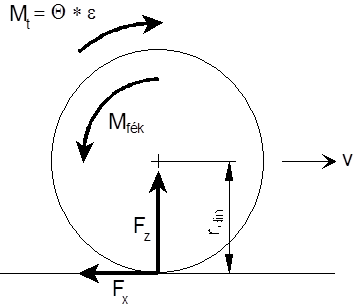
Ha a tapadási tényezőnek a 0 és 100% csúszás (a kerékblokkolása) között határozott maximuma (μmax) van, akkor ez a pont a függvényt stabil és labilis szakaszra osztja. A stabil szakaszban a fékezőnyomaték növelésre a kerék kismértékű csúszás növekedéssel és emiatt újabb, stabil fékezési munkapont kialakulásával reagál. Ha a fékezőnyomaték annyira növekszik, hogy a munkapont eléri a tapadási függvény maximumát, akkor a további fékezőnyomaték növekedéssel már csak a kerék lassuló forgásából adódó nyomaték tarthat egyensúlyt. Ez a fékezőnyomaték csökkentése nélkül a csúszás folyamatos növekedését és a kerék blokkolását eredményezi.
A kerékblokkolás nemkívánatos jelenség, mert
-
a blokkoló kerék által kifejtett fékező erő kisebb lassulást eredményez, mint a gördülő keréken létrejövő maximális kerületi erő,
-
a blokkoló keréken erőteljesen csökken az átvihető oldalerő nagysága, vagyis szinte megszűnik a kerekek oldalvezető képessége,
-
a blokkoló kerék fékerejét kizárólag az abroncs és a talaj közötti csúszó súrlódás határozza meg, vagyis itt nem érvényes a fékszerkezet működtető ereje (és ezzel a vezető által kifejtett vezérlő erő), illetve a kifejtett fékerő között a tapadási függvény stabil szakaszán fennálló és a vezető által megszokott összefüggés.
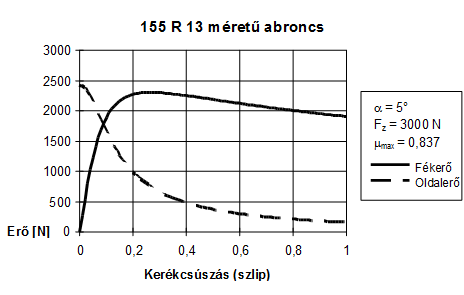
A fékerő és az oldalvezető erő közötti kapcsolatot szemlélteti a 13.7. ábra, melyen adott oldalkúszási szög (α) esetén a szlip függvényében egyidejűleg figyelhető meg az abroncs által átvitt hossz- és oldalirányú erő. Az oldalerő kialakulásában a kerék haladási iránya és saját síkja által bezárt, oldalkúszási szög (illetve annak szinusza) hasonló szerepet tölt be, mint a fékerők esetében a csúszás. Fordítva is igaz a (13.7. ábra) ábrán bemutatott összefüggés, vagyis a fékerő jelentős csökkenést mutat adott csúszás esetén, ha növekszik az oldalkúszási szög. A két erőkomponens, illetve a hossz- és keresztirányú csúszás mértéke tehát kölcsönösen befolyásolják egymást.
13.5. Fékerő felosztás
A gépjárművek üzemi fékrendszerének feladata a lehető legnagyobb lassulás biztosítása, a stabilitás és az irányíthatóság megőrzése mellett. Az elérhető legnagyobb lassulástól eltekintve az egyéb hosszirányú erőktől, a talaj és a gumiabroncsok közötti tapadástól függ:
ahol:
|
Fzi |
az i-edik kerék terhelése, |
|
|
μmaxi |
maximális tapadási tényező az i-edik keréknél, |
|
|
m |
a gépkocsi tömege, |
|
|
n |
a fékezett kerekek száma. |
A kerekek terhelése változik:
-
statikusan
a gépkocsi terhelésétől (utasok, rakomány),
az útpálya lejtésétől és dőlésétől,
-
dinamikusan
a tehetetlenségi erőktől (fékezés, kanyarodás),
az útegyenetlenségektől függően.
Az útfelület és a gumiabroncs közötti tapadási tényező is változik térben és időben, illetve az egyes kerekeknél különböző értékeket vehetnek fel. Szélsőséges esetben például száraz aszfalt és jég esetén a különbség nyolcszoros is lehet.
Hatékony lassítás csak akkor érhető el, ha az ehhez szükséges fékerő felosztása az egyes kerekek között a tapadási feltételeknek megfelelően történik. A gépkocsi jobb és bal oldalán a tömegközépponti függőleges tengely körüli forgatónyomaték, illetve a kormánykeréken jelentkező zavaró nyomaték keletkezésének elkerülése miatt nem célszerű lényegesen eltérő fékerőket megvalósítani.
Ha a gépkocsi két oldala, közötti különbségektől eltekintünk és homogén tapadási viszonyokat feltételezünk, a jármű futóművei közötti fékerő felosztásról beszélünk. Ez adott tapadási viszonyok mellett meghatározza a futóművek blokkolási sorrendjét. Egy kéttengelyes jármű esetén például a fékerők növelése esetén elvileg három eset fordulhat elő:
-
Az első kerekek blokkolnak először.
A kormányzott kerekeknél megszűnik az oldalvezető erő, a gépkocsi kormányozhatatlanná válik, de iránytartóan halad tovább.
-
A hátsó kerekek blokkolnak elsőször.
Ilyenkor már a legkisebb oldalerő hatására is a gépkocsi megperdül. Ez egy önerősítő folyamat, ezért a vezető kormánykorrekciója nélkül stabilitásvesztést eredményez.
-
Az első és a hátsó kerekek egyszerre blokkolnak.
A blokkolás határán valamennyi keréken azonos a tapadáskihasználás, azaz kifejthető a maximális fékerő, a gépkocsi viselkedése a blokkolás bekövetkezése után kiszámíthatatlan. Az útfelülettel párhuzamos síkban ható eredő erő és nyomaték nagyságától és irányától függően a sodródás és a pördülés tetszőleges kombinációja kialakulhat.
A konstruktőrök a fékrendszerek olyan kialakítására törekszenek, hogy a fékút a lehető legrövidebb legyen, és a gépkocsi eközben stabil maradjon. Ez az első kerekek enyhe túlfékezésével érhető el, vagy akkor, amikor az ABS megakadályozza a kerekek blokkolását.
A futóművek alul-, illetve túlfékezettségének és a tapadáskihasználás szemléltetésére az adhéziós diagramot használják. Ez a futóművek dinamikus terhelésre vonatkoztatott fajlagos lefékezettségét (tapadáskihasználását) ábrázolja a jármű fajlagos lassulása függvényében.
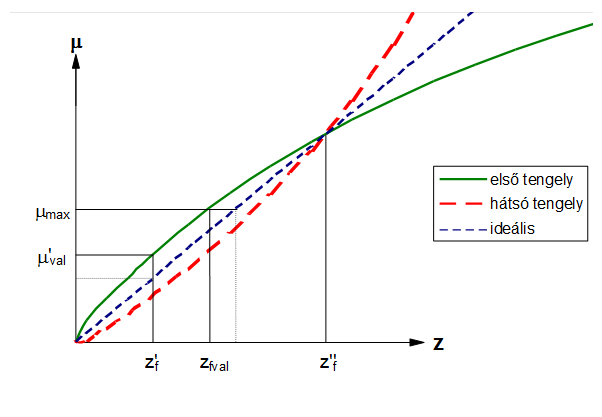
A diagram vízszintes tengelyén a „z” a lefékezettség vagyis a fajlagos lassulás.
ahol:
|
a |
– a gépkocsi lassulása fékezéskor, |
|
|
g |
– a gravitációs gyorsulás. |
– az i-edik tengely fajlagos lefékezettsége, vagy másként értelmezve tapadásigény
ahol:
|
Fxi |
– az i-edik tengely fékereje, |
|
|
Fzi |
– az i-edik tengely (dinamikus) terhelése. |
Az ábrában a kék színű, szaggatott vonal a fékezési lassulás szempontjából ideális fékrendszert jellemzi. Ekkor a kerekek lefékezettsége minden lassulásnál egymással és az adott tapadási viszonyok esetén elérhető maximális fajlagos lassulással megegyező. Ehhez a fékerőket a dinamikus tengelyterhelések arányában kell felosztani.
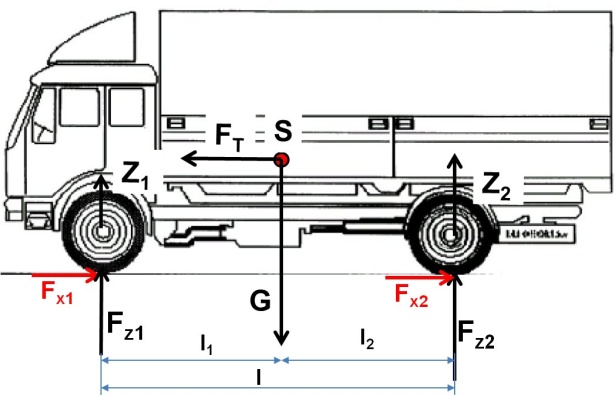
Sík úton fékezett kéttengelyes gépkocsi dinamikus tengelyterhelései a 13.9. ábra jelöléseit felhasználva a következő módon alakulnak:
ahol:
|
|
– a tehetetlenségi erő, |
|
|
|
– a gépkocsi súlyereje. |
Ezzel az ideális fékerő arány:
Ennek értéke a gépkocsi terhelési állapotától, a tömegközéppont helyzetétől és a pillanatnyi lassulástól függ. A fékrendszerek viszont állandó fékerőfelosztást valósítanak meg.
Az első és hátsó kerekek fékerői közötti állandó arány:
Az fékerők összege adott „” lassulás esetén:
Így:
|
és |
Ezzel a futóművek lefékezettsége (tapadási igénye) ilyen fékrendszer esetén:
A lefékezettség fenti összefüggések szerinti alakulását a 13.8. ábra vastag, folytonos vonalai szemléltetik. Az ideális esethez viszonyítva csökken az adott tapadási tényező (µmax) mellett realizálható lassulás (Zfval), illetve nő az adott lassuláshoz (Zf) szükséges tapadási tényező (µval). Természetesen a stabilitási viszonyok is megváltoznak. Az ideális fékerő-felosztású jármű kerekei a tapadási határt elérve egyszerre csúsznak meg, hiszen a tapadás kihasználtsága egyforma. Az állandó fékerő-felosztású járműnek viszont csak egyetlen esetben – lassulásnál – ilyen a viselkedése. Ennél kisebb lassulásnál az első futómű kerekei túlfékezettek, vagyis a tapadási tényező csökkenése, illetve a lassulás növelése esetén először ezek csúsznak meg. A -nél nagyobb lassulásoknál a helyzet fordított, azaz a hátsó futómű kerekei válnak túlfékezetté. Vagyis az ideális felosztás 45°-os egyenesétől felfelé a túl-, lefelé az alulfékezett tartomány található az adhéziós diagramban.
13.6. Ideális és effektív fajlagos fékerő eloszlás
Az adhéziós diagramban tetszőleges tengelyszámú jármű fékerő-felosztási viszonyai vizsgálhatók. A fajlagos fékerő diagram csak kéttengelyes járművek vizsgálatára alkalmas. Használata elsősorban a személygépkocsi fékrendszerekkel kapcsolatban terjedt el. Előnye, hogy itt az ideális fékerő eloszlást ábrázolja bonyolultabb (parabolikus) görbe, míg a tényleges felosztás ábrázolása általában egyenesekkel, illetve törtvonalakkal lehetséges. Vagyis az adott terhelési állapotára megszerkesztett ideális felosztás görbéjéhez viszonylag egyszerűen elvégezhető a különböző fékrendszer variánsok tényleges felosztási vonalainak illesztése.
A 13.9. ábra jelöléseit alkalmazva, írjuk fel az ábrán látható kéttengelyes gépkocsira ható vízszintes erők egyensúlyát!
mivel,
így
ebből a fajlagos lefékezettség
A tengelyenkénti fékerő:
mivel így
A tengelyenkénti fajlagos fékerők
ebből az ideális fajlagos fékerő karakterisztika egyenlete:
A pozitív előjel a fékezéskor, a negatív előjel a hajtáskor mutatja a járműre ható erőket.
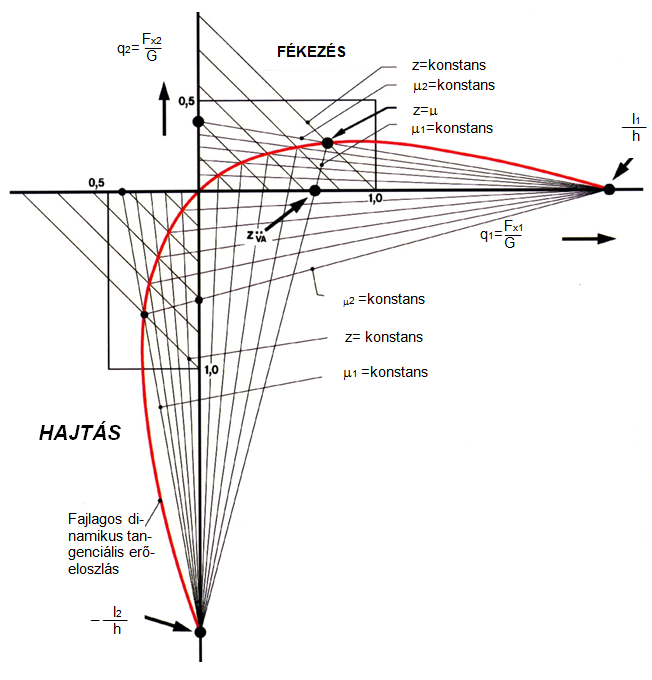
A fékezés folyamata a karakterisztika első síknegyedbeli része vonatkozik.
A gépkocsi fékberendezése által biztosított effektív fajlagos fékerők hidraulikus fékrendszernél.
Az első futóműnél:
A hátsó futóműnél
ahol:
|
η |
a hatásfok |
|
|
p |
a fékező nyomás |
|
|
c |
a kerékfékszerkezet belső áttétele |
|
|
r |
a súrlódó felület közepes sugara |
|
|
Rdin |
dinamikus gördülősugár |
|
|
A |
munkahenger felület |
Bevezetve és
az első, illetve a hátsó futómű fékszerkezetére jellemző fékkonstansokat kapjuk
|
ill. |
||
Fékerő módosító nélküli fékrendszernél a fékfolyadék nyomás az első és a hátsó fékkörben azonos, ezért:
így az effektív fajlagos fékerő függvény
A fékerő módosító nélküli fékrendszer fajlagos fékerő elosztás egyenes, melynek meredekségét az első és hátsó futóművek fékrendszerére jellemző konstansok aránya határozza meg.
Légfékrendszereknél az effektív fékerők
ahol ; a fékkar hossza és „l” a fékkulcs evolvens alapkör sugara.
A (13.11. ábra) ábrán az ideális fajlagos fékerő elosztási görbe fékezés mechanikai szempontból lényeges első síknegyedbeli része látható kiegészítve a konstans lefékezettségi, valamint a konstans ; egyenesekkel. Ugyanezen az ábrán tüntettük fel a fékerő módosító nélküli fékrendszer fajlagos effektív fékerőelosztási egyenesét.
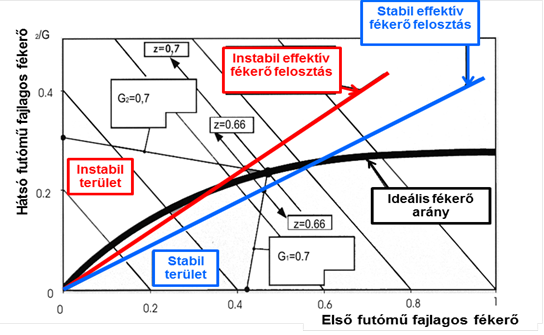
A (13.12. ábra) ábrán nyomásaránytartó fékerő módosítóval szerelt fékrendszer tört karakterisztikájú effektív fékerőelosztását szemlélteti.
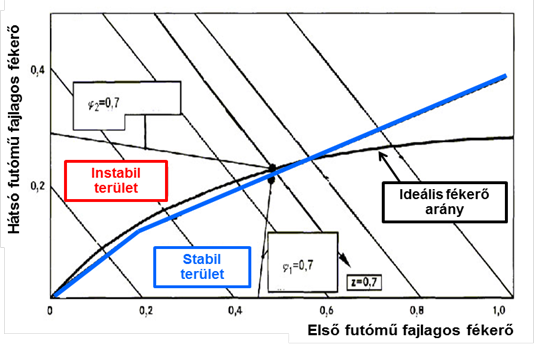
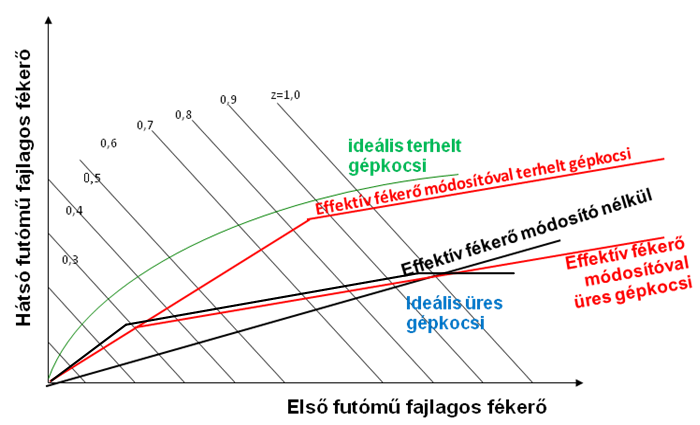
Az effektív fajlagos fékerőkarakterisztikák illesztése az ideálishoz úgy történik, hogy jó minőségű száraz beton úton haladva, amikor mindig az elsőtengely legyen túlfékezett, a hátsó pedig alulfékezett. Hidraulikus fékrendszernél üres terhelési állapothoz illesztünk, és teljesen terhelt állapothoz korrigálunk.
13.7. Fékezési stabilitás
A gépkocsik fékezés közbeni viselkedésének értékelésekor nagy jelentősége van a vészfékezésnek. Ha ilyenkor is stabilan uralható a gépkocsi, akkor van esély a baleset elkerülésére. Az instabillá váló gépkocsi uralhatatlan, megfarol és oldalával csapódik az akadálynak. Ez azért veszélyes mert, a kocsiszekrény oldala kevésbé alkalmas az ütközési energia deformációs munkává alakítására. A gyakorlatban a középkategóriás gépkocsinál 50 km/h sebességgel bekövetkező frontális ütközés még túlélhető. Az oldal irányú ütközés 30 km/h sebességgel a leggyakrabban már halálos kimenetelű. Ez is bizonyítja, hogy a fékezés közbeni stabilitás nagyon fontos követelmény. Függetlenül tehát a fékezés erősségétől a gépkocsi nyomtartó kell maradjon. A vezető minden különösebb kormánykorrekció nélkül, még zavaró körülmény fennállása esetén is meg kell tartsa ezt az állapotot.
A gépkocsi fékezés közbeni viselkedésének számítása
Az előzőekben leírt elvárás matematikai megfogalmazása az alábbi ábra alapján lehetséges. A gépkocsit egy kétkerekű járműmodell helyettesíti. Ennél a futóművek bal, illetve jobb oldali kerekei „összetoljuk” középre és csupán egy-egy kereket veszünk figyelembe a modellnél. Tekintettel vagyunk a β-val jelölt zavaró tényezőre, a gépkocsi „úszási szögére”. Ez a kerekek oldalkúszási szögéből αv-ből és az ah-ból adódik. A gépkocsit, a kerékfelfüggesztés rugalmasságát elhanyagolva egy merev testnek tekintjük. A gépkocsira ható erők a képen láthatók. A tömegközéppontban hat a tehetetlenségi erő Fx,g = z⋅Gg. Ezzel tartanak egyensúlyt a fékerők Fx,B,v az első futóműnél, Fx,B,h pedig a hátsó futóműnél.
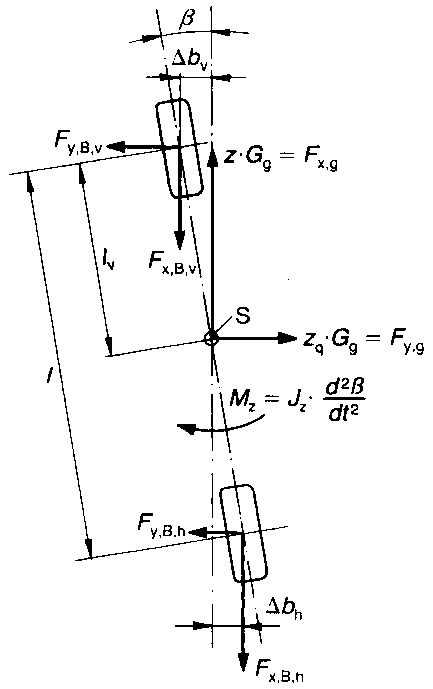
A tömegközéppont S.
Az első futómű felfekvési pontja β szöggel és ennek megfelelően Δbv szakasszal tolódott el. Ezzel ellentétes irányú a hátsó futóműnél a Δbh szakasz. A tömegközéppontban ható Fy,g = zq⋅Gg oldal irányú erő miatt az első keréken Fy,B,v oldalerő hat, és a hátsó keréken pedig Fy,B,h. Ezek okozzák a kerekek oldalcsúszását. A kerekek talppontjaiban ébredő nyomatékot is keltenek a függőleges tengely körül. Ezt a gépkocsi tehetetlenségi nyomatéka Jg,z (kg⋅m2) egyenlít ki. Ha feltételezzük, hogy β = αv = αh a következő egyenletek adódnak:
|
|
||
|
|
||
|
|
A (13.14. ábra) ábrából megállapítható, hogy:
|
|
||
|
|
Behelyettesítve az előző egyenletbe és elosztva l-el adódik:
|
|
Bevezetve a összefüggést és kissé átalakítva az alapegyenletet:
|
|
A nagy keréktávolságnak kedvező a hatása.
A tömegközéppont körüli szöggyorsulásnál a pozitív érték azt jelenti, hogy az úszási szög növekedésekor a gépkocsi instabillá válik és kitör. Negatív érték esetén, amikor csökken, a gépkocsi önmagától stabilizálódik, visszatér az eredeti nyomvonalra. A számszerű érték a reakció gyorsaságát fejezi ki. A nagyobb pozitív érték esetén még egy gyakorlott vezető sem tud kellően gyorsan beavatkozni. Jelentős szerepe van a gépkocsi tömegközépponti függőleges tengelyére vonatkozó tehetetlenségi nyomatéknak Jg,z. Minél kisebb, annál hajlamosabb lesz a gépkocsi a farolásra.
Ha a fenti összefüggésekkel üres és terhelt gépkocsira elvégezzük a számításokat, az eredményeket az alábbi ábra szemlélteti. Mindegyik terhelési állapotnak egy görbe felel meg. Ezek között látható az egyenes, amely az ideális merev kétkerekű modellt jellemzi. Az eredmény használható a gépkocsi fékezés közbeni viselkedésének megítélésére. A valóságos gépkocsinál a kerekek elaszto-dinamikus felfüggesztésével az önstabilizálás megvalósítható.
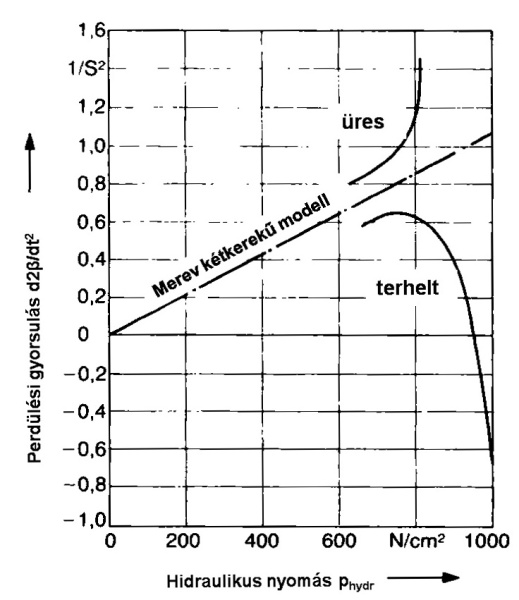
A fenti ábrán a középső egyenes pont-vonallal rajzolva a merev kétkerekű járműmodellre vonatkozik. 700 N/cm2 fékező nyomás felett a „üres” gépkocsi elkezd kitörni. A „terhelt” gépkocsi viszont 800 N/cm2 fékező nyomás felett stabilizálja magát. A negatív perdülési gyorsulás stabilizáló hatású.
Stabilizátorokkal a gépkocsi önkormányzási tulajdonsága javítható. Az üres gépkocsira vonatkozó görbénél 800 N/cm2 fékezőnyomás felett meredeken felfelé kanyarodik. Tehát a perdítő gyorsulás gyorsan növekszik, ezért a gépkocsi kitör. Ennél a terhelési állapotnál a gumiabroncs legnagyobb tapadási tényezője a kritikus lefékezettség feletti. A gumiabroncsok helyes megválasztásával kell biztosítani, hogy valamennyi lehetséges útviszonynál a kritikus lefékezettség a maximális tapadási tényező felett legyen. Csak ekkor alakul ki a kívánatos fékezési stabilitás.
A terhelt gépkocsi görbéje meredeken lefelé kanyarodik 900 N/cm2 nyomás felett. A perdülési gyorsulás negatív. A gépkocsi stabilizálódik. Ekkor az első kerekek blokkolnak. A kritikus lefékezettség jelentősen a maximális tapadási tényező felett van. A gépkocsi terhelésének jó hatása érvényesül.