3. fejezet - Koherens optikai erősítő
Vissza		Előre

3. fejezet - Koherens optikai erősítő

Tartalom

Ahhoz, hogy egy közegben egy adott átmeneten fényerősítést hozzunk létre indukált emisszióval - nem egyensúlyi betöltöttséget (azaz az egyensúlyi betöltöttséggel ellentétes betöltöttséget vagy populáció inverziót, azaz a nagyobb energiájú szinten nagyobb betöltöttséget) kell létesíteni. Ebben az esetben az átmenetnek (lásd (2.1) összefüggést) megfelelő frekvenciájú fotonnyaláb a nem egyensúlyi állapotban lévő közegen áthaladva koherensen fog erősödni.

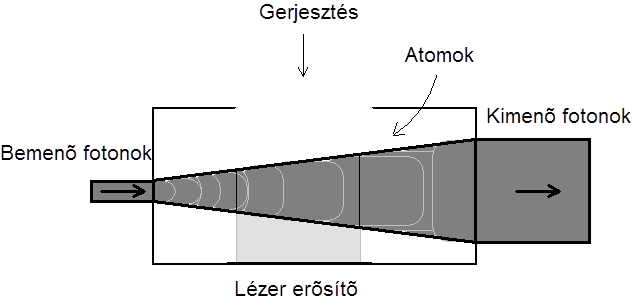
Koherens erősítő létrehozása. A gerjesztés hatására a nem egyensúlyi állapotban lévő atomok indukált emissziós fénykibocsátása a belépő fotonok koherens erősödését eredményezi

3.1. ábra - Koherens erősítő létrehozása. A gerjesztés hatására a nem egyensúlyi állapotban lévő atomok indukált emissziós fénykibocsátása a belépő fotonok koherens erősödését eredményezi

Egy ideális erősítő a bemenő harmonikus jelet úgy erősíti, hogy annak frekvenciája változatlan marad, amplitúdója lineárisan nő, fázisa a frekvencia lineáris függvényeként változik és az erősítés egy megadott frekvenciasávban állandó. Ezzel szemben a valóságban a reális erősítő frekvenciafüggő erősítésével és fázistolásával jellemezhető. Az erősítés csak kis amplitúdójú bemenő jelek esetén lineáris és egy adott jelszint felett pedig telítődik (3.2. ábra).

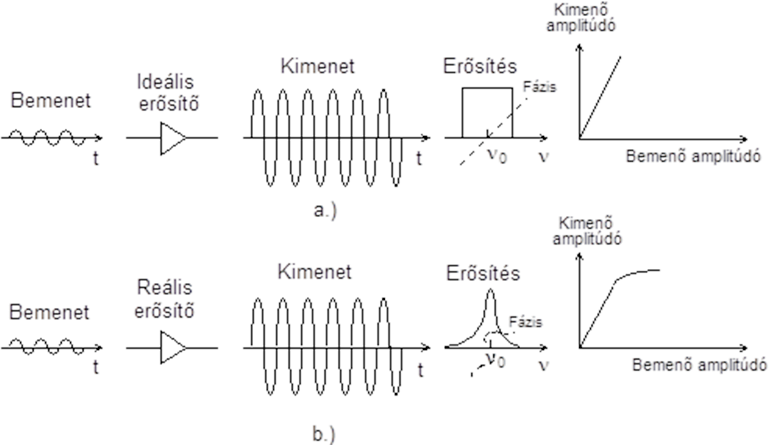
3.2. ábra - Ideális és reális erősítő összehasonlítása

3.1. Frekvenciafüggő erősítés

Legyen a gerjesztett állapotú közegbe belépő fotonnyaláb z irányban terjedő ν frekvenciájú monokromatikus síkhullám. A fotonnyaláb az intenzitással vagy a fluxussűrűséggel (2.4) jellemezhető.

3.3. ábra - A fluxussűrűség változása erősítő közegen való áthaladáskor

A közeg gerjesztett állapota az E₂ szint, a kiválasztott energiaátmenet a 2→1 szintek közötti, a rezonanciafrekvencia a (2.1) különbségnek megfelelően ν₀ és N₁, N₂ az egységnyi térfogatban lévő atomszám az adott energiaszinteken. Számítsuk ki a közeg egységnyi hosszának frekvenciafüggő γ(ν) erősítését.

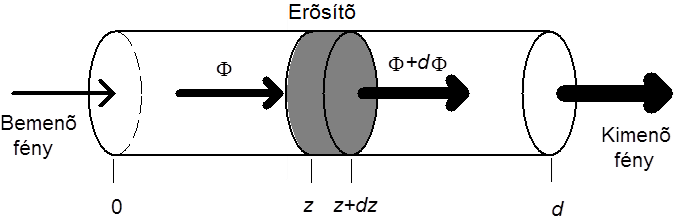
A gerjesztett közeg és a Φ(z) fluxussűrűségű elektromágneses tér között lejátszódó kölcsönhatási folyamatok:

abszorpció, N₁W_i az elnyelt fotonszám egységnyi időben és térfogatban, következmény: Φ(z) gyengülése,
indukált emisszió, N₂W_i a kibocsátott fotonszám egységnyi időben és térfogatban, következmény: Φ(z) erősödése,

az (N₂- N₁)W_i különbség pozitív vagy negatív volta dönti el, hogy a közeg erősítő vagy gyengítő lesz. A spontán emisszió, mely szintén jelen van, az erősítés szempontjából nem játszik szerepet, az erősítő zaját eredményezi. Az N=N₂- N₁ különbség az inverziósűrűség. Ha N>0, a közeg erősíti, ellenkező esetben gyengíti a belépő fénynyalábot. Egységnyi hosszúságú közegben a fluxussűrűség megváltozása felírható az inverziósűrűséggel és az indukált folyamatok valószínűségével:

	$d φ = N W_{i} d z$	(3.1)
	$\frac{d φ}{d z} = N W_{i} = N σ (ν) φ (z)$	(3.2)
	$γ (ν) = N σ (ν)$	(3.3)

ahol γ(ν) az egységnyi hossz erősítése. Megoldva (3.1)- et

$\begin{array}{l} φ (z) = φ (0) e^{γ (v) z} \\ I (z) = h v φ (z) = I (0) e^{γ (v) z} \end{array}$

(3.4)

z szakasz megtételével a fluxussűrűség vagy az intenzitás is exponenciálisan növekszik. A valóságban, mint látni fogjuk, az egységnyi hossz erősítése függ a fluxussűrűségtől, ezért a fluxussűrűség differenciálegyenletének a megoldása nem adható meg ilyen egyszerűen!

Az egységnyi hossz erősítésének frekvenciafüggését a hatáskeresztmetszet frekvenciafüggése adja. Homogén közeg esetén a hatáskeresztmetszet (2 .6) azaz Lorentz-alakú, inhomogén közegben pedig (2.7) azaz Gauss-alakú lesz.

3.2. Gerjesztési folyamatok

A gyakorlatban a gerjesztés (pumpálás) módja lehet: lámpa, kisülés vagy áram, vegyi folyamat, egy másik lézer, stb. A gerjesztéseket két fő csoportba szokás osztani: optikai és elektromos gerjesztések. Optikai gerjesztés során egy nagyteljesítményű fényforrás fényét abszorbeálja az aktív anyag, s így jön létre nem egyensúlyi állapot pl. szilárdtest lézerekben, ahol az atomi nívók sávokat hoznak létre, így a pumpálás széles sávban lehetséges; vagy folyadék (pl. festék) lézerekben. De lehetséges lézerrel is gerjeszteni lézert. Elektromos gerjesztés intenzív elektromos kisüléssel vagy árammal lehetséges például gázlézerekben, ahol a keskeny nívók optikai pumpálása nem megy, vagy félvezető lézerekben, ahol az árammal való gerjesztés egyszerűbb, mint optikailag pumpálni.

3.2.1. Optikai gerjesztés

Nagyteljesítményű inkoherens lámpa fényét megfelelő optikai közvetítő rendszerrel az aktív anyagba vezetik.

impulzus lézereknél 450-1500 torr Xe vagy Kr töltetű villanólámpát használnak, ahol egy nagy kapacitású kondenzátorban tárolt elektromos energiát sütnek ki a lámpába. A kisülést egy segédelektródára adott nagyfeszültségű trigger impulzus indítja, mely előionizálja a gázt, ezt követi a lámpa intenzív felvillanása. A fényimpulzus hosszát a kapacitás és az ellenállás szorzata szabja meg, általában 1 – 2 μs – 100 – 200 μs tartományba esik.
folytonos (continuous wave - cw) lézereknél nagy nyomású (4000 – 8000 torr ~ 5 – 10 atm) Kr vagy W - iodine lámpát használnak.

Geometriai elrendezések

Az aktív anyag rúd alakú, melynek átmérője 1 – 2 mm - néhány cm, hossza cm - néhányszor 10 cm tipikusan. Lehetséges elrendezések:

a lámpa csigavonalban körbeveszi a rudat, s a fény közvetlenül vagy a burkoló nagy reflexiójú hengeres felületről visszaverődve éri el az aktív anyagot,
elliptikus elrendezés az ábra szerint,

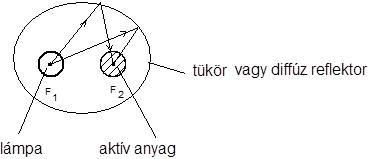3.4. ábra - Elliptikus elrendezés
szoros elrendezés az ábra szerint,

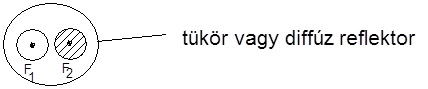3.5. ábra - Szoros elrendezés

diffúz reflektorként MgO, BaSO₄ port vagy fehér kerámiát használnak, ezek kicsit csökkentik a fényátvitel hatásfokát, de egyenletes megvilágítást eredményeznek,
bonyolultabb elrendezések is vannak 2 lámpával elliptikus és közeli elrendezésben.

Az optikai pumpálás hatásfoka

Több tényezőtől függ:

közvetítő rendszer hatásfoka, η_k, tipikus értéke 30-80 %,

η_k = az aktív anyagba belépő energia / a lámpa kisugárzott energiája
a lámpa sugárzási hatásfoka, η_e, tipikus értéke 25-50 %,

η_e = a kibocsátott fényenergia / a betáplált elektromos energia
abszorpciós hatásfok, η_a, tipikus értéke 10-60%,

η_a = az elnyelt hasznos energia / az aktív anyagba belépő energia
kvantumhatásfok, η_q, tipikus értéke 40-50 %

A teljes hatásfok, η_t

η_t = η_k η_e η_a η_q ~ 1 - 3 %

3.2.2. Elektromos gerjesztés

Itt csak a gázkisüléssel foglalkozunk. A félvezető lézerekkel egy későbbi fejezetben külön foglalkozunk. Az áram hatására a kisülésben ionok és szabad elektronok keletkeznek, melyek gyorsulnak és ütközéssel át is adják energiájukat, létrejön az atomok gerjesztése vagy ionizációja. Az elektronoknak van lényegesebb szerepük, nagyobb mozgékonyságuk miatt. Alacsony nyomású gázkisülésben cw gerjesztéssel rövid idő alatt kialakul egy egyensúlyi energiaeloszlás az elektronokra nézve, amelynek alapján megadható az átlagos elektronenergia vagy elektronhőmérséklet. Két fő folyamat van:

egykomponensű gáz esetén az elektronütközéses gerjesztés

e + X → X^* + e első fajú ütközés,
kétkomponensű gázban (a komponenseket jelölje A és B) rezonáns energiaátadással is lehetséges gerjesztés

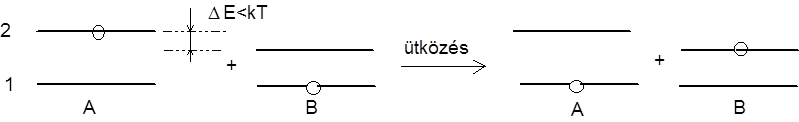
3.6. ábra - Rezonáns energiaátadású ütközés

A^* + B → A + B^* + ΔE másodfajú ütközés.

Különösen akkor jó ez a folyamat, ha az A atom 2 → 1 átmenete tiltott átmenet, vagyis az A 2-es szintje metastabil állapot, így mint egy energiatartály működik, s ha egyszer gerjesztődött, hosszú ideig gerjesztve is marad. Például He-Ne lézerben a He tölti be az "A" anyag szerepét, míg a Ne a "B" anyag. A hélium egy metastabil állapota játsza a főszerepet a Ne atom megfelelő szintjének (He-Ne lézer felső szintjének) a gerjesztésében.

3.3. Három és négy nívós közegek

Az irodalom kétfajta erősítő közeget az eddigieken felül is kiemelten tárgyal. Ezek az ún. három és négy nívós közegek. A kiemelést az indokolja, hogy a gyakorlatban a lézererősítők egy része megfeleltethető a három és négy nívós közegeknek.

Az adott atomi rendszernek több nívóját kell figyelembe venni, melyekre teljesülnie kell a (3.4. ábra és 3.5. ábra) ábrák szerinti feltételeknek.

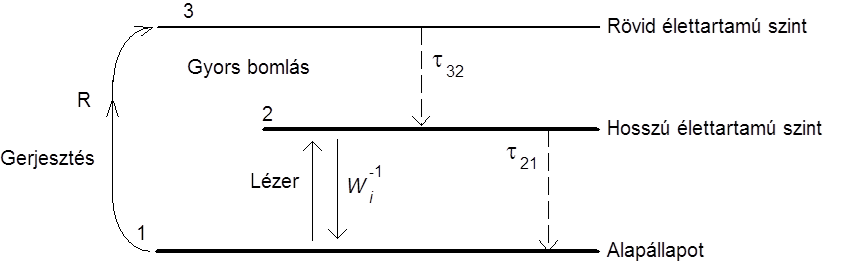
3.7. ábra - Háromnívós gerjesztési modell

Mivel az atomi szintek távolsága >> kT, (kivéve a molekulák rotációs szintjeit), ezért termikus egyensúlyban csak a legalacsonyabb szintek vannak betöltve. Ezért a 3 nívós esetben kezdetben N₁=N_t, ahol a t index az összes atomot jelenti. Az 1 és 2 szintek közötti inverz betöltöttséghez N_t/2+1 atom gerjesztése szükséges. Lehetséges olyan háromnívós gerjesztési model is, ahol a lézerátmenet a felső két szint között történik és a megfelelően nagy inverziókülönbséghez csak az alsó lézerszint gyors bomlását kell biztosítani.

3.8. ábra - Négynívós gerjesztési modell.

A 4 nívós esetben már egyetlen atom gerjesztésével létrejön az inverzió az 1 és 2 szintek között, ezért ebben az esetben kevesebb betáplált energiára van szükség az inverz betöltöttség létesítéséhez.

3.4. Példák

Klasszikus 3-nívós rendszer a rubinlézer (az első lézer volt 1960-ban). A természetben előforduló Al₂O₃ korund fekete színű kristály (ez a smirgli alapanyaga). Egykristályos szabályos változata a zafír, mely átlátszó. Krómmal szennyezve kapjuk a rubinkristályt, melyet Cr₂O₃+Al₂O₃olvadékából növesztenek. A krómdioxid az olvadékban 0,05 súlyszázalékban szerepel. Az így kapott kristály mélyvörös színe miatt kapta a rubin nevet.

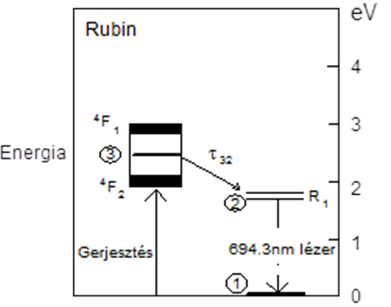3.9. ábra - Rubin kristály lézerműködéshez fontos nívói

A lézerműködés szempontjából fontos energiaszintek a háromnívós sémának felelnek meg. A rubin kristálynak kékben és zöldben két széles elnyelő sávja van (ezek okozzák a kristály piros színét), ezeket lehet lámpával gerjeszteni, a lézerátmenetek hullámhosszai: 0,6943 µm (erősebb átmenet) és 0,6928 µm. A 3→2 átmenet élettartama τ₃₂~ps nagyságrendű, a τ₂₁~t_sp≈3ms. Az átmenet homogén kiszélesedésű, Δν=60GHz (300K-en). A növesztett lézerkristály tipikus méretei: 5 - 20cm hosszú és 5 - 10mm átmérőjű.
Klasszikus 4-nívós rendszer a neodímium lézer. Szintén szilárdtest lézerfajta. A Nd ionokat YAG kristályba illetve üvegbe szennyezőként beépítve a Nd ion két nívója közötti átmeneten működik ~ 1,06µm körüli infravörös hullámhosszon. A lézerműködéshez szükséges energiaszintek a (3.10. ábra) ábrán láthatók.

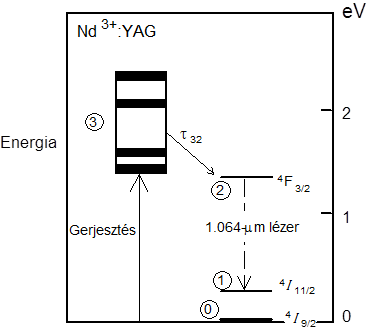3.10. ábra - Nd:YAG lézer nívói

A 3-mal jelölt szint 4 db ~ 30nm - es sávból áll: 0,810; 0,75; 0,58; 0,52μm körül, melyek rövid idő alatt ürülnek a lézer felső szintjére, a nívóélettartamok: τ₃₂ ~ 100ns, t_sp~ 1,2ms és τ₁ ~ 30ns.

A YAG - kristályos környezetben az átmenet homogén kiszélesedésű, Δν ≈ 120Ghz 300K -en, míg az üvegben a neodímium ionok szabálytalan környezete miatt az átmenet inhomogén kiszélesedésű, szobahőmérsékleten Δν ≈ 3000Ghz. Az üveg esetén a méretben nincs korlát. A ma ismert legnagyobb méretű lézer egy Nd:üveg lézer (NOVA lézer, melyet fúziós kisérletekhez fejlesztettek ki, 10⁵J energiájú 1ns - os impulzust ad).

A 3-as sávok hullámhossztartományában ma már nagy teljesítményű félvezető lézerek működnek, ezért a lámpás gerjesztések helyett ma már egyre inkább a 3.11. ábra ábra szerinti gerjesztés a jellemző.

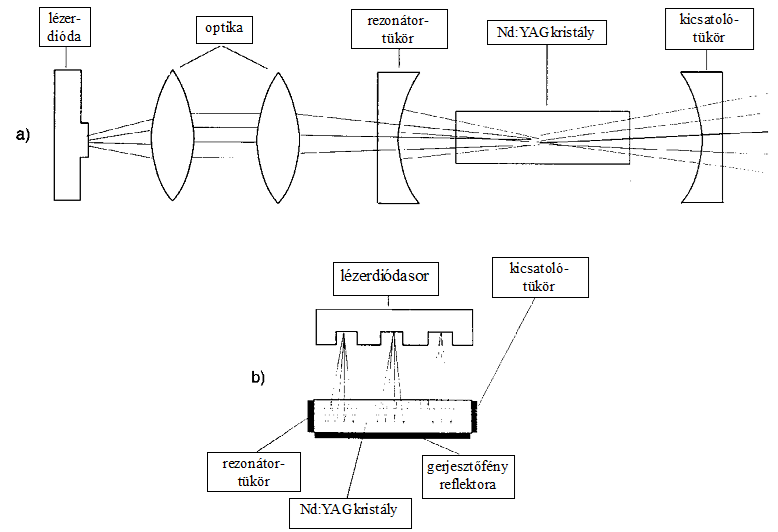3.11. ábra - Új típusú elrendezések az Nd:YAG lézerek gerjesztésére lézerdiódával, a) longitudinális, b) transzverzális.
A (3.12. ábra) ábrán egy hagyományos felépítésű He-Ne lézert láthatunk.

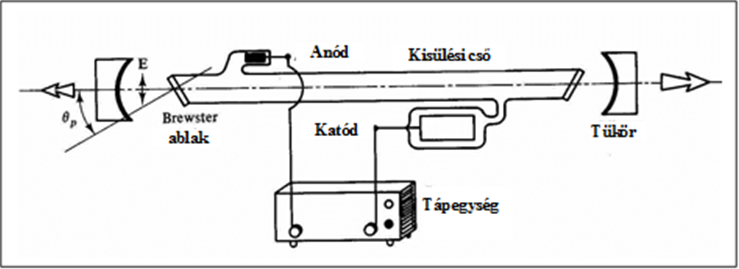3.12. ábra - Hagyományos felépítésű He-Ne lézer

A gáztartály kisnyomású (néhány mbar) tipikusan 5:1 keverékarányú He és Ne gázkeveréket tartalmaz. A Ne atomok gerjesztése gázkisüléssel történik. Közvetlen elektrongerjesztéssel, illetve a korábban említett másodfajú ütközéses energiacserével, amikor gerjesztett He atomok adják át energiájukat ütközés során alapállapotú Ne atomoknak. A wolframszál anód és a tipikusan Al ötvözetből készített katód között folyik a néhány mA nagyságú áram a vastag falú kapillárisban. A kisülés beindításához hossztól függő, de 5-10 kV nagyságú gyújtófeszültség szükséges. A lézer legismertebb hullámhossza a 0,6328 µm-es, de közeli infra hullámhosszai (1,15 és 3,39 µm), illetve zöld, sárga és egyéb piros hullámhosszai is ismertek. A (3.13. ábra) ábrán egy működő hagyományos felépítésű He-Ne lézert láthatunk.

3.13. ábra - Hagyományos He-Ne lézer működés közben

Néhány lézerátmenet jellemzői

Közeg	λ[μm]	σ₀[cm²]	t_sp	Δν	H hom. I inhom.	n
He-Ne	0,6328	1·10-¹³	0,7 μs	1,5 GHz	I	~1
Rubin	0,6943	2·10-²⁰	3 ms	60 GHz	H	1,76
Nd³⁺-YAG	1,064	4·10-¹⁹	1,2 ms	120 GHz	H	1,82
Nd³⁺:üveg	1,06	3·10-²⁰	0,3 ms	3THz	I	1,5
Er³⁺:üvegszál	1,55	6·10-²¹	10,0 ms	4 THz	H/I	1,46
Rodhamin 6G	0,56-0,64	2·10-¹⁶	3,3 ns	5 THz	H/I	1,33
Ti³⁺:Al₂O₃	0,66-1,18	3·10-¹⁹	3,2μs	100 THz	H	1,76
CO₂	10,6	3·10-¹⁸	2,9 s	60 MHz	I	~1
Ar⁺	0,515	3·10^-12	10,0 ns	3,5 GHz	I	~1

Vissza		Előre
2. fejezet - Fény és anyag kölcsönhatása (fénykibocsátás, fényelnyelés)	Főoldal	4. fejezet - Passzív optikai rezonátorok