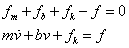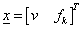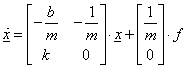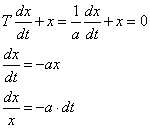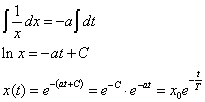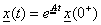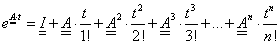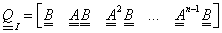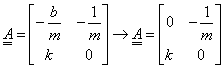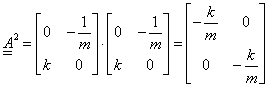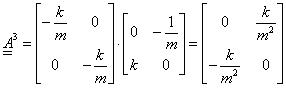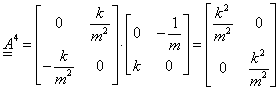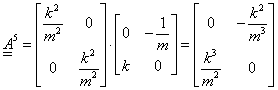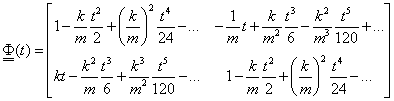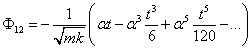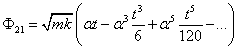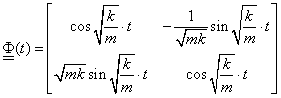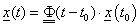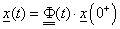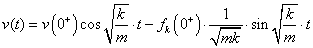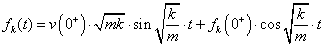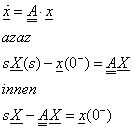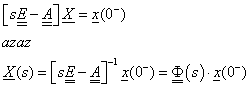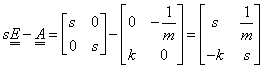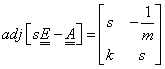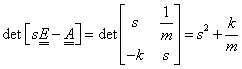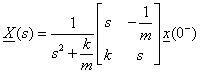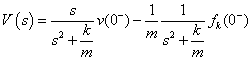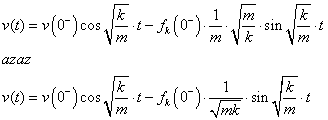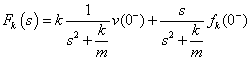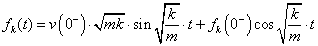5. fejezet - Az állapotegyenlet megoldása idő és operátor tartományban
A matematikai modellek felírását követően, a teljesség kedvéért bemutatjuk az állapotegyenlet megoldását idő- és operátor tartományban. E jegyzet terjedelme nem teszi lehetővé, hogy minden egyes mintapéldán elvégezzük ezeket a befejező lépéseket, de a kiválasztott, egyenes vonalú mozgást végző, másodrendű mechanikai rendszer alkalmas az állapotegyenletek megoldásának bemutatására.
A feladat egyszerű, és gyakori a gépészetben, hiszen a passzív rezgéscsillapító legegyszerűbb változatát modellezi. Azt, hogy a rezgéscsillapítás problémakörének egyetlen kis szelete mit jelent a valóságban, egy későbbi fejezetben módunk lesz részletesen megismerni.
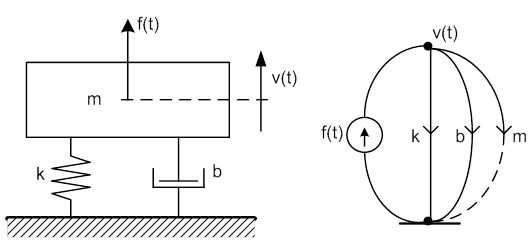
Az „m” tömeget egy „Kelvin-modell”, azaz egy valós, veszteséges rugó támasztja alá. Kétféle gerjesztés modellezi a valóságos folyamatokat: Erőgerjesztés, és a talaj (födém) sebesség gerjesztése. A példában a talaj sebességét egyenlővé tettük a referenciával, feltételezve annak teljes nyugalmi állapotát. A gráf mutatja, hogy a modell által „sugallt”, soros rendszer helyett egy párhuzamossal van dolgunk, hiszen a tömeg csak a referenciára vonatkoztatható.
A gráf alapján felírt csomóponti egyenlet alkalmas az állapottér modell megalkotására.
|
|
A két energiatároló meghatározza az állapotjelzőket, amelyek ebben az esetben „kanonikus” állapotjelzők [3.1.]:
|
|
A főegyenlet az állapotjelzők alkalmazásával az alábbi formát ölti:
|
|
Az alábbiakban az állapotegyenlet megoldására, az állapotváltozók időbeli lefolyásának meghatározására két utat mutatunk be. Az egyik út az időtartományban szemlélteti a lépéseket, a másik az operátor tartományban, ahonnan inverz Laplace transzformáció révén jutunk újra az időtartományba.
A műszaki gyakorlatban ezt a feladatot – lineáris esetben – a másodikként említett „kerülő úton”, az operátor tartományt igénybe véve szokás megoldani. A teljesség kedvéért azonban bemutatjuk az időtartománybeli megoldás folyamatát is, világossá téve, hogy még egy egyszerűnek mondható feladat esetében is milyen vesződségesen járható az „egyenes” út.
A feladatban annyi egyszerűsítést hajtunk végre, hogy a csillapítást kiiktatjuk a rendszerből. ha ezt nem tennénk, a megoldást rendkívül megnehezítené a periodikus és aperiodikus sorozat elemek szétválasztása.
5.1. Megoldás idő tartományban sorfejtéssel
Első lépésben emlékeztetünk arra, hogy egy változó esetében miként kapjuk időtartományban a megoldást.
Kiindulás az egyváltozós elsőrendű, lineáris, homogén differenciálegyenlet:
|
|
Az x(t) megoldáshoz integrálni kell mindkét oldalt, majd az „lnx” függvényt x-re kifejezni:
|
|
A fenti megoldás műszaki értelmezésében az integrálásból származó „C” konstans az x(t) függvény kezdeti értékének meghatározására szolgálhat.
Kihangsúlyozzuk, hogy az időfüggvények helyes megadásához nélkülözhetetlenek a jobboldali kezdeti értékek. Ha ezek nem állnak rendelkezésre, mert csak a baloldali, un. kiindulási értékek ismertek, akkor a kezdeti értékeket bizonyos gerjesztés típusok esetén ki kell számítani. A műszaki gyakorlatban általánosan elfogadható, hogy a kiindulási és a kezdeti értékek megegyeznek, hiszen a valóságban t(0-) és t(0+) „időtartam” alatt nem tudunk egy valós rendszer állapotjelzőinek feltöltöttségén változtatni. Más kérdés, hogy elméletben a Dirac-impulzus révén létrejövő x(0+) érték kiszámítható. A kérdéssel, Fodor György [3.1.]útmutatása alapján, részletesen foglalkozunk a 6.3. szakasz fejezetben.
Az egyváltozós differenciálegyenletre kapott megoldás analógiájaként az állapotegyenlet homogén megoldása a következő formájú lesz:
|
|
A fenti exponenciális függvény ebben az alakjában a „reménytelen esetek” kategóriájába tartozik. Az exponenciális mátrix helyett, a „használható” formában való alkalmazást a Taylor sorfejtés teszi lehetővé. Ennek segítségével az exponenciális mátrixot végtelen hatványsorrá lehet átalakítani.
|
|
Ugyanakkor sajnálatos dolog, de hatványsorból csak kellően nagy gyakorlattal lehetséges a megfelelő harmonikus és aperiodikus összetevők szétválasztása. Ezért jeleztük már korábban, hogy a modellben a csillapítási tényezőt nullának választjuk, és így kapott sor csak periodikus függvényhez tartozó elemeket fog tartalmazni. A befektetendő munka mennyisége könnyen elképzelhető, ha a feladatunkban megadott 2x2-es mátrixnál nagyobbakat kell hatványozni.
Ezen a helyen érdemes megjegyeznünk, hogy az állapotszabályozások esetében döntően fontos irányíthatósági feltétel hipermátrixában ugyancsak az alapmátrix hatványai jelennek meg, ennek oka a Taylor sorban rejlik. Ez természetes, hiszen az irányíthatóság esetében azt vizsgáljuk, hogy a bemenetek segítségével (a hatványsor szorzója „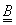
”) lehetséges-e az állapotjelzőket megadott kezdeti értékről tetszőleges értékre vezérelni, miközben figyelembe vesszük a rendszer dinamikai tulajdonságait is. A dinamikai tulajdonságok pedig éppen az „
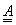” rendszermátrixba vannak „bekódolva”.
|
|
Az eredeti feladat rendszermátrixában zérussá tesszük a „b” csillapítási tényezőt, és ezzel átalakul a mátrix is, amint azt a jobboldali mátrixnál látjuk:
|
|
A sorozat felírásához szükséges mátrix hatványozást az alábbiakban mutatjuk be:
|
|
valamint
|
|
illetve
|
|
és
|
|
A kiszámított együtthatókkal már felírható a négy hatványsor első néhány tagja, amiből azonban már következtetni lehet a sor által helyettesített függvényre.
|
|
A mátrix Φ12 elemének sorozatából kiemelhető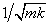
, a Φ21 elemének sorozatából pedig 
.
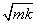Tekintettel arra, hogy az átalakítás nem egyszerű, néhány fontos lépését bemutatjuk. Ismeretes, hogy a csillapítatlan rendszer rezonancia körfrekvenciája a következő módon definiált: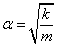 
.
A Φ12 elemet alkotó sorozatot úgy kell átalakítani, hogy a sorozat minden tagjában megjelenjék az „α” érték a „t” változónak megfelelő hatványon. Ha a hatványsort beszorozzuk α-val, és kiemeljük a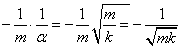 
szorzatot, akkor a Φ12 elemet alkotó sorozat az alábbi formájú lesz:
|
|
Hasonlóképpen járunk el a Φ21 elemben található sorozattal is, de itt a kiemelés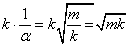 
formát ölt:
|
|
A kiemelés után felismerhető, hogy a mellékátló mindkét sorozata sinus, míg a főátló sorozatai cosinus függvény tagjait alkotják. Ezzel megkaptuk az alapmátrixot, vagy rezolvens mátrixot idő tartományban:
|
|
Az időtartománybeli megoldást az alapmátrix segítségével és a kezdeti értékek ismeretében kapjuk. Ez a megoldás a differenciálegyenlet- rendszer homogén megoldásait tartalmazza:
|
|
Egyszerűség kedvéért kezdődjön a vizsgálat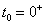 
időpillanatban (azaz zérus kiindulási értékekkel), és így az alábbi formát kapjuk:
|
|
A kijelölt mátrix-vektor műveleteket kifejtve látható lesz az állapotjelzők időbeli viselkedése, ha a vizsgálatot a jobboldali kezdeti értékekről indítjuk:
|
|
és
|
|
Az eredményt a szokásos módon dimenzió ellenőrzésnek vetjük alá, és megállapíthatjuk, hogy az eredmény helyes.
5.2. Megoldás operátor tartományban a kezdeti érték probléma figyelembe vételével
Nézzük ezek után, hogyan kell eljárni, ha az állapotjelzők időfüggvényét a Laplace transzformáció alkalmazásával határozzuk meg.
Az állapottér modell főegyenletének homogén részét Laplace transzformáljuk, és megfelelő átrendezés után kapjuk a megoldást. A deriválás Laplace transzformációs tétele tartalmazza az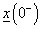 
kiindulási értéket. A későbbiekben látjuk majd, hogy éppen ez a tétel teszi lehetővé a kezdeti értékek „automatikus” meghatározását a transzformáció alkalmazása révén [3.1.].
|
|
Ügyelni kell a mátrix-vektor műveletek sorrendjére, mert a sorrend nem felcserélhető.
|
|
A szakirodalomban az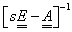 
inverz mátrixot gyakran „alapmátrixnak” nevezik, és 
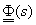-vel jelölik. Szerepe a dinamikai tulajdonságok leírásában igen jelentős, mert a nevezője a gyököket (pólusokat) meghatározó karakterisztikus polinom. Amikor az állapottér modell (ÁTM) rendszermátrixát vizsgáltuk, megjegyeztük, hogy a stabilitás egyik feltétele a főátló elemeinek negatív előjele. Íme, a magyarázat az állításra, ami az 
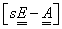kifejezésben rejlik. A rendszermátrix negatív előjelet kap, és így, az operátorral megszorzott egységmátrixból kivont, negatív előjelű főátló elemek mind pozitív előjelűek lesznek (lásd lejjebb, a példán). A Hurwitz stabilitási kritérium alapján ismert, hogy karakterisztikus polinom stabil esetben nem tartalmazhat nullánál kisebb együtthatót.
A feladat már ismert rendszermátrixával elvégezzük az első kijelölt műveletet:
|
|
A következő lépésben invertáljuk a kapott mátrixot! Ehhez meg kell határozni az adjungáltját és a determinánsát:
|
|
|
|
Ezekkel az inverz mátrix, és tulajdonképpen az állapotjelzők operátortérbeli függvényei is adottak. A keresett időtartománybeli alakhoz már csupán végre kell hajtani az inverz Laplace transzformációt.
|
|
tehát
|
|
Inverz Laplace transzformálás után a következő időfüggvényt kapjuk:
|
|
Látható, hogy a „kerülő út” használata ugyanazt az eredményt hozta, de lényegesen egyszerűbben. Ismételten le kell szögezni, hogy csillapított rendszer esetében – tehát, ha „b” nem zérus - az időtartományban az jelentene nagy gondot, hogy két sorozat szorzatának tagjaiból kellene szétválogatni, visszaállítani a harmonikus és az aperiodikus sor tagjait.
A másik állapotjelzővel is hasonlóan járunk el:
|
|
Végül a visszatranszformálás után ugyanazt a függvényt kapjuk, mint a sorfejtéssel:
|
|
A magyarázatot a kezdeti érték és a kiindulási érték közötti különbségre Fodor György többször idézett művében [3.1.]találjuk.
Láttuk, hogy a Laplace transzformáció alkalmazásával lényegesen egyszerűbben jutunk eredményhez. Fodor György a Laplace transzformáció további előnyeként mutatja be, hogy a transzformáció mintegy „automatikusan” előállítja az időtartománybeli megoldáshoz szükséges t(0+) kezdeti feltételeket is, elegendő a kiindulási értékeket ismerni.