A. függelék - Mechatronikai rendszerek hőtani és áramlástani modellezése
- A.1. Bevezetés
- A.2. Bevezetés a CM program használatába
- A.3. Felhasználó által definiált közönséges differenciálegyenlet-rendszer megoldása
- A.4. Hővezetés és hőátadás folyamatok hatásának vizsgálata egy szilárd test hőmérsékletének alakulására
- A.5. Vezetősínben kialakuló hőmérsékleti kép meghatározása (Joule törvény)
- A.6. Mérőperemben kialakuló áramlás vizsgálata
- A.7. Csőszigetelés vastagságának vizsgálata
- A.8. Hőmérő elhelyezés vizsgálata
A.1. Bevezetés
A még manapság is gyorsan fejlődő informatika lehetőséget teremt arra, hogy azon szimulációs technikák is a mindennapi mérnöki munka részéve váljanak, amelyek összetettebb geometriákban, komplex folyamatok viselkedésének időbeli lefutását is képesek megbízhatóan meghatározni. Az ilyen rendszerek vizsgálata esetén, már nincs szükség, vagy lényegesen kevesebb egyszerűsítés bevezetésére van szükség, mint ha a rendszer viselkedésére a klasszikus tökéletesen kevert egység, vagy az ideális kifolyású cső megközelítésmódokat alkalmaznánk.
A numerikus áramlástan (Computational Fluid Dynamics – CFD) az informatikával párhuzamosan fejlődött, fejlődik. Az utóbbi néhány évtizedben, ahogy a számítógépek már az életünk mind több területén megjelentek, lehetővé vált, hogy közönséges asztali számítógépeken is végezzünk CFD számításokat. A tudomány területhez kapcsolódóan született publikációk, mind az alkalmazási példák növekvő száma azt mutatja, hogy egy dinamikusan fejlődő területről van szó, amely egyre nagyobb teret hódít meg magának.
A következőkben egy nagyon rövid bemutatót adunk egy olyan jellegű szoftver alkalmazásához, mely CFD számítások elvégzésére is alkalmas, ez a COMSOL Multiphysics (CM). Egyszerű példákon keresztül kívánjuk megismertetni az olvasóval a szoftver alkalmazásának alapjait, de nem célunk a szoftver által használt, véges elemek módszerének részletes bemutatása, sem a transzport folyamatok alapjainak ismertetése. A választott példák elsősorban a mechatronikai rendszerekben lejátszódó hőtani és áramlástani jelenségek matematikai leírására és a kidolgozott modellek alapján elvégzett szimulációs vizsgálatok elvégzésére fókuszál.
A.2. Bevezetés a CM program használatába
A CM egy olyan szoftver, amely a CFD tudományterülethez tartozó mérlegegyenletekkel (főleg impulzusmérlegek), összefüggésekkel való számítások mellett, lehetőséget nyújt más jelenségek (anyag- és energiatranszport) folyamatok együttes vizsgálatára, összetett geometriák esetén is.
A legtöbb szimulációs szoftverhez hasonlóan, CM programban is, három részre bonthatjuk a problémamegoldás menetét:
-
Modellalkotás – vagy a felhasználó által definiált összefüggésekből, vagy az egyes jelenségek leírására alkalmas előredefiniált összefüggésekből, a probléma megoldásához szükséges modell felépítése. A matematikai modell megalkotását természetesen meg kell előzze a geometriai modell elkészítése. A modellalkotás folyamata a modellegyenletekben szereplő paraméterek (elsősorban a fázisok fizikai tulajdonságai), illetve a modell megoldásához szükséges peremfeltételek rögzítésével fejeződik be.
-
Modell megoldás – szimuláció lépésben a geometriai és matematikai modell elemzését követően véges számú elemre kell felosztani a definiált geometriát, azaz el kell végezni a diszkretizálást. A modellek elemzését a megoldás megbízhatósága szempontjából rendkívül körültekintően kell elvégezni, melynek során a vizsgált geometria azon részeiben, ahol a számítás elvégzését kritikusabbnak érezzük, a diszkretizálás során kisebb részekre való felosztást javasolt alkalmazni. A diszkretizálási lépést követően a szimulációs lépés következik, ahol a definiálnunk kell, hogy milyen szimulációs vizsgálatot, vizsgálatokat kívánunk elvégezni a létrehozott modellen.
-
Kiértékelés – mint minden szimulációs szoftverben, a CM programban is nagy hangsúlyt fektettek az eredmények hatékony kiértékelésére. A táblázatok, 2D-s és 3D-s ábrák készítése mellett, lehetőségünk van animációk készítésére is néhány kattintást követően. Az így kapott eredmények természetesen dokumentumokba is könnyen átemelhetők.
Az ismertetőben található példák a COMSOL Multiphysics 4.3.0.151 verziójával készültek.
A.3. Felhasználó által definiált közönséges differenciálegyenlet-rendszer megoldása
A CM program kezelőfelülete három főrészre osztható, ahogy az lejjebb (A.1. ábra) is látható, balról jobbra haladva ezek a következők:
-
Egy fastruktúrában (Model Builder) kerülnek megjelenítésre az elkészített modellek, a definiált vizsgálatok, illetve a kiértékelés fázisban létrehozott ábrák, táblázatok. A felhasználó által létrehozott összetett program struktúrában való hatékony navigálást teszi lehetővé.
-
Függően attól, hogy a fastruktúrának mely részét jelöltük ki, itt van lehetőség az általunk gondolt összefüggések, paraméter értékek megadására, a korábbi beállításaink módosítására, illetve a megalkotott matematikai vagy geometriai modell bővítésére, esetleg új vizsgálatok definiálására, ábrák készítésére.
-
Tovább bontható két részre, ahol a felső rész az ahol a létrehozott geometriai modell, illetve a számítások grafikus eredménye megjelenik. Itt is van lehetőségünk a geometriai modell manipulálására, ahol a geometria szerkesztésére navigálva megjelenő menüsorból tudjuk a legmegfelelőbb alakzatokat kiválasztva szerkeszteni a leképezett geometriát. Az alsó rész egy információs rész, ahol a program által felhasználónak küldött üzeneteket láthatjuk (Messages), az éppen futó szimuláció készültségi fokát követhetjük nyomon (Progress), a program által rögzített fontosabb információkat tekinthetjük meg (Log), illetve ha numerikus értékeket számoltatunk ki a programmal, azok jelennek meg itt (Results).
A program menüsora teljesen le van egyszerűsítve, és csak a más programokban is jól megszokott alapfunkciók kapnak itt helyet (pl. fájlok megnyitása, segítségkérés, program beállítások, stb.).
Annak érdekében, hogy elkezdjük az ismerkedést a programmal tekintsük az alábbi közönséges differenciálegyenleteket tartalmazó egyenletrendszert:
|
|
(A.1) |
|
|
|
(A.2) |
|
|
|
(A.3) |
Ezek az ún. Lorenz egyenletek, melyekben a σ=10; ρ=29; β=8/3 paraméterkészletet alkalmazva egy kaotikus viselkedés figyelhető meg. A fenti modell, az állapotváltozók csak az időbeli megváltozását írják le, azaz a teret homogénnek tekintik. Így ezen egyszerű példa esetén nincs szükség geometria megalkotására. Ez azt is jelenti, hogy a program által kínált hat lehetőség közül, melyek felülről lefelé haladva az alábbiak:
-
a modellezett objektum geometriája három dimenzióban kerül leképezésre (3D), nem használjuk ki, vagy nem tudjuk kihasználni a geometriában lévő szimmetria viszonyokat (koordináták: x, y, z);
-
a modellezett objektum hengerszimmetrikus (2D axisymmetric), s ezt kihasználva egyszerűsítjük a geometriai modellt (koordináták: r, x);
-
az objektum viselkedését egy síkban vizsgáljuk így annak geometriája két dimenzióban kerül leképezésére (koordináták: x, y);
-
a modellezett objektum gömbszimmetrikus (1D axisymmetric), s ezt kihasználva csökkentjük a térkoordináták számát (koordináták: r);
-
az objektum viselkedését csak egy koordináta mentén vizsgáljuk (1D), a többi koordináta mentén nem vesszük figyelembe az állapotváltozók alakulását (koordináták: x);
-
nincs geometriai modell (0D), a térben homogénnek tekintjük az objektumot (koordináták: -);
ebben az esetben a 0D beállítás kiválasztására van szükség. A modellalkotás következő lépésére, a kezelőfelült középső részének tetején található jobboldalra mutató kék nyíl segítségével ugorhatunk. Függetlenül attól, hogy mely dimenziót választottuk, a térkoordináták mellett, a modellegyenletekben szereplő független változók számát az idő is növeli, amennyiben dinamikus vizsgálatot végzünk.
Mivel ez esetben nem az előre definiált összefüggések közül építenénk fel a matematikai modellt, ezért a geometria kiválasztását követően Mathematics/ODE and DAE Interfaces/Global ODEs and DAEs útvonalon a kiválasztott összefüggésekhez (Selected Physics) adjuk hozzá az összefüggést a pluszjelre kattintva (vagy két a bal egérgombra kattintással az összefüggésre). Az ODE az Ordinary Differential Equation, azaz a közönséges differenciál egyenletek jelöli, míg a DAE a Differential Algebric Equation, azaz a differenciál algebrai összefüggéseket. A két kifejezés gyakorlatilag ugyanazt jelenti, csak az egyenletek formalizálásában különböznek az összefüggések.
Az összefüggés hozzáadását követését követően a nyíl segítségével továbbléphetünk az elvégzendő vizsgálat kiválasztására, amely ez esetben, mivel a felírt differenciálegyenletek a rendszer időbeli viselkedését írják le, dinamikus szimuláció (Time Dependent) lesz. Ezt kiválasztva kattintsunk a nyilak mellett lévő kockás zászlóra, így befejezve a modellalkotás első lépéseit. Amennyiben mindent megfelelően végeztünk, Model 1 és Study 1 jelent meg a struktúrában. A Model 1 pont alatt láthatjuk a modellben lévő összefüggés(eke)t, amennyiben újabb egyenletekkel akarjuk bővíteni a modellünk, úgy a Model 1 pontra jobb egérgombbal kattintva megjelenő menüben, az Add Physics menüponttal tehetjük ezt meg.
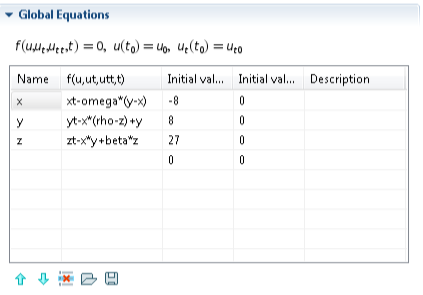
A következő lépés a differenciálegyenlet-rendszer leképezése a programba. Ehhez kattintsunk először Model 1/Global ODEs and DAEs/Global Equations 1 pontra a struktúrán belül. Az így megjelenő táblázatban tudjuk rögzíteni az összefüggéseinket differenciál algebrai egyenletek formájában, ennek megfelelően írjuk fel a modellegyenleteket:
|
|
(A.4) |
|
|
|
(A.5) |
|
|
|
(A.6) |
A táblázat első oszlopába az egyes összefüggésekből számítható változók nevét írjuk be, azaz sorrendbe x, y, z változókat. A táblázat második oszlopába írjuk be az (A.4-A.6) egyenleteket olyan formában, hogy ahol elsőrendű differenciálhányados szerepel, ott az adott változó neve mellé egy darab t-betűt, míg a másodrendű differenciálhányados esetén két darab t-betűt tegyünk. A táblázat harmadik oszlopába pedig az egyes differenciálegyenletek megoldásához megadott kezdeti értékeket rögzítsük. Amennyiben mindent helyesen írtunk be a táblázatnak az alább (A.2. ábra) látható módon kell kinéznie. Az így létrehozott modellegyenleteket a táblázat alatt lévő ikonok közül az utolsóra kattintva egy txt-fájlba menthetjük, s egy másik modellbe betölthetjük azokat, az utolsó előtt ikonra kattintva.
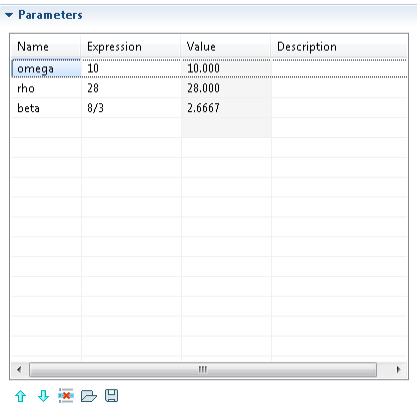
A modell megoldása előtt szükség van a modellparaméterek rögzítésére, ehhez a struktúrában kattintsunk a jobb egérgombbal a Global Definitons pontra, az így megjelenő menüben pedig válasszuk ki a Parameters menüpontot. Az így megjelenő táblázatba tudjuk felvenni a modell paramétereket, azok nevének (Name), illetve a számításukhoz szükséges összefüggések (Expressions) rögzítésével. Lehetőségünk van a létrehozott paraméterkészlet mentésére, illetve betöltésére is, hasonlóan az egyenletek esetén korábban már megismertekhez hasonlóan. Itt fontos megemlíteni, hogy a program lehetőséget ad, az egyes paraméterek mértékegységének megadására, ezt úgy tudjuk megtenni, hogy az összefüggés megadását követően egy szóköz kihagyásával szögletes zárójelben megadjuk az adott értékhez tartozó mértékegységet. A program a megadott mértékegységnek megfelelően fogja kezelni az értéket későbbiekben. A felvett paraméterek alább (A.3. ábra) láthatók.
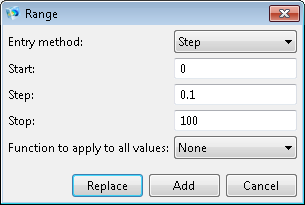
A modellalkotás fázisát befejeztük, s következhet a modell megoldása. Ennek érdekében a Study 1/Step 1: Time Dependent menüpontra kattintva a struktúrában adjuk meg a szimulációs időt, illetve, hogy mely időpillanatokban szeretnénk eredményeket kapni (Times). Esetünkben 100 s-ig végezzük a szimulációt és 0,1 s-ként akarunk eredményeket kapni. A range parancs argumentumának átírásával (range(0,0.1,100)), vagy a Times mellett lévő gombra (![]() ) kattintva megjelenő ablakban (lsd. A.4. ábra) adhatjuk ezt meg.
) kattintva megjelenő ablakban (lsd. A.4. ábra) adhatjuk ezt meg.
Ezt követően vagy az F8 gomb megnyomásával, vagy a program felső menüsorában megjelenő zöld egyenlőségjelre kattintva indíthatjuk a számítást. Amennyiben lefut a szimuláció a program automatikusan létrehoz egy ábrát (lsd. A.5. ábra), a három állapotváltozó időbeli alakulásának bemutatására.
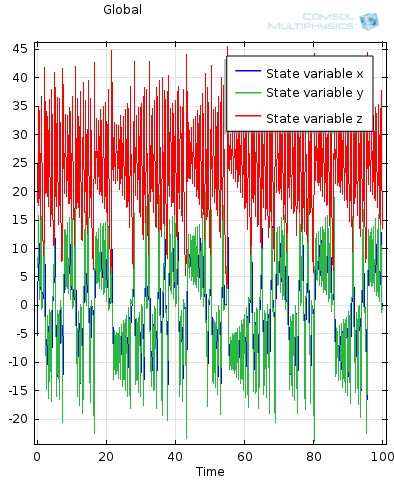
Látványosabb ábrák hozhatók létre, ha egy fázistérben mutatjuk be a rendszer viselkedését, ehhez x változó függvényében ábrázoljuk az y és z változókat. Ezt úgy tudjuk megtenni, hogy Results/1D Plot Group 1/Global 1 pontra kell kattintanunk a struktúrában. Itt először töröljük az y-tengelyhez rendelt adatsorok (y-Axis Data) közül az x változónkat (mod1.x – ahol mod1 a kidolgozott modell azonosítója) listából. Törölni a táblázat alatt lévő utolsó ikonnal tudunk. Változókat rendelni az y-tengelyhez pedig, vagy a változó nevének a táblázatban való megadásával, vagy a táblázat felett lévő két ikon valamelyikének megnyomását követően, a változókat tartalmazó listából kiválasztva.
Az x-tengely adatsorát (x-Axis Data) alatt tudjuk megtenni, a legördülő menüben az idő (Time) helyett válasszuk ki az összefüggést (Expression). Ezt követően rögzítsük a kifejezést, esetünkben ez mod1.x. Ha ezzel végeztünk vagy az F8 gomb megnyomásával, vagy a ![]() gombra kattintva frissíthetjük az ábrát. Amennyiben az eredmények kigyűjtésének lépésközét 0,01 s-re csökkentjük és frissítjük az előzőekben készített fázis diagramot, akkor az alább (A.6. ábra) látható görbéket kapjuk.
gombra kattintva frissíthetjük az ábrát. Amennyiben az eredmények kigyűjtésének lépésközét 0,01 s-re csökkentjük és frissítjük az előzőekben készített fázis diagramot, akkor az alább (A.6. ábra) látható görbéket kapjuk.
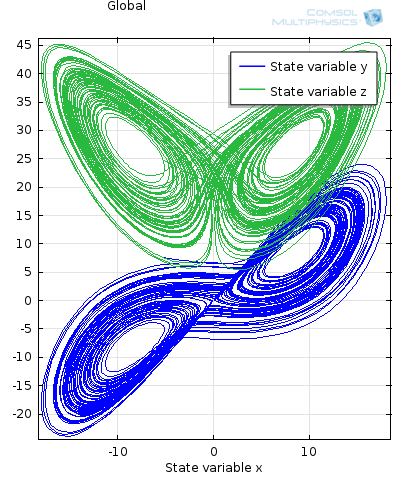
A.4. Hővezetés és hőátadás folyamatok hatásának vizsgálata egy szilárd test hőmérsékletének alakulására
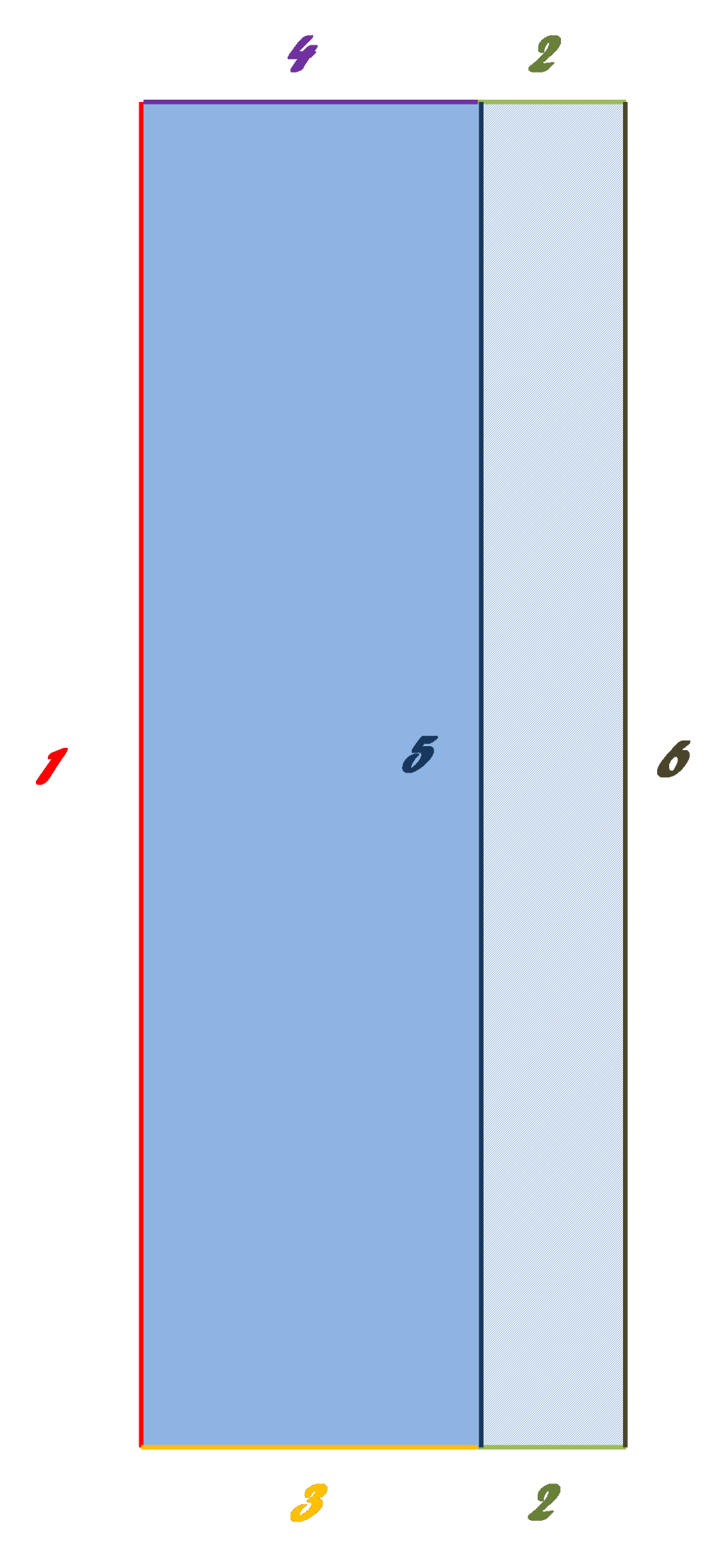
Ebben a fejezetben az alább (A.7. ábra) látható keresztmetszeti profillal rendelkező, szilárd testben kialakuló hőmérsékleti kép meghatározása a célunk. Feltételezzük, hogy a test kellően hosszú, s ennek folytán eltekinthetünk a test két végén lejátszódó folyamatok hatásától. Ennek eredményeképpen elegendő a test keresztmetszete mentén kialakuló hőmérsékleti kép számítására, ugyanis a feltételezés szerint, ez nem változik jelentősen a test hossza mentén.
A világos kék számok (A.7. ábra) jelölik a vizsgált alakzat főbb méreteit centiméterben, míg a többi színes szám az azonos színű peremek azonosítására szolgál. Az objektum belső kialakítása fiktív, amelynek a sötétebb része rézből, a világos körök szilika üvegből készült, míg a középső kisebb körben pedig telített gőz áramlik. Az peremfeltételek (Táblázat A.1) kerültek összefoglalásra.
|
Peremcsoport |
Peremfeltétel |
|---|---|
|
1 |
Állandó falhőmérséklet – 310 K |
|
2 |
Hőszigetelés - nincs hőtranszport a környezet felé, jQ=0W/m2 |
|
3 |
Van hőtranszport a környezet felé, jQ=500W/m2K·(293K−T) |
|
4 |
Állandó falhőmérséklet – 360 K |
|
5 |
A két szerkezeti anyag hőmérséklete megegyezik |
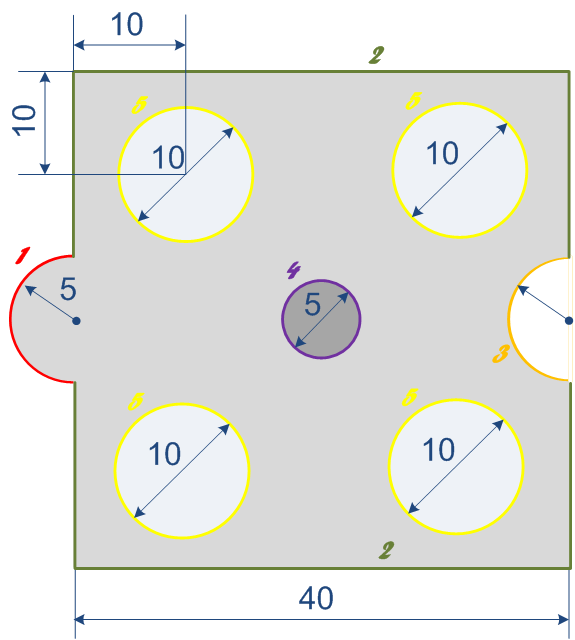
Mielőtt rátérnénk a modellalkotásra, nézzük meg részletesebben a peremfeltételeket (Táblázat A.1). A vizsgált objektum az 1-es peremcsoporton keresztül érintkezik közvetlenül a környezettel, amelynek végtelen hőkapacítása miatt, ezen perem mentén nem változik a környezet hőmérséklete. Az itt indukálódó hőátadási folyamat sebessége végtelen, így a perem mindkét oldalán azonos a hőmérséklet. A 3-as peremcsoporton ezzel szemben, nem végtelen nagy a transzport folyamat sebessége, de a környezet hőkapacítása itt is végtelen, ezért annak hőmérséklete itt sem változik. Az itt felírt hőátadási áramsűrűség első tagja a hőátadási tényező, amely azt adja meg, hogy egységnyi felületen, egységnyi hőmérsékletkülönbség hatására, mekkora hőáram indukálódik. A második tag ebben a szorzatban pedig a hajtóerő, amely hőátadási folyamat esetén a perem két oldalán kialakuló hőmérsékletek különbsége.
A 2-es peremcsoport mentén tökéletesen szigetelt az objektum, amely megakadályozza, hogy ezen peremeken keresztül hőáram indukálódjon az objektum környezete felé. A 4-es peremcsoport esetén ugyanazokat a megfontolásokat tehetjük, mint az 1-es peremcsoport esetén tettünk. Ez esetben azonban az állandó hőmérsékletet úgy is elképzelhetjük, hogy az itt felszálló telített gőz csak kondenzálódik, és emiatt nem változik jelentősen a hőmérséklete. Az 5-ös peremcsoporton érintkezik a két szerkezeti anyag közvetlenül, így ezen peremen nem lehet szakadás a hőmérsékleti profilban, ennek megfelelően a perem két oldalán a hőmérsékletet egyenlővé kell tennünk.
A vizsgált geometria (pl. A.7. ábra) kétdimenziós (2D), így a dimenzió megválasztásánál ezt válasszuk. Annak érdekében, hogy a hőmérséklet alakulását kiszámítsuk egy szilárd testben, olyan hőmérleg felvételére van szükség a modellbe, amelynek a makroszkopikus mozgás okozta hőtranszport folyamat, a konvektív hőáram matematikai leírása nem része:
|
|
(A.7) |
ahol a hővezetési hőáramsűrűség, ami a Fourier-törvény szerint:
|
|
(A.8) |
A geometria kiválasztását követően a Heat Transfer/Heat Transfer in Solids összefüggést kiválasztva adjuk hozzá az előbbi hőmérleget a modellhez. Jelen példában stacioner vizsgálatot akarunk elvégezni, így a következő lépésben a Stationery vizsgálatot válasszuk ki és fejezzük be a modellalkotás előkészítését. Az első példához képest annyi változott a modell struktúrában, hogy ezen példa esetén szükség van egy geometriai modell kidolgozására is, ezért a struktúrában megjelent a Geometry 1 pont. Emellett megjelent a Materials pont is, ahol az egyes tartományokhoz tudunk majd anyagokat rendelni a CM program adatbázisából, illetve saját magunk is definiálhatunk itt új anyagokat.
Jobb egérgombbal a Geometry 1 pontra kattintva válasszuk ki a négyzetet (Square) az előbukkanó menüből. Ennek eredményeképpen a geometriai modell bővül egy elemmel, amely méretét (Size), valamely kitüntetett pontjának pozícióját (Position), illetve elforgatásának szögét (Rotation) tudjuk megadni. Esetünkben, az A.7. ábra alapján, a négyzet oldalainak hossza 0,4 m, a bal alsó sarkának pozíciója pedig (0, 0). Ezen értékek rögzítését követően vagy az éppen kijelölt geometriai alakzatot (Build selected), vagy a teljes geometriai modellt (Build all) ábrázolhatjuk a rajzfelületre. Az alábbi táblázatban (Táblázat A.2) lévő alakzatokat adjuk hozzá a geometriai modellhez.
|
Alakzat |
Méret |
Pozíció |
Azonosító |
|---|---|---|---|
|
Négyzet |
l = 0,4 m |
Bal alsó sarok (0, 0) |
sq1 |
|
Kör |
r = 0,05 m |
Középpont (0, 0,2) |
c1 |
|
Kör |
r = 0,05 m |
Középpont (0,4, 0,2) |
c2 |
|
Kör |
r = 0,025 m |
Középpont (0,2, 0,2) |
c3 |
|
Kör |
r = 0,05 m |
Középpont (0,1, 0,1) |
c4 |
|
Kör |
r = 0,05 m |
Középpont (0,3, 0,1) |
c5 |
|
Kör |
r = 0,05 m |
Középpont (0,1, 0,3) |
c6 |
|
Kör |
r = 0,05 m |
Középpont (0,3, 0,3) |
c7 |
Az Táblázat A.2 utolsó oszlopában az egyes alakzatokhoz CM által automatikusan hozzárendelt azonosítókat láthatjuk (lsd. Geometry 1/Square (sq1)). Ezt követően végezzük el az alábbi Boolean-műveleteket:
-
képezzük a különbségét az sq1 és c2, c3 alakzatoknak, ehhez nyomjunk jobb egérgombot a Geometry 1 pontra, majd a menüben válasszuk ki a Boolean Operations/Difference menüpontot. A felső ablakhoz adjuk hozzá a négyzetet (sq1), az alsó ablakhoz pedig a jobbszélső (c2), illetve a négyzet közepén lévő (c3) kört. Az így létrejövő alakzat azonosítója dif1 lesz.
-
képezzünk úgy uniót az uni1 és c1 alakzatok között, hogy a belső peremeket nem tartjuk meg, ehhez az unióképzésnél (Boolean Operation/Union) vegyük ki a kijelölést a Keep interior boundaries sor elől. Az így létrejövő alakzat azonosítója uni1 lesz.
-
képezzünk uniót az uni1, c4, c5, c6, c7 alakzatok között a belső peremek megtartásával. Az így létrejövő alakzat azonosítója uni2 lesz.
Amennyiben a fentieknek megfelelően jártunk el, akkor az alább (A.8. ábra) látható alakzatot kapjuk eredményül.
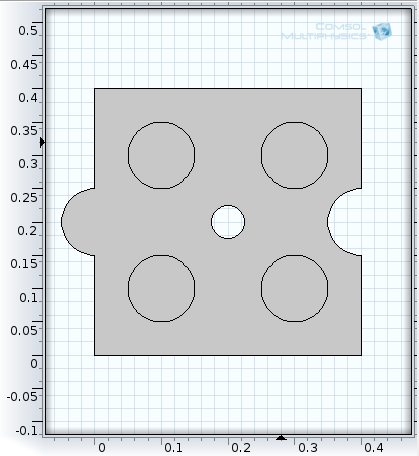
A geometria elkészítését követően, ahogy az fentebb (A.8. ábra) is látható, hogy öt tartományt (Domain) különböztethetünk meg, ezeket a program számokkal azonosítja (esetünkben 1-től, 5-ig). Ezekhez a Model 1/Materials pontra jobb egérgombbal kattintva, a CM adatbázisából rendeljünk hozzá anyagokat (Open Material Browser). Az adatbázisból (Built in), keressük ki a rezet (Copper) és a szilika üveget (Silica Glass), majd adjuk ezeket hozzá a modellhez (Add Material to Model). Miután az anyagok megjelentek a modellstruktúrában az anyagok alatt, hozzá kell ezeket rendelni a megfelelő tartományokhoz.
A rezet az 1-es, a szilika üveget pedig a többi tartományhoz kell rendelnünk, ennek érdekében töröljük a réz anyag hozzárendelései közül a 2-5 tartományokat, a szilika üveg anyag esetén pedig rendeljük ezeket hozzá. Amennyiben az egyes hozzáadott anyagok tulajdonságát módosítani szeretnénk, arra is itt van lehetőség. A program zöld pipával jelöli az anyag azon tulajdonságait, amely a tartományhoz való hozzárendelést követően, a modellben szereplő paraméterek megadásához szükséges. Abban az esetben, ha van olyan modell paraméter, amely nem áll rendelkezésre a tartományhoz rendelt anyag esetén, úgy azt a program a hiányzó paraméter megadásával fogja jelezni ezen a ponton. A modellbe épített hőmérleg esetén, a közeg hővezetési tényezőjének (Thermal conductivity – k), hőkapacításának (Heat capacity at constant pressure - cp) és sűrűségének (Density - ρ) megadására van szükség, amely látható, hogy mindkét kiválasztott anyag esetén rendelkezésre áll.
Miután minden tartományhoz rendeltünk anyagokat, amelyben rendelkezésre állnak a szükséges modell paraméterek, így ezek megadására nincs szükség (Model 1/Heat Transfer in Solids/Heat Transfer in Solids 1) alatt. Abban az esetben, ha nem rendelünk anyagokat a tartományokhoz, úgy ezen a ponton is rögzíthetjük ezeket. Ehhez az egyes tulajdonságok alatt/mellett lévő legördülő menükben válasszuk a felhasználó által definiált kifejezést (Used defined), majd az előbukkanó cellába adjuk meg az értéket, vagy a paraméterként definiált változó nevét.
A modellalkotás utolsó lépésében rögzítsük az megadott peremfeltételeket (Táblázat A.1), ehhez végezzük el az alább (Táblázat A.3) látható beállításokat a modellben. Jobb egérgombbal kattintva a Model 1/Heat Transfer in Solids pontra tudunk peremfeltételeket rendelni a mérlegegyenlethez. A 2-es peremcsoport esetén nincs szükség újabb peremfeltétel hozzárendelésére a mérleghez, ugyanis ez automatikusan felvételre kerül a hőmérleg alá, illetve az összes külső pereme a geometriának is hozzárendelésre kerül ehhez a peremfeltételhez. Ezen peremfeltételre kattintva láthatjuk, hogy vannak belső peremek (5-ös peremcsoport) is a geometriában, ezeket a program not applicable jelzővel látja el, azaz ezekre vonatkozóan nem kell rögzítenünk feltételt, ugyanis automatikusan egyenlővé teszi a program a perem két oldalán az állapotváltozókat. Amint felvesszük a több peremfeltételt és azokhoz peremeket rendelünk, úgy a Thermal Insulation 1 peremfeltétel esetén, ezen peremek mellett az overriden jelző jelenik meg, ami azt jelenti, hogy a sorrendben később álló peremfeltétel valamelyike ezt felülírta, és a modell megoldásánál az új peremfeltétel kerül figyelembevételére.
|
Peremcsoport |
Peremfeltétel |
Perem tulajdonsága |
Hozzárendelendő perem |
|---|---|---|---|
|
1 |
Temperature |
310 K |
7, 8 |
|
2 |
Thermal Insulation |
- |
1-6 |
|
3 |
Heat Flux |
500·(293-T) |
29, 30 |
|
4 |
Temperature |
360 K |
17-20 |
|
5 |
- |
- |
9-16, 21-28 |
A 3-as peremcsoport esetén meg kell jegyezni azt, hogy itt az adott peremen a tartományba befelé irányuló hőáram rögzítésére van lehetőség, azaz ennek megfelelően kell felírni a perem két oldala között létrejövő hőmérsékletkülönbséget, amely indukálja ezt a hőáramot. Esetünkben a környezet hőmérsékletéből (293 K) kell az objektum, a felírt hőmérleg alapján számított hőmérsékletét (T) kivonnunk. Gondoljunk bele, amennyiben az objektum hőmérséklete magasabb, mint a környezeté, így az így felírt hőmérsékletkülönbség negatív lesz, amely azt fogja eredményezni, hogy a hőátadási áramsűrűségre felírt összefüggés negatív lesz, azaz hő távozik a rendszerből. Ellenkező esetben a hőmérsékletkülönbség pozitív, amely pozitív hőátadási áramsűrűséget eredményez, azaz hő lép a rendszerbe a környezetből. Az 5-ös peremcsoport esetén, mivel ezek belső peremek, nincs szükség peremfeltétel megadására.
A modellalkotás fázisa ezzel befejeződött, következhet a modell megoldása. Először az előző példánál bemutatott módon alakítsuk ki a hálót az automatikus háló generálással. Jobb egérgombbal a Mesh 1 pontra kattintva előbukkanó menüből a Plot, illetve a Statistics menüpontokra kattintva láthatjuk a geometria felosztásának megfelelőségét és a kapott elemek minőségét (Element quality). Az egyik legfontosabb jellemző a minimális elem minőség (Minimum element quality), ugyanis elegendő egy rossz minőségű elem is, ahhoz, hogy a megoldásunk numerikusan instabillá váljon, s ne konvergáljon. Ebben az esetben az automatikus hálógenerálás mellett, normál (Normal) elem méretet rögzítve 2088 elemet kapunk, melyek átlagos jósága 0,9067, míg a legrosszabb elem jósága, 0,6926. A felosztást finomítva (Finer) nem nő jelentősen az elemek száma, mindössze 2464 elemre van szükség, azonban az elemek átlagos jósága 0,9519-re, míg a legrosszabb elem minősége 0,7047-re emelkedik. Jelen esetben ez elfogadható, ennek további javításához, vagy még kisebb elem méret beállítására van szükség az automatikus elemgenerálás esetén, vagy manuálisan kellene finomítani a geometria azon részeinek felosztásán, ahol az elemek minősége a legalacsonyabb. A megfelelő háló kialakítását követően indítsuk el a stacioner szimulációt, amely a számítógép teljesítményétől függően 5-30 s alatt be is fejeződik és az alább látható (A.9. ábra) stacioner hőmérsékleti képet adja eredményül.
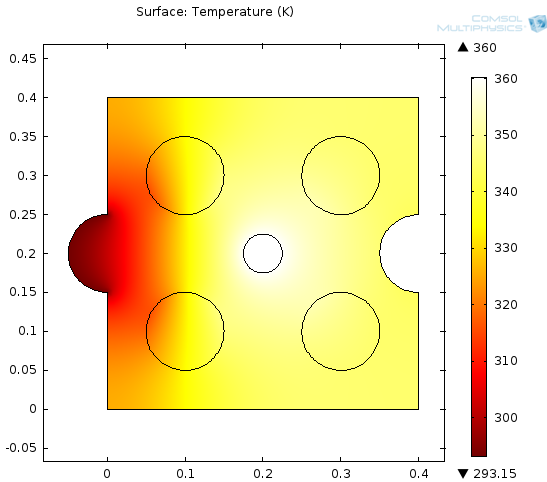
Feljebb (A.9. ábra) jól látható, hogy a vizsgált objektum legmelegebb rész a középső cső, amelyben a gőz kondenzálódik, míg a leghidegebb része az, ahol a környezeti hőmérséklet végtelen nagy hőátadási áram mellett csökkenti az objektum hőmérsékletét. A felület stacioner átlaghőmérsékletének meghatározásához az alábbi összefüggés megoldására van szükség:
|
|
(A.9) |
Mind a nevezőben, mind a számlálóban egy-egy felületi integrál számítására van szükség, ahol a számláló a hőenergia mennyiségét adja meg, míg a nevező a hőkapacitást adja eredményül. Esetünkben két anyagból álló objektumot vizsgálunk, amelyben lévő anyagok tulajdonságai nem függnek a hőmérsékletváltozásától, ily módon az összefüggés az alábbi formában írható fel:
|
|
(A.10) |
Ennek kiszámításához jobb egérgombbal kattintsunk a Results/Derived Values pontra, majd a megjelenő menüben válasszuk az Integration/Surface Integration menüpontot. Az összefüggést egyben nem tudjuk kiszámítani, így tagonként kell elvégeznünk a számítást, ehhez a megjelenő ablakbaa tartomány és az összefüggés beírását követően kattintsunk megjelenő ablak tetején lévő kiértékelés (Evaluate) gombra. Az alábbi táblázatban (Táblázat A.4) lévő módon végezzük a számítást.
|
Számítandó összefüggés |
Beírandó összefüggés |
Hozzárendelendő tartomány |
Eredmény |
|---|---|---|---|
|
385·8700·T |
1 |
1,434·108J/m |
|
|
385·8700 |
1 |
4.241·105J/K·m |
|
|
703·2203·T |
2-5 |
1,654·107J/m |
|
|
703·2203 |
2-5 |
4.865·104J/K·m |
A fentebbi táblázatban (Táblázat A.4) látható eredmények alapján már számítható az átlagos stacioner hőmérséklet:
|
|
(A.11) |
ami az A.9. ábra alapján hihető. A következőkben bemutatásra kerül, hogy hogyan tudjuk az átlag hőmérséklet időbeli alakulását számítani, ennek érdekében természetesen egy dinamikus vizsgálatot kell létrehoznunk, ennek érdekében jobb egérgombbal kattintsunk a Study 1 pontra jobb egérgombbal, majd az előbukkanó menüben válasszuk a Study Steps/Time Dependent menüpontot. Ezt követően a stacioner vizsgálatot deaktiválhatjuk (jobb egérgomb a Stationery ponton, majd Disable), vagy törölhetjük (jobb egérgomb a Stationery ponton, majd Delete) a vizsgálatok közül. A dinamikus szimuláció esetén állítsuk a szimulációs időt 1000 s-re, míg a mintavételezési időt 10 s-re.
Mielőtt elindítanánk a dinamikus szimulációt a fentebbi táblázatban (Táblázat A.4) lévő négy összefüggés számítására definiáljunk összefüggéseket. Mivel felületi integrálok is szerepelnek az összefüggésekben, ezért első lépésben ezeket kell felvennünk. Ehhez jobb egérgombbal kattintva a Model 1/Definitions pontra, majd Model Couplings/Integration menüpontot kell kiválasztanunk. A megjelenő ablakban felül adhatjuk meg a létrehozott függvény nevét (alapértelmezésben ez intop1), amellyel a későbbiekben meghívhatjuk az itt létrehozott függvényt. Ez alatt rögzíthetjük, hogy milyen típusú integrálási műveletet is szeretnénk elvégezni, esetünkben a felületi integrál számításához a Domain kiválasztása a megfelelő. Kiválasztási listához adjuk hozzá a réz tartományt. Vegyünk fel egy másik felületi integrált is a szilika üveg tartományokban való számításokhoz.
A felületi integrál függvények definiálását követően jobb egérgombbal a Model 1/Definitions pontra, majd a Variables menüpontot kiválasztva, hozzunk létre egy algebrai összefüggések definiálására szolgáló táblát. Itt a korábban, a paraméterek rögzítésére szolgáló tábla esetén megismerteknek megfelelően tudunk összefüggéseket definiálni, majd ezekre a későbbi számításokban az azonosítójuk alapján, hivatkozni. Az alábbi táblázatban (Táblázat A.5) látható összefüggéseket rögzítve számíthatjuk a felület átlaghőmérsékletét (Tatlag) adott időpillanatban.
|
Változó neve |
Beírandó összefüggés |
|---|---|
|
sz1 |
intop1(385·8700·T) |
|
n1 |
intop1(385·8700) |
|
sz2 |
intop2(703·2203·T) |
|
n2 |
intop2(703·2203) |
|
Tatlag |
(sz1+sz2)/(n1+n2) |
Ezt követően végezzük el a dinamikus szimulációt, majd a jobb egérgombbal a Results pontra kattintva, adjunk hozzá az eredményekhez egy egydimenziós ábracsoportot (1D Plot Group). Az ábracsoportra szintén jobb egérgombbal kattintva (Results/1D Plot Group 4), adjunk hozzá egy globális változók alakulását (Global) bemutató ábrát. Az ábrára pedig vegyük fel a Tatlag változó időbeli alakulását (Results/1D Plot Group 4/Global/y-Axis Data), s így a lentebbi (A.10. ábra) látható görbét kapjuk eredményül.
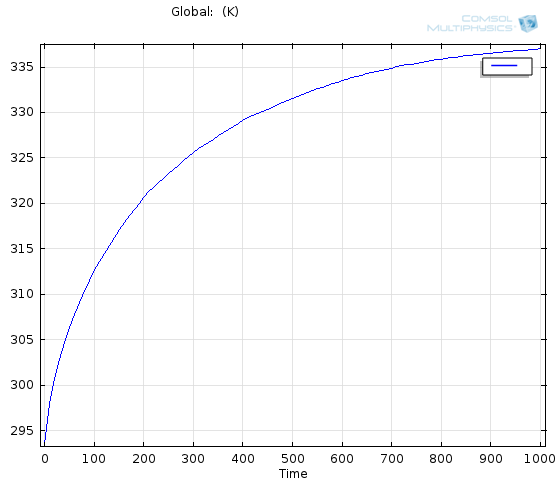
Fentebb (A.10. ábra) jól látható, hogy az átlaghőmérséklet időben nő, illetve az is látható, hogy 1000 s alatt sem jut el a rendszer a stacioner állapotba.
A.5. Vezetősínben kialakuló hőmérsékleti kép meghatározása (Joule törvény)
Ebben a részben arra látunk példát, hogy két különböző jellegű fizikai folyamat hatása a rendszer viselkedésére hogyan kezelhető egy CM modellben. Ehhez tekintsünk egy egyszerű példát, amelyben nagy áramok vezetésére alkalmas, ún. vezetősín háromdimenziós modelljét dolgozzuk ki. Lentebb (A.11. ábra) egy vezetősínre látunk példát.

Amikor egy homogén vezetőn elektromos áram halad keresztül, akkor az felmelegszik. A Joule törvény szerint a vezetőben felszabaduló hőmennyiség megegyezik a vezetéken keresztül folyó áramerősség négyzetének, a vezető elektromos ellenállásának és annak időtartamnak a szorzatával, amíg az áram keresztül folyik a vezetőn:
|
|
(A.12) |
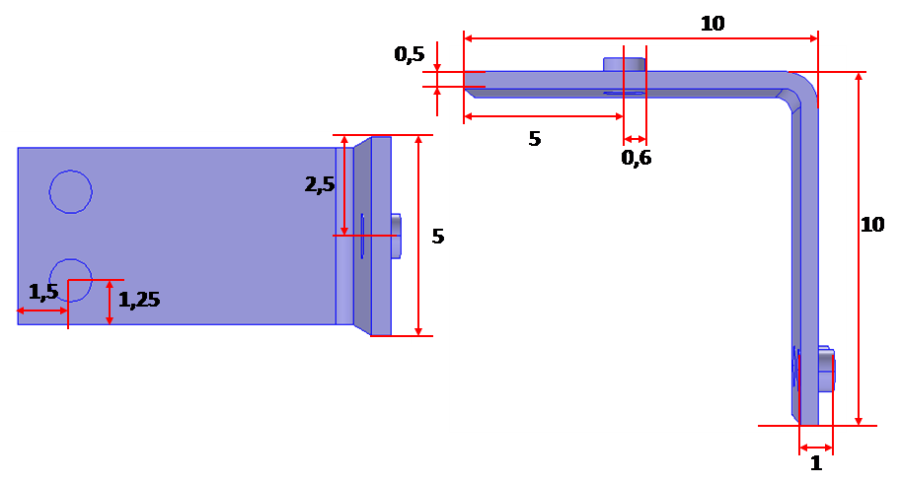
A vezetősínek főbb méreteinek meghatározásánál a legfontosabb szempont, az azon keresztül folyó áram. Alább (A.12. ábra) a vizsgált vezetősín főbb méretei láthatók centiméterben, emellett az is látszik, hogy ez esetben nem tudjuk csökkenteni a dimenziók számát, így a modellalkotás első lépésében a három dimenziót kell válasszuk. A feladat egy olya modell kidolgozása, amely alkalmas a vezetősínben kialakuló hőmérsékleti kép kiszámítására, ennek érdekében az előző példában alkalmazott hőmérleget egészítjük ki egy hőforrás taggal, amely hőáramot a Joule törvény alapján, az átfolyó áram alapján számítjuk.
A két különböző jellegű fizikai jelenség leírására használható modellek (elektromos vezetés – AC/DC/Electric Currents; hővezetés – Heat Transfer/Heat Transfer in Solids) integrált módon is elérhető a CM programban, ehhez a Heat Transfer/Electromagnetic Heating/Joule Heating összefüggéseket adjuk hozzá a modellhez. Mivel jelen példában a kialakuló stacioner hőmérsékleti képet kell meghatároznunk, így a modellegyenletek kiválasztását követően a stacioner vizsgálatot válasszuk, ezzel a modellalkotás előkészítő fázisát befejezve.
Egy háromdimenziós geometria létrehozása során a CM programban is lehetőség van, a más számítógépes tervező szoftverekben megismert munkasíkok létrehozására, majd ezekből kihúzással, vagy forgatással háromdimenziós testek létrehozására. Első lépésben hozzuk létre a sínt, amelyhez vegyünk fel egy munkasíkot jobb egérgombbal a Geometry 1 pontra kattintva, majd az előbukkanó menüben a Work Plane menüpontot választva. A munkasíkot a zx-síkban hozzuk létre. Ezt követően vegyünk fel két négyzetet, az egyiknek az oldalai 0,1 m, a másiké pedig 0,095 m legyen. A nagyobb négyzetből kivonva a kisebbiket, majd a sarkokat lekerekítjük (jobb egérgombbal a Geometry 1/Work Plane 1/Plane Geometry pontra kattintsunk, majd a felbukkanó menüben válasszuk a Fillet menüpontot). A belső sarokpont esetén 0,005 m-t, míg a külső sarokpont esetén 0,01 m-t alkalmazzunk. Ezt követően jobb egérgombbal a Geometry 1/Work Plane 1 pontra, majd a felbukkanó menüben válasszuk az Extrude menüpontot. 0,05 m távolságra húzzuk ki a munkasíkot.
A csavarok elhelyezéséhez szintén használhatunk munkasíkokat, az alábbi. táblázatban (Táblázat A.6) a három darab henger elhelyezéséhez szükséges méreteket és koordinátákat foglaltuk össze, valamint a henger forgástengely síkjának koordinátáit.
|
Henger |
Méretek (r, l) |
Koordináták (x, y, z) |
Tengely koordináták (x, y, z) |
|---|---|---|---|
|
1. |
(0,006, 0,1) |
(0,015, 0,0125, 0,0995) |
(0, 0, 1) |
|
2. |
(0,006, 0,1) |
(0,015, 0,0375, 0,0995) |
(0, 0, 1) |
|
3. |
(0,006, 0,1) |
(0,0995, 0,025, 0,05) |
(1, 0, 0) |
A geometriai modell bejezését követően definiáljuk a szerkezeti anyagokat az egyes tartományokba. A vezetősín rézből, míg a csavarok egy titán ötvözetből (Titanium beta-21S) készültek, rendeljük hozzá ezeket a megfelelő tartományokhoz.
Az 1. és 2. csavarok síntől távolabbi pereme (12 és 19 peremek) vannak földelve, míg a 3. csavar távolabbi peremére 20 mV elektromos potenciált kapcsolunk. A földelés megadásához jobb egérgombbal kattintsunk a Model 1/Joule Heating 1 pontra, majd az előbukkanó menüben válasszuk ki az Electric Currents/Ground menüpontot és rendeljük hozzá a megfelelő peremeket. Az elektromos potenciál az előzőekkel megegyező módon történik, de itt az Electric Potential peremfeltételt válasszuk és rendeljük hozzá a megfelelő peremet (43). A 20 mV megadásánál ne felejtsük el a szögletes zárójelet a mértékegység körül. Az objektum többi peremén egy környezet felé irányuló hőátadási áram indukálódik, ennek megadása az előző példában látott módon történik. Ez esetben a hőátadási tényező értéke 5 W/m2K, míg a környezet hőmérséklete 293 K.
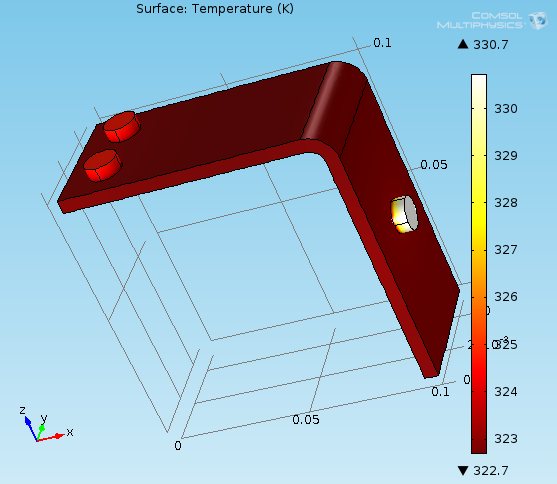
A modellalkotás fázisa a hőátadás peremfeltétel rögzítésével befejeződött, a hálógenerálást követően oldjuk meg a modellt. A számítás az alkalmazott számítógép teljesítményétől függően 5-20 s. A számított stacioner hőmérsékleti képet alább (A.13. ábra) láthatjuk. Ahogy az várható volt az objektum legmelegebb pontja azon csavar, amelyre a potenciált kötöttük. Mivel a földelés két, a harmadikkal megegyező méretű csavarra is rá lett kötve, így ezek esetén nem kell akkora hőmérsékletemelkedéssel számolni. Az így kapott szimulátor alkalmas vezetősínek főbb méreteinek meghatározására, a megismert modell pedig bármely elektromos vezető esetén melegedés számítására.
A.6. Mérőperemben kialakuló áramlás vizsgálata
A valós rendszerek üzemeltetése során nagyon fontos a megfelelő térfogatáram fenntartása. A folyamatos technológiák működésétől a csővezetékekben történő szállításig a gyártó technológiák szinte minden területén megjelennek áramlásmérő berendezések. Többféle módon mérhetünk térfogatáramot, vagy áramlási sebességet. Léteznek sebességmérő műszerek amelyek pontban, vagy síkban képesek a sebességértékek mérésére, mint például veloci, vagy anemométerek. Emellett a turbinás áramlásmérők valamilyen forgó elem segítségével mérik a térfogatáramot. A leggyakrabban használt módszerek a keresztmetszet változás kihasználásával működnek. A keresztmetszet változásával változni fog a sebesség, ez pedig a nyomás változásának mérésével jól nyomon követhető. A mérőperemek az áramlási sebesség mérésére szolgáló berendezések közé tartoznak. Alapvetően egy csőszűkítő elemet helyezünk el a csőben, és a perem előtti és utáni nyomáskülönbségből számítható az áramlási sebesség. Csőszerű geometriák esetében CM szoftverben alkalmazható az az egyszerűsítés, miszerint hengerszimmetrikus koordinátarendszert alkalmazunk, így kevesebb elemszámmal kisebb számítási teljesítmény mellett végezhetőek el a szimulációs vizsgálatok. A probléma alapvetően áramlási jellegű, és valamilyen áramlási modell segítségével írható le. Ebben a gyakorlatban egy mérőperemben kialakuló áramlási képet fogjuk meghatározni, valamint különböző módszerekkel megismerkedünk a CM különböző adatkinyerési eszközeivel, valamint parametrikus megoldó módszerekkel. A mérőperem, mint modellezett objektum segítségével tanulmányozhatóak az áramlási problémák. Az áramlás jellege miatt turbulens egyenletek beépítése is szükséges lehet.
Első lépésben definiáljuk a 2D axyssimmetric geometriát, majd a Fluid flow Single Phase Flow Laminar flow modellt. Mivel állandósult állapotban szeretnénk vizsgálni a rendszert ezért a Stationary menüpontot válasszuk.
|
Peremcsoport |
Peremfeltétel |
|---|---|
|
1 |
Szimmetriatengely |
|
2 |
Fal - nincs impulzustranszport a környezet felé, u=0 m/s |
|
3 |
Betáplálás (átlagsebesség u=uin) |
|
4 |
Elvétel (Súrlódásmentes nyomás elvétel p=0 Pa |
A geometriát és az alkalmazott peremfeltételeket az Táblázat A.7 és az A.14. ábra mutatja.
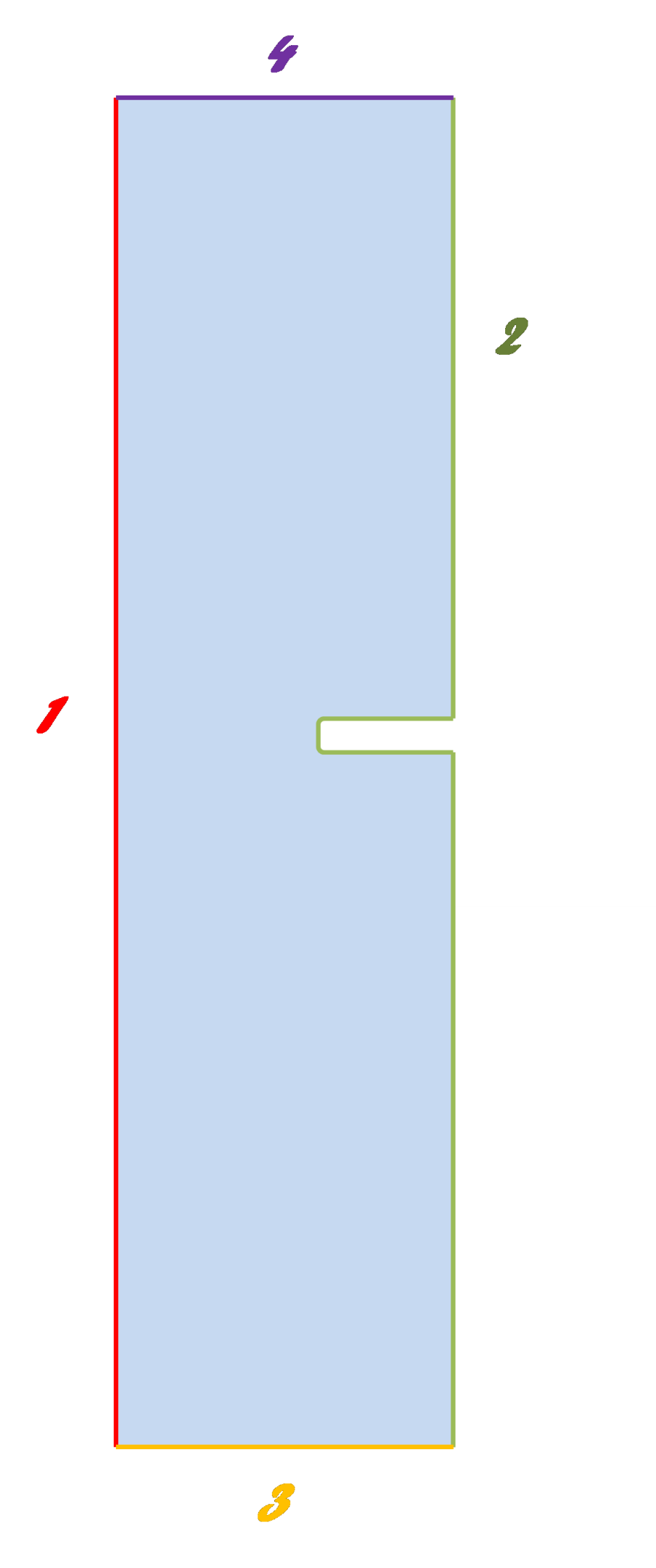
Az előzőekben megismerteknek megfelelően definiáljuk az anyagi tulajdonságokat Definitions/Variables fül alatt (rho=1000 kg/m3 eta=0.001 Pas). A betáplálási sebességet paraméterként definiáljuk a Global Definitions/Parameters fül alatt (uin=0.001 m/s). Ezáltal lehetővé válik a parametrikus vizsgálatnál a belépő sebesség használata paraméterként. A geometria esetében először a csövet kell megrajzolnunk (Rectangle-r1), majd az ebből kivágni kívánt peremet (Rectangle-r2). A harmadik lépés a két elem különbségének képzése, melyet a Geometry/Boolean Operations/Difference fülön érhetünk el. Figyeljünk rá, hogy felül (amiből kivonunk) a cső (r1), míg alul (amit kivonunk) a perem (r2) helyezkedjen el. Ezután már csak egy feladatunk van, a perem négyzetes felületének simítása, melyhez a Geometry/Fillet parancsot használjuk. A Fillet parancs sugaránál 0.01 m-t adjunk meg. Az egyes elemek pontos méreteit az Táblázat A.8 tartalmazza.
|
Alakzat |
Méret (l 1 ,l 2 ) |
Pozíció (r,z) |
Azonosító |
|---|---|---|---|
|
Téglalap |
(0,25 , 1) |
Bal alsó sarok (0, 0) |
r1 |
|
Téglalap |
(0,01 , 0,025) |
Középpont (0,15, 0,5) |
r2 |
Miután létrehoztuk a geometriát a következő lépés a modell paraméterek definiálása. A Laminar Flow/Fluid Properties fül alatt váltsuk át a Density és a Dynamic viscosity legördülő menünél User defined –re, és írjuk be a rho és eta változókat (amiket a korábbiakban definiáltunk). A Laminar Flow-ra jobb klikkelve adjunk hozzá egy Inlet peremet. Jelöljük ki a megfelelő peremet, majd a Velocity legördülő menü alatt a Normal inflow velocity alatt definiáljuk az uin paramétert. A Laminar Flow-ra jobb klikkelve adjunk hozzá egy Outlet peremet, majd jelöljük ki a megfelelő peremet. Ellenőrizzük, hogy az Axial Symmetry 1 peremen, valamint a Wall 1 peremeken minden adott tulajdonságú perem ki van jelölve. A Mesh és Study elemeket hagyjuk alapértelmezett értéken, majd a Study 1/Compute paranccsal futtassuk le a modellünket.
Amennyiben minden beállításunk megfelelő volt körülbelül 1 perc múlva az (A.15. ábra) ábrán látható sebességi mezőt ábrázoló diagramot láthatjuk.
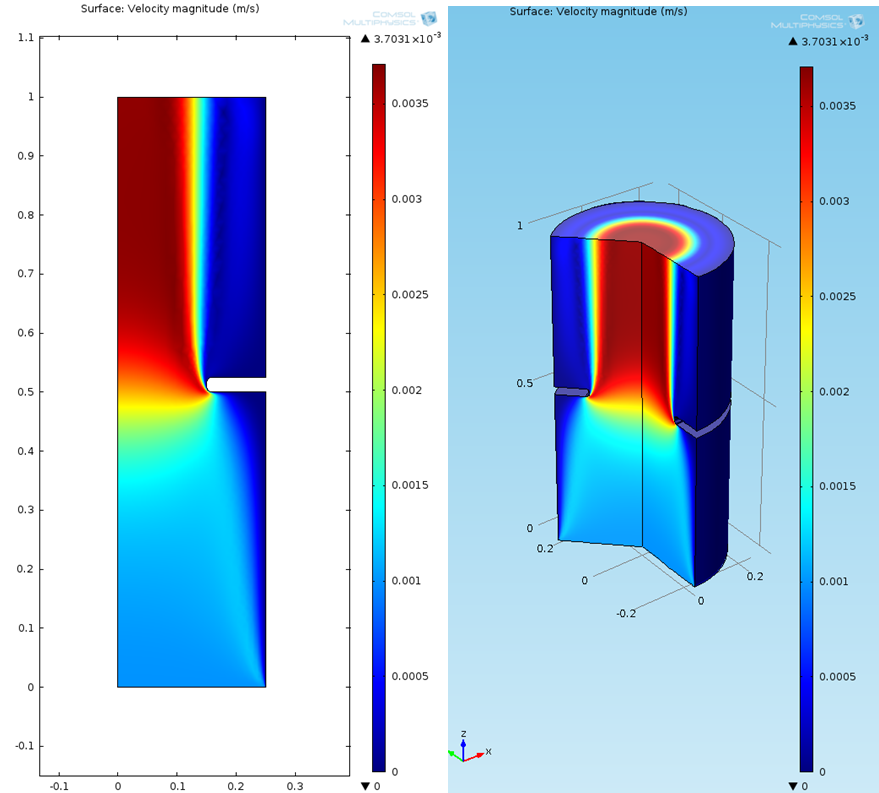
Szemléltetésképpen a hengerszimmetrikus ábra körbeforgatásával nyert (Velocity 3D fül alatt) látható ábrázolást is bemutatjuk az ábrán (A.15. ábra).
A következő lépésben állítsuk be a Parametrikus megoldó módszert. A Study 1/Parametric Sweep fülnél a Parameters name alatt klikkeljünk plusz jelre, ezáltal lehetővé válik a paraméterek hozzáadása, ahol adjuk hozzá az uin paramétert. Ezután a Parameter values list kitöltése következik. Klikkeljünk a jobb szélső Range ikonra. A Starthoz 0.001-es, a Stephez 0.001-et, a Stophoz pedig 0.01-et írjunk. A Study 1/Compute paranccsal futtassuk le a szimulációt. Az ábrán (A.16. ábra) figyeljük meg a megoldás menetét. A stacioner megoldó minden egyes paraméter értéknél kiszámítja a modell megoldását, majd lépteti a paramétert a parametrikus megoldóban.
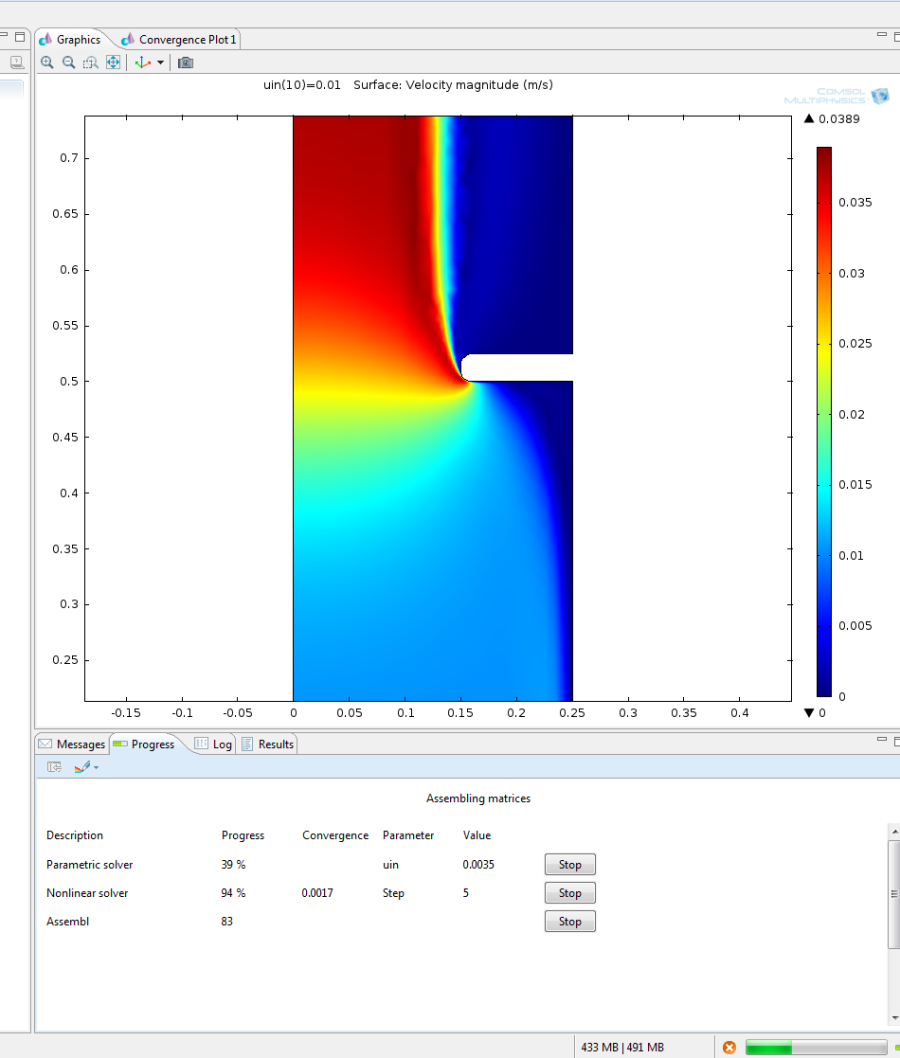
A következő lépésben vizsgáljuk meg a sebességértékek sugárirányú változását az egyes esetekben különböző metszeteknél. A Results/Data Sets menüpont lehetőségünk van különböző metszetek, megoldások definiálására. Választhatunk különböző pontokat, van lehetőség több pont, úgynevezett gridek definiálására a megoldásaink kiértékeléséhez. Természetesen az, hogy milyen kiértékelés választunk nagyban függ a tanulmányozott problémától, például pontszerű detektálás esetén érdemes a Cut point opciót választani. Mivel esetünkben egy sugárirányú metszetet szeretnénk számítani, ezért a Cut line opciót válasszuk. Természetesen a további választási lehetőség közül is választhatunk, azonban célszerű mindig az adott térdimenziónak megfelelő lehetőséget választani (Cut line 2D). A Point 2 r mezőbe írjunk 0.25-t, míg mindkét z mezőbe 0.5125-t, majd a plot paranccsal ellenőrizzük, hogy az általunk definiált vonal a perem közepén helyezkedik-e el. Amennyiben igen, akkor a Results/1 D Plot Group paranccsal definiáljunk egy vonalas ábrát. Jobb klikkeljünk az 1D plot Groupra, majd válasszul a Line Graph-ot. Az 1D Plot Group -nál a Data set legördülőmenüből válasszuk ki az előzőleg definiált Cut line 2D 1 metszetet, és hagyjuk a paramétereket alapértelmezett állapotban. A Plot ikonra kattintva ezután lehetőségünk van kirajzoltatni az ábrát, amely az egyes betáplálási sebességek függvényében mutatja a sebességprofilokat a mérőperemnél. Az adott rajzra specifikus beállításokat a Line Graph 1 fülön tehetjük meg. A Legends fület kibontva pipáljuk be a Show legends lehetőséget, majd ábrázoljuk újra a diagrammot. Természetesen van lehetőségünk párhuzamos metszetek definiálására, ezt a Cut Line 2D 1 – nél tehetjük meg bepipálva az Additional parallel lines jelölőnégyzet bepipálásával tehetünk meg. Azonban itt vigyázzunk, mivel a további párhuzamosok definiálása relatív, tehát a pozíciót az eredeti vonalhoz képest kell megadnunk. Definiáljunk összesen 5 párhuzamos metszetet -0.3 Start 0.15 Step és 0.3 Stop értékkel. Ebben az esetben Csak a legmagasabb sebességnél ábrázoljunk. A kapott eredményeket az A.17. ábra szemlélteti a középső metszet az összes sebesség paraméternél, valamint a párhuzamos metszetek a legnagyobb sebességértéknél.
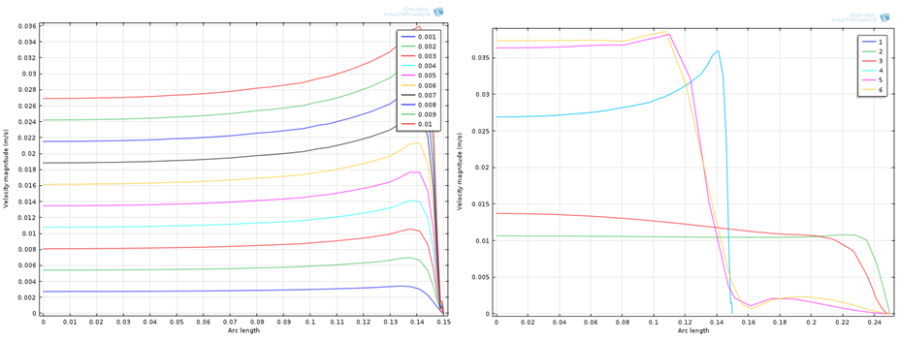
Sok esetben az alapszintű lamináris modellek nem képesek megfelelően leírni a berendezés belsejében lejátszódó folyamatokat, ilyenkor szükséges az áramlási jelleget jobban közelítő turbulencia egyenletek használata. A CM-ben a Reynolds átlagolt Navier-Stokes egyenletekkel leírt k-ε kétegyenletes turbulencia modellt alkalmazzuk a probléma leírására. A modell paramétereinek minimális változtatására van lehetőség. emellett a program támogatja más turbulencia modellek alkalmazását (k-ω modell, Spart-Allmanas modell), azonban bonyolultabb modelleket nem tartalmaz a turbulens áramlások leírására (pl. LES, vagy RSM modellek). A lamináris modellről turbulensre történő átváltás elég könnyen kivitelezhető CM-ben. Nem kell más tennünk, mint a Laminar Flow fülnél a Turbulence model type legördülő menünél kiválasztjuk a RANS (Reynolds averaged Navier-Stokes) egyenletet a None helyett. A modellünkre jobb klikkelve hozzunk létre egy új studyt, majd a Parameters fülön változtassuk 0.01 m/s-ra uin értékét, és futtassuk le a study 2-t.
A.7. Csőszigetelés vastagságának vizsgálata
Ebben a feladatban egy csőszigetelés vastagságának hatását vizsgáljuk a csőben létrejövő hőmérsékletprofilokra. A leképezett geometria belső része megegyezik az előző feladatban tárgyalt cső méreteivel. Ehhez adunk hozzá egy szigetelést, amit kerámiaként definiálunk. A peremeket az A.18. ábra, valamint Táblázat A.9 mutatja be. Alapvetően többféle folyamatot képezünk le. Lamináris impulzusmérleget alkalmazunk, mellyel a csőben való folyadékáramlást írjuk le (Laminar flow). Szükségünk van két további mérlegre a folyadékokban (Heat Transfer in Fluids - HTF), valamint a szilárd anyagokban (Heat Transfer in Solids - HTS) történő hőtranszport folyamatok leírására. A adott probléma definiálása és megoldása elvégezhető a CM GUI-ja használatával is, azonban ebben az esetben a Livelink to MATLAB (Livelink) használatát fogjuk bemutatni. A modell összeállítása, és egyszeri lefuttatása után. Válasszuk a File/Save Model as M file lehetőséget, és mentsük le a fájlunkat egy tetszőleges könyvtárba, természetesen követve a MATLAB előírásait a fájlnevekre.
|
Peremcsoport |
Peremfeltétel |
|---|---|
|
1 |
Szimmetriatengely |
|
2 |
Fal - nincs impulzustranszport a környezet felé, u=0 m/s Nincs hőtranszport a környezet felé |
|
3 |
Betáplálás (átlagsebesség u=0.001 m/s) Hőmérséklet (T=353 K) |
|
4 5 6 |
Elvétel (Súrlódásmentes nyomás elvétel p=0 Pa) Hőmérséklet kilépés Köztes perem a folyadék és a szilárd fázis között (A HTF modellben T=Tsolid, míg a HTS modelben T=Tfluid ) Külső hőmérséklet (T=293 K) |
A hőmérsékletként definiált peremek esetében az e végtelen hőátadási tényezőt definiáltunk. A megoldás stacioner, és mindhárom modellt együtt oldjuk meg. Erre azért van lehetőségünk, mivel mind a modellek, mind a közöttük lévő kapcsolatok nem túl komplexek. Figyeljük meg a Dependent variables változókat az egyes fizikai folyamatok leírásánál. Az impulzusmérlegnél a sebességvektorokat találjuk, valamint a nyomást, míg a hőmérlegeknél a mérlegekhez tartozó hőmérsékleteket. Ezeknek a változóknak akkor van a legnagyobb jelentőségük, amikor az egyes peremek közötti interakciót írjuk le. Így lehetséges például az impulzusmérleg megoldásának felhasználása a hőmérleg konvektív tagjának számítására. Hőátadás számításánál is felhasználhatóak ezek a függő változók, valamint minden esetben, amikor ábrázolunk, vagy valamilyen számítást végzünk ezekkel a változónevekkel tudunk hivatkozni az egyes modellek állapotjelzőire.
Az .m fájl létrehozása után indítsuk el a CM-et a with MATLAB végezetű ikonnal. Egy parancssor ablak fog megjelenni, ahol definiálnunk kell egy felhasználónevet és egy jelszót. Amint ezzel végeztünk, megnyílik egy MATLAB alkalmazás, ahol foglalkozhatunk a modellünkkel MATLAB környezetben. Célszerű függvényként használni a CM modellt, bemeneti paraméterként a falvastagságot, kimeneti paraméterként pedig a felületen integrált hőmérsékletet kapva. A továbbiakban a felhasznált kódot fogjuk feldolgozni, és áttekinteni, kiemelve a CM-ben megtalálható egyes részeket.
Az első lépés a függvény sor, ami tartalmazza a program nevét, a bementi változót (atm), valamint a kimeneti változót (h1). Ezután át kell alakítanunk a bemeneti változót szám változóból string változóra, mivel így tudjuk majd beírni a programba (a Livelink string változóként kezeli a változók egyes értékeit). A CM modell definiálása, valamint a munkakönyvtár beállítása a következő lépés.
function h1=program(atm)
atm=num2str(atm);
import com.comsol.model.*
import com.comsol.model.util.*
model = ModelUtil.create('Model');
model.modelPath(['L:\Proba);
model.modelNode.create('mod1');
Figyeljük meg az általános szintaktikát. A Livelink modellezés esetén az egyes parancsokat pontokkal választjuk el egymástól (model.modelPath). A CM-ben található azonosítók string változóként kerülnek definiálása (’Model’).
A modell létrehozása után a következő lépés a geometria létre hozása, a dimenzió, valamint a hengerszimmetria beállítása. Ezután létrehozzuk a modell egyes elemeit (mesh, fizikai folyamatok leírása, study stb.). Ez felel meg a CM felhasználói felületén a modellalkotás első lépéseinek, melyek a zászlóra való rányomásig telnek el.
model.geom.create('geom1', 2);
model.geom('geom1').axisymmetric(true);
model.mesh.create('mesh1', 'geom1');
model.physics.create('ht', 'HeatTransferInFluids', 'geom1');
model.physics.create('ht2', 'HeatTransfer', 'geom1');
model.physics.create('spf', 'LaminarFlow', 'geom1');
model.study.create('std1');
model.study('std1').feature.create('stat', 'Stationary');
model.study('std1').feature('stat').activate('ht', true);
model.study('std1').feature('stat').activate('ht2', true);
model.study('std1').feature('stat').activate('spf', true);
A következő lépések pedig teljesen azonosak a CM-ben történt egyes lépések leírásával. Definiáljuk a geometriát, két négyzetként. Ezután létrehozzuk parametrikusan a csőátmérő (atm), amit most már parametrikusan írunk be a megfelelő helyre. Ezután lérehozzuk a geometriát. Amennyiben ábrázolni szeretnénk ezt a geometriát az mphgeom parancs használata szükséges.
model.geom('geom1').feature.create('r1', 'Rectangle');
model.geom('geom1').feature('r1').setIndex('size', '0.25', 0);
model.geom('geom1').run('r1');
model.geom('geom1').run('r1');
model.geom('geom1').feature.create('r2', 'Rectangle');
model.geom('geom1').feature('r2').setIndex('size', 'dcso', 0);
model.param.set('dcso', atm);
model.geom('geom1').feature('r2').setIndex('pos', '0.25', 0);
model.geom('geom1').run('r2');
model.geom('geom1').run;
Az egyes fizikai folyamatok létrehozás, és paraméterezése következik. Szépen sorban definiáljuk az impulzusmérleg tartomány és peremfeltételeit. Ezután létrehozzuk a két hőmérleget, majd ezekkel kapcsolatban is definiáljuk a megfelelő peremfeltételeket. Az adott feature kijelölése után a peremfeltétel definiálása és számszerűsítése következik, majd ezután jelöljük ki a konkrét peremet. Figyeljük meg, hogy a szakasz utolsó sorában megjelenik a hőmérlegben az impulzusmérlegből számított sebesség, így kapcsolva össze a két modellt.
model.physics('spf').feature.create('inl1', 'Inlet', 1);
model.physics('spf').feature('inl1').selection.set([2]);
model.physics('spf').feature('inl1').set('U0in', 1, '0.001');
model.physics('spf').feature.create('out1', 'Outlet', 1);
model.physics('spf').feature('out1').selection.set([3]);
model.physics('ht').feature.create('temp1', 'TemperatureBoundary', 1);
model.physics('ht').feature('temp1').selection.set([2]);
model.physics('ht').feature('temp1').set('T0', 1, '353.15[K]');
model.physics('ht').feature.create('temp2', 'TemperatureBoundary', 1);
model.physics('ht').feature('temp2').selection.set([4]);
model.physics('ht').feature('temp2').set('T0', 1, 'T2');
model.physics('ht2').feature.create('temp1', 'TemperatureBoundary', 1);
model.physics('ht2').feature('temp1').selection.set([4]);
model.physics('ht2').feature('temp1').set('T0', 1, 'T');
model.physics('ht2').feature.create('temp2', 'TemperatureBoundary', 1);
model.physics('ht2').feature('temp2').selection.set([7]);
model.physics('ht').feature.create('ofl1', 'ConvectiveOutflow', 1);
model.physics('ht').feature('ofl1').selection.set([3]);
model.physics('ht').feature('fluid1').set('minput_velocity_src', 1, 'root.mod1.u');
Az anyagi jellemzők beállítása történhet többéle módon. Abban az esetben, ha paraméterként definiáljuk, vagy User Defined opcióval definiáljuk, akkor a megfelelő fizikai folyamatok leírásánál jelennek meg. Ha a beépített könyvtárból (Open Material Browser) vesszük az adott paramétert, abban az esetben egy eléggé szerteágazó, és terjedelmes adathalmazt kapunk. Figyeljük meg például a víz esetében (mat1) a polinomiális összefüggéseket, melyekkel az egyes tulajdonságok hőmérsékletfüggését írjuk le.
model.material.create('mat1');
model.material('mat1').name('Water');
model.material('mat1').set('family', 'water');
model.material('mat1').propertyGroup('def').set('dynamicviscosity', 'eta(T[1/K])[Pa*s]');
model.material('mat1').propertyGroup('def').set('ratioofspecificheat', '1.0');
model.material('mat1').propertyGroup('def').set('electricconductivity', '5.5e-6[S/m]');
model.material('mat1').propertyGroup('def').set('heatcapacity', 'Cp(T[1/K])[J/(kg*K)]');
model.material('mat1').propertyGroup('def').set('density', 'rho(T[1/K])[kg/m^3]');
model.material('mat1').propertyGroup('def').set('thermalconductivity', 'k(T[1/K])[W/(m*K)]');
model.material('mat1').propertyGroup('def').set('soundspeed', 'cs(T[1/K])[m/s]');
model.material('mat1').propertyGroup('def').func.create('eta', 'Piecewise');
model.material('mat1').propertyGroup('def').func('eta').set('funcname', 'eta');
model.material('mat1').propertyGroup('def').func('eta').set('arg', 'T');
model.material('mat1').propertyGroup('def').func('eta').set('extrap', 'constant');
model.material('mat1').propertyGroup('def').func('eta').set('pieces', {'273.15' '413.15'
'1.3799566804-0.021224019151*T^1+1.3604562827E-4*T^2-4.6454090319E-7
*T^3+8.9042735735E-10*T^4-9.0790692686E-13*T^5+3.8457331488E-16*T^6';
'413.15' '553.75' '0.00401235783-2.10746715E-5*T^1+3.85772275E-8*T^2-2.39730284E-11*T^3'});
model.material('mat1').propertyGroup('def').func.create('Cp', 'Piecewise');
model.material('mat1').propertyGroup('def').func('Cp').set('funcname', 'Cp');
model.material('mat1').propertyGroup('def').func('Cp').set('arg', 'T');
model.material('mat1').propertyGroup('def').func('Cp').set('extrap', 'constant');
model.material('mat1').propertyGroup('def').func('Cp').set('pieces', {'273.15' '553.75'
'12010.1471-80.4072879*T^1+0.309866854*T^2-5.38186884E-4*T^3+3.62536437E-7*T^4'});
model.material('mat1').propertyGroup('def').func.create('rho', 'Piecewise');
model.material('mat1').propertyGroup('def').func('rho').set('funcname', 'rho');
model.material('mat1').propertyGroup('def').func('rho').set('arg', 'T');
model.material('mat1').propertyGroup('def').func('rho').set('extrap', 'constant');
model.material('mat1').propertyGroup('def').func('rho').set('pieces', {'273.15' '553.75'
'838.466135+1.40050603*T^1-0.0030112376*T^2+3.71822313E-7*T^3'});
model.material('mat1').propertyGroup('def').func.create('k', 'Piecewise');
model.material('mat1').propertyGroup('def').func('k').set('funcname', 'k');
model.material('mat1').propertyGroup('def').func('k').set('arg', 'T');
model.material('mat1').propertyGroup('def').func('k').set('extrap', 'constant');
model.material('mat1').propertyGroup('def').func('k').set('pieces', {'273.15' '553.75'
'-0.869083936+0.00894880345*T^1-1.58366345E-5*T^2+7.97543259E-9*T^3'});
model.material('mat1').propertyGroup('def').func.create('cs', 'Interpolation');
model.material('mat1').propertyGroup('def').func('cs').set('funcname', 'cs');
model.material('mat1').propertyGroup('def').func('cs').set('interp', 'piecewisecubic');
model.material('mat1').propertyGroup('def').func('cs').set('extrap', 'const');
model.material('mat1').propertyGroup('def').func('cs').set('table', {'273' '1403'; '278' '1427';
'283' '1447'; '293' '1481'; '303' '1507'; '313' '1526';
'323' '1541'; '333' '1552'; '343' '1555'; '353' '1555'; ...
'363' '1550'; '373' '1543'});
model.material('mat1').propertyGroup('def').addInput('temperature');
model.material('mat1').set('family', 'water');
model.material('mat1').selection.set([1]);
model.material.create('mat2');
model.material('mat2').name('Alumina');
model.material('mat2').set('family', 'aluminum');
model.material('mat2').propertyGroup('def').set('thermalexpansioncoefficient', '8e-6[1/K]');
model.material('mat2').propertyGroup('def').set('heatcapacity', '900[J/(kg*K)]');
model.material('mat2').propertyGroup('def').set('density', '3900[kg/m^3]');
model.material('mat2').propertyGroup('def').set('thermalconductivity', '27[W/(m*K)]');
model.material('mat2').propertyGroup.create('Enu', 'Young''s modulus and Poisson''s ratio');
model.material('mat2').propertyGroup('Enu').set('poissonsratio', '0.222');
model.material('mat2').propertyGroup('Enu').set('youngsmodulus', '300e9[Pa]');
model.material('mat2').set('family', 'aluminum');
model.material('mat2').selection.set([2]);
Fontos, hogy megfelelően jelöljük ki az egyes tartományokat, hiszen ezek fogják meghatározni az anyagi jellemzőket.
model.physics('ht').selection.set([1]);
model.physics('ht2').selection.set([2]);
model.material('mat2').selection.set([2]);
model.material('mat2').propertyGroup('def').set('dynamicviscosity', {'1'});
Miután mindent definiáltunk, az utolsó lépés a megoldás előkészítése, és a módszerek beállítása. Alapértelmezetten is szükség van a solver (Stationary) definiálására, valamint a numerikus megoldók paramétereinek (például iterációk maximális száma, solver fajtája, kezdeti lépés) megadása. Ezután az attach paranccsal csatoljuk a megoldást a studyhoz, majd lefuttatjuk a modellt egybe számítva a három korábban említett mérleget.
model.sol.create('sol1');
model.sol('sol1').study('std1');
model.sol('sol1').feature.create('st1', 'StudyStep');
model.sol('sol1').feature('st1').set('study', 'std1');
model.sol('sol1').feature('st1').set('studystep', 'stat');
model.sol('sol1').feature.create('v1', 'Variables');
model.sol('sol1').feature('v1').set('control', 'stat');
model.sol('sol1').feature.create('s1', 'Stationary');
model.sol('sol1').feature('s1').feature.create('seDef', 'Segregated');
model.sol('sol1').feature('s1').feature.create('fc1', 'FullyCoupled');
model.sol('sol1').feature('s1').feature('fc1').set('initstep', 0.01);
model.sol('sol1').feature('s1').feature('fc1').set('minstep', 1.0E-6);
model.sol('sol1').feature('s1').feature('fc1').set('dtech', 'auto');
model.sol('sol1').feature('s1').feature('fc1').set('maxiter', 50);
model.sol('sol1').feature('s1').feature.create('d1', 'Direct');
model.sol('sol1').feature('s1').feature('d1').set('linsolver', 'pardiso');
model.sol('sol1').feature('s1').feature('fc1').set('linsolver', 'd1');
model.sol('sol1').feature('s1').feature('fc1').set('initstep', 0.01);
model.sol('sol1').feature('s1').feature('fc1').set('minstep', 1.0E-6);
model.sol('sol1').feature('s1').feature('fc1').set('dtech', 'auto');
model.sol('sol1').feature('s1').feature('fc1').set('maxiter', 50);
model.sol('sol1').feature('s1').feature.remove('fcDef');
model.sol('sol1').feature('s1').feature.remove('seDef');
model.sol('sol1').attach('std1');
model.sol('sol1').runAll;
A modell megoldása után lehetőségünk van különböző utófeldolgozási (Postprocessing) lépések elvégzésre. A Livelink esetében az egyes ábrákat a PlotGroup (’pg’) azonosítóval látjuk el. A PlotGroupok paraméterezését ugyanúgy a CM-ben megszokott elnevezéssel (Surface, Streamline stb. lehet definiálni). Létrehozunk egy numerikus integrálást, ami a kilépő peremen fogja a teljes felületre vonatkoztatott hőmérsékleti integrál értékét kiszámítani. A kapott eredményeket egy táblázatba íratjuk ki (tbl1), majd az utolsó sorban leírt getReal paranccsal átadjuk a kimeneti változónak, ami ezután tovább fogja adni a főprogramnak. A getReal parancs a táblázat valós részeit fogja átadni a programnak, így például az integrál neve (stringként) nem okoz további problémát, a változót számértékként tudjuk kezelni.
model.result.numerical.create('int1', 'IntLine');
model.result.numerical('int1').selection.set([3]);
model.result.numerical('int1').set('intsurface', 'on');
model.result.numerical('int1').set('expr', '1');
model.result.table.create('tbl1', 'Table');
model.result.table('tbl1').comments('Line Integration 1 (1)');
model.result.numerical('int1').set('table', 'tbl1');
model.result.numerical('int1').setResult;
model.result.numerical('int1').set('expr', 'T/0.19635 [m^2]');
model.result.table('tbl1').removeColumn(0);
model.result.numerical('int1').set('table', 'tbl1');
model.result.numerical('int1').appendResult;
h1=model.result.table('tbl1').getReal;
A legnagyobb előny a függvény alkalmazásában ebben az esetben az, hogy nem kell foglalkoznunk azzal, hogy az adott lépések milyen állapotban vannak a CM-ben, hiszen mindig újrahívjuk a CM-es modellt, így nem származik ütközés az egyes részek újra és újra létrehozásából. A főprogram pedig ezek után nem kell, hogy több adatot tartalmazzon legyen a falvastagságot tartalmazó vektornál, valamint egy ciklusnál, ami minden lépésben átadja a függvénynek a bemeneti paramétereket, valamint rögzíti és változóba gyűjti a kimeneti paramétereket.
D=0.1:0.01:0.5;
H=[];
for i=1:length(D);
atm=D(i);
h1=program(atm);
H(i)=h1;
end
A 6. gyakorlatban bemutatott metszetes ábrázolás természetesen ebben a feladatban is leképezhető. Definiálni kell a Data sets alatt egy új Cut line-t, majd beállítani a metszetet. Ebben az esetben a fal mellett definiálunk egy metszetet, és több paraméter értéknél vizsgáljuk a hőmérsékletprofilokat.
model.result.dataset.create('cln1', 'CutLine2D');
model.result.dataset('cln1').setIndex('genpoints', '0', 1, 0);
model.result.dataset('cln1').setIndex('genpoints', '0.24', 0, 0);
model.result.dataset('cln1').setIndex('genpoints', '0.24', 1, 0);
model.result.dataset('cln1').setIndex('genpoints', '1', 1, 1);
model.result.dataset('cln1').run;
Az ábrázoláshoz egy 1D PlotGroup-ra van szükség, aminek a segítségével vonalas ábrán tudjuk ábrázolni az adatsorainkat.
model.result.create('pg1', 'PlotGroup1D');
model.result('pg1').run;
model.result('pg1').set('data', 'cln1');
model.result.dataset('cln1').set('data', 'dset1');
model.result('pg1').run;
model.result('pg1').feature.create('lngr1', 'LineGraph');
model.result('pg1').run;
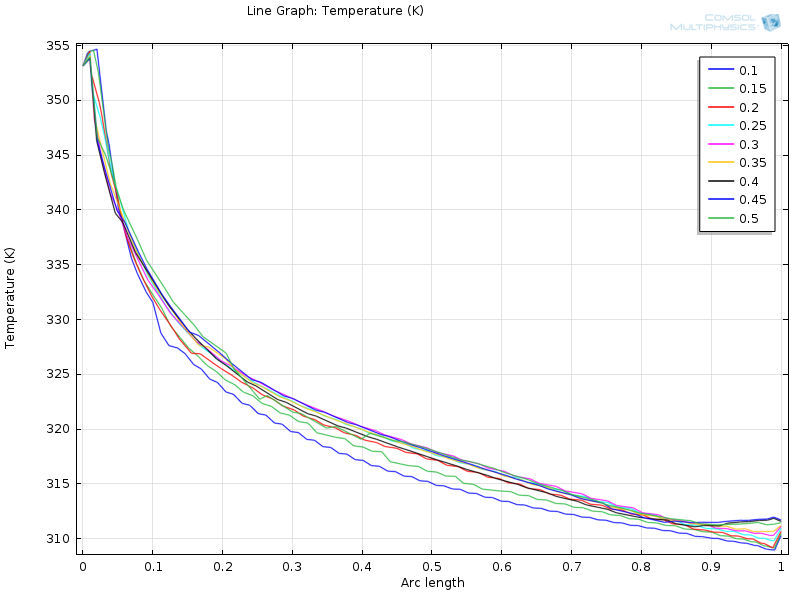
A kapott eredményeket ezután MATLAB környezetbe tudjuk leírni, így jóval kezelhetőbb adatsorokat kapunk. A kapott eredményeket az A.19. ábra szemlélteti. Látható, hogy a szigetelés vastagságának növelésével egy darabig nő a fal melletti hőmérséklet, majd elér egy közel állandó profilt, körülbelül 0.3 m vastagság után. Efölött a vastagság fölött már nincs hatása a szigetelés további növelésének.
Természetesen a Livelink alkalmazásának ez egy egyszerű példája volt. Használható bonyolultabb geometriák létrehozására, több paraméter vizsgálata, valamint még szélsőértékkeresési problémák megoldására is. Ami mindegyik esetben fontos, hogy gondoljuk át, és minél letisztultabb módon építsük meg a CM modellünket, majd ebből származtassuk az m fájlt. Ezt elősegíthetjük a CM File/Reset history menünpont alkalmazásával, melynek során az egyes tévutakat, valamint visszavonásokat, és újradefiniálásokat eliminálhatjuk a modellből.
A.8. Hőmérő elhelyezés vizsgálata
Ebben a komplex modellben felhasználjuk az eddig tanultakat a CM és a Livelink területén. Ezt a példát bonyolultsága miatt összegezve mutatjuk be a már ismert lépések kihagyásával. A tanult módszerek alkalmazásával, valamint az itt bemutatott kiegészítő lépések leképezésével a modell teljes egészében leképezhető.
A méréstechnikában hőmérő elhelyezés kapcsán ismert tény, hogy a hőmérőket áramlással szemben kell elhelyezni, minél jobban benyúlva az adott berendezésbe. Tipikusan csőkönyökökben szokták ezeket a hőmérőcsonkokat kialakítani. Ebben a feladatban különböző hőmérő pozíciók és kialakítások hatását vizsgáljuk a hőmérséklet mérés pontosságára. A fizikai rendszer esetében itt nem tehetjük meg azt az egyszerűsítést, hogy hengerszimmetrikus rendszer alkalmazunk, mivel ezt mind a csőkönyök, mind a hőmérő pozíciók vizsgálata kizárttá teszi. Az A.20. ábra a kialakított geometriát mutatja. A csőkönyök egyik oldalán betáplálunk, másik oldalán elvételt definiálunk. A mérőperemes példától eltérően itt nem tehetjük meg azt, hogy eltávolítjuk a törőlemezként viselkedő hőmérőcsonkot, mivel ebben az esetben a hőmérsékletmérés ezen a szilárd testen belül fog történni. A hőmérő elhelyezés vizsgálatához egy négyszögletű tartományt definiáltunk, ehhez a tartományhoz viszonyítva fogjuk vizsgálni a hőmérséklet mérés pontosságát.
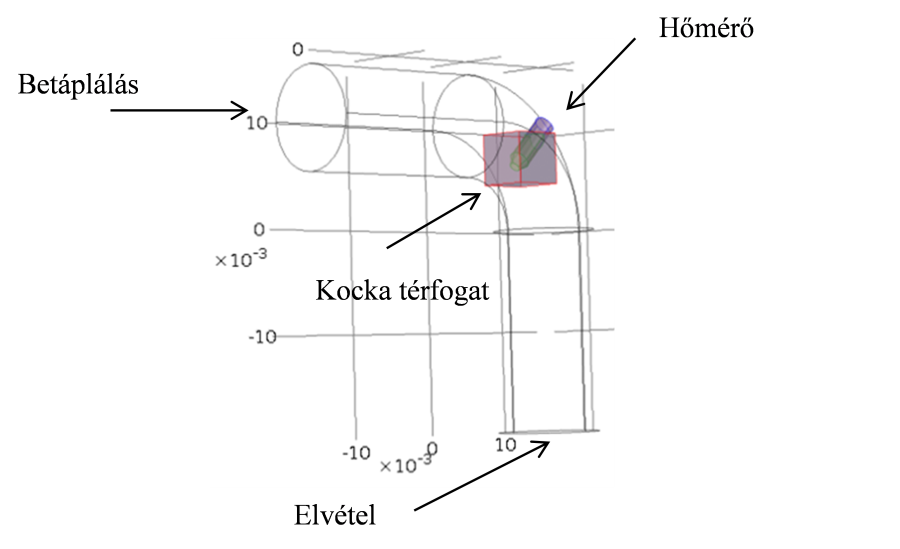
Áramló folyadékként vizet, a hőmérő szilárd anyagaként pedig rezet definiáltunk. Az anyagi tulajdonságok számításához ebben az esetben a CM program beépített anyagi tulajdonság könyvtárát alkalmaztuk. A következő paraméterek voltak szükségesek:
-
dinamikus viszkozitás (víz)
-
sűrűség (víz)
-
hővezetés (víz, és réz)
-
hőkapacitás (víz, és réz)
A hőmérséklet mérést egy úgynevezett Domain Point Probe definiálásával tehetjük meg. A hőmérséklet mérési pont definiálása a Definitions/Probes/Domain Point Probe paranccsal tehető meg. Ezek a pontszerű mérési lehetőségek nagyon jól használhatóak a hőmérséklet mérések mellett a modell futásának nyomon követésére. Alapértelmezett beállítás, hogy a pontszerű mérés változását a konvergencia diagramok mellett megjeleníti a program, így nyomon követhető az adott állapotváltozó változása, és nem megfelelő működés esetén leállítható a megoldás.
Ebben az esetben a nagyobb modell komplexitás, valamint a két mérleg jellege miatt két külön lépésre választjuk szét a megoldást. Az impulzusmérleget stacioner állapotban számoljuk, majd egy új megoldásban számítjuk a hőmérlegek megoldását egy dinamikus vizsgálatban végezzük. A dinamikus vizsgálatnál az impulzusmérleg változóit átvesszük a stacioner impulzusmérleg megoldásából (Study2/Time Dependent/Values of Dependent variables/Values of variables not solved for/Method=>Solution/Study=>Study1). Emellett a betáplálási hőmérséklet peremet lépcsőszerűen változtatjuk (Definitions/Functions/Step). Ezután lefuttatjuk a modellt, és elemezzük a dinamikus modell megoldását. Az A.21. ábra a) az áramlási képet mutatja a csőkönyökben, míg a b) ábra a hőmérsékleti képet mutatja. Mindkét modellt 3D-ben oldottuk meg, a 2D megjelenítés csak a jobb érthetőséget szolgálja.
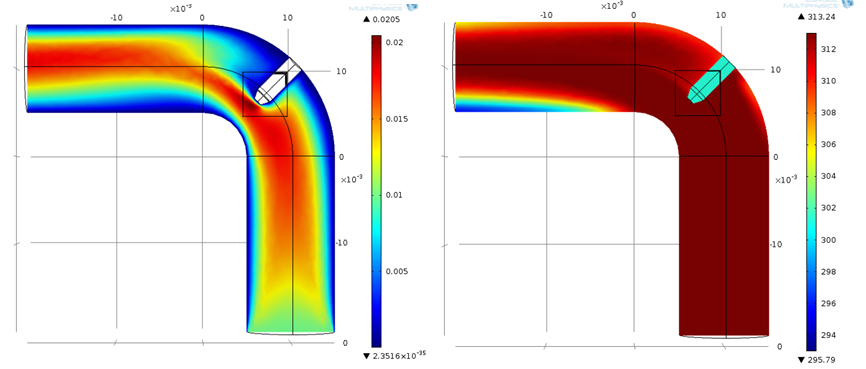
a) Az áramlási kép a csőkönyökben (m/s) . b) A hőmérsékleti tér a csőkönyökben (K)
A kifejlesztett modellben vizsgáltuk a mérési pont és a szondát körülvevő tér integrált hőmérsékletének a különbségét különböző betáplálási sebességeknél. Az eredményeket az A.22. ábra mutatja. Látható, hogy habár egy bizonyos sebességérték felett minimálisra csökken az eltérés, még mindig lesz valamennyi holtidő, amivel számolni lehet.
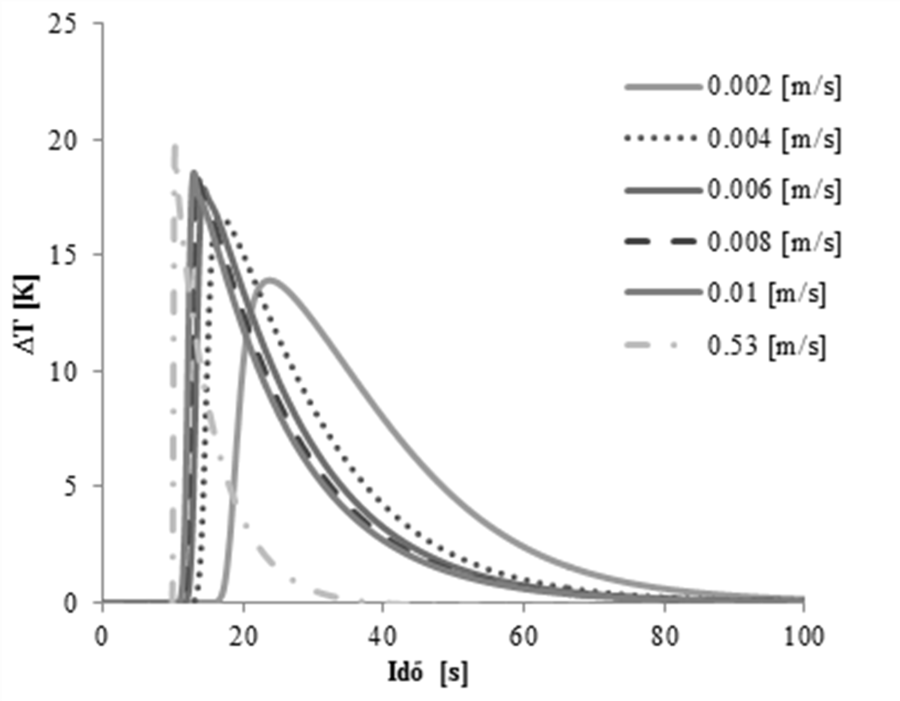
Az eredmények után tekintsük át azokat a külön részeket, amelyek megkülönböztetik ezt a modellt az előző feladattól. Az előző modell esetében egy egyszerű problémát oldottunk meg, ahol a geometria egy paramétere változott. Ebben az esetben három különböző szondageometriát vizsgálunk (sima, gömb, kúpos), valamint ezek különböző pozícióit. Ezek lesznek alapvetően azok a változók, amiket létre kell hozni. Ahhoz, hogy a geometriákat egyszerűen tudjuk kezelni, minden egyes szondaformát megrajzoltunk a CM felhasználói felületét alkalmazva (.mphbin kiterjesztés). Ezután ezeket a geometriákat fogjuk importálni a ciklus egyes lépéseiben. Emellett külön problémát jelent, hogy az egyes geometriák esetén különböző számú és azonosítójú peremet kell kezelnünk, ezért ezeket a peremeket definiálni kell minden egyes geometria esetén.
p=1;
n = {'gomb1.mphbin'};
x=3; % a különböző alakú elemek száma
for i2=1:x
q=num2str(i2)
k=horzcat('gomb',q)
k=horzcat(k,'.mphbin')
if i2==1
gomb_bound=[13 14 15 16 21 22 23 24];
gomb_bound_mesh_plot=[2 3 4 5 6 7 8 9 10 11 13 14 15 16 19 20 21 22 23 24];
elseif i2==2
gomb_bound=[13 14 15 16 19 22 23 24 25];
gomb_bound_mesh_plot=[2 3 4 5 6 7 8 9 10 11 13 14 15 16 19 20 21 22 23 24 25];
else
gomb_bound=[13 14 15 20 21];
gomb_bound_mesh_plot=[2 3 4 5 6 7 8 9 10 11 13 14 15 16 19 20 21];
end
Ami még újdonságot jelent az eddigiekhez képest az a Domain Point Probe definiálása. Ezt egy mérési pontot kell létrehozni a geometria megfelelő részén, majd társítani kell a megoldáshoz. Fontos megadnunk a koordinátáit ennek a mérési lehetőségnek, valamint a kiértékeléséhez egy numerikus értékelést (pev1) is létre kell hoznunk. Ezután a kapott eredményeket egy táblázatban tároljuk. Ami ebben az esetben különbség az előző példához képest, hogy itt nem függvényként kezeljük a CM megoldást, hanem egy fájlban számolunk. Így alkalmaznunk kell az egyes elemek eltávolítását (.remove) is, mivel minden esetben létrehozzuk az új elemeket (geometriát, hálót, megoldást stb.). Természetesen az itt közölt módszerek csak lehetőségek, többféleképpen oldhatunk meg egy adott problémát.
model.probe.create('pdom1', 'DomainPoint');
model.probe('pdom1').model('mod1');
model.probe('pdom1').setIndex('coords3', '0.01', 0, 0);
model.probe('pdom1').genResult('sol1');
model.result.numerical('pev1').set('table', 'tbl1');
model.result.numerical('pev1').set('innerinput', 'all');
model.result.numerical('pev1').set('outerinput', 'all');
model.sol('sol1').updateSolution;
model.probe('pdom1').genResult('sol1');
model.result.numerical('pev1').set('table', 'tbl1');
model.result.numerical('pev1').set('innerinput', 'all');
model.result.numerical('pev1').set('outerinput', 'all');
model.probe('pdom1').feature('ppb1').set('expr', 'T');
model.probe('pdom1').feature('ppb1').genResult('sol1');
model.result.numerical('pev1').set('table', 'tbl1');
model.result.numerical('pev1').set('innerinput', 'all');
model.result.numerical('pev1').set('outerinput', 'all');
model.result.numerical('pev1').setResult;
a=model.result.table('tbl1').getReal;
P(:,p)=a(:,2);
p=p+1;
Valamint az eredményeket itt egy futóindex segítségével számítjuk, és egy táblázatba gyűjtve tudjuk majd ábrázolni ebből a mátrixból.
A kapott eredmények azt a tapasztalatokat tükrözik, miszerint a megfelelő hőmérő pozíció az áramlási iránnyal szemben elhelyezkedő eset. Kiemelt szerepe a mérőegység kialakításának (gömb, sima, kúpos) nincsen. Természetesen ezek mellett a paraméterek mellett vizsgáltuk a betáplálási sebesség hatását is, azonban ezeknek az eredményeknek részletes bemutatására most nem térnék ki. Annyi mindenképpen kijelenthető, hogy a CM szoftver MATLABbal csatolva a következő előnyöket biztosítja:
-
stabilabb, gyorsabb működés
-
ciklusba szervezhetőség
-
az egyes változók, geometriák, valamint a teljes megoldás könnyebb manipulálhatósága
-
eredmények kiértékelése, vizsgálata részletesebb módon MATLAB környezetben
-
grafikák, diagramok vektoros kezelése
-
akár szélsőérték keresési és optimalizációs problémák megoldása kihasználva mindkét környezet lehetőséget
Ezáltal olyan keretrendszerek hozhatóak létre, melyek segítséget nyújthatnak komplex mérnöki feladatok megoldásában. Hátrányként talán a programnyelv sajátságait lehetne említeni, azonban könnyen belátható, hogy az egyfajta hibrid CM-MATLAB szintaktika nem bonyolult, valamint nem is tartalmaz olyan sok parancsot, ami miatt elsajátíthatósága nagy nehézségekbe ütközne.