9. fejezet - Golyósorsós átalakító dinamikai modelljei és tervezése
9.1. Golyósorsó átviteli tényezőjének meghatározása
Ez az energiaátalakító váltó, hiszen eltérő típusú fizikai rendszerek azonos típusú változóit köti össze. A golyósorsó, az egyéb menetes orsókkal ellentétben, olyan jó hatásfokkal rendelkezik (94-96%), hogy gyakorlatban is megközelíti az „ideális” átalakítót. Ha a hajtásláncban a hajtómű nem önzáró, azaz visszahatásmentes, akkor kimagasló hatásfok szükségesé teszi kikapcsolt állapotban az orsó megfelelő fékezését is.
A gyártók által közölt adatlapokon nem szerepel a váltó fontos jellemzőinek levezetése, csupán az értékeket közlik. Ezért a tervezéshez feltétlenül szükséges paramétereket bemutatjuk. A napjainkban, az internet által kínált lehetőségek mellett, a még elérhető nyomtatott katalógusok már nem mindig tartalmaznak magyarázó számításokat. Sokkal jellemzőbb, hogy a cégek, megfelelő díjazás ellenében, komplett számítási programokat bocsátanak rendelkezésre, ezek tartalmába viszont nem nyújtanak betekintést. Előfordul, hogy kínálnak ingyenesen letölthető 2D és 3D CAD rajzokat is, ezek megkönnyítik a konstrukcióhoz való illesztést, ilyeneket találunk például a www.thomsonlinear.com honlapon [9.1.].
Elsőként az átalakítási tényezőt kell meghatározni. A keresztváltozók közötti kapcsolat egyszerű, mert következik az orsó működéséből. Az átmenő változó esetében már óvatosabbnak kell lenni, nem szabad leegyszerűsítve kezelni az erő-erőkar és forgatónyomaték közötti összefüggést.
Az első ábra a golyósorsó géptervezésben szokásos jelölését mutatja, valamint a csapágyazásokat. Az orsót lehet az ábrán látható módon, de lehet csak az egyik végén is csapágyazni. Ezekre az esetekre a gyártók megfelelő faktorokat javasolnak figyelembe venni.

Az orsó menetemelkedését és a geometriából következő értékeket a (9.2. ábra) ábrán mutatjuk be.
Ideális esetet feltételezve írtuk, hogy az „Fs” súrlódó erő zérus. Alatta a keresztváltozók közötti kapcsolat látható. Ha az anya „x” értékkel mozdul el a hossztengely mentén, akkor ezt az elmozdulást az orsó „φ” szögelfordulása hozta létre. Az elmozdulást a „h” menetemelkedésre és a szögelfordulást a teljes „2π” körülfordulásra kell vonatkoztatni, és ebből az átalakítási tényező már adódik: h/2π. Ez a forma lehet reciprok is, esetünkben bemenetnek a forgást tekintjük.
A forgatónyomaték bemenő mennyiség és az anyára ható erő, mint kimenő mennyiség közötti kapcsolatot írja le a soron következő egyenlet. A nyomaték az orsó „r” közepes sugarán (ezen a sugáron támaszkodnak a golyók) „FK” kerületi erőt hoz létre. A keresett „FA” kimenő erő (anyára ható erő) és a kerületi erő közötti kapcsolatot a tangens szögfüggvény segítségével kapjuk. A hasonló háromszögek révén a kimenő (anyára ható) erő és a bemenő nyomaték között 2π/h lesz a kapcsolat.
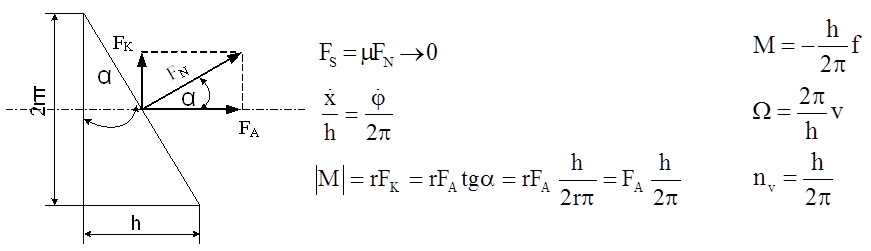
A gráf technikában szokásos módon, az átalakító egyenleteiben az átmenő változók között jelenik meg a negatív előjel, mintegy a négypólus bemenetek ellentétes irányultságának megfelelően. Értelmezhetjük ezt a visszahatás megjelenítéseként is.
Ha a golyósorsó bemenete nyomaték, illetve szögsebesség, akkor kapcsolat felírásához az alábbi formát célszerű választani:
Az ideális átalakító mellett modelleznünk kell a valós esetet is, mert az orsó-anya kapcsolat nyilvánvalóan rendelkezik eredő rugómerevséggel, nem elhanyagolható az orsó tehetetlenségi nyomatéka és a csapágyazások súrlódási tényezője sem.
9.2. Golyósorsós átalakító rugómerevségének számítása
Tervezés szempontjából a legtanulságosabb az eredő rugómerevség meghatározása. Nem mindegy, hogy a számítások során milyen rugalmasságokat veszünk figyelembe, de még ennél is fontosabb az, hogy a rugalmasságok eredőjét milyen módon állapítjuk meg. A katalógusokban általában az alábbi képletet közlik, ha egyáltalán szerepelnek ilyen részletes számítások. A rugómerevség jelölését meghagytuk, azonban a jegyzetünkben a „c” helyett a „k” a szokásos jelölés. A rugómerevségek alatt minden esetben transzlációs, axiális irányú (a pozícionálási hiba miatt ez a lényeges) rugómerevséget, vagy az erre történő átszámított értékeket értenek a katalógusok:
Ahol
|
ca |
anya-orsó kapcsolat közötti rugómerevség (függ attól, hogy osztott, vagy szimpla anyával dolgozunk) |
|
|
ceff |
az orsó effektív rugómerevsége, amely katalógus adat |
|
|
ccs |
a csapágy rugómerevsége, katalógus adat, vagy méréssel meghatározható |
|
|
ck |
az orsót befoglaló keretszerkezet rugómerevsége, amely legcélszerűbben végeselem számítással, vagy méréssel határozható meg. |
Néhol kisbetű, néhol nagybetű a jelölés, az előbbi transzlációs, az utóbbi általában rotációs rugómerevséget takar. A két forma között nem jelent gondot az átszámítás, hiszen az átalakítási tényező ismert.
Kérdés, hogy alkalmazható-e ez az összefüggés akkor, ha pozicionáló rendszert építünk? Mit takar ez az eredő számítás?
A katalógus szerinti eredő képlete gráfon ábrázolva a következő képen látható rendszert modellezi, azaz a sorosan kapcsolt rugómerevségek adják a katalógus szerinti eredőt.

Ez az eredő azt modellezi, hogy egy végtelen merevnek tekintett alapra elhelyezett, és keretbe csapágyazással foglalt orsón mozgó anya milyen rugalmassággal rendelkezik az alaphoz képest. Az anya alaphoz viszonyított sebességét vki-vel jelöltük. Ez a merevség a terhelhetőség miatt fontos a konstruktőr számára, és fontos a szabályozás pontossága szempontjából is, de a szabályozókör tervezésében is szerepet játszik.
A rendszert a következő ábrán mutatjuk be. A rajzon bizonyos nézetvonalakat és egyéb rajzi jelöléseket elhagytunk, hogy a lényeg bemutatását ne zavarják.
A vázlaton a tengelykapcsoló rugómerevségén kívül bejelöltük a katalógus szerinti transzlációs rugómerevségeket. A „v0” és „v1” sebességekkel és csomópontokkal azt illusztráltuk, hogy a csapágy és a keret rugalmassága (kcs és kk) miatt a tengely az alappal párhuzamos elmozdulásra képes, és ez iránya szerint hozzáadódik, vagy levonódik az anya pozíciójából.
Ez a jelenség „normál üzemben” nem jelentkezik, csak akkor, ha az asztal véghelyzetbe ütközik, és az orsó forgatása nem áll le. Szerepe lehet még a rezonancia hajlam meghatározásánál is, de ezt minden konstrukcióra külön kell elemezni. A modellezés során éppen ezért ennek a két rugómerevségnek a soros eredőjét „ke1” formában jelöltük, és végtelen nagynak fogjuk majd tekinteni.
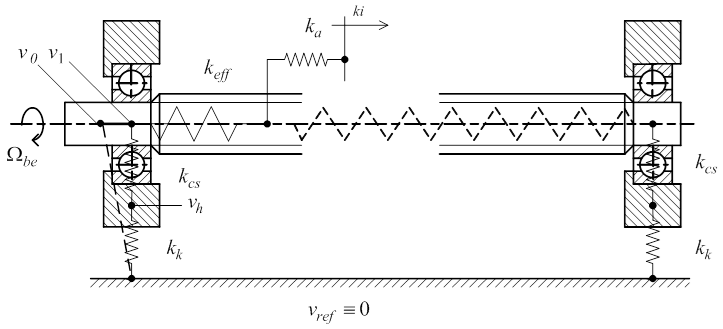
Az orsó torziós rugómerevsége helyett a katalógusok az átszámított transzlációs merevséget adják meg. Az előfeszített anya rugalmassága természetesen transzlációs.
A szerkezeti vázlat alapján készült a következő képen látható gráf. Ezen a gráfon egyszerűsítések nélkül, minden fontos paraméter és azok kapcsolódása megtalálható. A katalógusban szereplő egyenes vonalú rugómerevségekhez képest itt még vegyesen látunk forgó és egyenes vonalú elemeket, valóságos funkciójuknak megfelelően. Az átszámítás a szokásos módon természetesen lehetséges, és ezért a katalógus egyenes vonalú rugómerevség értékei felhasználhatóak.
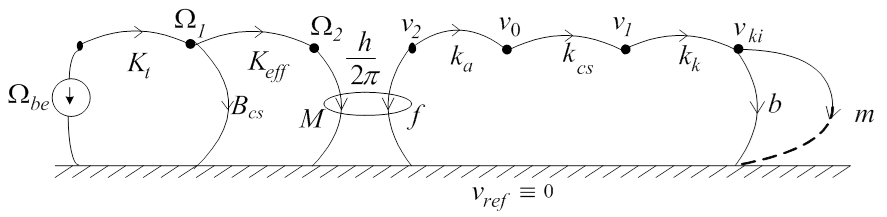
A bemenő mennyiség szögsebesség, általában a hajtómű kimenő mennyisége, ez egy torziós rugalmassággal is bíró tengelykapcsolóra kerül. A tengelykapcsoló szerepe a szög-és tengelyhiba kiegyenlítése. Ezután az orsó torziós rugómerevsége következik, és bejelöltük a csapágysúrlódást modellező „Bcs” csillapítási tényezőt is. Az előfeszített, kettős anya egyértelműen transzlációs rugómerevségéhez kapcsolódik a mozgatott asztal tömege és az egyenes vezeték súrlódását modellező csillapítási tényező. A szerkezeti vázlaton bejelölt két rugómerevséget, a csapágy és a keret két transzlációs irányú rugalmasságát, amelyek az asztal pozíciójában hibát okozhatnak, az anya rugalmasságával sorosan tüntettük fel, ahogy ezt korábban már jeleztük. A kétség kívül transzlációsként modellezhető rugalmasságokat egy váltó segítségével kötjük a tengelykapcsolóhoz. Vigyázat, a sebességek ebben az esetben nem kerületi sebességek, hanem az orsó (keret és csapágy rugalmasság okozta), illetve az anya transzlációs sebességét jelentik!
Annak érdekében, hogy az itt bemutatott tervezési modell ne csak elméleti fejtegetés maradjon, felhasználjuk az egyik gyártó régebbi, nyomtatott katalógusában szereplő méretezési útmutatásokat [9.2.]. A katalógusok általában a transzlációs rugómerevség számítására adnak módszert (N/μm). Ennek oka nyilvánvaló, és az eredő rugómerevség meghatározásának módjában keresendő, hiszen az anya transzlációs pozícionálási hibáját, illetve a mozgatott tömeg transzlációs rezgéseit észleljük, mint dinamikus pozícionálási hibát.
A gráfot átalakítjuk, és a torziós rugómerevségeket a váltók kiiktatásával transzlációsként modellezzük.
Az anya rugómerevségének meghatározása
-
Előfeszítés nélküli, szimpla anya esetében:
Ahol
N
az anya aktív menetszáma: 2,3,4,5,6,8
FN
feladat szerinti axiális erőterhelés
fm1
merevségi tényező a gyártótól (29,6 … 51,4)
fm2
merevségi tényező előfeszítetlen anyánál: 0,3
-
Előfeszített, kotyogásmentes (kettős) anya esetében:
A képlet változatlan, fm1 merevségi tényező is.
fm2
merevségi tényező: 0,6
FN=2,38 Fe
ahol Fe a feltételezett maximális axiális terhelés, erre méretezik az anya előfeszítését
N
az osztott anya aktív menetszáma: 2-2, 3-3, 4-4, 5-5, 6-6
Az orsó effektív rugómerevségének kiszámítása
A gyártó a következő képletet adja a merevség kiszámításához:
Ahol
|
f0 |
korrekciós faktor: 4, ha csapágyazás mindkét tengelyvégen, 1, ha csak az egyiken |
|
|
d1 |
orsó külső átmérője mm-ben |
|
|
d2 |
orsó magátmérője mm-ben |
|
|
l |
szabad orsóhossz mm-ben |
A csapágy rugómerevsége katalógus adat (de nem állandó, hanem függ a terheléstől), a keret rugómerevségét pedig legcélszerűbb a „drótmodellen” végzett mérésekkel ellenőrizni, de becsülhető végeselemes modellezés útján is. A csapágyak „Bcs” csillapítási tényezőjét a modellezésben nem vettük figyelembe, mert hatása az egyenes vezetésből adódó csillapításhoz képest elhanyagolható, figyelembe vételével ugyanakkor a számítás lényegesen bonyolultabbá válna.
A tervezésbe szükségszerűen be kell vonni a hajtómű kimenő tengelyét a golyósorsóval összekötő tengelykapcsolót. Különösen kisebb méretek esetén fordulhat elő, hogy a fenti rugómerevségeknél lényegesen kisebb a tengelykapcsoló torziós rugómerevsége. Ezeknek általában kettős szerep jut, ki kell egyenlíteniük a tengely-eltérést és az esetleges szöghibát. Úgy tervezik őket, hogy kellő torziós merevség mellett ennek a két hibának a kiküszöbölésére alkalmasak legyenek. A gyakorlati kivitelük általában csőmembrán-szerű, hullámos profillal, vagy vastag falú, hengeres, 120 fokkal eltolt bemetszésekkel. Tekintettel arra, hogy a legkisebb rugómerevség lesz a mértékadó, a tengelykapcsolót nem lehet figyelmen kívül hagyni a tervezés során.
A tengelykapcsoló még torziós rugómerevségként szerepel, hogy az átviteli függvény csomóponti módszerrel történő felírásához olyan rendszert kapjunk, amelyben a csomópontok függősége didaktikai okok miatt bemutatható.
A következő ábrán már egy olyan egyszerűsített gráf látható, amelyen „Bcs” nem szerepel, de még számolunk a „ke1” rugómerevség hatásával a rezonanciahajlam vizsgálatában.

A két csomóponti változó, Ωbe és vbe ugyanis nem függetlenek, így a hozzájuk kapcsolódóan felírható csomóponti egyenleteket egymásba kell majd helyettesíteni, a két változó közül csak az egyik maradhat.
A két soros eredő rugómerevséget össze kell vonni, és az eredőjüket a továbbiakban ke-vel fogjuk jelölni.
Elsőként határozzuk meg a rendszer átviteli függvényét csomóponti módszerrel, hiszen a keresett kimenő mennyiség keresztváltozó.
9.3. Átviteli függvény felírása csomóponti módszerrel
A 9.2. szakasz kiindulásnak tekinthető gráfját ebben az esetben szándékosan nem redukáltuk, hogy a csomópontok közötti összefüggés nyilvánvalóvá váljon.
A gráfon látható csomóponti változók Ωbe, vbe és vki. Valójában nincs három független változó, csak kettő, mert Ωbe, és vbe lineárisan összefüggenek, és ez az egyenletek egymásba építése során nyilvánvalóvá válik. A három csomóponti változóra felírt csomóponti egyenletek, valamint a két váltó egyenlete a következő:
A forgó rendszerrészhez tartozó egyenletet beépítjük a váltó csomóponti változók közötti összefüggésébe és felhasználjuk a keresztváltozók közötti egyenletet is:
A második és a harmadik csomóponti egyenlet a behelyettesítés után:
A továbblépéshez szükséges a Laplace transzformáció, mert így kapunk algebrai egyenletrendszert. Végül a mátrixos felírási mód:
Rövid dimenzió ellenőrzés után tovább lehet lépni. Az admittancia mátrix a11 eleme tulajdonképpen 2 db párhuzamosan kapcsolt rugómerevség eredő admittanciája, tehát a rugómerevségek összeadhatóak, de egy gyakorlati tanács: A inverz mátrix determinánsában (nevező) csak akkor látjuk a negatív előjelű tag „eltűnését”, ha a rugómerevségekkel külön-külön végezzük el a beszorzást, tehát az ilyen összevonásokat „nem kell elsietni”. Az következő egyenletben a redukció révén Kt–t transzlációs paraméterré számítottuk át, ez viszont célszerű:
Esetünkben csak a Vki(s) változó keresett, ezért célszerű a Cramer szabályt alkalmazni. A nevező miatt nem vontuk össze a rugómerevségeket:
A kijelölt műveletek elvégzése után az átviteli függvény egy lehetséges formáját alakítjuk ki úgy, hogy a két rugómerevség eredőjét most behelyettesítjük a kapott összefüggésbe.
A nevező operátortól független tagjával osztjuk a tört számlálóját és nevezőjét, ezzel a szokványos szabályozástechnikai alakot kapjuk:
A rendszer linearizált paraméterekkel másodrendű, de jól látható, hogy az átviteli függvényben két rugómerevség soros eredője szerepel:
Az átviteli függvény igen egyszerű alakot mutat, de nem szabad elfelejtenünk, hogy a paraméterek (m, b, k) összetett számítások eredményeként születtek.
9.4. Átviteli függvény felírása impedancia módszerrel
A 9.2. szakasz végén látható gráfon, a váltó baloldalán álló forrást és torziós rugómerevséget célszerű a jobb oldalra redukálni, átszámítani, ha impedancia módszerrel keressük a matematikai modellt.
Nagyon fontos kiemelni, hogy a transzlációs rendszerré egységesített rendszerben Vh forrás szerepel, és ez nem azonos a Ωh-val! Ennek az új forrás értéknek a kiszámítását igen gyakran elfelejtik, és ebből komoly hiba származik.
Látható, hogy a „ke1” rugómerevséget a modellben végtelen nagynak tekintjük, ezért a gráfon már nem szerepel.
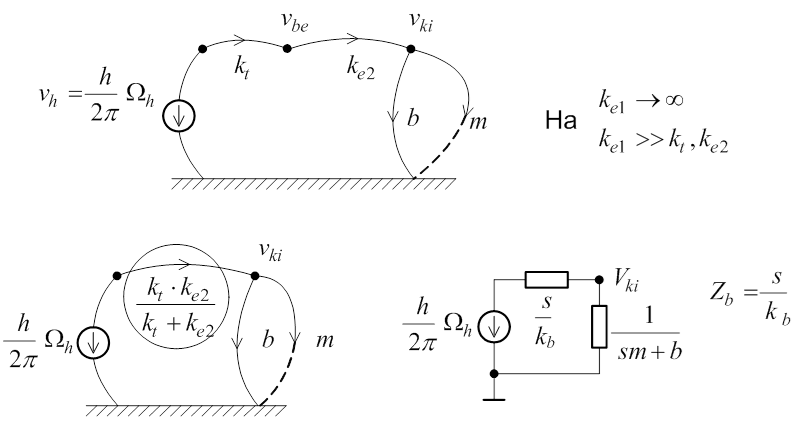
A csomóponti módszerrel kapott eredménnyel való összehasonlítás kínálkozik, ha felírjuk a keresztváltozó osztót, ami valójában a keresett átviteli függvény:
Láttuk már korábban, hogy törekedni kell a szabályozástechnikában alkalmazott átviteli függvény alakra, ezért végül az alábbi formát kapjuk:
Jól látható, hogy a két módszerrel kapott eredmény azonos. Az átviteli függvényből az állapottér modell visszavezetett (normál) alakja könnyen felírható, és ugyancsak felírható inverz Laplace transzformálás után vki(t)-re a másodrendű állandó együtthatós, lineáris differenciálegyenlet.
Ha a golyósorsós átalakítót pozícionálási feladatra alkalmazzuk, akkor az átviteli függvényt „Xki” változóra kell felírni, és tekintettel arra, hogy a sebesség és az elmozdulás között egy integrálási művelet van, az átviteli függvény nevezőjében megjelenik szorzóként az „s” operátor.
Szakirodalom
[9.1.] www.thomsonlinear.com.
[9.2.] Kugelgewindetriebe. FAG Lineartechnik.