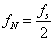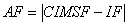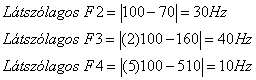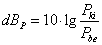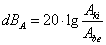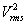8. fejezet - Bevezetés a digitális jelfeldolgozásba és analízisbe

A részletes elemzést végző könyvtáraknak az a feladatuk, hogy bejuttassák a berendezésekbe a nyers mérési adatokat. A nyers mérési adatok amint azt a 8.1. ábra ábra mutatja, nem mindig csak a közvetlen az információt hordozzák. Gyakran át kell alakítanunk a jelet, el kell távolítanunk belőle a zavarjeleket, ki kell javítanunk a hibás részeket, kompenzálnunk kell a káros környezeti hatásokat, mint például a hőmérséklet és a páratartalom változásának következményeit.

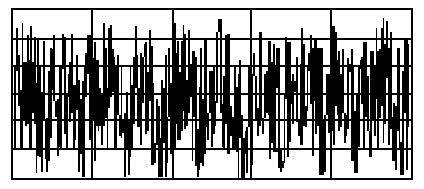
A digitális jel feldolgozásával és analízisével tudjuk „kibányászni” a felhasználható információt a zavarjellel terhelt mért jelből, és megjeleníthetjük egy olyan függvényként, amely jobban érthető, mint a nyers bejövő adatok (8.1. ábra).

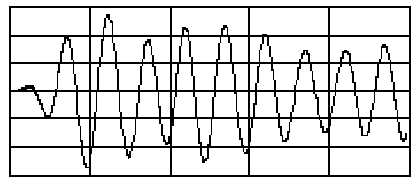
A LabVIEW blokkdiagramos programozási stílusa és a jel feldolgozásának helyes (pontos) beállítása , valamint a VI-s (Virtual Instrument) mérés lényegesen leegyszerűsítik a jeleket elemző alkalmazásokat.

A mai korszerű intelligens rendszereknél — úgy is mondhatjuk, mechatronikai rendszereknél — rendkívüli jelentősége van a mérésnek. Mérés nélkül nincs szabályozás, szabályozás nélkül pedig nincs intelligens rendszer. A legszemléletesebben ezt úgy lehet megérteni, ha megnézzük a különbséget a klasszikus gépészeti szemlélet és a korszerű mechatronikai szemléletmód között.

Egy jel frekvencia összetételének meghatározásához először digitalizálni kell a folytonos jelet. Ahhoz hogy alkalmazhassuk a digitális jelfeldolgozás módszereit, digitális formába kell (át)konvertálnunk az analóg jelet. A gyakorlatban ezt az átalakítást egy analóg-digitál (A/D) átalakítóval valósítják meg.

Tekintsünk egy analóg jelet x(t), amelyből minden h másodpercben veszünk mintát. A h időintervallum a mintavételi intervallum vagy mintavételi periódus . Ennek reciproka 1/h a mintavételi frekvencia . Mértékegysége: minta/másodperc. Az x(t) minden egyes függvényértéke diszkrét érték a t=0,h, 2h, 3h -nál és így tovább, ezek az egyes minták. Így x(0), x(h), x(2h), … az összes minta. Az x(t) jelet a mintavételezés után a mintavételi értékekből álló halmaz írja le:

A 8.4. ábra egy analóg jelet és a hozzá tartozó megfelelő mintavételi értékeket mutatja.

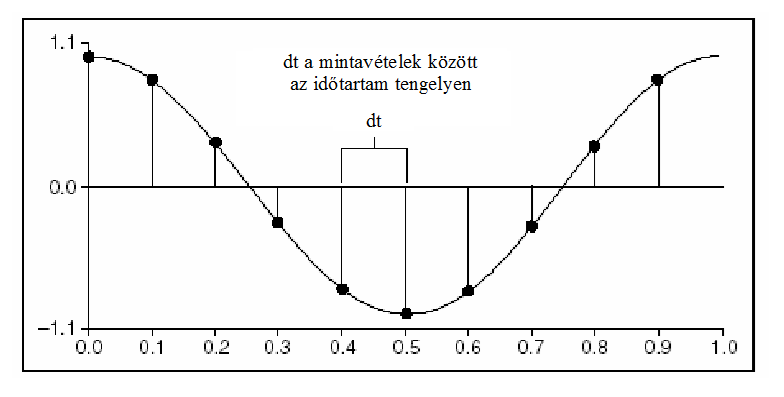
A következő kifejezés leírja az egyes mintavételi értékeket:

Ha az x(t) jelből N darab értéket veszünk, akkor x(t) előállítható a következő jelsorozatból:

A fenti sorozat x(t) digitális leképezése, vagyis x(t) mintavételezett alakja. Az  X = { x[k] } sorozat k egész értékei szerint van sorszámozva, és nem tartalmaz információt a mintavételezés gyakoriságáról. Tehát a mintáknak csak az értékét ismerjük, és nem tudjuk, hogy milyen frekvenciával történt a mintavételezés. Egy (digitális) számítógépes analóg bemenet egyik legfontosabb jellemzője hogy a mintavevő berendezés mekkora frekvenciával vesz mintát a bejövő jelből. Alacsony frekvenciájú mintavételezés alul mintavételezett jelet eredményezhet!

Ha a jel alul-mintavételezett, akkor minimális információt tartalmaz az analóg jelről. Az alul-mintavételezés eredményeként úgy tűnik, mintha egy megtévesztő kisebb frekvenciájú jel is megjelenne a mintavételezett jelben. A 8.5. ábra egy megfelelő módon mintavételezett és egy alul-mintavételezett jelet mutat be.

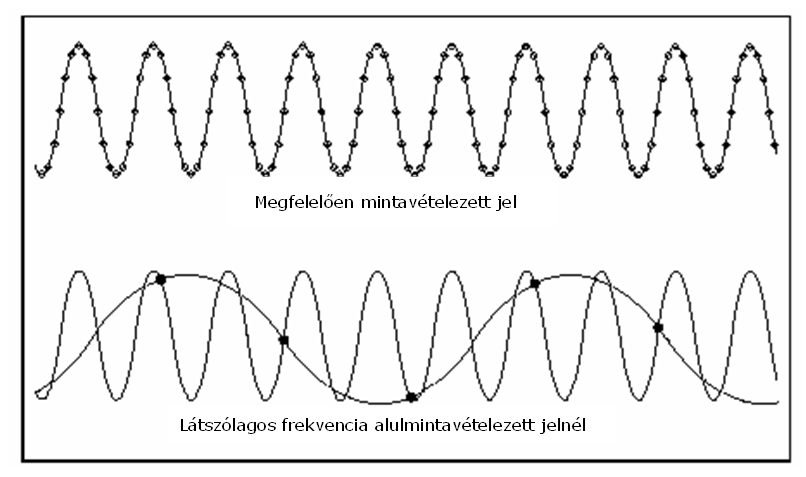
A (8.5. ábra) ábrán az alul-mintavételezett jelnél úgy tűnik mintha volna egy alacsonyabb frekvenciájú komponense is, ahol az eredeti tíz periódusból csak kettő látszik. Ha megnöveljük a mintavételi frekvenciát, ezzel megnöveljük a mintavételi pontok számát is az adott időtartam alatt. A nagyobb mintavételezési frekvencia az eredeti analóg jel egy jobb, több információt tartalmazó (átalakítása) megjelenítése, a kisebb frekvenciájú mintavételezéshez képest. Meg lehet adni egy olyan mintavételi frekvenciát, amellyel a mintavételezett jelben lévő maximális frekvenciát is mindig pontosan elő tudjuk állítani alul-mintavételezés (aliasing) nélkül, ez az úgynevezett Nyquist frekvencia .

A Nyquist frekvencia megegyezik az alkalmazott mintavételi frekvencia felével, amelyet a következő képlettel írhatunk le:

ahol

Az olyan jelek, amelyeknek bizonyos frekvencia komponensei a Nyquist frekvencia felett vannak, vonalasnak, szaggatottnak látszanak a tényleges és a Nyquist frekvencia között. A Nyquist frekvencia feletti komponensek az alatt látszanak a vonalas jelben. Például egy frekvencia komponens f _N <f ₀ <f _S ,  f _S- f ₀ frekvenciaként jelentkezik.

A (8.6. ábra) és (8.7. ábra) ábra illusztrálja az alul-mintavételezés jelenségét.

A 8.7. ábra a bejövő jel frekvencia komponenseit mutatja, és a mintavételi frekvenciát, amely 100 Hz.

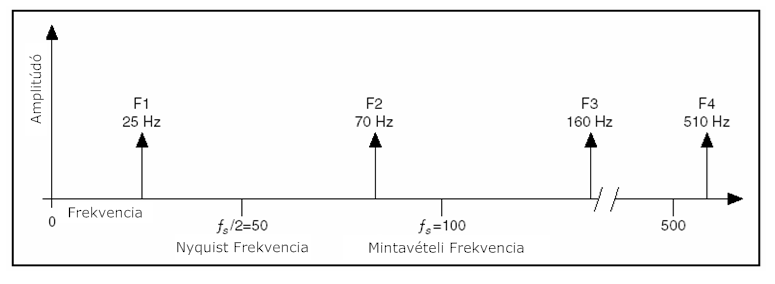
A 8.6. ábra a bejövő jel látszólagos és a tényleges frekvencia komponenseit mutatja.

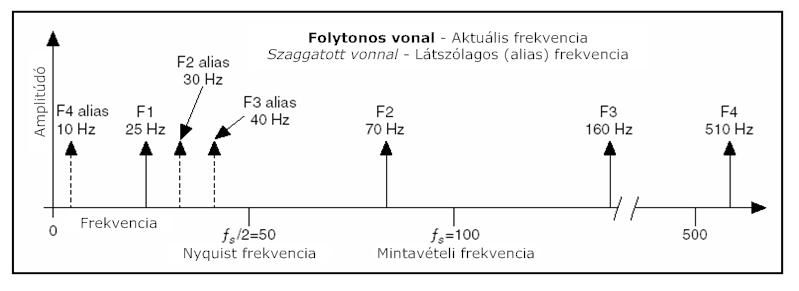
A 8.6. ábra szerint f _S /2=50Hz alatti komponensek helyesen vannak mintavételezve, például F1 jó helyen van. A Nyquist frekvencia feletti frekvenciájú komponensek viszont máshol látszódnak . Például az F2, F3 és F4 frekvencia komponensek 30 Hz-en, 40 Hz-en és 10 Hz-en látszanak külön-külön.

A látszólagos frekvencia értéke egyenlő a mintavételi frekvencia legközelebbi egészszámú többszöröse és a bejövő frekvencia különbségének abszolút értékével.

ahol

Például meghatározhatjuk a látszólagos frekvenciákat F2, F3 és F4-ből a következő képletek szerint:

A Shannon-féle mintavételi elv szerint (lásd 3.4.4. szakasz fejezetben) a mintavételi frekvenciának a minta-vételezett jel maximális frekvencia komponens legalább a duplájának kell lennie, hogy elkerüljük a látszólagos frekvencia jelenségét. A 8.8. ábra különböző mintavételi frekvenciák hatását mutatja be.

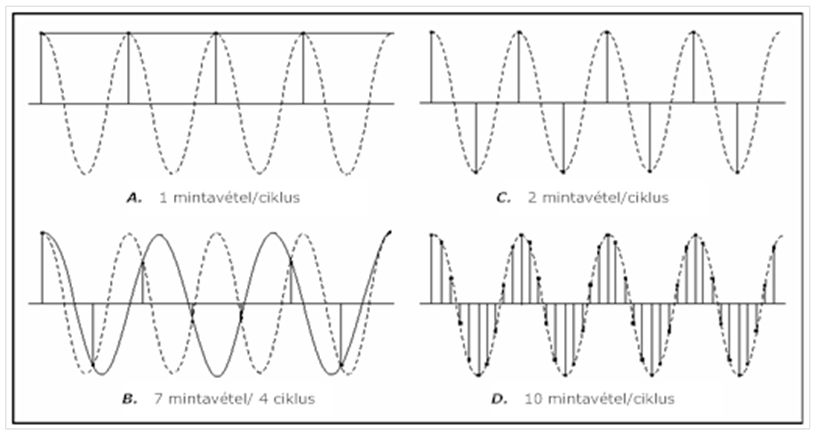
A 8.8. ábra szerinti A esetben az f _S mintavételi frekvencia egyenlő a mintavételezett szinusz hullám f frekvenciájával. f _S mértékegysége minta/másodperc. f mértékegysége periódus/másodperc. Tehát A esetben 1 mintavételi érték 1 periódusnak felel meg. A leképezett hullámforma az eredeti jel látszólagos frekvenciáját mutatja be, amely egy egyenfeszültség (minden mintavételezésnél állandó értékű jel).

A 8.8. ábra szerinti B esetben f _S =7/4f, azaz 7 minta esik 4 periódusra. A B esetben tehát a mintavételi gyakoriság növelésére emelkedik a hullám frekvencia. Azonban a látszólagos frekvencia kisebb mint az eredeti jel frekvenciája , 4 helyett csak 3 periódus jelenik meg.

A 8.8. ábra szerinti C esetben a mintavételi gyakoriság f _S =2f-re való növelésére a digitalizált hullámformát helyes frekvenciával kapjuk. A periódusok száma az eredeti jellel azonos. A C esetben az előállított hullámforma pontosabb leképezése az eredeti szinusz hullámnak, mint A vagy B esetben. Ha a mintavételi gyakoriságot kellő mértékben f fölé növeljük, például f _S =10f-re, azaz 10 minta/periódusra, akkor megfelelően és precízen mintavételeztük a jelet.

A 8.8. ábra szerinti D esetben a mintavételi frekvencia tízszerese az eredeti jel frekvenciájának, amelynek eredménye látható az ábrán.

A digitális átalakításnál a 0 és a Nyquist frekvencia közötti tartományban nem tudjuk megkülönböztetni a látszólagos frekvenciát a valóditól. Ha a mintavételi frekvencia éppen duplája a Nyquist frekvenciának, az elszórt jelekből eredő zavarjelek - például a villamos vezetékekből vagy a rádióadókból érkező jelek - tartalmazhatnak magasabb frekvenciájú komponenseket, mint a Nyquist frekvencia. Az elszórt jel Nyquist frekvencia feletti komponensei a vizsgáló jel által megkívánt frekvencia tartományába eshetnek és látszólagosan hibás eredményt hozhatnak létre. Ezért el kell tüntetnünk az analóg jelből a látszólagos frekvenciákat, mielőtt a jel A/D átalakítását elvégezzük.

Használjunk anti-aliasing analóg alul áteresztő szűrőt az A/D átalakítás előtt, hogy eltüntessük a Nyquist frekvenciánál magasabb látszólagos frekvenciákat. Egy alul áteresztő szűrő az alacsony frekvenciákat átengedi, de elnyomja a magas frekvenciákat. A Nyquist frekvenciánál magasabb frekvenciák gyengítésével az anti-aliasing alul áteresztő szűrő megelőzi a látszólagos komponensek mintavételezését. Az ilyen szűrő egy teljes frekvenciasávot le fog vágni, megfelelő nagyfrekvencia levágást az átmeneti sávban egy gyors lefutás biztosít . Mivel az anti-aliasing szűrőt az analóg jelhez alkalmazzuk mielőtt átalakítottuk volna digitális jellé, ezért ez a szűrő egy analóg szűrő.

8.8. ábra egy ideális és egy megvalósítható anti-aliasing szűrőt mutat be. A következő információk az ábrára vonatkoznak:

f ₁ a legnagyobb bejövő frekvencia.

f ₁ -nél kisebb frekvenciák, amelyeket át akarunk engedni.

f ₁ -nél nagyobb frekvenciák, amelyeket nem akarunk átengedni.

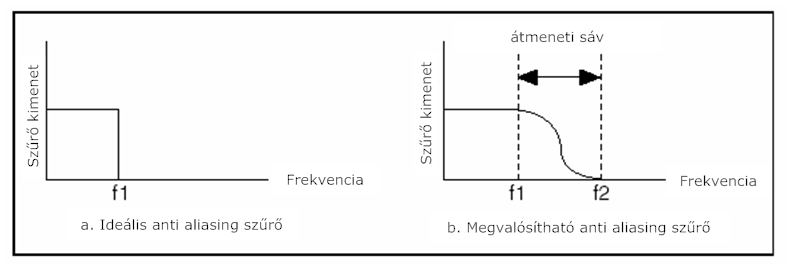
Egy ideális alul áteresztő szűrő, ahogy az a (8.9. ábra) ábrán látható, átengedi az összes alkalmazni kívánt bejövő frekvenciát, és levágja az összes nem kívánt komponenst. Az ideális alul áteresztő szűrő azonban fizikailag megvalósíthatatlan.

A (8.9. ábra) b ábra a megfelelő anti-aliasing szűrő viselkedését szemlélteti. Egy valós alul áteresztő szűrő minden f<f ₁ frekvenciát átenged, és minden f>f ₂ frekvenciát levág. Az f ₁ és f ₂ közötti tartomány az átmeneti sáv, ahol a bemenő frekvenciák fokozatos elnyomása történik. Habár mi csak f<f ₁ frekvenciájú jeleket akarjuk átereszteni, az átmeneti sávban lévő jelek előidézhetnek látszólagos frekvenciákat. Ezért a gyakorlatban több mint kétszeres mintavételező frekvenciát alkalmazunk, képlettel: f _S >2f ₁ .

Néhány berendezésen ki lehet íratni az amplitúdót lineáris és decibel(dB ) skálán egyaránt. A lineáris skála az amplitúdót tényleges értékét írja ki. A decibel skála egy arány kifejezése. A decibel skála egy transzformáció lineáris léptékről logaritmikus léptékre (lásd 3.4.3. szakasz fejezetet).

A következő egyenlőségek definiálják a decibel értékét. Az 8.7 egyenlet teljesítmény arányban írja le a deciBell (dB _P ) meghatározását.

ahol

Az 8.8 egyenlet pedig amplitúdók arányaként írja le a deciBell (dB _A ) értékét.

ahol

A 8.7 és 8.8 egyenletek igényelnek egy referencia értéket, hogy kifejezhessük a teljesítmény és az amplitúdó arányát decibel-ben. A vonatkoztatási érték adja a 0 (nulla) decibeles szintet. Különféle egyezmények léteznek a referencia érték megállapítására.

A következő megállapodásokkal meghatározható a referencia érték, és kiszámíthatók a decibel értékek.

Amikor a teljesítményt és amplitúdót úgy alkalmazzuk, mint ugyanaz a jel amplitúdó négyzete, akkor a decibel arány pontosan ugyanaz az érték. Ha a decibel arányt 2-vel megszorozzuk, ugyanazt érjük el, mintha az eredeti jelet négyzetre emeltük volna. Éppen ezért alkalmazhatjuk ugyanazt a decibel értéket és műszer beosztást, akár amplitúdó akár teljesítmény spektrumot mérünk.

Amplitúdó vagy teljesítmény spektrumot általában decibel skálán ábrázolnak. Decibel skálán ábrázolva e spektrumokat, áttekinthetővé válnak széles dinamikus értéktartományok, és apró jel összetevők jelenlétét is lehet látni a nagyok között. Például tegyük fel, hogy olyan jelet akarunk ábrázolni, amely amplitúdója 0.1 V és 100 V közötti értéket vehet fel, egy 10 cm magas kijelzős készüléken. Ha lineáris léptéket használunk, abban az esetben a berendezés teljes kijelző magasságát kitölti a 100 V, a kijelzőn 1 cm távolság 10 V-os amplitúdónak felel meg. Ha a műszerállandó 10 V/cm, akkor a 0.1 V amplitúdójú jel csak 0.1 mm nagyságú. Mivel a 0.1 mm távolság nehezen látható a képernyőn, ezért ember ezt a komponenst nem fogja észre venni.

A logaritmikus decibel lépték használata lehetővé teszi, hogy a 0.1 V amplitúdójú elemet is láthatóvá tegyük.

A Táblázat 8.2 táblázat bemutatja, hogyan lehet az amplitúdók széles tartományát összehúzni egy kisebb értékkészletbe a logaritmikus decibel léptékkel.