5. fejezet - Interferometria

A mérnöki optika, amely elsősorban az optikai jelenségek gyakorlati implementálásával foglalkozik, az optikai alapismeretek mellett műszertechnikai, finommechanikai, mechatronikai elvekre építve szintetizál. Az ilyen jellegű rendszerszintézis alkalmazott optikai eszköztára jellemzően a geometriai optikát fedi le. Azonban nem egy műszer, berendezés működése olyan elvekre épül, mely tárgyalásához a geometriai optika eszköztára már nem elegendő, hullámoptikai megközelítés szüksége. Ez két esetben nagyon markánsan érhető tetten. Egyrészt, amikor a képalkotás során a képalkotás minőségét már csak a diffrakció korlátozza, ilyenkor a geometriai optikai elvekre épülő analízis, illetve szintézis érvényességét veszti. Másrészt, amikor a geometriai optika alaptörvényei közül az, mely kimondja, hogy számtalan sugár vezethető át egyetlen ponton anélkül, hogy azok egymásra hatást gyakorolnának, bizonyos esetekben nem alkalmazható elv. Hiszen az interferometrikus berendezések pont azt a jelenséget használják ki, hogy a bennük terjedő hullámfrontok találkozásukkor egymásra hatva egy újabb jelenséget hoznak létre.

Az optikai jelenségek magyarázata az idők folyamán sokat változott, fejlődött. A nagy elődöknek sok hibás megközelítésen, téves elméleten át kellet verekedniük magukat, hogy a kérdéseikre tiszta, megállapodott válaszokat kapjanak. Mivel a hullámoptika és az általa magyarázható interferencia és diffrakció, mint jelenség ma már a korszerű méréstechnika egyik alapköve; alapfogalmainak ismerete a mérnöki optikát művelők számára elengedhetetlen. Ezért a következő fejezetekben a hullámoptikai megközelítés történeti fejlődését és annak alapfogalmait és jelenségeit tárgyaljuk.

Az fénytan, mint diszciplína, a fizika egyik legrégibbi területe; fejlődés­e rendkívül érdekes és tanulságos.  Az iránta tanúsított érdeklődés egyrészt visszavezethető arra, hogy az emberek nagy többsége környezetéből az ingerek szinte elsöprő hányadát látása útján szerzi úgy, hogy a forrásokból, tárgyakról érkező fény a szembe kerülve, onnan az agyba jutva egy nagyon bonyolult fiziológiai és kognitív pszichológiai folyamat útján válik hasznosítható információvá. A fokozott érdeklődés másik oka talán az lehetett, hogy a fénytani jelenségek hordozója és okozója, maga a fény mint jelenség sokáig maradt nehezen magyarázható.

Optikai ismeretekkel már a régi görögöknek is rendelkeztek [5.2.] . Időszámításunk előtt mintegy háromszáz esztendővel Euklidesz foglalta össze – mai tudásunkkal többé kevésbe általános érvényűnek tekinthető – megállapításait tapasztalati úton szerzett eredményei alapján. Platonra hivatkozva kifejti, hogy tárgyak láthatóságának oka az, hogy a szemből kiinduló látósugarak gyakorlatilag letapogatják a tárgyakat. Az Optika és Katoptrika című műveiben megmagyarázza, hogy ezen látósugarak érintői a vizsgált tárgynak, azok leírják annak körvonalát és az így keletkező látószögtől függ a tárgy látszólagos nagysága. Szintén ad magyarázatot a tárgyak látszólagos nagyságának annak helyzetétől és távolságától való függésére. Kimondja a geometriai optika alaptörvényét, mely szerint a fény egyenesvonal mentén terjed,  és helyesen írja le a visszaverődés törvényét. Tudjuk, hogy foglakozott a sík- és gömbtükrökkel, az optikai lencsékkel. Igazi különlegesség, hogy egy rendkívül előremutató gondolatot tudott időszámításunk előtt százhúsz körül megfogalmazni Herón, aki szerint a fénysugár által megtett út időminimumot elégít ki. Ennek szabatosabb formáját csak mintegy ezerhétszáz évvel később tudta megfogalmazni Pierre de Fermat (1601 – 1665). Herónnal szinte egy időben tanulmányozat a fénytörés jelenségét Ptolemaiosz, aki erre – ugyan nem teljesen helyes, de egészen Keplerig érvényes – matematikai összefüggés írt fel. A modern – hullámoptikai és korpuszkuláris – fényelméletek kezdetleges megfogalmazásai a görögöknél már szintén megjelentek. Arisztotelész az euklideszi látósugarak helyett egy hullámelmélet szerű magyarázatot adott, míg Epikurosz szerint a fényérzet a forrásból kilépő részecskék hatásával magyarázható, ami tulajdonképpen – az akkori kor ismereteinek szintjén – egy fajta korpuszkuláris fényelméletnek tekinthető.

A középkori arab optikai megfigyelések után az első igazán meghatározó eredmények Robert Bacon nevéhez fűződnek, aki az ezerkétszázas években meg tudta mérni a homorú tükrök fókusztávolságát, és leírta a szférikus aberráció, azaz a nyíláshiba jelenségét. Tőle származik a sötétkamra – camara obscura – gondolata, melyet Giovanni Battista della Porta egészített ki azzal, hogy, annak hatékonyságát egy a nyílásban elhelyezett lencsével lehet fokozni.

Az optikai műszerek építésének első jelentős korszakára meghatározó hatással volt az optikai üvegek előállításának és megmunkálási eljárásai­nak tökéletesedése. A tizenhetedik században járunk, ekkor találja fel Hans és Zacharias Jansen (egyes szakirodalmak Janssen-nek írják nevüket) a mikroszkópot [5.26.] , és készíti el Galileo Galilei (1564 – 1642) első távcsövét.

A fejlődés ekkorra érte el azt a szintet, ami világossá tette, hogy az optikai eszközök tervezésének, előállításának nagyobb tömegben történő gyártásának elengedhetetlen kelléke az, hogy az optikai jelenségek megértéséhez és alkalmazásához szabatos elméleti megközelítések szükségesek. E téren szerzett elévülhetetlen érdemeket Johannes Kepler (1571 – 1630) prágai csillagász, akit elsősorban a bolygómozgásokat leíró, róla elnevezett Kepler-törvények miatt ismerünk. Kepler egyik legjelentősebb munkája az 1611-ben megjelent Dioptrice volt, melyben lefektette az optika tudományos szintű tárgyalásának alapjait. Könyvében az általa szerkesztett Kepler-távcső mellett foglakozik a fénytöréssel és az optikai leképezéssel kapcsolatos eredményeivel. A kor színvonalának megfelelően írta le a szem működését, elemezte a látáshibákat, valamint magyarázatot adott a szemüveglencsék működésére vonatkozóan is [5.4.] . Eredménye a fénytörés tekintetében kimagasló jelentőségű, megállapítja az üvegre a teljes visszaverődés szögét. A róla elnevezett távcső szintén jelentős lépés az égi jelenségek megfigyelésének történetében.

A fénytörés törvényéhez érdekes tudománytörténeti adalék az, hogy ugyan az 1626-han elhunyt Willebrord Snel van Royen (1580 – 1626) holland matematikus – aki a Ledeni Egytem oktatója volt – hallgatói feljegyzései közt megtalálták azt a tanulmányt, amely már tartalmazta a fénytörés helyesen megfogalmazott törvényét. Az nem ismert, hogy René Descartes (1596 – 1650) olvasta-e ezt a tanulmányt, azonban tény, hogy a fény­törés törvényét elsőként ő közölte nyomtatásban. A mai szakirodalom is Snellius– Descartes törvényként jegyzi. Descartes további jelentős, optikai téren szerzett érdeme a szivárvány elméletének pontos megfogalmazása. A fénytörés jelenségének pontos megfogalmazása úttörő jelentőségű az optikai műszertervezés fejlődése szempontjából, hiszen ez által vált lehetővé az optikai rendszerekkel kapcsolatos számítások pontos elvégzése. Először 1693-ban Edmond Halley angol csillagász és matematikus végzett a lencsékre vonatkozóan általános – még mai szemmel is elfogadhatónak tűnő alaposságú – számításokat [5.2.] .

A hullámoptika, vagy más néven a fizikai optika igazi kezdete 1665-re tehető. Ebben az évben felfedezte fel Francesco Maria Grimaldi (1618 – 1663) olasz jezsuita szerzetes a fény diffrakcióját, és Robert Hooke (1635 – 1703)  az interferencia jelenségét, megállapítva, hogy a fény egy rezgés.

1666-ban Sir Isaac Newton (1642– 1710) kísérletileg valósítja meg a fehér fény spektrálisan felbontását, és kidolgozza a fény korpuszkuláris elméletét. 1672-ben Olaf Römer, (1644 – 1710) a Jupiter holdjainak fogyatkozását felhasználva megmérte a fény terjedési sebességét. 1669-ben dolgozta ki Christiaan Huygens (1629 – 1695) a fény hullámelméletét, szemben a newtoni korpuszkuláris elmélettel.

Ezen időszakkal bezárólag, gyakorlatilag tehát a tizenhetedik század végéig felfedezték azokat az alapvető és kiemelten fontos optikai jelen­ségeket, amelyek a fizikai fénytan, azaz a hullámoptika alapját jelentik, és egyben kísérleti úton ismertté váltak azok a fényjelenségek, amelyek a fény hullám­természetét alátámasztották és igazolták.

Annak ellenére, hogy ezen század második felének optikai jellegű eredményei a fény hullámtermészetét voltak hivatottak igazolni, a kor meghatározó és nagy tekintélyű fizikusa, Newton nem értett egyet ezzel az elmélettel. Mivel az általa ismert longitudinális hullámokkal nem tudta magyarázni a fény terjedését, ezért 1717-ben ismét felelevenítette fény részecske természetére vonatkozó, úgynevezett korpuszkuláris fényelméletét [5.27.] .  Ekkor az optikai eredmények születésének üteme hanyatlani kezdett, a tizennyolcadik században a korpuszkuláris elmélet dominált, annak ellenére, hogy például Leonhard Euler (1707 – 1783) Szentpétervárott dolgozó svájci matematikus, és Mihail Vasziljevics Lomonoszov (1711 – 1765), szintén Szentpétervárott dolgozó orosz fizikus és vegyész ismét előtérbe helyezték a fényjelenségek magyarázatára a hullámelméletet.

1793-ban nagy fontosságú megállapításokat tett a látás fiziológiájának értelmezésében Thomas Young (1773 – 1829) angol orvos és fizikus, aki 1801– 1804 között kidolgozta az interferencia elméletét a hullámelméletre alapozva.

Egy 1801-ben kiadott publikációjában részletesen és szabatosan leírta a fény hullámelméletének alapfeltevéseit [5.2.] :

Young ezirányú munkásságának talán legértékesebb eredménye, hogy elsőként utal a diffrakció jelenségére. Sikerül cáfolnia Huygens azon gondolatát, miszerint a hullámfelület oldalpontjaiból kiinduló, úgynevezett oldalhullámok fizikailag nem észlelhetők, így a fényhatároló elem széléről éles képet kapunk. Mint fogalmakat, Young bevezeti a hullámoptikát, a fényhullámhosszt, és elsõként kísérleti úton azt meg is méri [5.2.] . Kimondja, hogy fényinterferenciára csak koherens fényhullámok képesek.

A tizennyolcadik század végén, Étienne-Louis Malus (1775 – 1812) hadmérnök, fizikus és matematikus elévülhetetlen érdemeket szerez a kettőstörés jelenségének magyarázatával. Ismert tudománytörténeti érdekesség, hogy az ötlet Malus fejében akkor fogalmazódott meg, amikor egy este a Luxemburg-palota ablakainál egy kettőstörésű izlandi páton keresztül tanulmányozta a lenyugvó nap visszaverődő fényét, és meglepetésére két kép helyett csupán egyet látott [5.2.] .

Erre az időszakra esik Augustin-Jean Fresnel (1788 – 1824) francia fizikus meghatározó munkáinak megjelenése is [5.5.] , 1815-ben lefektette a diffrakció jelenségének új magyarázatát.

Michael Faraday (1791 – 1867) angol fizikus és kémikus, az elektrotechnika nagy alakja 1846-ban felfedezte – az optika történetében döntő fontosságú –, róla elnevezett effektust, amely szerint az elektromágneses tér az anyagokon való áthaladás közben elforgatja az áthaladó fény polarizációs síkját. Ahogy a Faraday-effektus, úgy az 1873-ban megjelent – a modern elektromágneses fényelmélet alapjait lefektető – James Clerk Maxwell (1831 – 1879) skót matematikus-fizikus által írt tanulmány mérföldkövet jelent a korszerű optika történetében.

Még mai is igaz, hogy az elektrodinamika az elméleti fizika egyik legfontosabb, gyakorlati szempontból is meghatározó, rendkívül érdekes fejezete. Joggal mondhatjuk, hogy a Maxwell által kidolgozott elektromágneses térelmélet a tizenkilencedik század fizikájának is az egyik legmeghatározóbb és legfontosabb eredménye, amely egyben utat nyitott a relativitáselmélet és a kvantumelmélet előtt. Maxwell nagy érdeme, hogy felismerte a közeg elektromos és mágneses jelenségekre gyakorolt befolyását. Az egzakt matematikai formába öntött törvényszerűségek egyértelművé teszik, hogy az elektromágneses – és ezen belül természetesen az optikai – jelenségek helye a tér, teljesen függetlenül attól, hogy azt mi tölti ki.

A fizikusokat már régóta foglalkoztató éter-elv kísérleti vizsgálatához kapcsolódik az úgynevezett  Michelson–Morley-kísérlet, melyet 1887-ben végeztek el Albert Abraham Michelson (1852 – 1931) és Edward Williams Morley (1838 – 1923) amerikai fizikusok a mai Case Western Reserve University-n. A kísérlet jelentőségét bizonyítja, hogy Albert Abraham Michelson 1907-ben Nobel-díjat kapott a Michelson–Morley-kísérletért. A kísérlet célja az volt, hogy megmérjék a Föld éterhez viszonyított sebességét. A lebonyolításhoz a Michelson által kifejlesztett Michelson-interferométert használták, amely a méréstechnikában mai is az egyik leggyakrabban alkalmazott interferometrikus elrendezés. E kísérlet – melyet az év folyamán többször is megismételtek, és döntő lökést adott a relativitáselmélet fejlődésének – eredményeként azt nyerték, hogy a keresett sebesség mindig nullával volt egyenlő.

A holográfia elvét a magyar, Gábor Dénes publikálta 1947-ben, módszerével teljes hullámfront rekonstrukció valósítható meg, kidolgozásáért 1971-ben fizikai Nobel-díjat kapott [5.28.] . Hullámoptika huszadik századi történetében fontos lépés volt Frits Zernike (1888 – 1966) holland Nobel-díjas fizikus és matematikus 1953-ban felfedezett fáziskontraszt mikroszkópja és a lézerek, azaz a fénykibocsátáshoz indukált emissziót használó fényforrások 1960-as fedezése, mely az amerikai Theodore Harold Maiman (1927 – 2007) nevéhez köthető. 1963-ban Yuri Nikolaevich Denisyuk (1927 – 2006) szovjet fizikus a Lippmann-emulzióra alapozva fehér fényben rekonstruálható hologramot készített. A kvantumelektronika területén a lézerelven működő oszcillátorok és erősítők létrehozásához vezető úton kifejtett tevékenységükért Charles Townes, Nikolay Basov és Aleksandr Prokhorov 1964-ben Nobel-díjat kaptak.

Az optika alapvető kérdéseire magyarázatot kereső természettudósokat az idők során folyamatosan foglalkoztatták a fény terjedésének körülményeire vonatkozó kérdések, de ezek között is kiemelt szerepet töltött be annak terjedési sebessége. Hosszú ideig tartotta magát az a nézet, mely szerint a fény esetében nem lehet beszélni terjedési sebességről, azaz ah­hoz, hogy a tér egyik pontjából a másikba jusson, nincs szük­sége időre. A fénysebesség mérésére már a kezdetekben is számos kísérlet történt, Galileo Galilei például két távoli hegycsúcson helyezett el fényforrásokat [5.3.] . A kísérlet során először Galilei nyitotta fel a fényforrás fedőlemezét, és mikor a másik hegycsúcson elhelyezkedő személy ezt észlelte, ő is felnyitotta a nála lévő fényforrás fedőlemezét. A kísérletet több különböző távolság esetén is megismételték, de az eltérést észlelni nem voltak képesek, sőt azt is megállapította Galilei, hogy a mérésben az idő jelentős részét az észlelő reakcióideje teszi ki. Csupán annyit következtetést tudott levonni, hogy a fénynek van terjedési sebessége, az igen jelentős. Később a kísérletet éjszaka elsütött ágyúk torkolattüze fényének egy tükörről történő visszaverődésének megfigyelésével próbálták pontosítani, azonban ezek a vizsgálatok sem vezettek használható eredményre. Galilei kísérletének igazi eredménye az a megállapítás volt, miszerint a fény sebessége igen nagy.

Első olyan kísérletet, amely a fény – rendkívül nagy –, de véges terjedési sebességére engedett következtetni 1672-ben Olaf Römer (Ole Christensen Rømer (1644 – 1710)) dán csillagász végezte el, nem földi objektumok felhasználásával. A Jupiter egyik holdját, az Iót figyelte meg távcsővel, és eltéréseket vett észre annak keringési periódusában; vizsgálta azt az időközt, amely a megfigyelt égitestnek a Jupiter árnyékából történő két egymás utáni kilépése között telik el [5.12.] . Megmérte tehát a keringési időt, és ebből kiszámította az árnyékból való kilépések feltételezett időpontjait. A Jupiter földközelben lévő állapotához tartozó számított eredmények és a fél évvel későbbiek között tizenhat perc és negyven másodpercet eltérést tapasztalt. Tehát egy félév múlva, amikor a Jupiter földtávolba került, holdjának kilépése az előre kiszámított időponthoz képest késett. Römer arra a következtetésre jutott, hogy e jelentős késés okát csak a fény terjedési sebessége okozhatja, mert a Földhöz képest a legtávolabbi és a legközelebbi Jupiter helyzet esetén az érkező fényeknek mintegy háromszáz millió kilométerrel – a földpálya átmérőjével – több utat kellett megtenniük. A távolság és a mért idő segítségével Römer kiszámította a fény sebességét, amire másodpercenként kettőszázhuszonhétezer kilométert kapott.

Römer okoskodása helyes volt, ugyanis az igen nagy terjedési sebességet csillagászati viszonyok mellett könnyebb meghatározni, mint a Földi körülmények között. Az utóbbira, azaz földi fényfor­rás segítségével történő fény terjedési sebesség meghatározásra első ízben Armand Hippolyte Louis Fizeau (1819 – 1896) francia fizikus tett javaslatot [5.12.] .

Fizeau, fénysebesség mérésére kifejlesztett berendezésében két, egymástól adott és ismert távolságokban elhelyezkedő mérőhelyeken egy – fókuszsíkjában tükröt tartalmazó – kollimátor és egy speciális távcső volt elhelyezve úgy, hogy egymás felé irányzottak és optikai tengelyeik egy közös tengelyre voltak felfűzve. A speciális távcsőben elhelyezett nagy fényerejű fényforrás fényét egy féligáteresztő tükör segítségével a kollimátor irányába terelte úgy, hogy a speciális távcső féligáteresztő tükre előtt egy vezérelhető fordulatszámú fogazott tárcsa helyezkedett el úgy, hogy annak fogai, illetve a fogak közötti nyílások a fénysugár útját kitakarták, vagy szabadon hagyták. A tárcsa fordulatszámának növelésével elérhető volt az az állapot, amikor a fényforrás fénye észlelhető volt a megfigyelő által, azaz ekkor az egyik fogaskerék nyílásnak a másik helyzetébe való befordulásához tartozó idő megegyezik a fénysugár teljes útjával. Ismerve a távcső és a kollimátor távolságát, a tárcsa fordulatszámát és a fogak számát; a fény sebessége maghatározható. Fizeau vizsgálatainak eredményeképpen a fény sebességére másodpercenként háromszáztizenháromezer kilométert kapott. Ő volt tehát az első, aki a fény sebességét (1849. július 23-án) földi, laboratóriumi körülmények között mérte meg. Az eljárás során a két opikai rendszer közötti távolság a nyolc kilométer volt.

Fizeau kísérletét később Jean Bernard Léon Foucault (1819 – 1868) a róla elnevezett – a Föld tengelye körüli forgását kimutató – ingáról híres francia fizikus tökéletesített formában megismételte, s 1862-ben már a fény által egy másodperc alatt megtett útra kettőszázkilencvennyolcezer kilométert kapott. Ez az érték igen közel áll a mai ismereteink szerint elfogadott 299 792 kilométerhez. Érdekesség, hogy Albert Abraham Michelson (1852 – 1931) 1926-ban, forgó tükrök használatával, és a kaliforniai Wilson-hegy és a San Antonio-hegy távolságát használva korrigálta a mérését, és a fény által egy másodperc alatt megtett útra 299 796 kilométert kapott [5.7.] .

A hullámoptika tárgya azon fényjelenséget vizsgálata [5.1.] , amelyek csak a fény hullámtermészetével értelmezhetőek és magyarázhatóak. A tárgyalásmód kívánalmainak megfelelően a terjedő fényt hullámként, az esetek jelentős részében periodikus hullámként értelmezzük, melyben egy vagy több fizikai mennyiség időben és térben periodikusan változik. A hullámoptikában előforduló jelenségek magyarázhatók az általános hullámtan fogalmai és törvényszerűségei alapján.

Azon mozgásokat, amelyek azonos időközönként ismétlik önmagukat, perio­di­kus mozgásoknak nevezünk. Szemléletes példaként egy spirálrugóra kötött tömeg moz­gá­sát lehet tárgyalni, mely során fellépő sajátos mozgást nevezzük egyszerű harmonikus mozgásnak vagy más szavakkal rezgőmozgásnak.

Definíció szerint az egyszerű harmonikus rezgőmozgást egy kör kerületén állandó se­bes­ség­gel mozgó pontnak a kör átmérőjére vetített mozgásával határozzuk meg. A maximális elmozdulást amplitúdónak, az egy teljes rezgés meg­té­te­léhez szükséges időt pedig periódusidőnek nevezzük. A rezgő test frekvenciáján a másodpercenkénti teljes rezgések számát értjük. A rezgés frekvenciája a periódusidő reciproka. Ha egy test rezgését a körmozgást végző pont segítségével írjuk le, ak­kor a frekvenciát a másodpercenkénti fordulatok száma adja meg, mértékegysége a Hertz (Hz).

A rezgőmozgást végző pont x irányú elmozdulását a következő összefüggés adja meg:

Felhasználva azt a mechanikai összefüggést, miszerint az idő a megtett út és a haladási sebesség hányadosa, a pont ω szögsebességét a periódusidő függvényében az alábbi össze­füg­gésekből kapjuk

A rezgőforrások demonstrálására szellemes példaként egy megnyújtott spirálrugót alkalmaznak, amely a feszítőerő hirtelen megszűnése után egyszerű harmonikus rezgőmozgással mozog tovább. Ilyen esetben a két egymást követő hullámforma azonos pontjainak távolsága a hul­lám­hossz, melyet a görög lambda λ betűvel jelölunk. Egy hullám­hossznyi a távolság két hullámhegy vagy két hullámvölgy között található. Egy időpontban a hullám bárme­lyik pontjának elmozdulását az egyen­sú­lyi helyzettől való távolsága adja meg. Ennek előjele megállapodás kérdése, de folyton változik pozitív és negatív értékek között. A hullám amp­li­tú­dó­ja az előbb definiált elmoz­du­lás maximális értéke.

Minden fényhullám transzverzális hullám, amely az a hullám, amelynek minden kis eleme a hullám terjedésének irá­nyá­ra merőleges mozgást végez. A legegyszerűbb hullámmozgások azok, amelyek hullámpontjainak  el­moz­dulását valamilyen egyenletesen változó mennyiség szinusza vagy ko­szi­nusza írja le. Hullámmozgás során a mindenkori elmozdulást és annak irányát az egységkörön mozgó pont helyzetével is jellemezhetjük, meghatározhatjuk. Az adott helyzetű pontot az origóval összekötő egyenes vízszintes tengellyel bezárt, az óramutató járásával el­len­tétes irányban mért szöge, meghatározza azt a pozíciót, amit általánosan fázis­szög­nek ne­vezünk.

A tömegpont helyzetét annak függőleges tengelyű vetülete határozza meg. Ez és a fentiek alapján

Ha pont állandó sebességgel halad, akkor az ω szögsebesség is ál­lan­dó, és a Θ szögre érvényes

Behelyettesítve és kiegészítve a fázisszöggel:

Az α szöget kezdeti fázisszögnek nevezzük és állandó. Az egyszerű harmonikus hullámok egyenleteiben az elmozdulásokat a körfrekvencia $\omega =2\pi \nu$ és a hullámszám $k=2\pi /\lambda$ függvényében ábrázoljuk.

A hullámcsúcs sebességére vonatkozóan gyakran alkalmazzák a hullámse­bes­ség­, vagy fázissebesség kifejezést.

A hullámok, terjedésük során energia hordozói, így definíció szerint az időegység alatt a mozgásra merőleges egység­nyi felületen áthaladó energiamennyiséget nevezzük a hullám intenzitásának. Ha a hul­lám állandó sebességgel terjed, akkor adott az egy­ségnyi térfogatra eső teljes energia, azaz az energiasűrűség [5.18.] . A terjedést biztosító közegben az egységnyi területen időegység alatt áthaladó energia egy adott hosszúságú és egységnyi alapfelületű hasábban található. Így az intenzitást a hasáb hossza és az energiasűrűség szor­za­ta adja, amely energiasűrűség, és az intenzitás arányos az amp­li­tú­dó, illetve a frekvencia négyzetével [5.16.] .

Rendkívül fontos tény, hogy minden hullámmozgást, amit valamilyen rezgő forrás hoz létre, a frekvenciája jellemez, és a kibocsátott hullá­mok frekvenciája megegyezik a forráséval. Egy adott közegben a hullám­hosszt a terjedési sebesség határozza meg, ami a sebesség és a frekvencia hányadosa. Az egyik közegből a másikba történő áthala­dás­kor a frekvencia változatlan marad, így a hullámhossz a sebesség változásával azonos arányban változik meg.

A hullámok egymásrahatásának egyik legismertebb megjelenési formája az interferencia, mely csak koherens interferáló hullámok esetén figyelhető meg. Mivel a fényforrások jelentős részénél a fénykibocsátás atomi folyamat, amely során az egyes atomok véletlenszerűen bocsátanak ki véges hosszúságú hullámvonulatokat, így azok nem koherensek. Ezért két, hagyományos fénykibocsátás elvén működő pontszerű fényforrás segítségével interferenciára jellemző térbeli intenzitáseloszlást létrehozni nem tudunk. Az ilyen, hagyományos fényforrások segítségével fényinterferenciát csak úgy tudunk megfigyelni, ha a fényforrás által kibocsátott hullámfrontokat osztjuk, majd újra egyesítünk, így tulajdonképpen a fényhullámot  önmagával interferáltatjuk [5.17.] .

Ha az interferencia létrejöttének feltételei teljesülnek, akkor az interferáló hullámok találkozásakor megfigyelhetjük az interferencia jelenségét. Ilyenkor a hullámok teljesen kiolthatják vagy erősíthetik egymást. Az interferencia jelensége akkor lesz folytonosan megfigyelhető, ha huzamos idő alatt nem változik meg az interferáló hullámok fáziskülönbsége [5.19.] .

A szuperpozíció elve egy olyan törvényszerűség, mely kimondja, hogy bármely pont elmozdulása azon el­moz­dulások összege, amelyeket az egyes hullámok külön-külön keltettek. Az ilyen formában megfogalmazott szuperpozíciós elvet, először Thomas Young (1773 – 1829) angol orvos és fizikus mondott ki először 1802-ben [5.8.] .

Két, azonos frekvenciájú szinuszhullám egymásra hatásának vizsgálata esetén a megoldandó feladat úgy is megfogalmazható, hogy milyen az az eredő mozgás, amely akkor keletkezik, amikor egy részecske két harmonikus rezgőmozgást végez egy idő­ben. A két hullám által okozott elmozdulásokat egy egyenes men­tén ábrázolva jelöljük az amplitúdókat a ₁ és a ₂ -vel, ezek lesznek tehát a részecskére illesztett két periodikus mozgás amplitúdói [5.1.] .

A szuperpozíció elve alapján – mely kimondja, hogy bármely pont elmozdulása azon el­moz­dulások összege, amelyeket az egyes hullámok külön-külön keltettek – a bekövetkező y elmozdulás egyszerűen az egyes elmozdulások összege, így írható, hogy:

A két szög különbségének szinuszára érvényes kifejezés segítségével:

Bevezetve az alábbi konstansokat:

Négyzetre emelve és összeadva:

Egyszerűsített alakban

Arányként felírva:

A fenti összefüggések alapján

amely a két szög különbségének szinuszát kifejező képlet alapján:

Ez az egyenlet megegyezik az egyszerű harmonikus rezgőmozgás egyenletével, de módosított A amplitúdót és Θ fázisállandót tartalmaz. Mindezek alapján megállapítható, hogy két, azonos frekvenciájú, egyszerű harmonikus rezgőmozgás össze­ge egy egyenes mentén egy velük azonos frekvenciájú, egyszerű har­monikus rezgőmozgás lesz. Az új rezgőmozgás amplitúdója és fázis­ál­lan­dója számítható a komponensek ampli­tú­dó­jából és fázis­állandójából.

Az eredő amplitúdó, az a ₁ és a ₂ amplitúdóktól és $\delta ={\alpha }_1-{\alpha }_2$fáziskülönbségtől függ. Két fénysugár találkozásakor a fény intenzitása bármely pontban arányos az eredő amp­litúdó négy­zetével.

Ha a fáziskülönbség $\delta =\mathrm{0,}2\pi ,4\pi \mathrm{...}$ akkor 4a ² -et kapunk, azaz bár­me­­lyik fénysugár intenzitásának 4-szeresét. Ha $\delta =\pi ,3\pi ,5\pi \mathrm{...}$ az intenzitás nul­la.

Az interferencia feltételeinek meglétekor [5.6.] fényhullámok találkozásakor interferencia jelenséget figyelhetünk meg. Alkalmasan megválasztott körülmények között a hullámok teljesen kiolthatják, és maximálisan erősíthetik egymást. Ahogy a fentiekben már kifejtésre került, az interferencia jelensége akkor lesz huzamosan megfigyelhető, ha e megfigyelés teljes időtartama alatt nem változik meg az interferáló hullámok fázisa, fáziskülönbsége. Az interferencia jelenségének méréstechnika alkalmazásához elengedhetetlen a nagy koherenciahosszú forrás alkalmazása. Ennek a feltételnek elsősorban a lézerek felelnek meg [5.14.] .

A fény igen sok tulajdonsága megmagyarázható, ha feltesszük, hogy a fényhullám önmagával vagy akár egy másik hullámmal képes interferálni. Az interferencia létrehozásának két lehetséges megvalósítási formája ismert; az egyiket hullámfrontosztással hozzuk létre, ahol a hullámfrontot oldalirányban tükrökkel vagy diafragmákkal szegmensekre osztjuk. A másik osztási mód megtartja eredeti hullám méretét, de csökkenti annak amplitúdóját. Michelson-Morley kísérlethez [5.8.] kidolgozott mérési elrendezés annyira sikeresnek bizonyult, hogy jelenleg is az egyik leggyakrabban alkalmazott [5.20.] az interferometrikus mérések során [5.23.] [5.24.] .

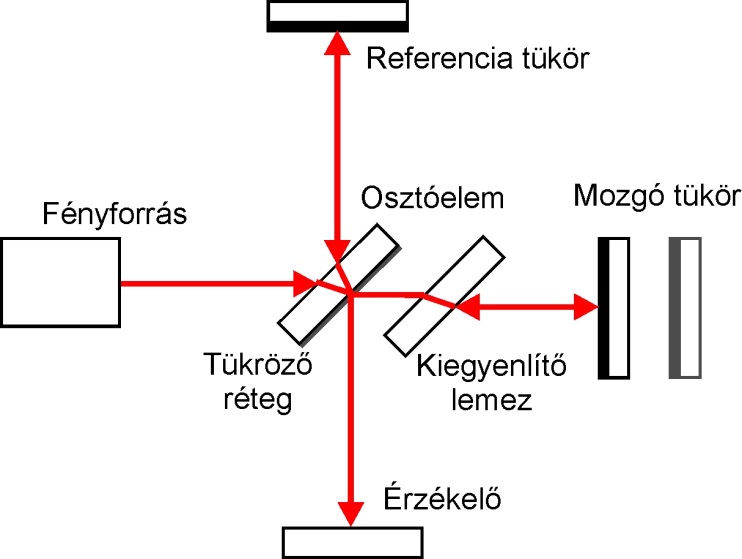
A Michelson-interferométer [5.21.] jó példája az amplitúdóosztás elvén működő interferometrikus eszközöknek. A amplitúdóosztás segítségével létrehozott két nyaláb különböző utakat jár be addig, míg elérik a síktükröket, melyekről reflektálódva újra egyesülnek. Számtalan mérési feladat ellátására alkalmasak, például hullámhossz, fizikai hosszúság, vagy egy anyag törésmutatójának mérésére alkalmas [5.15.] . Természetesen segítségével a forrás koherenciahossza is meghatározható [5.22.] .

Amennyiben a két tükör és a nyalábosztó között a fény útja azonos, ilyenkor a kilépő fényhullámok azonos fázisban találkoznak, azaz az interferometrikusa erősítik egymást. Ha valamelyik kar hosszúsága megváltozik, akkor az interferáló hullámok fáziskülönbsége is módosul, így a detektálható intenzitás is megváltozik. Ha a két tükör egymásra nem merőleges, akkor az interferáló hullámfrontok egymással szöget zárnak be, ami hatására az intenzitásmaximumok helyén világos csíkok figyelhetők meg, melyek távolságából a két hullámfront szöge, a hullámhossz ismeretében számolható.

A Michelson-interferométer felépítését tekintve tartalmaz egy monokromatikus fényforrást. Az innen kilépő – és esetleg kitágított – hullámfront eléri az osztóelemet, melyet elhagyva a keletkező hullámok egyrészt referencia, másrészt a mozgatható tükör irányába haladnak tovább. Ezekről reflektálódva az osztóelem túloldalán találkozva hozzák létre az interferencia jelenségét. Az egyik sugárútban található lemez az üveganyagban megtett sugárutak azonosságát hivatott biztosítani   [5.25.] .