7. fejezet - A mikroszkóp mint optikai rendszer

A környezetünkről nyerhető információ jelentős részének megszerzésében különleges és kiemelt szerepe van látásunknak. A látás útján történő érzékelés eszköze, a vizuális detektálást végző érzékszervünk teljesítménye rendkívül behatárolt [7.36.] , e határok kiterjesztésének hatékony eszközei optikaiak, e célra speciális műszereket használunk.

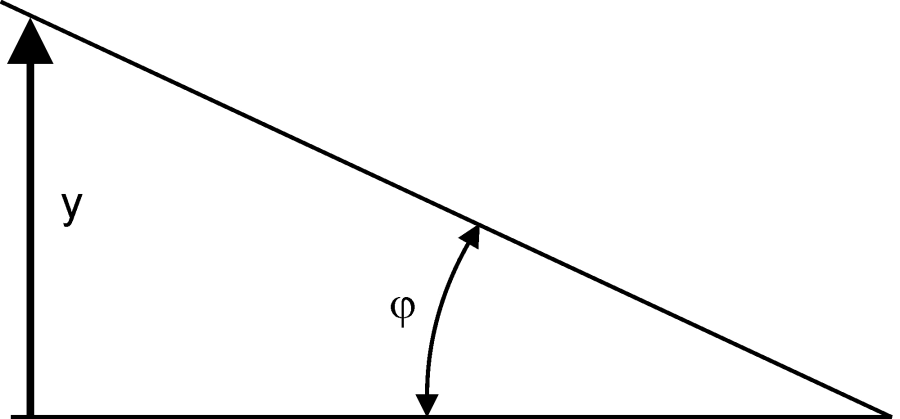
Szinte lehetetlen egy vizuálisan megfigyelt tárgy két szomszédos elemi pontját egymástól meg­különböztetni, ha a belőlük szemünkbe jövő fénysugarak két szögpercnél kisebb szöget zárnak be egymással [7.8.] . Ezen érték felénél kisebb látószögnél a részletek megkülönböztetése teljesen lehetetlen, azaz a tárgyrészleteket nem vagyunk képesek megkülönböztetni, szemünkkel feloldani [7.26.] . Ebben az esetben olyan speciális optikai rendszert vagyunk kénytelenek alkalmazni, amely megnöveli a látószöget, azaz olyan képalkotási elrendezést hoz létre, amelyben a vizsgált – és vizuálisan fel nem bontható – részleteket nagyobb látószög alatt látjuk, és így már azokat felbontani vagyunk képesek. Az ilyen – látószögnövelő – optikai berendezések a távcsövek, lupék, vagy mikroszkópok.

Ha a vizsgálandó (esetleg önmagában nagy) tárgy túl messze van, a rajta lévő – a vizsgálat tárgyát képező – részletek a szem felbontóképességének határszöge alatt vannak, tehát kicsi a részletek látószöge; ilyenkor úgynevezett távcsövet kell alkalmazunk. Fordított esetben, amikor a megfigyelést végző szemünkhöz közel lévő rendkívül kisméretű tárgyak részleteit nem látjuk, azaz ebben az esetben is azok a szem felbontóképességének megfelelő hátárszög alatt látszanak csak; lupét, vagy másképpen egyszerű nagyítót alkalmazunk, melynek feladat szintén a látószög növelése. Egyszerű megfontolások alapján beláthatjuk, hogy minél köze­lebb kerül szemünkhöz a megfigyelés tárgyát képező objektum vizsgált két részletpontja, annál nagyobb lesz azok látó­szöge. Azonban szemünk fontos paramétere a közelpont [7.8.] , amelynél közelebb levő térrészben megjelenő tárgypontokat már nem vagyunk képesek felbontani. Az ilyen esetben alkalmazott lupe szerepe az, hogy a közellevő – felbontott formában megfigyelendő – tárgypontok képét a tiszta látás távolságában hozza létre úgy, hogy a képpontoknak megegyezik a látószöge azzal, mint amikor közvetlenül szemlélnénk az élesen nem látható nagyon közeli pontokat.

7.1. ábra - A látószög értelmezése

Sajnos a lupék látószög növelő képessége igen korlátozott, a vizsgált tárgyat még ilyen eszközzel sem szemlélhetjük nagyon kicsi, a gyakorlatban tapasztalt körülbelül tíz milliméternél kisebb távolság­ból. Ha a vizsgált képpontok pozíciójából adódó látószög biztosításához ennél is kisebb szemlélési távol­ságra van igény, akkor összetett lupét, vagy más néven mikroszkópot kell alkalmazni. Ezt tükrözi az elnevezés is, hiszen az egy görög eredetű összetett szó; a mikrosz kicsit, míg a szkopein rnegfigyelést jelent [7.8.] . Tehát az elnevezés egyértelműen utal az ember képességeinek kibővítésére abban, hogy behatoljon a parányok világába, és onnan információt szerezzen.

A berendezés összetett jellege abban nyilvánul meg, hogy a megfigyelő szeme a tárgynak nem az objektív – a tárgylencse – által alkotott nagy nagyítású valós képét szemléli, hanem erről a valós képéről még egy különleges optikai rendszer, az okulár – vagy más néven szemlencse – által alkotott nagyított, egyenes állású, virtuális képet látja [7.24.] [7.25.] . Ilyen módon detektálni csak azt az információt tudjuk, amit tartalmaz a tárgyról az objektív által alkotott kép, ezért a mikroszkóppal alkotott kép minőségére döntő hatással van az objektív által alkotott kép minősége, azt az okulárral már tovább csak nagyítani, de javítani nem tudjuk.

A mikroszkópokat a tudomány, az ipar, a méréstechnika számos területén alkalmazzák. A feladat az esetek jelentős részében, elsősorban

tekintetében igen kiélezett, így ahhoz, hogy a mikroszkóp teljesítményét sikeresen tudjuk kihasználni, igen körültekintően kell eljárni. Másrészt azt is tudnia kell a felhasználónak, hogy a mikroszkóp egy igen összetett, speciális feladatoknak megfelelni képes, komoly technológiát maga mögött tudó eszköz, így a vele való bánásmód szintén nagy odafigyelést igényel az optimális élettartam elérése vonatkozásában. Ehhez elengedhetetlen a mikroszkóp felépítésének, működésének, kezelésének alaposan ismerete. A modern célmikroszkópok nagyon igényes műszerek, a finommechanika és az optika, mint tudomány és iparág legfejlettebb technológiáinak megtestesítői. Különösen igaz ez a megfelelő optikák kiválasztása és a megvilágítás helyes beállítása vonatkozásában [7.6.] [7.16.] [7.17.] .

Az optika egyéb fejezeteiből ismert, miszerint a fény transzverzális, elektromágneses hullám formájában terjed, amely a mikroszkópban a – speciális követelményeknek megfelelően kialakított megvilágító egységgel – helyesen kivilágított tárgypontból kilépve, áthalad a tubusban elhelyezett mikroszkópos kép­alkotó optikai rendszereken – az objektíven és az okuláron –, majd a megfigyelő szemébe jut, átadva a megfigyelt tárgypontokról a szükséges vizuális információt. Mindezen optikai, optimechanikai és finommechanikai elemeknek ad keretet a mikroszkóp állványa.

Ahogy azt a fentiekben már tisztáztuk; a tárgyról érkező fénysugarak az objektív által a tubusban egy elsődleges képet alkotnak, amiről az okulár által nagyított képet alkotunk a tárgyról. Ezt az objektív által alkotott képet az okuláron, mint egy lupén keresztül még jobban megnagyítva látjuk. Az objektív kiválasztása és helyes alkalmazása a továbbiak szempontjából meghatározó, mivel ez van döntő hatással a mikroszkópos kép minőségére.

A képalkotás folyamatának hullámoptikai alapokon történő vizsgálata ad választ számos olyan kérdésre, amely a mikroszkópok alkalmazhatóságát, paramétereik határait jelenti.

Ez a gyakorlatban azt jelenti, hogy a képalkotás folyamatának vizsgálata során a sugároptika által nyújtott lehetőségeken túl a hullámoptika eszköztárát is igénybe vesszük, azaz nem csak a geometriai optika alaptörvényeire építve követjük végig a rendszerben a fénysugár útját a tárgytértől a képtérig [7.11.] [7.19.] , hanem – az optikai kép­alkotás folyamatának finomabb részletei megismerésének céljából – figyeljük a tárgyból kilépő fényhullámok formájának és pozíciójának változását, alakulását a képalkotó optikán való áthaladása során. Ez a tárgyalásmód a szakirodalomban részletesen tárgyalt, felöleli az optikai rendszerek képalkotásának általános elméletét és az optikai rendszerek analízisének módszereit is [7.27.] [7.37.] . Ezzel a hullámoptikai leírásmóddal meg tudjuk álla­pítani, hogy milyen alsó határméret esetén képes a mikroszkóp tárgyrészleteket külön­választani vagy más szóval feloldani [7.27.] . Ezzel a hullámkövetési eljárással egyúttal magyarázatot kapunk azokra a jelenségekre, amelyeket az egyes mikroszkópos megfigyelési módszerek esetén előállnak. Ezek rendre:

Az a tény sem hagyható figyelmen kívül, mely szerint a mikroszkópnak, mint egy komplex mérőberendezésnek – optikai szempontból igényes korrekciójú – eleme az optikai leképző rendszere, megvilágító és fényterelő rendszere, és ugyancsak eleme egy igényes, precíziós kivitelű, fejlett technológiát képviselő finommechanikai szerkezet. Ennek ékes bizonyítéka az a tény is, hogy ezen eszközök előállítását végző iparágak vállalatai szorosan kapcsolódnak, együttműködnek és nem ritkán szerves egységet alkotnak.

A mikroszkópon belül a mechanikai szerkezeti elemek egymáshoz képesti pozíciójának állítási lehetőségei az ezredmilliméteres elmozdulási tartományban vannak, az ezekhez kapcsolódó vezetékek pontosságára vonatkozóan szintén hasonlóak az elvárások. A legkorszerűbb mikroszkópokban széles körben alkalmazzák a finommechanika, az optomechanika legújabb szerkesztési elveit, szerkezeti megoldásait és ezek gyártásához a legfejlettebb technológiákat és szerkezeti anyagokat. E tekintetben igen gazdag irodalom áll rendelkezésre [7.1.] [7.2.] [7.3.] [7.4.]

A mikroszkóp, mint finommechanika-optikai felépítésű, műszertechnikai szerkezet, minden eleme, alkatrésze, funkcionális egysége precíziós technikai hátterű tervezői munkát igényel.  Így a finommechanikai gyártás szigorú tűrései itt fokozottan érvényesülnek, ugyanis a műszeripari tűrésezés során azok méretére vonatkozóan igen szigorú megfontolások, és előírások szerint kell eljárni. A mikroszkópos technikában a tűrés, mint egy mérnöki-tervezési filozófiai alap, az elterjedt és ismert fogalom jól szemléltethető iskolapéldája. A mikroszkópos technikában, és általában a finommechanikában a tűrések nagyságrendje leggyakrabban a század­ vagy az ezredmilliméter környékére esik [7.1.] [7.6.] [7.8.] .

A mikroszkópban előálló kép észlelése általában vizuális úton történik. Ilyenkor lehet elvégezni a legalapvetőbb beállításokat, a helyes képkivágást, az élesre állást, a nagyítást. Természetesen a mikroszkópos kép szemlélése történhet megjelenítő eszközön keresztül is, ilyenkor a képet egy érzékelő detektálja, amit mintavételezés és kvantálás után, illesztve a megjelenítő bemenetéhez arra csatlakoztatni lehet. A látott objektum dokumentálása, vagy későbbi újravizsgálata céljából a mikroszkóp­ban látható képet elektronikusan vagy hagyományos módon rögzíthetjük, lefényképezhetjük. A mikroszkópos kép rögzítése által a képből történő újabb és mélyebb információk kinyerése céljából a rendszereket általában célorientált képfeldolgozó egységekkel egészítik ki, amelyek igen nagy számban tartalmazhatnak automatikus képjavító, rekonstruáló, szűrő, transzformáló, szegmentáló, alakfelismerő algoritmusokat. A mikroszkópos képek feldolgozásának algoritmusai és módszerei az utóbbi időben igen dinamikus fejlődésen mentek keresztül, ennek irodalma igen szerteágazó és gazdag [7.28.] .

Lehetőség van a térbeli információkat időbeli információkkal bővíteni a mikrokinematográfia, a mozgófényképezés, gyorsfilmezés eszközeivel a tárgy változásai, mozgásai, dinamikus viselkedései megörökítése útján. A fénymikroszkópok nagyítása a rendkívül szerény értékektől a mintegy kétezres értékig terjed [7.9.] . A nagyítások alsó határán a sztereomikroszkópok és mérő­mikroszkópok működnek, itt egyrészt a nagyítás fokozására nincs is szükség, másrészt a nagyítással csökkenő mélységélesség is korlátot jelent. Szintén fontos tény, hogy a nagyítás növekedése és a szabad tárgytávolság közötti kapcsolat is határt jelenthet az alkalmazhatóság tekintetében. A mérő­mikroszkópoknál gyakran nem a nagyítás a fontos, hanem az, hogy a tárgy képe egy – az okulár részét képező – beosztásos szállemezen keletkezik a tárgy méreteinek könnyű megmérése céljából. A nagyítások felső határán a biológiai vizsgálatokban alkalmazott mikroszkópok dolgoznak. A biológiai vizsgálatok során elsősorban az élő szervezetek alkotóelemeinek egyre kisebb és kisebb alkatrészeit analizálják, ami nagyobb nagyítást és jobb feloldóképességet igényel. Sajnos a látható fénnyel működő mikroszkópok a hullámoptikai korlátok miatt nem képesek az egymáshoz két tizedmikronnál közelebb levő tárgypontok feloldására. Könnyű belátni, hogy ilyen mértékű feloldáshoz mintegy ezerötszáz-kétezerszeres nagyítás szükséges. A két tizedmikronos tárgypont távolság ezerötszázszoros nagyításánál a kétszázötven milliméteres, tisztánlátási távolságból négy szögperc alatt látszik a két tárgypont, ami a szem feloldó­képesség gyakorlati határértékének felel meg [7.8.] .

A mikroszkóp feloldóképessége növelésének eszköze – ahogy a későbbiekben látni fogjuk – az objektív numerikus apertúrájának növelése, a hullámhossz csökkentése, illetve az elektronmikroszkóp alkalmazása. Itt a képalkotást nem fénysugarak, hanem nagy sebességgel mozgó negatív töltésű elektronok, elektronsugarak végzik. Az elektronsugarak pályáját külsőleg vezérelt elektron­lencsékkel, elektromos és mágneses erőterekkel úgy lehet irányítani, mint a fénysugarakat a hagyományos optikai elemekkel. A képalkotás is a hagyományos optikai mikroszkóphoz hasonlóan történik [7.8.] . Az elektronok egy elektronforrásból az úgynevezett katódból lépnek ki, nagyfe­szültségű téren haladnak át úgy, hogy közben felgyorsulnak, áthaladnak a tárgyon, majd az objektívnek és az okulárnak megfelelő két elektronlencse segítségével képet alkotnak. Az ernyő fluoreszkáló anyaggal van bevonva, a becsapódó elektronok mennyisége függvényében a kép, azon erősen vagy gyengén világít, ami szemmel látható, vizsgálható. Detektort helyezve a fluoreszkáló ernyő helyére, azon ugyanúgy fényképet kapunk, mint a hagyományos fénysugarakkal.

Mivel sajnos az elektronsugarak csak nagyon vékony rétegeken tudnak csak áthatolni, az elektronmikroszkópos minták előkészítése, kidolgozása jelentősen eltér­ az optikai mikroszkópnál megszokottaktól. Hatalmas nagy előny viszont, hogy az elektron­mikroszkóppal el lehet érni a több százezerszeres nagyítást és a fénymik­roszkópnál három nagyságrenddel nagyobb feloldóképességet.

A mikroszkópos megfigyelések nemcsak kvalitatív adatok megállapítására szolgálnak, hanem egyre inkább terjednek a mikroszkópos alapú kvantitatív vizsgálatok, mérések. Az ilyen jellegű mérések a tárgyak méreteinek meghatározásán túl, mennyiségi vizsgálatokra is kiterjednek. Mérhető például a törésmutató, az abszorpció, az extinkció, a fluoreszcencia, a refle­xió, a remisszió és a koncentráció, de a fáziskontraszt és a polarizációs mikroszkópia egyéb paraméterek kavalitatív és kvantitatív mérését is lehetővé teszi.

Az optikai mikroszkópok története szorosan összefügg az optika történetével, hiszen számos felfedezés gazdagította a mikroszkopizálás gyakorlatát, de fordítva is igaz, hiszen a mikroszkópok fejlesztése során megjelenő kihívások számtalan új, az optika szempontjából fontos felfedezés ösztönzői voltak. A mikroszkópok fejlődével kapcsolatos történelmi tények az irodalomban számtalan helyen [7.8.] fellehetők, az alábbiakban csak egy rövid kivonatot adunk ebből a nagyszerű tudománytörténeti fejezetből [7.20.] [7.29.] [7.30.] .

Az egyszerű mikroszkóp használatára vonatkozó első feljegyzések csak a 16. század végére tehetők annak ellenére, hogy a fénnyel kapcsolatok alapvető jelenségét már az ókorban is is­mertek voltak. Szintén a tizenhatodik századra tehető az első összetett, objektívből és okulárból álló mikroszkópok megjelenése is.

Az összetett mikroszkóp alkalmazásának elterjedését a színhibák korrekciója tette lehetővé. A mikroszkópia története nem választható el az egyetemes optika fejlődésétől, melynek lényegesebb momentumai – a teljesség igénye nélkül – az alábbiak.

Az optikai jellegű kísérletek kivitelezését és műszerek építését sokáig hátráltatta a megfelelő üvegválaszték, e tekintetben az első említésre méltó esemény a muranói üveggyár 1291-es alapítása. Természetesen az optikai tervezés vonatkozásában nagy jelentőséggel bíró és nagy szabadságfokot jelentő, gazdag üvegválasztékot előállító Schott üveggyár megalapítására még sokat kellet várni. A első összetett mikroszkópot Hans Janssen és fia Zacharias készítette el valamikor a tizenhatodik, illetve a tizenhetedik század fordulóján.

1623-ban Mansell flintüveget készített és két évre rá Faber alkalmazta először a mikroszkóp elnevezést. Az elméleti munkák tekintetében kimagasló jelentőségű az 1626-os esztendő, amikor Willebrord Snell a Leideni Egyetem tanáraként kimondta a fénytörés törvényét, amely egyik legfontosabb alapösszefüggése a geometriai optikának. Tőle talán függetlenül ugyanerre az eredményre jutott 1637-ben René Descartes. Az 1700-as évek elején Leeuwenhoek számtalan, különböző gyújtótávolságú lencsét csiszolt, elsősorban biológiai megfigyeléseihez.

Az egész optika szempontjából hatalmas jelentőségű Pierre Fermat 1657-ben kimondott elve az optikai úthosszak stacionáriusságáról. 1650-ban Francesco Grimaldi a fény diffrakciójáról írt, majd 1665-ben Robert Hook állványos mikroszkópot készített mesterséges megvilágítással. Ez az időszak az optikai megfigyelések szempontjából különös jelentőséggel bír, hiszen Sir Isaac Newton ekkor foglalkozott fénytani megfigyelésekkel, melyek elsősorban a fénytörésre, a színbontás jelentőségére és a diszperzióra (1666) vonatkoztak.

A következő esztendőben Christian Huygens összeállította a róla elnevezett okulárt, melyet ma is széles körben alkalmaznak. Erre az időszakra tehetők a mikroszkóppal kapcsolatos fontosabb fejlesztések; 1685-ben Tortoni átvilágításos mikroszkópja, 1691-ben Bonanni mikroszkópos megvilágítása fókuszálható kondenzorral, 1704-ben Marshall billenthető mikroszkópállványa, 1730-ból Culpeper mozgatható megvilágítótükre.

A mikroszkóp objektívek fejlődése tekintetében a nagy áttörés 1757-ben következett be, ugyanis a Dollond fívérek akromatikus lencsepárt készítettek sikerrel, cáfolva Newton ezirányú megállapításait. A színhibákkal terhelt optikai rendszerek korrekciója vonatkozásában a Dollond fívérek gyakorlati eredményeit Leonhard Euler szentpétervári matematikus 1762 és 1764 között végzett elméleti munkája zárta le, megoldva azaz akromatizálás kérdését. 1776-ban Adams a gyors objektívváltáshoz revolverszerkezetet tervezett.

Ramsden a geodéziában ma is széles körben alkalmazott teodolit feltalálója 1783-ban elkészítette a később róla elnevezett okulár típust. A modern mikroszkópia szempontjából nagy jelentőségű polarizáció jelenségére 1808-ben adott magyarázatot Etienne Malus, vizsgálva a fény polarizációját visszaverődés útján. 1818-ban Amici speciális, félgömb alakú objektív frontlencsét és katadioptrikus mikroszkópobjektívet készített.

1829-ben Talbot elkészítette az első polarizációs mikroszkópot.  1837-ben Ross korrekciós foglalatot tervezett a fedőlemez vastagság által okozott eltérések kiegyenlítésére. Szintén ugyanebben az esztendőben Reade sötét látóterű mikroszkópot készített.

A 1839-es esztendővel kezdődően komoly eredmények születtek, melyek meghatározó hatással voltak a fotográfia további fejlődésére. Jacques Daguerre kidolgozta a róla elnevezett Daguerrotypiát és a későbbiekben számtalan felvételt készített, melyek jelentősége kultúrtörténeti szempontból is kimagasló.

A bécsi Voigtlander cég megbízásából, a magyar származású bécsi matematikus Petzvál József 1841-ben fényerős objketívet tervezett, mellyel az addigi nagy expozíciós idők jelentősen csökkentek kimagasló képminőség mellett. Ez, az úgynevezett Petzvál-objektív volt az első olyan optikai rendszer, amelyet módszeresen terveztek, így tulajdonképpen Petzvál tekinthető a modern optikai tervezés, azaz a rendszerszintézis megalapítójának. Objektívje nagy távolságban elhelyezett légréses és ragasztott kéttag kombinációja, ma is számtalan rendszer kiindulási szerkezete. 1843-ban fogalmazat meg a képmezőhajlás és az asztigmatizmus korrekciójára vonatkozó feltételét; a Petzvál-összeg pedig a korszerű optikai tervezés egyik kiinduló feltétele még mai is. Petzvál megállapította, hogy egy leképző optikai rendszer esetén a képfelület akkor sík, ha a törésmutatók, és a lencsefelületek görbületi sugarainak kombinációja eleget tesz a róla elnevezett formulának. Petzvál szepességi német családban született, de mindig magyarnak vallotta magát. Pesten az Institutum Geometricum tanulója volt, itt szerzett mérnöki oklevelet, de később felsőbb matematikát tanított. 1837-ben Bécsben az egyetemen tanárrá nevezték ki. A Petzval-féle objektív szférikus aberrációja és longitudinális színhibája kicsi, ezért például vetítésre is alkalmas. Tőle származik a képmezőhajlásra vonatkozó általános összefüggés, melyet 1843-ban publikált. Optika mellett foglakozott ballisztikával és a hangtannal is, ezek körében is írt tanulmányokat. Saját szerkesztésű műszerével fotogrammetriai méréseket is végzett. Ő volt az első, aki kiterjedt közelítő számítások végzett optikai rendszerekre vonatkozóan méretezés céljából. Számításait nem publikálta, azért a harmadrendű hibaelmélet megalkotása Ludwig von Seidel nevéhez fűződik. A képmezőhajlás korrigálását biztosító feltétel felismerése azonban az ő érdeme, mely szerint a képmező görbületi sugara és az optikai rendszert alkotó lencsék fókusztávolságai, valamint törésmutatói között összefüggés áll fenn. Ugyanis az egy síkban fekvő, tengelyen kívüli tárgypontok képei görbült felületet alkotnak. A rendszer képmezeje általában görbült, amelyet Petzvál-görbületnek nevezünk. Ha nincs asztigmatizmus, akkor a szagittális és a meridionális képmezők egymásba egyesülnek. Ekkor csak képmezőhajlásról beszélünk. A Petzvál görbületet összefüggésében a lencsék vastagsága nem szerepel, tehát az összefüggés vékony rendszerre is alkalmazható.

1844-ben a felbontóképesség növelése céljából Amici kísérleteket végzett vízimmerziós objektívekkel. 1845-ben Chevalier alkalmazta először az elektromos ívlámpát mikroszkópos megvilágítás céljából fényforrásként. 1847-ben készítette el Carl Zeiss az első mikroszkópját.

1849-ben készítette el Kellner a ma is alkalmazott Kellner-féle és ortoszkopikus okulárt. A szem, mint optikai rendszer szintén az érdeklődés középpontjában állt, megfigyelésére Helmholtz 1850-ben szemtükröt szerkesztett. Ugyanebben az évben Porro olasz tüzértiszt elkészítette az első prizmás képfordító rendszert, és azt alkalmazta távcsövében.

A színtan területén végzett megfigyeléseket Helmholtz, a tudományterület szempontjából rendkívül fontos törvényeket 1853-ban Grassmann fogalmazta meg. Magyarázatot adott az additív színkeverés jelenségére. Ebben az évben publikálta az anyagi részecskéken végbemenő fényszóródással kapcsolatos eredményeit Tyndall.

A Petzvál József kapcsán említett harmadrendű aberrációk elméletét (a képmezőhajlás esetében Petzvál Józsefre hivatkozva) Ludwig von Seidel publikálta 1856-ban, megalapozva ezzel korszerű optikai tervezés módszertanát. James Clerk Maxwell 1864-ben ismertette az elektromos és mágneses mezők kölcsönhatását leíró elméletét. Eredményei meghatározó befolyással voltak a huszadik századi fizikára. Maxwell legfontosabb érdeme az, hogy kiterjesztette a korábbi eredményeket az elektromos és mágneses térre, azt egységes matematikai formulába öntötte. Ezek az – úgynevezett Maxwell-egyenletek – megmutatják az elektromos és mágneses mező a térben terjedésének mikéntjét.

1871-ben Lord Rayleigh kimutatta a fényszóródás hullámhossz-függését, amelyért 1904-ben Nobel-díjjal jutalmazták. 1873-ban Ernst Abbe megalkotta a mikroszkópos képalkotás elméletét, illetve levezette a mikroszkóp feloldóképességének függését a fény hullámhosszától és bevezette a numerikus apertúra fogalmát. 1884 meghatározó az optikai rendszerek tervezése és gyártása terén, ugyanis ebben az esztendőben alapította Otto Schott a jénai üveggyárat, mely széles üvegválasztékkal állt a tervezők rendelkezésére a törésmutató és a színbontó képesség tekintetében.  A jénai Zeiss műveknél Ernst Abbe 1886-ban alkotta meg az első, gyakorlatban is sikerrel alkalmazott apokromátot. 1888-ban Henrich Hertz kísérleti úton is kimutatta az elektromágneses hullámokat. Ugyanebben az évben alkalmazott először monobrómnaftalin immerziós objektívet Ernst Abbe. 1893-ban a mikroszkópos megvilágítás ma is alkalmazott elvét dolgozta ki August Köhler.

1930-ban kidolgozta a vákuumgőzölés módszerét Burch. 1933 az elektronmikroszkóp felfedezésének éve. 1934-ben Chrétien változtatható gyújtótávolságú (zoom) objektívet tervezett. Szintén ebben az évben publikálta a fáziskontraszt-eljárást Frits Zernike, aki ezért 1953-ban Nobel-díjat kapott. A jénai Zeiss műveknél alkalmaztak először 1935-ben reflexiócsökkentő bevonatot. 1938-ban mutatott be Boegehold plánakromát mikroszkópobjektívet. 1942-ben Zernike tanítványa Nijboer módszert mutatott a képhibák általános osztályozására, majd a következő esztendőben értelmezést adott a hullámaberráció fogalmának. 1947-ben Max Herzberger bevezette a pontszórás függvény, azaz a spot-diagram fogalmát.  

1948-ban matematikai módszerekkel alapozta meg Shannon az információelméletet, és alkotta meg Gábor Dénes a holográfia elméletét.  1950-ben Maréchal alkalmazta a térfrekvenciaszűrést, 1960-ban vezették be a kandelát a fényerősség alapegységeként, és alkotta meg Maiman az első rubin-lézert. Azóta napjainkig az optika fejlődése szinte töretlen, nem található olyan területe az életnek, a tudománynak és az iparnak, ahol ne alkalmaznák eredményeit széles körben. Szerepe a méréstechnikában szinte megkerülhetetlen.

(Balról jobbra, fentről lefelé). Johannes Kepler (1571–1630), Pierre de Fermat (1601 – 1665), Christiaan Huygens (1629 – 1695), Joseph von Fraunhofer (1787 – 1826), Leonhard Euler (1707 – 1783), Ludwig Wilhelm Seidel (1802 – 1894), Lord Rayleigh, (1842 – 1919), Ernst Karl Abbe (1840 – 1905), Petzval József (1807 – 1891)

7.2. ábra - A mikroszkópizálás történetének meghatározó alakjai

(Balról jobbra, fentről lefelé) James Clerk Maxwell (1831 – 1879), Carl Zeiss (1816 – 1888), Friedrich Otto Schott (1851 – 1935), Frits Zernike (1888 – 1966), Gábor Dénes (1900 – 1979)

7.3. ábra - A mikroszkópizálás történetének meghatározó alakjai

A mikroszkóp alkalmazásának alapgondolata az emberi szem viselkedésében keresendő. Annak anatómiai és fiziológiai tulajdonságai teszik a szemet képessé arra, hogy az érzékelést végző idegvégződésein a megfigyelt tárgy éles képét hozza létre, függetlenül attól, hogy a szemlélt tárgy hol helyezkedik el. Ez a folyamat, azaz a tárgy távolságához való illeszkedés az első képalkotás céljából az úgynevezett akkommodáció. A távolpont a legnagyobb tárgytávolság, amely­re akkommodálni kell a szemnek [7.8.] . A közelpont helye viszont attól függ, hogy a szem, szerkezetéből adódóan mennyire közeli tárgyra képes akkomodálni.

Ha erre valamilyen ok miatt nem képes, a közelpont szemléléséhez szem­üveget kell alkalmazni.

Egy tárgy akkor látszik nagyobbnak, ha közelebb van a szemhez. Ha ezt minden határon túl folytatjuk, akkor a tárgy a közelpontnál is közelebb kerülhet a szemhez. Ekkor azonban az már nem láthat­ó élesen, ilyenkor kerül sor lupe vagy összetett mikroszkóp alkalmazására.

A pupilla átmérője a környezeti világosságszintnek megfelelően változik, ez lényegében egy átmérő­re történő szabályozást jelent, azaz szem fényérzékelő képessége és érzékenysége is ehhez a világosságszinthez igazodik. A szemlencse a tárgy távolságának megfelelő alakot vesz fel [7.36.] .

Ismert és kísérleti úton igazolható tény, hogy a teljes adaptáció és akkommodáció állapotában a szem feloldó­képessége optimális, amin azt a legkisebb látószö­g értéket értjük, amely mellett sötét alapon levő két egyenlően világos, megfelelően kicsiny pont jól érzékelhetően szétválik (azaz a két pont együttes képe kellően „piskótásodott”). Az igen széleskörben elterjed egy szögperces érték különleges esetben előforduló maximumnak tekinthető, az átlag amivel a kísérletek, illetve a tervezés során számolni lehet valahol a két és a négy szögperc között található. Konkrét alkalmazásoknál célszerű a legrosszabb estet figyelembe venni [7.8.] , mivel az egyéni különbségek mellett a tárgyrészletek megkülönböztethetősége számtalan tényező függvénye. Ezek közé sorolható a világosság, a színezet, a kontraszt, a kontúrok alakja, összefüggősége, a textúra.

A körülmények miatti felbontóképesség ingadozást jól jellemzi az a tény is, hogy például két egyirányú vonaldarab esetén egymás folytatódásakor sokkal jobban meg tudjuk ítélni, hogy azok egybe esnek-e, vagy sem.

Kísérleti és tapasztalati úton is igazolt tény, hogy a perspektivikus elemeket tartalmazó vizuális ingerstruktúrák megfelelő értelmezése kulturális tényezőkre és tanulási folyamatra vezethető vissza. A térérzékelés tehát bizonyos tekintetben tanult folyamatnak tekinthető. Mivel vizuális érzékelés esetén az egyes szemek detektáló felületein keletkező képek kétdimenziósak, a harmadik dimenzióhoz kapcsolható információk előállításának e kétdimenziós képek bonyolult agyi tevékenységen alapuló értékelésén kell alapulniuk. A kognitív pszichológia szerint a térlátás, amely a két szemből érkező – és eltérő - képek agyi feldolgozásán nyugszik, a vizuális észlelés legmagasabb szintjének tekinthető. A térlátás elemei öt csoportba sorolhatók: a konvergencia, a retinális eltérés, az akkomodáció, a mozgás-parallaxis és a perspektivikus hatás.

A konvergencia a két szem látótengelye által bezárt szöggel áll kapcsolatban. E szög értéke a távolság növekedésével csökken, nagyságából az agy a tárgy távolságára következtet. A retinális eltérés oka, hogy a két retinán megjelenő, egymástól némileg eltérő kép értékelése alapján mélységérzet alakul ki. E jelenségen alapszik a sztereoszkóp, amelyben a két eltérő pozícióból készített két képet az agy egyetlen, térhatású képpé egyesíti. Az akkomodáció is hozzájárul a térlátás kialakulásához azáltal, hogy a szem közelebbi, vagy távolabbi tárgyra tekintés esetén alakot változtat, ezt értékeli az agy. A mozgási parallaxis azt jelenti, hogy az elmozdulás mértéke és a megfigyelő távolsága fordítottan arányos, így ismét egy agyi funkcióval a mozgási parallaxisból a tárgy távolságára is lehet következtetni. A perspektivikus hatást jelentik azok a mélységi információk, amelyek részei a képi tartalomnak;

Döntő fontosságú a térlátás kialakulása szempontjából az, hogy a szemlélt tárgyat és környezetét a jobb szemünk­kel jobbról, a ballal balról látjuk, tehát a két szem retináján eltérő képek keletkeznek, amit az agy egyetlen tér­beli látvánnyá köt össze [7.8.] .

A mikroszkopikus tartományok tárgyainak térbeli érzékeléséhez sztereomikroszkópokat célszerű használni, mely lényegében két független mikroszkóp egyesítve úgy, hogy azok a megfigyelő szemeinek tengelyei meghosszabbításában helyezkednek el. A tárgy egyik szemmel balról, a másikkal jobbról látható, azok képei a tisztánlátás távolságában jönnek létre, de eltérőek, így az érzékelés térbeli, sztereoszkopikus. A sztereomikroszkópot a biológiában és a szerelési technikában használják, azzal a mikroszkóp alá helyezett tárgyakon megfigyeléseket, műveleteket, beavatkozásokat lehet végezni. A szetereomikroszkóp nem összekeverendő a binokuláris mikroszkóppal, melybe szintén két szemmel lehet betekinteni, azonban mindkét kép ugyanaz, ezért a térbeli hatás létre nem jön. A binokuláris mikroszkóp alkalmazásának nagy előnye, hogy az észlelés nem fárasztó, a kétszemű nézés a fiziológiai egyensúlyt megtartja [7.8.] .

A tárgytér leképzéséből keletkező képtérbeli intenzitás-eloszlásban egy részlet felismerhetőségének kritériuma, hogy az a környezeté­től világosság vagy szín tekintetében az érzékelhetőség határán túli mértékben különbözzön. A részletek elkülönülésének ezt a tulajdonságát és az ebből származtatható képi tulajdonságot kontrasztbeli eltérésnek nevezzük. A kisméretű folt pontnak tűnik. Pszichológiai okok miatt eltérést mutat a sötét foltnak egy világos alapon való érzékelhetősége és világos foltnak sötét környezetben való érzékelhetősége [7.8.] . Kísérleti úton igazolható, hogy a világos pont érzékelhetősége a pont világosságától függ, de független a pont nagyságától, viszont a sötét folt érzékelhetősége függ a folt kiterjedésétől is. Természetesen az érzékelhetőség mértékét jelentős mértékben befolyásolják az észlelés emberi vonatkozásai, például a szem fáradtsága és az észlelésre fordított idő hossza is, a külső zavaró hatások, figyelemelterelő ingerek, azok gyakorisága.

Az érzékelhetőség szempontjából a kontrasztosság mellett szintén rendkívül fontos tulajdonság; a gradáció. A gradáció feltétele a képtulajdonságra vonatkozóan az, mely szerint a képen két szomszédos, érintkező elemi méretű ingert akkor látunk szétválasztottnak, ha egymás között is kontrasztosak. Ennek mértéke a kép gradációja. Más megfogalmazásban a képrészleteknek akkor van megfogalmazható alakjuk és méretük, ha világosságuk és a háttér világossága közötti átmenet gyors és határozott. Természetesen, ha színingerekről van szó, a helyzet hasonló módon és formában értelmezhető úgy. Az információt hordozó képrészlet és a háttér közötti átmenetek dinamikája, annak képbeni jelenléte jellemzi az egyik legfontosabb vizuális képtulajdonságot; a kép élességét. Szintén pszichológiai és neurológiai okokra vezethető vissza az a tény, hogy a vizsgált képen ugyan az előbb tárgyalt átmenetek szinte sohasem meredekek, de a látásunk ezeket a nem ugrásszerű, tehát akár folytonosnak tekinthető átmeneteket is értékeli. A képtérben megjelenő tárgyrészletek széleit nevezzük kontúroknak. Mivel ezek a kontúrok közvetlen kapcsolatban állnak az információt hordozó képrészlet és a háttér közötti átmenetek dinamikájával, az értékelt kép élességét elsősorban a kontúrélesség határozza meg.

Speciális hatását gyakorol az érzékelt kép tulajdonságaira a mélységélesség. Jelenti ez a gyakorlatban azt az esetet, amikor a tárgy a tárgytérben térbeli kiterjedésű, viszont a kép csak síkbeli. Tehát a tárgynak csak egy síkmetszete lesz ideálishoz közeli viszonyok mellett leképezve, az attól eltérők ugyanabban a képsíkban, de életlenül kerülnek ábrázolásra. A sztereómikroszkópok alkalmazása során a kellő mélységélesség biztosítására kellő hangsúlyt kell fektetni, ugyanis ebben az esetben a kis mélységélesség rendkívül zavaró [7.21.] [7.22.] [7.8.]

Az emberi szem tulajdonsága az is, hogy látómezőnknek csak egy kicsi részét képes élesen leképezni. Ezért az agy a szemet mindig a megfigyelni kívánt tárgyrészletre fordítja, és ekkor akkommodál, természetesen ilyenkor a többi leképzett tárgyrészlet életlen. A megbízható és jó észlelésnek feltétele továbbá, hogy a világosság és kontraszt is megfelelő legyen. Emiatt kulcsfontosságú a világosság-, kontrasztosság-és élesség képmezőn belüli eloszlása. A szemmel való jó leképzéshez az is szükséges, hogy a leképzendő tárgyrészlet elég nagy méretű legyen [7.11.] [7.20.] .

Megfelelő nagyítás esetén a részletek ugyan jól azonosíthatók, de esetleg éppen emiatt az átfogó tulajdonságok már nem érzékelhetők, ezért elengedhetetlen a kép megfelelő nagyításának biztosítása mellett a kép szükséges látómező mérete is.

A látás agyi szintű megvalósulása esetén egy integráló és differenciáló tevékenység valósul meg [7.8.] , melynél az integráló tevékenység a szomszédos képfoltok együttesének egy-egy nagyobb tárgyrészlet képének formájában történő láttatását biztosítja, míg a differenciáló tevékenység eredményeként az agy egyes képrészleteket és képrészlet csoportokat más részletektől és más részletcsoportoktól elválasztva egy-egy tárgyrészlet képeként láttatja. Ezek mellett jelentkezik az agy kiegészítő tevékenysége, amely azt jelenti, hogy ha valamely tárgyrészlet képe nem látszik, azt bizonyos kritériumokon belül oda lehet képzelni. Ezzel magyarázható például a kép rendezettsége. Az agy kiválasztó tevékenysége pedig a kiegészítő tevékenység ellentéte, amikor is egy tárgy képében megjelenő, oda nem illő tárgyrészletet agyi szinten le lehet a tárgytól választani. Ezzel a jelenséggel magyarázzák a kép tisztaságát.

A kép világosságának és kontrasztosságának értelmezéséhez elengedhetetlen a radiometria és fotometria fogalmainak helyes értelmezése. Radiometria-fotometria közötti összefüggés megértéséhez definiáljuk először a radiometriát, mely hullámhossz független érzékelést, tárgyalást jelent a szokásos energetikai egységekben.

A fotometria egy hullámhossz-függő érzékelés, melyet a világosra adaptált emberi szem láthatósági függvénye révén ír le. Az emberi szem érzékelése vonatkozásában megkülönböztetünk fotopikus látást, mely normális megvilágítás esetén érvényes; maximuma 555 nm-nél található. A szkotopikus látás gyenge megvilágítás esetén lép fel; maximuma 507 nm-nél van. A két előbbi között átmenetet jelenti a mezopos látás, melynél először a vörös színei tűnnek el, legtovább a kék színek maradnak meg. A fotometriai mennyiségek között alapmennyiség a fényerősség, mely egysége a kandela. A kandela annak az 540 THz (λ = ~555 nm) frekvenciájú monokromatikus sugárzást kibocsátó fényforrásnak adott irányban kibocsátott fényerőssége, amelynek sugárzáserőssége ebben az irányban 1/683 W/sr (Nemzetközi Súly- és Mértékügyi Bizottság 1979).

A fénysűrűség az a mérték, mely az emberi szemben a világító vagy a megvilágított felületek által keltett fényérzetet határozza meg, azaz a felületegységre jutó fényerősség. Mértékegysége a kandela/négyzetméter. A kép fénysűrűsége függ a tárgy fénysűrűségétől. A megvilágítás a megvilágított felületre eső fényáram és a megvilágított felület nagyságának hányadosa, nemzetközi egysége lux.

Lényegében a megvilágítás erőssége és a mikroszkóp objektív numerikus apertúrája tekinthethető a mikroszkópos kép világosságát leíró mértéknek [7.20.] [7.8.] .

A képvilágosság helyi változása meghatározó jelentőségű a mikroszkópos képek kontrasztjának értékelése szempontjából. A kontraszt definíciója [7.35.] :

A mikroszkópiában jelentőséggel bíró képtulajdonságok között a kontrasztosság talán az egyik legfontosabb. A jól értékelhető képhez nem elegendő, hogy a világos és éles legyen, ha alacsony a kontraszt, a képrészletek nem válnak el egymástól, nehezen megkülönböztethetőek. A kontrasztosság növelésnek célját szolgálja az összes festési eljárás. Ide tartozik továbbá a fáziskontraszt eljárás, az interferenciamikroszkóp, valamint a ferde és sötét látóterű megvilágítás is, hiszen ezen eljárásokkal a kontrasztnélküli, vagy fázistárgyakról jól megfigyelhető, kontrasztos képet tudunk előállítani.

A kép kontraszthűségén a kép tárgyéhoz viszonyított kontrasztosságát értjük, amely jelentős mértékben függ tárgy részleteinek méretétől és a tártérben található részletek térfrekvenciájától. Hiszen minél sűrűbb ráccsal modellezhető tárgyrészletet képezünk le, annál rosszabb lesz a kép kontrasztja. Ezt az összefüggést ábrázolja lényegében a kontrasztátviteli függvény [7.31.] [7.35.] is, mely a térfrekvencia függvényében ábrázolja a képtéri kontrasztot. A térfrekvencia pedig a leképzett periodikus struktúra egységnyi hosszra eső periodikus struktúráinak számát jelenti.

A mikroszkópos képalkotás, illetve a mikroszkópos kép használhatósága és értékelhetősége szempontjából kiemelten fontos a kép élessége, illetve a képélesség helyi változása. A kép élessége szempontjából fontos, hogy a képrészletek alakját meghatározó szélvonalakra, a kontúrokra merőlegesen a képvilágosság gyorsan változik. Az élességet lényegében az jelenti, hogy az átmenet mekkora út mentén történik. Gyakran a kontúrátmenetet leíró függvény emelkedő részét az inflexiós érintővel helyettesítik, és azt adják meg, hogy ez az egyenes mekkora utat tesz meg a legalacsonyabb és a legmagasabb világosságszintek között [7.8.] .

A képélesség helyi változásának okai az optikai rendszer aberrációi. Képi rögzítés esetén azonban az objektívnek a detektor egész felületére éles képet kell leképeznie. Ilyen célt szolgálnak a plánobjektívek: plánakromátok és plánapokromátok.  A mikroszkópos kép mélységélessége alatt a képen élesnek látszó legközelebbi és legtávolabbi tárgyrészlet távolságát értjük az optikai tengely mentén mérve [7.8.] .

Példa:

Egy felületi struktúra átmeneténél a legsötétebb helyen 0,12 a legvilágosabb helyen pedig 0,87 értékű reflexiós tényezőt mértünk. Határozzuk meg a kontrasztot!

Megoldás:

Tehát a struktúra átmenet 83%-os kontraszt értékű.

A a mikroszkópobjektív numerikus apertúrájának fogalmát [7.20.] Ernst Abbe vezette be, és azóta is fontos szerepet tölt be. Mértéke;

ahol, n a tárgy és az objektív frontlencséje között levő közeg törésmutatója; $\sigma$ pedig az apertúrasugár optikai tengellyel bezárt szöge a vizsgált térrészben.

Példa:

Határozzuk meg egy rendszer tárgyoldali numerikus apertúráját, ha a rendszer levegőben helyezkedik el, a tárgytávolság 20 mm és az apertúrasugár félkúpszöge 15 fok.

Megoldás:

Tehát a vizsgált rendszer numerikus apertúrája 0.2588.

A mélységélesség fogalmát már tisztáztuk, azonban mértékének kézben tartását befolyásoló paramétereket még nem tárgyaltuk. Megállapítható, hogy a mélységélesség növekvő apertúrával és nagyítással csökken. Ahogy azt már fentebb írtuk, a sztereomikroszkópikus megfigyelések esetén rendkívül zavaró – gyakran a térbeliség hatását gátló tényező – a kis mélységélesség, ezért sztereomikroszkópokat kis apertúrával és kis nagyítással készítik. Hasonló a helyzet a szerelő, illetve az orvosi alkalmazású mikroszkópok esetén is.

A mikroszkópos kép nagyításán a képnagyság és a tárgynagyság hányadosát értjük.

A kép látómezeje alatt a tárgyról alkotott kép azon részét értjük, ami a mikroszkóp okulárja által szemlélhető [7.8.] .

Felbontóképesség az optikai műszer képességeinek egyik legfontosabb mutatója, azt mutatja, hogy két különálló, tárgyrészletről készült képben azok különállónak tekinthetők-e. Fontos tudatosítani, hogy felbontóképesség nemcsak az optikai berendezéstől függ, hanem a leképzett tárgy tulajdonságaitól is. Különböző jellegű tárgyak eltérő felbontóképesség-értékeket adnak úgy, hogy a felbontóképesség függ a kép világosságától, kontrasztosságától és élességétől [7.8.] .

Az adott optikai rendszer felbontóképességét a képalkotás hullámoptikai elmélete alapján lehet számítani.

A Rayleigh-féle kritérium alapján [7.35.] egy objektív felbontóképessége két egyenlően fényes világos inkoherens pont esetén,

ahol $\lambda$, a használt fény hullámhossza,

NA az objektív Abbe szerint értelmezett numerikus apertúrája.

Az összefüggés matematikailag azt fejezi ki, hogy az egyik pont Airy-­féle elhajlási képének első sötét gyűrűje fedi a másik pont Airy-­féle elhajlási képét annak intenzitásmaximumot képviselő középpontján. Lényegében megállapítható tehát, hogy egy optikai rendszer – fenti összefüggés szerint értelmezett – felbontóképességének elméleti határa korlátos, függ a hullámhossztól és a numerikus apertúrától. A hullámhossz csökkentésével, illetve a numerikus apertúra növelésével javul az elméleti felbontóképesség. A valóságos felbontóképesség kisebb a fenti értéknél, hiszen azt a geometriai aberrációk rontják.

A mikroszkópos képalkotás tulajdonságait alapvetően meghatározó rendszerek minősítésére az optikai átviteli függvényt használják.

A képalkotó optikai rendszerek felbontó-képességét régebben egyetlen értékkel, a határfelbontással adták meg. A határfelbontás szubjektív jellege miatt jelenleg a komplexebb és rendszerszemléleti eszközökkel kezelt úgynevezett kontrasztátviteli függvénnyel jellemzik a képalkotó optikai rendszereket. Előnyük, hogy geometriai optikai módszerekkel, tehát valós sugárátvezetéssel számíthatók, a valóságos rendszereken jól mérhetők, és nem utolsó sorban szemléletesen jellemzik a rendszer képalkotási viselkedését.

Trigonometrikus alakjának abszolút értéke a modulációs átviteli függvény, melyet MTF-fel jelölnek, argumentuma pedig fázisátviteli függvény (PTF), melynek esetünkben jelentősége nem számottevő.

A legelterjedtebb ábrázolásban az MTF a térfrekvencia függvényében ábrázolja a kontraszt változását [7.35.] . A valóságos rendszerek kontrasztátviteli függvénye az ideális, azaz csupán a fényelhajlás jelensége által korlátozott rendszer kontrasztátviteli függvénye alatt helyezkedik el. Lefolyása jól jellemzi a rendszert. Természetesen a kontrasztátviteli függvény a kiterjedt képmezőben értelmezhető [7.31.] .

Egyszerű megfogalmazásban az optikai rendszer az adott térfrekvenciájú szinuszos eloszlású rácsot ugyanolyan frekvenciájú szinuszos eloszlású rácsba viszi át, azonban a különböző térfrekvenciájú szinuszos eloszlású rácsokat eltérő amplitúdóval képezi le. Mérése általában közvetlenül a rendszertechnikai modell, illetve periodikus teszttárgyak képeinek értékelése alapján történik.

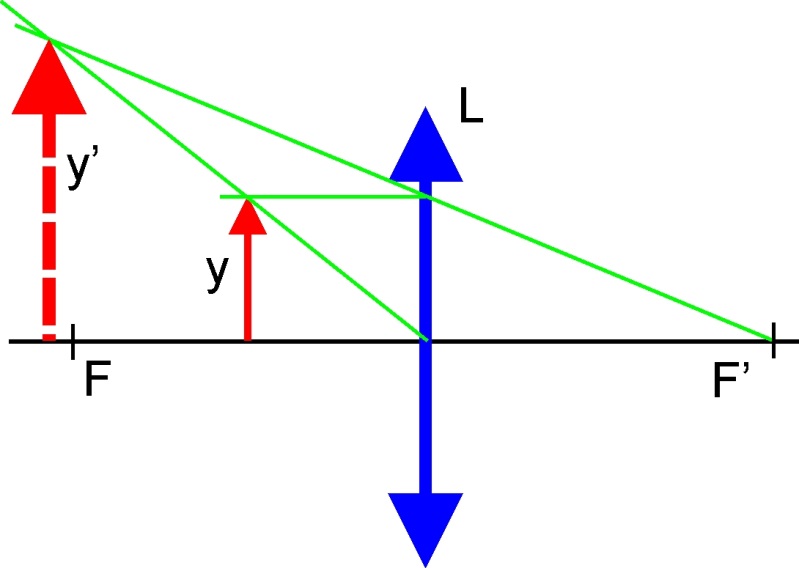
A geometriai optikai megfontolások alapján könnyen belátható, hogy egyetlen gyűjtő típusú rendszer, vagy akár egyetlen lencse a tárgyról képet alkot. Szabad szemmel történő megfigyelés esetén nagyított virtuális képre van szükségünk. Ehhez a geometriai elrendezés vonatkozásában arra van szükség, hogy a tárgy a tárgyoldali fókusz és a leképző rendszer között helyezkedjen el. Ismert tény, hogy ilyen esetben csak látszólagos nagyításról lehet beszélni, hiszen az optikai rendszeren keresztül szemlélt tárgy és az anélkül szemlélt tárgy látószögének eltérését tapasztaljuk. Ha az így kapott látószög a szabad szemmel történő szemlélés esetén fellépő látószögnél nagyobb, akkor látószög-növelésről, nagyításról beszélünk. Ilyen virtuális kép szerkesztése esetén a szerkesztő sugarak nem találkoznak, csupán azok virtuális meghosszabbításai. Az optikai eszközt nagyítónak, vagy lupénak nevezzük, és olyan műszerekben alkalmazzuk, ahol közvetlenül a tárgyat, vagy az arról létrehozott valós képet nagyobb látószög alatt kívánjuk szemlélni. Alkalmazása esetén a tárgyat a lencse tárgyoldali fókuszába helyezzük, ilyenkor a tárgyat 250 mm távolságban, a tisztánlátás távolságában adott szög alatt látjuk, ami nagyobb a lencse nélküli szemlélés esetén tapasztalható látószögnél. A szögnagyítás, azaz a lencse lupenagyítása e két szög tangensének aránya:

Az összefüggésből jól látható, hogy a lupe nagyítása a fókusztávolsággal fordítottan arányos. Az ilyen módon látószög-növelést végző lupe, vagy más néven egyszerű mikroszkóp alkalmazását korlátozza az, hogy a fókusztávolság csökkentésével a vizuális megfigyelés során technikai nehézségek lépnek föl, illetve az alkalmazhatóságot jelentős mértékben rontja az is, hogy a növekvő nagyítást a képminőség romlása és fényerő csökkenése kíséri. Ezért, ha látószög növelésének nagyobb mértékére van szükség, nagyobb nagyítású, jobb képalkotási tulajdonságokkal rendelkező, úgynevezett összetett mikroszkópot célszerű alkalmazni [7.16.] [7.17.] .

7.4. ábra - Az egyszerű mikroszkóp

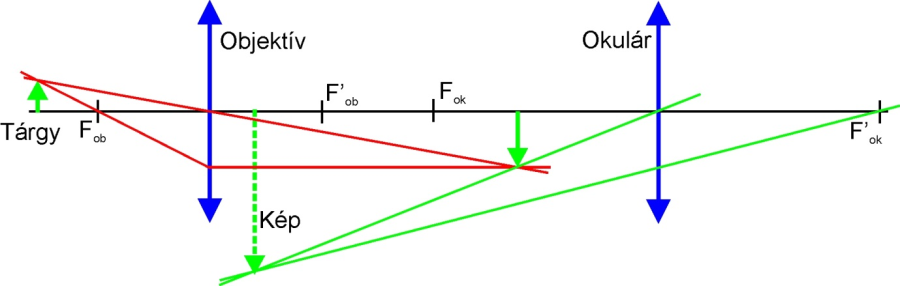
Az összetett mikroszkóp alkalmazása során a tárgy leképezése és nagyítása két egymástól elkülönítetten is kezelhető nagyítási folyamatnak tekinthető. Egyrészt a tárgyhoz viszonylag közel lévő, rövid fókusztávolságú leképző rendszer, az úgynevezett objektív, vagy tárgylencse a leképzendő tárgyról a képalkotás tulajdonságainak megfelelő, véges távolságban valós, fordított és nagyított képet alkot [7.12.] [7.18.] . Ezt a képet nevezzük közbenső képnek.  Megjegyzendő, hogy nem vizuális megfigyelés esetén, ezt a belső, közbenső képet detektálják és értékelik. Vizuális megfigyelés esetén ezt a valós fordított és nagyított képet egy következő optikai rendszeren, az úgynevezett okuláron, vagy szemlencsén keresztül szemléljük; megnagyítva a valós kép szemlélésének látószögét. Ezért a szemmel történő megfigyelés esetén a végső kép nagyított és virtuális, az eredeti tárgyhoz képest fordított állású [7.8.] .

Az objektívből és okulárból álló összetett mikroszkóp nagyításának meghatározása során ismerni kell az objektív és az okulár nagyítását, melyek szorzata az összetett mikroszkóp eredő nagyítása [7.11.] [7.12.] [7.13.] .

Gyakori feladat, hogy a mikroszkópizálás tárgyát képező objektumról valós képet kell alkotnunk, például mikroszkópos fényképezés vagy projekció esetén, ilyenkor a végső kép valós. Szerkezeti okok miatt ezt a valós képet úgy állítják elő, hogy a szemmel történő leképzéshez élesre állított mikroszkópot a tárgyhoz képest elmozdítják, így az új helyen keletkező képet az adott helyen elhelyezett fényérzékeny réteg, vagy elektronikus detektor síkjában felfogják.

Definíció szerint az objektív képoldali és az okulár tárgyoldali fókuszpontjai között mérhető távolság az optikai tubushossz, amit Δ-val jelölnek [7.8.] .

Mindezek alapján az összetett mikroszkóp nagyítása:

Az első hányados jelenti az alkalmazott okulár lupenagyítását, míg a második hányados az objektív nagyítását, ami az optikai tubushossz és az objektív fókusztávolságának aránya. Maga az optikai tubushossz egy előre meghatározott érték, ezáltal egy objektív tervezése során a képalkotási hibák korrekcióját mindig egy meghatározott távolságra, történetesen az optikai tubushosszra számítják.

Az okulárnak az a feladata, hogy az objektív által létrehozott nagyított, fordított állású, valós képet lupeszerűen tovább nagyítsa [7.13.] . Fontos szerkezeti eleme a mikroszkópnak a tubus, mely helyet ad az objektívnek és az okulárnak, biztosítja közöttük a távolság állandóságát [7.14.] . A valóságos objektívek és okulárok, a képalkotási hibák korrekciója miatt kiterjedt, több elemből álló összetett rendszerek, melyek közös foglalatban helyezkednek el. Az objektív és okulár közötti állandó távolságot egy meghatározott méretű mechanikai elem, a mikroszkóp mechanikai tubusa biztosítja. Az objektív illesztett peremes csavarmenettel foglalható a tubus végébe, az okulár pedig illesztett hüvelyen keresztül csatlakozik a tubushoz, pozícióját felfekvő váll jelöli ki [7.8.] .

Az objektív és okulár kapcsolatát biztosító mechanikus szerkezet hosszának, a mechanikai tubushossznak a mérete állandó, így az objektívek foglalatát úgy kell kialakítani, hogy a rájuk jellemző, és nagyításukat meghatározó fókusztávolságuktól függetlenül a közbenső képe a tubusban mindig ugyanazon a helyen jöjjön létre. Az objektívek felfekvő felületének a tárgytól való távolsága állandó, ez a távolságot a szakirodalom az objektív illesztési hosszának nevezi.

Az okulár tubussal való mechanikai kapcsolatát is úgy kell kialakítani, hogy annak tárgyoldali fókuszpontja mindig belessen a közbenső kép síkjába. Az okulárok foglalata tehát olyan, hogy annak felfekvő karimája és a tárgyoldali fókuszpontja közötti távolság, az úgynevezett okulár illesztési hossz állandó legyen. Mindezek alapján tehát az objektív építési hossza megegyezik az objektív illesztési hossza és a mechanikai tubushossz okulár illesztési hosszal csökkentett értékével [7.15.] .

Ez a megkötés biztosítja azt, hogy az összetett mikroszkóp nagyításának változtatásakor a képélesség nem változik meg. Tehát az objektív nagyításának mértéke

és az okulár lupenagyítása

Példa:

Egy mikroszkópos megfigyelés esetén 25 szörös nagyítású objektívet és 5 szörös nagyítású okulárt alkalmaztunk. Milyen nagyítású okulárt kell alkalmaznunk, hogy a nagyításunk 250 szeres legyen?

Megoldás:

Az eredő nagyítás az objektív és az okulár nagyításának szorzata:

Az új okulár nagyítása:

Tehát a 250 szeres nagyítás eléréséhez 10 szeres nagyítású okulárra van szükségünk.

7.5. ábra - Az összetett mikroszkóp

A mikroszkópizálás során vizsgált tárgyakat, objektumokat, melyek nem önálló fényforrások a következő képen csoportosítjuk [7.8.] :

Ismert tény, hogy a tárgypontban a megvilágítás erőssége négyzetesen növekszik a megvilágító sugárkúp apertúrájával, ez pedig annál nagyobb, minél na­gyobb a fényforrás felülete és minél közelebb van a tárgyhoz. Ez alapvetően határozza meg a mikroszkópos megvilágítás tervezésének szempontjait.

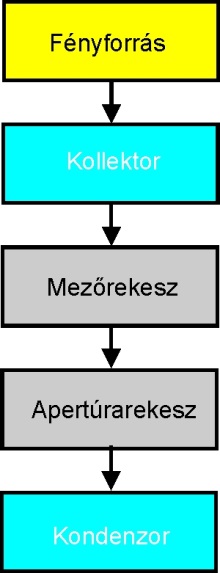
Mivel a fényforrás által kisugárzott hő miatt a csekély fókusztávolságú optikai rendszer fókuszsíkjában azt elhelyezni gyakorlatilag nem lehet, ezért ilyen esetben a fényforrás képét egy újabb optikai rendszer, a kollektor a kondenzor első fókuszsíkjába képezi. Az ilyen felépítésű megvilágító rendszer előnyei a következők:

Ahogy az előzőekben láttuk a minőségi mikroszkópos képalkotás fontos feltétele a kép optimális tulajdonságokkal rendelkező megvilágítása. Ennek legfontosabb szempontjai a következők [7.8.] :

E három rendkívül fontos feltétel körültekintő tervezést és beállítást igényel. Ilyen rendszert először 1893-ban A. Köhler, a Carl Zeiss művek munkatársa dolgozott ki. Ezt, a fenti feltételeknek eleget tevő megvilágítási elvet Köhler-féle megvilágításnak nevezik, és azóta a vizuális mikroszkópiában, és a mikroszkópos felvétel készítésben széles körben használják a megvilágítás módjától függetlenül [7.8.] [7.9.] [7.10.] .

A Köhler-féle megvilágítás optikai rendszerében a fényforrást egy gyűjtő típusú optikai rendszer, a kollektor a kondenzor első fókuszsíkjában fekvő szabályozható méretű apertúrarekeszre képezi, le úgy, hogy a fény­forrás képe a teljesen nyitott apertúrarekesz nyílását kitölti.

7.6. ábra - A Köhler-féle megvilágítás

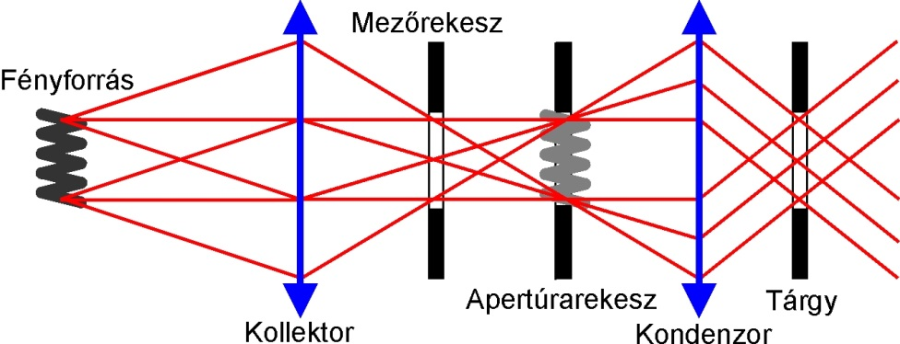
Könnyen belátható tehát, hogy a Köhler-féle megvilágítás egyik legfontosabb tulajdonsága, hogy alkalmazása esetén a tárgy és képhelyei, valamint a fény­forrás és világító felületének képei soha nem esnek ugyanazon helyre.

Az optikai rendszerek tervezésének elméletéből ismert, hogy egyetlen tagból álló optikai rendszer nem képes teljesíteni az elvárt képminőséggel szembeni elvárásokat, kívánalmakat. Ezt a gyakorlatban több tagból álló rendszerek generálásával oldják meg, több lencséből álló rendszert kell építeni. Az ilyen, összetett rendszerek elemei közös foglalatban helyezkednek el úgy, hogy optikai tengelyeik egybeesnek. Ez a gyártás során külön technológiai lépéssel biztosított. A teljes mikroszkópra vonatkozóan ezt a követelményt a mikroszkóp állvány biztosítja. A modern, nagy teljesítményű mikroszkópoknál a megvilágító egység, a kiegészítő optikai elemekkel az állványba van beépítve, így a munkaasz­talon való elmozdításakor nem kell a teljes megvilágítást újból beállítani.

7.7. ábra - A Köhler-féle megvilágítás vázlata

A mikroszkópban használt optikai rendszerek csoportosításukat tekintve lefedik az általános osztályozást, mely szerint az optikai rendszerek, optikai elemek két nagy osztályba sorolhatók. Ez a csoportosítás alkalmazás szerinti, és tartalmazza a képalkotó optikai rendszereket és a  nem-képalkotó optikai rendszereket.

A képalkotó optikai rendszerek a tárgy felületén tapasztalható intenzitáseloszlás módosított változatát hozzák létre a képsíkban, ahol elhelyezhető a detektor. A képalkotó rendszerek által alkotott kép legfontosabb tulajdonsága a felbontás, a kontraszt, és a geometriai aberrációk.  A nem-képalkotó optikai rendszerek funkciói közé sorolható a fény gyűjtése, fénysugarak irányítása, stb. Mikroszkópos alkalmazások esetén mindkét optikai rendszer típus részt vesz a folyamatban, egyrész a képalkotás, másrészt az energetikai viszonyok megfelelő biztosításában. A mikroszkópos képalkotás minőségére elsősorban a képalkotó rendszerek képalkotási hibái, illetve azok korlátozására van hatással. Ezek két nagy csoportra oszthatók, a monokromatikus és a kromatikus aberrációkéra [7.37.] . Az előbbi csoportba tartozik a szférikus aberráció, mely lényegében a metszéki távolság változását mutatja a belépő sugár magasságának függvényében. Jelenléte foltot eredményez, aminek nagysága hatással van a kép minőségére. A fénysugarak nem az elméleti pontban metszik az optikai tengelyt, hanem szóródási kört hoznak létre. Az üstököshiba, vagy koma ferde sugárköteg esetén hoz létre egy aszimmetrikus foltot, függ a rekesz helyétől is. Képmező elhajlás jelenléte esetén a tárgyról készült kép egy görbült felületre képződik le. Ezzel függ össze az asztigmatizmus, amely a meridionális és a szagittális síkban bekövetkező képmezőhajlások eredménye. A torzítás oka az, hogy az optikai rendszer nagyítása az optikai tengelyre merőleges irányban változik [7.32.] .

A kromatikus aberrációk oka eredendően az, hogy az alkalmazott üveganyagok törésmutatója a hullámhossz függvényében változik, így a különböző színű képek máshol és más méretben keletkeznek. Ezen hibák korrekciója különös jelentőséggel bír a mikroszkópos képalkotás során. A jó minőségű optikai rendszerek tervezése és gyártása időigényes és költséges folyamat eredménye, ami a termék árát a darabszám függvényében jelentősen meghatározza [7.32.] .

Az optikai rendszerek képalkotási hibáinak mértéke az őket alkotó elemek egymáshoz illesztésével, úgynevezett összetett lencserendszerek kialakításával kézben tartható, tehát az egyes tagok képesek egymás hibáit bizonyos határok között kiegyenlíteni. A szférikus aberráció korrekciójának lehetséges módja egy, például domború és egy homorú tag illesztése, ugyanis a gyűjtő és a szóró elem szférikus aberrációja ellentétes jelleget mutat. A kromatikus aberrációk kézben tartására, az üveganyagok eltérő színbontó képességét használják ki.

A mikroszkopizálás során a képalkotás folyamatában közvetlenül részt vevő optikai rendszerek közül kiemelt szerepet töltenek be az objektívek és az okulárok [7.8.] . Szerepük ismert; az összetett mikroszkópban a tárgy leképezése és a nagyítása két képalkotási folyamatnak tekinthető. Egyrészt a tárgyhoz viszonylag közel lévő, rövid fókusztávolságú leképző rendszer (objektív) a leképzendő tárgyról véges távolságban valós fordított és nagyított képet alkot. Ezt a képet nevezzük közbenső képnek.  Szemmel történő megfigyelés esetén ezt a valós fordított és nagyított képet egy következő optikai rendszeren (okulár) keresztül szemléljük; megnagyítva a valós kép szemlélésének látószögét. Ezért a szemmel történő megfigyelés esetén a végső kép nagyított és virtuális, az eredeti tárgyhoz képest fordított állású.

Az összetett mikroszkóp egyik legfontosabb optikai rendszere az objektív, hiszen tulajdonságai alapvetően határozzák meg a kép minőségét. Ez az elem az, amely az elsődleges, közbenső képet hozza létre. Az objektívek csoportosításukat tekintve lehetnek lencsékből, tükrökből építettek. A tükrös rendszerek nagy előnye, hogy mentesek a kromatikus aberrációktól, így a színhiba mentesítésére nem kell erőforrásokat átcsoportosítani. Hátrányuk viszont, hogy alkalmazásuk esetén a korrekció szabadságfoka igen korlátozott.

A fénytörésen alapuló mikroszkóp objektíveket elsősorban felépítésük és korrekciós állapotuk szerint szokás csoportosítani. Ezen tulajdonságaik azonban jelölésükben is megjelennek.  Szokásos csoportosítás kapcsolódik a fel­használásukhoz, itt elsősorban az áteső és ráeső fényben használt mikroszkóp objektíveket érdemes kiemelni, de természetesen önálló csoportot alkotnak például a polarizációs mikroszkópia objektívjei is.

7.8. ábra - Objektív tartó revolver

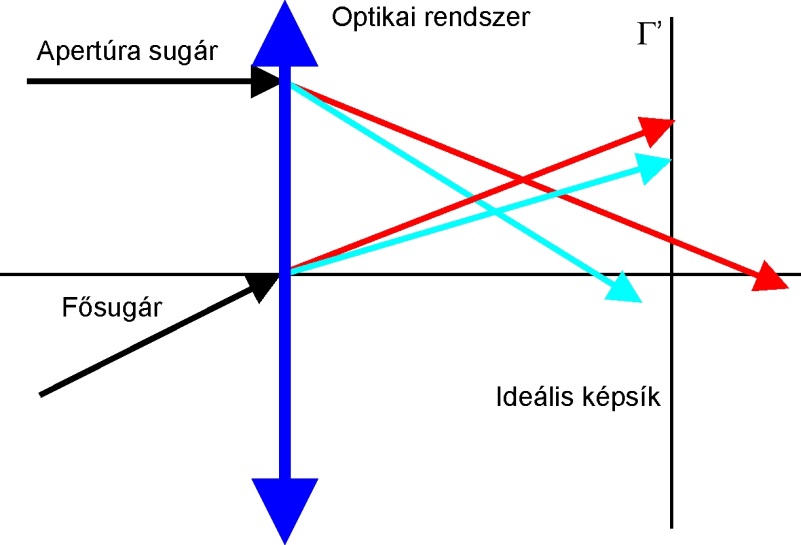
A mikroszkóp optikai viszonyainak tanulmányozása alapján könnyen kikövetkeztethető, hogy az objektív a szerény méretű tárgyat nagy nyílásszögű sugarakkal, az okulár viszont az így keletkezett nagy méretű közbenső képet kis nyílásszögű sugarakkal képezi le. Mindezek alapján megállapítható, hogy az objektíveknél és az okulároknál más és más típusú sugarak képalkotási hibáinak vizsgálata az elsődleges [7.8.] . Az objektíveknél figyelembe veendő [7.32.] :

Ha a képmező kitejedt tartományára vonatkozóan is korrigált állapotot írunk elő:

Ezek közül is jelentős az asztigmatizmus és a koma. Szemmel történő mikroszkópos megfigyelések esetén a képmezőhajlás és a torzítás nem okoz jelentős hibát, a tárgyrészletet a látó­mező közepére állítva, de a mikroszkópos kép rögzítése esetén ezekre is oda kell figyelni, korrekciós állapotukat kézben kell tartani.

Külön gondot okoz, hogy a longitudinális és a transzverzális színhiba egyszerre nehezen korrigálható, az egyik színhiba javí­tásával ugyanis a másik színhiba romolhat. Segítséget jelenthet az okulár, melyben az ellentétes maradék hiba az objektív hibáját kompen­zálja.

7.9. ábra - A longitudinális és a transzverzális színhiba szemléltetése

A mikroszkóp objektíveket színhibák korrekciója alapján a következők szerint csoportosítjuk:

Ez utóbbiak tekinthetők a legjobban korrigált mikroszkópobjektíveknek.

Annak függvényében, hogy a tárgy és a fedőlemez illetve az objektív első felülete közötti teret milyen közeg tölti ki, beszélhetünk:

Ha a vizsgálat során a tárgy nincsen fedőlemezzel lefedve, akkor a fénysugarak a levegőn keresztül jutnak az objektívbe, és a növekvő apertúrával alulkorri­gáltság lép fel, amit az objektív tervezése során túlkorrigálással lehet kompenzálni. A fordított eset is okozhat problémát, a 0,3 numerikus apertúra felett a fedőlemez okozta hiba olyan mértékű lesz, hogy hatása az objektív használatára már nem hagyható figyelmen kívül. Ezért a fedő­lemez vastagságát és anyagának törésmutatóját előre meg szokták határozni. A kialakult szokás szerint,

veszik a mikroszkóp objektívek gyártói.

Előnyös a korrekciós állapot szempontjából, ha a fénysugarak a tárgytól az objektív felületéig közel azonos törésmutatójú közegben futnak. Ez úgy valósítható meg, hogy a fedőlemez és a frontlencse üveganyagával azonos törésmutatójú folya­dékkal – úgynevezett immerziós folyadékkal – töltik ki a fedőlemez és frontlencse közötti teret [7.8.] . Az immerziós folyadék alkalmazása azonban további előnyt jelent, hiszen általa jelentősen növelhető az objektív numerikus apertúrája, ami közvetlen hatással van a felbontóképességre. A feloldóképességet az

numerikus apertúra jelentősen befolyásolja. Levegő (n = 1) esetén, a numerikus apertúra maximális elméleti értéke egy lehet, a gyakorlatban ez azonban a 0,95 értéket szinte sohasem haladja meg. Immerziós folyadék alkalmazása esetén a numerikus apertúra értéke az egynél is nagyobb lehet.

Az akromátok, minden hiányosságuk ellenére a széles körben alkalmazott mikroszkópobjektívek közé tartoznak. Az akromatizálás alapgondolata az, hogy a gyűjtő tag színhibáját az eltérő üveganyagú szóró lencse korrigálni tudja úgy, hogy az eredő rendszer gyújtótávolsága a kívánt értékű. Sajnos az akromátok színkorrekciója csak az ideális képhely két kitüntetett színre való egyezését biztosítja. Az akromatizálást vizuális rendszereknél általában a Fraunhofer-féle vonalak közül a C (656,3 nm) és az F (486,1 nm) színekre biztosítják. Ennek előnye az, hogy a két hullámhossz közötti színekre esik az emberi szem érzékenységi görbéjének a maximuma is [7.8.] .

A gyakorlati alkalmazásokhoz ebben a tarto­mányban a szferikus aberrációt is korrigálják a ragasztott, vagy légréses kéttag elemeinek alakfaktorai segítségével. Ha sikerül a színuszfeltétel megsértését is alacsony szinten tartani, akkor egy színre az aplanatizmus is biztosítottnak tekinthető. Sajnos, ahogy ezt már korábban említettük a longitudinális színhiba javításával a transzverzális színhiba értéke romlik. A színnagyítási hibát a mikroszkópiában a megfelelő nagysá­gú, de ellentétes hibával terhes okulár, az úgynevezett kompenzációs okulár tudja javítani. Az akromatikus mikroszkóp objektívek bizonyos mértékig az asztigmatizmusra és komára korrigáltaknak tekinthetők, sajnos azonban a szagittális és meridionális képmezőhajlás mértéke jelentős marad. Vizuálisan is jól felismerhető az akromát arról, hogy mivel azok színhibájának korrekciója csak két színre vonatkozik, a tárgy széleiről érkező ferde sugarak zavaró szekunder spekt­rumot mutatnak, azaz színesek.

Az apokromátok az akromátoktól abban különböznek, hogy a longitudinális színhiba három, a Fraunhofer-féle C(656,3 nm), D(589,3 nm) és F(486,1 nm) vonalra van korrigálva, azaz ezen színekre esnek egybe a paraxiális képpontok [7.33.] [7.34.] . Az ilyen rendszerek általában két színre egyben aplanatikusak is. A három színre megvalósított színkorrekció miatt a szekunder spektrum helyett ferde megvilágításnál egy annál jelentéktelenebb színhiba, a tercier spektrum jelenik meg, ennek mértéke azonban már nem zavaró [7.8.] . Sajnos ennek a jobb színkorrekciónak ára van, csak speciális üvegek és kristályok alkalmazásával valósítható meg. Az apokromátoknál a színhiba az objektív központ részén és a széleken egyaránt kiegyenlített. Az ilyen típusú mikroszkóp objektívek általában öt, vagy több tagból épülnek fel.

Az apokromátokhoz vizuális megfigyelésnél és képrögzítéses esetben is kompenzációs okulárokat kell illeszteni. Az adott esetben fellépő képmezőhajlás ebben az esetben is speciálisan az objektívhez tervezett okulárral korrigálható.

Külön csoportot képeznek a tükörobjektívek, melyek ugyan széles körben nincsenek igazán elterjedve, azonban jelentőségük még így is nagy. Két általános típusuk ismert szélesebb körben; a Schwarzschild-típusú rendszerben tisztán reflexió, míg Maksutov-típusú rendszereknél vegyesen, azaz reflexió és refrakció útján keletkezik a mikroszkópos kép [7.8.] . A Schwarzschild-típusú rendszerek előnye, hogy kierjedtebb hullámhossz tartományban is alkalmazhatók, színhiba nem terheli. A használhatóságukat növeli, hogy az objektív és a tárgy közötti szabad tárgytávolság lényegesen nagyobb, mint egy hasonló paraméterekkel rendelkező lencsés objektívnél, azonban a korrekció lényegesen nehézkesebb, hiszen az alkalmazható felületek száma igen korlátozott. Tükörobjektívhez áltlában hasonló felépítésű kondenzort használnak [7.32.] .

A mikroszkópos alkalmazásokhoz különlegesnek számítanak az úgynevezett a polarizációs objektívek, melyeket külön jelöléssel látnak el. Elvárás velük szemben, hogy ne tartalmazzanak belső feszültséget, ne legyen saját kettőstörésük, amely megzavarná a keletkezett polarizációs képet. Ez különösen érvényes a fluorit tagot tartalmazó objektívekre.

Külön csoportot képeznek a polarizációs mikroszkópia objektívjei, amelyekkel például a Fedorow-asztalon lehet méréseket végezni.

7.10. ábra - Fedorow-asztal

A fáziskontraszt objektíveknél a hátsó fókuszsíkba illesztik a fáziseltolást biztosító rétegeket.

Az összetett mikroszkóp másik legfontosabb optikai rendszere az okulár, amely alapesetben kétféle funkciót tud ellátni.

A helyesen alkalmazott okulár az objektív kilépőpupillájáról képet alkot, amely a rendszer kilépő pupillája. Vizuális megfigyelés esetén a szem pupilláját ebbe a kilépőpu­pillájába kell helyezni. Jelentősége van ezért a kilépő pupilla utolsó felülettől való távolságának, hiszen ez a kényelmes szemlélés szempontjából rendkívül fontos. Az okulár jellemzője a korábban definiált és leírt lupenagyitás, amit mikroszkóp okulár esetén belegravíroznak, vagy rányomtatnak annak foglalatára. A felhasználás szempontjából a nagyítás mellett legalább ilyen jelentőségű a tárgyból látott tárgymező nagysága is. A mikroszkóp közbenső képét az okulárban található úgynevezett látómezőrekesz határolja, annak milliméterben kifejezett nagysága látómezőszám [7.8.] .

Mivel az okulárok nyílásszöge viszonylag kicsi

szinte nem kell korrigálni. Viszont komoly hangsúlyt kell fektetni

kielégítő mértékű korrekciójára.

Az egyik legismertebb egyszerű okulár az úgynevezett Huygens-féle okulár. Nincs transzverzális színhibájuk, ezért szerény paraméterekkel rendelkező akromát objektívekhez célszerű használni. Az okulár, szerkezeti felépítését tekintve két síkdomború lencséből épül fel, mindkét lencse sík felülete a vizsgáló személy szeme felé áll. A közbenső kép a két síkdomború lencse között jön létre, ahol elhelyezkedik az oku­lár látómezőrekesze is.

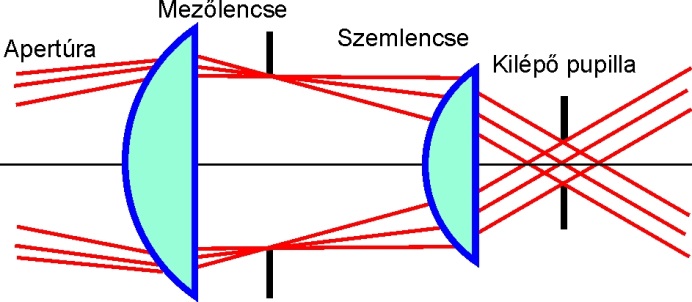
A másik ismert, és széles körben használt egyszerű kéttagú okulár a Ramsden-féle okulár, mely a Huygens-féle okulárhoz hasonlóan két síkdomború lencséből áll, azonban ezek domború felükkel egymás felé fordítottak. A mező­lencse és szemlencse fókusztávolságai egyenlők egymással és a két tag közötti távolsággal. Legnagyobb hátránya, hogy a közbenső kép az egyik lencse sík felületére képződik, így az esetleges szennyeződésekre rendkívül érzékeny, azok a képpel együtt látszanak, zavaróak. A szerkezetből adódó alkalmazástechnikai hiányossága az, hogy a kilépő pupilla zavaróan közel esik a második lencsetaghoz.

7.11. ábra - Ramsden-okulár

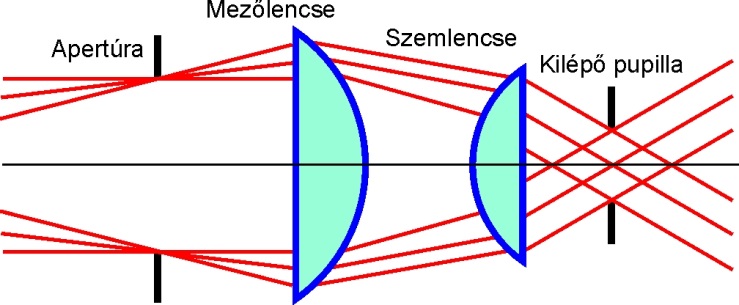
Ennek az okulár típusnak egy továbbfejlesztett változatának tekinthető a Kellner-okulár, amely abban különbözik, hogy a két lencse itt közelebb kerül egymáshoz, a kilépő pupilla távolabb kerül a szemlencsétől, és a fellépő színnagyítási hiba egy ragasztott kéttaggal korrigálva van.

A transzverzális színhiba az, amely az okulárok használata esetén a legtöbb problémát okozza. E hibát egyenlíti ki a kompenzációs okulár, mely az objektíven tapasztalható transzverzális színhibával azonos mértékű, de ellentétes irányú. Ezek lényegében a Huygens-féle okulárok továbbfejlesztett változatai, általában mindkét eleme ragasztott kéttag. A közepes és nagy nagyítású kom­penzációs okulárok az úgynevezett ortoszkopikus okulárok. Minden kedvező tulajdonságuk mellet bennük még a torzítás is korrigálva van, mérőokulárok céljára is sikeresen alkalmazhatók.

Ahogy azt már korábban említettük a mikroszkóp okulárokon feltüntetik a lupenagyítást, ellentétben a távcső okulárokkal, melyekre gyújtótávolságuk a jellemző.

7.12. ábra - A Huygens okulár

Egyre nagyobb a jelentőségük a változtatható nagyítású, úgynevezett pankratikus  okulároknak, melyek kényelmes és gyors megfigyelést tesznek lehetővé.

A méréstechnikai célokra fejlesztett okulárok látómezejében, pontosabb a látómező­rekesz síkjában egy úgynevezett okulármikrorméter-lemezt helyeznek el [7.8.] . Ez a lemez tartalmazza a feladathoz illesztett speciális osztást. Ezekben a szerkezetekben biztosítani kell, hogy az osztásvonalak képét, a szemlencse­foglalat menetes elmozdításával élesre lehessen állítani. Erre a célra általában az ortoszkopikus okulárt alkalmazzák, melyben – ahogy azt már fentebb részletesen kifejtettük – a torzítás ki van egyenlítve, látómezőrekesz a rendszer előtt fekszik, így a speciálisan tervezett és illesztett okulármikrométer a közbenső kép nagyságának a mérését közvet­lenül teszi lehetővé. Ezek továbbfejlesztett változatai az úgynevezett mozgószálas okulár­mikrométerek, melyekben a szálkereszt helyzete mikrométer­csavarral állítható, aktuális pozíciója a mikrométercsavar osztásai segítségével olvasható le.

Az okulárok foglalására általában egy hüvelyt használnak, melynek külső átmérője az esetek döntő többségében 23,2 mm, de kivételesen előfordul a 30 mm is. A lencsetagok pozíciója a foglalatban általában menetes gyűrűk segítségével biztosított. A foglalt optikai elemek a mikroszkóp tubusába becsúsztathatók. Az okulárok foglalatain feltüntetik a gyártót, a lupenagyitást és az okulár típusát. A komperzációs okulárokat K vagy C jelzéssel, a plán-objektívekhez használt kompen­zációs okulárokat Pk jelzéssel látják el.

7.13. ábra - Egy szerelt mikroszkóp okulár

A kondenzor ugyan nem tartozik a mikroszkóp közvetlen képalkotó rendszerei közé, viszont a megvilágításban és így közvetve az egész folyamatban betöltött fontos szerep miatt tárgyalásra érdemes. Az apertúrarekeszt és egy lencserendszert alkalmazó kondenzor feladata, biztosítani, hogy a tárgyat alkalmas apertúrájú sugárkúp világítsa meg. A kondenzorok korrigáltsági állapota azok felhasználhatósága szempontjából kulcsfontosságú. A Köhler-féle megvilágítás kellemes tulajdonságainak maradéktalan kihasználhatósága megköveteli a kondenzorokkal szemben, hogy a nagy apertúra mellett a szférikus aberráció is korrigálva legyen úgy, hogy amellett a színhibák is kézben legyenek tartva. A legjobb eredmény általában aplanatikus kondenzorokkal érhető el [7.8.] .