4. fejezet - Etológiai modellek implementációja fuzzy automatával
A fejezetben modellek fuzzy szabály-interpolációs automata (Hiba! A hivatkozási forrás nem található., Hiba! A hivatkozási forrás nem található., Hiba! A hivatkozási forrás nem található. és Hiba! A hivatkozási forrás nem található.) alapú megvalósítási lehetőségeit vizsgáljuk. Először az etológiai indíttatású ember-gép kapcsolatról, majd a viselkedés-alapú irányításról, végül pedig a fuzzy automatáról lesz szó. A leírni kívánt etológiai teszt folyamat bemutatása után a modell felépítését részletezzük. A fejezet végén példát láthatunk a fuzzy automata szabálybázisára és az ennek megfelelő futási eredményekre.
4.1. Etológiai indíttatású ember-gép kapcsolat
Az utóbbi években megnőtt az érdeklődés ember-gép kapcsolat alkalmazások iránt (Human-Robot Interaction - HRI). Általánossá vált a nézet, hogy az ember-gép kapcsolat javítható, ha ezen intelligens rendszerek valamilyen szocio-kognitív, vagy szocio-emocionális viselkedés kifejezésére képesek (lásd pl. Hiba! A hivatkozási forrás nem található.). A téma számos, a pszichológiát, a kognitív tudományokat, a szociológiát, a mesterséges intelligenciát, a számítástechnikát és robotikát is magába foglaló tudományterületet érint. A legfőbb cél az, hogy olyan megoldásokat találjunk, melyben ember az intelligens rendszerekkel a lehető leg természetesebb módon léphet kapcsolatba. Napjainkra az ember-gép kapcsolat felhasználó központúvá vált, azaz a rendszer hatékonyságát is a felhasználó szemszögéből kell értékelni. Ez a szemlélet erősíti azt is, hogy ma már egy robotnak nem csak egyes emocionális és kognitív képességeket kell mutatnia, hanem birtokában kell lennie az egyéniség kifejezés képességének is. Általában az egyébként szociális interakcióra képes robotok is alkalmatlanok hosszútávú emberi kapcsolatok kialakítására, így a kezdetben feléjük irányuló érdeklődés is hamar lelohad. A szociális interakcióra képes robotok tervezése számos kihívást rejt magában. Az eddigi fejlődés ellenére a természetes ember-robot interakció eléréséig sok még a megoldatlan feladat. A „borzongások völgye” hatás (Mori Hiba! A hivatkozási forrás nem található.) szerint, ha egy robot túlságosan emberszerűvé kezd válni, akkor van egy pont, ahol megnő annak a valószínűsége, hogy a vele kapcsolatba lépő emberből ellenérzéseket (félelmet) vált ki. Sokan vitatják ezt a hatást arra hivatkozva, hogy az elmélet nincs elég kutatással alátámasztva. Mások azt gondolják, hogy ha a hasonlóság átlép egy bizonyos határt, mint ahogy ez például az újabb számítógép grafikus karaktereknél történik, akkor a figurát az emberek elkezdik emberként kezelni Hiba! A hivatkozási forrás nem található.. Ugyanez a 3D robotok esetében már kevésbé egyértelmű, mivel a jelenlegi technológia túl nyers még a természetesnek tűnő viselkedés, érzelmek és párbeszédek megvalósításához. Azaz a „borzongások völgye” hatás a robotok esetében még megoldatlan kihívás.
A szociálisan interaktív robotok jelentős fejlődése ellenére motorikus és kognitív képességeik még mindig kívánnivalókat hagynak maguk után és az emberrel csak nagyon korlátozott interakcióra képesek. Ez a legfőbb probléma, mert a robotban a jelenleg rendelkezésre álló (hardver és szoftver) technológia mellett nem lehet elérni a kívánt emberszerű kognitív és motorikus képességeket. Emiatt van az, hogy a szociálisan interaktív robotok csak kevéssé keltik fel az emberek érdeklődését és az újdonság varázsának múltával még az is hamar eltűnik.
A biológiai, vagy pszichológiailag ihletett robotok tervezése és készítése azon múlik, hogy milyen mértékben értjük az emberi motorikus és mentális folyamatokat. Ezek azonban az élet leg összetettebb jelenségei. Ezért nagyon valószínű, hogy a szociálisan interaktív robotikához szükséges olyan emberi képességek, mint pl. a „megérzés”, vagy „emberi emlékezet, kellő szinten nem implementálható.
Ha a szociálisan interaktív robotot az ember képességeit alapul véve tervezzük, nem lesz lehetőségünk a szociális interakció embertől független általánosítására. Jelen esetben nem támaszkodhatunk az evolúcióra, ezért így csak a lehető leg emberibb robot elkészítését tűzhetjük ki célul.
Mindezen problémakör elkerülhető, ha etológiai indíttatású ember-gép kapcsolat modellt választunk. Az etológiai indíttatású ember-gép kapcsolat modell az állatok egymás közötti és az állatok ember felé irányuló interakciójának vizsgálatán alapul. Ez esetben az ember-gép kapcsolatban a robot a robot úgy viselkedik, mint egy az ember mellé szegődött állat társ. A paradigmának megfelelően a robotnak nem az embert és az ember-ember közti, hanem a biológiai rendszerekben már ismert fajok közötti kommunikációs sémákat kell követnie. A 20.000 éves ember-kutya kapcsolat Hiba! A hivatkozási forrás nem található. jó példa lehet erre a fajok közötti interakció paradigmára. Így természetesen a „borzongások völgye” hatás (Hiba! A hivatkozási forrás nem található.) is elkerülhető, hisz a robot nem lesz emberszerű.
Az ilyen robotoknak nem az ember szociális viselkedését kell másolnia (beleértve pl. a beszélt nyelvet is), hanem olyan minimális szociális viselkedéseket, melyek az ember-robot kooperációhoz elégségesek. Ezen alapmodell aztán bővíthető amennyiben az interakció összetettebbé válik.
Az etológiai modellekben jelentős állati viselkedéseket leíró tudás halmozódott. Ezen modellek általában verbális szakértői szabályok formájában adottak. A leíró szabály alapú tudásreprezentáció viszonylag könnyen átalakítható fuzzy szabályokká, azaz a verbális etológiai modellek viszonylag egyszerűen fuzzy modellekké alakíthatók. Problémát jelenthet azonban, hogy az etológiai modellek célja valamely jelenség szóbeli leírása és nem pedig implementálása. Azaz az etológiai modellek az implementáció szempontjából általában hiányosak. Ezen hiányosságok, azaz a nem teljes leírás miatt a klasszikus fuzzy következtetési módszerek nem alkalmazhatóak. A továbbiakban ezért fuzzy modellként alacsony számítás igényű fuzzy szabály interpolációs (Fuzzy Rule Interpolation - FRI) modelleket értünk (pl. FIVE Hiba! A hivatkozási forrás nem található.). A fuzzy interpolációs modellek ritka szabálybázisa jól illeszkedik az etológiai modellek „hiányos” leíró jellegű szabályformájához.
Az etológiai modellek fuzzy interpolációs modellekkel való leírásának legfőbb előnye az egyszerű szabályalapú tudásábrázolási forma. Emiatt a modell, még ha a modell a későbbiekben hangolásra kerül is, a szakértő (etológus) által könnyen értelmezhető, értékelhető és ellenőrizhető marad. Mindemellett az alacsony számítás igényű fuzzy szabály interpolációs módszerek könnyen implementálhatóak akár közvetlenül a robotokba is.
A továbbiakban az ember-gép kapcsolatra javasolt viselkedés-alapú szabályzási sémát vizsgáljuk.
4.2. Viselkedés-alapú szabályzás
A viselkedés-alapú szabályzás (Behaviour-based Control Hiba! A hivatkozási forrás nem található.) legfőbb építőelemei a viselkedéskomponensek. A viselkedéskomponensek tipikus emberi, állati, vagy mesterséges viselkedéseket másolhatnak. A rendszer aktuális viselkedése ezen viselkedéskomponenseknek az aktuális helyzethez leginkább illeszkedő kombinációja. A viselkedéskomponensek kódolása történhet pl. egyszerű reflexszerű ágens formában, az illető szituációban helyes cselekvéseket rendelve a megfigyelésekhez.
Ha egy helyzet megoldására több lehetséges viselkedéskomponens is alkalmas, akkor ezek közül vagy választanunk kell egyet, vagy valamilyen módon egyesítenünk kell őket. A viselkedéskomponensek egyesítése kétféleképpen történhet. Az első a versengéses eset, amikor viselkedéskomponensek pl. prioritást kapnak és azt választjuk, amelyiknek ez magasabb a másikat pedig figyelmen kívül hagyjuk. A második az együttműködő eset, amikor a viselkedéskomponenseket valamilyen szempont szerint egyesítjük.
A viselkedés-alapú szabályzásnak két fő feladata van. Az első a viselkedés koordináció, annak meghatározása, hogy az adott helyzet megoldására mely viselkedéskomponensek alkalmasak, a második a viselkedés fúzió. Az első feladat tekinthető a rendszer állapot becslésének, ahol az állapot nem más, mint az egyes viselkedés komponensek alkalmazhatóságának mértéke. A második, a viselkedés fúzió, a viselkedés komponensek egyesítése az alkalmazhatóságuk mértékének megfelelően. Jelen esetben mind a két feladat megoldható fuzzy interpolációs módszerekkel. Sőt, ha az egyes viselkedés komponenseket is fuzzy modellel írjuk le, az egész egy hierarchikus fuzzy rendszert alkot.
A fuzzy interpolációs modellnek köszönhetően a fuzzy szabályrendszer viszonylag egyszerűen megalkotható. Nem kell teljes szabályrendszert készítenünk, elég csak a lényegi szabályokat megadnunk. Ez esetben ugyanis az interpolációs modell azon esetekre is ad interpolált következtetést, amiket a szabályrendszerben nem határoztunk meg. Elég tehát a lényegi szabályokra koncentrálni, az ezekből kikövetkeztethető szabályokat akár szándékosan is ki lehet hagyni.
A fuzzy interpolációs modellek viselkedés-alapú szabályzásbeli alkalmazását a rendszer leginkább heurisztikus részén, a viselkedés koordináción mutatjuk be. A viselkedés koordináció feladata annak meghatározása, hogy az aktuális helyzet kezeléséhez milyen mértékben szükségesek az egyes viselkedéskomponensek.
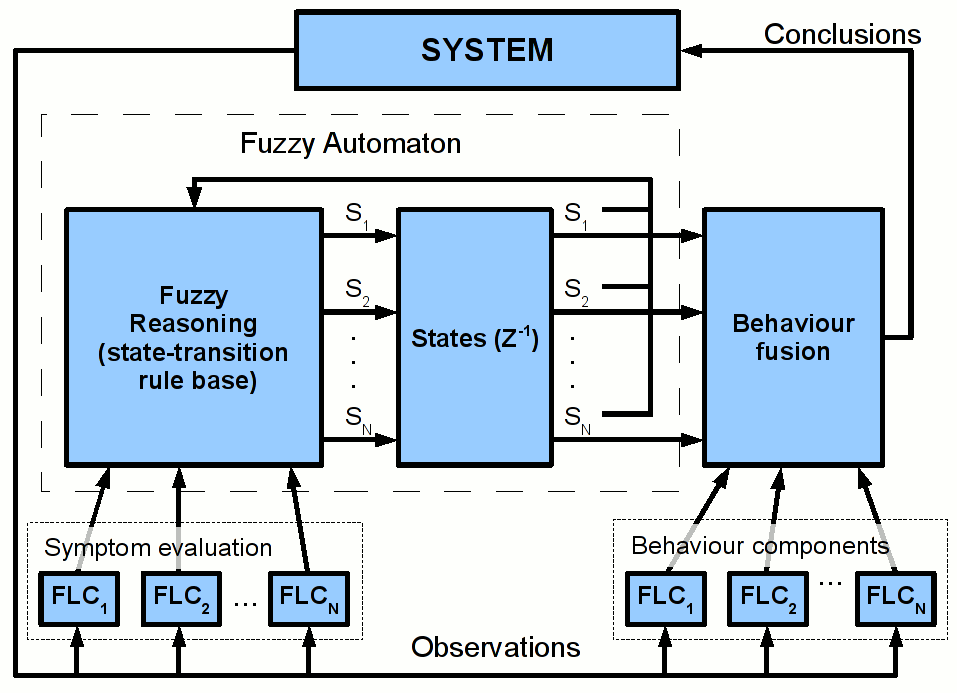
A javasolt viselkedés-alapú szabályzás struktúrában ez a feladat egy véges állapotú fuzzy automatára hárul Hiba! A hivatkozási forrás nem található. (lásd 4-1 ábrát és a következő fejezetet a részletekért), ahol fuzzy automata állapota az egyes viselkedéskomponensek szükségességének mértékét leíró vektor. Ez a megoldás azon a feltételezésen alapszik, hogy egy adott helyzetben a viselkedés komponensek szükségessége meghatározható az alkalmazhatóságuk mértékéből. Az alkalmazhatóságuk mértéke pedig megbecsülhető abból, hogy az adott helyzet mennyire hasonlít az illető viselkedés komponensek előfeltételeire. (Egy viselkedés komponens előfeltétele annak a helyzetnek a leírása, amelyben az illető viselkedés komponensek alkalmas a helyzet megoldására.) Ebben az esetben ahelyett, hogy a viselkedés komponensek szükségességét vizsgálnánk, elég azt néznünk, hogy egy adott helyzet mennyire hasonlít az egyes viselkedés komponensek előfeltételeire.
A teljes rendszer (lásd 4-1 ábra) a viselkedés koordináción kívül fuzzy modell alapú viselkedés fúziót és viselkedés komponenseket is tartalmaz (FLC). Az állapotváltozó (States) értéke határozza meg a komponens viselkedések szükségességének mértékét. Az állapot változásokat az állapot-átmeneti fuzzy szabályrendszer (state-transition rule base) irányítja. Az új állapot az aktuális állapot és a megfigyelések alapján kerül meghatározásra. Jelen esetben a fuzzy automata kimenete az új állapot, azaz a következő időpillanat aktuális állapota. Az aktuális állapot határozza meg a viselkedés fúzió során az egyes viselkedés komponensek súlyát. A viselkedés fúzió ugyancsak lehet fuzzy rendszer (pl. fuzzy szabály interpolációs következtetés), vagy egyszerűen csak egy súlyozott összeg. A szimptóma kiértékelés (symptom evaluation, 4-1 ábra), a hibadiagnosztikai rendszerek terminológiáját követve, egyfajta megfigyelés előfeldolgozást végez a fuzzy automata számára. Ezek a komponensek ugyancsak lehetnek fuzzy rendszerek (FLC).
Így a rendszer állapot becslés első lépése az aktuális helyzet és az egyes viselkedés komponensek előfeltételinek összehasonlítása. A szimptóma kiértékelés feladata ezen hasonlóságok meghatározása az aktuális szimptóma és az egyes viselkedés komponens előfeltételek szimptómái hasonlósága alapján. Ezen előfeltétel szimptómák jellemzik azt, hogy hozzájuk tartozó viselkedés komponens mely esetben helyes, azaz alkalmazható az illető helyzetben. A szimptóma kiértékelés nem más, mint az aktuális szimptóma és az összes viselkedés komponens előfeltétel szimptóma hasonlóságának meghatározása. Több lehetséges fuzzy megoldás is létezik a szimptóma kiértékelésre. Alkalmasak rá pl. a fuzzy klaszterezési módszerek, mint pl. a Fuzzy c-Means Hiba! A hivatkozási forrás nem található.. Ez esetben a klaszter középpontok lehetnek a viselkedés komponens előfeltétel szimptómák és a keresett hasonlóságok kiolvashatóak a fuzzy partíciós mátrixból, azaz az aktuális szimptómának az egyes klaszterekhez való tartozás mértékéből. Egyszerűbb esetben a szimptóma kiértékelés lehet fuzzy rendszer, vagy akár be is épülhet a fuzzy automata állapot-átmeneti szabályrendszerébe.
A rendszer állapot meghatározásánál fontos szempont, hogy a viselkedés komponens előfeltétel szimptómák függhetnek a rendszer aktuális viselkedésétől, azaz a rendszer állapotától. Mindegyik viselkedés komponens saját előfeltétel szimptóma rendszerrel rendelkezik, melyben szerepelhet az aktuális rendszer állapot is. Valójában a szimptóma kiértékelés állapotfüggősége miatt van szükség fuzzy automatára az állapot kiértékelés során. Az automata állapota a becsült rendszer állapot. Az állapot-átmenetek az állapot-átmeneti fuzzy szabályrendszer (lásd 4-1 ábra, “Fuzzy Reasoning (state-transition rule base)”) alapján a megelőző állapotnak és a szimptóma kiértékelésnek megfelelően hozott fuzzy szabály interpolációs következtetések.
4.3. Fuzzy automata
Ahogy arról az előző fejezetben is szó volt, az ember-gép kapcsolatra ajánlott modell a viselkedés-alapú szabályzásnak Hiba! A hivatkozási forrás nem található. megfelelő formát követi, azaz a rendszer aktuális viselkedése a komponens viselkedések a pillanatnyi helyzetre való alkalmasságuk mértékében fett fúziójaként jön létre. Az ajánlott modellben a viselkedés koordináció szerepét egy fuzzy automata tölti be. Számos fuzzy automata értelmezés lelhető fel az irodalomban Hiba! A hivatkozási forrás nem található.. Az egyik leg általánosabb forma a fuzzy véges állapotú automata (Fuzzy Finite-state Automaton FFA Hiba! A hivatkozási forrás nem található.), melyet az alábbi módon határozhatunk meg (Hiba! A hivatkozási forrás nem található., Hiba! A hivatkozási forrás nem található., Hiba! A hivatkozási forrás nem található.):
|
, |
(4.1) |
ahol Q a véges állapot halmaz, Q={q1,q2,...,qn}, Σ a véges bemeneti szimbólum halmaz, Σ={a1,a2,...,am}, az lehetséges kezdeti állapota, Z a kimeneti szimbólumok véges halmaza, Z={b1,b2,...,bn}, a fuzzy átmeneti függvény, mely az állapotot (aktuális állapot) a bemeneti szimbólum hatására egy másik állapothoz (következő állapot) rendeli, [0,1] értéket adva annak és a kimeneti függvény, mely kimenő értéket rendel az állapothoz.
A fuzzy véges állapotú automata koncepciót a fuzzy véges dimenziószámú automata koncepcióra kiterjesztve az alábbi formát kapjuk:
|
, |
(4.2) |
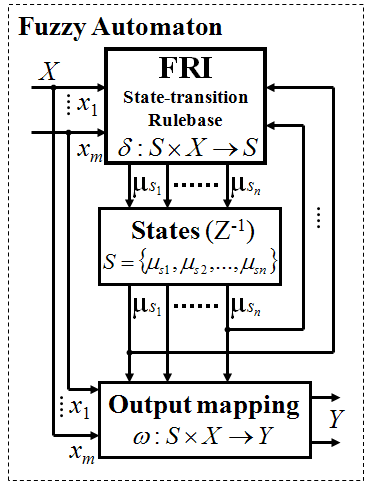
ahol S a véges fuzzy állapot halmaz, , X a véges dimenziószámú bemeneti vektor, , az fuzzy kezdeti állapota, Y a véges dimenziószámú kimeneti vektor, , a fuzzy állapot-átmeneti függvény, mely egy bemeneti érték hatására az aktuális fuzzy állapothoz az új fuzzy állapotot rendeli és a kimeneti függvény, mely kimenő értéket rendel a a bemenethez és a fuzzy állapothoz (lásd 4.2. ábra).
Az állapot-átmeneti függvény fuzzy szabályrendszerként megadása esetén a fuzzy szabályoknak dimenziós a feltétel és n dimenziós a következmény oldala. Klasszikus fuzzy következtetés és teljes szabályrendszer esetén a szabályok száma az alábbi:
|
, |
(4.3) |
ahol n az S fuzzy állapotvektor hossza, m a bemenet dimenziószáma, i az állapotvektor dimenziónként lehetséges nyelvi értékeinek száma, és j a bemenet dimenziónként lehetséges nyelvi értékeinek száma.
A fenti összefüggés (4.3) alapján, az állapot-átmeneti szabályrendszer szabályszáma exponenciálisan függ a fuzzy állapotvektor hosszától és a bemenetek számától. A fuzzy szabály interpolációs következtetési módszernek köszönhetően ez a szabályszám dramatikusan csökkenthető. Lásd pl. Hiba! A hivatkozási forrás nem található., ahol az eredetileg exponenciális szabályszám polinomiálissá volt alakítható a fuzzy szabály interpolációs következtetésnek köszönhetően.
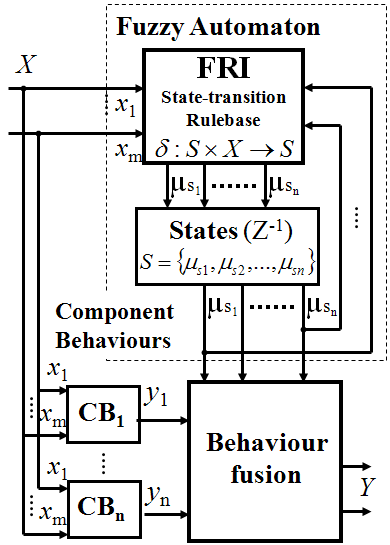
Könnyű belátni, hogy amennyiben a fuzzy véges dimenziószámú automata a kimeneti függvénye független párhuzamos komponens viselkedésekre és viselkedés fúzióra bontható, akkor a fuzzy véges dimenziószámú automata a viselkedés-alapú szabályzásnál megismert formára alakítható (lásd 43. és 41. ábrákat). Fuzzy automaták viselkedés-alapú szabályzási formában történő alkalmazásaira mutat további példákat Hiba! A hivatkozási forrás nem található., Hiba! A hivatkozási forrás nem található. és Hiba! A hivatkozási forrás nem található..
4.4. Az “Idegenhelyzet teszt” modellezése
Az itt bemutatott etológiai tesz folyamatot a kutya és gazdája kötődésének vizsgálatára dolgozták ki. Maga a teszt hét, egyenként két-két percig tartó szakaszból áll, ahol a kutya más-más helyzetbe kerül: először a gazdájával, majd egy idegennel, vagy egyedül (az előre meghatározott protokollnak megfelelően). A teszt folyamán a kutya viselkedését főleg a gazda közelségének keresése alapján értékelik Hiba! A hivatkozási forrás nem található..
Az első vizsgálati szakaszban a kutya és a gazdája együtt van egy a kutya számára ismeretlen szobában. A gazda eleinte passzív, majd játékot kezdeményez a kutyával. A második szakaszban egy idegen jön a szobába, majd ő is játékot kezdeményez a kutyával. Ezt követően a gazda elhagyja a szobát, azaz a harmadik szakaszban a kutyát elválasztják a gazdájától. A harmadik szakasz folytatásában az idegen újból játékot kezdeményez a kutyával, majd egy kis időre leül, majd megpróbálja megsimogatni a kutyát. A negyedik szakasz elején a gazda visszatér a szobába, ez az első újra egyesülés. Eközben az idegen elhagyja a szobát és két percig a kutya újra csak a gazdájával van együtt. Majd kimegy a gazda is, ez az ötödik szakasz, amikor a kutya egyedül van a szobában. A következő szakaszban az idegen visszajön, majd újból játékot kezdeményez, vagy megpróbálja megsimogatni a kutyát. A gazda újbóli visszatérése jelzi az utolsó szakasz kezdetét. Ebben az idegen kimegy, a gazda pedig két percig a kutyával próbál kapcsolatba lépni.
A teszt kiértékelése során az etológusok előre definiált viselkedés változókat figyelnek, hogy leírhassák a kutya gazdája felé és az idegen felé irányuló válaszait. Az így nyert adatokat elemezve keresnek lényegi különbségeket a kutya gazdája iránti és az idegen felé mutatott viselkedésében.
A korábban taglalt etológiai indíttatású ember-gép kapcsolat modell felépítésére példaként most ez az összetett etológiai modell kerül bemutatásra. A példában az etológiai modell által irányított ágens a kutya viselkedését szimulálja. A többi szereplőt a teszt folyamatban megadott szerepkörök irányítják. A szimulált ágens (kutya) a tesztnek megfelelően számos tevékenység végzésére alkalmas (valamilyen objektum felé halad, felveszi, vagy elejti a játékot, csóválja a farkát, stb.). Ezen tevékenységek közül egy néhány egyszerre is végrehajtható (együttműködő), míg mások kizárják egymást (versengő). Mindkét esetben a viselkedés fúzió végzi a viselkedés komponensek egyesítését.
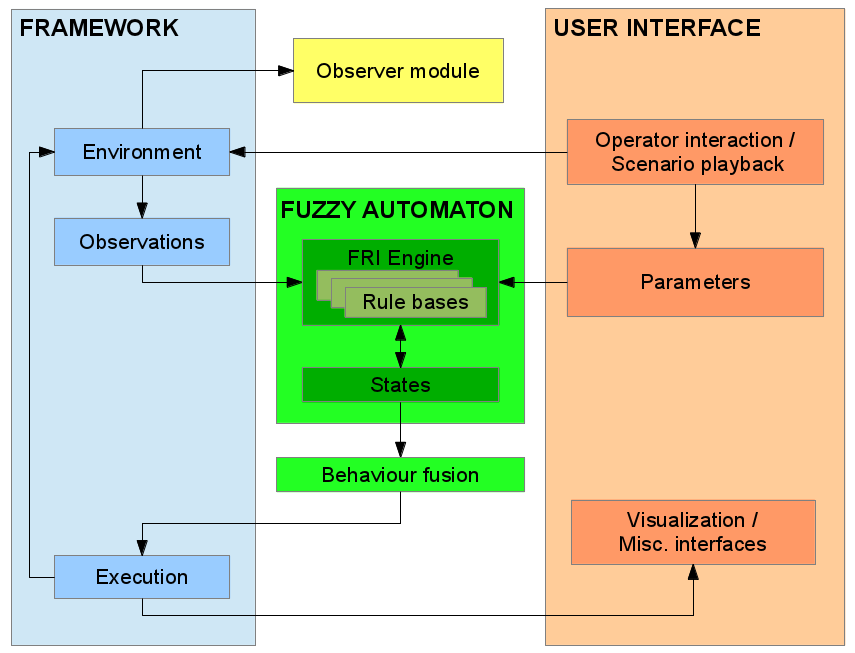
A most bemutatott modell eredetileg a kutya viselkedésének szimulációjára készült az idegenhelyzet tesztben (Strange Situation Test – SST Hiba! A hivatkozási forrás nem található.), de a modell elég rugalmas ahhoz, hogy etológiailag helyes módon reagáljon a teszt szakaszaitól eltérő helyzetekben is. A teljes SST szimulációs rendszer egyszerűsített blokkvázlatát az 44. ábra mutatja.
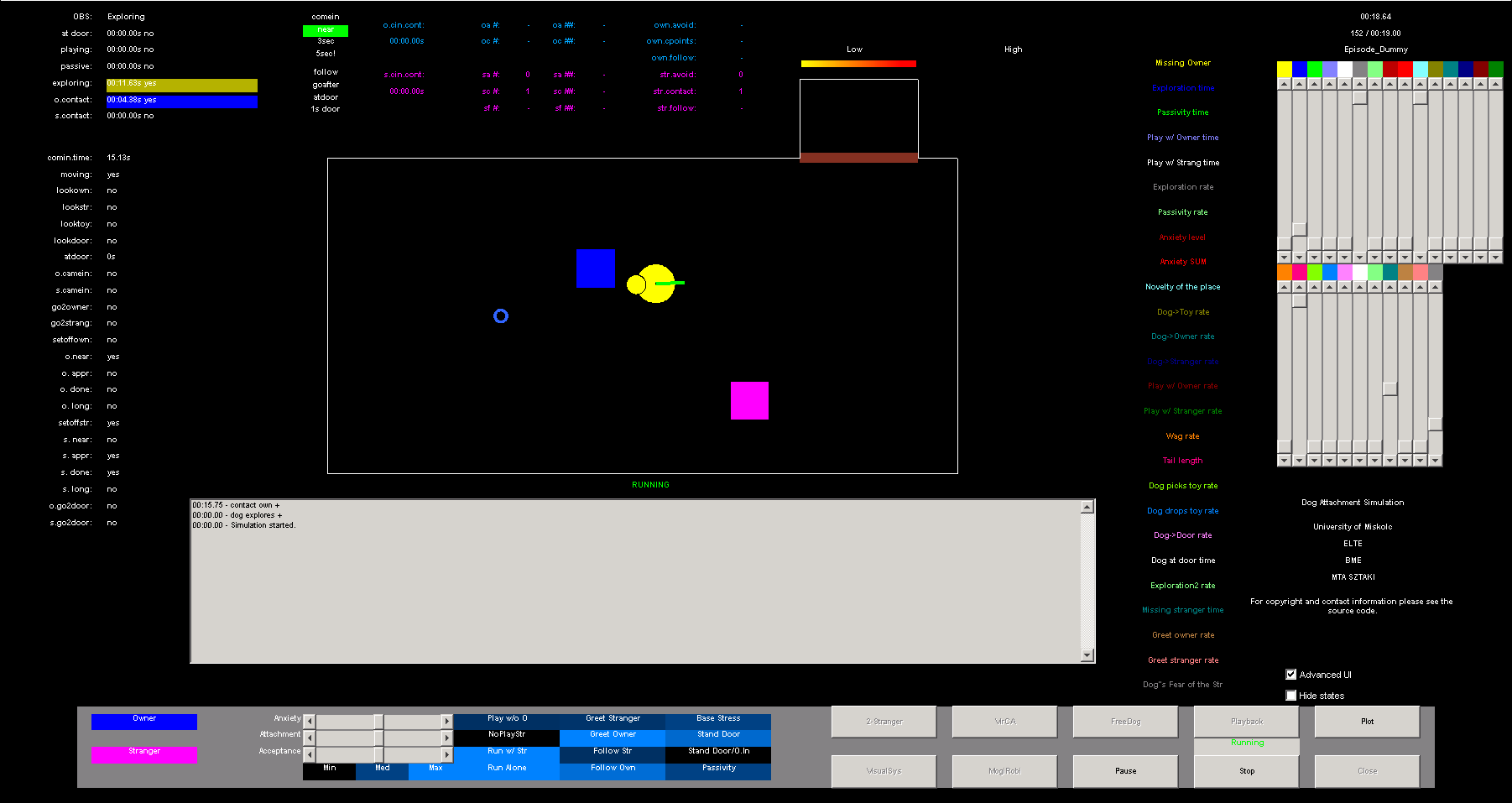
A 45. ábra az SST szimulációs rendszer egy lehetséges képernyőtervét mutatja, ahol a szoba, melyben az események zajlanak, felülről látszik. Az ember szereplőket négyzetek jelzik, kék a gazda, bíbor az idegen. A kutyát két kör jelzi, a nagyobbik a „teste”, a kisebbik a „feje”, ami a kutya figyelmének iránya meghatározása miatt szükséges. A kutyán a vékony zöld vonal a „farkat” jelöli, ezt a kutya „csóválhatja”, vagy változtathatja a hosszát. A szimulációban a kutya színe az izgatottságának megfelelően változik. A szobán van egy ajtó, ahol az ember szereplők elhagyhatják a szobát, illetve visszatérhetnek (a kutya nem hagyhatja el a helységet). Van ezen kívül még egy játék objektum (kis kék kör), amit valamennyi szereplő felvehet, vagy eldobhat.
A következőkben a modell néhány minta viselkedése és azok fuzzy automatának megfelelő definíciói kerülnek bemutatásra.
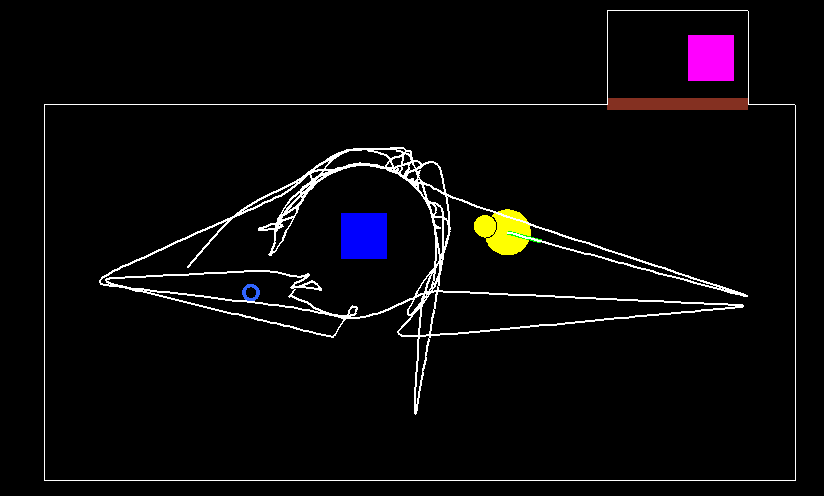
Az első minta viselkedés két viselkedés komponensből áll, úgymint ‘DogExploresTheRoom’ és ‘DogGoesToDoor’. A ‘DogExploresTheRoom’ a kutya felderítő tevékenysége, melyben a kutya „körbenéz” és megvizsgálja a számára ismeretlen helyet (lásd a fehér nyomvonalat a 46. ábrán). A ‘DogGoesToDoor’ egy egyszerű tevékenység, melyben a kutya az ajtóhoz megy, majd megáll (leül a gazdájára várva, hogy az újból megjelenjen). A minta viselkedéshez kapcsolódó fuzzy interpolációs automata állapot-átmeneti szabályrendszere felelős a viselkedés koordinációért.
A mintaviselkedéshez tartozó állapotok az alábbiak:
-
„Rejtett” állapotok, melyekhez nem kapcsolódik közvetlenül viselkedés komponens, de a viselkedés koordinációban szerepet játszanak: „A kutya gazda hiánya hangulata” (DogMissTheOwner) és a „A kutya nyugtalansági foka” (DogAnxietyLevel).
-
‘Normál’ állapotok, melyekhez közvetlenül is tarozik viselkedés komponens, jelen esetben a már korábban említett ‘DogExploresTheRoom’ és ‘DogGoesToDoor’: „A kutya ajtóhoz megy hangulata” (DogGoesToDoor) és a „A kutya felderíti a szobát hangulata” (DogExploresTheRoom).
Egy lehetséges állapot-átmeneti fuzzy szabályrendszer az alábbi formában adható meg (csak a példa állapotait kiemelve):
-
„A kutya gazda hiánya hangulata” állapotot meghatározó állapot-átmeneti fuzzy szabályrendszer:
If OwnerInTheRoom=False Then DogMissTheOwner=Increasing
If OwnerInTheRoom=True Then DogMissTheOwner=Decreasing
-
„A kutya nyugtalansági foka” állapotot meghatározó állapot-átmeneti fuzzy szabályrendszer:
If OwnerToDogDistance=Small And Human2ToDogDistance=High Then DogAnxietyLevel=Decreasing
If OwnerToDogDistance=High And Human2ToDogDistance=Low Then DogAnxietyLevel=Increasing
„A kutya ajtóhoz megy hangulata” állapotot meghatározó állapot-átmeneti fuzzy szabályrendszer:
If OwnerInTheRoom=False And DogMissTheOwner=High Then DogGoesToDoor=High
If OwnerInTheRoom=True Then DogGoesToDoor=Low
„A kutya felderíti a szobát hangulata”állapotot meghatározó állapot-átmeneti fuzzy szabályrendszer:
If DogAnxietyLevel=Low And OwnerStartsGame=False And ThePlaceIsUnknown=High Then DogExploresTheRoom=High
If ThePlaceIsUnknown=Low Then DogExploresTheRoom=Low
If DogAnxietyLevel=High Then DogExploresTheRoom=Low
A dőlt betűs szövegrészek a fuzzy szabályrendszer fuzzy nyelvi változói (azaz fuzzy halmazok). Itt kell megjegyeznünk, hogy a fenti szabályrendszer ritka, csak lényegi szabályokat tartalmaz, azaz fuzzy szabály interpolációs automata állapot-átmeneti szabályrendszere.
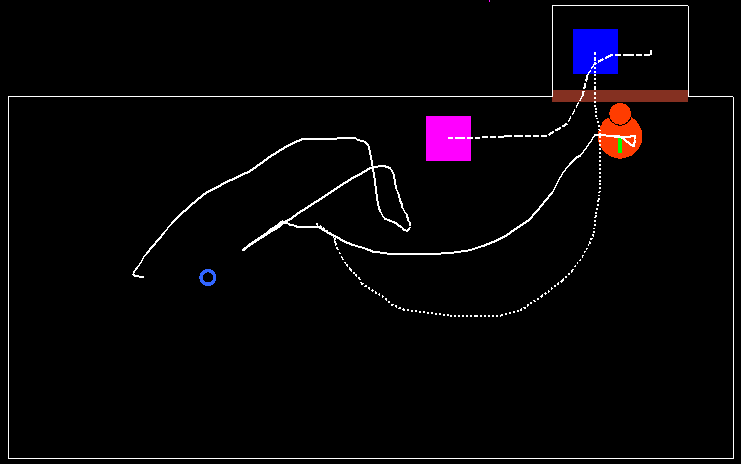
A példában bemutatott viselkedés egy lehetséges futási eredményét mutatja a 46. és 47. ábra. Az ábrákon bemutatott futatási példa kezdetén a gazda a szobában van, az idegen pedig kívül. A hely a kutyának ismeretlen (‘ThePlaceIsUnknown=High’ a szabályrendszerben). A fenti szabályrendszernek megfelelően a kutya elkezdi felderíteni a helységet (lásd 46. ábra). Egy kicsit később a kutya gazdája elhagyja a szobát, az idegen pedig bejön és bent marad (szaggatott fehér vonal a 47. ábrán). Az események következtében (a fenti állapot-átmeneti szabályrendszernek megfelelően), a kutya nyugtalanná válik és megemelkedik a „A kutya gazda hiánya hangulata” állapot tagsági értéke is, minek hatására a kutya az ajtóhoz megy (fehér vonal a 47. ábrán) és ott kezd várakozni, ahol a gazda elhagyta a szobát. Lásd az állapotváltozásokat a 48. ábrán.
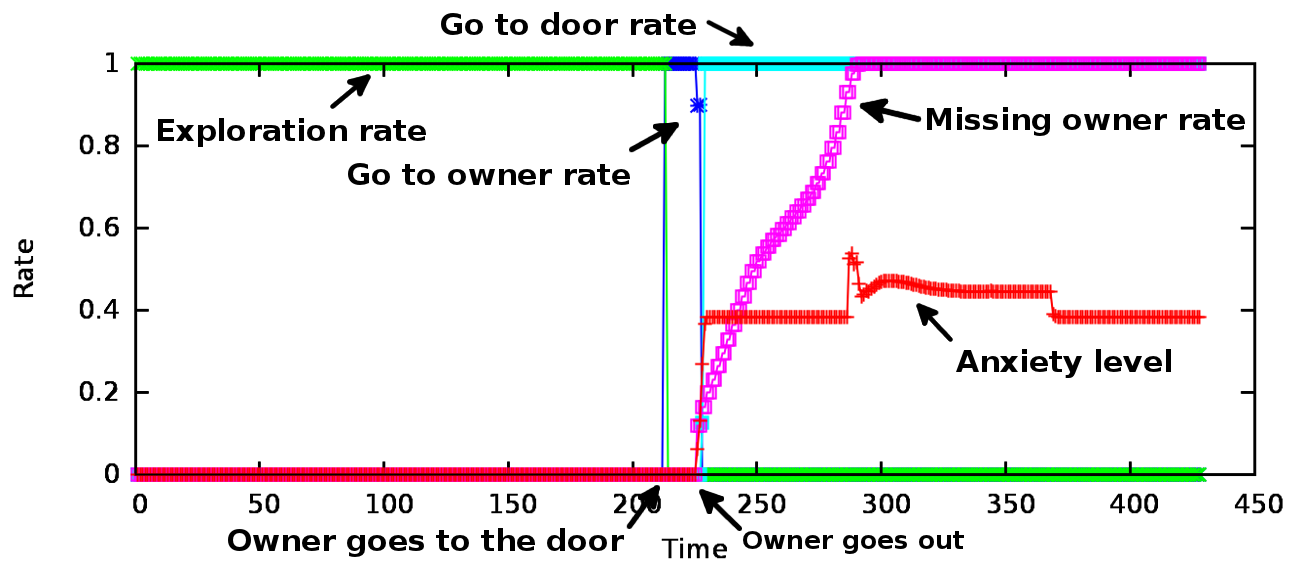
A 48. ábrán a mintapélda négy állapotváltozójának időbeli alakulását látjuk. Két azonnali változást a gazda mozgása vált ki. Az első, amikor a kutya észreveszi, hogy a gazda az ajtó felé tart (a 200. iterációs lépés körül). Ekkor a kutya felderítési kedve rohamosan csökkenni kezd, de a gazda követése hangulata (‘DogGoesToOwner’) még mindig magas addig, amíg a gazda el nem hagyja a szobát (a 250. iterációs lépés körül). Amikor a gazda elhagyja a szobát a ‘DogGoesToDoor’ viselkedéskomponens válik aktívvá, a ‘Missing the owner’ állapot emelkedésének következtében. Ugyanekkor a gazda hiánya miatt a kutya nyugtalansági szintje is emelkedik.
A második példában a ‘DogGoesToOwner’ viselkedés komponenst vizsgáljuk meg alaposabban egy az előző példától eltérő szemszögből. Ahogy azt az állapotváltozó neve is jelzi, a kutya gazdához közelítésének igényét fejezi ki, illetve a hozzá tartozó viselkedés komponens felelős azért, hogy a kutya a gazdához menjen. Az ezen állapotváltozóhoz tartozó állapot átmeneti szabálybázis jóval összetettebb az előző példánál. A teljes ‘DogGoesToOwner’ állapot-átmeneti szabályrendszert az Hiba! A hivatkozási forrás nem található.. táblázat mutatja, ahol az utolsó oszlop a szabály következmény, az azt megelőző oszlopok pedig a szabály feltétel dimenziók (a táblázatban ‘x’ jelöli, ha egy szabály nem függ valamely megfigyeléstől).
A szabálybázisban használt nyelvi értékek jelentése az alábbi (a „megfigyelés” a pillanatnyi környezetben mért érték, a „megelőző állapot” a megelőző iteráció állapot változókat illető következménye):
dgtd – megelőző állapot – a kutya az ajtóhoz megy hangulat (zero-large) – lásd 4-12. ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
dgto – megelőző állapot – a kutya a gazdához megy hangulat (zero-large) – lásd 4-12. ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
oir – megfigyelés – a gazda a szobában van (true-false) – lásd 4-9. ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
ddo – megfigyelés – a kutya és a gazda távolsága (zero-large) – lásd 4-10. for ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
dgtt – megelőző állapot – a kutya játékhoz megy hangulata (zero-large) – lásd 4-9. ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
dgro – megelőző állapot – a kutya üdvözli a gazdát hangulata (zero-large) – lásd 4-9. ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
dpmo – megelőző állapot – a kutya játszik a gazdával hangulata (zero-large) – lásd 4-9. ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
dpms – megelőző állapot – a kutya játszik az idegennel hangulata (zero-large) – lásd 4-9. ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
danl – megelőző állapot – a kutya nyugtalansági foka (zero-large) – lásd 4-11. ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
ogo – megfigyelés – a gazda kimegy a szobából (true-false) – lásd 4-9. ábrát a nyelvi értékekhez tartozó fuzzy partíciókért
dgto (consequent) – next state – a kutya a gazdához megy hangulat (zero-large) (kimenet)
|
# |
dgtd |
dgto |
oir |
ddo |
dgtt |
dgro |
dpmo |
dpms |
danl |
ogo |
dgto |
|
1 |
dgtdl |
x |
oirt |
x |
x |
x |
x |
x |
x |
x |
dgtoz |
|
2 |
dgtdz |
x |
oirt |
x |
dgttz |
dgrol |
x |
dpmsz |
x |
ogof |
dgtol |
|
3 |
dgtdz |
x |
oirt |
x |
dgttz |
x |
x |
dpmsz |
danll |
ogof |
dgtol |
|
4 |
dgtdz |
x |
oirt |
x |
dgttz |
x |
dpmol |
x |
x |
ogof |
dgtol |
|
5 |
dgtdz |
x |
oirt |
x |
x |
x |
x |
x |
x |
ogot |
dgtol |
|
6 |
dgtdz |
x |
oirt |
x |
x |
dgroz |
dpmoz |
x |
danlz |
ogof |
dgtoz |
|
7 |
x |
x |
oirf |
x |
x |
dgroz |
x |
x |
x |
ogof |
dgtoz |
|
8 |
dgtdz |
x |
x |
x |
dgtth |
dgroz |
x |
dpmsz |
x |
ogof |
dgtoz |
|
9 |
dgtdz |
x |
x |
x |
x |
dgroz |
x |
dpmsl |
x |
ogof |
dgtoz |
|
10 |
dgtdz |
dgtol |
oirt |
ddoz |
dgttz |
dgroz |
dpmoz |
dpmsz |
x |
ogof |
dgtoz |
|
11 |
dgtdz |
dgtol |
oirt |
ddol |
dgttz |
x |
x |
dpmsz |
x |
x |
dgtol |
A fenti szabályok sorrendben az alábbi szöveges formában értelmezhetők:
a kutya az ajtóhoz megy a kutya nem megy a gazdához
a kutyának üdvözölnie kell a gazdát a kutya a gazdához megy
a kutya nyugtalan a kutya a gazdához megy
a kutya gazdával való játékkedve magas a kutya a gazdához megy
a gazda kimegy a szobából a kutya a gazdához megy (a gazda követése)
a kutya nyugodt, nem játszi és nem üdvözöl a kutya nem megy a gazdához
a gazda nincs a szobában a kutya nem megy a gazdához (nem tud odamenni)
a kutya a játékhoz megy a kutya nem megy a gazdához
a kutya idegennel való játékkedve magas a kutya nem megy a gazdához
a kutya már a gazdához ment és mellette van a kutya nem megy a gazdához (már ott van)
a kutya már a gazdához ment de a gazda messze van a kutya a gazdához megy (továbbra is követi)
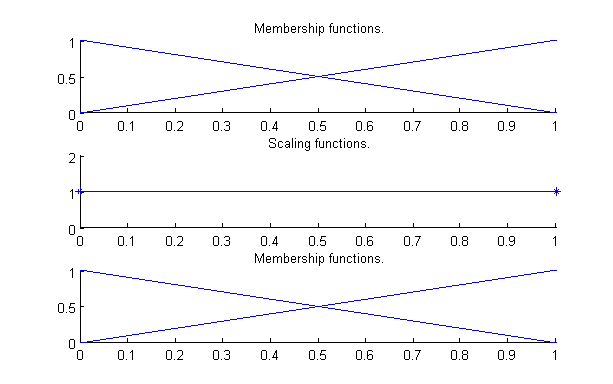
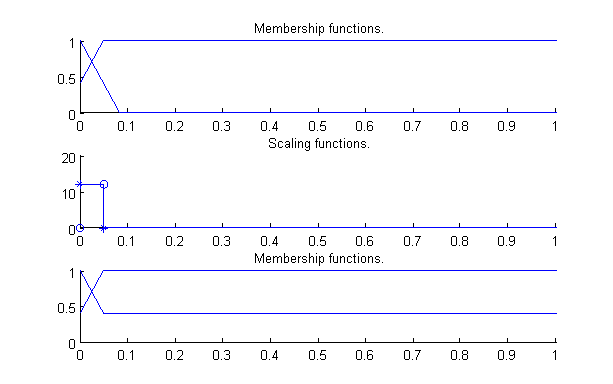
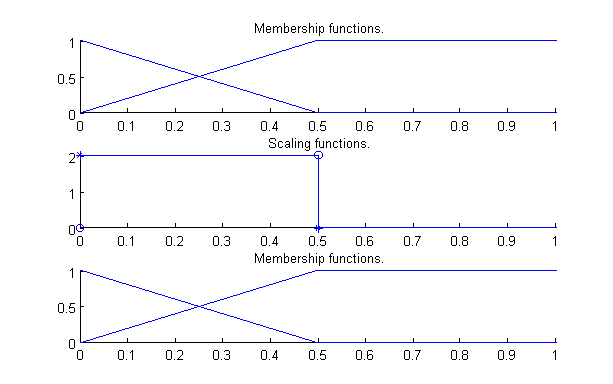
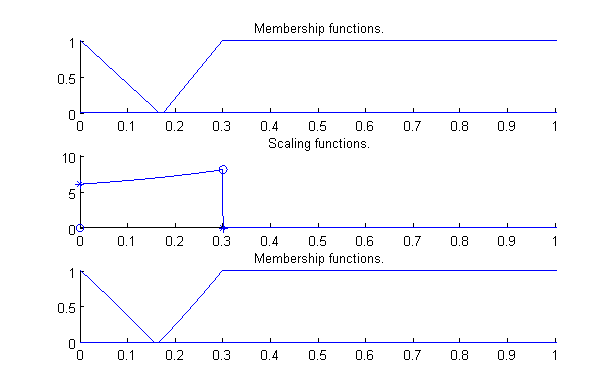
A fenti szabályrendszer egy összetett viselkedést ír le, a fuzzy szabály interpolációs következtetésnek köszönhetően mindössze tizenegy szabállyal annak ellenére, hogy a bemeneti dimenziószám igen magas (tíz változó). A 49. - 412. ábrák az egyes állapotváltozókhoz tartozó lehetséges nyelvi értékek fuzzy partícióit mutatják. Fentről lefelé az ábrákon az egyes görbék az illető fuzzy partíciót, a hozzá tartozó közelítő skálafüggvényt Hiba! A hivatkozási forrás nem található. és a közelítő skálafüggvény alapján rekonstruált fuzzy partíciót jelölik. Ahogy az az ábrákon is látszik, a legtöbb fuzzy partíció igen egyszerű (a kilenc szabály feltételből hat ugyan azt az egyszerű fuzzy partíciót használja). A legtöbb partíció csak két háromszög alakú nyelvi értéket (fuzzy halmazt) tartalmaz úgy, hogy a magjuk a 0 és 1 pozícióba esik és mindkét oldali meredekségük 1. Ez igaz a modell többi szabály rendszerére is, a legtöbb feltétel oldali változó a 49 ábrán bemutatott fuzzy partíciót használja.
A modell legtöbb viselkedés komponense a kutya mozgásirányáért felelős. A modellben ezen viselkedések fúziója az egyes elmozdulás vektorok súlyozott összegével történik, ahol a súlyok az illető viselkedés komponensekhez tartozó állapot értékek. A többi viselkedés komponens a mozgástól függetlenül is végrehajtható, így nem igényel különösebb viselkedés fúziót. Vanank olyan szabályrendszerek is, melyek olyan „rejtett” állapotok értékét határozzák meg, melyekhez nem kapcsolódik közvetlenül viselkedés komponens, de a viselkedés koordinációban szerepet játszanak. Ilyen pl. a ‘DogGreetsOwner’ állapotváltozó, melyhez közvetlenül nem tartozik viselkedés komponens, de ahogy azt az Hiba! A hivatkozási forrás nem található.. táblázat is mutatja, szerepet kap a ‘DogGoesToOwner’ állapotváltozó meghatározásában.
A modell különböző egyedi képességeket mutató kutyára is hangolható. Ez három [0,1] érték közé állítható faktor alapján történik (lásd 44 ábrán ‘Parameters’), úgy mint „Nyugtalanság”, „Idegen elfogadó készség” és „Kötődés”. A „Nyugtalanság” paraméter a kutya egyedi jellemzőit állítja a nyugodttól az idegesig. Az „Idegen elfogadó készség” a kutya idegenekkel szembeni viselkedését paraméterezi a barátságostól a barátságtalanig. A „Kötődés” a kutya gazda iránti kötődésének mértékét változtathatja a gyengétől az erős kötődésig. Valójában ezen módosító paraméterek nem jelennek meg közvetlenül a szabályrendszerekben, hanem másodlagos változókat állítanak, melyek több kapcsolódó szabályrendszert is módosítanak. A három külső paraméter („Nyugtalanság”, „Idegen elfogadó készség” és „Kötődés”) közvetlenül csak a másodlagos paramétereket meghatározó szabályrendszerekben szerepel. Ezen másodlagos paraméterek az alábbiak:
Játssz akkor is, ha nincs ott a gazda (ha a gazda nincs a szobában).
Ne játssz az idegennel (még akkor sem, ha lehetőség lenne rá).
Fuss körbe (a nyugtalanság miatt) ha az idegen a szobában van.
Fuss körbe (a nyugtalanság miatt) ha egyedül vagy.
Az idegen üdvözlésének alap szintje.
A gazda üdvözlésének alap szintje.
Az idegen követésének alap szintje, ha elhagyja a szobát.
A gazda üdvözlésének alap szintje, ha a szobába lép.
A stressz alap szintje (nyugtalanság).
Az ajtóban állás alap szintje.
Az ajtóban állás alap szintje akkor, ha a gazda a szobában van.
A passzivitás alap szintje.
A fentebb a külső paraméterek kapcsán bemutatott hierarchikus felépítés lényeges az egyes szabályrendszerek bemeneti dimenziószámának csökkentése érdekében (három helyett csak egy-egy változóval bővülnek az érintett szabályrendszerek), mert így csökkenthető a szabályok száma is. A másodlagos paramétereket is fuzzy interpolációs szabályrendszerek határozzák meg a három külső paraméter alapján. Ezek a rendszer inicializációja során kapnak értéket, de futásidőben is változtathatók, lehetővé téve, hogy a kutyák viselkedési formáit valamely tevékenység közben is megváltoztathassuk.
A modellhez tartozó lényeges, de attól függetlenül futó rendszer a „megfigyelő” (lásd 44 ábrát). Feladata, hogy a futás közben a valódi kutyákat érintő mérésekhez hasonlóan értékelje a modell működését. Ezért a megfigyelésit nem a modell állapotváltozóinak ismeretében hozza, hanem csak a környezet változóiból kikövetkeztetve (mint ahogy azt a valódi kutya esetén is teszi az etológus). A környezet megfigyelése alapján következtet a szimulált kutya állapotára, hogy az éppen „játszik”, „felfedez”, „az ajtóban áll”, vagy „passzív”. A megfigyelő az esetleges ember-kutya interakciót ugyancsak feljegyzi. A „látottakat” ugyan olyan módon pontozza, mint ahogy azt az etológusok teszik egy valódi kutyát megfigyelve az SST során. A megfigyelő rendszer által a modell működéséről készített mérési eredmények így más kutyák méréseivel így közvetlenül összevethetők.
Hivatkozások
|
[1] |
|
|
[2] |
D. Calisi, A. Censi, L. Iocchi és D. Nardi, „OpenRDK: a modular framework for robotic software development,” in Intelligent Robots and Systems, 2008. IROS 2008. IEEE/RSJ International Conference on, 2008. |
|
[3] |
|
|
[4] |
„OpenRTM-aist robot middleware hivatalos weboladal,” [Online]. |
|
[5] |
N. Ando, T. Suehiro, K. Kitagaki, T. Kotoku és W.-K. Yoon, „RT-middleware: distributed component middleware for RT (robot technology),” in Intelligent Robots and Systems, 2005.(IROS 2005). 2005 IEEE/RSJ International Conference on, 2005. |
|
[6] |
N. Ando, T. Suehiro és T. Kotoku, „A software platform for component based rt-system development: Openrtm-aist,” in Simulation, Modeling, and Programming for Autonomous Robots, Springer, 2008. |
|
[7] |
N. Ando, S. Kurihara, G. Biggs, T. Sakamoto, H. Nakamoto és T. Kotoku, „Software deployment infrastructure for component based rt-systems,” Journal of Robotics and Mechatronics, %1. kötet23, %1. szám3, 2011. |
|
[8] |
|
|
[9] |
M. Quigley, K. Conley, B. Gerkey, J. Faust, T. Foote, J. Leibs, R. Wheeler és A. Y. Ng, „ROS: an open-source Robot Operating System,” in ICRA workshop on open source software, 2009. |
|
[10] |
Domada, M. Ishde, K. Ohnishi, and T. Hori, „Disturbance observer-based motion control of dlrect drive motors,” IEEE Transactions on Energy Conversion, %1. kötet6, %1. szám3, pp. 553-559, 1991. |
|
[11] |
Iwasaki, M.; Shibata, T.; Matsui, N., „Disturbance-observer-based nonlinear friction compensation in table drive system,” IEEE/ASME Transactions on Mechatronics, %1. kötet4, %1. szám1, pp. 3-8, 1999. |
|
[12] |
ObserverLi, W.; Hori, Y., „Vibration Suppression Using Single Neuron-Based PI Fuzzy Controller and Fractional,” Order Disturbance IEEE Transactions on Industrial Electronics, %1. kötet54, %1. szám1, p. 117 – 126, 2007. |
|
[13] |
Tomita, M.; Senjyu, T.; Doki, S.; Okuma, S., „New sensorless control for brushless DC motors using disturbance observers and adaptive velocity estimations,” IEEE Transactions on Industrial Electronics, %1. kötet45, %1. szám2, pp. 274 - 282, 1998. |
|
[14] |
Radke, A.; Gao, Zhiqiang, „A survey of state and disturbance observers for practitioners,” in American Control Conference June 2006 Page(s):6, 14, 2006. |
|
[15] |
Katsura, S.; Matsumoto, Y.; Ohnishi, K., „Modeling of Force Sensing and Validation of Disturbance Observer for Force Control,” IEEE Transactions on Industrial Electronics, %1. kötet54, %1. szám1, p. 530 – 538, 2007. |
|
[16] |
McCann, R.A.; Islam, M.S.; Husain, I, „Application of a sliding-mode observer for position and speed estimation in switched reluctance motor drives.;,” IEEE Transactions on Industry Applications, %1. kötet37, %1. szám1, p. 51 – 58, 2001. |
|
[17] |
|
|
[18] |
T. Thomessen, P. K. Sannæs, and T. K. Lien, “Intuitive Robot Programming,” in 35th International Symposium on Robotics, 2004. |