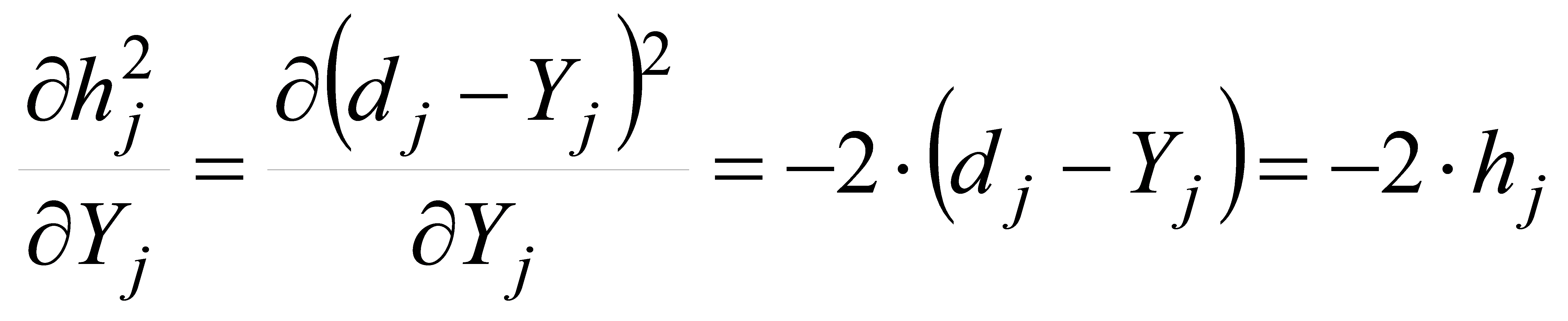9. fejezet - Emberszabású kéz Forma-Memória ötvözettel mozgatva
Abstract –Ezen dokumentum egy általános neurális hálózattal ellátott ügyes kéz gyakorlati alkalmazását tartalmazza, amely Forma-Memória ötvözetel kerül mozgatásra (Shape Memory Alloy-SMA) . Mivel az SMA karakterisztikája nagyon nem lineáris és a paramlterei a környezettől függenek (főként a hőmérséklettől), ezért a robotkéz egy általános neurális hálózat segíségével működtethető, amely képes arra, hogy megtanulja a robotkéz éppen aktuális nem lineáris karakterisztikáját. A kísérleti berendezés egy 20 szabadságfokú kézből áll, melyet egy SMA húr mozgat, mint mesterséges izom. A csatlakozások pozíciójának detektálására videokamerát használunk. A helyzetet ezután interneten keresztül elküldjük a kijelző számítógépnek, mely OpenGL segítségével megjeleníti a 3D-s kezet.
9.1. Bevezetés
Az emberek hat érzékkel képesek érzékelni a közvetlen környezetüket, de ezek közül csupán néhányat használnak telemanipuláció közben.
A telemanipuláció az emberi manipuláció kiterjesztése egy távoli helyre. Megfelelő visszajelzések segítségével a telemanipuláció jól megvalósítható veszélyes, vagy egyéb úton elérhetetlen területeken. Az emberek a feladataikat főképp kézzel végzik, ezért a master és slave eszközöknek illeszkednie kell a műveletet végző személy kezéhez. A telemanipuláció területén rengeteg HAPTIC eszköz lett kifejlesztve.
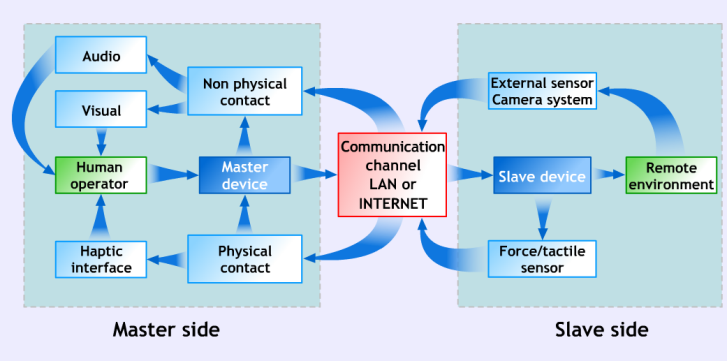 A kesztyű típusú master eszköz lehetővé teszi a legkomplexebb és ügyesebb manipulációt is. Az emberi kéz a legszélesebb körben alkalmazott szerszám. A végső cél, hogy egy olyan készüléket hozzunk létre, melynek segítségével az operátor úgy érzi, mintha csak hosszabb lenne a keze. A piacon jelenleg is rengeteg olyan érzékelős kesztyű kapható, mely nem képes a felhasználó számára “erő visszajelzést” adni.. A [7]-es dokumentum bemutat egy érzékelő kesztyűt, mely erő visszajelzéssel rendelkezik az operátor kezének mind a 20 kapcsolódására. Amennyiben az emberi kéz egy ilyen “kereskedelmi” kesztyűt használ többféle bonyolult feladat is elvégezhető az irányított területen, de a kereskedelmi kéz típusú slave eszközök nem elérhetőek. Ez a dokumentum bemutat egy kereskedelmi kéz típusú slave eszközt a precíz telemanipuláció végrehajtásához. Eddig még nem volt a rendszerbe az erő visszajelézés funkció implementálva, annak ellenére, hogy a berendezés jelentősen egyszerűbb, mint a 91. ábra –n lévő . A rendszer felhasználás a 92. ábra-n látható.
A kesztyű típusú master eszköz lehetővé teszi a legkomplexebb és ügyesebb manipulációt is. Az emberi kéz a legszélesebb körben alkalmazott szerszám. A végső cél, hogy egy olyan készüléket hozzunk létre, melynek segítségével az operátor úgy érzi, mintha csak hosszabb lenne a keze. A piacon jelenleg is rengeteg olyan érzékelős kesztyű kapható, mely nem képes a felhasználó számára “erő visszajelzést” adni.. A [7]-es dokumentum bemutat egy érzékelő kesztyűt, mely erő visszajelzéssel rendelkezik az operátor kezének mind a 20 kapcsolódására. Amennyiben az emberi kéz egy ilyen “kereskedelmi” kesztyűt használ többféle bonyolult feladat is elvégezhető az irányított területen, de a kereskedelmi kéz típusú slave eszközök nem elérhetőek. Ez a dokumentum bemutat egy kereskedelmi kéz típusú slave eszközt a precíz telemanipuláció végrehajtásához. Eddig még nem volt a rendszerbe az erő visszajelézés funkció implementálva, annak ellenére, hogy a berendezés jelentősen egyszerűbb, mint a 91. ábra –n lévő . A rendszer felhasználás a 92. ábra-n látható.
9.2. Kéz
A kéz elsősorban negyon finom mozgást igénylő műveletek elvégzésére szolgál a kéz és ujjpozíciók széles kombinációjának felhasználásával. Következésképpen, kölcsönhatás van a csuklóizületek pozíciója és az ujjmozdulatok hatékonysága között. A kézfej rengeteg stabil és mobil területtel rendelkezik, melyekhez nagyon komplex izom és “csukló-joint” mozdulatok tartoznak.
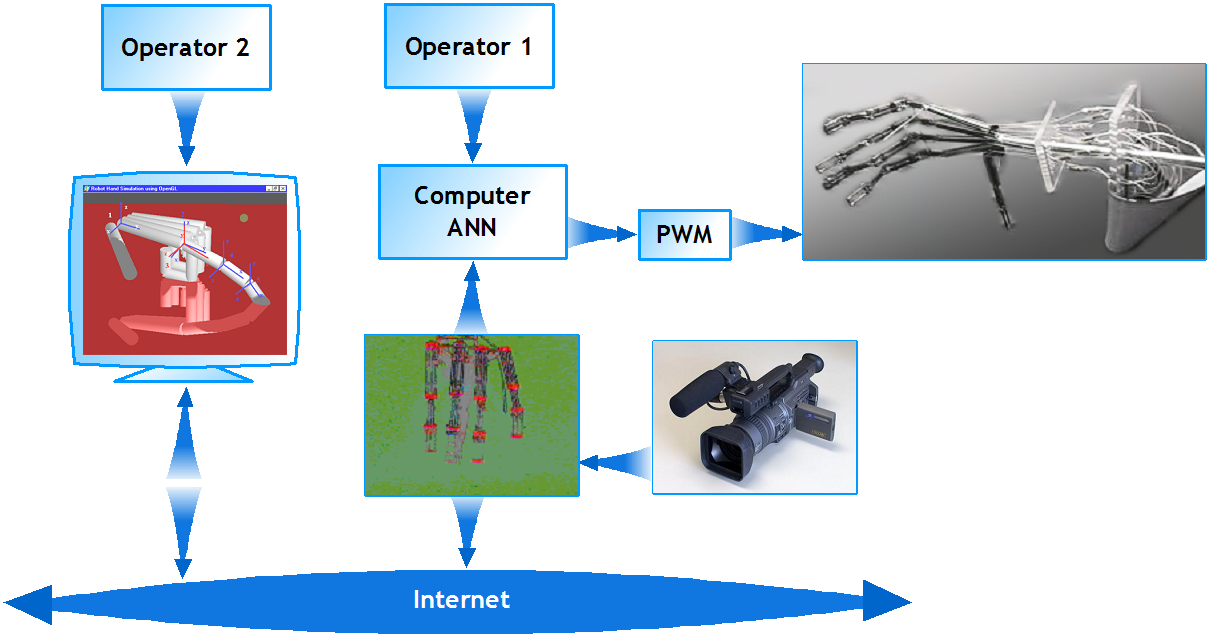
A robotkéz teljesen hasonló felépítésű az emberi kézhez, elméletileg az emberi kéz mozgásának mind a 20 szabadságfokával rendelkezik, de ebben az esetben csak 8-at használunk belőle.Nem szeretnénk külön irányítani a legfelső ujjperc mozgását, mert ezt az emberi kéz sem tudja jól irányítani. Mi csak a kis ujjpercet húzzuk és az magávalhúzza a középső ujjpercet is. A kéz felépítése a 93. ábra-n látható.

9.3. Általános neurális hálózat
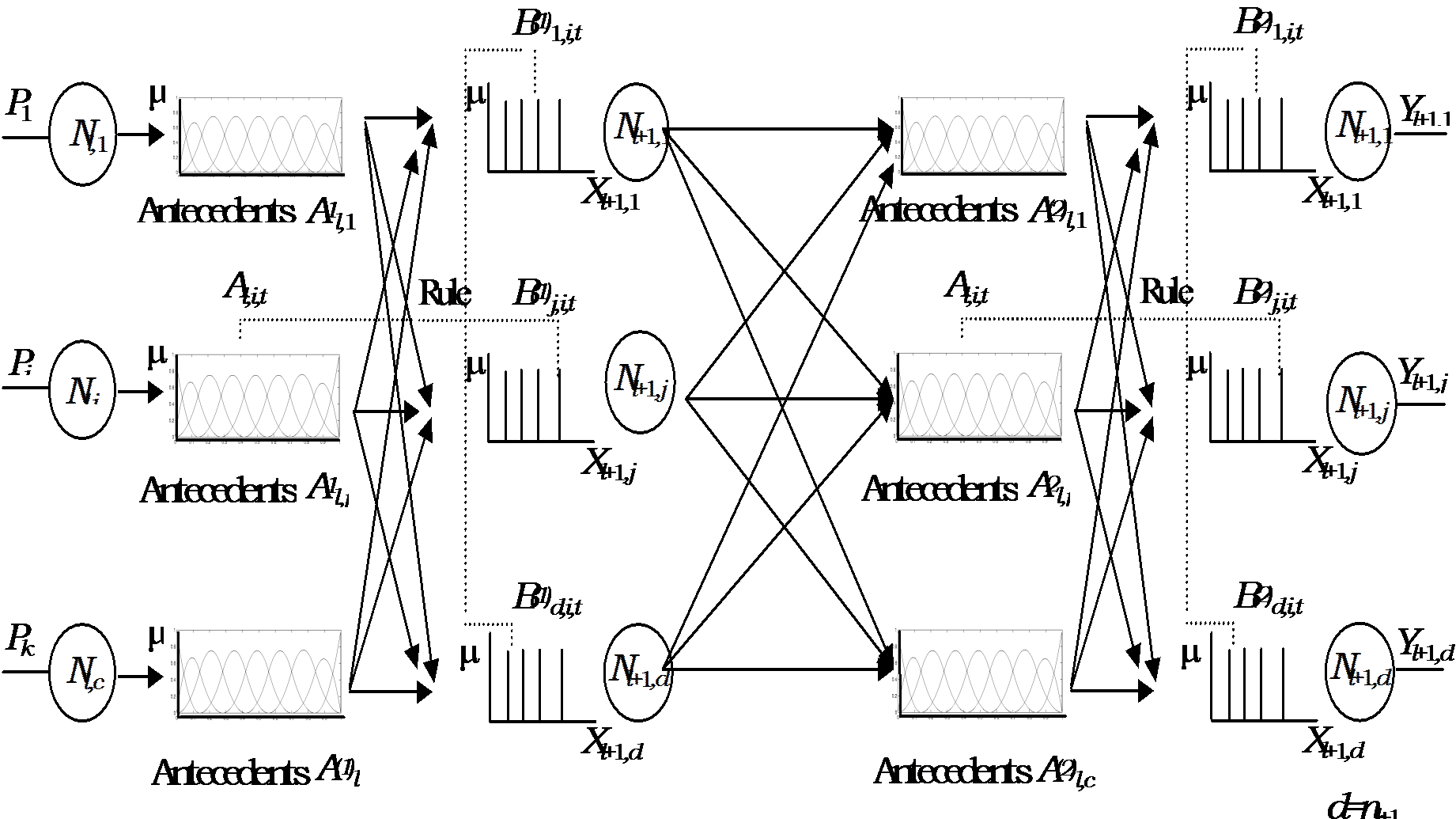
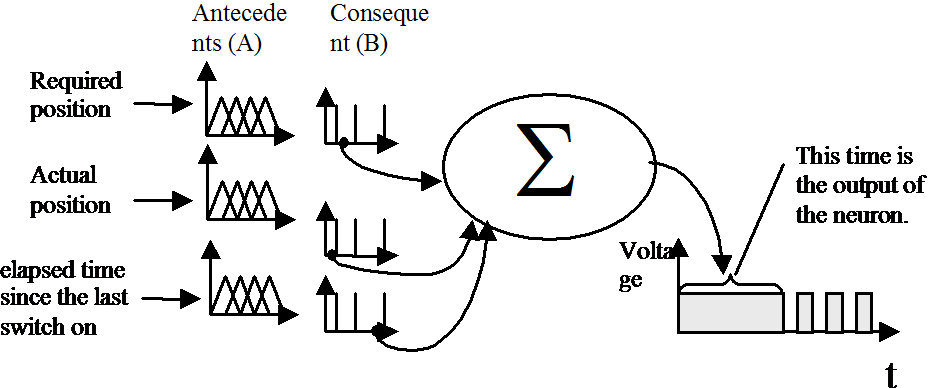
A kéz mozgatására általános neurális hálózatot használunk: A különbség a klasszikus és az általános neuron között, hogy a klasszikus neuron súlyát valós számokkal írjuk le, míg az általános neuron súlyát ebben az esetben “fuzzy” függvények adják. Egy egyszerű neuront mutat a 910. ábra és a többrétegű általános neurális hálózat in 97. ábra-n kerül kifejtésre.
A neuron minden egyes bemenetére van egy B set, melyet egy előző A set bocsát ki. Minden egyes előző set megfeleltehető egy következetes B set-nek , mely esetünkben egy egyedülálló set, ahogy azt a 94. ábra is mutatja. Ha az X0 bemenet eléri a rendszer X bemenetét ,akkor az kivág kettő vagy több előzményt is ( az előzmény függvény típusától függően, esetünkben háromszög set-eket feltételeztünk).Az előzményekhez tartozó B értékek súlyozva vannak és a tömegpontok a 94. ábra-n látható módon kerülnek kiszámításra:
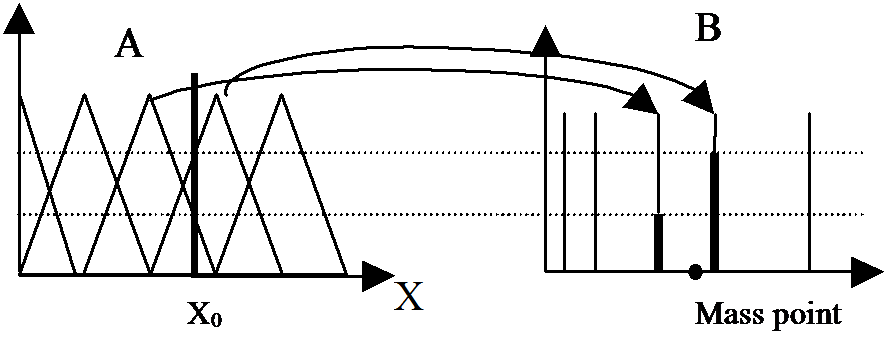
A súlypont értéke a neuron összegző részébe kerül (lásd: 910. ábra). A rendszer a következmény set-ek változtatásával tanítható (azaz B értékei).
Ha felrajzoljuk az előzmény A és következmény B értékeket egy koordinátarendszer két tengelyére, láthatóvá válik, hogy mi is történik: A legtöbb függvény (melyek a mérnöki gyakorlatban érdekeltek) közelíthető fuzzy függvényekkel. Az előzmény set-ek pozícióji meghatározzák a közelítendő függvény mintavételi pontjait. A B értékek mintavételezett értékek. Az előzmény tagsági függvény alakja meghatározza az interpolációs karakterisztikát a mintavételezett pontok között. Háromszög típusú előzmény függvényt használva a közelítő függvény szakaszonként lineáris lesz mint ahogy azt a 95. ábra mutatja.
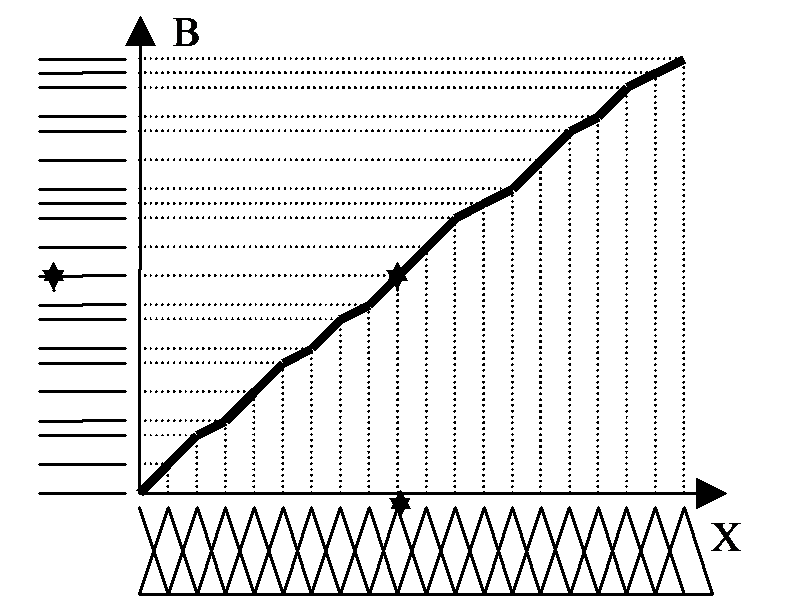
Szóval míg a normál neurális hálózat esetében minden esetre ugyanaz a nem lineáris függvény áll fenn, addig az általánosított neurális hálózat esetében minden bemenetre más és más nem lineáris függvényt kapunk. Még B értékének megváltoztatásával is könnyedén módosíthatjuk ezeket a nem lineáris függvényeket. Matematikai szemszögből vizsgálva: az eredeti neuron egy nem lineáris függvénnyal válaszol a bemenetre adott lineáris kombinációkra. Az általánosított neuron megadja a lineáris kombinációit a bemenetre adott nem lineáris függvénynek. A neuronok előzményei háromszög függvények, mert ezekhez szükséges a legkisebb számítási kapacitás. Az előzmények Ruspini-felbontást formálnak, ami azt jelenti, hogy a tagok összege bármely X helyen egyenlő 1-el. Ez a felbontás a 96. ábra –n látható.
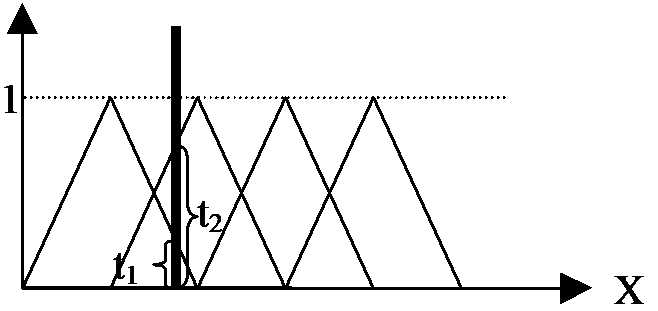
t1+t2 = 1 bármely X-re.
9.4. AZ ÁLTALÁNOS NEURÁLIS HÁLÓZAT TANÍTÁSA
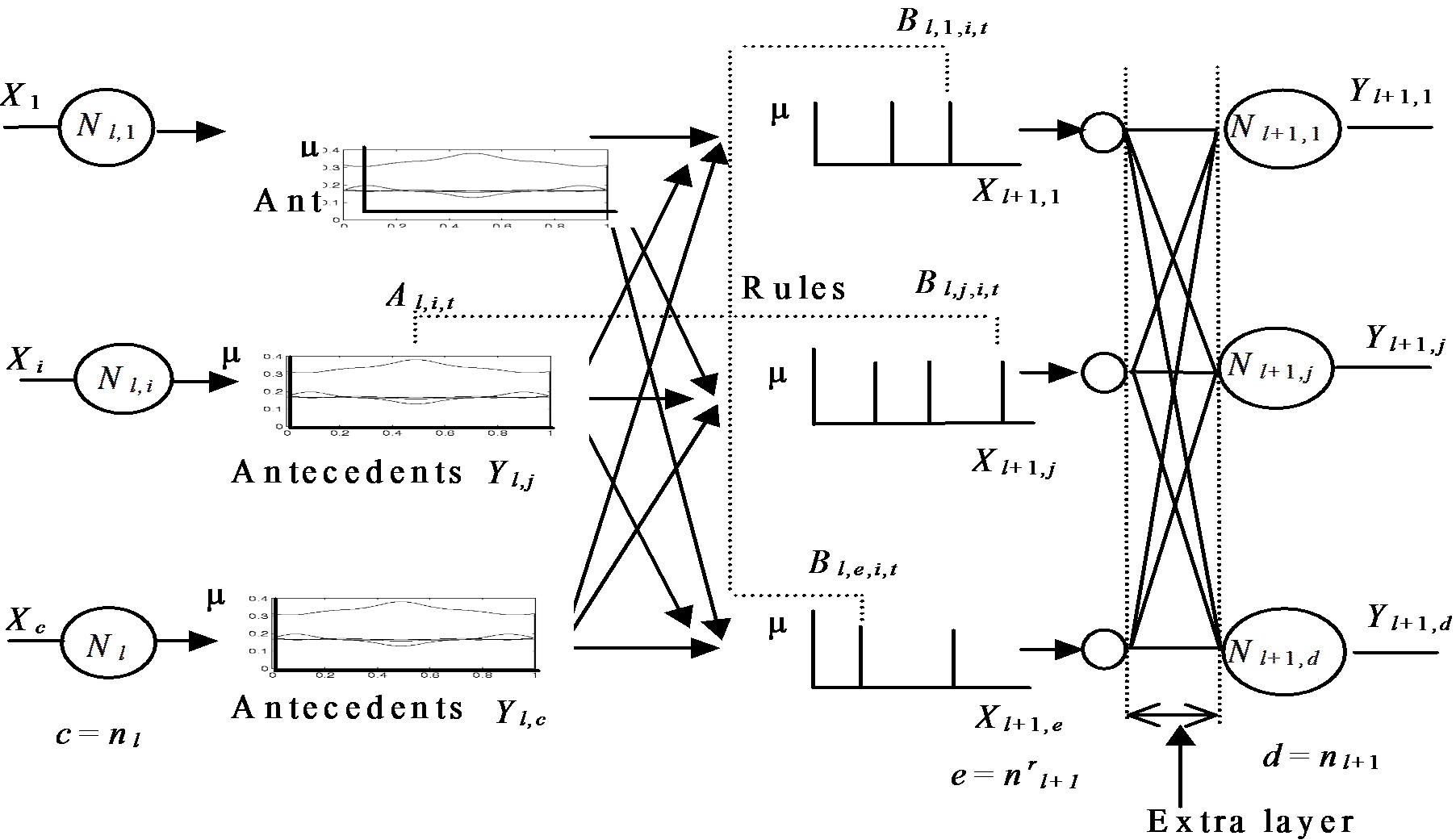
Az általános neurális hálózat a 97. ábra-n látható. A97. ábra jelöléseit felhasználva a neurális hálózat kimenetei a következőképpen számíthatóak:
|
|
( 9.1 ) |
ahol Xi az i neuron kimenete az első szinten/rétegen, a t-dik előzménye az i-dik bemenetnek a második szinten. Minden előzmény set összhangban van az összes neuronnal. a következmény set-je az által kibocsátott j-dik neuronnak.
|
|
( 9.2 ) |
Ahol k a bemenetek száma, t az előzmények száma, Pk pedig a k-dik bemenet.
A kérdés, hogy hogyan módosítjuk a Bk,i,t súlyát, ha a hiba h?
|
|
( 9.3 ) |
A hiba nem deriválható egyszerűen Bk,i,t miatt, ezért a láncszabályt kell alkalmazni , mint a Hátsó Terjedési Algoritmusban. A h hiba az Y kimenet szerint deriválható., a kimenet az X bemenet szerint deriválható, és végül pedig a bemenet a keresett B szerint deriválható. Így a következőt kapjuk:
h2 számítható, mint:
Általánosságban, ha a hiba az n-dik szinten történt h(n)j, akkor a hiba az n-1-dik szinten a következő módon számítható:
|
|
( 9.9 ) |
A súlyok a következőképpen módosulnak:
|
|
( 9.10 ) |
9.5. A KÉZ IRÁNYÍTÁSA
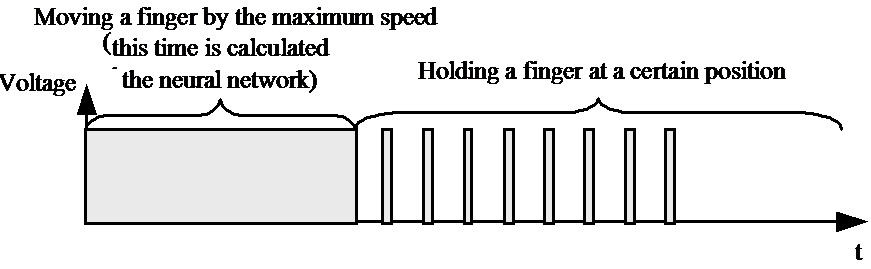
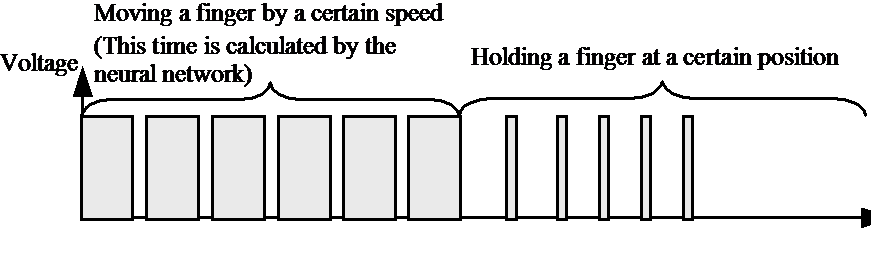
A kéz mozgásának szabályozásádra Pulzusszélesség Modulációt alkalmazunk (PWM). Két különböző kitöltési tényezőt használunk, egyet a kéz különböző részeinek mozgatására, a másikat pedig az egyes pozíciókban való tartásához. (lásd 98. ábra és 99. ábra). Amikor az operátor megváltoztatja a referencia pozícióját, a neurális hálózat kiszámítja , hogy mennyi ideig kell a vezetékre feszültséget kapcsolni, ahhoz hogy a kéz a kívánt pozícióba álljon (Lásd: 98. ábra és 99. ábra). Mivel a környezeti jellemzők (főként a hőmérséklet) jelentős hatást gyakorolnak az SMA vezetékek karakterisztikájára, a neurális hálózatot folyamatosan újra kell hangolni.
9.6. AZ ÁLTALÁNOS ALGORITMUS KOMPLEXITÁSÁNAK CSÖKKENTÉSE
Egyike a legnagyobb problémáknak, amikor fuzzy vagy neurális technikákat alkalmazunk a számítások komplexitása. A mérnökök gyakran szembesülnek ezzel a problémával különösen komplex feladatok esetén, valamint az információ visszakeresés területén, ahol teljes könyvtárak óriási információs térképeit vagy az internetet kell feldolgozni, minden egyes felhasználói kérésre. Ezek az alkalmazások használják az általánosított típusú neurális hálózatot. Engedjék meg a komplexitás tétel eredményeinek egy rövid bevezetését.
Lemma 1. A számítás összetettsége arányosan növekszik a neuronok párhuzamos szintjeinek számával.
Elhanyagolva a plusz műveletek számítási erőfeszítéseit, de figyelembe véve az eszköz működését, a számítási szükségletek a következőképpen realizálhatóak:
|
, |
( 9.11 ) |
ahol jelenti tagsági függvények számítását:
|
, |
( 9.12 ) |
ahol s jelenti egy előzmény set egy tagsági értékének számítását.
Ezen rész legfőbb feladata, hogy javaslatot tegyen egy olyan algoritmusra, mely képes kiszűrni a közös lineáris kombinációkat és csökkenteni képes az előzmény set-ek számát a súlyozó függvény transzformálására alapozva. A javasolt eljárás egyik legnagyobb előnye, hogy az egyszerűsítés hatékonysága a megadott hibaküszöb segítségével kerül irányításra.
Tétel 2.: Egyenlet (9.4) mindig átalakítható a következő alakra:
|
, |
( 9.13 ) |
ahol “r” jelöl “csökkentett”, továbbá és .
A egyszerűsített alak úgy jelenik meg, mint a neurális hálózat a 912. ábra-n. A technika további bizonyítékai a [9,10]-es pontban kerülnek további kifejtésre.
9.7. VISSZAHATÁS
Ahhoz, hogy a számítógéppel megtalálhassuk a kamera képén a csomópontokat, vörösre festettük őket. Azért ezt a színt választottuk, mert a három fő szín közül (Vörös, Zöld, Kék) ez a szín a legjellemzőbb.
Sajnos a kéz rézből készült, melynek szintén magas a vörös szín tartalma, ezért a kezet zöldre kellett festeni. A zöldet azéret választottuk, mert ez szintén egy alapszín és a filmtechinkában is használatos (annak ellenére, hogy a technikát “bluebox”-nak nevezik a kék színt csak tíz évvel ezelőttig hazsnálták, mikor is megváltoztatták zöldre, mert ez kedvezőbb hatással van a kamerák érzékenységére). Ezután észrevettük, hogy rengeteg vörös tárgy van a laboratóriumban, ezért létrehoztunk egy teljes green box-ot a kéz körül. Egy Sony Handicam-et használunk egy Genius Video Wonder II TV-kártyával. A számítógép egy Pentium-166 with 40 Mbyte RAM Windows 98 operációs rendszerrel. Azért ezt a konfigurációt választottuk, mert a TV-kártya programozása igen egyszerű Windows környezetben, a gyártó rendelkezésünkre bocsájt drivereket és nekünk csak az általuk előírt folyamatokat kell elvégeznünk. A program Borland Delphi 4-ben íródott. A video rögzítő program (eac401) az internetről került letöltésre (“Delphi Superpage”), és lett módosítva, hogy megfeleljen a mi elvárásainknak.
A kép méretét 160X120-ra választottuk, mivel ez a legkisebb standard méret.






Még ebben az esetben is rendkívül magas lehet a szükséges számítási kapacitás. A programban különböző kamera-tulajdonságok állíthatóak be, például fényerősség, kontraszt vagy telítettség. Ezen tulajdonságok állításával jobb képminőséget tudunk elérni. A képek javításának fázisai a 9-15. ábra-9-18. ábra- kon láthatóak.
9.8. VIZUÁLIS INTERFACE
A szoftver arra lett kifejlesztve, hogy egy képi visszajelzést adjon a kézről a telemanipuláció során. A vizuális visszajelzés célja, hogy egy megfelelően realisztikus képet szolgáltasson a környezetről és annak ellenére, hogy ez a környezet még messze van a teljestől, a program lehetőséget nyújt a felhasználónak, hogy teljes 3 dimenziós térben barangoljon.
A program úgy lett létrehozva, hogy helyileg teljes szimulációs módban fusson, vagy TCP/IP kapcsolaton keresztül, mint például Internet vagy Local Area Network. Szimulációs módban, a program lehetőséget ad, hogy az emberi kéz minden mozdulatát szimulálhassuk. Hogy ezt elérjük, mind az anatómiai és matematikai modelleket fel kellett építeni, mely modellek OpenGL-ben kerültek implementálásra. A matematikai levezetés a Denavit-Hartenberg jelzésrendszert használja, mert ez jól használható mindkét esetben és az OpenGL-ben is. A model sok alapfeltételezéssel él, melyek a következőek:
Az alap koordináta keret minden ujj esetében azonos. Ez azért került alkalmazásra, hogy egy teljesen általános esetet kapjunk, ahol az ujjbegyek koordinátái egy közös ponthoz képest kerülnek kiszámításra, mint például a csukló. Ezt a közös keret tekinthetjük a § pontnak. Ez a pont szolgál arra, hogy a rendszer a későbbiekben lehetőséget nyújtson arra, hogy a rendszert kiterjeszthessük, amennyiben ez szükségeltetik.
Egy ujj 3 pontot tartalmaz, az első két szabadságfokú, a másik kettőnek csak egy a szabadséágfoka, mely síkbeli forgást tesz lehetővé. Az első pont pozíciója l0 változó által kerül meghatározásra, mely a távolság az első pont és a közös koordinátarendszer középpontja között.
Egy ujj mentén a di értéke 0, ami azt jelenti, hogy a közös normálisok egy vonalba esnek.
Egy uj mentén ai érétke megegyezik a kapcsolat hosszávcal.
Az elfordulás szöge csak a bázis koordinátarendszerben van figyelembe véve, és az első “joint”-nál, mivel az ujjak oldalirányú mozgását is figyelembe kell venni.
Fontos, hogy a § koordináta minden ujjnál azonos lehgyen, és ez legyen az egész kéz közös referenciája is. A különböző i szögek és l0 változók meghatározzák a pontos pozícióját és orientációját a következő csuklópontban elhelyezkedő keretnek, minden ujj esetén. Két keret között a di értéke megegyezik a kapcsolat hosszával, l0. (Since joint 0 is of the revolute type, q0 is 1 the relationship between the two joints is xx.)
9.9. KÖVETKEZTETÉS
Ez a dokumentum egy ügyes kezet mutatott be, mely a telemanipuláció “slave” eszközeként szolgál. Forma memória ötvözeteket (SMA) felhasználva, mint „mesterséges izom” hatékonyan növeltük a robotmechanizmus szabadságfokainak számát, mely nagyobb rugalmasságot nyújtott , mint a széles körben alkalmazott pneumatikusan, vagy elektromos aktuátorokkal vezérelt kezek esetében. Az SMA vezetékek súlya és mérete jóval kisebb, mint az általában használatos aktuátoroké. A konstrukció sokkal egyszerűbb; és az ára sem magasabb az általánosabb eseteknél. Viszont SMA technológiát alkalmazva egy nagyon bonyolult irányítási problémához jutunk, mivel az SMA szolgáltatása erősen nem lineáris. Ez a dokumentum megmutatta, hogy az általánosított neurális hálózatok egyfajta megoldásul szolgálhatnak az SMA használatánál kialakuló irányítási problémára.