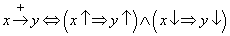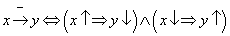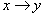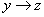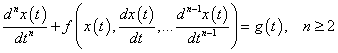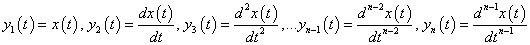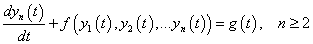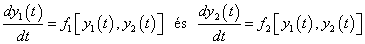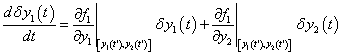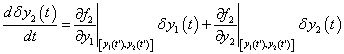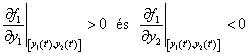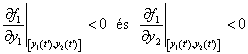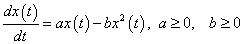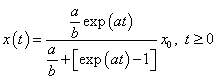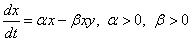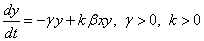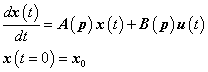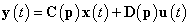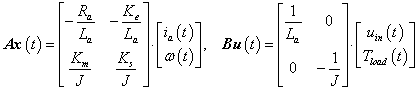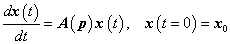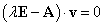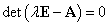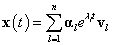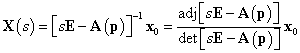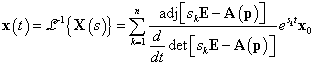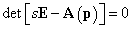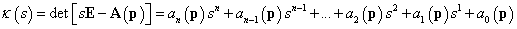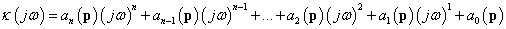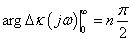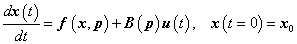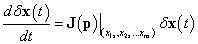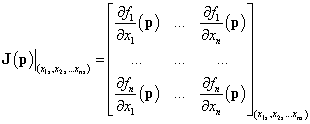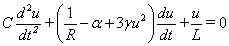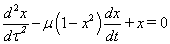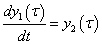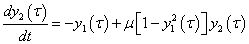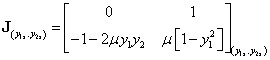3. fejezet - Kvalitatív rendszerdinamika és rendszerek stabilitása
3.1. Hatásalgebra és dinamikus rendszerek
3.1.1. Hatások és hatásgráfok
A mechatronikai rendszerek elemzésében, tervezésében és irányítási feladatainak megoldásában jelentős szerepet játszanak a rendszerek modelljei, melyek többnyire sok változót és a közöttük fellépő kölcsönhatásokat leíró algebrai és/vagy differenciálegyenleteket, valamint a rendszerekre vonatkozó korlátozásokat kifejező egyenlőtlenségeket tartalmaznak. A rendszerek kvantitatív vizsgálata, az egyenlet- és egyenlőtlenségrendszerek megoldásai adják meg a tervezési és irányítási problémák végső megoldásait, azonban a feladatok elemzésében, a rendszerek egyes minőségi tulajdonságainak és viselkedési formáinak vizsgálatában, valamint a többnyire meglehetősen összetett kvantitatív vizsgálatok előkészítésében a rendszerek kvalitatív analízise, kvalitatív tulajdonságainak és az azokat meghatározó körülmények felderítése sokszor alapvető a kedvező tervezési és üzemelési feltételek kimunkálásában
A rendszerben fellépő kölcsönhatások minőségi vizsgálatát a kvalitatív rendszerdinamika módszereivel végezhetjük, melynek célja annak meghatározása, hogy a rendszer változói, mint a rendszert alkotó fizikai objektumoknak és/vagy fizikai mennyiségeknek a modelljei milyen hatással vannak egymásra. Ez tehát a rendszerben fellépő hatások minőségi vizsgálatát jelenti, melynek feladata azon tényezők meghatározása, amelyek lényeges hatással lehetnek a rendszer viselkedésére.
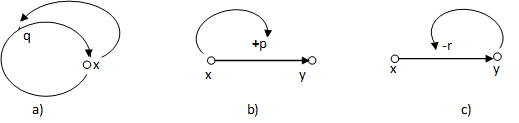
A kvalitatív elemzés geometriai segédeszköze a hatásgráf, amely lényegében egy irányított geometriai gráf, amellyel egyrészt megadjuk a rendszer egyes változó-párjai közötti
-
ok-okozati kapcsolatokat, másrészt az
-
okok által az okozatokban előidézett változások értékbeli irányait.
A hatásgráf két példáját mutatja be az 3-1. ábra, ahol az ok és okozat értékbeli változásainak irányától függően a hatások előjelét is megadtuk.
3.1 definíció. Az x változó pozitív hatással van az y változóra, ha az x változó mint ok az y változóban mint okozatban azonos irányú értékbeli változást idéz elő: azaz ha x növekszik, akkor y növekedését idézi elő, míg ha x csökken, akkor az y csökkenését okozza.
3.2 definíció. Az x változó negatív hatással van az y változóra, ha az x változó mint ok az y változóban mint okozatban ellenkező irányú értékbeli változást idéz elő: azaz ha x növekszik, akkor y csökkenését idézi elő, míg ha x csökken, akkor az y növekedését okozza.

A továbbiakban a változók változási irányait a változókhoz csatolt nyilakkal jelöljük, azaz azx↑ jelölés növekvő x változót jelent, míg az x↓ jelölés csökkenőt. Ezt felhasználva a fenti definíciót tömörebben az
|
|
(3.1) |
és
|
|
(3.2) |
módon fogalmazhatjuk meg.
A kvalitatív rendszerdinamika változóinak és két alapműveletének meghatározása után definiáljuk a hatás-algebra műveleti szabályait az 1. táblázatban megadott módon: ha ismertek az 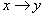 és
és 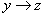 hatások, akkor milyen jellegű az eredő
hatások, akkor milyen jellegű az eredő 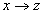 hatás?
hatás?
|
|
|
|
|
|
1 |
+ |
+ |
+ |
|
2 |
+ |
- |
- |
|
3 |
- |
+ |
- |
|
4 |
- |
- |
+ |
-
táblázat. A hatás-algebra műveleti szabályai
Az 1. táblázatban megadott műveleti szabályokat az alábbi képletekkel is megfogalmazhatjuk könnyen ellenőrizhető formában:
1) 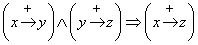 (3.3)
(3.3)
2) 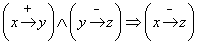 (3.4)
(3.4)
3) 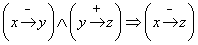 (3.5)
(3.5)
4) 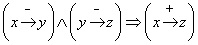 (3.6)
(3.6)
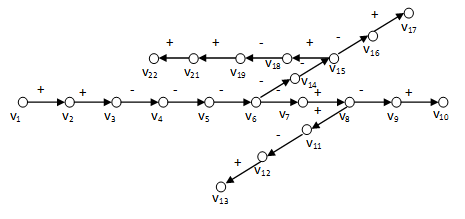
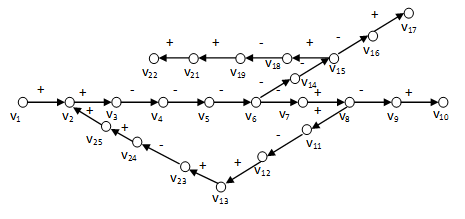
Természetesen az 1. táblázatban bemutatott két-elemű kapcsolatot, amely gyakorlatilag a két hatás soros kapcsolását jelenti, tetszőleges elemszámú, különböző elágazásokkal rendelkező hatásláncra bővíthetjük az 3-1. ábra által bemutatott módon. Ennek értékelését az 1-4 műveleti szabályok szekvenciális alkalmazásával érhetjük el, és meghatározhatjuk az ok-okozati kapcsolatok következetes végigkövetésével bármely két rendszerelem közötti eredő hatás értékét. Így könnyen megállapíthatjuk, hogy a v1 változó a v10 és v13 változókra negatív hatással van, míg v17 és v22 változókra az eredő hatás pozitív. Ezek az értékelések egy nagyon egyszerű szabály megfogalmazását engedik meg:
3.3 definíció. Ha egy hatásláncban a két rendszerelem között páros számú negatív hatás van függetlenül a pozitív hatások számától, akkor az eredő hatás pozitív, míg ha a negatív hatások száma páratlan, akkor a hatáslánc eredője negatív.
A 3-2. ábra elágazó nyílt hatásláncokat tartalmaz. Ezt bővítve: a 3-3. ábra és 3-4. ábra a 3-2. ábra nyílt hatásláncait a 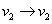 zárt hatásláncokkal egészítik ki. A zárt hatásláncokat a gráfok elméletéből ismerten irányított köröknek, vagy egyszerűen hurkoknak nevezzük. Ezek az apró bővítések azonban jelentős változást idéznek elő a rendszer viselkedésében, mivel a zárt hatásláncokbármelyik eleme visszahat önmagára. Így a
zárt hatásláncokkal egészítik ki. A zárt hatásláncokat a gráfok elméletéből ismerten irányított köröknek, vagy egyszerűen hurkoknak nevezzük. Ezek az apró bővítések azonban jelentős változást idéznek elő a rendszer viselkedésében, mivel a zárt hatásláncokbármelyik eleme visszahat önmagára. Így a 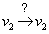 visszahatásnak jól meghatározott értéke van, ami természetesen függ a zárt hatásláncban szereplő egyes hatások értékeitől. Ahogy ezt a nyílt hatásláncok esetében láttuk, az eredő hatás értéke itt is lehet negatív és pozitív, amit a hurok polaritásának is nevezünk. A 3-3. ábra negatív polaritású hurkot mutat be, mivel páratlan számú negatív hatást lehet összeszámolni, míg a 3-4. ábra pozitív polaritású hurkot tartalmaz, ui. itt a negatív hatások száma páros.
visszahatásnak jól meghatározott értéke van, ami természetesen függ a zárt hatásláncban szereplő egyes hatások értékeitől. Ahogy ezt a nyílt hatásláncok esetében láttuk, az eredő hatás értéke itt is lehet negatív és pozitív, amit a hurok polaritásának is nevezünk. A 3-3. ábra negatív polaritású hurkot mutat be, mivel páratlan számú negatív hatást lehet összeszámolni, míg a 3-4. ábra pozitív polaritású hurkot tartalmaz, ui. itt a negatív hatások száma páros.
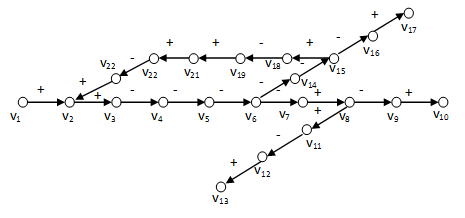
A zárt hatásláncok polaritásának azonban mélyebb értelme van: ugyanis a negatív polaritás lényegében a 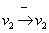 negatív visszahatást jelenti, azaz a v2 bármilyen irányú megváltozása a zárt hatásláncon keresztül ellenkező irányú hatást generál, azaz gyengíti önmaga változását, amit negatív visszacsatolásként értelmezünk. Ugyanakkor a pozitív polaritás a
negatív visszahatást jelenti, azaz a v2 bármilyen irányú megváltozása a zárt hatásláncon keresztül ellenkező irányú hatást generál, azaz gyengíti önmaga változását, amit negatív visszacsatolásként értelmezünk. Ugyanakkor a pozitív polaritás a 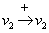 pozitív visszahatásból ered, azaz a v2 bármilyen irányú megváltozása a zárt hatásláncon keresztül azonos irányú hatást generál, azaz erősíti önmaga változását, aminek értelmezése a pozitív visszacsatolás. Ennek az a következménye, hogy a pozitív visszacsatolás a rendszerben mindaddig erősíti valamely változó, azaz ezen változó által modellezett fizikai mennyiség azonos irányú változását, amíg valamely ettől független hatás meg nem gátolja ezt vagy ellen nem hat ennek. Ugyanakkor a negatív visszacsatolás a rendszerben gyengíti valamely változó, azaz ezen változó által modellezett fizikai mennyiség bármely irányú változását.
pozitív visszahatásból ered, azaz a v2 bármilyen irányú megváltozása a zárt hatásláncon keresztül azonos irányú hatást generál, azaz erősíti önmaga változását, aminek értelmezése a pozitív visszacsatolás. Ennek az a következménye, hogy a pozitív visszacsatolás a rendszerben mindaddig erősíti valamely változó, azaz ezen változó által modellezett fizikai mennyiség azonos irányú változását, amíg valamely ettől független hatás meg nem gátolja ezt vagy ellen nem hat ennek. Ugyanakkor a negatív visszacsatolás a rendszerben gyengíti valamely változó, azaz ezen változó által modellezett fizikai mennyiség bármely irányú változását.
3.4 definíció. A negatív visszacsatolás a rendszert stabilizáló zárt hatáslánc, míg a pozitív visszacsatolás a rendszerben destabilizáló hatást eredményez. A kvalitatív értékelés egyik lényeges célja a visszacsatolások felderítése a rendszer stabilitásának elemzése érdekében.
Jegyezzük meg, hogy egy zárt hatáslánc bármelyik változójára ugyanolyan jellegű visszahatás, azaz visszacsatolás érvényesül, mivel ezt a hurok polaritása határozza meg.
Ha most gondolatban összevonjuk a 3-3. ábra és 3-4. ábra rendszervázlatait, akkor a v2 változóra egyidejűleg egy negatív és pozitív visszacsatolás is hat, ami azonban bizonytalanná teszi az értékelést, mivel azonnal felvetődik a kérdés: milyen értékű 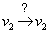 visszahatás? De ez a kérdés az 3-5. ábra rendszerében is felvetődik, ahol a v1 és v3 között az alsó kételemű lánc negatív eredő hatást ad, míg a felső háromelemű lánc eredője pozitív. Ismét: milyen értékű a
visszahatás? De ez a kérdés az 3-5. ábra rendszerében is felvetődik, ahol a v1 és v3 között az alsó kételemű lánc negatív eredő hatást ad, míg a felső háromelemű lánc eredője pozitív. Ismét: milyen értékű a 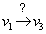 hatás? Ezekre a kérdésekre a választ a tiszta kvalitatív képhez egy kvantitatív adat hozzáadásával tudjuk megadni, ahogy ezt az 3-5. ábra b része jelöli, mégpedig egy-egy hatás értékéhez annak erősítésének, azaz erősítési tényezőjének megadásával. Ezzel a
hatás? Ezekre a kérdésekre a választ a tiszta kvalitatív képhez egy kvantitatív adat hozzáadásával tudjuk megadni, ahogy ezt az 3-5. ábra b része jelöli, mégpedig egy-egy hatás értékéhez annak erősítésének, azaz erősítési tényezőjének megadásával. Ezzel a 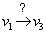 hatás eredő értéke attól függ, hogy a –(p·q)és +(a·b·c) szorzatok abszolút értékei közül melyik a nagyobb? Ezt úgy fejezzük ki, hogy a nagyobb abszolút értékkel rendelkező hatás a domináns. Ezzel természetesen már azt is meg tudjuk adni, hogy a 3-3. ábra. és 3-4. ábra sémáinak egyesítésével kapott rendszerben melyik visszacsatolás a domináns.
hatás eredő értéke attól függ, hogy a –(p·q)és +(a·b·c) szorzatok abszolút értékei közül melyik a nagyobb? Ezt úgy fejezzük ki, hogy a nagyobb abszolút értékkel rendelkező hatás a domináns. Ezzel természetesen már azt is meg tudjuk adni, hogy a 3-3. ábra. és 3-4. ábra sémáinak egyesítésével kapott rendszerben melyik visszacsatolás a domináns.

Az erősítési tényező értelmezésével egy további hatás-élt tudunk bevezetni a 3-6. ábraáltal bemutatott módon, amely az erősítési tényező modulálását jelenti a rendszer valamely változójának hatására. Ez alapjában véve a hatások szabályozását jelenti, amellyel egyes visszacsatolások erősítési tényezőit, sőt akár értékeit is meg tudjuk változtatni, azaz valamely pozitív visszacsatolást megszakítani vagy ellenkező értékűre változtatni a rendszer stabilitása érdekében.
Az eddigi vizsgálatok azt mutatják, hogy a hatásláncok elemzése során minden hatást egyidejűnek tételezünk fel. Azonban sok esetben szükséges lehet egy további elem explicit megfogalmazása, ami az egyes hatásokban előforduló időkésleltetéseket jelenti. Ezeket újabb változók és hatások bevezetésével eliminálhatjuk, de figyelembe kell vennünk, hogy jelentős hatásuk lehet a rendszer viselkedésére, ezért a kvantitatív vizsgálatok esetében figyelembe kell azokat venni.
A hatásgráfokkal történő elemzés által igényelt egyidejűség a dinamikus rendszerek esetében mind tranziens, mind állandósult állapotokban fennáll még abban az esetben is, ha a rendszer egyes hatásaiban jelentős időkésések fordulnak elő.
3.1.2. Hatásgráfok és elsőrendű közönséges differenciálegyenletek
A dinamikus rendszerek nagy csoportjának, ti. a koncentrált paraméterű dinamikus rendszereknek matematikai modelljeit elsőrendű közönséges differenciálegyenlet-rendszerek alkotják. Ez azt is jelenti, hogy tetszőleges rendű közönséges differenciálegyenlet átírható ekvivalens elsőrendű differenciálegyenlet-rendszer formába. Valóban, a
|
|
(3.7) |
n-ed rendű – lineáris vagy nemlineáris – differenciálegyenlet esetén sorban új változókat bevezetve az
|
|
(3.8) |
módon, és az új változókkal átírva az(3.7) egyenletet a
|
|
(3.9) |
formában, az (3.8)-(3.9)elsőrendű differenciálegyenlet-rendszer az (3.7)n-ed rendű differenciálegyenlettel ekvivalens egyenletrendszert alkot.
Vegyük tehát – az egyszerűség kedvéért – a két
|
|
(3.10) |
elsőrendű differenciálegyenletet, és vizsgáljuk meg annak viselkedését az 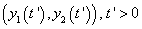 pont környezetében. E környezetben felírhatjuk az alábbi közelítő lineáris egyenleteket
pont környezetében. E környezetben felírhatjuk az alábbi közelítő lineáris egyenleteket
|
|
(3.11) |
|
|
(3.12) |
amelyből közvetlenül látszik, hogy az 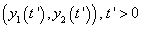 pont környezetében az együtthatók előjelei határozzák meg az y1 és y2 változók közötti hatások minőségét. A
pont környezetében az együtthatók előjelei határozzák meg az y1 és y2 változók közötti hatások minőségét. A
|
|
(3.13) |
egyenlőtlenségek például azt jelzik, hogy az 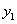 és
és 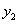 változók lokálisan az
változók lokálisan az 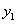 változóra pozitív, illetve negatív hatással vannak: az
változóra pozitív, illetve negatív hatással vannak: az 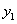 önmagára azonos irányú hatással van, ami
önmagára azonos irányú hatással van, ami 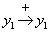 pozitív visszacsatolást jelent, míg az
pozitív visszacsatolást jelent, míg az 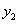 változásai az
változásai az 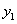 -ben éppen ellenkező irányú változásokat indukálnak, azaz
-ben éppen ellenkező irányú változásokat indukálnak, azaz 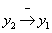 negatív hatást jelent. De hasonlóan értékelhetjük a szóban forgó változók hatásait az
negatív hatást jelent. De hasonlóan értékelhetjük a szóban forgó változók hatásait az 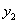 változóra is, így a
változóra is, így a
|
|
(3.14) |
egyenlőtlenségek azt jelzik, hogy az 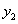 -re mind a két változó negatív hatással van, azaz
-re mind a két változó negatív hatással van, azaz
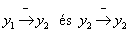
.
Természetesen a változók közötti hatásokat az (3.10) nemlineáris egyenletrendszer jobboldali tagjain keresztül globálisan is vizsgálhatjuk, ha azok a tagok konkrét formában adottak. Azonban a linearizálással kapott (3.11)-(3.12) egyenletrendszer csak lokálisan érvényes eredményekre vezet, de jobban érzékelteti a változók kölcsönhatásainak jellegét az egyes változók deriváltjainak előjelét vizsgálva.
3.1 példa. Vizsgáljuk meg az egyváltozós
|
|
(3.15) |
Verhulst egyenletet, amelynek az 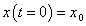 kezdeti feltétellel az
kezdeti feltétellel az
|
|
(3.16) |
analitikus megoldása is ismert.
Az(3.15) egyenlet jobboldalának első tagja az a>0 esetén az x-re pozitív visszacsatolást jelent, és a b=0 feltétellel a megoldást az 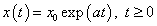 függvény adja, azaz korlátlan növekedést mutat.
függvény adja, azaz korlátlan növekedést mutat.
Az(3.15) egyenlet jobboldalának második tagja a b>0 esetén az x-re negatív visszacsatolást jelent, és az a=0 feltétellel az egyenlet megoldását az 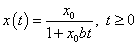 függvényként kapjuk meg. Ez a zérus értékhez történő aszimptotikus csökkenést mutatja.
függvényként kapjuk meg. Ez a zérus értékhez történő aszimptotikus csökkenést mutatja.
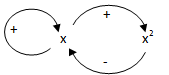
Az(3.15) egyenletet tehát két visszacsatolás, egy pozitív és egy negatív visszacsatolás kölcsönhatása határozza meg, ahogy ezt a 3-7. ábra illusztrálja. A két visszacsatolás kölcsönhatása eredményezi az egyensúlyra vezető (3.16) megoldást, amely a folyamat elején a pozitív visszacsatolás dominanciáját mutatja, de később a folyamat a negatív visszacsatolás dominanciájába csap át korlátos megoldáshoz vezetve.
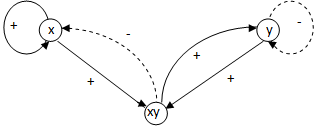
3.2 példa.Lotka-Volterra modell. Az ismert Lotka-Volterra modellt elsősorban biológiai populációk kölcsönhatásainak leírására használják. Ennek legegyszerűbb formájában az (x,y) változókat a
|
|
(3.17) |
|
|
(3.18) |
differenciálegyenletek határozzák meg az 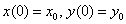 kezdeti feltételek mellett.
kezdeti feltételek mellett.
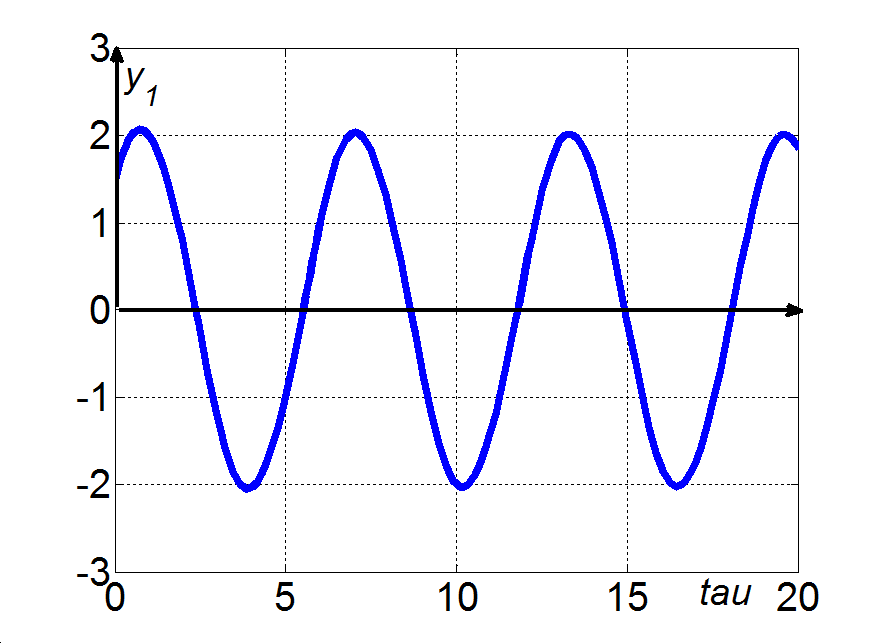
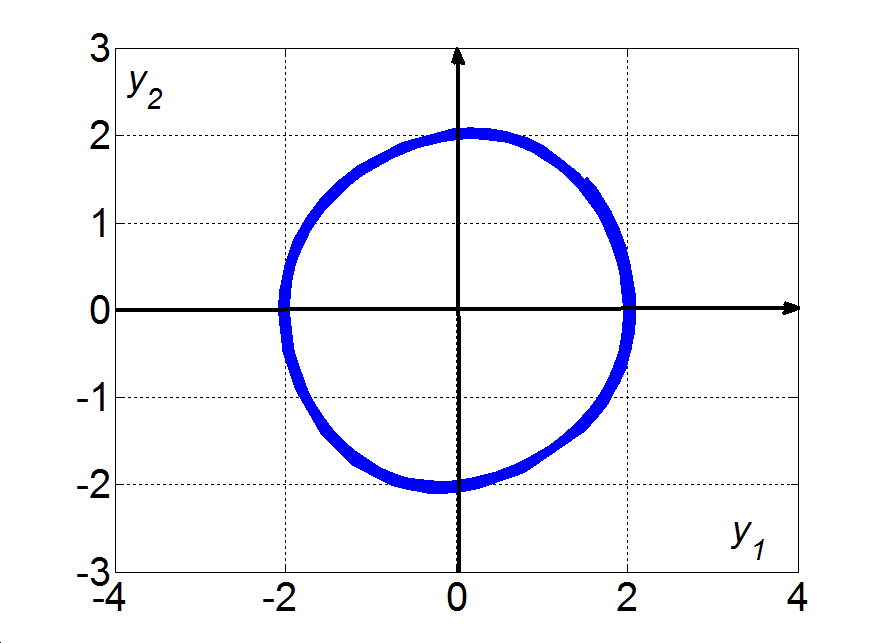
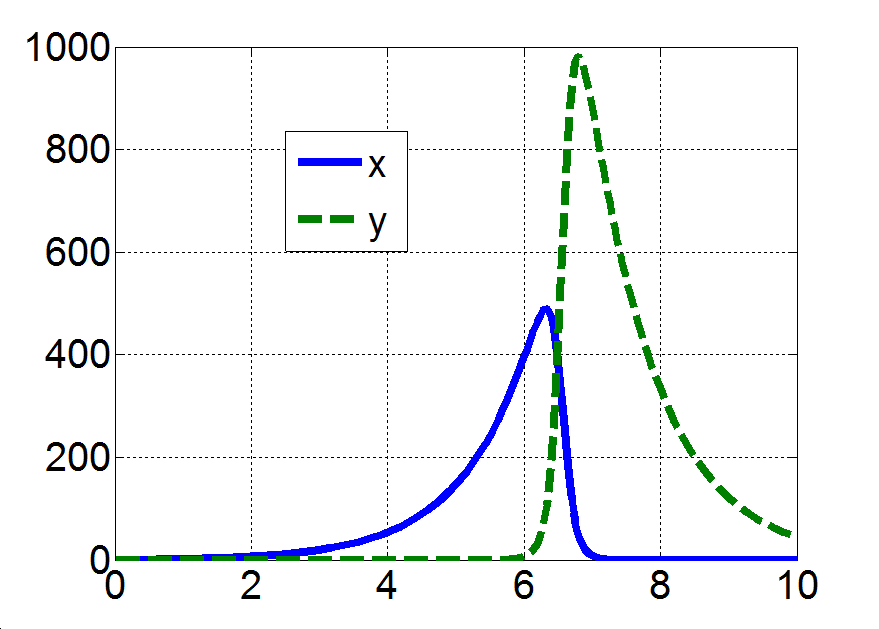
Az (3.17)-(3.18) egyenletrendszer a jobboldalon egy kvázilineáris tagot is tartalmaz, amely természetesen az x és y változók függvénye, így a rendszer hatásgráfjában önálló csomópontként célszerű ábrázolni, ahogy ezt a 3-8. ábra mutatja. Az ábrán azt látjuk, hogy a rendszer csak zárt hatásláncokat tartalmaz: az x körül egy pozitív visszacsatolás van, míg az y és xy változókat pozitív polaritású hurok köti össze. Ugyanakkor az y-ra egy negatív visszacsatolás hat, miközben az x és xy változók között negatív polaritású hurok található. Ez a tény lényegében jól magyarázza, hogy a (3.17)-(3.18) egyenletrendszernek a triviális 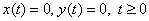 megoldáson kívül csak periodikus megoldásai vannak, ugyanis a kvázilineáris, vagy másképpen a nemlineáris tag miatt a pozitív és negatív visszacsatolások dominanciája az időben változik: a rendszerben periodikus mozgások jelennek meg. Egy ilyen periodikus megoldást mutat a 3-9. ábra, melynek egy kinagyított részletét mutatja a 3-10. ábra jól illusztrálva a két változó folyamatai közötti fáziskülönbséget is. □
megoldáson kívül csak periodikus megoldásai vannak, ugyanis a kvázilineáris, vagy másképpen a nemlineáris tag miatt a pozitív és negatív visszacsatolások dominanciája az időben változik: a rendszerben periodikus mozgások jelennek meg. Egy ilyen periodikus megoldást mutat a 3-9. ábra, melynek egy kinagyított részletét mutatja a 3-10. ábra jól illusztrálva a két változó folyamatai közötti fáziskülönbséget is. □
3.1.3. Dinamikus rendszerek elemzése hatásgráfokkal
A dinamikus rendszerek
|
|
(3.19) |
|
|
(3.20) |
lineáris állapottér modelljéből kiindulva az egyes változók, illetve általánosabban a 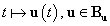 bemeneti változók,
bemeneti változók, 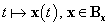 állapotváltozók,
állapotváltozók,  kimeneti változók és
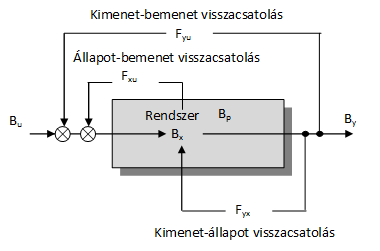
kimeneti változók és  paraméterek függvényterei közötti strukturális kapcsolatokat a 3-11. ábra mutatja be. Itt A a rendszermátrix, B a bementi mátrix, C a kimeneti mátrix és D az előrecsatolás mátrix.
paraméterek függvényterei közötti strukturális kapcsolatokat a 3-11. ábra mutatja be. Itt A a rendszermátrix, B a bementi mátrix, C a kimeneti mátrix és D az előrecsatolás mátrix.
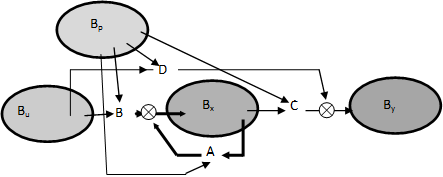
A 3-11. ábra jól illusztrálja, hogy az x állapotváltozók közötti kapcsolatok kivételével a többi változó között nyílt hatásláncokkal lehet a kapcsolatokat felvázolni, míg az állapotváltozók közötti közvetlen hatások lehetnek zárt hatásláncokkal jellemezhető visszacsatolások is. Ezeket alapjában véve az A rendszermátrix struktúrája és elemei határozzák meg és a rendszer belső változói – állapotváltozói – közötti belső visszacsatolásoknak nevezzük azokat. Ahogy ezt láttuk, ezek a zárt hatásláncok polaritásaitól függően lehetnek pozitív és negatív visszacsatolások is, és alapjában véve ezen visszacsatolások kölcsönhatásai határozzák meg a rendszer tulajdonságait és viselkedését, így többek között stabilitását is.
3.3 példa.Egy külső gerjesztésű egyenáramú motor matematikai modelljét az
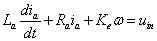
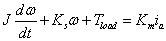
lineáris differenciálegyenlet rendszer alkotja. Elemezzük a rendszert annak hatásgráfja segítségével!
Az egyenáramú motorállapotváltozóit, amely lényegében egy villamos-mechanikai zsirátor, az armatúra ia árama és az ω körsebesség alkotja, azaz x=(ia,ω), és így az állapottér formát a
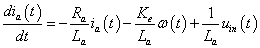
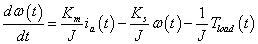
differenciálegyenletek alkotják, ahonnan
|
|
(3.21) |
és a kimeneti változót is az ω körsebességként kijelölve
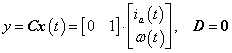
.
A rendszer hatásgráfját, melyet az (3.21) kifejezések alapján szerkeszthetünk meg, a 3-12. ábra illusztrálja. Az ábra jól mutatja, hogy mindkét állapotváltozó körül negatív visszacsatolás van, míg közöttük egy negatív polaritású hurok teremt kapcsolatot. A hatásgráf kitűnően ábrázolja a változók közötti kölcsönhatások szimmetriáját is, ami a motor mechatronikai-villamos zsirátorként való alkalmazhatóságát illusztrálja. □
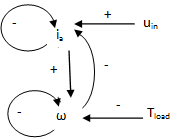
A 3-11. ábra jól illusztrálja, hogy a rendszer viselkedését a lényegileg meghatározó A rendszermátrix mellett az u bemeneti változók, valamint a Bu bemeneti hatások alkalmas megválasztásával tudjuk befolyásolni. Ez lehetővé teszi – többek között – az előző szakaszban említett szabályozott hatások megvalósítását, de sok esetben nem bizonyul elégségesnek ahhoz, hogy a rendszer viselkedését lényegileg is megváltoztassa. Így a rendszernek az A rendszermátrix struktúrájában meglévő belső visszacsatolások által okozott hatások kiküszöbölése sem igazán eredményes. Ezt – a rendszer belső világának átalakítása mellett – sok esetben további visszacsatolások létrehozásával lehet a legeredményesebben megvalósítani, ami viszont már a rendszeren kívül kialakítandó hatásláncok által történő visszacsatolásokat jelent.
A 3-12. ábra mutatja a lehetséges rendszeren kívüli visszacsatolásokat, amelyek közül elsősorban a belső tulajdonságokat, azaz az A rendszermátrix egyes komponenseit, tehát az előzőekben jelzett hatások erősítési tényezőit tudjuk megváltoztatni, viszont az A mátrix struktúráját, azaz a rendszer belső hatásláncainak szerkezetét nem. Ezek a rendszeren kívüli zárt hatásláncok a rendszer szabályozását jelentik, melyek többnyire nem csak teljesítmény-, hanem információkötéseket, azaz információcsatolásokat is tartalmazó hatásláncokon keresztül valósul meg.
3.2. Dinamikus rendszerek stabilitása
3.2.1. A stabilitás fogalma
A kvalitatív rendszervizsgálat azt mutatja, hogy a zárt hatásláncok kialakulása felveti a rendszerek stabilitásának problémáját. Ez azt jelenti, hogy ha valamelyik rendszerváltozó pozitív polaritású hurokba kerül, azaz valamilyen irányú megváltozását a pozitív visszacsatolás állandóan csak erősíti, akkor mi történik? Egy pozitív polaritású hurok mindegyik változójára pozitív visszacsatolást jelent, azaz egy ilyen hurokban nincs olyan mechanizmus, amely ezt az állandó irányú változást megakasztaná. Ezt jól érzékelteti a (3.15) Verhulst egyenlet hatásalgebrai vizsgálata, melyben a negatív visszacsatolás megszűnése az x változó korlátlan változását jelentette. Ugyanakkor a negatív visszacsatolás ellenirányú hatása ezt semlegesítheti és ez a kölcsönhatás állandósult egyensúlyra vezethet. Hasonlóan, a Lotka-Volterra modell is jól mutatja a pozitív és negatív visszacsatolások kölcsönhatásait, amelyek azonban itt a dominancia időbeli változásainak következtében a rendszer periodikus változásait eredményezik. Ugyanakkor a kezdeti értékek megváltoztatása minőségileg eltérő, azaz itt a triviális megoldást eredményezheti. Ez tehát azt a kérdést veti fel, hogy a rendszer valamely változójának vagy változóinak aktuális értékükből történő megváltozása milyen következményekkel jár, ami viszont a rendszerek stabilitásának a fogalmához vezet.
3.5 definíció.Az xsállapot Ljapunov-értelemben stabilis, ha bármely ε>0-ra létezik olyan δ(ε)>0 szám, hogy bármely 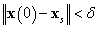 kezdeti feltétel esetén
kezdeti feltétel esetén 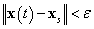 tetszőleges
tetszőleges 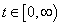 időpontra.
időpontra.
3.6 definíció.A rendszer xs állapota aszimptotikusan stabilis, ha 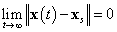 .
.
E definíciók alapján egy rendszer állapotainak stabilitását azzal vizsgáljuk, hogy a vizsgált állapot kismértékű perturbációja milyen mozgást indít el: ha ez a perturbáció növekedni kezd, akkor a vizsgált állapot pozitív polaritású hurokban található, azaz instabilis, ha viszont csökkenni kezd a zérus érték felé, akkor valamely negatív hatás a domináns, azaz az állapot stabilis. Korlátos megváltozás pozitív és negatív hatások egyensúlyát jelzi, így a vizsgált állapot ekkor is stabilis. Tehát az előzőekben vázolt egyszerű intuitív képpel jól értelmezhető ez a definíció.
A tényleges vizsgálatot természetesen nem e definíció alapján végezzük, hanem az – alapvető stabilitási tulajdonságokat rejtő zárt hatásláncokat reprezentáló A rendszermátrix megfelelő vizsgálatával. Ugyanakkor azt is érdemes megjegyezni, hogy egy lineáris rendszer összes állapota stabilis vagy nem stabilis, ezért magát a rendszert nevezhetjük stabilnak vagy instabilnak.
Az eddigiek alapján a dinamikus rendszer stabilitását vizsgálandó a (3.19) egyenlet helyett elégséges a
|
|
(3.22) |
homogén lineáris differenciálegyenlet vizsgálata.
3.7 tétel.Az(3.22)lineáris dinamikus rendszer Ljapunov-értelemben stabilis, ha minden megoldása korlátos.
3.8 tétel Az(3.22)lineáris dinamikus rendszer Ljapunov-értelemben aszimptotikusan stabilis, ha minden megoldása korlátos és nullához tart, ha t→∞.
E tétel k alapján a (3.19) lineáris dinamikus rendszer stabilitásának vizsgálatához a (3.22) egyenlet-rendszer megoldásait kell előállítanunk és azok korlátosságának a feltételeit kell megadni. Ehhez nézzük az A rendszermátrix sajátértékeit és sajátfüggvényeit, melyeket a
|
|
(3.23) |
egyenletből kapjuk meg. Ennek az egyenletnek akkor létezik a triviálistól különböző megoldása, ha érvényes a
|
|
(3.24) |
feltétel, amelynek megoldásai meg is adják a sajátértékeket.
A vl sajátfüggvények ismeretében létezik a kezdeti feltételnek olyan
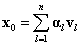
felbontása, hogy a (3.22)megoldásának
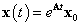
általános formáját egyszeres sajátértékek esetén
|
|
(3.25) |
alakban írhatjuk fel. A (3.25) már jól mutatja, hogy – mivel a 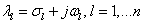 , sajátértékek komplex változók is lehetnek – az (3.25) forma akkor korlátos, ha
, sajátértékek komplex változók is lehetnek – az (3.25) forma akkor korlátos, ha 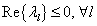 , és akkor tart zérushoz, ha
, és akkor tart zérushoz, ha 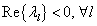 . Ha azonban létezik legalább egy
. Ha azonban létezik legalább egy 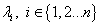 sajátérték, amelyre
sajátérték, amelyre 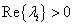 , akkor az (3.22) rendszer instabil.
, akkor az (3.22) rendszer instabil.
3.9 tétel .Az(3.22) lineáris dinamikus rendszer Ljapunov-értelemben stabilis, ha az A rendszermátrix összes 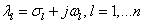 , sajátértékére érvényes a
, sajátértékére érvényes a 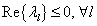 feltétel.
feltétel.
3.10 tétel .Az(3.22)lineáris dinamikus rendszer Ljapunov-értelemben aszimptotikusan stabilis, ha az A rendszermátrix összes 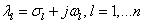 , sajátértékére érvényes a
, sajátértékére érvényes a 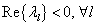 feltétel.
feltétel.
3.11 tétel .Az(3.22)lineáris dinamikus rendszer Ljapunov-értelemben instabilis, ha az A rendszermátrix 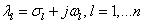 , sajátértékei között létezik legalábbegy
, sajátértékei között létezik legalábbegy 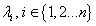 , amelyre fennáll a
, amelyre fennáll a 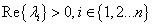 feltétel.
feltétel.
Ez tehát azt mutatja, hogy a (3.19) állapottér modellel adott lineáris dinamikus rendszer stabilitását az A rendszermátrix sajátértékeinek a vizsgálatából lehet levezetni. Azonban könnyen megmutatható, hogy az A rendszermátrix sajátértékei azonosak a rendszer karakterisztikus polinomjának gyökeivel. Képezve ugyanis (3.22) mindkét oldalának Laplace-transzformáltját
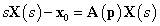
ahonnan az X(s)-t kifejezve az
|
|
(3.26) |
eredményre jutunk.
Az x(t) időfüggvényt a (3.26) inverz transzformációjával kapjuk meg, melyben alapvető szerepet játszanak a nevező 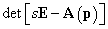 gyökei, azaz a (3.26) racionális törtfüggvény pólusai. Ha a
gyökei, azaz a (3.26) racionális törtfüggvény pólusai. Ha a 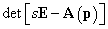 polinomnak csak egyszeres sk, k=1,2…n, gyökei vannak, akkor létezik a
polinomnak csak egyszeres sk, k=1,2…n, gyökei vannak, akkor létezik a
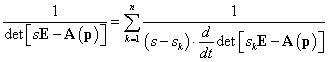
résztörtekre bontás. Mivel a (3.26)-ban a számláló a nevezőnél alacsonyabb fokú polinom, ezért az időfüggvényt az
|
|
(3.27) |
amely a (3.25) kifejezéssel ekvivalens forma, tehát alkalmazhatjuk az előző tétel kat.
Az(3.26) nevezőjében lévő 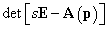 s-függvényt a rendszer karakterisztikus polinomjának nevezzük, míg annak gyökeit a
s-függvényt a rendszer karakterisztikus polinomjának nevezzük, míg annak gyökeit a
|
|
(3.28) |
karakterisztikus egyenlet megoldásaként kapjuk. Jól látszik, hogy (3.28) azonos az(3.24) egyenlettel, így a
|
|
(3.29) |
karakterisztikus polinom sk, k=1,2…n, gyökei azonosak az A rendszermátrix λj, j=1,2…n, sajátértékeivel.
3.2.2. Stabilitási kritériumok
A lineáris dinamikus rendszerek stabilitását kvalitatív értelemben a rendszer belső vissza-csatolásai, míg a kvantitatív vizsgálatban a rendszermátrix sajátértékeinek, vagy ezzel ekvivalens módon a karakterisztikus polinom gyökeinek valós részei határozzák meg, azaz a stabilitásvizsgálat alapesetben sajátértékek vagy gyökök meghatározását igényli. Ez egy n-ed rendű rendszer esetében n komplex érték kezelését igényli, ami megnehezíti a rendszerparaméterek hatásának szisztematikus vizsgálatát. Ha azonban ismert a karakterisztikus polinom, akkor a gyökök meghatározása nélkül, csak a polinom együtthatóinak ismeretében meg tudjuk határozni a rendszer stabilitásának mikéntjét. Erre itt egy algebrai és egy frekvenciamódszert mutatunk be, melyek tehát a (33) n-ed rendű, n≥1, karakterisztikus polinom ismeretében kerülnek meghatározásra.
Az algebrai módszert a Routh-Hurwitz kritérium szolgáltatja.
3.12 Tétel. Routh-Hurwitz kritérium. Az(3.19)dinamikus rendszer akkor és csak akkor aszimptotikusan stabilis, ha az(3.29) karakterisztikus polinomjának valamennyi együtthatója pozitív (azonos előjelű, ez a szükséges feltétel), és a Routh-tábla első oszlopának minden egyes eleme pozitív (ez az elégséges feltétel).
Az Routh-tábla első oszlopában az előjelváltások száma megadja a polinom pozitív valós részű gyökeinek számát.
Ha a rendszer instabilis, akkor a Routh-Hurwitz kritérium alkalmazásával megkaphatjuk azt is, hogy a polinomnak hány darab pozitív valós részű gyöke van, de azok értékeit természetesen csak a (3.28) karakterisztikus egyenlet megoldásával határozhatjuk meg.
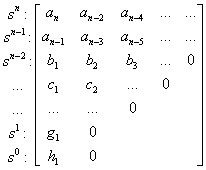
A Routh-tábla első két sorát közvetlenül a karakterisztikus polinom együtthatóiból képezzük a legmagasabb rendű tag együtthatójával kezdve és alá helyezve a következő rendű tag együtthatóját, majd így folytatva a két sort a következő tagokkal egészen a konstans tagig. A tábla első két sora, ha az n=2u páros az alábbi formájú
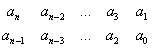
míg ha az n=2u-1 páratlan, akkor az utolsó oszlopot egy zérussal zárjuk le
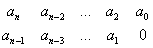
.
Ezt követően a következő sorokat a közvetlenül fölöttük lévő sorok tagjaiból képezzük sorban másodrendű determinánsokat alkotva az első oszloppal párosítva a következő oszlopokat és elosztva első oszlop alsó elemének negatív értékével. Ezeket a lépéseket folytatva a Routh-tábla a következő mátrix-formát eredményezi:
|
|
(3.30) |
ahol
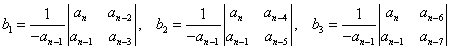
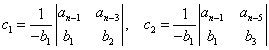
……………
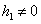
míg a következő sorban már az i1 első elem is zérus lenne, mivel
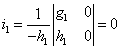
.
Ezzel záródik a Routh-tábla.
A következő lépés az első oszlopban található (an, an-1, b1, c1…g1, h1) elemek előjelének vizsgálata és a Routh-Hurwitz feltétel ellenőrzése.
3.4 példa.Legyen valamely lineáris dinamikus rendszer karakterisztikus polinomja a
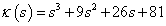
alakú. Megmutatjuk, hogy a rendszer stabilis.
A polinom teljes és mindegyik együtthatója pozitív, ezért a stabilitás szükséges feltétele teljesül. Az elégséges feltétel vizsgálatához létrehozzuk a Routh-táblát:
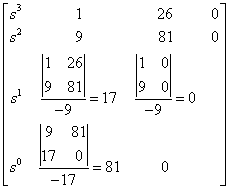
ahonnan az első oszlop elemei 1, 9, 17, 81 mind pozitívak, azaz az elégséges feltétel is teljesül, tehát a rendszer stabil. □
Előfordulhat, hogy az első oszlopban zérus jelenik meg, amely nem található a feltételek között. Ebben az esetben két módon léphetünk tovább:
-
Az első oszlop zérusa helyébe az ε≠0 kis mennyiséget helyettesítjük, ezzel végigszámoljuk a Routh-táblát és képezzük az ε→0 határértéket mind a pozitív és negatív értékek felöl. Ekkor ellenőrizhetjük az első oszlop előjeleit.
-
Behelyettesítve az (3.29)polinomba az 1/z változót és kiemelve az (1/z)n tényezőt a
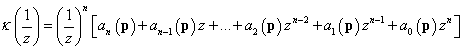
polinomot kapjuk, melynek gyökei az eredeti ( polinom gyökeinek reciprok értékeivel egyezik meg, így azonos előjelű valós részekkel rendelkeznek, ami a rendszer stabilitásáról az előzővel ekvivalens információt szolgáltat.
A Routh-Hurwitz kritérium a lineáris dinamikus rendszerek stabilitás-vizsgálatának algebrai módszerei közé tartozik. Egy másik módszertani csoportot alkotnak a frekvencia tartományban végzendő módszerek, melyek közül itt a Mihajlov-kritérium alkalmazását vizsgáljuk meg.
Vegyük ehhez a karakterisztikus polinom
|
|
(3.31) |
frekvencia-formáját, amelyet a
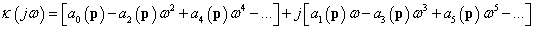
illetve
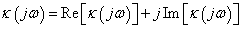
alakban is felírhatunk.
A 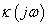 frekvenciafüggvényt ábrázolhatjuk a komplex változók síkján az körfrekvencia függvényében, és ezt a geometriai képet Mihajlov-hodográfnak nevezzük.
frekvenciafüggvényt ábrázolhatjuk a komplex változók síkján az körfrekvencia függvényében, és ezt a geometriai képet Mihajlov-hodográfnak nevezzük.
3.13 tétel. Mihajlov-kritérium. A (3.19) dinamikus rendszer aszimptotikus stabilitásának szükséges és elégséges feltétele, hogy a Mihajlov-hodográf az körfrekvenciát a 0≤<intervallumban változtatva pontosan n síknegyeden haladjon keresztül az óramutató járásával ellentétes irányban, azaz a 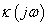 argumentumának változása legyen
argumentumának változása legyen
|
|
(.3.32) |
3.5 példa. Vegyük a 4. példában vizsgált harmadrendű rendszer
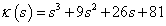
karakterisztikus polinomját, melyről a Routh-Hurwitz kritérium alkalmazásával megmutattuk, hogy stabilis rendszert reprezentál. Ennek a polinomnak és részeinek Mihajlov-hodográfjait mutatja be a 3-14. ábra, amely jól illusztrálja, hogy mindegyik redukció stabil rendszert reprezentál.
Az a) egyenes a 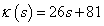 elsőrendű rendszer hodográfja, amely csak az első sík-negyeden halad át, és az ω→ limitnél a végpont által bezárt szög eléri a π/2 értéket.
elsőrendű rendszer hodográfja, amely csak az első sík-negyeden halad át, és az ω→ limitnél a végpont által bezárt szög eléri a π/2 értéket.
A b) jelű görbe a 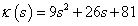 másodrendű rendszer hodográfja, míg a c) jelű görbe (hodográf) a
másodrendű rendszer hodográfja, míg a c) jelű görbe (hodográf) a 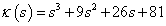 harmadrendű rendszert reprezentálja. □
harmadrendű rendszert reprezentálja. □
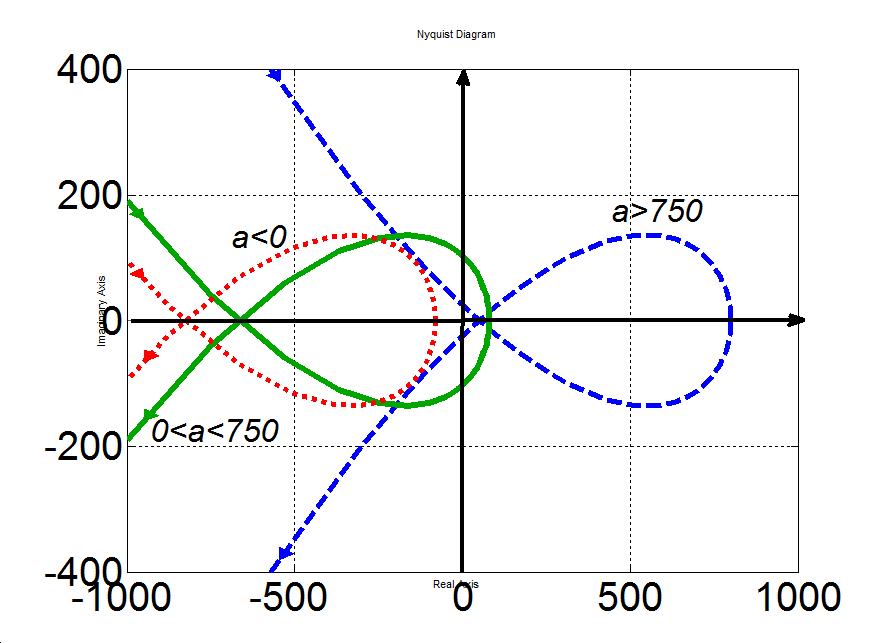
3.6 példa. Vizsgáljuk meg a
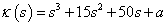
karakterisztikus polinommal adott harmadrendű rendszer stabilitását az α paraméter függvényében.
a) Alkalmazva a Routh-Hurwitz kritériumot az alábbi Routh-táblához jutunk
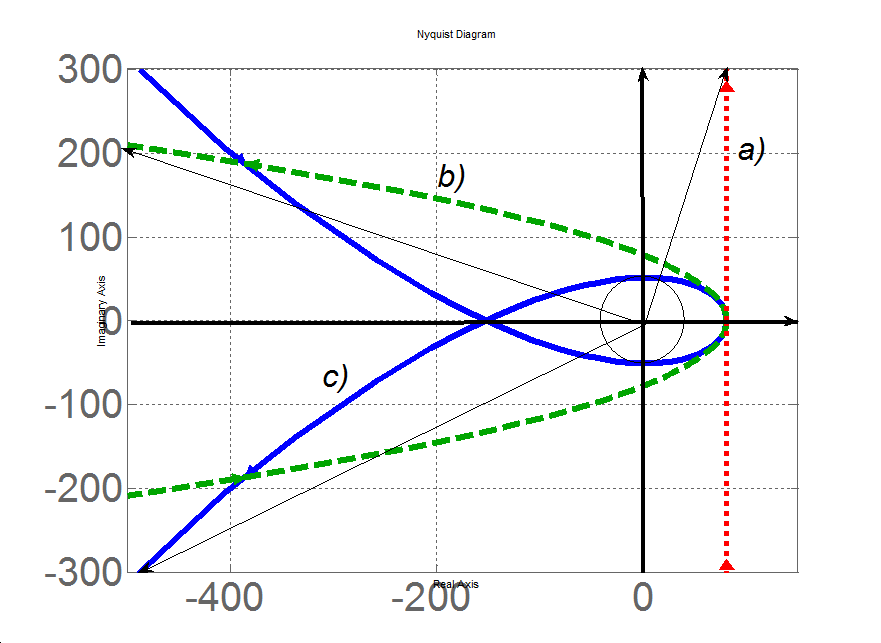
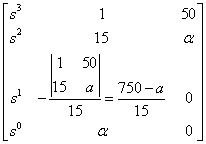
amelyből három esetet különböztetünk meg:
-
Ha a>750, akkor az első oszlopban csak az s1 sor első eleme negatív, azaz két előjelváltás van, ezért a rendszer instabil és a polinomnak két pozitív egész részű gyöke van.
-
Ha 0<a<750, akkor az első oszlop mindegyik eleme pozitív, azaz a rendszer stabil.
-
Ha a<0, akkor az első oszlop utolsó eleme negatív, azaz egy előjelváltást látunk, így a rendszer instabil és a polinomnak egy pozitív egész részű gyöke van.
b) Az egyes esetekhez tartozó Mihajlov-hodográfokat a 3-15. ábra mutatja be. Az 1) esetben a görbe úgy halad át az első negyedből a harmadikba, hogy kihagyja a sorrendben következőnek számító második negyedet, a 2) görbe a stabil rendszernek megfelelően halad át az első, második és harmadik síknegyeden, míg a 3) esetben a görbe eleve a második negyedből indul, így az első negyedbe el sem juthat.
3.2.3. A nemlineáris rendszerek stabilitásáról
A dinamikus rendszerek stabilitásának Ljapunov-féle definíciója a vizsgált rendszer valamely állapotának a stabilitására vonatkozik, azaz általános és mind lineáris, mind nemlineáris rendszerekre érvényes. Lineáris rendszerekben az egy állapotra meghatározott stabilitási tulajdonság az egész rendszerre érvényes, amit természetesen a rendszerparaméterek változásai is befolyásolnak, míg nemlineáris rendszerek esetében a különböző állapotok eltérő stabilitási tulajdonságokkal rendelkezhetnek, ezért azokat önállóan kell megvizsgálni. Ezt Ljapunov-első módszerének alkalmazásával tehetjük meg, amely lehetővé teszi a lineáris rendszerek stabilitásának vizsgálatára kidolgozott módszerek felhasználását nemlineáris rendszerek esetében is.
Ljapunov első módszere a következő definíción alapul.
3.14 tétel. A
|
|
(3.33) |
nemlineáris dinamikus rendszer 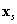 állapotának stabilitását a vizsgált állapot körül linearizált
állapotának stabilitását a vizsgált állapot körül linearizált
|
|
(3.34) |
lineáris állapottér modell stabilitása határozza meg, ahol 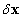 az
az 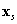 állapot körüli elég kis változót jelöli és a
állapot körüli elég kis változót jelöli és a
|
|
(3.35) |
Jacobi-mátrix a linearizált rendszer A rendszermátrixa.
Ljapunov első módszere tehát elvi alapot ad arra, hogy a nemlineáris rendszerek tetszőleges differenciálható állapotának stabilitási tulajdonságait meghatározzuk a lineáris rendszerekre kidolgozott módszerek alkalmazásával, ami az adott állapot infinitezimális környezetére érvényes. Itt természetesen erős hangsúly van a differenciálhatóságon, valamint azon, hogy ez a nemlineáris rendszerek csak egy-egy állapotára vonatkozik, azaz két egymástól véges távolságra található állapotot külön-külön kell megvizsgálni.
3.7 példa. Van der Pol egyenlet. Az alagút, vagy Esaki-dióda karakterisztikájának egy része – ahogy ezt a 3-16. ábra illusztrálja – negatív ellenállás jellegű, ami a karakterisztika nem-linearitásán túlmenően pozitív visszacsatolás forrása.
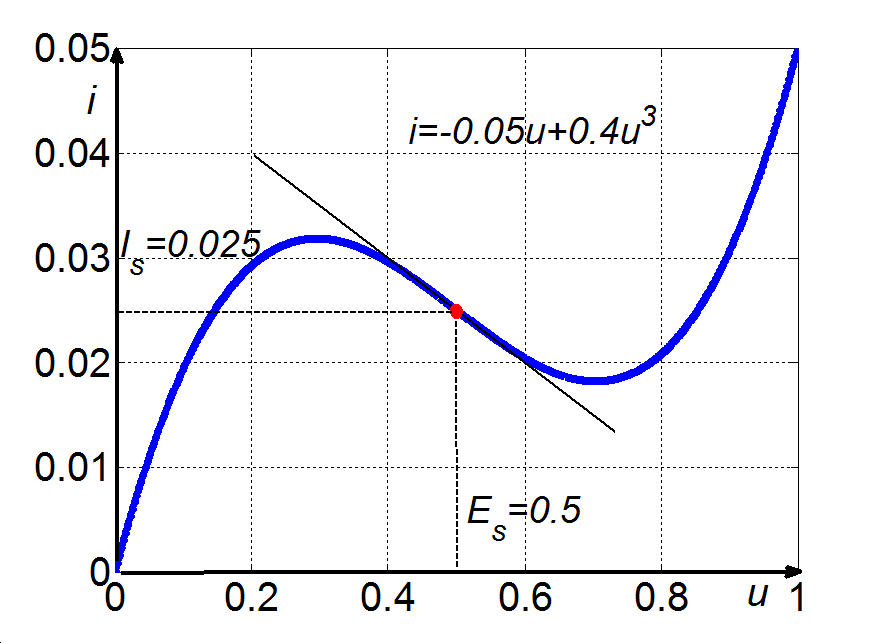
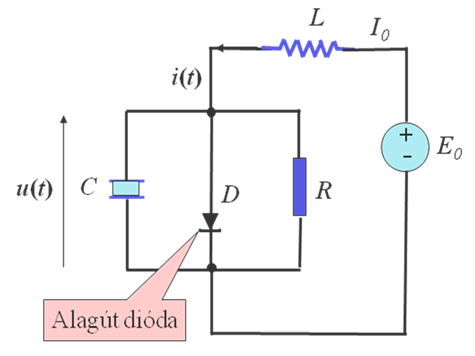
Vegyük tehát a 3-18. ábra által bemutatott egyszerű villamos kapcsolást, melynek modelljét – az alagút dióda 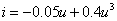 egyenlettel adott karakterisztikáját figyelembe véve – egyszerű számításokkal a 3-18. ábra jelöléseivel az u feszültségre
egyenlettel adott karakterisztikáját figyelembe véve – egyszerű számításokkal a 3-18. ábra jelöléseivel az u feszültségre
|
|
(3.36) |
másodrendű differenciálegyenletet kapjuk meg.
Vezessük be az 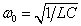 ,
, 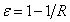 ,
, 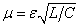 ,
, 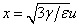 és
és 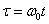 paramétereket és dimenziómentes változókat, akkor az(3.36) egyenlet a
paramétereket és dimenziómentes változókat, akkor az(3.36) egyenlet a
|
|
(3.37) |
formában jelenik meg. Ez az egyenlet az irodalomban a Van der Pol egyenletként ismert.
A megoldáshoz a (3.37) egyenletet az 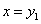 és
és 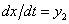 változók bevezetésével a
változók bevezetésével a
|
|
(3.38) |
|
|
(3.39) |
ekvivalens elsőrendű differenciálegyenlet-rendszerként írjuk át, melynek megoldását közvetlenül megkaphatjuk a Matlab alkalmazásával.
A (3.38)-(3.39) egyenletrendszer hatásgráfját mutatja be a 3-19. ábra, amely a különböző polaritású hurkokkal jelzi, hogy ez a nemlineáris egyenletrendszer, azaz a (3.36) másodrendű differenciálegyenlettel leírt villamos rendszer komplex dinamikus viselkedést mutathat.
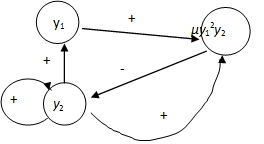
A (3.38)-(3.39) egyenletrendszer Jacobi-mátrixa a
|
|
(3.40) |
alakú, így a rendszer stabilitását a következő lépésekben vizsgáljuk meg: először meghatározzuk a (3.38)-(3.39) egyenletrendszer állandósult megoldását az adott paraméterérték esetén, majd ezt a megoldást behelyettesítve a (3.40) Jacobi-mátrixba meghatározzuk a Jacobi-mátrix sajátértékeit. A nemlineáris rendszer viselkedését ebben az állandósult állapotban a (3.38)-(3.39) egyenletek megoldásával vizsgáljuk meg. Ehhez a Matlab fsolve, eig és ode függvényeit használhatjuk fel.
Illusztrációképpen két paraméterértékre mutatjuk be az eredményeket. A paraméter 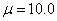 értéke esetén az állandósult megoldásokra az y1s=2.3060e-9 és y2s=0.0 értékeket, míg a sajátértékekre a pozitív valós λ1=1.0102e-1 és λ2=9.8990 értékeket kaptuk. A (3.38)-(3.39) nemlineáris rendszernek ez az állapota instabil, és – ahogy ezt a 3-20. ábra illusztrálja – a rendszerben relaxációs oszcillációk keletkeznek.
értéke esetén az állandósult megoldásokra az y1s=2.3060e-9 és y2s=0.0 értékeket, míg a sajátértékekre a pozitív valós λ1=1.0102e-1 és λ2=9.8990 értékeket kaptuk. A (3.38)-(3.39) nemlineáris rendszernek ez az állapota instabil, és – ahogy ezt a 3-20. ábra illusztrálja – a rendszerben relaxációs oszcillációk keletkeznek.
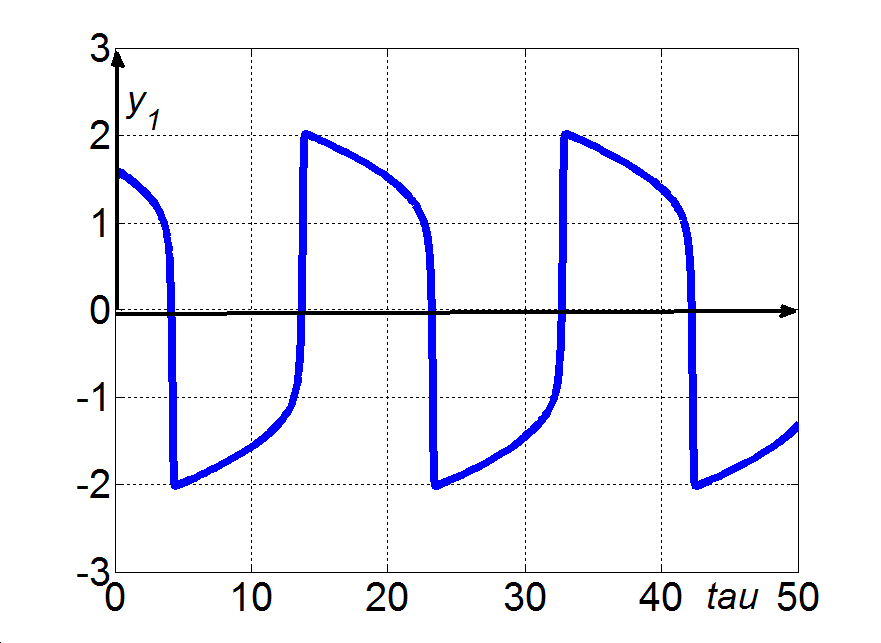
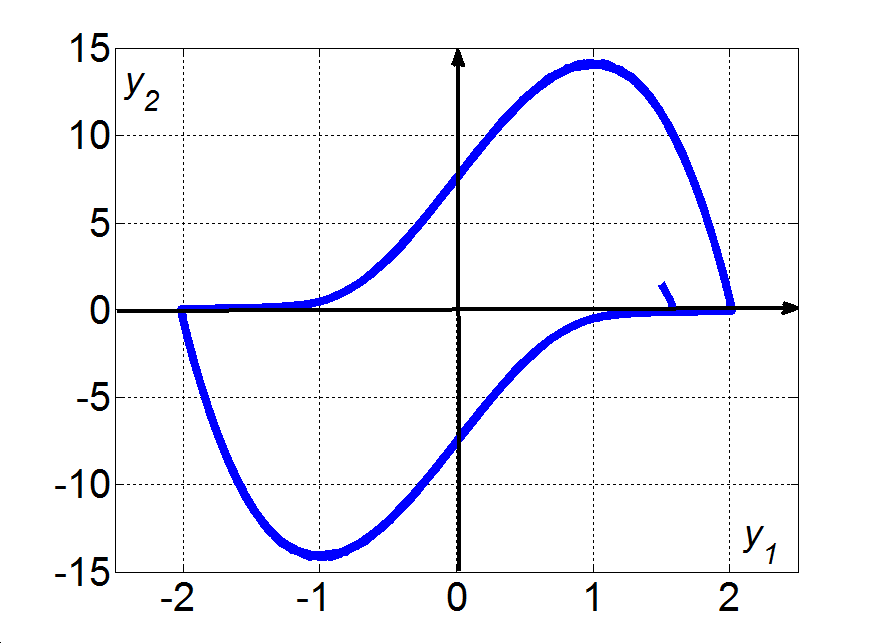
A paraméter 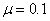 értéke esetén az állandósult megoldásokra az y1s=0.0 és y2s=0.0 érték-párt, míg a sajátértékekre a pozitív valós részű λ1=5.0e-2+j9.9875e-1 és λ2=5.0e-2-j9.9875e-1 konjugált komplex párt kapjuk. A (3.38)-(3.39) nemlineáris rendszernek ez az állapota is instabil. Ebben az esetben, ahogy ezt a 3-21. ábra illusztrálja, a rendszerben majdnem szinusz-jel alakú oszcillációk generálódtak.
értéke esetén az állandósult megoldásokra az y1s=0.0 és y2s=0.0 érték-párt, míg a sajátértékekre a pozitív valós részű λ1=5.0e-2+j9.9875e-1 és λ2=5.0e-2-j9.9875e-1 konjugált komplex párt kapjuk. A (3.38)-(3.39) nemlineáris rendszernek ez az állapota is instabil. Ebben az esetben, ahogy ezt a 3-21. ábra illusztrálja, a rendszerben majdnem szinusz-jel alakú oszcillációk generálódtak.