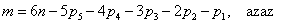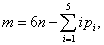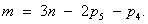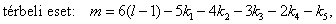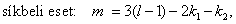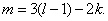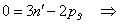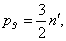4. fejezet - Mechanizmusok vizsgálati módszerei
Mechanizmus alatt egymással kényszerkapcsolatban lévő merev testekből álló ún. kinematikai láncot (mechanikai rendszert) értünk. A szerkezeti vizsgálat a mechanizmust felépítő szerkezeti elemtípusok és kényszerkapcsolatok számba vételét és végső soron a mechanizmus szabadsági fokainak meghatározását jelenti. Mindezek segítségével a mechanizmusokat majd különböző csoportokba sorolhatjuk.
A geometriai vizsgálat során a mechanizmust alkotó merev testek, ún. tagok pozíciójának és orientációjának leírása, az egyes koordináták közötti — a kényszerek által meghatározott — kapcsolatok megadása jelenti a feladatot. A koordináták és a kényszereket leíró összefüggések ismeretében már kiválasztható az egész mechanizmus pillanatnyi helyzetének egyértelmű leírásához szükséges, a mechanizmus szabadságfokának megfelelő számú általános koordináta.
A kinematikai vizsgálat az egyes tagok illetve azok kiválasztott pontjainak sebesség- és gyorsulásviszonyait, a pillanatnyi és véges mozgásokat elemzi, míg a dinamikai vizsgálat alkalmával a newtoni elvek alapján felírható mozgásegyenleteket próbáljuk megoldani és abból kiszámítani a tagokat, ízületeket terhelő erőket, nyomatékokat, az aktuátorok teljesítményigényét.
4.1. Szerkezeti vizsgálat
A mechanizmust alkotó merev testeket a mechanizmus tagjainak nevezzük, és rendszerint arab számokkal jelöljük azokat. Ide soroljuk a rögzített állványt, mint 0. tagot is, melyhez a mechanizmus mozgó tagjai által alkotott rész csatlakozik:
|
0. tag |
állvány |
|
1. tag 2. tag … |
mozgó tagok |
4.1.1. Kinematikai pár, szabadsági fok
Az egyes tagok közötti kapcsolatokat meghatározó kényszereket (pl. csukló) kinematikai pároknak nevezzük. A mechanizmus térbeli konfigurációjának egyértelmű leírásához szükséges független skalárfüggvények száma jelenti a rendszer szabadsági fokát, ami meghatározható a mozgó tagok száma és a kinematikai párok által lekötött szabadsági fokok alapján (ld. később). Az egymáshoz kinematikai párokkal kapcsolódó tagok sorát kinematikai láncnak nevezzük.
Szorosabb értelemben akkor beszélünk mechanizmusról, ha a tagok zárt kinematikai láncot alkotnak és csak egy vagy két szabadsági fok marad. Így az ezeknek megfelelő tagokra előírt mozgással (többnyire egy motor általi állandó fordulatszámú forgatással) a mechanizmus kiválasztott tagjainak adott pontjai egy bizonyos pályát írnak le.
Ezzel szemben a robotmechanizmusok tipikusan nyílt kinematikai lánccal rendelkeznek, több szabadságfokúak, és az ezeknek megfelelő számú aktuátor időben alkalmasan változó mozgatásával a kinematikai lánc végén levő ún. manipulátor tag tetszőleges pályát írhat le a munkatérben.
Kinematikai párok osztályozása
A kinematikai párokat az elvett szabadsági fokok (vagy kötöttségi fok) száma alapján osztályozhatjuk. Mivel egy tagnak mint merev testnek legfeljebb 6 szabadsági foka lehet a térben ezért 1., 2., 3., 4., és 5. osztályú kinematikai párokat különböztethetünk meg, például:
|
ötödosztályú |
síkcsukló, síkcsúszka (sín), gördülő kerék |
|
negyedosztályú |
görgős (sima) támasz, csúszó kerék |
|
harmadosztályú |
gömbcsukló, síkmozgás |
|
… |
(kevésbé jelentősek) |
4.1.1.1. Mechanizmus szabadságfoka (DoF, szf.), mobilitása
A mechanizmus szabadsági vagy mobilitási fokát 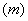 az előzőekben bevezetett fogalmak segítségével az alábbi formula szerint számíthatjuk:
az előzőekben bevezetett fogalmak segítségével az alábbi formula szerint számíthatjuk:
|
|
(4.1) |
ahol 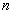 a mozgó tagok száma,
a mozgó tagok száma, 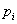 pedig az
pedig az 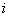 -ed osztályú kinematikai párok száma kinematikai láncban.
-ed osztályú kinematikai párok száma kinematikai láncban.
Síkbeli mechanizmus mobilitása ennek megfelelően:
|
|
(4.2) |
Szokás a kinematikai párokat a meghagyott szabadsági fokok szerint is csoportosítani illetve az állványt is a mechanizmus tagjai közé számítani és az azonos topológiájú kinematikai láncokat aszerint csoportosítani, hogy melyik tag az állvány. Ezzel a fenti képletek az alábbi alakot öltik:
|
|
(4.3) |
|
|
(4.4) |
ahol 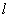 a kinematikai láncot alkotó összes tag száma,
a kinematikai láncot alkotó összes tag száma, 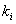 pedig az
pedig az 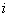 szabadságfokú kinematikai párok száma (azaz
szabadságfokú kinematikai párok száma (azaz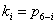 ).
).
Ha csak egy szabadsági fokú (azaz ötödosztályú) kinematikai párok találhatók kinematikai láncban, akkor kapjuk a mobilitásra vonatkozó Gruebler-féle formulát:
|
|
Példák forgattyús mechanizmus, Peaucellier-inverzor, …
4.1.2. Mechanizmusok csoportra bontása
A fenti képletek használata speciális geometriájú illetve ún. redundáns kényszereket tartalmazó mechanizmusok esetén ellentmondásra vezethet, azaz például egy láthatóan 1 szabadságfokú szerkezet esetén a képlet alapján 0 szabadságfokot kapunk. (Példa: parallel 4 csuklós mechanizmus kiegészítve egy harmadik párhuzamos csatlórúddal.)
Az ilyen paradoxonok magyarázata abban rejlik, hogy vannak ún. redundáns vagy passzív tagok, melyeknek nincs szerepe az input-output kapcsolat szabadságfokának meghatározásában és ezt a fenti képletek nem veszik figyelembe (azaz a redundáns tagokat elhagyva kinematikailag egyenértékű mechanizmust kapunk). Viszont, ha egy ilyen mechanizmus geometriáját kissé módosítjuk, akkor valóban a képlettel meghatározott szabadságfokot kapjuk. (A redundáns tagot tartalmazó parallel mechanizmus „befeszül”, ha a geometriát megváltoztatjuk.)
Bonyolultabb mechanizmusok szabadságfokának geometria függetlenségét csoportra bontással ellenőrizhetjük. Csoport alatt olyan 0 szabadságfokú kinematikai láncot értünk, amely nem bontható további 0 szabadságfokú részekre.
A kinematikai láncában megkülönböztethetünk a szabadságfokoknak megfelelő számú vezető (input) tagot és a többi tag által alkotott ún. vezetett részt. Ha a vezető tagokat rögzítjük, akkor a vezetett résznek nyilvánvalóan egy statikailag határozott szerkezetet kell alkotnia, azaz a vezetett rész szabadságfoka 0 kell, hogy legyen. Csak ötödosztályú kinematikai párokat tartalmazó síkbeli mechanizmus esetén tehát
|
|
(4.5) |
ahol 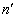 a vezetett rész tagjainak száma,
a vezetett rész tagjainak száma, 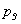 pedig a vezetett rész ötödosztályú kinematikai párjainak a száma. Mivel ezek egész számok, ezért az ilyen vezetett rész csak páros számú tagból állhat és 2, 4, 6, 8, stb. számú tag esetén az ötödosztályú kinematikai párok száma az alábbi táblázat szerint alakul:
pedig a vezetett rész ötödosztályú kinematikai párjainak a száma. Mivel ezek egész számok, ezért az ilyen vezetett rész csak páros számú tagból állhat és 2, 4, 6, 8, stb. számú tag esetén az ötödosztályú kinematikai párok száma az alábbi táblázat szerint alakul:
|
|
2 |
4 |
6 |
8 |
|
|
3 |
6 |
9 |
12 |
A mechanizmus tagjait megkülönbözethetjük aszerint is, hogy hány másik taghoz kapcsolódnak. Ennek megfelelően a 2, 3 illetve 4 másik taghoz kapcsolódó tagot bináris, ternáris illetve quaternáris tagnak nevezzük.
Példák A fenti táblázat szerint síkcsukló és síkcsúszka ötödosztályú kinematikai párokból 5 különböző kéttagú csoport alkotható. Egy négytagú csoport egy vagy két ternáris tagot (és 3 illetve 2 bináris tagot) tartalmaz. Egy hattagú csoportban 2 vagy 3 ternáris tag fodulhat elő.
Így egy egyszabadságfokú négytagú vagy egy kétszabadságfokú öttagú láncban egy kéttagú csoport alkotja a vezetett részt. Az egyszabadságfokú Watt- illetve Stephenson-féle hattagú kinematikai lánc vezetett része pedig két kéttagú vagy egy négytagú csoportból áll.
4.1.2.1. Kinematikai inverzió
Kinematikai inverziónak azt nevezzük, amikor ugyanazon kinematikai lánc más-más tagja lesz az állvány. Egy forgattyús mechanizmusnál elsőre látható az így kapott négy különböző működésű konstrukció.
A négycsuklós mechanizmus esetében a kinematikai inverzióval ugyan nem kapunk más topológiát, viszont a legrövidebb tagnak az állványhoz viszonyított helyzete alapján mégis három esetet különböztethetünk meg (a legrövidebb tag vagy az állványhoz kapcsolódik, vagy a csatló rúd szerepét tölti be, vagy maga az állvány). Amennyiben a hajtókart valamilyen motorral hajtjuk meg, fontos lehet annak eldöntése, hogy a 360 fokos körbe forgatásnak mi a feltétele. Ezt fejezi ki az alábbi, Grashof-féle összefüggés:
|
|
(4.6) |
ahol 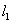 és
és 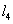 a legrövidebb illetve leghosszabb karok hosszai,
a legrövidebb illetve leghosszabb karok hosszai, 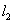 és
és 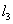 pedig a maradék két tag hosszúságát jelöli. Amennyiben ez a feltétel teljesül, akkor a mechanizmustGrashof-típusúnak is szokták nevezni.
pedig a maradék két tag hosszúságát jelöli. Amennyiben ez a feltétel teljesül, akkor a mechanizmustGrashof-típusúnak is szokták nevezni.
Az egyszabadságfokú hattagú láncok esetében kinematikai inverzióval kétféle Watt-típusú mechanizmust és háromféle Stephenson-típusú mechanizmust kapunk:
|
Watt-I. |
egy bináris tag az állvány |
|
Watt-II. |
egy ternáris tag az állvány |
|
Stephenson-I. |
egy bináris tag az állvány, melyhez két ternáris tag csatlakozik |
|
Stephenson-II. |
egy bináris tag az állvány, melyhez egy bináris és egy ternáris tag csatlakozik |
|
Stephenson-III. |
az állvány egy ternáris tag |