3. fejezet - Mozgások jellemzése és stabilitása

3. fejezet - Mozgások jellemzése és stabilitása
Vissza	2. rész - rész	Előre

Tartalom

3.1. Egy szabadsági fokú csillapított rezgések

3.1.1. Szabad rezgések
3.1.2. Gerjesztett rezgések

3.2. Mechanikai rendszerek egyensúlya

3.2.1. Virtuális teljesítmény elve
3.2.2. Dinamikus egyensúly
3.2.3. Stabilitási alapfogalmak

3.3. Holonom szkleronom rendszerek kis mozgásai

3.3.1. A mátrix differenciálegyenlet

3.3.2. Csillapítatlan rezgések

3.3.2.1. Sajátkörfrekvenciák, lengésképek

3.3.3. Stabilitás

3.3.3.1. A sajátvektorok ortogonalitása

3.3.4. A saját-körfrekvenciák becslési módszerei

3.3.4.1. A Rayleigh-hányados
3.3.4.2. Stodola-iteráció
3.3.4.3. Rayleigh-elv
3.3.4.4. Dunkerley-becslés

3.1. Egy szabadsági fokú csillapított rezgések

3.1.1. Szabad rezgések

A legtöbb egyszabadsági fokú mechanikai rendszer viselkedését kis kitérésű mozgásokra jól leírja a lineáris elemekből álló referencia modell mozgásegyenlete:

$m \ddot{x} + k \dot{x} + s x = 0 vagy \ddot{x} + 2 D α \dot{x} + α^{2} x = 0,$

ahol $α = \sqrt{s / m}$ az ún. csillapítatlan sajátkörfrekvencia és $D = k / 2 m α$ a relatív csillapítási tényező.

Az egyenlet megoldását a lineáris differenciálegyenletek elmélete alapján az alábbi alakban keressük:

$x (t) = A e^{ξ t} \Rightarrow (ξ^{2} + 2 D α ξ + α^{2}) A e^{ξ t} = 0.$

A nem triviális megoldást a zárójelben szereplő karakterisztikus polinom gyökeivel a következőképpen írhatjuk fel (a $D = 1$ eset kivételével, ld. később):

$x (t) = C_{1} e^{ξ_{1} t} + C_{2} e^{ξ_{2} t}, ahol ξ_{1,2} = - D α \pm α \sqrt{D^{2} - 1} \in ℂ és C_{1,2} \in ℂ .$

Vizsgáljuk meg az ún. gyökhelygörbét, ha $D$ változik:

mivel $| \sqrt{D^{2} - 1} | < | D |$ , $ℜ (ξ_{1,2}) \cdot D \leq 0$ továbbá $D = 0 \Leftrightarrow ℜ (ξ_{1,2}) = 0;$ vagyis, ha $D > 0,$ akkor a gyökök a komplex számsík baloldalán helyezkednek el, ha pedig $D < 0,$ akkor a jobboldalán;
$| D | < 1$ esetén komplex konjugált gyökpár a megoldás $(ξ_{1,2} = β \pm i γ),$ mégpedig az origó középpontú $α$ sugarú körön: $| ξ_{1,2} |^{2} = β^{2} + γ^{2} \equiv α^{2} (D^{2} + (1 - D^{2})) \equiv α^{2}$ .
$D = \pm 1$ esetén $ξ_{1,2} = β \equiv - D α$ kétszeres gyökök;
$D > 1$ esetén $ξ_{1} < ξ_{2} = - D α + α \sqrt{D^{2} - 1} < 0$ valósak;
$D < - 1$ esetén $0 < - D α - α \sqrt{D^{2} - 1} \equiv ξ_{1} < ξ_{2}$ valósak.

A továbbiakban csak a $D > 0$ esetekhez tartozó megoldásokat vizsgáljuk:

$D < 1$ : $γ = α \sqrt{1 - D^{2}}$ a csillapított sajátkörfrekvencia (a lengésidő $T = 2 π / γ$ ),

$x (t) = C_{1} e^{β t - i γ t} + C_{2} e^{β t + i γ t} \equiv \underset{2 ℜ (C_{1})}{\underset{︸}{(C_{1} + C_{2})}} e^{β t} \cos γ t + \underset{- 2 ℑ (C_{1})}{\underset{︸}{i (C_{2} - C_{1})}} e^{β t} \sin γ t,$

mivel $x (t) \in ℝ$ , azaz $C_{2} = {\bar{C}}_{1}$ (komplex konjugáltak). A csillapodó rezgés $x (t) = A e^{β t} \sin (γ t + δ)$ alakban is felírható, melynek segítségével értelmezhetjük a csillapodási hányados

$\frac{x (t)}{x (t + T)} = \frac{e^{β t}}{e^{β (t + T)}} \equiv e^{D α T}, illetve a Λ = D α T$

ún. logaritmikus dekrementum fogalmát.

$D = 1$ : aperiodikus határeset; a kétszeres gyök miatt a megoldás kvázipolinom alakú:

$x (t) = (C_{1} + t C_{2}) e^{β t} .$

$D > 1$ : $\tilde{γ} = α \sqrt{D^{2} - 1}$ , a jelenség exponenciálisan csökkenő aperiodikus mozgás:

$x (t) = C_{1} e^{ξ_{1} t} + C_{2} e^{ξ_{2} t} \equiv e^{β t} (A \cosh \tilde{γ} t + B \sinh \tilde{γ} t),$

ahol $2 C_{1} = A - B$ és $2 C_{2} = A + B$ .

Rajzoljuk fel $x (t)$ grafikonjait a $ξ$ komplex számsík néhány tipikus pontjában …!

3.1.2. Gerjesztett rezgések

A referencia modellt most kiegészítjük az $m$ tömegre ható $F (t) = F_{0} \cos ω t$ harmonikus gerjesztő erővel. Ezáltal a mozgásegyenlet új alakja:

$m \ddot{x} + k \dot{x} + s x = F_{0} \cos ω t vagy \ddot{x} + 2 D α \dot{x} + α^{2} x = α^{2} x_{st} \cos ω t,$

ahol $x_{st} = F_{0} / s$ az ún. statikus kitérés vagy deformáció, ami az $m$ tömeg statikus elmozdulását adja meg konstans $F_{0}$ esetén ( $ω = 0$ ).

A mozgásegyenlet most egy inhomogén közönséges differenciálegyenlet, melynek általános megoldását a homogén rész általános megoldásának és az inhomogén egyenlet partikuláris megoldásának összegeként kapjuk meg:

$x (t) = x_{h} (t) + x_{i h . p} (t) \underset{t \to \infty}{\to} x_{i h . p} (t) = X \cos (ω t - ϑ) \equiv X_{1} \cos ω t + X_{2} \sin ω t,$

mivel kvázipolinomiális gerjesztő függvény esetén a partikuláris megoldást is a megfelelő fokú és frekvenciájú függvény alakjában keressük.

A $x_{i h . p} (t)$ -t visszaírva a differenciálegyenletbe és $\cos ω t$ , $\sin ω t$ együtthatói szerint szétválasztva:

	$- ω^{2} X_{1} + 2 D α ω X_{2} + α^{2} X_{1} = α^{2} x_{st},$
	$- ω^{2} X_{2} - 2 D α ω X_{1} + α^{2} X_{2} = 0,$

illetve $α^{2}$ -tel való osztás után (a $ζ = ω / α$ frekvenciaviszony vagy hangolás bevezetésével) mátrix alakba rendezve:

$[\begin{matrix} 1 - ζ^{2} & 2 D ζ \\ - 2 D ζ & 1 - ζ^{2} \end{matrix}] [\begin{matrix} X_{1} \\ X_{2} \end{matrix}] = [\begin{matrix} x_{st} \\ 0 \end{matrix}] .$

Az egyenletrendszer megoldása:

$[\begin{matrix} X_{1} \\ X_{2} \end{matrix}] = \frac{1}{\det \dots} [\begin{matrix} 1 - ζ^{2} & - 2 D ζ \\ 2 D ζ & 1 - ζ^{2} \end{matrix}] [\begin{matrix} x_{st} \\ 0 \end{matrix}] \equiv \frac{x_{st}}{{(1 - ζ^{2})}^{2} + 4 D^{2} ζ^{2}} [\begin{matrix} 1 - ζ^{2} \\ 2 D ζ \end{matrix}],$

amiből kapjuk, hogy

$X = \sqrt{X_{1}^{2} + X_{2}^{2}} \equiv \frac{x_{st}}{\sqrt{{(1 - ζ^{2})}^{2} + 4 D^{2} ζ^{2}}}, \tan ϑ \equiv \frac{X_{2}}{X_{1}} = \frac{2 D ζ}{1 - ζ^{2}} .$

Innen a nagyítás: $N (ζ, D) = X / x_{st}$ , és $ϑ$ a fázisszög (vagy fáziskésés — a gerjesztéshez képest).

A nagyítás függvény szélsőértékhelye megegyezik a gyökjel alatti kifejezés szélsőértékhelyével (mivel a $ζ > 0$ tartományon az $1 / \sqrt{x}$ szigorúan monoton változik):

$- 4 ζ^{⋆} (1 - ζ^{⋆ 2}) + 8 D^{2} ζ^{⋆} = 0.$

Innen a $ζ^{⋆}$ szélsőértékhely és az $N^{⋆}$ szélsőérték:

$ζ^{⋆} = \sqrt{1 - 2 D^{2}}, N^{⋆} \equiv N (ζ^{⋆}) = \frac{1}{2 D \sqrt{1 - D^{2}}} .$

Ha $D ≪ 1$ , akkor $ζ^{⋆} \approx 1$ , és $N^{⋆} \approx 1 / 2 D$ – minőségi tényező, illetve $1 / N^{⋆} \approx 2 D$ – veszteségi tényező.

3.2. Mechanikai rendszerek egyensúlya

Egyensúly alatt a mechanikai rendszer tartós nyugalmi állapotát értjük, azaz ha ( $N$ anyagi pont esetén)

$v_{i} = 0, a_{i} \equiv 0 \Rightarrow v_{i} \equiv 0, r_{i} (t) \equiv r_{i}^{0} (i = 1, \dots, N) .$

(3.1)

Elnevezések: $r_{i}^{0}$ : egyensúlyi helyzet; $(r_{i}^{0}, v_{i} \equiv 0)$ : egyensúlyi állapot.

3.2.1. Virtuális teljesítmény elve

(Bernoulli, 1717; Galilei: „A mechanika aranyszabálya”):

Egy rendszernek az (ideális) kényszerekkel összeférő $r_{i}^{0}$ pozíciója egyensúlyi helyzet $\Leftrightarrow$ az $F_{k} (r_{i}, {\dot{r}}_{i}, t)$ szabaderők virtuális teljesítményének összege ott tartósan zérus:

$δ \equiv \sum_{k = 1}^{N} F_{k} (r_{i}^{0}, 0, t) \cdot δ {\dot{r}}_{k} = 0 (\forall t \geq t_{0} -ra)$

(3.2)

Bizonyítás: $δ = 0$ szükséges feltétel, hiszen a d'Alembert-elv alapján

$\sum_{k = 1}^{N} (- m_{k} {\ddot{r}}_{k} + F_{k} + K_{k}) \cdot δ {\dot{r}}_{k} = 0, {\ddot{r}}_{k} = 0, \sum_{k = 1}^{N} K_{k} \cdot δ {\dot{r}}_{k} = 0 \Rightarrow \sum_{k = 1}^{N} F_{k} \cdot δ {\dot{r}}_{k} = 0.$

Másrészt, ha $δ$ tartósan zérus egy $r_{i}^{0}$ helyzetben (és itt $f_{j} (r_{i}^{0}, t) \equiv {\hat{f}}_{j} (r_{i}^{0}) \equiv 0,$ azaz $\partial f_{j} (r_{i}^{0}, t) / \partial t = 0$ ), akkor megegyezik a ténylegesen lehetséges teljesítménnyel, mivel $δ {\dot{r}}_{i}$ megegyezik a lehetséges sebességekkel (vagyis az ilyen helyzet szkleronom, időtől független). Tehát

${δ |}_{e .h .} = |_{e .h .} = {\dot{T} |}_{e .h .}$

(3.3)

a teljesítménytétel értelmében. Viszont ha ez az $r_{i}^{0}$ helyzet nyugalmi helyzet — azaz a $T$ kinetikus energia zérus és egyben minimális, hiszen $T \geq 0$ — akkor a szabaderők zérus virtuális teljesítménye esetén a kinetikus energia változatlan, azaz zérus marad, tehát az adott helyzet tartós nyugalmi, vagyis egyensúlyi helyzet.

Általánosabban megfogalmazva: mivel a nyugalmi állapot megszűnése csak

$\dot{T} > 0, azaz δ > 0$

(3.4)

esetén következhet be, az egyensúly szükséges és elégséges feltétele, hogy

$δ \leq 0,$

(3.5)

ami egyenlőtlenséggel megadott kényszerfeltételek mellett is alkalmazható.

Következmény: holonom mechanikai rendszernek $q_{k} \equiv q_{k}^{0}$ ( $k = 1, \dots, n$ ) egyensúlyi helyzete $\Leftrightarrow$ ha ott az általános erők tartósan zérusok: $Q_{r} (q_{k}^{0}, {\dot{q}}_{k} \equiv 0, t) \equiv 0$ , mivel

$δ \equiv Q_{r} δ {\dot{q}}_{r} = 0$

(3.6)

és $δ {\dot{q}}_{r}$ a kényszerfeltételeket kielégítik, így tetszőlegesek (függetlenek), tehát $Q_{r} \equiv 0$ $(r = 1, \dots, n)$ .

Konzervatív holonom szkleronom mechanikai rendszerekben a $q_{k} \equiv q_{k}^{0}$ egyensúlyi helyzetben

$Q_{r} = {\frac{\partial U}{\partial q_{r}} |}_{q_{k}^{0}}$

(3.7)

és mivel $δ {\dot{q}}_{r}$ -k függetlenek és tetszőlegesek az egyensúly szükséges és elégséges feltétele, hogy

${\frac{\partial U}{\partial q_{r}} |}_{q_{k}^{0}} = 0$ $\forall r,$

(3.8)

vagyis, hogy az $U (q_{k})$ potenciál függvénynek az egyensúlyi helyzetben lokális szélsőértéke legyen.

3.2.2. Dinamikus egyensúly

Potenciálos erőtérben mozgó holonom (reonom) mechanikai rendszer mozgásegyenlete az $ℒ = T_{2} + ℒ_{1} + ℒ_{0}$ alakú kinetikus potenciállal:

$\underset{(\dots) {\ddot{q}}_{k} + (\dots) {\dot{q}}_{k}}{\underset{︸}{\frac{d}{d t} \frac{\partial T_{2}}{\partial {\dot{q}}_{k}} - \frac{\partial T_{2}}{\partial q_{k}}}} + \frac{d}{d t} \frac{\partial ℒ_{1}}{\partial {\dot{q}}_{k}} - \underset{(\dots) {\dot{q}}_{k}}{\underset{︸}{\frac{\partial ℒ_{1}}{\partial q_{k}}}} - \frac{\partial ℒ_{0}}{\partial q_{k}} = 0.$

(3.9)

Egyensúly esetén ( ${\dot{q}}_{k} = 0$ , ${\ddot{q}}_{k} = 0$ ) az első, a második és a negyedik tag eltűnik:

$\frac{d}{d t} a_{k} (q_{r}, t) - \frac{d}{d t} Ψ_{k} (q_{r}, t) - \frac{\partial T_{0} (q_{r}, t)}{\partial q_{k}} + \frac{\partial V_{0} (q_{r}, t)}{\partial q_{k}} = 0,$

(3.10)

mivel $ℒ_{1} = T_{1} - V_{1} \equiv a_{k} {\dot{q}}_{k} - Ψ_{k} {\dot{q}}_{k}$ és $ℒ_{0} = T_{0} - V_{0}$ . Az idő szerinti teljes deriválás után csak a parciális derivált marad meg (mert a másik tag ${\dot{q}}_{r}$ -tal szorzódna):

$\frac{\partial a_{k}}{\partial t} - \frac{\partial Ψ_{k}}{\partial t} - \frac{\partial T_{0}}{\partial q_{k}} + \frac{\partial V_{0}}{\partial q_{k}} = 0,$

(3.11)

és ennek az egyenletrendszernek a megoldása adja az egyensúlyi helyzetet. Ez persze nem függhet az időtől, ami tipikusan^[3] akkor teljesül, ha $r_{k} (q_{r}, t)$ , $Ψ_{k} (q_{r}, t)$ az időnek legfeljebb elsőfokú, $V_{0}$ pedig nulladfokú kifejezése. Ebben az esetben

$T_{0} = T_{0} (q_{r}), T_{1} = a_{k} (q_{r}, t) {\dot{q}}_{k}, V (q_{r}, t) = Ψ_{k} (q_{r}, t) {\dot{q}}_{k} + V_{0} (q_{r}) .$

(3.12)

Konzervatív erők (nem rendszer!) esetén $(V = V_{0} = U (q_{r}))$ pedig a

$\frac{\partial U}{\partial q_{k}} = \frac{\partial T_{0}}{\partial q_{k}}$

(3.13)

feltétel határozza meg a ${\dot{q}}_{k} \equiv 0$ , ${\ddot{q}}_{k} \equiv 0$ tulajdonsággal bíró $q_{k}^{0}$ dinamikus egyensúlyi helyzetet, hiszen itt ${\dot{r}}_{i} = v_{i} (q_{k}^{0})$ is lehetséges, ami alapján a kinetikus energia $T (q_{k}^{0},0, t) \equiv T_{0} (q_{k}^{0}) > 0$ , de az időben állandó (ld. kritikus fordulatszám legegyszerűbb modellje).

3.2.3. Stabilitási alapfogalmak

Azt mondjuk, hogy az $\dot{x} = f (x, t)$ differenciálegyenlet-rendszer ( $0 = f (x, t)$ egyenletrendszert kielégítő) $x^{⋆}$ egyensúlyi helyzete vagy pontmegoldása Ljapunov-stabilis, ha $\forall ε > 0$ számhoz $\exists δ > 0$ , hogy

$‖ x (t) - x^{⋆} ‖ < ε \forall ‖ x (t_{0}) - x^{⋆} ‖ < δ, t \geq t_{0} esetén .$

(3.14)

Azaz bármilyen kis $ε$ számhoz megadható az $x^{⋆}$ egyensúlyi helyzetnek egy valamilyen (esetleg $t_{0}$ -tól függő) $δ$ sugarú környezete, hogy az abból indított megoldások mindig az egyensúlyi helyzet $ε$ sugarú környezetében maradjanak.

Azt mondjuk, hogy az $\dot{x} = f (x, t)$ differenciálegyenlet-rendszer $x^{⋆}$ egyensúlyi helyzete vagy pontmegoldása aszimptotikusan stabilis, ha Ljapunov-stabilis és

$\lim_{t \to \infty} x (t) = x^{⋆} .$

(3.15)

Az $\dot{x} = A x$ állandó, valós együtthatós, homogén lineáris differenciálegyenlet-rendszer általános megoldása:

$x (t) = \sum c_{i} C_{i} e^{β_{i} t} + \sum c_{j} C_{j} e^{(β_{j} + i γ_{j}) t} + \sum {\bar{c}}_{j} {\bar{C}}_{j} e^{(β_{j} - i γ_{j}) t},$

(3.16)

ahol $c_{i}, β_{i}, β_{j}, γ_{j} \in ℝ$ , $C_{i} \in ℝ^{n}$ , $c_{j} \in ℂ$ , $C_{j} \in ℂ^{n}$ , továbbá $β_{i}$ valamint $β_{j} \pm i γ_{j}$ az $A$ együtthatómátrix valamelyik $λ_{k}$ sajátértékével egyezik meg (ha az összes $λ_{k}$ egyszeres gyök!).

Az $\dot{x} = A x$ rendszer $x \equiv 0$ (triviális) pontmegoldása (tetszőleges valós állandó $A$ mátrix esetén is)

aszimptotikusan stabilis, ha $Re λ_{k} < 0, \forall k $;$
Ljapunov-stabilis, ha $\forall Re λ_{k} \leq 0$ és a $Re λ_{k} = 0$ gyökök multiplicitása egyszeres $A$ mátrix minimálpolinomjában (ellenpélda:
egyébként pedig instabil.

Példa Ha

$A = [\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix}] \Rightarrow p (λ) = λ^{2}, de A = 0 csak p (A) \equiv A^{2} = 0,$

tehát $p (λ)$ a minimálpolinom és $x (t) = (c_{1} + c_{2} t, c_{2})$ nem korlátos megoldás. Viszont $A = 0$ esetén bár $p (λ) = λ^{2}$ ismét, de $\tilde{p} (λ) = λ$ lesz a minimálpolinom és korlátosak az $x (t) = (c_{1}, c_{2})$ alakú megoldások.

3.3. Holonom szkleronom rendszerek kis mozgásai

3.3.1. A mátrix differenciálegyenlet

Időtől független gerjesztés esetén a másodfajú Lagrange-egyenletek holonom szkleronom rendszernél az alábbi alakot öltik:

$\frac{d}{d t} \frac{\partial T}{\partial {\dot{q}}_{k}} - \frac{\partial T}{\partial q_{k}} + \frac{\partial D}{\partial {\dot{q}}_{k}} + \frac{\partial U}{\partial q_{k}} = Q_{k}^{⋆} (q_{i}, {\dot{q}}_{i}),$

(3.17)

ahol

	$T (q_{i}, {\dot{q}}_{i}) = T_{2} \equiv \frac{1}{2} a_{k j} (q_{i}) {\dot{q}}_{j} {\dot{q}}_{k} \equiv \frac{1}{2} {\dot{q}}^{⊤} A (q) \dot{q},$
	$D (q_{i}, {\dot{q}}_{i}, t) = \frac{1}{2} b_{k j} (q_{i}, t) {\dot{q}}_{j} {\dot{q}}_{k} \equiv \frac{1}{2} {\dot{q}}^{⊤} B (q, t) \dot{q} .$

Vizsgáljuk a rendszer $q_{i}^{0}$ egyensúlyi helyzetének környezetében történő mozgásokat (azaz $q_{i} \equiv q_{i}^{0}$ $\Rightarrow {\dot{q}}_{i} \equiv {\ddot{q}}_{i} \equiv 0$ megoldása a (3.17) egyenleteknek). Ekkor az $U$ potenciálfüggvény másodfokú tagokig történő és a $Q_{k}^{⋆}$ általános erők első fokig történő sorfejtése az egyensúlyi helyzet körül:

	$U (q_{i}, t) = U (q_{i}^{0}, t) + {\frac{\partial U}{\partial q_{k}} \|}_{q_{i}^{0}} (q_{k} - q_{k}^{0}) + \frac{1}{2} {\frac{\partial^{2} U}{\partial q_{k} \partial q_{j}} \|}_{q_{i}^{0}} (q_{j} - q_{j}^{0}) (q_{k} - q_{k}^{0}) + \dots,$
	$Q_{k}^{⋆} (q, \dot{q}) = Q_{k}^{⋆} (q^{0}, 0) + {\frac{\partial Q_{k}^{⋆}}{\partial q} \|}_{q^{0}, 0} \cdot (q - q^{0}) + {\frac{\partial Q_{k}^{⋆}}{\partial \dot{q}} \|}_{q^{0}, 0} \cdot \dot{q} + \dots,$

Tehát az egyensúlyi helyzetben ( ${\dot{q}}_{i} \equiv {\ddot{q}}_{i} \equiv 0$ miatt)

${\frac{\partial U}{\partial q_{k}} |}_{q^{0}} = Q_{k}^{⋆} (q^{0}, 0),$

(3.18)

amiből $q_{i}^{0}$ meghatározható.

Bevezetve a ${\tilde{q}}_{i}$ koordinátákat a $q_{i} = q_{i}^{0} + {\tilde{q}}_{i}$ összefüggés alapján, majd átparaméterezve az egyenleteket a ${\tilde{q}}_{i}$ koordinátákkal kifejezve és elhagyva a ~-t formailag a (3.17) egyenlettel azonos összefüggésre jutunk, azonban a vizsgált egyensúlyi helyzet a konfigurációs tér origójába kerül: $q_{i} = 0$ (eredetileg ${\tilde{q}}_{i}$ ). Azaz az általánosság megszorítása nélkül feltehetjük, hogy az általános koordináták mindig választhatók úgy, hogy egy egyensúlyi helyzetet (e.h.) a $q_{i} = 0$ koordinátaértékek azonosítsanak.

Módosítsuk $D$ -t és $U$ -t a következő módon:

$\tilde{D} (q_{i}, {\dot{q}}_{i}, t) = D - \frac{1}{2} {\frac{\partial Q_{k}^{⋆}}{\partial {\dot{q}}_{j}} |}_{e .h .} {\dot{q}}_{j} {\dot{q}}_{k} \equiv \frac{1}{2} (b_{k j} - {\frac{\partial Q_{k}^{⋆}}{\partial {\dot{q}}_{j}} |}_{e .h .}) {\dot{q}}_{j} {\dot{q}}_{k},$

(3.19)

$\tilde{U} (q_{i}, t) = U - {Q_{k}^{⋆} |}_{e .h .} q_{k} - \frac{1}{2} {\frac{\partial Q_{k}^{⋆}}{\partial q_{j}} |}_{e .h .} q_{j} q_{k} \equiv$

(3.20)

$\equiv {U (q_{i}, t) |}_{e .h .} + (\underset{0}{\underset{︸}{{\frac{\partial U}{\partial q_{k}} |}_{e .h .} - {Q_{k}^{⋆} |}_{e .h .}}}) q_{k} + \frac{1}{2} ({\frac{\partial^{2} U}{\partial q_{k} \partial q_{j}} |}_{e .h .} - {\frac{\partial Q_{k}^{⋆}}{\partial q_{j}} |}_{e .h .}) q_{j} q_{k} .$

Ezzel a másodfajú Lagrange-egyenletek kis mozgások esetén egy homogén lineáris másodrendű közönséges differenciálegyenlet-rendszert alkotnak, melyek az alábbi mátrix alakba rendezhetők:

$M \ddot{q} + K (t) \dot{q} + S (t) q = 0,$

(3.21)

ahol a tömeg-, csillapítási és merevségi mátrix rendre

$M = A (q^{0}) \equiv {[\frac{\partial^{2} T}{\partial {\dot{q}}_{k} \partial {\dot{q}}_{j}}]}_{e .h .}, K (t) = {[\frac{\partial^{2} D}{\partial {\dot{q}}_{k} \partial {\dot{q}}_{j}} - \frac{\partial Q_{k}^{⋆}}{\partial {\dot{q}}_{j}}]}_{e .h .}, S (t) = {[\frac{\partial^{2} U}{\partial q_{k} \partial q_{j}} - \frac{\partial Q_{k}^{⋆}}{\partial q_{j}}]}_{e .h .} .$

(3.22)

Időtől független esetben, vagyis állandó $M$ , $K$ , $S$ esetén a (3.21) egyenletnek a homogén általános megoldása

$q (t) = u e^{λ t}$

(3.23)

próbafüggvény (Ansatz) alakjában keresendő, amit ha beírunk a (3.21) mátrix differenciálegyenletbe, akkor egy homogén lineáris egyenletrendszerhez illetve sajátérték–sajátvektor feladathoz jutunk:

$(λ^{2} M + λ K + S) u e^{λ t} = 0,$

(3.24)

ami $e^{λ t}$ -től függetlenül kell, hogy teljesüljön. Viszont, ha $u = 0$ (nem triviális) megoldásokat (sajátvektorokat) keresünk, akkor az együttható mátrix determinánsának kell zérusnak lennie, azaz

$\det (λ^{2} M + λ K + S) = 0,$

(3.25)

ami a $λ$ sajátértékekre vonatkozó $2 n$ -edfokú karakterisztikus egyenlet.

A karakterisztikus egyenlet gyökei között lehetnek komplex konjugált párok, hasonló komplex konjugált sajátvektorokkal, vagyis

$β_{i} \in ℝ és β_{j} \pm i γ_{j} \in ℂ,$

úgy hogy

$q (t) = \sum_{i} c_{i} u_{i} e^{β_{i} t} + \sum_{j} c_{j} e^{β_{j} t} (u_{j} \sin (γ_{j} t + δ_{j}) + v_{j} \cos (γ_{j} t + δ_{j})),$

(3.26)

ahol már $u_{i}, u_{j}, v_{j} \in ℝ^{n}$ valós vektorok és $c_{i}, c_{j}, δ_{j}$ a kezdeti feltételektől függő $2 n$ darab valós szám (amennyiben a sajátértékek egyszeresek).^[4]

3.3.2. Csillapítatlan rezgések

3.3.2.1. Sajátkörfrekvenciák, lengésképek

Amennyiben a $K$ csillapítási mátrix zérus elemekből áll és az összes $q (t)$ megoldás korlátos (pl. konzervatív rendszerekben), akkor az

$M \ddot{q} + S q = 0$

(3.27)

hiányos másodrendű mátrix differenciálegyenlet sajátértékei tiszta képzetes gyökpárok lesznek, mivel a

$\det (λ^{2} M + S) = 0$

(3.28)

karakterisztikus egyenlet egy $λ^{2}$ -re $n$ -edfokú algebrai egyenlet lesz. Belátható, hogyha ennek gyöke egy $c$ pozitív valós szám, vagy egy $z$ konjugált képzetes gyökpár, akkor ezekhez tartozik pozitív valós részű $λ$ gyök ( $β > 0$ ), ami az exponenciális kitevőben $t \to \infty$ esetén a $q (t)$ megoldások korlátosságának ellentmond.

Viszont, ha $\forall λ_{j}^{2} < 0$ (valós szám), akkor $λ_{j} = \pm i α_{j}$ tiszta képzetes gyököket kapunk (ennek feltétele, hogy $S$ szimmetrikus pozitív definit mátrix legyen), aminek a

$q (t) = \sum_{j = 1}^{n} c_{j} u_{j} \sin (α_{j} t + δ_{j}) \equiv \sum_{j = 1}^{n} u_{j} (a_{j} \cos α_{j} t + b_{j} \sin α_{j} t)$

(3.29)

homogén általános megoldás felel meg, $c_{j}$ és $δ_{j}$ integrálási állandókkal. Tehát a megoldás harmonikus függvények lineáris kombinációja, melyeknek — azaz a magára hagyott rendszer szabad rezgéseinek — körfrekvenciája $α_{j}$ . Mivel ezek értéke csak az $M$ tömegmátrixtól és az $S$ merevségi mátrixtól függ — melyeket többnyire csak a rendszer fizikai, geometriai paraméterei határoznak meg, külső hatások nem —, ezért $α_{j}$ -t a csillapítatlan rendszer $j$ -edik sajátkörfrekvenciájának is nevezzük $(α_{j} < α_{j + 1})$ , a

$\det (- α^{2} M + S) = 0$

(3.30)

karakterisztikus egyenletet pedig frekvenciaegyenletnek.

Megfelelő kezdeti feltételekkel elérhető, hogy a megoldás tisztán az egyik vagy másik sajátkörfrekvenciájú rezgést tartalmazza. Ilyenkor az egyes általános koordináták értékeinek egymáshoz viszonyított arányai minden időpillanatban megegyeznek a megfelelő sajátvektor elemeinek egymáshoz képesti arányaival, és a koordináták egyszerre érik el a szélsőértékeiket illetve válnak zérussá. E fizikai tartalom miatt a sajátvektorokat az egyes sajátkörfrekvenciákhoz tartozó lengésképek vektorának is nevezzük.

3.3.3. Stabilitás

A mozgásegyenletet linearizálva a $q_{k}^{⋆}$ egyensúlyi helyzet körül, $q_{k} = q_{k}^{⋆} + x_{k}$ bevezetésével kapjuk a következő mátrix együtthatós differenciálegyenlet-rendszert:

$M \ddot{x} + S x = 0, ahol M = [{\frac{\partial^{2} T_{2}}{\partial {\dot{q}}_{i} \partial {\dot{q}}_{j}} |}_{q_{k}^{⋆}}], S = [{\frac{\partial^{2} U}{\partial q_{i} \partial q_{j}} |}_{q_{k}^{⋆}}] .$

(3.31)

Az $x (t) = u e^{λ t}$ próbafüggvényt behelyettesítve egy sajátérték-sajátvektor feladat homogén lineáris algebrai egyenletrendszerét kapjuk:

$(λ^{2} M + S) u = 0,$

(3.32)

melynek akkor létezik nemtriviális $(u \neq 0)$ megoldása, ha $\det (ξ M + S) = 0$ . Az utóbbi karakterisztikus egyenletnek a $ξ = λ^{2}$ gyökei valósak, mivel mind $M$ , mind $S$ valós szimmetrikus mátrixok, továbbá a megfelelő $u$ sajátvektorok is valós eleműek (vagy tiszta képzetes konjugáltak, ami persze nem jelent érdemi különbséget).

Mivel $ξ_{i} > 0$ gyök esetén $λ_{2 i - 1,2 i} = \pm \sqrt{ξ_{i}}$ , azaz az egyik gyök mindenképpen pozitív lenne és így

$e^{\sqrt{ξ_{i}} t} \underset{t \to \infty}{\to} \infty,$

(3.33)

azaz $x_{k} (t)$ nem marad korlátos az egyensúlyi helyzet bármilyen kis mértékű megzavarása esetén, ezért csak a $ξ_{i} = - α_{i}^{2} < 0$ gyökök esetén lehet a $q_{k}^{⋆}$ egyensúlyi helyzet stabilis. Ekkor $λ_{i} = \pm i α_{i}$ , azaz $Re λ_{i} = 0$ , és

$x (t) = \sum_{i = 1}^{n} c_{i} u_{i} \sin (α_{i} t + δ_{i}),$

(3.34)

ami eleget tesz a Ljapunov-féle stabilitási kritériumnak (de nem aszimptotikusan stabilis!).

Visszahelyettesítve az előbb karakterisztikus egyenlet $λ_{i}$ megoldását és a hozzátartozó $u_{i}$ sajátvektort a homogén lineáris egyenletrendszerbe és megszorozva azt balról $u_{i}^{⊤}$ -val, átrendezés után az alábbi kifejezéshez jutunk:

$λ_{i}^{2} = - \frac{u_{i}^{⊤} S u_{i}}{u_{i}^{⊤} M u_{i}} .$

(3.35)

Mivel a Ljapunov-féle stabilitáshoz $λ_{i}^{2} < 0$ szükséges és $M$ szimmetrikus pozitív definit mátrix, a számláló pozitivitásának elégséges feltételét jelenti, ha $S$ mátrix illetve az $U$ potenciálfüggvény kvadratikus alakja az egyensúlyi helyzet környezetében is pozitív definit, azaz $U$ -nak az egyensúlyi helyzetben lokális minimuma van. Tehát $S$ mátrix összes sajátértéke pozitív valós szám, ami a Sylvester-féle tétel értelmében igaz, $\Leftrightarrow$ ha $S$ összes sarokaldeterminánsa pozitív.

A pozitív definitség $S$ illetve $U$ esetében szükséges feltétel is egyben: minthogy $λ_{i}^{2} < 0$ az összes gyökre értendő, ami az $u_{i}^{⊤} S u_{i} > 0$ feltételt vonja maga után $(i = 1, \dots, n)$ , amiből viszont az $u_{i}$ sajátvektorok $M$ -re vonatkozó ortogonalitása miatt következik, hogy $a^{⊤} S a = - \sum λ_{i}^{2} a_{i}^{2} u_{i}^{⊤} M u_{i} > 0$ $(\forall a \equiv \sum a_{i} u_{i} \neq 0)$ .

3.3.3.1. A sajátvektorok ortogonalitása

Ha a $q (t) = u e^{i α t}$ megoldásokat behelyettesítjük a (3.27) egyenletbe, akkor a $j$ -edik illetve $k$ -adik sajátkörfrekvenciákhoz és $u_{j}$ illetve $u_{k}$ sajátvektorokhoz a következőket kapjuk:

$- α_{j}^{2} M u_{j} + S u_{j} = 0,$

(3.36)

$- α_{k}^{2} M u_{k} + S u_{k} = 0 .$

(3.37)

Az egyenleteket megszorozva balról $u_{k}^{⊤}$ -val illetve $u_{j}^{⊤}$ -vel majd kivonva őket egymásból:

$(α_{k}^{2} - α_{j}^{2}) u_{k}^{⊤} M u_{j} = 0,$

(3.38)

mivel $M$ és $S$ szimmetrikussága miatt

$u_{k}^{⊤} M u_{j} = u_{j}^{⊤} M u_{k} és u_{k}^{⊤} S u_{j} = u_{j}^{⊤} S u_{k} .$

A (3.38) egyenletből következik, hogy

$u_{k}^{⊤} M u_{j} = 0, ha j = k,$

(3.39)

azaz a sajátvektorok ortogonálisak az $M$ tömegmátrixra nézve.

3.3.4. A saját-körfrekvenciák becslési módszerei

3.3.4.1. A Rayleigh-hányados

Legyen $v = \sum c_{i} u_{i}$ a lengésképek valamilyen lináris kombinációjaként előállított tetszőleges vektor. Ekkor az

$R (v) = \frac{v^{⊤} S v}{v^{⊤} M v}$

(3.40)

hányadost Rayleigh-hányadosnak nevezzük.

A kinetikus energia pozitív definit kvadratikus alakjából következik a szimmetrikus $M$ mátrix pozitív definitsége. Így a korlátos, nem csillapodó rezgések kialakulásának feltétele, hogy a szimmetrikus $S$ mátrix is pozitív definit legyen:

$0 < v^{⊤} M v és 0 < v^{⊤} S v (\forall v = 0) .$

Rendezzük sorba az $α_{j}$ sajátkörfrekvenciákat úgy, hogy

$α_{1} \leq α_{2} \leq \dots \leq α_{n},$

(3.41)

és vizsgáljuk a Rayleigh-hányados számlálójában szereplő kifejezést:

$v^{⊤} S v \equiv v^{⊤} \sum_{i} c_{i} S u_{i} \equiv \sum_{i} c_{i} α_{i}^{2} \underset{c_{i} u_{i}^{⊤} M u_{i}}{\underset{︸}{v^{⊤} M u_{i}}} \equiv \sum_{i} α_{i}^{2} c_{i}^{2} u_{i}^{⊤} M u_{i} \geq α_{1}^{2} \underset{v^{⊤} M v}{\underset{︸}{\sum_{i} c_{i}^{2} u_{i}^{⊤} M u_{i}}},$

(3.42)

ahol $v^{⊤} M u_{i} = c_{i} u_{i}^{⊤} M u_{i}$ összefüggésben kihasználtuk a sajátvektorok ortogonalitását.

A (3.42)-ben megfogalmazott egyenlőtlenséget átrendezve kapjuk, hogy

$α_{1}^{2} \leq R (v) = \frac{v^{⊤} S v}{v^{⊤} M v} \leq α_{n}^{2},$

(3.43)

azaz az $R (v)$ Rayleigh-hányados tetszőleges $v$ vektor esetén felülről becsli az első (legkisebb) sajátkörfrekvencia négyzetét (a legnagyobb sajátkörfrekvenciájét pedig alulról). Természetesen minél jobb közelítést adunk $v$ -vel $u_{1}$ -re, az első lengésképre, $\sqrt{R}$ is annál jobban közelíti $α_{1}$ -et.

3.3.4.2. Stodola-iteráció

A (3.36) egyenletet az $S$ merevségi mátrix $C = S^{- 1}$ inverzével végigszorozva balról képezzük $j = 1$ esetén az alábbi iterációs eljárást:

$u_{1}^{(k + 1)} = {(α_{1}^{(k)})}^{2} C M u_{1}^{(k)} \equiv R (u_{1}^{(k)}) C M u_{1}^{(k)} .$

(3.44)

Megmutatjuk, hogy ez az iteráció konvergens, és tipikusan $u_{1}$ -hez, az első lengésképvektorhoz tart.

Az iterációnak több fixpontja is van, hiszen bármelyik $u_{i}$ sajátvektort behelyettesítve a frekvenciaegyenlet átírt formáját kapjuk vissza, amit $u_{i}$ -k kielégítenek.

$x^{(k + 1)} = f (x^{(k)}) \approx f (x^{⋆}) + {\frac{\partial f}{\partial x} |}_{x = x^{⋆}} (x - x^{⋆}) + h .o .t .$

(3.45)

iterációt az $x^{⋆}$ fixpont $(x^{⋆} = f (x^{⋆}))$ környezetében jól közelíti a ${grad}_{x} f$ derivált tenzorral megadott lineáris leképezés, ami akkor konvergens, ha ${grad}_{x} f$ mátrixának spektrálsugara

$ρ ({\frac{\partial f}{\partial x} |}_{x = x^{⋆}}) < 1,$

(3.46)

vagyis az összes sajátértéke a komplex egységkör belsejében található.

Képezzük tehát a Stodola-iteráció jobb oldalán szereplő kifejezés gradiensét:

$R (u_{1}) C M + \frac{\partial R (u_{1})}{\partial v} C M u_{1} \equiv α_{1}^{2} C M + 2 \frac{u_{1}^{⊤} M u_{1} u_{1}^{⊤} S - u_{1}^{⊤} S u_{1} u_{1}^{⊤} M}{{(u_{1}^{⊤} M u_{1})}^{2}} C M u_{1} \equiv α_{1}^{2} C M,$

(3.47)

mivel a második tagban a számláló zérus, hiszen $S u_{1} = α_{1}^{2} M u_{1}$ , továbbá $M$ és $S$ szimmetrikus mátrixok (másképpen: mivel az $R (v)$ Rayleigh-hányados $v = u_{1}$ esetén minimális, ezért ott a gradiense $0$ ).

Nézzük most az $α_{1}^{2} C M$ mátrix sajátértékeit:

$\det (α_{1}^{2} C M - λ I) \equiv α_{1}^{2 n} \det (C M - \tilde{λ} I) = 0 (λ = α_{1}^{2} \tilde{λ}) .$

(3.48)

Belátható, hogy ${\tilde{λ}}_{i}$ -k a $\det (- α^{2} C M + I) = 0$ frekvenciaegyenletből számítható sajátkörfrekvenciák négyzeteinek reciprokával egyenlőek:

${\tilde{λ}}_{i} = \frac{1}{α_{i}^{2}},$

amiből viszont

$λ_{i} = \frac{α_{1}^{2}}{α_{i}^{2}} \leq 1,$

(3.49)

és az egyenlőség csak $i = 1$ esetén áll fenn. Vagyis tetszőleges $v$ vektor esetén az $u_{1}$ sajátvektoron kívüli altérbe eső komponensek előbb-utóbb eltűnnek, és a Stodola-iterációval $v$ az $u_{1}$ lengéskép által meghatározott első sajátirányhoz tart.

3.3.4.3. Rayleigh-elv

Ha a csillapítatlan (konzervatív) rendszer első lengésképhez tartozó megoldását nézzük, illetve ha a rendszer tisztán az első sajátrezgésével rezeg, vagyis

$q (t) = u_{1} \cos α_{1} t és \dot{q} (t) = - α_{1} u_{1} \sin α_{1} t,$

(3.50)

akkor

$U_{max} = \frac{1}{2} u_{1}^{⊤} S u_{1},$

(3.51)

mivel a legnagyobb kitérésnél maximális az alakváltozási energia és ez egyben az $ℰ$ mechanikai összenergia is, hiszen a legnagyobb kitérésnél a kinetikus energia zérus $(\dot{q} = 0)$ .

A kinetikus energia $q = 0$ esetén lesz a legnagyobb (és ekkor $U = 0$ ):

$T_{max} = \frac{1}{2} α_{1}^{2} u_{1}^{⊤} M u_{1} \equiv α_{1}^{2} {\tilde{T}}_{max} .$

(3.52)

Mivel konzervatív rendszerről van szó, a mechanikai összenergia állandó:

$ℰ = T + U = U_{max} = T_{max} = állandó .$

(3.53)

Vagyis

$α_{1}^{2} = \frac{U_{max} (u_{1})}{{\tilde{T}}_{max} (u_{1})}$ $\equiv \frac{u_{1}^{⊤} S u_{1}}{u_{1}^{⊤} M u_{1}} \leq \frac{U_{max} (v)}{{\tilde{T}}_{max} (v)},$

(3.54)

ami a Rayleigh-hányados általánosításaként az első sajátfrekvenciára kínál becslést végtelen szabadságfokú (kontinuum) rendszerek esetén is. Azaz a legkisebb sajátfrekvenciához tartozó lengésalakot megfelelően közelítve (becsülve), a hozzá tartozó $U_{max}$ és ${\tilde{T}}_{max}$ kifejezések hányadosának gyöke $α_{1}$ -hez közeli értéket ad eredményül.

3.3.4.4. Dunkerley-becslés

Vizsgáljuk ismét a frekvenciaegyenletet:

$0 = \det (- α^{2} \underset{[d_{i j}]}{\underset{︸}{C M}} + I) \equiv | \begin{matrix} 1 - α^{2} d_{11} & - α^{2} d_{12} & \dots & - α^{2} d_{1 n} \\ - α^{2} d_{21} & 1 - α^{2} d_{22} & \dots & - α^{2} d_{2 n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ - α^{2} d_{n 1} & - α^{2} d_{n 2} & \dots & 1 - α^{2} d_{n n} \end{matrix} |$

(3.55)

$\equiv 1 - α^{2} D_{I} + α^{4} D_{I I} - α^{6} D_{I I I} + O (α^{8}) .$

A $D_{I}, D_{I I}, \dots$ együtthatók a $C M$ mátrix első, második, stb. skalárinvariánsait jelölik, tehát pl. $D_{I} = \sum d_{i i}$ , ami a $C M$ mátrix nyomának felel meg.

A váltakozó előjelű együtthatójú, csupa valós gyökkel bíró karakterisztikus polinom analízisével megmutatható, hogy az $α^{2}$ -nél magasabb fokú tagokat elhagyva az első két tag által alkotott másodfokú polinom az $α_{1}$ helyen negatív értéket vesz fel:

$1 - α_{1}^{2} \sum_{i = 1}^{n} d_{i i} < 0, azaz \frac{1}{α_{1}^{2}} < {(C M)}_{I},$

(3.56)

vagy másképpen

$\frac{1}{\sqrt{{(C M)}_{I}}} < α_{1} .$

(3.57)

Olyan különleges esetekben, amikor az $M$ tömegmátrix diagonális, akkor

${(C M)}_{I} = \sum_{i = 1}^{n} c_{i i} m_{i} és így$ $\frac{1}{α_{1}^{2}} < \frac{1}{α_{(I)}^{2}} + \dots + \frac{1}{α_{(N)}^{2}},$

(3.58)

ahol $α_{(i)}^{2} = {(c_{i i} m_{i})}^{- 1}$ az eredeti mechanikai rendszerből képzett olyan egyszabadságfokú rendszerek sajátkörfrekvenciái, ahol csak az $m_{i}$ tömeget tartottuk meg és a többit elhagytuk, és az így kapott részmodell rugómerevsége $s = 1 / c_{i i}$ lett.

Példa Vizsgáljuk egy rezgető motor $I E = 614 {Nmm}^{2}$ hajlítómerevségű tengelyére erősített $h = 4$ mm magasságú és $R = 2$ mm sugarú félhenger alakú $m = 0,2$ g-os rezgő tömeg alkotta rezgőrendszer sajátkörfrekvenciáit. A teljes henger tehetetlenségi nyomatéka $Θ_{z} = 1 / 4 (2 m) R^{2} + 1 / 12 (2 m) h^{2}$ lenne, ahol az első tag a két félhengernek a henger $x z$ szimmetriasíkjáraszámított $1 / 4 m R^{2}$ nagyságú tehetetlenségi nyomatékainak összegével egyezik meg. Ebből a félhengernek a $4 / 3 R / π$ távolságra levő súlypontján átmenő $x z$ síkkal párhuzamos síkra számított tehetetlenségi nyomatéka a Steiner-tételt visszafelé alkalmazva:

$\frac{1}{4} m R^{2} - m \frac{16 R^{2}}{9 π^{2}}, amibõl Θ_{z} = 0,07 m R^{2} + \frac{1}{12} m h^{2} \equiv 0,323 {gmm}^{2} .$

A továbbiakban az egyszerűség kedvéért feltesszük, hogy a tömeg súlypontja a motor tengelyén helyezkedik el, $l + h / 2 = 4$ mm távolságra a tengely csapágyazásától ( $l = 2$ mm a szabad tengelyhossz).

Az $l$ hosszúságú befogott rúd szabad végének $y$ lehajlása és $φ$ szögelfordulása a rúd végére ható $F$ koncentrált erő és $M$ erőpár hatására:

	$y = \frac{F l^{3}}{3 I E} + \frac{M l^{2}}{2 I E},$
	$φ = \frac{F l^{2}}{2 I E} + \frac{M l}{I E} .$

Így a szabad tengelyszakasztól $h / 2$ távolságra levő súlypont $y_{S}$ függőleges elmozdulása a ráható $F$ erő következtében:

$y_{S} = y + \frac{h}{2} \sin φ \approx \frac{F}{I E} (\frac{l^{3}}{3} + 2 \frac{h l^{2}}{4} + \frac{h^{2} l}{4}),$

mivel $M = F h / 2$ és $\sin φ \approx φ$ kis elmozdulások esetén.

Azaz az egyenértékű rugómerevség illetve az abból számítható sajátkörfrekvencia:

$s = \frac{F}{y_{S}} \equiv \frac{614 {Nmm}^{2}}{18, 67 {mm}^{3}} \equiv 32, 87 N/mm \Rightarrow α_{1} \approx \sqrt{\frac{s}{m}} \equiv 12820 \frac{rad}{s} (\approx 2040 Hz) .$
Ha a tehetetlenségi nyomatékot is figyelembe vesszük, akkor egy két szabadsági fokú rendszert vizsgálhatunk, melynek kinetikus illetve potenciális (alakváltozási) energiája:

$T = \frac{1}{2} m {\dot{y}}_{S}^{2} + \frac{1}{2} Θ_{z} {\dot{φ}}^{2} \equiv \frac{1}{2} m {\dot{y}}^{2} + \frac{m h}{2} \dot{y} \dot{φ} + \frac{1}{2} (Θ_{z} + m \frac{h^{2}}{4}) {\dot{φ}}^{2},$

$U = \int F (y, φ) d y + \int M (y, φ) d φ \equiv \int (d q^{⊤} C^{- 1} q) \equiv \frac{1}{2} q^{⊤} S q,$

ahol $S = C^{- 1}$ és

$q \equiv [\begin{matrix} y \\ φ \end{matrix}] = C [\begin{matrix} F \\ M \end{matrix}], vagyis C = \frac{1}{I E} [\begin{matrix} \frac{l^{3}}{3} & \frac{l^{2}}{2} \\ \frac{l^{2}}{2} & l \end{matrix}] \Rightarrow S = \underset{s_{0} \approx 230}{\underset{︸}{\frac{3 I E}{l^{3}}}} [\begin{matrix} 4 & - 2 l \\ - 2 l & \frac{4}{3} l^{2} \end{matrix}] .$

Az $M \ddot{q} + S q = 0$ mozgásegyenlet $M$ tömegmátrixa és $S$ merevségi mátrixa numerikusan:

$M = [\begin{matrix} 0, 2 & 0, 4 \\ 0, 4 & 1, 123 \end{matrix}], S = [\begin{matrix} 921 & - 921 \\ - 921 & 1228 \end{matrix}] 10^{6}$

és a karakterisztikus egyenlet:

$\det (- α^{2} M + S) \equiv (6, 451 {(\frac{α}{1000})}^{4} - 2016, 3 {(\frac{α}{1000})}^{2} + 282750) 10^{12} = 0,$

amiből $α_{1} = 11869$ rad/s (1890 Hz) és $α_{2} = 176389$ rad/s (28073 Hz).
Ha az első sajátfrekvenciával való rezgéshez tartozó rugalmas szál alakját a befogásnak megfelelő peremfeltételt $(Y (0) = 0, Y' (0) = 0)$ kielégítő legegyszerűbb $Y_{1} (x) = a_{0} x^{2}$ függvénnyel közelítjük, valamint

$y (x, t) = Y_{1} (x) \sin α_{1} t, φ (l, t) = Y_{1^{'}} (l) \sin α_{1} t és \max_{t} \dot{y} (x, t) = α_{1} Y_{1} (x), stb .,$

akkor

$U_{max} = \frac{1}{2} \int_{0}^{l} I E {(Y_{1^{″}} (x))}^{2} d x \equiv 2 I E a_{0}^{2} l és$

$T_{max} = \frac{1}{2} m α_{1}^{2} {(Y_{1} (l) + \frac{h}{2} Y_{1^{'}} (l))}^{2} \equiv \frac{1}{2} m α_{1}^{2} a_{0}^{2} l^{2} {(l + h)}^{2},$

amiből a Rayleigh-hányados szerint $α_{1} \leq 2 \sqrt{I E / m l} / (l + h) \equiv 13060$ rad/s $(\approx 2080 Hz)$ .
A kinetikus energia előbbi kifejezésébe beleszámítva a tehetetlenségi nyomatékot is:

$T_{max} = \frac{1}{2} m α_{1}^{2} {(Y_{1} (l) + \frac{h}{2} Y_{1^{'}} (l))}^{2} + \frac{1}{2} Θ_{z} α_{1}^{2} {(Y_{1^{'}} (l))}^{2} \equiv \frac{1}{2} α_{1}^{2} a_{0}^{2} l^{2} (m {(l + h)}^{2} + 4 Θ_{z}),$

és így az első sajátkörfrekvencia javított becslése (vö. két szabadságfokú eset)

$α_{1} \leq \sqrt{\frac{U_{max}}{T_{max}^{⋆}}} \equiv 2 \sqrt{\frac{I E}{l (m {(l + h)}^{2} + 4 Θ_{z})}} \equiv 12026 \frac{rad}{s} (1914 Hz) .$
A rugalmas szál alakját magasabb fokszámú, több ismeretlen paramétert tartalmazó polinommal vagy más függvénnyel (pl. $1 - \cos x$ ) is közelíthetjük. Legyen most $Y_{2} (x) = a_{0} x^{3} + a_{1} x^{2}$ , ami továbbra is megfelel a kinematikai peremfeltételnek. Ezzel

$Y_{2^{″}} (x) = 6 a_{0} x + 2 a_{1} és Y_{2^{'}} (l) = 3 a_{0} l^{2} + 2 a_{1} l .$

A potenciális energia maximuma most:

$U_{max} = 2 I E \int_{0}^{l} (9 a_{0}^{2} x^{2} + 6 a_{0} a_{1} x + a_{1}^{2}) d x \equiv 2 I E (3 a_{0}^{2} l^{3} + 3 a_{0} a_{1} l^{2} + a_{1}^{2} l),$

a kinetikus energia pedig

$T_{max} = \frac{1}{2} m α^{2} {(a_{0} l^{3} + a_{1} l^{2} + \frac{h}{2} (3 a_{0} l^{2} + 2 a_{1} l))}^{2} + \frac{1}{2} Θ_{z} α^{2} {(3 a_{0} l^{2} + 2 a_{1} l)}^{2} .$

Most is feltételezhetjük, hogy a sajátrezgések során a rezgő rendszer minden (anyagi) pontja egyszerre éri el a szélsőhelyzetét, amikor is $U = U_{max}$ és $T = 0$ , valamint $T = T_{m a x}$ esetén $U = 0$ , azaz

$U_{max} = T_{max} \Rightarrow \frac{1}{2} a^{⊤} S a - \frac{1}{2} a^{⊤} α^{2} M a \equiv \frac{1}{2} a^{⊤} (S - α^{2} M) a = 0,$

mivel $U_{max}$ és $T_{max}$ is homogén kvadratikus kifejezése az $a$ vektort alkotó $a_{1}$ és $a_{0}$ paramétereknek. Az $S = [s_{i j}]$ és $M = [m_{i j}]$ mátrixokat az $U_{max}$ és $T_{max}$ kifejezéseinek $a_{i}$ és $a_{j}$ szerinti paricális deriválásából kaphatjuk meg:

$S = 2 I E [\begin{matrix} 6 l^{3} & 3 l^{2} \\ 3 l^{2} & 2 l \end{matrix}] \equiv 614 [\begin{matrix} 96 & 24 \\ 24 & 8 \end{matrix}] 10^{6},$

$\begin{matrix} m_{11} & = & m l^{4} {(l + \frac{3}{2} h)}^{2} + Θ_{z} 9 l^{4} \equiv 251, 25, \\ m_{12} = m_{21} & = & m l^{3} (l + \frac{3}{2} h) (l + h) + Θ_{z} 6 l^{3} \equiv 92, 28, \\ m_{22} & = & m l^{2} {(l + h)}^{2} + Θ_{z} 4 l^{2} \equiv 33, 96. \end{matrix}$

Triviálistól eltérő, $a = 0$ vektort úgy kaphatunk, ha

$\det (S - α^{2} M) = 0, ahonnan \begin{matrix} α_{1} & \approx & 11869 \frac{rad}{s}, \\ α_{2} & \approx & 176389 \frac{rad}{s}, \end{matrix}$

vagyis visszakapjuk két szabadságfokú esetnél kiszámított eredményeket, ami nem meglepő, hiszen a köbös közelítés már elégséges a rugalmas szál pontos alakjához. Amennyiben a tengely tömege nem lenne elhanyagolható, a tengely $\frac{1}{2} \int ρ A α^{2} Y^{2} (x) d x$ mozgási energiáját is beszámítva a $T_{max}$ -ba az eredmények pontossága tovább javítható.

Példa Az ábrán egy $m_{1}$ tömegű $R$ sugarú tárcsa és a tetejére helyezett $h$ magasságú, $l$ hosszúságú homogén hasáb látható, melyet a hasáb végét és a falat összekapcsoló $s$ merevségű rugó tart egyensúlyban. A tárcsa gördül a talajon, és a hasáb sem csúszik meg a tárcsa felszínén a kis kitérésű mozgások alatt. Határozzuk meg, hogy milyen paraméterértékek esetén lesz stabilis az egyensúlyi helyzet!

3.1. ábra -

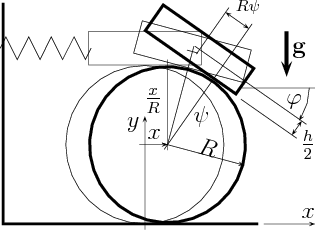
A stabilitás a rugó és a nehézségi erőtér potenciáljának pozitív definitásától függ. Mivel a tárcsa súlypontjának függőleges helyzete nem változik $(r_{S_{1}} = x i)$ , csak a hasáb súlyponti helyvektorára van szükségünk:

$r_{S_{2}} = [\begin{matrix} x + (R + \frac{h}{2}) \sin φ \\ R + (R + \frac{h}{2}) \cos φ \end{matrix}] + [\begin{matrix} - R ψ \cos φ \\ R ψ \sin φ \end{matrix}],$

ahol $ψ = φ - \frac{x}{R}$ , azaz $R ψ = R φ - x$

Feltéve, hogy a rugó az egyensúlyi helyzetben feszítetlen, a megnyúlása egy tetszőleges kitérés esetén:

$Δ l \approx \frac{l}{2} + x + (R + \frac{h}{2}) \sin φ - (R φ - x + \frac{l}{2}) \cos φ .$

Ezzel az $U$ potenciálfüggvény:

$U = m_{2} g (R + (R + \frac{h}{2}) \cos φ + (R φ - x) \sin φ) + \frac{1}{2} s Δ l^{2},$

melynek parciális deriváltjai és egyensúlyi helyzet körüli linearizálása:

	$\frac{\partial U}{\partial x} = - m_{2} g \sin φ + s (\frac{l}{2} \underset{\approx 0}{\underset{︸}{(1 - \cos φ)}} + x \underset{\approx 2}{\underset{︸}{(1 + \cos φ)}} + (R + \frac{h}{2}) \sin φ - R \underset{\approx φ}{\underset{︸}{φ \cos φ}}) \underset{\approx 2}{\underset{︸}{(1 + \cos φ)}},$
	$\frac{\partial U}{\partial φ} = m_{2} g (- \frac{h}{2} \sin φ + (R φ - x) \underset{\approx 1}{\underset{︸}{\cos φ}})$
	$+ s (x (1 + \cos φ) + (R + \frac{h}{2}) \sin φ - R φ \cos φ) ((R φ - x) \sin φ + \frac{h}{2} \cos φ)$
	$\approx m_{2} g ((R + \frac{h}{2}) φ - x) + s (2 x + \frac{h}{2} φ) \frac{h}{2} .$

A linearizált rendszer $S$ merevségi mátrixa tehát:

$S = [\begin{matrix} 4 s & s h - m_{2} g \\ s h - m_{2} g & m_{2} g (R - \frac{h}{2}) + s \frac{h^{2}}{4} \end{matrix}],$

és a determinánsa:

$4 s (m_{2} g (R - \frac{h}{2}) + s \frac{h^{2}}{4}) - {(s h - m_{2} g)}^{2} > 0 \Rightarrow 4 σ (1 - η + σ η^{2}) - {(2 σ η - 1)}^{2} \equiv 4 σ - 1 > 0,$

ahol $σ = s R / m_{2} g$ és $η = h / 2 R$ . Tehát a stabilitás feltételei ( $S$ sarokaldeterminánsai alapján):

$s > 0 és s > \frac{m_{2} g}{4 R} .$

^[3] azaz nem feltétlenül, de gyakran

^[4] A $j$ -edik konjugált gyökpárhoz tartozó megoldás alternatív alakja: $e^{β_{j} t} (a_{j} u_{j} + b_{j} v_{j}) \cos γ_{j} t +$ $e^{β_{j} t} (b_{j} u_{j} - a_{j} v_{j}) \sin γ_{j} t$

Vissza	Fel	Előre
2. fejezet - Merev test rendszerek dinamikája	Főoldal	4. fejezet - Mechanizmusok vizsgálati módszerei