1. fejezet - Példa – Robot manipulátor vezérlésére
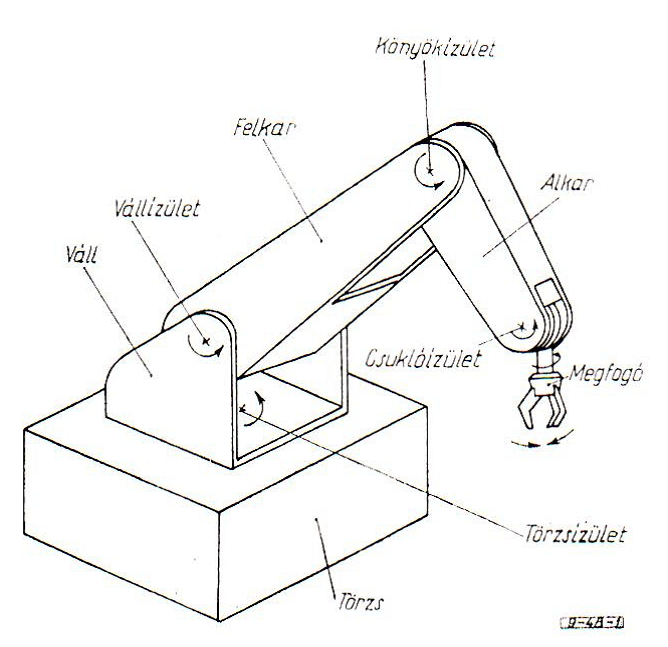
A robot manipulátor mechanikája öt részre tagolható (lásd a lenti ábrán). A manipulátor mozdulatlan része a törzs. A törzshöz a törzsízülettel kapcsolódik a váll. A vállhoz a vállízülettel a felkar, a felkarhoz a könyökízülettel az alkar kapcsolódik. Az alkarhoz a csuklóízület kapcsolja a megfogót. A csuklóízületet két független kúpkerék alkotja. A két kúpkerék egyidejű és megfelelő irányú mozgatása a megfogó egymástól független billenő és csavaró mozgását teszi lehetővé. A megfogó három nyitható-zárható rugalmas ujjból áll. A mozgást hat négyfázisú léptetőmotor végzi.
A vezérelt mozgás programozása alapvetően kétféle módon történhet. Az egyik lehetőség az, ha a mozgatni kívánt motorhoz rendelt billentyűk megfelelő sorrendű lenyomásával végigvezetjük a robot manipulátort a kívánt pályán, miközben a program a pálya bizonyos pontjaihoz rendelt koordinátákat tárolja.
A másik lehetőség a mozgás programozására az, ha a pálya pontjait világkoordinátákban közöljük a vezérlőprogrammal. A robot manipulátor jelenleg nincs érzékelőkkel ellátva, ezért bekapcsolás után vagy egy előre definiált (lásd a lenti ábrán) referenciahelyzetbe kell azt hozni, vagy világkoordinátákban közölni kell a programmal a robot manipulátor bekapcsolás pillanatában elfoglalt helyzetét.
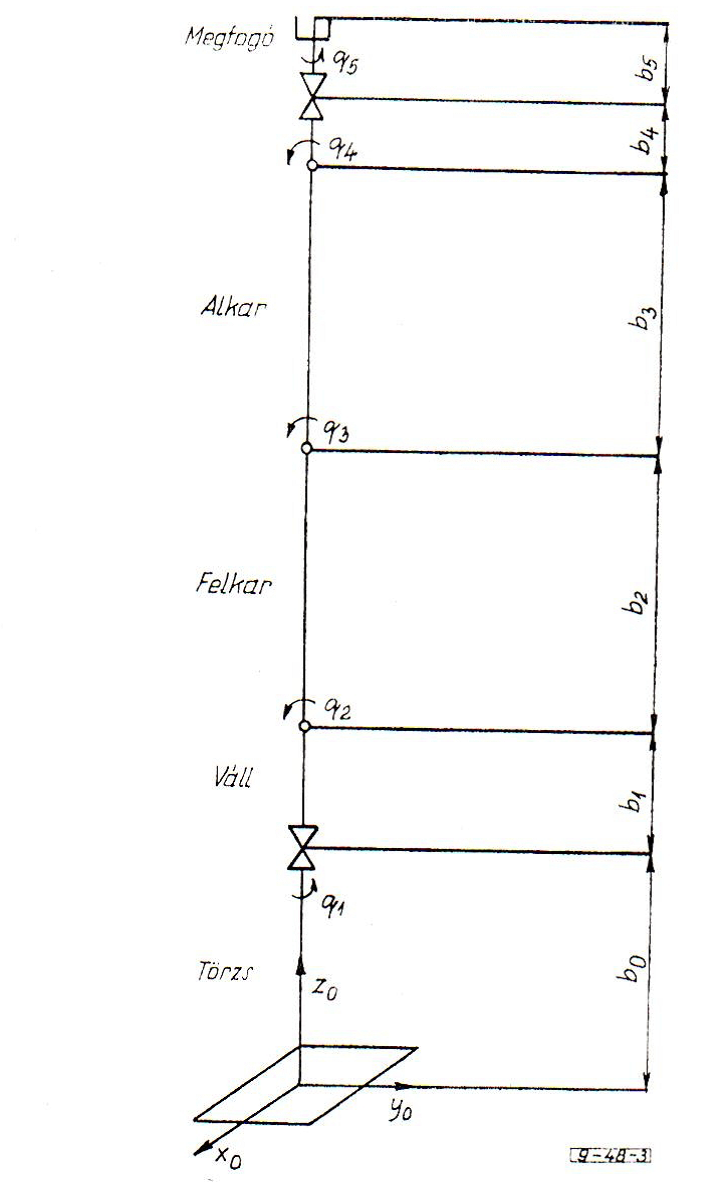
A robotirodalomban szokásos jelöléssel különböztettük meg a hajlító és a csavaró ízületeket. Az ízületi változókat ‑vel, az ízületek távolságát ‑vel jelöltük. A robot manipulátor Denavit‑Hartenberg leírási mód szerinti geometriai paramétereit az alábbi táblázatban közöljük.
|
Tagok |
0 |
1 |
2 |
3 |
4 |
5 |
|
[fok] |
- |
0 |
0 |
|||
|
[fok] |
- |
0 |
0 |
0 |
||
|
[mm] |
0 |
0 |
0 |
0 |
0 |
0 |
|
[mm] |
160 |
80 |
190 |
190 |
0 |
80 |
A referenciahelyzetben minden kartag tengelye merőleges az alapsíkra, az ízületi változók értéke nulla, a megfogó pozíciója [0, 0, 700].
A program mozgatása közben mindig azt tartja nyilván, hogy az egyes motorok hány lépés megtétele után kerülnek a robot manipulátor adott helyzetéből a referenciahelyzetbe. A programnak azt mindig tárolnia kell, hogy az egyes motorok milyen gerjesztési állapotban vannak.
A tárolt pályapontokon akár folyamatosan, akár pontonként előre-hátra pontonként vezethetjük végig a robot manipulátort, miközben lehetőségünk van a pálya módosítására, pontosítására.
A végigvezetéses pályatanítás közben a program akkor őriz meg egy pályapontot, ha
-
bármely motor az utolsó tárolt pályapont óta 121 lépésben többet tett meg (ez egy kartag kb. 6°-os elfordulását jelenti),
-
bármely motor mozgásiránya megváltozik (beleértve a motor elindulását és leállását),
-
egy fontosnak ítélt pontnál erre külön utasítást adunk.
1.1. Az inverz geometriai feladat bemutatása
Az inverz geometriai feladat megoldásakor a megfogó világkoordinátákban megadott állapotából (amelynek megadási módját a későbbiekben definiáljuk) az úgynevezett ízületi koordinátákat számítjuk ki. Az ízületi koordináták alatt az ízületeknek a referenciahelyzetből történő elmozdulásait értjük.
Tekintsük az alábbi ábrát, ahol feltüntettük a Denavit‑Hartenberg leírási módszer szerint választott ízületi koordinátarendszereket. A megfogó állapotát világkoordinátákban a pozíciójával, az orientációjával és az ujjai helyzetével adjuk meg.
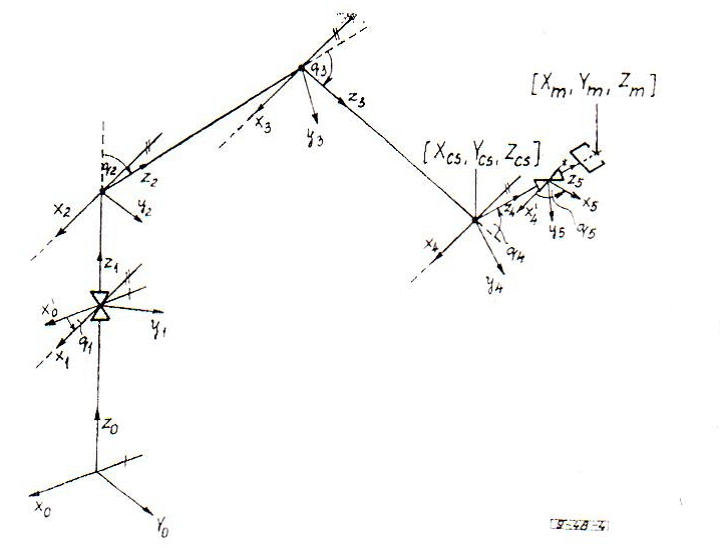
A pozíció három koordinátája a robot manipulátor munkaterén belül tetszőlegesen előírható.
Az orientációt az úgynevezett Euler-szögekkel adjuk meg (lásd alábbi ábra) amelynek a világ- és a megfogó koordinátarendszere között teremtenek kapcsolatot.
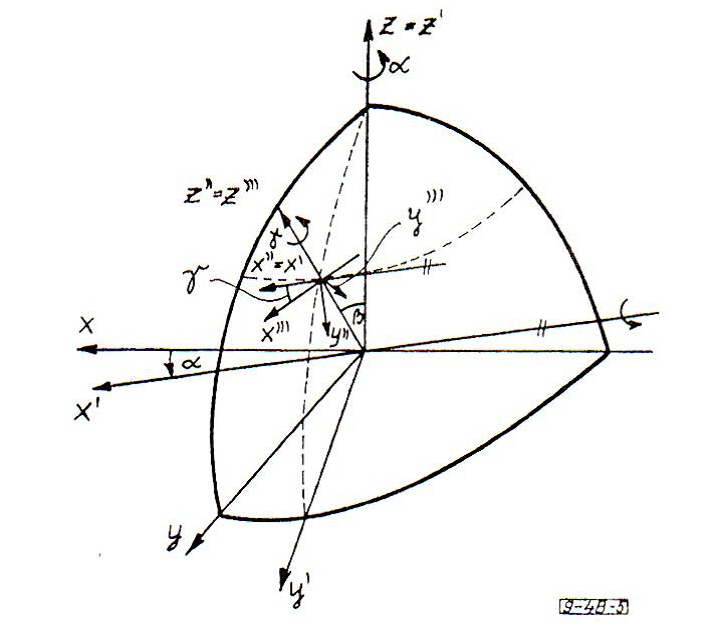
Mivel a robot manipulátor csak öt szabadságfokú, ezért az Euler-szögek csak a és választható tetszőlegesen. Az szöget a pozíció határozza meg.
A megfogó ujjak helyzetét azzal írjuk elő, hogy megadjuk annak a hengeres tárgynak az átmérőjét, amelyet még szorítás nélkül képes megfogni.
Ismeretes, hogy az inverz geometriai feladatnak általában több megoldása van. A program alapértelmezésben olyan megoldást keres, amikor a robot manipulátor a válltól előre nyúl, vagyis a váll koordinátarendszerében a megfogó pozíciójának koordinátája nem negatív értékű.
Továbbá az alapértelmezésben a könyök felső helyzetben van, tehát . A program lehetőséget nyújt arra, hogy mozgatás során a robot manipulátor az alapértelmezéstől eltérő helyzetbe kerüljön. A világkoordinátákban megadott és szögek megegyeznek a csuklóízület és elmozdulásaival.
Ha a megfogó pozícióját az síkra vetítjük (lásd alábbi ábra) és figyelembe vesszük a váll koordinátarendszerére tett kikötést, akkor törzselfordulást egyértelműen meghatározhatjuk.
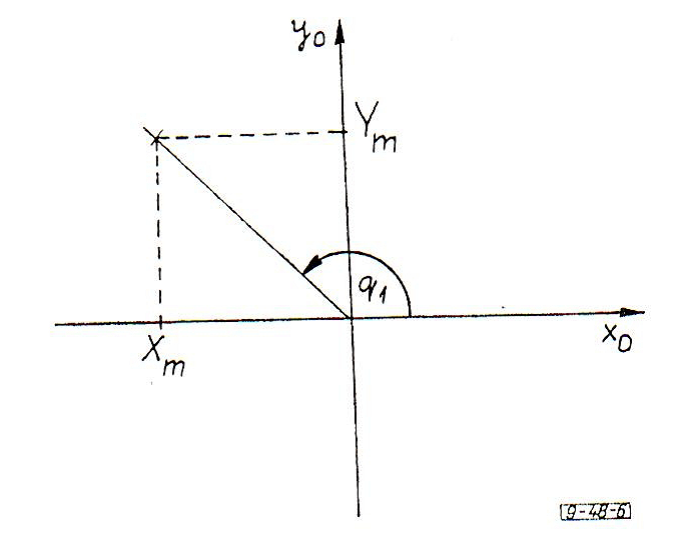
Ha , akkor
|
. |
(1.1) |
Ha , és , akkor értéke határozatlan. Ebben az esetben a törzs megtartja korábbi helyzetét.
A elmozdulással a megfogó orientációja is ismertté válik, így következtethetünk a csuklóízület [] pozíciójára
|
|
(1.2) |
Ha , és , akkor értéke határozatlan. Ebben az esetben a törzs megtartja korábbi helyzetét.
A elmozdulással a megfogó orientációja is ismertté válik, így következtethetünk a csuklóízület [] pozíciójára
|
|
(1.3) |
|
|
(1.4) |
|
|
(1.5) |
Az alkar, a felkar és a megfogó a váll koordinátarendszerében mindig a és tengelyek által kifeszített síkba esik. Rajzoljuk meg e síkban az említett kartagokat (lásd az alábbi ábra). A csukló-, a könyök- és a vállízület alkotta háromszög két oldalát konstrukciós adatokból ismerjük. A harmadik oldal meghatározása érdekében számítsuk ki a csuklóízület pozícióját a (lásd az alábbi ábra) koordinátarendszerében.
|
|
(1.6) |
|
|
(1.7) |
Térjünk át polár‑koordinátákra
|
|
(1.8) |
Ha , akkor
|
|
(1.9) |
|
|
(1.10) |
Ha és akkor
|
|
(1.11) |
A és eset nem lehetséges, kívül esik a robot manipulátor munkaterületén.
Az említett háromszögben a kiegészítő szögét a koszinusztétellel számítjuk ki. Figyelembe véve a könyök pozíciójára tett kikötést, a elmozdulást a következő egyenlettel kapjuk meg
|
|
(1.12) |
Mivel az alkar és a felkar hossza megegyezik, vagyis a vizsgált háromszög egyenlő szárú, a elmozdulás is könnyen meghatározható:
|
|
(1.13) |
Ezzel ismertté vált az összes ízületi elmozdulás nagysága, amelyeket az áttételek (beleértve a megfogó ujjak áttételét) ismeretében könnyen átszámíthatunk a motorok lépésszámaivá.
Két pályapont között a motorok állandó sebességgel mozognak. Ha azt szeretnénk, hogy az általunk megadott két pályapont között a robot manipulátor közelítőleg egyenes vonal mentén haladjon, akkor utasítást adhatunk arra, hogy a program a kezdő- és végpont közé generáljon adott számú az egyenes vonalú pályára eső pályapontot.
A program elsősorban oktatási céllal készült, ezért a felhasználó a számítógép képernyőjén mindig pontosan nyomon követheti a számításokat és a robot manipulátor helyzetét akár ízületi, akár világkoordináta-rendszerben. Az inverz geometriai feladat számítása közben a program ellenőrzi, hogy az adott ízületi elmozdulás nem ütközik-e a robot manipulátor konstrukciós korlátaiba, ugyanakkor jelzi a felhasználónak, ha a megfogó, vagy végberendezés adott állapotát a robot manipulátor az alapértelmezéstől eltérő módon is meg tudja valósítani.
A jövőben a robot manipulátort érzékelőkkel kívánjuk ellátni és az oktatási céloktól az ipari igények felé igyekszünk közelíteni.