5. fejezet - Komplex számok
- 5.1. Komplex számok bevezetése
- 5.2. Műveletek komplex számokkal
- 5.3. A komplex szám ábrázolása
- 5.4. Néhány a komplex számokra vonatkozó azonosság
- 5.5. Műveletek a trigonometrikus alakkal
- 5.6. A matematikai műveletek geometriai szemléltetése
- 5.7. A komplex számok exponenciális alakja
- 5.8. Gyökvonás komplex számok esetén
- 5.9. Néhány komplex függvény ábrázolása
- 5.10. Javasolt feladatok
- 5.11. Megoldások
5.1. Komplex számok bevezetése
A nincs értelmezve a valós számok halmazán. Bővítsük a szám fogalmát úgy, hogy és többszörösei is legyen része. Az egyszerűség kedvéért jelöljük j-vel.
Legyenek rá érvényesek a számok között definiált műveletek és az azokra vonatkozó szabályok:
|
Leírás |
Példák |
||||
|
Valós |
Valós és komplex |
||||
|
1. |
Minden a, b esetén összegük is szám: a+b=c |
1+2=3 |
j+2j=3j |
||
|
2. |
Az összeadás asszociatív: (a+b)+c=a+(b+c) |
(1+2)+3=1+(2+3) |
(j+2j)+3j=j+(2j+3j) |
||
|
3. |
Az összeadás kommutatív: a+b=b+a |
1+2=2+1 |
j+2j=2j+j |
||
|
4. |
Minden a, b esetén csak egy x van, amelyre a+x=b |
1+x=3x=2 |
1j+x=3jx=2j |
||
|
5. |
Minden a, b esetén szorzatuk is szám: a•b=c |
1•2=2 |
j•2j=-2 |
||
|
6. |
A szorzat asszociatív: (a•b)•c=a•(b•c) |
(1•2)•3=1•(2•3) |
(j•2j)•3j=j•(2j•3j) |
||
|
7. |
A szorzás kommutatív: a•b=b•a |
1•2=2•1 |
j•2j=2j•j |
||
|
8. |
Minden a, b esetén, ha a≠0 csak egy x van, amelyre ax=b |
1•x=2x=2 |
j•x=-2x=2j |
||
|
9. |
Minden a, b és c esetén fennáll a disztributivitás: a•(b+c)=a•b+a•c |
2•(1+3)=2•1+2•3 |
j•(2j+3j)=j•2j+j•3j |
||
A komplex szám általánosan két – egy valós és egy képzetes – részből áll. Jelölése: a+bj, ahol a és b valós számok, és a a valós, bj pedig a képzetes rész. Ez utóbbi azt jelenti, hogy a képzetes egységből b db van a számban (tehát bj=b•j). Szokás még a z=a+bj jelölés is. Erre az „összetett” z számra is igazak a táblázatban leírt szabályok. Meg kell azonban jegyezni, hogy a komplex számok halmaza nem rendezett, tehát nem mondhatjuk azt, hogy az egyik komplex szám nagyobb, mint a másik (azaz z1>z2 értelmetlen).
5.2. Műveletek komplex számokkal
A számítások során j-t ugyanúgy használjuk, mintha valós szám lenne, de ha előfordulnak a hatványai, akkor kihasználhatjuk, hogy j•j=j2=-1. Érdemes megfigyelni, hogy j hatványai négyes periódussal rendelkeznek:
j1=j
j2=j•j=-1
j3=j•j2=-j
j4=j•j3=1
j5=j•j4=jstb.
A fent említett jelölés (a+bj) a komplex szám algebrai, vagy kanonikus alakja. A későbbiekben az algebrai alak elnevezést fogjuk használni. A következőkben nézzünk néhány példát a négy alapművelet alkalmazására.
5.2.1. Összeadás
Általánosan:
z1=a+bj; z2=c+dj; z3=z1+z2=?
z3=a+bj+c+dj=(a+c)+(b+d)j=e+fj
(1+2j)+(0+j)=(1+0)+(2+1)j=1+3j
(5+2j)+(3+0j)=(5+3)+(2+0)j=8+2j
(1+0j)+(2+0j)=(1+2)+(0+0)j=3+0j=3
(2+j)+(3+2j)=(2+3)+(1+2)j=5+3j
(2+(-j))+(3+2j)=(2+3)+(-1+2)j=5+j
(1-2j)+(-1-3j)=(1-1)+(-2-3)j=-5j
5.2.1.1. Kivonás
Általánosan:
z1=a+bj; z2=c+dj; z3=z1-z2=?
z3=(a+bj)-(c+dj)=(a-c)+(b-d)j=e+fj
-
(1+2j)-(0+j)=(1-0)+(2-1)j=1+j
-
(5+2j)-(3+0j)=(5-3)+(2-0)j=2+2j
-
(1+0j)-(2+0j)=(1-2)+(0-0)j=-1+0j=-1
-
(2+j)-(3+2j)=(2-3)+(1-2)j=-1-j
-
(2+(-j))-(3+2j)=(2-3)+(-1-2)j=-1-3j
-
(1-2j)-(-1-3j)=(1+1)+(-2+3)j=2+j
5.2.1.2. Szorzás
Általánosan:
z1=a+bj; z2=c+dj; z3=z1•z2=?
z3=(a+bj)•(c+dj)=a•c+a•dj+bj•c+b•dj2=ac+ j• (ad+bc)+ j•bd•(-1)=(ac-bd)+(ad+bc)=e+fj
5.2.1.3. Osztás
-
(1+2j)•(0+j)=(1+2j)•j=j+2j2=j-2=-2+j vagy =(1•0-2•1)+(1•1+2•0)j=-2+j
-
(5+2j)•(3+0j)=(5+2j)•3=15+6j vagy =(5•3-2•0)+(5•0+2•3)j=15+6j
-
(1+0j)•(2+0j)=1•2=2 vagy =(1•2-0•0)+(1•0+0•2)j=2+0j=2
-
(2+j)•(3+2j)=(2•3-1•2)+(2•2+1•3)j=(6-2)+(4+3)=4+7j
-
(2+(-j))•(3+2j)=(2•3+1•2)+(2•2-1•3)j=(6+2)+(4-3)=8+j
-
(1-2j)•(-1-3j)=(-1•1-2•3)+(-1•3+2•1)j=(-1-6)+(-3+2)=-7-j vagy =-(1-2j)•(1+3j)=-(1•1+2•3)-(1•3-2•1)j=-(1+6)-(3-2)=-7-j
Általánosan:
z1=a+bj; z2=c+dj; z3=z1/z2=?
Kihasználjuk a következő – a valós számok köréből ismert – azonosságot:
x2-y2=(x+y)(x-y).
5.2.1.4. További szokásos jelölések
Re(z) jelenti valamely komplex szám valós, Im(z) pedig képzetes részét. Ha z=a+bj, akkor Re(z)=a és Im(z)=b. Fontos: mind a valós, mind a képzetes rész valós szám!
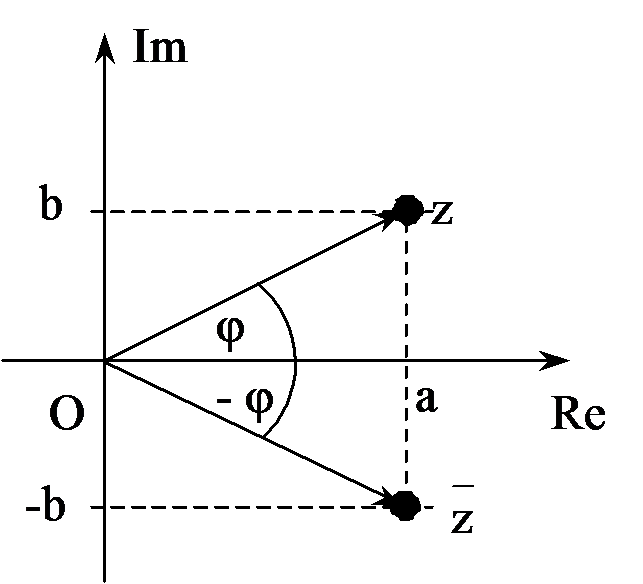
Valamely z komplex szám konjugáltja . Ha z=a+bj, akkor . Vegyük észre, hogy az osztáskor a nevező konjugáltjából álló törttel szoroztunk. Az ott látottak alapján megállapíthatjuk, hogy egy komplex számot megszorozva a konjugáltjával valós számot kapunk: (a+bj)•(a-bj)=a2+b2.
5.3. A komplex szám ábrázolása
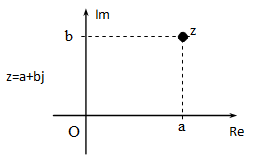
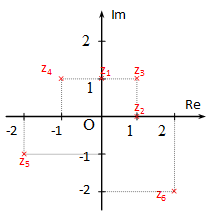
A valós számokat számegyenesen ábrázoljuk. Egy egyenes a komplex számok ábrázolására nem elegendő, mivel valós és képzetes részből állnak. Ki kell tehát lépnünk az egyenesből a síkba. Ezt a síkot komplex számsíknak nevezzük. Vegyünk fel egy derékszögű koordinátarendszert és a vízszintes tengelyen a komplex szám valós, a függőleges tengelyen pedig képzetes részét jelöljük.
Példák:
z1=0+jz2=1+0jz3=1+j
z4=-1+jz5=-2-jz6=2-2j
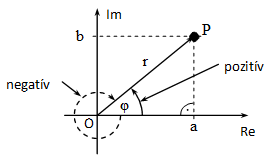
Az ábrázolás már sugallja, hogy a komplex számot vektorként is értelmezhetjük. Ebben az estben az OP vektor jelenti a z komplex számot. A vektor koordinátái rendre a komplex szám valós- és képzetes részei. Mint minden vektort, ezt is megadhatjuk a hosszával és a valós tengellyel bezárt szögével is. Ez utóbbit azonban pontosan definiálni kell, mivel a szög kétféle módon is értelmezhető. Pozitív az a szög, amelyet úgy kapunk, hogy a valós tengelyt az óramutató járásával ellentétes irányban az OP vektorra forgatjuk. A pozitív szög jelölése: arg z.
A vektor geometriai adatait könnyen felírhatjuk a komplex szám algebrai alakjának segítségével, ha felhasználjuk a derékszögű háromszögekről tanult összefüggéseket. A vektor hosszát a komplex szám abszolút értékének hívjuk. Ez a Pitagorasz tétel segítségével:
, a szög pedig: .
Érdemes az algebrai alak paramétereit (a és b) is kifejezni a geometriai alak paramétereivel:
Ez utóbbit a komplex szám trigonometrikus alakjának hívjuk, és gyakran használjuk, mert segítségével néhány művelet sokkal könnyebben elvégezhető, mint az algebrai alakkal.
5.4. Néhány a komplex számokra vonatkozó azonosság
|
Azonosság |
Bizonyítás |
|||
|
a, |
|
|
||
|
b, |
|
|
||
|
c, |
|
|
||
|
d, |
|
|
||
|
e, |
|
b, illetve d, felhasználásával |
||
|
f, |
e, általánosítható:
|
teljes indukcióval bizonyítható |
||
|
g, |
|
f, alapján, ha minden zi azonos (i=1,2,…,n) |
||
|
h, |
|
a jobboldalakból az állítás adódik |
||
|
i, |
|
|
|
|
5.5. Műveletek a trigonometrikus alakkal
5.5.1. Szorzás
A szükséges trigonometriai azonosságok:
Az abszolút értékeket tehát összeszorozzuk, a szögeket összeadjuk. Az, hogy az abszolút értékeket össze kell szorozni e,-ből is látható. A szögekre vonatkozó összefüggés (f,-hez hasonlóan) általánosítható:
arg(z1 z2 … zn)=arg z1+arg z2+…arg zn.
Ha azonban minden zi=z (ahol i=1,2,…,n), akkor arg zn=n arg z. Ennek és g,-nek a felhasználásával felírható zn összefüggése:
Ez az összefüggés Moivre tétele.
5.5.1.1. Osztás
Első lépésként nézzük meg, hogy mi lesz egy komplex szám reciproka:
a számláló z konjugáltja, a nevező pedig az abszolút értéke, így . Ebből . Ezzel az osztást visszavezettük szorzássá, már csak a konjugált abszolút értékét és szögét kell kifejezni z2 paramétereivel:
c, alapján és i, alapján .
. Tehát az abszolút értékeket osztjuk, a szögeket pedig kivonjuk egymásból!
Példák:
-
-
-
a,-ból
-
.
Tehát z az x3=1 egyenlet egyik gyöke.
5.6. A matematikai műveletek geometriai szemléltetése
z1=a+bjz2=c+dj
Összeadás Kivonás
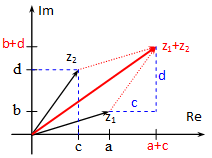
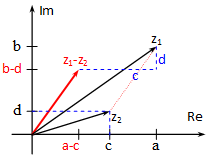
A geometriában tanult vektorösszegzési és kivonási szabályok itt is érvényesek, mint ahogy az ábrából is látszik.
5.6.1. Szorzás
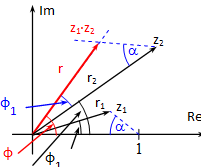
A következőkben a szorzat vektor megszerkesztésének módját ismerjük meg. Ehhez felhasználjuk a komplex számok szorzásáról tanultakat, azaz a szögek összeadódnak, az abszolút értékek összeszorzódnak.
amiből a szorzatvektor egyenese már megszerkeszthető.
Bizonyítsuk be, hogy az origó, 1, z1 és az origó, z2, z1z2 háromszögek hasonlóak. Elegendő azt belátni, hogy egy szöge, és ezen szögek szárainak aránya megegyezik. Az origónál levő szög mindkét háromszögben φ1 , tehát az egyik feltétel teljesül. Az oldalak aránya pedig: , ami igaz, hiszen a komplex számok abszolút értékeit össze kell szorozni. Ezek szerint a két háromszög tényleg hasonló, amiből viszont az következik, hogy minden szögük – tehát a z2-nél és 1-nél jelölt α szögek is – egyenlők. Így a szorzat már megszerkeszthető.
5.6.1.1. Osztás
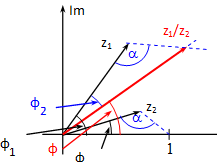
Nagymértékben építhetünk a szorzásnál tapasztaltakra, hiszen az osztás a szorzás ellentett művelete.
A hányados egyenesét úgy kaphatjuk, hogy z1 vektorát elforgatjuk –φ szöggel, mivel . Az előzőek alapján az origó, 1, z2 és az origó, z1/z2, z1 háromszögek hasonlóak, így az α szöget z1-nél felmérve a két egyenes metszéseként megkapjuk a keresett hányados vektort.
5.7. A komplex számok exponenciális alakja
Az áttérést az ún. Euler formula biztosítja. Ez a következő:
,
ahol e a természetes logaritmus alapszáma (≈2.718281828), -t pedig hatványnak tekintjük, ahol e az alap jφ pedig a kitevő.
A következőkben nem matematikai egzaktságú bizonyítással, hanem csak egy levezetéssel érzékeltetjük, hogy ami a valós számok között elképzelhetetlennek tűnik (egy hatvány függvény egyenlő a korlátos szinusz és koszinusz összegével), az a komplex számok körében valóság lehet.
A levezetéshez Maclaurin (nulla körüli Taylor) sorokat használunk fel. Bizonyítható, hogy az exponenciális függvény Maclaurin sora komplex változókkal is konvergens. Írjuk fel Maclaurin sorát, bontsuk ki:
A számlálóba írjuk be j hatványait, majd csoportosítsuk külön a valós, és külön a képzetes tagokat:
A két szummában sorban a koszinusz és a szinusz Maclaurin sorát kaptuk.
Az Euler formula tulajdonképpen egy egységnyi abszolút értékű komplex számot jelent, melynél az argumentum φ. Vizsgáljuk meg, hogy ez az egyezés fennáll-e a művelet végzés esetén is.
Szorzás:
Osztás:
Egész kitevős hatványozás:
Könnyen belátható, hogy az egyezés nem csak egységnyi abszolút értékű komplex számok esetén áll fenn. Egy komplex szám trigonometrikus alakból könnyen átírható exponenciális alakra az Euler formula alkalmazásával:
.
Példák:
Az előző feladatsor a, és e, feladatát oldjuk meg.
5.8. Gyökvonás komplex számok esetén
A problémát az jelenti, hogy egy komplex számnak több gyöke van. Tudjuk, hogy a hatványozás a gyökvonás ellentett művelete. Mivel hatványozni a legkényelmesebben a trigonometrikus alak segítségével lehet, ezért itt is azt használjuk.
Legyen és , valamint .
Ekkor a Moivre formula alapján:
.
Ez az egyenlőség csak akkor teljesül, ha az abszolút értékek és a szögek megegyeznek:
.
A gyökvonás összefüggése tehát:
ahol
Ez azt jelenti, hogy a komplex számok halmazán minden számnak n db n-edik gyöke van, hiszen mind a szinusz, mind a koszinusz 2π szerint periodikus.
Megvizsgálva a gyököket látjuk, hogy mindegyikük abszolút értéke azonos , és egymással bezárt szögük többszöröse. Ez azt jelenti, hogy a komplex számsíkon egy origó középpontú sugarú körön egyenletesen helyezkednek el. Ha ezen pontokat összekötjük, akkor egy n oldalú szabályos sokszöget kapunk.
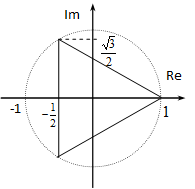
Példák:
A következő k-ra a szög 2π, ami a periodicitás miatt annyi mintha zérus lenne. Ekkor azonban ugyanazt az értéket kapjuk, mint k=0 esetén, Innentől kezdve tehát a gyökök ismétlődnek, így összesen három különböző gyök van.
Ábrázolva:
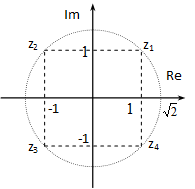
-
Ábrázolva:
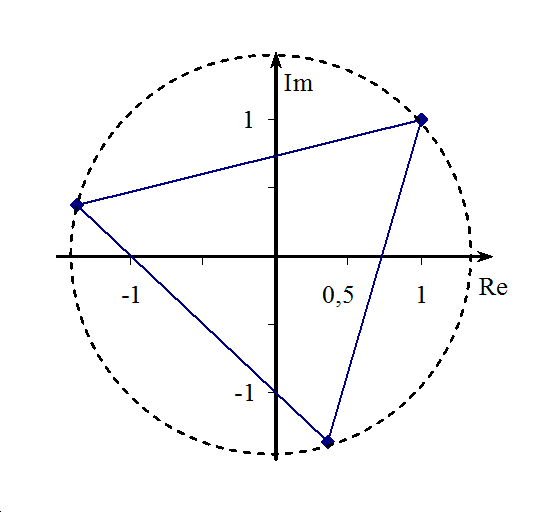
5-4. ábra Ábrázolás
5-5. ábra
Az eredmények meghatározásához a következőket vegyük figyelembe:
5.9. Néhány komplex függvény ábrázolása
A következő feladatokban az ω valós paramétertől függő komplex függvényeket ábrázolunk. Az ω a [0,∞] zárt intervallumba eső értékeket vesz fel.
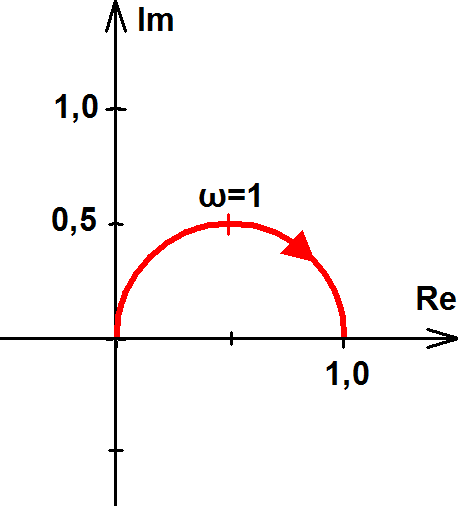
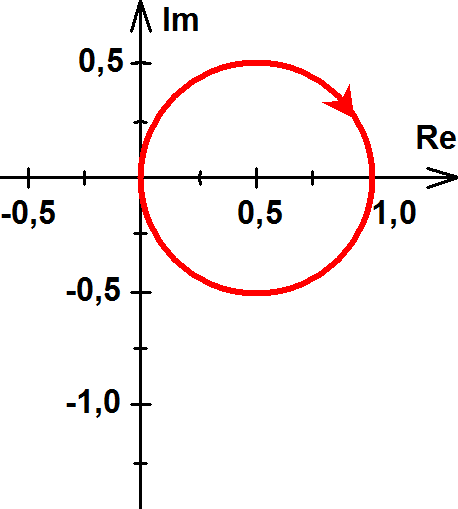
1.Legyen Y(ω)=ejω.
Ekkor Y(ω)=cos ω+jsin ω és Re(Y(ω))=cos ω; Im(Y(ω))=sin ω.
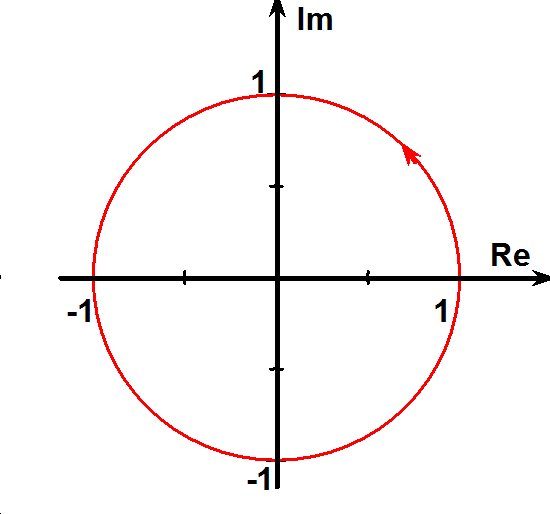
, tehát a függvény minden pontja azonos távolságra van az origótól, azaz a függvény képe kör, melynek sugara 1.
A körön a nyíl az ω növekedésének irányát jelzi.
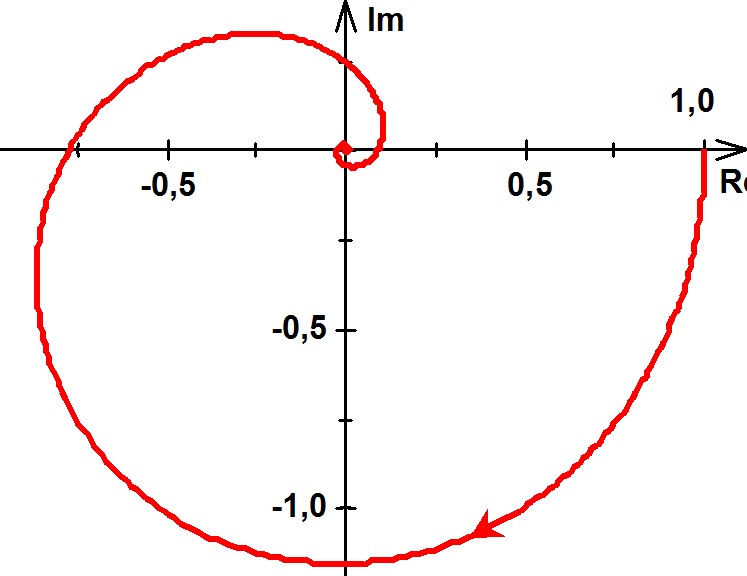
2.Legyen Y(ω)=2ejω.
Ekkor Y(ω)=2(cos ω+jsin ω) és Re(Y(ω))=2cos ω; Im(Y(ω))=2sin ω.
, tehát a függvény minden pontja azonos távolságra van az origótól, azaz a függvény képe kör, melynek sugara 2.
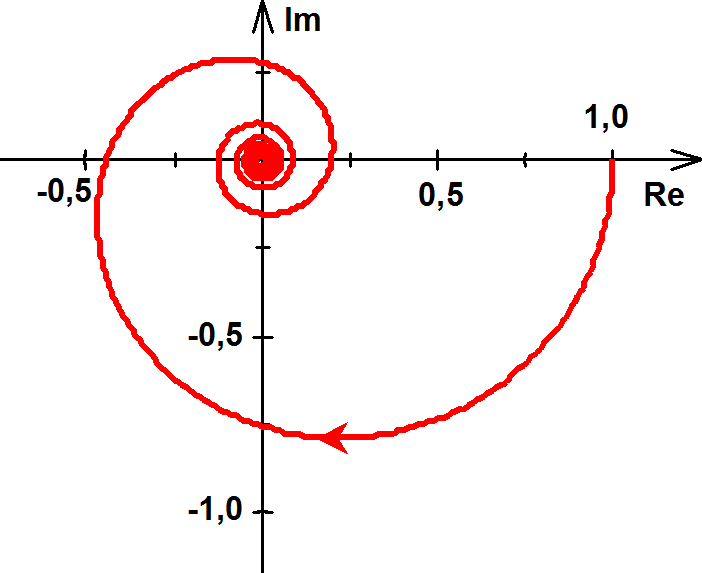
3.Legyen Y(ω)=ej2ω.
Ekkor Y(ω)=cos 2ω+jsin 2ω és Re(Y(ω))=cos 2ω; Im(Y(ω))=sin 2ω.
, tehát ez is kör – mint az 1, feladatban – de az ω növekedésével „gyorsabban haladnak” a függvény pontjai a körön.
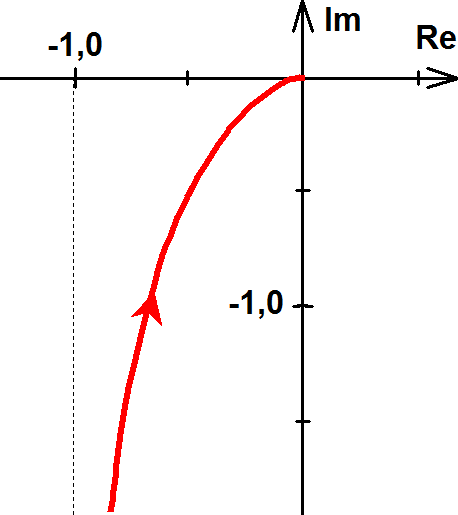
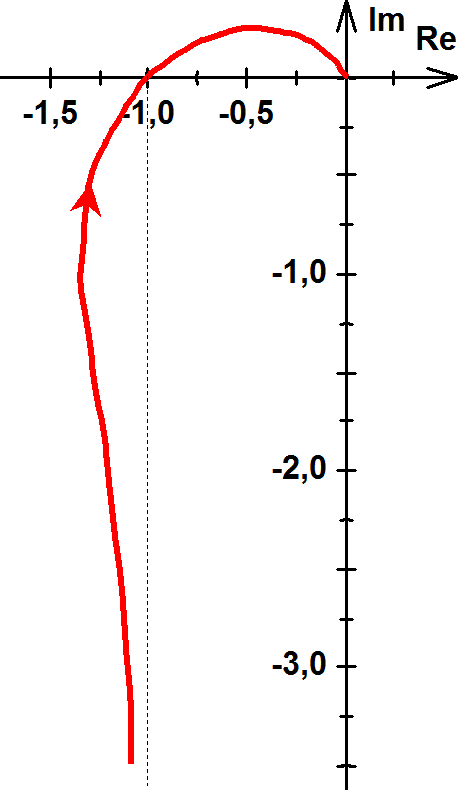
4.Legyen Y(ω)=1+j ω.
Ekkor Re(Y(ω))=1; Im(Y(ω))=ω, tehát valós része mindig 1.
.
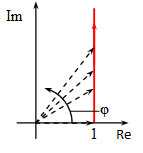
A komplex vektor hossza szigorúan monoton nő, legkisebb értéke egységnyi; szöge szintén szigorúan monoton nő, legkisebb értéke 0°, a legnagyobb pedig 90°. Ezek alapján megállapítható, hogy a függvény képe egyenes, mely a valós tengely 1 pontjából indul, és függőlegesen tart a végtelenbe.
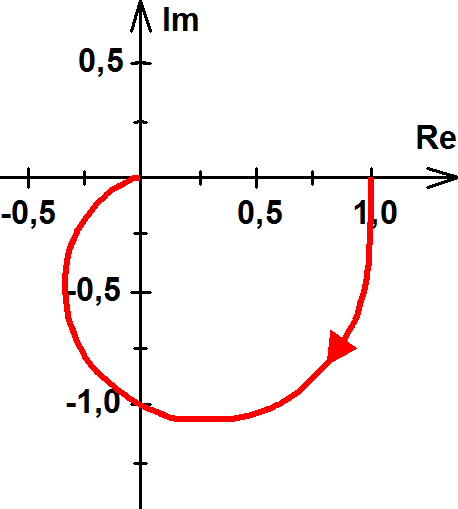
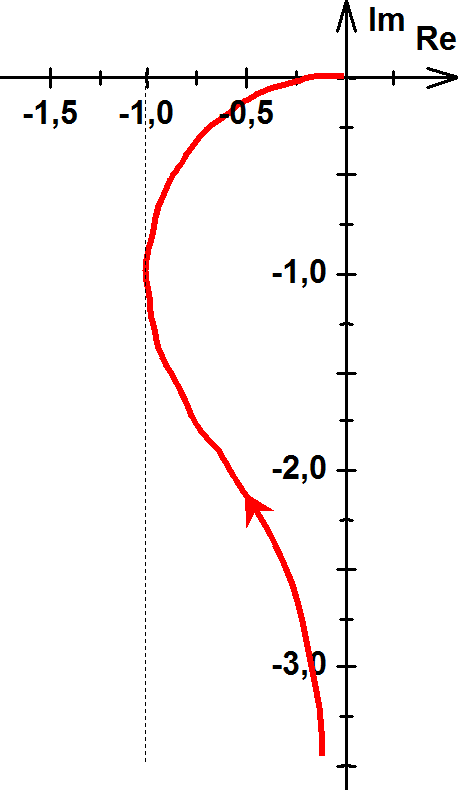
5. Legyen
Az ábrázolás előkészítéseként célszerű a függvényt az algebrai alaknak megfelelő formájúvá rendezni.
. Ebből az alakból könnyen kifejezhetjük az abszolút értéket és a szöget:
Ebből csak azt tudjuk megállapítani, hogy a szög 0°-tól –90°-ig nő, de az abszolút érték nem ad segítséget a függvény alakjának megállapításához. Vizsgáljuk inkább az Y1(ω)=Y(ω)-1 függvényt. Ha ezt sikerül ábrázolni, akkor az eredeti függvényünk képét egy egyszerű eltolással megkapjuk.
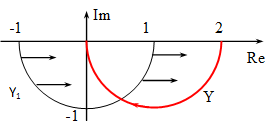
Megállapítható tehát, hogy az ω paramétertől függetlenül minden pont egységnyi távolságra van az origótól, azaz a függvény pontjai egy egységsugarú körön vannak. Mivel Im(Y1(ω)) minden pozitív ω esetén negatív, ezért a függvény képe egy origó középpontú egységsugarú félkör, amely a negatív képzetes félsíkon helyezkedik el.
Az eredeti függvényünk ennek +1-el való eltolásával adódik, így a félkör középpontja az 1+0j pont.
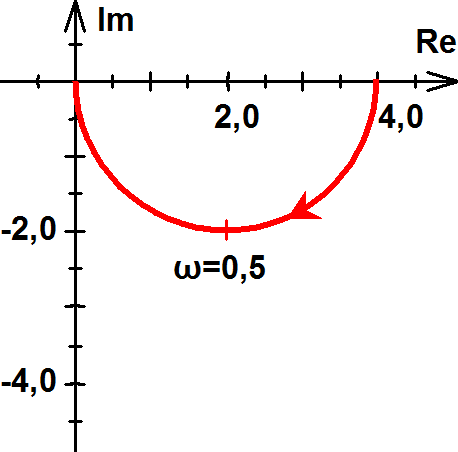
Javasolt feladat: vizsgálata. (Ez is egy félkör, de sugara: A/2, középpontja: A/2+0j. Érdekes még, hogy a függvény minimuma az ω=1/T helyen van, és itt a függvény értéke: A/2-jA/2.
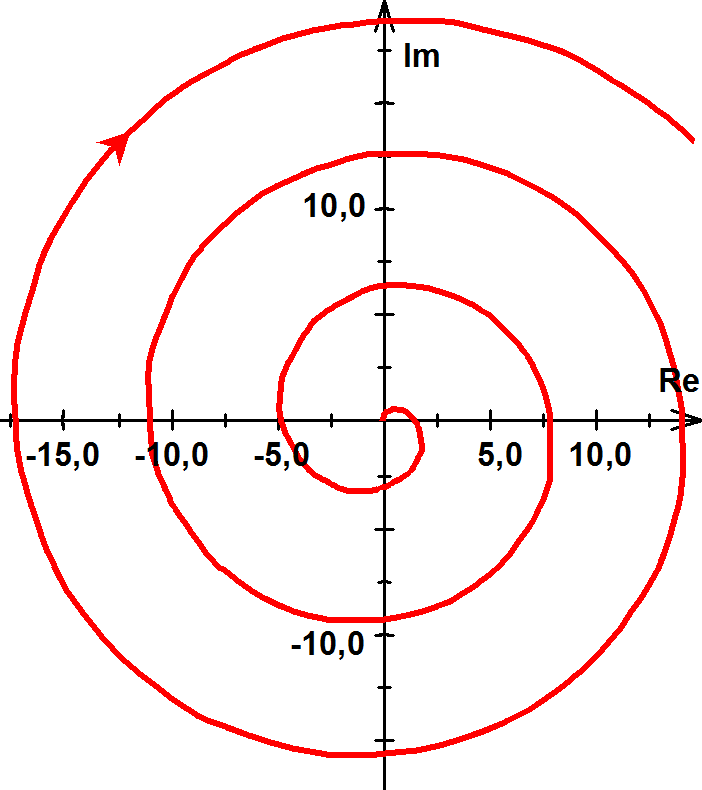
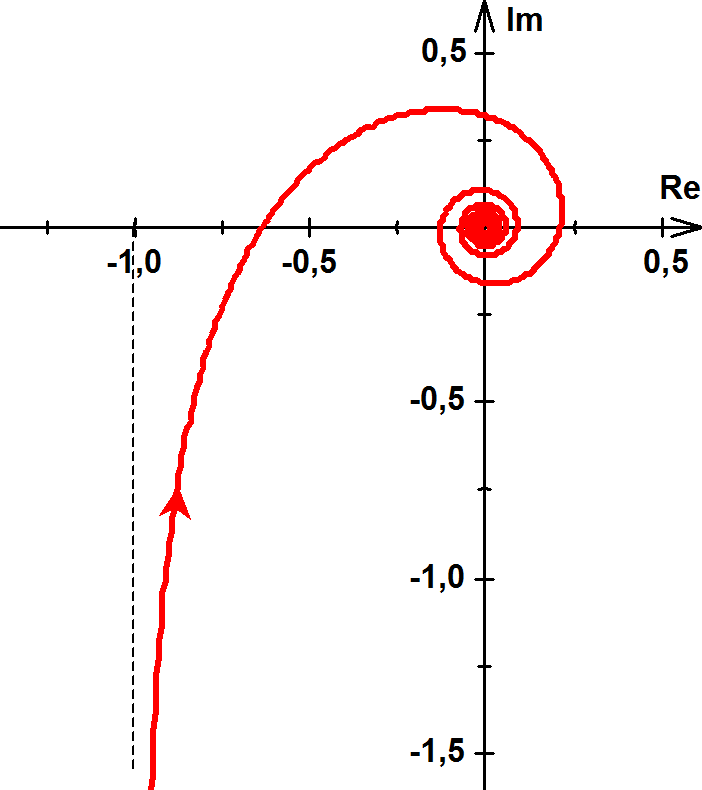
6.Legyen Y(ω)=e -0.1ω+jω.
Ekkor Y(ω)=e -0.1ω e jω = e -0.1ω (cos ω+jsin ω) és Re(Y(ω))= e -0.1ω cos ω; Im(Y(ω))= e -0.1ω sin ω.
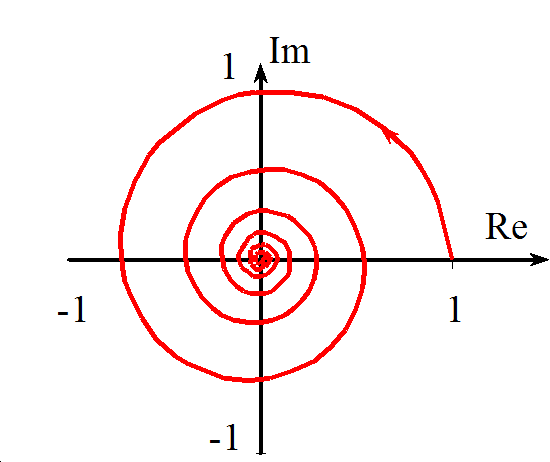
A szög megegyezik az 1. feladat szögével, tehát a komplex vektor itt is az origó körül fog forogni. Az abszolút értéket egy szigorúan monoton csökkenő, nullához tartó függvény írja le. Ebből arra lehet következtetni, hogy a függvény képe spirális, mely egyre jobban „rászorul” az origóra. Legtávolabb az origótól az ω =0 esetén lesz: 1+0j.
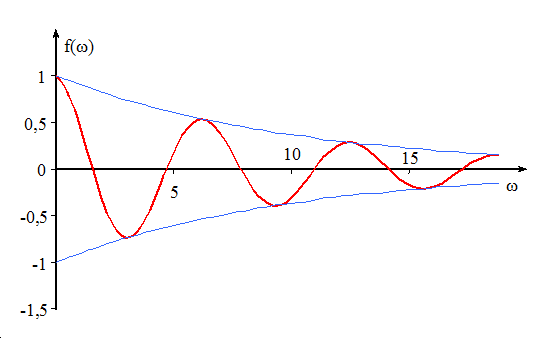
A későbbi tanulmányok miatt célszerű megvizsgálni a Re(Y(ω)) függvényt.
Legyen f(ω)= Re(Y(ω))=e -0.1ω cos ω, ez tehát egy valós függvény, amely két részből áll. Az egyik egy koszinusz, amely 1 és –1 között periodikusan „hullámzik”, a másik egy e-ad, amely negatív kitevője miatt szigorúan monoton tart nullához. Ez utóbbi alulról és felülről korlátok közé szorítja a koszinusz függvényt.
5.10. Javasolt feladatok
Rendezze algebrai alakra a következő komplex függvényeket:
Ábrázolja a következő komplex függvényeket pozitív ω esetén:
5.11. Megoldások
|
6. |
5-6. ábra |
7. |
5-7. ábra |
|
8. |
5-8. ábra |
9. |
5-9. ábra |
|
10. |
5-10. ábra |
11. |
5-11. ábra Megoldás |
|
12. |
5-12. ábra |
13. |
5-13. ábra |
|
14. |
5-14. ábra |
15. |
5-15. ábra |
|
16. |
5-16. ábra |
17. |
5-17. ábra |
|
18. |
5-18. ábra |
19. |
5-19. ábra |