2. fejezet - Robotok geometriai és kinematikai jellemzése

2. fejezet - Robotok geometriai és kinematikai jellemzése
Vissza	I. rész - rész	Előre

Tartalom

2.1. Homogén transzformációs mátrixok
2.2. Denavit‑Hartenberg paraméterek
2.3. Robotok kinematikai leírása

A bevezetőben elmondottak alapján a robotok csuklókkal összekapcsolódó kartagokból álló mechanikai rendszerek. Jelen jegyzeten belül csak olyan robotstruktúrákkal foglalkozunk, melyekben minden csukló csakis két kartagot kapcsol össze, vagyis a kartagok egymásutánja ún. nyílt kinematikai láncot alkot. Ellenkező esetben zárt kinematikai láncú, vagy párhuzamos működésű robotokról beszélhetünk.

A továbbiakban feltesszük, hogy hogy a kartagok ideális merev testek, a csuklók pedig holtjáték-, kotyogás-, és súrlódásmentesek. A fentieken túlmenően azzal a kikötéssel is élünk, hogy minden egyes csukló vagy csak lineáris, egyenes menti elmozdulás (transzlációt), vagy csak tengerkörüli elfordulást (rotációt) tesz lehetővé. Az előbbi P típusú (angolul: prismatic joint, P), az utóbbit R típusú (angolul: revolute joint, R) csuklónak is fogjuk nevezni. Egészen speciális estektől eltekintve a valóságos robotokban is csak ez a két csuklófajta fordul elő.

Ha egy robot kartagjairól és csuklóiról beszélünk, célszerű azokra valamilyen sorszámmal hivatkozni. Csaknem teljesen egységesen a robot (rögzített) törzsét 0. kartagnak szokás nevezni, a hozzá kapcsolódó kartag az 1. kartag, és az ezeket összekötő csukló az 1. csukló. Mind a kartagok, mind a csuklók sorszáma a törzstől a robotkéz felé haladva, és általánosságban az i. és az (i+1). kartagot az (i+1). csukló köti össze.

Mivel a robotok kinematikai jellemzésekor mozgásokat írunk le, be kell vezetnünk különböző vonatkoztatási rendszereket. Az egyik legkézenfekvőbb lehetőség a robottörzséhez (vagy a környezethez) rögzített koordináta rendszer felvétele. Ezen rendszerhez viszonyított adatokat leggyakrabban világkoordinátáknak (angolul: world coordinates) nevezzük.

Továbbá minden kartaghoz ugyancsak hozzárendelhetünk egy‑egy koordinátarendszert. Az így definiált Descartes-koordinátarendszerek tulajdonképpen már elegendőek lennének mindenfajta robotmozgatás leírására, azonban az esetek többségében rendkívüli számítástechnikai nehézségekkel járna, ha mindenáron a jól megszokott Descartes-koordinátákhoz ragaszkodnánk. Célszerű ezért bevezetni az ún. csuklókoordinátákat (angolul: joint coordinates), melyeket úgy értelmezünk, hogy a robot egy önkényesen megállapított konfigurációjában minden csuklóhoz zérus értéket rendelünk hozzá, majd a robotot ebből az alaphelyzetből (angolul: home position) kimozdítva minden csukló elmozdítását egy előjeles számmal fejezik ki. Ez a szám fizikailag P típusú csukló esetén a lineáris elmozdulás mértéke (pl. mm-ben), R típusú csukló esetén a szögelfordulás mértéke (pl. fokban).

Az eddigiekből kitűnik, hogy a robot bármely konfigurációja kifejezhető akár a csuklókoordináták aktuális értékeivel, akár a robotkéz pozícióját és orientációját jellemző (a világ-koordinátarendszerben értelmezett) adatokkal. A két fajta adathalmaz közötti kapcsolat megtalálása az egyik legbonyolultabb matematika probléma a robotikában. Egy hat csuklóval felszerelt, hat szabadságfokú robot egyes csuklóinak $q_{i}$ ‑vel jelölt csuklókoordinátáiból egy hat dimenziós vektort képezhetünk

$q = {[\begin{matrix} q_{1} & q_{2} & \dots & q_{6} \end{matrix}]}^{T}$ .

Ugyancsak hatdimenziós vektorral adható meg a robotkéz pozíciója és orientációja is, ezt a vektort p‑vel jelöljük. A p vektor meghatározása a q ismeretében az ún. direkt kinematikai feladat, míg az ezzel ellentétes irányú transzformációt inverz kinematikai feladatnak nevezzük. Az utóbbi probléma megoldását súlyosbítja az a körülmény is, hogy a robotkéz egy adott pozíciója és orientációja általában több különböző csuklószög helyzettel is megvalósítható, ilyenkor az inverz kinematikai feladat megoldása matematikailag nem egyértelmű.

Vizsgáljuk most meg kissé részletesebben két Descartes-koordinátarendszer egymáshoz viszonyított kölcsönös helyzetének leírását.

2.1. Homogén transzformációs mátrixok

Vegyünk fel térben tetszőleges helyen egy derékszögű koordinátarendszert az (2.1. ábra) ábrán látható módon!

2.1. ábra -

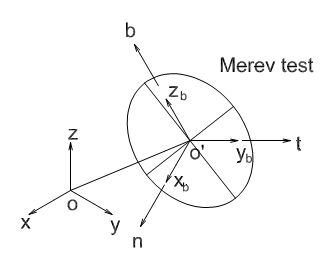
Legyen az ${O; x, y, z}$ koordinátarendszer a világ koordinátarendszer, melynek O az origója, tengelyei pedig rendre x, y és z. Helyezzünk el a tér tetszőleges helyén egy merev testet, ehhez az ${O^{'}; x_{b}, y_{b}, z_{b}}$ koordinátarendszert rendeljük (a merevtesthez rögzített koordináta rendszert body frame‑nek nevezi az angol terminológia). Az $x_{b}, y_{b} és z_{b}$ tengelyek irányába mutató egységvektorokat jelöljük rendre n‑, t‑ és b‑ vektorokkal jelöljük, továbbá az O világ koordináta rendszer origójából az $O^{'}$ merev testhez rögzített koordináta rendszer origójába az

$x_{0} = {[\begin{matrix} x_{0} & y_{0} & z_{0} \end{matrix}]}^{T}$

vektor mutat. Az $x_{0}$ vektor a két koordinátarendszer egymáshoz képes kölcsönös pozícióját írja le.

Vezessük be az R-rel jelölt 3×3-as mátrixot, amelynek oszlopvektorai rendre az n, t, b vektorok, ezáltal

$R = [\begin{matrix} n & t & b \end{matrix}]$ .

Fontos megjegyezni, hogy az n, t, b vektorok ortonormált bázist alkotnak, azaz a vektorok egymásra merőlegesek (ortogonalitás), valamint egységnyi hosszúak. Ezáltal az R mátrix inverze megegyezik a mátrix transzponáltjával

$R^{- 1} = R^{T}$ ,

ezáltal $R^{T} R = E$ , ahol E a 3×3-as egységmátrixot jelöli.

Válasszuk ki a tér egy tetszőleges P pontját, és keressük ennek koordinátáit az előzőekben definiált két koordinátarendszerben kifejezve. Legyen a P pont pozícióvektora a világ koordinátarendszerben

$x = {[\begin{matrix} x & y & z \end{matrix}]}^{T}$ ,

valamint a merevtesthez rögzített koordináta rendszerben

$x_{b} = {[\begin{matrix} u & v & w \end{matrix}]}^{T}$ .

Célunk, hogy kölcsönösen egyértelmű kapcsolatokat találjunk x és $x_{b}$ vektorok között. Az eddigiek alapján írhatjuk

$x = x_{0} + u n + v t + w b$ ,

(2.1)

továbbá

$x = x_{0} + R x_{b}$ .

(2.2)

Szorozzuk meg mindkét oldalát balról $R^{T}$ ‑tal, ezáltal az (2.2) egyenlet a következő formát ölti

$R^{T} x = R^{T} x_{0} + R^{T} R x_{b} = R^{T} x_{0} + x_{b}$ .

(2.3)

Az (2.3) egyenletből kifejezve $x_{b}$ vektort

$x_{b} = R^{T} x - R^{T} x_{0}$ .

(2.4)

Mivel az $x_{0}$ vektor a két koordinátarendszerben kölcsönös pozícióját, R mátrix pedig ezek kölcsönös orientációját fejezi ki, ezáltal az (2.4) egyenlet alkalmas két derékszögű koordinátarendszer közötti legáltalánosabb transzformáció leírására.

Speciális példaként tekintsük azt az esetet, amikor az ${O^{'}; x_{b}, y_{b}, z_{b}}$ koordinátarendszert az ${O; x, y, z}$ koordinátarendszerből úgy kapjuk, hogy azt annak z tengelye körül $γ$ szöggel elforgatjuk. A puszta forgatás miatt O pont egybeesik $O^{'}$ ‑vel, ezért $x_{0} = 0$ , az R mátrix pedig a következőképpen írható fel (bizonyítás nélkül)

$R = [\begin{matrix} \cos (γ) & - \sin (γ) & 0 \\ \sin (γ) & \cos (γ) & 0 \\ 0 & 0 & 1 \end{matrix}]$

Míg az $x_{0} = 0$ vektort az origók közötti transzlációt írja le, az R mátrix pedig kizárólag a forgatási transzformációt fejezi ki, ezért is nevezik rotációs mátrixnak. Az R mátrix elemeinek ismerete egyértelműen, de redundáns módon írja le két derékszögű koordinátarendszer kölcsönös orientációját, hiszen a mátrix kilenc elemet tartalmaz, az orientáció eltérés megadásához pedig, mint tudjuk, három független adat elegendő. Ezért érdemes megjegyezni, hogy az R mátrix elemei között csak három lineárison független elemet találhatunk.

A kölcsönös orientáció megadása három független (szög-) adattal többféleképpen is lehetséges. Az egyik lehetőség az orientáció megadása az ún. Euler-szögekkel. A 2.2. ábra és az alábbi gondolatmenet alapján belátható, hogy három alkalmasan megválasztott, egymást követő forgatással előállítható olyan koordinátarendszer, mely az eredetihez képest a lehető legáltalánosabb orientációjú.

2.2. ábra -

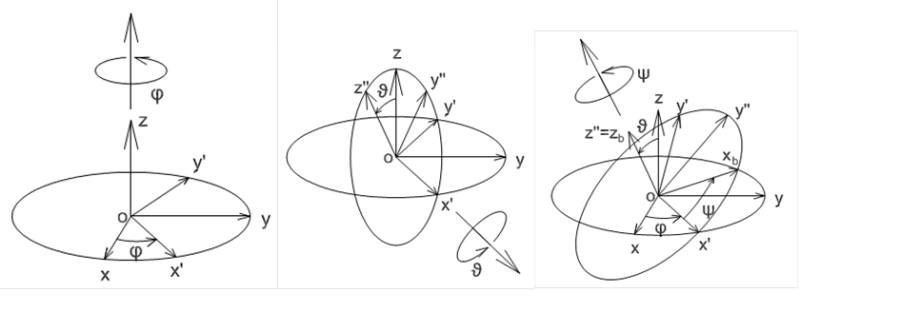
Az eredeti ${O; x, y, z}$ koordinátarendszert rendre a következő forgatási transzformációknak vetjük alá

Forgatás z tengely körül $φ$ szöggel, a forgatás után kapott koordináta rendszer ${O^{'}; x^{'}, y^{'}, z^{'}}$ , ahol $z \equiv z^{'}$ .
Forgatás $x^{'}$ tengely körül $ϑ$ szöggel, a forgatás után kapott koordináta rendszer ${O^{″}; x^{″}, y^{″}, z^{″}}$ , ahol $x^{″} \equiv x^{'}$ .
Forgatás $z^{″}$ tengely körül $ψ$ szöggel, a forgatás után kapott koordináta rendszer ${O; x_{b}, y_{b}, z_{b}}$ .

A fenti módon definiált $φ, ϑ, ψ$ szögeket nevezzük Euler-szögeknek. Természetesen a fenti forgatások mindegyikéhez hozzárendelhető egy-egy rotációs mátrix, melyek rendre

	$R_{z} (φ) = [\begin{matrix} \cos (φ) & - \sin (φ) & 0 \\ \sin (φ) & \cos (φ) & 0 \\ 0 & 0 & 1 \end{matrix}]$ ,	(2.5)
	$R_{x^{'}} (ϑ) = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos (ϑ) & - \sin (ϑ) \\ 0 & \sin (ϑ) & \cos (ϑ) \end{matrix}]$ ,	(2.6)
	$R_{z^{″}} (ψ) = [\begin{matrix} \cos (ψ) & - \sin (ψ) & 0 \\ \sin (ψ) & \cos (ψ) & 0 \\ 0 & 0 & 1 \end{matrix}]$	(2.7)

A három forgatás egymásutánja az $R (φ, ϑ, ψ) = R_{z} (φ) R_{x^{'}} (ϑ) R_{z^{″}} (ψ)$ eredő transzformációs mátrixszal írható le. Elvégezve a számításokat a következő formát kaphatjuk meg

$R = [\begin{matrix} c_{φ} c_{ψ} - s_{φ} c_{ϑ} s_{ψ} & - c_{φ} s_{ψ} - s_{φ} c_{ϑ} c_{ψ} & s_{φ} s_{ϑ} \\ s_{φ} c_{ψ} + c_{φ} c_{ϑ} s_{ψ} & - s_{φ} s_{ψ} + c_{φ} c_{ϑ} c_{ψ} & - c_{φ} s_{ϑ} \\ s_{ϑ} s_{ψ} & s_{ϑ} c_{ψ} & c_{ϑ} \end{matrix}]$ ,

ahol $c_{φ} = \cos (φ)$ , $c_{ϑ} = \cos (ϑ)$ , $c_{ψ} = \cos (ψ)$ , $s_{φ} = \sin (φ)$ , $s_{ϑ} = \sin (ϑ)$ , valamint $s_{ψ} = \sin (ψ)$ jelöléseket alkalmaztuk.

További lehetőséget az ún. hajómozgási szögekkel, vagy másképpen RPY szögekkel (Roll, Pitch, Yaw) való leírásmód ad

Az eredeti ${O; x, y, z}$ koordinátarendszert rendre a következő forgatási transzformációknak vetjük alá

Forgatás z tengely körül $α$ szöggel, a forgatás után kapott koordináta rendszer ${O^{'}; x^{'}, y^{'}, z^{'}}$ .
Forgatás y tengely körül $β$ szöggel, a forgatás után kapott koordináta rendszer ${O^{″}; x^{″}, y^{″}, z^{″}}$ .
Forgatás x tengely körül $γ$ szöggel, a forgatás után kapott koordináta rendszer ${O; x_{b}, y_{b}, z_{b}}$ .

A fenti módon definiált $α, β, γ$ szögeket nevezzük RPY-szögeknek. Természetesen a fenti forgatások mindegyikéhez hozzárendelhető egy-egy rotációs mátrix, melyek rendre

	$R_{z} (α) = [\begin{matrix} \cos (α) & - \sin (α) & 0 \\ \sin (α) & \cos (α) & 0 \\ 0 & 0 & 1 \end{matrix}]$ ,	(2.8)
	$R_{y} (β) = [\begin{matrix} \cos (β) & 0 & \sin (β) \\ 0 & 1 & 0 \\ - \sin (β) & 0 & \cos (β) \end{matrix}]$ ,	(2.9)
	$R_{x} (γ) = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos (γ) & - \sin (γ) \\ 0 & \sin (γ) & \cos (γ) \end{matrix}]$	(2.10)

A három forgatás egymásutánja az $R (α, β, γ) = R_{z} (α) R_{y} (β) R_{x} (γ)$ eredő transzformációs mátrixszal írható le. A számítások hasonló módon történnek, mint a korábban bemutatott Euler-féle szögekkel történő reprezentáció során.

A térbeli orientáció leírására további lehetőséget ad az ún. Tait‑Briant szögek alkalmazása is, miszerint az eredeti ${O; x, y, z}$ koordinátarendszert rendre a következő forgatási transzformációknak vetjük alá

Forgatás x tengely körül $φ$ szöggel, a forgatás után kapott koordináta rendszer ${O^{'}; x^{'}, y^{'}, z^{'}}$ , ahol $x \equiv x^{'}$ .
Forgatás $y^{'}$ tengely körül $ϑ$ szöggel, a forgatás után kapott koordináta rendszer ${O^{″}; x^{″}, y^{″}, z^{″}}$ , ahol $y^{″} \equiv y^{'}$ .
Forgatás $z^{″}$ tengely körül $ψ$ szöggel, a forgatás után kapott koordináta rendszer ${O; x_{b}, y_{b}, z_{b}}$ .

	$R_{x} (φ) = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos (φ) & - \sin (φ) \\ 0 & \sin (φ) & \cos (φ) \end{matrix}]$ ,	(2.11)
	$R_{y^{'}} (ϑ) = [\begin{matrix} \cos (ϑ) & 0 & \sin (ϑ) \\ 0 & 1 & 0 \\ - \sin (ϑ) & 0 & \cos (ϑ) \end{matrix}]$ ,	(2.12)
	$R_{z^{″}} (ψ) = [\begin{matrix} \cos (ψ) & - \sin (ψ) & 0 \\ \sin (ψ) & \cos (ψ) & 0 \\ 0 & 0 & 1 \end{matrix}]$ .	(2.13)

A három forgatás egymásutánja az $R (φ, ϑ, ψ) = R_{x} (φ) R_{y^{'}} (ϑ) R_{z^{″}} (ψ)$ eredő transzformációs mátrixszal írható le.

Az összetett transzformációk (transzláció és rotáció) tömör, kompakt leírására a robotikában is kiterjedten alkalmazzák a 4×4‑es ún. homogén transzformációs mátrixokat.

$H = [\begin{matrix} R & T \\ 0 & 1 \end{matrix}]$ ,

ahol R a 3×3‑as forgatási mátrix, T a 3×1‑as transzlációs vektor, valamint 0 az 1×3‑as nullvektor. Fontos megjegyezni, hogy a homogén transzformációs mátrixok alkalmazása során a korábban 3 elemű vektorokat ki kell bővíteni egy 1-es elemmel, máskülönben a számítások nem végezhetőek el.

Általánosan elterjedt továbbá az egyes kartagok saját koordinátarendszerének felvételére, valamint ezek kölcsönös helyzetének leírására az ún. Denavit‑Hartenberg‑féle reprezentáció.

2.2. Denavit‑Hartenberg paraméterek

A robotok geometriájának általános leírására Denavit és Hartenberg 1955‑ben publikáltak egy módszert. A módszer alkalmazásával a csuklókoordináták transzformálása a világkoordináta rendszerbe az un. Denavit‑Hartenberg féle transzformációs mátrixszal történik. A Denavit‑Hartenberg koordináta transzformáció során egy koordináta rendszer egy tetszőleges koordináta rendszerben átvihető, ha két eltolást és két elforgatást a megfelelő sorrendben alkalmazunk. A robotok leírása során a két távolságot d‑vel és a‑val, valamint a két elforgatást leíró paramétert $α$ ‑val, illetve q‑val jelöljük.

A konvencionális paraméterek bevezetéséhez első lépésként definiálnunk kell a robotok csuklóihoz rendelt koordináta rendszereket. Első lépésként az i‑edik és (i+1)‑edik csuklókra egy-egy derékszögű koordinátarendszert illesztünk, tehát a koordináta rendszerek origója a csukló középpontokba illeszkednek. A csuklókba illesztett koordináta rendszerek z tengelyei a csuklók irányába mutatnak.

A szabályrendszer értelmében az (i+1)‑edik csuklóba az ${O_{i}; x_{i}, y_{i}, z_{i}}$ koordináta rendszert rögzítjük. A korábbiak alapján a $z_{i}$ tengelyt az (i+1)‑edik csukló irányába helyezzük. Az $x_{i}$ tengelyt az (i+1)‑edik és i‑edik csuklók (z irányú) tengelyeinek közös normálisába (normál transzverzális) esik, és az (i+1)‑edik csukló felé mutat. Az $y_{i}$ tengelyt pedig úgy választjuk meg, hogy az ${O_{i}; x_{i}, y_{i}, z_{i}}$ koordináta rendszer jobbsodrású koordináta rendszert alkosson.

Továbbá az i‑edik csuklóba az ${O_{i - 1}; x_{i - 1}, y_{i - 1}, z_{i - 1}}$ koordináta rendszert rögzítjük. A korábbiak alapján a $z_{i - 1}$ tengelyt az i‑edik csukló irányába helyezzük. Az $x_{i - 1}$ tengelyt az (i‑1)‑edik és i‑edik csuklók (z irányú) tengelyeinek közös normálisába esik, és az i‑edik csukló felé mutat. Az $y_{i - 1}$ tengelyt pedig úgy választjuk meg, hogy az ${O_{i - 1}; x_{i - 1}, y_{i - 1}, z_{i - 1}}$ koordináta rendszer jobbsodrású koordináta rendszert alkosson. A robot többi tengely esetén hasonló módon járunk el.

A konvencionális paraméterek a következőek. Első paraméterként definiáljuk a $q_{i}$ paramétert rotációs csukló esetén az $x_{i - 1}$ tengely és az $x_{i}$ tengely között bezárt jobbcsavar irányú szög nagysága.

Második paraméterként vezessük be a $d_{i}$ paramétert, amely a korábban kijelölt csuklók normál transzverzálisainak távolságát jelöli, azaz a két normális közötti, az i‑edik csukló $z_{i - 1}$ tengelye mentén mért távolság.

Harmadik paraméterként az $a_{i}$ távolságot vezetjük be, miszerint az i‑edik és (i+1)‑edik csuklótengelyek közös normálisának a hossza, amelyet az $x_{i}$ tengely mentén mérünk.

Negyedik paraméterként a $α_{i}$ paramétert vezetjük be, amely az i‑edik csukló $z_{i - 1}$ tengelye, valamint az (i+1)‑edik $z_{i}$ tengelye között mért jobbcsavar irányú szög, az $a_{i}$ paraméterre merőleges síkban.

A Denavit‑Hartenberg transzformációs eljárás során két szomszédos koordináta rendszer, az átvihető egymásba a két transzlációs és két rotációs transzformáció megfelelő sorrendben történő végrehajtása segítségével. Általános esetben az ${O_{i - 1}; x_{i - 1}, y_{i - 1}, z_{i - 1}}$ koordináta rendszer átvihető az ${O_{i}; x_{i}, y_{i}, z_{i}}$ koordináta rendszerbe a következőképp

${}^{i - 1}D_{i} = D (q_{i}) D (d_{i}) D (a_{i}) D (α_{i})$ .

(2.14)

Első lépésben az ${O_{i - 1}; x_{i - 1}, y_{i - 1}, z_{i - 1}}$ $q_{i}$ szöggel a $z_{i - 1}$ tengely körül, egészen addig, amíg az $x_{i - 1}$ tengely az $x_{i}$ tengellyel párhuzamos nem lesz. A $q_{i}$ szöggel történő forgatás a következő homogén koordináta transzformációs mátrixszal írható le

$D (q_{i}) = [\begin{matrix} \cos (q_{i}) & - \sin (q_{i}) & 0 & 0 \\ \sin (q_{i}) & \cos (q_{i}) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$ .

(2.15)

Második lépésként a $z_{i - 1}$ tengely mentén $d_{i}$ nagysággal eltoljuk a koordináta rendszert, amíg a $z_{i - 1}$ tengely és az $x_{i}$ tengely nem metszi egymást. A $d_{i}$ paraméterrel történő eltolást a következő homogén koordináta transzformációs mátrixszal írható le

$D (d_{i}) = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & d_{i} \\ 0 & 0 & 0 & 1 \end{matrix}]$ .

(2.16)

Harmadik lépésként eltoljuk a koordináta rendszert $a_{i}$ nagysággal az $x_{i}$ tengely mentén, amíg a két koordináta rendszer origója nem metszi egymást, azaz az eltolást az $O_{i}$ origóig hajtjuk végre. Az $a_{i}$ paraméterrel történő eltolást a következő homogén koordináta transzformációs mátrixszal írható le

$D (a_{i}) = [\begin{matrix} 1 & 0 & 0 & a_{i} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$

(2.17)

Végezetül negyedik lépésként elforgatjuk a koordináta rendszert $x_{i}$ tengely körül $α_{i}$ szöggel, amíg a két koordináta rendszer fedésbe nem jön, azaz az $y_{i - 1}$ és $y_{i}$ tengelyek, valamint a $z_{i - 1}$ és $z_{i}$ tengelyek nem fedik egymást. Az $α_{i}$ szöggel történő forgatás a következő homogén koordináta transzformációs mátrixszal írható le

$D (α_{i}) = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos (α_{i}) & - \sin (α_{i}) & 0 \\ 0 & \sin (α_{i}) & \cos (α_{i}) & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$

(2.18)

Tehát két egymást követő rotációs csukló közötti transzformáció (általános esetben az (i‑1)‑edik csuklóból az i‑edik csuklóba), elvégezve a (2.14) egyenletben szereplő számításokat a következő rotációs csuklóhoz rögzített koordináta rendszer esetén a Denavit‑Hartenberg féle transzformáció mátrix a következő

${}^{i - 1}D_{i} = [\begin{matrix} \cos (q_{i}) & - \sin (q_{i}) \cos (α_{i}) & \sin (q_{i}) \sin (α_{i}) & a_{i} \cos (q_{i}) \\ \sin (q_{i}) & \cos (q_{i}) \cos (α_{i}) & - \cos (q_{i}) \sin (α_{i}) & a_{i} \sin (q_{i}) \\ 0 & \sin (α_{i}) & \cos (α_{i}) & d_{i} \\ 0 & 0 & 0 & 1 \end{matrix}]$ .

(2.19)

Amennyiben transzlációs csuklóra alkalmazzuk a Denavit‑Hartenberg féle konvenciókat, a következő változócseréket kell végrehajtanunk, miszerint az $a_{i}$ paraméter értéke zérus, a $d_{i}$ paraméter $q_{i}$ lesz, végezetül a rotációs csuklók leírásához használt szög pedig $θ_{i}$ paraméter lesz, azaz $a_{i} = 0$ , $d_{i} = q_{i}$ , $q_{i} = θ_{i}$ .

Felhasználva a bevezetett paraméter cseréket a (2.19) egyenlegben írt transzformációs mátrix transzlációs csuklók esetén a következő alakra módosul

${}^{i - 1}D_{i} = [\begin{matrix} \cos (θ_{i}) & - \sin (θ_{i}) \cos (α_{i}) & \sin (θ_{i}) \sin (α_{i}) & 0 \\ \sin (θ_{i}) & \cos (θ_{i}) \cos (α_{i}) & - \cos (θ_{i}) \sin (α_{i}) & 0 \\ 0 & \sin (α_{i}) & \cos (α_{i}) & q_{i} \\ 0 & 0 & 0 & 1 \end{matrix}]$

(2.20)

Ami után a korábban leírtak alapján minden csukló esetén meghatároztuk a Denavit‑Hartenberg féle transzformációs mátrixokat, azaz felírtuk minden (i‑1)‑edik csuklóból az i‑edik csuklóba meghatározhatjuk a robot álló (azaz a talajhoz rögzített pontjához rögzített koordináta rendszer) koordinátarendszere, valamint a végberendezés koordináta rendszere közötti transzformációs mátrixot. A transzformációs mátrixot az egymást követő csuklók Denavit‑Hartenberg féle mátrixok szorzata adja, azaz

${}^{0}T_{n} = {}^{0}D_{1} {}^{1}D_{2} ... {}^{n - 2}D_{n - 1} {}^{n - 1}D_{n}$ .

(2.21)

Az így kapott T mátrix a robot végberendezés szerszámközepének pozícióját és orientációját adja meg az álló koordináta rendszerben.

2.3. Robotok kinematikai leírása

A koordináta transzformációk áttekintése után rátérhetünk a robotok kinematikai leírásának kérdésére, vagyis a robotmozgások olyan jellegzetességével fogunk foglalkozni, amely a robotok mozgásának sebességeit írja le. A kinematikai jellemzést legegyszerűbb formában úgy fogalmazhatjuk meg, hogy keressük a kapcsolatot a robotkéz sebességének, illetve szögsebességének kapcsolatát a robot egyes csuklóinak sebessége illetve szögsebessége között.

A robotok kinematikai jellemzésének egyszerűbb tárgyalási módjának érdekében a (2.3. ábra) ábrán látható két szabadsági-fokú síkbeli manipulátort vizsgáljuk.

2.3. ábra -

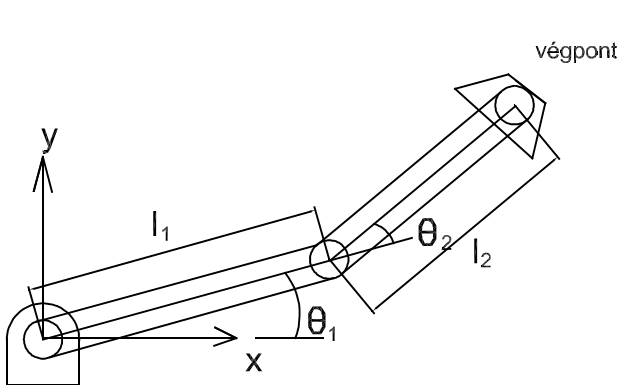
A manipulátor végpontjának koordinátája legyen x, y. Az ábra alapján az x, y koordinátákra vonatkozóan a következő egyenleteket írhatjuk fel, azaz

	$x (φ_{1}, φ_{2}) = l_{1} \cos (φ_{1}) + l_{2} \cos (φ_{1} + φ_{2})$ ,	(2.22)
	$y (φ_{1}, φ_{2}) = l_{1} \sin (φ_{1}) + l_{2} \sin (φ_{1} + φ_{2})$ .	(2.23)

Mivel célunk a mozgások időbeni lefolyásának vizsgálata, elő kell állítanunk a végpont sebességvektorát és a csukló szögsebességek vektorát. Ezért képezzük a fenti két egyenlet idő szerinti teljes deriváltját, miszerint

	$\frac{d x}{d t} = \frac{\partial x (φ_{1}, φ_{2})}{\partial φ_{1}} \frac{d φ_{1}}{d t} + \frac{\partial x (φ_{1}, φ_{2})}{\partial φ_{2}} \frac{d φ_{2}}{d t}$ ,	(2.24)
	$\frac{d y}{d t} = \frac{\partial y (φ_{1}, φ_{2})}{\partial φ_{1}} \frac{d φ_{1}}{d t} + \frac{\partial y (φ_{1}, φ_{2})}{\partial φ_{2}} \frac{d φ_{2}}{d t}$ .	(2.25)

Vegyük a korábbi két egyenletet, amelyet vektor‑mátrix formalizmussal is felírhatunk

$[\begin{matrix} \frac{d x}{d t} \\ \frac{d y}{d t} \end{matrix}] = [\begin{matrix} \frac{\partial x (φ_{1}, φ_{2})}{\partial φ_{1}} & \frac{\partial x (φ_{1}, φ_{2})}{\partial φ_{2}} \\ \frac{\partial y (φ_{1}, φ_{2})}{\partial φ_{1}} & \frac{\partial y (φ_{1}, φ_{2})}{\partial φ_{2}} \end{matrix}] [\begin{matrix} \frac{d φ_{1}}{d t} \\ \frac{d φ_{2}}{d t} \end{matrix}]$

(2.26)

amelyet a következő tömör alakban adhatjuk meg,

$v = J \dot{φ}$

(2.27)

ahol J jelöli az un. Jacobi‑mátrixot.

Az így definiált J mátrixot a manipulátor adott konfigurációjára érvényes Jacobi-mátrixnak nevezzük. A példánkban szereplő egyszerű manipulátorra nézve –könnyen belátható módon- a következő Jacobi-mátrix adódik

$J = [\begin{matrix} - l_{1} \sin (φ_{1}) - l_{2} \sin (φ_{1} + φ_{2}) & - l_{2} \sin (φ_{1} + φ_{2}) \\ l_{1} \cos (φ_{1}) - l_{2} \cos (φ_{1} + φ_{2}) & l_{2} \cos (φ_{1} + φ_{2}) \end{matrix}]$ .

(2.28)

A mozgások vizsgálata megköveteli, hogy az elemi (infinitezimális) elmozdulások sajátosságaival is megismerkedjünk. Figyelmünket a következőkben az elemi elforgatások vizsgálatára összpontosítjuk, mert – amint később látni fogjuk – ezek bizonyos mértékben eltérő tulajdonságokkal rendelkeznek a véges szögű elforgatáshoz képest.

Elemi elforgatásokat bármely térbeli tengely mentén végezhető, ezért célszerű azokat vektormennyiségeknek tekinteni. Ha definiálunk egy ${O; x, y, z}$ derékszögű koordinátarendszert, akkor abban bármely elemi elforgatás $d φ$ vektora három merőleges összetevőre bontható a következő alakban

$d φ = {[\begin{matrix} d φ_{x} & d φ_{y} & d φ_{z} \end{matrix}]}^{T}$ .

Végezzük el a $d φ$ szögű elemi elforgatást előállítani a $d φ_{x}, d φ_{y}, d φ_{z}$ elforgatás összetevők egymás utáni végrehajtásaként!

Vegyük sorra először az x tengelykörüli elforgatást, azaz végezzük el az elemi forgatást $d φ_{x}$ elemi szöggel. A $d φ_{x}$ szöggel történő forgatási mátrix

$R_{x} (d φ_{x}) = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos (d φ_{x}) & - \sin (d φ_{x}) \\ 0 & \sin (d φ_{x}) & \cos (d φ_{x}) \end{matrix}] \approx [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & - d φ_{x} \\ 0 & d φ_{x} & 1 \end{matrix}]$ .

(2.29)

A közelítő megoldás meghatározásakor kihasználtuk, hogy kis szögelfordulások esetén $\cos (d φ_{x}) \approx 1$ , valamint $\sin (d φ_{x}) \approx d φ_{x}$ .

az y tengelykörüli elforgatást, azaz végezzük el az elemi forgatást $d φ_{y}$ elemi szöggel. A $d φ_{y}$ szöggel történő forgatási mátrix

$R_{y} (d φ_{y}) = [\begin{matrix} \cos (d φ_{y}) & 0 & \sin (d φ_{y}) \\ 0 & 1 & 0 \\ - \sin (d φ_{y}) & 0 & \cos (d φ_{y}) \end{matrix}] \approx [\begin{matrix} 1 & 0 & d φ_{y} \\ 0 & 1 & 0 \\ - d φ_{y} & 0 & 1 \end{matrix}]$ .

(2.30)

Hasonlóan az x tengely körüli forgatás kapcsán írt kis szögekre vonatkozó összefüggéseket az y tengely körüli forgatásnál is felhasználtuk.

Végül a z tengelykörüli elforgatást vizsgáljuk, azaz végezzük el az elemi forgatást $d φ_{z}$ elemi szöggel. A $d φ_{z}$ szöggel történő forgatási mátrix

$R_{z} (d φ_{z}) = [\begin{matrix} \cos (d φ_{z}) & - \sin (d φ_{z}) & 0 \\ \sin (d φ_{z}) & \cos (d φ_{z}) & 0 \\ 0 & 0 & 1 \end{matrix}] \approx [\begin{matrix} 1 & - d φ_{z} & 0 \\ d φ_{z} & 1 & 0 \\ 0 & 0 & 1 \end{matrix}]$ .

(2.31)

Hasonlóan az x tengely körüli forgatás kapcsán bemutatott kis szögekre vonatkozó összefüggéseket a z tengely körüli forgatásnál is felhasználtuk.

Nézzük meg a két egymásra merőleges tengely körüli forgatást, példaképpen vizsgáljuk meg az x tengely, illetve y tengely körüli forgatást, miszerint

	$R_{x y} = R_{x} (d φ_{x}) R_{y} (d φ_{y})$ ,
	$R_{x y} = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & - d φ_{x} \\ 0 & d φ_{x} & 1 \end{matrix}] [\begin{matrix} 1 & 0 & d φ_{y} \\ 0 & 1 & 0 \\ - d φ_{y} & 0 & 1 \end{matrix}] = [\begin{matrix} 1 & 0 & d φ_{y} \\ d φ_{x} d φ_{y} & 1 & - d φ_{x} \\ - d φ_{y} & d φ_{x} & 1 \end{matrix}]$ .

Elemi forgatást alkalmazva két elemi szög szorzata „kellőképpen kicsi”, azaz $d φ_{x} d φ_{y} \approx 0$ , ezért a vegyes tagokat elhanyagoljuk, ezáltal az elemi forgatási mátrix a következő

$R_{x y} = [\begin{matrix} 1 & 0 & d φ_{y} \\ 0 & 1 & - d φ_{x} \\ - d φ_{y} & d φ_{x} & 1 \end{matrix}]$ .

(2.32)

Vizsgáljuk meg, hogy mi történik akkor, ha a fordított sorrendben forgatunk tengelyek körül, azaz

$R_{y x} = R_{y} (d φ_{y}) R_{x} (d φ_{x})$ ,

$R_{y x} = [\begin{matrix} 1 & 0 & d φ_{y} \\ 0 & 1 & 0 \\ - d φ_{y} & 0 & 1 \end{matrix}] [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & - d φ_{x} \\ 0 & d φ_{x} & 1 \end{matrix}] \approx [\begin{matrix} 1 & 0 & d φ_{y} \\ 0 & 1 & - d φ_{x} \\ - d φ_{y} & d φ_{x} & 1 \end{matrix}]$ .

(2.33)

Tehát, ha a két elemi elforgatást fordított sorrendben végezzük el, akkor a forgatás sorrendjétől függetlenül az elemi forgatási mátrixok megegyeznek, tehát a jelen példa esetén

$R_{x y} = R_{y x}$ .

Ebből tehát az következik, hogy két, egymásra merőleges tengelyek körüli elemi elforgatás tetszőleges sorrendben elvégezhető.

Ugyancsak könnyű belátni, hogy három, egymásra merőleges tengely körüli elemi elforgatás eredője is független attól, hogy az egyes elforgatásokat milyen sorrendben végeztük el. A fentiekkel ellentétben ugyanez nem mondható el a véges szögű elforgatásokkal kapcsolatban. Ha azonos alaphelyzetből kiindulva ugyanazon két tengely körül 90 – 90 fokos elforgatásokat végzünk, az eredmény forgatások sorrendjétől eltérő lesz a két lehetséges esetben.

A továbbiakban egy általános, hat szabadságfokú robot kinematikai leírásával foglalkozunk. Amint már a bevezetőben utaltunk rá, a robotkéz (end effector) pozícióját és orientációját tömören egy hatelemű vektorral fejezhetjük ki.

$p = {[\begin{matrix} x_{e} & φ_{e} \end{matrix}]}^{T}$

(2.34)

A robotkéz sebességét, és szögsebességét kifejező, ugyancsak hatelemű vektor a p vektor időszerinti deriválja lesz

$p = [\begin{matrix} {\dot{x}}_{e} \\ {\dot{φ}}_{e} \end{matrix}] = [\begin{matrix} v_{e} \\ ω_{e} \end{matrix}]$

(2.35)

Tudjuk továbbá, hogy egy hat szabadságfokú robot $q_{i}$ csuklókoordinátái ugyancsak egy hat elemű vektorban foglalhatóak össze.

$q = {[\begin{matrix} q_{1} & q_{2} & q_{3} & q_{4} & q_{5} & q_{6} \end{matrix}]}^{T}$

(2.36)

Fölmerülhet az a kérdés, hogy milyen kapcsolat van a végpont, az a robotkéz sebességének és szögsebességének $\dot{p}$ és a csukló sebességek $\dot{q}$ vektora között. A kapcsolat általános esetben is a (kétdimenziós esetre már bevezetett) J Jacobi-mátrix írja le az alábbi módon

$\dot{p} = J \dot{q}$ .

(2.37)

Annak érdekében, hogy a rendkívül tömör (2.37) összefüggés mögött rejlő fizikai tartalmat világosan lássuk, fel kell bontanunk az (2.37) egyenletben szereplő 6×6‑os Jakobi-mátrixot az alábbi módon

$J = [\begin{matrix} J_{L 1} & J_{L 2} & ... & J_{L 6} \\ J_{A 1} & J_{A 2} & ... & J_{A 6} \end{matrix}]$ .

(2.38)

Az (2.38) egyenlet szerinti szétbontás (ahol a $J_{L i}$ ‑k és $J_{A i}$ ‑k háromelemű oszlopvektorokat jelentenek) lehetővé számunkra, hogy az egyes csuklómozgásoknak a robotkéz mozgására kifejtett hatását különválasszuk aszerint, hogy az transzlációban, vagy rotációban nyilvánul meg. A $J_{L i}$ vektorok a transzlációt okozó hatást reprezentálják (az L betű az angol linear velocity kifejezésből adódik) a következő összefüggés szerint

$v_{e} = J_{L 1} {\dot{q}}_{1} + ... + J_{L 6} {\dot{q}}_{6}$ .

(2.39)

A korábbiakban leírt Denavit‑Hatenberg paraméterek alfejezet alapján ismeretes, hogy az i‑edik csukló tengelye az (i-1)‑edik $z_{i - 1}$ tengelyével esik egybe a Denavit‑Hartenberg‑féle jelölésrendszer szerint. Jelöljük a $z_{i - 1}$ pozitív irányában mutató egységvektort $b_{i - 1}$ ‑gyel! Ekkor P típusú (prizmatikus) csukló esetén a következő összefüggés lesz érvényes (az i‑edik csuklóra nézve)

$J_{L i} {\dot{q}}_{i} = b_{i - 1} {\dot{d}}_{i}$ ,

(2.40)

ahol ${\dot{d}}_{i}$ az i‑edik prizmatikus csukló változó Denavit-Hartenberg paraméterének idő szerinti deriváltja. Továbbá, ha az i‑edik csukló R típusú (rotációs), akkor a $z_{i - 1}$ tengely körüli forgás szögsebessége a következőképpen fejezhető ki

$ω_{i} = b_{i - 1} {\dot{Θ}}_{i}$ ,

(2.41)

ahol ${\dot{Θ}}_{i}$ az i‑edik csukló R típusú (rotációs) csukló idő szerinti deriváltja. (2.41) egyenletben felírt $ω_{i}$ szögsebesség a robotkéz lineáris elmozdulásához is hozzájárul. Jelöljük $r_{i - 1, e}$ ‑vel azt a helyvektort, amely az (i-1)‑edik kartag koordinátarendszerének origójából, $O_{i - 1}$ ‑ből (a $b_{i - 1}$ vektor kezdőpontjából) a robotkéz, vagy végberendezés koordinátarendszerének origójába mutat. Ekkor a következőt írhatjuk

$J_{L i} {\dot{q}}_{i} = ω_{i} \times r_{i - 1, e} = (b_{i - 1} \times r_{i - 1, e}) {\dot{Θ}}_{i}$ .

(2.42)

Az előzőekben említett „hatásszétválasztás” második lépéseként most a robotkéz szögsebességével fogunk foglalkozni, melyet az alábbi összefüggéssel fejezünk ki

$ω_{e} = J_{A 1} {\dot{q}}_{1} + ...... + J_{A 6} {\dot{q}}_{6}$ .

(2.43)

Az A betű most az angol angular velocity kifejezésből származik. Az (2.43) összefüggés fizikailag azt fejezi ki, milyen mértékben járulnak hozzá az egyes csuklósebességek a robotkéz szögsebességének kialakulásához.

Ha az i‑edik csukló prizmatikus, akkor a megfelelő $J_{A i}$ vektor minden eleme értelemszerűen zérus lesz, hiszen egyenes menti elmozdulás nem okoz elfordulást a robotkézen. Rotációs csuklóra ezzel szemben a következő összefüggés lesz érvényes

$J_{A i} {\dot{q}}_{i} = ω_{i} = b_{i - 1} {\dot{Θ}}_{i}$ .

(2.44)

Az eddigieket összefoglalva megállapíthatjuk, hogy az (2.38) egyenlettel definiált Jacobi‑mátrix i‑edik teljes (hatelemű) oszlopvektora

Prizmatikus csukló esetén

$[\begin{matrix} J_{L i} \\ J_{A i} \end{matrix}] = [\begin{matrix} b_{i - 1} \\ 0 \end{matrix}]$

(2.45)

rotáció csuklóra esetén

$[\begin{matrix} J_{L i} \\ J_{A i} \end{matrix}] = [\begin{matrix} b_{i - 1} \times r_{i - 1, e} \\ b_{i - 1} \end{matrix}]$ .

(2.46)

Ha ezek után feltesszük magunknak a kérdést, hogy mi az a legfontosabb, eredmény, amit az eddigiek során elértük, azt mondhatjuk, hogy a robot csuklókoordinátáinak és azok deriváltjának ismeretében meg tudjuk határozni a végpont pozícióját és orientációját, valamint a sebesség és szögsebesség vektorát. Ezt az ún. direkt kinematikai feladat.

A korábbiak tükrében felmerülhet az a kérdés, hogy képesek vagyunk-e az inverz kinematikai feladat megoldása is. A válasz az, hogy bizonyos esetekben, elvben képesek vagyunk megtalálni a megoldást. Ha ugyanis az (2.37) egyenlet mindkét oldalát balról formálisan megszorozzuk $J^{- 1}$ ‑vel, az inverz Jacobi mátrixszal, a következő összefüggést kapjuk

$\dot{q} = J^{- 1} \dot{p}$ .

(2.47)

A fenti, látszólag egyszerű összefüggés azonban a következő problémákat veti fel

A J Jacobi-mátrix függ a robot konfigurációjától. Minden robot karnál találunk olyan szinguláris konfigurációkat (pl: valamelyik kartag teljesen kinyújtott állapotban van), amikor a robotkar csupán öt szabadságfokú mozgás végzésére képes. Ilyen szinguláris esetben a Jacobi-mátrix nem invertálható.
Ha vizsgált eset nem szinguláris, akkor az (2.47) egyenlet matematikailag hatod fokú polinomhoz vezet, ezt a gyakorlatban a hatod fokú egyenlet gyökeinek megkeresését jelenti. Egy hatod fokú egyenlet gyökeinek meghatározására általános algebrai módszer nem létezik (nincs zárt alakú megoldó képlet), csak numerikusan tudjuk közelíteni.
Ha valamilyen speciális esetben találunk is algebrai megoldást, az sem lesz mindig egyértelmű, hanem általában véges sok (1…3) különböző megoldást kapunk.

A másodikként említett probléma feloldására D.L. PIEPER adott 1968-ban egy elégséges feltételt, amelynek teljesülése esetén az inverz kinematikai feladat algebrai úton megoldható. Amely szerint, ha egy robot rendelkezik három olyan egymást követő rotációs csuklóval, melyek tengelyei egy pontban metszik egymást, akkor az inverz kinematikai feladatnak létezik algebrai megoldása.

Ez esetben ugyanis az eredetileg hatod rendű probléma szeparálható (szétválasztható), azaz lebontható két harmadrendű polinom gyökeinek megkeresésére. Egy harmadfokú polinom gyökei pedig mindig meghatározhatok algebrai úton. A gyakorlatban alkalmazott ipari robotokat általában úgy konstruálják, hogy a három utolsó rotációs csukló tengelye egy pontban messe egymást (pl. a PUMA típusú robotok).

Vissza	Fel	Előre
1. fejezet - Bevezetés	Főoldal	3. fejezet - Robotok statikai jellemzése