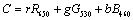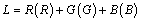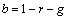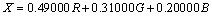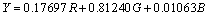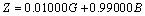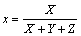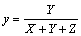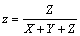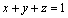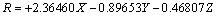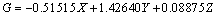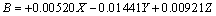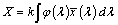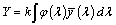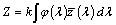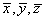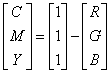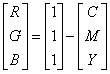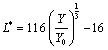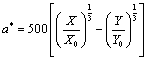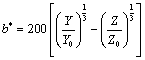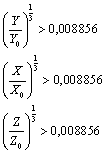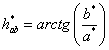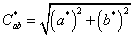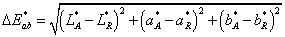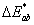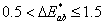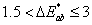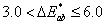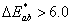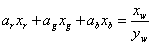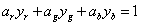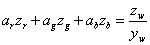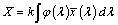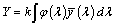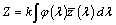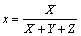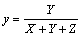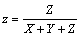2. fejezet - A háromdimenziós technikák optikai és interferometriai háttere
A háromdimenziós képalkotás alapja az emberi látásra vezethető vissza, inspirációja biológiai eredetű. Az emberi látás – és az élővilág egyedeinek jelentős része – úgynevezett binokuláris alapokon nyugszik, azaz a két szem által leképzett térrész síkbeli képeit az agy egy közös feldolgozási algoritmus segítségével együttesen értékeli, értelmezi. A legfontosabb momentum, hogy az adott objektumról a két érzékelő – adott esetben a szem –, eltérő térbeli pozíciója miatt, eltérő képeket regisztrál. A két szemmel látott két kép tehát nem pontosan ugyanolyan. Az agy e két kép közötti eltérésből számítja ki például a mélységet. Természetesen a folyamat ennél sokkal bonyolultabb, ugyanis a két eltérő kép értékelése egy összetett kognitív folyamat eredményeként hozza létre a háromdimenziós látás érzetét. A mindennapi életben ez biztosítja azt, hogy a minket körülvevő objektumokat, tárgyakat relatív pozíciójukkal tudjuk társítani, képesek vagyunk a minket körülvevő elemek relatív – bizonyos esetekben pedig akár az abszolút – pozícióját észlelni. Mindezek alapján viszont nyilvánvaló, hogy ezt a modellt alapul véve, a térhatású érzetet technikai eszközökkel egyszerűen reprodukálni tudjuk. Ha egy sík vagy görbült felületen a kódolt mélységi információkat tárolni tudjuk, akkor ezt közvetítve az agy felé, a térbeliség érzetét kelthetjük. Technikai részletnek tekinthető, hogy ennek alkalmas megvalósításához biztosítanunk kell, hogy a kódolt információk egy részét csak a bal, míg egy másik részét csak a jobb szemen keresztül jusson el az agyba. A sztereoszkópikus megjelenítők lényegében ezt az elvet valósítják meg, igen eltérő műszaki megoldások és technológiák felhasználásával.
2.1. A háromdimenziós megjelenítők - a feladat megfogalmazása
A térbeli megjelenítés lényegében az eredeti felületről érkező hullámfront, vagy a felületet helyettesítő másodlagos felületről érkező hullámfront rekonstruálását jelenti. Egy térbeli hatást keltő objektum valósághű szemlélése, körbejárása az élményen túl tudományos jelentőséggel is bír. Széleskörűen alkalmazható például a média, az orvostudomány bármely szegmensében. Futurisztikus esetben a módszer segítségével akár olyan virtuális események és térrészletek is létrehozhatók, amelyek lehetőséget nyújtanak időben és térben elválasztott pozícióváltásra, valamint térbeli manipulációkra.
E tekintetben egyre inkább előtérbe kerül – a virtualitás vonatkozásában – a számítógépes grafika, mely a felhasználó számára pillanatképeket készít a modellezett, háromdimenziós virtuális világról. Ez a pillanatkép - a generálás idejétől és helyétől függetlenül - alkalmas kimeneti eszközön – például az elektronikus számítógép megjelenítőjén – a vizuális valóság érzeteként láthatóvá tehető, megjeleníthető. A jelenség konstrukciója és szintézise szempontjából kulcsfontosságú ezen esetekben a térben található objektumok nagysága és alakja. A leképzés illetve az ábrázolás paraméterei az alkalmazott nézőponttól, és a megjelenítő felület alakjától és helyétől függenek. E technika egyik kulcsfogalma a virtuális kamera és annak pozíciója. A képgenerálási eljárások feladata, hogy a virtuális kamera nézőpontjából kétdimenziós képeket alkosson a háromdimenziós térről azzal a céllal, hogy a két kétdimenziós kép, az előbb említett bonyolult agyi mechanizmus után, a térbeliség élményévé szintetizálódjon. A grafikus eljárás műveletei többek között a képelemek összeállítása, a modell transzformáció, a látótéren kívül eső térrészek elhagyása, a nézőponti transzformáció, a képtérre történő vetítés és a megjelenítés.
A térbeli megjelenítés elméleti vizsgálata és gyakorlati megvalósítása korai eredetű, azonban elterjedése mindmáig korlátozott volt. Ennek elsődleges oka abban keresendő, hogy a generálás és a megjelenítés technikai háttere, eszközparkja szerény volt. Igazi lökést – a fokozott igény megjelenésén túl – a gyors számítástechnikai háttér és a korszerű, nagy teljesítményű és gyors optoelektronikai megjelenítési lehetőségek adtak. A felhasználók igényeinek megfelelően a fejlesztők és a gyártók arra koncentrálnak, hogy a tudományos és az ipari megvalósulásokon túlmenően, a hétköznapi élet és a kommunikáció részévé váljon a térhatású vetítés, valamint megjelenhessen az élet szinte minden területén.
2.2. A színek
A háromdimenziós megjelenítésben a színek kitüntetett szerepet töltenek be. Az élvezeti célú felhasználás esetén az igazi, mély alapcél a puszta térbeliségen túl olyan ingerek közlése a szemlélővel, amelyek a teljességen túl érzelmi hatást váltanak ki. Az élvezeti célú felhasználás mellett, a gyakorlati alkalmazások során a megfigyelt objektumról történő teljes információmennyiség megjelenítése a cél. Jelentheti ez azt, hogy a különböző látószögekből történő megfigyelés újabb információt ad, ahogy ez például a sztereo mikroszkópos megfigyelés esetén a mélységi méretek közvetett érzékeltetését jelenti. A manapság már nem igazán alkalmazott sztereo távolságmérő esetén pedig a – térbeli látás képességével rendelkező szemlélő – közvetlen, számszerűsíthető távolságadatokat tud kinyerni a berendezésből. Ha a megjelenítés során több érzékszervi hatást is ki tudunk használni, a kép teljesebbé válik. A háromdimenziós megjelenítés mellett közvetlen hatású a hang térbelisége, dinamikája, a figurális vagy éppen az életszerű hatások, képek. A lényeghez hozzátartozóan, de mélyebben fejtik ki hatásukat a színek, illetve azok tulajdonságai. Itt természetesen a színek tekintetében elsősorban nem azok meglétére vagy hiányára gondulunk. E hatás lehet technikai jellegű, amikor például az anaglif eljárás során a kiválasztott színpár, illetve a hozzájuk tartozó színszűrő pár közvetlen színdiszkriminációs hatása hozza létre a különböző látószögből készült képek szétválasztását. A hatás lehet emocionális jellegű is, amikor például meleg vagy hideg színű környezetbe helyezve a szemlélt objektumot, annak környezetében betöltött szerepét kívánjuk módosítani. A színpreferenciák, illetve a színharmóniák megfelelő és tudatos alkalmazásával a kívánt hatás érdekében még mélyebb érzelmi szintekre tudunk hatni. A fenti néhány példából is jól látható, hogy a színekkel történő műveletek helyes alkalmazásával a teljes és kívánt hatás szempontjából komoly erőfeszítéseket tudunk tenni. Mindehhez hozzátartozik az is, hogy a generálás, a képfeldolgozás illetve az egyes transzformációk során a színekre vonatkozó ismereteinket úgy legyünk képesek alkalmazni, hogy azok torzulása nélkül jöjjön létre a várt eredmény.
Fontos tudatosítani, hogy a színekkel kapcsolatos számszerűsíthető, racionalitáson alapuló megfontolások, műveletek mögött a színhasználat pszichológiai értelmezése is igen nagy és kiemelt jelentőséggel bír. A színeket a gyakorlati alkalmazások során nemegyszer az érzelmekkel hozzuk kapcsolatba, szemben a műszaki jellegű, figurális leírással, ábrázolással, amely racionális megközelítésű, és elsősorban az intellektussal hozható kapcsolatba. Tapasztalati tény, hogy a színek kimutatható érzelmi töltettel és hatással bírnak, valamint emocionális reakciókat váltanak ki. A színek projektív értelmezésének alaphipotézise az, hogy a színre, mint ingerre adott válasz érzelmileg színezett [2.1.] . A szín tehát szubjektív érzet, amely a fizikai ingerek belső, agyi, idegrendszeri leképeződéseként jön létre. Ezt a belső leképződést, érzetet befolyásolják a szín környezete, megnevezése és egyéb emlékezeti tényezők. Ez jut érvényre a színkontraszt hatásában, azaz színingerek csoportja egészen más hatást válthat ki, mint a csoportban lévő színingerek külön-külön. Ezt a hatást fokozhatja, vagy kiegészítheti a színáthangolódás jelensége, amely során a hosszú ideig tartó színingerhatás új, megváltozott színélményt eredményezi. Ám ez a jelenség egy idő után az úgynevezett színfáradtságot váltja ki, amely a szemlélőben a színlátás érzésének csökkenését idézi elő. Látható tehát, hogy a színek megjelenítés-technikai használatával kapcsolatos megfontolásoknál egyaránt figyelembe kell venni az emberi őstapasztalatokhoz, a kulturális és az individuális hatásukhoz, jelentésekhez kapcsolódó tartalmakat is.
2.3. Alapfogalmak
Az alábbi fejezetekben áttekintjük a színingerek érzékelésével és feldolgozásával kapcsolatos alapfogalmakat.
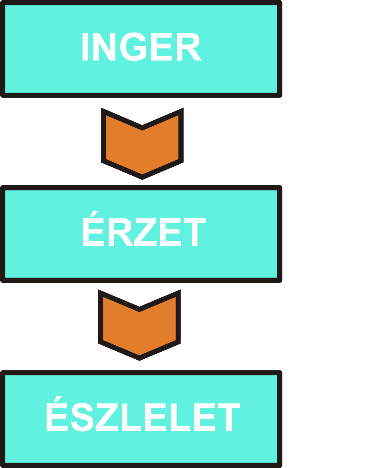
2.3.1. Inger, észlelet és érzéklet
Nem a szemünkkel, hanem az agyunkkal látunk [2.2.] . Ez természetesen az általános értelemben vett látáson belüli színlátásra is érvényes. A színinger lényegében a látás szervébe behatoló, fizikailag meghatározott hullámhosszú elektromágneses sugárzás [2.3.] hatására keletkező inger, amely a fiziológiai jellegű észlelet formájában kerül a pszichológiai szintű, agyi feldolgozásra, és váltja ki az érzékletet. A további vizsgálódásaink szempontjából a fény e hullámhossztartományának az emberi – teljes – idegrendszeri alapú látószervére gyakorolt fizikai, fiziológiai és pszichológiai hatásaként létrejövő színérzékletet jelenti [2.4.] .
A színekkel, mint fény okozta érzékletekkel és annak egyéb kapcsolataival foglalkozó tudományág a színtan, amely a jellegénél fogva szorosan összefügg a fizikával, a fiziológiával és a pszichológiával. Objektív értelemben sem az elektromágneses sugárzás kitüntetett hullámhossztartományának, sem a minket körülvevő tárgyaknak, fényforrásoknak nincs színük, csupán a szemünkkel és az agyunkkal látjuk azokat színeseknek. A színtan tehát a színérzéklet kialakulásának, számszerűsítésének és mérésének elméleti, módszertani és gyakorlati kérdéseivel foglakozik. Szintén nagy jelentőséggel bír a színek - kereskedelmi és egyéb alkalmazástechnikai vonatkozásaik miatt - tulajdonságainak valamint paramétereinek szabványosítása.
A továbbiakra vonatkozóan a színek osztályozásáról előrebocsátjuk, hogy a színérzet alapján nem tarka vagy semleges, illetve tarka színeket különböztetünk meg [2.5.] . A nem tarka színek csoportjába soroljuk a fehéret, szürkét, feketét, viszont a tarka színeket jelentik például a vörös, kék, sárga és ehhez hasonlók. Egy másik csoportosítás a forrásra vonatkozik, amely szerint egyes színek valódi fényforrásokból származnak, amilyenek például a Nap, a csillagok, egy viaszgyertya, egy halogén izzó, egy LED vagy egy izzólámpa. A nem önálló forrásként működő, nem világító tárgyakból származó színek az úgynevezett közvetett színek, amelyek például a testek, felületek színei. A közvetett színeket a szerint csoportosítjuk, hogy azok érzékelése reflexió vagy transzmisszió útján valósul meg, azaz visszaverten vagy átmeneti fényben szemléljük őket [2.6.] .
2.3.2. A szín, mint megnevezés
A szín szót többféle értelemben is használjuk. Általában a minket körülvevő tárgyak, festékanyagok, sugárforrások megjelölésére alkalmazzuk. A fizikában a forrásból – annak típusától és jellegétől függetlenül – kilépő elektromágneses sugárzás emberi szem által érzékelhető hullámhossztartományba eső részének jellemzését jelenti.
A szakkifejezések helyes – és itt elsősorban a „szín” szó – használata a műszaki-tudományos gyakorlatban elengedhetetlen. A színes látással, és az azt létrehozó komponensekkel, illetve részben azok számszerűsítésével a színingermetrika foglalkozik, amely bevett fogalmait az MSZ 9620 számú szabvány rögzíti. Színes tárgy látványakor agyi funkciók működnek – és ahogy ezt már kifejtettük –, a pszichológia számára ezt észlelést – színészlelet – jelent, és az ehhez kapcsolódó jelenségek tárgyalása során az észlelet szó használata a helyes. Továbblépve azt is megállapíthatjuk, hogy a színészleletek okozója maga az optikai sugárzás, mely energetikai kérdéseivel a radiometria foglalkozik. Az átlagos emberi észlelő tulajdonságaira alapozva vezethetjük be a szabványosított, és a világítástechnikában széles körben használatos fotometriai fogalmakat és mennyiségeket, melyek így színingermetrikai mennyiségeknek tekinthetők. A színingermetrikai mennyiségekkel kapcsolatos vizsgálatok, számítások során meg kell jelennie az inger szónak, amely ezáltal azt jelenti, hogy színingermetrikai tárgyalásmódról van szó [2.7.] . Az elmélet és a gyakorlat szempontjából tehát különösen fontos a színészlelet és a színinger közötti fogalmi különbség, azok helyes és megfelelő helyen való használata. Így a szín kifejezést önmagában a színingermetrika területén kerülni kell, vagy ha használata indokolt, akkor azt előzetesen definiálni szükséges.
2.3.3. A tarka színek jellemzői
A tarka színeket három fontos tulajdonsággal jellemezzük, amelyek a legismertebb besorolás szerint a színezet (amelyet színárnyalatnak, színjellegnek illetve színnek is nevezünk), a telítettség és a világosság.
A színezet szempontjából megkülönböztetünk úgynevezett ős, illetve közbülső színeket, melyek az ősszínekből összetettnek látszanak. Sajátságos szempontok – általában a hasonlóság – alapján a színárnyalatok visszatérő sorozatba, úgynevezett színkörbe rendezhetők. A spektrumszínek ismert sorrendje: vörös, narancs, sárga, zöld és kék. Egy ilyen színkörben az egymással szemközt található színek úgynevezett ellentétes színek. Természetesen a színkörben található színárnyalatok száma nem véges.
A másik fontos paraméter a telítettség, amely lényegében a tarka szín fehértartalmával függ össze. Annál telítettebb egy színárnyalat, minél kevesebb fehéret tartalmaz. A fehértartalom növelésével a telítettlenség fokozható. A legtelítettebbek a spektrumszínek, a telítettségi fokozatok megkülönböztethetőségének mértéke a szem egyik fontos paramétere.
A harmadik fontos paraméter a világosság, amely energetikai vonatkozású fogalom. Azonos spektrális energiaeloszlás esetén a szemünkbe jutó két fény közül az a világosabb, amely intenzitása nagyobb. Néhány kivételtől eltekintve megállapítható, hogy a tarka színek világossága a színérzetet viszonylag szerény mértékben befolyásolja.
2.3.4. Metaméria
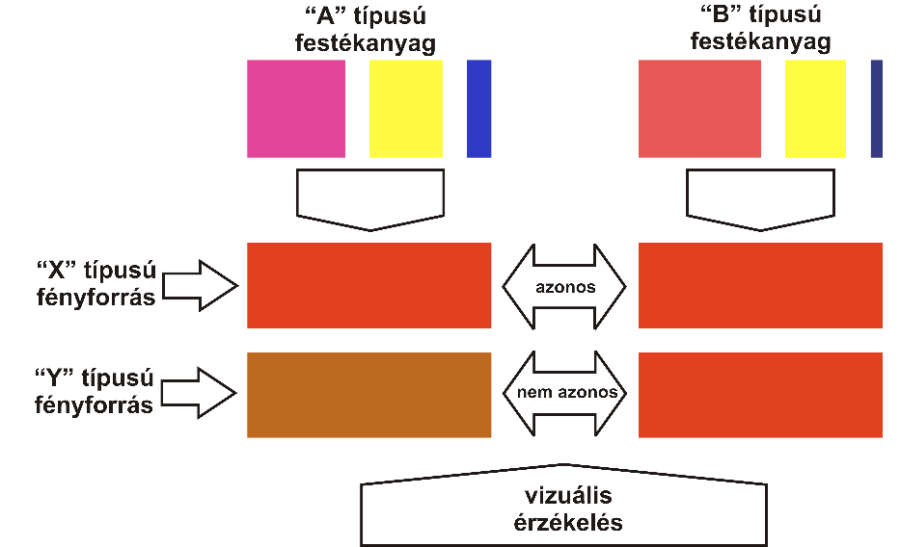
Ismert tény, hogy spektrálisan eltérő színek azonos színérzetet válthatnak ki [2.8.] . Ezt a jelenséget nevezzük metamériának [2.9.] , amely jellemzője, hogy két színárnyalat, egy adott megvilágításban egyformának tűnik, de más megfigyelési geometria vagy eltérő fényviszonyok esetén már különböznek [2.10.] . A metaméria a festék- és nyomdaipar komoly problémája, amely akkor lép fel, amikor a próbanyomat készítésénél fennálló fényviszonyok a felhasználásakor már nem állnak fenn. Kissé túlozva előfordulhat, hogy a műfénynél ellenőrzött próbanyomat kültéri felhasználásra kerül. A metaméria, mint hiba felléphet a szemlélő okán, mivel nincs két azonos színlátású ember. Így amit az egyik szemlélő azonosnak lát, azt egy másik ember, teljesen azonos körülmények között is eltérőnek észlelhet. Metaméria jellegű hibát okozhat a méretbeli eltérés is, ugyanis a látótér különböző részein érzékelt színek eltérőnek bizonyulhatnak. De ugyanígy különböző távolságokból vagy más látószög alatt szemlélt színek a kis területeken fellépő, eltérő fényviszonyok miatt különbözhetnek. Ez a jelenség elsősorban fémes csillogású festékek vagy hordozók, esetleg speciális bevonatok esetén fordulhat elő.
2.3.5. Színkeverési módok
A színkeverés során különböző spektrális összetételű elektromágneses sugárzásokat hozunk egymással kapcsolatba azzal a céllal, hogy újabb színeket hozzunk létre. A színkeverés két fő típusát különböztetjük meg, az additív (összeadó) és a szubtraktív (kivonó) színkeverést. Megjegyzendő, hogy a szakirodalom több fajta – nem igazán elterjedt – színkeverést is megkülönböztet [2.11.] . Párhuzamos színkeverés esetén, két vagy több szűrővel létrehozott akromatikus színinger egyidejűleg esik egy síknak ugyanarra a pontjára, és ezt látja az észlelő. Soros színkeverésnél egyetlen akromatikus fényinger két vagy több színes rétegen, egymás után halad át, az észlelő ezt is egy sík ugyanazon pontjában figyeli meg. Időbeli színkeverés esetén színingerek felváltva lépnek be a megfigyelő szemébe, de olyan frekvenciával, hogy az csak a keveréküket észleli. Foltok színkeverésekor kis alakzatokat készítünk úgy, hogy a megfigyelő nem tudja őket felbontani, így csak a színingerek keverékét látja.
2.3.5.1. Az additív színkeverés
Az additív színkeverés minden esetben színes fények keverését jelenti úgy, hogy további fény esetén világosabb fényt kapunk. Mivel az ilyen színes fények összeadódnak, összeadó színkeverésnek is nevezzük ezt az esetet. Szemléltetésének legegyszerűbb módja, ha három vetítőegység elé külön-külön sugárutakba vörös, zöld és kék üveget helyezünk, és ezeket egy fehér felületre vetítjük úgy, hogy a színes alakzatok részben fedjék egymást. Ebben az esetben az egymásra kerülő színek egy világosabb színt hoznak létre, a három szín pedig egymással keverve fehéret ad. A vörös és zöld összeadása sárgát, a vörös és kék bíbort, míg a zöld és kék türkizt eredményez. Mivel itt a sugárzások, vagyis a színek, és nem színes anyagok keverednek, az additív színkeverést optikai színkeverésnek is nevezzük. Additív színkeverés valósul meg akkor is, amikor a szem érzékelőjének ugyanazon helyét gyors időközökben, váltakozó színű fénysugarak érik, vagy a különféle színű felületrészeket a felbontóképességnél kisebb látószög alatt nézzük. Ekkor a szem a színeket már nem tudja különválasztani. A nyomdaiparban alkalmazott többszínnyomás felületén a szem nem ismeri fel a raszterpontok színét külön-külön, hanem csak a keverékszínt.
Összefoglalva, az additív, vagy más néven összeadó színkeverés elnevezése onnan származik, hogy a jelenség létrehozása szempontjából kiindulásnak tekinthető alapszínek fényenergiái összeadódnak. Az ilyen típusú színkeverés leggyakrabban tapasztalható esete például az optikai rendszerű, több vetítőegységből egy közös ernyőre történő vetítés. Ennek az esetnek feleltethető meg a színes monitor vagy televízió is, amelynél a forrásból kilépő elektronok vezérelt pályákon haladva a képcső elülső üvegfala belső felületén található speciális anyagnak ütközve színpontokat hoznak létre. Ha az additív színkeverés alapszíneinek megfelelő anyagokat gerjesztünk, akkor megfelelő elrendezés és méret esetén, kellő távolságból szemlélve, és a részleteket már nem felbontva additív keverékszínek jönnek létre a szemben. Hasonló a helyzet az autotípia (rácsfelbontásos) nyomtatásnál is, amikor az alapszínekkel nyomtatott pontok, azok közelsége miatt nem bonthatók fel az emberi szem által. Kicsit más eset, amikor a színes felületrészek gyors időbeni váltásakor,a tehetetlenség miatt jön létre az additív színkeverés. Az összeadó színkeverés mindegyik változatára jellemző, és az bennük a közös, hogy a különböző alapszínekből származó fénysugarak a szemben gyakorlatilag egy időben egy színérzékelő elemet ingerelnek.

2.3.5.2. A Grassmann-törvények
A Grassmann-törvények [2.12.] a színek additív keverésének törvényszerűségeit írják le. Kimondják,
-
hogy a színjellemzők meghatározására három független változó szükséges és elegendő,
-
hogy az additív színkeverés szempontjából a színek jellemzői számítanak, és nem azok spektrális összetétele,
-
ha a színek additív színkeverésében egy vagy több összetevőt folyamatosan változtatunk, az eredményül kapott jellemzők is folyamatosan változnak.
A Grassmann-törvények nem alkalmazhatók a perifériás, illetve a mezopos látás esetére, és akkor sem érvényesek, ha a vakítás jelensége lép fel. A jelentőségük megértése szempontjából értelmezésük különleges fontossággal bír. Az 1853-ban publikált Grassmann törvények azt jelentik a számunkra, hogy a keverékfény színét az összetevők színe szabja meg, és nem függ azok spektrális összetételétől. A gyakorlatban ez például azt jelenti, hogy a vörös és a zöld színek additív keverésével létrehozható sárga nem függ attól, hogy a létrehozó színkomponensek monokromatikusak-e, vagy sem, például keverékszínek. Minden színt három, matematikailag értelmezhető paraméterrel, a színezettel, a telítettséggel és az intenzitással lehet meghatározni. A keverés során az egyik összetevő folytonos változtatásakor a keverékszín is folytonosan változik, diszkrét lépések nélkül.
Összefoglalva és kissé más megfogalmazásban tehát a Grassmann-törvények kimondják, hogy egy szín leírásához három egymástól független adat szükséges és elégséges. A gyakorlatban ez például a színezetet, a telítettséget és a világosságot jelenti. Az adatok számára vonatkozó megkötés szerint három adat azért szükséges, mert a színlátás folyamata három különböző spektrális érzékenységű detektáló elemhez köthető. Az jellemzők kölcsönös függetlensége biztosítja, hogy azok közül kettőből matematikai módszerekkel a harmadik ne legyen meghatározható. Megjegyzendő, hogy a példaként említett világosság a három érzékelő elemtípus összegzett ingerültségi szintjét jelenti, valamint a becsapódó energia és a hozzá tartozó érzet logaritmikus összefüggést mutat. A fentebb tárgyalt metamer színek összeadó módszerrel kikevert színei szintén metamerek. Ennek gyakorlati jelentősége különösen nagy, mivel ez biztosítja, hogy például nyomtatásnál az előírtnak megfelelő színt állítsuk elő akkor is, ha a spektrális összetételek különbözőek. A keverés során a paraméterek folyamatos változtatásakor tapasztalható, az eredményül kapott színre vonatkozó jellemzők szintén folyamatosan változnak. Ennek következménye, hogy az additív színkeverésnél az egyik színből mindig el tudunk jutni egy másikba, a köztük lévő színárnyalatokon keresztül.
![Hermann Günther Grassmann (1809-1877) [2.26.]](images/image_II_4.png)
2.3.5.3. A szubtraktív színkeverés
A kivonó, vagy szubtraktív színkeverés esetén a fénysugár útjába kerülő színes anyagok módosítják annak spektrális összetételét. Ebben az esetben – az additive színkeveréstől eltérően – már egy meglévő fehér színből indulunk ki, és annak tulajdonságait az adott spektrális tartományban elnyelő vagy szóró eszközzel módosítjuk. Erre a célra a legtöbb esetben színszűrőket alkalmazunk, melyekre jellemző, hogy az összes színárnyalatot tartalmazó fehér fényből bizonyos hullámhossztartományokat átengednek, a többit viszont elnyelik, tehát a fehérből azokat kivonják, ez az új szín keletkezésének módja. A szubtraktív színkeverés törvényszerűségei természetesen az additív változaton alapulnak, arra vezethetők vissza.
A szubtraktív színkeverés leggyakrabban a festékek keverése, vagy azok egymásra történő nyomtatása során jön létre. A kivonó színkeverés egyik legismertebb, és szinte mindenki által megtapasztalható esete a színes film, illetve a színes fénykép keletkezése. Az alapszínek a cián, a magenta (bíborvörös) és a sárga, melyek teljes keveréke a fekete színt adja. A színhívásos elven működő színes filmek esetén a hordozóra egymás felett, az egyes additív színekre érzékeny anyaggal kevert zselatinréteget visznek fel. A fényérzékeny anyag általában valamilyen ezüsthalogén, mely az expozíció során energiát nyel el, és az érzékenységének megfelelő tartományban beérkező sugárzás hatására benne fotofizikai változások következnek be. Ennek során az ezüsthalogénben elemi ezűstcsíra gócok keletkeznek az elnyelt energiával arányos mennyiségben. Ez az úgynevezett látens kép, melyet egy színhívásnak vetnek alá, amely során az adott rétegben, a keletkezett elemi ezüstcsíra gócok mentén, az expozíció mennyiségével arányosan ezüst redukálódik ki, és a réteg érzékenységének megfelelő kiegészítő színű színezék is keletkezik. Következő lépésben az ezüstöt eltávolítva, megmarad a keletkezett színezék, amely a rajta áthaladó fehér fényből az eredeti szín kiegészítőjét hozza létre. A fenti esetben negatív filmet kapunk. A pozitív, az úgynevezett diakidolgozás esetén, az első lépés egy egyszerű redukció, amely során a rétegekben a beexponált helyeken ezüst keletkezik. Az ezüst eltávolítását követően a rétegekben az összes megmaradt ezüsthalogént beexponálják, majd ezután következik a színhívás, amely így az eredeti színeket fogja eredményezni, azaz pozitív kép keletkezik.
Nyomdatechnikában negyedik színként általában a feketét használják, mivel a nyomtatásban viszonylag sok a fekete színű felület. A három alapszínből történő összenyomásnál jobb minőségű a feketével történő nyomtatás. A valóságban általában nem tisztán additív vagy szubtraktív színkeveréssel magyarázhatjuk a színek keletkezését, hanem a kettő keveredésével. A nyomdatechnikában gyakran készítenek olyan színes nyomatokat, amelyek esetében az egymásra hordott festékek nem tökéletesen fedik egymást, azaz nem takarják ki az alattuk lévő színt, hanem átlátszóak.
A szubtraktív színkeverés alapkísérlete az egymás után elhelyezett – a feladatnak megfelelően megválasztott spektrális tulajdonságokkal rendelkező – színszűrőkkel vagy úgynevezett színes optikai ékekkel vitelezhető ki. Az egymás után elhelyezett szűrők esetén a fényforrás fehér fényéből az első színszűrő kivon egy részt azáltal, hogy a megfelelő rész elnyelődik. Ezután a megmaradó nyalábból a következő szűrő szintén kivon egy részt. Amennyiben ezeket, az egymást követő szűrőket sárga, bíbor és zöldeskék színűnek választjuk, akkor ezen szubtraktív alapszínek keverésével az additív színeket és a fekete színt is elő tudjuk állítani.
Például, a bíbor és zöldeskék szűrő kivonó jellegű alkalmazásával a kék additív színt kapjuk. Megjegyzendő, hogy ebben az esetben a példa nem általánosítható, mivel a kivonó színkeverés eredménye – nem úgy, mint az összeadó színkeverés esetén – függ az egyes szubtraktív szűrők spektrális eloszlásának tulajdonságaitól. A festékiparban elterjedt festéktípusok színes részecskéi, az úgynevezett pigmentek keveredésénél, azaz a festékkeverésnél a kivonó színkeverésnek megfelelően keletkezik az eredő szín. Például fehér alap esetén sárga és kék festék keverésével nem az összeadó keverés tulajdonságainak megfelelő fehér, hanem a szubtraktív módon létrejövő zöld keletkezik. Általános szabályként fogalmazható meg, hogy az észlelt tárgyszín mindig a felület által elnyelt szín kiegészítő színe lesz.
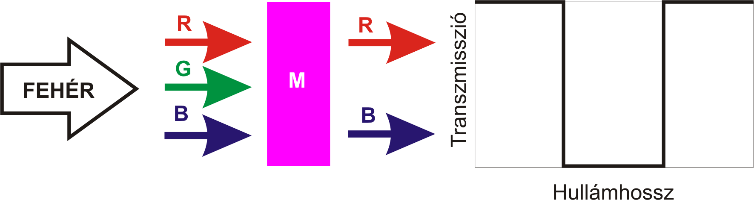
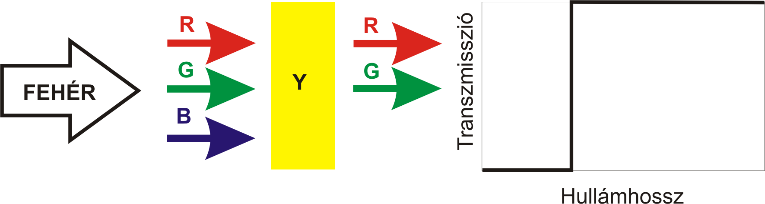
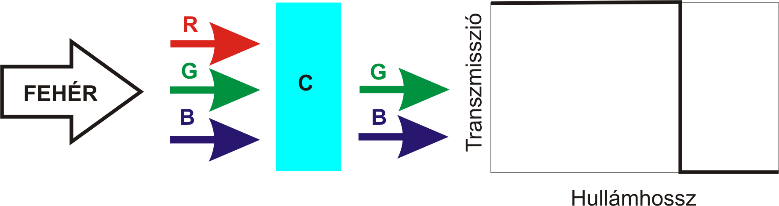
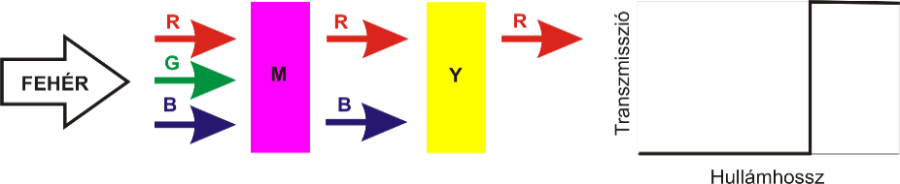
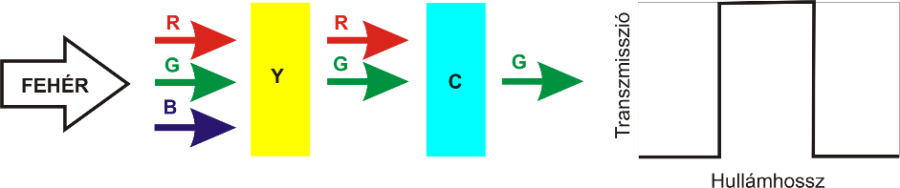
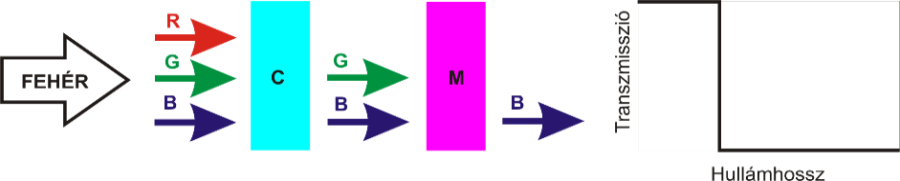
2.4. A CIE-féle színmérő rendszer
A Nemzetközi Világítástechnikai Bizottság (Commission Internationale de L’Éclairage) egyik fontos feladata módszerek és mérési technológiák kidolgozása a színek egyértelmű, objektív leírására és meghatározására. A szervezet első, az additív színkeverésen alapuló trikromatikus színmérő rendszerét 1931-ben fogadta el. A CIE additív színkeverési kísérletek alapján meghatározott függvények segítségével írja le a színeket. A Grassmann-törvényekre visszavezető tapasztalatra építve, additív módon három független alapszínből bármely szín kikeverhető, azok tetszőleges megválasztásának egyetlen feltétele a függetlenségük, azaz egyik se legyen kikeverhető a másik kettő lineáris kombinációjaként.
A CIE-színrendszere minden színhez egy-egy számhármast rendel, amely a szemünkben fellehető három színérzékelő receptor meglétére vezethető vissza. Itt jegyzendő meg, hogy vannak kísérletek e három – a vörösre érzékeny protos, a zöldre érzékeny deuteros és a kékre érzékeny tritos – színreceptor viselkedésére alapozott rendszer bevezetésére is, melynek alapja a színreceptorkra ható fény által kiváltott ingerek erőssége [2.13.] .
2.4.1. A színmeghatározás eredeti módszere
Az első mérésekre alapozott trikromatikus színleírás Wright [2.14.] és Guild [2.15.] nevéhez fűződik, akik egymástól függetlenül végeztek vizsgálatokat, és tettek javaslatot az eredményeik alapján. Az eredeti kísérletben a színkép monokromatikus színeit 2-fokos látószög alatt szemlélve, tizenhét megfelelőnek tekinthető színlátású személy kevert színekkel hasonlította össze 5 nm-es lépésközökben változtatva. Ez a változtatás a kevert színek fényerősségét érintette, melyeket három, 650, 530, 460 nm-es színszűrővel, 4800 K° színhőmérsékletű fényforrás mellett állítottak elő. Azok a fényerőkülönbségek, amelyek a színt, mint stimulusokat (gerjesztéseket) meghatározták, derékszögű koordináta-rendszerben ábrázolhatók, és a következő azonossággal jellemezhetők:
|
|
A kísérlet konkrét kivitelezése során zárt, fényszegény helyen elhelyezett berendezésben, a kék, zöld és vörös fényforrások változtatható fényintenzitással világították meg egy gipsz prizma matt fehér felületét. A prizma másik oldalára az adott színmintát helyezték el. Az ép színlátású vizsgálati személy a három fényforrás segítségével a színminta színét additív módon keverte ki, azaz a fények intenzitását addig állította, amíg a két oldalon színazonosság nem tapasztalt. Mérési adatként az adott színmintához tartozó, fényforrások által kibocsátott fénysűrűség-értékeket rögzítették. Ezzel a módszerrel, tapasztalati úton minden színt kimértek. A tapasztalat az volt, hogy előfordultak színek, amelyeknél a három szín keverésével színazonosság nem volt létrehozható. Ilyen esetben azt a megoldást alkalmazták, hogy a keverendő színekből egyet átvezettek a másik oldalra, azaz rávetítették a kikeverendő színmintára. Így a túloldalra vetített színmintához tartozó érték negatív előjelű lett. Ez az eredeti minta reprodukálásánál problémát jelentett. Természetesen ez azt a problémát vetette fel, hogy ebben az RGB rendszerben lévő negatív értékek miatt, az eredeti minta színeit – tisztán additív úton – nem lehetett visszaállítani.
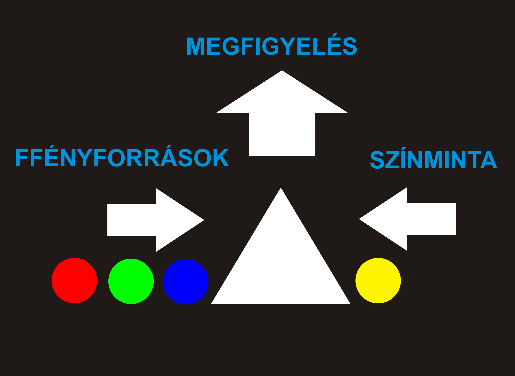
2.4.2. Az CIE RGB-színrendszere
Az eredeti kísérletekre alapozva a CIE által választott alapszínek a 700 nm hullámhosszúságú vörös (R), az 546,1 nm-es zöld (G) és a 435,8 nm-es kék (B) spektrumszínek lettek. Kísérletileg igazolták, hogy ha e vörös, zöld és kék alapszínek 1 : 4,5907 : 0,0601 arányban keverednek, akkor egy úgynevezett egyenlő energiájú fényforrás – azaz állandó spektrális teljesítmény-eloszlású, a 380-tól 780 nm-ig terjedő hullámhossztartományban ugyanakkora kisugárzott teljesítményű – fehér színt kapunk. Mindezek alapján az (R) = 0,176 97 lm, (G) = 0,812 40 lm és a (B) = 0,010 63 lm értékeket az alapszínek egységnyi R, G, B mennyiségeinek tekintjük. Megállapodás szerint egy egységnyi vörös, egy egységnyi zöld és egy egységnyi kék keveréke 1 lm fehéret eredményez. Ha egy megadott szín kikeveréséhez R, G, ill. B egységnyi kell az alapszínekből, akkor az eredő szín világosságára érvényes, hogy
|
|
Az együtthatók az úgynevezett trikromatikus összetevők. Az alapszínek egységei ismeretében kísérletileg meghatározhatók a spektrumszínek kikeveréséhez szükséges arányok. A színkép minden hullámhosszához három érték tartozik: r, g és b. Ilyen arányban kell az (R), (G), (B) alapszínegységeket keverni az adott hullámhosszú spektrumszín eléréséhez. Tehát a színkoordináták lehetővé teszik, hogy a színeket két dimenzióban ábrázolhatjuk úgy, hogy az egyik tengelyen például az r-et, másikon a g-t jelenítjük meg. A harmadik koordinátára érvényes, hogy
|
|
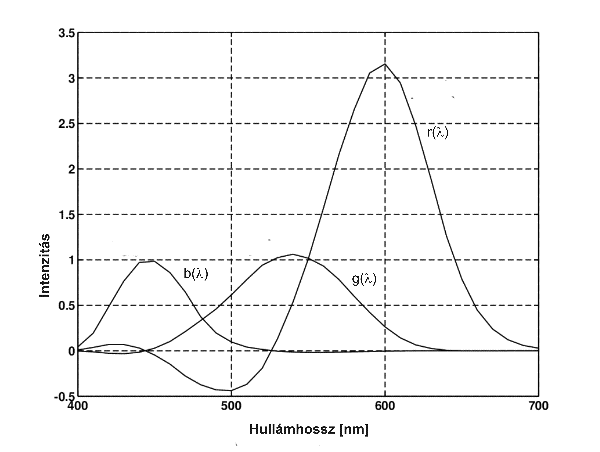
|
λ |
r |
g |
b |
|---|---|---|---|
|
400 |
0,00963 |
-0,00217 |
0,06237 |
|
420 |
0,05166 |
-0,01665 |
0,52396 |
|
440 |
0,01476 |
-0,00735 |
0,96395 |
|
460 |
-0,09622 |
0,07095 |
0,78554 |
|
480 |
-0,23780 |
0,24042 |
0,36195 |
|
500 |
-0,29500 |
0,49060 |
0,10749 |
|
520 |
-0,14768 |
0,91076 |
0,01331 |
|
540 |
0,41976 |
1,05120 |
-0,01219 |
|
560 |
1,22830 |
0,93783 |
-0,01461 |
|
580 |
2,27240 |
0,64930 |
-0,00993 |
|
600 |
2,87170 |
0,30069 |
-0,00427 |
|
620 |
2,37430 |
0,07468 |
-0,00151 |
|
640 |
1,25430 |
0,00450 |
-0,00014 |
|
660 |
0,44320 |
-0,00263 |
0,00023 |
|
680 |
0,12086 |
-0,00108 |
0,00005 |
|
700 |
0,02811 |
-0,00026 |
0,00002 |
|
720 |
0,00652 |
-0,00006 |
0,00001 |
2.4.3. Az XYZ-színrendszer
Az eredeti RGB a negatív előjelek miatt gyakorlati célokra nem használható, ezért célszerű rajta egy olyan matematikai transzformációt végrehajtani, amely eredményeként a már transzformált színrendszer csak pozitív színösszetevőket tartalmaz. Ebben eltűnnek a negatív előjelek, de túltelítetté válnak a színek, azaz a valóságban nem létező, virtuális színek jönnek létre [2.16.] . A Nemzetközi Világítási Bizottság 1931-ben ezért olyan szín-összehasonlító segédfüggvények bevezetését javasolta, amelyek segítségével Wright és Guild eredményei egy olyan téren belül helyezhetők el, ahol minden érték pozitív. Ezen felül a színkoordináták nemcsak vizuális összehasonlítással, hanem azok spektrális energia-eloszlása alapján, elméleti úton is meghatározhatók. Tehát a CIE javaslata az volt, hogy az (R), (G) és (B) alapszínek helyett minden valóságos színre kizárólag pozitív koordinátákat adó alapszínek kerüljenek bevezetésre. Az új alapszíneket úgy választották meg, hogy az általuk alkotott alakzat teljesen körülzárja a spektrumvonalat és a bíborvonalat, így az r, g, b rendszer analógiájára generált x, y, z rendszerben minden valóságos szín koordinátái pozitívak.
Az alakzat kiválasztására a CIE az alábbi követelményeket állította fel [2.17.] :
-
Az egyenlő energiájú fehér szín X, Y és Z színösszetevője legyen egymással egyenlő .
-
Minden szín Y színösszetevője adja meg a szín világosságát.
-
Az X, Y, Z alappontok essenek minél közelebb a spektrumvonalhoz.
-
Az egymástól minimálisan, de szemmel észrevehetően különböző színeket ábrázoló pontok távolsága az egész színtartományban lehetőleg egyforma legyen.
-
Azok a pontok, amelyek az r, g, b koordináta-rendszerben egy egyenes mentén fekszenek, az x, y, z rendszerben is egy egyenesre essenek.
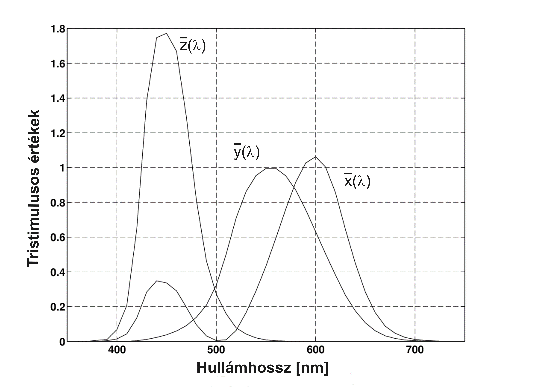
|
Hullámhossz |
x |
y |
z |
|---|---|---|---|
|
360 |
0,00013 |
3,92E-06 |
0,000606 |
|
380 |
0,001368 |
0,000039 |
0,00645 |
|
400 |
0,01431 |
0,000396 |
0,06785 |
|
420 |
0,13438 |
0,004 |
0,6456 |
|
440 |
0,34828 |
0,023 |
1,74706 |
|
460 |
0,2908 |
0,06 |
1,6692 |
|
480 |
0,09564 |
0,13902 |
0,81295 |
|
500 |
0,0049 |
0,323 |
0,272 |
|
520 |
0,06327 |
0,71 |
0,07825 |
|
540 |
0,2904 |
0,954 |
0,0203 |
|
560 |
0,5945 |
0,995 |
0,0039 |
|
580 |
0,9163 |
0,87 |
0,00165 |
|
600 |
1,0622 |
0,631 |
0,0008 |
|
620 |
0,85445 |
0,381 |
0,00019 |
|
640 |
0,4479 |
0,175 |
0,00002 |
|
660 |
0,1649 |
0,061 |
0 |
|
680 |
0,04677 |
0,017 |
0 |
|
700 |
0,011359 |
0,004102 |
0 |
|
720 |
0,002899 |
0,001047 |
0 |
|
740 |
0,00069 |
0,000249 |
0 |
|
760 |
0,000166 |
0,00006 |
0 |
|
780 |
4,15E-05 |
1,5E-05 |
0 |
|
800 |
1,03E-05 |
3,7E-06 |
0 |
|
820 |
2,52E-06 |
9,11E-07 |
0 |
Mindezek alapján a transzformációs formulák [2.18.] :
|
|
||
|
|
||
|
|
Az X, Y, Z színösszetevőkből számíthatók az x, y, z színkoordináták:
|
|
||
|
|
||
|
|
Können belátható, hogy
|
|
Az átszámítás fordított irányban is megvalósítható:
|
|
||
|
|
||
|
|
A színek kezelése, jellemzése és mérése során a rendszer jól vizsgázott, így jelenleg elfogadottnak tekinthető. Egy szín helye ebben a rendszerben az x, y színkoordinátákkal, világossága pedig az Y színösszetevővel jellemezhető. A színösszetevők a ɸ(λ) színinger-függvény ismeretében egyszerűen meghatározhatók:
|
|
||
|
|
||
|
|
Ahol
|
X, Y, Z |
a színösszetevők, |
|
|
|
spektrumszínek CIE színmegfeleltető függvényei, |
|
|
ɸ ( λ ) |
a színinger-függvény, |
|
|
λ |
a hullámhossz, |
|
|
k |
egy alkalmasan választott arányossági tényező. |
Ábrázolástechnikai érdekesség, hogy a CIE xyY színháromszögben meg szokták rajzolni a Planck vonalat, és a szabványos megvilágítások színpontjait (A,B,C) is
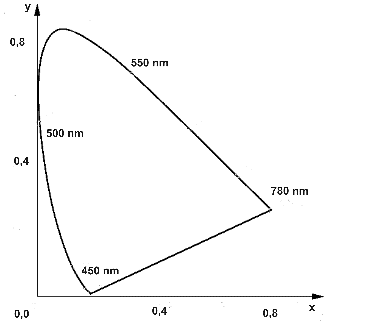
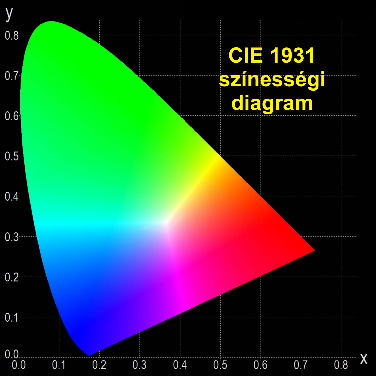
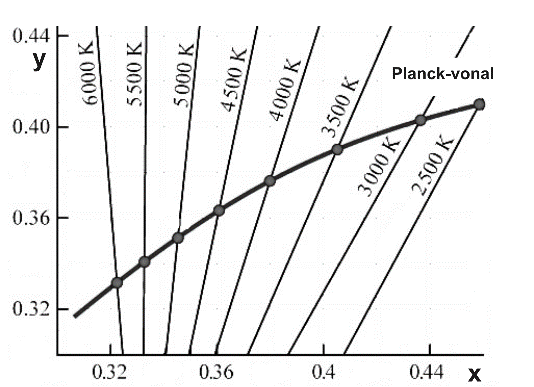
2.4.4. Az RGB színrendszer
Az RGB színrendszer a monitorok színképzése során lejátszódó jelenségekre alapozva jött létre.
A katódsugárcsöves, úgynevezett CRT monitorokban egy elektronágyú nyalábbal bombázza a foszforborítású üveglemez felületét. Az elektronnyalábot elektromágneses tér téríti ki, írányítja az ernyő megfelelő pontjába, ahol az a foszforborításba ütközik fényjelenséggel kísérve. E fényjelenség spektrális összetételét alapvetően a foszforborítás kémiai tulajdonságai határozzák meg. A színes CRT monitoroknak három alapszínük van: a vörös, a zöld és a kék (RGB). Ezek additív keverésével egyéb színek állíthatók elő. A fénysűrűség növelése az elektronok kinetikus energiájának növelésével történik. A monitor RGB komponenseivel azt határozzuk meg, hogy a vörös, zöld és kék érzetet keltő spektrumok milyen keverék hozza létre az elvárt színérzetet [2.19.] .
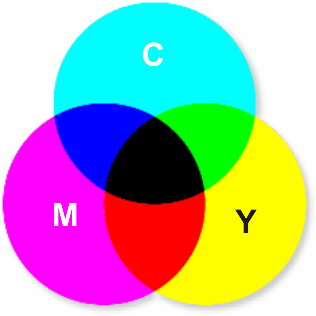
2.4.5. A CMY és a CMYK színrendszerek
A CMY, vagy más néven a szubtraktív színrendszer alapmodellje a nyomtatás során lejátszódó színkeverés. Ebben a rendszerben azt mondjuk meg, hogy mennyi kékeszöld (Cyan), bíbor (Magenta) és sárga (Yellow) színt kell kivonni a fehérből, hogy a keverék a kívánt színérzetet keltse [2.20.] , vagy a gyakorlatban mennyi ilyen festéket kell felvinni a fehér lapra a megkövetelt színérzet kiváltása céljából. A CMY színrendszer úgy származtatható RGB-ből, hogy a derékszögű koordináta-rendszerben történő ábrázolás esetén, a színek és inverzeik felcserélődnek. A koordináta-rendszer kezdőpontjában a fekete található, és az alapszínek a tengelyeken helyezkednek el. Az átalakítás összefüggései:
|
|
||
|
|
CMYK rendszer alkalmazását az indokolja, hogy a három alapszín csak elméletileg ad feketét, a gyakorlati kivitelezés során ez azonban csak sötétbarnának felel meg. A fekete festékanyag alkalmazásával ez a probléma orvosolható, továbbá a mély színek intenzitása fokozható. A fekete kulcsszín (Key) alkalmazása esetén az alapszíneket arányosan módosítani kell, ezért az eljárást alsószín-eltávolításnak (Undercolor Removal) is nevezzük [2.21.] :
2.4.6. A HLS színrendszer
Az RGB és CMY színrendszerek jellegükből és származtatásukból eredően fizikai megközelítést tükröznek, így nem tekinthetők igazán szemléletesnek. Közelebb áll az emberi gondolkodáshoz, ha a színt annak árnyalatával, fényességével és a telítettségével jellemezzük. Ebben a rendszerben a koordináta-tengelyeken elhelyezett testen ábrázolhatjuk a színeket úgy, hogy a főátlón lévő relatív távolságot a fényességnek (Lightness), a színárnyalatot meghatározó szöget az árnyalatnak (Hue), illetve a főátlótól a kocka széléig mért relatív távolságot pedig telítettségnek (Saturation) tekintjük. A főátlóra merőleges körökben a szürke középen helyezkedik el, arra nézve szimmetrikusan találhatók a komplementer színek, melyek keveréke a szürke (kivételes esetben fehér). A színkeverésben részt vevő sáv szélessége lényegében a telítettséget jelenti, értékének változása során a megadott szín távolabbi szomszédainak a szín kikeverésében való részvétele változik. A HSB modell a HLS modellel megegyezik, csak az L (fényesség) helyett a B (Brightness, világosság) szerepel.
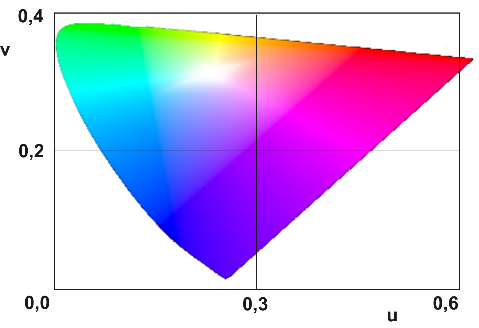
2.4.7. Egyenletes színterek
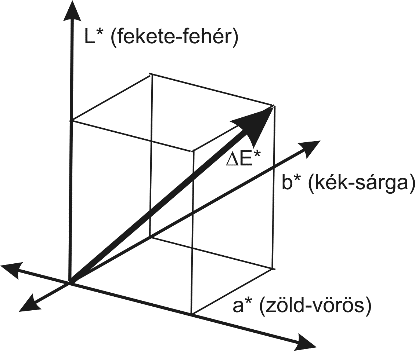
A szín(inger)tér a színingerek geometriai – általában háromdimenziós térben történő – szemléltetésére szolgál, azok valamilyen elv szerint definiált skála alapján való elrendezését mutatja. A színtest a színingertér azon része, amely a felületszíneket tartalmazza. A CIE 1931 XYZ szabvány egy színteret definiál, a neki megfelelő test magában foglalja az összes, az emberi szem által látható színt. Sajnos jelentős hátránya, hogy nem egyenletesen mutatja a színeket, tehát a színváltozásokhoz tartozó geometriai távolságok nem egyeznek meg. Tehát az a színtér, melyben az X, Y és Z értékekkel jellemezzük a színpontokat, nem egyenletes. Az egyenletes – ahol az azonos méretű elmozdulások mindig ugyanakkora színváltozást eredményeznek – színingertér megvalósítására való törekvés komoly múltra tekint vissza. Az egyik, már közel egyenletes eloszlású a CIELab [2.22.] színingertér, amely az ellentétes színpárok rendszerén alapul. Benne a pirosság vagy a zöldesség mértéke kifejezhető egyetlen koordinátával, az a-val. A kékesség, illetve a sárgaság pedig egy másikkal, a b koordinátával. A harmadik koordináta az L, a szín világosságának felel meg. Az X, Y és Z trikromatikus értékeket a CIELab színinger tér L*, b* és a* derékszögű koordinátákká transzformáló egyenletek egy neutrális fehér referencia mellett a következők:
|
|
||
|
|
||
|
|
ahol X, Y, Z a színes tárgy trikromatikus értékei, és X0, Y0, Z0 a szabványos fehér trikromatikus mérőszámai úgy, hogy teljesülnek az alábbi feltételek:
|
|
A fentiek alapján minden színhez egyértelműen hozzárendelhető a színtérben egy színpont, három koordinátával megadva. A CIELab színezeti szög a színpont színezetét jellemzi:
|
|
A CIELab króma a telítettség jellemzője, a színpontnak az L* tengelytől való távolsága:
|
|
A mintákhoz tartozó színpontok egymáshoz viszonyított geometriai távolságaiból [2.2.] a minták közötti színeltérés kiszámítható. A színingerkülönbséget a színtérben értelmezett A színpont és R etalon, vagy referencia, mint vonatkoztatási színpont közötti térbeli geometriai távolsággal adjuk meg [2.23.] .
|
|
Megjegyzendő, hogy a szakirodalomban az egyenletes színtérre vonatkozóan gyakran használják az érzethelyes jelzőt. A CIE ajánlásai szerint jelentőséggel bír még a CIE Luv is, melyben az u és a v értékek a CIE XYZ értékekből számíthatók [2.24.] .
|
|
Szemmel érzékelhető eltérés |
|
|
Nem érzékelhető |
|
|
Alig észrevehető. |
|
|
Észrevehető. |
|
|
Jól látható |
|
|
Nagy |
2.4.8. Színtranszformációk
Egy színes megjelenítő, például egy katódsugaras (CRT) monitor az egyes színingereket tristimulusos módon, azaz három komponensből keveri ki. Ennek oka lehet az is, hogy az emberi szemben additív módon zajlik a színkeverés, és az ember látószerve trikromatikus felépítésű, azonban emellett technológiai okok is felsorakoztathatók, ahogy az a színes nyomtatásnál egyértelmű. Működését tekintve a megjelenítő üvegből készült homlokfelületének belső részét – mátrixos elrendezésben – különböző spektrális tulajdonságú fénypor-keverék borítja, melyet vezérelt, és megfelelően eltérített elektronsugarakkal gerjesztünk. A fénypor összetevőit úgy választották meg a spektrális tulajdonságaik alapján, hogy segítségükkel széles tartományban nyíljon lehetőség a színingerek kikeverésére. Maga a keverés additív módon történik, azaz a mátrixba rendezett felületelemek az elektronsugaras gerjesztés hatására felvillannak. Kellő távolságból szemlélve, a megfigyelő számára az egyes mátrixelemek már nem különböztethetők meg, azaz a struktúra nem oldódik fel, így csupán az additív módon kikevert eredő színinger érzékelhető. Ha a megjelenítő különböző területein kikevert színingerek vizuális különbségét kívánjuk meghatározni, akkor annak saját rendszerében megadott, az egyes csatornákra vonatkozó értékeit – melyek az elektronnyaláb vezérléséért felelős DAC (digital-to-analog converter) értékekeit jelentik –, a megjelenítőnél alkalmazott fénypor-keverék spektrális tulajdonságai ismeretében egy eszközfüggetlen rendszerbe (CIE XYZ) kell konvertálni, majd ezen értékek segítségével egyenletes színtérben (CIE L*a*b*, vagy CIE L*u*v*) a különbség (ΔE) számítható.
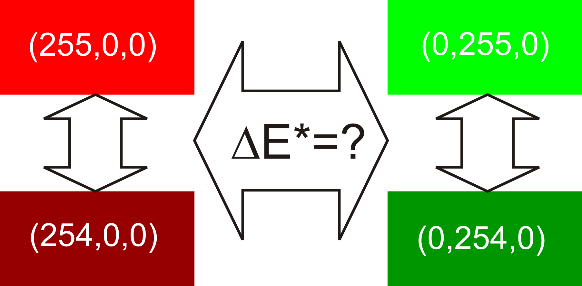
Példa:
Hozzunk létre katódsugaras (CRT) megjelenítőn egy-egy vörös és zöld színingerpárt úgy, hogy azok DAC értékei egységnyi különbségűek legyenek! Határozzuk meg, hogy mely színingerpár különbsége a nagyobb!

Megoldás:
Legyenek a beállított színingerpárok a monitor saját rendszerében R1(255;0;0), R2(254;0;0), illetve G1(0;255;0), G2(0;254;0). Az eszközfüggetlen rendszerbe történő transzformáció során szükségünk van az egyes csatornák színporkeverékei által gerjeszthető színingerek spektrális összetételére, ami spektrofotométerrel mérhető. Sajnos az estek jelentős részében ez nem áll rendelkezésre, vagy a mérés nem kivitelezhető. Ilyenkor a típusadatok alapján a konkrét megjelenítőre vonatkozó gyári adatok beszerzésére vagyunk kényszerítve. Ezek az adatok általában publikusak, ha nem is a konkrét spektrális összetétel, hanem az egyes csatornákra, illetve az azon megjeleníthető fehér színingerre vonatkozó CIE x,y,z adatok formájában.
![CRT monitor csatornáinak spektrális eloszlásfüggvényei [2.25.]](images/image_II_23.png)
A transzformációs mátrix elemeinek meghatározásához szükséges értékek:
|
xr, yr, zr |
||
|
xg, yg, zg |
||
|
xb, yb, zb |
||
|
xw, yw, zw |
Ha az Y relatív értéke egységnyi, akkor
|
|
||
|
|
||
|
|
Az így kapott 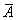 transzformációs mátrix lehetővé teszi a megjelenítő RGB-értékeinek XYZ-rendszerbe történő transzformációját, amiből a vizsgált színingerek színkülönbségei már számíthatók.
transzformációs mátrix lehetővé teszi a megjelenítő RGB-értékeinek XYZ-rendszerbe történő transzformációját, amiből a vizsgált színingerek színkülönbségei már számíthatók.
|
λ [nm] |
R [-] |
G [-] |
B [-] |
|---|---|---|---|
|
350 |
0,001482 |
0,001853 |
0,003054 |
|
360 |
0,001 |
0,000721 |
0,004163 |
|
370 |
0,001463 |
0,001504 |
0,010324 |
|
380 |
0,002252 |
0,001853 |
0,039576 |
|
390 |
0,001239 |
0,002598 |
0,088732 |
|
400 |
0,002204 |
0,004565 |
0,15395 |
|
410 |
0,003694 |
0,006498 |
0,2392 |
|
420 |
0,006824 |
0,010543 |
0,36657 |
|
430 |
0,008857 |
0,01487 |
0,49183 |
|
440 |
0,01039 |
0,018469 |
0,56028 |
|
450 |
0,010311 |
0,022723 |
0,56757 |
|
460 |
0,009983 |
0,029994 |
0,50862 |
|
470 |
0,01701 |
0,050423 |
0,40776 |
|
480 |
0,007753 |
0,098658 |
0,29973 |
|
490 |
0,017824 |
0,18414 |
0,19963 |
|
500 |
0,011093 |
0,29657 |
0,12449 |
|
510 |
0,00889 |
0,40732 |
0,076118 |
|
520 |
0,009602 |
0,48465 |
0,047458 |
|
530 |
0,011918 |
0,49941 |
0,030104 |
|
540 |
0,13073 |
0,47546 |
0,022944 |
|
550 |
0,012121 |
0,42357 |
0,01441 |
|
560 |
0,009065 |
0,35649 |
0,010385 |
|
570 |
0,012248 |
0,26477 |
0,007476 |
|
580 |
0,010583 |
0,1831 |
0,004995 |
|
590 |
0,059789 |
0,11959 |
0,004827 |
|
600 |
0,036581 |
0,080627 |
0,003169 |
|
610 |
0,050166 |
0,052528 |
0,002949 |
|
620 |
0,15703 |
0,035042 |
0,005033 |
|
630 |
0,3597 |
0,026878 |
0,009306 |
|
640 |
0,038894 |
0,012863 |
0,001098 |
|
650 |
0,017038 |
0,007922 |
0,000931 |
|
660 |
0,011249 |
0,005665 |
0,000868 |
|
670 |
0,013959 |
0,004285 |
0,000884 |
|
680 |
0,016805 |
0,002249 |
0,000945 |
|
690 |
0,038109 |
0,002236 |
0,001543 |
|
700 |
0,07625 |
0,002528 |
0,002447 |
|
710 |
0,12103 |
0,003164 |
0,003097 |
|
720 |
0,011686 |
0,00094 |
0,000728 |
|
730 |
0,005578 |
0,00081 |
0,000854 |
|
740 |
0,002852 |
0,000547 |
0,000459 |
|
750 |
0,002494 |
0,000473 |
0,000394 |
A csatornákra vonatkozó spektrális eloszlásfüggvények alapján, a CIE 1931 színmérő rendszer színingermegfeleltető függvényei segítségével az X, Y, Z értékek számíthatók.
|
|
||
|
|
||
|
|
Az így kapott X, Y, Z értékekből az egyes csatornákra, illetve az additív színkeverés miatt a fehér színingerre vonatkozó színkoordináták szintén számíthatók:
|
|
||
|
|
||
|
|
Értékeik:
|
R |
xr=0.64 |
yr=0.33 |
zr=0.03 |
|
G |
xg=0.29 |
yg=0.60 |
zg=0.11 |
|
B |
xb=0.15 |
yb=0.06 |
zb=0.79 |
|
Fehér |
xn=0.312713 |
yn=0.329016 |
zn=0.3581 |
A transzformációs mátrix:
|
|
A vizsgált színingerek és a fehér X,Y és Z értékei:
|
R1 |
R2 |
G1 |
G2 |
W |
|
|---|---|---|---|---|---|
|
X |
109.863 |
109.3724 |
87.108 |
86.7664 |
242.3520 |
|
Y |
56.6100 |
56.3880 |
180.2085 |
179.5018 |
255.0000 |
|
Z |
5.1510 |
5.1308 |
33.0480 |
32.9184 |
277.5675 |
Az L*, a* és a b* értékei:
|
R1 |
R2 |
G1 |
G2 |
|
|---|---|---|---|---|
|
L |
54.2386 |
54.1466 |
87.3244 |
87.1892 |
|
a |
81.3422 |
81.1659 |
-89.8741 |
-89.7456 |
|
b |
68.1504 |
68.0612 |
79.7545 |
79.6501 |
A fenti adatok segítségével végzett színkülönbség-meghatározások alapján, a vörös színingerpár színkülönbsége 0.2180, míg a zöld páré 0.2137. Megállapítható, hogy a két vörös színinger ugyan távolabb van egymástól, de mindkét színingerpár még az érzékelhető érték alatt helyezkedik el.
2.5. Ellenőrző kérdések:
-
Magyarázza meg példákkal az inger, az észlelet és az érzéklet fogalmakat!
-
A metaméria következtében két színárnyalat egy megvilágításban egyformának tűnik, de más megfigyelési geometria vagy eltérő fényviszonyok esetén már különböznek. Mondjon példát a gyakorlati életből!
-
Ismertesse és magyarázza el a Grassmann törvényeket!
-
Ismertesse és magyarázza el az additív és a szubtraktív színkeverés szabályait, mondjon rájuk példát a mindennapi életből!
-
Magyarázza meg az XYZ színrendszer kialakításánál a CIE által megfogalmazott követelményeket! Mi indokolta ezek előírását?
-
Mi a szerepe a Planck-vonalnak a korrelált színhőmérséklet értelmezésében?
-
Mi indokolja az egyenletes színterek generálását és az milyen alapokon nyugszik?
-
Mi módon generáljuk a színterek közötti transzformációt biztosító transzformációs mátrix egyes elemeit?
2.6. További irodalom a szakterület tanulmányozásához
-
Abney, W. de W. 1914. Researches in Colour Vision and the Trichromatic Theory. London: Longmans, Green.
-
Agoston, G. A. 1987. Color Theory and Its Application in Art and Design. Berlin: Springer.
-
Balinkin, I. 1941. Measurement and designation of small color differences. Bulletin of the American Ceramical Society 20:392–402.
-
Barasch, M. 1978. Light and Color in the Italian Renaissance Theory of Art. New York: New York University Press.
-
Bäuml, K. H. 2002. Color appearance of spatial pattern: the role of increments and decrements. Vision Research 42:1627–1637.
-
Bedford, R. E., and Wyszecki, G. 1958. Wavelength discrimination for point sources. Journal of the Optical Society of America 48:129–135.
-
Berlin, B., and Kay, P. 1969. Basic Color Terms. Berkley CA: University of California Press.
-
Berns, R. S. 1993. The mathematical development of CIE TC 1-29 proposed color difference equation. Proceedings of the 7th Congress of the International Colour Association,Vol. B: C19-1–C19-4.
-
Berns, R. S., and Billmeyer, F. W. 1985. Development of the 1929 Munsell Book of Color: A historical review. Color Research and Application 10:246–250.
-
Billmeyer, F.W., and Bencuya, A. K. 1987. Interrelation of Natural Color System and the Munsell color order system. Color Research and Application 12:243–255.
-
Boynton, R. M. 1983. Ten years of research with the minimally distinct border. In J. D.
-
Mollon and L.T. Sharpe, eds., Colour vision: Physiology and Psychophysics. London: Academic Press, pp. 193–206.
-
Brewster, D. 1831. A Treatise on Optics. London: Longman, Rees.
-
Brücke, E. 1866. Die Physiologie der Farben für die Zwecke der Kunstgewerbe. Leipzig: Hirzel.
-
Burnham, R. W. 1949. Comparison of color systems with respect to uniform visual spacing. Journal of the Optical Society of America 39:387–392.
-
Cheung, M., and Rigg, B. 1986. Colour-difference ellipsoids for five CIE colour centres.
-
Color Research and Application 11:185–195.
-
CIE 1964 (U*V*W*)-System. 1963. CIE Proccedings. Vienna, Austria: Commission Internationale de l’Éclairage.
-
CIE 1976 (L*u*v*)-System. 1986. No. 15.2, Colorimetry, 2nd ed. Vienna, Austria:
-
Commission Internationale de l’Éclairage.
-
CIE 1976 (L*a*b*)-System. 1986. No. 15.2, Colorimetry, 2nd ed. Vienna, Austria: Commission Internationale de l’Éclairage.
-
CIE 1987. International lighting vocabulary, 4th ed.Vienna,Austria: Commission Internationale de l’Éclairage.
-
CIE 1990. CIE 86, 2° Spectral Luminous Efficiency Function for Photopic Vision. Vienna: Commission Internationale de l’Éclairage.
-
Cohen, J. B. 2001. Visual Color and Color Mixture. Urbana: University of Illinois Press.
-
Cui, G., Luo, M. R., Rigg, B., Roesler, G., and Witt, K. 2002. Uniform colour spaces
-
based on the DIN99 colour-difference formula. Color Research and Application 27:282–290.
-
Derefeldt, G. 1991. Colour appearance systems. In P. Gouras, ed., The Perception of Colour. Boca Raton, FL: CRC Press.
-
Derefeldt, G., and Hedin, C. E. 1987. A color atlas for graphical displays. In B. Knave and P.G.Wiedebäck, eds.,Work with Display Units 86. Amsterdam: North-Holland.
-
DIN Farbenkarte, German Standard DIN 6164. 1962. Berlin: Beuth.
-
Evans, R. M. 1974. The Perception of Color. New York:Wiley.
-
Fairchild, M. D. 1998. Color Appearance Models. Reading, MA: Addison-Wesley.
-
Fairchild, M.D., and Pirotta, E. 1991. Predicting the lightness of chromatic object colors using CIELAB. Color Research and Application 16:385–393.
-
Fechner, G. T. 1860. Elemente der Psychophysik, Vols. 1 and 2. Leipzig: Breitkopf und
-
Gage, J. 1993. Color and Culture. Boston: Little, Brown.
-
Gage, J. 1999. Color and Meaning. Berkley: University of California Press.
-
Gerstner, K. 1986. The forms of color. Cambridge: MIT Press.
-
Gilchrist, A. L., ed. 1994. Lightness, Brightness, and Transparency. Hillsdale NJ: Erlbaum.
-
Goethe, J.W. v. 1810. Zur Farbenlehre. Tübingen: Cotta.
-
Guild, J. 1931. The colorimetric properties of the spectrum. Philosophical Transactions of the Royal Society (London) A230:149–187.
-
Helmholtz, H. v. 1891.Versuch einer erweiterten Anwendung des Fechnerschen Gesetzes im Farbensystem. Zeitschrift für Psychologie und Physiologie der Sinnesorgane 2:1–30.
-
Hunt, R. W. G. 1977. The specification of colour appearance. I. Concepts and terms. Color Research and Application 2:55–68.
-
Hunter, R. S. 1942. Photoelectric Tristimulus Colorimetry with Three Filters. Circular C429. National Bureau of Standards,Washington.
-
Hurvich, L. M. 1981. Color Vision. Sunderland: Sinauer.
-
Hurvich, L. M., and Jameson,D. 1955. Some quantitative aspects of an opponent-colors theory. II. Brightness, saturation, and hue in normal and dichromatic vision. Journal of the Optical Society of America 45:602–616.
-
Jameson,D., and Hurvich, L. M. 1964.Theory of brightness and color contrast in human vision. Vision Research 4:135–154.
-
Judd,D. B. 1932. Chromaticity sensibility to stimulus differences. Journal of the Optical Society of America 22:72–108.
-
Judd, D. B. 1940. The Munsell color system. Journal of the Optical Society of America 30:574–645.
-
Judd, D. B. 1969. Ideal color space. Palette 29:25–31, 30:21–28, 31:23–29.
-
Judd, D. B., MacAdam, D. L., and Wyszecki, G. 1964. Spectral distribution of typical
-
daylight as a function of correlated color temperature. Journal of the Optical Society of America 54:1031–1040.
-
Kim, D. H., and Nobbs, J. H. 1997. New weighting functions for the weighted CIELAB colour difference formula. Proceedings 8th Congress of the International Colour Association,Vienna: CIE, pp. 446–449.
-
Krauskopf, J. 1999. Higher order color mechanisms. In K. R. Gegenfurtner and L. T. Sharpe, eds. Color vision. Cambridge: Cambridge University Press.
-
Krauskopf, J., and Gegenfurtner, K. 1992. Color discrimination and adaptation. Vision Research 32:2165–2175.
-
Kuehni, R. G. 1982. Advances in color difference formulas. Color Research and Application 7:19–23.
-
Kuehni, R. G. 2000b. A comparison of five color order systems. Color Research and Application 25:123–131.
-
Kuehni, R. G. 2001c. Color space and its divisions. Color Research and Application 26:209–222.
-
Luneburg, R. K. 1950. The metric of binocular visual space. Journal of the Optical Society of America 40:627–642.
-
MacAdam, D. L. 1935. Maximum visual efficiency of colored materials. Journal of the Optical Society of America 25:361–367.
-
MacAdam, D. L. 1942. Visual sensitivities to color differences in daylight. Journal of the Optical Society of America 32:247–274.
-
MacAdam, D. L. 1965. Specification of color differences. Acta Chromatica 1:147–156.
-
MacAdam, D. L. 1974. Uniform color scales. Journal of the Optical Society of America 64:1691–1702.
-
MacAdam, D. L. 1978. Colorimetric data for samples of OSA uniform color scales. Journal of the Optical Society of America 68:121–130.
-
MacAdam, D. L. 1981. Color Measurement. Berlin: Springer.
-
Maxwell, J. C. 1860. Theory of compound colours, and the relations of the colours of the spectrum. Proceedings Royal Society (London) 10:57–84.
-
Munsell, A. H. 1907. Atlas of the Munsell Color System. Malden, MA: Wadsworth-Howland.
-
Munsell, A. H. 1915. Atlas of the Munsell Color System, 2nd ed. Malden:Wadsworth-Howland.
-
Newton, I. 1670. The Optical Papers of Isaac Newton: Vol. 1. The Optical Lectures 1670–1672, transl. ed. A. E. Shapiro. Cambridge: Cambridge University Press, 1984.
-
Newton, I. 1704. Opticks. London: Smith and Walford.
-
Stockman, A., MacLeod, D. I. A., and Johnson, N. E. 1993. Spectral sensitivities of the human cones. Journal of the Optical Society of America A10:2491–2521.
-
Stockman, A., and Sharpe, L. T. 1998. Human cone spectral sensitivities: a progress report. Vision Research 38:3193–3206.
-
Walraven, P. L., and Bouman, M. A. 1966. Fluctuation theory of colour discrimination of normal trichromats. Vision Research 6:567–586.
-
Wright, W. D., and Pitt, F. H. G. 1934. Hue discrimination on normal colour-vision. Proceedings of the Physical Society (London) 46:459–454.
-
Wyszecki, G. 1960. Farbsysteme. Göttingen: Musterschmidt-Verlag.
-
Wyszecki, G. 1963. Proposal for a new color-difference formula. Journal of the Optical Society of America 53:1318–1319.
Felhasznált irodalmak
[2.1.] A rajzvizsgálat pszichodiagnosztikai alapjai, Projekció, kifejezés, mintarajzok. Flaccus Kiadó. pp.415.. 2006.
[2.2.] Színmérés. Műszaki Könyvkiadó. Budapest . p.11.. 1982.
[2.3.] Színtan Színdinamika. Tankönyvkiadó. Budapest . p.10.. 1988.
[2.4.] Színmérés. Műszaki Könyvkiadó. Budapest . p.24.. 1982.
[2.5.] Általános színtan és színmérés. Közgazdasági és Jogi Könyvkiadó. Budapest . p.15.. 1956.
[2.6.] Kísérleti Fizika III. Tankönyvkiadó. Budapest . 1977.
[2.7.] A színingermetrika fogalmai. 27. Kolorisztikai Szimpózium. Tata . p.7-20.. 1999. szeptember 27-29.
[2.8.] Color Science, Concepts and Methods. Second edition. Wiley. New York . 1982.
[2.9.] Color Representation: Theory and Techniques. IMPA. p.4.. 1992.
[2.10.] Colorimetry, Understanding the CIE System. John Wiley & Sons, Inc.. p.70.. 2007.
[2.11.] Colour-Mixture Terminology. Color Research and Application. p. 93..
[2.12.] On the theory of compound colors. p.254-264.. 1854.
[2.13.] Optika. Panem. Budapest . p.486.
[2.14.] A re-etermination of the trichromatic coefficients of the spectral colours. Trans. Opt. Soc. 30. pp. 141-161. 1928-29.
[2.15.] The Colorimetric Properties of the Spectrum. Phil. Trans. Roy. Soc.. London . p. 149-187. 1931.
[2.16.] Optika. Panem. Budapest . p.487..
[2.17.] Optika. Panem. Budapest . p.488..
[2.18.] Színmérés. Műszaki Könyvkiadó. Budapest . p.142.. 1982.
[2.19.] Számítógépes grafika. ComputerBooks. Budapest . p.67.. 1999.
[2.20.] Számítógépes grafika. ComputerBooks. Budapest . p.67.. 1999.
[2.21.] Color and Its Reproduction. Graphics Arts Technical Foundation. pp. 320-329.. 1988.
[2.22.] Colorimetry, Understanding the CIE System. John Wiley & Sons, Inc.. p.64.. 2007.
[2.23.] Colorimetry, Understanding the CIE System. John Wiley & Sons, Inc.. p.84.. 2007.
[2.24.] Routine Test Method for Paper and Board. Instrumental Measurement of Colour. Paper technology and Industry. pp. 217-218. 1977, August.
[2.25.] A méréseket dr. Samu Krisztián bocsátotta rendelkezésemre nanométeres felbontásban, az adatokat tartalmazó táblázat csak tájékozató jellegű.
[2.26.] http://www-history.mcs.st-and.ac.uk/BigPictures/.