10. fejezet - H∞ szabályozó elméleti háttere
A szabályozási probléma megfogalmazása általános esetben a következő: adott a 10-1. ábrának megfelelő szabályozási struktúra [64]. A rendszer bemenetei a zavarok, zajok, parancsjelek, referencia és a szabályozó által előállított jelek.
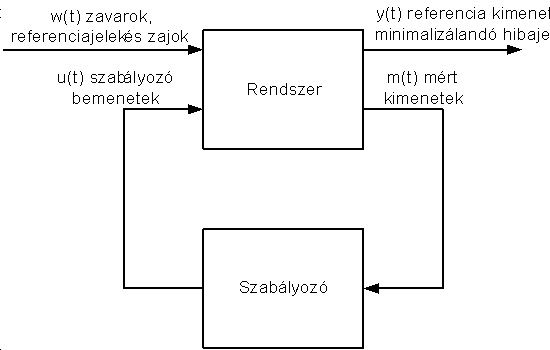
A rendszer kimenetei egyrészt a mért fizikai mennyiségek, másrészt az úgynevezett referencia kimenet, amelynek minimalizálása lesz a cél a szabályozó tervezési eljárás során. A rendszer viselkedését leíró állapottér egyenletek a következők:
|
|
(10.1) |
Ahol A a rendszermátrix, Bu a szabályozó bemenet bemeneti mátrixa, Bw a zavarok bemeneti mátrixa, Cy a kimeneti mátrix, Dyu a bemenet kimenetre gyakorolt hatását jellemzi, Cm a mérési mátrix és Dmw a mérési zajmátrix.
Teljesülniük kell továbbá a következő feltételeknek:
|
|
(10.2) |
|
|
(10.3) |
|
|
(10.4) |
|
|
(10.5) |
Az előbbi feltételek értelmében a rendszer bemenetein jelentkező zavarok és a mérési zajok eltérőek, a kimeneti egyenlet normalizálja a mérési zajokat, a referencia kimenet egy, csak az állapotoktól függő részből és egy, csak a szabályozó bemenettől függő részből áll és a szabályozó bemenettől függő rész maga a szabályozó bemenet vagy annak transzponáltja. További feltételezés, hogy a rendszer irányítható a szabályozó bemenet és a zavarok felől, megfigyelhető a mért kimenetek és a referencia kimenet felől (ez garantálja a rendszer stabilizálhatóságát visszacsatolás segítségével).
Probléma: A szuboptimális H∞ szabályozási probléma azon visszacsatolásos szabályozó megtalálása, amelyre az alábbi zárt kör átviteli függvényének normája korlátos adott intervallumon, azaz:
|
|
(10.6) |
A probléma megoldása két Riccati egyenlet megoldásával adható meg, A Riccati egyenletek megoldásai idővariáns mátrixokat lesznek. Az így kapott szabályozó becslő részének erősítése és az állapotvisszacsatoló részének erősítése állandósult állapotot érnek el bizonyos idő után, így olyan alkalmazási területeken, ahol az időbeli működési időtartomány nagy a tranziensek idejéhez képest, az idővariáns szabályozó helyett használhatók az állandósult állapotbeli értékek. Az állandósult állapotú H∞ szabályozó megoldása a következő szuboptimális szabályozási problémának.
Probléma: Feladat azon lineáris, időinvariáns szabályozó megtalálása, amelyet a Laplace tartományban a (10.7) egyenlet ír le és amely stabilizálja a zártkörű rendszert és a zárt kör normája korlátos (10.8).
|
|
(10.7) |
|
|
(10.8) |
A szabályozó kiszámítása ebben az esetben leegyszerűsödik a követekző két Riccati egyenlet megoldására megfelelően nagy esetén.
|
|
(10.9) |
|
|
(10.10) |
Ezeket a mátrixegyenleteket P-re illetve Q-ra kell megoldani. Ha a pozitív szemidefinit megoldásokra igaz, hogy és stabil, vagyis a mátrixok sajátértékeinek valós része negatív, valamint, azaz a spektrális rádiusz (a sajáértékek abszolútértékenek maximuma) korlátos akkor a szabályozó , amely a rendszerrel azonos rendű, a (10.11) állapottér reprezentációval adott és a mátrixai a (10.12)–(10.14) alapján számíthatók ki.
|
|
(10.11) |
|
|
(10.12) |
|
|
(10.13) |
|
|
(10.14) |
10.1. Szabályozó tervezése
Ebben a fejezetben az 8.5.2 fejezetben kapott modell segítségével szabályozó tervezésre kerül sor az aszinkron motorhoz. Mielőtt elkezdődne a tervezési eljárás, érdemes áttekinteni a H∞ szabályozási módnak az előnyeit, tulajdonságait, jobban rávilágítva annak lehetséges felhasználásai területére. A H∞ szabályozás a stabilitás, érzékenység tématerületeket célozza meg különös tekintettel a paraméteres bizonytalanságok kezelésére és különösen jól alkalmazható olyan esetekben, ahol a be és kimenetekre jól definiált korlátok adhatók. A H∞ szabályozás lineáris időinvariáns rendszerekre alkalmazható. Az 8.5.2 fejezetben bemutatott motor modell nagy hátránya a nemlinearitás, hiszen szerepelnek benne az állapotváltozók keresztszorzatai is, ezért a modellt a szabályozó tervezéséhez alkalmas lineáris alakra kell hozni.
Az egyszerűsítési lépések hasonlóak a korábbi fejezetekben látottakkal, itt azonban nem történik meg a megfelelő állórész árammal arányos és nem arányos tagok szétválasztása. Mint már a mezőorientált szabályozásról szóló fejezetben bemutatásra került, a motor folyamatos működése során fontos a fluxus konstans szinten tarása, a modell átalakítása ennek függvényében munkaponti linearizálással kerül levezetésre. A mezőorientált szabályozás során a szabályozási kör segítségével valósítható meg a fluxus konstans szinten tartása. Tegyük fel, hogy az előbbi követelménynek sikerült megfelelni. A (8.77) egyenletből ezért az következik, hogy ekkor a mágnesezési áram konstans.
|
|
(10.15) |
A (10.15) egyenletben ekkor = 0 (mivel konstans a mágnesezési áram) és e miatt isd = imr , továbbá imr konstans ezért . Az alábbi egyenlet ennek következtében nem differenciálegyenlet, hanem csak algebrai egyenlet.
|
|
(10.16) |
A motor dinamikus viselkedése így már két differenciálegyenlettel (10.17)–(10.18) leírható.
|
|
(10.17) |
|
|
(10.18) |
Az ismertetett feltételek mellett így a (10.19)–(10.20) összefüggések felhasználásával felírható ebből a szabályozó tervezéséhez az egyszerűsített modell.
|
|
(10.19) |
|
|
(10.20) |
|
|
(10.21) |
Felvetődik a kérdés: Mennyire pontosan írja le ez a modell a rendszer viselkedését? Érdemes észben tartani a feltételezéseket: a fluxus konstans, a fluxus szabályozó (d kör) feladata ennek biztosítása. Jól láthatóan az egyszerűsített modell alapján készített szabályozó a mező orientált szabályozásban látottaknak megfelelően csupán a q irányú szabályozást fogja elvégezni. Újabb kérdés vetődhet fel: Miért nem kerül alkalmazásra a d körhöz is H∞ szabályozó? Ennek legfőbb oka az, hogy a rendszerben jelentkező legnagyobb zavar (a terhelő nyomaték) ebben a részrendszerben jelenik csak meg, a cél ennek minél jobb ellensúlyozása, hiszen nem rendelkezünk semmilyen információval erről a mennyiségről, a rendszer viselkedését viszont jelentősen befolyásolja. A döntést az is indokolja, hogy a fluxus csak a tranziensek alkalmával változik meg a kereszthatások miatt, és a fluxus változási sebessége is kicsi (nagy időállandó miatt). A d kör PI szabályozójának legfőbb feladata a tranziensek alatt tapasztalható kismértékű változások kompenzálása.
A szabályozni kívánt rendszer általános esetben a következő egyenletekkel írható le:
|
|
(10.22) |
|
|
(10.23) |
Az egyszerűsított modellt (10.21) kell ilyen alakra hozni. A szabályozás egyik fontos célja az előírt referenciajel követése. Egyik lehetséges megoldás az lenne, ha a kimeneti egyenletben szerepelne a hibajel, vagyis a valós és a referencia sebesség különbsége, ez azonban nem lenne konisztens a (10.1)–(10.5) alakkal, hiszen a referenciakimenetben y(t) nem szerepelhet ilyen tag. A probléma megoldásához a legjobb módszer súlyfüggvények definiálása a referenciára és mérési zajra a 10-2 ábrának megfelelően. Ezáltal a két differenciálegyenletből álló rendszer (10.21) kiegészül még két differenciálegyenlettel és együtt egy negyedrendű rendszert alkotnak, ahol az új állapotváltozók xr és xv
A szabályozással szembeni további elvárás a nulla maradandó szabályozási eltérés elérése, ezért a referenciajel r1(s) súlyozó függvénye (10.24) alakú, ahol ε kicsi érték, továbbá a mérési zaj súlyozó függvénye (10.25) alakú.
|
|
(10.24) |
|
|
(10.25) |
Az kapott új állapotegyenlet:
|
|
(10.26) |
Ebben az esetben a11, a12,a21 értéke a (10.21)-ben szereplő értékeknek felelnek meg, míg ε hangolási paraméter, jellemzően kicsi érték (0.01). A (10.22)–(10.23) egyenleteknek megfelelő összeállítás eléréséhez a kimeneti egyenletet kell megfogalmazni.
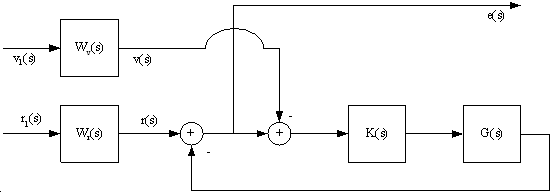
A mért érték a rendszerben a referenciasebesség és a valós sebesség különbsége a mérési zajjal terhelve, a referencia kimenet (a szabályozó ezt a kimenetet minimalizálja) egyrészt a sebességeltérésből (a mérési zaj nélkül), ennek súlyozása ctrack (szintén tervezési paraméter), másrészt a szabályozó jelből áll, ennek együtthatója csig szintén hangolási paraméter.
|
|
(10.27) |
A csig értéke kicsi, hiszen a szabályozó célja ezen érték véges szinten tartása, de nem szabad azt nulla szint közelébe hoznia. A másik két tervezési paraméter ctrack és ε segítségével a zajérzékenység állítható, ezek azonban egymástól nem állíthatók függetlenül, hiszen ha a rendszer érzékeny a sebességletérésre, akkor érzékeny lesz a mérési zajra is (ez ugyanolyan hibajelet generál). Elődleges szempont volt a jó referenciakövetés, ezért ctrack értéke alapján történt a hangolás. A (10.26)–(10.27) egyenletek megfelelőek a szabályozó előállításához, a következő fejezetekben használt szabályozó ezek alapján lett tervezve , valamint az optimálisnál 10%-kal nagyobb értékekkel. A Riccati egyenletek mogoldása a szimulációhoz is használt MATLAB programmal történt. A maradandó szabályozási eltérés eltüntetéséhez ad hoc módszerrel integrátor tag került előállításra a szabályozó átviteli függvényének nullához közeli pólusának origóba történő áthelyezésével. A következő fejezet az eljárás során kapott szabályozó és a rendszer együttes szimulációjával foglalkozik.
Szimuláció
Amint elkészült a követelményeknek megfelelő szabályozó, következhet a következő lépés, az előállított szabályozó működésének elemzése, megfigyelése. A szimulációs eljárás feladatata a későbbiekben implementálásra kerülő szabályozó megfelelő működésének biztosítása. A rendszer szimulációja a MATLAB/Simulink program segítségével történt az ábrának megfelelő összeállítás szerint. A rendszer átfogó képe a 10-4. ábrán látható. A motor modellje a 10-3. ábrán látható és a motor egyenleteinek megfelelő átviteli függvények megvalósításával történik a közös álló kétfázisú koordinátarendszerben.
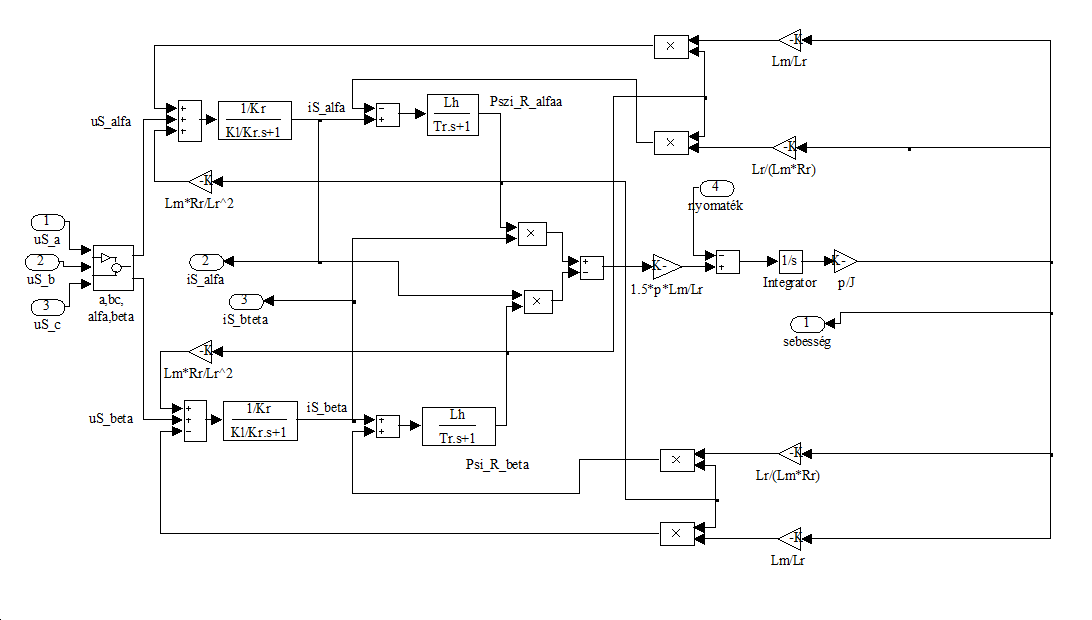
A motor bemenetei a stator feszültségek illetve a terhelő nyomaték, a kimenete a forgórész szögsebessége illetve a mért áramok. A szabályozó és motor közötti késleltetésnek a valós rendszerekben a szabályozó feszültséget előállító inverter működése során jelentekező késleltetések miatt van szükség. A fluxus modell biztosítja a mennyiségek elforgatásáshoz szükséges szöget illetve a becsült fluxusértéket, amely a d szabályozási körhöz szükséges.
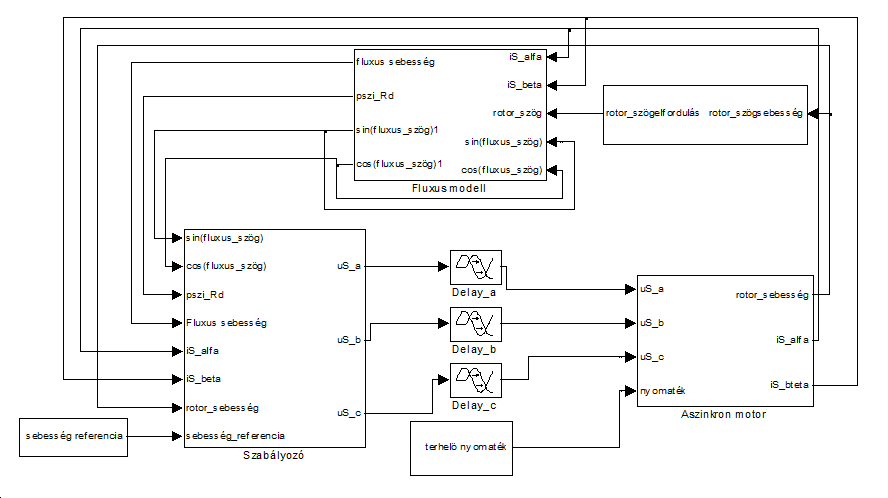
A szabályozó blokkon belül található a két különálló (d, q) szabályozási kör, a koordinátarendszerek közötti transzformációért felelős blokkok, valamint a mérési zajt előállító blokk és limitáló blokkok (pl. A szabályozóból kimenő állórész feszültség értéke nem léphet át egy bizonyos alsó és felső határt, a fluxus értéke nem süllyedhet egy minimális alsó határ alá). A szabályozás igényeinek való minél jobb megfelelés érdekében a q kör szabályozója az 3. fejezetben leírtaknak megfelelően integrátor tagot is tartalmaz, így nem lesz maradandó szabályozási eltérés. A szabályozó bemenete még a referenciasebesség.
Szimulációs eredmények
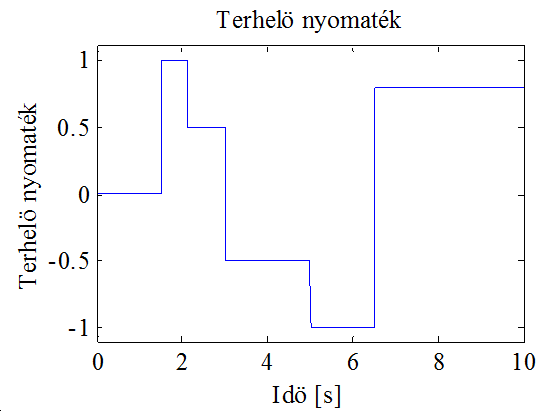
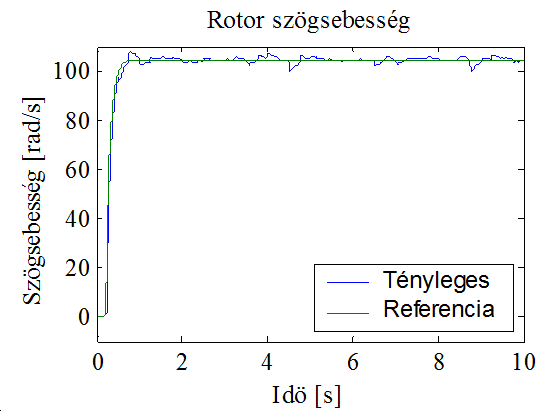
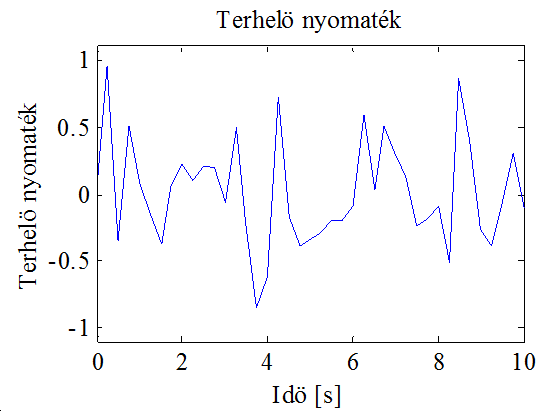
A szimulációs eljárás során az előző fejezetben bemutatott modell került tesztelésre. A szimuláció során lehetőség nyílik különböző referenciajelek esetén a rendszer várható viselkedését megfigyelni. Az alábbi ábrák a lefutatott szimulációk eredményeit mutatják. A 10-5. ábra a referenciakövetési tulajdonságot szemlélteti, kezdetben az előírt fluxus kialakulásáig nincs sem terhelő nyomaték, sem sebességreferencia, a szimulációhoz használt terhelő nyomaték a mellette látható ábrán található. Jól láthatóan a szabályozó teljesíti a tőle elvárt legalapvetőbb követelményt, vagyis jól követi a megadott referenciát.
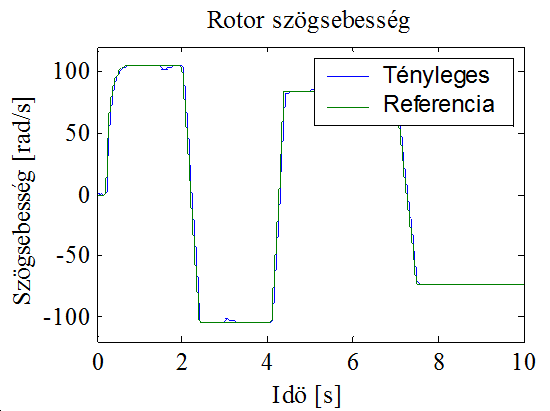
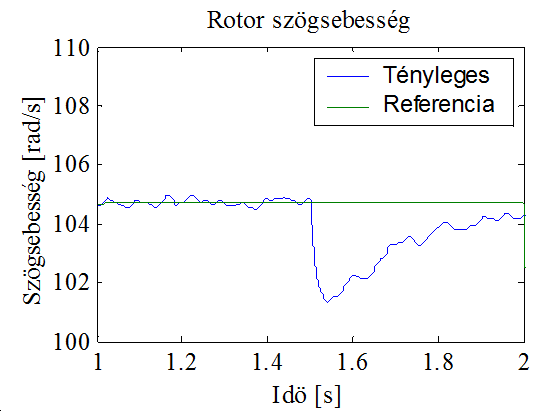
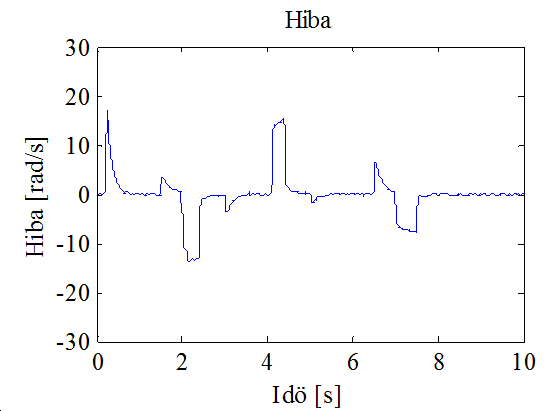
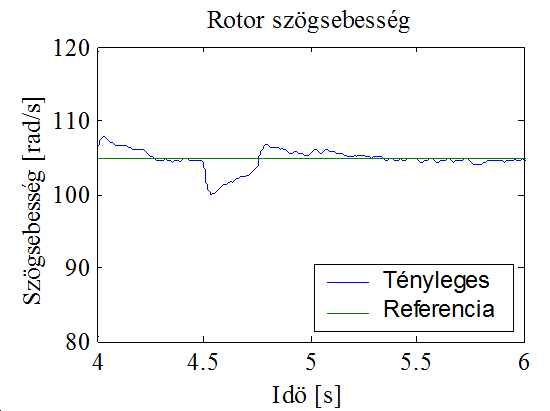
A 10-7. ábrán az 1 és 2 s közötti részt kinagyítva jól látható a terhelő nyomaték változásának hatása, a változás pillanatában a sebesség a változás irányától függően elmozdul a stacionárius állapotból valamilyen irányba, amíg a szabályozó a motor nyomatékát a kívánt értékre nem változtatja. A 10-8. ábra mutatja a szabályozás során előálló hibajelet, amely jól láthatóan stacionárius állapotban nullához tart.
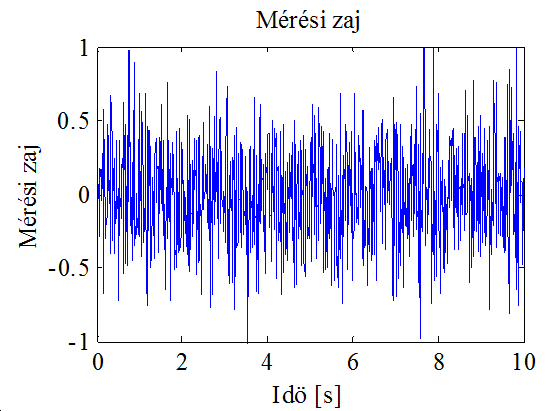
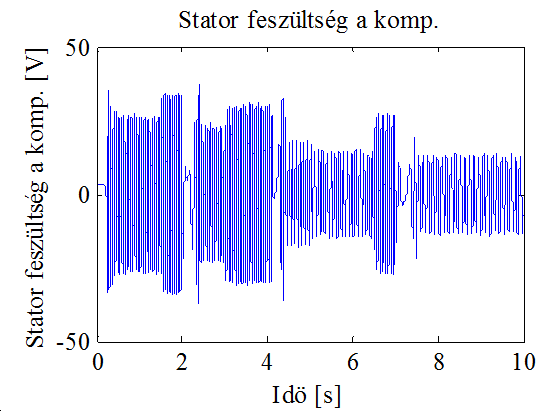
A 10-9. ábra és 10-10. ábra a mérési zajt illetve a motor bemenetén megjelenő állórész feszültség a komponensét mutatja, amelyen jól látszik a feszültség amplitúdójának és frekvenciájának változása a sebesség és a terhelés változása függvényében.
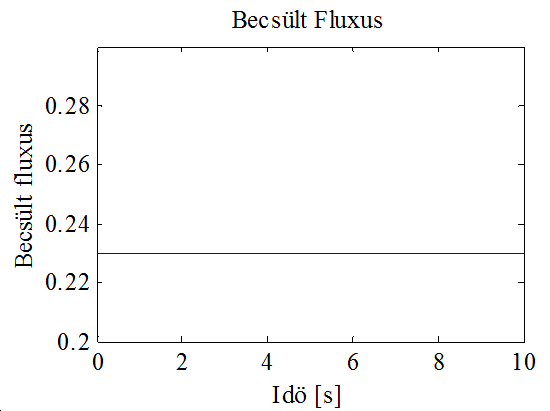
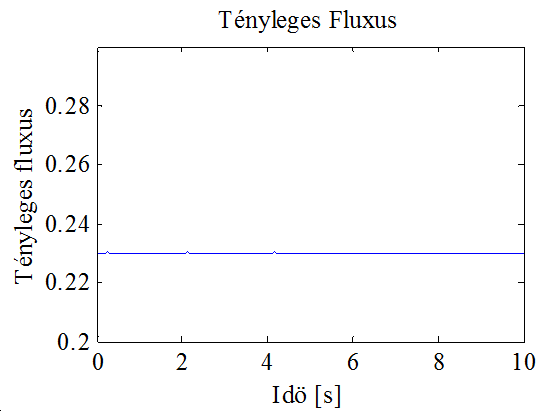
A 10-11. ábra és a 10-12. ábra a fluxus modell alapján becsült és a valós fluxus értékeket mutatják. Megállapítható, hogy sikerült a feltevésnek megfelelően a fluxus konstans szinten tartása. Az utolsó három ábra konstans sebességreferencia és gyorsan változó terhelő nyomaték mellett mutatja a sebességet. Ennek fontos szerepe lehet az alkalmazásokban, hiszen a sebesség szinten tartása fontos akkor is, ha a terhelő nyomaték időközben megváltozik. Ez utóbbi szimuláció jól mutatja a rendszer robusztusságát is.
Implementációs lépések
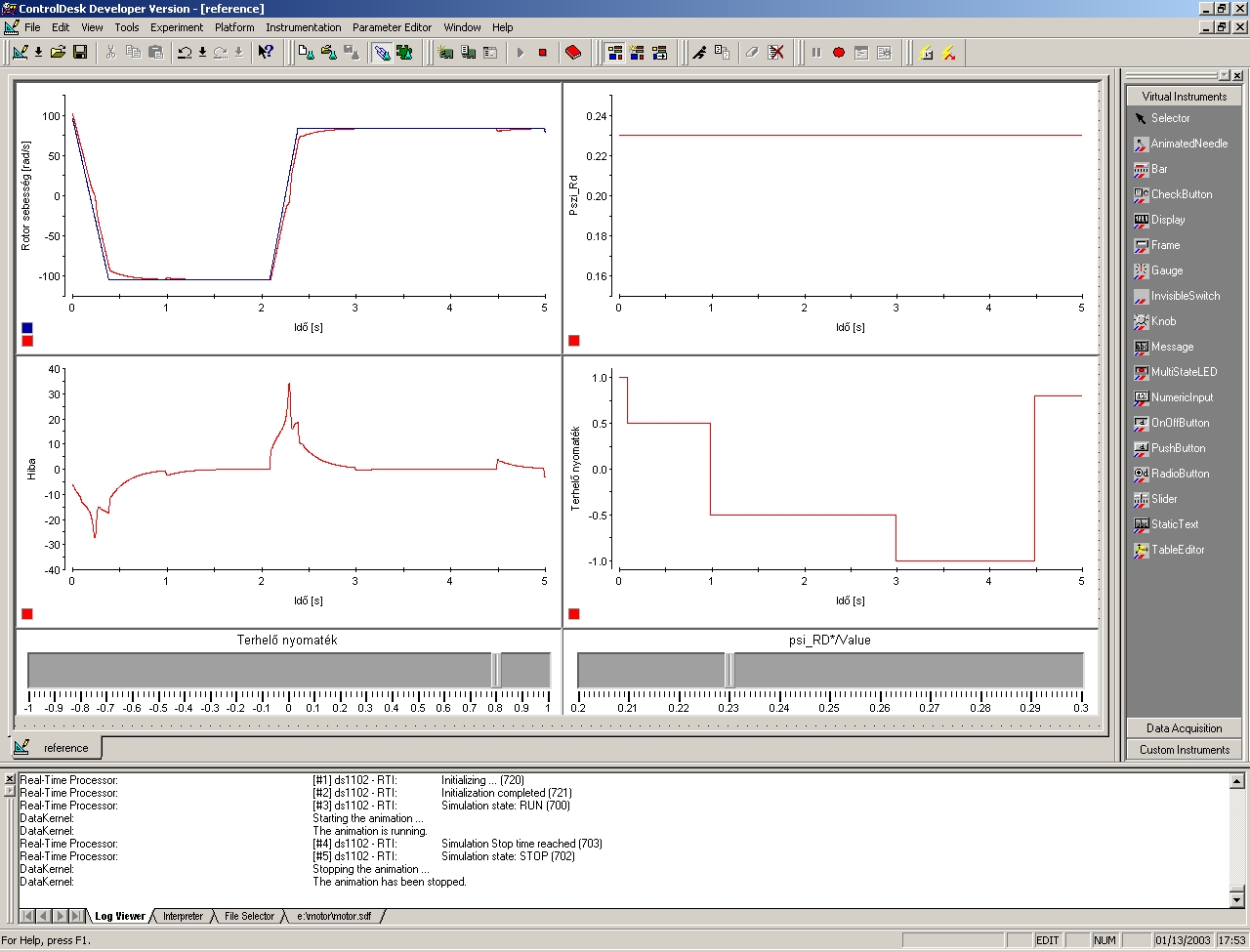
Az implementáció első lépéseit érdemes már az első sikeres szimulációk után megkezdeni.A MATLAB/ Simulink modellek készítésével párhuzamosan történik ezejn modellekből DSP processzoron futtatható kód generálása. A MATLAB/ Real Time Workshop Interfészen keresztül lehetőség nyílik a Simulink modellekből közvetlenül automatikus kódgenerálásra. A kód futtatása egy ISA foglalatos dSPACE DS1102-es kártyán történik, a fontos funkciók kezelése (kód futtatása, letöltése, adatok kirajzolása, paraméterek változtatása) a Controldesk nevű programmal lehetséges. A 10-16. ábrán látható a program kód futtatása és mérési eredmények kirajzolása közben, továbbá láthatók a paraméterek változtatására szolgáló gombok. Kezdeti lépésekben a szabályozó viselkedésének vizsgálata a motor elvi modelljével együtt történik (a MATLAB-ban használttal megegyező), majd a követelményeknek megfelelő eredmények elérése esetén a kártya hardverét kezelő blokkok felhasználásával (10-17. ábra) a jól működő Simulink modellben egyszerűen kicserélhető a motor elvi modellje a valós
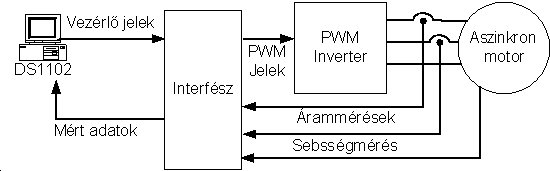
motor használatát lehetővé tevő blokkal így ezután már a kártya a valóságban is képes működtetni a motort a 10-18. ábra szerinti összeállításnak megfelelően. A blokkok kicserélése során a kártya ki- és bemeneteit kezelő blokkok és a PC-s kártya hardverfunkcióit kezelő egyéb blokkok kerülnek felhasználásra (megszakítások kezelése, stb). A 10-18. ábrának megfelelően a PC-s kártya közvetlenül egy interfész kártyával áll kapcsolatban, amely fogadja a PC-ből érkező jeleket és ezek alapján előállítja a PWM jeleket az inverter számára, amely a motor tápellátását biztosítja, valamint a mérési eredmények is ezen a kártyán keresztül jutnak vissza a DSP-re.
A Controldesk program fontos előnye, hogy a DSP-n futó programban a paraméterek on-line állíthatóak, így egyszerűvé válik az identifikált modell paraméterei változása hatásának vizsgálata a szabályozásra, valamint könnyűvé válik a paraméter beállítások közötti váltás is. Az implementáláskor feltétlenül elengedhetetlen a késleltetések szerepének figyelembe vétele, valamint a kártya és az inverter eltérő mintavételezési idejéből eredő hibák kiküszöbölése, amelyek befolyásolhatják a szabályozás minőségét (az alatt az idő alatt, amíg egy szabályozási ciklus lezajlik a kártyán, addig az inverter többször kapcsol, így szükséges az előállított szabályozó jeleket memóriában tárolni a következő ciklusig, majd azt egy hardveres megszakítás során felülírni).
Konklúzió k
A tervezett szabályozó sikeresen alkalmazva lett a háromfázisú aszinkronmotorhoz. A szimulációk során a komplett rendszer jó eredményeket mutat, teljesíti a tőle elvárt követelményeket (jó referenciakövetés, zavarok hatásainak csökkentése), zajos környezetben robusztus viselkedést mutat. A jó dinamikus viselkedés és egyszerűség alkalmassá teszik valós idejű alkalmazásokban történő használatra. Egy megfelelően beállított paraméterbecslő egység segítségével a rendszer tudása tovább bővíthető, hiszen ekkor nincs szükség a sebesség mérésére, helyette a becslő által szolgáltatott értékek használhatóak a szabályozás során.
Irodalmi hivatkozások BIBLIOGRAPHY \l 1038